Preprint
Review
Cellular Automata Modeling as Tool in The Corrosion Management
Altmetrics
Downloads
162
Views
67
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
24 June 2023
Posted:
25 June 2023
You are already at the latest version
Alerts
Abstract
Cellular automata (CA) models have emerged as a valuable tool in corrosion management. This manuscript provides an overview of the application of cellular automata models in corrosion research, highlighting their benefits and contributions to understanding the complex nature of corrosion processes. Cellular automata models offer a computational approach to simulate corrosion behavior at the microscale, capturing the intricate interactions between electrochemical reactions, material properties, and environmental factors generating a new vision of predictive maintenance. It discusses the key features of cellular automata, such as the grid-based representation of the material surface, the definition of state variables, and the rules governing cell-state transitions. The ability to model local interactions and emergent global behavior makes cellular automata particularly suitable for simulating corrosion processes. Finally, cellular automata models offer a powerful and versatile approach to studying corrosion processes, expanding models that can continue to enhance our understanding of corrosion and contribute to the development of effective corrosion prevention and control strategies.
Keywords:
Subject: Chemistry and Materials Science - Electrochemistry
1. Introduction
Corrosion refers to the irreversible reaction between a material and its environment, which can result in the degradation of the material and its properties. It is a natural process that occurs when a metal is exposed to oxygen and moisture [1]. It has a significant economic impact, representing approximately 3.4% of the global Gross Domestic Product (GDP) [2]. Moreover, corrosion can lead to disruptions in activities and decrease the efficiency and productivity of affected industries. While catastrophic failures due to corrosion have not been reported in solar thermal power plants, there are potential risks. For example, the Fukushima nuclear plant accident prompted the search for alloys that can withstand extreme operating conditions [3]. In the case of solar thermal power plants with thermal energy storage systems (TES), various corrosion mechanisms can occur, such as intergranular corrosion and mechanically assisted corrosion [4].
Cellular automata are computational models used to study the behavior of complex systems by simulating their evolution over time. Consist of a regular grid of cells, each of which can exist in a finite number of states and interact with its neighboring cells according to a set of rules. These rules govern the transition of cells from one state to another and can be based on simple local interactions or more complex global behaviors. The concept of cellular automata was first introduced by mathematician John von Neumann in 1940 [5], but it was cellular automaton pioneer John Conway popularized the idea in 1970. This manuscript recollects the main information about cellular automata models applied in corrosion management as an interesting tool for control and/or predictive maintenance of different types of corrosion, and factors that contribute to corrosion.
2. Cellular Automata as Tools in Corrosion Management.
Corrosion management refers to the systematic approach of preventing, controlling, and mitigating the effects of corrosion on materials and structures. It involves implementing strategies and practices to minimize the impact of corrosion, extend the service life, warrant safety, and reduce the maintenance and replacement of pieces or parts. Effective corrosion management includes preventive measures such as using corrosion-resistant materials, applying protective coatings or inhibitors, and proper new designs and considerations for regular inspection and maintenance. Corrosion management entails the proactive implementation of preventive measures, conducting regular inspections, performing thorough risk assessments, selecting appropriate materials, designing and constructing structures to minimize corrosion exposure, and employing a range of protective techniques, including coatings, corrosion inhibitors, cathodic protection systems, and other advanced technologies.
To effectively manage corrosion, a comprehensive understanding of the corrosion mechanisms associated with Hydrogen Evolution Reaction (HER), Oxygen Reduction Reaction (ORR), and Oxygen Evolution Reaction (OER) is crucial, along with a deep knowledge of the operating environment and the factors that can either accelerate or mitigate corrosion. Additionally, it is essential to consider the applicable regulations and safety standards from NACE [6] or another standard that can apply, pertaining to corrosion prevention across various industrial sectors, including petrochemicals [7], aeronautics [8], shipbuilding and maritime infrastructure [9,10,11,12], energy [13], mining [14], nuclear waste [15], microbial induced corrosion (MIC) [16], atmospheric corrosion [17], and among others. By incorporating this knowledge, industries can develop robust corrosion management strategies that ensure the safety, longevity, and optimal performance of their assets and infrastructure.
In the realm of corrosion management, the integration of computational techniques [18] and mathematical models [19] has emerged as an invaluable approach for comprehending and efficiently tackling the intricate behavior of corrosion processes. Among the array of techniques available, three stand out as particularly beneficial: cellular automata [20], Poisson processes [21], and Monte Carlo methods [22,23,24,25]. By harnessing these computational tools, researchers and engineers gain access to distinctive perspectives and capabilities, empowering them to simulate, analyze, and predict corrosion phenomena with remarkable precision and dependability.
The typical model such as Cellular Automata, Monte Carlo model, and Poisson processes are mathematical models that can be utilized in different aspects of corrosion management. In the field of corrosion, cellular automata have proven valuable information on the behavior of corrosion metals and alloys in contact with aggressive environments [26,27]. The cellular automata models generate interactions between electrochemical reactions, mechanical stresses, and material degradation, providing insights into the initiation, propagation, and evolution of various types of corrosion. Cellular Automata models considering the impact of environmental factors, in the optimization of corrosion-resistant materials.
Cellular automata models have proven to be valuable tools in corrosion management and mitigation strategies. They offer a computational framework for simulating and understanding the complex behavior of corrosion processes [28], enabling researchers and engineers to develop effective corrosion management techniques. The key applications of CA models in corrosion management are (i) predicting corrosion propagation, due which can simulate the propagation of corrosion in metallic structures, such as pipelines, bridges, or storage tanks [29]. These models can predict the spatial and temporal evolution of corrosion damage and help in identifying critical areas with corrosion and planning targeted inspection and maintenance activities [30], (ii) CA helps to understand the factors contributing to corrosion initiation, propagation, and the formation of localized corrosion features such as pits and crevices [31], (iii) CA can also be used to optimize corrosion management strategies by exploring different scenarios [32] and decision-making processes. These models can evaluate the cost-effectiveness of various corrosion control measures, optimize inspection and maintenance schedules, and assess the long-term performance and durability of materials under different environmental conditions, (iv) CA the assessment of corrosion-related risks in different scenarios, considering environmental parameters, material properties, and corrosion rules, these models can estimate the probability and severity of corrosion-induced failures, allowing for better risk mitigation and resource allocation [33], (v) and CA can serve as educational tools to enhance the understanding of corrosion processes among students and professionals in the field, due visualizing corrosion behavior and the effects of different factors [34], these models facilitate learning and provide a platform for exploring corrosion management strategies.
By utilizing Cellular Automata models in corrosion management, researchers and engineers can gain valuable insights into corrosion processes, optimize corrosion control measures, and develop proactive strategies to mitigate the detrimental effects of corrosion.
2.1. Fundamentals of Cellular Automata for Corrosion.
The AC model was initially proposed by John Von Neumann and corresponds to an idealization of a physical system where time and space are discrete and physical quantities take on a finite set of values [5]. Space is represented on a grid of cells, and each cell has a specific state. In a simplistic way, the state of a cell can be assigned as either alive or dead (0 and 1), indicating its characteristic.
To clarify, for an entity to be classified as a CA (Counter Argument), it must adhere to the following structure. A regular grid of cells that covers a part of a d-dimensional space.
A set of Boolean variables attached to each site r of the grid that gives the local state of each cell at time t = 0,1,2, …, n.
A rule R = {R1, R2, …, Rm} that specifies the time evolution of the states in the following form:
where denotes cells belonging to a specific neighborhood.
In the above definition, the rule R is applied to all sites simultaneously, leading to synchronous dynamics [34].
In the context of corrosion, the cell state can represent the presence of an element, a compound, or a corrosion product. The state of a cell changes over time depending on its own state and that of its nearest neighbors. Figure 1 shows a grid of cells where the cell undergoing a state change is represented in black, while the cells enclosed in a black frame (neighborhood) are the ones that influence this change, considering the state of their neighbors. This figure represents the three most used types of neighborhoods: Von Neumann, Moore, and Margolus. In the Von Neumann neighborhood (a), four neighbors are considered, located to the east, north, west, and south of the changing cell. On the other hand, in the Moore neighborhood (b), there are six neighbors surrounding the central cell. Finally, in the Margolus neighborhood, the change process is more complex as it depends on both space and time. Firstly, the space is divided into a 2x2 square. The first state change of cell lr occurs during an odd time, considering the neighbors in the upper square (ul, ur, ll, lr). In the next iteration, during even time, the state of cell lr is updated considering the neighbors in the square represented by dashed lines.
The neighborhood used traverses the entire grid, and through a set of transformation rules, the new state of each cell will be determined until the total update of the grid is completed, which represents the first generation (iteration) of the model. The rules and configuration of the AC model in corrosion simulations are specific for each phenomenon to be studied.
Table 1 presents a comprehensive summary of the results published in popular science journals, which have been utilized to support our bibliographic review.
2.1.1. Uniform Corrosion Model.
Fairén et al. [28] analyzed the evolution of surface roughness in the studied corroded metal. They examined the agreement between a classical macroscopic description and a mesoscopic approach that accounts for the development of such roughness. They studied how morphology could influence the modeling, finding that the model could simulate the mesoscopic heterogeneity of the electrode surface and its impact on the uniform corrosion process. Part of their study determined that further research was still needed to fully understand the relationship between the electrochemical mechanism involved, the steps determining corrosion rate, and the morphology of the electrode surface.
Badiali et al. [35,36,37] studied the formation of films on a surface in the presence of corrosion, diffusion, and precipitation at the growth front. Obtaining results that show that the growth of the layer follows a parabolic law and that the model can be useful for predicting and controlling corrosion growth in metallic structures, pipes, and equipment, as well as for developing new corrosion-resistant materials. Chen et al. [38,39] studied the corrosion and oxidation mechanism of stainless steel in lead-bismuth eutectic (LBE) environments, a liquid metal used as a coolant in some advanced nuclear reactors and accelerator-driven systems, and in [40] the medium was supercritical water. The model considered diffusion, reaction, and precipitation processes occurring on the steel surface, and a mesoscopic description was used to explore the general characteristics of the evolution of the involved processes. Additionally, they aimed to predict how oxide scale removal occurs and how it affects metal corrosion, concluding that the CA model is useful for understanding these mechanisms. Chen et al. [41] focused on simulating the growth of the oxide layer in chromium-containing stainless steels. Their objective was to verify whether the stochastic nature of the CA model for uniform corrosion would generate unstable or unreasonable results deviating from the deterministic model for uniform corrosion of steel in flowing LBE. Their results showed that the CA model is stable and reliable for simulating the thickness of the oxide layer. Chen et al [33] proposed a numerical simulation method to predict the evolution of uniform corrosion damage of the outer steel tube in concrete-filled tubular columns subjected to corrosive environments. They discussed the influence of solution concentration and the probability of dissolution of corrosive agents. The obtained results were compared with theoretical solutions and experimental findings. They concluded that different concentrations of corrosive agents have different impacts on the degree of corrosion damage. Ren et al. [42] simulated the uniform corrosion of aluminum in various environmental conditions. They defined corrosion rules based on the actual electrochemical reactions and examined the corrosion process at a mesoscopic scale. By studying the corrosion formation and modifying the rules for different concentrations of corrosive solutions and ambient temperatures, they gained insights into corrosion mechanisms. The simulation results contribute to a better understanding of corrosion and can aid in its prevention and mitigation, especially in aeronautical structures where corrosion can lead to fatigue-induced damage, compromising structural integrity. Li et al [43] sought to gain a better understanding of the corrosion evolution of marine structural steel in the tidal zone and how corrosion can be prevented or mitigated in this environment. Their objective was to comprehend the corrosion mechanisms in the tidal zone, identify the factors influencing the corrosion rate, and propose possible strategies to prevent or mitigate corrosion in structures and equipment used in marine environments, ultimately offering solutions to extend their lifespan. Wang et al [29,44] investigated the corrosion of a metal in molten chloride salt and explored methods to enhance its corrosion resistance. A simplified model was established based on the reactive diffusion of corrosive gas and the metallic substrate. Both experiments and simulations were conducted using the cellular automaton (CA) method.
The physical model from the experimental work determined that the main reactions involved are:
They assumed the presence of corrosive substances in the molten salt from the beginning, where O2 and H2O diffuse into the molten salt from the air, leading to the formation of HCl and Cl2 through a set of reactions. The dissolved O2 in the salt rapidly reacts with Cr (2). When the Cr content is insufficient, O2 reacts with Ni (3). The chloride containing Cr (mainly CrCl4) forms a protective spinel layer composed of MgCr2O4 through (4). On the other hand, Cl2 can react with Cr, resulting in a chromium-depleted layer (5).
To establish the CA model, the chemical reactions involved in the corrosion process were simplified by assigning letters to the compounds or elements present. A = Cr; B = Ni; O = O2; C = Cl2; D = CrCl4; Mg = MgO; P = MgCr2O4; BO = NiO.
The lattice sites were classified into fixed compounds (A, B, MgO, P, and BO) and mobile compounds (O, C, D). The interaction of mobile compounds within the lattice occurs through a probabilistic random walk process. As an example, Figure 2 shows four grid schematics of the CA model. In (a), a grid is depicted with the fixed compounds located. In (b), the location of mobile compounds that diffuse toward the metal is shown. In (c), the elements that can diffuse in the outer corrosion layer are present, and in (d), a lattice is shown where all compounds present in the process are located.
In reactions (6) to (9), the modified reaction and transformation rules for the CA model are shown.
The Margolus neighborhood was used to induce state changes in the different cells across generations. Figure 3 displays the results obtained by the model, where the left side (black color) represents the molten salt, while the right side (purple color) represents the metal under study. As the iterations progress, the growth of the oxide layer is observed. The number of iterations can be interpreted as representing an experimental time scale.
A comparison is shown in Figure 4 between the simulation results and a scanning electron microscopy (SEM) image. It was determined that 64,000 iterations correlate with the experimental results from 21 days of exposure, demonstrating that the AC simulation yields satisfactory results in the study of high-temperature corrosion of Fe-Cr alloys in the presence of molten salts.
2.1.2. Localized and pitting Corrosion model.
Localized corrosion encompasses corrosion processes that occur in specific areas of a material, leading to localized damage. Cellular automata simulate the initiation and propagation of localized corrosion, providing insights into factors influencing its occurrence, growth patterns, and evolution over time.
Di Caprio et al. [20,45] presented an electrochemical model for the corrosion of metals in contact with liquids, based on the description of chemical and electrochemical reactions occurring at the metal-liquid interface, which was simulated using CA. They investigated the corrosion process of each metallic site at the interface and compared the simulation results with experimental data. The proposed model reproduced experimental facts and trends without an explicit separation between anodic and cathodic sites. Overall, the study demonstrated that cellular automata-based models are a useful tool for simulating complex systems such as metal corrosion and can be adapted to include different rules and conditions according to the specific needs of the system under study. Cheng et al. [46] simulated the growth of metastable corrosion pits. The objective was to gain a better understanding of the mechanism behind the growth of these pits and compare the simulated results with experimental data. The researchers established a relationship between the current and current density of the pit over time to illustrate the mechanism of metastable pit growth. Additionally, they developed an optimal range of parameters for the simulation that allowed for visualizing the complete process of pit growth, including its geometry. The study built on previous work on the mechanism and electrochemical and mass transfer steps associated with the pitting corrosion process. Wang et al. [47] reproduced the interactions between metastable pits in stainless steel and analyzed how different factors affect their growth and stability. The model included corrosion, passivation, salt film hydrolysis, and hydrogen ion diffusion. Based on the model, they concluded that it is capable of accurately simulating the interactions between metastable corrosion pits in stainless steel. Wang et al. [48] investigated the interaction of metastable corrosion pits in stainless steel under mechano-electrochemical effects using an updated cellular automaton/finite element model, elucidating the mechanisms for pit interactions. In the study, they considered an electrochemical system where stainless steel is exposed to an aggressive chloride solution. The stainless-steel samples had passive layers of surface oxide, which can be damaged in the presence of chloride anions. Two breakdown locations in the passive film were included to study only the pit propagation and not its nucleation. They concluded that the cellular automaton/finite element model used was effective in predicting the interaction of corrosion pits on a mesoscopic scale. Torska et al. [49] discussed the fracture dynamics in the investigated areas and performed a comparative analysis of pitting corrosion rates under real and simulated conditions. They demonstrated that the simulation procedure using cellular automata accurately reproduced the physics of corrosion. The study proposed a new modeling algorithm and local transition rules for the automaton cells used in simulating pitting corrosion images. Hu et al. [50] simulated pitting corrosion in nickel alloys. The authors employed four fundamental elements of the model to simulate electrochemical reactions, chemical reactions, and diffusion processes. The obtained results were qualitatively and quantitatively compared with experimental data and analogous findings cited in the literature. The study suggested that this type of model could be useful in gaining a better understanding of corrosion processes and developing corrosion-resistant materials for various industrial applications. Fatoba et al. [51] employed a combination of cellular automata and finite element analysis to simulate the growth of localized corrosion under the influence of applied stress. The results demonstrated that mechanical effects, such as plastic deformation, accelerated the rate of localized corrosion development. The study focused on low-alloy steel, but the findings may be applicable to other materials as well. Rujin et al. [52] established a mathematical model based on a statistical approach to describe the evolution process of pitting corrosion. Additionally, they proposed a 3D stochastic CA model to replicate the simultaneous initiation and growth process of pits. The findings of the study can contribute to a better understanding of the laws governing pitting corrosion evolution and provide valuable insights into its prevention and control. To simulate localized corrosion, Pérez-Brokate et al. [31,53] aimed to gain a better understanding of hidden corrosion processes and pitting corrosion within corrosion cells by using a stochastic cellular automaton (CA) model. They studied the morphology, propagation, and influence of coupled diffusion within the corrosion cavity.
In the physical-chemical model, simplifications were made by assuming simplified electrochemical and chemical reactions (excluding contaminants and considering only H+ and OH-). Localized corrosion, being a multi-scale phenomenon, depends not only on atomic-scale surface phenomena but also on macroscopic environmental conditions.
The electrochemical reactions used:
Anodic reactions.
Cathodic reactions.
Authors called SJ reactions when the anodic and cathodic half reactions occur at the same location:
The anodic and cathodic sites are electrically connected through the metal and the solution. When they are separated, they are referred to as Spatially Separated Electrochemical (SSE) reactions. The diffusion of SSE reactions results in the generation of H+ and OH- ions, mimicking a random walk. When these ions interact, neutralization takes place, as depicted in the study through the following reaction:
The 3D lattice representation is depicted in Figure 5, illustrating a passivated metal in contact with a neutral electrolyte and the cathodic reaction takes place at a random point Figure 5a. The H+ and OH- ions generated in the first reaction diffuse in the electrolyte. Each lattice site was determined by the dominant species. In Figure 5b the solid sites represent the metal (M), the metal in contact with the electrolyte (R), and the oxide layer providing passivity to the metal (P). Additionally, the electrolyte sites were differentiated into three different states based on pH. An acidic site (A), a basic site (B), and a neutral site (E) were considered. The Moore neighborhood was employed for the simulation.
In Figure 6, they showed the evolution of the pit. They indicated the presence of an anodic half-reaction at the initial defect of the passive layer. The ions are dispersed randomly in the electrolyte, resulting in the growth of the pit when an H+ ion encounters the metal, leading to an electrochemical reaction. As the pit reaches a certain size, the concentration of acidic ions increases, causing instability and further enlargement of the pit.
The model was considered a valuable tool for gaining a better understanding of localized and pitting corrosion processes and developing more effective strategies for corrosion prevention and treatment.
2.1.3. Stress Corrosion Cracking (SCC) model
Stress corrosion cracking is a phenomenon where the combination of tensile stress and a corrosive environment leads to crack initiation and propagation in a material. Cellular automata modeling the complex interactions between mechanical stress, electrochemical processes, and material degradation, helping to understand the conditions under which SCC occurs and its progression.
Zhu et al. [54] focused on predicting the service life of concrete bridges and preventing chloride-induced corrosion. They utilized 3D-CA, which accurately simulates chloride diffusion in concrete. Multiple factors were considered, such as ambient relative humidity, temperature variations, stress, water-cement ratio (w/c), concrete degradation, corrosion propagation, cracks, and time. The study provides a useful tool for predicting the service life of the bridge and designing preventive measures against chloride-induced corrosion in concrete bridges. Liu et al. [55] modeled the SCC process in steel pipes. They employed a combination of finite element analysis and cellular automata techniques to simulate the initiation and propagation of cracks.
The electrochemical model used considered only the species H2O, Fe, Fe2+, H+ and FeOH+. The rules for corrosion evolution and cell diffusion were expressed in the following equations:
Based on the equations above, the authors formulated the rules of the AC model, where the diagram in Figure 7 represents the spatial layout of the model. The sites W represented a non-corrosive neutral solution (H2O), H represented a corrosive acidic solution (H+), the site M represented the metal, which dissolves to form site R after being in contact with the corrosive solution. The site R represents the active metal (Fe2+), and site P represents the corrosion product (FeOH+).
The evolution rules for corrosion in the CA model were formulated based on the previous equations. Figure 8 shows the rules for the oxidation of Fe and the hydrolysis of Fe2+ to FeOH+. When a site M is in contact with at least one site H, reaction 1 will occur with a corrosion probability Pcorr, transitioning from site M to site R. Additionally, when a site R is in contact with at least two sites W, Fe2+ hydrolyzes to FeOH+ with a probability PHyd, and both site R and the two W sites are replaced by the corrosion site P and two H sites, respectively.
The results demonstrated that prior to crack initiation, pitting corrosion was controlled by anodic reactions and mechanical factors, with electrochemical corrosion playing a significant role. During the crack propagation process, the mechano-chemical effects induced by plastic deformation promoted anodic dissolution at the crack tip, driving its propagation. This study may have significant implications for the pipe industry and help develop more effective strategies for corrosion prevention.
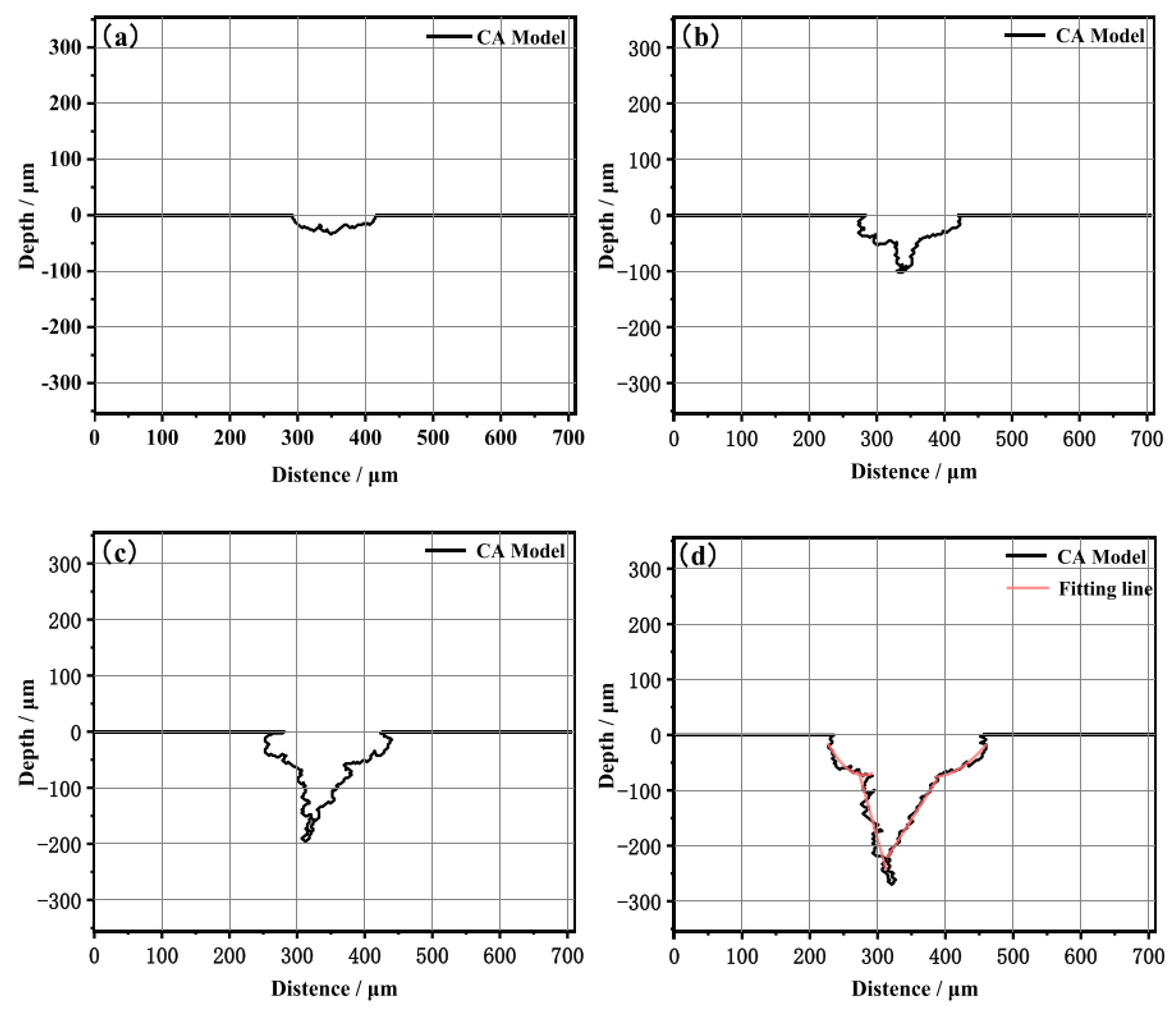
Figure 9.
Evolution process of cross-sectional stress corrosion profiles: (a) 30 h, (b) 60 h, (c) 90 h, and (d) 120 h [55].
Figure 9.
Evolution process of cross-sectional stress corrosion profiles: (a) 30 h, (b) 60 h, (c) 90 h, and (d) 120 h [55].

2.1.4. Intergranular Corrosion Model.
Intergranular corrosion occurs along the grain boundaries of a material, typically due to variations in composition or microstructure. Cellular automata can simulate the interactions between different grain boundaries, their susceptibility to corrosion, and the role of environmental factors in intergranular corrosion.
Chen et al. [56] developed a cellular automaton model to predict the susceptibility to intergranular corrosion in austenitic stainless steel and provide useful information on how to prevent or mitigate this problem. The results demonstrated how material properties change under different heat treatment and sensitization conditions. Additionally, they investigated factors affecting intergranular corrosion, such as the evolution of chromium-rich carbide precipitation and chromium concentration distribution [57]. They concluded that the CA model can be valuable for improving the design and performance of materials used in industrial applications.
Lishchuk et al. [58] utilized cellular automata to describe the propagation of intergranular corrosion and made simplifying assumptions that enabled them to predict the corrosion rate. The results of the model demonstrated good qualitative and quantitative agreement with experimental data regarding the advancement of the corrosion front.
Jahns et al. [59,60] develop a simulation to predict internal corrosion during high-temperature applications in metal alloys. They utilized the model to describe diffusion-controlled precipitation processes and enhance the understanding of high-temperature corrosion in metal alloys. The researchers' goal was to develop more effective strategies to prevent or mitigate corrosion.
Di Caprio et al. [61,62,63,64] conducted various studies on intergranular corrosion using 2D and 3D CA models. Their aim was to predict the rate and pattern of corrosion in stainless steel exposed to corrosive solutions. They quantitatively analyzed the surface morphology of the steel and grain boundary structures. They presented CA methodologies to understand and prevent corrosion, and experimental validation yielded positive results.
Wang et al. [65] focused on investigating the corrosion behavior of a nickel-based alloy in a molten chloride salt mixture. The CA model enabled them to reproduce the distribution of corrosion products and components, as well as changes in the morphology and thickness of the corrosion layer over time. The results of the study can help predict the corrosion behavior of different metals in similar molten salt environments.
The mechanism of high-temperature corrosion is relatively complex. In the study conducted by Wang et al. [44], due to the alloy being primarily composed of Cr, Fe, and Ni elements, which play a significant role in corrosion resistance and alloy microstructure, only Cr, Fe, and Ni were considered in the model, excluding other elements present in lower concentrations.
The mechanism considered by the authors primarily involved the migration of metallic elements, substance consumption, and generation of corrosion products through the following equations:
Like the presented studies in the uniform corrosion section, the physical model was simplified to facilitate the programming language.
where: AA = Ni, DD = Fe, EE = Cr, O = O2, c = Cl2, Y = Fe2O3, YY = Cr2O3, AO = NiO, D = CrCl4, and FF = FeCl3. All elements except for O, c, and D were considered fixed in the lattice. The positions of O and c were randomly predetermined with an assigned probability, and the sites AA, DD, and EE represent the alloy elements.
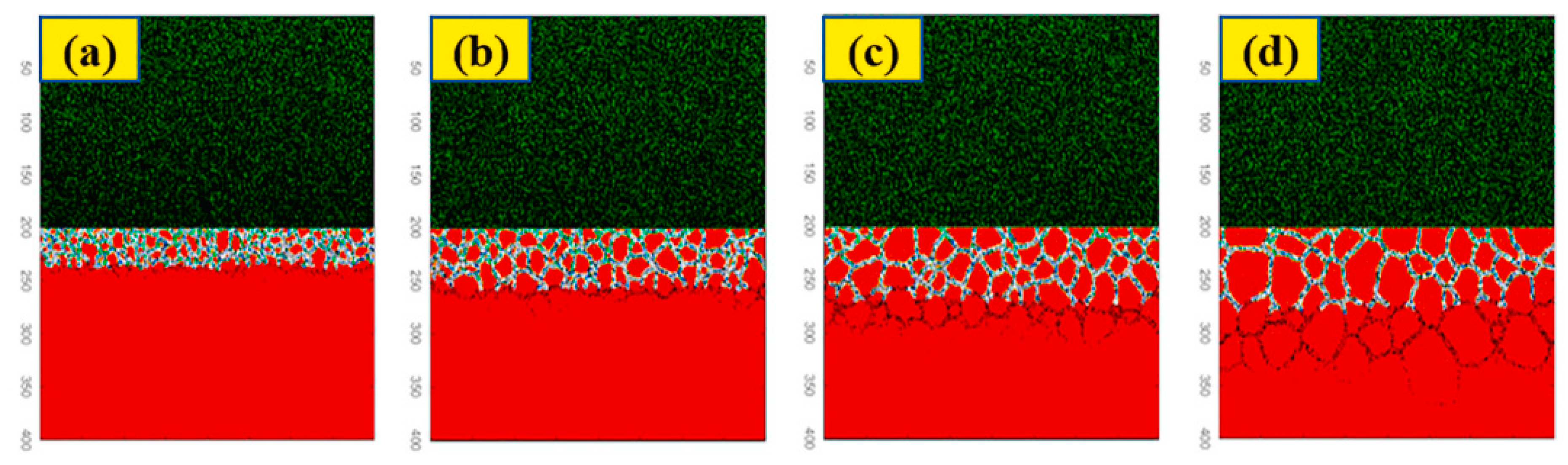
To consider the simulation of intergranular corrosion, the authors evaluated the effect of grain size. To obtain the initial structure, they simulated the grain growth process at different time steps Figure 10.
Therefore, their simulation of intergranular corrosion consisted of obtaining the initial microstructure model, which was combined with the AC model. The result of the model is shown in Figure 11, which displays different structures of the model at various iterations. The development of intergranular corrosion in the studied steel by the researchers can be observed.
3. Modeling approach and methodology for simulating corrosion phenomena
The methodology for simulating corrosion phenomena involves several key steps and considerations.
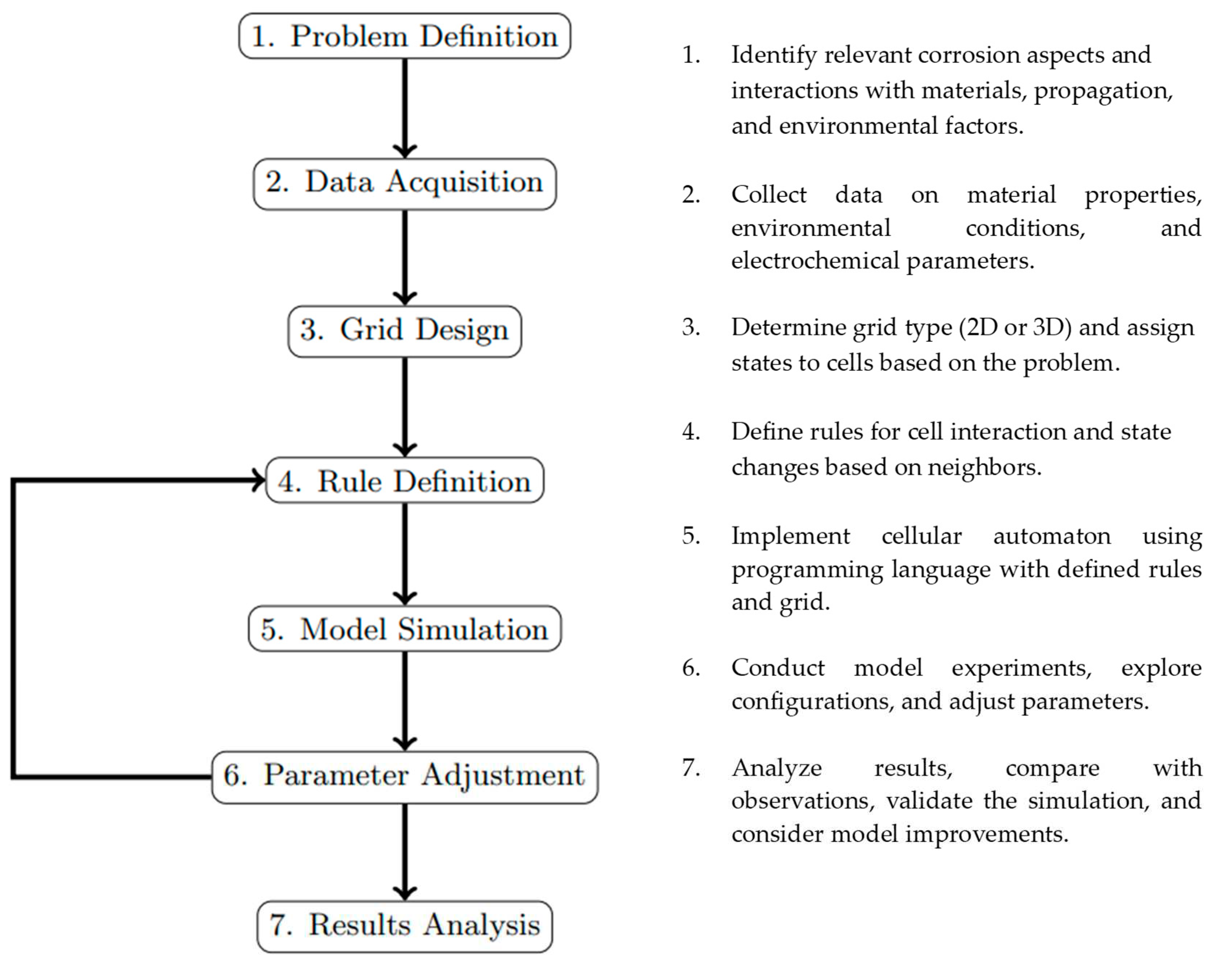
Figure 12.
Methodology for implementing a cellular cutomata model.

Table 1.
Summary of the results published.
| CA type | Neighborhood | Model type | Boundary | Lattice size | Rules | Cycles | Corrosion type | Environment | Material | Temperature (°C) | Exposure time (h) | Validation type | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LGAa | n-vector | Probabilistic | Periodic | - | - | - | - | - | - | - | - | Boltzmann hypothesis | [66] |
| 2D | n-vector | Probabilistic | Periodic | 200x160 | 3 | 48.000 | Kinetic of internal oxide precipitation | Oxygen | Metal | - | - | Theory of phase equilibrium | [67] |
| Theoretical | Moore | Probabilistic | Periodic | > 1000x1000 | 8 | - | Uniform | Electrolyte | Metal | - | - | Previous work data | [28] |
| 2D | Von Neumann | Probabilistic | Periodic | 2000x1000 | 2 | 10.000 to 90.000 | Uniform | Electrolyte | Metal | - | - | - | [35] |
| 2D | Von Neumann | Probabilistic | Periodic | 1000x1000 | 3 | 200.000 | Uniform | Solvent | Metal | - | - | Parabolic law | [36] |
| 2D | Von Neumann | Deterministic | Periodic | 600x20000 | 2 | 150 | Uniform | Electrolyte | Metal | - | - | Mott and Cabrera Parabolic’s law | [37] |
| 2D | Von Neumann | Probabilistic | Periodic | 1000x1000 | 2 | 25.000 | Uniform | Liquid lead alloy | Metal | 550 | 3.000 | Wagner theory | [38] |
| 3D | - | - | - | 100x100 | - | - | Intergranular | Sulfuric acid | Metal | 1100 | 0-400 | Electrochemical potentiodynamic reactivation | [56] |
| 2D | Moore | Probabilistic | - | 500x500 | 2 | 200.000 | Uniform | LBE | Metal | 535 | 3000 | Wargner theory | [39] |
| LGA-2D | Von Neumann | Probabilistic | - | 2000xLy | 3 | - | Pasivation | Solution | Metal | - | - | Passivation theory | [68] |
| 2D | Moore | Deterministic | - | 200x200 | 2 | 3 | Intergranular | Solution | Metal | 1100 | 2 | - | [57] |
| 2D | Von Neumann | Probabilistic | Periodic | - | 2 | 7.200.000 | Localised | Solution | Metal | 360 | - | Experimental | [45] |
| 2D | Von Neumann | Probabilistic | - | 1000x1000 | 399.577 | Localised | Solution | Metal | - | - | Pistorius experimental results | [46] | |
| 2D-3D | Moore | Probabilistic | Periodic | 640x320 – 240x280x240 | 3 | - | Intergranular | Solution | Metal | - | 144 | Eperimental | [58] |
| LGA-2D | Von Neumann | Probabilistic | - | 2000xLy | 2 | - | Pasivation | Solution | Metal | - | - | Passivation theory | [69] |
| 2D | Moore | Probabilistic | - | 500x500 | 2 | 5.000 | Uniform | Water | Metal | 600 | 1000 | Experimental | [40] |
| 2D | Von Neumann | Probabilistic | Periodic | 900x300 | 2 | 70.000 | Uniform, localised | Solution | Metal | 300-360 | - | Experimental | [20] |
| 2D | Von Neumann and Moore | Probabilistic | Periodic | 1000x1000 | 14 | 7.679 | Localised, passivation | Solution | Metal | - | - | Theoretical corrosion and passivity phenomena | [70] |
| 2D | Von Neumann and Moore | Probabilistic | Periodic | 1000x1000 | 11 | 4.000 | Crevice, passivation | Solution | Metal | - | - | Experimental | [71] |
| 2D | Moore | Probabilistic | - | 500x500 | 2 | 200.000 | Uniform | LBE | Metal | - | - | Chi-square of goodness-of-fit | [41] |
| 2D | Von Neumann and Moore | Probabilistic | - | 512x512 | 3 | 2.000 | Oxidation and nit | - | Metal | 1100 | 100 | Experimental data | [72] |
| 3D | Moore | Probabilistic | Periodic | 151x200x200 | 3 | 200 | Pitting | Solution | Metal | - | 0.5 | Experimental data | [73] |
| 2D | Von Neumann and Moore | Probabilistic | - | 512x512 | 3 | 20.000 | Oxidation and nitridation | Solution | Metal | 1100 | 100 | Experimental data | [74] |
| 3D | Moore | Probabilistic | Periodic | - | 4 | 124 | Pitting | Solution | Metal | - | 480 | Experimantal data | [75] |
| 2D | Moore and Von Neumann 2nd order | Probabilistic | - | 1000x1000 | 4 | 1.000 | Pitting | Solution | Metal | - | - | Experimental data | [76] |
| 2D | Von Neumann | Probabilistic | - | 1024x1024 | 2 | - | Pitting | Solution | Metal | - | - | Experimental data | [47] |
| 2D | Moore | Deterministic | Reflect | - | 2 | - | Pitting | Solution | Metal | - | - | Experimental data | [77] |
| 2D | Von Neumann | Probabilistic | Periodic | 1024x1024 | 5 | - | Pitting | Solution | Metal | - | - | Experimental data | [48] |
| 2D | Von Neumann 2nd order | Probabilistic | - | - | 3 | - | Pitting | Solution | Metal | Room | - | Experimental data | [49] |
| 2D | Von Neumann | Probabilistic | Periodic | 2000x2000 | 3 | 6.000 | Pitting | Water | Metal | - | 1.600 | Experimental data | [50] |
| 2D | Von Neumann and Moore | Probabilistic | - | 500x500 | 3 | 3.000 | Intergranular | Air | Metal | 1100 | 100 | Experimental data | [59] |
| 3D | Moore | Probabilistic | - | 512x512x512 | 4 | > 5.000 | Occluded, localized | Solution | Metal | - | - | Experimental data | [53] |
| 3D | - | Probabilistic | Periodic | 512x512x4096 | - | 4.000 | Intragranular | Solution | Metal | - | 7.000 | Experimental data | [61] |
| 2D | Von Neumann | Probabilistic | - | - | 3 | 25.000 | Electrochemical oxidation | Solution | Metal | 600 | 30 | Experimental data | [78] |
| 2D | Von Neumann and Moore | Probabilistic | - | 512x512 | 3 | - | Intergranular oxidation | Air | Metal | 1100 | 100 | Experimental data | [60] |
| 2D | Moore and Von Neumann extend | Probabilistico | Periodic | 1000x1000 | - | 2.000 | Uniform | Solution | Metal | - | - | Theoretical and experimental | [33] |
| 3D | Moore | Probabilistic | - | 256x256x256 | 7 | 45.000 | Pitting | Solution | Metal | - | - | Experimental data | [31] |
| 3D | Moore | Probabilistic | Periodic | 512x512x512 | 7 | 7.000 | Generalized | Solution | Metal | - | - | Experimental data | [79] |
| CA-FE-2D | Moore | Probabilistic | - | 2000x1000 | 4 | - | Localized | Solution | Metal | - | - | Experimental data | [80] |
| 3D | Von Neumann | Probabilistic | Constant and periodic | 100x100x100 | 4 | 400 | Atmospheric corrosion | Atmosphere | Metal | - | - | Theoretical and experimental data | [81] |
| 3D | Von Neumann | Deterministic | Periodic | 100x100x100 | 5 | 1.000 | Uniform | Solution | Metal | 20 | - | - | [42] |
| 3D | Von Neumann | Probabilistic | - | 7500x7500x1500 | - | - | Pitting | Salt-Spray | Metal | 35 | 1.440 | Experimental data | [52] |
| 2D | Margolus | Probabilistic | Rigid | 400x400 | 4 | 25.000 | Uniform | Solution | Metal | 600 | 504 | Experimental data | [29] |
| LGA-3D | Von Neumann | Probabilistic | Periodic | - | - | - | Passivation | Solution | Metal | - | - | Passivation theory | [82] |
| 3D | 12-neighbors | Probabilistic | Periodic | 1280x1280x1280 | - | - | Intergranular | Solution | Metal | - | 2.000 | Experimental data | [62] |
| 2D-bi plane | Von Neumann | Probabilistic | - | 500x500 | 5 | 100 | Pitting | Solution | Metal | - | - | Experimental data | [83] |
| 3D | - | - | - | 2048x2048x256 | 3 | 350 | Intergranular | Solution | Metal | - | - | Experimental data | [63] |
| 2D | Margolus | Probabilistic | Periodic | 400x400 | 7 | 70.000 | Uniform, intergranular | Solution | Metal | 600 | 504 | Experimental data | [44] |
| 3D | Margolus | Probabilistic | Periodic | 1280x1280x1280 | - | 21.555 | Intergranular | Solution | Metal | 111 | 17.783 | Experimental data | [64] |
| 2D-3D | Margolus | Probabilistic | Periodic | 40x400 - 100x100x100 | 10 | 50.000 | Intergranular, pitting | Solution | Metal | 700 | 168 | Experimental data | [65] |
| 3D | Von Neumann | Probabilistic | Periodic | 1000x1000x1000 | 5 | - | Uniform, pitting | Solution | Metal | 168 | Experimental data | [43] | |
| 2D | Moore | Probabilistic | - | 1024x1024x128 | 4 | 2.000.000 | Aqueous | Solution | Metal | 50 | 853 | Experimental data | [84] |
| 2D | Von Neumann | Probabilistic | - | 250x250 | 2 | 2.000 | Cracking | Solution | Metal | 27 | - | Experimental data | [55] |
| 3D | Von Neumann | Probabilistic | - | 2000x2000x1000 | 2 | - | Cracking | Concrete | Metal | 23 | 672 | Experimental data | [54] |
| 3D | Moore | Probabilistic | Periodic | 104x104x104 | 5 | - | Atmospheric corrosion | Atmosphere | Metal | - | - | Experimental data | [30] |
4. Future Perspectives and Emerging Trends.
Cellular automata models have emerged as powerful tools for analyzing various types of corrosion, offering valuable insights into their complex behavior. These models capture spatial and temporal variations, enabling a thorough examination of corrosion phenomena. Notably, cellular automata models have successfully analyzed specific corrosion types such as stress corrosion cracking, corrosion under insulation, marine corrosion, and more. Through these simulations, critical areas prone to corrosion can be identified, corrosion control measures can be evaluated, and corrosion-induced failures can be predicted, providing valuable perspectives for effective corrosion management.
When developing cellular automata models to simulate corrosion phenomena, it is crucial to consider a range of environmental parameters that have a substantial impact on corrosion performance. These parameters reflect the realistic conditions under which corrosion takes place. Firstly, the composition of the electrolyte solution surrounding the material holds the utmost importance in determining the corrosive environment. Factors such as pH, chloride concentration, dissolved oxygen levels, temperature, and other relevant chemical species all contribute to this environment. Secondly, the movement of the electrolyte solution, also known as flow or mass transport, plays a significant role in corrosion processes. It is imperative to account for these parameters in order to create accurate and comprehensive cellular automata models for studying corrosion behavior. Consideration of flow patterns, velocity, and diffusion rates within cellular automata models is essential to simulate the effects of convection, mass transfer, and concentration gradients on corrosion behavior. Thirdly, these models should account for the specific environmental exposure conditions relevant to the corrosion scenario, such as marine environments, industrial atmospheres, underground conditions, or exposure to specific chemicals. The inclusion of temperature as a critical environmental parameter is crucial, as thermal effects can impact corrosion rates by influencing electrochemical reaction kinetics, diffusion rates, and material properties. By incorporating temperature variations into the cellular automata model, a more comprehensive understanding of corrosion behavior under different thermal conditions can be achieved.
In some corrosion scenarios, such as atmospheric corrosion, humidity, and moisture levels play significant roles. A well-designed cellular automata model enables the simulation of localized corrosion phenomena related to moisture accumulation or the presence of electrolyte films. Additionally, it is important to consider the influence of ultraviolet (UV) radiation from sunlight, especially in outdoor environments. UV radiation can induce photochemical reactions, affect surface properties, and alter the electrochemical behavior of materials. Therefore, incorporating the effects of UV radiation into the cellular automata model provides a more accurate representation of corrosion behavior. By considering these various environmental parameters and incorporating them into the cellular automata models, a comprehensive and realistic simulation of corrosion behavior can be achieved, facilitating a deeper understanding of the corrosion processes and aiding in the development of effective corrosion mitigation strategies. Through the evaluation of corrosion mechanisms, the development of corrosion prevention strategies, and the assessment of material performance in specific environments by cellular automata models, researchers can obtain a more comprehensive understanding of corrosion processes and accurately simulate the behavior of materials under realistic conditions. The integration of data-driven approaches, such as machine learning and artificial intelligence, enhances corrosion monitoring, prediction, and decision-making are fundamental for a good future in the early detection of failures. These approaches leverage large datasets to identify patterns, anomalies, and correlations that can improve corrosion management strategies. Advances in remote sensing technologies and real-time monitoring systems enable continuous and remote monitoring of corrosion parameters and provide valuable data for proactive corrosion management, allowing for early detection of corrosion, timely interventions, and improved asset integrity management.
The future of cellular automata in corrosion research will be about the integration of advanced computational techniques, such as machine-learning algorithms, and data-driven approaches. This integration allows for more accurate and predictive corrosion models by leveraging large datasets and optimizing model parameters based on experimental or real-time monitoring data. In addition, the incorporation of electrochemical considerations in cellular automata models can better capture the fundamental mechanisms and behavior of corrosion, leading to more realistic simulations and predictions. The multi-scale modeling is a growing trend toward coupling cellular automata models with other modeling techniques, such as finite element analysis or computational fluid dynamics.
The integration of cellular automata in corrosion management generates models with corrosion monitoring and control systems that will enable real-time feedback and adaptive control strategies. This integration can enhance the effectiveness of corrosion prevention and mitigation measures by dynamically adjusting parameters based on the evolving corrosion behavior. Real-time monitoring techniques in cellular automata models allow for dynamic modeling of corrosion processes. By integrating data from sensors and monitoring systems, researchers can obtain more accurate and up-to-date information on corrosion behavior, enabling proactive corrosion management strategies. At the same time, the focus is on refining model parameters, algorithms, and simulation techniques to improve the accuracy and reliability of predictions, ultimately enabling more effective corrosion management strategies. CA models have the potential to be used in the design and optimization of corrosion-resistant materials used in storage energy by molten salts. Future perspectives in cellular automata models in molten salt corrosion involve the development of more sophisticated models that can accurately capture the complex corrosion mechanisms specific to molten salt environments. This includes considering factors such as electrochemical reactions, mass transport, and the interaction between molten salts and the material surface.
5. Conclusions
In conclusion, cellular automata offer a promising avenue for advancing corrosion management through their provision of a robust modeling and simulation framework. Their capacity to effectively capture the intricate dynamics of corrosion processes presents an opportunity to develop predictive models, corrosion-resistant materials, and real-time monitoring systems. Although challenges remain to be addressed, the prospects of utilizing cellular automata in corrosion management appear encouraging. Continued research and development in this field hold the potential for significant advancements in corrosion control and prevention.
- Most studies focus on uniform corrosion, localized corrosion, and intergranular corrosion. These three mechanisms account for almost 80% of all studies to date, leaving other types of corrosion, such as stress cracking corrosion, with only around 4% of the found studies. This indicates that there is a gap to be explored using cellular automaton for other existing corrosion mechanisms.
- On the other hand, it is observed that the CA model in all reviewed studies has a similar structure. It starts with a known phenomenon, either theoretical or experimental, which is sought to be simulated using CA. Then, the physicochemical or electrochemical model that governs the process is defined, and it is translated into a simplified language that facilitates programming. Each study generates its own reaction and transformation rules, dependent on the initially proposed physicochemical or electrochemical model so that these rules can simulate the desired process.
- There is variability in the mesh size used, the boundary conditions, the type of neighborhood utilized, or the number of transformation rules. Each study considers these aspects in a personalized manner, seeking the suitability of the result depending on the complexity of the corrosion process being studied. Therefore, there is still no single rule that encompasses all processes in a single comprehensive CA model.
- Most studies conclude that the CA model has tremendous potential for simulating the corrosion process of different alloys under different conditions. By using simple rules, it can generate complex patterns, and the obtained results closely match the experimental behavior. Furthermore, the model's ability to represent multiple types of physical phenomena makes it a powerful tool that can help researchers see the studied phenomena from a different perspective.
Author Contributions
The following statements should be used “Conceptualization, J.C.R.B. F.M.G.M, F.P and M.C.C ; methodology, J.C.R.B and F.M.G.M; validation J.C.R.B and F.M.G.M; formal analysis, , J.C.R.B. F.M.G.M, and M.C.C.; investigation, , J.C.R.B. F.M.G.M, M.H and M.C.C.; resources, J.C.R.B, M.C.C and F.M.G.M.; data curation, J.C.R.B and F.M.G.M.; writing—original draft preparation, J.C.R.B and F.M.G.M.; writing—review and editing, J.C.R.B. N.T, F.M.G.M, M.H, F.P and M.C.C.; visualization, J.C.R.B and F.M.G.M; supervision, F.M.G.M.; project administration, M.C.C.; funding acquisition, F.M.G.M, N.T and M.C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The author would like to the Programa de Doctorado en Energía Solar of the University of Antofagasta, Chile, and the authors are grateful for the support of the ANID through research grant Fondecyt 11230550.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lucas Granados, B.; Lucas Granados, B.; Sanchez Tovar, R. Corrosion; Editorial de la Universidad Politecnica de Valencia, 2018. ISBN 9788490487280.
- Koch, G.; Varney, J.; Thompson, N.; Moghissi, O.; Gould, M.; Payer, J. International Measures of Prevention, Application, and Economics of Corrosion Technologies Study. 2016.
- Xiao, Q.; Jang, C.; Kim, C.; Chen, J.; Jeong, C.; Kim, S.H. Corrosion behavior of Fe-based candidate accident tolerant fuel cladding alloys in spent fuel pool environment ― Effect of prior corrosion. J. Nucl. Mater. 2021, 548, 152845. [Google Scholar] [CrossRef]
- Walczak, M.; Pineda, F.; Fernández, Á.G.; Mata-torres, C.; Escobar, R.A. Materials corrosion for thermal energy storage systems in concentrated solar power plants. Renew. Sustain. Energy Rev. 2018, 86, 22–44. [Google Scholar] [CrossRef]
- Schwartz, J.T.; von Neumann, J.; Burks, A.W. Theory of Self-Reproducing Automata. Math. Comput. 1967, 21, 745. [Google Scholar] [CrossRef]
- Javaherdashti, R. Corrosion knowledge management for managers. Mater. Perform. 2016, 55, 58–61. [Google Scholar]
- Wan, Z.; Yang, J. Research on corrosion management technology of petroleum pipeline and pressure vessel. IOP Conf. Ser. Earth Environ. Sci. 2021, 692. [Google Scholar] [CrossRef]
- Jaya, A.; Tiong, U.H.; Clark, G. The interaction between corrosion management and structural integrity of aging aircraft. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 64–73. [Google Scholar] [CrossRef]
- Kurth, J.C.; Krauss, P.D.; Foster, S.W. Corrosion Management of Maritime Infrastructure. Transp. Res. Rec. 2019, 2673, 2–14. [Google Scholar] [CrossRef]
- Balamurugan, P.; Chandramohan, P.; Rao, T.S. Corrosion management of carbon steel material: Operational modes influence corrosion rate-an: In vitro study. RSC Adv. 2016, 6, 41122–41129. [Google Scholar] [CrossRef]
- Larché, N.; Dézerville, P.; Le Flour, D. Corrosion and corrosion management investigations in seawater reverse osmosis desalination plants. Desalin. Water Treat. 2013, 51, 1744–1761. [Google Scholar] [CrossRef]
- Liu, L.; Tan, E.; Cai, Z.Q.; Zhen, Y.; Yin, X.J. An Integrated Coating Inspection System for Marine and Offshore Corrosion Management. 2018 15th Int. Conf. Control. Autom. Robot. Vision, ICARCV 2018, 1536. [Google Scholar] [CrossRef]
- Choudhury, M.R.; Hsieh, M.K.; Vidic, R.D.; Dzombak, D.A. Corrosion management in power plant cooling systems using tertiary-treated municipal wastewater as makeup water. Corros. Sci. 2012, 61, 231–241. [Google Scholar] [CrossRef]
- Kamrunnahar, M.; Urquidi-Macdonald, M. Prediction of corrosion behavior using neural network as a data mining tool. Corros. Sci. 2010, 52, 669–677. [Google Scholar] [CrossRef]
- Beavers, J.A.; Sridhar, N.; Boomer, K.D. Corrosion management of the Hanford high-level nuclear waste tanks. Jom 2014, 66, 491–502. [Google Scholar] [CrossRef]
- Yazdi, M.; Khan, F.; Abbassi, R. Microbiologically influenced corrosion (MIC) management using Bayesian inference. Ocean Eng. 2021, 226, 108852. [Google Scholar] [CrossRef]
- Milazzo, M.F.; Piperopoulos, E.; Khaskhoussi, A.; Scionti, G. Investigation of the bottom corrosion of atmospheric storage tanks for the management of safety. 2022, 35–38.
- Shafeek, H.; Soltan, H.A.; Abdel-Aziz, M.H. Corrosion monitoring in pipelines with a computerized system. Alexandria Eng. J. 2021, 60, 5771–5778. [Google Scholar] [CrossRef]
- Hussain, M.; Zhang, T.; Seema, M.N.; Hussain, A. Application of big data analytics to energy pipeline corrosion management. Corros. Manag. 2021, 2021, 28–29. [Google Scholar] [CrossRef]
- di Caprio, D.; Vautrin-Ul, C.; Stafiej, J.; Saunier, J.; Chaussé, A.; Féron, D.; Badiali, J.P. Morphology of corroded surfaces: Contribution of cellular automaton modelling. Corros. Sci. 2011, 53, 418–425. [Google Scholar] [CrossRef]
- López De La Cruz, J.; Kuniewski, S.P.; Van Noortwijk, J.M.; Gutiérrez, M.A. Spatial Nonhomogeneous Poisson Process in Corrosion Management. J. Electrochem. Soc. 2008, 155, C396. [Google Scholar] [CrossRef]
- Verma, C.; Lgaz, H.; Verma, D.K.; Ebenso, E.E.; Bahadur, I.; Quraishi, M.A. Molecular dynamics and Monte Carlo simulations as powerful tools for study of interfacial adsorption behavior of corrosion inhibitors in aqueous phase: A review. J. Mol. Liq. 2018, 260, 99–120. [Google Scholar] [CrossRef]
- Vanaei, H.R.; Eslami, A.; Egbewande, A. A review on pipeline corrosion, in-line inspection (ILI), and corrosion growth rate models. Int. J. Press. Vessel. Pip. 2017, 149, 43–54. [Google Scholar] [CrossRef]
- Malki, B.; Baroux, B. Computer simulation of the corrosion pit growth. Corros. Sci. 2005, 47, 171–182. [Google Scholar] [CrossRef]
- Khaled, K.F. Monte Carlo simulations of corrosion inhibition of mild steel in 0.5 M sulphuric acid by some green corrosion inhibitors. J. Solid State Electrochem. 2009, 13, 1743–1756. [Google Scholar] [CrossRef]
- Cox, W.M. A strategic approach to corrosion monitoring and corrosion management. Procedia Eng. 2014, 86, 567–575. [Google Scholar] [CrossRef]
- Garcia, R.L.; Happ, P.N.; Feitosa, R.Q. Large scale semantic segmentation of virtual environments to facilitate corrosion management. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. - ISPRS Arch. 2021, 43, 465–470. [Google Scholar] [CrossRef]
- Córdoba-Torres, P.; Nogueira, R.P.; De Miranda, L.; Brenig, L.; Wallenborn, J.; Fairén, V. Cellular automaton simulation of a simple corrosion mechanism: Mesoscopic heterogeneity versus macroscopic homogeneity. Electrochim. Acta 2001, 46, 2975–2989. [Google Scholar] [CrossRef]
- Wang, W.; Guan, B.; Wei, X.; Lu, J.; Ding, J. Cellular automata simulation on the corrosion behavior of Ni-base alloy in chloride molten salt. Sol. Energy Mater. Sol. Cells 2019, 203, 110170. [Google Scholar] [CrossRef]
- Fan, Y.; Pan, J.; Wu, Z.; Li, B.; Wang, Z. A Method for Predicting the Corrosion Behavior of Structural Steel under Atmosphere. Buildings 2023, 13. [Google Scholar] [CrossRef]
- Pérez-Brokate, C.F.; di Caprio, D.; Féron, D.; de Lamare, J.; Chaussé, A. Pitting corrosion modelling by means of a stochastic cellular automata-based model. Corros. Eng. Sci. Technol. 2017, 52, 605–610. [Google Scholar] [CrossRef]
- D. di Caprio et al., “Morphology of corroded surfaces: Contribution of cellular automaton modelling,” Corros. Sci., vol. 53, no. 1, pp. 418–425, 2011. [CrossRef]
- Chen, M. cheng; Wen, Q. qing; Zhu, Q.; Huang, H.; Xie, L. Simulation of corrosion process for concrete filled steel tubular columns with the cellular automata method. Eng. Fail. Anal. 2017, 82, 298–307. [Google Scholar] [CrossRef]
- Chopard, B.; Droz, M. Cellular Automata Modeling of Physical Systems; Cambridge University Press: Cambridge, 1998; ISBN 9780521673457. [Google Scholar]
- Taleb, A.; Chaussé, A.; Dymitrowska, M.; Stafiej, J.; Badiali, J.P. Simulations of corrosion and passivation phenomena: Diffusion feedback on the corrosion rate. J. Phys. Chem. B 2004, 108, 952–958. [Google Scholar] [CrossRef]
- Saunier, J.; Chaussé, A.; Stafiej, J.; Badiali, J.P. Simulations of diffusion limited corrosion at the metal|environment interface. J. Electroanal. Chem. 2004, 563, 239–247. [Google Scholar] [CrossRef]
- Saunier, J.; Dymitrowska, M.; Chaussé, A.; Stafiej, J.; Badiali, J.P. Diffusion, interactions and universal behavior in a corrosion growth model. J. Electroanal. Chem. 2005, 582, 267–273. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Zhang, J. Cellular automaton modeling on the corrosion/oxidation mechanism of steel in liquid metal environment. Prog. Nucl. Energy 2008, 50, 587–593. [Google Scholar] [CrossRef]
- Tan, T.; Chen, Y. Scale removal cellular automaton oxidation models of metals in lead bismuth eutectic. J. Electroanal. Chem. 2009, 626, 89–97. [Google Scholar] [CrossRef]
- Lan, K.C.; Chen, Y.; Yeh, T.K.; Hung, T.C.; Liu, M. Lou; Yu, G.P. Scale removal oxidation behavior of metal in supercritical water modeled by cellular automaton. Prog. Nucl. Energy 2011, 53, 1034–1038. [Google Scholar] [CrossRef]
- Lan, K.C.; Chen, Y.; Hung, T.C.; Tung, H.M.; Yu, G.P. Simulation of the growth of oxide layer of stainless steels with chromium using cellular automaton model: Verification and parameter study. Comput. Mater. Sci. 2013, 77, 139–144. [Google Scholar] [CrossRef]
- Ji, H.; Ren, K.; Ding, L.; Wang, T.; Zhang, X.; Li, J.; Zhang, Z.; Guo, D. Three-Dimensional Cellular Automata Model of Uniform Corrosion for Aluminium Alloy; Springer Singapore, 2019; Vol. 459; ISBN 9789811333040.
- Chen, Z.; Sun, L.; Zhang, W.; Zheng, H.; Xia, W.; Zeng, H.; Chen, S.; Li, K.; Li, W. Corrosion behavior of marine structural steel in tidal zone based on wire beam electrode technology and partitioned cellular automata model. Corros. Commun. 2022, 5, 87–97. [Google Scholar] [CrossRef]
- Xu, Z.; Wei, X.; Lu, J.; Ding, J.; Wang, W. Simulation of corrosion behavior of Fe–Cr–Ni alloy in binary NaCl–CaCl2 molten salt using a cellular automata method. Sol. Energy Mater. Sol. Cells 2021, 231, 111301. [Google Scholar] [CrossRef]
- Di Caprio, D.; Vautrin-Ul, C.; Stafiej, J.; Chaussé, A.; Féron, D.; Badiali, J.P. Cellular automata approach for morphological evolution of localised corrosion. Corros. Eng. Sci. Technol. 2011, 46, 223–227. [Google Scholar] [CrossRef]
- Li, L.; Li, X.G.; Dong, C.F.; Cheng, Y.F. Cellular automaton model for simulation of metastable pitting. Corros. Eng. Sci. Technol. 2011, 46, 340–345. [Google Scholar] [CrossRef]
- Wang, H.T.; Han, E.H. Cellular automata simulation of interactions between metastable corrosion pits on stainless steel. Mater. Corros. 2015, 66, 925–930. [Google Scholar] [CrossRef]
- Wang, H.; Han, E.H. Computational simulation of corrosion pit interactions under mechanochemical effects using a cellular automaton/finite element model. Corros. Sci. 2016, 103, 305–311. [Google Scholar] [CrossRef]
- Rusyn, B.P.; Tors’Ka, R. V.; Pokhmurs’Kyi, A.Y. Modeling of the evolution of corrosion pitting with the use of cellular automata. Mater. Sci. 2015, 50, 74–80. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, J.; Wang, Y.; Zheng, M.; Zhang, Z. Simulation of pitting corrosion for Ni-based alloy using a cellular automata model. Xiyou Jinshu Cailiao Yu Gongcheng/Rare Met. Mater. Eng. 2015, 44, 2347–2352. [Google Scholar] [CrossRef]
- Fatoba, O.O.; Leiva-Garcia, R.; Lishchuk, S. V.; Larrosa, N.O.; Akid, R. Simulation of stress-assisted localised corrosion using a cellular automaton finite element approach. Corros. Sci. 2018, 137, 83–97. [Google Scholar] [CrossRef]
- Cui, C.; Ma, R.; Chen, A.; Pan, Z.; Tian, H. Experimental study and 3D cellular automata simulation of corrosion pits on Q345 steel surface under salt-spray environment. Corros. Sci. 2019, 154, 80–89. [Google Scholar] [CrossRef]
- Pérez-Brokate, C.F.; di Caprio, D.; Féron, D.; de Lamare, J.; Chaussé, A. Three dimensional discrete stochastic model of occluded corrosion cell. Corros. Sci. 2016, 111, 230–241. [Google Scholar] [CrossRef]
- Al-samawi, M.; Zhu, J.; Rong, W. Application of 3D cellular automata-based analysis to chloride diffusion process in concrete bridges. Structures 2023, 47, 500–519. [Google Scholar] [CrossRef]
- Gong, K.; Wu, M.; Liu, X.; Liu, G. Nucleation and propagation of stress corrosion cracks: Modeling by cellular automata and finite element analysis. Mater. Today Commun. 2022, 33, 104886. [Google Scholar] [CrossRef]
- Yu, X.; Chen, S. A simulation of Cr depletion in austenitic stainless steel with cellular automaton. Comput. Mater. Sci. 2009, 45, 899–904. [Google Scholar] [CrossRef]
- Yu, X.; Chen, S.; Liu, Y.; Ren, F. A study of intergranular corrosion of austenitic stainless steel by electrochemical potentiodynamic reactivation, electron back-scattering diffraction and cellular automaton. Corros. Sci. 2010, 52, 1939–1947. [Google Scholar] [CrossRef]
- Lishchuk, S. V.; Akid, R.; Worden, K.; Michalski, J. A cellular automaton model for predicting intergranular corrosion. Corros. Sci. 2011, 53, 2518–2526. [Google Scholar] [CrossRef]
- Jahns, K.; Balinski, K.; Landwehr, M.; Wübbelmann, J.; Krupp, U. Prediction of high temperature corrosion phenomena by the cellular automata approach. Mater. Corros. 2016, 68, 125–132. [Google Scholar] [CrossRef]
- Jahns, K.; Balinski, K.; Landwehr, M.; Trindade, V.B.; Wübbelmann, J.; Krupp, U. Modeling of Intergranular Oxidation by the Cellular Automata Approach. Oxid. Met. 2017, 87, 285–295. [Google Scholar] [CrossRef]
- di Caprio, D.; Stafiej, J.; Luciano, G.; Arurault, L. 3D cellular automata simulations of intra and intergranular corrosion. Corros. Sci. 2016, 112, 438–450. [Google Scholar] [CrossRef]
- Guiso, S.; di Caprio, D.; de Lamare, J.; Gwinner, B. Intergranular corrosion: Comparison between experiments and cellular automata. Corros. Sci. 2020, 177, 108953. [Google Scholar] [CrossRef]
- Guiso, S.; di Caprio, D.; de Lamare, J.; Gwinner, B. Influence of the grid cell geometry on 3D cellular automata behavior in intergranular corrosion. J. Comput. Sci. 2021, 53, 101322. [Google Scholar] [CrossRef]
- Guiso, S.; Brijou-Mokrani, N.; de Lamare, J.; Di Caprio, D.; Gwinner, B.; Lorentz, V.; Miserque, F. Intergranular corrosion in evolving media: Experiment and modeling by cellular automata. Corros. Sci. 2022, 205, 110457. [Google Scholar] [CrossRef]
- Xu, Z.; Lu, J.; Wei, X.; Ding, J.; Wang, W. 2D and 3D cellular automata simulation on the corrosion behaviour of Ni-based alloy in ternary molten salt of NaCl – KCl – ZnCl 2. Sol. Energy Mater. Sol. Cells 2022, 240, 111694. [Google Scholar] [CrossRef]
- Boon, J.P.; David, D.; Kapral, R.; Lawniczak, A. Lattice gas automata for reactive systems. Phys. Rep. 1996, 273, 55–147. [Google Scholar] [CrossRef]
- Zhou, L.; Wei, X. A randomwalk-cellular automaton model of precipitation of internal oxides. Scr. Mater. 1997, 37, 1483–1489. [Google Scholar] [CrossRef]
- di Caprio, D.; Stafiej, J. Simulations of passivation phenomena based on discrete lattice gas automata. Electrochim. Acta 2010, 55, 3884–3890. [Google Scholar] [CrossRef]
- Di Caprio, D.; Stafiej, J. The role of adsorption in passivation phenomena modelled by discrete lattice gas automata. Electrochim. Acta 2011, 56, 3963–3968. [Google Scholar] [CrossRef]
- Bartosik, Ł.; di Caprio, D.; Stafiej, J. Cellular automata approach to corrosion and passivity phenomena. Pure Appl. Chem. 2013, 85, 247–256. [Google Scholar] [CrossRef]
- Stafiej, J.; Di Caprio, D.; Bartosik, Ł. Corrosion-passivation processes in a cellular automata based simulation study. J. Supercomput. 2013, 65, 697–709. [Google Scholar] [CrossRef]
- Jahns, K.; Landwehr, M.; Wübbelmann, J.; Krupp, U. Numerical analysis of internal oxidation and nitridation by the cellular automata approach. Oxid. Met. 2013, 79, 107–120. [Google Scholar] [CrossRef]
- Van der Weeën, P.; Zimer, A.M.; Pereira, E.C.; Mascaro, L.H.; Bruno, O.M.; De Baets, B. Modeling pitting corrosion by means of a 3D discrete stochastic model. Corros. Sci. 2014, 82, 133–144. [Google Scholar] [CrossRef]
- Jahns, K.; Landwehr, M.; Wübbelmann, J.; Krupp, U. Numerical analysis of high temperature internal corrosion mechanisms by the cellular automata approach. Mater. Corros. 2014, 65, 305–311. [Google Scholar] [CrossRef]
- Qiao, G.; Hong, Y.; Ou, J. Quantitative monitoring of pitting corrosion based on 3-D cellular automata and real-time ENA for RC structures. Meas. J. Int. Meas. Confed. 2014, 53, 270–276. [Google Scholar] [CrossRef]
- Rusyn, B.; Tors’Ka, R.; Kobasyar, M. Application of the cellular automata for obtaining pitting images during simulation process of their growth. Adv. Intell. Syst. Comput. 2014, 242, 299–306. [Google Scholar] [CrossRef]
- da Silva, N.R.; Van der Weeën, P.; De Baets, B.; Bruno, O.M. Improved texture image classification through the use of a corrosion-inspired cellular automaton. Neurocomputing 2015, 149, 1560–1572. [Google Scholar] [CrossRef]
- Kireeva, A.E.; Sabelfeld, K.K.; Maltseva, N. V.; Gribov, E.N. Parallel implementation of cellular automaton model of the carbon corrosion under the influence of the electrochemical oxidation. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2017, 10421 LNCS, 205–214. [Google Scholar] [CrossRef]
- Pérez-Brokate, C.F.; di Caprio, D.; Féron, D.; de Lamare, J.; Chaussé, A. Probabilistic cellular automata model of generalised corrosion, transition to localised corrosion. Corros. Eng. Sci. Technol. 2017, 52, 186–193. [Google Scholar] [CrossRef]
- Fatoba, O.O.; Leiva-Garcia, R.; Lishchuk, S. V.; Larrosa, N.O.; Akid, R. Simulation of stress-assisted localised corrosion using a cellular automaton finite element approach. Corros. Sci. 2018, 137, 83–97. [Google Scholar] [CrossRef]
- Zhu, J.S.; Guo, X.Y.; Kang, J.F. 3D Cellular Automata Based Numerical Simulation of Atmospheric Corrosion Process on Weathering Steel. Maintenance, Safety, Risk, Manag. Life-Cycle Perform. Bridg. - Proc. 9th Int. Conf. Bridg. Maintenance, Saf. Manag. IABMAS 2018 2018, 30, 1791–1797. [Google Scholar] [CrossRef]
- Stępień, J.; di Caprio, D.; Stafiej, J. 3D simulations of the metal passivation process in potentiostatic conditions using discrete lattice gas automaton. Electrochim. Acta 2019, 295, 173–180. [Google Scholar] [CrossRef]
- Guo, Z. wei; Chen, H. Monte Carlo Simulation Method for Pit Erosion Process of Cable Wire Based on Bi-plane Cellular Automata. Int. J. Steel Struct. 2020, 20, 1527–1539. [Google Scholar] [CrossRef]
- Zenkri, M.; di Caprio, D.; Raouafi, F.; Féron, D. Cathodic control using cellular automata approach. Mater. Corros. 2022, 73, 1631–1643. [Google Scholar] [CrossRef]
Figure 1.
Most common neighboors. (a) Von Neumann. (b) Moore. (c) Margolus.
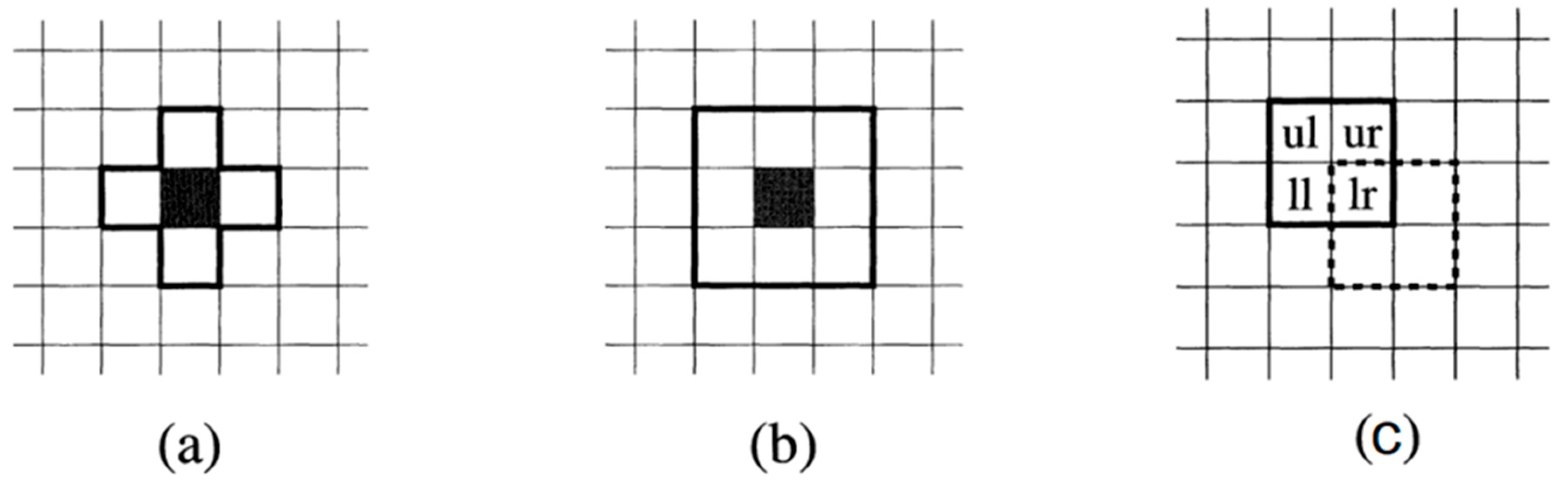
Figure 2.
Schematics of the CA model. (a) Grid of fixed sites. (b) Grid of mobile sites that diffuse towards the metal. (c) Grid of sites that can diffuse in the outer corrosion layer. (d) General scheme of the grid in the CA model [29].
Figure 2.
Schematics of the CA model. (a) Grid of fixed sites. (b) Grid of mobile sites that diffuse towards the metal. (c) Grid of sites that can diffuse in the outer corrosion layer. (d) General scheme of the grid in the CA model [29].
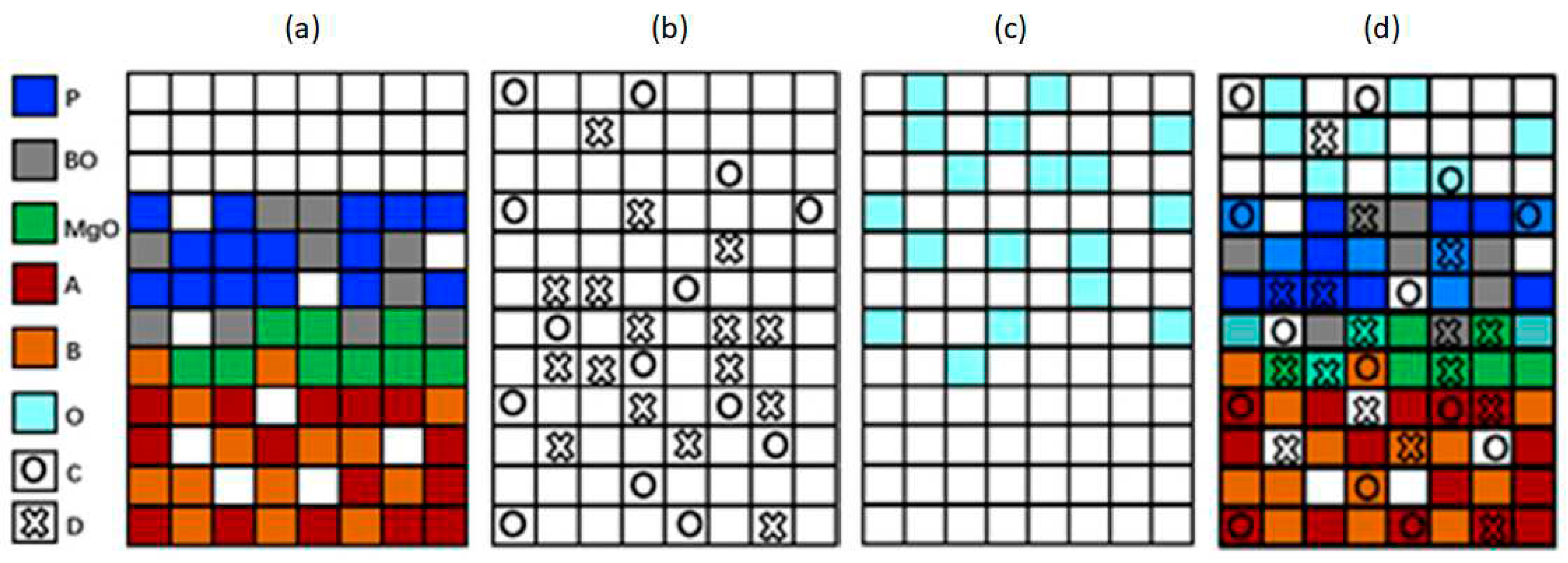
Figure 3.
Simulation of corrosion layer growth at different iterations. (a) 40 iterations. (b) 25,000 iterations. (c) 36,000 iterations [29].
Figure 3.
Simulation of corrosion layer growth at different iterations. (a) 40 iterations. (b) 25,000 iterations. (c) 36,000 iterations [29].
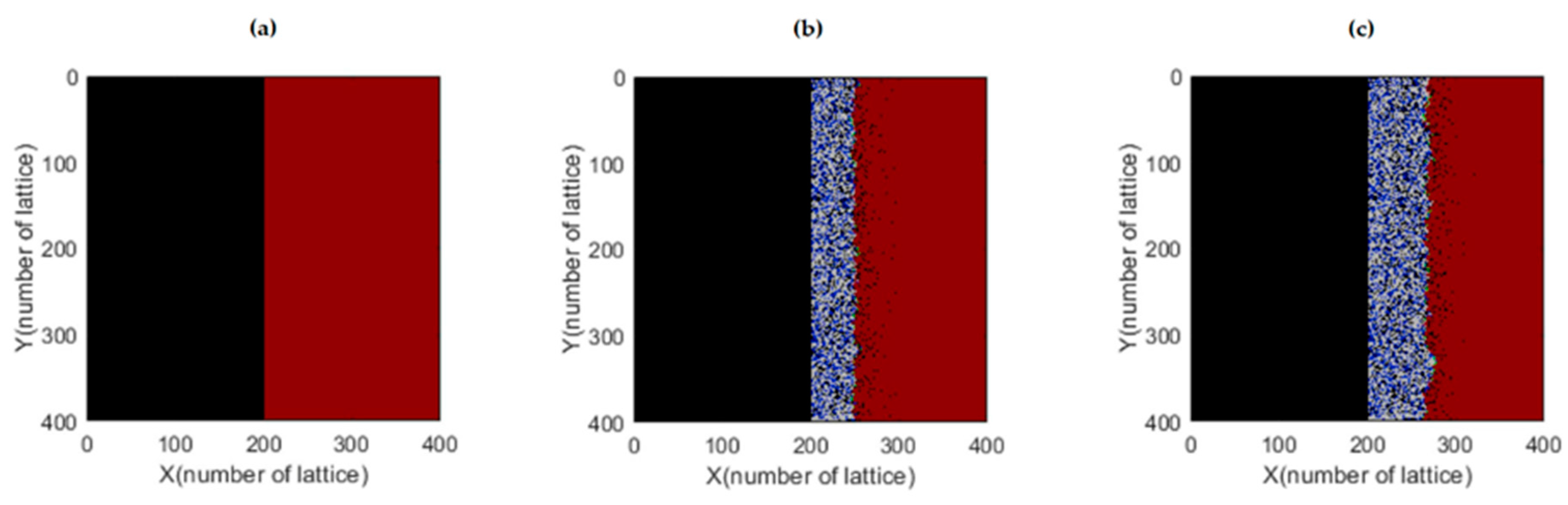
Figure 4.
Comparison of simulation morphology and experiment SEM photograph, (a) cross-sectional SEM photograph of In625 after 21 days immersion at 600 °C, (b) Snapshots of simulation results of corrosion morphology, for time steps Nt=25000 [29].
Figure 4.
Comparison of simulation morphology and experiment SEM photograph, (a) cross-sectional SEM photograph of In625 after 21 days immersion at 600 °C, (b) Snapshots of simulation results of corrosion morphology, for time steps Nt=25000 [29].
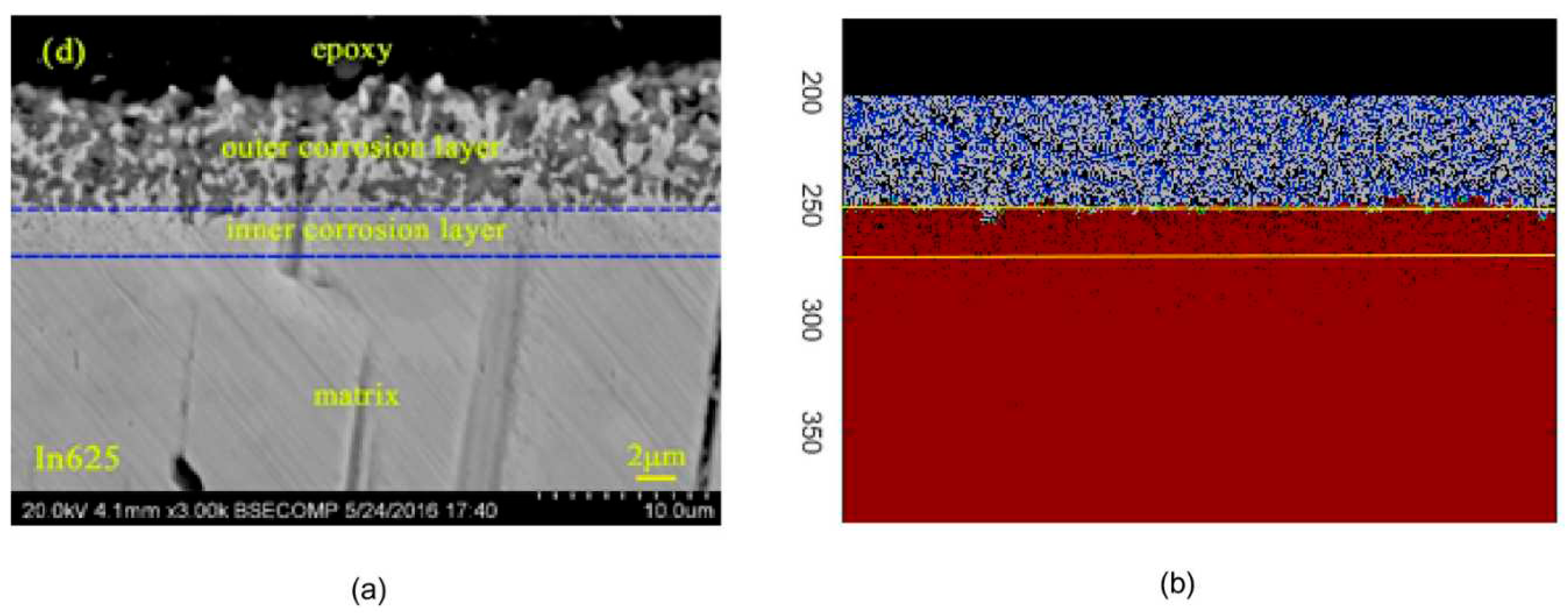
Figure 5.
Transversal view schema of (a) the initial global matrix and (b) after the development of the pit [30].
Figure 5.
Transversal view schema of (a) the initial global matrix and (b) after the development of the pit [30].
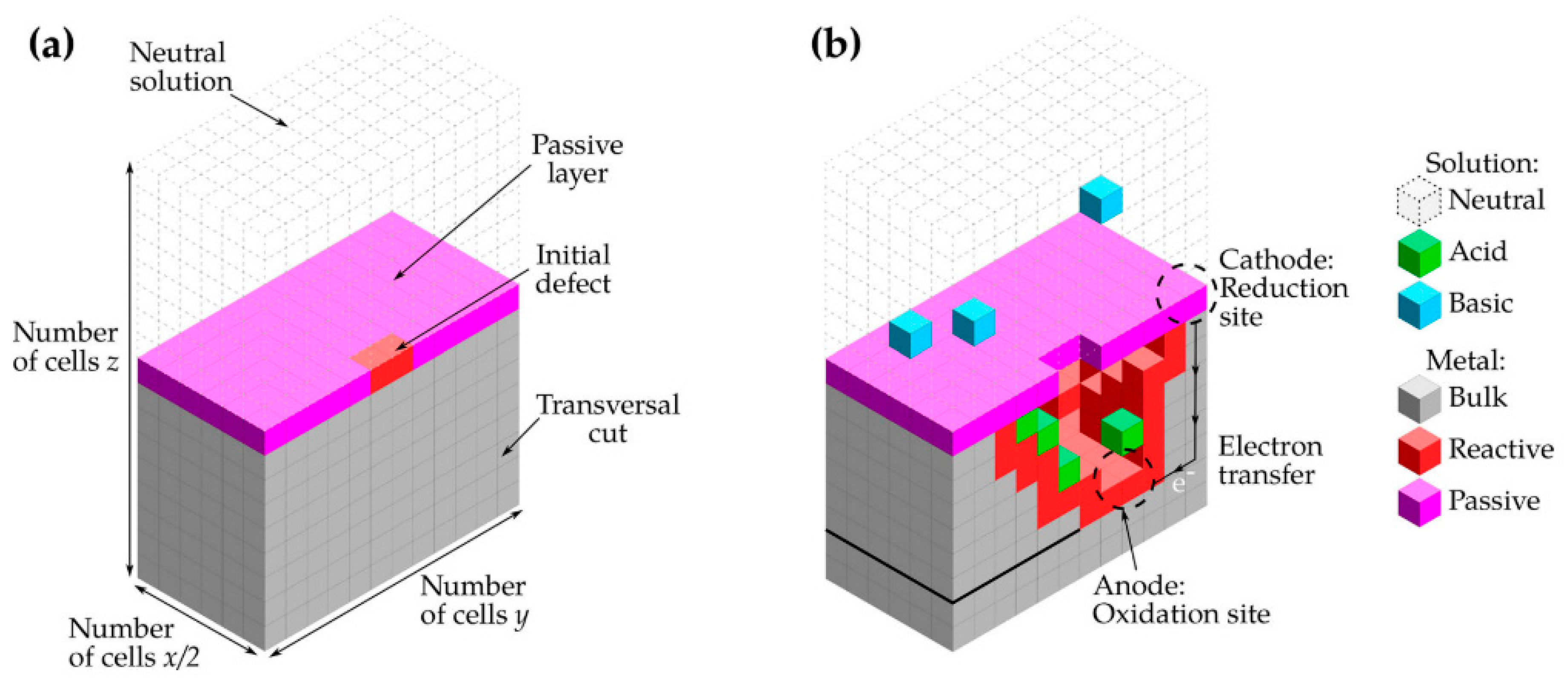
Figure 6.
Side views illustrating different pitting corrosion regimes (Ndiff = 2000): (a) initiation (for t ≤ 44,400), (b) growth instability phase (approximately 500 time steps, around t = 44,600), (c) stable growth (from t = 45,000) [30].
Figure 6.
Side views illustrating different pitting corrosion regimes (Ndiff = 2000): (a) initiation (for t ≤ 44,400), (b) growth instability phase (approximately 500 time steps, around t = 44,600), (c) stable growth (from t = 45,000) [30].
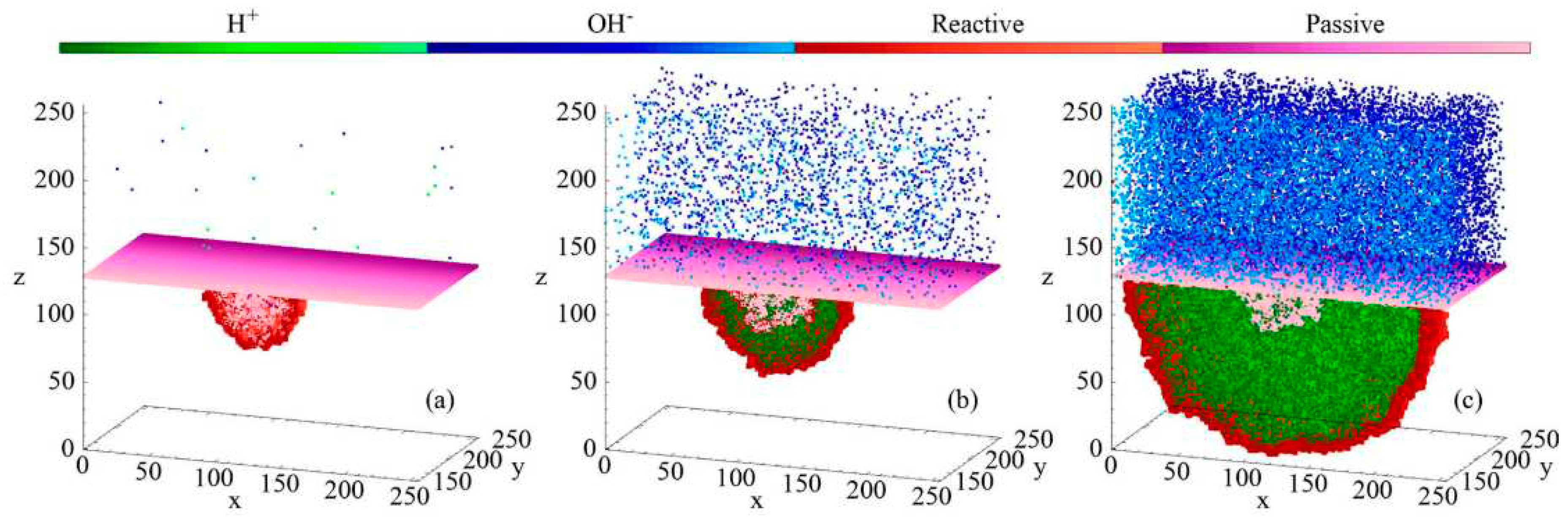
Figure 7.
Schematic diagramo f the cellular automata spatial model [55].
Figure 7.
Schematic diagramo f the cellular automata spatial model [55].
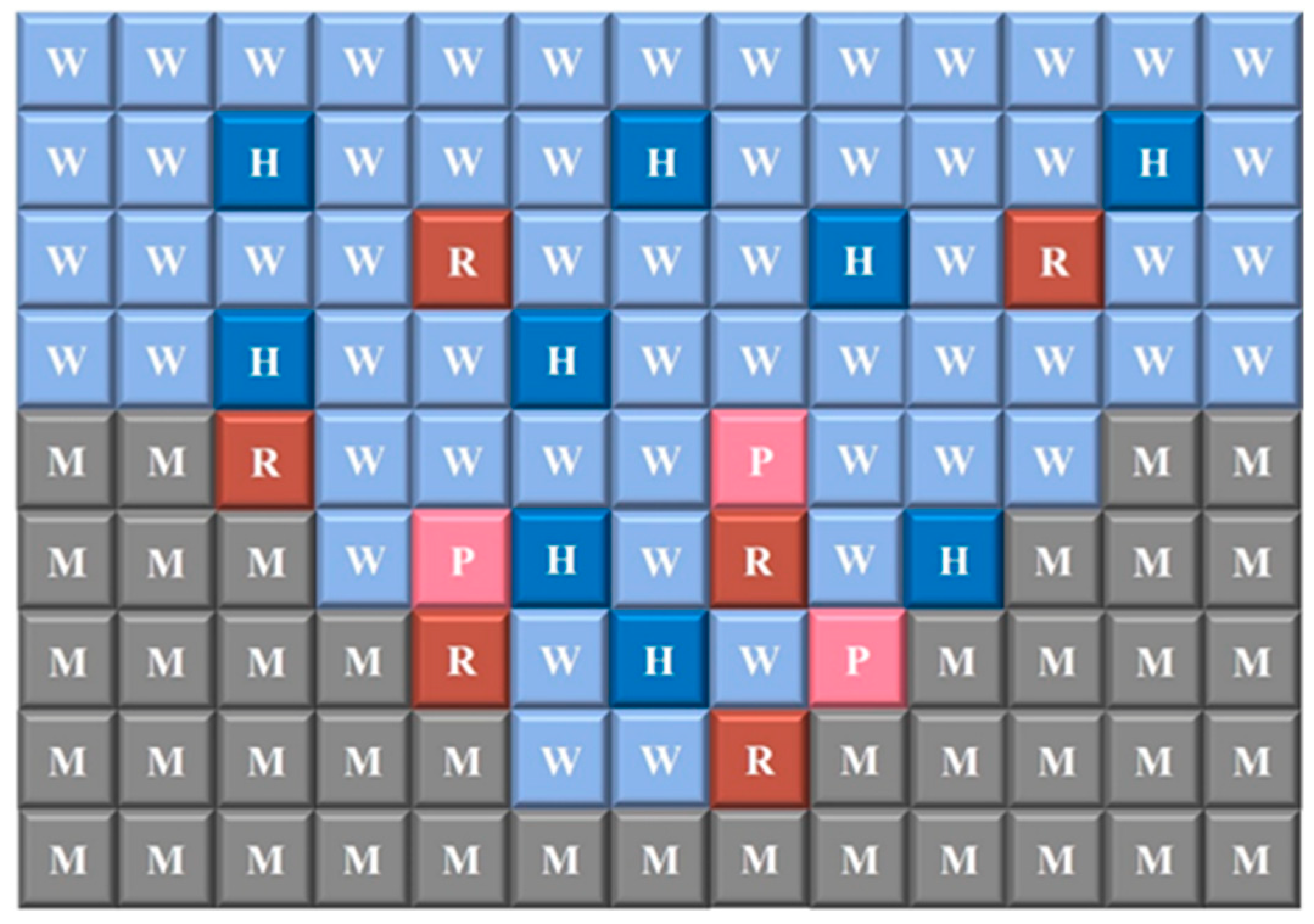
Figure 8.
CA corrosion evolutions rules: (a) Oxidation of Fe to Fe2+ ions. (b) hydrolyzes Fe2+ ions to FeOH+ [55].
Figure 8.
CA corrosion evolutions rules: (a) Oxidation of Fe to Fe2+ ions. (b) hydrolyzes Fe2+ ions to FeOH+ [55].
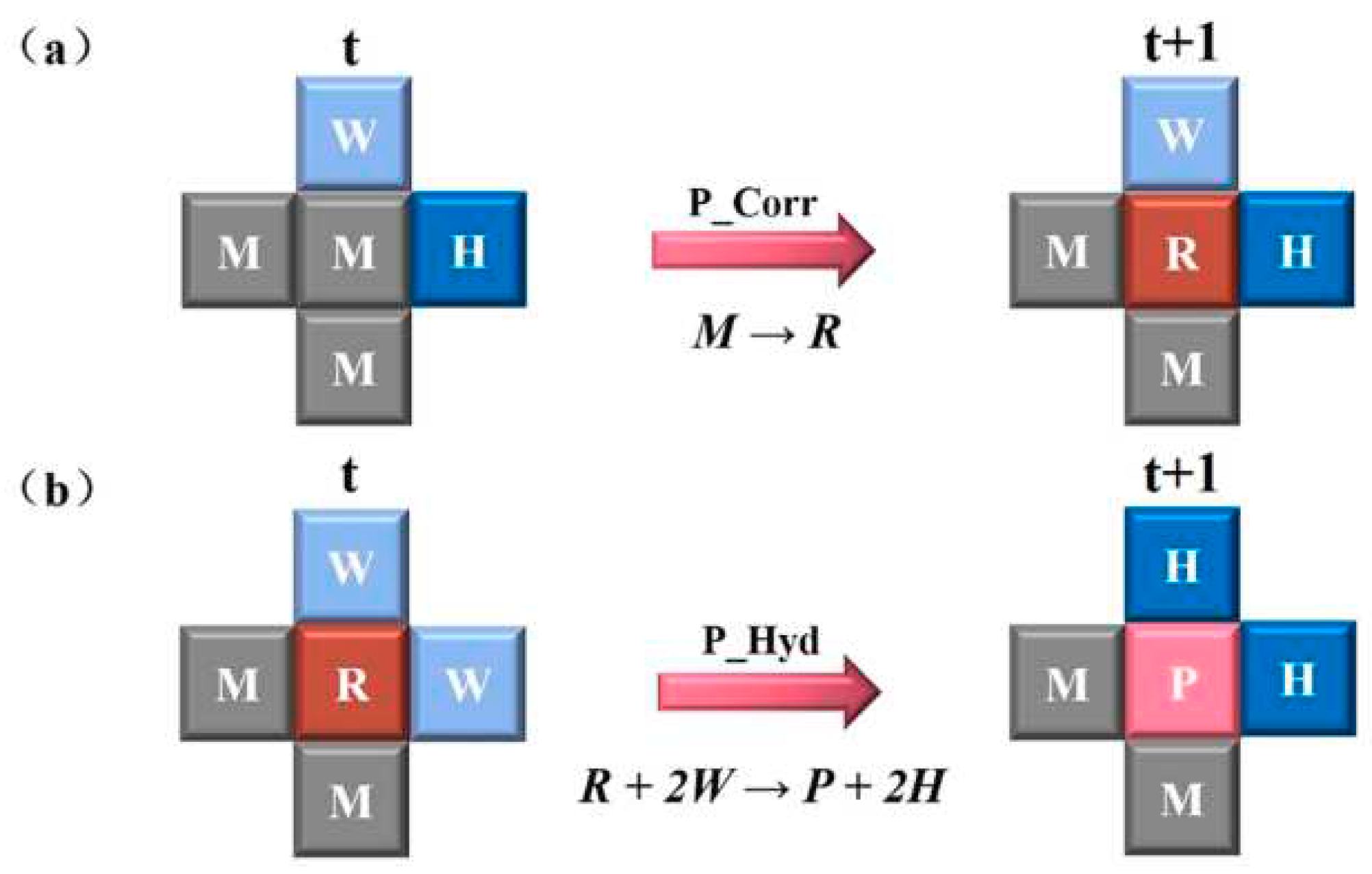
Figure 10.
Grain growth process at different simulation time steps [44].
Figure 10.
Grain growth process at different simulation time steps [44].

Figure 11.
The simulation results of intergranular corrosion (T = 70000) of the initial structure obtained at different simulation time steps:(a) T = 500 (b) T = 1000 (c) T = 2000 (d) T = 5000 [44].
Figure 11.
The simulation results of intergranular corrosion (T = 70000) of the initial structure obtained at different simulation time steps:(a) T = 500 (b) T = 1000 (c) T = 2000 (d) T = 5000 [44].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







