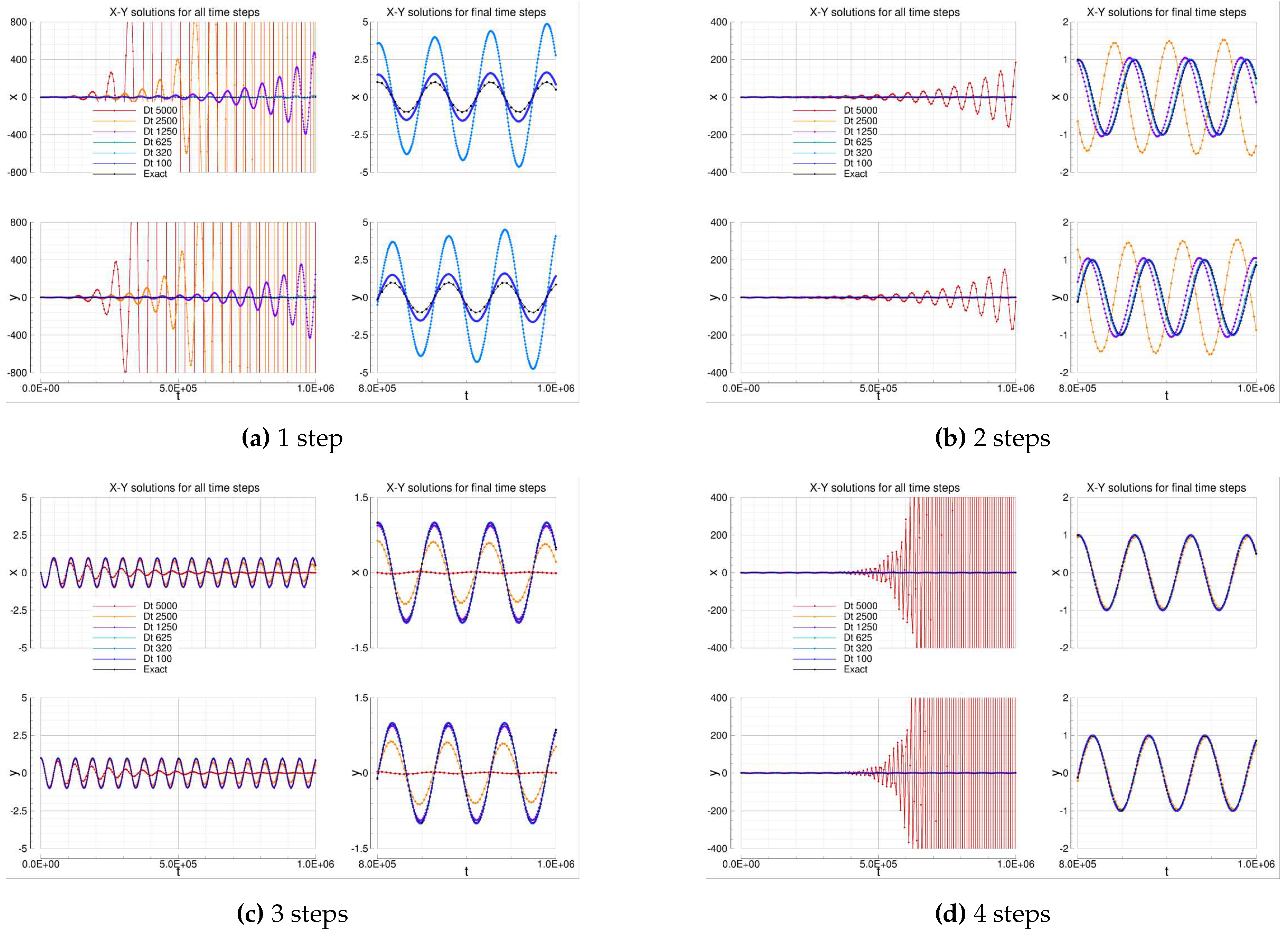
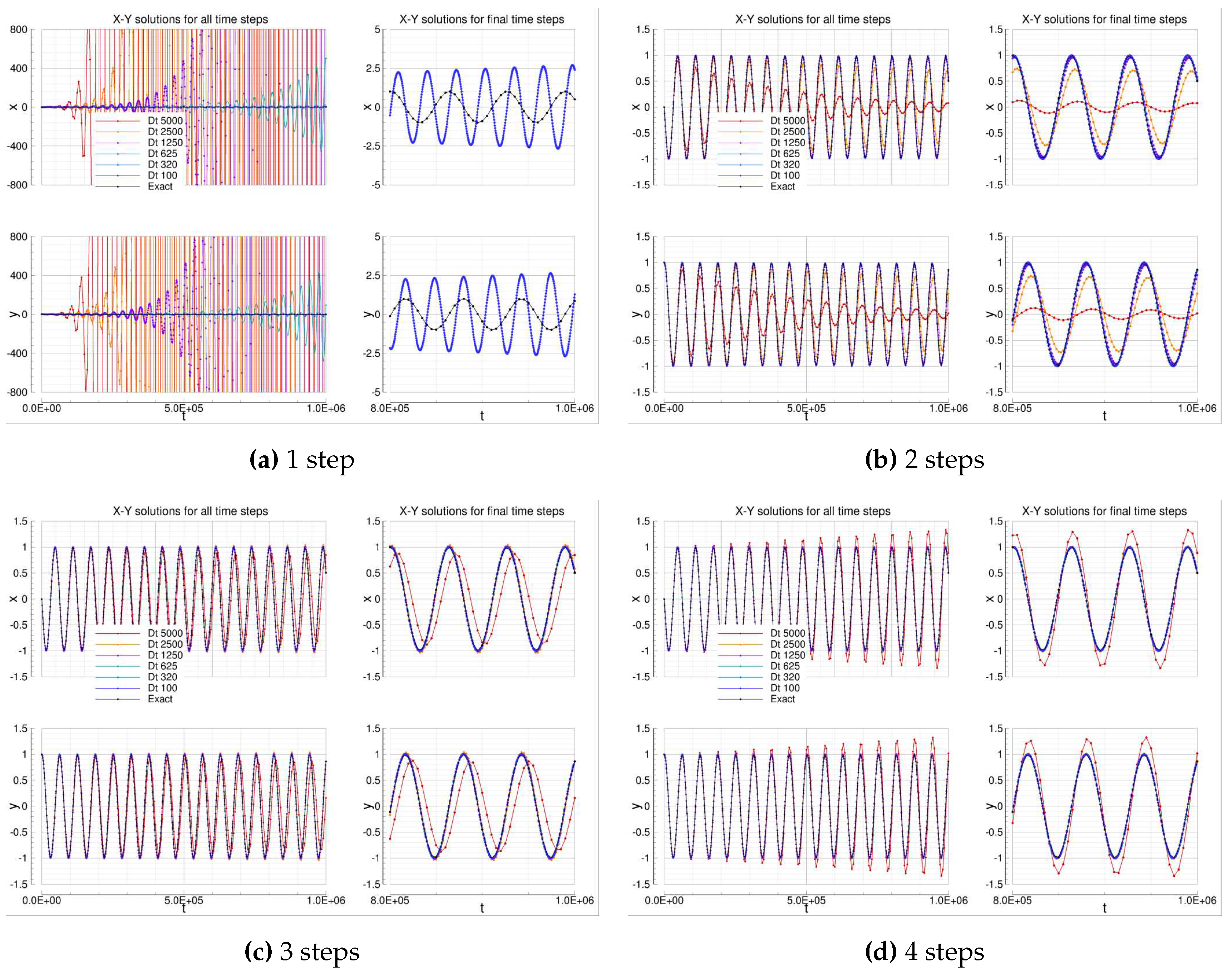
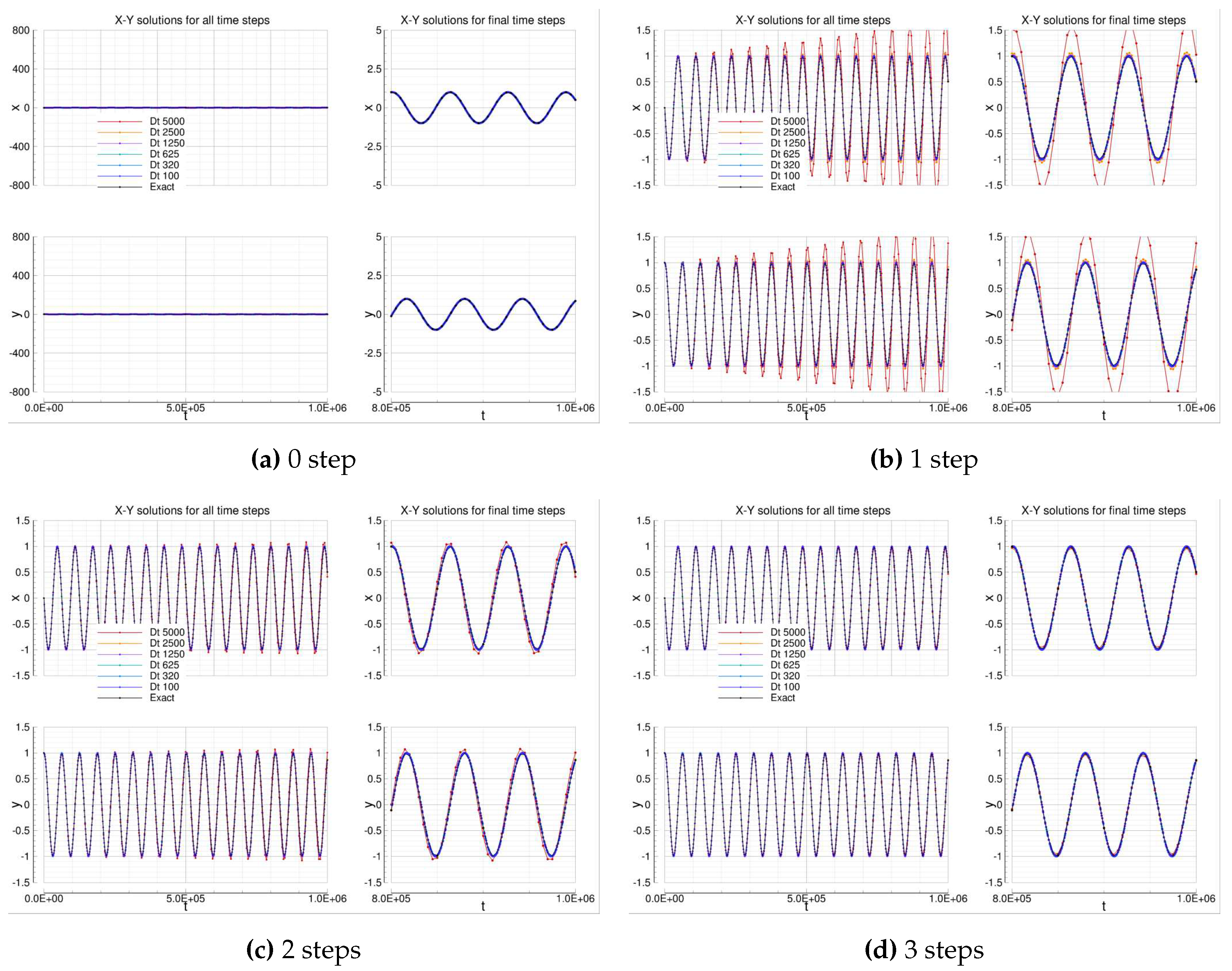
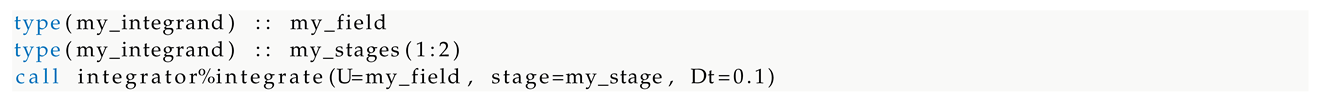2. Mathematical and Numerical Models
In many (most) circumstances, the solution of equation (
1) cannot be computed in a closed, exact form (even if it exists and is unique) due to the complexity and nature of the residuals functions, that is often non linear. Consequently, the problem is often solved relying on a numerical approach: the solution of system (
1) at a time
, namely
, is approximated by a subsequent time-marching approximations
where the relation
implies a
stepping, numerical integration from the time
to time
and
N is the total number of numerical time steps necessary to evolve the initial conditions toward the searched solution
. To this aim, many numerical schemes have been devised. Notably, the numerical schemes of practical usefulness must posses some necessary proprieties such as
consistency and
stability to ensure that the numerical approximation
converges to the exact solution as the numerical time step tends to zero. A detailed discussion of these details is out the scope of the present work and is omitted. Here, we briefly recall some classifications necessary to introduce the schemes implemented into the FOODIE library.
A non comprehensive classification of the most widely used schemes could distinguish between multi-step versus one-step schemes and between explicit versus implicit schemes.
Essentially, the multi-step schemes have been developed to obtain an accurate approximation of the subsequent numerical steps using the informations contained into the previously computed steps, thus this approach relates the next step approximation to a set of the previously computed steps. On the contrary, a one-step scheme evolves the solution toward the next step using only the information coming from the current time approximation. In the framework of one-step schemes family an equivalent accurate approximation can be obtained by means of a multi-stage approach as the one due to Runge-Kutta. The current version of FOODIE provides schemes belonging to both these families.
The other ODE solvers classification concerns with explicit or implicit nature of the schemes employed. Briefly, an explicit scheme computes the next step approximation using the previously computed steps at most to the current time, whereas an implicit scheme uses also the next step approximation (that is the unknown), thus it requires extra computations. The implicit approach is of practical use for stiff systems where the usage of explicit schemes could require an extremely small time step to evolve in a stable way the solution. Mixing together explicit and implicit schemes it is possible to build a family of predictor-corrector methods: using an explicit scheme to predict a guess for the next step approximation it is possible to use an implicit method for correcting this guess. Currently, FOODIE provides explicit solvers and predictor-correct ones.
FOODIE currently implements the following ODE schemes:
-
one-step schemes:
- -
explicit forward Euler scheme, it being 1st order accurate;
- -
-
explicit Runge-Kutta schemes (see [
9,
10]):
- *
-
TVD/SSP Runge-Kutta schemes:
2-stages, it being 2nd order accurate;
3-stages, it being 3rd order accurate;
5-stages, it being 4th order accurate;
- *
-
low storage Runge-Kutta schemes:
5-stages 2N registers schemes, it being 4th order accurate;
6-stages 2N registers schemes, it being 4th order accurate;
7-stages 2N registers schemes, it being 4th order accurate;
12-stages 2N registers schemes, it being 4th order accurate;
13-stages 2N registers schemes, it being 4th order accurate;
14-stages 2N registers schemes, it being 4th order accurate;
-
multi-step schemes (see [
11]):
- -
-
explicit Adams-Bashforth schemes:
- *
2-steps, it being 2nd order accurate;
- *
3-steps, it being 3rd order accurate;
- *
4-steps, it being 4th order accurate;
- -
-
implicit Adams-Moulton schemes:
- *
1-step, it being 2nd order accurate;
- *
2-steps, it being 3rd order accurate;
- *
3-steps, it being 4th order accurate;
- -
-
predictor-corrector Adams-Bashforth-Moulton schemes:
- *
1-step, it being 2nd order accurate;
- *
2-steps, it being 3rd order accurate;
- *
3-steps, it being 4th order accurate;
- -
-
explicit Leapfrog schemes
2:
- *
2-steps unfiltered, it being 2nd order accurate, but mostly unstable;
- *
2-steps Robert-Asselin filtered, it being 1st order accurate (on amplitude error);
- *
2-steps Robert-Asselin-Williams filtered, it being 3rd order accurate (on amplitude error);
2.1. The explicit forward Euler scheme
The explicit forward Euler scheme for ODE integration is probably the simplest solver ever devised. Considering the system (
1), the solution (approximation) of the state vector
U at the time
assuming to known the solution at time
is:
where the solution at the new time step is computed by means of only the current time solution, thus this is an explicit scheme. The solution is an approximation of 1
st order, the local truncation error being
. As well known, this scheme has an absolute (linear) stability locus equals to
where
contains the eigenvalues of the linear (or linearized) Jacobian matrix of the system.
This scheme is Total Variation Diminishing (TVD), thus satisfies the maximum principle (or the equivalent positivity preserving property, see [
12]).
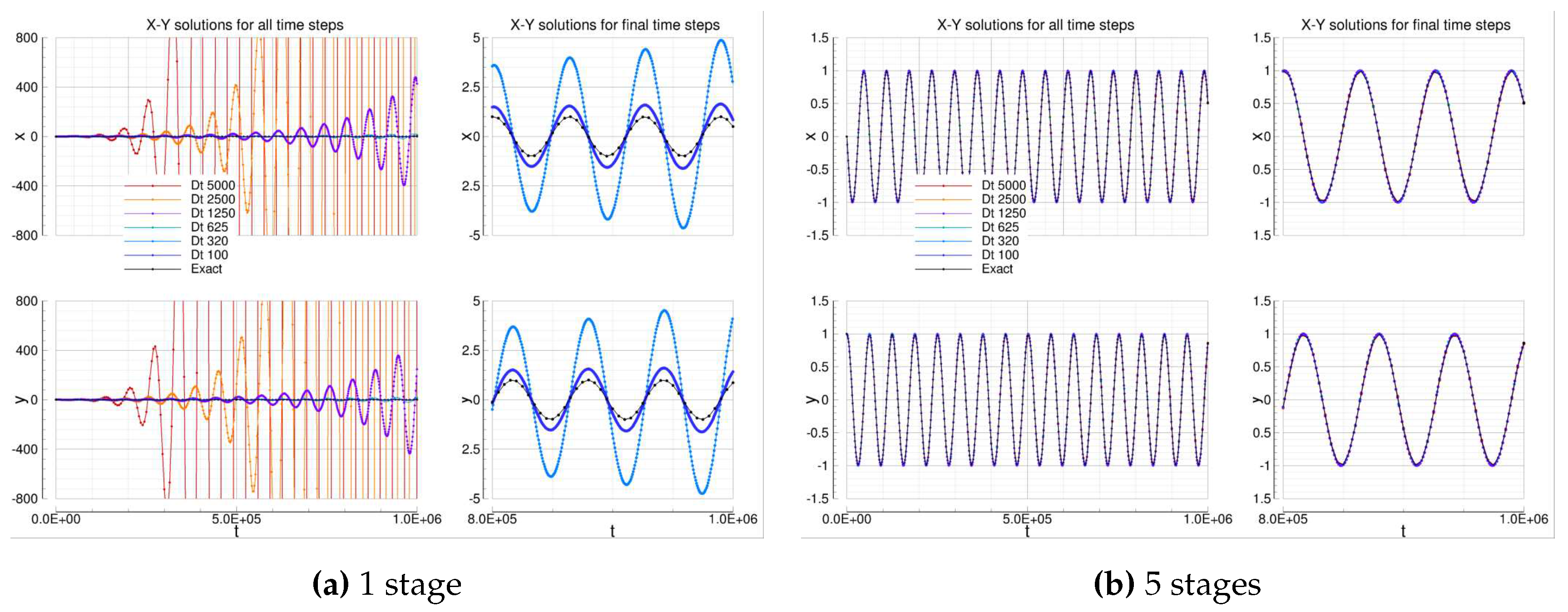
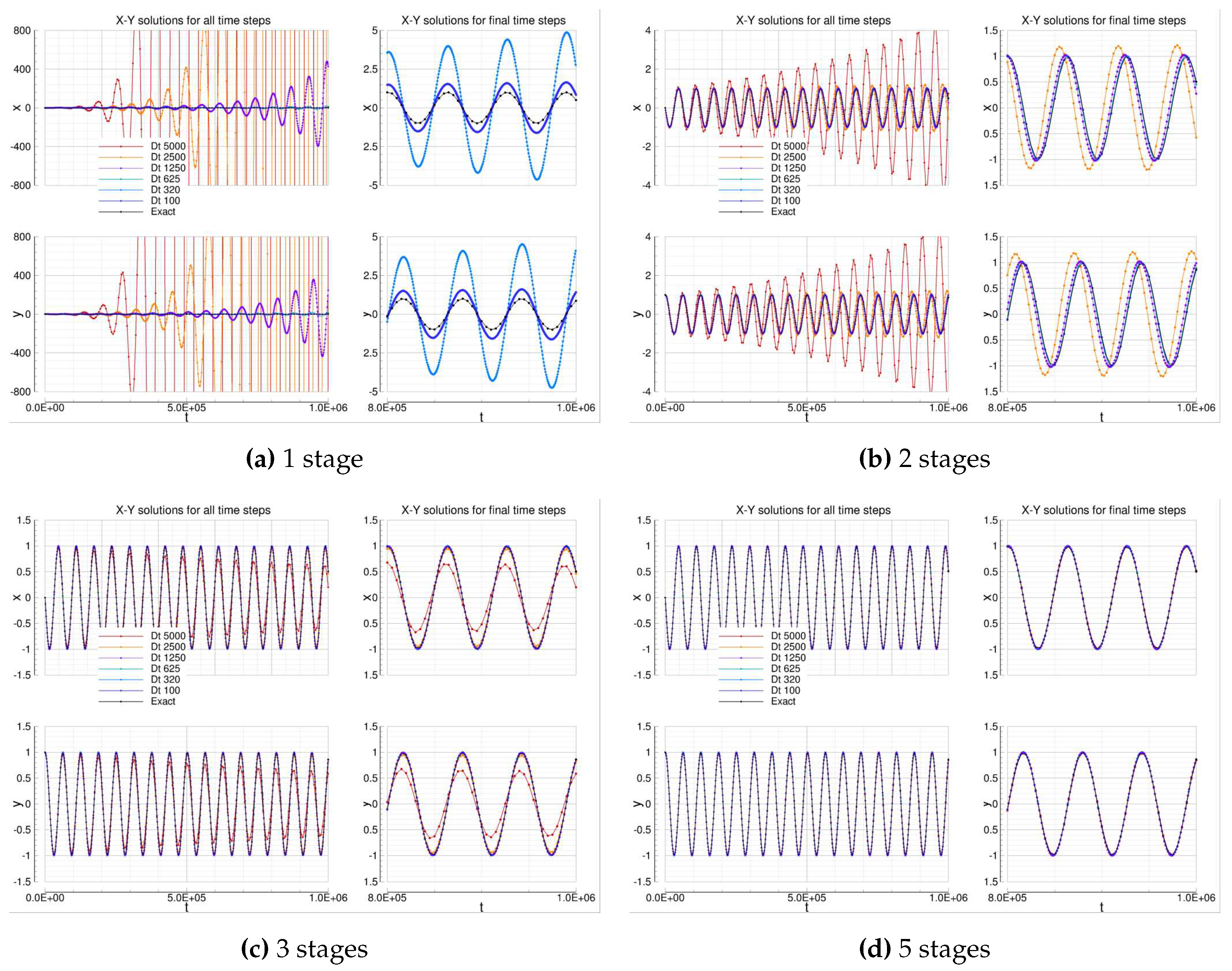
2.2. The explicit TVD/SSP Runge-Kutta class of schemes
Runge-Kutta methods belong to the more general multi-stage family of schemes. This kind of schemes has been designed to achieve a more accurate solution than the 1
st Euler scheme, but without increasing the number of time steps used, as it is done with the multi-step schemes, see [
10]. Essentially, the high order of accuracy is obtained by means of
intermediate values (the stages) of the solution and its derivative are generated and used within a single time step. This commonly implies the allocation of some auxiliary memory registers for storing the intermediate stages.
Notably, the multi-stage schemes class has the attractive property to be self-starting: the high order accurate solution can be obtained directly from the previous one, without the necessity to compute before a certain number of previous steps, as it happens for the multi-step schemes. Moreover, one-step multi-stage methods are suitable for adaptively-varying time-step size (that is also possible for multi-step schemes, but at a cost of more complexity) and for discontinuous solutions, namely discontinued solutions happening at a certain time (that in a multi-step framework can involve an overall accuracy degradation).
In general, the TVD/SSP Runge-Kutta schemes provided by FOODIE library are written by means of the following algorithm:
where
is the number of Runge-Kutta stages used and
is the
stage defined as:
It is worth noting that the equations (
3) and (
4) contain also implicit schemes. A scheme belonging to this family is operative once the coefficients
are provided. We represent these coefficients using the Butcher’s table, that for an explicit scheme where
has the form reported in
Table 1.
The equations (
3) and (
4) show that Runge-Kutta methods do not require any additional differentiations of the ODE system for achieving high order accuracy, rather they require additional evaluations of the residuals function
R.
The nature of the scheme and the properties of the solutions obtained depend on the number of stages and on the value of the coefficients selected. Currently, FOODIE provides 3 Runge-Kutta schemes having TVD or Strong Stability Preserving (SSP) propriety (thus they being suitable for ODE systems involving rapidly changing non linear dynamics) the Butcher’s coefficients of which are reported in
Table 2,
Table 3 and
Table 4.
The absolute stability locus depends on the coefficients selected, however, as a general principle, we can assume that greater is the stages number and wider is the stability locus on equal accuracy orders.
It is worth noting that FODDiE also provides a one-stage TVD Runge-Kutta solver that reverts back to the explicit forward Euler scheme: it can be used, for example, into a Recursive Order Reduction (ROR) framework that automatically checks some properties of the solution and, in case, reduces the order of the Runge-Kutta solver until those properties are obtained.
2.3. The explicit low storage Runge-Kutta class of schemes
As aforementioned, standard Runge-Kutta schemes have the drawback to require auxiliary memory registers to store the necessary stages data. In order to make an efficient use of the available limited computer memory, the class of low storage Runge-Kutta scheme was devised. Essentially, the standard Runge-Kutta class (under some specific conditions) can be reformulated allowing a more efficient memory management. Currently FOODIE provides a class of 2N registers storage Runge-Kutta schemes, meaning that the storage of all stages requires only 2 registers of memory with a word length N (namely the length of the state vector) in contrast to the standard formulation where registers of the same length N are required. This is a dramatic improvement of memory efficiency especially for schemes using a high number of stages () where the memory necessary is an half with respect the original formulation. Unfortunately, not all standard Runge-Kutta schemes can be reformulated as a low storage one.
Following the Williamson’s approach (see [
13,
14,
15,
16]) the standard coefficients are reformulated to the coefficients vectors
A,
B and
C and the Runge-Kutta algorithm becomes:
Currently FOODIE provides 5/6/7/12/13/14 stages, all 4
th order, 2N registers explicit schemes, the coefficients of which are listed in
Table 5.
Table 5.
Williamson’s table of low storage Runge-Kutta schemes.
Table 5.
Williamson’s table of low storage Runge-Kutta schemes.
Similarly to the TVD/SSP Runge-Kutta class, the low storage class also provides a fail-safe one-stage solver reverting back to the explicit forward Euler solver, that is useful for ROR-like frameworks.
2.4. The explicit Adams-Bashforth class of schemes
Adams-Bashforth methods belong to the more general (linear) explicit multi-step family of schemes. This kind of schemes has been designed to achieve a more accurate solution than the 1st Euler scheme using the information coming from the solutions already computed at previous time steps. Typically only one new residuals function R evaluation is required at each time step, whereas Runge-Kutta schemes require many of them.
In general, the Adams-Bashforth schemes provided by FOODIE library are written by means of the following algorithm (for only explicit schemes):
where
is the number of time steps considered and
are the linear coefficients selected.
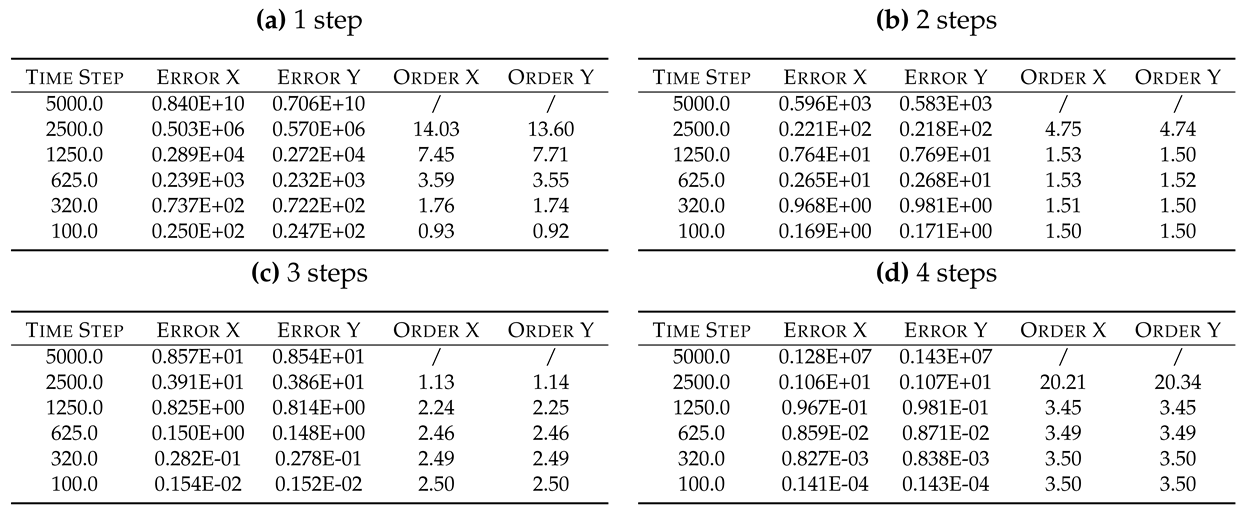
Currently FOODIE provides 2, 3, and 4 steps schemes having 2
nd, 3
rd and 4
th formal order of accuracy, respectively. The
coefficients are reported in
Table 6.
Similarly to the Runge-Kutta classes, the Adams-Bashforth class also provides a fail-safe one-step solver reverting back to the explicit forward Euler solver, that is useful for ROR-like frameworks.
It is worth noting that for the Adams-Bashforth class of solvers is not self-starting: the values of , , ..., must be provided. To this aim, a lower order multi-step scheme or an equivalent order one-step multi-stage scheme can be used.
2.5. The implicit Adams-Moulton class of schemes
Adams-Moulton methods belong to the more general (linear) implicit multi-step family of schemes. This kind of schemes has been designed to achieve a more accurate solution than the 1st Euler scheme using the information coming from the solutions already computed at previous time steps. Typically only one new residuals function R evaluation is required at each time step, whereas Runge-Kutta schemes require many of them.
In general, the Adams-Moulton schemes provided by FOODIE library are written by means of the following algorithm (for only implicit schemes):
where
is the number of time steps considered and
are the linear coefficients selected.
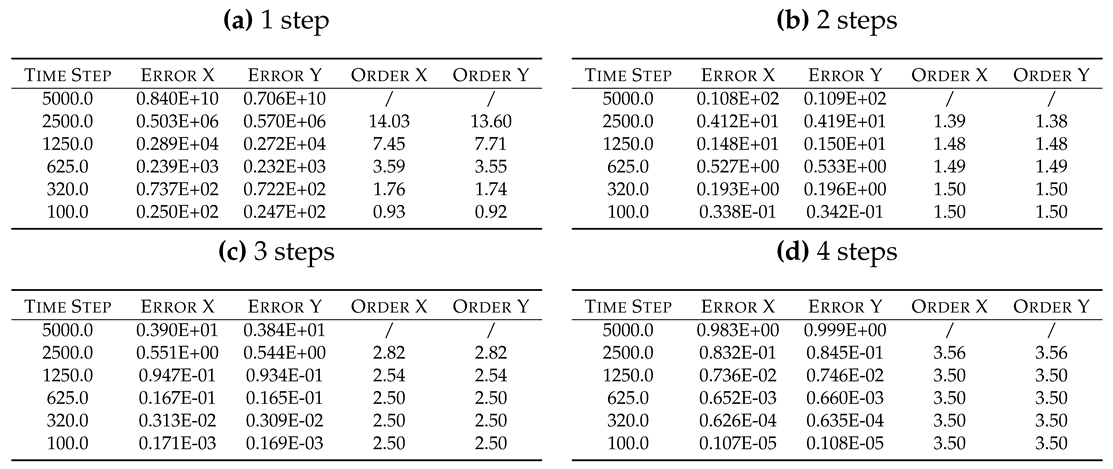
Currently FOODIE provides 1, 2, and 3 steps schemes having 2
nd, 3
rd and 4
th formal order of accuracy, respectively. The
coefficients are reported in
Table 7.
Similarly to the Runge-Kutta and Adams-Bashforth classes, the Adams-Moulton class also provides a fail-safe zero-step solver reverting back to the implicit backward Euler solver, that is useful for ROR-like frameworks.
It is worth noting that for the Adams-Moulton class of solvers is not self-starting: the values of , , ..., must be provided. To this aim, a lower order multi-step scheme or an equivalent order one-step multi-stage scheme can be used.
2.6. The predictor-corrector Adams-Bashforth-Moulton class of schemes
Adams-Bashforth-Moulton methods belong to the more general (linear) predictor-corrector multi-step family of schemes. This kind of schemes has been designed to achieve a more accurate solution than the 1st Euler scheme using the information coming from the solutions already computed at previous time steps. Typically only one new residuals function R evaluation is required at each time step, whereas Runge-Kutta schemes require many of them.
In general, the Adams-Bashforth-Moulton schemes provided by FOODIE library are written by means of the following algorithm:
where
is the number of time steps considered for the Adams-Bashforth predictor/Adams-Moulton corrector (respectively) and
are the corresponding linear coefficients selected. Essentially, the Adams-Bashforth prediction
is corrected by means of the Adams-Moulton correction resulting in
. In order to preserve the formal order of accuracy the relation
always holds.
Currently FOODIE provides
steps schemes having 2
nd, 3
rd and 4
th formal order of accuracy, respectively. The
coefficients are those reported in
Table 6 and
Table 7.
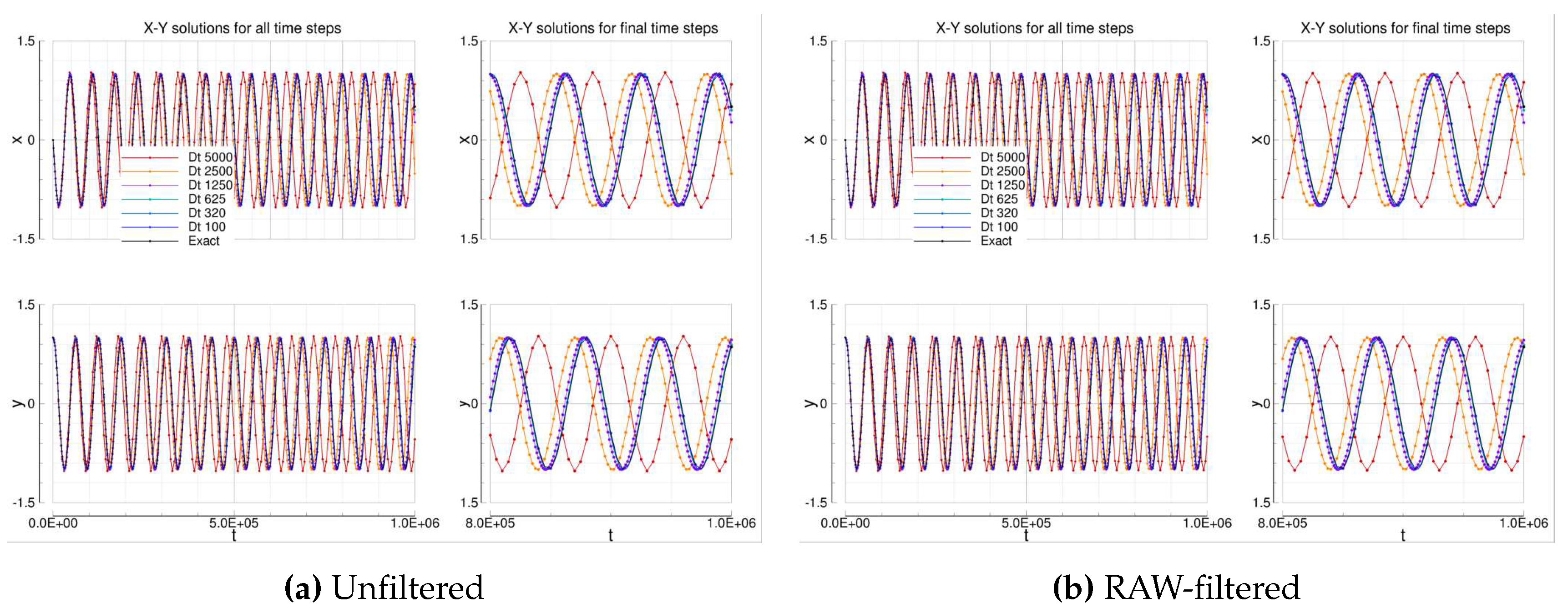
2.7. The leapfrog solver
The
leapfrog scheme belongs to the multi-step family, it being formally a centered second order approximation in time, see [
17,
18,
19]. The leapfrog method (in its original formulation) is mostly unstable, however it is well suited for periodic-oscillatory problems providing a null error on the amplitude value and a formal second order error on the phase one, under the satisfaction of the time-step size stable limit. Commonly, the leapfrog methods are said to provide a
computational mode that can generate unphysical, unstable solutions. As consequence, the original leapfrog scheme is generally
filtered in order to suppress these computational modes.
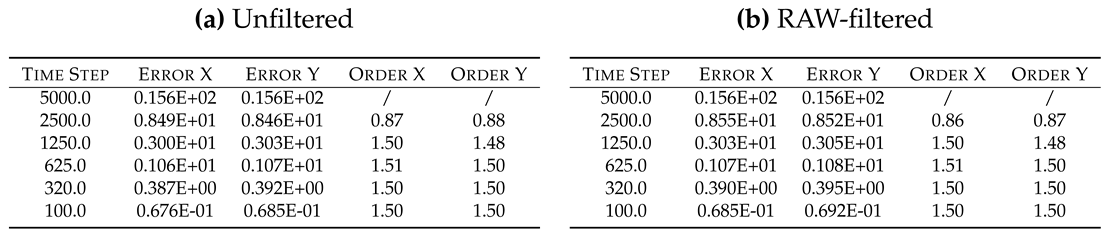
The unfiltered leapfrog scheme provided by FOODIE is:
FOODIE provides, in a
seamless API, also filtered leapfrog schemes. A widely used filter is due to Robert and Asselin, that suppress the computational modes at the cost of accuracy reduction resulting into a 1
st order error in amplitude value. A more accurate filter, able to provide a 3
rd order error on amplitude, is a modification of the Robert-Asselin filter due to Williams known as Robert-Asselin-Williams (RAW) filter, that filters the approximation of
and
by the following scalar coefficient:
The filter coefficients should be taken as and . If the filters of time and have the same amplitude and opposite sign thus allowing to the optimal 3rd order error on amplitude. The default values of the FOODIE provided scheme are , but they can be customized at runtime.
3. Application Program Interface
In this section we review the FOODIE API providing a detailed discussion of the implementation choices.
As aforementioned, the programming language used is the Fortran 2008 standard, that is a minor revision of the previous Fortran 2003 standard. Such a new Fortran idioms provide (among other useful features) an almost complete support for OOP, in particular for ADT concept. Fortran 2003 has introduced the abstract derived type: it is a derived type suitable to serve as contract for concrete type-extensions that has not any actual implementations, rather it provides a well-defined set of type bound procedures interfaces, that in Fortran nomenclature are called deferred procedures. Using such an abstract definition, we can implement algorithms operating on only this abstract type and on all its concrete extensions. This is the key feature of FOODIE library: all the above described ODE solvers are implemented on the knowledge of only one abstract type, allowing an implementation-style based on a very high-level syntax. In the meanwhile, client codes must implement their own IVPs extending only one simple abstract type.
It is worth noting that all FOODIE public entities (ADT and solvers) must be accessed by the FOODIE module, see Listing 1 for an example on how access to all public FOODIE entities.
|
Listing 1. usage example importing all public entities of FOODIE main module |
 |
3.1. The main FOODIE Abstract Data Type: the integrand type
The implemented ACP is based on one main ADT, the integrand type, the definition of which is shown in Listing 2.
|
Listing 2. integrand type definition |


|
The integrand type does not implement any actual integrand field, it being and abstract type. It only specifies which deferred procedures are necessary for implementing an actual concrete integrand type that can use a FOODIE solver.
As shown in listing 2, the number of the deferred type bound procedures that clients must implement into their own concrete extension of the integrand ADT is very limited: essentially, there are 1 ODE-specific procedure plus some operators definition constituted by symmetric operators between 2 integrand objects, asymmetric operators between integrand and real numbers (and viceversa) and an assignment statement for the creation of new integrand objects. These procedures are analyzed in the following paragraphs.
3.1.1. Time derivative procedure, the residuals function
The abstract interface of the time derivative procedure t is shown in Listing 3.
|
Listing 3. time derivative procedure interface |
 |
This procedure-function takes two arguments, the first passed as a type bounded argument, while the latter is optional, and it returns an integrand object. The passed dummy argument, self, is a polymorphic argument that could be any extensions of the integrand ADT. The optional argument t is the time at which the residuals function must be computed: it can be omitted in the case the residuals function does not depend directly on time.
Commonly, into the concrete implementation of this deferred abstract procedure clients embed the actual ODE equations being solved. As an example, for the Burgers equation, that is a Partial Differential Equations (PDE) system involving also a boundary value problem, this procedure embeds the spatial operator that convert the PDE to a system of algebraic ODE. As a consequence, the eventual concrete implementation of this procedure can be very complex and errors-prone. Nevertheless, the FOODIE solvers are implemented only on the above abstract interface, thus emancipating the solvers implementation from any concrete complexity.
Add citations to Burgers, Adams-Bashfort, leapfrog references.
3.1.2. Symmetric operators procedures
The abstract interface of symmetric procedures is shown in Listing 4.
|
Listing 4. symmetric operator procedure interface |
 |
This interface defines a class of procedures operating on 2
integrand objects, namely it is used for the definition of the operators
multiplication,
summation and
subtraction of integrand objects. These operators are used into the above described ODE solvers, for example see equations (
2), (
3), (
6) or (
9). The implementation details of such a procedures class are strictly dependent on the concrete extension of the integrand type. From the FOODIE solvers point of view, we need to known only that first argument passed as bounded one, the left-hand-side of the operator, and the second argument, the right-hand-side of the operator, are two integrand object and the returned object is still an integrand one.
3.1.3. Integrand/real and real/integrand operators procedures
The abstract interfaces of Integrand/real and real/integrand operators procedures are shown in Listing 5.
|
Listing 5. Integrand/real and real/integrand operators procedure interfaces |
 |
These two interfaces are necessary in order to complete the
algebra operating on the integrand object class, allowing the multiplication of an integrand object for a real number, circumstance that happens in all solvers, see equations (
2), (
3), (
6) or (
9). The implementation details of these procedures are strictly dependent on the concrete extension of the integrand type. From the FOODIE solvers point of view, we need to known only that first argument passed as bounded one, the left-hand-side of the operator, and the second argument, the right-hand-side of the operator, are an integrand object and real number of viceversa and the returned object is still an integrand one.
3.1.4. Integrand assignment procedure
The abstract interface of integrand assignment procedure is shown in Listing 6.
|
Listing 6. integrand assignment procedure interface |
 |
The assignment statement is necessary in order to complete the
algebra operating on the integrand object class, allowing the assignment of an integrand object by another one, circumstance that happens in all solvers, see equations (
2), (
3), (
6) or (
9). The implementation details of this assignment is strictly dependent on the concrete extension of the integrand type. From the FOODIE solvers point of view, we need to known only that first argument passed as bounded one, the left-hand-side of the assignment, and the second argument, the right-hand-side of the assignment, are two integrand objects.
3.2. The explicit forward Euler solver
The explicit forward Euler solver is exposed (by the FOODIE main module that must imported, see Listing 1) as a single derived type (that is a standard convention for all FOODIE solvers) named euler_explicit_integrator. It provides the type bound procedure (also referred as method) integrate for integrating in time an integrand object, or any of its polymorphic concrete extensions. Consequently, for using such a solver it must be previously defined as an instance of the exposed FOODIE integrator type, see Listing 7.
|
Listing 7. definition of an explicit forward Euler integrator |
 |
Once an integrator of this type has been instantiated, it can be directly used without any initialization, for example see Listing 8.
|
Listing 8. example of usage of an explicit forward Euler integrator |
 |
where my_integrand is a concrete (valid) extension of integrand ADT.
The complete implementation of the integrate method of the explicit forward Euler solver is reported in Listing 9.
|
Listing 9. implementation of the integrate method of Euler solver |
 |
This method takes three arguments, the first argument is an integrand class, it being the integrand field that must integrated one-step-over in time, the second is the time step used and the third, that is optional, is the current time value that is passed to the residuals function for taking into account the cases where the time derivative explicitly depends on time. The time step is not automatically computed (for example inspecting the passed integrand field), thus its value must be externally computed and passed to the integrate method.
3.3. The explicit TVD/SSP Runge-Kutta class of solvers
The TVD/SSP Runge-Kutta class of solvers is exposed as a single derived type named tvd_runge_kutta_integrator. This type provides three methods:
init: initialize the integrator accordingly the possibilities offered by the class of solvers;
destroy: destroy the integrator previously initialized, eventually freeing the allocated dynamic memory registers;
integrate: integrate integrand field one-step-over in time.
As common for FOODIE solvers, for using such a solver it must be previously defined as an instance of the exposed FOODIE integrator type, see Listing 10.
|
Listing 10: definition of an explicit TVD/SSP Runge-Kutta integrator |
 |
Once an integrator of this type has been instantiated, it must be initialized before used, for example see Listing 11.
|
Listing 11: example of initialization of an explicit TVD/SSP Runge-Kutta integrator |
 |
In the Listing 11 a 3-stages solver has been initialized. As a matter of facts, from the equations (
3) and (
4) a solver belonging to this class is completely defined once the number of stages adopted has been chosen. The complete definition of the
tvd_runge_kutta_integrator type is reported into Listing 12. As shown, the Butcher’s coefficients are stored as allocatable arrays the values of which are initialized by the
init method.
|
Listing 12: definition of tvd_runge_kutta_integrator type |


|
After the solver has been initialized it can be used for integrating an integrand field, as shown in Listing 13.
|
Listing 13: example of usage of a TVD/SSP Runge-Kutta integrator |
 |
where my_integrand is a concrete (valid) extension of integrand ADT. Listing 13 shows that the memory registers necessary for storing the Runge-Kutta stages must be supplied by the client code.
The complete implementation of the integrate method of the explicit TVD/SSP Runge-Kutta class of solvers is reported in Listing 14.
|
Listing 14: implementation of the integrate method of explicit TVD/SSP Runge-Kutta class |
 |
This method takes five arguments, the first argument is passed as bounded argument and it is the solver itself, the second is of an integrand class, it being the integrand field that must integrated one-step-over in time, the third is the stages array for storing the stages computations, the fourth is the time step used and the fifth, that is optional, is the current time value that is passed to the residuals function for taking into account the cases where the time derivative explicitly depends on time. The time step is not automatically computed (for example inspecting the passed integrand field), thus its value must be externally computed and passed to the integrate method.
It is worth noting that the stages memory registers, namely the array stage, must be passed as argument because it is defined as a not-passed polymorphic argument, thus we are not allowed to define it as an automatic array of the integrate method.
3.4. The explicit low storage Runge-Kutta class of solvers
The low storage variant of Runge-Kutta class of solvers is exposed as a single derived type named ls_runge_kutta_integrator. This type provides three methods:
init: initialize the integrator accordingly the possibilities offered by the class of solvers;
destroy: destroy the integrator previously initialized, eventually freeing the allocated dynamic memory registers;
integrate: integrate integrand field one-step-over in time.
As common for FOODIE solvers, for using such a solver it must be previously defined as an instance of the exposed FOODIE integrator type, see Listing 15.
|
Listing 15: definition of an explicit low storage Runge-Kutta integrator |
 |
Once an integrator of this type has been instantiated, it must be initialized before used, for example see Listing 16.
|
Listing 6: example of initialization of an explicit low storage Runge-Kutta integrator |
 |
In the Listing 16 a 5-stages solver has been initialized. As a matter of facts, from the equation (
5) a solver belonging to this class is completely defined once the number of stages adopted has been chosen. The complete definition of the
ls_runge_kutta_integrator type is reported into Listing 17. As shown, the Williamson’s coefficients are stored as allocatable arrays the values of which are initialized by the
init method.
|
Listing 17: definition of ls_runge_kutta_integrator type |
 |
After the solver has been initialized it can be used for integrating an integrand field, as shown in Listing 18.
|
Listing 18: example of usage of a low storage Runge-Kutta integrator |
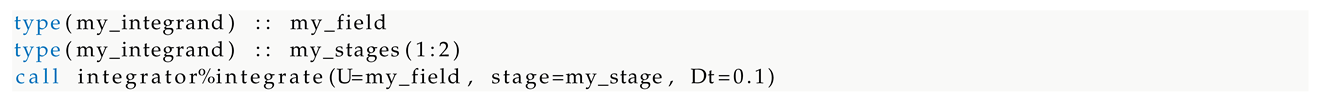 |
where my_integrand is a concrete (valid) extension of integrand ADT. Listing 18 shows that the memory registers necessary for storing the Runge-Kutta stages must be supplied by the client code, as it happens of the TVD/SSP Runge-Kutta class. However, now the registers necessary is always 2, independently on the number of stages used, that in the example considered are 5.
The complete implementation of the integrate method of the explicit low storage Runge-Kutta class of solvers is reported in Listing 19.
|
Listing 19: implementation of the integrate method of explicit low storage Runge-Kutta class |


|
This method takes five arguments, the first argument is passed as bounded argument and it is the solver itself, the second is of an integrand class, it being the integrand field that must integrated one-step-over in time, the third is the stages array for storing the stages computations, the fourth is the time step used and the fifth, that is optional, is the current time value that is passed to the residuals function for taking into account the cases where the time derivative explicitly depends on time. The time step is not automatically computed (for example inspecting the passed integrand field), thus its value must be externally computed and passed to the integrate method.
It is worth noting that the stages memory registers, namely the array stage, must be passed as argument because it is defined as a not-passed polymorphic argument, thus we are not allowed to define it as an automatic array of the integrate method.
3.5. The explicit Adams-Bashforth class of solvers
The explicit Adams-Bashforth class of solvers is exposed as a single derived type named adams_bashforth_integrator. This type provides three methods:
init: initialize the integrator accordingly the possibilities offered by the class of solvers;
destroy: destroy the integrator previously initialized, eventually freeing the allocated dynamic memory registers;
integrate: integrate integrand field one-step-over in time;
update_previous: auto update (cyclically) previous time steps solutions.
As common for FOODIE solvers, for using such a solver it must be previously defined as an instance of the exposed FOODIE integrator type, see Listing 20.
|
Listing 20: definition of an explicit Adams-Bashforth integrator |
 |
Once an integrator of this type has been instantiated, it must be initialized before used, for example see Listing 21.
|
Listing 21: example of initialization of an explicit Adams-Bashforth integrator |
 |
In the Listing 21 a 4-steps solver has been initialized. As a matter of facts, from the equation (
6) a solver belonging to this class is completely defined once the number of time steps adopted has been chosen. The complete definition of the
adams_bashforth_integrator type is reported into Listing 22. As shown, the linear coefficients are stored as allocatable arrays the values of which are initialized by the
init method.
|
Listing 22 definition of adams_bashforth_integrator type |
 |
After the solver has been initialized it can be used for integrating an integrand field, as shown in Listing 23.
|
Listing 23: example of usage of an Adams-Bashforth integrator |
 |
where my_integrand is a concrete (valid) extension of integrand ADT, times are the time at each 4 steps considered for the current one-step-over integration and previous are the memory registers where previous time steps solutions are saved.
The complete implementation of the integrate method of the explicit Adams-Bashforth class of solvers is reported in Listing 24.
|
Listing 24: implementation of the integrate method of explicit Adams-Bashforth class |
 |
This method takes five arguments, the first argument is passed as bounded argument and it is the solver itself, the second is of an integrand class, it being the integrand field that must integrated one-step-over in time, the third are the previous time steps solutions, the fourth is the time step used, the fifth is an array of the time values of the steps considered for the current one-step-over integration that are passed to the residuals function for taking into account the cases where the time derivative explicitly depends on time and the sixth is a logical flag for enabling/disabling the cyclic update of previous time steps solutions. The time step is not automatically computed (for example inspecting the passed integrand field), thus its value must be externally computed and passed to the integrate method.
It is worth noting that the method also performs the cyclic update of the previous time steps solutions memory registers. This can be disable passing autoupdate=.false.: it is useful in the framework of predictor-corrector solvers.
3.6. The implicit Adams-Moulton class of solvers
The implicit Adams-Moulton class of solvers is exposed as a single derived type named adams_moulton_integrator. This type provides three methods:
init: initialize the integrator accordingly the possibilities offered by the class of solvers;
destroy: destroy the integrator previously initialized, eventually freeing the allocated dynamic memory registers;
integrate: integrate integrand field one-step-over in time;
update_previous: auto update (cyclically) previous time steps solutions.
As common for FOODIE solvers, for using such a solver it must be previously defined as an instance of the exposed FOODIE integrator type, see Listing 25.
|
Listing 25 definition of an implicit Adams-Moulton integrator |
 |
Once an integrator of this type has been instantiated, it must be initialized before used, for example see Listing 26.
|
Listing 26: example of initialization of an implicit Adams-Moulton integrator |
 |
In the Listing 26 a 3-steps solver has been initialized. As a matter of facts, from the equation (
7) a solver belonging to this class is completely defined once the number of time steps adopted has been chosen. The complete definition of the
adams_moulton_integrator type is reported into Listing 27. As shown, the linear coefficients are stored as allocatable arrays the values of which are initialized by the
init method.
|
Listing 27: definition of adams_moulton_integrator type |
 |
After the solver has been initialized it can be used for integrating an integrand field, as shown in Listing 28.
|
Listing 28: example of usage of an Adams-Moulton integrator |
 |
where my_integrand is a concrete (valid) extension of integrand ADT, times are the time at each 4 steps considered for the current one-step-over integration and previous are the memory registers where previous time steps solutions are saved.
The complete implementation of the integrate method of the implicit Adams-Moulton class of solvers is reported in Listing 29.
|
Listing 29: implementation of the integrate method of explicit Adams-Moulton class |
 |
This method takes six arguments, the first argument is passed as bounded argument and it is the solver itself, the second is of an integrand class, it being the integrand field that must integrated one-step-over in time, the third are the previous time steps solutions, the fourth is the time step used, the fifth is an array of the time values of the steps considered for the current one-step-over integration that are passed to the residuals function for taking into account the cases where the time derivative explicitly depends on time and the sixth is a logical flag for enabling/disabling the cyclic update of previous time steps solutions. The time step is not automatically computed (for example inspecting the passed integrand field), thus its value must be externally computed and passed to the integrate method.
It is worth noting that the method also performs the cyclic update of the previous time steps solutions memory registers. This can be disable passing autoupdate=.false.: it is useful in the framework of predictor-corrector solvers.
3.7. The predictor-corrector Adams-Bashforth-Moulton class of solvers
The predictor-corrector Adams-Bashforth-Moulton class of solvers is exposed as a single derived type named adams_bashforth_moulton_integrator. This type provides three methods:
init: initialize the integrator accordingly the possibilities offered by the class of solvers;
destroy: destroy the integrator previously initialized, eventually freeing the allocated dynamic memory registers;
integrate: integrate integrand field one-step-over in time;
As common for FOODIE solvers, for using such a solver it must be previously defined as an instance of the exposed FOODIE integrator type, see Listing 30.
|
Listing 30: definition of an implicit Adams-Moulton integrator |
 |
Once an integrator of this type has been instantiated, it must be initialized before used, for example see Listing 31.
|
Listing 31: example of initialization of an implicit Adams-Moulton integrator |
 |
In the Listing 31 a 3-steps solver has been initialized. As a matter of facts, from the equation (
8) a solver belonging to this class is completely defined once the number of time steps adopted has been chosen. The complete definition of the
adams_moulton_integrator type is reported into Listing 32. As shown, the linear coefficients are stored as allocatable arrays the values of which are initialized by the
init method.
|
Listing 32: definition of adams_bashforth_moulton_integrator type |
 |
After the solver has been initialized it can be used for integrating an integrand field, as shown in Listing 33.
|
Listing 33: example of usage of an Adams-Bashforth-Moulton integrator |
 |
where my_integrand is a concrete (valid) extension of integrand ADT, times are the time at each 4 steps considered for the current one-step-over integration and previous are the memory registers where previous time steps solutions are saved.
The complete implementation of the integrate method of the predictor-corrector Adams-Bashforth-Moulton class of solvers is reported in Listing 34.
|
Listing 34: implementation of the integrate method of predictor-corrector Adams-Bashforth-Moulton class |
 |
This method takes four arguments, the first argument is passed as bounded argument and it is the solver itself, the second is of an integrand class, it being the integrand field that must integrated one-step-over in time, the third is the time step used, and the fourth is the current time. The time step is not automatically computed (for example inspecting the passed integrand field), thus its value must be externally computed and passed to the integrate method.
3.8. The leapfrog solver
The explicit Leapfrog class of solvers is exposed as a single derived type named leapfrog_integrator. This type provides three methods:
As common for FOODIE solvers, for using such a solver it must be previously defined as an instance of the exposed FOODIE integrator type, see Listing 35.
|
Listing 35: definition of an explicit Leapfrog integrator |
 |
Once an integrator of this type has been instantiated, it must be initialized before used, for example see Listing 36.
|
Listing 36: example of initialization of an explicit Leapfrog integrator |
 |
The complete definition of the leapfrog_integrator type is reported into Listing 37. As shown, the filter coefficients are initialized to zero, suitable values are initialized by the init method.
|
Listing 37: definition of leapfrog_integrator type |
 |
After the solver has been initialized it can be used for integrating an integrand field, as shown in Listing 38.
|
Listing 38: example of usage of a Leapfrog integrator |
 |
where my_integrand is a concrete (valid) extension of integrand ADT, previous are the memory registers where previous time steps solutions are saved, filter_displacement is the register necessary for computing the eventual displacement of the applied filter and times are the time at each 2 steps considered for the current one-step-over integration.
The complete implementation of the integrate method of the explicit Leapfrog class of solvers is reported in Listing 39.
|
Listing 39: implementation of the integrate method of explicit Leapfrog class |
 |
This method takes six arguments, the first argument is passed as bounded argument and it is the solver itself, the second is of an integrand class, it being the integrand field that must integrated one-step-over in time, the third are the previous time steps solutions, the fourth is the optional filter-displacement-register, the fifth is the time step used and the sixth is an array of the time values of the steps considered for the current one-step-over integration that are passed to the residuals function for taking into account the cases where the time derivative explicitly depends on time. The time step is not automatically computed (for example inspecting the passed integrand field), thus its value must be externally computed and passed to the integrate method. It is worth noting that if the filter displacement argument is not passed, the solver reverts back to the standard unfiltered Leapfrog method.
It is worth noting that the method also performs the cyclic update of the previous time steps solutions memory registers. In particular, if the filter displacement argument is passed the method performs the RAW filtering.
3.9. General Remarks
Table 8 presents a comparison of the relevant parts of equations (
2), (
3), (
4), (
5), (
6) and (
9) with the corresponding FOODIE implementations reported in Listings 9, 14, 19, 24 and 39, respectively. This comparison proves that the
integrand ADT has allowed a very high-level implementation syntax. The Fortran implementation is almost equivalent to the rigorous mathematical formulation. This aspect directly implies that the implementation of a ODE solver into the FOODIE library is very clear, concise and less-errors-prone than an
hard-coded implementation where the solvers must be implemented for each specific definition of the integrand type, it being not abstract.
5. Benchmarks on parallel frameworks
As aforementioned, FOODIE is unaware of any parallel paradigms or programming models the client codes adopt. As a consequence, the parallel performances measurements presented into this section are aimed only to prove that FOODIE environment does not destroy the parallel scaling of the baseline code implemented without FOODIE.
To obtain such a prove, the 1D Euler PDE system described previously is numerically solved with FOODIE-aware test codes that in turn exploit parallel resources by means:
CoArray Fortran (CAF) model, for shared and distributed memory architectures;
OpenMP directive-based model, for only shared memory architectures;
In order to measure the performances of the parallel-enabled FOODIE tests, the
strong and
weak scaling have been considered. For the strong scaling the
speedup has been computed:
where
N is the problem size,
K the number of parallel resources used (namely the physical cores),
is the CPU time of the serial code and
the one of the parallel code. The ideal speedup is linear with slop equals to 1. The efficiency correlated to the strong scaling measurement is defined as:
The maximum ideal efficiency is obviously the unity.
For the of weak scaling measurement the
sizeup has been computed:
where
is the minimum size considered and
is the size used for the test computed with
k parallel resources. If
is scaled proportional to
, the ideal sizeup is again linear and if
the slope is again linear. The efficiency correlated to the weak scaling is defined as:
The maximum ideal efficiency is obviously the unity.
The same 1D Euler PDEs problem is also solved by parallel-enabled codes that are not based on FOODIE: their solutions provide a reference for measuring the effect of FOODIE abstraction on the parallel scaling.
5.1. CAF benchmark
This subsection reports the parallel scaling analysis of Euler 1D test programs (with and without FOODIE) being parallelized by means of CoArrays Fortran (CAF) model. This parallel model is based on the concept of coarray introduced into the Fortran 2008 standard: the array syntax is extended introducing the so called codimension that is a new arrays indexing. Essentially, a CAF enabled code is designed to be replicated a certain number of times and all copies, conventionally named images, are executed asynchronously. Each image has its own set of data (memory) and the codimension indexes are used to access to the (remote) memory of the other images. The CAF approach allows the implementation of Partitioned Global Address Space (PGAS) model following the SPMD (single program, multiple data) parallelization paradigm. The programmer must take care of defining the coarray variables and of synchronizing the images when necessary. This approach requires the refactoring of legacy serial codes, but it allows the exploitation of both shared and distributed memory architectures. Moreover, it is a standard feature of Fortran (2008), thus it is not chained to any particular compiler vendors extension.
The benchmarks shows in this section have been done on a dual Intel(R) Xeon(R) CPU X5650 exacores workstation for a total of 12 physical cores, coupled with 24GB of RAM. In order to perform an accurate analysis 4 different codes have considered:
These codes (see A.1 for the implementation details) have been compiled by means of the GNU gfortran compiler v5.2.0 coupled with OpenCoarrays v1.1.0
4.
The Euler conservation laws are integrated for 30 time steps by means of the TVD RK(5,4) solver: the measured CPU time used for computing the scaling efficiencies is the average of the 30 integrations, thus representing the mean CPU time for computing one time step integration.
For the strong scaling, the benchmark has been conducted with 240000 finite volumes.
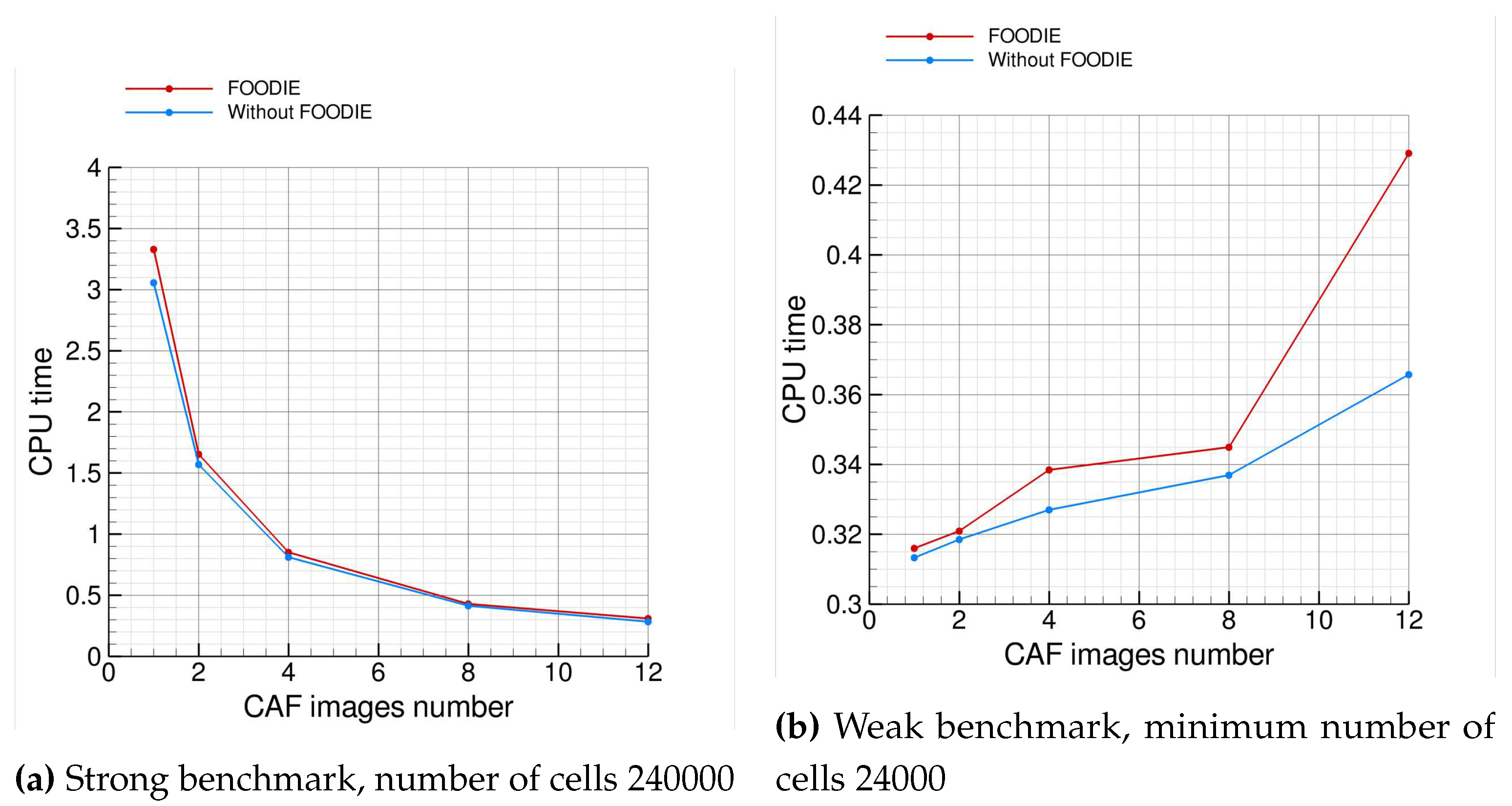
Figure 8a summarizes the strong scaling analysis: it shows that FOODIE-based code scales similarly to the baseline code without FOODIE.
For the weak scaling the minimum size is 24000 finite volumes and the size is scaled linearly with the CAF images, thus
cells.
Figure 8b summarizes the weak scaling analysis and it essentially confirms that FOODIE-based code scales similarly to the baseline code without FOODIE.
Both strong and weak scaling analysis point out that for the computing architecture considered the parallel scaling is reasonable up to 12 cores, the efficiency being always satisfactory.
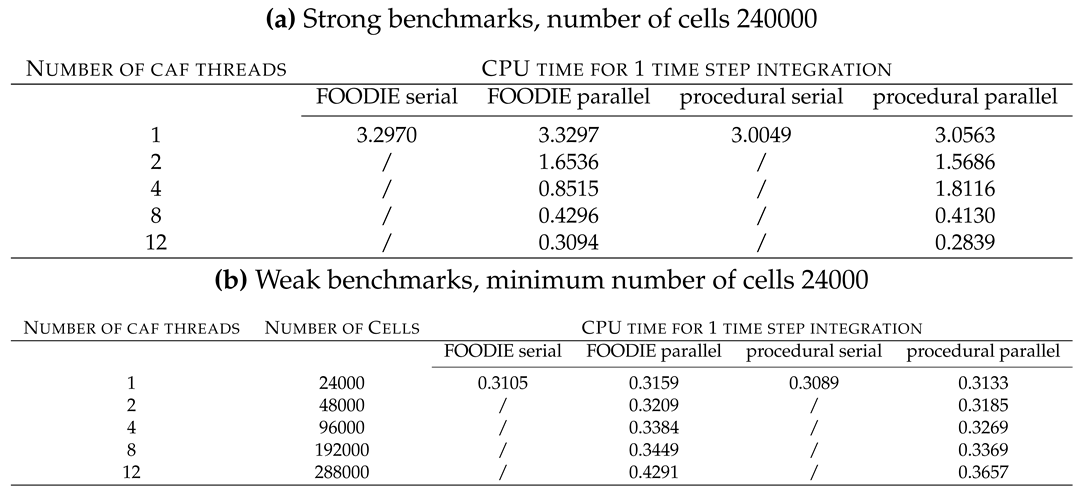
To complete the comparison, the absolute CPU-time consumed by the two families of codes (with and without FOODIE) must be considered.
Table 15 summarizes the benchmarks results. As shown, procedural and FOODIE-aware codes consume a very similar CPU-time for both the strong and the weak benchmarks. The same results are shown in
Figure 9. These results prove that the abstraction of FOODIE environment does not degrade the computational efficiency.
Table 15.
caf benchmarks results
Table 15.
caf benchmarks results
5.2. OpenMP benchmark
This subsection reports the parallel scaling analysis of Euler 1D test programs (with and without FOODIE) being parallelized by means of OpenMP directives-based paradigm. This parallel model is based on the concept of threads: an OpenMP enabled code start a single (master) threaded program and, at run-time, it is able to generate a team of (many) threads that work concurrently on the parallelized parts of the code, thus reducing the CPU time necessary for completing such parts. The parallelization is made by means of directives explicitly inserted by the programmer: the communications between threads are automatically handled by the compiler (through the provided OpenMP library used as back-end). OpenMP parallel paradigm is not a standard feature of Fortran, rather it is an extension provided by the compiler vendors. This parallel paradigm constitutes an effective and easy approach for parallelizing legacy serial codes, however its usage is limited to shared memory architectures because all threads must have access to the same memory.
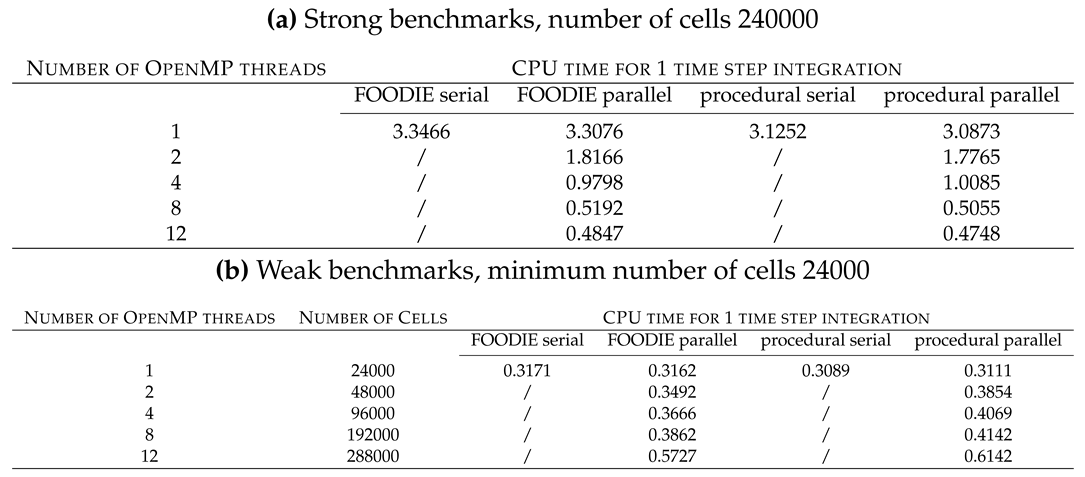
The benchmarks shown in this section have been done on a dual Intel(R) Xeon(R) CPU X5650 exacores workstation for a total of 12 physical cores, coupled with 24GB of RAM. In order to perform an accurate analysis 4 different codes have considered:
These codes (see A.1 for the implementation details) have been compiled by means of the GNU gfortran compiler v5.2.0 with -O2 -fopenmp compilation flags.
The Euler conservation laws are integrated for 30 time steps by means of the TVD RK(5,4) solver: the measured CPU time used for computing the scaling efficiencies is the average of the 30 integrations, thus representing the mean CPU time for computing one time step integration.
For the strong scaling, the benchmark has been conducted with 240000 finite volumes.
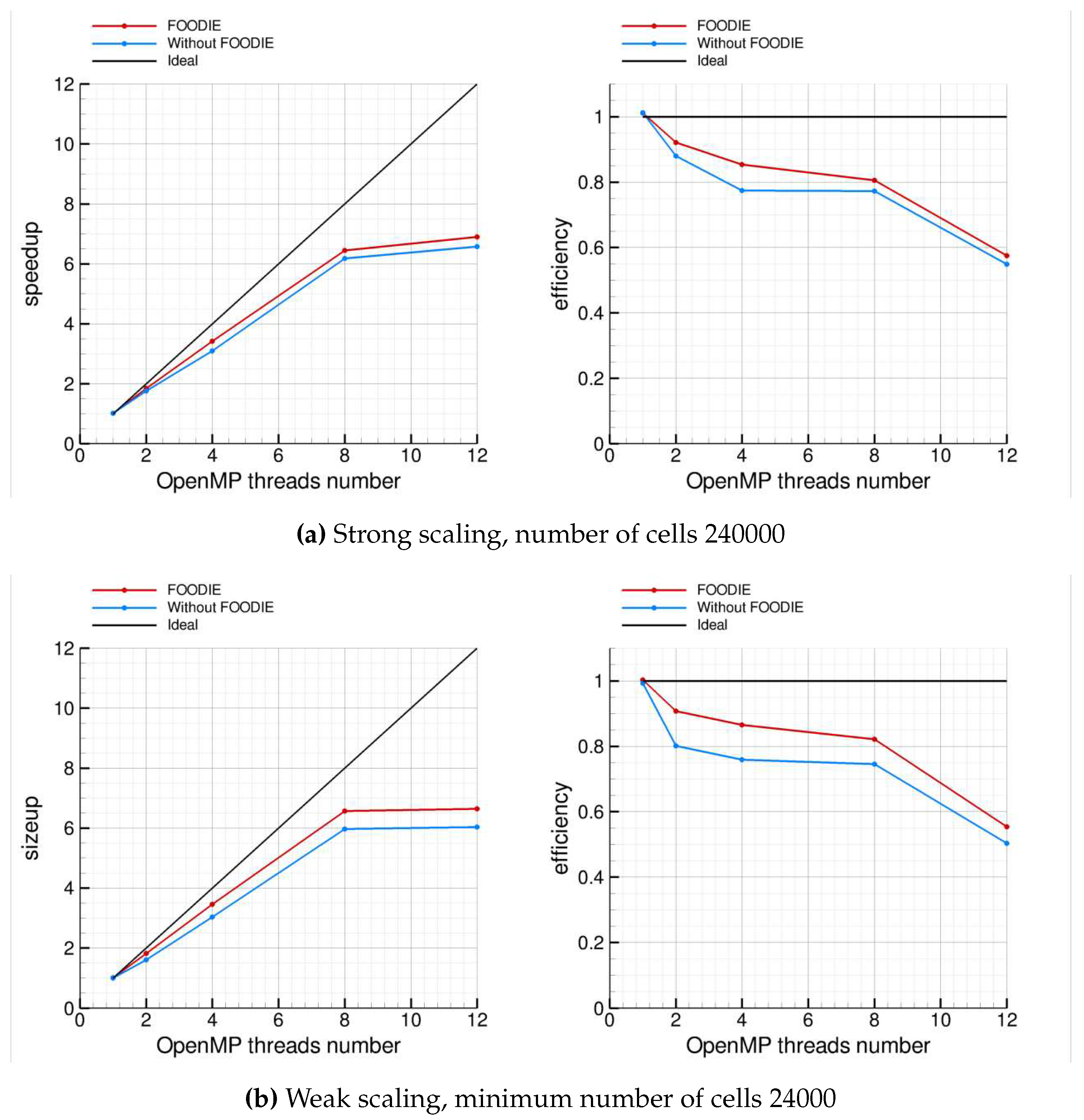
Figure 10a summarizes the strong scaling analysis: it shows that FOODIE-based code scales similarly to the baseline code without FOODIE.
For the weak scaling the minimum size is 24000 finite volumes and the size is scaled linearly with the OpenMP threads, thus
cells.
Figure 10b summarizes the weak scaling analysis and it essentially confirms that FOODIE-based code scales similarly to the baseline code without FOODIE.
Both strong and weak scaling analysis point out that for the computing architecture considered the parallel scaling is reasonable up to 8 cores: using 12 cores the measured efficiencies become unsatisfactory, reducing below the 60%.
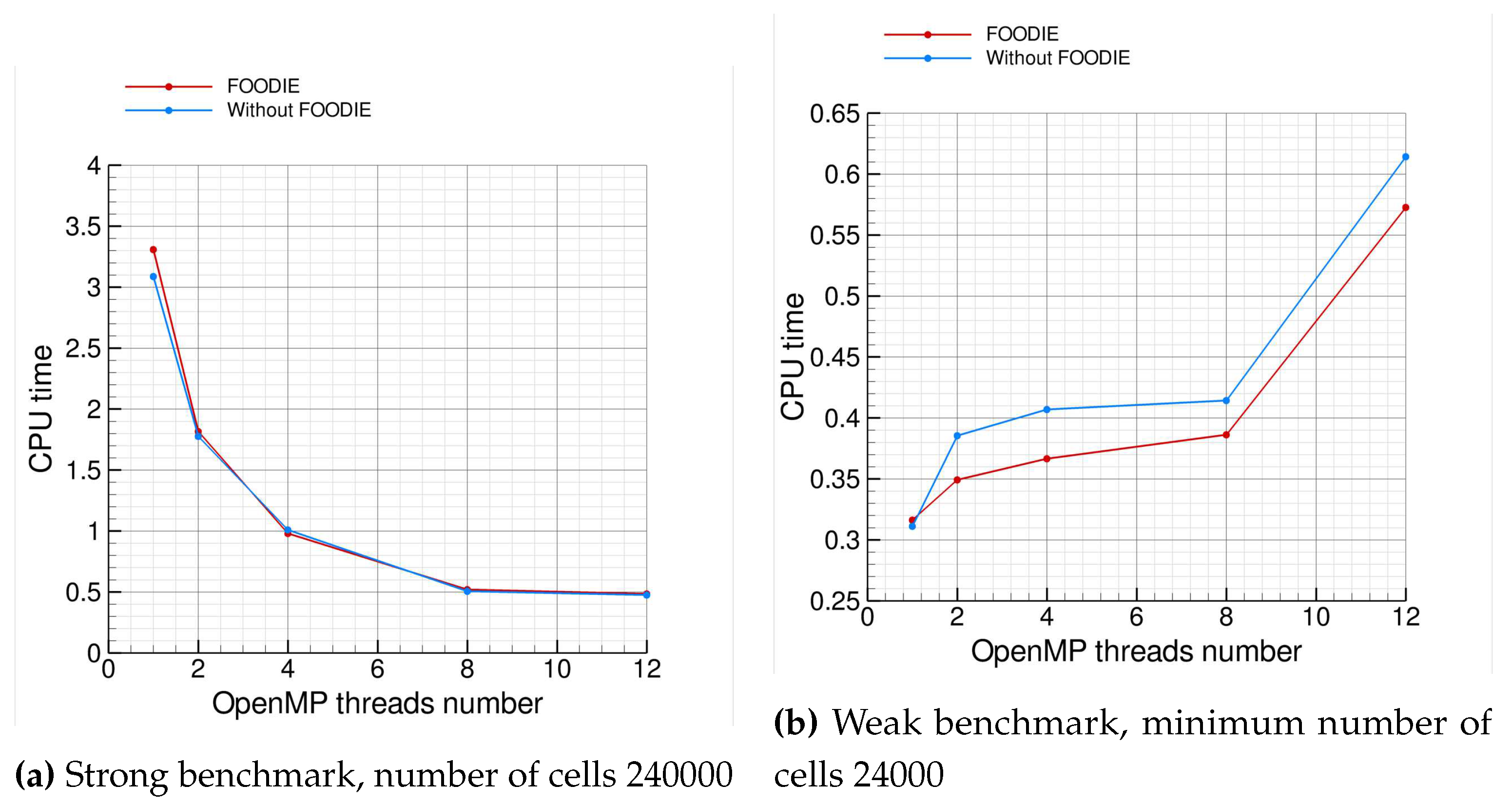
To complete the comparison, the absolute CPU-time consumed by the two families of codes (with and without FOODIE) must be considered.
Table 16 summarizes the benchmarks results. As shown, procedural and FOODIE-aware codes consume a very similar CPU-time for both the strong and the weak benchmarks. The same results are shown in
Figure 11. These results prove that the abstraction of FOODIE environment does not degrade the computational efficiency.
Table 16.
OpenMP benchmarks results
Table 16.
OpenMP benchmarks results