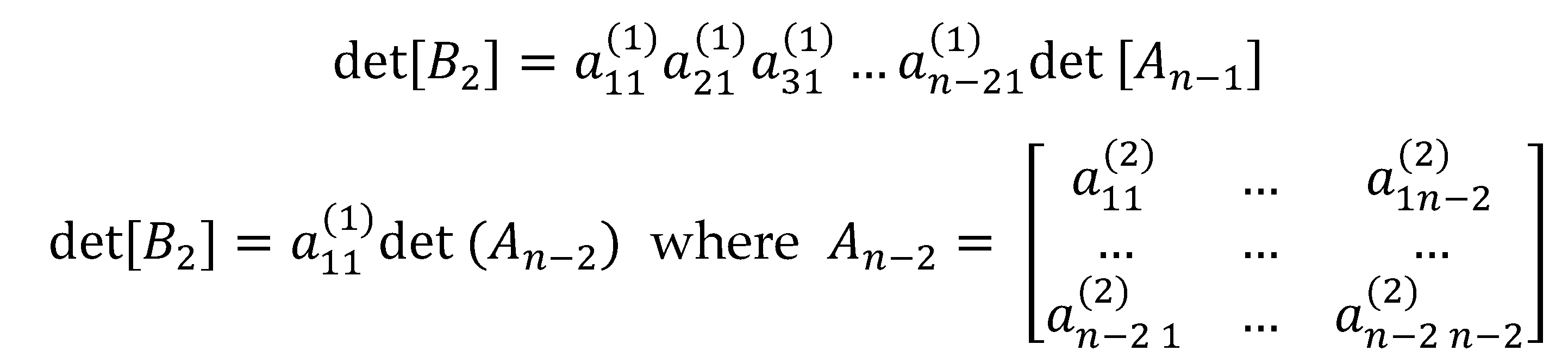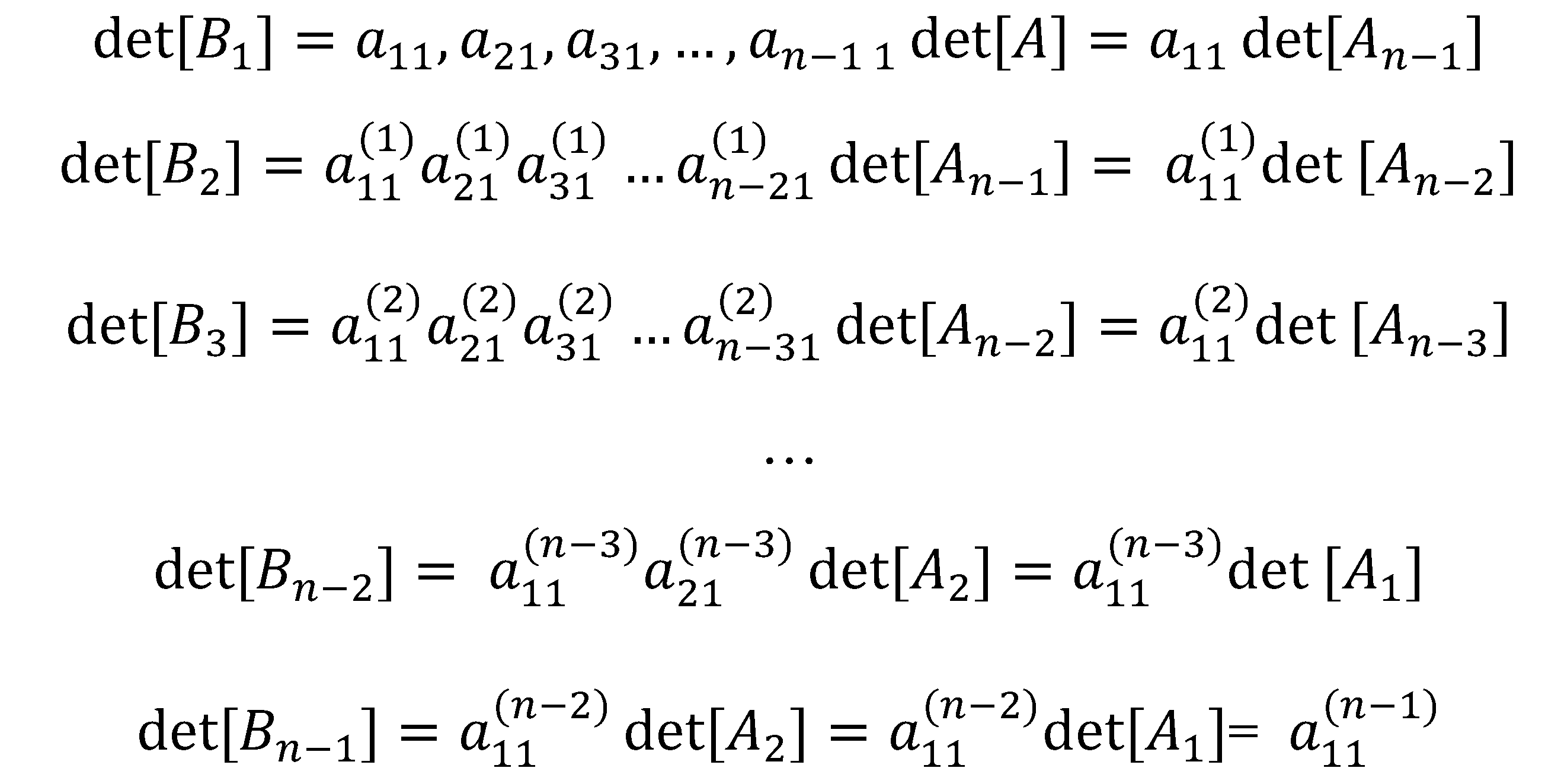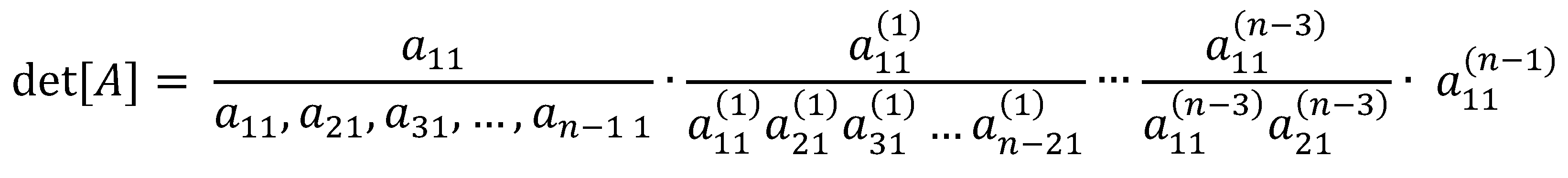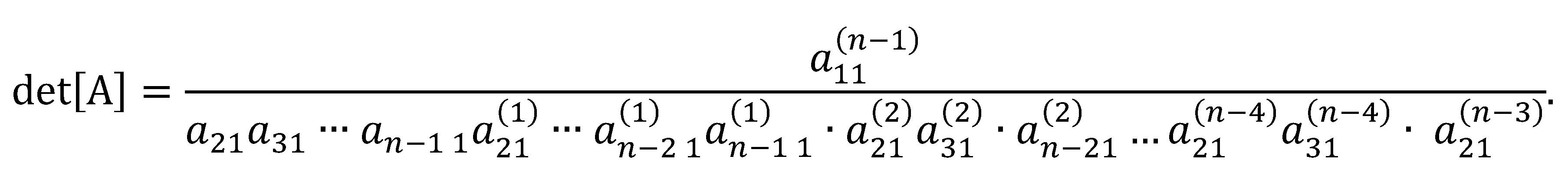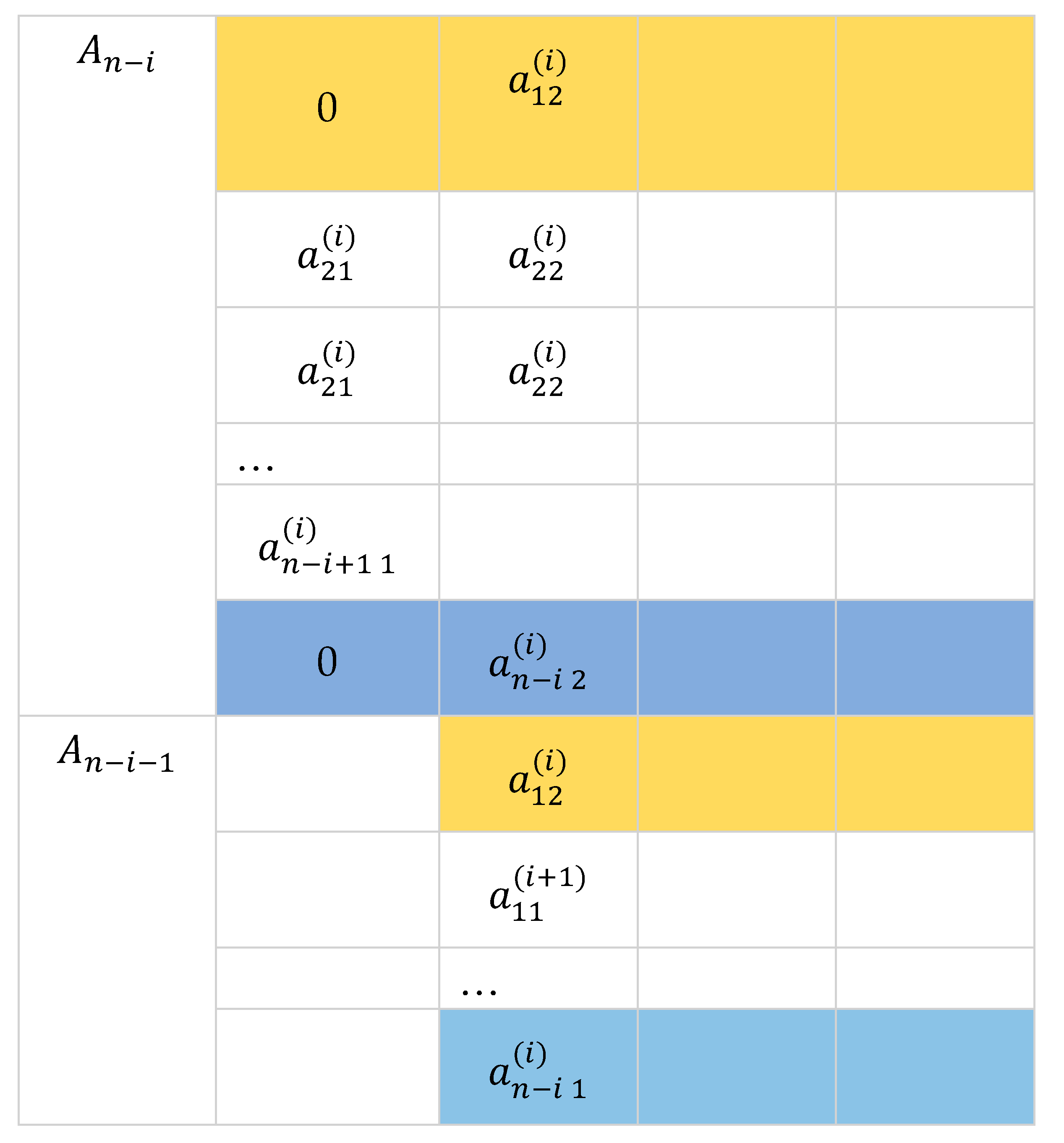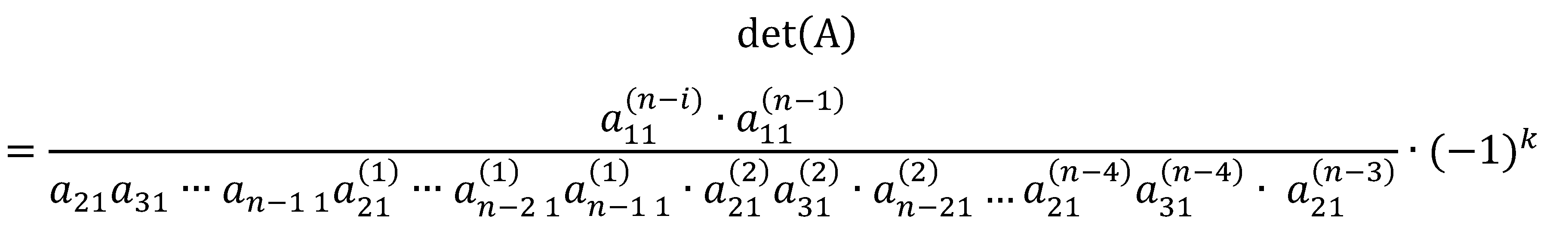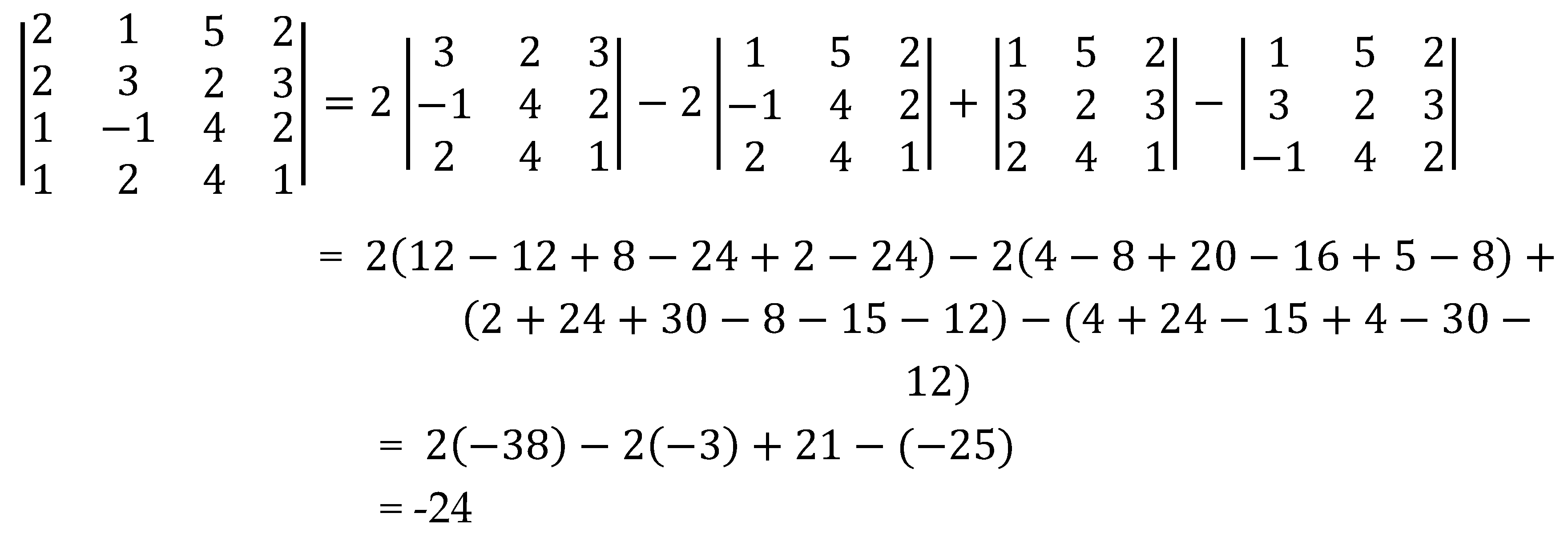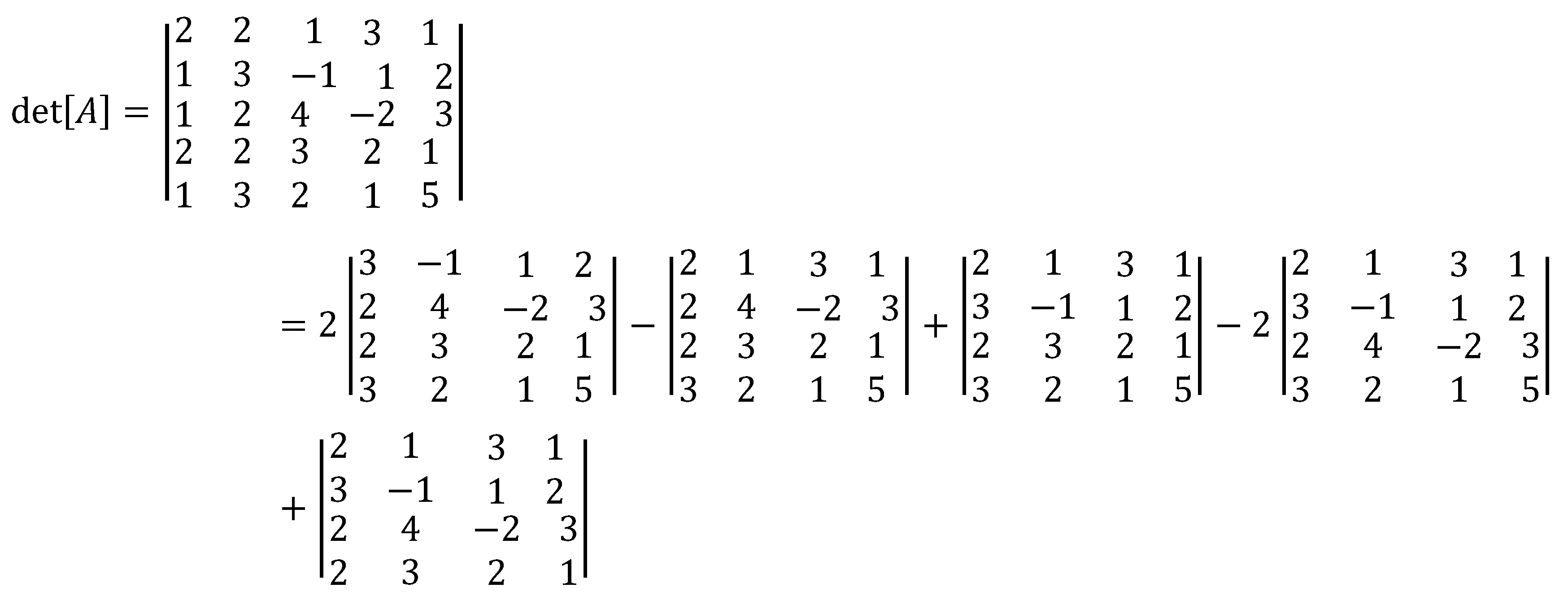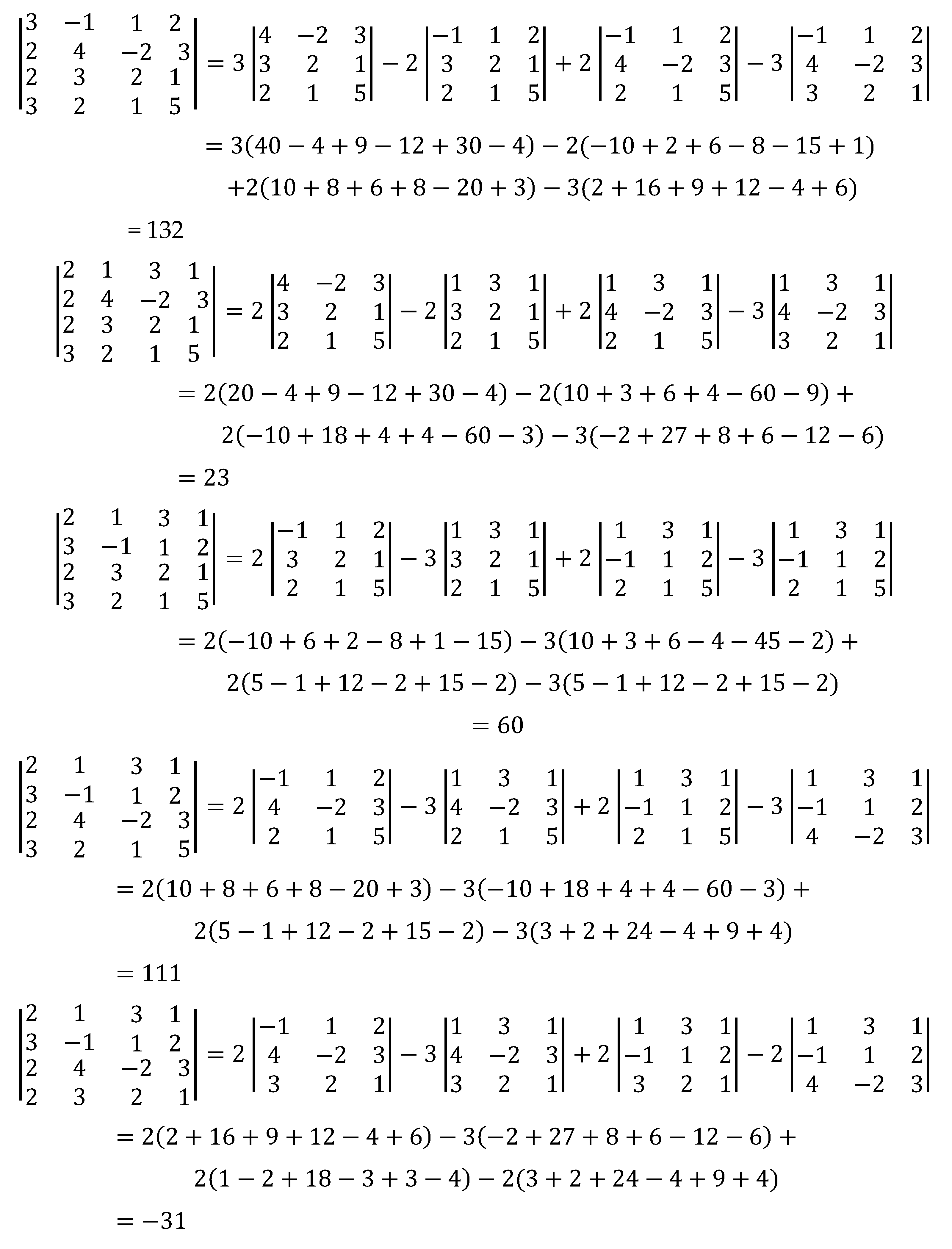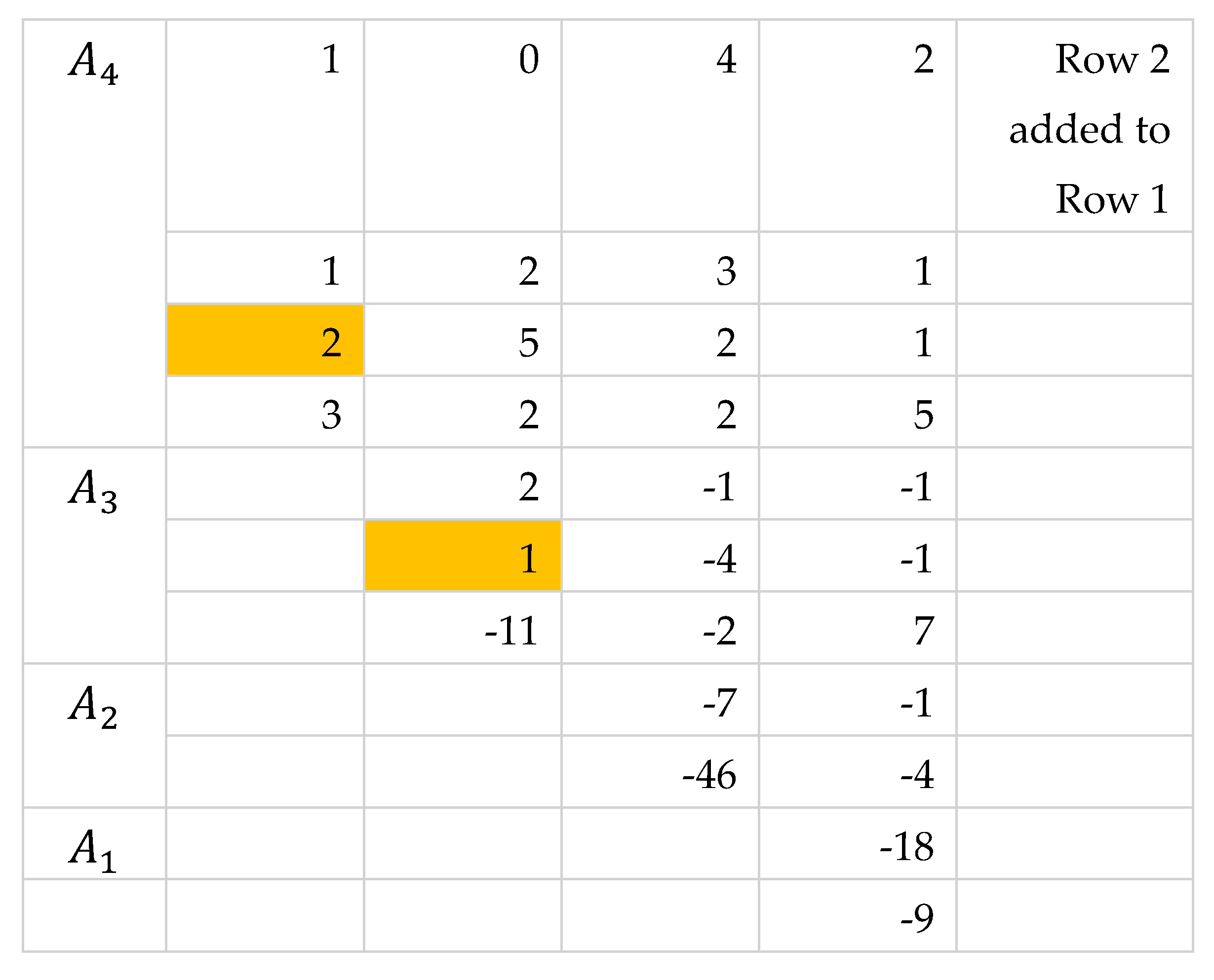1. Introduction
The determinant is a unique number that is associated with a square matrix [
1]. This determinant-square matrix one-to-one correspondence is a function
which assigns the number
|A| to a square matrix
A, the value of which is determined from the entries of
A. The methods of computing determinants usually presented in elementary linear algebra texts include the Leibniz’s definition, co-factor expansion, reduction by elementary row or column operations, and sometimes Dodgson’s condensation method.
Determinants by Definition
Definition 1.
The determinant of an matrix A denoted by or |A| is defined as
where
are column numbers derived from the permutations of the set
.
The sign is taken as + for even permutation and - for odd permutation [
1].
Accordingly, the determinants of simple matrices can be readily computed. The determinant of a single-entry matrix equals the entry itself,
. The butterfly method for
matrices is so-called as the movement of computation suggests the butterfly wings, that is,
. The Sarrus rule for
matrices provides the most efficient approach in computing the determinant [
2]. By Definition 1, the determinant of a
is expanded as
By extending the first two columns of the matrix to the right, the downward arrows give the positive terms and the upward arrows give the negative terms in the expansion of the formula.
Applying the definition in computing the determinant of
matrix which requires
terms with each containing
factors involving
multiplications implies a lengthy process in manually computing the determinants as matrix size becomes larger. Several approaches were proposed to extend Sarrus rule to
and
matrices [
2]. While these methods were shown to be efficient, the length of the process with added rules and number of factors in each term accumulate up as matrix size becomes larger.
Determinants by Cofactor Expansion
Two concepts defined below are essential in this method.
Definition 2.
The minor of an entry of an matrix A is the determinant of the submatrix of A obtained by deleting the of A. The co-factor of is a real number denoted by and is defined by
After computing the minor and its associated co-factor, we compute the determinant by expanding about an
ith row (the row containing all
):
or
jth column:
In co-factor expansion we “expand” the matrix about a certain row or column into submatrices each with rows and columns. This means at the first expansion, we compute minors and co-factors. For larger matrices, we may not readily compute the minors but have to perform second expansion of each of into submatrices each with rows and columns; that is, the process is repeated over the resulting submatrices until smaller submatrices with readily computed determinants are obtained. The determinant of the matrix is then computed by working backward.
Determinants by Row Operations
This alternative to computing the determinants employs elementary row operations to put the matrix into upper or lower triangular form in which the resulting entries in the main diagonal lead to the calculation of the determinant. Here, we revisit the three elementary row operations and their effect on the determinant of a given matrix [
1,
4].
Type 1. Multiplying a row through by a nonzero constant
Theorem 1. If is the matrix that results when a single row of is multiplied by a scalar , then .
Proof: Let be a scalar multiplier of ith row, , of . The definition denotes each entry of is a factor in each term of , so that yields .
Type 2. Interchanging two rows.
Theorem 2. If is the matrix that results when two rows of are interchanged, then .
Proof: Suppose we obtain an
matrix
by interchanging rows r and s of
so that
and
. By definition,
in terms of the entries of B and
in terms of the entries of A. Interchanging to rows denotes a single change within the permutation and produces a change in the number of inversions as to being odd or even; hence,
Type 3. Adding a constant times one row to another.
Theorem 3. If is the matrix that results when a multiple of a row of is added to another row , then .
Proof. Let
be a scalar multiplier
so that
;
and
. By definition,
Expanding the summation gives
Note that the first term and . The two equal factors denote two rows with same entries, thus . Finally,
By reducing a matrix into upper or lower triangular form and applying co-factor expansion, the determinant of the matrix is determined by the product of the entries in the main diagonal as stated in the following theorem.
Theorem 4. If A = is upper (lower) triangular, then det(A) = ; that is, the determinant of a triangular matrix is the product of the elements on the main diagonal.
Some methods along this approach include Chio’s condensation, triangle’s rule, Gaussian elimination procedure, LU decomposition, QR decomposition, and Cholesky decomposition (Sowabomo, 2016)
The English clergyman Rev. Charles Lutwidge Dodgson (1832-1898), famously known as Lewis Caroll for his literary works
Alice in Wonderland and
Through the Looking Glass, invented an algorithm for computing the determinant of a square matrix that is more efficient than Leibniz’s definition especially for larger matrices [
4,
5]. Dodgson’s method aims to ‘condense’ the determinant by producing an
matrix from an
matrix, then
until a
matrix is obtained. The condensation method is founded on Jacobi’s theorem [
5].
Theorem 5.
Jacobi’s Theorem. Let A be an matrix, let be an minor of , where , let be the corresponding minor of , and let be the complementary minor of A. Then:
With
, Dodgson realized that the determinant of
can be readily computed with
His algorithm consists of the following steps.
1. Check the interior of for a zero entry. The interior of A is an matrix that remains when the first row, last row, first column, and last column of A are deleted. We perform elementary row operations to remove all zeros from the interior of A.
2. Compute the determinant of every four adjacent terms to form a new matrix B.
3. Repeat Step 2 to produce an matrix. We then divide each term by the corresponding entry in the interior of the original matrix A, to obtain matrix C.
4. We continue the process of condensation with the succeeding matrices a matrix obtained which gives det A.
Note that Dodgson’s method employs division of entries in succeeding matrices beginning with matrix, a step which may magnify computational error especially for matrices with non-integral entries.
Some technology-based approaches are proposed to efficiently compute the determinant. Matrices with numerically very large or small entries are scaled down to optimize computing efficiency and space; which, however may affect accuracy. Hence, some methods are proposed such as computation of determinant of square matrices without division[
6]. Some matrices naturally take specialized forms which facilitate the development of formulas to compute the determinant. These include division-free algorithm to compute the determinant of quasi-tridiagonal matrices [
7], development of determinant formula for special matrices involving symmetry such as block matrices [
8]; break-down free algorithm for computing determinants of periodic tridiagonal matrices [
9]; and block diagonalization based algorithm of block k-tridiagonal matrices [
10].
The goal of this paper is to propose a more straightforward and mnemonical algorithm that can be applied to any numerical matrices.
2. Development of Proposed Algorithm
We start with an
matrix denoted by
with real entries
where the first entries are non-zero real numbers. Our goal is to produce a matrix in upper triangular form so as to readily compute the determinant by Theorem 4.
Reduction by Cross-Multiplication
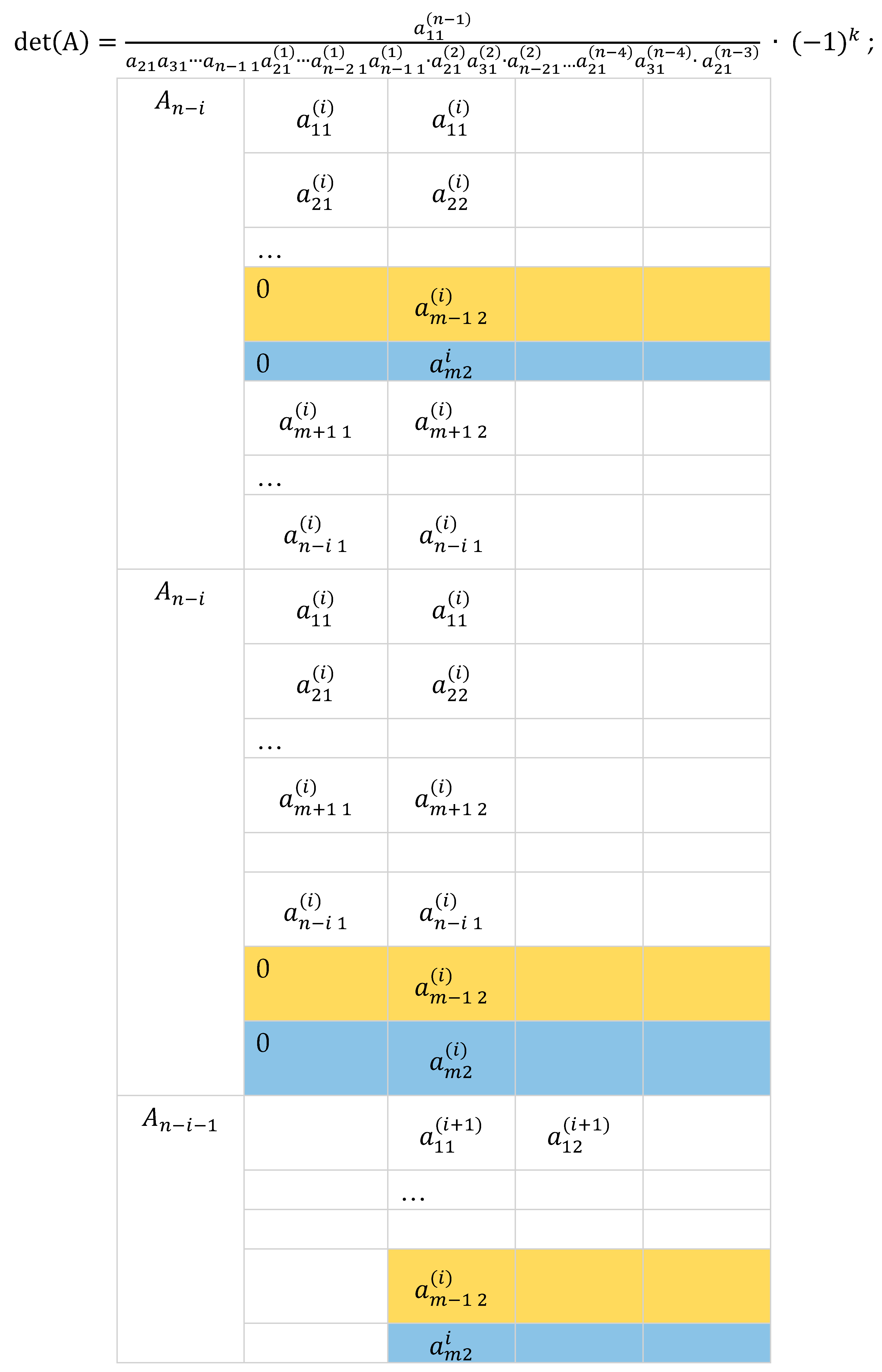
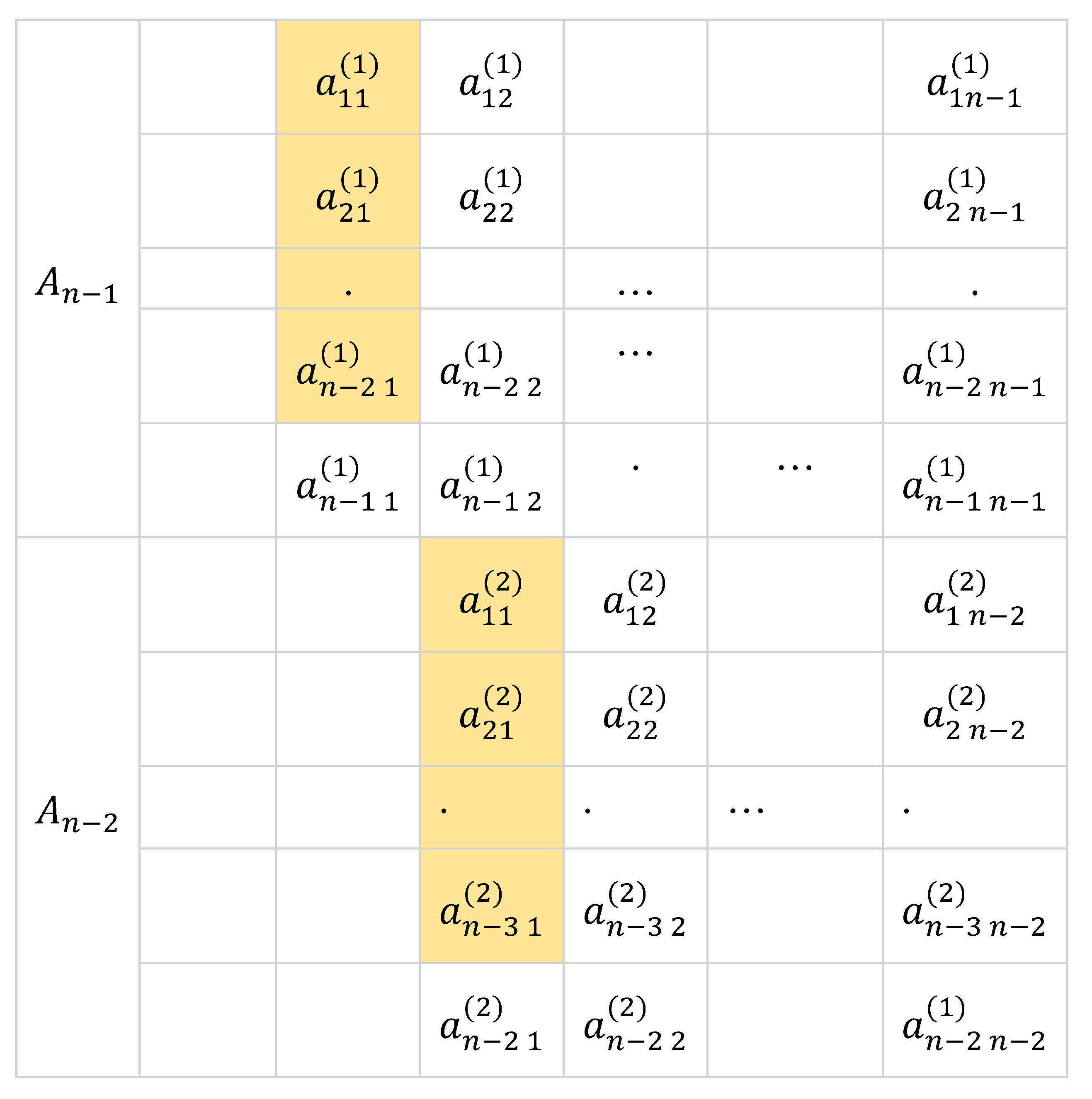
In this paper, we define reduction as the process of performing elementary row operations on a matrix to zero out entries under the first non-zero entry of the first row. A more straightforward way of zeroing out entries under in starting from the bottom row is through . By Theorem 3, the process introduces the factor into the determinant. Working our way up, we zero out the first entry of through which then introduces the factor into the determinant. By repeating the process upward until , we have introduced the following factors into the determinant of A: , At this stage, we obtain a matrix with rows and columns by excluding the first column at the left with zero entries. We specified the entries as follows:
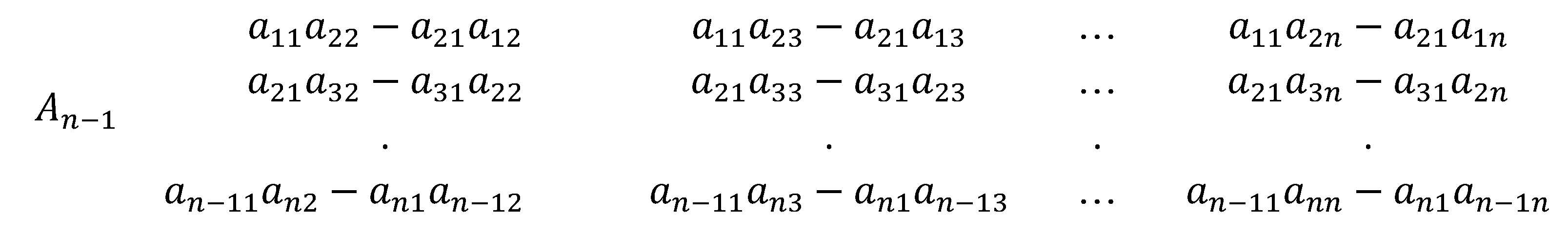
For the purpose of this algorithm, we do away with the usual matrix notation and we put the rows of under the given matrix.
The next stage is obtaining the rows for which is equivalent to zeroing out entries under by following similar process done in obtaining the rows for . The process also introduces the following factors into the determinant: , , … , , .
Assuming no first entries of each is zero, continuing the process of reduction leads to with an introduced factor of and eventually .
By taking the first row from each submatrix, we can reconstruct an matrix in upper triangular form that is row equivalent to the given matrix .
Since
is row equivalent to
and these factors
are introduced into the determinant of
in the process of forming
, then
from which,
Finally,
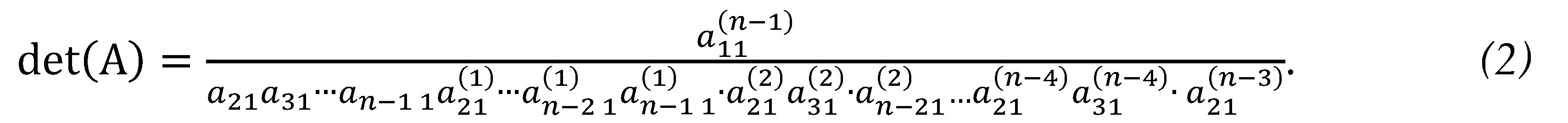
Examining the table below, the denominators are the in-between first entries in the submatrices.
Remarks. The expression for each entry suggests a cross-multiplication pattern involving the first entries of two adjacent rows of , and , and a pair of entries in the column, and such that a resulting entry denoted by in the submatrix is determined by where is the number of reductions performed. Hence, we name this method cross-multiplication. In for example, , , …, , and so on until
3. Cross-Multiplication and Dodgson’s Condensation Method in 3 x 3 Matrices
We now show the equivalence of Dodgson’s condensation method and cross-multiplication which as shown above is derived from elementary row operations for matrix.
Given where are nonzero. By Dodgson’s condensation method, we take four adjacent entries at a time, compute their determinants to form a matrix.
We then compute the determinant of the resulting matrix to obtain a matrix and divide the resulting entry by the corresponding entry of the interior of which is
With cancelled, this gives
Since is a common factor, then . By Definition 1, |A|= |. Thus, .
By exchanging columns 1 and 2 of we have and it can also be shown that .
By cross-multiplication
Here, is the common factor hence, which is consistent with Equation 2.
Similar to Dodgson’s approach, can be thought of as the determinant of matrix formed by the first entries of two adjacent rows and the pair of corresponding entries in the column; that is, . Here, we fix the first entries of two adjacent rows as the pivot in computing the determinants of consecutive matrices. By doing so, is the factor introduced into the original determinant, analogous to the corresponding entry of the interior matrix in the condensation method. By fixing the pivot at the first two entries, we can limit the number of divisions to be performed in preserving the determinant. With odgson’s method employs internal divisions while cross-multiplications only employs divisions at the final stage of calculations.
4. Alternate Proof of Cross-Multiplication Method
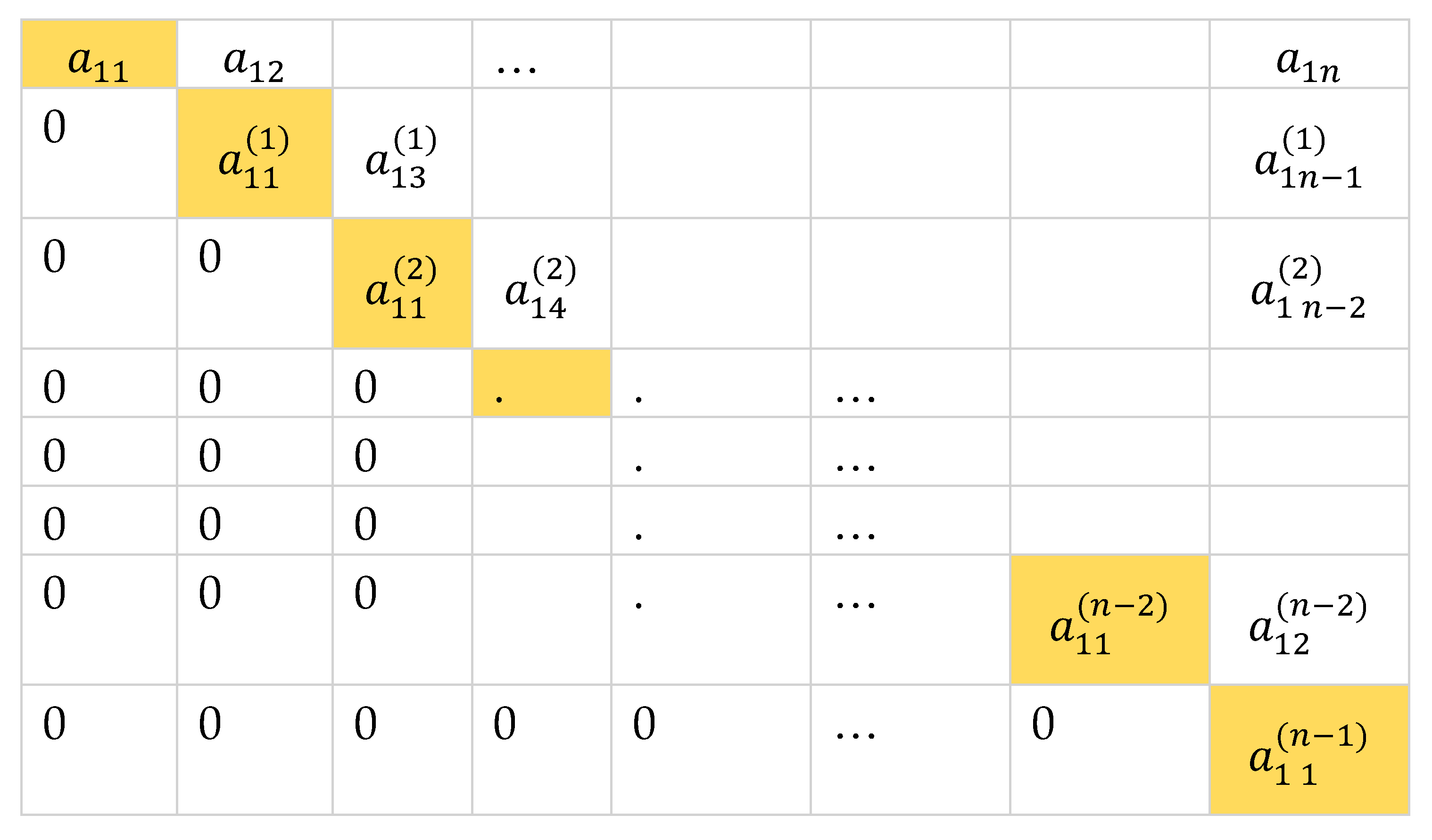
Suppose that B is an matrix where all entries under the first element of the first row are zeros,
By co-factor expansion . If , then to compute the determinant of the resulting submatrix requires a full co-factor expansion or elementary row operations. In deriving the proposed method, we first transform a given matrix into the form of through elementary row operations then apply the definition of co-factor expansion by expanding about the first column. We then repeat the process with the succeeding submatrices until a relatively smaller matrix is obtained where we can readily compute the determinant. By introducing the cross-multiplication, we only form one submatrix instead of submatrices in co-factor expansion.
Let be an matrix with real entries where
We zero out entries under through the process illustrated in this paper: With two successive rows and with first entries and , respectively, and by , a matrix is produced.
In the process, the factors are introduced into Thus by Theorem 1,
By cofactor expansion,
where .
We repeat the process of reduction on to form the matrix
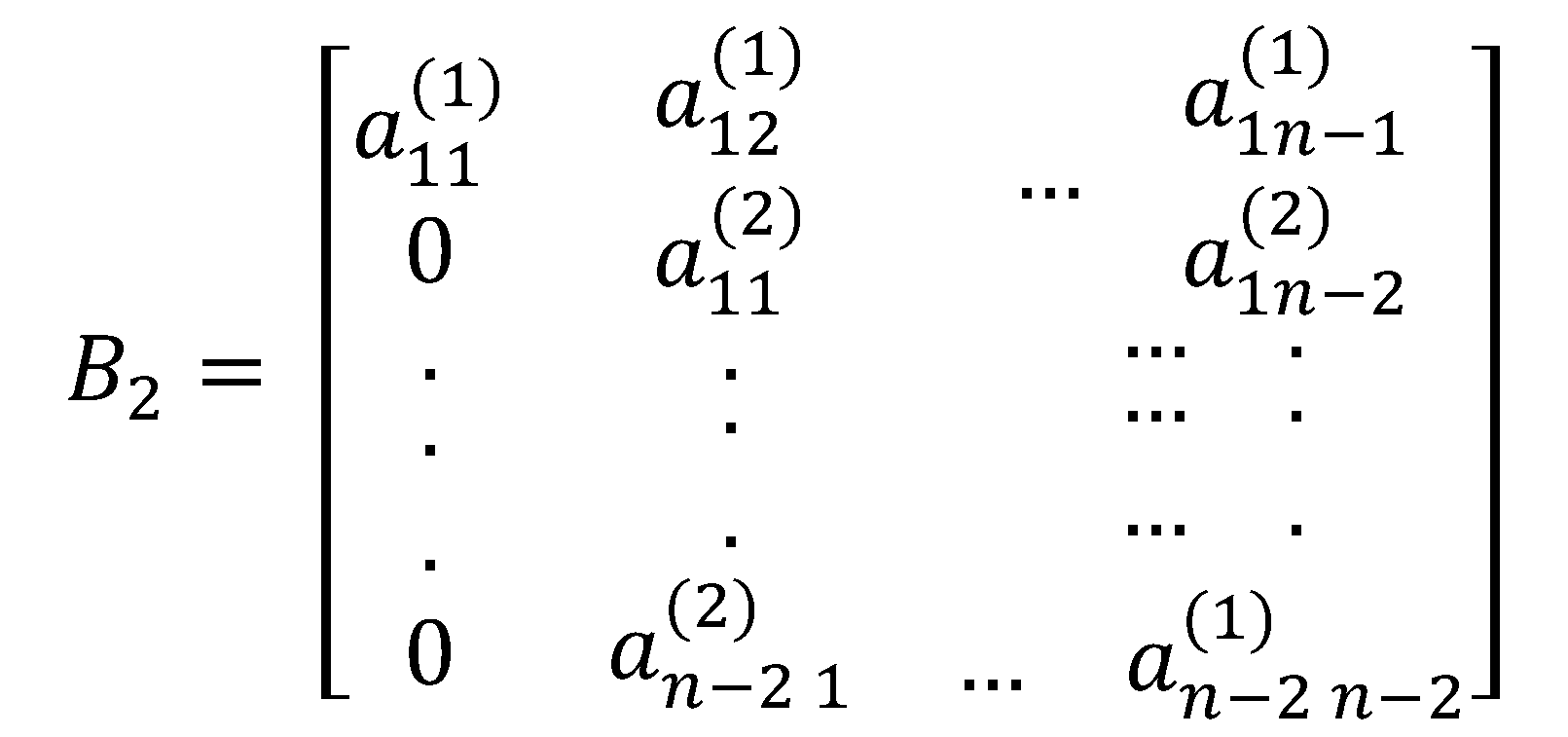
and which
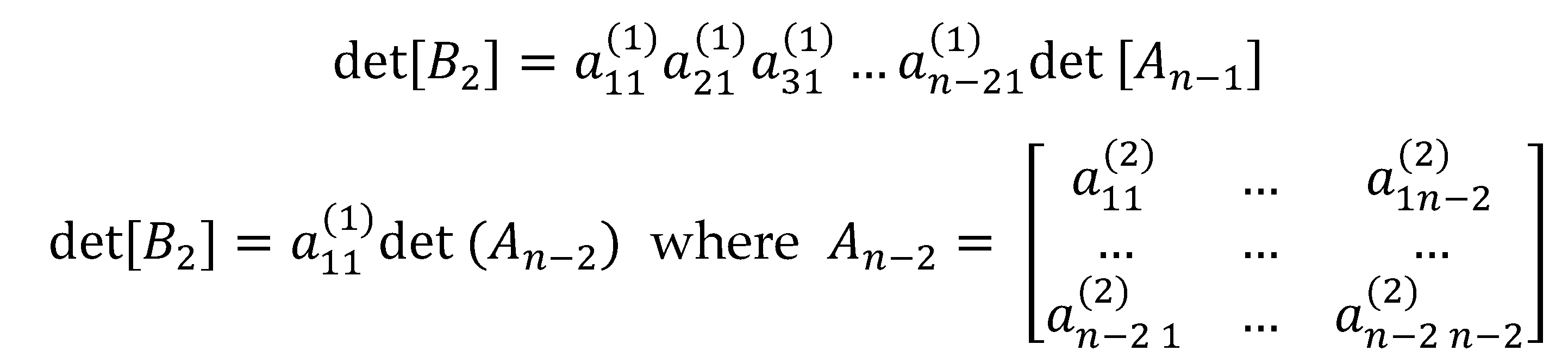
Continuing the reduction on subsequent submatrices we summarize the following results
Working backwards leads to
Hence,
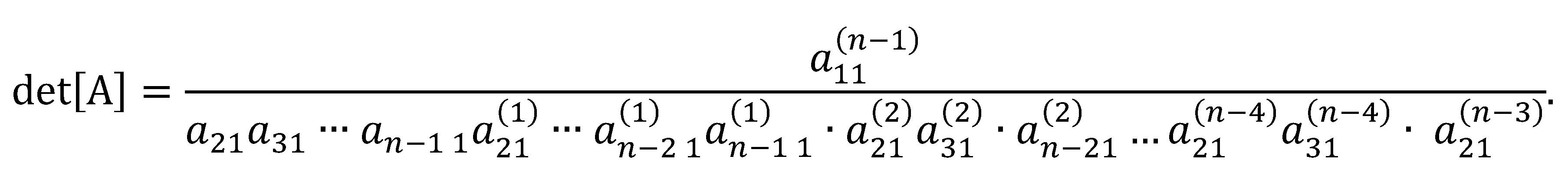
5. Some Special Cases
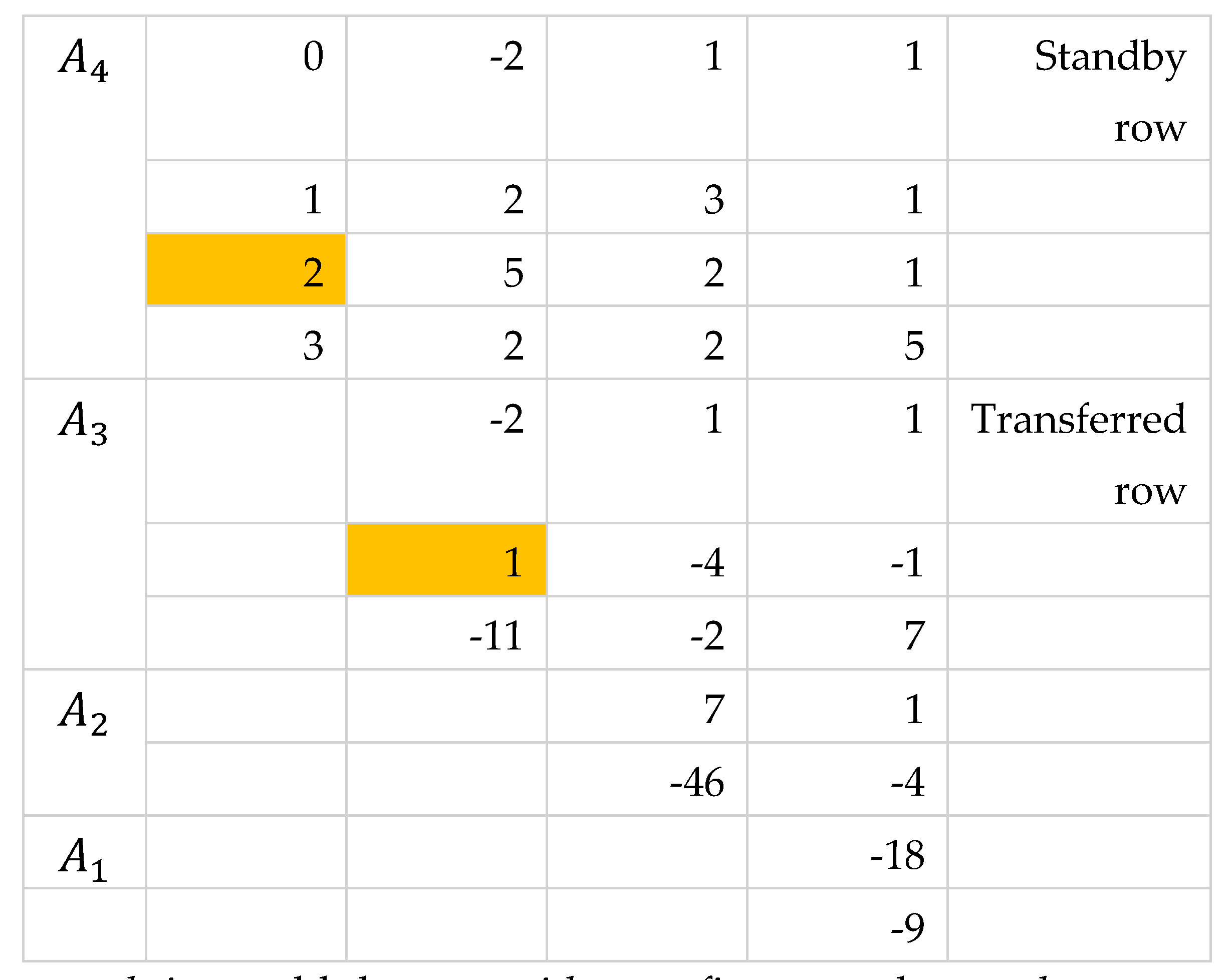
The equation in computing the determinant with the developed method holds if none of the first entries in any row is zero. Here we consider cases where there are zero first entries in any of the submatrices .
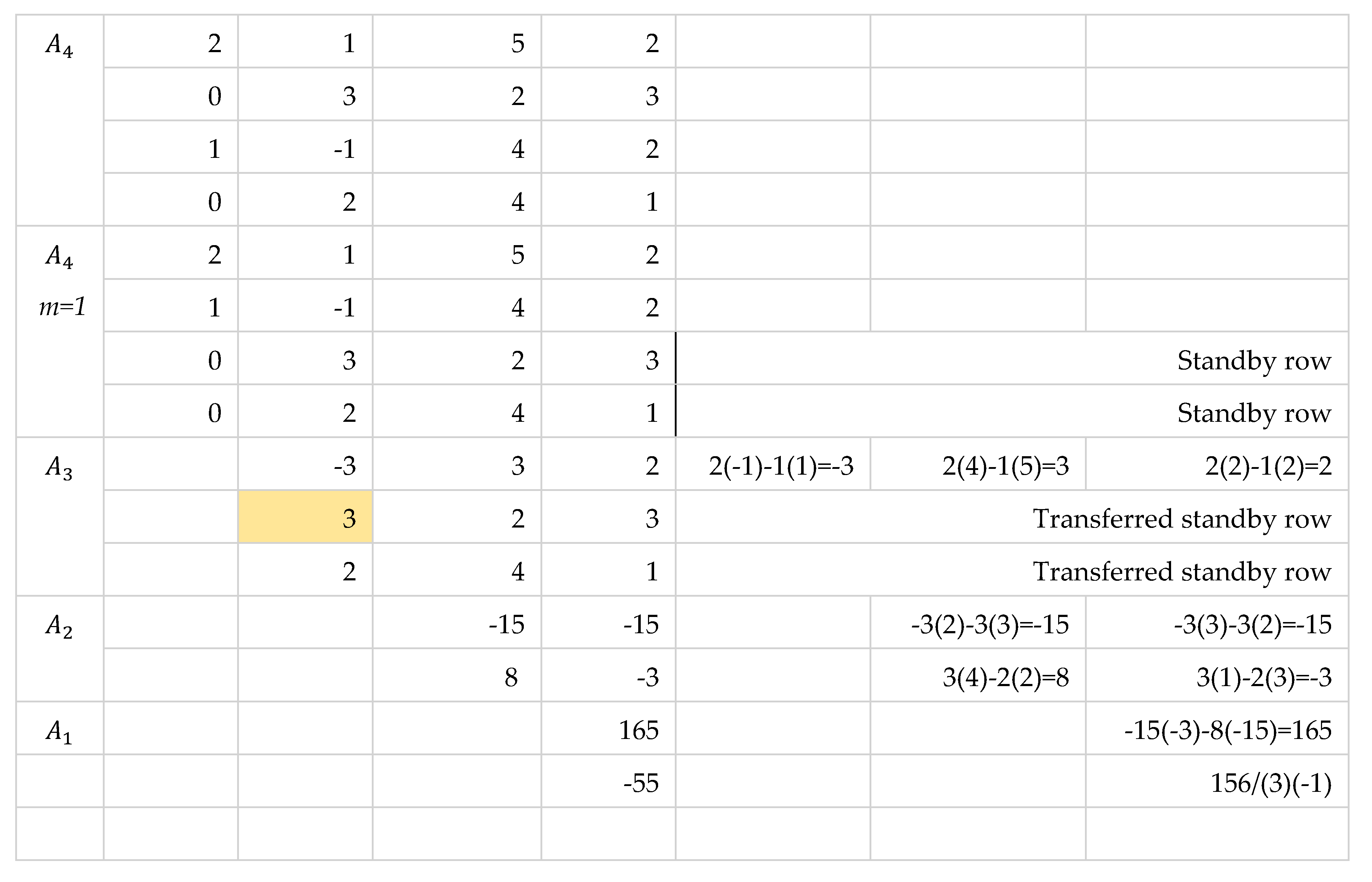
If the first entry of either first or last row of except the last submatrix is zero, then Equation 2 still holds. These rows with zero first entries are considered standby rows and do not participate in row reduction. They are then transferred to the next submatrix retaining their placement as first or last row.
By Theorem 3, we can also add any row with nonzero first entry to a row with zero first entry and go on with the usual process of reduction.
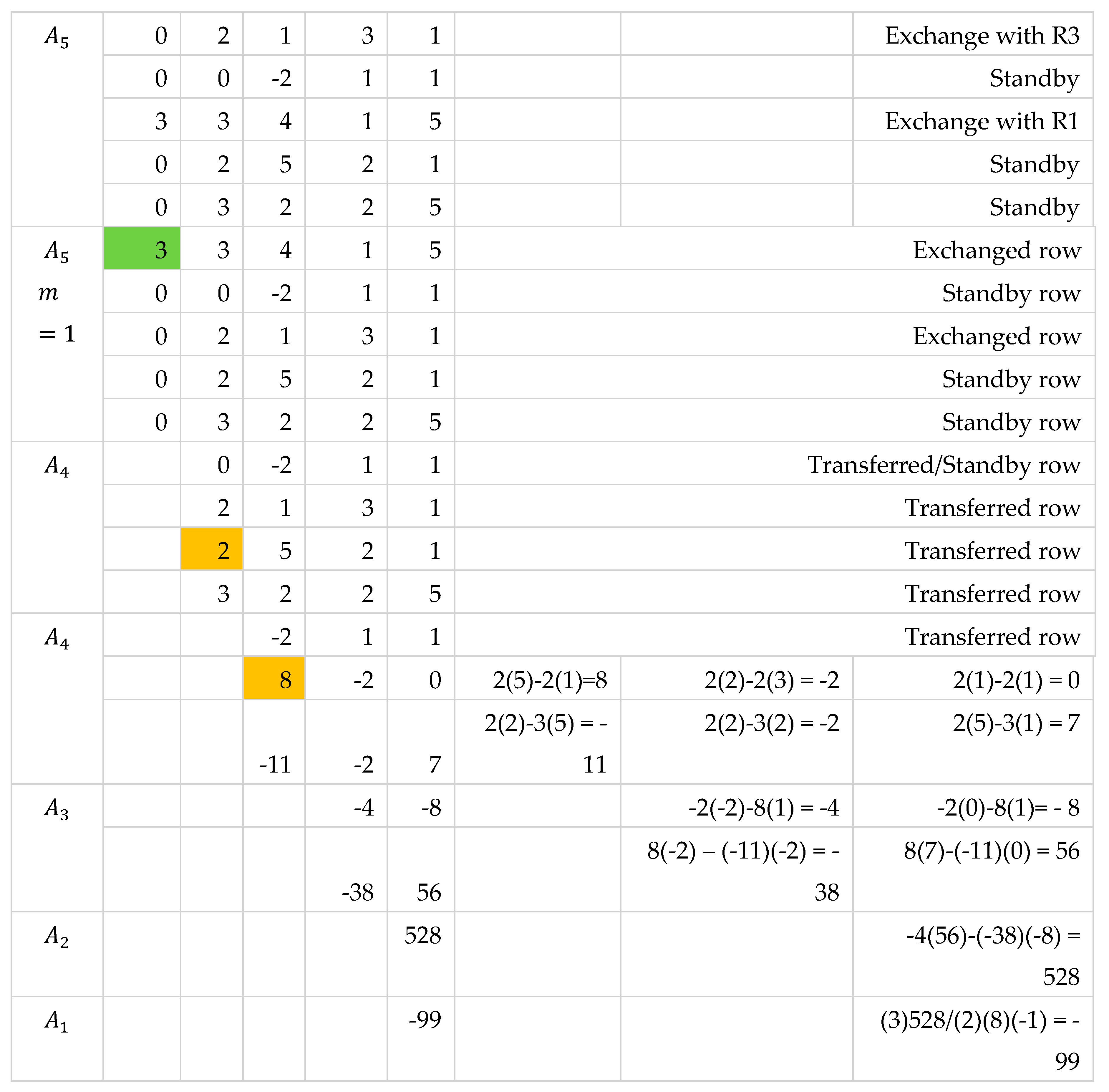
The general approach is to apply Theorem 3 by adding any row with nonzero first entry to a row with zero first entry. We can also apply Theorem 2 to lessen the number of operations especially when there are more rows with zero first entries than rows with nonzero first entries. If an th row of has , then the reduction is not possible since this will introduce a zero factor in the divisor of Equation 2. We reduce the entire submatrix by first moving the rows with zero first entries to the bottom part then perform reduction to rows with nonzero first entries. The rows with zero first entries are treated as “standby rows” and are then moved to the next submatrix in the same placement. Since , by Theorem 2, interchanging and the last row will lead to . We introduce the factor to Equation 2 where indicates the number of row exchanges performed.
If only one row of has non-zero first entry, we place this row as with first entry . No reduction is performed since the already takes the reduced form. By Theorem 4, is a diagonal entry thus this leads to the modified formula:
If all rows of have zero first entries, then no reduction is performed and since then by Equation 2,
6. Conclusions
The cross-multiplication method of computing the determinants is a mnemonical use of elementary row operations in reducing a matrix to lower triangular form by using the first entries of adjacent rows as scalar multipliers. Doing so retains the butterfly movement in computing the determinant of matrix as each entry is easily computed through or such that and are the pivot entries. The algorithm proceeds by computing each entry to produce a submatrix that is one row and one column less than the preceding submatrix until a matrix, [ is obtained. The determinant is then computed as to the following cases.
1. When all first entries in the rows of submatrices are nonzero, the determinant is solved by
where the factors in the denominator are the nonzero in-between first entries of submatrices, representing the factors introduced into the original determinant in the reduction process.
2. When some first entries in the rows are zero, the rows are transferred to the bottom of the submatrix and then transferred to the next submatrix. The determinant is solved by
where
is the number of row exchanges.
3. When rows with zero first entries are added by rows with nonzero first entries, the formula in (1) holds.
4. When each of the submatrices has exactly one row with nonzero first entry, we set these rows as first rows where necessary and compute the determinant by
where
is the number of row exchanges.
4. When all rows of a submatrix have zero first entries, then For , cross-multiplication and Dodgson’s condensation method are shown to be equivalent. Unlike the condensation method which employs internal divisions, the proposed method employs much fewer, , terminal divisions thus minimizing the propagation of computational errors. Both methods require row adjustments whenever there are zero pivot entries.
Compared to co-factor expansion which generates number of submatrices, then number of submatrices, and so on, the cross-multiplication method generates only one of each of , … submatrices.
The simplicity and efficiency of the proposed methods lies in the consistency and symmetry of of its iterative process. No procedural adjustments are introduced as the matrix size increases compared to other methods such as extension of Sarrus rule to matrices with
Acknowledgments
The author acknowledges the invaluable service of peer reviewers of this paper.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
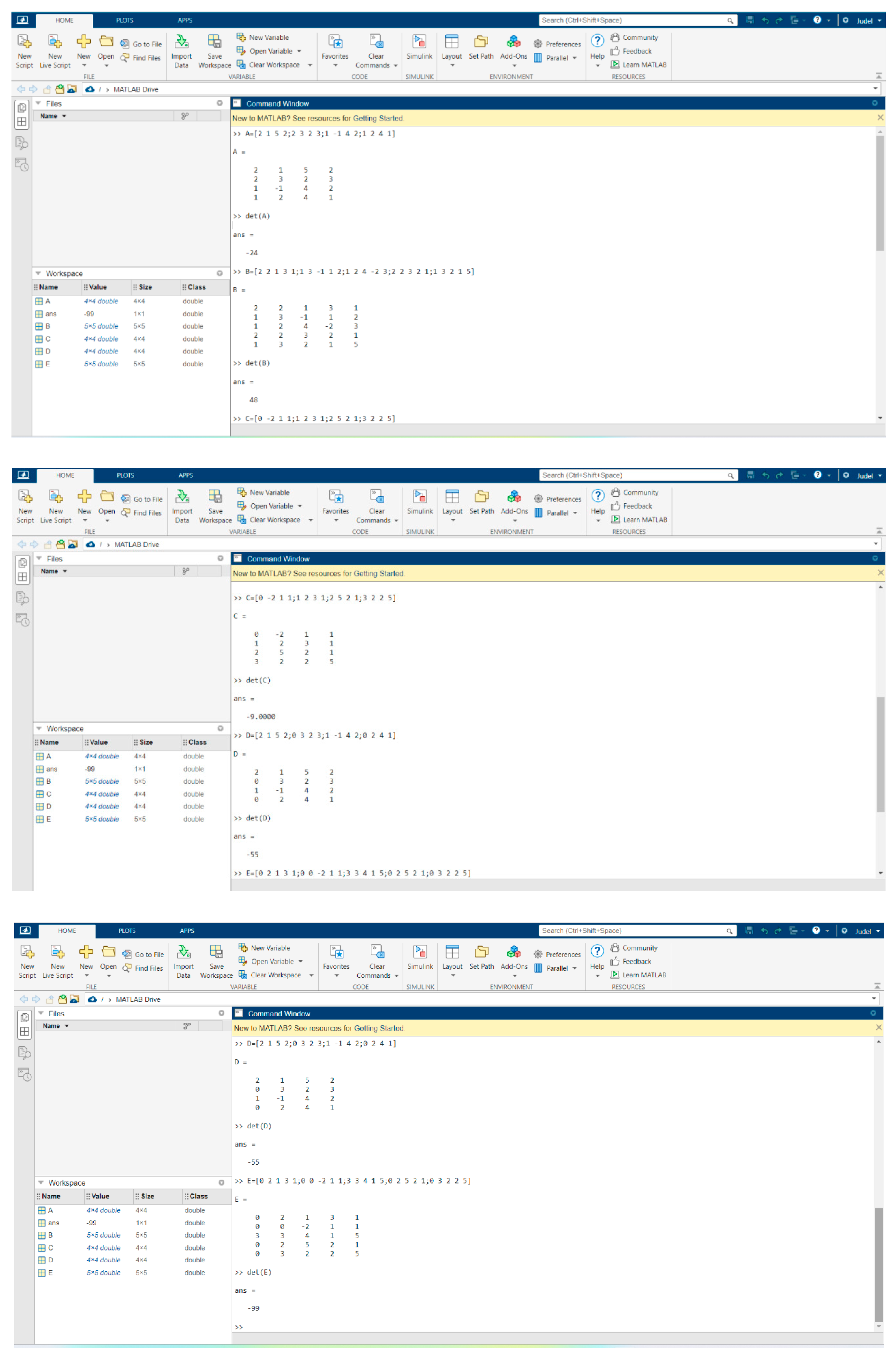
We provide illustrative examples for the proposed methods and we verify the results using co-factor expansion and Matlab (See Appendix B).
Illustration 1. matrix All First Entries Are Non-zeros
Solution by cross-multiplication method.
Solution by co-factor expansion
We expand at the first column to get
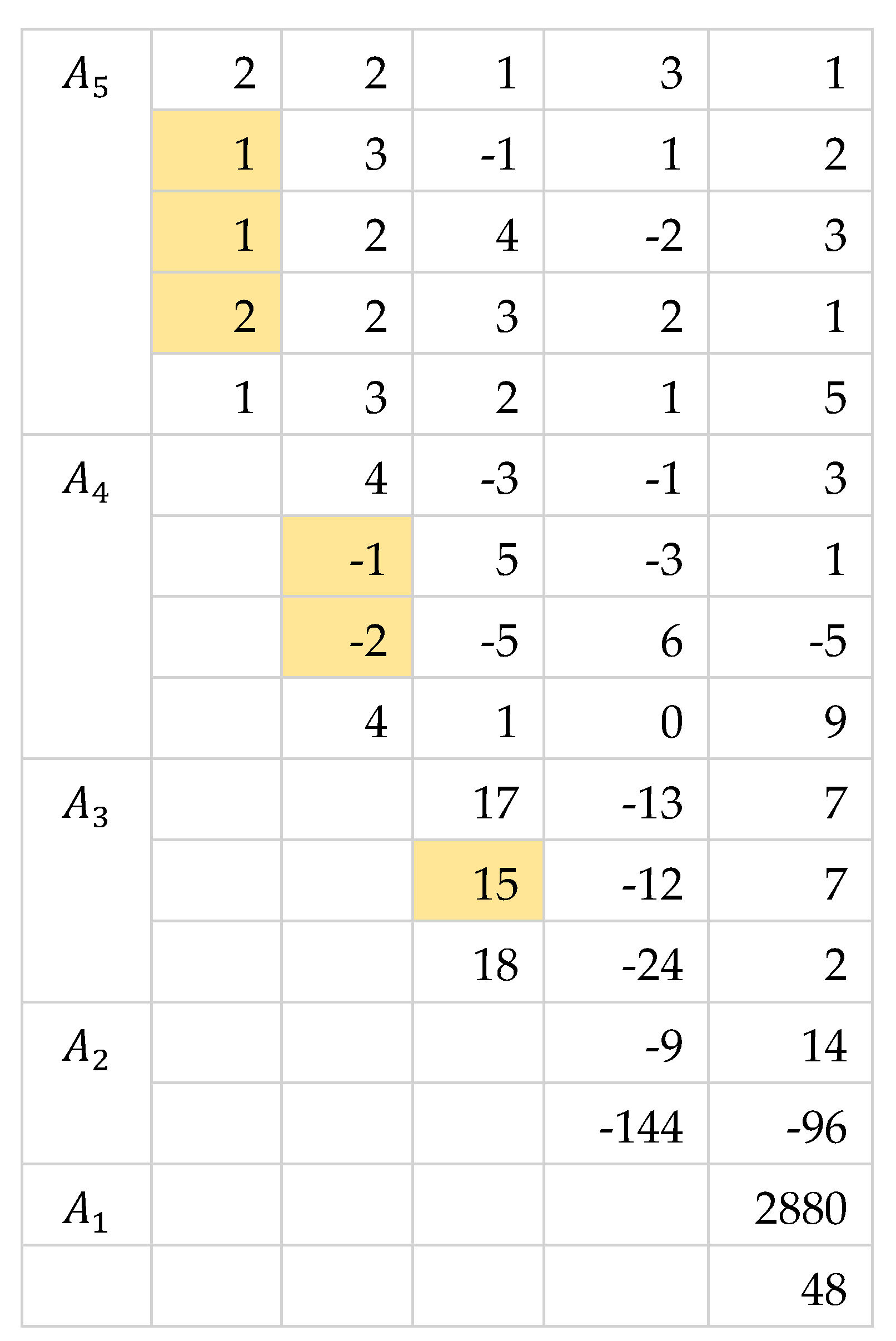
Illustration 2. matrix All First Entries Are Non-zeros
Computation of determinants by cross-multiplication method.
Verification of result by co-factor expansion.
We compute the determinant of each submatrix separately.
Thus,
Illustration 3. First Entry of First or Last Row is Zero
The other approach is to add the row with zero first entry by another row with nonzero first entry.
Illustration 4. Some In-between First Entries are Zeros
We apply similar technique as in Illustration 2.
Illustration 5. Only One Row Has Non-zero First Entry
References
- Kolman, B.; Hill, D. Elementary Linear Algebra with Applications 9th Ed; Pearson Education Ltd.: London, UK, 2014. [Google Scholar]
- Sobamowo, M. On the extension of Sarrus’. International Journal of Engineering Mathematics, 2016. [CrossRef]
- Anton, H.; Rorres, C.; Kaul, A. Elementary Linear Algebra, 12th Ed. John Wiley and Sons: NY, USA, 2019.
- Rice, A.; Torrence, E. ; Shutting up like a telescope: Lewis Carroll’s “Curious” Condensation Method for evaluating determinants. The College Mathematics Journal, 2007, 38, 85–95. [Google Scholar] [CrossRef]
- Harwood, R. C.; Main, M.; Donor, M. An elementary proof of Dodgson's condensation method for calculating determinants" Faculty Publications - Department of Mathematics and Applied Science, 2016.
- Seifullin, T. Computation of determinants, adjoint matrices, and characteristic polynomials without division. Cybernetics and Systems Analysis, 38, 2002.
- Ji-Teng, J.; Wang, J.; He, Q.; Yu-Cong, Y. A division-free algorithm to numerically evaluating the determinant of a special quasi-tridiagonal matrix. Journal of Mathematical Chemistry, 60, 2022.
- Bae, Y.; Lee, I. (2017). Determinant formulae of matrices with certain symmetry and its applications. Symmetry, 9, 2017.
- Ji-Teng, J. A breakdown-free algorithm for computing the determinants of periodic tridiagonal matrices. Numerical Algorithm, 83, 2020.s.
- Ji-Teng, J.; Yu-Cong, Y.; He, Q. A block diagonalization based algorithm for the determinants of block k-tridiagonal matrices. Journal of Mathematical Chemistry, 59, 2021.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
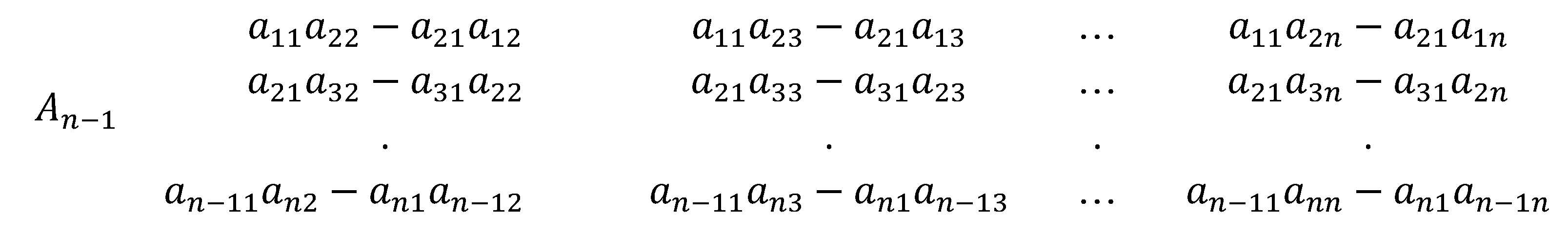
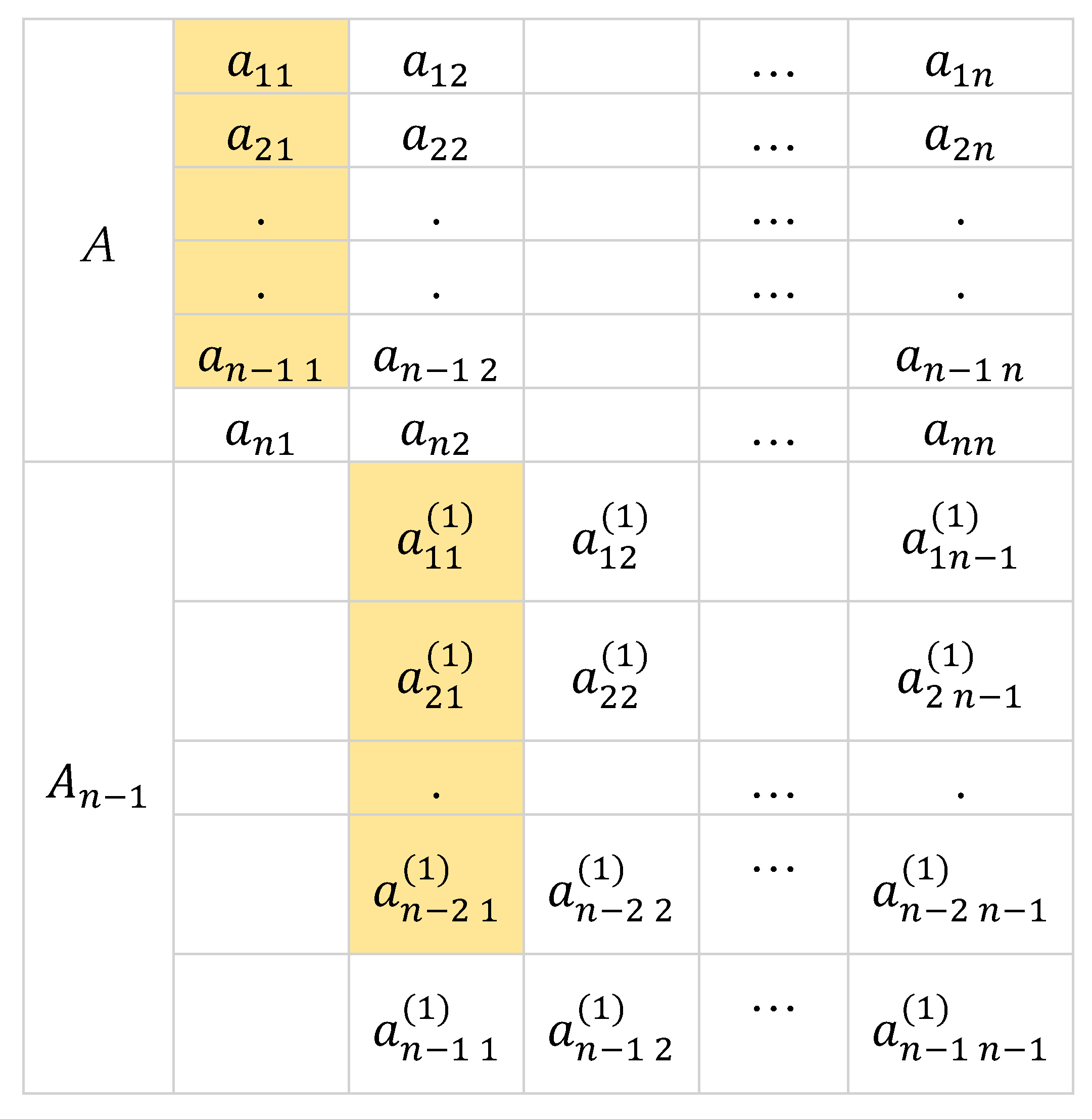

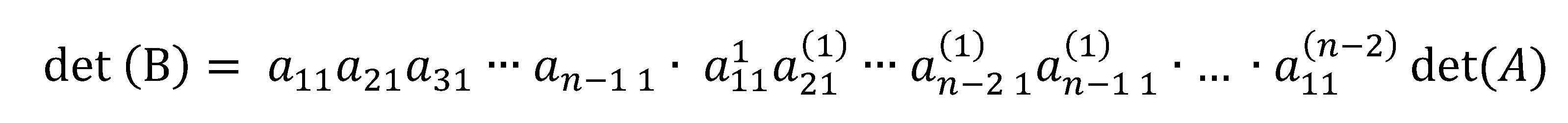
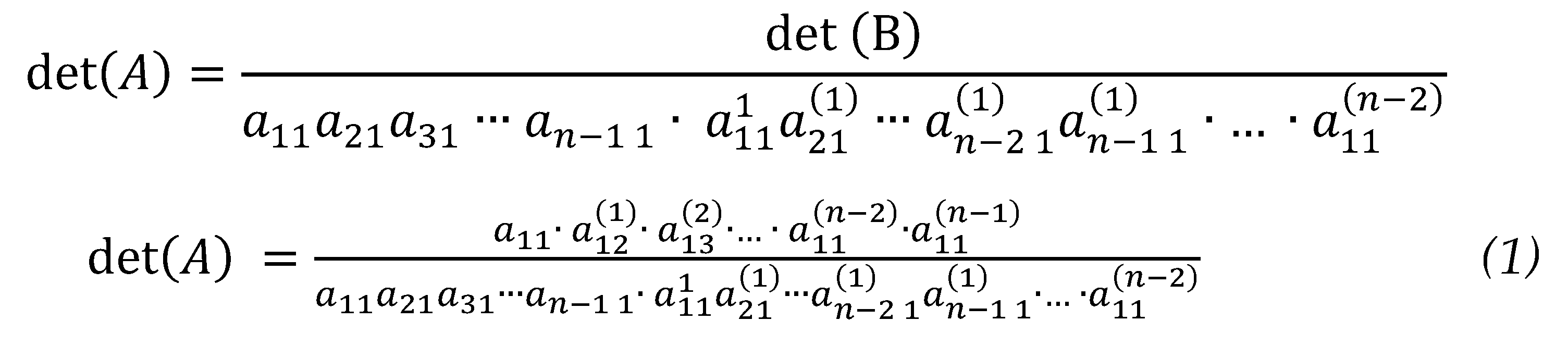
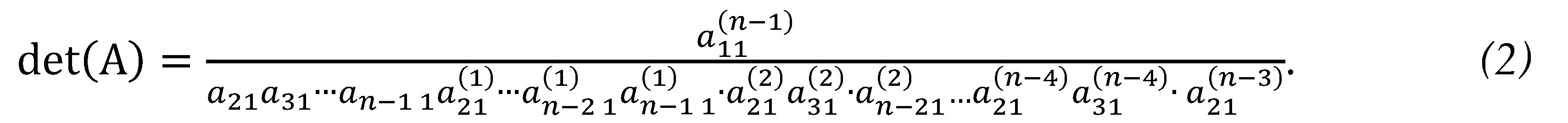

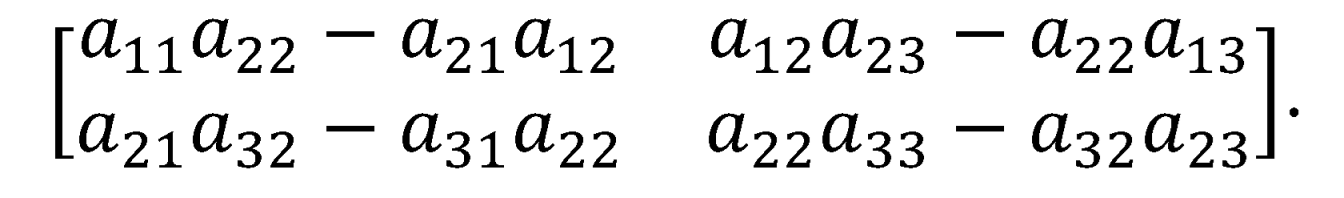
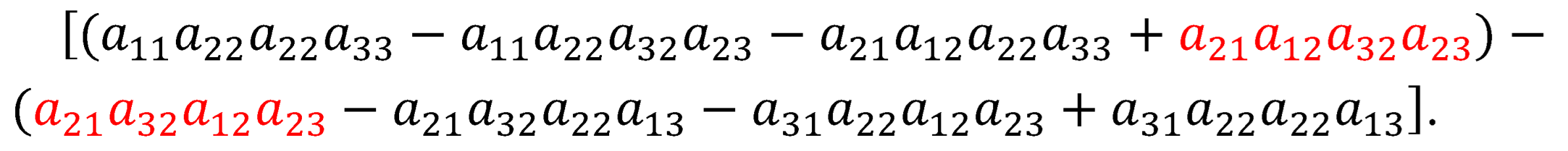

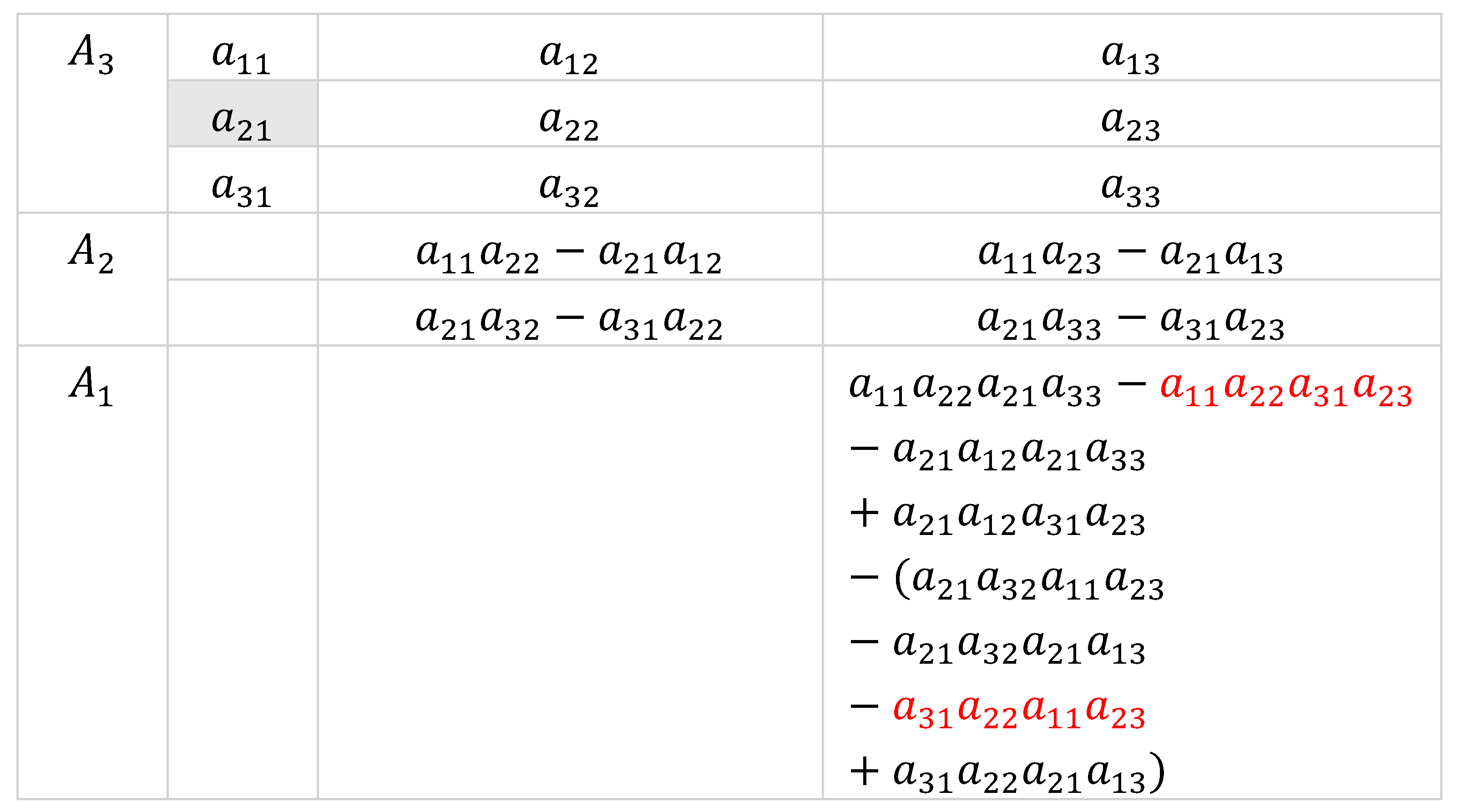
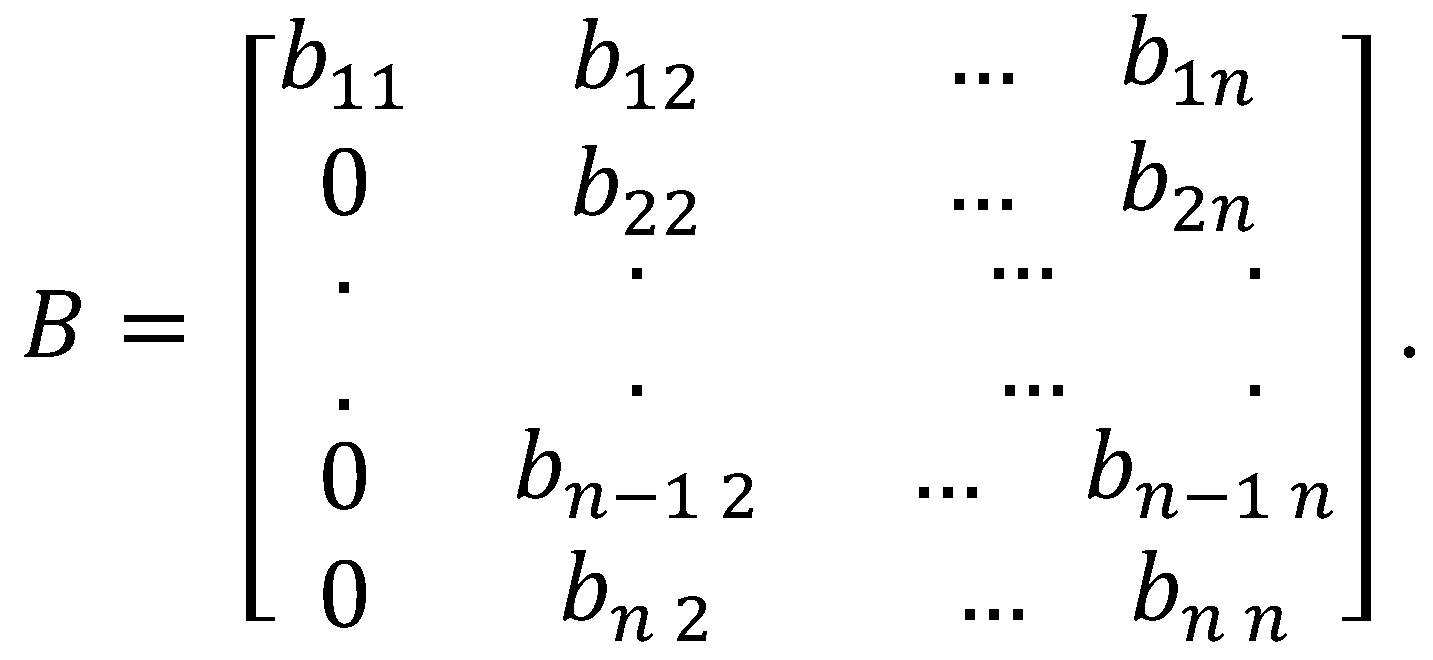
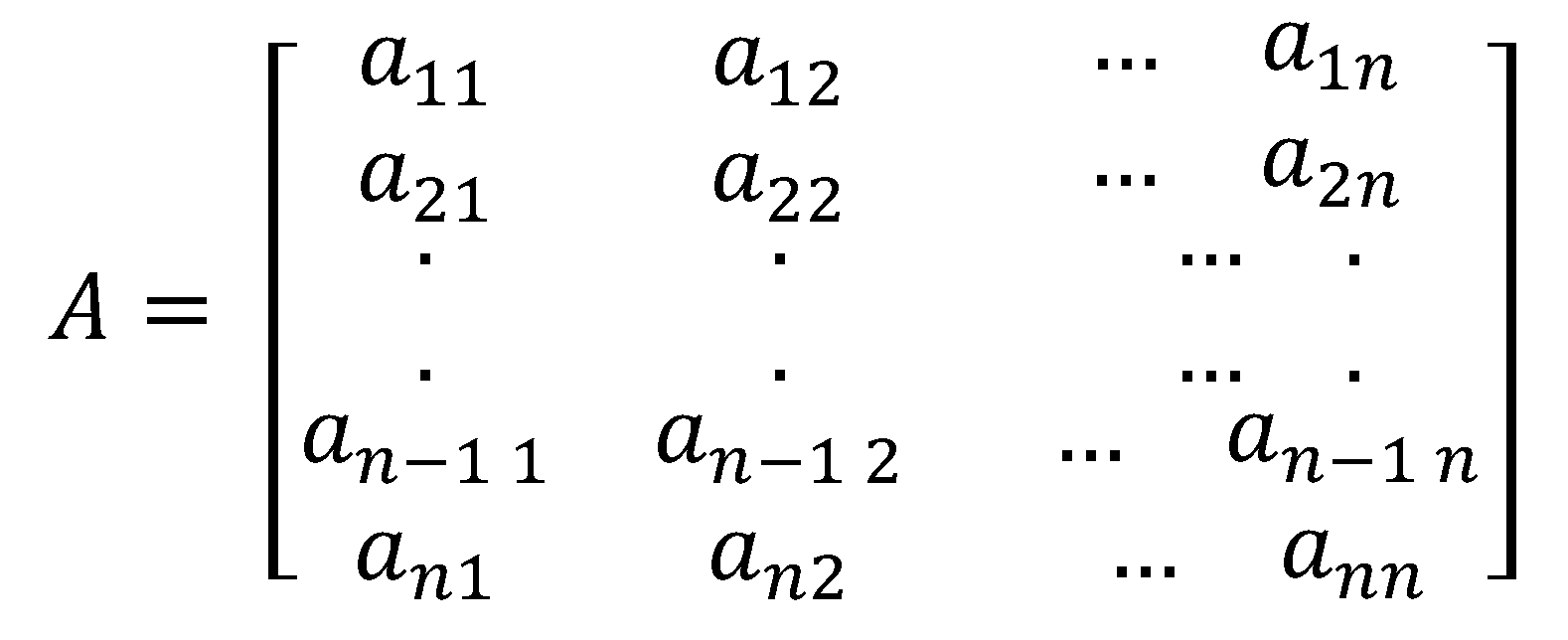
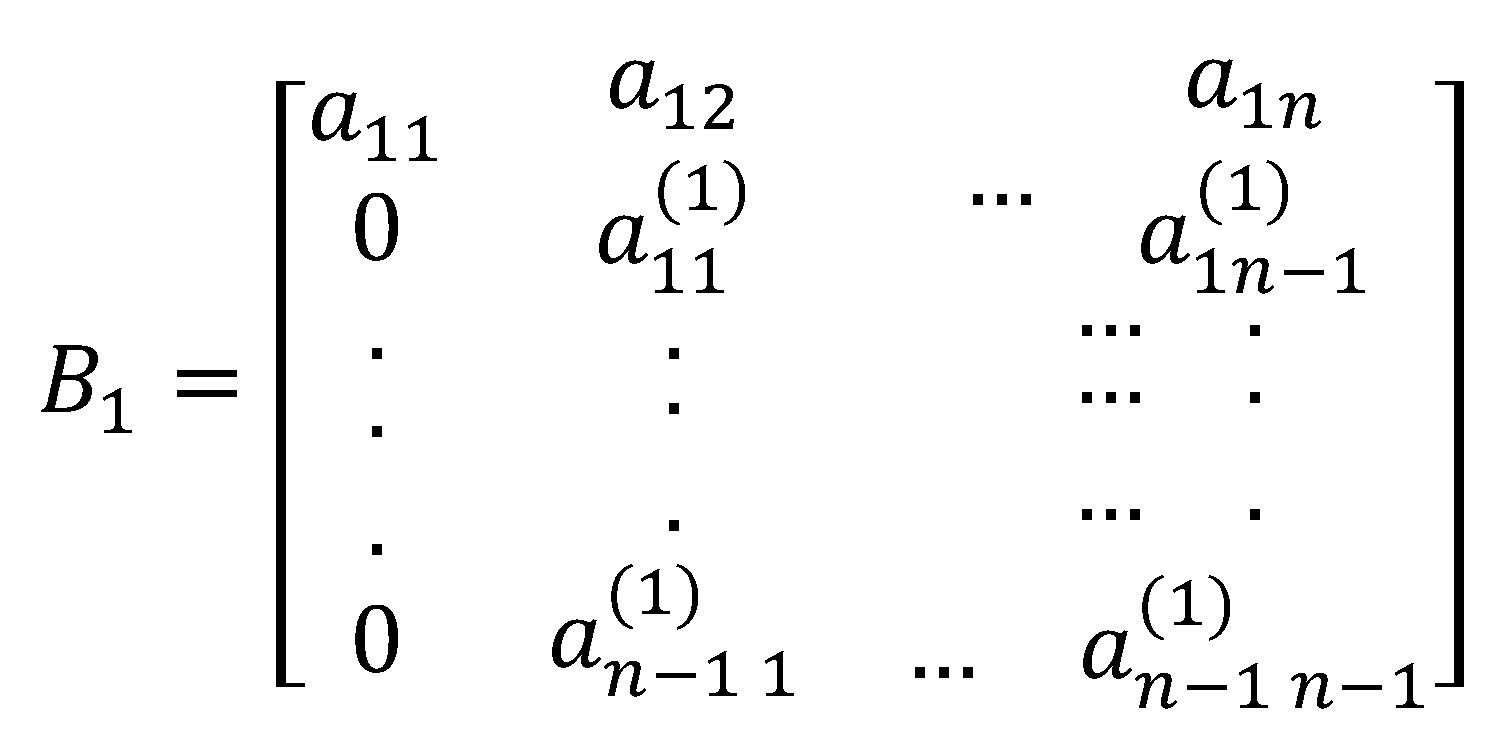
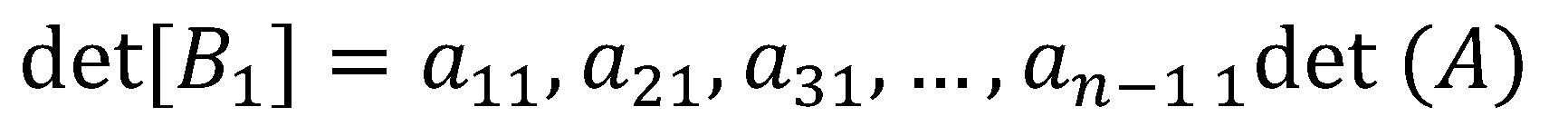
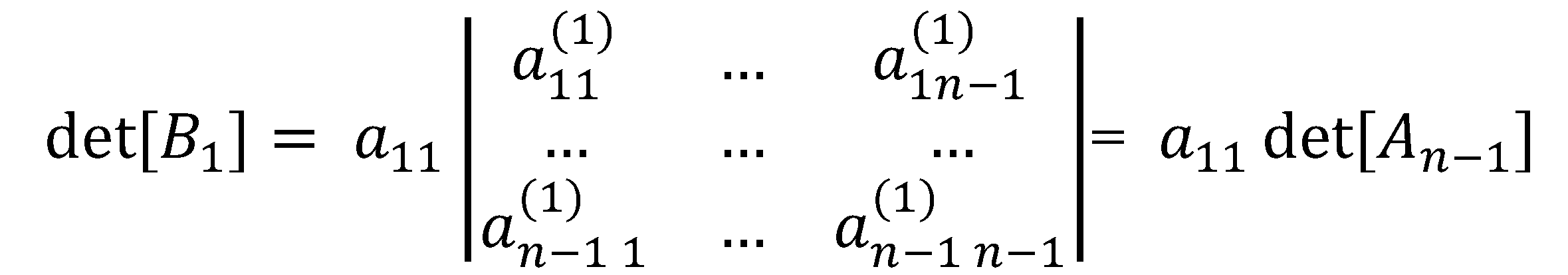
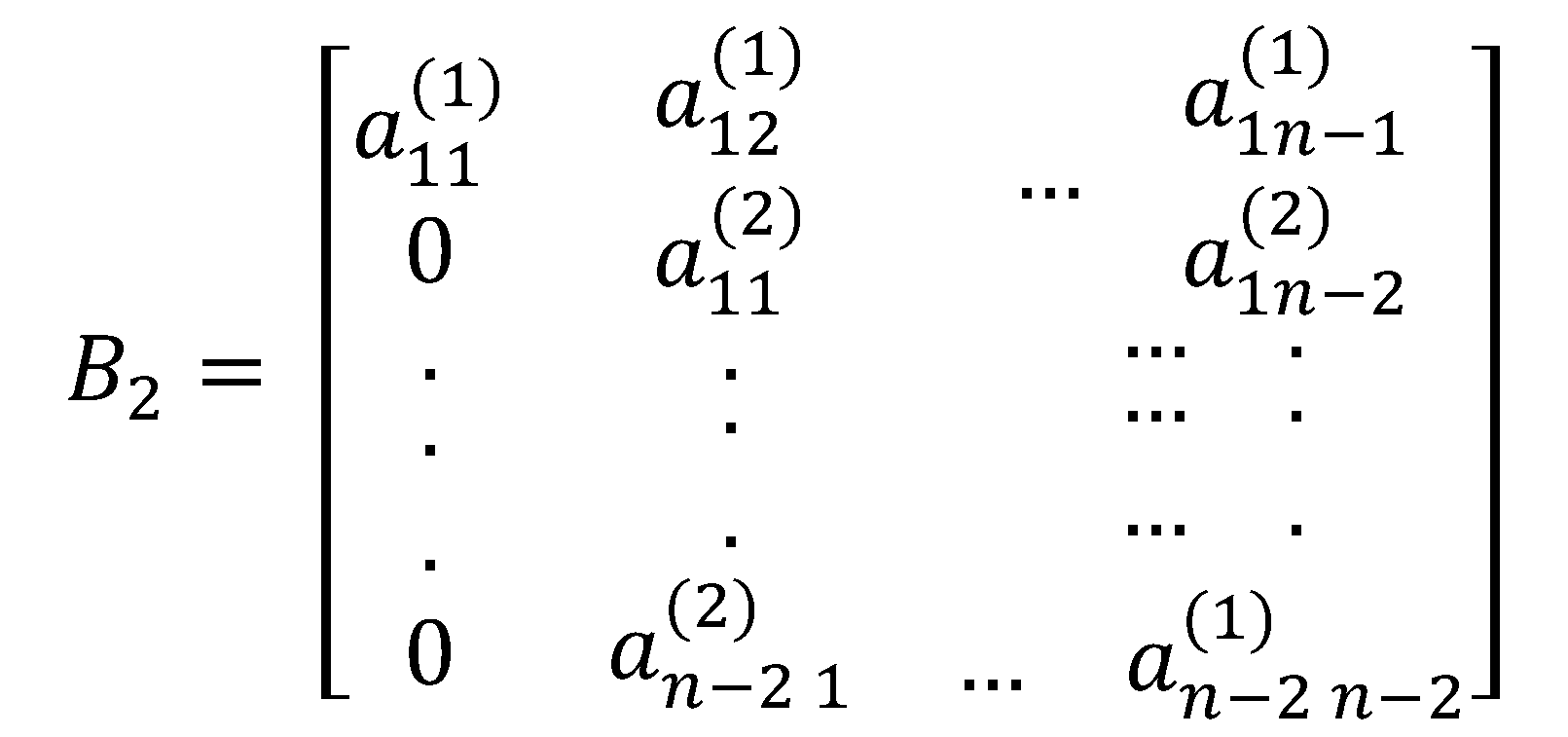 and which
and which