Preprint

Article

A Genetic Algorithms Enhanced Sensor Marks Selection Algorithm For Advanced Photolithography Process

Altmetrics

Downloads

135

Views

Comments

A peer-reviewed article of this preprint also exists.

Aris Magklaras^*,

Alefragkis Panagiotis

Alefragkis Panagiotis

Christos Gogos

,Christos Valouxis,

Alexios Birbas

This version is not peer-reviewed

Submitted:

23 June 2023

Posted:

26 June 2023

You are already at the latest version

Alerts

Abstract

In photolithography process, nanometer level precise, wavefront aberration models enable the machine to be able to meet the overlay (OVL) drift and critical dimension (CD) specifications. Software control algorithms take as input these models and correct any expected wavefront imperfections before reaching the wafer. In such way a near optimal image is exposed on the wafer surface. Optimizing the parameters of these models though, involves several time costly sensor measurements which reduce the throughput performance, in terms of exposed wafers per hour, of the machine. In that case, photolithography machines come across the trade-off between throughput and quality. Therefore one of the most common Optimal Experimental Design (OED) problems in photolithography machines (and not only) is how to choose the minimum amount of sensor measurements that will provide the maximum amount of information. Additionally, each sensor measurement corresponds to a point on the wafer surface and therefore we must measure uniformly around the wafer surface as well. In order to solve this problem, we propose a Sensor Marks Selection Algorithm which exploits Genetic Algorithms. The proposed solution first selects a pool of points that qualify as candidates to be selected in order to meet the uniformity constraint. Then, the point that provides the maximum amount of information, quantified by the Fisher based criteria of G, D and A-Optimality, is selected and added to the measurement scheme. This process though is considered "greedy", and for this reason Genetic Algorithms (GA) are exploited to further improve the solution. By repeating in parallel the "greedy" part several times we get an initial population that will be the input to our GA. This meta-heuristic approach outperforms the "greedy" approach significantly. The proposed solution is applied in a real life semiconductors industry use case and achieves interesting industry and academical results as well.

Keywords:

Subject: Engineering - Industrial and Manufacturing Engineering

1. Introduction

Moore’s law states that “every 24 months, the number of transistors that can be placed on a chip doubles” [1]. Of course, keeping up with Moore’s law is a very difficult task as it requires continues improvement in an already very advanced field. Despite this, recent advances in integrated circuits (ICs) manufacturing process and in photolithography specifically, enable the community to be able to meet this very strict requirements. Photolithography [2] is very important part of the whole process because it is responsible for transferring a desired pattern to a photosensitive material on the wafer surface (photo curable material; most typically, commercial photo resist [3]) by exposing it to ultraviolet (UV) or Extreme-UV (EUV) light. Successful photolithography will yield wafers with high overlay (OVL) and small critical dimension (CD). OVL and CD are the key performance indicators (KPI) for photolithography stage. Overlay is a measure of the correct alignment between the various layers of the wafer and CD is known as the minimum feature size which refers to the width of the lines, spaces, contact holes or dots of critical circuit patterns. The better the OVL and the smaller the CD, the smaller the exposed pattern and of course the smaller the exposed ICs on the wafer. This is why photolithography is the most important stage of ICs fabrication process. The stage that drives Moore’s law.

EUV photolithography, a technology entirely unique to ASML, is the State of the Art (SoA) in photolithography and the stepping stone to keep up with Moore’s Law. EUV light’s wavelength at 13.5 nanometers, 14 times shorter than DUV light, is key enabler for small CD and better OVL. Hence, from 2010 and onwards the EUV platforms (NXE) of ASML lead the race of keeping up with Moore’s law. In Figure 1 we see a visualization of the Moore’s law in terms of chip shrinkage together the photolithography machines that achieve these results as well.

In Figure 2 the full light path from EUV source to the silicon wafer is presented. The light is generated in the source, sent into the illuminator which controls the light beam, reflects off the mask with the chip pattern, before being focused in the projection optics and exposing the wafer. The projection optics box of the EUV machine, which is actually consisting of mirrors, is responsible for directing EUV light on the wafer surface. Ideally, the wavefront of the light reaches the wafer surfaces without any optical imperfections. This would expose a perfect wafer but of course this is almost never the case.

Platforms for new products such the one of ASML in Figure 3 are built on these breakthroughs. Platforms that are able to produce wafers with high performance (throughput), high precision at nanometer level (overlay) and optimized imaging capabilities (focus and critical dimension uniformity) [4].

Photolithography machines are some of the most complex, hardware and software wise, machines that exist in the industry. With more than fifty million lines of code-base and thousands of hardware modules, being able to orchestrate and control the machine such that it meets the extremely strict OVL and CD requirements is a very difficult task. Hardware itself can not achieve such perfection. For this reason a vital part of the machine is software control algorithms which deal with any kind of hardware imperfections. Software will enable the machine to meet the OVL and CD KPIs which will verify the quality of the machine. In principle the main idea behind this is that the machine is able to model accurately, at nanometer level, the expected wavefront anomalies. Then, by knowing what to expect, software will optimize the corresponding knobs on the machine, such as mirror positions for example, such that it compensates for the expected aberrations. In that case, the expected fingerprint will be corrected before reaching the wafer surface, which means that the desired pattern will be exposed with minimum imperfections. In this case we understand that being able to build accurate models is one of the most crucial and demanding tasks for the photolithography process. These models are the key enablers for a successful exposure.

Building such models though is also very time costly. During the model creation phase several sensor measurements are needed. These measurements will serve as a reference and the model parameters will be optimized based on them. Of course the more the measurements the bigger the accuracy but then we are against the throughput vs quality trade off. As mentioned above, throughput, in terms of wafers per hour (wph) is very important as well and chip manufacturers can not afford any throughput loss on photolithography process. Usually the number of points to measure is predetermined from the time budget of the process. Then we are called to find which points to measure such that the measurements in those points will provide the maximum amount of information needed to optimize the models. Hence, we are called to solve this specific optimization problem. How to select the best subset of points to measure out of a set of available locations on the wafer surface, in order to get the maximum information regarding the fingerprint estimation model without introducing significant throughput loss. This is a typical Optimal Experimental Design (OED) problem.

The Optimal Experimental Design (OED) problem has been in the center of interest of both academia and industry for a very long time already. Since the first scientific paper by Smith in 1918 [6] until today after numerous papers and research in this field, the advances in this area are quite remarkable. In our paper, as mentioned above, we examine a certain application of OED in the photolithography process. OED problems can be linear or non-linear based on the model nature. Non-linear models need to be solved with heuristic approaches. However, heuristics are not optimal especially for complex systems with high dimensionality, nonlinear responses and dynamics, multiphysics, and uncertain and noisy environments. OED for linear models [7,8] on the other hand are using criteria based on the information matrix derived by the model. These criteria can be calculated analytically and are different flavours of the dispersion of that matrix. The so called Fisher based criteria such as G, D and A-Optimality. The disadvantage of this approach however is that most of these algorithms are greedy and most of the times not optimal. In this paper, we are proposing a hybrid method incorporating both a deterministic part and a meta-heuristic Genetic Algorithms (GA) based part. On the one hand the stochasticity of GA can compensate for the greedy approach of the first step and on the other hand the GA can identify hidden patterns in the combination of good solutions created previously and exploit this information for creating the final solution. This innovative solution in combination with the real life use case from the industry serves as a promising alternative for similar problems.

An outline of the rest of the paper is as follows. Section 2 is regarding Problem Formulation discussing on the one hand the theory the basic concepts of OED problem and on the other hand presenting the specific photolithography OED use case. In Section 3 the proposed solution is presented and Section 4 exhibits the results of our solution. Finally Section 5 is regarding the conclusions and the future work.

2. Problem Formulation

2.1. Optimal Experimental Design (OED)

An experiment is a process carried out under carefully controlled conditions in order to establish some kind of knowledge over a specific topic. This knowledge is expressed by a model, which is the key element of an experiment. The model is relating the experimental responses, or the experimental observations, to the corresponding experimental factors. The purpose of the experiment itself is to define an accurate model. Experiments are designed for optimizing the parameters of a model or for estimating the responses of an already fitted model. In this paper we are interested in optimizing the parameters of an OVL model for example. An optimally designed experiment in this case will provide the maximum information in the most efficient way in order to gain knowledge about the model.

Even under the most protected laboratory environment though, it is often not possible to avoid random experimental errors. Such errors can either be small and harmless or can also be catastrophic for the experiments under certain conditions of noisy experiments, or highly dimensional models for example. For this reason, statistical methods are essential for the optimal design and analysis of the experiment, such that it will provide the maximum amount of information independently of those error factors. Optimal Experimental Design (OED) is a field between mathematics and computer science, which deals with this specific topic of designing optimal experiments exploiting various statistical methods.

Figure 4. OED and model relationship.

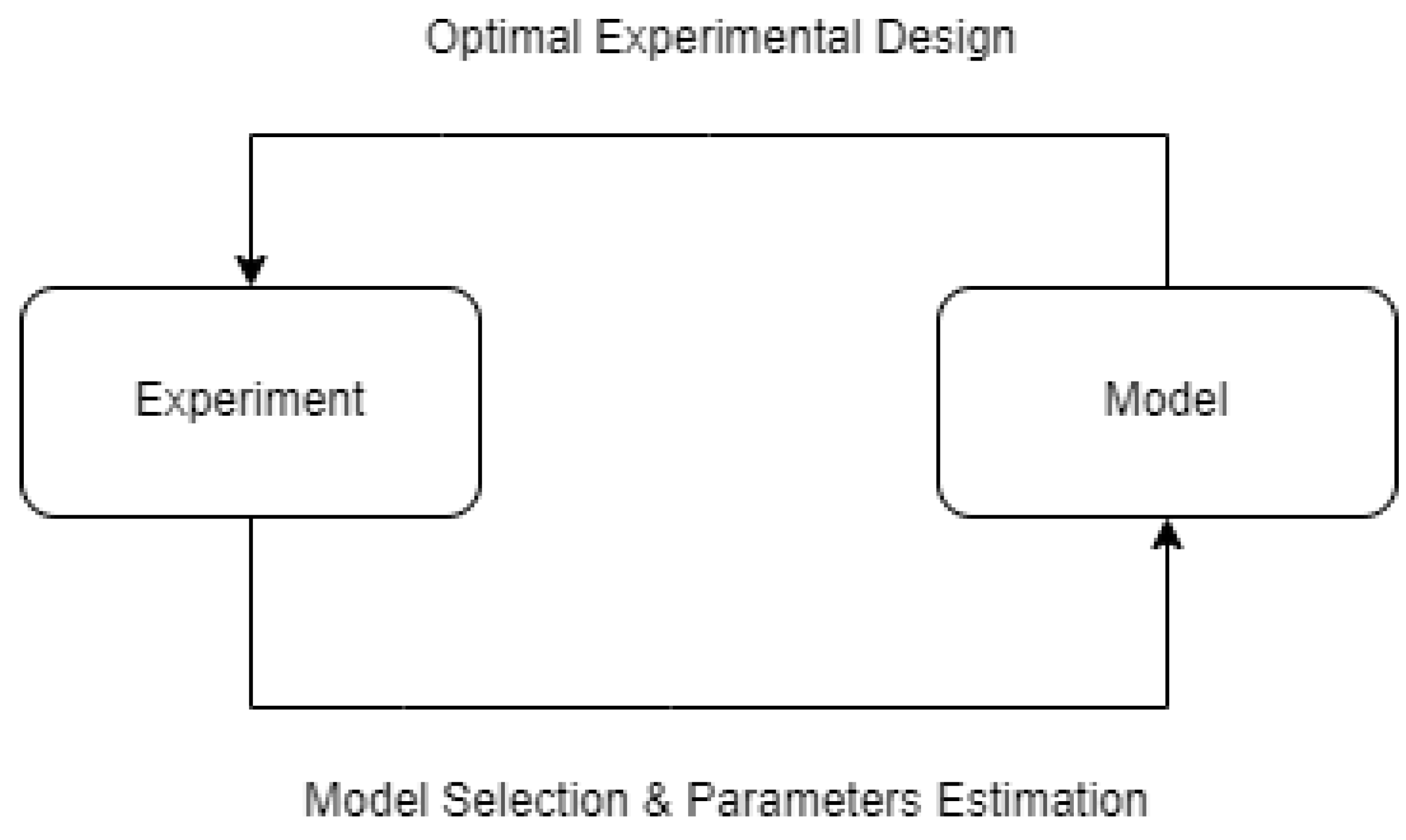
In OED problems the key input is the model. OED designs depend either on the model to be fitted to the data, or for linear models on the values of the parameters of the models. As mentioned above, the model is describing the relation between the observed response Y and the experimental factors X. Depending on the use case, models can be linear or non linear. In this paper, linear polynomial models are examined. More specifically, let us consider the linear model $Y = X b + ϵ$ with:

Y being an N-component column of experimental observations;
X being an $N \times p$ matrix of known elements known as information matrix
b being a vector of size p of unknown parameters
And $ϵ$ being an N component vector of residuals with $E (ϵ) = 0$ and $D (e) = {(σ)}^{2} I$ , where E and D stand for expectation operator and dispersion matrix respectively.

As mentioned above, the goal of the whole experiment is to build a model that is as close as possible to the reality. From the above model the information matrix X is the only known input. The information matrix is in reality the basis functions of the model polynomial. During the process of model selection, the corresponding basis functions are obtained and the information matrix is formed. This process is very interesting but it is out of the scope of this paper. In our work we consider the information matrix X as known. In that case, the unknown parts of the model equation are the b vector of unknown parameter and the noise

ϵ

. Hence, in order to build our model our real task is to estimate accurately the parameters vector b.

For parameter estimation there are different approaches depending on the model that is used. The most common and still very effective one for linear models is the Least Squares Method (LST).

In Figure 5 the whole process of parameter estimation is presented. On the top box, the real measurements take place. This is the experiment that takes place. The output of the measurements plus the added noise is the real value Y. The bottom box contains the modeling part. As we see, the information matrix X is already known and doesn’t change throughout the process. On the other hand the parameters vector b is the one that gets updated. On the right part of the schema the Least Squares Optimization (LST) takes place. Input to LST algorithm is the real measurement Y and the model output

\hat{Y}

. The output of the LST algorithm will be the updates of the parameters vector b such that the Least Squares of the differences between Y and

\hat{Y}

{∥Y - X \cdot b∥}^{2}

is minimized. This will mean that the parameters estimates are succesfull and our model output

\hat{Y}

is as close to real measurement Y as possible, hence our model is accurate.

All of this process though is highly dependent on the quality of the real measurements performed during the experiment. If the measurements are not informative enough, then the output of LST algorithm is also not trustworthy. And this results in bad model despite the rest of the process working fine. Additionally, in most of the use cases there is only a limited budget of "experiments" that can be performed. Here, by experiment we mean one measurement. In this cases, the problem of selecting the most informative subset of available measurements is crucial for the success or not of the process. Hence, the optimal design of the experiment is vital for ensuring the quality of the whole process of model optimization. The OED problem is defined as selecting an n-point design of a set of N candidate points to optimize for a certain design criterion. In most of the OED problems, as it is already mentioned above we assume to have:

A given model
An optimality criterion
A fixed sample size of n-points out of a candidate set of N-points

And the problem is how to take n independent observations of the given design space (candidate points). The solution of this problem is the Optimal Experiment Design (OED) which maximizes the confidence on the selected model parameters for providing maximum information[9]. Optimal Designs can be a) approximate or b) exact optimal designs. Approximate designs are obviously easier to extract since they are probability measures defined on a compact and known design space (set of N candidate points) [10]. This optimization problem finds the optimal probability measure in terms of a certain design criterion. The design criterion should reflect the amount of information gained if a certain experimental design is chosen.

2.2. Optimality Criteria

The final goal of an OED problem is to build an accurate model with optimized model parameters. As mentioned above though, the only input available to us is the information matrix X of size

N \times p

. By applying linear algebra computations, we can obtain

X^{'} X b

X^{'} Y

. The goal of the OED problem is to construct experimental designs that consist of choosing n rows of X out of set of candidate rows N in such a way that the information matrix

X^{'} X

is optimal in sense of the chosen optimality criterion [11].

Normalized Model Uncertainty (NMU) is a measure of the uncertainty in the model prediction due to the uncertainty in the model parameters. It is defined as the square root of the trace of the product of the variance-covariance matrix of the estimated parameters and the Hessian matrix of the model prediction function. The mathematical formula for Normalized Model Uncertainty (NMU) is:

\sqrt{trace [{(X^{T} X)}^{- 1} X^{T} Σ X {(X^{T} X)}^{- 1} H],}

where

X

is the design matrix, where each row represents a different design point and each column corresponds to a different predictor variable.

Σ

is the variance-covariance matrix of the estimated parameters of the model.

H

is the Hessian matrix of the model prediction function, evaluated at the design points. The trace operator returns the sum of the diagonal elements of a matrix. In this case, it returns the sum of the diagonal elements of the product of two matrices: the variance-covariance matrix and the Hessian matrix. The square root is taken of this sum to obtain the NMU. Normalized Model Uncertainty (NMU) is a measure of the model’s lack of fit, and it can be used as a criterion for experimental design optimization. However, NMU is not a direct criterion for experimental design, and it needs to be combined with an design criterion that represents the objective of the experiment.

The design criteria are used to analyze, evaluate and compare different design alternatives. These criteria are different flavours of the dispersion of the information matrix, which is the basis functions of the model. Assuming that

X^{'} X

is non-singular, the following optimality criteria (among others) can be involved for minimizing the functions of

(X^{'} X)

2.2.1. D-Optimality

D-optimality is a criterion for optimal experimental design that aims to minimize the determinant of the variance-covariance matrix of the estimated parameters. It focuses on good model parameter estimation [12] and further more makes both the variance and the covariance among the model parameter estimates very small.

This criterion ensures that the estimated parameters are as precise as possible and that the design provides the most information about the parameters by minimizing the determinant of the

| X^{T} {\cdot X |}^{- 1}

(D from determinant). In this formula,

X^{T}

is the transpose of the design matrix, and

X^{T} \cdot X

is the product of the transpose and the original design matrix. The inverse of this product,

| X^{T} {\cdot X |}^{- 1}

, represents the inverse of the variance-covariance matrix of the estimated parameters. The variance-covariance matrix of the estimated parameters represents the uncertainties and correlations between the parameters. The determinant of this matrix represents the overall magnitude of the uncertainty of the estimated parameters. Thus, by minimizing the determinant, the D-optimality criterion seeks to minimize the overall uncertainty of the estimated parameters.

D-optimality is commonly used in linear regression and other types of linear models, but it can also be used for nonlinear models and other types of statistical analyses.

2.2.2. A-Optimality

A-optimality seeks to minimize the trace of the inverse of the variance-covariance matrix of the estimated parameters

| X^{T} {\cdot X |}^{- 1}

. The A-optimality criterion is based on the principle of minimizing the average variance of the estimated parameters. Specifically, it seeks to minimize the trace of the inverse of the information matrix, which is the expected value of the variance-covariance matrix of the parameter estimates.A design that is A-optimal will result in parameter estimates that are expected to have the smallest average variance across all possible values of the true parameter values. A-optimal designs are particularly useful when all parameters are of equal interest and importance, and when the goal is to estimate them with equal precision.

2.2.3. G-Optimality

Another criterion that is used in experimental design to select an optimal design for a given model is G-Optimality. It is based on the principle of minimizing the maximum eigenvalue of the variance-covariance matrix of the estimated parameters. In other words, G-optimality seeks to minimize the maximum variance of the estimated parameters across all possible values of the true parameter values. A design that is G-optimal is one that minimizes the largest variance of the estimated parameters. Mathematically, G-optimality can be formulated as:

G (D) = min λ_{max} [{(X {(D)}^{T} X (D))}^{- 1}]

, where D is the set of design points,

X (D)

is the design matrix that contains the predictor variables at the design points and

λ_{max}

is the largest eigenvalue of the matrix. In practice, G-optimality is useful when the goal is to estimate the parameters with the most accuracy, regardless of their relative importance or the experimental resources available. However, it may not be the most appropriate criterion if some parameters are of greater interest than others, or if the experimental resources are limited and a smaller number of design points is required. In such cases, other criteria such as A-optimality or D-optimality may be more appropriate.

2.3. Fingerprint Estimation in Photolithography Process Use Case

As mentioned before the most important KPIs for a Photolithography machine are Overlay (OVL) and Critical Dimension (CD). OVL is a critical parameter in photolithography as it determines the alignment accuracy between the different layers being printed on the wafer. Overlay errors can result in misregistration between the different layers, which can cause defects in the final device and reduce the yield. Critical dimension (CD) is another important parameter in photolithography that refers to the size of the features being printed on the wafer. CD control is important because variations in CD can have a significant impact on the performance and yield of the final device.

In photolithography, fingerprint estimation (FE) refers to the process of characterizing the spatial variations in the critical dimensions (CD) and overlay (OVL) of the features being printed. These variations can arise from a variety of sources, such as imperfections in the mask or in the lithography process itself. Fingerprint estimation is typically performed using specialized metrology tools that can measure the CD and OVL of the features at various locations on the wafer. The resulting data is then analyzed to extract information about the spatial variations in the CD and OVL, which can be used to create a "fingerprint" of the lithography process. A vital part of the FE process involves the modelling of the OVL and CD. OVL and CD modelling involves developing mathematical and statistical models to predict the impact of different process parameters on OVL and CD. These models can be used to optimize the lithography process by adjusting the process parameters in real time to achieve the desired OVL and CD specifications. Overall, fingerprint estimation is an important tool in photolithography for ensuring high yield and consistent performance of the lithography process.

A model in general, and of course also OVL and CD models, is a mathematical or statistical representation of a system or process, a polynomial. A model consists of two key components: basis functions and parameters. The choice of basis functions depends on the nature of the problem and the characteristics of the data being modeled. Parameters of the model on the other hand, are the values that are estimated from the data and are used to define the model. The parameters determine the specific values of the basis functions that best fit the data.

In our specific use case, we need to provide the model for OVL. A linear model

m (x, y) = Φ \cdot p

is used for our purposes.

Φ

is the information matrix which consists of the basis function

ϕ (x, y)

and p are the parameters of our model. In the expanded version of the model below, each row corresponds to a certain point on the wafer surface. The first row for example describes the OVL in point

(1, 1)

. Hence, as we can see, the wafer consists of N available points on which we can measure. Furthermore, the OVL polynomial has P coefficients or parameters. As described above, the information matrix

Φ

is already known to us and in that case the goal of FE is to estimate the parameters p of our model.

[\begin{matrix} m_{1} (x_{1}, y_{1}) \\ m_{2} (x_{2}, y_{2}) \\ ⋮ \\ m_{N} (x_{N}, y_{N}) \end{matrix}] = [\begin{matrix} ϕ_{1} (x_{1}, y_{1}) & ϕ_{2} (x_{1}, y_{2}) & \dots & ϕ_{q} (x_{1}, y_{1}) \\ ϕ_{1} (x_{2}, y_{1}) & ϕ_{2} (x_{2}, y_{2}) & \dots & ϕ_{q} (x_{2}, y_{2}) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ ϕ_{1} (x_{N}, y_{1}) & ϕ_{2} (x_{N}, y_{2}) & \dots & ϕ_{q} (x_{N}, y_{N}) \end{matrix}] [\begin{matrix} p_{1} \\ p_{2} \\ ⋮ \\ p_{q} \end{matrix}]

In Figure 6 the process of FE is presented. Since the basis functions of the model

ϕ (x, y)

are already predefined the goal of the FE process is to get the best estimation of the model parameters p which are obtained by minimizing the

L 2

norm of the "real" measurements

m (x, y)

(on the top part of Figure 6) and the "modeled" results

\hat{m} (x, y)

, the Least Squares Optimization (LST). In this case, the inputs to the Least Squares algorithm are

m (x, y)

and

\hat{m} (x, y)

and the output is the update to the coefficients.

However, one of the key parts of the process is getting the real measurements

m (x, y)

. The quality of these measurements can directly affect the quality of the FE.

Unfortunately, these sensor measurements are time costly and are significantly affecting the throughput of the photolithography machine. Hence we do not have the budget of measuring on all available N points on the wafer. In most of the cases the maximum number of measurements that can be done is a very small subset of the available points. In this case we need to design our experimental space,i.e. the sensor measurements, such that even the small subset of available measurements can provide the maximum amount of information. Optimal Experimental Design (OED) can be used for optimizing the design of experiments when measuring the wafer surface by selecting an optimal subset n of all the available sampling points N.

So, the specific problem that we need to solve is, how to select n out of N points for measuring such that the measurements will provide us the maximum amount of information for fine tuning the parameters of our model. In our case

N = 933

and

n = 221

. Additionally, due to the nature of the problem, we have one constraint. We have to measure as uniformly as possible around the wafer surface and also not sample points that are too close to each other. In the following section of Materials and Methods the proposed solution to the above described problem is presented.

3. Materials and Methods

The only information that is available to us in this point is the matrix

Φ

, the information matrix. The goal of our algorithm is to provide an NMU design of our OED problem. As mentioned above, NMU can be calculated at any point

x, y

on the wafer:

\sqrt{trace [{(Φ^{T} Φ X)}^{- 1} Φ^{T} Σ Φ {(Φ^{T} Φ)}^{- 1} H]}

NMU Optimality though is not our only concern. We are also interested in sampling uniformly from the wafer. Hence, our optimality criteria are 1)NMU Optimal Design and 2) Uniform Sampling.

In this section, we present a method for solving the optimal experimental design (OED) problem of selecting

n = 221

out of

N = 933

available points on the wafer, which will provide the maximum amount of information to estimate the parameters of the OVL model. The high level diagram of the Genetic Algorithms Enhanced Sensor Marks Selection (GAESMS) is presented in Figure 7.

In the first two blocks we get the input to our OED problem

N = 933

and the size of the measurement scheme, or in other words the budget of our OED problem,

n = 221

. In the following block we need to determine the size of the initial population of the GA. In our case we set

size of population = 30

. In the following blocks we enter the core functionality of the GAESMS algorithm which will be described in details in the coming sub sections.

3.1. Sensor Marks Selection based on Poison-Disc Sampling and D-Optimality

In sensor marks selection problems, the goal is to select a subset of points from a larger set of candidate points such that the selected points provide the most informative measurements for a given application. Two important criteria for selecting these points are spatial randomness and sample uniformity. Spatial randomness refers to the evenness of the distribution of the selected points across the area of interest. A spatially random distribution of points helps ensure that the selected points are representative of the entire area, rather than being biased towards certain regions. This is important because biased samples can lead to inaccurate or incomplete measurements, which can ultimately impact the quality and reliability of the application. Sample uniformity, on the other hand, refers to the evenness of the distance between selected points. A uniform distribution of points helps ensure that each point contributes equally to the overall measurement and that the measurements are not biased towards certain areas. This is particularly important in applications where the measured quantity varies significantly across the area of interest, as a non-uniform sample may miss important features or over-represent certain regions.

In summary, both spatial randomness and sample uniformity are critical criteria for selecting sensor marks in order to ensure accurate and representative measurements. By considering these criteria, we can select a subset of points that provides the most informative measurements and improves the overall performance of the application.

In our problem as well, as already mentioned above, instead of only an NMU based criterion we also need to provide a uniform design. For this reason, we incorporate Poison-Disc sampling as part of the Sensor Marks Selection algorithm.

Poisson Disc Sampling with nearest neighbors is a method used for generating spatially random point sets on a two-dimensional surface [13,14]. This technique is particularly useful in sensor mark selection problems, as in our case, where it is essential to ensure both spatial randomness and sample uniformity. The goal is to generate a set of points that cover the area of interest while avoiding overlaps and producing a uniform distribution.

To ensure spatial randomness, the algorithm disqualifies the nearest neighbors of a point as candidate points. Specifically, for each new point, the algorithm checks the nearest neighbors of all existing points and removes them from the list of potential candidate points. This prevents points from being too close to each other and ensures a spatially random distribution. The algorithm continues this process, iteratively selecting new points until the entire surface is covered with a set of non-overlapping discs.

By adjusting the parameters of the algorithm, such as the number of nearest neighbors to be excluded, the user can control the spatial distribution and sample uniformity of the generated point set.

In summary, Poison Disc Sampling with nearest neighbors is a powerful algorithm that ensures both spatial randomness and sample uniformity in sensor mark selection problems. By generating a spatially random and uniform point set, this technique enables accurate and efficient sampling for a wide range of applications.

In Algorithm 1 the process of Sensor Marks Selection based on the Poison-Disc sampling and D-Optimality is presented. In the first step we get the coordinates

(x, y)

of the available points N. Then, we initialize the number of nearest neighbors to 32 and calculate the Euclidean distances between all points and their nearest neighbors. Next, we initialize an empty active points list and an empty inactive points list. We select a random point and add it to the active points list.

Algorithm 1 Algorithm: Sensor Marks Selection based on Poison-Disc Sampling and D-Optimality

1:: Get coordinates (x,y) of all candidate points N on the wafer surface
2:: Initialize the number of nearest neighbors - $N e a r e s t N e i g h b o o r s = 32$
3:: Calculate the Euclidean distances between all points and their nearest neighbors
4:: Initialize an empty $a c t i v e p o i n t s l i s t = []$
5:: Initialize an empty $i n a c t i v e p o i n t s l i s t = []$
6:: Select a random point and add it to the active points list
7:: while size of active points list < 221 do
8:: Initialize a list of $c a n d i d a t e p o i n t s = i n a c t i v e p o i n t s$ list
9:: Initialize an empty list of $d i s q u a l i f i e d p o i n t s = []$
10:: For each active point, add its $N e a r e s t N e i g h b o o r s$ to the $d i s q u a l i f i e d p o i n t s$ list
11:: Remove any disqualified points from the $c a n d i d a t e p o i n t s$ list
12:: if size of $c a n d i d a t e p o i n t s$ list $= = 0$ then
13:: $N e a r e s t N e i g h b o o r s = N e a r e s t N e i g h b o o r s - 4$
14:: Go to Step 10
15:: end if
16:: Calculate D-Optimality of the scheme for every point on the $c a n d i d a t e p o i n t s$ list
17:: Add to $a c t i v e p o i n t s$ list the point that contributes most to the D-Optimality of the scheme
18:: end while

In the main loop of the algorithm, we repeatedly add points to the active points list until we have selected 221 points. In each iteration of the loop, we first initialize a list of candidate points and a list of disqualified points. We add the nearest neighbors of all active points to the disqualified points list and remove any disqualified points from the candidate points list. If the candidate points list is empty, we decrease the number of nearest neighbors by 4 and repeat the loop.

Next, we calculate the D-Optimality of the scheme for every point on the candidate points list and add the point that contributes the most to the D-Optimality of the scheme to the active points list. As mentioned before NMU can not be used on its own since on the one hand it is not a direct criterion for experimental design and one the other hand it is computationally expensive. Finally, we repeat this process until we have selected 221 points.

In Figure 8 a nice visualization of the progress of the above algorithm is presented. In green, we see the points that qualifying as candidates at a specific iteration of the process while the blue ones are the points that are already part of the scheme. In this case, the k nearest neighbors of the already selected points are disqualified, with k depending on the iteration of the algorithm since we start with

k = 32

and this is reduced further. Hence the disqualified points are the ones belonging to the area that the red circles define. In a very careful look we notice that the red circles in the center are larger than the circles on the edge of the wafer. This is because the points in the center of the wafer were selected at an earlier stage of the points on the edge. Hence, at that step of the process the exclusion zone defined by the k disqualified neighbors is bigger (for enforcing uniforming) but as the process continues a large k yields no available points. In that case k decreases as described above, and the circle of exclusion zone becomes smaller.

In the end of the above process we get a scheme containing 221 selected points, uniformly sampled and with spatial randomness ensured, end at the same time the most important a near D-Optimal design.

3.2. Improving Solution with Genetic Algorithms (GA)

So far in the previous part of our algorithm we created an initial population of, in this case 30 solutions. The strategy though that we followed can be considered "greedy"since we add to the schemes the point that contributes more to the D-Optimality. A greedy algorithm makes locally optimal choices at each step with the hope of finding a global optimum, but it may not always lead to the best solution overall. It is important to strike a balance between the optimality criterion and practical considerations when designing an algorithm for a real-world problem. Hence, at this part of the algorithm we propose Genetic Algorithms to balance out the greedy approach. In fact, one of the strengths of GAs is that they can help to overcome local optima that might be encountered with a purely greedy approach.

Recently, real-world complicated problems originating from a variety of disciplines, including economics, engineering, politics, management, and engineering, have been solved using meta heuristic algorithms. These algorithms can be broadly divided into two categories: population-based meta heuristic algorithms and single solution algorithms (Figure 9).

Evolutionary algorithms, including Genetic Algorithms, have undergone significant advancements in recent years, resulting in the creation of efficient and dependable optimization tools. These algorithms have been applied to solve numerous optimization problems, such as the economic dispatch problem [16], optimal control problem [17], scheduling problem [18], energy harvesting problem [19], and others.

In our problem, after ensuring the uniformity of samples, we aim to find an optimal solution in terms of G, D, and A-Optimality, which is a multi-objective optimization problem. Multi-objective optimization seeks to find solutions that produce the best values for one or more objectives, typically having a series of compromise options known as Pareto optimal solutions rather than a single optimal solution. In our case, we simplify the multi-objective problem as a single objective by aggregating multiple objectives into one using a weighted sum. Our use case allows for this simplification since the three different objectives are very similar, representing different metrics of the same goal. Thus, the cost function of our Genetic Algorithm is the compound criterion of G, D, and A-Optimality, similar to the second step of the process.

The Genetic Algorithm draws its inspiration from the natural selection process. It is a population-based search algorithm that applies the survival of the fittest principle. The main components of the Genetic Algorithm are chromosome representation, selection, crossover, mutation, and fitness function computation. The Genetic Algorithm process involves the initialization of an n-chromosome population (Y), which is usually created randomly, but in our proposed strategy, the initial population is created using a deterministic approach, except for the first two random points. This detail plays a significant role in the quality of results and the robustness of the proposed algorithm. Then, the fitness of each chromosome in Y is calculated, and two chromosomes, designated

C 1

and

C 2

, are selected based on their compound criterion fitness value. The single-point crossover operator with crossover probability (

C p

) is applied to

C 1

and

C 2

to produce an offspring, O. The offspring O is then subjected to the uniform mutation operator with mutation probability (

M p

) to create

O^{'}

. The new progeny

O^{'}

is added to the new population, and this process is repeated until the new population is complete. GA dynamically modifies the search process using the probabilities of crossover and mutation to arrive at the best solution. GA can change the encoded genes, and it can evaluate multiple individuals to generate multiple ideal results, giving it higher ability for global search. The core part of the GA is the fitness function. In our solution we propose a compound criterion of G,D and A-Optimality instead of using only one type of optimality. Using a compound criterion that combines multiple types of optimality (such as D-, G-, and A-Optimality) in a GA fitness function can be beneficial for several reasons. Firstly, using a single type of optimality can result in the GA getting trapped in a local optima. Local optima are solutions that appear to be optimal in the immediate vicinity but are not the globally optimal solution. By using a compound criterion that considers multiple types of optimality, the GA can search for a solution that is not only locally optimal but also globally optimal. Secondly, a compound criterion can help balance different types of optimality. For example, a solution that is highly optimized for D-Optimality may not be optimized for G-Optimality or A-Optimality. By combining these different types of optimality, the GA can search for a solution that is optimized across all dimensions. Finally, a compound criterion can help ensure that the GA converges to a solution that is practical and usable in real-world situations. For example, a solution that is optimized for D-Optimality may not be feasible to implement due to other practical considerations such as cost or manufacturing constraints. By combining different types of optimality, the GA can search for a solution that is both optimal and feasible to implement. More specifically we define the fitness function as:

fitness = 0.4 \cdot G - Optimality + 0.3 \cdot D - Optimality + 0.3 \cdot A - Optimality

(1)

In this scenario, the multi-objective optimization problem requires that all objectives are taken into account equally while giving slightly more weight to G-Optimality. This is achieved by assigning a weight of 0.4 to G-Optimality, and weights of 0.3 to both D-Optimality and A-Optimality, in the compound criterion used for evaluating the fitness of the solutions generated by the GA. By giving more weight to G-Optimality, we can bias the optimization process towards generating solutions that have a good overall fit to the data, while still taking into account the other objectives. This can help to avoid the problem of getting trapped in local optima, since the GA will be better able to explore the search space and find better solutions that are not necessarily optimal in any one objective but are good overall. Furthermore, the use of multiple objectives in the fitness function can help to generate more diverse and robust solutions, since it allows the GA to explore a larger space of potential solutions. This can help to avoid over fitting to the training data and improve the generalization performance of the model. In the given fitness function, we have a constraint that the solution should not have more than 221 elements. If a solution violates this constraint, we need to penalize it to discourage the GA algorithm from selecting it. Penalizing a solution means assigning a high cost to it, which in turn lowers its fitness value. In our case for ensuring that we have 221 points in the final solution, the fitness function first checks if the sum of the elements in the solution is equal to 221. If it is not, we assign a penalty to the solution by adding a very high value (100000) to the sum of the elements in the solution. This will make the fitness value of the solution extremely low, which means it will have a very low chance of being selected by the GA algorithm. Finally the GA will have the following settings:

The initial population consists of 30 solutions, which were created using the Sensor Marks Selection based on Poison-Disc and D-Optimality technique described above.
The size of the population is set to 100, meaning that there will be 100 solutions in each generation.
The algorithm will run for 50 generations.
The probability of crossover is set to 0.6, meaning that there is a 60% chance that two parent solutions will be combined to produce a new offspring solution in each crossover event.
The probability of mutation is set to 0.05, meaning that there is a 5% chance that each gene in a solution will be mutated during a mutation event.
Elitism is enabled, which means that the best solution from the previous generation will always be included in the next generation.
The fitness function will be maximized, meaning that the algorithm will try to find solutions with the highest possible fitness value.

In our case, the Genetic Algorithm significantly improves the solution in terms of G, D, and A-Optimality, as demonstrated in the Experimental Results section.

4. Experimental Results

The newly proposed OED strategy is evaluated using G, D and A-optimality, the Fisher based criteria describing the different flavours of dispersion, and in accordance the amount of information that a certain solution can provide. As it is mentioned above, uniformity of the selected marks on the wafer is a requirement as well but since it already taken into account during the creation of the search space for our solution and consecutively assured from the Poison-Disc sampling part of the algorithm it is not needed to be included in the evaluation criteria.

In Figure 10 you can see a representation of the selected marks on the wafer surface. In red are the points that were finally selected to participate in the sampling scheme, while in gray you can see the points that were not. All together form the candidate points. From Figure 10 we can safely conclude that the solution satisfies the uniformity requirement.

In Table 1 the results of 10 different runs of our algorithm are presented. From this table we can draw two important conclusions. On the one hand, obviously the results are of high quality. As you can see, G-Optimality is in the worst case 0.106, while we can see that for the rest of the runs it is between 0.099 and 0.097.

From the theory of Optimal Experimental Design it is known that any G-optimality score below 1.00 is considered a satisfactory result. The proposed algorithm of Magklaras et.al. [20] achieves a G-Optimality of around 0.261 which is considered a very good result. This result is achieved without improving the solution. In our proposed strategy not only we achieve 10 times better result than the expected but also about 3 times better than Magklaras et.al. [20] by exploiting GAs in the final step. So, compared to previous work in the same problem, we can safely conclude for the success and superiority of our proposed solution.

Similarly, D-Optimality achieves high scores as well. In Figure 11 we see that there is an outlier of -93.555 and the rest of the run achieve a score less than -94.1. A-Optimality as well is around 0.31 with only one outlier at 0.337 as shown in Figure 11

The second important conclusion is that as you can see from Table 1 all G, D and A-Optimality scores are not only precise but also accurate. The dispersion of all three metrics is low and it seems that the Genetic Algorithm converges around certain values. For G-Optimality at 0.097, for D-Optimality around -94.373 and for A-Optimality around 0.314. The observation that the genetic algorithm (GA) converges to the same solution over multiple independent runs is an important finding. GA is a stochastic optimization algorithm, meaning that it uses randomization to explore the search space. As a result, the algorithm may find different solutions each time it is run, and the convergence to the same solution over multiple runs is not guaranteed. However, the fact that the GA converges to the same solution over multiple independent runs suggests that the proposed solution is robust, meaning that it is less sensitive to variations in the randomization used by the algorithm. The robustness of the solution is an important property because it indicates that the solution is more likely to be useful in practice. In real-world applications, the inputs and conditions can vary, and a robust solution is more likely to perform well across different scenarios. Additionally, the observation that the GA converges to the same solution over multiple runs increases the confidence in the optimality of the proposed solution, as it suggests that the solution is not just a lucky outcome of the randomization used by the algorithm.

Finally, we have to mention that our algorithm runs in a simple workstation (CPU Intel i5) in only 10 minutes and by using Python programming language. We understand that in a non-prototyping but in a real life industry scenario this performance can be improved drastically. This though not necessary since this is an offline process and there is no hard requirement on execution time.

5. Discussion and Future Work

The proposed algorithm is mixed since in the first part we follow a deterministic procedure for creating the initial population and in the second part we use a meta-heuristic approach in order to improve the solution we already have. A possible point of improvement could be reducing the execution time of our algorithm. Currently it is obtaining good results in 10 minutes but by applying certain parallelization techniques this can be further reduced. This is not a constraint though since our process runs offline and in this case execution time is not an issue.

In conclusion, the results obtained from this study are highly promising and satisfying for a real-life industry problem. The proposed genetic algorithm was able to converge to a robust solution that achieved significant improvements in the optimality criteria. This indicates the potential of the GA approach to be used in similar industrial applications. Additionally, the study provides valuable insights for future research on the optimization of the process parameters in the manufacturing industry. Overall, the results demonstrate the effectiveness of the proposed GA approach in tackling real-life industry problems and opens up possibilities for further research in this area.

References

"Moore’s Law Inspires Intel Innovation", www.intel.com/content/www/us/en /silicon-innovations/moores-law-technology.html.
Lee, K. Y., et al. "Micromachining applications of a high resolution ultrathick photoresist." Journal of Vacuum Science & Technology B: Microelectronics and Nanometer Structures Processing, Measurement, and Phenomena 13.6 (1995): 3012-3016. [CrossRef]
Jacobs, I. S. "Fine particles, thin films and exchange anisotropy." Magnetism (1963): 271-350.
Wester, Rogier, and John Koster. "The software behind Moore’s law." IEEE Software 32.2 (2015): 37-40.
S. Miller, “ASML’s NXE Platform for Volume Production”, 2013, presentation at Semicon West 2013, www.semiconwest.org.
Smith, Kirstine. "On the standard deviations of adjusted and interpolated values of an observed polynomial function and its constants and the guidance they give towards a proper choice of the distribution of observations." Biometrika 12.1/2 (1918): 1-85. [CrossRef]
V. V. Fedorov, Theory of Optimal Experiments, Academic Press, New York, NY, 1972.
A. C. Atkinson, A. N. Donev, and R. D. Tobias, Optimum Experimental Designs, With SAS, Oxford University Press, New York, NY, 2007.
Dobos, L., Z. Bankó, and J. Abonyi. "Optimal experiment design techniques integrated with time-series segmentation." 2010 IEEE 8th International Symposium on Applied Machine Intelligence and Informatics (SAMI). IEEE, 2010.
Mandal, Abhyuday, Weng Kee Wong, and Yaming Yu. "Algorithmic searches for optimal designs." Handbook of design and analysis of experiments (2015): 755-783.
Nguyen, Nam-Ky, and Alan J. Miller. "A review of some exchange algorithms for constructing discrete D-optimal designs." Computational Statistics & Data Analysis 14.4 (1992): 489-498. [CrossRef]
Wanyonyi, Samson & Okango, Ayubu & Koech, Julius. (2021). Exploration of D-, A-, I-and G-Optimality Criteria in Mixture Modeling. Asian Journal of Mathematics & Statistics. 12. 15-28. [CrossRef]
Cook, Robert L. "Stochastic sampling in computer graphics." ACM Transactions on Graphics (TOG) 5.1 (1986): 51-72. [CrossRef]
Mohamed S. Ebeida, Andrew A. Davidson, Anjul Patney, Patrick M. Knupp, Scott A. Mitchell, and John D. Owens. 2011. Efficient maximal poisson-disk sampling. ACM Trans. Graph. 30, 4, Article 49 (July 2011), 12 pages. 20 July. [CrossRef]
Katoch, Sourabh, Sumit Singh Chauhan, and Vijay Kumar. "A review on genetic algorithm: past, present, and future." Multimedia Tools and Applications 80 (2021): 8091-8126.
King, RTF Ah, K. Deb, and H. C. S. Rughooputh. "Comparison of NSGA-II and SPEA2 on the multiobjective environmental/economic dispatch problem." University of Mauritius Research Journal 16.1 (2010): 485-511.
El-Abbasy, Mohammed S., Ashraf Elazouni, and Tarek Zayed. "Finance-based scheduling multi-objective optimization: Benchmarking of evolutionary algorithms." Automation in Construction 120 (2020): 103392. [CrossRef]
Ciro, Guillermo Campos, et al. "A NSGA-II and NSGA-III comparison for solving an open shop scheduling problem with resource constraints." IFAC-PapersOnLine 49.12 (2016): 1272-1277. [CrossRef]
Foutsitzi, Georgia, et al. "Multicriteria Approach for Design Optimization of Lightweight Piezoelectric Energy Harvesters Subjected to Stress Constraints." Information 13.4 (2022): 182. [CrossRef]
Magklaras, Aris, et al. "Sampling Points Selection Algorithm For Advanced Photolithography Process." 2022 7th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM). IEEE, 2022.

Figure 1. Chip shrinkage and Photolithography machines of ASML. (Figure based on image (c) ASML [4,5].

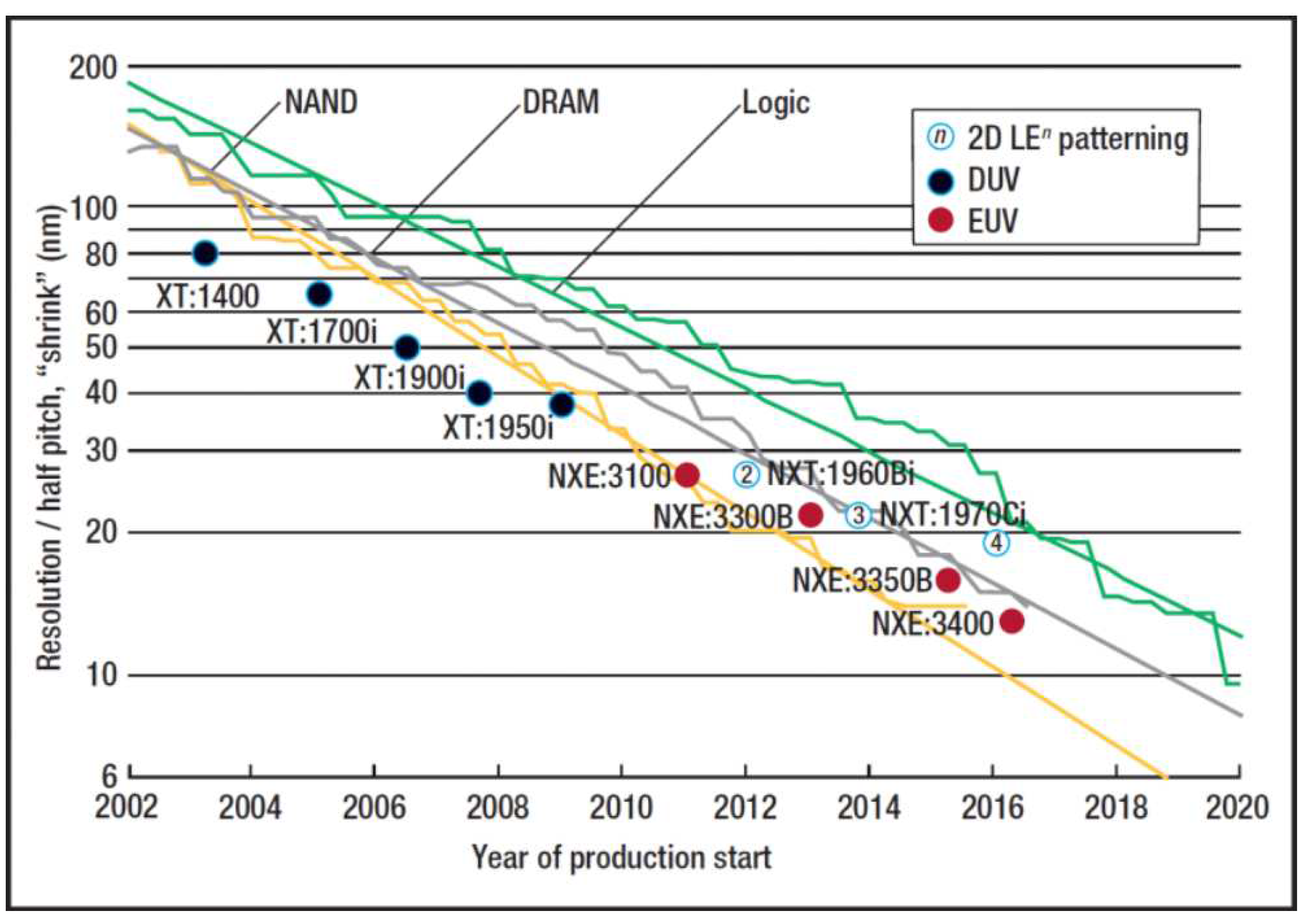
Figure 2. This sequence shows the full light path from EUV source to silicon wafer. The light is generated in the source (bottom right), sent into the illuminator (mid right) which controls the light beam, reflects off the mask with the chip pattern (top), before being focused in the projection optics (mid left) and exposing the wafer (mid bottom). (Figure based on image (c) ASML.

Figure 5. Parameter Estimation Process.

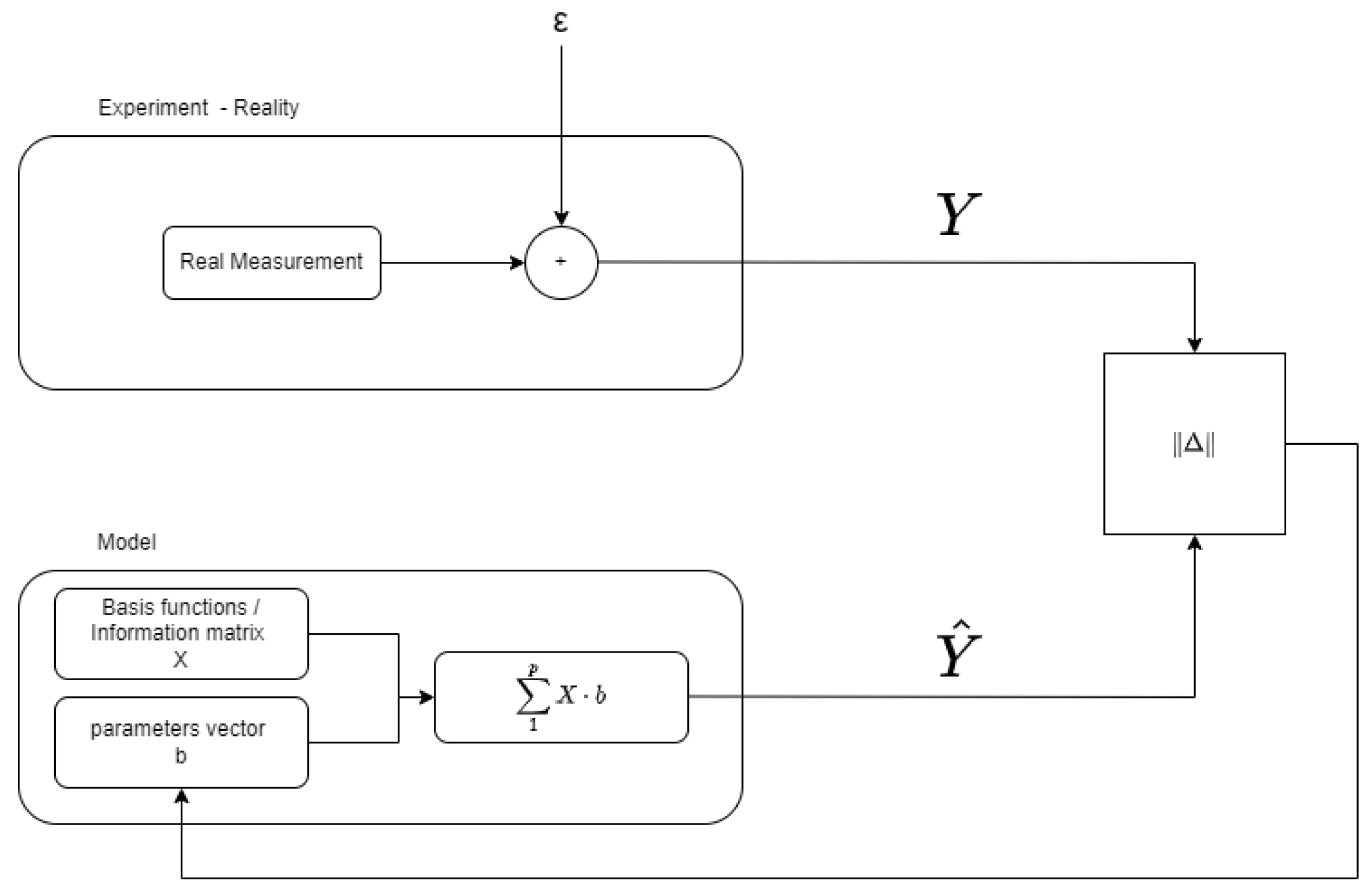
Figure 6. Fingerprint Estimation as a block diagram

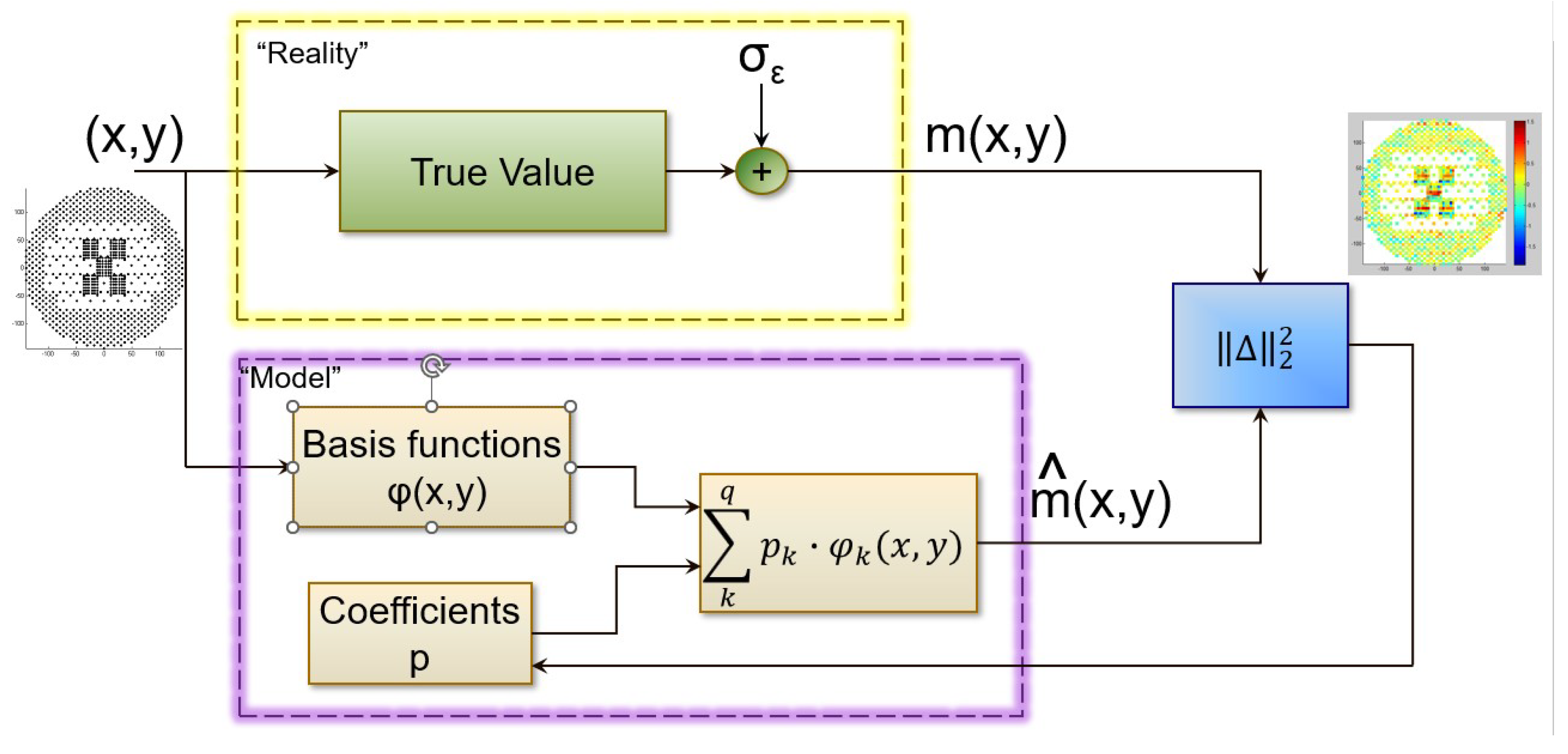
Figure 7. High Level Algorithm Diagram.

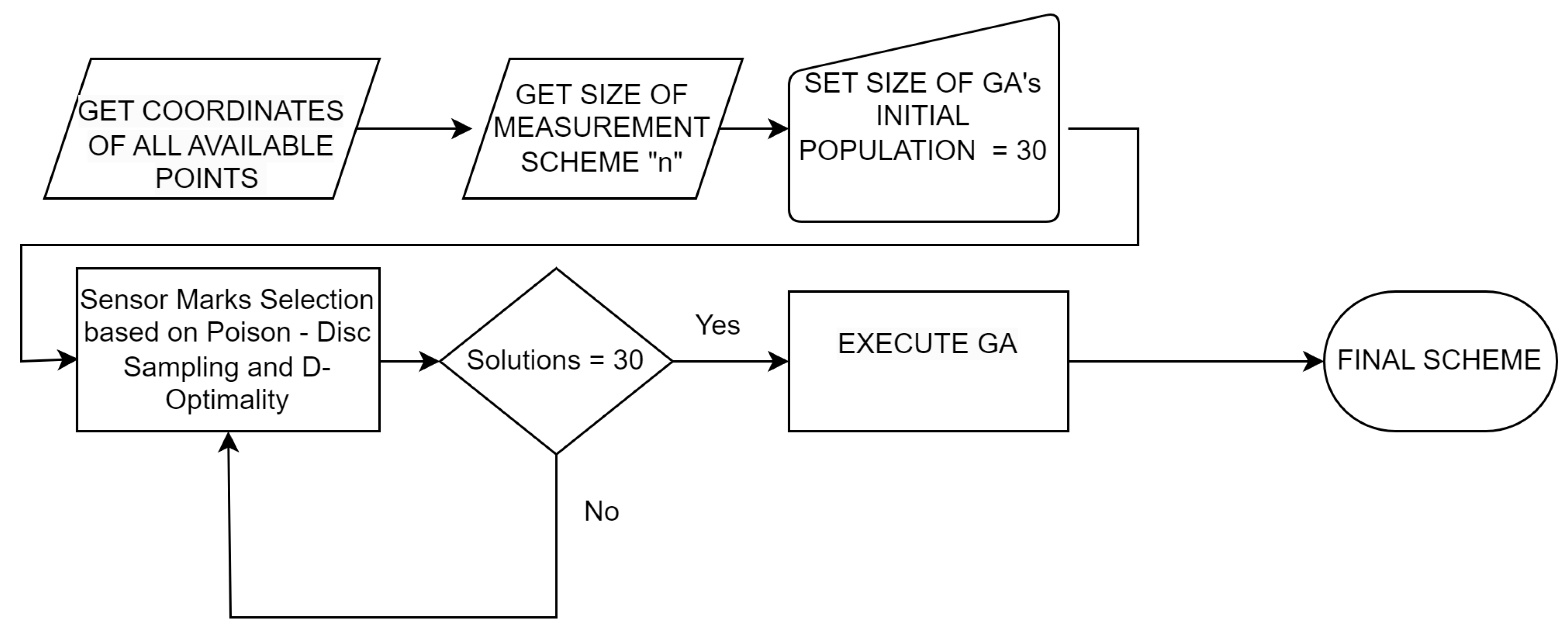
Figure 8. In green we see the feasible points that can be added to the sampling scheme.

Figure 9. Classification of metaheurisitics algorithms [15].

Figure 10. Solution representation on the wafer surface.

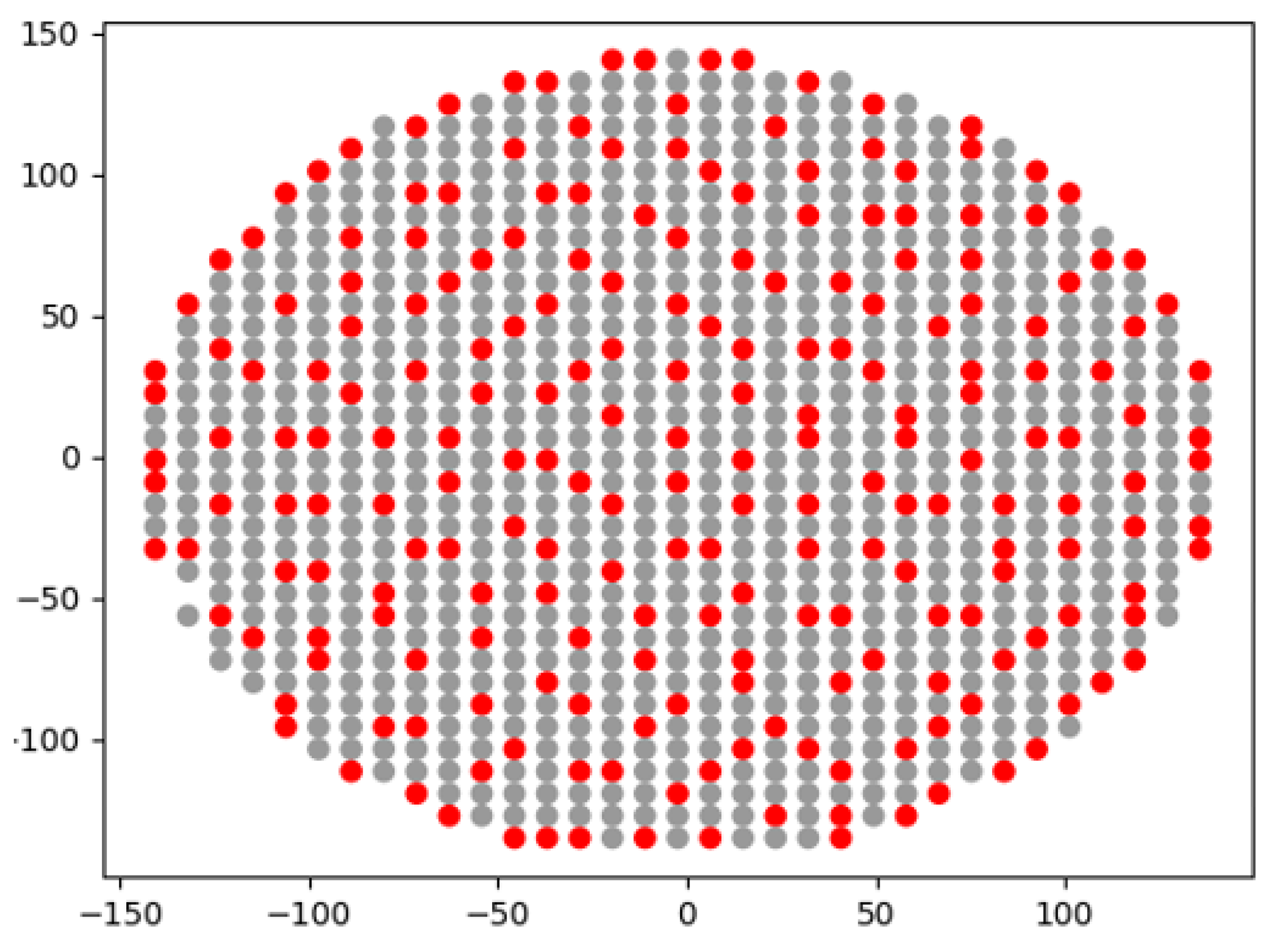
Figure 11. G, D, A-Optimality results bar plots.

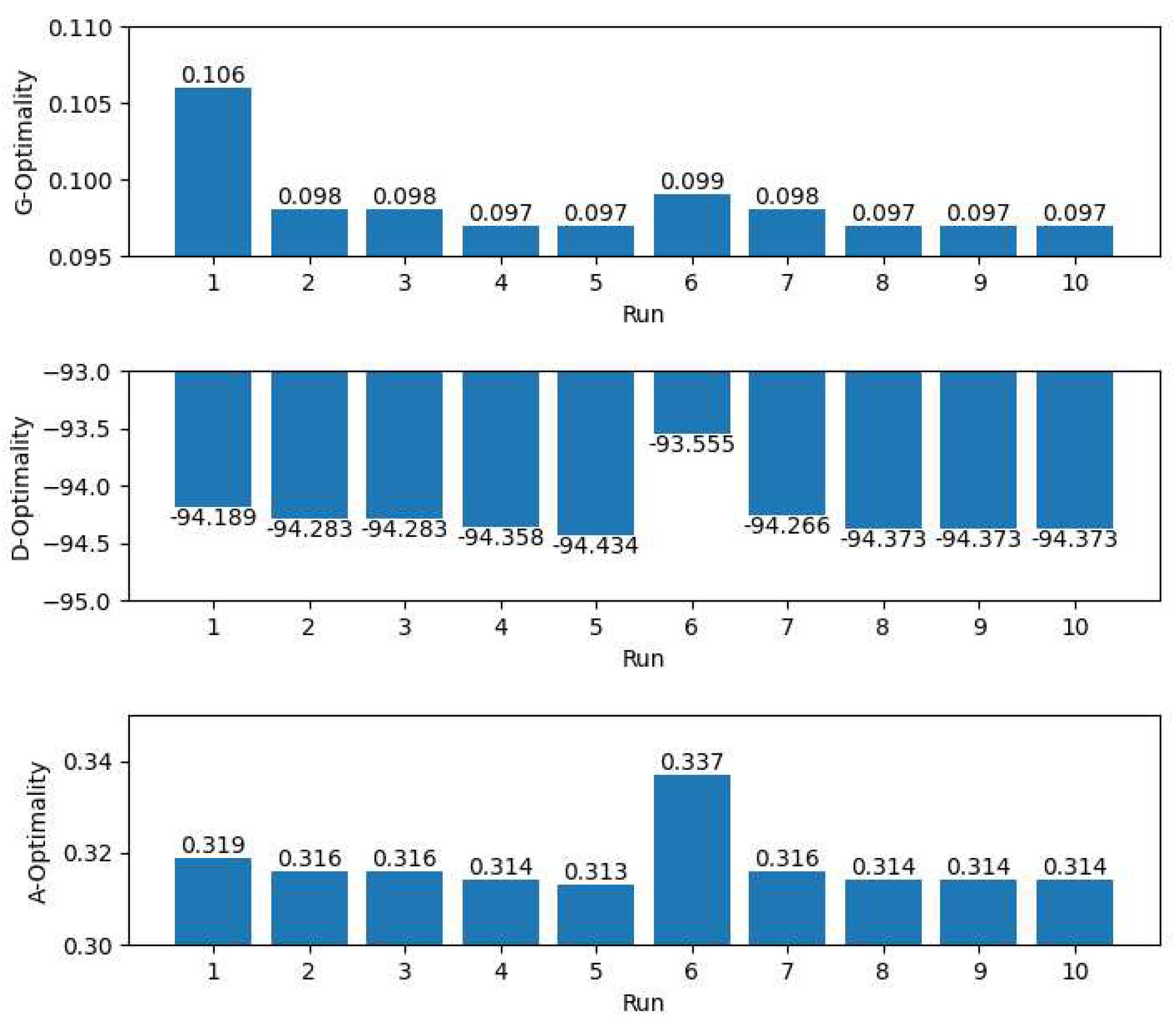
Table 1. Experimental results.

Run	G-Optimality	D-Optimality	A-Optimality
1	0.106	-94.189	0.319
2	0.098	-94.283	0.316
3	0.098	-94.283	0.316
4	0.097	-94.358	0.314
5	0.097	-94.434	0.313
6	0.099	-93.555	0.337
7	0.098	-94.266	0.316
8	0.097	-94.373	0.314
9	0.097	-94.373	0.314
10	0.097	-94.373	0.314

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer