Prerpints.org logo
Preprint
Article

Conversion of Polypropylene (PP) foams into Auxetic Metamaterials

Altmetrics

Downloads

99

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 June 2023

Posted:

26 June 2023

You are already at the latest version

Alerts
Abstract
In this work, a simple and environmentally friendly process combining low pressure (vacuum) and mechanical compression is proposed to convert recycled polypropylene (PP) foams (28 kg/m3) into low density foams (90-131 kg/m3) having negative tensile and compressive Poisson's ratios (NPR). The effect of processing conditions (vacuum time, temperature, and mechanical pressure) was studied. Based on the optimized conditions, the tensile Poisson’s ratio of the resulting auxetic foams reached −1.50, while the minimum compressive Poisson's ratios was −0.32 for the same sample. The foam structure was characterized via morphological analysis (SEM) to determine any changes related to the treatment applied. Finally, tensile and compressive properties (Young's modulus, strain energy, energy dissipation and damping capacity) are also presented and discussed. It was observed that the mechanical properties of the resulting auxetic foams were improved compared to the original PP foam (PP-O) for all tensile properties in terms of modulus (19.9 to 59.8 kPa), strength (0.298 to 1.43 kPa) elongation at break (28 to 77%), energy dissipation (14.4 to 56.3 mJ/cm3) and damping capacity (12 to 19%). Nevertheless, improvements were also observed under compression in terms of energy dissipation (1.6 to 3.6 mJ/cm3) and damping capacity (13 to 19%). These auxetic foams can find applications in sport and military protective equipment, as well as any energy mitigation system.
Keywords: 
Subject: Chemistry and Materials Science  -   Polymers and Plastics

1. Introduction

Polypropylene (PP) foams have a wide range of applications due to their unique properties, such as lightweight, high strength-to-weight ratio and excellent thermal insulation [1]. The main applications of PP foams are in packaging, automotive, building and construction, sports and leisure, as well as medical and healthcare [2,3]. PP foams are commonly used in protective packaging for fragile items, such as electronics, appliances and glassware. They are also extensively used in the automotive industry for sound/thermal insulation, vibration dampening and cushioning. Other specific uses are door panels, headliners, instrument panels and parts to improve comfort and reduce noise [2,3].
Today, millions of tons of plastics (include PP) are produced and consumed in the world every year leading to important problems to manage these large number of materials after their end of use generating environmental issues due to their long degradation time [4]. Recycling is one of the main methods to reduce the negative impact of these plastics waste. However, recycling PP foams can be challenging due to their low density, potential contamination and the lack of recycling infrastructure in several regions around the globe [5]. To increase the value of PP foam waste and promote its recycling, research and development efforts are needed to find simple and suitable methods. One possible approach is to develop technologies converting waste PP foams into valuable products or materials. This approach is associated with upcycling which is an innovative approach to create added-value by using low value wastes and transforming it into a higher quality product [6,7,8,9]. One interesting possibility for standard discarded PP foams is to convert them into metamaterials having superior mechanical properties compared to the original products. This process involves the conversion of the foam’s honeycomb cellular morphology into a re-entrant structure, resulting in foams with an auxetic behavior.
Over the years, researchers have successfully converted several types of polymer foams into auxetic ones having negative Poisson ratios. The list includes polyether urethane foam (PU) [10,11,12,13,14,15,16], polyethylene foam (PE) [7,8,17,18,19,20], polyester (PES) [21], and polyvinyl chloride (PVC) [19]. This process can create new materials having unique and interesting properties, such as increased elasticity and resistance towards different types of deformation or stress. This approach has the potential to significantly reduce the amount of waste ending up in landfills or incinerators. Unfortunately, no work was found on PP foams leading to a sustainable and low-cost solution to produce high-quality materials for a wide range of applications from automotive and aerospace engineering to medical devices and protective gears.
To create auxetic foams from conventional ones, the main idea is to convert the original honeycomb or polyhedral-shaped cell morphology into a re-entrant cellular structure [10,11,12,13,14,15,16,17,18,19,20,21]. This can be achieved through various methods including chemical, mechanical, physical and thermal treatments that can be applied alone or in combination. These processes often involve compressing the foam, heating above the polymer’s softening point and then cooling while maintaining compression.
Li et al. [22] developed a one-pot CO2 foaming method to produce closed-cell auxetic foams with different cellular structures (bimodal cell structure and homogeneous cell structure) directly from virgin PP. This foaming process involved the addition of NaCl as a hydrophilic additive. The results showed that under specific foaming conditions (159°C, CO2 pressure of 5 MPa and saturation time of 3 h with NaCl contents of 2%, 5% and 8% by weight), the Poisson’s ratio in tension ranged from –0.13 to –0.46. Another report described auxetic PP films extruded between 157°C and 230°C with a screw speed ranging from 0.525 to 2.10 rad/s and take-up speeds ranging from 0.0225 to 0.15 m/s [23]. By varying these processing parameters, it was possible to achieve a range of Poisson’s ratios in tension from positive (+0.4) to negative (–1.0). These auxetic PP fibers were later produced at an industrial scale [24].
Our previous works proposed two distinct methods to produce auxetic foams from waste foams. The first method involves a combination of solvent (ethanol) evaporation-condensation and mechanical compression (SECC) [7], while the second method uses vacuum and mechanical compression (VMC) [8]. In this study, the VMC method is used to convert recycled conventional PP foams (electronics packaging) into NPR materials. To the best of our knowledge, this is the first successful attempt to directly upcycle waste PP foams into auxetic metamaterials. In particular, the effect of mechanical stress, heating and vacuum time were investigated to optimize the final foam structure. From the samples produced, tensile and compressive properties were measured, especially the Poisson ratio. These findings will enhance our understanding on the production and properties of auxetic polymer foams in general.

2. Materials and Methods

2.1. Materials

In this study, PP foam samples from recycled low density electronics packaging was selected as in our previous studies [7,8,9]. These foams (different geometries) had an initial density of 28 kg/m3. To perform the treatments, a vacuum oven (Cole-Parmer OVV-400-24-120 Programmable Vacuum Oven, 24 L, Canada) was used.

2.2. Methods

The recycled PP foams were cut into 10 x 10 x 5.0 cm3 pieces using a doctor blade. Each sample was then placed inside the vacuum oven and heated for 1 h at temperatures ranging from 120 to 140°C. This temperature range is above the PP softening temperature (90-100oC), but below its melting temperature (142oC). Next, the oven was subjected to vacuum (maximum –0.88 bar) for 1-24 h at 120-140°C, followed by a rapid return to ambient pressure (fast decompression). Mechanical pressure (0-4.0 kPa) was also applied on the sample during the treatment by using a metal block of different weight. After treatment, the sample was left to cool inside the oven for 1-2 h still under mechanical pressure [8,9]. The final volume of the foam produced during the VMC process was determined by a balance between the foam’s expansion due to the elevated temperature and the vacuum/mechanical stress (weight) imposed.

2.3. Characterization

2.3.1. Characterization of the original PP foams

The bulk density of the foams (⍴f) was obtained from the ratio between its weight (Wf) and its volume (Vf ) calculated by measuring the length (L), width (W) and thickness (l) with a Mastercraft Digital Caliper (Vonore, USA). Each dimension was taken at four locations and averaged to calculate:
⍴ f = W f V f   = W f L   W   l
The porosity (P) was calculated as:
P = ⍴ l − ⍴ f ⍴ l − ⍴ a   ( 100 % )   
where ⍴a and ⍴l are the density of air (1.225 kg/m3) and unfoamed PP (910 kg/m3), respectively. The unfoamed (PP) volume ( V l ) is calculated as:
V l = ⍴ f − ⍴ a ⍴ l − ⍴ a   V f
while the gas phase (air) occupies a volume of:
V a = P   V f
Each sample was then immersed overnight in an ethanol bath. The volume of ethanol absorbed was calculated by using the weight gained (We), density of ethanol (⍴e = 789 kg/m3) and mass of polymer in the foam (Vl ⍴l) to give:
V e = W e − V l   ⍴ l ⍴ e
Finally, the open cell percentage (OCP) was obtained from the ratio between the volume of ethanol and air:
O C P = V e V a   ( 100 % )

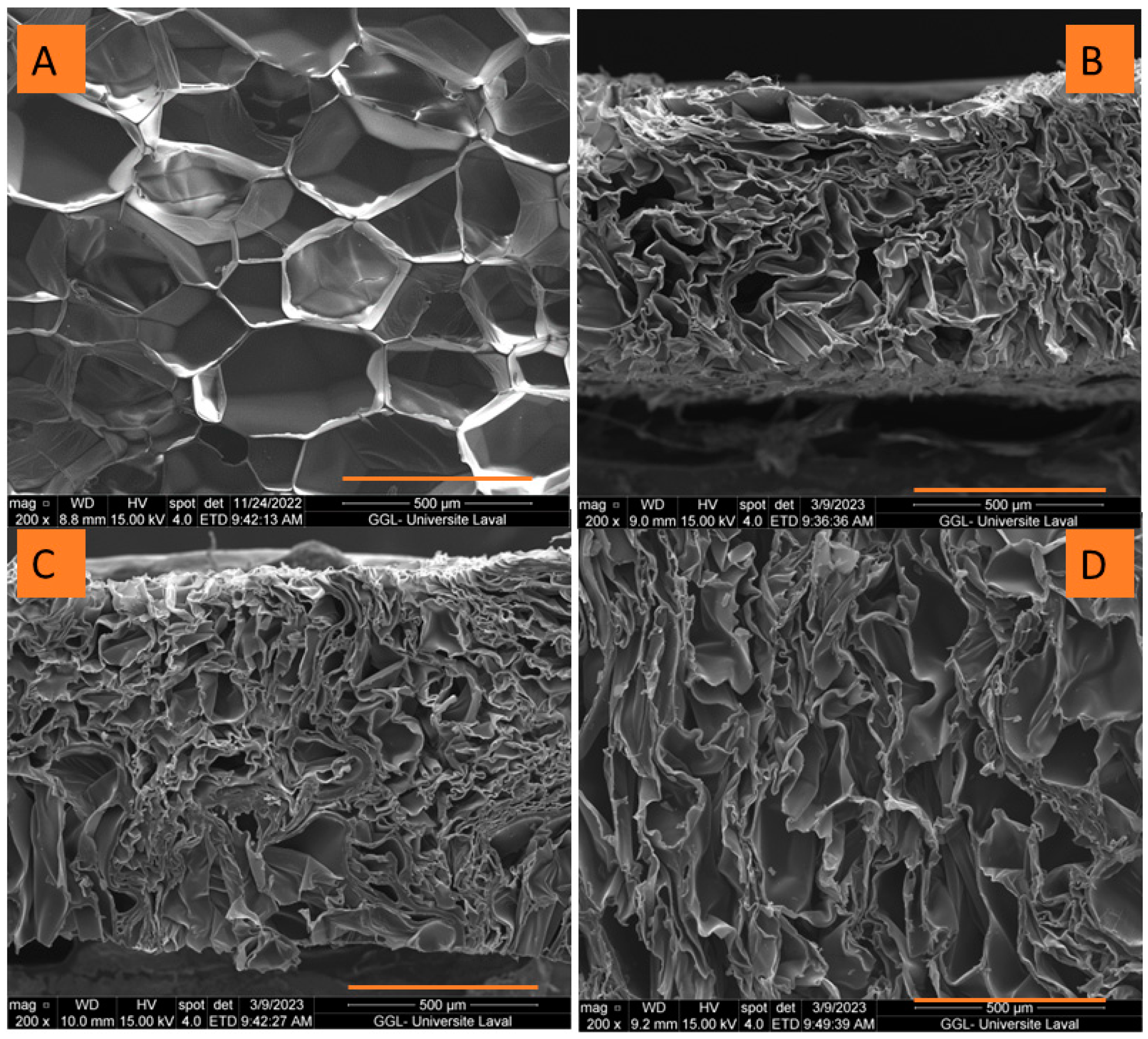
2.3.2. Foam morphology

The cell size of the PP foams was quantified by a scanning electron microscope (SEM) at 15-20 kV (Inspect F50, FEI, USA). The cross-section of each sample was obtained by cutting with a doctor blade slices 1.5 mm thick before coating with a conductive layer (Au-Pd). The images were then quantitatively analyzed (morphology analysis) to get the cell diameters via the Image J software (National Institutes of Health, USA).

2.3.3. Differential scanning calorimetry (DSC)

Differential scanning calorimetry (DSC) measurements were performed using a DSC 7 (Perkin Elmer, USA) coupled to the Pyris 1 software with samples weighting around 3–8 mg. The temperature increased at 10oC/min from 50 to 200oC before cooling back from 200 to 50oC and heating again to 200oC. All the runs were carried out under a constant rate (20 ml/min) of dry nitrogen. The crystallinity (Xc) was calculated as:
X c = △ H m △ H 100 ( 100 % )
where ΔHm is the enthalpy of the sample during the heating process, while ΔH100 is the enthalpy of 100% crystalline PP (207 J/g) [25].

2.3.4. Poisson’s ratio

The Poisson’s ratios were determined under tension and compression. The tests were done on a dynamic mechanical analyzer (DMA) RSA III (TA Instruments, USA). The deformation rate was fixed at 1.2 mm/min and the deformations were determined using a high-resolution video camera (SONY® FDR-AX53, Japan) in two perpendicular directions. The Poisson’s ratio (ʋ) was obtained as the negative ratio between the transverse (εy or εz) and axial (εx) deformations as [26]:
v = − Ɛ y Ɛ x o r − Ɛ z Ɛ x
More information on the methodology can be found in our previous publications [7,8].

2.3.5. Mechanical properties

A dynamic mechanical analyzer (DMA) RSA III (TA Instruments, USA) was used for quasi-static tests and determine the relationships between engineering stress and engineering strain. The tests were done at 1.2 mm/min for both tension and compression and module were determined by the slope in the linear region of stress-strain curves (below 5% deformation).
For hysteresis tests, a strain between 0.1% and 3% (up-and-down) was applied at 1 rad/s. The maximum potential energy (Ep), which represents the total strain energy in a cycle, was calculated by the area below the stress-strain curves as [27,28]:
E p = ∫ 0 ε m a x σ d ε
The dissipated energy (Ed) was quantified by calculating the energy loss resulting from internal forces over a complete loading cycle and calculated by the area enclosed by the hysteresis loop for one cycle as [27,28]:
E d = ∫ ε m i n ε m a x σ   d ε
Finally, the damping capacity (Ψ) was determined by the ratio between the energy loss divided by the total strain energy over a complete cycle as [29]:
= E d E p ( 100 % )

3. Results and discussions

3.1. Physical properties of the PP recycled foams

The density of the original (untreated) foam (PP-O) is 28.0 kg/m3. This material was used as the starting point for all the samples prepared as reported in Table 1. The nomenclature begins with “PP” for the type of foam, followed by Tx which represents the treatment temperature (120-140oC) and a number representing the vacuum time (1 to 24 h). Finally, Px represents the applied mechanical pressure (kPa). For example, sample PP-T130-15-P3.0 is a polypropylene foam that underwent treatment at 130°C for 15 h with a mechanical pressure of 3 kPa. Sample PP-O represents the original PP foam (untreated). All the samples were actually produced under the maximum oven vacuum (-0.88 bar) which was determined to be the best condition based on our previous studies [7,8].
Table 1. Physical properties of the original PP and auxetic foams.
Table 1. Physical properties of the original PP and auxetic foams.
Foam code Density (kg/m3) Porosity (%) OCP (%)
PP-O 28.0±1.1 97.1±3.0 3.1
PP-T130-15-P1.0 114.3±1.4 87.6±5.2 4.1
PP-T130-15-P2.0 116.4±1.5 86.8±2.7 4.3
PP-T130-15-P3.0 130.1±1.5 85.8±2.6 4.5
PP-T130-15-P4.0 131.3±1.6 85.5±2.7 5.2
PP-T120-15-P3.0 90.1±1.8 89.5±4.2 4.0
Table 1 also provides a summary of the physical properties of the foams, including foam density, porosity and open cell percent. According to Table 1, the density of the auxetic foams increased with increasing mechanical pressure, temperature and time. Additionally, the open cell percent (OCP) increased as the porosity decreased. These trends are expected since a higher temperature makes the sample easier to compress, leading to a higher density. For instance, the density of PP-T120-P3.0 was higher than that of PP-O, but less than that of PP-T130-15-P3.0. Furthermore, the porosity of PP-T120-P3.0 was lower than that of PP-O, but higher than that of PP-T130-15-P3.0. Overall, the OCP appears to be mostly linked to the mechanical pressure applied as a higher pressure produces more deformation on the closed cells, increasing their probability to create not only a re-entrant structure, but also cell wall breakup when excessive stress is imposed.
The DSC thermograms of the initial PP foams and after conversion are shown in Figure 1, and the results were compared to the original foams, as shown in Table 2. The two curves have only one peak indicating that no contamination or small molecules are present. The softening points were from 90-100°C and the peak melting points around of 142oC. Comparing the auxetic foams with their original counterparts, there was no significant difference between the melting points before and after conversion, but the crystallinity decreased from 39.8% to 35.8% after treatment. This indicates that during the VCM process, thermal and mechanical energies are applied to the original foam to produce the re-entrant morphology, but the level of long-range order was changed leading to lower crystallinity.
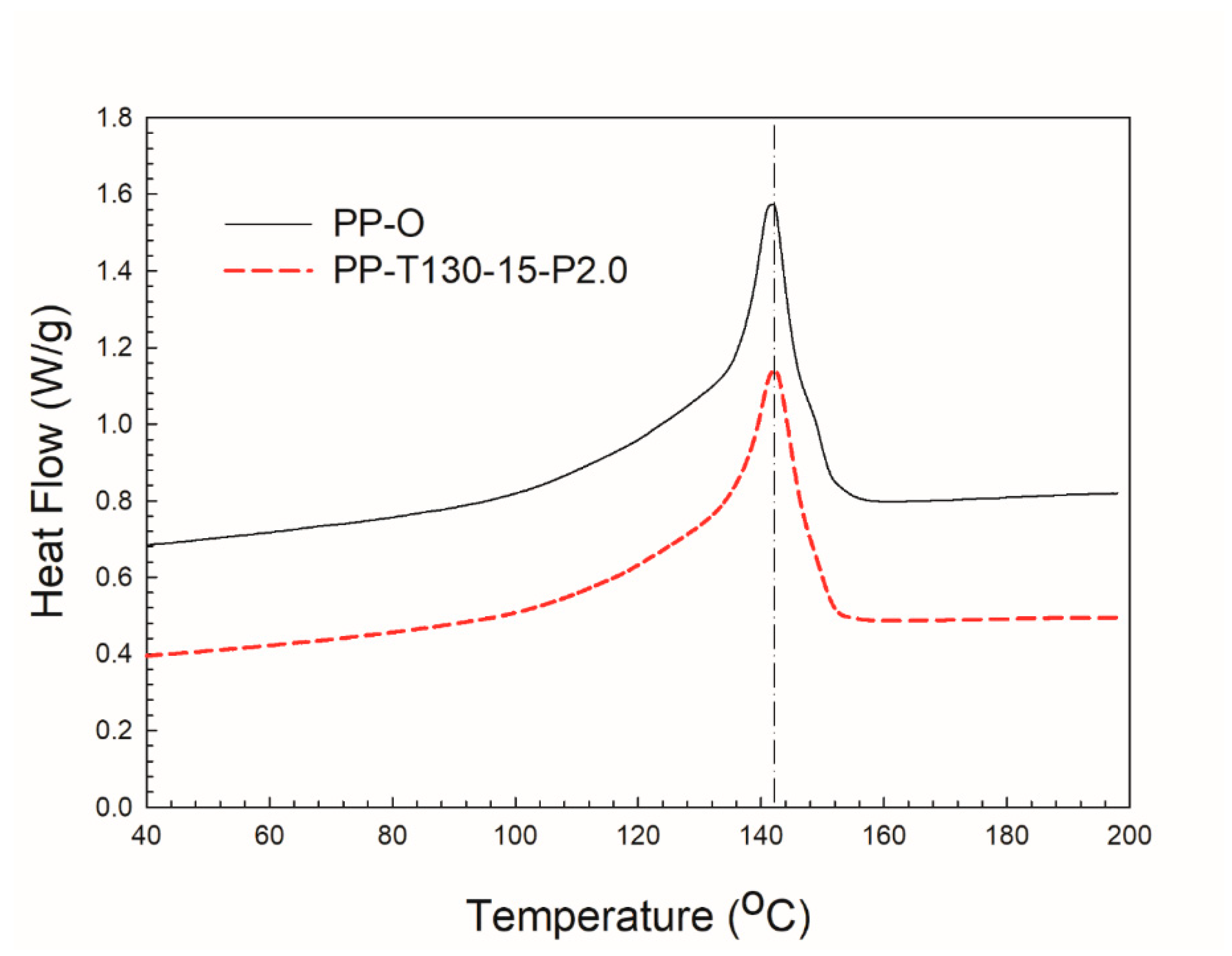
Preprints 77707 g001
Figure 1. Typical DSC curves (second heating) for the initial polypropylene and auxetic foams.
Figure 1. Typical DSC curves (second heating) for the initial polypropylene and auxetic foams.
Preprints 77707 g001
Table 2. DSC results (main peak) of the initial PP and auxetic foams.
Table 2. DSC results (main peak) of the initial PP and auxetic foams.
Sample Tm (oC) △Hm (J/g) Xc (%)
Initial PP foam (PP-O) 141.7 83.2 39.8
Auxetic foam (PP-T130-15-P2.0) 142.1 74.0 35.8

3.2. Auxetic foams

3.2.1. Morphology

PP foams have a cellular structure composed of a network of interconnected voids or cells separated by thin polymer walls. SEM micrographs of the PP foams cross-sections before and after modification are presented in Figure 2. The original foam shows a homogeneous distribution of fine cells across the sample with a mostly closed-cell honeycomb structure (Figure 2A). The average cell was 292±78 µm, which is similar to the literature [30]. It is clear that after treatment, the cells were modified and mostly have a re-entrant structure. Figure 2B-D shows that most of the cells collapsed inward (re-entrant structure) and it was difficult to quantify the cell size due to their complex geometry. These three samples were produced under the same temperature and vacuum time, but with different mechanical pressure. Nevertheless, they have a similar structure.
Preprints 77707 g002
Figure 2. Morphology (cross-section) of: (A) original foam (PP-O) as well as selected auxetic foams: (B) PP-T130-15-P1.0, (C) PP-T130-15-P2.0 and (D) PP-T130-15-P4.0.
Figure 2. Morphology (cross-section) of: (A) original foam (PP-O) as well as selected auxetic foams: (B) PP-T130-15-P1.0, (C) PP-T130-15-P2.0 and (D) PP-T130-15-P4.0.
Preprints 77707 g002

3.2.2. Poisson’s ratio

The Poisson’s ratio of the recycled PP foam was determined via tensile and compressive tests conducted in two directions, namely tangential (Y) and thickness (Z), while applying a deformation in the longitudinal direction (X). In our case, the recycled PP foam was rigid and isotropic with a density of 28 kg/m3. The tensile Poisson’s ratio was found to be 0.25-0.28 on average for both directions when the tensile elongation was up to 15-20%. In contrast, the average Poisson’s ratio in compression was only 0.008 for both directions, indicating that the recycled PP foam material was isotropic, with much higher resistance to deformation in compression compared to tension. This is in agreement with Rinde’s study reporting that for strains below 10%, the tensile Poisson’s ratio of PP foams was 0.25 with higher values in tension than compression, the latter being close to zero [31].
In order to maximize the negative Poisson’s ratio after treatment, an optimization of the processing conditions was carried out. During this process, the maximum vacuum level (−0.88 bar) was applied for all experiments. However, it was necessary to control the other parameters (temperature, vacuum time and mechanical pressure). Each factor is described next.
A. Treatment temperature
As previously stated, the treatment temperature must be above the polymer’s softening point, but below the melting point of the foam. Based on DSC results, the PP foam softening point is around 90-100oC with a melting point of 142oC. Therefore, the selected treatment temperatures were 120°C, 130°C, 135°C and 140°C.
Figure 3 displays the Poisson’s ratio as a function of tensile engineering strain for different treatment temperatures. These results were obtained without mechanical pressure and 1 h of heating time with 1 h of vacuum time. Negative Poisson’s ratios were obtained for all samples up to 80-110% deformation. Figure 3 also shows that the NPR was more negative at 130°C than for the other temperatures. In theory, a higher temperature would result in a softer foam, making the cell walls easier to deform and generate the re-entrant structure, resulting in a lower NPR. However, when the temperature is too high (140°C), the foam becomes too soft and completely collapse, making it too compact and not showing the re-entrant structure; i.e. losing the auxetic behavior above 130oC. In all cases, the Poisson’s ratios increased as the engineering strain increased. Based on these findings, a temperature of 130°C was selected for the subsequent steps.
Preprints 77707 g003
Figure 3. Poisson’s ratio (Z direction) as a function of engineering strain (tension) for auxetic foams treated at different temperatures under −0.88 bar vacuum and 1 h vacuum time.
Figure 3. Poisson’s ratio (Z direction) as a function of engineering strain (tension) for auxetic foams treated at different temperatures under −0.88 bar vacuum and 1 h vacuum time.
Preprints 77707 g003
B. Heating and vacuum time
Figure 4 presents the results for different vacuum periods (1, 3, 6, 15, 20 and 24 h). When the foam is under vacuum for a certain amount of time, the pressure inside the cells is reaching an equilibrium with the pressure outside the cells. When the oven is returned to ambient pressure, the air pressure outside the foam cells exceeds the one within the cells. This increased pressure compresses the foam, causing it to rapidly shrink resulting in partial cell wall collapse and the generation of a re-entrant structure. Once the sample cools back to room temperature, the generated cell structure is locked in. Thus, the driving force is the pressure differential between the outside and inside of the cells. In theory, longer vacuum periods imply that the force generating the re-entrant structure is more easily reached.
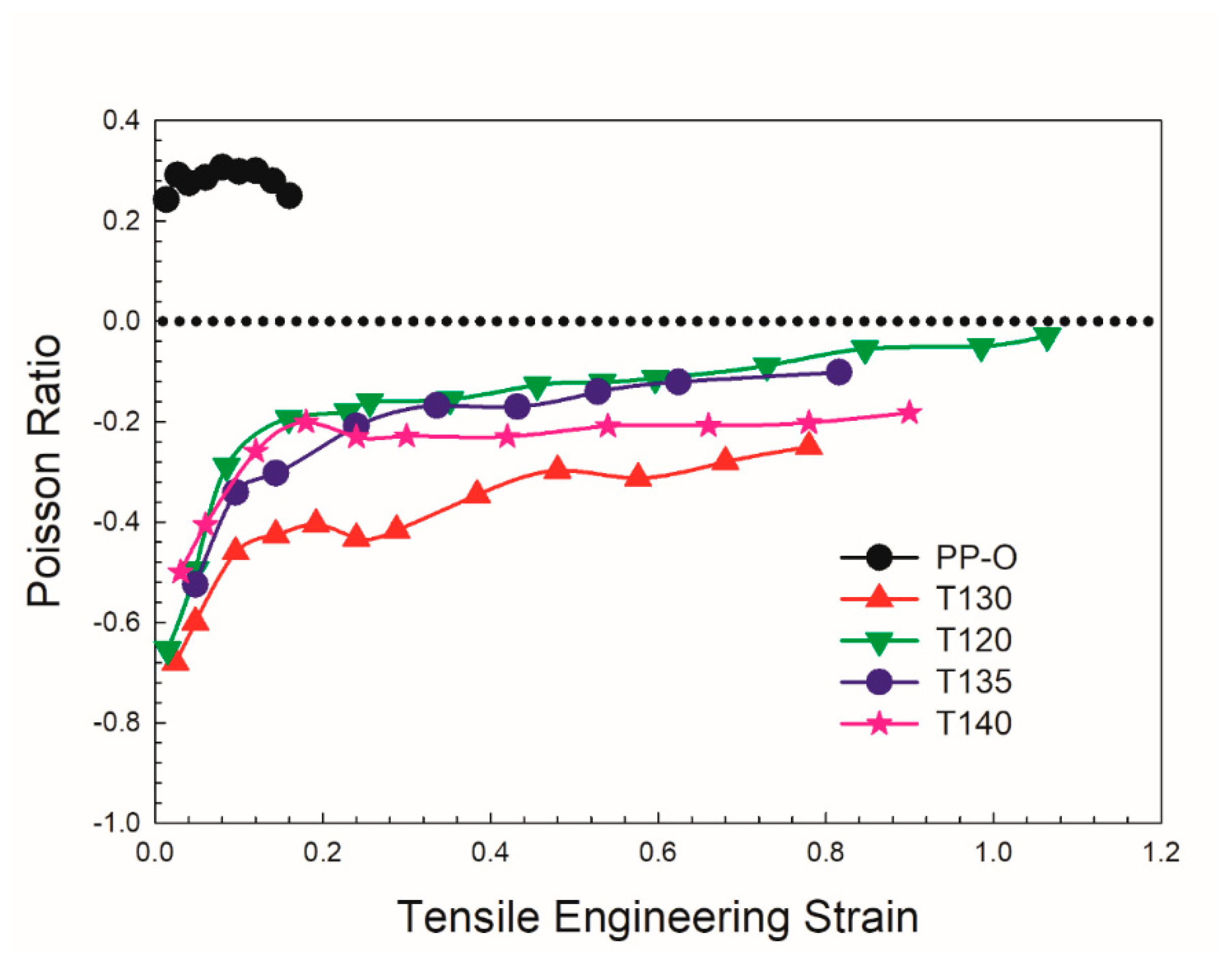
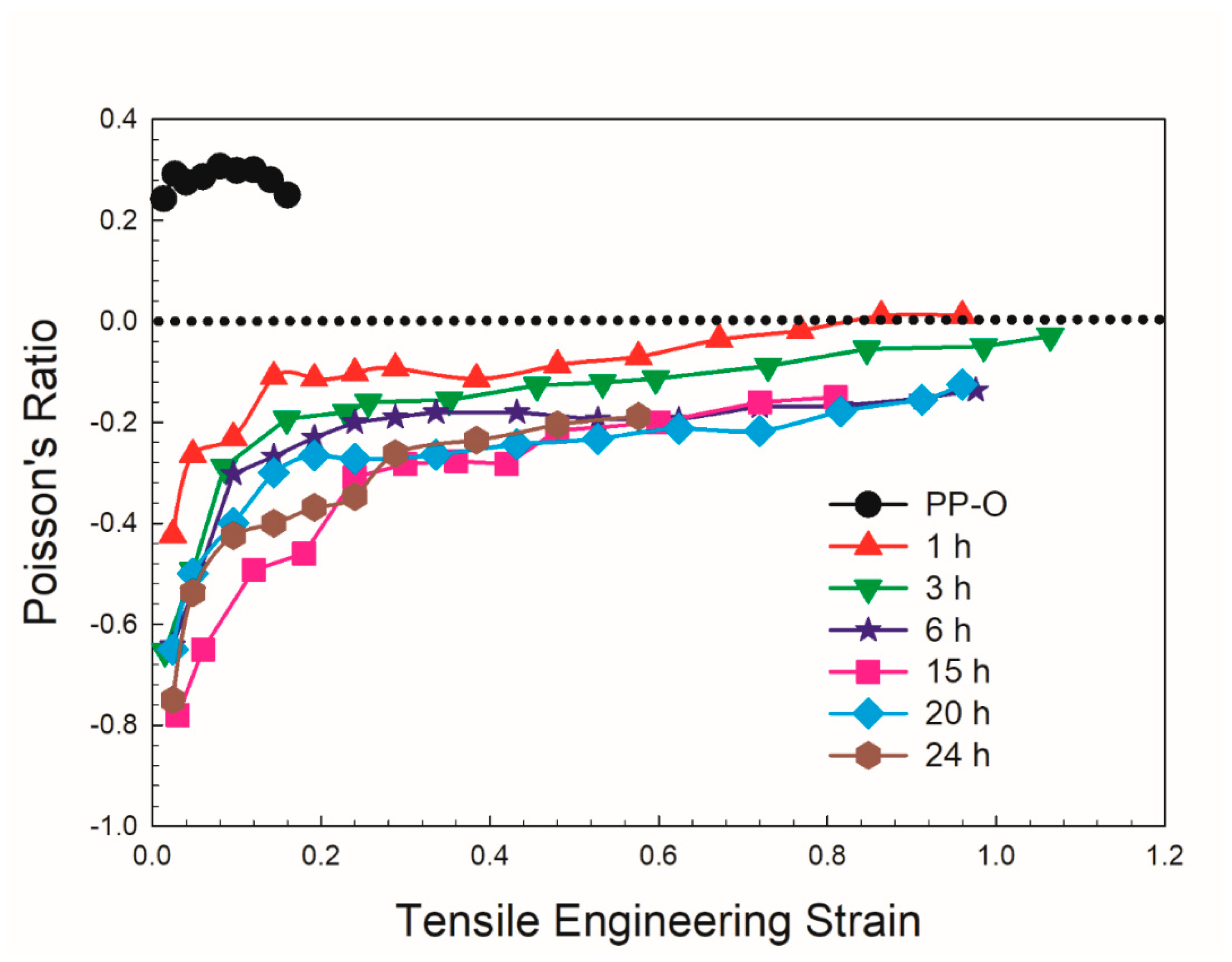
Preprints 77707 g004
Figure 4. Poisson’s ratio (Z direction) as a function of engineering strain (tension) for auxetic foams treated under different vacuum time at 130oC and −0.88 bar pressure.
Figure 4. Poisson’s ratio (Z direction) as a function of engineering strain (tension) for auxetic foams treated under different vacuum time at 130oC and −0.88 bar pressure.
Preprints 77707 g004
Based on the results obtained (Figure 4), it was observed that NPR values decreased with increasing vacuum time from 1 to 15 h, while the values for 20 to 24 h did not show significant differences. This is why 15 h was selected as the optimal time (equilibrium) for the next steps. This trend differs from our previous work on polyethylene (PE) foams, but is similar to polystyrene (PS) foams. For low density polyethylene (LDPE) foams, it was found that only 3 h of vacuum time was sufficient to achieve equilibrium [8]. This is attributed to the fact that PP and PS are more rigid (higher modulus) than LDPE [8]. Therefore, PP foams require more vacuum time to reach equilibrium (stable cellular structure) and fully convert into auxetic foams.
C. Mechanical pressure
The idea to impose mechanical pressure is to generate higher deformation and density to create the re-entrant structure. However, too much compression results in cell collapse destroying the re-entrant structure generated. This trend was also observed in our previous works [7,8].
To optimize the mechanical pressure for PP foams, four pressures (1, 2, 3 and 4 kPa) were applied under the maximum vacuum (−0.88 bar) and 15 h of vacuum at 130oC. Figure 5 presents the Poisson’s ratios as a function of tensile engineering strain for the different mechanical pressure applied. By comparing P2.0, P3.0 and P4.0, similar trends were obtained, and the minimum PR are very similar (–1.50, –1.45 and –1.48), but different than –0.78 for P1.0. This is why 2 kPa was selected to minimize the pressure imposed while producing the best NPR. Figure 5. Poisson’s ratio (Z direction) as a function of engineering strain (tension) for auxetic foams treated under different mechanical pressure at 130oC, 15 h of vacuum at −0.88 bar.
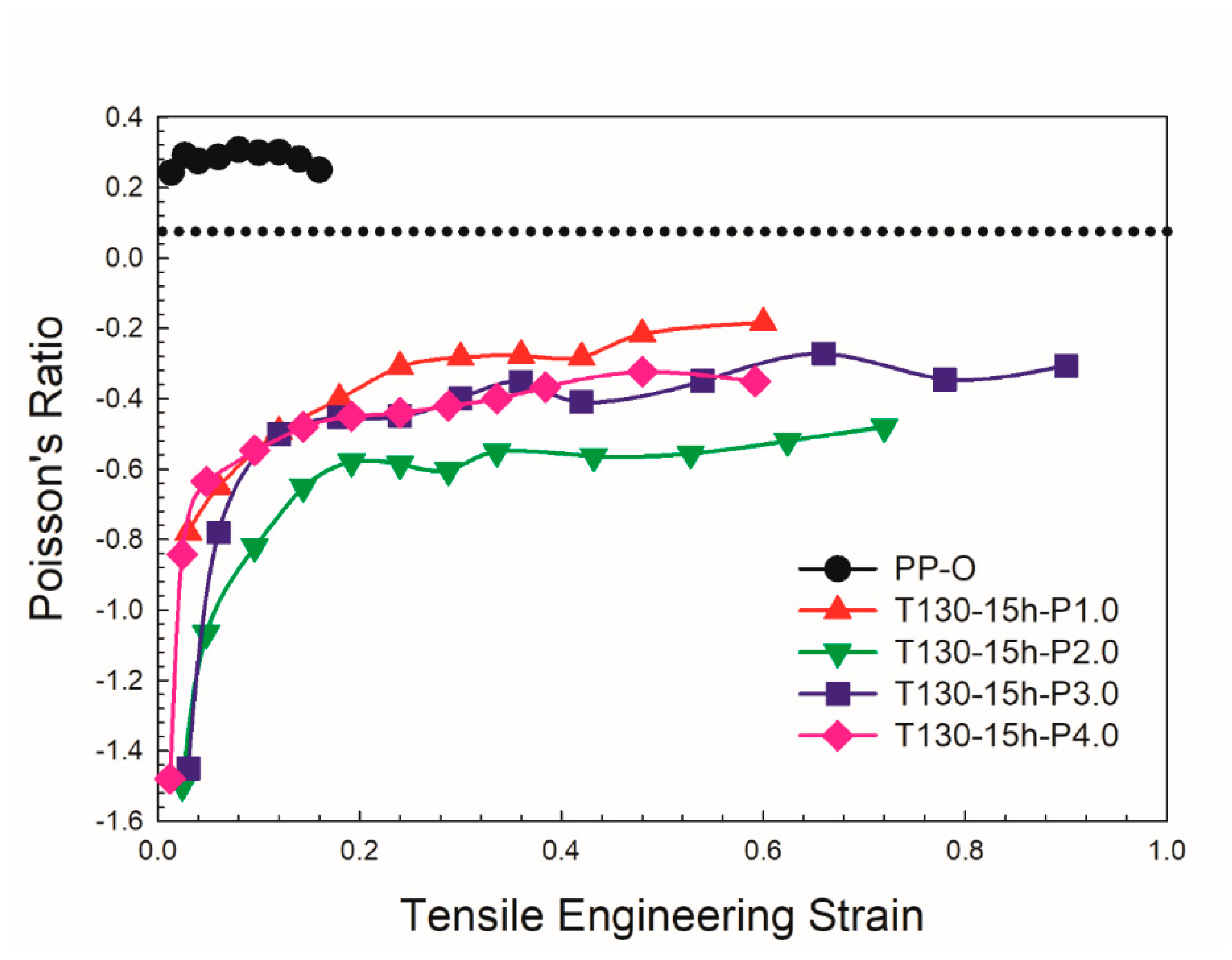
Preprints 77707 g005
Figure 5. Poisson’s ratio (Z direction) as a function of engineering strain (tension) for auxetic foams treated under different mechanical pressure at 130oC, 15 h of vacuum at −0.88 bar.
Figure 5. Poisson’s ratio (Z direction) as a function of engineering strain (tension) for auxetic foams treated under different mechanical pressure at 130oC, 15 h of vacuum at −0.88 bar.
Preprints 77707 g005
For the auxetic foams presented in Figure 5, the Poisson’s ratio was negative up to 65% of tensile engineering strain, as the PR increases with increasing engineering strain although all the curves are not linearly dependent on the axial strain. This behavior is similar to the results of Evans et al. [31] and Lake et al. [32] even if they used a different material (expanded polytetrafluoroethylene and mixed polyurethane-polyester foam, respectively) having a very different structure. But this trend has been reported several times in the literature for NPR foams [7,8,9,17,18,32,33,34]. Unfortunately, no data about PP auxetic foams have been reported in the literature to compare.
To complete the analysis, Figure 6 presents the Poisson’s ratio as a function of the compressive engineering strain for auxetic foams treated under different mechanical pressures (1.0-4.0 kPa). It can be seen that the NPR decreased from 1.0 to 2.0 kPa, but increased with increasing mechanical pressure from 3.0 to 4.0 kPa. In theory, high mechanical pressure should generate higher force to create a re-entrant structure. However, too much force compresses the foams and the cells collapse leading to higher densities (Table 1) and losing the auxetic behavior. So, again here, the optimum result is obtained at 2.0 kPa (similar to Figure 5 for tension). In this case, the PR increases with compressive engineering strain and remains negative up to a strain of 40%. This trend is consistent with the findings of Choi et al. [32] and Lisieck et al. [34], even if their original materials were a mixture of closed and open-cell polyurethane-polyester foam (density of 30 kg/m3) and open-cell PU foam (density of 25.3 kg/m3). The trend is also nonlinear with respect to the axial compressive strain owing to the complex relationships existing between the re-entrant structure (cell geometry and size), imposed deformation and resulting Poisson’s ratio.
Preprints 77707 g006
Figure 6. Poisson’s ratio as a function of engineering strain (compression) for PP-O and auxetic foams treated for different mechanical pressure at 130oC and 15 h vacuum time.
Figure 6. Poisson’s ratio as a function of engineering strain (compression) for PP-O and auxetic foams treated for different mechanical pressure at 130oC and 15 h vacuum time.
Preprints 77707 g006
Table 3 reports on the minimum PR under tension and compression as a function of the compression ratio. The best condition was found to be a compression ratio of 4.14 for PP-T130-15-P2.0 yielding a minimum PR of –1.50 in tension and –0.32 in compression. It is worth mentioning that the PR (absolute value) is always lower in compression compared to tension, which is similar as for rigid plastic foams [31].
Table 3. Properties of the auxetic samples based on PP foams.
Table 3. Properties of the auxetic samples based on PP foams.
Sample Final density (kg/m3) Compression ratio (⍴f/⍴o) Minimum PR (tension) Minimum PR (compression)
PP-O 28.0 1 0.28 (mean) 0.008 (mean)
PP-T130-15-P1.0 114 4.07 –0.78 –0.28
PP-T130-15-P2.0 116 4.14 –1.50 –0.32
PP-T130-15-P3.0 130 4.64 –1.45 –0.08
PP-T130-15-P4.0 131 4.68 –1.48 –0.02

3.2.4. Mechanical properties

In order to complete the mechanical analysis of the auxetic foams produced, Figure 7 compares the stress-strain curves and quasi-static cyclical curves in tension and compression before and after treatment. Figure 7A presents the tensile engineering stress as a function of engineering strain for both conventional and re-entrant foams. The corresponding values of tensile modulus, strength, strain at break and energy at break are listed in Table 4. The Young’s modulus of PP-O is 19.9 kPa, which is lower than that of all auxetic PP foams. This can be attributed to the higher final density of the treated samples. Additionally, the Young’s modulus, tensile strength and energy absorption all increase with increasing final foam density as expected for Young’s modulus, which is directly proportional to the amount of material (density) available to sustain the applied stresses [35,36,37]. The toughness (energy absorption) of the foams also increased with density [38]. Furthermore, substantially higher elongation at break for the auxetic foams (62-77%) was obtained compared to PP-O (28%).
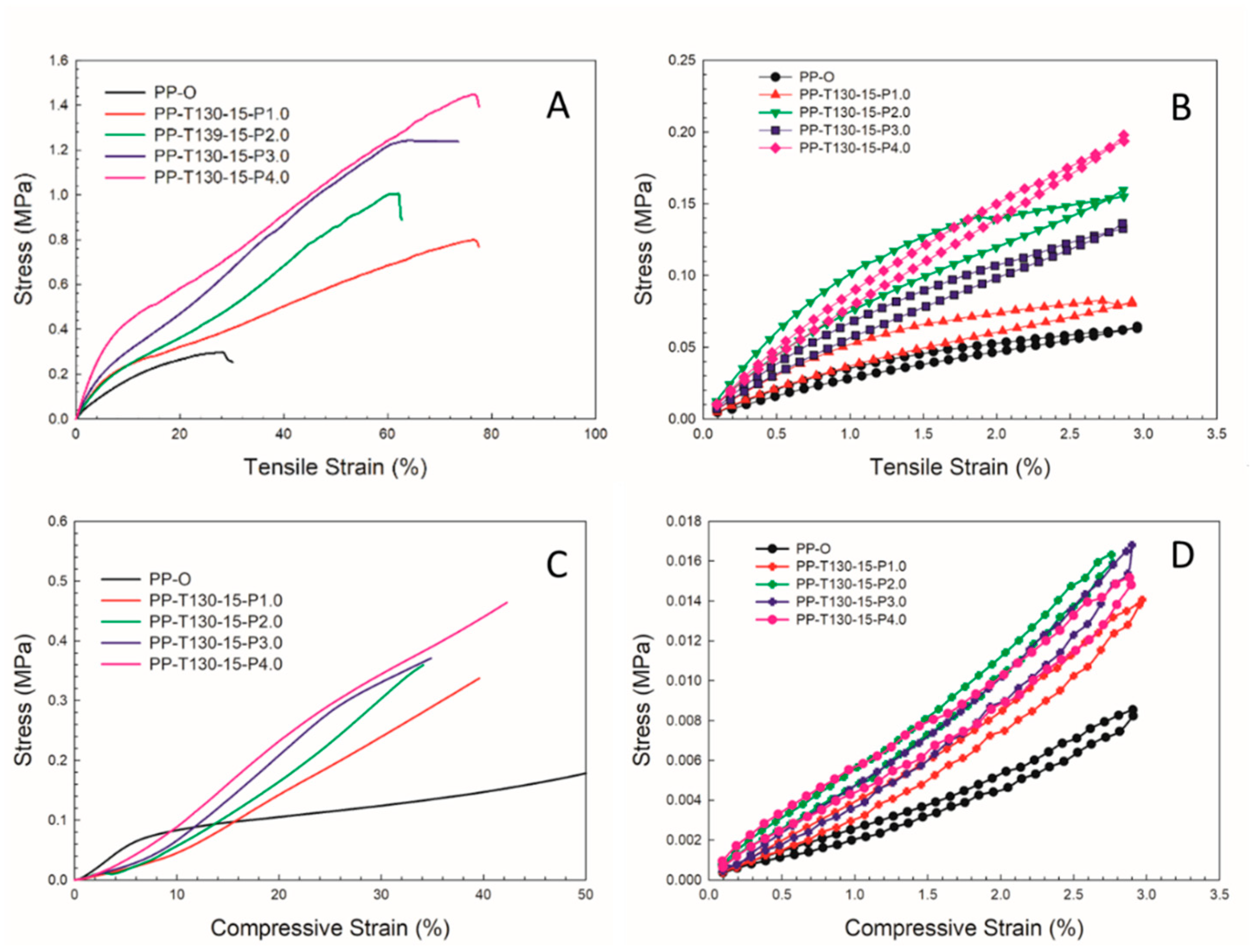
Preprints 77707 g007
Figure 7. Engineering stress as a function of compressive strain for the original and re-entrant (auxetic) foams: A) Tensile stress-strain plots, B) tensile hysteresis loops, C) compressive stress-strain plots and D) compressive hysteresis loops.
Figure 7. Engineering stress as a function of compressive strain for the original and re-entrant (auxetic) foams: A) Tensile stress-strain plots, B) tensile hysteresis loops, C) compressive stress-strain plots and D) compressive hysteresis loops.
Preprints 77707 g007
Table 4. Tensile and compressive properties of the PP auxetic foams produced.
Table 4. Tensile and compressive properties of the PP auxetic foams produced.
Samples Density
(kg/m3)		 Tension Compression
Modulus (kPa) Strength
(MPa)		 Strain at break
(%)		 Energy at break
(MPa)		 Modulus (kPa) Stress at 30% strain (kPa)
PP-O 28.0 21.9±2.8 0.30±0.07 28.1±3.2 6.10±0.61 10.8±2.5 125±43
PP-T130-15-P1.0 114 35.2±2.9 0.80±0.08 62.0±6.1 34.5±1.2 2.52±4.5 247±39
PP-T130-15-P2.0 116 40.3±7.3 1.00±0.09 76.7±5.8 37.5±2,6 2.72±4.9 308±41
PP-T130-15-P3.0 130 44.4±8.3 1.24±0.07 70.2±7.2 57.0±4.3 4.63±5.3 331±38
PP-T130-15-P4.0 131 51.1±6.9 1.43±0.08 72.9±6.9 68.1±5.4 8.06±6.7 349±39
For compressive tests (Figure 7C), the compressive modulus of PP-O was higher than that of all the auxetic foams. The curve of PP-O is composed of two regions: a linear elastic part and a plateau region. At small deformation, the stress and strain are proportional which is associated to cell walls bending. But at larger deformation (plateau region), the foam collapses under compression with negligible stress increase which is associated with cell walls buckling. This is why auxetic foams do not exhibit any plateau region since the ribs are already bend inwards (re-entrant structure) and only continue to bend rather than buckle. Therefore, the compressive modulus of the modified foams are lower. But the strength at 30% strain has a similar trend as in tension, which is increasing with increasing final foam density.
Quasi-static cyclic tensile and compressive tests were carried out to characterize the hysteresis cycle. Figure 7B,D present representative hysteresis cycles (stress-strain curves) for the original and auxetic foams. Table 5 shows that the maximum potential energy (Ep) depends on the sample density and cell structure (cell size and open cell percent). The values ranged from 120 to 170 and 316 kPa in tension for the original and auxetic foams. The energy loss (Ed) has a similar trend with strain energy which is improving from 14.4 to 50.3 mJ/cm3 leading to a damping capacity improvement from 12 to 19%. In compression, similar trends are observed for the strain energy (11.5 to 19.8 kPa) and energy loss (1.56 to 3.6 mJ/cm3). The presence of hysteresis loops (Figure 7B,D) confirms the typical energy dissipation (Ed) behavior of these materials under slow deformation. The damping capacity is the ability of a material to absorb vibration (cyclic stress) using internal friction and converting the mechanical energy into heat. The damping capacities in compression of the auxetic foams are higher or similar than those of the original foams.
Table 5. Strain energy, hysteresis properties (energy loss) and damping capacity of the samples produced.
Table 5. Strain energy, hysteresis properties (energy loss) and damping capacity of the samples produced.
Sample Tension Compression
Strain energy (Ep) (kPa) Energy loss
(Ed) (mJ/cm3)		 Damping capacity (Ψ) (%) Strain energy (Ep) (kPa) Energy loss
(Ed) (mJ/cm3)		 Damping capacity (Ψ) (%)
PP-O 120 14.4 12.0 11.5 1.56 13.6
PP-T130-15-P1.0 170 21.5 12.6 15.3 3.60 18.7
PP-T130-15-P2.0 166 31.7 19.2 19.8 1.97 10.0
PP-T130-15-P3.0 316 39.5 12.5 18.8 2.00 10.7
PP-T130-15-P4.0 309 50.3 16.2 19.0 3.34 17.5

4. Conclusions

In this study, a novel and eco-friendly approach was proposed to upcycle low density polypropylene (PP) foams (28 kg/m3) into auxetic foams having slightly higher densities (90-131 kg/m3). This was done by applying a thermo-mechanical treatment leading to the production of a re-entrant cellular structure. A systematic approach was used to optimize the effect of different processing conditions: 15 h of vacuum (–0.88 bar) at 130oC under 2 kPa of mechanical pressure.
The auxetic foams produced were shown to have superior mechanical properties compared to the original (non-auxetic) sample. Under tension, the auxetic foams exhibited a minimum tensile Poisson’s ratios of –1.50, while the values was only –0.32 under compression. More importantly, the tensile elongation at break increased from 28% up to 76%. Finally, the auxetic foams presented a hysteresis behavior under cyclic loading indicating that they are good materials for damping properties.
So these auxetic foams have high potential to be used as shock absorbers/energy mitigation in defense applications, such as behind armor padding, as well as in the production of protective sporting equipment (knee/elbow pads and helmet liners). However, more work is still required to apply these results to other polymers and for a wider range of density to further improve on their mechanical properties and potential applications.

Acknowledgments

This work was supported in part by funding from the Innovation for Defense Excellence and Security (IDEaS) program from the Department of National Defense (DND) of Canada, grant CFPMN1-032.

References

  1. Yang, C.; Zhang, Q.; Zhang, W.; et al. High thermal insulation and compressive strength polypropylene microcellular foams with honeycomb structure. Polym. Degrad. Stabil. 2021, 183, 109406. [Google Scholar] [CrossRef]
  2. Lee, Y.S.; Park, N.H.; Yoon, H.S. Dynamic Mechanical Characteristics of Expanded Polypropylene Foams. J. Cell. Plast. 2010, 46, 43–55. [Google Scholar]
  3. Polypropylene Foam Market Size, Share & Trends Analysis, By Type (Expanded polypropylene (EPP) foams, Extruded polypropylene (XPP) foams, Type (Density Basis)), By End Use (Automotive, Packaging, Consumer products), By Region and Forecast Period 2023–2030. https://straitsresearch.com/report/polypropylene-foam-market (access on 10 may,2023).
  4. Meran, C.; Ozturk, O.; Yuksel, M. Examination of the possibility of recycling and utilizing recycled polyethylene and polypropylene. Mater. Des. 2008, 29, 701–705. [Google Scholar] [CrossRef]
  5. Corvaglla, P.; Passaro, A.; Manni, O.; Barone, L. Recycling of PP-based Sandwich Panels with Continuous Fiber Composite Skins. J. Thermoplast. Compos. Mater. 2006, 19, 731–745. [Google Scholar] [CrossRef]
  6. Hamdi, O.; Rodrigue, D. Auxetic Polymer Foams: Production, Modeling and Applications. Curr. Appl. Polym. Sci. 2021, 4, 159–174. [Google Scholar] [CrossRef]
  7. Chen, X.Y.; Hamdi, O.; Rodrigue, D. Conversion of low-density polyethylene foams into auxetic metamaterials. Polym Adv Technol. 2023, 34, 228–237. [Google Scholar] [CrossRef]
  8. Chen, X.Y.; Underhill, R.S.; Rodrigue, D. A Simple Method to Convert Cellular Polymers into Auxetic Metamaterials. Appl. Sci. 2023, 13, 1148. [Google Scholar] [CrossRef]
  9. Chen, X.Y.; Rodrigue, D. Conversion of polystyrene foams into auxetic metamaterials. Polym Eng Sci. 2023, 1–11. [Google Scholar] [CrossRef]
  10. Bianchi, M.; Scarpa, F.; Banse, M.; Smith, C.W. Novel generation of auxetic open cell foams for curved and arbitrary shapes. Acta. Mater., 2011, 59, 686–691. [Google Scholar] [CrossRef]
  11. Bianchi, M.; Scarpa, F.; Smith, C.W. Stiffness and energy dissipation in polyurethane auxetic foams. J. Mater. Sci. 2008, 43, 5851. [Google Scholar] [CrossRef]
  12. Bianchi, M.; Scarpa, F.; Smith, C.W. Shape memory behaviour in auxetic foams: Mechanical properties. Acta Mater 2010, 58, 858–865. [Google Scholar] [CrossRef]
  13. Bianchi, M.; Frontoni, F.; Scarpa, F.; C. W. Smith, Density change during the manufacturing process of PU–PE open cell auxetic foams. Phys. Status Solidi B, 2011, 248, 30–38. [Google Scholar] [CrossRef]
  14. Zhang, Q.; Lu, W.; Scarpa, F.; et al. Large stiffness thermoformed open cell foams with auxeticity. Appl. Mater. Today, 2020, 20, 100775. [Google Scholar] [CrossRef]
  15. Zhang, Q.; Lu, W.; Scarpa, F.; et al. Topological characteristics and mechanical properties of uniaxially thermoformed auxetic foam. Mater. Des. 2021, 211, 110139. [Google Scholar] [CrossRef]
  16. Zhang, Q.; Yu, X.; Scarpa, F.; et al. Anisotropy in conventional and uniaxially thermoformed auxetic polymer foams. Composites Part B 2022, 237, 109849. [Google Scholar] [CrossRef]
  17. Duncan, O.; Allen,T. ; Birch, A.; et al. Effect of steam conversion on the cellular structure, Young’s modulus and negative Poisson’s ratio of closed-cell foam. Smart Mater. Struct. 2020, 30, 015031. [Google Scholar] [CrossRef]
  18. Duncan, O.; Leslie1, G.; Moyle, S.; et al. Developments on auxetic closed cell foam pressure vessel fabrications. Smart Mater. Struct. 2022, 31, 074002. [Google Scholar] [CrossRef]
  19. Fan, D.; Li, M.; Qiu, J.; et al. Novel Method for Preparing Auxetic Foam from Closed-Cell Polymer Foam Based on the Steam Penetration and Condensation Process. ACS. Appl. Mater. Interfaces 2018, 10, 22669–22677. [Google Scholar] [CrossRef]
  20. Martz, E.O.; Lee, T.; Lakes, R.S.; et al. Re-entrant transformation of methods in closed cell foams. Cellular Polymers 1996, 15, 229–249. [Google Scholar]
  21. Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
  22. Li, N.; Liu, Z.; Shi, X.; et al. Preparing Polypropylene Auxetic Foam by a One-Pot CO2 Foaming Process. Adv. Eng. Mater. 2022, 24, 2100859. [Google Scholar] [CrossRef]
  23. Chirima, G.; Ravirala, N.; Rawal, A.; et al. The effect of processing parameters on the fabrication of auxetic extruded polypropylene films. Phys. Stat. Sol. (b) 2008, 245, 2383–2390. [Google Scholar] [CrossRef]
  24. Alderson, K.; Nazaré, S.; Alderson, A. Large-scale extrusion of auxetic polypropylene fiber. Phys. Status. Solid. (b) 2016, 253, 1279–1287. [Google Scholar]
  25. Gee, D.R. and Melia, T.P. Thermal Properties of melt and solution crystallized isotactic polypropylene. Makromol. Chem. 1970, 132, 195. [Google Scholar] [CrossRef]
  26. Critchley, R. Corni, I.；Wharton, J.A.; et al. A review of the manufacture, mechanical properties and potential applications of auxetic foams. Phys. Status. Solid. 2013, 250, 1963. [Google Scholar] [CrossRef]
  27. Frioui, N.; Bezazi, A.; Remillat, C.; et al. Viscoelastic and compression fatigue properties of closed cell PVDF foam. Mech. Mater 2010, 42, 189. [Google Scholar] [CrossRef]
  28. Belaadi, A.; Bezazi, A.; Bourchak, M.; Scarpa, F. Tensile static and fatigue behaviour of sisal fibres. Mater. Des. 2012, 46, 76–83. [Google Scholar] [CrossRef]
  29. Panin, S.V.; Bogdanov, A.A.; Eremin, A.V.; et al. Estimating Low- and High-Cyclic Fatigue of Polyimide-CF-PTFE Composite through Variation of Mechanical Hysteresis Loops. Materials 2022, 15, 4656. [Google Scholar] [CrossRef]
  30. Andena, L.; Caimmi, F.; Leonardi, L.; Nacucchi, M. and De Pascalis, F. Compression of polystyrene and polypropylene foams for energy absorption applications: A combined mechanical and microstructural study. J. Cell. Plast. 2019, 55, 49–72. [Google Scholar] [CrossRef]
  31. Rinde, J.A. Poisson’s Ratio for Rigid Plastic Foams. J. Appl. Polym. Sci. 1970, 14, 1913–1926. [Google Scholar] [CrossRef]
  32. Caddock, B.D.; Evans, K.E. Microporous materials with negative Poisson’s ratios. I. Microstructure and mechanical properties. J. Phys. D. Appl. Phys. 1989, 22, 1877–1882. [Google Scholar] [CrossRef]
  33. Choi, J.B. and Lakes, R.S. Nonlinear properties of polymer cellular materials with a negative Poisson’s ratio. J. Materials Science 1992, 27, 4678–4684. [Google Scholar] [CrossRef]
  34. Lisiecki, J.; Błażejewicz, T.; Kłysz, S.; et al. Tests of polyurethane foams with negative Poisson’s ratio. Phys. Stat. Sol. B. 2013, 250, 250,1988–1995. [Google Scholar] [CrossRef]
  35. Li, D.W.; Zhou, L.W.; Wang, X.; He, L.J.; Yang, X. Effect of crystallinity of polyethylene with different densities on breakdown strength and conductance property. Materials. 2019, 12, 1746. [Google Scholar] [CrossRef] [PubMed]
  36. Bezazi, A.; Scarpa, F. Tensile fatigue of conventional and negative Poisson’s ratio open cell PU foams. Int J Fatigue. 2009, 31, 488–494. [Google Scholar] [CrossRef]
  37. Bianchi, M.; Scarpa, F.; Smith, C.W. Shape memory behaviour in auxetic foams: mechanical properties. Acta Mater. 2010, 58, 858–865. [Google Scholar] [CrossRef]
  38. Zhang, Y.L.; Rodrigue, D.; Ait-Kadi, A. High density polyethylene Foams. II. Elastic modulus. J Appl Polym Sci. 2003, 90, 2130–2138. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated