Prerpints.org logo
Preprint
Article

Prediction Mechanical Properties of Magnesium Matrix Composites with Regression Models by Machine Learning

Altmetrics

Downloads

149

Views

78

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 June 2023

Posted:

27 June 2023

You are already at the latest version

Alerts
Abstract
Magnesium matrix composites have attracted significant attention due to their lightweight nature and impressive mechanical properties. However, the fabrication process for these alloy compo-sites is often time-consuming, expensive, and labor-intensive. To overcome these challenges, this study employed machine learning (ML) techniques to predict the mechanical properties of magnesium matrix composites. Regression models were utilized to forecast the yield strength of magnesium alloy composites reinforced with various materials. The study incorporated previous research on matrix type, reinforcement type, heat treatment, and mechanical working. The re-gression models employed in this study included decision tree regression, random forest re-gression, extra tree regression, and XGBoost regression. Model performance was assessed using metrics such as RMSE and R2. The XGBoost Regression model out-performed others, exhibiting an R2 value of 0.94 and the lowest error rate. Feature importance analysis indicated that the rein-forcement particle form had the greatest influence on the mechanical properties. The study iden-tified the optimized parameters for achieving the highest yield strength, which was 186.99 MPa. Overall, this study successfully demonstrates the effectiveness of ML as a valuable tool for opti-mizing the production parameters of magnesium matrix composites.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Magnesium alloys are lightweight materials with many industrial applications due to their high rigidity, strength, and excellent castability. They are lighter (lower density) than other metals such as aluminum and steel, have excellent damping capacity, a high recycling rate, and are easy to machine. Additionally, they are a viable alternative material for aerospace and automotive components [1,2]. AE (Aluminum-Rare Metal Earth), AM (Aluminum-Manganese), AS (Aluminum-Silicon), and AZ (Aluminum-Zinc) are types of magnesium alloy-based element systems.
Aluminum-zinc elements are commonly used as magnesium alloying elements because they are advantageous, inexpensive, and highly soluble. The addition of aluminum to magnesium alloys can increase the strength and melting point of the alloy. In addition to aluminum, zinc can increase magnesium alloy strength without diminishing ductility, casting fluidity, or corrosion resistance [3,4,5]. AZ Magnesium alloys can be made into metal matrix composites by incorporating ceramic reinforcements in micro and/or nano forms, such as silicon carbide (SiC), tungsten carbide (WC), tungsten disulfide (WS2) and others [6,7,8,9]. Beside ceramic reinforcement, there is also graphene (carbon-based material) and eggshell (biomaterial) used for magnesium composite reinforcement [10,11].
In most cases, magnesium matrix composites are produced by stir casting, and there are some additional experimental methods to improve their mechanical properties, such as heat treatment and mechanical working (extrusion and equal channel angular pressing). [12,13]. Despite the potential for improvement through experimentation, the production of magnesium matrix composites poses some challenges, such as being time-consuming, expensive, and labor-intensive. Therefore, a new method is needed to address these challenges using machine learning, given the benefits of development magnesium matrix composites [14].
Machine Learning (ML) technology is a branch of artificial intelligence, and this is the current trend to develop research in materials. For the design and discovery of novel materials for a variety of applications, ML has been viewed as a promising tool. There are different types of ML algorithms that can be used to accelerate composite material research [15,16]. Regression methods are one of the method that can be used to predict the mechanical properties. There are several regression models from machine learning to predict such as decision tree regression, random forest regression, extra tree regressor, and xgboost regression; consequently, these model are used to obtain yield strength [17,18].
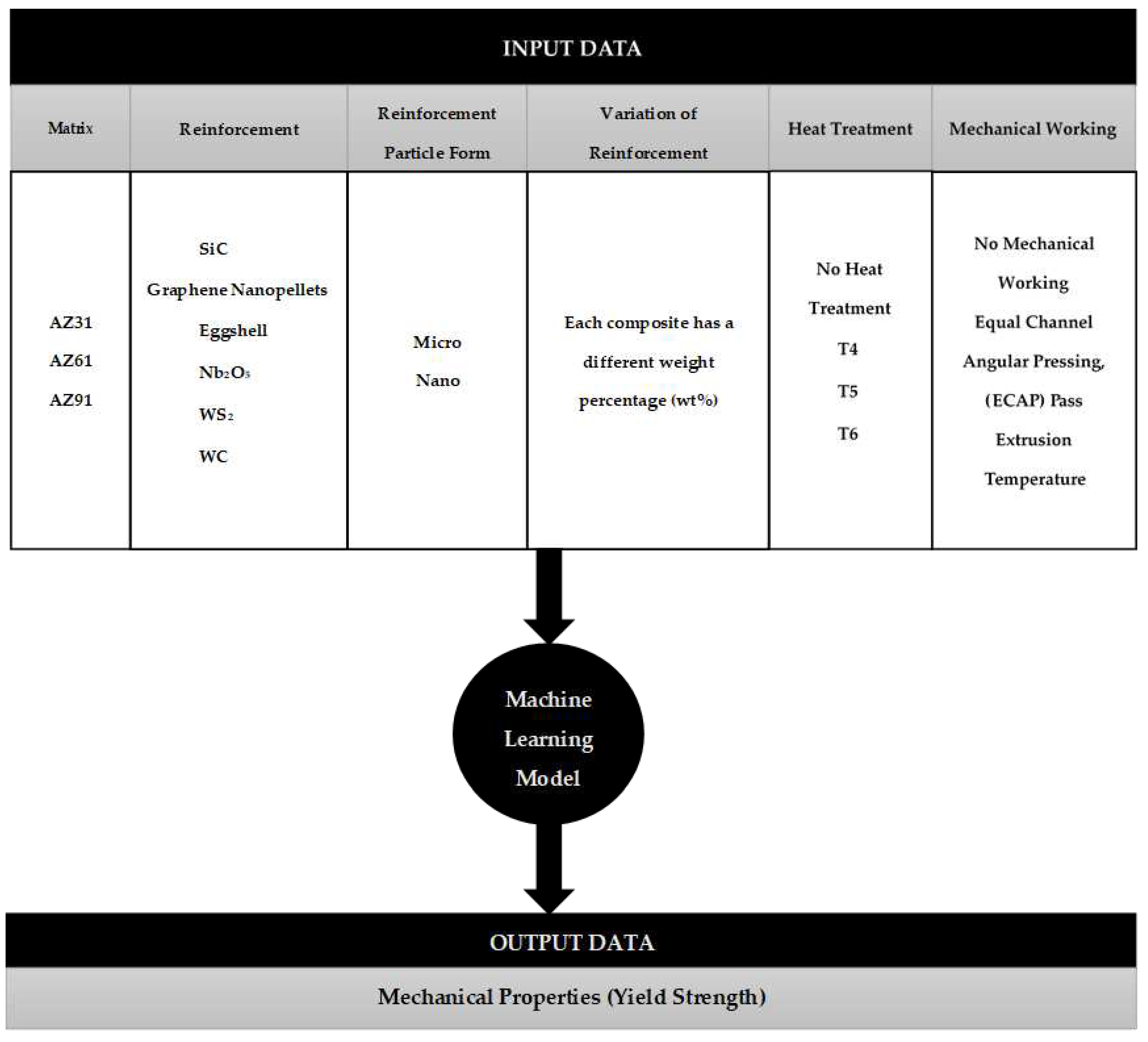
Various input parameters, including matrix type, reinforcement type, heat treatment, and mechanical working, can be used to predict the mechanical properties. The output parameters are the mechanical properties of the materials, such as yield strength. Each regression machine learning model has its own strengths and limitations. Therefore, in this research, machine learning will be employed to predict mechanical properties using the best regression model algorithm, which utilizes data from previous research.

2. Machine Learning Regression Algorithm Model

Regression algorithm models are used to predict mechanical properties because this model can establish relationships between independent variables such as matrix and reinforcement and then the dependent variable, such as mechanical properties (yield strength). Independent variables can be input parameters, and dependent variables can be output parameters. The output parameter, yield strength, is a continuous variable, so the regression model is fitted to predict continuous output [19,20,21]. The yield strength (YS) refers to the point at which a material undergoes plastic deformation and fails to revert to its initial shape once the applied stress is eliminated. This property is important because it characterizes the highest stress of the material before permanent deformation, and this property is always used by engineers [22].
There are several regression models that can be applied for prediction, including decision tree regression, random forest regression, extra tree regression, and XGBoost regression. These models have been successfully utilized in previous research to predict the mechanical properties of various materials. For instance, Rajput et al. [19] employed various regression algorithm models, including the four models mentioned earlier, to predict the mechanical properties of ultimate tensile strength in aluminum metal matrix hybrid composites. The best-performing model among them was decision tree regression, which achieved an R2 value of 0.92909. Similarly, Seungmi Kwak et al. [14] used a random forest regression model to predict the mechanical properties of titanium aluminum (TiAl) alloy, and the results were evaluated using R2 values for tensile strength, elongation, nanoindentation hardness, and interlamellar space, which were 0.9336, 0.9902, 0.8104, and 0.9810, respectively. 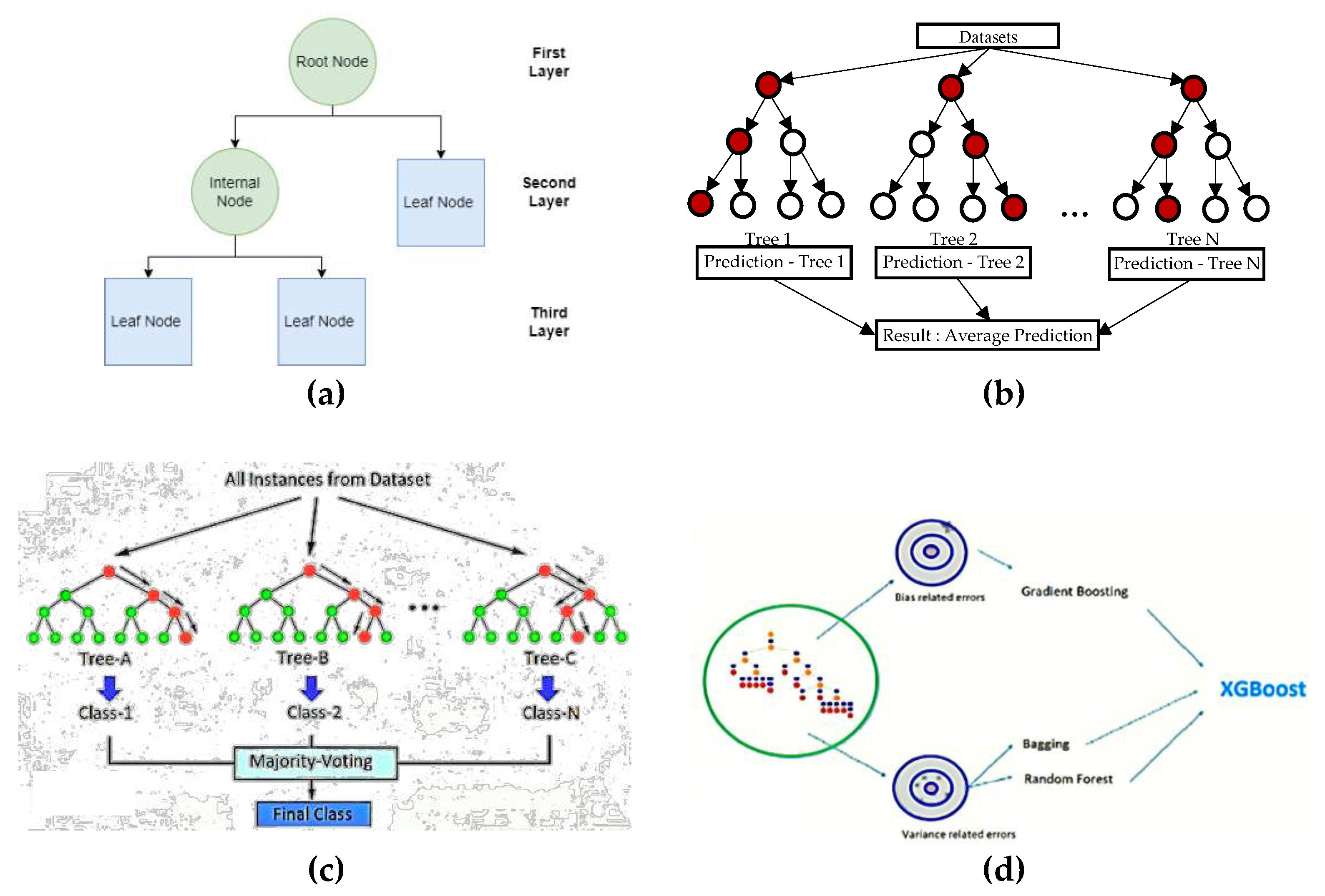Figure 1 displays the graphical representation of four different regression models.
The decision tree model can be visualized as a tree-like structure, as depicted in Figure 1a, where it mirrors a flowchart with nodes symbolizing the evaluation of features, as cited in [23]. Through this approach, it has the capacity to segregate a dataset into branches that together form an upside-down tree consisting of a root node, internal nodes, and leaf nodes. The root node signifies an initial decision that leads to the division of the entire data into two or more distinct groups. The internal nodes symbolize the subsequent choices made within the tree framework. Leaf nodes represent the final outcome achieved through a series of decisions.
Decision tree regression is a variant of the decision tree model specifically for dealing with complex non-linear relationships, in contrast to decision tree classification. The algorithm aims to divide the data in a manner that reduces the total sum of the squared differences between the data points and the average within each division. Through this method, the algorithm transforms a multifaceted decision-making procedure into a series of more manageable decisions, which are illustrated as a tree structure [26].
Random Forest Regression employs the foundational concept of decision trees, but takes it a step further by constructing multiple decision trees and their predictions to yield a more precise and robust estimation. It is adept at handling both classification and regression problems. As depicted in Table 2, the generalization error tends to plateau with an increase in the number of trees, indicating that Random Forest does not succumb to overfitting even when employing a larger number of trees [27].
Extra Tree Regression is a machine learning algorithm which is an extension of the Random Forest algorithm. However, similar to Random Forest, Extra Trees builds an ensemble of decision trees. However, while Random Forest uses bootstrapping to create different training datasets for each tree, Extra Trees trains each tree on the whole training dataset so making it less likely to overfit the data compared with random forest [25]. XGBoost is an advanced adaptation of the gradient boosting algorithm, and it is highly regarded for its high computations and outstanding performance. From Table 1, it is mentioned that XgBoost Regression is extremely fast because it combines the concept of Gradient Boosting Machine and cause based decision trees [26].
Table 1. Regression Models with Strengths and Limitations [27,28,29,30].
Table 1. Regression Models with Strengths and Limitations [27,28,29,30].
Algorithm Model Strengths Limitations
Decision Trees Regression Simple computation;
easy to understand and
interpret, 		Easy to overfit; Neglects
correlation among data
Extra Tree Regression Computational Efficiency Similar to Random Forest
Random Forest Regression It can be utilized for both predicting numerical values (regression) and categorizing data (classification) without the necessity to standardize the features
Clear of over-fitting.		 No Interpretability
Performance is not good when there is class imbalance.
XGBoost Regression Feature preparation, such as filling in missing values or tweaking the size and span of features, is not required.
It can be used for tasks like sorting data into categories, making predictions on numbers, or putting things in a specific order.
It is extremely fast and highly effective for its ability to do multiple calculations simultaneously		 For numeric features only.
Leads to overfitting if hyperparameters are not adjusted

3. Materials and Methods

3.1. Materials

In this study, we collected data from previous research papers on AZ31, AZ61, and AZ91 magnesium alloy composites with various reinforcements. All of these composites were fabricated using the stir casting process. The data collected from previous research had different parameters to obtain the mechanical properties, so these problems can be input as parameters for prediction with machine learning, and the collected data is presented in Table 2. The data consists of six input parameters: matrix, reinforcement, reinforcement particle form, variation of reinforcement, heat treatment, and mechanical working. The output parameter is the mechanical properties of the material, and the parameter diagram is shown in Figure 2.
Table 2. The Data from Previous Literature.
Table 2. The Data from Previous Literature.
Matrix Reinforcement Source
AZ31 SiC [7]
AZ31 Graphene Nanopellets [10]
AZ31 Eggshell [11]
AZ31 Nb2O5 (Niobium Pentoxide) [31]
AZ61 WS2 [32]
AZ61 SiC [33,34,35,36]
AZ91 WS2 [9,37,38]
AZ91 WC [8]

3.2. Methods

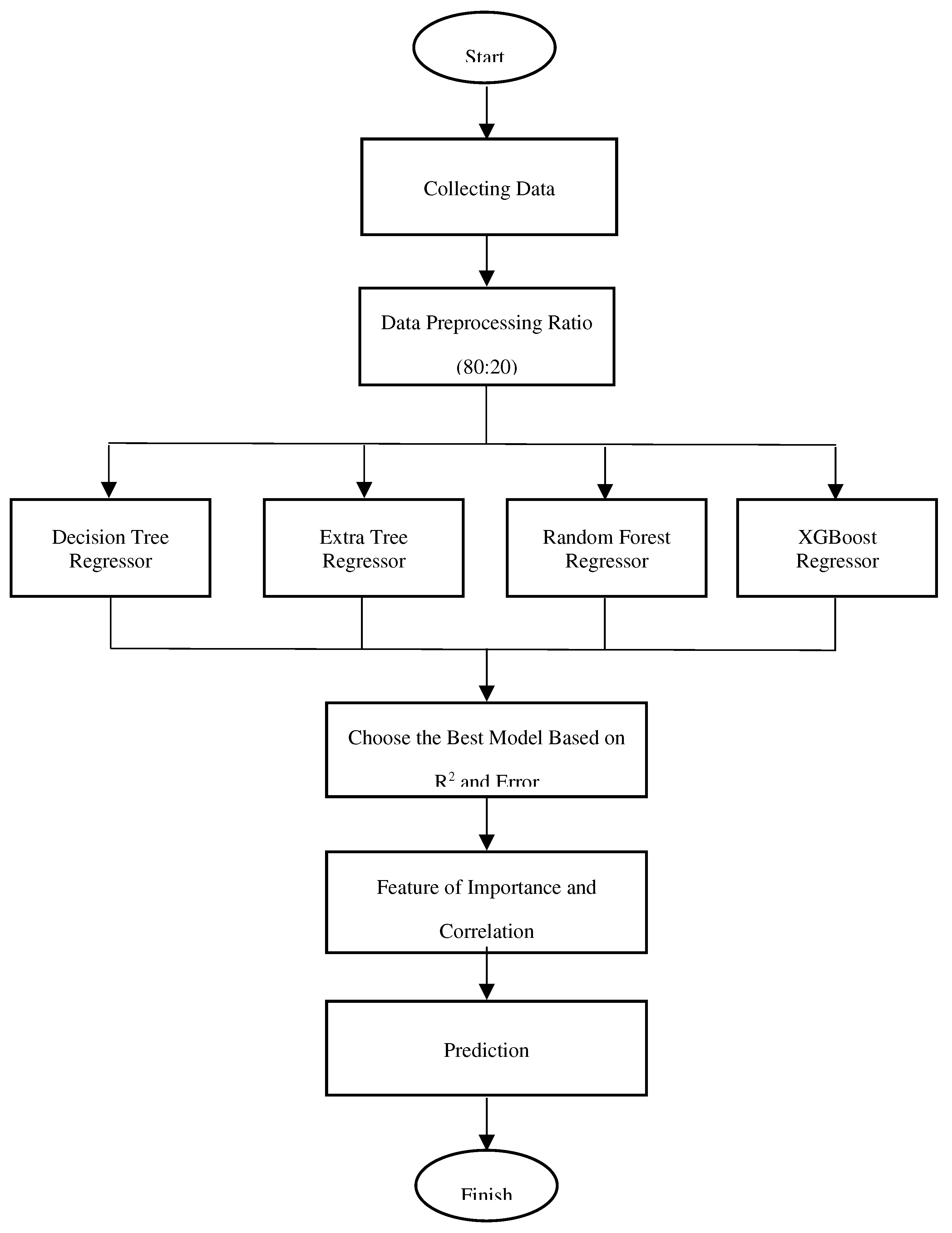
The data was analyzed using machine learning employing various regression methods, which are particularly adept at predicting continuous data, such as mechanical properties. The dataset was split into training and testing subsets in an 80:20 ratio and subjected to 10 random cycles. The Python programming language was used to implement the regression model algorithms. Through this research, we developed several regression models, including the Decision Tree Regressor, Extra Tree Regressor, Random Forest Regressor, and XGBoost Regressor. Figure 3 shows the flowchart of this study.
To determine which model offers the most accurate and reliable predictions, an evaluation of model performance was conducted. In this step, the previous regression models were assessed using various mathematical formulas. Within these formulas, Xi denotes the predicted ith value, while Yi represents the actual ith value from the ground-truth dataset. One of the equations used was the Mean Absolute Error (MAE), as shown in Equation 1, which calculates the average of the absolute differences between the predicted and actual values.
MAE = 1 m   ∑ i = 1 m X i − Y i
Equation (2) displays the RMSE, or root mean square error, which is the average root squared difference between the actual and predicted values, and equation 3 displays the coefficient of determination (R2 or R-squared), which can be interpreted as the proportion of the variance in the dependent variable that can be predicted from the independent variables (accuracy). Based on all model performance evaluations, the best model was chosen based on the highest R2 and smallest error [16,19,39].
RMSE = 1 m ∑ i = 1 m ( X i − Y i ) 2
R 2 = 1   -   ∑ i = 1 m ( X i − Y i ) 2 ∑ i = 1 m ( Y ¯ − Y i ) 2

4. Results and Discussion

4.1. Evaluation Based Error and R2

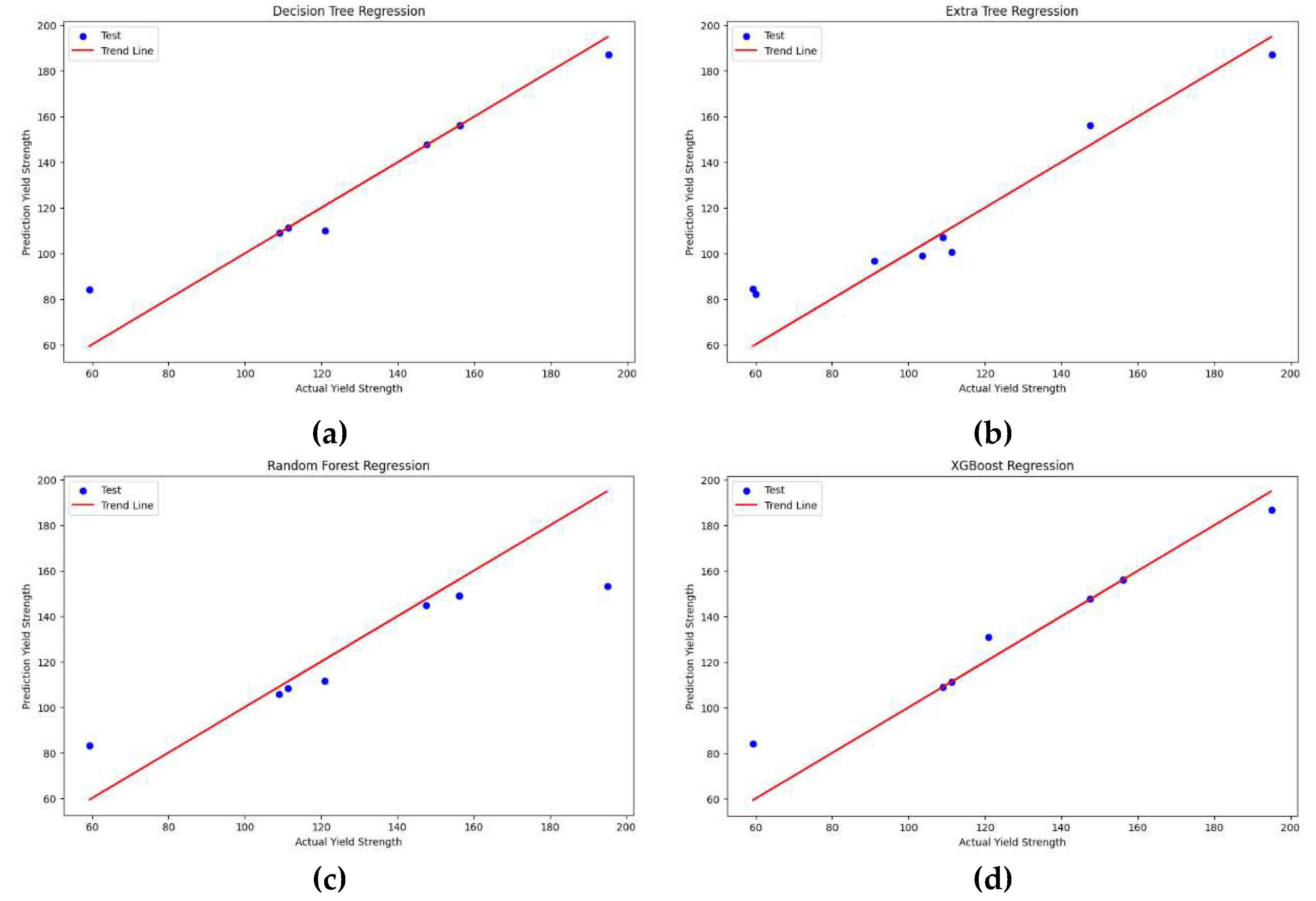
The datasets consist of six parameter input values and one parameter output value that were predicted with four different regression models. Each of the regression results has a different error and R2 value, so the best model was chosen to predict the data. The results of actual and predicted values can be seen in the Figure 4 with four different regression models. Each regression had a different prediction mechanical properties and affects the trend line of the graph (regression line). Based on the graph, it can be seen that the test data values on Figure 4b,c are not too close to the trend line. Meanwhile, the test data values on Figure 4a,d are closer to the trend line. These results can be related to the accuracy of the data that was scored by R2 (the coefficient of determination) [40].
Preprints 77641 g004
Figure 4. Graph of Predicted Yield Strength vs Actual Yield Strength with different regression model (a) Decision Trees Regression (b) Extra Tree Regression (c) Random Forest Regression (d) XGBoost Regression.
Figure 4. Graph of Predicted Yield Strength vs Actual Yield Strength with different regression model (a) Decision Trees Regression (b) Extra Tree Regression (c) Random Forest Regression (d) XGBoost Regression.
Preprints 77641 g004
The quality fit of the regression models was first assessed using R². The model with the highest accuracy will be selected as the best model. If the values of R² vary between 0 and 1, then the model partially predicts the outcome. If R² reaches 1, then the model perfectly predicts the outcome. Table 3 below shows how to interpret the value of R². The closer R² is to one, the greater the proportion of the total variation in the predicted values that is explained by the independent variable [41].
However, in this study, we also accommodate the error rates of each model using MAE and RMSE as they are the commonly used in machine learning studies. It’s important to note that evaluating the performance of regression models by considering the values of these error rates individually can be misleading. This is because each of these metrics provides a different perspective on the errors and does not give a complete picture of how well the model is performing [39]. Therefore, we were considering R² in conjunction with MAE and RMSE. R² provides insight into how much of the variability in the dependent variable can be explained by the model, while MAE and RMSE give perspectives on the magnitude and distribution of errors.
Table 4 shows the evaluation of four different regression models. The highest R2 in XGBoost regression was about 0.94, and this model also had the smallest error-based MAE, and RMSE of about 8.81 and 10.42. The smallest R2 in random forest regression with R2 was about 0.80, with the biggest error-based MAE and RMSE of about 18.63 and 14.21. Based on Table 3, it can be concluded that only the random forest regression model exhibits a high level of influence, as indicated by an R2 value below 0.82. Although the other models have closeness levels higher than 0.82, the XGBoost regression model stands out as the best among all the results. It exhibits the highest R2 value and the smallest error, making it the preferred choice for data prediction. Furthermore, a value closer to 1 indicates a strong fit with close agreement between the predicted values and the actual values [44].

4.2. Feature of Importance and Correlation Matrix

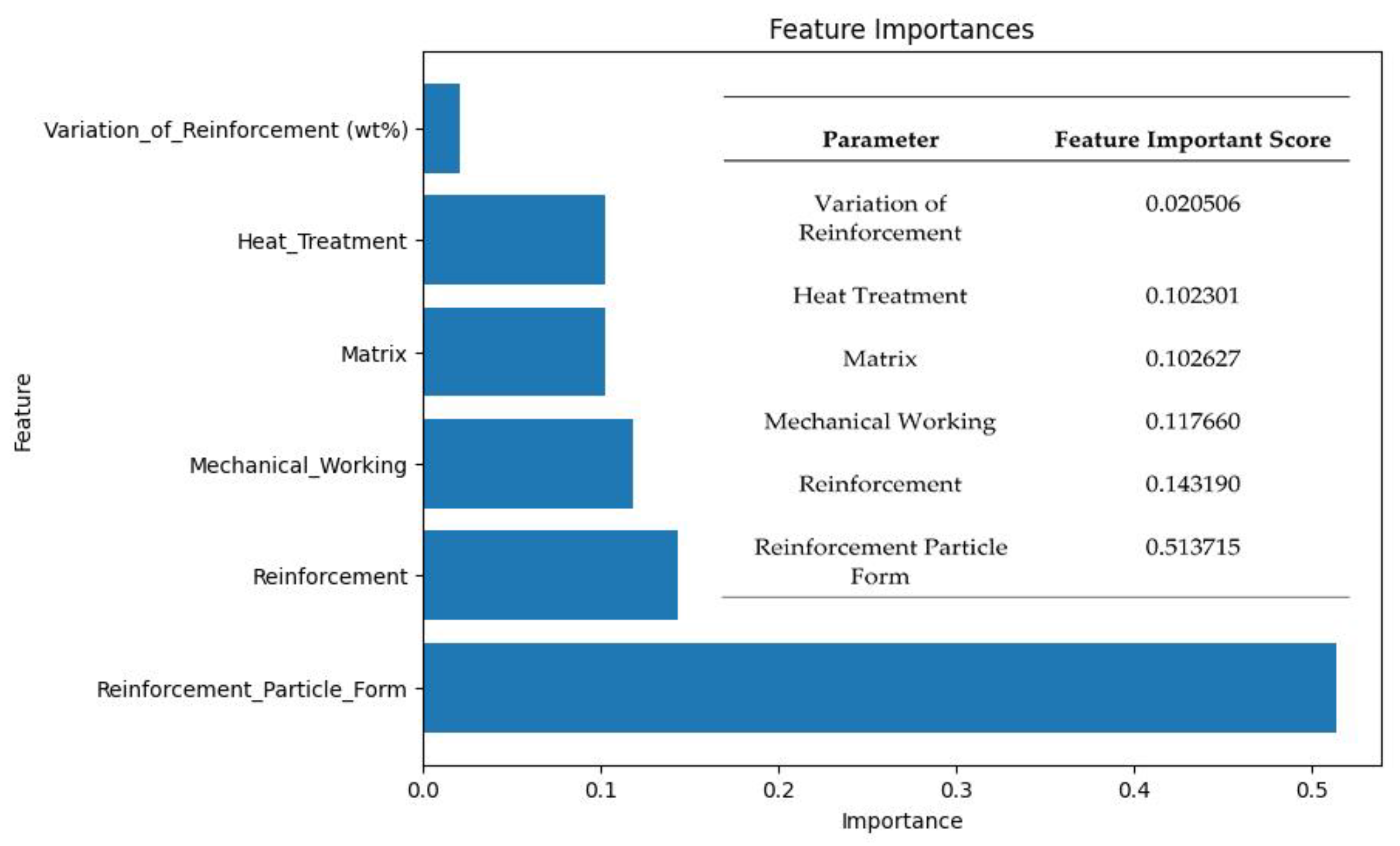
A feature of importance indicates the contribution of each feature (input parameter) to the model's output parameter [42]. The feature importance analysis from the best model (XGBoost regression) reveals that the parameter with the highest influence on the predicted mechanical properties was the reinforcement particle form, while the variation of reinforcement had the least influence. Figure 4 provides detailed information regarding the importance of the features.
The feature importance scores indicate that the reinforcement particle form had a score of 0.513715, indicating its strong impact on the properties. This finding is consistent with the review paper by Haotian Guan et al. [43] which concluded that the form of reinforcement particles, whether in micro or nano size, significantly influenced the mechanical properties of magnesium composites.
Preprints 77641 g005
Figure 4. Feature of Importance.
Figure 4. Feature of Importance.
Preprints 77641 g005
The reinforcement particle form in the dataset was classified as either micro or nano. In comparison to micro-sized particles, nano-sized particles are smaller. This size difference causes nano-sized particles to have a greater surface-to-volume ratio. As a result, nano-sized reinforcement particles tend to result in materials with enhanced mechanical properties. This is due to the fact that the increased surface area permits enhanced interfacial bonding and strengthening effects, resulting in improved mechanical performance.
On the basis of the feature importance analysis, it can be concluded that the selection of nano-sized reinforcement particles, with their associated higher surface volume ratio, significantly contributes to the improvement of the material's mechanical properties [44].
The second most influential parameter was reinforcement, with a score of 0.143190. The dataset for magnesium composites included reinforcements made of various materials, each with distinct properties [45]. These materials encompass ceramics, carbon-based materials, and biomaterial. Following reinforcement, the third most influential parameter was mechanical working, scoring 0.117660, followed by the matrix with a score of 0.102627. The fourth parameter was heat treatment with a score of 0.102301, and the fifth was the variation of reinforcement with a score of 0.020506.
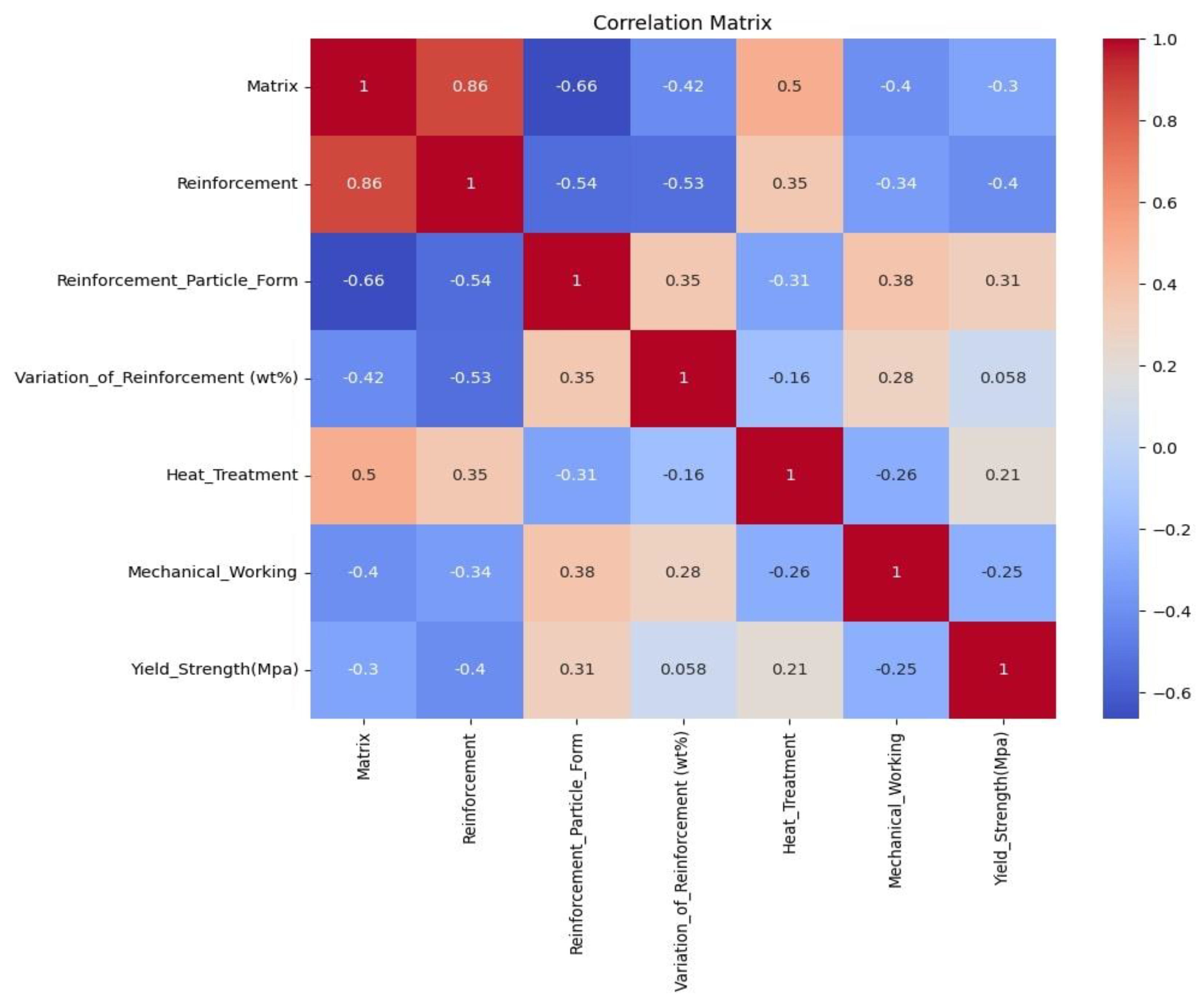
Figure 5 shows the correlation matrix, showcasing the correlation values among all parameters. The graph utilizes color coding to represent the values, with darker shades of red indicating a positive correlation (>0) between variables, and darker shades of blue indicating a negative correlation (<0). The correlation coefficient value is approximately 1. Notably, positive correlations were observed between matrix and heat treatment, reinforcement and heat treatment, reinforcement particle form and yield strength, mechanical working and variation of reinforcement, heat treatment and yield strength, mechanical working and variation of reinforcement, as well as yield strength and variation of reinforcement. These positive correlations suggest a strong relationship between these variables [46].

4.3. Prediction with Optimization

This study also involves predicting the optimization of materials through the regression model. It was found that the form of reinforcement particles is the most important feature for optimizing to achieve the highest yield strength, while variation in reinforcement is the least significant. Table 5 shows that the optimal parameters involve using an AZ31 matrix with Graphene Nanopellets (GNP) as reinforcement, in nanoparticle form, with 3 wt%, without heat treatment, and an extrusion temperature of 350°C for mechanical working. With these optimized parameters, we might achieve the highest yield strength predicted by the regression model, which is 186.99 MPa.
The results from the regression model support the theory of metal matrix composite material fabrication. Other research has mentioned that using graphene nano-pellets in the form of particles with a certain weight percentage might increase the mechanical properties [47]. The extrusion temperature also affects the mechanical properties, as using a specific temperature for mechanical working is important [48]. However, past studies haven't been able to link each parameter in order to achieve the highest yield strength. This study successfully utilizes the XGBoost Regression model to determine the optimal combination of parameters required for fabricating magnesium matrix composites using stir casting, incorporating the parameters obtained from this study.

5. Conclusions

This study focused on predicting the mechanical properties of magnesium matrix composites with four different regression model algorithms using machine learning with six input parameters and one output parameter. So, we can conclude:
  • XGBoost Regression proved to be the most effective in predicting the yield strength of magnesium alloy composites among the four regression models. It exhibited an R² value of approximately 0.94. Its superiority was further supported by the lowest error rates in MAE and RMSE, with values of 8.19 and 10.42, respectively.
  • Feature importance analysis revealed that the form of reinforcement particles, specifically nano-sized particles, had the most substantial influence on the mechanical properties of magnesium alloy composites. This is attributed to the increased surface-to-volume ratio of nano-sized particles which enhanced the strengthening effect of the composite.
  • The optimized parameters for achieving the highest yield strength in magnesium alloy composites were the use of the AZ31 matrix with Graphene Nano Pellets (GNP) as reinforcement, in nanoparticle form, with a 3 wt%. No heat treatment was applied, and the mechanical working was conducted at an extrusion temperature of 350°C.

Author Contributions

Conceptualization, S.-J.H., validation, S.-J.H. and Y.A.; formal analysis, S.-J. H., Y.A. and J.S.; Resources, Y.A. and J.S.; writing—original draft preparation, Y.A. and J.S.; writing—review and editing, S.-J.H. and Y.A.; visualization, Y.A. and J.S.; supervision, S.-J.H.; All authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Huang, S.; Subramani, M.; Alemayehu, D.B. THE EFFECT OF MICRO-SICP CONTENT ON THE TENSILE AND FATIGUE BEHAVIOR OF AZ61 MAGNESIUM ALLOY MATRIX COMPOSITES. International Journal of Metalcasting 2021, 15, 780–793, doi:10.1007/s40962-020-00508-0.
  2. Jeng, S.; Abbas, A.; Ballóková, B. Effect of CNT on Microstructure , Dry Sliding Wear and Compressive Mechanical Properties of AZ61. Integr Med Res 2019, 1–14, doi:10.1016/j.jmrt.2019.07.037.
  3. Gupta, M.; Sharon, N.M.L. MAGNESIUM , MAGNESIUM ALLOYS , AND MAGNESIUM COMPOSITES; 2011; ISBN 9780470494172.
  4. Somekawa, H. Review Effect of Alloying Elements on Fracture Toughness and Ductility in Magnesium Binary Alloys ; A Review. Mater Trans 2020, 61, 1–13, doi:10.2320/matertrans.MT-M2019185.
  5. Tan, J.; Ramakrishna, S. Applications of Magnesium and Its Alloys : A Review. 2021, doi:10.20944/preprints202105.0512.v1.
  6. Yadav, S.D.; Bhingole, P.P.; Chaudhari, G.P.; Nath, S.K.; Sommitsch, C. Hybrid Processing of AZ91 Magnesium Alloy/Nano-Al2O3 Composites. In Proceedings of the Key Engineering Materials; Trans Tech Publications Ltd, 2015; Vol. 651–653, pp. 783–788.
  7. Subramani, M.; Huang, S.J.; Borodianskiy, K. Effect of SiC Nanoparticles on AZ31 Magnesium Alloy. Materials 2022, 15, doi:10.3390/ma15031004.
  8. Karuppusamy, P.; Lingadurai, K.; Sivananth, V.; Arulkumar, S. A Study on Mechanical Properties of Tungsten Carbide Reinforced Magnesium Metal Matrix Composites for the Application of Piston. International Journal of Lightweight Materials and Manufacture 2021, 4, 449–459, doi:10.1016/j.ijlmm.2021.06.007.
  9. Huang, S.J.; Abbas, A. Effects of Tungsten Disulfide on Microstructure and Mechanical Properties of AZ91 Magnesium Alloy Manufactured by Stir Casting. J Alloys Compd 2020, 817, doi:10.1016/j.jallcom.2019.153321.
  10. Rashad, M.; Pan, F.; Liu, Y.; Chen, X.; Lin, H.; Pan, R.; Asif, M.; She, J. High Temperature Formability of Graphene Nanoplatelets-AZ31 Composites Fabricated by Stir-Casting Method. Journal of Magnesium and Alloys 2016, 4, 270–277, doi:10.1016/j.jma.2016.11.003.
  11. Ramanujam, N.; Muthukumaran, S.; Nagesawara Rao, B.; Ramarao, M.; Mangrulkar, A.L.; Ashraff Ali, K.S.; Pugazhendhi, L.; Markos, M. Experimental Investigations on Mechanical Properties of AZ31/Eggshell Particle-Based Magnesium Composites. Advances in Materials Science and Engineering 2022, 2022, doi:10.1155/2022/4883764.
  12. Saranu, R.; Chanamala, R.; Putti, S. Review of Magnesium Metal Matrix Composites. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing Ltd, November 9 2020; Vol. 961.
  13. Somekawa, H.; Watari, H.; Haga, T.; Koga, N.; Davey, K.; Tan, J.; Access, O.; Kaya, A.A.; Gupta, M.; Sharon, N.M.L.; et al. A Review on Developments in Magnesium Alloys. IOP Conf Ser Mater Sci Eng 2021, 11, 289–306, doi:10.3390/met4010065.
  14. Kwak, S.; Kim, J.; Ding, H.; Xu, X.; Chen, R.; Guo, J.; Fu, H. Machine Learning Prediction of the Mechanical Properties of γ-TiAl Alloys Produced Using Random Forest Regression Model. Journal of Materials Research and Technology 2022, 18, 520–530, doi:10.1016/j.jmrt.2022.02.108.
  15. Gomes, C.P.; Selman, B.; Gregoire, J.M. Artificial Intelligence for Materials Discovery. MRS Bull 2019, 44, 538–544, doi:10.1557/mrs.2019.158.
  16. Chen, C.T.; Gu, G.X. Machine Learning for Composite Materials. MRS Commun 2019, 9, 556–566, doi:10.1557/mrc.2019.32.
  17. Bhattacharya, S.; Kalita, K.; Čep, R.; Chakraborty, S. A Comparative Analysis on Prediction Performance of Regression Models during Machining of Composite Materials. Materials 2021, 14, doi:10.3390/ma14216689.
  18. Huang, S.J.; Mose, M.P.; Kannaiyan, S. A Study of the Mechanical Properties of AZ61 Magnesium Composite after Equal Channel Angular Processing in Conjunction with Machine Learning. Mater Today Commun 2022, 33, doi:10.1016/j.mtcomm.2022.104707.
  19. Rajput, R.; Raut, A.; Gangi Setti, S. Prediction of Mechanical Properties of Aluminium Metal Matrix Hybrid Composites Synthesized Using Stir Casting Process by Machine Learning. In Proceedings of the Materials Today: Proceedings; Elsevier Ltd, January 1 2022; Vol. 59, pp. 1735–1742.
  20. Singh Tumrate, C.; Roy Chowdhury, S.; Mishra, D. Development of Regression Model to Predicting Yield Strength for Different Steel Grades. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing Ltd, August 3 2021; Vol. 796.
  21. Kadam, V.S. Regression Techniques in Machine Learning &Applications: A Review. Int J Res Appl Sci Eng Technol 2020, 8, 826–830, doi:10.22214/ijraset.2020.32019.
  22. Li, D.; Thomas, J.; Leroux, P. A Better Measure Yield and Tensile Strength; 2020;
  23. Rahman, J.; Ahmed, K.S.; Khan, N.I.; Islam, K.; Mangalathu, S. Data-Driven Shear Strength Prediction of Steel Fiber Reinforced Concrete Beams Using Machine Learning Approach. Eng Struct 2021, 233, doi:10.1016/j.engstruct.2020.111743.
  24. Lou, Y.; Ye, Y.; Yang, Y.; Zuo, W.; Wang, G.; Strong, M.; Upadhyaya, S.; Payne, C. Individualized Empirical Baselines for Evaluating the Energy Performance of Existing Buildings. Sci Technol Built Environ 2023, 29, 19–33, doi:10.1080/23744731.2022.2134680.
  25. Ahmad, M.W.; Reynolds, J.; Rezgui, Y. Predictive Modelling for Solar Thermal Energy Systems: A Comparison of Support Vector Regression, Random Forest, Extra Trees and Regression Trees. J Clean Prod 2018, 203, 810–821, doi:10.1016/j.jclepro.2018.08.207.
  26. Shehadeh, A.; Alshboul, O.; Al Mamlook, R.E.; Hamedat, O. Machine Learning Models for Predicting the Residual Value of Heavy Construction Equipment: An Evaluation of Modified Decision Tree, LightGBM, and XGBoost Regression. Autom Constr 2021, 129, doi:10.1016/j.autcon.2021.103827.
  27. Huang, J.S.; Liew, J.X.; Ademiloye, A.S.; Liew, K.M. Artificial Intelligence in Materials Modeling and Design. Archives of Computational Methods in Engineering 2021, 28, 3399–3413, doi:10.1007/s11831-020-09506-1.
  28. Liu, H.; Lang, B. Machine Learning and Deep Learning Methods for Intrusion Detection Systems: A Survey. Applied Sciences (Switzerland) 2019, 9.
  29. Liu, J.; Wu, J.; Liu, S.; Li, M.; Hu, K.; Li, K. Predicting Mortality of Patients with Acute Kidney Injury in the ICU Using XGBoost Model. PLoS One 2021, 16, doi:10.1371/journal.pone.0246306.
  30. Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach Learn 2006, 63, 3–42, doi:10.1007/s10994-006-6226-1.
  31. Huanga, S.J.; Kannaiyan, S.; Subramani, M. Effect of Nano-Nb2O5 on the Microstructure and Mechanical Properties of AZ31 Alloy Matrix Nanocomposites. Adv Nano Res 2022, 13, 407–416, doi:10.12989/anr.2022.13.4.407.
  32. Huang, S.J.; Lin, C.C.; Huang, J.Y.; Tenne, R. Mechanical Behavior Enhancement of AZ31/WS2 and AZ61/WS2 Magnesium Metal Matrix Nanocomposites. Advances in Mechanical Engineering 2018, 10, doi:10.1177/1687814017753442.
  33. Huang, S.J.; Subramani, M.; Ali, A.N.; Alemayehu, D.B.; Aoh, J.N.; Lin, P.C. The Effect of Micro-SiCp Content on the Tensile and Fatigue Behavior of AZ61 Magnesium Alloy Matrix Composites. International Journal of Metalcasting 2021, 15, 780–793, doi:10.1007/s40962-020-00508-0.
  34. Zhao, W.; Huang, S.J.; Wu, Y.J.; Kang, C.W. Particle Size and Particle Percentage Effect of AZ61/SiCp Magnesium Matrix Micro- and Nano-Composites on Their Mechanical Properties Due to Extrusion and Subsequent Annealing. Metals (Basel) 2017, 7, doi:10.3390/met7080293.
  35. Huang, S.J.; Hwang, Y.M.; Huang, Y.S.; Huang, C.C. Mechanical Properties Enhancement of Particle Reinforced Magnesium Matrix Composites Used for Hot Extruded Tubes. In Proceedings of the Acta Physica Polonica A; Polska Akademia Nauk, April 1 2015; Vol. 127, pp. 1271–1273.
  36. Huang, S.J.; Hwang, Y.M.; Huang, Y.S. Grain Refinement of AZ61/SiCp Magnesium Matrix Composites for Tubes Extruded by Hot Extrusion Processes. In Proceedings of the Key Engineering Materials; Trans Tech Publications Ltd, 2013; Vol. 528, pp. 135–143.
  37. Abbas, A.; Huang, S.J. Investigation of Severe Plastic Deformation Effects on Microstructure and Mechanical Properties of WS2/AZ91 Magnesium Metal Matrix Composites. Materials Science and Engineering A 2020, 780, doi:10.1016/j.msea.2020.139211.
  38. Abbas, A.; Huang, S.J. ECAP Effects on Microstructure and Mechanical Behavior of Annealed WS2/AZ91 Metal Matrix Composite. J Alloys Compd 2020, 835, doi:10.1016/j.jallcom.2020.155466.
  39. Chicco, D.; Warrens, M.J.; Jurman, G. The Coefficient of Determination R-Squared Is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. PeerJ Comput Sci 2021, 7, 1–24, doi:10.7717/PEERJ-CS.623.
  40. Fox J Appendices to Applied Regression Analysis, Generalized Linear Models,; Third Edition.; SAGE, 2016; ISBN 978-1-4522-0566-3.
  41. Nurunnisha, G.A.; Rohmattulah, A.; Maulansyah, M.R.; Sinaga, O.; Maulansyah, R. Analysis Of Consumer Acceptance Factors Against Fintech At Bandung Smes-Palarch’s; Vol. 17;.
  42. Rengasamy, D.; Mase, J.M.; Kumar, A.; Rothwell, B.; Torres, M.T.; Alexander, M.R.; Winkler, D.A.; Figueredo, G.P. Feature Importance in Machine Learning Models: A Fuzzy Information Fusion Approach. Neurocomputing 2022, 511, 163–174, doi:10.1016/j.neucom.2022.09.053.
  43. Guan, H.; Xiao, H.; Ouyang, S.; Tang, A.; Chen, X.; Tan, J.; Feng, B.; She, J.; Zheng, K.; Pan, F. A Review of the Design, Processes, and Properties of Mg-Based Composites. Nanotechnol Rev 2022, 11, 712–730, doi:10.1515/ntrev-2022-0043.
  44. Wu, Q.; Miao, W.S.; Zhang, Y. Du; Gao, H.J.; Hui, D. Mechanical Properties of Nanomaterials: A Review. Nanotechnol Rev 2020, 9, 259–273, doi:10.1515/ntrev-2020-0021.
  45. Shahid Ul Islam, S.; Khan, N.Z.; Khan, M.M. Effect of Reinforcement on Magnesium-Based Composites Fabricated through Stir Casting: A Review. In Proceedings of the Materials Today: Proceedings; Elsevier Ltd, 2020; Vol. 46, pp. 6513–6518.
  46. Huo, W.; Zhu, Z.; Sun, H.; Ma, B.; Yang, L. Development of Machine Learning Models for the Prediction of the Compressive Strength of Calcium-Based Geopolymers. J Clean Prod 2022, 380, doi:10.1016/j.jclepro.2022.135159.
  47. Prashantha Kumar, H.G.; Anthony Xavior, M. Graphene Reinforced Metal Matrix Composite (GRMMC): A Review. In Proceedings of the Procedia Engineering; Elsevier Ltd, 2014; Vol. 97, pp. 1033–1040.
  48. Wu, S.P.; Feng, S.Y.; Wang, J.; Li, Q.L. Effects of Extrusion Temperatures on Mechanical Properties of B4C/Al Composites. In Proceedings of the IOP Conference Series: Materials Science and Engineering; Institute of Physics Publishing, January 3 2020; Vol. 715.
Preprints 77641 g001
Figure 1. Graphical of regression model (a) Decision Trees Regression [23] (b) Extra Tree Regression [24] (c) Random Forest Regression [23] (d) XGBoost Regression [23].
Figure 1. Graphical of regression model (a) Decision Trees Regression [23] (b) Extra Tree Regression [24] (c) Random Forest Regression [23] (d) XGBoost Regression [23].
Preprints 77641 g001
Preprints 77641 g002
Figure 2. Diagram of Input Parameters and Output Parameters.
Figure 2. Diagram of Input Parameters and Output Parameters.
Preprints 77641 g002
Preprints 77641 g003
Figure 3. Flowchart of This Study.
Figure 3. Flowchart of This Study.
Preprints 77641 g003
Preprints 77641 g006
Figure 5. Correlation Matrix.
Figure 5. Correlation Matrix.
Preprints 77641 g006
Table 3. Interpretation of Coefficient Determination [41].
Table 3. Interpretation of Coefficient Determination [41].
Value of Coefficient of Determination (R2) Level of Closeness
0.82-1 Very high
0.49 – 0.81 High influence
0.17 – 0.48 Quite strong influence
0.05 – 0.16 Low Impact
0 – 0.04 Very Low
Table 4. Evaluation of Four Different Regression Models.
Table 4. Evaluation of Four Different Regression Models.
Algorithm Model MAE RMSE R2
Decision Trees Regression 8.81 11.36 0.92
Extra Tree Regression 11.01 13.37 0.89
Random Forest Regression 18.63 14.21 0.80
XGBoost Regression 8.19 10.42 0.94
Table 5. Prediction with Optimization.
Table 5. Prediction with Optimization.
Matrix Reinforcement Reinforcement Particle Form Variation of Reinforcement (wt%) Heat Treatment Mechanical Working Yield Strength
AZ31 Graphene Nanopellets Nano 3 wt% No Heat Treatment Extrusion Temperature 3500C 186.99 MPa
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated