Submitted:
26 June 2023
Posted:
27 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Topology of decamerisation
2.2. Model construction
2.3. Isothermal titration calorimetry simulations
2.4. Parameter fitting
2.5. Simulations of the Prx in the Red blood cell
2.6. Horse radish peroxidase competition assay simulations
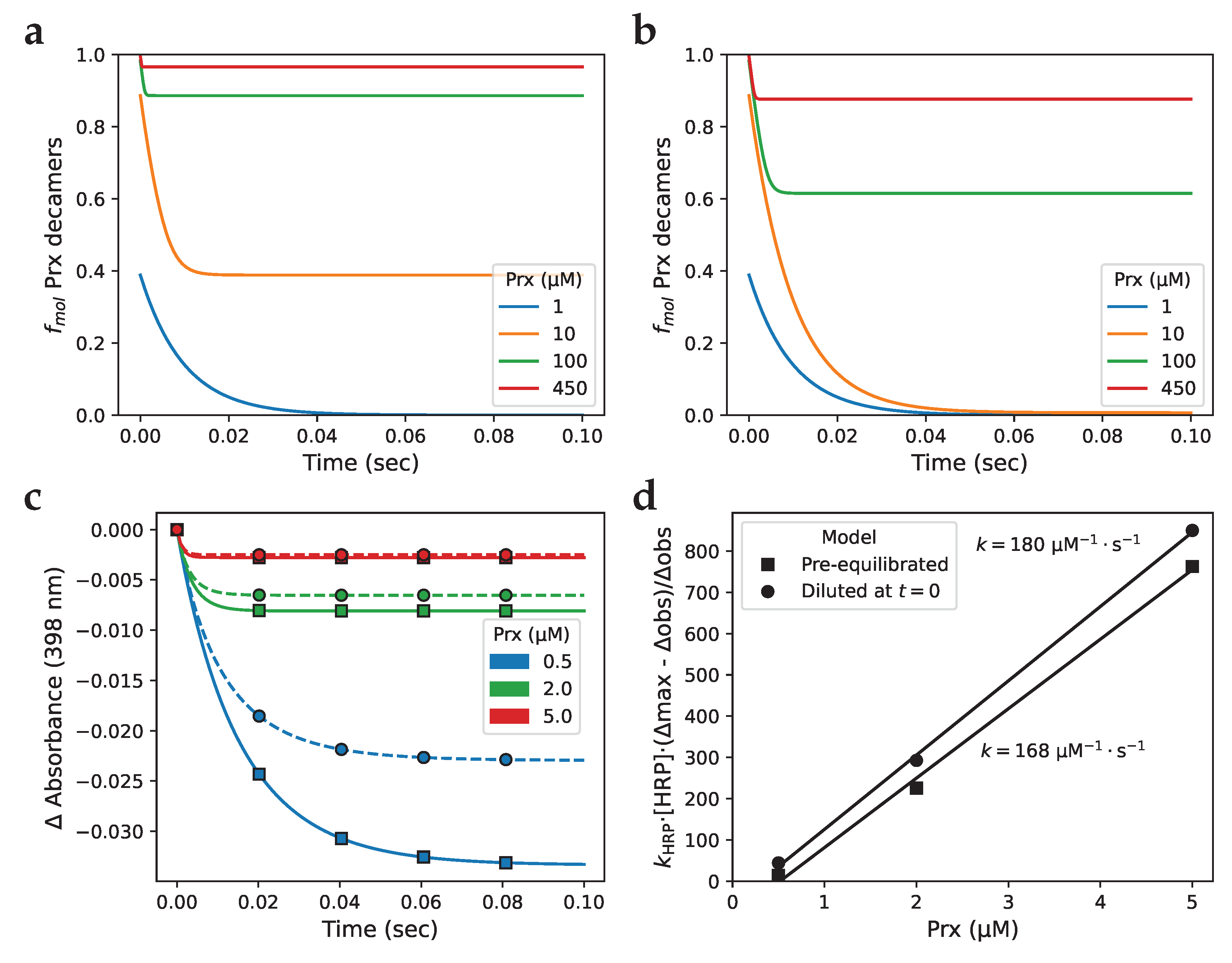
2.7. Time to reach equilibrium after dilution simulations
2.8. Whole system assay simulations
3. Results
3.1. Modelling Prx with and without decamer
3.2. Models of Prx decamerisation
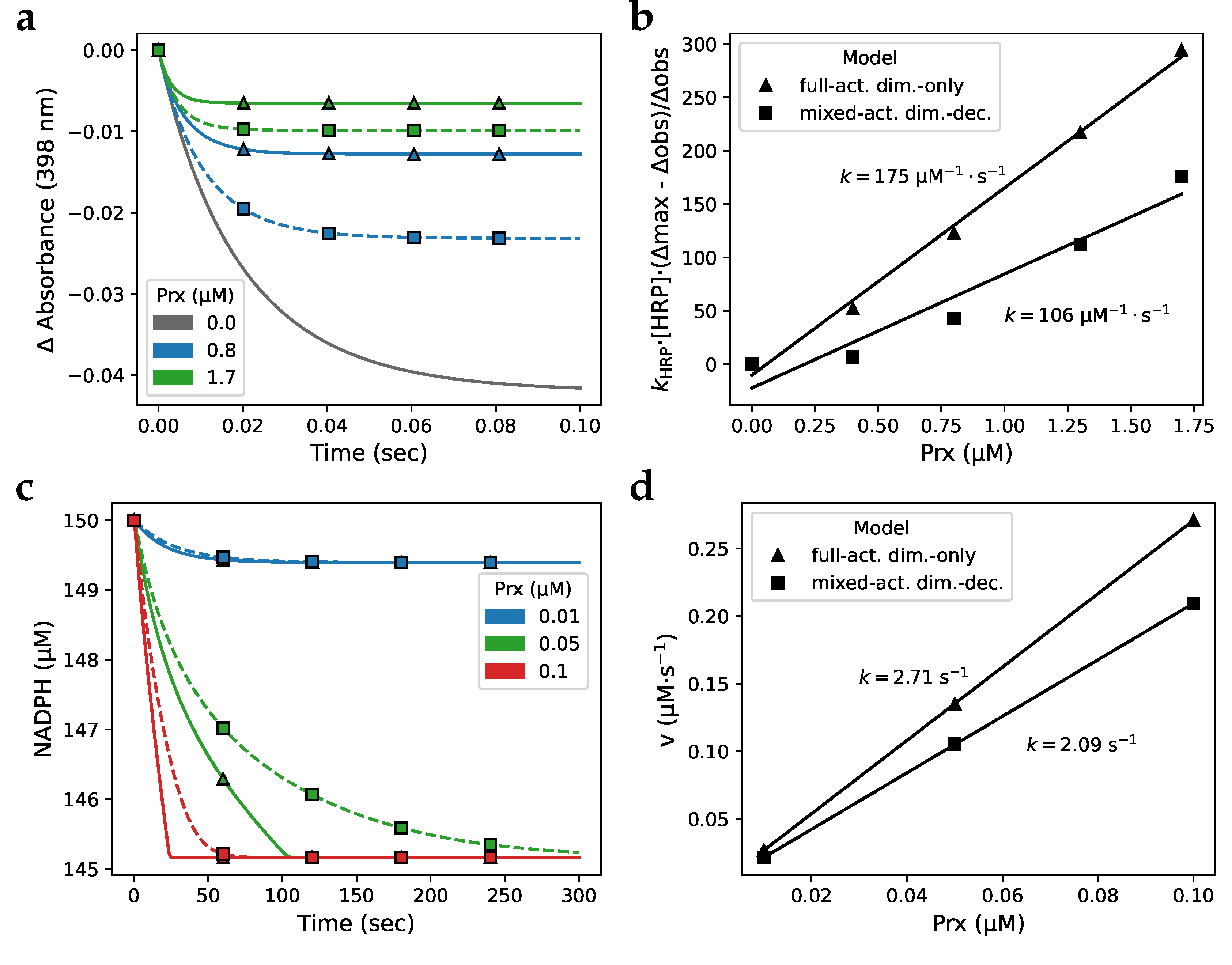
3.3. Isothermal titration calorimetry simulation
3.4. Fitting and
3.5. Enumerating the molecular states of decameric Prx
3.6. Comparing the Prx red blood cell model (Benfeitas et al. 2014) with and without decamerisation
3.7. Incorporating Prx decamers lowers activity
3.8. Diluting Prx can influence peroxidase activity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CTC | critical transition threshold |
| FF | fully folded |
| HRP | horse radish peroxidase |
| ITC | isothermal titration calorimetry |
| LU | locally unfolded |
| Prx | peroxiredoxin |
| RBC | red blood cell |
| SH | reduced peroxiredoxin site |
| SOH | sulfenilated peroxiredoxin site |
| SOOH | sulfinilated peroxiredoxin site |
| SS | disulfide-bridge peroxiredoxin site |
| TRR | thioredoxin reductase |
| Trx | thioredoxin |
References
- Harris, J. Release of a macromolecular protein component from human erythrocyte ghosts. BBA - Biomembranes 1968, 150, 534–537. [Google Scholar] [CrossRef]
- Chae, H.; Rhee, S. A thiol-specific antioxidant and sequence homology to various proteins of unknown function. BioFactors 1994, 4, 177–180. [Google Scholar]
- Schröder, E.; Littlechild, J.; Lebedev, A.; Errington, N.; Vagin, A.; Isupov, M. Crystal structure of decameric 2-Cys peroxiredoxin from human erythrocytes at 1.7 Å resolution. Structure 2000, 8, 605–615. [Google Scholar] [CrossRef]
- Alphey, M.; Bond, C.; Tetaud, E.; Fairlamb, A.; Hunter, W. The structure of reduced tryparedoxin peroxidase reveals a decamer and insight into reactivity of 2Cys-peroxiredoxins. Journal of Molecular Biology 2000, 300, 903–916. [Google Scholar] [CrossRef] [PubMed]
- Wood, Z.; Poole, L.; Hantgan, R.; Karplus, P. Dimers to doughnuts: Redox-sensitive oligomerization of 2-cysteine peroxiredoxins. Biochemistry 2002, 41, 5493–5504. [Google Scholar] [CrossRef]
- Parsonage, D.; Youngblood, D.; Sarma, G.; Wood, Z.; Karplus, P.; Poole, L. Analysis of the link between enzymatic activity and oligomeric state in AhpC, a bacterial peroxiredoxin. Biochemistry 2005, 44, 10583–10592. [Google Scholar] [CrossRef] [PubMed]
- Barranco-Medina, S.; Kakorin, S.; Lázaro, J.; Dietz, K.J. Thermodynamics of the dimer-decamer transition of reduced human and plant 2-cys peroxiredoxin. Biochemistry 2008, 47, 7196–7204. [Google Scholar] [CrossRef] [PubMed]
- Villar, S.; Dalla-Rizza, J.; Möller, M.; Ferrer-Sueta, G.; Malacrida, L.; Jameson, D.; Denicola, A. Fluorescence lifetime phasor analysis of the decamer–dimer equilibrium of human peroxiredoxin 1. International Journal of Molecular Sciences 2022, 23. [Google Scholar] [CrossRef] [PubMed]
- Munhoz, D.; Netto, L. Cytosolic thioredoxin peroxidase I and II are important defenses of yeast against organic hydroperoxide insult: Catalases and peroxiredoxins cooperate in the decomposition of H2O2 by yeast. Journal of Biological Chemistry 2004, 279, 35219–35227. [Google Scholar] [CrossRef]
- Ogusucu, R.; Rettori, D.; Munhoz, D.; Soares Netto, L.; Augusto, O. Reactions of yeast thioredoxin peroxidases I and II with hydrogen peroxide and peroxynitrite: Rate constants by competitive kinetics. Free Radical Biology and Medicine 2007, 42, 326–334. [Google Scholar] [CrossRef]
- Manta, B.; Hugo, M.; Ortiz, C.; Ferrer-Sueta, G.; Trujillo, M.; Denicola, A. The peroxidase and peroxynitrite reductase activity of human erythrocyte peroxiredoxin 2. Archives of Biochemistry and Biophysics 2009, 484, 146–154. [Google Scholar] [CrossRef] [PubMed]
- Low, F.; Hampton, M.; Peskin, A.; Winterbourn, C. Peroxiredoxin 2 functions as a noncatalytic scavenger of low-level hydrogen peroxide in the erythrocyte. Blood 2007, 109, 2611–2617. [Google Scholar] [CrossRef] [PubMed]
- Bayer, S.; Maghzal, G.; Stocker, R.; Hampton, M.; Winterbourn, C. Neutrophil-mediated oxidation of erythrocyte peroxiredoxin 2 as a potential marker of oxidative stress in inflammation. FASEB Journal 2013, 27, 3315–3322. [Google Scholar] [CrossRef] [PubMed]
- Benfeitas, R.; Selvaggio, G.; Antunes, F.; Coelho, P.; Salvador, A. Hydrogen peroxide metabolism and sensing in human erythrocytes: A validated kinetic model and reappraisal of the role of peroxiredoxin II. Free Radical Biology and Medicine 2014, 74, 35–49. [Google Scholar] [CrossRef] [PubMed]
- Tomalin, L.; Day, A.; Underwood, Z.; Smith, G.; Dalle Pezze, P.; Rallis, C.; Patel, W.; Dickinson, B.; Bähler, J.; Brewer, T.; et al. Increasing extracellular H2O2 produces a bi-phasic response in intracellular H2O2, with peroxiredoxin hyperoxidation only triggered once the cellular H2O2-buffering capacity is overwhelmed. Free Radical Biology and Medicine 2016, 95, 333–348. [Google Scholar] [CrossRef] [PubMed]
- Pérez, F.; Granger, B.E. IPython: A system for interactive scientific computing. Computing in Science & Engineering 2007, 9, 21–29. [Google Scholar] [CrossRef]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.E.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.B.; Grout, J.; Corlay, S.; et al. Jupyter Notebooks – a publishing format for reproducible computational workflows. In Positioning and Power in Academic Publishing: Players, Agents and Agendas. Proceedings of the 20th International Conference on Electronic Publishing; pp. 201687–90. [CrossRef]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; 2009.
- Olivier, B.G.; Rohwer, J.M.; Hofmeyr, J.H.S. Modelling cellular systems with PySCeS. Bioinformatics 2005, 21, 560–561. [Google Scholar] [CrossRef]
- van der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy array: A structure for efficient numerical computation. Computing in Science & Engineering 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P.; et al. SciPy: Open source scientific tools for Python, 2001.
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the Proceedings of the 9th Python in Science Conference; van der Walt, S.; Millman, J., Eds., 2010, pp. 56–61. [CrossRef]
- Newville, M.; Otten, R.; Nelson, A.; Stensitzki, T.; Ingargiola, A.; Allan, D.; Fox, A.; Carter, F. ; Michał. ; Osborn, R.; et al. lmfit/lmfit-py: 1.1.0 2022. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research 2011, 12, 2825–2830. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Computing in Science & Engineering 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Keating, S.M.; Waltemath, D.; König, M.; Zhang, F.; Dräger, A.; Chaouiya, C.; Bergmann, F.T.; Finney, A.; Gillespie, C.S.; Helikar, T.; et al. SBML Level 3: an extensible format for the exchange and reuse of biological models. Mol Syst. Biol. 2020, 16, e9110. [Google Scholar] [CrossRef] [PubMed]
- Wood, Z.; Schröder, E.; Harris, J.; Poole, L. Structure, mechanism and regulation of peroxiredoxins. Trends in Biochemical Sciences 2003, 28, 32–40. [Google Scholar] [CrossRef] [PubMed]
- Wood, Z.; Poole, L.; Hantgan, R.; Karplus, P. Dimers to doughnuts: Redox-sensitive oligomerization of 2-cysteine peroxiredoxins. Biochemistry 2002, 41, 5493–5504. [Google Scholar] [CrossRef]
- Yang, K.S.; Kang, S.; Woo, H.; Hwang, S.; Chae, H.; Kim, K.; Rhee, S. Inactivation of human peroxiredoxin I during catalysis as the result of the oxidation of the catalytic site cysteine to cysteine-sulfinic acid. Journal of Biological Chemistry 2002, 277, 38029–38036. [Google Scholar] [CrossRef]
- Chang, T.S.; Jeong, W.; Woo, H.; Sun, M.; Park, S.; Sue, G. Characterization of mammalian sulfiredoxin and its reactivation of hyperoxidized peroxiredoxin through reduction of cysteine sulfinic acid in the active site to cysteine. Journal of Biological Chemistry 2004, 279, 50994–51001. [Google Scholar] [CrossRef]
- Poole, L.; Michael Reynolds, C.; Wood, Z.; Andrew Karplus, P.; Ellis, H.; Li Calzi, M. AhpF and other NADH:peroxiredoxin oxidoreductases, homologues of low M(r) thioredoxin reductase. European Journal of Biochemistry 2000, 267, 6126–6133. [Google Scholar] [CrossRef]
- Cohen, S.D.; Hindmarsh, A.C. CVODE, a stiff/nonstiff ODE solver in C. Computers in Physics 1996, 10, 138–143. [Google Scholar] [CrossRef]
- Sgarlata, C.; Zito, V.; Arena, G. Conditions for calibration of an isothermal titration calorimeter using chemical reactions. Analytical and Bioanalytical Chemistry 2013, 405, 1085–1094. [Google Scholar] [CrossRef]
- Di Trani, J.M. Measuring Enzyme Kinetics Using Isothermal Titration Calorimetry. PhD thesis, McGill University, 2018.
- Rohatgi, A. Webplotdigitizer: Version 4.6, 2022. https://automeris.io/WebPlotDigitizer.
- Hayashi, Y.; Yamazaki, I. The oxidation-reduction potentials of compound I/compound II and compound II/ferric couples of horseradish peroxidases A2 and C. Journal of Biological Chemistry 1979, 254, 9101–9106. [Google Scholar] [CrossRef]
- VP-ITC MicroCalorimeter User’s Manual.
- Kantonen, S.; Henriksen, N.; Gilson, M. Evaluation and minimization of uncertainty in ITC binding measurements: Heat error, concentration error, saturation, and stoichiometry. Biochimica et Biophysica Acta - General Subjects 2017, 1861, 485–498. [Google Scholar] [CrossRef]
- Dalla Rizza, J.; Randall, L.; Santos, J.; Ferrer-Sueta, G.; Denicola, A. Differential parameters between cytosolic 2-Cys peroxiredoxins, PRDX1 and PRDX2. Protein Science 2019, 28, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Portillo-Ledesma, S.; Randall, L.; Parsonage, D.; Rizza, J.; Andrew Karplus, P.; Poole, L.; Denicola, A.; Ferrer-Sueta, G. Differential kinetics of two-cysteine peroxiredoxin disulfide formation reveal a novel model for peroxide sensing. Biochemistry 2018, 57, 3416–3424. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.M.; Goyette Jr., G.; Ravindranath, Y.; Ho, Y.S. Hemoglobin autoxidation and regulation of endogenous H2O2 levels in erythrocytes. Free Radical Biology and Medicine 2005, 39, 1407–1417. [Google Scholar] [CrossRef]
- Johnson, R.M.; Ho, Y.S.; Yu, D.Y.; Kuypers, F.A.; Ravindranath, Y.; Goyette, G.W. The effects of disruption of genes for peroxiredoxin-2, glutathione peroxidase-1, and catalase on erythrocyte oxidative metabolism. Free Radical Biology and Medicine 2010, 48, 519–525. [Google Scholar] [CrossRef] [PubMed]
- Jacob, H.; Ingbar, S.; Jandl, J. Oxidative hemolysis and erythrocyte metabolism in hereditary acatalasia. The Journal of Clinical Investigation 1965, 44, 1187–1199. [Google Scholar] [CrossRef] [PubMed]
- Cho, C.S.; Kato, G.J.; Yang, S.H.; Bae, S.W.; Lee, J.S.; Gladwin, M.T.; Rhee, S.G. Hydroxyurea-induced expression of glutathione peroxidase 1 in red blood cells of individuals with sickle cell anemia. Antioxidants and Redox Signaling 2010, 13, 1–11. [Google Scholar] [CrossRef]
- Nelson, K.; Parsonage, D. Measurement of peroxiredoxin activity. Current Protocols in Toxicology 2011. [Google Scholar] [CrossRef]
- Reeves, S.; Parsonage, D.; Nelson, K.; Poole, L. Kinetic and thermodynamic features reveal that Escherichia coli BCP is an unusually versatile peroxiredoxin. Biochemistry 2011, 50, 8970–8981. [Google Scholar] [CrossRef]
- Perkins, A.; Parsonage, D.; Nelson, K.; Ogba, O.; Cheong, P.Y.; Poole, L.; Karplus, P. Peroxiredoxin catalysis at atomic resolution. Structure 2016, 24, 1668–1678. [Google Scholar] [CrossRef]
- Pahl, P.; Berger, R.; Hart, I.; Chae, H.; Rhee, S.; Patterson, D. Localization of TDPX1, a human homologue of the yeast thioredoxin-dependent peroxide reductase gene (TPX), to chromosome 13q12. Genomics 1995, 26, 602–606. [Google Scholar] [CrossRef] [PubMed]
- Barranco-Medina, S.; Lázaro, J.J.; Dietz, K.J. The oligomeric conformation of peroxiredoxins links redox state to function. FEBS Letters 2009, 583, 1809–1816. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y. Applications of isothermal titration calorimetry in protein science. Acta Biochimica et Biophysica Sinica 2008, 40, 565–576. [Google Scholar] [CrossRef] [PubMed]
- Todd, M.; Gomez, J. Enzyme kinetics determined using calorimetry: A general assay for enzyme activity? Analytical Biochemistry 2001, 296, 179–187. [Google Scholar] [CrossRef]
- Di Trani, J.M.; Moitessier, N.; Mittermaier, A.K. Measuring rapid time-scale reaction kinetics using isothermal titration calorimetry. Analytical Chemistry 2017, 89, 7022–7030. [Google Scholar] [CrossRef] [PubMed]
- Transtrum, M.; Hansen, L.; Quinn, C. Enzyme kinetics determined by single-injection isothermal titration calorimetry. Methods 2015, 76, 194–200. [Google Scholar] [CrossRef] [PubMed]
- Cox, A.; Peskin, A.; Paton, L.; Winterbourn, C.; Hampton, M. Redox potential and peroxide reactivity of human peroxiredoxin 3. Biochemistry 2009, 48, 6495–6501. [Google Scholar] [CrossRef]
- Toledo Jr., J.; Audi, R.; Ogusucu, R.; Monteiro, G.; Netto, L.; Augusto, O. Horseradish peroxidase compound i as a tool to investigate reactive protein-cysteine residues: From quantification to kinetics. Free Radical Biology and Medicine 2011, 50, 1032–1038. [Google Scholar] [CrossRef]
- Nelson, K.; Knutson, S.; Soito, L.; Klomsiri, C.; Poole, L.; Fetrow, J. Analysis of the peroxiredoxin family: Using active-site structure and sequence information for global classification and residue analysis. Proteins: Structure, Function and Bioinformatics 2011, 79, 947–964. [Google Scholar] [CrossRef]
- Peskin, A.; Pace, P.; Winterbourn, C. Enhanced hyperoxidation of peroxiredoxin 2 and peroxiredoxin 3 in the presence of bicarbonate/CO2. Free Radical Biology and Medicine 2019, 145, 1–7. [Google Scholar] [CrossRef]
- Tipton, K.F.; Armstrong, R.N.; Bakker, B.M.; Bairoch, A.; Cornish-Bowden, A.; Halling, P.J.; Hofmeyr, J.H.; Leyh, T.S.; Kettner, C.; Raushel, F.M.; et al. Standards for Reporting Enzyme Data: The STRENDA Consortium: What it aims to do and why it should be helpful. Perspectives in Science 2014, 1, 131–137. [Google Scholar] [CrossRef]
- Swainston, N.; Baici, A.; Bakker, B.M.; Cornish-Bowden, A.; Fitzpatrick, P.F.; Halling, P.; Leyh, T.S.; O’Donovan, C.; Raushel, F.M.; Reschel, U.; et al. STRENDA DB: enabling the validation and sharing of enzyme kinetics data. FEBS J. 2018, 285, 2193–2204. [Google Scholar] [CrossRef] [PubMed]
- Lauterbach, S.; Dienhart, H.; Range, J.; Malzacher, S.; Spöring, J.D.; Rother, D.; Pinto, M.F.; Martins, P.; Lagerman, C.E.; Bommarius, A.S.; et al. EnzymeML: seamless data flow and modeling of enzymatic data. Nature Methods 2023, 20, 400–402. [Google Scholar] [CrossRef] [PubMed]

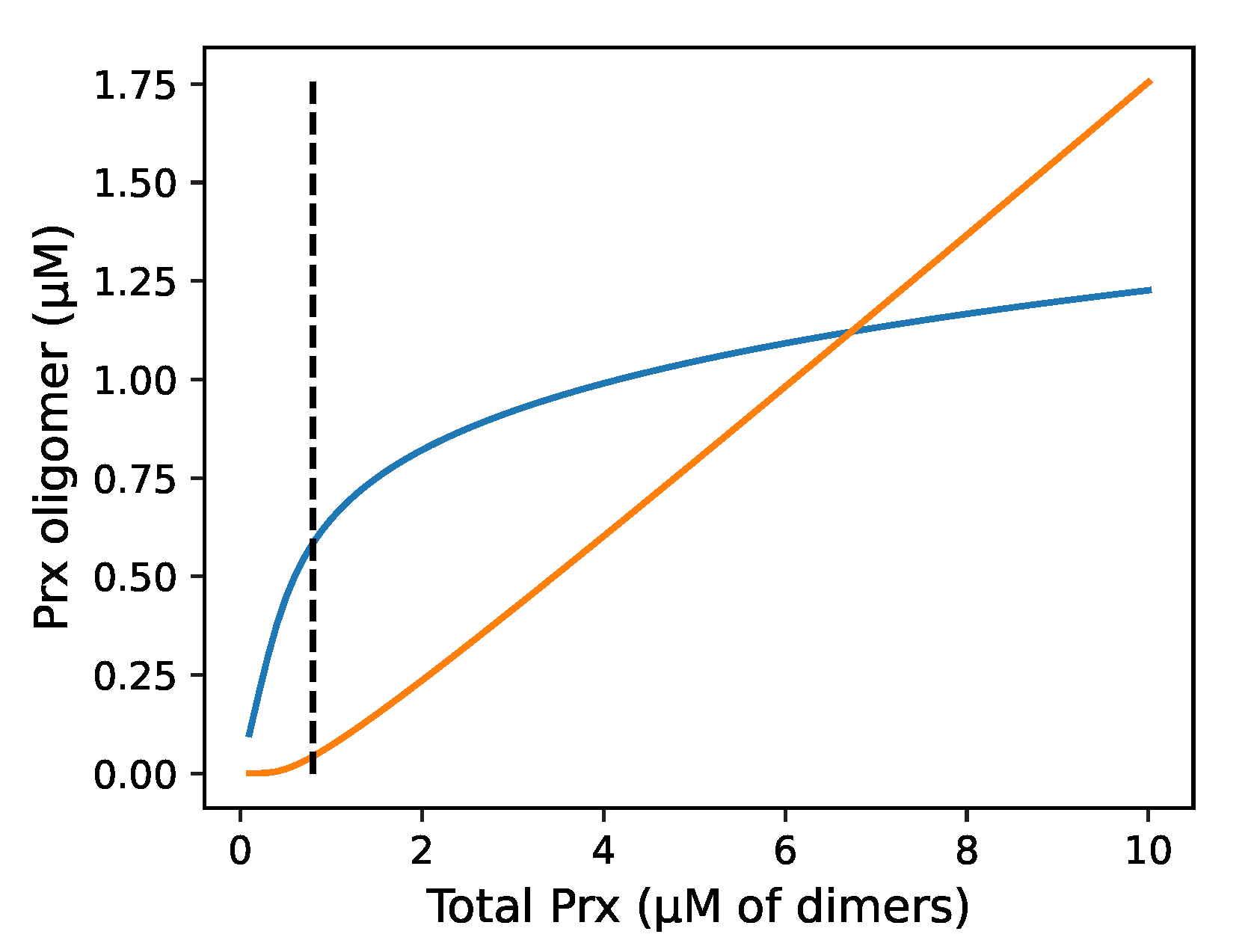
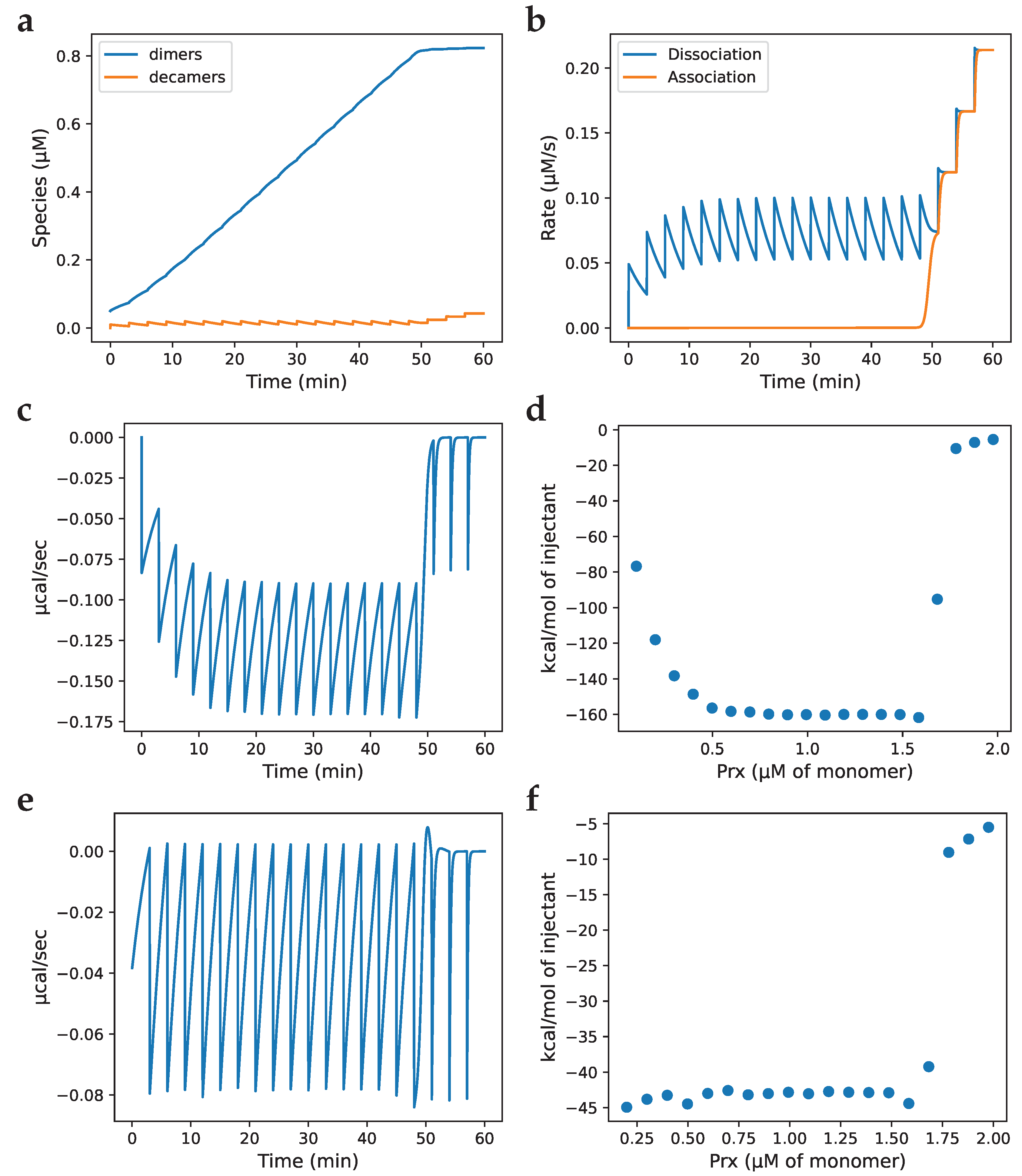
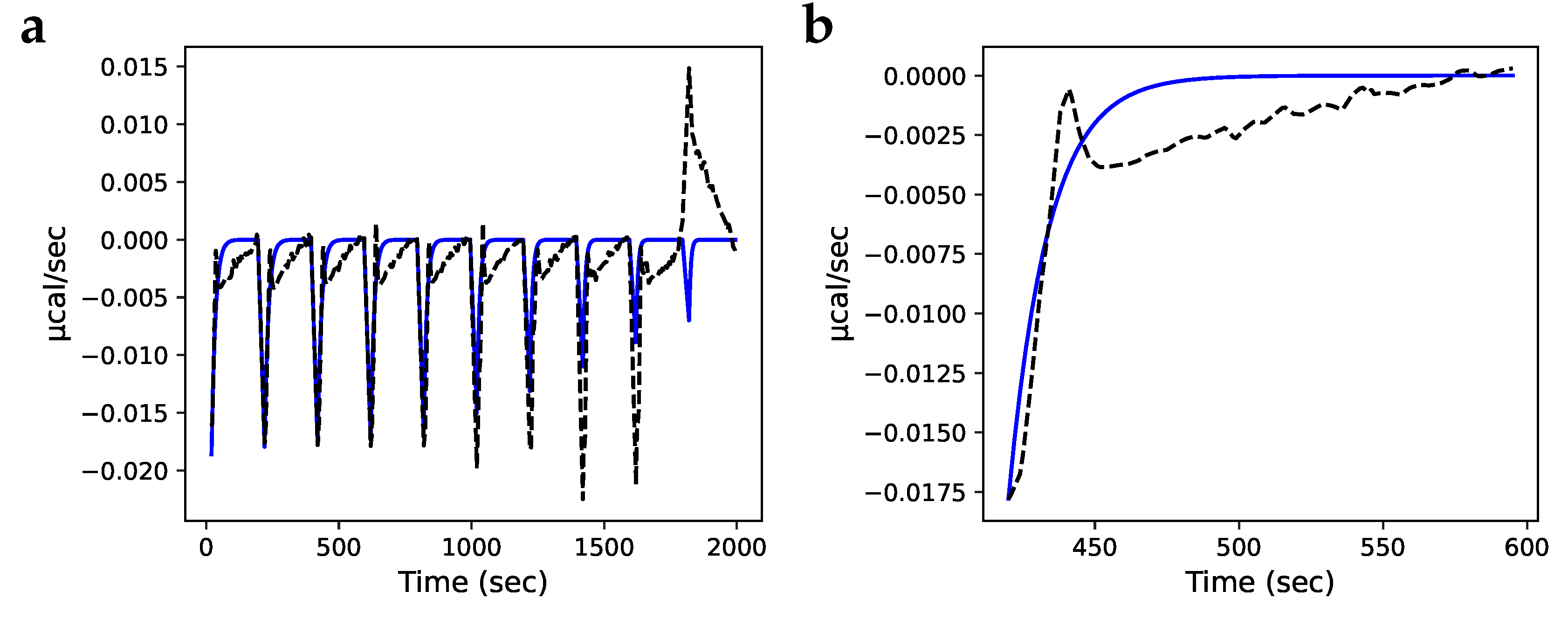
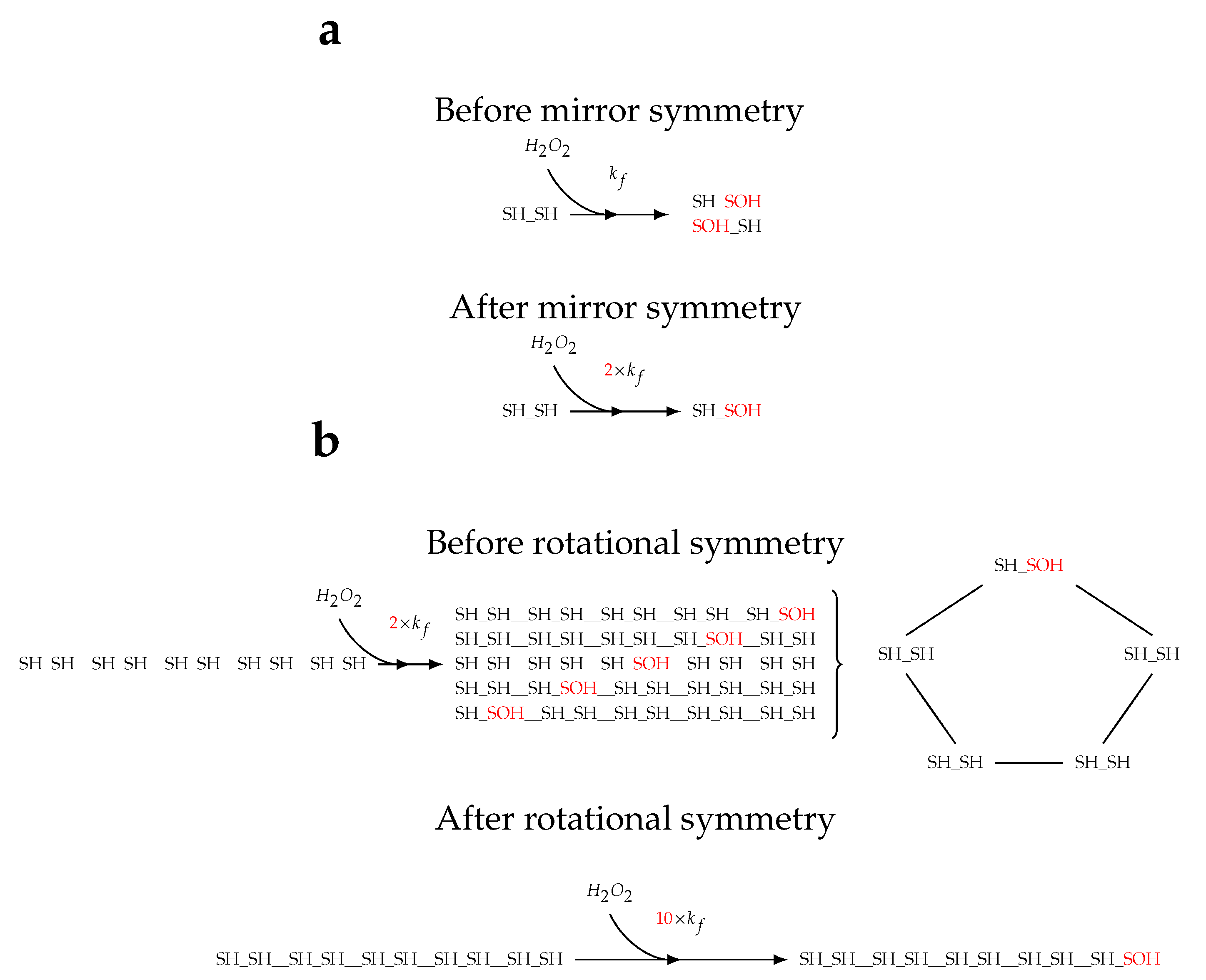
 ) fraction of Prx dimers with two disulphide-bridges; (—) fraction of Prx dimers with two sulfinic sites; (- -) fraction of Prx dimers with a disulphide-bridge and a sulfinic site.
) fraction of Prx dimers with two disulphide-bridges; (—) fraction of Prx dimers with two sulfinic sites; (- -) fraction of Prx dimers with a disulphide-bridge and a sulfinic site.
 ) fraction of Prx dimers with two disulphide-bridges; (—) fraction of Prx dimers with two sulfinic sites; (- -) fraction of Prx dimers with a disulphide-bridge and a sulfinic site.
) fraction of Prx dimers with two disulphide-bridges; (—) fraction of Prx dimers with two sulfinic sites; (- -) fraction of Prx dimers with a disulphide-bridge and a sulfinic site.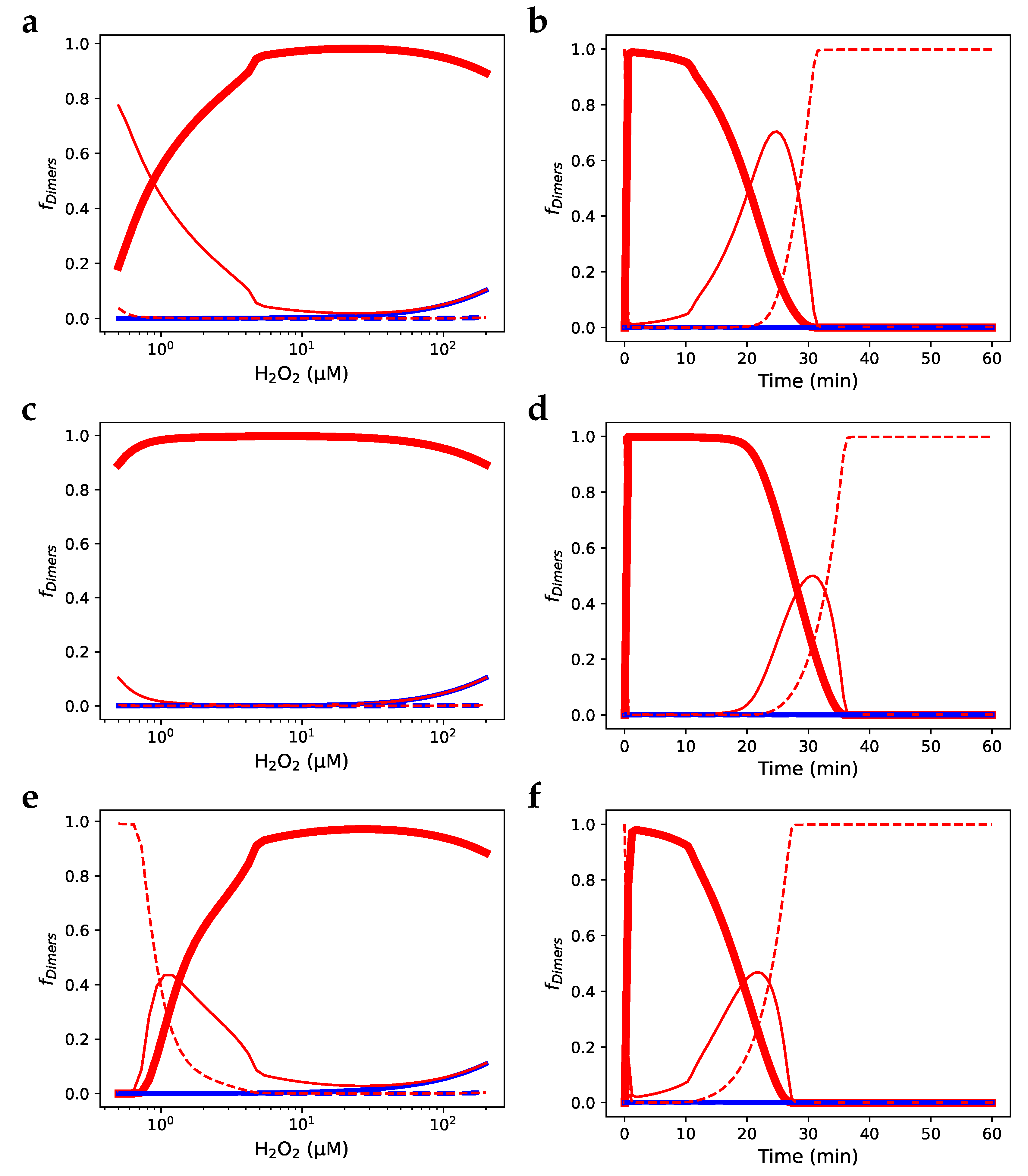
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




