Prerpints.org logo
Preprint
Article

Post-Covid-19 Pandemic Era and Sustainable Healthcare: Organization and Delivery of Health Economics Research (Principles and Clinical Practice)

Altmetrics

Downloads

138

Views

61

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Preprints on COVID-19 and SARS-CoV-2

Submitted:

26 June 2023

Posted:

27 June 2023

You are already at the latest version

Alerts
Abstract
Health services research is a multidisciplinary discipline that aims to improve population health by studying healthcare services' organization, delivery, and financing. Over time, the field has worked to define its boundaries and establish a set of core research topics and methods addressing population wellbeing, access, quality, and cost. Although the influence of health technology is significant, our literature survey on health services research showed that SCs in general—containing their management, cost, and policy—had received little attention. Importantly, our assessment also showed that the system’s readiness to handle supply policy and supply device deficiencies like those encountered during pandemic was hardly ever mentioned. Reduced open areas and water bodies, deteriorating infrastructure, and changes in the biological morphology all affect cities’ uncontrollable and unplanned growth. Urban amenities, facilities, and healthcare services were unevenly distributed due to this unchecked urban population development. In light of this, this research suggests two reliable models for site selection issues for one of Hong Kong’s main hospitals. Levels of uncertainty, infeasibility tolerance, and reliability are taken into consideration. Then, two categories of uncertainty—symmetric and bound-ed—were examined. As a result, the challenge of scheduling in uncertainty has been considered, and potential solutions have been presented using a specified probability distribution function. The paper concludes by introducing the specific justice and health problems and outlining four typical strategies. In order to ensure that medications and other healthcare supplies are produced, distributed, and given to patients, a vast network of systems, components, and procedures must be effectively managed. This research contributes in this regard. Also, its grantee fairness in health systems and the populations health locally, nationally, and globally. It highlights health inequity, advances the measurement of health inequity, and promotes public dialogues on health inequity.
Keywords: 
Subject: Public Health and Healthcare  -   Public Health and Health Services

1. Introduction

Researchers generally believe that the key to effectively ensuring the supply of emergency supplies lies in rational (LAP)1 and scientific planning of the (VRP)2. Moreover, there is an interdependent and interactional connection among LAP and VRP. Thus, it is necessary to design and optimise them as a whole system, that is, to study (LRP)3 in the emergency logistics system. LAP issue mainly refers to the decision-maker recognizing the amount and location of facilities in a specific geographical area based on the geographical distribution of customers and goods.
Hospital delivery throughout the world has been fraught with expensive, lower efficiency, and poorer quality patient care services, and thus Hong Kong is no exception in this regard. However, qualities of the services provided for the patients have been far from exemplary. As an example, it is common that waiting time for specific routine surgeries at public hospitals lasts 18 months. Another exacerbated issue would be population aging; that is, the number of individuals aged ≤65 has rapidly approached 15% of the general population in Hong Kong, so this figure has been enhancing by approximately 1% point annually.
The hospital under the present study is one of the major hospitals (MH) in Hong Kong under the Hospital Authority (HA) management. It provides residents of Hong Kong with a wide range of services. MH offers both inpatient and specialised outpatient medical services. However, the current constraints of QEH4 are summarized below:
➢
Hospital with a high volume of activities;
➢
Reach the limits of capacity;
➢
Heavily utilized and aged infrastructure.
Moreover, in line with HA’s speech at the Hospital Authority Convention, 2013, the growing demand for hospital beds in Hong Kong will be about 2600 by 2021 and about 6600 by 2031. Therefore, the long-term plan of the government is to expand healthcare capacity. MH plans to open a new special hospital ward (SHW) in Hong Kong. The most important issue is determining the right site for this new SHW.
The present study will represent a robust site selection model for MH. The location of the hospital is critical in minimizing economic hardship for both MH and HA and maximising the success of a Health Maintenance Organization (HMO) network since the location of the hospital definitely will have a direct effect on HMO utilization [1]. However, in site selection, the fixed and variable costs and the government budget to operate the hospital is uncertain while unexpectedly increasing the complexity of decision-making.
To address the issue of parameter uncertainty, novel robust optimisation protocol approaches are developing. The robust optimisation protocol would handle the parameter uncertainty, supposing unknown factors belonged to a set of bounded convex uncertainties. Therefore, it is possible to minimize the negative impacts on the objective values and guarantee the solutions [2]. However, a basic concept behind the robust optimisation protocol would be investigating the worst scenario with any particular distribution assumption. Notably, [3] has pioneered the works on the robust optimisation protocol and needs that each uncertain parameter reached its arrant case value that over-conserved the functional execution.
Moreover, [4,5,6] established several improvements with the ellipsoidal uncertainty set for adjusting conservatism levels and provided tractable mathematical reformulations. In addition, [7,8] investigated uncertainties via describing a polyhedron for all parameters. Consequently, they introduced the concept of “budget-of-uncertainty” for controlling conservation. Furthermore, [2] demonstrated one range for all parameters would cause overly conservative outcomes and illustrated uncertain parameters with numerous ranges. The other works followed a framework based on a scenario wherein uncertainty has been modelled by using some scenarios, which subsequently proposed the stochastic programming formulas [9].
Nonetheless, achieving precise probability data to distribute would be difficult, which varied times. Another study conducted via [10] and [6] developed a powerful deterministic alternative regarding the amount of data uncertainties, tolerance of in-feasibility, and levels of reliability as the probabilistic measurement has been applied. This protocol enjoys benefits like linearity and applicability. It also could be deterministically solved and easily controlled conservatism level. Therefore, the present robust optimisation protocol model has been designed concerning the work above in the field and specifically applied to the site selection model for MH.

2. A Review of the Literature

2.1. Cardiac care and its supply chain as the medical devices

Health services research (Health Serv. Res.), an expanding field, has tried to specify its boundaries as a multidisciplinary discipline involving population wellbeing, access, quality, and cost [11]. While there is awareness of the significance of the impact of health technologies and health technologies assessment (HTA), SCs5 containing their cost, policy, management, and influence on outcomes, receive relatively little attention in our examination of the Health Serv. Res. literature. Importantly, our assessment also showed that the system’s readiness to handle supply policy and supply device deficiencies like those encountered during COVID-19 was hardly ever mentioned.
We believe that infusing an SCM6 concentrate into Health Serv. Res. provides investigators with a nexus of theoretical frameworks integrating inter-organisational connections, micro and macro-economics, regulation, inter-mediation, and even a sociological component. Grennan et al. (2022), which examines a vital but frequently disregarded aspect of healthcare services: medical devices SC [12]. Even while the pandemic has increased interest in the SC, particularly in the device portion and its administration, research into this area began before the virus made an appearance [13]. Grennan et al. (2022) study’s contribution to understanding price variation for medical devices, our own research experiences bridging the gap between social science and Health Serv. Res. and our conviction that an SC perspective can enhance health services in the post-pandemic environment [12].
Effectively managing expensive medical goods, like implanted devices, has tremendous value for the health system because they are the second-largest expense category (after labour) [14]. At the same time, previous studies identified the variation in medical device prices [15] and their substantial variation [16]. Grennan et al. (2022), cardiac unit analysis, focusing on costs and management, is especially essential in the quest to untangle the causes for large levels of cost variance across some cardiac products and relatively little variation in others [12,17].
The rise of the worldwide interventional cardiology market, which was 14 bn.$ in 2019 and is anticipated to reach 16.2 bn.$ in 2027, illustrates the significance of a concentrates on cardiology device costs and cost variance [18]. We found significant price variations for stents between (2006-2014), one set of categories taken into account by Grennan et al. (2022), with bare-metal stent costs falling from roughly ($1000 to just over $600) and drug-eluting stent prices falling from approximately ($2300 to $1400) [12,19]. Stents' price variance is shown via Grennan et al. (2022) to be much lower than that of several other cardiac devices [12].
Gannon et al. (2019) contribute to understanding the underlying elements, such as variation [20]. They highlight the role of management in reducing costs in addition to a number of other factors, such as physician integration, standardization as it is connected to a smaller supplier base, efficient value analysis processes that bring clinicians together to agree on products and commit to a brand, and so forth. Their realization that purchasing more of the same product from the same vendor at the same hospital matters for savings attests to appropriate supplier base reduction, a crucial concept in SCM. This highlights the significance of including general management practices and practices tied to strategic management progressive practises via SC scholars—practices that can lead to a more successful medical device SC—into research design [13]. We go into further detail about a few of these approaches, which, if applied to study design, can aid health services scholars in providing clarity to this urgently needed field of research—not just for cardiology but also for other high-supply-cost growth sectors like spine and orthopedics.
Their contention that betters management practices are but one of several mechanisms to “chip away at the large potential savings in hospital purchasing” [12] and that investments in management practices may be appropriate to achieve future savings opens up the door for future health services and management studies into the mix of value-added management [21] practices and provides a reason for further consideration for SCM investment via hospital leadership.

2.2. Supply chain in healthcare and influencer factors

2.2.1. Innovation in medical device

Burne's analysis (2012) shows that in several areas of cardiology, innovation has slowed down during the past ten years as hospitals and payors have become more cost-conscious [22], highlights the huge price decreases that have occurred in a number of cardiac implant types in recent years. While drug-eluting stents have replaced metal-bare stents as the industry standard, the cost of biodegradable stents has dramatically increased. The contrasts among “commoditized items” (those with few differences and various suppliers) are discussed with the right product and fewer alternatives that clarify pricing disparities. Future studies that examine pricing and the rates at which practitioners embrace new technology are urgently required throughout the spectrum of medical device categories, including orthopedics and spine. It is also vital to realise that breakthroughs, such as those allowing for minimally invasive procedures, may affect practises, the value provided to patients, and as a result, changes in purchasing volumes and pricing.

2.2.2. Regulation and strategies towards cost reduction

Device costs for supply-intensive operations are intended to be impacted by bundled payments and gainsharing agreements. Some items are “pass-throughs,” meaning international reimbursement programmes do not cover them. Examining these components’ integration into the hospital and the effects of changing the incentives will help to understand how policies are evaluated and developed. Early research on drug-eluting stents showed that gainsharing decreased expenses for coronary stent patients while maintaining quality and access, serving as a crucial example for academics hoping to comprehend the advantages of incentive-based programmes [23].

2.2.3. Analyzing the value and comparative effectiveness of research

Assessing new products and product variety has become more methodical for healthcare organizations. However, study on comparable products within a category and pricing transparency is scarce [16]. However, suppose implantable device performance research becomes more thorough. In that case, it may help to demonstrate product equivalencies, giving buyers the ability to enter the market with commitments to huge volumes and the associated leverage to negotiate lower prices [24]. Studies on value-based purchasing and purchasing innovation are very helpful for future health services research on the influence of evidence-based purchasing and its impact on cost [25,26].

2.2.4. Preferences and clinician incentives

Physicians are surrogate buyers who use their professional experience and independence to choose items for hospitals and patients, particularly those in supply-intensive specialties like cardiology and orthopedics [27]. Physicians exercise great care in selecting the best medical devices and understand the significance of price as a selection factor. However, they also display little expertise and pay little attention to prices while choosing supplies [28]. Because of physicians' limited formal knowledge and information transparency regarding SCM, both during their training and once they are in practise, there is a lot of tension between the clinical domains and health care procurement [29]. Using AHA7 survey data as a proxy, via assigning physicians based on their being in “high-integration” affiliated organisations, Grennan et al. (2022) considers the impact of physician integration on cost [12]. According to our study, such a proxy may only scrape the surface of the issue of encouraging physicians to think about the cost and procurement implications of their product choices in a high-integration system [30,31,32]. As mentioned, participating in gainsharing and other incentives may significantly impact physicians’ use of expensive items.

2.3. Post-Pandemic health services research and supply chain perspective

In the COVID-19 era, every sector of the economy—from electronics to vehicles to agriculture to imported goods and vaccinations to everyday items like toilet paper—has at least one SC discussion. The same applies to healthcare. The “ailing supply chain” in healthcare has never been short of an opportunity or research questions [33]; SC concerns have risen to the top of the agendas and considerations of healthcare executives and politicians worldwide during the last two years. Expanding the emphasis beyond the SCs triple purpose of quality, cost, and outcomes to include SCRes8 and preparedness, as outlined below, in the mission statements of organisations in a sector with high resource dependence may be a starting point for change.

2.3.1. Risk assessment in supply chain

According to a company that handles and tracks SC risk for a variety of industries, disruptions from SC were 67 percent higher in 2020 than in 2019 [34]. In the healthcare industry and other sectors, there is a paradigm change taking place from a concentrate on SC efficiency (i.e., cost reduction) to one on SC robustness and contingency planning. Since SCs are now known to be more fragile than originally thought, other factors must take precedence above cost savings. Many medical devices to SCs are now vulnerable to disruptions as a result of the ubiquitous objectives in Six Sigma, Lean Management, and similar programmes that decrease inventory and costs over the past two decades. Talks on safety stock and business continuity planning are currently taking place at all levels of organisational governance, from departmental units to the highest levels of the federal government. Recent ideas for the engagement of local bodies establishing pooled safety stockpiles continue to characterise the SNS's9 role as a backup [35,36]. The health sector, which adopted JIT10 inventory and relied on suppliers and intermediates, must factor potential disruptions into their planning, readiness, and finance.

2.3.2. Identifying the risk of resource dependency

The dependence on other businesses and the resource dependence for health care products interact considerably. Medical gadgets reliant on semiconductors are expected to experience shortages and ensuing price increases. The WSJ11 highlighted the 2021 chip shortage for manufacturers of pacemakers, ultrasound equipment, and other devices [37]. In 2021, AdvaMed12, which represents distributors of medical devices, urged the DOC13 on the semiconductor industry to “ensure that it does not cause SC disruption that affects healthcare delivery in the USA [38].”

2.3.3. Integration of the supply chain

The focus on integration in healthcare systems in the long run ignores a heavily researched and significant topic of SCM integration, which can be divided into integration with peers, intermediaries, suppliers, customers, or between organisational units [39,40]. In order to encourage innovation, clinical research, and the development of new services and processes, buyer-supplier integration with suppliers and intermediaries such group purchasing organisations14 concentrates on partners that the hospital considers to be strategic [41]. When physician incentives influence supply selection decisions, for example, the physician-hospital integration could be viewed as a type of SC integration [31]. A strong case for horizontal SC integration to improve performance can usually be made with decentralised health systems [42] or recently merged systems. Nevertheless, numerous examples show that carrying out stated integration is difficult. SCM is among the most difficult areas to integrate. Years after the merger, numerous integrated systems continue to operate inefficient procurement processes (e.g., multiple supply information systems, separate procurement departments, multiple groups purchasing organisations, and overlapping contracts). Others have been able to integrate dispersed intermediaries by creating pools and consolidated service centres [30]. Health Serv. Res. might significantly increase clarity in this crucial area.

2.4. Approaches to examining access and justice in healthcare/Healthcare Disparities

Justice and health are two of the most important issues being discussed in today's social and political discourse. Large differences in health and access to healthcare still exist, even in wealthy nations with highly established health insurance systems [43,44]. Additionally, the sharp enhancement in healthcare expenditures has led to growing social pressure to illustrate some rationing in publicly financed systems [45], and this rationing may further exacerbate unfair disparities or inequities. In developing countries where economic disparities are larger, and people have to pay a large portion of their healthcare costs out of their pocket [46], the issue of justice becomes even more pressing [47,48,49,50,51].
What justice needs in health and healthcare settings is deeply contested [52,53,54,55,56]. It is not easy to distinguish clearly “justice” from “altruism” or “compassion”, but these are different concepts and the distinction matters. A reference to justice creates stronger entitlements than “compassion” [57], which has implications for the macro-debate about how to organise the healthcare system and the micro-relations between healthcare professionals and patients with their families. When faced with suffering, death and others are treated when presented with strong thoughts about how they and death. The treatment of people in the context of health is more an issue of “respect for human dignity” than in most other areas of social organisation. People might be profoundly injured in their self-respect and surprised via others’ lack of respect if they feel they have been treated unfairly. Given this context, it is not surprising that “justice and health” have been significant research issues across a variety of academic disciplines [58,59].

2.4.1. First strategy: Philosophical reflection

This strategy seeks to offer clear definitions of the importance of justice in health. instances of such queries contain: shall we be concerned about health or healthcare disparities, and if so, why (or why not)? What constitutes a "need" for health care? The specifics of the justice ideal have never been agreed upon and never will be. To come to a consensus is not the goal of philosophical reflection, though. Instead, it seeks to define the various ways that the idea of justice could be interpreted. Any meaningful scientific endeavour must start with conceptual clarity. A well-organized and cogent discussion of the rights and obligations of people in the area of health and healthcare also benefits from conceptual clarity. As a result, it plays a key role in every democratic decision-making process.

2.4.2. Second strategy: Based on real world solution

The second strategy of philosophical reflection is concerned with making conceptualizations of abstract justice operational and useful for understanding events in the real world, as opposed to the first method's focus on conceptualizations of abstract justice. For instance, reducing health disparities related to people's socioeconomic backgrounds can operationalize the abstract concept of justice and health. Under this operationalization, empirical analysis of justice and health needs: (a) trustworthy insights into the effects of various policy options (for example, which policy options are most effective to decrease socioeconomic disparities in health?); (b) approaches for measuring such socioeconomic disparities in health; and (c) applications of these measurement approaches to the current situation (for example, how large is socioeconomic disparities in health in a given society at a given point I What fundamental factors give rise to this inequality? Comparing the outcomes of empirical analyses based on various theories of justice is important for everyone, not just policymakers. The consequences of various justice concepts are sometimes best grasped when one is familiar with the policies they support.

2.4.3. Third strategy: Based on lay persons’ perceptions of justice

The last strategy concentrates on how society as a whole perceives justice. Specific policy proposals are more likely to have an impact on actual social opinions than impersonal conceptions of fairness. Instances of questions that employ the third tactic contain: What do people believe about justice? How may we interpret their responses to particular policy proposals? When are allusions to justice just a ruse to conceal personal interests? How do the contrasts between self-interest, justice, and compassion that are important in a normative theory also apply to describing behaviour? [60] The perceptions of less educated persons and the cohesive concepts developed by philosophers may differ significantly. The latter is most important for comprehending how society functions because philosophical theories seldom ever adequately account for behaviour. Focusing on real behaviour raises more queries. Are judgments of justice related to pure self-interest, and if so, how, and how do they relate to other values and impulses like fraternity or compassion?

2.4.4. Fourth strategy: investigation into the application of justice theories to actual policymaking

The fourth strategy analysis perceptions of justice at the level of political decision-making during the examination of the third method, perceptions of justice at the individual level. Only with the fourth method can we determine whether, and if so, how much, reasoned ideas factor into the actual decision-making process. Second technique enables us to advise which policy options shall be used to realise a certain vision of justice. Numerous factors outside of normative theories are probably at work to explain, for instance, the significant difference in health insurance systems between nations. In the real world, how do ideas of justice interact with other social norms and financial restrictions? Does this variety represent cultural variations, such as variations in how people view justice? How does the political system influence people's attitudes toward justice, as examined in the third technique above? How does the structure of a political system affect the results of political decision-making? Each of these queries is pertinent on its own. There are, however, also clear feedback loops. Undoubtedly, the political system has an impact on social interactions and how citizens view justice. A CNA15 may naively provide unexpected and undesired results if the unique characteristics of the political institutions are not adequately taken into account.

3. Robust Optimisation Protocol for General Integer and Mlip

Multiple works have been done on production schedules during the last few years. Most current works assume that each datum has known, fixed values. Nevertheless, uncertainty is prevalent in many scheduling problems [55] due to the absence of precise process models and variations in the procedure and environmental data. Therefore, new studies aimed to design techniques for addressing the scheduling problem based on uncertainty for creating reliable schedules that remained practicable in the exitance of the parameter uncertainty (refer to studies in [61] as well as [61,62]). Hence, various methods could be utilized for the scheduling problem based on uncertainties like the probabilistic, stochastic, and fuzzy programs [63].
The study by [64] addressed the scheduling problem based on the demand’s uncertainties. They employed a multi-stage stochastic MILP pattern wherein several decisions were made by ignoring uncertainty. Moreover, other decisions have been made when uncertainty is identified. Therefore, Balasubramanian and Grossmann introduced an approximation approach to solving some 2-phase models based on the shrinking horizon strategy. Additionally, [65] utilized the concept of sensitivity analyses based on inferences for the MILP problem to determine the prominence of various limitations and factors in their scheduling system [66]. This system provided a series of candidate time-tables for the unknown factors being considered.
Furthermore, [67] introduced a strategy for managing risks to schedule with uncertain demands. They utilized a 2-phase stochastic optimisation pattern, maximising the predicted profits and managing the risks explicitly via studying a novel aim as the measure for controls, which caused a multi-objective optimisation model. Then, [68] extended the above model to consider unknown processing time. Therefore, a 2-phase stochastic procedure has been employed wherein a weighted sum of the predicted makes-pan and predicted waiting for durations have been minimized; then, risks have been measured with various accuracy measures. Finally, [69] dealt with the extension of the 2-phase optimisation model for examining possible accurate estimating of several unknown factors. Then, the split and bound strategy was applied to solve the issue and was according to a partition of the unknown area and an approximation of the bounds in the Obj function.
The robust optimisation protocols have been designed for unknown information defined through multiple given distributions like a normal distribution, smooth dispersion, difference of 2 NDs16, BINDs17, GDD18, and Poisson dispersion. Our powerful optimisation protocol introduced little auxiliary parameters and further limitations in the genuine MILP problem, which generated a deterministic strong counter-part problem, providing an optimal and possible solution about the relative volume of unknown information and level of reliability well as feasibility tolerance. Consequently, a powerful optimisation protocol has been utilized for short-term scheduling issues based on uncertainties.
Now, general ILP with unknown factors will be studied. However, there is a concern about developing a strong optimisation protocol for generating “reliable” solutions to ILP immune to data uncertainty. Hence, a generic ILP with m × n parameters and m constraints would be considered:
M a x c x s . t . A x ≤ b , x ≥ 0 ,
So that A refers to an m × n integer matrix of rank m and b ∈ ℜ m . Moreover, uncertainty results from the left side variables of in-equality limitations b i , i = 1 , 2 , … , m . However, there are concerns about the feasibility of the limitations below in a robust optimisation protocol framework;
∑ j ∈ J a i , j x i , j ≤ b i .
Based on [6], when the nominal data have been partly worried, one or more constraints could be substantially violated. Therefore, current unit aimed to produce accurate solutions to a generic ILP problem that had immunity to uncertainty. Notably, our robust optimisation protocol was initially provided via [6] for the LP problem, which has unknown coefficients, and consequently [10] extended it for addressing a MILP problem. Notably, our introduction method of robustness into the original model was closely similar to the method employed in [10].

3.1. Bounded uncertainty

Let’s assume that uncertainty data have been in a range as the following interval:
a ˜ i , j − a ¯ i , j ≤ ε a ¯ i , j , b ˜ i − b ¯ i ≤ ε b ¯ i ,
where a ˜ i , j , b ˜ i represent true values and a ¯ i , j , b ¯ i refer to the nominal values (NVs). Moreover, ε stands for the level of uncertainty.
The present study provided its description of the precise solutions to the ILP problem with the finite unknown left-hand side variables:
Definition 1.1.
When the uncertainty in ILP is illustrated in a bounded state, it is called solution x correct if it meets this condition:
(i)
x would it be possible for nominal problems,
(ii)
if we have true values (say b ˜ i ) of uncertain parameters from intervals (3), therefore, x we should meet i − t h in-equality constraints with the error of Max δ max { 1 , b ¯ i } , wherein δ would be explained as a certain level of in-feasibility.
Particularly, condition (ii) could be written in this way:
∀ i ( a ˜ i , j − a ¯ i , j ≤ ε a ¯ i , j , b ˜ i − b ¯ i ≤ ε b ¯ i , ) : ∑ j ∈ J a ¯ i , j x i , j + ε ∑ j ∈ M J a ¯ i , j u i , j ≤ b ˜ i + δ ⋅ max { 1 , b ¯ i } .
Therefore, to derive a robust solution (RS), the worst values of the unknown variables have been used:
b ˜ i ≥ b ¯ i − ε b ¯ i ,
And substituted (5) into (4).
Hence, x it would be correct if and just if x would be one of the possible solutions for the optimisation problem below:
max c x s . t .   ∑ j ∈ J a i , j x i , j ≤ b ¯ i ∑ j ∈ J a ¯ i , j x i , j + ε ∑ j ∈ M J a ¯ i , j u i , j ≤ b ¯ i − ε b ¯ i + δ ⋅ max { 1 , b ¯ i } − u i , j ≤ x i , j ≤ u i , j x i , j ≥ 0 , ∀ i , j .
In addition, the calculated formulation (6) would be known as the “ ( ε , δ ) -Interval Robust Counter-part ( I R C [ ε , δ ] )” of the original ILP issue.

3.2. Symmetric uncertainty

Therefore, this sub-section supposed uncertain data a ˜ i , j , b ˜ i as a random and symmetric distribution surrounding the NVs a ¯ i , j , b ¯ i as follows:
a ˜ i , j = ( 1 + ε ξ i , j ) a ¯ i , j , b ˜ i = ( 1 + ε ς i ) b ¯ i ,
Where the perturbations ξ i , j , ς i represent the independent variables with symmetric distribution in the interval [ − 1 , 1 ] .
To provide the same description of the correct solution to the ILP problem with the finite uncertainty, transferring a deterministic version (ii) to the common probabilistic one would be very crucial. Hence, we defined a correct solution to the ILP problem with the symmetric unknown variables:
Definition 1.2.
When there is a symmetric uncertainty, the solution  x  would be called correct if it meets this condition:
(i)
x would it be possible for the nominal problems,
(ii)
for each i event probability of a limited violation; that is,
∑ j ∈ J a ˜ i , j   x i , j > b ˜ i + δ ⋅ max { 1 , b ¯ i } ,
It would be, at most κ , that δ > 0 refers to a certain impossible tolerance and κ > 0 a certain level of reliability.
Hence, a correct situation to ILP19 problem with the symmetric unknown parameters would be calculated via making solutions to ( ε , δ , κ )-robust counter-part (RC [ ε , δ , κ ]):
max c x ∑ j ∈ J a ¯ i , j x i , j ≤ b ¯ i ∑ j ∈ J a ¯ i , j x i , j + ε ∑ j ∈ M J a ¯ i , j u i , j + Ω ∑ j ∈ M J a ¯ i , j 2 v i , j 2 + b ¯ i 2 ≤ b ¯ i + δ max { 1 , b ¯ i } − u i , j ≤ x i , j − v i , j ≤ u i , j , ∀ i , j ， x i , j ≥ 0 , ∀ i , j ，
where Ω stands for a (+) parameter via κ = exp { − Ω 2 / 2 } . Therefore, the case considered here has been a specific kind of study conducted by [10]; hence, the procedure for deriving RC20 [ ε , δ , κ ] could be immediately called Lemma 1 and Theorem 2 reported by [10] study that has been ignored in the present research for simplicity.
Notably, according to the above explanation of the relatively correct formulation, relative variables of uncertainties ( ε ), reliability level ( κ ), and in-feasibility tolerance ( δ ) have been supposed to be single and common for simplification. Nonetheless, these new robust optimisation protocols could be readily extended for considering more general cases where such parameters depended on the constraints.

4. Site Selection Model for Qeh

The site selection model is concerned with choosing the right site for newly opened regional hospitals to maximize utilization. The involving model is related to three steps:
➢
Develop a utilization matrix;
➢
Specify constraints;
➢
Apply a robust optimisation protocol approach to select the best site.

4.1. Utilization Matrix

Estimating each choice’s potential utilization or “attractiveness” is necessary to locate a hospital optimally throughout a region. The mentioned utilization or “attractiveness” may be measured by the number of subscribers who select this site location under a dual-choice option.
The probability of the site selection as a function of travel time between the patient’s residence and hospital location and socioeconomic attributes. The utilization function gives the expected utilization u i , j from population unit i to facility location j for each i , j combination:
u i , j = n i p i , j ,
Where p i , j is the probability of utilization for a person from a population unit i location j as determined from the utilization function, and n i is the total population of the unit i . The utilization matrix also gives the Max expected utilization for each choice:
u j = ∑ i = 1 m u i , j ,

4.2. Constraints

Constraints are imposed on the model to limit expenses, ensure that hospitals exceed a Min utilization, assign each population unit to one and only one hospital, and restrict the number of hospitals.
The cost constraint could be considered in terms of fixed and variable costs. Fixed costs may represent set-up expenditures, including planning, capital outlays for equipment and facilities, and recruiting the necessary core staff. Variable costs are those expenditures that are a function of the number of subscribers.
∑ j = 1 n f j y j + ∑ j = 1 n v j ( ∑ i = 1 m u i , j ) x i , j ≤ C ,
where f j and v j are the fixed and variable costs, respectively, and C represents the total budget amount. The variables y j are 1 when a hospital is to be located at the site j and 0 otherwise.
It is believed that there exists a break-even point or Min utilization for a hospital.
∑ i = 1 m u i , j x i , j ≥ k y i ,
So that k is Min expected enrollment requirement before a hospital would be opened at the site j .
Each population unit would choose one and only one hospital, which could be expressed numerically as follows;
∑ j = 1 n x i , j ≥ 1.
Furthermore, the Max number of hospitals should be prescribed by HA managers,
∑ j = 1 n y j ≤ S .
Finally, the mathematical model to select the site to determine a location of new hospitals that maximises total utilization is presented below:
Maximise   E = ∑ i = 1 m ∑ j = 1 n u i , j x i , j s . t .   ∑ j = 1 n f j y j + ∑ j = 1 n v j ( ∑ i = 1 m u i , j ) x i , j ≤ C , ∑ i = 1 m u i , j x i , j ≥ k y i , ∑ j = 1 n x i , j ≥ 1 , ∑ j = 1 n y j ≤ S .

5. Robust Optimisation

It is possible to experience a direct application of the robust optimisation protocol models in Section 2 to the site selection problem with uncertain costs and budgets. Remembering the basic model (15) I R C [ ε , δ ] and R C [ ε , δ , κ ] application to this basic formulation has been considered. Considering the context of hotel revenue management, parameters b ¯ i in (6) and (8) would surely be positive. Therefore, it would be completely reasonable to assume the existence of less than one booking request arriving every day. HENCE, max { 1 , b ¯ i } = b ¯ i .
Consequently, the suggested robust site selection models can be converted into the following formulations:
Maximise   E = ∑ i = 1 m ∑ j = 1 n u i , j x i , j s . t .   ∑ j = 1 n f ¯ j y j + ∑ j = 1 n v ¯ j ( ∑ i = 1 m u i , j ) x i , j ≤ C ¯ , ∑ j = 1 n f ¯ j y j + ε ∑ j ∈ M J f ¯ j s j + ∑ j ∉ K J v ¯ j ( ∑ i = 1 m u i , j ) x i , j + ∑ j ∈ K J ( ( v ¯ j + ε v ¯ j ) ( ∑ i = 1 m u i , j ) x i , j ) ≤ ( 1 − ε + δ ) C ¯ ,
− s j ≤ y j ≤ s j ∑ i = 1 m u i , j x i , j ≥ k y i , ∑ j = 1 n x i , j ≥ 1 , ∑ j = 1 n y j ≤ S .
and
Maximise   E = ∑ i = 1 m ∑ j = 1 n u i , j x i , j s . t .   ∑ j = 1 n f ¯ j y j + ∑ j = 1 n v ¯ j ( ∑ i = 1 m u i , j ) x i , j ≤ C ¯ ,                                                               ∑ j = 1 n f ¯ j y j + ∑ j = 1 n v ¯ j ( ∑ i = 1 m u i , j ) x i , j + ε ∑ j = 1 n f ¯ j l j + Ω ∑ j ∈ M J f ¯ j 2 z j 2 + ∑ j ∈ M J v ¯ j 2 z j 2 + C ¯ 2 ≤ ( 1 + δ ) C ¯ , ∑ i = 1 m u i , j x i , j ≥ k y i , ∑ j = 1 n x i , j ≥ 1 , ∑ j = 1 n y j ≤ S .

5.1. Robust optimisation protocol to schedule under uncertainty

According to the research design, a robust optimisation protocol formulation21 has been utilized for 4 instance problems. Each instance has been run through GAMS software [70] on a 3.20 GHz Linux work-station. Then, CPLEX 8.1 utilised to solve the MILP problems, whereas DICOPT utilised to solve the MINLP [71].

5.1.1. Instance 1. Uncertainties via a Poisson distribution during the processing time

[72] initially designed an instance process utilized as a motivating instance in Section 1 of the article [10] on finite uncertainties. Therefore, 2 products have been generated through 3 feeds following the State-Task Network (Figure 1). Then, STN22 utilized 3 various kinds of tasks that could be done in 4 diverse units. Table 1 reports the corresponding data for this instance, including suitability, capacity, processing time, and storage limitation. It aimed at maximizing the profit from selling the products fabricated in the timetable equal to twelve hours.
Suppose that uncertainties during the processing time would have a Poisson distribution with the value equal to 5, the level of uncertainty ( ∈ ) equal to 5%, in0feasibility tolerance (δ) equal to 20%, and the reliability level (κ) equal to 24% (relative to λ-value equal to 6). When RC [ ∈ , δ, κ] problem has been solved, a “robust” schedule has been achieved (Figure 3) that investigated uncertainty in the processing time. Figure 2 depicts the nominal schedule.
Compared with the nominal solution (NS) achieved at the NVs of the processing duration, a correct situation exhibited many distinct scheduling approaches. For instance, even the sequence of tasks in the 2 reactors in Figure 3 experienced a significant deviation from Figure 1.
Moreover, compared with the NS attained at the NVs of the processing time, a correct situation was exhibited, so various scheduling approaches were used. For instance, even the task sequences in the 2 reactors in Figure 3 considerably deviated.
Sequences in NS in Figure 2. As seen, the correct solutions ensured the feasibility of a correct schedule with a given level of uncertainty, reliability, and infeasibility tolerance. Nonetheless, a reduction of the resultant profit from 3638.75 to 2887.19 has been reported, representing the effects of uncertainty on the overall production. Table 2 compares the pattern and solution statistics for robust and NSs.
Figure 4 is a summary of the outputs of the RC problem with numerous diverse mixes of infeasibility and uncertainty levels at enhancing values of the level of reliability. As shown, at a certain level of reliability, maximal profit, which could be gained, decreased by increasing the level of uncertainty, reflecting further conservative scheduling decisions due to uncertainty. Moreover, at the specific level of reliability, maximal profit increased by enhancing the tolerance level of infeasibility. It is possible to incorporate a more aggressive scheduling arrangement if violations of the pertinent timing constraints could be further tolerated. Additionally, at the specific level of uncertainty and infeasibility tolerance, profit increased by enhancing the level of reliability, reflecting that probable violation of uncertain constraints allowed for more aggressive scheduling. Therefore, the obtained outputs would be compatible with intuition and other approaches. Nevertheless, considering the powerful optimisation protocol, the impacts of uncertainties and the trade-off between the opposed goals would be effectively and rigorously quantified.

5.1.2. Instance 2. Uncertainty via a smooth distribution in the demand of the goods

According to instance 2, uncertainties have been considered with a smooth dispersion in demand for the goods for a similar procedure provided in instance 1. Nonetheless, the objective function has been to minimize the make-span for a certain demand equal to 70 for good 1 and 80 for good 2. The level of uncertainties ∈ equaled 10%, and in-feasibility tolerance (δ) equaled 5%. Moreover, the level of reliability (κ) has been 0%. Figure 5 demonstrates a nominal schedule with a make-span equal to 8.007. According to Figure 6, a robust schedule was achieved by solving the robust counter-part problem so that the corresponding make-span equaled 8.174. In the case of the execution of the obtained schedule, the make-span would be ensured to be at most 8.174 with a 100% probability in the exitance of 10% uncertainty in the product demand. Table 3 compares the pattern and solution statistics for a robust and NS.
Figure 7 represents a summary of the outputs of the RC problem with multiple diverse combinations of infeasibility as well as uncertainty levels at the enhancing values of the level of reliability. As observed, at a certain level of reliability, the Min make-span increased by enhancing the level of uncertainty, indicating more conservative scheduling decisions, which further lasted due to uncertainties in demand. Moreover, at the constant levels of reliability, the Min make-span decreased by increasing the level of infeasibility tolerance, meaning that scheduling arrangements with higher aggression could be included if a violation of the relevant demand limitations.
It could be further allowed. Put differently, at a certain level of uncertainty and infeasibility tolerance, make-span decreased by increasing reliability, reflecting that probable violations of uncertain constraints allowed for more aggressive scheduling. Hence, it is possible to quantify the effects of uncertainty on schedule using a robust optimisation protocol.

5.1.3. Instance 3. Uncertainty via normal distribution in the market price

For this instance, the level of uncertainty has been investigated via a normalized distribution in the market price for a similar procedure in instances 1 and 2. Nonetheless, the objective function has been to maximise profits in eight hours. The level of uncertainty ( ∈ ), infeasibility tolerance (δ), and level of reliability (κ) equaled 5, 5, and 5%. Figure 8 shows a nominal schedule with a profit equal to 1088.75. Moreover, the robust schedule has been achieved via solving the robust counter-part issue (Figure 9), and the corresponding advantage equaled 966.97. Upon the implementation of the schedule, the profit has been ensured to be not less than 966.97 with a 95% probability in the exitance of 5% uncertainty in the raw materials and product prices. Table 4 compares the pattern and solution statistics for a robust and NS.
Figure 10 represents a summary of RC problem outputs at multiple diverse levels of uncertainties and 0% in-feasibility tolerances at the enhancing amounts of level of reliability. As seen in the figure, at a certain level of reliability, maximal profit, which could be gained, decreased by enhancing the level of uncertainty, indicating more conservative scheduling decisions due to uncertainty. Moreover, at a certain level of uncertainty and infeasibility tolerance, profit increased by enhancing the level of reliability, demonstrating that with the increase of probable violation of uncertain constraint or κ, λ decreased, and the profit took on a greater value based on Equation (18):
P r o f i t ≤ ∑ s ∈ S p p s . S T F s − ∈ λ ∑ s ∈ S p p s 2 S T F s 2 + ∑ s ∈ S r p s 2 S T I s 2 + δ
So that λ = F − 1 1 − k   a n d   F n − 1 is the reverse distribution functions of the random variables with the standard normalized distribution.
Notably, the above instance considered uncertainties during the procedure time of missions for the industrial empirical report initially provided in the [73] study. Therefore, actual plant data has been utilized for determining the kinds and levels of uncertainty in the processing time. The industrial plant has been a multi-product chemical plant, which manufactured tens of various goods following a major 3-phase recipe and its changes with ten pieces of instrumentation. Therefore, the first sub-horizon in [73] study contained 5 days and 8 products. Hence, the objective function has been to maximise the general production described as the weighted sum of the substances aggregated after the sub-horizon minus a penalty term for the lack of satisfaction of the demands with mid-term deadlines. Finally, a processing recipe demonstrated in Figure 11 has been utilized for each product.
This plant consisted of 3 kinds of units, each corresponding to 1 of 3 major processing operations. Therefore, 4 types of 1 unit (units 1 to 4) have been utilized for operation 1, 3 types of 2 units (units 5 to 7) have been employed for operation 2, and 3 types 3 units (units 8 to 10) have been utilized for operation 3. Then, type 1 and type 3 units were applied in the batch mode, whereas type 2 units acted in a continual mode. Moreover, Table 5 presents the nominal processing duration or the processing rates of all tasks in the relative proper units.
Therefore, to determine the forms of uncertainties in the processing duration or rate, we addressed the analysis of the actual plant data. Hence, 2 various kinds of uncertainty have been selected based on the data: uncertainties via a normal distribution and finite uncertainties. For bounded uncertainty, ranges for unknown variables have been provided, and mean and standard deviation (SD) for uncertain parameters have been determined for normal uncertainty. Moreover, a total number of 23 uncertain parameters has been recognized, including 8 in units 1 to 4, 5 in units 5 to 7, and 10 in units 8 to 10. Table 6 summarizes all uncertain parameters’ characteristic NVs, mean, range, and SDs.
Strategy 2 for uncertainties in the processing duration or the rate in Section 3.2 would be utilized for the mentioned case study. Besides major sequencing constraints, the processing times appeared in 2 further constraints associated with timing operation 1 mission:
T s i ,   j ,   n + 1 ≤ T f i ,   j ,   n + H 2 − w v i ,   j ,   n − w v i ,   j ,   n + 1                                                                             ∀ i ∈ I r ,   j ∈ J i ,   n ∈ N ,   n ≠ N , T s i ,   j ,   n + 1 ≤ T f i ,   j ,   n + t c l i i ' + H 2 − w v i ,   j ,   n − w v i ' ,   j ,   n + 1                                                                             ∀ i ∈ I r ,   i ,   i ' ∈ I j , i ≠ i ' , n ∈ N ,   n ≠ N
So that Ir represents a series of operation 1 tasks. Jr refers to a collection of type 1 units appropriate for operation 1 tasks. When Tf (i, j, n) variables are substituted, further constraints have been proposed below for parameters via the bounded uncertainty for obtaining the robust counter-part issue:
                      T s i ,   j ,   n + 1 − T f i ,   j ,   n ≤ a i j L . w v i ,   j ,   n + β i j L . B i ,   j ,   n + H 2 − w v i ,   j ,   n − w v i ,   j ,   n + 1 + δ 2 ,
                                  T s i ,   j ,   n + 1 − T s i ' ,   j ,   n ≤ a i j L . w v i ' ,   j ,   n + β i j L . B i ' ,   j ,   n + t c l i i ' + H 2 − w v i ,   j ,   n − w v i ' ,   j ,   n + 1 + δ 2 ,
Here a i j L = 1 − ∈ a i j ,   β i j L = 1 − ∈ β i j ,   a n d   δ 2 represent a varied and correlate as followed with factor δ, which participated in further limitations relative to major sequencing limitations:
δ + δ 2 = a U − a L = 2. ∈ . a , o r   δ + δ 2 = β U − β L = 2. ∈ . β .
Accordingly, further limitations would be proposed for variables with normal uncertainties:
T s i ,   j ,   n + 1 − T s i ,   j ,   n ≤ 1 − ∈ λ i j a . σ i j a − μ i j a . a i j . w v i ,   j ,   n                                                   + 1 − ∈ λ i j β . σ i j β − μ i j β . β i j . β i ,   j ,   n                                                   + H 2 − w v i ,   j ,   n − w v i ,   j ,   n + 1 + δ 2 ,
T s i ,   j ,   n + 1 − T s i ' ,   j ,   n ≤ 1 − ∈ λ i ' j a . σ i ' j a − μ i j a . a i ' j . w v i ' ,   j ,   n                                       + 1 − ∈ λ i ' j β . σ i ' j β − μ i ' j β . β i ' j . β i ' ,   j ,   n + t c l i ' i                                       + H 2 − w v i ,   j ,   n − w v i ' ,   j ,   n + 1 + δ 2
So that δ2 would be described as:
δ + δ 2 = 2. ∈ λ . δ − μ .
As seen, the objective function for the above issue would be to maximise the production of the relative values of each state minus a penalty term for the lack of contentment of the demand at the intermediate due date:
γ ∑ s v a l d s v a l p s v a l m s S T F s − ∑ s ∑ n p r i s n S L s ,   n                                                                                               ∀ s ∈ S ,     n ∈ N
So that valds represent the corresponding values of the relative product reflecting the respective significance for fulfilling the future demands. In addition, valps refers to the relative value of the corresponding products representing the respective priority, and valms stands for the relative values of the state (s) in the materials sequences for the corresponding products. Moreover, STF(s) indicates the amounts of state (s) at the end of the horizon, and prisn refers to the demand priority25 [74] for the state (s) at the event point (n). Furthermore, SL (s, n) represents a slack variable for the number of states (s) which has not met the demand at the event point (n), and γ stands for a fixed coefficient applied for balancing the relative value of 2 terms in the Obj function.
It should be noted that this problem required additional sequencing constraints (19) to (21) for accurate scheduling of the operation 1 task. However, using such constraints to account for problem uncertainty led to a (MILP) problem because they only had one uncertain parameter, which produced linear deterministic types for typical unknown and constrained restrictions.

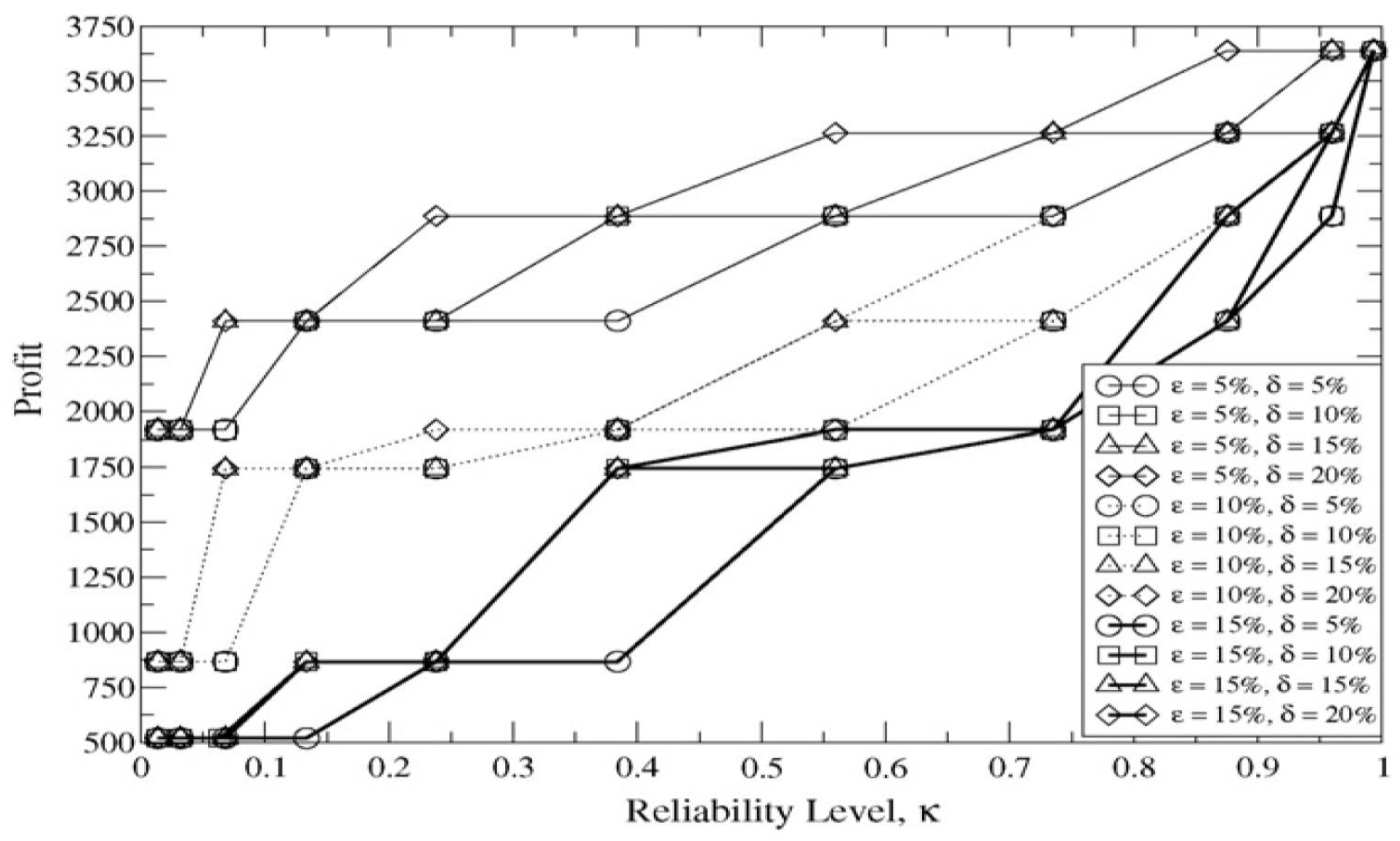
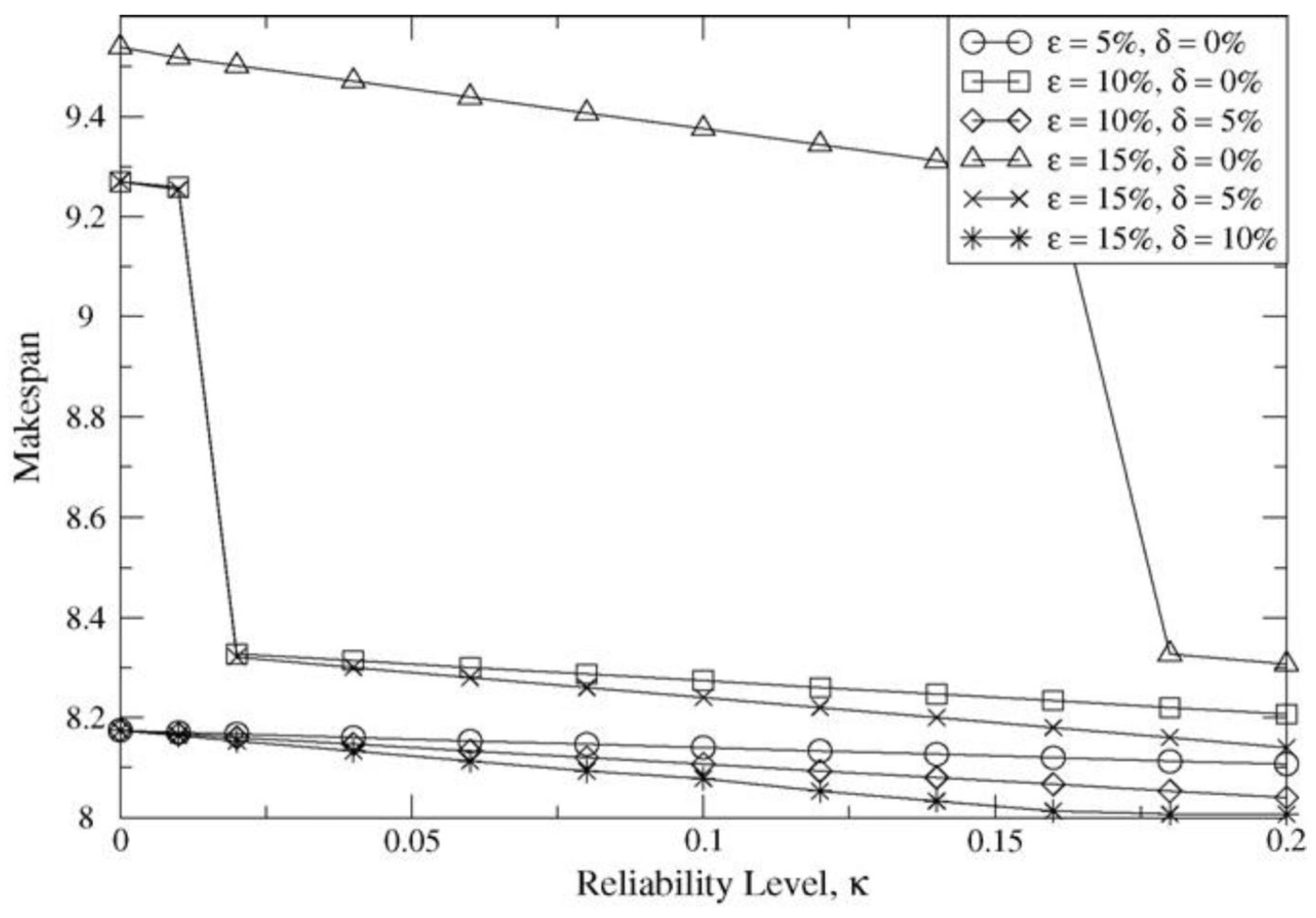
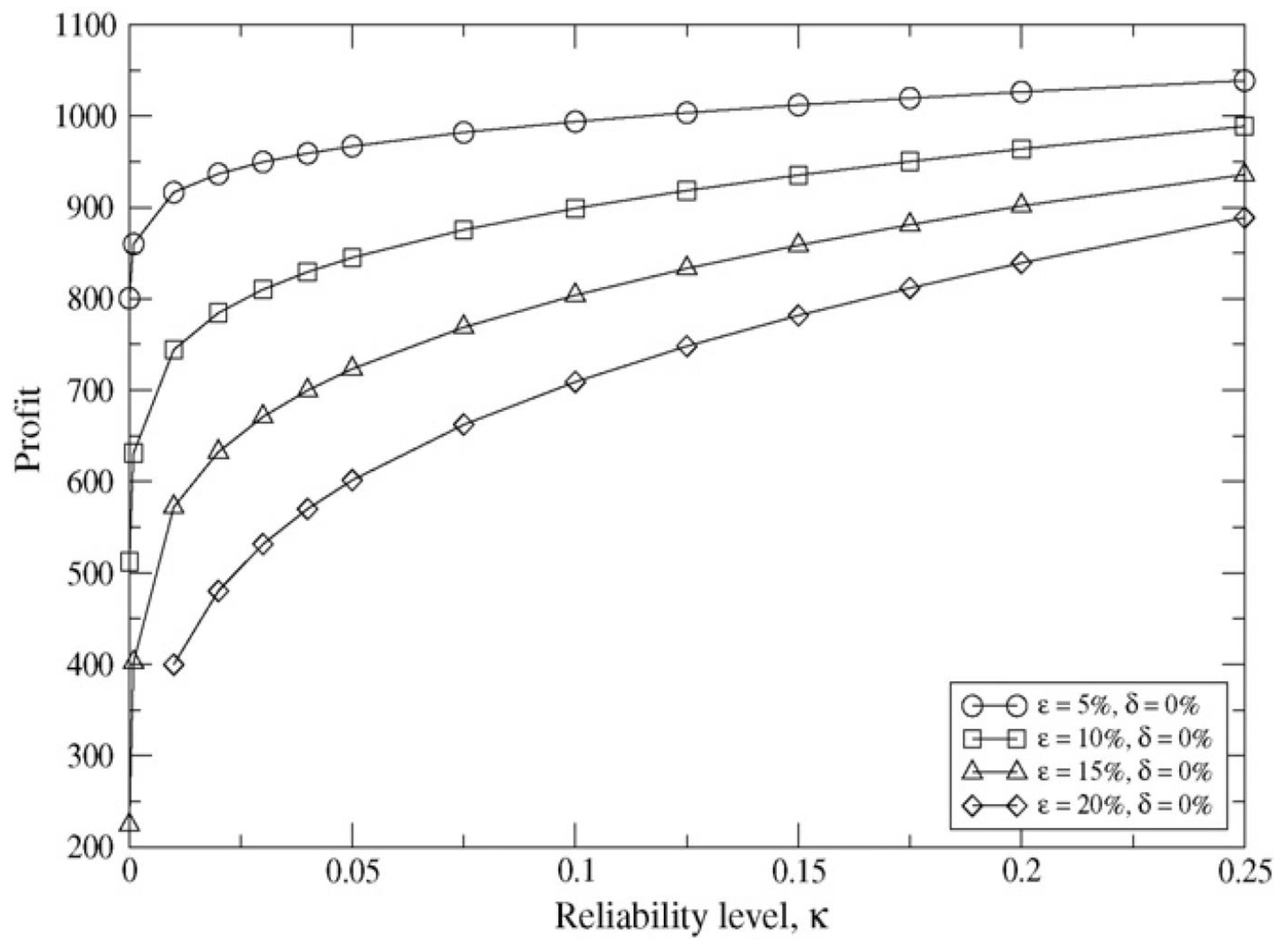
5.2. Computational outputs and discussion

Figure 12 depicts a NS for the problem with continual time formula and objective function values equaled 121.37. Figure 13 presents a solution to the correct respective problem with each of the 23 uncertain parameters at 10% (relative) in-feasibility tolerances (δ) for the finite unknown variables, 20% normal uncertain parameters, 5% level of uncertainty ( ∈ ), and 5% level of reliability (κ) for normal uncertain parameters reflecting just 5% violation of the constraints. As seen, the Obj function value has been 105.76, and the processing time of all uncertain tasks has been extended to ensure that the schedule would be feasible at the given level of uncertainty, reliability, and in-feasibility tolerances. Nonetheless, the value of the Obj function declined. Moreover, a more precise investigation of the term related to the Obj function indicated declining the Obj function value for a correct solution as the relative value of violating intermediate due-dates enhanced, whereas overall production diminished. Table 7 compares pattern and solution statistics for industrial evidence correct and NS. The published CPU times indicated the time for obtaining the most acceptable solution within a time limit of 2 h.
For a short-run timing problem examined in Part 5.1.1, the conservatism level observed in the resultant production time-table varied with the probability distribution function utilized for describing uncertain parameters. Comparing all types of uncertainties on each of the three uncertain constraints with various problem parameters for the example above problem revealed that I general discrete distributions have consistently been the least conservative, yielding the most reasonable Obj function values; binomial and Poisson distributions have consistently yielded the most conservative outputs, yielding the arrant Obj function values, and; among other kinds of distributions; that is, bounded, uniformed, and uniform distributions. Nonetheless, relative outputs for the 3 distributions strongly depended on the value of the level of reliability, κ. Therefore, when κ increased, indicating greater reliability, normal distribution became less conservative than the other two. For great κ, the normal distribution would be less conservation than the limited distribution.
Additionally, even though it is possible to use the robust optimisation protocol formulation for modelling the uncertainty in diverse MILP problems, several constraints of our approach, as an example, a series of probability distribution functions, could be just utilized for limitations containing a single uncertain variable; that is, uniform, binomial, and Poisson. Such a condition would be caused by limitations in the probability theory and not the introduced formulation. Moreover, it has not been possible for the robust optimisation protocol formulation to analyze the dependent uncertain parameters connected via general non-linear expressions; however, it could be used for linear dependence on uncertain parameters. Ultimately, our formulation could control the uncertainties in the linear constraints; therefore, further studies should address such issues.

6. Conclusion

The present research investigates the site selection problem for MH in Hong Kong. A robust optimisation protocol algorithm is employed to deal via uncertain parameters in a mathematical model. Two scenarios of uncertainty have been investigated. Therefore, the current study proposed a novel method for addressing timing based on the problem of uncertainties based on the correct optimisation protocol so that in a case of application to the MILP problems produced a “robust” solution, which had immunity against uncertainty in coefficient and the right-side variables of disparity limitations [75,76,77,78,79]. This strategy could address the issue of production scheduling with market demands, unknown processing duration, and the product and raw materials price [80,81,82]. Additionally, the new computational results show that our innovative approach offered one of the effective solutions for dealing with the timing issues brought on by uncertainty, producing accurate timetables and yielding useful data on the trade-offs between the conflicting aims. This technique could therefore resolve complex real-world problems with various uncertain factors as a result of its fruitful metamorphosis [10,73,83,84,85].
1
location Allocation Problem
2
Vehicle Routing Problem
3
Location-Routing Problem
4
Queen Elizabeth Hospital
5
Supply chains
6
Supply Chain Management
7
American Hospital Association
8
Supply Chain Resilience
9
Strategic National Stockpiles
10
Just-In-Time
11
Wall Street Journal
12
Advanced Medical Technologies Association
13
Department of Commerce
14
GPOs
15
Coherent normative analysis
16
Normal distributions
17
Binomial dispersion
18
General discrete distribution
19
Integer linear programming
20
Robust Counterpart
21
For more information about protocol formulation, see our other paper at (Heydari, M. et al., 2021).
22
State-Task Network
23
Binary variables
24
Continuous variables
25
Making choices about which treatments are covered by insurance and which are not is referred to as prioritising, or, negatively, as rationing. All insurance systems require these judgments, but publicly supported government systems are the most challenging. Cost-effectiveness analysis (CEA), which aims to "produce" the greatest number of quality-adjusted life years with a given government budget, is the dominant technique for making these judgments. This conventional method prioritises effectiveness above justice. But this is the very reason why it poses challenging justice questions. Individual patients will have uneven access to healthcare if they can pay for non-reimbursed therapies out of pocket. The same holds true in a less severe scenario when patients are required to make significant copayments for treatments that are only partially covered. The problem presented by uncommon diseases is particular. The so-called orphan pharmaceuticals, or medications for rare diseases, are rarely covered by insurance, and without government funding, the research and development of these medications is typically not profitable. However, it is challenging to argue that people with rare genetic disorders shouldn't be treated just because they are few from an ethical standpoint.

References

  1. Shuman, L.J.; Hardwick, C.P.; Huber, G.A. Location of ambulatory care centers in a metropolitan area. Health Services Research 1973, 8, 121. [Google Scholar] [PubMed]
  2. Düzgün, R.; Thiele, A. Robust optimization with multiple ranges: Theory and application to R&D project selection. In Proceedings of Proceedings of the 14th INFORMS Computing Society Conference Richmond. Virginia, USA: INFORMS; pp. 103–118.
  3. Soyster, A.L. Convex programming with set-inclusive constraints and applications to inexact linear programming. Operations research 1973, 21, 1154–1157. [Google Scholar] [CrossRef]
  4. Ben-Tal, A.; Nemirovski, A. Robust convex optimization. Mathematics of operations research 1998, 23, 769–805. [Google Scholar] [CrossRef]
  5. Ben-Tal, A.; Nemirovski, A. Robust solutions of uncertain linear programs. Operations research letters 1999, 25, 1–13. [Google Scholar] [CrossRef]
  6. Ben-Tal, A.; Nemirovski, A. Robust solutions of linear programming problems contaminated with uncertain data. Mathematical programming 2000, 88, 411–424. [Google Scholar] [CrossRef]
  7. Bertsimas, D.; Sim, M. Robust discrete optimization and network flows. Mathematical programming 2003, 98, 49–71. [Google Scholar] [CrossRef]
  8. Bertsimas, D.; Sim, M. The price of robustness. Operations research 2004, 52, 35–53. [Google Scholar] [CrossRef]
  9. Mulvey, J.M.; Vanderbei, R.J.; Zenios, S.A. Robust optimization of large-scale systems. Operations research 1995, 43, 264–281. [Google Scholar] [CrossRef]
  10. Lin, X.; Janak, S.L.; Floudas, C.A. A new robust optimization approach for scheduling under uncertainty:: I. Bounded uncertainty. Computers & chemical engineering 2004, 28, 1069–1085. [Google Scholar] [CrossRef]
  11. Lohr, K.N.; Steinwachs, D.M. Health services research: An evolving definition of the field. Health services research 2002, 37, 15. [Google Scholar] [CrossRef]
  12. Grennan, M.; Kim, G.H.; McConnell, K.J.; Swanson, A. Hospital management practices and medical device costs. Health Services Research 2022, 57, 227–236. [Google Scholar] [CrossRef]
  13. Schneller, E.S.; Smeltzer, L.R. Strategic management of the health care supply chain; Jossey-bass: 2006.
  14. Goodbaum, B. Streamlining the hospital supply chain: Just what the doctor ordered: As hospitals begin transforming to adapt to new healthcare initiatives, they are easing the pain by restructuring and streamlining supply chain operations. Inbound Logistics 2015. [Google Scholar]
  15. Robinson, J.C.; Pozen, A.; Tseng, S.; Bozic, K.J. Variability in costs associated with total hip and knee replacement implants. JBJS 2012, 94, 1693–1698. [Google Scholar] [CrossRef] [PubMed]
  16. Finance, U. MEDICARE Lack of Price Transparency May Hamper Hospitals’ Ability to Be Prudent. 2012.
  17. Schneller, E.; Abdulsalam, Y. Supply chain management and health services research: Aligning strange bedfellows. Health Services Research 2022, 57, 223–226. [Google Scholar] [CrossRef] [PubMed]
  18. Research, i. Interventional Cardiology Market Size, Share & COVID19 Impact Analysis | Global | 2021-2027 | MedSuite | Includes: Coronary Stent Market, Coronary Balloon Catheter Market, and 10 more. Available online: https://idataresearch.com/product/interventional-cardiology-market/ (accessed on 30 December 2021).
  19. Wenzl, M.; Mossialos, E. Prices for cardiac implant devices may be up to six times higher in the US than in some European countries. Health Affairs 2018, 37, 1570–1577. [Google Scholar] [CrossRef]
  20. Gannon, M.A.; Mackenzie, M.; Hand, D.J.; Short, V.; Abatemarco, D. Application of a RE-AIM evaluation framework to test integration of a mindfulness based parenting intervention into a drug treatment program. Maternal and Child Health Journal 2019, 23, 298–306. [Google Scholar] [CrossRef] [PubMed]
  21. Heydari, M.; Haghigh, E.M.; Danai, H. Value Added Production in the Company's Electrical Panel Builders West Based on Michael Porter's Value Chain. 2015.
  22. Burns, L.R. The business of healthcare innovation; Cambridge University Press: 2012.
  23. Ketcham, J.D.; Furukawa, M.F. Hospital-physician gainsharing in cardiology. Health Affairs 2008, 27, 803–812. [Google Scholar] [CrossRef]
  24. Epstein, A.J.; Ketcham, J.D.; Rathore, S.S.; Groeneveld, P.W. Variations in the use of an innovative technology by payer: The case of drug-eluting stents. Medical care 2012, 1–9. [Google Scholar] [CrossRef]
  25. Robinson, J.C. Purchasing medical innovation: The right technology, for the right patient, at the right price; Univ of California Press: 2015.
  26. Robinson, J.C. Value-based purchasing for medical devices. Health Affairs 2008, 27, 1523–1531. [Google Scholar] [CrossRef]
  27. Bhakoo, V.; Singh, P.; Sohal, A. Collaborative management of inventory in Australian hospital supply chains: Practices and issues. Supply Chain Management: An International Journal 2012, 17, 217–230. [Google Scholar] [CrossRef]
  28. Okike, K.; O’Toole, R.V.; Pollak, A.N.; Bishop, J.A.; McAndrew, C.M.; Mehta, S.; Cross III, W.W.; Garrigues, G.E.; Harris, M.B.; Lebrun, C.T. Survey finds few orthopedic surgeons know the costs of the devices they implant. Health Affairs 2014, 33, 103–109. [Google Scholar] [CrossRef] [PubMed]
  29. Burns, L.R.; Housman, M.G.; Booth Jr, R.E.; Koenig, A. Implant vendors and hospitals: Competing influences over product choice by orthopedic surgeons. Health care management review 2009, 34, 2–18. [Google Scholar] [CrossRef] [PubMed]
  30. Abdulsalam, Y.; Gopalakrishnan, M.; Maltz, A.; Schneller, E. The emergence of consolidated service centers in health care. Journal of Business Logistics 2015, 36, 321–334. [Google Scholar] [CrossRef]
  31. Abdulsalam, Y.; Gopalakrishnan, M.; Maltz, A.; Schneller, E. The impact of physician-hospital integration on hospital supply management. Journal of Operations Management 2018, 57, 11–22. [Google Scholar] [CrossRef]
  32. Abdulsalam, Y.; Schneller, E. Hospital supply expenses: An important ingredient in health services research. Medical Care Research and Review 2019, 76, 240–252. [Google Scholar] [CrossRef]
  33. McKone-Sweet, K.E.; Hamilton, P.; Willis, S.B. The ailing healthcare supply chain: A prescription for change. Journal of Supply Chain Management 2005, 41, 4–17. [Google Scholar] [CrossRef]
  34. Team, R.E. Report: Supply chain disruptions up 67% in 2020. Available online: https://www.resilinc.com/in-the-news/report-supply-chain-disruptions-up-67-in-2020/ (accessed on 23 April 2021).
  35. Roer, E.H.; Globus-Harris, I. A mechanism to reduce medical supply shortfalls during pandemics; RAND: 2020.
  36. Handfield, R.B.; Graham, G.; Burns, L. Corona virus, tariffs, trade wars and supply chain evolutionary design. International Journal of Operations & Production Management 2020, 40, 1649–1660. [Google Scholar] [CrossRef]
  37. Roland, D. Pacemaker, Ultrasound Companies Seek Priority Amid Chip Shortage. Available online: https://www.wsj.com/articles/pacemaker-ultrasound-companies-seek-priority-amid-chip-shortage-11633258802 (accessed on 3 October 2021).
  38. Intelligence, M. AdvaMed Calls on Commerce Department to Address Semiconductor Chip Shortage. Available online: https://www.medtechintelligence.com/news_article/advamed-calls-on-commerce-department-to-address-semiconductor-chip-shortage/ (accessed on 9 November 2021).
  39. Leuschner, R.; Rogers, D.S.; Charvet, F.F. A meta-analysis of supply chain integration and firm performance. Journal of Supply Chain Management 2013, 49, 34–57. [Google Scholar] [CrossRef]
  40. Walker, D.M.; McAlearney, J.S.; Sharma, L.; Kim, Y.H. Examining the financial and quality performance effects of group purchasing organizations. Health Care Management Review 2021, 46, 278–288. [Google Scholar] [CrossRef]
  41. Narasimhan, R.; Narayanan, S. Perspectives on supply network–enabled innovations. Journal of Supply Chain Management 2013, 49, 27–42. [Google Scholar] [CrossRef]
  42. Sreeramareddy, C.T.; Sathyanarayana, T. Decentralised versus centralised governance of health services. The Cochrane Database of Systematic Reviews 2019, 2019. [Google Scholar] [CrossRef]
  43. Van Doorslaer, E.; Masseria, C. Income-related inequality in the use of medical care in 21 OECD countries; OECD Paris: 2004; Vol. 14.
  44. Organization, W.H. Closing the gap in a generation: Health equity through action on the social determinants of health - Final report of the commission on social determinants of health. Available online: https://www.who.int/publications-detail-redirect/WHO-IER-CSDH-08.1 (accessed on 27 August 2008).
  45. Clement, F.M.; Harris, A.; Li, J.J.; Yong, K.; Lee, K.M.; Manns, B.J. Using effectiveness and cost-effectiveness to make drug coverage decisions: A comparison of Britain, Australia, and Canada. Jama 2009, 302, 1437–1443. [Google Scholar] [CrossRef] [PubMed]
  46. Schokkaert, E.; Van de Voorde, C. User charges. 2011.
  47. Asada, Y.; Schokkaert, E. Introduction to the special issue on justice and health: Different perspectives in different disciplines. Social Justice Research 2019, 32, 125–136. [Google Scholar] [CrossRef]
  48. Xiaohu, Z.; Heydari, M.; Lai, K.K.; Yuxi, Z. Analysis and modeling of corruption among entrepreneurs. REICE: Revista Electrónica de Investigación en Ciencias Económicas 2020, 8, 262–311. [Google Scholar] [CrossRef]
  49. Heydari, M.; Xiaohu, Z.; Keung, L.K.; Shang, Y. Entrepreneurial intentions and behaviour as the creation of business: Based on the theory of planned behaviour extension evidence from polish universities and entrepreneurs. Propósitos y representaciones 2020, 8, 46. [Google Scholar] [CrossRef]
  50. Heydari, M.; Lai, K.K.; Xiaohu, Z. Risk Management in Public-Private Partnerships; Routledge: 2020.
  51. Heydari, M.; Lai, K.K.; Xiaohu, Z. Corruption, Infrastructure Management and Public–Private Partnership: Optimizing through Mathematical Models; Routledge: 2021.
  52. Daniels, N. Just health: Meeting health needs fairly; Cambridge University Press: 2007.
  53. Powers, M.; Faden, R.R.; Faden, R.R. Social justice: The moral foundations of public health and health policy; Oxford University Press, USA: 2006.
  54. Ruger, J.P. Health and social justice. The Lancet 2004, 364, 1075–1080. [Google Scholar] [CrossRef]
  55. Segall, S. Health, luck, and justice. In Health, Luck, and Justice, Princeton University Press: 2009.
  56. Venkatapuram, S. Health justice: An argument from the capabilities approach; John Wiley & Sons: 2013.
  57. Hausman, D.M. Benevolence, justice, well-being and the health gradient. Public Health Ethics 2009, 2, 235–243. [Google Scholar] [CrossRef]
  58. Heydari, M.; Fan, Y.; Li, X.; Lai, K.K. Perceived Corruption in the Process of the Entrepreneurial Intention. In Concepts, Cases, and Regulations in Financial Fraud and Corruption, IGI Global: 2023; pp 97-143. [CrossRef]
  59. Heydari, M.; Lai, K.K.; Shi, V.; Xiao, F. Public Health Risk Evaluation through Mathematical Optimization in the Process of PPPs. International Journal of Environmental Research and Public Health 2023, 20, 1175. [Google Scholar] [CrossRef]
  60. Keshavarz, S.; Heydari, M.; Farsijani, H. The strategic factors of knowledge management success in achieving organizational agility on the model (APQC)(Case study: Automotive-related companies). European Online Journal of Natural and Social Sciences: Proceedings 2015, 4, 2309–2319. [Google Scholar]
  61. Floudas, C.A.; Lin, X. Mixed integer linear programming in process scheduling: Modeling, algorithms, and applications. Annals of Operations Research 2005, 139, 131–162. [Google Scholar] [CrossRef]
  62. Floudas, C.A.; Lin, X. Continuous-time versus discrete-time approaches for scheduling of chemical processes: A review. Computers & Chemical Engineering 2004, 28, 2109–2129. [Google Scholar] [CrossRef]
  63. Sahinidis, N.V. Optimization under uncertainty: State-of-the-art and opportunities. Computers & Chemical Engineering 2004, 28, 971–983. [Google Scholar] [CrossRef]
  64. Balasubramanian, J.; Grossmann, I. A novel branch and bound algorithm for scheduling flowshop plants with uncertain processing times. Computers & chemical engineering 2002, 26, 41–57. [Google Scholar] [CrossRef]
  65. Jia, Z.; Ierapetritou, M.G. Short-term scheduling under uncertainty using MILP sensitivity analysis. Industrial & Engineering Chemistry Research 2004, 43, 3782–3791. [Google Scholar] [CrossRef]
  66. Ozturk, C.; Ornek, M.A. Optimisation and constraint based heuristic methods for advanced planning and scheduling systems. International Journal of Industrial Engineering 2016, 23. [Google Scholar]
  67. Bonfill, A.; Bagajewicz, M.; Espuña, A.; Puigjaner, L. Risk management in the scheduling of batch plants under uncertain market demand. Industrial & engineering chemistry research 2004, 43, 741–750. [Google Scholar] [CrossRef]
  68. Bonfill, A.; Espuña, A.; Puigjaner, L. Addressing robustness in scheduling batch processes with uncertain operation times. Industrial & engineering chemistry research 2005, 44, 1524–1534. [Google Scholar] [CrossRef]
  69. Ostrovsky, G.M.; Datskov, I.V.; Achenie, L.E.K.; Volin, Y.M. Process uncertainty: Case of insufficient process data at the operation stage. AIChE Journal 2004, 49, 1216–1232. [Google Scholar] [CrossRef]
  70. Brooke, A.; Kendrick, D.; Meeraus, A.; Raman, R. GAMS: A user’s guide. South San Franciso, CA, 2003.
  71. Viswanathan, J.; Grossmann, I.E. DICOPT ++: A program for mixed-integer nonlinear optimization, user’s guide. Pittsburgh, Pennsylvania: Engineering Design Research Center, Carnegie Mellon University 1990.
  72. Kondili, E.; Pantelides, C.C.; Sargent, R.W. A general algorithm for short-term scheduling of batch operations—I. MILP formulation. Computers & Chemical Engineering 1993, 17, 211–227. [Google Scholar] [CrossRef]
  73. Lin, X.; Floudas, C.A.; Modi, S.; Juhasz, N.M. Continuous-time optimization approach for medium-range production scheduling of a multiproduct batch plant. Industrial & engineering chemistry research 2002, 41, 3884–3906. [Google Scholar] [CrossRef]
  74. Drummond, M.F.; Sculpher, M.J.; Claxton, K.; Stoddart, G.L.; Torrance, G.W. Methods for the economic evaluation of health care programmes; Oxford university press: 2015.
  75. Heydari, M.; Lai, K.K. A study on risk and expense evaluation of agility supply management of machinery. Discrete Dynamics in Nature and Society 2020, 2020. [Google Scholar] [CrossRef]
  76. Heydari, M.; Lai, K.K.; Zhou, X. Creating sustainable order fulfillment processes through managing the risk: Evidence from the disposable products industry. Sustainability 2020, 12, 2871. [Google Scholar] [CrossRef]
  77. Heydari, M.; Lai, K.K.; Xiaohu, Z. How to Manage Red Alert in Emergency and Disaster Unit in the Hospital? Evidence From London. Frontiers in Public Health 2021, 9. [Google Scholar] [CrossRef]
  78. Heydari, M.; Fan, Y.; Saeidi, M.; Lai, K.K.; Li, X.; Chen, Y.; Yang, J.; Cai, X.; Zhang, X. Emergency and Disaster Logistics Processes for Managing ORs Capacity in Hospitals: Evidence from United States. International Journal of Business and Management (IJBM) 2022, 1, 63–85. [Google Scholar] [CrossRef]
  79. Heydari, M.; Lai, K.K.; Fan, Y.; Li, X. A Review of Emergency and Disaster Management in the Process of Healthcare Operation Management for Improving Hospital Surgical Intake Capacity. Mathematics 2022, 10, 2784. [Google Scholar] [CrossRef]
  80. Ierapetritou, M.; Floudas, C. Effective continuous-time formulation for short-term scheduling. 1. Multipurpose batch processes. Industrial & engineering chemistry research 1998, 37, 4341–4359. [Google Scholar] [CrossRef]
  81. Ierapetritou, M.G.; Floudas, C.A. Effective continuous-time formulation for short-term scheduling. 2. Continuous and semicontinuous processes. Industrial & engineering chemistry research 1998, 37, 4360–4374. [Google Scholar] [CrossRef]
  82. Lin, X.; Floudas, C.A. Design, synthesis and scheduling of multipurpose batch plants via an effective continuous-time formulation. Computers & Chemical Engineering 2001, 25, 665–674. [Google Scholar] [CrossRef]
  83. Janak, S.L.; Floudas, C.A.; Kallrath, J.; Vormbrock, N. Production scheduling of a large-scale industrial batch plant. I. Short-term and medium-term scheduling. Industrial and Engineering Chemistry Research, 2006. in press.
  84. Janak, S.L.; Floudas, C.A.; Kallrath, J.; Vormbrock, N. Production scheduling of a large-scale industrial batch plant. II. Reactive scheduling. Industrial and Engineering Chemistry Research 2006, in press. [Google Scholar] [CrossRef]
  85. Lin, X.; Chajakis, E.D.; Floudas, C.A. Scheduling of tanker lightering via a novel continuous-time optimization framework. Industrial & engineering chemistry research 2003, 42, 4441–4451. [Google Scholar] [CrossRef]
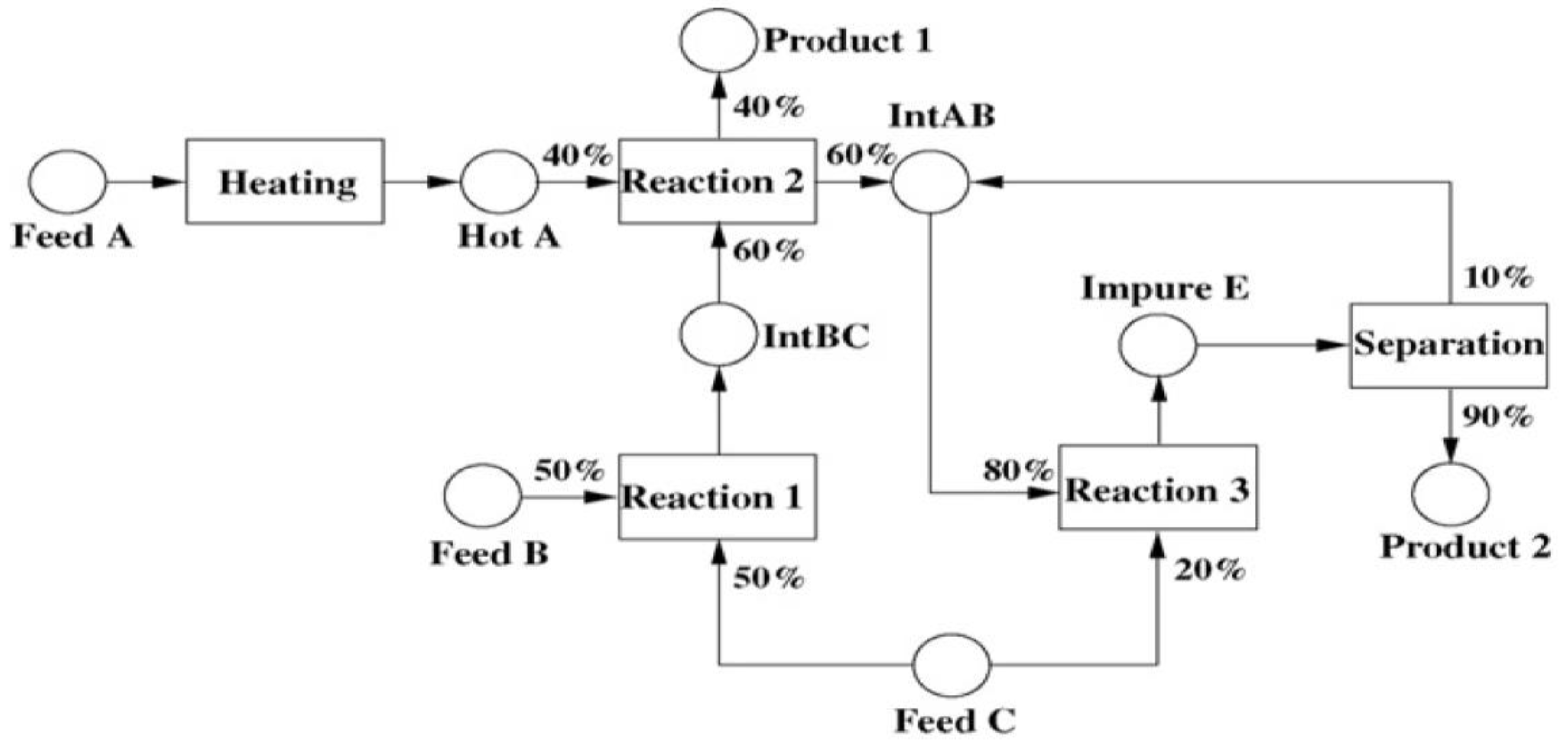
Preprints 77659 g001
Figure 1. The state task network, for instance, 1.
Figure 1. The state task network, for instance, 1.
Preprints 77659 g001
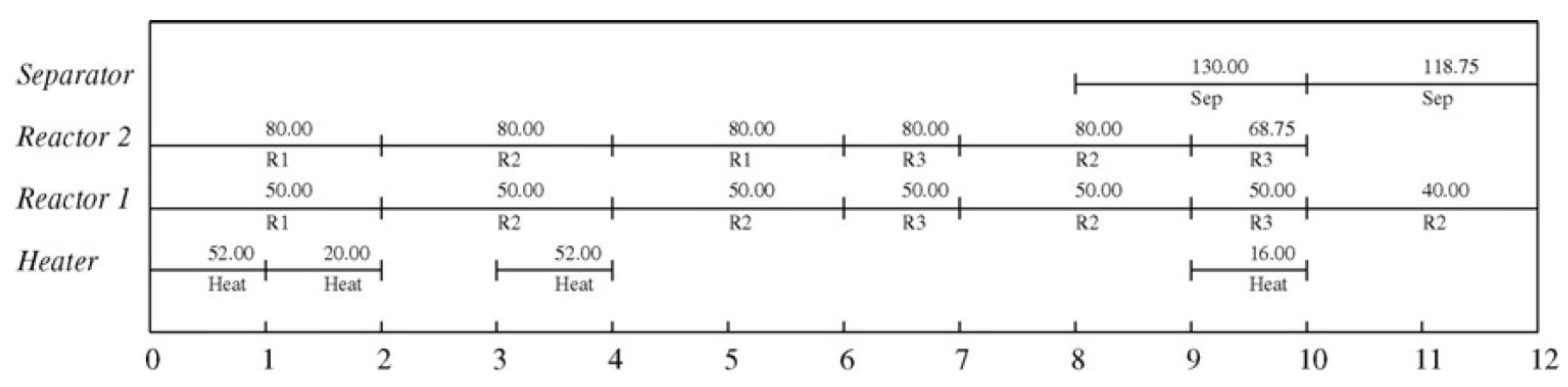
Preprints 77659 g002
Figure 2. An optimal solution via the nominal time for processing (profit=3638.75).
Figure 2. An optimal solution via the nominal time for processing (profit=3638.75).
Preprints 77659 g002
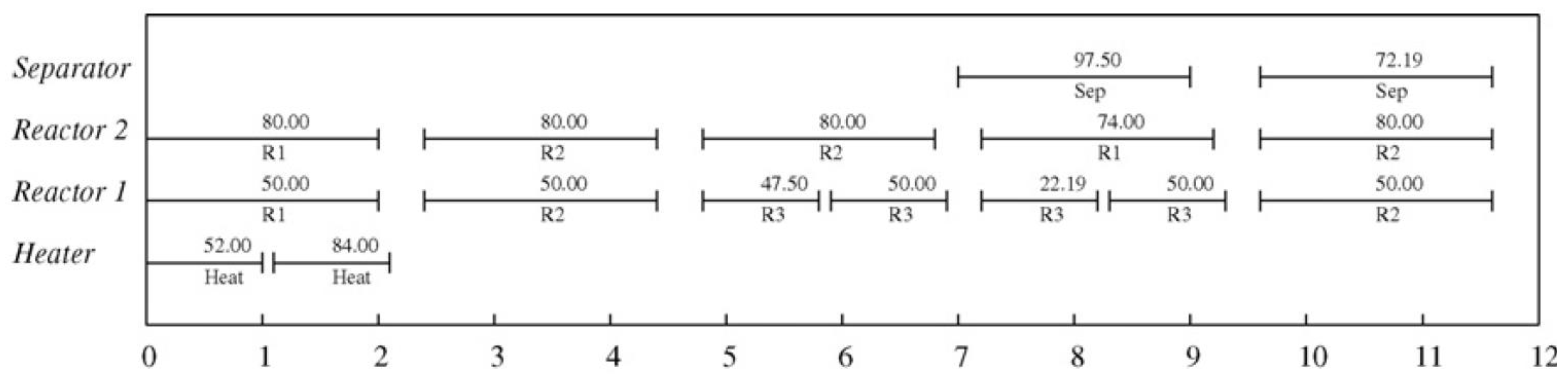
Preprints 77659 g003
Figure 3. A RS via uncertain processing time (profit=2887.19).
Figure 3. A RS via uncertain processing time (profit=2887.19).
Preprints 77659 g003
Preprints 77659 g004
Figure 4. Level of profit versus reliability at different.
Figure 4. Level of profit versus reliability at different.
Preprints 77659 g004
Preprints 77659 g005
Figure 5. Optimum solution via the nominal goods demands (make-span=8.007).
Figure 5. Optimum solution via the nominal goods demands (make-span=8.007).
Preprints 77659 g005
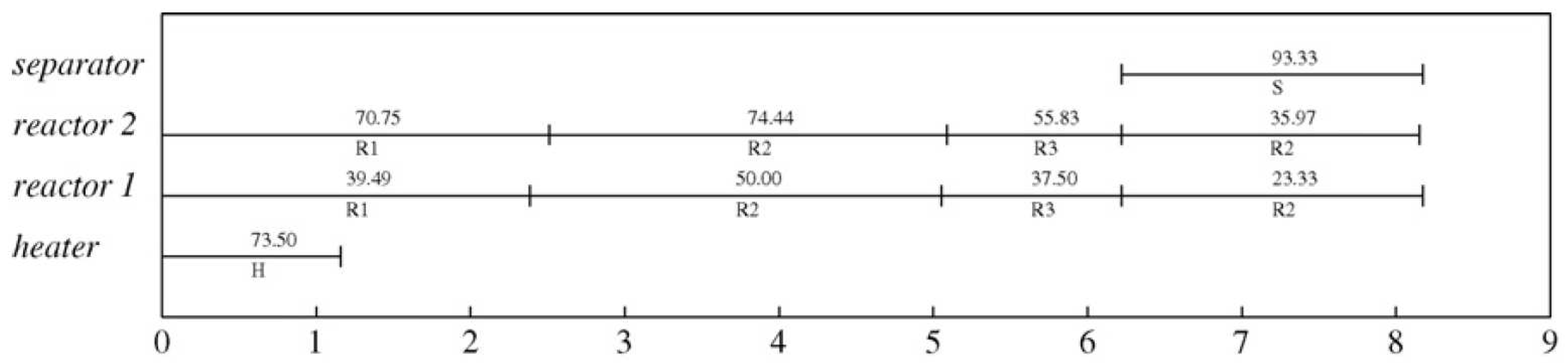
Preprints 77659 g006
Figure 6. A RS via unknown goods demand (make-span=8.174).
Figure 6. A RS via unknown goods demand (make-span=8.174).
Preprints 77659 g006
Preprints 77659 g007
Figure 7. The make-span versus the level of reliability at diverse levels of uncertainties as well as in-feasibility level, for instance, 2.
Figure 7. The make-span versus the level of reliability at diverse levels of uncertainties as well as in-feasibility level, for instance, 2.
Preprints 77659 g007
Preprints 77659 g008
Figure 8. The optimized solution via the nominal market price (profits =1088.75).
Figure 8. The optimized solution via the nominal market price (profits =1088.75).
Preprints 77659 g008
Preprints 77659 g009
Figure 9. A correct solution via unknown market price (profits =966.97).
Figure 9. A correct solution via unknown market price (profits =966.97).
Preprints 77659 g009
Preprints 77659 g010
Figure 10. For instance, the profit versus the reliability level at diverse uncertainties and in-feasibility levels, 3.
Figure 10. For instance, the profit versus the reliability level at diverse uncertainties and in-feasibility levels, 3.
Preprints 77659 g010
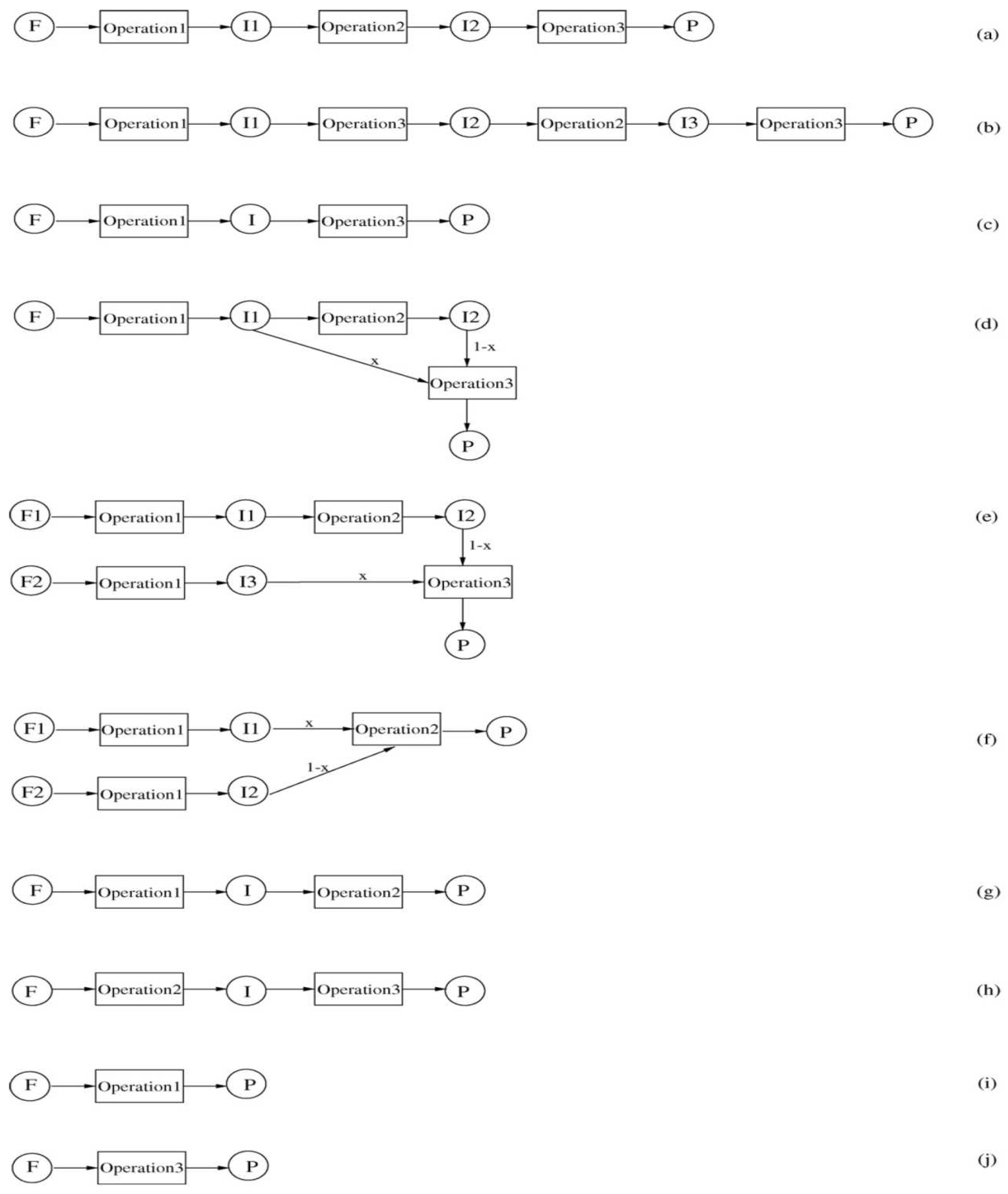
Preprints 77659 g011
Figure 11. The state-mission network of the production recipe in the industrial empirical report.
Figure 11. The state-mission network of the production recipe in the industrial empirical report.
Preprints 77659 g011
Preprints 77659 g012
Figure 12. The nominal in the case-report schedule (Obj) = 121.37, U1–U10; units I1 to I19: missions).
Figure 12. The nominal in the case-report schedule (Obj) = 121.37, U1–U10; units I1 to I19: missions).
Preprints 77659 g012
Preprints 77659 g013
Figure 13. The correct time in evidence (Obj=105.76, δ=10%, 20%, U1–U10, units I1 to I19, missions. End-point of all thick horizontal lines indicated the task end time based on nominal processing duration, whereas thin vertical lines represented the end time range because of uncertainty in the processing time.).
Figure 13. The correct time in evidence (Obj=105.76, δ=10%, 20%, U1–U10, units I1 to I19, missions. End-point of all thick horizontal lines indicated the task end time based on nominal processing duration, whereas thin vertical lines represented the end time range because of uncertainty in the processing time.).
Preprints 77659 g013
Table 1. The data, for instance, 1.
Table 1. The data, for instance, 1.
Units Adaptability Process period Capacity
Heater Heating 1.0 100
Reactor 1 R 1, 2, 3 2.0, 2.0, 1.0 50
Reactor 2 Reactions 1, 2, 3 2.0, 2.0, 1.0 80
Separator Separation 2.0 200
States Initial Amount Price Storage
Feed A Unbounded 0 Unbounded
Feed B Unbounded 0 Unbounded
Feed C Unbounded 0 Unbounded
Hot A 0 0 100
IntAB 0 0 200
IntBC 0 0 150
ImpureE 0 0 200
Product 1 0 10.0 Unbounded
Product 2 0 10.0 Unbounded
Table 2. The model and solution statistics, for instance, 1.
Table 2. The model and solution statistics, for instance, 1.
RS NS
Benefit
CPU time (s)
BIN variables
CON variables
Constraints		 2887.19 3638.75
11.33 0.46
96 96
442 442
777 553
Table 3. The model and solution statistics, for instance, 1.
Table 3. The model and solution statistics, for instance, 1.
RS NS
Make-span
CPU time (s)
BIN variables23
CON variables24
Constraints		 8.174 8.007
0.02 0.02
60 60
280 280
409 375
Table 4. The model and solution statistic, for instance, 3.
Table 4. The model and solution statistic, for instance, 3.
RS NS
Benefit
CPU time (s)
BIN variables
CON variables
Constraints		 966.97 1088.75
0.05 0.02
60 60
280 280
334 334
Table 5. The nominal processing rates and times in industrial evidence.
Table 5. The nominal processing rates and times in industrial evidence.
Units
Mission 1 2 3 4 5 6 7 8 9 10
1 0 0 0 9.5 -- -- -- -- -- --
2 -- -- -- -- 0 0 0.95 -- -- --
3 -- -- -- -- -- -- -- 12 12.8 12.5
4 0 10 10 10 -- -- -- -- -- --
5 -- -- -- -- 0.575 0.575 0.725 -- -- --
6 -- -- -- -- -- -- -- 12 12.8 12.5
7 6.09 6.09 6.09 11.1 -- -- -- -- -- --
8 -- -- -- -- 0.6 0.6 0.8 -- -- --
9 -- -- -- -- -- -- -- 12.5 13.8 12.9
10 6.09 6.09 6.09 11.1 -- -- -- -- -- --
11 -- -- -- -- 0.6 0.6 0.8 -- -- --
12 -- -- -- -- -- -- -- 12.5 13.8 12.9
13 6.09 6.09 6.09 11.1 0.6 0.6 0.8 -- -- --
14 -- -- -- -- -- -- -- -- -- --
15 -- -- -- -- -- -- -- 12.5 13.8 12.9
16 -- -- -- -- 0.6 0.6 0.8 -- -- --
17 -- -- -- -- -- -- -- 12.5 13.8 12.9
18 0 8.5 8.5 0 -- -- -- -- -- --
19 -- -- -- -- -- -- -- 0 15 16
20 0 0 8.38 9.5 -- -- -- -- -- --
Table 6. The bounded and normalized uncertainties in the processing duration and rate for the empirical report.
Table 6. The bounded and normalized uncertainties in the processing duration and rate for the empirical report.
Mission Unit NVs Uncertainty Rang Mean SD.
1 4 9.5 N -- 9.912 0.523
7,10,13 1-3 6.09 N -- 6.153 0.152
7,10,13 4 11.1 B 10.1-11.3 -- --
20 3 8.38 B 8.00-10.42 -- --
2 7 0.95 N -- 0.9611 0.112
8,11,14,16 5-6 0.60 B 0.344-0.853 -- --
3,6 9 12.8 B 10.5-19.3 -- --
9,12,15,17 9 13.8 B 12.0-16.3 -- --
9,12,15,17 10 12.9 N -- 12.100 0.760
Normal = N; Bounded = B.
Table 7. The model and solution statistics for the empirical report.
Table 7. The model and solution statistics for the empirical report.
RS NS
Obj
BIN variables
CON variables
Constraints
CPU time (s)
Nodes		 105.76 121.37
930 930
6161 6005
22931 18907
5910 3880
35640 15230
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated