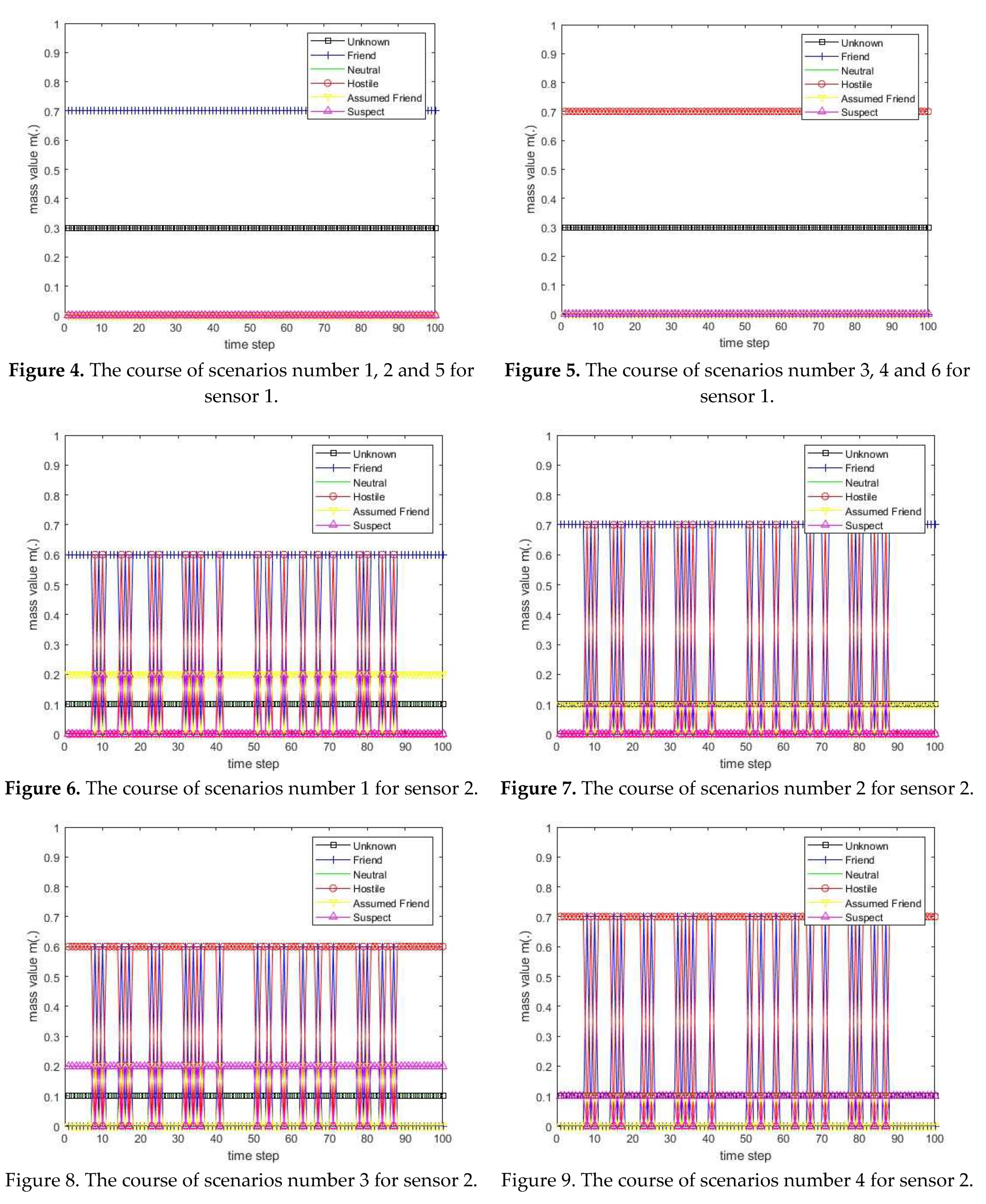
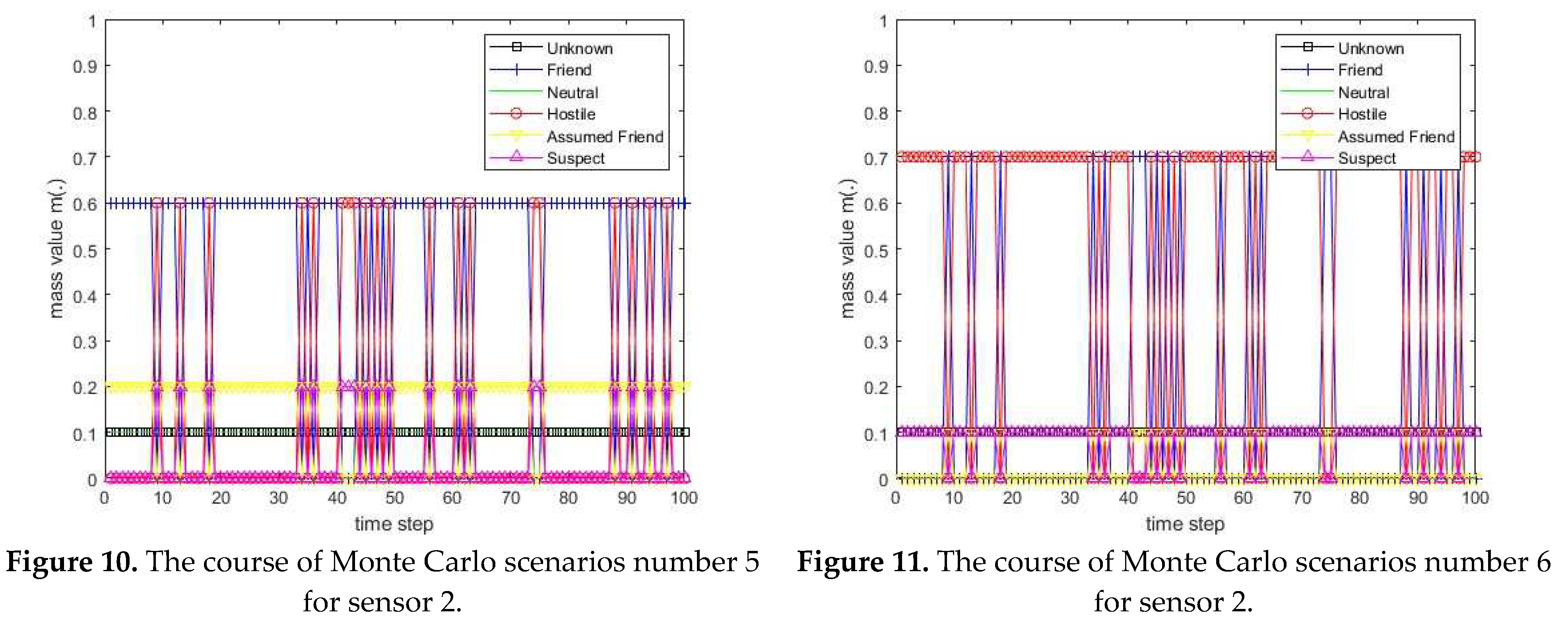
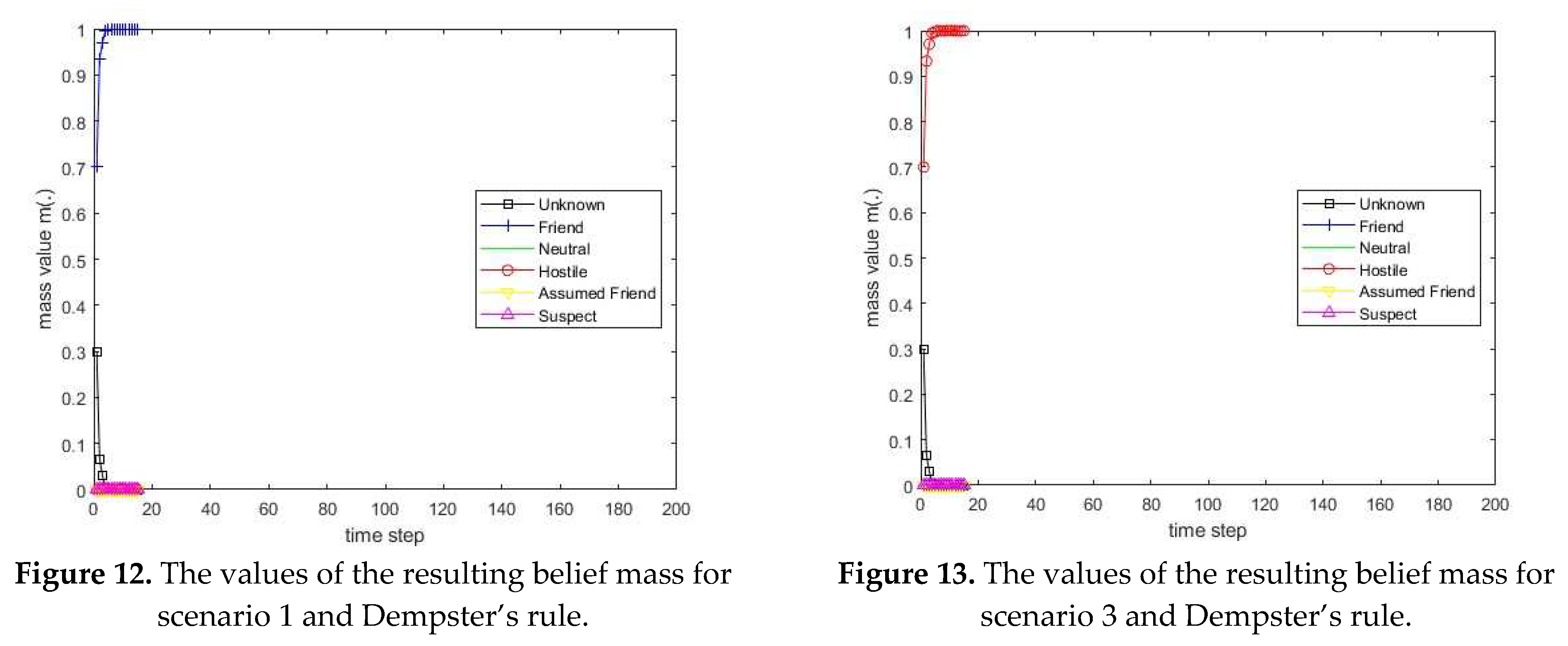
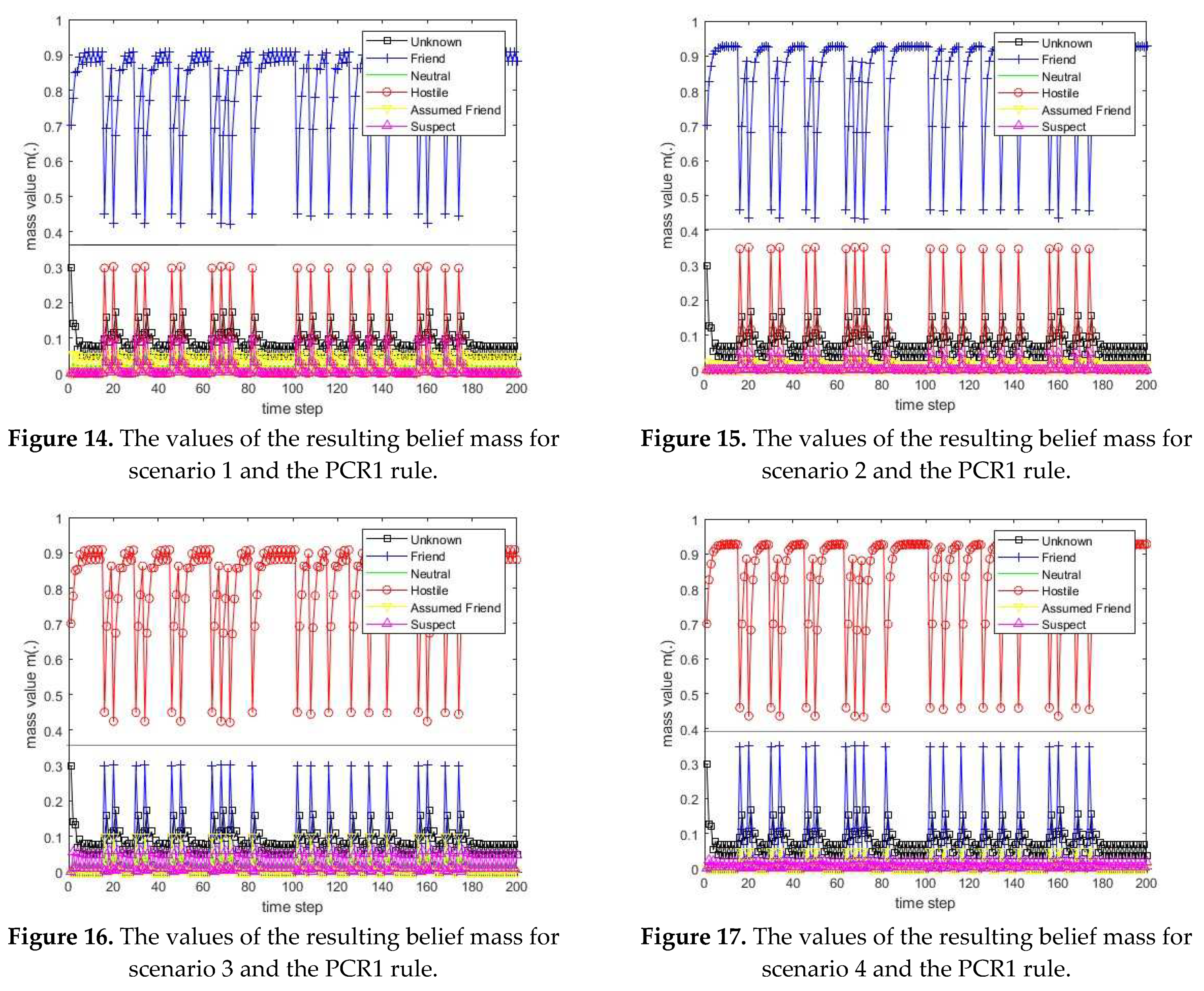
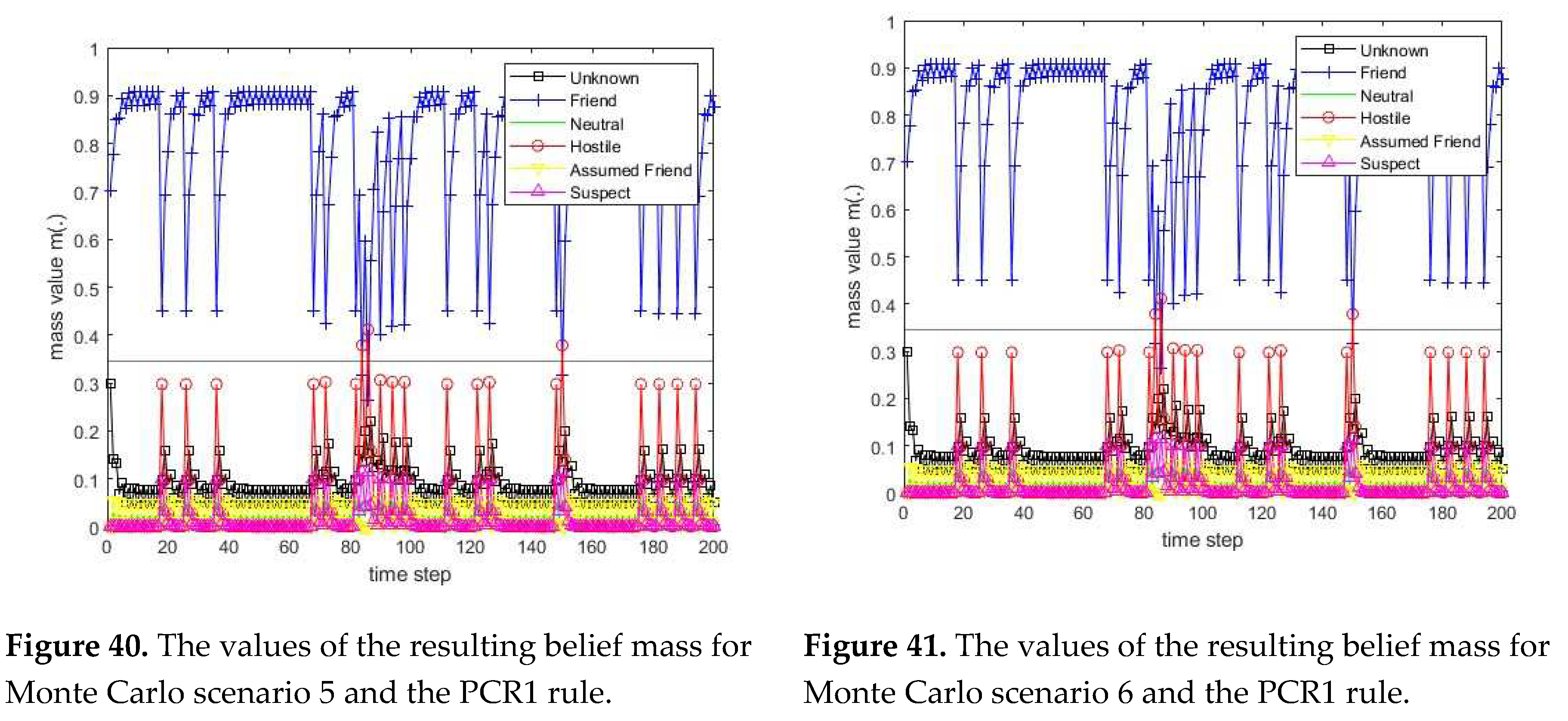
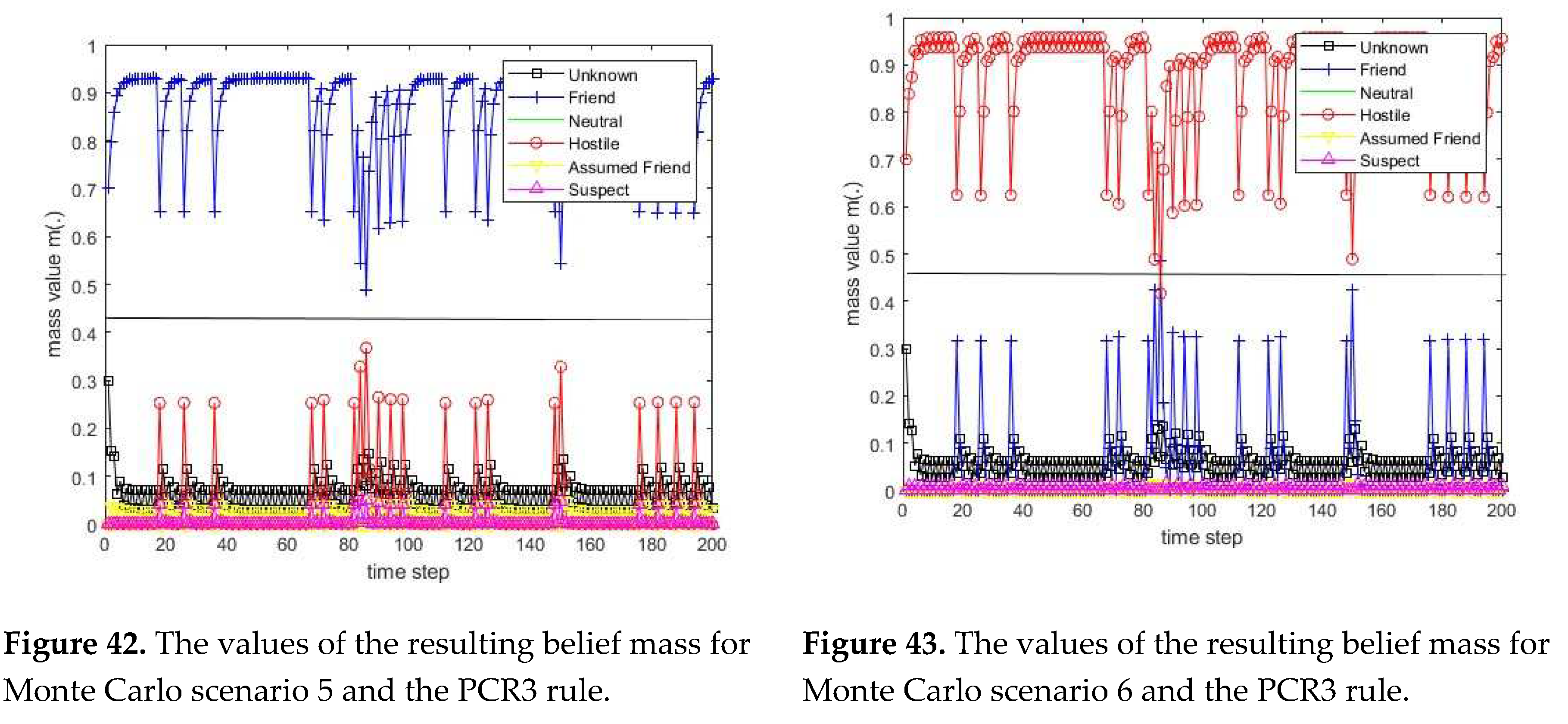
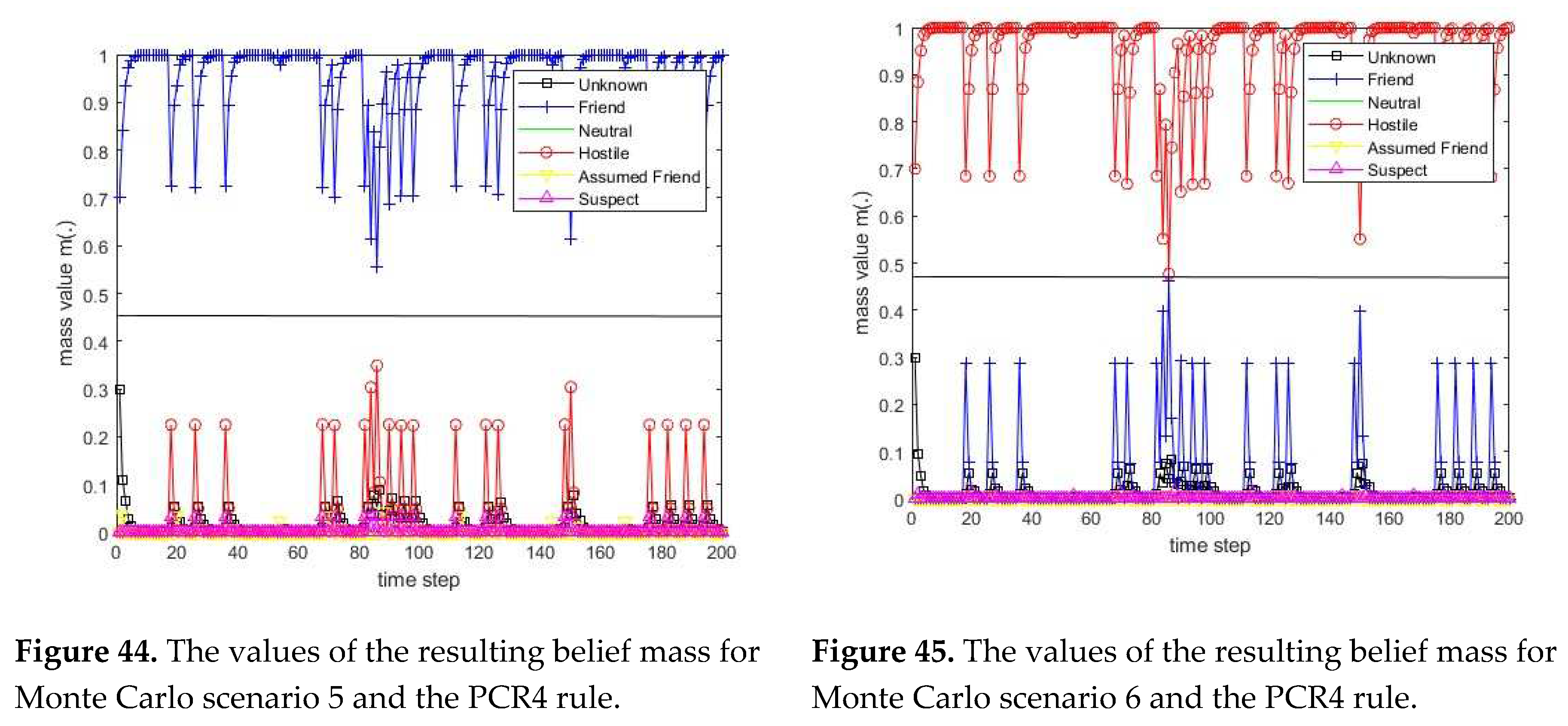
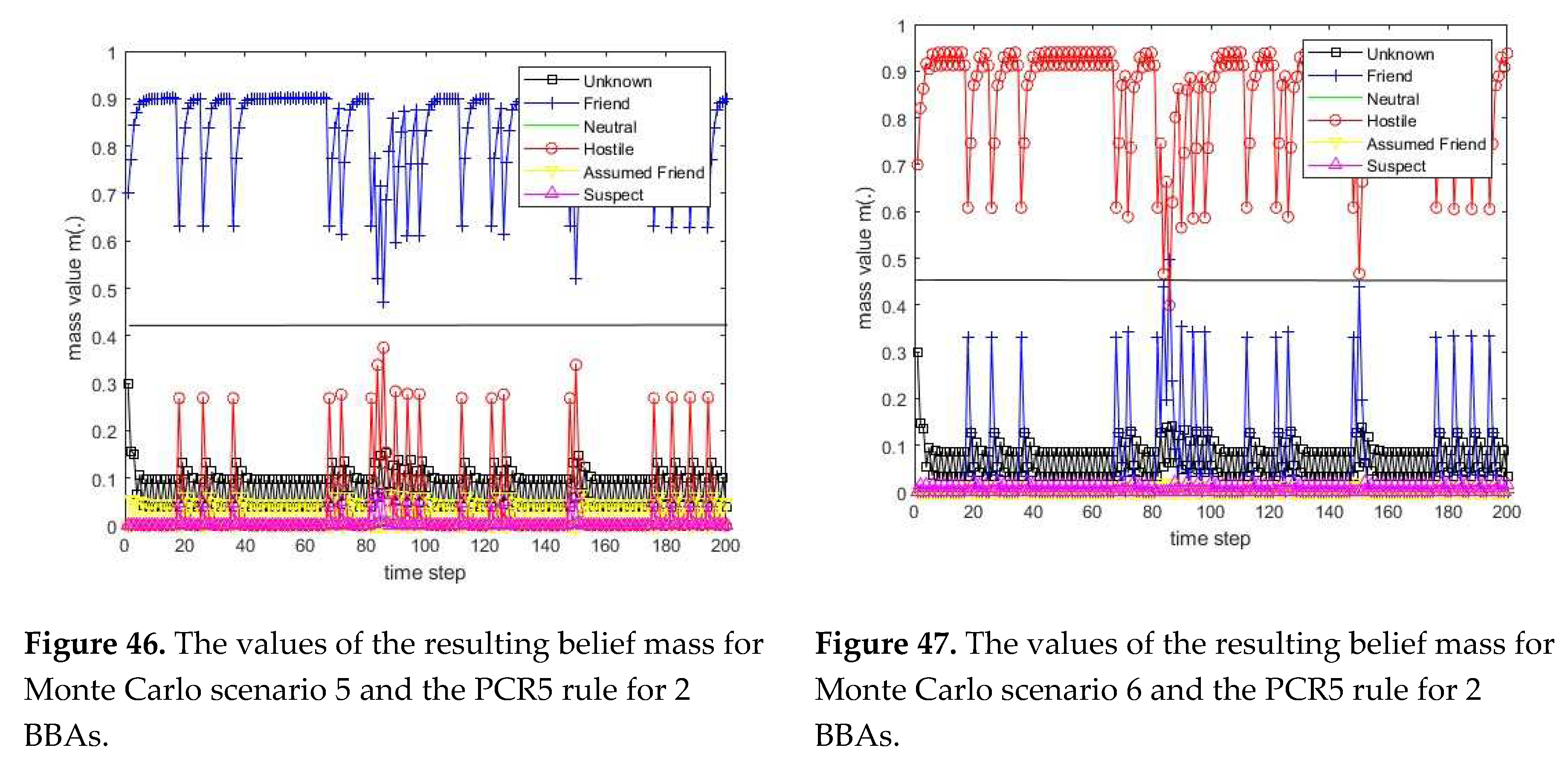
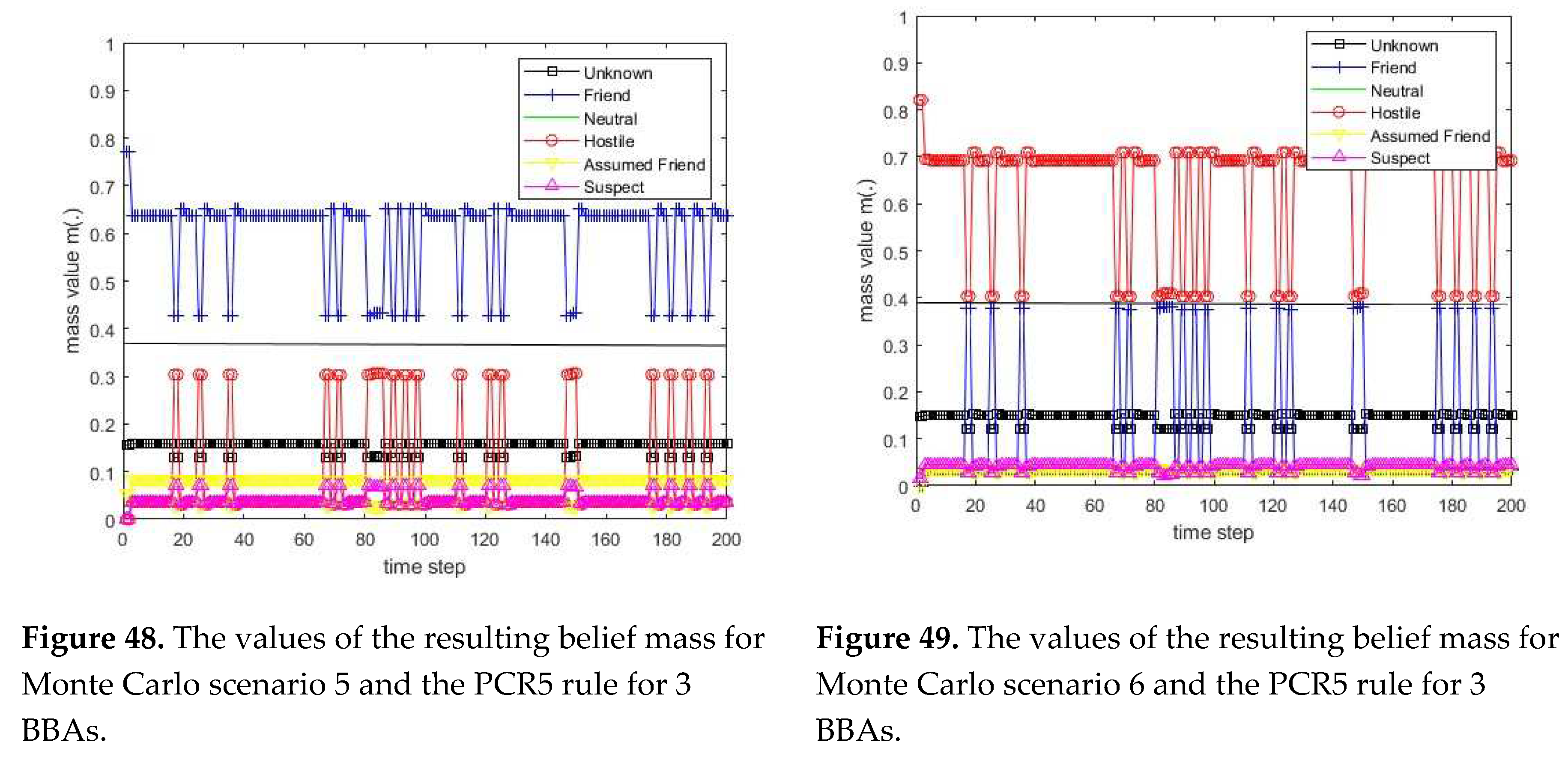
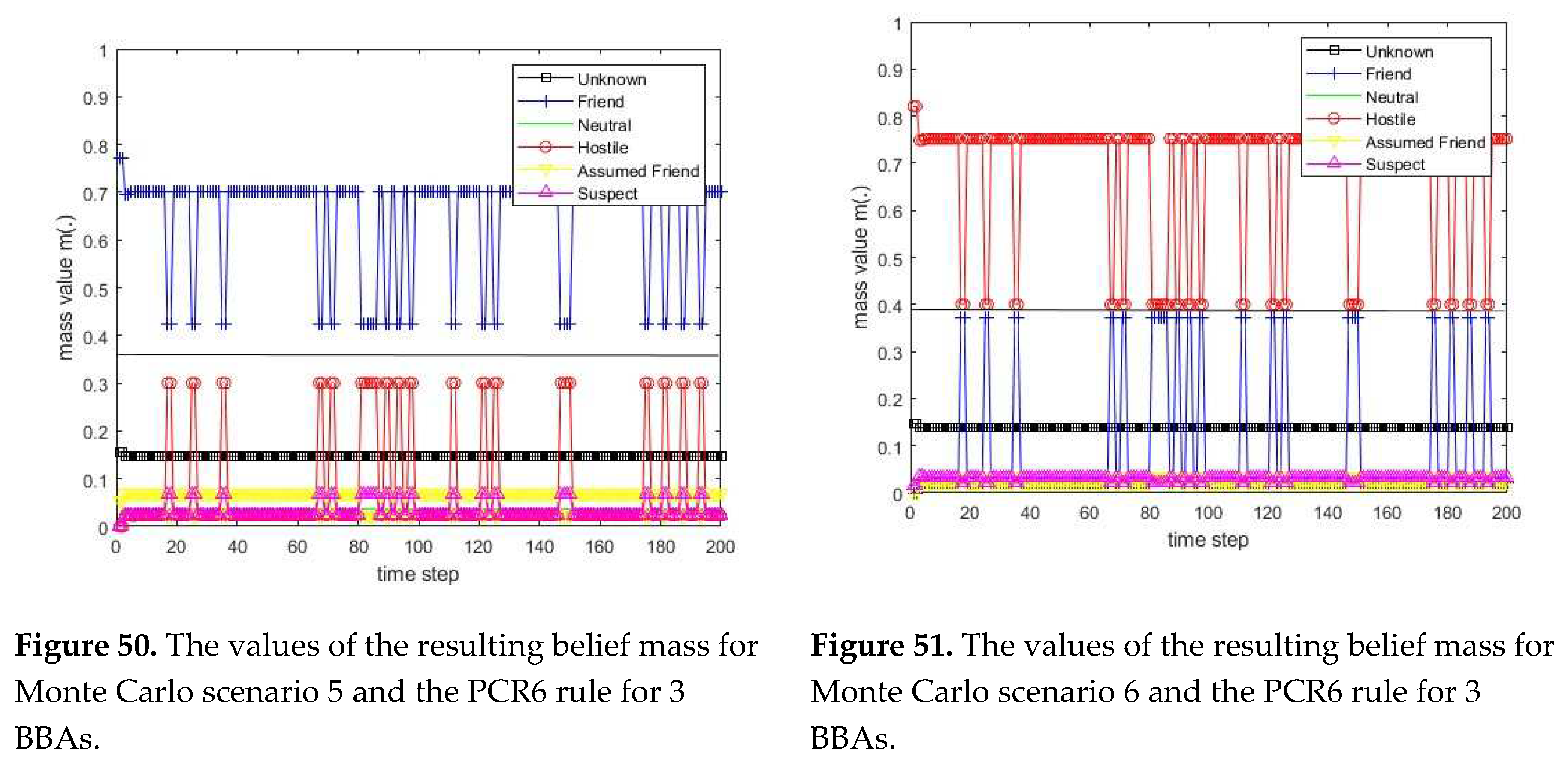
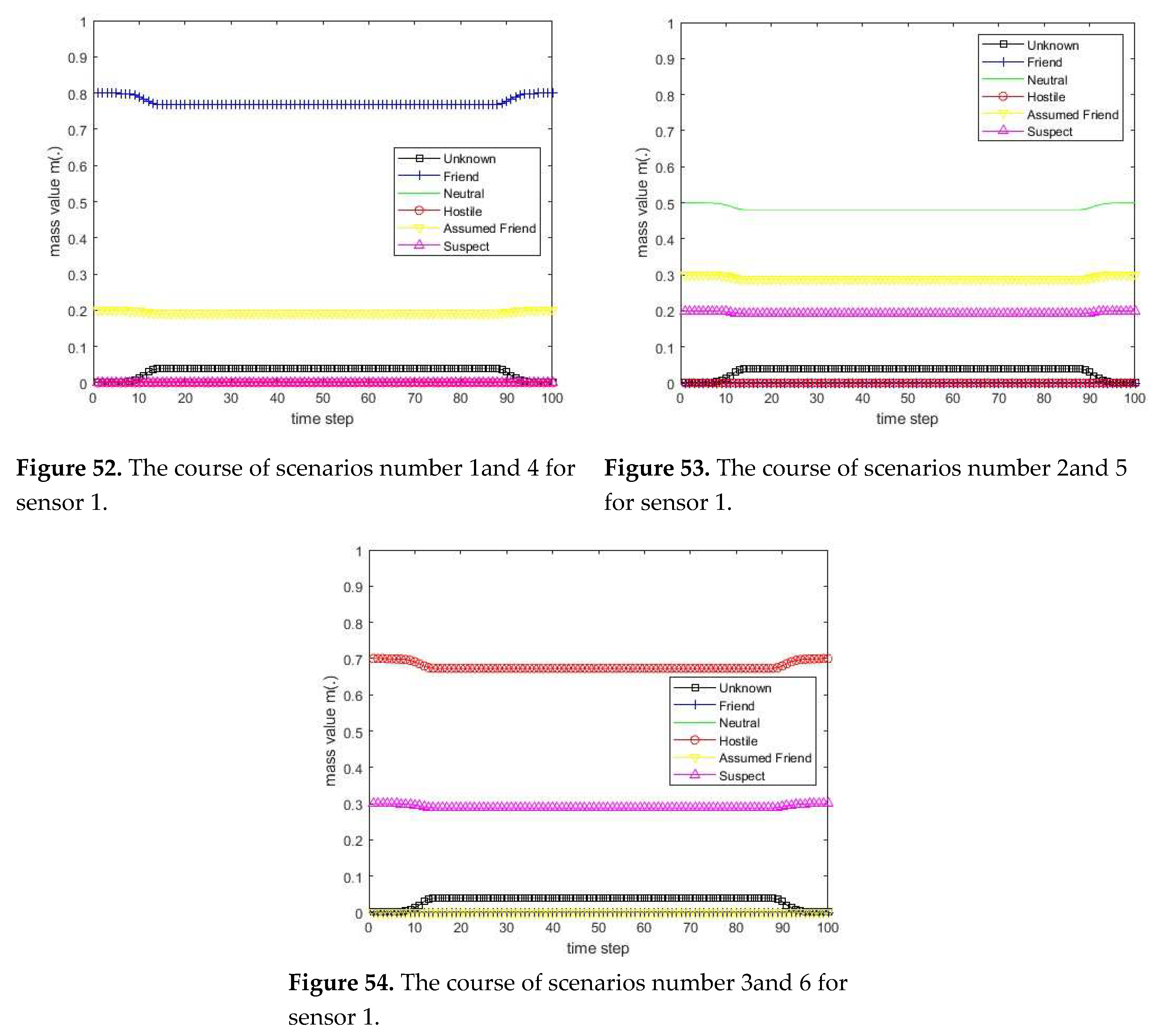
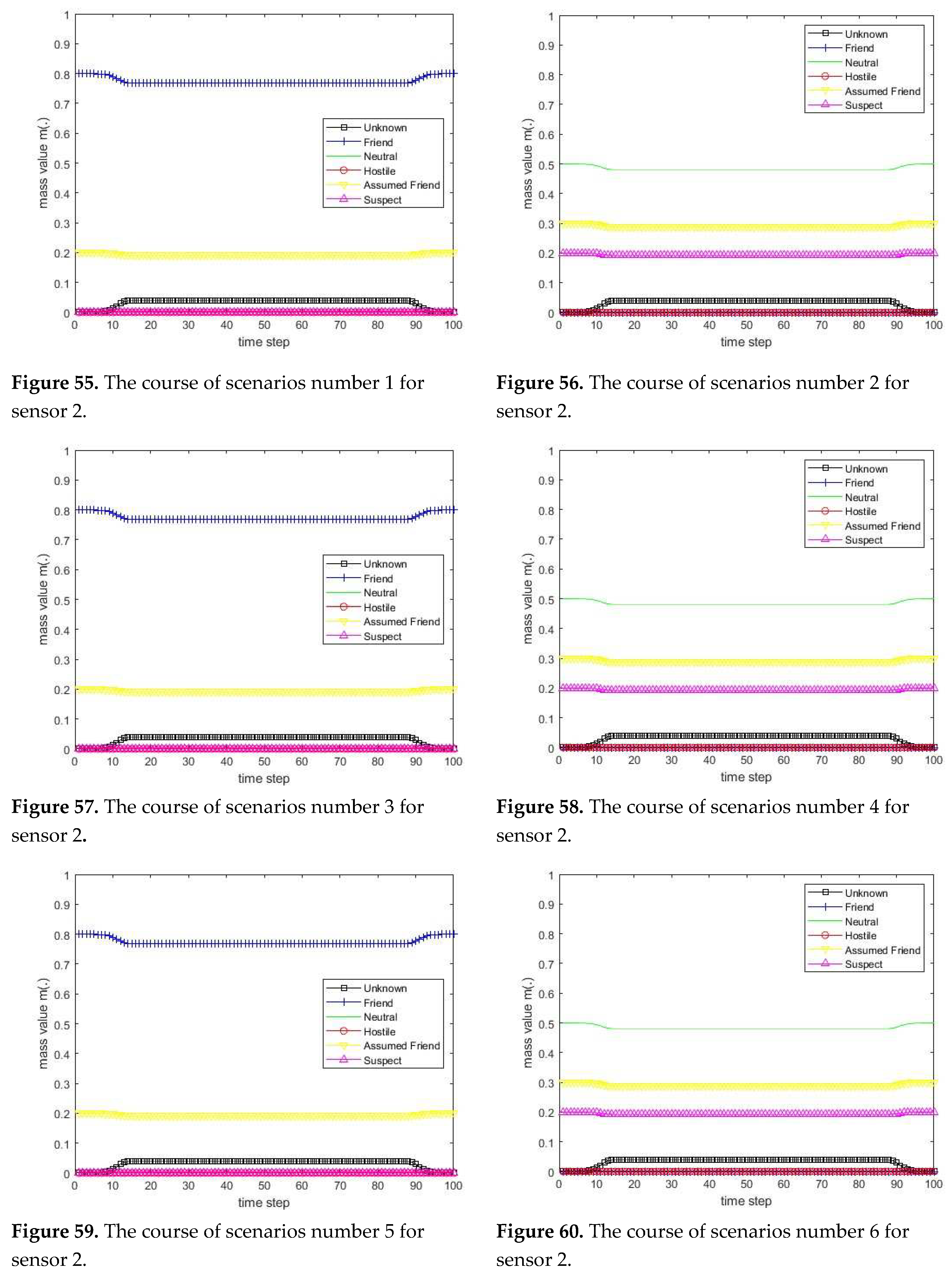
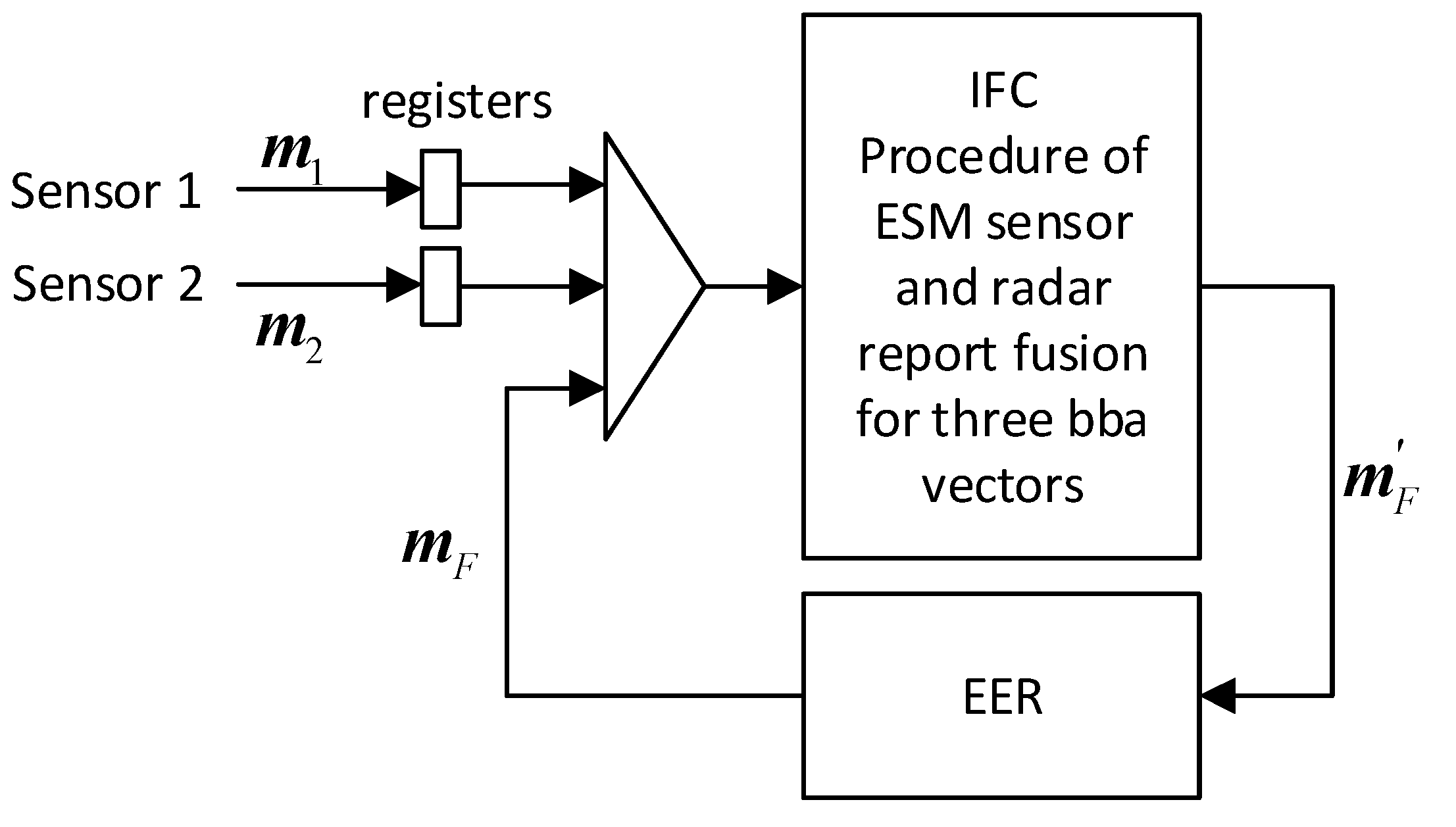
3.1. Diagram of the process of information fusion for two sensors in the information fusion center
In this work, it is assumed that ESM sensors send messages asynchronously to the information fusion center. These reports contain sensor decisions regarding the identification of objects emitting detected signals. The set of possible identifications is following:
wherein the following interpretation is used:
θ1 - FRIEND (F),
θ2 - HOSTILE (H),
θ3 - NEUTRAL (N),
θ4 - ASSUMED FRIEND(AF),
θ5 - SUSPECT(S).
θ6 - UNKNOWN (U),
According to
Figure 1, the hypotheses are mutually exclusive, i.e.
Each sensor with the number
i (
) sends its decisions as so-called soft decisions, i.e. as BBA measure vectors (BBA - basic belief assignment)
One should also introduce a vector of generalized BBA measures for the information fusion center
The paper adopts the Bayesian BBA model due to the fact that this model has been adopted as valid in the STANAG 4162 standard [
9]. This means that equation (5) applies in addition to (1) and (2).
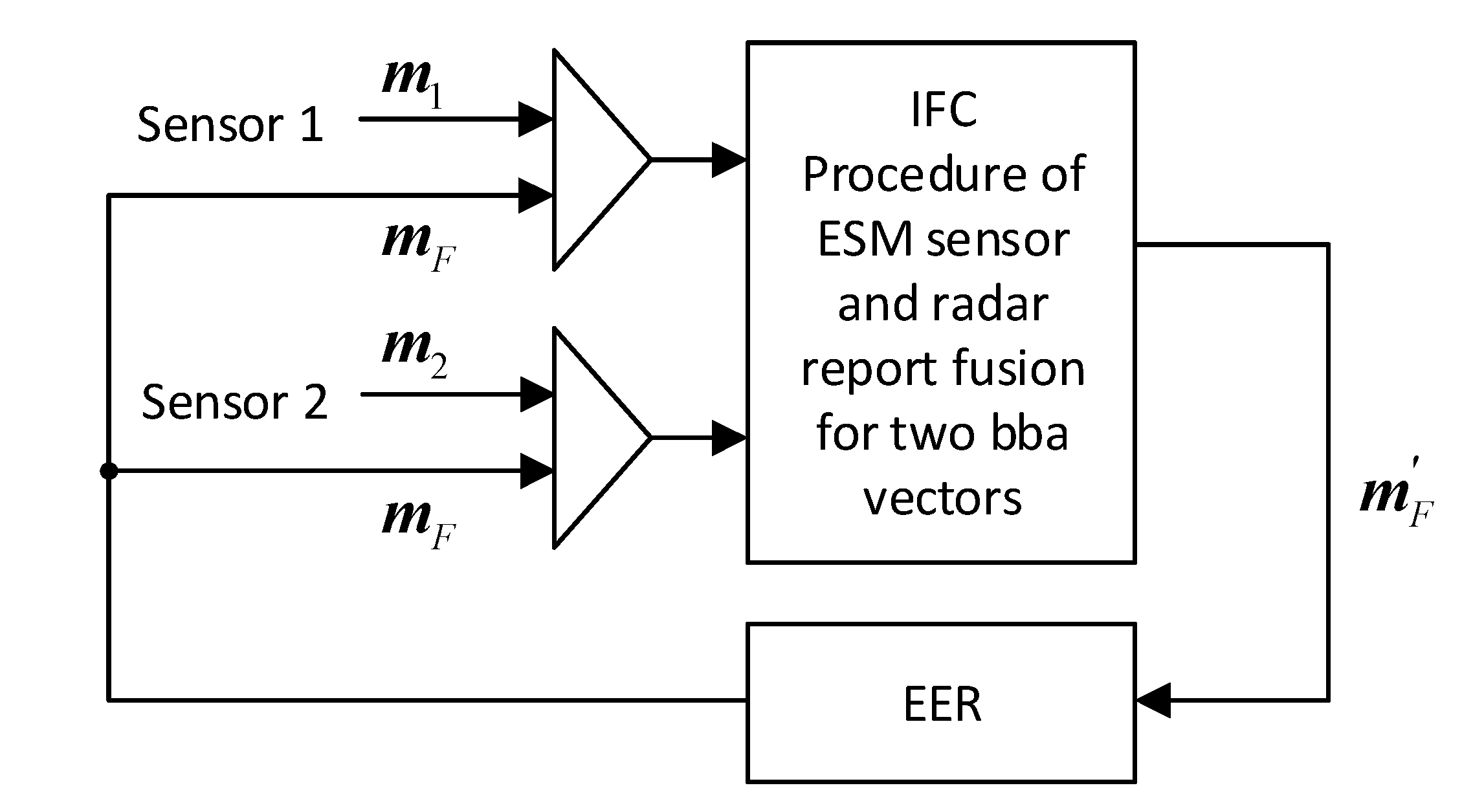
The first case will be considered when two sensors send, asynchronously in one cycle, one report each containing decisions regarding the BBA related to the target. The IFC system, after receiving the report from the sensor, fuses the information contained in the two vectors: in the current generalized BBA vector , and in the BBA vector from sensor 1 or in the BBA vector from sensor 2.
The information fusion procedure performed in the IFC is carried out in accordance with the following formula:
wherein
is a vector of the generalized BBA measure determined by the
rule based on the previous generalized BBA measure vector
and the new BBA measure vector
sent by the
i-th sensor. The diagram of the identification information fusion from the ESM sensors is shown in
Figure 2.
Figure 1.
The diagram of the information fusion process in the information fusion center IFC for two sensors. Explanations: mi – BBA measure vector of i-th sensor, mF – generalized BBA measure vector that is a part of the electronic entity record in IFC, EER – electronic entity record in IFC database.
Figure 1.
The diagram of the information fusion process in the information fusion center IFC for two sensors. Explanations: mi – BBA measure vector of i-th sensor, mF – generalized BBA measure vector that is a part of the electronic entity record in IFC, EER – electronic entity record in IFC database.
The second case will be considered when two sensors send, asynchronously in one cycle, one report each containing decisions regarding the BBA related to the target. The IFC system waits for reports from both sensors in one cycle, using registers. Only when both registers are full, the IFC system performs a fusion of the information contained in three vectors: BBA vector , and BBA vector from sensor 1, and BBA vector from sensor 2. It should be noted that this method has a drawback - the information stored in registers are losing credibility.
In this case, the information fusion procedure performed in the IFC is carried out in accordance with the following formula:
wherein
is a vector of the generalized BBA measure determined by the
rule based on the previous generalized BBA measure vector
and the new BBA measure vectors
and
sent by both sensors. The diagram of the identification information fusion from the ESM sensors is shown in
Figure 3.
In the further part of the paper, the combination rules of the BBA vector from the i - th sensor and the generalized BBA vector in the CFI are described.
3.2. The rules of combination of BBA measures vectors
This section presents formulas defining various combination rules for calculating basic belief assignments for the system shown in
Figure 2 and
Figure 3. The general forms are described in details in [
4,
11,
12]. The information fusion rules of the DSm theory are presented below with the following constraints:
Dempster’s rule
Dempster’s rule [
13,
14] of the BBA measure vector
mi sent by the
i-th sensor and the generalized BBA measure vector
mF s in IFC is described for each
θj ∈
Θ by the following formula:
wherein
the degree of conflict is defined by the formula:
while
From (12) it follows that if
then the degree of conflict is full.
If
then there is no conflict.
is Dempster-Shafer fusion result if and only if the denominator of the expression (8) is non-zero, i.e. the degree of conflict is less than 1.
The Proportional Conflict Redistribution rule PCR1
PCR1 rule is the simplest and the easiest version of proportional conflict redistribution rule. The concept of the PCR1 rule assumes the calculation of the total conflicting mass (not worrying about the partial conflicting masses). The total conflicting mass is redistributed to all non-empty sets of hypotheses proportionally with respect to their corresponding non-empty column sum of the associated mass matrix. The PCR1 rule is defined for every non-empty hypothesis in the following way:
where
is the non-zero sum of the column corresponding to the hypotheses
in the mass matrix
specified by the formula
where:
(i=1,2) is a row vector of the basic belief assignments masses of the i-th sensor's hypotheses ,
is a row vector of the basic belief assignments masses of the IFC system’s hypotheses,
is the degree of mass conflict specified by the formula
is the sum of all non-zero column sums of all non-empty sets
In our case
because
The Proportional Conflict Redistribution rule PCR2
In PCR2 rule, the total conflicting mass is distributed only to the non-empty sets involved in the conflict (not to all non-empty sets) and taken proportionally with respect to their corresponding non-empty column sum.
A non-empty set
is considered involved in the conflict if there exists another set
which is neither included in
nor includes
such that
and
. The PCR2 rule is defined for every non-empty hypothesis
in the following way:
where
Formula (23) can be written differently in the form (25), taking into account the definition of involvement in a conflict and formula (24) [
12]:
is the non-zero sum of the column corresponding to the hypotheses in the mass matrix M (16) specified by the formula
where:
(i=1,2) is a row vector of the basic belief assignments masses of the i-th sensor's hypotheses ,
is a row vector of the basic belief assignments masses of the IFC system’s hypotheses,
is the degree of mass conflict specified by the formula (18),
is the sum of all non-zero column sums of all non-empty sets only involved in the conflict
where
and
is defined by (24).
It will be shown below that in the case of data used in numerical experiments (section 6)
, this means that the PCR2 rule is equivalent to the PCR1 rule. The BBA vectors used there contain values less than 1, which means that
It follows that each BBA vector contains at least two non-zero components, that is
such that
From (31) and (32) it follows that if
, then there exists at least one value
such that
, which can be written in the following form
From (33) it follows that
Taking into account (34), (35) and (25) one can obtain
From (36) and (37) it follows that
This means that any hypothesis with a non-zero BBA value for any of the two sensors is involved in a conflict.
From (27) it follows that
Using (36), (37) and (40), the value
will be determined.
Because
we get
Considering (43), it can be said that in this case the PCR2 rule is equivalent to the PCR1 rule. For this reason, the results of the PCR2 rule are not presented in section 6, as they would be identical to the results of the PCR1 rule because we work only with Bayesian BBAs in this application.
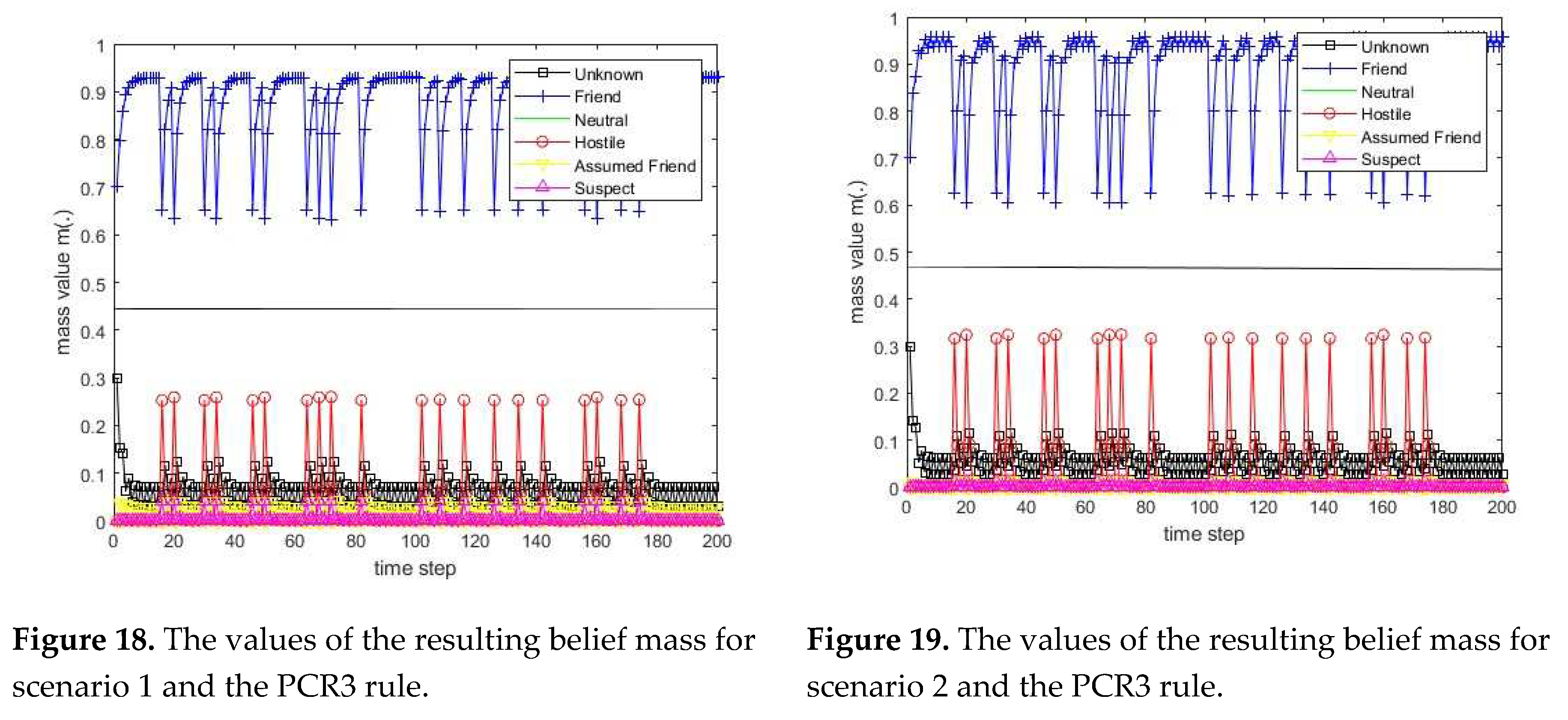
The Proportional Conflict Redistribution rule PCR3
In PCR3 rule, one distributes the partial conflicting masses, instead of the total conflicting mass , to the non-empty sets involved in the partial conflict. If an intersection is empty, for instance , then the mass of the partial conflict is transferred to the non-empty sets and proportionally with respect to the non-zero sum of masses assigned to and respectively to by the BBAs and . The PCR3 rule works if at least one set between and is non-empty and its column sum is non-zero.
The PCR3 rule is defined for every non-empty hypothesis
in the following way:
where
is the non-zero sum of the column corresponding to the hypotheses
in the mass matrix
M (16) specified by the formula
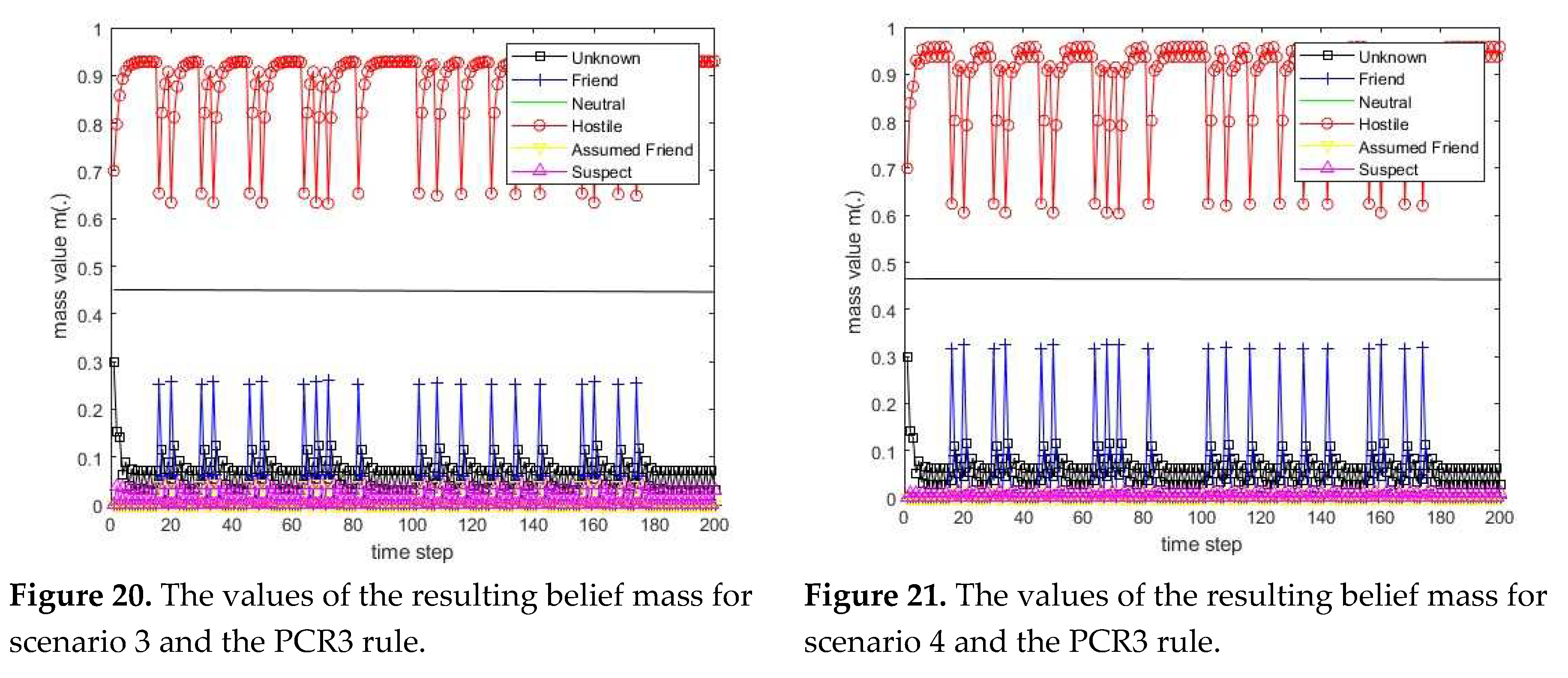
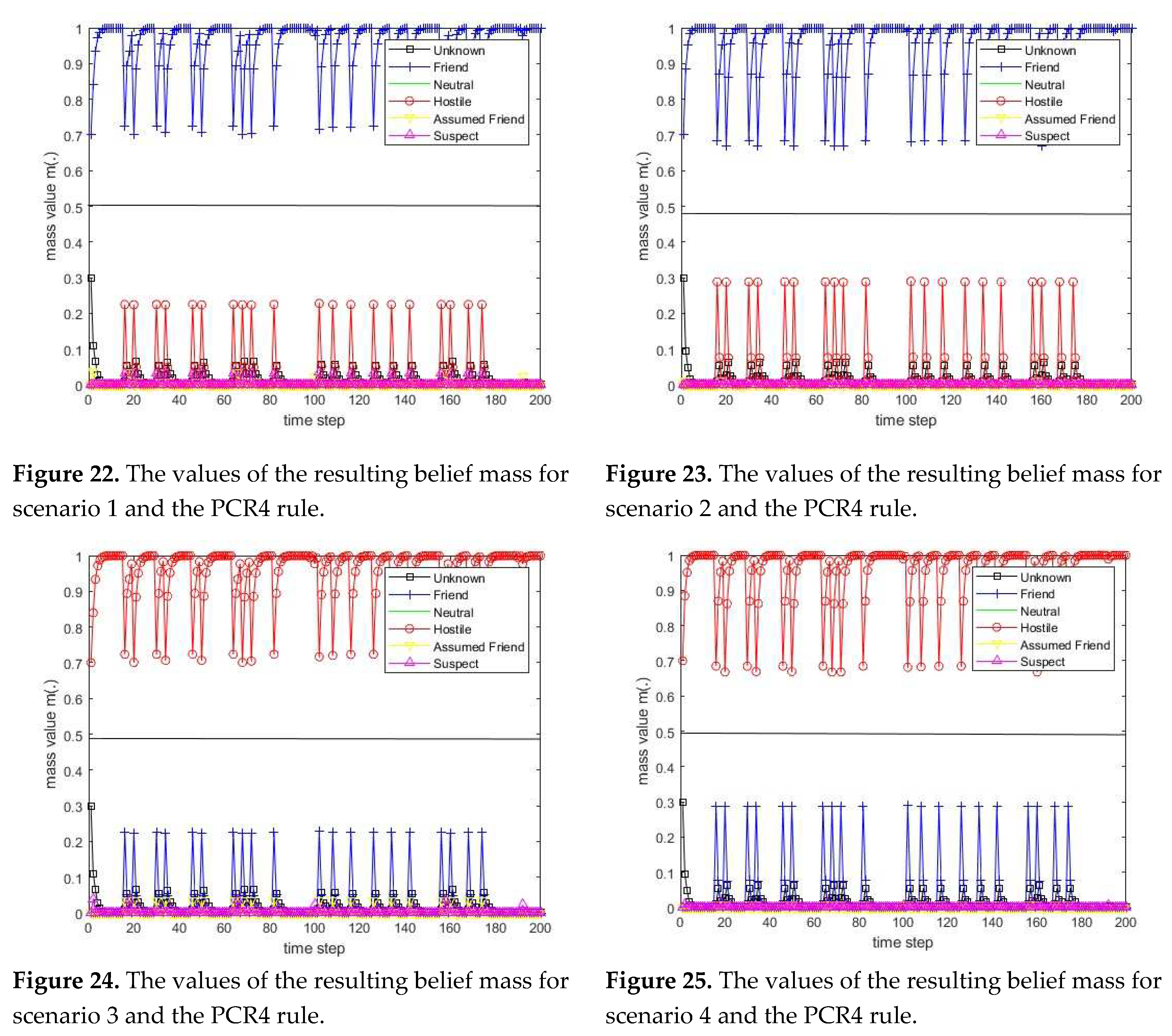
The Proportional Conflict Redistribution rule PCR4
The PCR4 rule redistributes the partial conflicting masses only to the sets involved in the partial conflict in proportion to the non-zero mass sum assigned to
and
by the conjunction rule according to the following formula:
where
wherein
If at least one of BBAs or is zero, the fraction is discarded and the mass is transferred to and proportionally with respect to their non-zero column sum of masses .
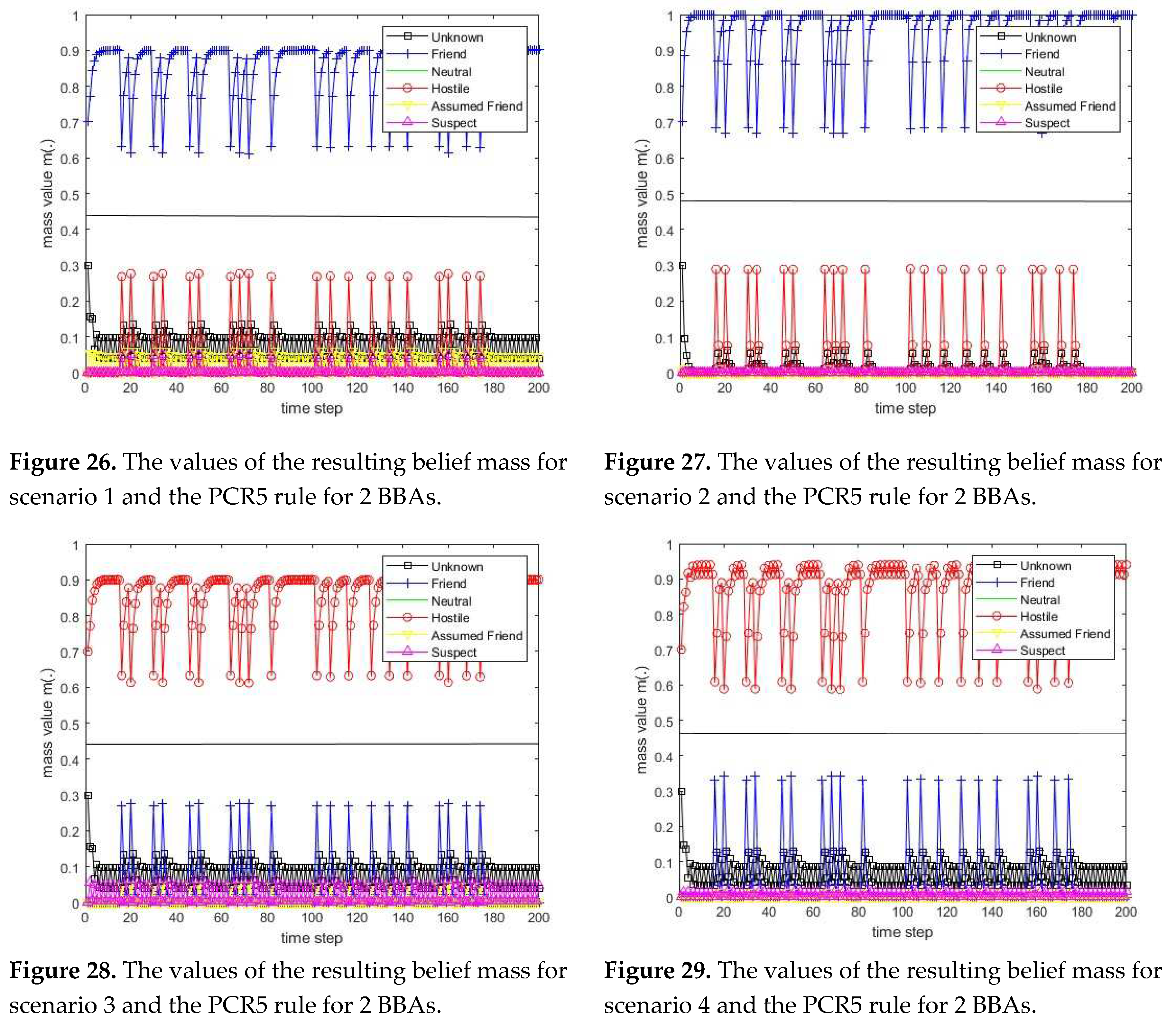
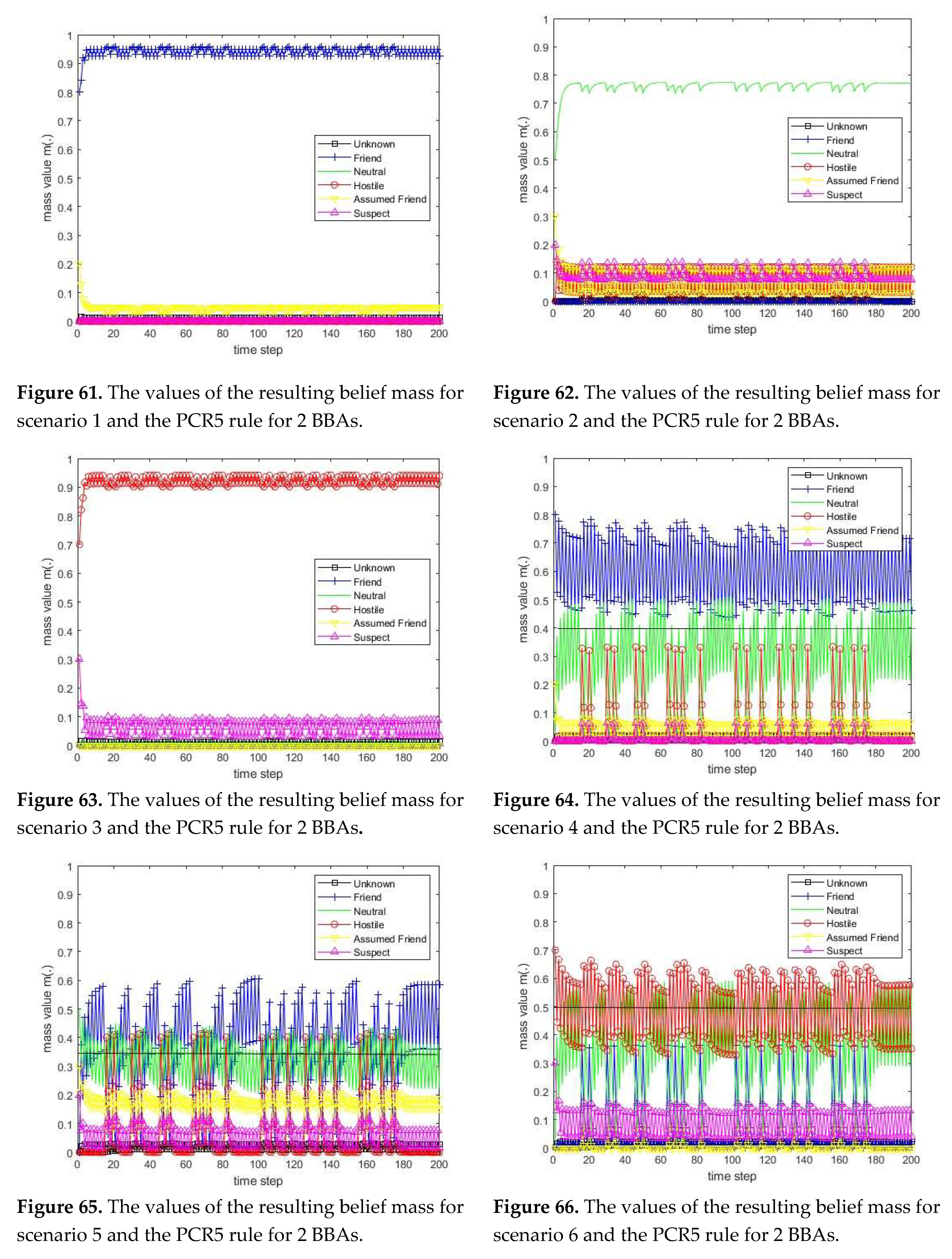
The Proportional Conflict Redistribution rule PCR5 for two BBAs (two sources)
Similarly to PCR2-PCR4 rules, PCR5 redistributes the partial conflicting mass to the hypothesis involved in the partial conflict. PCR5 provides the most mathematically precise [
4,
11,
12] redistribution of conflicting mass to non-empty sets in accordance with the logic of the conjunctive rule. However, it is more difficult to implementation. The PCR5 rule is defined for every non-empty hypothesis
in the following way:
where
wherein
In the formula (52), the component is equal to zero if both denominators are equal to zero. In the formula (53), if a denominator is zero, then component is discarded.
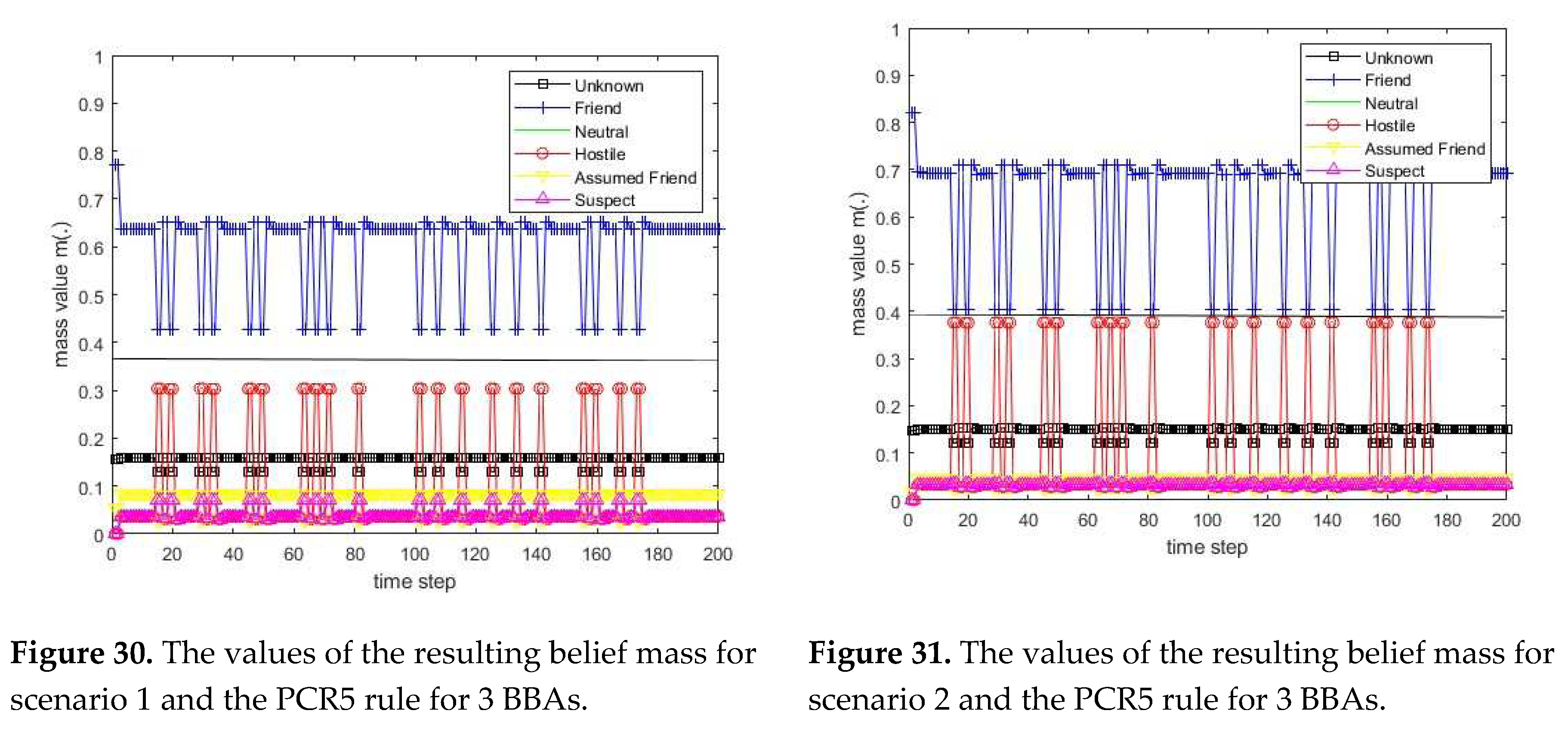
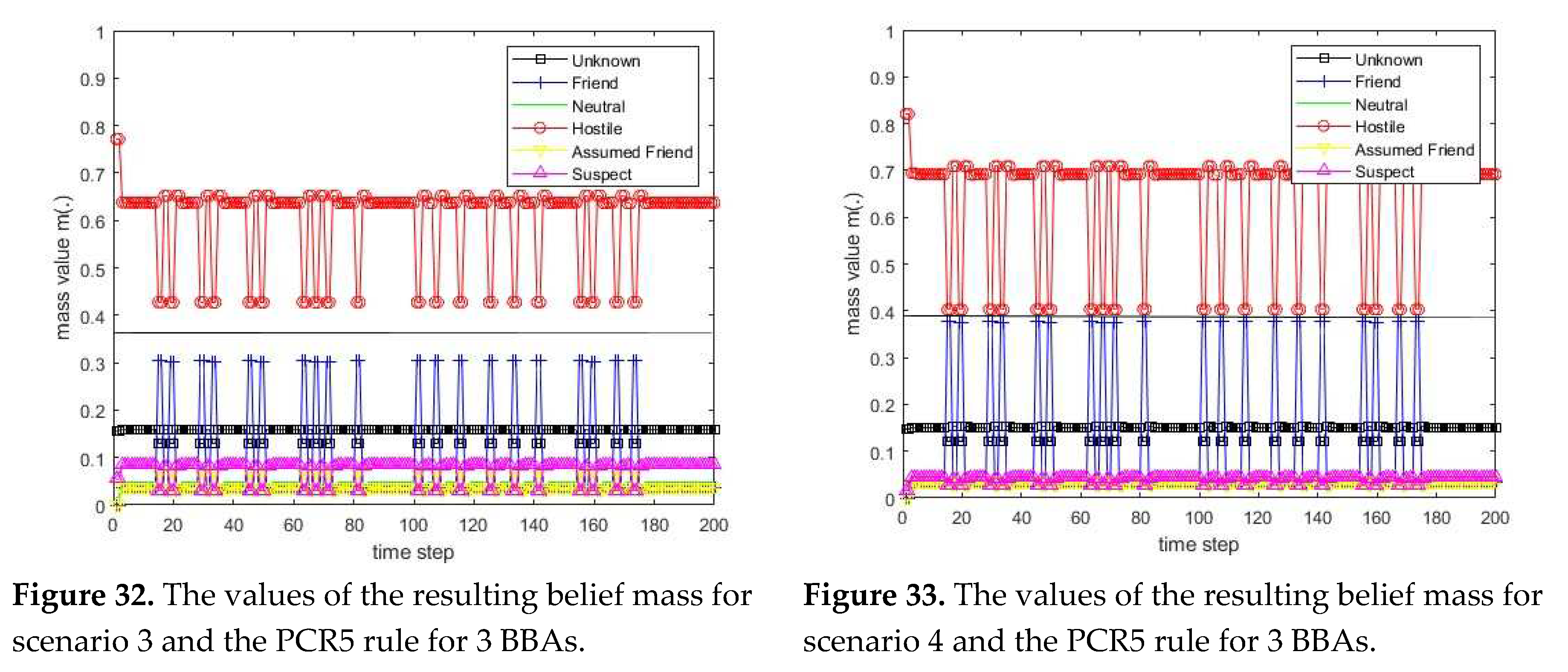
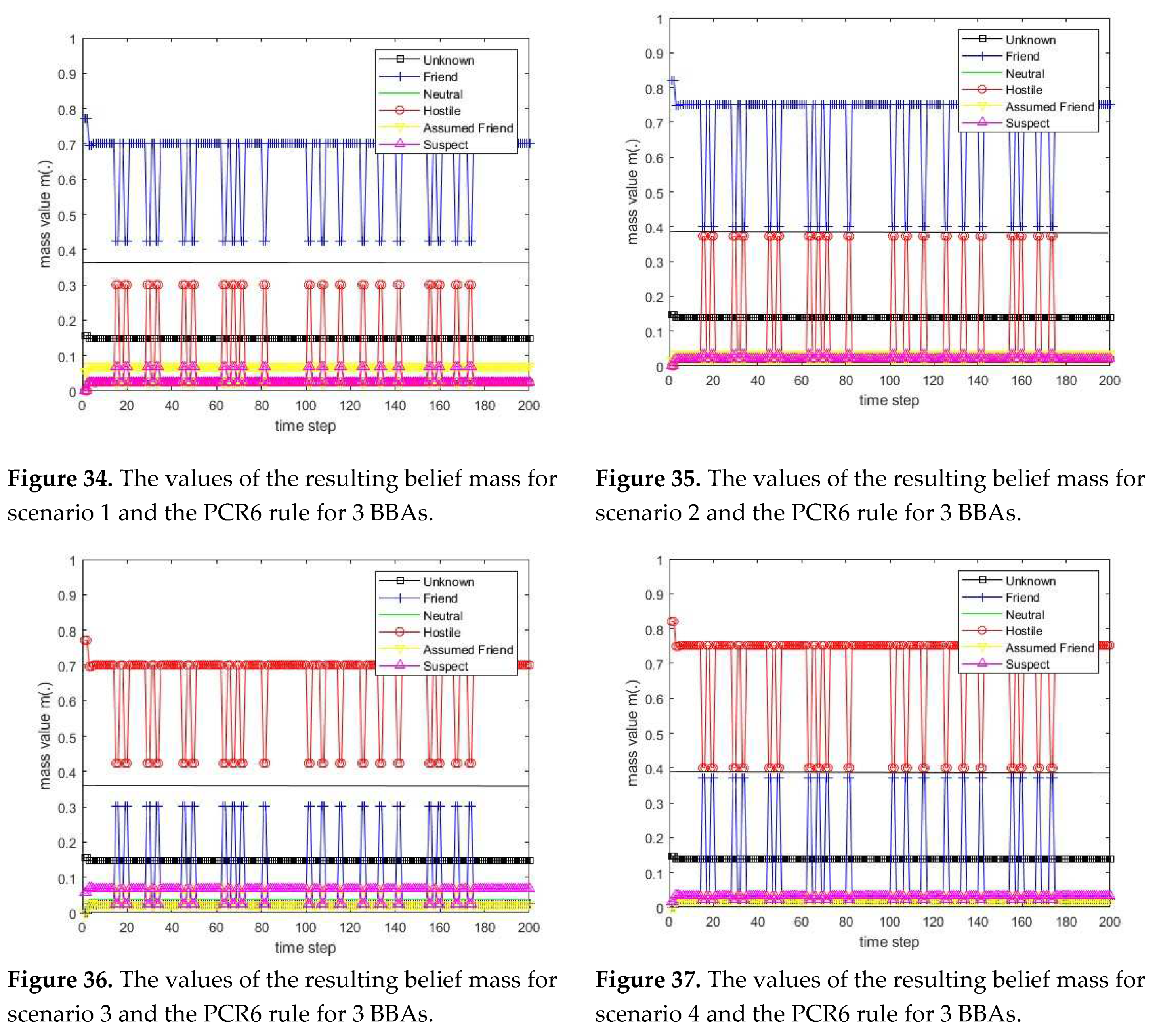
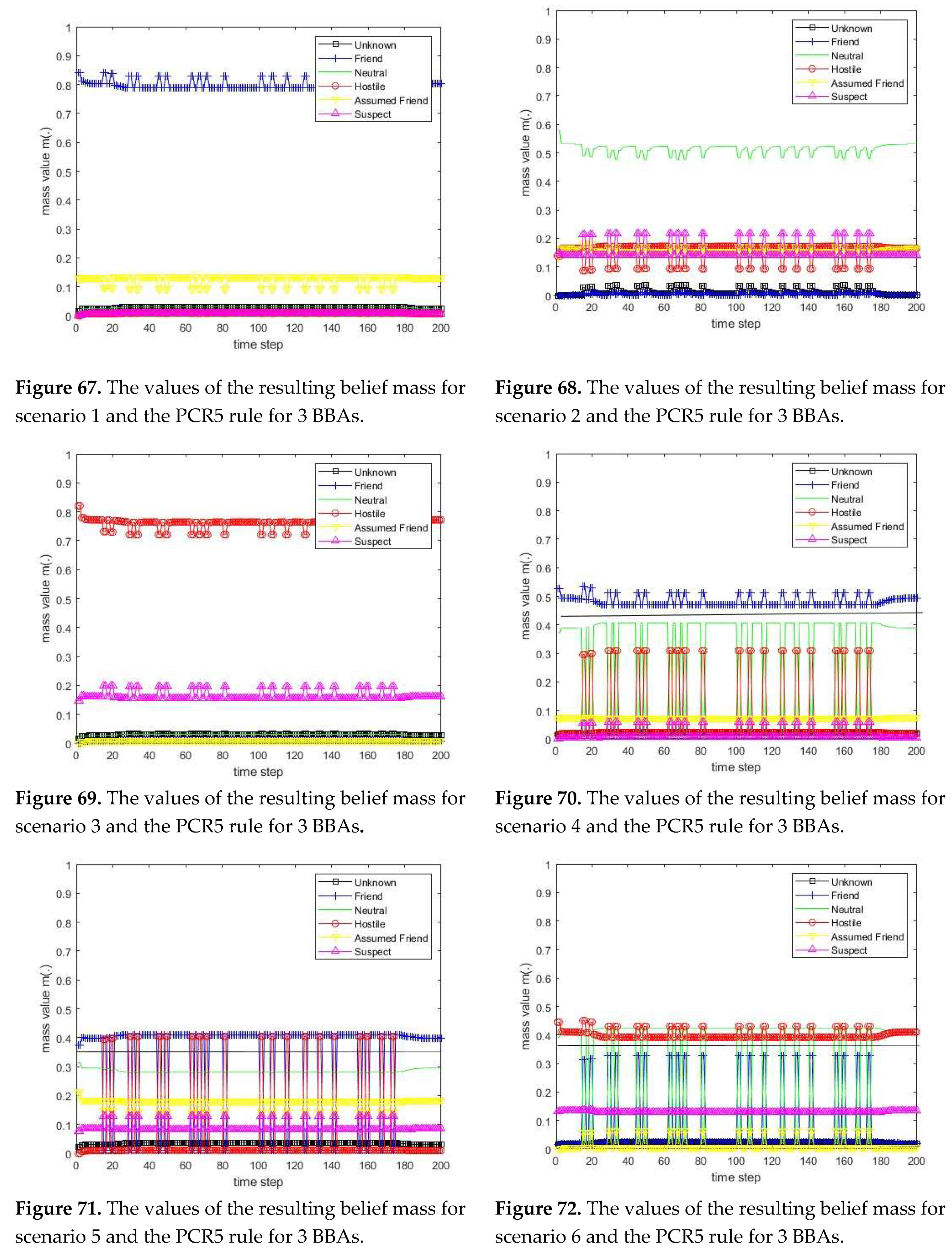
The Proportional Conflict Redistribution rules PCR5 and PCR6 for three BBAs (three sources)
In [
11,
12] improved proportional conflict redistribution rules of combination of basic belief assignments PCR6, PCR5+ and PCR6+ are presented. The authors point out that these rules should be applied if and only if we are to combine more than two BBAs. If we have only two BBAs to combine (s = 2) we always get
mPCR5 =
mPCR5+ =
mPCR6 =
mPCR6+ because in this case the PCR5, PCR5+, PCR6, and PCR6+ rules coincide. Below are the formulas that define the PCR5 and PCR6 rules for 3 BBAs.
The PCR5 rule for three BBAs (three sources) is defined for every non-empty hypothesis in the following way:
wherein
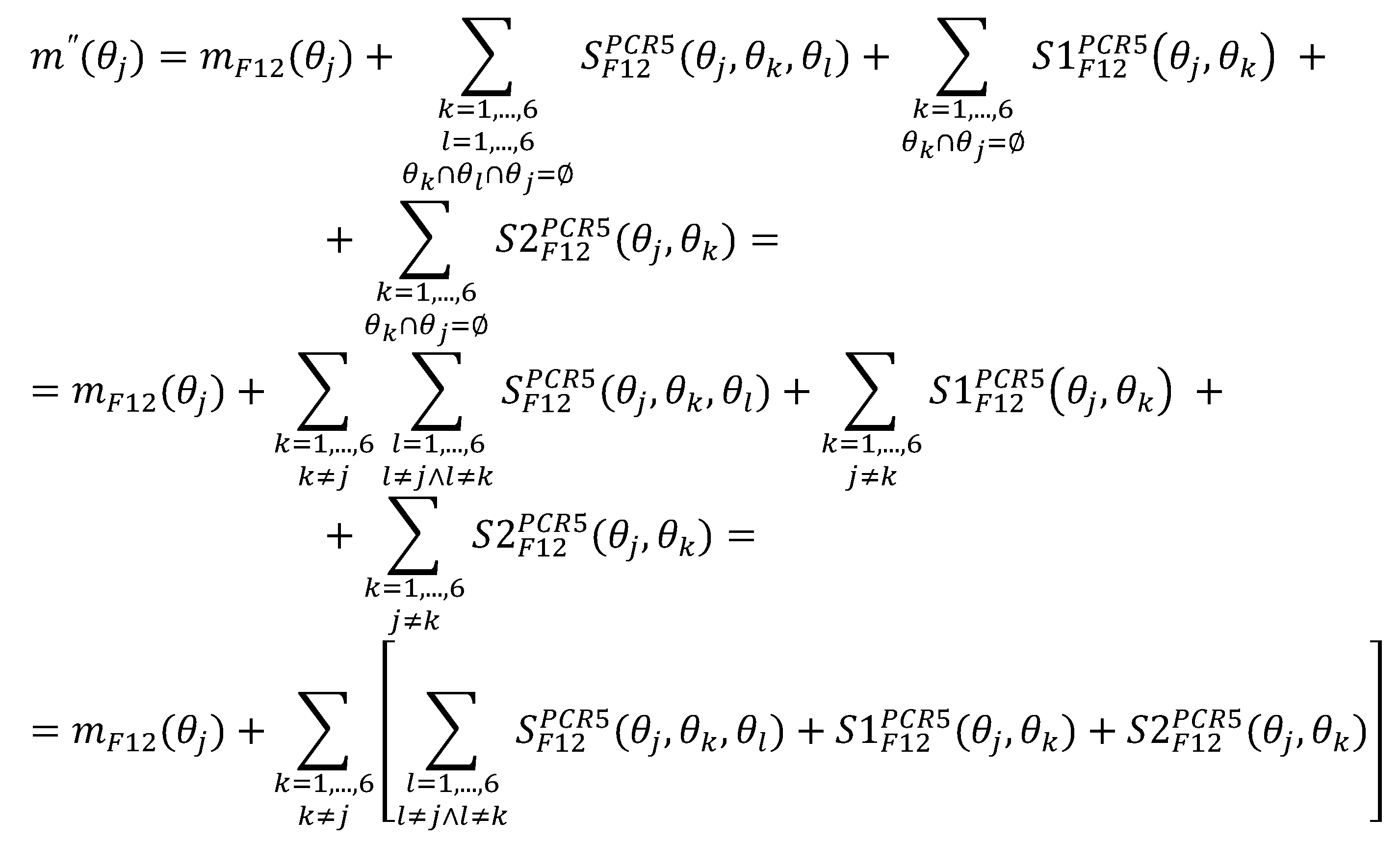
(56)
In the formulas (57)-(59), if a denominator is zero, then component is discarded.
The quotient in the formula (55) ensures the normalization of the BBA vector
, which ensures that
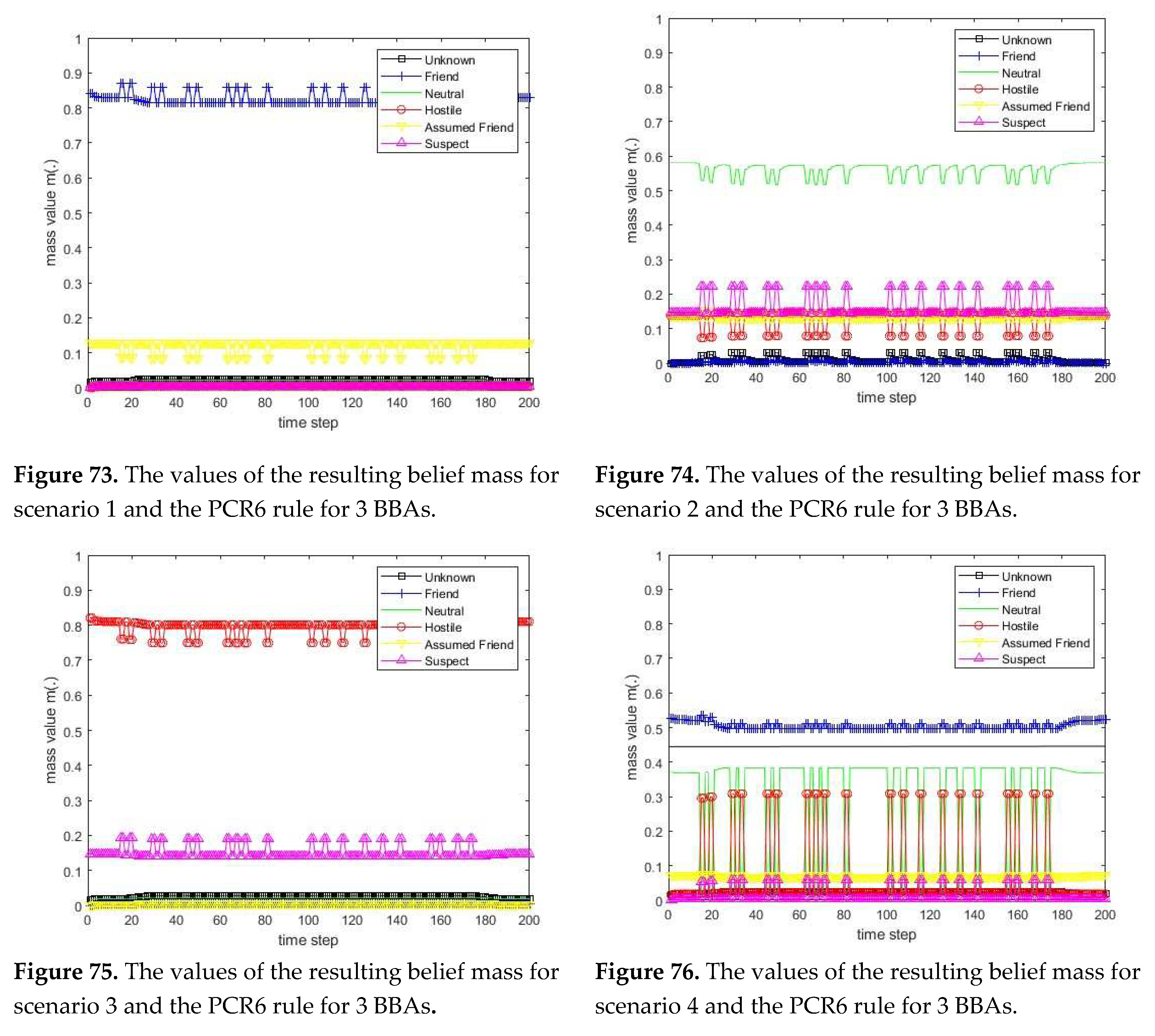
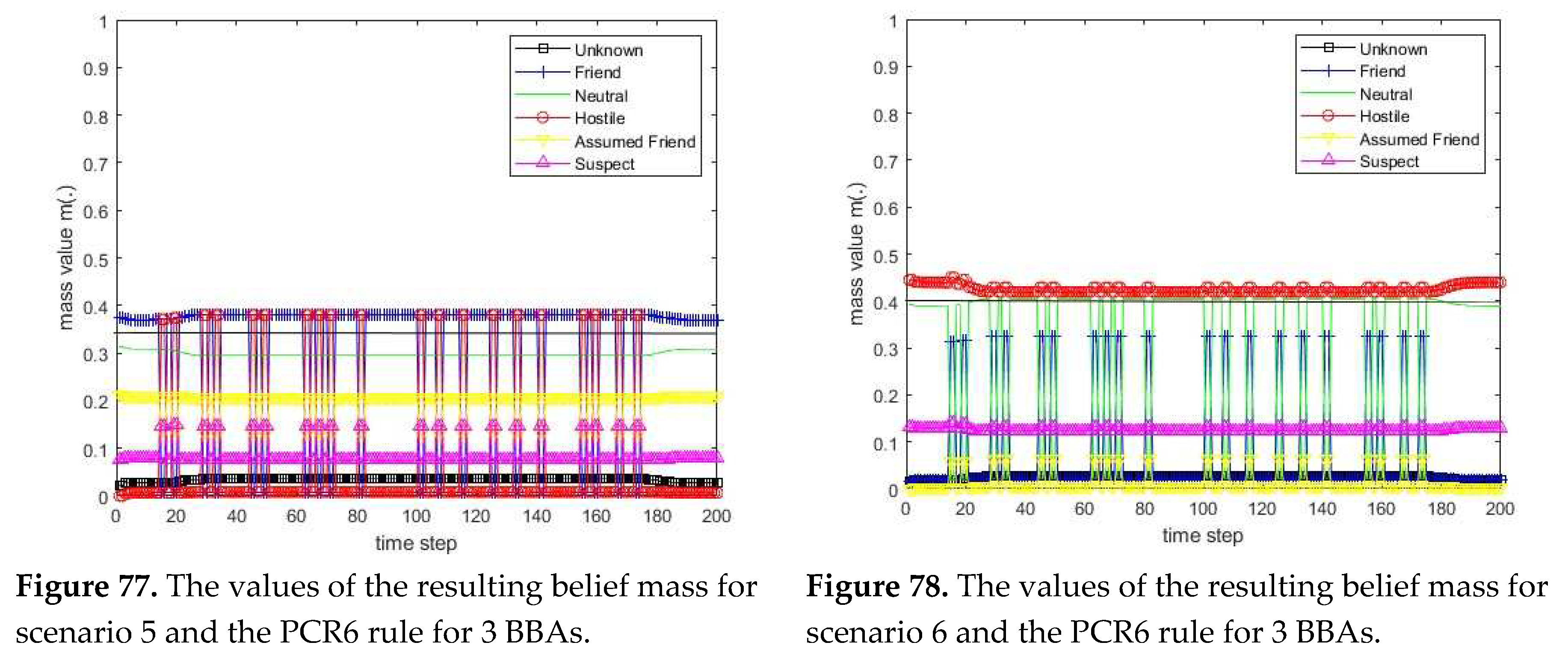
The PCR6 rule for three BBAs (three sources) is defined for every non-empty hypothesis
in the following way:
wherein
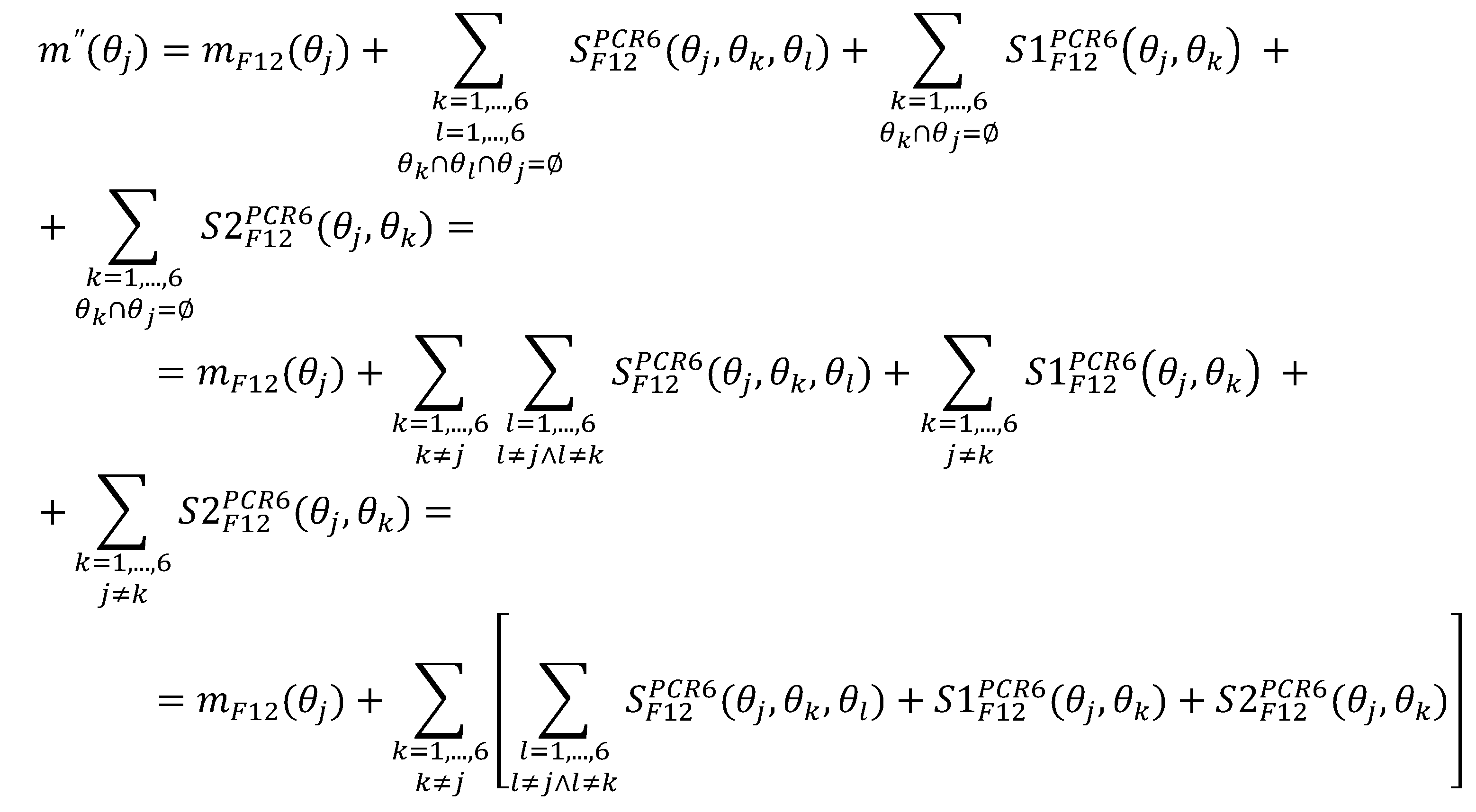
(62)
In the formulas (63)-(65), if a denominator is zero, then compent is discarded.
The quotient in the formula (61) ensures the normalization of the BBA vector
, which ensures that
Comparing the two fusion schemes (
Figure 2 and
Figure 3), it should be noted that sequential and global information fusion generally produces different results [
4], i.e.
In addition, the article experimentally verified the theorem on the inequality of the results of both PCR5 and PCR6 rules for three BBAs (three sources) presented in [
4]:
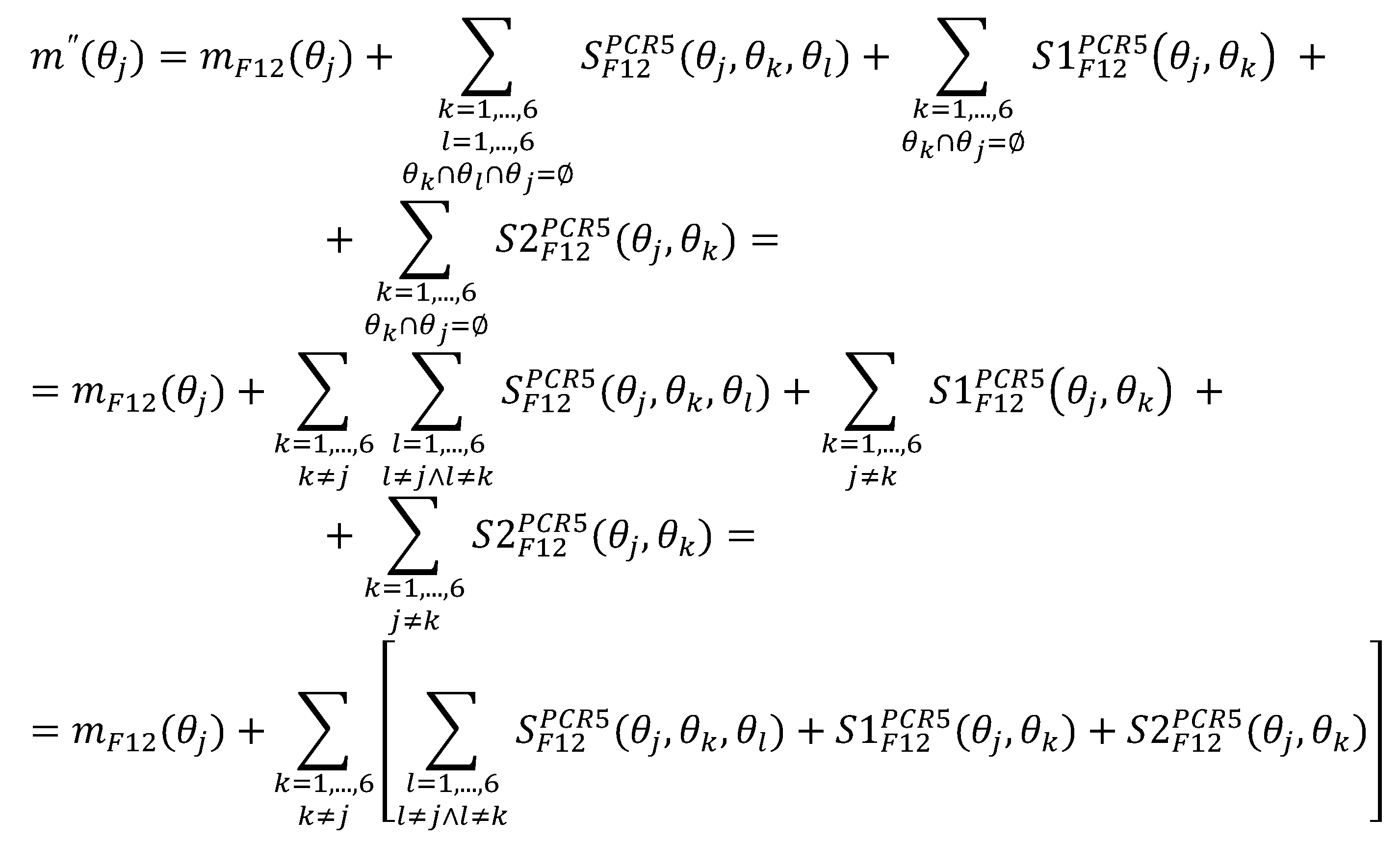 (56)
(56)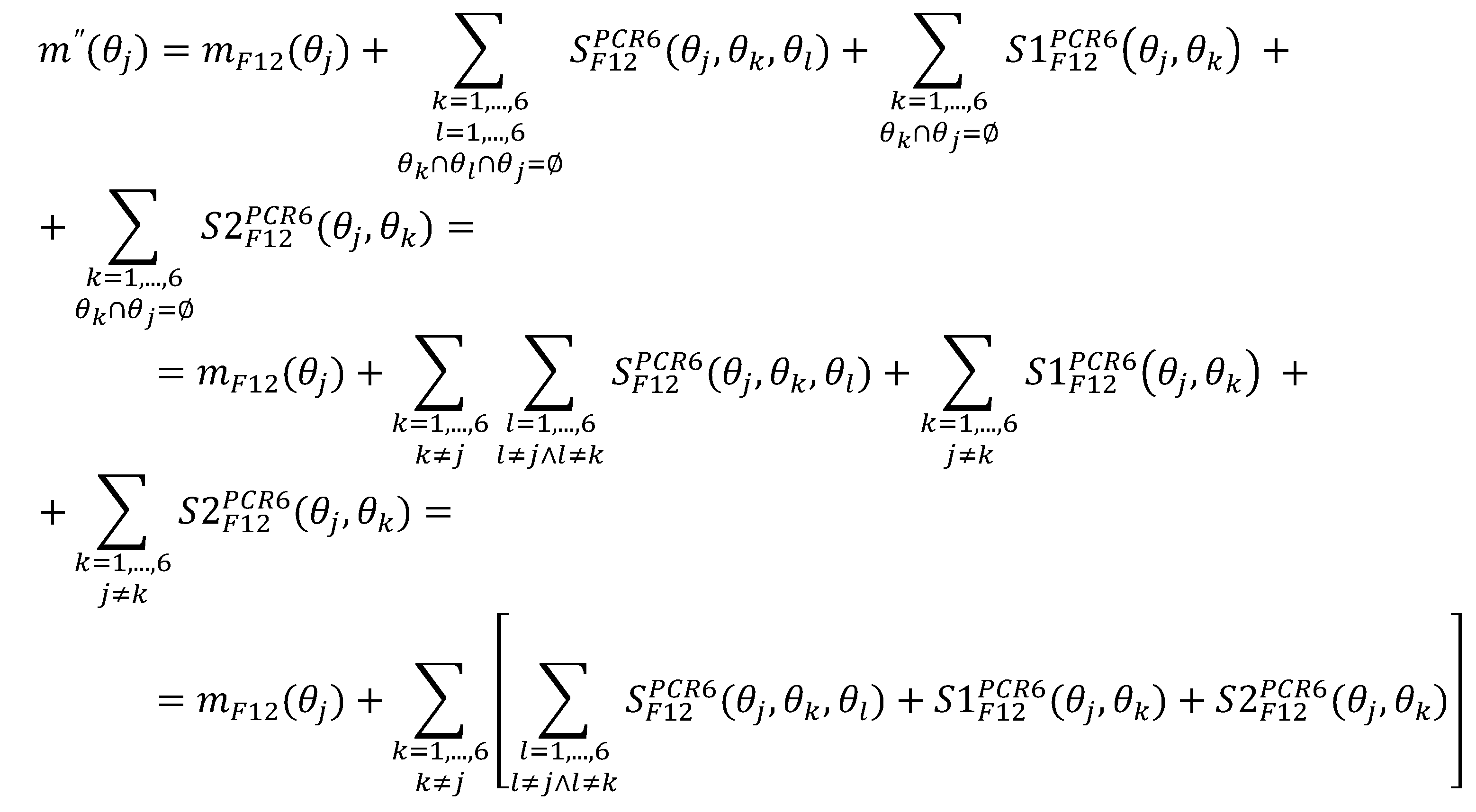 (62)
(62)