Prerpints.org logo
Preprint
Article

A Parameterized Multisplitting Iterative Method for Solving the PageRank Problem

Altmetrics

Downloads

91

Views

11

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 June 2023

Posted:

27 June 2023

You are already at the latest version

Alerts
Abstract
In this paper, a new multi parameter iterative algorithm is proposed to address the PageRank problem based on the multi-splitting iteration method described by Gu et al . The proposed method in each iteration needs to solve two linear subsystems by splitting the coefficient matrix, therefore, we consider inner and outer iteration to find the approximate solutions of these linear subsystems. It can be shown that the iterative sequence generated by the multi parameter iterative algorithm finally converges to the PageRank vector when the parameters satisfy the certain conditions. Numerical experiments show that the proposed algorithm has better convergence and numerical stability than the existing algorithms.
Keywords: 
Subject: Computer Science and Mathematics  -   Computational Mathematics

MSC:  65F10

1. Introduction

      Consider the following linear equation systems:
A x = x ,
with A is a convex combination Google matrix composed of matrix P and matrix E, and A = α P + ( 1 − α ) E , where α ∈ ( 0 , 1 ) denotes the damping factor that determines the weight given to the web link graph, and E = v e T ,  e = ( 1 , 1 , ⋯ , 1 ) T ∈ R n , and v = e n is a personalization vector or a teleportation vector. n is the dimension of P, and x is our desired eigenvector.
The system of linear equations in (1.1) above is what we refer to as the PageRank problem. Google’s PageRank algorithm has grown to be one of the most well-known algorithms in online search engines thanks to the rapid development of the internet, link analysis method called PageRank is used to rank online pages and assess their significance in relation to the link structure of Web, calculating the primary eigenvectors of the Google matrix, forms the basis of the PageRank algorithm. Although Google’s exact ranking technology and calculation techniques have gradually improved, the PageRank problem is still a major concern and has recently gained a lot of attention in the world of scientific and engineering computation.
To solve the PageRank problem, the power method is easy to calculate and the most classical algorithm, while all other eigenvalues of matrix A aside from the principal eigenvalues are simply scalar times the corresponding eigenvalues of matrix P. As a result, the power approach converges very slowly when the primary eigenvalue of matrix A is closely related to other eigenvalues, or when the damping factor is close to 1. The power method is not the ideal way to solve this problem, but a quicker and more logical way to solve the principal eigenvectors of the Google matrix is required to speed up the calculation of PageRank. The network graph is extremely large, with 1 billion or even 10 billion web page nodes. Additionally, a good search algorithm should minimize the lag time, which is the time from the search target proposed to the search result feedback to the web browser. In recent years, numerous researchers have proposed various methods to speed up the calculation of PageRank, among them, the design of power function method and its variant method for accelerating the solution of PageRank problem are favored by many researchers. For instance, Gleich et al. [4] proposed an inner outer iteration method combined with Richardson iteration, in which each iteration needs to solve a linear system whose algebraic structure is similar to the original system; Gu and Xie [5] proposed the PIO iteration algorithm, which combines the power method and the inner-outer iteration method, after that, Ma et al. [11] suggested a relaxed two-step splitting iteration strategy to address the PageRank problem based on [4] and [5], adding a new relaxation parameter; Gu et al. [8] introduced a two parameter iteration approach based on multiplicative splitting iteration in order to increase the possibility of optimizing the iterative process; based on the iteration framework [7] and relaxed two-step splitting (RTSS) iteration method [11], Two relaxed iteration techniques are presented by Tian et al. [12] for resolving the PageRank issue. Additionally, the PageRank problem can be solved by using Krylov subspace methods, which is a problem of solving linear equations. For instance, Wu and Wei propose a hybrid algorithm, power-Arnoldi algorithm [14], which combines its power technique and thick restart Arnoldi algorithm; as well as the Arnoldi-extrapolation method [26] and speeding the Arnoldi-type algorithm [23]. We cite [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] for a more in-depth theoretical study.
The structure of this essay is as follows: we briefly introduce the inner-outer iterative PageRank problem techniques in Section 2. In Section 3, we first examine the theoretical foundations of the multiplicative splitting iterative method before introducing our brand-new approach, the parameterized MSI iteration method. Section 4 reports on numerical testing and comparisons. Finally, Section 5 provides a few succinct closing notes.

2. The inner-outer method

First, we provide a brief summary of the methodological inside-out iteration procedure proposed by Gleich et al. [4], for computing the inside-out iteration of PageRank. It is clear that linear systems can be used to rewrite the eigenvector problem (1.1).
( I − α P ) x = ( 1 − α ) v ,
since e T x = 1 .
We observe that when the damping vector is small, it is simpler to solve the PageRank problem, Gleich et al. defined the outer iteration with a smaller damping factor β ( 0 < β < α ), rather than immediately resolving the equation (1.1). Therefore, the equations below are used to rewrite the linear system (1.1).
( I − β P ) x = ( α − β ) P x + ( 1 − α ) v .
So the stationary outer iteration scheme
( I − β P ) x ( k + 1 ) = ( α − β ) P x ( k ) + ( 1 − α ) v , k = 0 , 1 , 2 , … ,
For computing x ( k + 1 ) , define the inner linear system as
( I − β P ) y = f ,
where f = ( α − β ) P x ( k ) + ( 1 − α ) v , and compute x ( k + 1 ) via the Richardson inner iteration
y ( j + 1 ) = β P y ( j ) + ( α − β ) P x ( k ) + ( 1 − α ) v , j = 0 , 1 , 2 , . . . , l − 1 ,
where y ( 0 ) = x ( k ) , The l-th step inner solution y ( l ) is assigned to be the next new x ( k + 1 ) . The stopping criteria are given as follows, The outer iteration (2.1) terminates if
∥ ( 1 − α ) v − ( I − α P ) x ( k + 1 ) ∥ 2 < τ ,
while the inner iteration (2.5) terminates if
∥ f − ( I − β P ) y ( j + 1 ) ∥ < η , j = 0 , 1 , 2 , . . . , l − 1 ,
where η and τ are the inner and outer tolerances respectively.
The MSI iteration method
Gu et al. suggested the MSI approach in [8] to expedite the PageRank vector calculation. Here is a quick overview of the MSI approach, the MSI approach entails writing I − α P as
I − α P = ( I − β 1 P ) − ( α − β 1 ) P = ( I − β 2 P ) − ( α − β 2 ) P ,
here 0 < β 1 < α , 0 < β 2 < α , given an initial vector x ( 0 ) , for k = 0 , 1 , 2 , ⋯ , perform the following two-step iteration
( I − β 1 P ) u ( k + 1 ) = ( α − β 1 ) P x ( k ) + ( 1 − α ) v , ( I − β 2 P ) x ( k + 1 ) = ( α − β 2 ) P u ( k + 1 ) + ( 1 − α ) v .
until the sequence { x ( k ) } converges to the exact solution x * .
Theorem 2.1 
([8]). Let α be the damping factor in the PageRank linear system, and let M i = I − β i P , N i = ( α − β i ) P , ( i = 1 , 2 ) are the two splittings of the matrix I − α P . Then the iterative matrix H ˜ M S I ( β 1 , β 2 ) of the MSI method for PageRank computation is given by
H ˜ M S I ( β 1 , β 2 ) = ( I − β 2 P ) − 1 ( α − β 2 ) P ( I − β 1 P ) − 1 ( α − β 1 ) P ,
and its spectral radius ρ ( H ˜ M S I ( β 1 , β 2 ) ) is bounded by
σ ( β 1 , β 2 ) ≡ ( α − β 2 ) ( α − β 1 ) ( 1 − β 2 ) ( 1 − β 1 ) ,
therefore, it holds that
ρ ( H ˜ M S I ( β 1 , β 2 ) ) ≤ σ ( β 1 , β 2 ) < 1 , ∀ 0 ≤ β 1 < α , 0 ≤ β 2 < α .
the multiplicative splitting iteration method for PageRank computation converges to the unique solution x * ∈ C n of the linear system of equations.

3. The parameterized MSI iteration method

      The PageRank problem model is presented in this section, and it illustrates how the problem can be solved more simply by choosing a smaller damping factor α . We introduce a parameter ω based on the MSI method in order to further control the range of α , reduce the spectral radius, and speed up convergence, this results in a new iterative algorithm, denoted as the PMSI method below, that is described as follows.
The PMSI iteration method
( I − β 1 P ) u ( k + 1 ) = ( ω α − β 1 ) P x ( k ) + ( 1 − ω ) x ( k ) + ω ( 1 − α ) v , ( I − β 2 P ) x ( k + 1 ) = ( ω α − β 2 ) P u ( k + 1 ) + ( 1 − ω ) u ( k + 1 ) + ω ( 1 − α ) v .
with ω > 0 and 0 < β 1 < α < 1 ,  0 < β 2 < α < 1 . If ω = 1 , then the PMSI iteration method becomes the MSI iteration method.
Algorithm 1:PMSI method
Input: 
Parameters P, q, v, α , τ , η ;
1:
 
Output: 
x
2:
 
3:
x ⇐ ν , y ⇐ P x
4:
 
5:
if ∥ ( 1 − α ) v + α y − x ∥ 1 ≥ τ then
6:
 
7:
     f 1 = ( ω α − β 1 ) y + ( 1 − ω ) x + ω ( 1 − α ) v ;
8:
 
9:
    repeat
10:
 
11:
         x = β 1 y + f 1 ;
12:
 
13:
         y = P x ;
14:
 
15:
    until  ∥ f 1 + α y − x ∥ 1 < η
16:
 
17:
     f 2 = ( ω α − β 2 ) y + ( 1 − ω ) x + ω ( 1 − α ) v ;
18:
 
19:
    repeat
20:
 
21:
         x = β 2 y + f 2 ;
22:
 
23:
         y = P x ;
24:
 
25:
    until  ∥ f 2 + α y − x ∥ 1 < η
26:
 
27:
     x = β 2 y + f 2 ;
28:
 
29:
     y = P x ;
30:
 
31:
end if
32:
 
33:
x = α y + ( 1 − α ) v .
Remark 3.1. 
The computational cost of the PMSI iteration approach is somewhat higher than that of (2.8) since it simply requires an additional saxpy operation, ( 1 − ω ) u ( k + 1 ) Vector addition and the price ( ω α − β 1 ) P u ( k + 1 ) + ( 1 − ω ) u ( k + 1 ) each iteration of with o ( n ) flops.
In the sequel, we will analyze the convergence property of the parameterized MSI iteration method.
Lemma 3.1 
([8]). Let A ∈ C n × n , A = M i − N i ( i = 1 , 2 ) be two splittings of the matrix A , and let x ( 0 ) ∈ C n be a given initial vector. If x ( k ) is a two-step iteration sequence
M 1 x ( k + 1 2 ) = N 1 x ( k ) + b , M 2 x ( k + 1 ) = N 2 x ( k + 1 2 ) + b ,
then
x k + 1 = M 2 − 1 N 2 M 1 − 1 N 1 x k + M 2 − 1 ( I + N 2 M 1 − 1 ) b , k = 0 , 1 , 2 , …
Moreover, if the spectral radius ρ ( M 2 − 1 N 2 M 1 − 1 N 1 ) is less than 1, then the iteration sequence x ( k ) converges to the unique solution x * ∈ C n × n of the system of linear equation (2.1) for all initial vectors x ( 0 ) ∈ C n .
The multiplicative splitting iteration method for (2.1) is obviously related with the splitting of the coefficient matrix I − α P , and we will subsequently demonstrate that there exists a plausible convergent domain of two-parameters for the parameterized method.
I − α P = M i − N i ( i = 1 , 2 ) , M 1 = I − β 1 P , N 1 = ( ω α − β 1 ) P + ( 1 − ω ) I , M 2 = I − β 2 P , N 2 = ( ω α − β 2 ) P + ( 1 − ω ) I .
according to (3.1), The two-step iterative matrix corresponding to the multiplication split iterative method is as follows
G ˜ P M S I ( β 1 , β 2 ) = M 2 − 1 N 2 M 1 − 1 N 1 = ( I − β 2 P ) − 1 ( ω α − β 2 ) P + ( 1 − ω ) I ( I − β 1 P ) − 1 ( ω α − β 1 ) P + ( 1 − ω ) I ,
Now, we examine the convergence property of the multiplicative-splitting iterative method. By applying Lemma 3.1, we can obtain the following main theorem..
Theorem 3.1. 
Let α be the damping factor in the PageRank linear system, and let M i = I − β i P , N i = ( α − β 2 ) P + ( 1 − ω ) ( i = 1 , 2 ) are the two splittings of the matrix I − α P . Then the iterative matrix G ˜ P M S I ( β 1 , β 2 ) of the PMSI method for PageRank computation is given by
G ˜ P M S I ( β 1 , β 2 ) = ( I − β 2 P ) − 1 ( ω α − β 2 ) P + ( 1 − ω ) I ( I − β 1 P ) − 1 ( ω α − β 1 ) P + ( 1 − ω ) I ,
and its spectral radius ρ ( G ˜ P M S I ( β 1 , β 2 ) ) is bounded by
ψ ( β 1 , β 2 ) ≡ 1 − ( 1 − α ) ω [ 2 + ω ( 1 − α ) − β 2 − β 1 ] ( 1 − β 1 ) ( 1 − β 2 ) ,
therefore, it holds that
ρ G ˜ P M S I ( β 1 , β 2 ) ≤ ψ ( β 1 , β 2 ) < 1 , ∀ 0 ≤ β 1 < α , 0 ≤ β 2 < α .
the multiplicative splitting iteration method for PageRank computation converges to the unique solution x * ∈ C n of the linear system of equations.
Proof. From Lemma 3.1 we can obtain the iterative matrix of the PMSI method for PageRank computation Eq. (3.5)).
Let β = min { β 1 , β 2 } , since e T P = e T , β α ≤ ω ≤ 1 , then the matrix ( ω α − β i ) P + ( 1 − ω ) I ( i = 1 , 2 ) is a nonnegative matrix and the matrix G ˜ k is also nonnegative.
In addition, from (3.5) it turns out that
e T G ˜ P M S I ( β 1 , β 2 ) = e T [ ( I − β 2 P ) − 1 ( ω α − β 2 ) P + ( 1 − ω ) I ( I − β 1 P ) − 1 ( ω α − β 1 ) P + ( 1 − ω ) I ] ,
if λ i is an eigenvalue of P, The spectral radius of G ˜ P M S I ( β 1 , β 2 ) are
ρ ( G ˜ P M S I ( β 1 , β 2 ) ) = ( ω α − β 2 ) + ( 1 − ω ) ( ω α − β 1 ) + ( 1 − ω ) ( 1 − β 1 ) ( 1 − β 2 ) ,
for
( ω α − β 2 ) + ( 1 − ω ) ( ω α − β 1 ) + ( 1 − ω ) = ω ( α − 1 ) + 1 − β 2 ω ( α − 1 ) + 1 − β 1 = ( ω ( α − 1 ) ) 2 + ω ( α − 1 ) ( 2 − β 2 − β 1 ) + ( 1 − β 2 ) ( 1 − β 1 ) = ( 1 − β 2 ) ( 1 − β 1 ) − ( 1 − α ) ω [ 2 + ω ( 1 − α ) − β 2 − β 1 ] .
Since ( 2 + ω ( 1 − α ) − β 2 − β 1 ) > 0 , combining the above relations (3.9) and (3.10), we can get
ρ ( G ˜ P M S I ( β 1 , β 2 ) ) < 1 − ( 1 − α ) ω [ 2 + ω ( 1 − α ) − β 2 − β 1 ] ( 1 − β 1 ) ( 1 − β 2 ) < 1 .
So for any given constants β 1 and β 2 , 0 ≤ β 1 < α , 0 ≤ β 2 < α . The PMSI method converges to a unique solution to the linear system (2.1), the PageRank vector. □
Since 0 < β i < α < 1 ( i = 1 , 2 ) , then β α < ω < 1 . Immediately, a comparison result is obtained for the parameterized MSI iteration method compared with the MSI iteration method.
Theorem 3.2. 
Let 0 < β i < α < 1 ( i = 1 , 2 ) , β = min { β 1 , β 2 } , If β α < ω < 1 , then the parameterized MSI iteration method converges faster than the MSI iteration method.
Proof. From Eq (3.9), it follows that the spectral radius of the parameterized MSI iteration method is
ρ ( G ˜ P M S I ( β 1 , β 2 ) ) = ( ω α − β 2 ) + ( 1 − ω ) ( ω α − β 1 ) + ( 1 − ω ) ( 1 − β 1 ) ( 1 − β 2 ) .
Let ω = 1 in (3.12), then we obtain the spectral radius of the MSI iteration method as follows:
ρ ( H ˜ M S I ( β 1 , β 2 ) ) = ( α − β 2 ) ( α − β 1 ) ( 1 − β 1 ) ( 1 − β 2 ) .
For 0 < β i < α < 1 , β i α < ω < 1 ( i = 1 , 2 ) , from (3.12)-(3.13), it is clear that
ρ ( G ˜ P M S I ( β 1 , β 2 ) ) = ( ω α − β 2 ) + ( 1 − ω ) ( ω α − β 1 ) + ( 1 − ω ) ( 1 − β 1 ) ( 1 − β 2 ) = ( ω α − β 2 ) ( ω α − β 1 ) ( 1 − ω ) 2 ( 1 − β 1 ) ( 1 − β 2 ) < ( ω α − β 2 ) ( ω α − β 1 ) ( 1 − β 1 ) ( 1 − β 2 ) < ( α − β 2 ) ( α − β 1 ) ( 1 − β 1 ) ( 1 − β 2 ) = ρ ( H ˜ M S I ( β 1 , β 2 ) ) .
It is obvious that ρ ( G ˜ P M S I ( β 1 , β 2 ) ) < ρ ( H ˜ M S I ( β 1 , β 2 ) ) , and the proof is completed. □
Corollary 3.1. 
In the range of β α < ω < 1 , β = min { β 1 , β 2 } , 0 < β i < 1 ( i = 1 , 2 ) , when ω increases gradually within the value range, the smaller the iterative spectral radius of the PMSI algorithm, the faster the convergence speed.
Proof. According to Equation (3.9), we know that
ρ ( G ˜ P M S I ( β 1 , β 2 ) ) = ( ω α − β 2 ) + ( 1 − ω ) ( ω α − β 1 ) + ( 1 − ω ) ( 1 − β 1 ) ( 1 − β 2 ) .
Let
f ˜ ( ω ) = ( ω α − β 2 ) + ( 1 − ω ) ( ω α − β 1 ) + ( 1 − ω ) ( 1 − β 1 ) ( 1 − β 2 ) = ω ( α − 1 ) + 1 − β 2 ω ( α − 1 ) + 1 − β 1 ( 1 − β 1 ) ( 1 − β 2 ) = ( ω ( α − 1 ) ) 2 + ω ( α − 1 ) ( 2 − β 1 + − β 2 ) + ( 1 − β 1 ) ( 1 − β 2 ) ( 1 − β 1 ) ( 1 − β 2 ) .
It is easy one can obtain from above relation
f ˜ ′ ( ω ) = 2 ω ( α − 1 ) + ( α − 1 ) ( 2 − β 1 − β 2 ) ( 1 − β 1 ) ( 1 − β 2 ) ( 1 − β 1 ) ( 1 − β 2 ) 2 = 2 ω ( α − 1 ) + ( α − 1 ) ( 2 − β 1 − β 2 ) ( 1 − β 1 ) ( 1 − β 2 ) = ( α − 1 ) ( 2 ω + 2 − β 1 − β 2 ) ( 1 − β 1 ) ( 1 − β 2 ) .
since β α < ω < 1 , 0 < β i < α < 1 ( i = 1 , 2 ) , so we have ( 2 ω + 2 − β 1 − β 2 ) ) > 0 . we can get f ˜ ′ ( ω ) < 0 , we can see the PMSI iterative method may be more efficient when ω is large, the conclusion is proved. □

4. Numerical results

In this section, we compare the performance of the parameterized multisplitting (PMSI) iteration method to that of the inner-outer (IO) and multi-splitting (MSI) iteration methods, respectively. On dual-core processing, numerical experiments are carried out in Matlab R2018a (2.30 GHz, 8GB RAM). Four iteration parameters, the number of matrix vectors (denoted as MV), the iteration step size (denoted as IT), the calculation time in seconds (denoted as CPU), and the relative residual (denoted as res(k)) are used to test these iterative approaches, defined
r e s ( k ) = r k 2 ( 1 − α ) ν 2 , k = 0 , 1 , … .
where r k = ( 1 − α ) v ( I − α P ) x k .
Table 1 lists the properties of the test matrices P, where average non-zero refers to each row of non-zero elements, and
ρ d e n = n n z n × n × 100 .
All test matrices can be downloaded from https://www.cise.ufl.edu/research/sparse/matrices/list_by_id.htmlget. For the interest of fairness, we assume that the transfer vector x ( 0 ) = v ( 0 ) = e n ( e = ( 1 , 1 , … , 1 ) T ) is the initial guess for each test matrix. In all numerical tests, the damping factors are assumed to be α = 0.98 , 0.99, 0.995 , 0.997, 0.998 . The residual specification η = 0.01 , τ < 10 − 8 determines when all algorithms end.
Table 1. properties of test matrices
Table 1. properties of test matrices
Size n n n z ρ d e n
wb-cs-stanford 9914×9914 2 312 497 0.291 × 10 − 2
amazon0312 400,727×400,727 3200,440 1.993 × 10 − 3
Example 4.1. 
In this example, we compare the PMSI iteration method with the MSI iteration method. The test matrices are the wb-cs-stanford, and amazon0312 matrices, respectively. In order to verify the efficiency of the PMSI iteration method, we use
S P M S I = C P U M S I − C P U P M S I C P U M S I
to describe the speedups of the PMSI iteration compared with the MSI iteration associated with CPU time.
The numerical outcomes of the MSI and PMSI iterative procedures, where ω = 0.9 and β 1 = 0.9 and β 2 = 0.8 , are displayed in Tables 2 and 3. Tables 2 and 3 shows that the PMSI iterative technique performs better than the MSI iterative method in terms of IT, MV, and CPU time, especially for bigger α, such the α = 0.998 in Tables 2 and 3. As can be observed, most S P M S I values are more than 20%, sometimes even reaching 50%.
Table 2. Test results for the wb-cs-stanford matrix
Table 2. Test results for the wb-cs-stanford matrix
α   IO MSI PMSI S p t
IT(MV) 536 270(541) 228(457)
0.98 CPU 0.1261 0.1268 0.1079 14.90%
IT(MV) 1096 537(1075) 417(835)
0.99 CPU 0.2151 0.2274 0.1648 27.52%
IT(MV) 2168 1095(2191) 962(1525)
0.995 CPU 0.7280 0.3819 0.2942 22.96%
IT(MV) 3577 1806(3613 ) 1213(2427)
0.997 CPU 0.6380 0.5954 0.4350 26.93%
IT(MV) 5450 2698(5397) 1663(3327)
0.998 CPU 0.9354 0.8669 0.5862 32.37%
Table 3. Test results for the amazon0312 matrix
Table 3. Test results for the amazon0312 matrix
α   IO MSI PMSI S p t
IT(MV) 367 178(357) 170(341)
0.98 CPU 7.3867 6.8073 6.5658 3.54%
IT(MV) 733 363(727) 292(585)
0.99 CPU 15.7108 14.1045 12.0670 14.44%
IT(MV) 1436 723(1447) 5110(1021)
0.995 CPU 30.1137 29.4107 21.2650 27.69%
IT(MV) 2507 1164(2329) 717(1435)
0.997 CPU 30.1137 48.6659 27.8410 42.79%
IT(MV) 3630 1863(3727) 911(1823)
0.998 CPU 90.7846 75.3888 37.6927 50.00%
Example 4.2. 
With the test matrices being the wb-cs-stanford and amazon0312 matrix with various ω parameters, we will further examine the convergence performance of the PMSI iterative method in this example. We have set the ω value range to 0.4 − 0.9 . The numerical outcomes are shown in Figure 3, where β 1 = 0.9 and β 2 = 0.8 . According to the findings, the number of repetitions constantly lowers as ω rises. Because of this, we used ω = 0.9 in our studies, which is consistent with the finding in Corollary 3.1.
Example 4.3. 
Theorem 3.1 states that the PMSI method converges for any value of β 1 and β 2 , satisfying the conditions of 0 ≤ β 1 < α and 0 ≤ β 2 < α . This is what we take into consideration in this example. For two matrices, wb-cs-stanford and amazon0312, Tables 4 and 5 display the number of iterations of the PMSI approach. The values of β 1 and β 2 change from 0.1 to 0.9 and 0.1 to 0.9, respectively, when α = 0.99. From Tables 4 and 5, it can be inferred that, once one of the parameters β 1 and β 2 is determined, the number of iteration steps typically decreases first before increasing as more parameters are added. For instance, in Table 3, β 2 increased from β 2 of 0.8 to β 2 of 0.9. The number of iteration steps first declines, and then β 1 takes 0.1 to 0.5, and the number of iteration steps continues to rise. Finding an explicit link between β 1 and β 2 , or the ideal β 1 and β 2 , for the universal PageRank matrix, is quite difficult. Our considerable experience has shown that selecting β 1 =0.9 and β 2 =0.8 usually results in good performance. For this reason, in our studies, we used β 1 =0.9 and β 2 =0.8 in the PMSI approach.
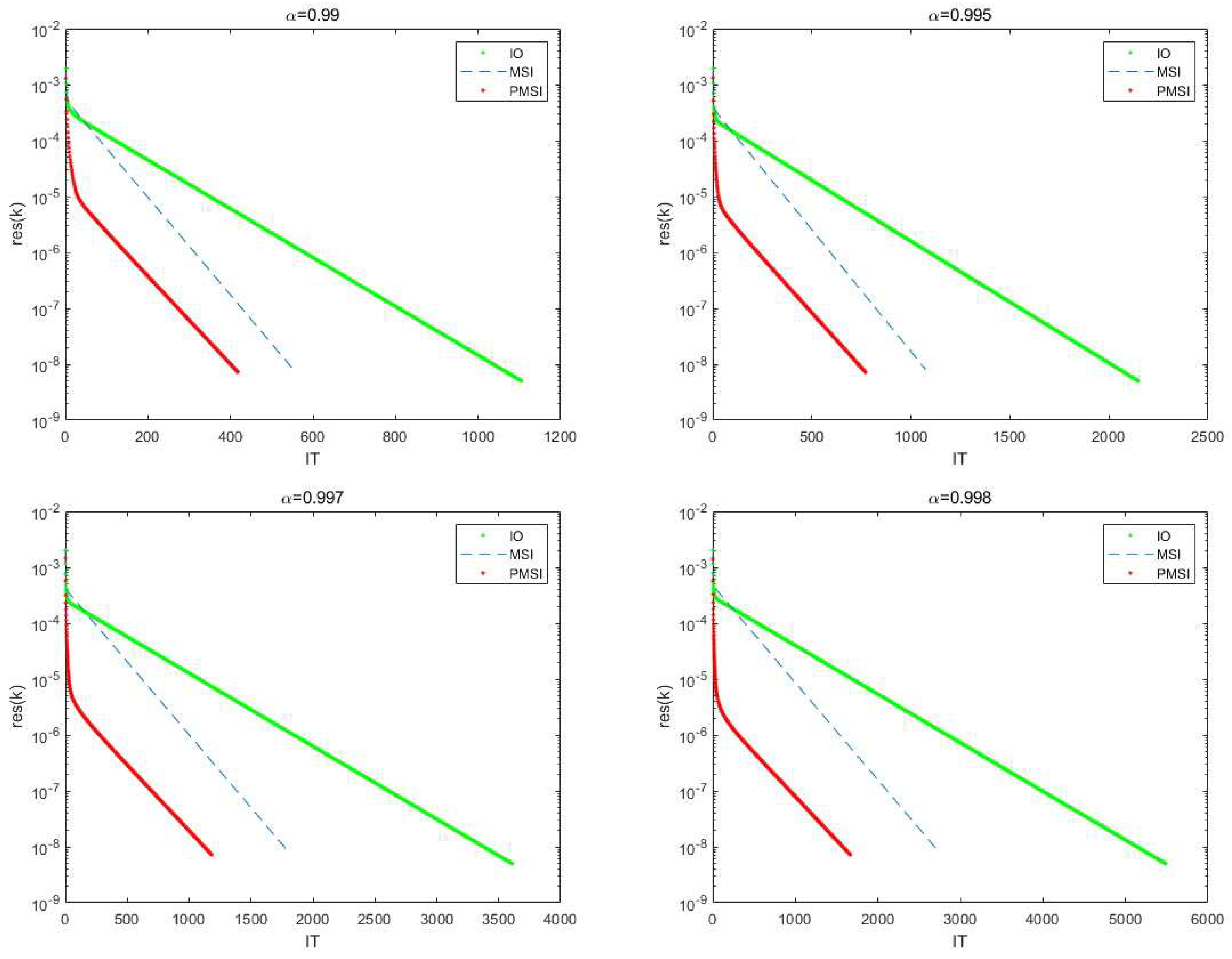
Preprints 77776 g001
Figure 1. Convergence effect of three algorithms for wb-cs-stanford matrix, τ = 10 − 8
Figure 1. Convergence effect of three algorithms for wb-cs-stanford matrix, τ = 10 − 8
Preprints 77776 g001
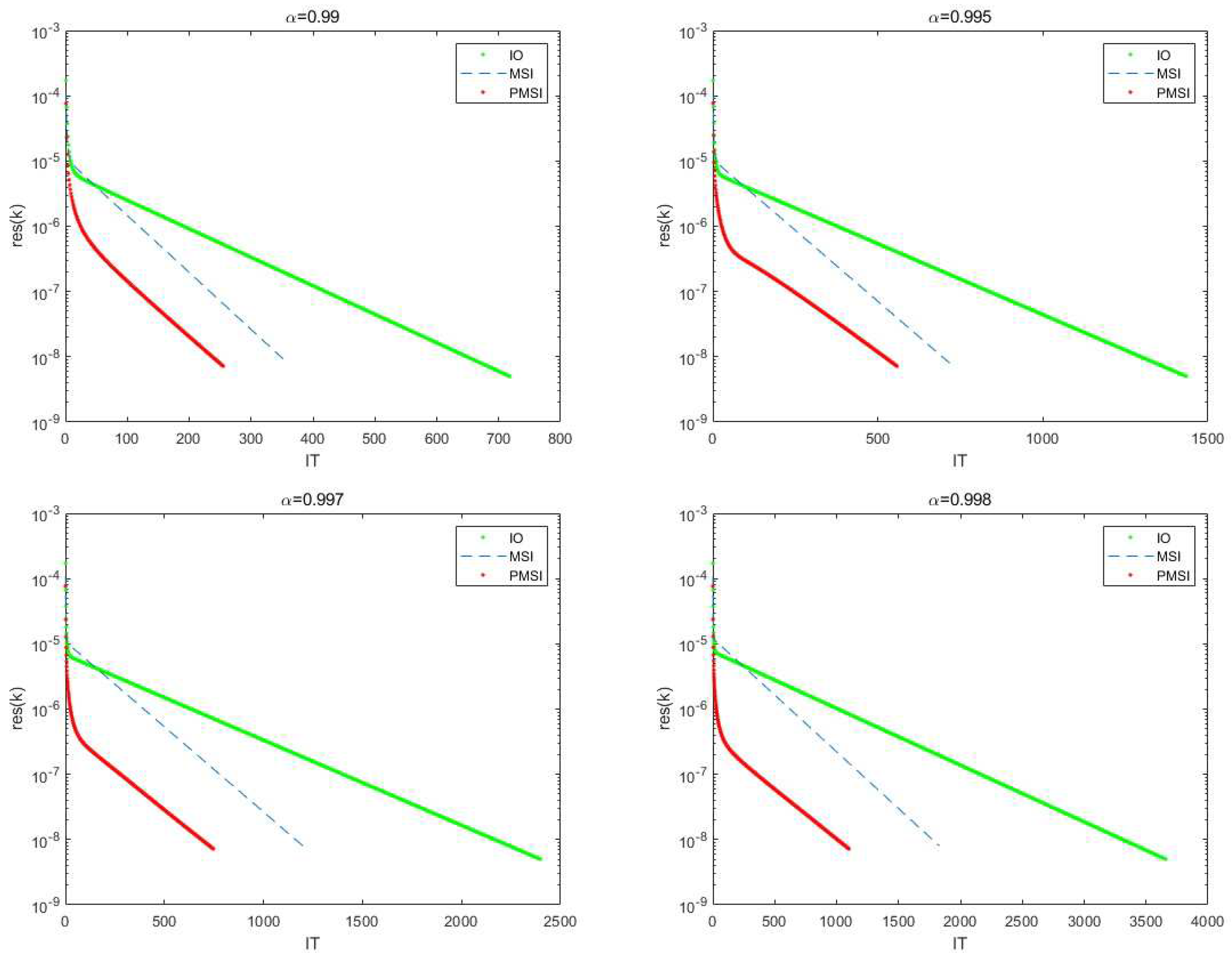
Preprints 77776 g002
Figure 2. Convergence effect of three algorithms for amazon0312 matrix, τ = 10 − 8
Figure 2. Convergence effect of three algorithms for amazon0312 matrix, τ = 10 − 8
Preprints 77776 g002
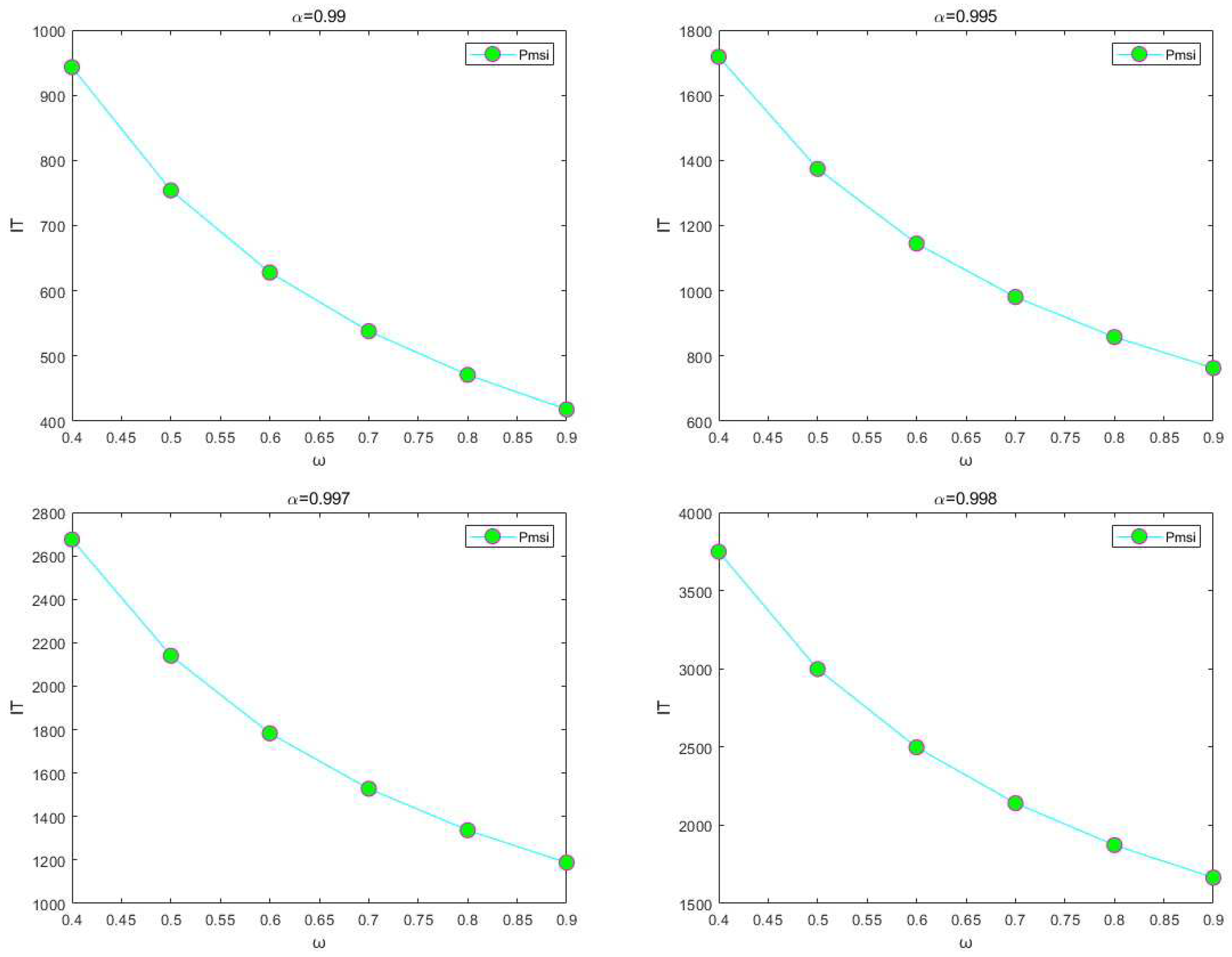
Preprints 77776 g003
Figure 3. Numerical results for the wb-cs-stanford matrix in Example 4.2
Figure 3. Numerical results for the wb-cs-stanford matrix in Example 4.2
Preprints 77776 g003
Preprints 77776 g004
Figure 4. Numerical results for the amazon0312 matrix in Example 4.2
Figure 4. Numerical results for the amazon0312 matrix in Example 4.2
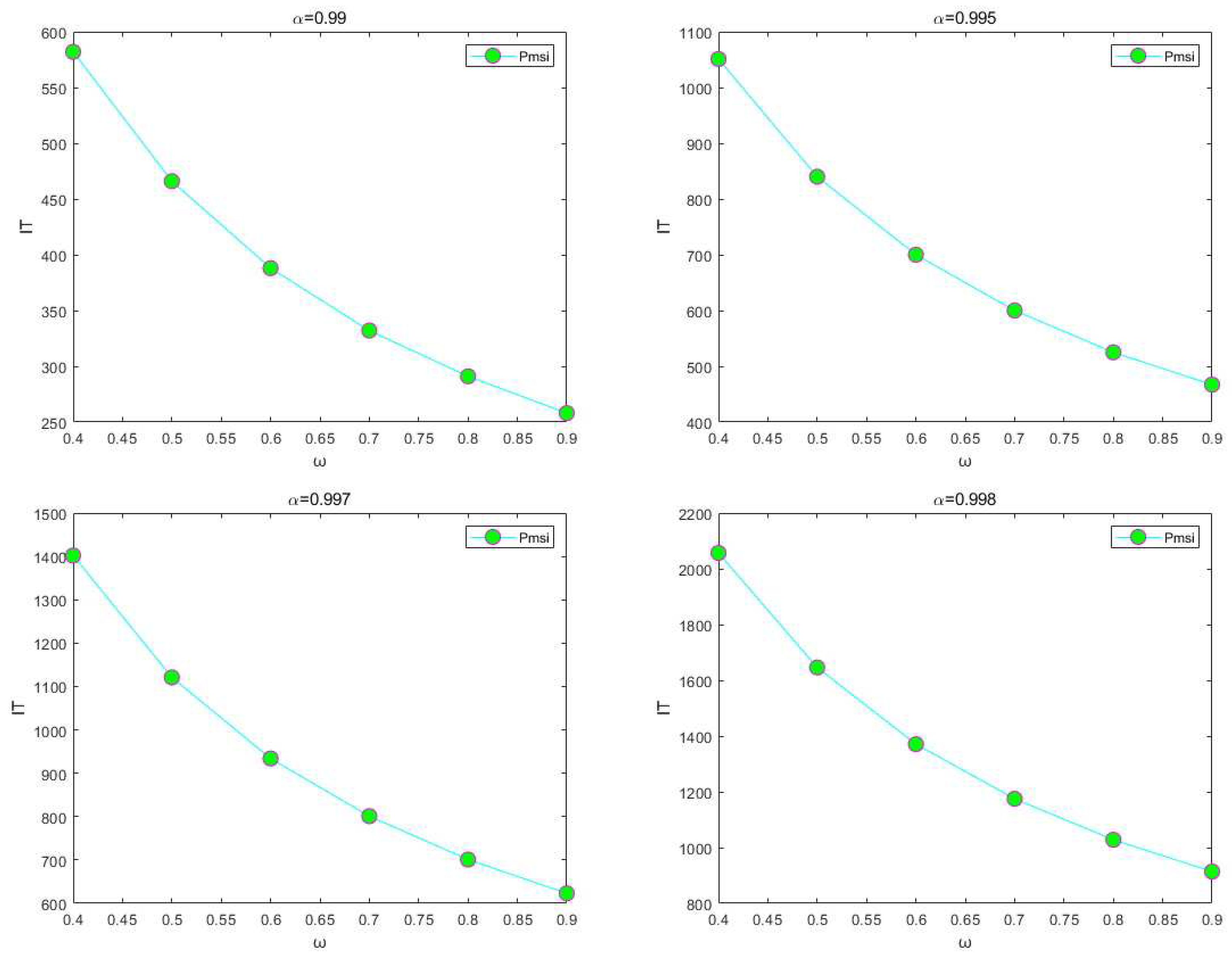
Preprints 77776 g004
Table 4. Numerical results for the wb-cs-stanford matrix in Example 4.3
Table 4. Numerical results for the wb-cs-stanford matrix in Example 4.3
β 2 ∖ β 1 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0.1 418(837) 410(821) 419(839) 419(839) 414(829) 422(845) 415(831) 417(835) 415(831)
0.3 416(833) 415(831) 418(837) 417(835) 420(841) 415(831) 426(853) 422(845) 417(835)
0.5 412(825) 420(841) 415(831) 416(833) 425(851) 411(823) 426(853) 424(569) 418(837)
0.7 418(837) 414(829) 417(837) 414(829) 419(839) 416(833) 412(825) 419(839) 417(835)
0.9 420(841) 422(845) 428(857) 420(841) 424(849) 422(845) 416(833) 417(835) 412(825)
Table 5. Numerical results for the amazon0312 matrix in Example 4.3
Table 5. Numerical results for the amazon0312 matrix in Example 4.3
β 2 ∖ β 1 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0.1 293(587) 275(551) 262(525) 302(605) 284(569) 269(539) 275(551) 277(555) 262(525)
0.3 262(525) 265(531) 294(589) 262(525) 263(527) 303(607) 271(543) 269(539) 258(517)
0.5 281(563) 257(535) 269(539) 308(617) 256(513) 276(553) 303(607) 284(569) 278(557)
0.7 322(665) 275(551) 303(607) 255(511) 301(603) 272(545) 269(539) 314(629) 264(529)
0.9 259(517) 276(553) 274(549) 270(541) 251(503) 274(549) 272(545) 272(545) 255(511)

5. Conclusions

In this paper, in order to further improve the two-step splitting iterative method, we propose a parameterized multisplitting iterative method to solve the PageRank problem by introducing a relaxation parameter ω , when ω = 1, the PMSI method reduces to the MSI method. Numerical experiments show that the sequence of iterations generated by the PMSI method converges to the PageRank vector when the parameters ω , β 1 , and β 2 satisfy specific requirements. The proposed method also has better convergence performance than IO and MSI methods. Since the new algorithms are parameter-dependent, how to obtain the optimal parameters in the general case remains to be studied.

References

  1. N.-A. Langville, C.-D. Meyer, Google’s PageRank and beyond: the science of search engine rankings. Princeton University Press, Princeton, NJ, 2006. 195-224.
  2. B. Philippe, Y. Saad, W.-J. Stewart, Numerical methods in Markov chain modeling. Oper. Res. 1992, 40, 1156–1179. [CrossRef]
  3. Golub, H. Gene, L. Van, F. Charles, Matrix computations, Johns Hopkins University Press. (1989). 569-784.
  4. D.-F. Gleich, A.-P. Gray, C. Greif, T. Lau, An inner-outer iteration for computing PageRank. SIAM J. Sci. Comput. 2010, 32, 349–371. [CrossRef]
  5. C.-Q. Gu, F. Xie, K. Zhang, A two-step matrix splitting iteration for computing PageRank. J. Comput. Appl. Math. 2015, 278, 19–28. [CrossRef]
  6. C. Wen, T.-Z. Huang, Z.-L. Shen, A note on the two-step matrix splitting iteration for computing PageRank. J. Comput. Appl. Math. 2017, 315, 87–97. [CrossRef]
  7. Z.-L. Tian, X.-J. Li, Z.-Y. Liu, A general multi-step matrix splitting iteration method for computing PageRank. Filomat 2021, 35, 679–706. [CrossRef]
  8. C.-Q. Gu, L. Wang, On the multi-splitting iteration method for computing PageRank. J. Comput. Appl. Math. 2013, 42, 479–490. [CrossRef]
  9. M.-Y. Tian, Y. Zhang, Y.-D Wang, Z.-L. Tian, A general multi-splitting iteration method for computing PageRank. Comput. Appl. Math. 2019, 38, 60. [CrossRef]
  10. X.-D. Chen, S.-Y. Li, A generalized two-step splitting iterative method modified with the multi-step power method for computing PageRank, (Chinese). J. Numer. Methods Comput. Appl. 2018, 39, 243–252.
  11. Y.-J. Xie, C.-F. Ma, A relaxed two-step splitting iteration method for computing PageRank. J. Comput. Appl. Math. 2018, 37, 221–233.
  12. Z.-L. Tian, Y. Zhang, J.-X. Wang, C.-Q. Gu, Several relaxed iteration methods for computing PageRank. J. Comput. Appl. Math. 2021, 388, 21.
  13. Z-L Tian, X.-Y. Liu, Y.-D. Wang, P.-H. Wen, The modified matrix splitting iteration method for computing PageRank problem. Filomat 2019, 33, 725–740. [CrossRef]
  14. G. Wu, Y.-M. Wei, A power-Arnoldi algorithm for computing PageRank. Numer. Linear Algebra Appl. 2007, 14, 521–546. [CrossRef]
  15. C.-Q. Gu, Y. Nie, J.-B. Wang, Arnoldi-PIO algorithm for PageRank, (Chinese). J. Shanghai Univ. Nat. Sci. 2017, 23, 555–562.
  16. Z-H. Qiu, C.-Q. Gu, A GMRES-RPIO algorithm for computing PageRank problem. J. Numerical Mathematics a Journal of Chinese Universities 2018, 40, 331–345.
  17. C.-Q. Gu, W.-W. Wang, An Arnoldi-MSI algorithm for computing PageRank problems, (Chinese). Numer. Math. J. Chinese Univ. 2016, 38, 257–268.
  18. C.-Q. Gu, C.-C. Shao, A GMRES-in/out algorithm for computing PageRank problems, (Chinese). J. Shanghai Univ. Nat. Sci. 2017, 23, 179–184.
  19. X.-M. Gu, S.-L. Lei, K. Zhang, Z.-L. Shen, C, Wen, B. Carpentieri, A Hessenberg-type algorithm for computing PageRank problems. Numer. Algorithms. 2022, 89, 1845–1863. [CrossRef]
  20. W.-K. X, X.-D. Chen, A Modified Multi-Splitting Iterative Method With the Restarted GMRES to Solve the PageRank Problem, (Chinese). Appl Math and Mechanics 2022, 43, 330–340.
  21. N. Huang, C.-F. Ma, Parallel multisplitting iteration methods based on M-splitting for the PageRank problem. Appl. Math. Comput. 2015, 271, 337–343.
  22. G. Wu, Y. Zhang, Y.-M. Wei, Accelerating the Arnoldi-type algorithm for the PageRank problem and the ProteinRank problem. J. Sci. Comput. 2013, 57, 74–104. [CrossRef]
  23. B.-Y. Pu, T.-Z. Huang, C. Wen, A preconditioned and extrapolation-accelerated GMRES method for PageRank. Appl. Math. Lett. 2014, 37, 95–100. [CrossRef]
  24. X.-Y. Tan, A new extrapolation method for PageRank computations. J. Comput. Appl. Math. 2017, 313, 383–392. [CrossRef]
  25. C. Wen, Q.-Y. Hu, B.-Y. Pu, Y.-Y. Huang, Acceleration of an adaptive generalized Arnoldi method for computing PageRank. AIMS Math. 2021, 6, 893–907. [CrossRef]
  26. G. Wu, Y.-M. Wei, An Arnoldi-extrapolation algorithm for computing PageRank. Comput. Appl. Math. 2010, 234, 3196–3212. [CrossRef]
  27. P.-C. Guo, S.-C. Gao, X.-X. Guo, A modified Newton method for multilinear PageRank. Taiwanese J. Math. 2018, 22, 1161–1171.
  28. B.-Y. Pu, C. Wen, Q.-Y. Hu, A multi-power and multi-splitting inner-outer iteration for PageRank computation. Open Math. 2020, 18, 1709–1718. [CrossRef]
  29. H.-F. Zhang, T.-Z. Huang, C. Wen, Z.-L. Shen, FOM accelerated by an extrapolation method for solving PageRank problems. J. Comput. Appl. Math. 2016, 296, 397–409. [CrossRef]
  30. C.-Q. Gu, G.-D. Ge, Two-splitting iteration method for computing higher-order PageRank, (Chinese). Appl. Math. Comput. 2018, 32, 581–587.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated