A Methodology for Assessing Airport Terminal Capacity Based on Service Resource Equilibrium

Preprint

Article

A Methodology for Assessing Airport Terminal Capacity Based on Service Resource Equilibrium

Altmetrics

Downloads

164

Views

Comments

This version is not peer-reviewed

Submitted:

27 June 2023

Posted:

27 June 2023

You are already at the latest version

Alerts

Abstract

To effectively estimate airport terminal area capacity and assess the maximum throughput the sector can achieve when the capacity is given, this research proposes an approach to assess the terminal area capacity from the viewpoint of service provision resources. Terminal area capacity is optimized based on the equilibrium of air traffic service resource supply and demand. The supply-demand nexus is examined in consideration of terminal area route structure, traffic flow characteristics, and safety regulations. A flight service probability matrix and a terminal area demand and supply service time model are constructed to quantify resource expenditure at varied capacity levels. A optimization model is then developed to apportion maximal capacity under resource limitations. Model computation and computation results demonstrate the deviation between estimated and amended capacities is under 0.3 flight sorties per hour. The outcomes are congruent with historical statistics, thereby validating the accuracy and reliability of the model proposed in this study. Given capacity parameters, the model can deduce the maximal aircraft quantity served concurrently in terminal areas during peak periods. These revelations indicate the submitted model furnishes theoretical foundation and reference for terminal area sector partition and traffic alerting.

Keywords:

Subject: Engineering - Transportation Science and Technology

1. Introduction

Air traffic flow management serves as a prerequisite for reducing flight delays [1], ensuring air traffic safety, and alleviating the workload of air traffic controllers [2,3] .When implementing air traffic flow management, an accurate and effective assessment of the terminal area is its primary task and a prerequisite. Therefore, research on terminal area capacity assessment algorithms is crucial for ensuring the safe, smooth, and efficient operation and management of airports and airspace. In the current state of research, terminal area capacity algorithms can be primarily classified into three distinct approaches: Constructing and computing mathematical models, rapid computer simulation modeling, and analyzing air traffic controller workload. Mitchell J et al. proposed an airspace route maximum capacity model through analyzing the geometry of airspace sectors and employing a stochastic weather model. They applied the maximum-flow and minimum-cut method to investigate this model [4]. Janic M et al. performed an airspace capacity assessment based on air traffic controller workloads. They investigated the influence of these workloads on airspace capacity from three aspects: control procedures, separation standards, and service policies [5]. After restructuring the route network, Kageyama K et al. employed computer simulation methods to model an air traffic controller workload-based airspace capacity assessment model [6].

In comparison, research specifically addressing airspace capacity assessment for terminal control areas in China is still scarce. Dong Xiangning et al. analyzed various approaches for evaluating air traffic controller workload. By optimizing the controller workload-based airspace capacity assessment model, they developed a new terminal area airspace capacity assessment model [7]. Taking into full account the dynamic factors of hazardous weather, Yang Shangwen et al. developed strategies for scheduling arriving and departing flights as well as planning hazardous weather avoidance routes. Using computer simulation techniques, they predicted dynamic airspace capacity thresholds [8]. Shen Linan et al. incorporated delay levels as an impact factor in terminal area airspace capacity assessment. They established a mathematical model quantifying the relationship between flight delays and aircraft count [9]. Huang Haiqing et al. analyzed and compared terminal area airspace capacity thresholds under military operations. They employed the maximum flow/minimum cut theory and an improved genetic algorithm [10]. Peng Ying et al. proposed a multi-input deep learning model for terminal area traffic prediction by incorporating weather factors. They integrated deep learning techniques with the consideration of meteorological characteristics [11]. Mao Limin et al. developed a random forest-based prediction model for terminal airspace operations. Their model took into account the impact of convective weather systems [12].

Traditional mathematical models for terminal area airspace capacity assessment are built upon one or more impact factors, which are treated as constraints to set corresponding objective functions for capacity calculation [13,14,15]. Different models consider different factors, leading to significant variability among them. While improving capacity estimation accuracy for specific scenarios to some extent, these models also increase the complexity of capacity assessment operations. Regarding model variables, most current models primarily employ stochastic factors like weather as constraint variables, with little consideration given to the balance between service resource supply and demand. The influence of service resources on capacity is overlooked.

Therefore, this paper proposes to analyze the operational environment of the airport terminal area as well as the characteristics of air traffic flows, considering the demand and supply relationship of air traffic service resources, a mathematical model for forecasting the capacity of the airport terminal area based on the equilibrium of service resource supply and demand has been established. Taking the terminal area of Hulunbuir Hailar Airport (ICAO: ZBLA) as an example, the capacity of the terminal area of this airport is computed according to statistics such as distribution of arriving and departing traffic flows and aircraft type proportion. Simultaneously, the effectiveness and reliability of the mathematical model are further verified based on Monte Carlo simulation.

2. Capacity and Service Resource Analysis of Terminal Areas

The airport terminal area, as the transition airspace for aircraft moving from the air route into airport arrival and departure, enables the connection between the two ends of air routes and airports, its capacity refers to the maximum number of aircraft that the airspace can safely and orderly serve within a unit time, under certain airspace structures, flight procedures, control regulations and safety standards, considering the influence of variable factors such as aircraft performance, human factors and meteorological conditions[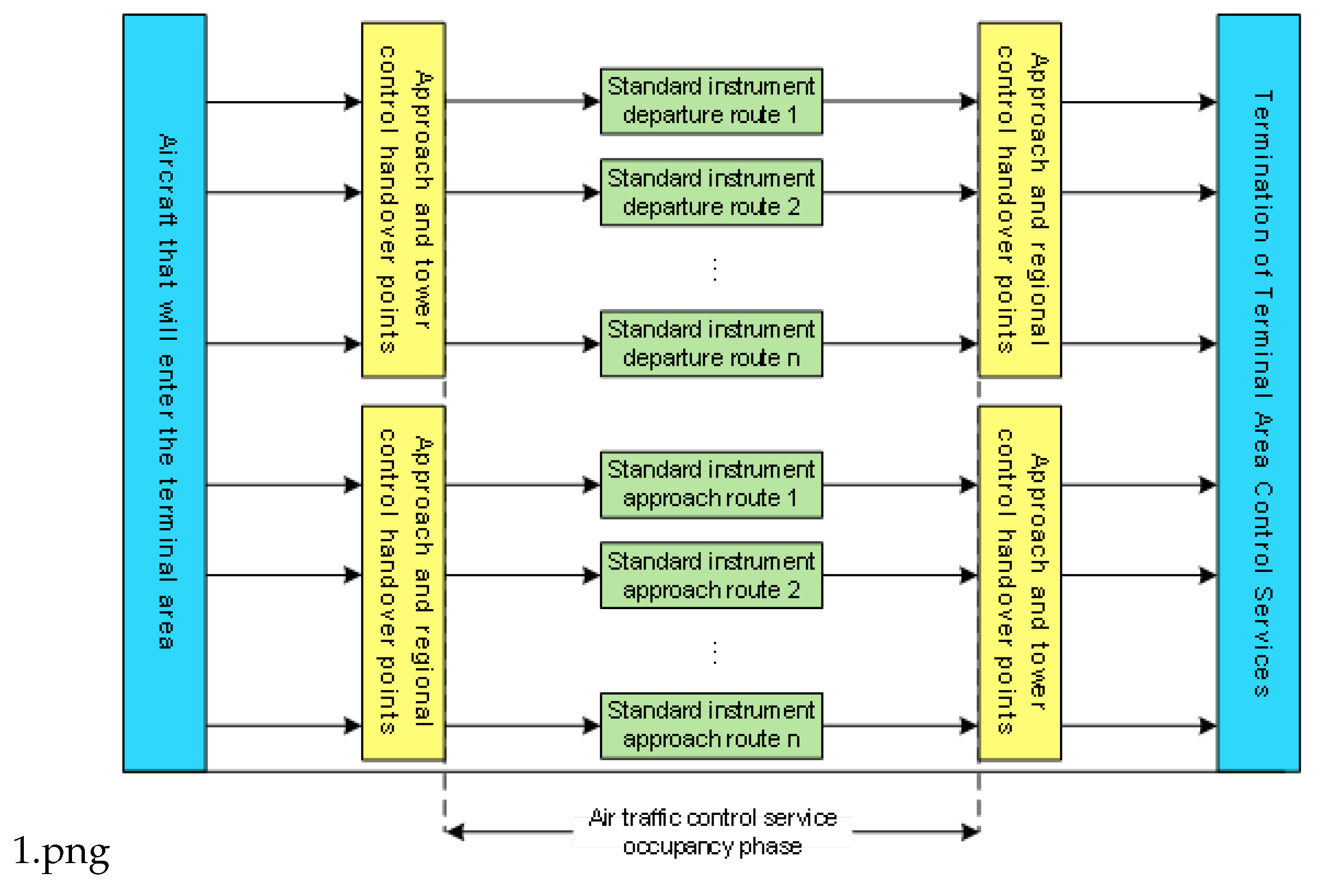1].The prerequisite for achieving the maximum capacity of terminal area is the prompt departure of the aircraft entering the terminal area after being serviced, thereby releasing the service resources of the area. Within the terminal area, demand refers to aircraft requiring control services, and supply refers to air route resources and control officer service resources. The process of aircraft entering the terminal area is depicted as the procedural flowchart shown in Figure 1.

The terminal area airspace includes airspace of approach control areas and aerodrome control zones, as illustrated in Figure 1. The airspace is divided by two control boundaries. The control boundary is a nonexistent spatial demarcation, indicating the control handover position where the airspace resources in current zone start/end to be occupied. When an aircraft enters the control zone, it means the aircraft begins to occupy part of the airspace resources of the area. Once the aircraft leaves the control zone, the resources occupied by the aircraft will be released immediately. Therefore, the two imaginary boundaries constitute the control transfer boundaries. During the flight process, the resource consumption includes not only the occupation of fixed resources such as air routes, but also the occupation of control service resources. Aircraft entering the terminal generates the demand for control services. While controllers provide services, they are under physical pressures and psychological stresses[16,17]. The physical operational pressure can be converted into time to relieve their own pressure and the demands of control tasks. The psychological stress determines the number of aircraft that controllers can safely handle under busy conditions, which remains unchanged within a certain period of time. The level depends mainly on the workload that controllers can bear and the number of aircraft in the terminal area. According to the Civil Aviation Air Traffic Management Rules (CCAR-93TM-R5), the number of aircraft receiving air traffic control services in a sector simultaneously shall not exceed the number that can be safely handled during peak times. Therefore, the higher the comprehensive abilities of controllers, the more aircraft sorties can be served under busy conditions, the greater the capacity of air traffic flow, and the higher the upper limit of terminal area capacity.

3. Mathematical Modeling

3.1. Model Assumptions

This study focuses on the capacity of arrival and departure in the terminal area of a single airport. There are many limiting factors that affect the capacity of the terminal area [1], and different definitions of terminal area capacity exist based on different limiting factors. According to the mathematical model developed in this study, the terminal area capacity is defined as follows: The maximum number of aircraft the terminal area can serve per unit time at an acceptable level of air traffic control service provision, balancing the supply and demand of service resources. Previous studies[10,11,12] have included some of the influencing factors as constraints. The construction of a mathematical model makes the computational model more relevant to the actual operating scenario. However, various influencing factors are potential risks in operation, and their occurrence probabilities are random. The complexity of the terminal area structure also limits the accuracy of the model results. This study simplifies the limiting factors and operational methods, introduces the supply and demand relationship of terminal area service resources, and establishes a mathematical model for terminal area capacity computation under the balance of service resource supply. To establish this model, the following assumptions have been made:

Any two arriving or departing aircraft are equipped with a minimum flight separation greater than that used in the control area where they are located.
In the terminal area, if the service for an aircraft has already started and has not yet finished, the service for another aircraft cannot begin.
Aircraft service requests in the terminal area are continuous, and the number of aircraft being served in the terminal area does not exceed the safe handling capacity.
Each aircraft flies according to its planned route and will not deviate from or change the planned route.
Each aircraft of the same type experiences the same flight time on the same air route.

3.2. Model Formulation

This model considers the supply-demand relationship among terminal area service resources. By analyzing the traffic flow characteristics of the terminal area, the terminal area capacity is finally obtained. It is assumed that the terminal area capacity of the airport is

C a p a c i t y

, and each airway and air route in this area is connected to airways and air traffic control transfer points. Each air route within the area, is connected to airways and air traffic control transfer points. There are i air routes within the terminal area, denoted as

R_{i}

t_{j}^{I N}

and

t_{j}^{O U T}

represent the times at which approaching/departing aircraft

f_{j}

enters the terminal area and leaves the terminal area, respectively. The terminal area service procedure for aircraft

f_{j}

is as follows: At time

t_{j}^{I N}

, aircraft

f_{j}

crosses the control transfer point to enter the control area from outside the terminal area. From time

t_{j}^{I N}

, it starts to occupy part of the service resources and flies along the planned route

R_{i}

. At time

t_{j}^{O U T}

, it crosses another control transfer point to leave the control area. At this moment, the service resources occupied by

t_{j}

are released. To differentiate different scenarios of service resource supply and demand, three mathematical models—demand model, supply model, and capacity solving model—are established respectively. The primary subject of the demand model is aircrafts entering the terminal area for service.

3.2.1. Demand Model

The approach/departure option model and terminal area route utilization, accumulated from aircraft operations are as follows:

\begin{matrix} A : D & = \frac{\sum f_{j}^{A R R}}{\sum f_{j}^{D E P}} \end{matrix}

(1)

\begin{matrix} a_{1} + a_{2} + \dots + a_{n} & = \sum a_{n} = 1, (n < i) \end{matrix}

(2)

\begin{matrix} d_{1} + d_{2} + \dots + d_{i - n} & = \sum d_{n} = 1, (n < i) \end{matrix}

(3)

Among Equations (1)–(3) , A represents the proportion of arriving aircraft

f^{A R R}

in the total traffic flow, and D represents the proportion of departing aircraft

f^{D E P}

in the total traffic flow.

a_{n}

indicates the utilization rate of the

n_{t h}

arriving air route, and

d_{i - n}

indicates the utilization rate of the

i - n_{t h}

departing air route; where among the i air routes in the terminal area, there are n arriving air routes and

i - n

departing air routes. The arriving and departing air routes are numbered sequentially in order.

All the aircrafts

f_{j}

under services are categorized into k types, then correspond to the following equation for the proportion

I_{i, k}

of each type of aircraft in different air routes :

I_{i, 1} + I_{i, 2} + \dots + I_{i, k} = \sum d_{n} = 1, (n < i)

(4)

In Equation (4),

I_{i, k}

represents the proportion of the

k_{t h}

type of aircraft in the total aircraft sorties operated on the

i_{t h}

terminal area air route. Through the above computations, the flight mission service probability matrix

P_{i k}

is obtained.

P_{i k} = [\begin{matrix} R_{1} \\ R_{2} \\ ⋮ \\ R_{i} \end{matrix}] \cdot [\begin{matrix} I_{1, 1} & I_{1, 2} & \dots & I_{1, k} \\ I_{2, 1} & I_{2, 2} & \dots & I_{2, k} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ I_{i, 1} & I_{i, 2} & \dots & I_{i, k} \end{matrix}]

(5)

P_{i k} = [\begin{matrix} P_{1, 1} & P_{1, 2} & \dots & P_{1, k} \\ P_{2, 1} & P_{2, 2} & \dots & P_{2, k} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ P_{i, 1} & P_{i, 2} & \dots & P_{i, k} \end{matrix}]

(6)

In Equation (5), the column vector

R_{i}

represents the list of probabilities of an aircraft selecting the

i_{t h}

service route in the terminal area. In Equation (6), the matrix

P_{i k}

stores the proportions of the

k_{t h}

type of aircraft operated on the

i_{t h}

air route in the total aircraft sorties in the terminal area system.

T_{i}^{k} = \frac{\sum (t_{f_{i}^{k}}^{O U T} - t_{f_{i}^{k}}^{I N})}{\sum f_{j}^{k}}

(7)

In Equation (7), when the aircraft

f_{j}

passes through the terminal area, it will generate two time points: the entry time

t_{j}^{I N}

and the exit time

t_{j}^{O U T} .

Based on these two time points, the expected flight time

T_{i}^{k}

of each type of aircraft

f_{j}

on different air route i can be computed statistically:

f_{i}^{k}

represents an aircraft operated on air route i and belongs to aircraft type k. The time at which the aircraft enters the terminal airspace is denoted by

t_{f_{i}^{k}}^{I N}

, and the time at which it exits the terminal airspace is denoted by

t_{f_{i}^{k}}^{O U T}

Equation (8) is the mathematical model for the expected demand service time

E (T_{i}^{k})

in the terminal area.

E (T_{i}^{k}) = \sum p_{i k} T_{i}^{k}

(8)

3.2.2. Demand Model

To describe the supply-demand relationship of service resources in the terminal area, the supply model is established. Equation (9) obtains the expected maximum supply service time

T_{s e r}

T_{s e r} = S_{m a x} T_{c a l}

(9)

The parameter

S_{m a x}

indicates the maximum aircraft handling capacity of an air traffic controller under peak circumstances.

T_{c a l}

refers to the length of time required for capacity calculation (typically 60 minutes).

3.2.3. Demand Model

The prerequisite for calculating terminal capacity is the balance between service supply and demand, which means that the maximum available service time should be greater than or equal to the estimated service time required. From the view of quantity, this translates to ensuring that the number of aircraft receiving services in the terminal area at any given time does not exceed the number that air traffic controllers can safely handle during peak periods. Equation (10) represents the capacity calculation model:

T_{s e r} \geq E (T_{i}^{k}) C a p a c i t y

(10)

Considering that air traffic control services cannot remain in a state of peak period indefinitely, it is necessary to add an utilization coefficient u to constrain it. Therefore, based on service supply and demand balance, the terminal area capacity mathematical model is as shown in Equation (11):

T_{s e r} = E (T_{i}^{k}) C a p a c i t y

(11)

As the utilization coefficient, u represents the probability that the number of aircrafts simultaneously receiving services in the terminal area within a unit of time does not exceed the number that can be safely handled under peak period conditions. When u is 1, the calculated capacity is the ultimate capacity. When u takes a value in [0,1), the calculated capacity is the operational capacity.

4. Empirical Analysis of the Proposed Model

4.1. Model Implementation Using ZBLA Airport Data

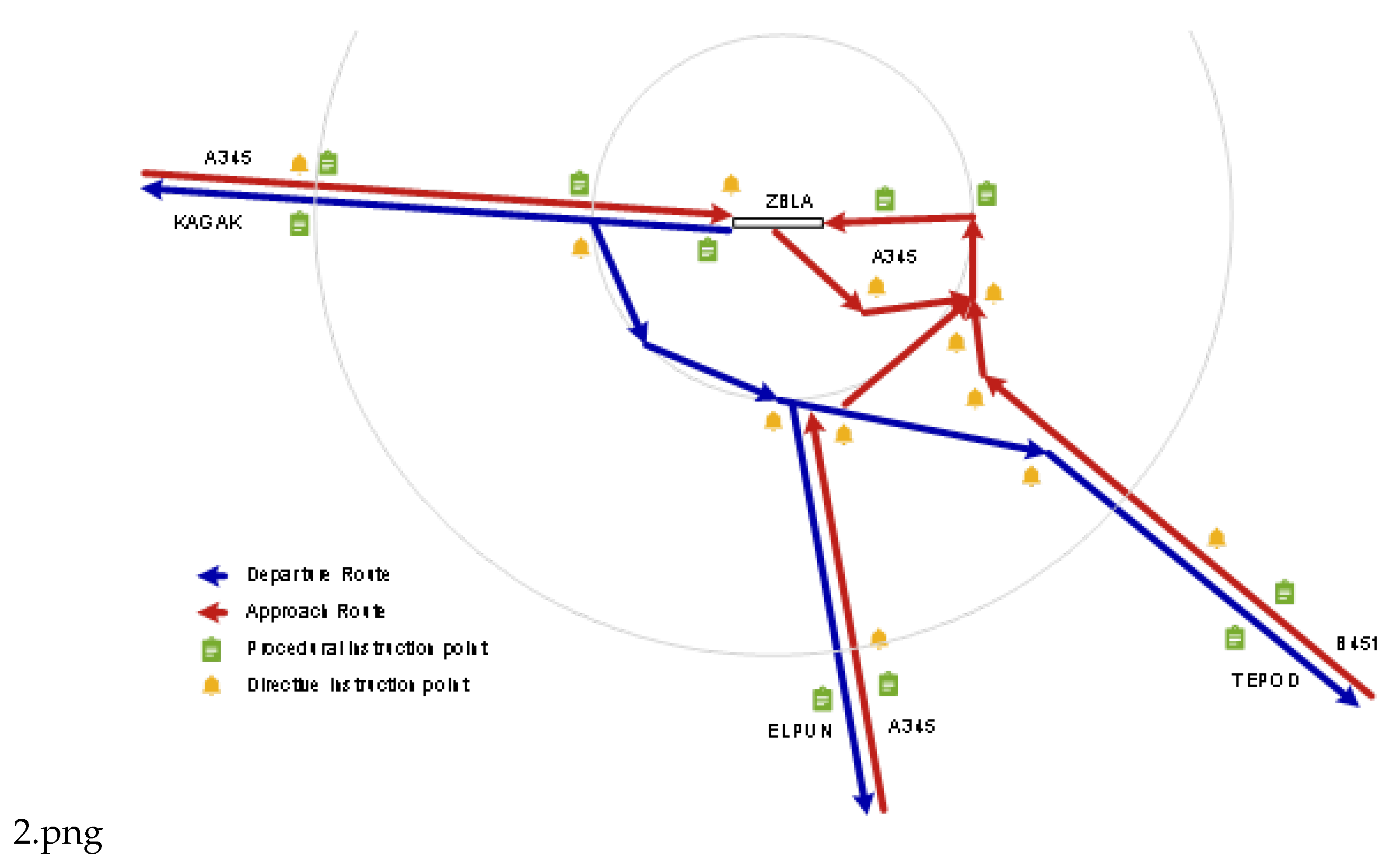
The terminal area of Hulunbuir Hailar Airport (ICAO: ZBLA) was selected as the subject for capacity calculation analysis. As shown in Figure 2, during the chosen time period, the terminal area employed procedural control and associated approach operation modes. A total of six arrival and departure routes are present in the area, consisting of three Standard Instrument Arrival (STAR) routes and three Standard Instrument Departure (SID) routes.

Based on the analysis of on-site collected data, aircraft types within the terminal area were categorized into three classes. The airport’s takeoff-to-landing ratio is 6:4. The approach and departure procedures KAGAK, TEPOD, and ELPUN are utilized in a proportion of 3:17:80. The distribution of aircraft types under different approach and departure procedures is presented in Table 1.

Under normal conditions, air traffic controllers at the terminal area of Hulunbuir Hailar Airport (ZBLA) can safely handle up to four aircraft at peak workload periods. Therefore, the supply model parameter $S_{m a x}$ is set to 4, and the calculation time $T_{c a l}$ is 1 hour.The continuous working time $T_{s e r}$ is calculated as:

$\begin{matrix} T_{s e r} & = s_{m a x} T_{c a l} \\ = 4 \times 60 \\ = 240 m i n \end{matrix}$
Considering that the average workload of air traffic controllers in China should not exceed 70% of the maximum workload threshold, the utilization coefficient u is set to 0.7 for this calculation.
When the utilization coefficient is unconstrained, the mathematical model can be expressed as:

$\begin{matrix} u T_{s e r} & = E (T_{i}^{k}) C a p a c i t y \\ = (0.408 \times 11.2 + 0.072 \times 14.4 + 0.086 \times 9 + 0.016 \times 11.5 + 0.010 \times 6.5 \\ + 0.005 \times 8 + 0.003 \times 7 + 0.272 \times 7.8 + 0.048 \times 10.1 + 0.057 \times 6 + 0.011 \times 7.7 \\ + 0.006 \times 12.3 + 0.004 \times 15.8 + 0.002 \times 22.2) C a p a c i t y \\ = 9.905 \times C a p a c i t y \end{matrix}$
When the utilization coefficient u assumes different values between 0.1 and 1, the workload and estimated terminal airspace capacity results vary accordingly. A higher u indicates a greater workload for air traffic controllers,thus,as shown in Figure 3, the $c a p a c i t y$ increases as u increases. In this study, a utilization coefficient of 0.7 is selected to represent a busy workload scenario for terminal airspace controllers at Hulunbuir Hailar Airport (ZBLA). Consequently, the calculated recommended operational capacity is 17 aircraft movements per hour.

4.2. Model Validation by Monte Carlo Simulation

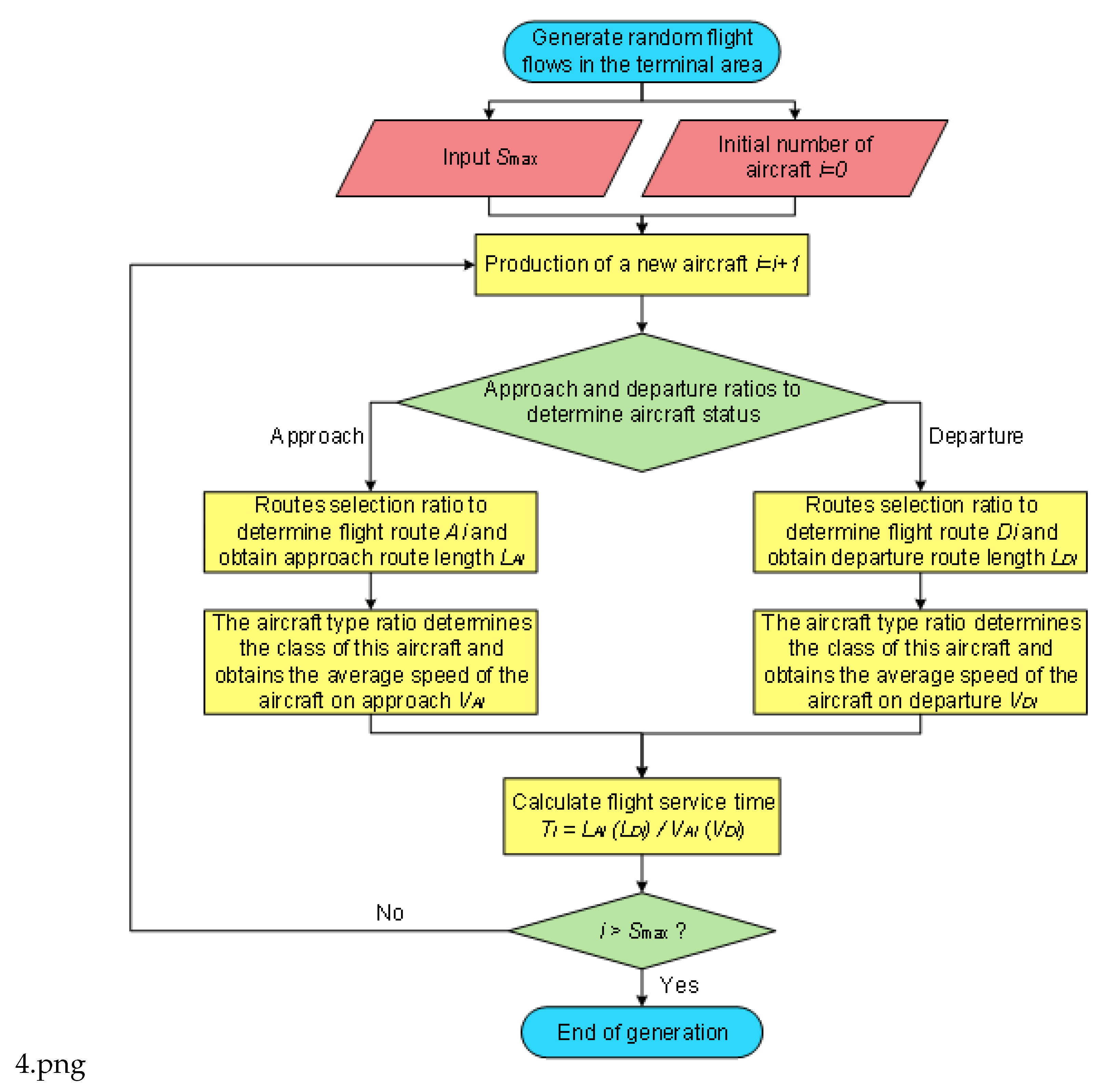
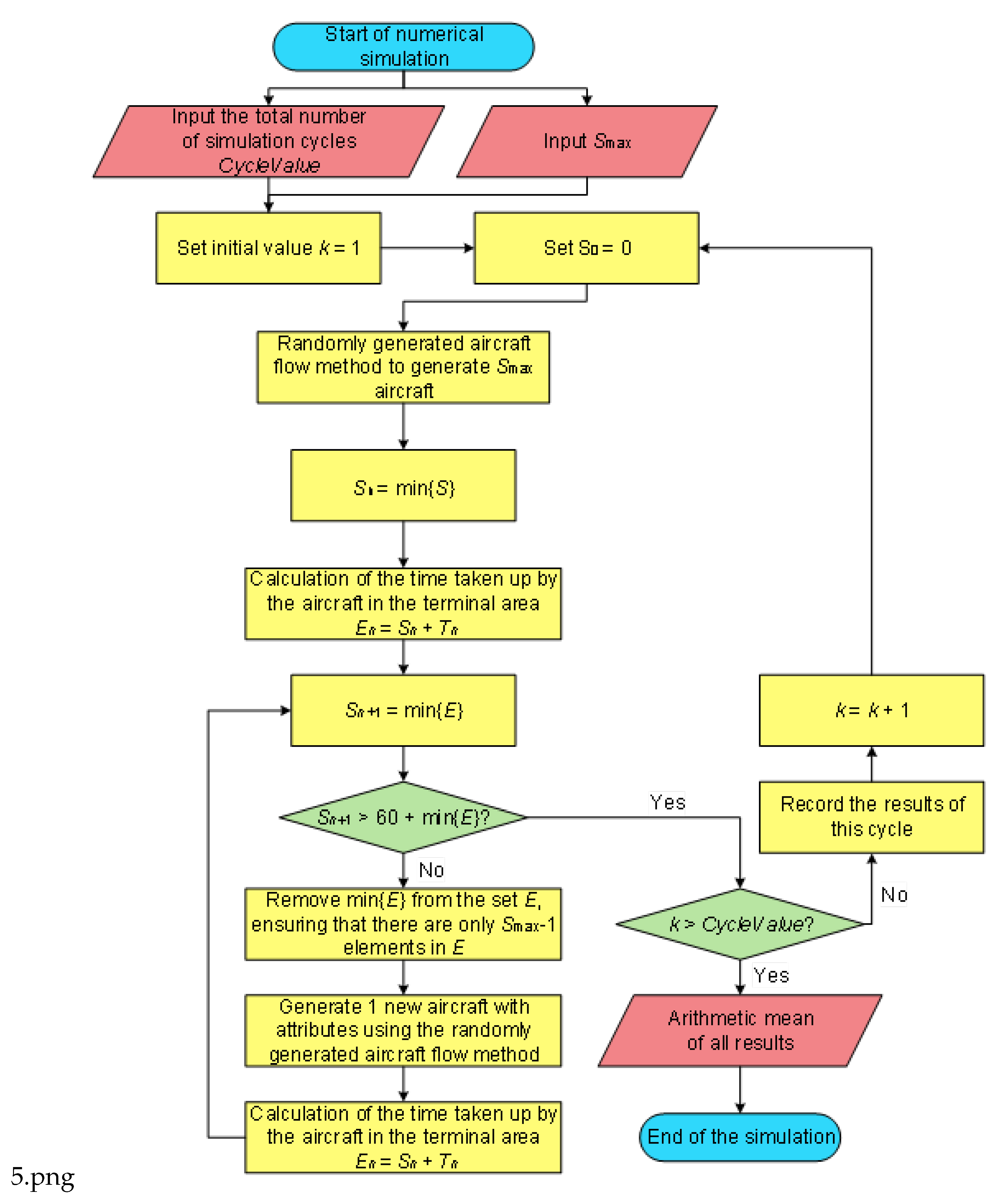
To verify the accuracy of the computation results obtained from the model , this study employs the Monte Carlo method [18] to develop and implement a numerical simulation program, which is subsequently used to assess the capacity of the terminal area at Hulunbuir Hailar Airport (ZBLA). The simulation process involves generating a random aircraft flow, which constitutes a critical step [19].The Monte Carlo method simulates the process of random aircraft flow generation in the terminal area by conducting multiple simulation runs. This proposed approach helps to ensure that the generated random aircraft flow aligns with actual operating conditions. It also maintains randomness for each simulation run. The detailed simulation procedure for aircraft flow generation is illustrated in Figure 4.

To eliminate the influence of the stochastic elements in generated aircraft flows with the simulation model, an averaging process has been utilized to satisfy the actual operational conditions. Derived from the random aircraft flow generation methodology, a statistical summarization of airspace and resources occupancy time was achieved in accordance with aircraft and airspace scenario calculation results. Each cycle corresponds to an averaging of the calculation results to minimize the impacts of random factors. The detailed simulation workflow is illustrated in Figure 5.

The detailed simulation procedure is illustrated below:

Random aircraft generation within the terminal area In the simulation, each aircraft needs to be randomly generated to operate in the airspace based on the take-off and landing ratios, the percentages of approach and departure procedures, and the percentages of aircraft types for different approach and departure procedures. The flight distance and speed are determined based on the selected approach, departure procedure, and aircraft type, resulting in the flight time for that aircraft. In each cycle, n aircrafts are first generated to meet the condition that no more than n aircrafts are under ATC control at the same time, which means n aircraft sorties in the terminal area are maintained as the limit case.
Confirmation upon aircraft’s proceeding out of the terminal Area As the simulation progresses, aircrafts fly along the selected approach and departure procedures until one of the aircrafts reaches the endpoint. The timing starts from aircraft’s proceeding out of the first aircraft until the cumulative time reaches 1 hour. The endpoints in this simulation are the points where arriving aircraft hand over control to the tower (for landing aircraft) or the approach control (for departing aircraft). In this simulation, the endpoints are: the transfer points where aircrafts in the approach control zone transfer control to the control zone (for landing aircrafts) or the Area Control Center (for departing aircraft).
Defining the Iteration Rules When an aircraft proceeds out of the endpoint, an aircraft is generated randomly in the scenario. This constantly maintains n aircrafts being operated within the terminal control area. Steps 2 and 3 are repeated until the cumulative time reaches 1 hour. After counting the total number of aircrafts present in this iteration, aircraft generation was ceased for this iteration.
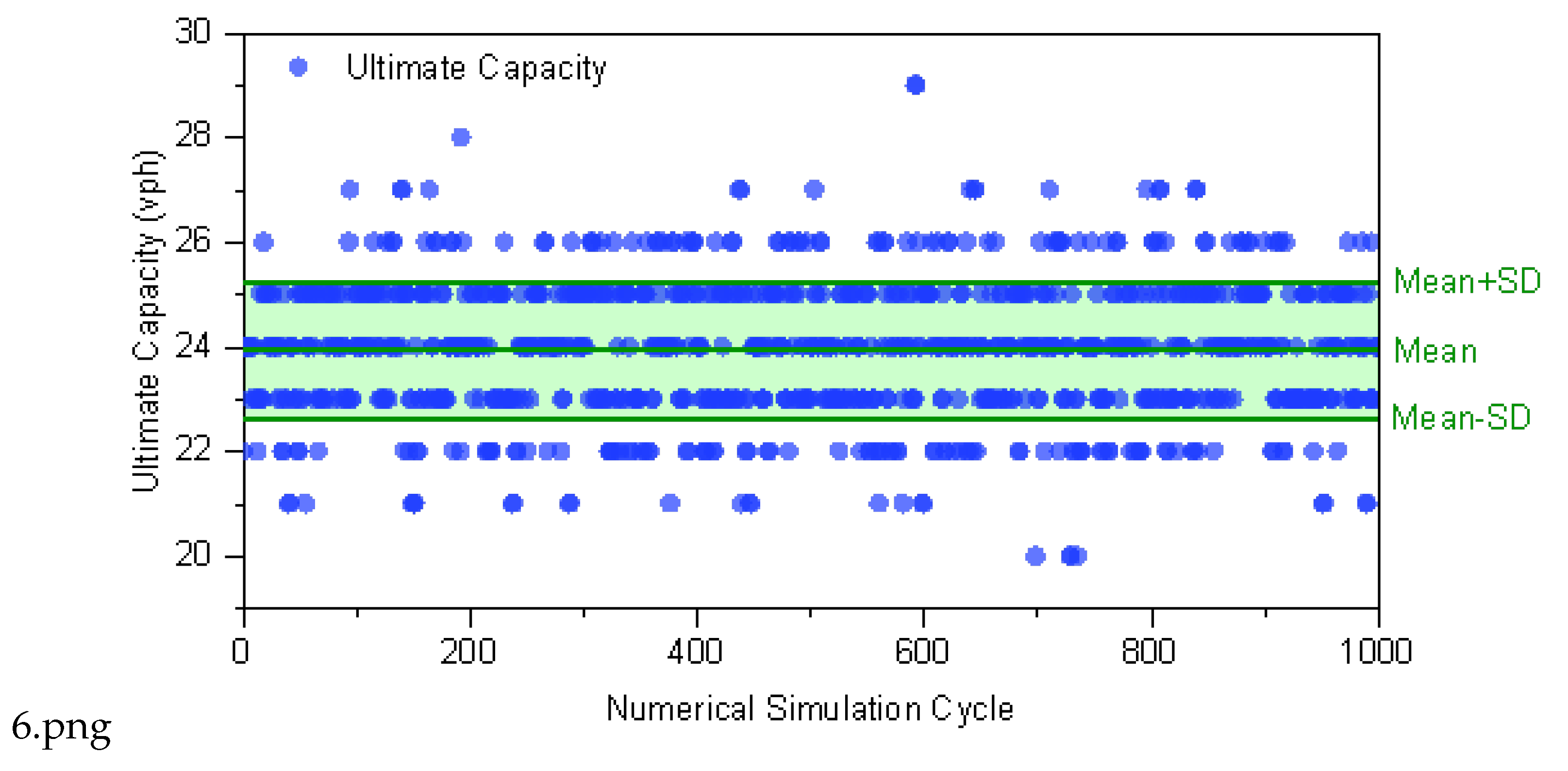
Defining the Integrated Iteration Rules Repeat Steps 1 through 3 until reaching the preset number of iterations. Take the arithmetic mean of the results as the numerical simulation capacity of the terminal area. The total number of iterations k is set to 1000. The approach and departure traffic distribution data, terminal area route selection ratios, and flight durations used in this simulation are the same as those in the previous model. The arithmetic mean of the results from these 1000 computational loops is used to determine the limit capacity of the terminal area. The final results are presented in Figure 6.

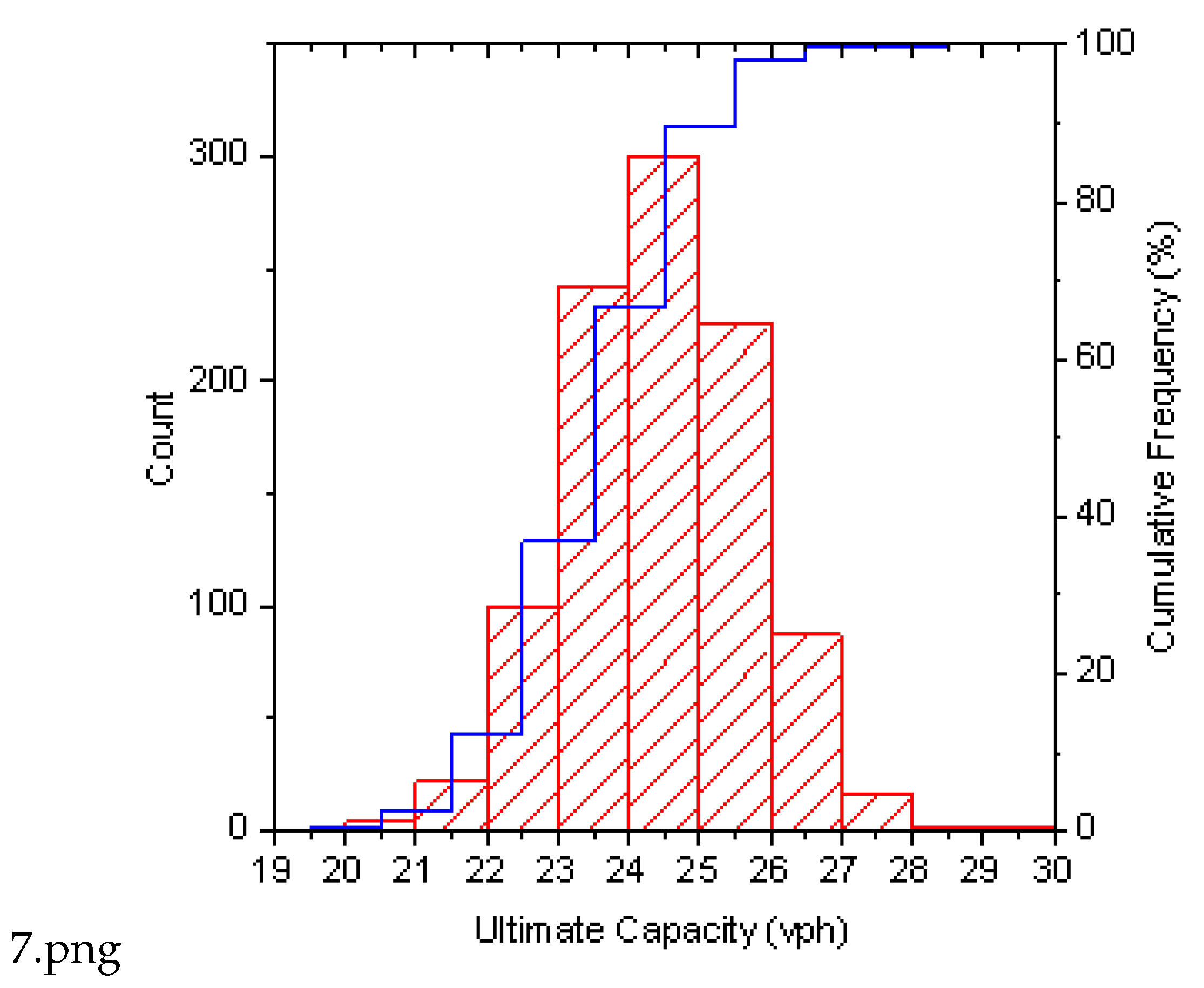
The data in Figure 6 and Figure 7 shows that the solutions of each computational iteration oscillate around the midpoint between 23 and 24, which demonstrates that within a fixed unit of time, factors including flight scheduling and types of aircrafts exert certain effects on the capacity. During the computation, the maximum throughput was 29 flight sorties per hour, whereas the minimum was 20 flight sorties per hour. Given the stochastic nature of each iteration, the arithmetic mean of results from all loops should be adopted as the simulated maximum capacity.

4.3. Quantitative Assessment and Extrapolation

After the assessment of the capacity of terminal area of Hailar Airport (ZBLA) with two methods in the paper and simulations on an ATC simulator, the results from the two methods and the simulator experiments were similar under the current operating mode, with the (terminal area) operating capacity being 17 flight sorties per hour. As shown in Table 2, the difference in maximum capacity was 0.291 flight sorties per hour, and the difference in operating capacity was 0.203 flight sorties per hour. In conventional capacity assessments, values after the decimal point are usually rounded to the nearest integer. Since the differences under the two methods were both less than 0.3, the results from the mathematical models can be validated to a certain extent.

The majority of contemporary studies on airport traffic management regard capacity as an invariant parameter [19,20]. In actuality, airport capacity is subject to variations contingent upon shifts in operating conditions. In actuality, airport capacity is subject to variations contingent upon shifts in operating conditions. 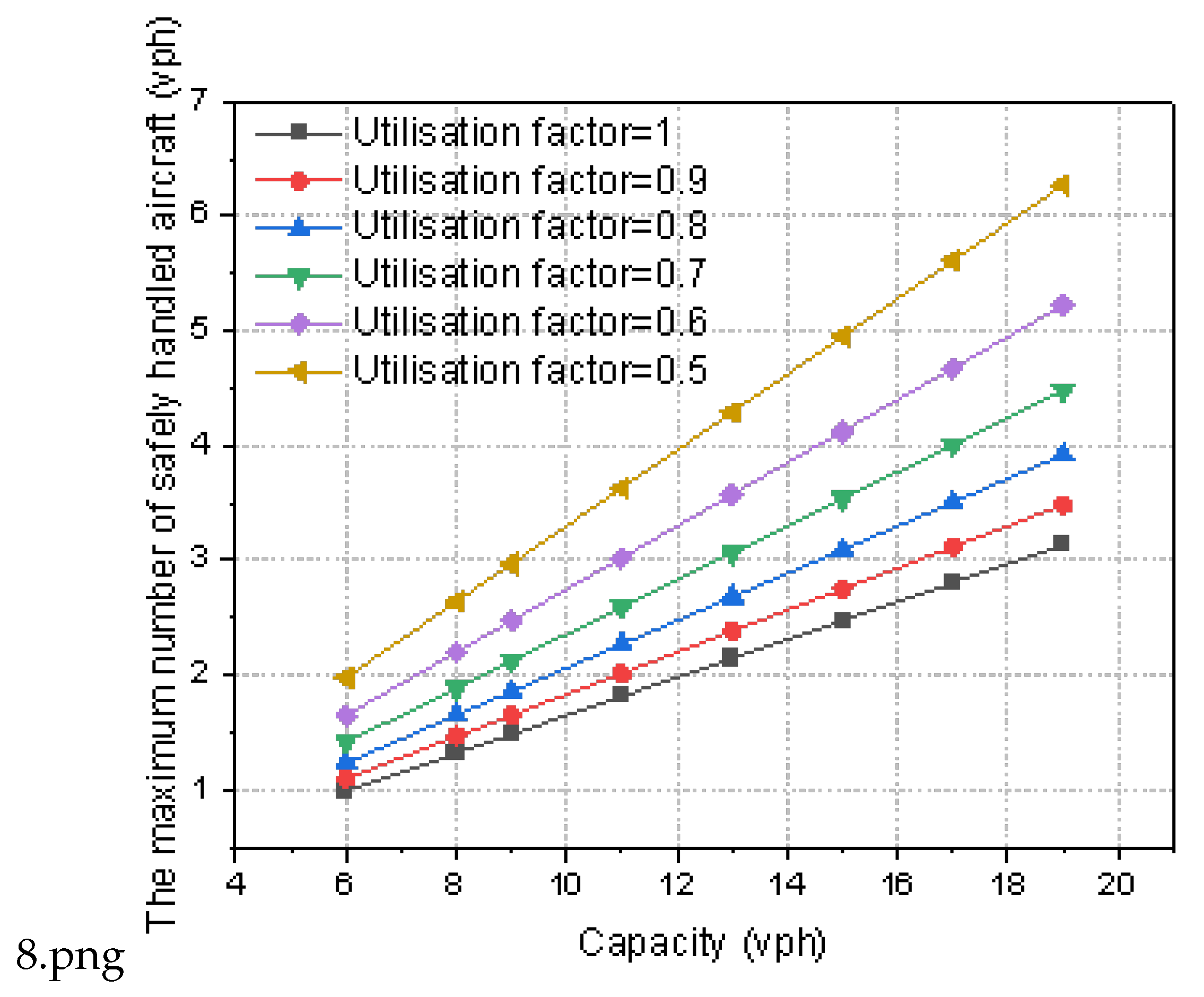Such an alerting approach necessitates substantial data aggregation and computation to derive relatively precise outcomes [21], which impedes the timely alerting. Disparities in time frames and flight flow characteristics engender deviations in both controller workload and the maximum number of aircrafts that can be safely handled. The fluctuating nature of air traffic also renders the maximum number of aircrafts that can be securely serviced by controllers under a safe workload constantly mutable. Therefore, in order to incorporate the workload component into air traffic alerting operations, the computational model established in this study was enhanced. Given determinate controller workload, terminal area configuration and flight flow characteristics within a particular temporal scope, the maximum number of aircraft that can be safely handled at peak periods is deduced. Taking the aforementioned airport terminal airspace as an example, the correlation between the maximum number of aircraft safely serviced and capacity during intervals of maximum controller workload is as follows:

S_{m a x} = \frac{E (T_{i}^{k})}{u T_{c a l}} C a p a c i t y

(12)

With the current capacity of 19 aircraft sorties per hour at the peak hours of the terminal area, the relationship between the maximum number of aircrafts safely handled and the area capacity was obtained by gradually adjusting the utilization coefficient and reducing the capacity at peak hours. As shown in Figure 8, the maximum number of aircrafts safely handled shows a decreasing trend with the decrease of terminal area capacity. This indicates that the bottleneck has shifted to the service ability of air traffic controllers as the traffic flow of the terminal area decreases.As mentioned above , under variant flow scenarios, it is viable to formulate an efficacious shift scheduling scheme for air traffic controllers . Furthermore, in view of serviceabilities of the terminal area, it is promising to devise terminal zone flow regulation strategies and tactics for discrete operational conditions.

5. Conclusion

Terminal area capacity computation constitutes one of the focal points in the preliminary phases of air traffic management and airport development planning. In order to determine the capacity of the terminal area, this study divides the service resources of the terminal area into supply resources and demand resources based on the relevant data. Through mathematical modeling, this study develops an optimized model to obtain the terminal area capacity based on the dynamic equilibrium between supply resources and demand resources. Through empirical studies, this model demonstrates solid applicability in estimating the capacity of airport terminal areas. Compared with other mathematical approaches, this model demonstrates broader applicability in statistical analysis of fundamental data and simulation of operational procedures for terminal areas. In summary, the key conclusions drawn from this study are as follows:

This study validates the computed results by using a Monte Carlo-based numerical simulation method, which demonstrates a close similarity between the simulated and actual results. This confirms the reliability of the capacity computations obtained through the proposed model. The findings indicate that the model can accurately and reasonably estimate the terminal area’s capacity, providing theoretical support for traffic management methods at airports and terminal areas.
By incorporating service resources and traffic alert operations, and examining the relationship between the maximum safe number of aircraft handled during peak periods and the capacity, this study broadens the utility of the mathematical model. It enables the prediction of the maximum safe number of aircrafts that controllers can handle during peak periods based on the determined terminal area capacity, offering guidance for shift scheduling of air traffic controllers and traffic flow management at Air Traffic Control (ATC) facilities.
Due to the lack of integration of influential factors such as meteorological elements, the proposed model requires further refinement to achieve higher fidelity to authentic operational circumstances.

6. Patents

A patent related to the work reported in this manuscript has been filed and granted in Mainland China. The patent, held by the Civil Aviation Flight University of China, was granted on April 21, 2023. [22]

Author Contributions

Conceptualization, Mou and Zhang; methodology, Mou and Zhang; software, Zhang; validation, Zhang, Mou and Yang; formal analysis, Zhang; investigation, Zhang; resources, Mou; data curation, Zhang and Yang; writing—original draft preparation, Zhang and Yang; writing—review and editing, Yang; visualization, Zhang and Yang; supervision, Mou; project administration, Mou; funding acquisition, Mou. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Fundamental Research Funds for the Central Universities (Grant No. ZHMH2022-002) and the Science and Technology Department of Sichuan Province (Grant No. 2022YFG0196).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data was obtained through field surveys conducted in Hailar Airport Project during 2021. The raw data contains sensitive information, so it will not be shared publicly to protect the privacy of organizations according to the principle of confidentiality.

Acknowledgments

This work was previously available as a preprint on Research Square [23].

References

Jiang,B.; Hu,M.; Tian,Y.;et al. Simulation method of airspace capacity eval-uation at terminal area. Journal of Traffic and Transportation Engineering 2003, 1, 97–100. [CrossRef]
Pan,W. ; Kang,R. Multi-airports Coordination Optimizing Model Based on Key Points Air Traffic Flow Limitation. Journal of Sichuan University Engineering Science Edition 2013, 45, 106–111. [CrossRef]
Zhang,J.; Zhang,J. Arriving and leaving aircrafts scheduling model based on dynamic optimize.Journal of Sichuan University Natural Science Edition 2012, 49, 90–96. [CrossRef]
Mitchell.J.; Polishchuk.V. ; Krozel.J. Airspace throughput analysis considering stochastic weather. In AIAA Guidance, Navigation, and Control Conference and Exhibit; AIAA; United States; p. 6770.2006. [CrossRef]
Janic, M. Modeling effects of different air traffic control operational procedures, separation rules, and service disciplines on runway landing capacity. Journal of Advanced Transportation 2014, 48, 556–574. [Google Scholar] [CrossRef]
Kageyama,K. ATC Procedures Modeling for Capacity Estimation of Japanese Airspace. In AIAA Modeling and Simulation Technologies Conference; AIAA; United States.2017. [CrossRef]
Dong, X.; Hu, M.; Su, J. Terminal Capacity Assessment Based on Workload of ATC. Aeronautical Computing Technique 2011, 41, 5–8. [Google Scholar] [CrossRef]
Li,Y.; Hu,M.; Peng,Y.; et al. Effect Mechanism of Multi-scenarios Terminal Capacity Based on Flow Decomposition Barrier. Journal of Southwest Jiaotong University 2014, 49, 928–934. [CrossRef]
Shen, L.; Xie, P. and Fu, C. Terminal Area Capacity Assessment Based on Certain Delay Level. Informatization Research 2017, 43, 24–27+36. https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C44YLTlOAiTRKibYlV5Vjs7iAEhECQAQ9aTiC5BjCgn0Rj41MJcFXPushonbYEMvaP7kA1m32PiOQOeoUjqE9Erw&uniplatform=NZKPT&src=copy.
Huang, H.; Gan, X. et al. Study on capacity assessment method of terminal area under the influence of military activities. Advances in Aeronautical Science and Engineering 2020, 11, 344–352. [CrossRef]
[Peng, Y.; Wang, H.; Mao, L. et al. Terminal Traffic Flow Prediction Method Under Convective Weather Using Deep Learning Approaches. Transactions of Nanjing University of Aeronautics and Astronautics 2021, 38, 634–645. [CrossRef]
Mao,L.; Peng,Y.;Li,J. et al. Random-forest based terminal capacity prediction under convective weather. Systems Engineering - Theory & Practice 2021, 41, 2125–2136. [CrossRef]
Yu, J.; Liu, H.; Xiong, Y. et al. An improved evaluation model of En route dynamic capacity. Journal of Sichuan University Natural Science Edition 2007, , 1005–1008. [CrossRef]
Li, X.; Zhang, Z. ; Wang, L. Terminal area capacity evaluation method based on following stability.Systems Engineering-Theory & Practice 2009, 29, 173–179. [CrossRef]
Zhang, Z. ; Wei, Z. A Model for Dynamic Terminal Airspace Capacity Estimation Considering Hazardous Weather.Science Technology and Engineering 2015, 346, 53–59+71. [CrossRef]
Liu, J.; Li, C.; Feng, S. et al. Assessment of Capacity Based on Air Traffic Controllers’ Workload Simulated on Airtop. Aeronautical Computing Technique 2018, 48, 8–12. [CrossRef]
Zhao, Z. Research on Airspace Capacity Assessment And Forecast. Master’s Thesis, https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CDFDLAST2016&filename=1016751873.nh. Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2015. [Google Scholar]
Xie, C.; Wang, X. Terminal Area Capacity Calculation Based on Monte-Carlo Simulation Method. Aeronautical Computing Technique 2009, 39, 1–4. [Google Scholar] [CrossRef]
Bowen, E.G.; Pearcey, T. Delays in the flow of air traffic. The Aeronautical Journal 1948, 52, 251–258. [Google Scholar] [CrossRef]
Blumstein, A. An analytical investigation of airport capacity. Technical Report, CORNELL AERONAUTICAL LAB INC BUFFALO NY, 1960. https://www.researchgate.net/publication/235022981_AN_ANALYTICAL_INVESTIGATION_OF_AIRPORT_CAPACITY.
Zhao, Y.; Chen, K.; Liu, G. and Yue, R. A New Flow Alert Index for Sector Congestion and Its Application. China Safety Science Journal 2009, 19, 103–107. [CrossRef]
Mou, Q.; Zhang, L.; Feng, X.; Li, M.; Wang, R. Patent No. CN114758528B. China Patent. Civil Aviation Flight University of China, assignee. Granted April 21, 2023. https://xueshu.baidu.com/usercenter/paper/show?paperid=1x1h0gj0f00y0cc0sr4u06k0me444570.
Mou, Q.; Zhang, L.; Fang, C. et al. Airport Terminal Area Capacity Calculation Based on Supply and Demand Balance of Service Resources. Preprint 2022. https://doi.org/10.21203/rs.3.rs-1505284/v2. [CrossRef]

Figure 1. Schematic diagram of the air traffic service process in the terminal area.

Figure 2. Schematic diagram of the terminal area structure at Hulunbuir Hailar Airport (ZBLA).

Figure 3. Line chart of the capacity computation results for the terminal area at ZBLA airport.

Figure 4. Flowchart of the random aircraft flow generation procedure.

Figure 5. Flow chart of Capacity Assessment for Numerical Simulation.

Figure 6. Computational Iteration Results versus Iteration Number based on the Monte Carlo Method.

Figure 7. Histogram of simulation results.

Figure 8. The Relationship between Maximum Number of Aircraft that can be Safely Handled and Airport Terminal Capacity.

Table 1. Distribution of aircraft types under different approach and departure procedures and corresponding flight times at Hulunbuir Hailar Airport (ZBLA).

Flight mission	Procedure	Aircraft Type	Proportion (%)	Mean time (min)
Departure	KAGAK	A320, B738	53%	6.5
		E190, CRJ, RRJ	30%	8
		ATR, Y12	17%	7
	ELPUN	A320, B738	85%	11.2
		E190, CRJ, RRJ	15%	14.4
		ATR, Y12	0%	20.2
	TEPOD	A320, B738	84%	9
		E190, CRJ, RRJ	16%	11.5
		ATR, Y12	0%	16.2
Approach	KAGAK	A320, B738	53%	12.3
		E190, CRJ, RRJ	30%	15.8
		ATR, Y12	17%	22.2
	ELPUN	A320, B738	85%	7.8
		E190, CRJ, RRJ	15%	10.1
		ATR, Y12	0%	14.2
	TEPOD	A320, B738	84%	6
		E190, CRJ, RRJ	16%	7.7
		ATR, Y12	0%	10.8

Table 2. Results of Capacity Assessment.

Assessment models	Ultimate capacity(fph)	Corrected capacity(fph)
Mathematical modeling	24.230	16.961
Numerical simulation	23.939	16.757
ATC simulator experiment	-	17

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Methodology for Assessing Airport Terminal Capacity Based on Service Resource Equilibrium

Abstract

1. Introduction

2. Capacity and Service Resource Analysis of Terminal Areas

3. Mathematical Modeling

3.1. Model Assumptions

3.2. Model Formulation

3.2.1. Demand Model

3.2.2. Demand Model

3.2.3. Demand Model

4. Empirical Analysis of the Proposed Model

4.1. Model Implementation Using ZBLA Airport Data

4.2. Model Validation by Monte Carlo Simulation

4.3. Quantitative Assessment and Extrapolation

5. Conclusion

6. Patents

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe