Quaternion Quantum Mechanics II: Unraveling the Mysteries of Gravity and Dirac Equation within the Planck-Kleinert Crystal

Preprint

Article

Quaternion Quantum Mechanics II: Unraveling the Mysteries of Gravity and Dirac Equation within the Planck-Kleinert Crystal

Altmetrics

Downloads

154

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 June 2023

Posted:

28 June 2023

You are already at the latest version

Alerts

Abstract

The correspondence between classical and quaternion quantum equations, permits considering the universe (vacuum) as an ideal elastic solid. Elementary particles would have to be standing or soliton-like waves. Tension induced by the compression and twisting of the elastic medium would increase the energy density, consequently generate a gravity forcing and affect the wave speed. Consequently the gravity could be described by an index of refraction. Theory was created by combining the Cauchy model of the elastic continuum with the Planck-Kleinert crystal hypothesis. The quaternion-imaginary Lagrange’an, the quaternion motion equation and the quaternionic oscillator allowed deriving: - The Schrödinger equation from the functional integral, which identifies the quaternion-imaginary quantum Hamiltonian. - The 2nd order wave equation system describing both the bosons and the gravity in terms of quaternionic Poisson equation. - The first order quaternionic wave equation system. - The family of the second order wave equation systems describing both the particles and the generated quaternionic force-fields (four-potentials). - The fundamental Planck and gravity constants. - The quaternionic continuity equation in an ideal elastic solid.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

Quaternion quantum mechanics, QQM, is ontic in the sense that it answers the central questions of interpretation of quantum mechanics; it is directly related to being (the Cauchy elastic continuum) as well as to the basic categories of being and their relations [1].

Quantum mechanics, where we are. From its beginning the “spooky action” irritated Einstein. Present explanations assume that the collapse of the wave function has no observable consequences and is philosophically permissible. However, the unsolved problem is what happens with the mass and energy of a particle when its wave-function collapses. The instantaneous jump is not expected in General Relativity and the “string theory” doesn’t help as well.

Schrödinger did not like the “probability” interpretation of the wave function and always considered the wave to be a real wave:

“Let me say at the outset, that in this discourse, I am opposing not a few special statements of quantum physics held today (1950), I am opposing as it were the whole of it, I am opposing its basic views that have been shaped 25 years ago, when Max Born put forward his probability interpretation, which was accepted by almost everybody.”[2].

David Bohm and Basil Hiley developed an interpretation of complex quantum mechanics (The complex quantum mechanics, more precisely may be called the operator quantum mechanics.), CQM, which gives a clear and intuitive interpretation of its meaning with no need of assuming a fundamental role for the human observer [3,4]. This deterministic interpretation is commonly considered as basically equivalent to the Copenhagen orthodox understanding. The importance of the Bohm approach, i.e., the fact that it consistently solves the measurement problem and allows the classical description of macroscopic objects, is frequently ignored. Unfortunately the predictive equivalence of the two theories was recently wiped out [5].

John Bell [6], despite his great impact to our understanding of CQM by verification that nonlocal features characterize natural processes, was also expressing dissatisfaction with the conceptual status of CQM [7]:

“Either the wavefunction, as given by the Schrödinger equation, is not everything, or it is not right.”

There are widely known remarks by Richard Feynman in 1964 [8]:

“It is safe to say that no one understands quantum mechanics”

and Murray Gell-Mann in his lecture at the 1976 Nobel Conference [9]:

“Niels Bohr brainwashed the whole generation of theorists into thinking that the job (of finding an interpretation of quantum mechanics) was done 50 years ago”.

There are several concepts that contradict the “probability” interpretation of CQM and are relevant to our QQM. It is known that certain nonlinear Schrödinger (NLS) equations, in one or more space dimensions, possess space-localized solutions

ψ = ψ (t, x),

e.g., solitons in the one-dimensional case. From numerous attempts we have selected a few considering such settings. Bodurov has shown that the space localized solutions happen for a large class of complex nonlinear wave equations and NLS equations [10,11]. Białynicki-Birula and Mycielski have found that NLS equations admit closed-form space localized solutions (gaussons) [12]. They have also shown that “...in every electromagnetic field, sufficiently small gaussons move like classical particles”. Weng’s results reveal that the quaternion space is appropriate to describe the gravitational features [13]. The Three Wave Hypothesis by Horodecki, which is based on de Broglie’s particle-wave duality, and the assumption of covariant æther [14,15] are also consistent with QQM. Close demonstrated a description of rotational waves in an elastic solid as the spin equivalent [16,17,18]

Regardless of the recent progress it is still safe to say that there has been insignificant advance in understanding of CQM.

Quaternion quantum mechanics today. The first suggestion of quaternion quantum mechanics came from Birkhoff and von Neumann [19]. Already in 1936 they mentioned that quaternion quantum mechanics has greater logical consistency than classical (complex, operator) quantum mechanics.

Yang [20] shows that it is not necessary to go beyond the three number systems, the real numbers

R

, complex numbers

C

and quaternions

Q

for the representation of quantum mechanics. Note that it is consistent with the Hurwitz theorem that the real numbers, complex numbers, quaternions and octonions 𝕆, are the only normed division algebras over the real numbers. In simple words, e.g., only

ℝ, ℂ, ℚ

and 𝕆 can be used in the models where energy,

ℝ,

is conserved. Finkelstein et al. [21] have shown that a quaternion calculus exists, and it is always possible to represent pure states of a system of quantum mechanics by rays in a vector space over the quaternions, but not so over the real and complex numbers. Recently, the global effects in quaternionic quantum field theory [22] were applied to analyze the experimental status of quaternionic quantum mechanics [23].

Adler studied downgraded quaternion Lagrangian [24], and the quaternionic group representations [25,26]. His idea of the trace dynamics relies on using a variational principle based on a Lagrangian constructed as a trace of noncommuting operator variables, making systematic use of cyclic permutation under the trace operation. Nottale’s used the bi-quaternion concept in suggesting an answer to the question of the origin of complex numbers, and Clifford algebra in quantum mechanics [27]. Recently Gantner demonstrated the equivalence of complex and quaternionic quantum mechanics [28].

Summing up, QQM has many new features which make it a much richer theory. It is caused generally by the noncommutativity of quaternion-valued wave functions. Our quaternion Klein–Gordon [29] and Schrödinger equations [1] carry much more physical information than their complex equivalents and make QQM a much richer theory. In this work, we combine the model of the Cauchy elastic continuum with the Planck–Kleinert Crystal hypothesis and will derive the first and extended second order differential equations of QQM.

The Planck–Kleinert crystal. Elastic waves play a remarkable function in physics. Thomas Young explained polarization of light as analogue to shear waves, Navier developed his equations by adding dissipative terms to the Cauchy equation of motion, Maxwell constructed the equations of electromagnetism by modelling a lattice of elastic cells, etc. [30]. The Cauchy model of elastic solids was already published [31] when Maxwell considered the crystal hypothesis. In “A Dynamical Theory of the Electromagnetic Field” [32] Maxwell explicitly remarked on the æther:

“On our theory, it (energy)… may be described according to a very probable hypothesis, as the motion and the strain of one and the same medium (elastic æther)”

and

”... what if these molecules, indestructible as they are, turn out to be not substances themselves, but mere affections of some other substance?” [33],

less known, if not entirely forgotten, is the remark on gravity:

“…assumption, therefore, that gravitation arises from the action of the surrounding medium leads to the conclusion that every part of this medium possesses, when undisturbed, an enormous intrinsic energy. As I am unable to understand in what way a medium can possess such properties, I cannot go any further in this direction in searching for the cause of gravitation.”

Maxwell idea of solid æther showing “enormous intrinsic energy” was unimaginable in the 19^th century.

We consider æther as the Planck-Kleinert crystal [38]. The macro properties of such a crystal are approximated by the Cauchy model of an elastic solid continuum in the quaternion representation.

The original arguments to implement the classical mechanics equations in the field of wave mechanics in crystalline, granular æther were given by Kleinert [34,35]. Soon it was shown that quantum gravity effects, when applied to a non-relativistic particle in a one-dimensional box, imply the quantization of length [36]. This result was interpreted as an indication of fundamental discreteness of space itself. Similarly, corrections to the Klein–Gordon and Dirac equations gave rise to area and volume quantizations, again indicative of the fundamentally grainy nature of space. Such an approach modifies all quantum mechanical Hamiltonians [37] and suggests that space itself is discrete, i.e., that all measurable lengths are quantized in units of a fundamental Planck length.

The building blocks of the Planck-Kleinert crystal are Planck particles, m_P, that obey the laws of mass, momentum and energy conservation [34]. Each particle exerts a short-range force at the Planck length, l_P. The Kleinert concept linked with the Cauchy model of the elastic continuum has later been analyzed with the arbitrary assumption of the complex potential field [38].

Recently, the Cauchy theory was rigorously combined with the Helmholtz decomposition and Planck-Kleinert crystal hypothesis. The quaternion representation of the deformation, σ, in the Cauchy displacement field, u, produced the system of 2^nd order wave (Klein–Gordon and Poisson) [29] and Schrödinger equations [1,39].

Dirac equation. Dirac’s equation on the one hand is a first order linear differential equation and, on the other hand, the iterated application of the equation yields the Klein-Gordon wave equation and consequently the invariance under Lorentz transformation. Because of its success in explaining both the electron spin and the fine structure of atomic energy levels, the utmost importance of Dirac’s discovery was evident. Several trials were made to avoid the operator method used by Dirac and to bring his equation into a form which could be interpreted in terms of normal vector analytical concepts. Cornel Lanczos made important progress and derived the first order differential equation using quaternion algebra.

Lanczos was with Einstein in Berlin, working with the great man to whom, in 1919, he dedicated his dissertation: a quaternionic field theory of classical electrodynamics [40]. Only year after Dirac had discovered his relativistic wave equation for the electron, Lanczos published a series of papers on Dirac’s equation [41,42]. He showed how to derive Dirac’s equation from a more fundamental system. He predicted that spin ½ particles should come in pairs and also the correct form of the wave equation of massive spin 1 particles that would be rediscovered by Proca in 1936. He foresaw the possibility of a nonlinear theory and the origin of mass exactly of the kind that would be developed almost thirty years later. In 1933 in his new derivation [43] there is a doubling in the number of solutions, which from four in Dirac’s theory (two for spin and two for particle/antiparticle) increases to eight, a feature that we can today interpret as isospin. The isospin partner of the proton — the neutron — was discovered in 1932. Nobody ever thought of using Lanczos’s doubling to explain the existence of isospin particles. His article, over eighty years later still contains a number of ideas which remain at the forefront of fundamental theory.

Sadly, the quaternions were non-popular and Lanczos articles were ignored by the vast majority of his contemporaries. Lanczos himself abandoned quaternions and never returned to quaternionic field theory for the rest of his life. He briefly referred to his quaternion articles of 1929 only twice [43,44]. Over eighty years later his papers contain ideas which remain at the frontline of fundamental theory. The whole series of Lanczos’s articles is a remarkable discussion of the fundamental problems of matter, fields, and the origin of mass, most of which is still pertinent today. The first problem of physical interpretation is due to the fact that Lanczos’s equation is much more general than Dirac’s. The trouble with Lanczos’s fundamental system (from which Dirac’s equation can be derived as a special case) is that it allows for spin

\frac{1}{2}

solutions (such as the electron), as well as for spin 0, 1 and

\frac{3}{2}

. Lanczos, like anybody at the time, was completely unaware of the abundance of the elementary particles. It seems that Lanczos was also not aware of the idea that covariance with respect to spatial reversal also had to be included in order to have full relativistic invariance.

Recently, Silvis applied the quaternion formalism to the Dirac equation by making a translation of the Dirac equation as usually stated to quaternion formalism. In his approach to the Dirac equation, a two-component biquaternion and one-component biquaternion wave equations were considered [45].

In the present paper, we solve the problem from a different point of view. We use the formalism which is well adapted to the problem and is based upon the “quaternions” introduced by Hamilton. We do not try to heuristically find analogies with the classical field equations. Using the quaternion algebra we combine the Planck-Kleinert crystal hypothesis and Cauchy theory of an ideal elastic solid. We construct a Hamiltonian with the use of the Cauchy–Riemann operator, acting on quaternionic valued functions.

The quaternion calculus has never really been adopted in physics. The ideas coming from the complex quantum theory remain almost completely unfamiliar to most mathematicians, mainly because of the absence of clear definitions and statements of the concepts involved. This paper attempts close some of these gaps in communication and starts with the fundamentals of the quaternion quantum theory, with the specification of what the theory is basically about.

2. The Quaternions

Hamilton created the

ℝ^{4}

analog of the complex numbers; his unquestionable motivation was the mechanics of solids and liquids. In Hamilton’s own words [46]:

”Time is said to have only one dimension, and space to have three dimensions. The mathematical quaternion partakes of both these elements; in technical language it may be said to be ’time plus space’, or ’space plus time’: and in this sense it has, or at least involves a reference to, four dimensions.”

The beauty of quaternions was immediately recognized. James Clerk Maxwell [47]:

“The invention of the calculus of quaternions is a step towards the knowledge of quantities related to space which can only be compared for its importance, with the invention of triple coordinates by Descartes. The ideas of this calculus are fitted to be of the greatest in all parts of science.”

The quaternions can be considered a physical reality; they allow the computation of processes in continua, in particular wave mechanics. The reformulation of basic principles in terms of quaternion algebra allows understanding of the classical as well as quantum mechanics. Our review of basic definitions and formulas of the quaternion numbers and functions is limited to those used in the paper [48].

The algebra of quaternions,

Q

, owns all laws of algebra with unique properties [48]. The essentials here are:

(1): the multiplication of quaternions is noncommutative,
(2): the quaternionic displacement potential (displacement four-potential), which is a relativistic vector function from which the displacement field can be derived. It combines both a compression scalar potential (pressure) and a torsion vector potential (twist) into a single quaternion (four-vector),
(3): the quaternionic displacement potential is Lorentz invariant.

In the original Hamilton notation, a quaternion is regarded as the sum of a real (scalar

q_{0}

) and imaginary (vector

\hat{q}

) parts:

q = q_{0} 1 + \hat{q} = [q_{0}, \hat{q}] \in ℚ

. The following algebraical notation is useful:

e_{0} = 1, e_{1} = i,

e_{2} = j,

e_{3} = k

. Thus an arbitrary quaternion q, i.e.,

q \in ℚ : = ℝ \otimes P

, can be written in terms of its basis components,

q = (q_{0}, q_{1}, q_{2}, q_{3}) = q_{0} 1 + q_{1} i + q_{2} j + q_{3} k \in ℚ

(1)

Because it is reserved for the scalar quantity (real), for the first component the notation l is used. The unit vector 1, behaves like the ordinary unit and can be ignored as a factor,

q = q_{0} + q_{1} i + q_{2} j + q_{3} k

. The remaining unit vectors

i, j, k

are usually called imaginary units.

Rigorously, in the mathematical way, the quaternion algebra

ℚ

can be defined as follows. Let

ℝ^{4}

be the four-dimensional Euclidean vector space with the orthonormal basis {e₀, e₁, e₂, e₃}, where e₀ = (1, 0, 0, 0), e₁ = (0, 1, 0, 0), e₂ = (0, 0, 1, 0), e₃ = (0, 0, 0, 1) and with the three-dimensional vector subspace P = span{e₁, e₂, e₃}.

The component wise addition and component wise scalar multiplication are the conventional operations. The multiplication is the fundamental operation that is defined by the multiplication of the unit vectors. The Hamilton product (multiplicative group structure) on the quaternions is defined by:

-: The real quaternion 1 is the identity element.
-: The real quaternions commute with all other quaternions, that is $a \cdot q = q \cdot a$ for every quaternion q and every real quaternion a.
-: The Hamilton product is not commutative: $p \cdot q \neq q \cdot p$ , but is associative: $p \cdot (q \cdot r) = (p \cdot q) \cdot r$ . Thus the quaternions form an associative algebra over the real numbers.
-: Every nonzero quaternion has an inverse with respect to the Hamilton product.
-: The product is first given for the unit vectors, and then extended to all quaternions.

The quaternions form division algebra. This means that the non-commutativity of multiplication is the only property that makes quaternions different from a real and complex numbers.

The unit vectors obey the following relations:

\begin{array}{l} i^{2} = j^{2} = k^{2} = - 1, i j = - j i = k, j k = - k j = i, k i = - i k = j, \\ i 1 = 1 i = i, j 1 = 1 j = j, k 1 = 1 k = k . \end{array}

(2)

A conjugate quaternion is defined as

q^{*} = q_{0} - q_{1} i - q_{2} j - q_{3} k

(3)

where the asterix means the following: one goes over to the “conjugate” of the quaternion, that is to say one gives the imaginary units the opposite sign. The conjugate mean one gives the vector components (the space part):

\hat{q} = q_{1} i + q_{2} j + q_{3} k

, the opposite sign:

q^{*} = q_{0} - \hat{q} = q_{0} - q_{1} i - q_{2} j - q_{3} k

(4)

It is easy to see that the quantity

q \cdot q^{*}

is simply a scalar number, all spatial components vanish, are equal zero. The multiplication is associative but not commutative. Instead of the simple commutative law,

p \cdot q = q \cdot p

, in quaternion algebra we have the law:

{(p \cdot q)}^{*} = q^{*} \cdot p^{*}

(5)

From Equations (2)–(5) it results that

q \cdot q^{*} = q^{*} \cdot q = \sum_{i = 0}^{3} q_{i}^{2}

and therefore the Euclidian norm

‖ q ‖ = \sqrt{q^{*} \cdot q}

(6)

Hence

ℚ

is a normed algebra.

From the multiplication law (5), follows the convenient formula

p \cdot q = (p_{0} q_{0} - \hat{p} \circ \hat{q}) e_{0} + \hat{p} \times \hat{q} + p_{0} \hat{q} + q_{0} \hat{p}

(7)

where

p = \sum_{i = 0}^{3} p_{i} e_{i}

q = \sum_{i = 0}^{3} q_{i} e_{i}

\in ℝ^{4}

;

\hat{p} = \sum_{i = 1}^{3} p_{i} e_{i}

\hat{q} = \sum_{i = 1}^{3} q_{i} e_{i}

\in P

and ◦, × mean the scalar and vector, i.e., cross, products in P, respectively:

\hat{p} \circ \hat{q} = \sum_{i = 1}^{3} p_{i} q_{i}

\hat{p} \times \hat{q} = \det [\begin{matrix} e_{1} & e_{2} & e_{3} \\ p_{1} & p_{2} & p_{3} \\ q_{1} & q_{2} & q_{3} \end{matrix}]

The multiplication given by (5) and (7) is noncommutative. The cross product of p and q relative to the orientation determined by the ordered basis i, j, and k is

p \times q = (p_{2} q_{3} - p_{3} q_{2}) i + (p_{3} q_{1} - p_{1} q_{3}) j + (p_{1} q_{2} - p_{2} q_{1}) k

(8)

p \times q = \frac{1}{2} (p \cdot q - q \cdot p)

(9)

The vector space

ℝ^{4}

with the multiplication (7) is a noncommutative algebra with unity usually denoted by

ℚ

and it is named the quaternion algebra. The commutator of two elements p and q is defined by

[p, q] = p \cdot q - q \cdot p = 2 p \times q

(10)

and can be looked at as the measure of noncommutativity. The noncommutativity of quaternion multiplication stems from the multiplication of vector quaternions. Two quaternions commute:

[p, q] = 0

, if and only if their vector parts are collinear.

Representations of quaternions. The quaternions can be represented as

-: matrices in such a way that quaternion addition and multiplication correspond to matrix addition and matrix multiplication, e.g., as 2 × 2 complex matrices and 4 × 4 real matrices [49]. There is a strong relation between quaternion units and Pauli matrices.

There is a strong relation between quaternion units and Pauli matrices.

-: exponent functions that have trigonometrical representation: $e^{q} = e^{q_{0}} (\cos | \hat{q} | + \hat{q} / | \hat{q} | \sin | \hat{q} |)$ .
-: rotors, the generalization of quaternions that represents a rotation about the origin and introduces the concept of bi-vectors. Only in $ℝ^{3}$ the number of basis bivectors equals the number of basis vectors, and each bivector can be identified as a pseudovector. In physics and mathematics, a pseudovector (or axial vector) is a quantity that is defined as a function of some vectors or other geometric shapes, that resemble to a vector, and behaves like a vector in many situations, but is changed into its opposite if the orientation of the space is changed, or an improper rigid transformation such as a reflection is applied to the whole figure. Geometrically, the direction of a reflected pseudovector is opposite to its mirror image, but with equal magnitude [50]. Rotors can be very useful for applications involving homogeneous coordinates, can be used to efficiently represent Lorentz boosts and to interpret formulas involving the gamma matrices.

Functions of a quaternion variable. Like functions of a complex variable, functions of a quaternion variable represent useful physical models. For example, the original electric and magnetic fields described by Maxwell are functions of a quaternion variable [48].

Let Ω ⊂

ℝ^{3}

be a bounded set. The so-called

ℚ

-valued functions may be written as

q (x) = q_{0} (x) 1 + q_{1} (x) i + q_{2} (x) j + q_{3} (x) k, x = (x_{1}, x_{2}, x_{3}) \in Ω

(11)

where the functions

q_{0} (x), q_{l} (x), l = 1, 2, 3

are real-valued.

Similarly, the functions

q (t, x)

depending on time t may be considered. Properties such as continuity, differentiability, integrability and so on, which are ascribed to

q

have to be possessed by all the components

q_{0} (t, x), q_{l} (t, x), l = 1, 2, 3

. In this manner, the Banach, Hilbert and Sobolev spaces of

ℚ

-valued functions can be defined [51], e.g., in the Hilbert space over

ℚ

L^{2} (Ω) = {q : Ω \to ℚ | \int_{Ω} = q_{0}^{2} d x < \infty, \int_{Ω} q_{l}^{2} d x < \infty, l = 1, 2, 3}

(12)

and we introduce the inner product as follows

〈 q_{1}, q_{2} 〉 = \int_{Ω} q_{1} \cdot q_{2} d x, q_{1}, q_{2} \in L^{2} (Ω)

(13)

In a similar way, the Sobolev spaces are defined

H^{k} (Ω) = {q : Ω \to ℚ | q, q^{(1)}, ..., q^{(k)} \in L^{2} (Ω)}, k \in ℕ

(14)

The definition of self-adjoint operators acting on these spaces is analogous as in the real and complex cases. Moreover, the theories of analytic functions, distributions, Fourier series, Lebesgue measure, Gelfand triples, Laplace transform and many others on the vector space of

ℚ

-valued functions over

ℚ

can be defined in a standard way as in the real and complex cases with analogous properties.

Remarks. Because it is possible to divide quaternions, they form a division algebra, the norm makes the quaternions into a normed algebra. The Hurwitz's theorem says that there are only four normed division algebras:

ℝ, ℂ, ℚ

and the octonions.

The Lagrange's four-square theorem in number theory states that every nonnegative integer is the sum of four integer squares. This theorem may have applications in different areas of mathematics, e.g., quaternion algebra.

Time is scalar and has only one dimension and space has three. Quaternion might be conceived as “time plus space” and in this sense it has reference to four dimensions.

2.1. Quaternions and Cauchy elastic continuum.

The displacement vector u has the standard definition

u : = x (X, t) - X

(15)

X denotes the position vectors of material points at t = 0 and x spatial position at other time t of the point that moved and was at X at t = 0. The velocity and acceleration are defined by

\dot{u} : = \frac{\partial x (X, t)}{\partial t}, \ddot{u} : = \frac{\partial^{2} x (X, t)}{\partial t^{2}}

(16)

The Cauchy theory describes the case when an infinitesimal line element dX of the reference configuration undergoes extremely small rotations and fractional change in length, in deforming to the corresponding line element dx, i.e., when

| \partial u_{i} / \partial X_{j} | < < 1

We now start with notation that is precise and convenient in a case of an ideal elastic continuum where only the compression and twist emerge:

p_{0} = σ_{0}

and a

\hat{p} = \hat{ϕ}

, explicitly:

p_{1} = ϕ_{1}

p_{2} = ϕ_{2}

and

p_{3} = ϕ_{3}

. We introduce the deformation that is a function of twist vector and compression:

σ = σ_{0} + \hat{ϕ} \in ℚ

(17)

where

σ_{0} = div u_{0}, \hat{ϕ} = rot u_{ϕ}

div \hat{ϕ} = div rot u_{ϕ} = 0

The commutator of two elements

σ^{1}

and

σ^{2}

equals

[σ^{1}, σ^{2}] = σ^{1} \cdot σ^{2} - σ^{2} \cdot σ^{1}

(18)

and we have the formulae

\begin{array}{l} σ^{1} \cdot σ^{2} = (σ_{0}^{1} σ_{0}^{2} - {\hat{ϕ}}^{1} \circ {\hat{ϕ}}^{2}) + σ_{0}^{1} {\hat{ϕ}}^{2} + σ_{0}^{2} {\hat{ϕ}}^{1} + {\hat{ϕ}}^{1} \times {\hat{ϕ}}^{2}, \\ σ^{2} \cdot σ^{1} = (σ_{0}^{2} σ_{0}^{1} - {\hat{ϕ}}^{2} \circ {\hat{ϕ}}^{1}) + σ_{0}^{2} {\hat{ϕ}}^{1} + σ_{0}^{1} {\hat{ϕ}}^{2} - {\hat{ϕ}}^{1} \times {\hat{ϕ}}^{2} . \end{array}

(19)

From Equations (18) and (19) follows that:

[σ^{1}, σ^{2}] = 2 {\hat{ϕ}}^{1} \times {\hat{ϕ}}^{2}

. Two quaternions commute,

[σ^{1}, σ^{2}] = 0

, if and only if their vector parts

{\hat{ϕ}}^{1} and {\hat{ϕ}}^{2}

are collinear.

We use here the Cauchy-Riemann operator D acting on the quaternion valued functions 𝜎:

D σ = - div \hat{ϕ} + grad σ_{0} + rot \hat{ϕ}

, where

grad σ_{0} = \frac{\partial σ_{0}}{\partial x_{1}} i + \frac{\partial σ_{0}}{\partial x_{2}} j + \frac{\partial σ_{0}}{\partial x_{3}} k

div \hat{ϕ} = \frac{\partial ϕ_{1}}{\partial x_{1}} + \frac{\partial ϕ_{2}}{\partial x_{2}} + \frac{\partial ϕ_{3}}{\partial x_{3}}

and

rot \hat{ϕ} = \det [\begin{matrix} i & j & k \\ \frac{\partial}{\partial x_{1}} & \frac{\partial}{\partial x_{2}} & \frac{\partial}{\partial x_{3}} \\ ϕ_{1} & ϕ_{2} & ϕ_{3} \end{matrix}]

Under the constraint,

div \hat{ϕ} = 0

, fundamental in the Cauchy model, D equals

D σ = grad σ_{0} + rot \hat{ϕ}

(20)

Note that

DD σ = - Δ σ

and hence D corresponds physically to the gradient in

ℝ^{3}

The exponent function has its trigonometrical representation

e^{σ} = e^{σ_{0}} (\cos | \hat{ϕ} | + \frac{\hat{ϕ}}{| \hat{ϕ} |} \sin | \hat{ϕ} |),

(21)

where

σ

is a

ℚ

valued function.

We also introduce a deformation four-potential as a single quaternion (four-vector)

σ : = (σ_{0}, \hat{ϕ})

(22)

It is the relativistic function defined by the displacement field, u. As measured in a given frame of reference, and for a given gauge (In physics, a gauge theory is a type of field theory in which the Lagrangian does not change (is invariant) under local transformations.)., the first component of the deformation four-potential is the compression scalar potential, and the other three components make up the twist vector potential. Note that while both the scalar and vector potential depend upon the frame, the deformation four-potential is Lorentz covariant.

3. Quaternion representation of the Cauchy classical theory of elasticity

In the following the mechanical reactions in the real FCC crystal are assessed by means of Cauchy continuum theory, i.e., we approximate the grainy continuum by field variables. The Cauchy model of an ideal elastic continuum [52] constitutes the consistent base used here since:

-: the macroscopic phenomena are expressed in terms of field variables [53];
-: from the beginning the model was applied in studying the elementary waves [54];
-: the proof of uniqueness of solutions [55] and the completeness proof are done [56].

We follow the Planck-Kleinert crystal hypothesis [38] and consider an ideal FCC structure, where the Poisson number

ν

= 0.25,

l_{P}

equals the Planck length and denotes the dimension of the FCC elementary cell that consists of four interacting Planck particles showing the Planck mass

m_{P}

. The density of such continuum equals

ρ_{P} = 4 m_{P} / l_{P}^{3}

We reduce the problem and the continuum is treated as a closed system occupying the constant volume

Ω \subset ℝ^{3}

. The Cauchy theory describes the case when any infinitesimal line element dX of the reference configuration undergoes extremely small rotations and fractional change in length, in deforming the corresponding line element dx, i.e., when

| \partial u_{i} / \partial X_{j} | < < 1

. Moreover:

The continuum density, $ρ_{P}$ , is high and we consider the small deformation limit only, $l_{P} ≅ c o n s t .$ , thus the density changes are negligible and $ρ_{P} = 4 m_{P} / l_{P}^{3} = c o n s t .$
The small deformation limit implies the invariant wave’s velocities. In particular the constant transverse wave velocity in Equation (24):

$c = \sqrt{0.4 Y / ρ_{P}} = c o n s t .$

(23)

where Y is the Young modulus [57].
We consider here the long evolution times, $t ≫ t_{P}$ , where $t_{P}$ is Planck time;
The quasi-stationary wave exists that may exhibit the velocity of its mass center, $υ$ [10,11].

In such a continuum, the equation of motion relates to local acceleration due to the displacement u, with the field variables, the compression

(div u)

and twist

(rot u)

\frac{\partial^{2} u}{\partial t^{2}} = 3 c^{2} grad div u - c^{2} rot rot u

(24)

where for the sake of simplicity we do not consider the external fields.

From Equation (24), the energy per mass unit in the deformation field follows [57,58]

e = \frac{ρ_{E}}{ρ_{P}} = \frac{1}{2} \dot{u} \circ \dot{u} + \frac{3}{2} c^{2} {(div u)}^{2} + \frac{1}{2} c^{2} rot u \circ rot u

(25)

where

\dot{u} = \partial u / \partial t

Equation (24) and relation (25) obey the Euler–Lagrange relation

\frac{\partial e}{\partial u} - \frac{d}{d t} (\frac{\partial e}{\partial \dot{u}}) = 0

and are sufficient to describe every deformation in the ideal elastic continuum. The Helmholtz theorem allows using quaternion algebra. The strong formulation of the Helmholtz’s decomposition theorem introduces the four-potential

\tilde{A}

F = D \tilde{A} = grad A_{0} + rot A_{ϕ}

(26)

where

\tilde{A} = A_{0} + A_{ϕ} = A_{0} 1 + i A_{1} + j A_{2} + k A_{3}

and

div A_{ϕ} = 0

Note that the Cauchy-Riemann operator D defined by the Eq. (20), acting on the quaternion valued potential

\tilde{A}

in an ideal elastic continuum corresponds physically to the force F in

ℝ^{3}

, see Equation (24). We will use here the weak formulation of the Helmholtz’s decomposition theorem. Every deformation can be expressed by the curl-free component,

u_{0}

, and a divergence-free component,

u_{ϕ}

, and if u belongs to the

C^{3}

class of functions then

u = u_{0} + u_{ϕ}

, where

rot u_{0} = 0

and

div u_{ϕ} = 0

[59]. Upon acting on Equation (24) by the divergence and rotation operators, we decompose it and get well known transverse and the longitudinal wave equations in the usual form

a_{t t} = k Δ a

\begin{array}{l} div (\frac{\partial^{2} u}{\partial t^{2}} = 3 c^{2} grad div u - c^{2} rot rot u) \Rightarrow \frac{\partial^{2}}{\partial t^{2}} div u_{0} = 3 c^{2} Δ div u_{0}, \\ rot (\frac{\partial^{2} u}{\partial t^{2}} = 3 c^{2} grad div u - c^{2} rot rot u) \overset{Δ u = \nabla (\nabla \cdot u) - \nabla \times (\nabla \times u)}{\Rightarrow} \frac{\partial^{2}}{\partial t^{2}} rot u_{ϕ} = c^{2} Δ rot u_{ϕ} . \end{array}

(27)

The Cauchy equation of motion combined with the Helmholtz decomposition theorem in (27) leads to four second-order scalar differential equations, “quattro cluster” and implies the transverse and longitudinal waves in the Cauchy elastic solid. Note that these equations remain coupled by the relation of the energy density (25) however, the more complex wave phenomena are not apparent in (27).

The Cauchy displacement field in the quaternion deformation representation shows the physical reality, the correspondence with Hamilton time-space continuum and complexity of wave phenomena. The Hamilton algebra

ℚ

allows coupling the curl-free and divergence-free components that are separated in (27). Upon denoting

σ_{0} = div u_{0}

and

\hat{ϕ} = rot u_{ϕ}

we get

\begin{array}{l} \frac{\partial^{2} σ_{0}}{\partial t^{2}} = 3 c^{2} Δ σ_{0}, \\ \frac{\partial^{2} \hat{ϕ}}{\partial t^{2}} = c^{2} Δ \hat{ϕ} \end{array}

(28)

and the energy density per mass unit (25) takes the form

e = 1 / 2 \dot{u} \circ \dot{u} + 3 / 2 c^{2} σ_{0}^{2} + 1 / 2 c^{2} \hat{ϕ} \circ \hat{ϕ}

(29)

The decomposition

u = u_{0} + u_{ϕ}

in (27) and change of variables results in four equations (28) and allows using the Hamilton quaternions. Namely, it implies the existence of the deformation field

σ = σ_{0} + \hat{ϕ}

that represents the twist and compression fields as a superposition of real (scalar compression

σ_{0}

) and imaginary (twist vector

\hat{ϕ}

) field parts at each point

σ = σ_{0} + \hat{ϕ} and σ^{*} = σ_{0} - \hat{ϕ} \in ℚ

(30)

where the Helmholtz decomposition implies the following constraint

d i v \hat{ϕ} = div rot u_{ϕ} = 0.

(31)

The Helmholtz decomposition theorem states that any sufficiently continuous vector field can be represented as the sum of the gradient of a scalar potential plus the curl of a vector potential [58],

σ = grad u_{0} + rot u_{ϕ}

(32)

where

σ_{0}

is the scalar potential and

\hat{ϕ}

is the vector potential. The gradient term in the decomposition has a zero rotation and is referred to as the irrotational part, while the rotation term has no divergence and is called solenoidal. This representation specifies three displacement components in terms of four potential components, and furthermore the divergence of

u_{0}

is arbitrary. It is common to choose

\hat{ϕ}

with zero divergence:

div \hat{ϕ} = 0

Adding equations in (28) and from (30), we get the quaternion form of the motion equation

\frac{1}{c^{2}} \frac{\partial^{2} σ}{\partial t^{2}} - Δ σ - 2 Δ σ_{0} = 0, where σ = σ_{0} + \hat{ϕ}

(33)

where

\hat{ϕ}

must obey constraint (31).

Since

\dot{u} \circ \dot{u} = \hat{\dot{u}} \circ \hat{\dot{u}} = - \hat{\dot{u}} \cdot \hat{\dot{u}} = \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*}

where

\hat{\dot{u}} = {\hat{\dot{u}}}_{1} i + {\hat{\dot{u}}}_{2} j + {\hat{\dot{u}}}_{3} k

and

\dot{u} = ({\dot{u}}_{1}, {\dot{u}}_{2}, {\dot{u}}_{3})

, the overall energy of the deformation field, the Formula (29) becomes in the quaternion form

e = \frac{1}{2} \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} + \frac{1}{2} c^{2} σ \cdot σ^{*} + c^{2} σ_{0}^{2}

(34)

The energy is conserved, so relation (34) leads to the nonlocal boundary condition for Eq. (33) [29].

Remark 3. The Cauchy theory of elastic continuum combined with the Helmholtz decomposition theorem and quaternion algebra results in second-order differential Equation (33) and constraint (31). It infers the transverse, longitudinal and complex forms of waves and shows Lorentz invariance. Equations (33) and (34) satisfy the Euler–Lagrange differential equation, i.e., satisfy the fundamental equation of the calculus of variations.

4. Quaternion Quantum Mechanics, the Planck-Kleinert model

We regard quantum space as an analog to the Cauchy elastic solid. The properties of ideal elastic æther are presented in Table 1. The fundamental new results, explicitly the ontology of Quaternion Quantum Mechanics, the appearance of imaginary numbers in Schrödinger equation and the family of waves in elastic continua were already published [1]. Already, upon adding Eqs. (28), we obtained quaternion form of the motion equation, Equation (33). Upon splitting Equation (33) into the system of the wave and Poisson type equations, the non-linear form of the wave equation follows [1,29].

In this section we present already published results. Namely, the use of the Hamilton algebra of quaternions [61], for combining the Cauchy model in

ℝ^{3}

[52] with Planck–Kleinert crystal hypothesis [1,29,34,38]. The relativistic waves in a Cauchy continuum follow from the postulate of existence of the stable wave showing the energy due to the motion and the strain of one and the same medium. Subsequently, Equation (33) can be written as a multisystem

{\begin{cases} \frac{1}{c^{2}} \frac{\partial^{2} σ}{\partial t^{2}} - Δ σ + k_{0}^{2} σ \cdot σ^{*} = 0, \\ - 2 Δ σ_{0} - k_{0}^{2} σ \cdot σ^{*} = 0, \end{cases}

(35)

where

k_{0} = 1 / λ_{0}

and the wavelength

λ_{0} = f (E)

. The system (35) is a hyperbolic-elliptic quaternion representation of a the wave and has solutions of the form

σ (t, x) = σ_{0} + \hat{ϕ} = σ_{0} + ϕ_{1} i + ϕ_{2} j + ϕ_{3} k \in ℚ

(36)

The second equation in (35) is the Poisson type equation [62], that describes/defines the compression potential as a function of energy density in a case of the particle showing the constant overall energy E (i.e., a constant equivalent mass:

m = E c^{- 2} = c o n s t

) [29]. In [38] we postulated

k_{0}^{2} = 8 π m / (m_{P} t_{P}^{2})

and the first equation above in (35) become

(\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}} - Δ) σ + \frac{8 π m}{ℏ t_{P}^{}} σ^{*} \cdot σ = 0

(37)

where

ℏ = m_{P} c^{2} t_{P} = 1.0545727 \times 10^{- 34}

The above 2^nd order equation fulfills the laws of special relativity, the Lorentz invariance and fixes the fundamental problems in complex formulations [63]. The energy computed using formula (34) is per definition always positive due to the constraint (31).

The second equation in (35) describes the irrotational potential of the displacement field. When expressed as a function of the local mass density [29]:

ρ = ρ_{E} / c^{2}

, where

ρ_{E} = m c^{2} σ \cdot σ^{*} / l_{P}^{3}

we get

c^{2} Δ σ_{0} = - 4 π ρ \frac{l_{P}^{3}}{m_{P} t_{P}^{2}} = - 4 π ρ G .

(38)

Using data in Table 1, the gravitational constant equals:

G = l_{P}^{3} / (t_{P}^{2} m_{P}) = 6.674082 \times 10^{- 11}

[m^{3} \cdot {kg}^{- 1} s^{- 2}] .

Remark 5. The low deformation limit allows for the simplified assumption of the constant mass density,

ρ_{P} ≅ c o n s t

, as well as the constant transverse wave velocity. Consequently, gravity in the simplified form of the Poisson equation follows. By considering the nonlinear dependence of the energy density on deformation and its impact on the wave velocity,

c : = c (ρ_{E})

, one can get a more general form of relation (38), i.e., the relations of general relativity [64].

4.1. The Diffusion of Energy in a Cauchy Continuum: the Quaternion Schrödinger Equation

We treat the wave as a particle in an arbitrary volume Ω [1]:

the overall wave energy, $E = E^{0} + Q$ , follows from the energy density, $E = \int_{Ω} ρ_{E} d x$ , where $E^{0}$ and Q are the ground and excess energies;
the equivalent mass is correlated to the overall wave energy [38,65]
the wave occupies a positive volume, has a mass center and the translation velocity $υ$ [10]

In the following, the labeled kinetic process will denote the wave translation in a continuum, i.e., the velocity of its mass center,

υ

. The motion will denote movements of the continuum itself, i.e., the lattice local velocity,

\hat{\dot{u}}

. From (34), upon substituting

{\tilde{σ}}_{0} = \sqrt{3} σ_{0}^{}

, the overall wave energy is expressed by

\begin{array}{l} E = E^{0} + Q = \int_{Ω} ρ_{E} d x = \int_{Ω} (\frac{1}{2} ρ_{P} \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} + ρ_{P} \frac{1}{2} c^{2} \tilde{σ} \cdot {\tilde{σ}}^{*}) d x \\ = c^{2} \int_{Ω} (\frac{ρ_{P}}{2 c^{2}} \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} + \frac{1}{2} ρ_{P} \tilde{σ} \cdot {\tilde{σ}}^{*}) d x \\ = c^{2} \int_{Ω} ρ_{P} k d x + c^{2} \int_{Ω} ρ_{P} s d x \\ = K + S, \end{array}

(39)

where

\tilde{σ} = {\tilde{σ}}_{0} + \hat{ϕ} = \sqrt{3} σ_{0} + \hat{ϕ} .

The overall mass of the particle, m, and the particle mass density, ρ, follow from (39),

m = \int_{Ω} ρ d x = \int_{Ω} ρ_{P} (\frac{1}{2 c^{2}} \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} + \frac{1}{2} \tilde{σ} \cdot {\tilde{σ}}^{*}) d x

(40)

We conclude that “the overall particle mass” follows from the relations (39) and (40) that imply:

m = E / c^{2} .

The mass is ontic in that sense that the particle mass is a “result” of the overall energy of the wave in the elastic continuum of the Planck-Kleinert crystal, see also [65]. Note that in general when Q > 0, m differs from the mass at the ground state.

The considered quasi-stationary wave satisfies the relations in (39) and (23). At every position, the energy density is a sum of the motion, k, and strain, s, energy terms:

ρ_{E} = c^{2} ρ_{P} (k + s) = 0.4 Y (k + s)

(41)

By using the extremum principle, namely the action concept, one can quantify the elementary properties of such particle waves. At every position in Ω:

the existence of the stable waves implies an equal duration of the s- and k-periodic cycles $Δ t$ in the whole volume occupied by the wave, $Δ t = c o n s t .$ Consequently this implies, that the s- and k-actions are equal everywhere

$\int_{t}^{t + Δ t} s (τ, x) d τ = \int_{t}^{t + Δ t} k (τ, x) d τ = γ (x) Δ t$

(42)
the sum of the overall strain, S, and the kinetic energy, K, in relation (39) equals the overall wave energy $E = E^{0} + Q$ , and, e.g., is time-invariant in the case of a free particle;
spans of the strain and the motion energy terms are equal,

$[0, \max {k (t, x)}] = [0, \max {s (t, x)}] = [0, ρ_{E} (t, x) / (c^{2} ρ_{P})] = [0, ρ_{E} (t, x) / (0.4 Y)]$

The relation (41) is valid for the whole Ω so

\int_{t}^{t + Δ t} \int_{Ω} s (τ, x) d x d τ = \int_{t}^{t + Δ t} \int_{Ω} k (τ, x) d x d τ = γ_{Ω} Δ t

(43)

and also for an arbitrary number of cycles:

t = n Δ t .

Thus, from assumptions 2 and 3 above and the relation (43), it follows that both actions in Ω can be approximated by the discrete formula

γ_{Ω} n Δ t = \int_{0}^{n Δ t} \int_{Ω} s d x d τ = \int_{0}^{n Δ t} \int_{Ω} k d x d τ

(44)

Taking into account that we consider time evolution in a case when

t ≫ Δ t

, the continuous expressions for both actions follow

γ_{Ω} t = \int_{0}^{t} \int_{Ω} s d x d τ = \int_{0}^{t} \int_{Ω} k d x d τ

(45)

Taking the time derivative of the relations in (45) we get:

\int_{Ω} s d x = \int_{Ω} k d x for t ≫ Δ t

(46)

Terms, s and k, in (46) oscillate and depend on time and position. We normalize the deformation term s in (39) with respect to the overall particle mass, relation (40). From the formulas (39), (40) and (46), the normalized particle mass density due to the motion, k, and strain energy density, s, equals

\int_{Ω} \frac{ρ_{P}}{m} \tilde{σ} \cdot {\tilde{σ}}^{*} d x = \int_{Ω} ψ \cdot ψ^{*} d x = 1, where ψ = \sqrt{\frac{ρ_{P}}{m}} \tilde{σ}

(47)

\int_{Ω} \frac{ρ_{P}}{m c^{2}} \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} d x = \int_{Ω} ψ \cdot ψ^{*} d x = 1, where ψ = \sqrt{\frac{ρ_{P}}{m}} \frac{\hat{\dot{u}}}{c}

(48)

Note that, the relations (39), (40) and (46) imply the relation between the overall energy of the wave, and equivalently the overall wave mass

E = m c^{2} .

The quaternionic particle mass density

ψ

can be called the quaternionic probability because the relation

\int_{Ω} ψ \cdot ψ^{*} d x = 1

in (47) and (48) is satisfied. Obviously, terms,

ψ = \sqrt{\frac{ρ_{P}}{m}} \tilde{σ} (t, x)

and

ψ \cdot ψ^{*},

vary in time. Consequently from (39), (46) and (47)

0 = \int_{Ω} (ρ_{P} c^{2} \tilde{σ} \cdot {\tilde{σ}}^{*} - E ψ \cdot ψ^{*}) d x

(49)

and also

0 = \int_{Ω} [ρ_{P} \hat{\dot{u}} \cdot {\hat{\dot{u}}}_{}^{*} - E ψ \cdot ψ^{*}] d x

(50)

The relations (39), (40) and (49) imply the relation between the overall energy E of the wave, the overall wave mass:

E = m c^{2}

. The wave periodicity implies that by solving the relation (50), one should expect only the discrete values of the excess energy Q. Both, the excess Q, and the ground

E^{0}

, energies are entangled in (49) and (50).

Particle in the time invariant potential field. We analyzed the evolution of the wave as in the relation (39) in the time invariant potential field [1], e.g., the wave in the field generated by other particles when the velocity of the wave mass center is low. The overall energy is now a sum of the ground and excess energy Q,

E = E^{0} + Q = \int_{Ω} (\frac{1}{2} ρ_{P} \hat{\dot{u}} \cdot {\hat{\dot{u}}}_{}^{*} + \frac{1}{2} ρ_{P} c^{2} \tilde{σ} \cdot {\tilde{σ}}^{*} + V (x) ψ \cdot ψ^{*}) d x

(51)

where

\sqrt{\tilde{σ} \cdot {\tilde{σ}}^{*}} = ‖ \tilde{σ} ‖

is q-potential amplitude.

We consider the low excess energies only,

υ ≪ c

. Consequently the impact of Q on the overall particle mass is marginal,

m ≅ m_{0}

, and the deformation

\tilde{σ}

in (51) can be normalized using the formulae (47). Thus relation (51) becomes

\begin{array}{l} E = E^{0} + Q = \int_{Ω} (\frac{1}{2} m c^{2} ψ \cdot ψ^{*} + \frac{1}{2} ρ_{P} \hat{\dot{u}} \cdot {\hat{\dot{u}}}_{}^{*} + V (x) ψ \cdot ψ^{*}) d x \\ = \frac{1}{2} m c^{2} + \int_{Ω} (\frac{1}{2} ρ_{P} \hat{\dot{u}} \cdot {\hat{\dot{u}}}_{}^{*} + V (x) ψ \cdot ψ^{*}) d x . \end{array}

(52)

Both, the

E^{0}

and m are constant, thus it is enough to minimize the relation

Q = \int_{Ω} (\frac{1}{2} ρ_{P} \hat{\dot{u}} \cdot {\hat{\dot{u}}}_{}^{*} + V (x) ψ \cdot ψ^{*}) d x

(53)

The above relation contains the unknown velocity due to the potential

V (x)

, i.e., contains two unknowns:

\hat{\dot{u}} = \partial \hat{u} / \partial t

and

ψ

. The Cauchy–Riemann operator D of the deformation can be understood, by means of the relation (20), as an analogy of the gradient in

R^{3}

. In the classical dynamics, the potential gradient results in acceleration. For the quaternion representation of the deformation field it is reasonable to guess that the local momentum in the lattice,

\hat{p} = m_{p} \hat{\dot{u}}

, is related to the Cauchy–Riemann operator of the deformartion,

D \tilde{σ} .

Namely, the local lattice velocity

\hat{\dot{u}}

is proportional to the force that is the normalized Cauchy–Riemann derivative of deformation

l_{P} D \tilde{σ}

, and to the transverse wave velocity

c

. Accordingly the momentum density equals

\hat{p} = - m_{P} c l_{P} D \tilde{σ} = - ℏ D \tilde{σ}

(54)

where we introduced the Planck constant

h = m_{P} c^{2} t_{P}

and

t_{P}

is the time that transverse wave travels at the lattice distance:

l_{P} = c t_{p}

The overall momentum balance requires

\hat{\dot{u}} = \frac{\hat{p}}{m} = - \frac{ℏ}{m} D \tilde{σ}

(55)

By introducing (55), the relation (53) becomes

Q = \int_{Ω} (ρ_{P} \frac{ℏ^{2}}{2 m^{2}} (D \tilde{σ}) \cdot {(D \tilde{σ})}^{*} + V (x) ψ \cdot ψ^{*}) d x

(56)

Finally, the normalization using (47) results in the functional

Q [ψ] = \int_{Ω} (\frac{ℏ^{2}}{2 m} (D ψ) \cdot {(D ψ)}^{*} + V (x) ψ \cdot ψ^{*}) d x

(57)

There are numerous methods solving above problem, e.g., the path integrals, the Hamilton Jacobi equation, etc. The functional

Q [ψ]

, that is the integral above, was minimized by as with respect to a quaternion function such that

ψ

satisfies the normalization introduced in the relation (47) [1].

In simple words, we looked for a differential equation that has to be satisfied by the

ψ

function to extremize (here minimize) the energies allowed by (57). Subsequently we have shown that the extremum problem leads to the quaternion analog of the time–independent diffusion equation.

Given the functional (57) and the constraint in (31), the conditional extreme was found using the Lagrange coefficients method and the Du Bois Reymond variational lemma [66]. The whole procedure is presented in [1]. It was found that there exists a multiplier

λ \neq 0

such that

ψ

minimizes the functional

\hat{Q} [ψ] = \int_{Ω} [\frac{ℏ^{2}}{2 m} (D ψ) \cdot {(D ψ)}^{*} + V (x) ψ \cdot ψ^{*} + λ (\frac{1}{| Ω |} - ψ \cdot ψ^{*})] d x .

(58)

In such a case

ψ

satisfies the time invariant diffusion equation

- \frac{ℏ^{2}}{2 m} Δ ψ + [V (x) - λ] ψ = 0

(59)

A constant factor

λ

on the right–hand side can be considered as an extra energy of the particle as a result of the field V = V(x). For

E = λ

, Eq. (59) is clearly the time independent Schrödinger equation satisfied by the particle in the ground state of the energy

E

- \frac{ℏ}{2 m} Δ ψ + \frac{1}{h} [V (x) - E] ψ = 0

(60)

that has to be satisfied together with the condition (31).

Upon using the NIST data [60] of Planck's natural units

m_{P}, l_{P}, t_{p}

and the light velocity c, the computed constant in (54) equals the Planck constant

ℏ = m_{P} c^{2} t_{P} = 6.626069311 \times 10^{- 34}

4.2. Time Dependent Diffusion Equation

By analogy to the complex time-dependent Schrödinger equation

i \frac{\partial Ψ}{\partial t} = - \frac{ℏ}{2 m} Δ Ψ + \frac{1}{h} V (x) Ψ

, we proposed the quaternion form [1]

\frac{i + j + k}{3} \frac{\partial Ψ}{\partial t} = - \frac{ℏ}{2 m} Δ Ψ + \frac{1}{h} V (x) Ψ

(61)

and demonstrated that in the diagonal case the quaternion (61) and complex time dependent Schrödinger equations are equivalent in same sense. Moreover, it was shown that by suitable natural substitution, the time-dependent Schrödinger equation (61) implies the quaternion stationary Schrödinger equation (60). Upon multiplying Eq. (61) by

- (i + j + k)

, it can be expressed also as

(\frac{i + j + k}{3} \frac{\partial Ψ}{\partial t} = - \frac{ℏ}{2 m} Δ Ψ + \frac{1}{ℏ} V (x) Ψ) \times (- i - j - k) \Rightarrow \frac{\partial Ψ}{\partial t} = Θ_{P} Δ Ψ - \frac{i + j + k}{ℏ} V (x) Ψ

(62)

where

Θ_{P} = (i + j + k) \frac{ℏ}{2 m} [\frac{m^{2}}{s}]

denotes the imaginary diffusion coefficient.

When the external potential

V (x)

is negligible, then it can be seen that we generated a quaternion form of the diffusion equation

\frac{\partial Ψ}{\partial t} = Θ_{P} Δ Ψ

(63)

Due to identity

Δ Ψ = - D D Ψ

it can be written in the flux form

\frac{\partial Ψ}{\partial t} = - Θ_{P} D D Ψ = D (- Θ_{P} D Ψ) \Rightarrow \frac{\partial Ψ}{\partial t} = D [J (Ψ)] where J (Ψ) = - Θ_{P} D Ψ .

(64)

Remark 6. We demonstrated that the energy conservation in the elastic Cauchy continuum implies a quaternion form of the Schrödinger equation, Eq. (60) and defines the Planck constant. The time dependent form (61) of the Schrödinger equation allows defining diffusive fluxes, Eq. (64). Both can be regarded as the fundamental diffusion equations. The excess, Q, and ground,

E^{0}

, energies are entangled and can’t be separated.

5. Results

5.1. Second Order Wave Systems of Equations

The Cauchy equation of motion as a sum of transverse (vector) and longitudinal (scalar) deformation waves, Eq. (28).

\begin{matrix} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) σ & - & 2 c^{2} Δ σ_{0} & = & 0, \\ [\begin{array}{l} Quaternion \\ wave term \end{array}] & - & [\begin{array}{l} Laplacian \\ term \end{array}] & = & 0. \end{matrix}

(65)

It looks like the Eq. (65) contains two matchless terms. By postulating the existence of a stable wave we already draw from (65) the Klein-Gordon equation [29] and subsequently the formulae relating the density of the wave

σ \cdot σ^{*}

, with density of the rate of momentum change

G_{0} (m) σ \cdot σ^{*}

{\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) σ + G_{0} (m) σ \cdot σ^{*} = 0, \\ 2 c^{2} Δ σ_{0} + G_{0} (m) σ \cdot σ^{*} = 0, \end{cases}

(66)

where the q-potential (four-potential) is given by

σ (σ_{0}, ϕ_{1}, ϕ_{2}, ϕ_{3}) = σ_{0} + \hat{ϕ}

and

G_{0} (m) \in ℝ

is a scalar function of the particle mass.

The system (66) represents a boson particle showing positive energy at rest,

m > 0

[29]. The real meaning of the system (66) is the postulate of the scalar coupling,

G_{0} (m) σ \cdot σ^{*},

between the longitudinal and transverse waves. Coupling is more evident upon expressing system (66) in the equivalent form

{\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) σ + G_{0} (m) σ \cdot σ^{*} = 0, \\ 2 c^{2} Δ σ_{0} + G_{0} (m) σ \cdot σ^{*} = 0, \end{cases} \Rightarrow {\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) \hat{ϕ} = 0, \\ (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) σ_{0} + G_{0} (m) σ \cdot σ^{*} = 0, \\ 2 c^{2} Δ σ_{0} + G_{0} (m) σ \cdot σ^{*} = 0, \end{cases} \Rightarrow {\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) \hat{ϕ} = 0, \\ (\frac{\partial^{2}}{\partial t^{2}} - 3 c^{2} Δ) σ_{0} = 0, \\ 2 c^{2} Δ σ_{0} + G_{0} (m) σ \cdot σ^{*} = 0. \end{cases}

(67)

Systems (66) and (67) are identical: 5 equations and 5 unknowns,

σ (σ_{0}, ϕ_{1}, ϕ_{2}, ϕ_{3})

and m. If mass is known, m it is the parameter in the Poisson equation above. In this section we further develop the coupling concept and present the family of second order quaternion wave equations.

Coupling coefficient. System (67) can be generalized to the following form:

{\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) \hat{ϕ} = 0, \\ (\frac{\partial^{2}}{\partial t^{2}} - 3 c^{2} Δ) σ_{0} = 0, \\ 2 (n - 1) c^{2} Δ σ_{0} - G_{0} (m) σ \cdot σ^{*} = 0 where n = 0, 2, 3, ... \end{cases}

(68)

It follows that harmonic oscillator implies the following relation:

2 (n - 1) c^{2} Δ σ_{0} - G_{0} (m) σ \cdot σ^{*} = 0 where n = 0, 2, 3, ...

(69)

It is evident that at n = 0 the coupling for boson particle follows: systems (66) and (67). For weaker coupling:

n = 2, 3, ...

the q-potentials (four-potentials

{\tilde{σ}}_{n}

) equal

{\tilde{σ}}_{n} = σ - n σ_{0} = (1 - n) σ_{0} + \hat{ϕ} where n = 2, 3, ...

(70)

Upon

{\tilde{σ}}_{n}

substitution in the system (68), the two wave equations are evident:

{\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) {\tilde{σ}}_{n} + G_{0} (m) σ \cdot σ^{*} = 0, \\ [n \frac{\partial^{2}}{\partial t^{2}} - (n + 2) c^{2} Δ] σ_{0} - G_{0} (m) σ \cdot σ^{*} = 0. \end{cases}

(71)

The function

G_{0} σ^{*} \cdot σ

\in ℝ

is the quaternionic oscillator with the following properties:

The q-potential $σ (t, x)$ represents the four deformations: the volume change $σ_{0} = div u,$ and twists in all three directions $ϕ (ϕ_{1}, ϕ_{2}, ϕ_{3}) = rot u,$ Eq. (70),
The q-potential components show common frequencies of the two harmonic oscillations: of the particle wave f and of the local process in the P-KC unit cell f_P. Oscillations energies obey the equipartition theorem.
The slowest process within the particle wave controls the velocity of the deformations propagation. In the system (71), the particle wave propagation depends on the velocity of the transverse wave c.
Following Cauchy, we neglect the dependence of the velocities of transverse and longitudinal waves on the energy density. That implies the constant Planck frequency: $f_{P} = 1 / t_{P} = c o n s t \neq f (m, σ)$ and $c = c o n s t$ .
The overall mass of the particle controls the frequency of the particle wave. Namely, the frequency of the compression and twists: $f = f (m)$ , where m might be known or computed.
The amplitudes of q-potentials, i.e., the Euclidian norms $‖ {\tilde{σ}}_{n} ‖ = \sqrt{{\tilde{σ}}_{n} \cdot {\tilde{σ}}_{n}^{*}} (t, x)$ , depend on the particle geometry, e.g., its volume, shape, the velocity of the particle center, etc. These are not discussed in this work.
We neglect as well the energy of the external field, $E_{Q F}$ , that is generated by the particle itself, i.e., we neglect the energy of the force fields generated by Poisson equations, Eqs. (66) and (71).

Every stable quaternionic wave showing the non-zero energy at rest, E_m > 0, and negligible velocity of its center will be called the free particle. The duration of the particle wave cycle

T = 1 / f

, i.e., the q-potential cycle, exceeds Planck cycle by many orders of magnitude:

f_{P} ≫ f .

We consider processes at

t > T ≫ t_{P},

i.e., a stable particles only and do not analyze processes at

T > t > t_{P}

, e.g., the collapse or interactions between particles. The Planck time is a least analyzed period of time and can be considered as the time unit in QQM.

5.2. The quaternionic oscillator

The quaternionic oscillator couples transverse and longitudinal waves in both cycles: f and f_P. The common frequency means that the periods of the compression cycle:

σ_{0} (t)

as well as all three twists cycles:

ϕ_{1} (t), ϕ_{2} (t)

and

ϕ_{3} (t)

are equal. One may compare the Cauchy motion equation in two representations: as the vectorial displacement in

ℝ^{3}

, Eq. (24) and as the q-potential, i.e., the quaternion deformation in

ℝ^{4}

, Eq. (65)

\begin{matrix} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} (grad div - rot rot)) u & - & 2 c^{2} grad div u & = & 0 & where u \in ℝ^{3}, \\ (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) σ & - & 2 c^{2} Δ σ_{0} & = & 0 & where σ \in ℝ^{4} . \end{matrix}

(72)

Comparison (72) suggests that the cycle duration is not affected by space dimensions:

ℝ^{4} vs . ℝ^{3}

. So, it allows to simplify the oscillator problem by analyzing the displacement u in

ℝ^{1}

and to apply the results to the deformations σ in

ℝ^{4}

The displacement

u (t, x)

of the Planck mass

m_{P}

in the unit cell is a function of two simultaneous harmonic processes:

f

and

f_{P}

. Namely, the displacement due to the Planck cycle

u_{P}

(decisive for propagation velocity) and due to the particle cycle

u_{λ}

. The same is valid in

ℝ^{1}

u (t, x) = f (u_{λ}, u_{P})

. The simultaneous displacements can be understood as the displacement during the Planck cycle occurring simultaneously with the displacement due to the particle wave, i.e., the Planck deformation of the element already deformed by the particle wave. In

ℝ^{1}

we write this in the following straightforward form

u (t, x) = {(u_{P})}_{λ} = {(u_{λ})}_{P}

(73)

where

{(u_{λ})}_{P}

is understood as Planck displacement of the element displaced by the particle wave, Figure 1.

Harmonic approximations. The displacement velocity is a direct measure of the momentum density per mass unit:

{\dot{u}}_{P} = \partial u_{P} / \partial t = p_{P} (t) / ρ_{P}

where

ρ_{P}

is the Planck density of the Cauchy continuum. Harmonic approximation, e.g., in Figure 1, infers the universal relation in

ℝ^{1}

between the arbitrary magnitude

| \dot{u} |

and the average value

\bar{\dot{u}}

of the displacement rate. The duration T of whole cycle does not depend on the velocity approximation:

T = 4 | u | / \bar{\dot{u}} = 2 π | u | / | \dot{u} | \Leftrightarrow | \dot{u} | = \frac{1}{2} π \bar{\dot{u}}

(74)

so, the sum of momentum changes

Δ_{T} | \dot{u} |

during the arbitrary harmonic cycle T equals

Δ_{T} | \dot{u} | = 4 \frac{1}{2} π \bar{\dot{u}} = 2 π \bar{\dot{u}}

(75)

Momentum magnitude during the Planck cycle_. Figure 1 shows the local process in the unit cell of the P-KC at the Planck frequency, f_P . Namely, the

ℝ^{1}

projection of the displacement

u_{P} (t)

The average velocity of the wave in the Planck volume, c in Eq. (71), is known:

c = l_{P} / t_{P}

. Thus, the magnitude of the displacement rate in the P-KC follows from (74):

| {\dot{u}}_{P} | = \frac{1}{2} π c .

(76)

From Figure 1 and (75) the sum of the momentum changes during the Planck cycle,

T_{P} = 4 t_{P}

, equals

Δ_{4 t_{P}} | {\dot{u}}_{P} | = \sum_{t = 0}^{4 t_{P}} | {\dot{u}}_{P} (t) | = 4 | {\dot{u}}_{P} |

, upon taking into account (76) it can be expressed by the wave velocity:

Δ_{4 t_{P}} | {\dot{u}}_{P} | = 2 π c

(77)

The average velocity of the wave in the Planck volume, c in Eq. (71), is known:

c = l_{P} / t_{P}

. Thus, the magnitude of the displacement rate in the P-KC follows from (74):

| {\dot{u}}_{P} | = \frac{1}{2} π c .

(76)

From Figure 1 and (75) the sum of the momentum changes during the Planck cycle,

T_{P} = 4 t_{P}

, equals

Δ_{4 t_{P}} | {\dot{u}}_{P} | = \sum_{t = 0}^{4 t_{P}} | {\dot{u}}_{P} (t) | = 4 | {\dot{u}}_{P} |

, upon taking into account (76) it can be expressed by the wave velocity:

Δ_{4 t_{P}} | {\dot{u}}_{P} | = 2 π c

(77)

The same result follows from integration:

Δ_{4 t_{P}} | {\dot{u}}_{P} | \overset{F i g .1}{=} 4 \int_{0}^{t_{P}} | \frac{\partial {\dot{u}}_{P}}{\partial t} | d t = 2 π \int_{0}^{π / 2} | \frac{\partial {\dot{u}}_{P}}{\partial α} | d α = 2 π c \int_{0}^{π / 2} \frac{\partial}{\partial α} | \cos α | d α = 2 π c {| \cos α | |}_{0}^{π / 2} = 2 π c,

(78)

where

{\dot{u}}_{1} (α) = \frac{π}{2} c \cos α

and

α (t) = \frac{π}{2} t / t_{P}

Total momentum change during the particle cycle, $Δ_{T} | {\dot{u}}_{λ} |$ . The rate of momentum change

\partial {\dot{u}}_{λ} / \partial t

is determined by the wave showing the frequency f. The momentum changes due to the particle wave cycle

T = f_{}^{- 1}

follow from the schema in Figure 2

From Figure 2 the average velocity of the particle wave equals

{\bar{\dot{u}}}_{λ} = λ / T

(79)

From (74) and (79) the magnitude of particle wave velocity equals

| {\dot{u}}_{λ} | = \frac{1}{2} π f λ

(80)

The schema in Figure 2 shows that the sum of the momentum changes solely due to the particle cycle equals

Δ_{T} | {\dot{u}}_{λ} | = 4 | {\dot{u}}_{λ} | = 2 π f λ

(81)

The Planck and particle displacements are simultaneous, relation (73), and the overall sum of the momentum changes during the particle cycle is a product

Δ_{T} | \dot{u} | = Δ_{T} | {\dot{u}}_{λ} | \times Δ_{4 t_{P}} | {\dot{u}}_{P} | = 4 π^{2} f λ c

(82)

By dividing relation (82) by the wave length, the average density of the momentum changes follows

\bar{\ddot{u}} = 〈 \frac{\partial^{2} u}{\partial t^{2}} 〉 = \frac{Δ_{T} | \dot{u} |}{λ} = 4 π^{2} f c

(83)

The amplitudes of the q-potential momentum. By dividing both sides of relation (83) by the Planck length l_P and noting that

c = l_{P} / t_{P}

we get

〈 \frac{\partial^{2}}{\partial t^{2}} (\frac{u}{l_{P}}) 〉 = 4 π^{2} \frac{1}{t_{P}} f = 4 π^{2} f_{P} f

(84)

where

〈 \frac{\partial^{2}}{\partial t^{2}} (\frac{u}{l_{P}}) 〉

means the average value of the normalized displacement acceleration.

By noting that:

σ_{0} = div u = div u_{0} = \lim_{Δ x \to l_{P}} \frac{Δ | u_{0} |}{Δ x}

we assume that relation (84) holds for deformation by compression and the average compression rate equals:

〈 \frac{\partial^{2} σ_{0}}{\partial t^{2}} 〉 = 〈 \frac{\partial^{2}}{\partial t^{2}} (\frac{u}{l_{P}}) 〉 = 4 π^{2} f_{P} f

(85)

The equipartition theorem allows extending the schemas in Figs. 1 and 2 for all q-potential components:

σ_{0}, ϕ_{1}, ϕ_{2}, ϕ_{3}

. Allows assuming that relation (85) is valid in

ℝ^{4}

〈 \frac{\partial^{2} σ}{\partial t^{2}} 〉 = 4 〈 \frac{\partial^{2} σ_{0}}{\partial t^{2}} 〉 = 16 π^{2} f_{P} f

(86)

Thus the estimated total power of the quaternionic oscillator is now:

G_{0}^{} (f) = 16 π^{2} f_{P} f

(87)

and the system (68) can be written as

{\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) \hat{ϕ} = 0, \\ (\frac{\partial^{2}}{\partial t^{2}} - 3 c^{2} Δ) σ_{0} = 0, \\ (n - 1) c^{2} Δ σ_{0} - 8 π^{2} f_{P} f σ \cdot σ^{*} = 0, \end{cases}

(88)

and also

{\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) {\tilde{σ}}_{n} + 16 π^{2} f_{P} f σ \cdot σ^{*} = 0, \\ n (\frac{\partial^{2}}{\partial t^{2}} - (1 + 2 / n) c^{2} Δ) σ_{0} - 16 π^{2} f_{P} f σ \cdot σ^{*} = 0, \end{cases}

(89)

where

f

is an unknown particle frequency that may be postulated or computed.

The particle frequency term as a function of free particle mass,

f (m_{0})

. We have already shown that P-KC model relates the free particle mass,

m_{0}

, and its wave energy,

E_{0} = m_{0} c^{2},

and that energy E₀ is the sum of the kinetic energies of all Planck masses

m_{P}

in the volume

Ω_{m}

occupied by the particle,

E_{0} (t) = 1 / 2 \sum_{i} p_{i}^{2} (t) / m_{P} .

We again simplified the problem and used the

ℝ^{1}

schema in relating the particle wave frequency f to the particle mass

m_{0}

The equipartition theorem implies the equality of the average moments of all Planck masses participating in particle:

{\bar{p}}_{i} = m_{P} \bar{\dot{u}}

, where i denotes the i-th Planck mass in the volume

Ω_{m}

occupied by the particle. The sum of moments of all particles forming Planck masses, m_P in

Ω_{m}

_, must be equal the momentum of particle m₀ itself. We will avoid laborious summing of all moments in all unit cells in

Ω_{m}

at arbitrary time t. Instead, we will estimate the average moment of the single Planck mass

m_{P}

, during the time period

T = f^{- 1}

, i.e., during the wave cycle. The cycle of the wave implies that every Planck mass returns to its initial conditions:

u_{P} (t) = u_{P} (t + T), {\dot{u}}_{P} (t) = {\dot{u}}_{P} (t + T)

and that the overall distance on which the moment of the mass m_P changes,

x \in [- l_{P}, l_{P}] .

The velocity of the Planck mass varies in the range:

{\dot{u}}_{P} \in [- | {\dot{u}}_{P} |, | {\dot{u}}_{P} |]

and the average velocity of the particle during cycle T of such a harmonic process equals

{〈 {\dot{u}}_{P} 〉}_{T} = 2 π l_{P} / T

. So, the average momentum of a Planck mass m_P is equivalent of the sum of moments of all particles in the wave is given by

p (m_{P}) = m_{P} \frac{2 π l_{P}}{T} = 2 π m_{P} l_{P} f .

(90)

The momentum of the particle m₀ is due to the wave propagation velocity c:

p (m_{0}) = m_{0} c

(91)

Both moments (90) and (91) must be equal and the frequency of particle wave equals:

2 π m_{P} l_{P} f = m_{0} c \Rightarrow f = \frac{m_{0} c}{2 π m_{P} l_{P}} = \frac{m_{0} c^{2}}{2 π m_{P} c^{2} t_{P}} = \frac{m_{0} c^{2}}{2 π ℏ} where ℏ = m_{P} c^{2} t_{P} .

(92)

Substituting

f = m_{0} c^{2} / (2 π ℏ)

and

f_{P} = 1 / t_{P}

in (87) the total power of the quaternionic oscillator equals:

G_{0} = 8 π \frac{m_{0} c^{2}}{ℏ t_{P}}

(93)

The above schema is valid not only for the free particles. Thus, in general:

G_{0} = 8 π m c^{2} / (ℏ t_{P})

and e.g., system (87) becomes:

{\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) σ + 8 π \frac{m c^{2}}{ℏ t_{P}} σ^{*} \cdot σ = 0, \\ c^{2} Δ σ_{0} + 8 π \frac{m c^{2}}{ℏ t_{P}} σ^{*} \cdot σ = 0. \end{cases}

(94)

All above relations were derived exclusively using the P-KC model. Upon substituting the relation

E_{0} = m_{0} c^{2}

[1] in (92) the Planck-Einstein relation follows:

E = h f where h = 2 π ℏ .

(95)

5.3. The 1st Order Wave Equation in P-KC

Complex quantum mechanics is based on the complex number algebra, the matrices and on the matrix algebra (Matrices lie at the heart of quantum mechanics nevertheless in this work we go along with Sir Arthur Eddington remark: “I cannot believe that anything as ugly as multiplication of matrices is an essential part of the scheme of nature” ), [67]. Canonical quantization starts from classical mechanics and assumes that the point particle is described by a "probabilistic wave function" that obeys the equation:

\frac{\partial ψ}{\partial t} + \frac{i}{ℏ} H (x, - i ℏ \frac{\partial}{\partial x}) ψ = 0, where ψ = ψ (t, x)

(96)

Dirac applied complex combinations of displacements and velocities in the linear problem of secondary quantization [68]. He replaced 2^nd order Klein-Gordon equation by an array of 1^st order equations, and as a result separated the different time scales. Dirac immediately recognized the problem of medium for transmission of waves: ”It is necessary to set up an action principle and to get a Hamiltonian formulation of the equations suitable for quantization purposes, and for this the aether velocity is required” [69]. We follow a different path and advance the quaternion quantum mechanics using simple heuristic considerations based on the concept of the medium as a solid “aether”, i.e., we consider the aether as the Planck-Kleinert crystal. We base it on:

1): Quaternion representation of the P-KC dynamics and canonical quantization (Canonical quantization in the sense that we develop quantum mechanics from quaternion representation of classical mechanics.) that yielded the Klein-Gordon equation [29]:

$\begin{matrix} \begin{array}{l} Cauchy equation of motion & \\ harmonic oscillator in ℝ^{4} \end{array} & \Rightarrow & \begin{array}{l} Klein - Gordon & Poisson \\ equations system in ℝ^{4} \end{array} \\ {\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) σ - 2 c^{2} Δ σ_{0} = 0, \\ 2 c^{2} Δ σ_{0} + G_{0} (m) σ \cdot σ^{*} = 0, \end{cases} & \Rightarrow & {\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) σ + G_{0} (m) σ \cdot σ^{*} = 0, \\ 2 c^{2} Δ σ_{0} + G_{0} (m) σ \cdot σ^{*} = 0, \end{cases} \end{matrix}$

(97)

where $σ = σ_{0} + \hat{ϕ} \in ℚ$ is deformation potential.
2): Postulate of the time invariant harmonic oscillator at the Planck scale $G_{0} (m)$ operating at the Planck frequency $f_{P} = 1 / t_{P} = c o n s t$ , see section 5.2.
3): Quaternion representation of deformations and velocities that yielded the Schrödinger equation and useful relations (39), (47) - (50):

$\int_{Ω} ρ_{P} (\frac{1}{2} \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} + \frac{1}{2} c^{2} \tilde{σ} \cdot {\tilde{σ}}_{}^{*}) d x = \int_{Ω} ρ_{E} (t, x) d x = c o n s t where \tilde{σ} = {\tilde{σ}}_{0} 1 + \hat{ϕ} = \sqrt{3} σ_{0}^{} 1 + \hat{ϕ}$

(98)

$\int_{Ω} s (t, x) d x = \int_{Ω} ρ_{P} c^{2} \tilde{σ} \cdot {\tilde{σ}}_{}^{*} d x \overset{t ≫ t_{0}}{\Rightarrow} \int_{Ω} (ρ_{P} c^{2} \tilde{σ} \cdot {\tilde{σ}}_{}^{*} - E ψ \cdot ψ^{*}) d x = 0, where ψ = \sqrt{ρ_{P} / m} \tilde{σ},$

(99)

$\hat{\dot{u}} = - \frac{ℏ}{m} D \tilde{σ}$

(100)

The deformations

σ_{0}

and

ϕ_{i}

are functions of the displacement vector

u = u_{0} + u_{ϕ}

σ_{0} = div u_{0}, \hat{ϕ} = rot u_{ϕ}

and

\hat{\dot{u}} = \hat{p} / ρ_{P} = {\dot{u}}_{1} i + {\dot{u}}_{2} j + {\dot{u}}_{3} k

is momentum per mass unit in quaternion representation. In (98) - (100) both, the velocity

\hat{\dot{u}}

and the deformation potential

\tilde{σ}

are written in quaternionic representation.

From the 2^nd order “electron wave” to the 1^st order equation. Schema of the secondary quantization:

Step 1:

\begin{matrix} \begin{array}{l} 2^{n d} o r d e r e q u a t i o n i n ℝ^{4}, v a r i a b l e : \\ q - potential \tilde{σ} = \sqrt{3} σ_{0} + \hat{ϕ} \end{array} \\ + & \Rightarrow & \begin{array}{l} 1^{s t} o r d e r e q u a t i o n i n ℝ^{3}, v a r i a b l e : \\ momentum per mass unit, \hat{\dot{u}} (t, x) \end{array} \\ P l a n c k frequency : f_{P} = 1 / t_{P} \end{matrix}

Step 2:

\begin{matrix} \begin{array}{l} C o n t i n u i t y e q u a t i o n i n ℝ^{3} : \\ \partial_{t} ρ_{P} = - div [ρ_{P} \dot{u} (t, x)] \end{array} & \begin{array}{l} T h e e l a s t i c c o m p r e s s i o n \\ i n ℝ^{4} : \partial_{t} σ_{0} (t, x) = f (σ), \end{array} \\ + & \Rightarrow & ⇓ \\ \begin{array}{l} I d e a l c o m p r e s s i o n \\ i n ℝ^{4} : ρ_{P} (t, x) = f (σ) \end{array} & \begin{array}{l} t h e q u a t e r n i o n i c f o r m o f \\ t h e R i c c a t i e q u a t i o n \end{array} \end{matrix}

Step 1. From quaternion potential

\tilde{σ}

to vectorial momentum

\hat{\dot{u}}

Using relations (68)-(71), the rearranged Cauchy system (35), where q-potential:

\tilde{σ} = {\tilde{σ}}_{0} + \hat{ϕ} = \sqrt{3} σ_{0} + \hat{ϕ}

[1] generates the following system:

\begin{matrix} \begin{array}{l} The Cauchy wave equations in ℝ^{4} \\ & harmonic oscillator : \\ σ = σ_{0} + \hat{ϕ} and n = 1 - \sqrt{3} \end{array} & \Rightarrow & {two 2}^{nd} order wave equations; \tilde{σ} = \sqrt{3} σ_{0} + \hat{ϕ} \\ {\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) \hat{ϕ} = 0, \\ (\frac{\partial^{2}}{\partial t^{2}} - 3 c^{2} Δ) σ_{0} = 0, \\ 2 (n - 1) c^{2} Δ σ_{0} - G_{0} (m) σ \cdot σ^{*} = 0, \end{cases} & \begin{array}{l} n = 1 - \sqrt{3} \\ \Rightarrow \end{array} & {\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) \tilde{σ} + G_{0} (m) σ \cdot σ^{*} = 0, \\ (1 - \sqrt{3}) [\frac{\partial^{2}}{\partial t^{2}} - \frac{3 - \sqrt{3}}{1 - \sqrt{3}} c^{2} Δ] σ_{0} - G_{0} (m) σ \cdot σ^{*} = 0. \end{cases} \end{matrix}

Thus, the system (97) for the deformation potential

\tilde{σ} = {\tilde{σ}}_{0} + \hat{ϕ} = \sqrt{3} σ_{0} + \hat{ϕ}

equals:

{\begin{cases} (\frac{\partial^{2}}{\partial t^{2}} - c^{2} Δ) \tilde{σ} + G_{0} (m) σ \cdot σ_{}^{*} = 0, \\ (1 - \sqrt{3}) (\frac{\partial^{2}}{\partial t^{2}} - \frac{3 - \sqrt{3}}{1 - \sqrt{3}} c^{2} Δ) σ_{0} - G_{0} (m) σ \cdot σ_{}^{*} = 0, \end{cases}

(101)

where c denotes the transverse wave velocity.

The relation (98) for the total energy of the free particle:

\int_{Ω} ρ_{P} (\frac{1}{2} \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} + \frac{1}{2} c^{2} \tilde{σ} \cdot {\tilde{σ}}_{}^{*}) d x = \int_{Ω} ρ_{E} (t, x) d x = c o n s t

(102)

and Cauchy-Riemann derivative (100):

D \tilde{σ} = - \frac{m}{ℏ} \hat{\dot{u}}

, hint at the displacement velocity (i.e., the normalized momentum

\hat{\dot{u}} .

). as an alternative variable:

\hat{\dot{u}} = - \frac{m}{ℏ} D \tilde{σ}

(103)

The particle is stable and its wave is at steady state. The local changes of deformation potential

\tilde{σ}

are only due to the wave propagation within the volume occupied by the particle. We know the propagation velocity c, thus the time derivative of the potential

\tilde{σ}

in (101) we express by:

\frac{\partial \tilde{σ}}{\partial t} = \frac{\partial x}{\partial t} \cdot (\frac{\partial \tilde{σ}}{\partial x})

(104)

The first term on the right hand side is the propagation velocity c and term in the bracket is the Cauchy-Riemann derivative. We have already proved that taking into account the obligatory restriction of the Cauchy continuum,

div \hat{ϕ} = 0

, at any time t the spatial distribution of deformation potential obeys the following set [1]:

{\begin{cases} D \tilde{σ} = grad {\tilde{σ}}_{0} + rot \hat{ϕ}, \\ div \hat{ϕ} = 0. \end{cases}

(105)

The next step might be called secondary quantization. When the

\partial x / \partial t

term is the known wave propagation velocity:

\frac{\partial x}{\partial t} = \frac{l_{P}}{t_{P}} = c

(106)

the relations (102) - (106) imply the following

\begin{array}{l} \frac{\partial \tilde{σ}}{\partial t} = c D \tilde{σ} = - \frac{m c}{ℏ} \hat{\dot{u}}, \\ D D \tilde{σ} = - D (\frac{m}{ℏ} \hat{\dot{u}}) = - \frac{m}{ℏ} D \hat{\dot{u}} . \end{array}

(107)

The relation between the deformation and kinetic energies in P-KC, relations (49) and (50) imply:

\hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} = c^{2} \tilde{σ} \cdot {\tilde{σ}}_{}^{*}

(108)

Introducing (107), (108) and

G_{0} = 8 π \frac{m c^{2}}{ℏ t_{P}}

in system (101) results in

{\begin{cases} \frac{m c}{ℏ} (- \frac{\partial}{\partial t} + c D) \hat{\dot{u}} + \frac{1}{c^{2}} 8 π \frac{m c^{2}}{ℏ t_{P}} \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} = 0, \\ (1 - \sqrt{3}) (\frac{\partial^{2}}{\partial t^{2}} - \frac{3 - \sqrt{3}}{1 - \sqrt{3}} c^{2} Δ) σ_{0} - G_{0} (m) σ \cdot σ_{}^{*} = 0, \end{cases}

(109)

and finally substituting relations:

ℏ = m_{P} c^{2} t_{P}

, (100) and (108)

{\begin{cases} (\frac{1}{c} \frac{\partial}{\partial t} - D) \hat{\dot{u}} - \frac{8 π}{t_{P} c^{2}} \hat{\dot{u}} \cdot {\hat{\dot{u}}}^{*} = 0, \\ (1 - \sqrt{3}) (\frac{\partial^{2}}{\partial t^{2}} - \frac{3 - \sqrt{3}}{1 - \sqrt{3}} c^{2} Δ) σ_{0} - G_{0} (m) σ \cdot σ_{}^{*} = 0 \end{cases} .

(110)

The relation (48),

ψ (t, x) = \sqrt{ρ_{P} / m} \hat{\dot{u}}

, implies that by multiplying the particle wave equation in system (110),

(\frac{1}{c} \frac{\partial}{\partial t} - D) \hat{\dot{u}} - \frac{8 π}{c^{2} t_{P}^{}} {\hat{\dot{u}}}^{*} \cdot \hat{\dot{u}} = 0,

\sqrt{ρ_{P} / m}

it will be expressed as a function of probability,

(\frac{1}{c} \frac{\partial}{\partial t} - D) ψ - \frac{8 π}{l_{P}^{}} \sqrt{\frac{m}{ρ_{P}}} ψ^{*} \cdot ψ = 0 where ψ (t, x) = \sqrt{ρ_{P} / m} \hat{\dot{u}} .

(111)

The Cauchy-Riemann derivative in (105) require the

σ_{0}

time dependence. This dependence will result from the continuity equation presented in the next section. Only upon neglecting the compression:

σ_{0} = c o n s t

, and we have

D \tilde{σ} = rot \hat{ϕ}

;

\hat{\dot{u}} = - \frac{ℏ}{m} rot \hat{ϕ}

and 1^st order Eq. (110) reduces to:

(\frac{1}{c} \frac{\partial}{\partial t} - D) \hat{\dot{u}} - \frac{8 π}{c^{2} t_{P}^{}} {\hat{\dot{u}}}^{*} \cdot \hat{\dot{u}} = 0 \Rightarrow (\frac{1}{c} \frac{\partial}{\partial t} - D) rot \hat{ϕ} - 8 π \frac{m_{P}}{m} rot {\hat{ϕ}}^{*} \cdot rot \hat{ϕ} = 0.

(112)

5.4. The Time Dependence Of Irrotational Deformation, $σ_{0} (t, x)$

In this section we combine the equations of the mass continuity, CE, and of the state to obtain the time dependence of the scalar potential

σ_{0}

(compression) in an ideal elastic solid (It can be considered as an quaternionic equivalent of the Riccati equation that usually it is written as:

(\partial / \partial t + \dot{u} \cdot \nabla) σ + σ \circ σ + σ_{p} = 0.

). Obviously simplified assumption of the constant Planck density is disobeyed (Consequently all the waves’ velocities depend on the displacement). The mass conservation in an ideal elastic solid in

ℝ^{3}

is affected only by displacements u:

\frac{\partial ρ_{P}}{\partial t} + ρ_{P} div \dot{u} = - \dot{u} \cdot grad ρ_{P} .

(113)

The density can be defined by:

ρ_{P} (t, x) = \lim_{Ω \to 0} m (Ω) / Ω (t, x),

(114)

where

m (Ω)

denotes the time-invariant mass contained in the deformed volume

Ω (t, x)

In an ideal elastic medium it depends exclusively on the irrotational deformation

(div u = div u_{0} = σ_{0})

. One can relate the deformation and density in a case of sphere in an ideal elastic continuum. In such a case the mass in a sphere does not depend on its radius:

m (Ω [r (t, x)]) = m = c o n s t

and the density is affected only by the radius:

ρ_{P} (t, x) = m / (\frac{4}{3} π {[r (t, x)]}^{3}) \Rightarrow d ρ_{P} = - m / (\frac{4}{3} π r^{3}) 3 \frac{d r}{r} = - 3 ρ_{P} \frac{d r}{r}

(115)

In an ideal elastic continuum

d σ_{0} = d r / r

and (115) in quaternionic notation becomes:

\frac{1}{ρ_{P}} d ρ_{P} = - 3 d σ_{0}

(116)

Consequently from (116) it follows:

\frac{1}{ρ_{P}} \frac{\partial ρ_{P}}{\partial t} = - 3 \frac{\partial σ_{0}}{\partial t} and \frac{1}{ρ_{P}} grad ρ_{P} = - 3 grad σ_{0} .

(116)

By introducing relations (116) and the identity

div \dot{u} = \frac{\partial}{\partial t} div u_{0} = \frac{\partial σ_{0}}{\partial t}

into the equation (113) we get:

- 3 \frac{\partial σ_{0}}{\partial t} + \frac{\partial σ_{0}}{\partial t} = 3 \dot{u} \cdot grad σ_{0},

(117)

by expressing the velocity as a function of the Cauchy-Riemann derivative, i.e., introducing (55) we finally get

\frac{\partial σ_{0}}{\partial t} = \frac{3}{2} \frac{ℏ}{m} (D σ) \cdot grad σ_{0} = \frac{3}{2} \frac{ℏ}{m} (rot \hat{ϕ} + grad σ_{0}) \cdot grad σ_{0} .

(118)

The quaternion form of the 1^st order wave equation presented in this work allows to get an insight into the Dirac equation and therefore spin ½. Spin ½ fermions are the cause of the Pauli Exclusion principle, and therefore it is important to understand the physical meaning of spin ½ in the Planck Kleinert model. In order to visualize this concept, a simple interactive simulation of a periodically twisting and compressing 3D grid illustrating spin ½ in an elastic solid for two particles is presented [70,71].

6. Summary

The presented quaternion representation of quantum mechanics allows its ontological interpretation. In simple words, the correspondence between classical and quaternion quantum equations, permits considering the universe (vacuum) as an ideal elastic solid. Elementary particles would have to be standing or soliton-like waves. Tension induced by the compression and twisting of the elastic medium would increase energy density, consequently:

- generate a gravity forcing and

- affect the wave speed. Consequently the gravity could be described by an index of refraction [72].

Theory was created by combining the Cauchy model of the elastic continuum with the Planck-Kleinert crystal hypothesis. The quaternion-imaginary Lagrange’an, the quaternion motion equation and the quaternionic oscillator allowed deriving:

-: A Schrödinger equation from the functional integral, which identifies the quaternion-imaginary quantum Hamiltonian.
-: The 2^nd order wave equation system describing both the bosons and the gravity in terms of quaternionic Poisson equation.
-: The first order quaternionic wave equation system.
-: The family of the second order wave equation systems describing both the particles and the generated quaternionic force-fields (four-potentials).

- The fundamental constants: Planck constant:

ℏ = m_{P} c^{2} t_{P} = 1.0545727 \times 10^{- 34}

and gravity constant:

G = l_{P}^{3} / (t_{P}^{2} m_{P}) = 6.674082 \times 10^{- 11}

[m^{3} \cdot {kg}^{- 1} s^{- 2}] .

-The quaternionic continuity equation in an ideal elastic solid.

The meaning of the particle mass center (particle ≡ wave) is assigned here to “space-localized” and is used in the sense given by the Bodurov definition [73]. A singularity-free multi-component function

σ = (σ_{0}, ϕ_{1}, ϕ_{2}, ϕ_{3}) \in ℚ

of the space

x = (x_{1}, x_{2}, x_{3})

and time t variables will be called space-localized if

‖ σ (t, x) ‖ \to 0

sufficiently fast when

‖ x ‖ \to \infty

, so that its Hermitean norm as given by Equation (13)

〈 σ, σ^{*} 〉 = \int_{Ω} (σ_{0}^{2} + \sum_{l = 1}^{3} ϕ_{l} \cdot ϕ_{l}^{*}) d x = \int_{Ω} σ \cdot σ^{*} d x < \infty

remains finite for all time.

The quaternion quantum mechanics has many new features which make it a much richer theory. Its great potential is visible, e.g., in:

-: The comparison of the 1^st order wave equations in quaternion formulation, Eq. (111) with the form in the Dirac algebra formalism:

$\begin{array}{l} Dirac algebra : (i γ^{μ} \partial_{μ} - \frac{m c}{ℏ}) ψ (t, x) = 0 where γ^{μ} \partial_{μ} = \frac{1}{c} \frac{\partial}{\partial t} + α_{1} \frac{\partial}{\partial x} + α_{2} \frac{\partial}{\partial y} + α_{3} \frac{\partial}{\partial z}, \\ Quaternion algebra : \partial_{\hat{μ}} ψ (t, x) - \frac{m c}{ℏ} β ψ^{*} \cdot ψ (t, x) = 0, where \partial_{\hat{μ}} = \frac{1}{c} \frac{\partial}{\partial t} - grad - rot \end{array}$

(119)

and $β = 8 π \frac{m_{P}}{m} \sqrt{\frac{m}{ρ_{P}}}$ .
-: A simple interactive simulation of a periodically twisting and compressing 3D grid illustrating spin ½ in an elastic solid for two particles is presented [70].

Symbols

u (u_{1}, u_{2}, u_{3})

displacement in

ℝ^{3}

;

u

displacement in

ℝ^{1}

;

u_{λ}

displacement by the particle wave in

ℝ^{1}

;

u_{P}

displacement by local process in unit cell in

ℝ^{1}

;

| u |

magnitude of u;

\bar{\dot{u}} or 〈 \dot{u} 〉

average value of the displacement rate

σ (σ_{0}, ϕ_{1}, ϕ_{2}, ϕ_{3})

q-potential in

ℝ^{4}

, the deformation quaternion;

‖ σ ‖ = \sqrt{σ \cdot σ^{*}} (t, x)

q-potential amplitude, i.e., the Euclidian norm of the deformation;

G_{0}

overall power of the quaternionicoscillator, i.e., the overall action;

G_{0} σ^{*} \cdot σ

density of the rate of the momentum change in

ℝ^{4}

, i.e., the quaternionic oscillator action;

σ^{*} \cdot σ

particle density;

ψ = \tilde{σ} \sqrt{ρ_{P} / m}

probability, i.e., the quaternionic particle mass density;

1 / (n - 1)

coupling coefficient,

n = 0, 2, 3, ...

l_{P}

Planck length;

f_{P} = 1 / t_{P}

Planck frequency, inverse of the Planck time;

m_{P}

Planck mass;

ν

Poisson number;

Y Young modulus;

c = l_{P} / t_{P}

transverse wave velocity in elastic continuum;

ρ_{P} = 4 m_{P} / l_{P}^{3}

Planck density, i.e., the mass density of the Cauchy continuum;

ρ

mass density

ρ = ρ_{E} / c^{2}

, as the equivalent of the energy density

ρ_{E}

;

ℏ

Planck constant in terms of angular frequency;

h Planck constant,

h = 2 π ℏ

;

m equivalent mass of the wave, i.e., mass of the particle;

λ

length of the particle wave;

f

frequency of the particle wave;

References

Danielewski, M.; Sapa, L. Foundations of the Quaternion Quantum Mechanics. Entropy 2020, 22, 1424. [Google Scholar] [CrossRef] [PubMed]
Schrödinger, E. The Interpretation of Quantum Physics; Ox Bow Press: Woodbridge, CN, USA, 1995. [Google Scholar]
Bohm, D. A. Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables. I and II. Phys. Rev. 1952, 85, 166–193. [Google Scholar] [CrossRef]
Bohm, D.; Hiley, B.J. The Undivided Universe: An Ontological Interpretation of Quantum Theory; Routledge: Philadelphia, PA, USA, 1993; p. 397. [Google Scholar]
Chen, P.; Kleinert, H. ; Kleinert, H. Deficiencies of Bohm Trajectories in View of Basic Quantum Principles. Electr. J. Theor. Phys. 2016, 13, 1–12. [Google Scholar]
Bell, J.S. ; On the Einstein Podolsky Rosen Paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
Bell, J.S. ; Schrödinger–Centenary Celebration of a Polymath; Kilmister, C.W., Ed.; Cambridge University Press: Cambridge, UK, 1987; pp. 41–52. [Google Scholar]
Feynman, R.P. The Character of Physical Law, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
Gell-Mann, M. The Nature of the Physical Universe; Huff, D., Prewett, O., Eds.; John Wiley & Sons: New York, NY, USA, 1979; p. 29. [Google Scholar]
Bodurov, T. Solitary Waves Interacting with an External Field. Int. J. Theor. Phys. 1996, 35, 2489–2499. [Google Scholar] [CrossRef]
Bodurov, T. Derivation of the Nonlinear Schrödinger Equation from First Principles. Ann. Fond. Louis Broglie 2005, 30, 343–352. [Google Scholar]
Białynicki-Birula, I.; Mycielski, I.J. Nonlinear Wave Mechanics. Ann. Phys. 1976, 100, 62–93. [Google Scholar] [CrossRef]
Weng, Zi-H. Field Equations in the Complex Quaternion Spaces. Adv. Math. Phys. 2014, 201, 450262. [CrossRef]
Horodecki, R. De Broglie Wave and its Dual Wave. Phys. Lett. 1981, 87A, 95–97. [Google Scholar] [CrossRef]
Horodecki, R. Superluminal Singular Dual Wave. Lett. Novo Cimento 1983, 36, 509–511. [Google Scholar] [CrossRef]
Close, R. Torsion Waves in Three Dimensions: Quantum Mechanics with a Twist. Foundations of Physics Letters 2002, 15, 71–83. [Google Scholar] [CrossRef]
Close, R. A. ; Exact Description of Rotational Waves in an elastic Solid. Adv.Appl. Clifford Algebras 2011, 21, 73–281. [Google Scholar] [CrossRef]
Close, R.A. Spin Angular Momentum and the Dirac Equation. EJTP 2015, 12, 43. [Google Scholar]
Birkhoff, G.; von Neumann, J. The Logic of Quantum Mechanics. Ann. Math. 1936, 37, 823–843. [Google Scholar] [CrossRef]
Yang, C.N. High Energy Nuclear Physics. In Proceedings of the Seventh Annual Rochester Conference, Rochester, NY, USA, 15–19 April 1957; Midwestern Universities Research Association, distributed by Interscience Publishing, Inc.: New York, NY, USA, 1957; p. IX-26. [Google Scholar]
Finkelstein, D.; Jauch, J.M.; Schiminovich, S.; Speiser, D. Foundations of Quaternion Quantum Mechanics. J. Math. Phys. 1962, 3, 207–220. [Google Scholar] [CrossRef]
Brumby, S.P.; Joshi, G.C. Global Effects in Quaternionic Quantum Field Theory. Found. Phys. 1996, 26, 1591–1599. [Google Scholar] [CrossRef]
Brumby, S.P.; Joshi, G.C. Experimental Status of Quaternionic Quantum Mechanics. Chaos Solitons Fract. 1996, 7, 747–752. [Google Scholar] [CrossRef]
Adler, S.L. Quaternionic Quantum Field Theory. Phys. Rev. Let. 1985, 55, 783–786. [Google Scholar] [CrossRef] [PubMed]
Adler, S.L. Mechanics and Quantum Fields; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
Adler, S.L. Quantum Theory as an Emergent Phenomenon; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
Nottale, L. Origin of Complex and Quaternionic Wavefunctions in Quantum Mechanics: The Scale-Relativistic View. Adv. Appl. Clifford Algebr. 2008, 18, 917–944. [Google Scholar] [CrossRef]
Gantner, J. On the Equivalence of Complex and Quaternionic Quantum Mechanics. Quantum Stud. Math. Found. 2018, 5, 357–390. [Google Scholar] [CrossRef]
Danielewski, M.; Sapa, L. Nonlinear Klein–Gordon equation in Cauchy–Navier elastic solid. Cherkasy Univ. Bull. Phys. Math. Sci. 2017, 1, 22–29. [Google Scholar]
Whittaker, E. A History of the Theories of Æther and Electricity; Philosophical Library: New York, NY, USA, 1951; Volume 1. [Google Scholar]
Cauchy, A.L. ; De la Pression ou Tension dans un Corps Solide. Exerc. Math. 1827, 2, 60–81. [Google Scholar]
Maxwell, J.C. ; A Dynamical Theory of the Electromagnetic Field. Phil. Trans. R. Soc. London 1865, 155, 459–512; [Google Scholar] [CrossRef]
Maxwell, J.C. Introductory lecture on experimental physics. In The Scientific Papers of James Clerk Maxwell, vol. II; Niven, W.D., Ed.; Dover: New York, NY, USA, 1965; pp. 241–255. [Google Scholar]
Kleinert, H. Gravity as Theory of Defects in a Crystal with Only Second–Gradient Elasticity. Ann. Phys. 1987, 44, 117–119. [Google Scholar] [CrossRef]
Kleinert, H. Emerging Gravity from Defects in World Crystal. Brazilian Journal of Physics 2005, 35. [Google Scholar] [CrossRef]
Deb, S.; Das, S.; Vagenas, E.C. Discreteness of Space from GUP in a Weak Gravitational Field. Phys. Lett. B 2016, 755, 17–23. [Google Scholar] [CrossRef]
Ali, A.F.; Das, S.; Vagenas, E.C. Discreteness of Space from the Generalized Uncertainty Principle. Phys. Let. B, 2009, 678, 497–499. [Google Scholar] [CrossRef]
Danielewski, M. The Planck–Kleinert Crystal. Z. Naturforsch. 2007, 62, 564–568. [Google Scholar] [CrossRef]
Danielewski, M.; Sapa, L. Diffusion in Cauchy Elastic Solid. Diff. Fundam. 2020, 33, 1–14. [Google Scholar]
Lanczos, C.; Die Funktionentheoretischen Beziehungen der Maxwellschen Æthergleichungen-Ein Beitrag zur Relativitäts und Elektronentheorie (Verlagsbuchhandlung Josef Németh, Budapest, 1919) 80 pp. Handwritten and lithographed in 50 copies). Reprinted in C. Lanczos Collected Published Papers With Commentaries, W.R. Davis et al., eds., (North Carolina State University, Raleigh, 1998) Vol. VI, pp A1-A82.
Lanczos, C. Die tensoranalytischen Beziehungen der Diracschen Gleichung (The tensor analytical relationships of Dirac’s equation). Zeits. f. Phys. 1929, 57, 447–473. [Google Scholar] [CrossRef]
Lanczos, C. Zur kovarianten Formulierung der Diracschen Gleichung (On the covariant formulation of Dirac’s equation). Zeits. f. Phys. 1929, 57, 474–483. [Google Scholar] [CrossRef]
Lanczos, C. Die Wellenmechanik als Hamiltonsche Dynamik des Funktionraumes. Eine neue Ableitung der Dirak-schengleichung (Wave mechanics as Hamiltonian dynamics of function space. A new derivation of Dirac’s equation). Zeits. f. Phys. 1933, 81, 703–732. [Google Scholar] [CrossRef]
Lanczos, C. Electricity as a natural property of Riemanian geometry. Phys. Rev. 1932, 39, 716–736. [Google Scholar] [CrossRef]
Silvis, M.H. A quaternion formulation of the Dirac equation, report, (Centre for Theoretical Physics, Univ. of Groningen 2010.
Graves, R.P. Life of Sir William Rowan Hamilton; Hodges, Figgis, & Co.: Dublin, Ireland, 1989. [Google Scholar]
Maxwell, J.C. Remarks on the Mathematical Classification of Physical Quantities. Proc. London Math. Soc. 1869, 3, 224–233. [Google Scholar] [CrossRef]
Gürlebeck, K.; Sprössig, W. Quaternionic and Clifford calculus for physicists and engineers. In Mathematical methods in practice; Wiley: New York, NY, USA, 1997; ISBN 0-471-96200-7. [Google Scholar]
Altmann, S.L. Rotations, quaternions, and double groups; Clarendon Press: New York, NY, USA, 1986; ISBN 0-19-855372-2. [Google Scholar]
Dorst, L., Fontijne, D. and Mann, S., Geometric Algebra for Computer Science (Elsevier 2007). [CrossRef]
Gürlebeck, K.; Sprößig, W. Quaternionic Analysis and Elliptic Boundary Value Problems; Akademie-Verlag: Berlin, Germany, 1989. [Google Scholar]
Cauchy, A.L. De la Pression ou Tension dans un Corps Solide. Exerc. Math. 1827, 2, 60–81. [Google Scholar]
Todhunter, I. A History of the Theory of Elasticity and of the Strength of Materials; Pearson, K.; Ed.; Cambridge University Press: Cambridge, UK, 2014. [CrossRef]
Poisson, D. Mémoire sur L'équilibre et le Mouvement des Corps Élastiques. Mém. Acad. Sci. Paris 1829, 8, 357–570. [Google Scholar]
Neumann, F. Vorlesungen über die Theorie der Elasticität der Festen Körper und des Lichtäthers; B.G. Teubner: Leipzig, Germany, 1885. [Google Scholar]
Duhem, P. Sur l'intégrale des équations des petits mouvements d'un solide isotrope. Mém. Soc. Sci. Bordeaux Ser. V 1898, 3, 316. [Google Scholar]
Love, A.E.H. Mathematical Theory of Elasticity, 4th ed.; Dover Publications Inc.: New York, NY, USA, 1944; p. 8. [Google Scholar]
Landau, L.D.; Lifshitz, E.M. Theory of Elasticity, 3rd ed.; Butterworth-Heinemann Elsevier Ltd.: Amsterdam, Holland, 1986. [Google Scholar]
Helmholtz, H.v. Über Integrale der hydrodynamischen Gleichungen, welche den Wirbel-bewegungen entsprechen. Crelle J. 1858, 55, 25–55. [Google Scholar]
National Institute of Standards and Technology. Available online: http://physics.nist.gov (accessed on Nov 10th 2018).
Hamilton, W.R. On Quaternions, or on a New System of Imaginaries in Algebra. London Edinb. Dublin Phil. Mag. J. Sci. 1844, 25, 10–13. [Google Scholar] [CrossRef]
Ulrych, S. Higher Spin Quaternion Waves in the Klein-Gordon Theory. Int. J. Theor. Phys. 2013, 52, 279–292. [Google Scholar] [CrossRef]
Weinberg, S. The Quantum Theory of Fields, Volume 1; Cambridge University Press: Cambridge, UK, 1995; pp. 7–8. [Google Scholar]
Weng, Z.-H. Field Equations in the Complex Quaternion Spaces. Advances in Mathematical Physics 2014, 2014, 2014–450262. [Google Scholar] [CrossRef]
Krasnoholovets, V. Reasons for the Gravitational Mass and the Problem of Quantum Gravity. In Æther, Spacetime and Cosmology, Volume 1; Duffy, M.J., Levy, J., Krasnoholovets, V., Eds.; PD Publications: Liverpool, UK, 2008. [Google Scholar]
Zeidler, E. Nonlinear Functional Analysis and Its Applications II/A: Linear Monotone Operators; Springer: New York, NY, USA, 1990; p. 18. [Google Scholar]
Hays, J. Tracing the History of Clifford Algebra. https://web.archive.org/web/ 20040810155540/ jonhays/clifhistory.htm.
Dirac, P.A.M. The Quantum Theory of the Electron. Proc. Roy. Soc. London A 1928, 117, 610. [Google Scholar]
Dirac, P.A.M. Is There an Aether? Nature 1952, 169, 702. [Google Scholar] [CrossRef]
Snoswell, M. personal communications 2022.
Roth, C.; Simulation of electron spin: https://elastic-universe.org/.
Evans, J.C.; Alsing, P.M.; Giorgetti Nandi, K.K. Matter waves in a gravitational field: An index of refraction for massive particles in general relativity. Am. J. Phys. 2001, 69, 1103–1110. [Google Scholar] [CrossRef]
Bodurov, T. ; Generalized Ehrenfest Theorem for Nonlinear Schrödinger Equations. Int. J. Theor. Phys. 1988, 37, 1299–1306. [Google Scholar] [CrossRef]

Figure 1. The harmonic displacement in the Planck volume of the ideal elastic continuum. The displacement is visualized by its

ℝ^{1}

projection:

u_{P} (t) = u_{P} [α (t)] = | u_{P} | \sin α (t)

of the circular motion

α (t) = \frac{1}{2} π f_{P} t .

| {\dot{u}}_{P} | = \frac{1}{2} π c

is the magnitude of the displacement rate, Eq. (74).

Figure 1. The harmonic displacement in the Planck volume of the ideal elastic continuum. The displacement is visualized by its

ℝ^{1}

projection:

u_{P} (t) = u_{P} [α (t)] = | u_{P} | \sin α (t)

of the circular motion

α (t) = \frac{1}{2} π f_{P} t .

| {\dot{u}}_{P} | = \frac{1}{2} π c

is the magnitude of the displacement rate, Eq. (74).

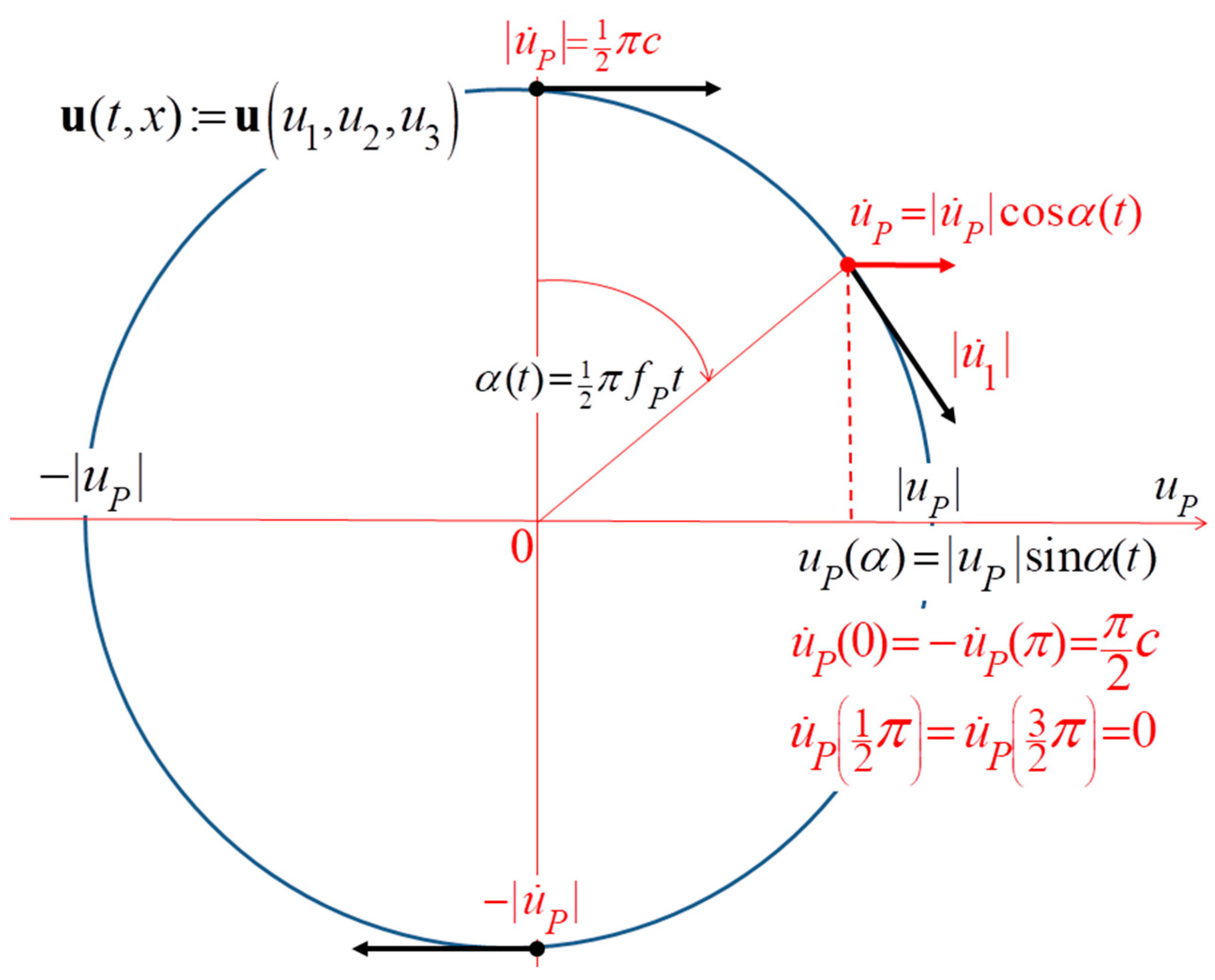
Figure 2. The harmonic displacement in the elastic continuum. The displacement is visualized as the

ℝ^{1}

projection:

u_{λ} (t) = u_{λ} (α) = \frac{1}{4} λ \sin α (t)

of the circular motion

α (t) = 2 π f t;

where

λ

denotes the particle wave length.

Figure 2. The harmonic displacement in the elastic continuum. The displacement is visualized as the

ℝ^{1}

projection:

u_{λ} (t) = u_{λ} (α) = \frac{1}{4} λ \sin α (t)

of the circular motion

α (t) = 2 π f t;

where

λ

denotes the particle wave length.

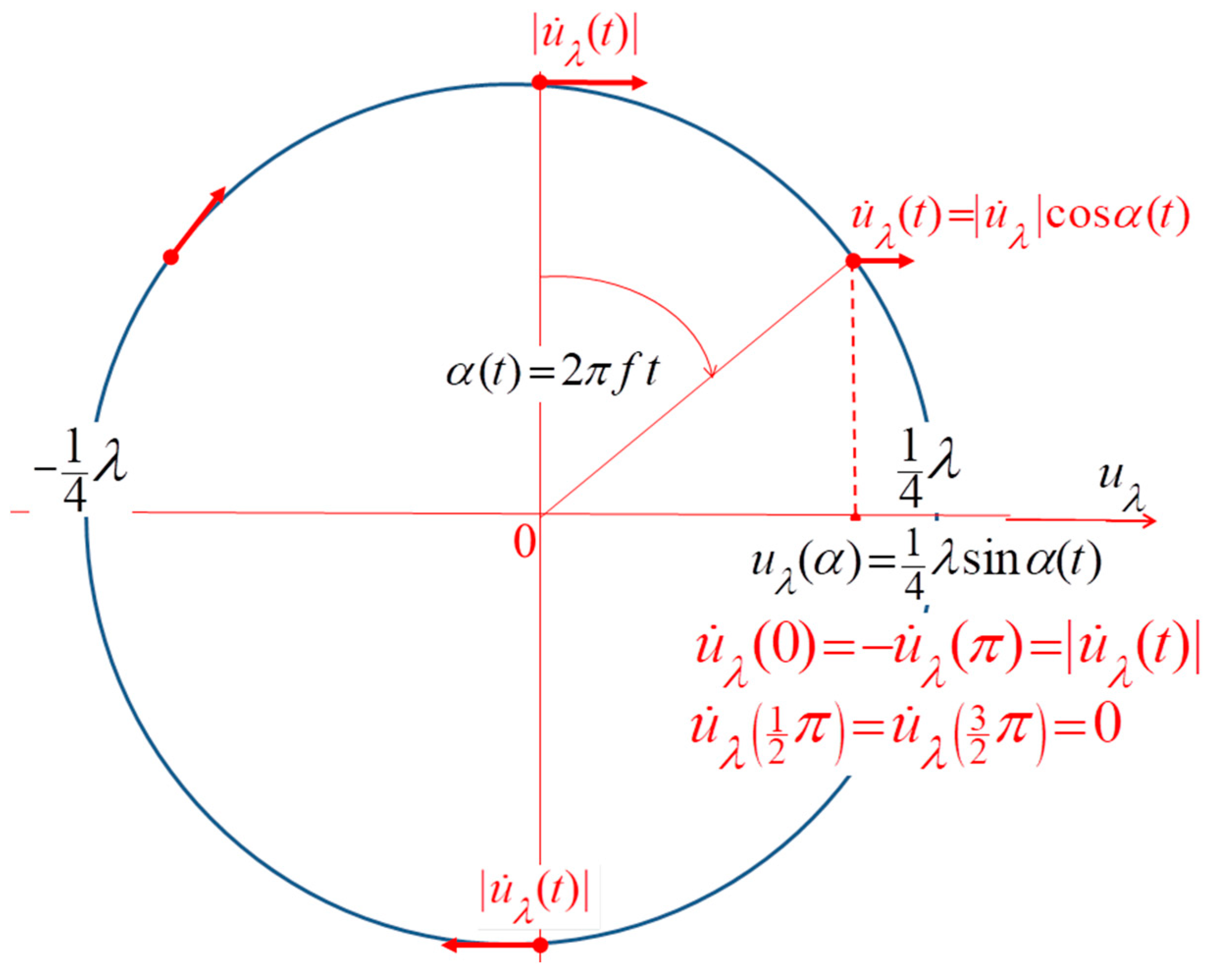
Table 1. The physical constants of the Planck–Kleinert crystal (fcc ideal isotropic crystal).

Label Used in This Work	Planck Constants	Symbol for Unit	Value	SI Unit	Reference
Lattice parameter	Planck length	$l_{P}$	1.616229(38)×10⁻³⁵	m	[60]
Poisson ratio		$ν$	0.25	-	[60]
Mass of the Planck particle	Planck mass	$m_{P}$	2.176470(51)×10⁻⁸	kg	[60]
Planck–Kleinert crystal density		$ρ_{P}$	2.062072×10⁹⁷	kg∙m⁻³	[60]
Duration of the internal process	Planck time	$t_{P}$	5.39116(13) ×10⁻⁴⁴	s⁻¹	[60]
Young modulus,intrinsic energydensity		Y	4.6332447×10¹¹⁴	kg∙m⁻¹s⁻²	$c = \sqrt{0.4 Y / ρ_{P}}$
Transverse wave velocity	Light velocityin vacuum	c	$2.99792458 \times 10^{8}$	m∙s⁻¹	[60]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quaternion Quantum Mechanics II: Unraveling the Mysteries of Gravity and Dirac Equation within the Planck-Kleinert Crystal

Abstract

1. Introduction

2. The Quaternions

2.1. Quaternions and Cauchy elastic continuum.

3. Quaternion representation of the Cauchy classical theory of elasticity

4. Quaternion Quantum Mechanics, the Planck-Kleinert model

4.1. The Diffusion of Energy in a Cauchy Continuum: the Quaternion Schrödinger Equation

4.2. Time Dependent Diffusion Equation

5. Results

5.1. Second Order Wave Systems of Equations

5.2. The quaternionic oscillator

5.3. The 1st Order Wave Equation in P-KC

5.4. The Time Dependence Of Irrotational Deformation, σ 0 ( t , x )

6. Summary

References

MDPI Initiatives

Important Links

Subscribe

5.4. The Time Dependence Of Irrotational Deformation, $σ_{0} (t, x)$