Prerpints.org logo
Preprint
Article

Rastall Gravity and the Impact of Particle Creation

Altmetrics

Downloads

168

Views

55

Comments

0

A peer-reviewed article of this preprint also exists.

  ‡ These authors contributed equally to this work.

This version is not peer-reviewed

Submitted:

25 June 2023

Posted:

29 June 2023

You are already at the latest version

Alerts
Abstract
We investigate the Friedmann–Lemaitre–Robertson–Walker cosmological models within the framework of Rastall gravity incorporating particle creation. The modified field equations for Rastall gravity are derived and exact solutions are obtained under various choices of scale factors. The qualitative behaviour of our solutions depends on the Rastall coupling parameter ψ=kλ. Following the literature, we have restricted the Rastall coupling parameter ψ(k=1) to the range −0.0001 < ψ < 0.0007 at 68% CL from CMB+BAO data. Further, we have discussed the distinct physical behaviour of the derived models in detail.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

Researchers have always been curious for understanding the universe from the past to the future scientifically. Einstein presented the general theory of relativity and gained considerable attention due to its success in building cosmological models. Currently, modifications of Einstein’s gravity or extensions of Einstein’s general theory of gravity are being studied to solve some of the problems presented by Einstein’s general theory of relativity to study cosmology. The Λ CDM model seems to be sufficient to describe the current scenario of the universe, although there are some unresolved issues. One of the critical ingredients of Einstein’s theory of relativity is the covariant conservation of energy-momentum. A number of modified theories of gravity have been proposed in the last few decades, such as f ( T ) gravity [1,2,3], f ( Q ) gravity [4,5,6], f ( Q , T ) gravity [7,8,9], R 2 gravity [10,11,12], f ( G ) gravity [13,14,15], f ( R , G ) gravity [16,17,18], f ( R ) gravity [19,20,21,22,23,24], f ( R , T ) gravity [25,26,27]. In the present study we are interested in Rastall gravity theory. Rastall gravity theory was developed in 1972. Modified theories of gravity, may or may not satisfy the conservation law. Thus, one of the possible ways of extending general relativity is through relaxing the conservation law. In curved space time, the conservation law may or may not hold [28]. In response to this, Rastall [28] proposed that the covariant divergence of the energy-momentum tensor might not be vanishing, but should be determined by the curvature of space-time through a coupling parameter, so that general relativity can be recovered at zero coupling. The expression for Rastall gravity is given by [28,29]. It is precisely this non-conservation that allows for particle creation.
R μ ν − λ 2 g μ ν R = k T μ ν
T μ ν ; μ = 1 − λ 2 k R , ν = 1 − λ 2 ( 1 − 2 λ ) T , ν
where, λ is a free parameter called the Rastall parameter. Rastall theory of gravity is a non-conservative extension of Einstein’s general relativity. The energy-momentum tensor of matter has a divergence proportional to the gradient of the Ricci scalar. This violation of the energy-momentum conservation equation allows us to construct a possible Lagrangian formulation of this theory. Recenty, Moraes and Santos [30] proposed the Lagrangian formalism of Rastall gravity by a non-minimal coupling between geometry and matter fields. Shabani and Ziaie [31] developed the Lagrangian formulation for Rastall theory under the influence of perfect fluid matter content and linear equation of state in the framework of f ( R , T ) gravity.
Rastall theory gained attention in the last few decades due to its diverse research in standard cosmology [32,33,34], Brans-Dicke theory [35], Kaluza-Klein theory [36] and loop quantum gravity [37]. Researchers [38,39] have reproduced a phenomenological method of examining quantum effects in gravitational systems. Batista et al. [40] has pointed out that the two fluid (vacuum energy and baryons plus cold dark matter) cosmological models have the same cosmological scenario both at background and linear perturbation levels except for the fact that dark energy may cluster in this theory. Using Rastall theory, Kumar et al [41] investigated the shadows of black holes surrounded by an anisotropic fluid. Several studies [42,43,44,45] have been conducted on rotating and non-rotating black hole solutions in Rastall gravity. Moradpour et al. [46] developed the traversable asymptotically flat wormholes solution in view of Rastall gravity. Ziaie et al. [47] described spherically symmetric gravitational collapse in Rastall gravity for homogeneous perfect fluids. Both Visser [48] and Darabi et al. [49] differ in their perspectives when comparing general relativity with Rastall gravity. It was pointed out by Visser [48] that general relativity and Rastall gravity are equivalent, while Darabi et al. [49] suggest that they are not. Cosmologists [50,51,52] developed the models to study the thermodynamical aspects of Rastall gravity. The Newtonian-Janis approach is used to compute the charged black string solution in the framework of Rastall gravity [53]. Also, they investigate the graphical representation of Hawking temperature through the event horizon to check the stability conditions of charged black strings under the influence of Rastall gravity. The Wormhole solutions are investigated with the phantom regime ( ω < − 1 ) through conformal symmetry, and they explored the physical aspects of the epicyclic frequencies to explore the self-gravitating system [54]. Mustafa et al.[55] explored the existence of wormhole solutions using conformal symmetries in Rastall’s theory of gravity. For this purpose, they considered the spherically symmetric model filled with matter distribution as an anisotropic fluid.
In this study, our primary focus is on the study of particle creation in Rastall gravity. Particle creation remains one of the most important unsolved problems in cosmology. Several cosmologists have discussed this phenomenon and its effects on the evolution of the universe. Furthermore, they developed a cosmological model to discuss the thermodynamical aspects of the universe by using the mechanism of particle creation. A detailed exploration of the thermodynamics of particle creation with the change of specific entropy has been discussed [56,57,58]. Hamil et al. [59] discussed the mechanism of particle creation in the absence of a time-like singularity in the emergent universe scenario. Various modified theories of gravity such as cubic gravity [60], f ( T ) gravity [61], f ( R ) gravity, [62] f ( R , T ) gravity [63], f ( G ) gravity [64], f ( G , T ) gravity [65], and the alternative theories such as Brans-Dicke theory [66] and Lyra’s geometry [67] are used to investigate different aspect of the particle creation mechanism. Lyth et al. [68] discussed the cosmological consequences of particle creation during the inflationary era of the universe. Particle creation arises due to a change of space-time metric at the end of an inflationary era at the time of the early universe [69]. The nature and origin of quantum fields are due to the back reaction of particle creation by deriving the effective action of a scalar field [70]. The time dependence of particle creation is due to a quantised, massless, minimally coupled scalar field in two-dimensional flat space–time with an accelerating mirror [71]. Recently, Bishi and Lepse [72] studied the influence of the deceleration parameter with the particle creation mechanism.
Following the above-stated research work based on Rastall gravity and the particle creation mechanism, we were motivated to investigate the impact of particle creation in Rastall gravity by considering different types of scale factors a ( t ) such as a ( t ) = − 1 t + 1 + ( t + 1 ) 2 , a ( t ) = a 0 ( k + e μ t ) , a ( t ) = e x p ( m t l ) , a ( t ) = t b e β t , a ( t ) = a 0 exp ( μ t − λ 0 t n ) , and a ( t ) = σ ( e μ t − τ e − μ t ) m .

2. Field Equations

The modified field equations of Rastall gravity are expressed as [41]
R μ ν − 1 2 g μ ν R = k ( T μ ν − λ g μ ν R ) .
It can be rewritten in the form
R μ ν + ( ψ − 1 2 ) g μ ν R = k T μ ν ,
where k is the Rastall gravitational coupling constant and ψ = k λ is treated as Rastall coupling parameter. Li et al. [73] have constrained the Rastall coupling parameter ψ = 0.163 ± 0.001 ( 68 % C L ) with the help of the 118 galaxy–galaxy strong gravitational lensing systems. Further using CMB+BAO data, Akarsu et al. [74] determined ψ = k λ in the range − 0.0001 < ψ < 0.0007 ( 68 % CL) for k = 1 . The Rastall coupling parameter measures the deviation from general relativity ( ψ = 0 i.e. λ = 0 ). To illustrate the physical parameters, we have used these constrained values. In fact, all vacuum solutions of general relativity are Rastall solutions as well. Rastall gravity has important aesthetic advantages since the non-vacuum solutions depend on the Rastall coupling parameter and differ significantly from their corresponding solutions in General Relativity [41]. Let us consider the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric
d s 2 = − d t 2 + R 2 ( t ) d r 2 1 − κ r 2 + r 2 ( d θ 2 + sin 2 θ d ϕ 2 )
where κ = 0 , + 1 and − 1 represents the flat, closed and open universes, respectively. In the presence of creation of matter, the energy momentum tensor is given by
T i j = ( ρ + p + p c ) u i u j + ( p + p c ) g i j
where ρ and p are the energy density and pressure, respectively, p c is the creation pressure, u i the fluid-four velocity vector such that u i u i = − 1 and g i j is the metric tensor. The trace of the energy momentum tensor is given as
T = − ρ + 3 ( p + p c )
Adiabatic particle production means that particle as well as the entropy S (with entropy per particle ( σ = S N ) being constant) have been produced in the space time. The certain creation pressure in case of conserved specific entropy σ (that is, entropy per particle σ = S N ) is given by [75,76,77]
p c = − ( ρ + p ) Γ 3 n H
Here Γ = 3 η H n is the parameterization of the source function (See [78] and refs. there in). It determines whether particles are produced or annihilated. n refer to the particle number density and 0 ≤ η ≤ 1 is a constant. The positive, negative and zero values of the source function represent particle production, particle annihilation and no particle production respectively. With the help of the parameterization of the source function Γ , expression (8) leads to
p c = − ( ρ + p ) η
The modified gravitational field equations (4) with the help of (5) and (6) yield
λ 1 H ˙ + λ 2 H 2 + κ a 2 = − λ 3 ρ H ˙ + λ 4 H 2 + λ 5 κ a 2 = λ 6 ( p + p c )
where λ 1 = 2 ψ 2 ψ − 1 , λ 2 = 4 ψ − 1 2 ψ − 1 , λ 3 = k 3 ( 2 ψ − 1 ) , λ 4 = 3 2 λ 2 , λ 5 = 6 ψ − 1 6 ψ − 2 , λ 6 = k 6 ψ − 2
Using (9) in (10), the modified gravitational field equations take the form
λ 1 H ˙ + λ 2 H 2 + κ a 2 = − λ 3 ρ H ˙ + λ 4 H 2 + λ 5 κ a 2 = λ 6 [ ( 1 − η ) p − η ρ ]
From (11) we get the general expressions for energy density ρ , pressure p, and creation pressure p c
ρ = − ( λ 2 H 2 + λ 1 H ˙ ) a 2 + κ λ 3 a 2
p = ( λ 1 λ 6 η − λ 3 ) λ 3 λ 6 ( η − 1 ) H ˙ + λ 2 λ 6 η − λ 3 λ 4 λ 3 λ 6 ( η − 1 ) H 2 + κ ( λ 6 η − λ 3 λ 5 ) a 2 ( λ 3 λ 6 ( η − 1 ) )
p c = − η λ 1 λ 6 − λ 3 λ 3 λ 6 ( η − 1 ) H ˙ + λ 2 λ 6 − λ 3 λ 4 λ 3 λ 6 ( η − 1 ) H 2 + κ ( λ 6 − λ 3 λ 5 ) a 2 λ 3 λ 6 ( η − 1 )

3. Solution of the Modified Field Equations

3.1. Model I

let us consider the scale factor of the form
a = − 1 ( t + 1 ) + ( t + 1 ) 2
The Hubble parameter takes the form
H = 2 t 3 + 6 t 2 + 6 t + 3 t 2 + 3 t + 3 t t + 1
The deceleration parameter q for the scale factor (15) is given by
q = − 2 t 2 + 3 t + 3 2 t 2 2 t 3 + 6 t 2 + 6 t + 3 2
We get the energy density ρ , pressure p and particle creation pressure p c by using (16) and (15) in (12) to (14) as follows:
ρ = 2 ( λ 1 − 2 λ 2 ) t 6 + 12 ( λ 1 − 2 λ 2 ) t 5 + ( − k + 30 λ 1 − 60 λ 2 ) t 4 + 4 ( − k + 12 λ 1 − 21 λ 2 ) t 3 + 6 ( − k + 9 λ 1 − 12 λ 2 ) t 2 + 4 ( − k + 9 λ 1 − 9 λ 2 ) t − k + 9 λ 1 − 9 λ 2 λ 3 t 2 ( t 2 + 3 t + 3 ) 2 ( t + 1 ) 2
p = p 7 t 6 + p 8 t 5 + p 9 t 4 + p 10 t 3 + p 11 t 2 + p 12 t + p 13 t 2 ( t 2 + 3 t + 3 ) 2 ( t + 1 ) 2
p c = η [ p 14 t 6 + p 15 t 5 + p 16 t 4 + p 17 t 3 + p 18 t 2 + p 19 t + p 20 ] t 2 ( t 2 + 3 t + 3 ) 2 ( t + 1 ) 2
p 1 = η λ 1 λ 6 − λ 3 λ 3 λ 6 η − 1 p 2 = λ 2 λ 6 η − λ 3 λ 4 λ 3 λ 6 η − 1 p 3 = k λ 6 η − λ 3 λ 5 λ 3 λ 6 η − 1 p 4 = λ 1 λ 6 − λ 3 λ 3 λ 6 η − 1 p 5 = λ 2 λ 6 − λ 3 λ 4 λ 3 λ 6 η − 1 p 6 = k − λ 3 λ 5 + λ 6 λ 3 λ 6 η − 1
p 7 = − 2 p 1 + 4 p 2 = − 4 λ 4 + 2 λ 3 − 2 η λ 6 λ 1 − 2 λ 2 λ 3 λ 6 η − 1 p 8 = − 12 p 1 + 24 p 2 = − 24 λ 4 + 12 λ 3 − 12 η λ 6 λ 1 − 2 λ 2 λ 3 λ 6 η − 1 p 9 = − 30 p 1 + 60 p 2 + p 3 = − k λ 5 − 60 λ 4 + 30 λ 3 + η λ 6 k − 30 λ 1 + 60 λ 2 λ 3 λ 6 η − 1 p 10 = − 48 p 1 + 84 p 2 + 4 p 3 = − 4 k λ 5 − 84 λ 4 + 48 λ 3 + 4 η λ 6 k − 12 λ 1 + 21 λ 2 λ 3 λ 6 η − 1 p 11 = − 54 p 1 + 72 p 2 + 6 p 3 = − 6 k λ 5 − 72 λ 4 + 54 λ 3 + 6 η λ 6 k − 9 λ 1 + 12 λ 2 λ 3 λ 6 η − 1 p 12 = − 36 p 1 + 36 p 2 + 4 p 3 = − 4 k λ 5 − 36 λ 4 + 36 λ 3 + 4 η λ 6 k − 9 λ 1 + 9 λ 2 λ 3 λ 6 η − 1 p 13 = − 9 p 1 + 9 p 2 + p 3 = − k λ 5 − 9 λ 4 + 9 λ 3 + η λ 6 k − 9 λ 1 + 9 λ 2 λ 3 λ 6 η − 1
p 14 = 2 p 4 − 4 p 5 = 4 λ 4 − 2 λ 3 + 2 λ 6 λ 1 − 2 λ 2 λ 3 λ 6 η − 1 p 15 = 12 p 4 − 24 p 5 = 24 λ 4 − 12 λ 3 + 12 λ 6 λ 1 − 2 λ 2 λ 3 λ 6 η − 1 p 16 = 30 p 4 − 60 p 5 − p 6 = k λ 5 + 60 λ 4 − 30 λ 3 − λ 6 k − 30 λ 1 + 60 λ 2 λ 3 λ 6 η − 1 p 17 = 48 p 4 − 84 p 5 − 4 p 6 = 4 k λ 5 + 84 λ 4 − 48 λ 3 − 4 λ 6 k − 12 λ 1 + 21 λ 2 λ 3 λ 6 η − 1 p 18 = 54 p 4 − 72 p 5 − 6 p 6 = 6 k λ 5 + 72 λ 4 − 54 λ 3 − 6 λ 6 k − 9 λ 1 + 12 λ 2 λ 3 λ 6 η − 1 p 19 = 36 p 4 − 36 p 5 − 4 p 6 = 4 k λ 5 + 36 λ 4 − 36 λ 3 − 4 λ 6 k − 9 λ 1 + 9 λ 2 λ 3 λ 6 η − 1 p 20 = 9 p 4 − 9 p 5 − p 6 = k λ 5 + 9 λ 4 − 9 λ 3 − λ 6 k − 9 λ 1 + 9 λ 2 λ 3 λ 6 η − 1
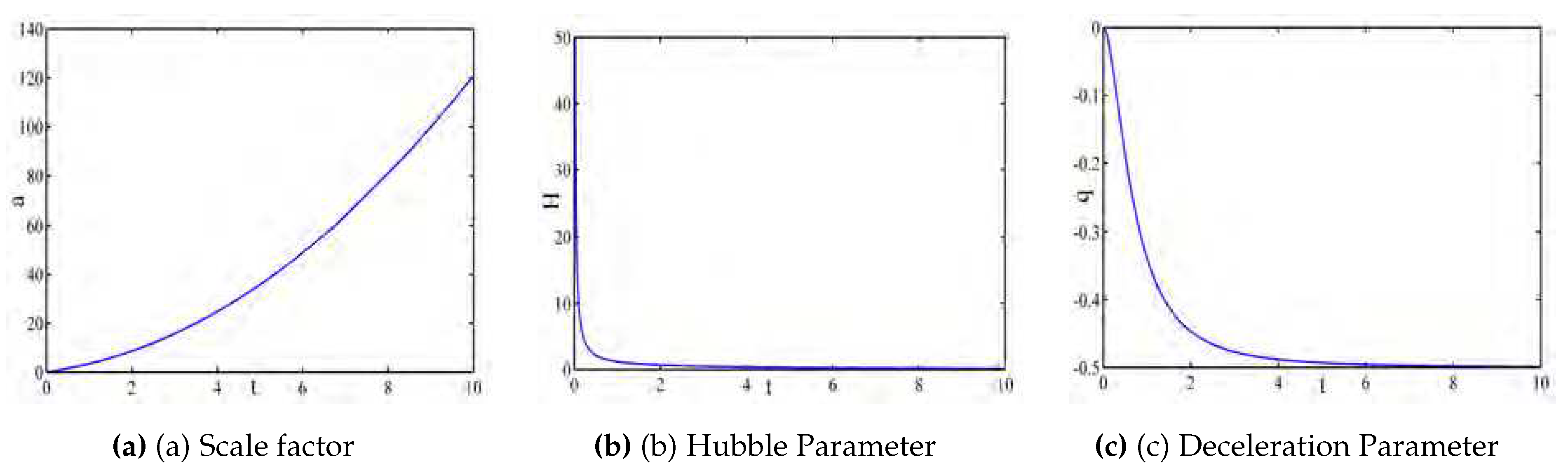
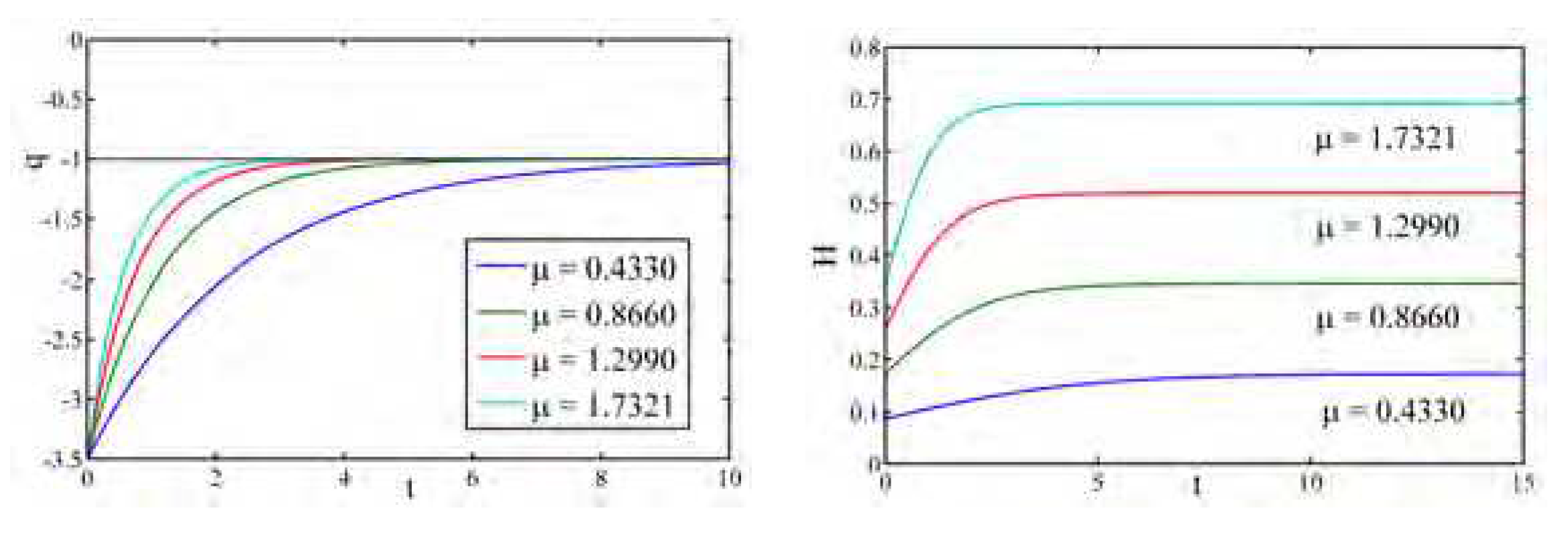
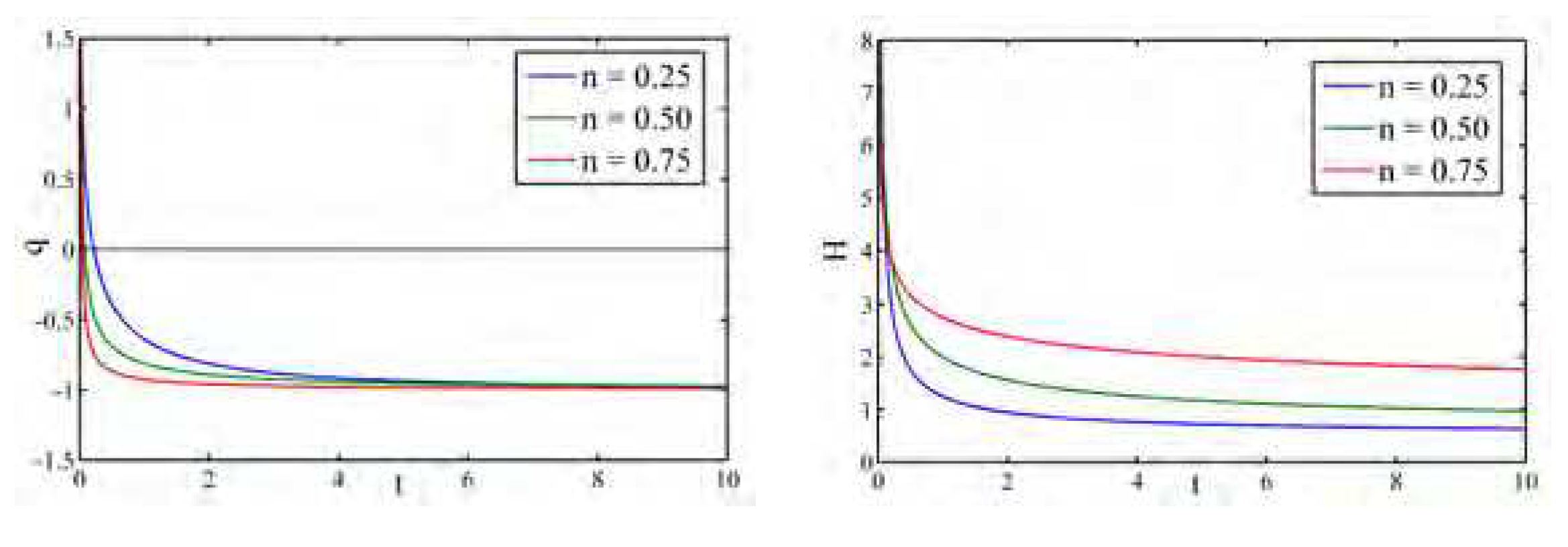
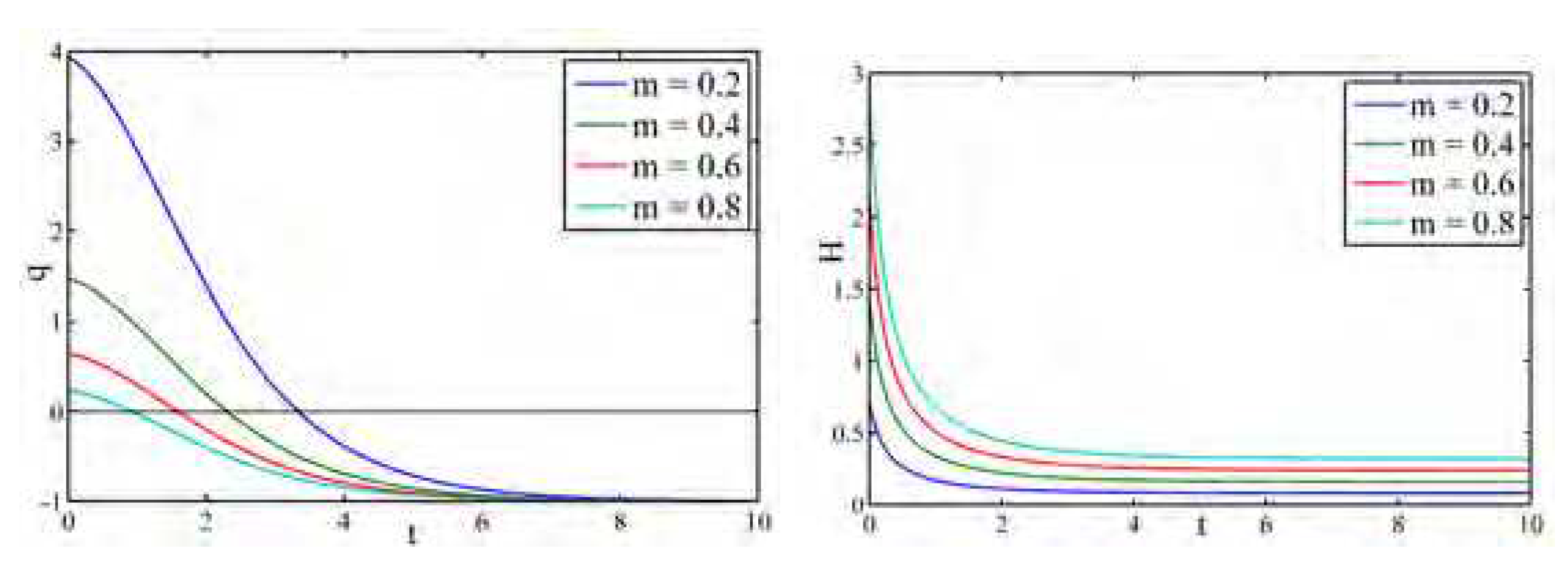
Figure 1 indicate the profiles of the scale factor, Hubble parameter and deceleration parameter. The scale factor is an increasing function of cosmic time and a → ∞ when t → ∞ . The Hubble parameter H is a decreasing function of cosmic time. Further it follows that H → ∞ when t → 0 and H → 0 when t → ∞ . The deceleration parameter is negative and approaches to − 0.5 at late times.
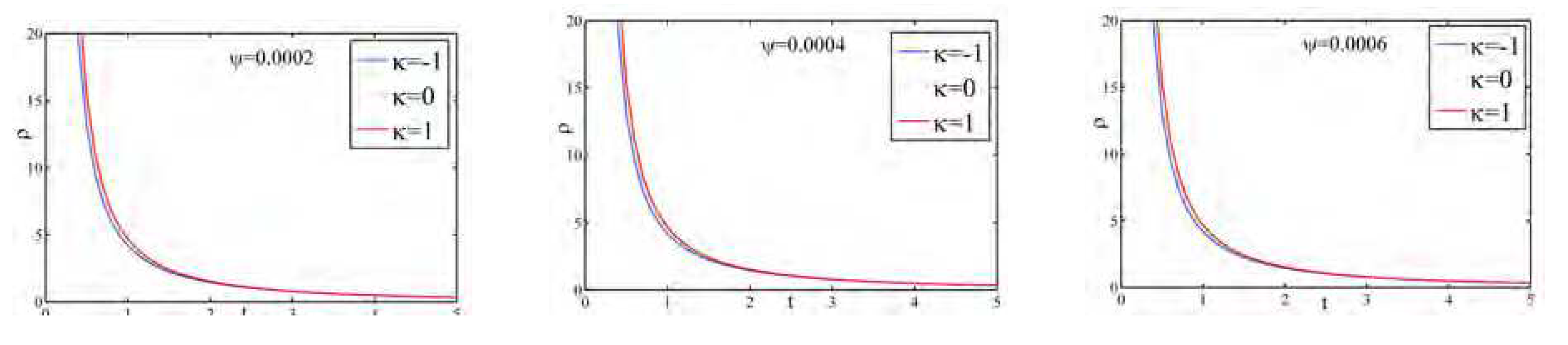
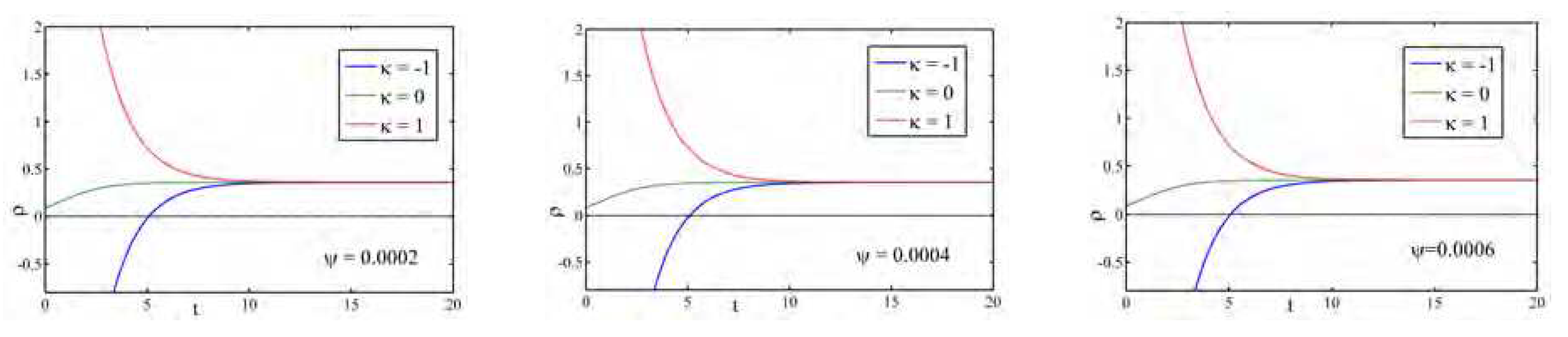
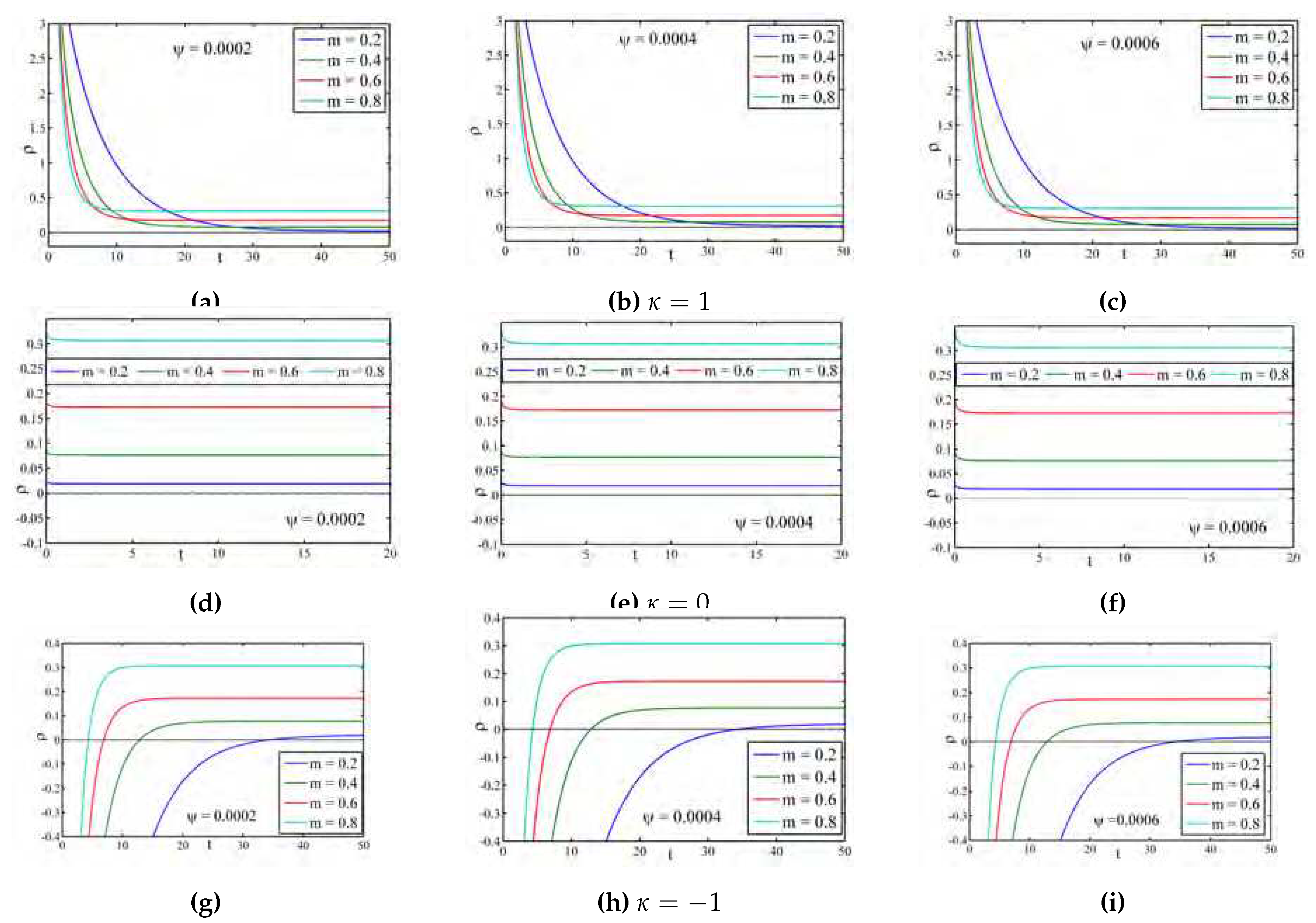
Figure 2 represent the profiles of the energy density ρ for different universes (open,flat and closed) with different ψ . In all the universes, ρ is a decreasing function of cosmic time and tends to zero at late times.
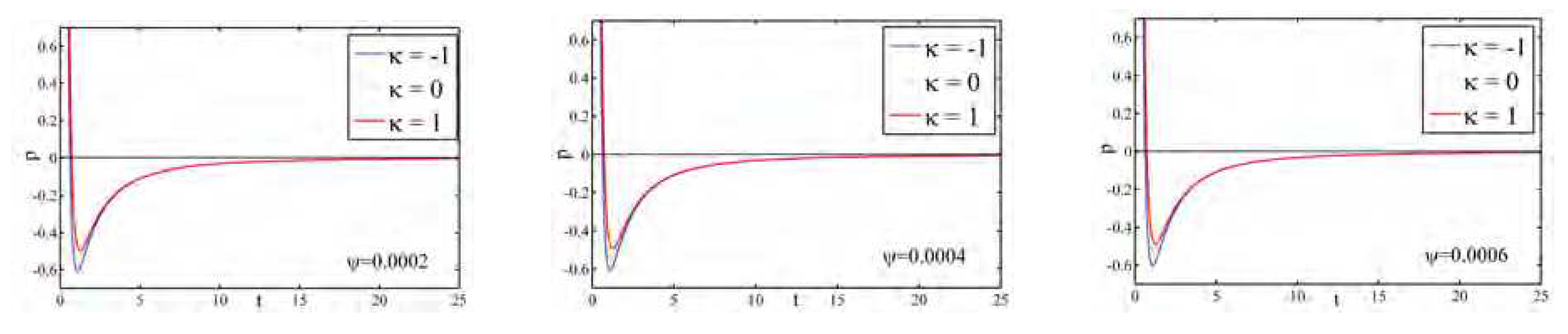
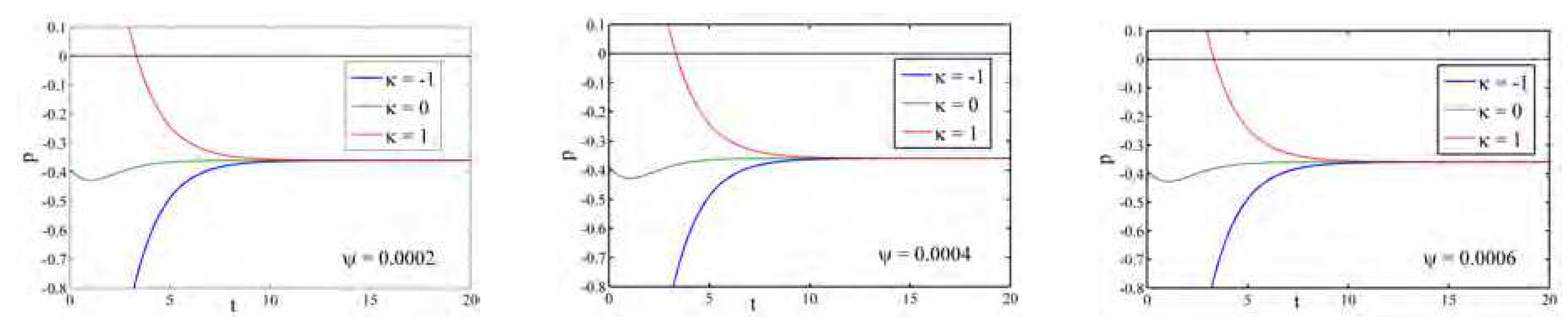
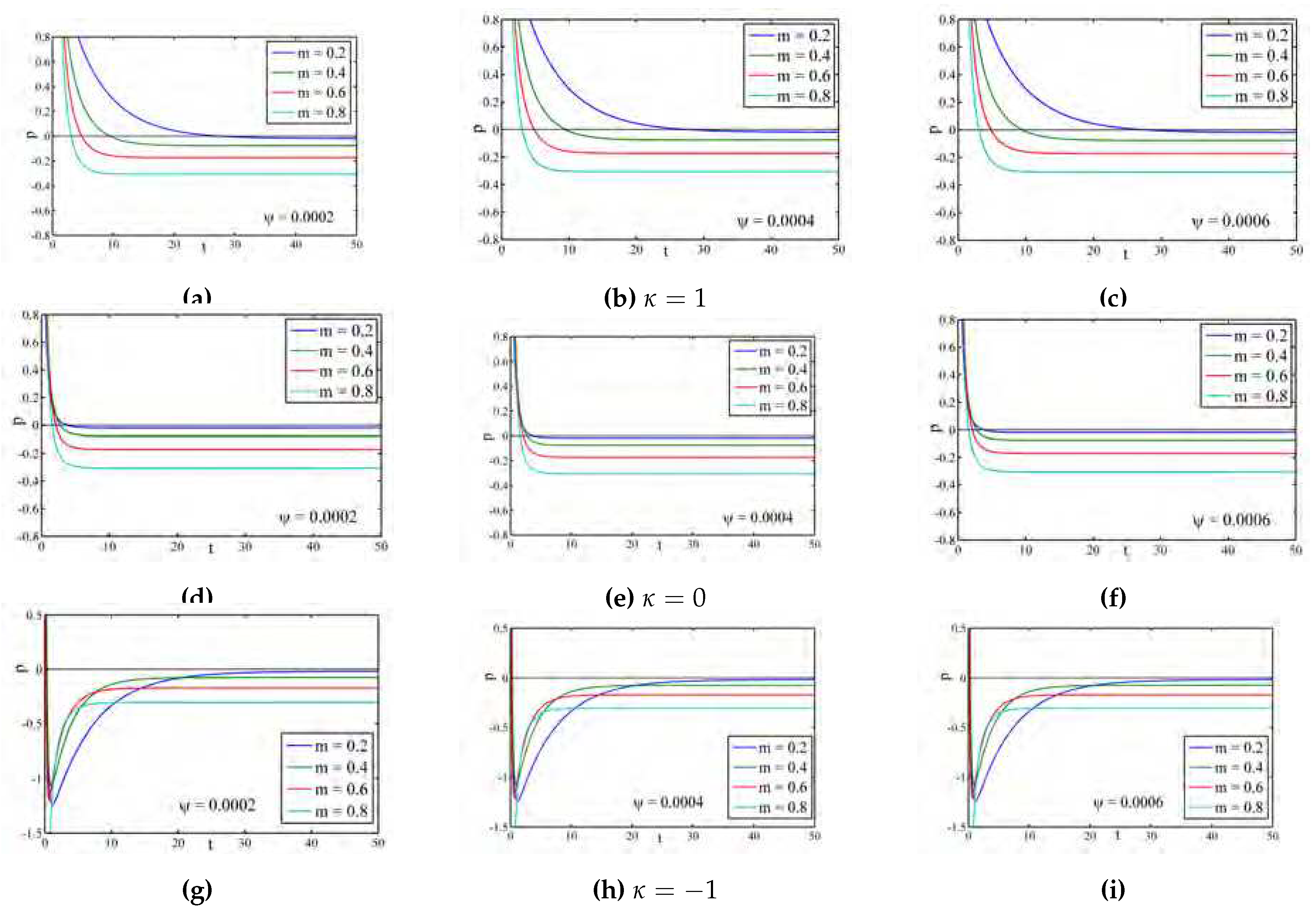
Figure 3 shows the profile of pressure p for different universes (open,flat and closed) with different ψ . Initially, the pressure is positive and after that it increases with cosmic time. It tends to zero at late times for different ψ .
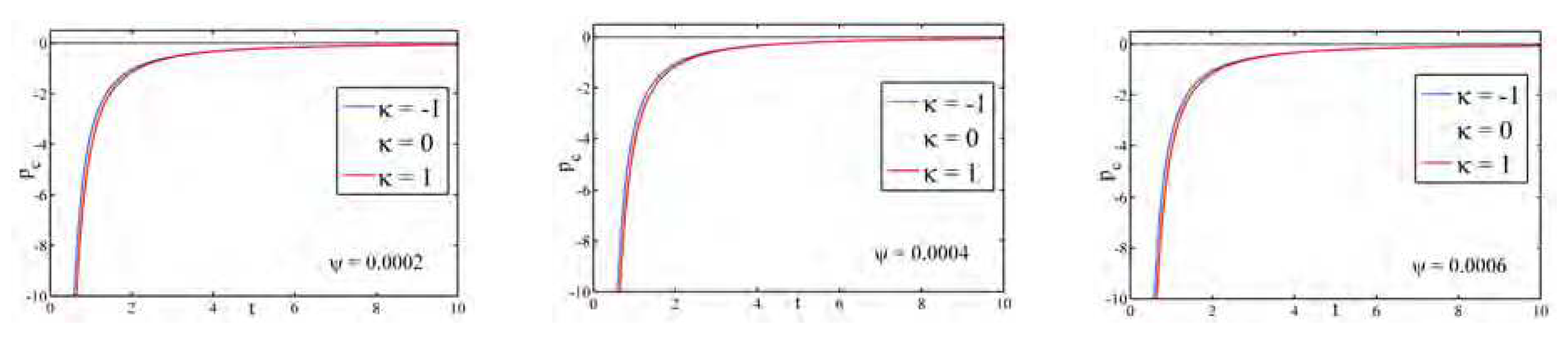
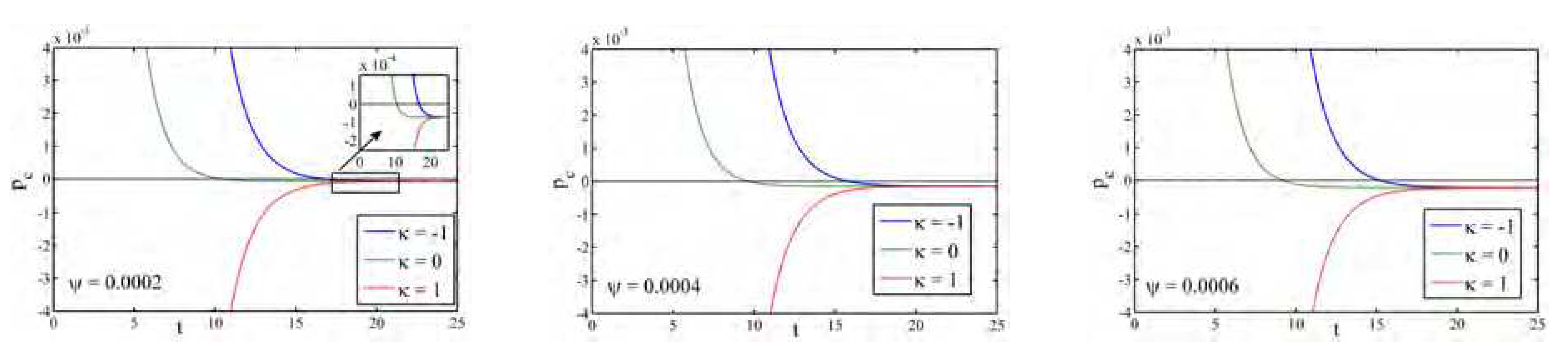
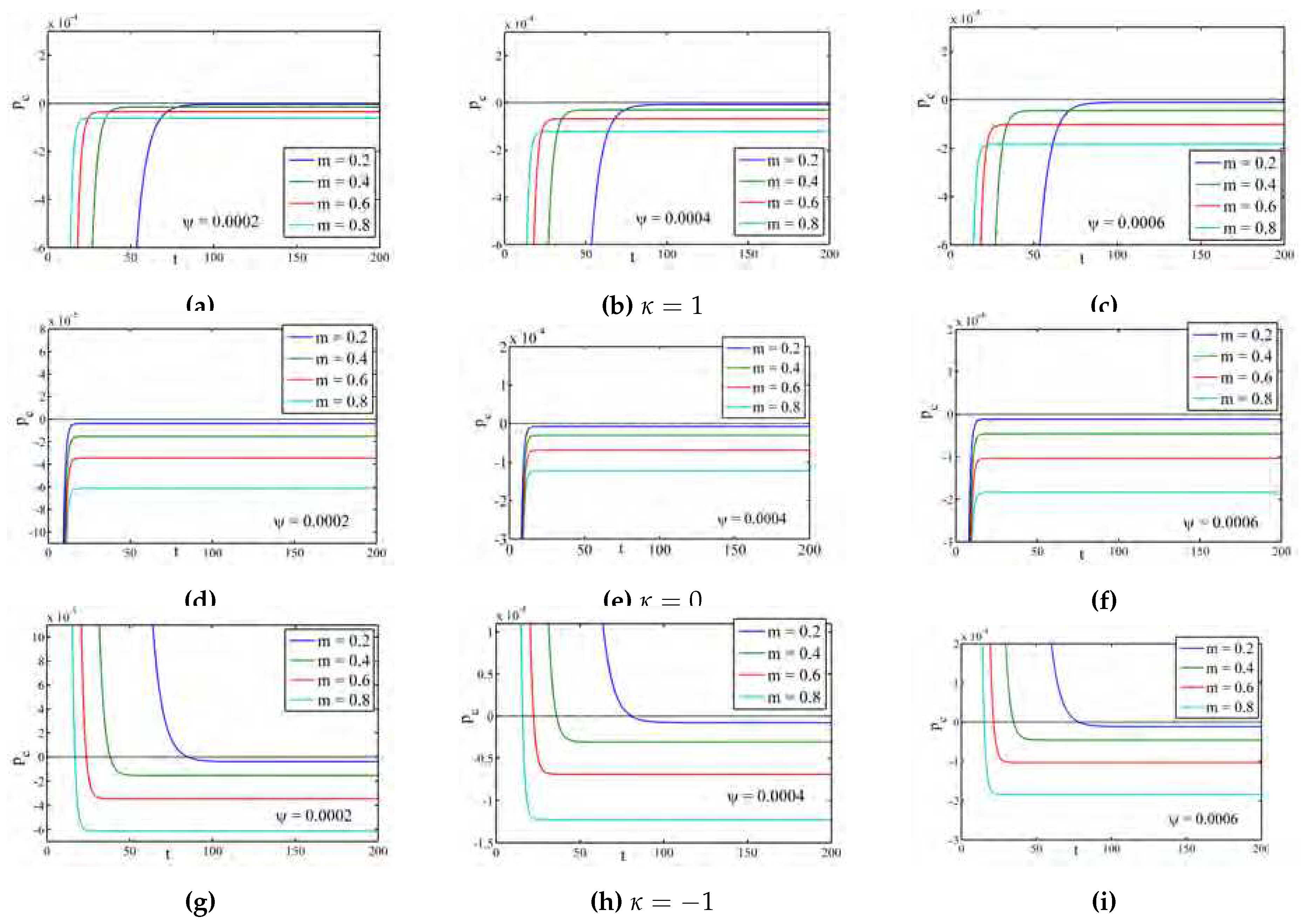
Figure 4 illustrates the profile of the particle creation pressure p c for different universes (open,flat and closed) with different ψ . It is noticed that, p c < 0 , for all the universes and different ψ .

3.2. Model II

The emergent form of scale factor
a = a 0 ( k 0 + e μ t ) ν
where a 0 , k 0 , μ , ν are any positive constant. The above-stated form of the scale factor is popularly used for various types of matters in general relativity and other gravity theories to develop cosmological models of the universe [82,83]. The model of the emergent universe by using the particle creation mechanism is formulated in the context of the flat FLRW space-time with perfect fluid by satisfying the barotropic equation of state [84]. The emergent form of the scale factor is considered to study the thermodynamical stability of the FLRW universe having a system of non-interacting diffusive fluids with a variable equation of state parameter [85]. The Hubble parameter is given by
H = μ ν e μ t k 0 + e μ t
The deceleration parameter for the emergent universe takes the form
q = − 1 − k 0 ν e μ t
Here the deceleration parameter is time dependent in the emergent scenario case and when t → ∞ we get q → − 1 . We get the energy density ρ by using (21) and (22) in (12)
ρ = − 1 λ 3 κ ( e μ t + k 0 ) − 2 ν a 0 2 + e μ t μ 2 ν ( λ 1 k 0 + λ 2 e μ t ν ) ( e μ t + k 0 ) 2
With the help of equations (21) and (22) in (13), the pressure p can be calculated as
p = 1 λ 3 λ 6 ( η − 1 ) [ e μ t μ 2 ν ( k 0 ( λ 1 λ 6 η − λ 3 ) + e μ t ν ( λ 2 λ 6 η − λ 3 λ 4 ) ) ( e μ t + k 0 ) 2 + κ ( e μ t + k 0 ) − 2 ν ( λ 6 η − λ 3 λ 5 ) a 0 2 ]
By incorporating (21) and (22) into (14), we get the particle creation pressure p c as
p c = − [ ( e μ t + k 0 ) − 2 ν η ( − a 0 2 e μ t ( e μ t + k 0 ) − 2 + 2 ν μ 2 ν ( ( λ 3 − λ 1 λ 6 ) k 0 + e μ t ( λ 3 λ 4 − λ 2 λ 6 ) ν ) + κ ( λ 6 − λ 3 λ 5 ) ) ] a 0 2 λ 3 λ 6 ( η − 1 )
Figure 5 portrays the profile of the deceleration parameter q and the Hubble parameter H against cosmic time t for different μ ( = 0.4330 , 0.8660 , 1.2990 , 1.7321 ). Here the deceleration parameter shows negative behavior and the Hubble parameter shows positive behavior. We can see that as t increases, H also goes on increasing and then maintains a constant value.
Figure 6 illustrates the profile of energy density ρ w.r.t cosmic time t for different ψ . For different ψ values, the energy density is positive valued in the case of flat and closed universes, whereas negative to positive valued for open universes. Furthermore, Figure 7 is the profile of pressure p against cosmic time t for different ψ . It is negative valued in the case of flat and open universes, whereas positive to negative valued for closed universes with respect to different ψ . The profile of the creation pressure p c is given in Figure 8. We can observe that p c shows positive to negative values for flat and open universes, whereas negative valued for closed universes with respect to different ψ .

3.3. Model III

Borrow [86] has studied the intermediate expansion law in cosmology for the first time. The intermediate form of the scale factor has an exponential function of time as
a = exp ( m t l )
where m > 0 and 0 < l < 1 are constants. An ample amount of research work based on the intermediate scale factor in the isotropic and anisotropic metric backgrounds has been studied in various gravity theories [88,89,90]. It will be interesting to study the intermediate form of the scale factor in the framework of Rastall gravity with particle creation. The Hubble parameter is given by
H = m l t l − 1
The deceleration parameter for the emergent universe takes the form
q = − 1 − l − 1 m l t l
We get the energy density ρ by using (27) and (28) in (12)
ρ = − 1 λ 3 e − 2 m t l κ + l m t l − 2 ( λ 1 ( l − 1 ) + λ 2 l m t l )
With the help of equation (27) and (28) in (13), the pressure p can be calculated as
p = e − 2 m t l ( λ 6 η ( κ t 2 + e 2 m t l l m t l ( λ 1 ( l − 1 ) + λ 2 l m t l ) ) − λ 3 ( e 2 m t l l m t l ( l − 1 + λ 4 l m t l ) + κ t 2 λ 5 ) ) λ 3 λ 6 ( η − 1 ) t 2
By incorporating (27) and (28) into (14), we get the creation pressure p c as
p c = e − 2 m t l η ( e 2 m t l ( λ 3 − λ 1 λ 6 ) ( l − 1 ) l m t l + e 2 m t l ( λ 3 λ 4 − λ 2 λ 6 ) l 2 m 2 t 2 l + κ t 2 ( λ 3 λ 5 − λ 6 ) ) λ 3 λ 6 ( η − 1 ) t 2
Figure 9 is the profile of the deceleration parameter q and the Hubble parameter H for different m. We can observe that q is a decreasing function of cosmic time t. At the initial stage q starts with positive values and then later on it takes negative values. In other words, we can say that a phase transition takes place, and the model transits from deceleration to acceleration. The Hubble parameter is also a decreasing function of the cosmic time t for different m.
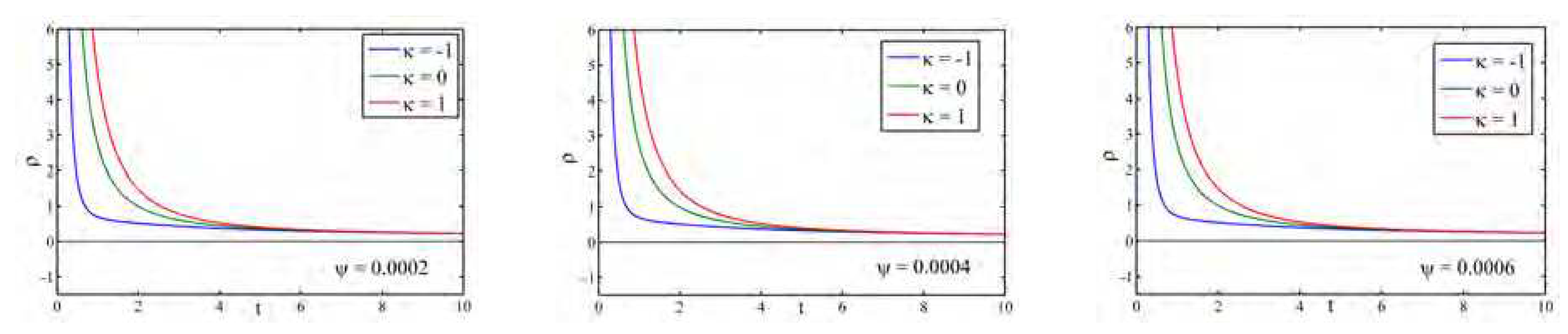
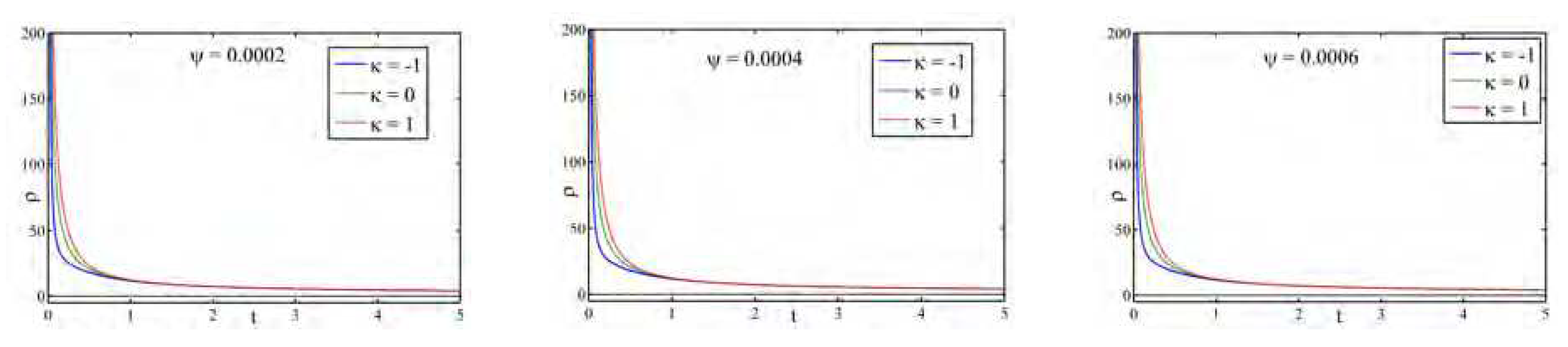
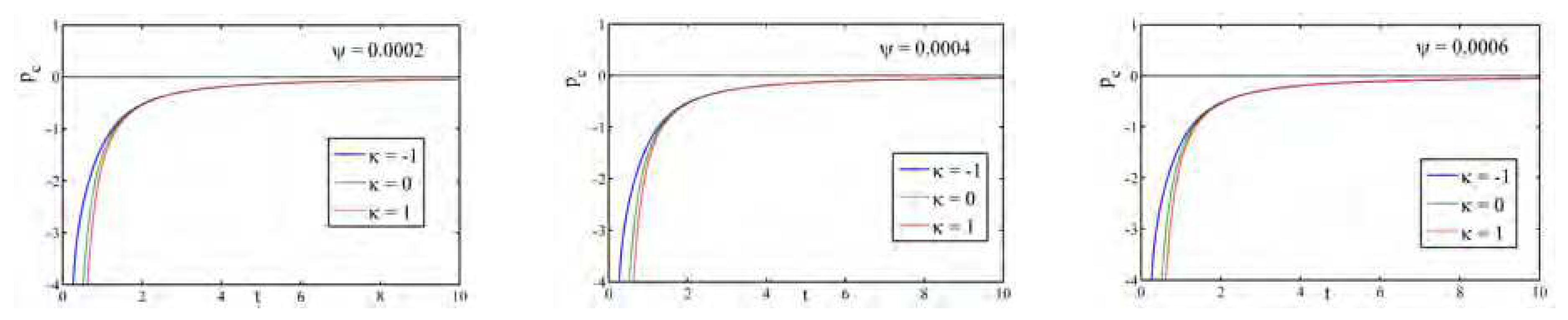
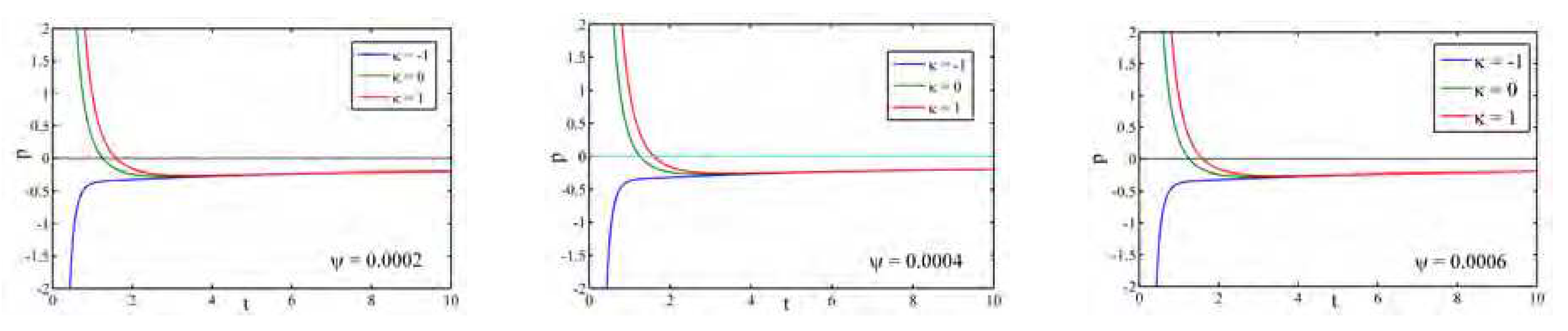
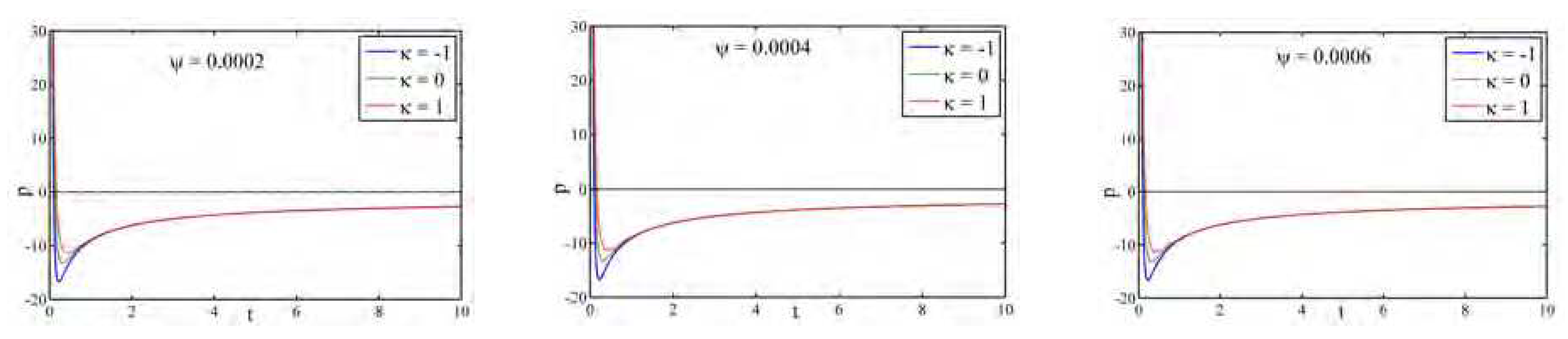
Figure 10 portrays the variation of the energy density ρ against cosmic time t for different ψ . Here we observe that the energy density ρ is positive, and a decreasing function of cosmic time t with respect to different values of ψ for all the universes (flat, open and closed). Figure 11 delivers the profile of pressure p against cosmic time t with respect to different ψ for all the universes (flat, open and closed). At the initial phase, it takes positive values and after that it takes negative values for different values of ψ . 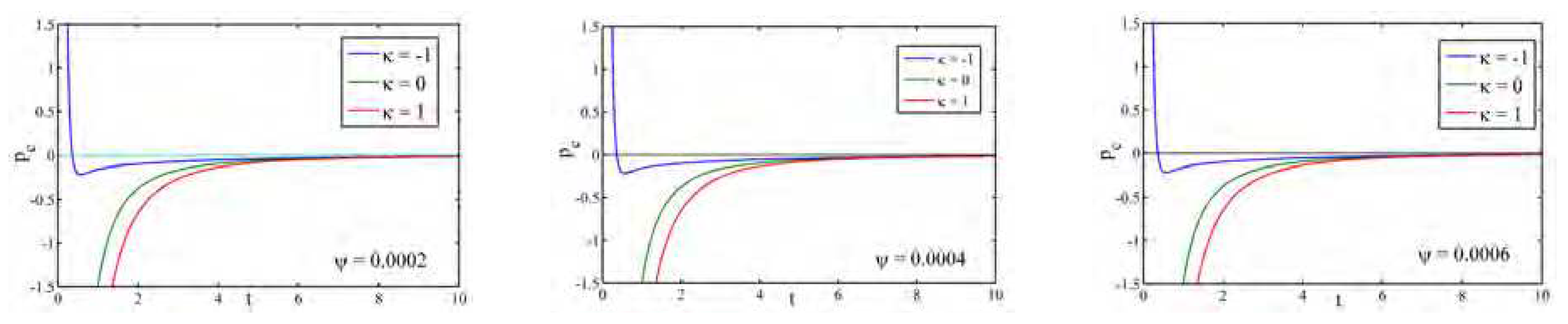Furthermore, the profile of the creation pressure p c is shown in Figure 12. In all the universes (flat, open and closed), the particle creation pressure is an increasing function of cosmic time and approaches zero for different ψ .

3.4. Model IV

The hybrid expansion law is the generalized form of the power-law and exponential law forms of the scale factor. Researchers developed cosmological models by considering the hybrid expansion law [91,92]. It is exciting to explore the hybrid expansion law in Rastall gravity theory with the particle creation mechanism. In order to study the particle creation mechanism during the stages of cosmic evolution, we take the scale factor as
a ( t ) = t b e β t
where b ≥ 0 and β ≥ 0 are some constants. As special cases, the hybrid expansion law mimics the power-law form a ( t ) = t b for β = 0 and for b = 0 , exponential law a ( t ) = e β t [79]. The Hubble parameter is given by
H = β + b t
The deceleration parameter for the hybrid form of the scale factor is expressed as
q = − 1 − b ( b + β t ) 2
We get the energy density ρ by using (33) and (34) in (12)
ρ = − 1 λ 3 λ 2 β + b t 2 − λ 1 b t 2 + e − 2 β t κ t − 2 b
With the help of equation (33) and (34) in (13), the pressure p can be calculated as
p = b ( λ 3 − λ 1 λ 6 η ) − ( λ 3 λ 4 − λ 2 λ 6 η ) ( b + β t ) 2 + e − 2 β t κ t 2 b − 2 ( λ 6 η − λ 3 λ 5 ) λ 3 λ 6 ( η − 1 ) t 2
By incorporating (33) and (34) in (14) we get the creation pressure p c as
p c = − e − 2 β t η t − 2 b ( e 2 β t ( λ 2 λ 6 − λ 3 λ 4 ) β + b t 2 t 2 b + b e 2 β t ( λ 1 λ 6 − λ 3 ) t 2 b − 2 + κ ( λ 6 − λ 3 λ 5 ) ) λ 3 λ 6 ( η − 1 )
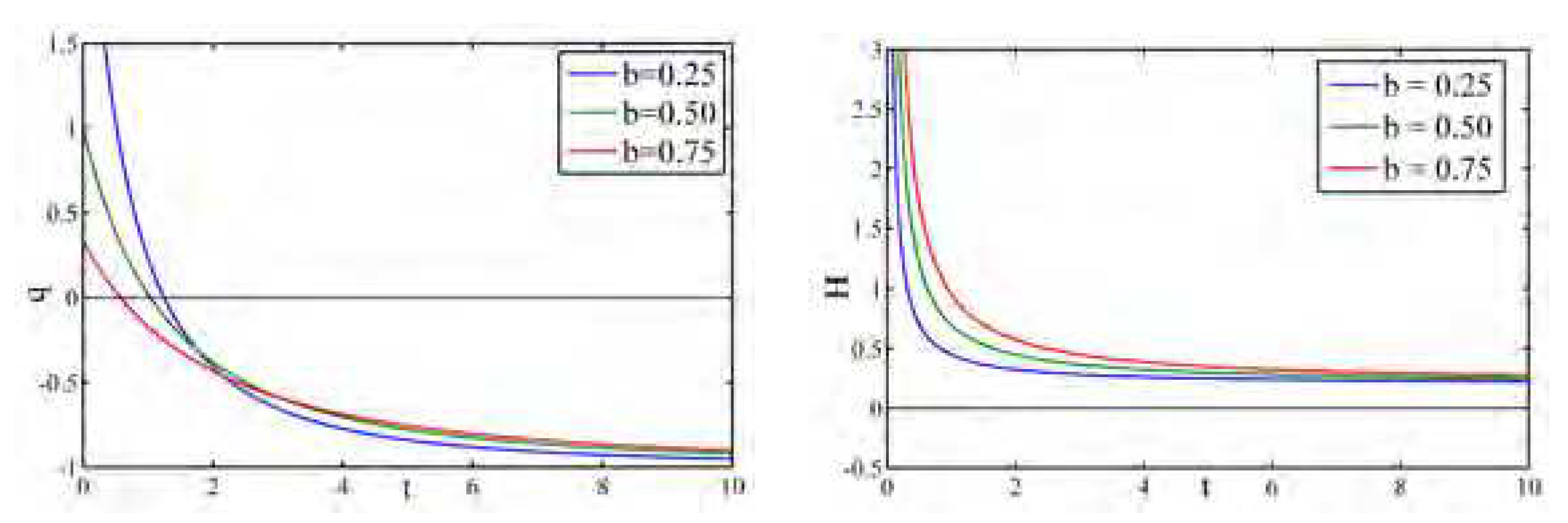
Figure 13 illustrates the profile of the deceleration parameter q and the Hubble parameter H against cosmic time t for different values of b. Here we can observe that as t increases. q shows transitional behavior and H is a decreasing function of cosmic time.
The profile of the energy density ρ against cosmic time t is depicted by Figure 14. Here the energy density is positive and shows decreasing behavior for different values of ψ . Figure 15 is the profile of the pressure p against cosmic time t with different values of ψ . In case of flat and closed universes, it is a decreasing function of cosmic time and takes positive to negative values, whereas it is negative valued and increasing in open universe for different ψ .
Figure 16 portrays the profile of the creation pressure p c against cosmic time t for different values of ψ . For different ψ in flat and closed universes, p c is negative valued and an increasing function of cosmic time whereas in open universes, it takes values from positive to negative, and is a decresing function of cosmic time. In all the universes, p c approaches zero at late times.

3.5. Model V

The non-linear flow equation is a widely used approach for exploring the inflationary behaviour of the universe. It has been accepted that the observable stage of inflation provides the initial condition for a flat universe, as well as the cosmic microwave background (CMB) and the large scale structure (LSS). An inflationary solution is important to avoid the flatness, horizon and isotropic problems and is accelerated and expanding. Zhou [93] discussed the intermediate inflationary scenario by introducing a scale factor of the form:
a ( t ) = a 0 exp ( μ t − λ 0 t n )
where a 0 > 0 , λ 0 , μ and n are constants. For an expanding process, we have several restrictions on t, μ , λ 0 and n, which is discussed in detail in Zhou [93]. As per our requirement, we considered t ≥ 0 for λ 0 < 0 , 0 < n < 1 and μ ≥ 0 . For graphical representation of the physical parameters, we choose λ 0 = − 3 , μ = 0.5 , a 0 = 1 , n = 0.5 and η = 0.5 . The scale factor (27) is used to study the cosmic inflation scenario [86,94,95]. The Hubble parameter is given by
H = μ − λ 0 n t n − 1
The deceleration parameter is expressed as
q = − 1 + λ 0 ( n − 1 ) n t n ( λ 0 n t n − t μ ) 2
We get values for the energy density by using (39) and (40) in (12)
ρ = − 1 λ 3 e 2 λ 0 t n − 2 μ t a 0 2 κ + λ 2 ( λ 0 n t n − μ t ) 2 − λ 1 λ 0 ( n − 1 ) n t n t 2
With the help of equation (39) and (40) in (13), the pressure p can be calculated as
p = [ ( n − 1 ) n λ 0 ( λ 3 − λ 1 λ 6 n ) t n − 2 + ( λ 2 λ 6 η − λ 3 λ 4 ) ( μ − n λ 0 t n − 1 ) 2 + e 2 λ 0 t n − 2 μ t κ ( λ 6 η − λ 3 λ 5 ) a 0 − 2 ] λ 3 λ 6 ( η − 1 )
By incorporating (39) and (40) in (14) we get the creation pressure p c as
p c = − η [ ( n − 1 ) n λ 0 ( λ 3 − λ 1 λ 6 n ) t n − 2 + ( λ 2 λ 6 η − λ 3 λ 4 ) ( μ − n λ 0 t n − 1 ) 2 + e 2 λ 0 t n − 2 μ t κ ( λ 6 η − λ 3 λ 5 ) a 0 − 2 ] λ 3 λ 6 ( η − 1 )
Figure 17 portrays the behavior of the deceleration parameter q and the Hubble parameter H against cosmic time t for different n and appropriate values of other parameters. We observe that q is a decreasing function of cosmic time and shows transitional behavior with the evolution of cosmic time and different n. The Hubble parameter H is a positive valued and a decreasing function of cosmic time for different n. Figure 18 indicates the profile of the energy density ρ versus cosmic time for different values of ψ . Here we notice that ρ > 0 , a decreasing function of cosmic time and ρ → 0 when t → ∞ for all the universes and different values of ψ .
Figure 19 represents the profile of the pressure p versus cosmic time t for different values of ψ . At the initial stage, the pressure shows positive values and later negative values as t increases for all the universes and different values of ψ . Furthermore, Figure 20 portrays the creation pressure p c against cosmic time t for different ψ . We notice that the creation pressure p c is increasing and negative valued for all the universes and different values of ψ .

3.6. Model VI

Recently, there is upsurge of interest in alternative theories of gravity in the context of inflationary cosmology. Therefore the study of cosmological models in Rastall gravity may be relevant for inflationary models, apart from particle creation processes and late time acceleration. Zhou [93] discussed the scale factor as follows.
a ( t ) = σ ( e μ t − τ e − μ t ) m
where σ > 0 , τ , μ and m are suitable constants. For an expanding process, we have several restrictions on t, σ > 0 , τ , μ and m which are discussed in detail in Zhou [93]. As per our requirement, we considered t ≥ 0 for μ > 0 and 0 ≤ τ ≤ 1 . For graphical representation of the physical parameters, we choose λ 0 = − 3 , μ = 0.5 , a 0 = 1 , n = 0.5 and η = 0.5 . The Hubble parameter is given by
H = m μ 1 + 2 τ ( e 2 μ t − τ )
The deceleration parameter for the hybrid universe takes the form
q = − 1 + 4 e 2 μ t τ m ( e 2 μ t + τ ) 2
We get the energy density ρ by using (45) and (46) in (12)
ρ = − 1 λ 3 κ ( e μ t − e − μ t τ ) − 2 m σ 2 + m ( λ 2 m ( e 2 μ t + τ ) 2 − 4 λ 1 e 2 μ t τ ) μ 2 ( e 2 μ t − τ ) 2
With the help of equation (45) and (46) in (13), the pressure p can be calculated as
p = [ ( σ − 2 κ ( e μ t − e − μ t τ ) − 2 m ( λ 6 η − λ 3 λ 5 ) ) + μ 2 ( e 2 μ t − τ ) − 2 m ( λ 2 λ 6 m η ( e 2 μ t + τ ) 2 − 4 e 2 μ t ( λ 3 ( λ 4 m − 1 ) + λ 1 λ 6 η ) τ ) − λ 3 λ 4 m 2 μ 2 ] λ 3 λ 6 ( η − 1 )
By incorporating (45) and (46) in (14), we get the particle creation p c as
p c = − η [ λ 3 − 1 [ ( e 2 μ t − τ ) − 2 m τ ( λ 2 λ 6 m ( e 2 μ t + τ ) 2 ) μ 2 − 4 e 2 μ t ( λ 1 λ 6 + λ 3 ( λ 4 m − 1 ) ) + σ − 2 κ ( e μ t − e − μ t τ ) − 2 m ( λ 6 − λ 3 λ 5 ) − λ 4 m 2 μ 2 ] ] λ 6 ( η − 1 )
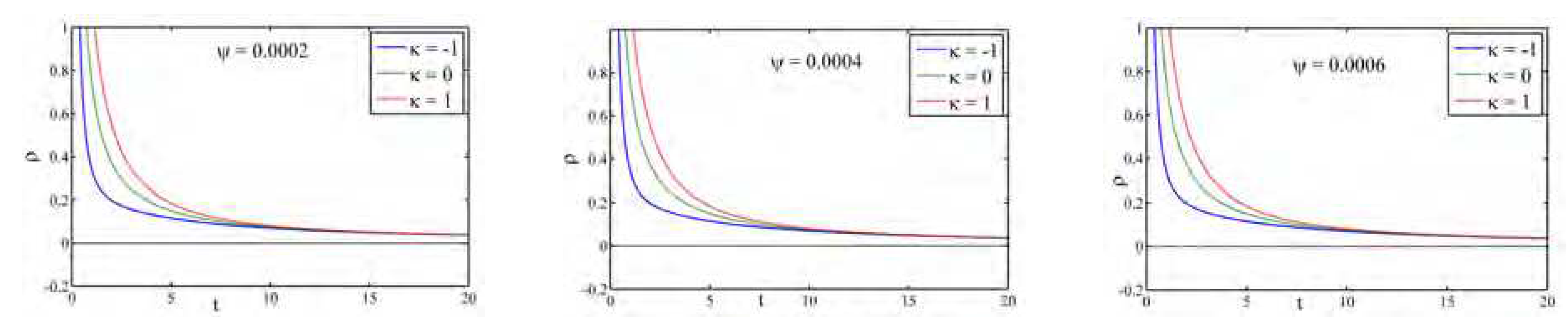
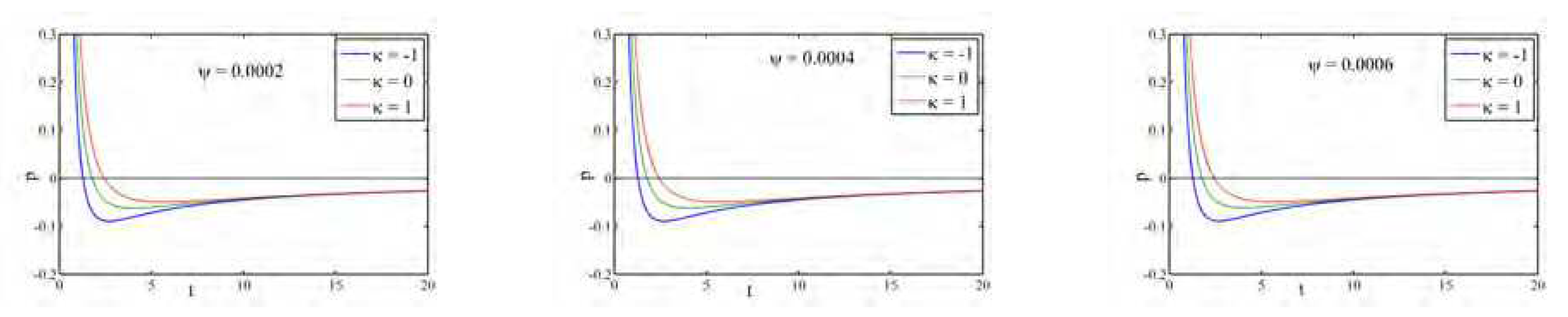
The profile of the energy density ρ against time t is indicated in Figure 21 for different ψ . We notice that ρ > 0 is a decreasing function of cosmic time for flat and closed universe, whereas a negative to positive valued increasing function of cosmic time with respect to different m and ψ . Figure 22 portrays the profile of the pressure against cosmic time t for different m and ψ . Here the pressure p is an increasing function of cosmic time and p < 0 in open universes whereas a positive to negative valued decreasing function of cosmic time with respect to different m and ψ . 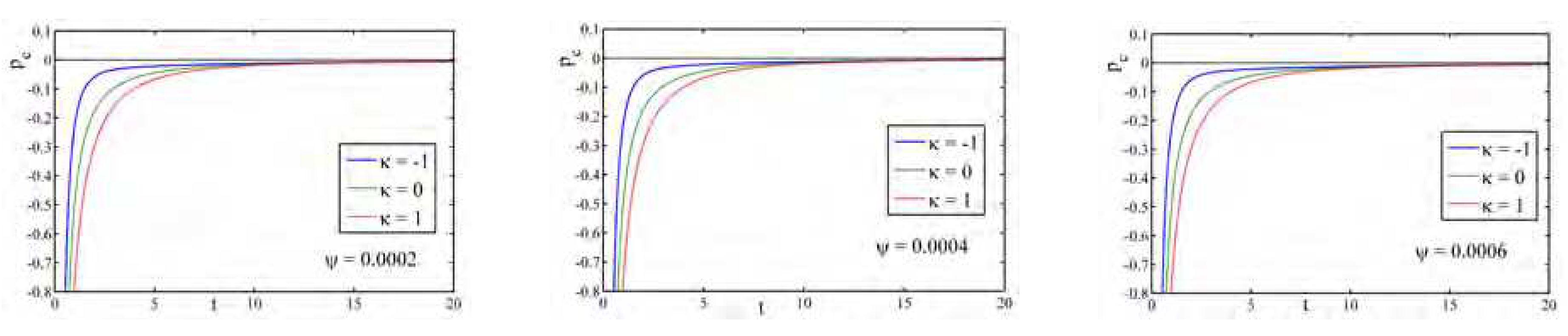Figure 23 portrays the profile of particle creation p c against cosmic time t for different m and ψ . One can notice that p c < 0 is increasing for flat and closed universes, whereas a positive to negative valued decreasing function of cosmic time in open universes with respect to different m and ψ .
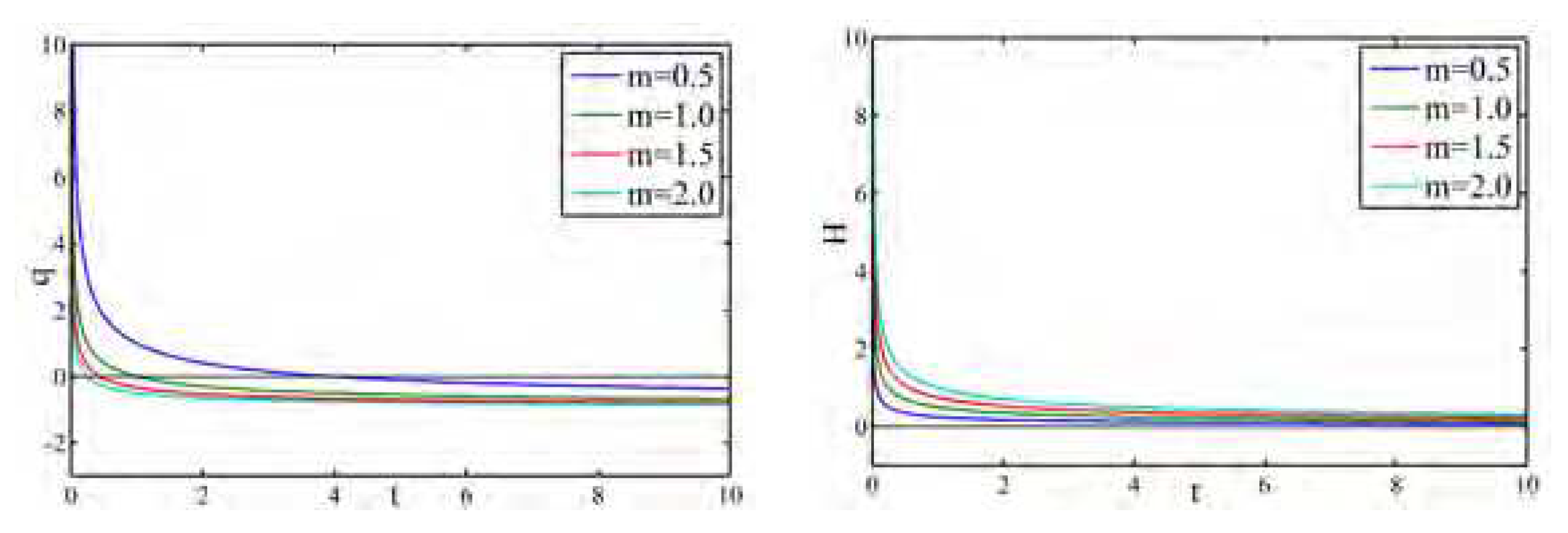
Figure 24 illustrates the profile of the deceleration parameter q and the Hubble parameter H versus cosmic time for different m( = 0.2 , 0.4 , 0.6 , 0.8 ). We observe that q takes positive to negative values with the evolution of cosmic time, which indicates a transitional behaviour for different m. It is well known that the crucial quantity in explaining the evolution of the universe is the deceleration parameter q. Table 1 illustrates the complete scenario of the deceleration parameter q for different parameters involved. The Hubble parameter H is a decreasing function of cosmic time for different values of m.

4. Conclusions

In this manuscript, we have examined particle creation in the context of Rastall gravity. Particle creation mechanisms in the considered modified gravity models permit us to understand particle production and annihilation in the universe. There are many periods during the evolution of the universe when particle creation can arise. When Poincare symmetry is broken very early in the universe, then the quantum field could absorb energy from the background and this can give rise to quantum particle creation (see [97] for an excellent review). It is also possible to obtain an estimate for particle creation. Particle creation can arise during the change from the inflationary period to the radiation dominated period, the change from radiation to matter eras, and thereafter also during the change to the accelerated area. Several authors that noted that anisotropic expansion can lead to enhanced particle creation. Some ideas of how to measure particle creation have also been put forward. Hence, it is important to study this process.
Rastall gravity is a non-conservative theory, and an extension of general relativity. This non-conservation is associated with particle creation. The key element of this theory is that non-vacuum solutions are dependent on the Rastall coupling parameter and are significantly different from the corresponding solutions in general relativity. The flat Friedmann-Lemaitre-Robertson-Walker models were considered for all values of the curvature, viz., open, closed and flat models. We derived and solved the Rastall gravity field equations under six different forms of the scale factor. We illustrated the scale factor, Hubble parameter, deceleration parameter, energy density and pressure for different values of the coupling parameter ψ . The deceleration parameter q portrays negative behaviour for all the models, indicating accelerating universes. Here, we can observe that all the models have positive energy density ρ . Furthermore, we get negative, positive to the negative and negative to the positive behavior of the pressure p. If the energy density is positive, the associated negative pressure will reflect accelerated expansion of the universe. This results in all the models having accelerated expansion. In the case of model III (the Barrow intermediate exponential law), model IV (hybrid law), model V (exponential of the linear sum of two power laws of time) and model VI (sum of power law and exponential) there is a transition from deceleration to acceleration as reflected in the graph of q (positive to negative). Hence, all these models can describe the current universe, without the need for a cosmological constant. Also, for the particle creation pressure, its presence or absence is indicated by zero or negative particle creation pressure p c . As a result, particle creation p c occurs in all the models for different values of the Rastall coupling parameter ψ ( = 0.0002 , 0.0004 , 0.0006 ) with κ = 1 , 0 , − 1 .
In conclusion, we can say that Rastall gravity is well worth studying as it entails particle creation as reflected in the non-conservation of the energy momentum tensor, and gives rise to a transition from deceleration to acceleration for a non-zero set of values of the parameters. We wish to constrain the models against observations, and this has been done to some extent for many of the scale factors considered here, but such an investigation is beyond the scope of this work.

5. Patents

No patents result from the work reported in this manuscript.

Author Contributions

Conceptualization, B. K. Bishi and A. Beesham; methodology, B. K. Bishi and A. Beesham; software, P. V. Lepse; writing—original draft preparation, B. K. Bishi and P. V. Lepse ; writing—review and editing, A. Beesham

Funding

A. Beesham acknowledges the financial support provided by National Research Foundation of South Africa (Grant Numbers:118511). Binaya K. Bishi thanks University of Zululand, South Africa, for providing a post doctoral fellowship and necessary facilities.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

There are no new data associated with this article.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Capozziello, S.; Cardone, V.F.; Farajollahi, H.; Ravanpak, A. Cosmography in f(T) gravity. Phys. Rev. D 2011, 84, 043527. [Google Scholar] [CrossRef]
  2. Myrzakulov, R. Accelerating universe from f(T) gravity. Eur. Phys. J. C 2011, 71, 1–8. [Google Scholar] [CrossRef]
  3. Yang, R. New types of f(T) gravity. Eur. Phys. J. C 2011, 71, 1–8. [Google Scholar] [CrossRef]
  4. Jimenez, J.B.; Heisenberg, L.; Koivisto, T.; Pekar, S. Cosmology in f(Q) geometry. Phys. Rev. D 2020, 101, 103507. [Google Scholar] [CrossRef]
  5. Mandal, S.; Sahoo, P.K.; Santo, J.R.L. Energy conditions in f(Q) gravity. Phys. Rev. D 2020, 102, 02405. [Google Scholar] [CrossRef]
  6. Shekh, S.H. Models of holographic dark energy in f(Q) gravity. Phys. Dark Universe 2021, 33, 100850. [Google Scholar] [CrossRef]
  7. Najera, A.; Fajardo, A. Fitting f(Q,T) gravity models with a CDM limit using H(z) and Pantheon data. Phys. Dark Universe 2021, 34, 100889. [Google Scholar] [CrossRef]
  8. Zia, R.; Maurya, D.C.; Shukla, A.K. Transit cosmological models in modified f(Q,T) gravity. Int. J. Geom. Methods Mod. 2021, 18, 2150051. [Google Scholar] [CrossRef]
  9. Bhattacharjee, S.; Sahoo, P.K. Baryogenesis in f(Q,T) gravity. Eur. Phys. J. C 2020, 80, 1–6. [Google Scholar]
  10. Cembranos, J.A. Dark matter from R2 gravity. Phys. Rev. Lett. 2009, 102, 141301. [Google Scholar] [CrossRef]
  11. Sahoo, P.K.; Moraes, P.H.R.S.; Sahoo, P. Wormholes in R2-gravity within the f(R,T) formalism. Eur. Phys. J. C 2018, 78, 1–7. [Google Scholar] [CrossRef]
  12. Pi, S.; Zhang, Y.L.; Huang, Q.G.; Sasaki, M. Scalaron from R2-gravity as a heavy field. J. Cosmol. Astropart. Phys. 2018, 2018, 042. [Google Scholar] [CrossRef]
  13. De Felice, A.; Tsujikawa, S. Construction of cosmologically viable f(G) gravity models. Phys. Lett. B 2009, 675, 1–8. [Google Scholar] [CrossRef]
  14. Myrzakulov, R.; Saez-Gomez, D.; Tureanu, A. On the CDM Universe in f(G) gravity. Gen. Relativ. Grav 2011, 43, 1671–1684. [Google Scholar] [CrossRef]
  15. Abbas, G.; Momeni, D.; Ali, M.A.; Myrzakulov, R; Qaisar, S. Anisotropic compact stars in f(G) gravity. Astrophys. Space Sci. 2015, 357, 1–11. [Google Scholar]
  16. De Laurentis, M.; Paolella, M.; Capozziello, S. Cosmological inflation in F(R,G) gravity. Phys. Rev. D 2015, 91, 083531. [Google Scholar] [CrossRef]
  17. De la Cruz-Dombriz, A.; Saez-Gomez, D. On the stability of the cosmological solutions in f(R,G) gravity. Class Quantum Gravity 2012, 29, 245014. [Google Scholar] [CrossRef]
  18. Atazadeh, K.; Darabi, F. Energy conditions in f(R,G) gravity. Gen. Relativ. Grav 2014, 46, 1–14. [Google Scholar] [CrossRef]
  19. Akbar, M.; Cai, R.G. Friedmann equations of FRW universe in scalar–tensor gravity, f(R) gravity and first law of thermodynamics. Phys. Lett. B 2006, 635, 7–10. [Google Scholar] [CrossRef]
  20. Capozziello, S.; Nojiri, S.I.; Odintsov, S.D.; Troisi, A. Cosmological viability of f(R)-gravity as an ideal fluid and its compatibility with a matter dominated phase. Phys. Lett. B 2006, 639, 135–143. [Google Scholar] [CrossRef]
  21. Nojiri, S.I.; Odintsov, S.D. Modified f(R) gravity consistent with realistic cosmology: From a matter dominated epoch to a dark energy universe. Phys. Rev. D 2006, 74, 086005. [Google Scholar] [CrossRef]
  22. Hendi, S.H.; Momeni, D. Black-hole solutions in f(R) gravity with conformal anomaly. Eur. Phys. J. C 2011, 71, 1–9. [Google Scholar] [CrossRef]
  23. Sharif, M.; Arif, S. Non-vacuum static cylindrically symmetric solution and energy distribution in f(R) gravity. Astrophys. Space Sci. 2012, 342, 237–243. [Google Scholar] [CrossRef]
  24. Jamil, M.; Mahomed, F.M.; Momeni, D. Noether symmetry approach in f(R)–tachyon model. Phys. Lett. B 2011, 702, 315–319. [Google Scholar] [CrossRef]
  25. Harko, T.; Lobo, F.S.; Nojiri, S.I.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
  26. Singh, V.; Beesham, A. Plane symmetric model in f(R,T) gravity. Eur. Phys. J. Plus 2020, 135, 1–15. [Google Scholar] [CrossRef]
  27. Singh, V.; Beesham, A. . LRS Bianchi I model with constant expansion rate in f(R,T) gravity. Astrophys. Space Sci. 2020, 365, 1–8. [Google Scholar] [CrossRef]
  28. Rastall, P. Generalization of the Einstein Theory. Phys. Rev. D 1972, 6, 3357. [Google Scholar] [CrossRef]
  29. Bronnikov, K.A.; Fabris, J.C.; Piattella, O.F.; Santos, E.C. Static, spherically symmetric solutions with a scalar field in Rastall gravity. Gen. Relativ. Grav 2016, 48, 1–15. [Google Scholar] [CrossRef]
  30. De Moraes, W.A.G.; Santos, A.F. Lagrangian formalism for Rastall theory of gravity and Gödel-type universe. Gen. Relativ. Grav 2019, 51, 167. [Google Scholar] [CrossRef]
  31. Shabani, H.; Ziaie, A.H. A connection between Rastall-type and f(R, T) gravities. EPL 2020, 129, 20004. [Google Scholar] [CrossRef]
  32. Fabris, J.c.; Daouda, M.H.; Piattella, O.F. Note on the evolution of the gravitational potential in Rastall scalar field theories. Phys. Lett. B 2012, 711, 232. [Google Scholar] [CrossRef]
  33. Batista, C. E. M.; Daouda, M. H.; Fabris, J. C.; Piattella, O. F.; Rodrigues, D. C. Rastall cosmology and the ΛCDM model Phys. Rev. D 2012, 85, 084008. [Google Scholar] [CrossRef]
  34. Moradpour, H. Thermodynamics of flat FLRW universe in Rastall theory. Phys. Lett. B 2016, 757, 187. [Google Scholar] [CrossRef]
  35. Smalley, L. L. Gravitational theories with nonzero divergence of the energy-momentum tensor. Phys. Rev. D 1975, 12, 376. [Google Scholar] [CrossRef]
  36. Wolf, C. Non-Conservative Gravitation and Kaluza Klein Cosmology. Phys. Scripta 1986, 34, 193. [Google Scholar] [CrossRef]
  37. Silva, G. F.; Piattella O., F.; Fabris J., C.; Casarini, L.; Barbosa T., O. Bouncing solutions in Rastall’s theory with a barotropic fluid. Grav. Cosmol. 2013, 19, 156. [Google Scholar] [CrossRef]
  38. Koivisto, T. A note on covariant conservation of energy–momentum in modified gravities. Classical Quantum Gravity 2006, 23, 4289. [Google Scholar] [CrossRef]
  39. Minazzoli, O. Conservation laws in theories with universal gravity/matter coupling. Phys. Rev. D 2013, 88, 027506. [Google Scholar] [CrossRef]
  40. Batista, C. E. M.; Daouda, M. H.; Fabris, J. C.; Piattella, O. F.; Rodrigues, D. C. Rastall cosmology and the ΛCDM model Phys. Rev. D 2012, 85, 084008. [Google Scholar] [CrossRef]
  41. Kumar, R.; Singh, B.P.; Ali, M.S.; Ghosh, S.G. Shadows of black hole surrounded by anisotropic fluid in Rastall theory. Phys. Dark Universe 2021, 34, 100881. [Google Scholar] [CrossRef]
  42. Heydarzade, Y.; Darabi, F. Black hole solutions surrounded by perfect fluid in Rastall theory. Phys. Lett. B 2017, 771, 365–373. [Google Scholar] [CrossRef]
  43. Heydarzade, Y.; Moradpour, H.; Darabi, F. Black hole solutions in Rastall theory Can. J. Phys. 2017, 95, 1253–1256. [Google Scholar]
  44. Kumar, R.; Ghosh, S. G. Rotating black hole in Rastall theory. Eur.Phys. J. C 2018, 78, 750. [Google Scholar] [CrossRef]
  45. Ma, M. S.; Zhao, R. Noncommutative geometry inspired black holes in Rastall gravity. Eur. Phys. J. C 2017, 77, 629. [Google Scholar] [CrossRef]
  46. Moradpour, H.; Sadeghnezhad, N.; Hendi, S. H. Traversable asymptotically flat wormholes in Rastall gravity. Can. J. Phys. 2017, 95, 1257. [Google Scholar] [CrossRef]
  47. Ziaie, A. H.; Moradpour, H.; Ghaffari, S. Gravitational Collapse in Rastall Gravity, Phys. Lett. B 2019, 793, 03055. [Google Scholar] [CrossRef]
  48. Visser, M. Rastall gravity is equivalent to Einstein gravity. Phys. Lett. B 2018, 782, 83. [Google Scholar] [CrossRef]
  49. Darabi, F.; Moradpour, H.; Licata, I.; Heydarzade, Y.; Corda, C. Einstein and Rastall theories of gravitation in comparison. Eur. Phys. J. C 2018, 78, 25. [Google Scholar] [CrossRef]
  50. Bamba. , K.; Jawad, A.; Rafique, S; Moradpour, H. Thermodynamics in Rastall gravity with entropy corrections. Eur. Phys. J. C 2018, 78, 1–12. [Google Scholar]
  51. Cruz, M.; Lepe, S.; Morales-Navarrete, G. A thermodynamics revision of Rastall gravity. Class Quantum Gravity 2019, 36, 225007. [Google Scholar] [CrossRef]
  52. Moradpour, H.; Salako, I.G. Thermodynamic analysis of the static spherically symmetric field equations in Rastall theory. Adv. High Energy Phys. 2016. [Google Scholar] [CrossRef]
  53. Ali, R.; Babar, R.; Asgher, M.; Shah, S.A.A. Gravity effects on Hawking radiation from charged black strings in Rastall theory. Ann. Physics 2021, 432, 168572. [Google Scholar] [CrossRef]
  54. Javed, F.; Mustafa, G.; Övgün, A.; Shamir, M.F. Epicyclic frequencies and stability of thin shell around the traversable phantom wormholes in Rastall gravity. Eur. Phys. J. Plus 2022, 137, 1–16. [Google Scholar] [CrossRef]
  55. Mustafa, G.; Waheed, S.; Zubair, M.; Xia, T.C. Non-commutative wormholes exhibiting conformal motion in Rastall gravity. Chin. J. Phys. 2020, 65, 163–176. [Google Scholar] [CrossRef]
  56. Prigogine, I.; Géhéniau, J.; Gunzig, E.; Nardone, P. Thermodynamics of cosmological matter creation. Proc. Natl. Acad. Sci. 1988, 85, 7428–7432. [Google Scholar] [CrossRef]
  57. Lima, J.A.S. Thermodynamics of decaying vacuum cosmologies. Phys. Rev. D 1996, 54, 2571. [Google Scholar] [CrossRef]
  58. Gunzig, E.; Maartens, R.; Nesteruk, A.V. Inflationary cosmology and thermodynamics. Class Quantum Gravity 1998, 15, 923. [Google Scholar] [CrossRef]
  59. Hamil, B.; Merad, M.; and Birkandan, T. Particle creation in the context of the emergent universe. Rev. Mex. de Fis. 2021, 67, 219–225. [Google Scholar] [CrossRef]
  60. Jawad, A.; Maqsood, S. Gravitationally induced particle creation in cubic gravity. Int. J. Geom. Methods Mod. 2021, 18, 2150106. [Google Scholar] [CrossRef]
  61. Setare, M. R; Houndjo, M.J.S. Particle creation in flat Friedmann–Robertson–Walker (FRW) universe in the framework of f(T) gravity. Can. J. Phys. 2013, 91, 168–174. [Google Scholar] [CrossRef]
  62. Appleby, S.A.; Battye, R.A.; Starobinsky, A.A. Curing singularities in cosmological evolution of F(R) gravity. J. Cosmol. Astropart. Phys. 2010, 2010, 005. [Google Scholar] [CrossRef]
  63. Singh, J.K.; Nagpal, R.; Pacif, S.K.J. Statefinder diagnostic for modified Chaplygin gas cosmology in f(R,T) gravity with particle creation. Int. J. Geom. Methods Mod. 2018, 15, 1850049. [Google Scholar] [CrossRef]
  64. Rashidi, R.; Ahmadi, F.; Setare, M.R. Particle creation in the framework of f(G) gravity. Astrophys. Space Sci. 2018, 363, 1–8. [Google Scholar] [CrossRef]
  65. Zubair, M.; Rahseed, M.; Saleem, R.; Abbas, G. Particle creation from thermodynamics point of view in f(G,T) gravity. Int. J. Geom. Methods Mod. 2021, 18, 2150177. [Google Scholar] [CrossRef]
  66. Singh, G.P.; Beesham, A. Bulk viscosity and particle creation in Brans–Dicke theory. Aust. J. Phys. 1999, 52, 1039–1049. [Google Scholar] [CrossRef]
  67. Bishi, B.K.; Lepse, P. V; Beesham, A. Impact of particle creation in Lyra’s geometry. Indian J. Phys. 2022; 1–13. [Google Scholar]
  68. Lyth, D.H.; Roberts, D.; Smith, M. Cosmological consequences of particle creation during inflation. Phys. Rev. D 1998, 57, 7120. [Google Scholar] [CrossRef]
  69. Ford, L.H. Gravitational particle creation and inflation. Phys. Rev. D 1987, 35, 2955. [Google Scholar] [CrossRef]
  70. Calzetta, E.; Hu, B.L. Dissipation of quantum fields from particle creation. Phys. Rev. D 1989, 40, 656. [Google Scholar] [CrossRef]
  71. Good, M.R.; Anderson, P.R.; Evans, C.R. 2013. Time dependence of particle creation from accelerating mirrors. Phys. Rev. D 1989, 88, 025023. [Google Scholar] [CrossRef]
  72. Bishi, B.K.; Lepse, P.V. Particle creation and quadratic deceleration parameter in Lyra geometry. New Astron. 2021, 85, 101563. [Google Scholar] [CrossRef]
  73. Li, R.; Wang, J.; Xu, Z.; Guo, X. Constraining the Rastall parameters in static space–times with galaxy-scale strong gravitational lensing. Mon. Not. Royal Astron. Soc. 2019, 486, 2407–2411. [Google Scholar] [CrossRef]
  74. Akarsu, O.; Katırcı,N. ; Kumar, S.; Nunes, N.C.; Ozturk, B.; Sharma, S. Rastall gravity extension of the standard ΛCDM model: theoretical features and observational constraints. Eur. Phys. J. C 2020, 80, 1050. [Google Scholar] [CrossRef]
  75. Calvao,M. O.; Lima J. A. S.; Waga, I. On the thermodynamics of matter creation in cosmology. Phys. Lett. A 1992, 162, 223. [Google Scholar]
  76. Lima J. A., S.; Germano A. S., M. On the equivalence of bulk viscosity and matter creation. Phys. Lett. A 1992, 170, 373. [Google Scholar] [CrossRef]
  77. Lima J. A., S.; Calvao M., O.; Waga,I. Cosmology, Thermodynamics and matter creation. Front. Phys. 1990. [Google Scholar]
  78. Hulke, N.; Singh, G.P.; Bishi, B.K.; Singh, A. Bianchi type-I Universe with Cosmological constant and periodic varying deceleration parameter. New Astron. 2020, 77, 101357. [Google Scholar] [CrossRef]
  79. Singh, G.P.; Hulke, N.; Singh, A. Cosmological study of particle creation in higher derivative theory. Indian J. Phys. 2020, 94(1), 127–141. [Google Scholar] [CrossRef]
  80. Amirhashchi, H.; Chouhan, D.S.; Pradhan, A. Interacting and Non-interacting Two-Fluid Atmosphere for Dark Energy in FRW Universe. Electron. J. Theor. Phys. 2014; 11. [Google Scholar]
  81. Kotambkar, S.; Singh, G.P.; Kelkar, R.; Bishi, B.K. Commun. Theor. Phys 2017, 67, 222.
  82. Mulryne, D.J.; Tavakol, R.; Lidsey, J.E.; Ellis, G.F. 2005. An emergent universe from a loop. Phys. Rev. D 2017, 71, 123512. [Google Scholar] [CrossRef]
  83. Nunes, N.J. . Inflation: a graceful entrance from loop quantum cosmology. Phys. Rev. D 2005, 72, 103510. [Google Scholar] [CrossRef]
  84. Chakraborty, S. Is emergent universe a consequence of particle creation process? Phys. Lett. B 2014, 732, 81–84. [Google Scholar] [CrossRef]
  85. Maity, S.; Bhandari, P.; Chakraborty, S. Universe consisting of diffusive dark fluids: thermodynamics and stability analysis. Eur. Phys. J. C 2019, 79, 1–8. [Google Scholar] [CrossRef]
  86. Barrow, J.D.; Saich, P. The behaviour of intermediate inflationary universes. Phys. Lett. B 1990, 249, 406–410. [Google Scholar] [CrossRef]
  87. Barrow, J.D.; Hervik, S. Anisotropically nflating universes. Phys. Rev. D 2006, 73, 023007. [Google Scholar] [CrossRef]
  88. Rendall, A.D. Intermediate inflation and the slow-roll approximation. Class Quantum Gravity 2005, 22, 1655. [Google Scholar] [CrossRef]
  89. Khatua, P.B.; Debnath, U. Int. J. Theor. Phys 2011, 50, 799. [CrossRef]
  90. Farajollahi, H.; Ravanpak, A. Tachyon field in intermediate inflation on the brane. Phys. Rev. D 2011, 84, 084017. [Google Scholar] [CrossRef]
  91. Moraes, P.H.R.S.; Sahoo, P.K. The simplest non-minimal matter–geometry coupling in the f(R,T) cosmology. Eur. Phys. J. C 2017, 77, 1–8. [Google Scholar] [CrossRef]
  92. Singh, G.P.; Bishi, B.K. Bianchi type-I transit Universe in f(R,T) modified gravity with quadratic equation of state and Λ. Astrophys. Space Sci. 2015, 360, 1–8. [Google Scholar] [CrossRef]
  93. Xiao-Hua, Z. Some characteristics of three exact solutions of Einstein equations minimally coupled to a Quintessence field. Chin. Phys. B 2009, 18, 3115. [Google Scholar] [CrossRef]
  94. Barrow, J.D.; Liddle, A.R. Perturbation spectra from intermediate inflation. Phys. Rev. D 1993, 47, 5219. [Google Scholar] [CrossRef] [PubMed]
  95. Barrow, J.D.; Nunes, N.J. Dynamics of “logamediate” inflation. Phys. Rev. D 2007, 76, 043501. [Google Scholar] [CrossRef]
  96. Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder—a new geometrical diagnostic of dark energy. J. Exp. Theor. Phys. Lett. 2003, 77, 201–206. [Google Scholar] [CrossRef]
  97. Ford, L.H. Cosmological particle production: a review. Phys. Rep. bf 2021, 84, 116901. [Google Scholar] [CrossRef]
Preprints 77586 g001
Figure 1. Profile of Scale factor, Hubble parameter and Deceleration parameter for Model-I
Figure 1. Profile of Scale factor, Hubble parameter and Deceleration parameter for Model-I
Preprints 77586 g001
Preprints 77586 g002
Figure 2. Profile of energy density for Model-I with different ψ
Figure 2. Profile of energy density for Model-I with different ψ
Preprints 77586 g002
Preprints 77586 g003
Figure 3. Profile of Pressure for Model-I with different ψ
Figure 3. Profile of Pressure for Model-I with different ψ
Preprints 77586 g003
Preprints 77586 g004
Figure 4. Profile of creation pressure for Model-I with different ψ
Figure 4. Profile of creation pressure for Model-I with different ψ
Preprints 77586 g004
Preprints 77586 g005
Figure 5. Profile of q and H for Model-II against time for different μ
Figure 5. Profile of q and H for Model-II against time for different μ
Preprints 77586 g005
Preprints 77586 g006
Figure 6. Profile of energy density for Model-II against time for different ψ
Figure 6. Profile of energy density for Model-II against time for different ψ
Preprints 77586 g006
Preprints 77586 g007
Figure 7. Profile of pressure for Model-II against time for different ψ
Figure 7. Profile of pressure for Model-II against time for different ψ
Preprints 77586 g007
Preprints 77586 g008
Figure 8. Profile of particle creation pressure for Model-II against time for different ψ
Figure 8. Profile of particle creation pressure for Model-II against time for different ψ
Preprints 77586 g008
Preprints 77586 g009
Figure 9. Profile of q and H for Model-III against time for different m
Figure 9. Profile of q and H for Model-III against time for different m
Preprints 77586 g009
Preprints 77586 g010
Figure 10. Profile of energy density for Model-III against time for different ψ
Figure 10. Profile of energy density for Model-III against time for different ψ
Preprints 77586 g010
Preprints 77586 g011
Figure 11. Profile of pressure for Model-III against time for different ψ
Figure 11. Profile of pressure for Model-III against time for different ψ
Preprints 77586 g011
Preprints 77586 g012
Figure 12. Profile of particle creation pressure for Model-III against time for different ψ
Figure 12. Profile of particle creation pressure for Model-III against time for different ψ
Preprints 77586 g012
Preprints 77586 g013
Figure 13. Profile of q and H for Model-IV against time for different b
Figure 13. Profile of q and H for Model-IV against time for different b
Preprints 77586 g013
Preprints 77586 g014
Figure 14. Profile of energy density for Model-IV against time for different ψ
Figure 14. Profile of energy density for Model-IV against time for different ψ
Preprints 77586 g014
Preprints 77586 g016
Figure 15. Profile of pressure for Model-IV against time for different ψ
Figure 15. Profile of pressure for Model-IV against time for different ψ
Preprints 77586 g016
Preprints 77586 g015
Figure 16. Profile of particle creation pressure for Model-IV against time for different ψ
Figure 16. Profile of particle creation pressure for Model-IV against time for different ψ
Preprints 77586 g015
Preprints 77586 g017
Figure 17. Profile of q and H for Model-V against time for different n
Figure 17. Profile of q and H for Model-V against time for different n
Preprints 77586 g017
Preprints 77586 g018
Figure 18. Profile of energy density for Model-V against time for different ψ
Figure 18. Profile of energy density for Model-V against time for different ψ
Preprints 77586 g018
Preprints 77586 g019
Figure 19. Profile of pressure for Model-V against time for different ψ
Figure 19. Profile of pressure for Model-V against time for different ψ
Preprints 77586 g019
Preprints 77586 g020
Figure 20. Profile of particle creation pressure for Model-V against time for different ψ
Figure 20. Profile of particle creation pressure for Model-V against time for different ψ
Preprints 77586 g020
Preprints 77586 g021
Figure 21. Profile of energy density for Model-VI against time for different ψ
Figure 21. Profile of energy density for Model-VI against time for different ψ
Preprints 77586 g021
Preprints 77586 g022
Figure 22. Profile of pressure for Model-VI against time for different ψ
Figure 22. Profile of pressure for Model-VI against time for different ψ
Preprints 77586 g022
Preprints 77586 g023
Figure 23. Profile of Particle creation pressure for Model-VI against time for different ψ
Figure 23. Profile of Particle creation pressure for Model-VI against time for different ψ
Preprints 77586 g023
Preprints 77586 g024
Figure 24. Profile of q and H for Model-VI against time for different m
Figure 24. Profile of q and H for Model-VI against time for different m
Preprints 77586 g024
Table 1. The nature of the deceleration parameter q for the different values of τ , m and μ
Table 1. The nature of the deceleration parameter q for the different values of τ , m and μ
τ m μ q Nature of q
0.2 0.2 > 0 +ve to -ve valued Phase transition
0.4 > 0 +ve to -ve valued Phase transition
0.6 > 0 -ve valued Accelerating
0.8 > 0 -ve valued Accelerating
1 > 0 -ve valued Accelerating
10 > 0 -ve valued Accelerating
0.4 0.2 > 0 +ve to -ve valued Phase transition
0.4 > 0 +ve to -ve valued Phase transition
0.6 > 0 +ve to -ve valued Phase transition
0.8 > 0 +ve to -ve valued Phase transition
1 > 0 -ve valued Accelerating
10 > 0 -ve valued Accelerating
0.6 0.2 > 0 +ve to -ve valued Phase transition
0.4 > 0 +ve to -ve valued Phase transition
0.6 > 0 +ve to -ve valued Phase transition
0.8 > 0 +ve to -ve valued Phase transition
1 > 0 -ve valued Accelerating
10 > 0 -ve valued Accelerating
0.8 0.2 > 0 +ve to -ve valued Phase transition
0.4 > 0 +ve to -ve valued Phase transition
0.6 > 0 +ve to -ve valued Phase transition
0.8 > 0 +ve to -ve valued Phase transition
1 > 0 -ve valued Accelerating
10 > 0 -ve valued Accelerating
1 0.2 > 0 +ve to -ve valued Phase transition
0.4 > 0 +ve to -ve valued Phase transition
0.6 > 0 +ve to -ve valued Phase transition
0.8 > 0 +ve to -ve valued Phase transition
1 > 0 -ve valued Accelerating
10 > 0 -ve valued Accelerating
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated