Prerpints.org logo
Preprint
Review

Gamma Ray Pulsars and Opportunities for the MACE Telescope

This version is not peer-reviewed.

Submitted:

27 June 2023

Posted:

29 June 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Rapidly rotating neutron stars with very strong surface magnetic fields are observed to emit pulsed emission in the whole range of electromagnetic spectrum from radio to high energy gamma-rays. These so called pulsars are known for their exceptional rotational stability. The radio emission from pulsars is generally believed to be powered by the rotational energy of neutron stars. More than 3000 pulsars have been currently known from radio observations, however, it is observed that a large population of pulsars is also bright in optical, X-rays and gamma-rays. The Fermi-LAT observations in the energy range above 100 MeV have discovered about 300 pulsars. However, origin of high energy non-thermal radiation from pulsars is not completely understood and remains an active area of research. In this contribution, we report a summary of observational features of the gamma-ray pulsars and perform pulsar population study to predict their detectability for the MACE gamma-ray telescope, which has just started its regular science operation at Hanle in India.
Keywords: 
Subject: 
Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

A high energy phenomena, the so called supernova explosion, takes place at the end of stellar evolution cycle of massive stars [49]. A huge amount of energy, released by the gravitationally collapsing stellar core, produces shocks that eject the outer layers of the progenitor star. This leads to the formation of relativistic compact objects such as a white dwarf, a neutron star or a black hole with a very high matter density [2]. The masses of white dwarfs and neutron stars are in the range 0.18-1.3M ⊙ and 1-3M ⊙ respectively. The white dwarfs are approximately Earth-sized while neutron stars have radius around 10km [3,4]. Such objects reach extreme physical conditions of density, temperature, pressure, strong surface magnetic fields and fast rotations. Generally, neutron stars are formed after the core collapse of stars with initial masses in the range 8-20M ⊙ and the corresponding supernova explosion asymmetrically ejects the matter at a very high velocity of ∼ 10 7 m s − 1 [5,6]. Asymmetric ejection of matter imparts natal kicks to the neutron star due to conservation of momentum. Consequently, the resulting kick force causes the rotation of neutron star unless it is exerted exactly head-on at the center of star. However, the exact physical process which kicks the neutron star initially at birth has not been clearly understood and is still under debate [7,8,9]. Rapidly spinning/rotating neutron stars with a surface magentic field strength above ∼ 10 8 G are referred to as pulsars [10,11]. The strength and structure of magnetic field play a significant role in describing the observational properties and ages of pulsars. Numerical simulations suggest that isolated pulsars (spherical neutron star with dipole magnetic field) follow the spin-down law of the form [12]
P P ˙ = 8 π 2 μ 2 3 I c 3 s i n 2 ( α )
where P is spin period of the pulsar, P ˙ is time-derivative of P or spin-down rate, μ and I are respectively the magnetic dipole moment and moment of inertia of the neutron star, α is the angle between magnetic and rotation/spin axes and c is speed of light in vacuum. Angle α is also referred to as the magnetic angle or the magnetic obliquity of the neutron star. The values of α close to 0 ∘ and 90 ∘ correspond to the aligned and orthogonal pulsars respectively. The field lines of strong magnetic field of pulsar are anchored to the outer crust of the neutron star. Resulting which, the rotation axis and frequency of rotation of the surface magnetic field are same as the pulsar rotation axis and its spin frequency respectively. A strong electric potential is produced along the magnetic poles due to the co-rotation of the magnetic field lines near the surface and outer crust of the neutron star. This electric potential generates a powerful current of charged particles traveling along the field lines in the magnetosphere [13,14]. The charged particles moving along the magnetic field lines create a radiation cone which is centered on the magnetic axis. Since, the magnetic axis does not coincide with the spin/rotation axis, series of periodic pulses are detected due to rotation of neutron star if the radiation cone sweeps past our line of sight. Therefore, the pulsars are considered as astronomical lighthouse. The pulsed radiation measured from pulsars spans over the entire electromagnetic spectrum rangeing from radio to high energy gamma-rays and is very precisely characterized by their spin period (P).
Historically, the first pulsar C P 1919 (CP:Cambridge Pulsar) or P S R B 1919 + 21 with P = 1.34s was discovered by Jocelyn Bell and Antony Hewish in 1967 at the Cambridge University using an array of diploes tuned to 81.5 MHz radio frequency. However, the official announcement was made in the February 24, 1968, edition of the prestigious Nature journal [10] and the Nobel Prize in Physics was awarded to Antony Hewish in 1974 for the discovery of pulsars. This breakthrough result was interpreted as the radial pulsations of either a neutron star or a white dwarf. Subsequently, about 30 pulsars were detetced using radio observations in a span of two years and a sudden decrease in the pular spin period (pulsar glitch) by about 3 parts in a million was also discovered in 1969 [15,16]. The discovery of first binary pulsar PSR B1913+16 by Russell Hulse and Joe Taylor in 1974 provided the first accurate measurement of neutron star mass [17]. The next important discovery of a millisecond pulsar PSR B1937+214 with P = 1.558ms resolved the puzzle of extremely steep radio spectrum of pulsars in 1982 [18]. A unique binary radio pulsar PSR J0737–3039A/B with P = 22ms and an orbital period of 2.4 hours was discovered in 2003 [19]. This binary system comprises two neutron stars of different ages and their orbit can be viewed exactly edge-on. Discovery of this eclipsing binary pulsar system is hailed as a milestone both in observational search as well as exploring the fundamental physics. Over the past 50 years, the pulsar astronomy has made a very impressive progress as the number of known pulsars in our Milky-Way Galaxy has rapidly grown to more than 3000 including isolated and binary pulsars with diverse characteristics over the entire electromagentic spectrum1. The distribution of latitudes and longitudes of the known pulsar population in the Milky-Way Galaxy are shown in Figure 1. It is evident that the Galactic latitude of most of the pulsars is close to zero. This suggests that the Galactic plane is populated with the pulsars. The peak of longitude at 0 ∘ or 360 ∘ implies that the pulsar population in the Galactic plane is concentrated in the region facing the Galactic Centre. A vast majority of these pulsars are observed in radio waveband and many have been detected in the optical, X-ray and high energy gamma-ray bands [20].
On the basis of plausible physical processes involved in the emission of radiation, pulsars are classified in three types: rotation powered pulsars, accretion powered pulsars and internal energy powered pulsars [21]. In the rotation powered pulsars, emission of electromagnetic radiation is attributed to the loss of rotational kinetic energy of neutron star due to the magnetic braking. This group of pulsars are further classified as classical radio pulsars, millisecond radio pulsars, and mildly recycled pulsars depending upon the spin period (P) and strength of neutron star surface magnetic field ( B p ). The classical radio pulsars exhibit P ∼ 1s and B p ∼ 10 11 − 10 14 G. Whereas millisecond radio pulsars and mildly recycled pulsars have P ≤ 20s, B p ≤ 10 10 G and P ∼ 20–100ms, B p ≤ 10 11 G respectively [22]. In the accretion powered pulsars, material accretion on to the neutron star is responsible for emission of energetic radiation. These pulsars are generally observed as a binary system consisting of a neutron star as a compact object and a main sequence companion star as a donor star. Depending on the mass of companion star, the accretion powered pulsars are classified as low-mass X-ray binary and high-mass X-ray binary. In low-mass X-ray binary pulsars, the surface magnetic field of neutron star is weak ( B p ≤ 10 11 G) due to extended phase of accretion [23]. Thermonuclear X-ray burst, accretion-powered millisecond pulsations, kHz quasi-periodic oscillations, broad relativistic iron lines, and quiescent emission are the main physical processes taking place in low-mass X-ray binary systems. On the other hand, high-mass X-ray binaries harbour neutron stars with relatively strong surface magnetic field B p ∼ 10 12 . These objects are mostly observed in X-rays with hard spectrum [24]. The X-ray emission from such pulsars has the signatures of Comptonisation due to interaction of accretion plasma with the magnetic field of neutron star and presence of Cyclotron broad absorption lines referred to as the Cyclotron Resonance Scattering Feature. Finally, the internal energy powered pulsars form a new class where exact physical mechanism for emission of radiation is not known. However, it is assumed that internal energy reservoir in the form of strong magnetic field decay or residual cooling powers the observed emission [25]. Magnetars, soft gamma ray repeaters and anomalous X-ray pulsars are believed to be member of the group of internal energy powered pulsars [26]. Another classification of known pulsars is also proposed on the basis of their measured spin period. According to this classification, pulsars are of two types: millisecond pulsars (MSP) and normal pulsars (NP). MSPs exhibit P ≤ 20ms and B p ∼ 10 8 − 10 14 G, whereas NPs have P > 20ms and B p ∼ 10 10 − 10 12 G. It is believed that MSPs in binary systems are spun up by accreting matter and angular momentum from companion stars in a so called recycling process [27].
The launch of large area telescope onboard the Fermi satellite in 2008 has led to the discovery of a number of gamma-ray pulsars. However, only a few of them have been detected so far by the ground-based gamma-ray instruments. In this paper, we mainly focus on the gamma-ray pulsars and explore the potential of recently commissioned MACE (Major Atmospheric Cherenkov Experiment) telescope to detect the pulsed emission above 20GeV. The outline of paper is the following. In Section 2, we discuss the empirical properties of pulsars. A brief review of gamma-ray pulsars is given in Section 3. In Section 4, we describe salient features of the MACE telescope. We discuss the results from the feasibilities studies for pulsar observations with MACE in Section 5. Finally we summarize in Section 6.

2. Pulsar Characteristics

A complete understanding of the underlying physical processes involved in the pulsed electromagnetic emission and geometry of the emission region is far from complete. Soon after the pulsar discovery, it was argued that, on the basis of observed features, the powerhouse of pulsar is a fast spinning/rotating neutron star with strong surface magnetic field [11]. The periodic nature of pulsar emission observed on Earth, with incredible timing accuracy comparable to the atomic clock, is understood in the frame-work of a lighthouse model as the magnetic axis of rotating neutron star sweeps across the line of sight of an observer. The emission mechanism is linked to the magnetic field affected co-rotating plasma in the pulsar magnetosphere with less understood structure and dynamics. It is still not clear whether the emission region is located out in the magnetosphere or close to the neutron star [28,29].
The spin-down law, given by Equation 1, is generally valid for any moment in the lifetime of the pulsars. Moreover, among the three parameters I, μ , and α , atleast two are expected to change for a real pulsar. Therefore, B p suffers a slow decay due to the Ohmic dissipation of electric currents in the neutron star crust [30]. The time evolution of obliquity angle α is given by
d α d t ∝ B p 2 P 2 s i n ( α ) c o s ( α )
Measurements from radio observations suggest that α evolves on a timescale of 10 7 years [31]. This can lead to a situation where α becomes zero and magnetic axis of an isolated pulsar eventually aligns with its rotation axis on a timescale of P / P ˙ . The moment of inertia I varies slightly only during sudden small changes in the rotation velocity of pulsar, generally referred to as pulsar-glitches [32]. This is attributed to the transfer of angular momentum between the crust and another component of the neutron star. The pulsar period P also changes continuously for the rotation powererd pulsars due to the loss of kinetic energy. Therefore, most of the pulsars slow down over the time despite their P being very stable and the slow-down rate is given by P ˙ . The parameters such as P, P ˙ and higher order time-derivatives of P are determined from the pulse time-of-arrival measurements over long intervals ranging from hours to decades [33]. The precision in the measurement of the pulse time-of-arrival critically decides the amount of useful information that can be extracted for a pulsar observationally. The measured pulse time-of-arrival by a telescope on Earth corresponds to a non-inertial frame of reference measurement. Therefore, pulse time-of-arrivals are first translated to an inertial reference frame, normally the solar-system barycentre (an appropriate inertial reference frame), to remove the effects of Earth’s rotational and orbital motion. A barycentric pulse arrival time is estimated for individual time-of-arrival on the basis of a model for the intrinsic properties of the pulsar including its astrometric, rotational, propagation effects in interstellar medium and other parameters. The difference between estimated and observed pulase arrival times is referred to as the timing residual and its study is very important for all pulsar timing measurements.
From the long-term pulsar timing measurements, the slow-down rate is derived as
P ˙ = d P d t = − 1 ν 2 d ν d t
where ν = 1 / P is the pulse freqeuncy or spin-frequency of the pulsar. The intrinsic rotation of an isolated pulsar can be expressed by the Taylor-series expansion of ν or P about a reference time t 0 as [33]
ν ( T ) = ν 0 + d ν 0 d t ( T − t 0 ) + d 2 ν 0 d t 2 ( T − t 0 ) 2 2 + . . . . .
or
P ( T ) = P 0 + d P 0 d t ( T − t 0 ) + d 2 P 0 d t 2 ( T − t 0 ) 2 2 + . . . . .
where T is pulsar proper time, ν 0 = 1 / P 0 is the initial spin frequency at reference epoch t 0 . The number of rotations completed by the neutron star from t 0 is known as pulsar phase ( ϕ ). The fractional part of ϕ at a given epoch carries the information on orientation of pulsar at that time. Pulses with same fraction of ϕ are measured when pulsar orientation is aligned with the observer. Distribution of ϕ attributed to each event recorded by a detector/telescope is known as pulsar phase diagram or phasogram. This describes the pulsar rotation model in a reference frame comoving with the pulsar or pulsar-ephemeris which takes into account the changes in spin frequency with time due to the rotational energy loss. The pulsar spin down contributes to the time-derivatives of ν 0 or P 0 . From Equation 4, pulse number N can be written as [34]
N = N 0 + ν 0 ( T − t 0 ) + 1 2 d ν 0 d t ( T − t 0 ) 2 + 1 6 d 2 ν 0 d t 2 ( T − t 0 ) 3 + . . . . .
where N 0 is the number of pulses at t 0 . The pulsar proper time T corresponds to its time at solar-system barycentre of infinite frequency up to a constant and is expresses as [34]
T = t t + t c − D × D M f 2 + Δ R + Δ S + Δ E
where t t is pulse arrival time at telescope, t c is relative time correction, ( D × D M / f 2 ) is dispersion correction, f is observation frequency, Δ R is delay due to Earth-motion around Sun, Δ S is the Shapiro delay due to space-time curvature, and Δ E is the Einstein delay. For a pulsar in binary system, extra time delays caused by the orbital motion of neutron star and gravitational field of the companion star are also included in T.
The distribution of P ˙ versus P or P − P ˙ diagram is used to identify the underline physical process in the distinct group of pulsars [35]. For rotation powered pulsars (i.e. NPs), values of P (0.3-3 s) and P ˙ ( ∼ 10 − 15 s s − 1 ) are measured with high accuracy through the pulsar-timing measurements. For MSPs (mostly observed in binary systems), P is mostly less than 20ms and P ˙ ranges from 10 − 18 s s − 1 to 10 − 22 s s − 1 . The smaller values of P ˙ for MSPs imply that their P is more stable than that of NPs on a longer timescale. The knowledge of P and P ˙ is also used to estimate the magnetic field at the pulsar surface as [36]
B p ≈ 10 12 P 1 s P ˙ 10 − 15 s s − 1 G
assuming a magnetic-dipole field structure. However, the actual B p could be much stronger due to presence of higher order magnetic poles at the neutron star surface. The spin-down history of an isolated pulsar can be captured by its P and P ˙ . If the initial spin period P 0 is much less than P, (Equation 5), we have the characteristic age of pulsar given by [30]
τ c h = P 2 P ˙
This corresponds to the time since the pulse period was zero and is used to estimate the true pulsar age ( τ p ). The lines of constant τ c h in the P − P ˙ diagram are known as death line. A simplified view of pulsars suggests that the evolution of radio pulsars proceeds along the line of constant magnetic field and descends towards the death line in the P − P ˙ diagram. After crossing the death line, a pulsar becomes radio quiet. The true age of a rotation powered pulsar is expressed as
τ p = 2 τ c h n − 1 − τ 0
where τ 0 is initial spin-down timescale and n is the braking-index which describes the secular spin down of pulsar. The braking-index is defined as [37]
n = ν ν ¨ ν ˙ 2 = 2 − P P ¨ P ˙ 2
It is a characteristic tool to probe the magnetic field evolution. n = 3 and 5 correspond to the braking due to the magnetic-dipole and gravitational wave emission respectively. Braking by pulsar winds, which deform the magnetosphere, is characterized by the value of n ranging between 1.0 to 3.0. It is also used to describe the spin-down of neutron star or pulsar using the torque equations as
ν ˙ = − K ν n
where K is a proportionality constant related to energy loss mechanism of pulsar [38]. In case of a rotating magnetic dipole approximation, the spin-down luminosity ( L s d ) of pulsar is given by the rotation energy loss of the neutron star, i.e.
L s d = − d d t E r o t = 4 π 2 I P ˙ P − 3
where E r o t is the rotational kinetic energy of neutron star and I is its moment of inertial [4]. This expression can be further simplified as
L s d = 4 π 2 I P 0 2 ( n − 1 ) τ 0 1 + τ p τ 0 − ( n + 1 ) ( n − 1 )
and
τ 0 = 3 c 3 I P 0 2 4 π 2 B p 2 R 6
where R is the radius of neutron star. For magnetic dipole braking ( n = 3 ), Equation 14 simply reduces to
L s d ≈ 1.1 × 10 34 τ p 10 6 y r − 2 e r g s − 1
This suggests that the braking timescale, over which loss of rotational energy of neutron star will slow down the pulsar spin, is ∼ 10 6 years. Since L s d also depends on B p 2 , MSPs are more lumnious than NPs for a given surface magnetic field strength of the neutron star [36].
Thermal emission from the surface of neutron star can be distinguished from the non-thermal emission arising from the pulsar magnetosphere in the X-ray band. Due to strong gravitational field of neutron star, general relativistic effects should be invoked in the interpretation of the observed X-ray luminosity of a pulsar [39]. The apparent bolometric thermal luminosity measured by a distant observer is given by
L o b s t h = L t h ( 1 + z b ) − 2
where L t h is the thermal luminosity emitted from the surface of neutron star and z b is the surface gravitational redshift. The apparent radii of neutron star is
R o b s = R ( 1 + z b )
and the atmosphere redshifted effective temperature is
T o b s = T 1 + z b
For a canonical neutron star, R = 10km, M = 1.4 M ⊙ , and z b ≈ 0.15 , the general relativistic effects may be important because the distantly observed thermal luminosity will be larger than the intrinsic luminosity by a factor of 1.32 or 32% higher.

3. Gamma-ray Pulsars

First gamma-ray pulsation at energies above 50MeV was detected from the Crab pulsar (NP 0532) in 1971 by a detector consisting of a multiplate spark chamber in a balloon-borne experiment [40]. These gamma-ray pulsations were observed at the radio period ( P ≈ 33ms) of the source. Launch of Small Astronomy Satellite (SAS-2) in 1972 confirmed the pulsed gamma-ray emission from the Crab and Vela pulsars [41,42]. The number of radio pulsars increased rapidly after their first discovery, but Crab and Vela remained only known gamma-ray pulsars for more than two decades after their first detection. Subsequently, EGRET (Energetic Gamma Ray Experiment Telescope), onboard the Compton Gamma Ray Observatory, was launched in 1991 to search for more gamma-ray pulsars apart from exploring the high energy Universe. It detected a total of six gamma-ray pulsars (Crab, B1509-58, Vela, B1706-44, B1951+32, Geminga, and B1055-52) and a few plausible candidates during its operation. Finally, the large area telescope, onboard the Fermi satellite, has been able to discover about 300 gamma-ray pulsar above 100 MeV energies in a time span of approximately 15 years since its launch in 2008 [43].

3.1. Fermi-LAT Pulsars

Until 2008, pulsed gamma-ray emission was mainly detected from pulsars that were initially observed in lower energy bands. Therefore, discovery and identification of new gamma-ray sources was the main science goal of the Fermi-LAT [44]. Due to its large field of view of ∼ 2.4sr, the Fermi-LAT completes continuous mapping of whole sky in about 3 hours in survey mode. Therefore, observations of a few weeks to few months are sufficient to build an average pulse profile for confirming a gamma-ray source as pulsar. The photon collection by the Fermi-LAT, with an accuracy better than 1 μ s, helps in the detection of even rapid pulsations from millisecond pulsars. The first Fermi-LAT pulsar catalog containing 46 high-confidence pulsed detections in the energy range 0.1-300 GeV was released in 2010 using only the first six months of its observation [45]. This included discovery of 16 new gamma-ray pulsars and confirmation of pulsed gamma-ray emission from 24 known pulsars. Subsequently, 117 gamma-ray pulsars with high-confidence detection at energies above 0.1 GeV were reported in the Second Fermi-LAT pulsar catalog using first three years of data [46]. This sample of 117 gamma-ray pulsars was divided into three classes: MSPs, young radio-loud, and young radio-quiet pulsars. The more recent 12-year Fourth Source Catalog of the Fermi-LAT identifies about 300 gamma-ray pulsars [43] which is approximately 10% of the total pulsar population2. The increase in number of gamma-ray pulsars detected by the Fermi-LAT so far is depicted in Figure 2. It is evident that the population of gamma-ray pulsars has continued to grow after the launch of Fermi satellite. The P − P ˙ diagram of the gamma-ray pulsars suggests that a large fraction of Fermi-LAT detected pulsars can be identified as rotation powered radio-loud MSPs [47]. Also, a significant fraction of these pulsars exhibit no emission in the radio band hence the name radio-quiet pulsars. A comparative study of this relatively large population has led to new understanding of the emission process and geometry of the gamma-ray pulsars [48]. The differential energy spectra of pulsars in the energy range 0.1 GeV-1 TeV, measured by the Fermi-LAT, are significantly curved and can be well fitted with a super-exponential cutoff power law of the form [43]
d N d E = K E E 0 d b − Γ s e x p d b 2 1 − E E 0 b
where K is normalization (flux density at the reference energy E 0 ), b and d are referred to as exponential index and spectral curvature respectively, and Γ s is the spectral slope. Γ s and d are designated as spectral shape parameters.

3.2. Gamma-Ray Emission

The availability of a good statistics and high quality data on gamma-ray pulsars over the last 50 years has provided a better perspective on the properties of their gamma-ray emission. The primary radiative processes for bulk γ -ray emission from pulsars are the synchrotron-curvature radiation and inverse Compton scattering due to relativistic charged particles in the magnetosphere of neutron star. Therefore, the problem of high energy emission from pulsars is two fold: acceleration of charge particles to relativistic energies and radiative processes associated with the relativistic charge particles. According to the famous Goldreich-Julian model, the neutron star is considered to be a uniformly magnetised perfectly conducting sphere with an internal magnetic field and an external dipole magnetic field [13]. The external magnetic field of neutron star affects the pulsar magnetosphere which is filled with ultra-relativistic electron-positron pairs and is assumed to be in ideal magnetohydrodynamic state or an ideal plasma with infinite conductivity. However, the exact structure and dynamics of pulsar magnetosphere are poorly understood. The charged particles at the surface of neutron star experience a Lorentz force due to its rotation. Since the neutron star is assumed to be perfect condutor, the surface charges are redistributed so that the electric force counter balances the magnetic force, leading to a charge separation. The external electric field requires a continuous electric potential at the surface of neutron star and the electric force on surface charges greatly exceeds the gravitational attraction. This suggests that the accelerating electric field extracts particles from the surface of neutron star and fills the magnetosphere. The number density of charge particles at the surface of neutron star is given by [13]
n e = 7 × 10 − 2 B p P c m − 3
This simple model has several challenges such as the problem of charge supply (considered only from the surface of neutron star) and question of return current or charge neutrality & its inherent instability despite many successes. Pair-production mechanisms, in the extreme environments of pulsars, are invoked to ensue the particle-photon cascades [50]. One photon pair-production ( e ± -pair) may take place in the presence of a strong magnetic field (B) if the following threshold condition is satisfied [51]
E γ B s i n θ ≥ 10 12.76
where E γ is the photon energy in units of m e c 2 and θ is angle between direction of photon propagation and magnetic field. Collision between two high energy photons may produce an e ± -pair in a region devoid of magnetic field, if their energies satisfy the threshold condition [52]
E γ 1 E γ 2 = 2 ( m e c 2 ) 2 ( 1 − c o s θ )
where E γ 1 & E γ 2 are energies of two photons undergoing collision and θ is the angle between their momenta. The photon-photon collision may also lead to e ± -pair production in the presence of strong magnetic field provided the e ± -pair have non-zero velocity to ensure the conservation of parallel momentum and energy.
An electric field is required to accelerate the charge particles along the neutron star magnetic field lines to explain the observed non-thermal high energy radiation from pulsars. But the electric field, perpendicular to the magnetic field lines everywhere in the magnetosphere, implies no acceleration of charged particles. Geometrically, there exist several popular sites with non-zero electric field component parallel to the magnetic field lines due to breaking down of the ideal magnetohydrodynamic conditions in the pulsar magnetosphere. These privileged regions are considered as the accelerating and dissipative sites of the magnetospheric plasma and their locations play an important role in the high energy γ -ray emission from pulsars which is generally described by Equation 20.
Absence of plasma in vacuum gaps (often called accelerating gaps) provides three profound regions namely Polar Cap, Outer Gap and Slot Gap with non-zero electric field for acceleration of charge particles in the pulsar magnetosphere. These scenarios are primarily based on the Goldreich-Julian model [13] for the case of an aligned rotator (a neutron star with magnetic dipole moment along its rotation axis). The dipolar magnetic field lines inside the light cylinder (a boundary where an object co-rotating with the neutron star would need to move at the speed of light to maintain co-rotation) form closed loops or closed field lines. On the other hand, the magnetic field lines outside the light cylinder cannot form loops and are referred to as open field lines. Inside the light cylinder, particles move along the closed field lines and make the so called co-rotating magnetosphere. The electric potential corresponding to each magnetic field line is associated with the latitude of the origin of field lines on the neutron star surface. For an aligned rotator, field lines originate close to the equator (low latitude) correspond to very high electric potential. If these field lines are open, the positively charged particles tend to move along these lines and stream outward. The open field lines originating above the equator (high latitude) correspond to low electric potential. This causes negatively charged particles to move outward along the field lines. The charge density calculations in the magnetosphere suggest that it consists of separate conical regions of negatively and positively charged particles. With this brief description of the pulsar magnetosphere, different acceleration models (also known as vacuum gap models) are summarized below:
  • Polar Cap: Historically, this is the first model considered for acceleration of charge particles in the pulsar field by considering the case of an anti-aligned rotator (magnetic dipole vector and rotation vector are directly opposite each other) wherein the charge density and electric potential corresponding to the magnetic field lines are flipped. This causes the positively charge particles to move outward along the open field lines. A charge density depletion in the conical regions near the magnetic poles of neutron star provides a large electric potential for acceleration of charge particles [53]. Particles are accelerated along the open field lines to altitudes where they attain high enough Lorentz factors to emit gamma-ray photons. However, the strong magnetic field near the poles causes the absorption of high energy gamma-ray photons via magnetic pair-production. This leads to a gamma-ray spectra of the form given by Equation 20 with a cutoff energy in the range 1-10 GeV. Therefore, this model is not able to explain gamma-ray emission above 10 GeV from many pulsars deteced by the Fermi-LAT [46].
  • Outer Gap: This model is based on the case of an aligned rotator wherein positively charged particles move along the open field lines outside the light cylinder. Resulting which, a gap, extending along the last closed field line up to the light cylinder, is created. A charge density depletion leads to a large electric field component parallel to the magnetic field for accelerating the particles to relativistic energies required to emit high energy gamma-rays by the curvature emission [54]. These models require no polar cap pair-production and are invoked to explain the gamma-ray spectra of most of the Fermi-LAT pulsars [46].
  • Slot Gap: This scenario is assumed to lie between the polar cap and outer gap. The slot gap is considered as a narrow set of magnetic field lines near the boundary between open and close field lines [55]. In this model, charged particles, originating from the neutron star surface, are accelerated from the polar cap along the last open field lines up to high altitudes (of the order of the radius of light cylinder). But, later works show that this model is not able to explain the observed gamma-ray spectra of pulsars [56].
An alternative model to the above vacuum gap models is the current sheet model where acceleration of particles is attributed to the magnetic reconnection process [57]. This model is based on Monte-Carlo simulations employing Particle-In-Cell scheme of the plasma physics. It has now been firmly established that the magnetosphere of a non-aligned rotator entails a current sheet outside its light cylinder. The rotating distribution pattern of this current sheet moves at linear superluminal speed and emits the high energy radiation [58]. This provides a reasonable explanation for non-thermal broadband radiation measured from pulsars with a phase lag between the radio and gamma-ray peaks [59]. This model has first time provided an acceptable fit to the exceptionally broad gamma–ray spectrum of the well known Crab pulsar [60]. Therefore, it is utterly important to detect high energy gamma-ray emission above from a large sample of pulsars to discriminate between different emission models. Pulsed emission above 50 GeV has been detected from a number of pulsars but only four very high energy gamma-ray pulsars (Crab, Vela, Geminga, PSR B1706-44) have been detected in the GeV-TeV range by the ground-based state-of-the-art gamma-ray telescopes. Thus dedicated gamma-ray monitoring of pulsars with low energy threshold ground-based telescopes is one the main science drivers of the very high energy gamma-ray astronomy at present.

4. MACE Telescope

Major Atmospheric Cherenkov Experiment (MACE) is an extremely large state-of-the-art gamma-ray telescope located at an altitude of ∼4.3 km at Hanle, Ladakh in India. The telescope was commissioned in September 2021 after its successful first light from the standard candle Crab Nebula in April 2021 [61]. Subsequently, various operating parameters of the telescope were optimized and tuned using a large number of engineering runs and repeated observations of the Crab Nebula. The telescope has been deployed for science data collection for more than one year. During this period, it has successfully detected high energy gamma-ray photons from a number candidate sources including the recent giant flaring episode of the radio galaxy NGC 1275 in December 2022 and January 2023 [62,63]. The MACE telescope is designed to cover the high energy gamma-ray band above 20 GeV with a point source sensitivity better than the existing stand-alone imaging atmospheric Cherenkov telescopes in the world [64,65]. At present, the telescope is capable of detecting the high energy gamma-ray photons from Crab Nebula with a sensitivity of 5 σ in a few minutes (internal communication) in the energy range above 50 GeV. A picture of the MACE telescope at Hanle is shown in Figure 3. It is equipped with a big quasi-parabolic light reflector of 21 m diameter and 25 m focal length. This offers a total light collection area of ∼ 340 m 2 . Such a large area is achieved by using a tessellated structure comprising 356 mirror panels of size 0.986 m × 0.986 m each. Each panel consists of 4 square-shaped spherical metalic mirror facets of size 0.488 m × 0.488 m each [66] with similar focal length. The reflecting surface of the mirror facets, coated with a protection layer of S i O 2 of thickness ∼ 120 nm, has an average reflectance of ∼ 85%. An active mirror alignment control system employing linear actuators and diode-lasers fitted on each panel is used to obtain best possible parabolic approximation and optimum focusing in all orientations of the basket. An imaging camera at the focal plane has an optical field of view of 4 . 36 ∘ × 4 . 03 ∘ and a uniform pixel resolution of 0.125 ∘ . It consists of 1088 photo-multiplier tubes (PMTs) with high quantum efficiency (above 30%) and medium gain (∼10 4 ). The MACE camera is custom-designed, event-driven system with state-of-the-art technologies for in-house signal processing electronics and high-speed data acquisition. The entire telescope structure is supported by an altitude-azimuth drive system. With telescope’s moving weight of 180 ton, the drive system enables pointing and tracking of a gamma-ray source with an accuracy of ∼ 1 arcmin in the presence of wind blowing at a speed of up to 45 km/h. A data archival storage system with a capacity of 80 TB is housed in the control room at the telescope site for safe and secure storage of the MACE data as a large data volume of ∼ 50 GB is generated during every hour of observation.
Combination of large light collector of the telescope and high altitude of the site offers a unique opportunity to achieve a low gamma-ray energy threshold close to ∼ 20 GeV of MACE. It helps in exploring the gamma-ray Universe beyond a redshift z ≥ 2 [67]. The low threshold energy of MACE makes it an ideal instrument for observation of gamma-ray pulsars detected by the Fermi-LAT.

5. Pulsars with MACE

The gamma-ray spectra of most of the pulsars, observed by the Fermi-LAT, have cutoff energy in the range 1-10 GeV. Due to this, the gamma-ray flux at higher energy end of the spectrum decreases very fast. Therefore, ground-based telescopes with better sensitivity than Fermi-LAT in the energy range above 50 GeV play crucial role in determining the pulsar spectra in very high energy band. With this motivation, we have developed a formalism based on following arguments to select a sample of Fermi-LAT pulsars for their observation with the MACE telescope.
In general, pulsar light curves or phasograms exhibit two peak structure. The first peak position at phase P 1 is attributed to the radio emission and is therefore referred to as main pulse. This is assigned zero phase and the position of second peak at phase P 2 is calculated with respect to P 1 . However, there exist pulsars like Geminga which have only one peak in their phasogram. The pulse amplitude corresponding to these peaks changes with the energy and P 2 peak is observed to dominate with increasing energy. Therefore, observation of pulsars in very high energy range by the ground-based telescopes like MACE is governed by the detection of pulse at P 2 at 5 σ confidence level in their phasogram over the huge isotropic cosmic ray background mainly due to protons. Thus, if a gamma-ray pulsar is residing within the nebula, both gamma-rays from nebula and cosmic ray protons will act as background for pulsar detection with ground-based telescopes. These background events lack in periodicity and hence no phase, whereas photons originating from the pulsars have well defined phase associated with their rotation. Thus, the background events are uniformly distributed in the light curve or phasogram of a pulsar and gamma-ray signal from a pulsar will pile up in a particular phase-bin. If N b i n s is the number of bins in the phasogram of a pulsar, then background will get reduced by a factor of N b i n s . For N b i n s = 30, the observation time required for detection of dominant gamma-ray peak ( T P ) in the phasogram of a pulsar at 5 σ statistical significance level with the MACE telescope is estimated as
T P ( h o u r s ) = 0.025 × 1.66 × 10 − 9 I P 2
where I P is the integral flux of dominating peak above 30 GeV in units of p h c m − 2 s − 1 . We apply this methodology to two well known gamma-ray pulsars Crab and Geminga for estimating the expected time for MACE observations as their gamma-ray spectra are available in the energy range covered by the MACE telescope.

5.1. Crab Pulsar

Crab pulsar (PSR J0534+2200) is the most studied pulsar in all energy bands from Radio to TeV and also the first pulsar detected by any ground-based gamma-ray telescope. It is normal pulsar with P = 33 ms and P ˙ = 4.2 × 10 − 13 s s − 1 . It is among the few pulsars that have been detected across the entire electromagnetic spectrum from radio up to gamma rays of beyond 1 TeV [68]. Its emission profile has three components: two dominant pulses separated by 0.4 in observed from radio to TeV gamma-rays and third, bridge component. The main pulse corresponding to P 1 at phase 0 dominates at radio frequencies. The second pulse corresponding to P 2 at phase 0.4 (also referred to as interpulse) is weaker at radio frequnecies and becomes dominant at very high energy gamma-rays. The bridge component (defined as the pulse phase between the main pulse and the second pulse) is observed in gamma-rays up to 150 GeV [68]. The stereoscopic MAGIC telescope has detected signal at 6.6 σ and 8.8 σ for P 1 and P 2 respectively in 152 hours of carb pulsar observations at zenith angles below 35 ∘ . The differential energy spectra of gamma-ray photons corresponding to P 1 and P 2 are described by a power law in the range 70 GeV to 1.5 TeV. The P 2 spectrum is relatively hard and corresponding integral flux is two times that of P 1 . For I P = I P 2 = 3.35 × 10 − 11 p h c m − 2 s − 1 , the corresponding detection time for MACE is estimated to be T P ∼ 61.38 hours using Equation 24.

5.2. Geminga

Geminga pulsar (PSR J0633+1746) is a radio-quiet gamma-ray pulsar with P = 237 ms and P ˙ = 1.1 × 10 − 14 s s − 1 . Located at a distance of 250 pc from Earth, it is one of the closest gamma-ray pulsar. The MAGIC telescope has detected pulsed gamm-ray signal from Geminga at 6.3 σ statistical significance level in 80 hours of observations [69]. Only P 2 peak is observed to be dominant in the phasogram in the energy range 15-75 GeV. The corresponding integral flux is estimated as I P = I P 2 = 2.18 × 10 − 11 p h c m − 2 s − 1 . For this flux level, the total observation time required for MACE observations in the energy range 30 GeV-5 TeV is calculated to be T P ∼ 144 hours.

5.3. Pulsar Catalog for MACE

As discussed in Section 3.1, the current population of gamma-ray pulsars detected by the Fermi-LAT is ∼ 300. The distribution of integral energy flux in the energy range 0.1–100 GeV for all the Fermi-LAT pulsars is shown in Figure 4. It is observed that majority of the pulsars have high energy flux ∼ 1.4 × 10 − 11 e r g c m − 2 s − 1 which is typically two order less than the corresponding crab pulsar flux. The Fermi-LAT spectra of most of the pulsars are described by Equation 20. The cutoff energy can be approximately calculated as
E c = E 0 × b 2 d 1 b
The distribution of cutoff energy ( E c ) for all the Fermi-LAT pulsars is reported in Figure 5. It is found that most of the pulsars have cut-off energy close to 0.8 GeV whereas only 33 pulsars (out of 292) have E c ≥ 2 GeV.
Applying the visibility criteria of the astrophysical sources from a given observatory, only 96 Fermi-LAT pulsars are found to be visible from the MACE site at hanle (32.8 ∘ N, 78.9 ∘ E). Next criteria is the identification of pulsars which have E c ≥ 2GeV. This constrain further reduces the number of pulsars from 96 to 8. At last, we check for the significance of pulsation in the energy range 10-30 GeV, overlapping with MACE, to be more than 2 σ . Based on the above criterion, we are left with only 6 pulsar candidates (other than Crab and Geminga) from the 4FGL-DR3 catalog for MACE observations. A summary of these sources is given in the Table.

6. Summary and Outlook

Gamma-ray pulsars represent a dominant poupulation of Galactic sources in the Universe. However, emission of very high energy gamma-ray photons from pulsars remains a fundamental problem in astrophysics even after more than 50 years of discovery. Individual pulsars of the Fermi-LAT catalog have not been observed so far by the ground-based telescopes except a few which have exhibit giant pulses such as Crab, Geminga and Vela. In this work, we have briefly reviewed the different aspects of the gamma-ray pulsars and outline the importance of recently commissioned MACE telescope in this field. A total of 6 pulsars, other than very high energy gamma-ray pulsars Crab and Geminga, have been identified as probable candidates for MACE observations in upcoming times.

Author Contributions

A. Pathania, Conceptualization, Data Curation and original draft preparation; K. K. Singh, Conceptualization and original draft preparation; K. K. Yadav, Review and editing

Funding

“This research received no external funding”

Conflicts of Interest

“The authors declare no conflict of interest.”

References

  1. Janka, H. -Th. Theory of core-collapse supernovae. Phy Rep 2007, 442, 38–74. [Google Scholar] [CrossRef]
  2. Shapiro, S. L. Black holes, white dwarfs, and neutron stars: The physics of compact objects.John Wiley & Sons 1983.
  3. Miller, M. C. The masses and spins of neutron stars and stellar-mass black holes. Phy Rep 2015, 548, 1–34. [Google Scholar] [CrossRef]
  4. Singh, K. K. Properties of white dwarf in the binary system AR Scorpii and its observed features. MPLA 2021, 36, 2150096. [Google Scholar] [CrossRef]
  5. Woosley, S. E. The evolution and explosion of massive stars. Rev Mod Phys 2002, 74, 1015–1071. [Google Scholar] [CrossRef]
  6. Müller, B. Hydrodynamics of core-collapse supernovae and their progenitors. LRCA 2020, 6, 3. [Google Scholar] [CrossRef]
  7. Spruit, H. Birth kicks as the origin of pulsar rotation. Nature 1998, 393, 139–141. [Google Scholar] [CrossRef]
  8. Janka, H. -Th. Supernova Fallback as Origin of Neutron Star Spins and Spin-kick Alignment. ApJ 2022, 926, 9. [Google Scholar] [CrossRef]
  9. Coleman, M. S. B. Kicks and induced spins of neutron stars at birth. MNRAS 2022, 517, 3938–3961. [Google Scholar] [CrossRef]
  10. Hewish, A. Observation of a rapidly pulsating radio source. Nature 1968, 217, 709. [Google Scholar] [CrossRef]
  11. Gold, T. Rotating neutron stars as the origin of the pulsating radio sources. Nature 1968, 218, 731. [Google Scholar] [CrossRef]
  12. Spitkovsky, A. Time-dependent Force-free Pulsar Magnetospheres: Axisymmetric and Oblique Rotators. ApJL 2006, 648, L51–L54. [Google Scholar] [CrossRef]
  13. Goldreich, P. Pulsar Electrodynamics. ApJ 1969, 157, 869. [Google Scholar] [CrossRef]
  14. Arons, J. Relativistic Particle Acceleration in Plerions. ApJS 1994, 90, 797. [Google Scholar] [CrossRef]
  15. Radhakrishnan, V. Detection of a Change of State in the Pulsar PSR 0833-45. Nature 1969, 222, 228. [Google Scholar] [CrossRef]
  16. Reichley, P. E. Observed Decrease 1n the Periods of Pulsar PSR 0833-45. Nature 1969, 222, 229. [Google Scholar] [CrossRef]
  17. Hulse, R. A. Discovery of a pulsar in a binary system. ApJL 1975, 195, L51–L53. [Google Scholar] [CrossRef]
  18. Backer, D. C. A millisecond pulsar. Nature 1982, 300, 615–618. [Google Scholar] [CrossRef]
  19. Burgay, M. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 2003, 426, 531–533. [Google Scholar] [CrossRef]
  20. Manchester, R. N. The Australia Telescope National Facility Pulsar Catalogue. AJ 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
  21. Konar, S. Neutron Star Physics in the Square Kilometre Array Era: An Indian Perspective. JoAA 2016, 37, 36. [Google Scholar] [CrossRef]
  22. Tauris, T. M. Five and a Half Roads to Form a Millisecond Pulsar. ASPC 2011, 447, 285. [Google Scholar]
  23. Bhattacharyya, S. Measurement of neutron star parameters: A review of methods for low-mass X-ray binaries. ASR 2010, 45, 949–978. [Google Scholar] [CrossRef]
  24. Caballero, I. X-ray pulsars: a review. MmSAI 2012, 83, 230. [Google Scholar]
  25. Kaspi, V. M. Grand unification of neutron stars. PNAS 2010, 107, 7147–7152. [Google Scholar] [CrossRef] [PubMed]
  26. Thompson, C. The Soft Gamma Repeaters as Very Strongly Magnetized Neutron Stars. II. Quiescent Neutrino, X-Ray, and Alfven Wave Emission. ApJ 1996, 473, 322. [Google Scholar] [CrossRef]
  27. Lorimer, D. R. Binary and Millisecond Pulsars. LRR 2008, 11, 8. [Google Scholar] [CrossRef]
  28. Baring, M. G. High-energy emission from pulsars: the polar cap scenario. ASR 2004, 33, 552–560. [Google Scholar] [CrossRef]
  29. Harding, A. K. High-Altitude Emission from Pulsar Slot Gaps: The Crab Pulsar. ApJ 2008, 680, 1378–1393. [Google Scholar] [CrossRef]
  30. . Igoshev, A. P. Evolution of Neutron Star Magnetic Fields. Universe 2021, 7, 351. [Google Scholar] [CrossRef]
  31. Tauris, T. M. On the Evolution of Pulsar Beams. MNRAS 1998, 298, 625–636. [Google Scholar] [CrossRef]
  32. Haskell, B. Models of pulsar glitches. IJMPD 2015, 24, 1530008. [Google Scholar] [CrossRef]
  33. Manchester, R. N. Pulsar timing and its applications. JPCS, 2017, 932, 012002. [Google Scholar] [CrossRef]
  34. Damour. T. Strong-field tests of relativistic gravity and binary pulsars. PRD, 1992, 45, 1840–1868. [Google Scholar] [CrossRef] [PubMed]
  35. Hobbs, G. Developing a Pulsar-Based Time Standard. Highlights Astronomy, 2015, 16, 207–208. [Google Scholar] [CrossRef]
  36. Pétri, J. Pulsar gamma-ray emission in the radiation reaction regime. MNRAS, 2019, 484, 5669–5691. [Google Scholar] [CrossRef]
  37. Igoshev, A. P. Braking indices of young radio pulsars: theoretical perspective. MNRAS, 2020, 499, 2826–2835. [Google Scholar] [CrossRef]
  38. Lyne, A. G. 45 years of rotation of the Crab pulsar. MNRAS, 2015, 446, 857–864. [Google Scholar] [CrossRef]
  39. Mitra, A. Thermal Radiation from Compact Objects in Curved Space-Time. Universe, 2022, 8, 504. [Google Scholar] [CrossRef]
  40. Browning, R. Detection of Pulsed Gamma Radiation from the Crab Nebula. NPS, 1971, 232, 99–101. [Google Scholar] [CrossRef]
  41. Kniffen, D. A. Gamma radiation from the Crab Nebula above 35 MeV. Nature, 1974, 251, 397–399. [Google Scholar] [CrossRef]
  42. Thompson, D. J. SAS-2 high-energy gamma-ray observations of the Vela pulsar. ApJL, 1975, 200, L79–L82. [Google Scholar] [CrossRef]
  43. Abdollahi, S. Incremental Fermi Large Area Telescope Fourth Source Catalog. ApJS, 2022, 260, 53. [Google Scholar] [CrossRef]
  44. Atwood, W. B. The Large Area Telescope on the Fermi Gamma-Ray Space Telescope Mission. ApJ, 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
  45. Abdo, A. A. The First Fermi Large Area Telescope Catalog of Gamma-ray Pulsars. ApJS, 2010, 187, 460–494. [Google Scholar] [CrossRef]
  46. Abdo, A. A. The Second Fermi Large Area Telescope Catalog of Gamma-Ray Pulsars. ApJS, 2013, 208, 17. [Google Scholar] [CrossRef]
  47. Limyansky, B. The Third Fermi Pulsar Catalog. AAS, 2019, 17, 109. [Google Scholar]
  48. Harding, A. K. The neutron star zoo. FrPhy, 2013, 8, 679–692. [Google Scholar] [CrossRef]
  49. Goldreich, P. Pulsar Electrodynamics. ApJ, 1969, 157, 869. [Google Scholar] [CrossRef]
  50. Daugherty, J. K. Electromagnetic cascades in pulsars. ApJ, 1982, 252, 337. [Google Scholar] [CrossRef]
  51. Sturrock, P. A. A Model of Pulsars. ApJ, 1971, 164, 529. [Google Scholar] [CrossRef]
  52. Gould, R. J. Opacity of the Universe to High-Energy Photons. PRL, 1966, 16, 252–254. [Google Scholar] [CrossRef]
  53. Ruderman, M. A. Theory of pulsars: polar gaps, sparks, and coherent microwave radiation. ApJ, 1975, 196, 51–72. [Google Scholar] [CrossRef]
  54. Cheng, Energetic Radiation from Rapidly Spinning Pulsars. I. Outer Magnetosphere Gaps. ApJ, 1986, 300, 500. [Google Scholar]
  55. Arons, J. Pair creation above pulsar polar caps : geometrical structure and energetics of slot gaps. ApJ, 1983, 266, 215–241. [Google Scholar] [CrossRef]
  56. Hirotani, K. Outer-Gap versus Slot-Gap Models for Pulsar High-Energy Emissions: The Case of the Crab Pulsar. ApJL, 2008, 688, L25. [Google Scholar] [CrossRef]
  57. Uzdensky, D. A. Physical Conditions in the Reconnection Layer in Pulsar Magnetospheres. ApJ, 2014, 780, 3. [Google Scholar] [CrossRef]
  58. Philippov, A. Pulsar Magnetospheres and Their Radiation. ARA&A, 2022, 60, 495–558. [Google Scholar]
  59. Ardavan, H. Radiation by the superluminally moving current sheet in the magnetosphere of a neutron star. MNRAS, 2021, 507, 4530–4563. [Google Scholar] [CrossRef]
  60. Ardavan, H. Congruity of the Crab Pulsar’s γ-ray spectrum with the spectral distribution of tightly focused caustics. A&A, 2023, 672, A154. [Google Scholar]
  61. Yadav, K. K. Commissioning of the MACE gamma-ray telescope at Hanle, Ladakh, India. Current Science, 2022, 123, 1428–1435. [Google Scholar] [CrossRef]
  62. Yadav, K. K. MACE detection of very high energy gamma-ray flare from the radio galaxy NGC 1275. ATel, 1582. [Google Scholar]
  63. Yadav, K. K. Detection of Renewed Gamma-Ray Flare from the Radio Galaxy NGC 1275 with the MACE telescope. ATel, 1585. [Google Scholar]
  64. Singh, K. K. 20 Years of Indian Gamma Ray Astronomy Using Imaging Cherenkov Telescopes and Road Ahead. Universe, 2021, 7, 96. [Google Scholar] [CrossRef]
  65. Singh, K. K. Gamma-ray astronomy with the imaging atmospheric Cherenkov telescopes in India. JoAA, 2022, 43, 3. [Google Scholar] [CrossRef]
  66. Dhar, V. K. Development of a new type of metallic mirrors for 21 meter MACE γ-ray telescope. JoAA, 2022, 43, 17. [Google Scholar]
  67. Tolamatti, A. Feasibility study of observing γ-ray emission from high redshift blazars using the MACE telescope. JoAA, 2022, 43, 49. [Google Scholar] [CrossRef]
  68. Ansoldi, S. Teraelectronvolt pulsed emission from the Crab Pulsar detected by MAGIC. A&A, 2016, 585, A133. [Google Scholar]
  69. Acciari, V. A. Detection of the Geminga pulsar with MAGIC hints at a power-law tail emission beyond 15 GeV. A&A, 2020, 643, L14. [Google Scholar]
1
https://www.atnf.csiro.au/research/pulsar/psrcat/
2
https://www.atnf.csiro.au/research/pulsar/psrcat/
Preprints 77810 g001
Figure 1. Distribution of Galactic latitude and longitude of more than 3000 known pulsars.
Figure 1. Distribution of Galactic latitude and longitude of more than 3000 known pulsars.
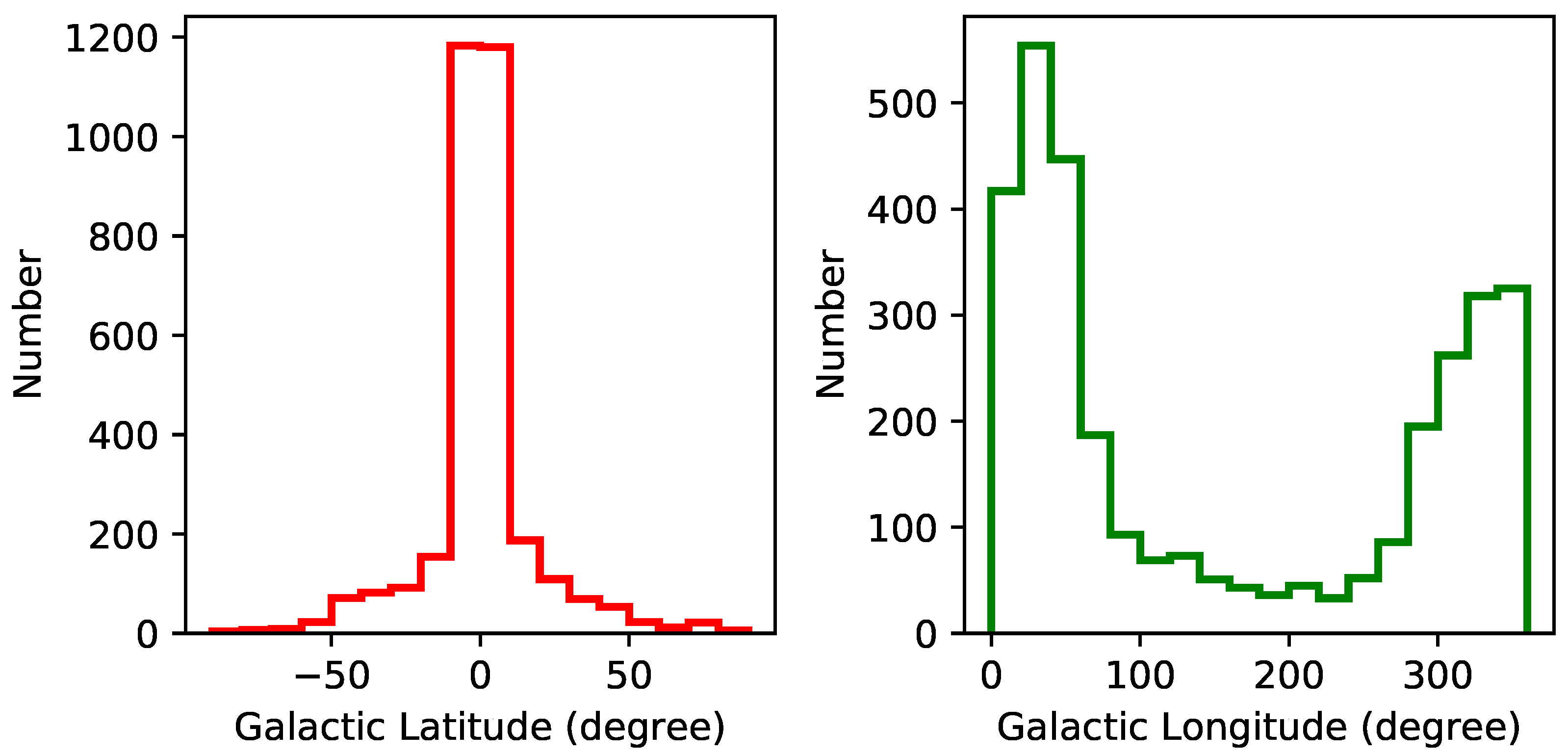
Preprints 77810 g001
Preprints 77810 g002
Figure 2. Evolution of number of gamma-ray pulsars in the successive Fermi-LAT source catalogs.
Figure 2. Evolution of number of gamma-ray pulsars in the successive Fermi-LAT source catalogs.
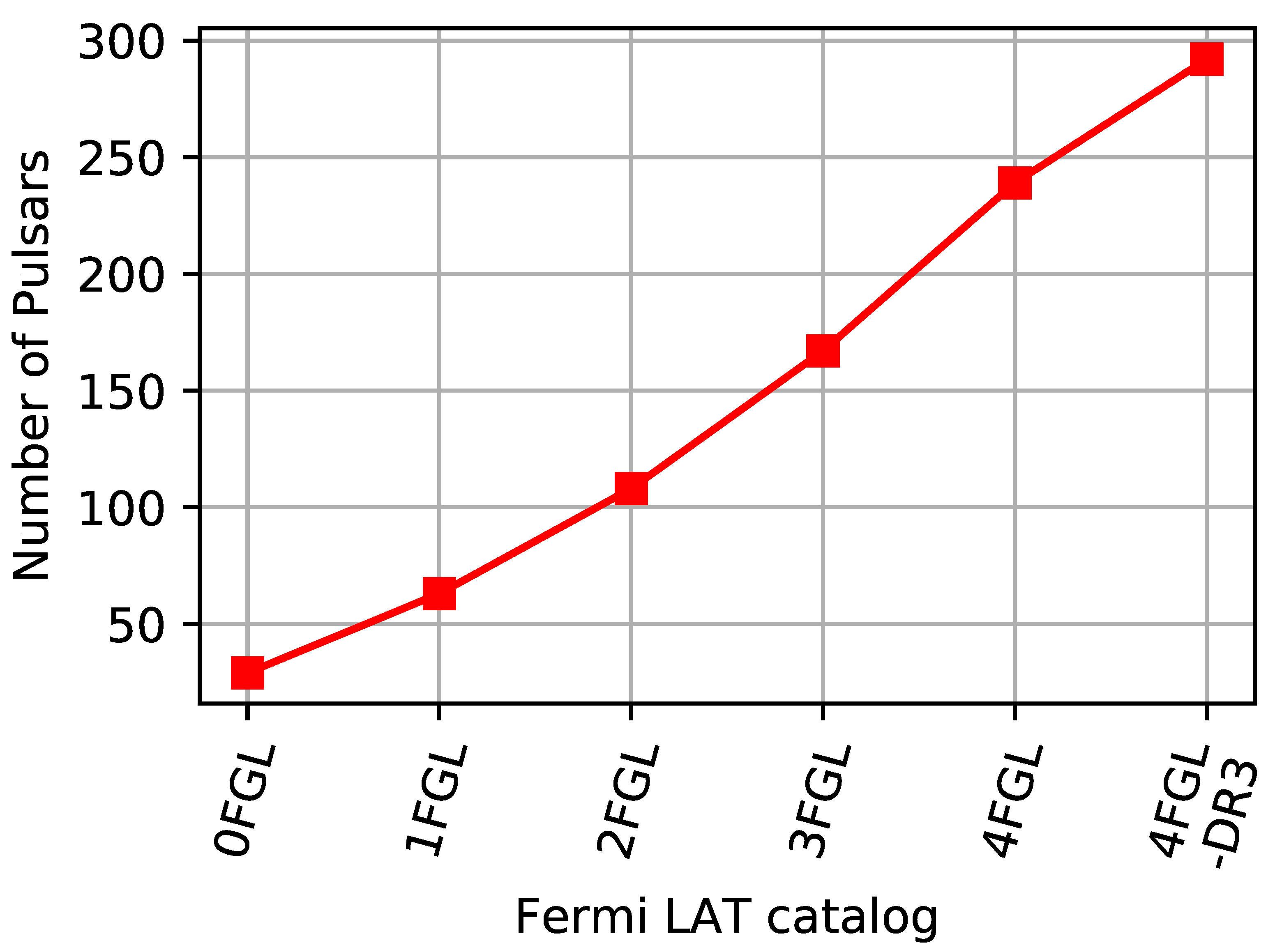
Preprints 77810 g002
Preprints 77810 g003
Figure 3. MACE gamma-ray telescope at Hanle, Ladakh, India.
Figure 3. MACE gamma-ray telescope at Hanle, Ladakh, India.
Preprints 77810 g003
Preprints 77810 g004
Figure 4. Histogram of energy flux of Fermi-LAT pulsars in the energy range 0.1-100 GeV.
Figure 4. Histogram of energy flux of Fermi-LAT pulsars in the energy range 0.1-100 GeV.
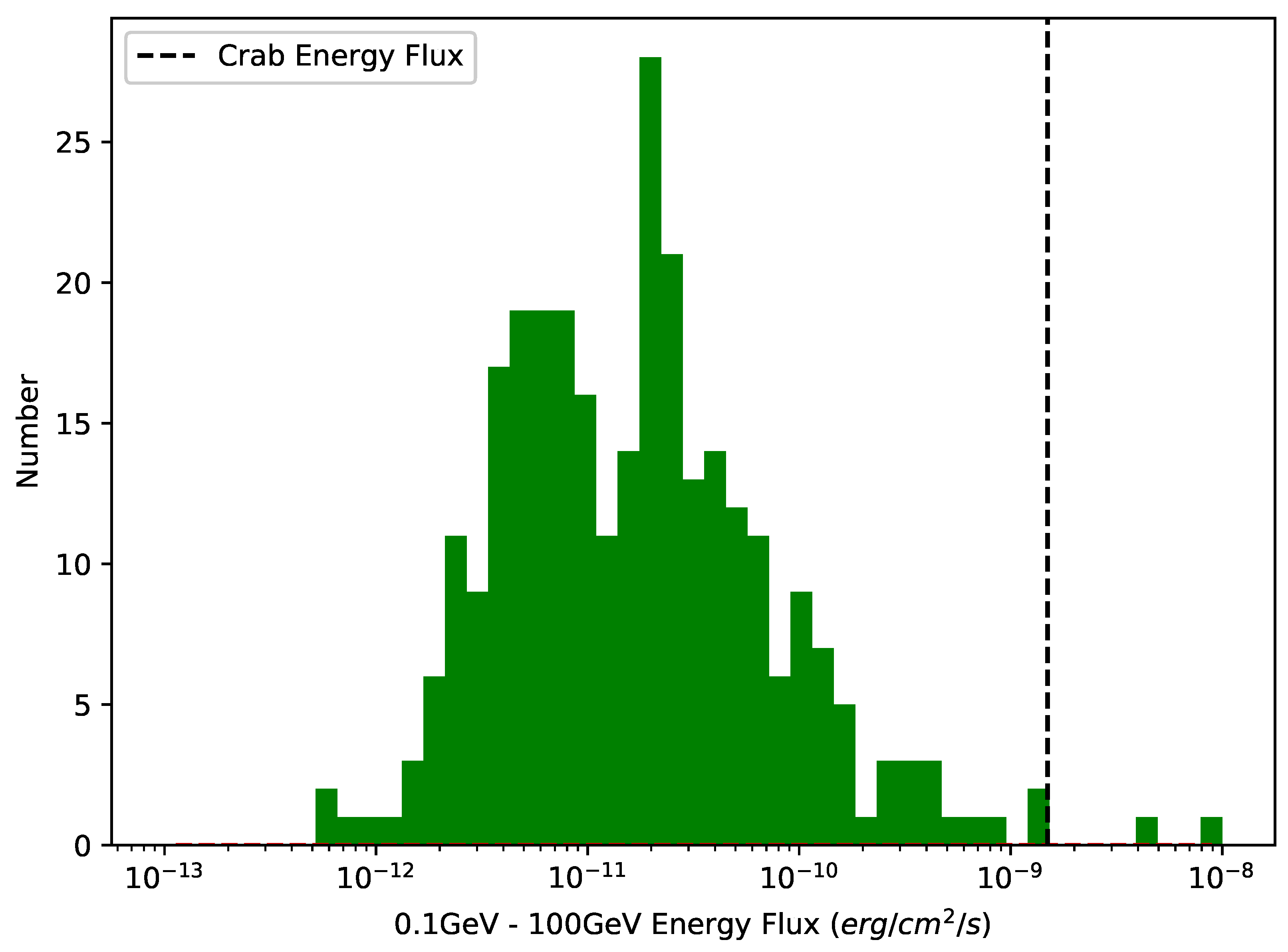
Preprints 77810 g004
Preprints 77810 g005
Figure 5. Histogram of cut-off energy of Fermi-LAT pulsars. The vertical dotted line indicates E c = 2 GeV.
Figure 5. Histogram of cut-off energy of Fermi-LAT pulsars. The vertical dotted line indicates E c = 2 GeV.
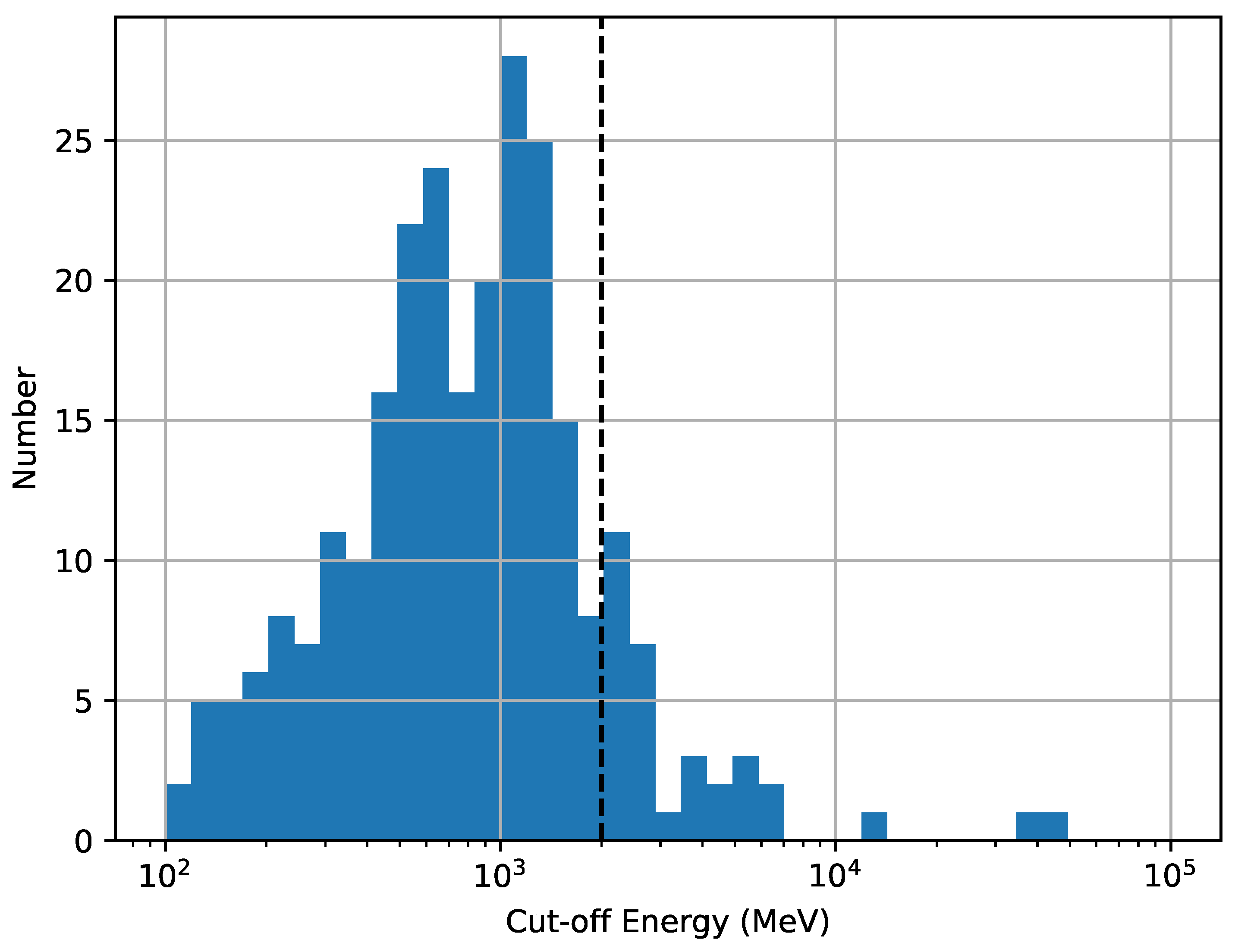
Preprints 77810 g005
Table 1. List of gamma-ray pulsar candidates derived from the 4FGL-DR3 catalog for observations with the MACE telescope.
Table 1. List of gamma-ray pulsar candidates derived from the 4FGL-DR3 catalog for observations with the MACE telescope.
Sr. No. Name P(s) P ˙ E c (GeV) Significance (10GeV - 30GeV)
1 J1807.1+2822 0.015084 3.75E-20 6.434 2.17 σ
2 J1908.9+2103 0.002564 1.38E-20 2.063 4.26 σ
3 J1913.3+1019 0.035909 3.36E-15 37.886 7.23 σ
4 J2047.3+1051 0.004290 2.1E-20 2.722 3.52 σ
5 J2052.7+1218 0.001985 6.7E-21 3.595 3.18 σ
6 J2302.7+4443 0.005192 1.38E-20 2.077 12.64 σ
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated