Prerpints.org logo
Preprint
Article

Forecasting Snowmelt Season Temperatures in the Mountainous Area of Northern Xinjiang of China

Altmetrics

Downloads

89

Views

20

Comments

0

This version is not peer-reviewed

Accessing and Analyzing Air Quality and Atmospheric Environment

Submitted:

27 June 2023

Posted:

28 June 2023

You are already at the latest version

Alerts
Abstract
The mountains in northern Xinjiang of China were studied during the snowmelt season. Multi-source fusion live data Chinese Land Data Assimilation System (CLDAS,0.05°× 0.05°,hourly data) were used as real data, and Central Meteorological Observatory guidance forecast (SCMOC,0.05°× 0.05 °,forecasting the following 10 days in 3 h intervals) was used as forecast data, both issued by the China Meteorological Administration. The dynamic linear regression and the average filter correction algorithms were selected to revise the original forecast products SCMOC.Based on conventional temperature forecast information,we designed four temperature rise prediction algorithms for essential factors affecting snowmelt.Temperature rise prediction algorithms included the daily maximum temperature algorithm, daily temperature rise range algorithm, snowmelt temperature algorithm, and daily snowmelt duration algorithm.Four temperature rise prediction algorithms values were calculated of each prediction product.Root-mean-square error algorithm and temperature prediction accuracy algorithm were used to compare and test each prediction algorithm value from the time sequence and spatial distribution.Comprehensive tests show that the forecast product revised by the average filter algorithm was superior to revised by the dynamic linear regression algorithm as well as the original forecast product.Through these algorithms, the more suitable temperature rise forecast value for each grid point in the study area can be obtained at different prediction times. The comprehensive and accurate temperature forecast value in mountainous snowmelt season can provide an accurate theoretical basis for effective prediction of the runoff in snowmelt areas and prevention of snowmelt flooding.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Northern Xinjiang is one of the three areas with a seasonal snow cover in China (Zhong et al.,2021;Zhang et al.,2022;Zhou et al.,2022). The snow covered on the Ertysi River basin is particularly deep in winter, where the source area snow depth reached 197 cm during the winter of 2021/2022. In northern Xinjiang, seasonal snowmelt water is the main local water resource, and snowmelt runoff can supply more than 75 % of rivers in spring (Li et al., 2021; Xiang et al., 2017).The temperature variation in mountains in spring is the major determining factor of snowmelt runoff formation and snowmelt flood occurrence (Wang et al., 2019; Jeelani et al., 2012; Cho et al., 2020; Sadro et al., 2018). The positive temperature change was more favorable to snow ablation (Wang et al., 2021; Hanati et al., 2021; 2019). The analysis based on the annual maximum flood peak records in the last 50 years and the frequency of warming snowmelt (ice) floods in the last 20 years in Xinjiang indicated that rising temperatures in the mountains led to the early melting of glaciers in surrounding areas (Mao et al., 2012; Laudon et al., 2004; Zhang et al., 2021). The continuous rapid rise temperature caused snowmelt floods in Xinjiang (Tian et al., 2011).The temperature had become an important element of snowmelt (Qin et al., 2021). Several studies made dynamic evaluations and forecasts on the occurrence of snowmelt flooding in spring (Zhou et al., 2021; Mercado-Bettín et al., 2021; Yan et al., 2012). All of these analyses confirmed a direct relationship between snowmelt and the temperature, with all research based on data from meteorological observation stations.The distances between meteorological observation stations in Xinjiang amount to several hundred kilometers, and there are even fewer observation stations in mountainous areas. Thus, the stations data alone cannot timely and accurately characterize the temperature changes in mountainous areas. Therefore, SCMOC, a grid forecasting product (0.05°×0.05°, forecasting the following 10 days in 3 h intervals), was used in this study to carry out full-coverage forecast for mountainous areas, and to accurately forecast temperature detail changes in mountainous areas.
Numerous studies showed that numerical weather predictions provide early warnings with extended lead time (Kim et al.,2013;Battisti et al.,2017;Liu et al., 2019) and improve the reservoir’s flood control and water supply objectives (Nayak et al., 2018;Jiang et al.,2018;Krainer et al.,2021). In catchments with seasonal snow cover, snowmelt is an important flood-generating process. Hence, high-quality air temperature data are important to accurately forecast streamflows (Hegdahl et al.,2019). In recent years, intelligent grid point temperature prediction technology had become an important field, and numerous scholars studied its localization correction algorithms to improve the accuracy of local temperature forecasting in time (Regonda et al., 2006; Zhang et al., 2022;Fan et al.,2023;Zhang et al.,2023). Dai et al. used unary linear regression algorithm and Kriging interpolation algorithm (Dai et al., 2019) and Hao et al. used sliding training algorithm and optimized variable weights algorithm(Hao et al., 2019) trained the temperature data of ECMWF fine grid forecast products(Hou et al.,2022). Wei and Wan et al. tested and evaluated the products of the intelligent grid prediction (SCMOC) service and the ECMWF fine grid (Wei et al., 2020 and Wan et al., 2018).Li et al. established horizontal, longitudinal, and horizontal and longitudinal integrated forecast models (Li et al., 2020) and Liu et al. used the wavelet analysis, sliding training algorithm, and optimal fusion algorithm to correct the temperature forecast products of intelligent grid forecast (SCMOC) (Liu et al., 2020). Analysis results show that these algorithms have the partial ability to revise the temperature prediction in their study area.These revision algorithms few considered mountain areas,which specifically forecast the future temperature of the snowmelt and snowmelt temperature rise range. Due to the lack of meteorological observation data in mountainous areas, the weather physical process in mountainous areas has its particularity, and the numerical prediction model faces difficulty dealing with the steep and complex terrain, so that it is difficult to forecast the temperature in mountainous areas.The prediction accuracy of the temperature in mountainous areas is evidently lower than that in plain areas.Therefore, improving the accuracy of temperature forecast in mountainous areas is of utmost importance.
In this study, two aspects were considered to design the correction algorithms. First,dynamic linear regression algorithm,due to the abrupt change of altitude in mountain areas, the temperature changes dramatically, so for the forecast value of each prediction time of each grid point,base on the linear regression algorithm to design the correction algorithm of dynamically changing the slope and constant value. Secondly,the average filter correction algorithm,due to the large amount of grid prediction products, base on average error of forecast in previous days as forecast values error to revision forecast value of each prediction time of each grid point in order to reduce the calculation and facilitate the rapid services.
In this research, we study the intelligent grid temperature prediction technology of temperature rise during spring snowmelt period in the mountainous area of northern Xinjiang.Two temperature prediction correction algorithms were designed to correct the original forecast product SCMOC respectively.After correcting,two new forecast products were obtained.In order to focus on the influence of temperature rise prediction accuracy during spring snowmelt period,based on the temperature forecast information,four innovative temperature rise prediction algorithms were designed to more accurately describe the physical quantity index of the snowmelt process.Temperature rise prediction algorithms included prediction algorithms of the daily maximum temperature, daily temperature rise range, snowmelt temperature, and daily snowmelt duration.The values of four temperature rise prediction algorithms for each forecast product were calculated.Though multiple indexes were used to compare and test the value of each temperature rise prediction algorithm and temperature prediction from the time sequence and spatial distribution, the suitable forecast product were selected in mountainous areas.

2. Data and methods

The study area includes mountainous areas with altitudes above 1300 m in northern Xinjiang, ranging from 42.25°to 49.20°N and 79.85° to 96.50° E, with a total of 7371 grid points and a spatial resolution of 0.05º × 0.05º, as shown in Figure 1.
The original temperature forecast product (XJ) was obtained from the temperature guidance forecast product of the China Meteorological Administration (SCMOC) with a spatial resolution of 0.05° × 0.05°. The temperature forecast future 240h in 3 h intervals value , and reported starting from 08 AM Beijing time every day,during March to May 2021.
Real data were obtained from Chinese Land Data Assimilation System (CLDAS) hourly data with a spatial resolution of 0.05° × 0.05°. The advantage of the real product was the combination of multi-source fusion data, such as ground and satellite data. After evaluation by the Meteorological Information Center of China, the temperature of CLDAS was in good agreement with the actual ground observation values (Meteorological Center 2017). After Liu Ying et al. evaluating the temperature of CLDAS-V2.0 in Xinjiang, the results showed that the non-independence test of CLDAS was 0.972, the independence test was 0.950, the mean deviation was -0.271 ℃, the RMSE was 2.406 ℃, and the mean absolute error was 1.588 ℃ (Liu et al., 2021).

2.1. Temperature revision method

2.1.1. Dynamic unitary linear regression (HG) revision scheme

Based on the temperature forecast products (XJ) in the mountainous area of northern Xinjiang in spring from March to May 2021, the unary regression correction model was established dynamically by each grid and each forecast time, respectively, and a new forecast data product (HG) was generated after revision. The revised model formula of the dynamic regression equation was as follows:
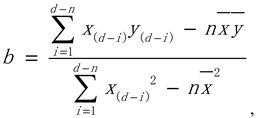
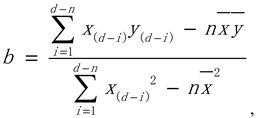
Preprints 77846 i001
a = y ¯ − b x ¯ ,
Y = a X + b ,
The forecast value of one grid at the forecast time on the day revised by the following steps. In Equations (1) ,n represents the number of days of dynamic training in the previous days,according to previous experiments on observation stations, n=6 was chosen in this paper,x represent the temperature forecast value (XJ) and y represent the actual value of the corresponding time,d represents the day the forecast began,i stands for integer value 1-n, (d-i) indicates the previous i day, x ¯ represent the temperature forecast average value (XJ), y ¯ represent the average actual value of the corresponding time.Equation (1) calculates the value of b. According to x ¯ , y ¯ ,b calculated by Equation (1), the value of a is calculated by Equation (2).In Equation (3), X was the original forecast value (XJ), and Y was the forecast value after regression correction (HG).According to b of formula (1) and a of formula (2), the correction value Y is computed by formula (3).
There were 7371 grid points in this study area. One grid point had forecast the following 240h in 3 h intervals every day, so 80 forecast value per day. The each grid forecast value were revised according to the above steps.

2.1.2. Average filtering (PJ) revision scheme

Both the original temperature forecast product (XJ) and the real product CLDAS were grid data with spatial resolution of 0.05°× 0.05°. The average filtering algorithm was used to correct the original forecast temperature, and the revised temperature forecast product marked as PJ was obtained.The forecast value of one grid at the forecast time on the day revised by average filtering algorithm as follows steps :
① Calculation of model prediction error:
b ( d ) = f ( d ) − a ( d ) ,
In Equation (4) : b(d) was the prediction error value,which was defined as the prediction error between the prediction data f(d) of a certain prediction time and the corresponding live data a(d).
② Daily sliding forecast error model:
B ( d ) = b ( d − 1 ) + b ( d − 2 ) + ... + b ( d − n ) n ,
In Equation (5) : B(d) was the corrected error of the model forecast, which was the arithmetic average of the temperature forecast error of the same grid at the same forecast time every day for n days before the forecasting date. Through numerous experiments conducted by meteorological observation stations in different regions, different values of n were found to have great influence on B(d). Based on previous period studies and reference materials (Zhang et al., 2022), this study selected n = 6.
③ Model forecast error revision:
F ( d ) = f ( d ) − B ( d ) ,
In Equation (6), B(d) was obtained by Equation (5), f(d) was the forecast value of the original temperature forecast product (XJ) , and F(d) was the revised forecast value.
Equations (4-6) refers to the process of correcting at specific forecast time of the same grid. Equations (4-6) was used to correct the temperature every forecast time of 7371 grid points in mountainous areas. After the correction, a new temperature forecast product (PJ) in 3 h intervals for the following 10 days forecasted from 8 AM every day was generated.

2.2. Temperature forecast method

2.2.1. Forecast of daily maximum temperature

In the forecast for the next 10 days in 3 h intervals from 8 AM Beijing time every day, the maximum temperature was selected as the daily maximum temperature forecast value from the eight forecast times of each 24 h interval, such as 0–24 h and 24–48 h, and the daily maximum temperature forecast values in the future 1–10 days (d) were calculated similarly. The method for selecting the real maximum temperature was the same. The daily maximum temperature was selected from the corresponding eight real values of the forecast obtained during the day.

2.2.2. Forecast of temperature rise range

First, the daily maximum temperature of grid points was calculated, followed by the daily temperature rise range during the temperature rise period.
U P i = H o u i − Q i a n i ,
U P s k = H o u s k − Q i a n s k ,
b t u p i = U P i − U P s k ,
In Equations (7) and (8), i represents XJ, HG and PJ forecast products respectively, sk represents the grid value obtained from CLDAS, Hou represents the daily maximum temperature of the following day, and Qian represents the daily maximum temperature of the previous day. For example, if a grid temperature exhibits a four-day continuous rise, the grid has three daily temperature rise values. The calculation of the daily forecast temperature rise was the same as the real temperature rise, and the error of the forecast temperature rise was calculated from the above Equation (9).

2.2.3. Forecast of snowmelt temperature and daily snowmelt duration

Taking 0 ℃ as the critical index of snowmelt temperature, the temperature ≥ 0 ℃ satisfies the snowmelt temperature condition. In this study, when the forecast temperature reaches above 0 ℃, it was defined as the snowmelt temperature.
The duration of daily snowmelt was directly related to its speed. In the critical period of spring snowmelt, the duration of the temperature ≥ 0 ℃ within 24 hours of one day (08:00– 08:00, Beijing time) was the duration of daily snowmelt, expressed in hours (h). Because the grid temperature forecast interval was 3 h, there were eight values in the 24 h forecast time of 08:00 to 08:00. The eight temperature forecast values were identified one by one. The times when the snowmelt temperature index was reached were added up and multiplied by three to obtain the daily snowmelt duration hours of the day.Therefore, based on the temperature forecast of the next 10 days by 24 h interval, the daily snowmelt duration forecast of the next 1–10 days can be calculated respectively.To test the forecast data, the real daily snowmelt duration was calculated from the corresponding eight time temperatures of CLDAS temperature. Forecast of daily duration of snowmelt (FS), the formula is as follows:
d = t × 3 ,
FS = ∑ j = 1 N d ( j ) N ,
In Equation (10), t were the times at which the temperature ≥ 0 ℃, predicted by a single grid within a specific 24 h forecast time; d represented the predicted snowmelt duration of a single grid point within a specific 24 h forecast time.In Equation (11), N were the grid number of reaching the forecast snowmelt temperature in the study area. FS were the predicted duration of snowmelt within 24 h in the study area.

2.3. Inspection Index

The root mean square error (RMSE) and prediction accuracy (TT：temperature forecast accuracy or TS:prediction accuracy of the snowmelt temperature) were used as test indexes, and the value of the corresponding correction technique value (SS) that measure the effect value of the revised forecast relative to the original forecast.The prediction effect of the three grid temperature forecast products (XJ, HG, and PJ) was compared and tested.
The RMSE was given by:
RMSE = ∑ t = 1 N ( x ( t ) − y ( t ) ) 2 N ,
where x(t) and y(t) were the predicted and real values of factors, respectively, and N was the number of samples involved in the test.
The temperature forecast accuracy was given as follows:
TT = N A N A + N B × 100 ,
where NA was the number of samples whose absolute error of the forecast value is less than 2 ℃, and NB is the number of samples whose absolute error of the forecast value was above 2 ℃.
The prediction accuracy of the snowmelt temperature was given as follows:
T S = N C N C + N D + N E × 100 ,
where NC was the number of correctly forecasting samples, ND was the number of empty forecasting samples when the forecast value reaches the target but the real value was not reached, and NE was the number of missing forecasting samples when the forecast value did not reach the target, but the real value was reached.
Value of correction technique (SS): The RMSE(SS_RMSE*:the values of various root mean square error correction techniques) and prediction accuracy (SS_TT/TS) were calculated by the following formula:
S S _ R M S E * i = R M S E * X J − R M S E * H G / P J ,
S S _ T T / T S i = T T / T S H G / P J - T T / T S X J
In Equations (15) and (16), subscript HG/PJ represented the index value of the revised forecast product by dynamic unary regression correction/average filtering correction, while subscript XJ represented the index value of the original forecast guidance product. RMSE* standed for RMSEDF,RMSEUP or RMSE_Max, where RMSEDF was the RMSE of daily snowmelt duration forecast,RMSEUP was the RMSE of daily temperature rise amplitude forecast, and RMSE_Max was the RMSE of the daily maximum temperature forecast.In Equation (15), the RMSE correction technique of the corresponding prediction algorithm yielded value (original forecast XJ minus the revised forecast HG/PJ).In Equation (16), the prediction accuracy correction technique of the corresponding prediction algorithm yielded value(the revised forecast HG/PJ minus original forecast XJ ).When SS was positive, the correction technique was positive, and vice versa.

2.4. Test method

The time series test method calculated and compared index values during 10 days in 3 h intervals of the three kinds of grid temperature forecast products.
The spatial distribution test method calculated and compared the index values during the whole forecast time of 10 days or a certain range of forecast time of three kinds of grid temperature forecast products.

3. Tests of various temperature prediction algorithms

3.1. Temperature forecast test

3.1.1. Time series comparison of temperature forecast

Figure 2a and Table 1 show that the mean root errors of XJ, HG, and PJ products are 5.17, 6.77, and 4.59 ℃, respectively. Compared with XJ, the root-mean-square errors of HG and PJ were increased by 1.6 ℃ and decreased by 0.58 ℃, respectively, and the correction effect was better within 72 h.The RMSE of PJ forecast products was lower than that of XJ, and the correction technique values were positive than that of HG. The forecast time was shorter than 33 h, mainly at 14:00,17:00 Beijing time, the RMSE of HG and PJ was 0.6 and 1.93 ℃ lower than XJ, respectively. The forecast time was shorter than 81 h, mainly at 11:00, 14:00, 17:00, 20:00, and 23:00 Beijing time, the RMSE of HG and PJ forecast products increased by 0.23 ℃ and decreased by 1.74 ℃ compared with XJ, respectively.
Figure 2b and Table 1 show that the average accuracy of temperature forecast for XJ, HG, and PJ are 35.52, 41.65, and 41.83 %, respectively. Compared with XJ, the temperature forecast accuracy of HG and PJ increased by 9.13 and 9.30 % respectively; the positive prediction accuracy correction techniques values of HG and PJ within 129 and 165 h respectively, which the temperature forecast accuracy of HG and PJ increased by 22.68 and 25.17 %, respectively; the accuracy correction effect of PJ is better than that of HG.

3.1.2. Spatial distribution comparison of temperature forecast

Table 1 and Figure 3 show the temperature prediction accuracy of XJ, HG, and PJ in 24 h forecast time as 40.15, 55.36, and 58.04 %, respectively, with PJ having the highest prediction accuracy. After 72 h, the temperature forecast accuracy of the three products was below 50 %. Figure 3 below shows the RMSE distribution of temperature forecast for XJ, HG, and PJ in the following 24, 48, and 72 h.
As shown in Table 1, compared with the forecast product (XJ), there were 2496, 1536, and 1219 grid points where the RMSE correction technique of HG was positive in 24, 48, and 72 h, which account for 33.9, 20.8, and 16.5 % of the temperature forecast in northern Xinjiang. Meanwhile, there were 5592, 5068, and 4747 grid points where RMSE correction techniques of PJ forecast products were positive in 24, 48, and 72 h forecast time, accounting for 75.9, 68.8, and 64.4 % of the temperature forecast in northern Xinjiang.Compared with HG, PJ forecast product correction techniques had evident advantages.
Figure 3 shows a total of 5592 grid points where the RMSE correction technique value of PJ in the future 24 h temperature forecast has a positive effect, 748 grid points where the RMSE correction technique value exceeds 3 ℃, and 220 grid points where the RMSE correction technique value exceeds 5 ℃, accounting for 75.9, 10.1, and 3.0 % of the mountainous areas in northern Xinjiang, respectively. The grid points with positive effect of RMSE correction were distributed in most of the mountainous areas of northern Xinjiang. The grid points with the correction effect exceeding 5 ℃ were distributed in the areas with elevations above 3000 m in the Kharketau Mountain and 2000 m in the source region of Burjin River in northern Altai.

3.2. Daily maximum temperature test

3.2.1. Time series comparison of daily maximum temperature forecast

Figure 4 and Table 2 show the average root-mean-square errors of the daily maximum temperature forecast of XJ, HG, and PJ in the following 1–10 days as 5.11, 7.85, and 4.61 ℃, respectively. Compared with the guide forecast product (XJ), HG increased by 2.74 ℃, exhibiting a negative effect on the whole, where only the correction technique value in the prediction of one day was positive; PJ decreased by 0.50 ℃ on average, whereas the correction technique values for 1–10 days in the future were all positive. The root-mean-square errors of the daily maximum temperature forecast of PJ in the following 1, 2, and 3 days were 2.26, 2.54, and 2.87 ℃, compared with XJ, the root-mean-square errors being reduced by 1.48, 1.29, and 1.1 ℃, respectively.
Figure 4 and Table 2 show the forecast accuracy of the daily maximum temperature of XJ, HG, and PJ in during 1–10 days as 32.77, 35.00 and 43.7 %, respectively.
Figure 4 shows that compared with the guide forecast product (XJ), the accuracies of HG and PJ were increased by 2.23 and 10.96 %, respectively. The correction technique values were both positive, and PJ was higher. The forecast accuracies of the daily maximum temperature of PJ for the following 1, 2, and 3 days were 71.61, 65.88, and 58.12 %, respectively, increased to be 29.19, 24.25, and 18.04 % higher than that of XJ, respectively. The accuracy correction technique of the PJ daily maximum temperature forecast in the mountainous areas of northern Xinjiang was obviously superior to that of HG.

3.2.2. Spatial distribution comparison of daily maximum temperature forecast

Figure 5 shows that there are 3056, 1736, and 992 grid points where the RMSE correction technique of HG the daily maximum temperature forecast for the following 1, 2, and 3 days had positive effects, accounting for 47.6, 23.6, and 13.5 % of the mountains in northern Xinjiang.There were 6164, 5430, and 4920 grid points where the RMSE correction technique value of PJ the daily maximum temperature forecast for the following 1, 2, and 3 days had positive effects, accounting for 83.6, 73.7, and 66.7 % of the mountainous areas in northern Xinjiang. Compared to HG, the areas where the RMSE correction technique values of PJ the daily maximum temperature forecast for the following 1, 2, and 3 days were positive increased by 42.0, 48.0, and 47.9 %, respectively, indicating that the correction technique value had evident advantages in the spatial area.
Figure 5 shows there are 5322, 1505 and 603 grid points with RMSE correction techniques value for daily maximum temperature forecasts of PJ for the following day exceeding 0, 3, and 5 ℃, respectively, accounting for respective 72.2, 20.4, and 8.2 % of the mountains in northern Xinjiang. The grid points with a positive effect of the RMSE correction technique value of the PJ daily maximum temperature forecast were distributed in most of the mountainous areas of northern Xinjiang, while the areas with a negative effect of correction technique value were located at 1300–1500 m south of Mulei in the eastern Changji Prefecture. The grid points with the PJ correction effect exceeding 5 ℃ were distributed in the areas with elevations above 3000 m in Kharketawu Mountain and 2000 m in the source region of the Burjin River in northern Altai.

3.3. Prediction and test of temperature rise

From April 23rd to 30th 2021, 7371 grid points for the daily maximum temperature average rise reached 25.63 ℃ in the mountainous area of northern Xinjiang, among which the single grid maximum temperature rise was 32.96 ℃, 559 grid points had a temperature rise of more than 30 ℃, 3894 grid points had a temperature rise of more than 25 ℃ but less than or equal to 30 ℃, and 2388 grid points had a temperature rise of more than 20 ℃ but less than or equal to 25 ℃. The continuous temperature rise period was selected for the daily temperature rise amplitude forecast test.

3.3.1. Forecast time series comparison of daily temperature rise amplitude

Figure 6 and Table 3 show the average root-mean-square errors of the forecast daily temperature rise amplitude of XJ, HG, and PJ for the following 1–10 days as 4.87, 6.41, and 4.25 ℃, respectively. Compared with XJ, the RMSE of HG increased by 1.54 ℃, while that of PJ decreased by 0.62 ℃. As shown in Figure 6, compared with the guidance product (XJ), the root-mean-square errors of the daily temperature rise amplitude forecast of HG for the following 1, 2, and 3 days increased by 1.32, 0.61, and 0.69 ℃, and PJ was reduced by 1.50, 1.31, and 0.97 ℃, respectively. The root-mean-square errors of the daily temperature rise amplitude forecast of PJ for the following 1, 2, and 3 days in the mountainous area of northern Xinjiang were 1.69, 2.10, and 2.53 ℃, respectively, and the forecast is significantly improved.

3.3.2. Spatial distribution comparison of temperature rise amplitude forecast

Figure 7 and Table 3 show that compared with XJ, there were 2768, 2875, and 2762 grid points where RMSE correction techniques of the HG daily temperature rise amplitude forecast for the following 1, 2, and 3 days were positive, accounting for 37.6, 39.0, and 37.5 % of the mountainous areas in northern Xinjiang, respectively. Meanwhile, there were 5322, 5108, and 4545 grid points with positive correction technique values of the PJ forecast product for the following 1, 2, and 3 d, accounting for 72.2, 69.3, and 61.7 % of the mountainous areas in northern Xinjiang, respectively. Compared with the prediction results of HG, the number of grid points with a positive effect increased by 34.6, 30.3, and 24.2 %, respectively, and the positive effect areas of PJ was significantly larger than that of HG.
Figure 7 shows that there were 5322, 1505, and 603 grid points with RMSE correction techniques of the PJ daily temperature rise amplitude forecast in the following day exceeding 0, 3, and 5 ℃, respectively, accounting for 72.2, 20.4, and 8.2 % of the mountainous areas in northern Xinjiang. The positive results were found in most of the mountainous areas in northern Xinjiang, while the correction techniques of Yili Zhaosu at an altitude of 1500–2000 m and some areas in the south of Urumqi showed negative results.

3.4. Snowmelt temperature testes

3.4.1. Time series comparison of snowmelt temperature

From March to May in spring 2021, the average snowmelt temperature forecast accuracies of XJ, HG, and PJ were 79.36, 74.10, and 81.99 %, respectively. Compared with guidance product (XJ), the forecast accuracy of HG decreased by 5.4 %, while the PJ scheme increased by 2.45 % (Figure 8 and Table 4).In a total of 80 forecast times during the 10 days forecast period, the positive correction technique values of HG and PJ the snowmelt temperature forecast accuracy was in 13 and 77 times respectively, and the correction technique values of PJ was relatively high. At 02:00, 11:00, 14:00 and 17:00 Beijing time, the correction technique values of HG were higher than those of XJ. The average accuracy of the snowmelt temperature forecast of XJ and HG at these times was 82.16 and 84.36 %, respectively.
At 02:00, 11:00, 14:00 and 17:00 Beijing time, the correction technique values of HG were relatively high. The average accuracies of the snowmelt temperature forecast of XJ and HG at these times were 82.16 and 84.36 %, respectively. At 11:00, 14:00, 17:00, and 23:00 Beijing time, the correction technique of PJ was relatively high, the prediction accuracies of the snowmelt temperature of XJ and PJ at these times were 84.59 and 91.60 %, respectively.

3.4.2. Spatial distribution comparison of snowmelt temperature

The number of correct snowmelt grid points in CLDAS, XJ, HG, and PJ were 7324, 6609, 6641, and 6598, respectively.
Figure 9 and Table 4 show that compared to the original prediction (XJ), the average correction technique values of the PJ algorithm at 24, 48, and 72 h were 3.29, 3.11, and 2.42, respectively, and the positive correction technique values had 3109, 3115, and 3194 grid points, respectively. The average correction technique values of the HG algorithm at 24, 48 and 72 h were –9.8, –12.28 and –14.77 respectively, among which there were 1475, 1054, and 980 positive correction grid points, respectively.
At 24 h, positive correction technique value grid points of the PJ algorithm were concentrated in the areas including the Yili Prefecture 1500–2000 m above sea level, Irenhabirgaa and Borokonu mountains at 2000–3500 m above sea level, and 3000 m above sea level for central Tianshan reaches east to Igo, except for the Tomulti Peak, North Tower Mountain northward 1500 m above the Altai Mountains, and Northwest of Tachen to the area of Hobuxell. Correction technique values greater than five had 2180 grid points concentration areas, which are located in the Borokonu Mountain, the Green River, and the Bukser region.

3.5. Daily snowmelt duration tests

3.5.1. Time series comparison of snowmelt duration

Figure 10 and Table 5 show the root-mean-square errors of the XJ, HG, and PJ snowmelt duration forecast for the following 1–10 days as 2.22, 1.4, and 1.29 h, respectively. Compared with XJ, the mean square errors of HG and PJ daily snowmelt durations were decreased by 0.81 and 0.93 h, respectively. Figure 10 shows that the root-mean-square errors of HG forecast products for the following 1, 2, and 3 days were 0.72, 0.93, and 1.03 h, respectively, which reduced by 1.18, 0.98, and 0.9 h relative to XJ. The root mean square errors of PJ prediction products for the following 1, 2, and 3 days were 0.66, 0.80, and 0.92 h, respectively, which were reduced by 1.24, 1.11, and 1.01 h relative to XJ, and 0.06 h, 0.13, and 0.11 h relative to HG, respectively. Thus, the RMSE correction technique of the PJ snowmelt duration in the mountainous area of northern Xinjiang was superior.

3.5.2. Spatial distribution comparison of snowmelt duration forecast

Figure 11 and Table 5 show that, compared with XJ forecast products, there were 4373, 3964, and 3778 grid points where the RMSE correction technique values of HG daily snowmelt duration forecast products was positive in the following 1, 2, and 3 d, accounting for 59.3, 53.8, and 51.3 % of the northern mountainous areas of Xinjiang, respectively. Compared with XJ, 4445, 4143, and 3952 grid points with positive correction techniques of PJ forecast products for the following 1, 2, and 3 days accounted for 60.3, 56.2, and 53.6 % of the mountainous areas in northern Xinjiang, respectively. Compared with HG, the areas of PJ forecast products positive correction technique values in the following 1, 2, and 3 days increased by 1.0, 2.4, and 2.4 %, respectively.
Figure 11 shows that the grid with the RMSE correction technique of PJ daily snowmelt duration forecast for the following day covers all study areas, among which there were 334 grid points with the correction technique exceeding 5 h, concentrated in the areas with 3000 m altitude above in Yili region, upper Burtin River in the northern Altai Mountains, and partial areas 3000 m above sea level at the eastern end of Mount Borokonu.

4. Conclusions

4.1. Algorithms test results

Through the above comparative test analysis, we obtain the following conclusions.
(1) Temperature forecast test by forecast time: In the 10-day with 3 h interval forecast, compared with the guidance forecast product (XJ), the Root-mean-square errors of the HG and PJ temperature forecast products increases by 1.6 ℃ and decreases by 0.58 ℃, respectively, and the temperature forecast accuracy increases by 9.13 and 9.30 %, respectively. The Root-mean-square errors and prediction accuracy of the temperature forecast, as well as the effects of the PJ intelligent grid temperature forecast correction technique were significantly better than those of HG.
(2) Test of daily maximum temperature forecast: In the 10-day forecast, compared with the guidance forecast product (XJ), the RMSE of the daily maximum temperature of the HG and PJ temperature forecast products increases by 2.74 ℃ and decreases by 0.5 ℃, respectively, and the temperature forecast accuracy increases by 2.23 and 10.96 %, respectively. The accuracy correction technique of the PJ daily maximum temperature forecast in the mountainous areas of northern Xinjiang evidently outperformed HG.
(3) Daily temperature rise prediction test: In the 10-day forecast, compared with the guidance forecast product (XJ), the RMSE of the daily temperature rise amplitude of HG increases by 1.55 ℃, and the correction technique exhibits a negative effect on the whole, while PJ decreases by 0.62 ℃, which exhibits a positive effect on the whole.
(4) Test of snowmelt temperature forecast: In the 10-days with 3 h interval forecast, compared with the guidance forecast product (XJ), the accuracy of snowmelt temperature forecast of HG and PJ decreased by 5.4 % and increased by 2.45 %, respectively. Among the 80 forecasts within 10 days, the positive correction techniques of HG and PJ were 13 and 77 times, respectively, and the accuracy correction techniques of PJ were relatively high.
(5) Test of snowmelt daily duration forecast: In the 10-day forecast, compared with the guidance product (XJ), the mean square error of HG and PJ snowmelt duration forecast decreased by 0.81 h and 0.93 h, respectively. The effect of the PJ correction technique was superior to that of HG.
According to the comprehensive test of time series and spatial distribution,the original forecast products corrected by the average filter algorithm were superior to those corrected by the dynamic unary regression algorithm and the original forecast products.

4.2. Limitations and Novelty

Herein,SCMOC was selected as the original forecast product and used to design two correction algorithms. The dynamic linear regression and the average filter correction algorithms were selected by numerous experiments in the meteorological observation stations forecast. Only the average filtering algorithm has strong adaptability, which effectively reduces the prediction error of grid prediction products. Though other correction algorithms exist, all of which must forecast and test the temperature rise process of snowmelt in mountainous areas to determine its suitability in the mountains.
These innovative correction algorithms (the dynamic regression algorithm and average filtering algorithm) designed in this study, and the forecast algorithms of daily maximum temperature, daily temperature rise range, snowmelt temperature and daily snowmelt duration in mountain areas, and the methods of comparing and testing each prediction algorithm from time series and spatial distribution by using multiple indexes,can be applied to forecast and test the snowmelt temperature rise in other mountainous areas.
We study an intelligent grid temperature prediction technology for snowmelt warming in mountainous areas during spring. Our algorithms yield the most suitable temperature forecast for each grid point at different prediction times in the study area. Efforts to obtain optimal grid point temperature forecasting products during snowmelt in mountainous areas contribute to a more solid technical support for predicting snowmelt flood time and flood peak discharge. To monitor and forecast the temperature rise change process of each grid in the mountainous areas during snowmelt season, we provide a scientific assessment of the snowmelt time, speed, and snowmelt quantity, a quantitative analysis of snowmelt flood changes in the river basin, and provide scientific basis for guiding agricultural production layout, water resource management, and accurate disaster prevention and avoidance.

Author Contributions

Z.Z.: Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing-Original Draft; W.M.: Writing- Original Draft; Funding Acquisition, Resources; M.W.: Conceptualization, Data Curation, Supervision, Writing-Review & Editing; W.Z.: Visualization, Investigation; C.J.: Supervision, Validation; M.A.: Validation; D.A.: Investigation. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China(2019YFC1510501), National Natural Science Foundation of China (NSFC)(41975146).

Data Availability Statement

Supplementary data to this article can be found online at http://data.cma.cn/.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Battisti, A.;Acevedo,O.C.;Costa,F.D.;et al.2017.Evaluation of Nocturnal Temperature Forecasts Provided by the Weather Research and Forecast Model for Different Stability Regimes and Terrain Characteristics. Boundary-Layer Meteorol 162, 523-546. [CrossRef]
  2. Cho,E.;& Jacobs,J.M.2020.Extreme value snow water equivalent and snowmelt for infrastructure design over the contiguous United States. Water Resources Research, 56, e2020WR028126. [CrossRef]
  3. Dai,Y.;He,N.;& Fu,Z.Y.2019.Beijing intelligent grid temperature objective prediction method (BJTM) and verification of forecast result. Journal of Arid Meteorology,37(2): 339-344. [CrossRef]
  4. Fan,H.;Liu,Y.;Li,Y.;Liu,Y.;Duan,J.;Li,L.;Huo,Z.Y.2023.A deep learning method for predicting lower troposphere temperature using surface reanalysis,Atmospheric Research,283. [CrossRef]
  5. Hanati,G.L.M.R.;Zhang,Y.;Su,L.D.;& Hu,K.K.2021. Response of water and heat of seasonal frozen soil to snow melting and air temperature. Arid Land Geography 44(4): 889-896. [CrossRef]
  6. Hanati,G.L.M.R.;Helili,H.M.D.;Liu,Q.Q.;&Su,L.D.2019.Dynamic snowmelt process and its relationship with air temperature in a small watershed in the West Tianshan Mountains. Arid Zone Research 36(4): 801–808. [CrossRef]
  7. Hao,C.;Zhang,Y.X.;Wang,Z.W.;&Fu,Z.Y.2019.Application of analog ensemble rectifying method in objective temperature prediction. MeteorMon 45(8):1085-1092. [CrossRef]
  8. Hegdahl,T.J.;Engeland,K.;Steinsland,I.;&Tallaksen,L.M.2019.Streamflow forecast sensitivity to air temperature forecast calibration for 139 Norwegian catchments, Hydrology and Earth System Sciences 23:723-739. [CrossRef]
  9. Hou,Z.L.;Li,J.P.;Wang,L.;Zhang,Y.Z.;Liu,T.2022.Improving the forecast accuracy of ECMWF 2-m air temperature using a historical dataset,Atmospheric Research 273. [CrossRef]
  10. Jiang,Z.;Xu,T.&Mariethoz,G.2018.Numerical investigation on the implications of spring temperature and discharge rate with respect to the geothermal background in a fault zone. Hydrogeol J 26:2121–2132. [CrossRef]
  11. Jeelani,G.;Feddema,J.J.;VanderVeen,C.J.;&Stearns,L.2012.Role of snow and glacier melt in controlling river hydrology in Liddar watershed (western Himalaya) under current and future climate, Water Resources Research 48, W12508. [CrossRef]
  12. Kim,Y.;Sartelet,K.;Raut,J.C.;et al.2013.Evaluation of the Weather Research and Forecast/Urban Model Over Greater Paris. Boundary-Layer Meteorol 149,105-132. [CrossRef]
  13. Krainer,K.;Winkler,G.;Pernreiter,S.;et al.2021.Unusual catchment runoff in a high alpine karst environment influenced by a complex geological setting (Northern Calcareous Alps, Tyrol, Austria). Hydrogeol J 29:2837-2852. [CrossRef]
  14. Li,J.;Zhang,Y.T.;& Zhang,Y.Y.2021. Impact of seasonal snowmelt on snowpack at woodland, grassland and bare land in North Slope of Tian Mountain. Journal of Irrigation and Drainage40(1): 106-114. [CrossRef]
  15. Laudon,H.;Seibert,J.;Köhler,S.;& Bishop,K.2004.Hydrological flow paths during snowmelt: Congruence between hydrometric measurements and oxygen 18 in meltwater, soil water, and runoff, Water Resources Research 40, W03102. [CrossRef]
  16. Li, G.;Yang,X.Z.;Liu,Y.H.;Chen,Z.H.;Yu,Q.;&Wu,C.H.2020. Forecast of maximum temperature based on refined guidance SCMOC data in Guizhou Province. Journal of Arid Meteorology 38(3): 457-464. http://www.ghqx.org.cn/CN/Y2020/V38/I03/457.
  17. Liu,X.W.;Duan,B.L.;Huang,W.B.;Duan,M.J.;Li,R.;Di,X.H.;&Wei,S.J.2020.Application of objective prediction method based on wavelet analysis in intelligent grid high and low temperature prediction. Trans Atmos Sci 43(3): 577-584. [CrossRef]
  18. Liu,Y.;Shi, C. X.;Wang,H.J.;&Han,S.2021. Applicability assessment of CLDAS temperature data in China. Trans Atmos Sci 44(4): 540-548. [CrossRef]
  19. Liu,L.;Xu,Y.P.;Pan,S.L.;&Bai,Z.X.2019.Potential application of hydrological ensemble prediction in forecasting floods and its components over the Yarlung Zangbo River basin, China, Hydrol. Earth System Science Data 23: 3335-3352. [CrossRef]
  20. Mao,W.Y.;Fan,J.;Shen,Y.P.;Yang,Q.;Gao,Q.Z.;Wang,G.Y.;Wang,S.D.;&Wu,S.F.2012.Variations of extreme flood of the rivers in Xinjiang region and some typical watersheds from Tianshan Mountains and their response to climate change in recent 50 years. Journal of Glaciology and Geocryology 34(5): 1037–1046. http://www.bcdt.ac.cn/CN/Y2012/V34/I5/1037.
  21. Mercado-Bettín,D.;Clayer,F.;Shikhani,M.;Moore,T.N.;Frías,M.D.;Blake,L.J.;Sample,J.;Lturbide,M.; Herrera,S.;French,A.S.;Norling,M.D.;Rinke,K.;&Marcé,R.2021.Forecasting water temperature in lakes and reservoirs using seasonal climate prediction, Water Research 201:0043-1354. [CrossRef]
  22. Meteorological Center, C.M.A.;CLDAS2.0 dataset description. http://data.cma.cn/data/detail/dataCode/NAFP_CLDAS2.0_NRT.html [2017-01-19].
  23. Nayak,M.A.;Herman,J.D.;&Steinschneider,S.2018.Balancing flood risk and water supply in California: Policy search integrating short-term forecast ensembles with conjunctive use. Water Resources Research 54:7557-7576. [CrossRef]
  24. Qin,Y.;Zhao,Q.D.;Liu,Y.Q.;&Ding,J.L.2021.Response of snow hydrological processes to climate change in the Hutubi river basin on the North Slope of Tian shan mountains. Journal of Soil and Water Conservation 35(3): 190-199. [CrossRef]
  25. Regonda,S.K.;Rajagopalan,B.;Clark,M.;&Zagona,E.2006.A multimodel ensemble forecast framework: Application to spring seasonal flows in the Gunnison River Basin. Water Resources Research 42, W09404. [CrossRef]
  26. Sadro,S.;Sickman,J.O.;Melack,J.M.;&Skeen,K.2018.Effects of climate variability on snowmelt and implications for organic matter in a high-elevation lake. Water Resources Research 54: 4563–4578. [CrossRef]
  27. Tian,H.;Yang,X.D.;Zhang,G.P.;Zhao,L.N.;Wang,Z.;&Zhao,L.Q.2011.The possible weather causes for snowmelt flooding in Xinjiang in Mid-March 2009. Meteor Mon 37(5): 590-598. [CrossRef]
  28. Tian,D.;Wood,E.F.;&Yuan,X.2017.CFSv2-based sub-seasonal precipitation and temperature forecast skill over the contiguous United States. Hydrology and Earth System Sciences 21: 1477-1490. [CrossRef]
  29. Ji, Q.;Ma, Z.;Xu,J.;Yan,S.;Li,X.A Snowfall Detection Algorithm for Fengyun-3D Microwave Sounders with Differentiated Atmospheric Temperature Conditions. Water 2023,15, 2315. [CrossRef]
  30. Wang,X.Q.;Lu,X.Y.;Ma,Y.;&Wang,X.2019.Study on snow disaster assessment method and snow disaster regionalization in Xinjiang. Journal of Glaciology and Geocryology 41(4): 836-844. [CrossRef]
  31. Wang,H.;Wang,M.X.;Wang,S.L.;&Yu,X.J.2021.Spatial-temporal variation characteristics of snow cover duration in Xinjiang from 1961 to 2017 and their relationship with meteorological factors. Journal of Glaciology and Geocryology 43(1): 61-69. [CrossRef]
  32. Wei,Q.;Dai,K.;Lin,J.;&Zhao,R.X.2020.Evaluation on the 2016-2018 finegrid dedprecipitation and temperature for ecastion. Meteor Mon 46(10): 1272-1285. [CrossRef]
  33. Wang,F.J.;Zhao,C.H.;Ma,Y.;&Xia,Z.Y.2018.Prediction effectiveness verification of ECMWF Fine grid model for air temperature in Qingdao region. Meteorological Science and Technology 46(1): 112–120. [CrossRef]
  34. Xiang,Y.Y.;Wang,Z.Z.;Zhang,W.;&Chen,Y.Y.2017.Study of snowmelt runoff simulation in arid regions: Progress and prospect. Journal of Glaciology and Geocryology 39(4): 892-901. [CrossRef]
  35. Yan,J.;Liao,G.Y.;Gebremichael,M.;Shedd,R.;&Vallee,D.R.2012.Characterizing the uncertainty in river stage forecasts conditional on point forecast values. Water Resources Research 48, W12509. [CrossRef]
  36. Zhang,J.L.;Luo,J.;&Wang,R.M.2021.Combined analysis of the spatiotemporal variations in snowmelt(ice) flood frequency in Xinjiang over 20 years and atmospheric circulation patterns. Arid Zone Research 38(2): 339–350. [CrossRef]
  37. Zhou,G.;Cui,M.Y.;Li,Z.;&Zhang,S.Q.2021.Dynamic evaluation of the risk of the spring snowmelt flood in Xinjiang. Arid Zone Research 38(4): 950-960. [CrossRef]
  38. Zhang,Z.L.;Mao,W.Y.;Zhang,S.Q.;Wang,M.Q.;Tang,Y.;Mushajiang,A.D.T.L.d;&Yusupu,T.R.G.2022.Correction and verification for grid refined forecast of temperature and frost in spring in Northern Xinjiang. Meteor Mon 48(11): 1460–1474. [CrossRef]
  39. Zhang,W.;Jiang,Y.;Dong,J.;Song,X.J.;Pang,R.B.;Guoan,B.Y.;Yu,H.2023.A deep learning method for real-time bias correction of wind field forecasts in the Western North Pacific,Atmospheric Research 284. [CrossRef]
  40. Zhang,H.;Wang,F.T.;Zhou,P.2022.Changes in climate extremes in a typical glacierized region in central Eastern Tianshan Mountains and their relationship with observed glacier mass balance,Advances in Climate Change Research,13(6):909-922. [CrossRef]
  41. Zhou,Y.;Li,G.Y.;Jin,H.J.;Marchenko,S.S.;Ma,W.;Du,Q.S.;Li,J.M.;Chen,D.2022.Viscous creep of ice-rich permafrost debris in a recently uncovered proglacial area in the Tianshan Mountains, China,Advances in Climate Change Research,13(4):540-553. [CrossRef]
  42. Zhong,X.Y.;Zhang,T.J.;Su,H.;Xiao,X.X.;Wang,S.F.;Hu,Y.T.;Wang,H.J.;Zheng,L.;Zhang,W.;Xu,M.;Wang,J.2021.Impacts of landscape and climatic factors on snow cover in the Altai Mountains, China,Advances in Climate Change Research,12(1):95-107. [CrossRef]
Preprints 77846 g001
Figure 1. Overview map of mountainous areas in Northern Xinjiang.
Figure 1. Overview map of mountainous areas in Northern Xinjiang.
Preprints 77846 g001
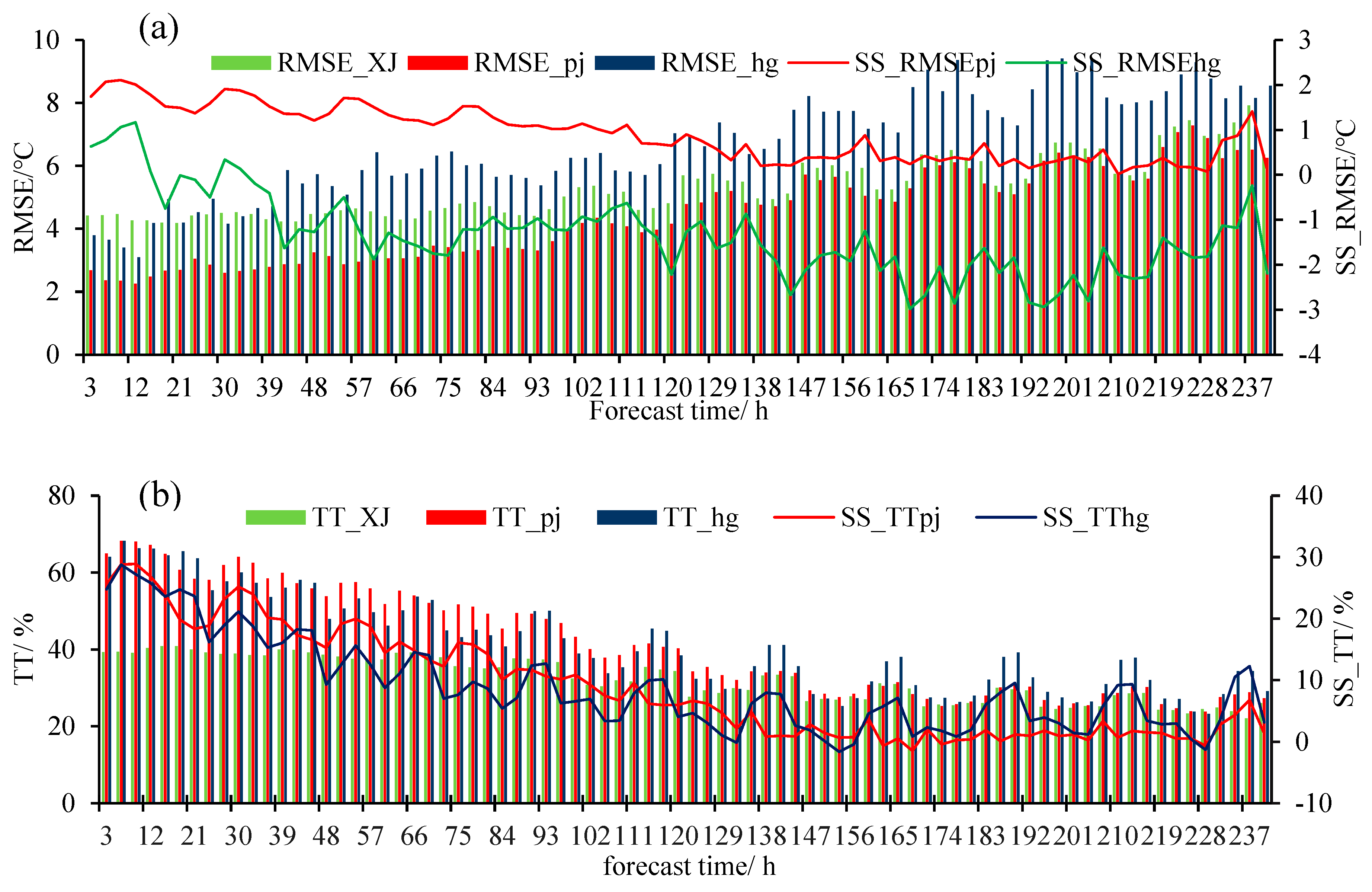
Preprints 77846 g002
Figure 2. Time series distribution of RMSE(a), forecast accuracy(b) and correction techniques of three temperature forecast products in the mountainous areas of northern Xinjiang.
Figure 2. Time series distribution of RMSE(a), forecast accuracy(b) and correction techniques of three temperature forecast products in the mountainous areas of northern Xinjiang.
Preprints 77846 g002
Preprints 77846 g003
Figure 3. Spatial distribution of RMSE for 0–24, 24–48, and 48–72 h temperature forecasts. (Column: XJ, HG, and PJ forecast from left to right; Rows: 0–24, 24–48, and 48–72 h from top to bottom).
Figure 3. Spatial distribution of RMSE for 0–24, 24–48, and 48–72 h temperature forecasts. (Column: XJ, HG, and PJ forecast from left to right; Rows: 0–24, 24–48, and 48–72 h from top to bottom).
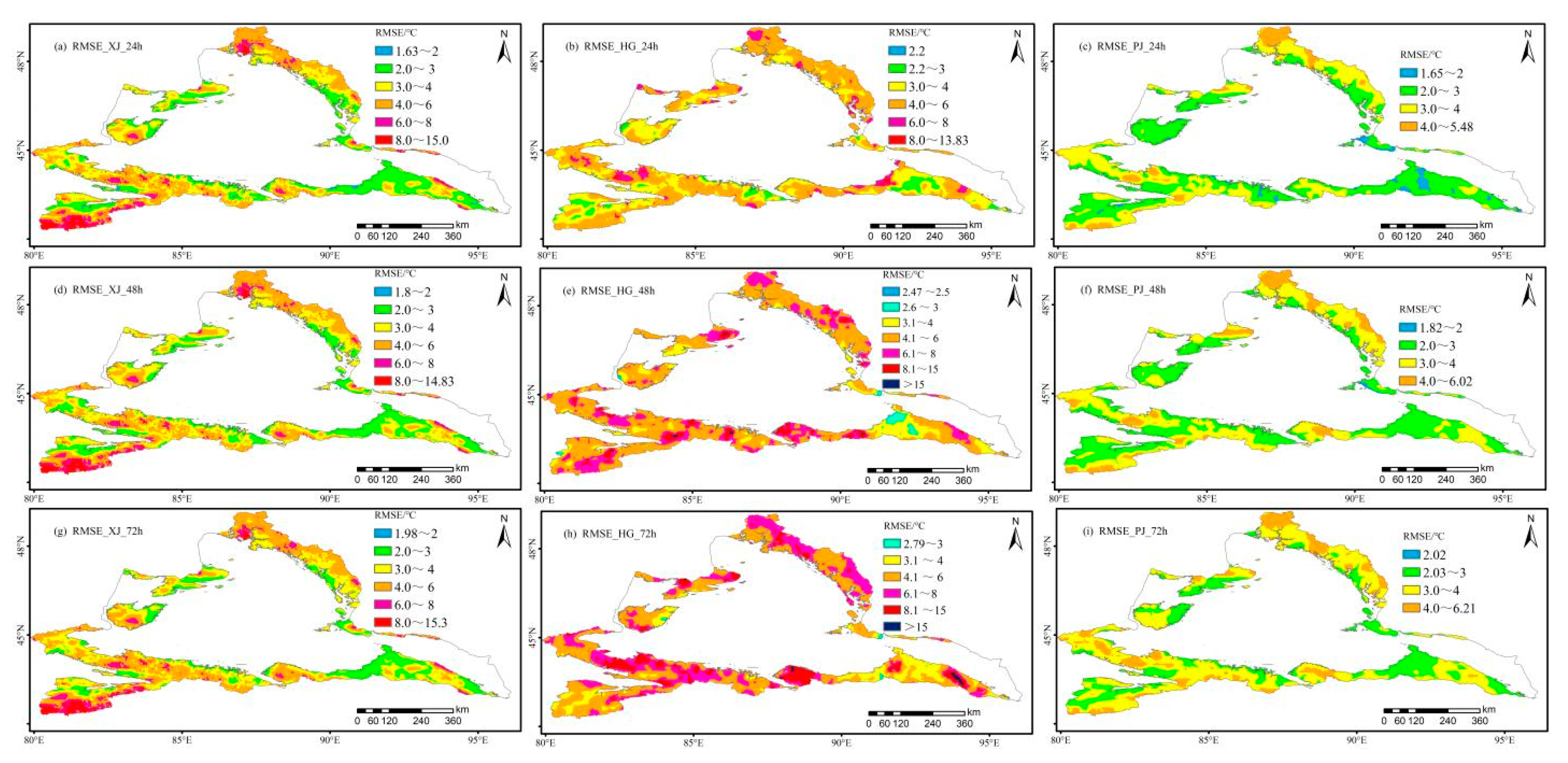
Preprints 77846 g003
Preprints 77846 g004
Figure 4. Time series distribution of root-mean-square errors and prediction accuracy during 1–10 days of daily maximum temperature forecasts in mountainous areas of northern Xinjiang.
Figure 4. Time series distribution of root-mean-square errors and prediction accuracy during 1–10 days of daily maximum temperature forecasts in mountainous areas of northern Xinjiang.
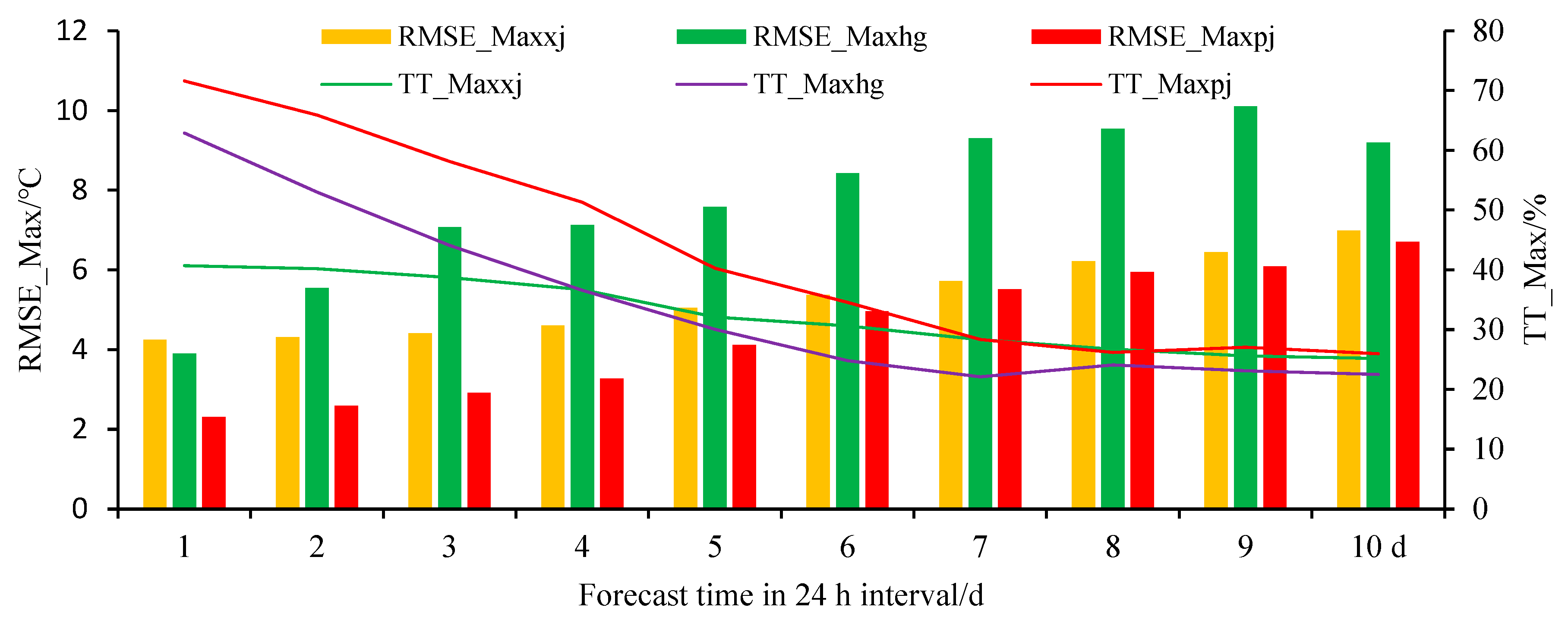
Preprints 77846 g004
Preprints 77846 g005
Figure 5. Spatial distribution of root-mean-square errors in the following 1, 2, and 3 days for daily maximum temperature forecasts in the mountainous areas of northern Xinjiang. (Column: XJ, HG, and PJ forecast from left to right; Rows: 1, 2, and 3 days from top to bottom).
Figure 5. Spatial distribution of root-mean-square errors in the following 1, 2, and 3 days for daily maximum temperature forecasts in the mountainous areas of northern Xinjiang. (Column: XJ, HG, and PJ forecast from left to right; Rows: 1, 2, and 3 days from top to bottom).
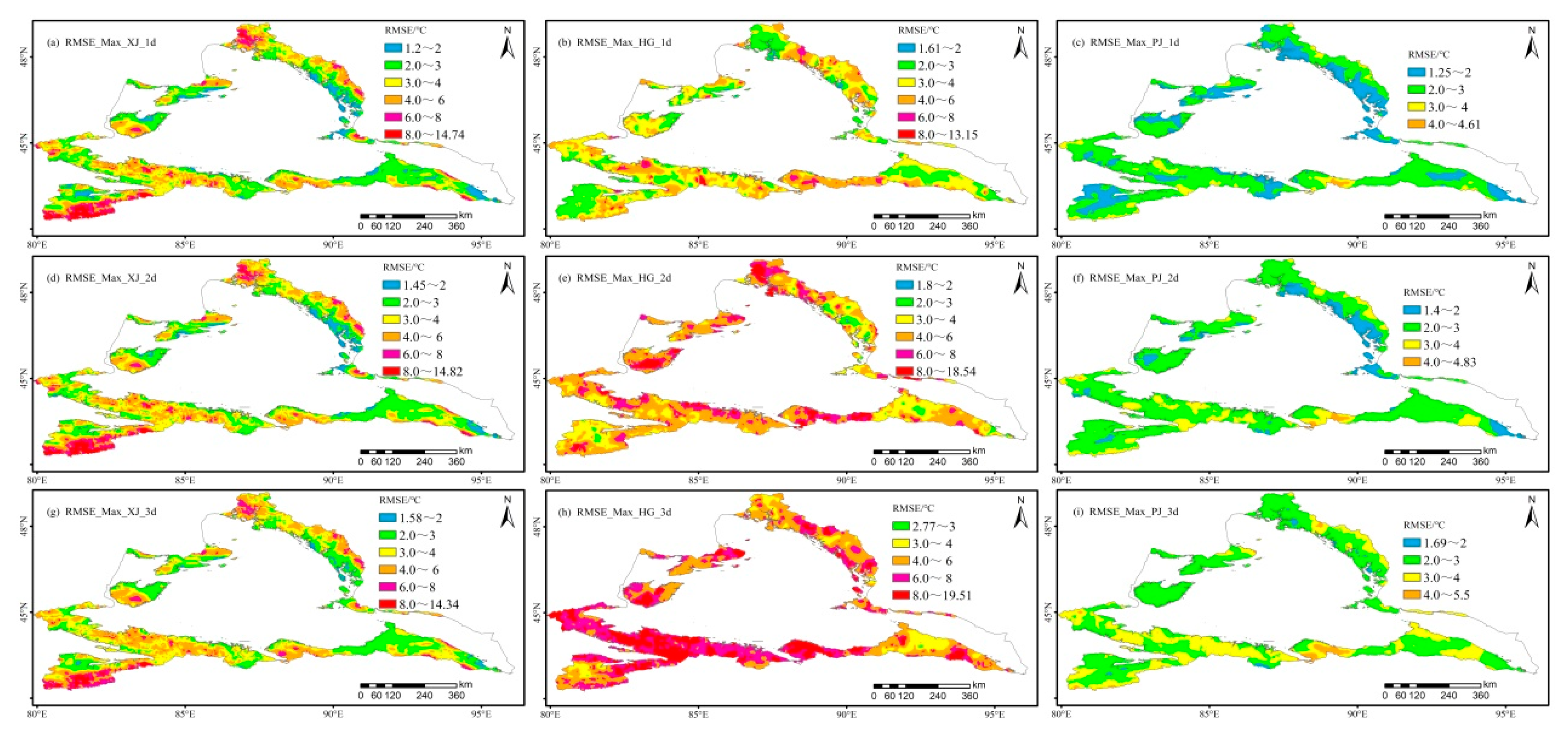
Preprints 77846 g005
Preprints 77846 g006
Figure 6. Time series distribution of root-mean-square errors and correction technique of daily temperature rise amplitude forecast for the following 1–10 days in mountainous areas of northern Xinjiang.
Figure 6. Time series distribution of root-mean-square errors and correction technique of daily temperature rise amplitude forecast for the following 1–10 days in mountainous areas of northern Xinjiang.
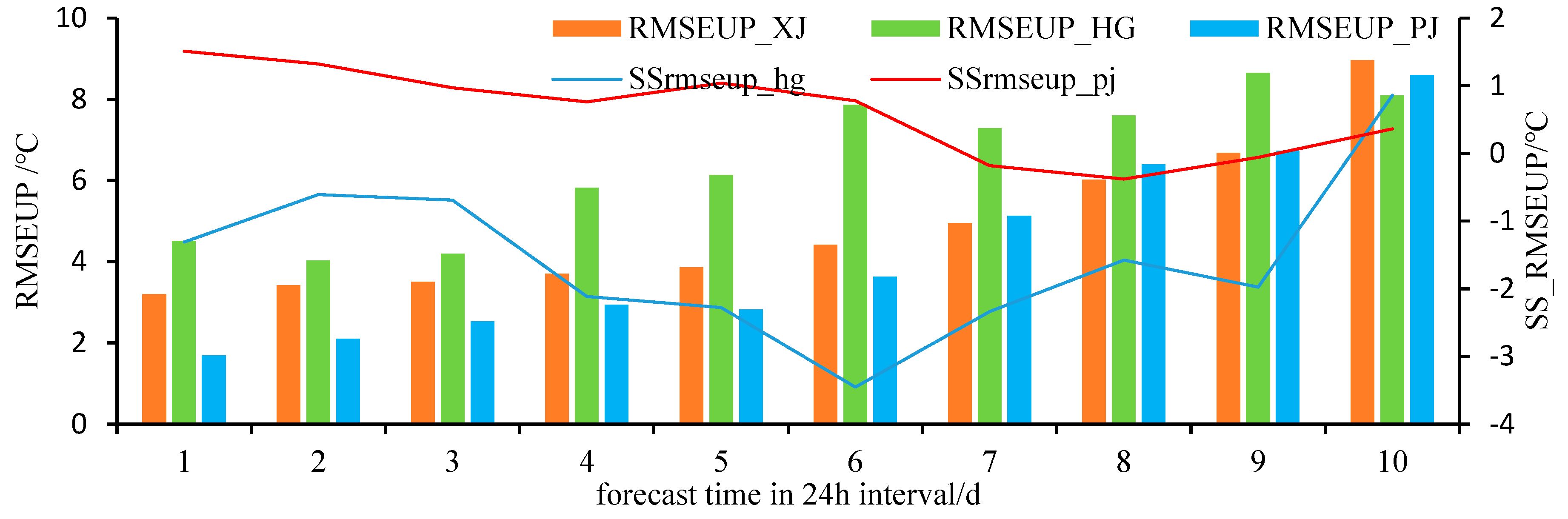
Preprints 77846 g006
Preprints 77846 g007
Figure 7. Spatial distribution of root-mean-square errors for daily temperature rise amplitude forecast for the following 1, 2 and 3 days in the mountainous areas of northern Xinjiang. (Column: XJ, HG, and PJ forecast from left to right; Rows: 1, 2, and 3 days from top to bottom).
Figure 7. Spatial distribution of root-mean-square errors for daily temperature rise amplitude forecast for the following 1, 2 and 3 days in the mountainous areas of northern Xinjiang. (Column: XJ, HG, and PJ forecast from left to right; Rows: 1, 2, and 3 days from top to bottom).
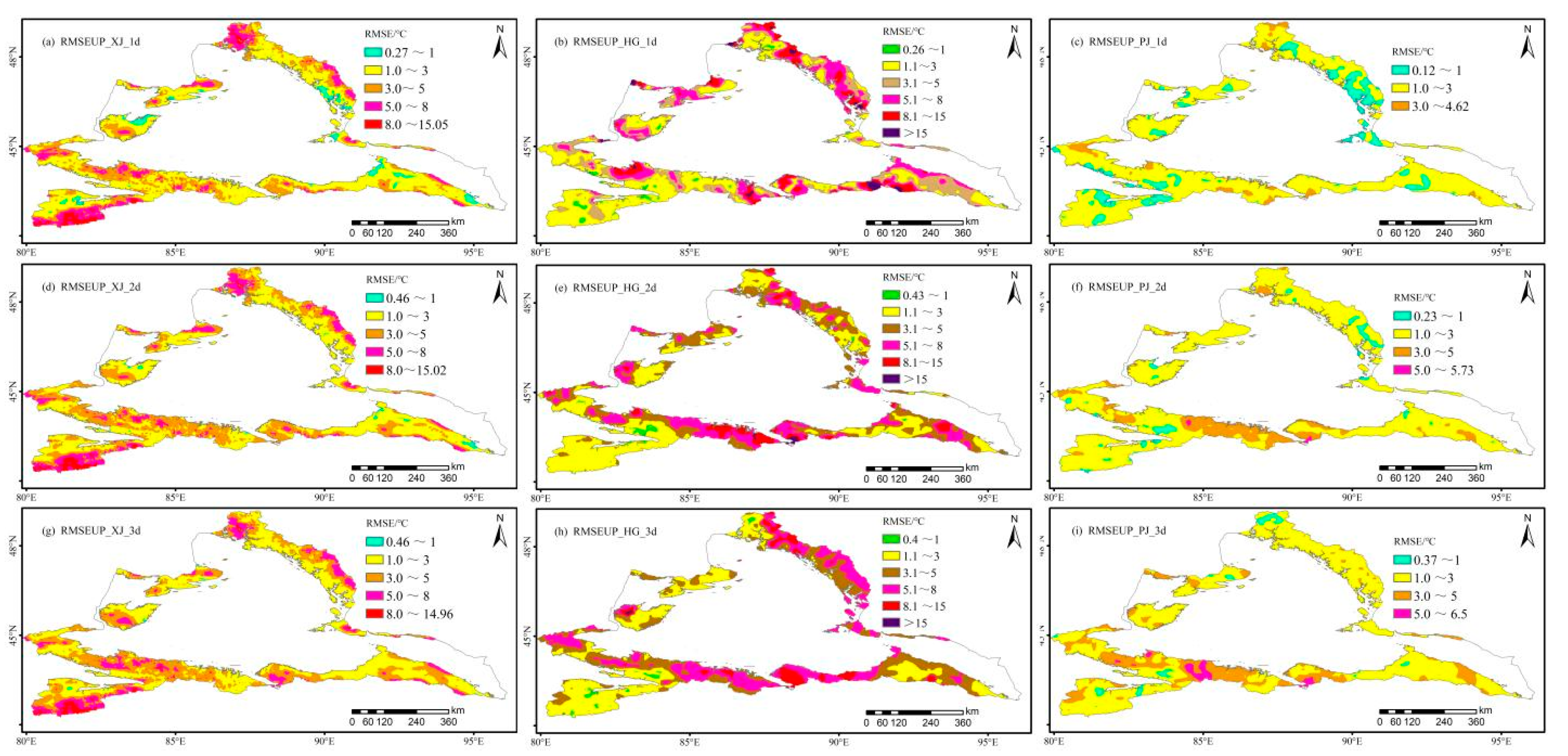
Preprints 77846 g007
Preprints 77846 g008
Figure 8. Time series of snowmelt temperature forecast accuracy and correction techniques values of three kinds forecast products in spring in mountainous areas of northern Xinjiang within 10 days forecast time.
Figure 8. Time series of snowmelt temperature forecast accuracy and correction techniques values of three kinds forecast products in spring in mountainous areas of northern Xinjiang within 10 days forecast time.
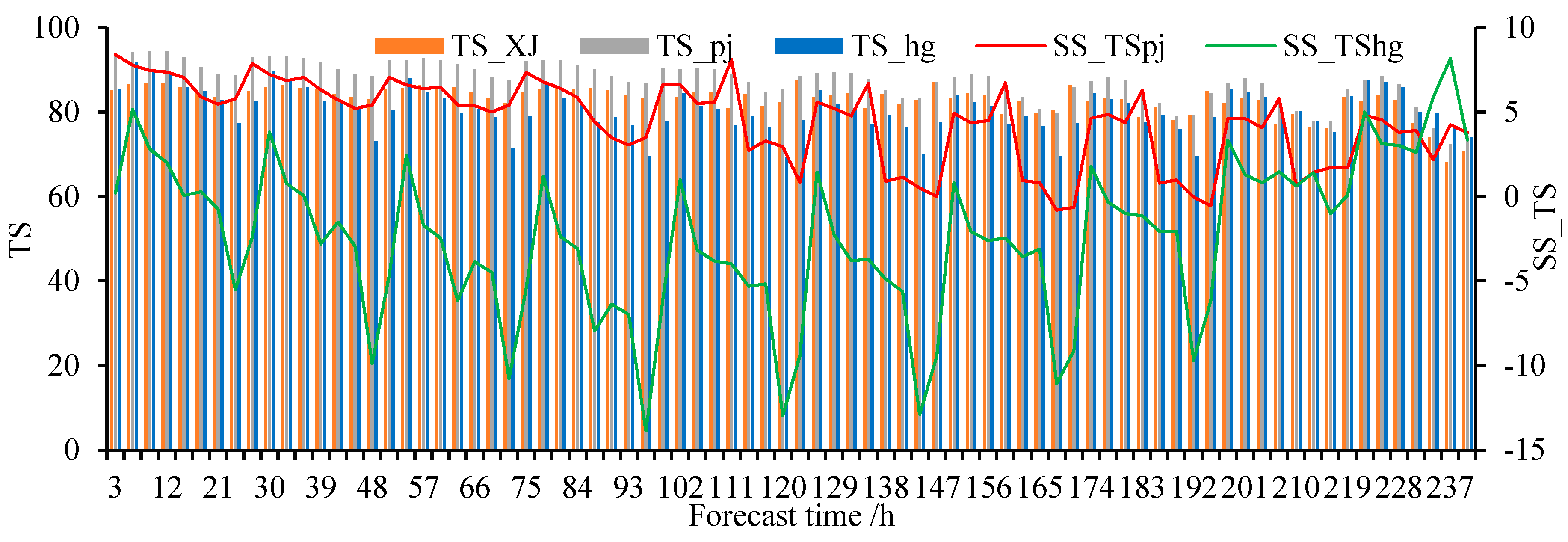
Preprints 77846 g008
Preprints 77846 g009
Figure 9. Spatial distribution of snowmelt temperature forecast accuracy at 24, 48, and 72 h (Columns: XJ, HG and PJ forecast from left to right; Rows: 24h, 48h and 72h forecast times from top to bottom, respectively).
Figure 9. Spatial distribution of snowmelt temperature forecast accuracy at 24, 48, and 72 h (Columns: XJ, HG and PJ forecast from left to right; Rows: 24h, 48h and 72h forecast times from top to bottom, respectively).
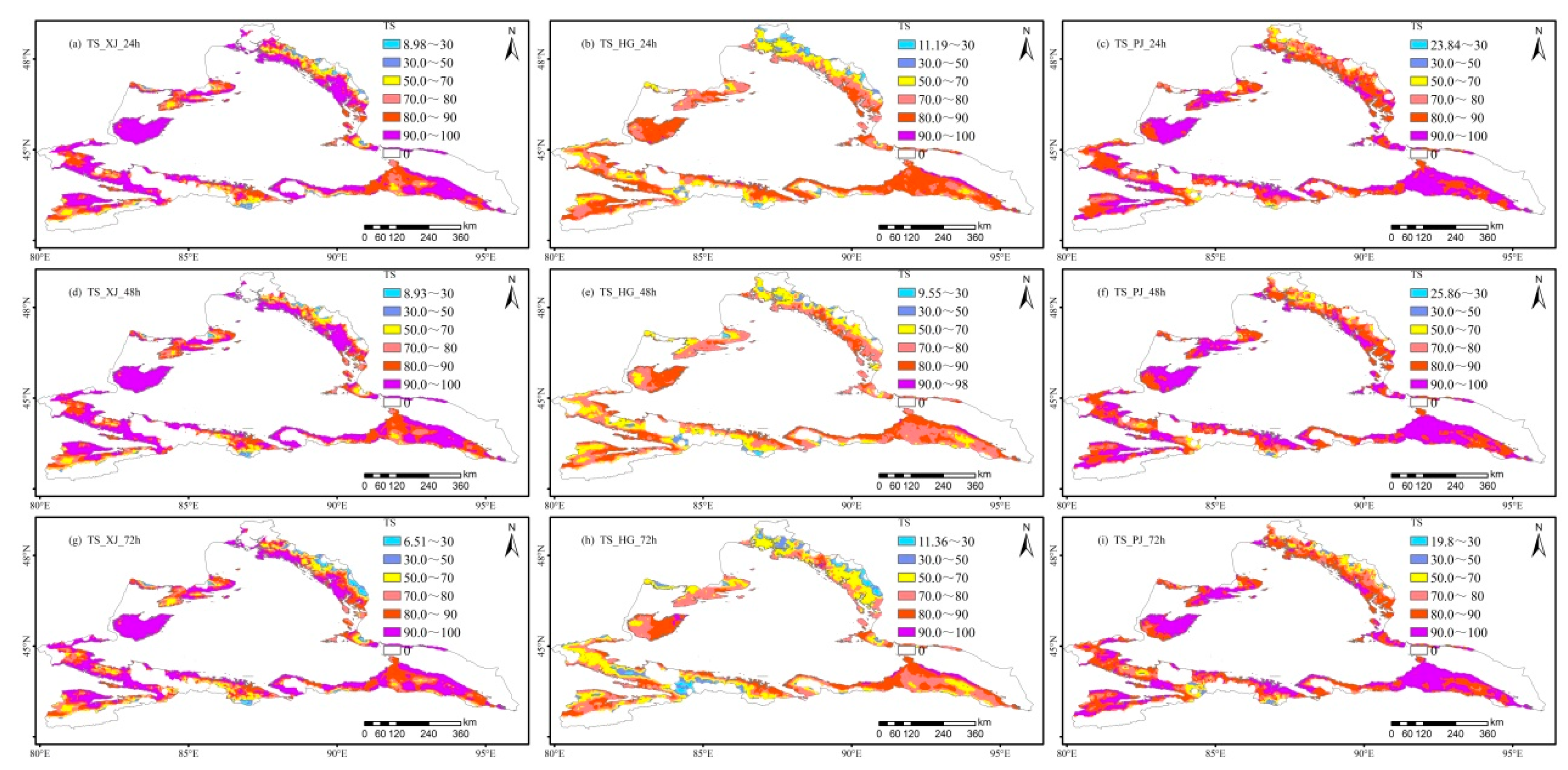
Preprints 77846 g009
Preprints 77846 g010
Figure 10. Daily distribution of Root-mean-square errors of daily snowmelt duration forecast for the following 1–10 days in the mountainous areas of northern Xinjiang.
Figure 10. Daily distribution of Root-mean-square errors of daily snowmelt duration forecast for the following 1–10 days in the mountainous areas of northern Xinjiang.
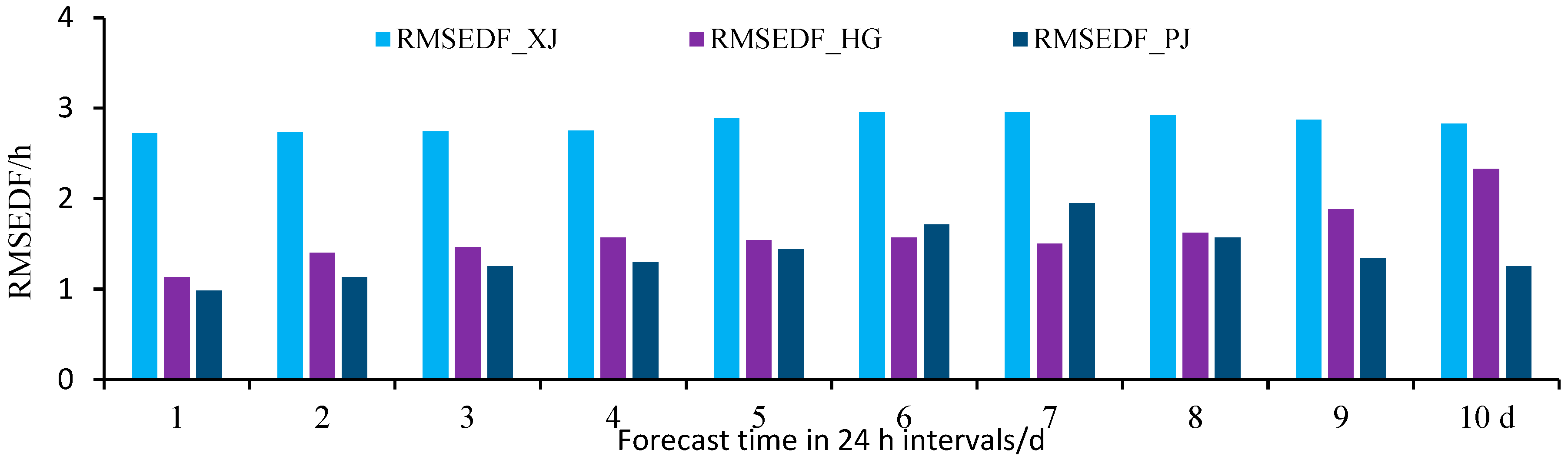
Preprints 77846 g010
Preprints 77846 g011
Figure 11. Spatial distribution of Root-mean-square errors of daily snowmelt duration forecast for the following 1, 2, and 3 days in the mountainous areas of northern Xinjiang (Columns: XJ, HG, and PJ forecast from left to right; Rows: 1, 2, and 3 days from top to bottom).
Figure 11. Spatial distribution of Root-mean-square errors of daily snowmelt duration forecast for the following 1, 2, and 3 days in the mountainous areas of northern Xinjiang (Columns: XJ, HG, and PJ forecast from left to right; Rows: 1, 2, and 3 days from top to bottom).
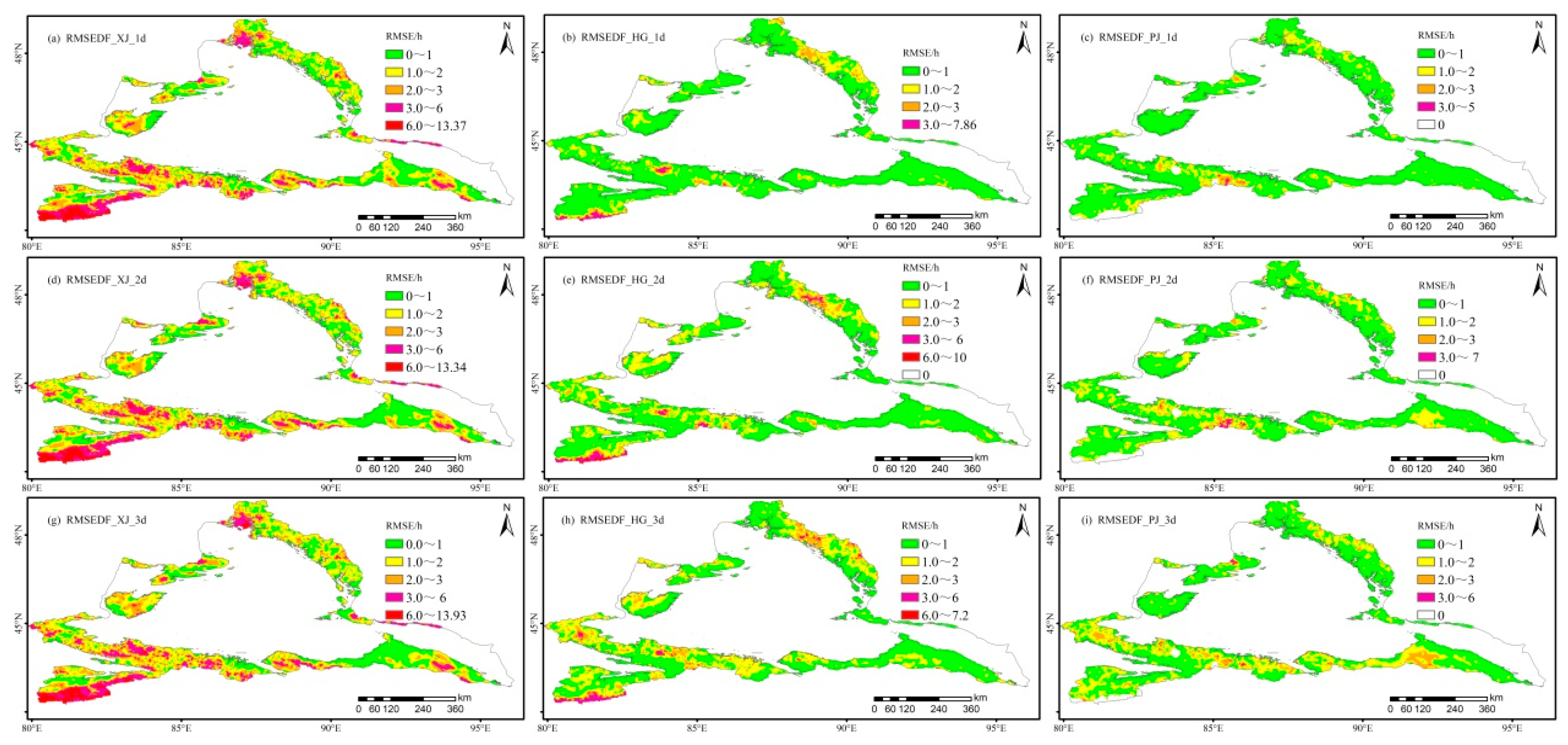
Preprints 77846 g011
Table 1. Test effect of root mean square error, temperature prediction accuracy, and its correction techniques of three prediction products.
Table 1. Test effect of root mean square error, temperature prediction accuracy, and its correction techniques of three prediction products.
Average value of the forecast time 0–240 h Correction techniques 0–24 h 24–48 h 48–72 h 72–96 h 96–120 h 120–240 h
RMSE_XJ/℃ 5.17 4.04 4.11 4.22 4.3 4.55 6.19
RMSE_HG/℃ 6.77 –1.60↓ 4.37 5.37 5.9 5.47 6.66 8.01
RMSE_PJ/℃ 4.59 0.58↑ 2.97 3.18 3.39 3.54 4.11 6.21
TT_XJ/ % 32.52 40.15 39.37 38.82 37.19 34.56 26.24
TT_HG/ % 41.65 9.13↑ 55.36 47.9 44.92 42.91 38.39 29.14
TT_PJ/ % 41.83 9.30↑ 58.04 53.82 50.1 46.8 40.3 27.31
Table 2. RMSE and prediction accuracy of daily maximum temperature forecast in mountainous areas of northern Xinjiang.
Table 2. RMSE and prediction accuracy of daily maximum temperature forecast in mountainous areas of northern Xinjiang.
Average value of forecast time in 24 h interval 240 h Correction techniques 1 d 2d 3 d 4 d 5 d 10 d
RMSE_Max_XJ/℃ 5.11 3.74 3.83 3.97 4.20 4.75 6.82
RMSE_Max_HG/℃ 7.85 –2.74↓ 3.68 5.16 6.64 6.82 7.33 8.96
RMSE_Max_PJ/℃ 4.61 0.50↑ 2.26 2.54 2.87 3.23 4.06 6.68
TT_Max_XJ/% 32.77 42.47 41.63 40.08 37.77 32.66 25.27
TT_Max_HG/% 35.00 2.23↑ 62.91 53.02 44.11 36.59 30.05 22.52
TT_Max_PJ/% 43.73 10.96↑ 71.61 65.88 58.12 51.30 40.25 25.97
Table 3. Root-mean-square errors in the daily temperature rise amplitude forecast for mountainous area of northern Xinjiang.
Table 3. Root-mean-square errors in the daily temperature rise amplitude forecast for mountainous area of northern Xinjiang.
Average value of the forecast time in 24 h interval Range 1–10 d correction techniques 1 d 2 d 3 d 4 d 5 d
RMSEUP_XJ/ ℃ 2.4–714.68 4.87 3.19 3.41 3.50 3.70 3.85
RMSEUP_HG/ ℃ 2.96–20.14 6.41 –1.54↓ 4.51 4.02 4.19 5.81 6.13
RMSEUP_PJ/ ℃ 2.84–7.35 4.25 0.62↑ 1.69 2.10 2.53 2.94 2.82
Table 4. Regional and times division comparison of snowmelt temperature forecast accuracy for three kinds of forecast products.
Table 4. Regional and times division comparison of snowmelt temperature forecast accuracy for three kinds of forecast products.
Average forecast time Range 240 h Correction techniques 24 h 48 h 72 h 96 h 120 h 240 h
TS_XJ 0.09–99.84 79.36 82.35 82.65 80.94 82.64 82.1 66.29
TS_HG 0.26–99.07 74.1 –5.4↓ 71.72 68.8 65.93 63.6 64.68 68.01
TS_PJ 1.45–98.98 81.99 2.45↑ 85.12 84.78 83.22 83.06 81.71 66.75
Table 5. Root-mean-square errors in the daily snowmelt duration forecast for mountainous areas of northern Xinjiang.
Table 5. Root-mean-square errors in the daily snowmelt duration forecast for mountainous areas of northern Xinjiang.
Average value of the forecast time in 24h interval Range 1–10d Correction techniques 1 d 2 d 3 d 4 d 5 d 10 d
RMSEDF_XJ/ h 0–14.62 2.22 1.90 1.91 1.93 1.97 2.07 2.04
RMSEDF_HG/ h 0–7.2 1.40 0.81↑ 0.72 0.93 1.03 1.07 1.03 1.85
RMSEDF_PJ/ h 0–5.68 1.29 0.93↑ 0.66 0.80 0.92 0.95 1.10 0.81
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated