Prerpints.org logo
Preprint
Article

Finite Element Analysis using Crack Strain Separation Model for Reinforced Concrete Membrane

Altmetrics

Downloads

85

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 June 2023

Posted:

29 June 2023

You are already at the latest version

Alerts
Abstract
This paper presents a finite element analysis of the bi-directional orthogonal model, which incorporates individual crack strain separation and tracking. The objective of the research is to expand the current shear friction model to manage bi-directional cracking at any angle, allowing for a more universal model that can be applied to intricate structures and non-proportional loading cases. The proposed model was initially developed as a total strain-based model, with the assumption that crack strains are equivalent to total strains, but was subsequently recalculated to improve accuracy by separating crack strains from total strains. Furthermore, a separate crack strain formulation was created to account for strains in the concrete's uncracked portions and locked-in crack strains. The article then discusses the testing of various convergence methods and loading programs to achieve high convergence. Comparative analyses of the generalized shear friction model with other models for crack orientation and loading cases similar to those of a reinforced concrete membrane are also presented. The MATLAB program successfully applied the bi-directional cracking model for one finite element under a uniform cyclical strain state, using a secant stiffness formulation.
Keywords: 
Subject: Engineering  -   Architecture, Building and Construction

1. Introduction

The finite element analysis for the reinforced concrete is primarily dependent on steel and concrete constitutive relationship development out of which a cracked reinforced concrete behaviour is accurately modelled. However, it is important to note that the task is not simple because the stress-strain relationship between the cracked concrete, reinforcing steel as well as their interaction are not linear. The issues may include reverse loading and unloading relationships for illogical loading, tension stiffening effect within cracked concrete for modelling the reinforcement’s bond-slip behaviour as well as shear transfer using shear friction through a crack. Studies have been conducted on these. Therefore, choosing robust and accurate modelling methods for the analysis of finite element that can capture desirable behaviours is very important. Finite-element modelling is ultimately aimed at providing formulations that are stable, easily implemented and computationally efficient and whose results are accurate and reasonable.
Analysis of finite element reinforced concrete membrane structures is faced with a number of issues that have not been completely developed. Models which are pertinent to particular structures’ monotonic loading like a uniform shear modulus that uses shear retention factor (β), crack surface degradation and interlock, smeared shear modulus as the function of the principal strains and stresses, corresponding continuum behaviour that denotes a local crack slip and local shear stress check on crack surfaces have resulted in better accuracy [1,2,3,4]. However, the process providing sufficient behaviour simulations under non-uniform loading conditions like reverse-cyclical loading are limited [5,6]. In addition, some essential material model sections do not capture cracked reinforced concrete behaviour in an accurate manner [7]. Most importantly, one of the problems is that derivation of most of the models is based on experimental data fitting instead of basic physical principles. Researchers have proposed orthogonal shear friction model that uses a modified newton-raphson method (MNRM) formulation [8]. There is an assumption that divergence is caused by total strains which are purely crack strains that are made within the model. This assumption disregards the fact that some of the strains can be emanating from the concrete’s uncracked portions. The absence of slip shear stress in computing doesn’t matter because the equation is regarded as the uncracked concrete equation τb=GγTotal. On the other hand, slip limits cannot be correct if they are solved through the use of total strains rather than crack strains thus making the model to flip-flop and diverge. This shows that it is necessary to separate crack strains from total strains and then tracked them during the analysis process [9]. This paper proposes a new bi-directional shear friction model with crack strains that separate out. The paper then compares Vecchio models and uniform shear modulus (βG) with BSFT bearing crack strain separated (CSS) model.

2. Research Significant

Two significant areas are a bond-slip relationship between reinforcement and concrete for various loading and an appropriate model for the shear strength and stiffness in cracked concrete. To robust the convergence of the bi-directional cracked concrete model, this study focused on a new formulation for the bi-directional shear friction model using crack strain separation to improve the convergence of the bi-directional cracked reinforced concrete membrane.

3. Crack Opening Path Model

This is a model that is based on the slip-separation relationship γ = a ε and crack opening model which is a constitutive model that uses affiliation between crack friction coefficient, μ u p , μ d o w n and tension stress that is normal to crack separation and crack surface. This coefficient differs from the traditional friction coefficient as its definition is relative to the crack opening path slope but not the crack surface. As such, a regular friction coefficient is achieved instead of the one which differs from the crack opening path slope. Dilatancy and friction effects are separated thus making the friction coefficient to be nearly constant [10,11,12,13,14]. The friction coefficient definition leads to values that vary to a small extent in terms of slip. Furthermore, the definition enhances the computation of a friction coefficient for the two slip directions due to the fact that it is difficult to push a block uphill in comparison with pushing it downhill. Friction coefficients μdown and μup are defined as crack opening path angle θ and a distinct crack path friction coefficient μ’. 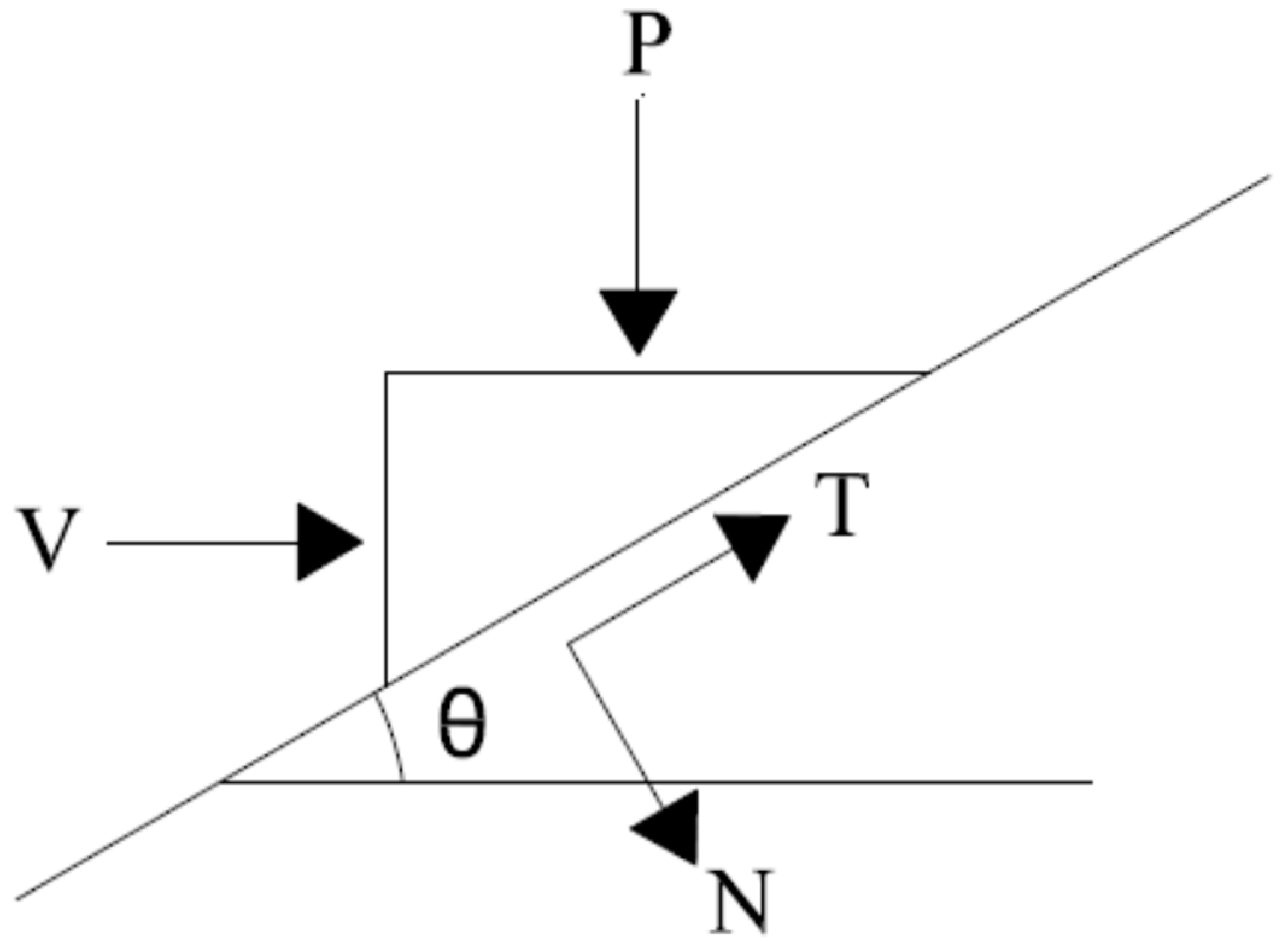Figure 1 shows the relationships of the coefficient of fraction. μ’=T/N and μ=V/P, where μ' is the coefficient of friction relative to the surface of the hill and μ is the coefficient of friction corresponding to the applied forces V and P. It is convenient to define the friction coefficient, μ, in terms of the friction coefficient relative to the crack opening path, μ’. Reference 13 provides the detailed crack formulation. Therefore, it is essential to define the key concepts of the crack strain separated model.

4. Crack Strain Separated (CSS) Bi-directional Shear Friction Model

The bilinear rectangular element is a key element in this model. It is a simple 4-noded element with eight degrees of freedom, which allows it to translate horizontally and vertically. The boundary conditions, DOFs, and geometries of the model are all defined using this element [8]. The crack coordinate system remains to be “1-2” whereas the global coordinate system is in the “x-y” direction. The definitions of bi-directional cracking are similarly kept in such a way that the first crack can be formed out of the global coordinate system at angle θ. The direction of principal tension defines it. On the other hand, the second crack can be formed perpendicular to the first crack thus making multiple crack coordinate systems unnecessary. The smearing of cracks and material properties is done throughout the element. Crack strains are however considered to be unequal to the total strains, but a single crack may only be active at ago. The model can now give an account of locked-in crack slip. Integration of the linear crack opening path with the model is done with the aim of enforcing the slip-separation relationship. The definition of an effective strain is done out of the crack opening path. It justifies the crack surface state. Enforcement of shearing stress limits helps in determining whether the crack surface slips. It also helps in defining the crack’s shear stiffness because of friction.
MNRM enhanced the achievement of non-linear property convergence within the model [8]. There was pure shear loading from MNRM which was applicable to the vertical load. This was determined by applied displacements. A proportional load vector enforced pure shear loading thus ensuring that a constant strain and stress state is maintained. Presentation of more details on model definitions just like that of separated crack strain formulations.

5. CSS Stress-Strain Formulations

The formulations are aimed at putting stress-strain relationships with regard to crack strains while maintaining the ability to formulate secant stiffness matrices on the basis of the total strains for analysis. There is a similarity in development between the total strains and a reasonable strain cracking simplification which is put into consideration when the slip is defined along the crack’s surface. The slip beside the crack was initially defined as the total shearing strain within the crack’s orientation γ12. To separate out the cracking shear strain, the total shear strain should be defined as follows:
γ 12 = γ c r + γ c
where γ c denotes the concrete shearing strain and refers to the cracking shear strain compared to concrete shear modulus (G). The crack’s locked-in slip can be justified by introducing the net shearing strain, γn concept. Calculation of the total shearing strain portion which has not been previously locked-in the crack provides the net shearing strain as illustrated in the following equation.
γ n = γ 12 − γ c r o l d
These definitions are only applicable to a situation in which the crack direction is one. For the locked-in shear strain to be considered in 2 crack directions, it is very important to consider net shearing strain for 2 cracks i.e. γ n 1 , γ n 2 with the number representing the first or the second crack. As such, the crack shear strain is allowed to be renewed for the active crack. Active crack γ n 1 would play a key role in defining the net shear strain for another crack shear strain to be obtained for the first crack. This implies that Equation 3 may define crack shear strain if either the first or the second crack is active. Individual crack strains and the total strains are currently separated from each other for the bi-directional shear friction model.
γ c r ( 1,2 ) = γ n ( 1,2 ) − γ c
The effective strain concept is necessary for implementing the slip-separation relationship. In addition, effective strain is a very important element as it helps in defining the crack surface state i.e. compression or tension. The state of the crack enables the determination of shear friction behaviour. However, there is a need for changing effective strain formulas because the crack slip drives the crack opening path. It is important to note that effective strain must be incorporated with crack shear strain and not the total shear strain. As such, effective strain is determined through the subtraction of crack slip separation from the normal strain due to the crack as indicated in the following equation.
ε 1,2 e = ε 1,2 − γ c r ( 1,2 ) a
Normal concrete stress curves are defined using the effective strain. Positive effective strain values imply that the surface of the crack does not touch the crack. It ensures the existence of tension throughout the crack. On the other hand, negative effective strain values ensure the existence of compression throughout the surface of the crack. Normal concrete stress curves in compression and tension should be equal as far as the bi-directional shear friction model is concerned. Equations should however be changed to incorporate include crack strain separation from total strains. Equations (5) and (6) listed below represent the normal concrete stress which is formulated for crack one [13]. However, Crack two equations may be obtained through the replacement of that of Crack one with that of Crack two for strain and stress notations eε1≤ εcr (concrete cracking strain):
σ 1 = E c ε 1 e = E c ε 1 − γ c r ( 1 ) a e
(a) eε1>εcr:
σ 1 = f c r 1 + 200 ε 1 e

5.1. Shearing Stress in the compression and tension throughout the crack

A bi-directional shear friction model is used to formulate shearing stress equations which incorporate separating crack strain from the total strain. There are 2 main categories of shearing stresses i.e. when the crack’s normal stress is compressive and when the crack’s normal stress is tensile. A presentation of the shear friction limit which is only considered in a compressive crack is made. However, the shear stress for the crack surface with tension is indicated in Equation 7. This is based on the assumption that the dowel action of reinforcement that crosses the crack resists the shearing stress if either the first or the second crack is active:
τ 12 = β ’ G γ n ( 1,2 ) 1 + β ’
The idea of low stiffness when cracks aren’t in contact with each other, is a weak spring. Reformulation of normal stress equations for tension throughout the crack can be done since shear stress has been defined. The following equation (8) may be formulated in case of a positive shear strain;
σ 1,2 = E 1,2 ε 1,2 − E 1,2 a 1 − β ’ 1 + β ’ γ n ( 1,2 )
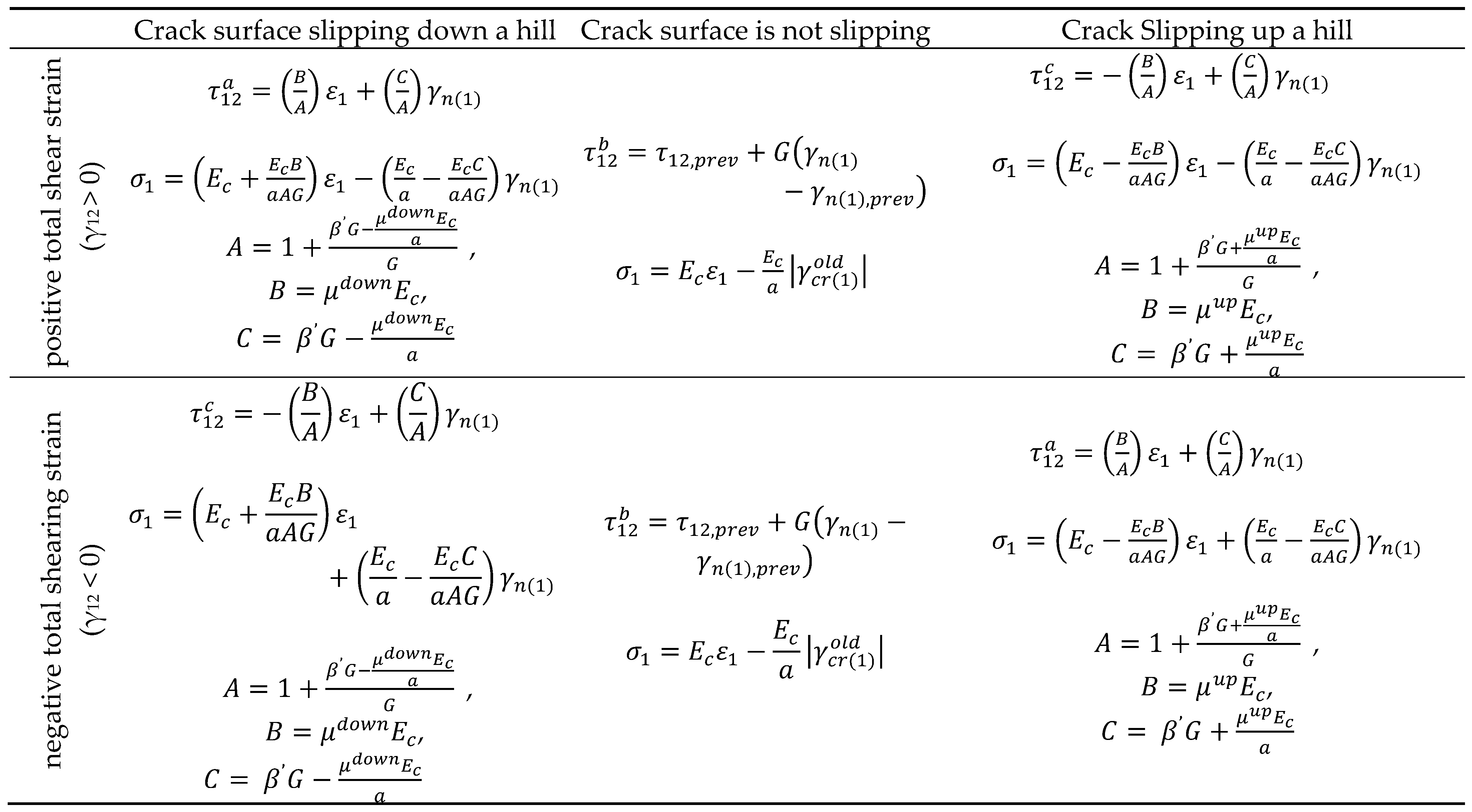
For crack surfaces that are in contact with each other with compression throughout the crack, equations that have been presented in this section are used to determine the shear stress. The first and the second crack are represented by the following derivations: (γ12< 0) and (γ12> 0) for negative and positive shearing strains respectively. There are 3 cases that are mostly put under consideration and whose derivations are presented in Table 1: (a) The crack surface that doesn’t slip, (b) The crack surface that slip downhill, and (c) The crack surface that slips uphill. The non-slip equation is used to determine shear stress, τ12 in any shear strain, γ12. However, it is restricted by the highest (τa12) and lowest (τc12) shear stresses as indicated in the following equation:
τ 12 a ≤ τ 12 = τ 12 b ≤ τ 12 c
Upper and lower shear stress limits (τa and τc) denote the stress that is necessary for overcoming friction force throughout the crack thus initiating slip. The limits of shear stress for the 2 cracks help in the determination of the crack that is active (τc1, τc2, τa1 andτa2). An active crack is said to be the first crack to reach the limits due to the fact that it is where the slip is first initiated thus resulting in behavioural control.

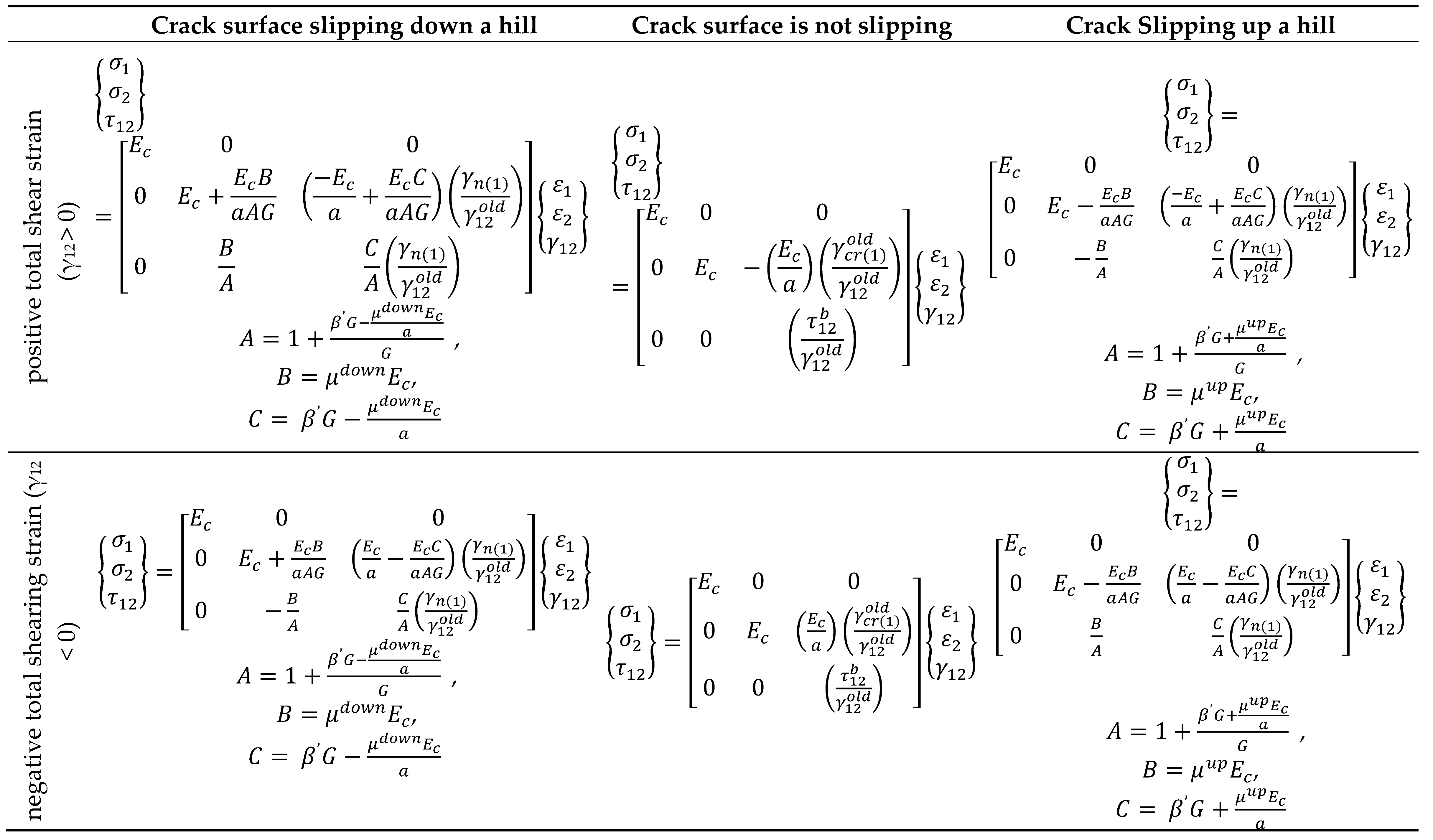
5.2. Formulation of Secant Stiffness Matrix: Net Shearing Strain

Net shearing strain is the basis for which normal and shearing are formulated. This is done with the aim of separating crack strain from the total strain thus enhancing the formulation of secant stiffness matrices which are divided into two major categories i.e. Crack one active and Crack two active. E1 and E2 represent the concrete’s secant moduli for the 1 and 2 crack directions. In addition, γn and total shear strain, γ12 are pre-multiplied in the equations for the stress equations to be written in terms of the aggregate strain.

5.2.1. Case One: Crack Direction 1 Active

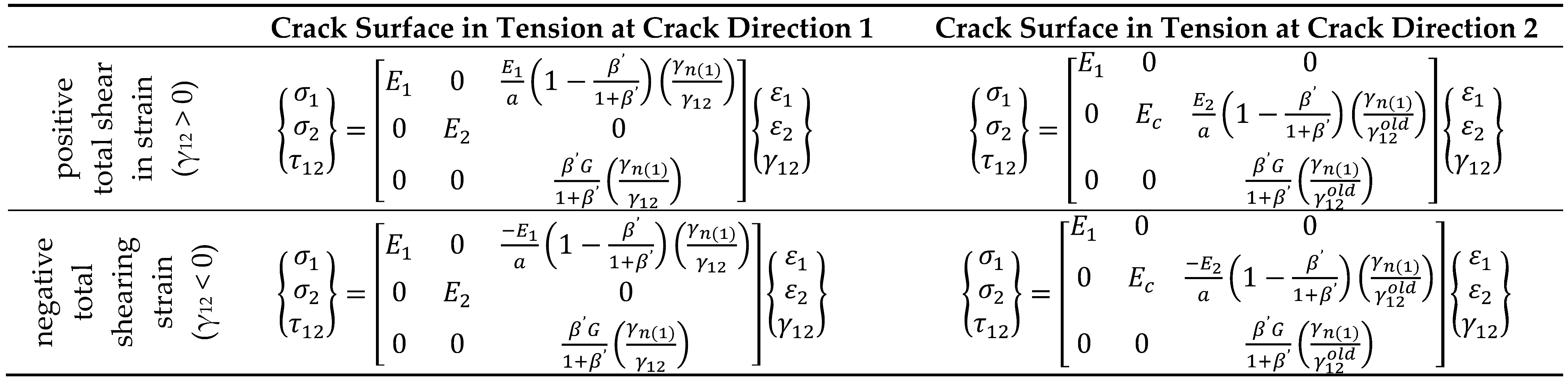
After the formation of Crack 1, stiffness cases should be put into consideration. For the crack surface that is said to be in tension, the stress-strain relationship is positive shearing strain and negative shearing strain, γ12 as illustrated in Table 2. However, the definition of a secant stiffness matrix is based on a number of shear stress cases for the crack surface that is in compression. Normal stress and shearing stress equations can as well be presented there. Table 3 shows the cases for both negative total shear strain (γ12<0) and positive total shear strain (γ12>0).

5.2.2. Case Two: Crack Direction 2 Active

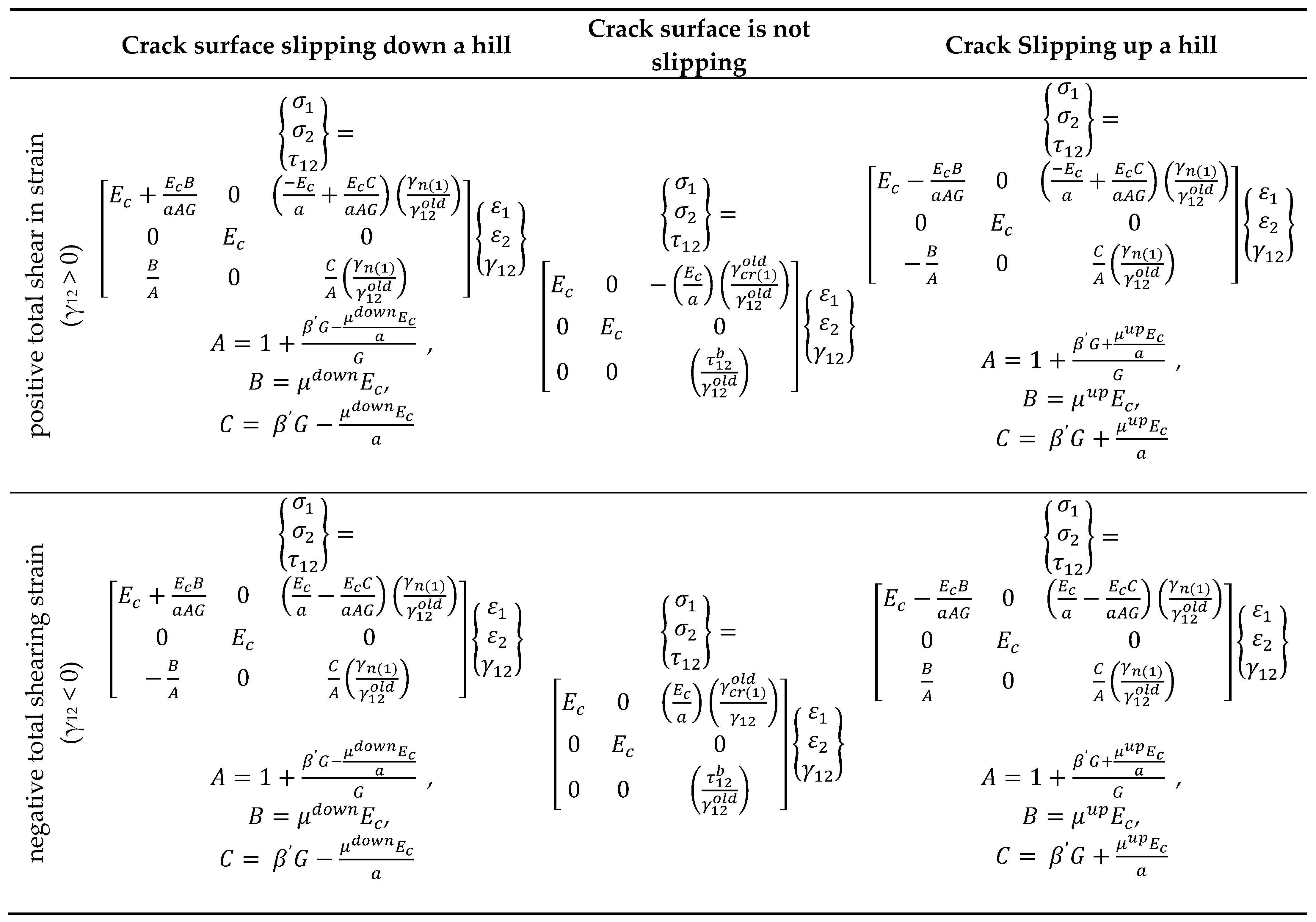
After the formulation of Crack 2, the following stiffness cases should be put into consideration for active Crack 2. For the crack surface that is said to be in tension, the stress-strain relationship is positive shearing strain and negative shearing strain, γ12 as illustrated in Table 2. However, the definition of secant stiffness matrix is based on a number of shear stress cases for the crack surface that is in compression. Calculation of A, B, and C constants was done within the derivations for the cases of shear stress in the preceding. Normal stress and shearing stress equations can as well be presented there. Table 4 indicates the cases for both negative total shear strain (γ12<0) and positive total shear strain (γ12>0).

5.2.3. Active Crack Criteria

One established crack direction may only be active at ago as previously stated. This makes it necessary to establish rational active crack criteria. The bi-directional shear friction model was newly formulated with the aim of separating crack strain from the total strain. However, there is a need to change some of the criteria that were previously established. Epsilon effective was used in determining if the crack experienced compression or tension. The new effective strain formation however makes it necessary that the shear strain of the crack is recognized. It is hard to determine the shear strain of the crack until the right equation of the shear stress is determined. The following is the newly established criteria for determining the crack state.
For tensional crack surface, τ 12 = β ’ G γ c r a n d γ n = ( τ 12 / G ) + γ c r . Providing a cracking shear stress solution result in: γ c r = γ n / ( 1 + β ’ ) . Epsilon effective equation can be plugged into this leads us to the following equation.
ε e = ε − γ n a 1 + β ’
The value obtained from Equation 9 above is positive if the tension assumption was accurate. However, a negative value is yielded in case of a wrong assumption. As such, the cracked surface is said to be in compression. After determining the nature of the value obtained, a similar active crack criterion is applicable just like that used for the bi-directional shear friction model.

6. Results and Discussions

The bi-directional shear friction model’s CSS (Crack Strain Separated) formulation was used to analyze a single four-node component. The MATLAB Program was used to insert the Modified Newton-Raphson Method with the model’s CSS [9]. Analysis was done on a single four-node rectangular component in the relative load vector loading. The concrete membrane measured 50.8 mm thick, 254 mm wide, and 254 mm tall with a shear retention factor, β’, of 0.05. On the other hand, the compressive strength, f’c, of the concrete was about 41.4 MPa. Shear modulus, G, and elastic modulus Ec were 13.8 GPa and 27.6 GPa in that order. The strength of the reinforcement yield was about 414 MPa with the steel’s modulus elasticity, Es, being 206.8 GPa. Additionally, there was a horizontal and vertical reinforcement ratio of 2% and 0.5% respectively. The concrete was pre-cracked with the crack coordinates having been placed at 45º from the universal coordinate system. Friction coefficients, μdown, and μup were 0.2 and 1.2 respectively with linear crack opening path inverse slope, a being set at 2.0. Additionally, vertical load, v, was originally set at 8.9kN.
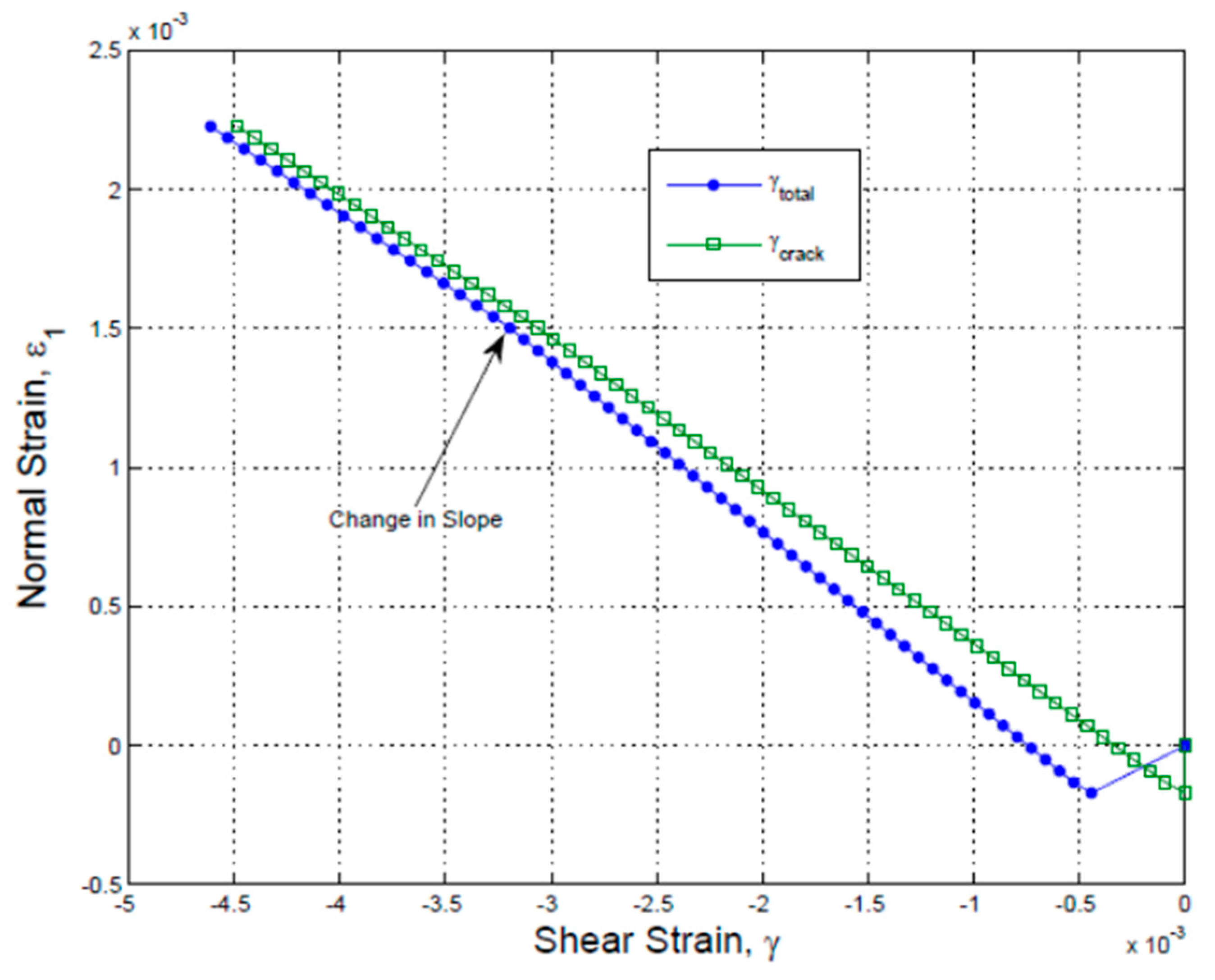
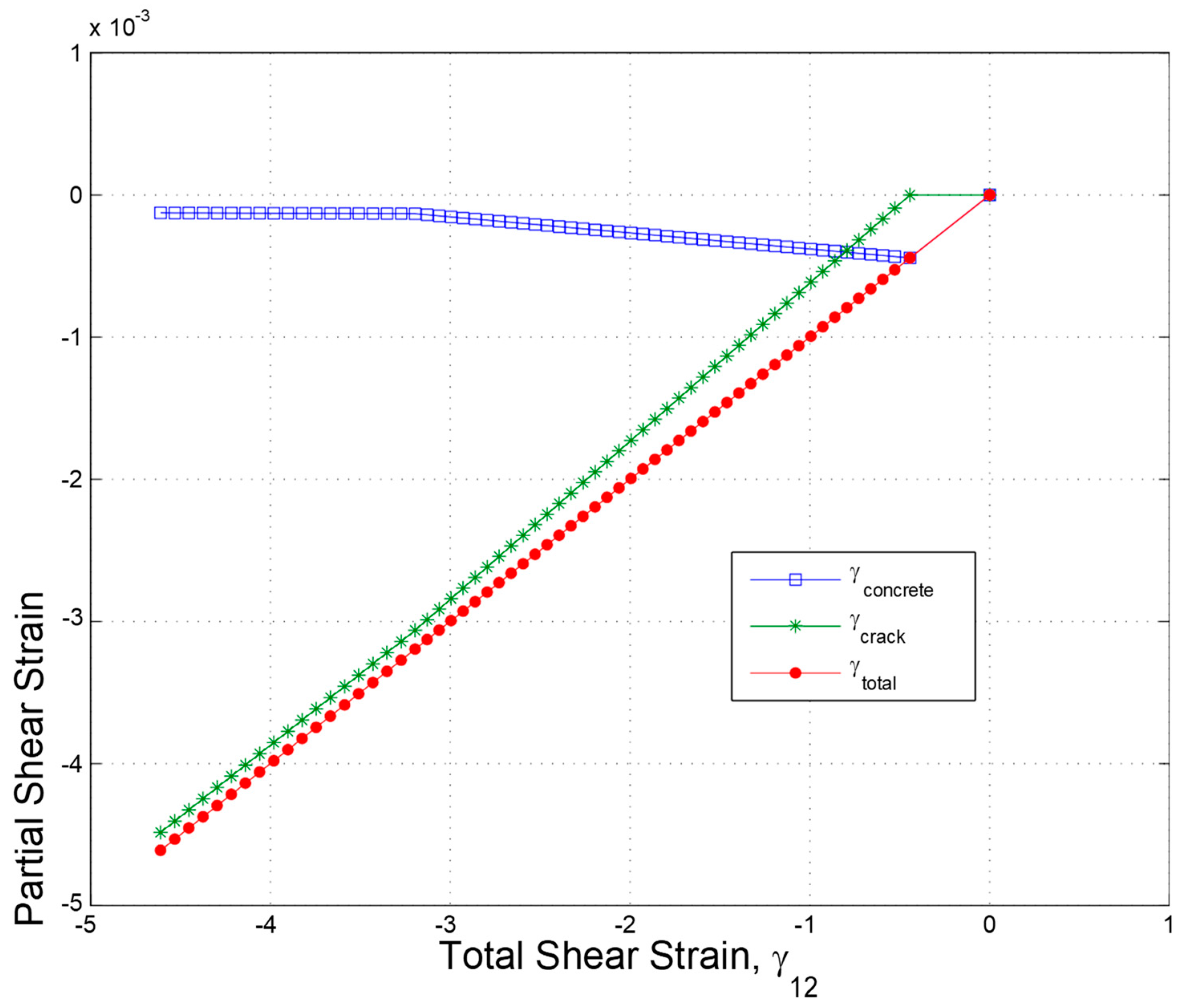
The loading analysis effectively converged in a single direction while the solution diverged when unloading began. Figure 2, Figure 3 and Figure 4 indicate the CSS analysis results with Figure 2 illustrating the total shear strain, γ12 and crack shear strain,γcr, versus normal strain, ε1. The affiliation indicates a crack opening path. Most importantly, 2 different slopes are noted when the total shear strain is plotted against the normal strain. On the other hand, one slope was noticed when the normal strain and the crack shear strain (crack opening path) were plotted against each other thus confirming that the crack opening path is enforced by crack shear strain. 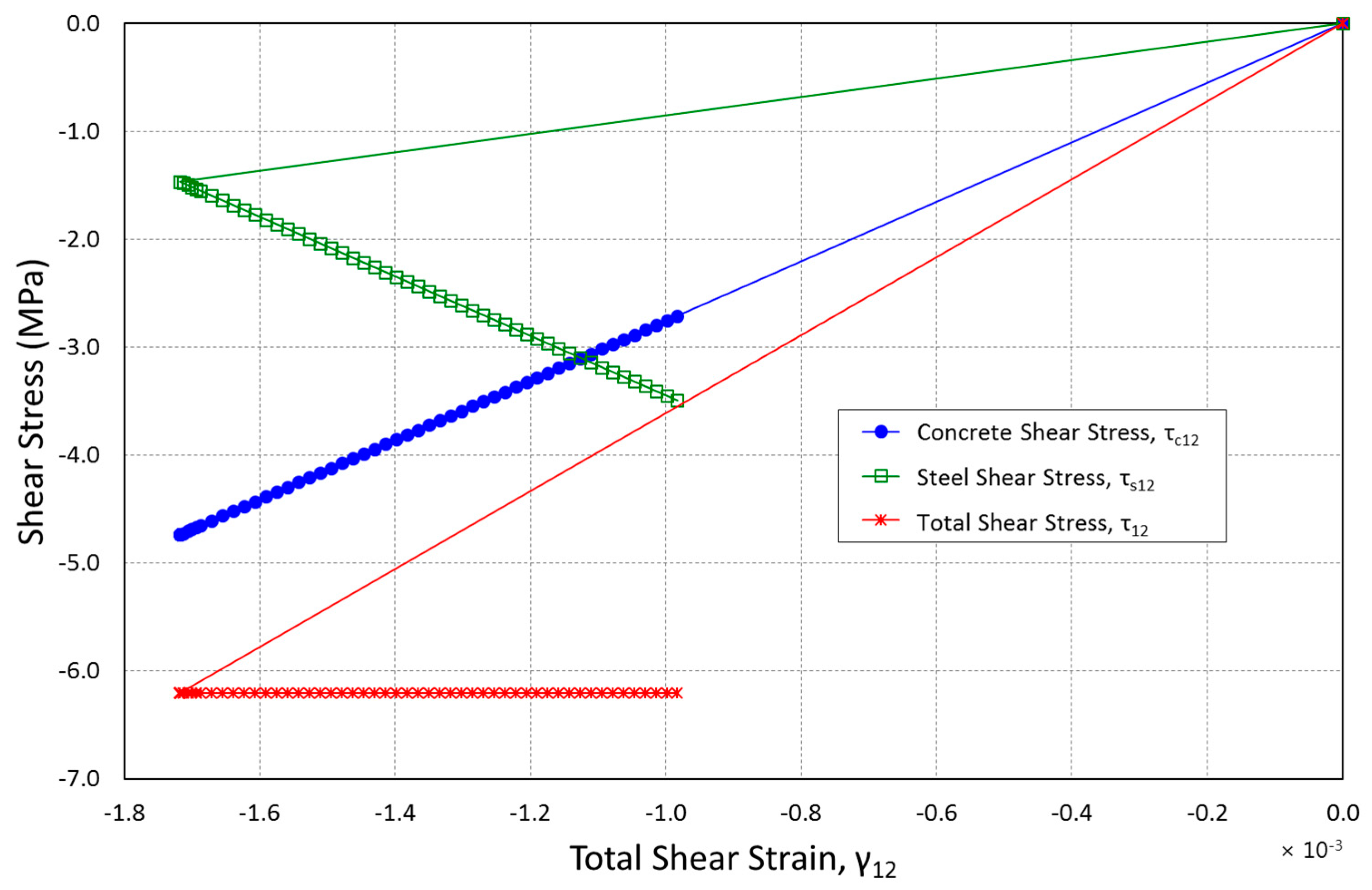The concrete and crack shear strains against the total shear strain are illustrated in Figure 3. As the analysis began, the crack shear strain is zero while the crack state is “no slip”. However, there is an increase in the concrete shear strain. The crack surface finally starts to “slip uphill” while the crack shear strain rises as the concrete shear strain approaches zero thus enforcing the fact that nearly all the cracked concrete strains are crack strains.
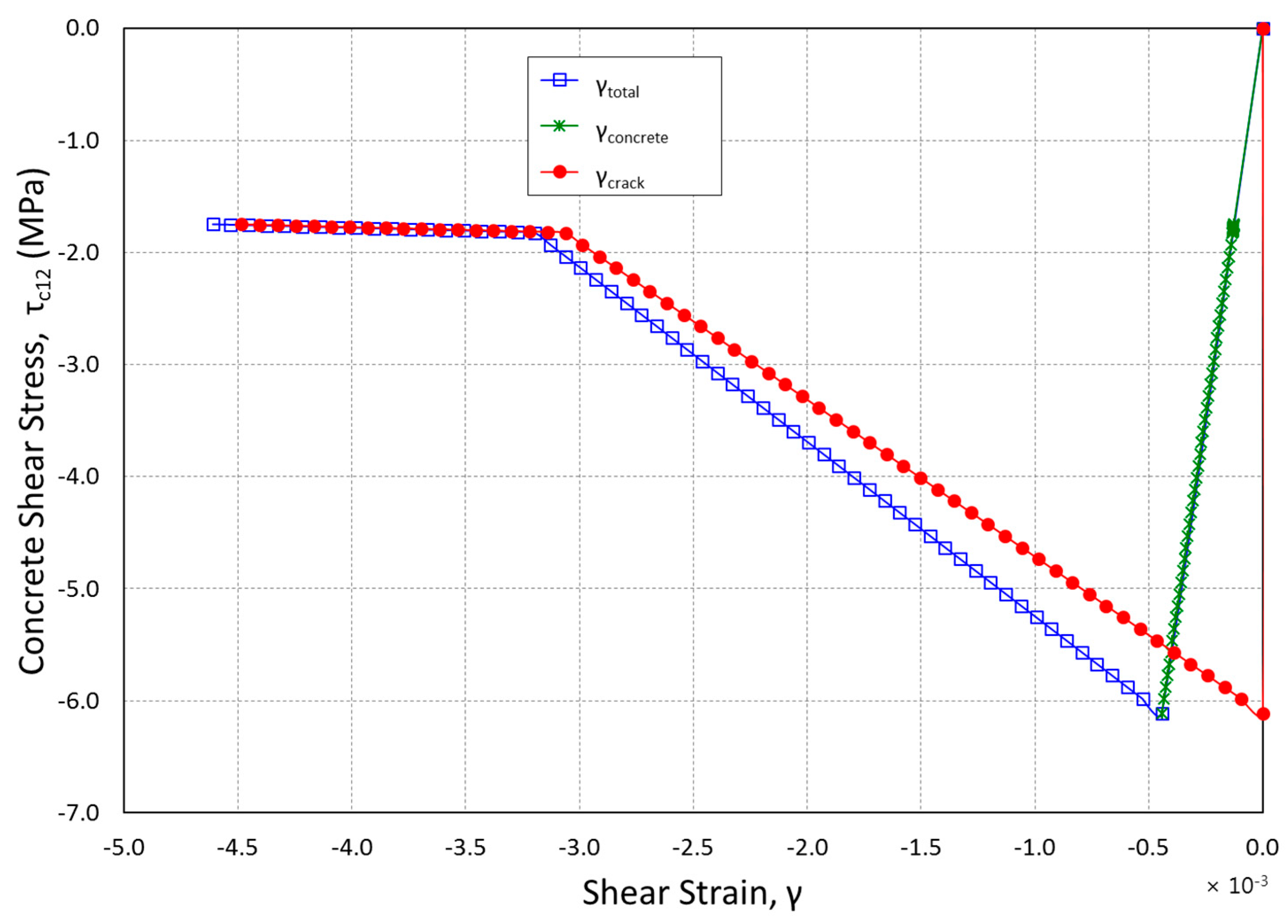
The concrete shear stress versus the concrete, crack and total shear strains is illustrated in Figure 4. It is evident that the curve’s “no slip” portion (shear modulus, G) is only followed by concrete shear strains which get to the highest value at the onset of analysis as shown in Figure 3. It then moves back to zero. According to the data presented in Figure 5, crack strains begin at point zero and rises after the crack surface starts slipping. This is a point at which the shear strength starts becoming functional to the shear friction that is created throughout the crack. 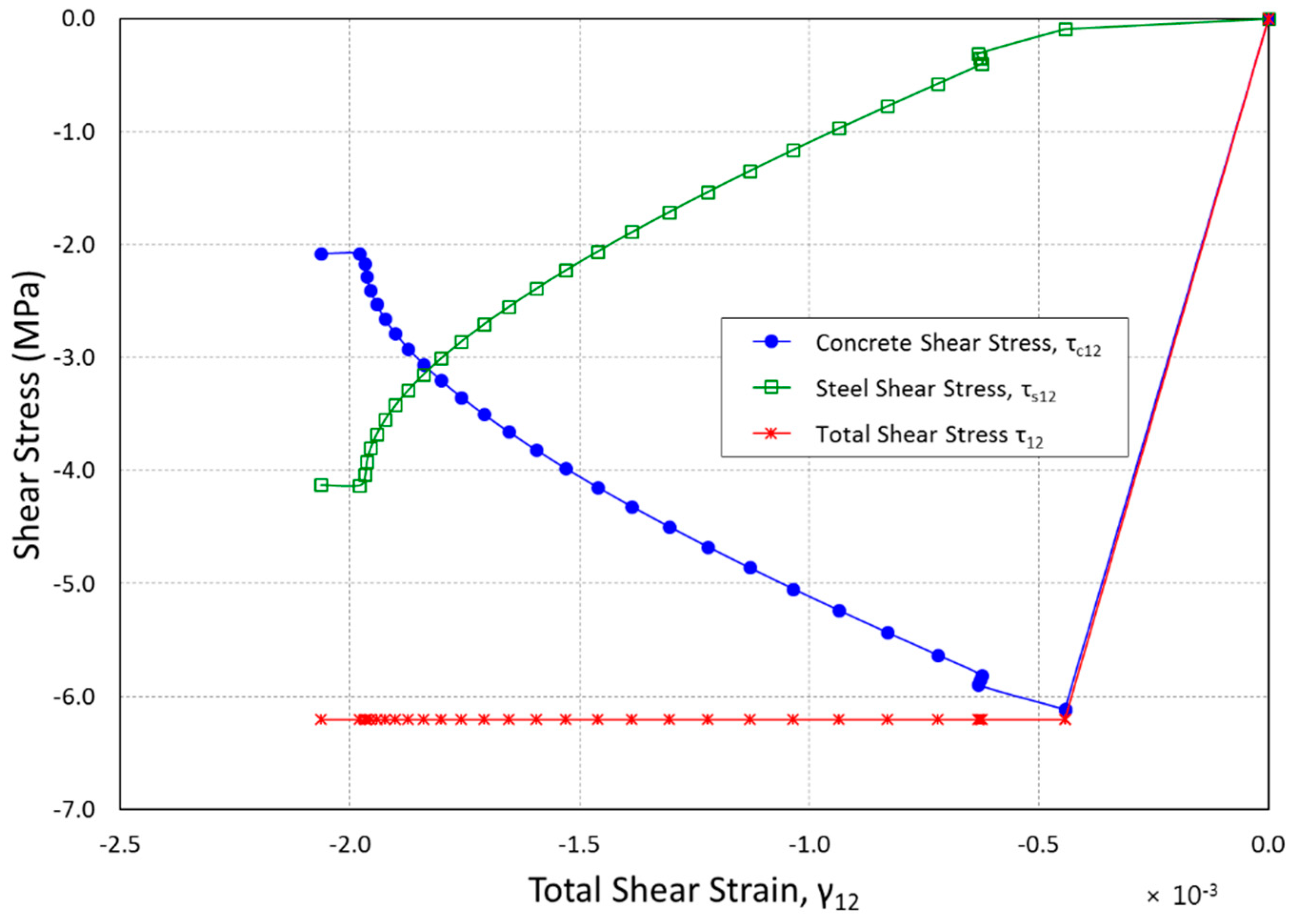Also, the Figure 4 shows that crack and concrete shear strain additions are the same as the total shear strains thus validating the Crack Strain Separated model imposed relationship. Comparisons were made between the results obtained from the analysis of CSS and other models that are mostly used to model the stiffness of reduced shear for cracked reinforced concrete as shown in the following section.

7. Comparison of MCFT and βG models with CSS Results

Crack Strain Separated analysis results were compared with the cracked reinforced concrete model results. It was found that the observed results were significantly different. MCFT (Modified Compression Field Model) that was proposed by Vecchio [14] and a basic βG models were used in the comparison. The two modes are said to have a similar tension stiffening curve with CSS analysis for approximation of cracked concrete non-linear behaviour. In addition, the models are secant stiffness formulations, including Crack Strain Separated formulation. The reduced cracked concrete shear stiffness is handled by basic βG model through multiplication of hear modulus, G, by a random factor, β, that is between 0 and 1. Vecchio’s [14] model changes secant shear stiffness for it to be a secant stiffness value function for principal stress directions.
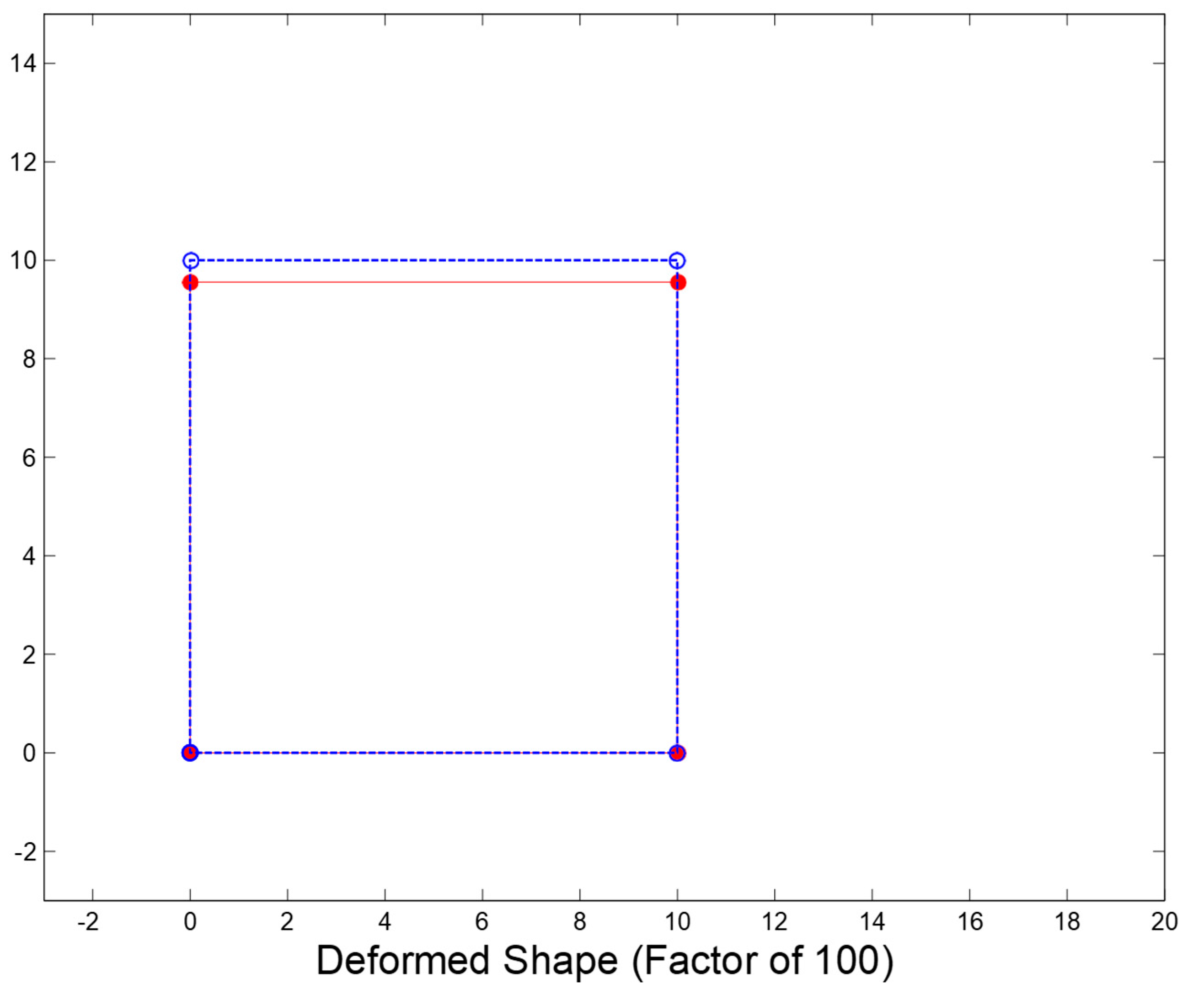
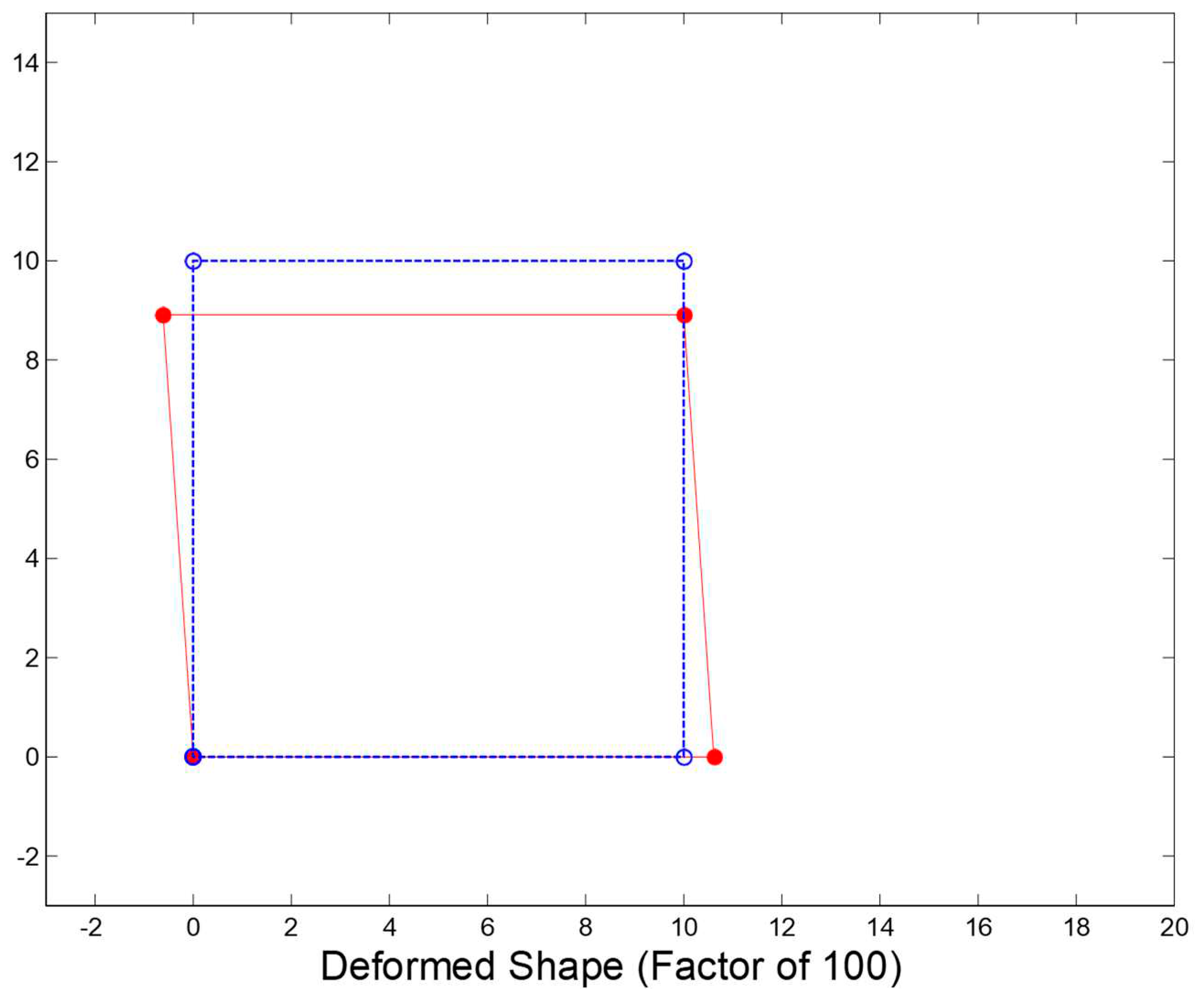
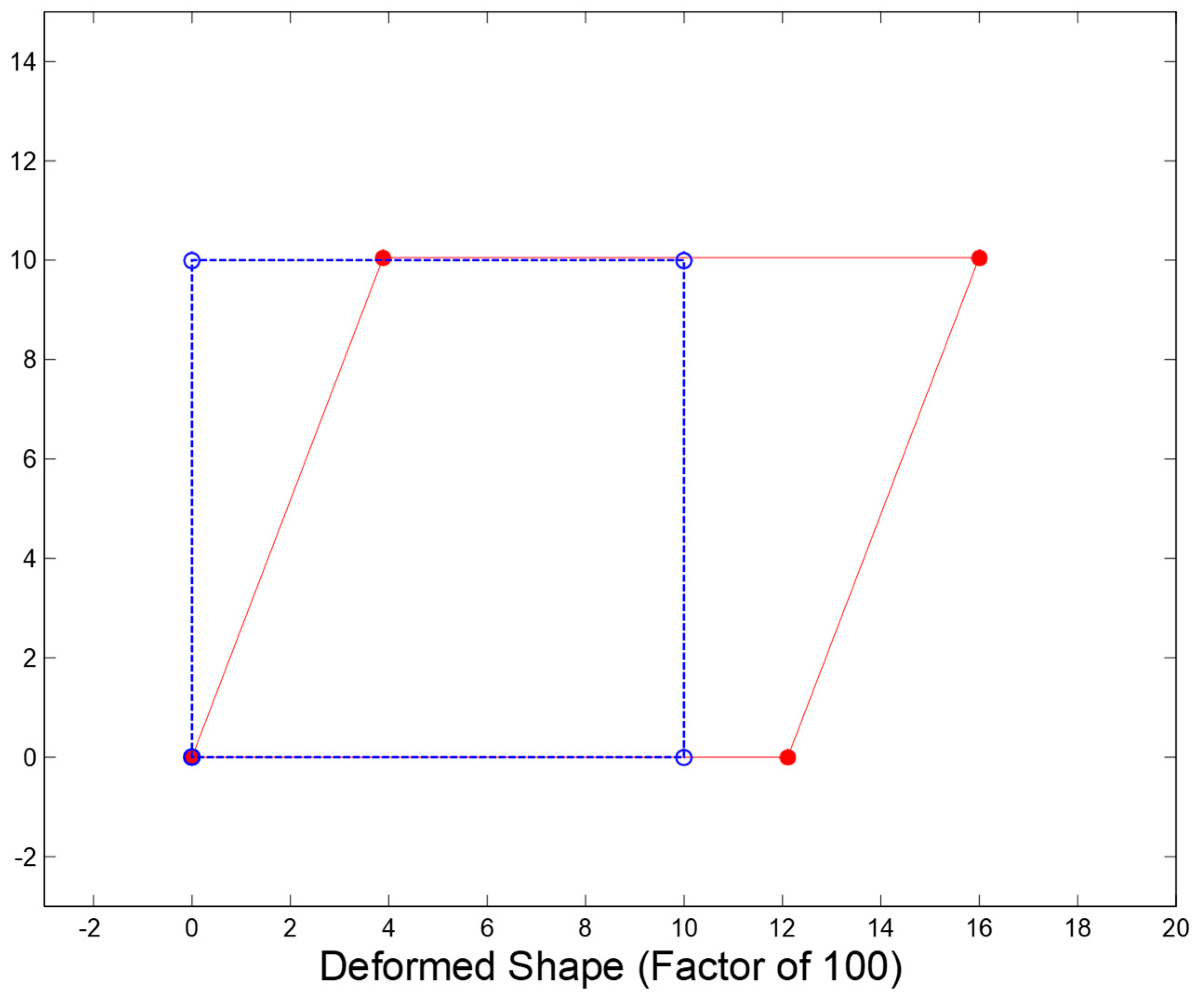
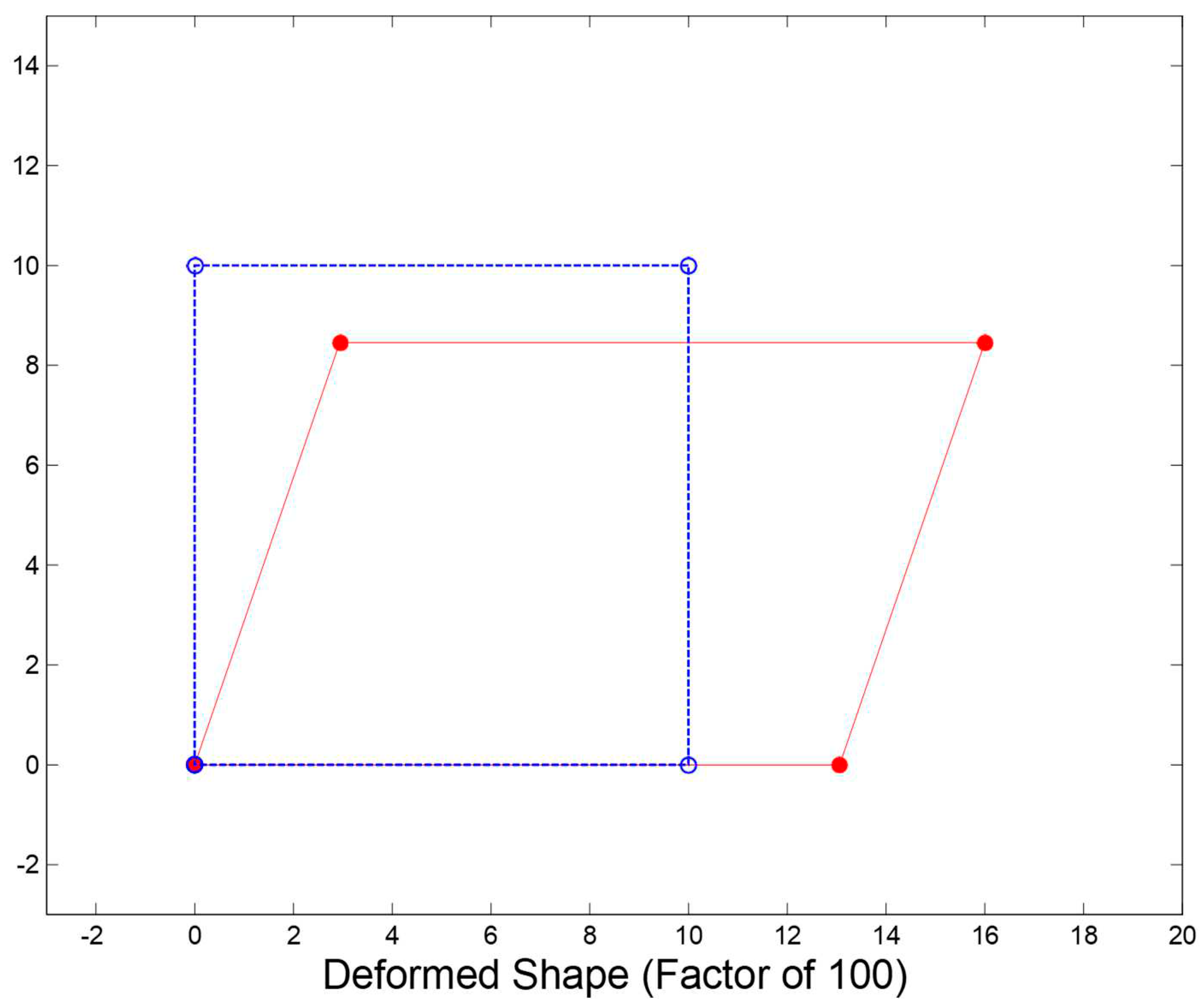
One component was subjected to analysis in a given group of loads under the control of a prescribed displacement just like the crack strain separated analysis. The element was applied with 80 kips constant vertical load and horizontal shear through the proportional load vector so as to make sure that the stress state is uniform. There was a reinforcement in global vertical and horizontal directions with vertical direction’s reinforcement ratio being 0.2% while that of horizontal direction is 2%. On the other hand, β in the βG model was set at 0.2. However, Poisson’s ratio was ignored in order to make it easy to interpret and implement results. The stress strain and other material constant relationships were equal to the crack strain separated analysis. The model was originally analyzed with displacement of prescribed DOF set at zero so as to establish behavioural differences for simple cases. The 3 models’ deformed shape whose prescribed displacement is zero is indicated in Figure 5, Figure 6 and Figure 7. The nodes’ un-deformed position is denoted by open circles while the nodes’ deformed position is represented by solid circles. All displacements are measured in terms of inches and then multiplied by a factor whose value is 100.
Both Vecchio and CSS models have almost the same behaviour whereas the βG model’s results are very different. This is because of the effect of a false Poisson’s ratio which results from reduced shear stiffness. Researchers argue that elastic relationships between elastic modulus, shear modulus and Poisson’s ratio are violated by reduced shear modulus. Rotation of stiffness matrix into a global direction result in the production of a non-diagonal stiffness matrix despite the fact that Poisson’s ratio is ignored within the stiffness formulation of crack orientation. Diagonal stiffness matrix rotation from crack orientation into global direction also leads to the production of a diagonal stiffness matrix if it is true that elastic modulus, Poisson’s ratio and shear modulus are elastically related. As such, Vecchio and CSS models have no horizontal expansion. However, they have vertical contraction which results from the compressive load. The state of the crack strain separated model is of ‘no crack slip’. Therefore, the stiffness matrix within the crack orientation has uncracked concrete’s full shear and elastic modulus. Vecchio model is the same as the concrete’s elastic modulus for a specific loading state is not reduced for shear modulus to remain to be the uncracked concrete’s true shear modulus. In addition, this is the reason why Vecchio and CSS models’ results are almost identical for a specific loading state.
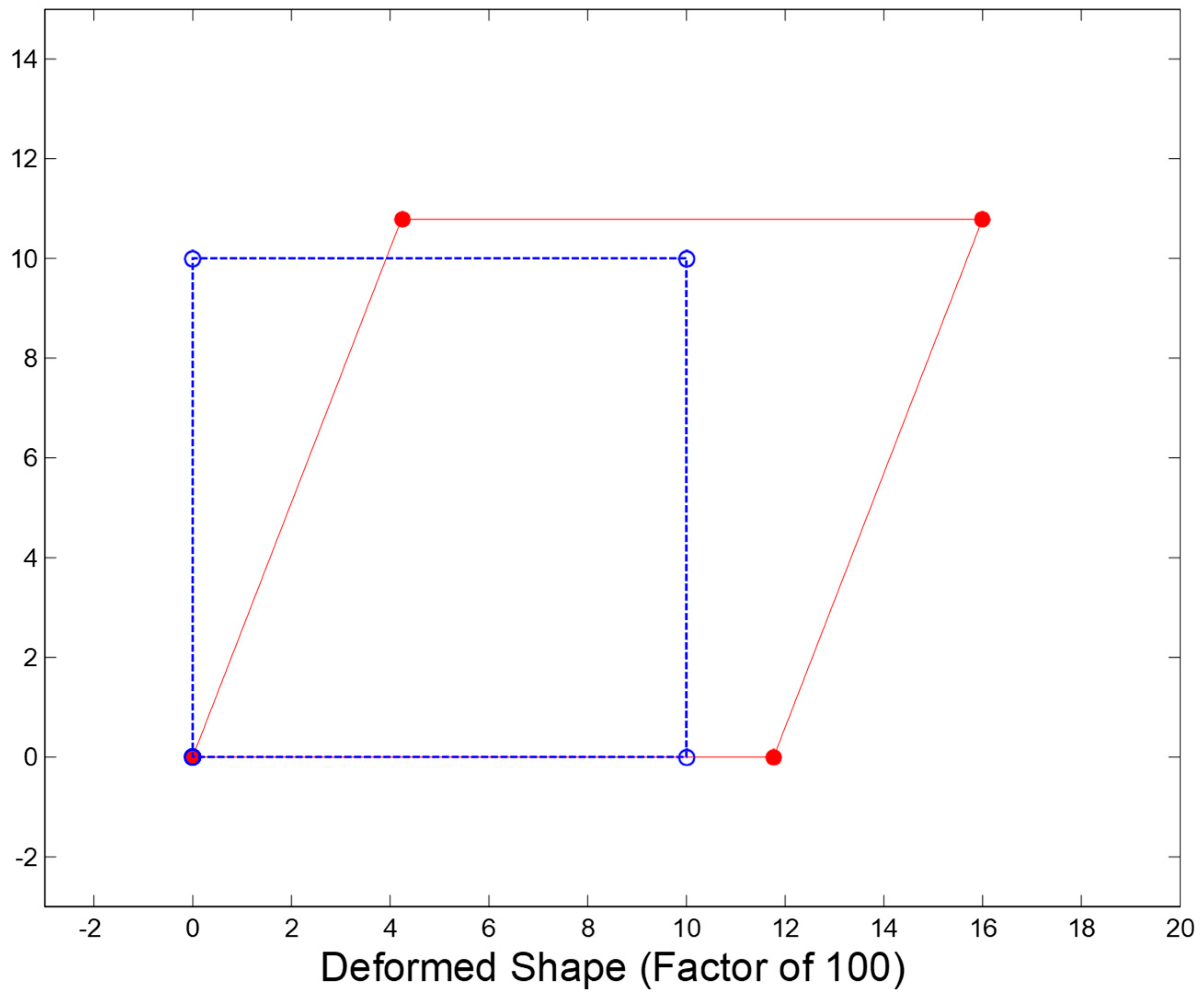
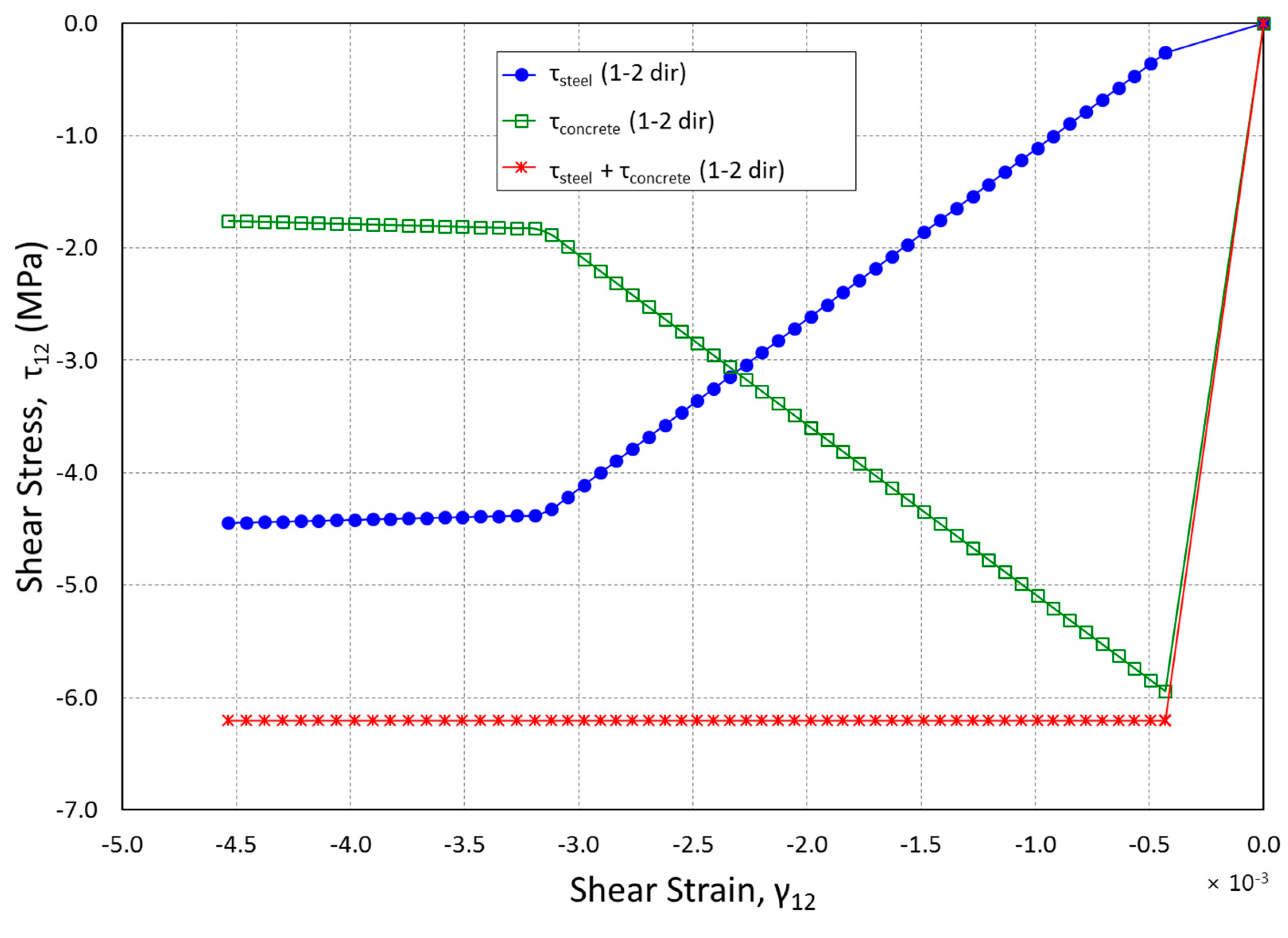
A comparison was then made between the three models and the identical horizontal displacement sets. The element’s prescribed DOF in every model was increasingly displaced to about 1.524mm. Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 present the three different models’ results with Figure 8 indicating the steel, concrete and total shear stresses against the βG model’s total shear stress. The vertical load that was applied resulted in a large first step. One may realize that as the element is further displaced, the steel starts taking more shear stress. On the other hand, reduced shear modulus, βG, slope is followed by the concrete. Furthermore, an increase in horizontal displacement results in the reduction of ‘slip’ or shear strain because the ratio of steel is higher within the horizontal direction compared to the vertical direction as evident in the deformed shape. The ultimate deformed shape whose prescribed displacement is 1.524 mm with a factor whose value is 100 is shown in Figure 9.
Data obtained from the analysis of Vecchio is presented in Figure 10 and Figure 11 whereas the data obtained from the analysis of CSS is presented in Figure 12 and Figure 13. The comparison between Figure 10 and Figure 12 indicates some level of agreement with shear stresses within the crack direction between CSS and Vecchio models. Shear strains within the crack strain separated model are nearly two times Vecchio model’s shear strains. Predicted displacements also differ as evident in the comparison between Figure 11 and Figure 13. Totally different results are generally produced by 3 different cracked reinforced concrete models. 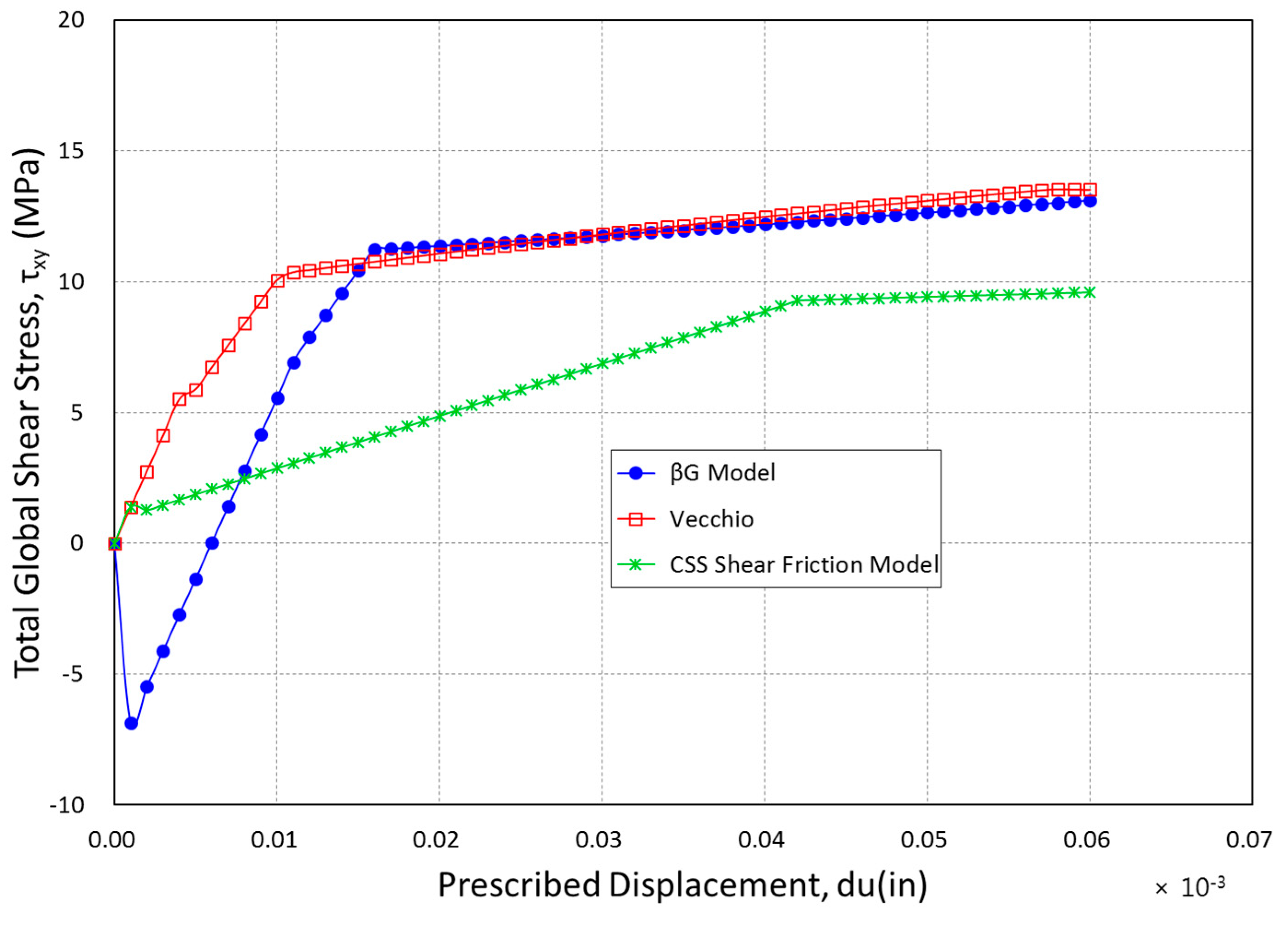Figure 14 further presents the difference in the 3 models which compares every model’s prescribed displacement against the total shear stress thus showing every model’s predicted shear stress versus the same displacements. Vecchio and βG models evidently have the same maximum predicted shear stress whereas the crack strain separated shear stress is very low. It is also evident that steel yielded displacement varies with the models. This may be clear where the curves’ slope is smaller. The difference in the DOF’s vertical displacements varied greatly even though the comparison of prescribed DOF’s identical horizontal displacement results are shown in Figure 14. Comparing these results is very critical in that the predicted design values differ significantly between the fundamental load case models just like the one that may be seen by a shear wall. From the results, establishment of a testing program that confirms finite element models’ accuracy is necessary for the cracked reinforced concrete membranes that are frequently subjected to the loading pattern.

8. Conclusions

Models that use CSS Model had the ability to capture some reinforced concrete’s complex and unique behaviour. The uniqueness of the models is that they can help in predicting cracked reinforced concrete’s stiffness using rational physical behaviour but not random constants. In addition, they can limit the shear’s strength as a reinforcing steel yielding function which is provided throughout the cracks based on recognized concrete behaviour and ACI Building Code provisions [15]. In addition, the models are capable of capturing composite interaction between the reinforcing concrete and steel. A simple model is used to capture the complex behaviour.
  • Formulation of CSS of the Bi-directional shear friction model had the ability to capture essential shear friction behaviors. Strains were successfully separated by the model because of the uncracked concrete and the cracks thus resulting in increased accuracy in the overall model. The model can also handle a number of crack orientations.
  • Comparing the CSS Model with other models such as Modified Compression Field Model and basic βG models indicate that the level of inconsistency is very high. Predicted displacements and shear stresses varied greatly for the three models under comparison. It was evident that every model showed varying interactions between the steel and the concrete because of the differences in the cracked concrete’s predicted stiffness.
  • There are some elements that were examined by the three models. They were also subjected to horizontal shear and vertical compression. They had earlier on developed diagonal cracks. The reinforced concrete membrane loading can directly be applied in shear wall design and behavioral prediction.
To improve the model’s overall accuracy the shear friction model should include damage parameters for cyclical loading or fatigue of materials. In addition, the degradation of the crack opening path should be included as the rough protrusions on the crack surface could tend to smooth out under cyclical loading. This would change the “up” and “down” coefficients of friction as well as the angle of the crack opening path.

Author Contributions

J.P.M. and Y.-J.K. conceived and formulated the equations and base model; J.P.M. and Y.-J.K. performed the base model with Matlab; J.P.M. and S.-U.C. analyzed the output data; J.P.M. and S.-U.C. contributed reagents/materials/analysis tools; J.P.M., S.-U.C., M.E.A., and Y.-J.K. wrote the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by Research Grant No. DGE-0538541 from the National Science Foundation.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article.

Acknowledgments

J.P.M. would like to thank the National Science Foundation for the GK-12 Fellowship that funded this research and provided invaluable experiences.

Conflicts of Interest

The authors declare no conflict of interest.

List of Symbols

a a parameter that defines the slope of the crack opening path,
γtotal the total shear strain,
γ12 the shear strain,
γcr the cracking shear strain,
γc the concrete shear strain,
γcrold the previous converged value of locked-in crack slip,
γn the net shearing strain,
γn(1 or 2) the net shearing strain in the 1 or 2 direction,
γ12old the previous converged value of shear strain,
eε the effective concrete crack strain,
eε1 or 2 the effective concrete crack strain in the 1 or 2 direction,
ε1 or 2 the concrete crack strain in the 1 or 2 direction,
μup the friction coefficient defined relative to crack surface in the uphill direction,
μdown the friction coefficient defined relative to crack surface in the downhill direction,
𝜎1 the concrete stress in the 1 direction,
𝜎2 the concrete stress in the 2 direction,
τ12 the shear stress,
τa12 the minimum shear stress,
τb12 the outside upper limit shear stress,
τc12 the maximum shear stress,
fcr the concrete crack stress,
Ec the modulus of elasticity of concrete,
E1 or 2 the secant modulus of concrete in the direction 1 or 2,
G the concrete shear modulus,
β’ the dowel action shear retention factor,
β a random factor that is between 0 and 1,
V and P the applied forces,
T and N the normal forces.

References

  1. Vecchio, F. J., and Collins, M. P. The Modified Compression-Field Theory for Reinforced Concrete Elements Subjected to Shear. ACI Struct. J., 1986, 83, 219-231.
  2. So, M. Total-Strain Based Bond/Slip and Shear/Friction Membrane Model for Finite Element Analysis of Reinforced Concrete. Ph.D. thesis, Washington University in St. Louis, St. Louis, MO., USA, 2008.
  3. Zhu, R. R. H., Hsu, T. T. C., and Lee, J. Y. Rational Shear Modulus for Smeared-Crack Analysis for Reinforced Concrete. ACI Struct. J., 2001, 98, 443-450.
  4. Walraven, J. C. Rough Cracks Subjected to Earthquake Loading. J. Struct. Eng., 1994, 120, 1510-1524. [CrossRef]
  5. Palermo, D., and Vecchio F. J. Simulation of Cyclically Loaded Concrete Structures Based on the Finite-Element Method. J. Struct. Eng., 2007, 133, 728-738. [CrossRef]
  6. Stevens, N. J., Uzumeri, S. M., Collins, M. P., and Will, G. T. Constitutive Model for Reinforced Concrete finite Element Analysis. ACI Struct. J., 1991, 88, 49-59. [CrossRef]
  7. Pang, X. B, and Hsu, T. T. C. Behavior of Reinforced Concrete Membrane Elements in Shear. ACI Struct. J., 1995, 92, 665-677. [CrossRef]
  8. Mitchell, P.J, Cho B.Y. and Kim Y.J., Analytical Model of Two-Directional Cracking Shear-Friction Membrane for Finite Element Analysis of Reinforced Concrete. Materials. 2021, 14, 1-20. [CrossRef]
  9. Mitchell, P.J. Two-direction Cracking Shear-Friction Membrane Model for Finite Element Analysis of Reinforced concrete. M.S. thesis, Washington University in St. Louis, St. Louis, MO., USA, 2010.
  10. Harmon, T.G., Ramakrishnan, S. and Wang, E.H. Confined Concrete Subjected to Uniaxial Monotonic Loading. J. Eng. Mech., 1998, 124, 1303-1309. [CrossRef]
  11. Kim, Y.J., You, B., Sriraman, V., and Kotwal, A. Confined Concrete with Variable Crack Angle-Part I: Analytical Model. Mag. Concr. Res., 2014, 66, 1075-1083. [CrossRef]
  12. Kim, Y.J., Sriraman, V. Kotwal, A., and You, B. Confined Concrete with Variable Crack Angle-Part II: Shear Friction Model. Mag. Concr. Res., 2014, 66, 967-974. [CrossRef]
  13. Chorzepa, M., Kim, Y.J., Yun, G.J., Harmon, G.T. and Dyke, S. Cyclic Shear-Friction Constitutive Model for Finite Element. ACI Struct. J., 2011, 108, 324-331. [CrossRef]
  14. Vecchio, F. J. Reinforced Concrete Membrane Element Formulations. J. Struct. Eng., 1990, 116, 730-750. [CrossRef]
  15. Mattock, A. H., and Hawkins, N. M. 1972. Shear Transfer in Reinforced Concrete−Recent Research. PCI J., 1972, 17, 55-75. [CrossRef]
Preprints 78010 g001
Figure 1. Schematic of a block slipping “up the hill” at an inclination, θ.
Figure 1. Schematic of a block slipping “up the hill” at an inclination, θ.
Preprints 78010 g001
Preprints 78010 g002
Figure 2. Normal Strain vs. Crack Shear Strain and Total Shear Strain.
Figure 2. Normal Strain vs. Crack Shear Strain and Total Shear Strain.
Preprints 78010 g002
Preprints 78010 g003
Figure 3. Crack Shear Strain and Concrete Shear Strain vs. Total Shear Strain.
Figure 3. Crack Shear Strain and Concrete Shear Strain vs. Total Shear Strain.
Preprints 78010 g003
Preprints 78010 g004
Figure 4. Concrete Shear Stress vs. Total, Concrete and Crack Shear Strains.
Figure 4. Concrete Shear Stress vs. Total, Concrete and Crack Shear Strains.
Preprints 78010 g004
Preprints 78010 g005
Figure 5. Deformed Shape for zero prescribed displacement, CSS model (mm).
Figure 5. Deformed Shape for zero prescribed displacement, CSS model (mm).
Preprints 78010 g005
Preprints 78010 g006
Figure 6. Deformed Shape for zero prescribed displacement, Vecchio model (mm).
Figure 6. Deformed Shape for zero prescribed displacement, Vecchio model (mm).
Preprints 78010 g006
Preprints 78010 g007
Figure 7. Deformed Shape for zero prescribed displacement, βG model (mm).
Figure 7. Deformed Shape for zero prescribed displacement, βG model (mm).
Preprints 78010 g007
Preprints 78010 g008
Figure 8. Concrete, Steel and Total Shear Stresses vs. Total Shear Strain, βG model.
Figure 8. Concrete, Steel and Total Shear Stresses vs. Total Shear Strain, βG model.
Preprints 78010 g008
Preprints 78010 g009
Figure 9. Deformed Shape for a prescribed displacement of 1.524 (mm), βG model.
Figure 9. Deformed Shape for a prescribed displacement of 1.524 (mm), βG model.
Preprints 78010 g009
Preprints 78010 g010
Figure 10. Concrete, Steel and Total Shear Stresses vs. Total Shear Strain, Vecchio model.
Figure 10. Concrete, Steel and Total Shear Stresses vs. Total Shear Strain, Vecchio model.
Preprints 78010 g010
Preprints 78010 g011
Figure 11. Deformed Shape for a prescribed displacement of 1.524 (mm), Vecchio model.
Figure 11. Deformed Shape for a prescribed displacement of 1.524 (mm), Vecchio model.
Preprints 78010 g011
Preprints 78010 g012
Figure 12. Concrete, Steel and Total Shear Stresses vs. Total Shear Strain, CSS model.
Figure 12. Concrete, Steel and Total Shear Stresses vs. Total Shear Strain, CSS model.
Preprints 78010 g012
Preprints 78010 g013
Figure 13. Deformed Shape for a prescribed displacement of 1.524 (mm), CSS model.
Figure 13. Deformed Shape for a prescribed displacement of 1.524 (mm), CSS model.
Preprints 78010 g013
Preprints 78010 g014
Figure 14. Comparison of Global Shear Stress vs. Prescribed Displacement for βG, Vecchio and CSS models.
Figure 14. Comparison of Global Shear Stress vs. Prescribed Displacement for βG, Vecchio and CSS models.
Preprints 78010 g014
Table 1. Equations for Compression Across the Crack.
Table 1. Equations for Compression Across the Crack.
Preprints 78010 i001
Table 2. Secant Stiffness Matrices at Crack Direction 1 and 2 Active (the crack surface is in tension).
Table 2. Secant Stiffness Matrices at Crack Direction 1 and 2 Active (the crack surface is in tension).
Preprints 78010 i002
Table 3. Secant Stiffness Matrices at Crack Direction 1 Active (the crack surface is in compression).
Table 3. Secant Stiffness Matrices at Crack Direction 1 Active (the crack surface is in compression).
Preprints 78010 i003
Table 4. Secant Stiffness Matrices at Crack Direction 2 Active (the crack surface is in compression).
Table 4. Secant Stiffness Matrices at Crack Direction 2 Active (the crack surface is in compression).
Preprints 78010 i004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated