Prerpints.org logo
Preprint
Article

Characteristic Length for Pinning Force Density in Nb3Sn

Altmetrics

Downloads

82

Views

83

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 June 2023

Posted:

29 June 2023

You are already at the latest version

Alerts
Abstract
The pinning force density FpJc,B=Jc×B (where Jc is the critical current density and B is the applied magnetic field) is one of the main parameters that characterize the resilience of a superconductor to carry a dissipative-free transport current in an applied magnetic field. Kramer (1973 J. Appl. Phys. 44 1360), and Dew-Hughes (1974 Phil. Mag. 30 293) proposed a widely used scaling law for the pinning force density amplitude: FpB=Fp,max×p+qp+qppqq×BBc2p×1-BBc2q, where Fp,max, Bc2, p, and q are free-fitting parameters. Since the late 1970-s till now, several research groups have reported experimental data on the dependence of Fp,max on the average grain size, d, in Nb3Sn-based conductors. Godeke (2006 Supercond. Sci. Techn. 19 R68) proposed that the dependence obeys the law Fp,maxd=A×ln1d+B. However, this scaling law has several problems, for instance, the logarithm is taken from a non-dimensionless variable, and Fp,maxd<0 for large grain sizes, and Fp,maxd→∞ for d→0. Here, we reanalysed the full inventory of publicly available Fp,maxd data for Nb3Sn conductors and found that the dependence can be described by Fp,maxd=Fp,max0×exp-dδ law, where the characteristic length, δ, varies within a remarkably narrow range, that is, δ=175±13 nm, for samples fabricated by different technologies. The interpretation of the result is based on the idea that the in-field supercurrent flows within a thin surface layer (thickness of δ) near the grain boundary surfaces (similar to London’s law, where the self-field supercurrent flows within a thin surface layer with a thickness of the London penetration depth, λ, and the surface is a superconductor-vacuum surface). An alternative interpretation is that δ represents the characteristic length of the exponential decay flux pinning potential from the dominant defects in Nb3Sn superconductors, which are grain boundaries.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Multifilamentary superconducting Nb3Sn-based wires are used in many high-energy physics and fusion energy projects, including international mega-science projects such as the Large Hadron Collider (LHC) [1] and International Thermonuclear Experimental Reactor (ITER) [2]. The Nb3Sn-based superconductors should, first of all, have high current-carrying capacity in high magnetic fields. In particular, the modernization of LHC [3] involves the replacement of a part of NbTi conductors with Nb3Sn-based conductors. Particularly, to create high-field large-aperture quadrupole MQXF [4] and high-field 11-T dipoles [5] for the high-luminosity LHC Upgrade Project, the development of a new generation of high-field Nb3Sn-based superconductors is required for the effective use of the advantages of Nb3Sn wires over previously used NbTi, to provide a minimum critical current of approximately 360 A and higher in a field of 15 T at 4.2 K [3]. The critical current density J c of the modern designed Nb3Sn strand has achieved record values of non-Cu J c B = 12 T ,   T = 4.2   K = 3000   A / m m 2 and J c B = 15 T ,   T = 4.2   K = 1700   A / m m 2 [6]. However, to create a Future Circular Collider (FCC) at CERN, Nb3Sn-based wires with J c B = 16   T ,   T = 4.2   K = 1500   A / m m 2 or J c B = 12   T ,   T = 4.2   K = 3500   A / m m 2 are required [7].
For thermonuclear power engineering, bronze-processed Nb3Sn-based wires were developed for superconducting magnets of the ITER project, providing a Jc of approximately 750 A/mm2 and higher in a field of 12 T [2]. The next mega-science project after the ITER should be the DEMO experimental facility, the primary goal of which is to demonstrate the possibility of obtaining a positive power balance from a thermonuclear reactor as the whole system. This goal requires the development of superconducting Nb3Sn-based conductors with even better characteristics [8].
Extensive (nearly five decades) R&D studies of Nb3Sn-based conductors have shown that the key factors affecting the in-field critical current in these wires are the local composition, structure, and morphology of the superconducting A-15 phase [9,10,11,12,13,14,15,16,17].
These studies also showed that at high magnetic fields, the main pinning centers in Nb3Sn-based composites are grain boundaries, and the conventional approach to increasing J c B ,   T , in Nb3Sn is to increase the density of grain boundaries, that is, to ensure grain refinement. To achieve this, various manufacturing methods and designs of multifilamentary wires have been proposed [7], targeting the creation of small average grain sizes in the superconducting phase [18,19,20,21].
Superconducting wires based on Nb3Sn are produced by one of the following methods: bronze route, internal tin (IT), and power in tube (PIT) [22,23,24]. In the bronze route, an initial billet formed of Nb, Nb-Ti or Nb-Ta rods assembled in a bronze Cu-Sn matrix and external copper tube is extruded and drawn to a small diameter. The Nb3Sn phase is formed by Sn diffusion from the matrix to Nb filaments under heat treatment (HT), which is usually referred to as diffusion annealing. The solid-state diffusion of Sn at relatively low temperatures of HT prevents excessive grain growth and increases the pinning efficiency. The main disadvantage of the bronze method is the limited solubility of Sn in the bronze matrix when the Sn concentration increases to more than 8 mass. %, brittle phases are precipitated, which impedes plastic deformation and leads to cracking of the composite wire at the manufacturing stage. Therefore, to ensure a sufficient amount of Sn for the formation of the Nb3Sn phase, the ratio of the volume fractions of bronze and niobium should not be less than 3:1. Owing to these restrictions, bronze-processed wires have lower Jc-values than those potentially possible for the Nb3Sn phase. An important step in the development of bronze technology was the development of the Osprey method for producing high-tin bronze, which retains its plasticity up to 15–17 mas. % Sn. Using such bronze makes it possible to increase the number of Nb filaments in the strand, provide a complete transformation of Nb filaments into the superconducting phase, and increase the Sn concentration in the Nb3Sn layers, which results in an increase of Jc [25]. However, even in the Nb3Sn strands fabricated using a high-Sn bronze matrix, it is not possible to avoid large Nb3Sn composition gradients across the superconducting layer. These gradients, in turn, produce large gradients in the superconducting properties that limit the overall current density, particularly in high fields [9]. The deficiency of tin leads to the formation of a relatively large fraction of non-stoichiometric Nb3Sn compounds [26], which are stable from 18 to 25 at. % Sn, and the low-tin part of superconducting layers loses its superconductivity in high fields [27].
The IT process was developed to avoid frequent in-process annealing during wire drawing and to enhance the available Sn concentration with respect to the bronze process using separate Sn, Cu, and Nb billet stacking elements rather than specially melted high-Sn bronze matrix alloys [28]. The modified design of modern IT strands (e.g. strands with distributed diffusion barriers) makes it possible to obtain Jc beyond 2200 A/mm2 and achieve a record-braking value of 3000 A/mm2 (non-copper, l2 T, 4.2 K) [12,29]. The highest critical current density strands have Nb3Sn layers with minimal chemical and microstructural inhomogeneity and a high fraction of the close to stoichiometric phase.
To increase the Jc of superconductors designed to operate in high magnetic fields (15-16 T and higher), new designs of superconducting strands are created based on the IT technology, which are referred to as high-Jc strands. According to Ref. [30], the OST company produces high-Jc strands using the so called Restacked Rod Process (RRP) design of the wires. In the RRP strands, the many Cu-clad niobium filaments surrounding the tin source inside the subelement grow through the inter-filamentary Cu and formed a single Nb3Sn tube in the volume of the strand. Each subelement was surrounded by a Nb-Ta diffusion barrier, which was designed to partially react, and Jc values of these strands were approximately 3000 A/mm2. The compositional analysis of the high-current wires indicated that the Sn content was relatively uniform at approximately 24 ± 1 at. % Sn in the A15 volume [31].
The PIT process [32] combines an abundant Sn source with a relatively high current density (over 2500 A/mm2) and fine filaments (approximately 35 μm). The abundant Sn source results in a relatively high Sn content in the A15 phase. This indicates that the PIT wires contained a relatively large A15 fraction rich in Sn. The maximum non-Cu Jc is from 2600 A/mm2 (at 12 T, 4.2 K) in 1.25 mm wires, for superconducting wires, which were developed for the Next European Dipole (NED) program. The main advantages of the PIT process are shorter heat treatments because of the close location of the Sn source to the niobium, no pre-heating treatment is required compared to other methods, and relatively small filaments (30–50 µm) can be obtained, which leads to low hysteresis losses. The main disadvantage of the PIT manufacturing routine is its higher cost compared with other fabrication technologies [33,34].
The resilience of any superconducting wire to carry a dissipative-free transport current at an applied magnetic field can be quantified by the pinning force density, F p → , (defined as a vector product of the transport critical current density,   J c → , and the applied magnetic field, B → ):
F p → J c , B = J c → ⊗ B → .
For an isotropic superconductor and maximal Lorentz force geometry, i.e. when J c → ⊥ B → , Kramer [35] and Dew-Hughes [36] proposed a widely used scaling expression for the amplitude of the pining force density [37]:
F p → B = F p , m a x × p + q p + q p p q q × B B c 2 p × 1 − B B c 2 q ,
where F p , m a x , B c 2 , p, and q are free-fitting parameters, and B c 2 is the upper critical field, and F p , m a x is pinning force density amplitude.
Figure 1 shows a typical F p → B , 4.2   K for Nb3Sn superconductors reported by Flükiger et al [38], where the data fit to Equation (2) and deduced free-fitting parameters, F p , m a x , B c 2 , p, and q are shown.
While the upper critical field, B c 2 , is one of the fundamental parameters for a given superconducting phase, three other parameters in Equation (2), that is, F p , m a x , p, and q, depend on the superconductor microstructure, presence of secondary phases, and so on. In accordance with the approach proposed by Dew-Hughes [36], the shape of the F p → B (defined by p and q) reflects the primary pinning mechanism in a sample. Dew-Hughes [36] calculated theoretical characteristic values for p and q for different pinning mechanisms, in particularly for point defect (PD) and grain boundary (GB) pinning.
The evolution of the dominant pinning mechanism from GB- to PD-pinning in Nb3Sn under neutron irradiation was recently reported by Wheatley et al [39], who showed that the unirradiated Nb3Sn alloy exhibits F p → B , T form indicating the dominance of the GB-pinning, and after the neutron irradiation the F p → B , T form transforms towards the PD-pinning mode.
The fourth parameter in Equation (2), which is the F p , m a x , represents the maximal performance of a given superconductor in an applied magnetic field. It is well-established experimental fact [38,40,41,42,43,44,45,46] that the F p , m a x in Nb3Sn depends on the average grain size, d , of the material. The traditional approach to representing the F p , m a x vs. d dependence is to use a reciprocal semi-logarithmic plot (Figure 2). Godeke [41] proposed the following form for the F p , m a x vs. d dependence:
F p , m a x d = A × l n 1 / d + B ,
where free-fitting parameter A = 22.7 and B = − 10 .
Following traditional methodology [37], Godeke [41] proposed that because grain boundaries are primary pinning centers in Nb3Sn, there is an optimum grain size, d o p t , at which the maximum performance for a given wire can be achieved for a given applied magnetic field, B. This field [41] is equal to the flux line spacing in the hexagonal vortex lattice, a h e x a g o n a l [47], at the applied field B , which can be designated as the matching field, B m a t c h , at the maximum pinning force density:
d o p t = a h e x a g o n a l = 4 3 1 / 4 × ϕ 0 B m a t c h 1 / 2 ,
where ϕ 0 = h 2 e is superconducting flux quantum.
Here, we show that neither Equation (3) nor Equation (4) provides a valuable description of the available experimental F p , m a x d data measured over several decades in Nb3Sn conductors. We also propose a new model to describe a full set of publicly available experimental datasets on the maximum pinning force density vs. grain size, F p , m a x d .

2. Problems associated with current models

Equation (4) implies that if the grain size, d o p t , in some Nb3Sn conductors has been determined, then the matching applied magnetic field, B m a t c h , can be calculated as:
B m a t c h d o p t = 4 3 1 / 2 × ϕ 0 d o p t 2 .
Following this logic [41], one can expect that the maximal performance in magnetic flux pinning, that is, F p , m a x , should be observed at B m a t c h :
B m a t c h d o p t = B F p . m a x d o p t = 4 3 1 / 2 × ϕ 0 d o p t 2 .
In Figure 1, we fitted F p → B data [38] to Equation (1) for Nb3Sn conductors with different grain sizes, d , from which the B F p . m a x , e x p d were extracted. In Figure 3, we show B F p . m a x , e x p d and calculated B F p . m a x , c a l c d (Equation (6)), from which it can be concluded that the traditional understanding of the primary mechanism governing dissipative-free high-field current capacity in Nb3Sn conductors [41] is incorrect.
The validity of the F p , m a x d scaling law proposed by Godeke (Equation (3) [41]) was analyzed and it was concluded that there are at least three fundamental problems with the law:
1. The logarithmic function used in Equation (3), as well as all other mathematical functions, can operate only with the dimensionless variable, whereas the variable in Equation (3) has the dimension of inverse length. For instance, the variable B in the Kramer-Dew-Hughes scaling law (Equation (2)) has the dimension cancelation term 1 B c 2 . The same general approach can be found for all equations in Ginzburg-Landau [47], Bardeen-Cooper-Schrieffer [48], and other physical theories [49], all of which implement this general rule.
For instance, the lower critical field, B c 1 , in superconductors has traditional form [50]:
B c 1 T = ϕ 0 4 π λ 2 T × ln ⁡ λ T ξ T + α λ T ξ T ,
where
α κ = α ∞ + e − c 0 − c 1 × l n λ T ξ T − c 2 × l n λ T ξ T 2 ± ε ,
where λ T is the London penetration depth, ξ T is the superconducting coherence length, α ∞ = 0.49693 , c 0 = 0.41477 , c 1 = 0.775 , c 2 = 0.1303 , and ε ≤ 0.00076 . Equations (7), (8) were recently simplified to the following form [51]:
B c 1 T = ϕ 0 4 π λ 2 T × ln ⁡ 1 + 2 λ T ξ T ,
In Equations (7) and (9) the variable under the logarithm is dimensionless. The same can be found in the equation for the universal self-field critical current density, J c s f , T , in thin film superconductors [52]:
J c T = ϕ 0 4 π μ 0 λ 3 T × ln ⁡ λ T ξ T + 0.5 ,
where μ 0 is the permeability of the free space. It should be noted that Equation (10) was recently confirmed by Paturi and Huhtinen [53] for YBa2Cu3O7-d thin films that exhibit different mean-free paths for charge carriers.
The same principle is implemented in all general physics laws, for instance, in Planck’s law [49]:
B ν ν , T = 2 h ν 3 c 2 × 1 e h ν k B T − 1 ,
where B ν ν , T is the spectral radiance of a body, h is the Planck constant, ν is the frequency, c is the speed of light in the medium, k B is the Boltzmann constant, and where the variable under the exponential function, h ν k B T , is dimensionless.
Based on all above, Equation (3) has a fundamental mistake based on a simple fact that l n 1 / d is an absurdum expression.
2. Even if the problem mentioned above (i.e. in #1) is omitted, there are two other problems associated with Equation (3). One problem is the limit of Equation (3) for a large grain size. In Figure 4, we replotted F p , m a x d data from Figure 2 in a linear-linear plot and showed both side extrapolations of Equation (3) within the range of 20   n m ≤ d ≤ 800   n m , which is the usual range of grain sizes in Nb3Sn conductors. In Figure 2 and Figure 4 one can see that:
F p , m a x d   d ≥ 550   n m = A × l n 1 / d + B d ≥ 550   n m < 0 ,
which is the absurdum. We also noted that the free-fitting parameters deduced by us ( A = 21.9 ± 1.2   , B = − 9.9 ± 2.7 ) from the fit of the F p , m a x d dataset to Equation (3), are different from the values reported by Godeke [41], A = 22.7 , B = − 10 , who analysed the same F p , m a x d dataset.
3. A similar validity problem of Equation (3) is for small grain sizes:
lim d → 0 ⁡ F p , m a x d = lim d → 0 ⁡ A × l n 1 / d + B = ∞ ,
which is unphysical because when d becomes comparable to the double coherence length (which is the size of a normal vortex core):
d m i n 4.2   K ≅ 2 × ξ T = 2 × ξ 0 1 − T T c = 2 × 3.0   n m 1 − 4.2   K 18   K = 6.9   n m ,
where ξ 0 = 3.0   n m [54] and T c = 18   K [54] were used, a further decrease in the grain size d should not cause any changes in the magnetic flux pinning, and thus in F p , m a x d amplitude.

3. Results

By experimenting with many analytical functions that can approximate F p , m a x d dependence shown in Figure 2 and Figure 4, we found a remarkably simple, robust, heuristic, and physically sounded expression:
F p , m a x d = F p , m a x 0 × e − d δ ,
where F p , m a x 0 and δ are free fitting parameters. This function exhibits physically sounded limits:
lim d → ∞ ⁡ F p , m a x d = lim d → ∞ ⁡ F p , m a x 0 × e − d δ = 0 ,
lim d → 0 ⁡ F p , m a x d = lim d → 0 ⁡ F p , m a x 0 × e − d δ = F p , m a x 0 < ∞ .
We proposed interpretations for F p , m a x 0 and of δ parameters in the Discussion Section. Before that, in this Section we show the robustness of Equation (15) to fit publicly available datasets for Nb3Sn conductors. Data fitting was performed in Origin2017 software.

3.1. Bronze technology samples

Bronze technology for Nb3Sn-based wires has been described in detail elsewhere [1]. For our analysis, we used F p , m a x d dataset reported by Godeke [41]. Godeke [55] pointed out that Fischer [40] collected raw F p , m a x d data (shown in Figure 2 and Figure 4), and these data are “all pre-2002 results” and this dataset includes Fischer’s [41] “the non-Cu area” data.
In Figure 5, we fitted this largest publicly available dataset for Nb3Sn conductors fabricated using bronze technology to Equation (15). The deduced parameters were F p , m a x 0 = 74 ± 3   G N m 3 , and δ = 175 ± 12   n m . The parameters have low dependence (~ 0.87), which indicates that our model (Equation (15)) is not over-parameterized.

3.2. Powder-in-tube technology samples

Powder-in-tube technology for Nb3Sn-based wires has been described in detail elsewhere [1]. For our analysis, we used F p , m a x d dataset reported by Fischer [40] and Xu et al [56]. In Figure 6, we show the results of the fit of this dataset to Equation (15).
It is interesting to note that the deduced δ = 175   ± 13   n m is in remarkable agreement with its counterpart deduced for samples fabricated by bronze technology. The deduced parameters also have low dependence (~ 0.87), which is an additional indication that our model (Equation (15)) is not over-parameterized.

3.3. Samples fabricated by Flükiger et al by bronze technology [38]

Flükiger et al [38] reported full F p → B curves, which we analysed in Figure 1, for four samples fabricated using bronze technology. It should be noted that this research group utilized a different normalization procedure for the absolute value of the pinning force density from that used by other research groups [40,42,43,44,45,46]. Therefore, we analyzed this dataset separately (Figure 7). Although this dataset has only four F p , m a x d data points, we fitted this dataset to Equation (15) to estimate the robustness of our approach for extracting the characteristic length, δ , from limited F p , m a x d datasets. The deduced δ = 146 ± 15   n m is in the same ballpark as the δ values deduced from the fits to Equation (15) for large datasets (Figure 5 and Figure 6).

4. Discussion

Primary result of our analysis is that Nb3Sn conductors exhibit fundamental length constant, δ , which is in the range of 146   n m   ≤ δ ≤   175   n m , and which characterizes maximal intrinsic in-field performance of real world multifilamentary Nb3Sn-based wires.
Our current understanding of this unexpected result can be explained by two hypotheses, both of which are based on the interpretation that one of the two multiplication terms in the formal definition of the pinning force density (Equation (1)), F p → J c , B = J c → ⊗ B → , exhibits exponential decay with characteristic length δ . Thus, there are two possible scenarios/mechanisms:

4.1. Exponential dependence of the J c → vs grain size at F p , m a x

This interpretation is based on an analog to the exponential decay ~ e − x λ (more accurately ~ c o s h x λ c o s h d λ dependence, where d is the slab half-thickness and the layer thickness λ is London penetration depth [54]) of the self-field transport current density from the superconductor-vacuum interface, which is the London’s law. Considering that under high-field conditions, the interfaces in polycrystalline Nb3Sn are grain boundaries, we naturally came to Equation (15), where the thickness of the layer (where the dissipative-free transport current flows at the condition of the pinning force maximum) is the characteristic length δ .
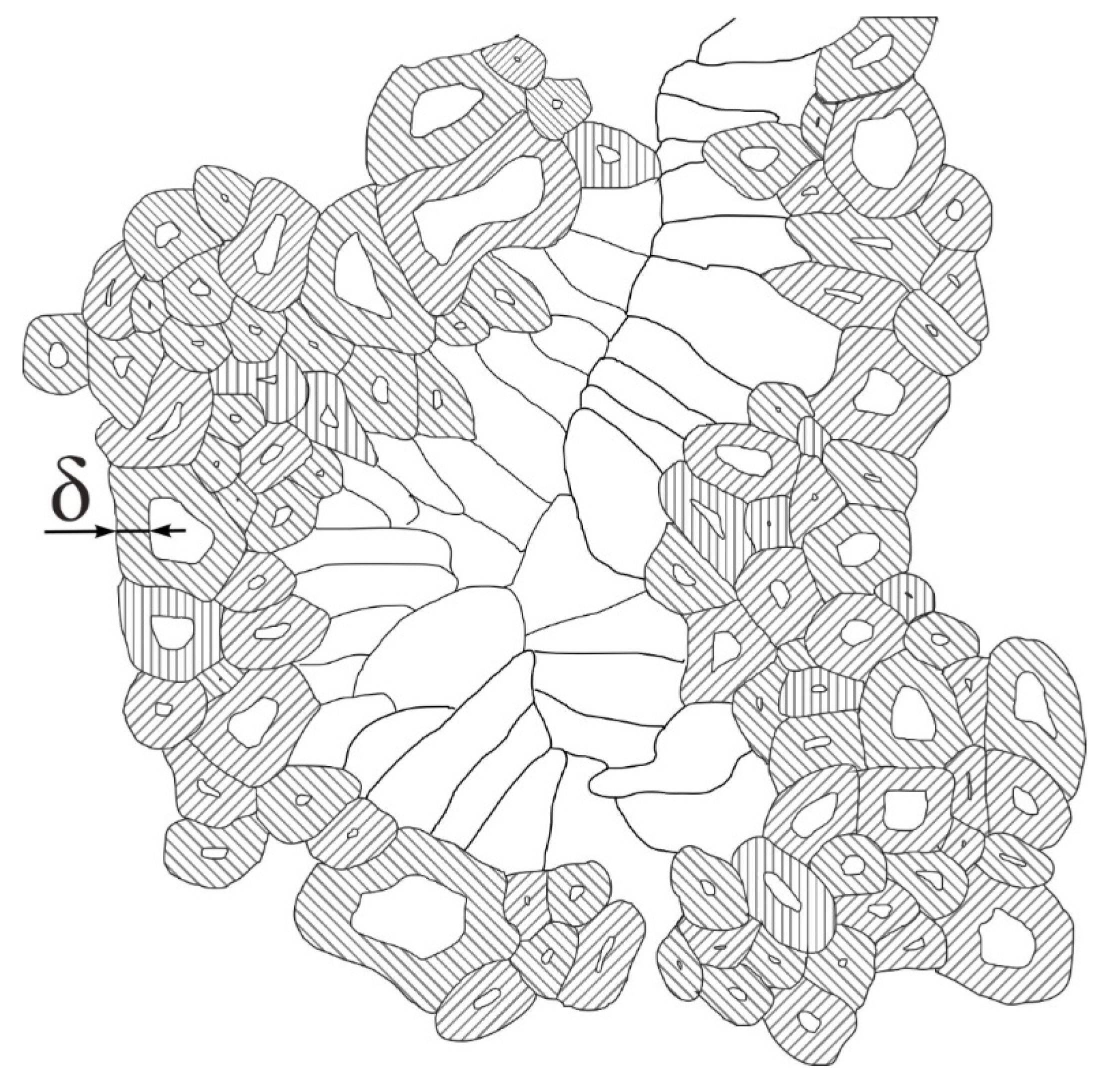
A schematic representation of δ -layers in the polycrystalline Nb3Sn phase, where we drew the δ -layer, is shown in Figure 8.
In this interpretation, large-size grains, d ≫ δ , are less effective areas to carry dissipative-free transport current, because central areas of these large grains do not contribute in transferring the transport current (Figure 8), and the current density is reduced by the exponential law. At the same time, small grains, d ≤ δ , are very effective areas for carrying dissipative-free transport current flow (Figure 8), because the full grain cross-section area works with approximately the same efficiency.

4.2. Exponential dependence of the B → vs grain size at F p , m a x

Alternative interpretation is based on an assumption that the flux pinning potential has exponential dependence ~ e − x δ . As a result, the dissipative-free current can flow only within a thin layer (the thickness of δ ) from both sides of grain boundaries, because the flux pinning is strong there and vortices can be hold by the potential vs the Lorentz force. In this interpretation, central areas of large-size grains, d ≫ δ , also do not contribute to transfer dissipative-free in-field transport current, because vortices are not hold strong enough vs the Lorentz force. While, the small-size grains, d ≤ δ , are very effective to carry dissipative-free transport current flow (Figure 8), because vortices are pinned by pinning potential across full grain area cross-section.
It is interesting to note that the schematic for the effective areas that can carry dissipative-free transport current is the same for both scenarios (Figure 8).
Thus, our current interpretation of the result is that the highest performance of the in-field transport current capacity of Nb3Sn wires is determined by the thin layer with characteristic thickness of δ ≅ 175   n m which surrounds the grain boundaries from both sides.

5. Conclusions

Finning force maximum, F p , m a x J c , B , represents global maximum of the vector product of the transport critical current density,   J c → , and the applied magnetic field, B → , and it can be derived as from F p B [35,36,37], as from F p J c [57] projections of the F p J c , B function (Eq. 1).
In this report we re-analysed experimental data on the dependence of the maximum pinning force density, F p , m a x d , T = 4.2   K (deduced from the F p B [35,36,37] projection) from the average grain size in practical low-Tc multifilamentary Nb3Sn conductors [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,38,39,40,41,42,43,44,45,46,55,56,58] fabricated by bronze and power-in-tube technologies.
The primary result of our analysis is that Nb3Sn conductors at their maximum in-field performance exhibit characteristic length δ = 175   n m , which is the same for samples fabricated by bronze and powder-in-tube technologies, which we interpreted as the characteristic thickness of the layer surrounding the grain boundary network, where a dissipative-free transport current flows.

Author Contributions

E.F.T. conceived the work and proposed exponential dependence for F p , m a x d , E.F.T. and E.G.V.-Z. searched publicly available experimental data and performed data fit and calculations, E.F.T. proposed to interpret δ as the characteristic thickness for transport current flow, E.G.V.-Z. proposed to interpret δ as the characteristic length for flux pinning potential. All authors discussed results. E.G.V.-Z. prepared final figures. E.F.T. wrote the manuscript, which was revised by E.G.V.-Z., I.L.D. and E.N.P.

Funding

The research was carried out within the state assignment of Ministry of Science and Higher Education of the Russian Federation (theme “Pressure” No. 122021000032-5). E.F.T. thanks the research funding from the Ministry of Science and Higher Education of the Russian Federation (Ural Federal University Program of Development within the Priority-2030 Program).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Rossi, L.; Bottura, L. Superconducting Magnets for Particle Accelerators. Rev. Accel. Sci. Technol. 2012, 05, 51–89. [Google Scholar] [CrossRef]
  2. Tronza, V.I.; Lelekhov, S.A.; Stepanov, B.; Bruzzone, P.; Kaverin, D.S.; Shutov, K.A.; Vysotsky, V.S. Test Results of RF ITER TF Conductors in the SULTAN Test Facility. IEEE Trans. Appl. Supercond. 2014, 24, 1–5. [Google Scholar] [CrossRef]
  3. Ambrosio, G. Nb3Sn High Field Magnets for the High Luminosity LHC Upgrade Project. IEEE Trans. Appl. Supercond. 2015, 25, 1–7. [Google Scholar] [CrossRef]
  4. Ferracin, P.; Ambrosio, G.; Anerella, M.; Borgnolutti, F.; Bossert, R.; Cheng, D.; Dietderich, D.R.; Felice, H.; Ghosh, A.; Godeke, A.; et al. Magnet Design of the 150 Mm Aperture Low-β Quadrupoles for the High Luminosity LHC. IEEE Trans. Appl. Supercond. 2014, 24, 1–6. [Google Scholar] [CrossRef]
  5. Karppinen, M.; Andreev, N.; Apollinari, G.; Auchmann, B.; Barzi, E.; Bossert, R.; Kashikhin, V. V.; Nobrega, A.; Novitski, I.; Rossi, L.; et al. Design of 11 T Twin-Aperture Nb3Sn Dipole Demonstrator Magnet for LHC Upgrades. IEEE Trans. Appl. Supercond. 2012, 22, 4901504. [Google Scholar] [CrossRef]
  6. Parrell, J.A.; Zhang, Y.; Field, M.B.; Meinesz, M.; Huang, Y.; Miao, H.; Hong, S.; Cheggour, N.; Goodrich, L. Internal Tin Nb3Sn Conductors Engineered for Fusion and Particle Accelerator Applications. IEEE Trans. Appl. Supercond. 2009, 19, 2573–2579. [Google Scholar] [CrossRef]
  7. Ballarino, A.; Bottura, L. Targets for R&D on Nb3Sn Conductor for High Energy Physics. IEEE Trans. Appl. Supercond. 2015, 25, 1–6. [Google Scholar] [CrossRef]
  8. Lelekhov, S.A.; Krasil’nikov, A. V.; Kuteev, B. V.; Kovalev, I.A.; Ivanov, D.P.; Ryazanov, A.I.; Surin, M.I.; Shavkin, S. V.; Vysotsky, V.S.; Potanina, L. V.; et al. Further Developments of Fusion-Enabling System in Russia: Suggestions on Superconductors and Current Leads for DEMO-FNS Reactor. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
  9. Lee, P.J.; Larbalestier, D.C. Microstructural Factors Important for the Development of High Critical Current Density Nb3Sn Strand. Cryogenics 2008, 48, 283–292. [Google Scholar] [CrossRef]
  10. Sanabria, C.; Field, M.; Lee, P.J.; Miao, H.; Parrell, J.; Larbalestier, D.C. Controlling Cu–Sn Mixing so as to Enable Higher Critical Current Densities in RRP® Nb3Sn Wires. Supercond. Sci. Technol. 2018, 31, 064001. [Google Scholar] [CrossRef]
  11. Segal, C.; Tarantini, C.; Sung, Z.H.; Lee, P.J.; Sailer, B.; Thoener, M.; Schlenga, K.; Ballarino, A.; Bottura, L.; Bordini, B.; et al. Evaluation of Critical Current Density and Residual Resistance Ratio Limits in Powder in Tube Nb3Sn Conductors. Supercond. Sci. Technol. 2016, 29, 1–10. [Google Scholar] [CrossRef]
  12. Pong, I.; Hopkins, S.C.; Fu, X.; Glowacki, B.A.; Elliott, J.A.; Baldini, A. Microstructure Development in Nb3Sn(Ti) Internal Tin Superconducting Wire. J. Mater. Sci. 2008, 43, 3522–3530. [Google Scholar] [CrossRef]
  13. Xu, X.; Sumption, M.; Wan, F.; Peng, X.; Rochester, J.; Choi, E.S. Significant Reduction in the Low-Field Magnetization of Nb3Sn Superconducting Strands Using the Internal Oxidation APC Approach. Supercond. Sci. Technol. 2023, 36, 085008. [Google Scholar] [CrossRef]
  14. Xu, X.; Peng, X.; Wan, F.; Rochester, J.; Bradford, G.; Jaroszynski, J.; Sumption, M. APC Nb3Sn Superconductors Based on Internal Oxidation of Nb–Ta–Hf Alloys. Supercond. Sci. Technol. 2023, 36, 035012. [Google Scholar] [CrossRef]
  15. Pfeiffer, S.; Baumgartner, T.; Löffler, S.; Stöger-Pollach, M.; Hopkins, S.C.; Ballarino, A.; Eisterer, M.; Bernardi, J. Analysis of Inhomogeneities in Nb3Sn Wires by Combined SEM and SHPM and Their Impact on Jc and Tc. Supercond. Sci. Technol. 2023, 36, 045008. [Google Scholar] [CrossRef]
  16. Senatore, C.; Bagni, T.; Ferradas-Troitino, J.; Bordini, B.; Ballarino, A. Degradation of Ic Due to Residual Stress in High-Performance Nb3Sn Wires Submitted to Compressive Transverse Force. Supercond. Sci. Technol. 2023, 36, 075001. [Google Scholar] [CrossRef]
  17. Rochester, J.; Ortino, M.; Xu, X.; Peng, X.; Sumption, M. The Roles of Grain Boundary Refinement and Nano-Precipitates in Flux Pinning of APC Nb3Sn. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
  18. Deryagina, I.; Popova, E.; Patrakov, E.; Valova-Zaharevskaya, E. Structure of Superconducting Layers in Bronze-Processed and Internal-Tin Nb3Sn-Based Wires of Various Designs. J. Appl. Phys. 2017, 121, 233901. [Google Scholar] [CrossRef]
  19. Deryagina, I.L.; Popova, E.N.; Patrakov, E.I.; Valova-Zaharevskaya, E.G. Effect of Nb3Sn Layer Structure and Morphology on Critical Current Density of Multifilamentary Superconductors. J. Magn. Magn. Mater. 2017, 440, 119–122. [Google Scholar] [CrossRef]
  20. Popova, E.N.; Deryagina, I.L. Optimization of the Microstructure of Nb3Sn Layers in Superconducting Composites. Phys. Met. Metallogr. 2018, 119, 1229–1235. [Google Scholar] [CrossRef]
  21. Deryagina, I.; Popova, E.; Patrakov, E. Effect of Diameter of Nb3Sn-Based Internal-Tin Wires on the Structure of Superconducting Layers. IEEE Trans. Appl. Supercond. 2022, 32, 1–5. [Google Scholar] [CrossRef]
  22. Bottura, L.; Godeke, A. Superconducting Materials and Conductors: Fabrication and Limiting Parameters. Rev. Accel. Sci. Technol. 2012, 05, 25–50. [Google Scholar] [CrossRef]
  23. Uglietti, D.; Abacherli, V.; Cantoni, M.; Flukiger, R. Grain Growth, Morphology, and Composition Profiles in Industrial Nb3Sn Wires. IEEE Trans. Appl. Supercond. 2007, 17, 2615–2618. [Google Scholar] [CrossRef]
  24. Banno, N. Low-Temperature Superconductors: Nb3Sn, Nb3Al, and NbTi. Superconductivity 2023, 6, 100047. [Google Scholar] [CrossRef]
  25. Abächerli, V.; Uglietti, D.; Seeber, B.; Flükiger, R. (Nb,Ta,Ti)3Sn Multifilamentary Wires Using Osprey Bronze with High Tin Content and NbTa/NbTi Composite Filaments. Phys. C Supercond. 2002, 372–376, 1325–1328. [Google Scholar] [CrossRef]
  26. Abächerli, V.; Uglietti, D.; Lezza, P.; Seeber, B.; Flükiger, R.; Cantoni, M.; Buffat, P.A. The Influence of Ti Doping Methods on the High Field Performance of (Nb, Ta, Ti)3Sn Multifilamentary Wires Using Osprey Bronze. IEEE Trans. Appl. Supercond. 2005, 15, 3482–3485. [Google Scholar] [CrossRef]
  27. Godeke, A.; Haken, B. ten; Kate, H.H.J. ten; Larbalestier, D.C. A General Scaling Relation for the Critical Current Density in Nb3Sn. Supercond. Sci. Technol. 2006, 19, R100–R116. [Google Scholar] [CrossRef]
  28. Lee, P.J.; Squitieri, A.A.; Larbalestier, D.C. Nb3Sn: Macrostructure, Microstructure, and Property Comparisons for Bronze and Internal Sn Process Strands. IEEE Trans. Appl. Supercond. 2000, 10, 979–982. [Google Scholar] [CrossRef]
  29. Pong, I.; Oberli, L.-R.; Bottura, L. Cu Diffusion in Nb3Sn Internal Tin Superconductors during Heat Treatment. Supercond. Sci. Technol. 2013, 26, 105002. [Google Scholar] [CrossRef]
  30. Godeke, A. Advances in Nb3Sn Performance. In Proceedings of the Workshop Accelerator Magnet Superconductors, Design and Optimization; CERN: Geneva, Switzerland, 19–23 May 2008; pp. 24–27.
  31. Barzi, E.; Bossert, R.; Caspi, S.; Dietderich, D.R.; Ferracin, P.; Ghosh, A.; Turrioni, D. RRP Nb3Sn Strand Studies for LARP. IEEE Trans. Appl. Supercond. 2007, 17, 2607–2610. [Google Scholar] [CrossRef]
  32. Godeke, A.; den Ouden, A.; Nijhuis, A.; ten Kate, H.H.J. State of the Art Powder-in-Tube Niobium–Tin Superconductors. Cryogenics 2008, 48, 308–316. [Google Scholar] [CrossRef]
  33. Hawes, C.D.; Lee, P.J.; Larbalestier, D.C. Measurements of the Microstructural, Microchemical and Transition Temperature Gradients of A15 Layers in a High-Performance Nb3Sn Powder-in-Tube Superconducting Strand. Supercond. Sci. Technol. 2006, 19, S27–S37. [Google Scholar] [CrossRef]
  34. Cantoni, M.; Scheuerlein, C.; Pfirter, P.-Y.; Borman, F. de; Rossen, J.; Arnau, G.; Oberli, L.; Lee, P. Sn Concentration Gradients in Powder-in-Tube Superconductors. J. Phys. Conf. Ser. 2010, 234, 022005. [Google Scholar] [CrossRef]
  35. Kramer, E.J. Scaling Laws for Flux Pinning in Hard Superconductors. J. Appl. Phys. 1973, 44, 1360–1370. [Google Scholar] [CrossRef]
  36. Dew-Hughes, D. Flux Pinning Mechanisms in Type II Superconductors. Philos. Mag. 1974, 30, 293–305. [Google Scholar] [CrossRef]
  37. Ekin, J.W. Experimental Techniques for Low-Temperature Measurements; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
  38. Flükiger, R.; Senatore, C.; Cesaretti, M.; Buta, F.; Uglietti, D.; Seeber, B. Optimization of Nb3Sn and MgB2 Wires. Supercond. Sci. Technol. 2008, 21, 054015. [Google Scholar] [CrossRef]
  39. Wheatley, L.E.; Baumgartner, T.; Eisterer, M.; Speller, S.C.; Moody, M.P.; Grovenor, C.R.M. Understanding the Nanoscale Chemistry of As-Received and Fast Neutron Irradiated Nb3Sn RRP® Wires Using Atom Probe Tomography. Supercond. Sci. Technol. 2023, 36, 085006. [Google Scholar] [CrossRef]
  40. Fischer, C.M. Investigation of the Relationships between Superconducting Properties and Nb3Sn Reaction Conditions in Powder-in-Tube Nb3Sn Conductors, Master Thesis, University of Winsconsin-Madison, 2002.
  41. Godeke, A. A Review of the Properties of Nb3Sn and Their Variation with A15 Composition, Morphology and Strain State. Supercond. Sci. Technol. 2006, 19, R68–R80. [Google Scholar] [CrossRef]
  42. Marken, K.R. Characterization Studies of Bronze-Process Filamentary Nb3Sn Composites, PhD Thesis, Wisconsin Univ., Madison, USA, 1986. [Google Scholar]
  43. West, A.W.; Rawlings, R.D. A Transmission Electron Microscopy Investigation of Filamentary Superconducting Composites. J. Mater. Sci. 1977, 12, 1862–1868. [Google Scholar] [CrossRef]
  44. Shaw, B.J. Grain Size and Film Thickness of Nb3Sn Formed by Solid-State Diffusion in the Range 650–800 °C. J. Appl. Phys. 1976, 47, 2143–2145. [Google Scholar] [CrossRef]
  45. Schauer, W.; Schelb, W. Improvement of Nb3Sn High Field Critical Current by a Two-Stage Reaction. IEEE Trans. Magn. 1981, 17, 374–377. [Google Scholar] [CrossRef]
  46. Scanlan, R.M.; Fietz, W.A.; Koch, E.F. Flux Pinning Centers in Superconducting Nb3Sn. J. Appl. Phys. 1975, 46, 2244–2249. [Google Scholar] [CrossRef]
  47. Tinkham, M. Introduction to Superconductivity, 2nd ed.; Dover Publications: Mineola, New York, USA, 2004. [Google Scholar]
  48. Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
  49. Kittel, C. Introduction to Solid State Physics, 8th ed.; Wiley: Hoboken, New Jersey, USA, 2004. [Google Scholar]
  50. Brandt, E.H. The Vortex Lattice in Type-II Superconductors: Ideal or Distorted, in Bulk and Films. Phys. Status Solidi B 2011, 248, 2305–2316. [Google Scholar] [CrossRef]
  51. Talantsev, E.F. The Electron–Phonon Coupling Constant and the Debye Temperature in Polyhydrides of Thorium, Hexadeuteride of Yttrium, and Metallic Hydrogen Phase III. J. Appl. Phys. 2021, 130, 195901. [Google Scholar] [CrossRef]
  52. Talantsev, E.F.; Tallon, J.L. Universal Self-Field Critical Current for Thin-Film Superconductors. Nat. Commun. 2015, 6, 7820. [Google Scholar] [CrossRef]
  53. Paturi, P.; Huhtinen, H. Roles of Electron Mean Free Path and Flux Pinning in Optimizing the Critical Current in YBCO Superconductors. Supercond. Sci. Technol. 2022, 35, 065007. [Google Scholar] [CrossRef]
  54. Poole, C.P.; Farach, H.; Creswick, R.; Prozorov, R. Superconductivity, 2nd ed.; Academic Press: London, UK, 2007. [Google Scholar]
  55. Godeke, A. Performance Boundaries in Nb3Sn Superconductors, PhD Thesis, University of Twente, Enschede, Netherlands, 2005. [Google Scholar]
  56. Xu, X.; Sumption, M.D.; Peng, X. Internally Oxidized Nb3Sn Strands with Fine Grain Size and High Critical Current Density. Adv. Mater. 2015, 27, 1346–1350. [Google Scholar] [CrossRef]
  57. Talantsev, E.F. New Scaling Laws for Pinning Force Density in Superconductors. Condensed Matter 2022, 7, 74. [Google Scholar] [CrossRef]
  58. Tarantini, C.; Kametani, F.; Balachandran, S.; Heald, S. M.; Wheatley, L.; Grovenor, C. R. M.; Moody, M. P.; Su, Y.-F.; Lee, P.J.; Larbalestier, D. C. Origin of the enhanced Nb3Sn performance by combined Hf and Ta doping. Scientific Reports 2021, 11, 17845. [Google Scholar] [CrossRef]
Preprints 78046 g001
Figure 1. Pinning force density Fp versus B for bronze-route wires of different average grain sizes, d: (a) d = 35 nm; deduced Fp,max = 7.19 ± 0.02 GN/m3, Bc2 = 19.2 ± 0.3 T, p = 0.68 ± 0.01, q = 2.7 ± 0.1; fit quality is 0.9997; (b) d = 74 nm; deduced Fp,max = 4.99 ± 0.03 GN/m3, Bc2 = 23 ± 1 T, p = 0.84 ± 0.03, q = 3.5 ± 0.3; fit quality is 0.9982; (c) d = 143 nm; deduced Fp,max = 3.52 ± 0.02 GN/m3, Bc2 = 21.4 ± 0.4 T, p = 0.55 ± 0.02, q = 1.8 ± 0.1; fit quality is 0.9987; (d) d = 191 nm; deduced Fp,max = 2.45 ± 0.01 GN/m3, Bc2 = 23.5 ± 0.3 T, p = 0.42 ± 0.01, q = 1.50 ± 0.07; fit quality is 0.9986. The p and q parameters for the fit were determined using the Kramer-Dew-Hughes equation (Equation (2)). Raw data reported by Flükiger et al [38]. 95% confidence bands are shown by pink shadow areas.
Figure 1. Pinning force density Fp versus B for bronze-route wires of different average grain sizes, d: (a) d = 35 nm; deduced Fp,max = 7.19 ± 0.02 GN/m3, Bc2 = 19.2 ± 0.3 T, p = 0.68 ± 0.01, q = 2.7 ± 0.1; fit quality is 0.9997; (b) d = 74 nm; deduced Fp,max = 4.99 ± 0.03 GN/m3, Bc2 = 23 ± 1 T, p = 0.84 ± 0.03, q = 3.5 ± 0.3; fit quality is 0.9982; (c) d = 143 nm; deduced Fp,max = 3.52 ± 0.02 GN/m3, Bc2 = 21.4 ± 0.4 T, p = 0.55 ± 0.02, q = 1.8 ± 0.1; fit quality is 0.9987; (d) d = 191 nm; deduced Fp,max = 2.45 ± 0.01 GN/m3, Bc2 = 23.5 ± 0.3 T, p = 0.42 ± 0.01, q = 1.50 ± 0.07; fit quality is 0.9986. The p and q parameters for the fit were determined using the Kramer-Dew-Hughes equation (Equation (2)). Raw data reported by Flükiger et al [38]. 95% confidence bands are shown by pink shadow areas.
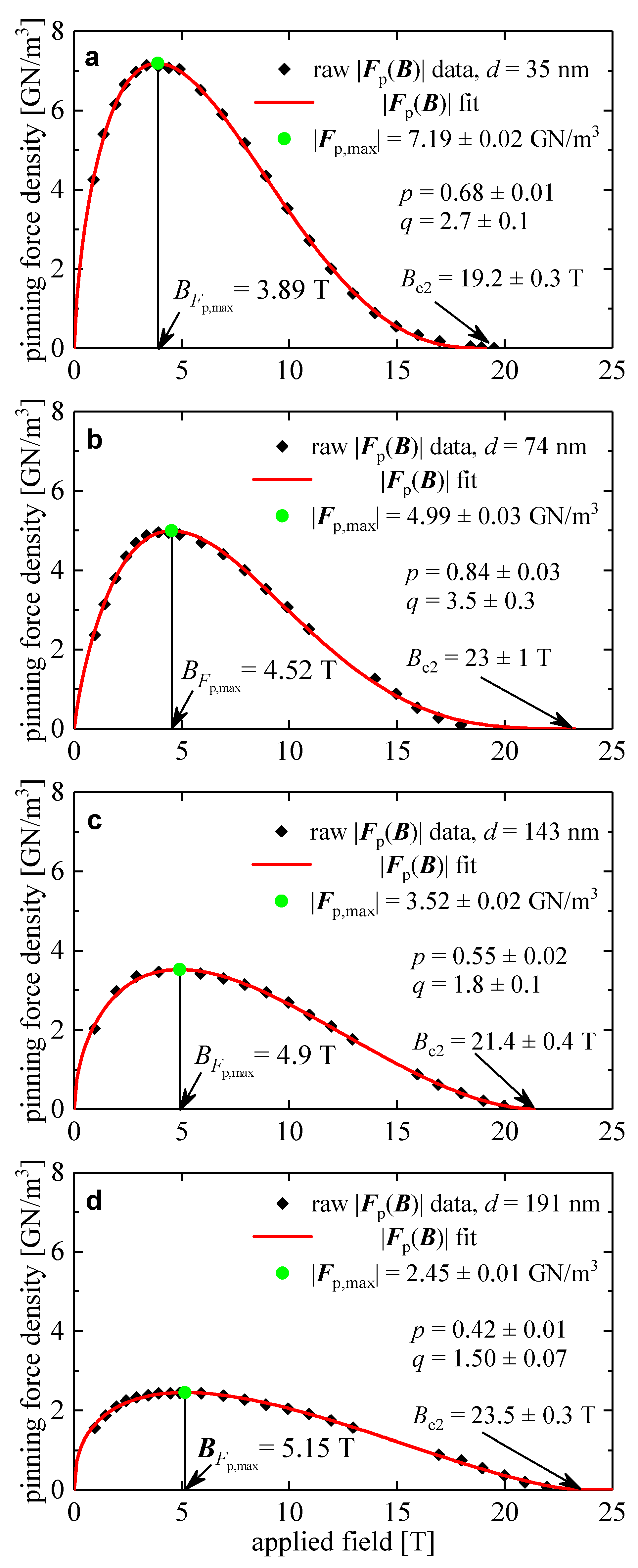
Preprints 78046 g001
Preprints 78046 g002
Figure 2. Maximum pinning force density, F p , m a x , vs. reciprocal average grain size, 1 / d , for datasets reported by Marken [42], West et al [43], Fischer [40], Shaw [44], Schauer et al [45], and Scanlan et al [46]. Fitting curve (Equation (3)) was proposed by Godeke [41], who also presented full dataset in the log-linear plot.
Figure 2. Maximum pinning force density, F p , m a x , vs. reciprocal average grain size, 1 / d , for datasets reported by Marken [42], West et al [43], Fischer [40], Shaw [44], Schauer et al [45], and Scanlan et al [46]. Fitting curve (Equation (3)) was proposed by Godeke [41], who also presented full dataset in the log-linear plot.
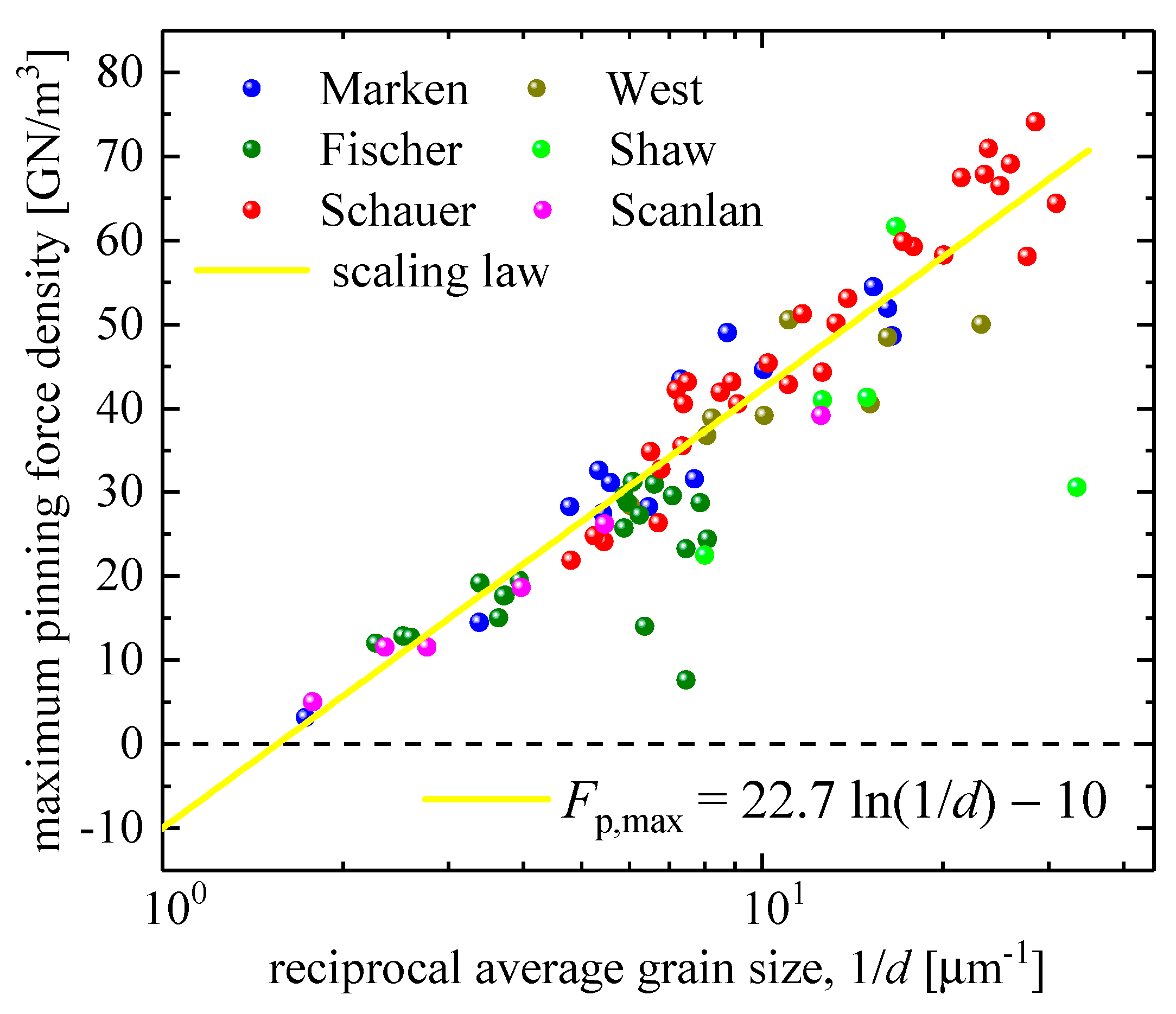
Preprints 78046 g002
Preprints 78046 g003
Figure 3. B F p . m a x , c a l c was calculated using Equation (4) (red) [41] and B F p . m a x , e x p was extracted from experimental data reported by Flükiger [38] for Nb3Sn conductors fabricated by bronze technology.
Figure 3. B F p . m a x , c a l c was calculated using Equation (4) (red) [41] and B F p . m a x , e x p was extracted from experimental data reported by Flükiger [38] for Nb3Sn conductors fabricated by bronze technology.
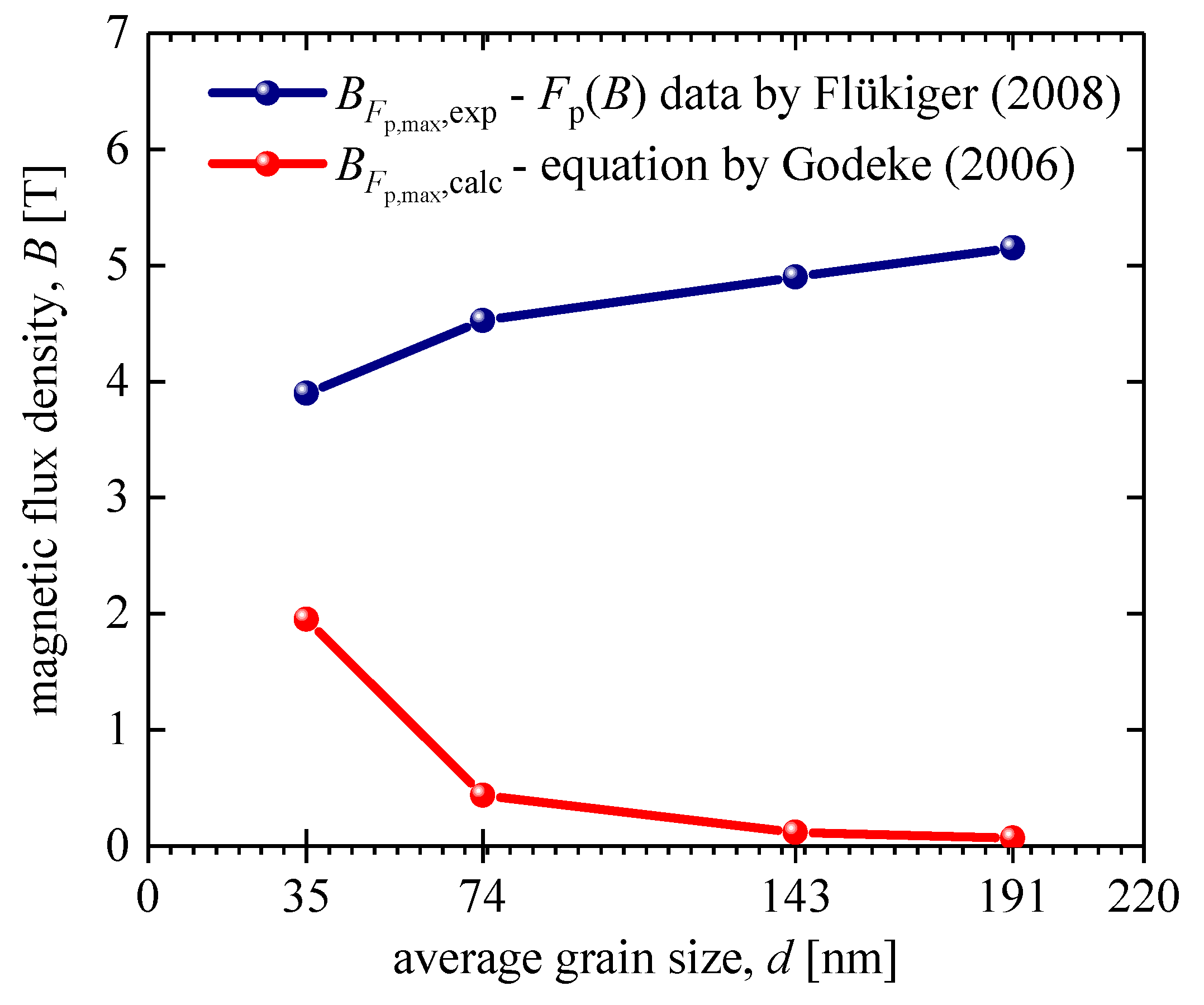
Preprints 78046 g003
Preprints 78046 g004
Figure 4. F p , m a x d data from Figure 2 (reported by Fischer [40] and Godeke [41]) in linear-linear plot, and the fitting curve to Equation (3) [41], where we also showed both side extrapolations within the average grain size range of 20   n m ≤ d ≤ 800   n m of Nb3Sn. Raw data reported by Marken [42], West et al [43], Fischer [40], Shaw [44], Schauer et al [45], and Scanlan et al [46].
Figure 4. F p , m a x d data from Figure 2 (reported by Fischer [40] and Godeke [41]) in linear-linear plot, and the fitting curve to Equation (3) [41], where we also showed both side extrapolations within the average grain size range of 20   n m ≤ d ≤ 800   n m of Nb3Sn. Raw data reported by Marken [42], West et al [43], Fischer [40], Shaw [44], Schauer et al [45], and Scanlan et al [46].
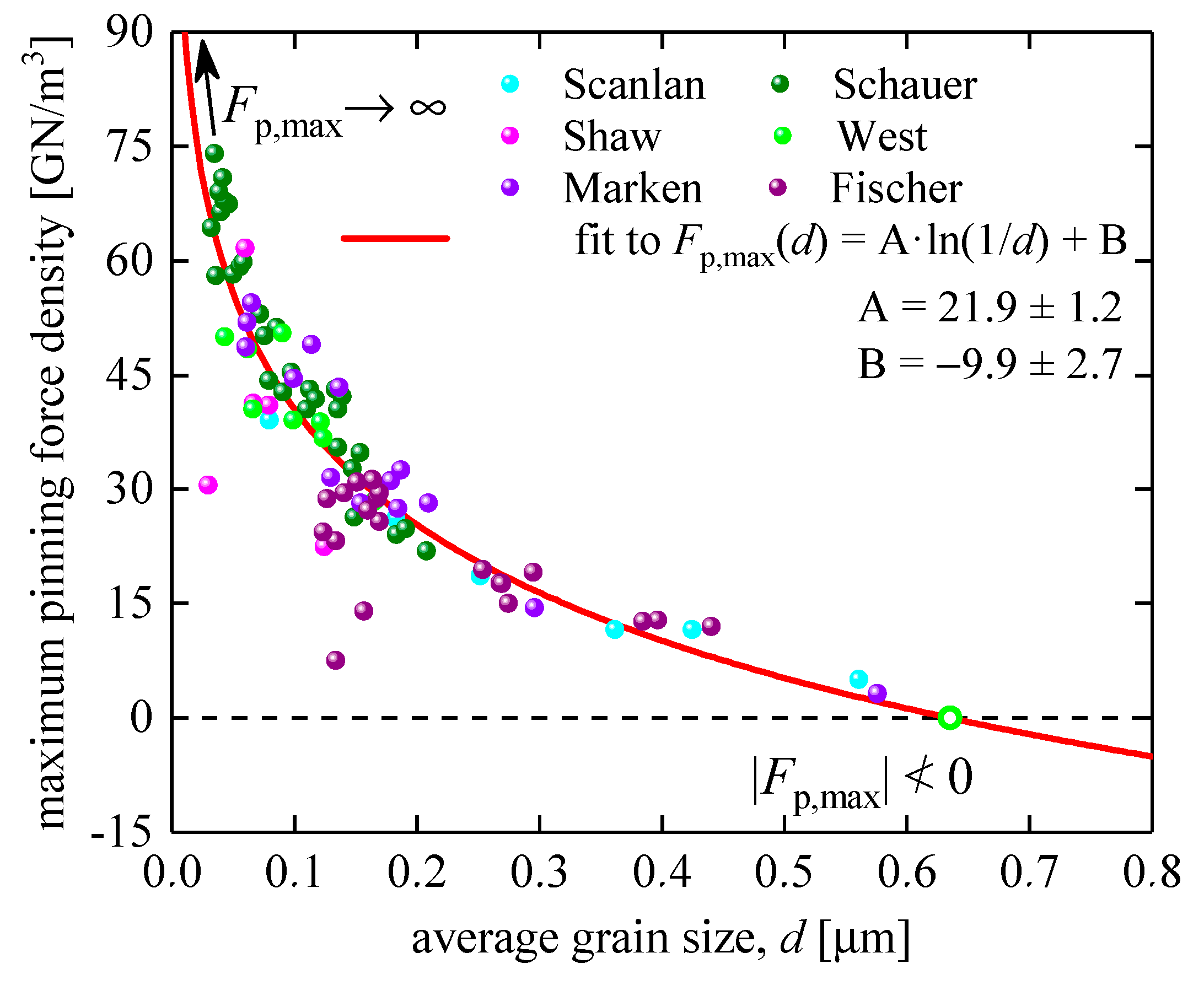
Preprints 78046 g004
Preprints 78046 g005
Figure 5. Maximum pinning force density, F p , m a x d , vs average grain size, d , for the non-Cu Nb3Sn wires and data fit to Equation (15). Raw data reported by Marken [42], West et al [43], Fischer [40], Shaw [44], Schauer et al [45], and Scanlan et al [46]. Nb3Sn conductors were fabricated by bronze technology. Deduced parameters are F p , m a x 0 = 74 ± 3   G N m 3 , δ = 175 ± 12   n m ; fit quality is 0.9248. 95% confidence bands are shown by grey shadow areas.
Figure 5. Maximum pinning force density, F p , m a x d , vs average grain size, d , for the non-Cu Nb3Sn wires and data fit to Equation (15). Raw data reported by Marken [42], West et al [43], Fischer [40], Shaw [44], Schauer et al [45], and Scanlan et al [46]. Nb3Sn conductors were fabricated by bronze technology. Deduced parameters are F p , m a x 0 = 74 ± 3   G N m 3 , δ = 175 ± 12   n m ; fit quality is 0.9248. 95% confidence bands are shown by grey shadow areas.
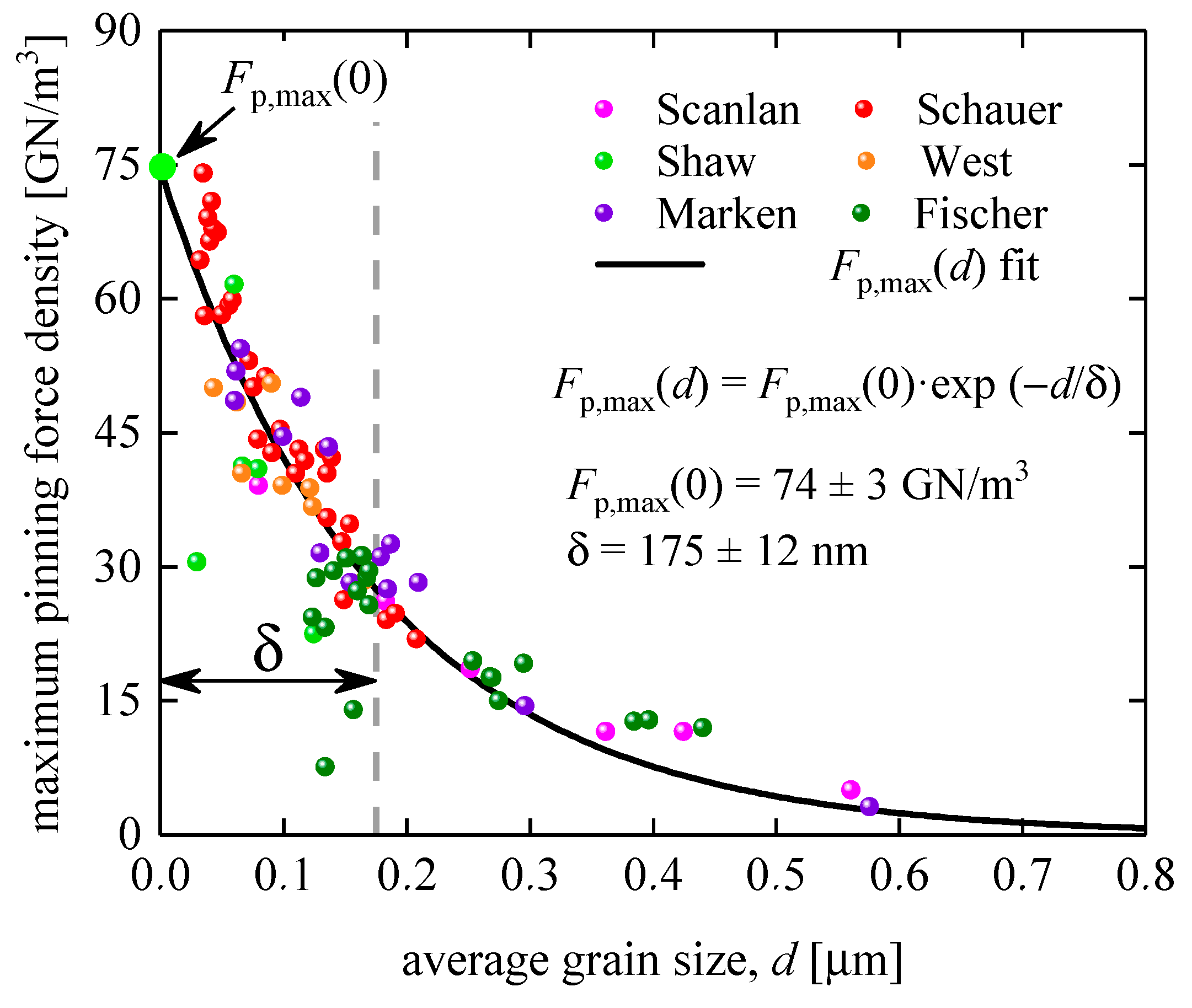
Preprints 78046 g005
Preprints 78046 g006
Figure 6. Maximum pinning force density, F p , m a x d , vs average grain size, d , for the A15 layer fabricated by powder-in-tube technology [40,56]. Raw data reported by Fischer [40] and Xu et al [56]. Deduced parameters are F p , m a x 0 = 189 ± 11   G N m 3 , δ = 175 ± 13   n m ; fit quality is 0.9093. 95% confidence bands are shown by pink shadow areas.
Figure 6. Maximum pinning force density, F p , m a x d , vs average grain size, d , for the A15 layer fabricated by powder-in-tube technology [40,56]. Raw data reported by Fischer [40] and Xu et al [56]. Deduced parameters are F p , m a x 0 = 189 ± 11   G N m 3 , δ = 175 ± 13   n m ; fit quality is 0.9093. 95% confidence bands are shown by pink shadow areas.
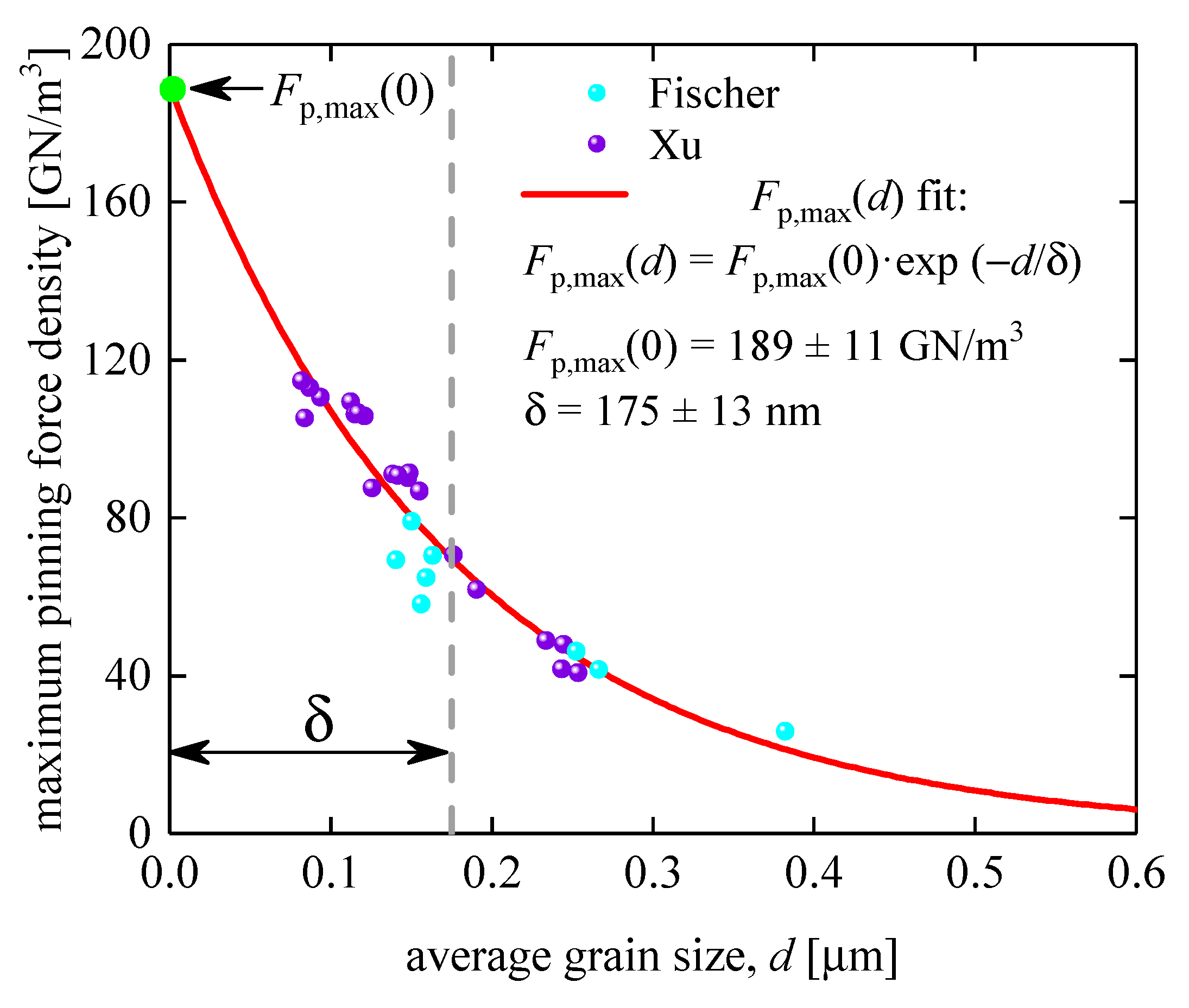
Preprints 78046 g006
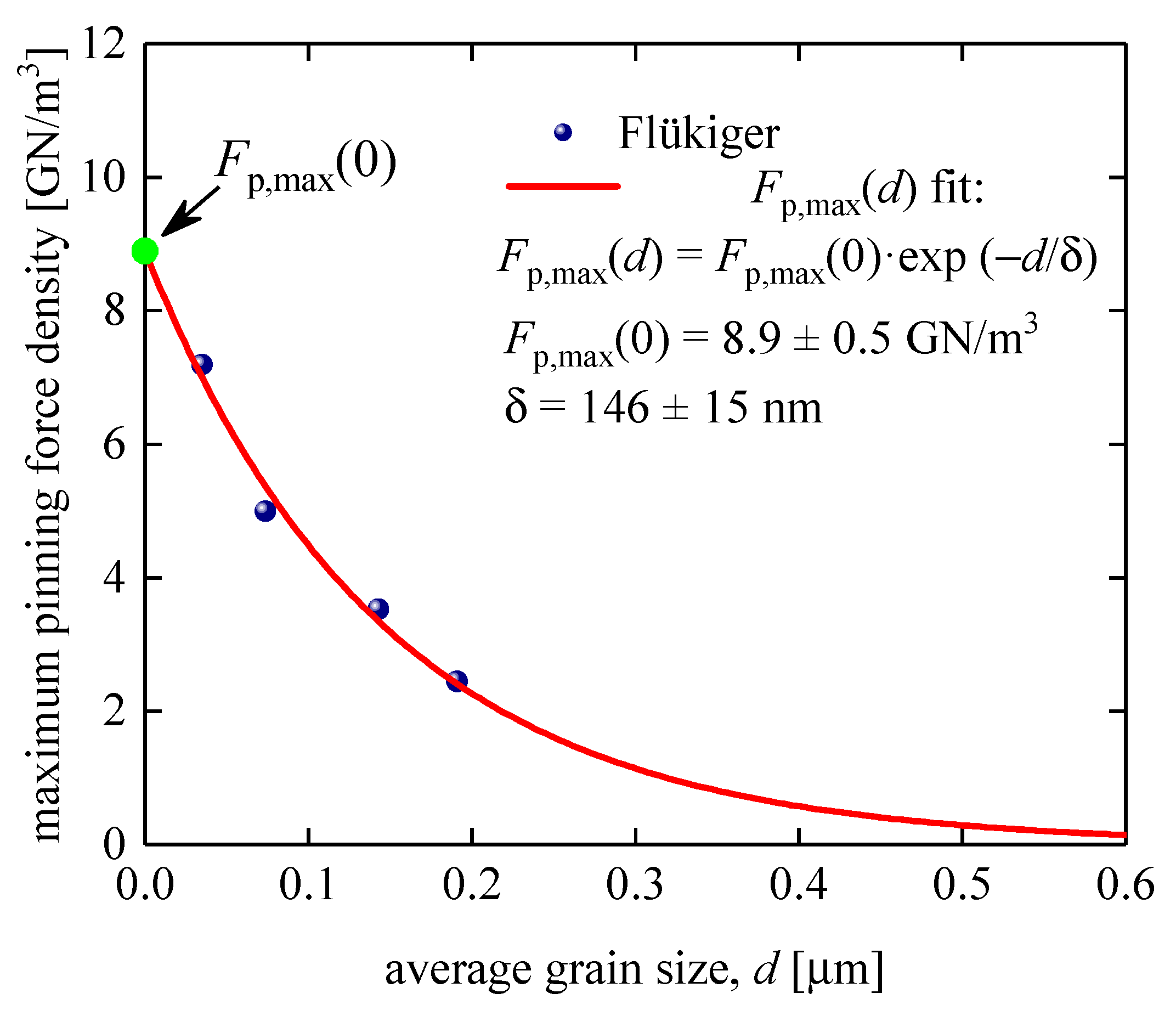
Preprints 78046 g007
Figure 7. Maximum pinning force density, F p , m a x d , vs average grain size, d , for samples fabricated by bronze technology and data fit to Equation (15). Raw data reported by Flükiger et al [38]. Deduced parameters are F p , m a x 0 = 8.9 ± 0.5   G N m 3 , δ = 146 ± 15   n m . fit quality is 0.9837. 95% confidence bands are shown by pink shadow areas.
Figure 7. Maximum pinning force density, F p , m a x d , vs average grain size, d , for samples fabricated by bronze technology and data fit to Equation (15). Raw data reported by Flükiger et al [38]. Deduced parameters are F p , m a x 0 = 8.9 ± 0.5   G N m 3 , δ = 146 ± 15   n m . fit quality is 0.9837. 95% confidence bands are shown by pink shadow areas.
Preprints 78046 g007
Preprints 78046 g008
Figure 8. Schematic representation of the effective areas ( δ -layer) in a cross-section of the eqiaxed Nb3Sn layer.
Figure 8. Schematic representation of the effective areas ( δ -layer) in a cross-section of the eqiaxed Nb3Sn layer.
Preprints 78046 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated