Preprint
Article
Homer-Based Multi-Scenario Collaborative Planning for Grid-Connected Pv-Storage Microgrids With Electric Vehicles
This is a preprint, it has not been peer-reviewed.
Submitted:
29 June 2023
Posted:
30 June 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
Microgrid is one of the important ways to accommodate distributed PV generation. However, the optimal planning scheme of microgrids is closely related to solar resources, load characteristics, and the key components of microgrid systems. This paper uses HOMER software to conduct collaborative planning for grid-connected PV-storage microgrids with electric vehicles in multiple scenarios. Specifically, we construct a multi-scenario capacity optimization model for PV generation, energy storage, and converters, considering both the cleanliness and economic performance of microgrids. The performance is quantified using indices such as net present cost, levelized cost of electricity, and carbon dioxide emission under multiple scenarios. Finally, we conduct extensive case studies on a business park in Wuhan, China, to compare and discuss the planning performance under multiple scenarios, as well as sensitivity analysis with specific cases.
Keywords:
-
1. Introduction
In recent years, the proportion of photovoltaic (PV) generation, wind power generation, and other renewable energy sources in the grid has been increasing, and the planning and construction of future renewable-dominated power systems have become the key to building a modern energy system [1]. Although renewable generation has the advantages of environmental protection, energy saving, and emission reduction, it relies on external environmental conditions and shows the characteristics of uncertainties in power output [2]. Large-scale grid integration of renewable generation will cause many adverse effects on the normal operation of traditional power systems [3]. Microgrid, as a combination of distributed renewable generation, energy storage devices, and various types of loads into a small power network, provides a promising tool for renewable accommodation. Microgrids not only serve as a bridge for energy exchange between distributed power sources and distribution grids, but also plays a positive role in load redistribution [4,5]. Optimal planning of microgrids coordinating resources and loads is an important issue.
As electric vehicles (EVs) gain popularity and the share of EV charging load is continuously increasing, characteristics of loads in microgrids show diversity [6]. Compared with conventional electricity load, EV charging load shows significant randomness and fluctuation in spatial and temporal distribution, and EV charging decision is susceptible to real-time electricity price, weather, road conditions, battery state of charge, and other factors [7,8]. Users' travel habits and usage habits also make EV charging load present a certain dispersion, and the operation and charging characteristics of different types of EVs also differ greatly, thus bringing more uncertainty to microgrid operation [9]. Microgrids with only conventional loads considered in the planning stage might fail to accommodate the massive access of EVs, and the electricity quality and economic performance of microgrids will be significantly impacted by EV loads [10]. The large-scale access of EVs to the microgrid system will lead to load growth and affect the microgrid load architecture and characteristics, and the simultaneous access of a large number of EVs will also lead to a surge in the microgrid power supply pressure and deterioration of power quality [11,12], which will affect operation stability and economy of the microgrid. In this context, the necessity of taking into account EV charging loads in microgrid planning is enhanced.
The problem of optimal planning of microgrids has been widely studied. In the literature [13], the objective function of minimizing active power fluctuation is established to derive the optimal configuration of microgrid energy storage capacity with minimum active power fluctuation. In the literature [14], an off-grid microgrid economic optimization model was established, mainly considering the effects of battery capacity decay and temperature. The results showed that the overall economy of the microgrid system was effectively improved. In literature [15], the optimal allocation of PV and energy storage in rural microgrids is achieved based on the second-generation non-dominated ranking genetic algorithm with the optimization objectives of maximum PV utilization and optimal economy, considering the load characteristics of rural areas, local environmental factors and various economic factors. In literature [16], the optimal planning of isolated hybrid systems is derived with total NPV minimization as the optimization objective and based on an improved genetic algorithm. However, these studies mainly focused on economic factors and did not adequately consider other important indicators such as renewable energy resource utilization and carbon emissions. In literature [17], a microgrid system with renewable resources and batteries is constructed, and the electric vehicle load is generated based on Monte Carlo algorithm, with the lowest probability of power loss and the lowest life cycle cost as the optimization objectives, and finally the optimal configuration of the system is derived based on particle swarm optimization algorithm. The aforementioned literature conducts studies by establishing optimization models and seeking solution algorithms. In addition, HOMER as one of the commercial software, provides an efficient platform for tailored microgrid planning. In literature [18], HOMER software was employed to perform the technical-economic assessment of hybrid renewable energy systems to electrify three off-grid remote villages in Columbia. And the most economical system was proposed for each village based on net present cost (NPC), levelized cost of electricity (LCOE), and initial capital cost. In literature [19], Rahman used the Canadian Ontario region as a study, set up seven generation scenarios based on the percentage of renewable energy and applied HOMER for a hybrid energy generation design that can meet a peak load of 772 kW and an average load of 4.4 kWh/day. In addition, the carbon dioxide penalty cost is also considered in the total cost components and solar surface radiation, wind speed, diesel price and carbon dioxide penalty cost are analyzed as sensitive variables.The simulation results show that the percentage of renewable energy is 100%, 80%, 65%, 50%, 35%, 21%, and 0%, and the corresponding electricity costs are $1.48/kWh, $0.62/kWh, $0.54/kWh, $0.42/kWh, $0.39/kWh, $0.37/kWh, and $0.36/kWh, respectively. In literature [20], based on HOMER software, an optimal configuration of a diesel-battery-wind-PV hybrid system was proposed considering NPC and LCOE. In literature [21], HOMER Pro software was used to develop a stand-alone microgrid system with a mixture of wind power, PV power, diesel generators, and batteries to meet the agricultural load requirements using minimized NPC as the objective function and resources, technology, reliability, and emissions as constraints. Overall, the effectiveness of HOMER software is verified in several scenarios. However, existing studies using HOMER did not comprehensively consider the technical, economic, and environmental-friendly performance of different components in microgrids, especially with multiple operating scenarios with EVs.
In this paper, we use HOMER software to carry out multi-scenario collaborative planning for grid-connected PV-storage microgrids with EVs. Specifically, we build a multi-scenario optimization model considering both the economic and cleanliness performance of EV-connected microgrids. Based on HOMER software, we build multi-type EV charging load and consider the stochasticity of multi-type EV charging load. The performance is quantified using indices such as NPC, LCOE, and carbon dioxide emission under multiple scenarios. Extensive case studies on a business park in Wuhan, China, are conducted to compare and discuss the planning performance under multiple scenarios, as well as sensitivity analysis with specific cases.
The remainder of this paper is structured as follows. Section 2 presents the modelling of each component of the grid-connected PV-storage microgrid based on HOMER. Section 3 presents the multi-scenario collaborative planning model. Section 4 conducts an extensive case analysis based on a business park in China. Section 5 concludes this paper.
2. Grid-connected PV-storage microgrids based on HOMER software
2.1. Topology of grid-connected PV-storage microgrids
The grid-connected PV-storage microgrid system consists of PV modules, battery packs, converters, and conventional loads. Meanwhile, considering the growing access of EV charging load in the microgrid, EV charging piles are added to the microgrid system. The topology of a grid-connected PV-storage microgrid with EVs is built in HOMER, as shown in Figure 1.
2.2. Distributed PV power generation model
HOMER software calculates the available output power of distributed PV generation in microgrids based on input parameters, such as PV array size, ambient temperature, and solar radiation intensity, using equation (1), and continuously optimizes the final optimal power of PV [22].
where PPV is the output power of PV panel, YPV is the PV array output power (kW) under standard test conditions, fPV is the PV array derating factor, is the solar radiation incident on the PV array, is the solar radiation under standard test conditions, ap is the power temperature coefficient, Tc is the ambient temperature during the current time period, Tc,STC is the temperature under standard test conditions.
2.3. Battery storage model
In the HOMER model, the operating characteristics of the battery are represented by the KiBam dynamic battery model [23]. In the KiBam model, the power limits for the charging and discharging rate of the battery are as follows:
where is the maximum charging power of the battery (kW);is the maximum discharging power of the battery (kW); is the maximum charging power of the battery in each time step (kW); is the maximum charging power of the battery in the maximum charging rate limit (kW); is the maximum charging power of the battery in the maximum charging current limit (kW); is the maximum discharging power of the battery within each time step (kW); is the charging efficiency of the battery (%); is the discharging efficiency of the battery (%); is the available energy of the battery (kJ); is the maximum storage energy of the battery (kJ); is the rate constant of the battery; is the capacity ratio of the battery; is the maximum charging rate of the battery (Ah); is the total number of series and parallel connections of the battery; is the rated voltage of the battery (V); is the maximum charging current (Ah).
2.4. Converter parameters
The conversion of the DC part and AC part of the microgrid is considered, and the converter configuration is incorporated into the planning model. The investment cost and replacement cost of converters are set 5393.54 Yuan/kW and 4800 Yuan/kW, respectively, and the maintenance cost is 60 Yuan/year/kW. The operating life of converters is set as 15 years, and the conversion efficiency is set as 95%.
2.5. Load characteristics
In addition to the conventional load in the microgrid, the charging load brought by the EVs is also considered. The types of EVs and their corresponding charging characteristics are set. Then, by setting the number of charging piles in the microgrid and their rated power, the charging load demand of EVs is simulated for 8760 hours.
3. HOMER-based multi-scenario collaborative planning for grid-connected PV-storage microgrids
In this paper, we develop a multi-scenario collaborative planning strategy for grid-connected PV-storage microgrids with EVs based on HOMER software. Specifically, multiple scenarios under two categories of indices, i.e., the cleanliness index and economic index, are considered. On this basis, a multi-scenario collaborative planning model is constructed.
3.1. Cleanliness and economic performance indices
3.1.1. Indices for cleanliness performance
In this paper, based on HOMER software, the cleanliness performance of the grid-connected PV-storage microgrid is evaluated in terms of two indicators: renewable energy share and carbon dioxide emission. The percentage of non-renewable energy is calculated as shown in equation (10), and the percentage of renewable energy is calculated as shown in equation (11) [24].
where is the amount of electricity purchased from the grid in the microgrid system (kWh/year), and is the annual electrical load in the microgrid system (kWh/year). and are the ratios of non-renewable energy generation and renewable energy generation, respectively. When the value of is 0, it means that the electric load in the microgrid is supplied entirely by the main grid, while when the value of is 1, it means that the electric load in the microgrid is supplied entirely by distributed PV.
For grid-connected PV-storage microgrids, the purchased power from the distribution network also indirectly causes carbon dioxide emissions in the power grid. Carbon dioxide emissions are calculated as shown in equation (12).
where is the carbon dioxide emission (kg/kWh) from the grid-connected PV-storage microgrid, and is the carbon emission factor, which is 0.632 kg/ kWh.
3.1.2. Indices for economic performance
In this paper, the NPC and the LCOE are selected as the economic indicators of grid-connected PV-storage microgrids.
The LCOE is the cost of generation calculated by leveling the cost and generation over the life cycle of the system [25], which is calculated as shown in equation (13):
where is the total annualized cost of the system (Yuan/year) [26], which is calculated as shown in equation (14):
where is the total net present value cost of the microgrid, including all costs as well as revenues generated during the project life cycle, such as initial investment costs, operation and maintenance costs, replacement costs, salvage value, and revenue from power sales; denotes the capital recovery factor, which is used to convert the present value into equivalent annual cash flows [27]. is calculated as shown in Equation (15):
where
nd
re the discount rate and project life cycle, respectively.
The NPC of a system is the present value of all costs incurred by the system over its lifetime minus the present value of all revenues earned by the system over its lifetime. The cost component includes investment costs, replacement costs, operation and maintenance costs, carbon dioxide emission penalties, and the cost of purchasing power from the grid. The revenue component includes the residual value of the equipment and the revenue from the sale of electricity from the microgrid to the larger grid [28]. It is calculated as shown in equation (16):
3.2. Optimal planning of grid-connected PV-storage microgrids
In this paper, we consider three scenarios for optimal capacity configuration of grid-connected PV-storage microgrids.
Scenario I: Only the economic performance of the microgrid is considered, i.e., minimizing the and indices. The objective function of collaborative planning is:
where
nd are the weights of and indices, respectively.
Scenario II: Only the cleanliness performance of the microgrid is considered, i.e., minimizing
nd ndices. In this scenario, the objective function is:
Scenario III: Both the economic and cleanliness performance of microgrids are considered. In this scenario, the objective function is:
where (, 2, 3, 4) is the weighting factor for the th index.
The multi-objective function is constructed by determining the weights of each index in (19) based on the entropy weighting method [29]. Entropy is a measure of uncertain information, and from the perspective of information entropy, the dispersion of an index can be measured by its entropy value. The lower its information entropy, the higher its dispersion is, and the more significant impact it exerts on the comprehensive assessment. The main steps include the construction of a decision matrix, data normalization, information entropy calculation, and the final determination of indicator weights [30].
(1) Initialization of the decision matrix. When there are alternatives to be evaluated based on decision indicators, the decision matrix is shown in equation (20):
where
s the index value of the th decision index of the h alternate solution.
(2) Normalization of the decision matrix. Since the units of measurement of the decision indicators are not uniform, they need to be normalized before calculating the integrated weights. Specifically, the positive indicators are normalized as shown in equation (21), and the negative indicators are normalized as shown in equation (22) [31]:
(3) Calculation of information entropy. The information entropy of the decision indicator is calculated by equation (23):
where s the information entropy of decision indicators, is the weight of the indicator value of option under decision indicators, and its calculation formula is shown in equation (24) :
(4) Calculation of weighting factors. Based on the information entropy of the decision indicator, the weight value of the decision matrix can then be derived by equation (25).
4. Case analysis
4.1. Case parameters settings
In this paper, a grid-connected PV-storage microgrid located in a commercial area of Wuhan, China, is selected for case analysis. The annual frost-free period in this area is generally 211-272 days, the total annual sunshine hours are 1810-2100 hours, the total annual radiation is 104 kcal/cm2-113 kcal/cm2, the annual solar radiation intensity is shown in Figure 2, and the annual average temperature is 15.8 °C-17.5 °C, as shown in Figure 3.
The load demand in this business park includes conventional load demand and EV charging load. The annual average conventional load is about 2619.91 kWh/day, with an average power of 109.16 kW and a maximum daily load of 376.19 kW, as shown in Figure 4. Figure 5 shows a typical daily conventional load profile for the business park, with the peak hours of the day from 9:00 am to 8:00 pm. The EV charging load includes SUV EVs and small electric cars with the parameters shown in Table 1. Four charging piles are used in this microgrid, with a rated power of 12kW for each charging pile, and the EV charging scale is set at 6. The annual EV charging load is shown in Figure 6, and the typical daily EV charging load is shown in Figure 7. The average annual EV charging load is 290 kWh/day, and in this business park, the EV charging load is mainly concentrated between 8:00 and 16:00. The microgrid sets a limit target for carbon dioxide emissions, stipulating that the portion exceeding 300000 kg/year is penalized at 250 Yuan per ton.
In terms of cost parameters, the unit investment cost and replacement cost of the PV modules is 9599.26 Yuan/kW, and the operational life is set to 25 years. Among them, the derating factor for PV arrays is 80%. In addition, a horizontal axis continuous tracking strategy is adopted for the PV generation system with a ground reflectivity of 20% and a temperature coefficient of -0.5, with an operating temperature of about 47°C and a flat panel efficiency of about 13%. The price for this microgrid to purchase electricity from and sell electricity to the distribution grid is 1.5 Yuan/kW and 0.4 Yuan/kW, respectively, and the carbon emission of electricity generation in the distribution grid is 632 kg/kWh.
4.2. Multi-scenario collaborative planning results
Considering the three scenarios set in Section 3.2 in this paper, this section carries out the planning of grid-connected PV-storage microgrids with EVs based on HOEMER. The NPC, LCOE, non-renewable energy ratio, and carbon emission of the microgrid are used as the decision indicators. In Scenario III, the weights of each indicator based on the entropy weight method are derived, as shown in Table 2.
The planning results and corresponding costs for the three scenarios are shown in Table 3 Table 4, respectively. It can be seen that the installed capacity of PV generation, battery energy storage, and converters in Scenario I are the smallest compared with that in the other two scenarios. The NPC and LCOE indices in Scenario I are the lowest in comparison with Scenario II and Scenario III, and the NPC and LCOE are 22.3 million Yuan and 1.471 Yuan/kWh, respectively. However, the cleanliness index in Scenario I is poor, with a reduction of 25.08% in the share of renewable energy and carbon dioxide emissions of 199675.3 kg/year compared to the results in Scenario II. In Scenario II, the installed PV capacity and battery capacity are the highest, and Scenario II has the highest renewable energy ratio and the lowest carbon dioxide emissions. This is because the cleanliness performance is taken into account in the planning objective in Scenario II, which, however, leads to poor economic performance with its NPC and LCOE respectively increasing by 126.01% and 28.69% compared with that in Scenario I. In Scenario III, both the economic and cleanliness performance of the grid-connected PV-storage microgrid are considered, and the optimal planning scheme is with 2195 kW PV generation, 637 kW converter, and no battery energy storage. Compared with Scenario I, the installed PV capacity in Scenario III is much larger, but the battery energy storage reduces to 0 kWh, which decreases the LCOE by 34.09%, although the NPC increased by 39.46%. In the meantime, the renewable energy ratio in Scenario III reaches 85.62%, and carbon dioxide emissions also decrease to 199178.9 kg/year, demonstrating a better cleanliness performance. And compared with Scenario II, although the carbon dioxide emissions are larger and the renewable energy share is reduced by 13.24%, the NPC and the LCOE are reduced by 62.06% and 72.56%, respectively, showing a better economic performance. Collaborative planning in Scenario III achieves an optimal trade-off that meets both system economic and cleanliness requirements.
The investment and operation cost of the grid-connected PV-storage microgrid under each scenario are shown in Table 5, and the parameters of different components are shown in Table 6. The optimal planning schemes for all 3 scenarios do not cause load-shedding. Compared to the other two scenarios, the PV capacity and the battery energy storage capacity in Scenario I are the minimum. Therefore, the PV investment costs as well as the system operation and maintenance costs in Scenario I are the lowest. But the lower PV capacity leads to a higher amount of electricity purchased from the distribution grid and higher carbon dioxide emissions. The lower PV capacity also leads to a lower percentage of PV power spillage, accounting for 15.12% of the total energy consumption. The amount of electricity sold to the grid is 110,542.8 kWh. The optimal planning scheme in Scenario II has the largest PV capacity and the highest investment cost and operation and maintenance cost. Consequently, the highest annual PV power generation is observed in Scenario II, reaching 3419029 kWh/year. With a higher energy storage capacity, the grid-connected PV-storage microgrid in Scenario II has the least purchased electricity and the most sold power, at 996,154.8 kWh. The PV power spillage accounts for 36.15% of the total energy consumption. Nevertheless, the higher PV output and larger battery energy storage capacity in Scenario II contributes to a better cleanliness performance but less economic performance. In Scenario III, the optimal planning scheme includes no energy storage, causing a higher PV power spillage compared with Scenario I, which accounts for 27.60% of the total electricity consumption. Moreover, deploying no energy storage greatly reduces the system investment and operation and maintenance costs. The cost of purchasing electricity from the distribution grid is 0.24% less than that in Scenario I, but the income from selling electricity to the distribution grid increases by 922.15%.
4.3. Sensitivity Analysis
We analyze the impacts of EV charging demand, unit investment costs of PV modules and battery energy storage, and carbon dioxide emissions on the optimal planning scheme for grid-connected PV-storage microgrids. We take minimizing the NPC as the planning objective. Specifically, we set the unit investment costs parameters in Section 4.1 as the base case, then the values of the parameters to be analyzed are adjusted step by step in the HOMER software.
Figure 8 presents the sensitivity of microgrid planning to EV charging demand and carbon dioxide emission limits under different unit investment costs. The region below the lines in Figure 8 represents the optimal planning results consisting of only PV modules with no battery energy storage. The region above the lines denotes the optimal planning results with both PV modules and battery energy storage. As shown in Figure 8, with the base case parameters, when the carbon dioxide emission limit reaches about 310 t/year or more, the optimal planning scheme of the grid-connected PV-storage microgrid contains only PV modules and converters with no energy storage. As the carbon dioxide emission limit gradually increases, the dependence of microgrid on renewable energy decreases accordingly, and since the cost of power purchase is lower than the cost of deploying battery energy storage, microgrid does not need to allocate energy storage in order to pursue a lower NPC index. In the meantime, as the EV charging demand increases, the lines under unit investment cost parameters show a slightly increasing trend, revealing the dependence of increased EV charging on energy storage. When the unit investment costs of PV modules and energy storage decrease from the base case to 60%, the boundary of the optimal planning scheme changes from the carbon dioxide emission limit value of about 310 t/year to 290 t/year. The optimal planning scheme of a grid-connected PV-storage microgrid with EV load is less prone to the impacts of the EV load scale. Specifically, the change in the scale of EV charging load does not increase the dependence of the microgrid system on energy storage, and the optimal planning scheme change boundary also tends to be stable. The optimal planning scheme of the microgrid under 60% unit investment cost is stable and less affected by EV charging scale, while the optimal planning scheme of the microgrid under unit investment cost is more affected by EV charging scale.
The sensitivity of the microgrid to EV charging demand and carbon dioxide emission limits when the unit investment costs of different components reduce to 60% is shown in Figure 9. When the unit investment cost of PV modules decreases to 60%, and the battery unit cost remains unchanged, the optimal planning scheme change boundary decreases to the carbon dioxide emission limit value of about 280 t/year. This is because the decrease in the unit cost of PV modules increases the affordable PV capacity with the same investment budget, thus reducing the amount of electricity purchased from the distribution network and reducing the required storage capacity, thus enabling the microgrid to operate economically and environmentally at a lower carbon dioxide limit. When the unit investment cost of battery energy storage decreases to 60%, and the PV module unit cost remains the same as the base case, the optimal planning scheme change boundary rises to the carbon dioxide emission limit of about 330 t/year. Comparing the change of planning schemes with different component investment costs, it further demonstrates that the impact of the unit investment cost of PV modules is greater than that of the battery energy storage.
The impacts of influential factors on the system NPC are shown in Figure 10 and Figure 11. It can be observed that when the unit investment cost multiplier for PV module and battery is 1, the system NPC will gradually increase with the increase of EV charging scale and the decrease of carbon dioxide emission limit. The increase of the PV penetration rate in grid-connected PV-storage microgrid is necessary to meet the increase of EV charging load under the fixed carbon emission limit, so the system NPC increases gradually with the increase of charging scale under the fixed carbon emission limit. And under the fixed EV charging scale, the system NPC gradually decreases as the carbon emission limit increases. Because the increase in carbon emission limit makes the microgrid less dependent on renewable energy, and the unit cost of purchasing electricity from the distribution grid is lower than the cost of installing battery energy storage and PV modules, the increase in carbon emission limit leads to increased power exchange amount with the distribution grid and thus reduce the system NPC. When the PV and battery module unit cost multiplier is 0.6, the trend of system NPC is similar. However, the NPC is reduced by the decrease in the unit cost of PV and battery modules for the same carbon emission limit.
5. Conclusions
This paper uses HOMER software to carry out the collaborative planning of a PV-storage microgrid with EVs. Multiple scenarios comprising different performances, e.g., economic and cleanliness performance of the microgrid, are incorporated into the collaborative planning. A case study on a business park in Wuhan, China, is implemented to compare and analyze the optimal PV-storage configuration of the microgrid. The economic and cleanliness performance under different scenarios are discussed, and sensitivity analysis is conducted. Through case studies, the following conclusions can be drawn.
1) Based on the proposed economic and cleanliness indices, the optimal planning scheme of grid-connected PV-storage microgrids under three different scenarios is obtained. The comparison of the planning results shows that, when only the economic index is considered (Scenario I), the configured microgrid contains a lower percentage of renewable energy and is less clean, but shows the best economic performance. When only the cleanliness index is considered (Scenario II), the economic performance of the microgrid is poor, and the LCOE reaches 1.893 Yuan/kWh, which is 28.69% higher than the LCOE in Scenario I, but the cleanliness index is the highest. When both the economic and cleanliness indices are considered (Scenario III), the obtained optimal planning scheme balances the economic and cleanliness performance.
2) Sensitivity analysis demonstrates that, the NPC of the microgrid is jointly determined by the unit investment of equipment, EV charging demand, and carbon emission limits. The NPC gradually increases as the EV charging demand increases and the allowed carbon dioxide emission limits decrease. As the EV charging demand increases, the energy storage capacity required in the microgrid gradually increases, while the carbon dioxide emission limit is negatively correlated with the energy storage capacity demand. In addition, the unit investment cost of PV and battery modules can significantly affect the optimal configuration of the microgrid. A lower unit investment cost of battery energy storage leads to a larger energy storage capacity in the planning schemes, while a lower unit investment cost of PV modules results in lower demand for energy storage in microgrids. The unit investment cost of PV module units has a greater impact on the optimal system configuration than the cost of batteries. The optimal planning scheme of the microgrid under 60% unit investment cost is stable and less affected by EV charging scale, while the optimal planning scheme of the microgrid under unit investment cost is more affected by EV charging scale. The increase in the scale of EV charging at unit investment cost will increase the reliance of the microgrid on energy storage.
Acknowledgments
Project Supported by Technical Standard of Shanghai 2020 “Technology Innovation Action Plan” (20DZ2205400).
Conflicts of Interest
The authors declare that they have no conflict of interest.
Nomenclature
| Levelized cost of energy (Yuan/ kWh) | |
| Net present cost (million Yuan) | |
| Output power of PV panel (kW) | |
| PV array output power (kW) | |
| PV array derating factor | |
| Solar radiation incident on the PV array during the current time period | |
| Solar radiation under standard conditions | |
| Power temperature coefficient | |
| PV array temperature during the current time period | |
| PV array temperature under standard test conditions | |
| The maximum charging power of the battery (kW) | |
| The maximum discharging power of the battery (kW) | |
| The maximum charging power of the battery in each time step (kW) | |
| The maximum charging power of the battery in the maximum charging rate limit (kW) | |
| The maximum charging power of the battery in the maximum charging current limit (kW) | |
| The maximum discharging power of the battery within each time step (kW) | |
| The charging efficiency of the battery (%) | |
| The discharging efficiency of the battery (%) | |
| Available energy of the battery (kJ) | |
| The maximum storage energy of the battery (kJ) | |
| The rate constant of the battery | |
| Capacity ratio of the battery | |
| The maximum charging rate of the battery (Ah) | |
| The total number of series and parallel connections of the battery | |
| Rated voltage of the battery (V) | |
| The maximum charging current (Ah) | |
| Percentage of non-renewable energy (%) | |
| Percentage of renewable energy (%) | |
| The amount of electricity purchased from the grid (kWh/year) | |
| Annual electrical load(kWh/year) | |
| Carbon dioxide emission (kg/kWh) | |
| Power purchased from the grid (kW) | |
| Carbon emission factor | |
| Total annualized cost of the system (Yuan/ year) | |
| Levelized cost of electricity (Yuan/ kWh) | |
| Net present cost of the microgrid system (million Yuan) | |
| Capital recovery factor | |
| Discount rate | |
| Project life cycle (year) | |
| The index value of the th decision index of the th alternate solution | |
| Information entropy of decision indicators | |
| The weight of indicator value of option under decision indicators | |
| The weight value of the decision matrix | |
| Percentage of non-renewable energy (%) | |
| Percentage of renewable energy (%) |
References
- Ren, G.R.; Liu, J.F.; Wan, J.; Guo, Y.F.; Yu, D. Overview of wind power intermittency: Impacts, measurements, and mitigation solutions. Applied Energy 2017, 204, 47–65. [Google Scholar] [CrossRef]
- Ding, X.; Ma, H.; Yan, Z.; Xing, J.; Sun, J. Distributionally robust capacity configuration for energy storage in microgrid considering renewable utilization. Frontiers in Energy Research 2022, 10, 896. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, C.; Wu, X. Statistical machine learning model for uncertainty analysis of photovoltaic power. Frontiers in Energy Research 2022, 971. [Google Scholar] [CrossRef]
- Nara, K. Next-generation power delivery system with resiliency and environmental affinity. Global Energy Interconnection 2022, 5, 274–280. [Google Scholar] [CrossRef]
- Hou, H.; Wang, Z.; Hou, T.; Fang, R.; Tang, J.; Xie, C. Optimal schedule of 100% renewable energy microgrid considering demand response of EVs. Energy Reports 2023, 9, 1743–1750. [Google Scholar] [CrossRef]
- Chai, Y.T.; Che, H. S.; Tan, C.K.; Tan, W.N.; Yip, S.C. A two-stage optimization method for Vehicle to Grid coordination considering building and Electric Vehicle user expectations. International Journal of Electrical Power & Energy Systems 2023, 148, 108984. [Google Scholar]
- Meng, S.X.; Qian, K.J.; Wang, H.; Yuan, J.; Zhou, H.; Shi, X.C. Electric vehicle charging strategy considering harmonics and the effect on current-carrying capacity and thermal life of distribution network cables. High Voltage Technology 2020, 46, 1269–1280. [Google Scholar]
- Meng, T.; Ai, X. The operation of microgrid containing electric vehicles//Asia-Pacific Power and Energy Engineering Conference. IEEE Computer Society 2011, 1–5. [Google Scholar]
- Hu, Z.C.; Song, Y.H.; Xu, Z.W.; Luo, Z.W.; Zhan, K.Q.; Jia, L. Impact and utilization of electric vehicle access to power grid. Chinese Journal of Electrical Engineering 2012, 32, 1–10. [Google Scholar]
- Strnad, I.; Prenc, R. Optimal sizing of renewable sources and energy storage in low-carbon microgrid nodes. Electrical Engineering 2018, 100, 1661–1674. [Google Scholar] [CrossRef]
- Gong, Q.; Midlam-Mohler, S.; Marano, V.; Rizzoni, G. Study of PEV charging on residential distribution transformer life. IEEE Transactions on Smart Grid 2011, 3, 404–412. [Google Scholar] [CrossRef]
- Gómez, J.C.; Morcos, M.M. Impact of EV battery chargers on the power quality of distribution systems. IEEE transactions on power delivery 2003, 18, 975–981. [Google Scholar] [CrossRef]
- Xu, D.M.; Kang, L.C.; Chang, L.C.; Cao, B.G. Optimal sizing of standalone hybrid wind/PV power systems using genetic algorithms. Canadian Conference on Electrical and Computer Engineering 2005, 1722–1725. [Google Scholar]
- Goodall, G.; Scioletti, M.; Zolan, A.; Suthar, B. Optimal design and dispatch of a hybrid microgrid system capturing battery fade. Optimization and Engineering 2019, 20, 179–213. [Google Scholar] [CrossRef]
- Yuan, H.; Ye, H.; Chen, Y.; Deng, W. Research on the optimal configuration of photovoltaic and energy storage in rural microgrid. Energy Reports 2022, 8, 1285–1293. [Google Scholar] [CrossRef]
- Bernal-Agustín, J.L.; Dufo-López, R.; Rivas-Ascaso, D.M. Design of isolated hybrid systems minimizing costs and pollutant emissions. Renewable Energy 2006, 31, 2227–2244. [Google Scholar] [CrossRef]
- Sadeghi, D.; Naghshbandy, A.H.; Bahramara, S. Optimal sizing of hybrid renewable energy systems in presence of electric vehicles using multi-objective particle swarm optimization. Energy 2020, 209, 118471. [Google Scholar] [CrossRef]
- Mamaghani A, H.; Escandon S A, A.; Najafi, B.; Shirazi, A.; Rinaldi, F. Techno-economic feasibility of photovoltaic, wind, diesel and hybrid electrification systems for off-grid rural electrification in Colombia. Renewable Energy 2016, 97, 293–305. [Google Scholar] [CrossRef]
- Fazelpour, F.; Soltani, N.; Rosen, M.A. Economic analysis of standalone hybrid energy systems for application in Tehran, Iran. International journal of hydrogen energy 2016, 41, 7732–7743. [Google Scholar] [CrossRef]
- Fazelpour, F.; Farahi, S.; Soltani, N. Techno-economic analysis of hybrid power systems for a residential building in Zabol, Iran. IEEE 2016, 1–6. [Google Scholar]
- Elkadeem, M.R.; Wang, S.; Sharshir, S.W.; Atia, E.G. Feasibility analysis and techno-economic design of grid-isolated hybrid renewable energy system for electrification of agriculture and irrigation area: A case study in Dongola, Sudan. Energy Conversion and Management 2019, 196, 1453–1478. [Google Scholar] [CrossRef]
- Turkdogan, S. Design and optimization of a solely renewable based hybrid energy system for residential electrical load and fuel cell electric vehicle. Engineering Science and Technology, an International Journal 2021, 24, 397–404. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G. Lead acid battery storage model for hybrid energy systems. Solar energy 1993, 50, 399–405. [Google Scholar] [CrossRef]
- Milone, D.; Curto, D.; Franzitta, V.; Guercio, A.; Cirrincione, M.; <monospace> </monospace>Mohammadi, A. An economic approach to size of a renewable energy mix in small Islands. Energies, 2022, 15, 2005. [Google Scholar] [CrossRef]
- Podder, A.K.; Das, A.K.; Hossain, E.; Kumar, N.M.; Roy, N.K.; Alhelou, H.H.; Al-Hinai,A. Integrated modeling and feasibility analysis of a rooftop photovoltaic systems for an academic building in Bangladesh. International Journal of Low-Carbon Technologies 2021, 16, 1317–1327. [Google Scholar] [CrossRef]
- Riayatsyah, T.M.I.; Geumpana, T.A.; Fattah, I.M.R.; Rizal, S.; Mahlia, T.I. Techno-Economic Analysis and Optimisation of Campus Grid-Connected Hybrid Renewable Energy System Using HOMER Grid. Sustainability 2022, 14, 7735. [Google Scholar] [CrossRef]
- Cartland, R.; Sendegeya, A.M.; Hakizimana, J.D.K. Performance Analysis of a Hybrid of Solar Photovoltaic, Genset, and Hydro of a Rural-Based Power Mini-Grid: Case Study of Kisiizi Hydro Power Mini-Grid, Uganda. Processes 2023, 11, 175. [Google Scholar] [CrossRef]
- Arabzadeh, S.M.; Fazelpour, F.; Soltani, N.; Rosen, M.A. Performance analysis of a photovoltaic/wind/diesel hybrid power generation system for domestic utilization in winnipeg, manitoba, Canada. Environmental Progress & Sustainable Energy 2019, 38, 548–562. [Google Scholar]
- Lu, J.; Wang, W.; Zhang, Y.; Cheng, S. Multi-objective optimal design of stand-alone hybrid energy system using entropy weight method based on HOMER. Energies 2017, 10, 1664. [Google Scholar] [CrossRef]
- Li, J.; He, Z.; Wang, Y.; Lv, J.; Zhao, L. A two-dimensional cloud model for condition assessment of HVDC converter transformers. Energies 2012, 5, 157–167. [Google Scholar] [CrossRef]
- Ji, Y.; Huang, G.H.; Sun, W. Risk assessment of hydropower stations through an integrated fuzzy entropy-weight multiple criteria decision making method: A case study of the Xiangxi River. Expert Systems with Applications 2015, 42, 5380–5389. [Google Scholar] [CrossRef]
Figure 1.
Topology of a grid-connected PV-storage microgrid.
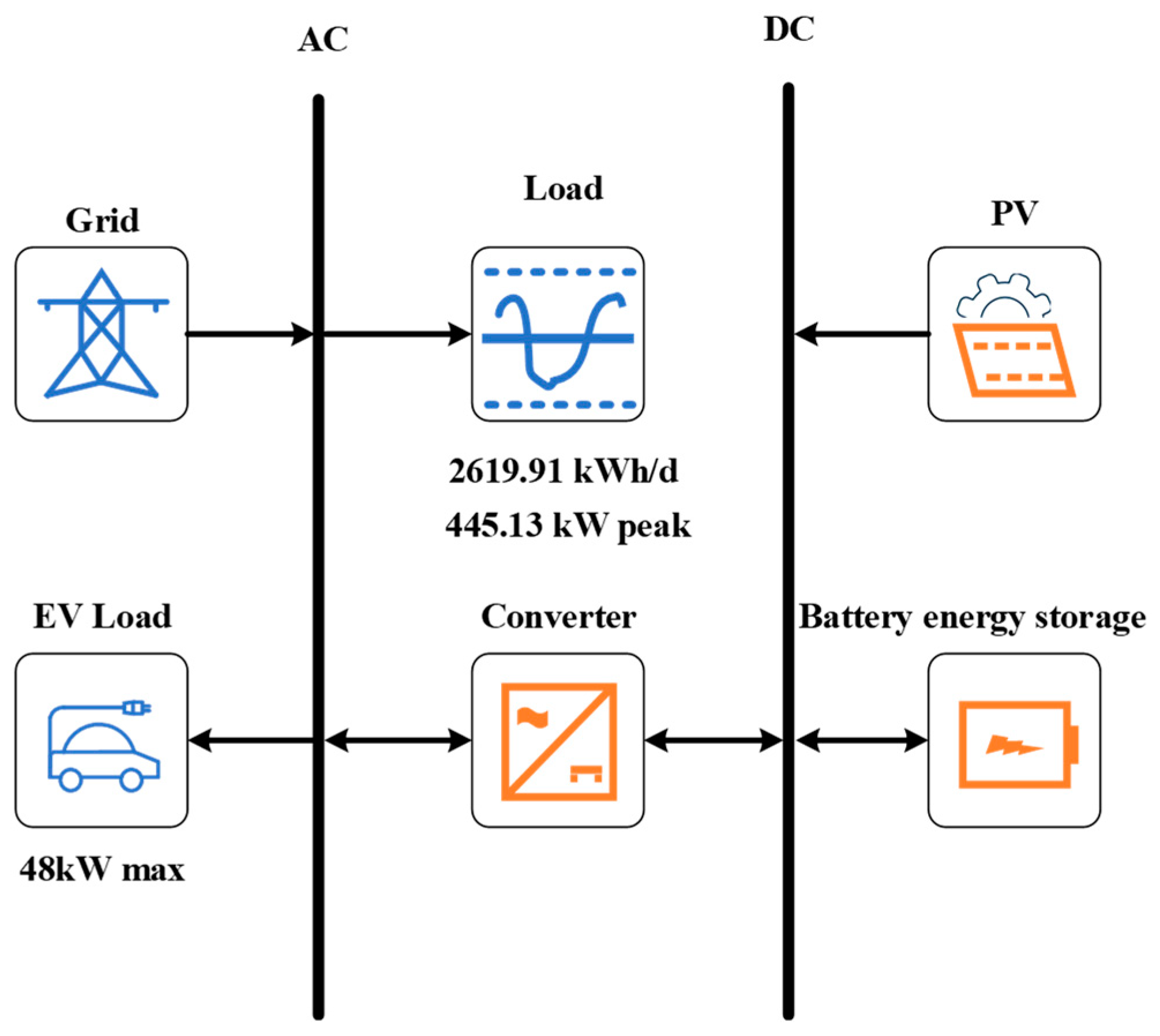
Figure 2.
Annual solar radiation.
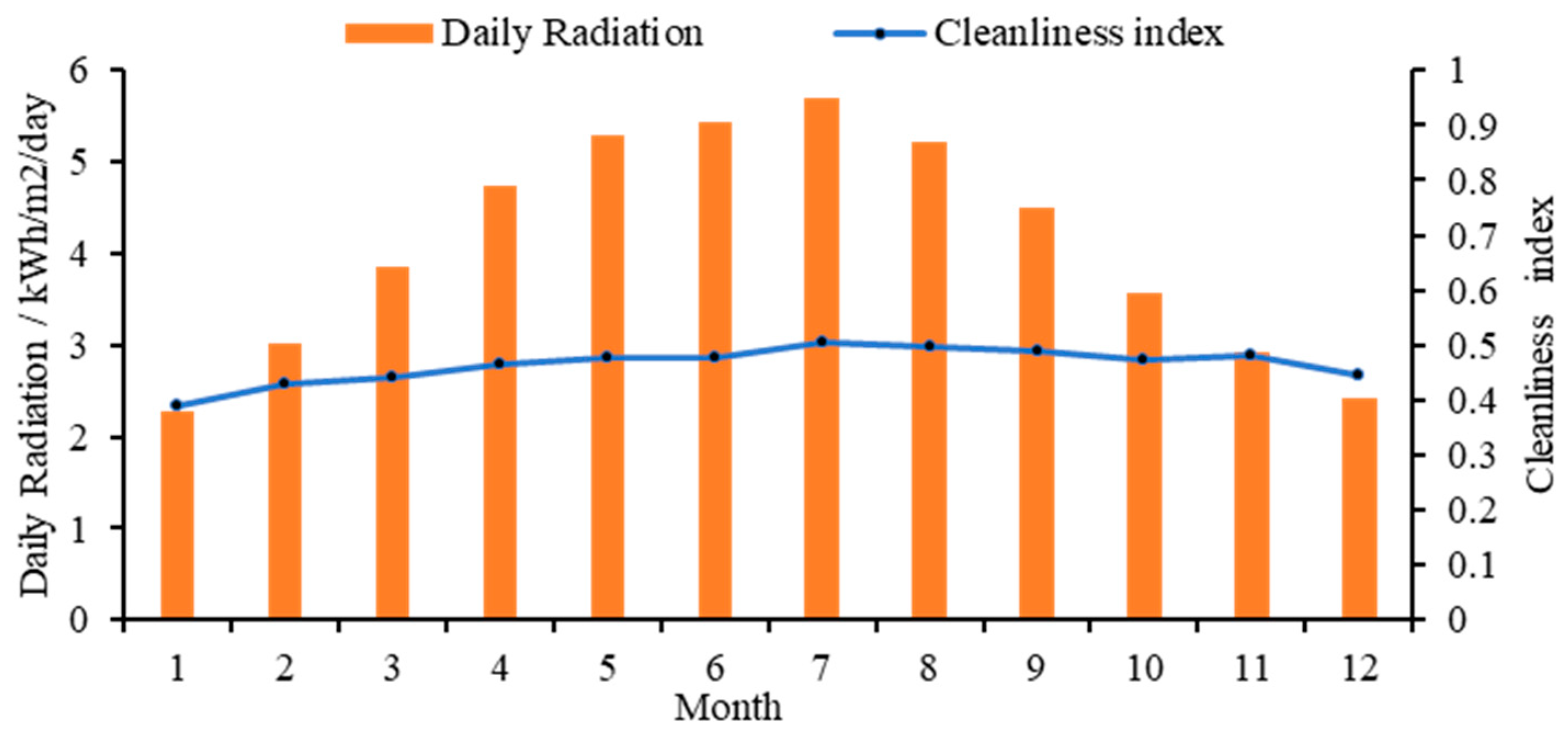
Figure 3.
Annual temperature parameters.
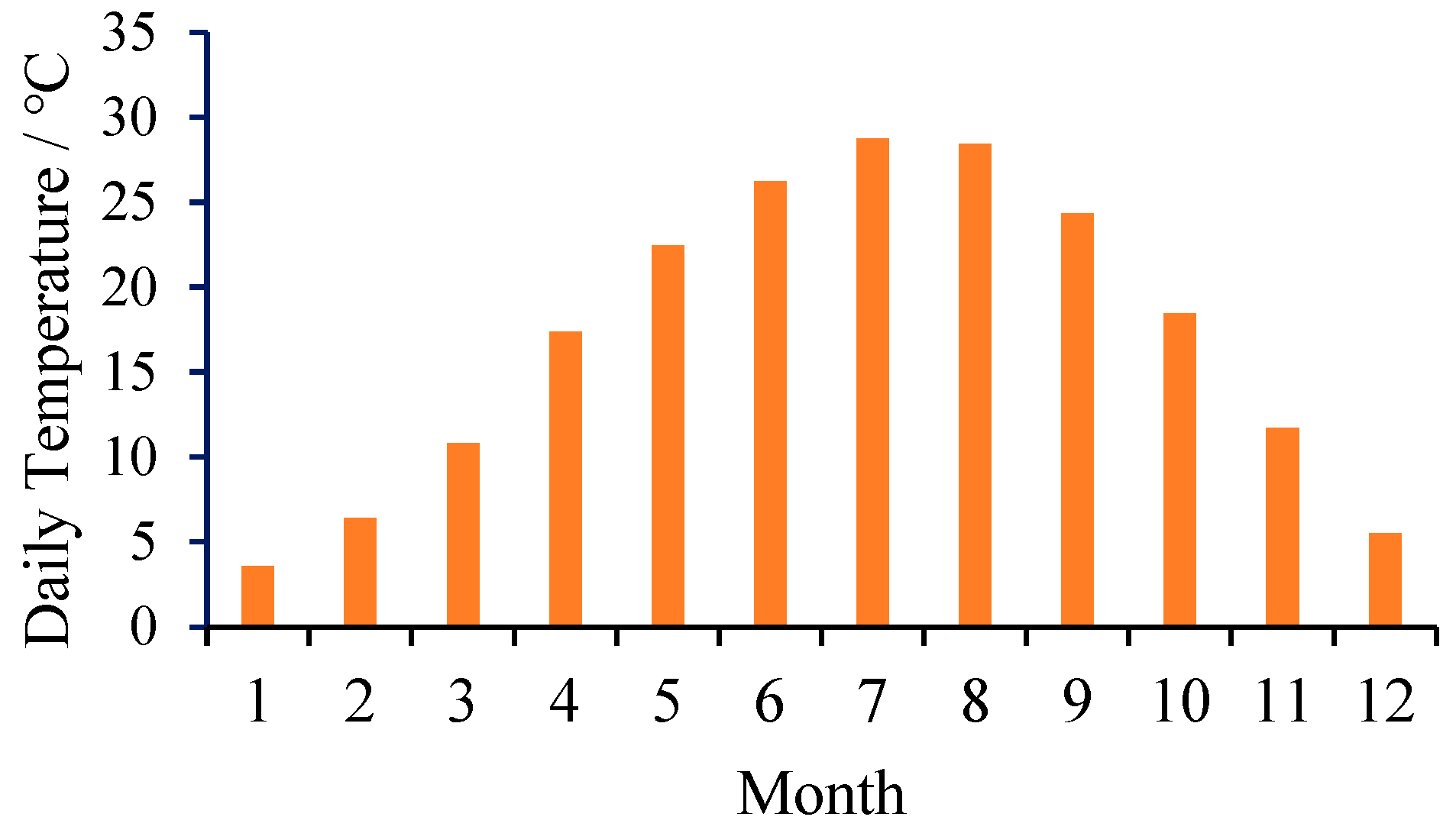
Figure 4.
Annual conventional load curve.
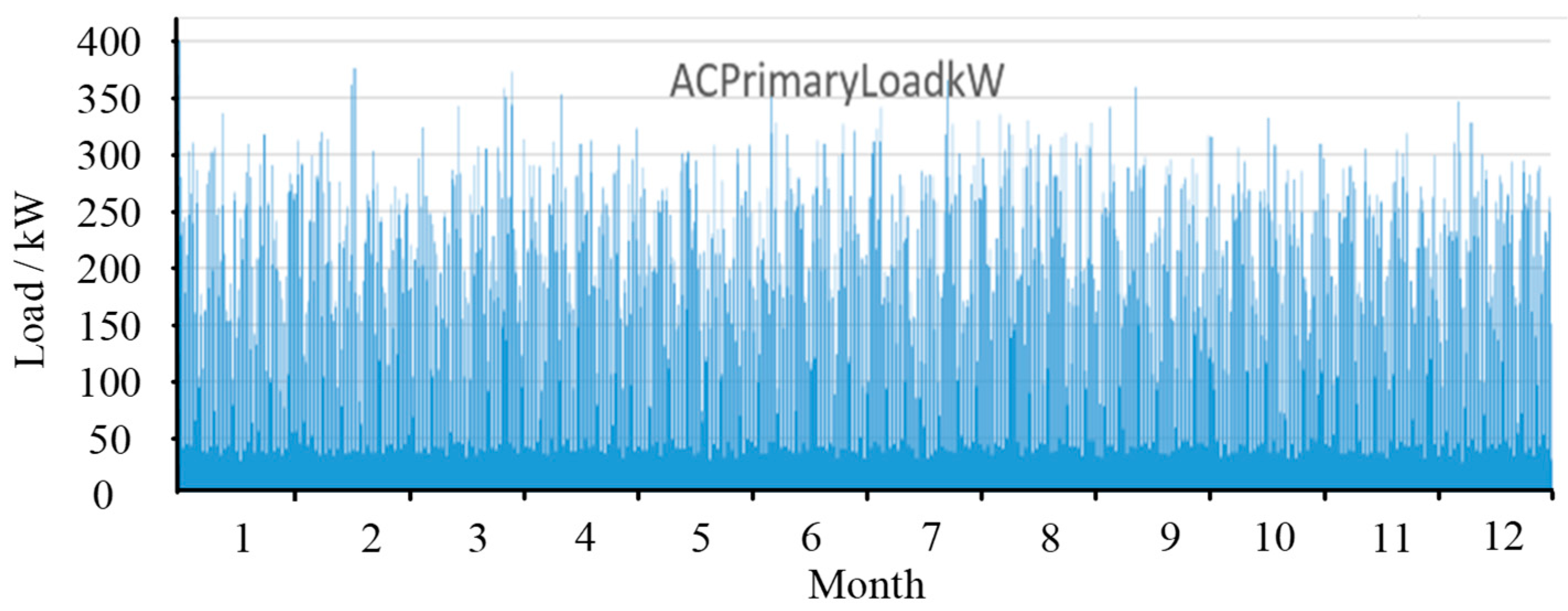
Figure 5.
Typical daily conventional load curve.
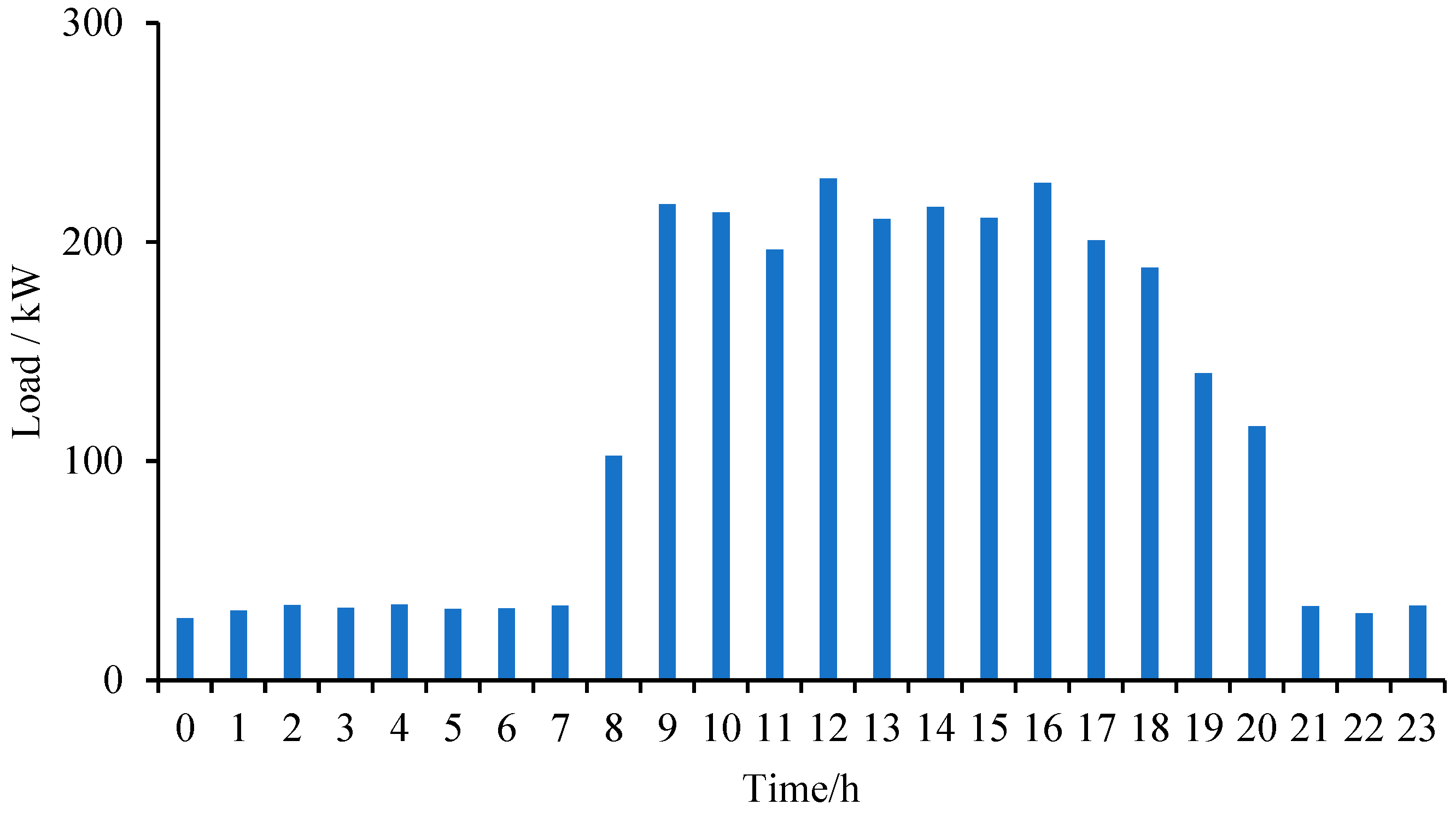
Figure 6.
Annual EV charging load curve.
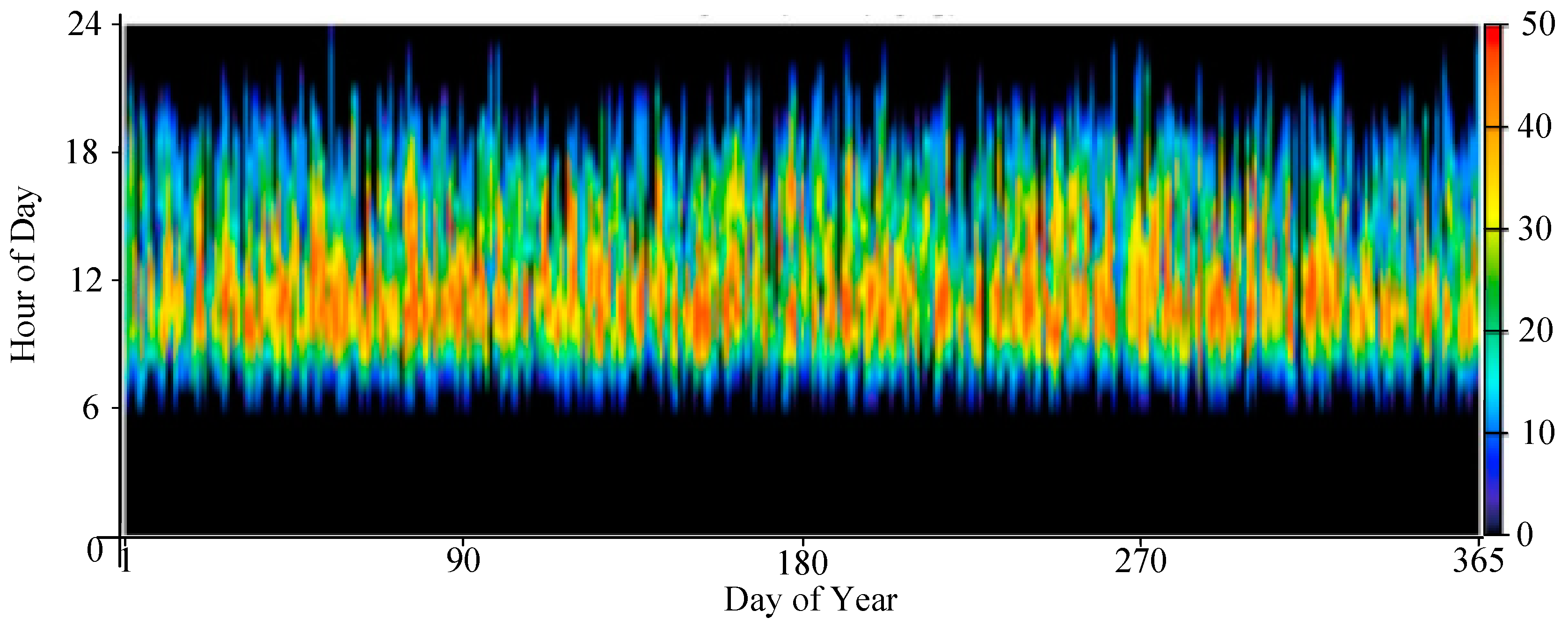
Figure 7.
Typical daily EV charging load curve.
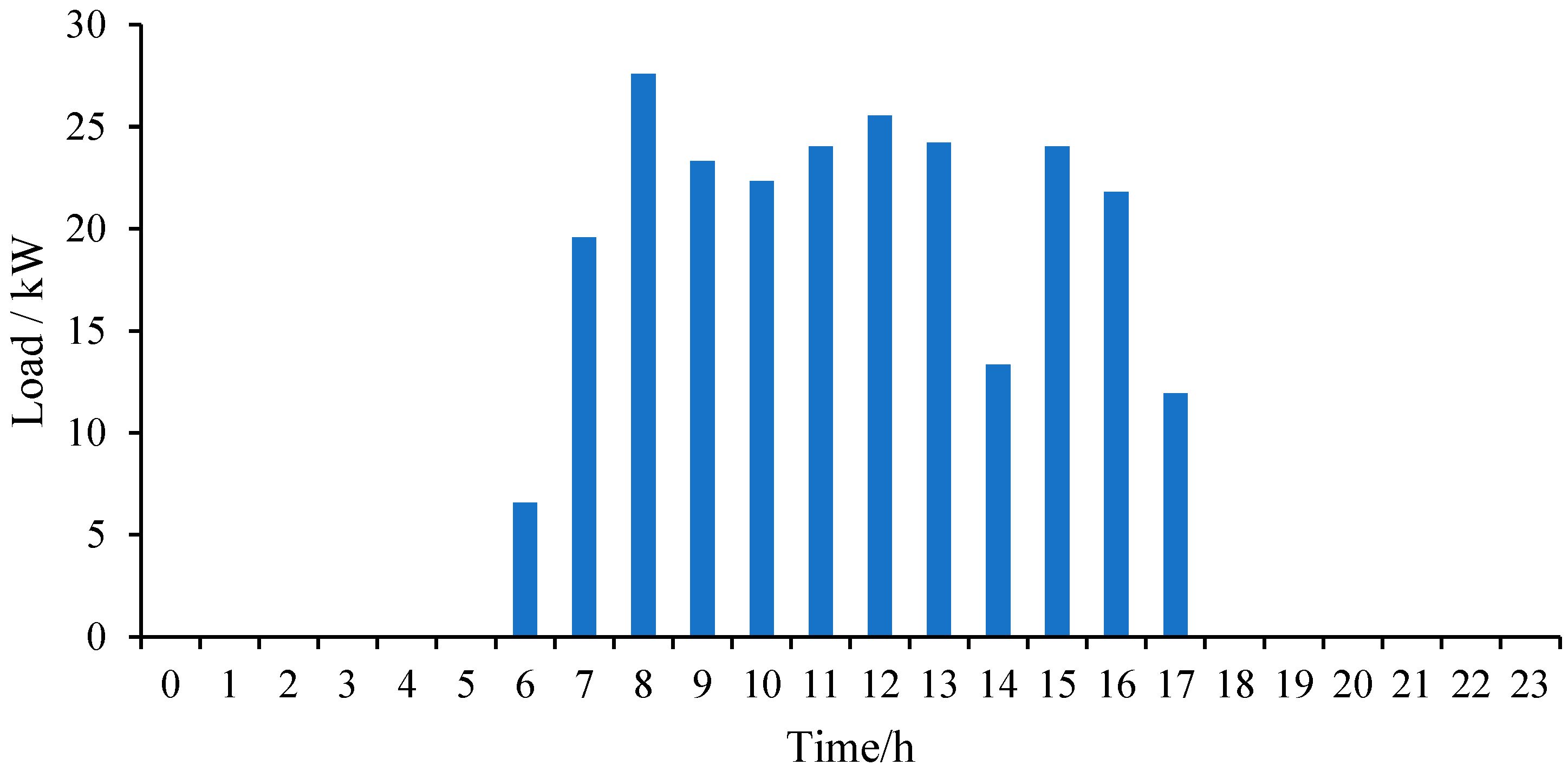
Figure 8.
Sensitivity to EV charging demand and CO2 emission limits at different unit investment costs.
Figure 8.
Sensitivity to EV charging demand and CO2 emission limits at different unit investment costs.
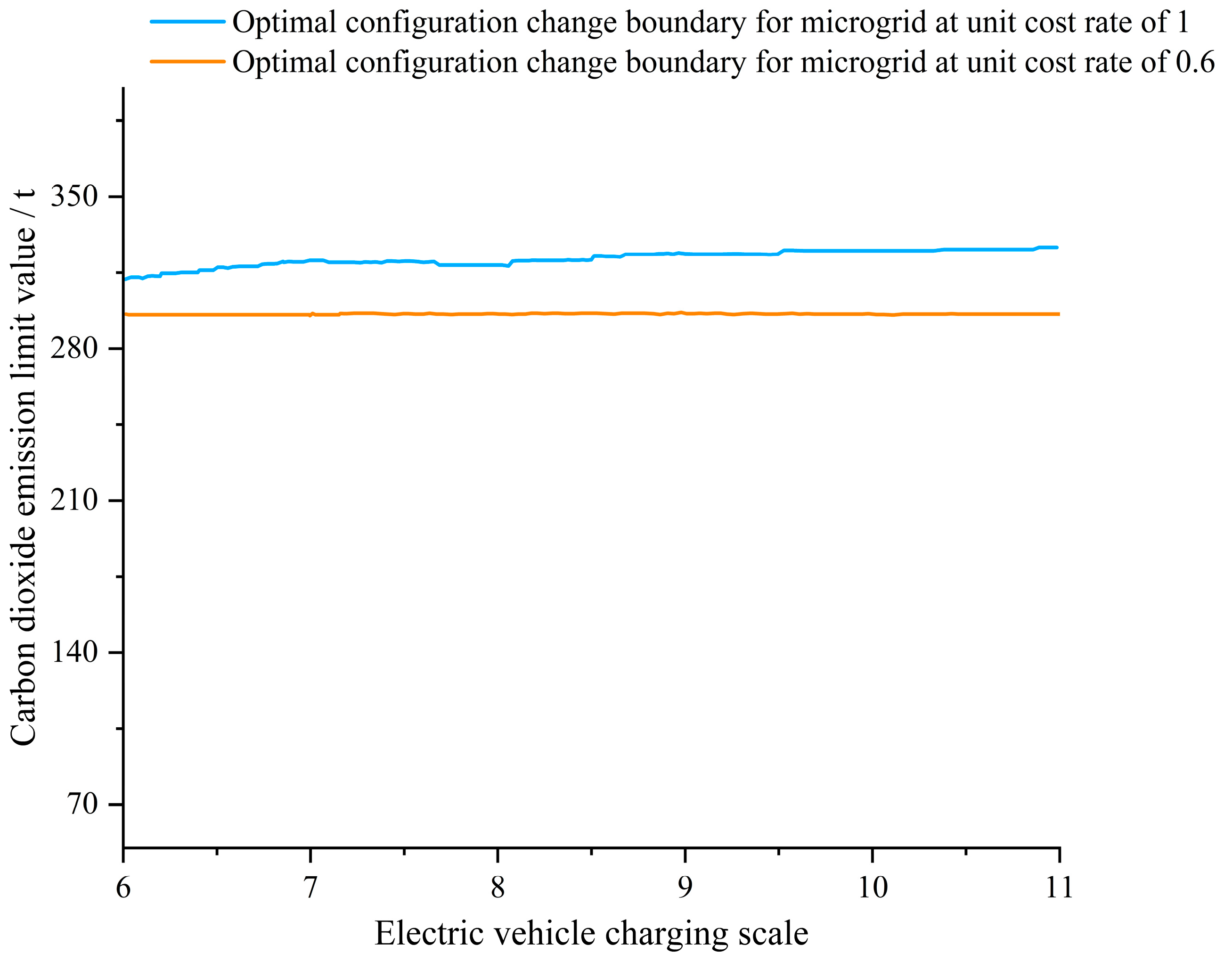
Figure 9.
Sensitivity of microgrid to EV charging demand and CO2 emission limits when the individual component cost multiplier is reduced to 0.6.
Figure 9.
Sensitivity of microgrid to EV charging demand and CO2 emission limits when the individual component cost multiplier is reduced to 0.6.
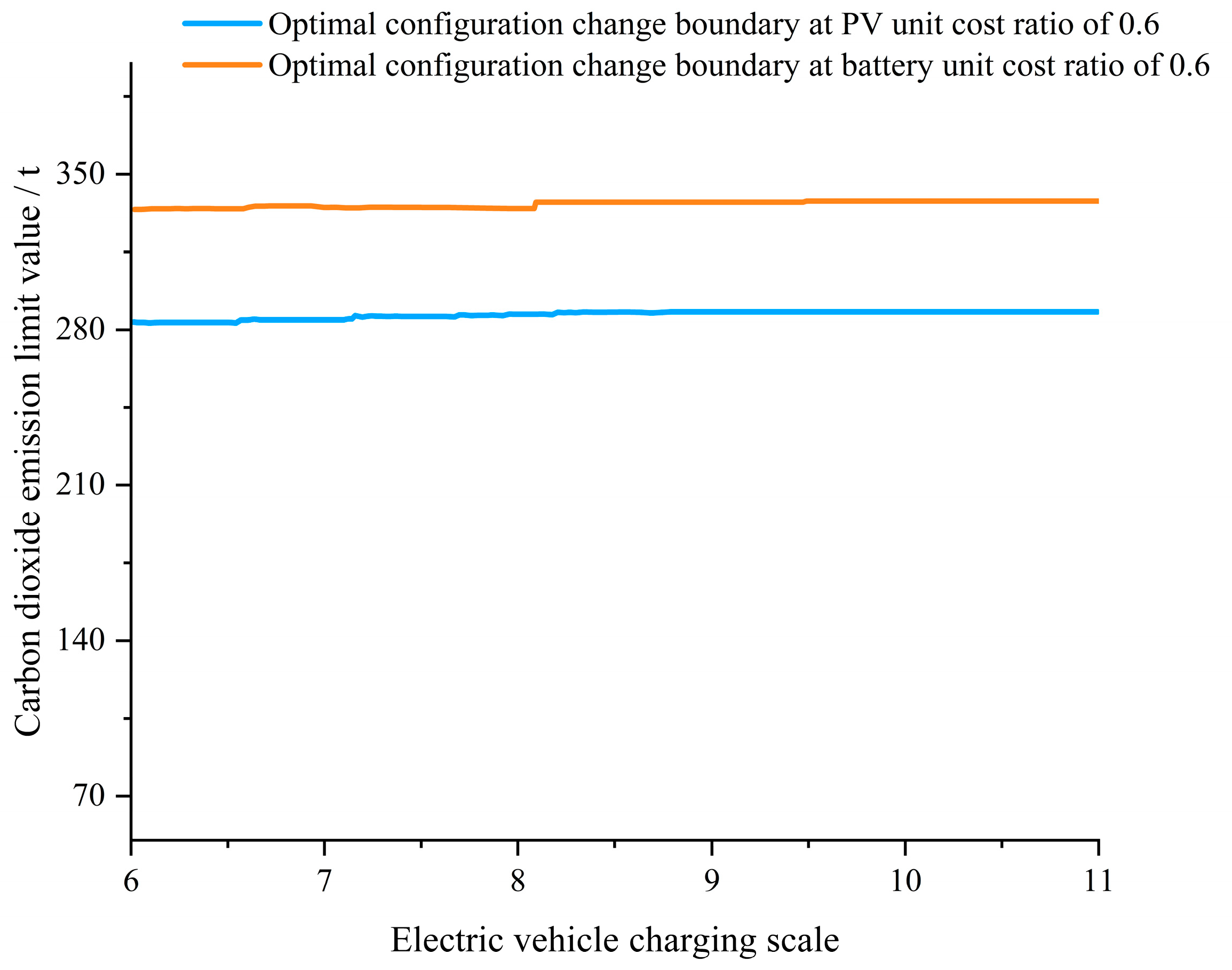
Figure 10.
System NPC surface with unit investment cost multiplier of 1.
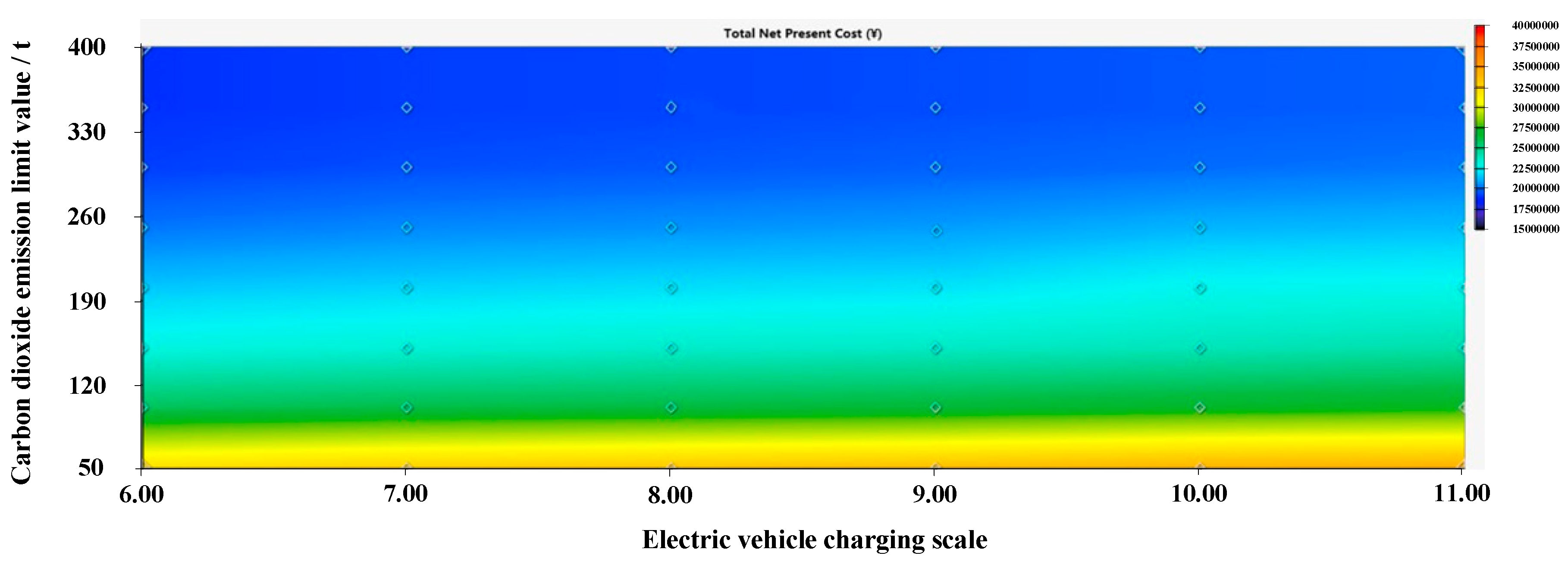
Figure 11.
System NPC surface with unit investment cost multiplier of 0.6.
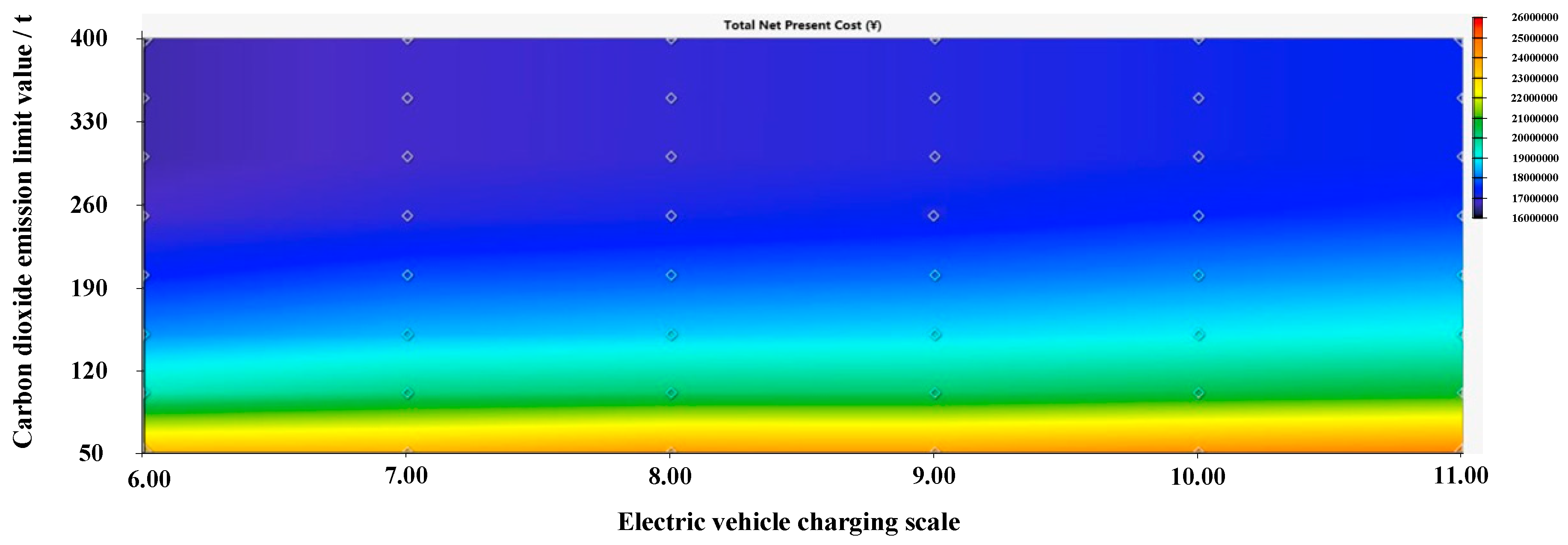
Table 1.
Electric vehicle technical parameters.
| Type of car | Percentage (%) | Maximum charging power (kW) | Average charging time (min) |
|---|---|---|---|
| SUV Electric Vehicles | 30 | 150 | 260 |
| Small electric cars | 70 | 50 | 260 |
Table 2.
Weight of each index in Scenario III.
| Indicator | Information entropy value | Information utility value | Weight |
|---|---|---|---|
| NPC | 0.988 | 0.012 | 4.971% |
| LCOE | 0.994 | 0.006 | 2.714% |
| NRF | 0.931 | 0.069 | 29.134% |
| [M1] | 0.851 | 0.149 | 63.181% |
Table 3.
Planning results for the grid-connected PV-storage microgrid.
| System Component | System component parameter | Configuration result | ||
|---|---|---|---|---|
| Scenario I | Scenario II | Scenario III | ||
| PV | Installed capacity (kW) | 874.88 | 2634 | 2195 |
| Battery bank | Nominal capacity ×string (kWh) | 800 | 4400 | 0 |
| Converter | rated power (kW) | 297.27 | 637 | 637 |
Table 4.
Economic and cleanliness performance of the grid-connected PV-storage microgrid.
| Index | Scenario I | Scenario II | Scenario III |
|---|---|---|---|
| NPC (million Yuan) | 2230 | 5040 | 3110 |
| LCOE (Yuan/kWh) | 1.471 | 1.893 | 1.097 |
| RF (%) | 73.06 | 98.86 | 85.623 |
| (kg/year) | 199675.3 | 14857.95 | 199178.9 |
Table 5.
Investment and operation and investment costs under different scenarios.
| Scenario I | Scenario II | Scenario III | |
|---|---|---|---|
| PV module investment cost (million Yuan) | 839.88 | 2530 | 2110 |
| System operation and maintenance costs (million Yuan) | 1160 | 3750 | 2450 |
Table 6.
Component parameters under different scenarios.
| Indicator | Scenario I | Scenario II | Scenario III |
|---|---|---|---|
| Excess Electricity (kWh/year) | 219546.2 | 1244603 | 873389.2 |
| Excess Electricity (%) | 15.12481 | 36.15364 | 27.60093 |
| Load shedding (%) | 0 | 0 | 0 |
| PV/Production (kWh/year) | 1135621 | 3419029 | 2849191 |
| 100LI/Annual Throughput (kWh/year) | 133973.5 | 307623.8 | \ |
| Energy Purchased (kWh) | 315941.9 | 23509.41 | 315156.4 |
| Energy Sold (kWh) | 110542.8 | 996154.8 | 1129914 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







