1. Introduction
The carcinogenesis of colorectal cancer is a heterogeneous process encompassing a series of genetic, epigenetic and molecular changes in the cells that line the colonic mucosa [
1,
2]. These changes are influenced by dietary, environmental, and microbiotic factors and the host's immune response [
3,
4]. The successive activation of oncogenes (KRAS, NRAS, BRAF, PIK3CA, ERRB2) while inactivating tumour suppressor genes (APC, TP53, PTEN, TGF-β, DCC) guides the adenoma-carcinoma transition [
5,
6]. KRAS is a gene of the RAS/MAPK pathway. RAS proteins are a family of proteins expressed in all cells within the intracellular cascade associated with tyrosine-kinase receptors. This pathway stimulates cell proliferation, differentiation, adhesion, apoptosis and migration [
7]. Up to 60-80% of colorectal cancers overexpress EGFR (Epidermal Grow Factor Receptors), which are tyrosine-kinase receptors, and this is an important component in the initiation and progression of colorectal cancer [
8,
9]. The anti-EGFR antibodies (cetuximab or panitumumab) has a therapeutic effect in patients with colorectal cancer. When there is a mutation in this pathway, such as KRAS mutation, these therapies cannot be employed because it confers resistance to EGFR antibodies. The KRAS mutation is present in 30-50% of colorectal cancers [
9], and this mutation is associated with worse survival, so it is considered as a negative prognostic factor [
10,
11].
Radiomics is the transformation of radiological images into structured data that can be used to support decision making in day-to-day clinical practice. Data that are not visible to the human eye are taken into account through radiomic analysis of a radiological image [
12,
13]. The development of radiomics has been more pronounced in the field of oncology. There are several studies published in recent years using radiomics in different cancers and using different imaging modalities, such as magnetic resonance imaging (MRI), ultrasound and CT [
14].
This article aims to predict the presence of KRAS mutation in colorectal cancer patients using a CT-based radiomics model. To achieve this goal, it is necessary to extract the radiomics features from the CT images and automatically classify the patients as KRAS + or KRAS- using machine learning algorithms belonging to different classifiers families, such as support vector machine, neural network, linear discriminant analysis, decision trees and ensembles, among others. A second objective of this article is to explore the performance of clinical data and whether it can improve the radiomic model when both are combined. To this purpose, data such as tumour location, presence of hepatic or pulmonary metastases, as well as tumour stage and differentiation are included. The results were compared with the anatomopathological analysis of the tumour using Cohen's Kappa statistic, sensitivity and specificity.
Anatomopathological analysis of the tumour is the gold standard for determining KRAS mutation, but it is an invasive test, and it only analyses a portion of the tumour. Radiomics is a non-invasive method that can help determine KRAS status by localizing the area of the tumour most likely to have a KRAS mutation and guiding the biopsy.
2. Materials and Methods
2.1. Radiomics workflow
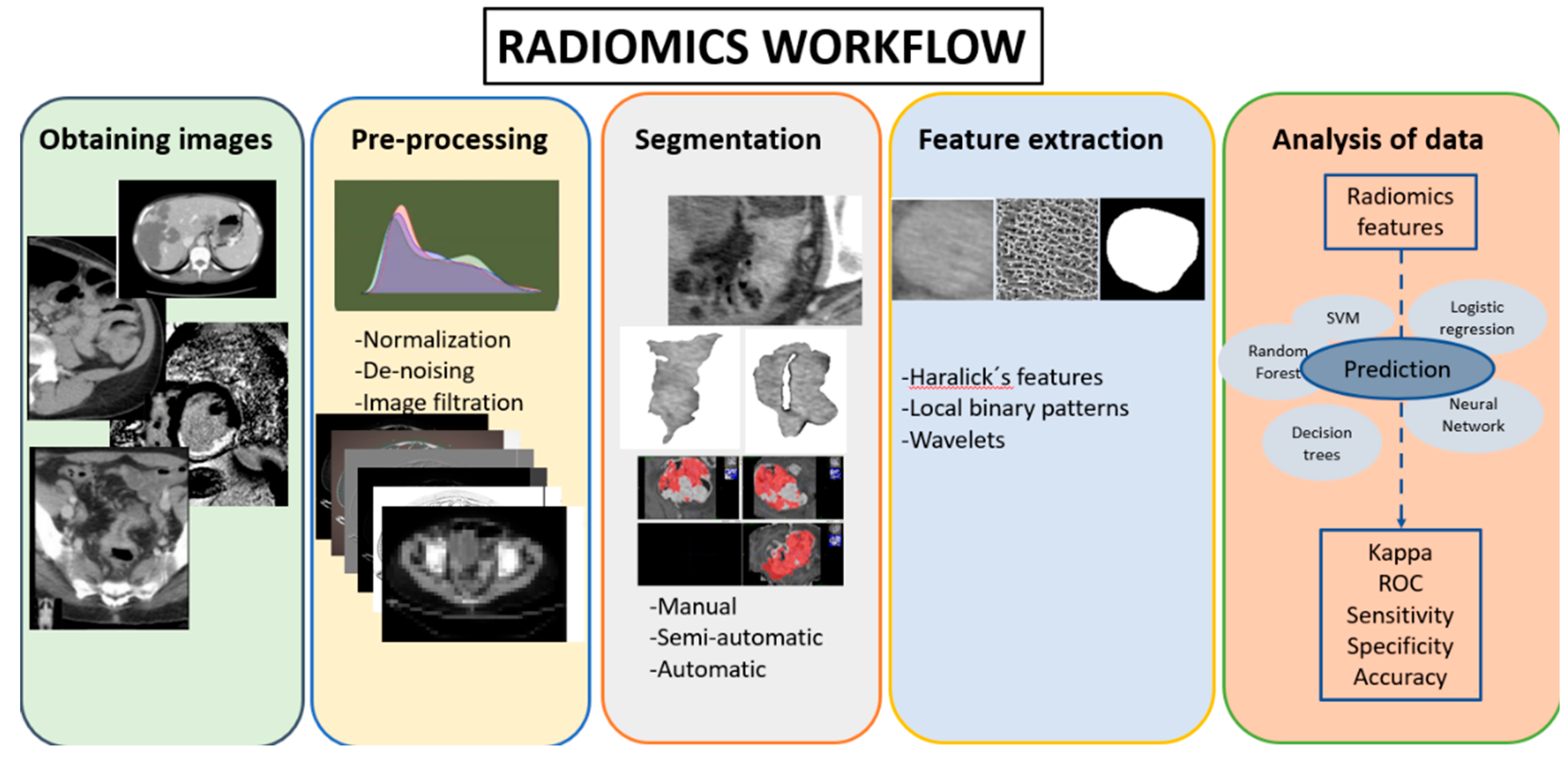
Radiomics workflow consists of five sequential steps: image acquisition, pre-processing, region of interest segmentation, feature extraction and analysis [
Figure 1]][
13,
14].
2.2. Patient selection and obtaining imaging
For this retrospective study, 56 patients from the Santiago de Compostela Health District were selected. The inclusion criteria were defined as follows: (1) colorectal cancer patients with anatomopathological confirmation of KRAS status by biopsy between 2016 and 2019 (30 KRAS+ and 26 KRAS- patients, respectively); (2) intravenous CECT performed before any treatment; (3) CT images with a slice thickness of less than 5 mm. The exclusion criteria were as follows: (1) patients with colorectal cancer in which the anatomopathological analysis was performed after any type of treatment; (2) CT with a slice thickness other than that specified; (3) patients with a tumour difficult to delineate. The conduct of this research has been approved by the Ethics Committee.
2.3. Segmentation
The segmentation performed was a manual segmentation by an expert abdominal radiologist. The software used for the segmentation was Sectra IDS7 visualization program, which is the software used by the radiology department of the Clinic Hospital of Santiago de Compostela.
Three slices of the tumour were selected, the slice with the largest tumour area (central slice), and the slices immediately cranial and caudal to that central slice. For each slice, 4 images were obtained, 2 of them with the tumour manually segmented. A total of 12 images were obtained for each patient. The images were saved in “.tiff” format.
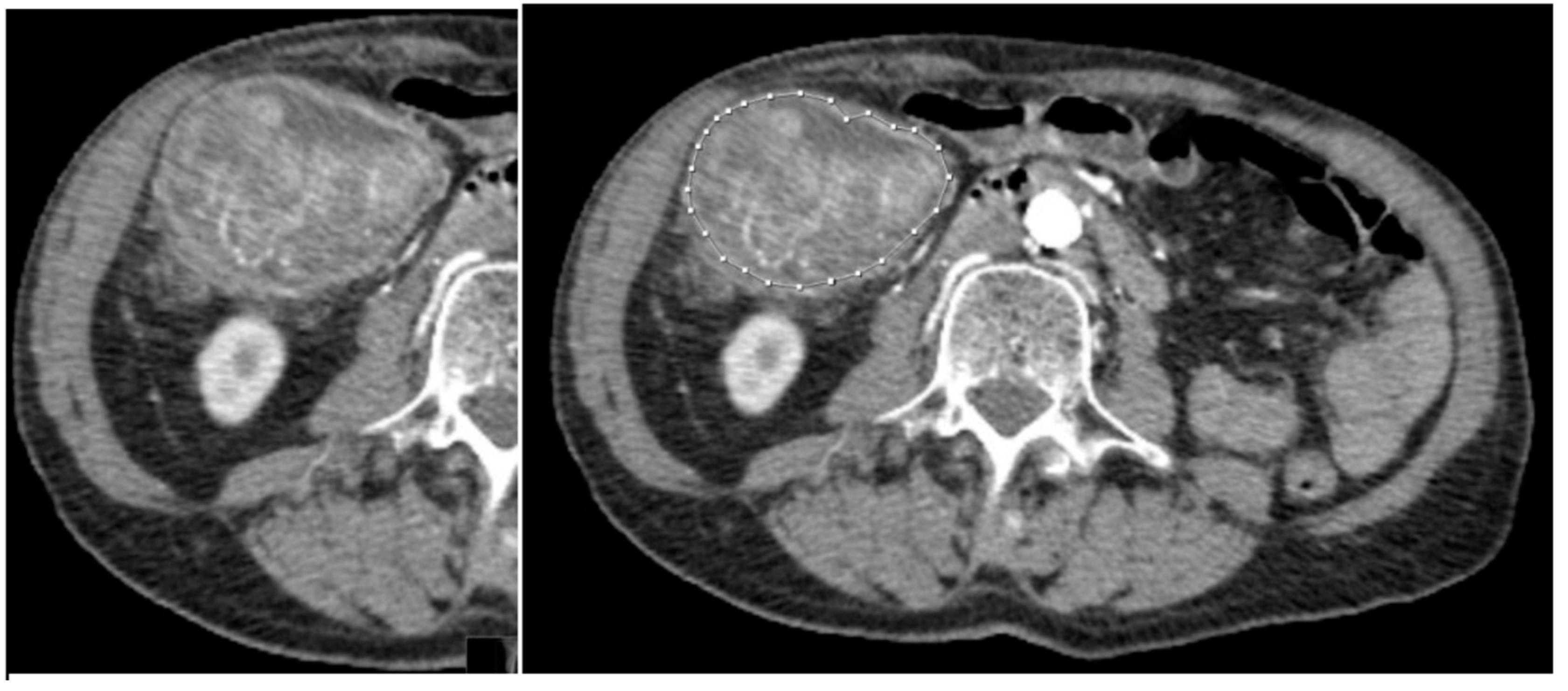
Figure 2.
58-year-old patient with KRAS mutated CRC. a) Tumour without any segmentation. b) Tumour manually segmented by an expert abdominal radiologist.
Figure 2.
58-year-old patient with KRAS mutated CRC. a) Tumour without any segmentation. b) Tumour manually segmented by an expert abdominal radiologist.
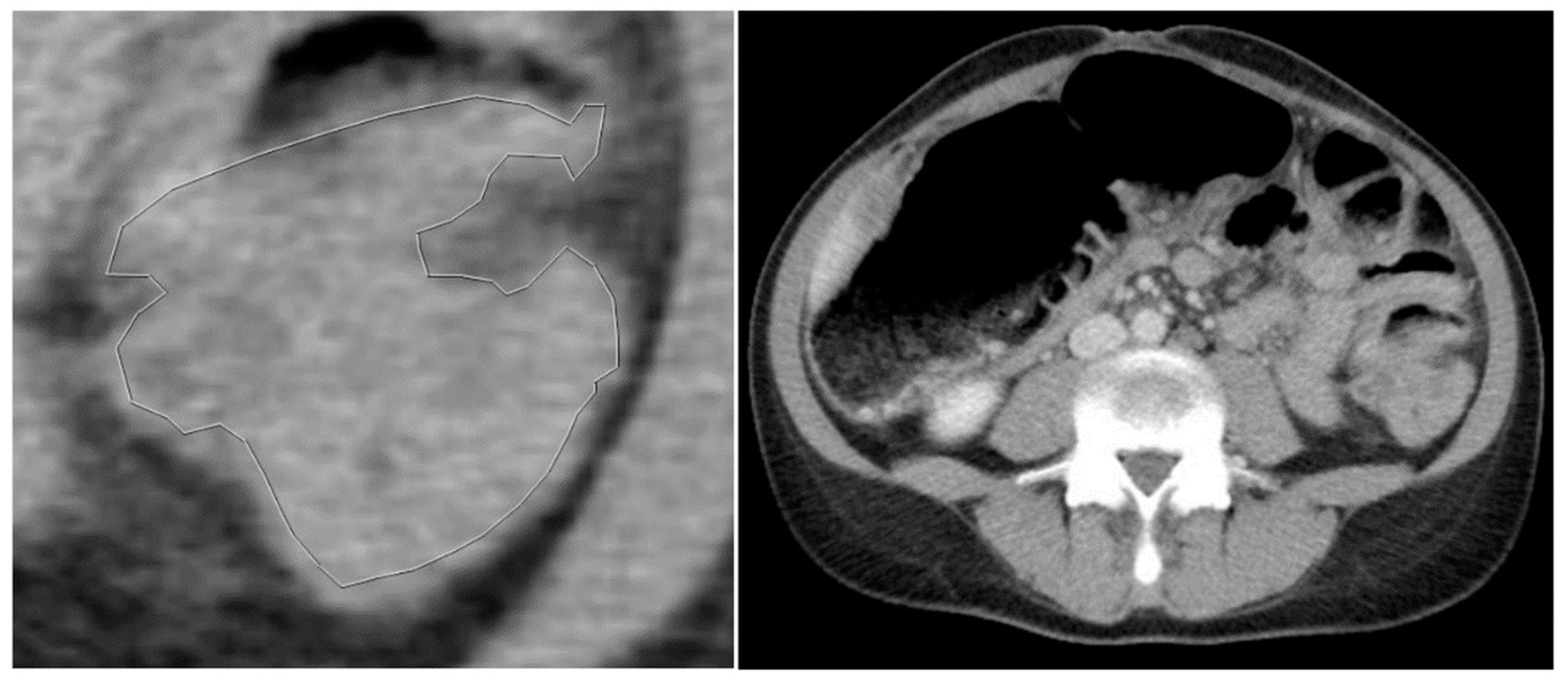
Figure 3.
a) Manually segmented non-mutated KRAS tumour. b) Abdominal contrast-enhancement CT of the same patient.
Figure 3.
a) Manually segmented non-mutated KRAS tumour. b) Abdominal contrast-enhancement CT of the same patient.
2.4. Pre-processing and Feature extraction
The texture is a visual image property related to the spatial distribution of grey level of pixels [
15], which may be used for image classification. The feature extraction algorithms transform an image or region of interest (ROI) in the image into a feature vector, which will be used to do the classification. Some of the techniques provided in the literature can only be applied to rectangular or even squared regions [
16], and they are not suitable for our problem, in which the cancer tumors are irregular regions. In previous works, some popular texture extraction techniques were adapted to operate over irregular ROIs [
19,
21]. For example, the frequency techniques, like Gabor or Fourier filters, are global techniques and cannot be adapted to operate on irregular regions. Among the statistical techniques, we use in this study the Haralick coefficients and the local binary patterns (LBP), which are described in our previous work [
19]. Let
G={0, 1, …,
Ng-1} the number of grey levels,
S a finite set of pixels specifying the region of interest (ROI) to be analysed (in our case, the tumour),
I(
x,
y) ∈
G the grey level in the pixel (
x,
y) ∈
S. To compute Haralick coefficients [
17], the grey level cooccurrence matrix, M, count the occurrence of pixel
(xi , yi) ∈ S and
(xj , xj)∈ S with a grey level
gi and
gj ∈
G in a specific orientation
θ and scale, i.e., different distance,
d={1,2,3}, from one pixel to each other. The matrices M, of dimension
Ngx
Ng, are calculated for different orientations and scales. Normally, the matrices M for different orientations are averaged in order to achieve rotation invariance. The energy, correlation, contrast, homogeneity and entropy are derived from the matrix M for each scale. Eight Haralick vectors Hf
dm are calculated varying the distance
d, to be
d={1, 2, 3} pixels, alongside with another vector concatenating the previous three distances,
d=123, and the number of Haralick coefficients
m={4, 5} depending of entropy coefficient is included or not: {Hf
dm,
d=1, 2, 3, 123,
m=4, 5}.
The local binary patterns (LBP) [
20] algorithm extracts the dependence of pixels in a neighborhood comparing the grey level of central pixel with the surrounding ones. Among the variants proposed in the literature, we use the LBP uniform patterns, i.e., patterns which a limited number of transitions from 0 to 1 or vice versa, lower, or equal than two. Four texture feature vectors, called LBP
R, one for each radius
R={1,2,3} using a neighborhood of
P=8 pixels. The LBP
R contains 10 features for each scale or radius, representing a histogram of the number of transitions in the pixels (
x,
y)∈
S. The feature vector LBP
123 with 30 features for the concatenation of the previous three LBP
R vectors: {LBP
R,
R=1, 2, 3, 123}.
The Discrete Wavelet Transform (DWT) is another very popular spectral technique for texture extraction, which is normally applied on a squared region whose side is a power of 2. A multi-scale decomposition is obtained applying recursively low-pass and high-pass filters and downsampling to the image. Statistical measures over the transform coefficients for each sub-band and decomposition level are normally used to encode texture information. The measured used are mean, energy, entropy, and standard deviation, calculated in the pixels (x,y)∈ S. We compute the vector DWT using three levels of decomposition and calculating the energy, entropy, mean, and standard deviation measures over all subbands developing a vector with 52 features.
We derive texture descriptors from the wavelet decomposition in different ways (see our reference [
21] for a detailed description):
Applying Haralick coefficients over the different wavelet decomposition levels using a distance d=1, due to the scale is implicitly included in the downsampling. We compute four vectors, called WDCFfm, varying the number of Haralick coefficients m={4,5} and the type of decomposition f={LL, All} using a distance d = 1: {WDCFfm, f=LL, All, m=4,5}.
Another way to capture multiscale information would be calculating the cooccurrences matrices on the first level of decomposition. We compute the following six vectors (WCFdm) varying the distance d={1,2,3} to calculate the cooccurrences matrices and the number of Haralick’s coefficients m={4,5}: {WCFdm, d=1, 2, 3, m=4, 5}.
The multiscalar information can also be captured calculating the LBP signature using a radius of one pixel over low-pass wavelet decompositions of the original image. Specifically, the four vectors LBPs considering one level of wavelet decomposition s={1, 2, 3} is computed, developing feature vectors of 10 features. The concatenation of the three previous vectors is called LBP123 with 30 features: {LBPs, s=1, 2, 3, 123}.
2.5. Machine learning models
Machine Learning is widely used in medicine to predict different indicators. Our attempt is the prediction of KRAS status, in which there are two possible labels, patient with KRAS+ or KRAS-, being the former considered as a “positive event” to be detected. So, this prediction is an case of binary classification. Among the classifiers proposed in the literature, we have selected a reduced number among the best-performing classifiers in our exhaustive comparison [
21] from all the classifier families. The classifiers are trained to learn from the input data (texture features and patient clinical information, see below) how to predict the output (KRAS+ or KRAS-). In this training process the classifier uses a collection of examples composed by input data and desired output (gold standard). The trained classifier can predict, with more or less reliability, the genetic disease of unseen patients. In the current experimental work, we use a collection of 34 classifiers implemented in the programming languages Matlab, Octave, Python and R, belonging to the families: support vector machine, neural network, decision tree, bagging, ensemble and linear discriminant analysis, among others. The
Table 1 list the information about the classifiers used in this work.
The classifier performance is assessed by the Cohen’s kappa value (K), which measures the agreement between the true and predicted categories labels excluding the agreement by chance [
22]. Other performance measures are the accuracy, sensitivity or recall, specificity, positive predictivity or precision, F1 and area under the receiver operating curve (AUC), see our reference [
16] for a description of these measures.
3. Experimental setup and Results
3.1. Experimental setup
The information related to each patient is of two types:
Vector clinical, containing information related to patient life and its histopathology status before any treatment, composed by the following nine values: liver metastasis, pulmonary metastasis, sex (dicotomical variable), age, location of the tumour, T staging (0, 1, 2, 3 or 4), N staging (0, 1 or 2), M staging (0 or 1) and tumour differentiation (stages 1 to 4).
Texture feature vectors, with features extracted from each slice of the CT, in our case three slices of the tumour for each patient (56 patients multiplied by 3 cuts per patient).
The classifier performance is assessed using the leave-one-patient-out cross-validation approach. This methodology uses one patient (i.e., three cuts) to test the model and the remaining ones to train the model and to adjust its tunable hyper-parameters (see in
Table 1 the values of the tunable parameters of each model). All the inputs are pre-processed to have zero mean and standard deviation one. This process is repeated as many times as patients, each time using a different test patient. Finally, the performance is calculated comparing the label predicted by the classifier and the gold standard for determining KRAS mutation for each patient. In the case of texture feature vectors, we have an input vector for each cut of the patient’s tumor, and then a classifier output (or prediction) for each cut. The classifier prediction is selected by most voted among the three predictions, one for each cut.
3.2. Results
We developed experiments applying the 34 classifiers using as input: 1) the clinical vector; 2) the 27 texture feature vectors; and 3) the combinations of clinical vector and the 27 texture feature vectors. The texture feature vectors used are: eight Haralick vectors Hfdm, {Hfdm, d=1, 2, 3, 123, m=4, 5}, four LBPR, {LBPR, R=1, 2, 3, 123}, four LBPs, {LBPs, s=1, 2, 3, 123}, vector DWT, six WCFdm, {WCFdm, d=1, 2, 3, m=4, 5}, and four WDCFfm vectors {WDCFfm, f=LL, All, m=4,5}. Overall, we performed 34(1+27+27) = 1,870 experiments.
Table 2 shows the list of top-10 best combination of a feature vector and classifier to predict the KRAS mutation. The highest kappa value (53.7%) and accuracy (76.8%) was achieved by the the
adaboost (adaptive boosting ensemble) classifier implemented in Python using the
clinical vector. The best performance using only feature texture vectors (image information) was provided using the combination of wavelet and Haralick’s coefficients (feature vector WDCF
fm with
f=All bands and
m=4), achieving a kappa=46.0% and accuracy=73.2%. The combination of clinical and imaging information did not exceed the results achieved by the clinical information alone.
Table 3 shows the confusion matrix for the best performance for clinical and imaging information. Although the difference between both confusion matrices is small, they lead to a large difference in kappa, 53.7% and 46% using clinical (up) and WDCF
fm (down). However, the difference in accuracy (76.8% and 73.2%) is much smaller. In the best result, achieved by adaboost using the clinical vector (up), the terms outside the diagonal (5 and 8 false negatives and positives, respectively) are much smaller than terms in the diagonal (22 and 21 true positive and negatives, respectively).
Other performance metrics for the best classification are reported in
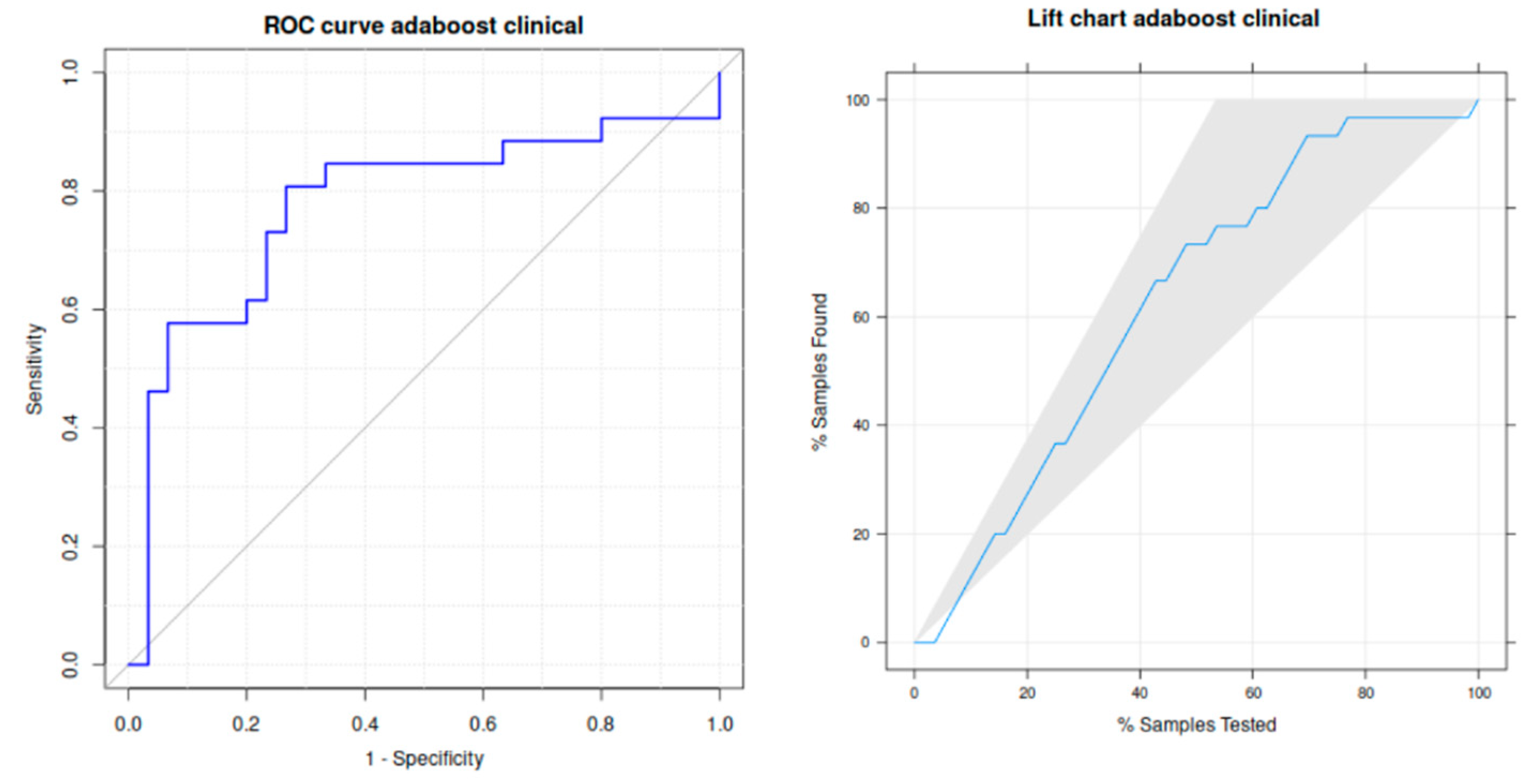
Table 4. Specifically, adaboost achieves a high sensitivity (73.3%), specificity (80.8%) and area under the receiver operating curve (ROC), that is (in %) 77.8%. The left panel of
Figure 4 plots this curve, that is quite near to the upper left corner that identifies ideal classification. The right panel plots the lift curve, where the black line inside the gray shadowed area is also fairly near to the left border of this area identifying the ideal classification.
In order to analyse the behaviour of different texture features families,
Table 5 shows the best performance achieved by a vector of each descriptor family. The highest kappa (46%) and accuracy (73.2%) is achieved by the combination of Haralick coefficients and wavelets using all bands (WDCF
fm vector with
f=All and
m=4 or m=5) using the rpart classifier (recursive partitioning decision tree), implemented in the R language. Indeed, four of 6 best results were achieved by classification trees (ctree and rpart). The other way to compute Haralick coeficients over wavelet decomposition (vectors WCF
dm) achieved much lower performance (kappa=28.2%). The local binary patterns (LBP
R and LBP
S vectors) provided similar results (kappa=35.0% and 36.9% respectively), but also much lower than WDCF
fm vector. The worst texture descriptor is the DWT vector (kappa=12% using diagonal linear discriminant analysis).
Table 6 shows the performance achieved using
clinical and texture feature vectors concatenated as input to the classifier. The performance increased in almost all the texture families, but it is still lower than the performance achieved using only the
clinical vector. The highest kappa is achived by the combination of
clinical and Hf
dm vector (using
d=123 and
m=4) and the mlp (multi-layer perceptron) classifier implemented in Python. Nevertheless, all the combinations provided quite similar results (kappa value higher than 42%), except to DWT (kappa=34.7%) and WDCF
fm (38.8%). It's a surprise that WDCF
fm concatenated with
clinical vector decreased its performance compared to WDCF
fm alone (kappa=46% in
Table 5 and 38.8% in
Table 6).
4. Discussion
This study demonstrates that it is possible to predict KRAS mutation in CRC patients using a CT-based radiomics features. There is a relationship between the quantitative features obtained from the images and the KRAS oncogene mutation. The value of Cohen's Kappa coefficient shows that the relationship is not simply justified by chance. Compared to our previous investigations [
19], we have increased the number of patients and tried a larger and more diverse collection of classifiers, including also patient clinical features. In the current work, the results achieved using only clinical information, only radiomics information and combined (clinical and radiomics) were similar, but slightly better using only clinical information. This demonstrates that clinical variables also provide useful information that can be unified with radiomic data to create a more effective combined model. The implementation of clinical data into radiomic studies is a growing field in recent years. Studies that combine clinical and radiomics features are becoming increasingly common. These studies often show improved results with clinical-radiomic association. For instance, Yuntai Cao et al. [
23] developed a model that combines radiomic parameters with other clinical parameters such as age, CEA (carcinoembryonic antigen) level and clinical stage for the prediction of KRAS status. They achieved results similar than ours. His AUC, sensitivity and specificity was higher with the combined model (0.772, 0.792 and 0.646 respectively). Our results, together with those published in the literature, reflect the need for further research into the development of a combined model and the search for the best clinical-radiomic combination.
A recent revision published by our research group shows that studying the KRAS status is an expanding field. There are numerous studies published on this topic between 2018 and 2022 [
14]. In December 2022, Jia et al. [
24] performed the first meta-analysis on this topic which includes 29 articles published between February 2014 and March 2022. Approximately 60% were recent (2020 and 2021). This review reflects the multiple imaging modalities to which KRAS status analysis is applicable (CT, PET, MRI). MRI was the most widely used, but the meta-analysis concluding that the diagnostic performance of CT is higher. Only one prospective design was included. The main criticisms of meta-analysis studies can be summarized in two aspects: low quality and heterogeneity. The sample size and segmentation methods are sources of variability between studies. The conclusion is that radiomics is at an early stage in terms of determining KRAS status, therefore prospective multicenter studies with standardized protocols are needed to achieve effective implementation in routine clinical practice.
Comparing with other similar studies, several aspects of our research should be highlighted. All the studies compared are retrospective. The sample size of our study is similar to other similar published studies, like Taguchi et al. [
25], who created a model to predict KRAS mutation in CRC. They obtained an AUC between 0.4 and 0.7 with 40 patients. The slice thickness varies between 1 and 5 mm depending on the study. KRAS is the oncogene analyzed in all the studies, but Yang et al. [
26] analyzes as well NRAS and BRAF mutations. They obtained an AUC, sensitivity and specificity of 0.869, 0.757 and 0.833. Yu Li et al. also seeks to detect perineural invasion. They obtained an AUC of 7.793 and 0.862 in the prediction of perineural invasion and KRAS mutation [
27].
Anatomopathological analysis will remain the gold standard for mutational analysis. However, it has limitations that could be solved if complemented by radiomic analysis. Radiomics based on CT images would cover the entire tumour area and possible metastatic sites, thus avoiding the false negatives associated with analyzing a single tumour fragment [
28]. There is also a percentage of patients with primary resistance to anti-EGFR monoclonal antibodies. In addition, almost all of those who initially respond to these therapies will eventually become refractory to treatment [
29]. Therefore, serial radiomic CT scans throughout the course of the disease would offer the possibility of detecting new mutations in KRAS that cause this resistance.
The limitations of our study do not differ from those mentioned by other authors. Firstly, we started from a small sample size obtained retrospectively from the records of a single center. Secondly, despite having an advanced electronic medical record system, it is difficult to filter which patients could meet the inclusion criteria for the study, as there are no databases of patients diagnosed with colorectal cancer in our autonomous community. This could lead to patient selection bias and hinder the applicability of radiomics in the future. As regards technical parameters, over the years the reconstruction of the images has evolved. The first slices compiled for this study were 5 mm and are now less than 2.5 mm. The trend is to use increasingly thinner slices, as this is one of the parameters that provides the greatest variability in radiomic studies. Finally, the segmentation is manual, which is associated with a high time consumption in the delimitation of the regions of interest and high level of subjectivity.
Lastly, we should consider extending mutational analysis to other genes such as BRAF, NRAS, mismatch repair genes and even to other sites such as metastases. This approach would be more integrative and would facilitate the use of radiomics throughout the entire period of the disease, from diagnosis to the evolution of metastases.
5. Conclusions
CT-based radiomics can predict the KRAS status. Specifically, the recursive partitioning classification trees trained on texture features extracted from the CT images (Haralick and Wavelet coefficients) achieve Cohen kappa and accuracy of 46% and 73.2%. These results prove the correlation between texture patterns and KRAS mutational status. The patient clinical parameters (including liver and pulmonary metastasis, location of the tumour, N and M staging, and tumour differentiation) further improved the performance of the radiomics model up to a Cohen kappa and accuracy of 53.7% and 76.8%, sensitivity and specificity of 73.3% and 80.8%, and area under ROC of 77.8% achieved by the adaboost ensemble classifier. This clinical information should be also taken into account for the application of radiomics in daily clinical practice. Radiomics is not intended to replace current diagnostic methods such as biopsy and pathological analysis, but rather to complement them by analyzing the entire area of the primary tumour from the time of diagnosis and throughout the course of the disease.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.
Author Contributions
Conceptualization, J.P.A, R.A.M. and M.S.B.; methodology, E.C., M.F.D. and V.G.C.; software, E.C., M.F.D. and V.G:C.; validation, E.C., M.F.D., V.G.C., S.B.G., R.G.F., M.S.B.; formal analysis, J.P.A., S.B.G. and R.G.F.; investigation, J.P.A., E.C., R.A.M., M.F.D., V.G.C.; resources, E.C., M.F.D., V.G.C.; data curation, E.C., M.F.D.; writing—original draft preparation, J.P.A., R.A.M.; writing—review and editing, E.C. and S.B.G.; visualization, E.H.Z., R.G.F., J.R.A.L. and M.S.B.; supervision, E.G., E.H.Z., S.B.G., J.R.A.L. and M.S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee of Santiago-Lugo (protocol code 2019/356, 22/10/2019).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
This work has received financial support from Xunta de Galicia (ED431G-2019/04) and the European Regional Development Fund (ERDF), which acknowledges the CiTIUS - Centro Singular de Investigación en Tecnoloxías Intelixentes da Universidade de Santiago de Compostela as a Research Center of the Galician University System.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Silva, M.; Brunner, V.; Tschurtschenthaler, M. Microbiota and Colorectal Cancer: From Gut to Bedside. Front. Pharmacol. 2021, 12. [Google Scholar] [CrossRef] [PubMed]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- O'Keefe, S.J.D. Diet, microorganisms and their metabolites, and colon cancer. Nat. Rev. Gastroenterol. Hepatol. 2016, 13, 691–706. [Google Scholar] [CrossRef] [PubMed]
- Nosho, K.; Sukawa, Y.; Adachi, Y.; Ito, M.; Mitsuhashi, K.; Kurihara, H.; Kanno, S.; Yamamoto, I.; Ishigami, K.; Igarashi, H.; et al. Association of Fusobacterium nucleatum with immunity and molecular alterations in colorectal cancer. World J. Gastroenterol. 2016, 22, 557–66. [Google Scholar] [CrossRef]
- Fearon, E.R.; Vogelstein, B. A genetic model for colorectal tumorigenesis. Cell 1990, 61, 759–767. [Google Scholar] [CrossRef]
- Vergara, É., Alvis, N. and Suárez, A. ¿Existen ventajas clínicas al evaluar el estado de los genes KRAS, NRAS, BRAF, PIK3CA, PTEN y HER2 en pacientes con cáncer colorrectal? Revista Colombiana de Cirugía 2017, 32, 45–55. [CrossRef]
- Currais, P.; Rosa, I.; Claro, I. Colorectal cancer carcinogenesis: From bench to bedside. World J. Gastrointest. Oncol. 2022, 14, 654–663. [Google Scholar] [CrossRef]
- Afrăsânie, V.-A.; Marinca, M.V.; Alexa-Stratulat, T.; Gafton, B.; Păduraru, M.; Adavidoaiei, A.M.; Miron, L.; Rusu, C. KRAS, NRAS, BRAF, HER2 and microsatellite instability in metastatic colorectal cancer – practical implications for the clinician. Radiol. Oncol. 2019, 53, 265–274. [Google Scholar] [CrossRef]
- Garcia-Carbonero, N.; Martinez-Useros, J.; Li, W.; Orta, A.; Perez, N.; Carames, C.; Hernandez, T.; Moreno, I.; Serrano, G.; Garcia-Foncillas, J. KRAS and BRAF Mutations as Prognostic and Predictive Biomarkers for Standard Chemotherapy Response in Metastatic Colorectal Cancer: A Single Institutional Study. Cells 2020, 9, 219. [Google Scholar] [CrossRef]
- Zhu, G.; Pei, L.; Xia, H.; Tang, Q.; Bi, F. Role of oncogenic KRAS in the prognosis, diagnosis and treatment of colorectal cancer. Mol. Cancer 2021, 20, 143. [Google Scholar] [CrossRef]
- Schirripa, M.; Nappo, F.; Cremolini, C.; Salvatore, L.; Rossini, D.; Bensi, M.; Businello, G.; Pietrantonio, F.; Randon, G.; Fucà, G.; et al. KRAS G12C Metastatic Colorectal Cancer: Specific Features of a New Emerging Target Population. Clin. Color. Cancer 2020, 19, 219–225. [Google Scholar] [CrossRef] [PubMed]
- Limkin, E.J.; Sun, R.; Dercle, L.; Zacharaki, E.I.; Robert, C.; Reuzé, S.; Schernberg, A.; Paragios, N.; Deutsch, E.; Ferté, C. Promises and challenges for the implementation of computational medical imaging (radiomics) in oncology. Ann. Oncol. 2017, 28, 1191–1206. [Google Scholar] [CrossRef] [PubMed]
- Gillies, R.J.; Kinahan, P.E.; Hricak, H. Radiomics: Images Are More than Pictures, They Are Data. Radiology 2016, 278, 563–577. [Google Scholar] [CrossRef] [PubMed]
- Porto-Álvarez, J.; Barnes, G.T.; Villanueva, A.; García-Figueiras, R.; Baleato-González, S.; Huelga Zapico, E.; Souto-Bayarri, M. Digital Medical X-ray Imaging, CAD in Lung Cancer and Radiomics in Colorectal Cancer: Past, Present and Future. Appl. Sci. 2023, 13, 2218. [Google Scholar] [CrossRef]
- Sonka, M.; Václav, H.; Boyle, R. Image processing, analysis and and machine vision. Thomson 2008. https://dl.acm.org/doi/abs/10.5555/1537182. 5555. [Google Scholar]
- Cernadas, E.; Fernández-Delgado, M.; González-Rufino, E.; Carrión, P. Influence of normalization and color space to color texture classification. Pattern Recognit. 2017, 61, 120–138. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- González-Castro, V.; Cernadas, E.; Huelga, E.; Fernández-Delgado, M.; Porto, J.; Antunez, J.R.; Souto-Bayarri, M. CT Radiomics in Colorectal Cancer: Detection of KRAS Mutation Using Texture Analysis and Machine Learning. Appl. Sci. 2020, 10, 6214. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- González-Rufino, E.; Carrión, P.; Cernadas, E.; Fernández-Delgado, M.; Domínguez-Petit, R. Exhaustive comparison of colour texture features and classification methods to discriminate cells categories in histological images of fish ovary. Pattern Recognit. 2013, 46, 2391–2407. [Google Scholar] [CrossRef]
- McHugh, M.L. Interrater reliability: the kappa statistic. Biochem Med 2012, 22, 276–82. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, J.; Huang, L.; Zhao, Z.; Zhang, G.; Li, H.; et al. Development and Validation of Radiomics Signatures to Predict KRAS Mutation Status Based on Triphasic Enhaced Computed Tomography in Patients with Colorectal Cancer. Research Square 2022. [CrossRef]
- Jia, L.-L.; Zhao, J.-X.; Zhao, L.-P.; Tian, J.-H.; Huang, G. Current status and quality of radiomic studies for predicting KRAS mutations in colorectal cancer patients: A systematic review and meta-analysis. Eur. J. Radiol. 2023, 158, 110640. [Google Scholar] [CrossRef] [PubMed]
- Taguchi, N.; Oda, S.; Yokota, Y.; Yamamura, S.; Imuta, M.; Tsuchigame, T.; Nagayama, Y.; Kidoh, M.; Nakaura, T.; Shiraishi, S.; et al. CT texture analysis for the prediction of KRAS mutation status in colorectal cancer via a machine learning approach. Eur. J. Radiol. 2019, 118, 38–43. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Dong, D.; Fang, M.; Zhu, Y.; Zang, Y.; Liu, Z.; Zhang, H.; Ying, J.; Zhao, X.; Tian, J. Can CT-based radiomics signature predict KRAS/NRAS/BRAF mutations in colorectal cancer? Eur. Radiol. 2018, 28, 2058–2067. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Eresen, A.; Shangguan, J.; Yang, J.; Benson, A.B., 3rd; Yaghmai, V.; Zhang, Z. Preoperative prediction of perineural invasion and KRAS mutation in colon cancer using machine learning. J. Cancer Res. Clin. Oncol. 2020, 146, 3165–3174. [Google Scholar] [CrossRef] [PubMed]
- Jian, C.; Guorong, W.; Zhiwei, W.; Zhengyu, J. CT Texture Analysis: A Potential Biomarker for Evaluating KRAS Mutational Status in Colorectal Cancer. Chin. Med Sci. J. 2020, 35, 306–314. [Google Scholar] [CrossRef]
- Leto, S.M.; Trusolino, L. Primary and acquired resistance to EGFR-targeted therapies in colorectal cancer: impact on future treatment strategies. J. Mol. Med. 2014, 92, 709–722. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).