Application of the Fuzzy Approach to Evaluation and Selection of Relevant Objects, Features and their Ranges

Preprint

Article

Application of the Fuzzy Approach to Evaluation and Selection of Relevant Objects, Features and their Ranges

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Wiesław Paja^*

This version is not peer-reviewed

Submitted:

29 June 2023

Posted:

30 June 2023

You are already at the latest version

Alerts

Abstract

Significant attribute selection in machine learning is one of the key aspects aimed at simplifying the problem and reducing its dimensionality, and consequently speeding up computation. This paper proposes new algorithms for selecting not only relevant features but also for evaluating and selecting a subset of relevant objects in a dataset. Both algorithms are mainly based on the use of a fuzzy approach. The research presented here yielded preliminary results of a new approach to the problem of selecting relevant attributes and objects, and, in fact, to selecting appropriate ranges of their values. Detailed results obtained on the Sonar dataset show the positive effects of this approach. Moreover, the observed results may suggest the effectiveness of the proposed method in terms of identifying a subset of truly relevant attributes from among those identified by traditional feature selection methods.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

One of the main challenges and goals of machine learning and data-mining methods is to identify relationships, connections between the features describing an object, an example, and the category, class to which that example belongs. In other words, the relationships between the dependent variable and the independent variables. In most real-world data sets, only a subset of the describing features actually have a specific relationship with the dependent variable. This is the set of so-called relevant features, i.e. those carrying information that allows us to identify the value of the dependent variable (class). The rest of the features are referred to as non-relevant features, i.e. those that do not affect the determination of the value of the dependent variable, and only cause an increase in the dimensionality of the problem and thus the time complexity of computational methods. Many of the non-relevant characteristics are difficult to identify a priori, they may have little effect on the dependent variable which is difficult to identify. Relevant features may also be redundant and carry the same information, so to speak. In addition, they may be dependent on each other, i.e. a particular feature may show relevance only in the presence of another feature. For the aforementioned reasons, many different feature selection methods, more or less specialized, have been developed [1]:

filter-based methods: These methods evaluate the relevance of features independently of the specific machine learning task [2]. Examples include analysis of variance (ANOVA), Pearson correlation coefficient, informative chi-square coefficient, Gini measure, etc. These methods are fast and model-independent, but may not take into account relationships between features.
wrapper-based methods: These methods use a specific machine learning model as a black box, assessing the quality of features in the context of a given model [3]. Examples include Recursive Feature Elimination, Backward Stepwise Selection, Forward Stepwise Selection, etc. These methods can take into account dependencies between features, but are more computationally expensive.
embedded methods: these methods take into account feature selection in the model learning process [4]. Examples include L1 regularization (Lasso), L2 regularization (Ridge), Decision Trees with Feature Selection, etc. These methods combine the process of model learning and feature selection, which can be more effective, but limits the possibility of model reuse without feature selection.
methods based on Principal Component Analysis (PCA) [5]: PCA is a dimensionality reduction technique that projects data into new non-covariates so as to maximize variance. By selecting the principal components, the dimension of the data can be reduced. PCA is not a direct feature selection method, but it can help extract relevant information from the data.
methods based on information metrics: These methods measure the informational relationship between features and the target variable. An example is the Information Gain factor, which is used in decision trees. These methods help assess which features will contribute the most information to the model.

Various hybrid feature selection methods and techniques that adapt to specific problems and data are also used in practice [6]. The choice of an appropriate feature selection method depends on the specifics of the problem, the available data and the requirements for model efficiency and interpretability.

2. Materials and Methods

One of the key problems is to reduce the input data in such a way as to select only relevant data for further operations. Three types of data reduction can be distinguished, so to speak: selection of relevant attributes/characteristics, selection of relevant ranges of feature values, and selection of relevant objects from the data. Selection of relevant attributes is a typical step in the process of analysis and machine learning. However, the other two types, which are equally important, are the purpose of this research. Assessing the relevance of value ranges has been the subject of previous research [7,8,9]. On the basis of such an assessment, algorithms for the selection of both significant attributes and significant objects in the data can be defined.

In a variety of machine learning applications, input data are arranged in a tabular form that is called a decision table

D T = (U, A, D)

, where

$U = \{U_{1}, U_{2}, U_{3}, . . ., U_{m}\}$ is the non-empty, finite set of m cases,
$A = \{A_{1}, A_{2}, A_{3}, . . ., A_{n}\}$ is the non-empty, finite set of n descriptive (condition) attributes describing cases,
$D = \{D\}$ is the non-empty, finite set of decision attributes classifying cases from U to decision classes.

For each attribute, the set of its values is determined. Thus, the algorithm for fuzzy selection of a subset of relevant features is presented in the form of pseudocode (see Algorithm 1 - Fuzzy Feature Selection). The aforementioned

D T

decision table in which attributes have continuous values is used as input. Several key stages can be distinguished in the algorithm. First, the input data is discretized resulting in a set of discrete

A_{D I S C}

values. Then, using the chosen fuzzification method, we determine the membership function and, based on it, the set of fuzzy linguistic variables LVs

A_{F U Z Z}

. The next important step is the selection of significant linguistic variables from the set of

A_{F U Z Z}

using the selected feature selection method, the result is the set of

A_{F U Z Z_{S E L}}

. The obtained selection results are used to convert the attribute set A into

A_{B I N A R Y}

binary form representing the relevance of individual attribute values in a binary manner considering the

A_{F U Z Z_{S E L}}

set. The binary set is the basis for assessing the relevance and selection of relevant attributes and relevant objects for the Fuzzy Object Selection algorithm (see Algorithm 2). To assess the relevance of a given attribute, it is necessary to determine how many relevant intervals are in the binary set. For this purpose, a threshold is defined (see Equation 1), which is equal to the product of the m number of objects in the set and the EPS (epsilon) parameter, which is the interval span.

t h r e s h o l d = E P S * m,

(1)

Algorithm 1: Fuzzy Feature Selection

EPS has values ranging from 0 to 1. Using specific values of the EPS parameter, we determine the value of the threshold, e.g. for a value of

E P S = 0.01

the threshold will be the smallest so all relevant features

A_{i}

will remain in the selected set FS, while as the value of EPS increases the value of the threshold increases, which causes the number of features

A_{i}

in the selected set to decrease. As EPS increases, the optimal threshold value can be selected, which will select the optimal subset of features with the best classification quality values.

The algorithm for fuzzy selection of a subset of relevant objects works similarly (Algorithm 2). It works horizontally, so to speak, i.e. we use the number of features n to determine the threshold (see Equation 2), and in a loop each of the objects

U_{i}

from the set U is checked. The result of the operation is a subset of relevant objects OS.

t h r e s h o l d = E P S * n,

(2)

Algorithm 2: Fuzzy Object Selection

2.1. The dataset used

The classification quality of the presented ceh and object selection algorithms was obtained on a dataset called Sonar [?]. This dataset came from the UCI repository and was added to the core collection by Terry Sejnowski (Salk Institute and University of California, San Diego). The tested data set contains 111 patterns obtained by reflecting off a metal cylinder at different angles and under different conditions. The transmitted sonar signal is frequency modulated, with increasing frequency. The data includes signals obtained at different angles, 90 degrees for the cylinder and 180 degrees for the rock. Each pattern in this data set is a set of 60 numbers ranging (V1-V60) from 0.0 to 1.0. Each number expresses the energy in a specific frequency band, which is consolidated over a specific time. The consolidation aperture for higher frequencies takes place later, as these frequencies are sent later via the chirp. In addition, for each record, the data includes whether the object is a rock (R) or a mine (M), i.e., a metal cylinder. The provided operations will be illustrated on the basis of the variable V9 from the Sonar set and the results of its processing.

2.2. Discretization algorithm

To determine the ranges of descriptive attribute values underlying the fuzzification process (DiscretizationAlgorithm), a supervised discretization that depends on local distinguishability heuristics [10] was used. This discretization gives us locally semi-optimal cut sets consistent with the input decision table. The cuts divide entire ranges of descriptive attribute values into disjoint sub-ranges that correspond to the linguistic values assigned to these attributes. linguistic values assigned to these attributes (see Table 1). In the fuzzification process, the centers of the subintervals are determined and then the membership functions are defined. and then the membership functions are defined. and then the membership functions are defined. The local strategy is implemented through a decision tree. This strategy is based on finding the best cut and dividing the set of cases into two subsets of cases, repeating this processing for each set of cases separately until it is satisfied. The quality of the cut depends on the number of cases recognized by the cut, in the local strategy calculated locally on the subset of cases.

2.3. Fuzzification algorithm

One of the methods used is fuzzification, so it should be first mentioned the idea of a fuzzy set.

Definition 1

([11]). A fuzzy set R in

X \neq \emptyset

R = {(x, R (x)) | x \in X}

(3)

where

R : X \to [0, 1]

and

R (x)

is the recognized grade of membership of the x to the R.The collection of all fuzzy sets in X will be denoted by

F S (X)

To convert variables with continuous values into linguistic variables LV (FuzzificationAlgorithm), the selected triangular membership function was used. Let

[m i n, m a x]

be the entire range of values for a given attribute a the dataset under study. In the fuzzification process, three steps are performed:

For each descriptive attribute a, for each linguistic value l assigned to a, determine the center of the interval corresponding to l (the means are calculated based on the intervals into which the entire range of attribute values $[m i n, m a x]$ is divided).
For each descriptive attribute a, for each linguistic value l assigned to a, define a membership function based on the means of the intervals determined earlier.
For each descriptive attribute a, calculate the values of the fuzzy descriptive attributes corresponding to a based on the membership functions defined previously.

Many different membership functions can be used to determine the linguistic values of individual variables. In the present experiments, they are limited to a typical triangular function, which becomes a trapezoidal function at the edges of the interval.

Let

{c_{1}, c_{2}, . . ., c_{k}}

be the set of interval centers defined for the i-th descriptive attribute.

The triangular membership functions are defined according to Equations 4–6. In fact, the first and last membership functions are trapezoidal:

For

j = 1

μ_{c_{j}} (x) = \{\begin{matrix} 1, & if x \geq a and x \leq c_{j}, \\ \frac{c_{j + 1} - x}{c_{j + 1} - c_{j}}, & if x > c_{j} and x \leq c_{j + 1}, \\ 0, & otherwise . \end{matrix}

(4)

For

j > 1

and

j < k

μ_{c_{j}} (x) = \{\begin{matrix} \frac{x - c_{j - 1}}{c_{j} - c_{j - 1}}, & if x \geq c_{j - 1} and x \leq c_{j}, \\ \frac{c_{j + 1} - x}{c_{j + 1} - c_{j}}, & if x > c_{j} and x \leq c_{j + 1}, \\ 0, & otherwise . \end{matrix}

(5)

For

j = k

μ_{c_{j}} (x) = \{\begin{matrix} \frac{x - c_{j - 1}}{c_{j} - c_{j - 1}}, & if x \geq c_{j - 1} and x \leq c_{j}, \\ 1, & if x > c_{j} and x \leq b, \\ 0, & otherwise . \end{matrix}

(6)

An example of a triangular membership function for the variable V9 from the Sonar dataset is shown in Figure 1. Based on the corresponding linguistic variables and their values (see Table 1).

2.4. Feature selection algorithm

The obtained membership values for each created interval of attribute values constitute a set, which is subjected to evaluation and selection of significant value intervals (FeatureSelectionAlgorithm). For this purpose, a method based on the random forest paradigm [12] was used. This method is a wrapper method and is a ranking method, i.e. in the process of assessing the significance of features, a ranking of features is created based on a measure of importance. This measure is calculated based on the created set of decision trees. Each tree in such a set is created based on a random sample of data from the original set. In this way, correlation between dependent variables is minimized. In addition, divisions within the tree are also created based on random subsets of attributes. The tree structure created makes it possible to estimate the importance of an attribute based on decreasing measures of accuracy when an attribute is removed from a node. Since attributes for nodes are selected according to a criterion (in this case, the impurity of the Gini coefficient), we can estimate how each attribute reduces the impurity of a given distribution. The attribute with the largest decrease is placed in the node under consideration. Using this relationship, we can assess the impact of each attribute on the quality of the distributions in the set of trees and thus its significance.

Such methodology is used in the Boruta package [13,14], which allows identifying all relevant attributes from a dataset. It works on an extended dataset containing attributes with a random value that have no correlation with the dependent variable. The maximum MSA score among the random attributes (shadow attributes) is then determined, which is taken as a threshold for evaluating the importance of features. Attributes whose importance is significantly higher than the MSA are placed in the essential attribute group (confirmed features), while those whose importance is significantly lower than the MSA are placed in the irrelevant attribute group (rejected features), see Figure 2. This procedure is repeated until all attributes achieve the estimated significance or the algorithm reaches a set limit of random forest runs. Information on the relevance of linguistic variables (LVs) allows to narrow down and indicate relevant subsets of attribute values, see Figure 3.

The information about the relevance or irrelevance of the ranges is the basis for creating a binary version of the decision table (see Figure 4). In this table, individual values of the original data are checked for their presence in the relevant (green, value 1) or irrelevant (red, value 0) range.

3. Results

In accordance with the earlier description of the various algorithms and procedures, a series of computational experiments were planned and carried out using the described Sonar database. Table 2 and Figure 5 contain the aggregate results of the Fuzzy Feature Selection algorithm, while Table 3 and Figure 6 contain the aggregate results of the Fuzzy Object Selection algorithm. In both experiments, the Leave-One-Out Cross Validation approach was applied in the context of splitting into learning and test sets. Decision tree models and Quinlan’s C5.0 algorithm [15] were used to evaluate the quality of classification. Accuracy (ACC), Sensitivity (True Positive Rate, TPR), Specificity (True Negative Rate, TNR), Precision (Positive Predictive Value, PPV), as well as Matthews Correlation Coefficient (MCC) and F1 score (F1) were used as measures of classification quality. The calculation formulas for each parameter are presented below:

A c c u r a c y = \frac{T P + T N}{T P + T N + F P + F N}

(7)

S e n s i t i v i t y = \frac{T P}{T P + F N}

(8)

S p e c i f i c i t y = \frac{T N}{F P + T N}

(9)

P r e c i s i o n = \frac{T P}{T P + F P}

(10)

M C C = \frac{T P * T N - F P * F N}{\sqrt{(T P + F P) (T P + F N) (T N + F P) (T N + F N)}}

(11)

F 1 = \frac{2 * T P}{2 * T P + F P + F N}

(12)

where: TP is a number of results that correctly indicates the presence of a condition or characteristic, TN is a number of results that correctly indicates the absence of a condition or characteristic, FP - is the number results which wrongly indicates that a particular condition or attribute is present and FN is a number of results which wrongly indicates that a particular condition or attribute is absent.

Analysis of the obtained results of the FFS algorithm identifies a full subset of all relevant attributes, which includes 24 features (Table 2). Such a subset allows us to obtain an ACC of 0.75 and other parameters at a better level than for the original set of 60 features (Figure 5), which allows us to obtain an ACC of 0.64. With an increase in the EPS coefficient and consequently the threshold, we observe an improvement in the classification evaluation parameters up to a subset of 16 features, which appears to be the optimal subset. But both from Table 2 and Figure 5 we can see that equally good results can be obtained using a subset of 9, 12 and 19 relevant features.

On the other hand, analysis of the obtained results of the FOS algorithm allows us to identify a full subset of all relevant features, which includes 204 objects (Table 3). Such a subset allows us to obtain an ACC of 0.7 and other parameters at a level similar to that of the original set of 208 objects (Figure 6), which allows us to obtain an ACC of 0.73. With the increase of the EPS coefficient and, consequently, the threshold, we observe an improvement of the classification evaluation parameters up to a subset of 145 learning objects, which appears to be the optimal subset. Moreover, from both Table 3 and Figure 6 it can be seen that equally good results can be obtained using a subset of 109 relevant objects.

The experimental results presented here allow us to identify a subset of relevant descriptive attributes and a subset of relevant objects in the dataset. This raises the idea of combining these results to identify sub-tables with dimensions suggested by the selected subsets. So, based on the results, four suggested dimensions were selected and classification was performed by determining similar parameters (see Table 4). The results thus obtained clearly show that the most optimal combination is 187 objects and 19 describing attributes. For this combination, almost all parameters were better than the original dataset. Classification accuracy increased to a value of 0.83 from a value of 0.73 for the original dataset.

4. Discussion

The research presented here yielded preliminary results of a new approach to the problem of selecting relevant attributes, and in fact to selecting appropriate ranges of their values. In addition, a method for evaluating and selecting a subset of significant objects from the dataset was proposed. These methods are based on evaluating the relevance of ranges of attribute values by applying fuzzy logic. Detailed results obtained on the Sonar dataset show the positive effects of this approach. Out of 208 objects, the algorithm identifies subsets of about 145, 187 relevant cases, and out of 60 features, it identifies about 9, 12 or 19 relevant features, thus significantly reducing the dimensionality of the problem and simplifying measurements. Moreover, the observed results may suggest the effectiveness of the proposed method in the context of identifying a subset of truly relevant attributes among those identified by traditional feature selection methods.

This approach may find application in datasets where there is a need to identify specific ranges of continuous attribute values. Such datasets exist in the area of medical data, where only selected, narrow ranges of values of diagnostic test results have a significant impact on determining a disease diagnosis. Another area may be the field of spectrometry [16], in which only certain ranges of wavelengths have a significant relationship with the dependent variable.

5. Conclusions

This section is not mandatory, but can be added to the manuscript if the discussion is unusually long or complex.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available in a publicly accessible repository that does not issue DOIs Publicly available datasets were analyzed in this study. This data can be found here: [https://data.world/uci/connectionist-bench-sonar-mines-vs-rocks].

Conflicts of Interest

The authors declare no conflict of interest.

References

Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Computers & Electrical Engineering 2014, 40, 16–28. 40th-year commemorative issue, doi:https://doi.org/10.1016/j.compeleceng.2013.11.024. [CrossRef]
Sánchez-Maroño, N.; Alonso-Betanzos, A.; Tombilla-Sanromán, M. Filter Methods for Feature Selection – A Comparative Study. Intelligent Data Engineering and Automated Learning - IDEAL 2007; Yin, H.; Tino, P.; Corchado, E.; Byrne, W.; Yao, X., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2007; pp. 178–187. doi:10.1007/978-3-540-77226-2_19. [CrossRef]
Yang, P.; Liu, W.; Zhou, B.B.; Chawla, S.; Zomaya, A.Y. Ensemble-Based Wrapper Methods for Feature Selection and Class Imbalance Learning. Advances in Knowledge Discovery and Data Mining; Pei, J.; Tseng, V.S.; Cao, L.; Motoda, H.; Xu, G., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2013; pp. 544–555. doi:10.1007/978-3-642-37453-1_45. [CrossRef]
Lal, T.N.; Chapelle, O.; Weston, J.; Elisseeff, A., Embedded Methods. In Feature Extraction: Foundations and Applications; Guyon, I.; Nikravesh, M.; Gunn, S.; Zadeh, L.A., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2006; pp. 137–165. doi:10.1007/978-3-540-35488-8_6. [CrossRef]
Jolliffe IT, C.J. Principal component analysis: a review and recent developments. Philosophical transactions. Series A, Mathematical, physical, and engineering sciences 2016, 374. doi:10.1098/rsta.2015.0202. [CrossRef]
Ben Brahim, A.; Limam, M. A hybrid feature selection method based on instance learning and cooperative subset search. Pattern Recognition Letters 2016, 69, 28–34. doi:https://doi.org/10.1016/j.patrec.2015.10.005. [CrossRef]
Pancerz, K.; Paja, W.; Sarzyński, J.; Gomuła, J. Determining Importance of Ranges of MMPI Scales Using Fuzzification and Relevant Attribute Selection. Procedia Computer Science 2018, 126, 2065–2074. doi:10.1016/j.procs.2018.07.245. [CrossRef]
Paja, W.; Pancerz, K.; Pękala, B.; Sarzyński, J. Application of the Fuzzy Logic to Evaluation and Selection of Attribute Ranges in Machine Learning. 2021 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), 2021, pp. 1–6. doi:10.1109/FUZZ45933.2021.9494515. [CrossRef]
Paja, W. Identification of Relevant Medical Parameter Values in Information Systems using Fuzzy Approach. Procedia Computer Science 2021, 192, 3915–3921. Knowledge-Based and Intelligent Information & Engineering Systems: Proceedings of the 25th International Conference KES2021, doi:https://doi.org/10.1016/j.procs.2021.09.166. [CrossRef]
Bazan, J.G.; Nguyen, H.S.; Nguyen, S.H.; Synak, P.; Wróblewski, J. Rough Set Algorithms in Classification Problem. In Rough Set Methods and Applications: New Developments in Knowledge Discovery in Information Systems; Polkowski, L.; Tsumoto, S.; Lin, T.Y., Eds.; Physica-Verlag: Heidelberg, 2000; pp. 49–88. doi:10.1007/978-3-7908-1840-6_3. [CrossRef]
Zadeh, L. Fuzzy sets. Information and Control 1965, 8, 338–353. doi:10.1016/S0019-9958(65)90241-X. [CrossRef]
Breiman, L. Random Forests. Machine Learning 2001, 45, 5–32. doi:10.1023/A:1010933404324. [CrossRef]
Kursa, M.; Rudnicki, W. Feature Selection with the Boruta Package. Journal of Statistical Software 2010, 36. doi:10.18637/jss.v036.i11. [CrossRef]
Kursa, M.B.; Jankowski, A.; Rudnicki, W. Boruta - A System for Feature Selection. Fundam. Informaticae 2010, 101, 271–285. doi:10.3233/FI-2010-288. [CrossRef]
Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993.
Guleken, Z.; Tuyji Tok, Y.; Jakubczyk, P.; Paja, W.; Pancerz, K.; Shpotyuk, Y.; Cebulski, J.; Depciuch, J. Development of novel spectroscopic and machine learning methods for the measurement of periodic changes in COVID-19 antibody level. Measurement 2022, 196. doi:https://doi.org/10.1016/j.measurement.2022.111258. [CrossRef]

Figure 1. An example of defining a triangular membership function of the value of the variable V9 from the Sonar dataset based on the designated discretization intervals.

Figure 2. Graph of the average importance value of linguistic variables for the V9 attribute from Sonar dataset. Green variables are those confirmed relevant, while red variables are those rejected.

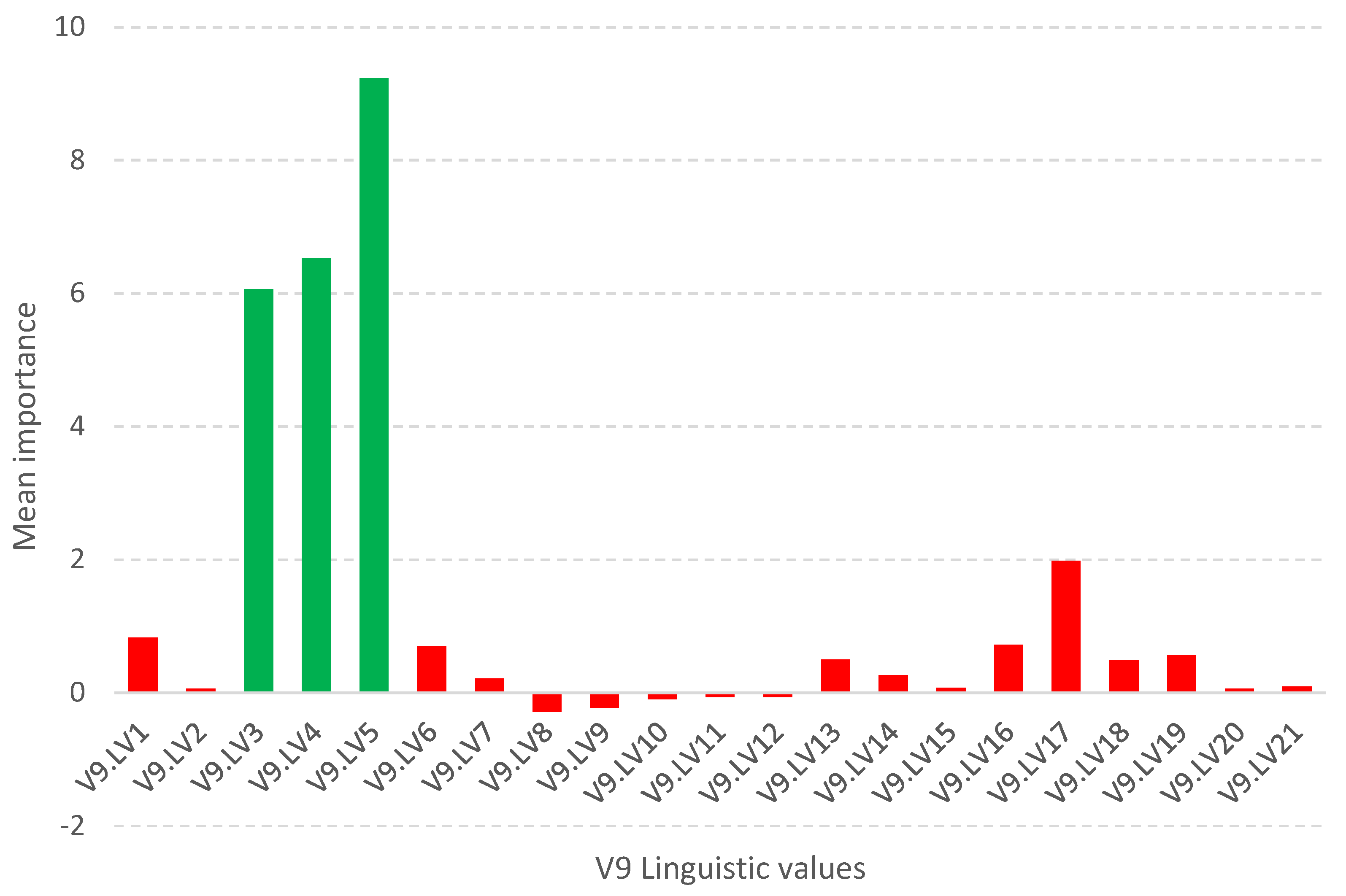
Figure 3. The range of values of the V9 original variable (red color) and the range of values after selection including linguistic variables (green color).

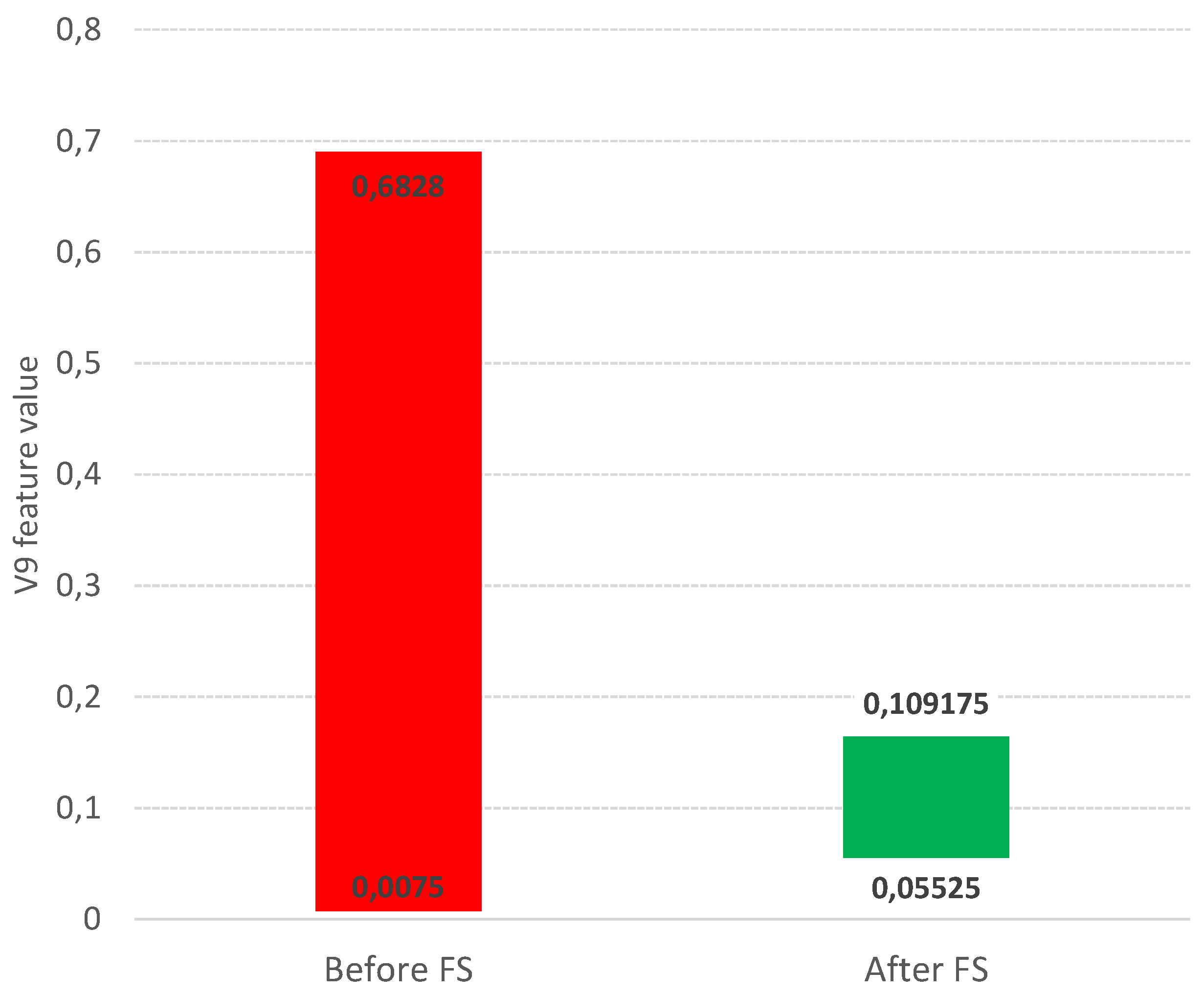
Figure 4. Part of the binary table obtained for the Sonar dataset. The green fields (value 1) indicate the value of an attribute that is in the relevant value range, the red fields (value 0), on the other hand, are the values that are considered irrelevant.

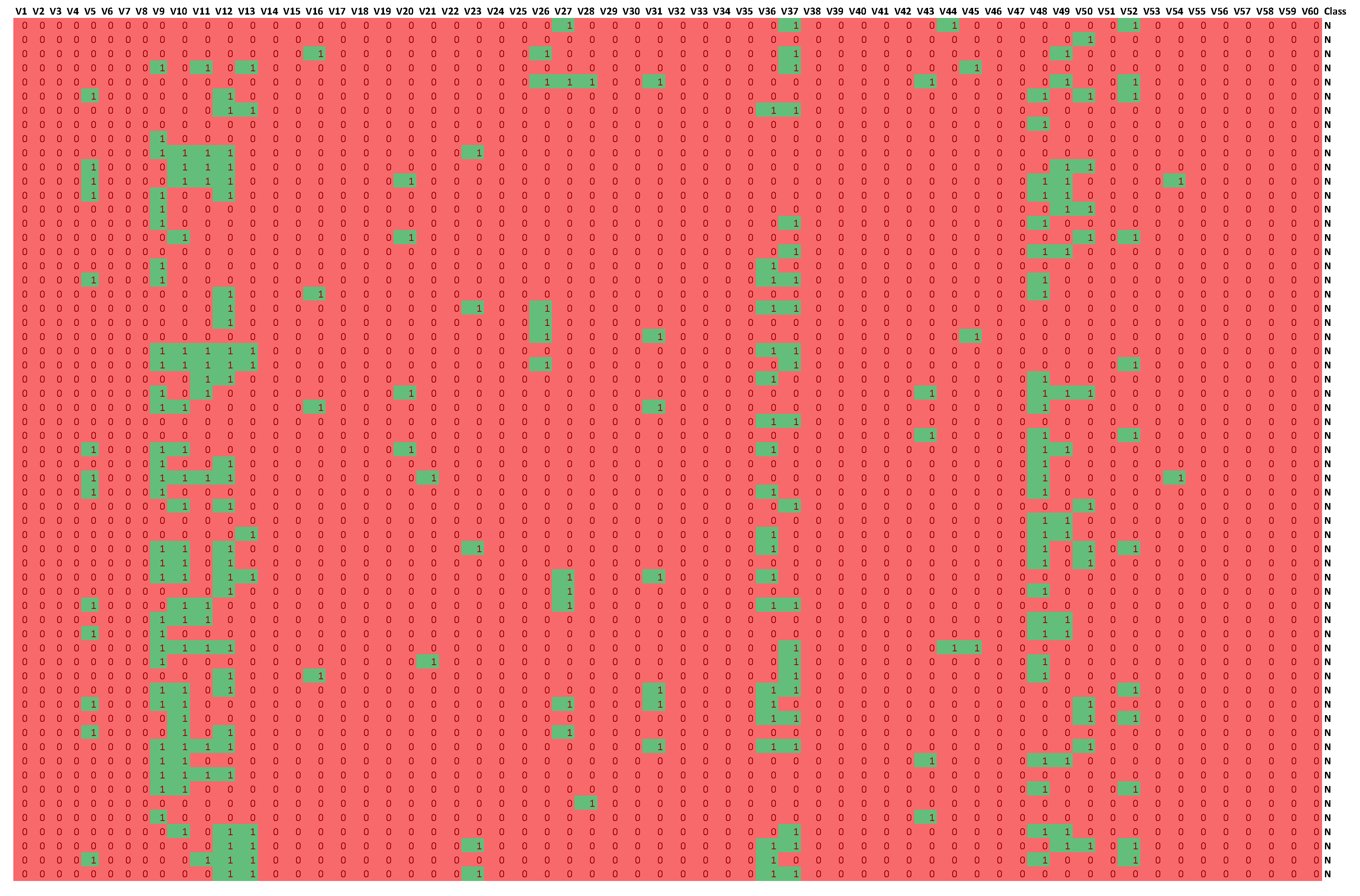
Figure 5. The results of the Fuzzy Feature Selection algorithm obtained using Sonar dataset for different values of the EPS parameter, along with parameters for assessing the quality of classification of the model built on the subset. Red color indicates the result for the original set.

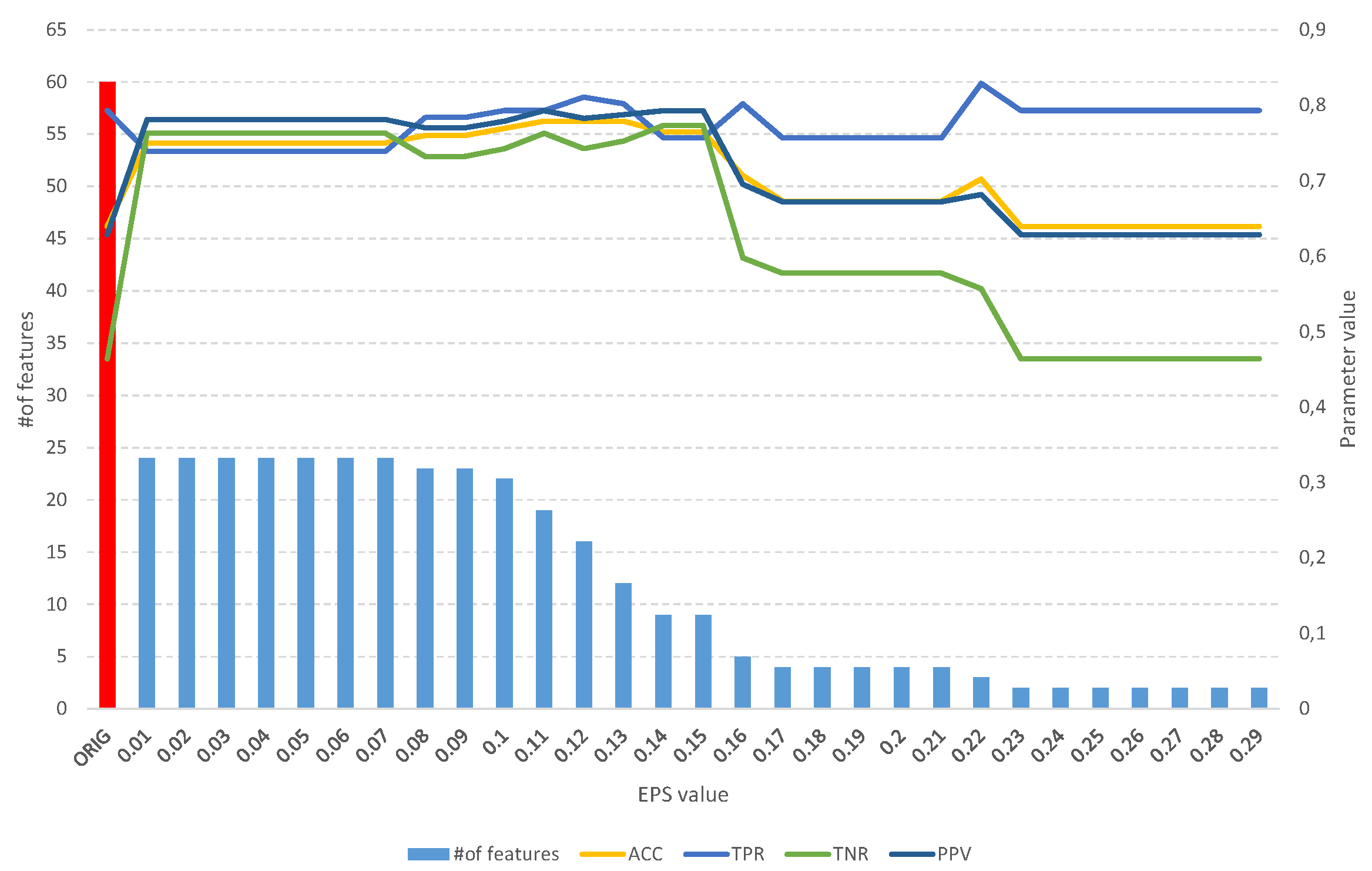
Figure 6. The results of the Fuzzy Object Selection algorithm obtained using Sonar dataset for different values of the EPS parameter along with the parameters for assessing the classification quality of the model built on the subset. The result for the original set is marked in red.

Table 1. The discretization intervals of the V9 variable and the corresponding linguistic variables and their minimum and maximum values.

V9 Intervals	Linguistic Values
0.0075	name	min	max
0.0488	V9.LV1	0.0075	0.05525
0.0617	V9.LV2	0.02815	0.068525
0.07535	V9.LV3	0.05525	0.079025
0.0827	V9.LV4	0.068525	0.092325
0.10195	V9.LV5	0.079025	0.109175
0.1164	V9.LV6	0.092325	0.1202
0.124	V9.LV7	0.109175	0.127875
0.13175	V9.LV8	0.1202	0.134775
0.1378	V9.LV9	0.127875	0.1436
0.1494	V9.LV10	0.134775	0.1541
0.1588	V9.LV11	0.1436	0.16075
0.1627	V9.LV12	0.1541	0.17025
0.1778	V9.LV13	0.16075	0.17865
0.1795	V9.LV14	0.17025	0.1908
0.2021	V9.LV15	0.17865	0.2168
0.2315	V9.LV16	0.1908	0.2502
0.2689	V9.LV17	0.2168	0.2794
0.2899	V9.LV18	0.2502	0.299525
0.30915	V9.LV19	0.2794	0.33355
0.35795	V9.LV20	0.299525	0.520375
0.6828	V9.LV21	0.33355	0.6828

Table 2. The results of the Fuzzy Feature Selection algorithm obtained using Sonar dataset for different values of the EPS parameter, along with parameters for assessing the quality of classification of the model built on the subset.

#of features	EPS	threshold	ACC	TPR	TNR	PPV	MCC	F1
24	0.01	2.08	0.75	0.74	0.76	0.78	0.5	0.76
24	0.02	4.16	0.75	0.74	0.76	0.78	0.5	0.76
24	0.03	6.24	0.75	0.74	0.76	0.78	0.5	0.76
24	0.04	8.32	0.75	0.74	0.76	0.78	0.5	0.76
24	0.05	10.40	0.75	0.74	0.76	0.78	0.5	0.76
24	0.06	12.48	0.75	0.74	0.76	0.78	0.5	0.76
24	0.07	14.56	0.75	0.74	0.76	0.78	0.5	0.76
23	0.08	16.64	0.76	0.78	0.73	0.77	0.52	0.78
23	0.09	18.72	0.76	0.78	0.73	0.77	0.52	0.78
22	0.1	20.80	0.77	0.79	0.74	0.78	0.54	0.79
19	0.11	22.88	0.78	0.79	0.76	0.79	0.56	0.79
16	0.12	24.96	0.78	0.81	0.74	0.78	0.55	0.8
12	0.13	27.04	0.78	0.8	0.75	0.79	0.56	0.79
9	0.14	29.12	0.76	0.76	0.77	0.79	0.53	0.77
9	0.15	31.20	0.76	0.76	0.77	0.79	0.53	0.77
5	0.16	33.28	0.71	0.8	0.6	0.7	0.41	0.74
4	0.17	35.36	0.67	0.76	0.58	0.67	0.34	0.71
4	0.18	37.44	0.67	0.76	0.58	0.67	0.34	0.71
4	0.19	39.52	0.67	0.76	0.58	0.67	0.34	0.71
4	0.2	41.60	0.67	0.76	0.58	0.67	0.34	0.71
4	0.21	43.68	0.67	0.76	0.58	0.67	0.34	0.71
3	0.22	45.76	0.7	0.83	0.56	0.68	0.4	0.75
2	0.23	47.84	0.64	0.79	0.46	0.63	0.27	0.7
2	0.24	49.92	0.64	0.79	0.46	0.63	0.27	0.7
2	0.25	52.00	0.64	0.79	0.46	0.63	0.27	0.7
2	0.26	54.08	0.64	0.79	0.46	0.63	0.27	0.7
2	0.27	56.16	0.64	0.79	0.46	0.63	0.27	0.7
2	0.28	58.24	0.64	0.79	0.46	0.63	0.27	0.7
2	0.29	60.32	0.64	0.79	0.46	0.63	0.27	0.7
original set	-	-	0.64	0.79	0.46	0.63	0.27	0.7

Table 3. The results of the Fuzzy Object Selection algorithm obtained using Sonar dataset for different values of the EPS parameter, along with parameters for assessing the quality of classification of the model built on the subset.

#of objects	EPS	threshold	ACC	TPR	TNR	PPV	MCC	F1
204	0.01	0.6	0.7	0.76	0.64	0.7	0.4	0.73
187	0.02	1.2	0.73	0.69	0.76	0.75	0.46	0.72
187	0.03	1.8	0.73	0.69	0.76	0.75	0.46	0.72
145	0.04	2.4	0.77	0.72	0.8	0.72	0.52	0.72
109	0.05	3	0.77	0.68	0.82	0.66	0.49	0.67
109	0.06	3.6	0.77	0.68	0.82	0.66	0.49	0.67
72	0.07	4.2	0.69	0.48	0.8	0.52	0.28	0.5
72	0.08	4.8	0.69	0.48	0.8	0.52	0.28	0.5
37	0.09	5.4	0.76	0.14	0.9	0.25	0.05	0.18
37	0.1	6	0.76	0.14	0.9	0.25	0.05	0.18
21	0.11	6.6	0.81	0	0.94	0	-0.09	-
original set	-	-	0.73	0.73	0.72	0.75	0.45	0.74

Table 4. Classification results obtained for selected combinations of the number of relevant objects and the number of relevant features.

#of objects	#of features	ACC	TPR	TNR	PPV	MCC	F1
187	9	0.8	0.84	0.77	0.78	0.61	0.81
187	19	0.83	0.87	0.8	0.81	0.67	0.84
145	9	0.81	0.86	0.73	0.82	0.6	0.84
145	19	0.81	0.85	0.75	0.83	0.6	0.84
original set		0.73	0.73	0.72	0.75	0.45	0.74

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Application of the Fuzzy Approach to Evaluation and Selection of Relevant Objects, Features and their Ranges

Abstract

1. Introduction

2. Materials and Methods

2.1. The dataset used

2.2. Discretization algorithm

2.3. Fuzzification algorithm

2.4. Feature selection algorithm

3. Results

4. Discussion

5. Conclusions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe