1. Introduction
A growing consensus from governments and civil engineering communities worldwide has identified Building Information Modelling (BIM) as a highly-efficient method within the construction industry that offers enhanced ways of working throughout the life cycle of a structure [
1,
2]. This process aims to generate an information model that functions as a digital description of the individual components of the structure. The model is built on information generated collaboratively and updated throughout various key stages of the project. While BIM in the planning and design phase is initially based on virtual models that describe the building to be realized (Project Information Models), the models in the life cycle must be further developed into as-built or as-is models that reflect the actual built condition of the structure, that are also the basis of Asset Information Models for operation. For operations, however, the concept of the digital twin is currently being discussed intensively. In a digital twin, the real asset is coupled with its digital representation. A bidirectional connection enables the exchange of information and knowledge between both representations. The construction of a digital twin is achieved by integrating different digital models (information models, physical models, sensor models,
.). An essential model can be the as-is BIM model, which describes the actual geometric-semantic situation as well as the position and height of the structure [
3].
The complexities across major infrastructure projects have demonstrated for quite some time the need to develop a single model that reflects all components of the entire project. Consequently, one can argue that applying BIM in infrastructure projects provides a much needed solution to this particular problem. This is similar to the single source of truth (SSOT) concept applied in information science, where data from many systems is aggregated and edited in one place. When needed, this data can also be recalled by reference. Some of the multiple advantages of this procedure include avoiding the duplication of data entries and building a complete view of the project’s performance.
The main modelling scenarios of an infrastructure project can be categorized into greenfield and brownfield.
Greenfield is categorized by creating new information about built assets from design through construction, resulting in what is called an as-built model. Ideally, the as-built model is identical to the as-planned model. However, in most of the cases there are deviations between those two models [
4]. By comparing the as-built model with the as-planned model these deviations can be uncovered. On the other hand, in
Brownfield scenarios the information of an already existing asset must consider the nature and quality of the information required for the project. In terms of safety, the advanced age and relevance of most infrastructure projects makes this a very common scenario. In rare cases, the digital models of existing assets are available, but there is a need to update them due to modifications, damages and repairs [
3].
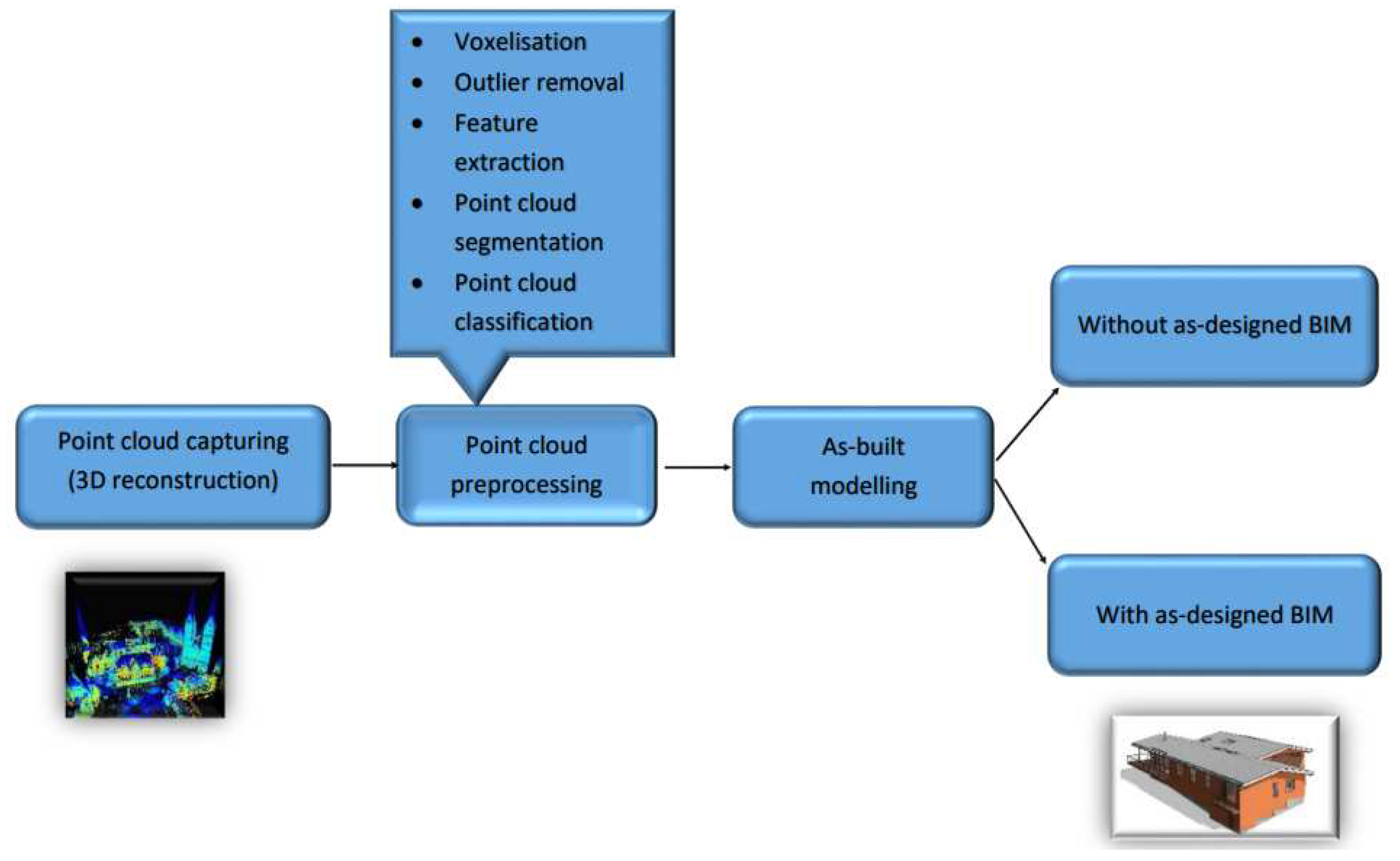
In order to update the as-planned model to an as-built model during the construction in the greenfield scenario, geometric information of an existing structure today can be captured with high resolution using 3D laser scans or photogrammetry and then imported in specific software to create the 3D as-is model. This crucial step is often called Scan to BIM (Scan2BIM). The workflow of the scan to BIM process taken from literature is shown in Figure 1.1. Firstly, various capturing devices are employed to collect 3D points of an object. However, the resulting 3D representation typically includes redundant points, causing noise in the scene and offering limited semantic information. Secondly, further processing is conducted to obtain a more informative 3D representation of the scene, which involves the use of different point cloud preprocessing techniques. This preprocessing stage begins with converting the unordered 3D points into structured 3D grids known as voxels, which provides a regular and efficient way of processing and analyzing 3D point clouds. Voxelization can also be utilized for point cloud downsampling, whereby the number of points is reduced by averaging the values of points within a voxel. Additionally, preprocessing involves the elimination of outliers that are not part of the 3D points representing the object, and extraction of semantic information via feature extraction. The point cloud is then segmented and classified into distinct categories to represent the entire scene. Utilizing these classified segments, various surface construction algorithms are employed to generate 3D models of the object [
5,
6]. Extracting geometric-semantic models from the point cloud is the fundamental aspect of 3D modelling for BIM. Finally, an as-is built model of the structure is generated. An overview of the as-is built modelling process is presented in the following literature [
7].
Figure 1.
Scan to BIM workflow to create as built model starting from point cloud capturing; after [
7].
Figure 1.
Scan to BIM workflow to create as built model starting from point cloud capturing; after [
7].
One widespread technology for Scan2BIM is 3D laser scanning. There are different techniques for capturing 3D data of the built environment using 3D laser scanners. Two of the most frequently used techniques are Terrestrial Laser Scanning (TLS) and Mobile Laser Scanning (MLS), with varying advantages depending on their application. TLS is used as a reality capture system that is ground-based. Placed on a static tripod, these systems are able to scan multiple positions and are therefore particularly useful when capturing data points from engineering structures, building interiors or areas with especially dense vegetation. MLS on the other hand is a surveying method, characterized by placing laser systems onto moving vehicles or carrying by hand. It is useful for kinematically capturing large structures and areas, whereas TLS has delivers point clouds at a much higher resolution and with lower of noise. MLS is thus suitable for large infrastructure objects, while TLS is to be preferred in scenarios with good visibility (fewer scan positions required) and high accuracy requirements. Figure 1.2 highlights exemplary for two scanner systems in the acquisition and processing time, as well as resolution based on the application of both methods in cultural heritage sites.
Figure 2.
Exemplary comparison of acquisition and processing time, as well as resolution, between MLS (Lynx mobile mapper) and TLS (Trimble GX) on 3D point cloud from cultural heritage sites [
8].
Figure 2.
Exemplary comparison of acquisition and processing time, as well as resolution, between MLS (Lynx mobile mapper) and TLS (Trimble GX) on 3D point cloud from cultural heritage sites [
8].
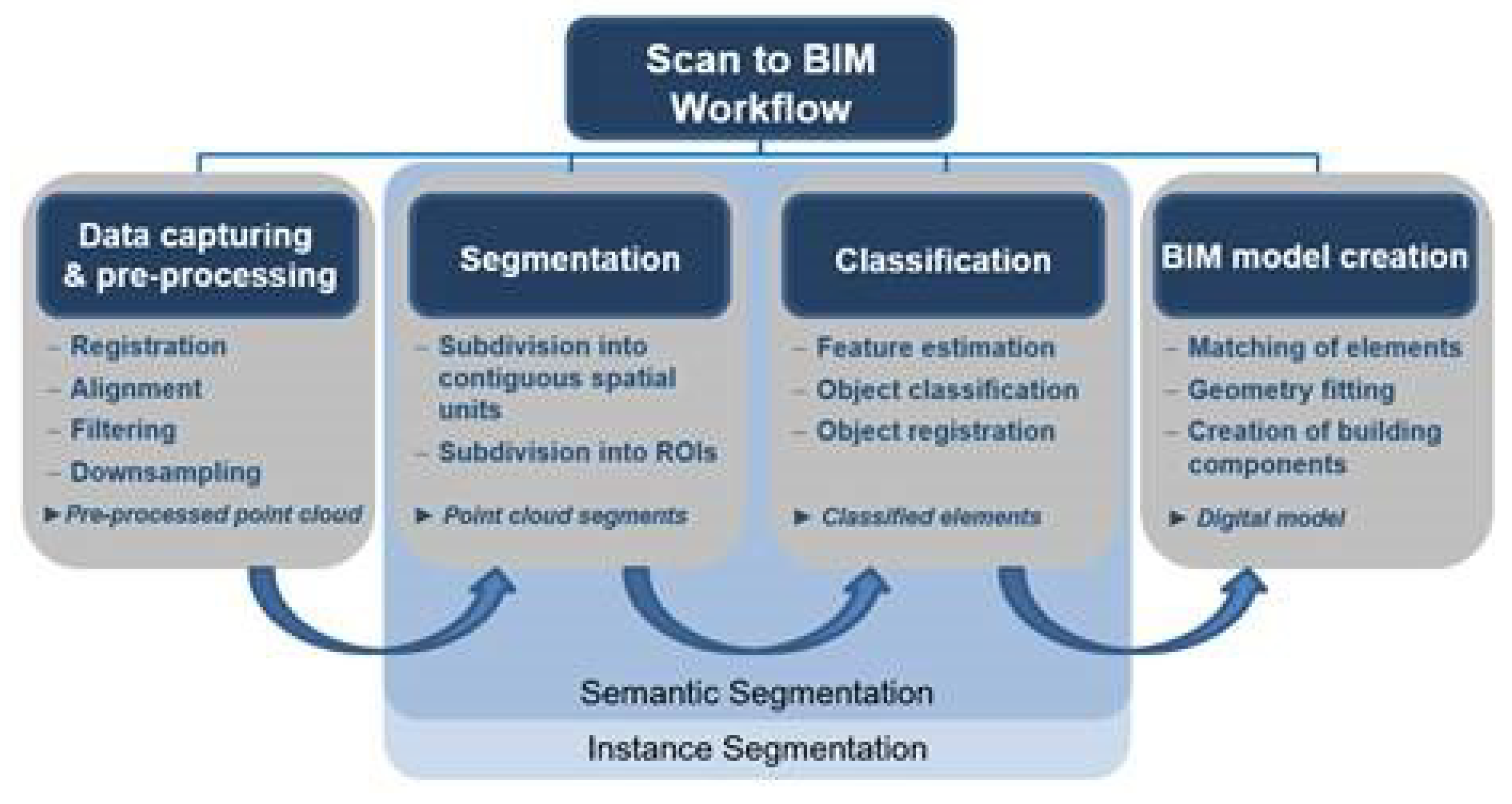
The process of creating a 3D model from a point cloud in practice is a highly manual-driven task. Considering how much time is required to conduct this step manually in order to represent complex geometries accurately, one could conclude that manual Scan2BIM is particularly difficult work [
9]. The aim of this study is to automate this process through the segmentation and classification of captured points, which in turn reduces, at least partially, the manual work involved. Segmentation focuses on partitioning the scene into multiple segments without understanding their meaning. This step is crucial for subsequent modeling efforts, as it provides a way to filter out irrelevant points and focus on the Region of Interests (ROI). On the other hand, classification assigns each point to a specific label based on the meaningful representation of its segment in the scene to give semantic meaning to the segment. Various names have been used in the literature to refer to segmentation and classification of point cloud, including semantic segmentation, instance segmentation, point labeling, and point-wise classification [
10,
11,
12]. The main difference between semantic segmentation and instance segmentation of 3D point clouds is that semantic segmentation focuses on assigning semantic labels to points based on their object or class, while instance segmentation goes a step further by distinguishing individual instances of objects within the same class, providing a more detailed scene understanding. However,for the sake of simplification, we will adopt the term "semantic segmentation" throughout this work. Figure 1.3 illustrates the workflow of Scan2BIM showing where our approach for the automatic semantic segmentation of the 3D points fits. A general overview of the as-is modelling process is provided showing the capability of various techniques from different research fields (computer vision, surveying and geoinformatics, construction informatics, architecture,
.) to automate the as-is modelling process [
7]. The overview is based on different relevant works, that discussed the potential of these techniques and the large overlap of the modelling process with the geometry processing field. As a result these approaches will be discussed in detail in this work..
Figure 3.
Steps of Scan to BIM showing where our approach fits in the automation of the semantic segmentation stage for 3D point clouds.
Figure 3.
Steps of Scan to BIM showing where our approach fits in the automation of the semantic segmentation stage for 3D point clouds.
Recently, there has been an increasing interest in investigating different techniques to automate the Scan2BIM process by automating the stages of point cloud semantic segmentation. A notable scientific investigation explored different approaches for segmenting and generating BIM models from point cloud data. The study introduced the VOX2BIM method, which involved converting point clouds into voxel representations and employing diverse techniques to automate the process of BIM model generation [
13]. Other research investigations have explored the automation of the workflow for point cloud processing, which is an essential step in the Scan2Bim process [
14]. The automatization aimed in our work can be achieved by segmenting and classifying the point cloud, using machine learning algorithms, which can complete this task efficiently and in reasonable time [
15,
16]. Machine learning algorithms (including deep learning, neural network,
) generate models that are based on, but not specific to, a training data set that allows the algorithms to learn how to classify information.
Two broad categories of machine learning are often discussed: classical machine learning and deep learning [
17]. Classical machine learning refers to traditional machine learning algorithms that typically rely on handcrafted features and are trained on data sets using statistical models. In contrast, deep learning involves neural networks that automatically learn features from raw data and are trained on larger data sets using optimization techniques.
In point cloud semantic segmentation, one of the challenges is to assign every 3D point to a correct label or class in the observed scene (car, bridge,
). After the segmentation, the 3D point cloud can be classified into different categories which are present in the scene [
18]. Our process of automatic semantic segmentation of 3D point clouds employs classical machine learning methods which can be broken down into three primary stages. The first stage is selecting a group of points around a 3D point, a step that can be completed manually or automatically. Each group contains information and spatial relations between its points which should be described using different methods. The second stage is extracting different features from each group and passing these features to the machine learning algorithms for the training process. The key factor in this stage is to discover which features may be more characteristic for each group among other features based on good understanding of the scene. In the third stage, the training stage, a training data set is used to train the classification model. The training data set is fed to the model in the form of features assigned with labels of the different classes. Here the model learns the correlations between these features and be able to separate the different classes in the feature space. Finally, a new 3D point cloud, a so called test set, can be segmented and classified automatically based on the learned features. The classified test set reflects the performance of the model which can be used to segment and classify any other data sets captured by comparable sensors.
2. Related Work
Research in the literature revealed several studies which show that outdoor 3D point cloud semantic segmentation, specifically urban and rural scenes, using machine learning techniques has become an established research topic. That is similar to the application of machine learning in the field of automated driving. There, machine learning techniques have been applied in order to allow cars to capture data from their surroundings through sensors and cameras. The algorithm is then able to interpret the collected data and decide on next actions, which allows cars to perform tasks equally well as human beings [
19,
20].
During the data acquisition process, 3D point clouds are obtained using various laser scanning techniques. For the semantic segmentation of these point clouds using classical machine learning methods, diverse strategies can be employed at each stage of the processing workflow. Firstly, certain subsets of 3D points are selected, which correspond to a specific part of the scene and referred to as neighborhoods. Several techniques are used to obtain an appropriate representation of the neighborhood in the scene. Then, the characteristic features that describe these neighborhoods are extracted, and the machine learning model is trained with these features as input data. Finally, the trained model is tested on various data sets and the categories in the scene are classified. In contrast, for semantic segmentation using deep learning methods, the input point clouds are fed to the model, and the model extracts the features and generates initial output. The learning process is supervised using a loss function to optimize the network performance by minimizing the defined loss function in a predefined number of iterations (epochs) until a minimum value of loss function is achieved. In the following sections, we describe the step-by-step process of both methods and provide examples from previous studies to illustrate their advantages and limitations.
2.1. Classical Machine Learning Method
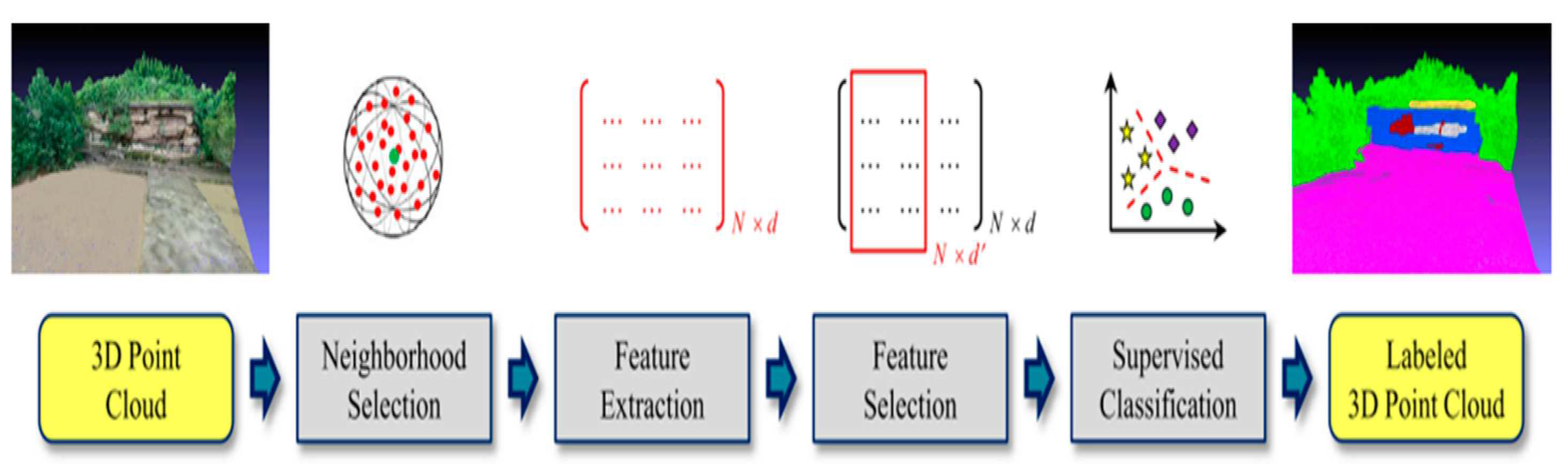
The process of semantic segmentation using classical machine learning methods entails three fundamental stages, as described earlier. In order to obtain a complete comprehension of the workflow, it is essential to provide a concise discussion of each stage, emphasizing the techniques that have been previously applied in related literature. Furthermore, we will review the prior studies that have utilized various methods to tackle the semantic segmentation of distinct objects present in a given scene.
Figure 4.
Workflow of point cloud semantic segmentation using classical machine learning method [
21].
Figure 4.
Workflow of point cloud semantic segmentation using classical machine learning method [
21].
2.1.1. Neighborhood Selection
Selecting a respective neighbourhood containing all relevant 3D points around a given point is particularly crucial to define the local features for machine learning algorithms. There are different forms of neighborhood definitions. The most commonly applied ones are spherical neighborhood, cylindrical neighborhood and K-nearest neighborhood. Spherical neighborhood definition refers to the local neighborhood that is formed by all 3D points inside a sphere of a fixed radius [
22]. In the definition for cylindrical neighborhoods, the neighborhood is defined by the 2D projections of all 3D points that fall within the sphere of a fixed radius [
23]. K-nearest neighborhoods are characterised by a particular number of 3D points within a specific area [
24,
25]. It is argued that from a purely conceptual stance, radius neighborhood definition should be the appropriate procedure to describe a group of 3D points [
26], although it could be less useful when the point density shows strong variations [
27]. The three common definitions will be discussed in detail in
Section 3.2.1 to show the difference between each of them and which definitions are applied in this work.
To date, studies have examined two approaches for neighborhood scale selection using the above mentioned neighborhood definitions. The first approach is to use a
fixed scale parameter (usually either
k or the radius) to select the neighborhood around a 3D point. This scale parameter is frequently selected to be identical across all 3D points and relevant to each 3D data set. The main drawbacks of this approach is that in 3D point cloud semantic segmentation most of the outdoor scenes contain objects that vary in size and one can thus argue that using fixed scales inadequately capture this information. Moreover, fixed scale approach is sensitive to the point cloud densities, which is a feature that defines the number of points located in a specific neighborhood. The second approach, which was developed in order to avoid the major drawback of the first approach, considers the point cloud density by identifying an
individual neighborhood for each 3D point. It is an optimization for the fixed scale approach, which selects the scale parameters based on local point density, as well as local 3D structure. Besides, this approach offers a solution for the problem of selecting the fixed scale parameter via heuristic or empirical knowledge on the scene, which is the case in the first approach [
28,
29]. The two most common selection methods for the scale parameter are Eigenentropy based selection [
28,
30] and dimensionality based selection [
29]. The advantages as well as the disadvantages of the two approaches will be mentioned in the methods section showing the ability of the second approach to define a representative neighborhood.
2.1.2. Feature Extraction
Based on the neighborhood defined, a suitable description of a 3D point
X is required for the point cloud semantic segmentation. Each neighborhood is characterized by unique features, which can be extracted at a
single scale or
multi-scale. If a single scale approach is used, one has to make sure that a suitable scale is selected. Extracting features at different scales is a better alternative to a single scale approach, where the behaviour of the local 3D geometry is described through different scales. It has been argued that this approach is significantly more effective, regardless of whether it is used with k-nearest neighborhood [
31], with spherical/cylindrical neighborhoods [
25,
26] or with a combination of all neighborhood types [
32]. However, the common drawback between this approach and the first one is the selection of the different scales and the spacing between them, as well as its computational time due to the variation of point densities at each scale. It is suggested that defining a multiscale neighborhood ensures sufficient density at each scale without distortion of the features [
18]. From a mathematical point of view, the extracted features occupy different positions in a high dimensional space and are represented by a feature vector. This mathematical aspect is important when trying to distinguish between different classes using different machine learning algorithms like SVM, Random forests,
. Different feature types are used to define this vector:
- • parametric
features, which are used for the extraction of surfaces. The surface parameters are estimated by clustering as well as locating the maxima in the parameter space. It is only used for shapes that can be described with few parameters only (e.g. cylinders, spheres or planes) [
33].
- • sampled
features, in which the geometric relations between 3D points within the local neighborhood are sampled. As a result, a description of the local context is obtained. Histograms represent the different relations, such as angles and angular variations, as well as distances. Blomley et al. [
34] emphasis the difficulty for humans to interpret the entries of these resulting feature vectors.
- • metrical
features, such as shape measures. In this type, a single value, which specifies one particular property, represents each feature. Calculating the 3D structure tensor from the 3D coordinates of all the points in a given neighborhood, generates interpretable features. For more details on structure tensor, see
Section 3.2.1.2 on selecting scale of the neighborhood. The use of eigenvalues of this 3D structure tensor introduces features describing various structures (linear, planar or volumetric) [
35]. One can also add even further geometric features to the standard geometric features (such as anisotropy or omnivariance) [
36]. In some cases more metrical features like full wave and echo based features are added to the feature vector in order to distinguish between classes, which have large similarity in terms of geometric features [
37].
2.1.3. Semantic Segmentation
In terms of segmentation and classification of point clouds, one usually differentiates between three types of machine learning approaches, namely, unsupervised, semi-supervised and supervised learning. In
unsupervised learning techniques, the algorithm will analyze the data for the features within it, to determine features that actually correlate between two data items. This approach is being used for clustering, dimensionality reduction and feature learning tasks. A survey on unsupervised machine learning algorithms for different proposes is presented by Khanum et al. [
38]. As indicated by its name,
semi-supervised learning is partially linked to both supervised and unsupervised learning. It minimizes the input of the user and at the same time maximizes the generalization ability of the classifier. In this case, the algorithm makes use of the labeled and unlabelled data to improve the learning accuracy and thus improving the classification performance of the model. The literature suggests that this learning method can be used for point cloud semantic segmentation tasks where there is difficulty to get robust supervision information [
39]. An up-to-date overview of semi-supervised learning methods focusing on semi-supervised classification is introduced by Van Engelen, Jesper E. and Hoos, Holger H. [
40]. In a
supervised approach, the classification model will find the separation between categories based on the training samples given to the model, which contain the features and their categories. The strength of this method is that the outputs always have a probabilistic interpretation and the algorithm can be regularized to avoid overfitting.
Supervised machine learning algorithms have shown reasonable results when dealing with point cloud semantic segmentation processes [
28,
41]. This method is also applied by Brodu, Nicolas and Lague, Dimitri [
26] to segment and classify complex natural scenes using features derived from different scales.
Figure 5.
Result of the classification process for the mountain river data set. A) Original river scene, B) Classification( green: vegetation, gray: bedrock, red: gravel, blue: water) [
26].
Figure 5.
Result of the classification process for the mountain river data set. A) Original river scene, B) Classification( green: vegetation, gray: bedrock, red: gravel, blue: water) [
26].
There are different supervised machine learning algorithms (random forest, k-nearst neighbor, naive bayes,
) that are used for 3D point cloud semantic segmentation. Support Vector Machine (SVM) is among the most preferred methods for these tasks, due to its high performance on linear and non linear problems. In the field of computer vision and image processing SVM showed high accuracy in identification and classification tasks [
42,
43]. SVM was also investigated along with various algorithms for point cloud semantic segmentation and delivered a reasonable performance [
28,
41]. In other scientific fields, Osisanwo et al. [
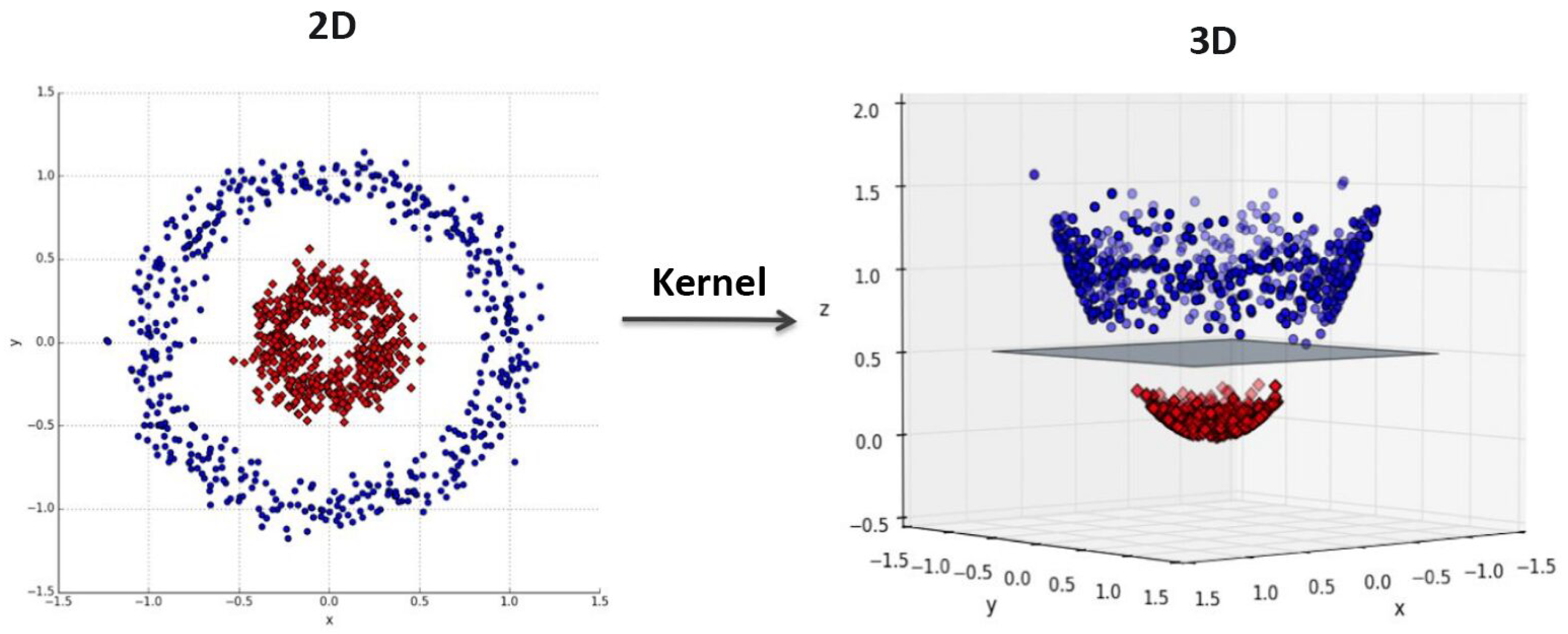
44] investigated different supervised machine learning techniques and compared between different classification algorithms, based on the data set given, to show which algorithm give the best performance. The comparison between seven algorithms showed that SVM was found to be the algorithm with the most accuracy. Using the Kernel trick, it is possible to map the input features into high dimensional feature spaces, in order to identify the optimal hyperplane separating all samples of each category [
45], thus, achieving better results, see Figure 2.3.
Figure 6.
Using kernel function to map the data set from 2D space to 3D space and constructing a separating surface between two classes [
46].
Figure 6.
Using kernel function to map the data set from 2D space to 3D space and constructing a separating surface between two classes [
46].
3D point cloud of infrastructure scenes usually contains more than two objects (vegetation, roads, bridges,
), meaning it is a multi-class classification task. As such, a suitable strategy is needed to solve this kind of tasks using supervised binary classifiers, which differentiate only between two classes. Multi-class classification problems can be reduced into multiple numbers of binary classification problems using different numbers of binary classifiers. This is done by training each binary classifier to distinguish between two classes in a scene, thus covering all the classes of an infrastructure asset. Such a strategy is known as transformation to binary [
47]. Two techniques are developed to reduce the multi-class problem. The first technique is called
one vs one. Here, each class is compared to another class, resulting in a number of classifiers that can be calculated using the following equation:
where
n is number of classes in the scene. The multi-class classification is split into one binary classification problem for each pair of classes. The second technique is called
one vs rest, where each class is compared to all other classes and the number of classes is equal to the number of classifiers. Here, the multi-class classification is split into one binary classification problem per class. This technique was used in the following literature [
48].
The two techniques discussed above are applied in road inventory studies, where the 3D point cloud of basic structures obtained from MLS is classified [
49]. In that work a hierarchical segmentation and classification was adapted, where the scene is firstly rough segmented into two main categories based on the major differences between their features (e.g. ground and above ground objects). Afterwards, the objects located in each category will be further classified to sub-classes by assigning a label to each segment based on its properties. The scene is thus semantically segmented through different stages.
As a binary classifier, SVM was used in several works to solve multi-class classification tasks using the different techniques mentioned previously [
48,
50]. An idea was introduced to use SVM classifier with multi-class classification problems by combining it with a decision tree approach [
50].
2.2. Deep Learning Method
State-of-the-art point cloud semantic segmentation approaches are based on deep learning techniques [
51,
52]. The workflow of these techniques can be summarized into three main steps shown in the following figure.
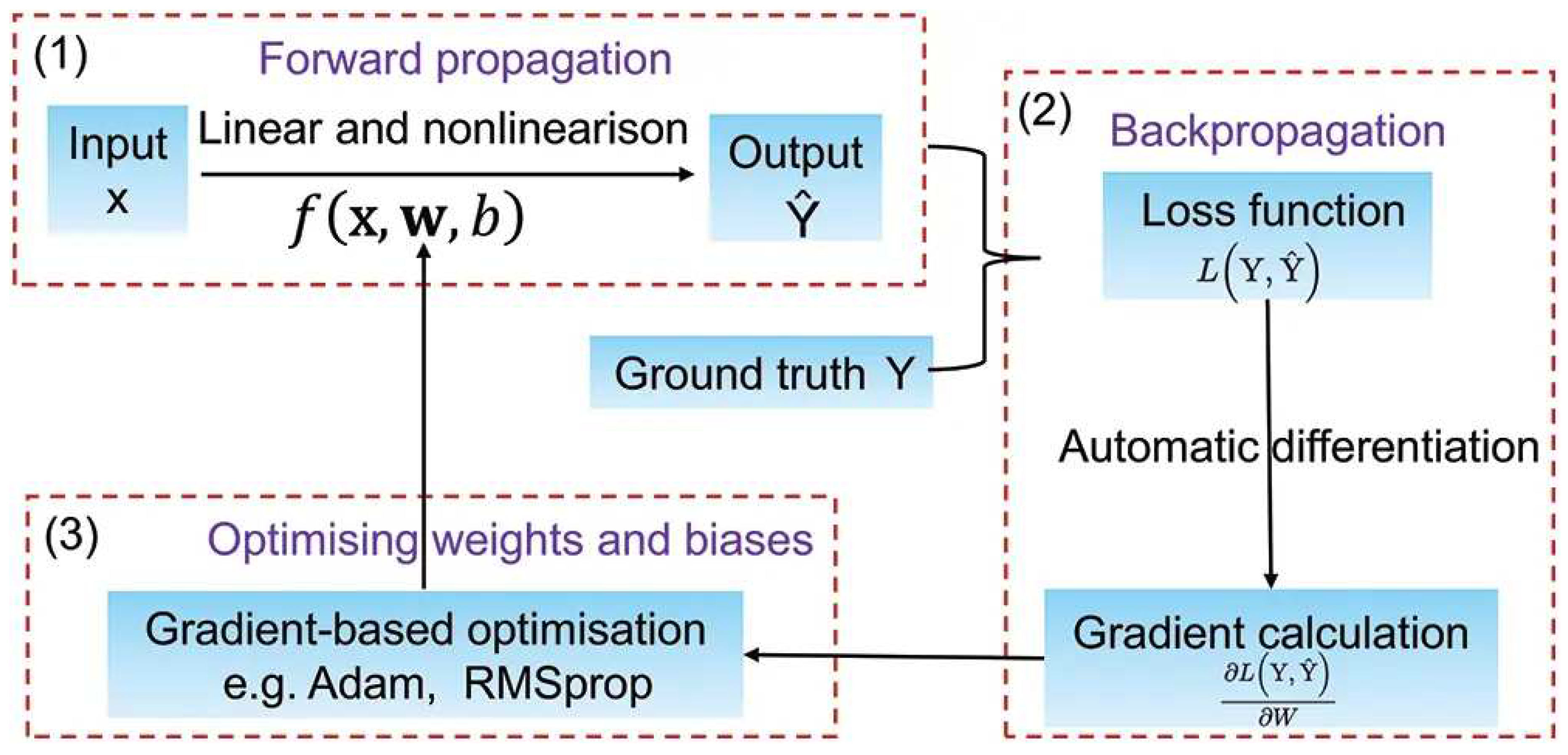
Figure 7.
Deep learning workflow showing the three main steps [
53].
Figure 7.
Deep learning workflow showing the three main steps [
53].
- • forward propagation,
where the input point cloud is fed into the deep learning model and the model generates an output. During this step, the point cloud is transformed into a set of feature maps, which are then passed through multiple layers of the neural network to generate a final prediction.
- • backward propagation,
the error calculated from the loss function is propagated back through the network to adjust the weights and biases of each layer in the model. This involves calculating the gradient of the loss function with respect to the weights and biases and using this information to update the values of these parameters.
- • optimization,
an optimization algorithm, such as stochastic gradient descent (SGD) or Adam, to adjust the weights and biases of the neural network based on the gradients calculated in the backward propagation step. The objective is to find the values of the parameters that minimize the loss function.
The most common problem of points in a point cloud is that these points are irregular and cannot easily be handled. Most researchers have to transform these points to different forms, such as 3D voxel grid [
54] or collection of images before passing these data to a deep net architecture. Since this transformation has drawbacks, another way for handling this problem is using a unified architecture called PointNet. PointNet is a pioneering architecture that processes set of points without voxelization by using multi-layer perceptrons to extract features for each point [
55,
56]. Then all point features are accumulated using a symmetric function. Finally, the information of neighboring points is effectively handled jointly. However, PointNet does not detect local features induced by the points in the metric space limiting its ability to generalize complex scenes. To address this drawback, an extension of PointNet, called PointNet++, is designed [
57]. PointNet ++ applies PointNet recursively on a portioning of input point cloud to capture local features at different scales. The architectures of PointNet and PointNet++ utilize a Multi Layer Perceptron (MLP) based method, which has been previously employed in the literature for various classification and segmentation tasks. MLP is a type of feedforward neural network that consists of multiple layers of perceptrons or nodes, each of which performs a linear transformation on the input followed by a non-linear activation function. This allows for the MLP to model non-linear relationships between input and output data.
Other deep learning-based methods have been proposed in the literature for point cloud semantic segmentation [
51,
52].
2.3. Advantages and Limitations
Although deep learning approaches deliver good results, they still have some shortcomings, such as their requirement of large data sets and computational resources during the training stage and the difficulty of interpreting deep networks [
58].
Classical machine Learning methods might be useful to address these shortcomings. Zhang et al. [
59] proposed a machine learning method, called the PointHop method, for the semantic segmentation of point cloud.
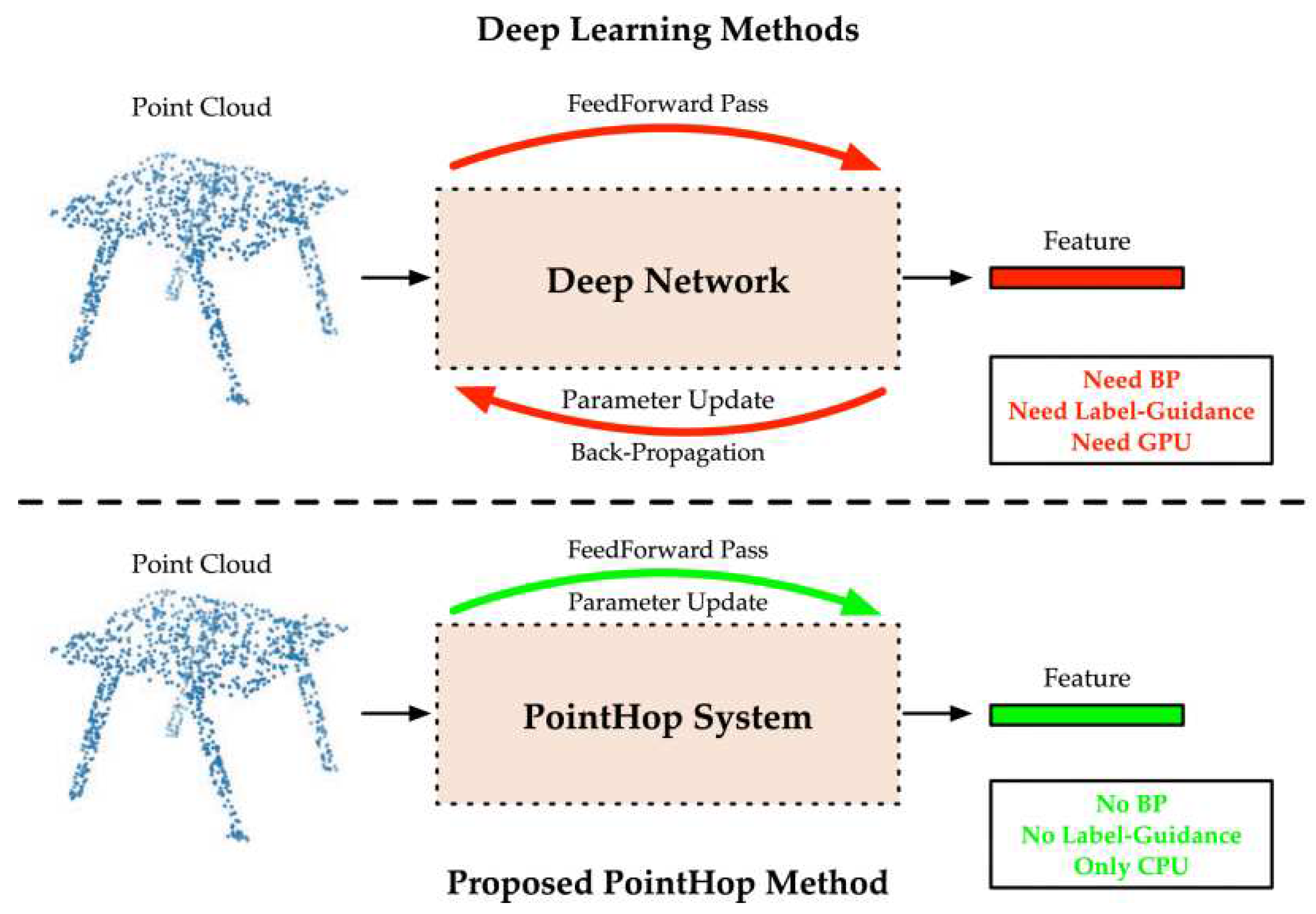
Figure 8.
Comparison between deep learning based methods and PointHop method showing that PointHop requires only one forward pass to learn parameters of the system [
59].
Figure 8.
Comparison between deep learning based methods and PointHop method showing that PointHop requires only one forward pass to learn parameters of the system [
59].
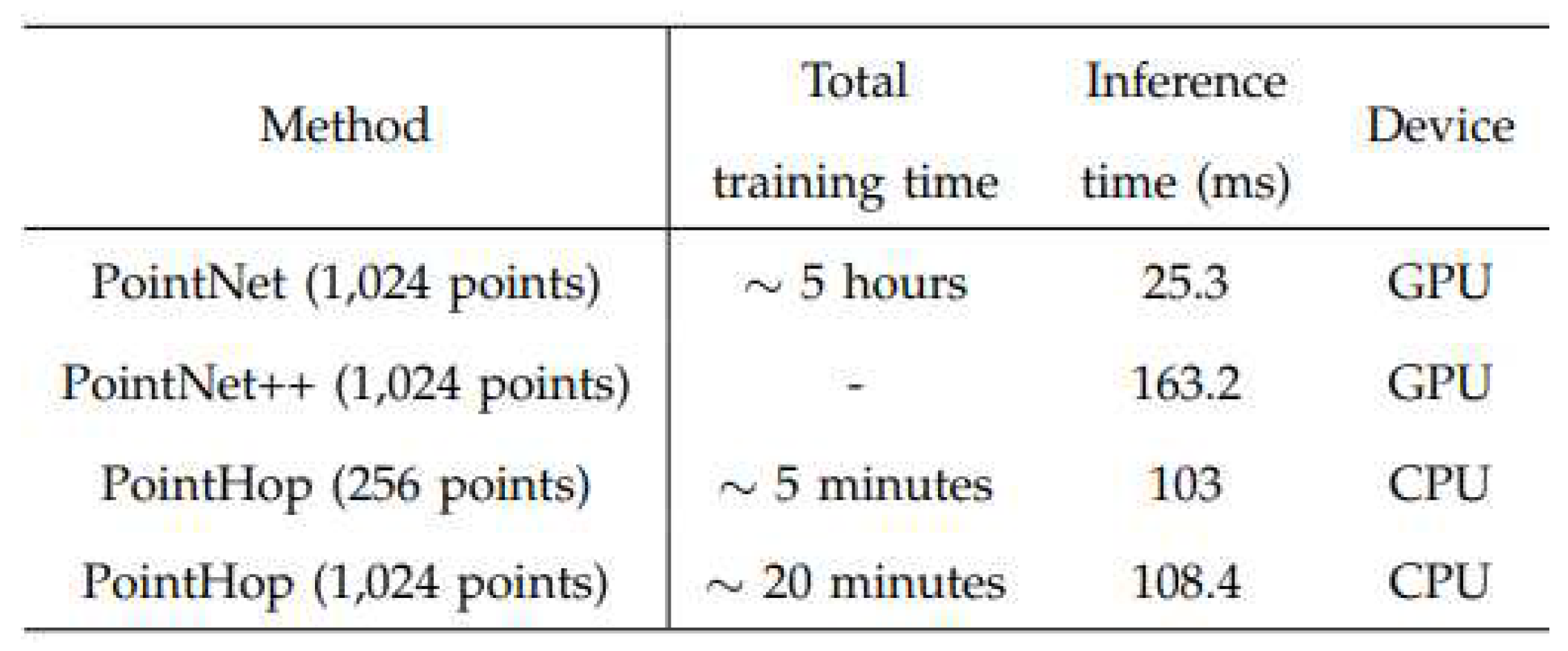
In terms of time complexity, PointHob system was compared to deep learning based methods, see Figure (2.6). The training time need by the developed system was significantly lowen than the other methods.
Figure 9.
Comparison of the time complexity between Pointnet, Pointnet++ and PointHop method [
59].
Figure 9.
Comparison of the time complexity between Pointnet, Pointnet++ and PointHop method [
59].
SVM as a classical machine learning algorithm was investigated alongside two other artificial neural networks, Recurrent Neural Networks (RNN) and Feed Forward Neural Networks (FFNN), in the field of autonomous driving [
19]. The task aimed to compare all three techniques within the context of lane change behaviour by humans in a simulated environment. The different approaches were evaluated using different feature combinations and the results showed that SVM generated the best outcomes and was able to successfully define the most appropriate feature combinations. This shows that under the right conditions, SVMs can compete with or even outperform deep learning techniques.
In point cloud semantic segmentation different classical machine learning algorithms were implemented and compared to deep learning models [
28]. The results of the study indicated that, with regard to the utilization of characteristic features, classical methods may outperform deep learning models.
3. Methods
In this work, 3D point clouds of bridges are semantically segmented based on classical supervised machine learning, where a training data set is required. For supervised learning approaches, standard supervised classifiers are applied, such as Support Vector Machine [
48] or Random Forest [
37]. Having demonstrated the usefulness of SVM in a road context and computer vision field in the previous sections, one may conclude that it could be equally useful for infrastructure in general. For these reasons, the application of support vector machine algorithm in road context will be extended in this work to include the semantic segmentation of 3D point cloud of the infrastructure asset.
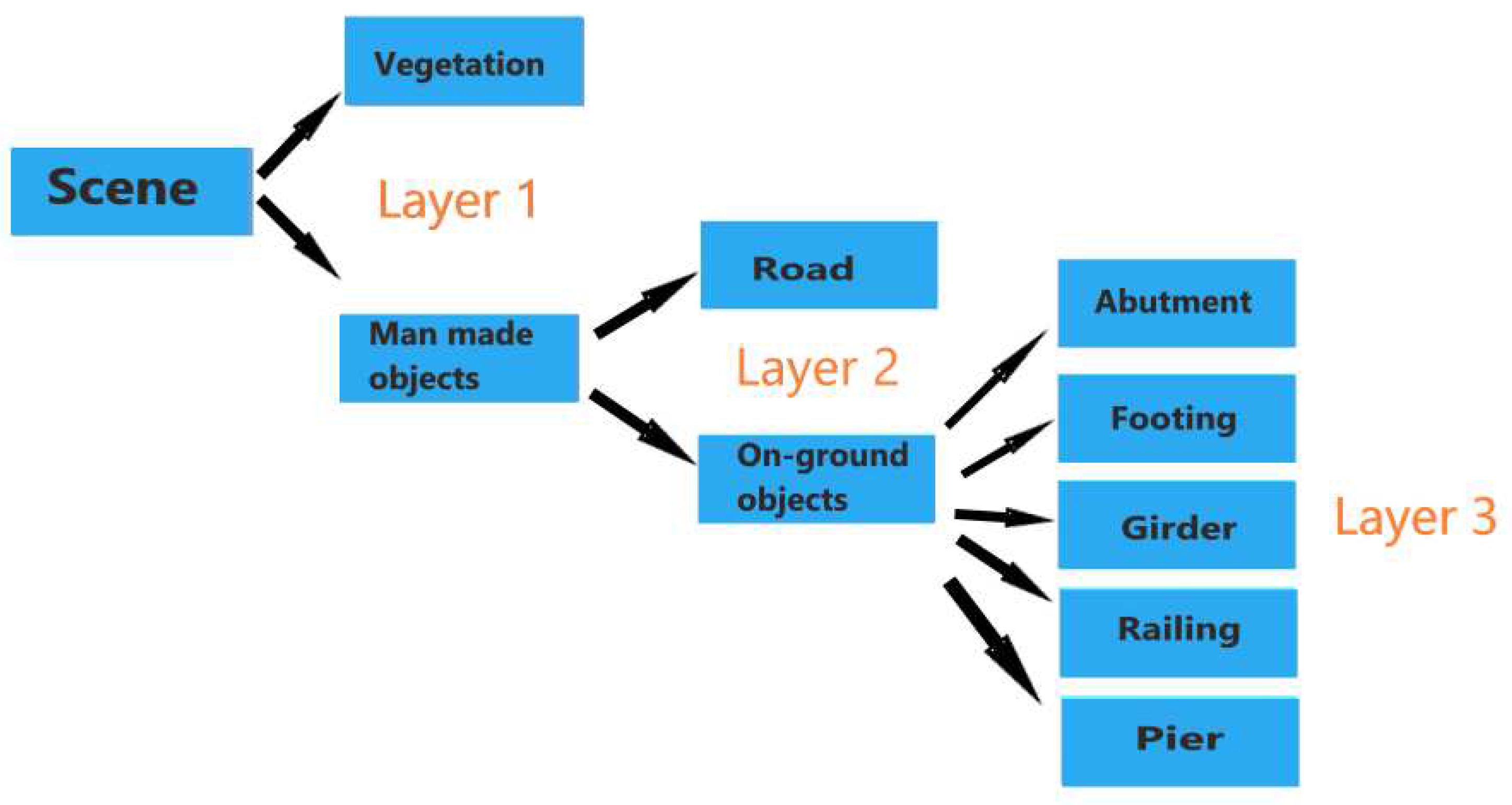
3.1. Hierarchy Support Vector Machine Approach
In 3D point cloud semantic segmentation using supervised learning methods, the necessary inputs for the model are features and the ground truth labeling. As a supervised machine learning model, SVM is used in this work to semantically segment the 3D point cloud of the infrastructure scene. Using the two techniques mentioned in
Section 2.1.3, one vs one and one vs rest, the whole scene can be segmented using a hierarchical approach derived from knowledge-based rules or insights about the scene. In this approach the 3D point cloud is semantically segmented through three layers, see Figure 3.1. At each layer different features and different techniques are used to separate between the multiple categories in that layer. In the first layer, the scene is classified into two categories, namely vegetation and man made objects, using one vs one technique. In the second layer, the classifier differentiates between ground and above ground objects using the same technique in the previous layer. Lastly, the 3D point cloud of the above ground objects is semantically segmented into different segments as abutment, footing, girder, railing and pier. In this layer, SVM classifier is applied using one vs rest technique.
Figure 10.
The hierarchy classification approach combining SVM solutions and decision tree framework.
Figure 10.
The hierarchy classification approach combining SVM solutions and decision tree framework.
3.2. Neighborhood Selection
This section presents the method used to determine the neighborhood of a 3D point in point cloud semantic segmentation. Traditional methods often rely on randomly selected scale parameters, such as
r or
k, based on empirical knowledge of the scene. In contrast, our approach, inspired by [
28], leverages the local 3D structure of the neighborhood to define the optimal scale parameter for each 3D point. This integration between neighborhood’s parameter selection and its local 3D structure ensures that each point’s neighborhood is the most representative, or optimal, for that specific point.
3.2.1. Optimal Neighborhood Definition
The concept of an optimal neighborhood refers to the largest cluster of spatially proximal 3D points that belong to the same category as a point of interest. The process of determining this neighborhood involves answering two primary questions: (1) what type of neighborhood should be used, and (2) what is the appropriate scale for this neighborhood? In the following sections, each of these questions will be discussed in detail to provide a comprehensive understanding of the process.
3.2.1.1. Neighborhood Type
For better understanding of the type of the neighborhood applied in this work it is worth to discuss the main difference between the common types. Unlike spherical and cylindrical neighborhoods, k-nearest neighborhoods do not include fixed spatial neighborhood sizes. Moreover, the selection of k points is based on the nearest euclidean distance to reference point X, both in 2D and 3D [
24,
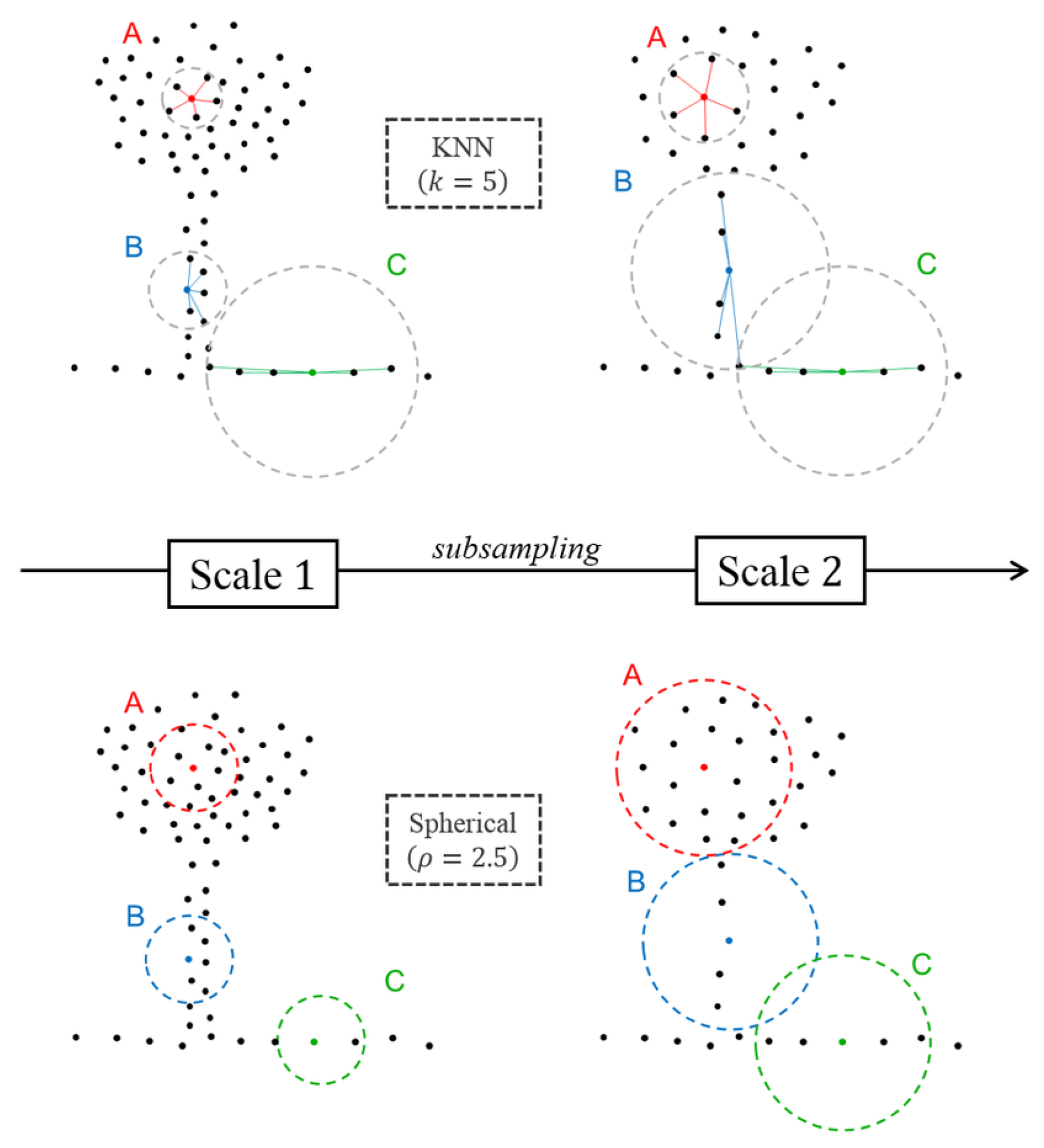
25]. On the other hand, the radius neighborhood definitions correspond to a specific part of the space and this property is a vital component to assign a more consistent geometrical meaning to the features. For these reasons, k-nearest neighborhood type was excluded for the semantic segmentation task in this work. Figure 3.2 shows the difference between the behaviour of spherical neighborhood and k-nearest neighborhood under two different scales.
Due to the characteristic of the cylindrical neighborhoods, this type of neighborhoods is found to be useful for delivering robust height information when the scene contains vertical man-made objects ( buildings, facades). As a result, this type will be applied in this work along with the spherical neighborhood definition.
Figure 11.
Behavior of the KNN and spherical neighborhoods under two different scales (scale 1, scale 2) at three different locations in the scene (A, B, C) [
18].
Figure 11.
Behavior of the KNN and spherical neighborhoods under two different scales (scale 1, scale 2) at three different locations in the scene (A, B, C) [
18].
Under the Euclidean norm, the spherical neighborhood
of point
at scale
r is defined as the set of points
verifying:
3.2.1.2. Selecting Scale of the Optimal Neighborhood
Selection of the radius of 3D point neighborhood is considered a heuristic or an empiric selection and specific to each data set. This means that the decision about the suitability of a neighborhood from a geometrical point of view is delayed to the classifier after obtaining the results. Showing the usefulness of the individual neighborhood, discussed in
Section 2.1.1, a generic selection of the neighborhood scale may be an alternative allowing a generalization of data sets and results in obtaining an optimal neighborhood.
The optimization of the parameter selection may be based on different criteria. The methodology introduced in this work aims to find automatically the optimal neighborhood radius based on the entropy feature (
). The idea is to find the optimal radius that achieves the best separation among the three main geometric patterns (linearity, planarity, scatter). Using Shannon entropy [
60] to find the distribution of these three geometric behavior, an energy function can be developed to define the optimal radius:
This energy function is based on the covariance matrix, which is also called 3D structure tensor and is calculated from the 3D coordinates of the neighborhood (
).
,
and
represent linearity, planarity and scatter, respectively, and can be calculated using the eigenvalues of the covariance matrix. The following equation can be used to calculate the 3D structure tensor:
where
denotes the center of gravity of
,
is the spherical neighborhood around reference point
.
Denoting the eigenvalues of the 3D structure tensor by
, where
, the three geometric features (
,
,
) can be calculated as follows:
The lower
in equation (3.2) is, the more one dimensionality prevails over the two other ones. This criterion allows to define an optimal radius
that minimizes
in the [
] space:
where
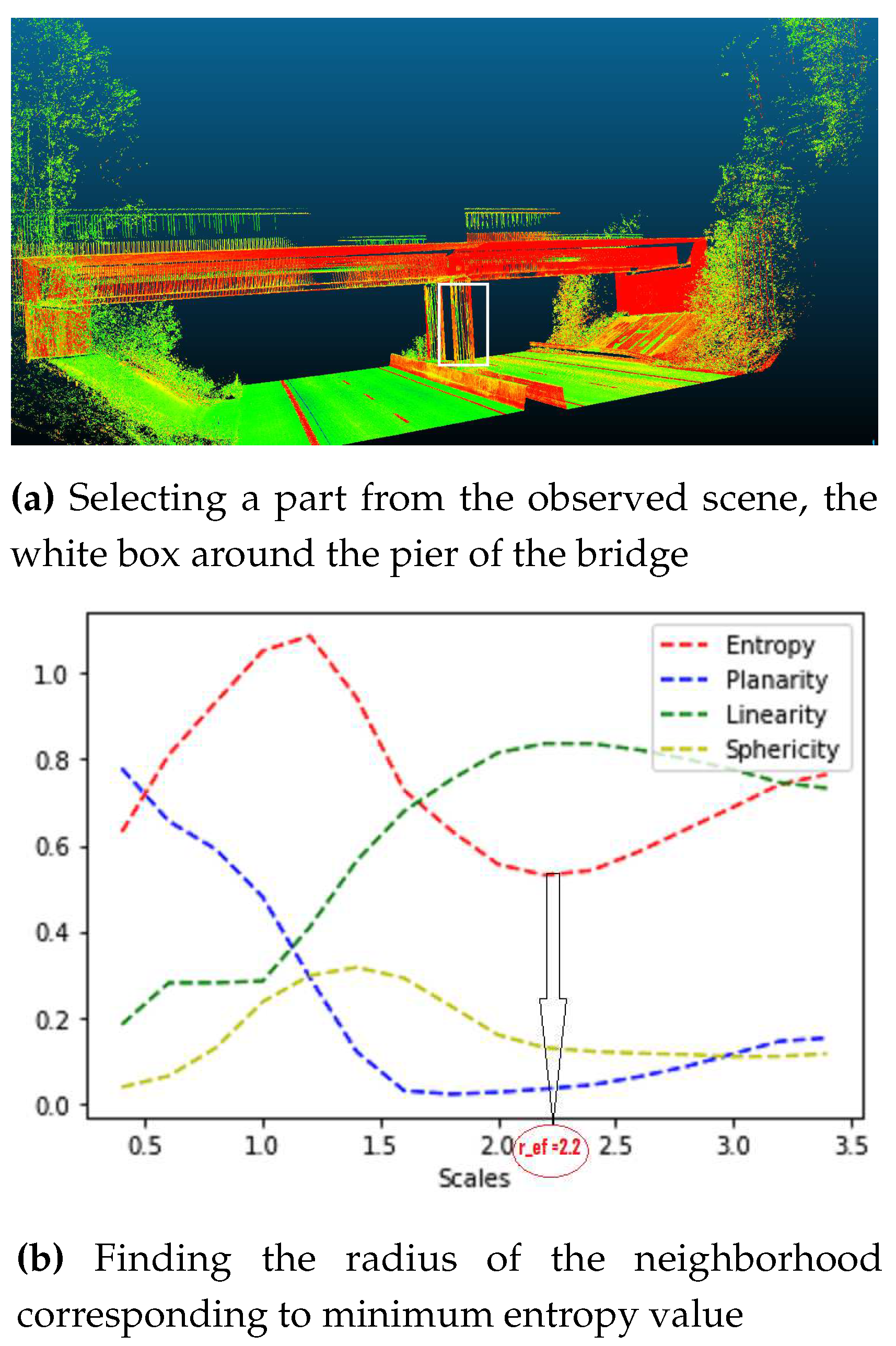
An illustration of the neighborhood selection can be shown in Figure 3.3. Here, the optimal scale that achieves the best separation between the three main geometric features for the selected part from the scene, the white box in Figure 3.3.a, is determined. This value corresponds to the lowest value of in Equation 3.2. One can observe that by increasing the scale, the pier of the bridge looks more linear and the linearity feature dominates over the other two features.
Figure 12.
Finding the optimal neighborhood around the pier of the bridge.
Figure 12.
Finding the optimal neighborhood around the pier of the bridge.
It is challenging to choose the boundaries of the radius, i.e,
, because they depend on multiple characteristics of the given data and are therefore specific for each data set. In one piece of literature, where TLS and MMS data set are investigated, 16 values were selected to represent the [
] space [
29]. There, the choice of the upper boundary was not critical and was selected based on the largest object in the scene, facades (3m). However, the selection of the lower boundary was found to depend on different aspects such as: the noise in the point cloud, the specifications of the sensor and the computational constraints. These different aspects were addressed in detail in the original work. Given that the radius of interest is frequently close to the (
), r values are not increased linearly but with a square factor instead. As a result, one notices an increase in samples near the radius of interest and a decrease of sample when reaching maximal values.
The paragraphs above highlighted the problem of point density and the scale of the neighborhood used. The problem concerning the lower boundary can be solved by controlling the number of points in each scale. An approach was introduced to avoid the strong variations of point density at different scales using the following relation [
18]:
where
is point density,
l is the size of the grid cell used for downsampling the point cloud and
r is the radius of neighborhood.
3.3. Feature Extraction
After the neighborhood is selected, the features of each neighborhood are extracted at different scales and combined together to identify a feature vector in the feature space. Metrical features are investigated in this work, each being represented by an individual value that specifies a particular property. In
Section 2.1.2, the most popular feature types in 3D scene analysis are introduced. In this work, two feature types are extracted and used during the different stages of the semantic segmentation process. The first type consists of geometric features, also referred to as 3D eigenvalue based features. The second type consists of height based features.
3.3.1. Geometric Features
Using the eigenvalues obtained from the 3D structure tensor, mentioned in
Section 3.2.1.2, different geometric features are extracted describing the spatial distribution of points in the neighborhood
of a 3D point
. One can use variety of geometric features [
36]. Planarity, linearity and sphericity features were sufficient for delivering good results.
In order to describe the verticality of the objects in the scene, the angle between the normalized normal vector and an "up"-vector (0,0,1) is calculated.
refers to the third component of the normal vector.
3.3.2. Height Based Features
Since the scene contains a variety of vertical objects, a cylindrical neighborhood search is very helpful to deliver decent height information in most of the cases. However, in some cases where a cylindrical neighborhood of an object contains noise from other classes, due to the location of that object in the scene, spherical neighborhood produces better height information. To make sure that robust height information is obtained, both neighborhoods are used parallel to each other depending on the location of an object in the scene. For each 3D point the following height features are extracted:
• maximal height features between any two points in the neighborhood
:
• using the statistical moments to give robust height feature. The standard deviation of the height is calculated using the following equation:
3.4. Learning Strategy
The 3D point cloud is semantically segmented using trained SVM classifiers. In the training stage, the feature vector constructed from geometric and height features, is utilized. To identify the optimal hyperparameters of the SVM classifier, a validation set is employed. During the training process, two critical considerations must be taken into account: Firstly, to enhance model generalization and prevent overfitting, the training data set should be evenly distributed. Secondly, the optimal strategy for labeling the neighborhood provided to the model during training must be established.
When faced with an imbalanced dataset, various methods exist to mitigate this issue. This study employs two such techniques. The first involves resampling the dataset so that each class contains an equal number of samples. This is accomplished by duplicating instances from the underrepresented class until balance is achieved. The second technique involves utilizing appropriate performance metrics to evaluate the quality of the model developed using an imbalanced dataset.
The process of assigning a label to a group of points in the training stage can take one of two forms. One approach is to label the neighborhood based on the predominant class among the points within it, which usually yields satisfactory results. Another option is to label the neighborhood relative to a specific reference point, which corresponds to the point of search of this specific neighborhood.
4. Results
This chapter reports the evaluation of the performance of the implemented classification algorithms and examines the influence of different feature sets on the overall performance of the Support Vector Machine (SVM) model. The results are contrasted with those of the PointNet deep learning model, with the aim of illuminating both the advantages and limitations of each method. Moreover, the two learning strategies of neighborhood labelling used during the training of the SVM model are evaluated and the results are summarized.
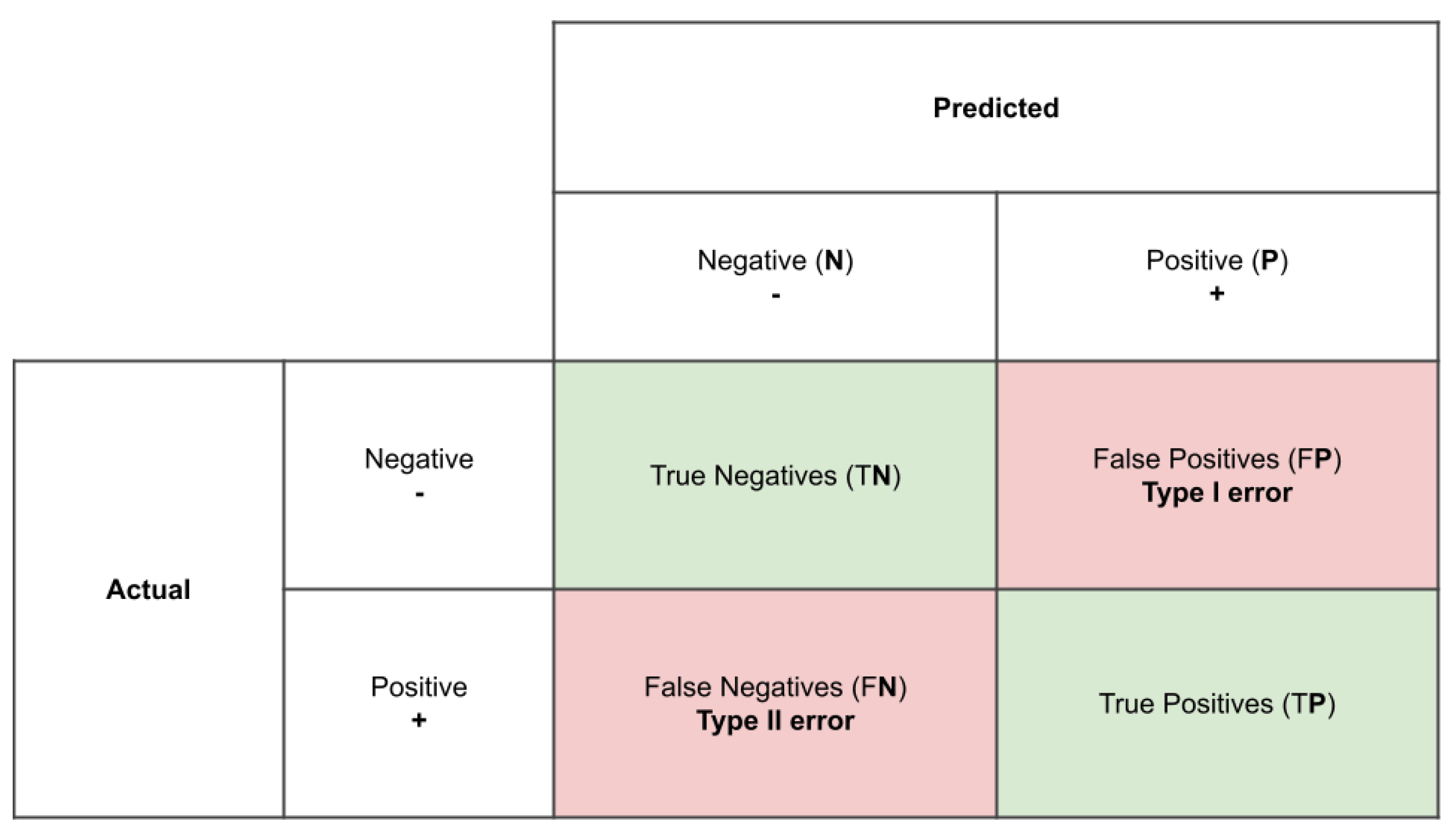
Since the predicted label of the test sample is either consistent or inconsistent with the true label, four possible outcomes can be reported from a prediction process. In the first case, the test sample is correctly predicted either true positive (TP) or true negative (TN). In the other case, the test sample is incorrectly predicted either false negative (FN) or false positive (FP). These four outcomes are summarized in the confusion matrix in Figure 4.1.
In order to quantitatively verify the quality of the results, the confusion matrix of each data set is obtained and different performance metrics are derived. These are: precision, confusion matrix, recall and overall accuracy. Observing the accuracy of each class, instead of relying on the overall accuracy of the classifier, leads to a more realistic evaluation of the model.
- (i)
precision (measure of correctness)
- (ii)
recall (measure of completeness)
- (iii)
accuracy (measures overall performance of the model)
Figure 13.
Confusion matrix .
Figure 13.
Confusion matrix .
4.1. Implementation Details/Tools
The workflow of 3D point cloud semantic segmentation described above, is implemented in Python. Scikit-learn [
61] offers a variety of tools to adjust and tune the parameters of the SVM classifier. It also contains several metrics to evaluate the model performance. Matplotlib [
62] offers different options for visualizing the results and provides an overview of the distribution of the classes in the data set. For the implementation of PointNet, Pytorch library has been used [
63].
4.2. Evaluation Data Sets
To assess the effectiveness of the hierarchical semantic segmentation method employing SVM algorithm and the deep learning method using Pointnet architecture, several real-world data sets of infrastructure objects are utilized. These data sets contain different types of scenes from Straßen NRW Nord in Germany. One type of scene displays roads without bridges and the second type of scene illustrates roads with bridges (see Figure 4.2 and 4.3, respectively). All scenes were captured using MLS.
Nevertheless, certain differences exist between the evaluation of the two methods with respect to the characteristics of the data sets utilized as well as the number of points employed for training and testing the models.
Figure 14.
Data set, scene one: Noise barriers, road, vegetation and signs in the scene of Straßen NRW with laser scan intensities shown in gray scale color.
Figure 14.
Data set, scene one: Noise barriers, road, vegetation and signs in the scene of Straßen NRW with laser scan intensities shown in gray scale color.
Figure 15.
Data set, scene two: bridge, vegetation and road in the scene of Straßen NRW with laser scan intensities shown in gray scale color.
Figure 15.
Data set, scene two: bridge, vegetation and road in the scene of Straßen NRW with laser scan intensities shown in gray scale color.
4.2.1. SVM Data Sets
In order to assess the efficacy of the SVM algorithm, two data sets from different scenes were utilized for training and testing. In the training phase, each class was represented by 1000 points, yielding a total of 5000 points for scene one and 7000 points for scene two, respectively. During the validation process, a total of 209,400 points were used for scene one and 149,114 points were used for scene two. Notably, the validation data sets were independent from the training data sets. The ground truth label of these scenes contained a total of 9 classes, encompassing all infrastructure buildings present in the scene. Table 4.1 summarizes the classes and number of points used in training and validation stages.
Table 1.
Summary for data points used in the training and validation of SVM model
Table 1.
Summary for data points used in the training and validation of SVM model
| Data set |
Classes |
Training () |
Validation () |
| scene one |
plant, road, railing, noise barrier, signs |
1000 |
209,400 |
| scene two |
plant, road, railing, abutment, girder, pier, footing |
1000 |
149,114 |
4.2.2. Pointnet Data Sets
The evaluation of the PointNet model was performed using 22 data sets comprising the objects of scene one. It is noteworthy that the PointNet model utilized a significantly greater number of points for both training and evaluation than the Support Vector Machine (SVM) model. Specifically, 8,691,712 points were employed for training the PointNet model and 1,634,304 points for evaluation.
4.3. Hierarchical Support Vector Machine Approach
Our developed approach was divided into three classification layers and is explained in detail in
Section 3.1. In the following table, the features used in each classification layer are summarized, along with the number of classifiers. Moreover, during the training process of the classifiers two different labelling strategies are employed and their performance is evaluated in this section.
Table 2.
Hierarchy classification features at each layer with the number of classifiers for the first scene
Table 2.
Hierarchy classification features at each layer with the number of classifiers for the first scene
| Classification layer |
Features |
Number of classifiers |
| layer 1 |
planarity, linearity, sphericity |
1 |
| layer 2 |
planarity, linearity, sphericity, maximal height, standard deviation of height |
1 |
| layer 3 |
planarity, linearity, sphericity, maximal height, standard deviation of height, verticality |
3 |
The first scene from the data set captures a high way and contains 5 classes. The overall accuracy of the SVM model for this scene was 93.94% . The classification performance for each class is shown in detail in the following table.
Table 3.
Performance metrics of all classes for HSVM semantic segmentation approach for scene one
Table 3.
Performance metrics of all classes for HSVM semantic segmentation approach for scene one
| Classes |
Precision[%] |
Recall[%] |
| plant |
80.7 |
100 |
| road |
98.1 |
97.7 |
| railing |
97.2 |
67.6 |
| noise barrier |
95.4 |
94.63 |
| signs |
98.3 |
97.4 |
Figure 16.
The semantic segmentation result of Straßen NRW data set for scene one, using Hierarchical SVM approach.
Figure 16.
The semantic segmentation result of Straßen NRW data set for scene one, using Hierarchical SVM approach.
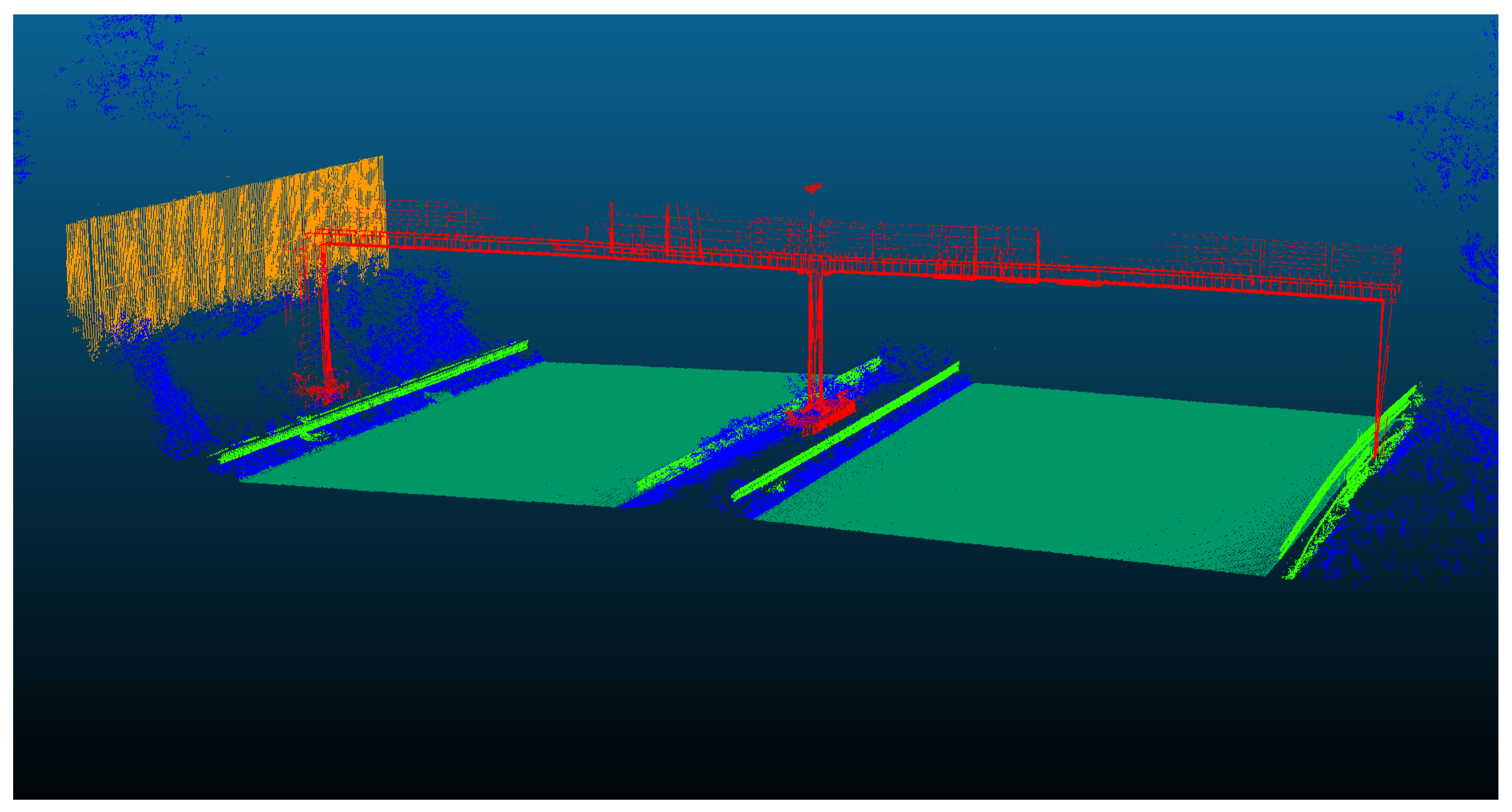
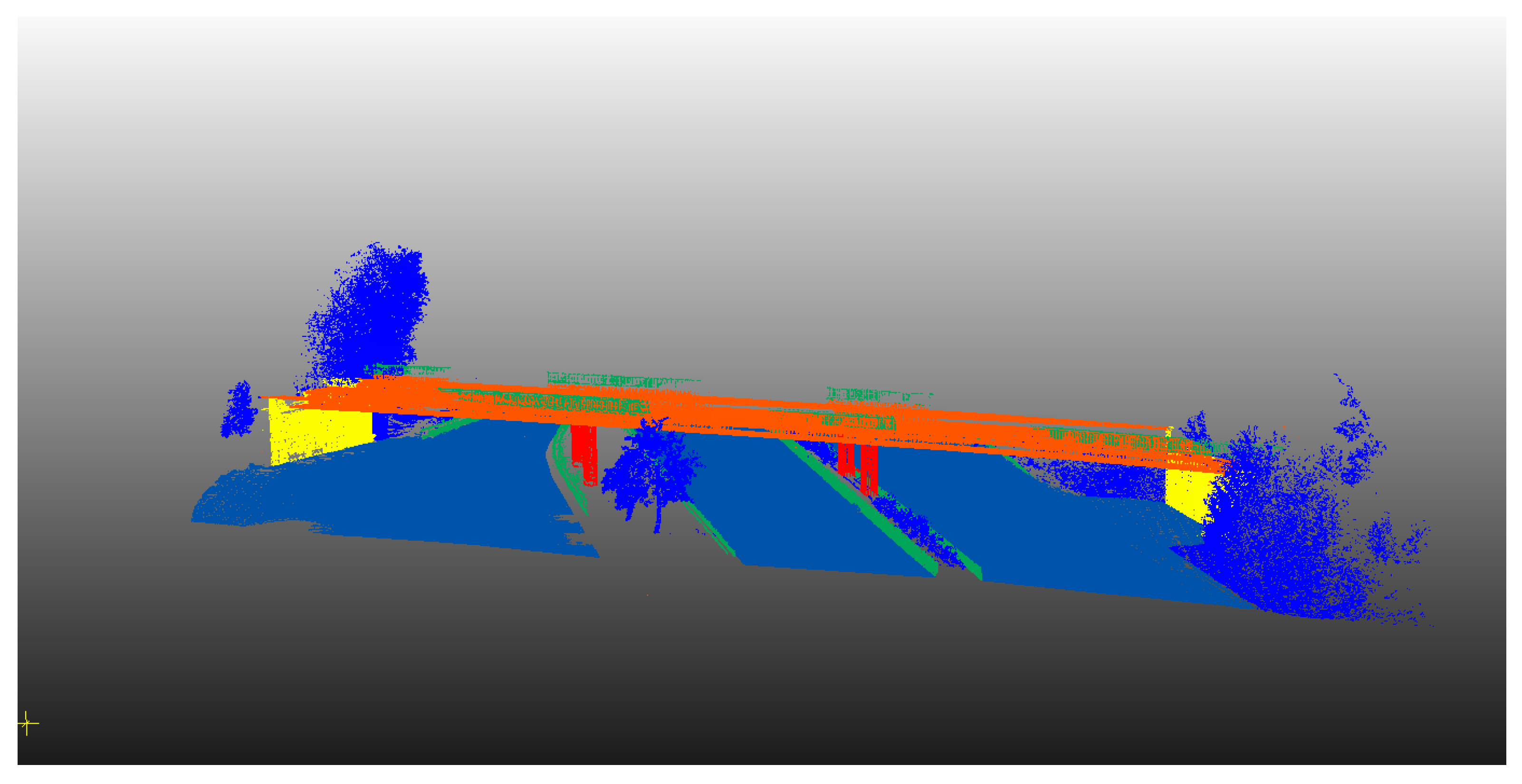
The second scene contains more classes due to the presence of the bridge elements. The performance of the SVM approach along with the evaluation metrics for each class are shown in Table 4.4 and Figure 4.5, respectively.
Table 4.
Performance metrics of all classes for HSVM semantic segmentation approach for scene two.
Table 4.
Performance metrics of all classes for HSVM semantic segmentation approach for scene two.
| Classes |
Precision[%] |
Recall[%] |
| plant |
90.00 |
81.67 |
| road |
95.52 |
100 |
| railing |
79.81 |
85.84 |
| abutment |
96.70 |
99.11 |
| girder |
79.61 |
100 |
| pier |
97.06 |
99.85 |
| footing |
94.01 |
90.93 |
Figure 17.
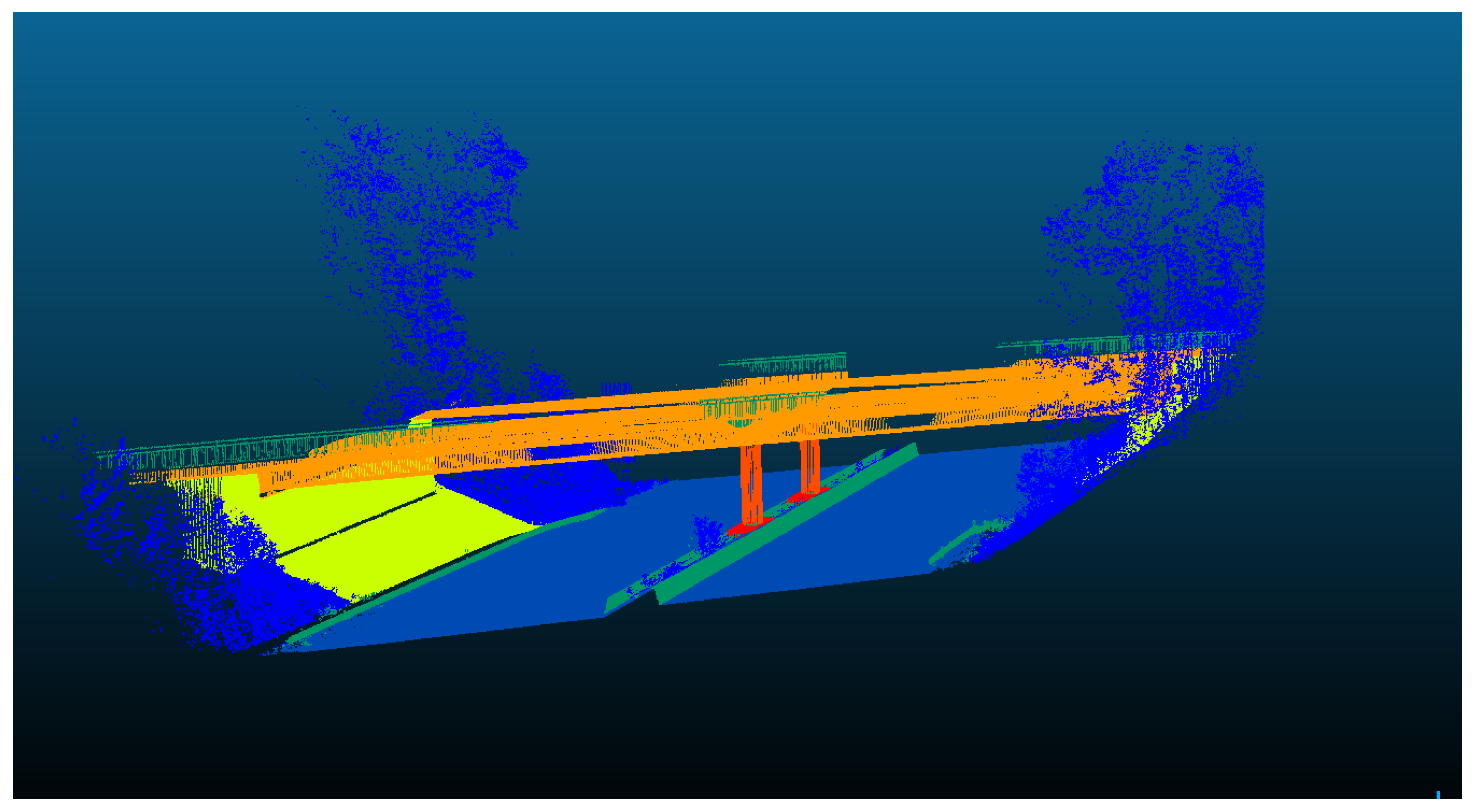
The semantic segmentation result of Straßen NRW data set for scene two, using Hierarchical SVM approach.
Figure 17.
The semantic segmentation result of Straßen NRW data set for scene two, using Hierarchical SVM approach.
4.3.1. Evaluating Hierarchical SVM Approach Using Different Learning Strategies
To explore the effects of the employed learning strategies during the training phase of the HSVM approach, the second data set of scene two was utilized. In each layer, the model was trained on both strategies, and the evaluation results based on each training method are presented in the following figures.
Figure 18.
Comparison between both learning strategies employed in the training process of the HSVM approach for data set of scene two.
Figure 18.
Comparison between both learning strategies employed in the training process of the HSVM approach for data set of scene two.
4.3.2. Evaluating Hierarchical SVM Approach on Additional Data Sets
The trained SVM model is applied to additional point clouds from infrastructure scenes and the results are shown in the figures below. Two data sets are used with total number of 296,141 points. Table 5 summarizes the classes and number of points used for the evaluation for each data set. These data sets are evaluated using different scales for the neighborhoods. The ranges of the radii were set to 0.5 () and 1 (). These scales were chosen heuristically based on the characteristics and the quality of each data set. The data sets are shown in following figures.
Table 5.
Additional data sets used to evaluate the model.
Table 5.
Additional data sets used to evaluate the model.
| Data set |
Classes |
Evaluation () |
| additional scene 1 |
plant, road, railing, abutment, girder, pier, footing |
201,029 |
| additional scene 2 |
plant, road, railing, noise barrier, signs |
95,112 |
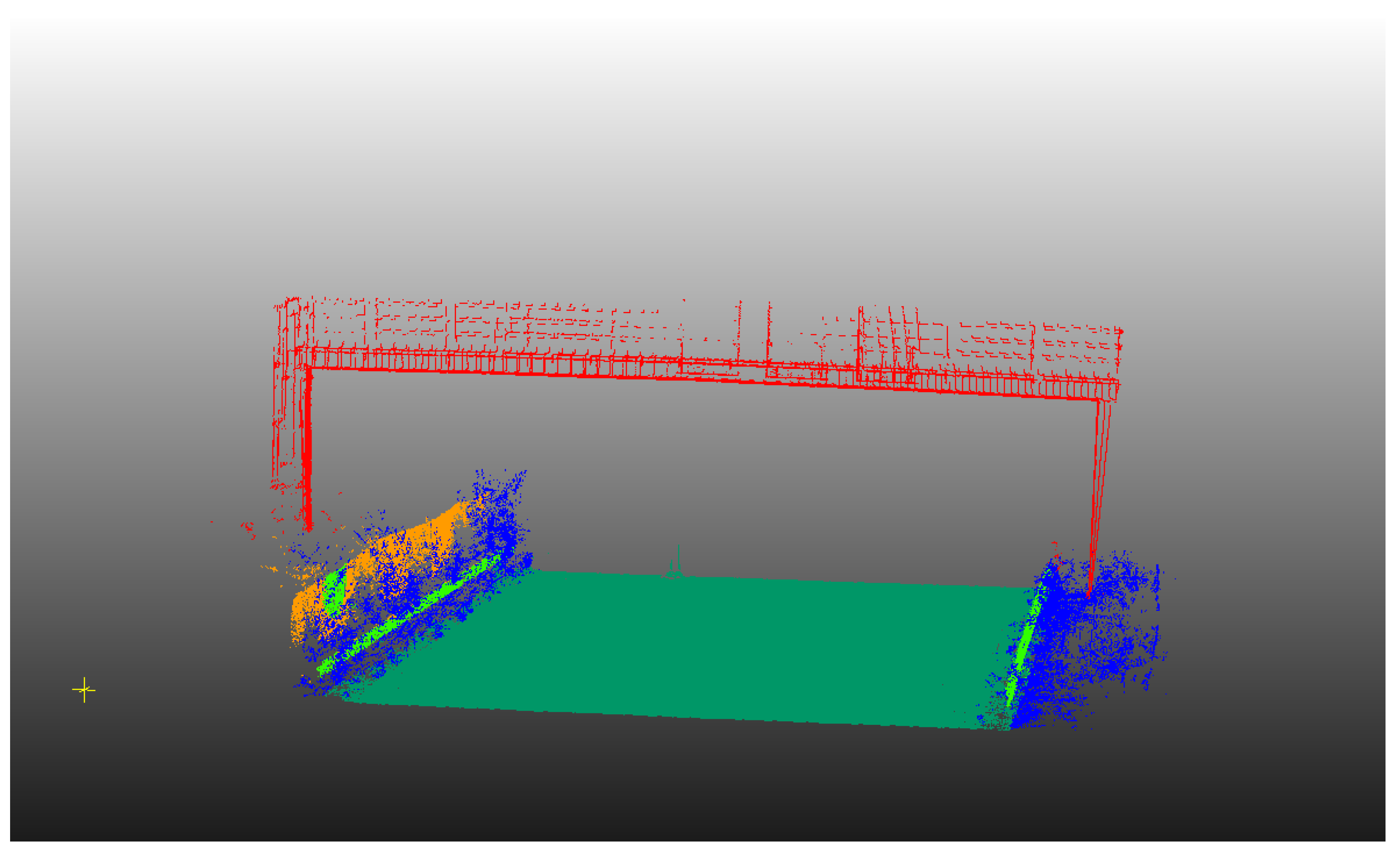
Figure 19.
Classification results of additional data set 1 of infrastructure scene containing 7 classes.
Figure 19.
Classification results of additional data set 1 of infrastructure scene containing 7 classes.
Figure 20.
Classification results of additional data set 2 of infrastructure scene containing 5 classes.
Figure 20.
Classification results of additional data set 2 of infrastructure scene containing 5 classes.
4.4. PointNet Model
Despite the simplicity of the input feature vector for the PointNet model, consisting solely of the raw x, y, and z coordinates of each point in the 3D point cloud, the results of its semantic segmentation performance are noteworthy and exhibit its ability to accurately segment objects in a scene. Despite this success, the optimization of its parameters remains a laborious task with further potential for improvement. The direct impact of these parameters on the model’s performance makes their definition highly significant.
4.4.1. Hyperparameters of Pointnet Model
- • Learning rate:
is a hyperparameter that determines the speed at which the model learns from the training data, and can have a significant impact on the accuracy and convergence of the model.
- • Batch size:
is a hyperparameter that defines the number of training examples used in one iteration.
- • Number of points in each batch:
the number of points in each batch refers to the quantity of down-sampled points extracted from the original point cloud and presented to the model as batches. These points should be representative of the characteristics of the original point cloud within the voxel, thereby ensuring that the down-sampling process retains the essential features of the original data.
- • Epochs:
an epoch refers to a single iteration through the entire training data set during the training of a neural network. The number of epochs determines the number of times that the learning algorithm will work through the entire training data set.
The parameters employed in the training of the model are detailed in the accompanying table.
Table 6.
Training parameters of the PointNet model.
Table 6.
Training parameters of the PointNet model.
| Parameters |
Values |
| learning rate |
0.001 |
| batch size |
32 |
| number of points in each batch |
4096 |
| epochs |
500 |
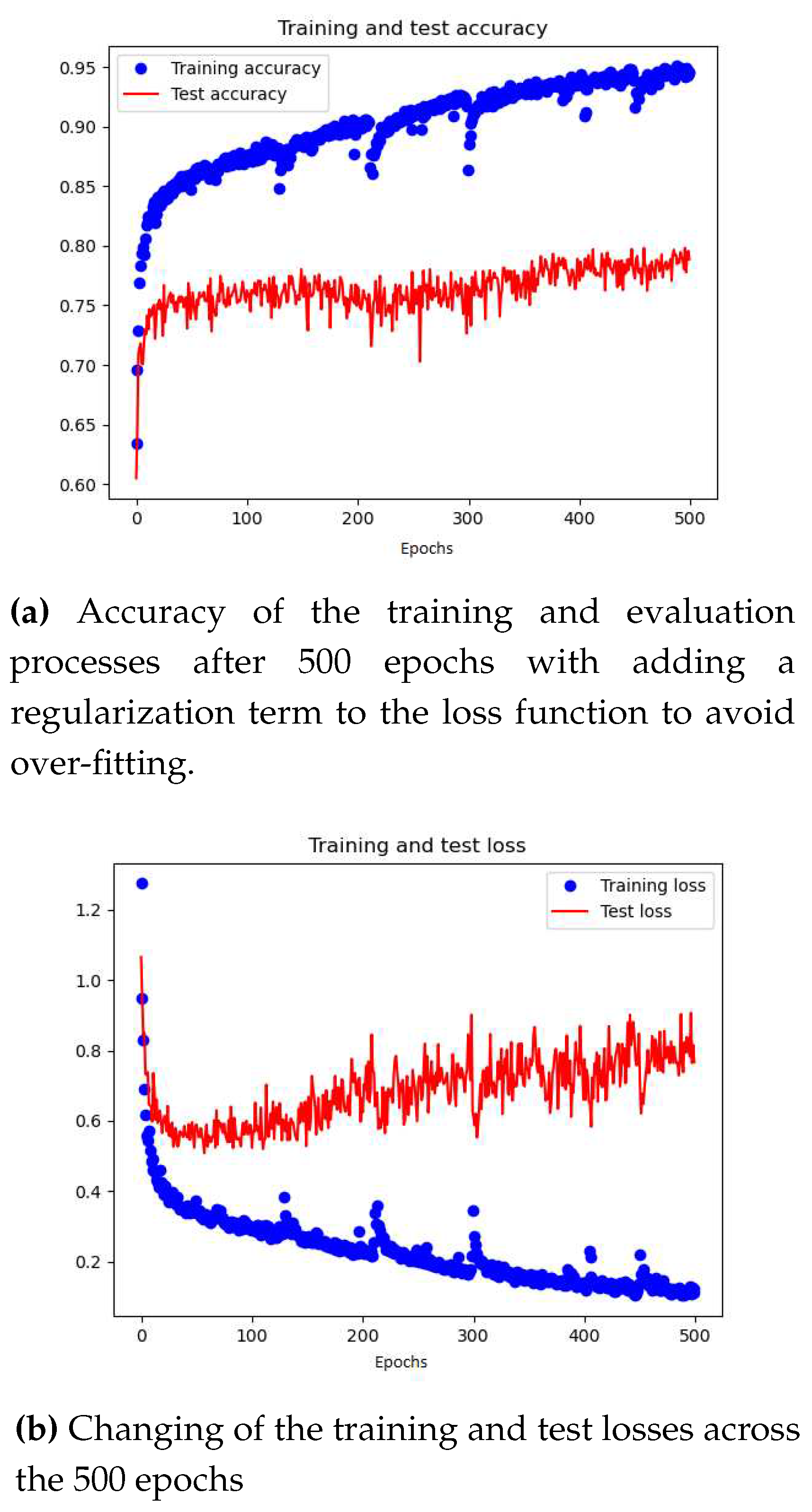
The results of the training and evaluation stages of the PointNet model are summarized in Figure 4.5, where the accuracy of the model is presented.
Figure 21.
Performance of the PointNet model using the raw xyz coordinates of each point as an input feature vector.
Figure 21.
Performance of the PointNet model using the raw xyz coordinates of each point as an input feature vector.
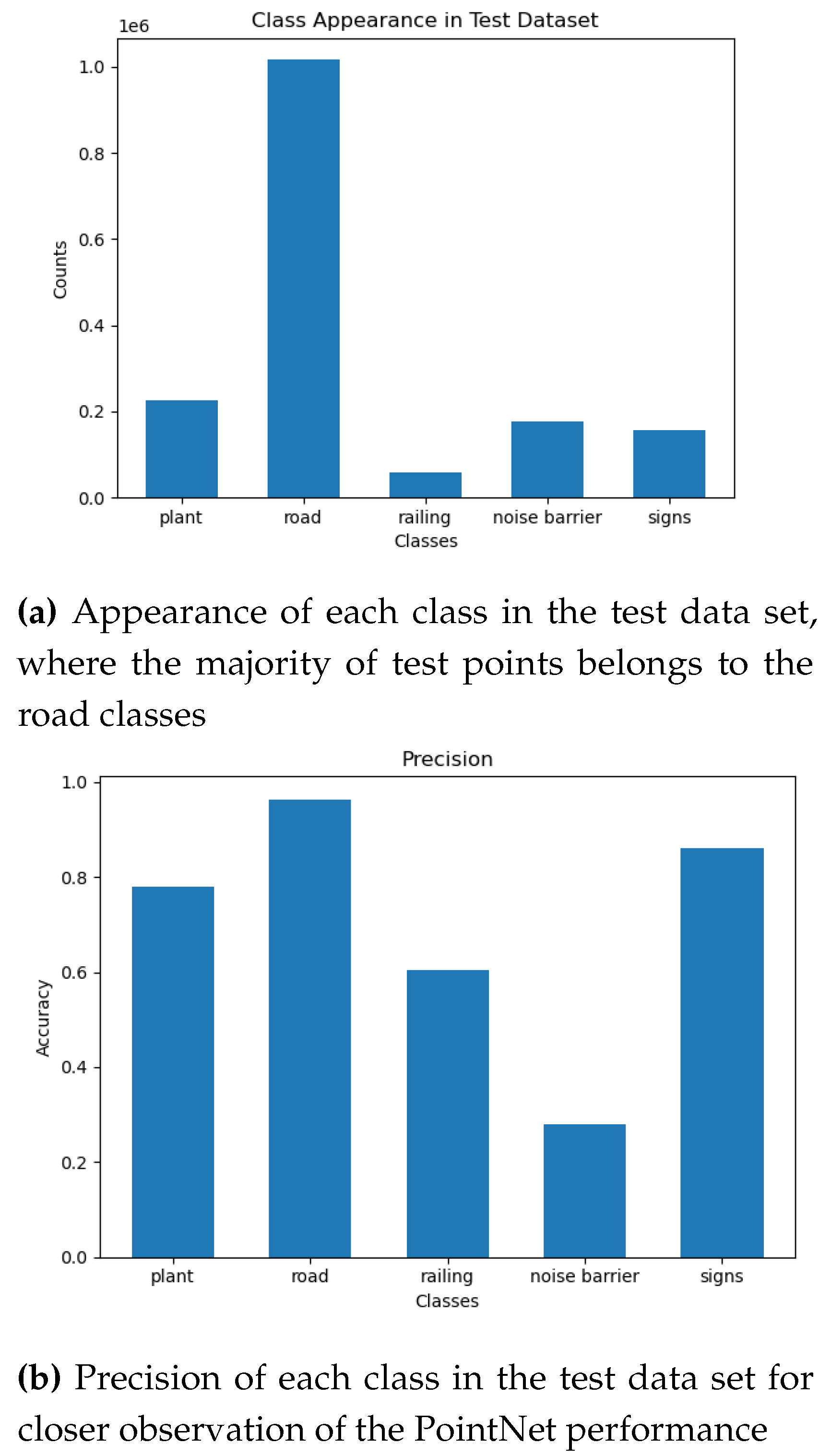
As evidenced by the figures presented above, the training accuracy of the model is 95%, demonstrating the proficiency of its deep learning architecture in capturing intricate relationships within the data. Conversely, the test accuracy is approximately 80%, indicating the potential of the model to generalize to unseen data sets. Given the imbalanced nature of the training and test data sets, it is more informative to examine the accuracy of each class in the test data set to gain a comprehensive understanding of the model’s performance. The following figures present the distribution of each class in the test data set and the respective precision scores.
Figure 22.
Imbalanced test data set and different precision values indicating the performance of the model which is also trained on imbalanced data set.
Figure 22.
Imbalanced test data set and different precision values indicating the performance of the model which is also trained on imbalanced data set.
5. Discussion
The introduced semantic segmentation approach produced notable results based on three significant techniques. The first technique involved defining an optimal neighborhood for each object to extract remarkable features. The second technique utilized the nature of the Support Vector Machine (SVM) classifier as a binary classifier for the development of a hierarchical semantic segmentation workflow. The third technique involved using a suitable learning strategy for labeling the neighborhood during the model training process.
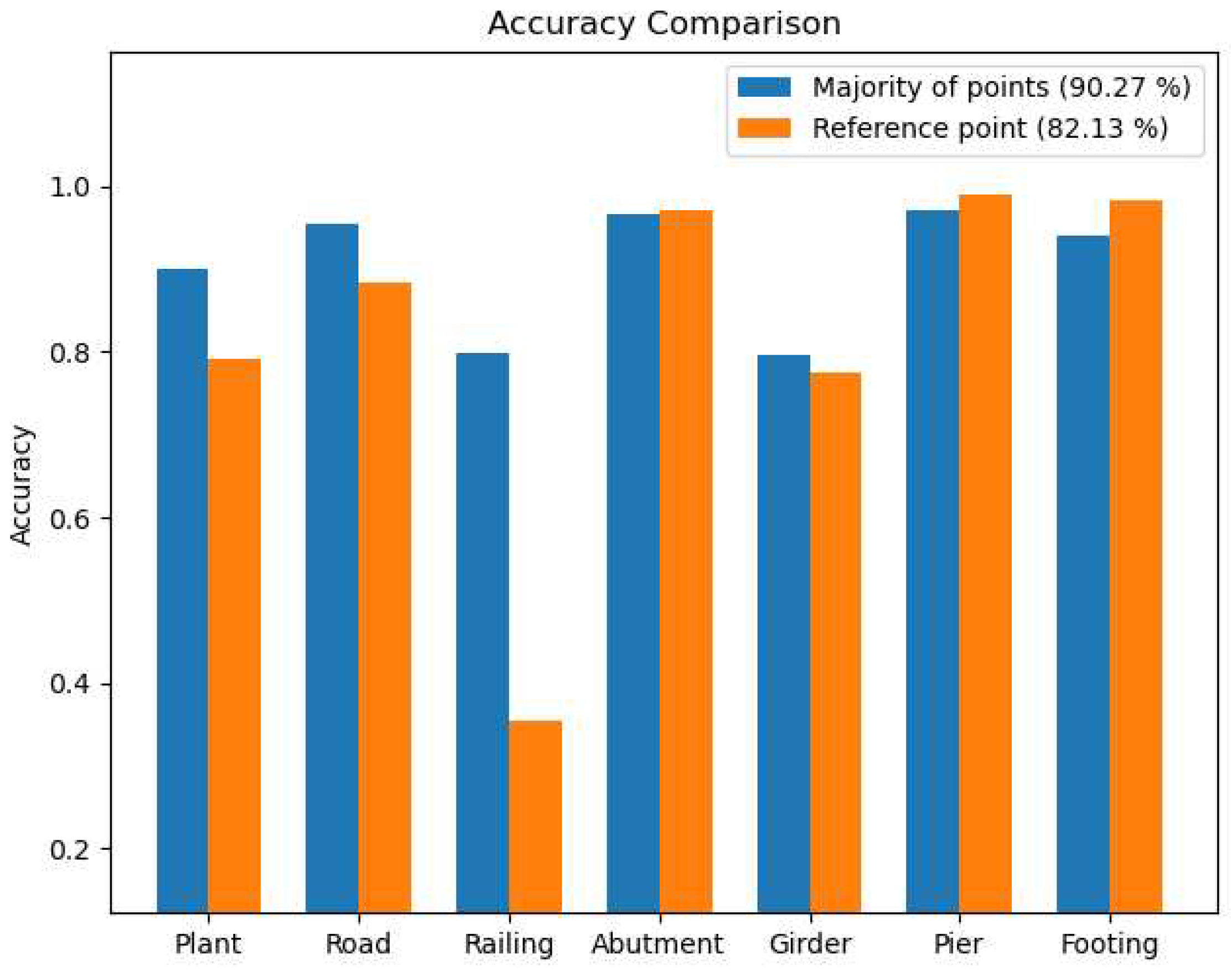
The use of an optimal radius for the neighborhood surrounding a point resulted in the extraction of higher quality geometric features without the need for features at multiple scales. This created a more robust feature vector for training the SVM model, which had a significant impact on each layer of the segmentation process. The feature vector provided valuable semantic information for both natural and man-made objects in the scene. Additionally, labeling the neighborhood according to the majority of points it contains improved the performance of the hierarchical semantic segmentation approach, with the majority of points often being the reference point, see Figure 4.6.
The hierarchical semantic segmentation method exhibited a high level of effectiveness in accurately segmenting and categorizing various objects in the scene, with an average accuracy of 93.94% and 90.27% for the first and second data sets, respectively. This success can be attributed to the selection of a suitable feature vector for each segmentation layer. The first layer utilized a robust feature vector that reflects the planar and linear nature of man-made objects, as well as the dense distribution characteristic of plants, represented by a high value of the sphericity feature. Subsequently, the feature vector in the subsequent layers incorporated height information of man-made objects, allowing for the distinction between ground and above-ground objects.
The Hierarchical SVM approach was also investigated using additional data sets comprising bridge and non bridge scenes.In the first data set some of the bridge railing points at large scales are generalized as a part of the girder. This is due to majority of girder points at these scales, which has an impact on the classification strength of the model, see Figure 4.7. On the other hand, most of the noise barrier in the second data set at large scales are displayed as a planar vertical objects, thus the majority of these points are correctly classified. However, at small scale these characteristic features could not be well recognized and thus classified as a linear object, specifically as a railing class, see Figure 4.8.
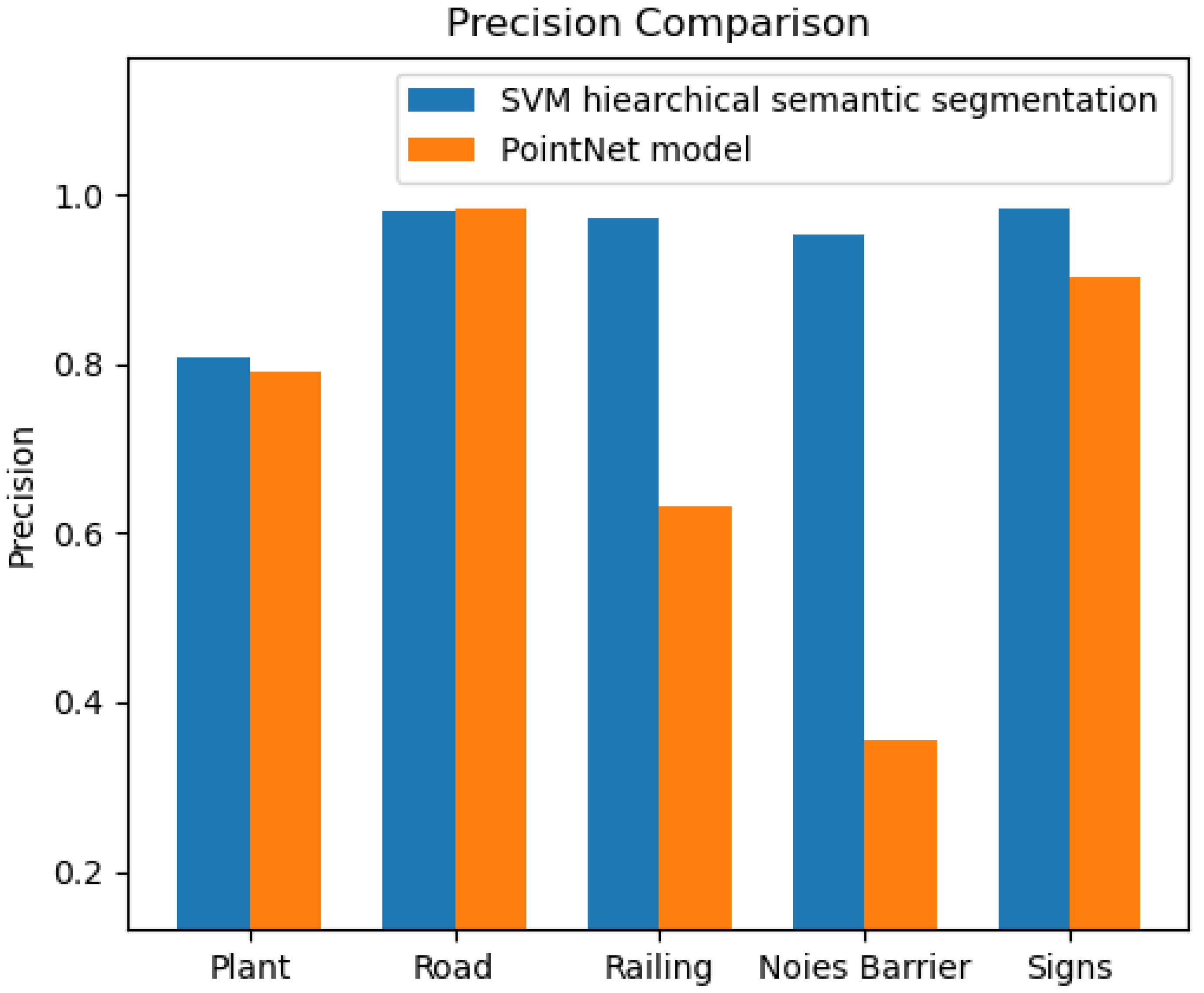
Comparison of the results of the SVM semantic segmentation method with those of the PointNet model showed that the utilization of diverse feature sets at each classification layer in the hierarchical approach led to an improved segmentation of the 3D points. The SVM classifier’s training process was aided by employing remarkable features between two or more classes in each layer as a feature vector to train the model. This feature vector significantly separated the classes in the feature space, thereby enhancing the SVM classifier’s performance (93.94%).
Figure 23.
Comparison between HSVM approach and Pointnet in terms of precision values for classes in data set of scene one.
Figure 23.
Comparison between HSVM approach and Pointnet in terms of precision values for classes in data set of scene one.
Although the PointNet model was trained on a large data set (8,691,712 points), its overall performance, (72.4%), still lags behind that of the approach employed in this study, which utilized a significantly smaller training data set. In regards to the segmentation of man-made objects in the scene, the PointNet model achieved satisfactory results for the road and sign classes. However, it performed poorly when it came to the railing and noise barrier classes, see Figure 5.1. This can be attributed to the imbalanced nature of the training data set and the use of a feature vector that only consisted of raw x, y, and z coordinates, which may not be sufficient to provide better results for these classes.
Optimizing hyperparameters such as learning rate, batch size, and number of epochs is crucial to improve the performance of the PointNet model. A high learning rate may cause the model to diverge, while a low learning rate may result in slow convergence. The optimal batch size depends on data set size, memory, and model complexity. Increasing the number of epochs can improve accuracy on the training set but overfitting may occur if the number of epochs is too high. Balancing these parameters is a challenging yet crucial task for optimal performance of the PointNet model.
6. Conclusions
This work investigated the idea of the automatic semantic segmentation of 3D point cloud for infrastructure objects, obtained by 3D laser scanners in order to generate a 3D model that contains geometric and semantic information of the asset according to BIM requirements. This automatic point cloud semantic segmentation is achieved by using machine learning techniques, a time-efficient method in the process of 3D point cloud modelling. The machine learning model assigns each 3D point to a specific class from number of classes in the scene, based on the correlations between inputs and outputs as defined in the training stage. In this paper, SVM was used as the primary classical machine learning algorithm, due to its high performance in the field of computer vision and 3D image processing. The performance of the proposed point cloud semantic segmentation approaches are primarily dependent on the features that are used to train the SVM classifier.
Different types of features were extracted and combined, constructing various numbers of feature sets. On the one hand, geometric features were generated describing the local 3D structure of the scene. On the other hand, height based features were defined, using statistical moments to complement the geometric features and obtain robust feature vectors. Although texture features were not investigated in this work, they could still be added for making the classification model more robust.
The Hierarchy semantic segmentation method was used dividing the scene into different categories. In this approach, the SVM was applied to the framework of a decision tree flow chart. As a result, classes were classified at each node of the decision three, thus eventually leading to increased performance accuracy of the model.
Features used in the training were extracted at different scales to describe the behavior of the neighborhood across the different scales. Since these scales are usually selected based on empiric or heuristic knowledge of the scene, the selection criteria discussed in this work depends on the local 3D structures of the neighborhood, also referred to as "dimensionality based scale selection" [
29]. The neighborhood defined based on this scale selection criteria is commonly known as optimal neighborhood and can be an alternative to multi-scale feature extractions. It can therefore be interpreted as a form of presegmentation, because the neighborhood itself can be representative of the characteristic features of the object. It is worth noting, however, that the scale boundaries defined in this selection approach are challenging and must be carefully chosen. The lower boundary is determined by various factors, including point cloud noise, sensor specifications and computational constraints [
29]. Furthermore, it can be argued that selecting a neighborhood scale that is too small, leads to fewer points and exhibits strong variation in point density. Selection of the upper boundary on the other hand is not as static and can be adjusted with the knowledge of the largest object in the scene.
In the learning stage, two approaches were implemented for neighborhood labeling. The first approach involved labeling the neighborhood based on the predominant class of points present in the area. In the second approach, the neighborhood was labeled based on a reference point. The first technique offers the ability to define features for specific classes on a large scale, even when points from other classes are present within that large scale neighborhood. This allows for more precise classification of features at different scales.
A comparative evaluation of the semantic segmentation results generated by SVM and PointNet was carried out to gain a deeper understanding of the strengths and weaknesses of each approach. The results revealed that the SVM approach was more efficient in terms of the required size of the training data set, as it produced better results with fewer points. This comparison sheds light on the trade-off between processing speed and accuracy, and enables researchers to choose the most suitable approach for a given task. The comparison can also contribute to the development of novel and improved algorithms for semantic segmentation. One potential avenue for improvement is to extract additional features and pass them to the PointNet model, or to integrate both approaches such that the SVM is used to pre-process the 3D point cloud into major groups, which are then passed to the PointNet model for further processing based on different geometric and texture features.
The semantic segmentation algorithms developed for point cloud data can only be applied to classify specific types of point cloud data sets that have similar properties to the data sets used in the training process. The models are trained to identify the average or specific properties of each class of an infrastructure asset, such as a bridge, and are thus only appropriate for filtering data sets that pertain to bridge components. The characteristics of each class learned by the models are dependent on the data acquisition technique used, such as the type of sensor and the flight plan, as well as the structure of the captured scene. Consequently, it is necessary to refine or retrain the classification models when encountering new types of point cloud data sets. Future works could explore the impact of various data acquisition techniques on the characteristics of each class to better understand the limitations of these models.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BIM |
Building Information Modeling |
| SVM |
Support Vector Machine |
| IoT |
Internet of Things |
| MLS |
Mobile Laser Scanning |
| TLS |
Terrestrial Laser Scanning |
| MMS |
Mobile Mapping System |
References
- Bryde, D.; Broquetas, M.; Volm, J.M. The project benefits of Building Information Modelling (BIM). International Journal of Project Management 2013, 31, 971–980. [Google Scholar] [CrossRef]
- Wong, A.; Wong, F.; Nadeem, A. Attributes of Building Information Modelling Implementations in Various Countries. Architectural Engineering and Design Management 2010, 6, 288–302. [Google Scholar] [CrossRef]
- Vilgertshofer, S.; Borrmann, A.; Martens, J.; Blut, T.; Becker, R.; Blankenbach, J.; Göbels, A.; Beetz, J.; Celik, F.; Faltin, B.; König, M. TwinGen: Advanced technologies to automatically generate digital twins for operation and maintenance of existing bridges. 2022.
- Ndekugri, I.; Braimah, N.; Gameson, R. Delay Analysis within Construction Contracting Organizations. Journal of Construction Engineering and Management-asce 2008, 134, 692–700. [Google Scholar] [CrossRef]
- Huang, Z.; Wen, Y.; Wang, Z.; Ren, J.; Jia, K. Surface Reconstruction from Point Clouds: A Survey and a Benchmark. 2022; arXiv:cs.CV/2205.02413. [Google Scholar]
- Sharma, R.; Abrol, P. Parameter Extraction and Performance Analysis of 3D Surface Reconstruction Techniques. International Journal of Advanced Computer Science and Applications 2023, 14. [Google Scholar] [CrossRef]
- Pătrăucean, V.; Armeni, I.; Nahangi, M.; Yeung, J.; Brilakis, I.; Haas, C. State of research in automatic as-built modelling. Advanced Engineering Informatics 2015, 29, 162–171, Infrastructure Computer Vision. [Google Scholar] [CrossRef]
- Rodríguez-Gonzálvez, P.; Jiménez Fernández-Palacios, B.; Muñoz-Nieto.; Angel.; Arias, P.; González-Aguilera, D. Mobile LiDAR System: New Possibilities for the Documentation and Dissemination of Large Cultural Heritage Sites. Remote Sensing 2017, 9, 189. [Google Scholar] [CrossRef]
- Ariyachandra, M.; Brilakis, I. Understanding the challenge of digitally twinning the geometry of existing rail infrastructure. 2019. [CrossRef]
- Grilli, E.; Menna, F.; Remondino, F. a Review of Point Clouds Segmentation and Classification Algorithms. ISPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2017, 42W3, 339–344. [Google Scholar] [CrossRef]
- Li, Q.; Yuan, P.; Lin, Y.; Tong, Y.; Liu, X. Pointwise classification of mobile laser scanning point clouds of urban scenes using raw data. Journal of Applied Remote Sensing 2021, 15, 024523. [Google Scholar] [CrossRef]
- Lu, H.; Shi, H. Deep Learning for 3D Point Cloud Understanding: A Survey. CoRR 2020, abs/2009.08920. [Google Scholar]
- Martens, J.; Blankenbach, J. VOX2BIM+ - A Fast and Robust Approach for Automated Indoor Point Cloud Segmentation and Building Model Generation. PFG – Journal of Photogrammetry, Remote Sensing and Geoinformation Science 2023. [Google Scholar] [CrossRef]
- Martens, J.; Blankenbach, J. An evaluation of pose-normalization algorithms for point clouds introducing a novel histogram-based approach. Advanced Engineering Informatics 2020, 46, 101132. [Google Scholar] [CrossRef]
- Thomson, C.; Boehm, J. Automatic Geometry Generation from Point Clouds for BIM. Remote Sensing 2015, 7, 11753–11775. [Google Scholar] [CrossRef]
- Anandakumar, R.; Nidamanuri, R.; Krishnan, R. Semantic labelling of Urban point cloud data. 2014, Vol. XL-8. [CrossRef]
- Mukhamediev, R.I.; Symagulov, A.; Kuchin, Y.; Yakunin, K.; Yelis, M. From Classical Machine Learning to Deep Neural Networks: A Simplified Scientometric Review. Applied Sciences 2021, 11. [Google Scholar] [CrossRef]
- Thomas, H.; Goulette, F.; Deschaud, J.E.; Marcotegui, B.; LeGall, Y. Semantic Classification of 3D Point Clouds with Multiscale Spherical Neighborhoods. 2018 International Conference on 3D Vision (3DV); IEEE: Verona, 2018; pp. 390–398. [Google Scholar] [CrossRef]
- Dogan, Ü. ; Edelbrunner, J.; Iossifidis, I. Autonomous driving: A comparison of machine learning techniques by means of the prediction of lane change behavior. 2011 IEEE International Conference on Robotics and Biomimetics, 2011, pp. 1837–1843. [Google Scholar] [CrossRef]
- Lu, Z.; Happee, R.; Cabrall, C.D.; Kyriakidis, M.; de Winter, J.C. Human factors of transitions in automated driving: A general framework and literature survey. Transportation Research Part F: Traffic Psychology and Behaviour 2016, 43, 183–198. [Google Scholar] [CrossRef]
- Yang, S.; Hou, M.; Li, S. Three-Dimensional Point Cloud Semantic Segmentation for Cultural Heritage: A Comprehensive Review. Remote Sensing 2023, 15. [Google Scholar] [CrossRef]
- Lee, I.; Schenk, T. Perceptual organization of 3D surface points. In: The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. XXXIV, Part 3A, 2002, pp. 193–198.
- Filin, S.; Pfeifer, N. Neighborhood Systems for Airborne Laser Data. Photogrammetric Engineering & Remote Sensing 2005, 71, 743–755. [Google Scholar] [CrossRef]
- Linsen, L.; Prautzsch, H. Local Versus Global Triangulations. Eurographics 2001 - Short Presentations. Eurographics Association, 2001. [CrossRef]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Contextual classification of lidar data and building object detection in urban areas. ISPRS Journal of Photogrammetry and Remote Sensing 2014, 87, 152–165. [Google Scholar] [CrossRef]
- Brodu, N.; Lague, D. 3D terrestrial lidar data classification of complex natural scenes using a multi-scale dimensionality criterion: Applications in geomorphology. ISPRS Journal of Photogrammetry and Remote Sensing 2012, 68, 121–134. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. FAST SEMANTIC SEGMENTATION OF 3D POINT CLOUDS WITH STRONGLY VARYING DENSITY. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2016, pp. 177–184. [Google Scholar]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS Journal of Photogrammetry and Remote Sensing 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Demantké, J.; Mallet, C.; David, N.; Vallet, B. DIMENSIONALITY BASED SCALE SELECTION IN 3D LIDAR POINT CLOUDS. ISPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2012, XXXVIII-5/W12, 97–102. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Mallet, C. Semantic 3D scene interpretation: A framework combining optimal neighborhood size selection with relevant features. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences 2014, II3, 181–188. [Google Scholar] [CrossRef]
- Pauly, M.; Keiser, R.; Gross, M. Multi-scale Feature Extraction on Point-Sampled Surfaces. Computer Graphics Forum 2003, 22, 281–289. [Google Scholar] [CrossRef]
- Blomley, R.; Jutzi, B.; Weinmann, M. CLASSIFICATION OF AIRBORNE LASER SCANNING DATA USING GEOMETRIC MULTI-SCALE FEATURES AND DIFFERENT NEIGHBOURHOOD TYPES. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences 2016, III-3, 169–176. [Google Scholar] [CrossRef]
- Vosselman, G.; Gorte, B.; Sithole, G.; B, T. Recognising structure in laser scanner point clouds. Inter. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2004, 46. [Google Scholar]
- Blomley, R.; Weinmann, M.; Leitloff, J.; Jutzi, B. Shape distribution features for point cloud analysis and A geometric histogram approach on multiple scales. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences 2014, II-3, 9–16. [Google Scholar] [CrossRef]
- Jutzi, B.; Groß, H. NEAREST NEIGHBOUR CLASSIFICATION ON LASER POINT CLOUDS TO GAIN OBJECT STRUCTURES FROM BUILDINGS. 2009.
- Weinmann, M.; Jutzi, B.; Mallet, C. Feature relevance assessment for the semantic interpretation of 3D point cloud data. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences 2013, II-5/W2, 313–318. [Google Scholar] [CrossRef]
- Chehata, N.; Guo, L.; Mallet, C. AIRBORNE LIDAR FEATURE SELECTION FOR URBAN CLASSIFICATION USING RANDOM FORESTS. Laserscanning; , 2009.
- Khanum, M.; Mahboob, T.; Imtiaz, W.; Ghafoor, H.A.; Sehar, R. A survey on unsupervised machine learning algorithms for automation, classification and maintenance. International Journal of Computer Applications 2015, 119. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Lin, Y.; Jiang, M.; Huang, Y.; Lei, Y. Consistency-Based Semi-Supervised Learning for Point Cloud Classification. 2021 4th International Conference on Pattern Recognition and Artificial Intelligence (PRAI), 2021, pp. 440–445. [CrossRef]
- Van Engelen, J.E.; Hoos, H.H. A survey on semi-supervised learning. Machine Learning 2020, 109, 373–440. [Google Scholar] [CrossRef]
- Park, Y.; Guldmann, J.M. Creating 3D City Models with Building Footprints and LiDAR Point Cloud Classification: A Machine Learning Approach. Computers Environment and Urban Systems 2019, 75, 76–89. [Google Scholar] [CrossRef]
- Hu, J.; Li, D.; Duan, Q.; Yueqi, H.; Chen, G.; Si, X. Fish species classification by color, texture and multi-class support vector machine using computer vision. Computers and Electronics in Agriculture 2012, 88, 133–140. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wu, L. Classification of Fruits Using Computer Vision and a Multiclass Support Vector Machine. Sensors (Basel, Switzerland) 2012, 12, 12489–505. [Google Scholar] [CrossRef]
- Osisanwo, F.; Akinsola, J.; Awodele, O.; Hinmikaiye, J.; Olakanmi, O.; Akinjobi, J. Supervised machine learning algorithms: classification and comparison. International Journal of Computer Trends and Technology (IJCTT) 2017, 48, 128–138. [Google Scholar]
- Murty, M.N.; Raghava, R. Kernel-Based SVM. In Support Vector Machines and Perceptrons: Learning, Optimization, Classification, and Application to Social Networks; Springer International Publishing: Cham, 2016; pp. 57–67. [Google Scholar] [CrossRef]
- Hachimi, M.; Kaddoum, G.; Gagnon, G.; Illy, P. Multi-stage Jamming Attacks Detection using Deep Learning Combined with Kernelized Support Vector Machine in 5G Cloud Radio Access Networks. 2020.
- Rivolli, A.; Read, J.; Soares, C.; Pfahringer, B.; de Carvalho, A.C. An empirical analysis of binary transformation strategies and base algorithms for multi-label learning. Machine Learning 2020, 109, 1509–1563. [Google Scholar] [CrossRef]
- Chen, C.; Li, X.; Belkacem, A.N.; Qiao, Z.; Dong, E.; Tan, W.; Shin, D. The Mixed Kernel Function SVM-Based Point Cloud Classification. International Journal of Precision Engineering and Manufacturing 2019, 20, 737–747. [Google Scholar] [CrossRef]
- Pu, S.; Rutzinger, M.; Vosselman, G.; Oude Elberink, S. Recognising basic structures from mobile laser scanning data for road inventory studies. Photogrammetry & Remote Sensing 2011, 66, 528–539. [Google Scholar]
- Madzarov, G.; Gjorgjevikj, D. Multi-class classification using support vector machines in decision tree architecture. IEEE EUROCON 2009, 2009, pp. 288–295. [Google Scholar] [CrossRef]
- He, Y.; Yu, H.; Liu, X.; Yang, Z.; Sun, W.; Wang, Y.; Fu, Q.; Zou, Y.; Mian, A. Deep learning based 3D segmentation: A survey. arXiv preprint arXiv:2103.05423, 2021. [Google Scholar]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3d point clouds: A survey. IEEE transactions on pattern analysis and machine intelligence 2020, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Qu, T.; Di, S.; Feng, Y.T.; Wang, M.; Zhao, T.; Wang, M. Deep Learning Predicts Stress–Strain Relations of Granular Materials Based on Triaxial Testing Data. Computer Modeling in Engineering & Sciences 2021, 128, 129–144. [Google Scholar] [CrossRef]
- Hinks, T.; Carr, H.; Truong-Hong, L.; Laefer, D.F. Point cloud data conversion into solid models via point-based voxelization. Journal of Surveying Engineering 2013, 139, 72–83. [Google Scholar] [CrossRef]
- Yao, X.; Guo, J.; Hu, J.; Cao, Q. Using Deep Learning in Semantic Classification for Point Cloud Data. IEEE Access 2019, 7, 37121–37130. [Google Scholar] [CrossRef]
- Ruizhongtai Qi, C.; Su, H.; Mo, K.; Guibas, L. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation 2016.
- Qi, C.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. NIPS, 2017.
- Thompson, N.C.; Greenewald, K.; Lee, K.; Manso, G.F. The Computational Limits of Deep Learning. 2022; arXiv:cs.LG/2007.05558. [Google Scholar]
- Zhang, M.; You, H.; Kadam, P.; Liu, S.; Kuo, C.C.J. PointHop: An Explainable Machine Learning Method for Point Cloud Classification. IEEE Transactions on Multimedia 2020, 22, 1744–1755. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; Perrot, M.; Duchesnay, E. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research 2011, 12, 2825–2830. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Computing in Science & Engineering 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; Desmaison, A.; Kopf, A.; Yang, E.; DeVito, Z.; Raison, M.; Tejani, A.; Chilamkurthy, S.; Steiner, B.; Fang, L.; Bai, J.; Chintala, S. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc., 2019; pp. 8024–8035.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).