Preprint
Article
The Effects of Flexible Cylinder Structural Dynamics to the Near Wake Turbulence
Altmetrics
Downloads
92
Views
21
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
29 June 2023
Posted:
30 June 2023
You are already at the latest version
Alerts
Abstract
A rigid protruding surface, agitator and vortex generator often dissipate more energy than to produce a satisfied turbulence production. In contrast, a passively-oscillating flexible protruding surface has the ability in generating greater turbulence level. In the current study, a circular finite cylinder (cantilever) was used as the geometry of the rigid and protruding surface. They were varied through the aspect ratio (AR) and materials. Also, a local Reynolds number within the subcritical flow range (102<ReD<105) was considered. The results from the rigid protruding surface (finite cylinder) is served as a validation to the published results and benchmark to the improve-ment of the turbulence generated by the flexible protruding surface. It was mentioned in the pre-vious work that the increment of turbulence production by the flexible cylinder is speculated to be oscillation, this work investigates the validity of the speculation through manipulating the struc-tural stiffness of the flexible cylinder by employing different materials. The results have further demonstrated that the flexible cylinder is capable of generating a greater turbulence through the examination of turbulence intensity, turbulence production term and Reynolds stress. All the flex-ible cylinders that oscillate show increment in turbulence production but at a different percentage. The cylinders studied in this work ranged from the least structural stiffness (EVA), moderate (al-uminium) to the highest structural stiffness (carbon steel). Through studying the normalized am-plitude responses graph of the flexible cylinder, it is identified that the oscillating motion does in-deed contribute to increment. A further investigation into the results, it is found that the factor which governs the increment is the structural velocity instead of just oscillating motion alone.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
The ability of vortex-induced vibration (VIV) to increase the strength of vortices shed through the vibration (e.g. see [1,2,3]) could promote the turbulence generated by flexible protruding surface. Vortex shedding (typically Kármán vortex) happens when flow past a bluff body. Under condition where the structure is rigid enough (high stiffness) to resist the different pressure distribution on the structure caused by the unsymmetrical vortices, it experiences little to negligible motion (oscillation or vibration as their meaning are interchangeable in this context). As is the same with rigid protruding surface, some portion of the oncoming fluid loses kinetic energy as it meets the rigid protruding surface. Given a flexible body with low Young modulus properties and a geometry with low second moment of area, the bending stiffness will inherently be lower. Therefore, smaller fluid force is needed to drive the vibration in order for the VIV to happen.
The main component that determines the flexibility or elasticity of the flexible cylinder is the structural stiffness, as shown in Figure 1. Stiffness relies on material properties and geometry. Therefore, it is the combination of the material’s Young’s modulus, E and the element’s second moment of inertia, I.
Under general situations, there are two types of vortex shedding that can affect the oscillation mode of the VIV and one of which is perhaps more commonly known than the other – the Kármán vortex shedding. The Kármán vortex street consists of the alternately shed vortices due to the asymmetric vortex shedding behaviour. It is the asymmetric vortex shedding behaviour that alters the pressure distribution on the surface of each side of the cylinder, thus, leading to the vibration of the cylinder in transverse direction to the flow. This type of vibration is also widely known as cross-flow motion. The second type of vortex shedding is the symmetric vortex shedding. As the name suggests, it consists of a pair of symmetrical vortices when shed in one cycle. The vibration mode of this shedding is in-line or parallel to the flow, hence the name of in-line VIV. Under certain conditions, in-line VIV accompanied by symmetric vortex shedding may occur at lower flow velocities than the Kármán vortex shedding [4]. Another type of shedding that would happen in addition to either the Kármán vortex shedding or symmetric vortex shedding, is the tip vortex shedding. It happens whenever the free end of the cylinder is exposed to the flow. These tip vortices are generally shed at a frequency one-third the Kármán vortex shedding and may cause large amplitude vibrations.
The back and forth motion, which are lift and drag, is due to vortex shedding at which the vortex shedding frequency, fs was close to the cylinder natural frequency, fn at the velocity. The Strouhal number, St is the frequency of the excitation force in the lift direction whereas the frequency of the excitation force in the drag direction is normally two times the lift direction. The lift force can be explained as a group of vortices shed to one side of the cylinder once per cycle and the other side. The lift force, which appears when the vortex shedding starts to occur, causes the cross-flow motion (perpendicular to the fluid flow direction). Similarly, the drag force appears as a result of vortex shedding but with all vortices shed downstream. In-line motion (in the same direction as the fluid flow) of the cylinder is caused by drag force. Since all the vortices are shed downstream of the cylinder in the drag direction, the drag force associated with vortex shedding occurs at twice the frequency of the lift force, as explained by [5].
Higher amplitudes of vibration in cross-flow direction have been documented by various experimental results in [5,6]. When the amplitude reaches its maximum, lock-in is said to happen. Lock-in occurs when the natural frequency of the structure, fn is in proximity with the vortex shedding, fv, or in mathematical expression, = 1. Both frequencies synchronise and large amplitude vortex induced structural vibration can occur. The vortices in lock-in condition can pack a colossal amount of energy. Besides the increase in vortex strength, consequences of lock-in also increase correlation length, in-line drag force, and lock-in bandwidth; all of which result in the increase of maximum amplitude. The lock-in bandwith was found to increase with increasing response amplitude [7]. It is easy to see that the lower mass ratio cylinders, require lesser energy to make vibration of the cylinder because it is lighter compared to higher mass ratio cylinders. Thus, it is able to achieve the maximum amplitude (lock-in) more effortlessly at a wider range of reduced velocity, as opposed to the higher mass ratio cylinders.
The wake structure differs according to below and above the critical aspect ratio. The AR of the cylinder is defined by its length over diameter ratio, AR = L/D. From the various studies by several authors, the value of critical aspect ratio seems to be sensitive to experimental conditions, especially the relative thickness of the boundary layer [8,9]. The critical aspect ratio varied from AR = 1-7 in many literatures, which is a wide range. When a cylinder at a very low AR is immersed in an atmospheric boundary layer, the vortex formation length, the width of the near wake and the value of Strouhal number at mid-height are reduced, comparable to the case of small relative thickness of the boundary layer [10,11]. Liu et al. [12] supported that a two-dimensional region exists when the AR is greater than the critical aspect ratio but the area of the two-dimensional region decreases when the Re increases. It should however be noted that the range of critical aspect ratio is only loosely defined based on the observation of the wake structure. It can be seen that the critical aspect ratio is sensitive and scales with the boundary layer thickness and Re because the AR has to be large enough in order to sustain the two-dimensional region. A lower AR or AR lower than the critical aspect ratio that is put in a higher Re and a thicker boundary layer signify that the region of free end effects will engulf the whole span of the cylinder, supressing the two-dimensional region.
Tip vortices are known to have more turbulent energy than the regular Kármán vortices. The turbulence intensity has also been reported to increase considerably at the free end of the cylinder. In the recent work of [13], they demonstrated that the streamwise turbulence intensity (u’/U) and wall-normal turbulence intensity (w’/U) are indeed higher at the free end and within the recirculation region on the wake centreline (y/D = 0). On the other hand, Park and Lee [14] also showed in their results, that the turbulent kinetic energy is at its highest level at the free end for cylinder of AR = 6 at ReD = 7,500. Rostamy et al. [13] noticed that the elevated turbulence intensity extends into the downwash region. One noticeable distinct pattern that separates the cylinder of AR = 3 from the rest is that the location of the highest wall-normal turbulence intensity moves downward and further away to a distance of x/D = 2. The location of the highest wall-normal turbulence intensity appears to remain at x/D < 2 as the AR of the cylinder increases.
Similarly, the Reynolds shear stress (-) are also reported to be at a higher value in the experimental work from [13]. They noticed a region of positive shear stress and a region of negative shear stress at an evaluated value near the wake region. However, the region of positive shear stress is absent below the free end, leaving only the region of negative shear stress for cylinder of AR = 3. On the contrary, the positive shear stress is dominating the region just below the free end for AR = 9 but slowly decreasing in size and level as the AR decreases until it disappears at AR = 3. In their results, the Reynolds shear stress are found be at highest for cylinder of AR = 9 with the peak at 0.018. However, the Reynolds shear stress decreases as AR decreases. Besides, according to Figure 2, [8] also showed in their experimental results that the vorticity contour is immensely elevated near the free end. Thus, the tip vortices can greatly improve the quality of mixing. However, due to the downwash phenomenon that is always present at the free end, the tip vortices are always brought downwards to the ground plane. Therefore, its influence could only impinge on fluid in the very near wake. The mean velocity, turbulence intensity and Reynolds shear stress distributions are similar for cylinders above the critical aspect ratio but dissimilar for cylinders below the critical aspect ratio [15].
The Reynolds normal () and shear () stress of a flexible cylinder has also been reported by [16] to increase significantly compared to that of rigid cylinder. They first investigated the Reynolds shear stress of a rigid cylinder and compared with the results from [17]. The periodic part of Reynolds normal and shear stress of both authors are a near match though the experiment conducted by [17] was much higher at Re = 140,000. The peak total Reynolds stress is however much higher for the higher Re experiments. Govardhan and Williamson [16] therefore concluded that the periodic part of Reynolds stress, which is generated from the repeatable large-scale coherent structures, holds true over the range of Re = 3,900 to 140,000. As the other component of total Reynolds stress – random part of Reynolds stress, gain strength from the increasing strength of the Kelvin-Helmholtz instability of the separating shear layer as Re increases, the total Reynolds stress value increases. They also compared the Reynolds normal and shear stress value of vibrating cylinder to that of rigid cylinder and found that the largest increase in periodic part of Reynolds stress ()max increases by 485%, ()max increases by 100% and ()max increases by 125% in the lower branch.
It was shown in the previous work [6,18,19] that the flexible cylinders bring significant changes to the turbulence in the near wake – the x-deflection of the flexible cylinders increases the turbulence wake region, which effectively increase the region of turbulent activities; and the aspects of the structural motion such as oscillating amplitude, oscillating frequency and the oscillating motion are able to enhance the turbulence energy production as demonstrated by the production term (in the kinetic energy budget) and the Reynolds stresses. Despite the remarkable findings, it is unable to confirm which parameter(s) of the structural motion could bring effects to the enhancement of turbulence energy in the near wake. It is therefore, this work mainly investigates the influence of different properties of the flexible cylinders to bridge the gap. As an effort to encourage an organized oscillating motion, material properties such as aluminium and carbon steel with moderately high stiffness and low damping coefficient are employed in this studies. The metal group flexible cylinders are performed at Reynolds number of 2,500 due to the limitation of the highest possible freestream velocity the water tunnel could provide. Apart from that, AR = 12 and 14 of polymer based EVA flexible cylinders at Reynolds number of 4,000, 6,000 and 8,000 will also be investigated in this work.
2. Materials and Methods
These objectives are achieved by conducting experimentally in an open channel water tunnel, as shown in Figure 3. In order to gain insights of the flow behaviour, Ultrasonic Velocity Profiler (UVP), capable of measuring velocity vector as a function of both space and time in an unidimensional Eulerian frame, was used to obtain the velocity vectors. The calibration of the 2 MHz transducer was carried by positioning it at a trajectory angle that has the minimum Doppler angle error possible which is used in speed calculations. As stated by Yokoyama et al. [20], at least two transducers are needed in measuring two-dimensional flow and three transducers for three-dimensional flow. This is because each transducer is needed to measure each velocity component at one spatial point in order to form a vector. The vector is therefore obtained from any two non-parallel measured components. As the vector component is an orthogonal projection of a true vector into a measuring line (Figure 4), therefore, a large projection angle in between the two transducers is encouraged to avoid large inaccuracy in direction estimation. In other words, a two-dimensional flow or three-dimensional flow measurements, unlike the technique of one-dimensional flow measurements, relies solely on the orthogonal composition technique which in turn can only be achieved at their respective intersection points. Further details on the experimental set-up and UVP description can be referred in [19,21].
With that in mind, the projection angle between two transducers is orthogonal (90° in between the two transducers) when measuring the u and w velocity components behind the finite cylinder. For each of the measurements, 4069 samples were taken at a sampling rate of 100 Hz. Though proven mathematically that the sampling rate must be twice the highest frequency contained in the analogue signal, researchers normally would opt for a sampling rate more than twice the highest frequency contained in the analogue signal if plausible, to be safer, the 100 Hz sampling rate chosen in this experimental work was the highest sampling rate that could be selected after sacrificing the repetition to only 64 pulse. When considering the St for a cantilever, the St is approximately 0.14 ~ 0.18 [8]. Based on the Strouhal number equation, , selecting the maximum St, freestream velocity and the minimum diameter give the opportunity in accounting for the maximum vortex shedding frequency available in this work. Taking into consideration, the sampling rate chosen is twice as big than the maximum vortex shedding frequency calculated ~ 40 Hz.
A traverse is important as it guides the UVP accurately. The basic design of traverse can be seen in Figure 5 and Figure 6. It can be extended in x and z directions. The main body of the traverse was taken from a drawer slides as it can be extended with minimum friction and the extension was perfectly guided so it could travel in a straight line. The extension can be made up to 25 cm long. The extension had a resolution of a ruler, which is 1 mm, as a 50 cm long ruler was fitter on the guiding rail. The drawer slides were made to sit on a steel frame that provide stability to the traverse. All the joints were bolted using hexagonal nuts and bolts to ensure the sturdiness of the structure. In order to account for the ability to move in the z direction, 4 hollow bars were welded onto the 2 inch flat bars. The UVP transducer was attached to the holder that were moved and guided by the square hollow bar. When the transducer reaches a desired location, the holder was jammed by the bolts so that it would stay in place. The UVP probe emits sound waves in z direction (top to bottom) and x-direction (streamwise). They are free to move in x and z direction to collect the velocity around the cylinder upstream and downstream.
A set of experiments was performed to investigate the boundary layer and properties of the flow prior to the finite and flexible cylinder experiments. The boundary layer thickness, δ was defined as the point where the local mean velocity was 99% of the freestream velocity while the displacement thickness, δ* was defined as the boundary layer displacement thickness. The momentum thickness, δθ on the other hand, was defined as the distance by which the boundary should be displaced to compensate for the reduction in momentum of the flowing fluid on account of boundary layer formation. The shape factor, Hδ which is the ratio of the displacement thickness over the momentum thickness provides information on the nature of the flow. Tables below show a summary of the boundary layer measurements on the ground plane at different freestream velocity. x/D = 0 (350 mm from the leading edge of the flat plate) indicates the location of the cylinder. The ReL is based on the distance across the leading edge to the location of interest. The specifications of the boundary layer of U = 0.33 m/s, 0.49 m/s and 0.65 m/s are shown in Table 1 to Table 3. The cylinders were partially immersed in the boundary layer (δ/H ranged from 0.3 to 0.5) for both rigid and flexible cylinder under all Re. As previously mentioned, /H would greatly alter the critical aspect ratio where the vortex shedding at the free end is suppressed. Therefore, it is with great care in making sure the boundary layer is small enough such that the free end of the cylinder does not submerge in the boundary layer.
To ensure success of the present study, the investigations were conducted in a systematic and organized manner. The tests were divided into two categories: rigid cylinder cantilever and flexible cylinder cantilever. Flow in the lower subcritical Reynolds number regime ~ x103 is selected as the regime of interest as it is more compatible in most of the engineering applications. Given the height of the test section is only 20 cm, overall length of the structure to be less than 18 cm were conducted. Firstly, a series of tests was performed on a rigid cantilever in fluid. It served as an insight of flow behaviour influenced by the free end and can later be used to justify the change in flow behaviour caused by flexible cantilevers. Secondly, a series of tests was performed on a flexible cantilever in fluid where it provided a picture of the flow behaviour of the complex problems. The movement of the flexible cantilever was not limited by any means and was intended to vibrate freely as the flow past through it. Two governing parameters, namely Reynolds numbers (based on cylinder diameter), and structural stiffness were varied throughout the tests. The variation of structural stiffness could be achieved by different material selections of different Young Modulus and also the geometry. Since the geometry was fixed in this research, different AR will be manipulated to achieve different stiffness for the same material. Full details on the finite rigid and flexible cylinders specifications can be found in [6]. Table 4-5 show the specifications of the models used in the experiments.
The stiffness rating and the deflection is seen to be governed by the Young Modulus, E, second moment of inertia, I, overall length of the cantilever, L, and also the spanwise location of the cantilever, y. It is collectively a function of material properties. In order to vary the Young Modulus, different materials of cantilever cylinder are adopted in this research – aluminium, carbon steel and Ethylene vinyl acetate (EVA). The variation of the geometry can be achieved by changing the length or shape of the object as it affects the second moment of inertia. To increase the flexibility of the cylinders, one could replace the material with high Young Modulus value with a lower Young Modulus value – EVA. Other method is to adopt a very large length to diameter ratio (lower I and longer L) in order to compensate for the materials (aluminium and carbon steel) that have high Young Modulus value.
The behavior of fluctuation quantities can be described by applying the Reynolds decomposition method to the Navier–Stokes equations and after a series of simplifications [22] the kinetic energy budget which describes the energy of turbulence is formed. Since the kinetic energy budget provides insight on how the turbulence is distributed after being produced from the mean flow, there exists the kinetic energy budget for the mean flow and the kinetic energy budget for the turbulent flow, both of which compliment each other in the process of examining the transfer of turbulence energy. The kinetic energy budget of mean flow is given by:
whilst the kinetic energy budget of turbulent flow is given by the following equation:
The production term is generally positive in the kinetic energy budget of turbulent flow, signifying an energy supply from the mean flow to the turbulent flow. When comparing the Equations (1) and (2), it can be understood that the transfer of energy between the mean and turbulent flow can only be done through the fifth term on the RHS, and therefore is often labelled as the production term. The kinetic energy budget equations are useful in ‘visualizing’ the nature of turbulence and are especially useful in examining the level of turbulence energy produced by the rigid and flexible cylinders through evaluating the production term. In the current work, attention is given to the production term to understand the distribution of the energy by the rigid and flexible cylinders.
In order to examine the strength of the turbulence, the Reynolds averaged statistics, which is important as it gives insight on the transport of momentum within the flow because velocity fluctuations give turbulent flow extra kinetic energy and hence generate extra momentum transfer. Reynolds stress is used to account for turbulent fluctuations in fluid momentum. Hence, the fluctuating components of the instantaneous flow was determined from each velocity field in the x–z plane. Since the Reynolds stress is the component of the total stress tensor in a fluid obtained from the averaging operation over the Navier-Stokes equations, the Reynolds averaged Navier-Stokes equation can be written as:
where is the Reynolds stress tensor. The instantaneous and mean velocity can be extracted directly from the Met-Flow Software Version 3 except the fluctuation velocity, so the fluctuation velocities of 4096 data points at one location were calculated by subtracting the mean from instantaneous. The u component fluctuation velocities were then multiplied by each other before averaging was performed in order to calculate the normal stress, contributed by u component. The same procedure is valid for w component. To calculate the Reynolds shear stress, , the u fluctuation velocities were multiplied with the w component before averaging. The uncertainty analysis has been discussed in [19].
As this project is fully based on experimental work, the results have to be assured to be of high integrity. The uncertainty analysis is performed to give a quantitative estimation of the reliability of the measured value generated from a series of experiments. The uncertainty estimation for the different parameters are calculated based on the Coleman and Steele [23] approach at a 90 % confidence level.
3. Results and Discussion
Based on the analysis of [18], it can be discerned that the wake region of the flexible cylinder is generally larger than that of the rigid cylinder. A larger wake region translates to a larger region where turbulence activities can happen effectively. Therefore, the increase of wake region can be denoted as a direct evidence of turbulence enhancement, in terms of the effectiveness of the region where turbulence activities take place. In addition, it is speculated that the increase of wake region is caused by the bending of flexible cylinder. On the other hand, the turbulence intensity, production term term and Reynolds stress have also seen huge increment in flexible cylinder [6,19]. It is speculated that the increment is not caused by the bending but oscillating motion. So, this work investigates the validity of the speculation through manipulating the structural stiffness of the flexible cylinder by employing different materials.
3.1. Time-Averaged Velocity Distribution
Figure 7, Figure 8 and Figure 9 and Figure 10, Figure 11 and Figure 12 show the time-averaged streamwise velocity profile () and wall-normal velocity profile () of flexible cylinders of AR = 12 and 14 on the wake centreline (y/D = 0) at Re = 4,000, 6,000 and 8,000, respectively. The distance measured of each velocity profile behind the cylinder are one diameter apart at x/D = 3, 4 and 5. The deflection downstream of the flexible cylinders have resulted in the increment of wake region nearly identical as the cylinder’s height as indicated by the point where strong velocity gradient happens. The tip effects for both flexible cylinders of AR = 12 and 14 at all Re can be seen only influential to z/D ≈ AR - 1, consistent with the postulation of wake region increment due to cylinder’s deflection.
The time-averaged () and () of flexible cylinders of AR = 50 and 54 on the wake centreline (y/D = 0) at Re = 2,500 are shown at Figure 13 and Figure 14 and Figure 15-16 respectively. The () and () for both materials at AR = 50 and 54 have hinted the influence of downwash, as indicated by the higher localize negative w component velocity than the u component at very near wake at x/D = 1 and 2 (compare Figure 13 and Figure 15 for aluminium and carbon steel cylinder of AR = 50 for example). Due to the extremely long AR (AR = 50 and 54), the influence of downwash is only affected from the free end to circa 7D from the free end at the near wake of x/D = 1 and 2 for both materials and AR while the span below that region is considered to be of two-dimensional flow region which is free from the tip vortex.
It is observed that all the cylinders did not succumb to the incoming force exerted on it by the oncoming fluid and deflect due to the relatively higher stiffness properties of both materials. Though the aluminium cylinders of both AR are not deflected in the x-direction (too negligible), they do however, oscillate/vibrate transversely. Downwash phenomenon is seen associated with all the metal group cylinders – carbon steel which acts like a rigid cylinder and aluminium which barely has any deflection but oscillates. As a result, it can be confirmed that the downwash phenomenon is caused by the deflection of the cylinder alone and not by the oscillation. Table 6 shows the average wake region based on the point of the greatest velocity gradient from the () profiles of EVA, aluminium and carbon steel cylinders. It is apparent to see from the Table 6 that there is an increase in the wake region of the deflected cylinders; roughly equivalent to the deflected height of the cylinder.
In general, the () velocity profile might look similar for all the cylinders. However, the localized velocity for aluminium cylinders of both AR near the free end is slightly slower than that of carbon steel cylinders (see Figure 13 and 14). The lower velocities of the aluminium cylinders could be due to the transverse oscillation of the cylinders (see [6]). As the cylinder is oscillating transverse to the flow, more energy from the mean flow is needed to account for the higher fluctuation velocities due to the higher shear rate and hence, the lower velocities. On the contrary, throughout the experiment, it is observed that no oscillation phenomenon occurs for the carbon steel cylinders of both AR. As a result, the carbon steel cylinder is behaved in the same manner as the rigid cylinder.
3.2. Turbulence Intensity
The distributions of the streamwise turbulence intensity (u’/U) and the wall-normal turbulence intensity (w’/U) of cylinders of AR = 12 and 14 at Re = 4,000, 6,000 and 8,000 in the wake centreline (y/D = 0) are analyzed. Though both the EVA cylinders are of the same material but the AR is different, therefore, affecting the stiffness of the cylinders; hence, it is suspected that there will be differences in the magnitude of the (u’/U). In general, all of the cylinders have experienced an increment over the rigid cylinder of AR = 10 at Re = 4,000, which is (/U) ≈ 26.14 %. They show an elevated region at near z/D = AR - 3, corresponding to the region where the cylinder oscillates most. In spite of that, the magnitude of (/U) is very different for each cylinder. AR = 12 has a localized (/U) ≈ 42.14 %, 48.44 % and 41.66 % at increasing Re (Figure 17). On the other hand, AR = 14 has a localized (/U) ≈ 52.39 %, 64.48 % and 43.64 % at increasing Re (Figure 18).
It is observed that the localized (/U) of AR = 12 and 14 at Re = 8,000 suffer from huge increment. It is therefore clear that the increment of the (u’/U) does not depend directly on the AR or Re; instead it is the oscillating motion that is subjected to different AR or Re as it affects the structural stiffness. Mittal and Kumar [24] concluded that the motion of the cylinder alters the flow field significantly in their simulation in an attempt to investigate the VIV of a light circular cylinder in a uniform flow.
The distributions of the streamwise turbulence intensity (u’/U) and the wall-normal turbulence intensity (w’/U) of aluminium and carbon steel cylinders of AR = 50 and 54 at Re = 2,500 in the wake centreline (y/D = 0) are also analysed and shown in Figure 19 and 20. It is noticeable that the localized (/U) of the metal group flexible cylinders is at approximately 5D from the free end at x/D = 2, unlike the EVA flexible cylinders. Beyond x/D = 2, the (u’/U) quickly subsides. This suggest that the downwash phenomenon due to no deflection of the metal group flexible cylinders; has direct most of the vortical activities downward as the vortical activities follow the flow.
According to Figure 19 of aluminium cylinder, the localized (/U) is scattered around 1/3 of the cylinder’s span near the free end at z/D ≈ 33D to the free end. In contrast to that, the localized (/U) produced by the carbon steel cylinder (see Figure 20) is seen to concentrate only at the region from the free end to z/D ≈ AR - 10D; a smaller area of elevated turbulence intensity compared to the aluminium cylinder. The reason of the smaller area of augmented turbulence intensity could be due to the carbon steel cylinders that behaved exactly as the rigid cylinder. Despite not having a x-deflection for the aluminium cylinder, it did vibrate at a comparatively high oscillating frequency (see Figure 21 and 22). As the vibration takes place greatest at the free end and subside along the span (its local stiffness is the least stiff at the free end and slowly increasing along the span towards the fixed end), the region where the vibration takes place have augmented the turbulence intensity; hence the larger area of elevated turbulence intensity for aluminium cylinder. This finding is also in agreement with the findings from Thulukkanam [25] where VIV (vibration of cylinder caused by the vortices shed) has the ability to increase the strength of the vortices shed.
Since the carbon steel flexible cylinder is behaving similarly as the rigid cylinder. Therefore, it is expected that it will have a similar performance as the rigid cylinder. The local (/U) of the carbon steel of AR = 50 and 54 are (/U) ≈ 23.0 % and 24.2 % respectively, slightly lesser than the (/U) produced by rigid cylinder of AR = 10 and 16 at Re = 4,000. The local (/U) of the aluminium flexible cylinder of AR = 50 and 54 are (/U) ≈ 52.9 % and 57.8 %.
3.3. Turbulence Kinetic Energy Budget
The flexible cylinder has the ability to enhance the turbulence generation; therefore, it can be seen that the normalized production term, generated by the flexible cylinders of AR =12 and 14 at all Re have increased with reference to the rigid cylinder (see Figure 23 for Re = 4,000 for example). Similarly, the localized maximum production occurs in the vicinity of the free end where the shear layer instability is the strongest. It is evident that the production term values do not scale with the AR alone (though the values do indeed vary with the AR); instead, it is the different structural motion generated by the flexible cylinders at different AR which result in a different structural stiffness.
Similarly, the localized production term occurs in the vicinity of the free end for both aluminium and carbon steel cylinders at both AR of 50 and 54 (Figure 24 and 25). Besides, it can be seen that the localized production term occurs at x/D = 2 in the wake region where the region is approximately close to the dividing streamline of the flow as indicated by the negative () at x/D = 2 and positive () at x/D = 3 of the velocity profile in Figure 13 and Figure 14. A dividing streamline is the boundary which separates downward dominant flow and downstream dominant flow [13]. Beyond x/D = 2, the normalized production term quickly subsides as the flow are less chaotic due to the downwash that directs most of the vertical activities downwards instead of downstream.
The production term of carbon steel cylinder remains at a lower magnitude than the aluminium cylinder (Figure 25). As mentioned, the carbon steel cylinder is behaving like a rigid cylinder due its high structural stiffness; therefore, it is can serve as a reference/benchmark to the increment of the aluminium cylinder that oscillates. Increment of the production term by the aluminium cylinder of AR = 50 and 54 that oscillates can be seen from the graphs (Figure 24). They both have a rather similar pattern in terms of the evolution of turbulence production. The contributor of this increment is suspected to be the higher oscillating amplitude (see Figure 21 and 22) by AR = 54 as its structural stiffness is slightly lower than that of AR = 50.
3.4. Reynolds Stresses
The Reynolds stresses for the flexible cylinders has seen a major increase over the rigid cylinders. The increment ranged from approximately 4.5 % for flexible cylinder of AR = 10 at Re = 8,000 to over 150.0 % for flexible cylinder of AR = 16 at Re = 6,000 under similar condition case basis. Also, as demonstrated by the (u’/U) and the production term generated by the EVA cylinders of AR = 12 and 14, it is expected that the , and will gain as well. The Reynolds stresses, , and of the EVA flexible cylinder of AR = 12 and 14 at Re = 4,000, 6,000 and 8,000 are presented in Figure 26–31 to provide insight on the turbulent fluctuations in the flow. As anticipated, the of AR = 12 and 14 at all Re show increment. The is also consistent to the production term where the peak intensity coincides with each other near the free end, and is also evident in the high shear rate (high velocity gradient) of the mean flow. It shows good agreement that the energy from the mean flow is being passed on to the fluctuating components by the mechanism of shear. Likewise, the shows a peak intensity in the regions of strong velocity gradient and it can be imagined that it is where the separated shear layer is. The localized max is located near the free end where the tip vortices are generated. The u’ in the near wake are more energetic than the w’, hence the magnitude of component is much larger than the component. The evaluated Reynolds shear stress can be said to stem from the since the are more energetic than the in that region. The production term shows that the increment of turbulence production does not strictly follow the AR or Re pattern; increase in turbulent production as the AR or Re increase. Same phenomenon can also be seen throughout the of the cylinders.
The Reynolds stresses, , and along the span of the aluminium and carbon steel cylinder of AR = 50 and 54 at Re = 2,500 at the wake centreline (y/D = 0) are presented in Figure 32-35. The local peak Reynolds shear stress of the aluminium cylinder of AR = 50 and 54 near the free end shows an approximate 128 % and 131 % increment for AR = 50 and 54 over the carbon steel flexible cylinder which behave the same as rigid cylinder. Their increment over the rigid cylinder of AR = 10 at Re = 4,000 is approximately 14 % and 26 % for AR = 50 and 54, which shows a great deal of increment considering it is operating at Re = 2,500. The enlargement in the region can also be seen from the (u’/U) and production graphs. The local peak for the carbon steel cylinder of AR = 50 and 54 however, suffer from any increment as they behaved exactly like the rigid cylinder throughout the experiments.
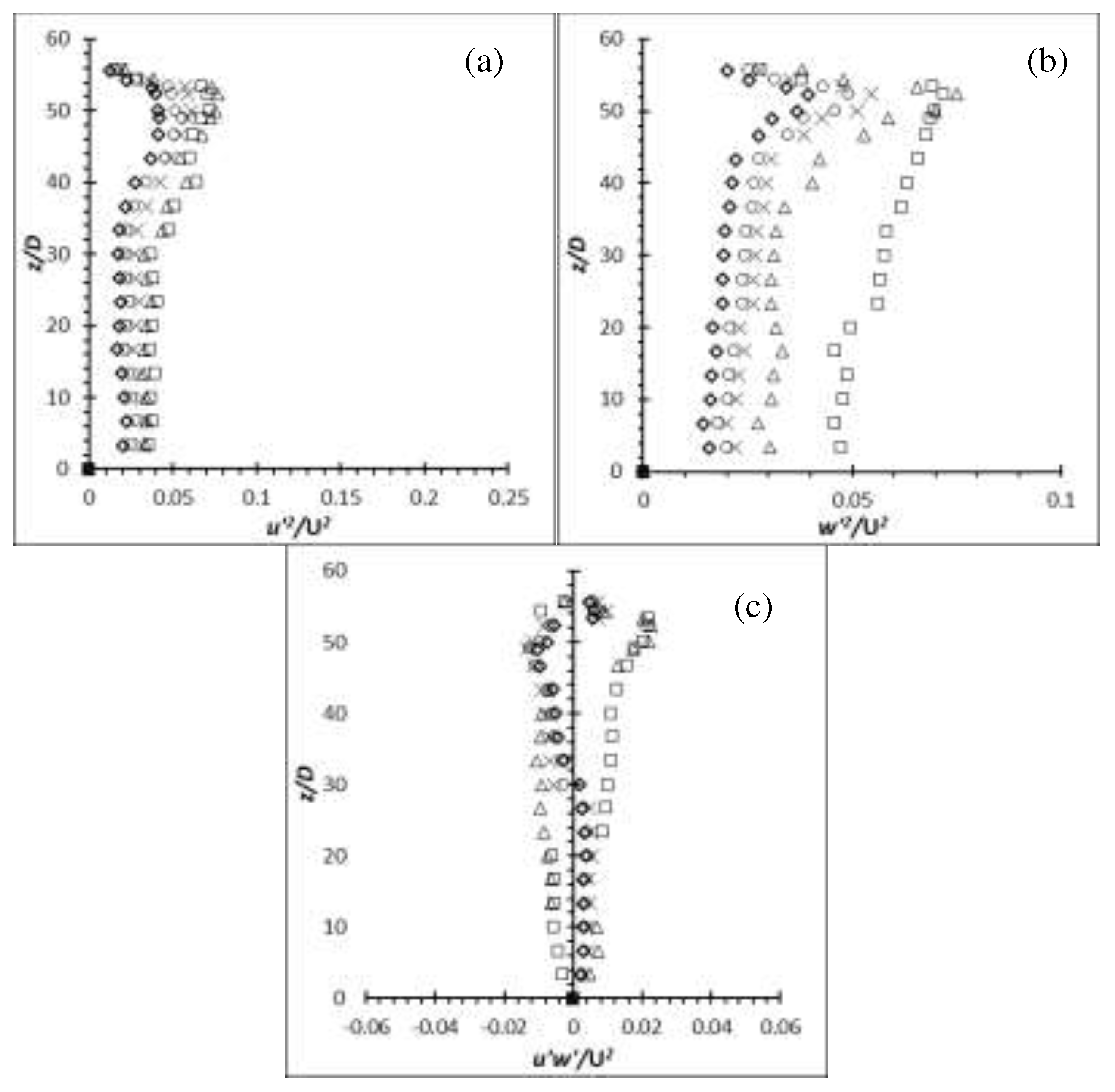
Figure 29.
Reynolds stress profiles for cylinder of AR = 14 at Re = 4,000: (a) (b) (c) .
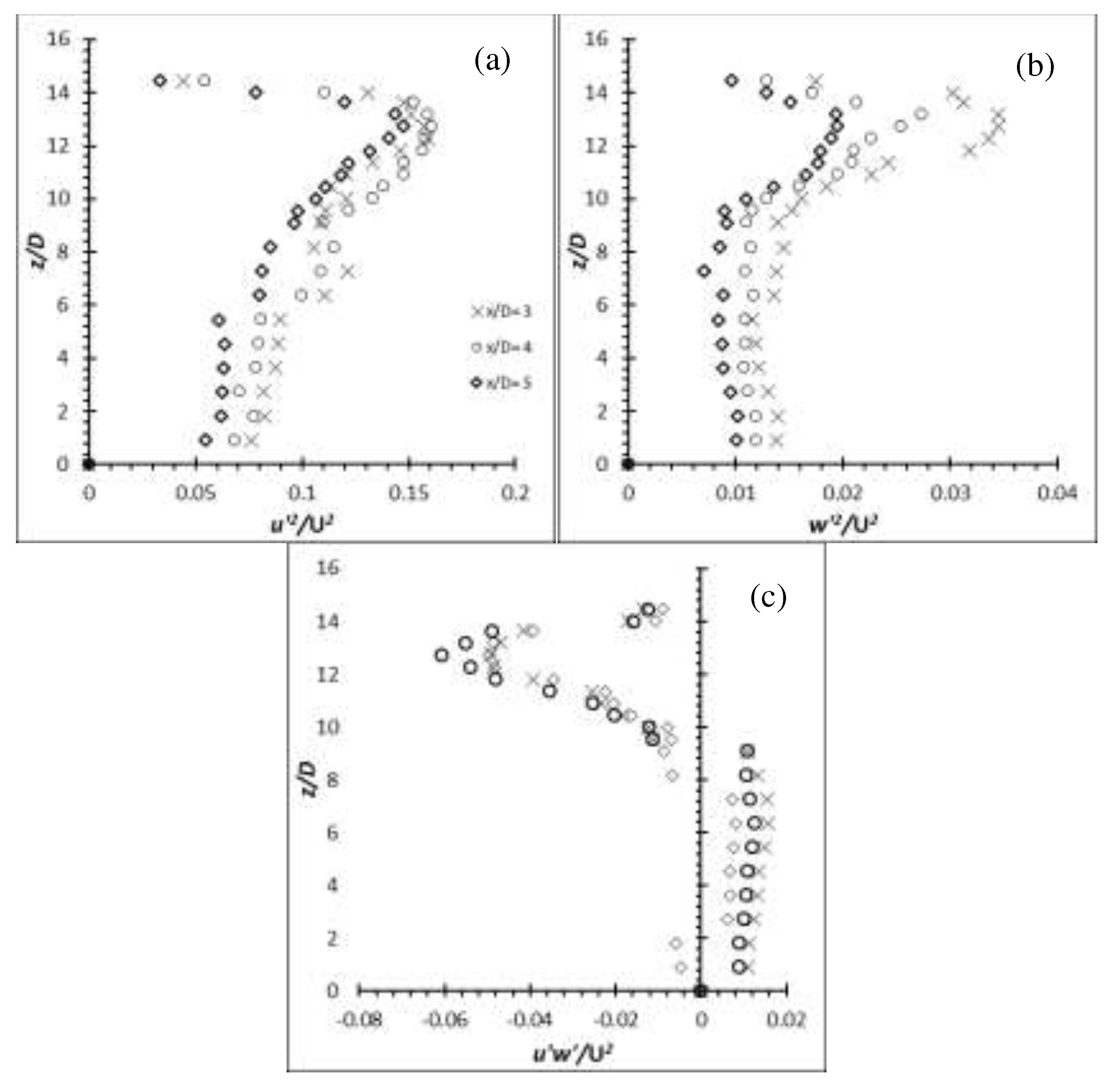
Figure 30.
Reynolds stress profiles for cylinder of AR = 14 at Re = 6,000: (a) (b) (c) .
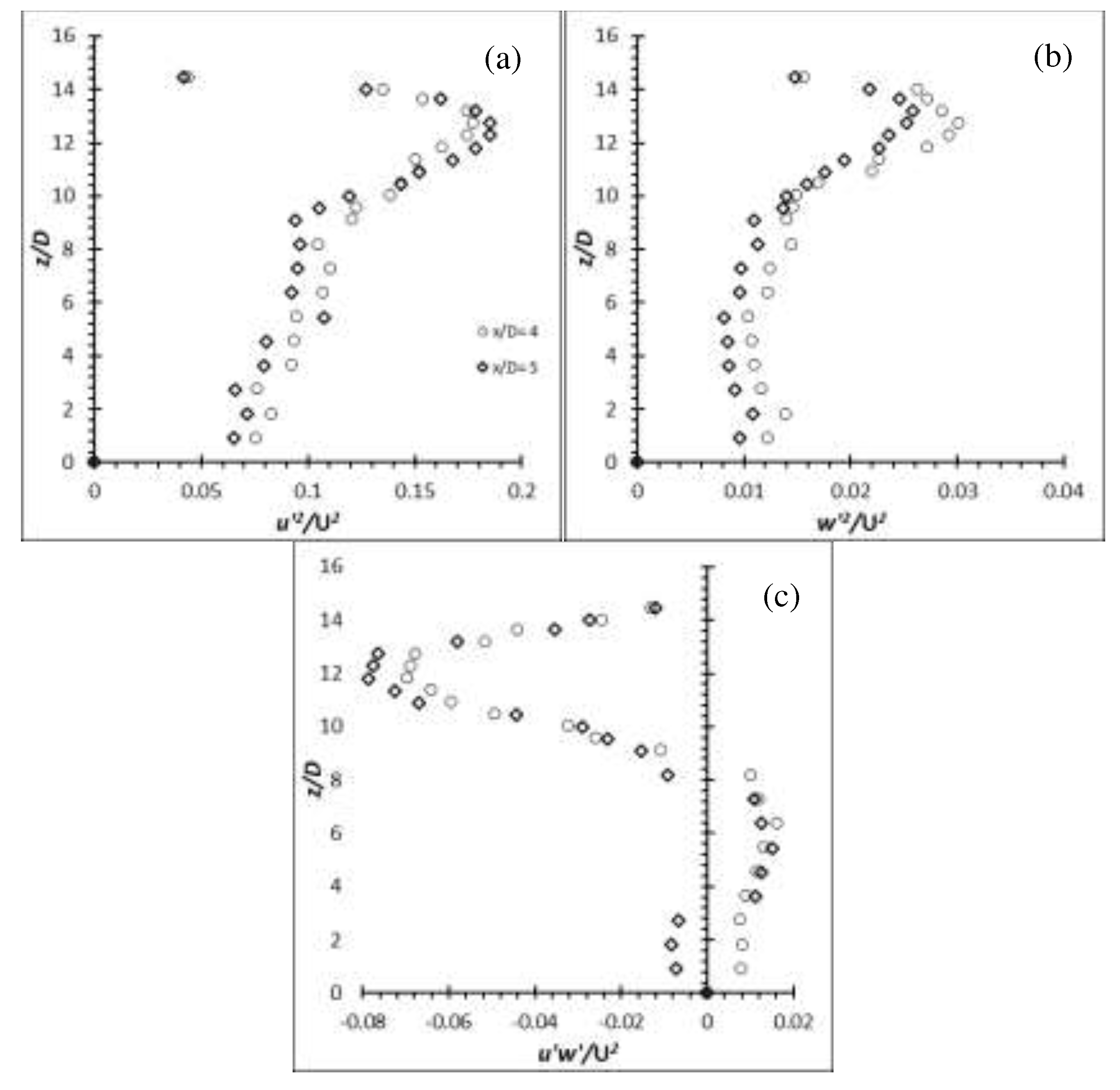
Figure 31.
Reynolds stress profiles for cylinder of AR = 14 at Re = 8,000: (a) (b) (c) .
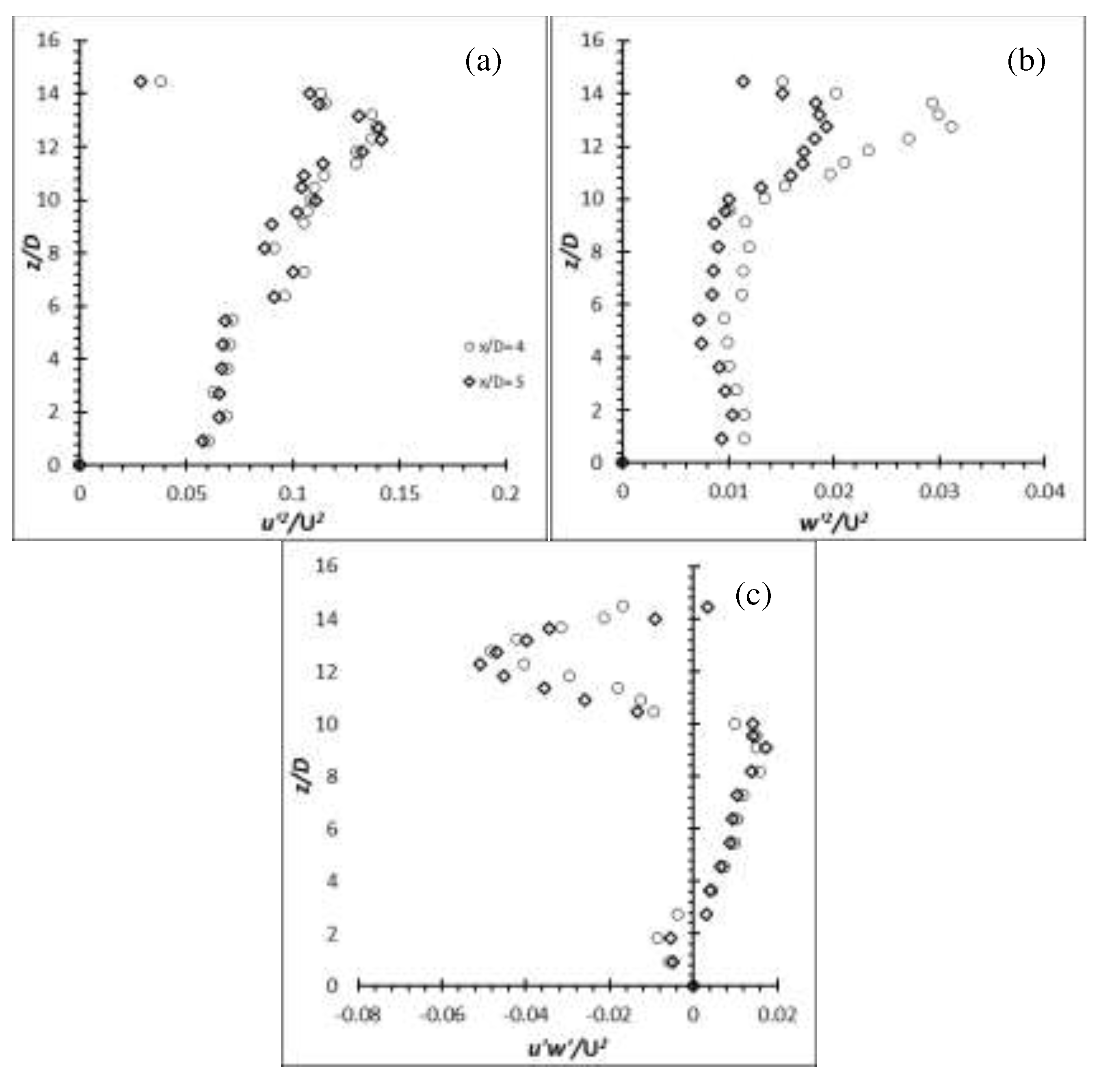
Figure 32.
Reynolds stress profiles for Aluminium flexible cylinder of AR = 50 at Re = 2,500: (a) (b) (c) .
Figure 32.
Reynolds stress profiles for Aluminium flexible cylinder of AR = 50 at Re = 2,500: (a) (b) (c) .
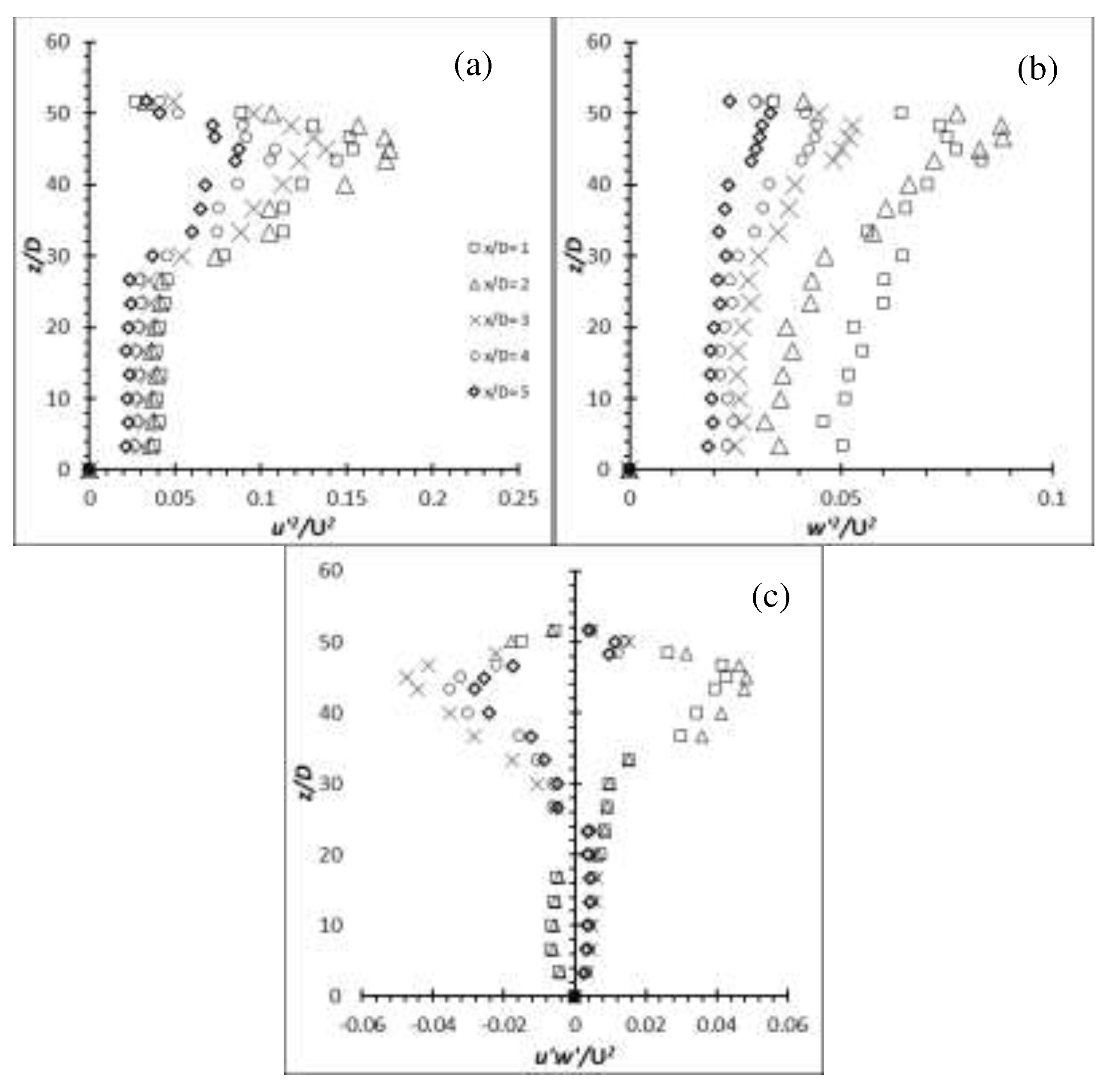
Figure 33.
Reynolds stress profiles for Aluminium flexible cylinder of AR = 54 at Re = 2,500: (a) (b) (c) .
Figure 33.
Reynolds stress profiles for Aluminium flexible cylinder of AR = 54 at Re = 2,500: (a) (b) (c) .
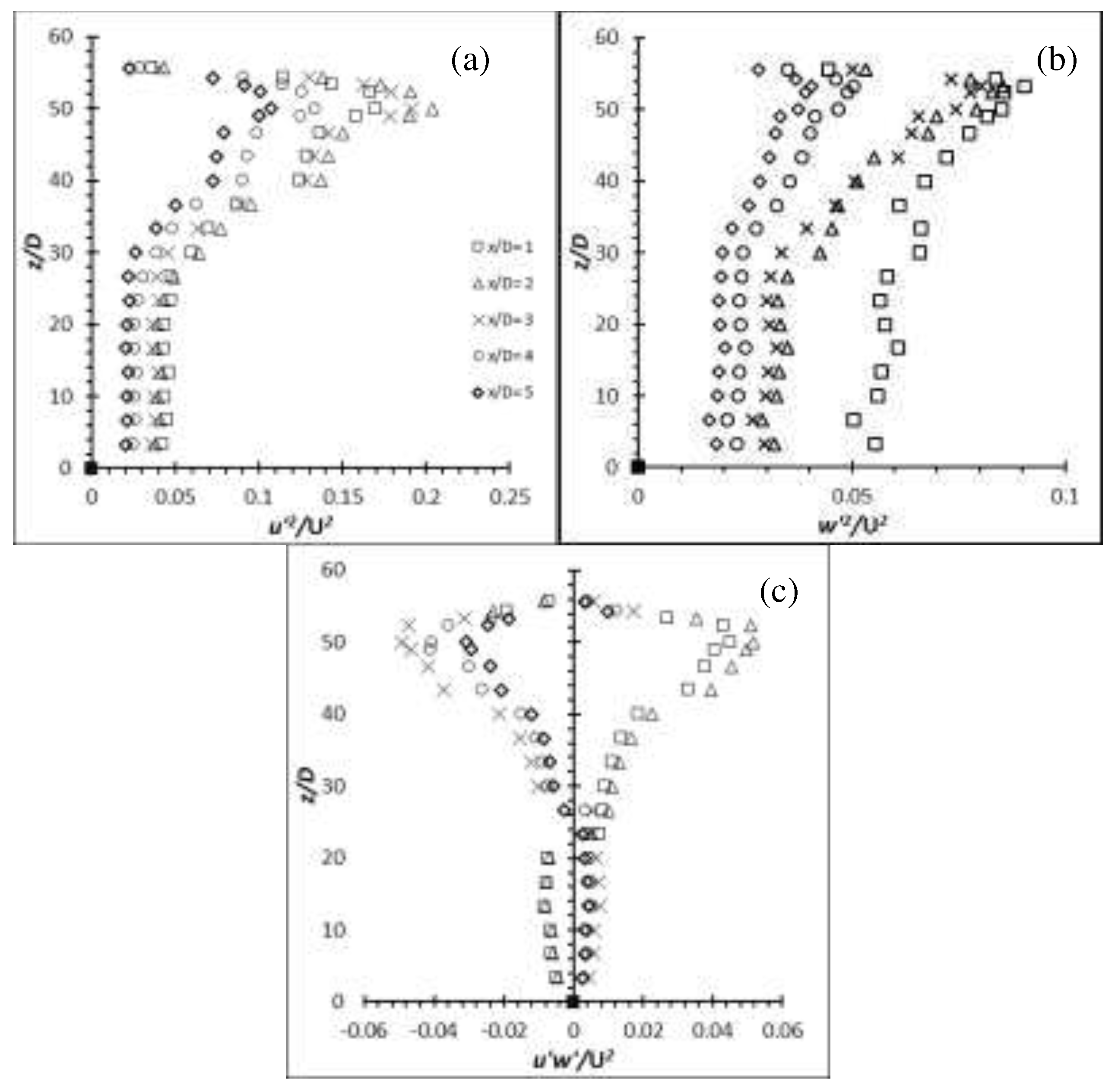
Figure 34.
Reynolds stress profiles for Carbon steel flexible cylinder of AR = 50 at Re = 2,500: (a) (b) (c) .
Figure 34.
Reynolds stress profiles for Carbon steel flexible cylinder of AR = 50 at Re = 2,500: (a) (b) (c) .
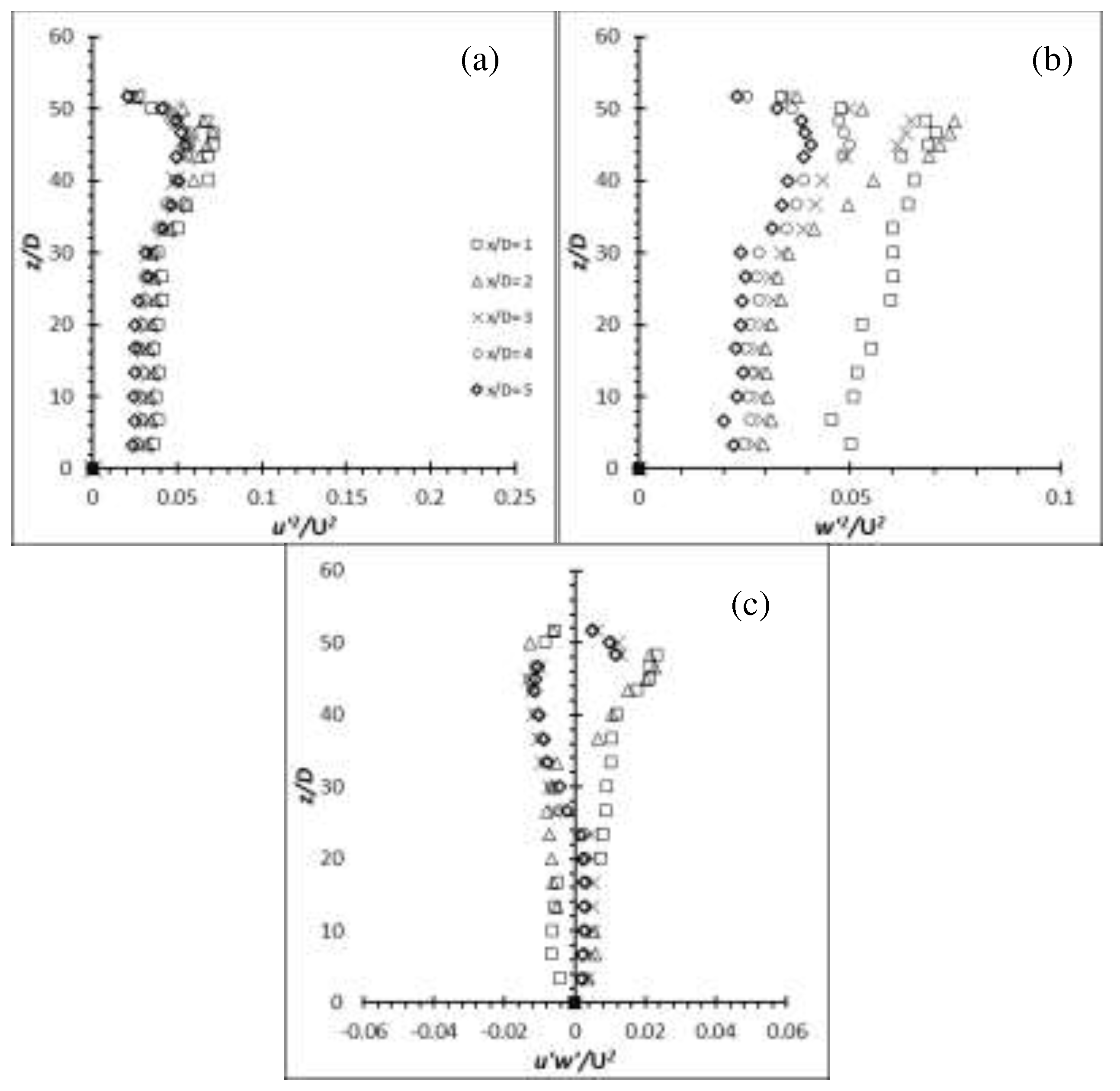
Figure 35.
Reynolds stress profiles for Carbon steel flexible cylinder of AR = 54 at Re = 2,500: (a) (b) (c) .
Figure 35.
Reynolds stress profiles for Carbon steel flexible cylinder of AR = 54 at Re = 2,500: (a) (b) (c) .
3.5. Roles of oscillation of the flexible cylinder on the turbulence enhancement
The results have clearly shown that the turbulence production of the flexible cylinder is greater than the rigid cylinder. The turbulence intensity, production term from the Turbulence Kinetic Energy budget equations and the Reynolds stresses have revealed that the turbulence enhancement depends on the structural dynamics or the motion of the oscillating cylinder rather than the AR or Re itself.
With reference to the production term of the EVA cylinder of AR = 12 and 14, the increment gained by the cylinder at Re = 8,000 is the least. A look at the (y/D) of AR = 12 and 14 at Re = 8,000 show that the cross-flow oscillations/motions are disorganized. Furthermore, both exist an abrupt change of amplitude and vortex shedding which latch on to a certain cycle. The abruptness of the cross-flow oscillations suggests that there could be a possibility of mode-change between two or more modes of vortex shedding. It has been established by William and Roshko [26] regarding the vortex pattern in response to the oscillating motion of the vibrating cylinder. Apart from that, Mittal and Kumar [24] also confirmed the existence of mode-change of vortex shedding in relation to the cylinder’s motion mentioned above. They discovered the large amplitude of cross-flow oscillations correspond to anti-symmetric shedding. Despite that, no associated turbulence characteristics have been reported. Thus, the results generated in these experiments also serve to provide insights into the turbulence characteristics by the different oscillating motion of the flexible cylinders. Besides the above-mentioned features, it is also observed that the oscillations of AR = 16 at Re = 8,000 are off-axis from the (y/D) graph. The same phenomenon was noticed by [24] in their results at high Re which the wake is bias towards a particular side, away from the centre line. This is also evident by the fact that the cylinder is oscillating in favour of one side. It is suggested that the disorganized cross-flow oscillations which happen at Re = 8,000 is due to the relatively low structural stiffness against the relatively strong fluid force (U = 0.65 m/s); thus, the flow becomes more complex.
Next, through the examination of AR = 12, 14 and 16 at Re = 6,000, which coincidentally have the highest turbulence enhancement amongst each AR respectively, one can notice that the cross-flow oscillations are fairly organized. In other words, the oscillations have a fairly consistent frequency and amplitude. The (y/D) of AR = 12, 14 and 16 at Re = 4,000 show fairly organized cross-flow oscillations as well except their oscillating amplitude is lower than their respective AR operating at higher Re. The frequency of AR = 12 and 14 is close to regular and is in a more temporally periodic state. AR = 16 shows an occasion of higher amplitude in a certain cycle which could be due to the different mode-change. It is believed that the cross-flow oscillations/motions of AR = 12 and 14 behave in this manner because its structural stiffness is relatively high in comparison to the relatively weak fluid force (U = 0.33 m/s) and hence the cross-flow oscillations are more predictable but lower amplitude. Therefore, the flow field is quite similar to that of a rigid/stationary cylinder [24]. Nevertheless, despite the similarity, the vibration of cylinder has proven to enhance the turbulence production.
Through the analysis above, it can be concluded that the vibration/oscillation/motion of the cylinder can alters the fluid flow significantly. The oscillation of the cylinder very much depends on the structural stiffness of the cylinder and the Re or fluid force more specifically. At a relatively high structural stiffness against relatively weak fluid force, the oscillations are fairly organized but the amplitudes are small. Turbulence enhancement is noticeable at this stage though not as significant. On the contrary, in the opposite condition, the flow becomes more complex and the cylinder undergoes fairly large amplitude but disorganized oscillation. Turbulence enhancement is also noticeable but at a low efficiency. The (y/D) graphs suggest the possibility of mode-change of vortex shedding. Mittal & Kumar [24] observed that under chaotic flow condition, a large number of small vortices are seen shed alongside the large vortex and the flow field is very different from the rigid cylinder. It is at a suitable range of the structural stiffness and the fluid force only will the oscillations become fairly organized and at a high amplitude. The turbulence enhancement associated to this oscillation is significant.
It shows that the
max corresponds to the highest structural velocity (i.e. velocity of the oscillation by the flexible cylinder under the same Re). However, it can be observed that the structural velocity at Re = 8,000 is lower compared to the structural velocity of the same AR under lower Re. This is because the structural stiffness is too low for the fluid force. It causes the cylinder to oscillate at a disorganized motion. The frequent lower frequency and amplitude at certain cycles contribute to the lower structural velocity.
Since the vortex pattern depends heavily on the oscillation, it is suspected that the energy feeding process to the vortex must have been altered – it no longer follows the normal condition (classical Kármán vortex) where the vortex only sheds off when it has received sufficient energy. The mode-change competition by the flexible cylinder could have interrupted the normal vortex formation for better or worse. Based on the performance of the turbulence enhancement by cylinders at Re = 8,000, it can be confirmed that the alteration to the normal vortex formation at this Re is less than ideal as the improvement in max is quite low. It is recommended that the relationship between the motion of the cylinder and the vortex shedding mode to be further studied or refined to further explore the effects of shedding mode on the vortex strength. Fortunately, regardless of the performance of the turbulence enhancement, the adoption of flexible cylinder still proves to have a higher turbulence production than the rigid cylinder.
4. Conclusions
This work gives the conclusions of the key findings on the wake region modification by the flexible cylinder and the turbulence characteristics improved by the flexible cylinder over the rigid cylinder. The metal based flexible cylinder namely aluminium and carbon steel cylinder did not experience the similar increment found in the EVA cylinder; instead, it’s wake region is approximately the same as the rigid cylinder. Through the analysis of the structural behaviour, it is found that the cause of the increment in wake region is due to the diminishing of the downwash that is presented in all cantilever cylinder. The reason of the disappearance is because the EVA flexible cylinder is deflected to the x-direction due to the fluid force. As the metal based vibrating cylinders have a relatively higher stiffness property, it did not succumb to the bending; hence no deflection and thereby, the wake region remain the same as rigid cylinder.
Therefore, a greater deflection can greatly weaken the influence of downwash. The rigid cylinder of AR = 10 at Re = 4,000 has produced a localized (/U) ≈ 26 %. The turbulence intensity produced by other rigid cylinder at different AR and Re do not deviate much from 26 %. In contrast to that, the increment of the localized (/U) produced by the flexible cylinder ranged from 36 % to 99 %. The carbon steel flexible cylinder however, did not experience any gain in value of the turbulence intensity as they behaved exactly like a rigid cylinder. The results show that the production term generated by the flexible cylinder is higher than that of rigid cylinder. Similarly, the Reynolds shear stress have produced a similar pattern of results. The Reynolds shear stress is seen gained massively through the employment of flexible cylinder. However, the increment of the Reynolds shear stress does not strictly follow the AR or Re pattern. This suggest that the turbulence enhancement is neither influenced by the geometry factor (AR) nor the Re. Instead, it is closely linked to the structural dynamics of the cylinder that is governed by the AR and Re.
References
- Abdullah, Abdul Qader, Abid Abdul Azeez, Sharul Sham Dol, Mohammad Khan, and Mior Azman Meor Said. "SIMULATION STUDY ON VORTEX-INDUCED VIBRATION AIR WAKE ENERGY FOR AIRPORT RUNAWAY APPLICATION: A PRELIMINARY ANALYSIS." Platform: A Journal of Engineering 4, no. 3 (2020): 38-47.
- Azeez, Abid Abdul, Sharul Sham Dol, and Mohammad S. Khan. "Effects of cylinder shape on the performance of vortex induced vibration for aquatic renewable energy." In 2019 Advances in Science and Engineering Technology International Conferences (ASET), pp. 1-4. IEEE, 2019.
- Zahari, M., H. B. Chan, T. H. Yong, and S. S. Dol. "The effects of spring stiffness on vortex-induced vibration for energy generation." In IOP Conference Series: Materials Science and Engineering, vol. 78, no. 1, p. 012041. IOP Publishing, 2015.
- Nakamura, Tomomichi, Shigehiko Kaneko, Fumio Inada, Minoru Kato, Kunihiko Ishihara, Takashi Nishihara, Njuki W. Mureithi, and Mikael A. Langthjem, eds. Flow-induced vibrations: classifications and lessons from practical experiences. Butterworth-Heinemann, 2013.
- Bai, Yong, and Qiang Bai, eds. Subsea pipelines and risers. Elsevier, 2005.
- Yong, T. H., H. B. Chan, S. S. Dol, S. K. Wee, and S. A. Sulaiman. "Experimental Investigation on Effects of Elastic Agitator to Turbulence Enhancement." Journal of Applied Fluid Mechanics 14, no. 2 (2020): 361-373.
- Khing, T. Yui, M. A. Zahari, and S. S. Dol. "Application of vortex induced vibration energy generation technologies to the offshore oil and gas platform: The feasibility study." International Journal of Aerospace and Mechanical Engineering 9, no. 4 (2015): 661-666. [CrossRef]
- Sumner, D., J. L. Heseltine, and O. J. P. Dansereau. "Wake structure of a finite circular cylinder of small aspect ratio." Experiments in Fluids 37, no. 5 (2004): 720-730. [CrossRef]
- Luo, S. C. "Flow past a finite length circular cylinder." In The Third International Offshore and Polar Engineering Conference. OnePetro, 1993.
- TANIGUCHI, Seiichi, Hiroshi Sakamoto, and Mikio Arie. "Flow around circular cylinders of finite height placed vertically in turbulent boundary layers." Bulletin of JSME 24, no. 187 (1981): 37-44. [CrossRef]
- Park, Cheol-Woo, and Sang-Joon Lee. "Flow structure around a finite circular cylinder embedded in various atmospheric boundary layers." Fluid Dynamics Research 30, no. 4 (2002): 197. [CrossRef]
- Liu, Yang, R. M. C. So, and Z. X. Cui. "A finite cantilevered cylinder in a cross-flow." Journal of fluids and structures 20, no. 4 (2005): 589-609.
- Rostamy, N., D. Sumner, D. J. Bergstrom, and J. D. Bugg. "Local flow field of a surface-mounted finite circular cylinder." Journal of Fluids and Structures 34 (2012): 105-122.
- Park, C. W., and S. J. Lee. "Effects of free-end corner shape on flow structure around a finite cylinder." Journal of Fluids and Structures 19, no. 2 (2004): 141-158.
- Adaramola, M. S. (2008). The wake of an exhaust stack in a crossflow. Ph.D. Thseis, Department of Mechanical Engineering, University of Saskatchewan, Saskatoon, Canada.
- Govardhan, R., and C. H. K. Williamson. "Mean and fluctuating velocity fields in the wake of a freely-vibrating cylinder." Journal of Fluids and Structures 15, no. 3-4 (2001): 489-501.
- Cantwell, Brian, and Donald Coles. "An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder." Journal of fluid mechanics 136 (1983): 321-374.
- Yong, T. H., H. B. Chan, S. S. Dol, S. K. Wee, and P. Kumar. "The flow dynamics behind a flexible finite cylinder as a flexible agitator." In IOP conference series: materials science and engineering, vol. 206, no. 1, p. 012033. IOP Publishing, 2017.
- Dol, Sharul Sham, Tshun Howe Yong, Hiang Bin Chan, Siaw Khur Wee, and Shaharin Anwar Sulaiman. "Turbulence Characteristics of the Flexible Circular Cylinder Agitator." Fluids 6, no. 7 (2021): 238. [CrossRef]
- Yokoyama, Kaoru, Naoya Kashiwaguma, Tomoyuki Okubo, and Yasushi Takeda. "Flow measurement in an open channel by UVP." Proceedings, ISUD 4 (2004): 204-210.
- Dol, Sharul Sham. 2021. “Application of Ultrasonic Velocity Profiler (UVP) in the Vortex-Induced Vibration Experiments”. Novel Perspectives of Engineering Research Vol. 4, December, 142-52.
- Park, C.W.; Lee, S.J. Free end effects on the near wake flow structure behind a finite circular cylinder. J. Wind. Eng. Ind. Aerodyn. 2000, 88, 231–246.
- Coleman, H. W., and W. G. Steele. "Experimentation and Uncertainty Analysis for Engineers Second Edition." (1999): 38-84. [CrossRef]
- S. MITTAL, V. KUMAR, FLOW-INDUCED VIBRATIONS OF A LIGHT CIRCULAR CYLINDER AT REYNOLDS NUMBERS 103 TO 104, Journal of Sound and Vibration, Volume 245, Issue 5, 2001.
- Thulukkanam, Kuppan. "Classification of Heat Exchanger." Heat Exchanger Design Handbook, 2nd ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA (2013): 1-27.
- 26. C.H.K. Williamson, A. Roshko, Vortex formation in the wake of an oscillating cylinder, Journal of Fluids and Structures,Volume 2, Issue 4, 1988, Pages 355-381.
Figure 1.
(a) A rigid cantilever cylinder subject to fluid force, FU (b) A flexible cantilever cylinder subject to fluid force, FU.
Figure 1.
(a) A rigid cantilever cylinder subject to fluid force, FU (b) A flexible cantilever cylinder subject to fluid force, FU.
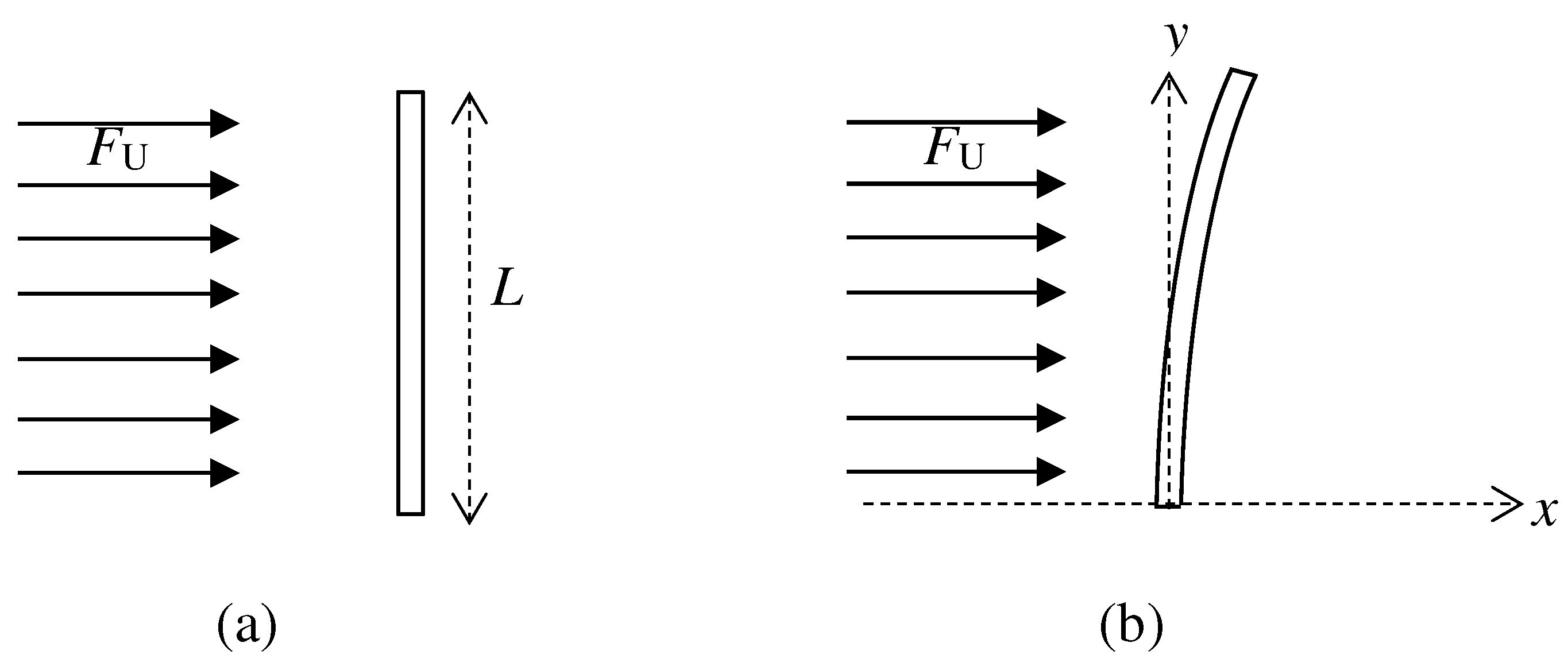
Figure 2.
The non-dimensional, time-averaged, streamwise vorticity field at x/D = 6 (a) AR = 9, (b) AR = 7, (c) AR = 5 and (d) AR = 3. Vorticity contour increment is 0.05 and minimum vorticity contour is ± 0.05, solid lines represent positive counter-clockwise [15].
Figure 2.
The non-dimensional, time-averaged, streamwise vorticity field at x/D = 6 (a) AR = 9, (b) AR = 7, (c) AR = 5 and (d) AR = 3. Vorticity contour increment is 0.05 and minimum vorticity contour is ± 0.05, solid lines represent positive counter-clockwise [15].
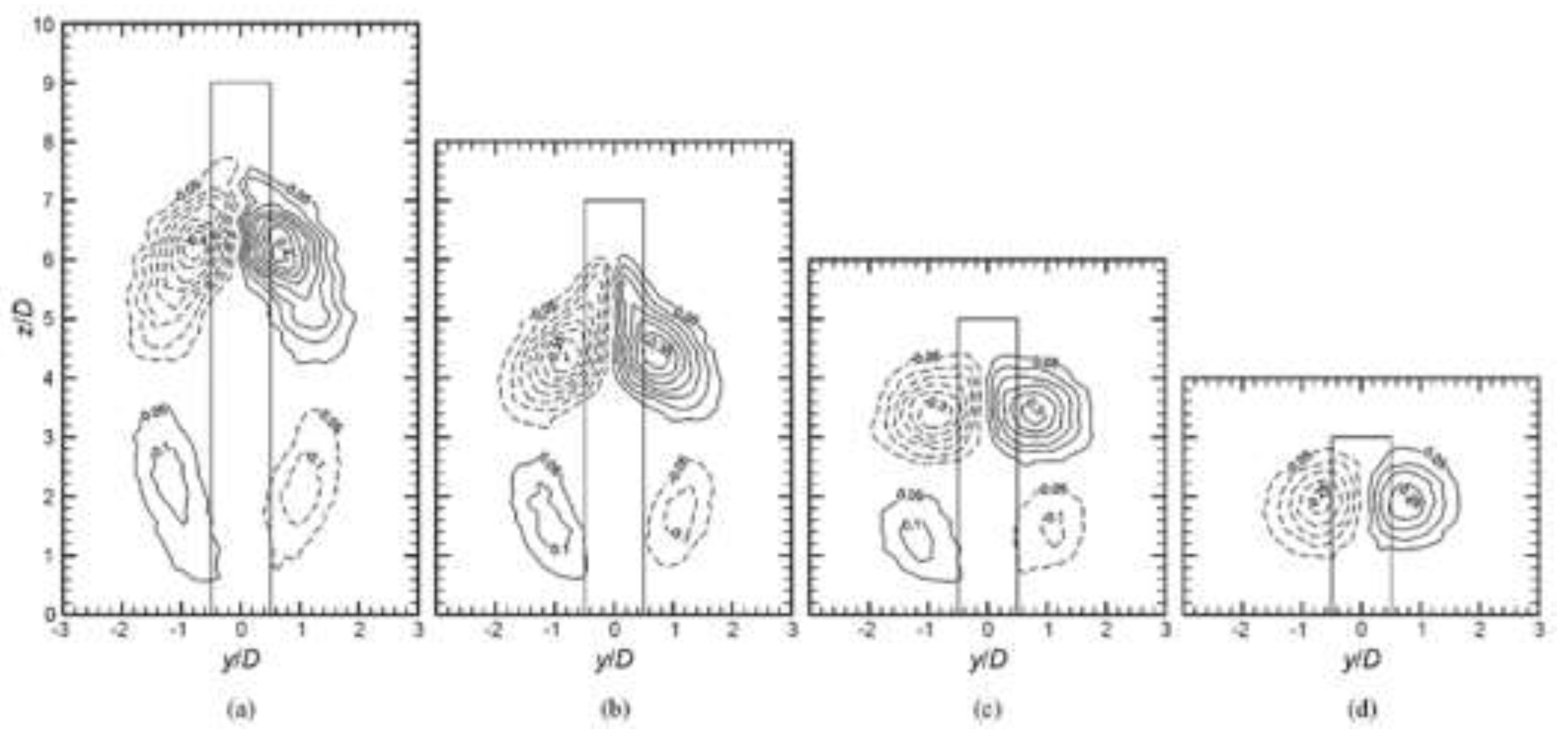
Figure 3.
The water tunnel with the test section made of Plexiglas for visualization purpose.

Figure 4.
Vector orthogonal composition technique.
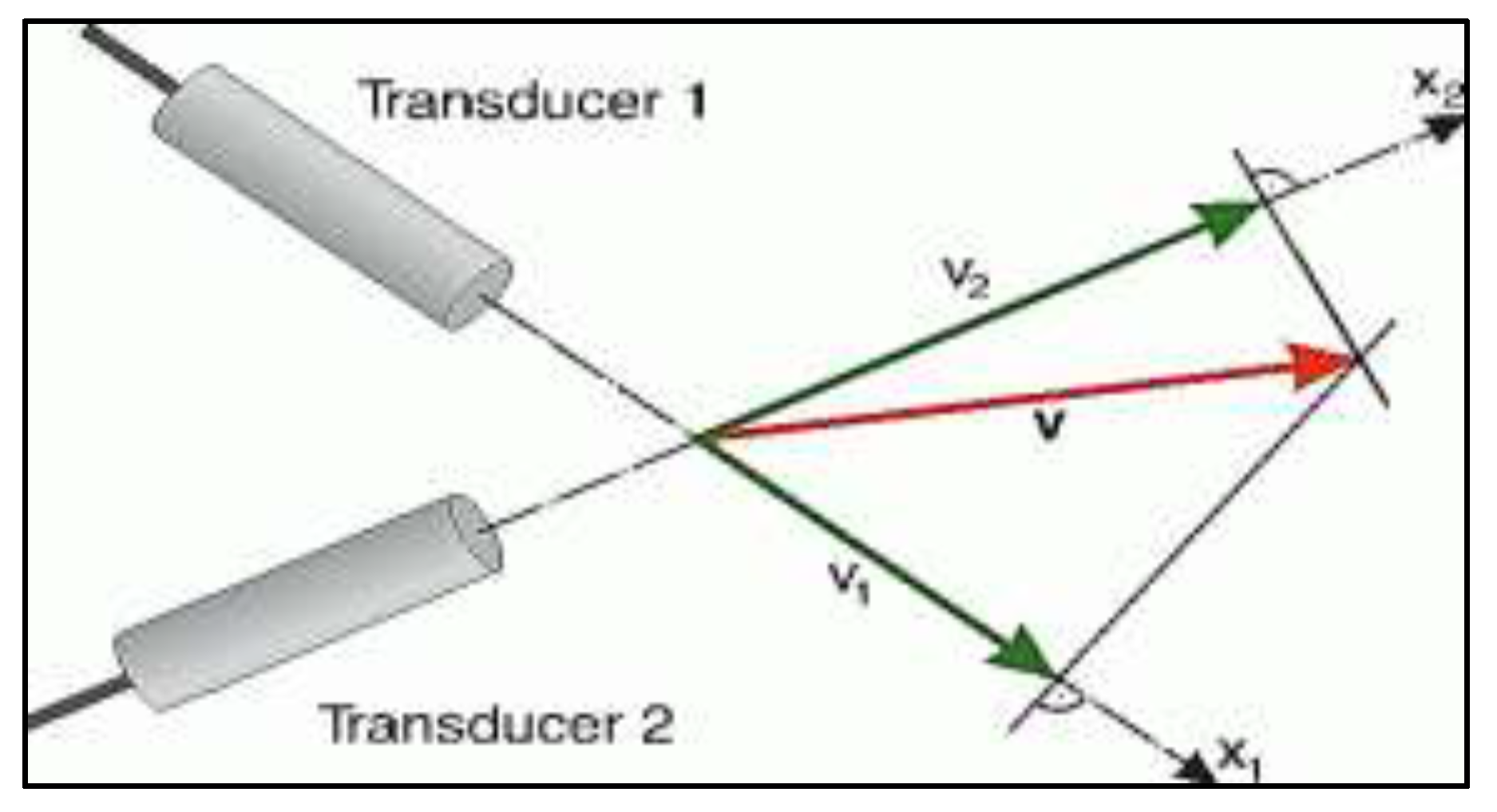
Figure 5.
UVP traverse system.

Figure 6.
UVP traverse and transducer.

Figure 7.
Time-average streamwise velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 4,000.
Figure 7.
Time-average streamwise velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 4,000.
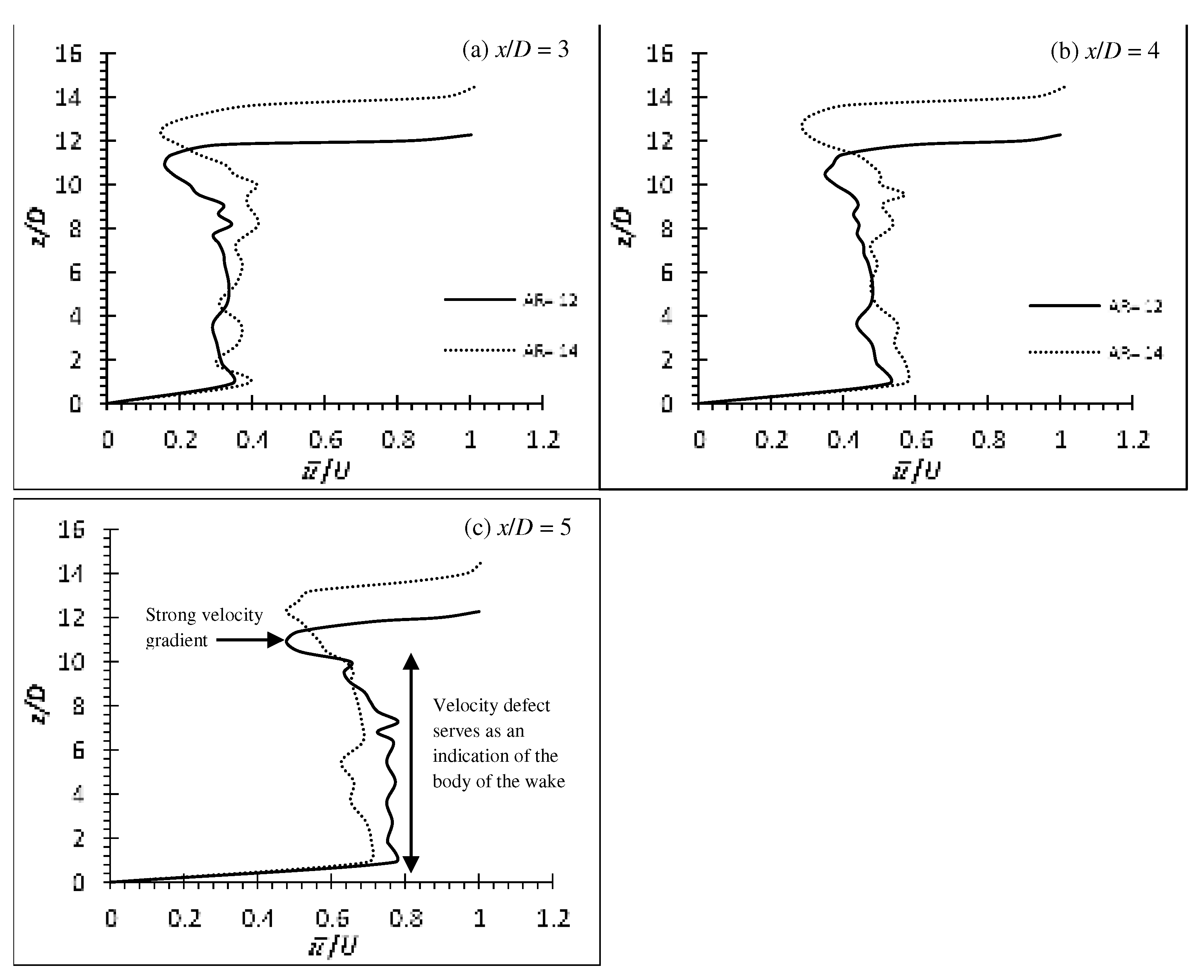
Figure 8.
Time-average streamwise velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 6,000.
Figure 8.
Time-average streamwise velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 6,000.
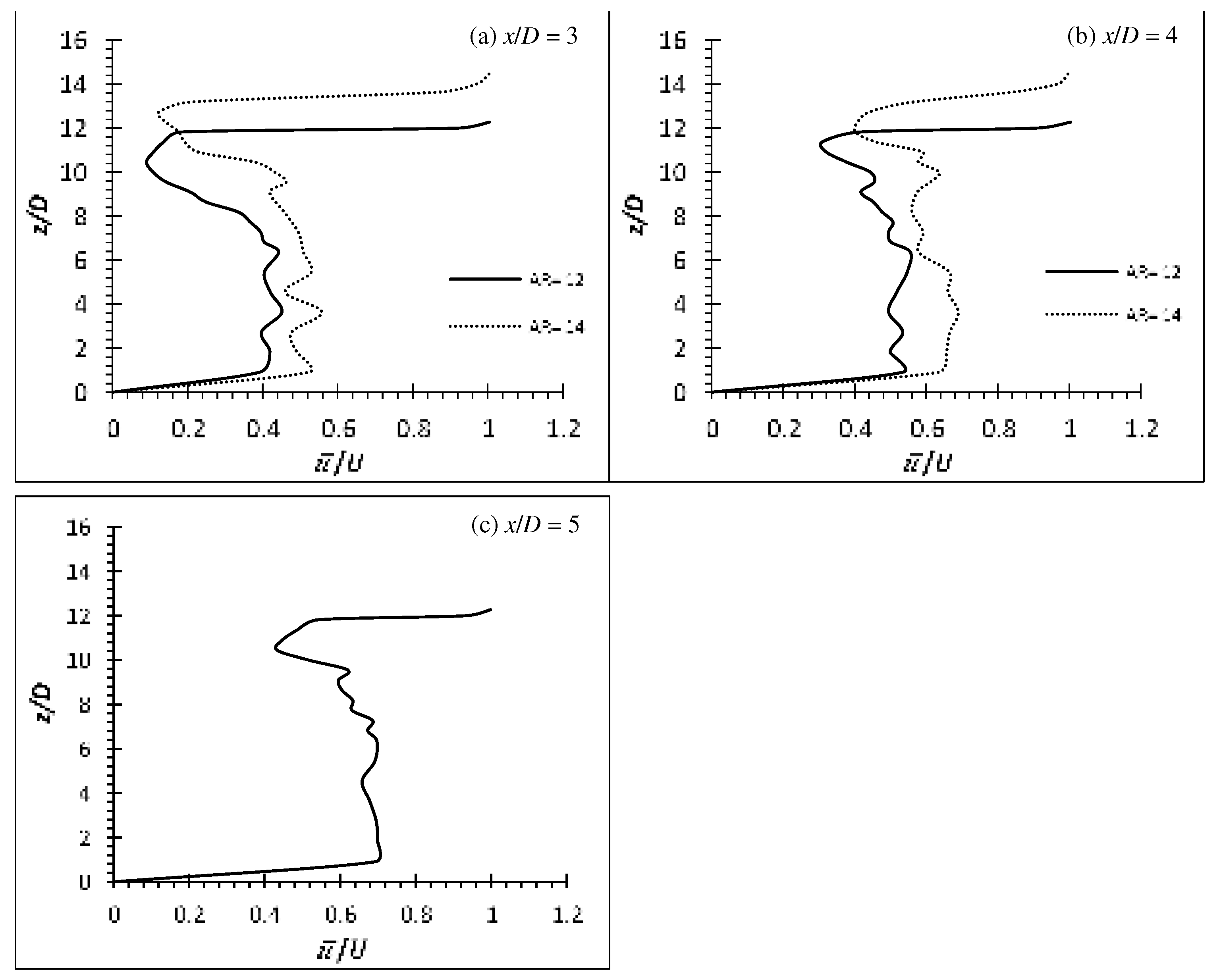
Figure 9.
Time-average streamwise velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 8,000.
Figure 9.
Time-average streamwise velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 8,000.
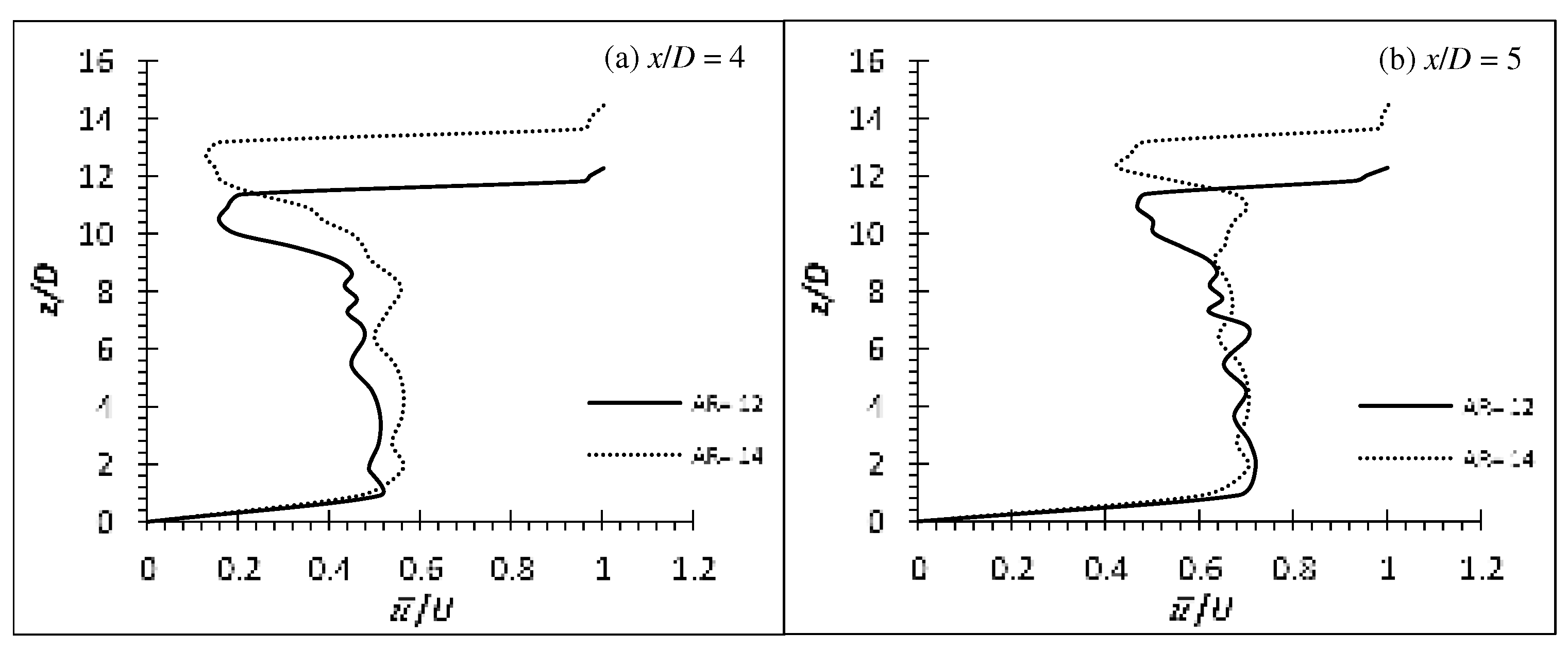
Figure 10.
Time-average wall-normal velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 4,000.
Figure 10.
Time-average wall-normal velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 4,000.
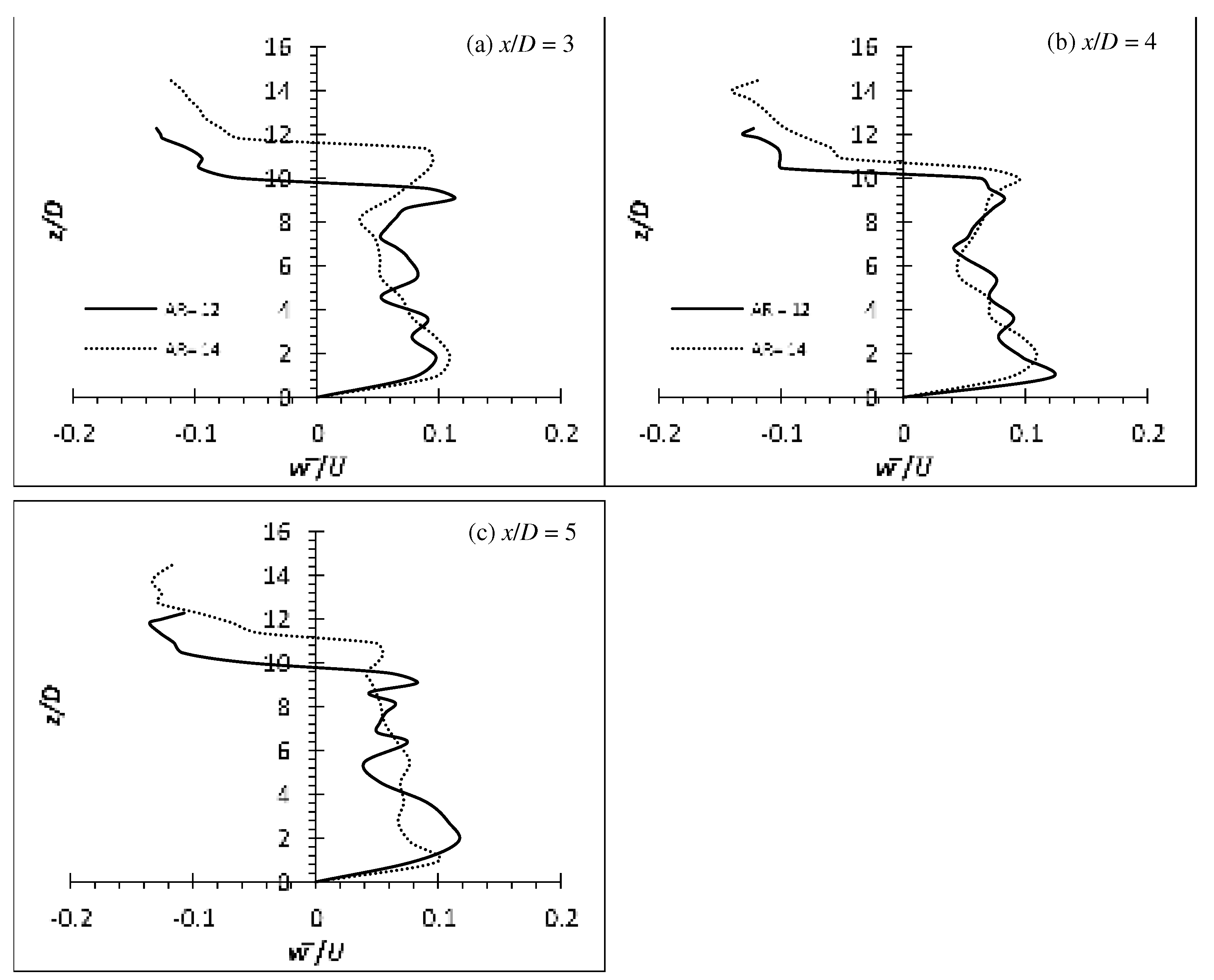
Figure 11.
Time-average wall-normal velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 6,000.
Figure 11.
Time-average wall-normal velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 6,000.
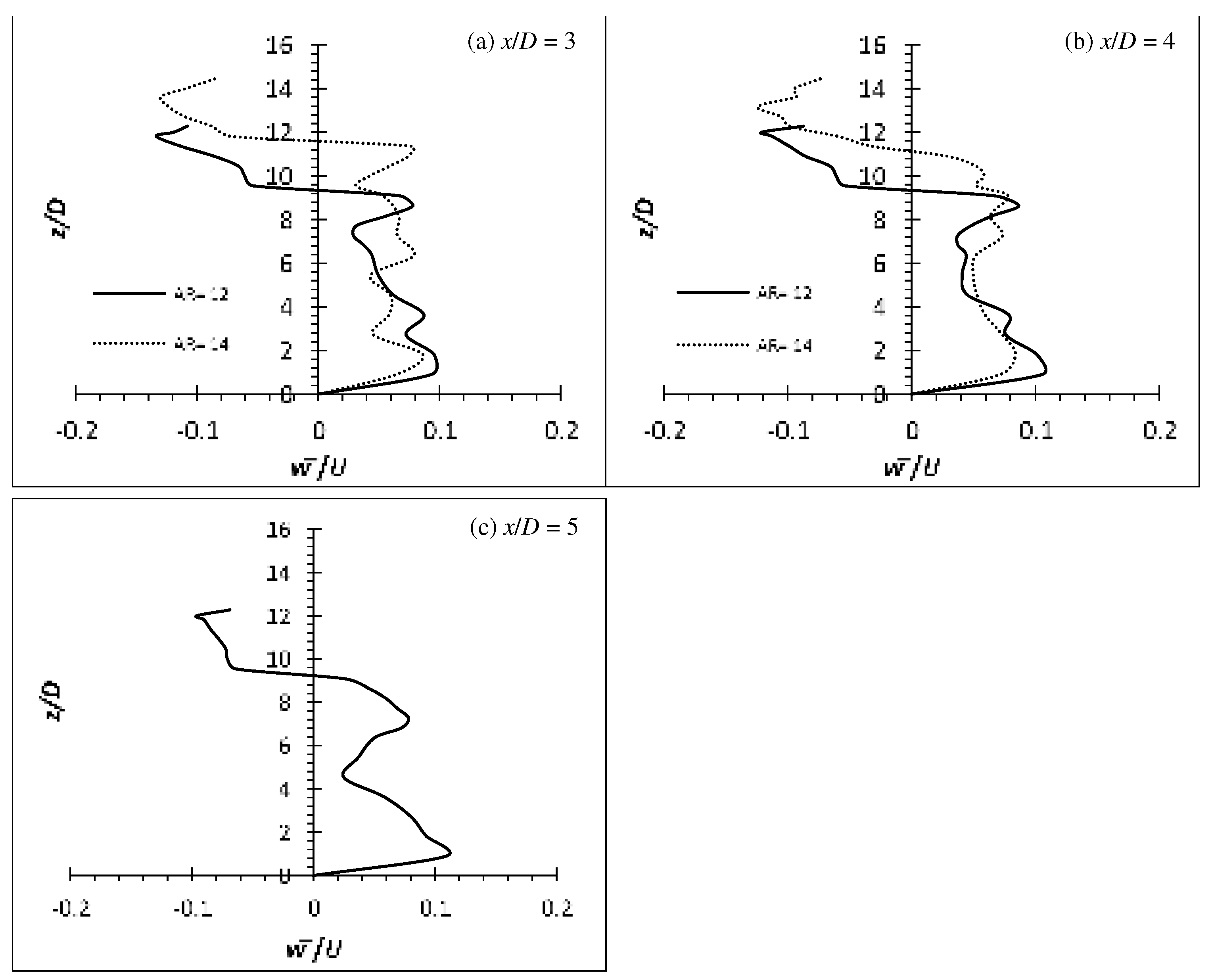
Figure 12.
Time-average wall-normal velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 8,000.
Figure 12.
Time-average wall-normal velocity profile of flexible finite cylinder of AR = 12 and 14 at wake centreline (y/D = 0) for Re = 8,000.
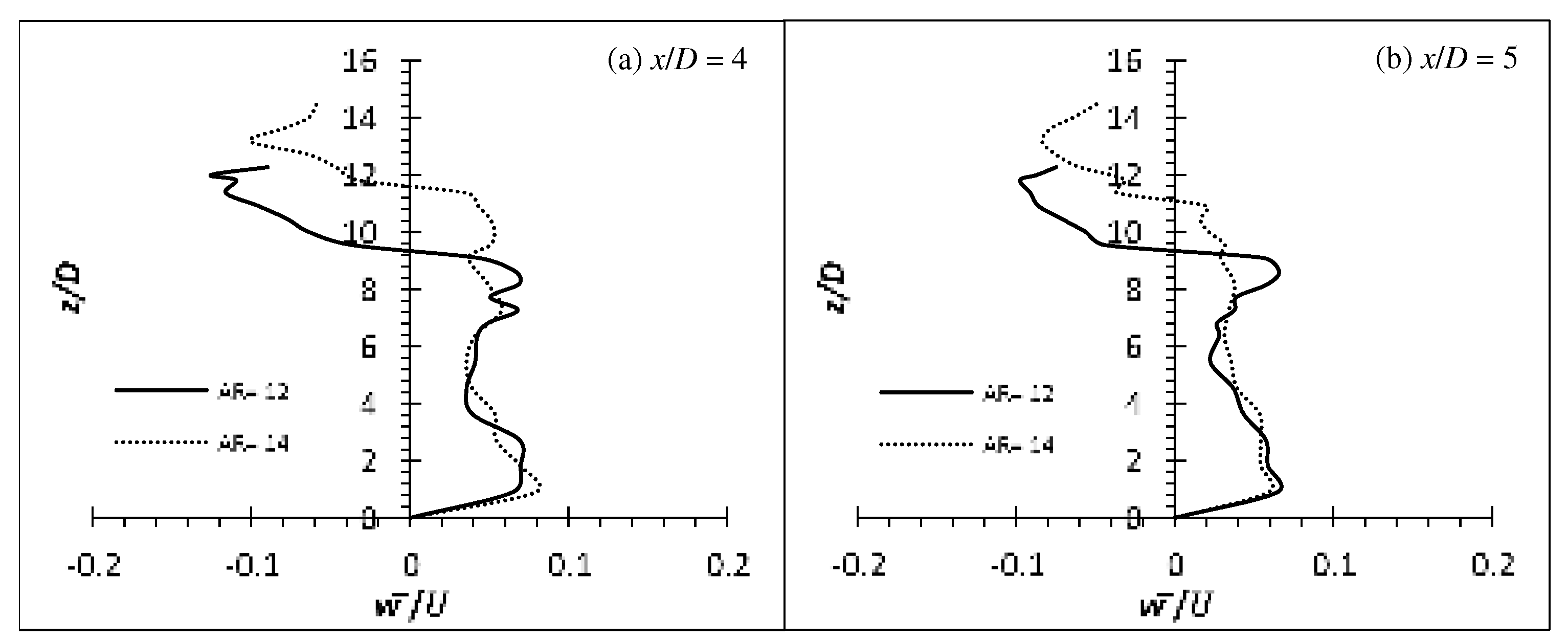
Figure 13.
Time-average streamwise velocity profile of flexible finite cylinder (Aluminium and Carbon Steel) of AR = 50 at wake centreline (y/D = 0) for Re = 2,500. Aluminium denotes Al while Carbon Steel denotes CS.
Figure 13.
Time-average streamwise velocity profile of flexible finite cylinder (Aluminium and Carbon Steel) of AR = 50 at wake centreline (y/D = 0) for Re = 2,500. Aluminium denotes Al while Carbon Steel denotes CS.
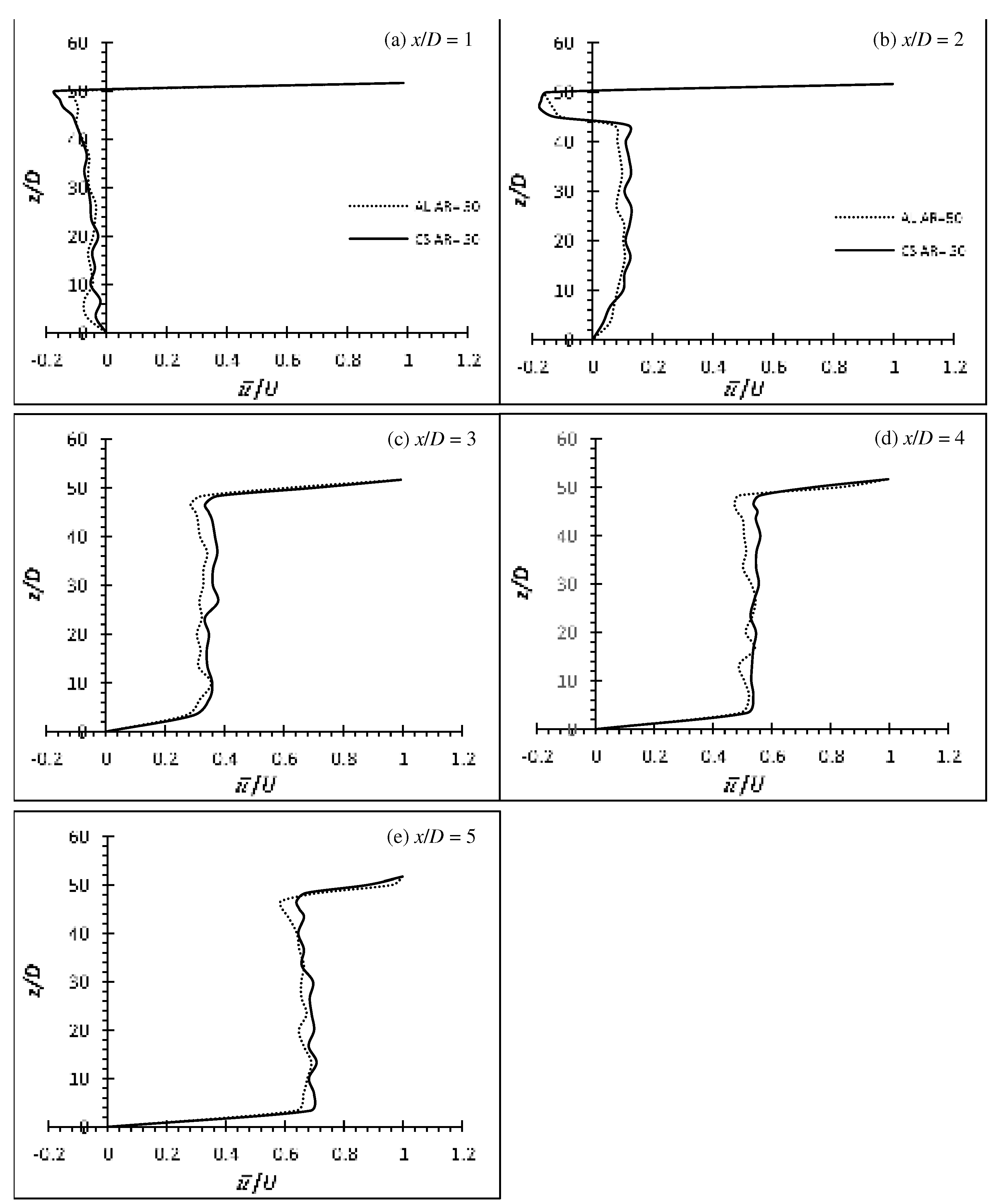
Figure 14.
Time-average streamwise velocity profile of flexible finite cylinder (Aluminium and Carbon Steel) of AR = 54 at wake centreline (y/D = 0) for Re = 2,500. Aluminium denotes Al while Carbon Steel denotes CS.
Figure 14.
Time-average streamwise velocity profile of flexible finite cylinder (Aluminium and Carbon Steel) of AR = 54 at wake centreline (y/D = 0) for Re = 2,500. Aluminium denotes Al while Carbon Steel denotes CS.
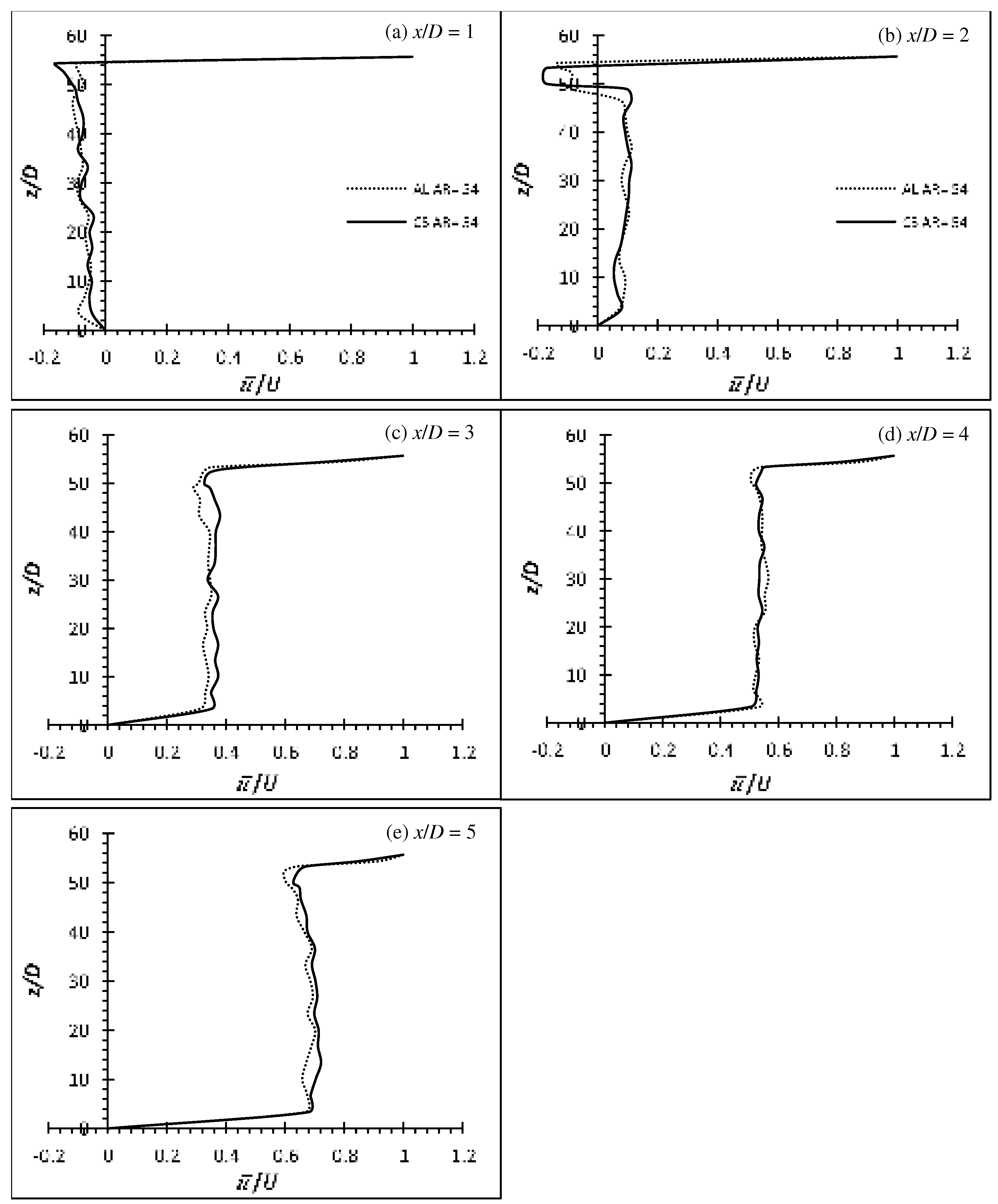
Figure 15.
Time-average wall-normal velocity profile of flexible finite cylinder (Aluminium and Carbon Steel) of AR = 50 at wake centreline (y/D = 0) for Re = 2,500. Aluminium denotes Al while Carbon Steel denotes CS.
Figure 15.
Time-average wall-normal velocity profile of flexible finite cylinder (Aluminium and Carbon Steel) of AR = 50 at wake centreline (y/D = 0) for Re = 2,500. Aluminium denotes Al while Carbon Steel denotes CS.
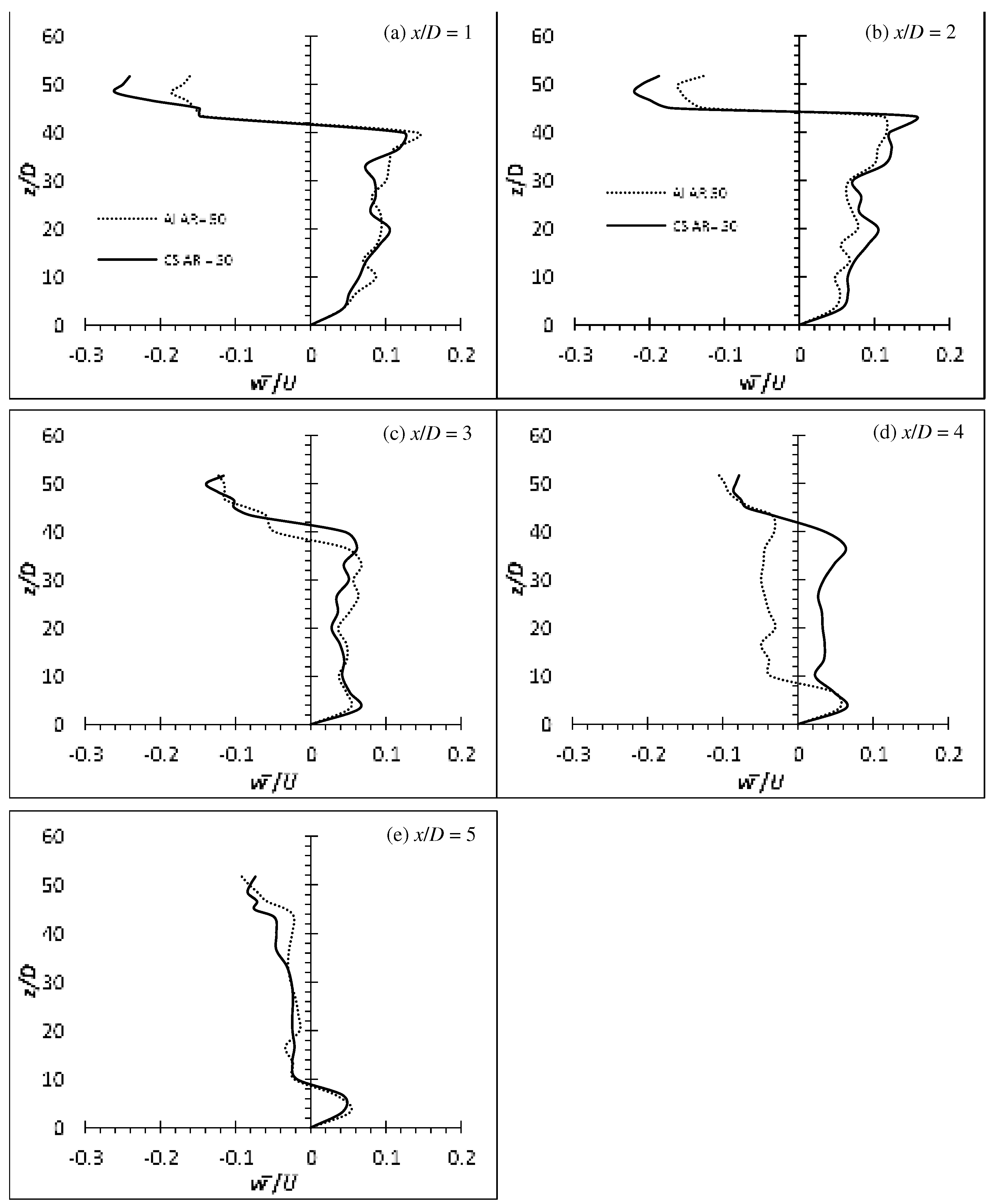
Figure 16.
Time-average wall-normal velocity profile of flexible finite cylinder (Aluminium and Carbon Steel) of AR = 54 at wake centreline (y/D = 0) for Re = 2,500. Aluminium denotes Al while Carbon Steel denotes CS.
Figure 16.
Time-average wall-normal velocity profile of flexible finite cylinder (Aluminium and Carbon Steel) of AR = 54 at wake centreline (y/D = 0) for Re = 2,500. Aluminium denotes Al while Carbon Steel denotes CS.
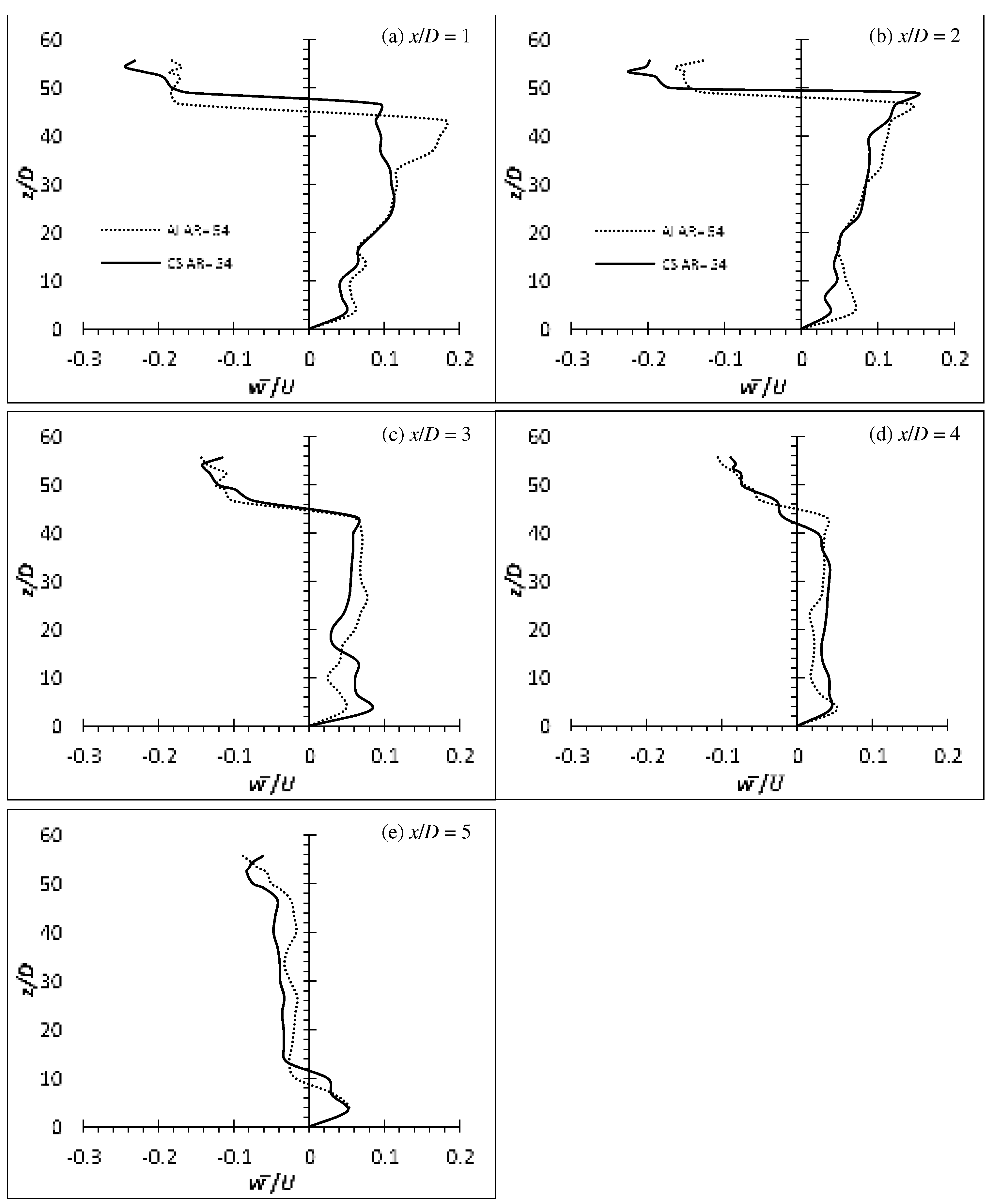
Figure 17.
Turbulence intensity distribution for AR = 12 at (a) Re = 4,000; (b) Re = 6,000.
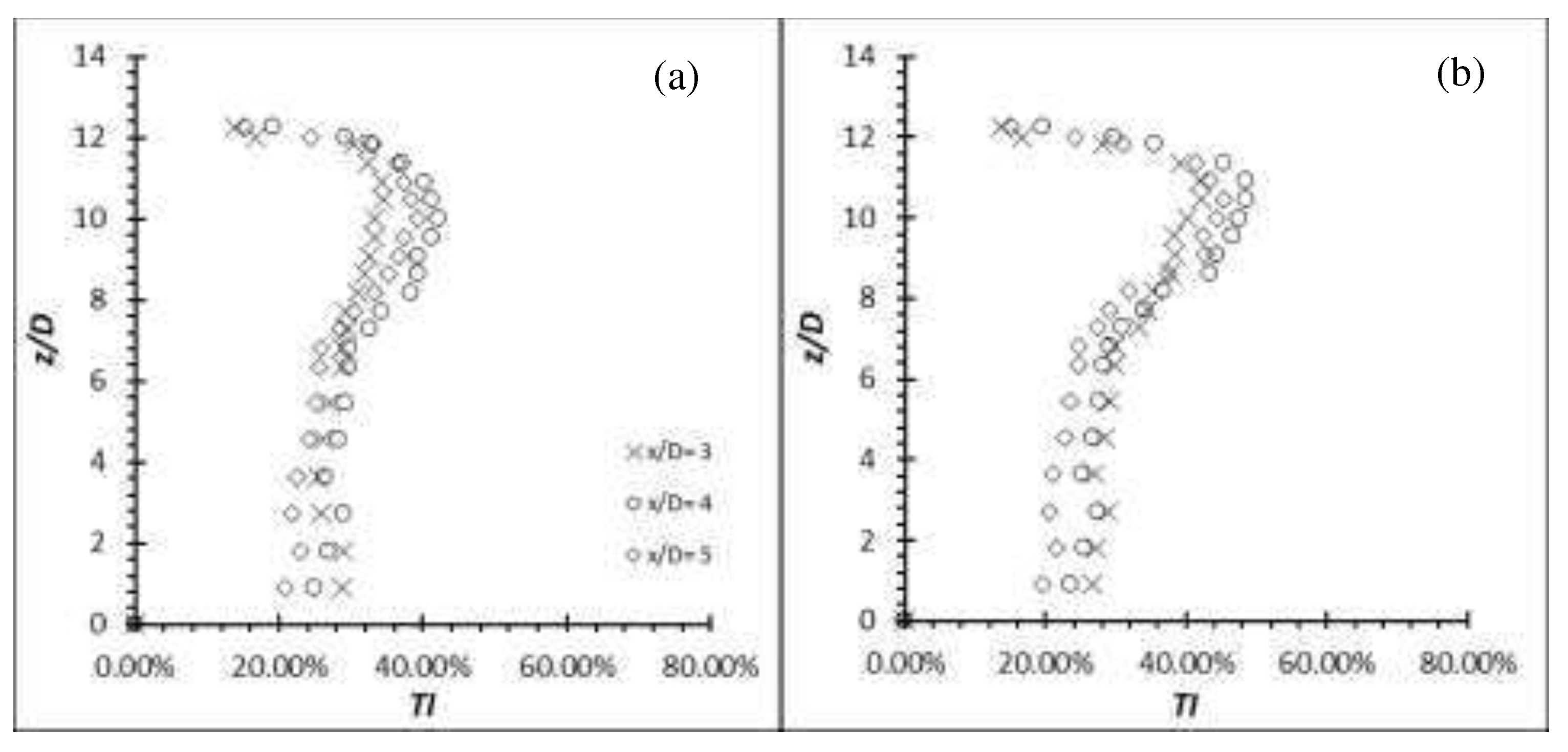
Figure 18.
Turbulence intensity distribution for AR = 14 at (a) Re = 4,000; (b) Re = 6,000.
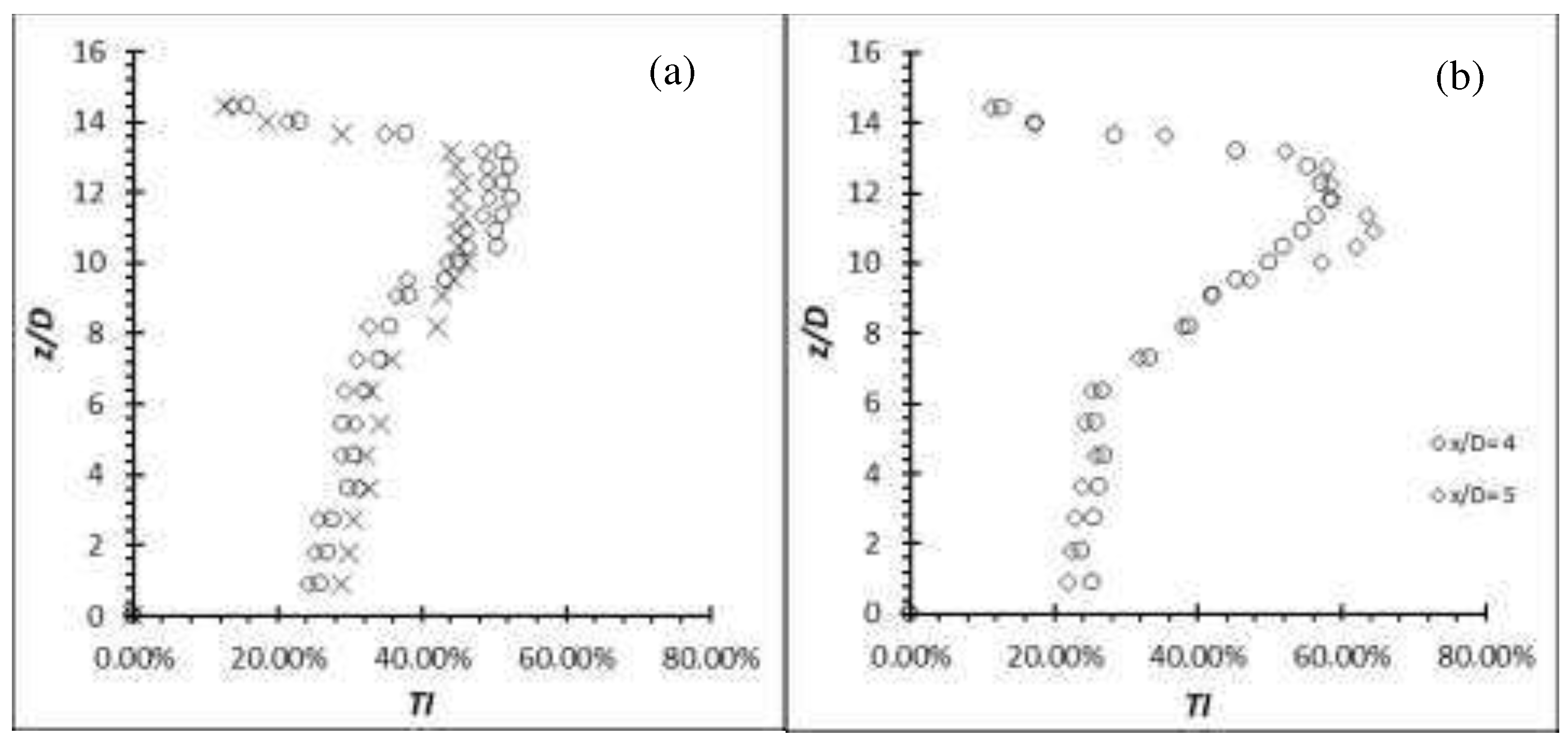
Figure 19.
Turbulence intensity distribution for aluminium cylinder at Re = 2,500 (a) AR = 50; (b) AR = 54.
Figure 19.
Turbulence intensity distribution for aluminium cylinder at Re = 2,500 (a) AR = 50; (b) AR = 54.
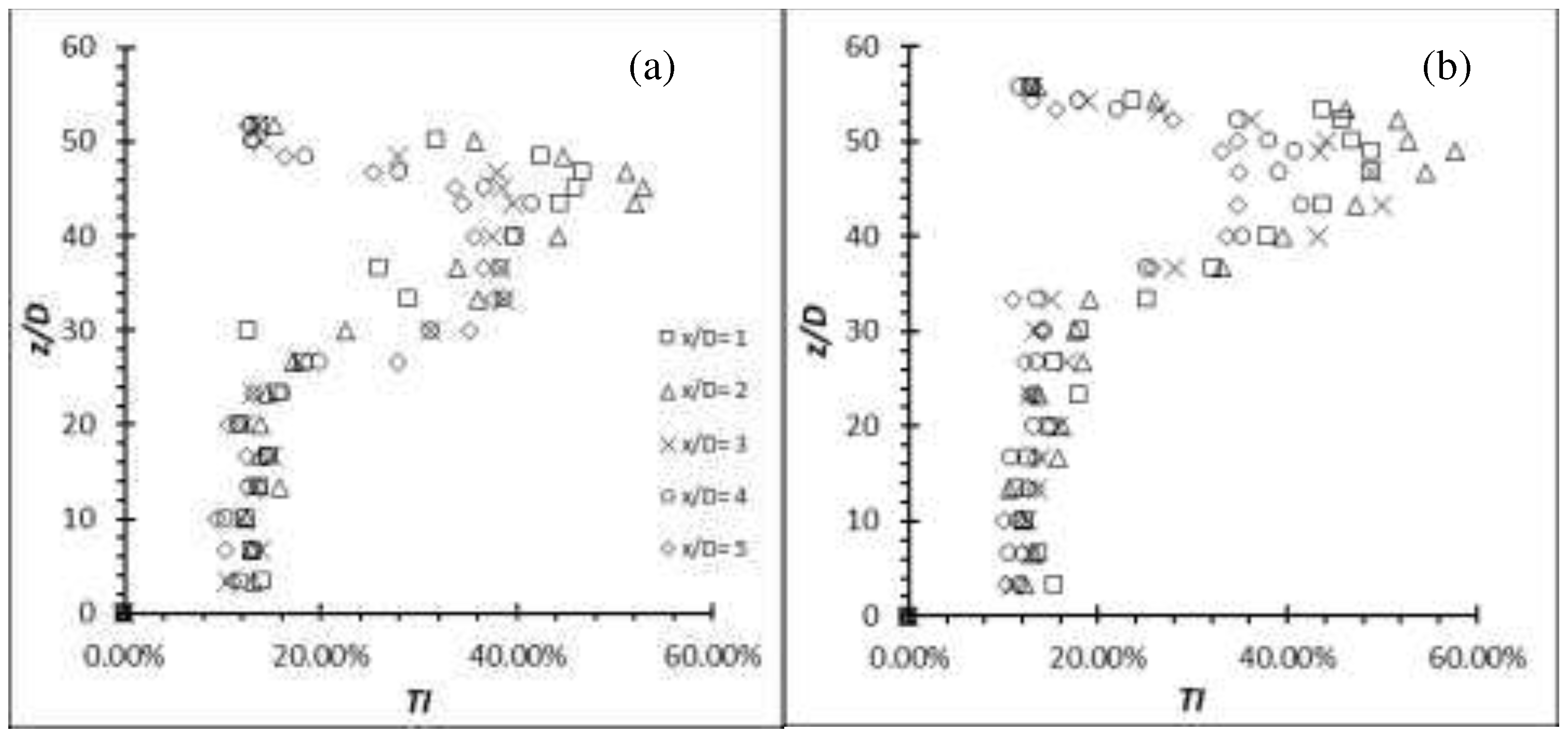
Figure 20.
Turbulence intensity distribution for carbon steel cylinder at Re = 2,500 (a) AR = 50; (b) AR = 54.
Figure 20.
Turbulence intensity distribution for carbon steel cylinder at Re = 2,500 (a) AR = 50; (b) AR = 54.
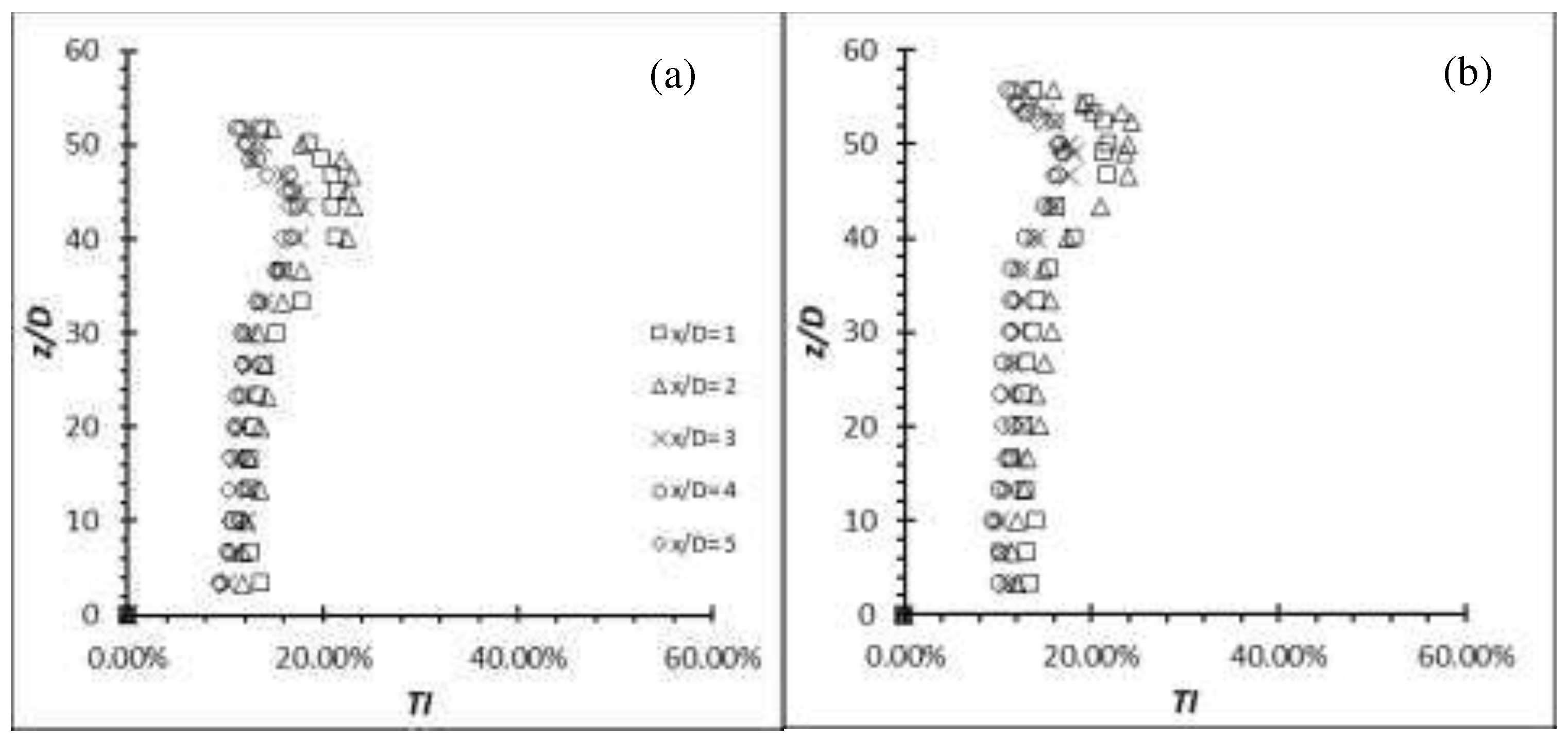
Figure 21.
Oscillation of aluminium flexible cylinder of AR = 50 at Re = 2,500.
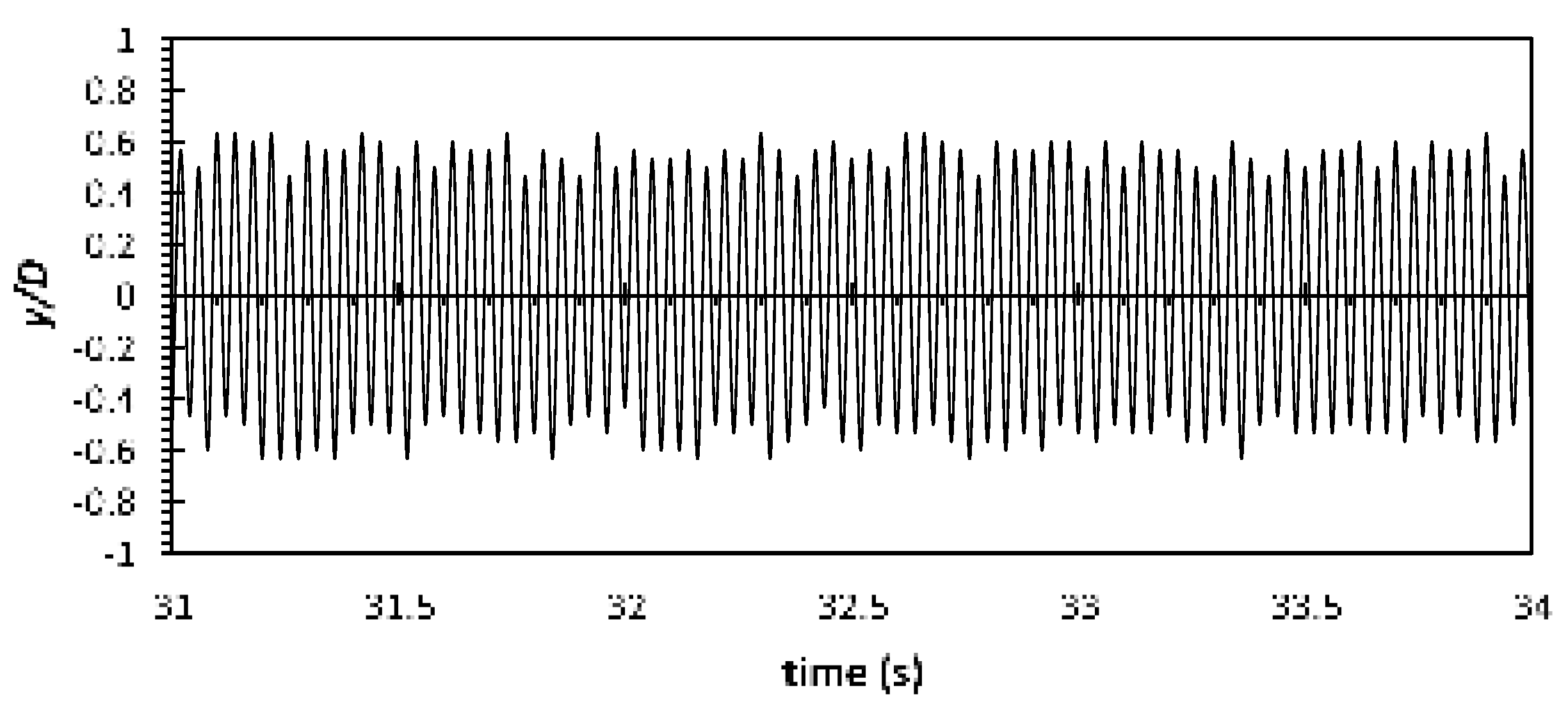
Figure 22.
Oscillation of aluminium flexible cylinder of AR = 54 at Re = 2,500.
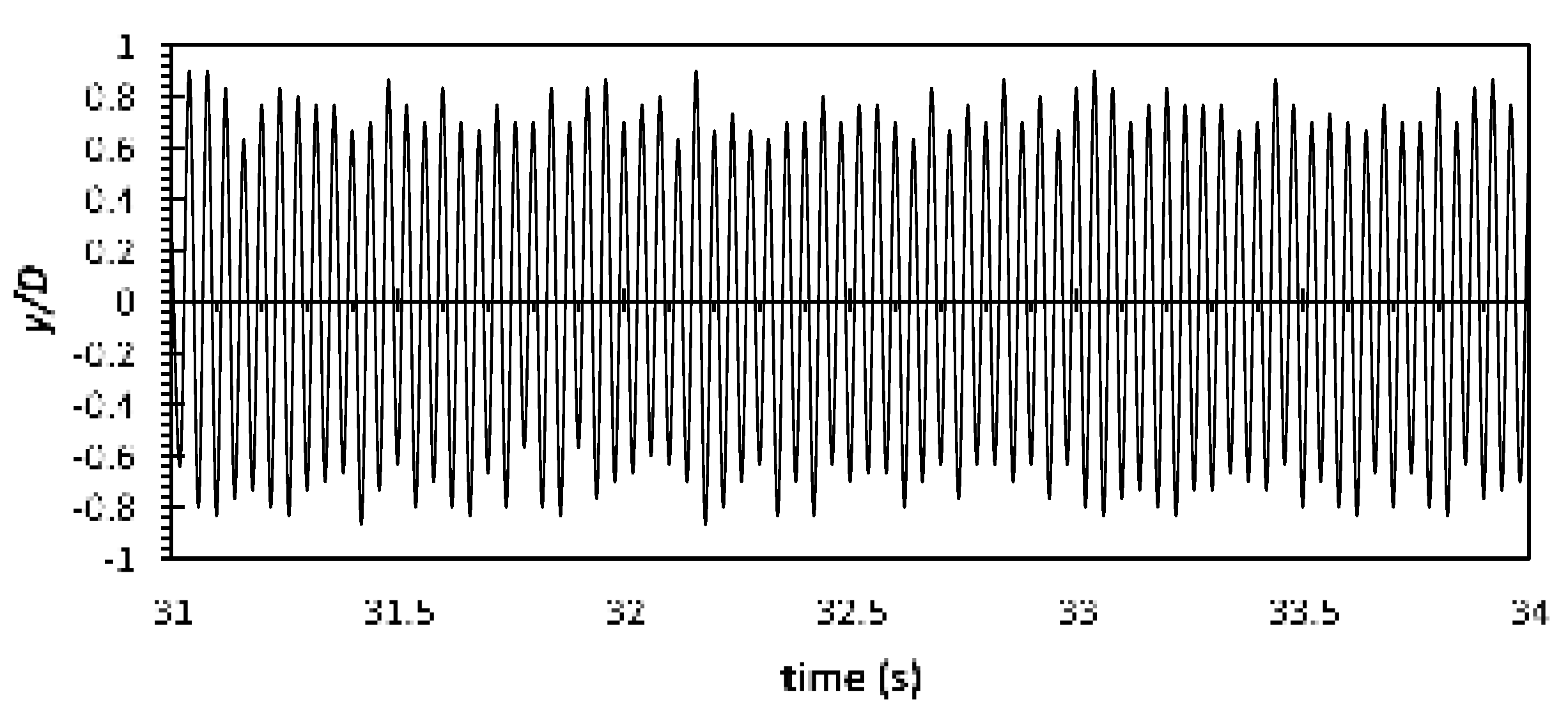
Figure 23.
Production term, for flexible cylinder at Re = 4,000 for (a)AR = 12; (b)AR = 14.
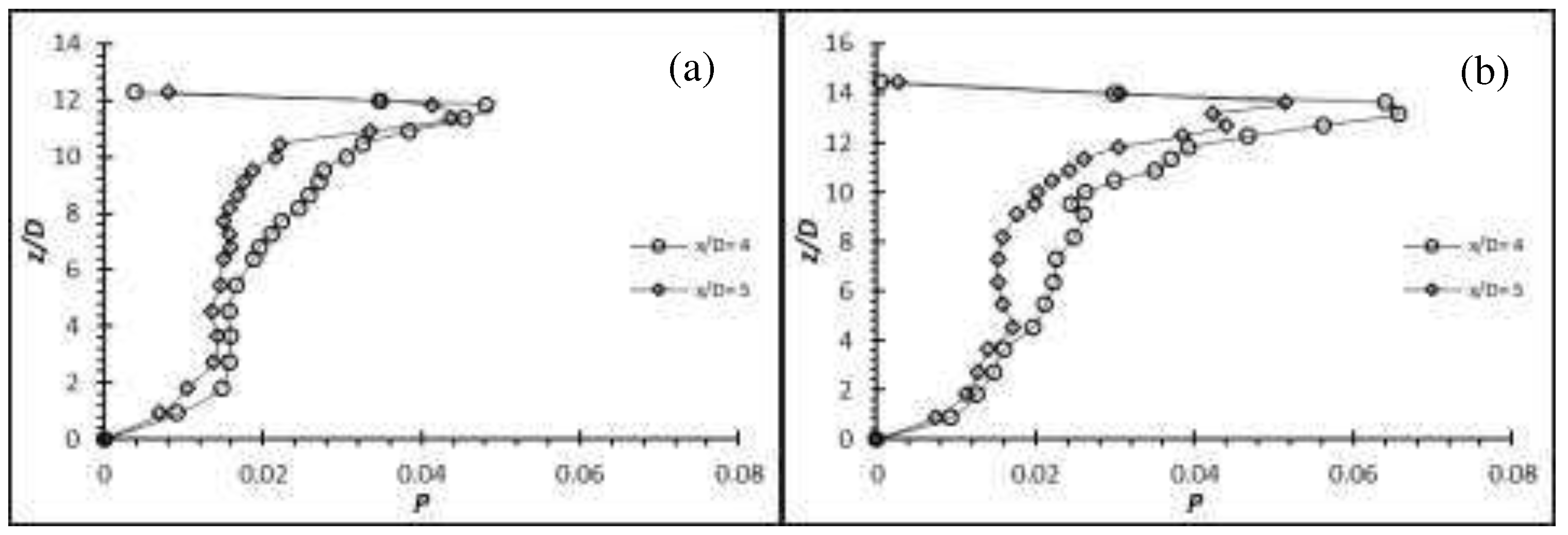
Figure 24.
Production term, for flexible aluminium cylinder of (a) AR = 50 and (b) AR = 54 at Re = 2,500.
Figure 24.
Production term, for flexible aluminium cylinder of (a) AR = 50 and (b) AR = 54 at Re = 2,500.
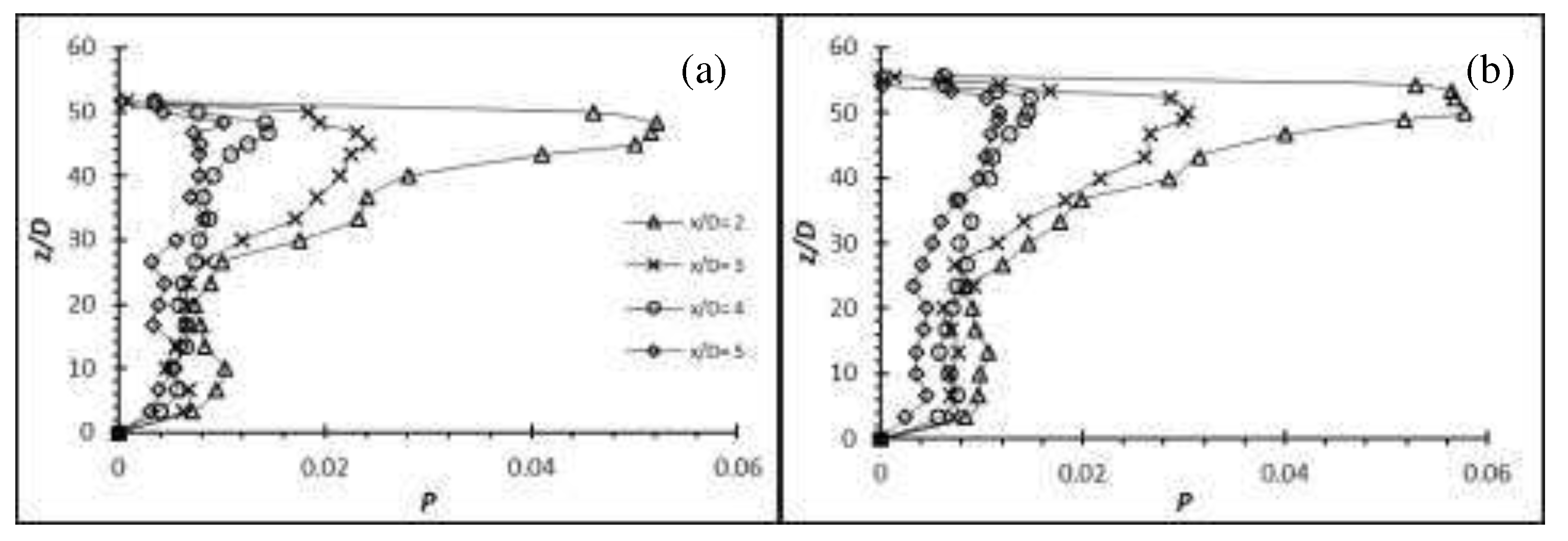
Figure 25.
Production term, for flexible carbon steel cylinder of (a) AR = 50 and (b) AR = 54 at Re = 2,500.
Figure 25.
Production term, for flexible carbon steel cylinder of (a) AR = 50 and (b) AR = 54 at Re = 2,500.
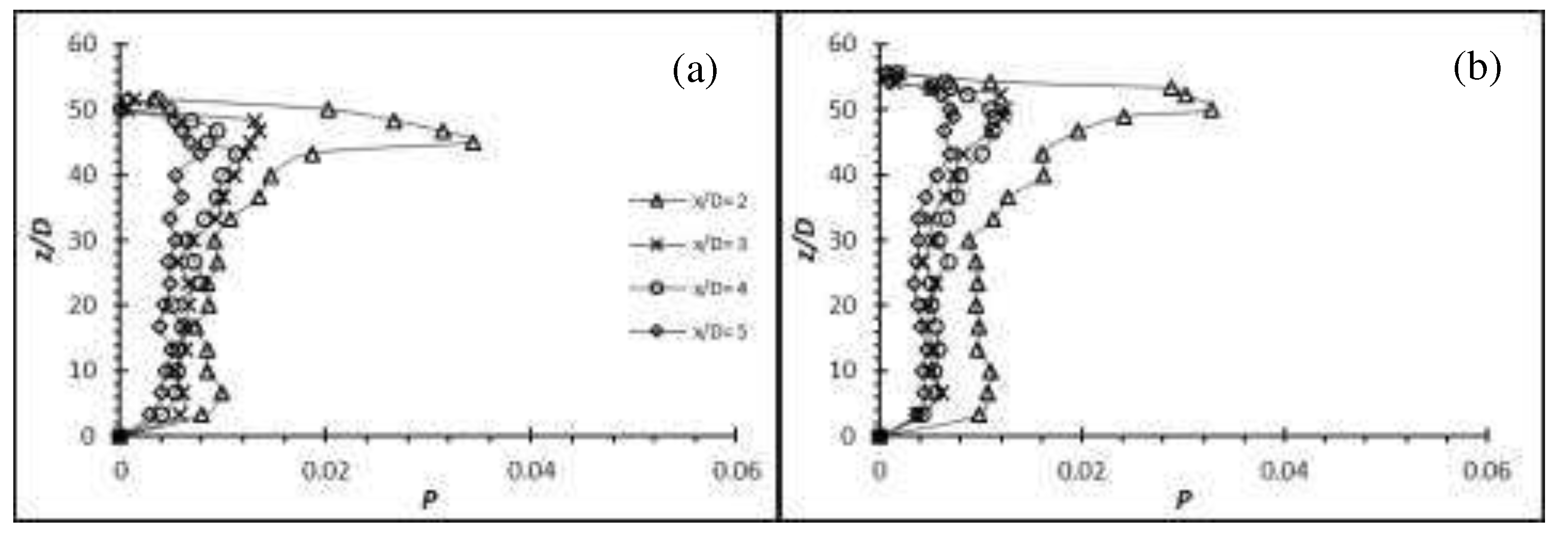
Figure 26.
Reynolds stress profiles for cylinder of AR = 12 at Re = 4,000: (a) . (b) (c) .
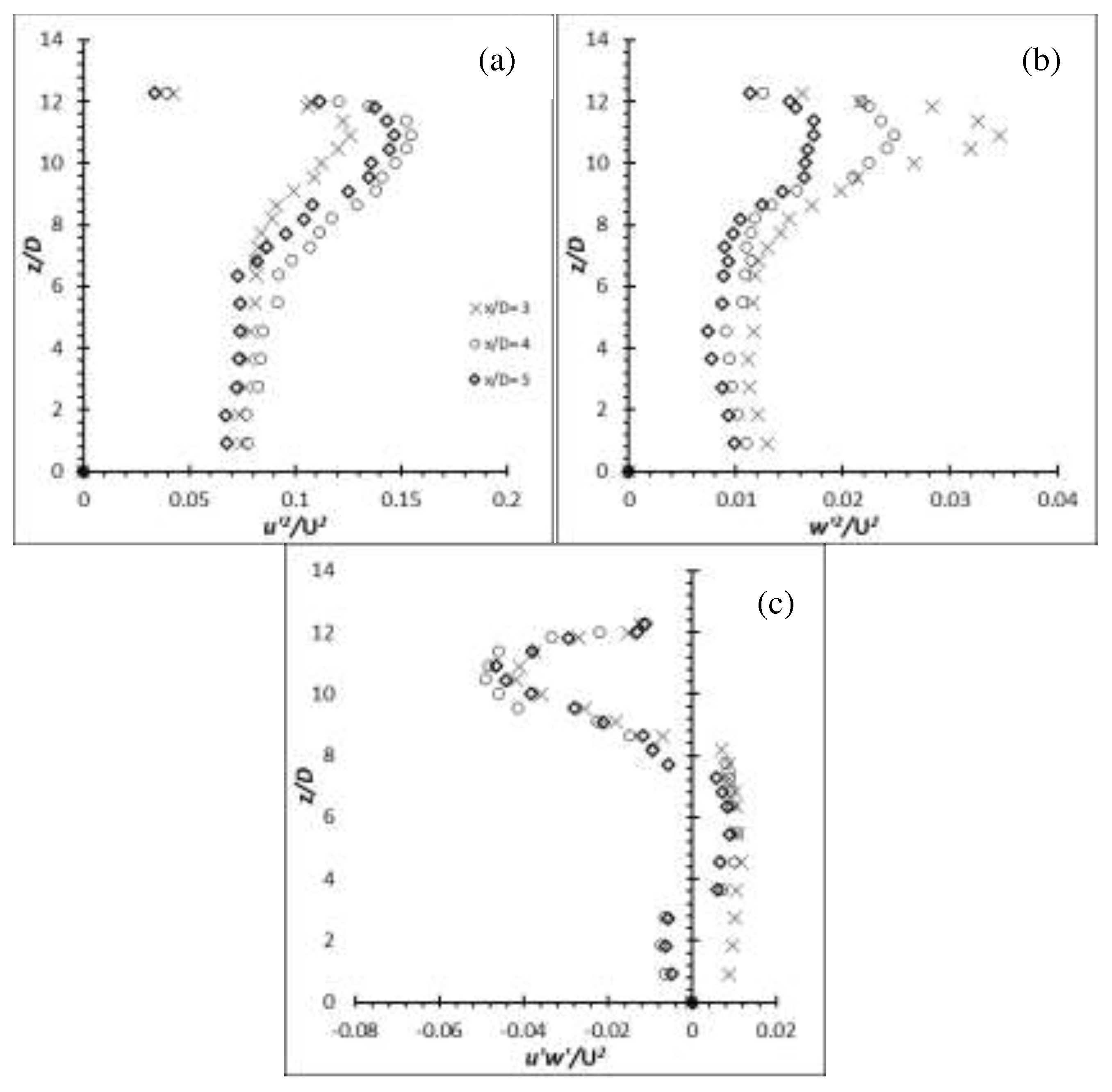
Figure 27.
Reynolds stress profiles for cylinder of AR = 12 at Re = 6,000: (a) (b) (c) .
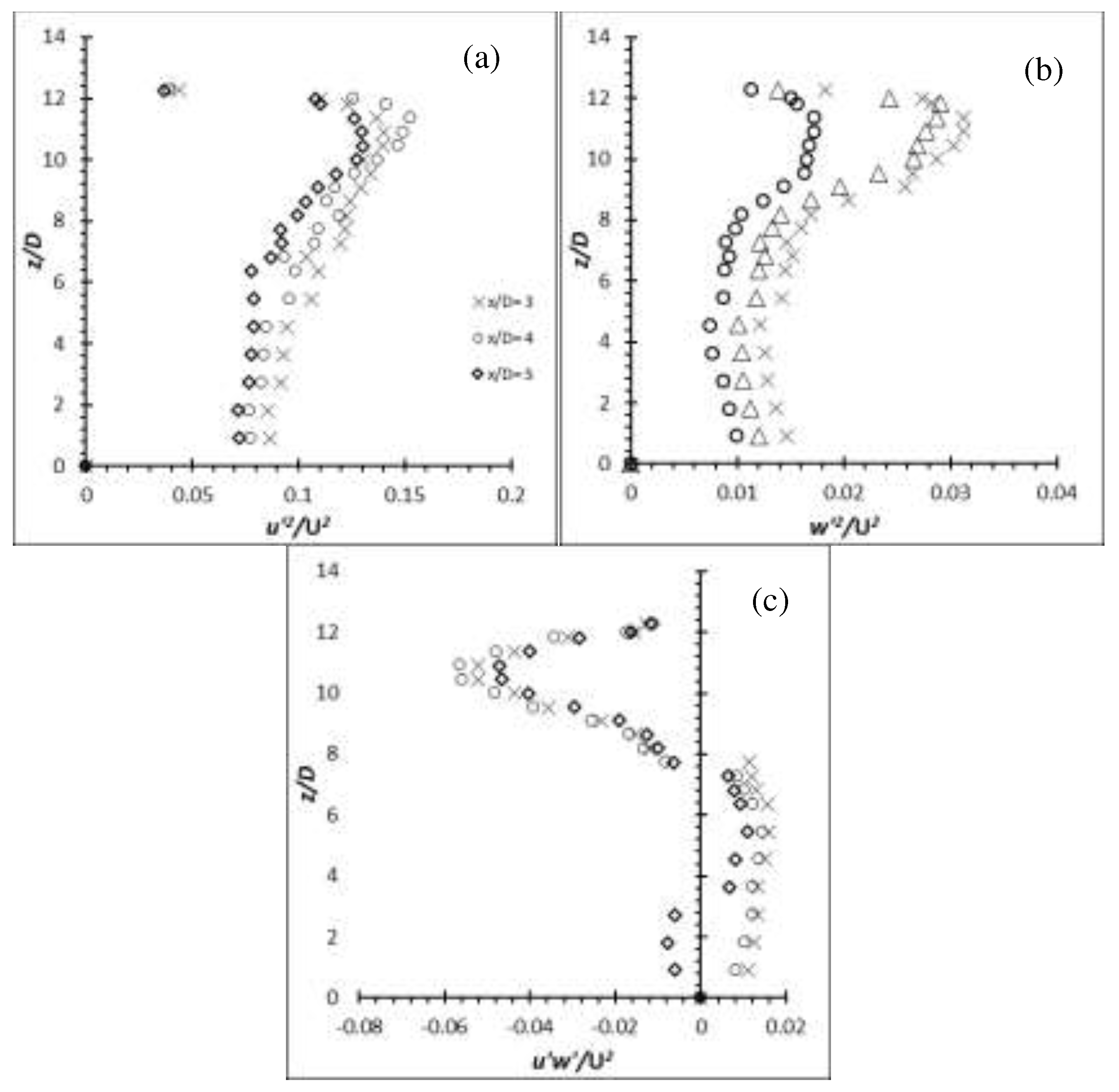
Table 1.
Boundary layer measurements on the ground plane at U = 0.33 m/s.
| Location x/D | δ (mm) | δ* (mm) | δθ (mm) | Hδ | ReL x 105 |
|---|---|---|---|---|---|
| -10 | 50 | 11.6 | 8.9 | 1.30 | 0.80 |
| 0 | 54 | 11.9 | 9.9 | 1.20 | 1.28 |
| +10 | 61 | 12.0 | 10.0 | 1.20 | 1.76 |
Table 2.
Boundary layer measurements on the ground plane at U = 0.49 m/s.
| Location x/D | δ (mm) | δ* (mm) | δθ (mm) | Hδ | ReL x 105 |
|---|---|---|---|---|---|
| -10 | 52 | 11.7 | 10.1 | 1.15 | 1.19 |
| 0 | 58 | 11.9 | 9.9 | 1.20 | 1.90 |
| +10 | 67 | 12.3 | 10.2 | 1.20 | 2.61 |
Table 3.
Boundary layer measurements on the ground plane at U = 0.65 m/s.
| Location x/D | δ (mm) | δ* (mm) | δθ (mm) | Hδ | ReL x 105 |
|---|---|---|---|---|---|
| -10 | 54 | 11.9 | 9.0 | 1.30 | 1.58 |
| 0 | 56 | 11.9 | 9.3 | 1.30 | 2.52 |
| +10 | 60 | 12.0 | 9.4 | 1.30 | 3.45 |
Table 4.
Summary of the specifications of finite rigid circular models.
| AR | 10 | 16 |
|---|---|---|
| D (mm) | 13.0 ± 0.5 | 11.0 ± 0.5 |
| L (mm) | 130.0 ± 1 | 176.0 ± 1 |
| δ/D | 4.15, 4.46, 4.30 | 4.90, 5.27, 5.09 |
| δ/H | 0.41, 0.44, 0.43 | 0.30, 0.32, 0.31 |
| Blockage ratio (%) | 4.2 | 4.8 |
| ReD | 4 x103, 6 x103, 8 x103 | 4 x103, 6 x103, 8 x103 |
| Material | Aluminium | Aluminium |
| Young Modulus (GPa) | 65 | 65 |
Table 5.
Summary of the specifications of finite flexible circular models.
| Group | Metal | Polymer |
|---|---|---|
| AR | 50 and 54 | 10, 12, 14 and16 |
| D (mm) | 3.0 ± 0.5 | 11.0 ± 0.5 |
| L (mm) | 150.0 ± 1, 160.2 ± 1 | 110.0 ± 1, 132.0 ± 1, 154.0 ± 1, 176.0 ± 1 |
| δ/D | 25.0, 26.0 | 4.90, 5.27, 5.09 |
| δ/H | 0.46 – 0.52 | 0.30 – 0.52 |
| Blockage ratio (%) | 1.1 and 1.2 | 3.0, 3.6, 4.2, 4.8 |
| ReD | 2.5 x103 | 4 x103, 6 x103, 8 x103 |
| Material | Aluminium and AISI 12L14 carbon steel | EVA |
| Young Modulus (GPa) | 65 and 200 | 0.0015 |
Table 6.
The average wake region (in approximation) behind the rigid and flexible cylinders at different conditions.
Table 6.
The average wake region (in approximation) behind the rigid and flexible cylinders at different conditions.
| Average wake region | |||
|---|---|---|---|
| Material | AR | Re | Average Wake Region |
| EVA | 12 | 4,000 | ~10.45 D |
| 6,000 | ~11.30 D | ||
| 8,000 | ~10.90 D | ||
| 14 | 4,000 | ~12.27 D | |
| 6,000 | ~12.27 D | ||
| 8,000 | ~12.72 D | ||
| Aluminium | 50 | 2,500 | ~46.67 D |
| 54 | ~51.30 D | ||
| Carbon Steel | 50 | ~46.67 D | |
| 54 | ~50.00 D | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







