Prerpints.org logo
Preprint
Article

Remote Sensing Image Scene Classification in Hybrid Classical-Quantum Transferring CNN with Small Samples

Altmetrics

Downloads

203

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 June 2023

Posted:

04 July 2023

You are already at the latest version

Alerts
Abstract
Deep learning is improving by leaps and bounds in remote sensing images (RSIs) analysis, pre-trained convolutional neural networks (CNNs) have shown remarkable performance in remote sensing image scene classification (RSISC). Nonetheless, pre-trained CNNs require massive annotated data as samples for data training. When labeled samples are not sufficient, the most common solution is to the pre-trained CNNs using a great deal of natural image dataset (e.g. ImageNet). However, these pre-trained CNNs require a large quantity of labelled data for training, which is often not feasible in RSISC, especially when the target RSIs have different imaging mechanisms from RGB natural images. In this paper, we proposed an improved hybrid classical-quantum transfer learning CNNs composed of classical and quantum elements to classify open-source RSI dataset. The classical part of the model is made up of a ResNet network which extracts useful features from RSI datasets. To further refine the network performance, a tensor quantum circuit is subsequently employed by tuning parameters on near-term quantum processors. We tested our models on open-source RSI dataset. In our comparative study, we have concluded that the hybrid classical-quantum transferring CNN has achieved better performance than other pre-trained CNNs based RSISC methods with small training samples. Moreover, it has been proved that the proposed algorithm improves the classification accuracy while greatly decreasing sum of model parameters and sum of training data.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In recent times with the rocketing progress of the earth observation capability and the intelligent computing technology, the progression and innovation of remote sensing(RS) is more important than ever. RS image data processing is now developing towards RS Big Data Era, which relies on data model by data-driven intelligent analysis [1]. Machine learning(ML) plays an essential role in extracting underlying features or a probability distribution of patterns in RSI datasets, such as trend prediction, target recognition, change detection, or image classification in hitherto unknown domains [2]. In particular, deep learning (DL) has proven to be a technological innovation and a historic milestone in many fields [3]. It emphasizes neural networks (NNs) involving multiple hidden layers, which use feature representations learned exclusively from the data, instead of handcrafted features that are designed based mainly on domain-specific knowledge. DL has widely used in various research topics, for example data analysis tasks, including semantic segmentation, image classification, target detection, scene classification, change detection and three-dimensional reconstruction.
Deep learning algorithms has opened up an entirely novel frontier of learning algorithms including CNNs techniques that have been adopted in the RS image recognition and image classification [6]. Various deep learning models have been developed with outstanding performance for RSISC on RSI datasets in multiple applications [8–10]. But the CNN architecture construction requires skill in both DL methodology and professional expertise [11], the efficiency of CNN models remains a huge challenge. CNNs can extract hierarchical and insightful features automatically from massive size of image data [7]. Early studies involving RSISC in CNN were transplanted from natural image data, which led to increase the difficulty of RSISC task in complex RSIs [4], and handmade architecture design is troublesome and fallible, experienced and mature professionals in both DL and the investigated domain are often not available in practical applications. Since then, researchers have aimed to replace hand-engineered features with trainable multilayer networks, so enhancement capability of feature representation has become the main research technique [5].
Most studies on CNN-based RSISC have used pre-trained CNN models as features extractors to extract high semantic features. Researchers have utilized networks that are pre-trained on different networks, for instance AlexNet [12], VGGNet [13], GoogleNet [14], and ResNet [15], stand out among numerous DL-based methods due to closely related powerful features extraction performance. Although both assignments involve RSIs data and the pre-trained networks can easily be operated for transferring in RSISC, these methods have limitation: It has no advantage if significant domain differences exist between source and target datasets. Furthermore RSIs differ significantly in terms of spectral resolutions, spatial resolution, and radiometric resolution etc.[16].
Fine-tuning CNN-based models is an effective tool for RSISC. However, such approaches still have limitations in three perspectives related to datasets, models, and labels. These limitations are discussed below.
Firstly, the dataset plays a important role in advancing RSISC. The Size-Similarity Matrix of dataset determines the choices of the pre-trained model. This matrix classifies the strategies based on the size of the dataset and its similarity to the dataset in which the pre-trained model was trained. Due to the matrix transformation conducted in the fully connected layers, the dataset must be transformed into a certained fixed size. The most common approach is to crop and interpolate the original image, which inevitably results in a loss of fine information from the original RSIs. Unfortunately, either of these approaches can be detrimental to the performance of RSISI. Therefore, the selection of the pre-trained models depends on the dataset's size and size-similarity. The RSIs dataset must be transformed into a special fixed size [17].
Secondly, from a modeling perspective, most pre-trained models can achieve excellent classification performance. However, these models also have some limitations. The learned feature may be not entirely satisfactory for the properties of targets datasets and per-trained treatments applied between heterogeneous networks require manual manipulations of layer combinations, depending on type of task. The RSISC task, in particular, requires a massive tuning procedure to achieve optimal classification performance.
Thirdly, many scene images with same exteriors have different but correlated scene categories, which can lead to the label paradox. Because a RSI contains various objects, such as water, mountains, nudation and buildings etc, which may be covered in a residential scene as shown in Figure 1. The variance and complex spatial distributions of ground objects cause the diversity of RSISC. As a result of the different varieties in the exteriors of ground objects within the similar semantic information, traditional methods of RSISC often fail to achieve satisfactory classification accuracy due to low sort separability caused by the presence of the same objects within different scene sorts or the high semantic superimposed between different scene categories. Another important difficulty of RSISC is the large variance of object scales caused by sensor imaging altitude variation. Furthermore, the label distribution of ground objects in dataset is often unavailable in original training dataset and needs to be modeled label paradox, which is typically caused by resembling sample dataset that have different but correlated labels, as can be seen in Figure 1 [18].
Quantum computing are emergent techniques that have the potential to transform the research and application of remote sensing. Quantum computing can provide significant advantages in terms of improving the performance of classification techniques. The great potential of quantum computing in ML has been actively investigated. In specific cases, traditional machine learning tasks can be improved with exponential speedups when it operates on a quantum computer [21,22]. The Harrow-Hassidim-Lloyd (HHL) algorithm is a quantum computing that has been successfully implanted in conventional ML theories and topics, such as data mining, artificial neural networks, computational learning theory, etc., as shown in [23,24,25,26,27]. HHL-based algorithms is based on the quantum phase estimation algorithm, which operates in a high depth quantum circuit [28]. To bypass this strict requirement of hardware, classical-quantum hybrid algorithms containing a low depth quantum circuit for instance the variational quantum eigensolver (VQE) and the quantum approximate optimization algorithm (QAOA) have been suggested [29,30]. The idea of a hybrid algorithm is to divide the problem into two components, either of which can be operated on a quantum and a classical computer separately. Cai verified the feasibility of K-Means algorithm on a quantum computer [31]. Otgonbaatar proposed a parameterized quantum circuit (PQC) with only 17 quantum bits for classifying a two-label Sentinel RSI dataset. A quantum-based pseudo-labelling for hyperspectral imagery classification is demonstrated by R. U. Shaik. Noisy intermediate-scale quantum (NISQ) devices are a advanced quantum computing technology providing solutions for large-scale and complex practical quantum computation, such as solving high-complexity problems or supporting ML algorithms. An NISQ device is termed a variational quantum circuit (VQC) when it has parameterized quantum gates and parameterized quantum circuit. Sometimes, the VQC is a supervised learning algorithm in which quantum neural networks (QNNs) are trained to perform a classification mission. The transfer learning approach in the quantum domain has been largely unexplored, with only very little applications such as modeling quantum many-body system (MBS), associated with classical autoencoders to a quantum Boltzmann machine, and initializing variational quantum networks. In the paper, a innovative, self-designed and systematic theory through a concept of tensor quantum circuits and pre-trained networks is proposed.
Our study demonstrate that hybrid classical-quantum transferring CNN models can significantly enhance the efficient and performance of RSISC with small training samples and investigate the feasibility of the hybrid classical-quantum(CQ) transferring CNN model for RSISC. In this paper, we focus on the hybrid models scenario and proposed an improved hybrid classical-quantum(CQ) transfer learning CNNs composed of classical and quantum elements that can extract high informative feature efficiently with a VQC.
The remaining sections of this work are introduced as follows: Section 2 introduces some notations about hybrid classical-quantum networks. Section 3 outlines the architecture of the hybrid classical-quantum transferring CNN. Section 4 reports the evaluation an results of our model. Finally, the paper is concluded in Section 5.

2. Hybrid Classical-Quantum Networks

2.1. Vairiational Quantum Circuits

VQCs usually can define a subcircuit, which is a basic circuit architecture where complex VQCs can be constructed through repeating layers. Circuits consists of multiple rotating logic gates as well as CNOT logic gates that entangle each qubit with its neighbouring qubit. We also need a line to encode the classical data onto the quantum state, so that the output of the line measurement is related to the input. In this case, we encode the binary input onto the qubits of the corresponding order.
VQC can define a quantum layer similar to the classical neural network. Furthermore, arbitrary VQC U can be demonstrated
L = U w | x
where w denotes variational parameters, a unitary operation is realized acting on the input state |x〉of nq quantum subsystems.
The depth d of a VQC is a superposition of different quantum circuits and match the product of various parameterized unitaries with different weights:
L = L d ∘ . . . L 2 ∘ L 1
The first step is transformation of the classical image dataset into quantum state, the process denotes quantum state coding (QSE). This operation can be realized through a variational circuits depending on x. Single-qubit rotations or single mode displaces parameter x. And the quantum layer ε maps classical vector space into Hilbert space.
On other hand, for extraction of a classical output y we can measure the expectation values of nq local obervables ẑ=[ẑ1,ẑ2,...ẑn]. The process is known as a measurement layer, which maps a quantum state to a classical dataset.:
Μ ∶ = x z ^ x
The initial quantum layers and the final measurement state in the quantum circuits can be globally written as follows
Q = M∘L∘ε

2.2. Tensor Quantum Circuits

The VQC algorithm is limited to parameters adjustment, using the quantum computer as feedback circuits to adjust the parameters in the parameterized circuits to optimal values. It can only optimize the structure of the fixed circuit, cannot change its own structure, nor increase the number of entanglement operations or change the entanglement characteristics expressed, so the algorithm still means the quantum chip entanglement operation. For complex Hamiltonian, such as correlated systems, this common method performs not well.
Tensor quantum circuits adopt the classical quantum hybrid algorithm.The classical part adopts the form of tensor network to process the higher order tensor into the form of multiple lower order tensor compressors. The quantum part adopts VQC to adjust the parameters. Tensor quantum circuits consist of n qubits, and consisting of k layers. Parameterized eiθX⊗X gates are between each neighboring qubit in each layer, then followed by a series of single-qubit parameterized Z and X rotations..
Preprints 78152 g002
Figure 2. An illustration of tensor quantum circuits.
Figure 2. An illustration of tensor quantum circuits.
Preprints 78152 g002

3. Hybrid Classical-Quantum Transferring CNN

In the following section we introduce the concept of transferring prior “knowledge” from classical to quantum. A hybrid classical-quantum transferring CNN for RSISC proposal on the basis of two networks A and B is defined in Figure 3.
A hybrid classical-quantum transferring CNN for RSISC proposal (as shown in Figure 3.) A pre-trained network A on a dataset DA for a task CA is CNN’. Then the final layers are removed. The reduced network A’ can be taken as feature extractor. A new trainable network B can integrate closely the pre-trained network A’. The parameters of network B can adjust finely on the specific dataset.
DA=ImageNet：ImageNet Large Sclae Visual Recognition Challenge (ILSRC) with many classes [32].
A = ResNet34: a pre-trained residual neural network [33].
CA =Image Classification .
A’= ResNet34 a residual neural network without the final layer.
DB = RSI datasets
B = Q = L4→2ºQºL512→4 :i.e., 4-qubit tensor quantum circuits and outputs.
CB = RSISC.
The strategy of feature extraction is much more general than what we needed in this work. In the context for transfer learning, the reduced pre-trained network A’ is interpretered as a feature extractor, after removing the final layer of A. A’ can produce features that are not problem-specific. In hybrid structure, the network A is classical and the network B is quantum.
Nowadays classical hybrid transfer learning is perhaps the definitely efficient and mature tools of DL in the current technological era of ML. It is commonly validated as the successful ML algorithms, especially for RSISC.
The quantum circuits model in Equation (5) demonstrates the concept. We assume quantum circuits of 4 qubits and utilize the following model:
Q ~ = L 4 → 2 ∘ Q ∘ L 2 → 4
where L2→4 implies residual networks using the activation function tanh φ = tanh, Q is VQC, and L4→2 denotes residual networks without activation function. The strategy of quantum encoding establishes linkages between the image dataset input x and its quantum state |x〉. The chosen embedding map from the classical image dataset input vector can be written as Equation (7)：
ε x = ⨂ i = 1 4 R y π x i H | 0 ⨂ 4 = c o s π x 1 s i n π x 1 ⨂ c o s π x 2 s i n π x 2 ⨂ c o s π x 3 s i n π x 3 ⨂ c o s π x 4 s i n π x 4
L x : | x → | y = K ⨂ i = 1 4 R y π x i | x
where H denotes a single Hadamard gate. The quantum circuits consists of 4 variational circuits. And K indicates an entangling unitary operation of 3 CNOT gates. The model in the red frame demonstrates CNOT gates and 3 rotation gates RX,RY,RZ. The CNOT gates force quantum entanglement between any 2 quantum circuits, allowing the qubits from the circuits can be entangled.
Then the measurement operators should be projected by measuring the expectation values of 4 observables, locally estimated for each qubit:
z ^ = z ^ 1 , z ^ 2 , z ^ 3 , z ^ n
Μ : z = x z ^ x
In the final classification stage, the cost function was used as cross entropy and via a LogSoftMax layer. The flowchart of our proposed method is shown in Figure 4, and numerical simulations were conducted using the PyTorch interface and the PennyLane software.
Table 1. The Algorithm of the hybrid classical-quantum transferring CNN.
Table 1. The Algorithm of the hybrid classical-quantum transferring CNN.
Algorithm Hybrid classical-quantum transferring CNN
  • INPUT: RSI data as training data, rest RSIs dataset as test data.
  • OUTPUT: Generate the predicted category labels.
  • Prepare a ResNet 34 network with the autoencoder.
  • Encode the RSI dataset .
  • Traning: a 4-qubits tensor quantum circuit.
  • Feed the RSI dataset to the tensor quantum circuit.
  • Testing:
  • Feed the rest RSI dataset to the tensor quantum circuit.
  • STOP ALGORITHM.

4. Evaluation an Results

In this section, we assess the hybrid classical-quantum transferring CNN in terms of performance gains for RSI scene classification.

4.1. Data Profile

Our proposed method was evaluated using two challenging RSI datasets: the EuroSat dataset and the Aerial Image dataset (AID) [19,20,38]. The EuroSat dataset contains images taken from the Sentinel-2 satellite, categorizing the ground objects into ten distinct land cover categories. The collection includes approximately 27,000 images divided across 10 classes, with patches measuring 64 × 64 pixels. The data was originally hyperspectral images captured with 13 spectral bands, but we used only RGB channels. he AID dataset includes 10,000 images of size 600×600 pixels, classified into 30 scene classes, with varying numbers of images for each label ranging from 220 to 420. The ground resolution also varies from approximately 8m to 0.5m per pixel. Figure 6 shows examples of the AID dataset.
Preprints 78152 g005
Figure 5. This outline shows all sample images of all 10 categories covered in the EuroSAT dataset. The images size has 64 × 64 pixels. Each category contains 2000 to 3000 images. In sum, the dataset has 27,000 georefenced images [19,20].
Figure 5. This outline shows all sample images of all 10 categories covered in the EuroSAT dataset. The images size has 64 × 64 pixels. Each category contains 2000 to 3000 images. In sum, the dataset has 27,000 georefenced images [19,20].
Preprints 78152 g005

4.2. Evaluation Criteria

There exist two extensively used evaluation criteria in RSISC: overall accuracy (OA) and confusion matrix. OA is an evaluating indicator of the classifier’s performance on the whole test data set and is defined as the sum of accurately classified samples divided by the sum of tested samples. It’s a commonly used to evaluate the performance of RSISC. The confusion matrix is an informative table used to analyse all the errors and confusions between different classes, generated by comparing the performance of correct and incorrect classification of each single classifier.
The definition of the calculation of OA can be expressed as follow:
O A = ∑ i = 1 n ∑ j = 1 k P i j T
where Pij is the correct prediction of each single label, and n, k represents the sum of each label and the sum of labels. T is the sum of test dataset.

4.3. Experimental Setup

We split two different RSI datasets in different training-test ratios (10/90 ratio and 20/80 ratio) class-wise. The RGB images vast majority of all aerial and RSI datasets. For performance measurement, we compare with the performance of the proposed algorithm, the Bag-of-Viusal-Words(BoVW) approach with SIFT features, a trained SVM and other deep learning algorithms for accuracy evaluation. Furthermore, we trained a shallow CNN, a ResNet50 and a GoogleNet model on the training dataset [32,33,34,35,36]. For our proposed method, we trained a ResNet34 model and the tensor quantum circuit with the model for 60 epochs over the training dataset, with a quantum depth of 6 and an initial learning rate of η =0.0006. The model was validated with respect to the test dataset after each epoch, and overall classification on the datasets was calculated.
We used many commonly used RSISC for instance ResNet50 [15],DCNNs [73], AlexNet [44] and VGG-VD16 [47] as criteria to assess the performance improvement of our proposed method. The aforementioned models were pre-trained on ImageNet dataset and then fine-tune them to adopt them to the RSIs. For the open source AID dataset [37], the training-test ratios were set to 20%/80% and 50%/50%.

4.4. Performance Comparison

Furthermore, in order to further verify the efficiency and feasibility of the proposed algorithm in this paper, the proposed algorithm was also compared with other RSISC algorithms for experimental analysis and validated on the validation set. The results showed that the proposed algorithm achieved the best classification result (%), as shown in Table 2.
As can be seen from Table 2, we can analysis the performance of different approaches on the EuroSAT RGB dataset using various training-test splits. We evaluated four frequently used methods, including BovW, CNN, ResNet50, and GoogleNet, as baselines to assess the performance improvement of the hybrid classical-quantum transferring CNN. We used these pre-trained models on the ImageNet dataset and fine-tuned them on the EuroSAT dataset. For ResNet50 and GoogleNet, we replaced the flatten layer, maintaining the original image sizes. The proposed method exhibited better classification accuracy than other methods and significantly reduced model complexity.
To quantitatively evaluate the performance of our proposed method, we adopt the OA and confusion matrix as the evaluation metrics. OA is recorded as the number of correctly classified samples divided by the total number of samples. In the confusion matrix, each column denotes the prediction results, and each row denotes the actual ground objects of the class data. It can display the distribution of each class, and can be recommended for the analysis of miscalssification results between different classes.
Preprints 78152 g007
Figure 7. Confusion matrix of the proposed method on the EuroSAT dataset in a training and a test set (10/90 ratio) using RSIs in the RGB color space.
Figure 7. Confusion matrix of the proposed method on the EuroSAT dataset in a training and a test set (10/90 ratio) using RSIs in the RGB color space.
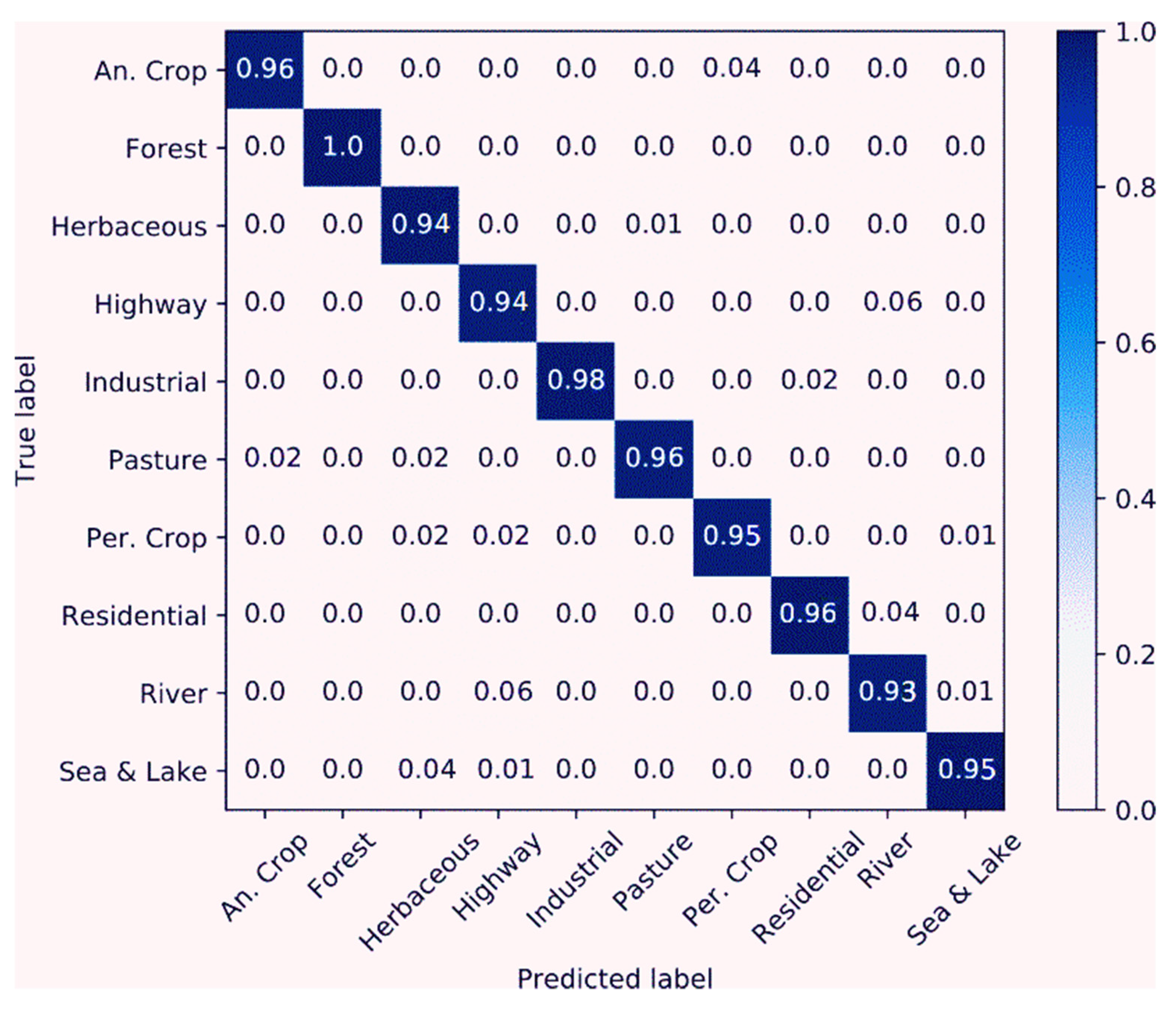
Preprints 78152 g007
As can be seen from Table 2, all CNN algorithms surpassed the BoVW method and the classification result of whole deep CNNs perform better than the classification result of shallow CNNs. Nevertheless, the proposed method achieved a classification result of up to 95.81% in a training and a test dataset (10/90 ratio) for the EuroSAT RSISC. The optimization process is demonstrated in Figure 8. As can be seen from Figure 9, the images of two scene labels are absolutely alike to each other, resulting in imperfect classification results compared with other labels.
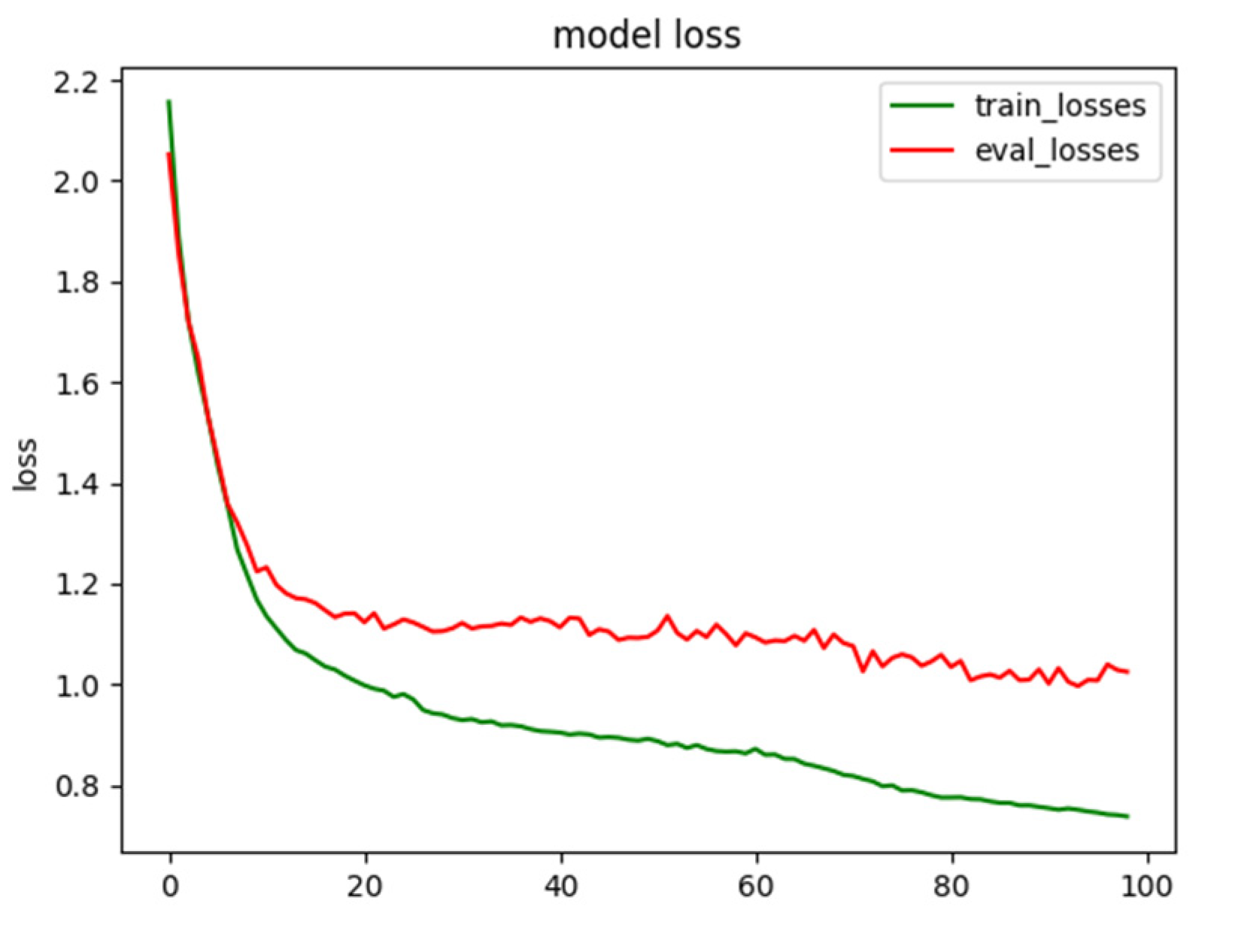
Preprints 78152 g008
Figure 7. Relation between the loss function and training step of the proposed method.
Figure 7. Relation between the loss function and training step of the proposed method.
Preprints 78152 g008
Table 2 shows the resulted classification accuracies for the best performing DL models CNN models、 GoogLeNet、ResNet50 and the proposed method. In experiments with the GoogLeNet、ResNet50、CNN models and the proposed method, all models were pre-trained on the EuroSAT dataset. For a better comparison of performance of all fine-tuning models, we trained the last layer with a learning rate between 0,01 and 0,0001. Using the proposed method, we achieved a classification accuracy of about 17% better than the pre-trained model GoogleNet which have been trained on the EuroSAT dataset in the same training-test dataset ratio setting.
Preprints 78152 g009
Figure 9. The images misclassified as others. (a,b) The images of highways misclassified as rivers. (c,d) The images of rivers misclassified as highways.
Figure 9. The images misclassified as others. (a,b) The images of highways misclassified as rivers. (c,d) The images of rivers misclassified as highways.
Preprints 78152 g009
Furthermore, we compared the proposed algorithm with other pre-trained CNN-based classification methods for different training-test ratios on the RSI dataset. As shown in the table below, the hybrid classical-quantum transferring CNN achieved higher accuracy than other pre-trained CNN-based classification methods. The proposed algorithm can also enhance the classification result for the large scale of input images and performs better than all of the other algorithms under the training ratio of 20% and 50%, and “*” indicates the best result among all methods. The best classification results can be obtained by the algorithm that achieves 97.33% and 98.82% for the training ratios of 20% and 50%, respectively. Our proposed approach exhibits the performance of the most advanced methods.
Table 3. Contrast of the classification accuracies (%) of different training-test ratios on the AID dataset（training ratio=20% and 50%).
Table 3. Contrast of the classification accuracies (%) of different training-test ratios on the AID dataset（training ratio=20% and 50%).
Method 20/80 50/50
VGG-VD16[38] 86.59 89.64
GoogLeNet [38] 83.44 86.39
AlexNet+MSCP [39] 88.99 92.36
VGG-VD16+MSCP [39] 91.52 94.42
AlexNet+SPP [40] 87.44 91.45
RADCNet [41] 88.12 92.53
AlexNet+SAFF [42] 87.51 91.83
VGG-VD16+SAFF [42] 90.25 93.83
AlexNet+RIR [43] 91.95 94.56
VGG-VD16+RIR [43] 93.34 95.57
ResNet50+RIR [43] 94.95 96.48
DCNN [44] 90.82 96.89
CBAM [45] 94.66 96.90
MSCP [46] 92.21 96.56
Two-Stream Fusion [47] 92.32 94.58
RTN [48] 92.44 _
GCFs+LOFs [49] 92.48 96.85
CapsNet [50] 91.63 94.74
ARCNet [51] 88.75 93.1
SCCov [52] 93.12 96.1
KFBNet [53] 95.50 97.40
GBNet [54] 92.20 95.48
MG-CAP [55] 93.34 96.12
EAM [56] 94.26 97.06
EAM [56] 93.64 96.62
F2BRBM [57] 96.05 96.97
MBLANet [58] 95.60 97.14
GRMANet [59] 95.43 97.39
IDCCP [60] 94.80 96.95
MSANet [61] 93.53 96.01
CTNet [62] 96.25 97.70
LSENet [63] 94.41 96.36
DFAGCN [64] _ 94.88
MGML-FENet [65] 96.45 98.60
ESD-MBENet-v1[66] 96.20 98.85*
ESD-MBENet-v2[66] 96.39 98.40
SeCo-ResNet-50[67] 93.47 95.99
RSP-ViTAEv2-S [68] 96.91* 98.22
ISP(ViT) [69] 96.24 97.95
ISSP(ViT) [70] 95.82 97.98
RingMo(ViT-200W-200E) [71] 96.54 98.38
ISP(Swin) [72] 96.24 98.03
ISSP(Swin) [73] 96.54 97.95
RingMo(Swin-200W-200E) [71] 96.90 98.34
Ours 97.33 98.82
We have implemented these networks using a neural network library named Pytorch and a cross-platform Python library for quantum computing named PennyLane [74,75]. The experiments have been operated on a computer graphics workstation equipped with a single AMD Ryzen Threadripper PRO 3945WX 12-Cores CPU and a single NVIDIA GeForce NVIDIA RTX A5000 24GB GPU.

5. Conclusions

Over the past decade, rapid development has provided us with massive remote sensing datasets for intelligent earth observation using RSIs. However, the lack of publicly available “big data” of RSIs severely limits the development of new approaches especially quantum machine learning methods. This work first presents the background of classical networks, variation quantum circuits and tensor quantum circuits. Then, a hybrid classical-quantum transferring CNN applied to RSISC is proposed. The main advantage of the proposed method is that it allows the input images to be of various shapes and sizes dispense with resizing of such images prior to the processing. It preserves key feature information in high spatial resolution images, which is greatly beneficial to ultimately achieve better classification performance. In comparison to other deep learning methods with the same number of training samples, the proposed method has achieved amazing scene classification results. Data annotation must be done manually by skilled professionals of the area of RSISC. When RSI dataset is massive, data annotation can become more complicated because of the huge diversities and variations in RSIs. Most of these models require a large-scale labeled dataset and numerous iterations to train their parameter sets. The experimental results show that the proposed method can achieve satisfied classification results with fewer number of training samples. This means that in the application of RSISC, the increased workload of data annotation can be reduced manually by skilled professionals. In order to improve classification accuracy, the sum of the CNNs layer has expanded from few layers to hundred layers. Usually the vast majority of models have huge parameters, moreover operation of the CNN models require a enormous labeled datasets for models training and powerful equipment wtih high-performance GPUs for notable performance improvements of operation, which severely limits the development of RSISC methods. However, in compare with huge CNNs, the proposed method is a compact、lightweight and efficient RSISC model with fewer parameters. On the other side, the proposed method is extremely expensive and time-consuming due to the limitations of cross-platform for differentiable programming of quantum computers. In the future, the method should be improved in quantum circuit simulators with support for automatic differentiation, just-in-time compiling, hardware acceleration, and vectorized parallelism. Especially when the quantum circuit size or the batch dimension is large, the new platform can bring speedup in quantum circuit simulation.

Author Contributions

Conceptualization, Z.Z. ; methodology, Z.Z.; software, Z.Z. and P.L.; validation, X.M. and Z.Z.; formal analysis, Z.Z.; investigation, Z.Z.; resources, Z.Z.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z.; visualization, Z.Z.; supervision, J.Y.; project administration, X.M.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key R&D Program of China (2019YFE0127300).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to thank Xingfa Gu, Tao Yu and Tianhai Cheng (Aerospace Information Research Institute, Chinese Academy of Sciences) for their valuable comments and contributions to enhance their letter..

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. S. Otgon; M. Datcun, B. Classification of Remot Sensing Images With Parameterized Quantum Gates. IEEE Geoscience and Remote Sensing Letters, 2022; Volume 19, pp. 154–196.
  2. Xiao Xiang Zhu; Devis Tuia; . Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geoscience and Remote Sensing Magazine, 2022, Volume:5,Issue:4, pp.8-36. phrase indicating stage of publication (submitted; accepted; in press). [CrossRef]
  3. Author 1, A.B. (University, City, State, Country); Author 2, C. (Institute, City, State, Country). Personal communication, 2012.
  4. Weiquan Wang, Yushi Chen, . Transferring CNN With Adaptive Learning for Remote Sensing Scene Classification, IEEE Transactions on Geoscience and Remote Sensing, Volume:60, 2022. [CrossRef]
  5. Gong Chen, Jun Wei. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proceedings of the IEEE, Volume: 105, Issue: 10, October 2017.
  6. Y. LeCun, Y. Bengio, and G. Hinton. “Deep learning,” Nature, vol. 521, no. 7553, pp. 436-444, 2015.
  7. C. Broni-Bediako, Y. Murata, and L. G.B. Mormille, “Searching for CNN Architectures for Remote Sensing Scene Classification,” IEEE Transactions on Geoscience and Remote Sensing, vol. No, pp. ,2021. [CrossRef]
  8. X. X.Zhu et al., “Deep learning in remote sensing :A comprehensive review and list of resources,” IEEE Geosci. Remote Sens. Mag., vol. 5, no.4, pp. 8-36, Dec. 2017. [CrossRef]
  9. Krizhevsky, I. Sutskever, and G. E. Hintion, “ImageNet classification with deep convolutional neural neural networks,” in Advances in Neural Information Processing Systems. Red Hook, NY, USA: Curran Associates, 2012, pp.1097-1105.
  10. L. Ma, Y. Liu, X. Zhang, and Y. Ye, “Deep learning in remote sensing applications: A meta-analysis and review,” ISPRS J. Photogramm. Remote Sens., vol. 152, pp. 166-177, Jun.2019. [CrossRef]
  11. Y. Sun, B. Xue, M. Zhang, and G.G. Yen, “Completely automated CNN architecture design based on blocks,” IEEE Trans. Neural Netw. Learn. Syst., vol. 31, no.4.pp. 1242-1254, Apr. 2019. [CrossRef]
  12. Krizhevsky, I. Sutskever, and G.E. Hinton, “ImageNet classification with deep convolutional neural networks,” in Proc. Adv. Neural Inf. Process. Syst. (NIPS), vol.25. Stateline, NV, USA, Dec. 2012, pp. 1097-1105.
  13. M. D. Zeiler and R. Fergus, “Visualizing and understanding convolutional networks,” in Proc. Eur. Conf. Comput. Vis., Sep. 2014, pp.818-833.
  14. C.Szegedy et al., “Going deeper with convolutions,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2015, pp. 1-9.
  15. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2016, pp.770-778. [CrossRef]
  16. J.A.Richards and X. Jia, “Sources and characteristics of remote sensing image data,” in Remote Sensing Digital Image Analysis Image Analysis:An Introduction. Berlin, Germany: Springer 1999, pp. 1-38.
  17. J. Coelho, “ Solve any Image Classification Problem Quickly and Easily”, https://github.com/pmarcelino/blog.
  18. G. Cheng，X. Xie，and J. Han， “Remote Sensing Image Scene Classification Meets Deep Learning: Challenges, Methods, Benchmarks, and Opportunities”, IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 13, Jun. 2020, pp.3735 - 3756.
  19. P. Helber, B. Bischke and A. Dengel, “Eurosat: A novel dataset and deep learning benchmark for land use and land cover classification”, IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019. [CrossRef]
  20. P. Helber, B. Bischke and A. Dengel, “Introducing EuroSAT: A Novel Dataset and Deep Learning Benchmark for Land Use and Land Cover Classification”, IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium,2018,pp.204-207. [CrossRef]
  21. P.W. Shor, SIAM J. Comput. 26,1484(1997).
  22. M.A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information.(Cambridge University Press, Cambridge,2010). [CrossRef]
  23. Y.Jeong,and J. Yu,“Bulk scanning method of a heavy metal concentration in tailings of a gold mine using SWIR hyperspectral imaging system,”Int. J. Appl. Earth Obs.,vol.102, pp. Oct. 2021.
  24. T. Yue, Y. Liu, Z. Du, “Quantum machine learning of eco-environmental surfaces.” Science Bulletin 67, pp.1031-1033. 2022. [CrossRef]
  25. R. Uddien Shaik, A. Unni and W. Zeng, “Quantum Based Pseudo-Labelling for Hyperspectral Imagery: A Simple and Efficient Semi-Supervised Learning Method for Machine Learning Classifiers”, Remote Sens. 2022, 14(22). [CrossRef]
  26. Mari, T. R. Bromley and J. Izaac, “Transfer learning in hybrid classical-quantum neural networks.”arXiv preprint arXiv:1912.08278,2019. [CrossRef]
  27. J. Qi, J. Tejedor, “Classical-to-Quantum Transfer Learning for Spoken Command Recognition Based on Quantum Neural Networks.”arXiv preprint arXiv:2110.08689,ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP),2022. [CrossRef]
  28. V. Dunjko, & H. J. Briegel. Machine learning & artificial intelligence in the quantum domain: a review of recent progress. Rep. Prog. Phys. 81, 074001(2018). [CrossRef]
  29. A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik, and J. L. OBrien, Nature Communications 5, 4213 (2014).
  30. E. Farhi, J. Goldstone, and S. Gutmann, arXiv:1411.4028 [quant-ph] (2014), arXiv: 1411.4028.
  31. X. Cai, D. Z. Li, X. Liu, “Experimental Realization of a Quantum Support Vector Machine,” PhysRevLett.114.140504, 2015.
  32. V. Havlíček, A. D. Córcoles,“Supervised learning with quantum-enhanced feature spaces,” Nature, volume 567, pp.209–212. 2019.
  33. J. Deng, W. Dong, and R. Socher. ImageNet: A large-scale hierarchical image database. In 2009 IEEE Conference on Computer Vision and Pattern Recognition, pp.248-255. IEEE, 2009.
  34. K. He, X. Zhang, and S. Pradhan. Quanvolutional neural networks: powering image recognition with quantum circuits. Quantum Machine Intelligence, 2(1), Feb. 2020.
  35. C. Szegedy, S. Ioffe, V.Vanhoucke, and A. Alemi. Inception-v4, inception-resnet and the image recognition. arXiv preprint arXiv:1409.1556,2014.
  36. C. Szegedy, W.Liu, Y.Jia, P.Sermanet, S.Reed, D.Anguelov, D.Erhan, V.Vanhoucke, and A.Rabinovich. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1-9,2015.
  37. C.Segedy, V.Vanhoucke, S. Ioffe, J. Shlens, and Z. Wojna,. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2818-2826, 2016.
  38. Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
  39. He, N.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Remote sensing scene classification using multilayer stacked covariance pooling. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6899–6910. [Google Scholar] [CrossRef]
  40. Han, X.; Zhong, Y.; Cao, L.; Zhang, L. Pre-trained alexnet architecture with pyramid pooling and supervision for high spatial resolution remote sensing image scene classification. Remote Sens. 2017, 9, 848. [Google Scholar] [CrossRef]
  41. Bi, Q.; Qin, K.; Zhang, H.; Li, Z.; Xu, K. RADC-Net: A residual attention based convolution network for aerial scene classification. Neurocomputing 2020, 377, 345–359. [Google Scholar] [CrossRef]
  42. Cao, R.; Fang, L.; Lu, T.; He, N. Self-Attention-Based Deep Feature Fusion for Remote Sensing Scene Classification. IEEE Geosci. Remote. Sens. Lett. 2021, 18, 43–47. [Google Scholar] [CrossRef]
  43. Qi Kunlun, Yang Chao, Hu Chuli, Shen Yonglin, Shen Shengyu, Wu Huayi. Rotation invariance regularization for remote sensing image scene classification with convolutional neural networks. Remote Sensing, 2021, 13(4), 569.
  44. G. Cheng, C. Yang, X. Yao, L. Guo, and J. Han, “When deep learning meets metric learning: Remote sensing image scene classification via learning discriminative cnns,” IEEE transactions on geoscience and remote sensing, vol. 56, no. 5, pp. 2811–2821, 2018. [CrossRef]
  45. S. Woo, J. Park, J.-Y. Lee, and I. S. Kweon, “Cbam: Convolutional block attention module,”in Proceedings of the European conference on computer vision (ECCV), pp. 3–19, 2018.
  46. N. He, L. Fang, S. Li, A. Plaza, and J. Plaza, “Remote sensing scene classification using multilayer stacked covariance pooling,” IEEE Transactions on Geoscience and Remote Sensing, vol. 56, no. 12, pp. 6899–6910, 2018. [CrossRef]
  47. Y. Yu and F. Liu,“A two-stream deep fusion framework for high-resolution aerial scene classification,” Computational intelligence and neuroscience, vol. 2018, 2018. [CrossRef]
  48. Z. Chen, S. Wang, X. Hou, L. Shao, and A. Dhabi, “Recurrent transformer network for remote sensing scene categorisation.,”in BMVC, vol. 266, 2018.
  49. D. Zeng, S. Chen, B. Chen, and S. Li, “Improving remote sensing scene classification by integrating globalcontext and local-object features,” Remote Sensing, vol. 10, no. 5, p. 734, 2018. [CrossRef]
  50. W. Zhang, P. Tang, and L. Zhao, “Remote sensing image scene classification using cnn-capsnet,” Remote Sensing, vol. 11, no. 5, p. 494, 2019.
  51. Q. Wang, S. Liu, J. Chanussot, and X. Li, “Scene classification with recurrent attention of vhr remote sensing images,” IEEE Transactions on Geoscience and Remote Sensing, vol. 57, no. 2, pp. 1155–1167, 2018. [CrossRef]
  52. N. He, L. Fang, S. Li, J. Plaza, and A. Plaza, “Skipconnected covariance network for remote sensing scene classification,” IEEE transactions on neural networks and learning systems, vol. 31, no. 5, pp. 1461–1474, 2019. [CrossRef]
  53. F. Li, R. Feng, W. Han, and L. Wang, “High-resolution remote sensing image scene classification via key filter bank based on convolutional neural network,”IEEE Transactions on Geoscience and Remote Sensing, vol. 58, no. 11, pp. 8077–8092, 2020. [CrossRef]
  54. H. Sun, S. Li, X. Zheng, and X. Lu, “Remote sensing scene classification by gated bidirectional network,”IEEE Transactions on Geoscience and Remote Sensing, vol. 58, no. 1, pp. 82–96, 2019. [CrossRef]
  55. S. Wang, Y. Guan, and L. Shao, “Multi-granularity canonical appearance pooling for remote sensing scene classification,” IEEE Transactions on Image Processing, vol. 29, pp. 5396–5407, 2020. [CrossRef]
  56. Z. Zhao, J. Li, Z. Luo, J. Li, and C. Chen, “Remote sensing image scene classification based on an enhanced attention module,” IEEE Geoscience and Remote Sensing Letters, vol. 18, no. 11, pp. 1926–1930, 2020.
  57. X. Zhang, W. An, J. Sun, H. Wu, W. Zhang, and Y. Du, “Best representation branch model for remote sensing image scene classification,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 14, pp. 9768–9780, 2021.
  58. H. Chen, Z. Qi, and Z. Shi, “Remote sensing image change detection with transformers,” IEEE Transactions on Geoscience and Remote Sensing, 2021. [CrossRef]
  59. B. Li, Y. Guo, J. Yang, L. Wang, Y. Wang, and W. An,“Gated recurrent multiattention network for vhr remote sensing image classification,” IEEE Transactions on Geoscience and Remote Sensing, 2021.
  60. S. Wang, Y. Ren, G. Parr, Y. Guan, and L. Shao,“Invariant deep compressible covariance pooling for aerial scene categorization,” IEEE Transactions on Geoscience and Remote Sensing, vol. 59, no. 8, pp. 6549–6561, 2020.
  61. G. Zhang, W. Xu, W. Zhao, C. Huang, E. N. Yk, Y. Chen, and J. Su, “A multiscale attention network for remote sensing scene images classification,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 14, pp. 9530–9545, 2021.
  62. P. Deng, K. Xu, and H. Huang, “When cnns meet vision transformer: A joint framework for remote sensing scene classification,” IEEE Geoscience and Remote Sensing Letters, vol. 19, pp. 1–5, 2021. [CrossRef]
  63. Q. Bi, K. Qin, H. Zhang, and G.-S. Xia, “Local semantic enhanced convnet for aerial scene recognition,” IEEE Transactions on Image Processing, vol. 30, pp. 6498–6511, 2021. [CrossRef]
  64. K. Xu, H. Huang, P. Deng, and Y. Li, “Deep feature aggregation framework driven by graph convolutional network for scene classification in remote sensing,”IEEE Transactions on Neural Networks and Learning Systems, 2021. [CrossRef]
  65. Q. Zhao, S. Lyu, Y. Li, Y. Ma, and L. Chen, “Mgml: Multigranularity multilevel feature ensemble network for remote sensing scene classification,” IEEE Transactions on Neural Networks and Learning Systems, 2021. [CrossRef]
  66. Q. Zhao, Y. Ma, S. Lyu, and L. Chen, “Embedded selfdistillation in compact multi-branch ensemble network for remote sensing scene classification,” arXiv preprint arXiv:2104.00222, 2021.
  67. Ma˜nas, A. Lacoste, X. Giro-i Nieto, D. Vazquez, and P. Rodriguez, “Seasonal contrast: Unsupervised pre-training from uncurated remote sensing data,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 9414–9423, 2021.
  68. D. Wang, J. Zhang, B. Du, G.-S. Xia, and D. Tao, “An empirical study of remote sensing pretraining,” IEEE Transactions on Geoscience and Remote Sensing, 2022.
  69. Dosovitskiy, L. Beyer, A. Kolesnikov, D. Weissenborn, X. Zhai, T. Unterthiner, M. Dehghani, M. Minderer, G. Heigold, S. Gelly, et al., “An image is worth 16 × 16 words: Transformers for image recognition at scale,”arXiv preprint arXiv:2010.11929, 2020.
  70. G. Cheng, C. Yang, X. Yao, L. Guo, and J. Han, “When deep learning meets metric learning: Remote sensing image scene classification via learning discriminative cnns,” IEEE transactions on geoscience and remote sensing, vol. 56, no. 5, pp. 2811–2821, 2018.
  71. X. Sun, P.Wang, W. Lu, Z. Zhu, X. Lu, Q. He, J. Li, X. Rong, Z. Yang, H. Chang, Q. He, G. Yang, R. Wang, J. Lu and K. Fu. RingMo: A remote sensing foundation model with masked image modeling. IEEE Transactions on Geoscience and Remote Sensing[J]. 2022. [CrossRef]
  72. Z. Liu, Y. Lin, Y. Cao, H. Hu, Y. Wei, Z. Zhang, S. Lin, and B. Guo, “Swin transformer: Hierarchical vision transformer using shifted windows,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 10012–10022, 2021.
  73. Z. Xie, Z. Zhang, Y. Cao, Y. Lin, J. Bao, Z. Yao, Q. Dai,and H. Hu, “Simmim: A simple framework for masked image modeling,” arXiv preprint arXiv:2111.09886, 2021. [CrossRef]
  74. Pointer. Programming PyTorch for Deep Learning. Creating and Deploying Deep Learning. O'Reilly, 2019-11-4.
  75. V. Bergholm et al. PennyLane: Automatic differentiation of hybrid quantum-classical computations. 2018. arXiv:1811.04968.
Preprints 78152 g001
Figure 1. Limitations of RSISC, which include (a) low sort separability, (b) complex variance of scene scales (c) coexist of multiple objects. The sources are from Eurosat dataset [19,20].
Figure 1. Limitations of RSISC, which include (a) low sort separability, (b) complex variance of scene scales (c) coexist of multiple objects. The sources are from Eurosat dataset [19,20].
Preprints 78152 g001
Preprints 78152 g003
Figure 3. A hybrid classical-quantum transferring CNN for RSISC. ResNet network is utilized as features extraction and tensor quantum circuits is applied as fully connected layer for RSISC.
Figure 3. A hybrid classical-quantum transferring CNN for RSISC. ResNet network is utilized as features extraction and tensor quantum circuits is applied as fully connected layer for RSISC.
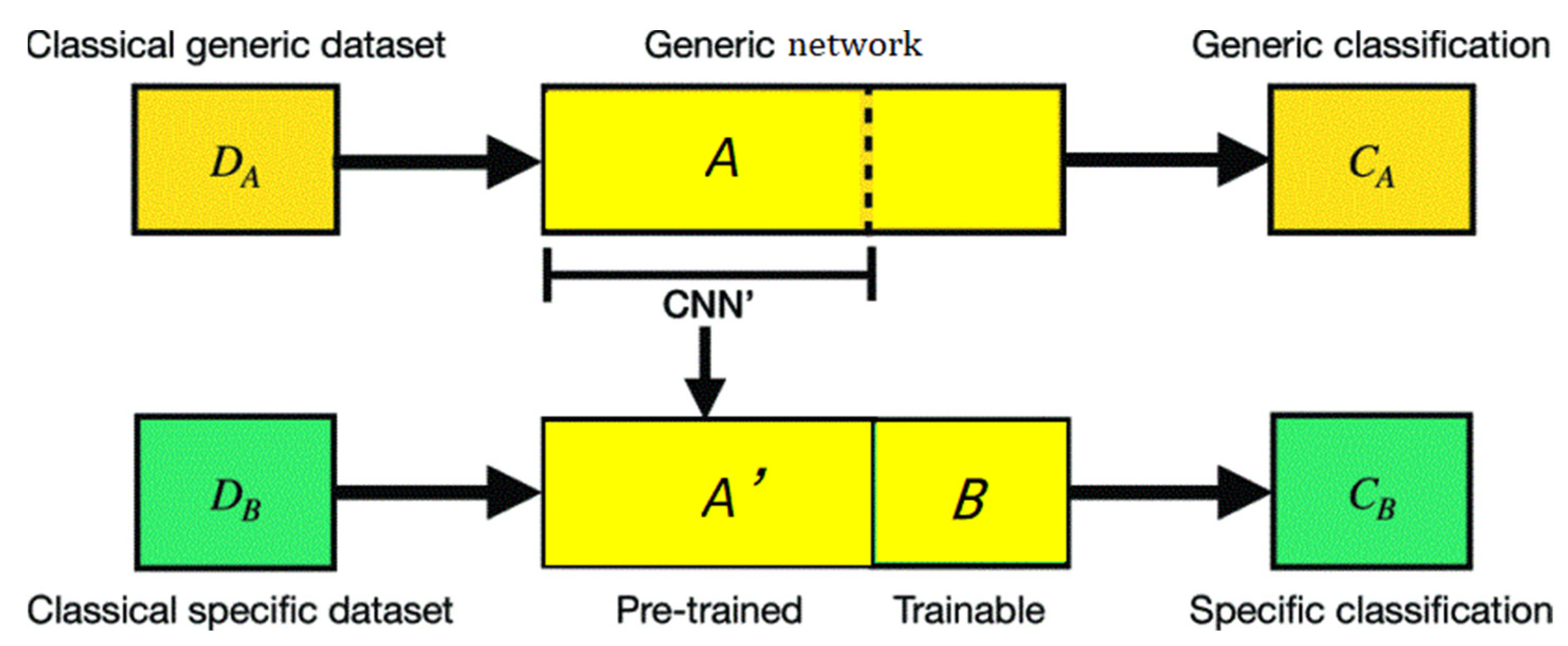
Preprints 78152 g003
Preprints 78152 g004
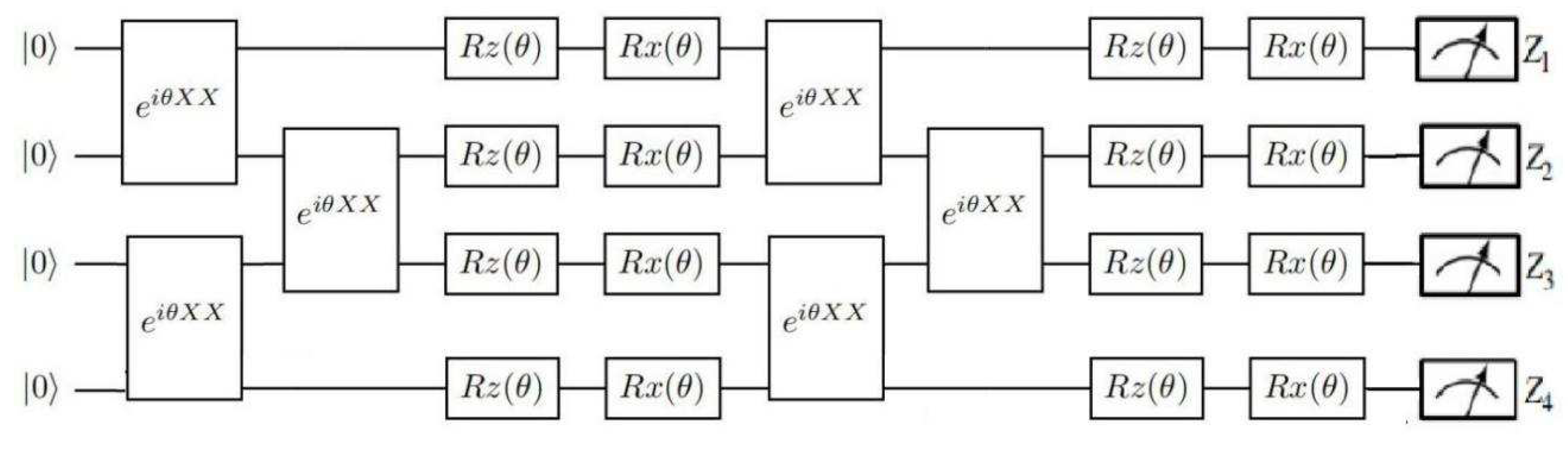
Figure 4. Top: general scheme for the hybrid classical-quantum transferring CNN for RSISC, Middle: detailed scheme for classifying the scene image dataset, Bottom: architecture of the tensor quantum circuit with inputs of 4 qubits. Rx(•),Ry(•) and Rz(•) separately denote Pauli rotation X, Y, Z gates.
Figure 4. Top: general scheme for the hybrid classical-quantum transferring CNN for RSISC, Middle: detailed scheme for classifying the scene image dataset, Bottom: architecture of the tensor quantum circuit with inputs of 4 qubits. Rx(•),Ry(•) and Rz(•) separately denote Pauli rotation X, Y, Z gates.
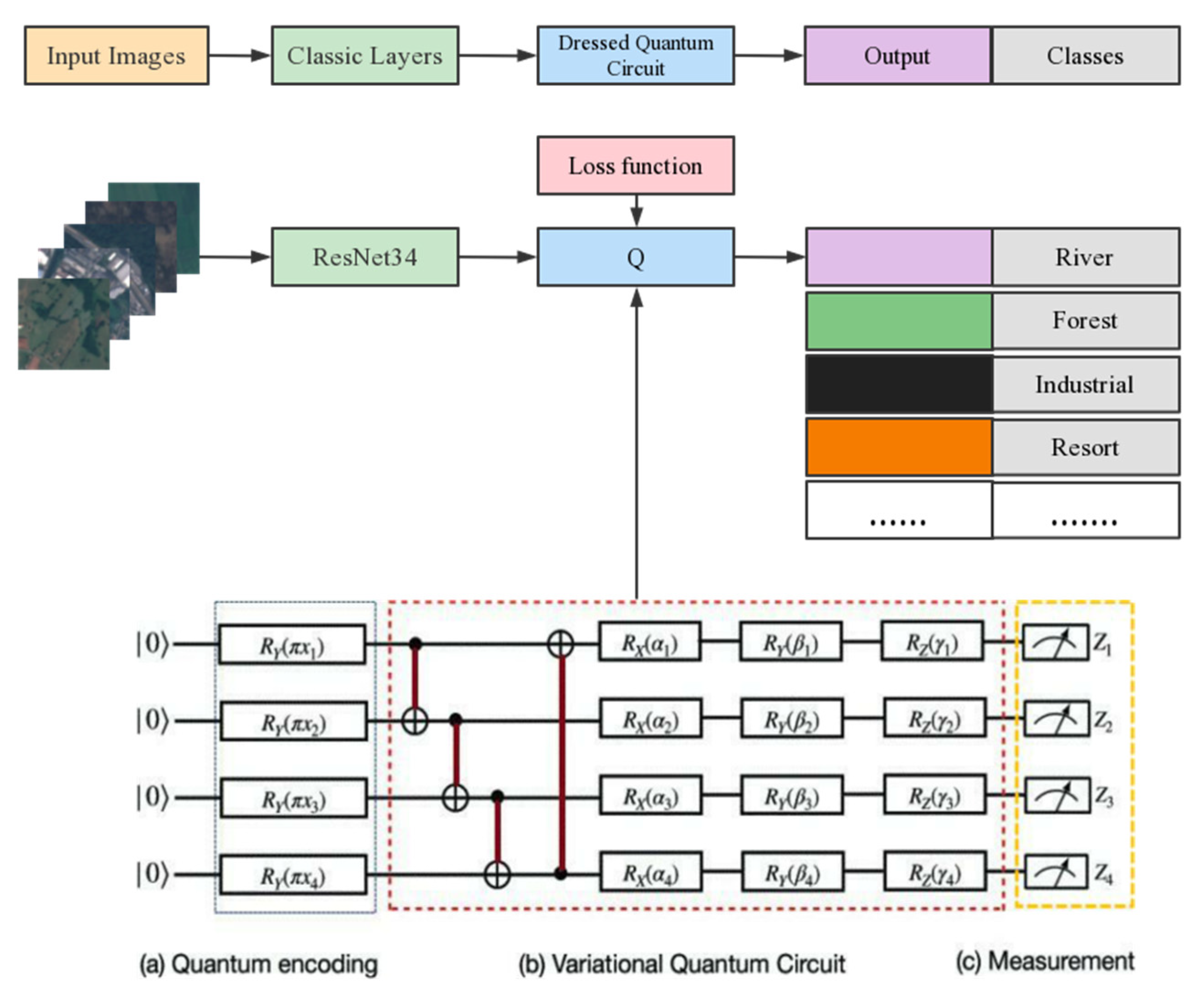
Preprints 78152 g004
Preprints 78152 g006
Figure 6. This outline shows all sample images of all 30 categories covered in the AID dataset. The images size has 600×600 pixels. Each category contains 220 to 420 images. In all, the dataset has 10,000 georefenced images [37].
Figure 6. This outline shows all sample images of all 30 categories covered in the AID dataset. The images size has 600×600 pixels. Each category contains 220 to 420 images. In all, the dataset has 10,000 georefenced images [37].
Preprints 78152 g006
Table 2. Overall accuracy(%) of different training-test ratios on the EuroSAT dataset classification（training ratio=10% and 20%).
Table 2. Overall accuracy(%) of different training-test ratios on the EuroSAT dataset classification（training ratio=10% and 20%).
Method(%) 10/90 20/80 Number of Parameters
BoVW(SVM, SIFT, k=10) 54.54 56.13 _
BoVW(SVM, SIFT, k=100) 63.07 64.80 _
BoVW(SVM, SIFT, k=500) 65.62 67.26 _
CNN(two layers) 75.88 79.84 50.5K
ResNet-50 75.06 88.53 25.6M
GoogleNet 77.37 90.97 6.8M
Ours 95.81 96.62 21.28 M
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated