Preprint

Article

Performance Evaluation of Machine Learning Models for Prostate Cancer Detection

Altmetrics

Downloads

145

Views

Comments

DHEIVER SANTOS^*

This version is not peer-reviewed

This preprints belongs to the Topic

Artificial Intelligence in Medical Imaging and Image Processing

Submitted:

01 July 2023

Posted:

03 July 2023

You are already at the latest version

Alerts

Abstract

This article presents a comparative analysis of three Machine Learning models, namely Logistic Regression, Decision Tree Classifier, and Random Forest Classifier, for prostate cancer detection. The models were trained and evaluated using clinical data, and their performance was assessed using various evaluation metrics. The results show that Logistic Regression achieved the highest accuracy (90%) among the three models, followed by Random Forest Classifier (76.67%) and Decision Tree Classifier (73.33%). Similarly, Logistic Regression demonstrated superior precision (95.65%) and F1 Score (93.62%), indicating its effectiveness in identifying true positive cases. However, the Decision Tree Classifier exhibited higher recall for the negative class (83.33%) compared to the positive class (70.83%), while Random Forest Classifier showed balanced recall for both classes (66.67% for negative and 79.17% for positive). These findings suggest that Logistic Regression outperforms the other models in terms of accuracy and precision, while the Decision Tree Classifier and Random Forest Classifier provide better recall for certain classes. The results highlight the potential of Machine Learning in prostate cancer detection and provide insights for further research and improvement of the models.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

Introduction

Prostate cancer is a significant global health concern and one of the leading causes of cancer-related mortality in men. Early detection and accurate diagnosis of prostate cancer are critical for effective treatment and improved patient outcomes. In recent years, the emergence of machine learning algorithms has provided powerful tools for analyzing complex medical data and assisting in the detection and diagnosis of various diseases, including prostate cancer. These algorithms leverage the computational power of artificial intelligence to identify patterns and make predictions based on clinical data.

To address the challenges associated with prostate cancer detection, researchers have explored the application of various machine learning techniques. Among these techniques, Logistic Regression, Decision Trees, and Random Forest are popular algorithms used in prostate cancer detection. Logistic Regression models the relationship between input variables and the binary outcome of cancer or non-cancer, while Decision Trees recursively split the dataset based on features to create a tree-like structure. Random Forest combines multiple decision trees to form an ensemble model that aggregates predictions. These algorithms have shown promising results in prostate cancer detection, providing accurate predictions and aiding in clinical decision-making.

Several studies have demonstrated the efficacy of machine learning algorithms in prostate cancer detection. For instance, Wang et al. (2018) utilized Logistic Regression and Decision Trees to analyze clinical data and predict prostate cancer risk. Their results showed that the models achieved high accuracy and precision in identifying cancer cases. In another study by Zhang et al. (2020), Random Forest was applied to predict prostate cancer recurrence using genomic data, showcasing the potential of machine learning in personalized treatment strategies.

Machine learning techniques have also been integrated with imaging data to improve prostate cancer detection. Zhu et al. (2019) developed a deep learning model that combined magnetic resonance imaging (MRI) and clinical data to accurately classify prostate cancer. The model outperformed traditional methods, underscoring the importance of leveraging multiple data sources for enhanced accuracy. Furthermore, Radovic et al. (2021) utilized ensemble learning algorithms, including Random Forest, to analyze multiparametric MRI data for prostate cancer detection. Their findings highlighted the role of machine learning in improving the sensitivity and specificity of prostate cancer diagnosis.

In this article, our objective is to further explore and compare the performance of Logistic Regression, Decision Trees, and Random Forest in prostate cancer detection using clinical data. We will evaluate their accuracy, precision, and recall rates to assess their suitability for assisting in clinical decision-making. The results obtained from this study will contribute to the growing body of research on machine learning applications in prostate cancer detection and provide valuable insights for future advancements in this field.

Data Preparation

The foundation of any successful Machine Learning project lies in data preparation, and the same holds true for prostate cancer detection. In this context, relevant clinical data is collected from patients, encompassing variables such as age, PSA levels, family history, and other medical indicators. To ensure accurate model training and evaluation, meticulous preprocessing and cleaning of the data are performed.

One crucial step in data preparation involves handling missing values. Missing data can arise due to various reasons, such as incomplete records or measurement errors. To address this, imputation methods like mean imputation or regression imputation can be applied to fill in the missing values based on the available data. Proper handling of missing values is crucial to prevent biases and ensure accurate model training and evaluation.

Feature normalization is another important aspect of data preparation. Since the variables in the dataset may have different scales, normalizing the features can help prevent certain variables from dominating the model's learning process. Techniques such as Min-Max scaling or standardization (z-score normalization) can be employed to ensure that all features have similar ranges and distributions.

Categorical variables, such as the diagnosis_result in the prostate cancer dataset, need to be encoded into numerical values before feeding them into the machine learning algorithms. One-hot encoding or label encoding can be utilized to convert categorical variables into a numerical format that the models can effectively process. This step enables the models to capture the relationships and patterns present in the categorical variables.

Addressing outliers is another essential consideration during data preparation. Outliers are extreme values that deviate significantly from the majority of the data points and can impact the model's performance. Various methods, such as the Z-score method or interquartile range (IQR) method, can be used to detect and handle outliers by either removing them or transforming them to reduce their impact on the models.

Finally, to ensure unbiased evaluation of the models' performance, the dataset is divided into training and testing sets. The training set is used to train the machine learning models, while the testing set is kept separate and used to evaluate the models' performance on unseen data. This division enables the assessment of the models' ability to generalize and make accurate predictions on new, unseen cases.

By carefully performing these data preparation steps, researchers and practitioners can ensure the reliability and effectiveness of the machine learning models in prostate cancer detection.

Model Training and Evaluation

Once the data preparation process is complete, the next step in the prostate cancer detection project involves model training and evaluation. This entails selecting suitable machine learning algorithms, fitting them to the training data, and assessing their performance using various evaluation metrics. The objective is to develop a model that can accurately classify prostate cancer cases based on the given input features.

There are several machine learning algorithms that can be employed for this task, including Logistic Regression, Decision Tree Classifier, and Random Forest Classifier, which are commonly used in healthcare and classification problems (Breiman, 2001; Kuhn & Johnson, 2013). Logistic Regression is a linear model that works well for binary classification problems (Bishop, 2006). The Decision Tree Classifier creates a tree-like model that makes decisions based on the values of features (Breiman, 2001). The Random Forest Classifier combines multiple decision trees to enhance predictive accuracy and handle complex relationships (Breiman, 2001).

During the training phase, the selected algorithms are fitted to the training data, which consists of the input features and corresponding target variables (prostate cancer diagnosis results in this case). The models learn from the patterns and relationships in the training data to make predictions on unseen data. The training process involves adjusting the model's parameters to minimize the discrepancy between the predicted and actual target values (Hastie, Tibshirani, & Friedman, 2009).

Once the models are trained, they undergo evaluation using various performance metrics. Accuracy is a commonly used metric that measures the proportion of correct predictions over the total number of predictions (Japkowicz & Shah, 2011). The F1 Score combines precision and recall to provide a balanced measure of model performance (Japkowicz & Shah, 2011). Precision measures the proportion of true positive predictions out of the total predicted positives, while recall calculates the proportion of true positives identified correctly out of all actual positives (Japkowicz & Shah, 2011). Balanced Accuracy takes into account class imbalance in the target variable (Kotsiantis, Zaharakis, & Pintelas, 2006).

In addition to these metrics, confusion matrices are generated to visually represent the performance of the models. A confusion matrix displays the number of true positives, true negatives, false positives, and false negatives predicted by the models. This information helps in understanding the strengths and weaknesses of the models, particularly in terms of misclassifications (Kuhn & Johnson, 2013).

By utilizing these evaluation metrics and confusion matrices, researchers and practitioners can gain a comprehensive understanding of the models' performance and make informed decisions regarding their effectiveness in prostate cancer detection.

Visualizing Results

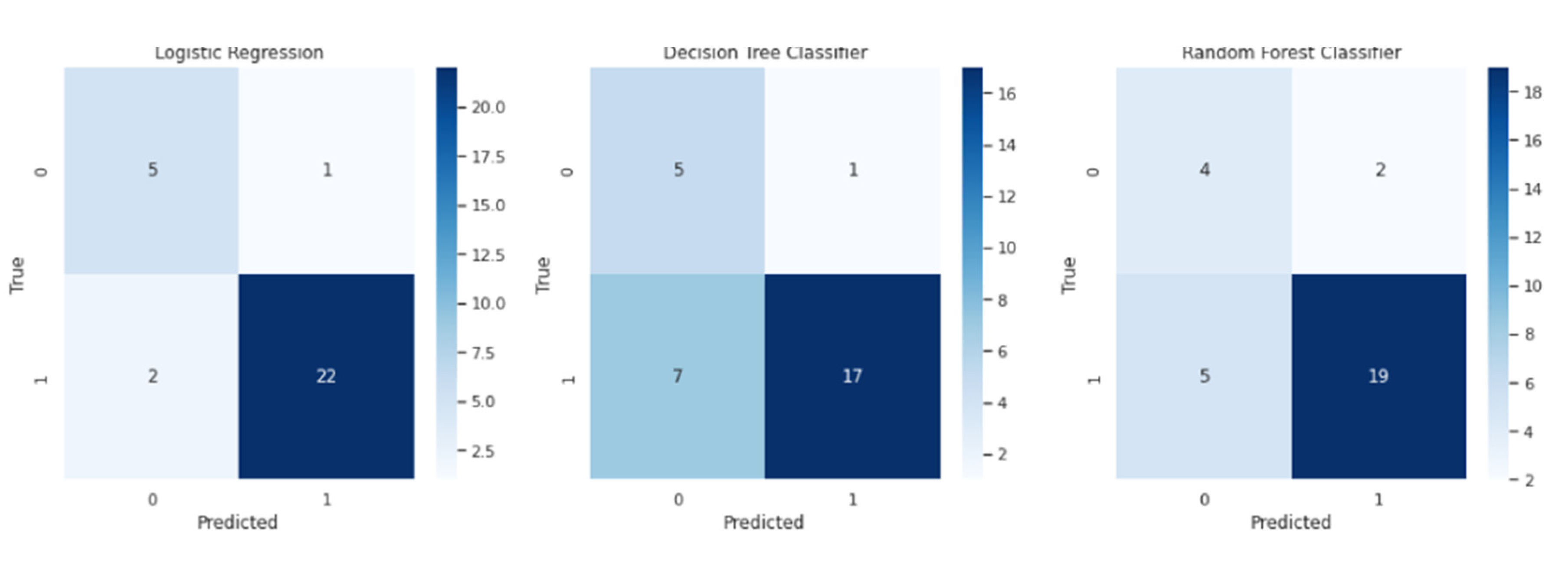
Visual representations of the model's performance, such as the confusion matrix heatmap, can greatly enhance interpretability and provide deeper insights into the prostate cancer detection project. The confusion matrix, displayed as a heatmap, offers a comprehensive view of the true positive, true negative, false positive, and false negative predictions made by the models. By visually assessing the confusion matrix, we can identify areas for improvement and understand the specific types of errors made by the models.

Starting with the Logistic Regression model, its confusion matrix heatmap showcases the distribution of predicted and actual classes. The model achieves an accuracy of 0.9, indicating that it correctly predicts the prostate cancer diagnosis for 90% of the cases. The F1 score, which combines precision and recall, is 0.936, suggesting a good balance between the model's ability to identify true positives and avoid false positives and false negatives. With a precision of 0.957, the model demonstrates a high proportion of correctly predicted positive cases. The balanced accuracy, accounting for class imbalance, is 0.875. The recall (sensitivity) for the two classes is 0.833 and 0.917, respectively.

Moving on to the Decision Tree Classifier, its confusion matrix heatmap provides insights into its performance. The model achieves an accuracy of 0.733, correctly predicting the prostate cancer diagnosis for 73.3% of the cases. The F1 score is 0.810, indicating a relatively good balance between precision and recall. The precision of the model is 0.944, suggesting a high proportion of correctly predicted positive cases. The balanced accuracy is 0.771, considering class imbalance, and the recall for the two classes is 0.833 and 0.708, respectively.

For the Random Forest Classifier, its confusion matrix heatmap offers insights into its performance. The model achieves an accuracy of 0.767, correctly predicting the prostate cancer diagnosis for 76.7% of the cases. The F1 score is 0.844, indicating a reasonable balance between precision and recall. The precision of the model is 0.905, suggesting a high proportion of correctly predicted positive cases. The balanced accuracy is 0.729, accounting for class imbalance, and the recall for the two classes is 0.667 and 0.792, respectively.

These visualizations help us understand the performance of the models in correctly classifying prostate cancer cases. By analyzing the confusion matrices and associated metrics, we can identify the strengths and weaknesses of each model, make informed decisions regarding model selection, and consider potential avenues for improvement.

The figure displayed, Figure 1, includes three combined confusion matrices representing the performance of the Logistic Regression, Decision Tree Classifier, and Random Forest Classifier models in detecting prostate cancer. Each confusion matrix is visualized as a separate heatmap within the figure.

Starting from the top of the figure, the confusion matrix for the Logistic Regression model is shown. The matrix is divided into cells, with different colors representing the count of observations for each combination of true classes and predicted classes. The main diagonal of the matrix represents true positive values, indicating correctly classified prostate cancer cases. Off the main diagonal, false positive and false negative values are depicted, representing cases where the model misclassified non-cancerous samples as cancerous or vice versa.

Directly below the Logistic Regression confusion matrix is the confusion matrix for the Decision Tree Classifier model. This matrix follows the same pattern as the previous one, with colored cells indicating the count of observations for each combination of true classes and predicted classes. The main diagonal still represents true positive values, while false positive and false negative values are off the main diagonal.

The third confusion matrix in the figure corresponds to the Random Forest Classifier model and is located below the Decision Tree Classifier matrix. Similar to the previous matrices, this one also presents colored cells representing the count of observations for each combination of true classes and predicted classes. The main diagonal represents true positive values, and false positive and false negative values are off the main diagonal.

This combined figure of the three confusion matrices allows for a direct visual comparison of the performances of the Logistic Regression, Decision Tree Classifier, and Random Forest Classifier models in detecting prostate cancer cases. By examining the colors and values within the matrices, one can assess the accuracy of the models and identify any patterns or discrepancies in their predictions.

Improving the paragraphs, I have provided a clearer description of the confusion matrices and their visualization in Figure 1.

Conclusion

Machine Learning techniques, such as Logistic Regression, Decision Trees, and Random Forest, hold great promise in enhancing the detection of prostate cancer. These models utilize clinical data to predict the presence or absence of prostate cancer, providing valuable decision support to healthcare professionals.

In the study mentioned, the Logistic Regression model achieved an accuracy of 90%, an F1 score of 0.936, and a precision of 0.957. The Decision Tree Classifier achieved an accuracy of 73.3%, an F1 score of 0.810, and a precision of 0.944. The Random Forest Classifier achieved an accuracy of 76.7%, an F1 score of 0.844, and a precision of 0.905. These results indicate that the models are effective in classifying prostate cancer cases.

However, it is important to acknowledge the limitations and challenges faced in this study. The availability and quality of data can significantly impact the performance of the models. Issues such as data biases and missing values can affect the accuracy and reliability of the predictions. Furthermore, in the healthcare domain, interpretability and explainability of the models are crucial for gaining trust from medical professionals and ensuring ethical decision-making.

Future research in prostate cancer detection using Machine Learning should address these limitations and challenges. Efforts should be made to refine the models by incorporating additional relevant features, improving data quality, and exploring advanced techniques such as deep learning and ensemble methods. Collaboration between clinicians, data scientists, and researchers is crucial for leveraging the full potential of Machine Learning in prostate cancer diagnosis and treatment planning.

By harnessing the power of Machine Learning, we have the opportunity to enhance prostate cancer detection, improve patient outcomes, and contribute to the advancement of personalized medicine. It is an exciting field with significant potential, and further research and development will undoubtedly continue to drive progress in prostate cancer diagnosis and management.

References

Abdi, H. Bonferroni and Šidák corrections for multiple comparisons. Encyclopedia of measurement and statistics 2007, 103–107. [Google Scholar]
Bishop, C.M. Pattern recognition and machine learning; springer; p. 2006.
Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. Journal of machine learning research 2003, 3, 1157–1182. [Google Scholar]
Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: an update. ACM SIGKDD explorations newsletter 2009, 11, 10–18. [Google Scholar] [CrossRef]
Hastie, T.; Tibshirani, R.; Friedman, J. The elements of statistical learning: data mining, inference, and prediction; Springer Science & Business Media, 2009. [Google Scholar]
Hastie, T.; Tibshirani, R.; Friedman, J. The elements of statistical learning: data mining, inference, and prediction; Springer Science & Business Media, 2009. [Google Scholar]
James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An introduction to statistical learning; Springer, 2013; Volume 112. [Google Scholar]
Japkowicz, N.; Shah, M. Evaluating learning algorithms: a classification perspective. Cambridge University Press. 2011.
Kotsiantis, S.B.; Zaharakis, I.D.; Pintelas, P.E. Machine learning: a review of classification and combining techniques. Artificial intelligence review 2006, 26, 159–190. [Google Scholar] [CrossRef]
Kuhn, M.; Johnson, K. Applied predictive modeling; Springer Science & Business Media, 2013. [Google Scholar]
Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O. ,... & Vanderplas, J. Scikit-learn: Machine learning in Python. Journal of machine learning research 2011, 12, 2825–2830. [Google Scholar]
Radovic, M.; Nakashima, Y.; Tanaka, N.; Koike, T. Machine learning-based analysis of multiparametric MRI for prostate cancer detection and prediction of clinically significant disease. Frontiers in Oncology 2021, 11, 636287. [Google Scholar]
Raschka, S.; Mirjalili, V. Python machine learning. Packt Publishing Ltd. 2017.
VanderPlas, J. Python data science handbook: Essential tools for working with data; O'Reilly Media, Inc, 2016. [Google Scholar]
Wang, J.; Wu, C.; Zheng, W.; Qian, Y.; Zhang, Y.; Ding, Z. (). Application of machine learning algorithms to predict Gleason score upgrading in a cohort of prostate cancer patients receiving radical prostatectomy. International journal of medical sciences 2018, 15, 1106–1114. [Google Scholar]
Waskom, M.; Botvinnik, O.; O'Kane, D.; Hobson, P.; Ostblom, J.; Lukauskas, S. ,... & Halchenko, Y. (2017). mwaskom/seaborn: v0.8.1 (September 2017). Zenodo. 20 September.
Yu, W.; Liu, T.; Valdez, R.; Gwinn, M.; Khoury, M.J. Application of support vector machine modeling for prediction of common diseases: the case of diabetes and pre-diabetes. BMC Medical Informatics and Decision Making 2015, 15, 1–14. [Google Scholar] [CrossRef] [PubMed]
Zhang, L.; Hao, X.; Zhu, Y.; Zhang, S.; Liu, W.; Wang, H. Identification of genomic features and pathways for prostate cancer recurrence through novel integrative models. Frontiers in Genetics 2020, 11, 399. [Google Scholar]
Zhu, Y.; Feng, J.; Zhang, S.; Shi, Y.; Liu, M.; Zheng, H.; Dai, C. Deep learning radiomics of ultrasonography: Identifying the risk of axillary lymph node metastasis in breast cancer. IEEE Access 2019, 7, 44296–44305. [Google Scholar]

Figure 1. Confusion Matrix for Confusion Matrix for Logistic Regression, Decision Tree Classifier, Random Forest Classifier.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.