Prerpints.org logo
Preprint
Article

Boosting the Self-Trapped Exciton Emission in Cs4SnBr6 Zero-Dimensional Perovskite via Rapid Heat Treatment

Altmetrics

Downloads

124

Views

54

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 June 2023

Posted:

04 July 2023

You are already at the latest version

Alerts
Abstract
Zero-dimensional (0D) tin halide perovskites feature extraordinary properties, such as broadband emission, high photoluminescence quantum yield, and self-absorption-free characteristics. The innovation of synthesis approaches for high-quality 0D tin halide perovskites has facilitated the flourishing development of perovskite-based optoelectronic devices in recent years. However, discovering an effective strategy to further enhance their emission efficiency remains a considerable challenge. Herein, we report a unique strategy employing rapid heat treatment to attain efficient self-trapped exciton (STE) emission in Cs4SnBr6 zero-dimensional perovskite. Compared to the pristine Cs4SnBr6, rapid thermal treatment (RTT) at 200°C for a duration of 120 seconds results in an augmented STE emission with photoluminescence (PL) quantum yield rising from an initial 50.1% to a substantial 64.7%. Temperature-dependent PL spectra analysis, Raman spectra, and PL decay traces reveal that the PL improvement is attributed to the appropriate electron-phonon coupling as well as the increased binding energies of STEs induced by the RTT. Our findings open up a new avenue for efficient luminescent 0D tin-halide perovskites toward the development of efficient optoelectronic devices based on 0D perovskites.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

In recent years, zero-dimensional (0D) metal halides have attracted significant attention due to their remarkable photoluminescence (PL) quantum yields (QY) and adjustable emissions. These materials, characterized by the confinement of luminescent metal halide octahedra by organic or inorganic cations, offer great potential for various optoelectronic applications, including LEDs, solar cells, scintillators, sensors, and thermal imaging systems [1,2,3,4,5]. In these materials, the Jahn-Teller distortion of metal halide octahedra upon photoexcitation leads to the localization of excitons, enhancing radiative emission by preventing exciton migration to defects. This phenomenon, known as self-trapping of excitons (STEs), contributes to high PL QY and improved stability [6,7]. While significant progress has been made in exploring efficient 0D metal halides, the use of lead-based compounds such as Cs4PbBr6 is limited by the toxicity of lead, posing environmental and health concerns [8,9,10]. To address this issue, tin (Sn2+) has emerged as a promising alternative to lead (Pb2+) due to its similar electronic properties and environmentally-friendly nature [11,12,13]. Numerous studies have probed into the intriguing properties of 0D tin halide perovskites, including Cs4SnX6 (where X = Br, I), and demonstrated their potential for optoelectronic applications [14,15,16]. For instance, the work conducted by Kovalenko and his team presented the compelling discovery of an efficient green-yellow emission derived from self-trapped excitons in Cs4SnBr6, with the achievement of a notable PL QY of 15±5% at room temperature [14]. Intriguingly, through strategic substitution of Cs+ with Rb+ or K+ and Br- with I-, both the PL peak position and Stokes shift can be simultaneously adjusted [14]. Quan et al. synthesized high-quality Cs4SnX6 (X = Br, I) nanocrystals that exhibit well-defined shapes and narrow size distributions, culminating in an impressive PL QY of up to 21% for Cs4SnBr6 nanocrystals [16]. However, a persistent obstacle facing tin halide perovskites is their lack of stability in air, a problem primarily attributed to the oxidation of Sn2+ to Sn4+, leading to a consequential decline in luminescent performance [17,18]. To overcome this issue, Zhang et al. implemented an innovative solution by introducing SnF2 as a tin source, which replaced the easily oxidizable SnBr2, and successfully enhanced the structural stability of Cs4SnBr6 perovskite by utilizing fluorine to suppress Sn2+ oxidation effectively [19]. Despite the remarkable PL performance displayed by 0D tin halide perovskites, the quest for their commercialization necessitates considerable efforts to further enhance both their PL efficiency and stability.
0D perovskites generally display wide-band emission with a large Stokes shift. Numerous researchers have employed the STEs model to elucidate the wide-band emission and large Stokes shift induced by octahedral distortions in 0D perovskites upon light excitation [20,21,22,23,24]. Strong electron-phonon coupling and a malleable lattice are widely considered the cornerstone factors driving the emission of STEs. Particularly within the context of 0D perovskites, excitons, when photoexcited, induce swift distortions in the lattice of the excited state, culminating in the formation of localized STEs [22,23,24,25,26]. Previous investigations have revealed that the lattice distortion in zero-dimensional metal halide perovskites can be manipulated by adjusting factors such as the chemical composition, temperature, and pressure. Such modulation enables precise control of the STE states, which in turn optimizes luminescence performance [22,23,24,25,26,27]. For example, the introduction of varying metal ions into 0D metal halide perovskites can amplify the distortion of [BX6]4− octahedra and bolster electron-phonon coupling, consequently enhancing the density of STE states and boosting luminescence efficiency [26]. In previous work, we successfully expanded the emission spectra and amplified the emission efficiency of STEs in Cs4SnBr6 through an innovative Mn2+ doping strategy [28]. This approach imbued the Mn2+-doped Cs4SnBr6 with remarkably enhanced PL QY of up to ~75%, a broader emission spectrum, and increased thermal stability.
Rapid thermal treatment (RTT) is a widely used technique to modify the micro-nano structure and enhance the optoelectronic properties of materials [29]. RTT involves rapid heating and cooling, characterized by short heating times and accelerated cooling rates. This transient process can induce changes in the structural order of metal halide octahedra, which plays an important role in the formation of STEs. However, the influence of RTT on the PL properties of 0D Cs4SnBr6 has not been fully explored. In this study, we propose a novel strategy based on RTT to enhance the emission of STEs in lead-free Cs4SnBr6. We systematically investigate the effects of RTT on the optical properties of Cs4SnBr6. Compared to pristine Cs4SnBr6, we find that RTT at 200°C for 120 seconds leads to enhanced STE emission, with the PL QY escalating from an initial 50.1% to a substantial 64.7%. The improvement in PL is discussed in terms of electron-phonon coupling and increased binding energies of STEs induced by RTT.

2. Materials and Methods

Cs4SnBr6 samples were synthesized through water-assisted wet ball-milling. Cesium bromide (4 mmol, CsBr, Aladdin, 99.9%), stannous fluoride (1 mmol, SnF2, Macklin, 99.9%), and ammonium bromide (1 mmol, NH4Br, Aladdin, 99.99%) were employed as reactant precursors. To achieve Cs4SnBr6, the molar ratios of CsBr, SnF2, and NH4Br were maintained at 4, 1, and 2 mmol, respectively. Initially, the precursors were loaded into a jar and combined with 60 μL of deionized water. Subsequently, a ball milling process was conducted for 30 min at a speed of 600 rpm. The resulting product was then dried in a vacuum-drying oven for 120 min at room temperature and annealed at various temperatures ranging from 100 to 300 °C using a straightforward RTT process. The RTT process was executed on a rapid thermal processor, heating the sample to the annealing temperature at a rate of 10 °C s−1. After maintaining the annealing temperature for 30, 90 and 120 s, respectively, the system was rapidly cooled to room temperature. Upon cooling, the Cs4SnBr6 powder was acquired via ball milling for 30 min at a speed of 600 rpm. PL measurements were conducted using an Edinburgh Instrument FLS1000 PL spectrometer (Livingstone, UK). The PL spectra were obtained at different temperatures to investigate the temperature-dependent behavior. PL excitation (PLE) spectra and time-resolved PL spectra were also recorded using the same instrument. The crystal structures of Cs4SnBr6 were analyzed using X-ray diffraction (XRD) with a Bruker D8 Advance instrument (Karlsruhe, Germany). XRD measurements were performed at 35 kV and 35 mA to determine the crystal structure of the samples. The compositions of Cs4SnBr6 were determined by energy dispersive spectroscopy (EDS) using a Bruker EDS QUANTAX system (Karlsruhe, Germany). Scanning electron microscopy (SEM) (A Hitachi SU5000 SEM instrument, Tokyo, Japan) was employed to investigate the surface morphology and microstructure of Cs4SnBr6.

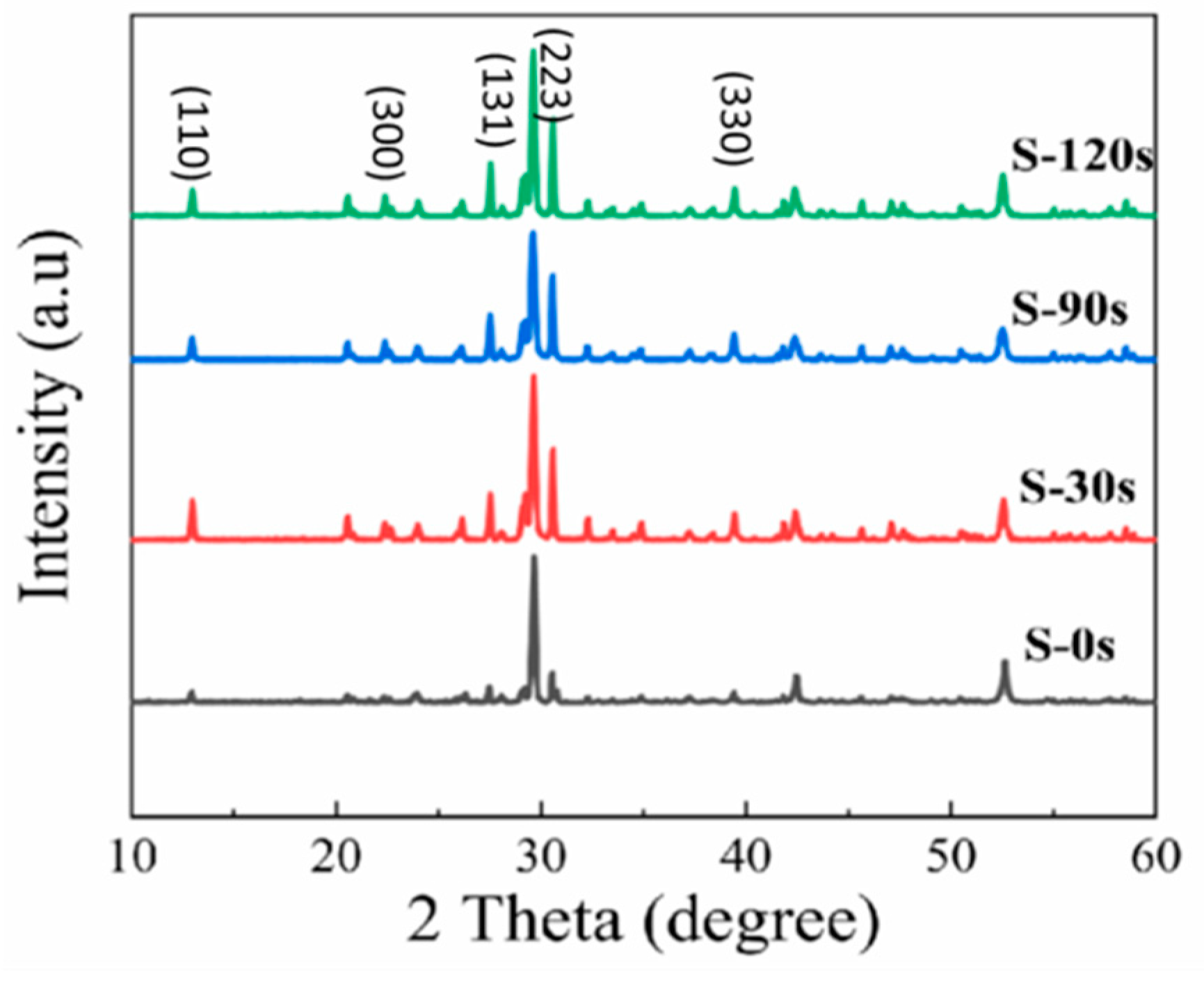
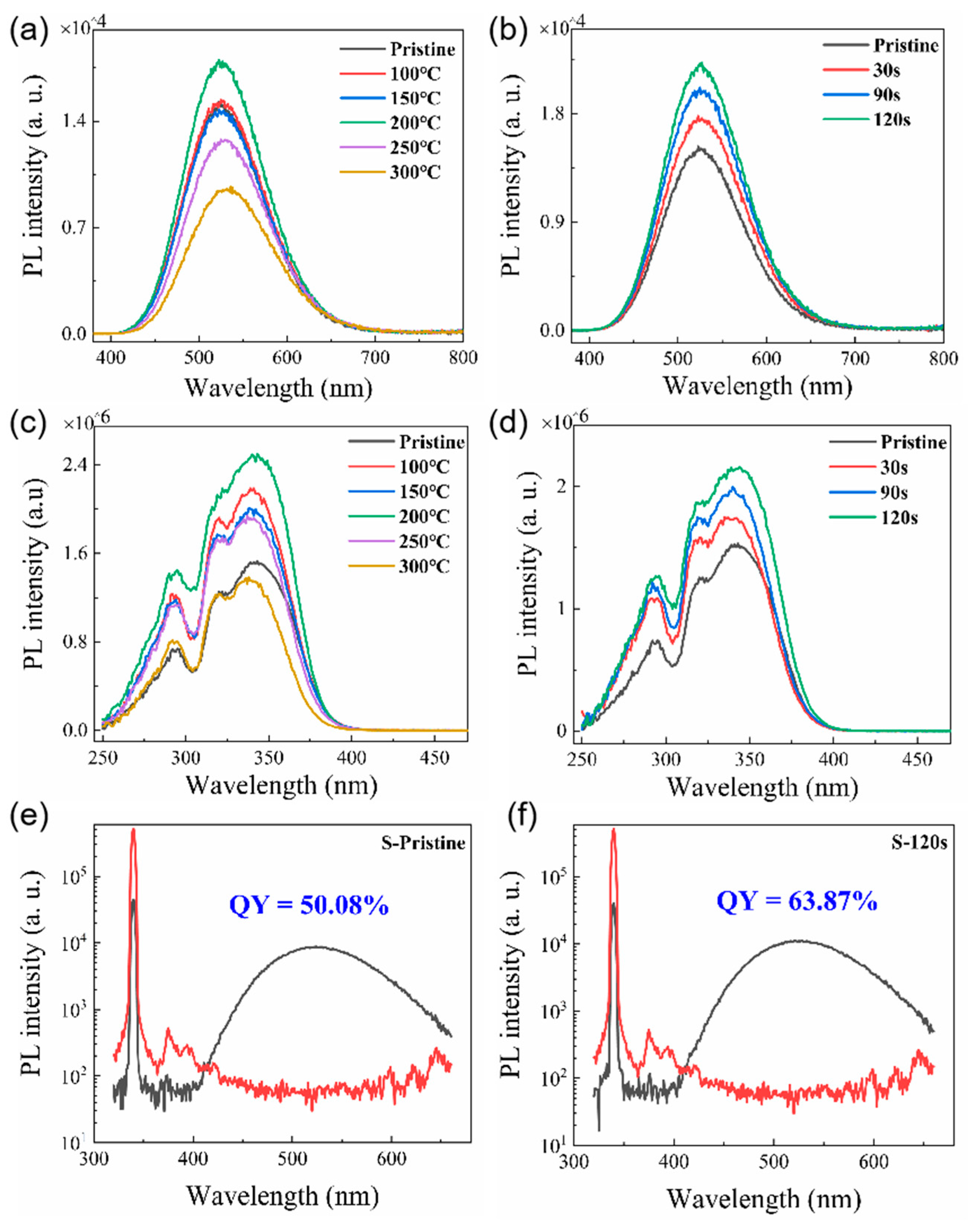
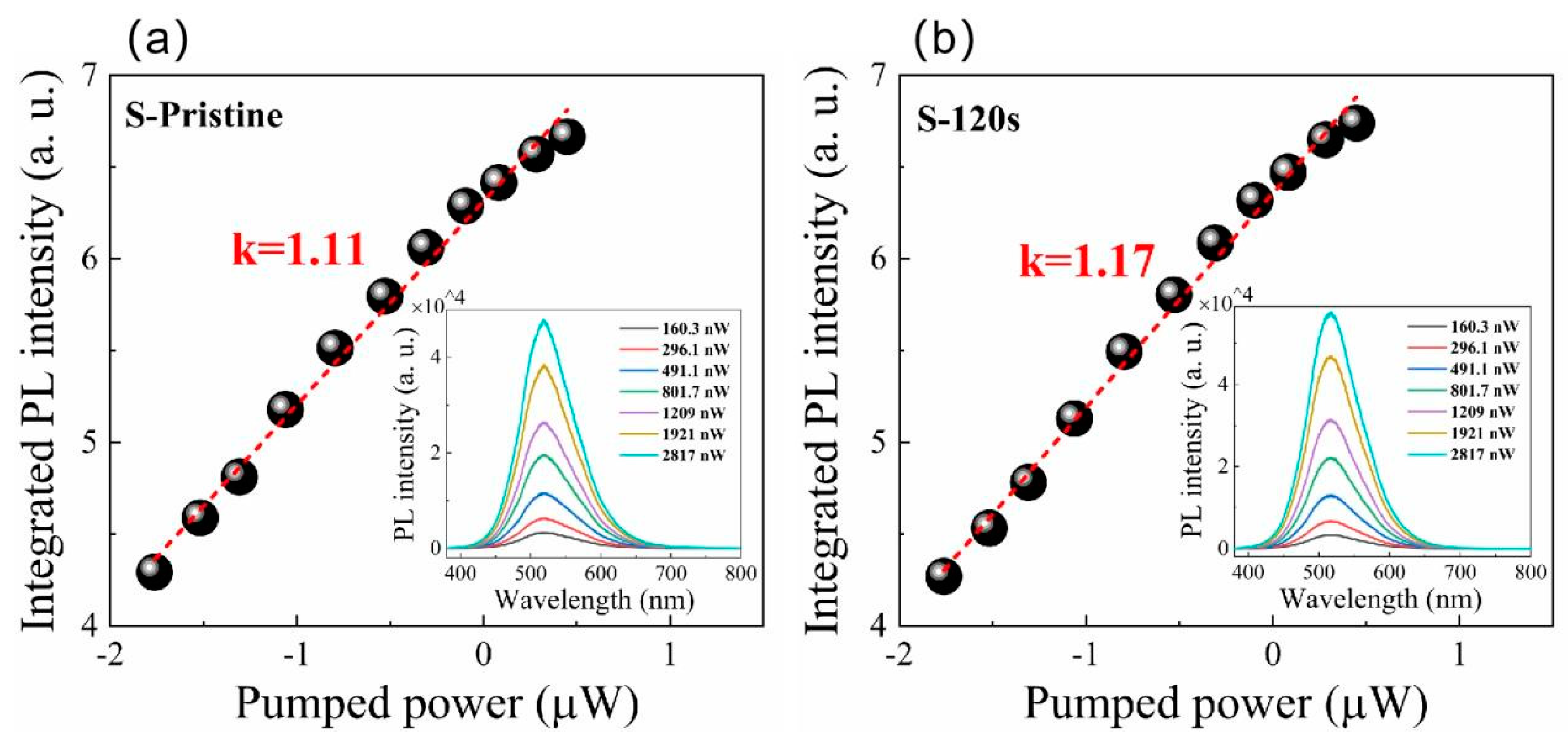
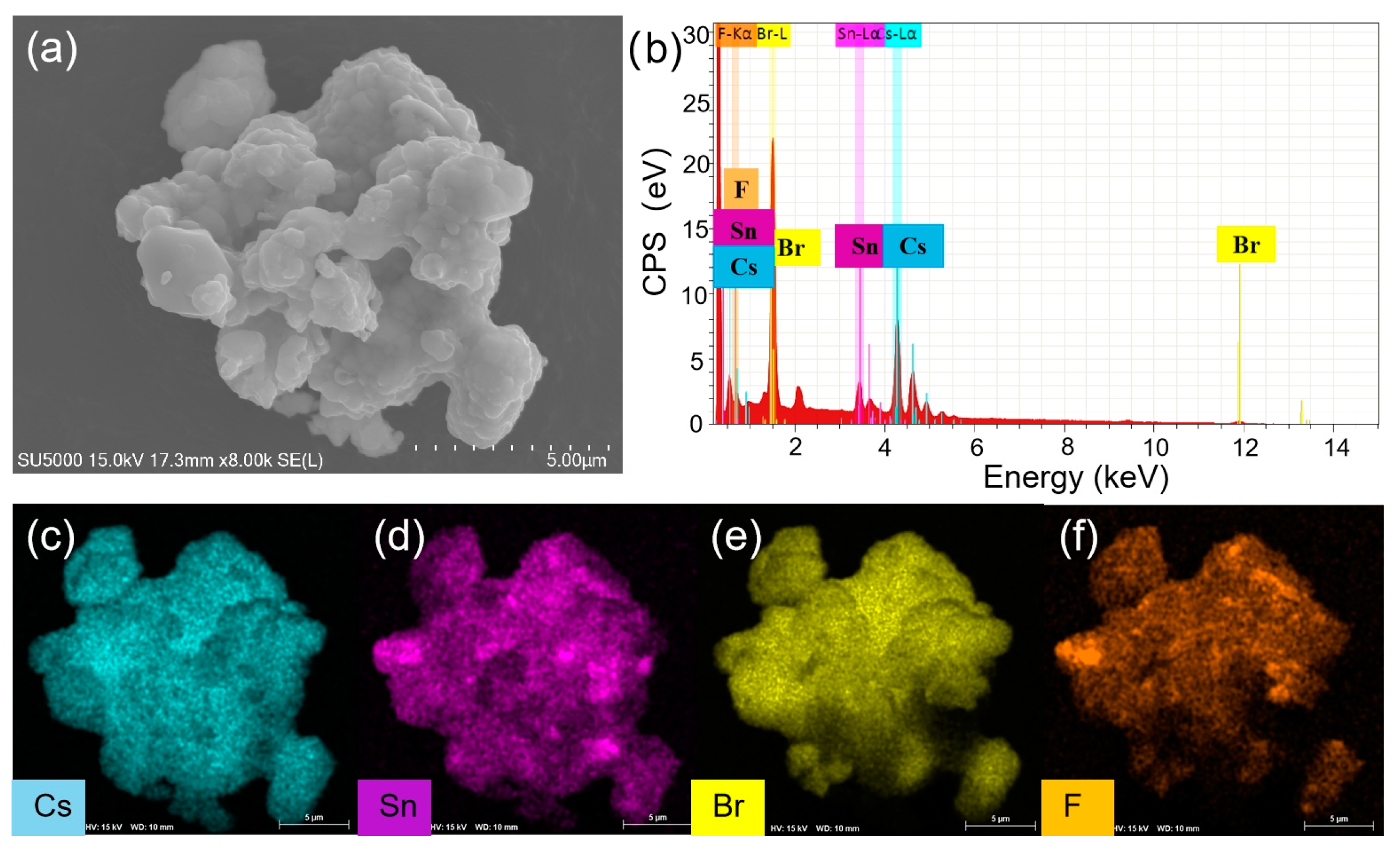
3. Results and discussion

The PL spectra of pristine Cs4SnBr6 sample and samples subjected to RTT at different temperatures are shown in Figure 1(a). Both types of samples exhibited a broad emission with a peak at approximately 530 nm. The emission band had a large full width at half maximum (FWHM) of approximately 105 nm. Additionally, a significant Stokes shift of around 1.30 eV was observed, as illustrated in Figure 1(c) and 1(d). It is evident that RTT at temperatures below 150°C had minimal influence on the PL intensity of Cs4SnBr6 samples. However, a notable increase in PL intensity was observed when the RTT temperature was raised to 200°C. Conversely, as the RTT temperature was further increased to 300°C, the PL intensity of Cs4SnBr6 samples decreased rapidly. Figure 1(b) showcases PL spectra of Cs4SnBr6 samples annealed at a RTT temperature of 200°C over diverse durations. The observed PL intensity of the Cs4SnBr6 samples appears to increment gradually with the prolongation of RTT duration from 30 to 120 seconds. Notably, as depicted in Figure 1(e) and 1(f), the PL QY takes a significant leap from 50.1% to 64.7% following the annealing of the unprocessed Cs4SnBr6 at an RTT temperature of 200°C for a span of 120 seconds. Figure 2a and Figure 2b display the excitation power dependence of PL for both the pristine sample and sample-120s. The insets of Figure 2a and Figure 2b demonstrate that an increase in excitation power, from 160 to 2817 nW, is accompanied by a corresponding enhancement in PL intensity. Nevertheless, the PL peak position maintains consistent, unaffected by variations in the excitation power. Additionally, a distinct linear correlation emerges between the integrated PL intensity and the excitation power within the range of 160 to 2817 nW. The excitation power-dependent PL intensity is commonly employed to determine the underlying mechanism of light emission in semiconductors. As per the literature [30], the PL intensity (I) can be described by the equation I = η I 0 k , where I0 denotes the excitation power, η symbolizes the emission efficiency, and the exponent k is affiliated with the radiative recombination process. A linear fit of ln(I/η) in contrast to ln(I0) allows the estimation of the k parameter values as 1.11 and 1.17 for the pristine sample and sample-120s respectively. This deduction strongly suggests that the green emission in both samples is engendered by the recombination of excitons. Given the large Stokes shift of ~1.30 eV, coupled with a broad FWHM of the emission band approximating ~105 nm, and further considering the long radiative lifetime of ~1μs, as illustrated in Figure 5, the green emission can be ascribed to the radiative recombination STEs, which is prompted by Jahn–Teller distortion of [SnBr6]4- octahedra in 0D perovskite [31,32,33].
To understand the enhanced PL, the structure and compositions of Cs4SnBr6 samples were evaluated via SEM and EDS, respectively. Figure 3(a) showcases the SEM image obtained from the pristine Cs4SnBr6 sample. The EDS spectrum reveals the presence of Cs, Sn, Br, and F elements in Cs4SnBr6, which are uniformly distributed, as demonstrated in the EDS mapping of Figure 3(c)-3(f). The Cs, Sn, Br, and F elements maintain this uniform distribution even after Cs4SnBr6 was annealed at an RTT temperature of 200°C for a duration of 120 s, as shown in Figure 4(c)-4(f). This result indicates that the elemental distribution of Cs4SnBr6 remained unaltered when subjected to RTT at 200°C for a duration of 120 s.
In Figure 5, we present the XRD patterns obtained for different samples. The XRD pattern of pristine Cs4SnBr6 sample (S-0s) reveals the coexistence phase of Cs4SnBr6 and CsBr due to incomplete consumption of CsBr powder precursors in the solid-state reaction. Apart from the prominent diffraction peak at 29.7°, attributed to the CsBr phase, we observe that the diffraction peaks of S-0s from the Cs4SnBr6 phase are consistent with those reported for Cs4SnBr6-SnF2[19,34]. This consistency suggests that the substitution of Br- with smaller F- effectively suppresses the oxidation of Sn2+ in Cs4SnBr6. Notably, the diffraction peaks corresponding to crystal planes (110), (300), (131), (223), and (330) of the Cs4SnBr6 phase become more pronounced and well-defined as the RTT time increases from 0 s to 120 s [34]. This strongly indicates an enhanced crystallinity of the Cs4SnBr6 powders after the RTT process.
Preprints 78201 g005
Figure 5. XRD patterns of the pristine Cs4SnBr6 sample and the samples annealed at a RTT temperature of 200°C for 30s, 90s, and 120s, respectively.
Figure 5. XRD patterns of the pristine Cs4SnBr6 sample and the samples annealed at a RTT temperature of 200°C for 30s, 90s, and 120s, respectively.
Preprints 78201 g005
To better comprehend the PL characteristics, we employed an excitation wavelength of 375 nm (facilitated by 70 ps excitation pulses from a laser) to measure the PL decay curves, as illustrated in Figure 6. The PL decay curve associated with the green emission yielded a sound fit when we employed a biexponential decay function [35]:
I t = I 0 + A 1 e x p − t τ 1 + A 2 e x p − t τ 2
where I0 represents the background level, τ1 and τ2 represent the lifetimes of each exponential decay component, and A1 and A2 denote the corresponding amplitudes. The intensity-weighted averaged PL lifetimes are then determined by A 1 ∗ τ 1 2 + A 2 ∗ τ 2 2 / A 1 ∗ τ 1 + A 2 ∗ τ 2 [35]. As depicted in Figure 6, the green emission in all samples exhibits a slow decay with a long radiative lifetime of approximately 1 μs. Notably, the lifetime remains nearly unchanged despite variations in the RTT conditions, even though the crystallinity of the Cs4SnBr6 samples improves after the RTT process. These findings suggest that the PL enhancement does not exclusively arise from a reduction in nonradiative recombination centers.
In order to gain insights into the influence of electron-phonon coupling, the temperature-dependent PL spectra of the samples were measured in the range of 100 to 300 K. As shown in Figure 7(a) and (b), a decrease in temperature led to an increase in PL intensity and a reduction in the FWHM for both the pristine sample and sample-120s. According to the theory proposed by Stadler [36], the FWHM of the PL peak is closely related to the electron-phonon coupling and can be described by the following equation:
F W H M T = 2.36 S ћ ω coth ћ ω 2 k B T
where S is the Huang-Rhys factor, ℏω is the energy of the phonon mode, T is the temperature, and kB is Boltzmann's constant. By fitting the temperature-dependent FWHM of the PL peaks using the equation 2, we can calculate the value of the Huang-Rhys factor S, which is commonly used to describe the exciton-phonon coupling. For the pristine sample, it was found that the value of S is as large as 63.7 (see Figure 7(c)), which is significantly higher than that reported in Cs4SnBr6. Generally, a larger S value indicates a stronger electron-phonon coupling, which is more favorable for the formation of STEs. However, a high S value also increases the probability of non-radiative recombination [24]. The Raman spectrum shown in the inset of Figure 7(c) reveals two dominant phonon modes, corresponding to the Sn-Br stretching vibrational modes at approximately 130 cm-1 and 220 cm-1 [37,38], respectively, which may be involved in the electron-phonon coupling and thus result in the S value as large as 63.7. After annealing the sample at a RTT temperature of 200°C for 120 s, the value of S is significantly reduced to 46.1, which closely resembles that observed in Cs4SnBr6 [28]. This reduction can be attributed to the disappearance of the Sn-Br stretching vibrational mode near 240 cm-1 (see the inset of Figure 7(d)) resulting from the enhanced crystallinity of the Cs4SnBr6 powders after the RTT process, as evidenced by the X-ray diffraction (XRD) patterns (refer to Figure 5). The fitted data in Figure 7(d) provide an optical phonon energy (ELO) of 16.7 meV (134 cm-1), which corresponds well with the Sn-Br stretching vibrational mode near 130 cm-1 in Cs4SnBr6 (see the inset of Figure 7(d)) [37,38]. This suggests that the electron-phonon coupling only involves the dominant phonon mode near 130 cm-1, which corresponds to the Sn-Br stretching vibrational mode near 130 cm-1. On another note, the PL QY of STEs highly depends on the exciton binding energy. The detrapping of STEs due to thermal activation results in a decreased radiative recombination rate. The exciton binding energy of STEs can be determined by analyzing the temperature-dependent integrated PL intensity (IPL) using the Arrhenius equation [33]:
          I P L   T = I P L   T 0 1 + β e x p − E b / k B T
where IPL(T0) is the integrated PL intensity at 80 K, β is a constant related to the density of radiative recombination centers, kB is Boltzmann's constant, and Eb is the exciton binding energy. Through fitting the experimental data with the Arrhenius equation, we can obtain the exciton binding energy Eb of 227 meV and 409 meV for the pristine sample and sample S-120, respectively (see Figure 7(e) and Figure 5(f)). It is noteworthy that the Eb value in sample S-120 substantially exceeds the 227 meV found in the pristine sample. This infers that the detrapping of STEs via thermal activation has been effectively suppressed in sample S-120, resulting in an augmented emission from the STEs. Therefore, based on the above analyses, we deduce that optimal electron-phonon coupling, compounded by the enhanced exciton binding energy elicited by the RTT, is responsible for the enhanced STE emission discerned in sample S-120.

4. Conclusions

In conclusion, our study systematically investigated the impact of RTT on the PL properties of lead-free Cs4SnBr6. The results showed that RTT at 200°C for 120 seconds significantly enhanced the emission from STEs, with the photoluminescence quantum yield increasing up to 64.7%. Through analysis of temperature-dependent PL spectra, Raman spectra, and PL decay traces, we propose that the improvement in photoluminescence is due to appropriate electron-phonon coupling and increased binding energies of STEs induced by the RTT. Our study offers a new approach for the development of efficient luminescent 0D tin-halide perovskites, which holds significant implications for the future advance.

Author Contributions

H.W. (Haixia Wu): investigation, formal analysis, writing - original draft. Z.L.: investigation, formal analysis. J.Song.: investigation. Y.Z.: investigation, Y.G.: investigation, W.Z.: investigation, R.H.: writing—review and editing, formal analysis, funding acquisition. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Guangdong Basic and Applied Basic Research Foundation (2020A1515010432), Project of Guangdong Province Key Discipline Scientific Research Level Improvement (2021ZDJS039, 2022ZDJS067), Special Innovation Projects of Guangdong Provincial Department of Education (2019KTSCX096, 2020KTSCX076), Advanced Materials and Devices Laboratory(623012).

Data Availability Statement

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Li, M.; Xia, Z. Recent progress of zero-dimensional luminescent metal halides. Chem. Soc. Rev. 2021, 50, 2626–2662. [Google Scholar] [CrossRef] [PubMed]
  2. Akkerman, Q.A.; Abdelhady, A. L.; Manna, L. Zero-dimensional cesium lead halides: history, properties, and challenges. J. Phys. Chem. Lett. 2018, 9, 2326–2337. [Google Scholar] [CrossRef] [PubMed]
  3. Zhou, C.; Xu, L.J.; Lee, S.; Lin, H.; Ma, B. Recent Advances in Luminescent Zero-Dimensional Organic Metal Halide Hybrids. Adv. Opt. Mater. 2021, 9, 2001766. [Google Scholar] [CrossRef]
  4. Sun, S.; Lu, M.; Gao, X.; Shi, Z.; Bai, X.; Yu, W.W.; Zhang, Y. 0D perovskites: Unique properties, synthesis, and their applications. Adv. Sci. 2021, 8, 2102689. [Google Scholar] [CrossRef] [PubMed]
  5. Yakunin, S.; Benin, B.M.; Shynkarenko, Y.; Nazarenko, O.; Bodnarchuk, M.I.; Dirin, D.N.; Hofer, C.; Cattaneo, S.; Kovalenko, M.V. High-resolution remote thermometry and thermography using luminescent low-dimensional tin-halide perovskites. Nat. Mater. 2019, 18, 846–852. [Google Scholar] [CrossRef]
  6. Tan, Z.; Chu, Y.; Chen, J.; Li, J.; Ji, G.; Niu, G.; Gao, L.; Xiao, Z.; Tang, J. Lead-free perovskite variant solid solutions Cs2Sn1–xTexCl6: bright luminescence and high anti-water stability. Adv. Mater. 2020, 32, 2002443. [Google Scholar] [CrossRef]
  7. Chang, T.; Wei, Q.; Zeng, R.; Cao, S.; Zhao, J.; Zou, B. Efficient energy transfer in Te4+-doped Cs2ZrCl6 vacancy-ordered perovskites and ultrahigh moisture stability via A-site Rb-alloying strategy. J. Phys. Chem. Lett. 2021, 12, 1829–1837. [Google Scholar] [CrossRef]
  8. Chen, D.; Wan, Z.; Chen, X.; Yuan, Y.; Zhong, J. Large-scale room-temperature synthesis and optical properties of perovskite-related Cs4PbBr6 fluorophores. J. Mater. Chem. C 2016, 4, 10646–10653. [Google Scholar] [CrossRef]
  9. Fan, Q.; Biesold-McGee, G.V.; Ma, J.; Xu, Q.; Pan, S.; Peng, J.; Lin, Z. Lead-free halide perovskite nanocrystals: crystal structures, synthesis, stabilities, and optical properties. Angew. Chem. Int. Ed. 2020, 59, 1030–1046. [Google Scholar] [CrossRef]
  10. Li, X.; Gao, X.; Zhang, X.; Shen, X.; Lu, M.; Wu, J.; Shi, Z.; Colvin, V.L.; Hu, J.; Bai, X.; Yu, W.W.; Zhang, Y. Lead-Free Halide Perovskites for Light Emission: Recent Advances and Perspectives. Adv. Sci. 2021, 8, 2003334. [Google Scholar] [CrossRef]
  11. Wang, A.; Guo, Y.; Zhou, Z.; Niu, X.; Wang, Y.; Muhammad, F.; Li, H.; Zhang, T.; Wang, J.; Nie, S.; Deng, Z. Aqueous acid-based synthesis of lead-free tin halide perovskites with near-unity photoluminescence quantum efficiency. Chem. Sci. 2019, 10, 4573–4579. [Google Scholar] [CrossRef] [PubMed]
  12. Wang, X.; Zhang, T.; Lou, Y.; Zhao, Y. All-inorganic lead-free perovskites for optoelectronic applications. Mater. Chem. Front. 2019, 3, 365–375. [Google Scholar] [CrossRef]
  13. Liu, Q.; Yin, J.; Zhang, B.B.; Chen, J.K.; Zhou, Y.; Zhang, L.M.; Wang, L.M.; Zhao, Q.; Hou, J.; Shu, J.; Song, B.; Shirahata, N.; Bakr, O.M.; Mohammed, O.F.; Sun, H.T. Theory-guided synthesis of highly luminescent colloidal cesium tin halide perovskite nanocrystals. J. Am. Chem. Soc. 2021, 143, 5470–5480. [Google Scholar] [CrossRef] [PubMed]
  14. Benin, B.M.; Dirin, D.N.; Morad, V.; Wörle, M.; Yakunin, S.; Rainò, G.; Nazarenko, O.; Fischer, M.; Infante, I.; Kovalenko, M. V. Highly emissive self-trapped excitons in fully inorganic zero-dimensional tin halides. Angew. Chem. Int. Ed. 2018, 57, 11329–11333. [Google Scholar] [CrossRef] [PubMed]
  15. Zhang, X.; Wang, H.; Wang, S.; Hu, Y.; Liu, X.; Shi, Z.; Colvin, V.L.; Wang, S.; Yu, W.W.; Zhang, Y. Room temperature synthesis of all inorganic lead-free zero-dimensional Cs4SnBr6 and Cs3KSnBr6 perovskites. Inorg. Chem. 2019, 59, 533–538. [Google Scholar] [CrossRef]
  16. Tan, L.; Wang, W.; Li, Q.; Luo, Z.; Zou, C.; Tang, M.; Zhang, L.; He, J.; Quan, Z. Colloidal syntheses of zero-dimensional Cs4SnX6 (X= Br, I) nanocrystals with high emission efficiencies. Chem. Commun. 2020, 56, 387–390. [Google Scholar] [CrossRef]
  17. Jellicoe, T.C.; Richter, J.M.; Glass, H.F.; Tabachnyk, M.; Brady, R.; Dutton, S.E.; Rao, A.; Friend, R.H.; Credgington, D.; Greenham, N.C.; Böhm, M.L. Synthesis and optical properties of lead-free cesium tin halide perovskite nanocrystals. J. Am. Chem. Soc. 2016, 138, 2941–2944. [Google Scholar] [CrossRef]
  18. Kang, C.; Rao, H.; Fang, Y.; Zeng, J.; Pan, Z.; Zhong, X. Antioxidative stannous oxalate derived lead-free stable CsSnX3 (X= Cl, Br, and I) perovskite nanocrystals. Angew. Chem. Int. Ed. 2021, 60, 660–665. [Google Scholar] [CrossRef]
  19. Zhang, Q.; Liu, S.; He, M.; Zheng, W.; Wan, Q.; Liu, M.; Liao, X.; Zhan, W.; Yuan, C.; Liu, J.; Xie, H.; Guo, X.; Kong, L.; Li, L. Stable Lead-Free Tin Halide Perovskite with Operational Stability > 1200 h by Suppressing Tin (II) Oxidation. Angew. Chem. Int. Ed. 2022, 61, e202205463. [Google Scholar] [CrossRef]
  20. Zhou, C.; Lin, H.; He, Q.; Xu, L.; Worku, M.; Chaaban, M.; Lee, S.; Shi, X.; Du, M.H.; Ma, B. Low dimensional metal halide perovskites and hybrids. Mater. Sci. Eng. R Rep. 2019, 137, 38–65. [Google Scholar] [CrossRef]
  21. Smith, M.D.; Connor, B.A.; Karunadasa, H.I. Tuning the luminescence of layered halide perovskites. Chem. Rev. 2019, 119, 3104–3139. [Google Scholar] [CrossRef] [PubMed]
  22. Lin, H.; Zhou, C.; Tian, Y.; Siegrist, T.; Ma, B. Low-dimensional organometal halide perovskites. ACS Energy Lett. 2017, 3, 54–62. [Google Scholar] [CrossRef]
  23. Hu, T.; Smith, M.D.; Dohner, E.R.; Sher, M.J.; Wu, X.; Trinh, M.T.; Fisher, A.; Corbett, J.; Zhu, X.Y.; Karunadasa, H.I.; Lindenberg, A.M. Mechanism for broadband white-light emission from two-dimensional (110) hybrid perovskites. J. Phys. Chem. Lett. 2016, 7, 2258–2263. [Google Scholar] [CrossRef] [PubMed]
  24. Li, S.; Luo, J.; Liu, J.; Tang, J. Self-trapped excitons in all-inorganic halide perovskites: fundamentals, status, and potential applications. J. Phys. Chem. Lett. 2019, 10, 1999–2007. [Google Scholar] [CrossRef] [PubMed]
  25. Dohner, E.R.; Jaffe, A.; Bradshaw, L.R.; Karunadasa, H.I. Intrinsic white-light emission from layered hybrid perovskites. J. Am. Chem. Soc. 2014, 136, 13154–13157. [Google Scholar] [CrossRef] [PubMed]
  26. Han, P.; Luo, C.; Yang, S.; Yang, Y.; Deng, W.; Han, K. All-inorganic lead-free 0D perovskites by a doping strategy to achieve a PLQY boost from< 2% to 90%. Angew. Chem. 2020, 132, 12809–12813. [Google Scholar]
  27. Ma, Z.; Liu, Z.; Lu, S.; Wang, L.; Feng, X.; Yang, D.; Wang, K.; Xiao, G.; Zhang, L.; Redfern, S.A.; Zou, B. Pressure-induced emission of cesium lead halide perovskite nanocrystals. Nat. Commun. 2018, 9, 4506. [Google Scholar] [CrossRef]
  28. Ulloa, J.M.; Llorens, J.M.; Alén, B.; Reyes, D.F.; Sales, D.L.; González, D.; Hierro, A. High efficient luminescence in type-II GaAsSb-capped InAs quantum dots upon annealing. Appl. Phys. Lett. 2012, 101, 253112. [Google Scholar] [CrossRef]
  29. Lin, Z.; Wang, A.; Huang, R.; Wu, H.; Song, J.; Lin, Z.; Hou, D.; Zhang, Z.; Guo, Y.; Lan, S. Manipulating the sublattice distortion induced by Mn2+ doping for boosting the emission characteristics of self-trapped excitons in Cs4SnBr6. J. Mater. Chem. C 2023, 11, 5680–5687. [Google Scholar] [CrossRef]
  30. Bergman, L.; Chen, X.B.; Morrison, J.L.; Huso, J.; Purdy, A.P. Photoluminescence dynamics in ensembles of wide-band-gap nanocrystallites and powders. J. Appl. Phys. 2004, 96, 675–682. [Google Scholar] [CrossRef]
  31. Guo, Q.; Zhao, X.; Song, B.; Luo, J.; Tang, J. Light Emission of Self-Trapped Excitons in Inorganic Metal Halides for Optoelectronic Applications. Adv. Mater. 2022, 34, 2201008. [Google Scholar] [CrossRef] [PubMed]
  32. Sun, C.; Jiang, K.; Han, M.F.; Liu, M.J.; Lian, X.K.; Jiang, Y.X.; Shi, H.S.; Yue, C.Y.; Lei, X.W. A zero-dimensional hybrid lead perovskite with highly efficient blue-violet light emission. J. Mater. Chem. C 2020, 8, 11890–11895. [Google Scholar] [CrossRef]
  33. Wang, X.; Zhang, X.; Yan, S.; Liu, H.; Zhang, Y. Nearly-Unity Quantum Yield and 12-Hour Afterglow from a Transparent Perovskite of Cs2NaScCl6: Tb. Angew. Chem. Int. Ed. 2022, 61, e202210853. [Google Scholar] [CrossRef] [PubMed]
  34. Chiara, R.; Ciftci, Y.O.; Queloz, V.I.; Nazeeruddin, M.K.; Grancini, G.; Malavasi, L. Green-emitting lead-free Cs4SnBr6 zero-dimensional perovskite nanocrystals with improved air stability. J. Phys. Chem. Lett. 2020, 11, 618–623. [Google Scholar] [CrossRef]
  35. Lin, K.H.; Liou, S.C.; Chen, W.L.; Wu, C.L.; Lin, G.R.; Chang, Y.M. Tunable and stable UV-NIR photoluminescence from annealed SiOx with Si nanoparticles. Opt. Express 2013, 21, 23416–23424. [Google Scholar] [CrossRef]
  36. Stadler, W.; Hofmann, D.M.; Alt, H.C.; Muschik, T.; Meyer, B.K.; Weigel, E.; Müller-Vogt, G.; Salk, M.; Rupp, E.; Benz, K.W. Optical investigations of defects in Cd1−x Zn x Te. Phys. Rev. B 1995, 51, 10619. [Google Scholar] [CrossRef]
  37. Kuok, M.H.; Tan, L.S.; Shen, Z.X.; Huan, C.H.; Mok, K.F. A Raman study of RbSnBr3. Solid State Commun. 1996, 97, 497–501. [Google Scholar] [CrossRef]
  38. Qin, Z.; Dai, S.; Hadjiev, V.G.; Wang, C.; Xie, L.; Ni, Y.; Wu, C.; Yang, G.; Chen, S.; Deng, L.; Yu, Q.; Feng, G.; Wang, Z.M.; Bao, J. Revealing the origin of luminescence center in 0D Cs4PbBr6 perovskite. Chem. Mater. 2019, 31, 9098–9104. [Google Scholar] [CrossRef]
Preprints 78201 g001
Figure 1. (a) PL spectra and (c) PLE spectra of both the unprocessed Cs4SnBr6 sample and samples treated with RTT at varying temperatures. (b) PL spectra and (d) PLE spectra of Cs4SnBr6 samples annealed at a RTT temperature of 200 °C for distinct durations. The PL QY derived from the excitation and emission spectra for (e) the pristine Cs4SnBr6, and (f) Cs4SnBr6 sample annealed at a RTT temperature of 200 °C for a span of 120 seconds.
Figure 1. (a) PL spectra and (c) PLE spectra of both the unprocessed Cs4SnBr6 sample and samples treated with RTT at varying temperatures. (b) PL spectra and (d) PLE spectra of Cs4SnBr6 samples annealed at a RTT temperature of 200 °C for distinct durations. The PL QY derived from the excitation and emission spectra for (e) the pristine Cs4SnBr6, and (f) Cs4SnBr6 sample annealed at a RTT temperature of 200 °C for a span of 120 seconds.
Preprints 78201 g001
Preprints 78201 g002
Figure 2. The integrated PL intensity under different excitation powers: (a) pristine sample, (b) sample-120s. The red solid lines are theoretical fitting curves. Insets in Figure 2a and 2b show the PL spectra from pristine sample and sample-120s under different excitation powers, respectively.
Figure 2. The integrated PL intensity under different excitation powers: (a) pristine sample, (b) sample-120s. The red solid lines are theoretical fitting curves. Insets in Figure 2a and 2b show the PL spectra from pristine sample and sample-120s under different excitation powers, respectively.
Preprints 78201 g002
Preprints 78201 g003
Figure 3. (a) SEM image, (b) EDS spectrum, and (c)-(f) EDS elemental maps of Cs, Sn, Br, and F for a typical pristine Cs4SnBr6 sample, respectively.
Figure 3. (a) SEM image, (b) EDS spectrum, and (c)-(f) EDS elemental maps of Cs, Sn, Br, and F for a typical pristine Cs4SnBr6 sample, respectively.
Preprints 78201 g003
Preprints 78201 g004
Figure 4. (a) SEM image, (b) EDS spectrum, and (c)-(f) EDS elemental maps of Cs, Sn, Br, and F for Cs4SnBr6 sample S-120s annealed at a RTT temperature of 200°C for 120 s, respectively.
Figure 4. (a) SEM image, (b) EDS spectrum, and (c)-(f) EDS elemental maps of Cs, Sn, Br, and F for Cs4SnBr6 sample S-120s annealed at a RTT temperature of 200°C for 120 s, respectively.
Preprints 78201 g004
Preprints 78201 g006
Figure 6. Time-resolved PL decay traces, captured at 525 nm, in both the pristine Cs4SnBr6 sample and the samples subjected to annealing at a RTT temperature of 200°C for varying durations. Each measurement was conducted under an excitation wavelength of 375 nm, employing 70 ps excitation pulses from a laser.
Figure 6. Time-resolved PL decay traces, captured at 525 nm, in both the pristine Cs4SnBr6 sample and the samples subjected to annealing at a RTT temperature of 200°C for varying durations. Each measurement was conducted under an excitation wavelength of 375 nm, employing 70 ps excitation pulses from a laser.
Preprints 78201 g006
Preprints 78201 g007
Figure 7. Temperature-dependent PL spectra measured in the range of 100 to 300 K for (a) pristine sample, (b) sample S-120s annealed at a RTT temperature of 200°C for 120 s. Temperature-dependent PL linewidth observed for (c) pristine sample and (d) sample S-120s (solid symbols), and the fitting of the experimental data (red line) by using Eq. (1). The insets in Figure (c) and (d) show the Raman spectrum of pristine sample and sample S-120s, respectively. Integrated PL intensities measured for (e) pristine sample and (f) sample S-120s at different temperatures (green solid symbols). Also shown is the fitting of the corresponding experimental data (red dashed curve) of the pristine sample and sample S-120s.
Figure 7. Temperature-dependent PL spectra measured in the range of 100 to 300 K for (a) pristine sample, (b) sample S-120s annealed at a RTT temperature of 200°C for 120 s. Temperature-dependent PL linewidth observed for (c) pristine sample and (d) sample S-120s (solid symbols), and the fitting of the experimental data (red line) by using Eq. (1). The insets in Figure (c) and (d) show the Raman spectrum of pristine sample and sample S-120s, respectively. Integrated PL intensities measured for (e) pristine sample and (f) sample S-120s at different temperatures (green solid symbols). Also shown is the fitting of the corresponding experimental data (red dashed curve) of the pristine sample and sample S-120s.
Preprints 78201 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated