Prerpints.org logo
Preprint
Article

Group Theory of Messenger RNA Metabolism and Disease

Altmetrics

Downloads

205

Views

236

Comments

1

A peer-reviewed article of this preprint also exists.

supplementary.pdf (372.06KB )

Submitted:

19 October 2023

Posted:

23 October 2023

You are already at the latest version

Alerts
Abstract
Our recent work has focused on the application of infinite group theory and related algebraic geometric tools in the context of transcription factors and microRNAs. We were able to differentiate between “healthy" nucleotide sequences and disrupted sequences that may be associated with various diseases. In this paper, we extend our efforts to the study of messenger RNA metabolism, showcasing the power of our approach. We investigate (i) mRNA translation in prokaryotes and eukaryotes, (ii) polyadenylation in eukaryotes, which is crucial for nuclear export, translation, stability, and splicing of mRNA, (iii) miRNAs involved in RNA silencing and post-transcriptional regulation of gene expression, and (iv) the identification of disrupted sequences that could lead to potential illnesses. To achieve this, we employ (a) infinite (finitely generated) groups fp, with generators representing the r+1 distinct nucleotides and a relation between them [e.g., the consensus sequence in the mRNA translation (i), the poly(A) tail in item (ii), and the miRNA seed in item (iii)], (b) aperiodicity theory, which connects “healthy groups" fp to free groups Fr of rank r and their profinite completion F^r, and (c) the representation theory of groups fp over the space-time-spin group SL2(C), highlighting the role of surfaces with isolated singularities in the character variety. Our approach could potentially contribute to the understanding of the molecular mechanisms underlying various diseases and help develop new diagnostic or therapeutic strategies.
Keywords: 
Subject: Biology and Life Sciences  -   Biochemistry and Molecular Biology

1. Introduction

Genome-scale metabolic pathways [1,2], genome–environment interactions [3], the immune response [4], post-transcriptional regulatory mechanisms [5] and oncohistones [6] represent aspects of a research field connecting the heritable genetic code to other biological codes.
The aforementioned genetic code is defined precisely as a non-injective map from the 64 codons to the 20 amino acids. Both finite groups [7,8,9] and quantum groups [10] play a leading role in modeling this code. More explicitly, in our paper [8], complete quantum information is encoded in the 22 irreducible characters of the small group ( 240 , 105 ) ≅ Z 5 ⋊ 2 O , with 2 O the binary octahedral group. The characters are put in correspondence with the DNA multiplets encoding the proteinogenic amino acids and the multiplicity is reflected in the dimension of the character representation. Further developments are explored in [11] showing that the small group ( 336 , 118 ) ≅ Z 7 ⋊ 2 O is another model of the genetic code reflecting the symmetry of Lsm 1 − 7 complex in the spliceosome. The 8-fold symmetric histone complex is investigated in [12] with the character table of the group ( 384 , 5589 ) ≅ Z 8 ⋊ 2 O . The latest papers inaugurate the role played by a specific algebraic surface called the Kummer surface in the quantum modeling of the genetic code.
From now, we refer to the “epigenetic code" as all processes that reveal and execute gene expression. This includes DNA methylation processes [13], mRNA translation preparation, the poly(A) tail, the RNA-induced silencing complex (RISC) — a vital tool in gene regulation comprising single strands of RNA (ssRNA) and double strands of small interfering RNA (siRNA) — and other regulatory nucleotide sequence fragments that are discarded after splicing. For a relation between the epigenetic code and morphogenesis, see [14].
Chemical modifications in RNA also drive the metabolism of transcription of the genetic information. Post-transcriptional regulation in gene expression is a hot topic known as epitranscriptomics. There are more than 170 known types of RNA methylation processes but the most common in eukaryotes is the possible methylation of A ̲ = m 6 A on sites with a specific short sequence R R A ̲ C H ( R = A or G, H = A , U or C), see e.g. [15,16,17].
For studying the epigenetic code (hereinafter referred to as the e-code), we employ infinite (finitely generated) groups denoted by f p , and their representations over the ( 2 × 2 ) matrix group S L 2 ( C ) , where the entries are complex numbers [19]. The significance of this group extends across all fields of physics as it represents a space-time-spin group. In this study, we apply a mathematical field known as algebraic geometry to define the e-code. This has never been done before.
Our crucial observation is that an f p group associated with a "healthy" sequence usually approximates a free group F r , where the rank r equals the number of distinct nucleotides (nt) minus one. A sequence deviating from this may suggest a potential e-code deregulation leading to a disease. However, an f p group closely resembling a free group does not provide sufficient assurance against a disease. Additional examination of the S L 2 ( C ) representations of f p — termed the character variety— specifically, its basis — called a Groebner basis G — is necessary.
The Groebner basis comprises a set of surfaces. A surface within G containing isolated singularities indicates another potential disease that can be identified specifically, e.g., relating to an oncogene or a neurological disorder [19]. The e-code we define comprises such algebraic geometric characteristics.
An additional attribute of “healthy" sequences, which leads to a group f p approximating the free group F r and not mentioned in [19], is their connection to aperiodicity. Schrödinger’s book [20] proposes aperiodicity of living “crystals". Our paper [21] characterizes aperiodic DNA sequences. We further this concept by introducing the so-called profinite completion F ^ r of the free group F r . A sequence f p ( l ) of finitely generated groups approaching F r emerges by applying l repeated substitutions to the generators of f p . However, all distinct groups f p ( l ) should possess the same profinite completion F ^ r . Profinite groups F ^ 1 (corresponding to sequences containing two distinct nt) and F ^ 2 (corresponding to sequences containing three distinct nt) have been examined in a prominent algebraic geometry treatise [22]. We present the details below in a manner that is accessible to a non-specialist reader.
In Section 2, we illustrate our mathematical concepts through a few simple pedagogical examples. In Section 3, we apply these concepts to the cases of mRNA translation, microRNAs and m 6 A methylation. In Section 4, we provide additional comments, a summary diagram and perspectives.

2. Methods and Preliminary Results

2.1. Infinite Finitely Generated Groups f p and Free Groups F r

The TATA Box

We’ll start with a simple example of an infinitely finitely generated group taken from the context of introns. The DNA sequence located in the core promoter region of many eukaryotic genes is the Goldberg-Hogness sequence, also known as the TATA box. This sequence contains a non-coding segment with repeated T and A base pairs. The TATA box serves as the binding site for the TATA-binding protein and other transcription factors in some eukaryotic genes. Its consensus sequence takes the form rel=TATAAAA. Variations in this consensus sequence, resulting from genetic polymorphism, can lead to diseases like Gilbert’s syndrome and immune suppression [23].
In our methodology, we define the group f p = A , T | r e l , which contains infinitely many elements. There are numerous ways to investigate this group, but we opted for a specific one. This method involves calculating the number of conjugacy classes of subgroups of index d of f p (a sequence we’ll refer to as the card seq of f p ). The card seq of f p for the selected TATA sequence is [ 1 , 1 , 2 , 3 , 2 , 8 , 7 , 10 , 18 , 28 ⋯ ] . Interestingly, the group H 3 = A , T | A 2 = T 3 shows a similar card seq (at least up to the highest index we can reach with the calculations). The group H 3 , as defined, is isomorphic to the so-called modular group P S L ( 2 , Z ) – the group of ( 2 × 2 ) matrices of determinant 1 with integer entries. This group has an intriguing topological interpretation as the fundamental group of the trefoil knot manifold. Thus, we find that the group f p is ’close’ to H 3 since the card seq of both groups is the same, but we can easily verify that f p and H 3 are not isomorphic.
In paper [25], we discovered that Hecke groups H q = A , T | A 2 = T q , with q = 3 or 4, have a card seq corresponding to ’healthy’ TATA box sequences. The f p group for a TATA box with a card seq resembling that of Hecke groups, with q ≠ 3 or q ≠ 4 , or even that of groups slightly different from H 3 and H 4 , signifies Gilbert’s syndrome.

Polyadenylation Signals

For our second example, we select a sequence from the context of eukaryotic polyadenylation [24]. Polyadenylation involves the addition of a poly(A) tail to an RNA transcript, usually a messenger RNA (mRNA). A consensus poly(A) sequence takes the form rel1=AAUAAA. This corresponds to a two-generator group of the form f p = A U | r e l 1 . The card seq of such a group is found to be [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , ⋯ ] , implying a single conjugacy class for each index. It appears that the free group F 1 = A , U | A U , of rank 1, has the same card seq as the f p group with relation rel1, even though both groups are not isomorphic.
Another consensus poly(A) sequence takes the form rel2=UGUAA. This corresponds to a three-generator group of the form f p = A , U , G | r e l 2 . The card seq of such a group is found to be [ 1 , 3 , 7 , 26 , 97 , 624 , 4163 , ⋯ ] . Intriguingly, the free group F 2 = A , U , G | A U G , of rank 2, has the same card seq as the f p group with relation rel2, despite both groups not being isomorphic.
From our perspective, DNA/RNA sequences that lead to f p groups closely resembling a free group are considered ’healthy’ sequences [19,21,25]. The standard poly(A) sequences mentioned earlier play a regulatory role in producing mature mRNA during translation. Sequences that generate an f p group diverging from a free group F r may be indicative of a disease.

2.2. Aperiodic Sequences, Their Attached Groups f p and Free Groups

In this subsection, we’ll elucidate how a group f p , with a card seq identified to be close to a free group F r , can be linked to an aperiodic sequence and the profinite completion F ^ r . We introduced the concept of aperiodic groups and sequences in our earlier papers [25] and [21].
Consider the motif r e l = T T T A T T A , which serves as a consensus sequence for the transcription factor of the DBX gene in Drosophila melanogaster (fruit flies). This gene is involved in neuronal specification and differentiation. The group f p = A , T | r e l has the same card seq as the free group F 1 of rank 1. Furthermore, by splitting rel into two segments r e l = r e l A r e l T and applying the substitution maps A → r e l A = T T T A , T → r e l T = T T A , we generate the substitution sequence
S D B X = A , T , A T , T T T A T T A , T T A T T A T T A T T T A T T A T T A T T T A , ⋯ . Upon inspection, it’s straightforward to observe that all finitely generated groups f p ( l ) , with their generators being
A T , T T T A T T A , T T A T T A T T A T T T A T T A T T A T T T A , ⋯ , respectively, possess the card seq of F 1 .
As per Reference [25], a substitution rule to be considered aperiodic must satisfy two conditions: (1) the substitution matrix M must be primitive, meaning it should be a strictly positive matrix (all entries > 0 ), irreducible, and M k should be strictly positive for some k. This condition is denoted as M > > 0 , and (2) the Perron-Frobenius λ P F eigenvalue must be irrational. It’s worth noting that the Perron-Frobenius eigenvector of an irreducible non-negative matrix is the only one whose entries are all positive.
The aforementioned sequence has a substitution matrix M = 1 3 1 2 . One can verify that M is primitive since M 2 > > 0 and λ P F = ( 3 + 13 ) / 2 . Conditions (1) and (2) are satisfied, implying that the substitution S D B X is aperiodic.
Numerous other genes have transcription factors with a motif rel generating an aperiodic sequence [21].

2.3. Aperiodic Sequences and the Profinite Groups F ^ r

This section can be skipped without affecting the comprehension of the rest of the paper. It endeavors to answer the following question: why do the aforementioned groups f p ( l ) produce the same card seq as that of the free group F 1 ? The tentative answer to this question is that the profinite completion of all groups f p ( l ) is the profinite group F ^ 1 . By making this observation, we align the aperiodicity of sequences with profinite groups. Profinite groups were introduced by Grothendieck in the context of algebraic geometry [22]. Here, we describe the necessary ingredients for the layperson, focusing first on F ^ 1 and then on F ^ 2 , and their relevance to our present work.
A group G can be considered a ’topological group’ by applying the ’discrete topology’, in which the elements of G are points of a ’discrete space’, form a ’discontinuous sequence’ and are isolated from each other. Every subset is ’open’ in the discrete topology. A profinite group is a topological group that, in a certain sense, is assembled from a system of finite groups. A profinite group requires a system of finite groups and group homomorphisms between them.
Given a group G, there is a related profinite group G ^ defined as the inverse limit G ^ = lim ← G / N , of the groups G / N , where N runs through the normal subgroups of G of finite index [a normal subgroup is a subgroup that remains invariant under conjugation by members of the group]. Each finite quotient group corresponds to a normal subgroup N of G and the profinite completion G ^ can be perceived as containing an analogue of each of these normal subgroups.
The profinite group G ^ exhibits several properties: it is non-abelian, residually finite [meaning that for any non-identity element g in G ^ , there exists a finite quotient of G ^ in which g is not the identity], and totally disconnected [meaning that the only connected subsets of G ^ are singletons, sets containing only one element].
In general, an explicit construction of profinite groups G ^ cannot be obtained. However, F ^ 1 and F ^ 2 are not overly complex to handle.

About the Profinite Group F ^ 1

Let’s begin with F ^ 1 . The free group F 1 on a single generator can be described as a group with one generator, say a, and no relations. It consists of all possible finite strings that can be formed by combining the generator and its inverse. It is the infinite cyclic group Z = { 1 , a , a − 1 , a 2 , a − 2 , a 3 , a − 3 , ⋯ } . Now, let’s discuss the profinite completion of F 1 . The profinite group F ^ 1 is isomorphic to the group of all units of the commutative ring of p-adic integers Z p , across all primes p. It is often denoted as Z p * since it corresponds to the elements of Z p with a valuation of zero. The p-adic integers are a special class of numbers utilized in number theory and algebraic geometry.

About the Profinite Group F ^ 2

Let’s briefly discuss F ^ 2 . This topic was initiated in [22]. The subject is complex. It’s connected to the so-called Belyi theorem, a fundamental result that establishes a connection between algebraic curves defined over the algebraic closure of the rationals, Q ¯ , and certain rational functions called Belyi functions.
An algebraic curve defined over Q ¯ can be represented as a branched covering of the Riemann sphere (the complex projective line P 1 ( C ) ) branched only over three points (usually taken as 0, 1, and ∞) if and only if the curve itself is defined over a number field, which is a finite extension of the field of rational numbers Q .
In other words, the Belyi theorem implies that an algebraic curve defined over a number field can be mapped to the Riemann sphere in such a way that the ramification (branching) is restricted to just three points. The rational functions that provide these branched coverings are known as Belyi functions.
The significance of the Belyi theorem lies in the fact that it provides a method to study algebraic curves defined over number fields by analyzing their ramified coverings and the associated dessins d’enfants, which are combinatorial objects encoding the ramification data.
Specifically, we have the crucial result that
π ^ 1 ( P 1 ( C ) ∖ { 0 , 1 , ∞ } ) ≅ F ^ 2 ,
i.e., the so-called étale fundamental group for the triply branched projective line is the profinite group F ^ 2 .

2.4. S L 2 ( C ) Representations of Groups f p and a Groebner Basis G

While the previous section about profinite groups showcases the importance of algebraic geometry in the context of DNA/RNA sequences, it remains somewhat abstract. To address this, we can consider the representations of an f p group over the space-time-spin group S L 2 ( C ) , as we did in [18,19,21].
Representations of f p in S L 2 ( C ) are homomorphisms ρ : f p → S L 2 ( C ) with character κ ρ ( g ) = t r ( ρ ( g ) ) , g ∈ f p . The notation t r ( ρ ( g ) ) signifies the trace of the matrix ρ ( g ) . The set of characters is employed to determine an algebraic set by taking the quotient of the set of representations ρ by the group S L 2 ( C ) , which acts by conjugation on representations[26,27].
In such papers, we elaborated that the character variety of f p is a set comprised of a sequence X of multivariate polynomials. A particular basis related to X is the Groebner basis G ( X ) , whose factors define hypersurfaces.
Our precursor paper [18] focused on a possible algebraic approach of topological quantum computing. Later, in [19,21], we could investigate S L 2 ( C ) representations of short DNA/RNA sequences (e.g. the consensus sequence of a transcription factor or the seed of a microRNA) and relate them to a potential disease.
For a two-generator group f p , the factors are three-dimensional surfaces. In general, these surfaces can be classified by mapping them to a rational surface across five categories [19]. Often encountered surfaces are degree p Del Pezzo surfaces where 1 ≤ p ≤ 9 . A rational surface may either be non-singular, ’almost non-singular’, having only isolated singularities, or singular. Almost non-singular surfaces are crucial in our context. A simple singularity is referred to as an A-D-E singularity and must be of the type A n , n ≥ 1 , D n , n ≥ 4 , E 6 , E 7 or E 8 .
The A-D-E type is mirrored in the notation we employ. For instance, S ( l A 1 , m A 2 , n A 3 , ⋯ ) denotes a surface containing l type A 1 , m type A 2 , n type A 3 singularities, etc. A generic surface is the Cayley cubic we encountered in our previous papers, defined as S ( 4 A 1 ) = x y z + x 2 + y 2 + z 2 − 4 ([19] Figure 5).
For a three-generator group f p , the factors of G ( X ) are seven-dimensional surfaces of the form S a , b , c , d ( x , y , z ) . Some of them belong to the Fricke family ([19] Equation 3), which is associated with the four-punctured sphere. But for a chosen set of parameters a , b , c , d , the hypersurface reduces to an ordinary three-dimensional surface.
For a four-generator group f p , the factors of G ( X ) are 14-dimensional surfaces containing 4 copies of the form S ( x , y , z ) , S ( x , u , v ) , S ( y , u , v ) and S ( z , v , w ) for selected choices of 8 parameters.

Groebner Basis for the TATA Box

The Groebner basis for the character variety associated with the f p group of generator rel=TATAAAA of the TATA box, studied in subSection 2.1, is found to be:
G T A T A = ( z 4 − x y 2 − x y z + x 2 + y 2 + y z − 3 z 2 + x − 2 ) ( x 2 z − x y − x z + y − z ) S ( A 2 ) S ( A 4 ) ( x 3 − z 2 − 3 x + 2 ) ,
where S ( A 2 ) = x 2 y − z 3 − x z − y + 3 z and S ( A 4 ) = x z 2 − x 2 − y z − x + 2 are degree 3 Del Pezzo surfaces.
The Groebner basis G T A T A comprises a degree 2 Del Pezzo surface (see Figure 1, up), and a rational scroll whole analytic expression is in the first row. Both surfaces are singular. The second row consists of two surfaces with simple singularities of type A 2 and A 4 , respectively. The last term represents a curve (not a surface).

Groebner Basis for Polyadenylation Signals

For the first polyadenylation signal considered in subSection 2.1, the relation of the f p group is rel1=AAUAAA. The corresponding Groebner basis is:
G r e l 1 = 3 r a t i o n a l s c r o l l s × P 2 × S ( 4 A 1 ) S ( A 1 ) × c u r v e .
The Groebner basis G r e l 1 contains three rational scrolls, a surface birationally equivalent to the projective plane P 2 , the Cayley cubic S ( 4 A 1 ) , the degree 3 Del Pezzo surface S ( A 1 ) = x 2 y − x z 2 − x z + y z + x − y (see Figure 1, down) and a curve.
For the second polyadenylation signal considered in subSection 2.1, the relation of the f p group is rel2=UGUAA. The factors of G ( X ) are seven-dimensional hypersurfaces S a , b , c , d ( x , y , z ) . However, choosing specific parameters, such as S 0 , 0 , 0 , 0 ( x , y , z ) or S 1 , 1 , 1 , 1 ( x , y , z ) , we obtain three-dimensional surfaces. These are found to be degree 3 Del Pezzo surfaces with simple singularities of the form S l A 2 , with l=1, 2 or 3, quadrics, or curves.

Groebner Basis for the Transcription Factor of DBX Gene

For the DBX gene studied in Section 2.2, the Groebner basis takes the form
G D B X = s c r o l l × P 2 × S ( A 4 ) × S ( A 2 ) × S ( 4 A 1 ) × c u r v e , where scroll= y 2 z − x y − y z + x − z and P 2 = z 4 − x 2 y + x z − 4 z 2 + y + 2 are singular. The other factors are D P 3 surfaces with isolated singularities that are S ( A 4 ) = y z 2 − y 2 − x z − y 2 , S ( A 2 ) = z 3 − x y 2 + y z + x − 3 z , the Cayley cubic S ( 4 A 1 ) and curve = y 3 − z 2 − 3 y + 2 .

3. Further Results

In this section, we produce further results related to mRNA metabolism and miRNA.

3.1. Algebraic Geometry of mRNA Translation

The Shine-Dalgarno Box

Ribosomal RNA (rRNA) – a type of non coding RNA– is the main component of a macromolecular machine, called the ribosome, whose role is to ensure mRNA translation. The initiation of translation needs the recognition of the appropriate sequences on the m-RNA by the ribosome. A major factor in this recognition is an mRNA-rRNA interaction first proposed by Shine and Dalgarno [28]. They proposed that the ribosomal nucleotides recognize the complementary purine-rich sequence rel3=AGGAGGU, which is found around 8 bases upstream of the start codon AUG in a number of mRNAs found in viruses that affect Escherichia coli.
Let us study the group f p = A , G , U | r e l 3 . The card seq of f p is found to be the same than that of the free group F 2 .
The S L 2 ( C ) chararacter variety is a scheme X whose a Groebner basis G ( X ) is made of of 7-dimensional surfaces S a , b , c , d ( x , y , z ) . By projecting to 3 dimensions, one gets surfaces like S 0 , 0 , 0 , 0 ( x , y , z ) and S 1 , 1 , 1 , 1 ( x , y , z ) as in Section 2.4. We find degree 3 Del Pezzo surfaces with isolated singularities S ( A 1 ) = x 2 y + y z 2 + 4 x z + 4 y and x 2 y + y z 2 + x 2 + z 2 + 6 x z + 5 y − 6 z − 7 , S ( A 2 ) = x y z + 2 x 2 + z 2 + 4 and S ( A 4 ) = x y z + 3 x 2 + z 2 − 5 z , quadrics and curves.

Kozak Consensus Sequence

The Kozak consensus sequence is a nucleotide motif that functions as the protein translation initiation site in most eukaryotic mRNA transcripts [29]. The small (40S) subunit of eukaryotic ribosomes bind, initially at the capped 5 ′ -end of messenger RNA and then migrate, stopping at the first AUG codon in a favorable context for initiating translation. In eukaryotes, the Kozak sequence ensures that a protein is correctly translated from the genetic message, mediating ribosome assembly and translation initiation. A sequence logo of the most conserved bases around the initiation codon AUG for human mRNAs may be found in the first caption of [30] as r e l 4 = A C C A U G G C .
Let us study the group f p = A , C , G , U | r e l 4 . The card seq of f p is found to be the same than that of the free group F 3 of rank 3. This group can be linked to an aperiodic sequence by following the steps given in Section 2.2.
By splitting rel4 into four segments r e l 4 = r e l A r e l C r e l G r e l U and applying the substitution maps C → r e l C = A , A → r e l A = C C A U G , U → r e l U = G , G → r e l G = C , we generate the substitution sequence
S K o z a k = C , A , U , G , C A U G , A C C A U G G C , C C A U G A 2 C C A U G G C 2 A , ⋯ .
Upon inspection, it’s straightforward to observe that all finitely generated groups f p ( l ) , with their generators being
C A U G , A C C A U G G C , C C A U G A 2 C C A U G G C 2 A , ⋯ , respectively, possess the card seq of F 3 .
The aforementioned sequence has a substitution matrix M = 0 2 0 1 1 1 0 0 0 1 0 0 0 1 1 0 . One can verify that M is primitive since M 4 > > 0 and λ P F ≈ 2.2055694 is the only real (and irrational) solution of the equation x 3 − 2 x 2 − 1 . Conditions (1) and (2) of Section 2.2 are satisfied, implying that the substitution S K o z a k is aperiodic. See [31] for a connection of the later Perron-Frobenius eigenvalue to random Fibonacci sequences.
Mutation of a purine at position − 3 with respect to the AUG codon is kwown to be associated to a disease such as a type of thalassemia due to a bad initiation of α -globin [29]. In our approach the mutation from rel4 to rel4’=CCCAUGGC leads to a substitution M ′ that is no longer primitive so that the property of aperiodicity of the sequence is lost. However the cardseq of the associated f p group is still that of the free group F 3 . No other substitution in the sequence rel4’ can be found to restore the aperiodicity.

3.2. Algebraic Geometry of miRNAs

A microRNA (miRNA) is a small, single-stranded, non-coding RNA molecule containing approximately 22 nucleotides. miRNAs play crucial roles in RNA silencing and post-transcriptional regulation of gene expression by specifically targeting certain mRNAs for degradation and translational repression [32,33]. miRNA genes are typically transcribed by RNA polymerase II (Pol II), which binds to a promoter located near the DNA sequence, encoding what will become the hairpin loop of a pre-miRNA (for precursor-miRNA). The pre-miRNAs are approximately 70 nucleotides in length and fold into imperfect stem-loop structures.
A miRNA consists of a duplex comprising two strands (-5p and -3p). However, a single strand is selected into the RNA-induced silencing complex to serve as a template during the transcript of a complementary mRNA [34,35]. For details about the miRNA sequences, we use the Mir database [36,37,38].
It should be emphasized that a given miRNA may have hundreds of different mRNA targets, and a single target might be regulated by multiple miRNAs.
For previous results about how to define a f p group from the seed of a miRNA, the reader may consult ([19] Section 4.3).
Below, we focus on other examples.

miRNA hsa-mir-122

Mir-122 is a tissue specific miRNA which is highly expressed in liver [39]. It is involved in cholesterol accumulation and fathy acid metabolism. It has a leading role in controlling hapatitis C virus (HCV) [40,41].
The seed region for mir-122-5p is seed0=GGAGUGU. The corresponding group f p = C , G , U | s e e d 0 has the card seq of the free group F 2 .
Let us first check if the seed sequence is aperiodic. By splitting seed0 into three segments seed0= seedAseedGseedU and applying the substitution maps A → s e e d A = G G , G → s e e d G = A G U , U → s e e d U = G U , one can check that the finitely generated groups f p ( l ) with generators
G G A G U G U , A G U A G U G G A G U G U A G U G U , ⋯
possess the card seq of the free group F 2 . Following the method described in Section 2.2, one gets the (primitive) substitution matrix M = 0 1 0 2 1 1 0 1 1 whose characteristic polynomial λ 3 − 2 λ 2 − 2 λ + 2 has three real roots. The largest one is the (irrational) Perron-Frobenius eigenvalue λ P F ≈ 2.481194 . One concludes the sequence seed0 is aperiodic.
Let us now look at the Groebner basis for the S L 2 ( C ) representation of f p with the method described in Section 2.4. One obtains G m i r − 122 − 5 p ( 0 , 0 , 0 , 0 ) = 8 y z ( 2 − z 2 ) and G m i r − 122 − 5 p ( 1 , 1 , 1 , 1 ) = − 4 z 2 ( x − z 2 + z + 1 ) ( y + z 3 − z 2 − 2 z ) . One can check that for all values of the parameters G a , b , c , d ( x , y , z ) only contains factors which are curves (not surfaces).

miRNA hsa-mir-503

The slowest evolving miRNA gene in the human species (hsa) is hsa-mir-503 [37]. It regulates gene expression in various pathological processes of diseases, including carcinogenesis, angiogenesis, tissue fibrosis, and oxidative stress [42].
The seed region for mir-503-5p is seed1=AGCAGCGG. The corresponding group f p = A , C , G | s e e d 1 has the card seq of the free group F 2 . For this group, the Groebner basis with parameters ( a , b , c , d ) = ( 0 , 0 , 0 , 0 ) is quite simple: G m i r − 503 − 5 p ( 0 , 0 , 0 , 0 ) = S ( 4 A 1 ) ( x , y , z ) , which is the already mentioned Cayley cubic.
For ( a , b , c , d ) = ( 1 , 1 , 0 , 0 ) , G m i r − 503 − 5 p ( 1 , 1 , 0 , 0 ) = − 3 x y z κ 3 ( x , y , z ) , where κ 3 ( x , y , z ) is the Fricke surface found in [43]. For ( a , b , c , d ) = ( 1 , 1 , 1 , 1 ) , there are several more polynomials. One of them defines the Fricke surface x y z + x 2 + y 2 + z 2 − 2 x − y − 2 .
The considered seed region for mir-503-3p is GGGUAUU. The surfaces in the Groebner basis are very simple in this case, and no simple singularities exist within them.

miRNA hsa-mir-146a

Mir-146 is primarily involved in the regulation of inflammation and other processes functioning in the innate immune system. It plays a role in neuropathogenesis.
The considered seed region for hsa-mir-146a-5p is seed2=GAGAAC [37]. Again the corresponding group f p = A , C , G | s e e d 2 has the card seq of the free group F 2 .
The Groebner basis with parameters ( a , b , c , d ) = ( 0 , 0 , 0 , 0 ) is
G h s a − 146 a − 5 p ( 1 , 1 , 1 , 1 ) = ( x z + y + 2 ) ( y − z 2 + 2 ) 2 ( x 2 + z 2 − 2 y − 4 ) S ( 3 A 2 ) , where S ( 3 A 2 ) = z 3 − x y − 2 y z − 2 x − 4 z .
The Groebner basis with parameters ( a , b , c , d ) = ( 1 , 1 , 1 , 1 ) is of the form
G h s a − 146 a − 5 p ( 1 , 1 , 1 , 1 ) = D P 4 × f ( 2 A 2 ) × quadric × curves, where D P 4 is a degree 4 del Pezzo surface.

miRNAs and Disease

As we announced earlier (see also [19]), a potential disease is associated with f p groups which fail to satisfy at least one of three requirements (1) the card seq of f p should be that of a free group F r , (2) the generating sequence should be aperiodic, (3) the S L 2 ( C ) character variety of f p should have a Groebner basis devoid of isolated singularities (even though the f p group may have the card seq of a free group ([19] Figure 6)).
Following this criteria, the sequence hsa-mir-122-5p is healthy while the sequences hsa-mir-503-5p and hsa-mir-146a-5p are not since the criterion (3) is not satisfied. Additional examples can be found in ([19] Table 3).
Besides isolated singularities, the Groebner basis may contain singular surfaces that are not simply singular. The D P 4 surface in G h s a − 146 a − 5 p ( 1 , 1 , 1 , 1 ) is an example of a singular surface. Further mathematical techniques are required to investigate these surfaces [44]. However, we will not discuss these methods in this paper.

4. Discussion

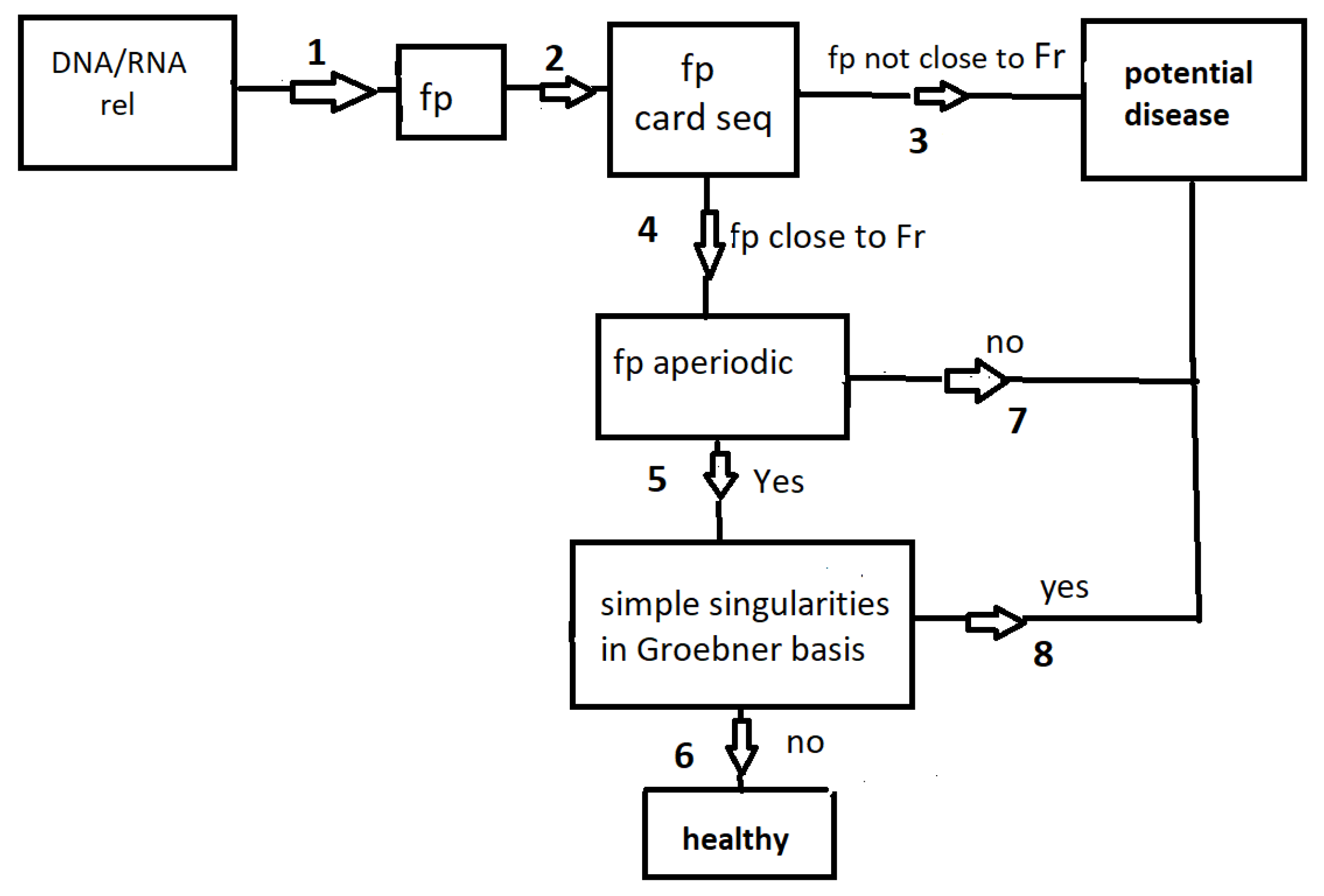
In this section, we summarize our paper by referring to the diagram in Figure 2. Given a short DNA/RNA sequence, rel, which represents a consensus sequence in a transcription factor, the seed of a miRNA, or a relevant sequence in mRNA recognition and processing, we construct a finitely generated group, f p . The architecture of subgroups, card seq, within this group is computed (see Section 2.1). If the f p card seq matches that of the free group F r (of rank r equal to nt-1), we proceed to path 4; otherwise, a potential disease could be in sight (path 3). After reaching path 4, the next step involves checking the aperiodicity of rel and the corresponding f p group, as described in Section 2.2. The final step is to examine the presence (or absence) of isolated singularities in the Groebner basis G for the S L 2 ( C ) character variety associated with f p , as outlined in Section 2.4. For a healthy sequence, the path concludes at 6, while a potential disease may be indicated if the path ends at 3, 7 or 8.
In Table 1, we provide several examples of paths. All three checks can be performed, even if paths 4 or 5 are not followed. For instance, the termination { 7 , 8 } signifies that the sequence fails both in being aperiodic and in being devoid of simple singularities.
For sequences with 4 distinct nucleotides (like the sequence of transcription factor FOX or the Kozak sequence rel4), it is difficult to conclude about the risk of a disease. The generic Groebner basis G (x,y,z) always contains surfaces with isolated singularities such as S ( 4 A 1 ) and S ( 3 A 1 ) and there are four copies of them. The termination { 6 , 8 } applies for this case.

Algebraic Geometry of m 6 A Modifications

As mentioned in the introduction, a subfield of epigenetics deals about post-transcriptional mRNA modifications. N 6 -methyladenosine ( m 6 A ) is the most frequent modification in most eukaryotes. But m 6 A is also present in bacteria with the consensus motif G C C A G [48,49]. An interesting aspect is that the mRNA m 6 A motif in bacteria is distinct from the consensus motif in eukaryotes (RRACH). This features the evolutionary machinery present in the last eukaryotic common ancestor (LECA) compared to the last universal common ancestor (LUCA) ([50] Fig. 2).
In Table 2, we provide details about the group generated by these sequences, when the sequence is aperiodic and/or has a Groebner basis of its character variety containing an isolated singularity. As in Table 1, the path in the diagram of Figure 2 is shown.
We clearly read that only the bacterial sequence leads to a path terminating at the edge 6 of the diagram of Figure 2. In the closest eukaryotic sequence GGACA (from the viewpoint of group analysis), isolated singularities are found, such as the degree 3 Del Pezzo surface S ( A 2 A 2 ) = y 3 − 2 x z − 4 y . The other sequences are not aperiodic. On the biological point of view, it is known that an appropriate level of m 6 A methylation is beneficial but it may be a risk to drive it in an artificial way because it may destroy the delicate balance of regulations performed within the messenger RNA.
Our approach is quite comprehensive and can be applied in numerous contexts beyond those we have considered thus far. It has the potential to impact the search for underlying causes of diseases and aid in the discovery of therapeutic strategies. The e-code, the processes that reveal and execute gene expression, has a sophisticated structure, which our mathematical approach aims to elucidate.

Author Contributions

Conceptualization, M.P., F.F. and K.I.; methodology, M.P., D.C. and R.A.; software, M.P.; validation, R.A., F.F., D.C. and M. M.A..; formal analysis, M.P. and M. M.A.; investigation, M.P., D.C., F.F. and M. M.A.; writing–original draft preparation, M.P.; writing–review and editing, M.P.; visualization, F.F. and R.A.; supervision, M.P. and K.I.; project administration, K.I..; funding acquisition, K.I. All authors have read and agreed to the published version of the manuscript.

Funding

Funding was obtained from Quantum Gravity Research in Los Angeles, CA.

Data Availability Statement

Computational data are available from the authors.

Acknowledgments

The first author would like to acknowledge the contribution of the COST Action CA21169, supported by COST (European Cooperation in Science and Technology).‌

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gu, C.; Kim G., B.; Kim, W. J.; Kim, H. U.; Lee, S. Y. Current status and applications of genome-scale metabolic models. Genome Biology 2019, 20, 121. [Google Scholar] [CrossRef]
  2. Romão, L. mRNA metabolism in health and disease. Biomedicines 2022, 10, 2262. [Google Scholar] [CrossRef] [PubMed]
  3. Peedicayil, J. Genome–environment interactions and psychiatric disorders. Biomedicines 2023, 11, 1209. [Google Scholar] [CrossRef] [PubMed]
  4. Scharf, S.; Ackerman, J.; Bender, L.; Wurzel, P.; Schäfer, H.; Hansmann, M. L.; Koch, I. Holistic view on the structure of immune response: Petri net model. Biomedicines 2023, 11, 452. [Google Scholar] [CrossRef] [PubMed]
  5. Marques, A. R.; Santos, J. X.; Martiniano, H.; Vilela, J.; Rasga, C.; Romão, L.; Vicente, A. M. Gene variants involved in nonsense-mediated mRNA decay suggest a role in autism spectrum disorder. Biomedicines 2022, 10, 665. [Google Scholar] [CrossRef] [PubMed]
  6. Wan, Y. C.E. Histone H2B Mutations in Cancer. Biomedicines 2021, 9, 694. [Google Scholar] [CrossRef] [PubMed]
  7. Fimmel, E.; Giannerini, S.; Gonzalez, D. L.; Strüngmann. Circular codes, symmetries and transformations. J. Math. Biol. 2014, 70, 1623–16434. [Google Scholar] [CrossRef] [PubMed]
  8. Planat, M.; Aschheim, R; Amaral, M. M.; Fang, F; Irwin, K. Complete quantum information in the DNA genetic code. Symmetry 2020, 12, 1993. [CrossRef]
  9. Sanchez, R.; Barreto, J. Genomic abelian finite groups. Available online. [CrossRef]
  10. Frappat, L.; Sciarrino, A.; Sorba; P. Crystalizing the Genetic Code. J. Biol. Phys. 2001, 27, 1–34. [Google Scholar] [CrossRef]
  11. Planat, M.; Chester,D.; Aschheim, R; Amaral, M. M.; Fang, F; Irwin, K. Finite groups for the Kummer surface: the genetic code and quantum gravity. Quantum Rep 2021, 3, 68–79. [CrossRef]
  12. Planat, M.; Aschheim, R; Amaral, M. M.; Fang, F; Irwin, K. Quantum information in the protein codes, 3-manifolds and the Kummer surface. Symmetry 2021, 13, 1146. [CrossRef]
  13. Sanchez, R.; Mackenzie, S. A. On the thermodynamics of DNA methylation process. Scient. Rep. 2023, 13, 8914. [Google Scholar] [CrossRef]
  14. Bessonov, N.; Butuzova, O.; Minarsky, A.; Penner, R.; Soulé, C; Tosenberger, A.; Morozova, D. Morphogenesis software based on epigenetic code concept. Comp. Struct. Biotech. J. 2019, 17, 1203–1216. [Google Scholar] [CrossRef]
  15. Vissers, C.; Sinha, A.; Ming, G. l.; Song, H. The epitranscriptome in stem cell biology and neural development. Neurobiol. Dis 2020, 146, 105139. [Google Scholar] [CrossRef]
  16. Wang, S.; Lv, Wei, Lv.; Li, T.; Zhang ,S.; Wang, H.; Li, X.; Wang, L.; Ma, D.; Zang, Y.; Shen, J. Xu, Y.; Weii W. Dynamic regulation and functions of mRNA m6A modification. Cancer Cell Int. 2022, 22, 48.
  17. Widagdo, J.; Wong, J. J.L.; Anggono, V. The m6A-epitranscriptome in brain platicity, learning and memory. Seminars In Cell and Devt Biol. 2022, 125, 110–121. [Google Scholar] [CrossRef]
  18. Planat, M.; Amaral, M. M; Fang, F.; Chester, D.; Aschheim, R.; Irwin, K. Character varieties and algebraic surfaces for the topology of quantum computing. Symmetry 2022, 14, 915. [Google Scholar] [CrossRef]
  19. Planat, M.; Amaral, M. M; Irwin, K. Algebraic morphology of DNA–RNA transcription and regulation. Symmetry 2023, 15, 770. [CrossRef]
  20. Schrödinger, E. What Is Life? The Physical Aspect of the Living Cell; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
  21. Planat, M.; Amaral, M. M; Fang, F.; Chester,D.; Aschheim R.; Irwin, K. DNA sequence and structure under the prism of group theory and algebraic surfaces. Int. J. Mol. Sci. 2022, 3, 13290.
  22. Grothendieck, A. Esquisse d’un programme 1984, in Geometric Galois Actions I: Around Grothendieck’s Esquisse D’un Programme, London Mathematical Society Lecture Note Series, vol. 242, Cambridge University Press Schneps and Lochak 1997, pp. 243-283. Avalaible online: http://matematicas.unex.es/∼ navarro/res/esquisseeng.pdf.
  23. TATA Box: Available online:. Available online: https://en.wikipedia.org/wiki/TATA_box (accessed on 1 September 2021).
  24. Polyadenylation: Available online:. Available online: https://en.wikipedia.org/wiki/Polyadenylation (accessed on 1 May 2023).
  25. Planat, M.; Amaral, M. M; Fang, F.; Chester,D.; Aschheim R.; Irwin, K. Group theory of syntactical freedom in DNA transcription and genome decoding. Curr. Issues Mol. Biol. 2022, 44, 1417–1433. [Google Scholar] [CrossRef] [PubMed]
  26. Goldman, W.M. Trace coordinates on Fricke spaces of some simple hyperbolic surfaces. Eur. Math. Soc. 2009, 13, 611–684. [Google Scholar]
  27. Ashley, C.; Burelle, J.P.; Lawton, S. Rank 1 character varieties of finitely presented groups. Geom. Dedicata 2018, 192, 1–19. [Google Scholar] [CrossRef]
  28. Jacob, W. F. Jacob, Santer, M., Dahlberg, A. E. A single-base change in the Shine-Dalgarno region of 16 rRNA of Escherichia colo affects translation of many proteins. Proc. Natl. Acad. Sci. USA 1987, 84, 4257–4761. [Google Scholar] [CrossRef]
  29. Kozak, M. The scanning model for translation: an update. J. Cell Biology 1989, 108, 229–241. [Google Scholar] [CrossRef] [PubMed]
  30. Kozak consensus sequence: Available online:. Available online: https://en.wikipedia.org/wiki/Kozak_consensus_sequence (accessed on 1 January 2023).
  31. Rittaud, B. On the average groth of random Fibonacci sequences. J. Int. Seq. 2007, 10. [Google Scholar]
  32. microRNA. Available online: https://en.wikipedia.org/wiki/MicroRNA (accessed on 1 September 2022).
  33. Fang, Y.; Pan, X.; Shen, H. B. Recent deep learning methodology development for RNA–RNA interaction prediction. Symmetry 2022, 14, 1302. [Google Scholar] [CrossRef]
  34. Medley, C. M.; Panzade, G.; Zinovyeva, A. Y. MicroRNA strand selection,: unwinding the rules. WIREs RNA 2021, 12, e1627. [Google Scholar] [CrossRef] [PubMed]
  35. Dawson, O.; Piccinini, A. M. miR-155-3p: processing by-product or rising star in immunity and cancer? Open Biol. 2022, 12, 220070. [Google Scholar] [CrossRef] [PubMed]
  36. Kozomara, A.; Birgaonu, M.; Griffiths-Jones, S. miRBase: from microRNA sequences to function. Nucl. Acids Res. 2019, 47, D155–D162. [Google Scholar] [CrossRef]
  37. miRBase: the microRNA database. Available online: https://www.mirbase.org/ (accessed on 1 November 2022).
  38. Fromm, B.; Billipp, T.; Peck. L. E.; Johansen, M.; Tarver, J. E.; King, B. L.; Newcomb, J. M.; Sempere, L. F.; Flatmark, K.; Hovig, E.; Peterson, K. J. A uniform system for the annotation of human microRNA genes and the evolution of the human microRNAome. Annu. Rev. Genet. 2015, 23, 213–242.
  39. Ludwig, N.; Leidinger, P.; Becker, K.; Backes, C. Fehlmann, T.; Palleasch, C.; Rheinheimer, S.; Meder, B.; Stähler, C.; Meese, E.; Keller, A. Distribution of miRNA expression across human tissues. Nucl. Acids Res. 2016, 44, 3865–3877. [Google Scholar] [CrossRef]
  40. Girard, M.; Jacquemin, E.; Munnich, A.; Lyonnet, S.; Henrion-Caude, A. miR-122, a paradigm for the role of microRNAs in the liver. J. Hepatology 2008, 48, 648–656. [Google Scholar] [CrossRef]
  41. Hu, J.; Xu, Y.; Hao, J. Wang, S.; Li, C.; Meng S. MiR-122 in hepatic function and liver diseases. Protein & Cell 2012, 3, 364–371. [Google Scholar]
  42. He, Y.; Cai, Y.; Paii, P. M.; Ren, X.; Xia, Z. The Causes and Consequences of miR-503 Dysregulation and Its Impact on Cardiovascular Disease and Cancer. Front. Pharmacol. 2021, 12, 629611. [Google Scholar] [CrossRef]
  43. Planat, M.; Chester, D.; Amaral, M.; Irwin, K. Fricke topological qubits. Quant. Rep. 2022, 4, 523–532. [Google Scholar] [CrossRef]
  44. Planat, M.; Amaral, M. M.; Chester, D.; Irwin, K. SL(2,C) scheme processsing of singularities in quantum computing and genetics. Axioms 2023, 12, 233. [Google Scholar] [CrossRef]
  45. Mir-132. Available online: https://fr.wikipedia.org/wiki/Micro-ARN_7 (accessed on 1 June 2023).
  46. Sonkoly, E.; Stahle, M. Pivarsci, A. MicroRNAs and immunity: novel players in the regulation of normal immune function and inflammation. Sem. in Cancer Biol. 2008, 18, 131–140. [Google Scholar] [CrossRef] [PubMed]
  47. Micro-ARN 7. Available online: https://en.wikipedia.org/wiki/MiR-132 (accessed on 1 June 2023).
  48. Deng, X.; Chen, K.; Luo, G. Z.; Weng, X.; Ji, Q.; Zhou, T. He, C. Widespread occurrence of N6-methyladenosine in bacterial mRNA. Nucl. Acids Res. 2015, 43, 6557–6567. [Google Scholar] [CrossRef]
  49. Gao, R.; Shi, H.; Zhang, Y.; Shao, X.; Deng, X. N6-methyladenosine modification in bacterial mRNA. Clin. Microbiol. 2016, 5, 1000256. [Google Scholar] [CrossRef]
  50. Liu, C.; Cao, J.; Zhang, H.; Yin, J. Evolutionary history of RNA modifications at N6-adenosine originating from the R-M System in eukaryotes and prokaryotes. Biology 2022, 11, 214. [Google Scholar] [CrossRef]
Preprints 88245 g001
Figure 1. Up: The degree 2 Del Pezzo surface within G T A T A . Down: The degree 3 Del Pezzo surface S ( A 1 ) within G r e l 1 .
Figure 1. Up: The degree 2 Del Pezzo surface within G T A T A . Down: The degree 3 Del Pezzo surface S ( A 1 ) within G r e l 1 .
Preprints 88245 g001
Preprints 88245 g002
Figure 2. A diagram illustrating the main results discussed in the text. For example, for the transcription factor of the gene EGR1, rel=GCGTGGGCG ([25] Section 4.1.2), the path is 1 → 2 → 4 → 5 → 6 showing no risk of disease. But for the transcription factor of gene DBX (see Section 2.2 and Section 2.4), rel= TTTATTA, the path is 1 → 2 → 4 → 5 → 8 meaning a potential disease (see Table 1).
Figure 2. A diagram illustrating the main results discussed in the text. For example, for the transcription factor of the gene EGR1, rel=GCGTGGGCG ([25] Section 4.1.2), the path is 1 → 2 → 4 → 5 → 6 showing no risk of disease. But for the transcription factor of gene DBX (see Section 2.2 and Section 2.4), rel= TTTATTA, the path is 1 → 2 → 4 → 5 → 8 meaning a potential disease (see Table 1).
Preprints 88245 g002
Table 1. A few possible paths in the diagram of Figure 2 terminating at 6 (healthy) or (3)-(7)-(8) (potential disease). The set { 6 , 8 } denotes a lack of a clear conclusion about the existence of an isolated singularity. The selected examples are taken in three parts that are transcription factors (group 1), regulating elements in introns (group 2) and miRNAs (group 3). Details are given in the text. Otherwise a reference is provided.
Table 1. A few possible paths in the diagram of Figure 2 terminating at 6 (healthy) or (3)-(7)-(8) (potential disease). The set { 6 , 8 } denotes a lack of a clear conclusion about the existence of an isolated singularity. The selected examples are taken in three parts that are transcription factors (group 1), regulating elements in introns (group 2) and miRNAs (group 3). Details are given in the text. Otherwise a reference is provided.
Sequence rel path
EGR1 [25] GCGTGGGCG 1 → 2 → 4 → 5 → 6
FOS [25] TGAGTCA 1 → 2 → 4 → 5 → { 6 , 8 }
Nanog [25] TAATGG 1 → 2 → 4 → { 7 , 8 }
DBX TTTATTA 1 → 2 → 4 → 5 → 8
TATA TATAAAA 1 → 2 → 3 → ( 7 , 8 )
poly(A) (rel1) AAUAAA 1 → 2 → 4 → { 7 , 8 }
poly(A) (rel2) UGUAA 1 → 2 → 4 → { 7 , 8 }
Shine-Dalgarno (rel3) AGGAGGU 1 → 2 → 4 → 5 → 8
Kozak (rel4) ACCAUGGC 1 → 2 → 4 → 5 → { 6 , 8 }
Kozak (rel4’) CCCAUGGC 1 → 2 → 4 → 7
hsa-mir-122-5p [41] (seed0) GGAGUGU 1 → 2 → 4 → 5 → 6
hsa-mir-132-5p [45] CCGUGGC 1 → 2 → 4 → 5 → 6
hsa-mir-503-5p (seed1) [42] AGCAGCGG 1 → 2 → 5 → 8
hsa-mir-146a-5p (seed2) [46] GAGAAC 1 → 2 → { 7 , 8 }
hsa-mir-7-5p [47] GGAAGA 1 → 2 → { 3 , 7 , 8 }
hsa-mir-7-5p GGAAGAC 1 → 2 → 4 → 5 → 6
hsa-mir-7-3p AACAAAU 1 → 2 → 4 → 7
hsa-mir-155-3p [35,46] UCCUAC 1 → 2 → 4 → { 7 , 8 }
hsa-mir-155-3p UCCUACA 1 → 2 → 3
Table 2. A detailed group theoretical analysis of m 6 A modifications for bacteria (the sequence GCCAG) and eukaryotes (sequence R R A ̲ C H ( R = A or G, H = A , U or C) ). Column 2 is the group closer to the f p group generated by the sequence in column 1 ( F r is for the free group of rank r, H 3 is for the modular group P S L ( 2 , Z ) . If the sequence is aperiodic, the Perron-Frobenius eigenvalue λ P F is given in column 3. The type of isolated singularity, if any, is in column 4. The path in the diagram of Figure 2 is shown in column 5.
Table 2. A detailed group theoretical analysis of m 6 A modifications for bacteria (the sequence GCCAG) and eukaryotes (sequence R R A ̲ C H ( R = A or G, H = A , U or C) ). Column 2 is the group closer to the f p group generated by the sequence in column 1 ( F r is for the free group of rank r, H 3 is for the modular group P S L ( 2 , Z ) . If the sequence is aperiodic, the Perron-Frobenius eigenvalue λ P F is given in column 3. The type of isolated singularity, if any, is in column 4. The path in the diagram of Figure 2 is shown in column 5.
Sequence group aperiodic Groebner basis path
bacterial
GCCAG F 2 1.83928 no 1 → 2 → 4 → 5 → 6
eukaryote
AAACA F 1 no S ( A 2 ) , S ( A 1 A 2 ) 1 → 2 → 4 → { 7 , 8 }
AAACC H 3 no no 1 → 2 → { 3 , 7 }
AAACU F 2 no no 1 → 2 → 4 → 7
GGACA F 2 1.83928 S ( A 2 ) , S ( A 2 A 2 ) 1 → 2 → 4 → 5 → 8
GGACC F 2 no no 1 → 2 → 4 → 7
GGACU F 3 no unknown 1 → 2 → 4 → 7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated