Prerpints.org logo
Preprint
Article

A Novel Approach-Based Sparsity for Damage Localization in Functionally Graded Material

Altmetrics

Downloads

105

Views

60

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 July 2023

Posted:

04 July 2023

You are already at the latest version

Alerts
Abstract
Model-based approaches form the basis of the majority of damage detection and localization studies; however, built-in online detection technique can offer an alternative for future structural health monitoring technologies. Thus, in this paper, we present a dynamic localization algorithm for damage localization in functionally graded plates. The method depends on the creation of a grid matrix that contains the dynamic response of the structure over time. Subsequently, an optimization process is carried out via a linear equation representing the information contained within the grid to achieve accurate localization of damage. Due to the inherent sparsity of the localization nature, the FISTA algorithm has been employed as a problem solver. The approach is tested in the case of the functionally graded plate under clamped free boundary conditions. Several, damage scenarios were investigated for the case of damage signals on and off the grid. The results show that the proposed approach is capable of accurately predicting damage position and can be suitable for use in low size data systems.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Composite materials are widely employed in various civil and mechanical engineering fields such as building construction and infrastructure rehabilitation, mainly due to their exceptional properties including lightweight, high strength, high modulus, high fatigue resistance, and corrosion. However, composites are more easily damaged, and delaminate under excessive inter-laminar stresses, additionally, they cannot tolerate high temperatures. As a class of composite materials, functionally graded material (FGM) overcome the limitations of traditional composites by comprising two or more materials with gradual variation from surface to surface. The conventional FGMs are formed from metal and ceramic and the material properties of FGMs are a mixture of well thermal resistance of ceramic [1], high strength and superior fracture toughness of metal [2]. Numerous investigations have been conducted by researchers to elucidate the mechanical characteristics of functionally graded materials (FGMs). However, it is noteworthy that a substantial portion of the existing literature predominantly focuses on the examination of unidirectional FGMs, wherein the material properties exhibit a discernible variation along a single direction, specifically spanning from the top to the bottom surface [3,4,5,6,7]. However, it is imperative to address the exposure of advanced living structures to external loads in multiple directions. To meet this requirement, the development of multi-directional Functionally Graded Materials (FGMs) becomes crucial. These FGMs exhibit varying material properties along different directions, including the thickness and in-plane directions.
FGM-based structures, like other types of structures, are exposed to various loads during operation that can result in different types of damage. Failing to spot and localize these damages can eventually lead to a catastrophic failure with feline consequences. Therefore, it is imperative to identify and detect any potential damages in FGM structures. Damage detection plays a vital role in guaranteeing the safety and dependability of structures, particularly in scenarios where failure could lead to severe consequences. Nonetheless, the existence of graded disparities in material properties within FGM structures can present challenges in the detection and characterization of damage. Numerous techniques have been developed to address the issue of damage detection in FGM structures. One approach is to use non-destructive testing (NDT) methods such as ultrasonic testing [8,9,10], eddy current tomography [11,12,13,14,15], and X-ray computed tomography (CT) [16]. These methods can detect damage by analyzing changes in the properties of the material, such as changes in acoustic properties or changes in magnetic fields.
An alternative methodology involves the implementation of sensor-based structural health monitoring (SHM) systems to detect alterations in the structural response of the functionally graded material (FGM) structure. These SHM systems commonly rely on a network of sensors, including accelerometers, strain gauges, and temperature sensors, to continuously monitor the dynamic behaviour of the structure in real-time [17,18,19,20,21,22,23]. The detection of structural damage can be inferred from alterations in the response of the system. Moreover, analytical and numerical modelling methodologies can be employed to forecast the behaviour of functionally graded material (FGM) structures under various loading scenarios and to simulate the progression of damage. Such models are instrumental in identifying vulnerable regions within the structure that are susceptible to damage, consequently aiding in the formulation of strategies for damage mitigation. The detection of damage in FGM structures represents a multifaceted challenge necessitating a multidisciplinary approach incorporating non-destructive testing (NDT), structural health monitoring (SHM), and analytical and numerical modelling techniques.
There are several algorithms available for damage detection in structures. The most investigated methods in the literature are the modal-based algorithms [24], which involve measuring changes in modal parameters such as natural frequencies, mode shape curvature [25], structure damping [23], and strain energy [26] to identify damage in the FGM structure. The efficacy of this particular approach in detecting damage in Functionally Graded Materials (FGMs) has been well-established; however, it is worth noting that its performance may be influenced by the presence of noise in the measured response. An alternative technique considered for damage detection in FGMs is the Frequency Response Function (FRF) method [27], which includes analyzing the curvature of the FRF to identify changes in the dynamic properties of the structure. The FRF technique can be further refined using the Modal Assurance Criterion (MAC) in the frequency domain [28], in which quantitative measures of mode shape similarity can be utilized to ascertain the location of the damages. Additionally, employing the coupling response measurement technique enables the determination of damage location and extent through the analysis of output responses of a structure under diverse loading conditions [29]. This methodology holds significant potential for the detection of damage in intricate FGM structures, surpassing the capabilities of conventional techniques. Each of these methods possesses inherent advantages and limitations, and the selection of an appropriate approach is contingent upon multiple considerations, including the nature and magnitude of the damage, the material properties inherent to the FGM structure, and the accessibility of relevant data. Thorough evaluation and comparison of diverse approaches are imperative to ascertain their efficacy and appropriateness within a specific application.
The use of Artificial Neural Networks (ANNs) for detecting damage in FGM structures has gained popularity and is being extensively studied. ANNs work by collecting data from the structure and constructing a mathematical model that can predict the presence and location of damage [18,30,31,32,33]. The acquisition of data for training ANNs commonly involves visual inspections or vibration tests. ANNs offer the advantage of obviating the requirement for high-fidelity system models. Nonetheless, ANNs necessitate substantial quantities of training data and may lack adequate reliability in the absence of appropriate training. To address this concern, this research paper introduces an innovative methodology founded on the dynamic response exhibited by the impaired structure. The suggested approach uses a matrix grid to store the signal response of an FGM plate for every damage, and by using a sparse algorithm, the position of the damage can be identified. The Finite Element Method (FEM) is considered to analyze the accuracy and reliability of the proposed procedure in localizing damage when the damage is on-the-grid and off the grid.
The present research paper is organized as follows: Section 1 presents the mathematical formulation of the structure being investigated. The subsequent section, namely section 2, presents the outcomes and results derived from the approach employed in this study. Finally, concluding remarks are provided to summarize the findings.

2. Materials and Methods

2.1. FGM Constitutive Equations

Let’s consider an FGM material made of two separate isotropic material based, which are in our case, a ceramic and a metal. The effective material properties of the FGM are mainly estimated using the well-known rule of mixture (ROM) which describes the effective property P as the sum of the ratio of each constituent as below [33]:
P = P m   V m + P c   V c
where V is the volume fraction. c and m are indexes that respectively represent the metal and ceramic parts. In the present work, we presume that the metal material varies through the thickness of the structure following the power law formula as below:
Vc =〖(1/2+z/h)〗^k,
Vm=1-Vc
where h is the thickness of the structure, and k is the power law index, which governs the volume fraction outline through the thickness. It is worth to be mentioned that the variation of the material is proceeding symmetrically to the mid surface which means that the material on the bottom surface (z=-h/2) is pure metal and at the top surface (z=h/2) is entirely ceramic.

2.2. Equation of Motion

The FE equations of the FGM plate can be described in terms of nodal displacement {U}, while each node includes its corresponding degree of freedom. Thus, the equation of motion in a global system coordinate is assembled ad presented as follows:
M u u U ¨ + C u u U ˙ + K u u U = F
where K u u is the stiffness matrix, M u u is the mass matrix, C u u is the damping matrix, and {F} is the structural loads.
The Newmark beta schema is used to solve Equation (3). The schema is adopted for the required time Domaine. The displacement, velocity and acceleration are calculated using the following integration formula
U t + δ t = U t +   δ t U ˙ t + ( δ t 2 / 2 ) ( 1 − 2 β ) U ¨ t + ( δ t 2 / 2 ) β U ¨ t + δ t                                                                 U ˙ t + δ t = U ˙ t + δ t 1 − γ U ¨ t + δ t γ U ¨ t + δ t                                                                                                               U ¨ t + 1 = M − 1 ( F t + δ t − C U ˙ t + δ t − K U ¨ t + δ t                                                                                                
γ and β are Newmark beta integration parameters that are given below:
β = 1 4 1 − γ 2 γ = 1 2 − α                
where α is a parameter that controls the numerical dissipation of the method.

2.3. Finite Element Model

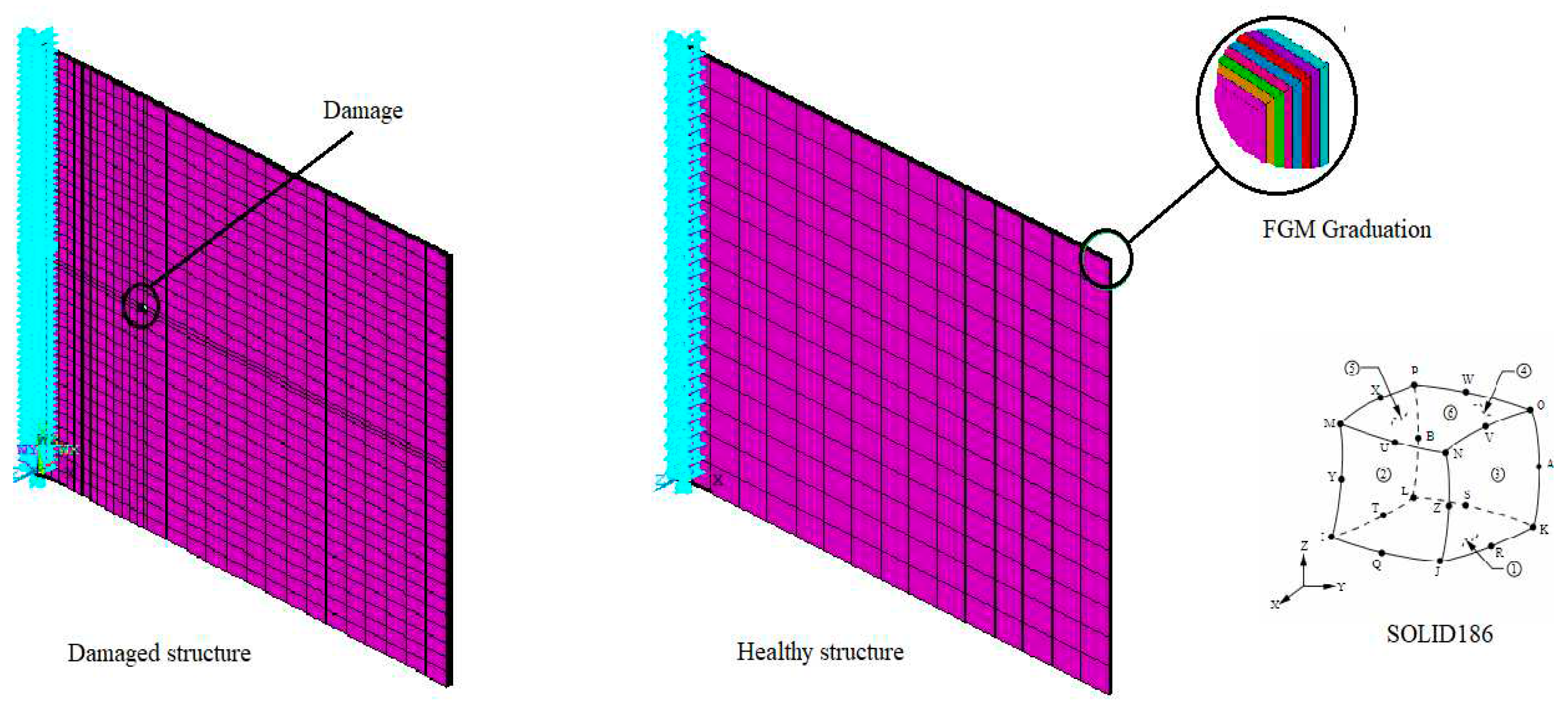
This section presents a comprehensive account of the implementation of the finite element model. The Ansys APDL package is utilized for modelling and conducting the analysis. The modelling approach incorporates a series of macro files specifically tailored for each procedural step. A macro file, in this context, is defined as a function encompassing a custom-designed command written in APDL. The modelling process encompasses various stages such as geometry implementation, material assignment, meshing, load application, boundary condition specification, and ultimately, the analysis. The specific focus of this study revolves around a plate composed of Functionally Graded Material (FGM).
The modelling approach commences with the utilization of the block command to generate a three-dimensional (3D) model of the plate structure. Subsequently, the damage geometry is introduced by subtracting it from the primary BLOCK using the Boolean command VSBV. For meshing purposes, the SOLID186 element, a 3D solid element, is employed. This element comprises 20 nodes, each possessing three translation degrees of freedom, and supports various analysis types. To ensure greater control over the mesh size and quality, the LSEL and LESIZE commands are utilized. The assignment of the Functionally Graded Material (FGM) is accomplished through a *Do loop in conjunction with a power law function (eq.1). The loop iterates through the elements in the z-direction and assigns the necessary parameters to each element, considering the element length as an argument.
The code developed for the incorporation of the FGM is presented in Algorithm 2. Of course, this approach can not insure a complete continuous distribution of the graded material but it is as far the best method to border on the real-life material distribution when an appropriate number of elements is used [34,35]. The suitable boundary conditions are allocated using NSEL and D commands.
Algorithm 1. Implementation of FGM in Ansys APDL
*Create, mat_fgm
       z_coord = arg1
      grad_common = (a_z*z_coord)**k
      E_fgm     = (E_t-E_b)*grad_common + E_b
      den_fgm    = (dens_t-dens_b)*grad_common + dens_b
*End !mat_fgm_pol
counter = 0
*Do, j, 1, ele_numb_z, 1
           z_coord = length_e_z*(j-0.5)
counter = counter + 1
           *use, mat_fgm,z_coord
           mp, ex,   counter, E_fgm
           mp, dens, counter, den_fgm
           esel, s, CENT, Z,-b/2+length_e_z*(counter-1),
          - b/2+length_e_z*counter, 1 emodif, all, mat, counter           esel, all
*Enddo 		*Create a function named mat_fgm
*Take z_coord as a variable
*Calculate the volume fraction (eq.2)
*Calculate the The effective Youngs Modulus(eq.1)
*Calculate the The effective Density(eq.1)
Start the loop through the z-direction element
Assign the variable the needed value
Use the function mat_fgm
Redefine the Youngs modulus
Redefine the density
Select the elements that receive the new properties. Modify the element material properties to calculate one
End the loop
Preprints 78346 g001
Figure 1. Finite element model.
Figure 1. Finite element model.
Preprints 78346 g001

2.4. Damage Detection Based on Sparse Regression

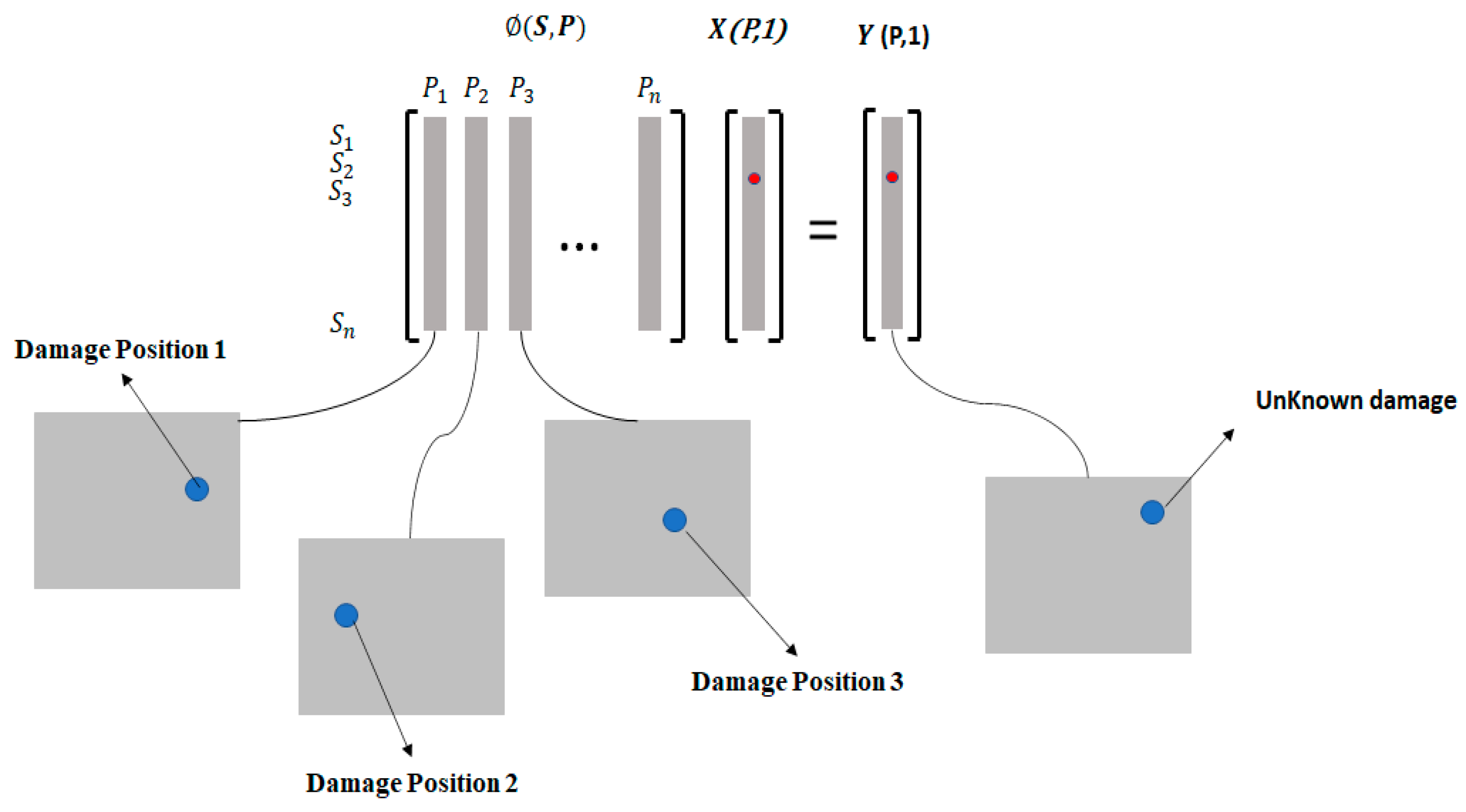
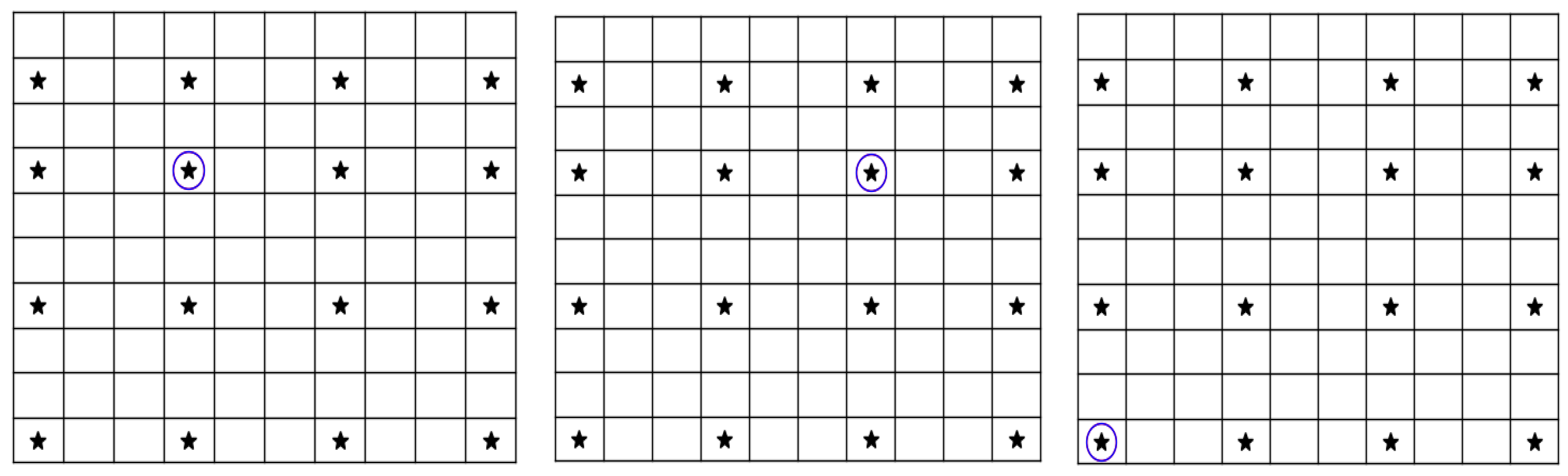
Models that are parametrically based can generally be described by a set of linear equations that define the relationship between the model inputs and outputs. Usually, such linear models are addressed using regression algorithms. A regression is said to be sparse when some components in the model are non-zero while others are explicitly set to zero. This approach enables variable selection, effectively determining which variables are included or excluded. In this study, we employ a sparsity approach to define our problem. Therefore, we capture the time history deflections of the fibre-reinforced (FG) plate for various damage locations. We subtract the retrieved signals from the undamaged deflections and then plug the results into a matrix grid. Thus, the problem is formulated as follows:
∅ X = Y
∅ ∈ R n × p is a matrix container, where each column ∅ is the normalized substruction between damage and undamaged responses for a p damage location. The raw of ∅ is the n time simples of the retrieved data which are in our case the plate deflections.
X ∈ R p × 1 is a sparse vector pointer that defines the damage locations. The element in X is taken to be zero when there is no damage and non-zero when the damage exists.
Y ∈ R n × 1 is a normalized substruction between the damaged and undamaged response vector for an unknown damage location. Figure 2 illustrates the idea.
Equation (6) can be handled as an optimization problem concerning X as follows:
a r g m i n x ∅ X − Y
In Equation (7), l 1 norm is found to be the best choice because it promotes sparsity, which fits our damage identification approach. Hence, our problem is reformulated as an optimization problem using l 1 as fellow:
a r g m i n x ∅ X − Y 2 + γ X 1
where X 1 defined as the sum of the absolute values of the X elements. γ is the regularization parameter governing the sparsity of the vector X . In the case of multiple damages. The test signal is treated as the sum of the signals acquired from the structures with different damages. As stated by [29], this assumption remains true only in the case of small damages. To solve Equation (8), we use the FISTA Algorithm proposed by [36].
Algorithm 2. Implementation of the FISTA algorithm
Set       L = 2 λ σ max ⁡ ∅ T ∅
Take   t 1 = 1 ,  k = 1 ;  ε > 0 &  y 1 = x 0 ∈ R n (i.e., x 0 is an arbitrary real-valued n-dimensional starting point)
while  x k − x k − 1 > ε do 
            z = y k − 1 L f ∇ f y k = y k − ∅ T ∅ y k m a x ⁡ ∅ T ∅  
            x k = m i n x x − u 2 + L f 2 x − z 2 = L f z + 2 u 2 + L f   t k + 1 = 1 + 1 + 4 t k 2 2
            y k + 1 = x k + t k − 1 t k + 1 x k + x k − 1  
            k = k + 1
End while

3. Results

3.1. Validation

To validate the present model, two sets of analyses are performed. The material properties used in the analysis are presented in Table 2. The model implementation follows the same procedure described in Subsection 2.3. It is worth mentioning that a sensitivity analysis is performed for each analysis, and a total of 1800 elements are used.
In the first analysis, we consider a square FGM plate made of Al/ZrO2-1 with a dimension of 0.4 × 0.4 × 0.5 mm following Clamped Free Free Free boundary conditions. The plate is subjected to modal analysis and the first six frequencies are extracted and compared with those presented by [36]. The results are shown in Table 3. It can be seen that the predictions are in good agreement with those found in [36]. In the second validation process, an Al/ZrO2-2 fully clamped FGM plate is considered. The plate is subjected to a uniform pressure loading p 0 . The nondimensional central deflection is retrieved for two sets of length-to-thickness ratios and three values of k index. The results are presented in Table 4 and compared with those presented by [37,38]. It is observed that the results are in close agreement, which proves the accuracy of the present model.

3.2. Damage Detection

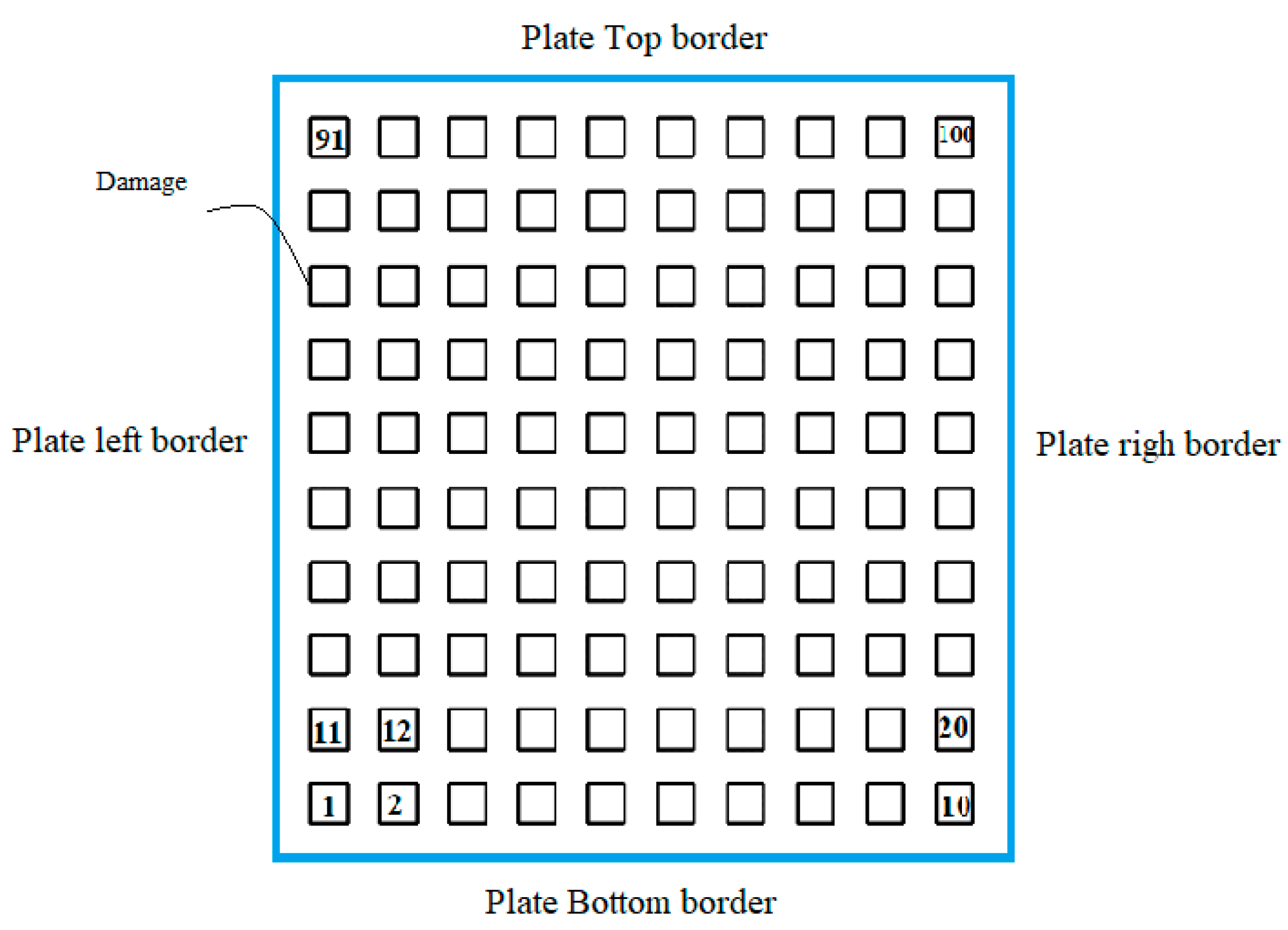
In the present section, we examine the proposed damage identification schema. Hence, a plate as a structure involving FGM materials was used as a use case. A through-all damage having a length of 2   m m is incorporated in the plate to represent the damage. The location of the damage is repeatedly changed 100 times. Thought, The damage was uniformly distributed across the plate and labelled as shown in Figure 3. This numbering procedure avoids the use of floating values for the location in the x and y direction, which helps simplify the problem.

3.2.1. Case Study

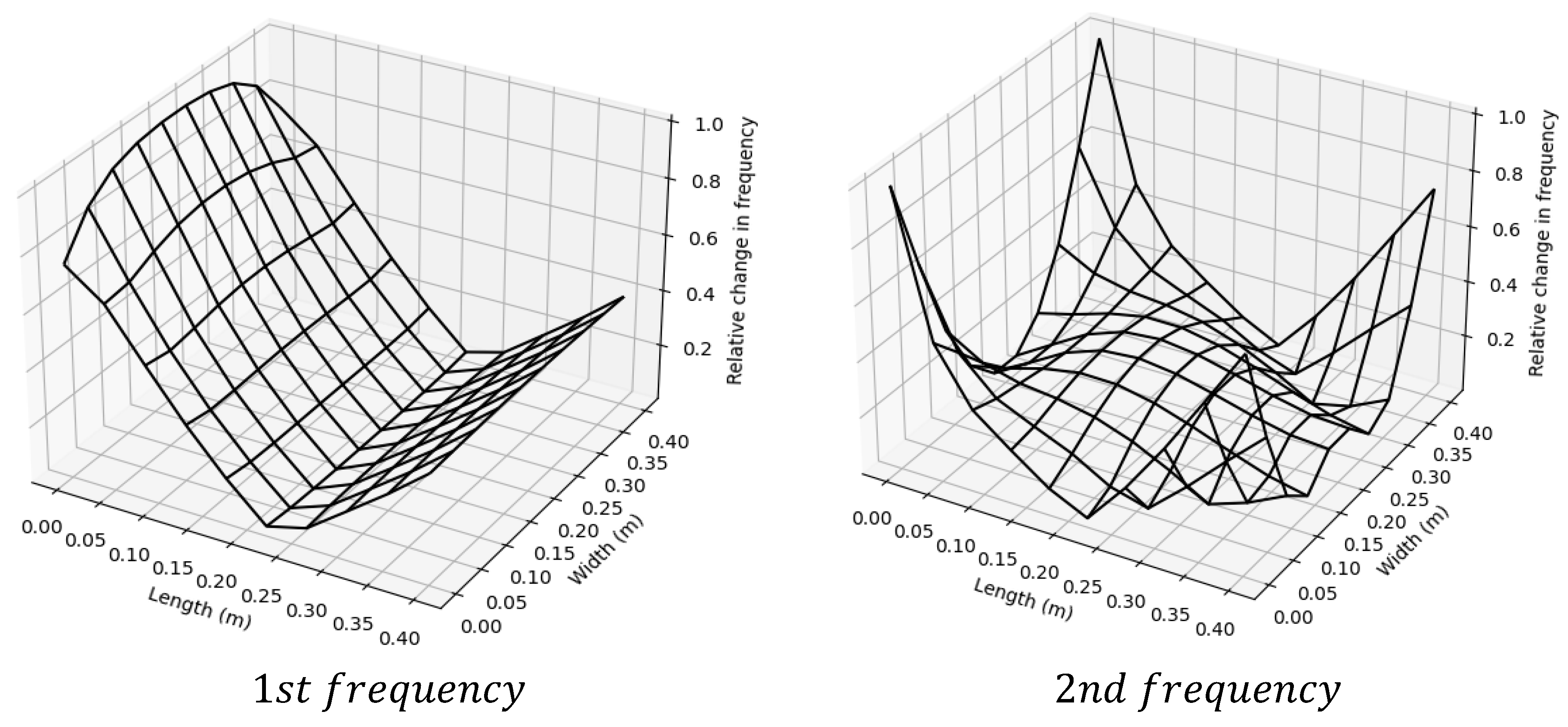
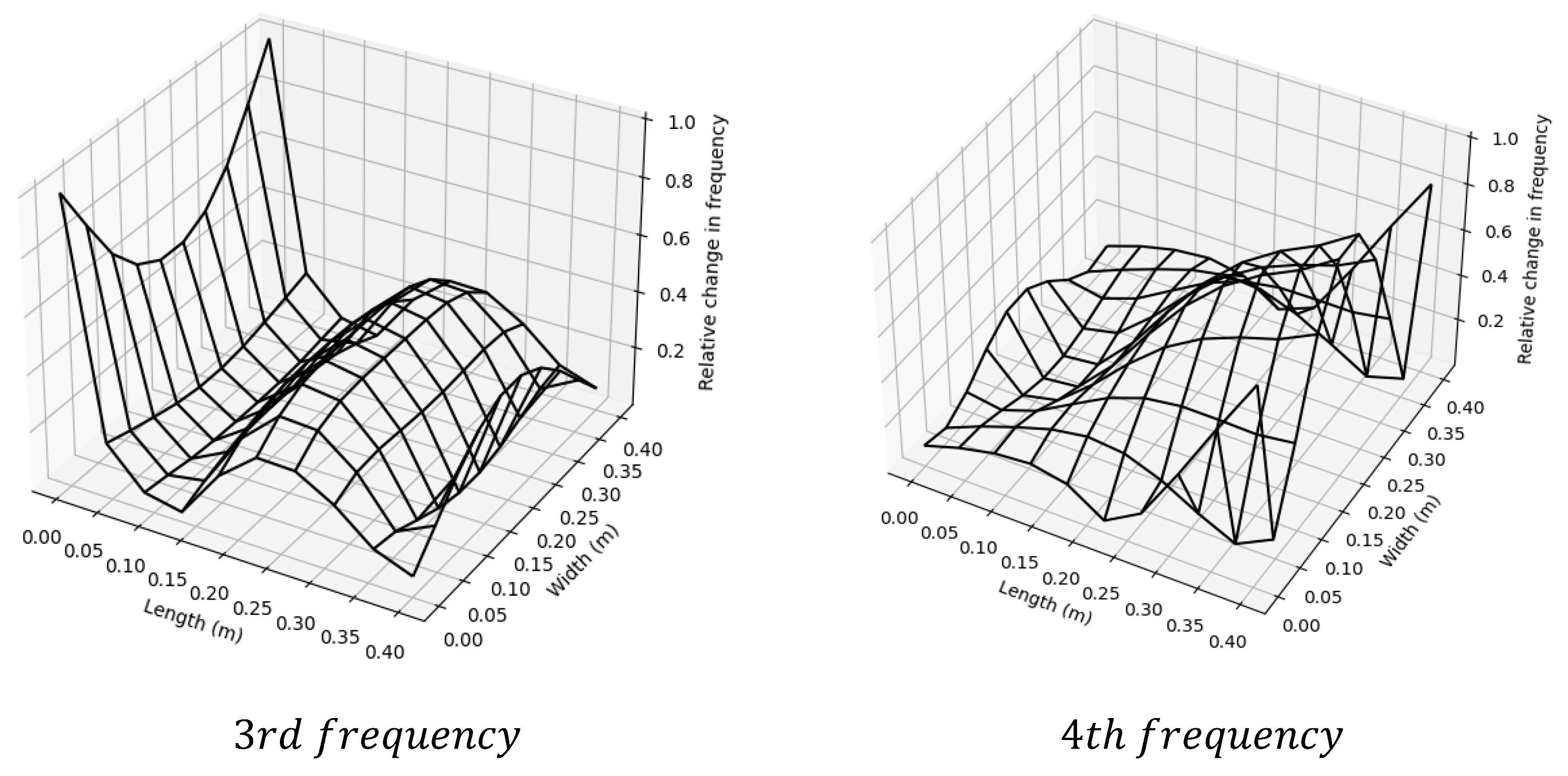
An FGM Al/ZrO2-1 square plate having a length of 0.4   m and thickness of 0.5   m m is implemented using APDL following the modelling procedure presented in subsection 2.3. A modal analysis was performed and the first six frequencies were extracted. Three power law indexes k = 0.5,1 , 2 were investigated. The relative change in frequencies for each damage position is depicted in Figure 4. For the case of brevity, only the first four frequencies with k = 1 are presented. It can be seen that the structure is sensitive to the damaged position while the change can be significant when it is located out of the mode shape neural line.
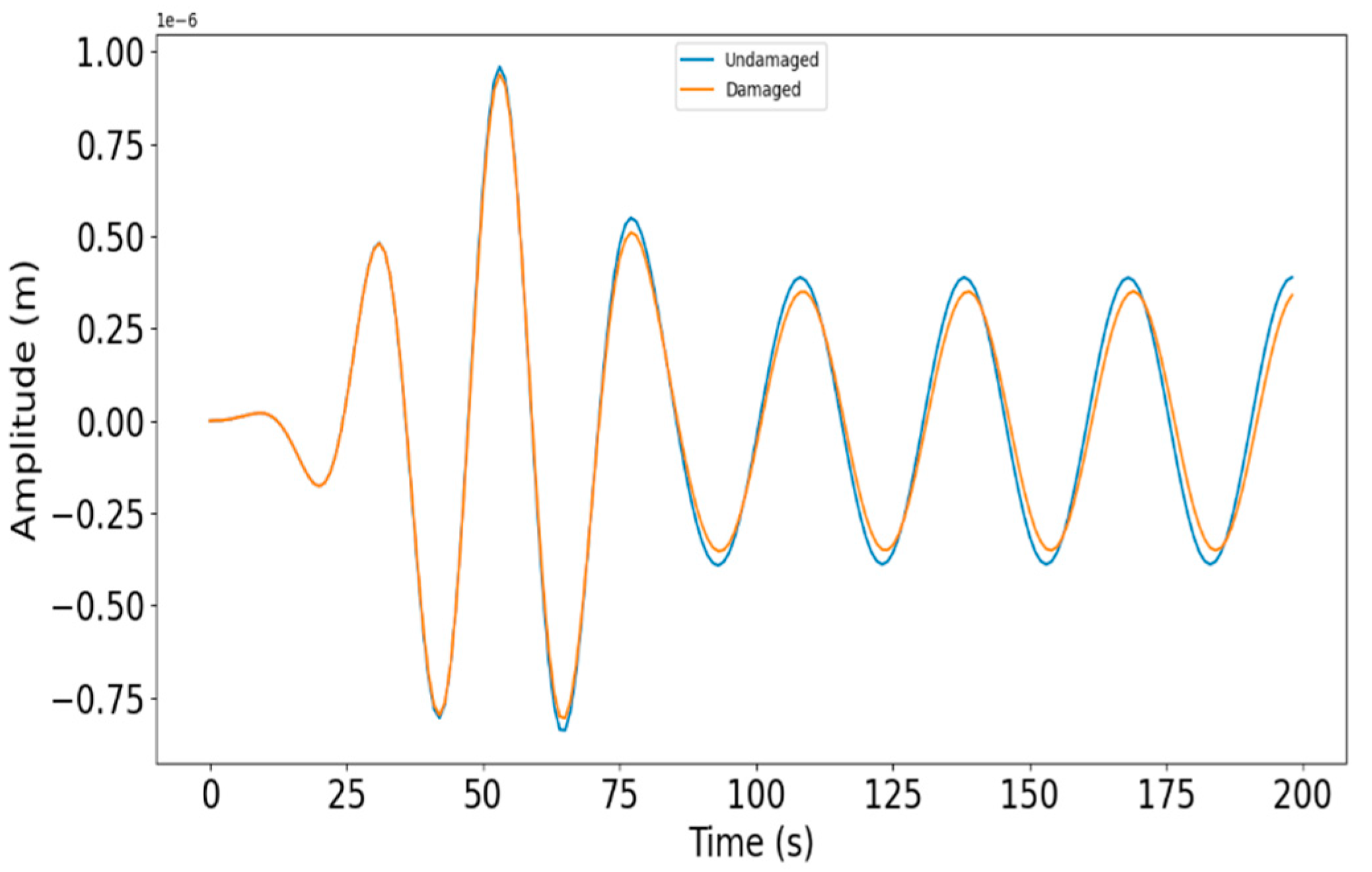
To construct the grid according to the specifications outlined in subsection 2.4 of the research paper, a nodal transient load is imposed on the unrestrained end of the Plate. For this investigation, a 5-cycle tone burst load with a suitable central frequency of 50Hz is considered. The selection of this central frequency is based on the resonance modes of interest, specifically the first three modes in our particular scenario. Subsequently, the deflections of the functionally graded (FG) plate are recorded. This procedure is repeated for a total of one hundred locations while ensuring that the load position and the node at which the deflections are obtained remain consistent. Figure 5 displays the representative deflection profiles observed for both the damaged and undamaged plates.
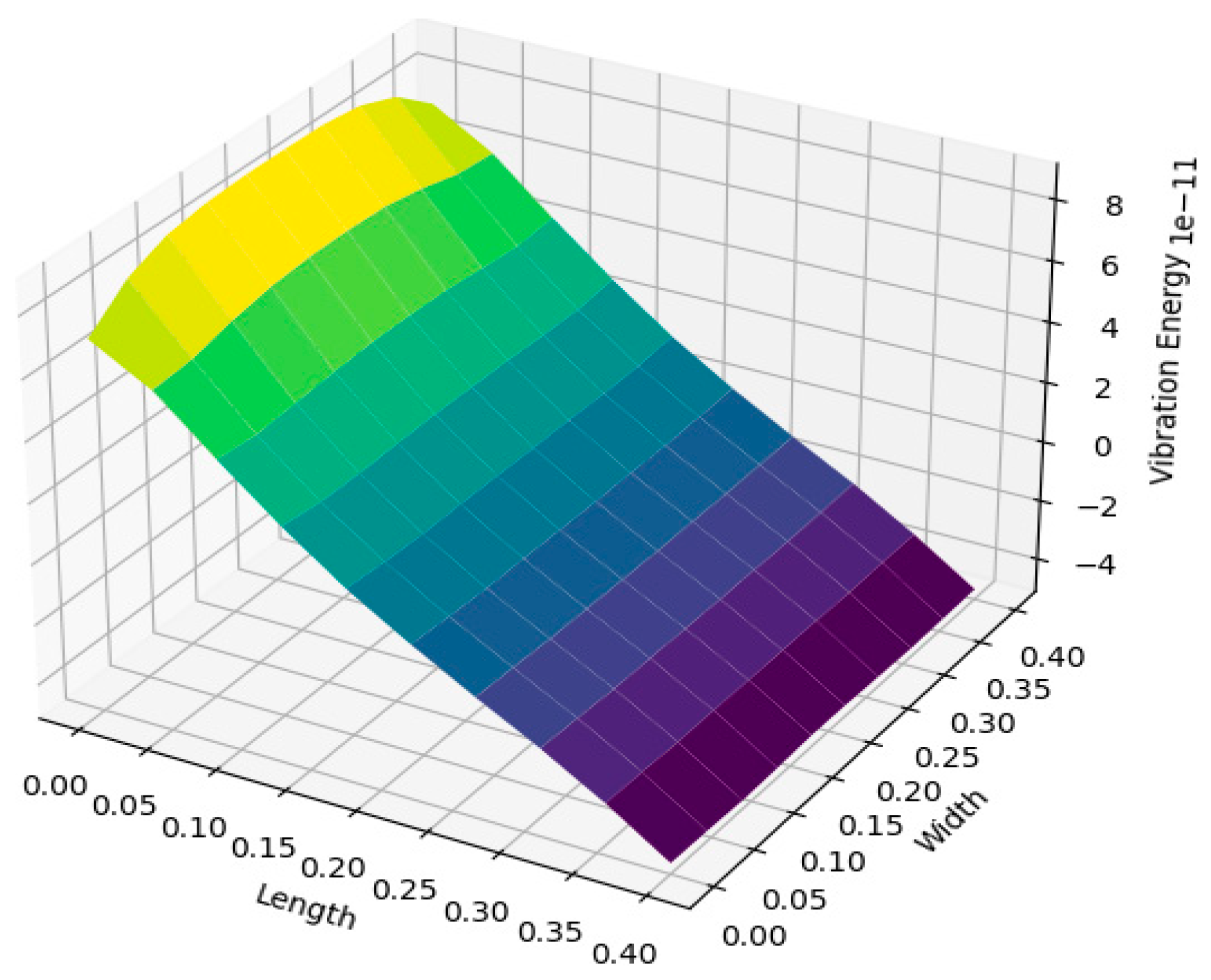
The damage was quantified using the relative vibration energy which is just the normalized subtraction of the energy vibration of healthy and damaged cases. The normalized vibration energy is given as follows:
δ E n e r g y   =   ∫   U h U h T − ∫   U d U d T   ∫   U h U h T
where U h and U d are the time history displacements of the FG plate.
Figure 6 depicted the relative vibration energy reduction for each damage position. it is clearly shown that the vibration energy reduction is significantly large when it is closed to the clamped area of the FG plate.
In this research paper, a total of 199 samples were obtained for each registered deflection. The construction process of the grid involved subtracting the deflections observed in damaged cases from those recorded in the responses of the healthy structure. These subtracted values were subsequently normalized. To construct the grid, the time deflections from 16 randomly selected damage positions were utilized, while the remaining positions were considered degraded.
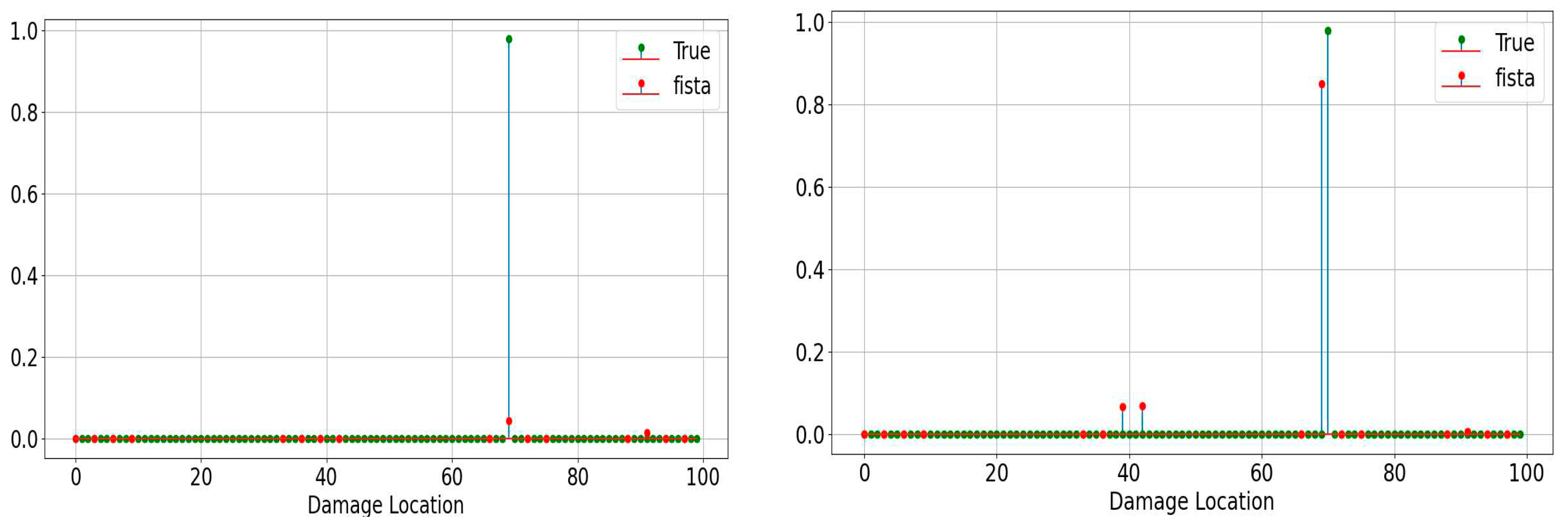
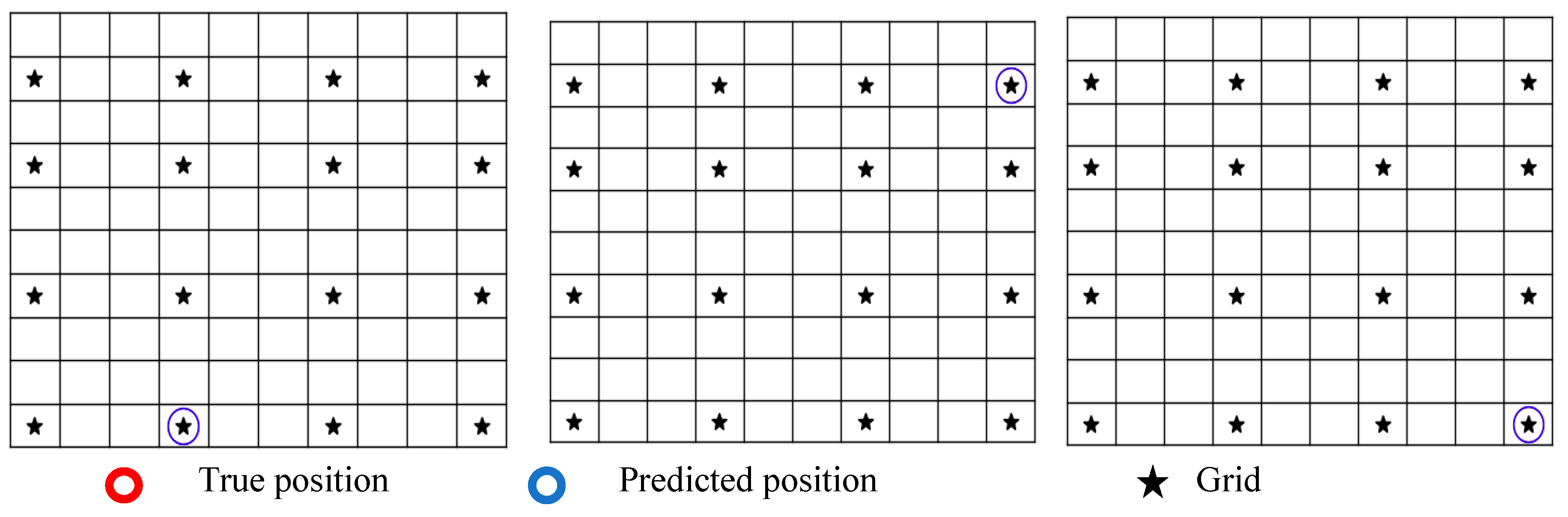
To evaluate the methodology, two cases were examined. The first case involved damage located within the grid, while the second case involved damage positioned outside the grid, which we will refer to as “off the grid.” From Figure 7, it is evident that the algorithm successfully identified the location of the damage (in this case, damage 70) within the grid. However, for the off-the-grid position (specifically position 71), the algorithm determined the nearest position within the grid to the actual damage.
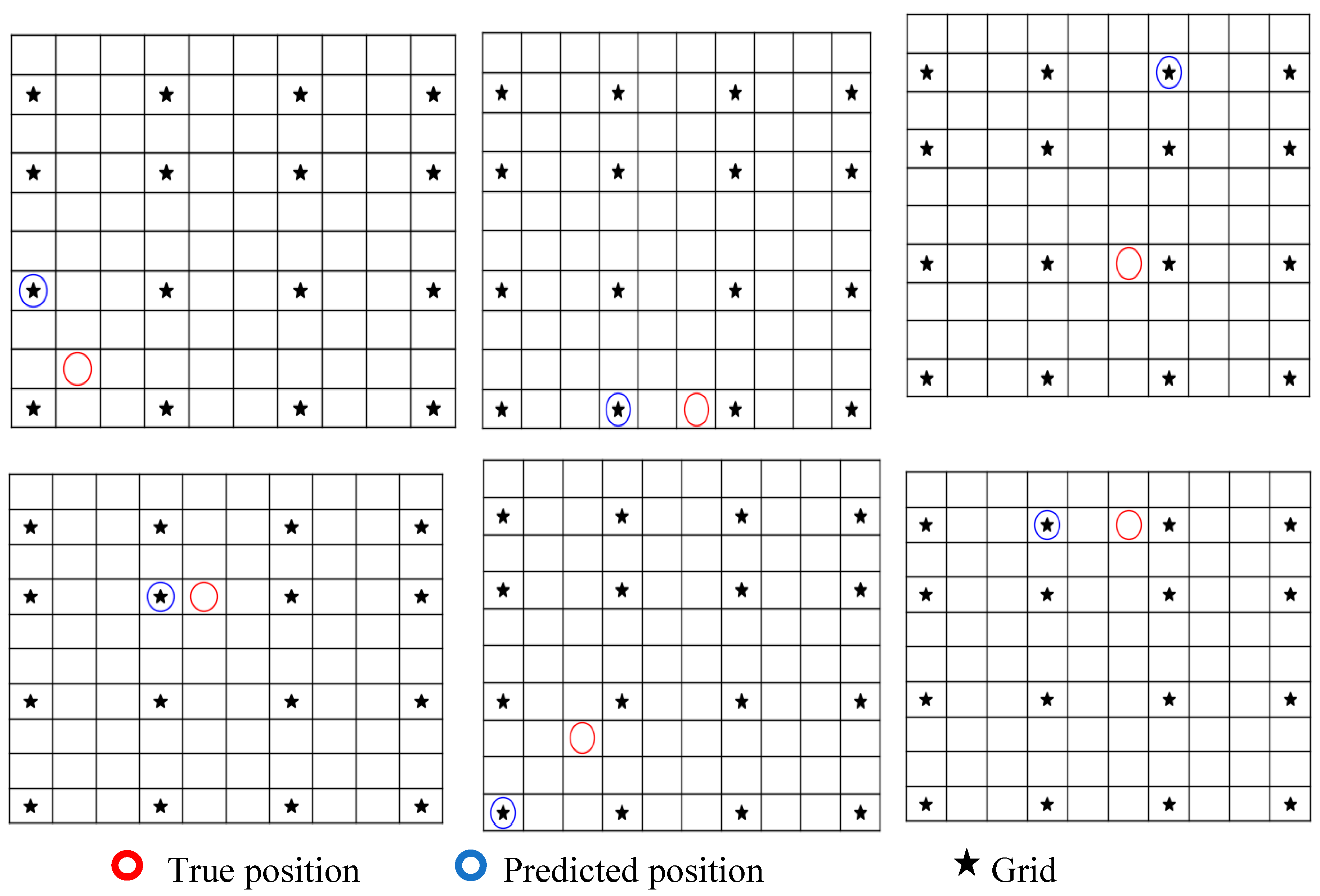
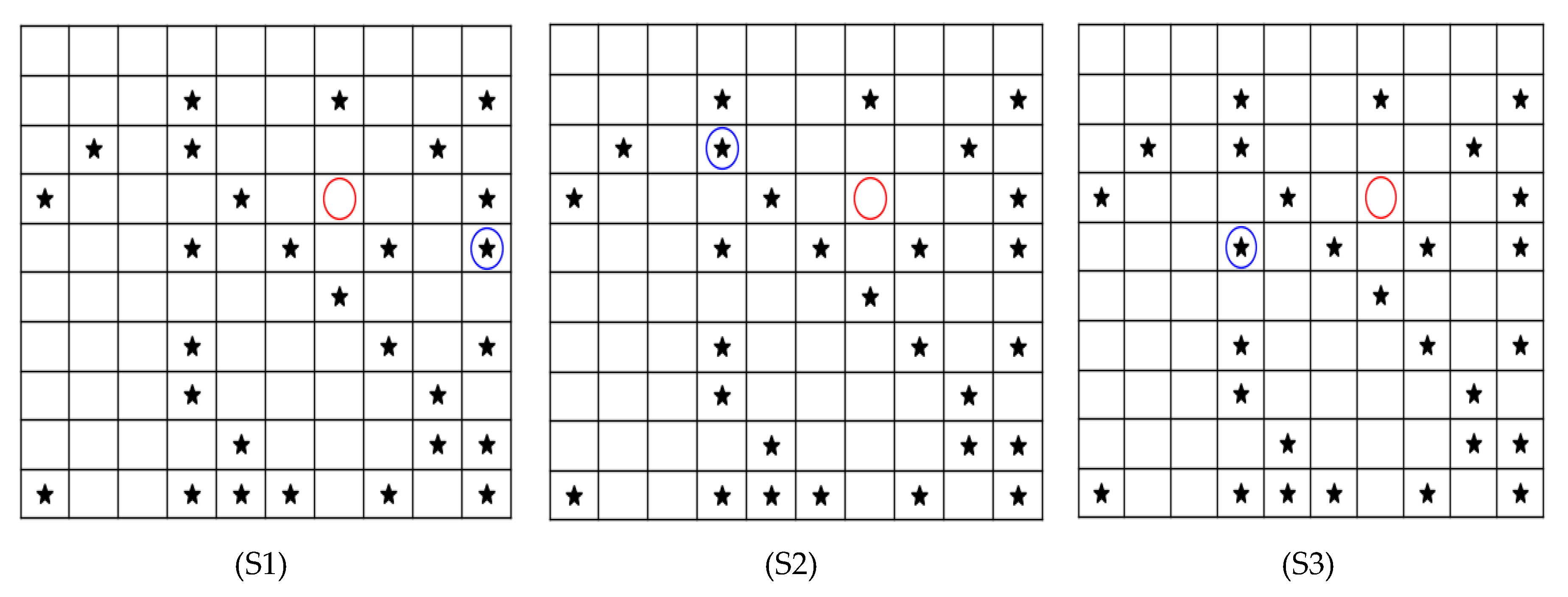
The algorithm underwent additional testing to evaluate its performance across multiple cases, and the outcomes are presented in Figure 8. As anticipated, in all instances where the target positions were within the grid, the algorithm demonstrated perfect accuracy in predicting the locations of damage. However, for instances where the target positions were situated outside the grid, the algorithm’s findings are depicted in Figure 9. In such cases, the algorithm highlighted the closest grid location it identified.

3.2.2. Damage Localization Sensitivity

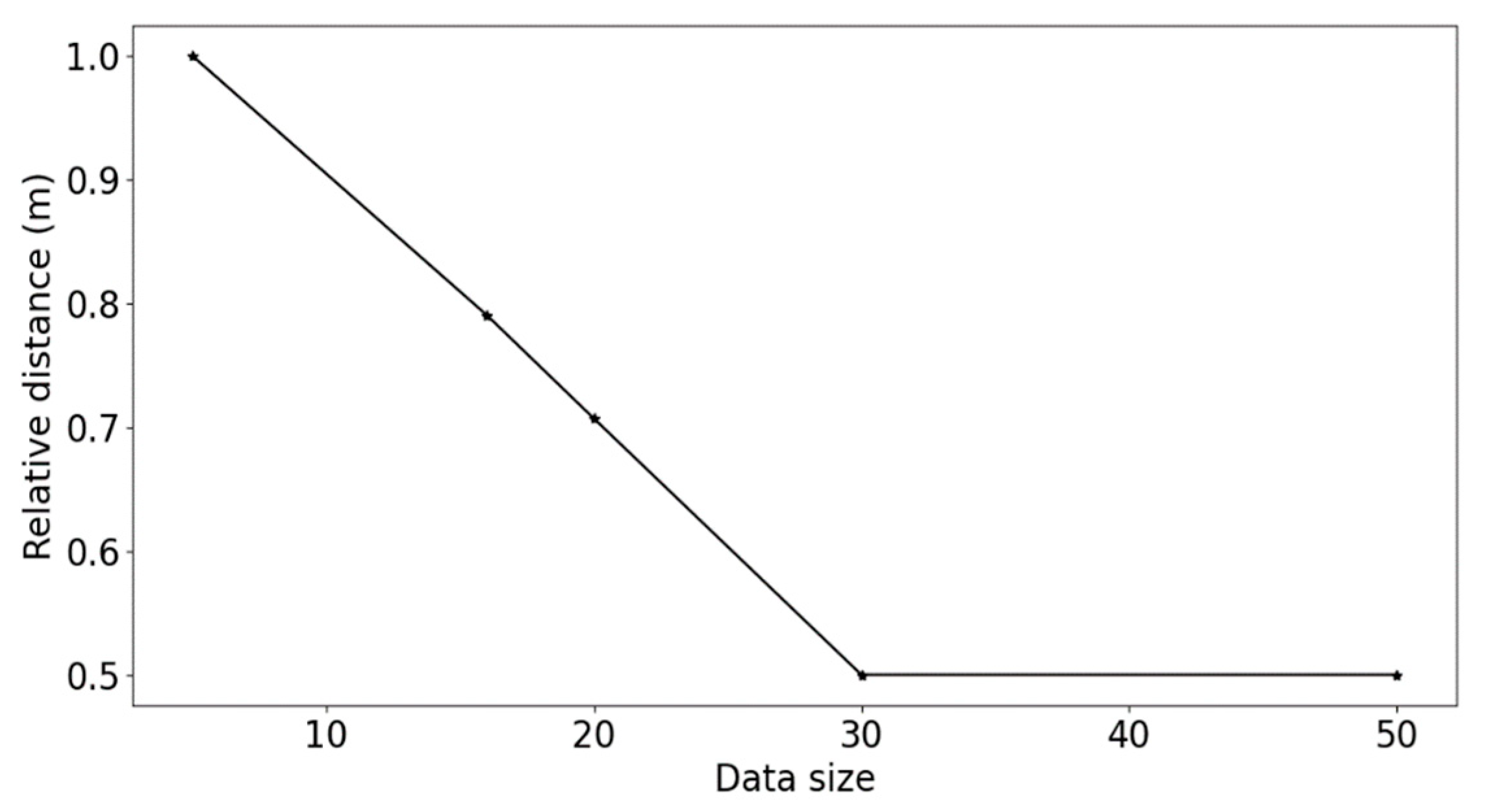
The accuracy of the sparsity-based algorithm is highly dependent on the data size used [40]. To evaluate the impact of grid size on the algorithm’s accuracy, we analyzed six different data size scenarios: 5, 10, 16, 20, 30, and 50 damage positions, respectively. In all scenarios, the same unknown damage position was utilized.
We determined the accuracy of damage localization by measuring the distance between the predicted damage position and the true position. The distance was calculated using a simple Pythagorean equation, as depicted in Figure 10.
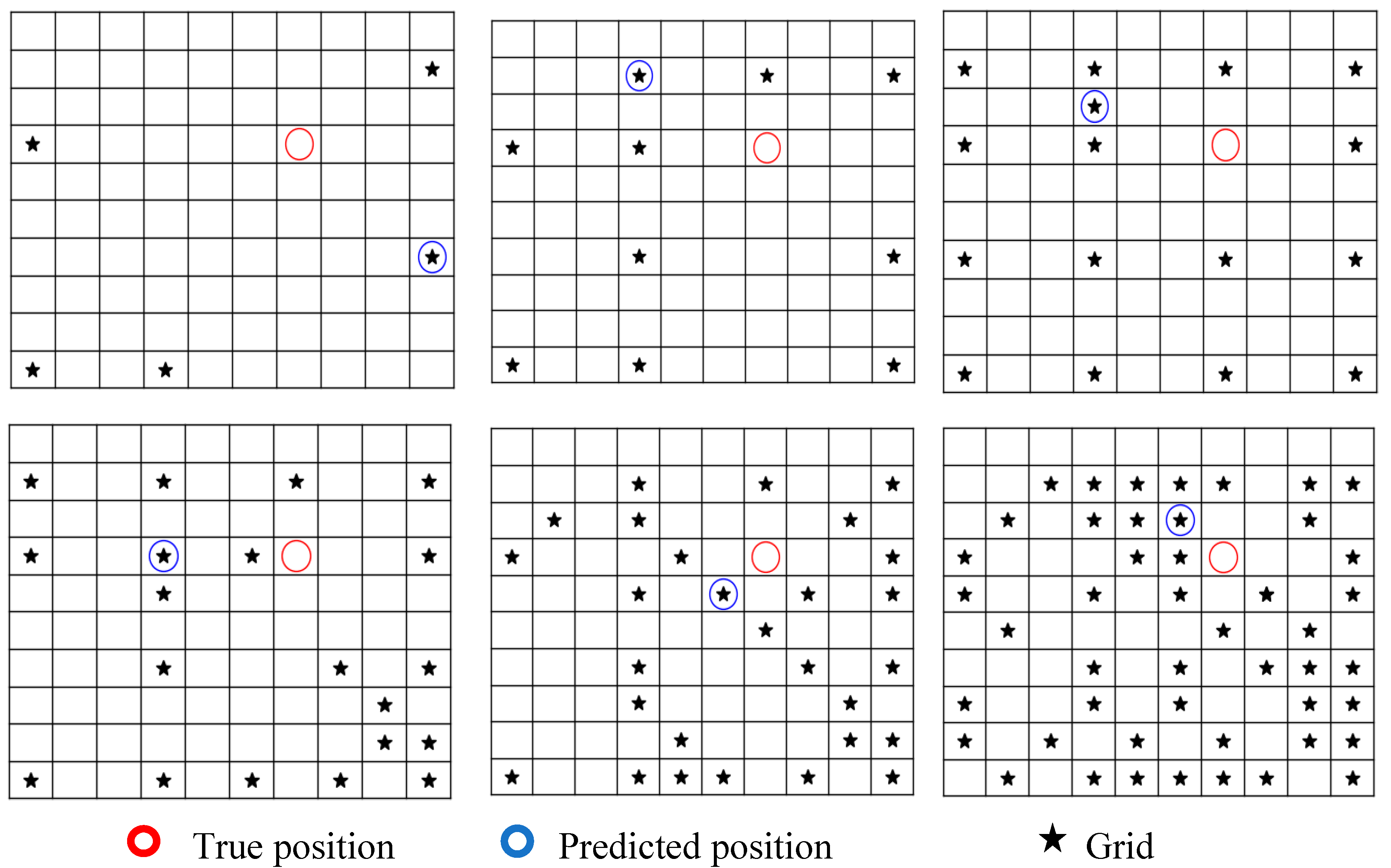
The true and predicted damage positions for each data size scenario are given in Figure 11. As the figures clearly show, the accuracy of the present algorithm is highly sensitive to data size. The prediction error decreases with respect to the amount of data. However, increasing the data will also rise computational time. Therefore, optimizing the used data concerning the prediction performance can significantly enhance the reliability of the proposed algorithm. Figure 12 shows that in our case, the prediction error decreases linearly until reaching 30 damage points, and then the results stabilize.

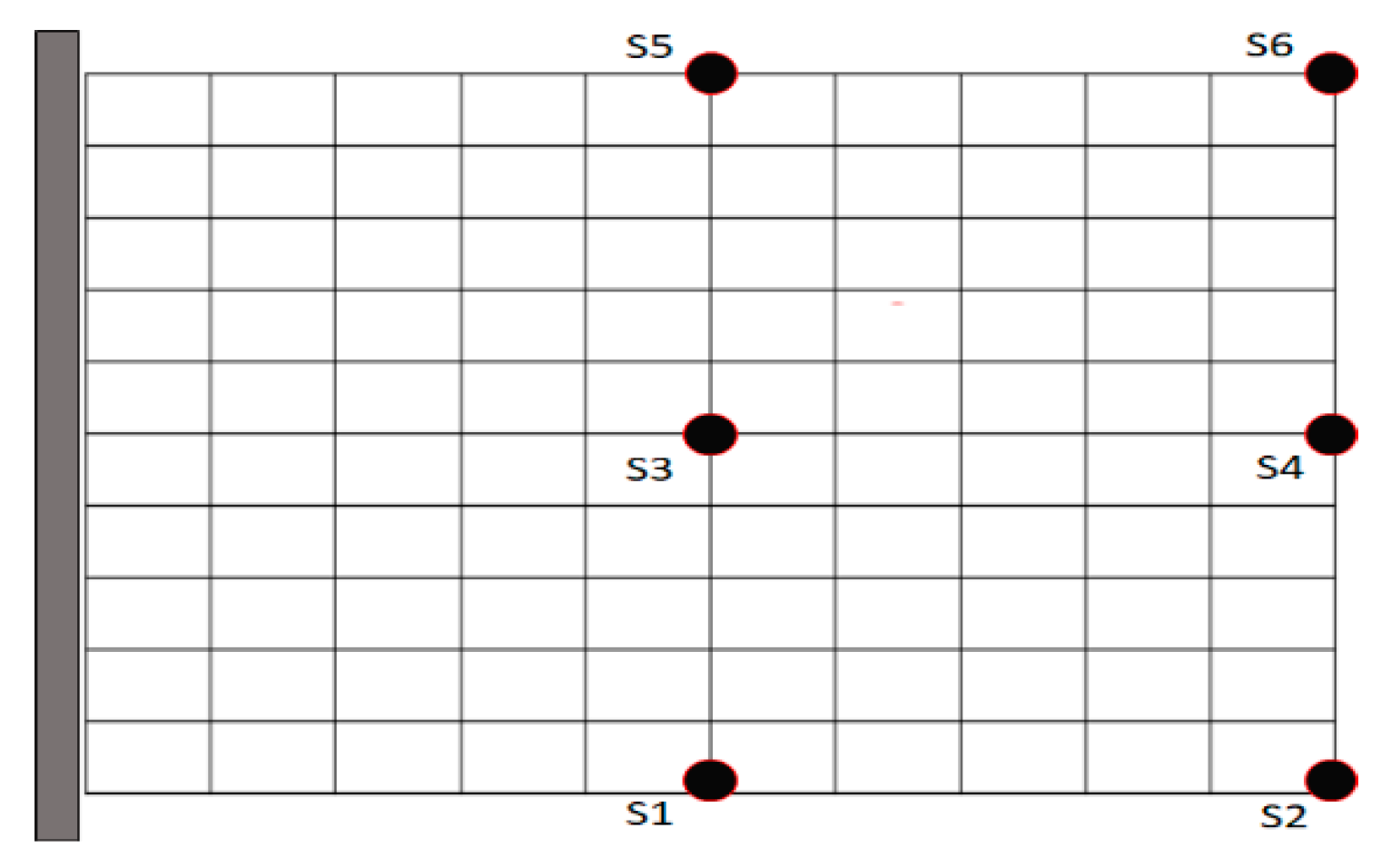
3.2.3. Effect of Observation Nodes

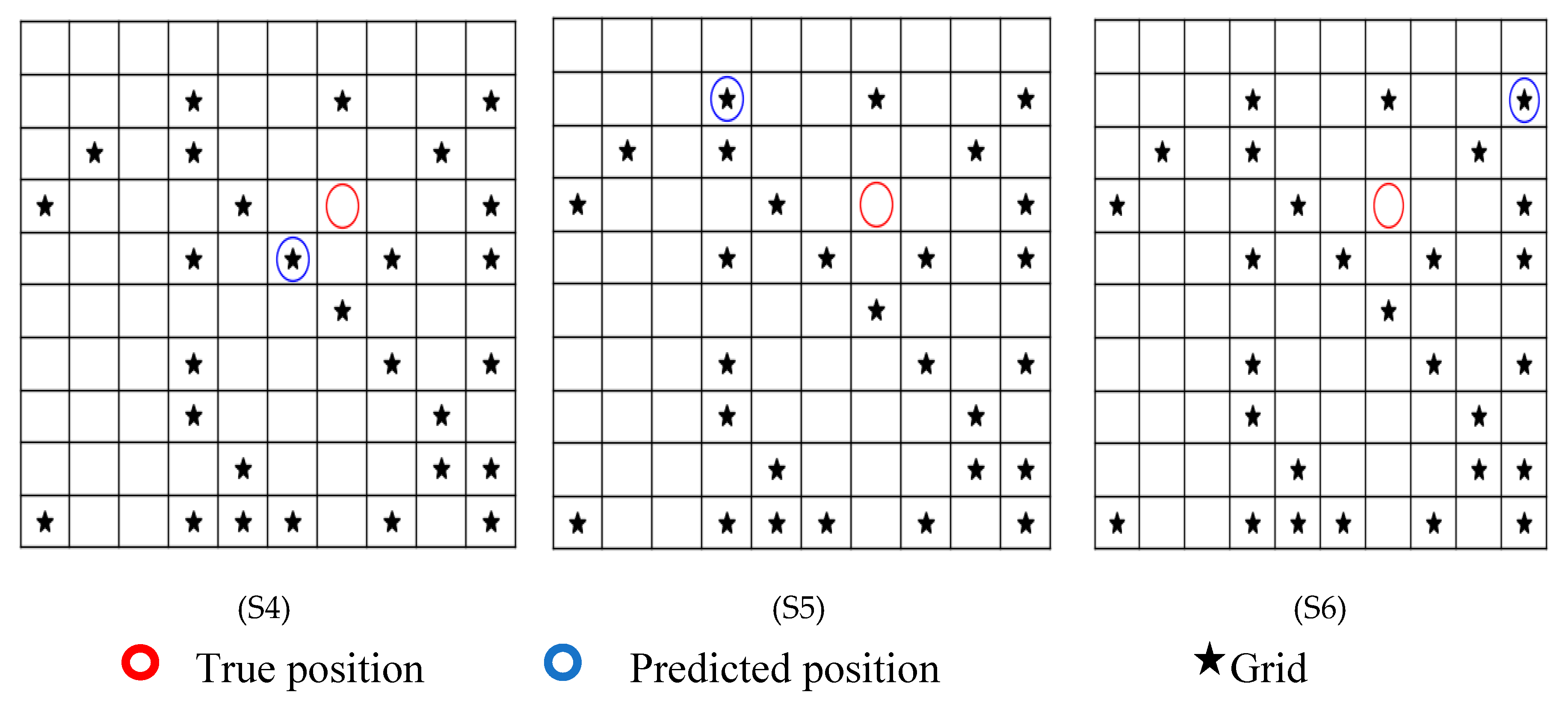
In this section, our focus is to analyze the effect of the deflection measuring point on the performance of the algorithm for localizing multiple damages. Thus, we excite the plate using the same excitation as before, placing it in the middle of the free end of the plate. We select six measuring points, as shown in Figure 13. Based on the findings in subsection 3.2.2, we construct a grid using 30 randomly chosen damage positions. However, the sought-after damage position is intentionally chosen to be off the grid, specifically at location 72 in our case. We run the algorithm for each measuring point and present the results in Figure 14. From the figures, we observe a significant improvement in accuracy when the measuring points coincide with the excitation point, which is visible in Figure 14(S4).

4. Conclusions

This paper suggests a dynamic algorithm for accurate damage localization in functionally graded plates. The algorithm utilized a grid matrix to capture the dynamic response of the structure and an optimization process incorporating the information from the grid to precisely locate damage. Our approach demonstrated its suitability for application in low-size data systems by accurately predicting the position of damage in experimental tests on a functionally graded plate.
The validation process confirmed the accuracy of our proposed model by comparing the predicted frequencies and deflections with those obtained from previous studies, showing good agreement and supporting its reliability. The damage detection experiments further demonstrated the sensitivity of the structure to damaged positions and the effectiveness of our algorithm in localizing damage. The algorithm identified the location of damage within the grid and determined the nearest grid location for off-the-grid positions.
Additionally, our algorithm’s performance was evaluated for different data sizes and observation nodes, revealing that increasing the data size improved the accuracy of damage localization but also resulted in longer computational time. Therefore, optimizing the data used for prediction can enhance the algorithm’s reliability. Moreover, we found that the algorithm performed better when the measuring points coincided with the excitation point.
We observed that our approach is time-dependent, making it suitable for online tracking of damages. The algorithm exhibited high sensitivity to data size, emphasizing the importance of choosing appropriate data for achieving accurate results. Furthermore, the choice of measuring point significantly improved the algorithm’s accuracy. Notably, our approach outperformed an ANN-based approach when the training data was limited.

Author Contributions

Emad Ghandourah and Kouider Bendine; Conceptualization, software, investigation, writing—original draft preparation. Samir Khatir, Brahim Benaissa; methodology, software, Essam Mohammed Banoqitah, Abdulsalam Mohammed Alhawsawi, Essam B. Moustafa; writing—review, editing and funding acquisition.

Funding

This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 1878-135-1443).

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article [and its Supplementary Materials].

Acknowledgments

This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 1878-135-1443) Therefore, authors gratefully acknowledge the technical and financial support from the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. M. Koizumi, « FGM activities in Japan », Composites Part B: Engineering, vol. 28, no 1-2, p. 1-4, 1997.
  2. D. K. Jha, T. Kant, et R. K. Singh, « A critical review of recent research on functionally graded plates », Composite structures, vol. 96, p. 833-849, 2013. [CrossRef]
  3. T. Cuong-Le, K. D. Nguyen, J. Lee, T. Rabczuk, et H. Nguyen-Xuan, « A 3D nano scale IGA for free vibration and buckling analyses of multi-directional FGM nanoshells », Nanotechnology, vol. 33, no 6, p. 65703, 2021. [CrossRef]
  4. C. Le Thanh, T. N. Nguyen, T. H. Vu, S. Khatir, et M. Abdel Wahab, « A geometrically nonlinear size-dependent hypothesis for porous functionally graded micro-plate », Engineering with Computers, p. 1-12, 2020. [CrossRef]
  5. T. Cuong-Le, K. D. Nguyen, N. Nguyen-Trong, S. Khatir, H. Nguyen-Xuan, et M. Abdel-Wahab, « A three-dimensional solution for free vibration and buckling of annular plate, conical, cylinder and cylindrical shell of FG porous-cellular materials using IGA », Composite Structures, vol. 259, p. 113216, 2021.
  6. K. K. Żur, M. Arefi, J. Kim, et J. N. Reddy, « Free vibration and buckling analyses of magneto-electro-elastic FGM nanoplates based on nonlocal modified higher-order sinusoidal shear deformation theory », Composites Part B: Engineering, vol. 182, p. 107601, 2020. [CrossRef]
  7. S. Sahmani, A. M. Fattahi, et N. A. Ahmed, « Analytical treatment on the nonlocal strain gradient vibrational response of postbuckled functionally graded porous micro-/nanoplates reinforced with GPL », Engineering with Computers, vol. 36, p. 1559-1578, 2020.
  8. W. Fang, L. Cheng, H. Wang, L. Yang, et R. Liao, « High Power Ultrasonic Testing Method for Agglomeration of Nanoparticles in Nanocomposite Dielectrics », in 2021 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), IEEE, 2021, p. 347-351. [CrossRef]
  9. M. Aslam et J. Lee, « Numerical Investigation of Nonlinear Guided Wave Propagation in a Functionally Graded Material », in Fiber Reinforced Polymeric Materials and Sustainable Structures, Springer, 2023, p. 191-198.
  10. M. Aslam, J. Park, et J. Lee, « Microcrack inspection in a functionally graded plate structure using nonlinear guided waves », in Structures, Elsevier, 2023, p. 666-677. [CrossRef]
  11. H. Haddar, Z. Jiang, et M. K. Riahi, « A robust inversion method for quantitative 3D shape reconstruction from coaxial eddy current measurements », Journal of Scientific Computing, vol. 70, p. 29-59, 2017. [CrossRef]
  12. H. Haddar et M. K. Riahi, « Near-field linear sampling method for axisymmetric eddy current tomography », Inverse Problems, vol. 37, no 10, p. 105002, 2021.
  13. M. K. Riahi et I. A. Qattan, « On the convergence rate of Fletcher-Reeves nonlinear conjugate gradient methods satisfying strong Wolfe conditions: Application to parameter identification in problems governed by general dynamics », Mathematical Methods in the Applied Sciences, vol. 45, no 7, p. 3644-3664, 2022.
  14. M. K. Riahi, « A new approach to improve ill-conditioned parabolic optimal control problem via time domain decomposition », Numerical Algorithms, vol. 72, p. 635-666, 2016. [CrossRef]
  15. B. Benaissa, S. Khatir, M. S. Jouini, et M. K. Riahi, « Optimal Axial-Probe Design for Foucault-Current Tomography: A Global Optimization Approach Based on Linear Sampling Method », Energies, vol. 16, no 5, p. 2448, 2023. [CrossRef]
  16. L. Zhu, F. Dang, Y. Xue, W. Ding, L. Zhang, et X. Xiong, « Meso-scale damage detection and assessment of concrete under dynamic compression loading using X-ray computed tomography », Materials Characterization, vol. 176, p. 111149, 2021. [CrossRef]
  17. A. Khatir et al., « A new hybrid PSO-YUKI for double cracks identification in CFRP cantilever beam », Composite Structures, vol. 311, p. 116803, 2023. [CrossRef]
  18. E. Ghandourah, S. Khatir, E. M. Banoqitah, A. M. Alhawsawi, B. Benaissa, et M. A. Wahab, « Enhanced ANN Predictive Model for Composite Pipes Subjected to Low-Velocity Impact Loads », Buildings, vol. 13, no 4, p. 973, 2023. [CrossRef]
  19. M. Slimani et al., « Improved ANN for Damage Identification in Laminated Composite Plate BT—Proceedings of the International Conference of Steel and Composite for Engineering Structures », R. Capozucca, S. Khatir, et G. Milani, Éd., Cham: Springer International Publishing, 2023, p. 186-198.
  20. S. Khatir, S. Tiachacht, B. Benaissa, C. Le Thanh, R. Capozucca, et M. Abdel Wahab, « Damage Identification in Frame Structure Based on Inverse Analysis », in Proceedings of the 2nd International Conference on Structural Damage Modelling and Assessment: SDMA 2021, 4–5 August, Ghent University, Belgium, Springer, 2022, p. 197-211.
  21. M. Slimani, T. Khatir, S. TIACHACHT, D. BOUTCHICHA, et B. Benaissa, « Experimental sensitivity analysis of sensor placement based on virtual springs and damage quantification in CFRP composite », Journal of Materials and Engineering Structures «JMES», vol. 9, no 2, p. 207-220, 2022.
  22. A. Kahouadji, S. Tiachacht, M. Slimani, A. Behtani, S. Khatir, et B. Benaissa, « Vibration-Based Damage Assessment in Truss Structures Using Local Frequency Change Ratio Indicator Combined with Metaheuristic Optimization Algorithms BT—Proceedings of the International Conference of Steel and Composite for Engineering Structures », R. Capozucca, S. Khatir, et G. Milani, Éd., Cham: Springer International Publishing, 2023, p. 171-185.
  23. A. Banerjee, B. Panigrahi, et G. Pohit, « Crack modelling and detection in Timoshenko FGM beam under transverse vibration using frequency contour and response surface model with GA », Nondestructive Testing and Evaluation, vol. 31, no 2, p. 142-164, 2016.
  24. D. Dinh-Cong et T. Nguyen-Thoi, « An effective damage identification procedure using model updating technique and multi-objective optimization algorithm for structures made of functionally graded materials », Engineering with Computers, vol. 39, no 2, p. 1229-1247, 2023.
  25. J. Xiang, T. Matsumoto, Y. Wang, et Z. Jiang, « Detect damages in conical shells using curvature mode shape and wavelet finite element method », International Journal of Mechanical Sciences, vol. 66, p. 83-93, 2013. [CrossRef]
  26. C. Liang, Z. Yaw, et C. W. Lim, « Thermal strain energy induced wave propagation for imperfect FGM sandwich cylindrical shells », Composite Structures, vol. 303, p. 116295, 2023.
  27. J. Xiang, Y. Lei, Y. Wang, Y. He, C. Zheng, et H. Gao, « Structural dynamical monitoring and fault diagnosis », Shock and Vibration, vol. 2015. Hindawi, 2015. [CrossRef]
  28. P. Ghannadi, S. Khatir, S. S. Kourehli, A. Nguyen, D. Boutchicha, et M. A. Wahab, « Finite element model updating and damage identification using semi-rigidly connected frame element and optimization procedure: An experimental validation », in Structures, Elsevier, 2023, p. 1173-1190. [CrossRef]
  29. D. Sen, A. Aghazadeh, A. Mousavi, S. Nagarajaiah, et R. Baraniuk, « Sparsity-based approaches for damage detection in plates », Mechanical Systems and Signal Processing, vol. 117, p. 333-346, 2019. [CrossRef]
  30. M. Irfan Shirazi, S. Khatir, B. Benaissa, S. Mirjalili, et M. Abdel Wahab, « Damage assessment in laminated composite plates using modal Strain Energy and YUKI-ANN algorithm », Composite Structures, vol. 303, p. 116272, 2023. [CrossRef]
  31. B. Benaissa, N. A. Hocine, S. Khatir, M. K. Riahi, et S. Mirjalili, « YUKI Algorithm and POD-RBF for Elastostatic and dynamic crack identification », Journal of Computational Science, vol. 55, p. 101451, 2021. [CrossRef]
  32. S. Ishihara, K. Ishihara, M. Nagamachi, et Y. Matsubara, « An automatic builder for a Kansei Engineering expert system using self-organizing neural networks », International Journal of Industrial Ergonomics, vol. 15, no 1, p. 13-24, 1995. [CrossRef]
  33. A. Zara, I. Belaidi, S. Khatir, A. O. Brahim, D. Boutchicha, et M. A. Wahab, « Damage detection in GFRP composite structures by improved artificial neural network using new optimization techniques », Composite Structures, vol. 305, p. 116475, 2023. [CrossRef]
  34. K. Bendine, B. F. Boukhoulda, M. Nouari, et Z. Satla, « Structural modeling and active vibration control of smart FGM plate through ANSYS », International Journal of Computational Methods, vol. 14, no 04, p. 1750042, 2017. [CrossRef]
  35. E. Martínez-Pañeda, « On the finite element implementation of functionally graded materials », Materials, vol. 12, no 2, p. 287, 2019.
  36. M. Saadatmorad, R.-A. Jafari-Talookolaei, M.-H. Pashaei, et S. Khatir, « Damage Detection in Rectangular Laminated Composite Plate Structures using a Combination of Wavelet Transforms and Artificial Neural Networks », Journal of Vibration Engineering & Technologies, vol. 10, no 5, p. 1647-1664, 2022. [CrossRef]
  37. S. Kapuria, M. Patni, et M. Y. Yasin, « A quadrilateral shallow shell element based on the third-order theory for functionally graded plates and shells and the inaccuracy of rule of mixtures », European Journal of Mechanics-A/Solids, vol. 49, p. 268-282, 2015. [CrossRef]
  38. J. S. Moita, V. F. Correia, C. M. M. Soares, et J. Herskovits, « Higher-order finite element models for the static linear and nonlinear behaviour of functionally graded material plate-shell structures », Composite structures, vol. 212, p. 465-475, 2019. [CrossRef]
  39. K. Y. Dai, G. Liu, X. Han, et K. M. Lim, « Thermomechanical analysis of functionally graded material (FGM) plates using element-free Galerkin method », Computers & structures, vol. 83, no 17-18, p. 1487-1502, 2005. [CrossRef]
  40. D. Di Lorenzo, V. Champaney, C. Germoso, E. Cueto, et F. Chinesta, « Data Completion, Model Correction and Enrichment Based on Sparse Identification and Data Assimilation », Applied Sciences, vol. 12, no 15, p. 7458, 2022.
Preprints 78346 g002
Figure 2. Illustration of the structural response estimation for unknown damage.
Figure 2. Illustration of the structural response estimation for unknown damage.
Preprints 78346 g002
Preprints 78346 g003
Figure 3. Damage location numbering.
Figure 3. Damage location numbering.
Preprints 78346 g003
Preprints 78346 g004aPreprints 78346 g004b
Figure 4. Relative change in frequency along the plate surface for first four frequencies: case k = 1.
Figure 4. Relative change in frequency along the plate surface for first four frequencies: case k = 1.
Preprints 78346 g004aPreprints 78346 g004b
Preprints 78346 g005
Figure 5. A typical deflection response for damaged and undamaged cases.
Figure 5. A typical deflection response for damaged and undamaged cases.
Preprints 78346 g005
Preprints 78346 g006
Figure 6. A typical deflection response for damaged and undamaged cases.
Figure 6. A typical deflection response for damaged and undamaged cases.
Preprints 78346 g006
Preprints 78346 g007
Figure 7. Values of the elements of the sparse vector x obtained for damage location: 70 on the grid. 71 off the grid.
Figure 7. Values of the elements of the sparse vector x obtained for damage location: 70 on the grid. 71 off the grid.
Preprints 78346 g007
Preprints 78346 g008aPreprints 78346 g008b
Figure 8. Damage localization for the case of on grid.
Figure 8. Damage localization for the case of on grid.
Preprints 78346 g008aPreprints 78346 g008b
Preprints 78346 g009
Figure 9. Damage localization for the case of off-grid.
Figure 9. Damage localization for the case of off-grid.
Preprints 78346 g009
Preprints 78346 g010
Figure 10. Distance between the true and predicted damage positions.
Figure 10. Distance between the true and predicted damage positions.
Preprints 78346 g010
Preprints 78346 g011
Figure 11. Offgrid damage prediction for different data sizes.
Figure 11. Offgrid damage prediction for different data sizes.
Preprints 78346 g011
Preprints 78346 g012
Figure 12. Relative distance vs data size.
Figure 12. Relative distance vs data size.
Preprints 78346 g012
Preprints 78346 g013
Figure 13. displacements Lecture points.
Figure 13. displacements Lecture points.
Preprints 78346 g013
Preprints 78346 g014aPreprints 78346 g014b
Figure 14. Distance between the true and predicted damage positions.
Figure 14. Distance between the true and predicted damage positions.
Preprints 78346 g014aPreprints 78346 g014b
Table 2. Material and geometrical proprieties.
Table 2. Material and geometrical proprieties.
Property Aluminum (Al) Zirconia-1 (ZrO2-1) Zirconia-2
(ZrO2-2)
Young’s Modulus E (GPa)
Density
Poisson coefficient 		70
2700
0.3		 151
3000
0.3		 200
5700
0.3
Table 3. Natural frequencies (Hz) of a cantilever plate for different power law k index.
Table 3. Natural frequencies (Hz) of a cantilever plate for different power law k index.
p Mode no 1 2 3 4 5 6
0 [39]
Present		 36.715
37.06		 89.111
90.503		 226.25
227.03		 286.77
289.66		 326.05
329.16		 569.32
575.14
0.2
 [39]
Present		 34.969
35.217 		84.864
86.006		 215.54
215.74		 273.11
275.27		 310.54
312.81		 542.21
546.59
1
 [39]
Present		 31.774
31.792		 77.156
77.642		 195.97
194.7		 248.12
248.49		 282.30
282.39		 492.78
493.44
5
 [39]
Present		 29.915
29.797		 72.675
72.746		 184.44
182.51		 233.55
232.85		 265.76
264.56		 463.87
462.19
inf [39]
Present		 26.933
26.675		 65.345
65.140		 166.12
163.41		 210.18
208.49		 239.11
236.92		 417.27
413.96
Table 4. Non-dimensional deflections of the fully clamped plate with different power law k index.
Table 4. Non-dimensional deflections of the fully clamped plate with different power law k index.
P S Present [37] [38]
0.5
 5
10		 0.1016
0.0707		 0.1060
0.0772		 0.0978
0.0706
1
 5
10		 0.1198
0.0833		 0.1236
0.0892		 0.1150
0.0830
2 5
10		 0.1416
0.0962		 0.1422
0.1003		 0.1351
0.0957
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated