1. Introduction
In recent years, there has been a significant amount of research interest in unmanned aerial vehicles (UAVs) due to their impressive features, such as their maneuverability, ease of positioning, versatility, and the high likelihood of line-of-sight (LoS) air-to-ground connections [
1,
2]. UAVs are feasibly exploited to alleviate a wide range of challenges in commercial and civilian sectors [
3,
4]. It is expected that forthcoming wireless communication networks will need to provide exceptional service to meet the demands of users. This presents difficulties for traditional terrestrial-based communication systems, particularly in hotspot areas with high traffic [
5,
6,
7]. UAVs have the potential to serve as flying base stations, providing support to the land-based communication infrastructure without the need for costly network construction [
8]. In addition, their ability to be easily relocated makes them particularly highly beneficial in the aftermath of natural disasters [
9,
10]. UAVs can also be deployed as intermediaries between ground-based terminals, improving transmission link performance and enhancing reliability, security, coverage, and throughput [
11,
12]. As such, UAV-assisted communications are becoming increasingly vital in developing future wireless systems.
UAV-aided wireless communications possess a distinct advantage owing to the controllable maneuverability of UAVs, which allows for flexible trajectories. This added degree of freedom significantly boosts the system’s performance. Therefore, optimizing the UAV’s trajectory is an indispensable area of focus in this field, as it is paramount to exploit the potential of UAV-assisted wireless communications fully [
13]. Several studies have looked into improving system performance through trajectory design. One study, for example, optimized the trajectory of a UAV to gather received signal strength measurements efficiently and improve the accuracy of spectrum cartography [
14]. Another study proposed a method for planning the trajectory of a UAV to provide emergency data uploading for large-scale dynamic networks [
15]. Multi-hop relay UAV trajectory planning is also crucial in UAV swarm networks [
16]. Joint optimization of the UAV’s trajectory and user association was suggested in [
17] to maximize total throughput and energy efficiency. Another study examined joint UAV trajectory design and time allocation for aerial data collection in NOMA-IoT networks [
18]. In a cluster-based IoT network, joint optimization of the UAV’s hovering points and trajectory was studied to achieve minimal age-of-information data collection [
19]. Autonomous trajectory planning solutions were proposed in [
20] to enable UAVs to navigate complex environments without GPS while fulfilling real-time requirements. Lastly, the trajectory of a UAV was optimized in [
21] to minimize propulsion energy and ensure the required sensing resolutions for cellular-aided radar sensing.
Traditional methods rely on optimization mathematical models that require precise information about the system, including the number of users in different areas and network parameters when designing a UAV trajectory. However, this approach may not be feasible in real-world situations due to the constantly changing environment and limited battery life, making it difficult to solve these problems using traditional techniques [
22]. On the other hand, artificial intelligence (AI) techniques, such as machine learning (ML) and reinforcement learning (RL), have proven to be effective in addressing challenges related to sequential decision-making. By equipping UAVs with AI capabilities (AI-enabled UAVs), they can attain a remarkable level of self-awareness, transforming wireless communications [
23]. With AI, UAVs can effectively comprehend the radio environment by discerning and segregating the explanatory factors that are concealed in low-level sensory signals [
24]. However, most ML and RL methods are not capable of adjusting to new situations that were not included in their initial training. This limitation in generalizing requires extensive retraining efforts, which can pose challenges for real-time prediction and decision-making [
25].
When AI-enabled agents sense and interact with their environment, they struggle with structuring the knowledge they gather and making logical decisions based on it. One way to address this is through knowledge representation and reasoning techniques inspired by human problem-solving to handle complex tasks effectively [
26]. Causal probabilistic graphical models are a prime example of such techniques, which are highly effective in capturing the hidden patterns in sensory data obtained from the environment. These models also provide a seamless way to integrate sensory data from various sources [
27]. By statistically structuring the data, they can describe different levels of abstraction that can be applied across different domains. For instance, when learning a language, one must learn how sounds form words, how words form sentences, and how grammar characterizes a language. At every level, the learning process requires making probabilistic inferences within a structured hypothesis space. Dealing with uncertainty is a common challenge in AI and decision-making, as many real-world problems have incomplete or ambiguous information. Probabilistic representation is an effective technique that leverages probability theory to model and reason with uncertainty, enabling AI agents to make better decisions and operate more efficiently [
28].
Active inference is a mathematical framework that helps us understand how living organisms interact with their environment [
29]. It provides a unified approach to modelling perception, learning, and decision-making, aiming to maximise Bayesian model evidence or minimise free energy [
30]. Free energy is a crucial concept that empowers agents to systematically assess multiple hypotheses concerning behaviors that can effectively achieve their desired outcomes. Moreover, active inference governs our expectations of the world around us. Specifically, it posits that our brains utilize statistical models to interpret sensory information [
31]. By using active inference, we can modify our sensory input to conform to our preconceived notions of the world and rectify any inconsistencies between our expectations and reality. Probabilistic graphical models are used to represent active inference models because they provide a clear visual representation of the model’s computational structure and how belief updates can be achieved through message-passing algorithms [
32].
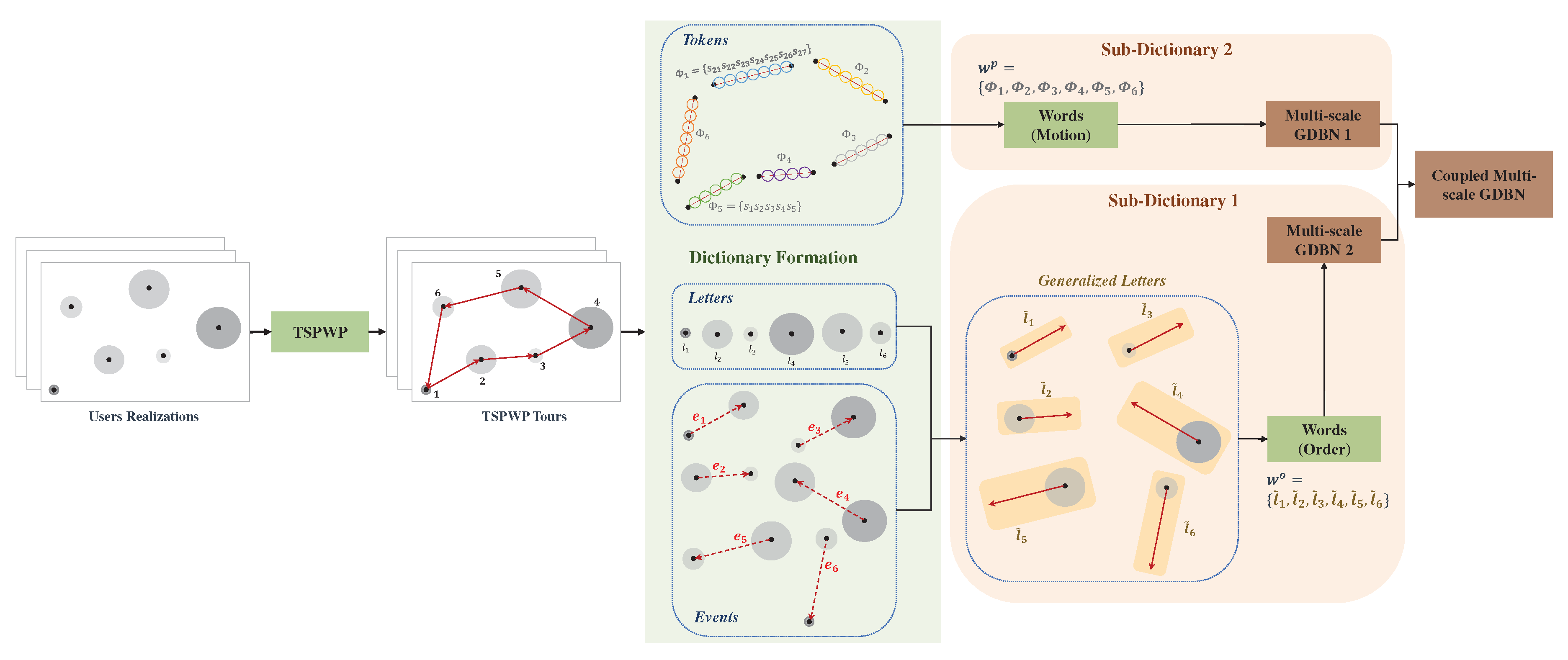
Motivated by the previous discussion, we propose a goal-directed trajectory design framework for UAV-assisted wireless networks based on active inference. The proposed approach involves two key computational units. The first unit meticulously analyzes the statistical structure of sensory signals and creates a world model to gain a comprehensive understanding of the environment. The second is the decision-making unit seeking to perform actions minimizing a cost function and generating preferred outcomes. The two components are linked by an active inference process. To create the world model, the UAV was trained to complete various flight missions with different realizations (such as the locations of hotspots and users’ access requests) using the conventional travel salesman problem with profit (TSPWP) [
33] with 2-OPT local search algorithm in an offline manner. The TSPWP instances (trajectories) were turned into graphs and used to build a global dictionary with two sub-dictionaries. The first sub-dictionary represents the hotspots the UAV needs to serve and their order of travel. In contrast, the second sub-dictionary shows the trajectories to follow between two adjacent nodes. The global dictionary consists of letters at multiple levels, tokens, and words. The world model is created by coupling the two sub-dictionaries, constructing a detailed representation of the environment at different hierarchical levels and time scales. The world model is structured in a Coupled Multi-Scale Generalized Dynamic Bayesian Network (C-MGDBN). This model builds upon the Single-Scale GDBN, which is a statistical model that explains how hidden states drive time series observations. However, unlike the conventional GDBN [
34,
35,
36], which can only model single-scale data, our enhanced GDBN representation can encode the dynamic rules that generate observations at different temporal resolutions, making it far more versatile than traditional GDBNs. With this superior model, we can simultaneously model a UAV’s behaviour at different time scales. The decision-making unit relies on active inference to select actions based on the current state of the environment as inferred from the world model. The proposed framework explains how UAVs navigate their surroundings with a goal in mind, choosing actions that minimize unexpected or unusual observations (abnormalities), which are measured by how much they deviate from the expected goal.
The main contributions of this paper can be summarized as follows:
We developed a global dictionary during training to discover the TSPWP’s best strategy for solving different realizations. The dictionary comprises letters representing the available hotspots, tokens representing local paths, and words depicting the complete trajectories and order of hotspots. By studying the dictionary, we can comprehend the decision-maker’s grammar (i.e., the TSPWP strategy) and how it uses the available letters to form tokens and words.
We have designed a novel hierarchical representation structuring the acquired knowledge (the global dictionary) to accurately depict the properties of the TSPWP graphs at various levels of abstraction and time scales.
We tested the proposed method on different scenarios with varying hotspots. Our method outperformed traditional Q-learning by providing fast, stable, and reliable solutions with good generalization ability.
The remainder of the paper is organized as follows: the literature review is presented in
Section 2. The system model and problem formulation are presented in
Section 3. The proposed goal-directed trajectory design method is explained in
Section 4.
Section 5 is dedicated to the numerical results and discussion, and finally
Section 6 concludes this paper by highlighting the future directions.
Notations: Throughout the paper, capital italic letters denote constants, lowercase bold letters denote vectors, capital boldface letters denote matrices. The shorthand is used to denote a Gaussian distribution with mean and covariance . If represents a matrix, the element in its ith row and jth column is denoted by , and its ith row vector is represented by .
2. Literature Review
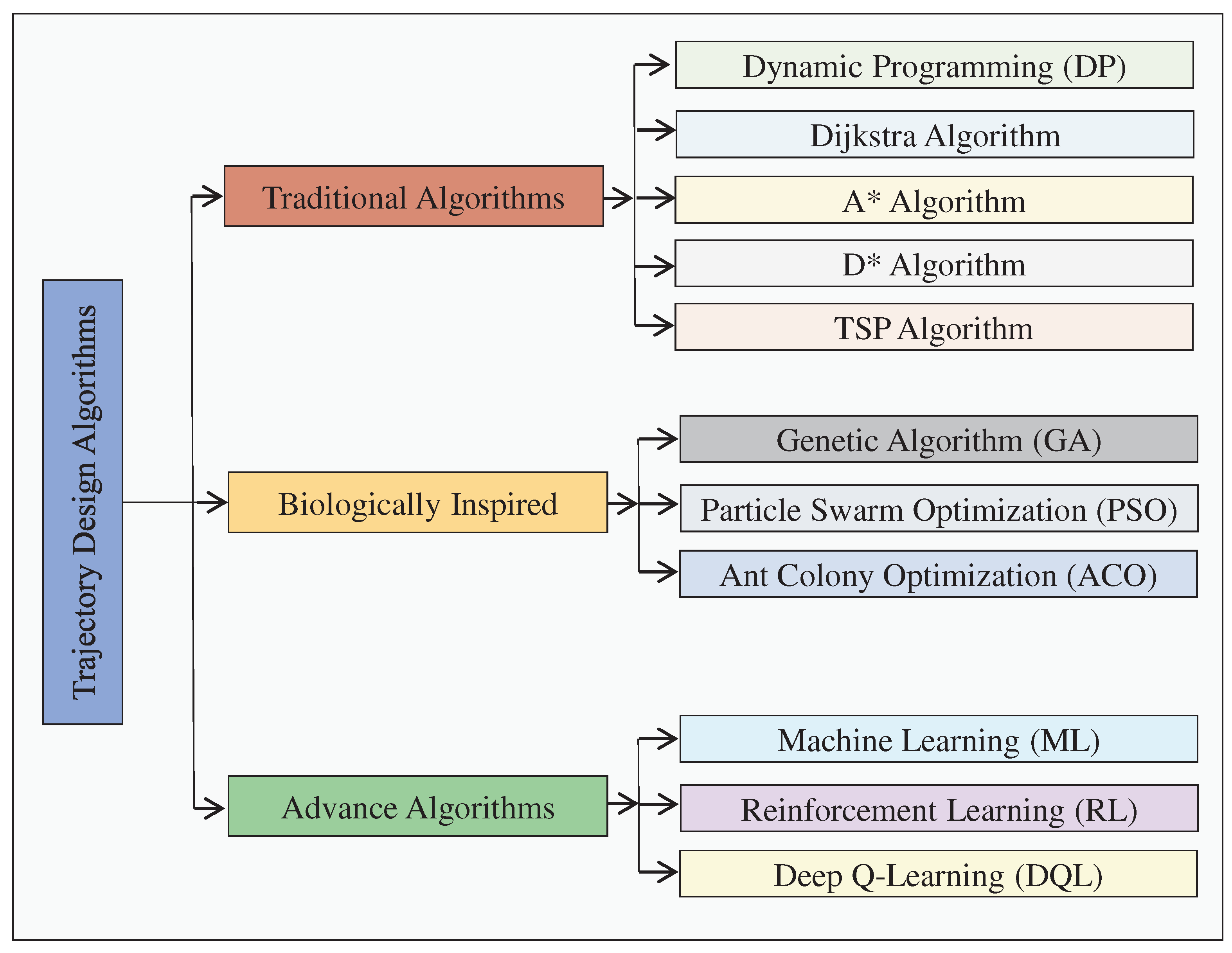
Solving the trajectory design problem is a crucial and leading research topic in AI-enabled wireless UAV networks. This problem involves determining the optimal shortest path for a UAV to cover all targeted hotspot zones (nodes) in a dynamic wireless environment while adhering to time and mission completion constraints. This section discusses various techniques proposed in the literature for UAV trajectory design to optimize communication performance efficiently in a flexible wireless environment. These techniques can be categorized as classical and modern optimization algorithms.
In order to meet time constraints for all ground users, a feasible UAV trajectory was proposed in [
37] using traditional dynamic programming (DP). However, due to an increase in hovering nodes, it may not align with time constraint criteria and may not be suitable for real-time environments. DP was also used to optimize the UAV trajectory in [
38] for accessing multiple wireless sensor nodes (WSNs) and collecting data under time constraints. However, the algorithm was inefficient in recognizing and iterating through repeated grids, requiring high-order gridding for accuracy and resulting in computational complexity. In the study referenced as [
39], the problem of the UAV trajectory has been formulated as a mixed integer linear program (MILP). The trajectory planning is carried out in discrete time steps, where each step represents the dynamic state of the UAV in the environment. The algorithm is designed for offline planning to ensure a feasible trajectory is available before the UAV performs its tasks. However, this algorithm has limitations as it can easily get stuck due to its blind nature and cannot generate long trajectories in a complex environment. The Dijkstra algorithm proposed in [
40] enables UAVs to perform environmental tasks efficiently by using the optimal battery level and reaching the target point in the shortest possible time. However, as the network scale increases, the algorithm takes a long time to provide a solution, making it unsuitable for real-time trajectory planning. The A* algorithm, as discussed in [
41], selects suitable node pairs and evaluates the shortest path for UAVs based on feasible node pairs in a known static environment to address this issue. Although the A* algorithm does not provide a continuous path, it ensures that the shortest path is followed in the direction of the targeted node. However, this algorithm is not practical in a dynamic environment. To overcome this, the D* algorithm and its variants, as reviewed in [
42], are efficient tools for quick re-planning in a cluttered environment. The D* algorithm updates the cost of new nodes, allowing the use of prior paths instead of re-planning the entire path. However, D* and its variants do not guarantee the quality of the solution in a large dynamic environment.
Figure 1.
An overview of existing trajectory design algorithms.
Figure 1.
An overview of existing trajectory design algorithms.
In order to design an effective path planning model for a UAV, the discrete space-based travelling salesman problem (TSP) [
43] is utilized to search for the optimal shortest path for the UAV to travel through a fixed number of cities, with each city only being visited once. The UAV must also return to the starting city within a fixed flight time for battery charging. However, the TSP is an offline algorithm, so when a new city appears in the UAV’s path, the cost of the new city is updated from the starting point, resulting in the entire path being replanned from the start to the new end, which is a major drawback. The TSP is a challenging NP-hard problem and can be difficult to solve in polynomial time unless P=NP. Two approaches are available when dealing with the challenging NP-hard problem in TSP. The first involves using heuristics, such as 2-OPT and 3-OPT, to quickly generate near-optimal tours through local improvement algorithms [
44]. The second approach is to utilize evolutionary optimization algorithms, such as genetic algorithm (GA), particle swarm optimization (PSO), and ant colony optimization (ACO), which have proven to be effective in minimizing the total distance travelled by the salesman in real-world scenarios [
45]. While the GA is a good solution for obtaining an appropriate path for a UAV, it can be relatively slow, making it inefficient for modern path planning problems that require fast performance [
46]. On the other hand, the PSO is good at local optimization and can be used in combination with a GA that is good at global optimization [
47]. The ACO is also effective in solving the UAV path planning problem, but it requires a significant amount of data to find the optimal solution, has a slow iteration speed, and demands much more simulation time [
48]. Therefore, a combination of these algorithms may be necessary to effectively solve the UAV path planning problem.
Reinforcement learning (RL) is a popular AI tool used to tackle complex problems like trajectory design and sum-rate optimization, which are critical challenges due to the continuous environmental variation over time. Indeed, solving mathematical optimization models is only possible when a priori input data is available or requires too high complexity and computational time. Recent studies [
49,
50,
51] proposed optimal trajectory design for UAV using Q-learning to maximize the sum rate [
49], increase QoE of users [
50], and enhance the number and fairness of users served [
51]. However, Q-learning has a drawback in that the number of states increases exponentially with the number of input variables, and its memory usage also increases sharply. Due to the mobility of both ground and aerial users, the curse of dimensionality can cause Q-learning to fail. As a result, solving the trajectory design problem in a large and highly dynamic environment is a challenging task. A machine learning (ML) technique has been proposed in [
52] to optimize the flight path of UAVs in order to meet the needs of ground users within specific zones during set time intervals. Another study in [
53] explored a multi-agent Q-learning-based method to design the UAV’s flight path based on predicting the movement of the user to maximize the sum rate. Additionally, a meta-learning algorithm was introduced in [
54] to optimize the UAV’s trajectory while meeting the uncertain and variable service demands of the GUs. However, these reinforcement learning-based solutions can only work in certain environments and are unsuitable for highly dynamic and unpredictable environments. A deep Q-learning (DQL) algorithm was introduced in [
55] to enable UAVs to provide network service for ground users in rapidly changing environments autonomously. However, the user mobility model in this algorithm is simple and does not account for ground users moving to different positions multiple times, resulting in inadequate trajectory results for different paths.
In this work, we approached the task of designing a UAV trajectory as a TSP with profit problem. To solve this problem optimally offline, we used the 2-OPT local search algorithm. We converted the resulting TSP instances from various examples into graphs and used them to train the UAV. This allowed the UAV to capture the TSP graphs’ properties and form a world model consisting of a hierarchical and multi-scale representation. With this model, the UAV can realise the TSP’s strategy for solving the problem and implicitly discover the objective function. Our approach allows the UAV to deduce optimal routes when facing a new realization based on its belief encoded in the world model. This helps the UAV determine the best solution when there are deviations between what it knows and what it sees.
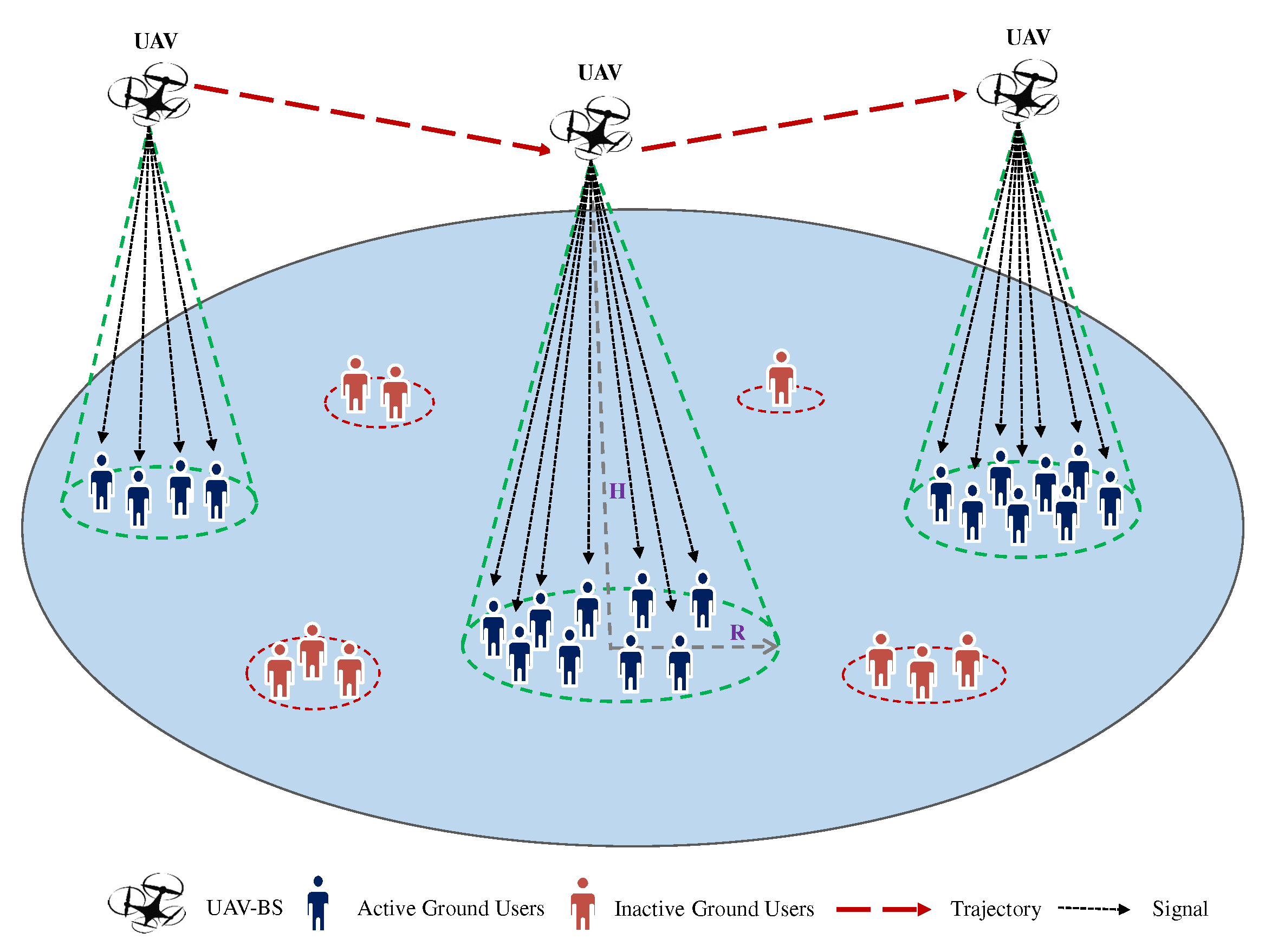
3. System Model and Problem Formulation
Consider a UAV-assisted wireless network, as shown in
Figure 2, with a single UAV acting as a flying base station (FBS) to serve
U ground users (GUs) distributed randomly across a geographical area and requesting uplink data service. GUs that demand the data service are introduced as active users; others are so-called inactive users, as illustrated in
Figure 2. It is assumed that the GUs are partitioned into
N distinct groups, each of which is defined as a hotspot area. The UAV’s mission is to fly from a start location, move towards hotspots with high data service requests, and then return to the initial location within a time period
T for battery charging. Thus, the UAV’s initial (
) and final (
) locations are predefined, represented by
. It is important to note that the variable
T is directly proportional to the number of available hotspots (
N). As
N increases,
T also increases and vice versa. The UAV adjusts its deployment location at each flight slot according to the users realization forming a trajectory denoted by
. The sequence tracing UAV’s travels among the available hotspots during the flight time duration is given by
, where
is the
nth hotspot served by the UAV and
is the total number of the hotspots served along the trajectory. Let
be the set of all possible trajectories the UAV might follow and
be the probability to move toward hotspot
after being in
(visited at time
) where
is the remaining time to go back to the original location after serving
. The set of available hotspot areas is denoted as
and GUs across the total geographical area are denoted as
, where
is the set of users belonging to the
nth hotspot and each GU belongs to a single hotspot where the coordinate of each GU is given by
. Each hotspot
n is characterized by its center
, radius
representing the coverage range and the average data rate
that depends on the number of active users in hotspot
n where
such that
.
To capture the dynamic nature of the network, the UAV flight time (T) is discretized into a set of M equal time slots where the length of each time slot is . Due to its short duration, the UAV’s location, uplink data requests and channel conditions are considered fixed in each t. Further, in the considered network, the UAV assigns a set of uplink resource blocks (RBs) to serve the active GUs in a specific hotspot (one RB for each active GU) who transmit their data over the allocated RBs using the orthogonal frequency division multiple access (OFDMA) scheme.
In our network, the air-to-ground signal propagation is adopted and a probabilistic path loss model subject to random line-of-sight (LoS) and Non-line-of-sight (NLOS) conditions is considered [
56]. Thus, the channel gain between GU (
) and UAV (
u) can be expressed as:
where
,
is the carrier frequency,
c is the speed of light,
is the path loss exponent,
and
are the LoS and NLoS probabilities, respectively.
and
are additional attenuation factors to the free-space propagation for LoS and NLoS links. The distance between GU (
) and the UAV at time slot t is given by:
The average achievable data rate of the set of users in hotspot
n is calculated as:
where
is the bandwidth of the RB allocated to GU (
),
is the transmit power of GU (
), and
is the power spectral density of the additive white Gaussian noise (AWGN).
In this work, we focus on UAV trajectory design that can maximize the total sum-rate in the cell. Therefore, our optimization objective can be formulated as:
Constraint (4b) indicates that each GU belongs to a specific hotspot. (4c) implies that the UAV must go back to the initial location before
T, where
T is directly proportional to
N. If
N increases,
T will also increase; if
N decreases,
T will also decrease. Furthermore, (4e) represents the sum-rate requirement for each GU and (4f) depicts the power allocation constraint. It is worth noting that in this paper, the number of hotspots remains constant in a certain mission (realization). No new hotspots emerge nor do any existing hotspots disappear while the UAV is solving a specific realization.
The symbols used in the article and their meanings are summarized in Table 1. 5. Numerical Results and Discussion
In this section, we will thoroughly assess how well the proposed framework performs in designing a trajectory for the UAV that effectively allows it to attain the highest total sum-rate possible with the cell. In our simulations, we are looking at a situation where a single UAV is providing service to several users who are located in different hotspots across a square geographic area of
. The main simulation parameters are listed in
Table 2. It is assumed that the altitude of the UAV remains constant at
m [
59]. Throughout the training process, we place a total of
hotspots in various random locations across the geographical area. The frequency of user presence and requests within each hotspot adheres to the Poisson distribution. We generate a training set
that consists of
M examples corresponding to different realizations. Each realization (
m) consists of 7 hotspots picked randomly from the
N total hotspots and the users’ requests in each hotspot are generated following Poisson distribution. The TSPWP method is used to solve the
M examples in
, generating
M trajectories (TSPWP instances) and
M sequences of the order in which the hotspots are visited, which are saved in
and
, respectively.
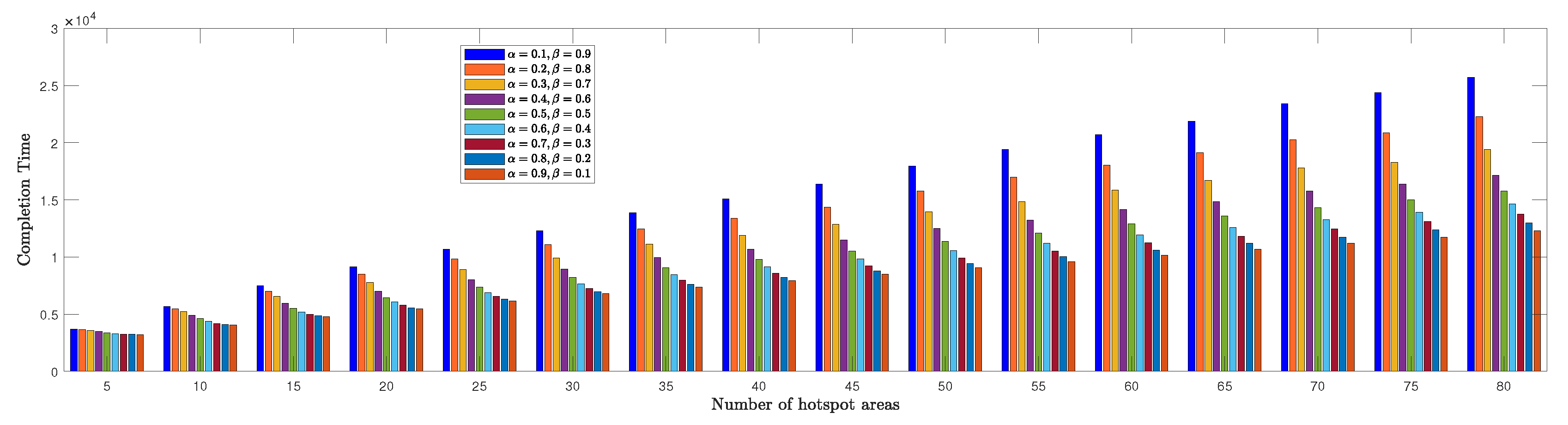
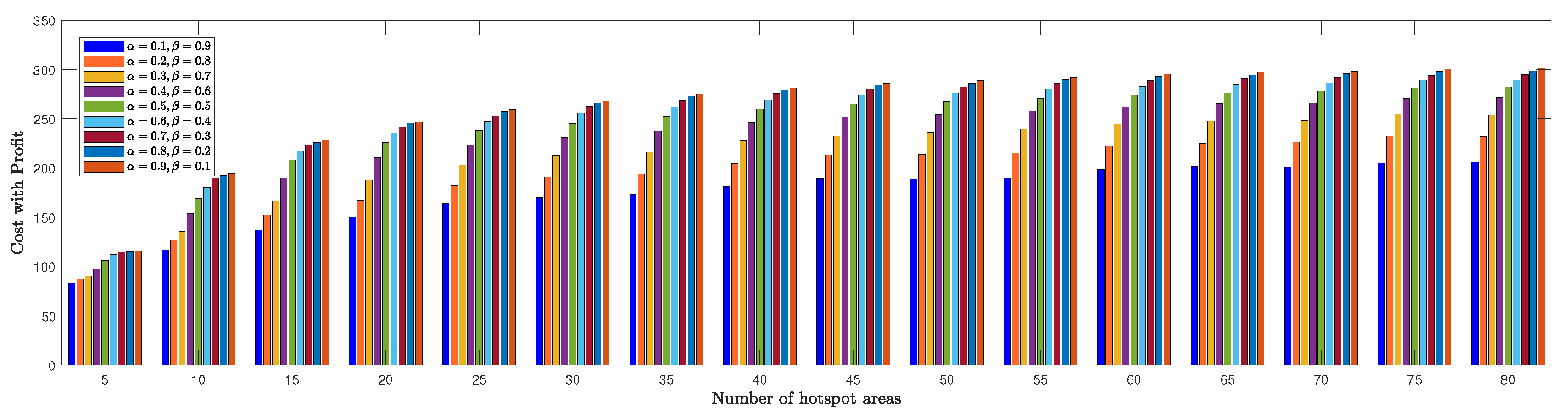
We evaluate the TSPWP performance by conducting a thorough analysis of completion time and cost with profit metrics for different numbers of hotspots to determine the optimal
and
values mentioned in (
6a). In
Figure 8, we see how the completion time of TSPWP is impacted by various
and
values, as well as changes in the number of hotspots. Meanwhile,
Figure 9 displays the TSPWP performance in terms of cost with profit for different
and
settings while also altering the number of hotspots. It is evident from
Figure 8 that the completion time increases as the number of hotspots increases, as having more hotspots makes the trajectory longer. It is worth noting that the cost with profit rises gradually as the number of hotspots increases, especially between five and twenty, as shown in
Figure 9. However, after twenty hotspots, the cost with profit slightly rises due to the reduction of profit (i.e., the accumulated sum-rate) from the cost (i.e., the travelling distance between the hotspots). This effect becomes stable for higher hotspots and has a minimal impact on the overall cost with profit. By analyzing the data, we have found that the ideal
and
values for achieving both minimal completion time and maximum profit with cost are
and
, respectively. Therefore, we will use these values when implementing TSPWP.
To solve each realization
m, we use the TSPWP with
and
, as previously mentioned. The TSPWP gives us the solution (i.e., the TSPWP instance), which includes the trajectory and the order of the hotspots to visit. We then create two sub-dictionaries from the
M TSPWP instances. The first sub-dictionary comprises all the words that make up the TSPWP trajectories, which use letters to represent the hotspots (explained in
Section 4.2.1). The second sub-dictionary contains all the tokens that show the path between two adjacent letters (hotspots), as described in
Section 4.2.1.
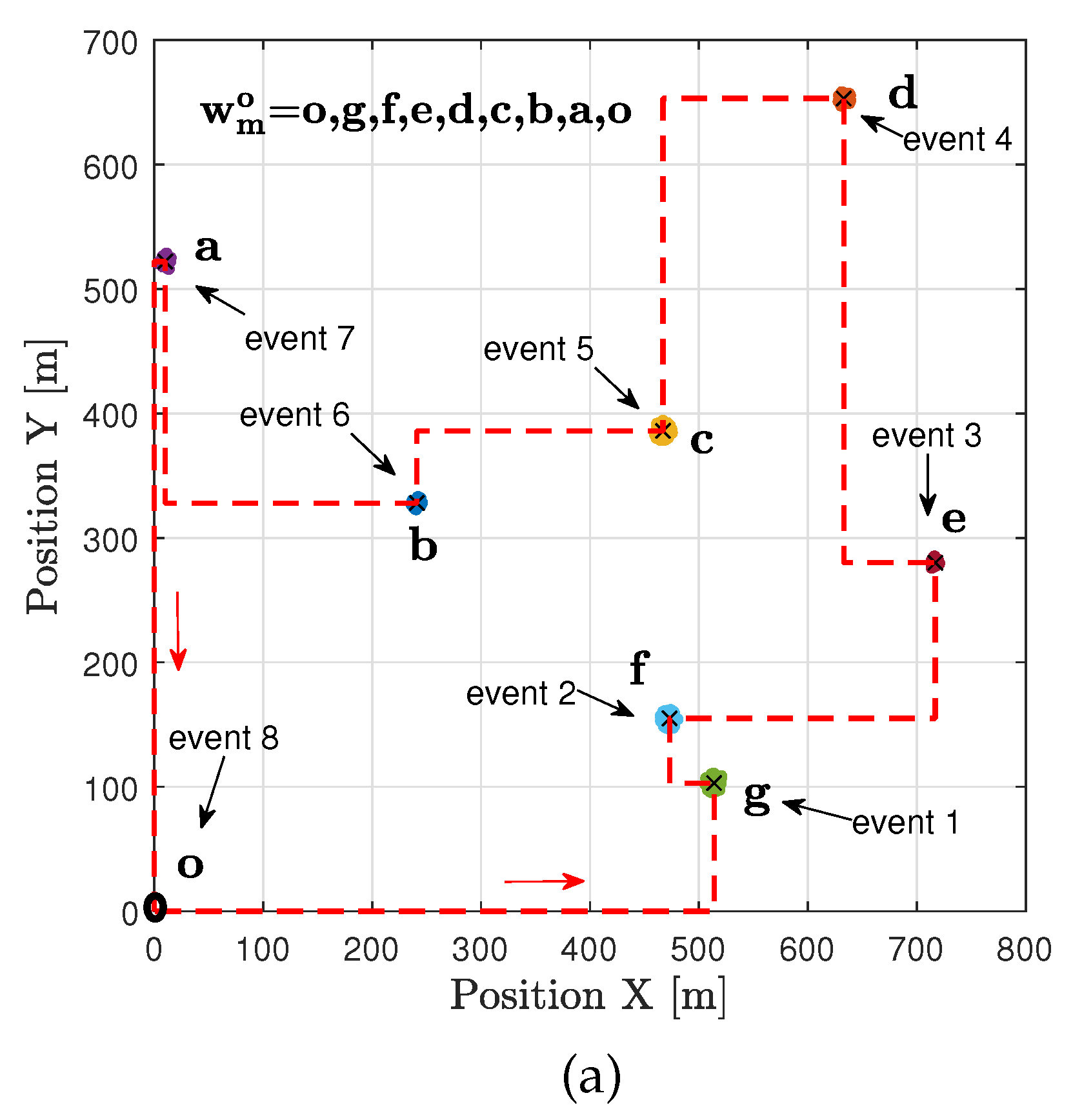
In the example shown in
Figure 10-(a), there is one realization with seven hotspots scattered randomly in the geographic area. Each hotspot has some active users who need resources. The goal is to start from the initial station at the origin, visit each hotspot only once, serve the users there, and then return to the origin within a specific time frame. Give the realization depicted in
Figure 10-(a) to the TSPWP method. It will produce the TSPWP instance, which includes the trajectory and the order of visited hotspots, as demonstrated in
Figure 10-(b). To create the global dictionary, TSPWP instances from
M examples are utilized, which include sub-dictionary 1 and sub-dictionary 2. Sub-dictionary 1 records the events that take place during the flight mission, such as when the UAV reaches hotspot
j after departing from hotspot
i. The process of detecting different events and forming a word representing the sequence of hotspots served during a flight mission is illustrated in
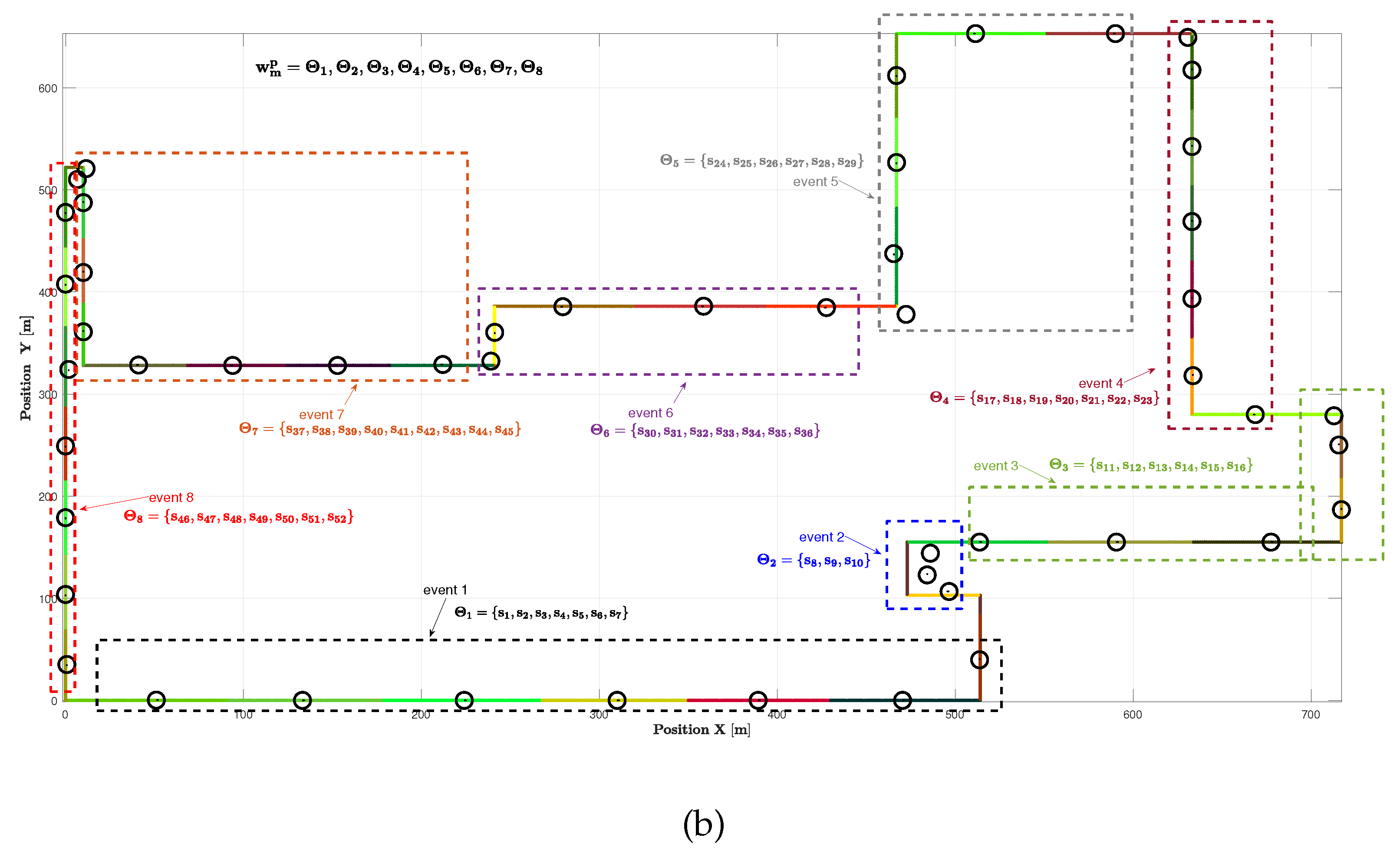
Figure 11-(a). In this process, hotspots are considered as letters, and the full trajectory represents a word. The first event occurs after reaching the letter "g" starting from "o". The second event occurs after reaching "f" from "g", and so on for the third and subsequent events. The final event occurs when the UAV returns to the initial location, represented by the letter "o", starting from "a". Therefore, the word describing the mission is defined as "w=o,g,f,e,d,c,b,a,o". In contrast, if we cluster the trajectory data (which includes positions and velocities), we can see the resulting clusters in
Figure 11-(b). Each event that was previously detected will be linked to the set of clusters that form the path from one letter to another, as illustrated in
Figure 11-(b). A token is created for each event, and all the tokens are combined to form the resulting word, which represents the path followed during the mission. Throughout the training process, the same procedure is done for
M examples in order to create the words that indicate the sequence of targeted hotspots and the words that describe the movement from one hotspot to the next. These two sets of words are coupled statistically to create a world model that the UAV will use during the active inference (testing) process to plan a suitable trajectory based on encountered situations (realizations).
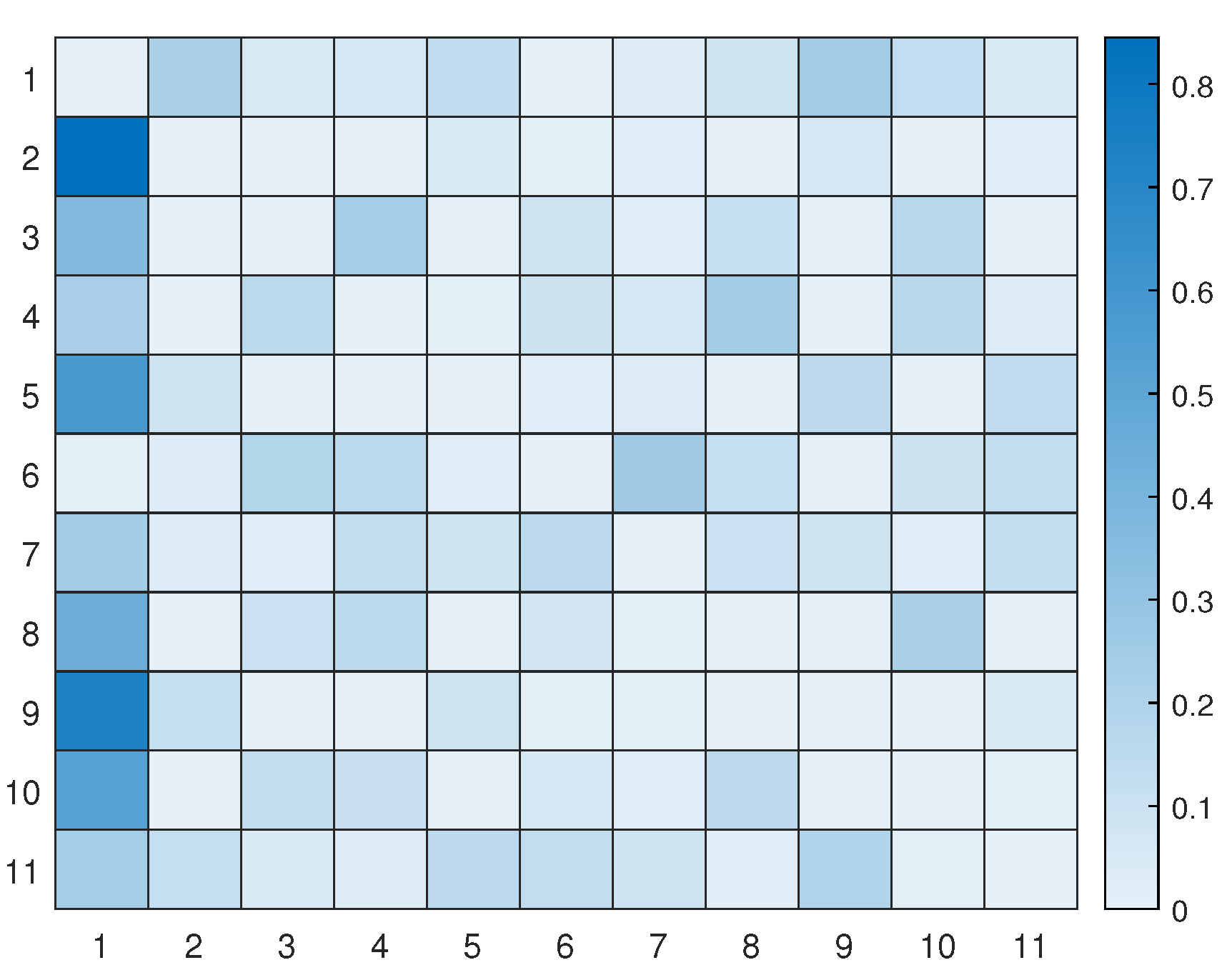
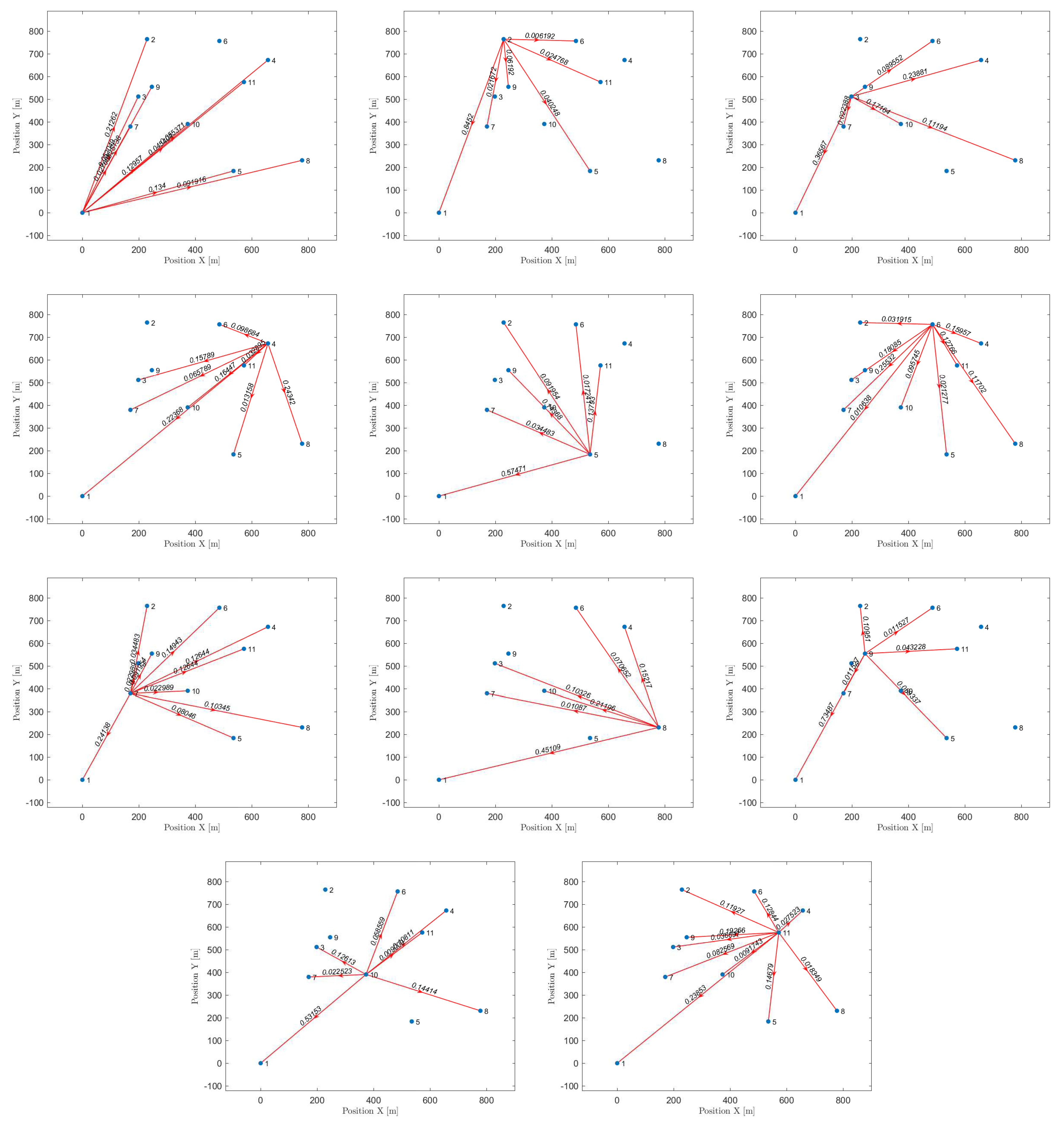
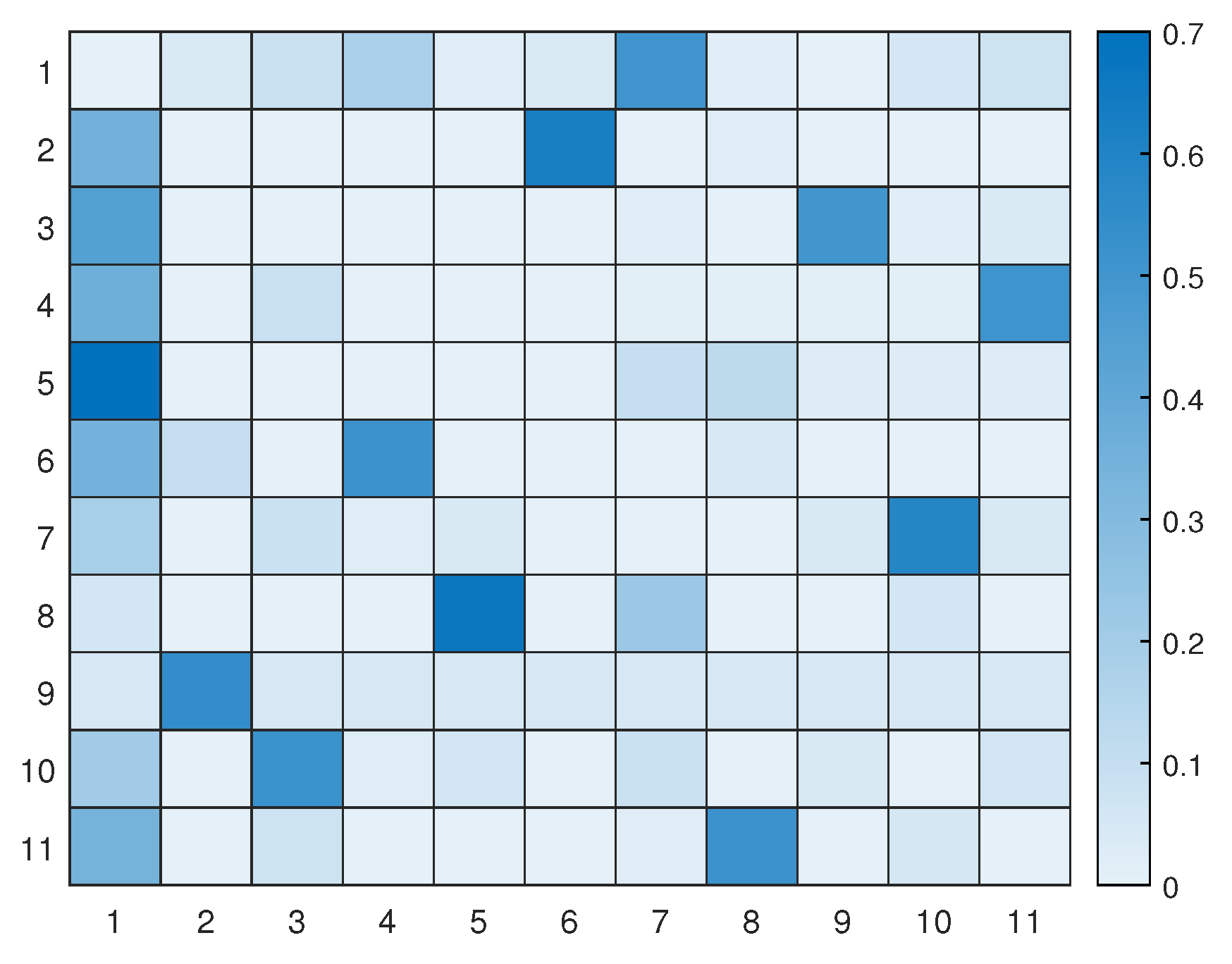
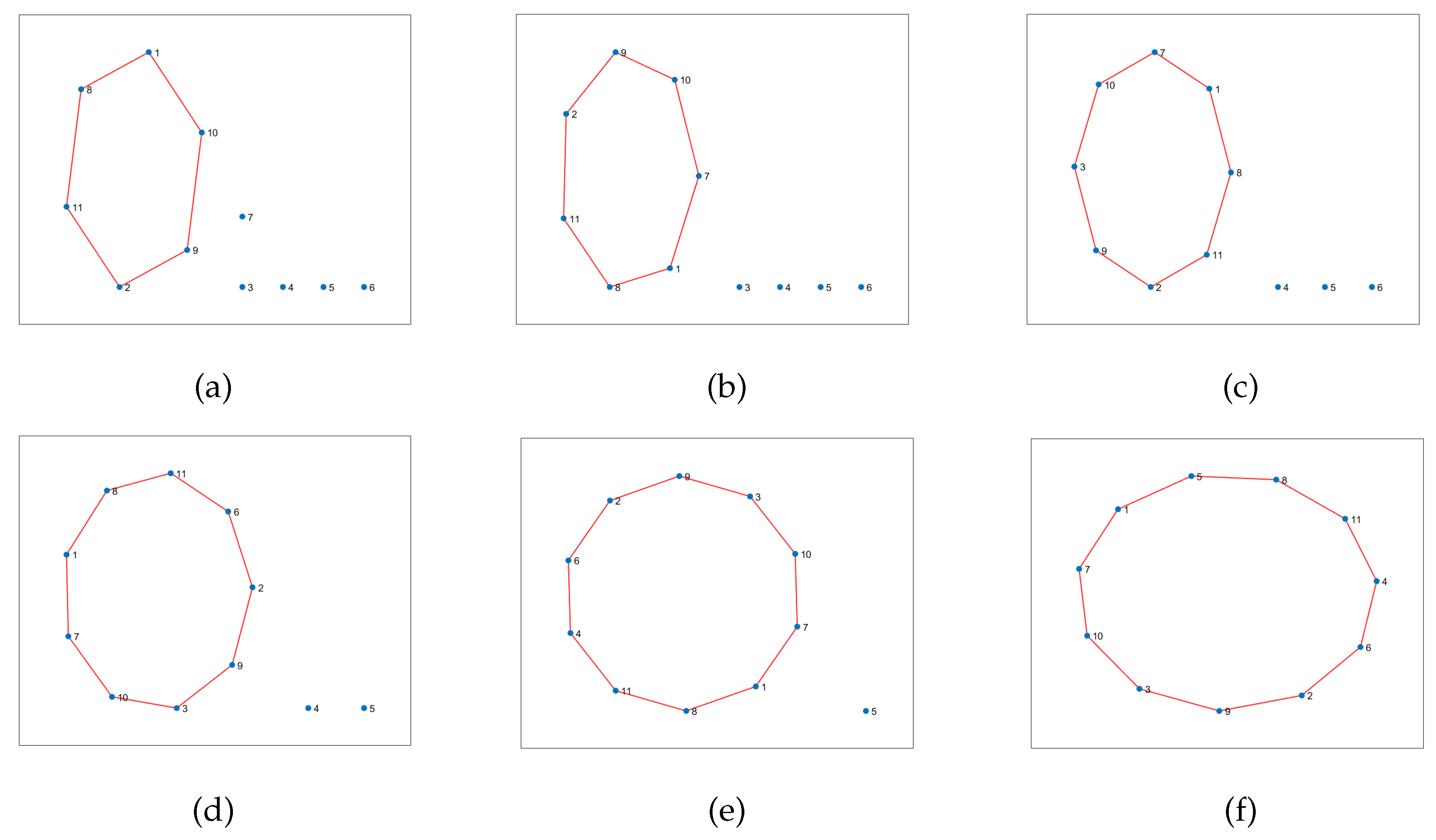
Let’s take a look at how a UAV, using active inference, completes a mission. For instance, suppose there are 10 hotspots in a given testing scenario. The UAV will rely on the world model, made up of two sub-dictionaries, that it learned during training to successfully navigate the testing scenario. Firstly, the UAV examines the current letters and matches them against the words listed in sub-dictionary 1. This process helps to establish how closely they resemble each other in the current testing scenario. After that, the UAV chooses the closest word from the dictionary and uses it as a starting point to create the initial graph. The goal is to expand the graph by adding new letters to form a word that enables an efficient trajectory to reach all hotspots (letters) and serve their users as quickly as possible. To achieve this, one letter is added during each iteration, with the number of iterations depending on the size of the reference graph and the number of new letters required to include all available letters in the current configuration. To update the graph and make it directed, one link must be removed from the reference graph, and two links must be added to the newly added letter or node at every iteration. The transition matrix, which encodes the probabilistic relationships among the letters, is crucial at each step and can be found in
Figure 12. This matrix determines whether it is possible to transition from a letter already present in the reference graph to the newly added letter. The transition matrix is learned after solving
M examples during training and allows for the generation of words based on probability entries.
Figure 13 displays all the available pathways from the 11 hotspots to other letters. Depending on the current letter, you can determine which letters are reachable. For instance, if you start at letter 1 (the initial location), you cannot transition to letter 6, but you can transition to the other 9 letters with varying probabilities. Similarly, if you reach letter 2, you cannot go towards letters 3, 4, 8, and 10, and so on. It’s worth noting that the probability values provided by the world model prevent unnecessary transitions that won’t help the UAV reach its desired goal.
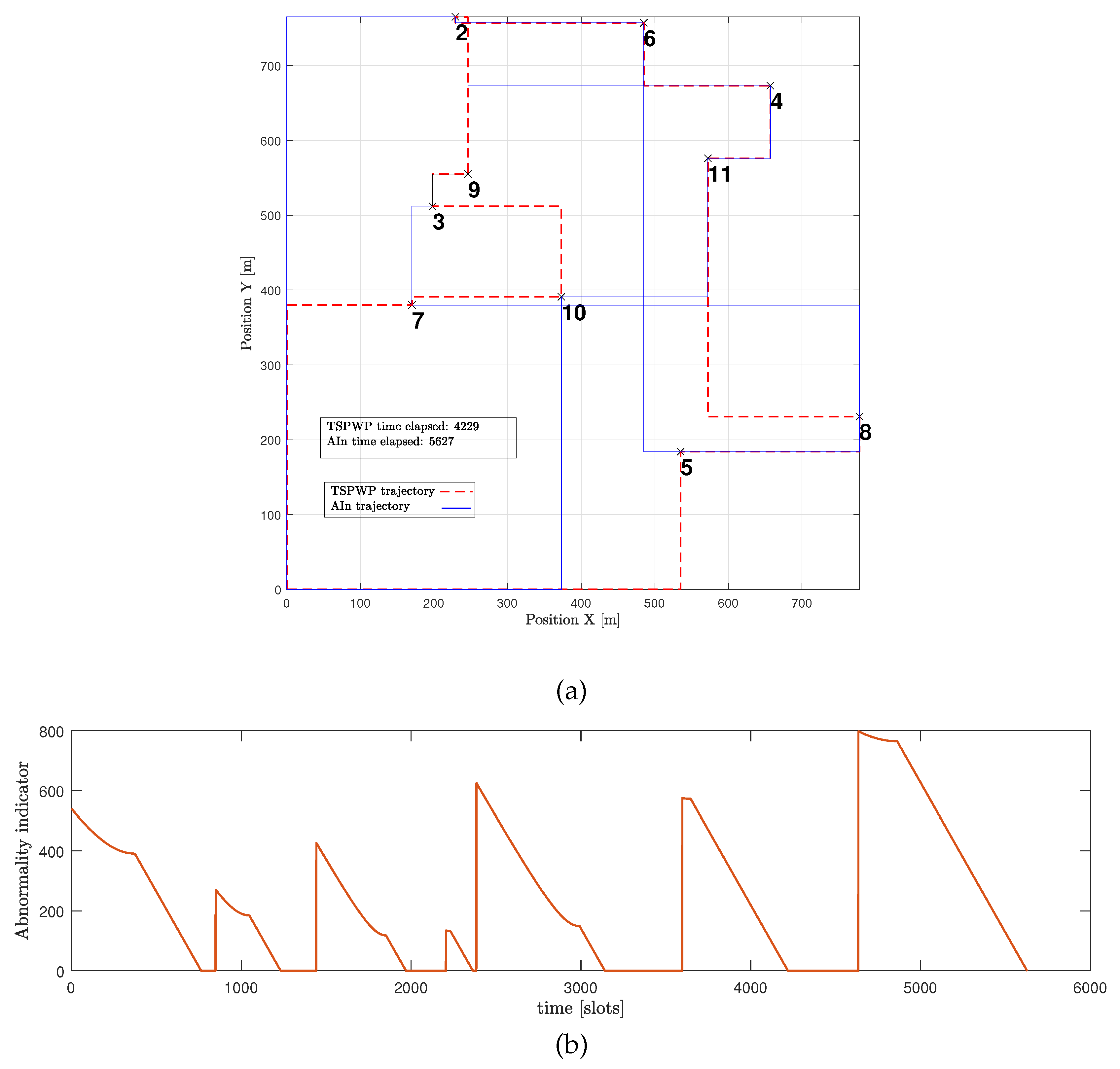
The example shown in
Figure 14-(a) expresses a word generated by the UAV through the proposed method but before it fully converged. The generated word is not optimal as it contains hotspots in the wrong order, which causes the mission to take longer and increases the time needed to return to the initial location. Furthermore,
Figure 14-(b) shows that the UAV detected abnormalities during most of the operation events. When the UAV detects abnormalities in its position, it is usually because it is not close enough to its goal. The UAV aims for a specific letter that represents its target. It is drawn towards that goal and then assesses its distance from the goal after each continuous action that represents its velocity. If there are any abnormalities, the UAV can use prediction errors to correct its actions and adjust its path to reach the targeted letter. For instance, during event 1, the UAV perceived high abnormalities and prediction errors while it was still far from the intended letter, with the starting letter being 1 and the targeted being 10. However, utilizing the prediction error, the UAV was able to adjust its actions and reach the destination faster. This resulted in the abnormality signals gradually decreasing until they reached zero, indicating that the UAV had indeed arrived at the targeted destination.
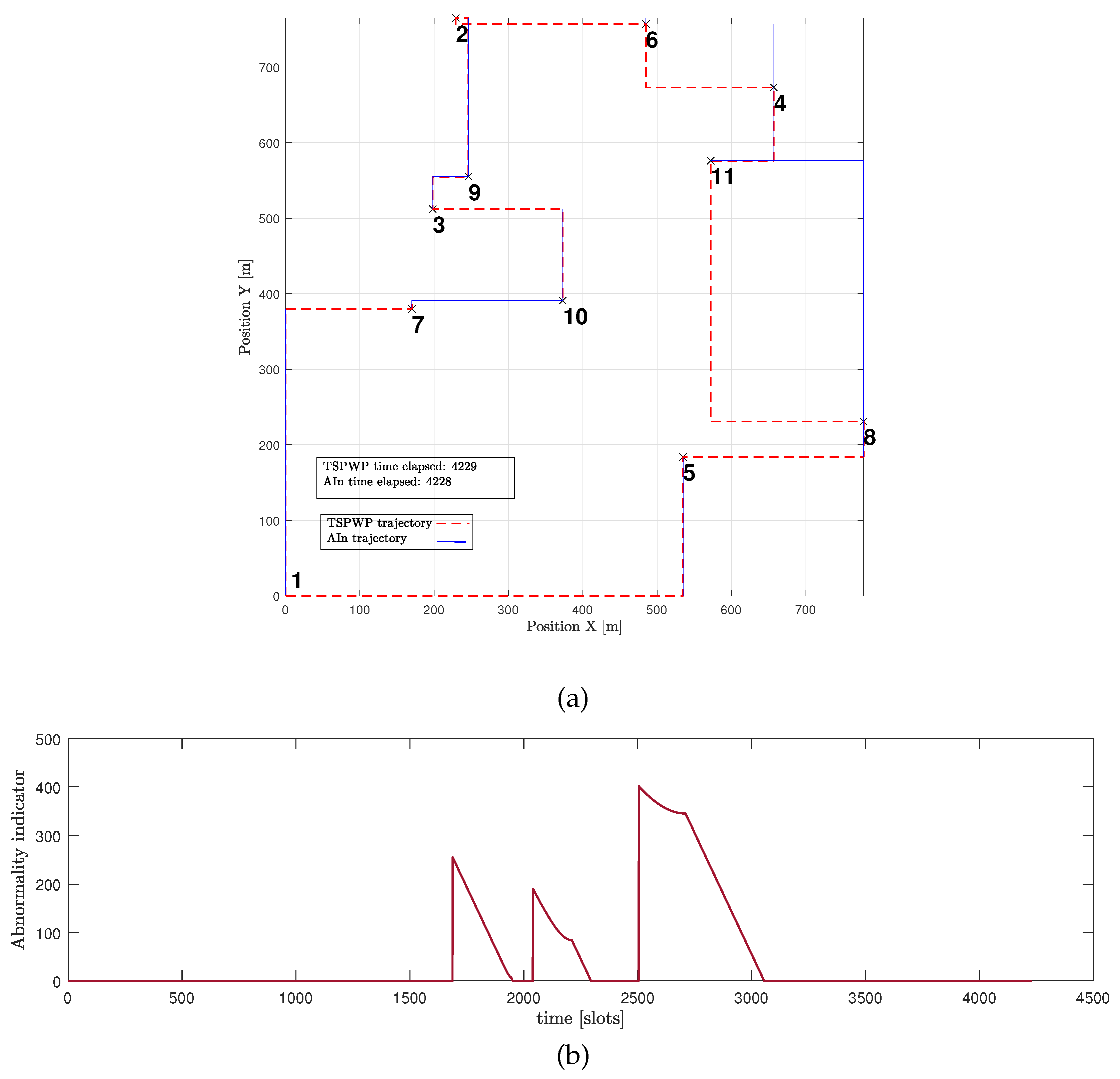
Figure 15-(a) presents another example of a word created by the UAV after convergence. The proposed approach enabled the UAV to design a trajectory that is comparable to the one generated by the TSPWP, with a similar completion time. It is noticeable that the UAV was successful in reducing high abnormalities in various events, as depicted in
Figure 15-(b), compared to the example shown before convergence. This reduction is due to the UAV’s ability to differentiate between similar events encountered before and deduce the optimal path immediately.
Figure 16 displays the updated transition matrix for 11 letters, which includes corrected probability entries detailing the possible transitions between the available letters. This updated transition matrix was rectified using the one exhibited in
Figure 12.
The process of creating new words is shown in
Figure 17. The first step is to select a reference word from the dictionary by comparing the available letters in the current realization with the encoded words in the dictionary. The UAV selects the word with the highest probability of being a match based on the similarity of its letters to the available ones. The matching letters from the most similar word are then used as a reference for creating new words. This reference word is represented graphically as a closed loop, as demonstrated in
Figure 17-(a). The initial graph is expanded by adding one letter at a time, as illustrated in the figure. This insertion approach dramatically reduces the likelihood of the UAV needing to determine the optimal visiting order. For instance, if there are 11 nodes to visit, and each node must be visited only once, there are approximately
(
million) possible word combinations to find the correct order, which is a time-consuming and challenging task, particularly when using a trial-and-error method. However, the proposed word formation mechanism decreases the number of possible combinations from
to just 40. In
Figure 17-(a), there are 6 potential ways to create a new word by adding the first letter to the reference graph.
Figure 17-(b) has 7 possible words, while the other graphs feature 8, 9, and 10 options. The total number of combinations is 40, which is calculated by adding the number of edges in each graph.
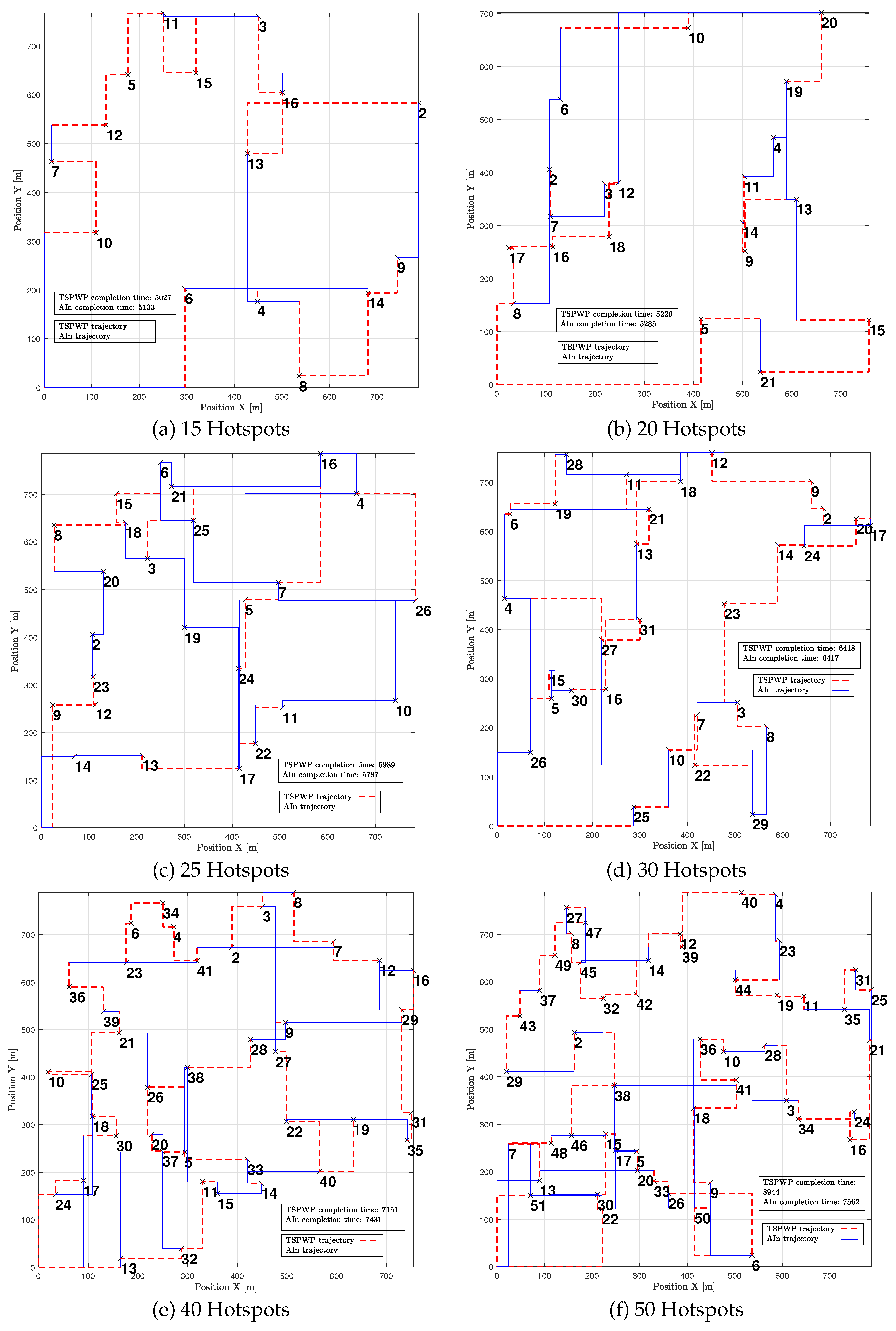
In
Figure 18, you can see different examples with different numbers of hotspot areas. The trajectories generated by the proposed method (AIn) and the TSPWP using 2-OPT are also shown, along with their respective completion times. It is evident that the proposed approach produces alternative solutions when compared to the TSPWP. In some cases, it also results in a quicker completion time as shown in
Figure 18-(c)-(d)-(f). This highlights the adaptability of the proposed method in deriving reasonable solutions that surpass those of the TSPWP.
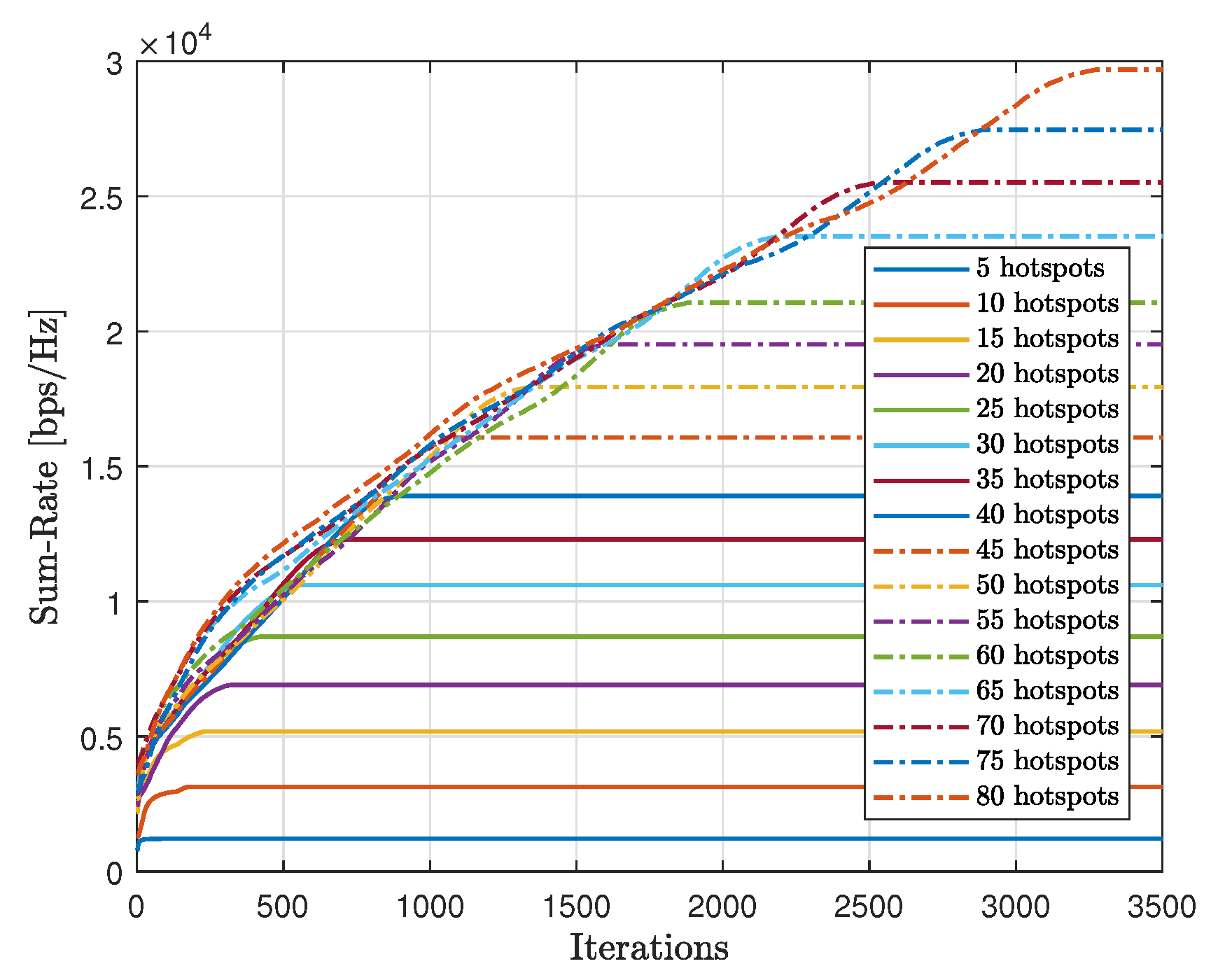
In
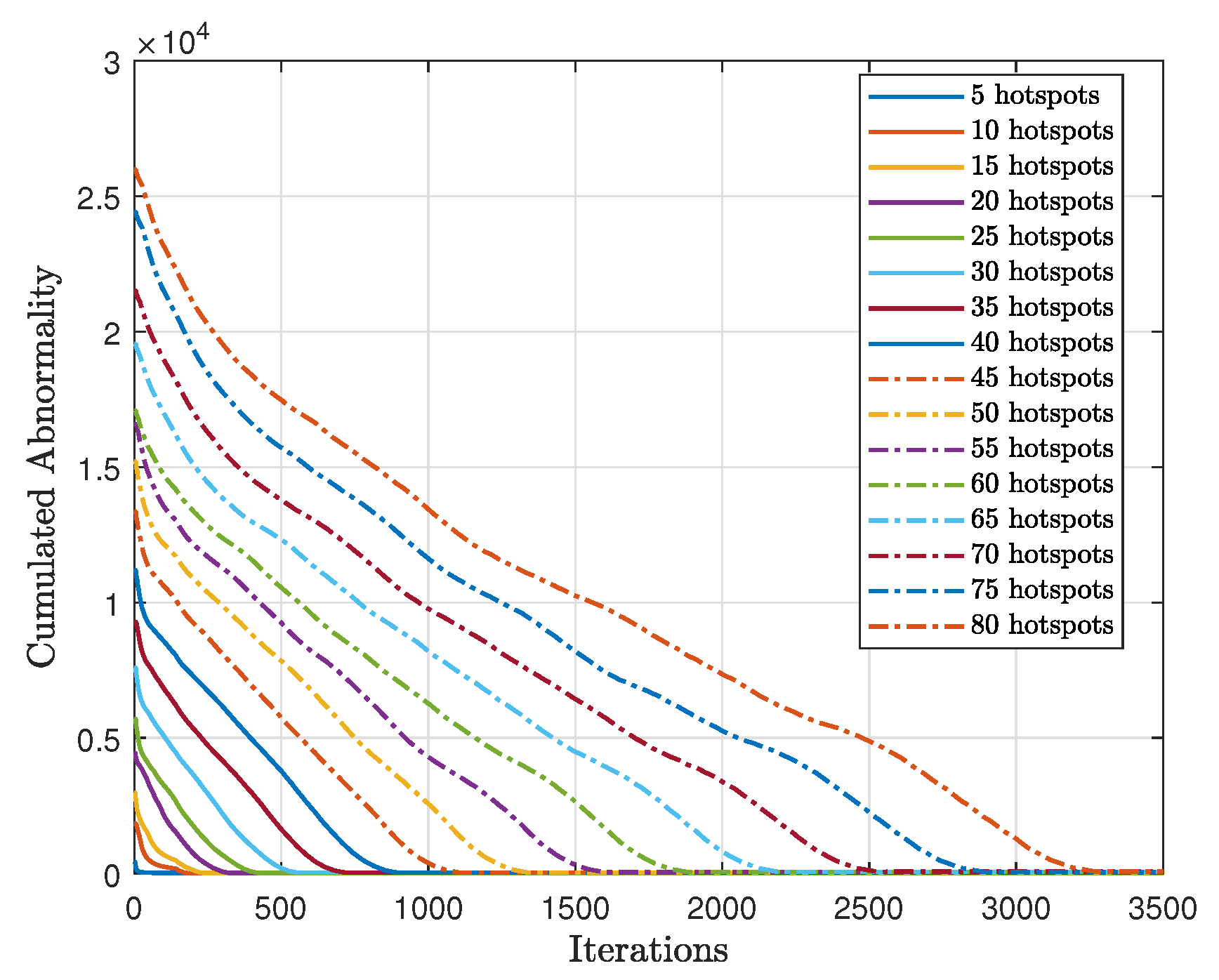
Figure 19, we tested the scalability of the proposed method (AIn) and compared the cumulative sum-rate convergence for various hotspots. We observed that as the number of hotspots increased, the cumulative sum-rate also increased. However, it took longer to find the best solution and reach convergence with more hotspots. This is because there were more possible generated words to test, which takes longer. In contrast,
Figure 20 shows the cumulative abnormality for various numbers of hotspots. The trend of the cumulative abnormality is contrary to the cumulative sum-rate. It begins with high values and gradually decreases until reaching quasi-zero at convergence. As the number of hotspots increases, the time taken to reach quasi-zero abnormality also increases.
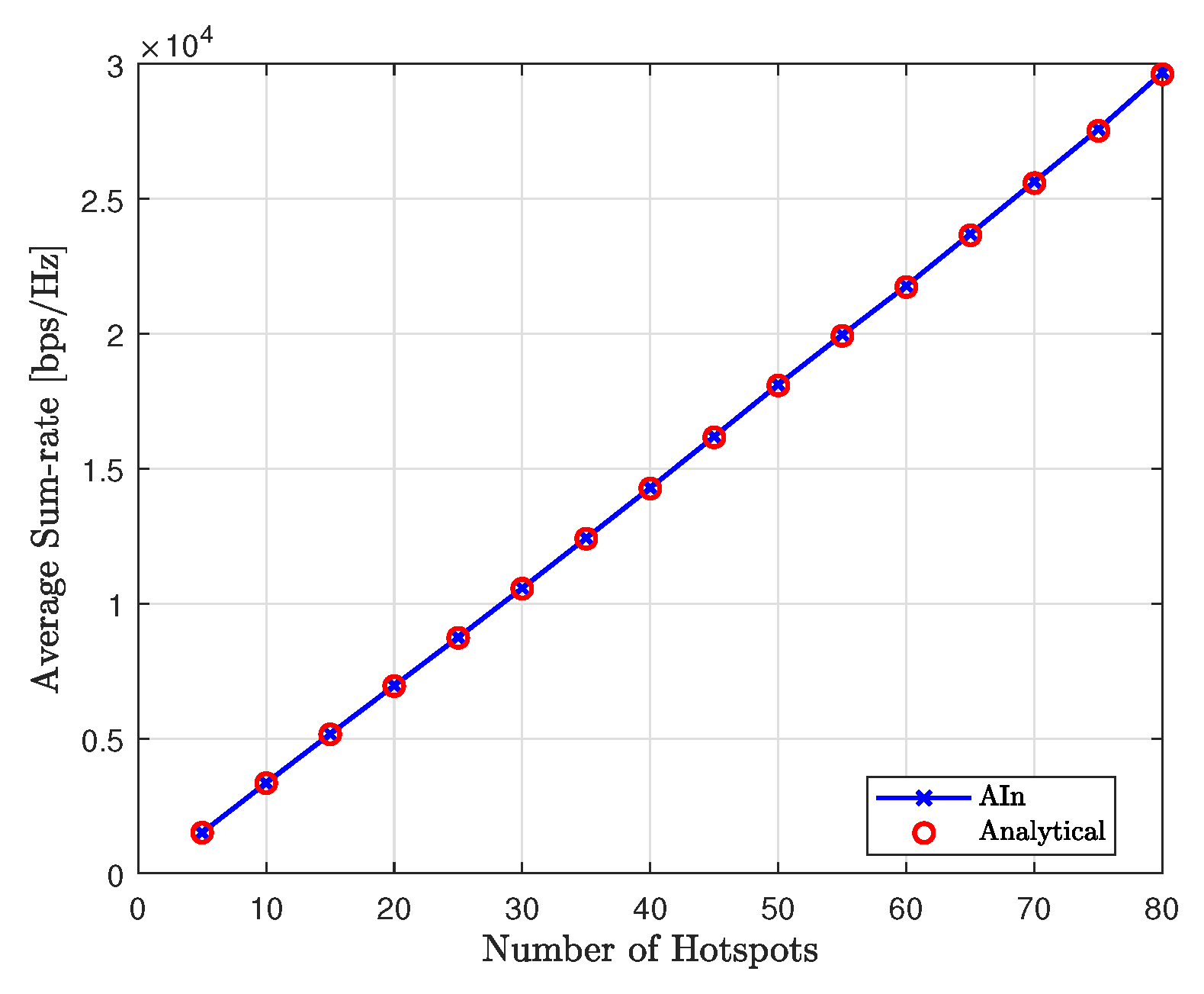
In
Figure 21, we can see the average sum-rate of the proposed method at convergence for various numbers of hotspots, compared to the analytical sum-rate. It’s clear that the proposed approach achieves the expected analytical sum-rate after convergence, regardless of the number of hotspots.
5.1. Comparison with modified Q-learning
In this section, we are comparing the performance of the proposed approach (AIn) with a modified version of the conventional Q-learning (QL) [
60]. To ensure a fair comparison, the modified-QL follows the same logic as the proposed approach. Thus, the modified version uses two probabilistic q-tables - one for mapping discrete states (hotspots) to discrete actions (targeted letters) and another for mapping discrete environmental regions to continuous actions (velocity). Unlike traditional QL, the q-values in these tables are represented as probability entries that range between 0 and 1.
As in the proposed method, we can see that the discrete states stand for the letters, and the discrete environmental regions stand for the clusters. In addition, the available letters during a specific realization make up the discrete action space, while four continuous actions representing different directions (Up, Down, Left, Right) make up the continuous action space. The reward function in modified-QL was designed using the TSPWP instances. If the modified-QL behaves similarly to the TSPWP, it will receive a positive reward (+1). Otherwise, the reward is zero.
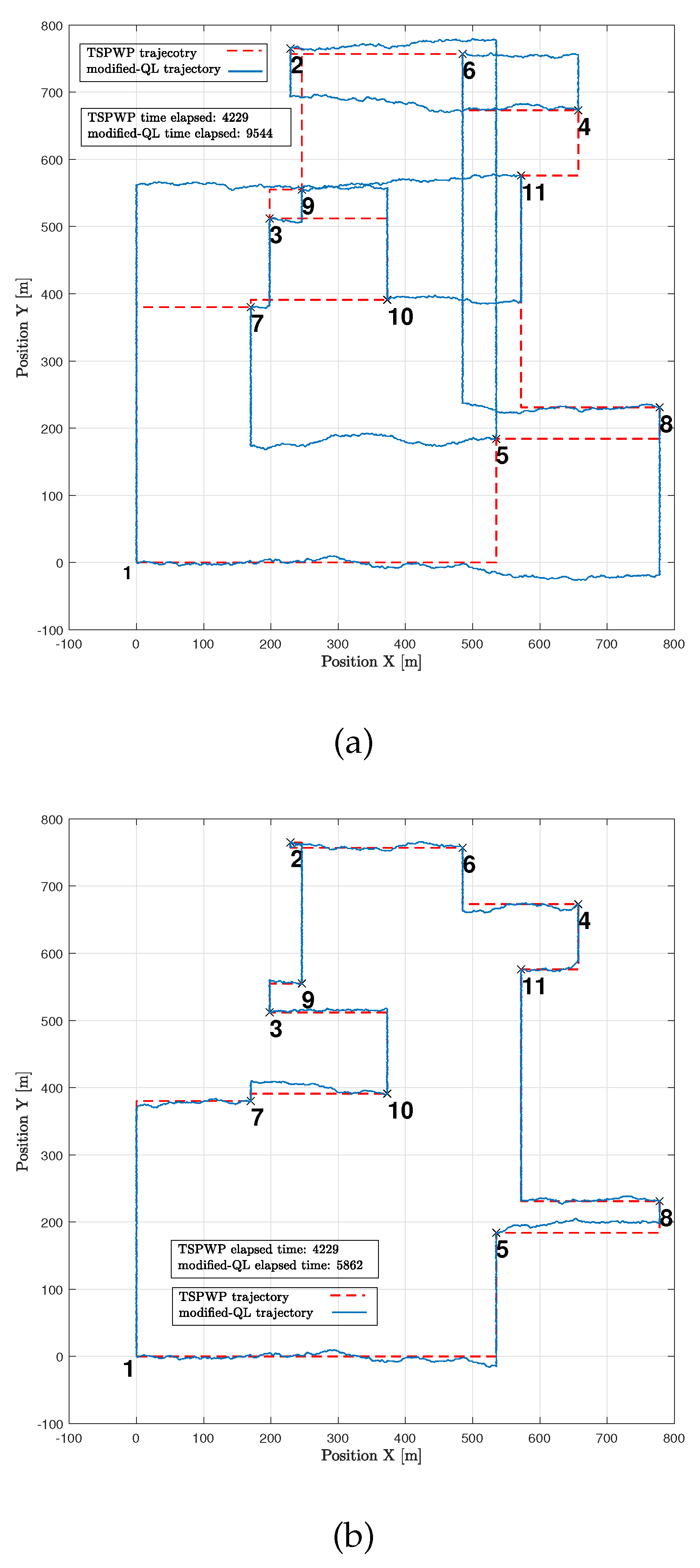
In
Figure 22, an example similar to the one in
Figure 10-(a) is shown to illustrate how the modified-QL algorithm solved the mission both before and after convergence. Prior to convergence (
Figure 22-(a)), the modified-QL selected the wrong order of letters to visit, leading to a longer completion time. However, after convergence (
Figure 22-(b)), the algorithm discovered the correct order of letters, resulting in a reduced completion time, although it still fell short of the completion time achieved by the TSPWP due to a slight deviation from the correct path. It’s important to note that the agent’s movement was limited to travelling between two boundaries to simplify the process, which reduced the environmental states it could discover. Consequently, the modified-QL agent’s movements were guided by the TSPWP through positive and zero rewards.
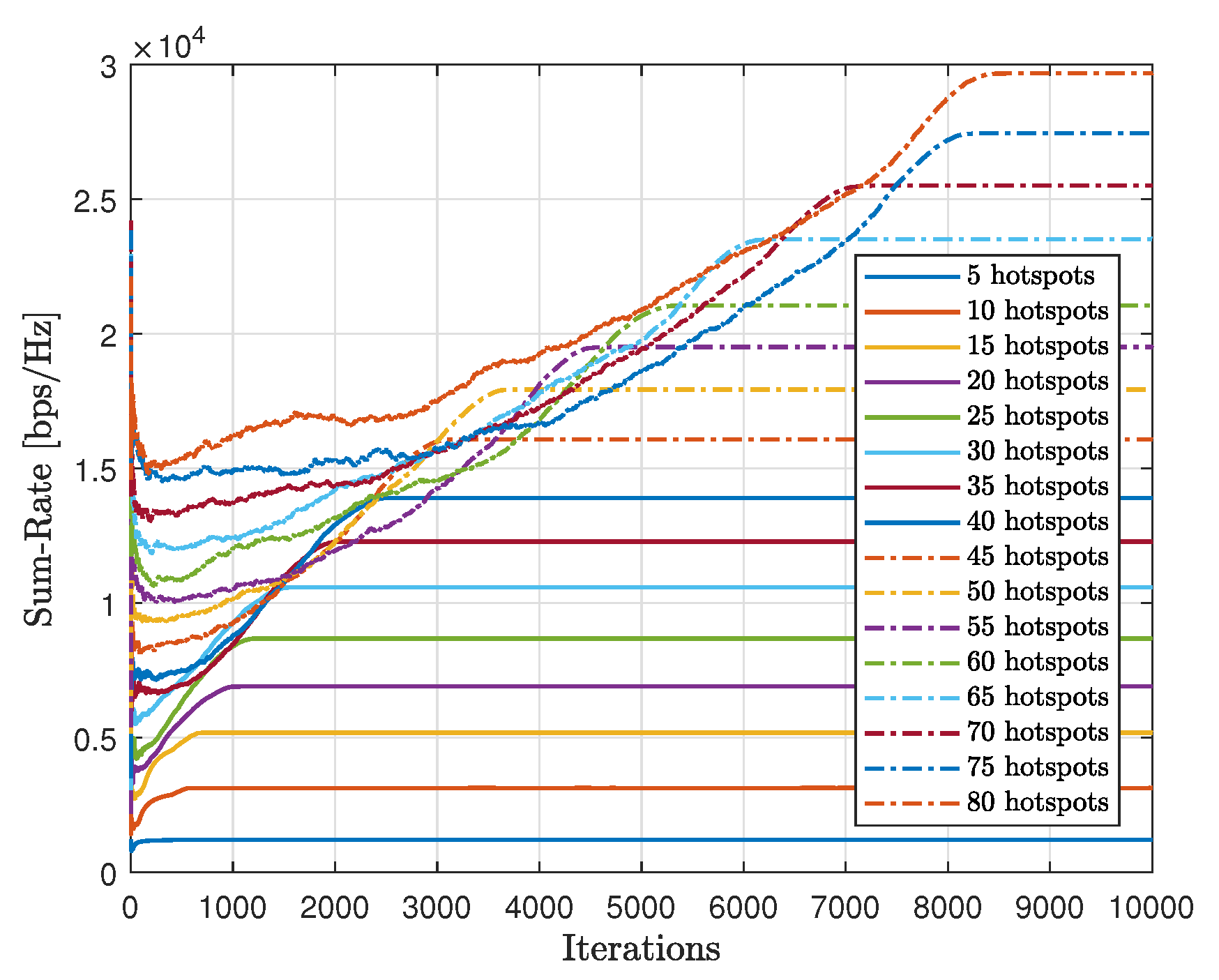
Figure 23 displays the gathered sum-rate in relation to the number of iterations, providing insight into the modified-QL’s overall performance and scalability with varying numbers of hotspots. It is clear that as the number of hotspots increases, both the collected sum-rate and the time to converge will also increase with the modified-QL. Despite requiring more iterations, the modified-QL achieves the same sum-rate at convergence as the proposed method.
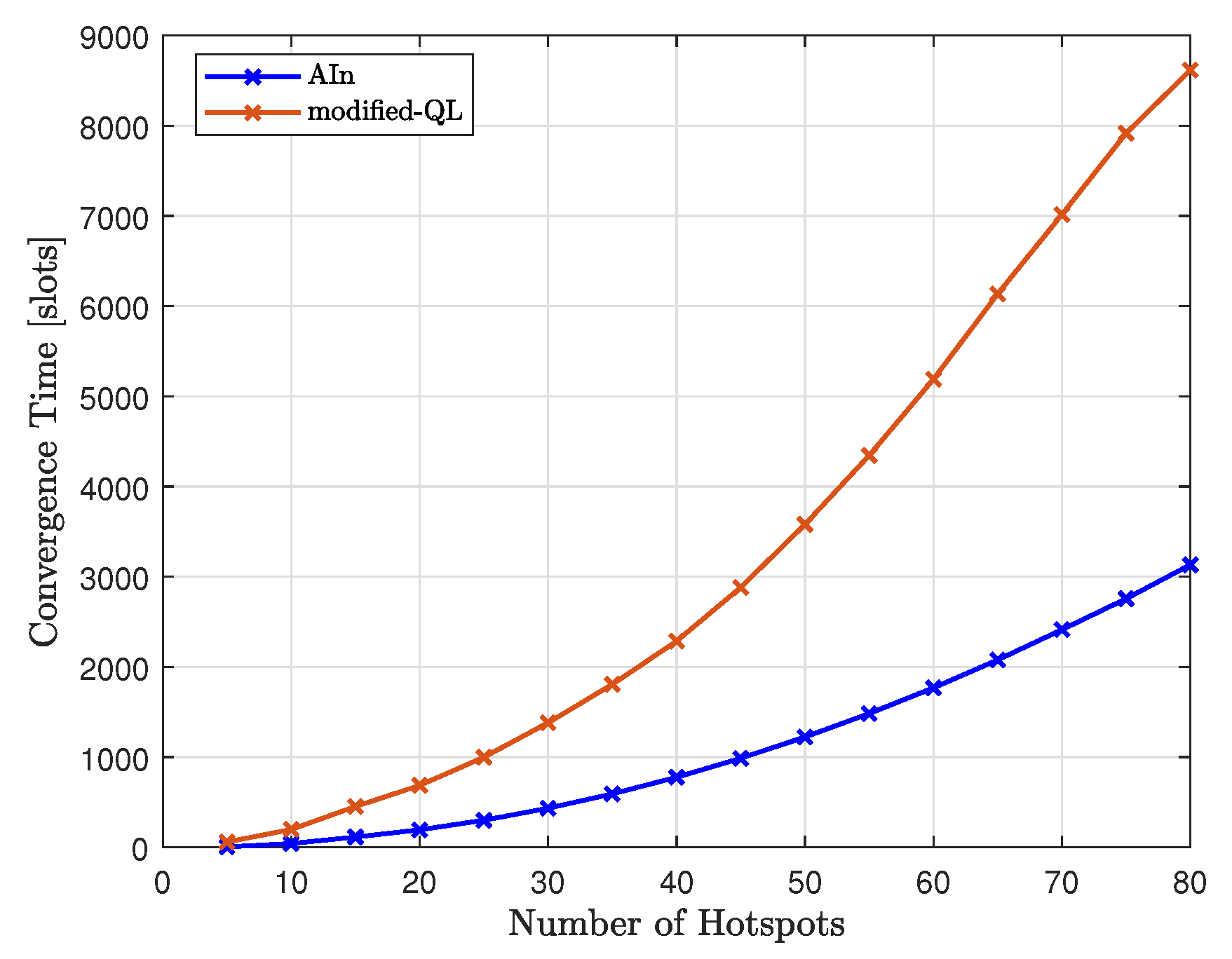
In
Figure 24, we compared the convergence time of the proposed method (AIn) to that of the modified-QL, as we varied the number of hotspots. The results showed that the proposed method requires less time to converge than the modified-QL. This difference is more noticeable as we increase the number of hotspots, with the gap between the two trends increasing. The modified-QL takes longer to converge as we increase the number of hotspots, and it does so at a faster rate than AIn due to its random nature, which leads to a higher number of possible words to try compared to AIn.
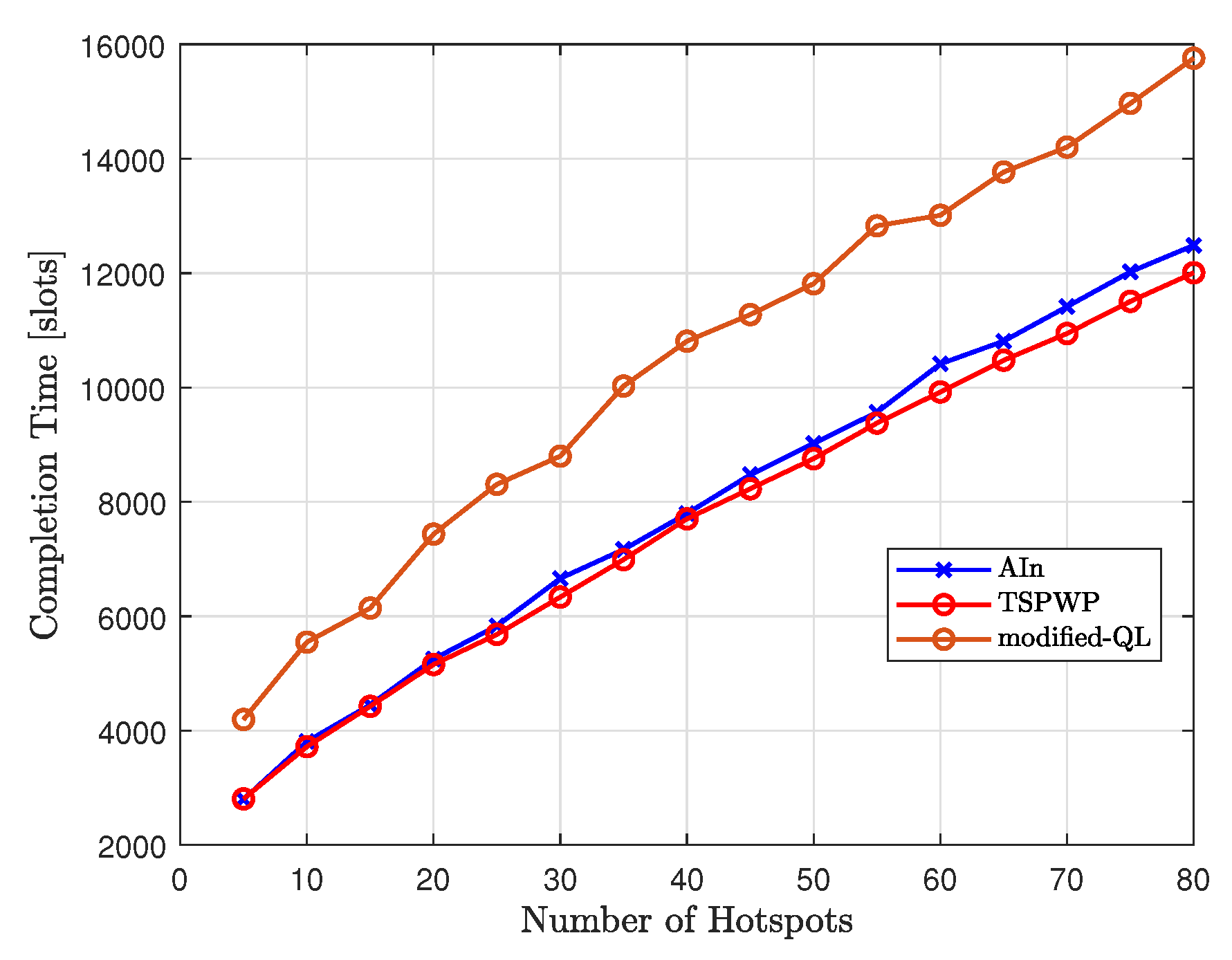
Figure 25 compares the completion time of our proposed method, AIn, to that of modified-QL and TSPWP as the number of hotspots varies. The results show that modified-QL takes longer to complete the missions due to slight deviations from the reference trajectories designed by TSPWP. These deviations are caused by the random actions performed before the convergence. On the other hand, AIn is able to complete missions faster than modified-QL thanks to its ability to deduce certain paths based on the world model and calculate prediction errors to correct continuous actions. This allows AIn to reach the target destination more quickly.
Figure 2.
Illustration of the system model.
Figure 2.
Illustration of the system model.
Figure 3.
The procedure to form the global dictionary.
Figure 3.
The procedure to form the global dictionary.
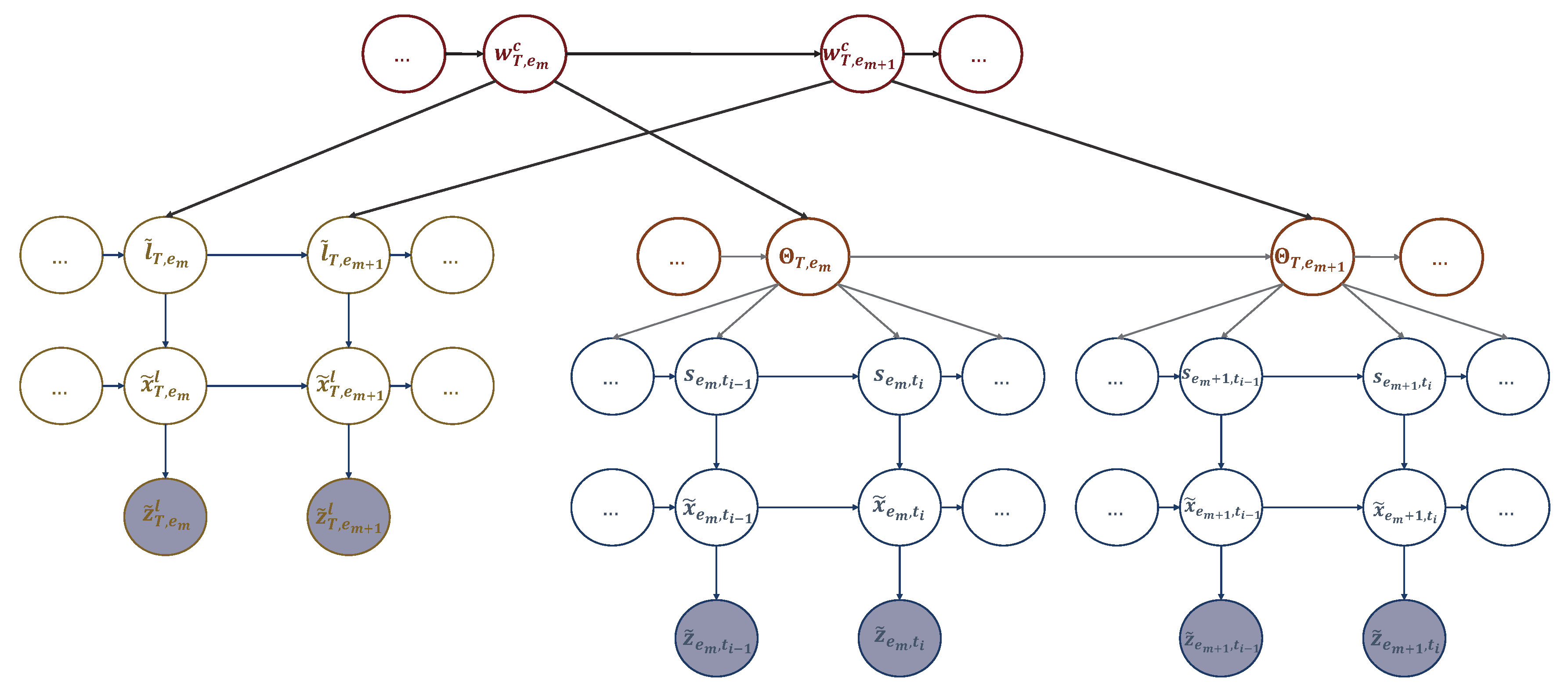
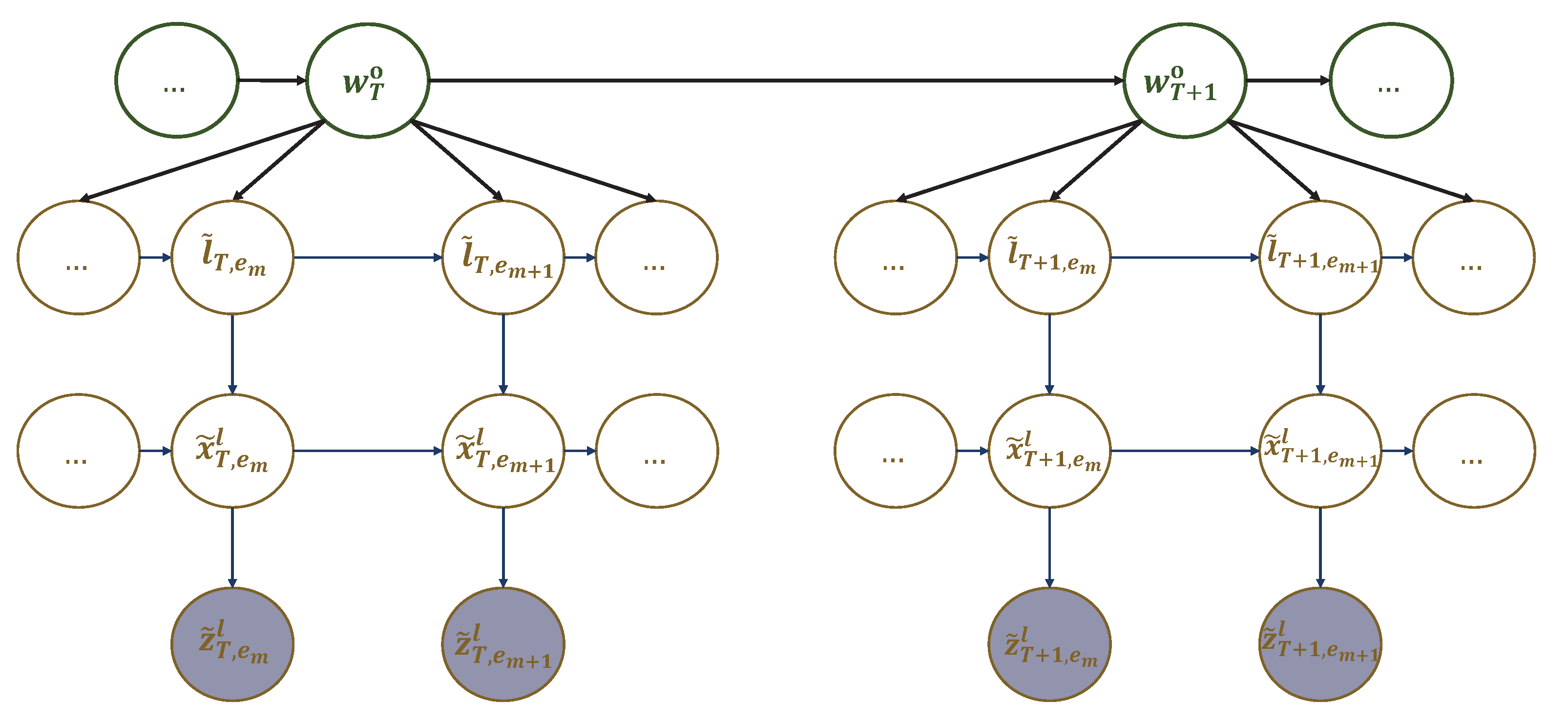
Figure 4.
A multi-scale GDBN representing sub-dictionary 1 that encodes the dynamic rules generating UAV’s hotspots sequence in different experiences.
Figure 4.
A multi-scale GDBN representing sub-dictionary 1 that encodes the dynamic rules generating UAV’s hotspots sequence in different experiences.
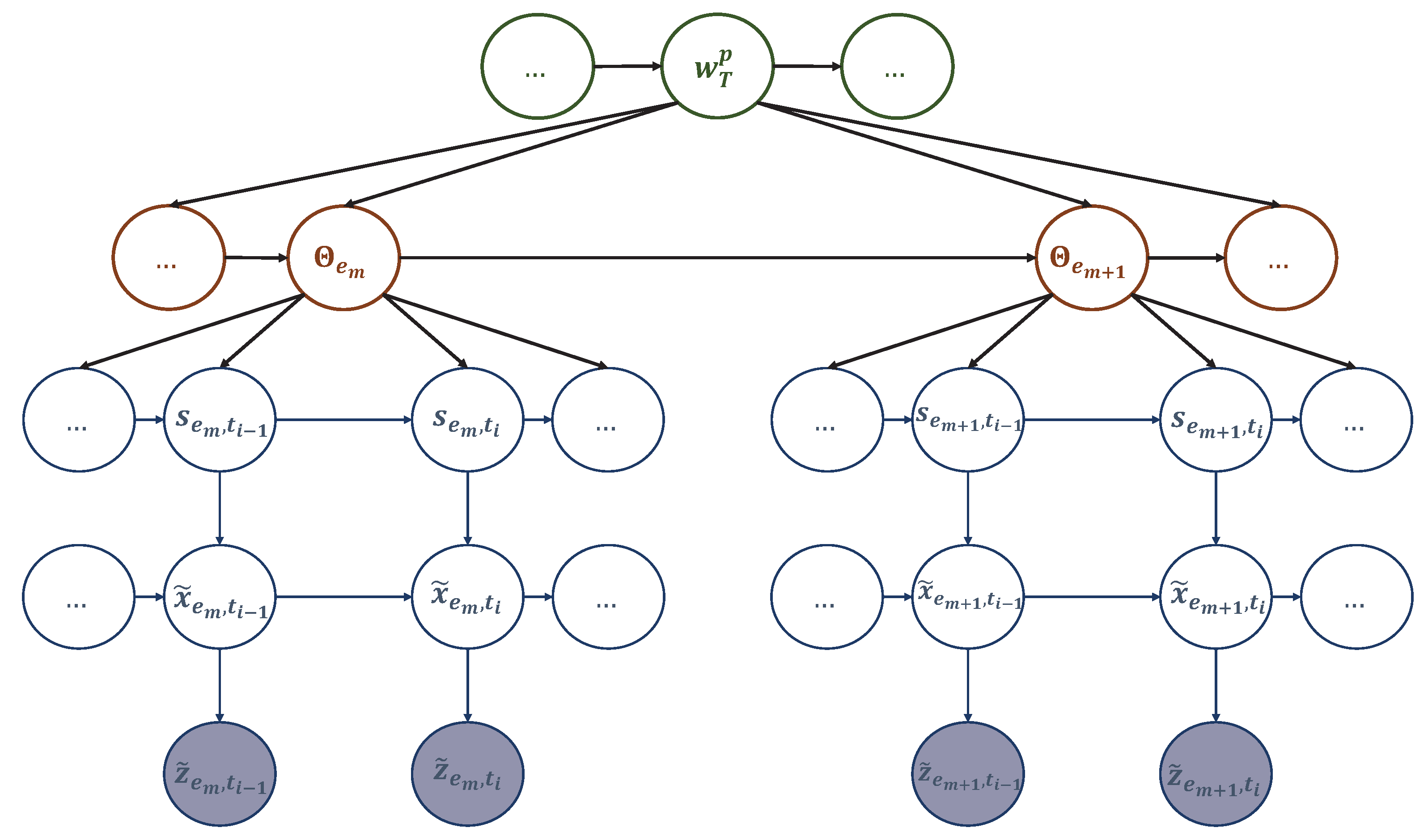
Figure 5.
A multi-scale GDBN representing sub-dictionary 2 that encodes the dynamic rules generating UAV’s positions to travel among the hotspots in different events.
Figure 5.
A multi-scale GDBN representing sub-dictionary 2 that encodes the dynamic rules generating UAV’s positions to travel among the hotspots in different events.
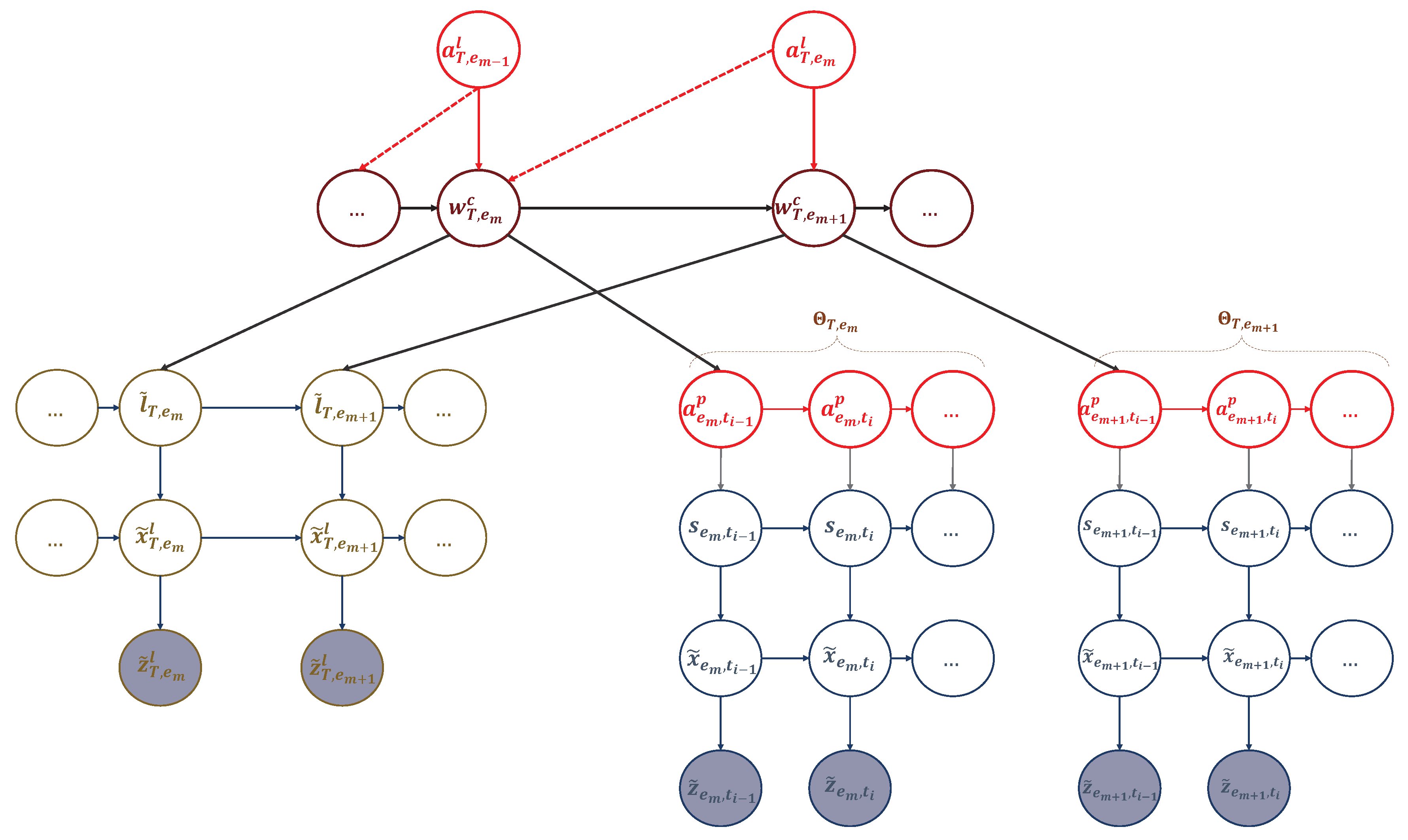
Figure 7.
An Active multi-scale GDBN involving the active states representing the actions that the UAV can perform and affect the dynamic rules generating UAV’s positions to travel among the hotspots in different events.
Figure 7.
An Active multi-scale GDBN involving the active states representing the actions that the UAV can perform and affect the dynamic rules generating UAV’s positions to travel among the hotspots in different events.
Figure 8.
TSPWP’s completion time performance for varying alpha and beta values, as well as changes in the number of hotspots.
Figure 8.
TSPWP’s completion time performance for varying alpha and beta values, as well as changes in the number of hotspots.
Figure 9.
TSPWP’s cost with profit performance for varying alpha and beta values, as well as changes in the number of hotspots.
Figure 9.
TSPWP’s cost with profit performance for varying alpha and beta values, as well as changes in the number of hotspots.
Figure 10.
An example of one realization: (a) Seven hotspots scattered randomly across the geographical area labeled with different letters, and each has a varying number of active users requesting service. (b) The trajectory provided by the TSPWP.
Figure 10.
An example of one realization: (a) Seven hotspots scattered randomly across the geographical area labeled with different letters, and each has a varying number of active users requesting service. (b) The trajectory provided by the TSPWP.
Figure 11.
The process of forming the dictionary: (a) The events that have been occurred during the flight and the generated word consisting of the letters visited by the UAV. Event 1 occur after reaching letter g starting from letter o. Event 2 occur after reaching letter f from g. Event 3 occur after reaching letter e from f. Event 4 occur after reaching letter d from e. Event 5 occur after reaching letter c from d. Event 6 occur after reaching letter b from c. Event 7 occur after reaching letter a from b. Event 8 occur after returing to the origin from a. (b) The clusters obtained after clustering the trajectory. Clusters are labeled as letters. The generated tokens each consisting of several letters corresponds to a specific event and so explaining the path to follow between two adjacent letters.
Figure 11.
The process of forming the dictionary: (a) The events that have been occurred during the flight and the generated word consisting of the letters visited by the UAV. Event 1 occur after reaching letter g starting from letter o. Event 2 occur after reaching letter f from g. Event 3 occur after reaching letter e from f. Event 4 occur after reaching letter d from e. Event 5 occur after reaching letter c from d. Event 6 occur after reaching letter b from c. Event 7 occur after reaching letter a from b. Event 8 occur after returing to the origin from a. (b) The clusters obtained after clustering the trajectory. Clusters are labeled as letters. The generated tokens each consisting of several letters corresponds to a specific event and so explaining the path to follow between two adjacent letters.
Figure 12.
The transition matrix encoding the probabilities of passing from one letter to another based on the examples solved during training.
Figure 12.
The transition matrix encoding the probabilities of passing from one letter to another based on the examples solved during training.
Figure 13.
The transition probabilities suggested by the world model to generate a word that might solve the current realization: (a) Possible letters to target starting from letter 1. (b) Possible letters to target starting from letter 2. (c) Possible letters to target starting from letter 3. (d) Possible letters to target starting from letter 4. (e) Possible letters to target starting from letter 5. (f) Possible letters to target starting from letter 6. (g) Possible letters to target starting from letter 7. (h) Possible letters to target starting from letter 8. (i) Possible letters to target starting from letter 9. (j) Possible letters to target starting from letter 10. (k) Possible letters to target starting from letter 11.
Figure 13.
The transition probabilities suggested by the world model to generate a word that might solve the current realization: (a) Possible letters to target starting from letter 1. (b) Possible letters to target starting from letter 2. (c) Possible letters to target starting from letter 3. (d) Possible letters to target starting from letter 4. (e) Possible letters to target starting from letter 5. (f) Possible letters to target starting from letter 6. (g) Possible letters to target starting from letter 7. (h) Possible letters to target starting from letter 8. (i) Possible letters to target starting from letter 9. (j) Possible letters to target starting from letter 10. (k) Possible letters to target starting from letter 11.
Figure 14.
A word generated using active inference before convergence: (a) The trajectory followed by the UAV based on active inference before the convergence. (e) The abnormalities occured during the fligth mission.
Figure 14.
A word generated using active inference before convergence: (a) The trajectory followed by the UAV based on active inference before the convergence. (e) The abnormalities occured during the fligth mission.
Figure 15.
A word generated using active inference after convergence: (a) The trajectory followed by the UAV based on active inference before the convergence. (e) The abnormalities occured during the fligth mission.
Figure 15.
A word generated using active inference after convergence: (a) The trajectory followed by the UAV based on active inference before the convergence. (e) The abnormalities occured during the fligth mission.
Figure 16.
The updated transition matrix encoding the probabilities of passing from one letter to another after convergence.
Figure 16.
The updated transition matrix encoding the probabilities of passing from one letter to another after convergence.
Figure 17.
This is a graphic explanation of the process for creating new words from a base word found in the dictionary: (a) The reference word represented graphically, and the new letters encountered in the new situation should be added to the reference graph. (b) The updated graph (word) after adding letter 7. (c) The updated graph (word) after adding letter 3. (d) The updated graph (word) after adding letter 6. (e) The updated graph (word) after adding letter 4. (f) The updated graph (word) after adding letter 5.
Figure 17.
This is a graphic explanation of the process for creating new words from a base word found in the dictionary: (a) The reference word represented graphically, and the new letters encountered in the new situation should be added to the reference graph. (b) The updated graph (word) after adding letter 7. (c) The updated graph (word) after adding letter 3. (d) The updated graph (word) after adding letter 6. (e) The updated graph (word) after adding letter 4. (f) The updated graph (word) after adding letter 5.
Figure 18.
The figure displays various examples with varying numbers of hotspot areas, along with the solutions produced by the proposed method (AIn) and the TSPWP utilizing 2-OPT.
Figure 18.
The figure displays various examples with varying numbers of hotspot areas, along with the solutions produced by the proposed method (AIn) and the TSPWP utilizing 2-OPT.
Figure 19.
Convergence of the proposed approach (AIn) in terms of sum-rate for different number of hotspots.
Figure 19.
Convergence of the proposed approach (AIn) in terms of sum-rate for different number of hotspots.
Figure 20.
Cumulative abnormality convergence of the proposed approach (AIn) for different number of hotspots.
Figure 20.
Cumulative abnormality convergence of the proposed approach (AIn) for different number of hotspots.
Figure 21.
The average sum-rate of the proposed approach (AIn) compared to the analytical value for various number of hotspots.
Figure 21.
The average sum-rate of the proposed approach (AIn) compared to the analytical value for various number of hotspots.
Figure 22.
An example of the realization shown in
Figure 10-(a): (
a) The trajectory followed by the UAV using the modified-QL before convergence. (
b) The trajectory followed by the UAV using the modified-QL after convergence.
Figure 22.
An example of the realization shown in
Figure 10-(a): (
a) The trajectory followed by the UAV using the modified-QL before convergence. (
b) The trajectory followed by the UAV using the modified-QL after convergence.
Figure 23.
Convergence of the modified-QL in terms of sum-rate for different number of hotspots.
Figure 23.
Convergence of the modified-QL in terms of sum-rate for different number of hotspots.
Figure 24.
The convergence time of the proposed approach (AIn) compared to the convergence time of the modified-QL for different number of hotspots.
Figure 24.
The convergence time of the proposed approach (AIn) compared to the convergence time of the modified-QL for different number of hotspots.
Figure 25.
The performance of the proposed approach (AIn) in terms of completion time after convergence compared with TSPWP for different number of hotspots.
Figure 25.
The performance of the proposed approach (AIn) in terms of completion time after convergence compared with TSPWP for different number of hotspots.
Table 1.
Variables Description.
Table 1.
Variables Description.
| Symbol |
Meaning |
|
Ground Users (GUs) |
| N |
Number of hotspots |
| T |
battery life time |
|
UAV’s initial location |
|
UAV’s final location |
|
UAV’s trajectory |
|
Sequence of hotspots served by the UAV |
|
nth hotspot serverd by the UAV |
|
total number of hotspots served along the trajectory |
|
set of possible trajectories to follow by the UAV |
|
Probability to move toward hotspot after visiting at time
|
|
Remaining time to go back to the original location after serving
|
|
The set of available hotspot areas |
|
The set of GUs distributed across the total geographical area |
|
The set of GUs belonging to the nth hotspot |
|
The coordinate of GU belonging to the
|
|
Center of nth hotspot |
|
Radius of the nth hotspot |
|
The set of the average data rate of all the available hotspots |
|
Data rate of the nth hotspot |
| t |
Time slot |
| u |
UAV |
|
Channel gain between GU () and UAV (u) |
|
Channel factor |
|
Carrier frequency |
| c |
Speed of light |
|
Path loss exponent |
|
Probability of Line of Sight |
|
Probability of Non Line of Sight |
|
Additional attenuation for line of sight links |
|
Additional attenuation for non line of sight links |
|
Distance between GU and UAV u at time t
|
|
Achievable data rate in hotspot n
|
|
The bandwidth of the resource block (RB) allocated to user
|
|
Transmit power of user
|
|
Power spectral density of the additive white Gaussian noise |
|
Training set of realizations representing M examples |
|
Set of the sequences of hotspots selected by TSPWP to solve M examples |
|
Set of trajectory instances generated by TSPWP |
|
Set of clusters generated by GNG |
|
Generalized letter |
|
Adjacency matrix |
|
Global adjacency matrix |
|
Global transition matrix |
|
Degree matrix |
|
Tokens |
|
Tokens transition matrix |
|
Words on order |
|
Words on motion |
|
Coupling word |
Table 2.
Simulation Parameters.
Table 2.
Simulation Parameters.
| Parameter |
Value |
Parameter |
Value |
|
1 W |
|
2 |
|
180 KHz |
|
dBm |
|
3 |
|
23 |
| N |
80 |
M |
1000 |