Prediction of Pubertal Mandibular Growth in Males with Class II Malocclusion by Utilizing Machine Learning

The goal was to create a novel machine learning (ML) model which can predict the magnitude and direction of pubertal mandibular growth in males with Class II malocclusion. Lateral cephalometric radiographs of 123 males at three time points (T1: 12, T2: 14, T3: 16 years old) were collected from an online database of longitudinal growth studies. Each radiograph was traced, and 7 different ML models were trained using 38 data points obtained from 92 subjects. 31 subjects were used as a test group, to predict post-pubertal mandibular length and Y-axis using input data from T1 and T2 combined (2-year prediction), and T1 alone (4-year prediction). Mean absolute errors (MAEs) were used to evaluate the accuracy of each model. For all ML methods tested using the 2-year prediction, the MAEs for post-pubertal mandibular length ranged from 2.11-6.07mm and 0.85-2.74° for the Y-axis. For all ML methods tested with 4-year prediction, the MAEs for post-pubertal mandibular length ranged from 2.32-5.28 mm and 1.25-1.72° for the Y-axis. Besides its initial length, the most predictive factors for mandibular length were found to be chronological age, upper and lower face heights, upper and lower incisor positions and inclinations. For the Y-axis, the most predictive factors were found to be Y-axis at earlier time points, SN-MP, SN-Pog, SNB and SNA. Whilst the potential of ML techniques to accurately forecast future mandibular growth in Class II cases is promising, a requirement for more substantial sample sizes exists to further enhance the precision of these predictions.

Keywords:

Subject: Medicine and Pharmacology - Dentistry and Oral Surgery

1. Introduction

The post-natal growth of the human mandible holds great significance within the field of orthodontics, as it boasts the highest growth potential among craniofacial structures [1]. The majority of mandibular growth takes place during adolescence, which coincides with the common treatment period for orthodontic patients [2]. Normal mandibular growth is typically observed in Class I patients, where the development of the mandible proceeds without significant deviations or abnormalities. Unanticipated mandibular growth can notably influence outcomes, particularly in Class III patients where excessive growth poses challenges. Conversely, in Class II cases, there is often a prominent deficiency in mandibular growth, characterized by insufficient horizontal and/or vertical development [3,4]. This deficiency limits the potential for self-correction without the intervention of orthodontic treatment [5]. To address these challenges, growth modification therapies have been utilized for decades to enhance mandibular growth while concurrently restricting maxillary growth [6]. If orthodontists had the ability to accurately predict mandibular growth, this would hold immense value as it would enable clinicians to anticipate and plan orthodontic treatment effectively, allowing for timely interventions to guide and optimize mandibular development, resulting in improved treatment outcomes and long-term stability.

In the 1960’s, Bjork sought to understand normal growth variation by placing metallic implants in the jaws of developing children [7,8,9]. His approach aimed to unravel the mysteries of mandibular growth, enabling the prediction of both the magnitude and direction of growth with greater precision [10]. Through his research, Bjork deduced that the mandible exhibits a predominant downward and forward growth pattern, with the condyle serving as the primary site of substantial growth [10]. Skieller et al made significant contribution to mandibular growth prediction through longitudinal studies and cephalometric analysis. Their research focused on establishing growth patterns predictions based on intermolar angle, shape of the lower border of the mandible, inclination of the symphysis, and mandibular inclination [11]. Though Skieller et al’s methods were thought to have high accuracy, subsequent clinical evaluation exhibited notable inaccuracy and limitations [12]. Thereafter, Ricketts and his colleagues [13,14] proposed an arcial prediction method which exhibited promising clinical utility when subjected to preliminary testing with a limited sample size, subsequently earning recognition as a prediction method currently integrated into the Dolphin Imaging 11.0 Software. But ultimately, predictions derived from anatomical structures have demonstrated inconsistent accuracy.

In the pursuit of more accurate predictions, several mathematical models have been developed. Rudolph et al incorporated Bayes theorem and Gaussian distribution to develop a statistical model that predicted mandibular growth based on observed variables and their probabilistic relationships [15]. Their approach leveraged both prior knowledge and the data at hand to estimate and predict mandibular growth. However, this method demonstrated a prediction accuracy of only 82%. Buschang et al developed a mathematical model that involved comparing the average yearly growth velocities with a population based growth curve [16]. Their findings demonstrated a prediction accuracy of 76%; the researchers acknowledged the presence of bias due to anticipated growth variations that could not be fully accounted for by the prediction methods employed. In 2021, Jiménez-Silva et al’s systematic review investigating Class II mandibular growth reached a significant conclusion, highlighting the overall low to moderate methodological quality of existing predictors and underscoring the pressing need for reliable prediction methods [17]. Numerous studies were found to possess an elevated risk of bias and employed broad sample selections, further emphasizing the need for rigorous investigation. As a result, this systematic review advocated for the implementation of a meticulously designed longitudinal cohort study based on lateral cephalometric radiographs, one that adheres to stringent quality standards, to address this research gap and provide more accurate predictions. Despite concerted efforts, it remains challenging for human made models to comprehensively account for intricate and multifaceted variations in human beings.

Walker was one of the first in the field of orthodontics to postulate and conduct mandibular predictions using computer software [18]. Since then, technology has advanced so significantly that artificial intelligence (AI) and machine learning (ML) have been utilized in almost every aspect of our life. AI is the development of computer systems able to perform tasks that normally require human intelligence [19]. Within AI, ML utilizes a set of inputs and outputs to create an algorithm to process the data and correctly predict the output [20]. AI and ML have been utilized for several tasks in orthodontics such as to automated cephalometric analyses [21,22,23,24,25], predict extraction vs. non-extraction treatment decision [26,27,28,29,30,31,32,33,34], predict orthodontic extraction patterns [35], determine the need for surgery in Class III patients [36], and growth assessment [37,38,39,40,41,42,43,44,45]. However, there has been little research conducted on using AI to predict mandibular growth. Niño-Sandoval et al. utilized automated learning techniques to predict mandibular morphology in Class I, II and III patients [46]. The study used the coordinates of craniofacial landmarks as variables for Artificial Neural Networks and Support Vector Regression (SVR) to predict the morphological outcome. This research yielded exceptional predictability, showcasing the remarkable ability of AI to accurately forecast jaw morphology. The same group of researchers used AI to classify skeletal patterns through craniomaxillary variables selected on the mandible for forensic use [47]. This resulted in 74% accuracy in correctly predicting skeletal patterns. In an unpublished master thesis, Jiwa et al. employed deep learning techniques to construct an algorithm for mandibular growth prediction [48]. Their approach involved utilizing predictions based on the X and Y coordinates of 17 mandibular landmarks on selected cephalograms and comparing them with Rickett’s growth prediction. However, this proved to be generally inaccurate highlighting the necessity for larger and more targeted sample populations to enhance the predictive capabilities. Recently, Wood et al. utilized 39 linear and angular measurements from lateral cephalograms to predict mandibular growth in untreated Class I male patients [49]. This study employed 7 distinct ML algorithms to analyze the measurements, predict the magnitude and direction of the mandible, and subsequently compare the results to the final cephalogram of each patient. They were able to predict mandibular growth within 3 mm and Y-axis within 1°. To the best of our knowledge, there has been no prior research investigating the application of ML in accurately predicting the magnitude and direction of mandibular growth in adolescent males with a Class II malocclusion during the circumpubertal period. Achieving this breakthrough in the field of orthodontics would be a significant advancement. This project aims to develop a ML algorithm capable of reliably and accurately forecasting the amount and direction of mandibular growth in this specific group of patients.

2. Materials and Methods

2.1. Ethics

This retrospective study was approved as a non-human subjects research (NHSR) by the Institutional Review Board (IRB) of Indiana University Human Research Protection Program (HRPP) (Protocol #14987)

2.2. Study Sample

The sample of this study consisted of digital cephalometric radiographs from subjects in the American Association of Orthodontists Foundation (AAOF) Craniofacial Legacy Collection, which includes data from the Bolton Brush Growth, Burlington Growth, Denver Growth, Fels Longitudinal, Forsyth Twin, Iowa Growth, Matthews Growth, Michigan Growth, and Oregon Growth studies [50]. Inclusion criteria consisted of males with Class II malocclusion or an ANB>3.5 with pre-pubertal (T1) (Mean age ± SD: 12.0 ± 0.29 years), pubertal (T2) (Mean age ± SD: 14.1 ± 0.27 years) and post-pubertal (T3) (Mean age ± SD: 15.9 ± 0.48 years) cephalograms. Subjects with craniofacial anomalies, apparent skeletal asymmetries, missing teeth (excluding third molars), missing cephalometric records or lateral cephalograms lacking necessary structures were excluded from this study. A total of 123 cases met the inclusion criteria and were selected for this study.

2.3. Sample Size Justification

The study used 92 of the cases for training and remaining 31 for the testing set. With this sample size, the 95% confidence interval for the intra-class correlation coefficients (ICCs) has a width of 0.28, extending from 0.62 to 0.90, if the ICC is 0.80; higher ICCs have shorter confidence interval widths.

2.4. Data Collection

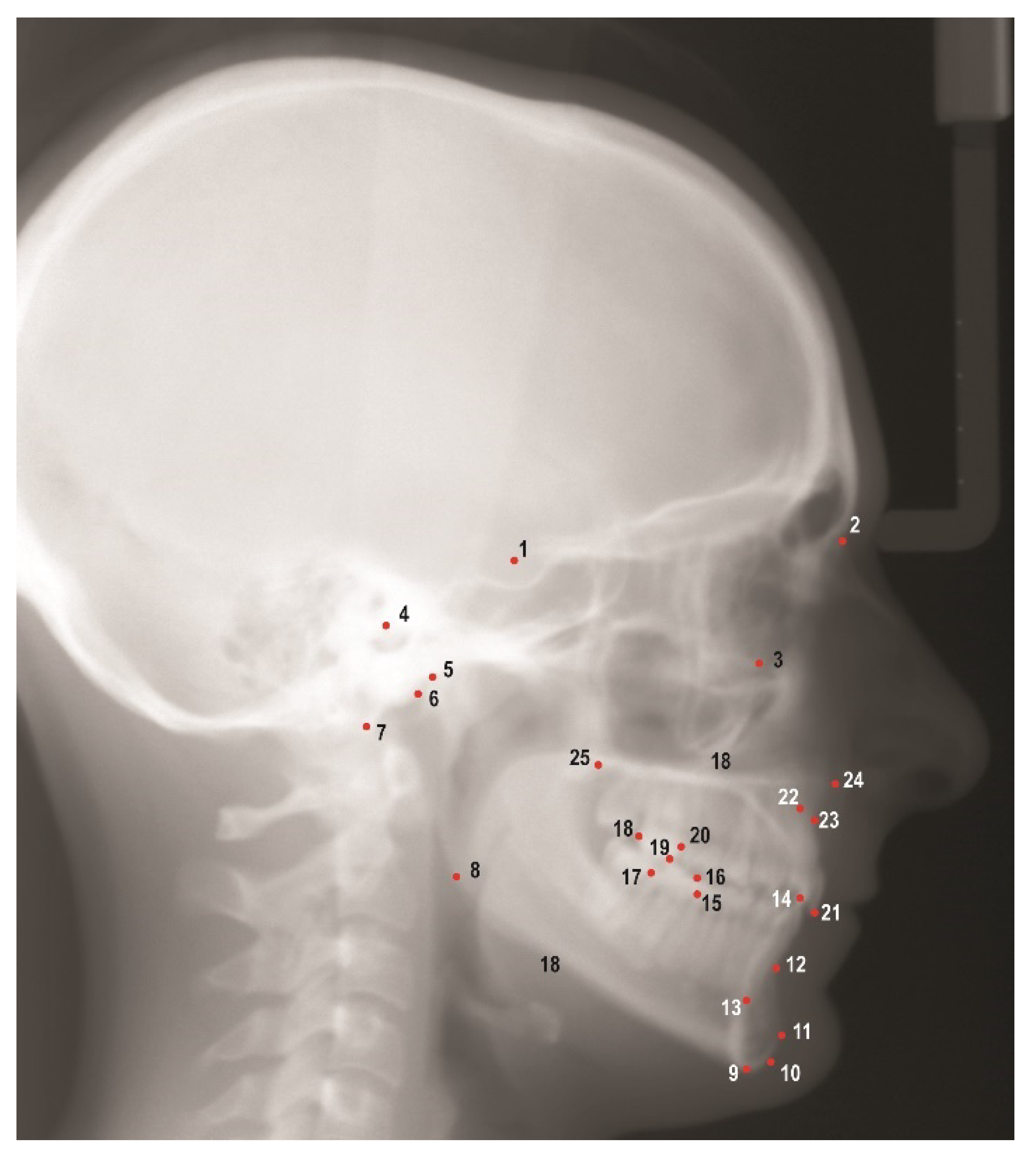
Images obtained from the AAOF collection were then imported into Dolphin Imaging V. 11.95 (Dolphin Imaging and Management Solutions, Chatsworth, CA, USA) for further analyses. A solitary investigator (G.Z.) identified and marked 25 hard tissue landmarks on each image (Figure 1), thereby enabling the calculation of 38 linear and angular measurements (Table S1). Several cephalograms did not show adequate soft tissue therefore, soft tissue landmarks and associated cephalometric measurements were not included in the study.

The AAOF provided dots-per-inch (DPI) calibration for measurements; however, when magnification discrepancies were detected, images were printed at 1:1 scale and ruler length verified for accuracy, whereafter the digital ruler was employed to recalibrate measurements. Demographic and cephalometric data were then compiled and stored in a secure cloud service (OneDrive, Microsoft Co., Redmond, WA, USA). For intra-examiner repeatability assessment, a research randomizer was utilized to randomly choose 20 images for retracing. ICCs were utilized to evaluate the measurements’ repeatability.

2.5. Algorithm Training and Testing

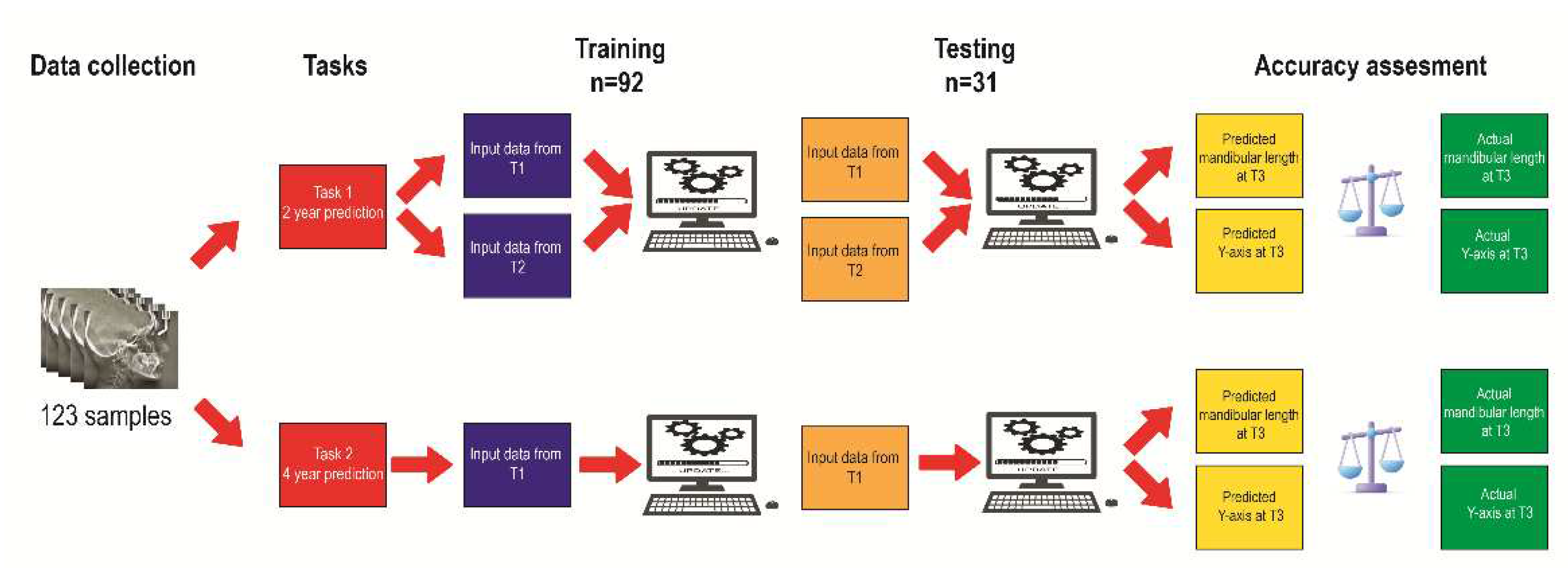
The data was randomly partitioned into a training and a testing set, with 75% of the samples (92) allocated to the former and 25% (31) to the latter. The training set’s purpose was to impart knowledge to the ML models so they could accurately forecast the post-pubertal mandibular length and Y-axis. To this end, input data obtained both from T1 and T2 were used for 2-year prediction, whereas input data from T1 only were utilized for 4-year prediction (Figure 2).

Least squares (linear), Ridge, Lasso, Elastic Net, XGBoost, Random Forest, and Multilayer Perceptron (MLP) were used. All experiments were conducted in Spyder 4.1.5, utilizing the programming language Python 3.7.9 (Python Software Foundation, Fredricksburgh, VA, US). To carry out the experiments, following packages were used: sklearn version 1.0.2 (NumFOCUS, Austin, TX, US) for least squares, Ridge, Lasso, Elastic Net, and Random Forest; XGBoost version 1.5.0 (DMLC, US) for XGBoost; and Keras version 2.4.0 (Keras, Mountain View, CA, US) in the TensorFlow version 2.4.3 (Keras, Mountainview, CA, US) platform for the neural network.

2.6. Statistical Analysis

The mean absolute error (MAE), root mean square error (RMSE), mean error (ME), ICCs, and Bland-Altman plots were calculated for each technique to evaluate the agreement between the predicted and actual outcome measurements. The accuracy percentage of the methods were calculated using the formula (1-(MAE/Actual Value) x 100). The directional and absolute differences between the predicted and actual measurements were calculated and compared between models using analysis of variance (ANOVA), with random effects to correlate data from the same patient. Paired t-tests were used to test for a significant mean directional difference between predicted and actual measurements. A two-sided 5% significance level was used for all tests. All analyses were performed using SAS version 9.4 (SAS Institute, Inc., Cary, NC, USA).

3. Results

3.1. Reliability Analysis

The results of the reliability analysis are given in Table S2. Most variables exhibited excellent repeatability (ICCs>0.90), with the remainder having good repeatability (0.75<ICC<0.90) [51]. The only measurement revealed poor repeatability (ICC<0.50) was L1-MP.

3.2. Descriptive Statistics

Table S3 presents the descriptive statistics for the cephalometric variables at T1, T2, and T3, encompassing measures such as the mean, standard deviation, minimum, and maximum. A significant increase in mandibular length was observed between T1 and T2, with an average growth of 15.11 mm. Furthermore, between T2 and T3, the mandible exhibited continued growth, adding an additional 5.78 mm. In total, there was a cumulative increase of 20.89 mm in mandibular length between T1 and T3.

In comparison to mandibular length, the Y-axis demonstrated relatively minimal changes throughout puberty. Between T1 and T2, there was an average decrease of 0.14° in the Y-axis. Furthermore, an additional decline of 0.34° was observed between T2 and T3, resulting in a cumulative decrease of 0.48° in the Y-axis over the entire observation period (T1-T3).

3.3. Prediction of the Post-Pubertal Mandibular Length

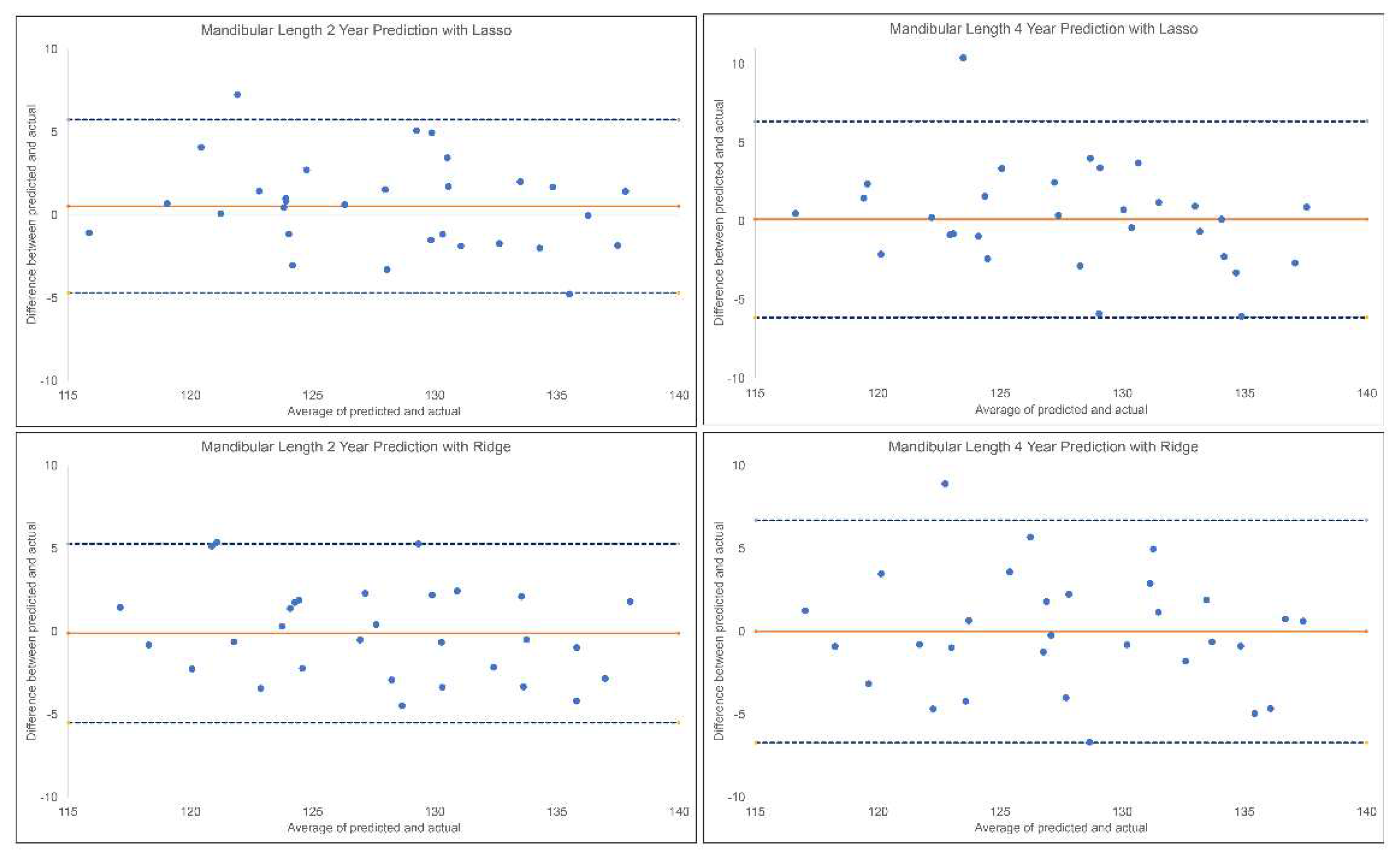
The results for the 2-year and 4-year predictions of post-pubertal mandibular length are given in Table 1 and Figure 3. For the 2-year prediction, MAEs ranged from 2.11 mm to 6.07 mm, with Lasso being most accurate and Linear Regression the least. Accuracy percentages ranged from 95.26% to 98.35% between models employed. Lasso, Ridge and MLP models demonstrated an excellent correlation between predicted and actual values (0.90<ICCs), while XGBoost, Random Forest and SVR showed good correlations (0.75<ICCs<0.90). Linear Regression was the only model with moderate correlation between the predicted and actual values (ICC: 0.58). Similarly, 4-year prediction MAEs ranged from 2.32 mm to 5.28 mm, with Lasso being most accurate and Linear Regression the least. All methods demonstrated moderate to good correlation between predicted and actual values (0.67< ICCs < 0.84). Accuracy percentages ranged from 95.88% to 98.19%.

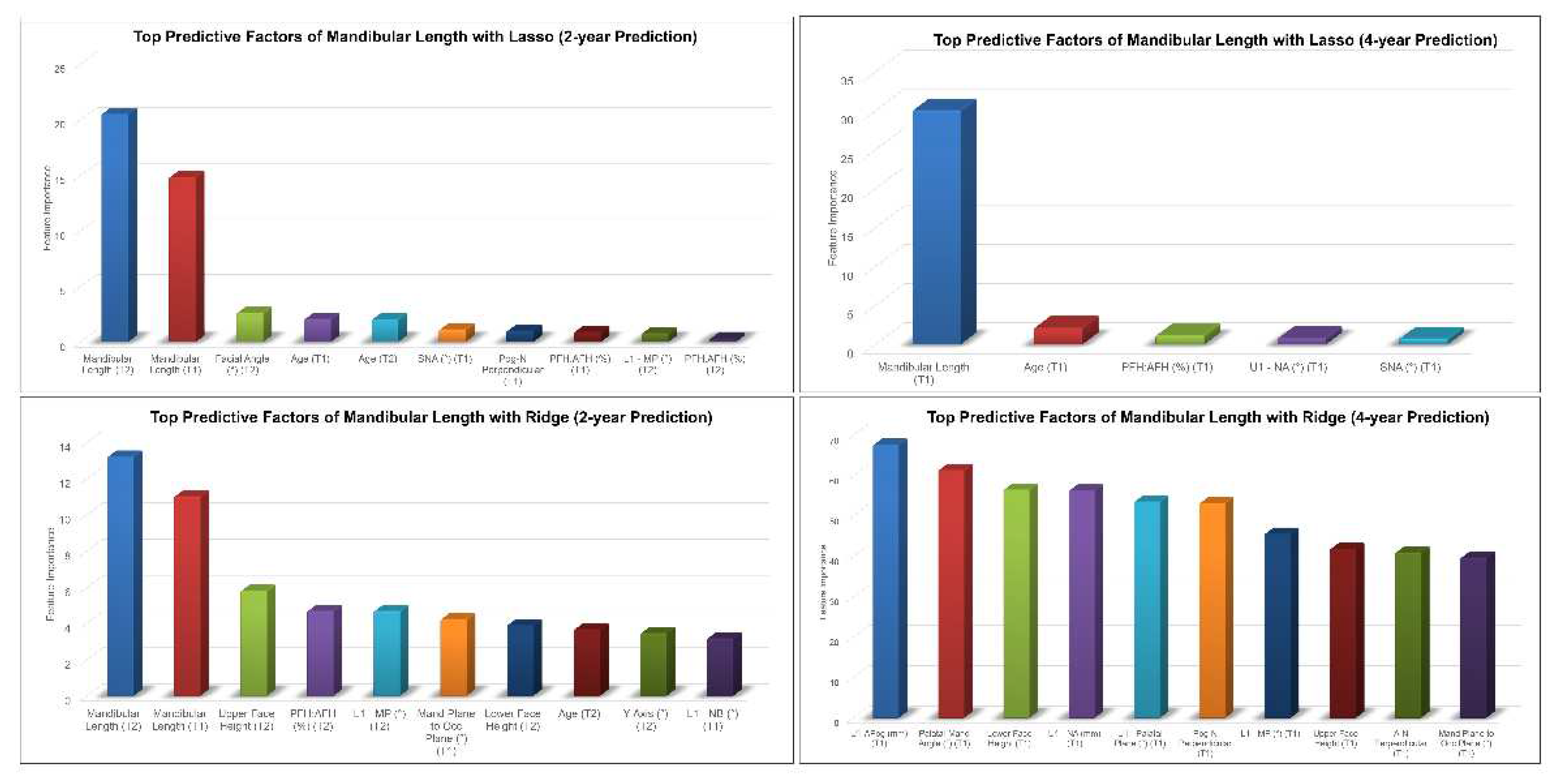
Mandibular length, age, PFH:AFH and SNA at earlier timepoints were among the top predictive factors for 2-year and 4-year predictions of post-pubertal mandibular length using Lasso (Figure 4). On the other hand, Ridge model picked up U1 to APog distance, mandibular length, upper and lower face heights, L1-MP and mandibular plane to occlusal plane angles as the most predictive factors of post-pubertal mandibular length.

3.4. Prediction of the Post-Pubertal Y-axis

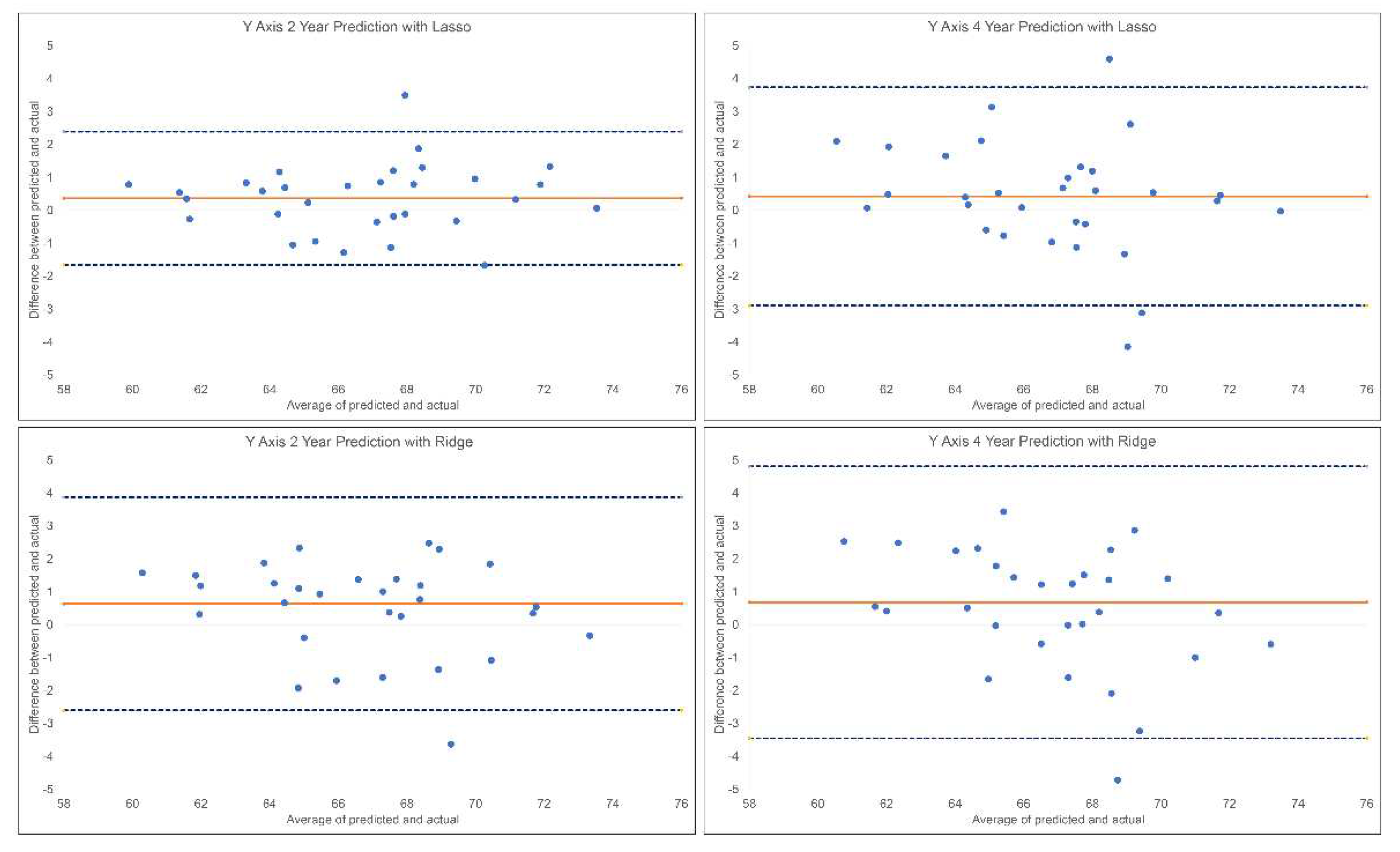
The results of the 2-year and 4-year predictions of the post-pubertal Y-axis are shown in Table 2 and Figure 5. For the 2-year prediction, MAEs ranged from 0.85° to 2.74°, with Lasso being most accurate and Linear Regression the least. Random Forest and Lasso demonstrated an excellent correlation between predicted and actual values (0.90<ICCs), while XGBoost, Ridge, SVR and MLP showed good correlations (0.75<ICCs<0.90). Linear Regression was the only model with moderate correlation between the predicted and actual values (ICC: 0.63). Accuracy percentages ranged from 96.02% to 98.76% between models employed. For the 4-year prediction, MAEs ranged from 1.25° to 1.72°, with Lasso being most accurate and Random Forest and SVR the least. All methods demonstrated good correlation between predicted and actual values (0.76< ICCs <0.86). Accuracy percentages ranged from 97.50% to 98.18%.

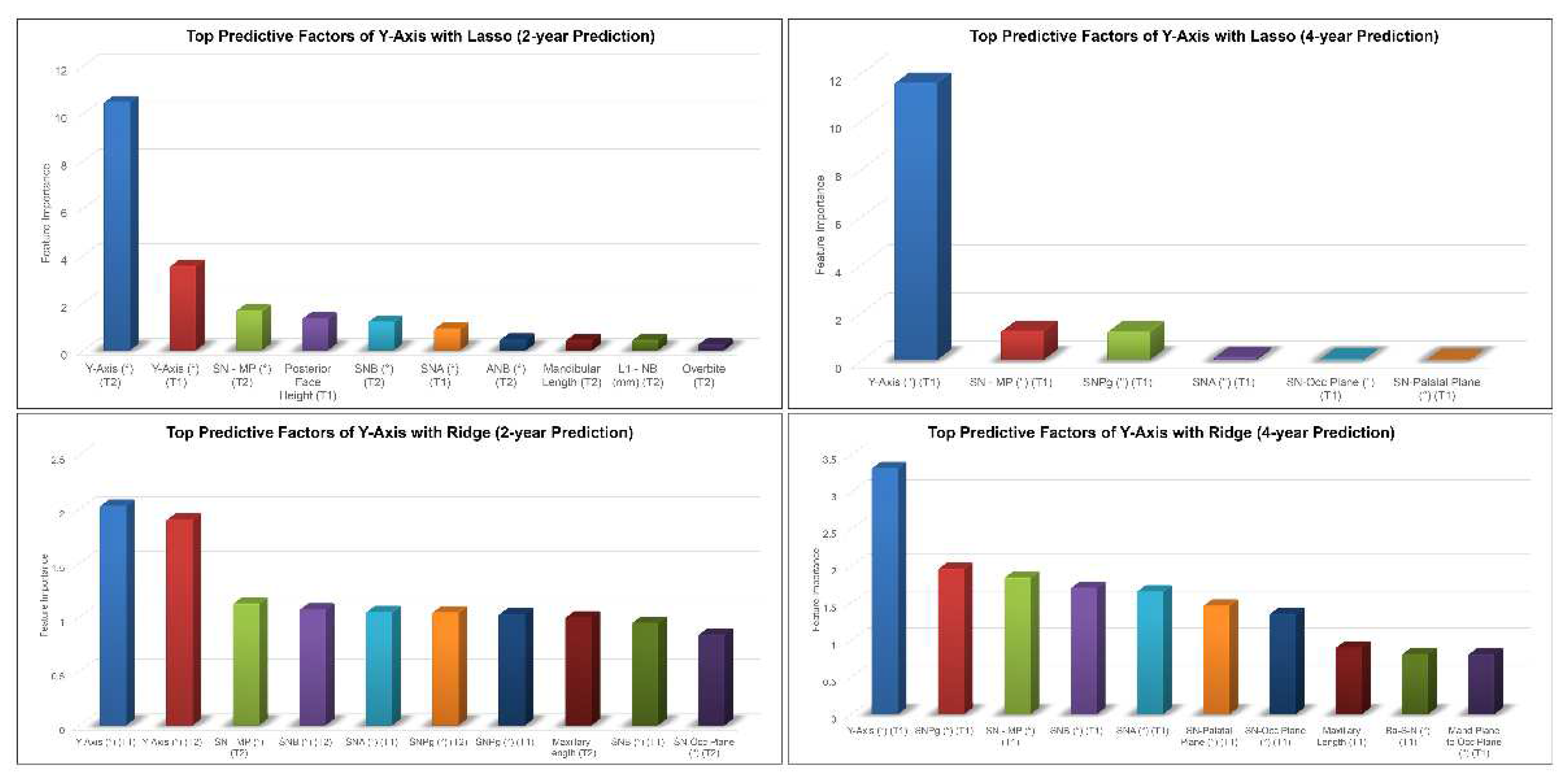
Y-axis, SN-MP, SNA angles at earlier timepoints among the top predictive factors for 2-year and 4-year predictions of post-pubertal Y-axis using Lasso (Figure 6). In addition to these features, Ridge model picked up SN-Pog, SNB, SN-Occlusal Plane angles as the most predictive factors of post-pubertal Y-axis.

3.5. Method Comparison

Directional and absolute difference comparisons between ML methods for 2-year prediction of post-pubertal mandibular length are given in Table 3. Linear Regression showed significantly larger absolute differences from the actual values compared to all other methods (P<.05). Additionally, SVR exhibited significantly larger absolute differences from the actual values compared to Lasso and Ridge (P<.05). In the case of a 4-year prediction for male mandibular growth, Linear Regression demonstrated significantly larger absolute differences from the actual values compared to all other methods, while Random Forest and SVR showed significantly larger absolute differences compared to Lasso (P<.05) (Table 4).

In terms of Y-axis prediction for the 2-year prediction, Lasso exhibited significantly smaller absolute differences from the actual values compared to Linear Regression, Random Forest, Ridge, and SVR (P<.05) (Table 5). Conversely, for the 4-year projection, Linear Regression had significantly larger absolute differences from the actual values compared to all other methods (P<.05) (Table 6).

When comparing the prediction methods for both 2-year and 4-year predictions of mandibular length, no significant differences were found in terms of absolute differences or directional differences for any of the methods (P>.05) (Table 7). However, when considering the Y-axis, the absolute differences between the predicted and actual values were significantly larger when using the 2-year prediction compared to the 4-year prediction for Linear Regression (P<.001) (Table 8). Additionally, the directional differences between the predicted and actual values on the Y-axis were significantly smaller when using the 2-year prediction compared to the 4-year prediction for Linear Regression (P<.05). Specifically, the predicted values were on average higher than the actual values for 4-year prediction, but slightly lower on average than the actual values for 2-year prediction. Moreover, the Y-axis absolute differences between the predicted and actual values were significantly larger when using the 4-year prediction data compared to the 2-year prediction data for Random Forest (P<.05) (Table 8).

4. Discussion

There exists a significant degree of variability in both the magnitude and direction of pubertal mandibular growth across different genders, races, and even among individuals of the same age and gender [52]. To thoroughly investigate the complex growth patterns of the mandible, we employed a targeted approach by selecting specific samples based on malocclusion, gender, and age. This study specifically focused on analyzing records exclusively from Class II males in the circumpubertal stage. By utilizing data from individuals aged 11 to 16 years, we were able to examine the peak growth and maturation stages that most males experience, capturing a more stable estimate of the final position of the mandible as growth approaches its plateau. Our intention was to create a novel ML model which can predict the magnitude and direction of pubertal mandibular growth in males with Class II malocclusion.

This study is a vital contribution to an extensive series of investigations utilizing advanced ML techniques to forecast the intricate process of mandibular growth. Baumrind et al conducted a study in which orthodontists attempted to forecast the mandibular growth of Class II patients, ultimately leading to the conclusion that human predictions fare no better than chance [53]. Conversely, our study achieved an elevated level of precision by accurately predicting the post-pubertal mandibular length within a margin of 2.5 mm. In a similar vein, Wood et al. successfully predicted mandibular length among Class I males with an accuracy within 3 mm [49]. ML exhibited an exceptional capability in accurately predicting the Y-axis within a narrow range of 1 degree. Notably, Wood et al also predicted Y-axis in a range of 1 degree [49].

Different predictors were prominent for each ML model. In terms of mandibular length, significant predictors that were identified include chronological age, upper and lower face heights, and upper incisor position. The strong predictive power of chronological age is inherently logical, given that the patients were situated within the circumpubertal age, a period characterized by accelerated growth and development. It is noteworthy that the algorithm likely detected the average peak height velocity, which typically transpires around the age of 14, enabling more accurate predictions [2]. Lower face height also contributed significantly to precise predictions. Hypodivergent patients with a short lower face height tend to exhibit more forward growth while hyperdivergent patients with a long lower face height exhibit more vertical growth [54]. Furthermore, upper incisor position plays a role in this regard. Class II Division 1 malocclusion is typified by protruded maxillary incisors, whereas Class II Division 2 patients exhibit retruded maxillary incisors. Since Class II Division 2 patients commonly have shorter lower face height [54], the algorithm may have leveraged this information to identify them as forward growers. These predictive factors indicate that the ML algorithms were possibly capable of differentiating between Class II Division 1 and Class II Division 2 patients to discern the appropriate growth pattern more accurately.

Regarding Y-axis, the most predictive factors were identified as SN-MP, SN-Pog, SNB, SNA, and SN-Palatal plane. SN-MP is a measurement of the mandibular plane angle relative to the cranial base. The SN-MP angle provides the mandibular rotation model indicating hypodivergent, normodivergent, or hyperdivergent. The larger the SN-MP angle, the more the mandible tends to become steeper and the more the chin move backward [55]. The Y-axis is another cephalometric measurement used to assess the direction of the mandibular growth; downward and backward or downward and forward. Both the SN-MP angle and the Y-axis angle are used to evaluate the skeletal and growth patterns in orthodontics and orthognathic surgery. They help orthodontists and surgeons understand the vertical dimensions of the face, the inclination of the mandible, and the overall skeletal relationships between the cranial base and the jaws. So, it is understandable that the vertical relationship of the mandible to the cranial base helped predict the vertical direction of growth via Y-axis. This is in agreement with Schudy who found that SN-MP is closely associated with the growth and morphology of the mandible when he sought to identify the specific increments of growth responsible for rotation of the mandible [55]. Schudy found that the larger the SN-MP angle, the more the mandible tends to become steeper and the more the chin moves backward and the smaller the angle, the greater the tendency of the mandible to become flatter and the chin to grow forward [55]. Additionally, the ML models utilized anterior-posterior measurements such as SNA and SNB to predict Y-axis. A larger SNB may indicate more forward mandibular growth. By assessing these sagittal measurements, AI could make predictions about how the mandible will likely grow in relation to the rest of the face.

When comparing the ML techniques to one another, none showed a clear superiority to the others. However, Linear Regression may have performed worse than others due to its inherent limitations. Linear regression assumes a linear relationship between the predictor variables and the response variable, which may not accurately capture the non-linearities present in human growth patterns [56]. On the other hand, Lasso and Ridge techniques incorporate regularization, which helps address issues of overfitting and model complexity. Lasso performs both variable selection and regularization by imposing a penalty on the absolute values of the coefficients, effectively shrinking less important predictors to zero [56]. This feature helps in identifying the most relevant predictors for growth prediction. Ridge, on the other hand, adds a penalty term based on the square of the coefficients, which allows for a better balance between bias and variance [57]. By considering non-linear relationships and incorporating regularization techniques, Lasso and Ridge are better equipped to handle the complexities involved in predicting human growth with AI. When assessing overall performance, the authors would consider further studies using Lasso prediction model.

The authors acknowledge certain limitations in the current study. First, the sample size was relatively small due to the constraints of the available records in the AAOF Legacy Collection. It is worth noting that when employing ML techniques, a larger sample size is desirable as it allows for a more representative and diverse dataset. This, in turn, increases the likelihood of capturing the true underlying patterns and characteristics of the population, thereby reducing sampling bias and enhancing the model’s ability to make predictions on unseen data. Moreover, a larger sample size would help mitigate the impact of random variation and minimize instances of overfitting. Another limitation is that many images did not include sufficient facial tissue in the lateral cephalogram, which could have potentially improved the accuracy of the prediction methods. Additionally, the utilization of automated cephalometric landmark identification methods could have ensured consistency in cephalometric analyses.

5. Conclusions

ML algorithms tested were able to predict post-pubertal mandibular length within 2.5 mm and Y-axis within 1° range. Besides its initial length, the most significant predictors for mandibular length were identified as chronological age, upper and lower face heights, upper and lower incisor position and inclination. Similarly, for the Y-axis, the most predictive factors were identified as Y-axis at earlier timepoints, SN-MP, SN-Pog, SNB and SNA. Whilst the potential of ML techniques to accurately forecast future mandibular growth in Class II cases is promising, a requirement for more substantial sample sizes exists to further enhance the precision of these predictions.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Table S1: Cephalometric variables and their definitions. Table S2: Intra-examiner repeatability of the measurements. Table 3: The descriptive statistics of the cephalometric measurements at T1, T2, and T3, including mean, standard deviation, and minimum/maximum values.

Author Contributions

Conceptualization, Grant Zakhar, George Eckert, Ariel Wong, Sarkhan Badirli and Hakan Turkkahraman; Data curation, Grant Zakhar, Samir Hazime, Sarkhan Badirli and Hakan Turkkahraman; Formal analysis, Grant Zakhar, George Eckert, Sarkhan Badirli and Hakan Turkkahraman; Investigation, Grant Zakhar, Sarkhan Badirli and Hakan Turkkahraman; Methodology, Grant Zakhar, Sarkhan Badirli and Hakan Turkkahraman; Project administration, Hakan Turkkahraman; Resources, Grant Zakhar and Hakan Turkkahraman; Software, George Eckert and Sarkhan Badirli; Supervision, Hakan Turkkahraman; Validation, Grant Zakhar, George Eckert, Sarkhan Badirli and Hakan Turkkahraman; Visualization, Hakan Turkkahraman; Writing—original draft, Grant Zakhar, Ariel Wong, Sarkhan Badirli and Hakan Turkkahraman; Writing—review & editing, Grant Zakhar, Samir Hazime, George Eckert, Ariel Wong, Sarkhan Badirli and Hakan Turkkahraman.

Funding

This research received no external funding.

Institutional Review Board Statement

This study was approved as a non-human subjects research (NHSR) by the Institutional Review Board (IRB) of Indiana University (Protocol #14987 March 30.2022).

Informed Consent Statement

Not applicable

Data Availability Statement

The data underlying this article are available in the article. The datasets were derived from sources in the public domain from the AAOF Legacy Collection at https://www.aaoflegacycollection.org/.

Acknowledgments

This study was made possible by the American Association of Orthodontists Foundation Craniofacial Growth Collection managing the Oregon Growth Study, Denver Growth Study, Forsyth Twin Study, Fels Longitudinal study, Bolton Brush Growth Study, Iowa Growth Study, Michigan Growth Study and Matthews Growth Study. This study was also made possible using material from the Burlington Growth Centre, Faculty of Dentistry, University of Toronto, which was supported by funds provided by Grant (1) (No. 605-7-299) National Health Grant (Canada), (data collection); (2) Province of Ontario Grant PR 33 (duplicating) and (3) the Varsity Fund (for housing and collection).

Conflicts of Interest

The authors declare no conflict of interest.

References

Manlove, A.E.; Romeo, G.; Venugopalan, S.R. Craniofacial growth: current theories and influence on management. Oral Maxillofac Surg Clin North Am 2020, 32, 167–175. [Google Scholar] [CrossRef]
Tsutsui, T.; Iizuka, S.; Sakamaki, W.; Maemichi, T.; Torii, S. Growth until Peak Height Velocity Occurs Rapidly in Early Maturing Adolescent Boys. Children (Basel) 2022, 9. [Google Scholar] [CrossRef]
McNamara, J.A., Jr. Components of class II malocclusion in children 8-10 years of age. Angle Orthod 1981, 51, 177–202. [Google Scholar] [CrossRef] [PubMed]
Sayin, M.O.; Türkkahraman, H. Cephalometric evaluation of nongrowing females with skeletal and dental Class II, division 1 malocclusion. Angle Orthod 2005, 75, 656–660. [Google Scholar] [CrossRef] [PubMed]
Stahl, F.; Baccetti, T.; Franchi, L.; McNamara, J.A., Jr. Longitudinal growth changes in untreated subjects with Class II Division 1 malocclusion. Am J Orthod Dentofacial Orthop 2008, 134, 125–137. [Google Scholar] [CrossRef] [PubMed]
Türkkahraman, H.; Sayin, M.O. Effects of activator and activator headgear treatment: comparison with untreated Class II subjects. Eur J Orthod 2006, 28, 27–34. [Google Scholar] [CrossRef]
Bjork, A. Variations in the growth pattern of the human mandible: longitudinal radiographic study by the implant method. J Dent Res 1963, 42 Pt 2, 400–411. [Google Scholar] [CrossRef]
Björk, A. The use of metallic implants in the study of facial growth in children: method and application. Am J Phys Anthropol 1968, 29, 243–254. [Google Scholar] [CrossRef]
Björk, A. Prediction of mandibular growth rotation. Am J Orthod 1969, 55, 585–599. [Google Scholar] [CrossRef]
Björk, A. Prediction of mandibular growth rotation. American journal of orthodontics 1969, 55, 585–599. [Google Scholar] [CrossRef]
Skieller, V.; Björk, A.; Linde-Hansen, T. Prediction of mandibular growth rotation evaluated from a longitudinal implant sample. American journal of orthodontics 1984, 86, 359–370. [Google Scholar] [CrossRef] [PubMed]
Leslie, L.R.; Southard, T.E.; Southard, K.A.; Casko, J.S.; Jakobsen, J.R.; Tolley, E.A.; Hillis, S.L.; Carolan, C.; Logue, M. Prediction of mandibular growth rotation: assessment of the Skieller, Björk, and Linde-Hansen method. American journal of orthodontics and dentofacial orthopedics 1998, 114, 659–667. [Google Scholar] [CrossRef] [PubMed]
Ricketts, R.M. A principle of arcial growth of the mandible. Angle Orthod 1972, 42, 368–386. [Google Scholar] [CrossRef] [PubMed]
Mitchell, D.L.; Jordan, J.F.; Ricketts, R.M. Arcial growth with metallic implants in mandibular growth prediction. Am J Orthod 1975, 68, 655–659. [Google Scholar] [CrossRef] [PubMed]
Rudolph, D.J.; White, S.E.; Sinclair, P.M. Multivariate prediction of skeletal Class II growth. Am J Orthod Dentofacial Orthop 1998, 114, 283–291. [Google Scholar] [CrossRef]
Buschang, P.; Tanguay, R.; LaPalme, L.; Demirjian, A. Mandibular growth prediction: mean growth increments versus mathematical models. The European Journal of Orthodontics 1990, 12, 290–296. [Google Scholar] [CrossRef]
Jiménez-Silva, A.; Carnevali-Arellano, R.; Vivanco-Coke, S.; Tobar-Reyes, J.; Araya-Díaz, P.; Palomino-Montenegro, H. Craniofacial growth predictors for class II and III malocclusions: A systematic review. Clin Exp Dent Res 2021, 7, 242–262. [Google Scholar] [CrossRef]
Walker, G.F. A new approach to the analysis of craniofacial morphology and growth. American Journal of Orthodontics 1972, 61, 221–230. [Google Scholar] [CrossRef]
Vilone, G.; Longo, L. Explainable artificial intelligence: a systematic review. arXiv preprint arXiv:2006.00093 2020. arXiv:2006.00093 2020.
Rajkomar, A.; Dean, J.; Kohane, I. Machine learning in medicine. New England Journal of Medicine 2019, 380, 1347–1358. [Google Scholar] [CrossRef]
Panesar, S.; Zhao, A.; Hollensbe, E.; Wong, A.; Bhamidipalli, S.S.; Eckert, G.; Dutra, V.; Turkkahraman, H. Precision and Accuracy Assessment of Cephalometric Analyses Performed by Deep Learning Artificial Intelligence with and without Human Augmentation. Applied Sciences 2023, 13, 6921. [Google Scholar] [CrossRef]
Bulatova, G.; Kusnoto, B.; Grace, V.; Tsay, T.P.; Avenetti, D.M.; Sanchez, F.J.C. Assessment of automatic cephalometric landmark identification using artificial intelligence. Orthod Craniofac Res 2021, 24 Suppl 2, 37–42. [Google Scholar] [CrossRef]
Kim, J.; Kim, I.; Kim, Y.J.; Kim, M.; Cho, J.H.; Hong, M.; Kang, K.H.; Lim, S.H.; Kim, S.J.; Kim, Y.H.; et al. Accuracy of automated identification of lateral cephalometric landmarks using cascade convolutional neural networks on lateral cephalograms from nationwide multi-centres. Orthod Craniofac Res 2021, 24 Suppl 2, 59–67. [Google Scholar] [CrossRef]
Lindner, C.; Wang, C.W.; Huang, C.T.; Li, C.H.; Chang, S.W.; Cootes, T.F. Fully Automatic System for Accurate Localisation and Analysis of Cephalometric Landmarks in Lateral Cephalograms. Sci Rep 2016, 6, 33581. [Google Scholar] [CrossRef]
Popova, T.; Stocker, T.; Khazaei, Y.; Malenova, Y.; Wichelhaus, A.; Sabbagh, H. Influence of growth structures and fixed appliances on automated cephalometric landmark recognition with a customized convolutional neural network. BMC Oral Health 2023, 23, 274. [Google Scholar] [CrossRef]
Xie, X.; Wang, L.; Wang, A. Artificial neural network modeling for deciding if extractions are necessary prior to orthodontic treatment. Angle Orthod 2010, 80, 262–266. [Google Scholar] [CrossRef] [PubMed]
Suhail, Y.; Upadhyay, M.; Chhibber, A.; Kshitiz. Machine Learning for the Diagnosis of Orthodontic Extractions: A Computational Analysis Using Ensemble Learning. Bioengineering (Basel) 2020, 7. [Google Scholar] [CrossRef]
Ryu, J.; Kim, Y.H.; Kim, T.W.; Jung, S.K. Evaluation of artificial intelligence model for crowding categorization and extraction diagnosis using intraoral photographs. Sci Rep 2023, 13, 5177. [Google Scholar] [CrossRef] [PubMed]
Real, A.D.; Real, O.D.; Sardina, S.; Oyonarte, R. Use of automated artificial intelligence to predict the need for orthodontic extractions. Korean J Orthod 2022, 52, 102–111. [Google Scholar] [CrossRef] [PubMed]
Mason, T.; Kelly, K.M.; Eckert, G.; Dean, J.A.; Dundar, M.M.; Turkkahraman, H. A machine learning model for orthodontic extraction/non-extraction decision in a racially and ethnically diverse patient population. Int Orthod 2023, 21, 100759. [Google Scholar] [CrossRef]
Li, P.; Kong, D.; Tang, T.; Su, D.; Yang, P.; Wang, H.; Zhao, Z.; Liu, Y. Orthodontic Treatment Planning based on Artificial Neural Networks. Sci Rep 2019, 9, 2037. [Google Scholar] [CrossRef] [PubMed]
Kapoor, S.; Shyagali, T.R.; Kuraria, A.; Gupta, A.; Tiwari, A.; Goyal, P. An artificial neural network approach for rational decision-making in borderline orthodontic cases: A preliminary analytical observational in silico study. J Orthod 2023, 14653125231172527. [Google Scholar] [CrossRef] [PubMed]
Jung, S.K.; Kim, T.W. New approach for the diagnosis of extractions with neural network machine learning. Am J Orthod Dentofacial Orthop 2016, 149, 127–133. [Google Scholar] [CrossRef] [PubMed]
Etemad, L.; Wu, T.H.; Heiner, P.; Liu, J.; Lee, S.; Chao, W.L.; Zaytoun, M.L.; Guez, C.; Lin, F.C.; Jackson, C.B.; et al. Machine learning from clinical data sets of a contemporary decision for orthodontic tooth extraction. Orthod Craniofac Res 2021, 24 Suppl 2, 193–200. [Google Scholar] [CrossRef]
Leavitt, L.; Volovic, J.; Steinhauer, L.; Mason, T.; Eckert, G.; Dean, J.A.; Dundar, M.M.; Turkkahraman, H. Can we predict orthodontic extraction patterns by using machine learning? Orthod Craniofac Res 2023. [Google Scholar] [CrossRef]
Lee, H.; Ahmad, S.; Frazier, M.; Dundar, M.M.; Turkkahraman, H. A novel machine learning model for class III surgery decision. Journal of Orofacial Orthopedics/Fortschritte der Kieferorthopädie 2022, 1-11.
Radwan, M.T.; Sin, Ç.; Akkaya, N.; Vahdettin, L. Artificial intelligence-based algorithm for cervical vertebrae maturation stage assessment. Orthod Craniofac Res 2022. [Google Scholar] [CrossRef] [PubMed]
Mohammad-Rahimi, H.; Motamadian, S.R.; Nadimi, M.; Hassanzadeh-Samani, S.; Minabi, M.A.S.; Mahmoudinia, E.; Lee, V.Y.; Rohban, M.H. Deep learning for the classification of cervical maturation degree and pubertal growth spurts: A pilot study. Korean J Orthod 2022, 52, 112–122. [Google Scholar] [CrossRef] [PubMed]
Liao, N.; Dai, J.; Tang, Y.; Zhong, Q.; Mo, S. iCVM: An Interpretable Deep Learning Model for CVM Assessment Under Label Uncertainty. IEEE J Biomed Health Inform 2022, 26, 4325–4334. [Google Scholar] [CrossRef]
Li, H.; Chen, Y.; Wang, Q.; Gong, X.; Lei, Y.; Tian, J.; Gao, X. Convolutional neural network-based automatic cervical vertebral maturation classification method. Dentomaxillofac Radiol 2022, 51, 20220070. [Google Scholar] [CrossRef]
Kök, H.; Izgi, M.S.; Acilar, A.M. Determination of growth and development periods in orthodontics with artificial neural network. Orthod Craniofac Res 2021, 24 Suppl 2, 76–83. [Google Scholar] [CrossRef]
Kim, D.W.; Kim, J.; Kim, T.; Kim, T.; Kim, Y.J.; Song, I.S.; Ahn, B.; Choo, J.; Lee, D.Y. Prediction of hand-wrist maturation stages based on cervical vertebrae images using artificial intelligence. Orthod Craniofac Res 2021, 24 Suppl 2, 68–75. [Google Scholar] [CrossRef]
Atici, S.F.; Ansari, R.; Allareddy, V.; Suhaym, O.; Cetin, A.E.; Elnagar, M.H. AggregateNet: A deep learning model for automated classification of cervical vertebrae maturation stages. Orthod Craniofac Res 2023. [Google Scholar] [CrossRef] [PubMed]
Atici, S.F.; Ansari, R.; Allareddy, V.; Suhaym, O.; Cetin, A.E.; Elnagar, M.H. Fully automated determination of the cervical vertebrae maturation stages using deep learning with directional filters. PLoS One 2022, 17, e0269198. [Google Scholar] [CrossRef] [PubMed]
Amasya, H.; Yildirim, D.; Aydogan, T.; Kemaloglu, N.; Orhan, K. Cervical vertebral maturation assessment on lateral cephalometric radiographs using artificial intelligence: comparison of machine learning classifier models. Dentomaxillofac Radiol 2020, 49, 20190441. [Google Scholar] [CrossRef] [PubMed]
Niño-Sandoval, T.C.; Pérez, S.V.G.; González, F.A.; Jaque, R.A.; Infante-Contreras, C. Use of automated learning techniques for predicting mandibular morphology in skeletal class I, II and III. Forensic science international 2017, 281, 187. e181-187. e187. [Google Scholar] [CrossRef]
Niño-Sandoval, T.C.; Perez, S.V.G.; Gonzalez, F.A.; Jaque, R.A.; Infante-Contreras, C. An automatic method for skeletal patterns classification using craniomaxillary variables on a Colombian population. Forensic Science International 2016, 261, 159. e151-159. e156. [Google Scholar] [CrossRef]
Jiwa, S. Applicability of deep learning for mandibular growth prediction. Boston University, 2020.
Wood, T.; Anigbo, J.O.; Eckert, G.; Stewart, K.T.; Dundar, M.M.; Turkkahraman, H. Prediction of the Post-Pubertal Mandibular Length and Y Axis of Growth by Using Various Machine Learning Techniques: A Retrospective Longitudinal Study. Diagnostics 2023, 13, 1553. [Google Scholar] [CrossRef]
AAOF Craniofacial Growth Legacy Collection. Available online: https://www.aaoflegacycollection.org/aaof_home.html (accessed on June 19, 2023).
Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. Journal of chiropractic medicine 2016, 15, 155–163. [Google Scholar] [CrossRef]
Ochoa, B.K.; Nanda, R.S. Comparison of maxillary and mandibular growth. Am J Orthod Dentofacial Orthop 2004, 125, 148–159. [Google Scholar] [CrossRef]
Baumrind, S.; Korn, E.L.; West, E.E. Prediction of mandibular rotation: an empirical test of clinician performance. Am J Orthod 1984, 86, 371–385. [Google Scholar] [CrossRef]
Karlsen, A.T. Craniofacial growth differences between low and high MP-SN angle males: a longitudinal study. The Angle Orthodontist 1995, 65, 341–350. [Google Scholar] [CrossRef] [PubMed]
Schudy, F.F. The rotation of the mandible resulting from growth: its implications in orthodontic treatment. The Angle Orthodontist 1965, 35, 36–50. [Google Scholar] [CrossRef] [PubMed]
Su, X.; Yan, X.; Tsai, C.L. Linear regression. Wiley Interdisciplinary Reviews: Computational Statistics 2012, 4, 275–294. [Google Scholar] [CrossRef]
McDonald, G.C. Ridge regression. Wiley Interdisciplinary Reviews: Computational Statistics 2009, 1, 93–100. [Google Scholar] [CrossRef]

Figure 1. Cephalometric landmarks used in this study. 1. Sella (S), 2. Nasion (N), 3. Orbitale (Or), 4. Porion (Po), 5. Condylion (Co), 6. Articulare (Ar), 7. Basion (Ba), 8. Gonion (Go), 9. Menton (Me), 10. Gnathion (Gn), 11. Pogonion (Pog), 12. B point (B), 13. Lower incisor root apex (L1a), 14. Lower incisor incisal edge (L1i), 15. Mesial of lower first molar (L6m), 16. Mesiobuccal cusp of lower first molar (L6mb), 17. Distal of lower first molar (L6d), 18. Distal of upper first molar (U6d), 19. Mesiobuccal cusp of upper first molar (U6mb), 20. Mesial of upper first molar (U6m), 21. Upper incisor incisal edge (U1i), 22. Upper incisor root apex (U1a), 23. A point (A), 24. Anterior nasal spine (ANS), 25. Posterior nasal spine (PNS).

Figure 2. Algorithm training and testing workflow.

Figure 3. Bland-Altman plots for 2-year and 4-year predictions of post-pubertal mandibular length using Lasso (top) and Ridge (bottom). The blue dashed lines represent upper and lower bounds of the 95% confidence intervals. Orange solid line represents mean difference between predicted and actual mandibular length. .

Figure 4. Top predictive factors for 2-year and 4-year predictions of post-pubertal mandibular length using Lasso (top) and Ridge (bottom).

Figure 5. Bland-Altman plots for 2-year and 4-year predictions of post-pubertal Y-axis using Lasso (top) and Ridge (bottom). The blue dashed lines represent upper and lower bounds of the 95% confidence intervals. Orange solid line represents mean difference between predicted and actual Y-axis.

Figure 6. Top predictive factors for 2-year and 4-year predictions of post-pubertal Y-axis using Lasso (top) and Ridge (bottom).

Table 1. Results of 2-year and 4-year prediction of post-pubertal mandibular length.

	2-Year Prediction					4-Year Prediction
Models	MAE	RMSE	ME	ICC	Accuracy %	MAE	RMSE	ME	ICC	Accuracy %
XGBoost	2.80	3.29	-0.42	0.88	97.81	3.20	3.97	0.02	0.81	97.50
Random Forest	2.83	3.58	-0.56	0.83	97.79	3.55	4.39	0.34	0.71	97.23
Lasso	2.11	2.68	-0.54	0.91	98.35	2.32	3.13	-0.12	0.87	98.19
Ridge	2.29	2.71	0.10	0.91	98.21	2.62	3.37	-0.01	0.87	97.95
Linear Regression	6.07	7.65	2.32	0.58	95.26	5.28	6.33	0.84	0.67	95.88
SVR	3.55	4.14	-0.29	0.78	97.23	3.41	4.01	-0.70	0.74	97.33
MLP	2.65	3.08	-0.46	0.90	97.93	3.09	3.90	-1.74	0.84	97.59

MAE: Mean absolute error, RMSE: Root mean square error, ME: Mean error, ICC: Intra-class coefficient.

Table 2. Results of 2-year and 4-year prediction of the post-pubertal Y-axis.

	2-Year Prediction					4-Year Prediction
Models	MAE	RMSE	ME	ICC	Accuracy %	MAE	RMSE	ME	ICC	Accuracy %
XGBoost	1.20	1.55	-0.87	0.89	98.26	1.52	1.93	-0.62	0.82	97.79
Random Forest	1.17	1.45	-0.66	0.90	98.30	1.72	2.10	-0.79	0.77	97.50
Lasso	0.85	1.08	-0.37	0.95	98.76	1.25	1.72	-0.42	0.86	98.18
Ridge	1.41	1.74	-0.64	0.86	97.95	1.68	2.18	-0.68	0.77	97.56
Linear Regression	2.74	3.78	0.32	0.63	96.02	1.66	2.24	-0.62	0.81	97.59
SVR	1.31	1.75	-0.39	0.86	98.10	1.72	2.25	-0.45	0.76	97.50
MLP	1.30	1.62	0.00	0.89	98.11	1.49	1.91	-0.38	0.83	97.83

MAE: Mean absolute error, RMSE: Root mean square error, ME: Mean error, ICCL Intra-class correlation coefficient.

Table 3. Directional and absolute difference comparisons between ML models for 2-year prediction of post-pubertal mandibular length.

Directional Difference		Absolute Difference
Result	P-value	Result	P-value
Lasso > Linear Regression	<.001	Lasso < Linear Regression	<.001
Lasso & MLP	0.922	Lasso & MLP	0.336
Lasso & Random Forest	0.971	Lasso & Random Forest	0.196
Lasso & Ridge	0.407	Lasso & Ridge	0.752
Lasso & SVR	0.745	Lasso < SVR	0.010
Lasso & XGBoost	0.882	Lasso & XGBoost	0.213
Linear Regression < MLP	<.001	Linear Regression > MLP	<.001
Linear Regression < Random Forest	<.001	Linear Regression > Random Forest	<.001
Linear Regression < Ridge	0.004	Linear Regression > Ridge	<.001
Linear Regression < SVR	0.001	Linear Regression > SVR	<.001
Linear Regression < XGBoost	<.001	Linear Regression > XGBoost	<.001
MLP & Random Forest	0.893	MLP & Random Forest	0.739
MLP & Ridge	0.464	MLP & Ridge	0.517
MLP & SVR	0.820	MLP & SVR	0.105
MLP & XGBoost	0.959	MLP & XGBoost	0.777
Random Forest & Ridge	0.386	Random Forest & Ridge	0.327
Random Forest & SVR	0.717	Random Forest & SVR	0.197
Random Forest & XGBoost	0.853	Random Forest & XGBoost	0.961
Ridge & SVR	0.614	Ridge < SVR	0.024
Ridge & XGBoost	0.496	Ridge & XGBoost	0.352
SVR & XGBoost	0.860	SVR & XGBoost	0.181

Table 4. Directional and absolute difference comparisons between ML models for 4-year prediction of post-pubertal mandibular length.

Directional Difference		Absolute Difference
Result	P-value	Result	P-value
Lasso & Linear Regression	0.171	Lasso < Linear Regression	<.001
Lasso < MLP	0.021	Lasso & MLP	0.115
Lasso & Random Forest	0.508	Lasso < Random Forest	0.013
Lasso & Ridge	0.876	Lasso & Ridge	0.536
Lasso & SVR	0.405	Lasso < SVR	0.027
Lasso & XGBoost	0.846	Lasso & XGBoost	0.075
Linear Regression < MLP	<.001	Linear Regression > MLP	<.001
Linear Regression & Random Forest	0.478	Linear Regression > Random Forest	0.001
Linear Regression & Ridge	0.225	Linear Regression > Ridge	<.001
Linear Regression < SVR	0.028	Linear Regression > SVR	<.001
Linear Regression & XGBoost	0.239	Linear Regression > XGBoost	<.001
MLP > Random Forest	0.003	MLP & Random Forest	0.357
MLP > Ridge	0.014	MLP & Ridge	0.337
MLP & SVR	0.137	MLP & SVR	0.518
MLP > XGBoost	0.013	MLP & XGBoost	0.834
Random Forest & Ridge	0.613	Random Forest & Ridge	0.061
Random Forest & SVR	0.136	Random Forest & SVR	0.783
Random Forest & XGBoost	0.639	Random Forest & XGBoost	0.476
Ridge & SVR	0.323	Ridge & SVR	0.109
Ridge & XGBoost	0.970	Ridge & XGBoost	0.243
SVR & XGBoost	0.305	SVR & XGBoost	0.662

Table 5. Directional and absolute difference comparisons between ML methods for the 2-year prediction of Y-axis.

Directional Difference		Absolute Difference
Result	P-value	Result	P-value
Lasso & Linear Regression	0.096	Lasso < Linear Regression	<.001
Lasso & MLP	0.374	Lasso & MLP	0.121
Lasso & Random Forest	0.483	Lasso & Random Forest	0.270
Lasso & Ridge	0.514	Lasso & Ridge	0.052
Lasso & SVR	0.968	Lasso & SVR	0.109
Lasso & XGBoost	0.229	Lasso & XGBoost	0.228
Linear Regression & MLP	0.434	Linear Regression > MLP	<.001
Linear Regression < Random Forest	0.018	Linear Regression > Random Forest	<.001
Linear Regression < Ridge	0.021	Linear Regression > Ridge	<.001
Linear Regression & SVR	0.088	Linear Regression > SVR	<.001
Linear Regression < XGBoost	0.004	Linear Regression > XGBoost	<.001
MLP & Random Forest	0.113	MLP & Random Forest	0.651
MLP & Ridge	0.124	MLP & Ridge	0.692
MLP & SVR	0.353	MLP & SVR	0.960
MLP < XGBoost	0.037	MLP & XGBoost	0.727
Random Forest & Ridge	0.961	Random Forest & Ridge	0.396
Random Forest & SVR	0.508	Random Forest & SVR	0.615
Random Forest & XGBoost	0.614	Random Forest & XGBoost	0.917
Ridge & SVR	0.540	Ridge & SVR	0.729
Ridge & XGBoost	0.580	Ridge & XGBoost	0.456
SVR & XGBoost	0.244	SVR & XGBoost	0.690

Table 6. Directional and absolute difference comparisons between ML models for the 4-year prediction of Y-axis.

Directional Difference		Absolute Difference
Result	P-value	Result	P-value
Lasso & Linear Regression	0.337	Lasso < Linear Regression	0.013
Lasso & MLP	0.823	Lasso & MLP	0.133
Lasso & Random Forest	0.070	Lasso < Random Forest	0.004
Lasso & Ridge	0.203	Lasso < Ridge	0.008
Lasso & SVR	0.891	Lasso < SVR	0.004
Lasso & XGBoost	0.339	Lasso & XGBoost	0.093
Linear Regression & MLP	0.237	Linear Regression & MLP	0.314
Linear Regression & Random Forest	0.390	Linear Regression & Random Forest	0.705
Linear Regression & Ridge	0.753	Linear Regression & Ridge	0.880
Linear Regression & SVR	0.411	Linear Regression & SVR	0.721
Linear Regression & XGBoost	0.997	Linear Regression & XGBoost	0.407
MLP < Random Forest	0.042	MLP & Random Forest	0.167
MLP & Ridge	0.135	MLP & Ridge	0.247
MLP & SVR	0.718	MLP & SVR	0.173
MLP & XGBoost	0.239	MLP & XGBoost	0.858
Random Forest & Ridge	0.585	Random Forest & Ridge	0.820
Random Forest & SVR	0.093	Random Forest & SVR	0.983
Random Forest & XGBoost	0.387	Random Forest & XGBoost	0.228
Ridge & SVR	0.256	Ridge & SVR	0.837
Ridge & XGBoost	0.750	Ridge & XGBoost	0.327
SVR & XGBoost	0.413	SVR & XGBoost	0.236

Table 7. Comparisons of the directional and absolute differences between the 2-year and 4-year predictions of post-pubertal mandibular length.

	Directional Difference		Absolute Difference
Method	Result	P-value	Result	P-value
XGBoost	2-year & 4-year	0.577	2-year & 4-year	0.495
Random Forest	2-year & 4-year	0.250	2-year & 4-year	0.213
Lasso	2-year & 4-year	0.595	2-year & 4-year	0.724
Ridge	2-year & 4-year	0.889	2-year & 4-year	0.563
Linear Regression	2-year & 4-year	0.062	2-year & 4-year	0.169
SVR	2-year & 4-year	0.603	2-year & 4-year	0.811
MLP	2-year & 4-year	0.107	2-year & 4-year	0.437

Table 8. Comparisons of the directional and absolute differences between the 2-year and 4-year predictions of post-pubertal Y-axis.

	Directional Difference		Absolute Difference
Method	Result	P-value	Result	P-value
XGBoost	2-year & 4-year	0.500	2-year & 4-year	0.214
Random Forest	2-year & 4-year	0.724	2-year < 4-year	0.036
Lasso	2-year & 4-year	0.886	2-year & 4-year	0.126
Ridge	2-year & 4-year	0.912	2-year & 4-year	0.305
Linear Regression	2-year < 4-year	0.012	2-year > 4-year	<0.001
SVR	2-year & 4-year	0.863	2-year & 4-year	0.125
MLP	2-year & 4-year	0.314	2-year & 4-year	0.455

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer