Preprint
Article
Multi-NDE Technology Approach to Improve Interpretation of Corrosion in Concrete Bridge Decks Based on Electrical Resistivity Measurements
Altmetrics
Downloads
81
Views
23
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
28 June 2023
Posted:
04 July 2023
You are already at the latest version
Alerts
Abstract
This research aimed to improve the interpretation of electrical resistivity (ER) results in concrete bridge decks by utilizing results from multiple nondestructive evaluations (NDE) techniques in machine learning algorithms. To achieve this, a parametric study was first conducted using numerical simulations to investigate the effect of various parameters on ER measurements, such as the degree of saturation, corrosion length, delamination depth, concrete cover, and the moisture condition of delamination. A data set from this study was used to build a machine-learning algorithm based on the Random Forest methodology. This algorithm was then implemented on data collected from a bridge deck in the BEAST® facility. The presented results demonstrate an improvement in the interpretation of ER measurements using data from other NDE technologies.
Keywords:
Subject: Engineering - Civil Engineering
1. Introduction
Using nondestructive evaluation (NDE) techniques to identify corrosion in bridge decks early on can help reduce overall management costs. Several NDE technologies can be used for this purpose, such as electrical resistivity (ER) and half-cell potential (HCP), galvanostatic pulse measurements (GPM), and linear polarization resistance (LPR). For example, ER is used for assessing corrosive environments and to them related anticipated corrosion rates, while HCP is used to determine the likelihood of active corrosion in reinforcing steel bars. However, it's important to note that NDE technologies can have limitations when it comes to detecting certain types of defects and deterioration, as the accuracy of their detection and characterization can be influenced by various parameters.
Electrical resistivity (ER) is a commonly used NDE technique that can be used to assess the durability of concrete structures (Layssi et al., 2015). It can also be useful for structural health monitoring and quality control, as it can detect the presence of cracks and measure chloride penetration (Sengul and Gjørv, 2008) (Cristina Silva et al., 2011) (Sengul, 2014).
Electrical resistivity (ER) measurements can be influenced by various factors that can significantly impact the measured values. For example, ER measurements can be affected by factors like moisture content (Robles et al, 2022)(Azarsa and Gupta, 2017)(Hornbostel et al., 2013), temperature (Marquez, 2015)(Elkey and Sellevold, 1995), and carbonation(Gowers and Millard, 1999). Several studies have demonstrated that an increase in moisture content can lead to a decrease in electrical resistivity (Weiss et al., 2013). However, it is noted that further research is needed to better understand the effect of partial saturation on the electrical resistivity of concrete. The electrical resistivity of a material is influenced by its characteristics, which can change over time, such as porosity and the level of void interconnections (Lataste and Breysse, 2013). In addition, the characteristics of cracks and delamination in concrete, like the delamination depth or crack orientation, can also affect ER measurement values (Khudhair and Gucunski, 2018). Thus, this study has been conducted to investigate the changes in the ER measurements in a presence of different parameters and how can improve the interpretation of the collected data of the ER technology by using different NDE technologies. In addition, the ER measurement results are corrected for reference conditions to enable objective comparison of the results from periodical surveys on the same bridge, or the results from surveys on different bridges. The following sections describe the evaluation of the effects of different parameters on ER results using finite element simulations, and the development and utilization of machine learning techniques to improve the interpretation of ER data based on the results from other NDE techniques.
2. Algorithm Development
2.1. Finite Element Modeling:
Three-dimensional finite element models have been built to simulate multiple NDE techniques with COMSOL Multiphysics® software. Each NDE technique has its unique characteristics, parameters, and requirements that must be taken into consideration when constructing a model. Yet, the ultimate aim of this study was to develop a comprehensive model capable of simulating all of the studied NDE techniques in a single reinforced concrete volume simultaneously.
Three non-destructive evaluation (NDE) techniques were simulated: impact echo (IE), for delamination detection and characterization (Gucunski et al., 2005)(Gucunski et al., 2012), electrical resistivity (ER), and half-cell potential (HCP). These techniques are based on distinct physical phenomena, but COMSOL Multiphysics® software's ability to integrate them into a single model allows for the simultaneous implementation of all three techniques on the target domain, mimicking the use of multiple NDE techniques in real-life situations.
The layout of the model components with the positioning of various NDE probes is illustrated in Figure 1. These components show the probe locations and boundary conditions for each NDE technique utilized in the simulation. Although this single model represents all three techniques, the domain was divided around each technique for meshing purposes, enabling finer element meshes for each technique to be obtained during the solution process, as shown in Figure 2.
The three technologies have been simulated to be deployed simultaneously on a concrete slab with different parameters which led to the production of 1008 unique models. These parameters are the degree of saturation (DoF), rebar corrosion length (CL), delamination depth (DD), concrete cover (CC) thickness, and moisture condition of the delamination. Below are the descriptions of these parameters in more detail:
- Degree of saturation (DoS): Seven values have been chosen to represent the degree of saturation, which are 20%, 30%, 40%, 50%, 60%, 70%, and 80%. This range of values represents different moisture conditions in the slab.
- Corrosion length (CL): A set of four values that represent the corrosion length of the steel rebar. These lengths are used as the anode segment in the corrosion process, which are 2.5 cm, 5 cm, 10 cm, and 15 cm.
- Delamination depth (DD): The delamination depth has been simulated to represent a crack at various depths. A set of six values has been selected: 40mm, 50mm, 60mm, 70mm, 80mm, and 90mm.
- Concrete cover (CC) thickness: a set of four values has been selected to simulate the concrete cover thickness, which was 38mm, 51mm, 63mm, and 76mm.
- The moisture condition of the delamination: Two different conditions have been chosen to represent the moisture condition of the delamination inside the concrete. The first one is air-filled delamination (AFD) which represents completely dry delamination, and the second condition is water-filled delamination (WFD), which represents fully saturated delamination.
2.1.1. Impact Echo Simulation
A concrete slab with dimensions of 1.0m x 1.0m x 0.2m was used as a domain for the impact echo (IE) test simulation. The slab had Perfect Match Layers (PML) elements on its sides to prevent the reflection of elastic waves. The domain included a loading plate and measurement points, which represented the impact area and transducer location, respectively. The transducer was placed 5 cm away from the impact point, as shown in Figure 1. A cross-section of a slab with a 1 mm wide delamination at a depth of 50 mm from the surface is shown in Figure 3. Also, the concrete Poisson's ratio, P-wave, and S-wave are 0.2, 4000 m/s, and 2312 m/s, respectively.
The acceleration time history for a sound concrete model is plotted in Figure 4a, while the corresponding frequency spectrum is illustrated in Figure 4b. The frequency spectrum of the IE test on the sound concrete model in Figure 4b indicates that the dominant frequency is 10,000 Hz. Using this information and Eq. (1), the thickness of the slab is calculated to be 0.192 m, which is very close to the actual thickness of 0.2 m.
On the other hand, Figure 5a shows the waveform and frequency analysis for a model with a 5 cm deep delamination. The dominant frequency due to the defect is 34,900 Hz, as shown in Figure 5b. By applying Eq. (1), the calculated depth of the delamination in the concrete slab is found to be 0.055 m, which is very close to the known defect depth of 0.050 m.
The IE test involved the application of a half-sine wave pulse with an intensity of 1 N and a duration of 50 microseconds. The IE method is effective in determining the thickness of plate-like structures. This can be achieved by analyzing the dominant frequency in the slab and using the velocity of P-waves in the medium (Sansalone and Streett, 1997), as shown below:
where:
2.1.2. Electrical Resistivity Simulation
The model of the concrete slab used for ER simulation is the same as the one used for IE simulation. However, since ER relies on different physical phenomena, an additional boundary condition must be applied to the edges of the model to simulate the continuous boundaries of the concrete block on all four sides. For this purpose, the essential (or Dirichlet) boundary has been used to model the ground electrical continuity. It is often used in models of electrical circuits, electronic devices, and heat transfer systems. The center region of the ER model includes the probe contact zone, which is represented by four electrodes spaced 5 cm apart, as shown in Figure 1. The concrete slab block was meshed using free tetrahedral elements, with a finer mesh used in the ER probe region to achieve a precise value at the measurement points. The maximum element size for the free tetrahedra near the point sources was set to 0.001 m, with a growth factor of 1.2, as shown in Figure 2.
The simulation of ER was performed by mimicking the operation of the Proceq Resipod probe (according to the Proceq Resipod manual from 2017). In this probe, a current of 200 μA is injected from the two outer electrodes, while the two inner electrodes are used to measure the potential difference in the generated electric field, as shown in Figure 6. Specifically, the current intensity is +200 μA in probe No. 1 and -200 μA in probe No. 4, as shown in Figure 10. The electrical conductivity values for concrete, water, and air used in the modeling are listed in Table 1. The used conductivity of concrete is 0.002 S/m is the reciprocal of a resistivity of 500 Ω.m.
The resistivity of the concrete is calculated based on three variables: the potential difference (voltage), the electrical current, and the spacing of probes. These variables are related according to the following equations:
where:
ρ=k V/I
k=2aπ
ρ= Electrical resistivity
k= Geometrical factor of a Wenner acquisition array
V= Potential measured (Voltage)
I= Electrical current applied
a= Spacing between the probes
The electrical potential distribution measured in (mV) at the C-C cross-section (Figure 1) for the sound concrete is shown in 7. Figure 8 shows that the relationship between electrical resistivity and degree of saturation is inversely proportional, meaning that as one variable increases, the other decreases. This is because water is more conductive than concrete. When concrete is dry, the resistance to electric flow increases as the number of free electrons available to carry the current decreases. Distributions for the model containing air-filled delamination (AFD) and water-filled delamination (WFD) are shown in Figure 9 and Figure 10, respectively. The delamination dimensions are 50cm×50cm×0.1cm with a depth of 80 mm. It can be inferred that the air-filled delamination serves as an insulating barrier that prevents the current flow, as air has a much higher resistance than concrete. In contrast, water-filled delamination facilitates the current flow as water has a much lower resistance than concrete.
2.1.3. Half-Cell Potential Simulation
A half-cell can be represented by an electrode immersed in an electrolyte. The potential difference can be measured by using a reference electrode with a known potential on the concrete surface. The FE model for HCP simulation is the same concrete slab that has been used for IE and ER, as shown in Figure 1. Cross-section A-A, shown in Figure 11, illustrates the steel bar inside the concrete, the cathodic zone, and the anodic zone (corrosion zone).
The equipotential lines between the anode and cathode from the simulation results demonstrate a high sensitivity to certain parameters, such as the presence of shallow delamination and the degree of saturation of the delamination. Due to this sensitivity, different modeling cases are presented to illustrate the potential outcomes of the electrochemical process of corrosion within the concrete. Figure 12 illustrates the potential distribution inside the concrete due to a 10 cm length of corrosion in steel rebar with a 40% degree of saturation and no delamination. In contrast, the potential distribution inside the concrete with the same parameters but with the presence of a 40 mm deep delamination is shown in Figure 13 and Figure 14. Figure 13 illustrates the effect of air-filled delamination (AFD), while Figure 14 illustrates the effect of water-filled delamination (WFD). Looking closely into the potential distributions, a more pronounced effect on the near-surface potentials can be observed in the AFD model.
2.2. Machine Learning Algorithm
2.2.1. Random Forest Algorithm
The Random Forest algorithm can be used for both regression and classification tasks. It has a high success rate as a general-purpose algorithm due to its use of multiple decision trees to make predictions on the training data set. In a regression task, the final prediction is the mean value of the individual tree predictions. In a classification task, the final prediction is the class chosen by the majority of the trees. Figure 15 illustrates the Random Forest algorithm for regression and classification tasks, marked in black and red respectively. The algorithm was first introduced in 1995 by Tin Kam Ho (Ho, 1995) and further developed in 2001 by L. Breiman (Breiman, 2001). The basic principles of the algorithm are described using the following equations (Biau and Scornet, 2016):
where:
Equation (4) represents a random input vector that is observed in the general framework that considers a nonparametric regression estimation of the algorithm.
where:
Equation (5) represents the square-integrable random response which can be predicted by estimating the regression function defined by equation (6)
where:
The data set defined by equation (8) is used to construct a regression function estimate defined by equation (7). Hence, the regression function estimate is consistent if (Biau and Scornet, 2016):
The multitude of M randomized regression trees construct the Random Forest predictor for the jth tree in the family. The predicted value at the query point x is defined by:
where:
In the other word, the mathematical expression of the estimate for the jth tree is denoted by (Biau and Scornet, 2016):
where:
Moreover, the finite forest estimate can be constructed by combining all the trees as follows (Biau and Scornet, 2016):
Simulations of the (NDE) technologies in three dimensions were used to develop a machine-learning algorithm using the Random Forest method. The simulation generated 1008 models with specific values for the simulated NDE technologies, resulting in a dataset of 1008 instances that will be used to train the machine learning algorithm. This algorithm was designed to electrical resistivity correct measurement values affected by five specific parameters discussed earlier in section 2.1. The correction of the measurements is based on a reference model with DoS=40%, DD=0, CC=63mm, and CL=0 (no rebar corrosion). The algorithm was created using Orange®, an open-source software for machine learning, data mining, and data visualization. The regression algorithm used in this study is based on a dataset with 9 types of attributes. These attributes play different roles in the process and can be classified as Feature, Meta, or Target, as described below:
- Degree of Saturation: the attribute is Numerical variable that has a Feature role.
- Length of Corrosion: the attribute is Numerical variable that has a Meta role.
- Delamination Depth: the attribute is Numerical variable that has a Feature role
- Concrete Cover: the attribute is Numerical data variable that has a Feature role
- Delamination M.C: the attribute is Categorical variable that has a Meta role
- Measured Resistivity: the attribute is Numerical variable that has a Feature role
- Measured HCP: the attribute is Numerical variable that has a Feature role
- Actual Resistivity: the attribute is Numerical variable that has a Target role
In this study, the algorithm was used to predict the values of Actual Resistivity (kOhm.cm) based on reference models with no delamination, a concrete cover of 63mm, and a degree of saturation of 40%. The algorithm serves as a correction tool, adjusting the measured values to provide more accurate predictions of the electrical resistivity for reference conditions. Figure 16s shows the workflow of the algorithm.
When analyzing the results of the algorithm, it was found that the coefficient of determination (R2) was 0.81, indicating a strong positive correlation between the predicted and actual values. Additionally, the coefficient of variation of the root mean squared error (CVRSM) was found to be 23.931.
Figure 17 illustrates the correlation between the actual values on the x-axis and the predictions made by the Random Forest algorithm on the y-axis for electrical resistivity (ER) values. The chart displays the correlation in three different colors: blue for instances with no delamination, red for instances with AFD (a type of damage), and green for instances with WFD (another type of damage). The red instances have the highest value of r, which is 0.92, while the other r values are 0.90, 0.88, and 0.90 for the blue, green, and overall instances, respectively. While the results are very close, they indicate that the algorithm's predictions are slightly more accurate for ER technology applied to sound and concrete slabs with AFD than those with WFD.
3. Algorithm Implementation
The algorithm was implemented on data obtained from an NDE survey on an actual bridge deck. The raw data were collected on a bridge structure with a concrete deck installed in the BEAST® (Bridge Evaluation and Accelerated Structural Testing) facility on the Rutgers’ Livingston campus. The bridge structure is approximately 15 meters long and 8.4 meters wide. The BEAST® facility allows exposure of the concrete deck to different environmental conditions, such as freezing and thawing, deicing salt exposure, and continuous traffic loading, to accelerate the deterioration of the bridge deck. The traffic loading is simulated by a dual-axle carriage that applies a load of approximately 60,000 pounds, as illustrated in Figure 18, and makes about 15,000 passes per day over the bridge. Also, NDE data were collected on a 0.3m X 0.3m (1ft X 1ft) grid, as shown in Figure 18.
The data for this study were collected periodically, typically on a monthly basis, using three primary NDE technologies: impact echo, electrical resistivity, and half-cell potential, as shown in Figure 19. In addition, the degree of saturation of the concrete was measured using the MOIST-Scan, as shown in Figure 19a. This device uses microwave technology to nondestructively determine the residual moisture content of the concrete. The collected values from the MOIST-Scan device were distributed between 0% and 100%. Ground penetrating radar (GPR) was used to evaluate the concrete cover thickness.
The data for each technology was analyzed and presented in terms of condition maps before applying the machine learning algorithm. This was done to compare the results of the data interpretation with and without the use of the algorithm. The DoS, ER, and HCP condition maps for the BEAST deck are shown in Figure 20.
The delamination map from IE is shown in Figure 21. All delamination found was shallow, with a depth of less than approximately 3 cm (1.25 inches). The delamination occurred at the top reinforcement level. The concrete cover thickness was obtained from the GPR survey, as shown in the same figure.
To use the algorithm, the values of the five parameters were input into the prediction table of the algorithm for each point on the BEAST deck test grid. The collected data for the five parameters was organized in an Excel sheet for 1,127 points on the BEAST grid. A new set of plots were generated based on the corrected values of the algorithm. Figure 22 shows ER plots before and after using the algorithm for ER. There are significant differences in the values of ER measurements between Figure 22a (before applying the algorithm) and Figure 22b (after applying the algorithm). The measurements changed from around 12 kOhm.cm to approximately 25 kOhm.cm, with the lowest resistivity after using the algorithm being located in the middle of the slab. These changes are primarily due to the influence of the DoS parameter and the effects of delamination. The values seen in Figure 20 of the DoS have a significant impact on the ER values shown in Figure 22b. The algorithm appears to attempt to counteract the effects of DoS by raising the resistivity in areas with high DoS and lowering it in areas with low DoS. Additionally, the IE condition assessment map in Figure 21 shows the location of delamination, which is reflected in the corrected ER values in Figure 22b. The algorithm incorporates the impact of delamination on ER measurement values by decreasing the resistivity value for the delaminated area, which is mainly located in the middle section of the deck.
4.Conclusions
The measurement of electrical resistivity is essential for assessing the potential for corrosion-induced deterioration of reinforced concrete structures. However, ER measurements are greatly influenced by a variety of factors. The degree of saturation, rebar corrosion, and the depth and moisture condition of delamination are all factors that can have a significant impact on the accuracy of ER measurements. These factors must be taken into account when interpreting the results of ER measurements.
One way to address this is by utilizing machine learning techniques to develop a measurement correction tool. This tool could be designed to take into account the impact of all of the influencing parameters. This tool could be beneficial for improving the interpretation of ER measurements and for better understanding the relationships between the parameters. Overall, this study highlights the importance of considering the various factors that can affect ER measurements and the benefits stemming from the multi-NDE technology approach in the condition assessment of reinforced concrete structures.
References
- Azarsa, P.; Gupta, R. Electrical Resistivity of Concrete for Durability Evaluation: A Review. Adv. Mater. Sci. Eng. 2017, 2017, 1–30. [Google Scholar] [CrossRef]
- Biau, G. and Scornet, E. (2016) ‘A random forest guided tour’, Test, 25(2), pp. 197–227.
- Breiman, L. (2001) ‘Random forests’, Machine learning, 45(1), pp. 5–32.
- Cristina Silva, P. , Miguel Ferreira, R. and Figueiras, H. (2011) ‘Electrical Resistivity as a Means of Quality Control of Concrete – Influence of Test Procedure’, XII DBMC Int. Conf. Durab. Build. Mater. Components, pp. 1–8. Available at: http://www.irbnet.de/daten/iconda/CIB22513.pdf.
- Elkey, W. and Sellevold, E. J. (1995) ‘Electrical resistivity of concrete’.
- Gowers, K. and Millard, S. (1999) ‘Measurement of concrete resistivity for assessment of corrosion’, ACI Materials Journal, 96(5).
- Gucunski, N.; Romero, F.A.; Shokouhi, P.; Makresias, J. Complementary Impact Echo and Ground Penetrating Radar Evaluation of Bridge Decks on I-84 Interchange in Connecticut. In Proceedings of the Geo-Frontiers Congress 2005, Austin, TX, USA, January 2005. [Google Scholar]
- Gucunski, N.; Yan, M.; Wang, Z.; Fang, T.; Maher, A. Rapid Bridge Deck Condition Assessment Using Three-Dimensional Visualization of Impact Echo Data. J. Infrastruct. Syst. 2012, 18, 12–24. [Google Scholar] [CrossRef]
- Hamed Layssi, Pouria Ghods, Aali R. Alizadeh, and M. S. and T (2015) ‘Electrical Resistivity of Concrete’, Concrete Internationals, (02), pp. 293–302.
- Ho, T. K. (1995) ‘Random decision forests’, in Proceedings of 3rd international conference on document analysis and recognition. IEEE; pp. 278–282.
- Hornbostel, K.; Larsen, C.K.; Geiker, M.R. Relationship between concrete resistivity and corrosion rate – A literature review. Cem. Concr. Compos. 2013, 39, 60–72. [Google Scholar] [CrossRef]
- Khudhair, M. J. and Gucunski, N. (2018) ‘Effects of Concrete Delamination and Cracking on Electrical Resistivity Measurement Results’, in NDE/NDT for Highways & Bridges: SMT 2018.
- Lataste, J.-F.; Breysse, D. A Study on the Variability of Electrical Resistivity of Concrete. 2011; 255–261. [Google Scholar] [CrossRef]
- Robles, K.P.V.; Yee, J.-J.; Kee, S.-H. Electrical Resistivity Measurements for Nondestructive Evaluation of Chloride-Induced Deterioration of Reinforced Concrete—A Review. Materials 2022, 15, 2725. [Google Scholar] [CrossRef]
- Sanchez Marquez, J. M. (2015) ‘Influence of Saturation and Geometry on Surface Electrical Resistivity Measurements’. Concordia University.
- Sansalone, M. J. and Streett, W. B. (1997) ‘Impact-echo. Nondestructive evaluation of concrete and masonry’.
- Sengul, O. Use of electrical resistivity as an indicator for durability. Constr. Build. Mater. 2014, 73, 434–441. [Google Scholar] [CrossRef]
- Sengul, O. and Gjørv, O. E. (2008) ‘Electrical resistivity measurements for quality control during concrete construction’, ACI Materials Journal, 105(6), p. 541.
- Weiss, J.; Snyder, K.; Bullard, J.; Bentz, D. Using a Saturation Function to Interpret the Electrical Properties of Partially Saturated Concrete. J. Mater. Civ. Eng. 2013, 25, 1097–1106. [Google Scholar] [CrossRef]
Figure 1.
Figure 1. Model components
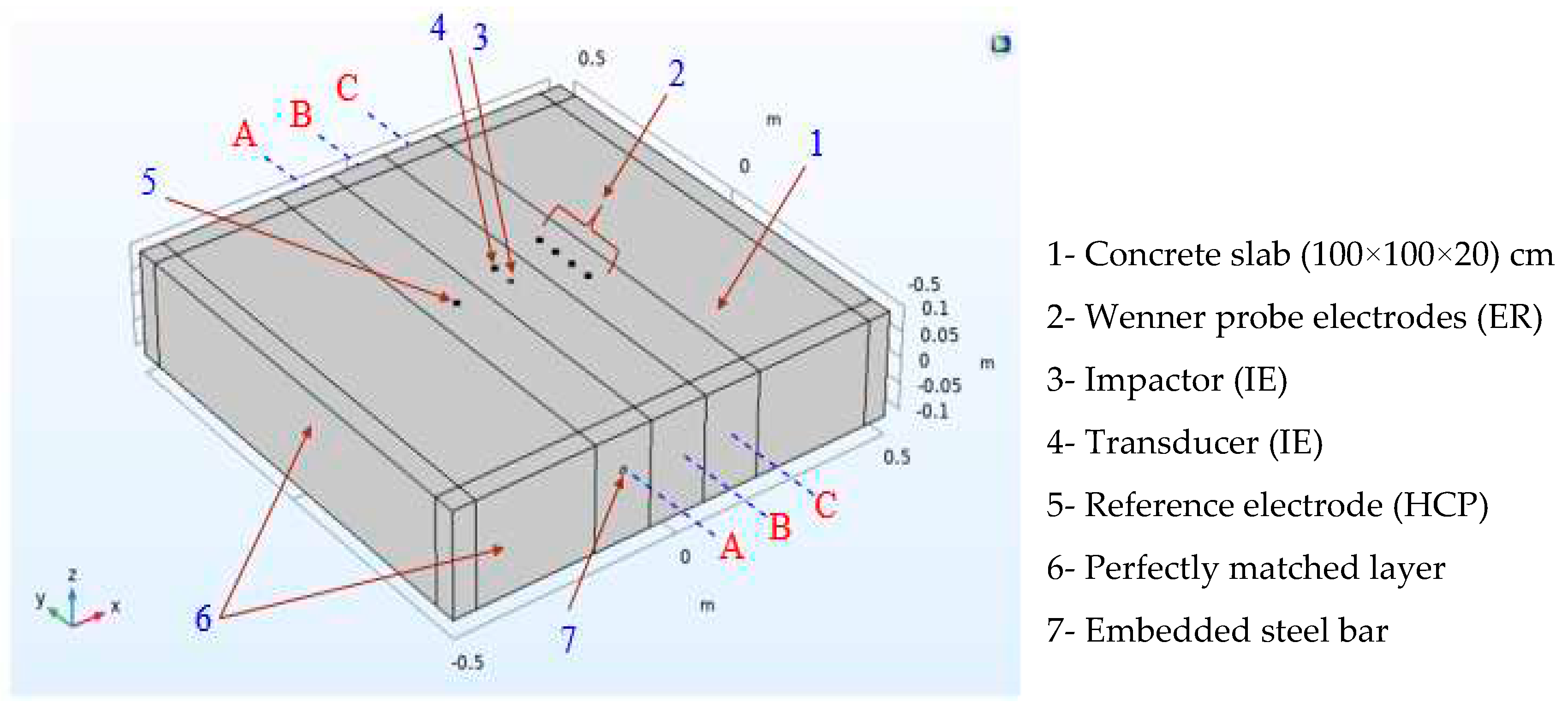
Figure 2.
Model meshing.
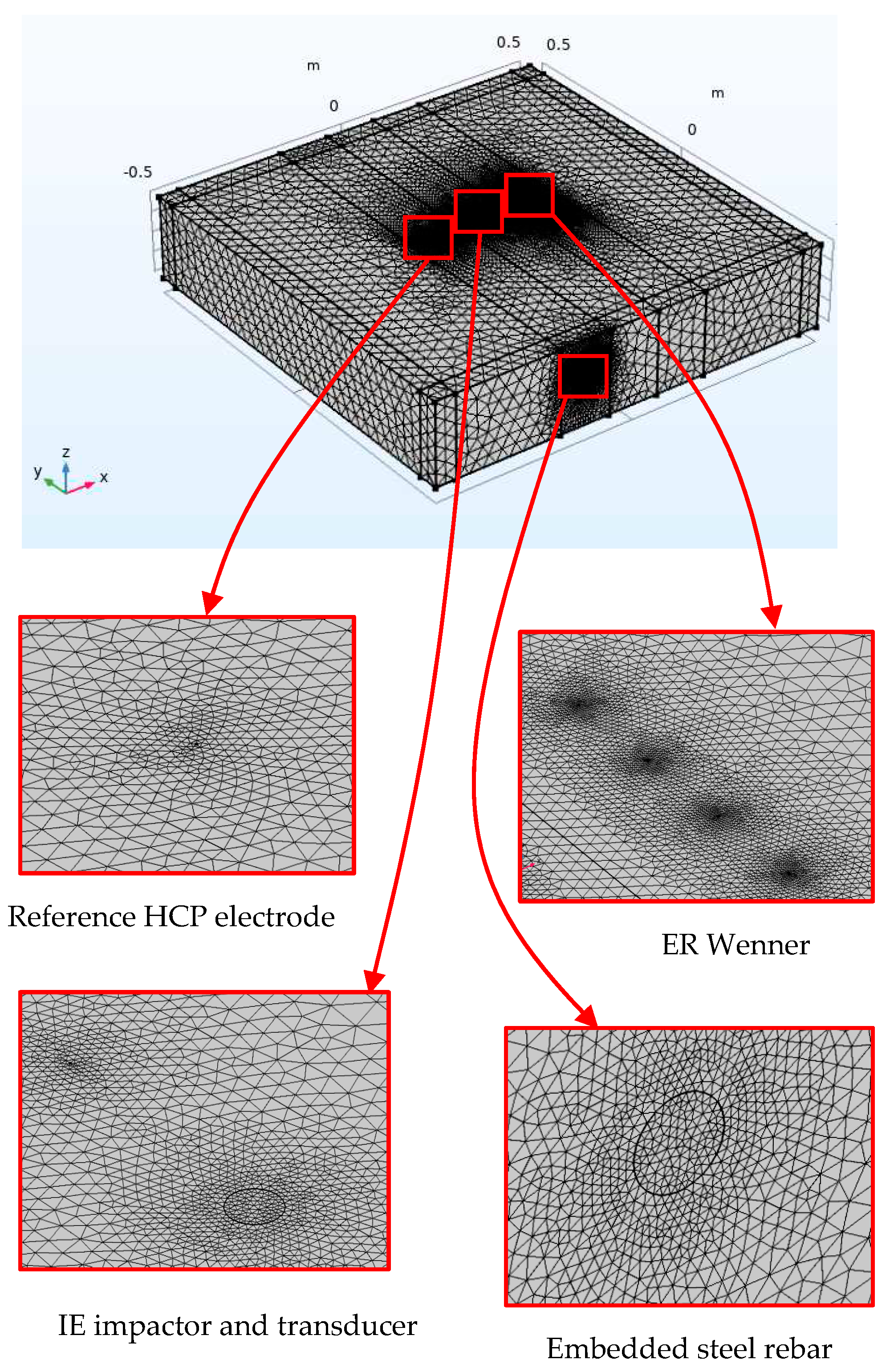
Figure 3.
B-B cross section for defective concrete
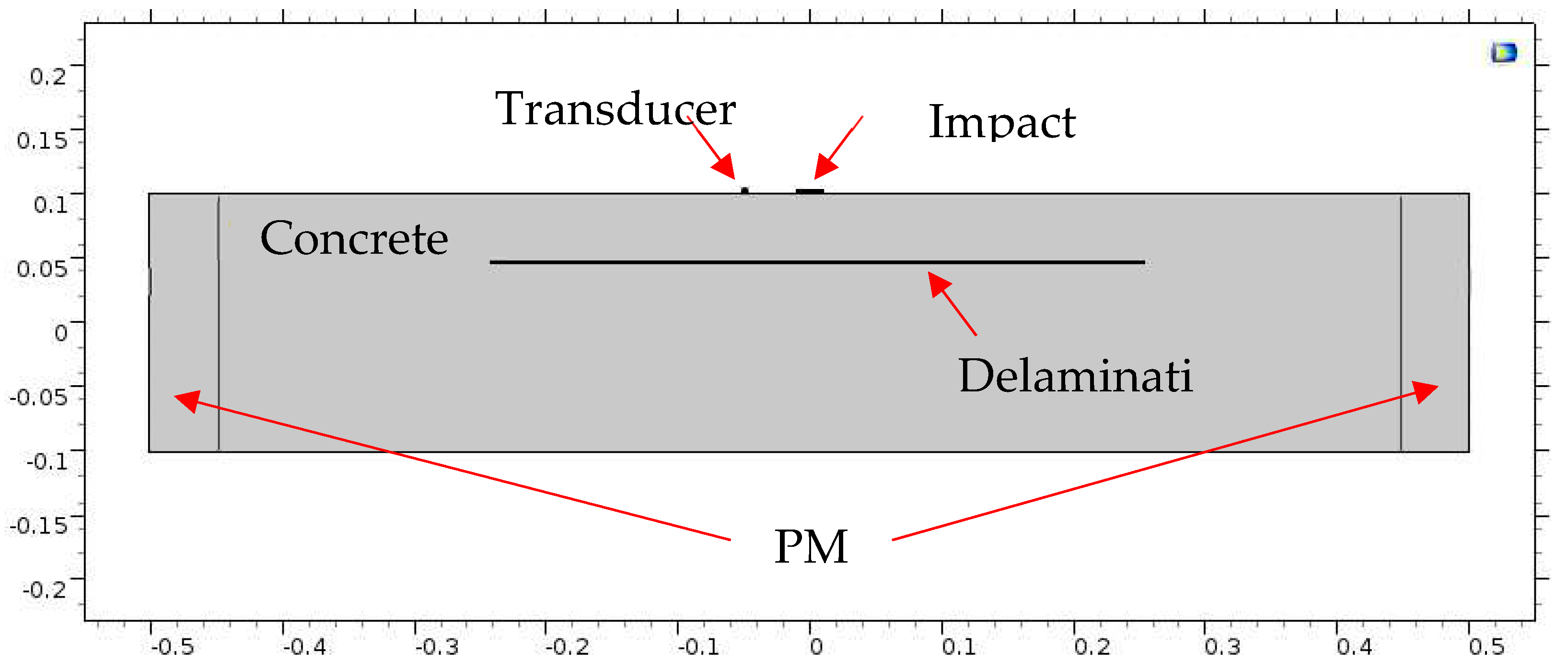
Figure 4.
The sound concrete model: (a) The acceleration time history, and (b) frequency spectrum.
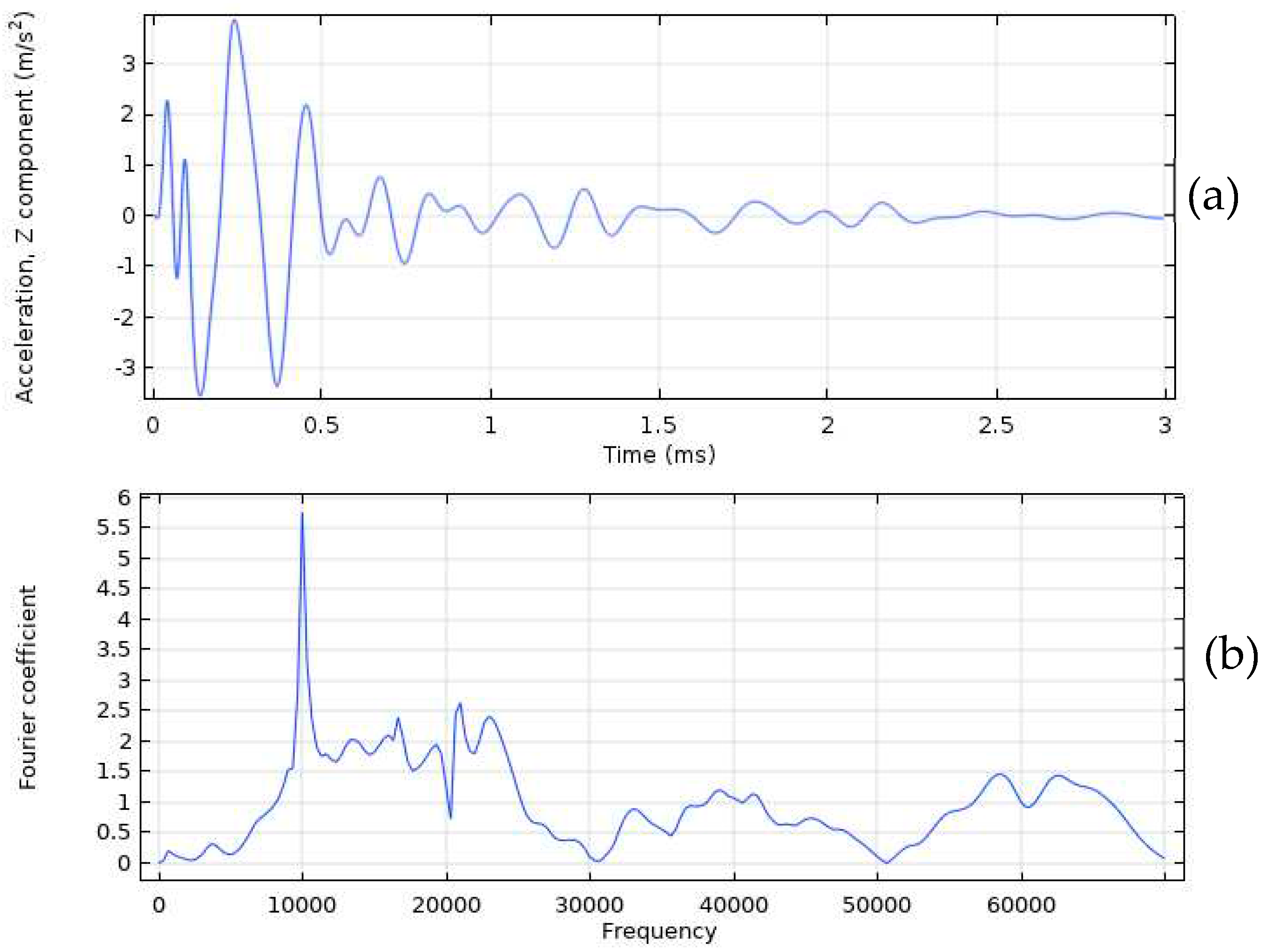
Figure 5.
The defected concrete model: (a) The acceleration time history, and (b) frequency spectrum.
Figure 5.
The defected concrete model: (a) The acceleration time history, and (b) frequency spectrum.
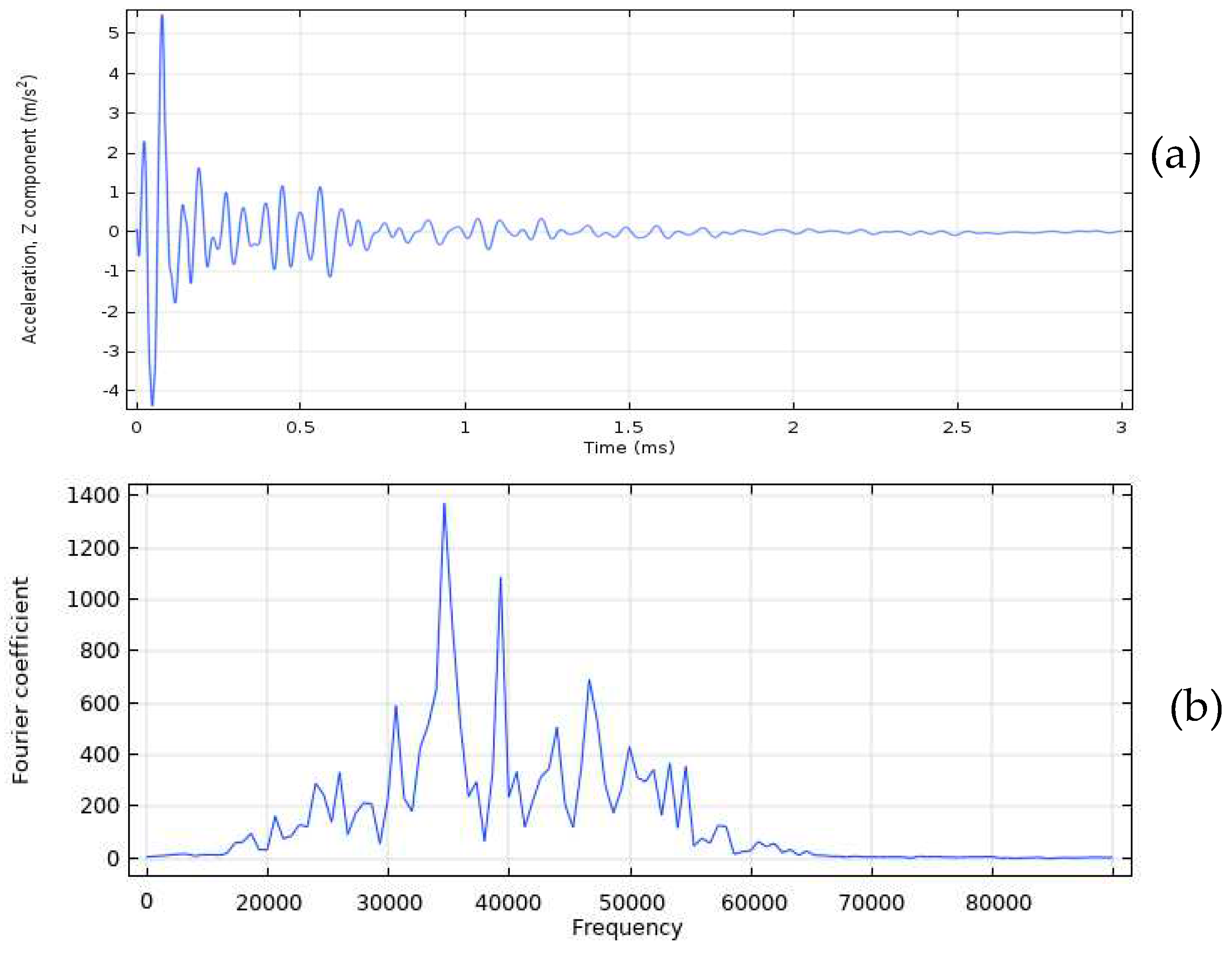
Figure 6.
C-C cross section.
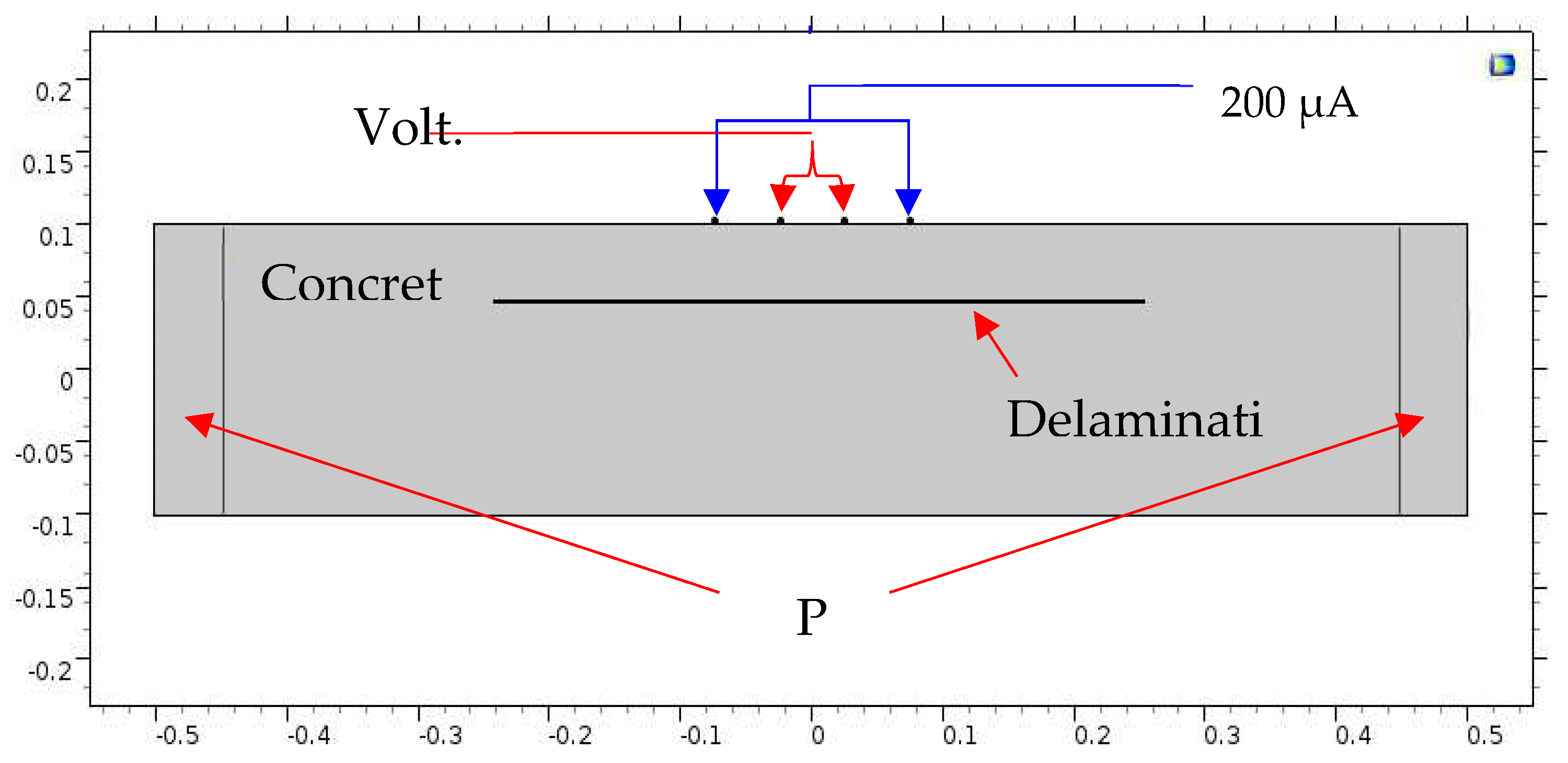
Figure 7.
Sound concrete potential distribution from ER simulation.
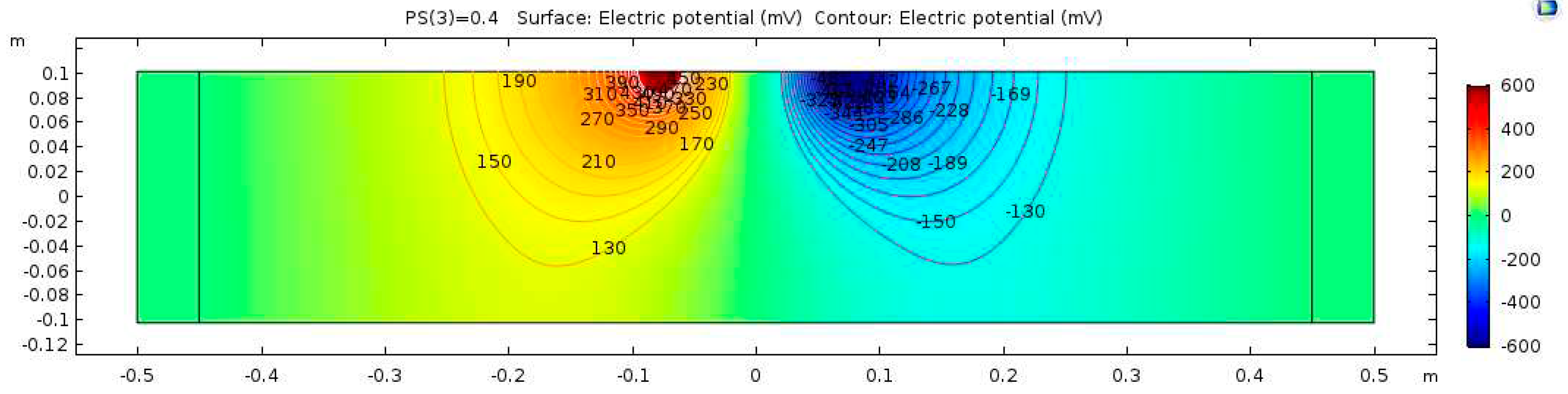
Figure 8.
ER for the models with WFD, AFD, and sound concrete.
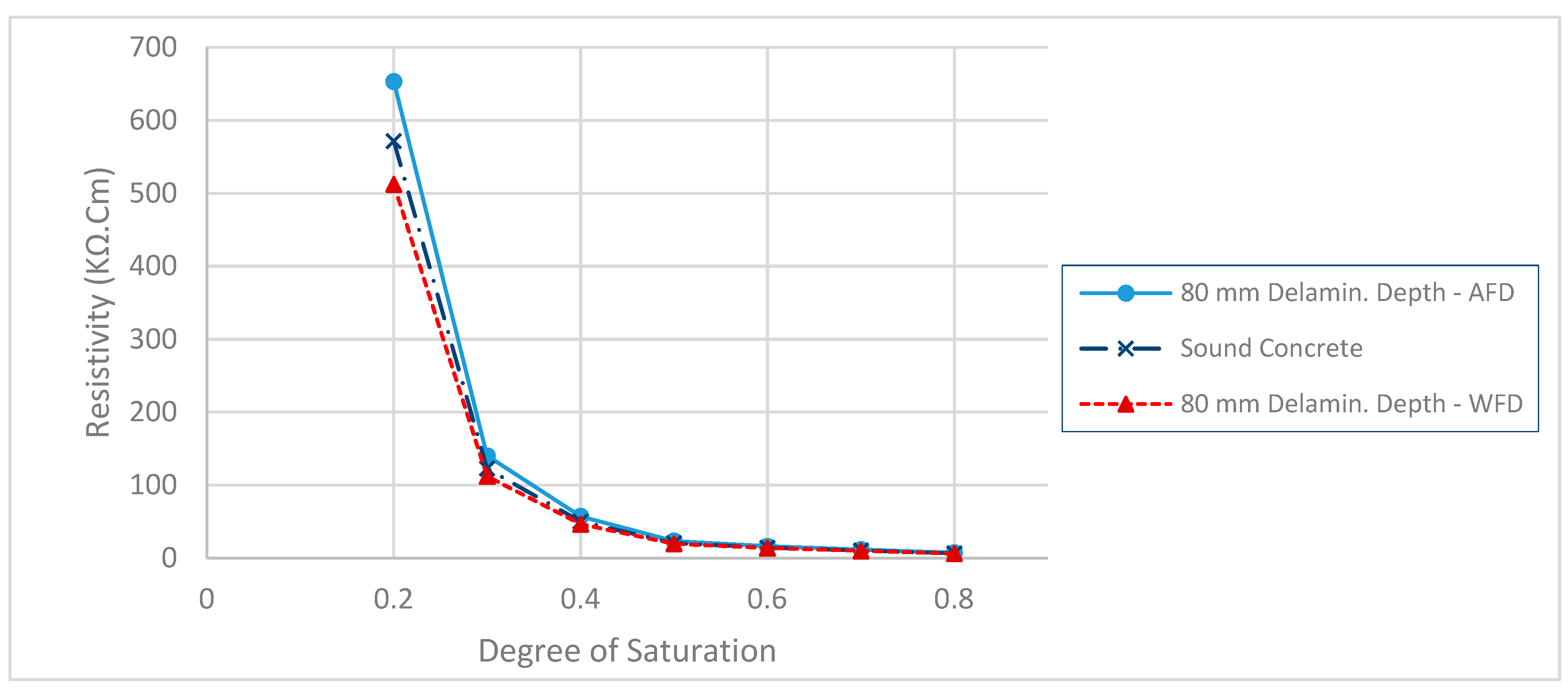
Figure 9.
Defective concrete potential distribution from ER simulation - AFD
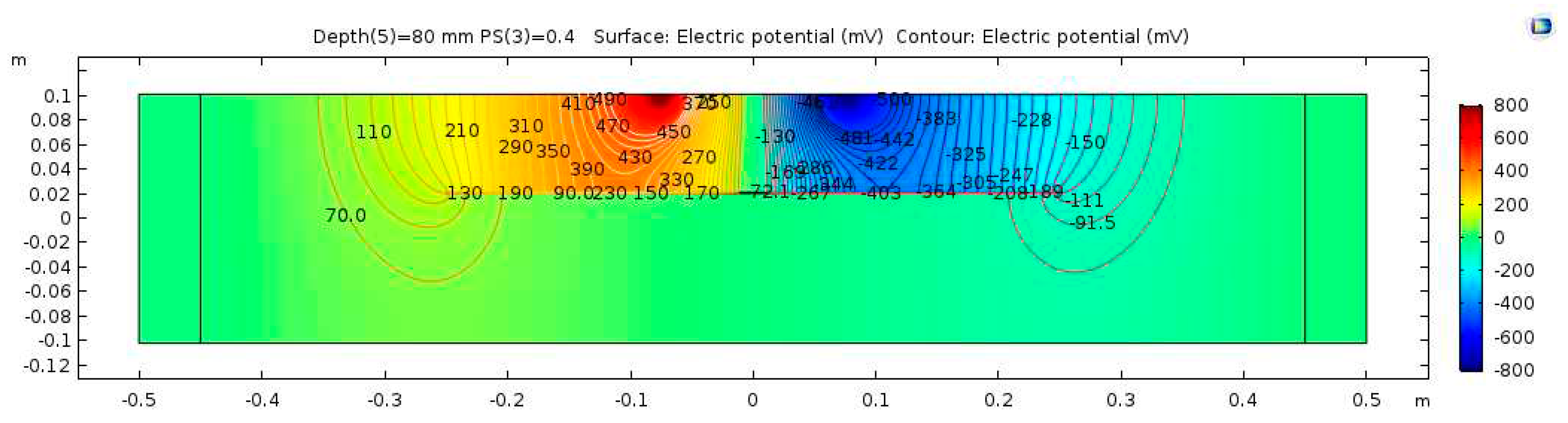
Figure 10.
Defective concrete potential distribution from ER simulation - WFD
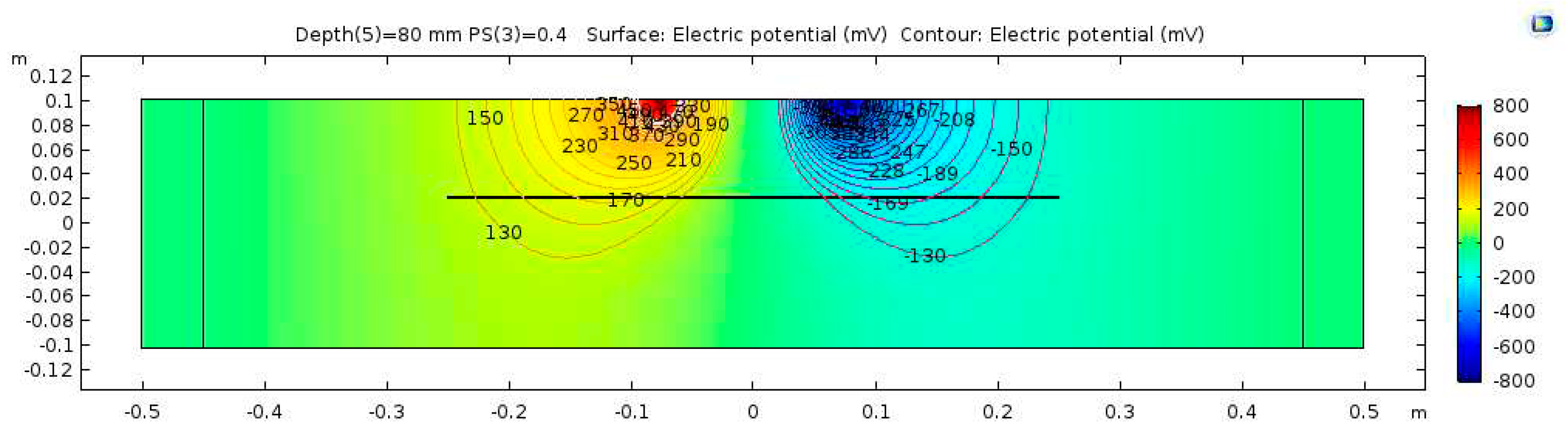
Figure 11.
A-A cross section.
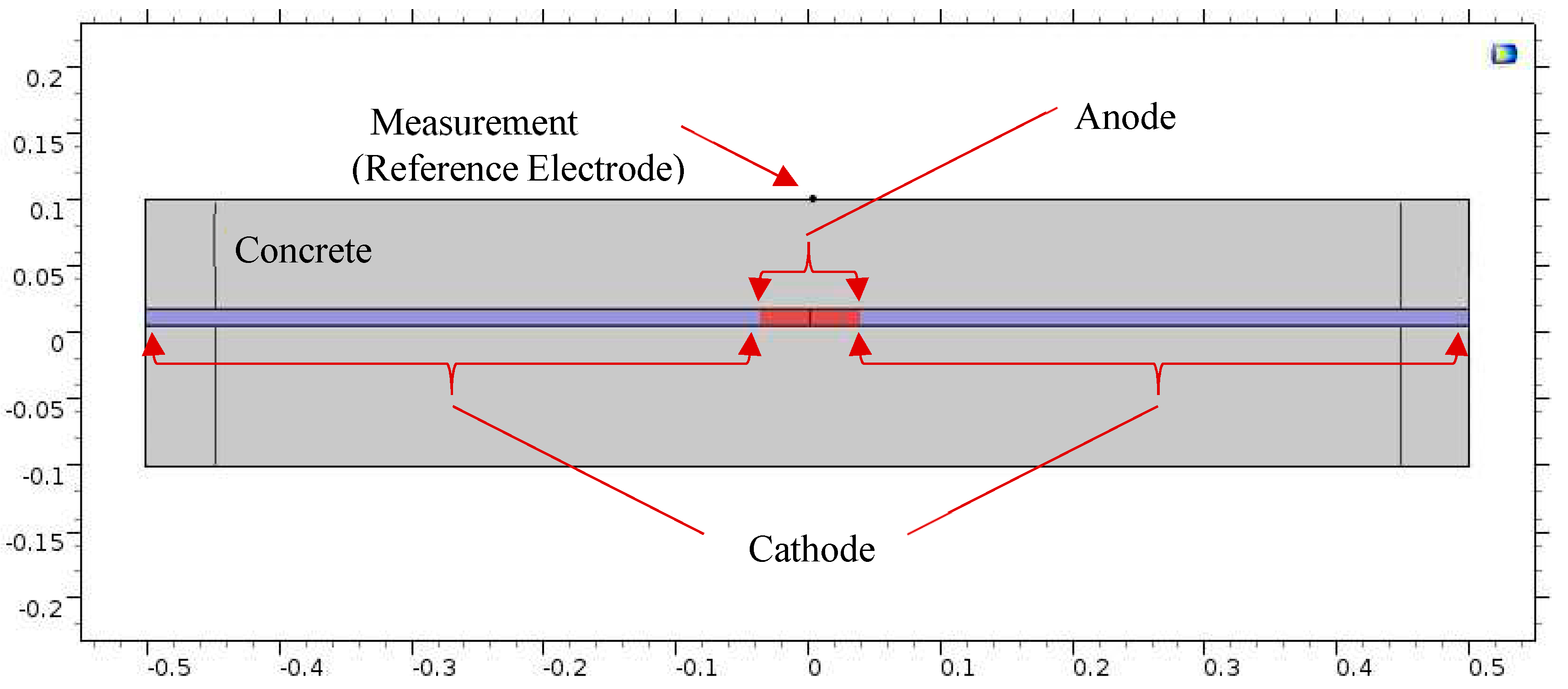
Figure 12.
Potential distribution for: 10 cm corrosion length, no delamination
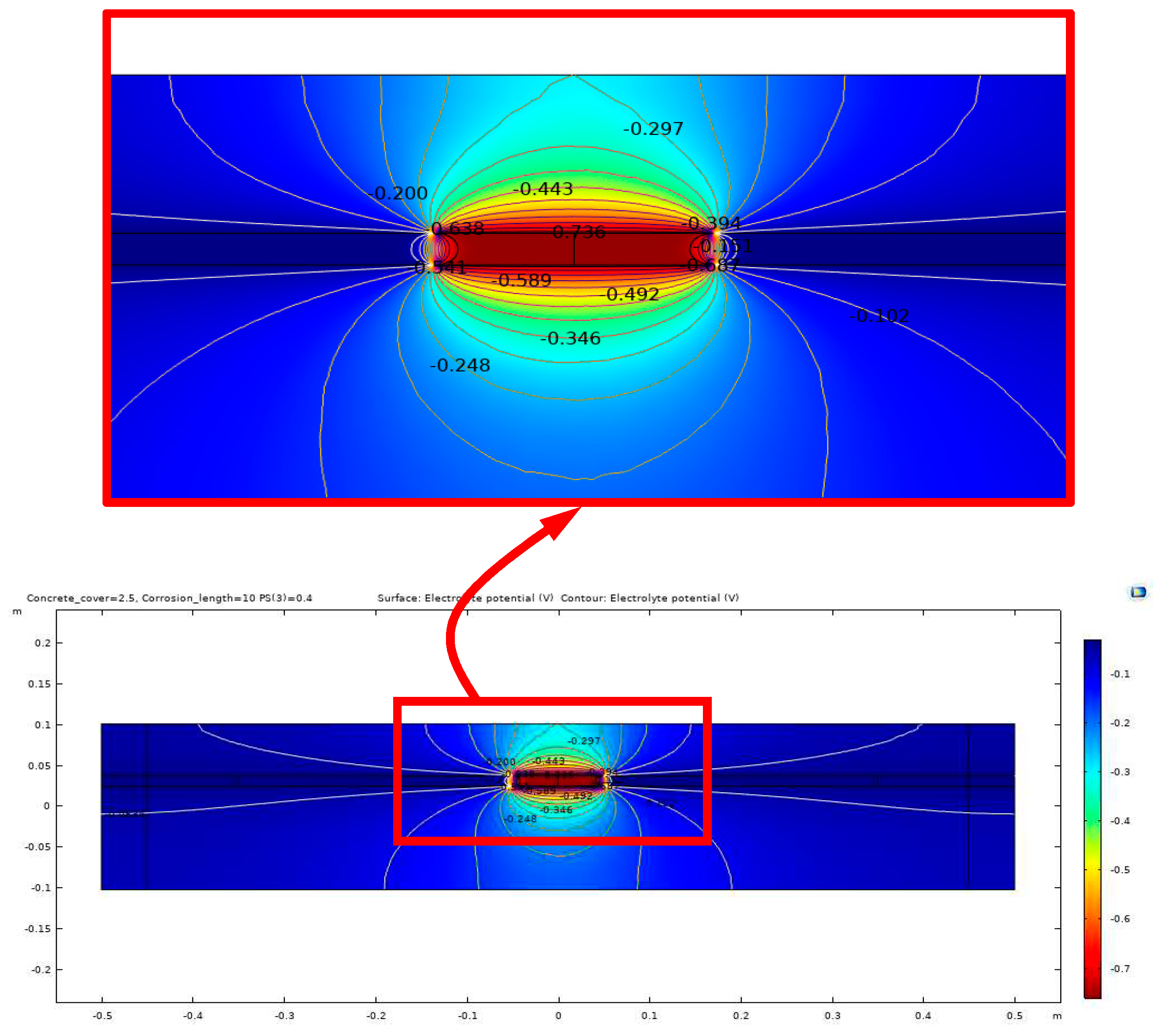
Figure 13.
Potential distribution for 10 cm corrosion length, AFD.
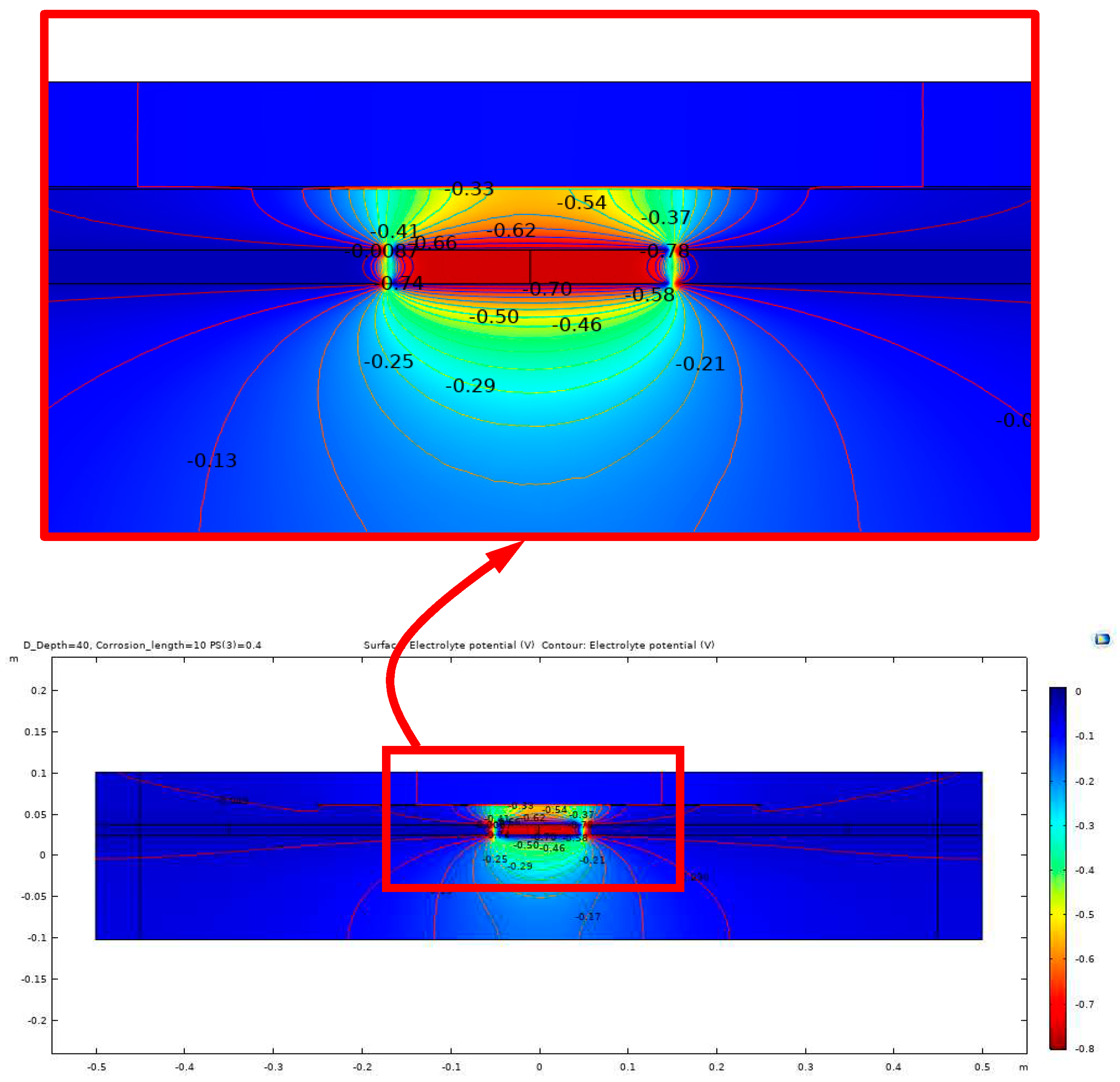
Figure 14.
Potential distribution for 10 cm corrosion length, WFD

Figure 15.
Scheme of random forest regression (black), and classification (red).
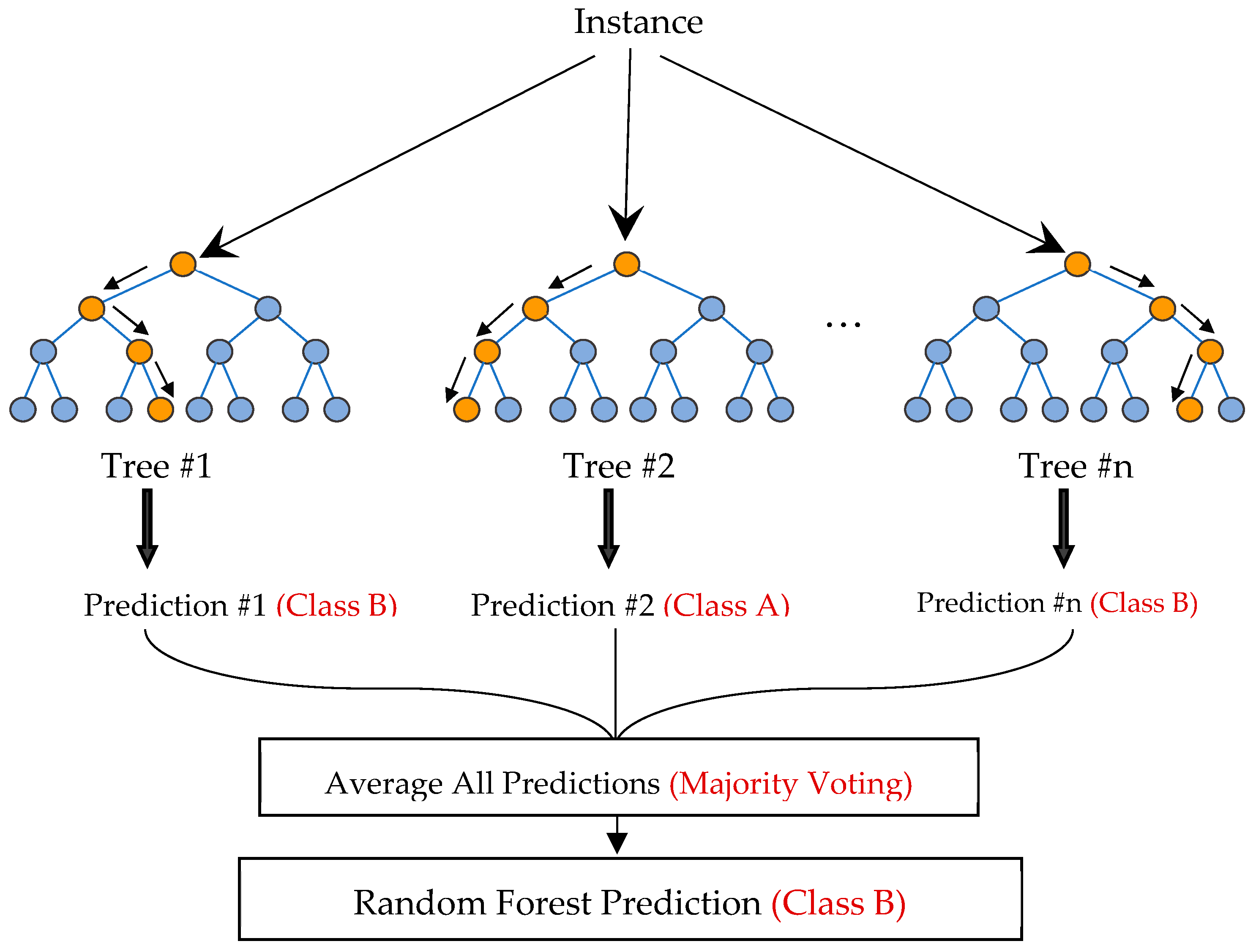
Figure 16.
Workflow diagram for the algorithm.
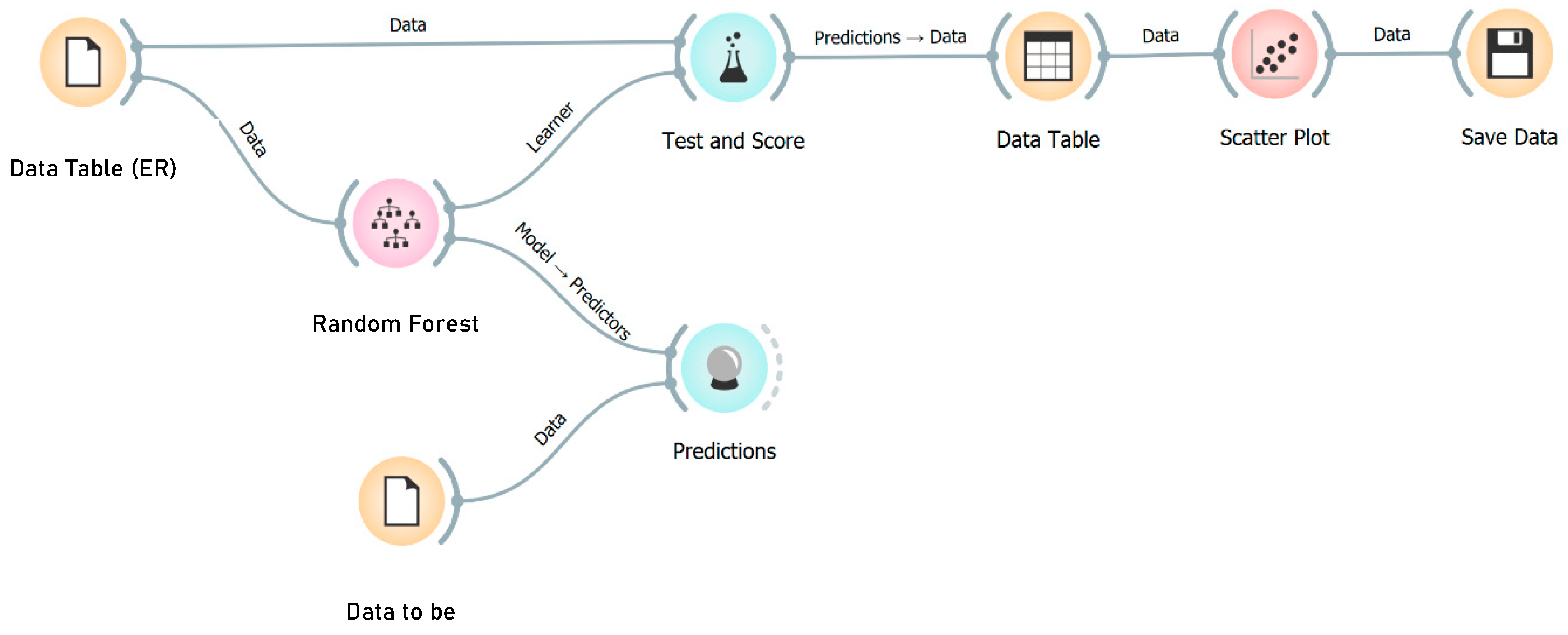
Figure 17.
Scatter plot for the Random Forest predictions against the Actual Resistivity.
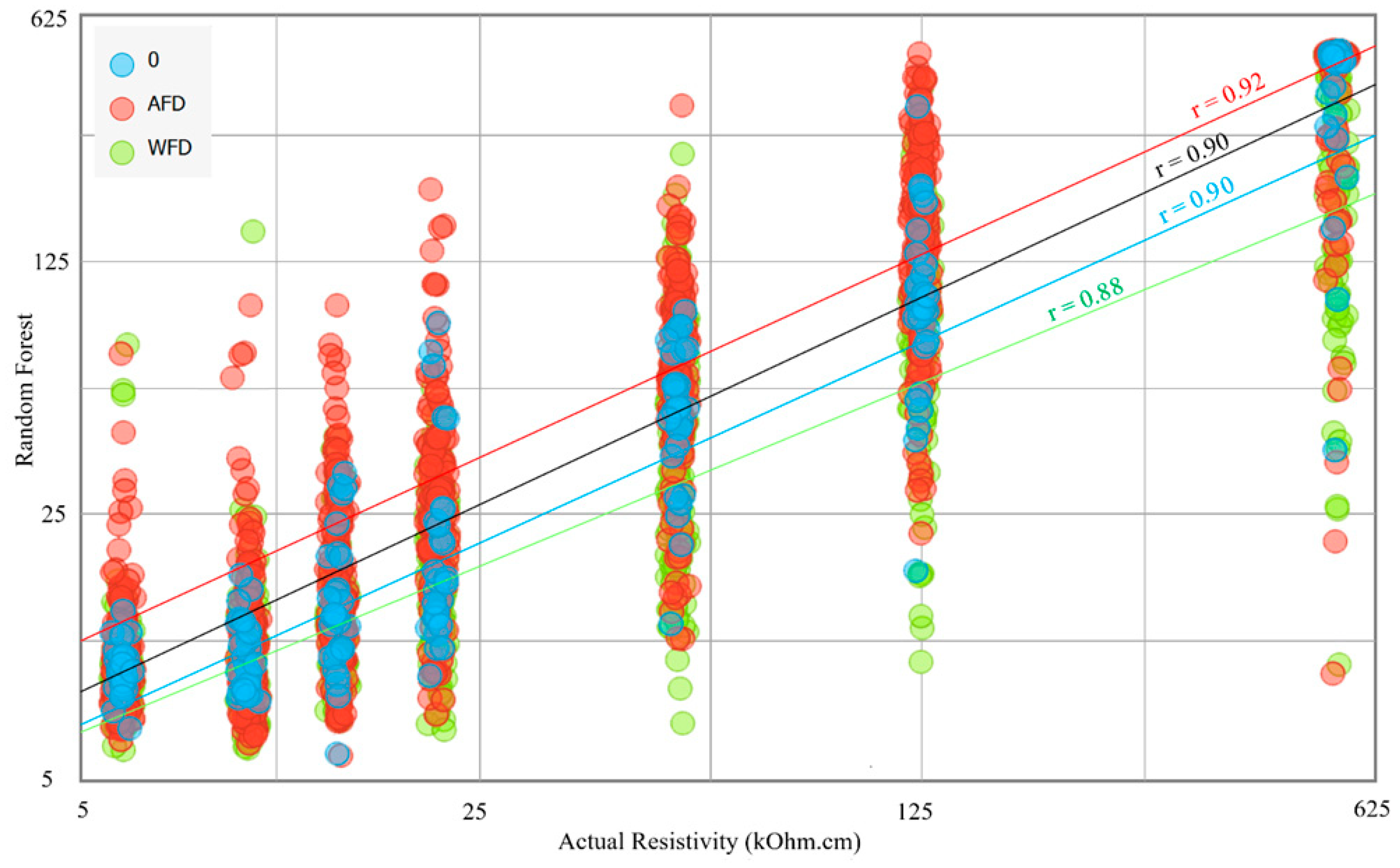
Figure 18.
The bridge deck in the BEAST facility (left) and the dual-axle carriage (right).

Figure 19.
NDE data collection on the BEAST deck: (a) MOIST-Scan, (b) Impact echo, (c) Half-cell potential, and (d) Electrical resistivity.
Figure 19.
NDE data collection on the BEAST deck: (a) MOIST-Scan, (b) Impact echo, (c) Half-cell potential, and (d) Electrical resistivity.

Figure 20.
Degree of saturation (top), electrical resistivity (middle), and half-cell potential (bottom) maps from the BEAST slab survey.
Figure 20.
Degree of saturation (top), electrical resistivity (middle), and half-cell potential (bottom) maps from the BEAST slab survey.
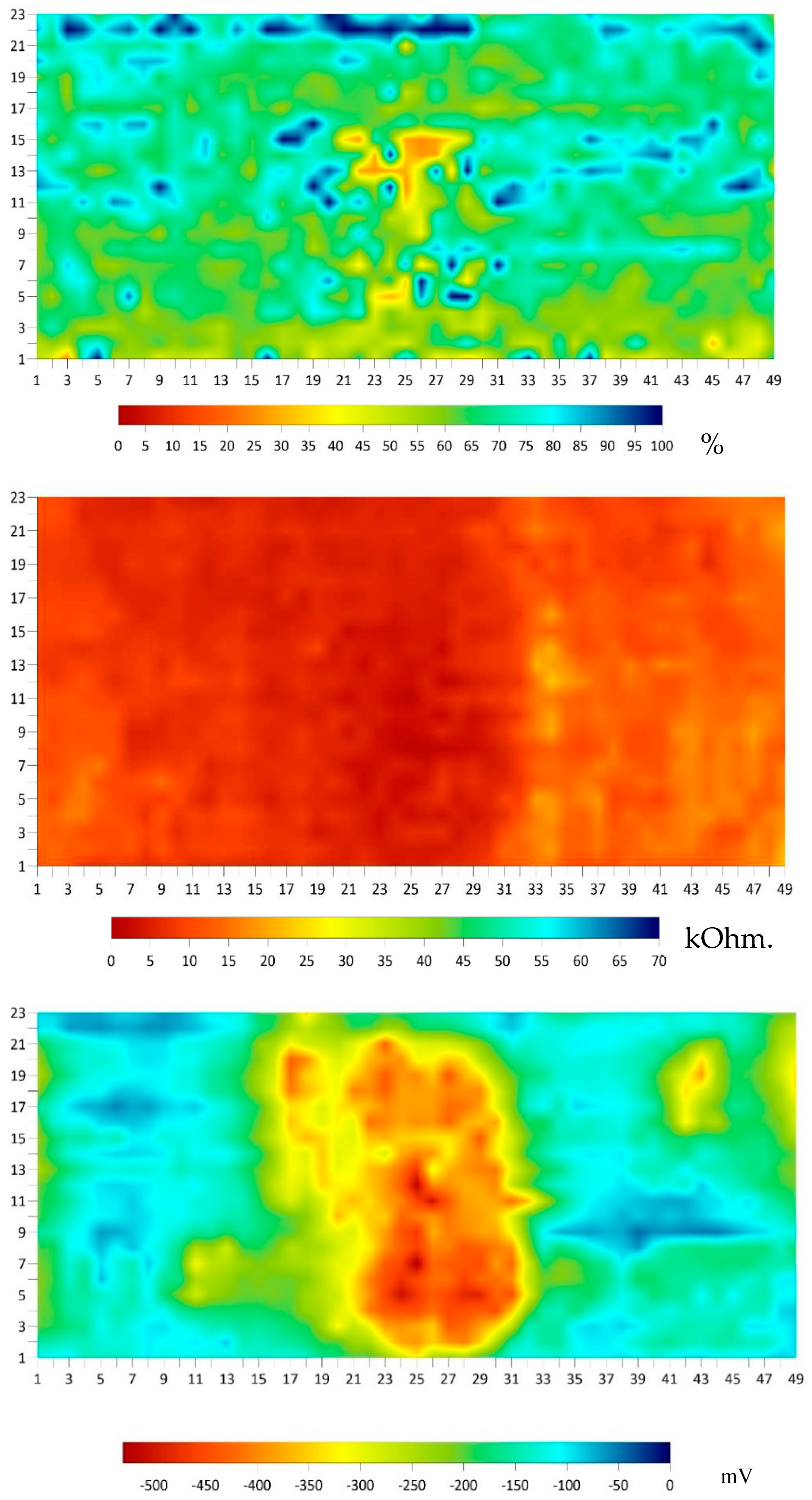
Figure 21.
Delamination (top) and concrete cover thickness map (bottom) of the BEAST deck..
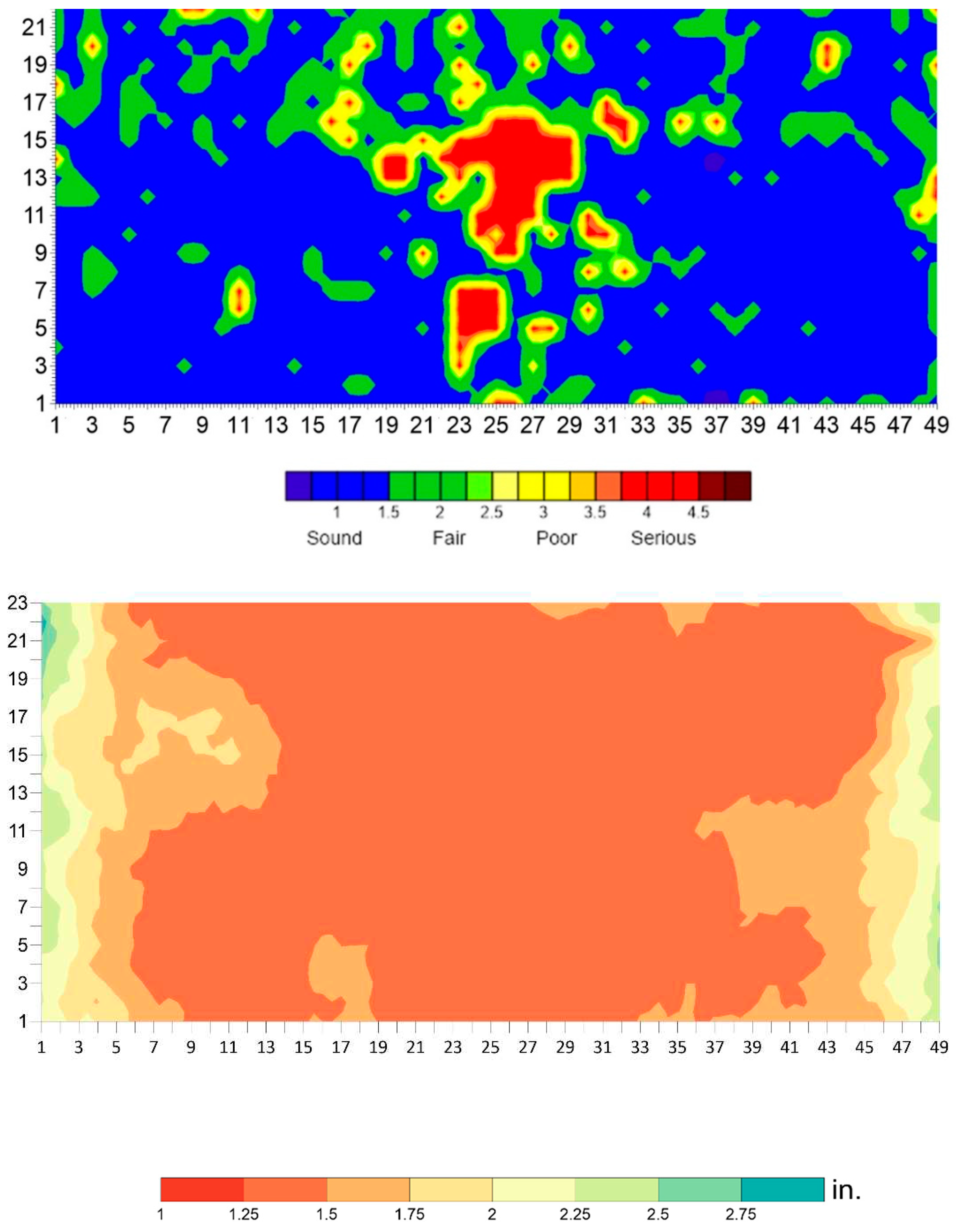
Figure 22.
Electrical resistivity results comparison. (a) Before and (b) after application of the regression algorithm.
Figure 22.
Electrical resistivity results comparison. (a) Before and (b) after application of the regression algorithm.
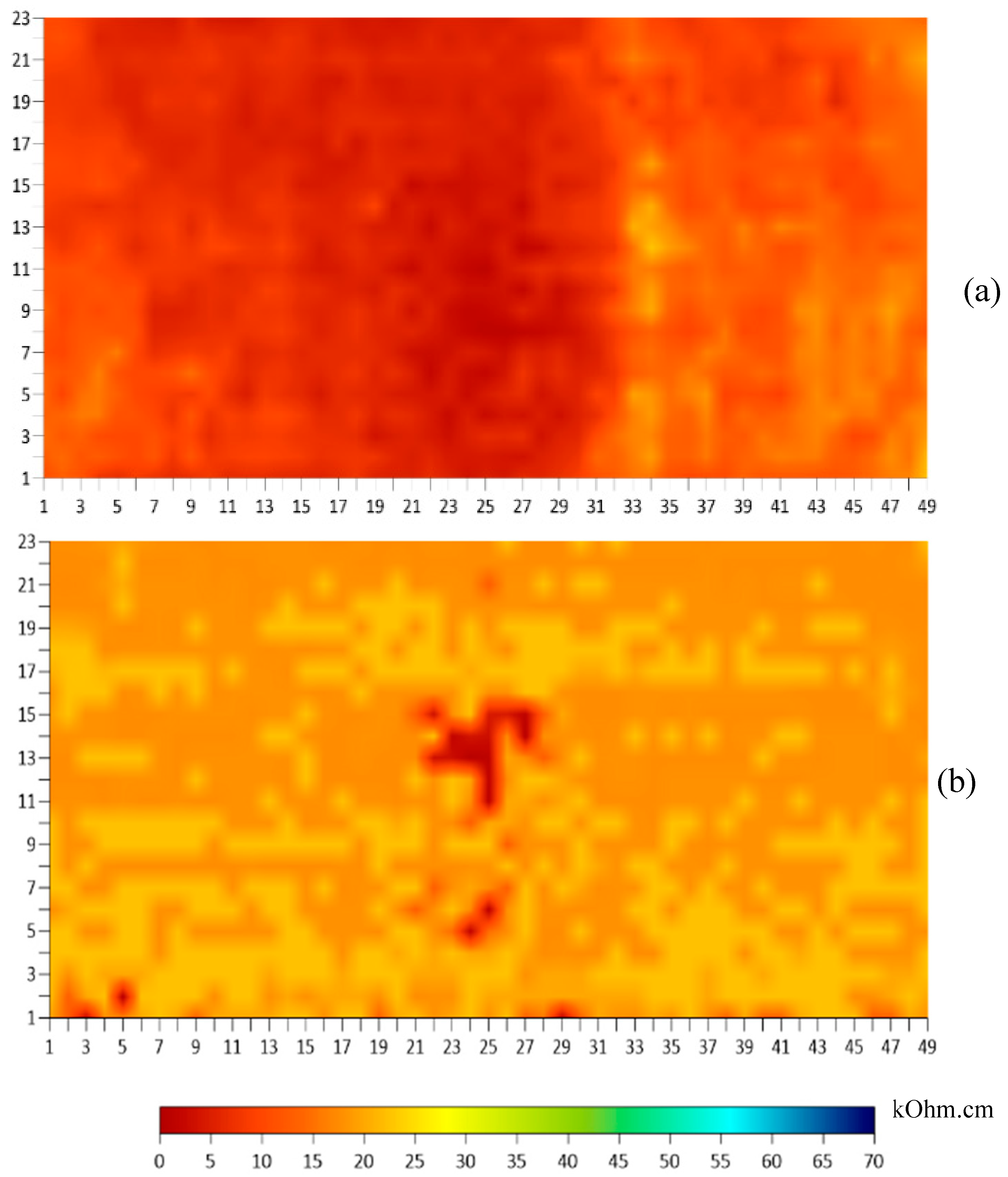
Table 1.
Material properties.
| Materials | Properties | |
|---|---|---|
| Electrical conductivity (S/m) |
Relative permittivity | |
| Concrete | 0.002 | 4.5 |
| Water* | 0.5 | 88.1 |
| Air* | 3×10−15 | 1 |
| *Used to fill the delamination. | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






