Prerpints.org logo
Preprint
Article

Transaction Entropy: An Alternative Measurement of Market Performance

Altmetrics

Downloads

115

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 July 2023

Posted:

04 July 2023

You are already at the latest version

Alerts
Abstract
Market uncertainty has a significant impact on market performance. Previous studies put much efforts in investigations on market uncertainty related to information asymmetry and risk. However, they have neglected the uncertainty inherent in market transactions, which is also an important aspect of market performance, besides quantity of transactions and market efficiency. In this paper, we put forward the concept of transaction entropy to measure the market uncertainty and see how it changes with price. The definition of transaction entropy is the ratio of total information entropy of all traders to quantity of transactions, reflecting the level of uncertainty in making transactions. And the transaction entropy is the lowest at equilibrium, it will be decreasing in a shortage market, and increasing in a surplus market. Additionally, we make a comparison of total entropy of the centralized market with that of the decentralized market, revealing that the price filtering mechanism could effectively reduce market uncertainty. Overall, the introduction of transaction entropy enriches our understanding of market uncertainty and facilitates a more comprehensive assessment of market performance.
Keywords: 
Subject: Business, Economics and Management  -   Economics

1. Introduction

The concept of the market holds great significance in economics and serves as a fundamental basis for research of economics [1]. Understanding the mechanisms by which markets function has profound implications for decision-making, policy formulation, and economic development. Presently, research on market functioning primarily focuses on two key aspects: price formation and market efficiency.
In the context of market price, it is determined by the interaction between supply and demand curves. Therefore, factors that influence these curves, such as the competitive state of the market and information dissemination, also impact the level of market price. When considering market efficiency, an important indicator for assessing it is market surplus. Market surplus represents total welfare generated by transactions between sellers and buyers. An increase in market surplus signifies improved efficiency in market transactions and a more optimal allocation of resources.
However, both analysis of price formation and the derivation of market surplus are typically conducted through simplified analyses under the assumption of ideal conditions, without accounting for the uncertainties faced by participants in market transactions. Several studies have verified the existence of uncertainties in market transactions [2,3]. During an actual transaction process, each participant has limited access to information and cannot obtain complete knowledge about the counterparty's information or the overall market situation. This inherent imperfection in information significantly influences the decision-making and behavior of both parties involved, thereby increasing transactional uncertainty, which subsequently impacts market prices and market surplus. Therefore, while the mechanisms of price formation and market surplus analysis have become the cornerstones of economic analysis, we contend that incorporating uncertainty analysis in the market can provide a more accurate description of market functioning. The analysis of uncertainty can enrich our understanding of real market transactions and their operational mechanisms.
Actually, there has long been recognition among economists, particularly in the fields of information economics and experimental economics, regarding the presence of uncertainty in market performance. This recognition is evident in the seminal works of Akerlof and Smith, respectively. Akerlof highlighted the role of asymmetric information in generating uncertainty in market transactions [4], while Smith conducted experiments to demonstrate how participants' trading behavior is influenced by factors such as market competition, thereby introducing uncertainty into market transactions and impacting market outcomes [5]. These contributions provide a solid research foundation to examining the role of uncertainty in market performance. In the latter research, some economists have narrowed their focus to financial markets, exploring the uncertainty within them. Connolly et al. and Segel et al. argued that the relationship between market uncertainty and market outcomes in stock and asset markets, respectively [6,7]. Their studies confirmed the influence of market uncertainty on market outcomes. Segel subdivided uncertainties into two parts: good and bad, revealing that these uncertainties have opposite impacts on market outcomes. Based on the aforementioned research, it becomes apparent that lots of studies have underscored the significance of uncertainty in markets from various perspectives. Therefore, it is necessary to put forward an indicator that can effectively measure the uncertainty in the market. Dzielinski has introduced a novel measure of economic uncertainty based on the frequency of internet searches, which has been applied to the stock market, and demonstrated a significant relationship between overall stock returns and volatility [8]. However, this indicator lacks universality and rigorous mathematical verification, particularly in capturing quantity uncertainty in the mechanisms of market functioning.
In order to enhance our understanding of the mechanisms of market functioning further, we integrate the concept of information entropy into the analysis of the market performance as the indicator to measure uncertainty. Information entropy is an important concept of information theory, which represents the degree of disorder or uncertainty of information. As more information is available, uncertainty decreases, resulting in a decrease in entropy. Conversely, when there is less information and higher uncertainty, the entropy increases. Based on the information entropy, various related terms have been developed, such as transfer entropy and conditional entropy. Among them, transfer entropy can measure the information transfer or information flow between two-time series, and it can be used to analyze information transfer and the influence of decisions in markets [9,10]. Conditional entropy measures the uncertainty of one random variable given some known information [11]. These different concepts of entropy play crucial roles in information theory, aiding us to comprehensively understand the nature and transmission of information.
In the financial market, information entropy has become an important component to measure the market performance. One of the representative applications of information entropy in the financial market is the measurement of market volatility, which can indicate market risk. Billio et al. developed an early warning signal for the systemic risk of the banking system using a variety of entropies, including information entropy [12]. They demonstrated that entropy metrics have the ability to foretell and predict banking crises by estimating the entropy of marginal systemic risk measures including Marginal Expected Shortfall, Delta CoVaR, and network connectivity. According to Pele et al. empirical analysis can forecast daily Value-at-Risk by using the entropy of the distribution of intraday returns as a predictor [13]. Entropy was found to be negatively correlated with both intraday Estimated Shortfall and intraday Value-at-Risk. Another application of entropy in the financial market is reflected in portfolio selection. The mean-entropy approach was first put forth by Philippatos and Wilson, who claimed that entropy is broader and more suited for portfolio selection [14]. Since then, many economists have improved how entropy is used in portfolio selection. In order to underline that there was an optimal portfolio for a specific probability of return, Ou et al. developed incremental entropy [15].
Based on the analysis presented, the current application of entropy in measuring uncertainty caused by incomplete market information, as well as its utilization in characterizing asset portfolios and risk assessment in the financial domain, does not provide a comprehensive understanding of the usage of entropy in mechanisms of market operation. In particular, there is no equivalent concept of entropy to express the uncertainty of participants’ trade in the market. Thus, we came up with the concept of transaction entropy to represent the uncertainty of market trade. We investigate how the transaction entropy changes with price. The results show that the equilibrium market corresponds to not only the highest amount of trade and the greatest market surplus, but also the lowest entropy. Additionally, we also compared total entropy between centralized and decentralized markets, where the key distinction lies in the presence or absence of a price filtering mechanism. The result shows that the total entropy is lower in the centralized market than in the decentralized market. This finding highlights the effectiveness of price filtering in reducing market uncertainty, and emphasizes the importance of integrating a price filtering mechanism in the trading process to ensure market transaction stability.
The contributions of this paper can be summarized as follows: (1) Proposing the concept of “transaction entropy” to measure the level of uncertainty in the process of transactions. By introducing the concept of transaction entropy, we are able to better understand and quantify market uncertainty, providing a new perspective for in-depth analysis of the mechanism of market function; (2) Adding the consideration of market uncertainty dimension based on the existing framework of market function analysis. Through investigating the evolution of entropy with respect to price change, we find that the state of market equilibrium not only corresponds to the highest volume of transaction, maximum market surplus, but also the minimum level of uncertainty, indicated by the lowest entropy; (3) Comparing the level of total entropy between centralized and decentralized markets, revealing that the presence of a price filtering mechanism enhances successful transactions and promotes market efficiency; (4) Identifying the assumptions of reverse rank matching between sellers and buyers during the process of transaction in the market, where the information of willingness prices is publicly available. By contrasting the ideal assumptions of traditional analysis with the real process of market transactions, we highlight the importance of incorporating market uncertainty into our analysis of market operations.
The remaining sections of this paper is organized as follows. Section 2 formulates the functions of supply and demand by introducing the concept of willingness price. In section 3, we analyze the transaction quantity first and then explore the market transaction entropy and market surplus by use of rationing rate. Section 4 compares the level of entropy with and without the mechanism of price filtering. Section 5 illustrates the matching pattern in the market transaction also have an impact on market uncertainty, and compare the level of uncertainty and entropy with parallel-rank matching and reverse-rank matching. Section 6 is conclusion.

2. The Expression of Demand and Supply with Willingness Price

Partial equilibrium analysis (PEA) is a widely used tool in understanding market performance. It argues that supply and demand collectively represent two sides of traders in a market, making it simple to analyze the consequence of their interaction by tracing the equilibrium point. However, the PEA also needs to be improved, since it fails to identify clearly how sellers and buyers constitute supply and demand curves correspondingly. To identify this problem, Wang and Eugene introduced the concept of willingness price and formulated the supply and demand functions to restate the PEA in a goods market [16]. The major advantage of this approach is that the laws of supply and demand can be derived directly, and the efficiency of market equilibrium can be strictly proved.
In this paper, we follow their approach to describe supply and demand. In a goods market, buyers and sellers exchange various goods, including final goods, intermediary goods. Supposing that each trader is willing to make a trade of one unit of the good and has a willingness price before participating the trade. For one seller, the willingness price is defined as the minimum price that he is willing to sell one unit of the good. On the other side, the willingness price of a buyer is defined as the maximum price that he is willing to buy for one unit of the good. Considering that a seller with willingness price v s meets a buyer with willingness price v b , and their deal can be made only if v b > v s is valid. Although we cannot identify all traders’ willingness prices in the real markets, we know that they exist there and govern whether a deal can be made or not.
As all participants’ willingness prices are exogenously given, the willingness prices of sellers and buyers must have a distribution correspondingly. It is reasonable to assume that willingness prices spread over the domain of (0, + ∞ ). The spread can be characterized by probability density functions f s ( v ) , f B ( v ) for sellers and buyers respectively. Suppose the numbers of sellers and buyers are given exogenously, denoted as N S and N B respectively, then we can use F s ( v ) = N s × f s ( v ) and F B ( v ) = N B × f B ( v ) to characterize such distributions. From normalization condition, we have the integrals of F s ( v ) and F B ( v ) over the whole region of willingness prices are N s and N B respectively,
∫ 0 ∞ F s ( v ) d v = N s ,
∫ 0 ∞ F B ( v ) d v = N B .
For anyone seller, he will make his choice by comparing the willingness price and actual market price, that is to say, only if the willingness price of the seller is lower than the actual price, he will sell in the market. Therefore, given the actual market price p , the necessary condition for the seller to sell one unit of the good can be expressed as
p ≥ v S .
Otherwise, the seller will withdraw his offer.
Regarding all sellers, Inequation (3) implies that only the sellers whose willingness price are not greater than the actual market price is willing to sell his goods. Combining (1) and (3), we can obtain the supply function with a given market price Q S p , which can be written as
Q S p = ∫ 0 p F s v d v .
The above rationale can also be applied to derive the demand function. For a buyer, only if his willingness price v B is higher or equal to the actual market price p , he will buy one unit of the good in the market., i.e.,
p ≤ v B .
Otherwise, he will give up to buy one unit of the good in the market. Combining (2) and (5), we can get demand function with a given market price Q D p of the market, which is given by
Q D p = ∫ p ∞ F B v d v .
As is well known, there are many factors can affect supply and demand in the market. From the expressions of supply and demand given by Equations (4) and (6), the implicit governing factor of supply and/or demand are the willingness prices of market participants. Thus, we can infer that most relevant factors take their effects through the willingness prices of sellers and buyers. As a result, any change in all variables that impacts the willingness prices will have an indirect impact on supply and demand of goods. In addition, the extent of markets determines total quantities of goods demanded and supplied, which also has an impact on supply and demand functions.
Another important inference of supply and demand functions is that we can prove the laws of supply and demand by taking derivative of these two formulas. The first derivatives of supply and demand functions can be expressed respectively as the following,
ⅆ Q S ⅆ p = F s p > 0 ,
ⅆ Q D ⅆ p = − F B p < 0 .
The results show that the relationship between quantity supplied and market price is positive. In other words, the higher market price, the more goods supplied in the market. On the contrary, the relationship between quantity demanded and market price is negative. The less goods are demanded as price rises.
The interaction of supply and demand determines the equilibrium price level and transactions quantity. Combining Equations (4) and (6), we can have the equilibrium price p = p * . The equilibrium transaction quantity T* can be derived directly, which can be expressed as
T * = ∫ 0 p * F s v d v = ∫ p * ∞ F B v d v .
Figure 1 illustrates supply and demand curves in a commodity market. The supply curve is upward-sloping, and the demand curve is downward-sloping. The cross point of these two curves specifies the market equilibrium, which corresponds to the equilibrium quantity and price of the goods market.

3. The Market Performance with Formulated Supply and Demand Functions

In this section, we examine the market performance based on the newly formulated supply and demand functions, focusing on two traditional market indicators: transaction quantity and market surplus. Here we introduce a new dimension of market performance, namely market uncertainty.

3.1. The Transaction Entropy

The supply and demand of goods represent two parties of the goods market, and their interaction determines not only the market price but also the transaction quantity. In this section, we set the market price as given exogenously, and investigate how the transaction quantity is determined by the supply and demand as the price varies.
The state of the market depends on the level of market price. The market is in equilibrium when the level of price is equal to the equilibrium level. Otherwise, the state of the market is disequilibrium. The disequilibrium can be divided into two cases, one is shortage and the other is surplus. When the price level is lower than the equilibrium one, it corresponds to a state of shortage where there is more quantity demanded than quantity supplied in the market. When the price level is higher than the equilibrium price, it corresponds to a state of surplus where there is more quantity supplied than quantity demanded in the market.
According to the short-side principle, the realized quantity of transaction is determined by the short side. The short side refers to the trading parties with less willing exchanges, and those with more are at the long side. In the market equilibrium, the quantity supplied is equal to the quantity demanded. In this case, the quantity of realized transactions T * as shown in Equation (9), is equal to the quantity supplied and demanded.
In the shortage market, the quantity demanded exceeds the quantity supplied. Therefore, the quantity of realized transactions is determined by the quantity supplied. The expression of realized quantity of transactions in the shortage market T S T p can be expressed as
T S T p = ∫ 0 p F s v d v p < p * .
For the surplus market, the quantity demanded is less than the quantity supplied. In contrast, the quantity of realized transactions in the surplus market T S P p can be written as follows
T S P p = ∫ p ∞ F B ( v ) d v p > p * .
Based on the preceding analysis, the transaction quantity in the various state of market can be given by,
T p = ∫ 0 p F s v d v p < p * , ∫ 0 p * F s v d v = ∫ p * ∞ F B ( v ) d v p = p * ∫ p ∞ F B ( v ) d v p > p * . ,
Based on the expression (12), the relationship between transaction quantity and market price can be illustrated by Figure 2.
Obviously, the transaction quantity is growing as market price increases when p < p * ，and the transaction quantity decreases with the increase of market price when p > p * . The transaction quantity reaches the maximum when the market price attains its equilibrium level.

3.2. Market Surplus

3.2.1. The Introduction of Rationing Rate

According to the short side principle, we can know that all participants at the long side are willing to make transactions, nevertheless, some of them could not achieve their desired outcome. Thus, we define rationing rate as the ratio of the quantity of actual transactions to the desired exchange quantity. The definition of rationing rate can be used in the following analysis of market surplus and transaction entropy. The expressions of sellers’ and buyers’ rationing rates ( G s and G B ) are given as follows, respectively
G s = T Q S ,
G B = T Q D .
According to their definitions, it is obvious that G s and G B a r e in the range of [0, 1]. The quantities supplied and demanded will change with the variation of market price. Therefore, the level of rationing rate will alter as market price varies. When market price equals the equilibrium one, rationing rates of either sellers or buyers equals one. So we have
G s ( p * ) = G B ( p * ) = 1 .
In the shortage market, p < p * , all sellers can fulfill their willing exchange, where only a portion of buyers can successfully match with sellers and achieve their desired transactions. As a result, the sellers' rationing rate is one, while the buyers' rationing rate would be less than 1. Thus, we have
G s ( p ) = 1 ,
G B p < 1 .
Meanwhile, with the increasing market price, there are more commodities supplied and less demanded. The rationing rate of sellers remains constant with the increase of price, while the rationing rate of buyers is increasing. We then have
d G s p d p = 0 .
d G B p d p ≥ 0 .
In contrast, the above rationale can also be applied to the surplus market where p > p * . The rationing rate of sellers is lower than 1, and the buyers' rationing rate is one. Then we get
G S p < 1 ,
G B ( p ) = 1 .
The relationship between the rationing rate and market price in the surplus market also can be derived. In this case, as the market price increases, sellers are less likely to get their rations because supply is increasing while demand is decreasing. Meanwhile, the rationing rate of buyers will not change. The derivatives of the seller and buyer rationing rates have the following properties,
d G s p d p ≤ 0 ,  
d G B p d p = 0 .
Figure 3 depicts the dependence of rationing rates on market price. The blue line represents G s p , while the orange line is G B p . As shown in this figure, as the market is in shortage, the rationing rate of buyers is less than one, whereas the rationing rate of sellers is equal to one. In contrast, the rationing rate of sellers is smaller than 1, while buyers' rationing rate equals one as the market is in surplus. When the market is in equilibrium, the rationing rates of either sellers or buyers are one.

3.2.2. The Formulation of Market Surplus

Market surplus, used to measure market efficiency, is another essential component of traditional market performance analysis. The surplus of one seller or one buyer can be defined as the difference between the actual (willingness) price and the willingness (actual) price. In the goods market transactions, only a portion of the participants will be able to realize their willing exchange, and their surplus will be generated. Therefore, it is reasonable to take rationing rates into account when formulizing the surplus of the market.
For the sellers, given the market price p, the total realized surplus of the sellers ( Z s r )   in the market could be calculated as follow
Z s r ( p ) = ∫ 0 p F s ( v ) ( p − v ) G s ( p ) d v .
On the other side, given the market price p , the total realized surplus of the buyers ( Z B r )   in the market could be given by
Z B r ( p ) = ∫ p ∞ F B ( v ) ( v − p ) G B ( p ) d v .
The total realized market surplus for price Z r ( p )   is the sum of them, i.e.,
Z r ( p ) = ∫ 0 p F s ( v ) ( p − v ) G s ( p ) d v + ∫ p ∞ F B ( v ) ( v − p ) G B ( p ) d v .
Taking the first derivatives of Equation (26), the expression of relationship between the derivation of surplus and market price can be expressed as
∂ Z r p ∂ p = ∫ 0 p F s v G s p d v − ∫ p ∞ F B v G B p d v + ∫ 0 p F s ( v ) ( p − v ) ∂ G s ( p ) ∂ p d v + ∫ p ∞ F B ( v ) ( v − p ) ∂ G B ( p ) ∂ p d v .
Combining with Equations (4) (6) and (13) (14), Equation (27) can be rewritten as
∂ Z r p ∂ p = ∫ 0 p F s ( v ) ( p − v ) ∂ G s ( p ) ∂ p d v + ∫ p ∞ F B ( v ) ( v − p ) ∂ G B ( p ) ∂ p d v .
When the market is in shortage, we can get the following expression by combining Equations (18), (19), and (28),
∂ Z r ( p ) ∂ p ≥ 0 .
When the market is in surplus, we can obtain the following expression by combining Equations (22), (23), and (28),
∂ Z r ( p ) ∂ p ≤ 0 .
Figure 4 shows the relationship between market price and market surplus. We can find that the market surplus is increasing when p < p * , decreasing when p > p * . As a result, we can draw the conclusion that when the market is in equilibrium, the market surplus attains its maximum.

3.3. Market Uncertainty

Except for traditional market performance, which focuses on quantity transactions and market surplus, we also consider market uncertainty as an additional dimension of market performance.

3.3.1. Transaction Entropy of One Transaction

Information entropy is a commonly used tool to measure the level of disorder and uncertainty, and its extension has been widely applied in the field of economics and finance [17,18]. In this section, we introduce a new kind of information entropy named as transaction entropy to characterize market uncertainty and investigate how transaction entropy changes as market price varies.
To figure out the information entropy of one participant, we need to identify the transaction procedure which is shown in Figure 5. At first, the participant has to make sure whether he satisfies the price filtering mechanism given by Equation (3) and (5). At this stage, there are only two filtering results for the participants: remain in or exit the market. The exiting participant refers to one whose willingness price does not satisfy the condition of trade in the market, while the remaining participant refers to those who satisfy the trading conditions. It is worth noting that it is possible to fail in the trade for the remaining participants. Only the traders in the short side can make a deal.
In one word, the possibility of making a deal for the participant is uncertain. Therefore, we can use the information entropy to present the uncertainty of the trader's transaction in the market. The definition of information entropy for individual traders H E can be written as
H E = − [ E * l n E + 1 − E * ln ⁡ 1 − E ] ,
where E is the possibility of a successful trade. Please note that the possibility of successful trade in this case is the rationing rate referred in the former subsection. Therefore, the respective information entropy of one seller H s and one buyer H B can be given by, respectively
H s p = − [ G s ( p ) * l n G s ( p ) + 1 − G s ( p ) * ln ⁡ 1 − G s ( p ) ] ,
H B p = − [ G B ( p ) * l n G B ( p ) + 1 − G B ( p ) * ln ⁡ 1 − G B ( p ) ] .
We assume that a trader is willing to make an exchange with one unit of the good, so Equations (32) and (33) can also present the information entropy of his willingness exchange quantity. The willingness exchange quantities of remaining sellers and buyers are denoted as QS and QB. Combining supply and demand functions given by Equations (4) and (6), then the total information entropy T S of the whole market takes the following form,
T S = ∫ 0 p F s v H s p d v + ∫ p ∞ F B ( p ) H B p d v .
From Equations (16) and (17), we have that the rationing rate of sellers G s p = 1 , and the rationing rate of buyers G B ( p ) < 1 when p < p * . As a result, we can derive that H s p = 0 a n d H B p ≠ 0 directly from Equations (32) and (33). The total information entropy of the market equals the information entropy of buyers. When the p > p * , the rationing rate of sellers G s p < 1 , and the rationing rate of buyers G B ( p ) = 1 based on Equations (20) and (21), So H B p = 0 , H s p ≠ 0 . In this case, the total information entropy of the whole market equals the information entropy of sellers, which can be obtained from Equation (34). And the rationing rates of sellers and buyers are equal to one when p = p * given by Equation (15), the information entropy of sellers and buyers is equal to zero. Thus, Equation (34) can be rewritten as
T S = ∫ p ∞ F B ( v ) H B p d v p < p * 0 p = p * ∫ 0 p F s v H s p d v p > p * .
The expression indicates that the resulting information entropy contains contributions of all actual transactions. To eliminate the effect of market scale on information entropy, we define the transaction entropy generated by one transaction to measure market performance. Then the transaction entropy takes the following form
S = T S T = H B p G s p p < p * 0 p = p * H s p G B p p > p * .
For the sake of simplicity, we denote G ( p ) = m i n { G s , G B } . The minimum rationing rate of buyers and sellers G ( p ) is presented in Figure 6 based on the relationship between G s a n d G B which is shown in Figure 3.
Then, we transform Equation (35) into the Equation (36) where we denote G p = m i n   G S , G B .
S = − G p * l n G p + 1 − G p * ln ⁡ 1 − G p G p .
According to the equation, it is obvious to identify that the level of transaction entropy S is non-negative. According to L'Hospital's rule, the entropy tends to be positive infinity when the market price tends to positive infinity or zero. The statistical expression of them can be given by
lim p → 0 ⁡ S = lim p → 0 ⁡ ln ⁡ ( 1 G ( p ) − 1 ) = + ∞ ,
lim p → + ∞ ⁡ S = lim p → + ∞ ⁡ ln ⁡ ( 1 G ( p ) − 1 ) = + ∞ .
Taking the first derivation of Equation (37), we can have
∂ S ∂ p = G ' p G 2 p * l n ⁡ ( 1 − G p ) .
When the market price is lower than the equilibrium one, the relationship between the transaction entropy and market price is negative, which can be expressed as
∂ S ∂ p < 0 .
When the market price is greater than the equilibrium one, the relationship between the transaction entropy and market price is positive, which can be presented as
∂ S ∂ p > 0 .
Figure 7 depicts the relationship between transaction entropy and market price. We can see that the slope is down-ward when p < p * , while it is upward in the case of p > p * f r o m t h i s f i g u r e . Moreover, the single equilibrium transaction entropy corresponds to zero when p = p * .

3.3.2. Total Entropy in Centralized and Decentralized Markets

In this section, we redirect our focus from analyzing the entropy generated by once transaction (S) to examining the total entropy (TS) within two distinct market structures: a centralized market and a decentralized market. The difference between these two markets is the presence of price filtering or not. The centralized market can be regarded as the transaction with price filtering, while the decentralized market is the transaction without price filtering. By comparing the entropy in these two market types, we can reveal the role of price filtering in mitigating market uncertainty.
Firstly, we examine total entropy in a centralized market. The centralized market is characterized by the presence of a central authority or intermediary that set one order book to collect bid-ask prices of traders, thereby facilitating all trading activities within the market [19,20]. It is worth noting that in our previous analysis of transaction entropy, we assumed that a given market price serves as the reference condition for transactions, which is consistent with the key assumption of a centralized market. Therefore, we can conduct a total entropy analysis in the centralized market based on the existing results from the previous section.
For the sake of simplicity, we make the following assumptions: (1) the number of sellers is equal to the number of buyers, denoted as N; (2) the willingness prices of sellers and buyers are ranging from [a, b]; (3) the supply and demand functions are linear. With these assumptions we can easily obtain F S v = F B v = k , where k is a constant variable. As for the total entropy, we rewrite Equation (35) with above assumptions, it can be given by
T S = ∫ p b F B v H B p d v a < p < p * 0 p = p * ∫ a p F s v H s p d v p * < p < b .
Additionally, we can express the supply and demand functions in the centralized market, denoted as Q S C p and Q D C p respectively, as follows:
Q S C p = ∫ a p F S v d v = k p − a ,
Q D C p = ∫ p b F B v d v = k b − p .
Taking the derivation of (44) and (45), we obtain that the derivative of the supply and demand functions are constant, which can be expressed as:
Q S C ' p = F s p = k ,
Q D C ' p = − F B p = − k .
By substituting Equations (14) and (33) into (43), the total entropy as shown in Equation (43) can be rewritten as
T S = − Q S C p ln ⁡ Q S C p + Q D C p − Q S C p ln ⁡ Q D C p − Q S C p − Q D C p ln ⁡ Q D C p a < p < p * 0 p = p * − Q D C p ln ⁡ Q D C p + Q S C p − Q D C p ln ⁡ Q S C p − Q D C p − Q S C p ln ⁡ Q S C p p * < p < b .
To clarify the concavity of the total entropy, we can differentiate Equation (48) based on Equations (46) and (47). As a result, we can find that l i m p → a T S ' = + ∞ ， l i m p → p * − T S ' = − ∞ ,and l i m p → p * + T S ' = + ∞ , l i m p → b T S ' = − ∞ , where T S ' is the derivative of TS. Moreover, it can be observed that the second derivative of TS is negative as shown in Appendix A, indicating a concave shape. And there are three price levels corresponding to total entropy is down to zero, that is, p = a , p = b , and p = p * .
Then we turn our attention to the exploration of total entropy in decentralized market. The decentralized market operates without a centralized authority or intermediary, enabling participants to engage in direct transactions with one another [21]. The key characteristic of the decentralized market is the random matching of sellers and buyers for one period at a time, along with anonymous pairwise meetings involving bargaining [22,23]. The transaction process in the decentralized market is illustrated in Figure 8 below.
The orange circles represent sellers, while the blue circles represent buyers, each having its own willingness prices. In this decentralized and random trading environment, every seller and buyer has an equal opportunity to engage in trading with one another. A transaction will only materialize if the buyer’s willingness price surpasses the seller’s willingness price; otherwise, the trade will not take place.
In order to make a comparison of the level of total entropy in different markets, we keep the core assumptions presented in the centralized market. Suppose that traders in the market only trade for once time with one unit of good in random way. The probability of a successful transaction for a buyer with willingness price v ' is the ratio of the number of the sellers with willingness price lower than v ' to the total number of sellers. Similarly, the probability of a successful transaction for a seller with a willingness price v ' is the ratio of number of the buyers with price higher than v ' to the total number of buyers. Therefore, the respective expressions for the probability of a successful transaction for a seller ( E s ) and a buyer ( E B ) with a willingness price v ' are as follows,
E s = ∫ v ' b F B v ⅆ ν ∫ a b F B v ⅆ ν ,
E B = ∫ a v ' F s v ⅆ ν ∫ a b F s v ⅆ ν .
At this time, the total entropy in the decentralized market with random matching T S d e is the sum of buyers’ entropy and sellers’ entropy, which can be expressed as,
T S d e = ∫ a b F S v d v * H S E S + ∫ a b F B v d v * H B E B = ∫ a b F S v * H S v d v + ∫ a b F B v * H B v d v
The result shows that the total entropy in the decentralized market with random matching is a constant variable, as detailed calculations can be find in the Appendix B. This constant entropy can be expressed as:
T S d e = k ( b − a ) .
This result indicates that the total entropy is closely related to the market scale in this market with the willingness prices of sellers and buyers would not change due to the assumption of traders only trade for one time.

3.3.3. Comparison of Total Entropy in Centralized and Decentralized Markets

By investigating the characteristic of the centralized and decentralized markets, it is obvious that the most prominent difference of these two market structure lies in the role of price in market transaction. In the centralized market, the difference between the willingness price and the market price acts as a criterion for sellers and buyers to enter the market. Conversely, in the decentralized market, there is no market price to guide market participants, they trade by random matching. Therefore, the decentralized market can be seen as operating without price filtering.
By comparing the different levels of total entropy in the centralized and decentralized markets, we can shed light on the role of price filtering on the transaction uncertainty in the market. As discussed earlier in the analysis of the centralized market, the total entropy exhibits a symmetrical double-humped downward profile. Therefore, there exist two price levels at which the total entropy reaches its maximum. These price levels can be derived by solving the equation for the derivative of total entropy with respect to price, i.e., T S ' p = 0 . The resulting expressions for the prices corresponding to maximum entropy are as follows, which detailed derivation can be found in the Appendix C,
p 1 = 5 − 5 b + 5 + 5 a 10 , p 2 = 5 + 5 b + 5 − 5 a 10 ,
By substituting Equation (53) into Equation (48), we can obtain the maximum total entropy as follows,
T S M A X = k * ( b − a ) 2 * l n 5 + 5 5 − 5 .
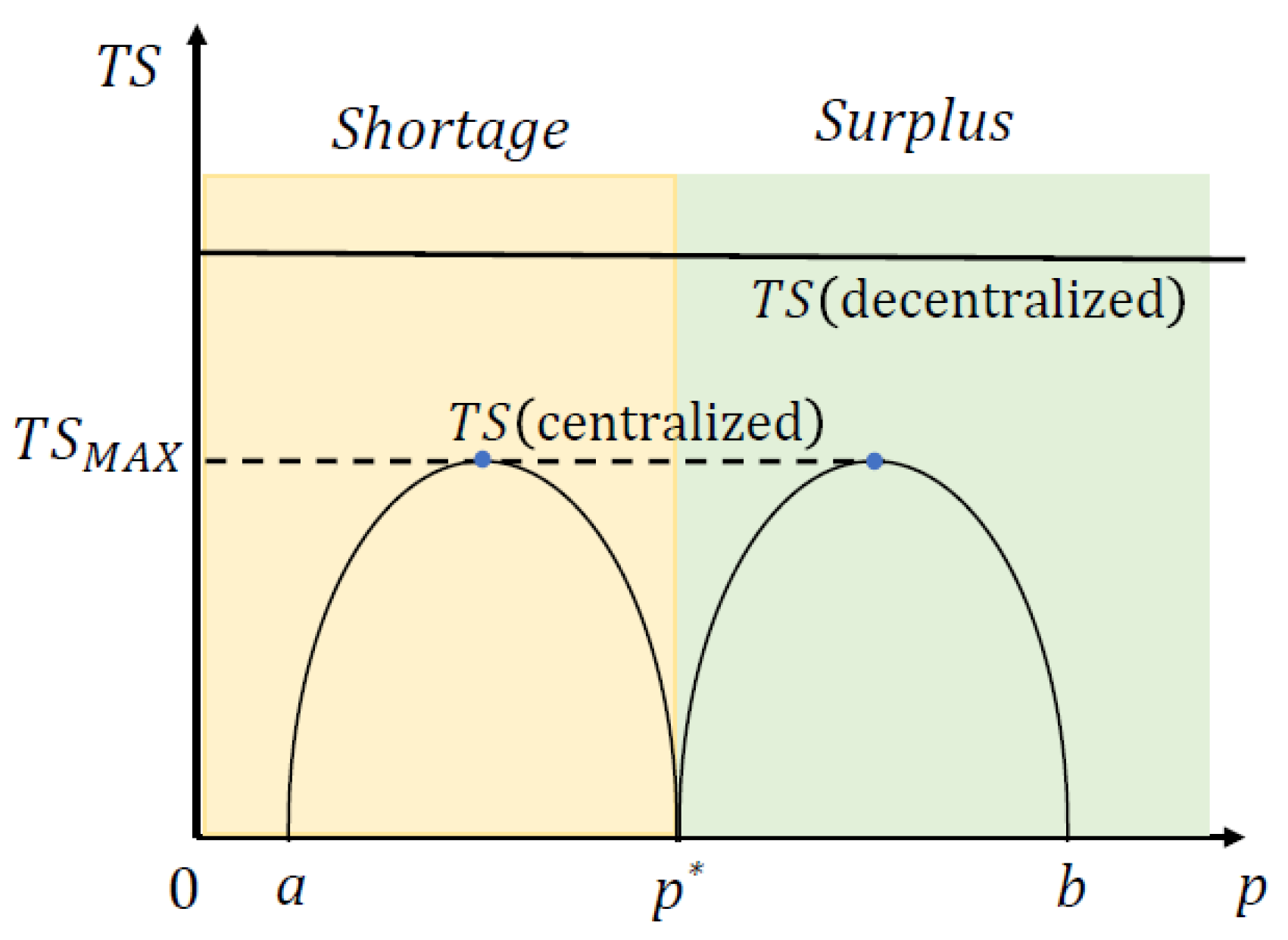
Comparing Equations (52) and (54), we can find that the total entropy of the decentralized market surpasses that of the centralized market for all prices. This result indicates that there is a higher uncertainty in transactions within the random matching market compared to transactions with price filtering. Thus, it is evident that the filtering mechanism plays an effective role in reducing transaction uncertainty and ensuring successful trade in the centralized market. Figure 9 illustrates the comparison of total entropy in the centralized and decentralized markets. The double-humped curve is total entropy in the centralized market, and the horizontal line is total entropy in the decentralized market.

4. Discussion

Market equilibrium is a fundamental concept in economic analysis, and its research involves two primary theories: Walrasian general equilibrium theory and Marshallian partial equilibrium theory. Walrasian general equilibrium theory assumes that there is an auctioneer who acts as an information center during the trading process. Prices are gradually adjusted in response to changes in supply and demand until equilibrium is achieved across all markets. However, the existence of the fictional Walrasian auctioneer has been criticized for its inconsistency with reality [24,25]. In contrast, Marshallian partial theory has been widely accepted by economists in analyzing the market equilibrium with supply and demand curves. It focuses on individual markets and takes producers and consumers as market participants, who are matched in a reverse rank during the transactions [26,27]. The reverse rank matching refers to willingness bids to buy are typically arranged from high to low in the order book, and willingness asks to sell are arranged from low to high. This way of matching implies that the information of traders' willingness prices is public, leading to transparent transactions and the absence of uncertainty in the transactions. As a result, the concept of transaction entropy, which measures market uncertainty, is not applicable in this case. However, except for certain call auction markets, the willingness prices of traders are private information in most markets. Therefore, the partial equilibrium theory has limited applications.
In this paper, we argue that traders' willingness prices are private information, and the transaction process can be depicted as a random matching of the market participants in the market. Specifically, in a centralized market, the price maker can just know who has entered the market after setting the market price, but is not aware about the willingness prices of the existing traders. Likewise, in a decentralized market the willingness prices of traders, which guide them to make transactions, are not known for each other no matter they have successfully make a deal or not. Therefore, we can see that inherent uncertainty exists in actual transactions due to the unavailability of traders' willingness prices. It is necessary to introduce the concept of transaction entropy to characterize market uncertainty, when the willingness prices are private information.

5. Conclusions

Following the statistical approach from Wang and Eugene [16], in which the concept of willingness price was introduced to formulate supply and demand functions as well as market surplus in a goods market, we expand metrics of market performance by introducing a new kind of information entropy to measure transaction uncertainty in a market.
The first metric of market performance is realized quantity of transaction. Given a market price in the centralized market, the realized quantity of transaction can be derived from supply and demand functions. According to the short-side principle, the transactions quantity is governed by the quantity supplied when the market is in shortage; while when the market is in surplus, the realized quantity is governed by the quantity demanded. And when the market is at equilibrium, the quantity of transactions is determined by the cross point of supply and demand curves. We find that the quantity of transactions reaches its maximum at equilibrium, it will decrease when the market price departs from the market-clearing point to shortage or surplus.
The second metric is market surplus, which is a traditional index of market efficiency. In the calculation of realized market surplus, the rationing rate is indispensable, which is defined as the ratio of actual transaction quantity to desired one. Sellers and buyers have their rationing rates, which are dependent on the market status. It can be proved that the realized market surplus is at its highest when the market is in equilibrium since it is increasing in the shortage and decreasing in the surplus.
We argue that the transaction uncertainty is a new dimension of market performance. To measure this kind of uncertainty, we first introduce the concept of transaction entropy which reflects the level of uncertainty in individual transactions. When a market is at equilibrium, the transaction entropy is zero. Otherwise, we will have positive transaction entropy when a market is in disequilibrium. It has a decreasing trend in shortage but has an increasing trend in surplus. The results indicate that there is no transaction uncertainty in equilibrium, and disequilibrium leads to higher transaction uncertainty. We then make a comparison of total entropy in centralized and decentralized markets and find that it is lower in the centralized market than in the decentralized market. This means that the price filtering mechanism plays a key role in reducing market uncertainty.
Finally, we argue that the market uncertainty is necessary in analyzing market performance, since the willingness prices are private information. Traditional methods of market equilibrium analysis are assuming that information of willingness prices of traders is public, and traders engage in a reverse rank matching when they make transactions. However, these assumptions are unrealistic, the willingness prices of traders can only guide them to choose entering market or not. Once they have entered the market, they are randomly matched to transact with each other, which must incur uncertainty in transactions.

Author Contributions

Conceptualization, H.Z. and X.H.L.; methodology, X.H.L. formal analysis, H.Z. and Y.G.W.; investigation, H.Z. and X.H.L.; writing—original draft preparation, H.Z.; writing—review and editing, X.H.L. and Y.G.W.; visualization, H.Z.; supervision, Y.G.W. All authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. The Derivation of Concavity of Total Entropy in the Centralized Market

As shown in Equation (49), the total entropy when a < p < p * can be expressed as:
T S = − Q S C p ln ⁡ Q S C p + Q D C p − Q S C p ln ⁡ Q D C p − Q S C p − Q D C p ln ⁡ Q D C p .
Taking the first derivation of Equation (49), which can be expressed as
T S ' = − Q S C ' p ln ⁡ Q S C p − ln ⁡ Q D C p − Q S C p + Q D C ' p ln ⁡ Q D C p − Q S C p − ln ⁡ Q D C p = Q S C ' p ln ⁡ Q D C p − Q S C p − ln ⁡ Q S C p − Q D C ' p ln ⁡ Q D C p − Q S C p − ln ⁡ Q D C p = F S C p ln ⁡ Q D C p − Q S C p − ln ⁡ Q S C p + F B C p ln ⁡ Q D C p − Q S C p − ln ⁡ Q D C p = 2 k * ln ⁡ Q D C p − Q S C p − k * ln ⁡ Q S C p − k * ln ⁡ Q D C p
Then, we can identify the concavity of the TS function by taking the second derivative as follows,
T S ' ' = − 2 k 2 Q D C p − Q S C p − k 2 Q S C p + k 2 Q D C p = − 1 Q D C p − Q S C p * Q S C p * Q D C p * [ 2 k 2 * Q S C p * Q D C p + k 2 * Q D C p * Q D C p − Q S C p − k 2 * Q S C p * Q D C p − Q S C p ] = − k 2 Q D C p − Q S C p * Q S C p * Q D C p * Q S C p + Q D C p 2 < 0 .
Therefore, TS is a concave function when a < p < p * . With the similar derivation process, we can deduce that there are two concave curves symmetric about p = p * within the interval [a, b].

Appendix B. The Total Entropy in the Decentralized Market

To facilitate obtaining an integral expression of Equation (51), we split it into two components, that is, the sellers’ total entropy T S S d e = ∫ a b F S v H S v d v and buyers’ total entropy T S B d e = ∫ a b F B v H B v d v . Combining with Equation (31), we derive buyers’ market entropy first, which can be expressed as,
    T S B d e = ∫ a b F B v − 1 [ E B l n E B + ( 1 − E B ) l n ⁡ ( 1 − E B ) ] ⅆ ν = − k ∫ a b ( v − a b − a l n v − a b − a + b − v b − a ln ⁡ b − v b − a ) ⅆ ν = − k b − a ∫ a b v − a ln ⁡ v − a + b − v ln ⁡ b − v − b − a ln ⁡ b − a ⅆ ν = − k b − a ∫ a b v − a ln ⁡ v − a + b − v ln ⁡ b − v d v + k b − a ln ⁡ b − a
Supposing x = v − a , t = b − v , Equation (57) can be rewritten as
T S B d e = − k b − a [ ∫ 0 b − a x ln ⁡ x d x + ∫ 0 b − a t ln ⁡ t d t ] + k b − a ln ⁡ b − a = 2 − k b − a ∫ 0 b − a x ln ⁡ x d x + k b − a ln ⁡ b − a
where 2 ∫ 0 b − a x ln ⁡ x d x = b − a 2 ln ⁡ b − a − 1 2 b − a 2 . Therefore, the final total entropy of buyers in the market with random matching can be derived as
T S B d e = − k b − a b − a 2 ln ⁡ b − a − 1 2 b − a 2 + k b − a ln ⁡ b − a = 1 2 k ( b − a )
Then, we can derive the final total entropy of sellers’ total entropy through a similar derivation process, given by
T S S d e = 1 2 k ( b − a )
Summing up Equations (59) and (60), we obtain the final expression of total entropy in the decreolization market, as shown in Equation (52).

Appendix C. The Prices Which Correspond the Maximum Total Entropy in the Centralized Market

According to Appendix 7.1, we can know that the condition of the maximum total entropy in the centralized market is T S ' = 0 . According to the equation (56), we have
( Q D C p − Q S C p ) 2 = Q D C p * Q S C p .
Combined (62) with equation (45) and (46), we can get the price when the total entropy is max, which is
p 1 = 5 − 5 b + 5 + 5 a 10 , a < p < p * .
With the similar derivation process, we have
p 2 = 5 + 5 b + 5 − 5 a 10 ,           p * < p < b .

References

  1. Buzzell, R.D. Market Functions and Market Evolution. J. Mark. 1999, 63, 61–63. [Google Scholar] [CrossRef]
  2. Jurado, K.; Ludvigson, S.C.; Ng, S. Measuring Uncertainty. Am. Econ. Rev. 2015, 105, 1177–1216. [Google Scholar] [CrossRef]
  3. Sniazhko, S. Uncertainty in Decision-Making: A Review of the International Business Literature. Cogent Bus. Manag. 2019, 6, 1650692. [Google Scholar] [CrossRef]
  4. Akerlof, G.A. The Market for "Lemons": Quality Uncertainty and the Market Mechanism. Q. J. Econ. 1970, 84, 488–500. [Google Scholar] [CrossRef]
  5. Smith, V.L. An Experimental Study of Competitive Market Behavior. J. Polit. Econ. 1962, 70, 111–137. [Google Scholar] [CrossRef]
  6. Connolly, R.; Stivers, C.; Sun, L. Stock Market Uncertainty and the Stock-Bond Return Relation. J. Financ. Quant. Anal. 2005, 40, 161–194. [Google Scholar] [CrossRef]
  7. Segal, G.; Shaliastovich, I.; Yaron, A. Good and Bad Uncertainty: Macroeconomic and Financial Market Implications. J. Financ. Econ. 2015, 117, 369–397. [Google Scholar] [CrossRef]
  8. Dzielinski, M. Measuring Economic Uncertainty and Its Impact on the Stock Market. Financ. Res. Lett. 2012, 9, 167–175. [Google Scholar] [CrossRef]
  9. Dimpfl, T.; Peter, F.J. Using Transfer Entropy to Measure Information Flows between Financial Markets. Stud. Nonlinear Dyn. Econom. 2013, 17, 85–102. [Google Scholar] [CrossRef]
  10. Liu, A.; Chen, J.; Yang, S.Y.; Hawkes, A.G. The Flow of Information in Trading: An Entropy Approach to Market Regimes. Entropy 2020, 22, 1064. [Google Scholar] [CrossRef]
  11. Li, S.; Zhuang, Y.; He, J. Stock Market Stability: Diffusion Entropy Analysis. Physica A. 2016, 450, 462–465. [Google Scholar] [CrossRef]
  12. Billio, M.; Casarin, R.; Costola, M.; Pasqualini, A. An Entropy-Based Early Warning Indicator for Systemic Risk. J. Int. Financ. Mark. Inst. Money. 2016, 45, 42–59. [Google Scholar] [CrossRef]
  13. Pele, D.T.; Lazar, E.; Dufour, A. Information Entropy and Measures of Market Risk. Entropy 2017, 19, 226. [Google Scholar] [CrossRef]
  14. Philippatos, G. C.; Wilson, C. J. Entropy, market risk, and the selection of efficient portfolios. Appl. Econ. 1972, 4, 209–220. [Google Scholar] [CrossRef]
  15. Ou, J. Theory of portfolio and risk based on incremental entropy. J. Risk Finance 2005, 6, 31–39. [Google Scholar] [CrossRef]
  16. Yougui, Wang; H. E. Stanley. Statistical approach to partial equilibrium analysis. Physica A: Stat. Mech. Appl. 2009, 388, 1173–1180. [Google Scholar] [CrossRef]
  17. Zhou, R.; Cai, R.; Tong, G. Applications of Entropy in Finance: A Review. Entropy 2013, 15, 4909–4931. [Google Scholar] [CrossRef]
  18. Carruthers, B. G. (2013). From uncertainty toward risk: The case of credit ratings. Socio-Economic Review, 11(3), 525-551. [CrossRef]
  19. Miao, J. A Search Model of Centralized and Decentralized Trade. Rev. Econ. Dyn. 2006, 9, 68–92. [Google Scholar] [CrossRef]
  20. Peivandi, A.; Vohra, R.V. Instability of Centralized Markets. Econometrica 2021, 89, 163–179. [Google Scholar] [CrossRef]
  21. Malamud, S.; Rostek, M. Decentralized Exchange. Am. Econ. Rev. 2017, 107, 3320–3362. [Google Scholar] [CrossRef]
  22. Rubinstein, A.; Wolinsky, A. Decentralized Trading, Strategic Behaviour and the Walrasian Outcome. Rev. Econ. Stud. 1990, 57, 63–78. [Google Scholar] [CrossRef]
  23. Blouin, M.R.; Serrano, R. A Decentralized Market with Common Values Uncertainty: Non-Steady States. Rev. Econ. Stud. 2001, 68, 323–346. Available online: https://www.jstor.org/stable/2695931. [Google Scholar] [CrossRef]
  24. De Fraja, G.; Sakovics, J. Walras Retrouvé: Decentralized Trading Mechanisms and the Competitive Price. J. Political Econ. 2001, 109, 842–863. Available online: https://www.journals.uchicago.edu/doi/10.1086/322087. [Google Scholar] [CrossRef]
  25. Tesfatsion, L. Walrasian Equilibrium: A Critique, Class Lecture Notes, Department of Economics, Iowa State University, 2004.
  26. Plott, C.; Roy, N.; Tong, B. Marshall and Walras, Disequilibrium Trades and the Dynamics of Equilibration in the Continuous Double Auction Market. J. Econ. Behav. Organ. 2013, 94, 190–205. [Google Scholar] [CrossRef]
  27. Hudik, M. The Marshallian Demand Curve Revisited. Eur. J. Hist. Econ. Thought 2020, 27, 108–130. [Google Scholar] [CrossRef]
Preprints 78485 g001
Figure 1. The supply and demand curves in the market.
Figure 1. The supply and demand curves in the market.
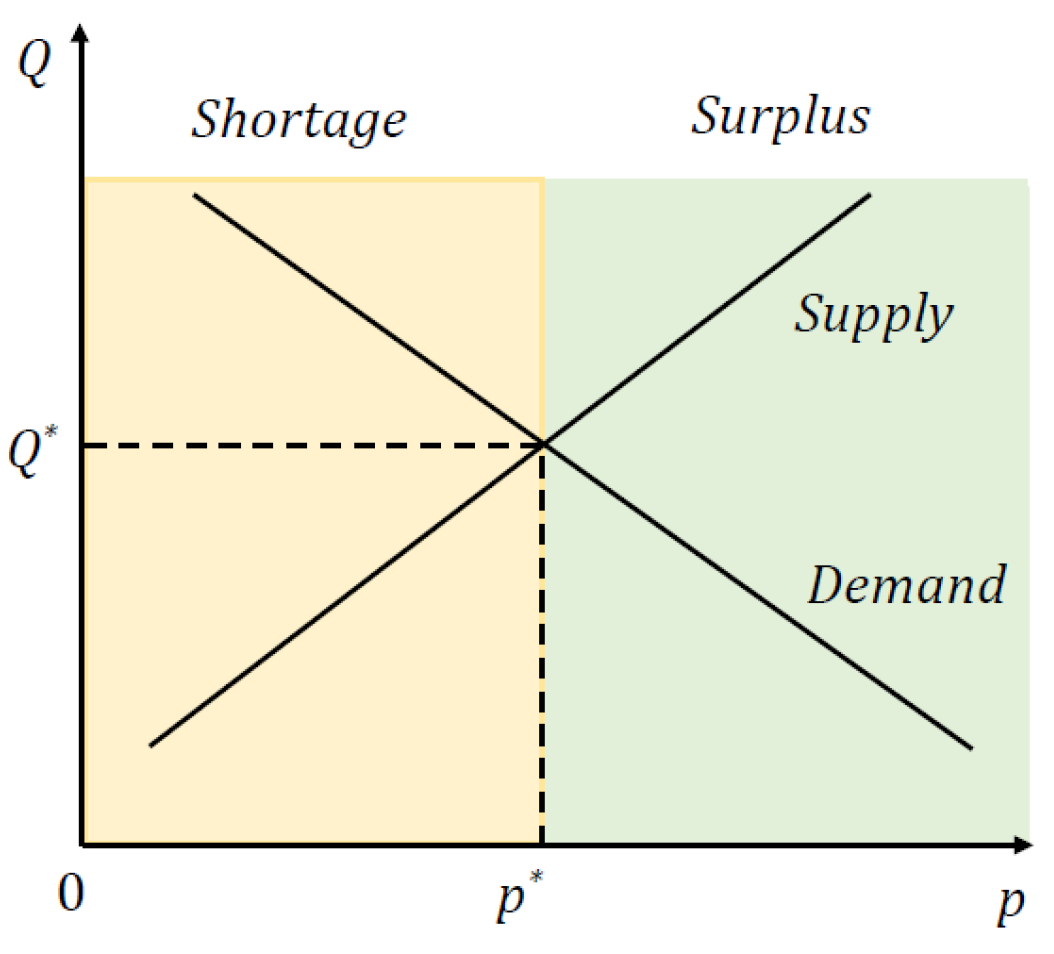
Preprints 78485 g001
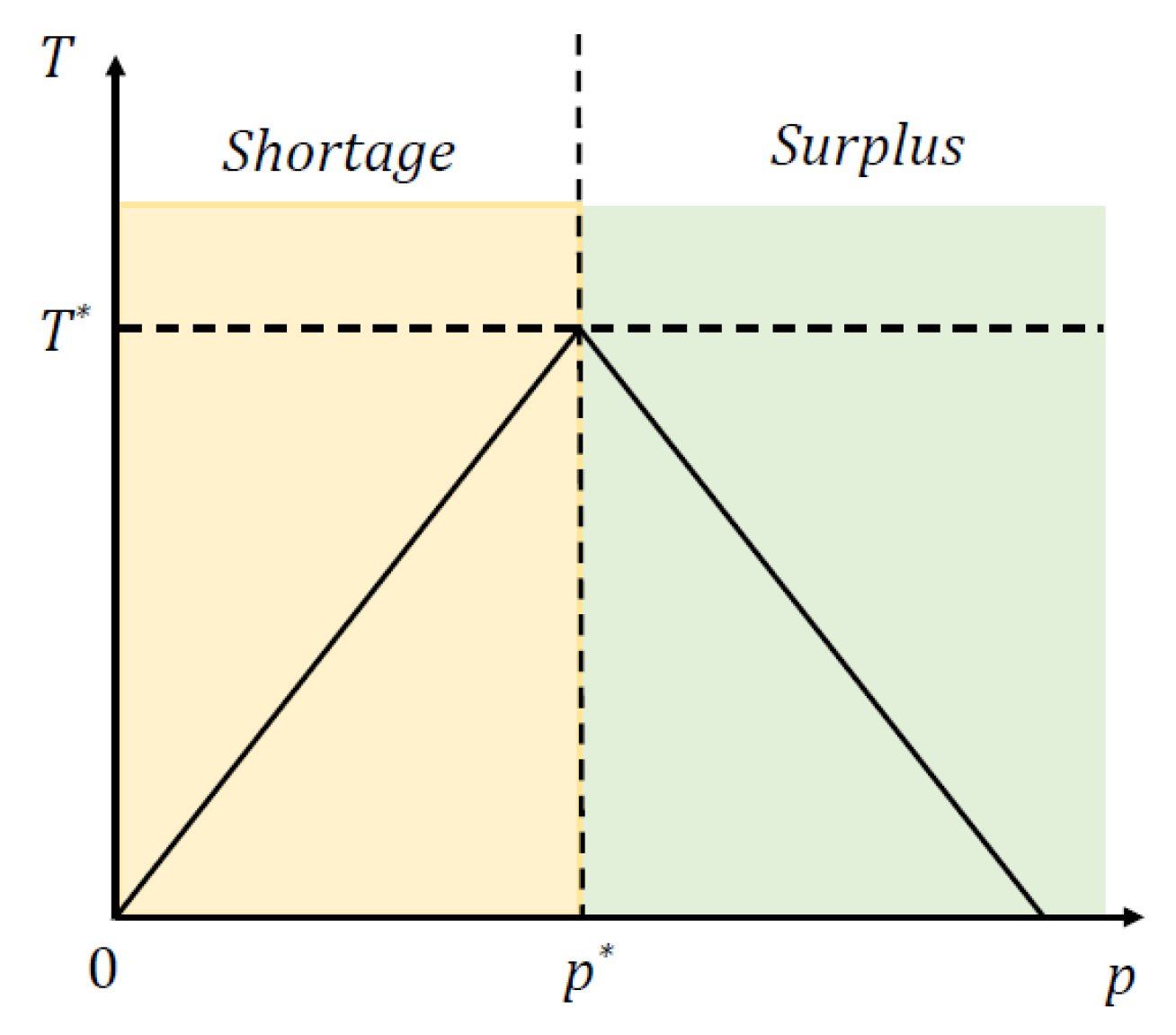
Preprints 78485 g002
Figure 2. The relationship between transaction quantity and market price.
Figure 2. The relationship between transaction quantity and market price.
Preprints 78485 g002
Preprints 78485 g003
Figure 3. The relationship between rationing rates and market price.
Figure 3. The relationship between rationing rates and market price.
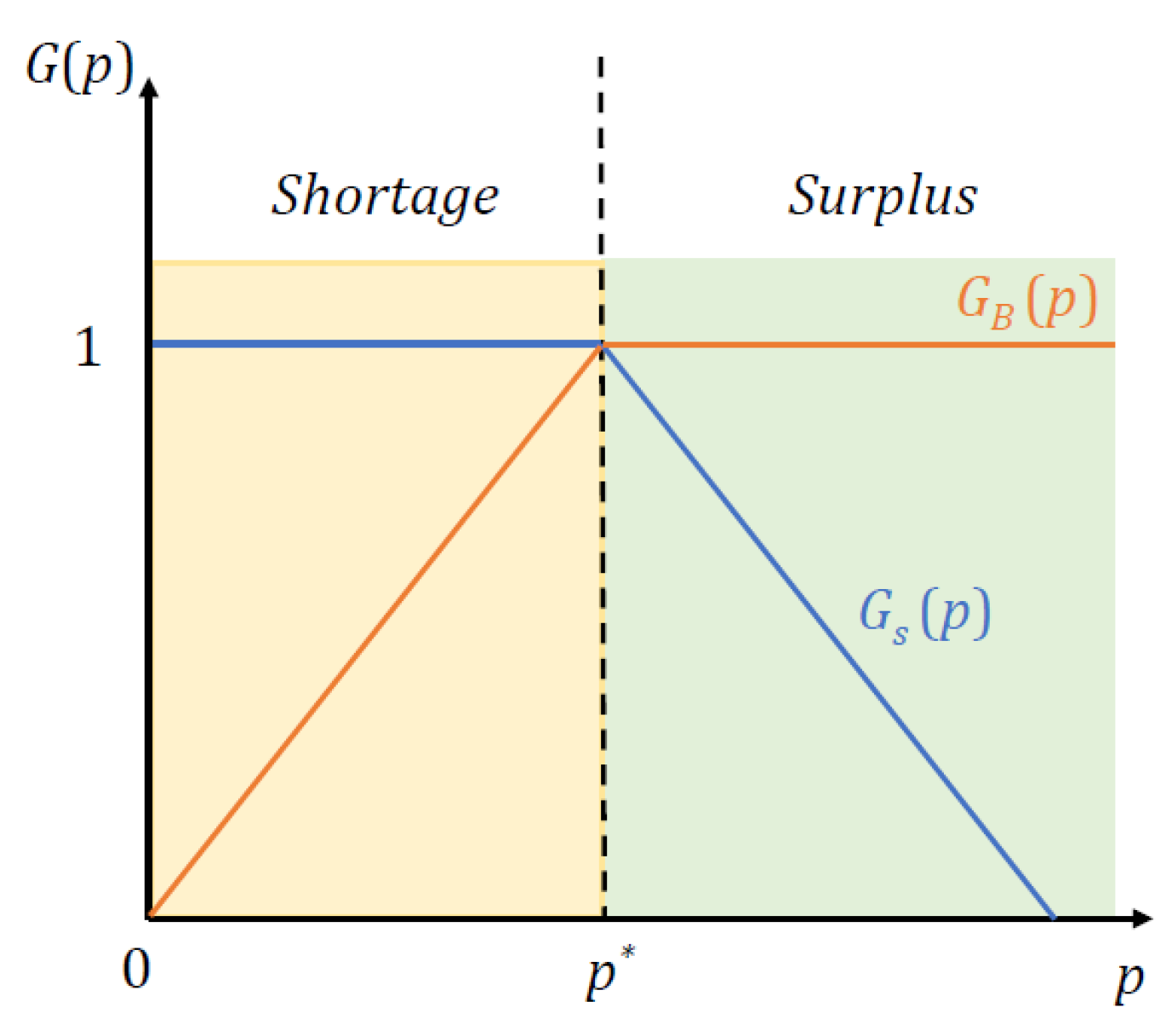
Preprints 78485 g003
Preprints 78485 g004
Figure 4. The relationship between the market price and market surplus.
Figure 4. The relationship between the market price and market surplus.
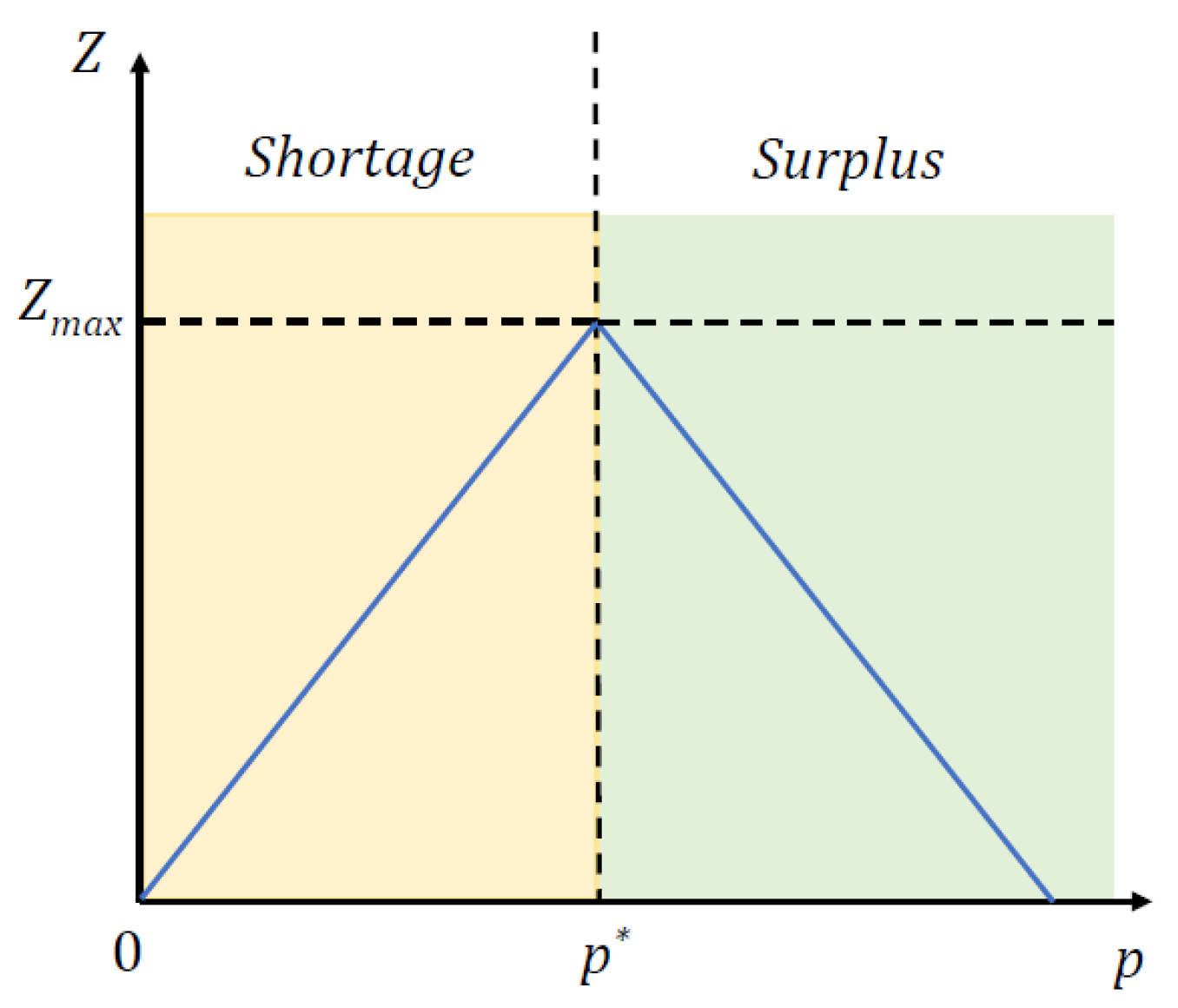
Preprints 78485 g004
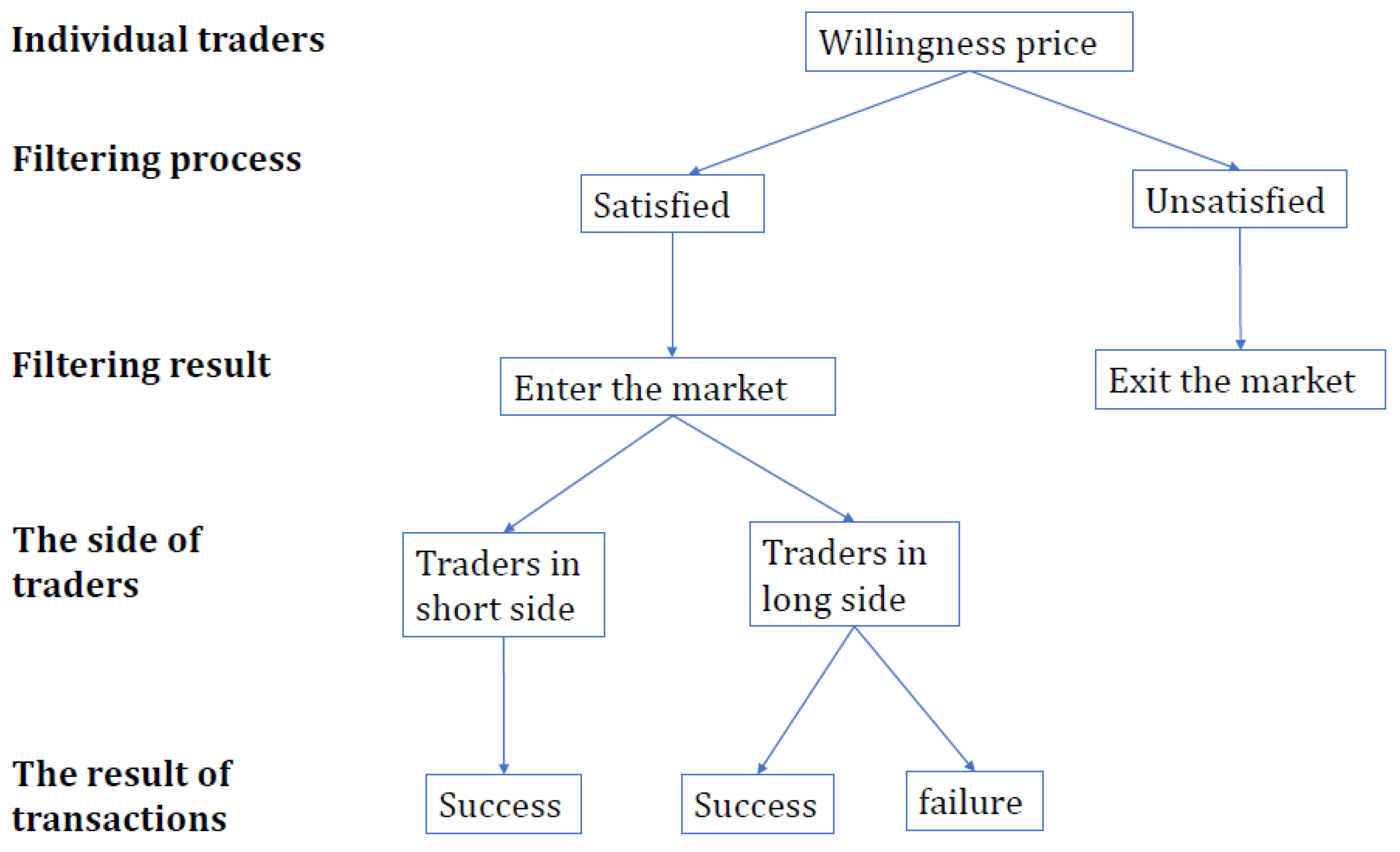
Preprints 78485 g005
Figure 5. The transaction process of one participant trade in the market.
Figure 5. The transaction process of one participant trade in the market.
Preprints 78485 g005
Preprints 78485 g006
Figure 6. The minimum of rationing rates of buyers and sellers.
Figure 6. The minimum of rationing rates of buyers and sellers.
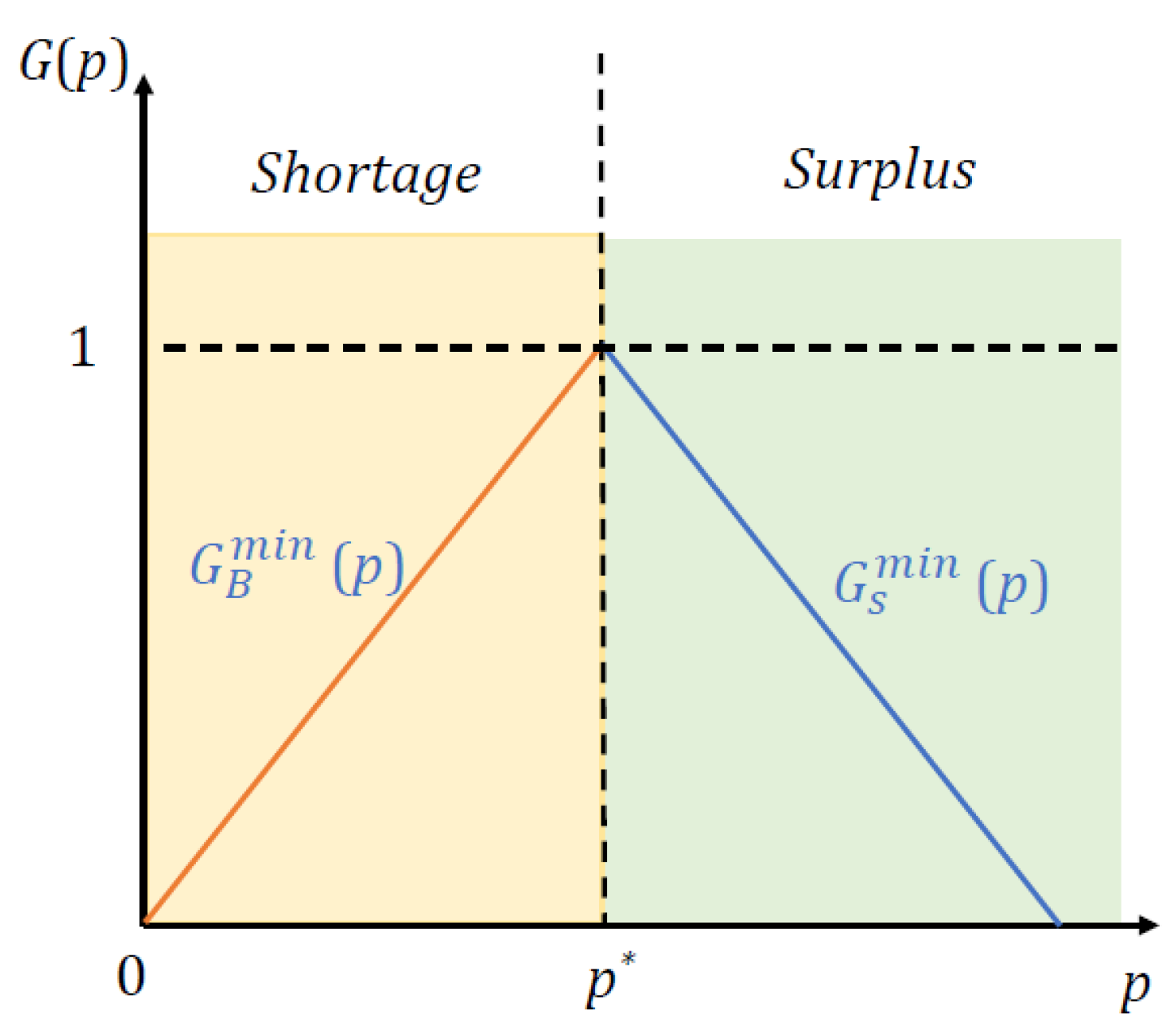
Preprints 78485 g006
Preprints 78485 g007
Figure 7. The dependence of transaction entropy on market price.
Figure 7. The dependence of transaction entropy on market price.
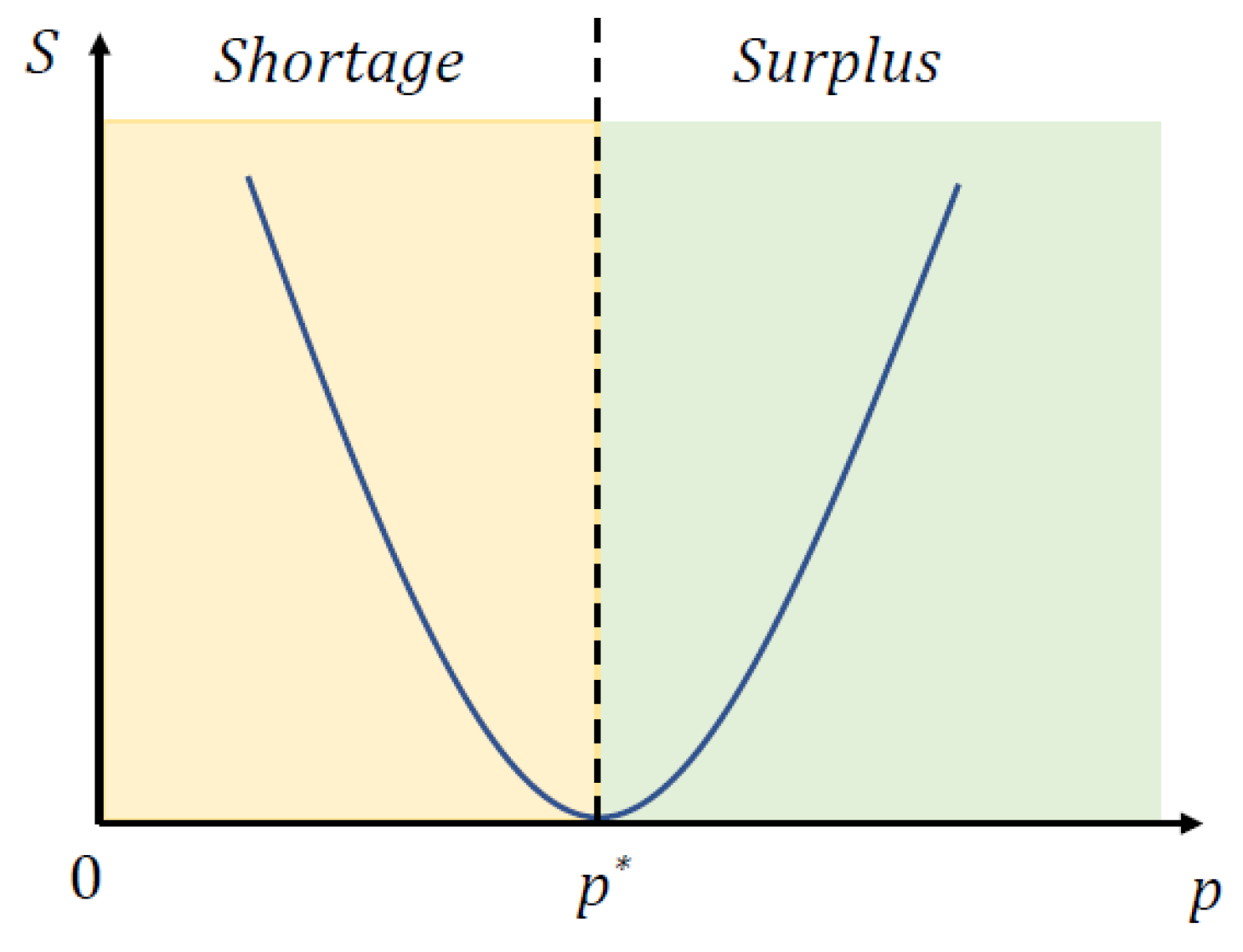
Preprints 78485 g007
Preprints 78485 g008
Figure 8. Random matching of a transaction process in a decentralized market.
Figure 8. Random matching of a transaction process in a decentralized market.
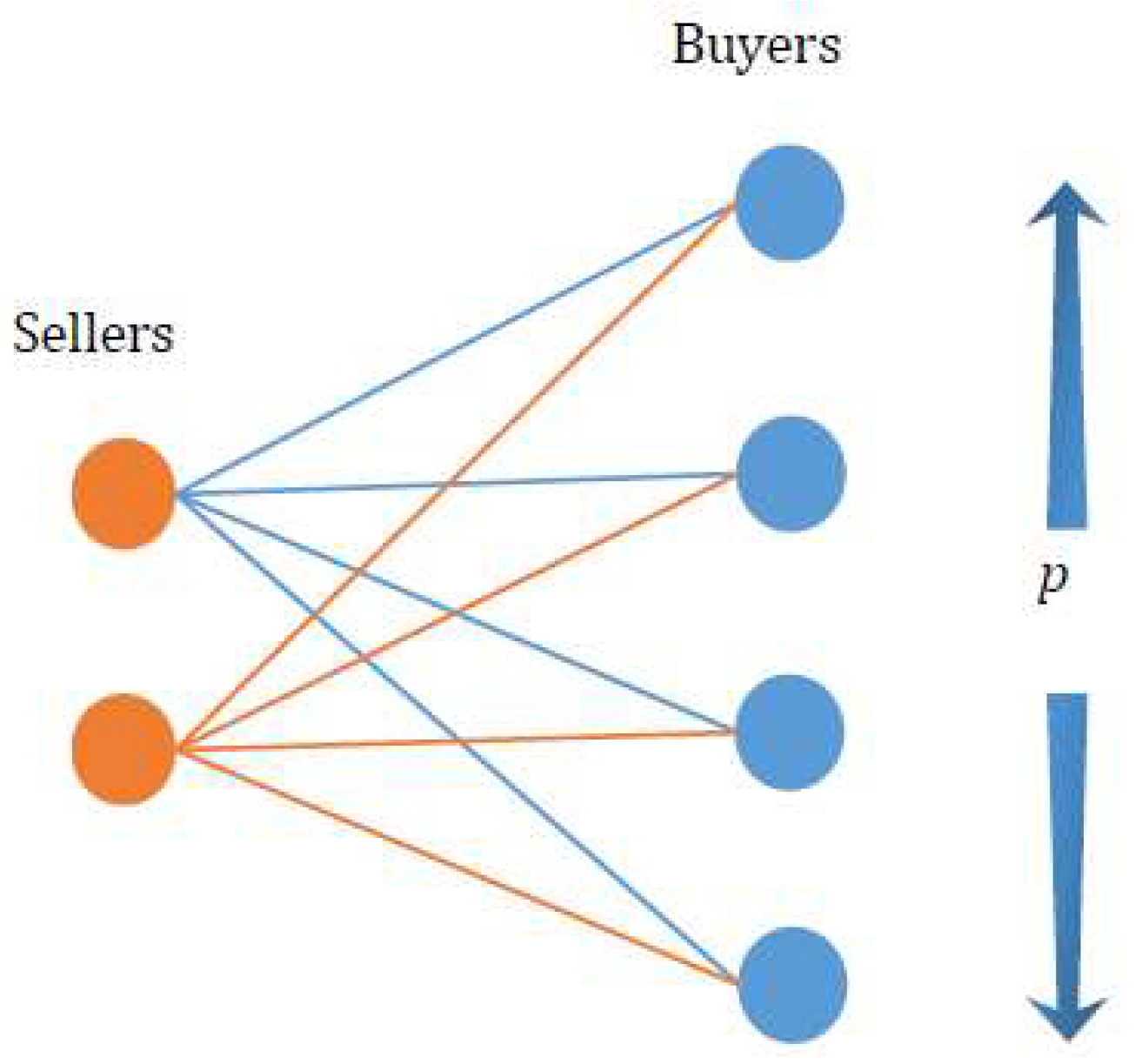
Preprints 78485 g008
Preprints 78485 g009
Figure 9. Comparison of total entropy in centralized and decentralized markets.
Figure 9. Comparison of total entropy in centralized and decentralized markets.
Preprints 78485 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated