Preprint
Article
Statistical Analyses of a Class of Random Cyclooctatetraene Chain Networks with Respect to Several Topological Properties
Altmetrics
Downloads
63
Views
10
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
04 July 2023
Posted:
04 July 2023
You are already at the latest version
Alerts
Abstract
In recent years, there has been a wave of research on complex networks. The purpose of this paper is to study the graph theoretic mathematical properties of random cyclooctatetraene chain. We obtain the explicit analytical expressions for the variances of the Gutman index, Schultz index, multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index of a random cyclooctatetraene chain with $n$ octagons, which plays a crucial role in the research and application of topological indices.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
1. Introduction
In this paper, we only consider simple and finite connected graphs, we refer to [1] and the references cited therein. Chemistry has been widely studied and applied in graph theory. The chemical compounds can be described in chemical graph theory, vertices represent the atoms and edges stand for the covalent bonds between atoms.
The molecular formula of a compound can represent different molecular structures and characteristics, but theoretical chemists are concerned about the physical and chemical properties of a compound and its relationship with the molecular formula of a compound. The topological index is considered as one of the most important methods to establish the relationship between molecular structure and its physicochemical properties in chemical graph theory.
In reality, chemical molecules are various. The same element has different shapes, and the same molecule has different expression names. Hydrocarbons are a kind of very important substances, and their synthesis has always been an important research topic in the field of organic chemistry. Cyclooctatetraene is a typical unsaturated hydrocarbon, so more and more people study its structure and properties, and the research in chemical graph theory is more and more in-depth. In this article, we consider four kinds indices of cyclooctatetraene chains with n octagons. And we simply consider the situation that is Starting from a vertex of a Cyclooctatetraene chain,connecting an edge to another octagon. For more information, we can refer to [16,17,24,29].
Let be a graph, whose vertex is set and the edge is set . Then let (or for short), which represents the distance between two vertices u and v (of G) , that is, in G is the shortest path between them. The famous Wiener index (or transmission) of is the sum of distances between all vertex pairs of vertices of G. It was created by H.Wiener in 1947 [34], that is
The Wiener index is one of the best studied, most understood, and widely used molecular shape descriptors, which is based on graph theory. Moreover, it becomes more and more widely used and studied, see [3,8,10,39].
A weighted graph [38] is a graph together with the weight function : . Let ⊕ denote one of the four arithmetic operations . Therefore, the weighted Wiener index is defined as
Clearly, if and ⊕ represents the operation ×, then .
If ⊕ represents the operation × and , then (2) is equivalent to
It is just the Gutman index. For the study of the possible chemical applications of Gutman index, and similar quantities, as well as their theoretical studies, polycyclic molecules are more difficult cases, see [14].
If ⊕ denotes the operation + and , then (2) is equivalent to
And it is just the Schultz index. More articles on developing such a topology indexes of the [6,11,19,35], such as mathematical properties, discrimination and applications refer to [30].
The effective resistance distance is the potential difference between x and y (of G) induced by the unique flow with an intensity of 1 that satisfies Kirchhoffs cycle law [12], for more detailed information in [4,13,20,23]. The Wiener index for non-trees is the Kirchhoff index, this distance funtion proposed by Klein and Randić [25], defined as
There are introduced the eccentric distance sum and the eccentricity resistance-distance sum, refer to [18,22,26].
The multiplicative degree-Kirchhoff index is proposed by Chen and Zhang in 2007 [7], see [33] to study some details about it, which is defined as
thus, the invariance of this graph is represented as
where are the eigenvalues of . Furthermore, is the normalized Laplacian matrix of the graph G, which was proposed by Chung [9]. The normalized Laplacian index and multiplicative degree-Kirchhoff index have important applications in mathematical chemistry and statistics. Their research has attracted more and more researchers’ attention.
The additive degree-Kirchhoff index is introduced by Gutman, Feng and Yu in 2012 [15], we refer the papers [32,36], which is defined as
In this paper,we mainly talk about the cyclooctatetraene chain with n octagons, which are constructed by the following way.
Firstly, is an octagon and is the Figure 1 graph with 2 octagons.
Secondly, The random cyclooctatetraene chain with n octagons is constructed by attaching a new terminal octagon to . We demonstrate this process by Figure 2. As demonstrated in Figure 3, we can attach the terminal hexagon to in four ways and denote the resulted figures by , , , respectively.
At each step, a random selection is made from one of the following possible constructions:
- with probability ,
- with probability ,
- with probability ,
- with probability ,
We consider four random variables as our choice. If our choice is , we let , otherwise , , we can easily obtain that
and .
By the above processes, we obtain a random polyphenylene chain . We always abbreviate to .
Noting that is a random graph, , , and are all random variables in probability. In the view of probability, one problem appears naturally. When n is big enough, whether the distribution of , , and will look like a distribution in probability or not.
In this paper, we make the following hypothesis.
Hypothesis 1.1. Our choice of attaching the new terminal hexagon to , are random and independently. In more accurate words, the series of random variables are independently and have the same law (9). For some , we have . Under Hypothesis 1.1, we give analytical expressions for the variances of , , and
2. The variances for the Gutman index and Schultz index of a random cyclooctatetraene chain
For a random cyclooctatetraene chain , the Gutman index and Schultz index are random variables. In this section, we will consider the variances of and . In fact, is linked to a new terminal octagon by an edge, where is spanned by vertices , , , , , , , , and the new edge is ; see Figure 1. On the hand, for all , one has
On the other hand,
In [40] Theorem 1, the author proves that
Now we introduce the first main result in this section.
Theorem 1.
If Hypothesis 1.1 is true, the following results are obtained. The variance of , which is the Gutman index of the random cyclooctatetraene chain , is given by
where
Recalling that ,,,are random variables in Section 1 which indicate our choice in the construction of from . We have the following four equalities.
Equality 1.
If , the above equality is obvious. So we only need to consider the case , which implies . In this case, (of ) coincides with the vertex labelled or (of ), see Figure 4. In this situation, becomes
in the above, we have used (10)-(12). Thus, we conclude the desired equality.
Equality 2.
As that in the proof of Equality 1, we only consider the case , that is . The proof is similar and we omit the details.
Equality 3.
we only consider the case , that is . The proof is the same as Equality 1 and we omit the details.
Equality 4.
we only consider the case , that is . The proof is also similar and we omit the details.
Noting that , by the above discussions, it holds that
where for each n,
. Therefore, by (15) we obtain
By direct calculation, one sees that, , , where for any two random variablesX, Y, . By the properties of variance and interchanging the order of sums, it follows that
With the help of a computer, the above equality implies the desired result .
Now, we discuss the variance of the Schultz index of a random cyclooctatetraene chain.
In [40] Theorem 2.3, we have
Then we state our results.
Theorem 2.
Assume Hypothesis 1.1, then the following results hold. The variance of , which is the Schultz index of the random cyclooctatetraene , is given by
where
With similar discussion, we have the following four equalities.
Equality 1.
If , the above equality is obvious. So we only need to consider the case , which implies . In this case, (of ) coincides with the vertex labelled or (of ),see Figure 4. In this situation, becomes
in the above, we have used (10)-(12). Thus, we conclude the desired equality.
Equality 2.
As that in the proof of Equality 1, we only consider the case , that is . The proof is similar and we omit the details.
Equality 3.
we only consider the case , that is . The proof is the same as Equality 1 and we omit the details.
Equality 4.
we only consider the case , that is . The proof is also similar and we omit the details.
Noting that ,by the above discussions, it holds that
where for each n,
. Therefore, by (15)
If we replace by in the proof of Theorem 1, the rest proof of this theorem is the same as that in the proof of Theorem 1 and we omit the details.
3. The variances of multiplicative and additive degree-Kirchhoff indices of a random cyclooctatetraene chain
In this section, we talk about the variances for and . For a random cyclooctatetraene chain , the multiplicative degree-Kirchhoff index and the additive degree-Kirchhoff index are random variables.
Recall that is obtained by attaching a new terminal octagon by an edge, where is spanned by vertices , , , , , , , , and the new edge is ; see Figure 1. On the hand, for all , one has
On the other hand,
In [40] Theorem 3, we have
Now we introduce the first main result in this section.
Theorem 3.
Assume Hypothesis 1.1, then the following results hold. The variance of , which is the multiplicative degree-Kirchhoff index of the random cyclooctatetraene , is given by
where
Recalling that are random variables in Section 1 which indicate our choice in the construction of from . We have the following four equalities.
Equality 1.
If , the above equality is obvious. So we only need to consider the case , which implies . In this case, (of ) coincides with the vertex labelled or (of ), see Figure 4. In this situation, becomes
in the above, we have used (17)-(19). Thus, we conclude the desired equality.
Equality 2.
As that in the proof of Equality 1, we only consider the case , that is . The proof is similar and we omit the details.
Equality 3.
we only consider the case , that is . The proof is the same as Equality 1 and we omit the details.
Equality 4.
we only consider the case , that is . The proof is also similar and we omit the details.
Noting that , by the above discussions, it holds that
where for each n,
. Therefore, by (22)
Now we consider , in [40] Theorem 3.3, we have
The variance of , is given by
Theorem 4.
where
Recalling that are random variables in Section 1 which indicate our choice in the construction of from . We have the following four equalities.
Equality 1.
If , the above equality is obvious. So we only need to consider the case , which implies . In this case, (of ) coincides with the vertex labelled or (of ), see Figure 4. In this situation, becomes
in the above, we have used (17)-(19). Thus, we conclude the desired equality.
Equality 2.
As that in the proof of Equality 1, we only consider the case , that is . The proof is similar and we omit the details.
Equality 3.
we only consider the case , that is . The proof is the same as Equality 1 and we omit the details.
Equality 4.
we only consider the case , that is . The proof is also similar and we omit the details.
Noting that , by the above discussions, it holds that
where for each n,
. Therefore, by (25)
If we replace by in the proof of Theorem 1, the rest proof of this theorem is the same as that in the proof of Theorem 1, we simply omit the details.
4. Concluding remarks
In this paper, we obtain the explicit analytical expressions for the variances of the Gutman index, Schultz index, multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index of a random cyclooctatetraene chain with n octagons. All these results will contribute to the study of the Gutman index, Schultz index, multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index of graphs.
With the continuous development and progress of science, more and more molecules are discovered and created.In chemical graph theory, the matter of polygonal chain is being widely studied by researchers. The molecular structures of polygonal chemicals are various and its physicochemical properties also become more and more important which are referenced to [2,5,27,31]. It is possible to establish exact formulas for the variances of some indices of a random polygon chain with n regular polygons.
References
- J.A. Bondy, U.S.R. Murty, Graph Theory, Springer, New York, 2008.
- Willis B. Person, George C. Pimentel, Kenneth S. Pitzer, The Structure of Cyclooctatetraene, J. Am. Chem. Soc. 74 (13) (1952) 3437-3438.
- F. Buckley, F. Harary, Distance in Graphs, Addison-Wesley, Reading, 1989.
- Z. Cinkir, Deletion and contraction identities for the resistance calues and the Kirchhoff index, Int. J. Quantum Chem. 111 (2011) 4030-4041. [CrossRef]
- Arthur C. Cope, Ronald M. Pike, Cyclic Polyolefins. Cyclooctatetraene Derivatives from Copolymerization and Side Chain Modification, J. Am. Chem. Soc. 75 (13) (1953) 3220-3223. [CrossRef]
- S. Chen, Modified Schultz index of zig-zag polyhex nanotubes, J. Comput. Theor. Nanosci. 6 (7) (2009) 1499-1503. [CrossRef]
- H. Chen, F. Zhang, Resistance distance and the normalized Laplacian spectrum, Discrete Appl. Math. 155 (5) (2007) 654-661. [CrossRef]
- A.L. Chen, F.J. Zhang, Wiener index and perfect matchings in random phenylene chains, MATCH Commun. Math. Comput. Chem. 61 (2009) 623-630.
- F.R.K. Chung, Spectral Graph Theory, American Mathematical Society Providence, RI, 1997.
- R.C. Entringer, D.E. Jackson, D.A. Snyder, Distance in graphs, Czechoslovak Math. J. 26 (1976) 283-296.
- M.R. Farahani, Hosoya, Schultz, modified Schultz polynomials and their topological indices of benzene molecules: first members of polycyclic aromatic hydrocarbons (PAHs), Int. J. Theor. Chem. 1 (2) (2013) 9-16.
- A. Georgakopoulos, Uniqueness of electrical currents in a network of finite total resistance, J. Lond. Math. Soc. 82 (1) (2010) 256-272. [CrossRef]
- S. Gupta, M. Singh, A.K. Madan, Eccentric distance sum: A novel graph invariant for predicting biological and physical properties, J. Math. Anal. Appl. 275 (2002) 386-401. [CrossRef]
- I. Gutman, Selected properties of the Schultz molecular topological index, J. Chem. Inf. Comput. Sci. 34 (1994) 1087-1089. [CrossRef]
- I. Gutman, L. Feng, G. Yu, Degree resistance distance of unicyclic graphs, Trans. Comb. 1 (2) (2012) 27-40. [CrossRef]
- Marco Garavelli, Fernando Bernardi, Alessandro Cembran, Cyclooctatetraene Computational Photo- and Thermal Chemistry: A Reactivity Model for Conjugated Hydrocarbons, J. Am. Chem. Soc. 124 (46) (2002) 13770-13789. [CrossRef]
- Donald H.Lo, M.A. Whitehead, Molecular geometry and bond energy. III. Cyclooctatetraene and related compounds, J. Am. Chem. Soc. 91 (2) (1969) 238-242. [CrossRef]
- F.G. He, Z.X. Zhu, Cacti with maximum eccentricity resistance-distance sum, Discrete Appl. Math. 219 (2017) 117-125. [CrossRef]
- A. Heydari, On the modified Schultz index of C4C8(S) nanotubes and nanotorus, Digest. J. Nanomater. Biostruct. 5 (1) (2010) 51-56. [CrossRef]
- S.B. Huang, J. Zhou, C.J. Bu, Some results on Kirchhoff index and degree-Kirchhoff index, MATCH Commun. Math. Comput. Chem. 75 (1) (2016) 207-222.
- G.H.Huang, M.J.Kuang, H.Y.Deng, The expected values of Kirchhoff indices in the random polyphenyl and spiro chains, Ars Math. Contemp. 9 (2) (2015) 197-207. [CrossRef]
- Z.W. Huang, X.Z. Xi, S.L. Yuan, Some further results on the eccentric distance sum, J. Math. Anal. Appl. 470 (1) (2019) 145-158. [CrossRef]
- S.B. Huang, J. Zhou, C.J. Bu, Some results on Kirchhoff index and degree-Kirchhoff index, MATCH Commun. Math. Comput. Chem. 75 (1) (2016) 207-222.
- Ryan J. Schwamm, Mathew D. Anker, Matthias Lein, Reduction vs. Addition: The Reaction of an Aluminyl Anion with 1,3,5,7-Cyclooctatetraene, J. Chem. 58 (5) 2019 1489-1493. [CrossRef]
- D.J. Klein, M. Randić, Resistance distance, J. Math. Chem. 12 (1) (1993) 81-95.
- S.C. Li, W. Wei, Some edge-grafting transformations on the eccentricity resistance-distance sum and their applications, Discrete Appl. Math. 211 (2016) 130-142.
- G. Luthe, J.A. Jacobus, L.W. Robertson, Receptor interactions by polybrominated diphenyl ethers versus polychlorinated biphenyls: a theoretical structure-activity assessment, Environ. Toxicol. Pharm. 25 (2008) 202-210. [CrossRef]
- L.Ma, H.Bian, B.J.Liu, H.Z.Yu, The expected values of the Wiener indices in the random phenylene and spiro chains, Ars Combin. 130 (2017) 267-274. [CrossRef]
- Nicholas Milas, John Nolan, Jr., Petrus H.L. Otto, Notes-Ozonization of Cyclooctatetraene, J. Org. Chem. 23 (4) (1958) 624-625. [CrossRef]
- S. Mukwembi, S. Munyira, MunyiraDegree distance and minimum degree, Bull. Aust. Math. Soc. 87 (2013) 255-271.
- F. Scott Mathews, William N. Lipscomb, The Structure of Silver Cyclooctatetraene Nitrate, J. Phys. Chem. 63 (6) (1959) 845-850. [CrossRef]
- M. Somodi, On the Ihara zeta function and resistance distance-based indices, Linear Algebra Appl. 513 (2017) 201-209. [CrossRef]
- M. Tang, C.E. Priebe, Limit theorems for eigenvectors of the normalized Laplacian for random graphs, Ann. Statist. 46 (5) (2018) 2360-2415. [CrossRef]
- H. Wiener, Structrual determination of paraffin boiling points, J. Am. Chem. Soc. 69 (1947) 17-20. [CrossRef]
- Z. Xiao, S. Chen, The modified Schultz index of armchair polyhex nanotubes, J. Comput. Theor. Nanosci. 6 (5) (2009) 1109-1114. [CrossRef]
- Y.J. Yang, D.J. Klein, A note on the Kirchhoff and additive degree-Kirchhoff indices of graphs, Z. Naturforsch. A 70 (6) (2015) 459-463. [CrossRef]
- W.Yang, F.Zhang, Wiener index in random polyphenyl chains, MATCH Commum. Math. Comput. Chem. 68 (2012) 371-376.
- Leilei Zhang, Qishun Li, Shuchao Li, Minjie Zhang, The expected values for the Schultz index, Gutman index, multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index of a random polyphenylene chain, J. Discrete Applited Mathematics. 282 (2020) 243-256. [CrossRef]
- Q.N. Zhou, L.G. Wang, Y. Lu, Wiener index and Harary index on Hamilton-connected graphs with large minimum degree, Discrete Appl. Math. 247 (2018) 180-185. [CrossRef]
- Jinfeng Qi, Jinbo Ni, Xianya Geng, The expected values for the Kirchhoff indices in the random cyclooctatetraene and spiro chains, J. Discrete Applited Mathematics. 321 (2022) 240-249. [CrossRef]
Figure 1.
Graph .

Figure 2.
The construction of from and .
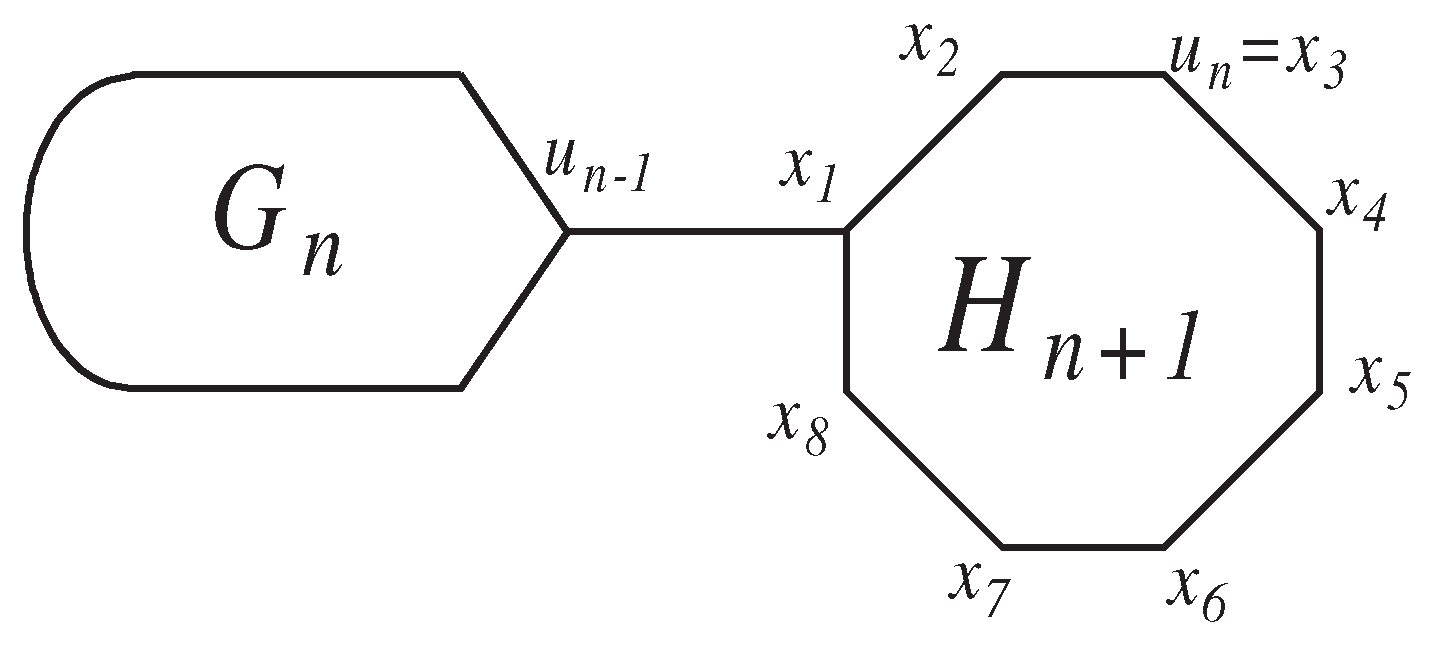
Figure 3.
Four ways to attach the new terminal hexagon to .
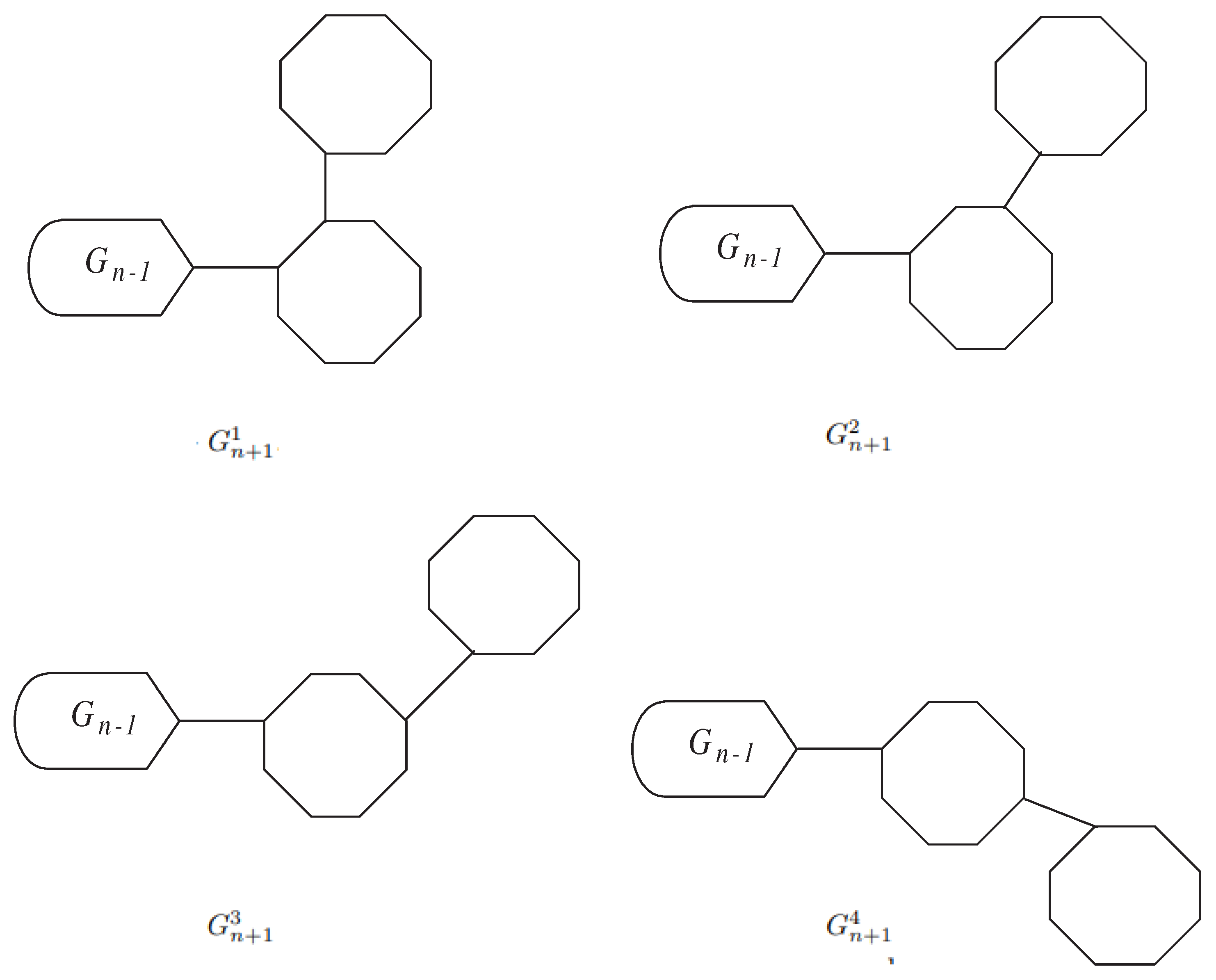
Figure 4.
.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





