A Stope Mining Design with Consideration of Hanging Wall When Transitioning from Open Pit Mining to Underground Mining for Sepon Gold Mine Deposit, Laos

This study investigates the transition from surface to underground mining at the Sepon Gold mine. The stability of surface slopes is assessed prior to commencing underground operations. Stope mining is adopted based on ore body characteristics and geological features. Finite element numerical analysis, employing the Generalized Hoek-Brown criterion, evaluates slope stability for surface slopes and opening stopes. The pit design comprises a 70° slope angle, 20 m height, and 10-15 m safety berm, meeting stability requirements with a factor of safety of 2.46. Underground mining design includes a 62° ore body dip, 50 m thick crown pillar to prevent surface subsidence, and 5 m wide, 5 m high stopes. Sill pillars are left for support after each level excavation. Rock bolts are employed in specific stope areas where is necessary, with continuous monitoring for surface deformation. The study analyzes the influence of stope sizes on pit wall and pit bottom stability, identifying slope failures near the hanging wall close to the pit bottom during underground mining. A slight increase in the displacement zone is observed on the upper crest of the top footwall. Overall, the findings demonstrate successful stability in the transition from surface to underground mining at Sepon Gold mine.

Keywords:

Subject: Engineering - Mining and Mineral Processing

1. Introduction

To continue mining operations and to obtain greater productivity, a transition from surface mining to underground stopping is necessary as the costs associated with waste removal and management experience a significant exponential increase [1]. Bakhtavar et al. [2] determined the optimal transition depth from open pit to underground mining in cases where combined mining methods are feasible. A methodology is proposed that utilizes economical block models of open-pit and underground methods, considering their respective Net Present Values (NPVs). They also focused on the optimization of the transition from open-pit to underground mining for near-surface deposits with a vertical extent [3]. It employs (0-1) integer programming to maximize profits and make informed decisions regarding the transition depth. The model incorporates the block economic value of open-pit and underground mining. A hypothetical example is used to evaluate the effectiveness of the model. Canadian open-stope mining is the primary method used in underground, hard-rock mines. It involves small, fast-turnaround stopes (20,000 to 100,000 tons) with poor to fair rock-mass conditions. Stability is ensured through stope dimensions, cable bolting, and diligent dilution control. The orebodies are typically deep, irregularly shaped, and high grade. Pillarless or early pillar recovery strategies prevent overstressing, and stopes are filled, often with a cemented fill. This study highlights the commonalities in Canadian open-stope mines [4]. Chung et al. [5] proposed a mixed-integer programming model for the optimization and planning of shallow deposits in mines that can be extracted using both open-pit and underground methods. The model aims to find the best transition point and period, taking into account factors such as crown pillar placement and development cost, to maximize the net present value of the project. Through a case study, the optimal transition points and periods were generated for various scenarios. These findings indicate that the transition points range from 315 to 360 m below the surface. However, the transition from open-pit to underground mining presents challenges in terms of geotechnical aspects, infrastructure definition, and meeting project deadlines and production targets [6]. Eberhardt et al. [7] conducted an implementation that addressed the challenges and risks associated with transitioning from surface to underground mass mining. It employs remote sensing, numerical modeling, and monitoring technologies to study rock engineering interactions and surface deformations caused by cave propagation. These findings improve the understanding of mass-mining-induced subsidence and enhance subsidence prediction.

To address these concerns, we conducted a parametric study to investigate the design and influence of the stope, not only in the vicinity of the excavation but also in relation to open-pit displacement, particularly at the pit bottom and pit walls in Sepon gold mine. According to the classification by previous report [8], The transition scenario can be categorized into three types. The first involves transitioning from open-pit mining to underground mining, where both operations are carried out simultaneously. The second type involves underground mining below or adjacent to an existing open pit, indicating that open-pit mining ceased in that area. The third type involves open-pit mining that extends through existing underground workings, often expanding the scale of mining to include high-grade zones, and reopening closed historical underground mines. In the context of these three scenarios, the second type is specifically relevant and has been implemented in the case of Sepon gold mine deposits. In 1988, Potvin identified three fundamental aspects of engineering rock mechanics design of open stopes. These aspects include the characteristics of the rock mass; effects of stress fields on the rock mass; and physical conditions determined by the size, geometry, and orientation of the rock mass and stress field. There are three main types of opening stopes that differ from those of other underground extraction methods. The first type is an opening stope with a non-entry method, followed by stopes that remain open until the final dimensions are achieved. Finally, underground excavations are designed for stability rather than caving methods [9]. Among these, the second type is utilized in the Sepon gold mine deposit. Moreover, in underground mining operations, the primary consideration is the impact of stress on an open stope. Stress relaxation in a rock mass is a time-dependent phenomenon characterized by the reduction in stress at a constant strain, which leads to deformation or weakening of the rock mass over time [10]. This study investigates the transition from surface to underground mining at the Sepon Gold mine.

2. Geology of Gold and Copper Mineralization at Sepon Mineral District

2.1. Sepon Mineral District

Sepon is located in the Vilabouly district, Savannakhet province, in the south-central part of Laos. The Sepon project comprises 1,947 km² located approximately 40 km north of the town of Sepon. The study area was selected from the Sepon Basin, Vilabouly District, Savannakhet Province, Lao PDR. The Sepon Basin is well known for the copper-gold mineralization district, as shown in Figure 1 the location of project, and the Cu-Au mineralization within the SMD occurred along the east-trending corridor, approximately 40 km long and 10 km wide. The open-pit gold and copper mining activities and productions in the SMD were commenced in late 2002 and late 2004, respectively, within indicated and inferred resources of 83 Mt @ 1.8 g/t Au for 4.75 Moz plus 100 Mt @ 2% Cu for 2.0 Mt [11,12].

2.2. Geology and the structural geology

Geological assessment of the Indochina plate throughout geological time has played a crucial role in creating a favorable environment for the formation of copper-gold deposits in the Sepon region. The mineralization process in this area is controlled by a normal fault, that exhibits a steep inclination and vertical dip. This fault configuration provides ideal conditions for hydrothermal fluids to migrate along the fault plane and permeate into the surrounding rocks. Additionally, strike-slip faults that traverse the region have also contributed to the formation of Cu and Au mineralization, along with associated minerals, such as malachite, azurite, and chalcocite. The Figure 2 shows the Schematic model of mineralisation styles in the Sepon Mineral District (after Sillitoe 1990).

The in-situ supergene enrichment of sulfide minerals, particularly chalcocite, has resulted in the formation of a high-grade chalcocite enrichment blanket. Directly beneath this blanket, is a zone rich in high-grade copper oxides, including minerals such as malachite, azurite, cuprite, and small amounts of native copper [13].

2.3. Geotechnical rock mass characterization

Before commencing mining operations, it is crucial to have a comprehensive understanding of the geological strength of the rock mass. In this study, the rock mass was evaluated using the Geological Strength Index (GSI) owing to its extensive applicability in underground mining research. The GSI system, developed by Hoek in 1994, is a widely employed method for the effective, efficient, and simple characterization of rock masses. This approach was established by combining observations of rock mass conditions (relying on Terzaghi's descriptions) with relationships derived from extensive experience gained through the utilization of the Rock Mass Rating (RMR) system. The average GIS value can be determined by establishing a connection between the structure of the rock mass and the circumstances surrounding rock discontinuities. Based on the core log samples, it can be observed that the Rock Quality Designation (RQD%) demonstrates a relatively good average ranging from 80% to 100% at depths exceeding 100 to 500 m. As part of the assessment process, fieldwork and geotechnical logging were conducted on the core, as shown in Figure 3 (a) and (b).

Laboratory studies were performed to evaluate the quality of intact rock. Among the initial strength tests conducted, Triaxial Compressive Strength Test was conducted. This involved using three sets of specimens obtained from a generally undisturbed rock sample, for pre-test and post-test illustrated in Figure 4 (a) - (c) illustrate the pre-test and post-test specimens, respectively. The results of the triaxial tests are shown in Figure 5 (a) - (c). The findings indicate that the ore sample exhibited the highest uniaxial compressive strength (UCS) with a measurement of 224.92 MPa. Ryodacite porphyry (RDP), followed by a UCS of 82.58 MPa, and Nodular Shale with 66.59 MPa. The highest strength value corresponds to the core sample with the highest strength. Furthermore, the test results also include the calculation of Young's modulus, expressed in GPa. It is worth noting that the general densities of all the three rock types were nearly identical.

3. Numerical Analysis

3.1. The input parameters

To determine the value of the entire rock, or the rock with the core specimen as fresh rock without weathering, the fundamental input parameters were established using the rock lab application, as indicated in Table 1. The parameter for the Geological Strength Index provided in [14,15] is used. Various Geological Strength Index (GSI) values were calculated between 35 and 55, which indicate blocky rock masses with fair joint surface quality and extremely blocky rock masses with good joint surface quality.

3.2. Model Construction

A finite element plastic numerical analysis utilizing the Generalized Hoek-Brown criterion was performed using RS2 software to assess the stability of the surface slopes and underground stope in a simplified model. The active underground section encompasses a former open-pit area. Figure 6 illustrates the segments of the pit bottom with an orebody dip angle of 62° connecting the footwall and hanging wall at the midpoint. The dimensions of the model were 520 m along the short axis and 700 m along the long axis. The y-and x-directions have fixed horizontal and vertical boundaries, while the upper part of the model is left free to allow for deformation movement. In terms of design, a safety berm was retained, and the slope had a height of 20 m and a slope angle of 70°. The overall slope had an inclination of approximately 47° and the total height was approximately 80 m.

The specific measures are taken in the design to prevent surface subsidence, such as incorporating a crown pillar thickness of approximately 50 meters [16]. The stope was 5 m wide and 5 m high. The mining sequence involved leaving sill pillars after five excavations at each level to provide support for the working floor, followed by backfilling. In certain areas of stopes, additional support through shotcreting and rock bolting, along with continuous monitoring, is necessary for stability management. With a GSI of 62 and a vein dip of 62°, mining operations utilize the overhand-cut method. Unlike conventional mining sequences that progress from the bottom to the top, leaving a 5-meter-thick sill pillar between each excavation, the overhand cut method starts from the bottom and moves upward to the top. This process is depicted in Figure 7, with the first group of excavations comprising of five steps. Once the initial group of excavations was complete, the method was repeated for subsequent excavations using the overhand-cut approach. This mining sequence continued until the final excavation was completed.

4. Results and Discussion

In terms of rock mechanics and rock engineering. The displacement and yielded elements were tracked in this study based on a numerical model to assess stability with a criteria based on plastic strain, it specifies that a 2.5% plastic strain is an indicator of failure in a non-entry stope [17] . As a result, the goal of this study was to examine how a designed stope might affect the slope face and pit bottom. The results of the analysis in a two-dimensional numerical model showed that stresses and stope deformation occurred more on the side of the hanging wall than on the footwall.

4.1. Surface and slope deformations

The stability of the slopes was examined using monitoring locations near the pit surface, which resulted in a factor of safety (FoS) of approximately 2.46, as shown in Figure 8. Underground mining operations must be continuously monitored once the surface slopes have finished. According to the results in Figure 9, a high displacement mostly occurred in the hanging wall. The displacement monitoring pins placed every ten meters along the surface are shown. The display revealed that the footwall was unaffected, but the bench's high displacement on the hanging wall side dramatically grew to pit bottom.

4.2. Comparison of different vein widths

4.2.1. Yielded elements

To assess and choose the best design based on geological conditions and ore recovery, there are six different design factors that are carried out in different sizes as open stope dimensions. The elements produced were used by numerous researchers to assess the likely failure zone [18,19,20]. Therefore, this study was conducted in the yielded zone to evaluate the potential failure zones.

According to the results, the failure zone is in a tiny location, as indicated in the yielded elements, and the first step of the excavation is 3 × 15m and comprises five minor steps. Figure 10(a) shows the small-scale propagation surrounding an open stope with a size of 3 × 15 m (wide and high). Each tiny step in the mining sequence was 3 × 3 m in size, using an overhand cut that was adequate for the rock mass and considered the orebody's GIS orebody value of 62. The ore recovery is reduced, and the first design is rather narrow, but it exhibits great stability around the open stope and has no impact on the crown pillar. The results in Figure 10(b) also demonstrate small-scale spreading around the open stops, but the size of the stope was slightly different, being 3 × 25 m for the initial step of excavation, which is made up of five smaller steps, each of which is 3 × 5 m high. In this situation, the failure zone increases more than the result in Figure 10(a) for the initial design. However, even though the stability was slightly higher than before, the crown pillar was unaffected. However, the ore recovery has improved. The design shown in Figure 10(c) utilized an excavation 5 × 25 m in size as its initial phase. The failure zone primarily formed around the first excavation to the fourth excavation, more so than in the previous two designs, according to the results. As shown in Figure 10(b), the failure zone increased twice as much as that of the design. Additionally, there was a propensity for failure on the higher slope due to open stope failure, but there was no response along the crown pillar. However, the ore recovery has improved. Figure 10(d), (e), and (f) almost all have the same failure zone, which starts to grow from 10(e) to 10(f). According to the findings, it is evident that large open stopes can result in significant failure zones, particularly around the hanging wall and crown pillar failures at designs as large as 20 × 25 m.

4.3.2. Displacement

Mining operations induce volumetric and stress-strain changes in rock masses. As the deformation exceeds the limits set by the rock strength, instability develops around the excavation area. It is crucial to monitor the stability of the surrounding rocks to prevent unforeseen failures. Therefore, careful observation and monitoring of the stability of rocks encircling stopes are essential. In contrast to real-time monitoring during active mining operations, where automatic monitoring occurs intermittently and occasionally using reference points, in this simulation, the monitoring points were strategically placed at critical locations in the model. The evaluation of displacements in the ongoing underground Sepon Mine revealed significant deformation conditions that could lead to failure. Based on these results, it can be observed that the displacements along the surface were pinned every 10 m, as shown in Figure 11. The highest displacement occurred on the hanging wall, predominantly on the crest, whereas the footwall side exhibited relatively lower displacements. This can be attributed to the stronger rock mass on the footwall side and the weaker rock mass on the hanging wall. This study examined six different designs for an open stope. The wider open stope design (20 m × 25 m) resulted in a larger failure zone and higher displacement. Conversely, a stope with dimensions of 3 × 15 m exhibited the lowest potential failure zone. The results indicated that the displacement gradually increased with increasing stope size.

Figure 12 illustrates the displacement, indicating that the highest displacement occurred during the third and fourth excavation steps, particularly on the hanging wall. However, on the footwall, the displacement remained generally low. Additionally, the safety factor remained relatively stable throughout the excavation process, with an approximate value of 1.67. According to the results, the first step of excavation showed the lowest displacement, with a value of 2.37 mm. The second open stope excavation exhibited a gradual increase in the displacement to 2.63 mm. Similarly, the third and fourth steps of the excavation showed further increases in displacement, measuring 3.25 mm and 3.78 mm, respectively. It can be observed that as the excavation depth increases, the predominant displacement also increases. Furthermore, the highest displacement occurred on the hanging wall side, whereas the footwall side displayed a slightly higher displacement, especially on the crest, as shown in Figure 13.

Based on the data displayed in Figure 14, the monitoring sites were positioned along the side of the open stope. High displacements were generally observed on the hanging wall side, which can be attributed to the lower strength of the rock mass compared to the footwall side. Specifically, the hanging wall side exhibited a Geological Strength Index (GSI) of 51, indicating a relatively weaker rock mass, whereas the footwall side had a GSI of 72, indicating a stronger rock mass. Consequently, due to this and the favorable geometry, low displacements were recorded on the footwall side in this scenario.

4.4. Determined of the various stress ratio

According to the results, it can be observed that the instability around the open stope is relatively low at a K ratio of 0.5 compared to other stress ratios, as shown in Figure 15 (a). In Figure 15 (b), it can be observed that the predominant failure starts developing around the open stope with a K ratio of 1. The failure zone was more pronounced on the hanging wall side because of the weak rock mass with a GSI of 51. When the K ratio increased to 1.5, more failure zones began to develop, as shown in Figure 15 (c). Furthermore, as shown in Figure 15 (d), (e), and (f), when the K ratio was increased from 2 to 3, the instability dramatically increased, and the most significant failure zone occurred at the highest K ratio of 3, surpassing the failure zones observed at K ratios of 2 and 2.5. However, the sill pillar remained stable for K ratios of 0.5 and 1. At a K ratio of 1.5, the sill pillar was affected, along with the crown pillar. Additionally, for K ratios of 2 to 3, both the sill pillar and crown pillar are significantly affected. Based on the result of the horizontal displacement graph in Figure 16, it can be said that the low displacement depends on the stress ratio. In this study, a K ratio of 0.5, with a displacement of 8.32 mm, followed by a K ratio of 1, which has a double increase of 16.7 mm as double increased. While when K ratio with 1.5 and its result on displacement was 35.4 mm and almost double increased to 62.8 mm with K ratio of 2. However, when the K ratio increased to 2.5, the displacement slightly increased to 87.9 mm. In addition, it increased dramatically to 135 mm with a K ratio of 3. Consequently, the highest displacement occurred with the highest stress ratio. However, the lowest displacement occurred along with the lowest stress ratio.

4.5. Different GSI values

According to the outcome depicted in Figure 17, the geological strength index (GIS) affects the safety factor. As can be seen from the displays, underground mining that complies with a GSI of 35 is considered safe when a factor of 1.3 is used. However, when the GSI is lower than 35, the safety factor falls below 1.3, which fails to meet the requirements. However, it is evident from the horizontal displacements shown in Figure 18 that the lowest GSI value resulted in displacements of up to 15 cm, as illustrated by the highest displacement at GSI 30 and below. However, as the GIS values increase, higher GSI values correspond to smaller horizontal displacements. This confirms that a high GSI value leads to a high level of stability, particularly in surface mining and open stopes. Thus, the GSI value plays an important role in the numerical simulation of the safety of the factors and horizontal displacements.

The results obtained from the simulation presented in Figure 19 provide valuable insights into the behavior of the open stope under different GSI conditions. In Figure 19(a), the lowest GSI of 25 leads to the occurrence of a considerable failure zone, primarily affecting the hanging wall side, with a relatively minor impact on the crown pillar. This suggests that the stability of the open stope was significantly compromised at this GSI level. As shown in Figure 19(b), an increase in the GSI to 30 resulted in a slight improvement in the failure zone. Although there was a marginal reduction in the extent of failure, the hanging wall region continued to exhibit a dominant failure behavior. Notably, even a moderate increase in GSI had a limited effect on stabilizing the open stope. However, the scenario changed significantly as GSI continued to increase. From the GSI values of 35 to 50, there was a noteworthy decrease in the failure zone size and extent. Notably, Figure 19(e) and (f) show that when the GSI reached 45 and 50, respectively, the impact on the failure zone was the least pronounced. These figures indicate that the open stope exhibited improved stability with a considerable reduction in the occurrence of failures, particularly in the hanging wall portion.

Overall, the simulation results presented in Figure 19 highlight the critical role of GSI in determining the stability of the open stope. A lower GSI, such as 25, led to a significant failure zone, primarily affecting the hanging wall side, whereas higher GSI values, such as 45 and 50, resulted in improved stability and a substantial decrease in the failure zone. These findings underscore the importance of considering the GSI as a crucial factor in designing and managing open stopes to ensure their long-term stability and safety.

5. Conclusions

A study was conducted to assess the impact of an open stope excavation beneath an existing open pit. The objective was to understand the patterns of slope deformation and the influence of the open stope beneath the open pit bottom as crucial mining characteristics. A 2D isotropic plastic numerical model using RS2 was created to represent both portions of the mine (underground and open pits) throughout the investigation. Based on the displacements and generated elements, this study demonstrated that underground mining can have various consequences on the slope face and pit bottom of an open pit. Underground mining had a greater impact on the slope wall above the hanging wall than on the wall above the footwall. Furthermore, in terms of open stope design, it can be concluded that smaller stope dimensions result in smaller failure zones, whereas larger open stope dimensions lead to larger failures around the stope, particularly on the hanging wall and upper part, known as the crown pillar. However, the footwall side was less affected by the excavation. To gain a better understanding of the impact of underground mining on the overall stability of mines, a comprehensive analysis that examines both underground and open-pit sections is required.

Author Contributions

Conceptualization, P.S. and H.S.; Data curation, P.S. and A.H.; Formal analysis, P.S.; Methodology, P.S., H.S.; Software RS2, P.S. and A.H.; Supervision, H.S. and T.S.; Validation, H.S.,T.S.,A.H.; Visualization, P.S., Writing—original draft, P.S., Writing—review and editing, H.S.,T.S.,A.H.,P.Ph.,Sh.S.,S.Kh; Materials, H.S.,T.S., A.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research work is part of a doctoral program supported by JICA.

Informed Consent Statement

Informed consent was obtained from all the subjects involved in the study.

Data Availability Statement

Research data will be provided upon request from the first author.

Acknowledgments

We sincerely thank JICA for the scholarship funding that has facilitated this research. Laboratory for providing the RS2 software used for analysis and test results of rock mechanics from the Spon Company.

Conflicts of Interest

The authors declare no conflict of interest.

References

Soltani Khaboushan, A. , Osanloo, M., & Esfahanipour, A. Optimization of open pit to underground transition depth: An idea for reducing waste rock contamination while maximizing economic benefits. Journal of Cleaner Production 2020, 277, 123530. [Google Scholar] [CrossRef]
Bakhtavar, E. , Shahriar, K., & Oraee, K. Transition from open-pit to underground as a new optimization challenge in mining engineering. Journal of Mining Science 2009, 45, 485–494. [Google Scholar] [CrossRef]
Bakhtavar, E. , Shahriar, K., & Mirhassani, A. Optimization of the transition from open-pit to underground operation in combined mining using (0-1) integer programming. Journal of the Southern African Institute of Mining and Metallurgy 2012, 112, 1059–1064. [Google Scholar]
Potvin, Y. , & Hudyma, M. Open Stope Mining in Canada OPEN STOPE MINING IN CANADA Yves Potvin and Marty Hudyma Australian Centre for Geomechanics, (January 2000).
Chung, J. , Asad, M. W. A., & Topal, E. Timing of transition from open-pit to underground mining: A simultaneous optimisation model for open-pit and underground mine production schedules. Resources Policy 2022, 77, 102632. [Google Scholar] [CrossRef]
Olavarría, S., Adriasola, P., & Karzulovic, A. Transition from open pit to underground mining at chuquicamata, Antofagasta, Chile. International Symposium of Stability of Rock Slopes in Open Pit Mining and Civil Engineering 2015, 421–434.
Eberhardt, E., Woo, K., Stead, D., & Elmo, D. Transition from surface to underground mining : Integrated mapping , monitoring and modeling data to better understand complex rock mass interaction. ISRM Congress 2015 Proceedings - Int’l Symposium on Rock Mechanics 2007, I.
Hamman, E., Cowan, M., Venter, J., & de Souza, J. (2020). Considerations for open pit to underground transition interaction, 1123–1138. [CrossRef]
Potvin, Y. (1988). Empirical open stope design in canada a thesis submitted in partial fulfillment of the requirements for the degree of doctor of philosophy in the faculty of graduate studies department of mining and mineral process engineering, (November).
Hudson, J. A., & Harrison, J. P. 13-Rock dynamics and time-dependent aspects. Engineering rock mechanics. Oxford: Pergamon 1997, 207–221.
Smith, S., Olberg, D., & Manini, T. (2005). The Sepon gold deposits, Laos: exploration, geology and comparison to Carlin-type gold deposits in the Great Basin. In Geological Society of Nevada Symposium, Reno, Nevada (pp. 899–915).
Cannell, J., & Smith, S. (2008). High-grade supergene enriched and exotic copper deposits in the Sepon Mineral District, Lao PDR. In Proceedings of PACRIM Congress (pp. 355–361).
Loader, S. E. (1999). Supergene enrichment of the Khanong copper resource, Sepon project, Lao PDR. In PACRIM (Vol. 99, pp. 263–270).
Marinos, P. , & Hoek, E. (2018). GSI: A geologically friendly tool for rock mass strength estimation. ISRM International Symposium 2000, IS 2000.
Hoek, E. , Carter, T. G., & Diederichs, M. S. Quantification of the geological strength index chart. 47th US Rock Mechanics / Geomechanics Symposium 2013, 3, 1757–1764. [Google Scholar]
Sasaoka, T. , Takamoto, H., Shimada, H., Oya, J., Hamanaka, A., & Matsui, K. Surface subsidence due to underground mining operation under weak geological condition in Indonesia. Journal of Rock Mechanics and Geotechnical Engineering 2015, 7, 337–344. [Google Scholar] [CrossRef]
Vakili, A. An improved unified constitutive model for rock material and guidelines for its application in numerical modelling. Computers and Geotechnics 2016, 80, 261–282. [Google Scholar] [CrossRef]
Thae, C., Dyson, O., Takashi, M., & Hideki, S. Design and Stope Stability Analysis of Multiple Concurrent Excavated Veins in Underground Mine ; Case Study of Hermyingyi Tin - Tungsten ( W - Sn ) Mine. Geotechnical and Geological Engineering 2022, 0123456789. [CrossRef]
Dintwe, T. K. M. , Sasaoka, T., Shimada, H., Hamanaka, A., Moses, D., Liu, S., & Meng, F. Effects of Sublevel Open Stope Underground Mining on Surface and Open Pit Slopes. Journal of Geoscience and Environment Protection 2021, 09, 121–131. [Google Scholar] [CrossRef]
Purwanto,, Shimada, H. , Sasaoka, T., Wattimena, R. K., & Matsui, K. Influence of Stope Design on Stability of Hanging Wall Decline in Cibaliung Underground Gold Mine. International Journal of Geosciences 2013, 04, 1–8. [Google Scholar] [CrossRef]

Figure 1. Location of Sepon Project.

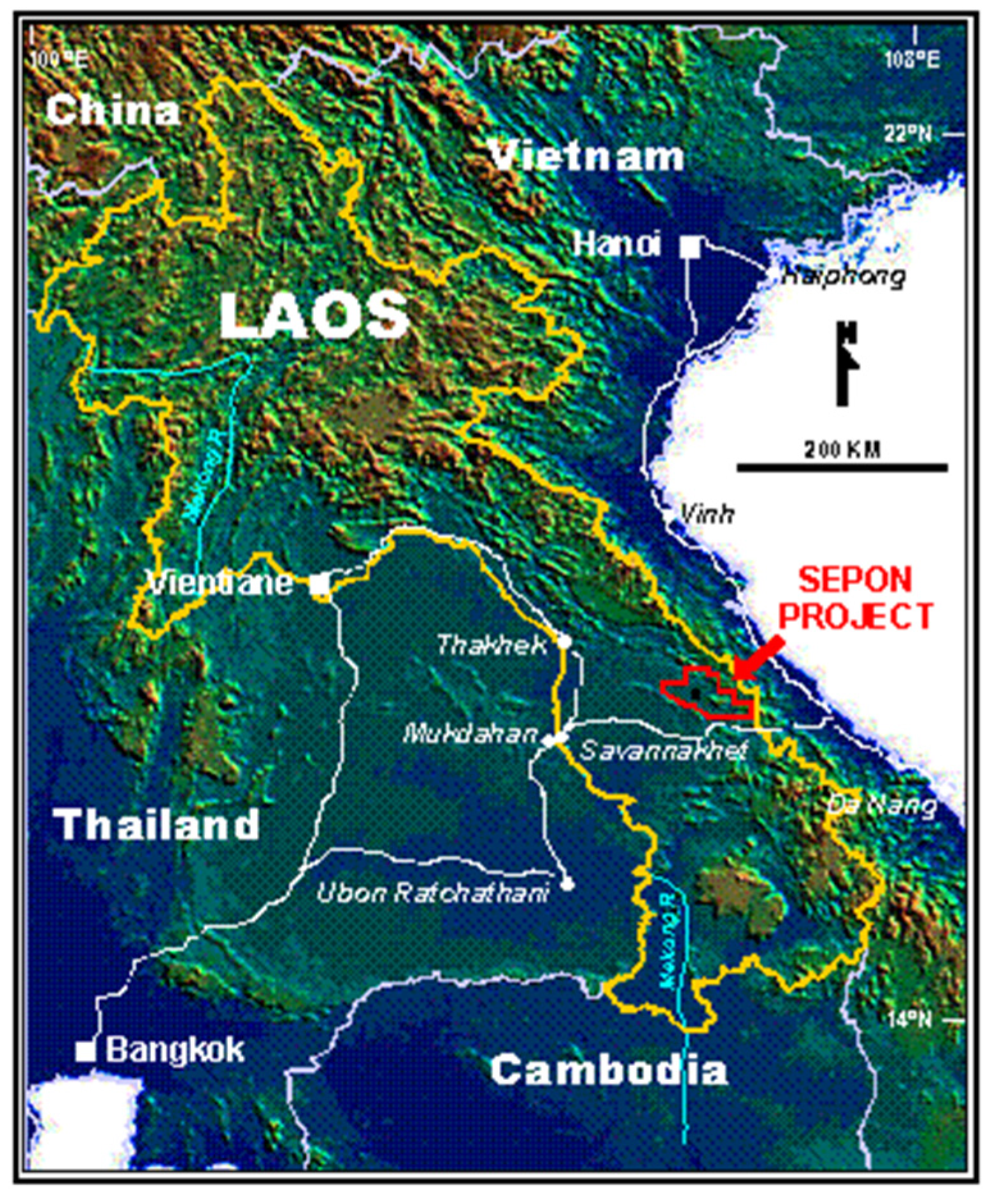
Figure 2. Schematic model of mineralisation styles in the Sepon Mineral District (after Sillitoe 1990).

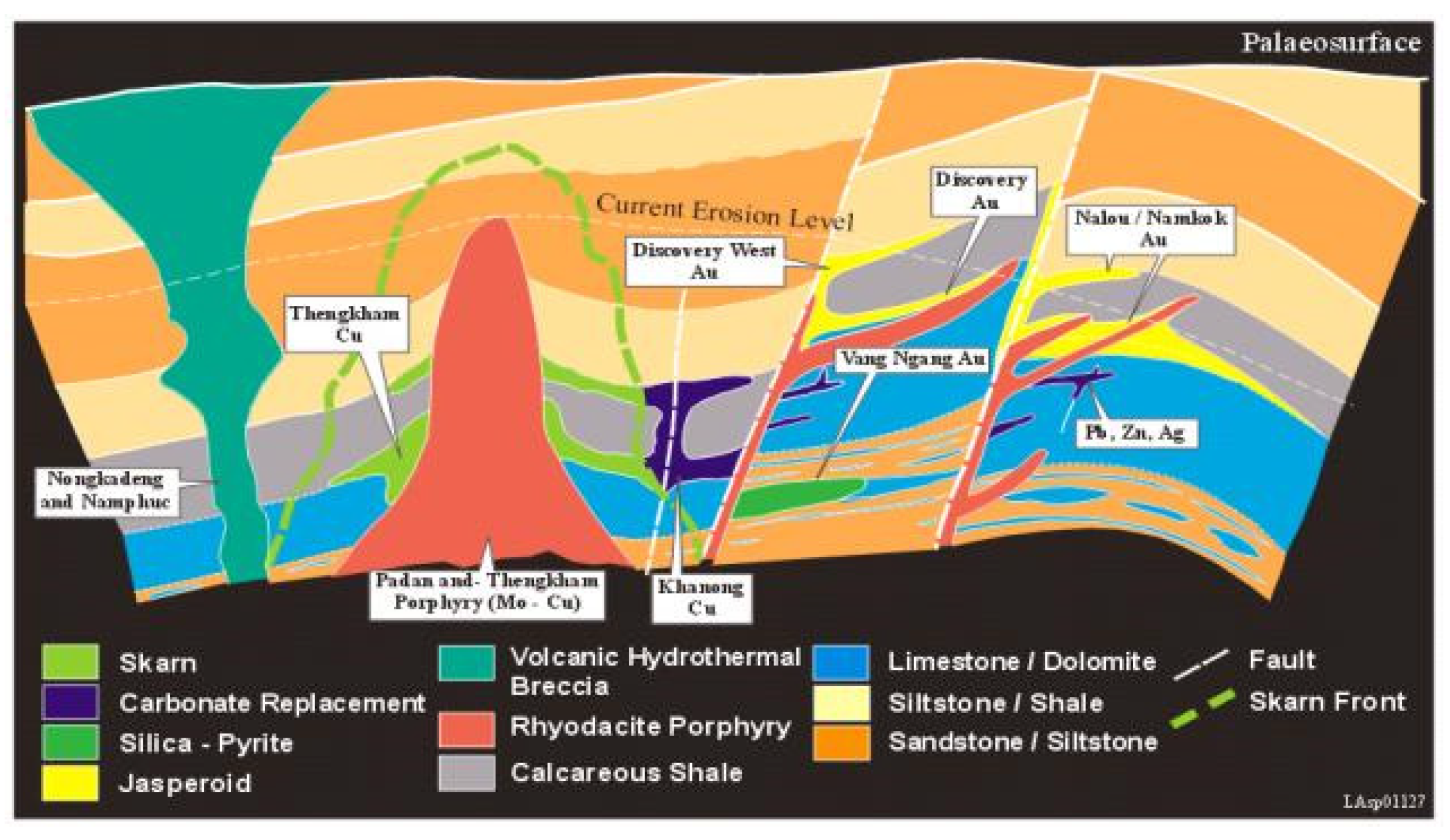
Figure 3. Evaluation of the geotechnical characteristics of the rock mass in Sepon Mine.

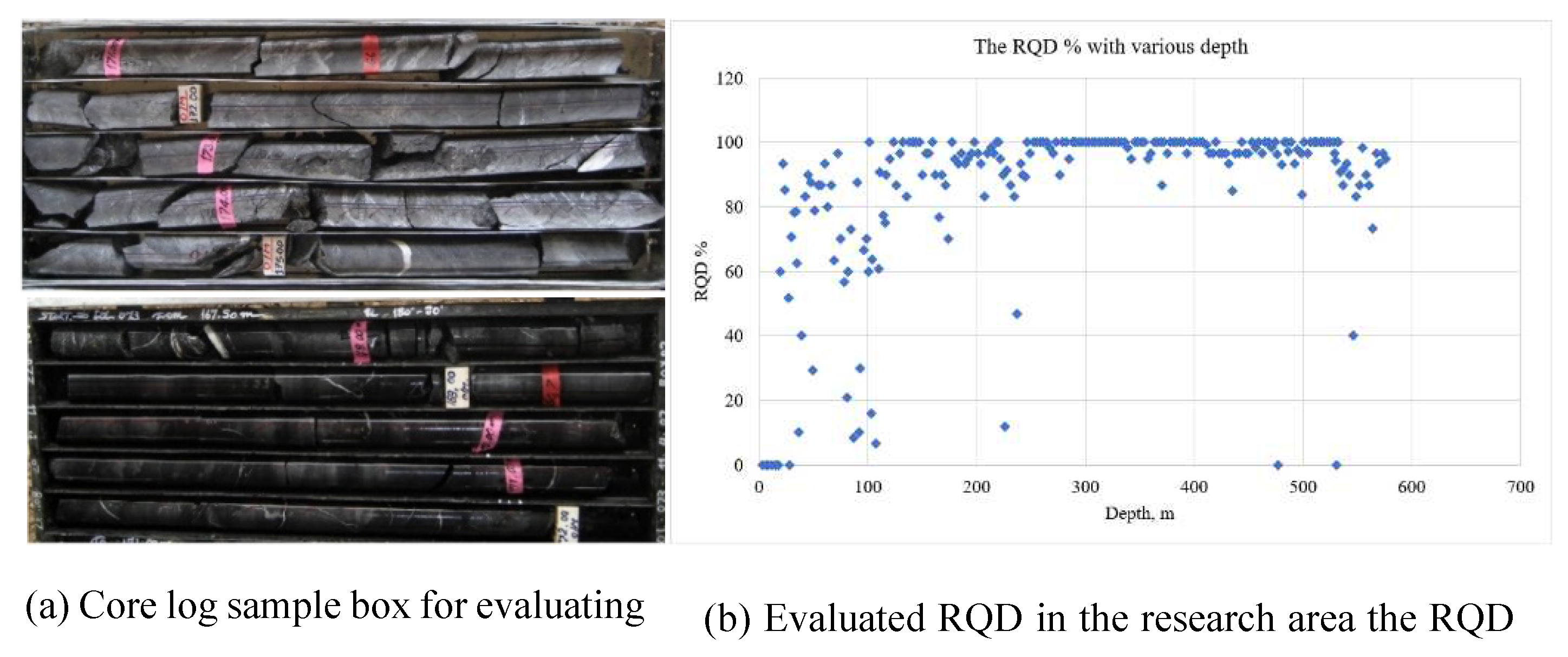
Figure 4. The pre-test and post-test by using triaxial compressive strength test; (a) Nodular shale, (b) Ore, (c) RDP.

Figure 5. The result of the lab test for triaxial compressive strength; (a) Nodular shale, (b) Ore, (c) RDP.

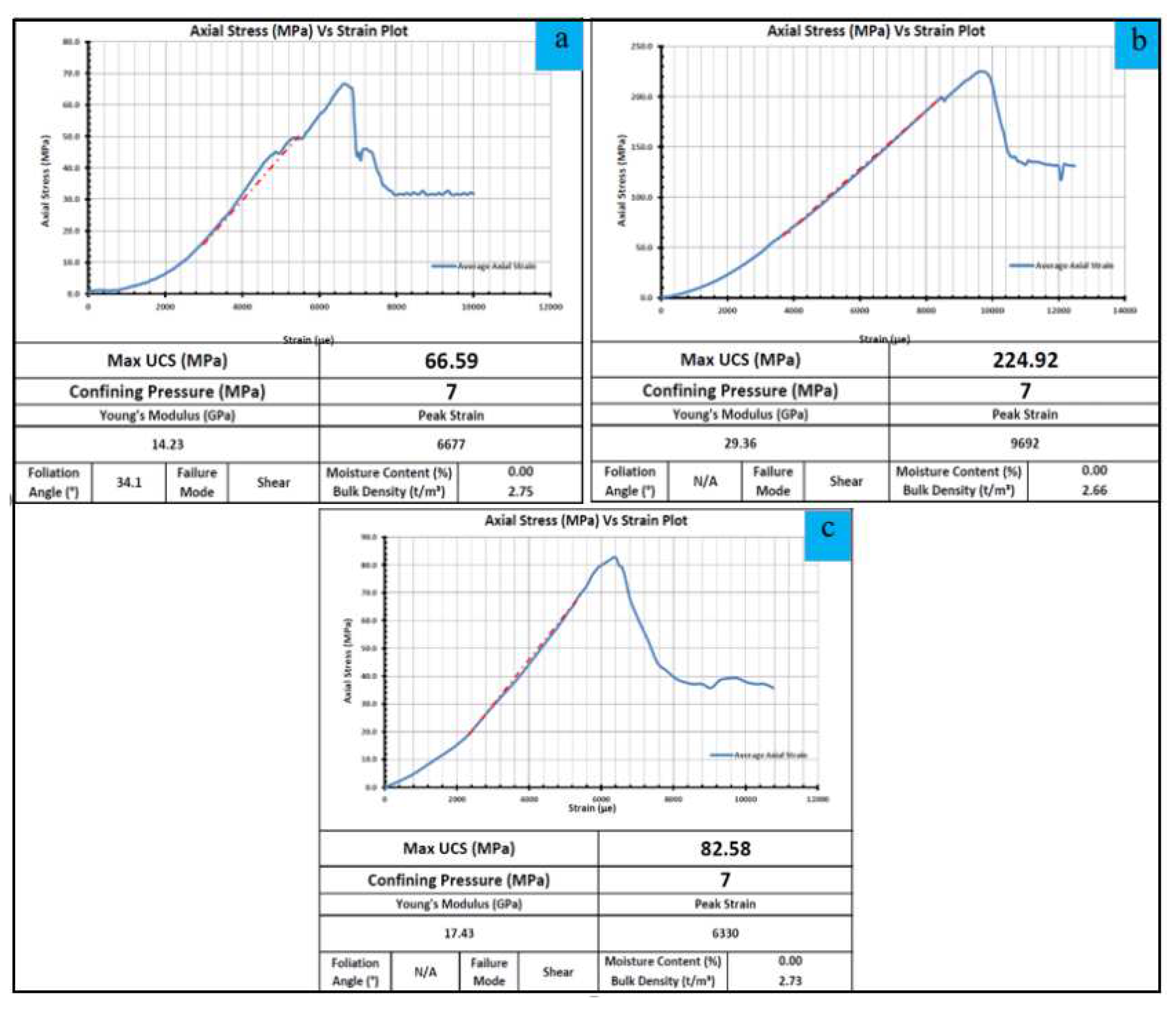
Figure 6. Simplified model set up showing dimensions.

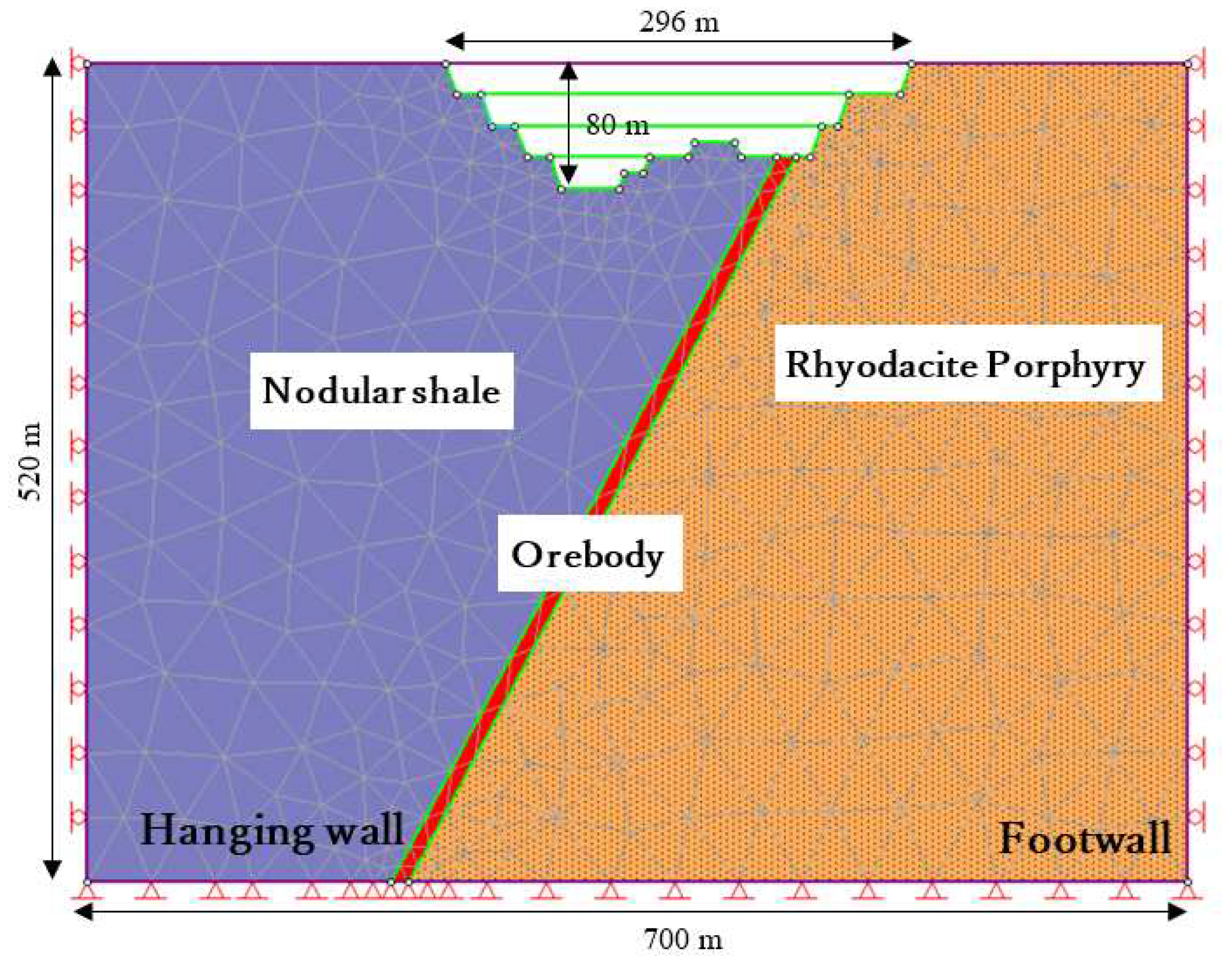
Figure 7. The mining consequence.

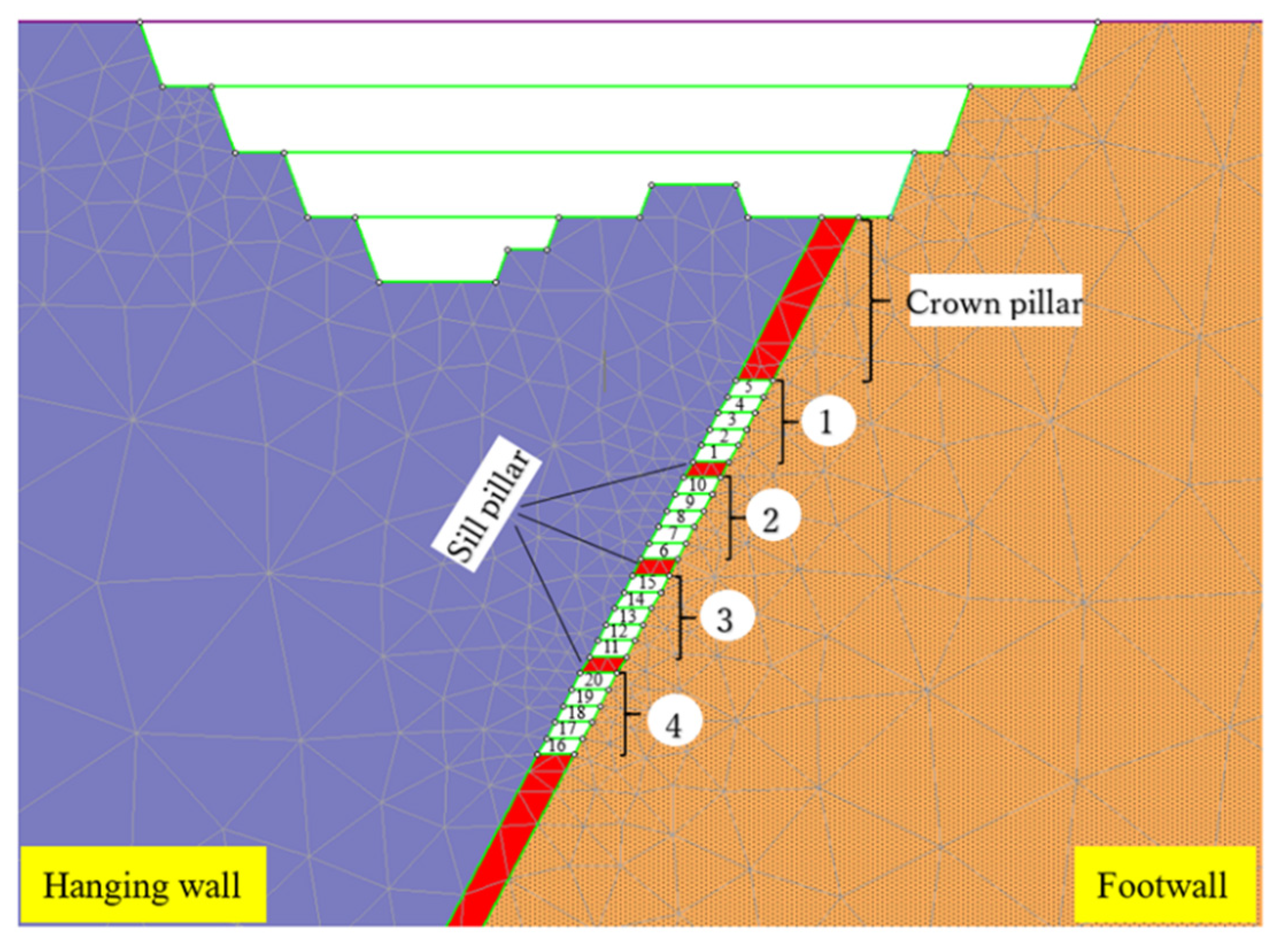
Figure 8. Slope stability before beginning an underground mining operation.

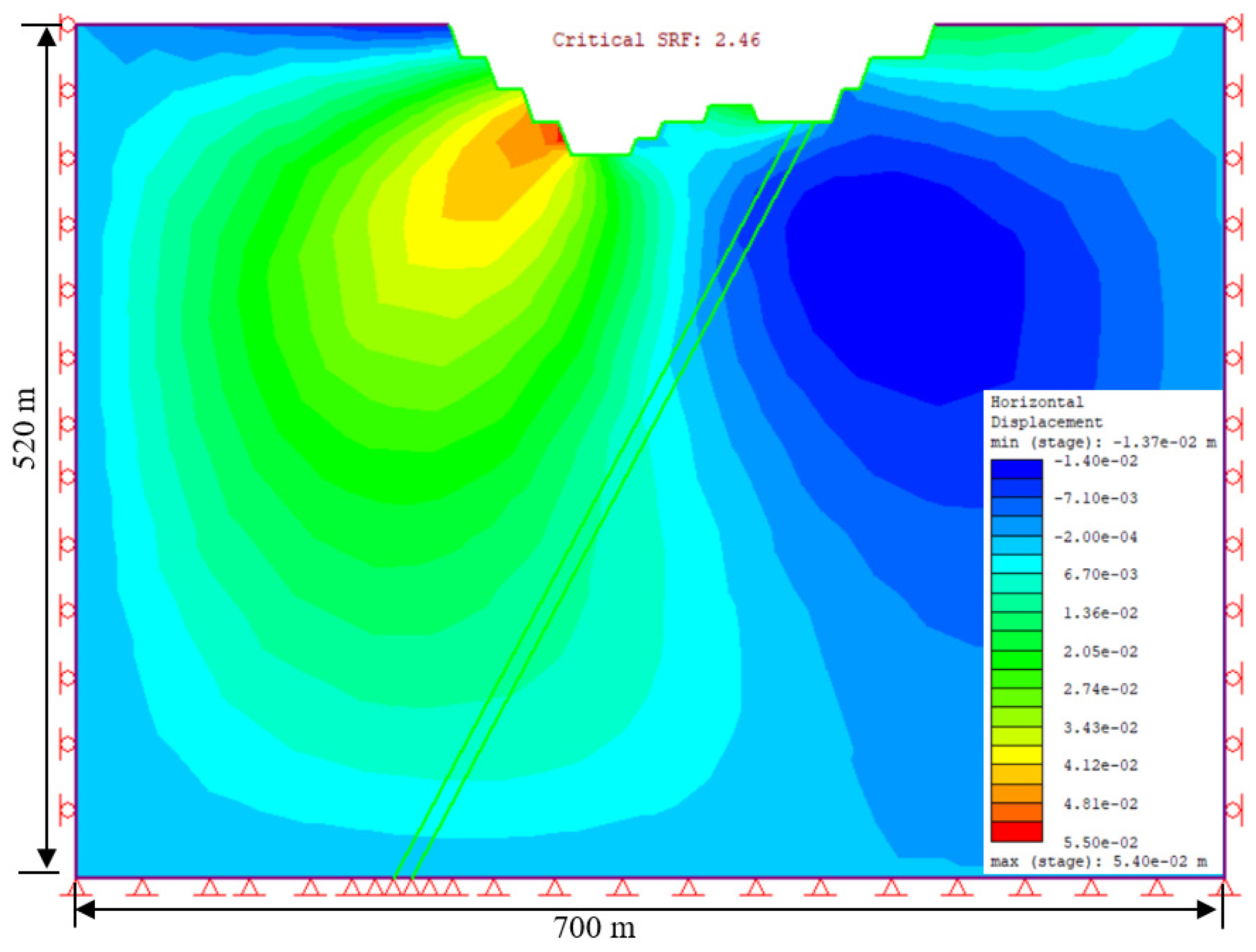
Figure 9. The monitoring point along the surface displaying displacement.

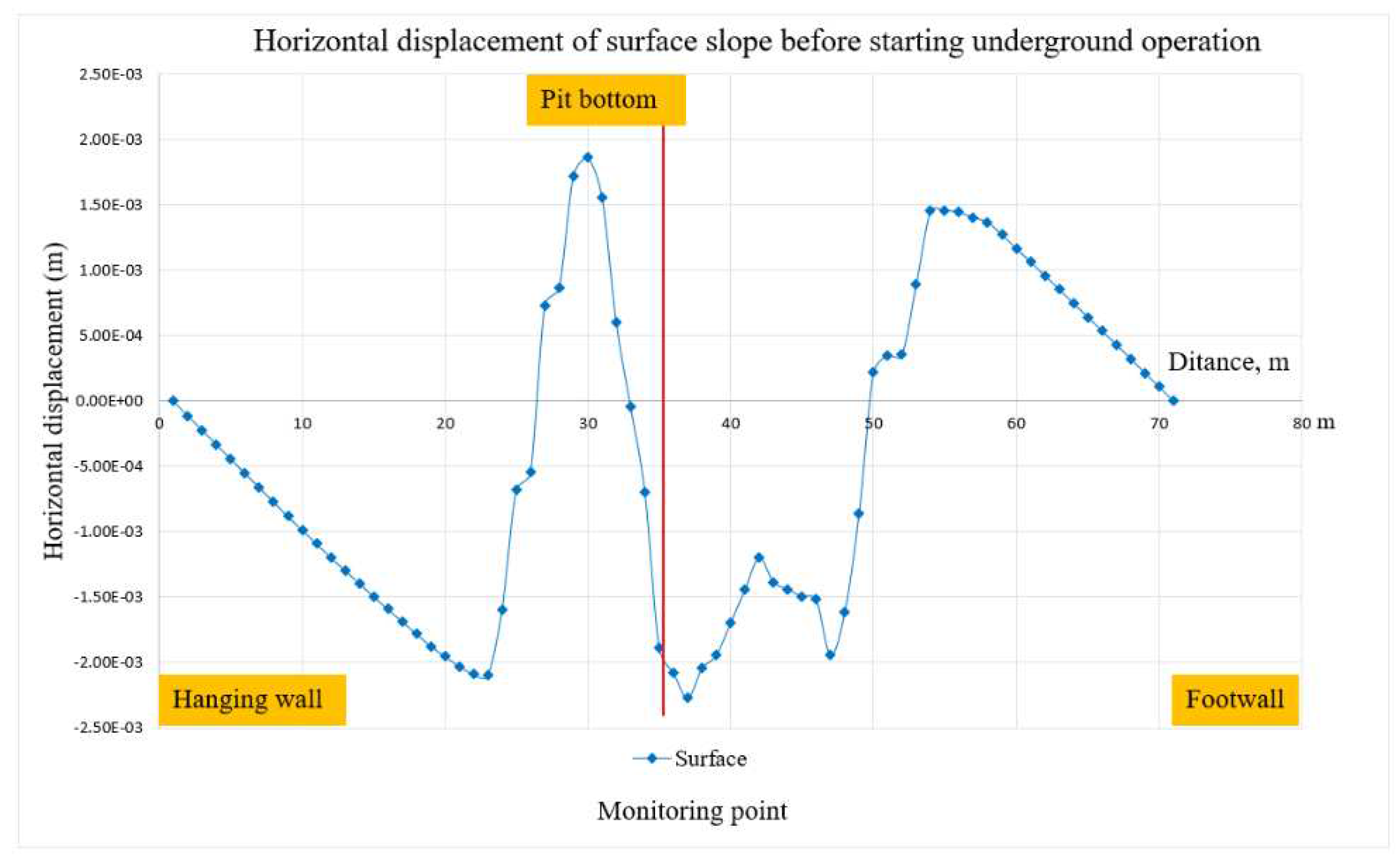
Figure 10. Various design of open stop dimension.

Figure 11. Comparison of the displacement of six different stope size.

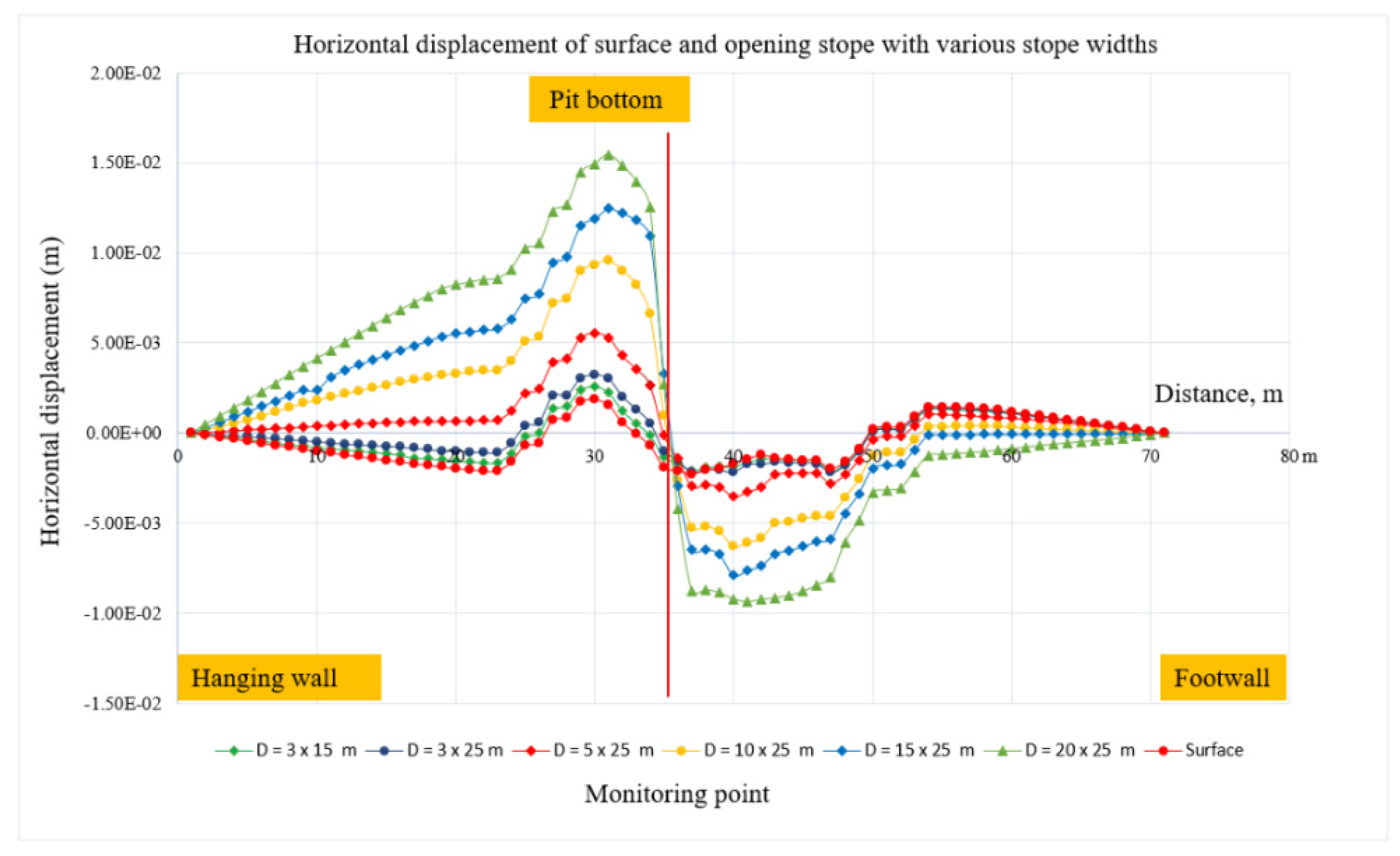
Figure 12. The displaying displacement in open stope.

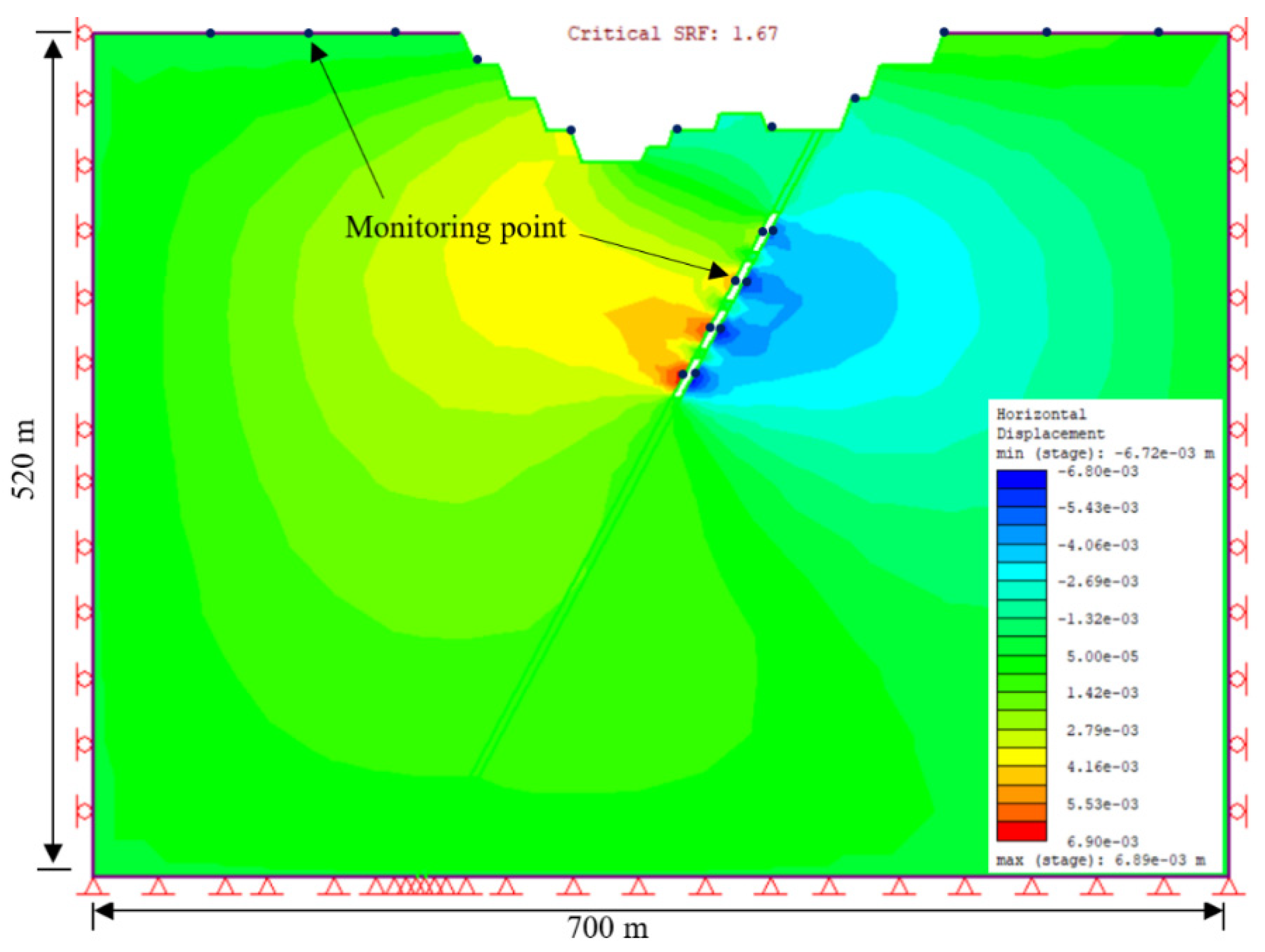
Figure 13. Horizontal displacement of surface and various excavation level.

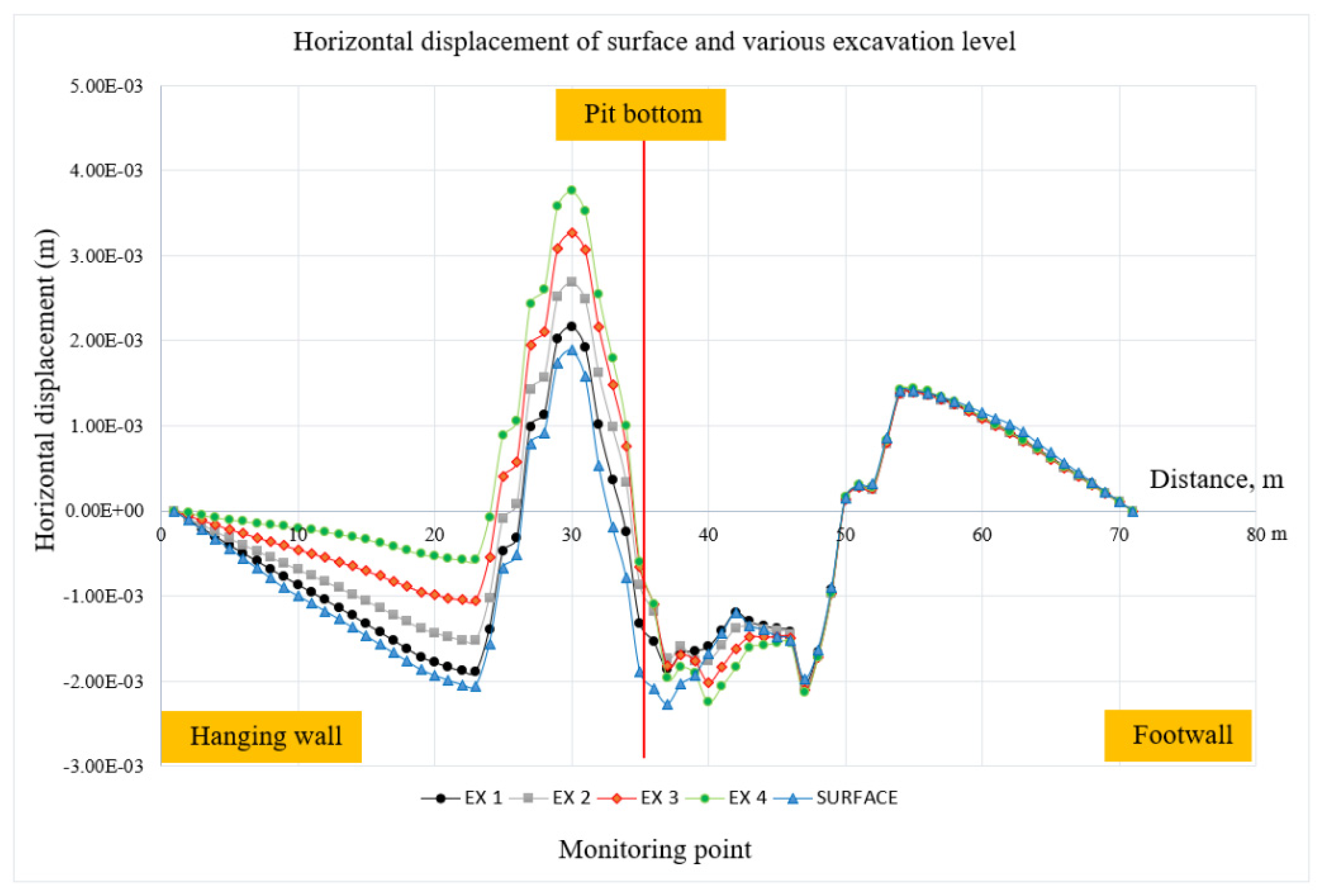
Figure 14. The horizontal displacement in each stope excavation.

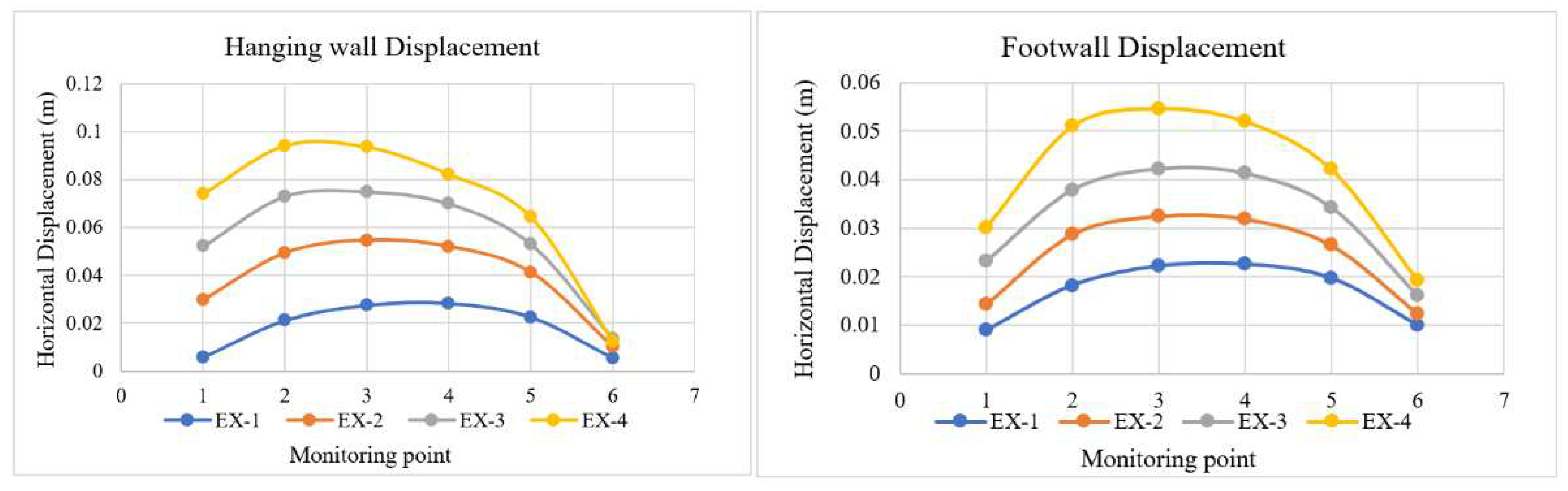
Figure 15. Depict the result of study area under different stress ratio under yielded element.

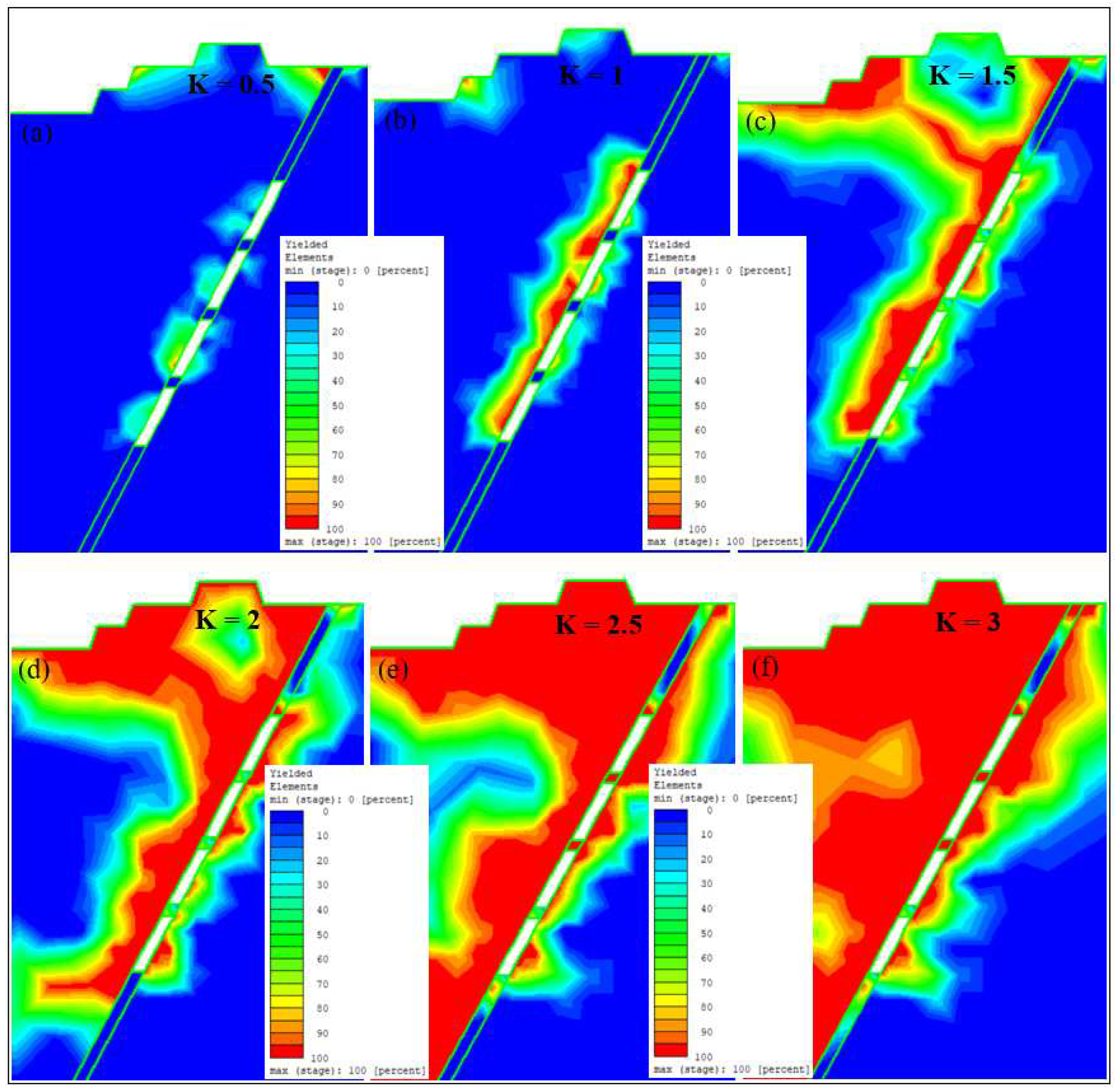
Figure 16. The horizontal displacement with various stress ratio.

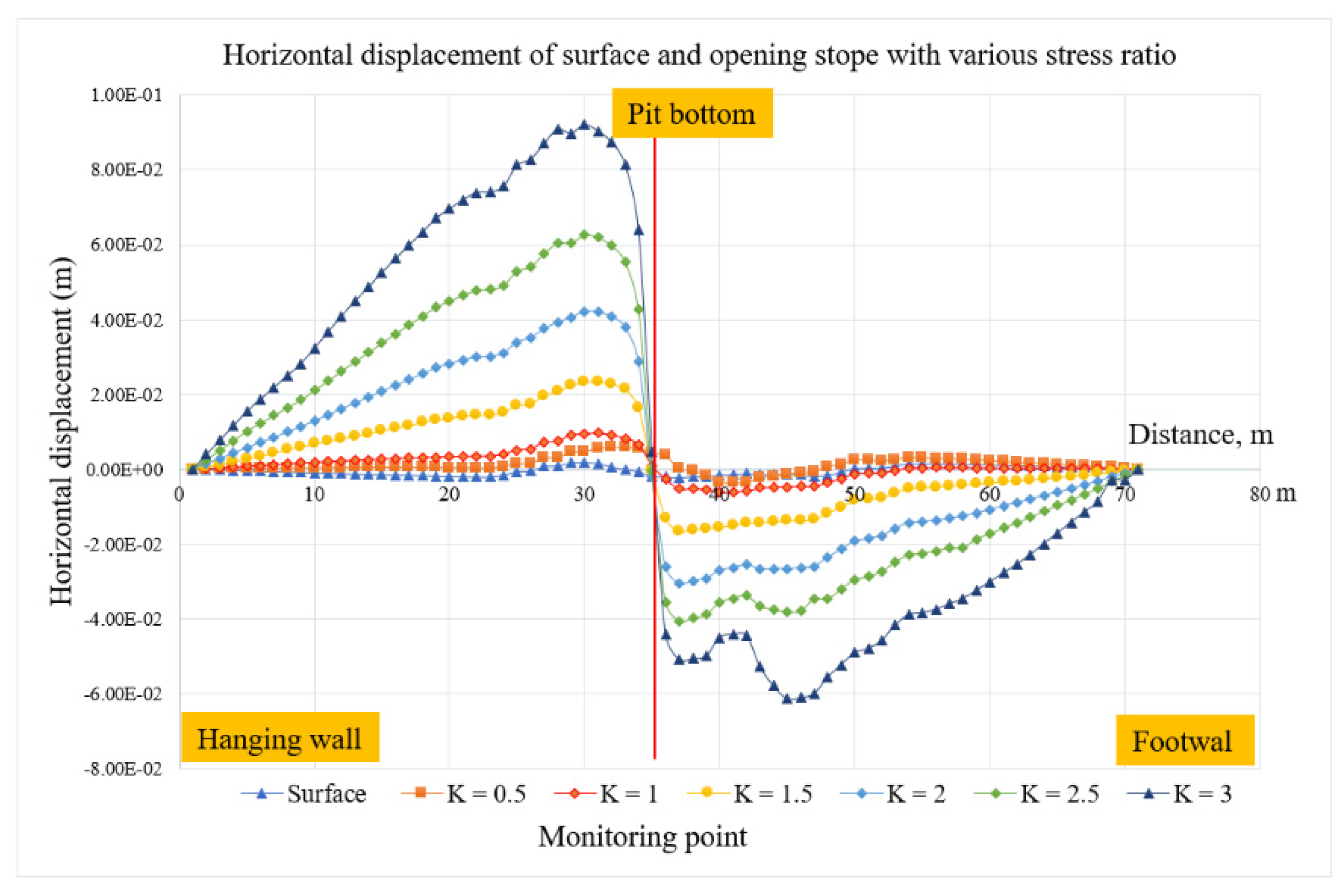
Figure 17. Strength reduction factor with various GSI value.

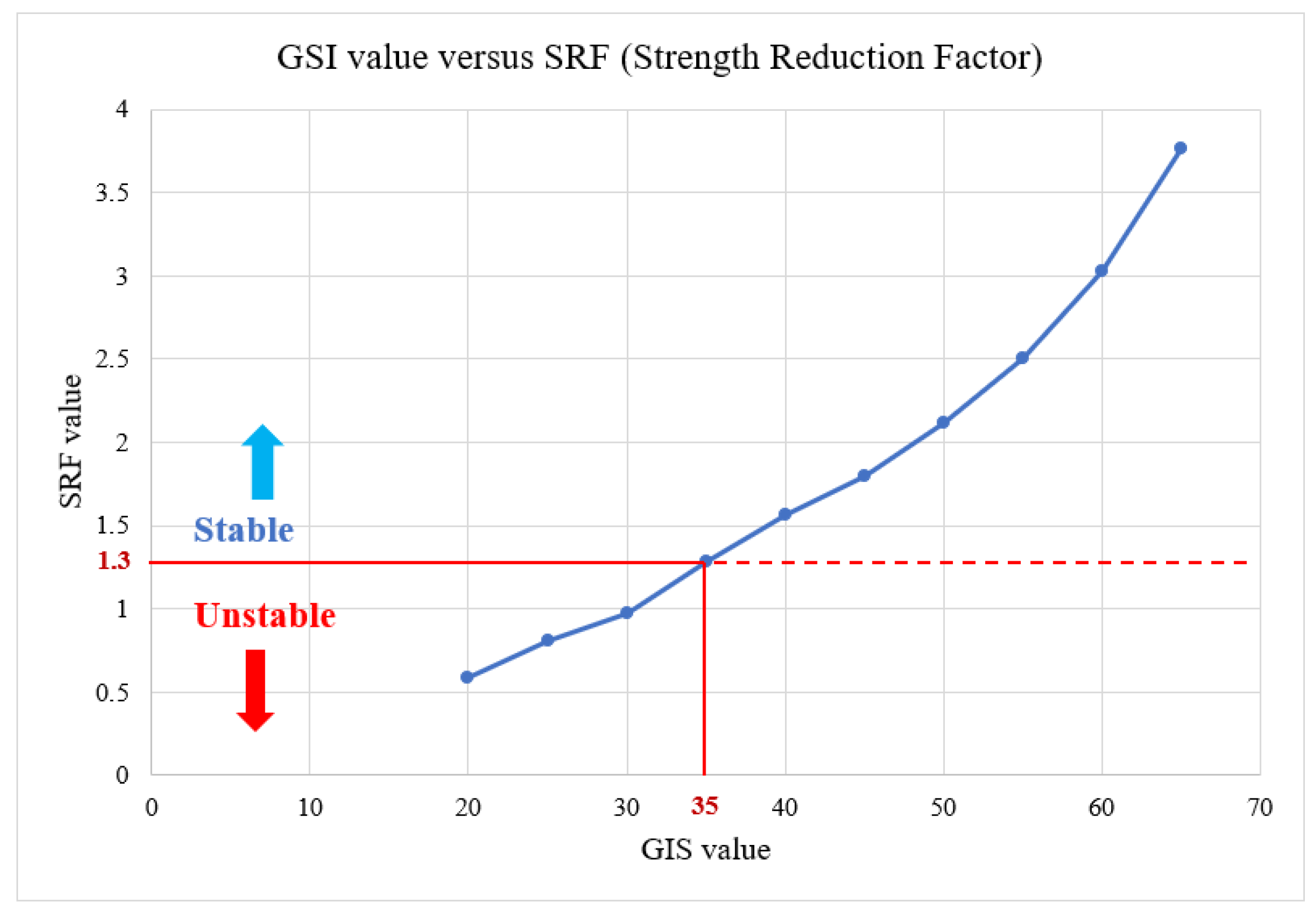
Figure 18. Horizontal displacement with various GSI value.

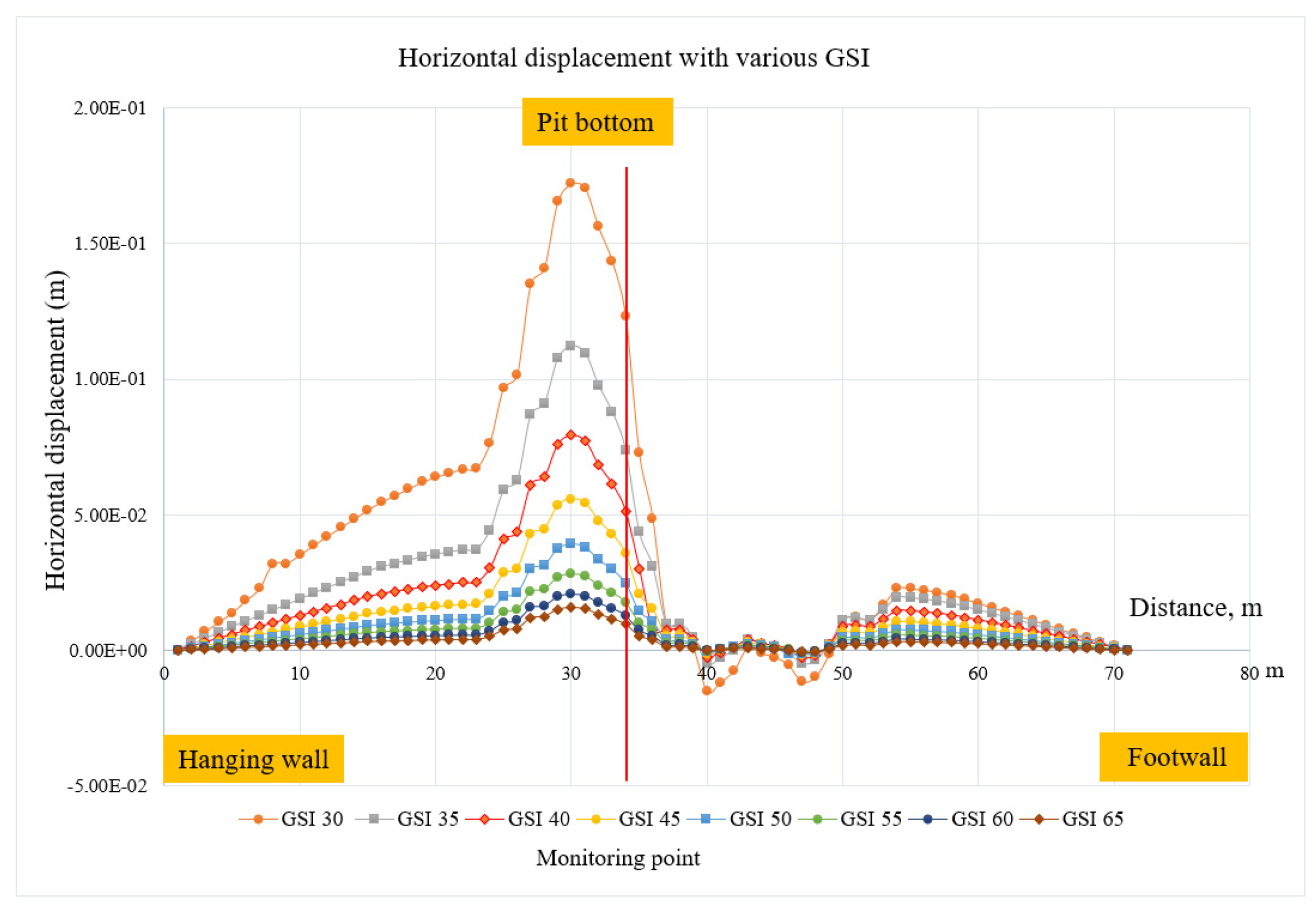
Figure 19. The effect of various GSI value to open stope.

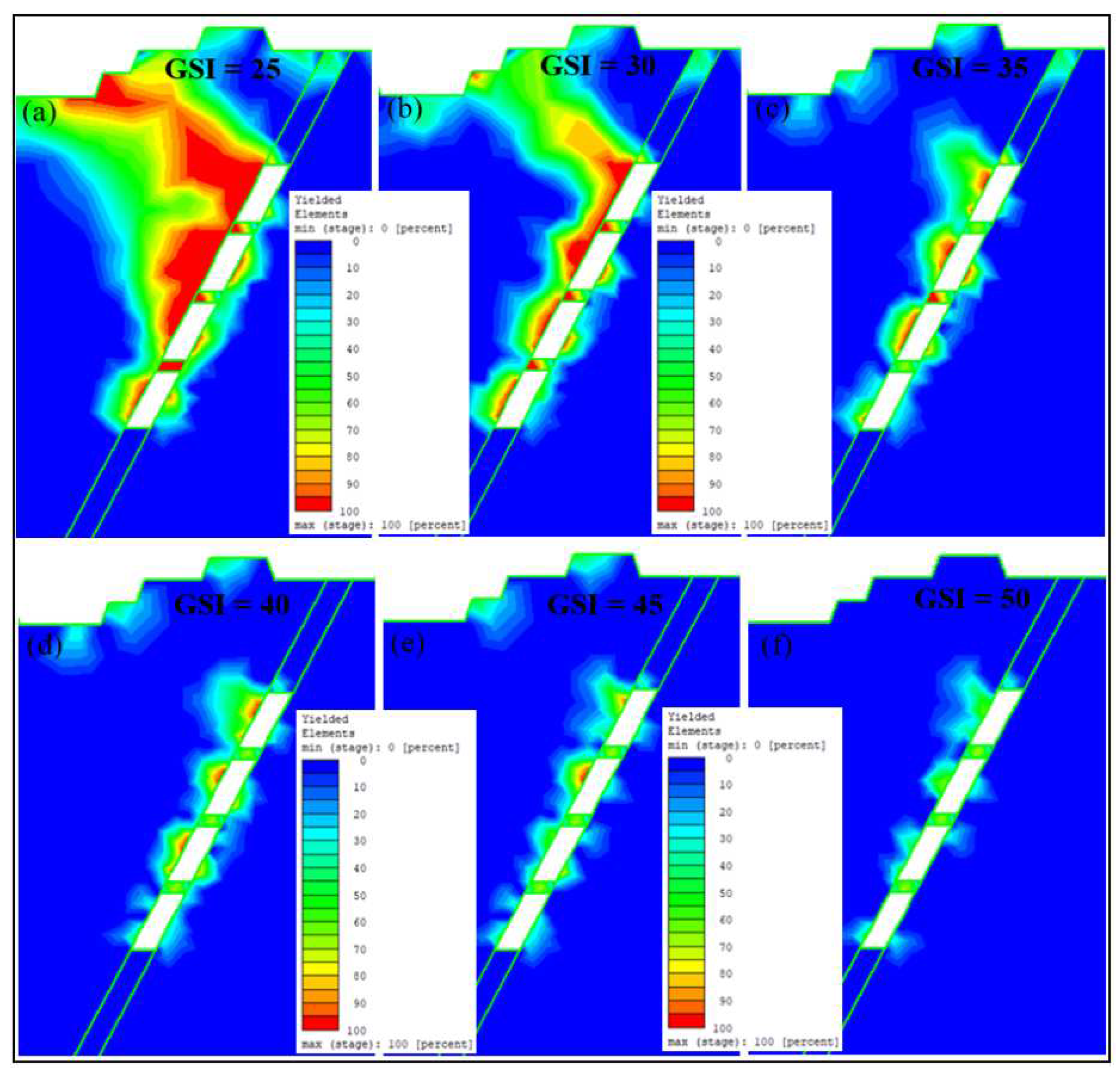
Table 1. The geotechnical properties of rock at Sepon gold mine deposit.

Geological Strength Index (GSI)	Zone/Rock type	Unit Weight (MN/m³)	σ_ci (MPa)	Tensile strength (MPa)	E_rm (GPa)	v (-)	Hoek Brown Parameter
Geological Strength Index (GSI)	Zone/Rock type	Unit Weight (MN/m³)	σ_ci (MPa)	Tensile strength (MPa)	E_rm (GPa)	v (-)	m_b	s	a
72	Footwall RDP	0.0275	82.58	15.59	17.43	0.3	6.167	0.0315	0.501
62	Ore body	0.0266	224.92	13.81	29.36	0.3	2.656	0.010	0.502
51	Hanging wall Nodular shale	0.0279	66.59	11.66	14.23	0.35	0.898	0.0019	0.505

Notes: σ_ci = uniaxial compressive strength of intact rock material; m_b, s, a = material constant for Hoek-Brown Failure criterion; E_rm = Young’s modulus of rock mass; and v = Poisson’s ratio.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer