Prerpints.org logo
Preprint
Article

High Efficient Anchor-Free Oriented Small Objects Detection for Remote Sensing Images via Periodic Pseudo-Domain

Altmetrics

Downloads

86

Views

15

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 July 2023

Posted:

05 July 2023

You are already at the latest version

Alerts
Abstract
With the continuous progress of remote sensing image object detection tasks in recent years, researchers in this field have gradually shifted the focus of their research from horizontal object detection to the study of object detection in arbitrary directions. It is worth noting that some properties are different from the horizontal object detection during oriented object detection that researchers have yet to notice much. This article presents the design of a straightforward and efficient arbitrary-oriented detection system, leveraging the inherent properties of the orientation task, including the rotation angle and box aspect ratio. In the detection of low aspect ratio objects, the angle is of little importance to the orientation bounding box, and it is even difficult to define the angle information in extreme categories. Conversely, in the detection of objects with high aspect ratios, the angle information plays a crucial role and can have a decisive impact on the quality of the detection results. By exploiting the aspect ratio of different targets, this letter proposes a ratio-balanced angle loss that allows the model to make a better trade-off between low-aspect ratio objects and high-aspect ratio objects. The rotation angle of each oriented object, which we naturally embed into a two-dimensional Euclidean space for regression, thus avoiding an overly redundant design and preserving the topological properties of the circular space. The performance of the UCAS-AOD, HRSC2016, and DLR-3K datasets show that the proposed model in this paper achieves a leading level in terms of both accuracy and speed. The code is released at https://github.com/minghuicode/Periodic-Pseudo-Domain.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

LLMs(Large Language Models) such as ChatGPT and IndustrialGPT [1] exhibit notable performance in both language and vision tasks, however, their extensive memory consumption and computational burden impede their applicability in various tasks under limited computational resources. As a fundamental task in computer vision and remote sensing, object detection has achieved continuous progress. In recent years, researchers in this field have paid more attention from horizontal object detection to arbitrary object attention [2,3,4]. For some densely arranged rectangular objects, arbitrary orient object detection method can match boundary better and distinguish those objects from each other.
To describe a rotated box, it is common practice to add the rotation angle parameter to the horizontal box [3] or to describe the coordinates of all 4 points [4]. Diverging from traditional bounding boxes, the description of arbitrarily oriented bounding boxes, commonly referred to as OBBs (oriented bounding boxes), poses significant challenges in the form of PoA (Periodicity of Angular) and EoE (Exchangeability of edges) problems. Furthermore, the existence of square or circular targets poses an additional challenge in that they frequently do not necessitate, and in some instances, cannot identify their orientation angle.
To address the aforementioned problems related to predicting oriented bounding boxes, various methods have been proposed. For instance, R2CNN [5] and oriented RCNN [6] employs redundant anchors alongside regression of orient box offsets, while CSL [7] tackles the problem by converting it from regression into a classification question. Guo et al. [8] use a convex hell to represent the oriented boxes. PIoU [9] computes a novel pixel-iou loss for obb targets. R3Det [10] proposes a rotation detector using a coarse-to-fine approach. GWD [11] and KLD [12] convert oriented boxes into 2-d Gaussian Distribution and Kullback-Leibler Divergence, respectively. Moreover, CFC [13] directly computes the rotation angle loss utilizing the tan θ function.
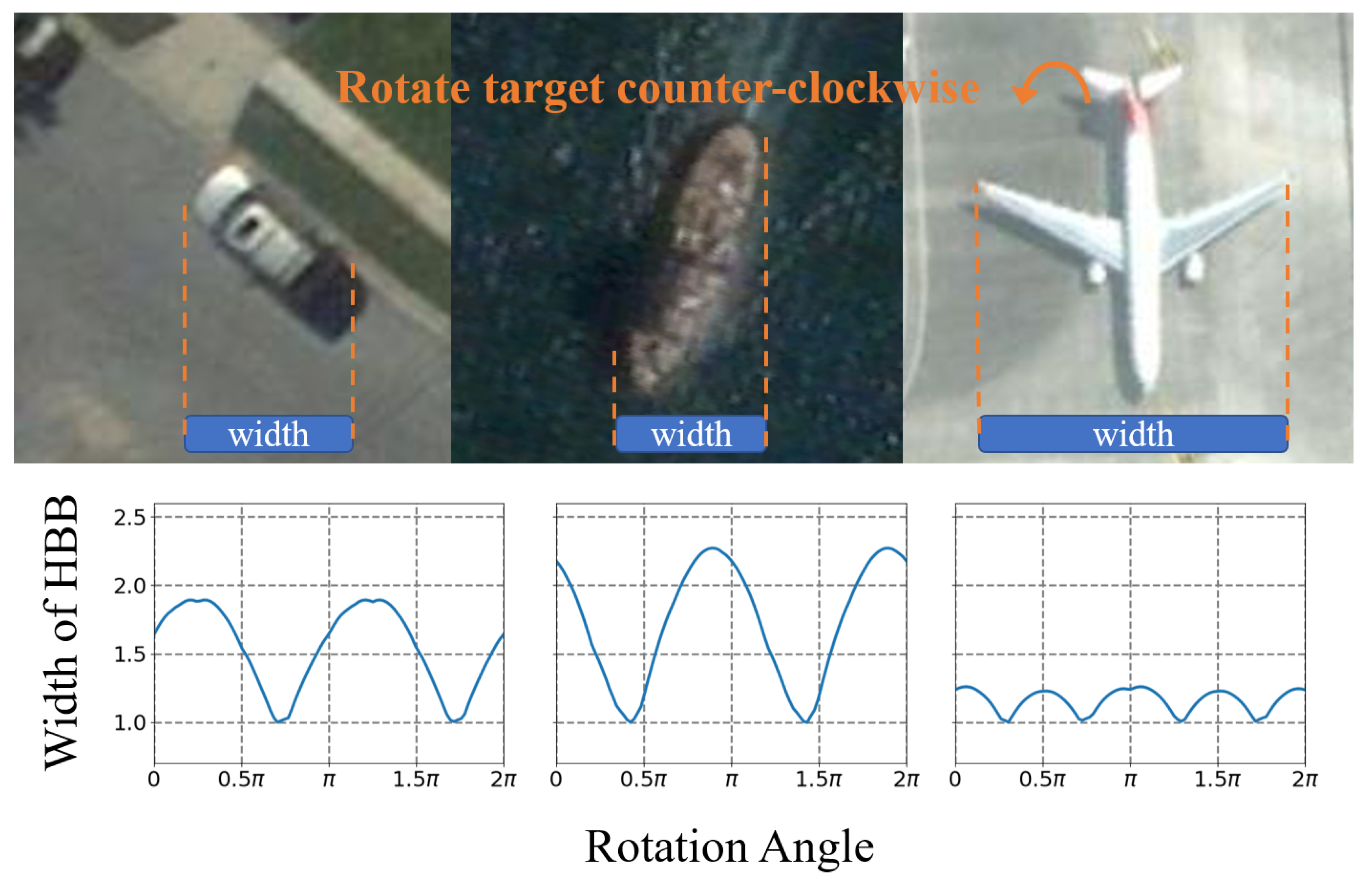
As shown in Figure 1, for targets with a high aspect ratio, the rotation angle is not only important but also accompanied by an evident visual feature. Nevertheless, two more points need to be made clear: first, the evident periodic is π but not 2 π ; Second, for targets with a low aspect ratio, the rotation angle is not only unimportant, but also, the visual features are relatively messy. Our work is motivated by these two points.
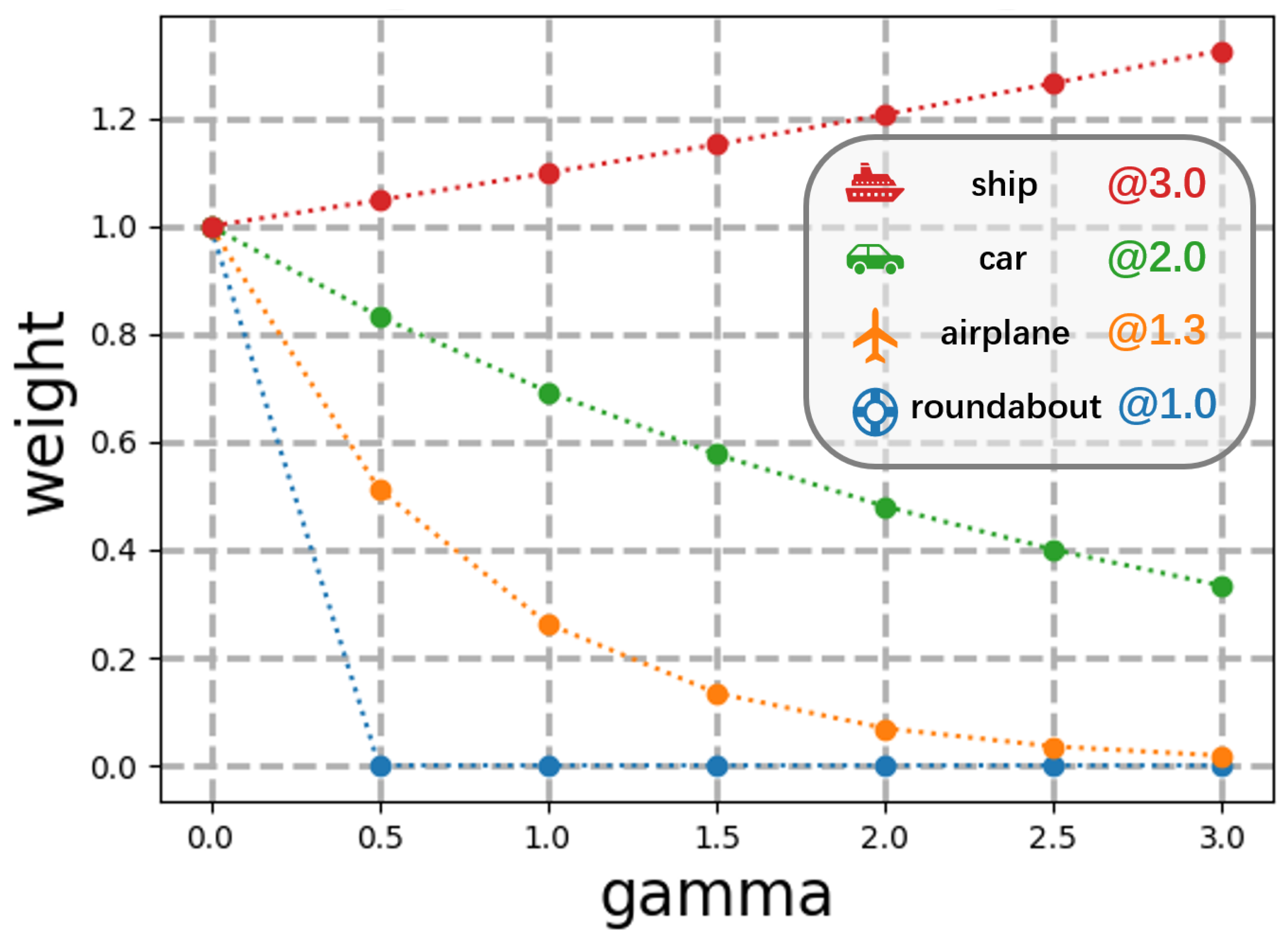
This paper proposes a topology-based detection method that utilizes a periodic pseudo-domain. In topology, it is well-known that the genus of the real number axis is zero, whereas the genus of the circular space is one. Consequently, using a single real number to regress the angular value accurately is not feasible. Instead, we utilize the natural embedding of the circular space in a two-dimensional Euclidean space to precisely estimate the angles of the oriented boxes. The weight assigned to the angle is determined according to the ratio of the height and width of the targets, as demonstrated in Figure 4.
In the ensuing section, some work related to object detection and oriented object detection will be described. Later, a detailed explanation of the regressor’s definition and loss function can be found. In Section 4, our method’s performance and speed are evaluated through experiments on UCAS-AOD [14], HRSC2016 [15], and DLR 3K [16]. Section 5 provides a discussion of the benefits and drawbacks of the approach.

2. Related Work

As a fundamental task in computer vision, object detection has a wealth of research papers. In the following, we will describe the representative research work on object detection and then some recent work on oriented object detection.

2.1. Object Detection Method

The goal of object detection is to find the location of the interested target in the image and use a bounding box to describe the pixel dimensions and coordinates of the target. In general, two pairs of line segments parallel to the horizontal and vertical axes of the image are used to form the minimum bounding boxes of the target. The most mainstream methods of current object detection are the two-stage and one-stage methods. We will describe the advantages and disadvantages of these methods and their representative work, respectively.
The two-stage work uses a convolutional network named RPN(Region Proposal Network) to propose candidate regions in the first stage, after which each proposal is evaluated and refined in the second stage to obtain the final detection results. The most well-known two-stage models include R-CNN [17], fast-RCNN [18], faster-RCNN [19] and R-FCN [20]. Faster RCNN achieved state-of-the-art results on the PASCAL VOC dataset [21] during that period and became a standard for two-stage models. Thousands of proposals need to be extracted in the first stage, thus ensuring accuracy while making the two-stage methods more time-consuming.
The most famous one-stage methods are YOLO [22], YOLO9000 [23], YOLOv3 [24], SSD [25] and RetinaNet [26]. The one-stage methods are more straightforward: they divide the image into grids and predict the target’s confidence, center offset, width, and height within each grid. The one-stage methods infer much faster than the two-stage methods but also has a relatively lower accuracy than the two-stage methods for targets with significant intra-class variations.
In addition to the proposal-based two-stage methods and the grid-based one-stage methods, researchers have proposed many other approaches. For instance, CornerNet [27] estimates the bounding box of an object by predicting a pair of points in the upper left and lower right corners of the target. And CenterNet [28] uses a triplet of object centroid and a pair of corner points to predict the bounding box of an object. ExtremeNet [29] uses five key points to estimate the bounding box.

2.2. Oriented Object Detection

The purpose of oriented object detection is also to find the location of the interested target and label it. But the difference is that the two pairs of line segments are no longer parallel to the horizontal and vertical axes of the image. As shown in Figure 9, oriented bounding boxes may fit objects closer. Even in dense scenes, oriented bounding boxes rarely overlap with those of surrounding targets. Oriented object detection is generally most used in scene text [2,5,30], and aerial image [3,4,13].
Influenced by faster-RCNN [19], oriented object detection has many two-stage methods. For example, oriented R-CNN [6] is a typical one, which includes an oriented RPN(Region Proposal Network) in the first stage. Pan et.al. [31] develop a dynamic refine network for dense objects. The advantages and disadvantages of the two-stage method in oriented object detection are similar to the two-stage way in a horizontal one.
In addition to the oriented proposal, many point-based arbitrary orient detection approaches exist. Li et.al. [32] represents the original oriented bounding boxes by dynamically assigning multiple points to the boundaries. Zand et.al. [33] and APS-Net [34] utilize 5 and 9 points to represent an oriented bounding box separately. Guo et.al. [8] tried to find a convex hull representation for the oriented bounding boxes. [35,36] are also point-based work.
Another common idea is to develop the loss function for arbitrary-oriented object detection. For example, [37] use smooth L1 loss; PIoU [9] use Pixels-IoU loss; RAIH-Det [38] use cyclical focal loss; [39,40] use GIoU loss.
There are also a lot of Gaussian-like methods. Such as [11,41,42,43] use Gaussian Heatmap for the arbitrary-oriented object detection task. KLD [12] represent oriented boxes as Kullback-Leibler Divergence.
One interesting thing about obb is that Cheng et.al. [44] found that obb(oriented bounding boxes) only appears diagonally from the hbb(horizontal bounding boxes) if these two do not coincide. Awareness of this fact can help one to propose proposals more efficiently. Nie et.al. [45] use two hbbs to represent an obb.

3. Materials and Methods

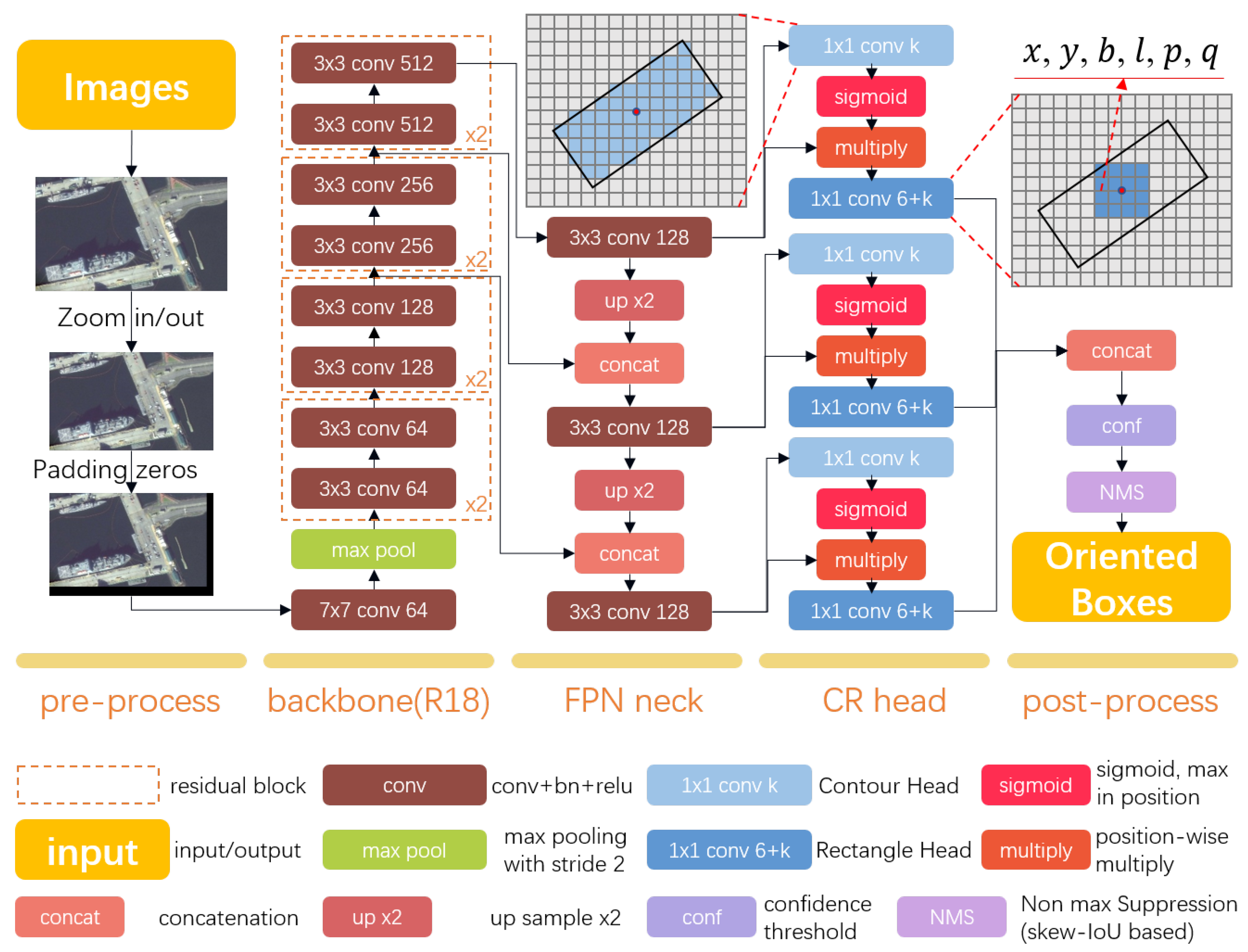
Our proposed approach for oriented object detection in aerial imagery applies an anchor-free trainable network. As shown in Figure 3, we introduce the end-to-end method framework in Section 3.1. The details in our detection head and loss functions are explained in Section 3.2 and Section 3.3, separately.

3.1. Framework

The main process of our method is shown in Figure 3. There are a total of 5 steps between input images and output-oriented boxes which were displayed column by column. In pre-process and post-process steps, there have no trainable parameters. All deep neural network computations are calculated during the second step and fourth steps.
In the pre-processing step, we process the image to make sure it can be fed into GPU correctly. First, if the image size is larger than the setting value, we resize the image and keep the aspect ratio. Then we padded zeros at the right and bottom edge of the scaled image to make sure both image height and width can be divided by 32.
Our method use a pre-trained deep neural network as backbone, which may include but is not limited to resnet18, reset50, resnet101, and darknet53 [24,46]. The backbone may largely determine the model speed, performance, convergence time, and others.
We pass the visual feature at 1/8, 1/16, and 1/32 resolutions from backbone to FPN (feature pyramid network) neck [47]. Feature vector at each position of those resolutions represents a grid that has 8x8, 16x16, and 32x32 pixels, separately. We unify the dimension of the above feature and concatenate different level features before feeding them into heads.
In CR head step,, we use both contour and rectangle heads at each FPN level. We classify the foreground and background for each category at the contour head, and regress the center offset, breadth, length and rotate angle of the rectangle at the other head. The proposed CR head will be introduce in detail in the next section.
Preprints 78499 g004
Figure 4. The penalty loss to the pseudo-domain is to apply a smaller weight for targets with low aspect ratios, like roundabouts and airplanes, and a larger weight for targets with high aspect ratios, such as cars and ships.
Figure 4. The penalty loss to the pseudo-domain is to apply a smaller weight for targets with low aspect ratios, like roundabouts and airplanes, and a larger weight for targets with high aspect ratios, such as cars and ships.
Preprints 78499 g004
After model infer, we concat all predict rectangle together. Then we use confidence threshold and skew-IoU [2] based non-max-suprresion to the predict boxes. It’s worth mentioning that calculating for skew-IoU is much more time-consuming than horizontal IoU, such that we also calculate it on GPU.

3.2. CR Head and Pseudo-Domain

Two issues need to be addressed to design an arbitrary direction object detector, i.e. periodicity and degeneration.
The first issue is how to express and predict the angle. As we all know, the degree of the angle has its periodic, but the real number axis has an ordered structure. That means the ring space and 1-dim linear space are topologically different. So the angle of the oriented object bounding box cannot be determined by predicting a single real number. To address this issue, we use the natural embedding of the circular space in a two-dimensional Euclidean space to regress the degree of the angle. It is noteworthy that the periodic in rotate rectangle is π instead of 2 π . More specifically, for a given angle θ , we predict cos 2 θ and sin 2 θ in a pseudo-domain.
And the other issue is that different kinds of remote-sensing object have different aspect ratios. For example, the aspect ratio of objects such as cars and ships may reach 2:1, 3:1, or even higher, while the aspect ratio of objects such as airplanes, storage tanks, roundabout may be very close to 1:1, and sometimes the the angle of the target may not even be defined. In the former, the angle of the oriented bounding box is essential and distinctive, while in the latter, the angle of the bounding box is irrelevant and weakly distinctive. In the next subsection, we will propose an angle loss to address the degeneration issue and make a trade-off between those two kinds of objects.
To better encode the rotate rectangle information, we use both the contour head as well as rectangle head. For k given category, we predict k float numbers in each grid at contour head and k + 6 float numbers in each grid at rectangle head.
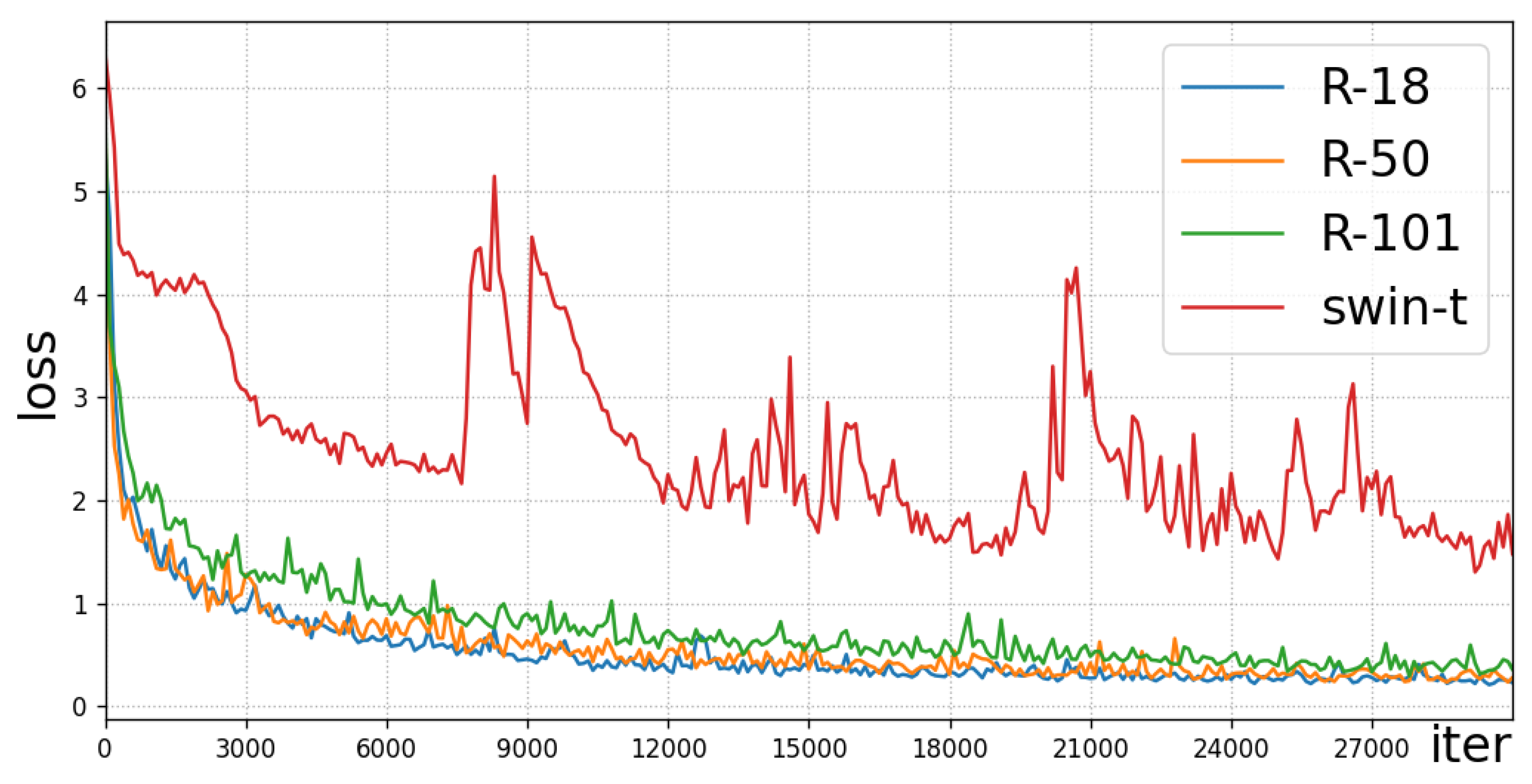
Preprints 78499 g005
Figure 5. Training loss with different backbone. The shown loss was averaged for every 100 iters.
Figure 5. Training loss with different backbone. The shown loss was averaged for every 100 iters.
Preprints 78499 g005
The contour head is a binary classification approach, each category has its own heatmap. The target is set to be 1 if the grid center locates in a rectangle, otherwise 0.
The rectangle head predicts k + 6 float number in each grid, where the first k float numbers denote the confidence of the rectangle for each category, separately. The 6 extra float number ( x , y , b , l , cos 2 θ , sin 2 θ ) in this head represents the rectangle shape, where x, y predict offset at x and y axis for rectangle center, b, l predict the breadth and length of the rectangle, and the last two float numbers represent the rotation angle of the rectangle.

3.3. Loss Function

Our arbitrary-oriented method has 3 contour heads and 3 rectangle heads. We compute loss at each head and add them together to get the joint loss.
At both rectangle and contour heads, we use the cross-entropy loss for each category, separately. And also, this is the only loss computed by contour heads.
L c o n f = − ∑ k = 1 K ∑ i ∈ G k + log s k i | G k + | + λ ∑ i ∈ G k * log ( 1 − s k i ) | G k * |
where G k + is the set of all grids whose target is set to be 1 in category k, G k * is the set of all grids whose target is set to be 0 in category k, K is category numbers, s k i is the grid confidence for category k in grid i, and λ is a given constant.
At rectangle heads, we regress the angle in a pseudo-domain to address its periodicity and degeneration issues.
L a n g = 1 | G + | ∑ i ∈ G + log ( l i * b i * ) γ | p i − cos 2 θ i * | + | q i − sin 2 θ i * |
where p i , q i is the predict result, b i * , l i * denote the breadth and length of the rectangle, θ i represents the rotate angle between the long side and x axis, γ is a given constant.
As shown in Figure 4, the angle gets more loss when the aspect ratio is larger. In response to this, for circular and square objects, angle loss gets less weight. We use a penalty loss, as shown below, to constrain the parameters ( p , q ) within a periodic pseudo-domain rather than the entire 2-dimensional Euclidean space:
L p e n = 1 | G + | ∑ i ∈ G + log ( l i * b i * ) ( | p i 2 + q i 2 − 1 | )
The regression loss for offset parameters at each rectangle head is computed in each grid separately as below
L o f f = 1 | G + | ∑ i ∈ G + ∑ t ∈ { x i , y i } ( t − t * ) 2 + 1 | G + | ∑ i ∈ G + ∑ t ∈ { b i , l i } ( log t − log t * ) 2
where G + is the set of all grids whose target is set to be 1, x i * , y i * is the ground truth for rectangle center offset at x-axis and y-axis in grid i, b i * , l i * is the ground truth for breadth and length for rectangle in grid i, x i , y i , b i , l i is the corresponding predict result in grid i.
The final joint loss is computed as below:
L o s s = ∑ h ∈ C L c o n f h + ∑ h ∈ R L c o n f h + L a n g h + L p e n h + L o f f h
where C represents the set of contour heads and R represents the set of rectangle heads.
Figure 5 shows the training loss with different backbone.

4. Results

All experiment was implemented on a single Titan X with 12GB GPU memory, Intel(R) Core(TM) i5-7500 CPU @ 3.40GHz with 16GB CPU memory. We write the code under the software environment Python 3.9.0 and torch 2.0.0. All image scaling maintains the aspect ratio. We use graying, rotation, crop, and multiscale for data augmentation.

4.1. Dataset and Metrics

We evaluate our model performance on three public remote sensing datasets: UCAS-AOD, HRSC2016 and DLR3K. The object in the above datasets was labeled by oriented bounding boxes.
UCAS-AOD [14] dataset has 1000 plane images and 510 vehicle images. We randomly chose 755(50%) images for training, 302(20%) images for validation, and 453(30%) images for test.
HRSC2016 [15] dataset is a challenging ship detection dataset, which provides 436, 181, and 444 images for training, validation, and testing separately.
DLR3K dataset [16] is a set of UAV images captured by a 3K+ camera system that has 10 raw images of size 5616x3744 and labels. We adopt 5 images and the corresponding labels for training and the other 5 for the test.
We use the VOC 2012 mAP metrics to evaluate the model performance, and compute iou as same as SkewIou [2]. To evaluate the model inference speed, we use the key ms/Mpx to denote milliseconds per million pixels.

4.2. Ablation study

We tested different γ values for the pseudo adaptive on the UCAS-AOD dataset and trained all models using Adam for 300 epochs. The results, shown in Table 2, indicate that using the pseudo-domain method has the potential to help models balance both high and low aspect ratio targets. The performance of backbone swin-t [51] is weak, thus demonstrating swin transformer backbone does not work well in small datasets such as UCAS-AOD. It is interesting to note that through the ablation study, we have discovered that redundant network structures may negatively affect model performance when the dataset size is limited.
Preprints 78499 g006
Figure 6. Example of dataset images. Top 2 rows: UCAS-AOD dataset; Third row: HRSC2016 dataset; Last row: DLR-3K dataset. The images are cropped and zoomed.
Figure 6. Example of dataset images. Top 2 rows: UCAS-AOD dataset; Third row: HRSC2016 dataset; Last row: DLR-3K dataset. The images are cropped and zoomed.
Preprints 78499 g006
Preprints 78499 g007
Figure 7. Results on the UCAS-AOD dataset, speed test on a single Titan X.
Figure 7. Results on the UCAS-AOD dataset, speed test on a single Titan X.
Preprints 78499 g007
Table 1. Performance on UCAS-AOD dataset. Key: ms/Mpx = millisecond per million pixels.
Table 1. Performance on UCAS-AOD dataset. Key: ms/Mpx = millisecond per million pixels.
method backbone car plane mAP ms/Mpx
CFC-Net [13] resnet50 89.29% 88.69% 89.49% 135.52
DAL [48] resnet50 89.25% 90.49% 89.87% 113.97
SLA [49] resnet50 88.57% 90.30% 89.44% 72.94
ours resnet18 89.24% 96.76% 93.00% 16.21
resnet50 81.96% 93.03% 87.50% 63.16
resnet101 71.14% 90.95% 81.04% 83.54
swin-t 21.56% 57.81% 39.69% 69.23

4.3. Performance

We assessed the mAP of our models on the three datasets mentioned above. The inference speed of our methods, as well as that of the compared methods, was tested on a single Titan X GPU. The detection results are shown in Figure 9. All categories of mAP in compared methods are reported in their own paper.
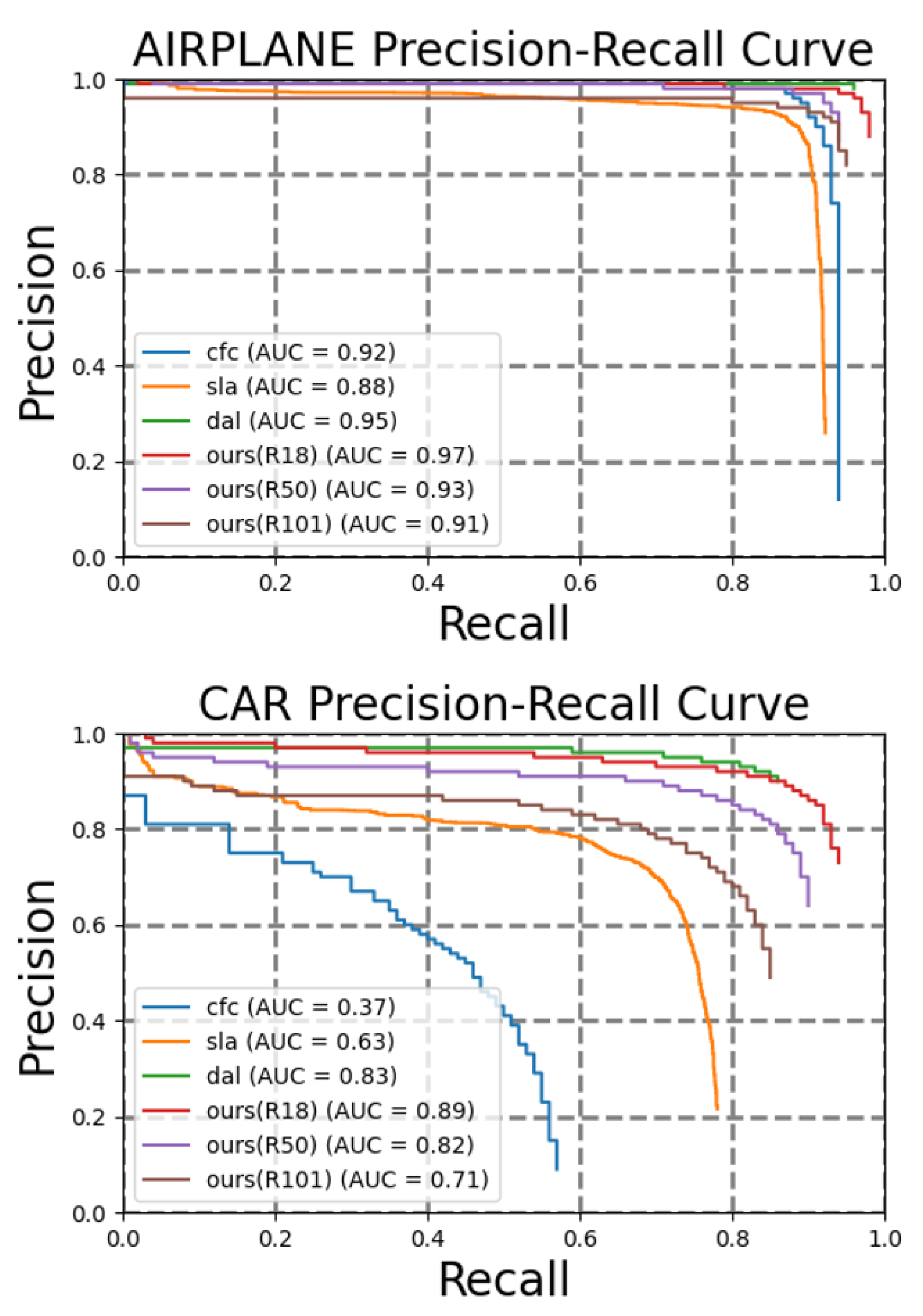
Result on UCAS-AOD Our models were trained using Adam for 300 epochs, while γ was set to be 3 . 0 . The results in Table 1 and Figure 7 demonstrate that our method is competitive in both speed and performance. The precision-recall curves for the airplane and car categories can be observed in Figure 8.
Table 2. The ablation result of our methods at different settings on UCAS-AOD dataset.
Table 2. The ablation result of our methods at different settings on UCAS-AOD dataset.
backbone γ car plane mAP ms/Mpx
resnet18 1.0 84.48% 97.44% 90.96% 16.21
2.0 86.41% 95.60% 91.00%
3.0 89.24% 96.76% 93.00%
resnet50 1.0 83.84% 96.61% 90.22% 63.16
3.0 81.96% 93.03% 87.50%
resnet101 2.0 77.29% 92.97% 85.13% 83.54
3.0 71.14% 90.95% 81.04%
swin-t 3.0 21.56% 57.81% 39.69% 69.23
Table 3. Performance on HRSC2016 and DLK 3K dataset.
Table 3. Performance on HRSC2016 and DLK 3K dataset.
dataset method backbone mAP ms/Mpx
HRSC2016 CFC-Net [13] resnet50 88.6% 148.78
DAL [48] resnet50 88.60% 118.75
SLA [49] resnet50 87.14% 838.47
MRDet [50] resnet101 89.94% 1249.36
ours resnet18 78.07% 17.53
resnet50 73.59% 65.87
DLR 3K ours resnet18 83.99% 13.64
resnet50 69.79% 62.26
resnet101 71.99% 80.59
Result on HRSC2016 The result of HRSC2016 is reported in Table 3. The 181 images in the val part are not used for training. The results reveal that the accuracy of our method is relatively poor when dealing with targets that have high height-width-ratio targets but also have a good processing speed.
Result on DLR3K We evaluate our model on the small and dense arranged oriented detection dataset DLR 3K, the result is shown in Table 3 and Figure 9.
Preprints 78499 g008
Figure 8. Results on the UCAS-AOD dataset, compared with our methods.
Figure 8. Results on the UCAS-AOD dataset, compared with our methods.
Preprints 78499 g008
What is more, we also test the above UCAS-AOD dataset-trained model on aerial video frames of busy parking lot surveillance 1. The results are shown in Figure 10, Figure 11 and Table 4.

5. Discussion

One of the primary characteristics of the proposed technique is its speed. As shown in Figure 7, the straightforward architecture enables our method to surpass other methods in terms of speed. Another contradictory outcome, as demonstrated in Table 2, suggests that an increase in the complexity of the model backbone leads to a decrease in the model’s performance and speed. This phenomenon can be explained by the restricted size of the dataset and the use of a simple architecture in the detection method.
Preprints 78499 g009
Figure 9. Detection results. Top 2 rows: UCAS-AOD dataset; Third row: HRSC2016 dataset; Last row: DLR-3K dataset. The images are cropped and zoomed.
Figure 9. Detection results. Top 2 rows: UCAS-AOD dataset; Third row: HRSC2016 dataset; Last row: DLR-3K dataset. The images are cropped and zoomed.
Preprints 78499 g009
Preprints 78499 g010
Figure 10. Detection result on aerial video frames without training. Top: frame-A; Second: frame-B; Bottom: frame-C.
Figure 10. Detection result on aerial video frames without training. Top: frame-A; Second: frame-B; Bottom: frame-C.
Preprints 78499 g010
Preprints 78499 g011
Figure 11. Detection result on aerial video frames without training. Top: frame-D, Second: frame-E; Bottom: frame-F.
Figure 11. Detection result on aerial video frames without training. Top: frame-D, Second: frame-E; Bottom: frame-F.
Preprints 78499 g011
Table 4. Performance on video frame.
Table 4. Performance on video frame.
TP FP TN Accuray Recall F1 score
frame-A 482 17 8 0.9659 0.9837 0.9747
frame-B 491 16 7 0.9684 0.9859 0.9771
frame-C 481 17 9 0.9659 0.9816 0.9737
frame-D 487 16 10 0.9682 0.9799 0.9740
frame-E 479 15 12 0.9696 0.9756 0.9726
frame-F 477 17 14 0.9656 0.9715 0.9686
Another crucial attribute of the method is its ability to reconcile the significance of angular information for targets possessing varying aspect ratios. As an illustration, the UCAS-AOD dataset consists of two categories- cars and airplanes. The former classifies as a high aspect ratio target, whereas the latter does not possess such a characteristic. It follows that for the former category, the angular information of the orientation frame plays a significant role, while for the latter category, it is inconsequential. As shown in Table 1, our method balances these two categories favorably.
In addition to this, one of the disadvantages of our approach is that its efficacy is comparatively lower for larger targets than for smaller ones. As shown in Table 3, although our method is also fast in handling large targets, the accuracy will be somewhat lower than the comparison methods. This suggests that in the case of oriented object detection for larger targets, albeit redundant candidates may consume additional time, they can offer a relatively favorable performance boost at this phase.

6. Conclusions

In this paper, we proposed a simple mathematical method to detect arbitrary direction objects in aerial images using a deep neural network. For more details, we embedded the rotation angle of each oriented object into a two-dimensional Euclidean space and regressed them with the deep network. That method not only preserves the typological properties of the circular space but also avoids an overly redundant design. What’s more, we notice that the importance of rotate angle in high-aspect and low-aspect ratio objects are different, thus we made a trade-off between those two kinds of objects. The detection results of the neural network are fed into a skew-iou based NMS method to get the final result. The experiment on several remote sensing objects shows our arbitrarily oriented detection method makes a good performance in both speed and precision.

Author Contributions

Conceptualization, M.W., Q.L. and Y.G.; methodology, M.W., Q.L. and J.P.; software, M.W.; validation, Q.L. and J.P.; formal analysis, M.W.; investigation, M.W.; resources, Q.L.; data curation, Y.G.; writing—original draft preparation, M.W.; writing—review and editing, Q.L.; visualization, M.W.; supervision, Y.G. and J.P.; project administration, Y.G. and J.P.; funding acquisition, Q.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 62201209 and Natural Science Fund of Hunan Province under Grant 2022JJ40092.

Data Availability Statement

All data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

We gratefully thank the two anonymous reviewers for their valuable comments.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ouyang, L.; Wu, J.; Jiang, X.; Almeida, D.; Wainwright, C.; Mishkin, P.; Zhang, C.; Agarwal, S.; Slama, K.; Ray, A.; et al. Training language models to follow instructions with human feedback. Advances in Neural Information Processing Systems 2022, 35, 27730–27744.
  2. Ma, J.; Shao, W.; Ye, H.; Wang, L.; Wang, H.; Zheng, Y.; Xue, X. Arbitrary-Oriented Scene Text Detection via Rotation Proposals. IEEE Transactions on Multimedia 2018. [CrossRef]
  3. Ding, J.; Xue, N.; Long, Y.; Xia, G.; Lu, Q. Learning RoI Transformer for Oriented Object Detection in Aerial Images. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2019, pp. 2844–2853. [CrossRef]
  4. Yang, X.; Liu, Q.; Yan, J.; Li, A. R3Det: Refined Single-Stage Detector with Feature Refinement for Rotating Object. In Proceedings of the AAAI, 2021. [CrossRef]
  5. Jiang, Y.; Zhu, X.; Wang, X.; Yang, S.; Luo, Z. R 2 CNN: Rotational Region CNN for Arbitrarily-Oriented Scene Text Detection. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), 2018. [CrossRef]
  6. Xie, X.; Cheng, G.; Wang, J.; Yao, X.; Han, J. Oriented R-CNN for object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 3520–3529. [CrossRef]
  7. Yang, X.; Yan, J. Arbitrary-oriented object detection with circular smooth label. In Proceedings of the European Conference on Computer Vision. Springer, 2020, pp. 677–694. [CrossRef]
  8. Guo, Z.; Liu, C.; Zhang, X.; Jiao, J.; Ji, X.; Ye, Q. Beyond bounding-box: Convex-hull feature adaptation for oriented and densely packed object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 8792–8801. [CrossRef]
  9. Chen, Z.; Chen, K.; Lin, W.; See, J.; Yu, H.; Ke, Y.; Yang, C. Piou loss: Towards accurate oriented object detection in complex environments. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part V 16. Springer, 2020, pp. 195–211.
  10. Yang, X.; Yan, J.; Feng, Z.; He, T. R3det: Refined single-stage detector with feature refinement for rotating object. In Proceedings of the AAAI conference on artificial intelligence, 2021, Vol. 35, pp. 3163–3171. [CrossRef]
  11. Yang, X.; Yan, J.; Ming, Q.; Wang, W.; Zhang, X.; Tian, Q. Rethinking rotated object detection with gaussian wasserstein distance loss. In Proceedings of the International Conference on Machine Learning. PMLR, 2021, pp. 11830–11841.
  12. Yang, X.; Yang, X.; Yang, J.; Ming, Q.; Yan, J. Learning High-Precision Bounding Box for Rotated Object Detection via Kullback-Leibler Divergence 2021. [CrossRef]
  13. Ming, Q.; Miao, L.; Zhou, Z.; Dong, Y. CFC-Net: A critical feature capturing network for arbitrary-oriented object detection in remote-sensing images. IEEE Transactions on Geoscience and Remote Sensing 2021. [CrossRef]
  14. Zhu, H.; Chen, X.; Dai, W.; Fu, K.; Ye, Q.; Jiao, J. Orientation robust object detection in aerial images using deep convolutional neural network. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP). IEEE, 2015, pp. 3735–3739. [CrossRef]
  15. Liu, Z.; Yuan, L.; Weng, L.; Yang, Y. A high resolution optical satellite image dataset for ship recognition and some new baselines. In Proceedings of the International conference on pattern recognition applications and methods. SciTePress, 2017, Vol. 2, pp. 324–331. [CrossRef]
  16. Liu, K.; Mattyus, G. Fast multiclass vehicle detection on aerial images. IEEE Geoscience and Remote Sensing Letters 2015, 12, 1938–1942. [CrossRef]
  17. Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2014, pp. 580–587. [CrossRef]
  18. Girshick, R. Fast r-cnn. In Proceedings of the IEEE international conference on computer vision, 2015, pp. 1440–1448. [CrossRef]
  19. Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Advances in neural information processing systems 2015, 28. [CrossRef]
  20. Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object detection via region-based fully convolutional networks. Advances in neural information processing systems 2016, 29.
  21. Everingham, M.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes challenge 2007 (voc 2007) results (2007), 2008.
  22. Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 779–788. [CrossRef]
  23. Redmon, J.; Farhadi, A. YOLO9000: better, faster, stronger. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 7263–7271. [CrossRef]
  24. Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv preprint arXiv:1804.02767 2018. [CrossRef]
  25. Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11–14, 2016, Proceedings, Part I 14. Springer, 2016, pp. 21–37. [CrossRef]
  26. Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE international conference on computer vision, 2017, pp. 2980–2988. [CrossRef]
  27. Law, H.; Deng, J. Cornernet: Detecting objects as paired keypoints. In Proceedings of the European conference on computer vision (ECCV), 2018, pp. 734–750. [CrossRef]
  28. Duan, K.; Bai, S.; Xie, L.; Qi, H.; Huang, Q.; Tian, Q. Centernet: Keypoint triplets for object detection. In Proceedings of the IEEE/CVF international conference on computer vision, 2019, pp. 6569–6578. [CrossRef]
  29. Zhou, X.; Zhuo, J.; Krahenbuhl, P. Bottom-up object detection by grouping extreme and center points. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 850–859. [CrossRef]
  30. Liao, M.; Shi, B.; Bai, X. TextBoxes++: A Single-Shot Oriented Scene Text Detector. IEEE Transactions on Image Processing 2018, 27, 3676–3690. [CrossRef]
  31. Pan, X.; Ren, Y.; Sheng, K.; Dong, W.; Yuan, H.; Guo, X.; Ma, C.; Xu, C. Dynamic refinement network for oriented and densely packed object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 11207–11216. [CrossRef]
  32. Li, W.; Chen, Y.; Hu, K.; Zhu, J. Oriented reppoints for aerial object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 1829–1838. [CrossRef]
  33. Zand, M.; Etemad, A.; Greenspan, M. Oriented bounding boxes for small and freely rotated objects. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–15. [CrossRef]
  34. Zhou, J.; Zhang, R.; Zhao, W.; Shen, S.; Wang, N. APS-Net: An Adaptive Point Set Network for Optical Remote Sensing Object Detection. IEEE Geoscience and Remote Sensing Letters 2022. [CrossRef]
  35. Fu, K.; Chang, Z.; Zhang, Y.; Sun, X. Point-based estimator for arbitrary-oriented object detection in aerial images. IEEE Transactions on Geoscience and Remote Sensing 2020, 59, 4370–4387. [CrossRef]
  36. Chen, X.; Ma, L.; Du, Q. Oriented object detection by searching corner points in remote sensing imagery. IEEE Geoscience and Remote Sensing Letters 2021, 19, 1–5. [CrossRef]
  37. Wei, L.; Zheng, C.; Hu, Y. Oriented Object Detection in Aerial Images Based on the Scaled Smooth L1 Loss Function. Remote Sensing 2023, 15, 1350. [CrossRef]
  38. Song, F.; Ma, R.; Lei, T.; Peng, Z. RAIH-Det: An End-to-End Rotated Aircraft and Aircraft Head Detector Based on ConvNeXt and Cyclical Focal Loss in Optical Remote Sensing Images. Remote Sensing 2023, 15, 2364. [CrossRef]
  39. Qian, X.; Zhang, N.; Wang, W. Smooth giou loss for oriented object detection in remote sensing images. Remote Sensing 2023, 15, 1259. [CrossRef]
  40. Cui, M.; Duan, Y.; Pan, C.; Wang, J.; Liu, H. Optimization for Anchor-Free Object Detection via Scale-Independent GIoU Loss. IEEE Geoscience and Remote Sensing Letters 2023, 20, 1–5. [CrossRef]
  41. Hua, Z.; Pan, G.; Gao, K.; Li, H.; Chen, S. AF-OSD: An Anchor-Free Oriented Ship Detector Based on Multi-Scale Dense-Point Rotation Gaussian Heatmap. Remote Sensing 2023, 15, 1120. [CrossRef]
  42. Hou, L.; Lu, K.; Yang, X.; Li, Y.; Xue, J. G-rep: Gaussian representation for arbitrary-oriented object detection. Remote Sensing 2023, 15, 757. [CrossRef]
  43. Huang, Z.; Li, W.; Xia, X.G.; Tao, R. A general Gaussian heatmap label assignment for arbitrary-oriented object detection. IEEE Transactions on Image Processing 2022, 31, 1895–1910. [CrossRef]
  44. Cheng, Y.; Xu, C.; Kong, Y.; Wang, X. Short-Side Excursion for Oriented Object Detection. IEEE Geoscience and Remote Sensing Letters 2022, 19, 1–5. [CrossRef]
  45. Nie, G.; Huang, H. Multi-Oriented Object Detection in Aerial Images With Double Horizontal Rectangles. IEEE Transactions on Pattern Analysis and Machine Intelligence 2022. [CrossRef]
  46. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778. [CrossRef]
  47. Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 2117–2125. [CrossRef]
  48. Ming, Q.; Zhou, Z.; Miao, L.; Zhang, H.; Li, L. Dynamic anchor learning for arbitrary-oriented object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, 2021, Vol. 35, pp. 2355–2363. [CrossRef]
  49. Ming, Q.; Miao, L.; Zhou, Z.; Song, J.; Yang, X. Sparse label assignment for oriented object detection in aerial images. Remote Sensing 2021, 13, 2664. [CrossRef]
  50. Qin, R.; Liu, Q.; Gao, G.; Huang, D.; Wang, Y. MRDet: A multihead network for accurate rotated object detection in aerial images. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–12. [CrossRef]
  51. Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 10012–10022. [CrossRef]
1
https://www.youtube.com/watch?v=yojapmOkIfg
Preprints 78499 g001
Figure 1. Three curves for width at different rotate angles(car, ship, airplane). The y-coordinate denotes the width of the object bounding boxes, i.e., the length of the object’s projection on the horizontal axis, where the minimum projection length is standardized to 1. For high aspect ratio targets, the width curve is closer to the trigonometric function. Otherwise, the width curve is more messy.
Figure 1. Three curves for width at different rotate angles(car, ship, airplane). The y-coordinate denotes the width of the object bounding boxes, i.e., the length of the object’s projection on the horizontal axis, where the minimum projection length is standardized to 1. For high aspect ratio targets, the width curve is closer to the trigonometric function. Otherwise, the width curve is more messy.
Preprints 78499 g001
Preprints 78499 g002
Figure 2. (Left) HBB: Horizontal bounding boxes. (Right) OBB: Oriented bounding boxes.
Figure 2. (Left) HBB: Horizontal bounding boxes. (Right) OBB: Oriented bounding boxes.
Preprints 78499 g002
Preprints 78499 g003
Figure 3. Framework of the proposed method with backbone resnet18. k means the number of categories. At CR(Contour and Rectangle) head, the confidence for each category is computed separately. x,y denote the rectangle center offset at x and y axis. b, l denote the breadth and length of the rectangle. p, q are the regressors of cos 2 θ and sin 2 θ , where θ represents the rotate angle between the long side and x axis.
Figure 3. Framework of the proposed method with backbone resnet18. k means the number of categories. At CR(Contour and Rectangle) head, the confidence for each category is computed separately. x,y denote the rectangle center offset at x and y axis. b, l denote the breadth and length of the rectangle. p, q are the regressors of cos 2 θ and sin 2 θ , where θ represents the rotate angle between the long side and x axis.
Preprints 78499 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated