Prerpints.org logo
Preprint
Article

Interaction of Hoechst 33342 with Lipid Membranes at Different pH Values

Altmetrics

Downloads

155

Views

88

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (1.12MB )

Submitted:

03 July 2023

Posted:

04 July 2023

You are already at the latest version

Alerts
Abstract
Hoechst 33342 (H33342) is a fluorescent probe that is commonly used to stain DNA of living cells. To do so, it needs to interact with and permeate through cell membranes. The pH of biological media may vary quite significantly and this influences H33342 ionization state, and may change its rate of permeation through biomembranes. In this work, we address the effect of pH in the association of H33342 with lipid bilayers using a combined experimental and computational approach. The partition of H33342 to 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipid membranes was experimentally quantified using fluorescence spectroscopy and isothermal titration calorimetry (ITC) measurements. Quantum chemical calculations were performed to select the most stable isomer of H33342 for the overall charges 0, +1, and +2, expected to predominate across the 5 < pH < 10 range. The interaction of these isomers with POPC bilayers was then studied by both unrestrained and umbrella sampling molecular dynamics simulations. While probe insertion occurs for all ionization states, with similar overall equilibrium location, orientation was found to depend on the probe charge, with the neutral form lying mostly parallel and the doubly charged displaying a significant tilt relative to the membrane plane. Both experimental results and computational free energy profiles indicate that the partition coefficient of H33342 displays a small variation over a wide pH range, not exceeding one order of magnitude. The enthalpy of interaction is negative and is larger at lower pH values. This suggests efficient hydrogen bonding between the probe and the lipid, namely for the protonated +2 form. The relatively high lipophilicity obtained for the charged species contrasts with the decrease in their general hydrophobicity as estimated from water and octanol partition. This highlights the distinction between lipophilicity and hydrophobicity, and the importance of considering association with lipid bilayers when predicting the affinity for biomembranes.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

1. Introduction

Hoechst 33342 (H33342) is a bis-benzimidazole derivative fluorescent dye which associates with DNA, allowing its visualization by optical microscopy. This dye can be used to stain the DNA of living cells [1,2], which requires fast permeation through cell membranes. Although H33342 transport has been reported to occur by active influx [3] and/or efflux [3,4,5] depending on the cells, a relatively fast passive permeation has also been shown, which allows equilibration through the membrane to occur within a few minutes [1]. The specificity of H33342 to DNA and its fast permeation have recently extended the use of this popular probe as a targeting moiety in drugs directed towards cell DNA [6]. The high permeability of H33342 is quite unexpected because at physiological pH it is expected to have an overall positive charge [7].
In addition to its interest in DNA staining and targeting, H33342 transport by P-glycoprotein has been extensively used in competition assays to characterize the transport of drugs by this efflux transporter [8,9]. To be transported by P-glycoprotein, the substrates must access the binding pocket from the inner face of the cell membrane [10]. Therefore, molecules added to the medium outside the cell must first associate with the membrane outer leaflet and permeate the lipid bilayer towards the inner leaflet. These processes will be affected by the ionization state of the protein substrates, altering the overall efflux transport. To understand the details in the protein activity, it is therefore important to know how the ionization state of the H33342 as substrate for P-glycoprotein affects its interaction with lipid membranes.
The characterization of the effect of H33342 ionization on its interaction with lipid membranes extends well beyond this fluorescent probe and its use to stain DNA or characterize P-gp’s activity. In fact, the knowledge obtained may be of relevance for drugs containing the imidazole and benzimidazole groups, some of which are already present in the market [11,12].
Figure 1a shows the molecular structure of H33342, highlighting the three ionizable groups, two benzimidazole groups in the central region and an aliphatic tertiary amine in one of the ends of the molecule. Usually, the aliphatic tertiary amines are relatively strong bases, and are protonated at physiological pH (≈7). Quantum mechanical calculations carried out for H33342 indicated that one of the benzimidazole groups shows higher basicity than the other, with a pKa difference of 2 units [7]. The attribution given for the ionization constants in that work was made based on the acid/base properties of imidazole, resulting in pKa values for H33342 on the order of 5 and 7, or 7 and 9, dependent on which group is considered to have an acid/base behaviour similar to the reference imidazole base. Therefore, a global charge between +1.5 and +2.5 is predicted for H33342 at neutral pH, with a large variation within the range of physiological pH values [13].
In this work we characterize the interaction of H33342 with lipid membranes of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC; structure in Figure 1b) in the pH range between 3 and 11. This lipid was chosen due to the high abundance of phosphatidylcholines in biological membranes [14,15,16,17,18], and the prevalence of the combination of palmitoyl and oleoyl acyl chains in the membrane phospholipids [19]. H33342 partition coefficient (KP) was obtained from changes in its fluorescence intensity, and fluorescence anisotropy. Isothermal titration calorimetry (ITC) was also used to characterize the partition coefficient, from the heat evolved in the interaction between H33342 and the lipids in the bilayer. In addition to the partition coefficient, with this methodology the enthalpy variation (ΔHo) associated with the interaction is also obtained, providing important insight regarding the nature of the interactions established. More negative enthalpy variations reflect the establishment of favourable interactions with the membrane, while associations favoured by an increase in entropy are mostly due to the hydrophobic effect [20,21,22,23,24].
The experimental results were complemented by Molecular Dynamics (MD) simulations. Quantum mechanical calculations were carried out for all different possible isomers of H33342 with overall charges 0, +1 and +2, enabling determination of the most stable one in each case. These selected isomers were then simulated in the presence of POPC bilayers, to acquire molecular detail of the interactions established [25,26,27]. While interactions of H33342 with proteins [28,29,30,31] or DNA [32] have been previously characterized using MD simulations, this powerful methodology has, to our best knowledge, not yet been applied to the interactions between H33342 and lipid membranes. In the present work, we use unrestrained MD simulations to characterize several properties of the interaction of H33342 at different protonation states with POPC membranes, namely transverse localization, preferred orientation of solute in the bilayers and the possibility of hydrogen bonding between solute and lipid bilayers components. Umbrella sampling (US) simulations were also performed to obtain the Potential of Mean Force (PMF) across the POPC bilayer, providing insights on the effect of protonation on the rate of permeation through the membrane.
Altogether, this work provides the identification of key properties that allow H33342 to interact efficiently with cell membranes and to have a fast permeation despite its high global charge. The exploration of these properties in drug design may contribute to the development of new drugs with improved bioavailability.

2. Results and discussion

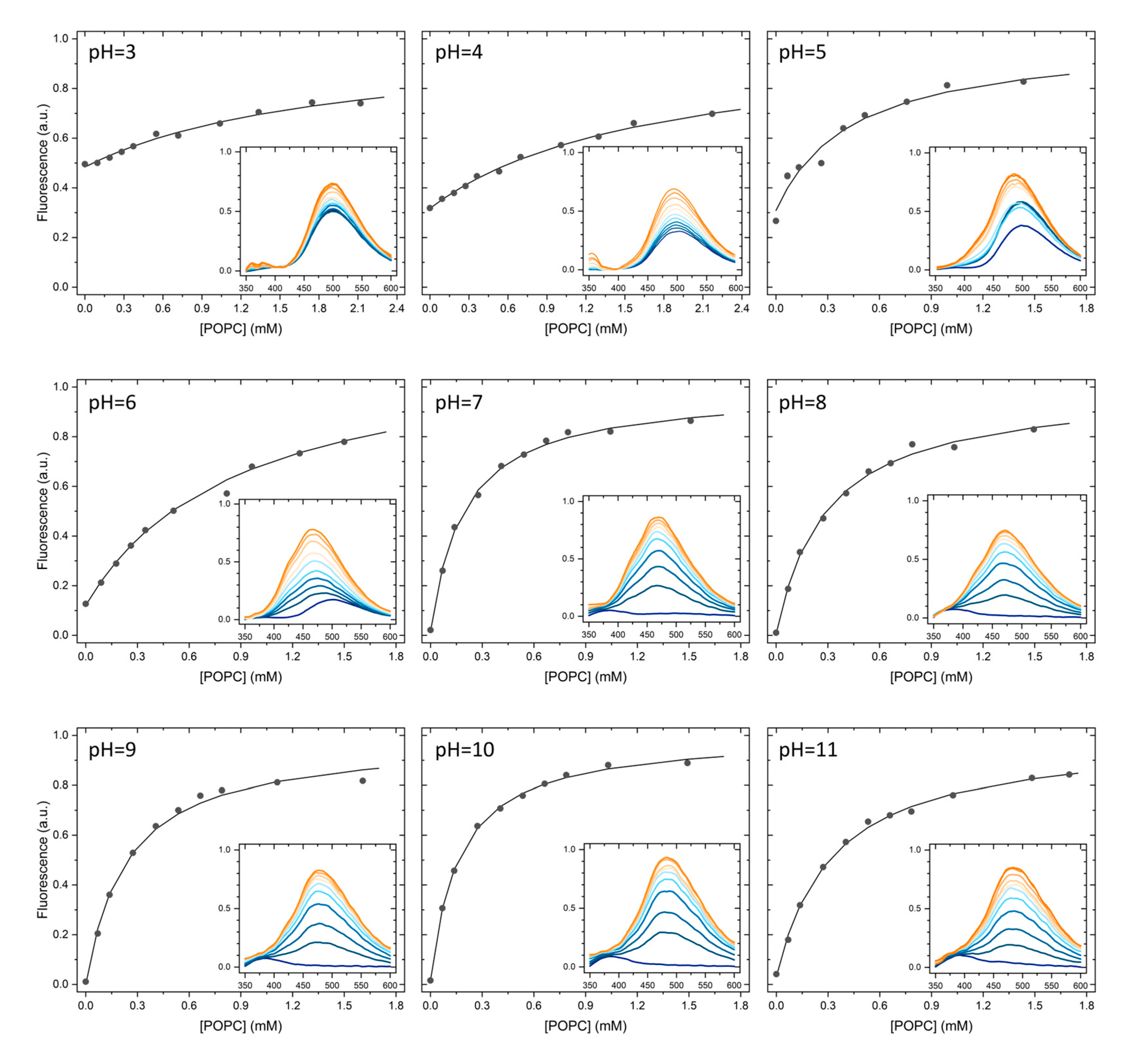
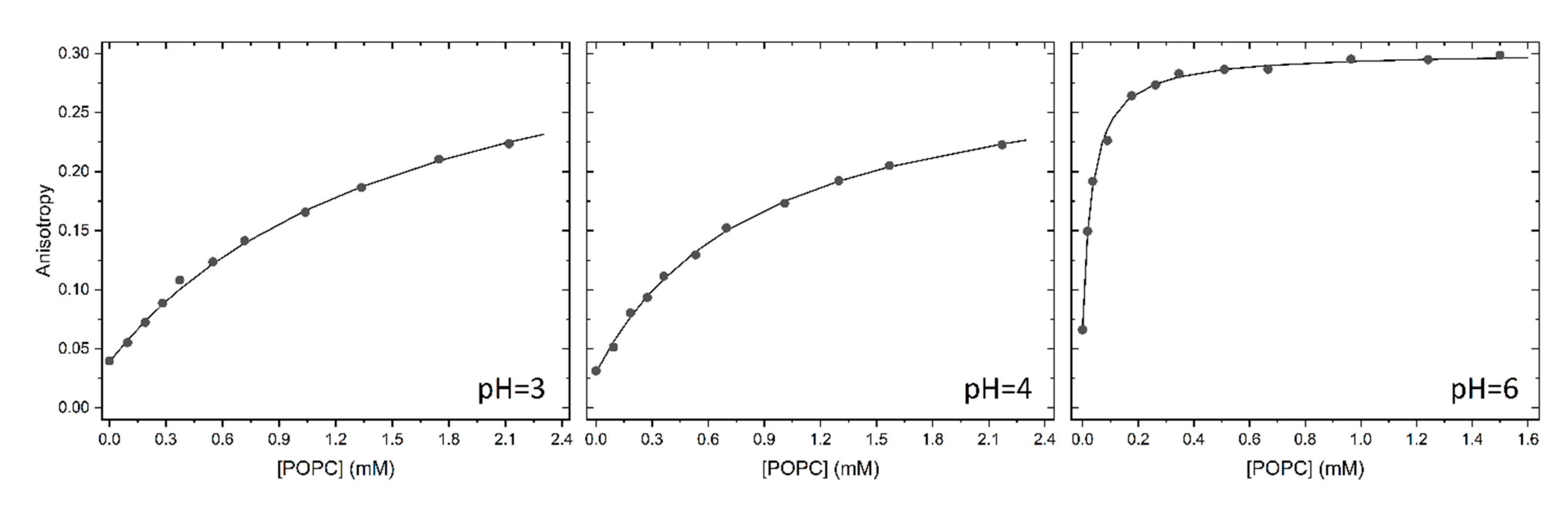
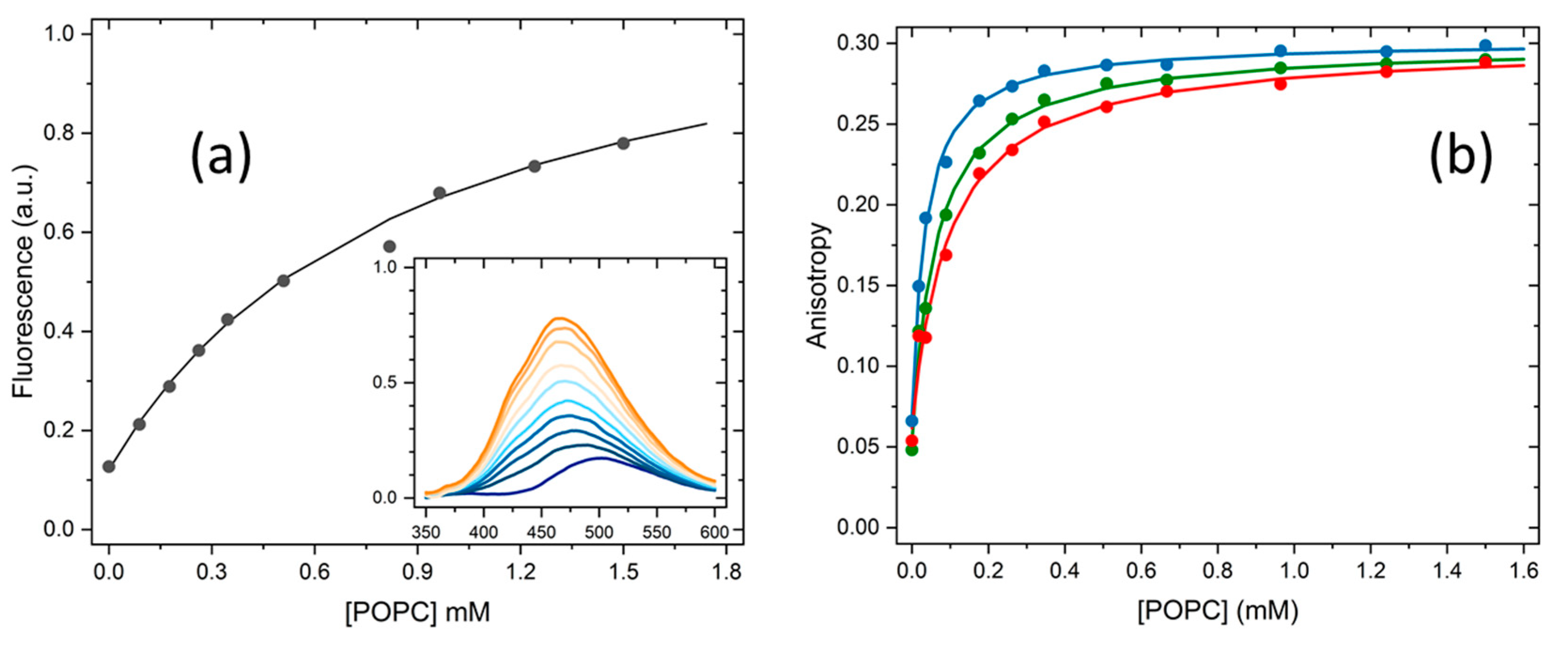
2.1. Partition to POPC LUVs

As explained in detail in the Section 3.5, the partition of H33342 to POPC LUVs was characterized from the variation in the fluorescence intensity and from the variation in the fluorescence anisotropy. At pH ≥ 6, association with the membrane leads to a large increase in the fluorescence intensity, allowing to directly obtain the amount of H33342 in both media. However, for pH ≤ 6 the major species in the aqueous media has a large fluorescence quantum yield, and only a small variation is observed upon association with the membrane. Under these conditions, the quantification of the partition coefficient from the variation of the fluorescence intensity has a large uncertainty. On the other hand, interaction with the membrane imposes constraints in H33342 mobility, leading to a significant increase in the fluorescence anisotropy. The variation observed in the fluorescence anisotropy at a given volume of membrane is however not a direct measure of the amount of H33342 in each media. Instead, it reflects the relative fluorescence intensity from the probe molecules in both media. To validate the methodology based on the fluorescence anisotropy, both approaches were followed at pH=6. Typical results obtained at this pH are shown in Figure 2. The fluorescence anisotropy depends much strongly on the POPC concentration because the anisotropy is dominated by the H33342 associated with the membrane. That is, the ratio between the fluorescence intensity from the probe in the membrane and that from the probe in the aqueous phase ( α M ) is much larger than 1. This parameter is larger at shorter wavelengths because the spectrum of probe associated with the membrane is blue-shifted when compared to that for the probe in the aqueous media. Thus, the fluorescence anisotropy increases more abruptly with the lipid concentration for fluorescence detection at lower wavelengths (Figure 2b). When the variation in the fluorescence anisotropy is weighted by α M ( α M =13 in the range 450-470 nm, 8 in the range 470-490 nm, and 5 in the range 490-510 nm), the obtained partition coefficient is essentially independent on the detection wavelength. Statistically equivalent values are also obtained from the analysis of the fluorescence intensity (equation (2)) and the fluorescence anisotropy (equation (3)).
Typical results obtained at all pH values studied are shown in Figure A1 and Figure A2 of Appendix A, and the average values of KP obtained are provided in Table 1. The partition coefficient obtained at neutral pH is in excellent agreement with the values reported in literature for partition to DMPC membranes in the liquid disordered phase [5], and to the lipid bilayer of inside-out vesicles of Lactococcus lactis [33]. A maximal value of KP is observed at pH=10, in agreement with the higher abundance of the neutral form, predicted in literature studies [7,34,35] and also by the MarvinSketch software [36]. The affinity for the POPC bilayers is essentially unaffected by the pH when the latter varies between 7 and 11, although it is predicted that at pH=7 the most abundant species is the monocation. A significant decrease is observed for acidic pH values. However, this variation is still relatively modest, with only one order of magnitude decrease between pH=10 and 3. This result is unexpected, given that the most abundant species is +3 at pH=3.
The partition of H33342 to the POPC membranes was also characterized by ITC to obtain the enthalpy of interaction. The enthalpy variation obtained directly from the thermogram includes contributions from the interactions established between the solute and the medium where it is dissolved (aqueous medium or membrane), as well as from changes in solute ionization upon partition, the latter also including contributions from changes in the ionization of the buffer [21,38,39]. The phosphate buffer used in the ITC experiments has a very low ionization enthalpy [40], thus with a negligible contribution to the observed enthalpy variation. Therefore, the overall value obtained for the enthalpy variation reflects only changes in H33342, interactions established with the aqueous medium and the lipid membrane, and possible changes in ionization upon partition. Figure 3 shows typical titration curves obtained at different pH values. The partition coefficients obtained are in good agreement with those obtained from changes in H33342 fluorescence properties, although somewhat lower. This may be due to the higher concentration used in the ITC experiments, to incomplete equilibration of H33342 between the two bilayer leaflets during the titration [20], or to a small preference for membranes with a higher curvature [41]. This was not further explored because the enthalpy variation is the most relevant parameter from those experiments.
It is observed that the interaction of H33342 with the POPC membranes shifts from being stabilized by enthalpy at acidic pH values (ΔHo = -54 ± 7 kJ/mol and TΔSo = -38 kJ/mol at pH=5.3), to equal contribution from enthalpy and entropy at alkaline pH values (ΔHo = -9 ± 2 kJ/mol and TΔSo = 9 kJ/mol at pH=8.2). This suggests that the association of the neutral form of H33342 with POPC membranes is mostly stabilized by the hydrophobic effect, while stabilizing electrostatic interactions are established between the cationic forms of H33342 and the membrane, even in the case of membranes containing only zwitterionic lipids such as POPC. To further elucidate on the nature of the interactions established, computational studies were performed with H33342 in distinct protonation states. The results obtained are presented in the next sections.

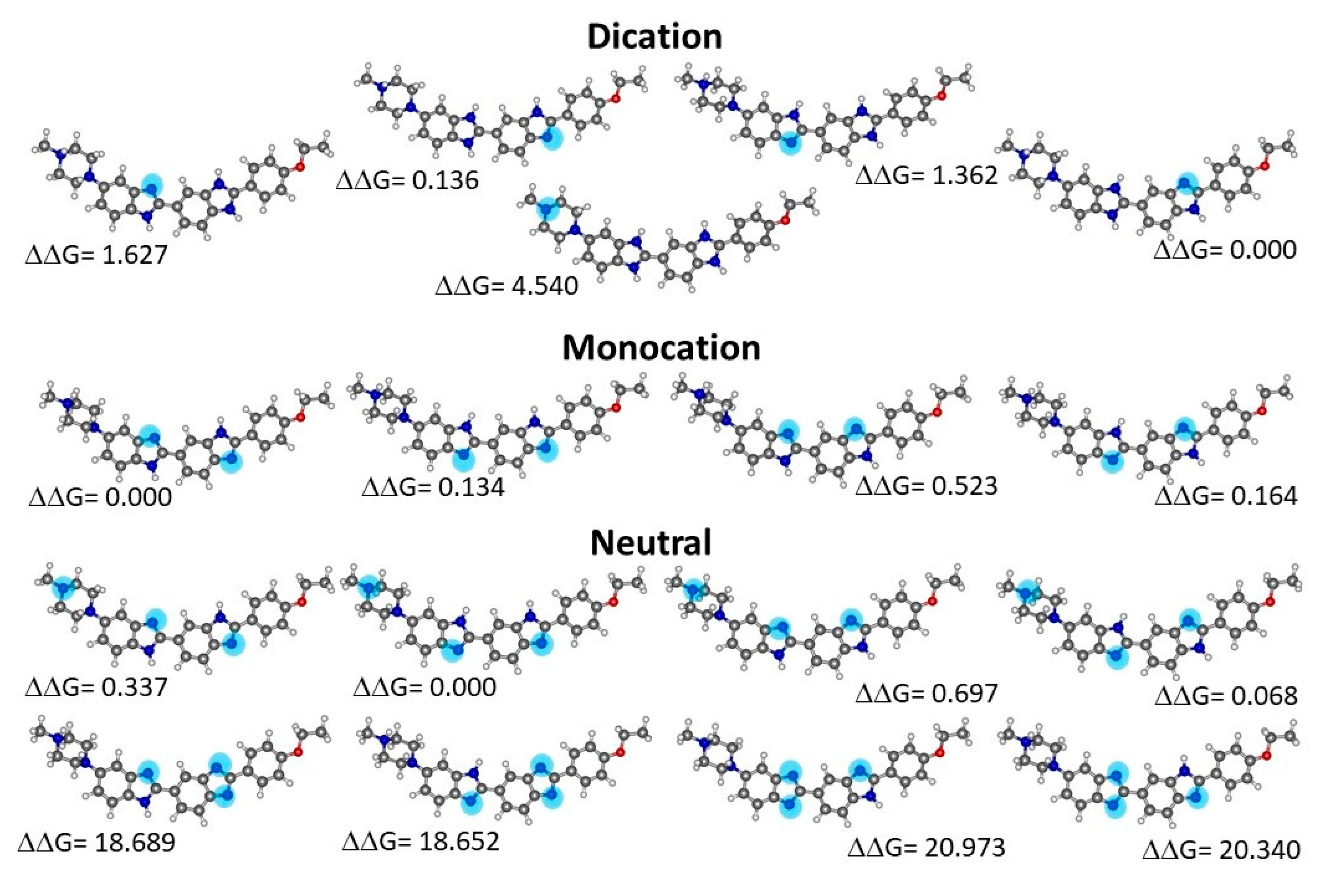
2.2. Quantum Chemical Determinations of Isomer Relative Stability

Geometry optimizations were conducted for the monocationic form of H33442 (H(+1)), its neutral form (H(0)), obtained by removal of one proton, and for the doubly charged molecular cation (H(+2)), obtained by further protonation relative to the monocation. For each of the different charge values there are several protonation/deprotonation possibilities corresponding to different isomers. From a total number of 17 molecular species, the most stable structures of the neutral, mono-charged, and double-charged cations, respectively, were selected by calculating their relative Gibbs energy in solution and were used to conduct the MD simulation. Figure 4 presents the optimized isomers thus obtained, together with relative free energies in aqueous solution.

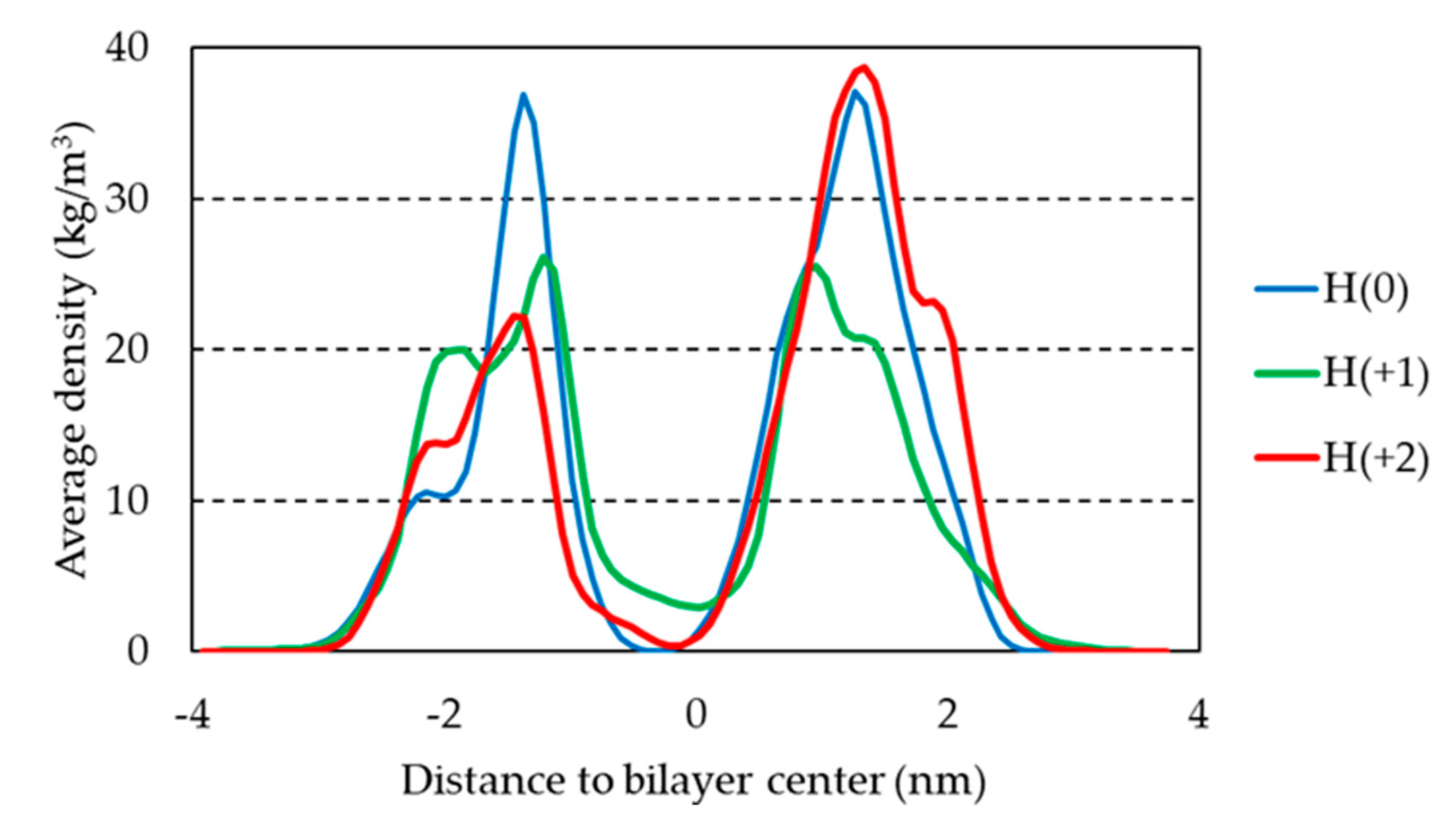
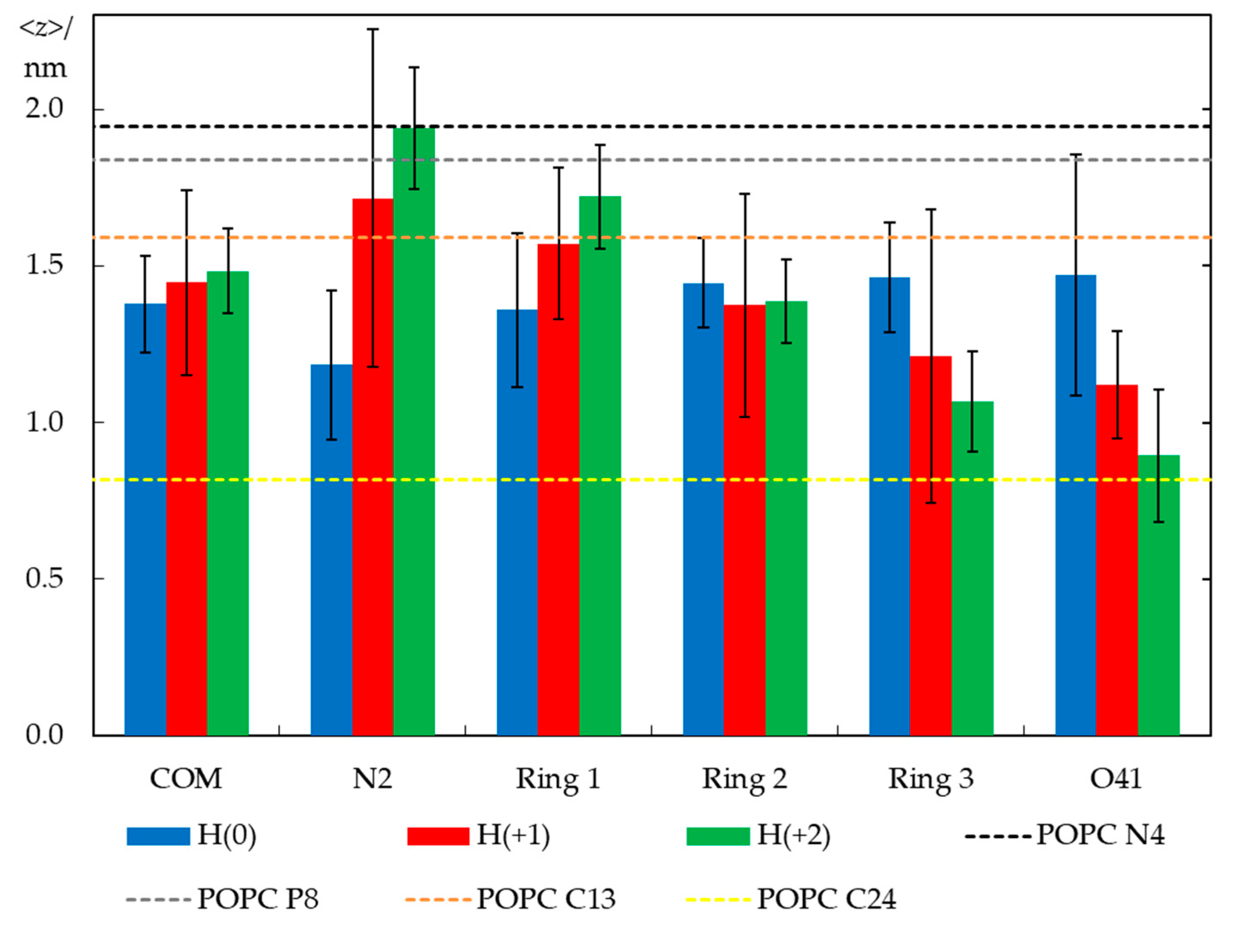
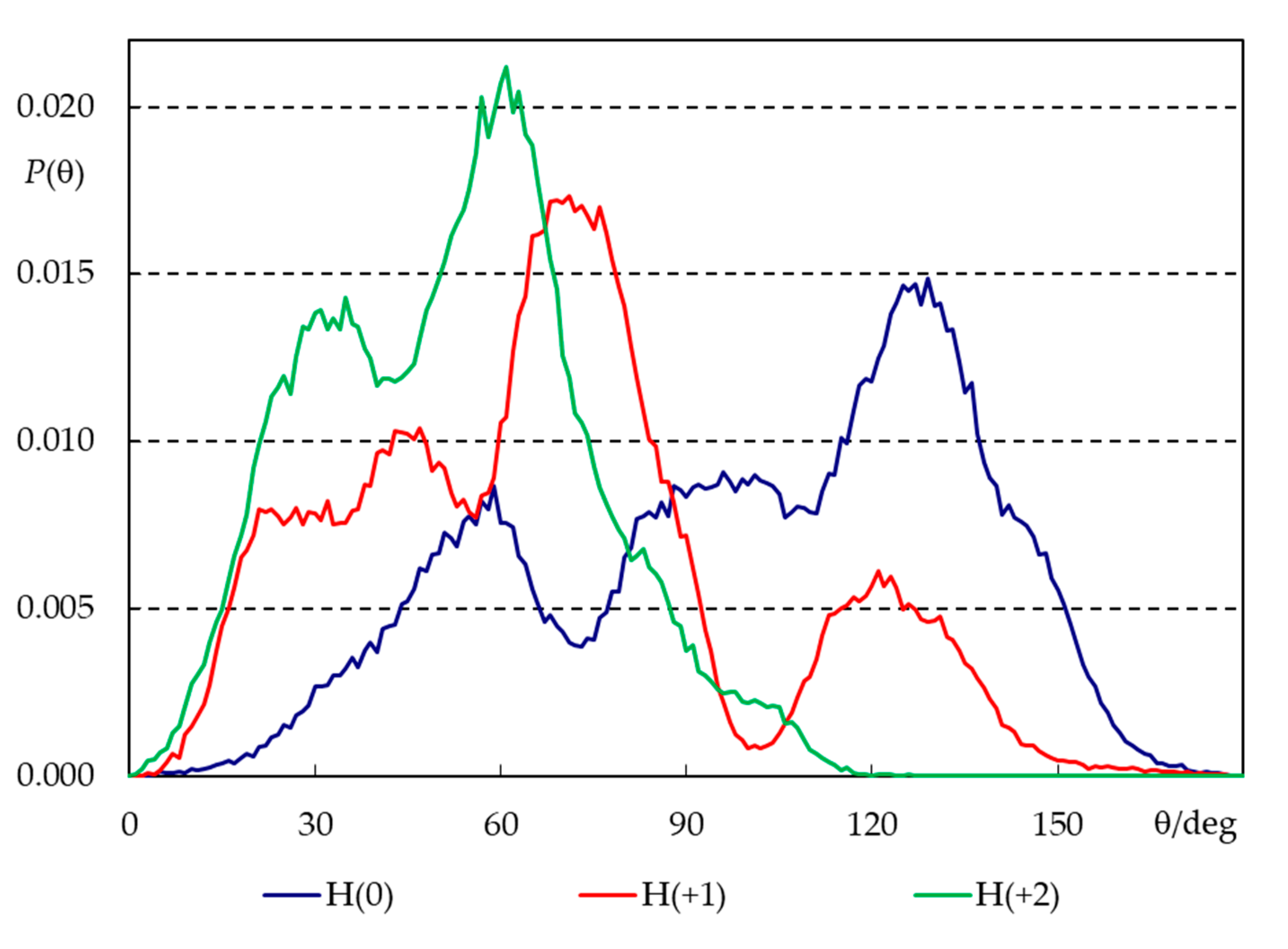
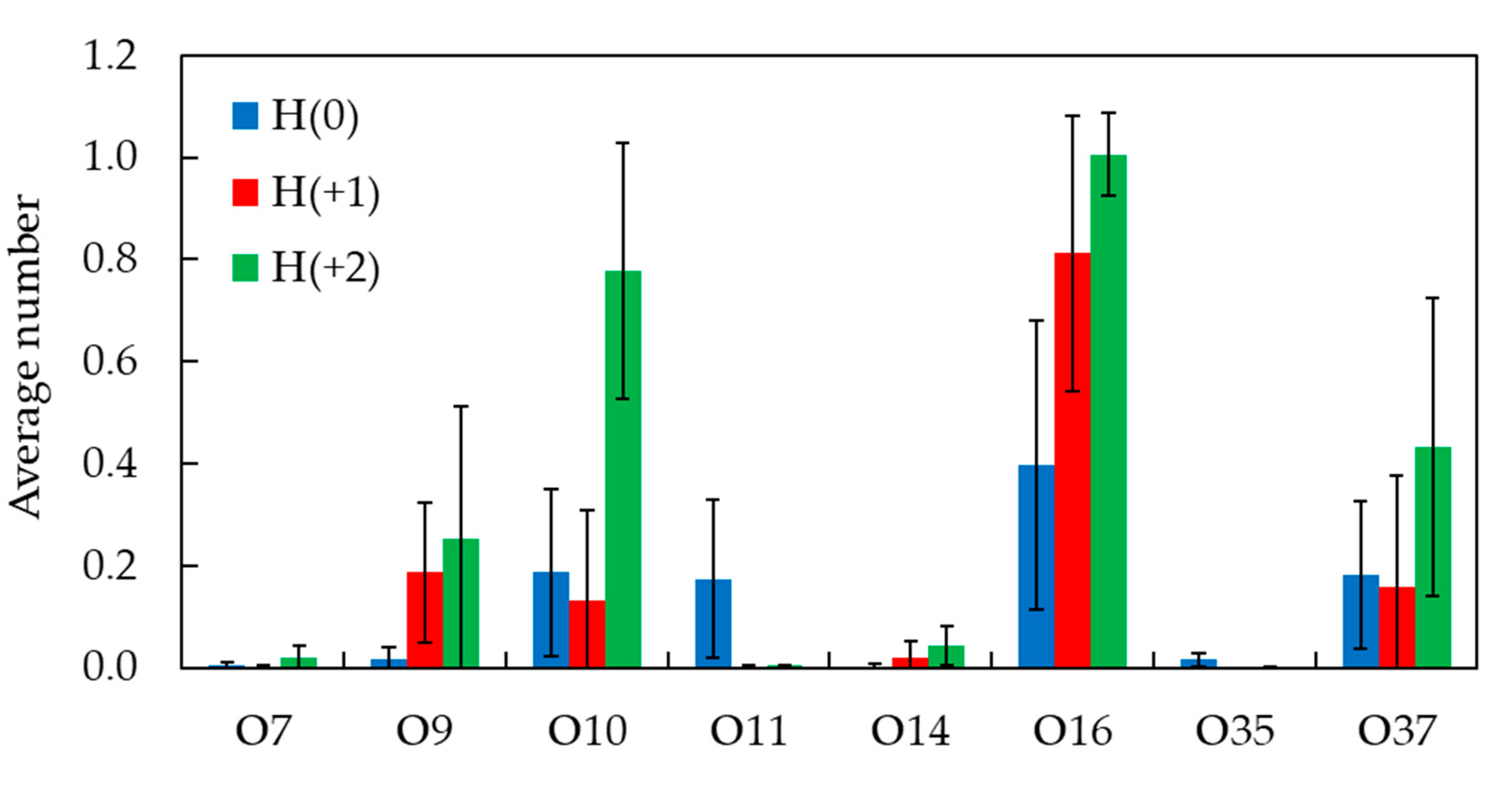
2.3. Unrestrained MD Simulations

As described in the methods section, the single most stable structures obtained from the quantum chemical calculations for H(0), H(+1) and H(+2) were parameterized for MD simulations and simulated in triplicate for 200 ns, in the presence of a POPC bilayer. Figure 5 depicts final snapshots in each simulation (run 1 and 2 refers to the system with probe molecules initially placed in the water phase, while in run 3 the probe molecules were initially placed in the bilayer midplane). Even though they only depict a single configuration state, some general features can already be observed. All molecules, irrespective of the ionization state, interact with the lipid bilayer. H(+2) molecules often adopt an orientation perpendicular to the membrane plane, where they insert the region of the molecule bearing no protonated sites (ring 3, ethoxy substituent) into the bilayer, while keeping the protonated region (ring 1, piperazine) in the upper headgroup region or even protruding into the water. This tendency is progressively lost for lower ionization states. Figure 5 reveals that two molecules in run 1 of H(+1) aggregate (average distance between centers of mass is 0.90 nm in the last 150 ns of simulation, with minimal distance of 0.36 nm; the dimer is clearly visible in the lower leaflet). Aggregation markedly affects probe interactions with the bilayer, and because we believe that this is a result of the relatively high probe:lipid ratio (1:32) necessary for simulating an adequate number of solute molecules, we excluded these two molecules from subsequent analyses. Therefore, whereas in the H(0) and H(+2) analyses twelve molecules were used for averaging, only ten were considered for H(+1).
The time evolution of the center of mass vertical position (z) for the four individual molecules in each run (Figure S1) shows that z converges rapidly in the simulations that start with the molecules in the bilayer midplane (z = 0, replicate 3), mostly to values in the 1 nm < |z| < 1.5 nm range. However, in replicates 1 and 2, where H33342 molecules were initially placed in the water/headgroup interface, insertion of some molecules is still occurring after 50 ns. Some molecules in these systems appear to not actually having inserted by the end of the simulations, residing at |z| ≈ 2 nm. Despite these different behaviors, all molecules (except the aggregated pair in run 1 of H(+1), as previously explained) were included for subsequent analyses, after discarding the first 100 ns of each simulation.
The mass density of H33342 along the z direction is shown in Figure 6 for the three ionization states. Overall, no pronounced differences are observed, with the preferred location being around 1.5 nm from the bilayer center for all forms. This was already suggested by the similar position of the center of mass (Figure S1). Curiously, H(+1) shows a more internal peak than both H(0) and H(+2), but it has a wider density profile.
Despite this similarity, the molecules clearly change their average orientation in the bilayer in response to varying their degree of protonation. We looked at orientation differences in two ways: by calculating average positions of different structural groups (Figure 7) and angular distributions for the H33342 long axis (defined in Figure 1a) tilt relative to the bilayer normal (Figure 8).
Figure 7 shows average transverse positions of groups and atoms of H33342, in comparison with those determined for selected atoms of POPC in a probe-free system (as shown in Figure S2, the presence of H33342 leads to very slight changes in POPC atom locations, <1.5% for those included in Figure 7). Globally, it illustrates that the probe has similar vertical localization in the membrane for all ionization states, corresponding to the upper acyl chain/carbonyl/glycerol region of the bilayer. The center of mass position appears to show a very slight dependence on the ionization state, and slightly more external locations are observed for progressively increased overall charge. However, the difference is ultimately very small and well within the estimated uncertainty, in accordance with the density profile analysis above. Still, there is a larger difference in positions of particular H33342 atoms/groups, which, while not entirely significant at the 95% confidence level considered in the figure error bars, appears to be sufficiently consistent overall to allow the following considerations. The uncharged species prefers to adopt an almost horizontal orientation, in the plane of the bilayer. The average positions of the different atoms of H(0) lie in a narrow bilayer region (between ~1.2 and 1.5 nm) for this ionization state, with the piperazine ring (N2) slightly more internal than other parts of the molecule. This contrasts with the behavior observed for H(+2). For this species, the most internally located part is the ethoxy group, with the O41 atom located on average at z = (0.89 ± 0.21) nm. Conversely, the opposite end of the molecule (the piperazine ring) has a very external transverse location in the headgroup region (z = (1.94 ± 0.19) nm), implying that in this ionization state, H33342 spans ~1 nm in the direction normal to the bilayer plane. An intermediate scenario is observed for H(+1), with specific atoms/groups located on average between z = (1.12 ± 0.17) nm (for O41) and (1.71 ± 0.54) nm (for N2).
The long axis tilt distributions (Figure 8) confirm these patterns. All distributions are very wide, illustrating the flexibility in the orientation of H33342 in the bilayer as well as distinct behaviors of different molecules (some of which actually do not insert properly in the course of the simulation, as pointed out above). Still, the widest distribution is clearly that corresponding to H(0), which displays significant probability density both for θ < 90º (piperazine pointing towards water) and θ > 90° (piperazine pointing towards center of bilayer), though the latter dominates slightly, and the average tilt angle for this state is <θ> = 100°. The opposite behavior is verified for H(+2). This form favors orientation of piperazine towards water and insertion of the opposing end, with <θ> = 52°. Again, H(+1) displays intermediate behavior (<θ> = 74°).
To obtain further details on the interactions established between H33342 and the lipid molecules, and how they may depend on the probe ionization state, we studied the fractional frequency of hydrogen bonding between NH donor groups of H34442 and oxygen acceptor atoms of POPC (Figure 9). Globally, it is observed that H bonding to glycerol O atoms (O14 and O35 for sn-2 and sn-1 lipid acyl chains, respectively) is low in all cases (<2% of total for the three forms), and only bonding to POPC O atoms from the phosphate (O7, O9, O10, and O11, mainly the three latter atoms) and carbonyl (O16 and O37 for sn-2 and sn-1 lipid acyl chains, respectively) groups need to be considered.
It must be noted that the higher the probe charge, the larger the number of NH donors available for H bonding. H(0) has two NH groups, one in each of the benzimidazole rings. H(+1) has one more NH group, in the piperazine ring, while H(+2) has that group and an additional one, in the benzimidazole ring closest to the piperazine. The fractional frequency of H-bonding summed across all POPC acceptor atoms reflects this obvious fact, and increases in the order 0.98 (H(0)) < 1.31 (H(+1)) < 2.53 (H(+2)). When these values are divided by the actual number of NH donor groups, similar values are obtained for H(0) and H(+1) (0.49 and 0.44, respectively), whereas the one for H(+2) is slightly higher (0.63). Overall, these results indicate that H33342 NH groups are roughly involved in H bonding to lipid O acceptors 40-60% of the time. The fractions of bonding to the phosphate (39%, 25% and 41% for H(0), H(+1) and H(+2), respectively) or carbonyl POPC O atoms (59%, 74% and 57% for H(0), H(+1) and H(+2), respectively) are similar for the three forms. The fact that maximal bonding to the phosphate occurs for H(+2) (41%) reflects perhaps the more external position of piperazine and benzimidazole ring 1, all with NH donors. However, in general, the transverse location of the NH donor groups is around z ~1.5 nm (Figure 7), enabling efficient H bonding to carbonyl POPC atoms, which are the dominant interactions.
The higher number of hydrogen bonds from H33342 NH to POPC acceptor atoms, as H33342 protonation increases, may be correlated with the increase observed in the interaction enthalpy as the pH is decreased (Figure 3). Those favourable interactions can also explain the relatively small variation observed in the affinity for the membrane, despite the large decrease in the hydrophobicity of the protonated charged forms of H33342.

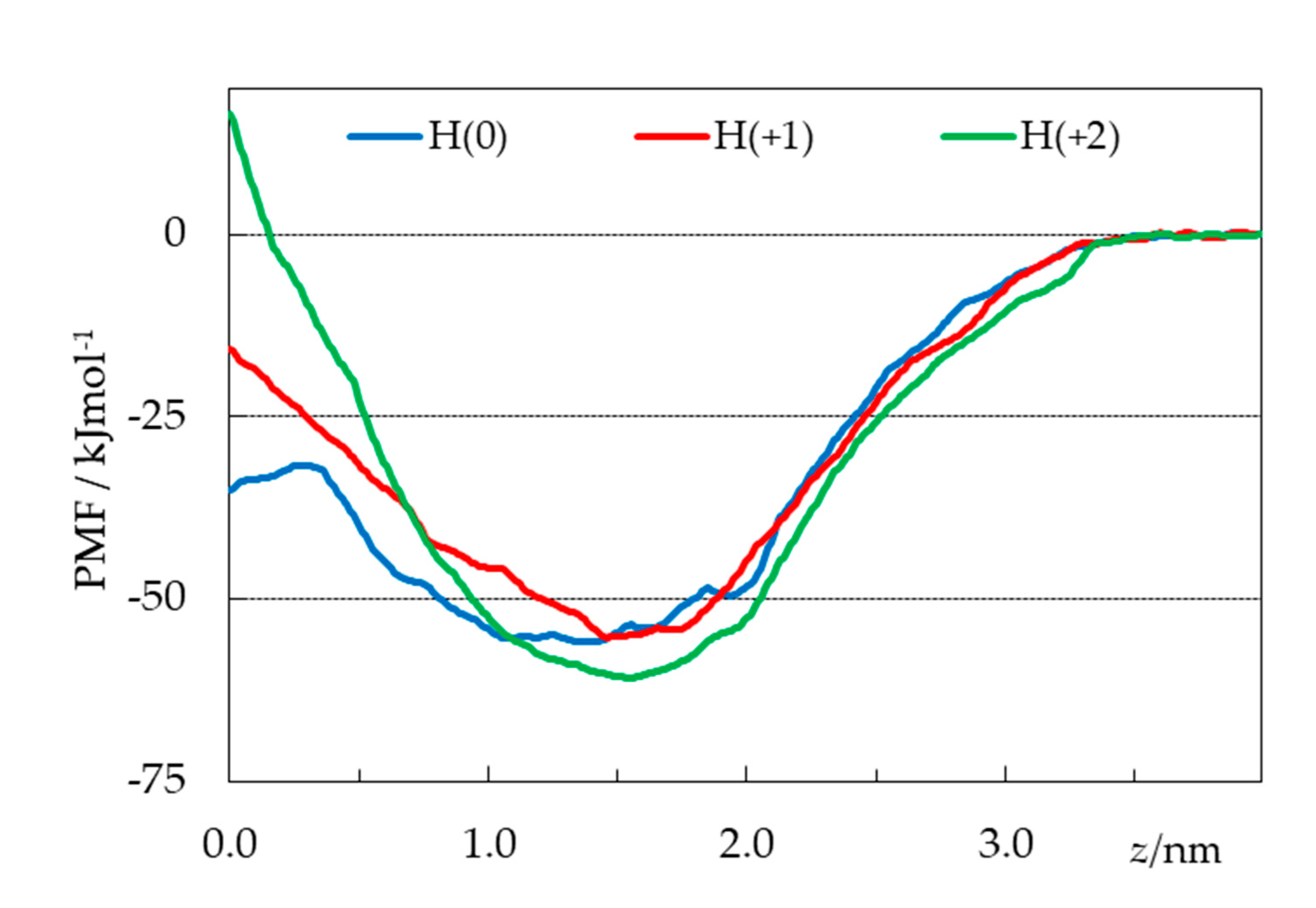
2.4. Free Energy Profiles from Umbrella Sampling MD

From umbrella sampling simulations, free energy profiles were calculated for the three considered H33442 forms, as described in detail in the Methods section. The potential of mean force (PMF) curves are shown in Figure 10, whereas Figures S3-S5 depict uncertainty estimates and convergence analysis (PMF profiles obtained using different regions of the 0 < t < 120 ns simulation time range, following the procedure of reference [42]) for the different curves.
As expected for amphiphilic solutes [42,43,44,45,46], the free energy is reduced when they interact with the lipid bilayer, coming from the aqueous medium. Energy minima are observed for the three ionization states at depths close to those obtained from the unrestrained simulations and shown in Figure 7, again similar for all forms (slightly more interior for the neutral form). The minimal ordinate values are also similar for the three states. Whereas the value calculated for H(+2) form is lower than those obtained for the other ones by ~5-6 kJmol-1, this difference is smaller than the uncertainty of approximately ±10 kJmol−1 indicated from bootstrapping analysis (Figs. S3E-S5E). In the absence of clearcut distinction in the regions around the equilibrium locations, the most striking difference in the three free energy profiles occurs for the regions nearest the center of the bilayer (z ≈ 0). Neutral H33442 displays a 24 kJmol-1 energy barrier for crossing from the free energy minimum to a maximum located at z = 0.26 nm, before decreasing by 3.5 kJmol-1 between the latter location and z = 0. In recent studies by our group, free energy plateaus or slight decreases near the bilayer center have been obtained for neutral solutes such as cholesterol [43], neutral rhodamine dyes [44] or undissociated fatty acids [45]. This feature is not observed in the profiles of the charged H(+1) and H(+2), for which maxima are observed at z = 0, with free energy barriers (of 40 and 78 kJmol-1, respectively) that increase with the charge of the solute.
Following the procedure used in recent studies [44,47,48,49,50,51], these calculated free energy profiles may be used to obtain computational estimates of the partition coefficient:
K P ∝ ∫ 0 a exp ⁡ ( − Δ G ( z ) / R T ) d z
Because of different underlying reference states in the experimental and calculated KP, as well as arbitrariness in the location of the bulk water/lipid interphase in the simulations, here considered to be a = 4.0 nm, no attempt is made to calculate absolute KP values. Still, we can compare relative values of computational estimates of KP for the three simulated forms. From the PMF profiles, the lowest KP value was obtained for the H(+1) state, below the corresponding ones for H(0) and H(+2) by 0.3 and 1.0 log units, respectively. This order does not fully coincide with the one resulting from the experimental determinations (Table 1), which point to a steady ~2-fold (or 0.4 log units) increase in KP as pH is increased from 5 to 9, with dominant protonation state varying between +2 and 0 [7,34,35] Still, both experimental and computational values agree in the fact that KP shows low sensitivity across a wide range of pH values.

3. Materials and Methods

3.1. Materials

The lipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) was acquired from Avanti Polar Lipids, Inc. (Alabaster, Alabama, USA). Hoechst 33342 (H33342) was acquired from Sigma - Aldrich Química S.A. (Sintra, Portugal). The water used to prepare the solutions was first distilled, and deionized by ion exchange cartridges and activated carbon filters (ARIOSO UP, from Human, Seoul, Republic of Korea), with a final resistance ≥ 18 MΩ. Reagents and solvents used were analytical grade or with higher purity.

3.2. Preparation of Large Unilamellar Vesicles (LUVs)

The LUVs were prepared by extrusion as previously described [52]. For the partition experiments followed by H33342 fluorescence properties, the aqueous buffer used to hydrate the lipid film contained 3.3 mM Trizma, 3.3 mM citric acid, 3.3 mM ammonium phosphate, 150 mM NaCl, and 0.02 % m/v sodium azide, with the pH previously adjusted to the required value by addition of HCl or NaOH (pH between 3 and 11). Large Unilamelar Vesicles (LUVs) were prepared from the MLVs obtained after hydration of the lipid film by freeze-thaw and extrusion through two stacked polycarbonate filters (with a pore diameter of 100 nm (for ITC experiments) or 50 nm (for fluorescence experiments). The smaller size used in the fluorescence-based experiments was required to decrease the contribution from light scatter. The liposomes were allowed to stabilize overnight before use, to allow the dissipation of the stress imposed by extrusion, and their effective size was analyzed by dynamic light scattering (Zetasizer Nano ZS, Malvern). The average diameter was 77 ± 2 nm or 112 ± 7 when filters with pore diameter of 50 or 100 nm were used for extrusion. The final lipid concentration was quantified using the Bartlett method. The liposome samples were stored at 4 to 8 °C and used within 2 weeks.

3.3. Partition of Hoechst 33342 to POPC LUVs

A stock of H33342 was first prepared in methanol and quantified by UV-vis absorption (Spectronic Unicam UV500) assuming a molar absorptivity of 4.7×104 M-1 cm-1 at 343 nm [53]. The required volume of this solution was then evaporated to prepare a stock of H33342 in DMSO at a concentration of 50 µM. An aliquot from this stock was squirted under vortex to a buffer solution (previously heated to 37 °C), to obtain a final solution with 2 % DMSO and Hoechst 33342 at 1 µM. The fluorescence intensity spectra and/or the fluorescence anisotropy were obtained (Carry Eclipse, Varian) for excitation at 340 nm. Aliquots of the LUV suspension were then added, and the fluorescence signal was obtained, with 10 min equilibration between each LUV addition.
At pH ≥ 6, partition of H33342 to the lipid bilayer leads to a strong increase in the fluorescence intensity and a red shift in the spectra. The partition coefficient (KP) was calculated from the dependence of the fluorescence intensity at 470 nm with the lipid concentration, equation (2):
I = I W + I M K P V ¯ POPC POPC 1 + K P V ¯ POPC POPC
where I W and I M are the fluorescence intensity obtained when all H33342 is the aqueous medium or associated with the membrane, respectively. A molar volume ( V ¯ POPC ) of 0.8 dm3/mol was considered, and it was assumed that all lipid is accessible (corresponding to full translocation of Hoechst during the 10 min equilibration).
At lower pH values, the fluorescence intensity from H33342 in the aqueous medium increases significantly with a maximum emission at 500 nm, being similar in both media (aqueous and membrane). Due to the small variation in the fluorescence intensity, the estimates of KP obtained from equation (2) have a large uncertainty. In these conditions, association with the membrane is followed more accurately through the variation in the fluorescence anisotropy, equation (3):
r = r W + α M   r M K P V ¯ POPC POPC 1 + α M   K P V ¯ POPC POPC
where r W and r M correspond to the fluorescence anisotropy when H33342 is all in the aqueous medium or in the membrane, and r is that observed at a given lipid concentration. The parameter α M is the ratio between the fluorescence emission intensity when H33342 is in the membrane and in the aqueous medium, as exemplified in Figure 11. This parameter was estimated from the trend observed in the fluorescence intensity.
The association of H33342 with the POPC membranes was also characterized by Isothermal Titration Calorimetry (ITC) to obtain the enthalpy of the interaction. Titrations were performed on a VP-ITC from MicroCal (Northampton, MA) at 25 °C, with injection speed 0.5 µL/s, stirring speed 459 rpm, and reference power 10 µcal/s. The LUVs (at a lipid concentration of 10 mM) were placed in the syringe and added to H33342 (at a concentration of 5 µM) in 10 µL aliquots. The solvent was saline phosphate buffer (10 mM phosphate with 150 mM NaCl, previously equilibrated at different pH values from 5.3 to 8.2) containing 2 % (v/v) DMSO. All solutions were previously degassed for 10 min. The thermogram was integrated using the data analysis software Origin 7.0 as modified by MicroCal for ITC experiments. The heat evolved was analyzed assuming simple partition and considering that all lipid is available for interaction with H33342. The fitting parameters, K P and Δ H o , were obtained using the Solver Add-In from Excel® with the spreadsheet provided in reference [54].

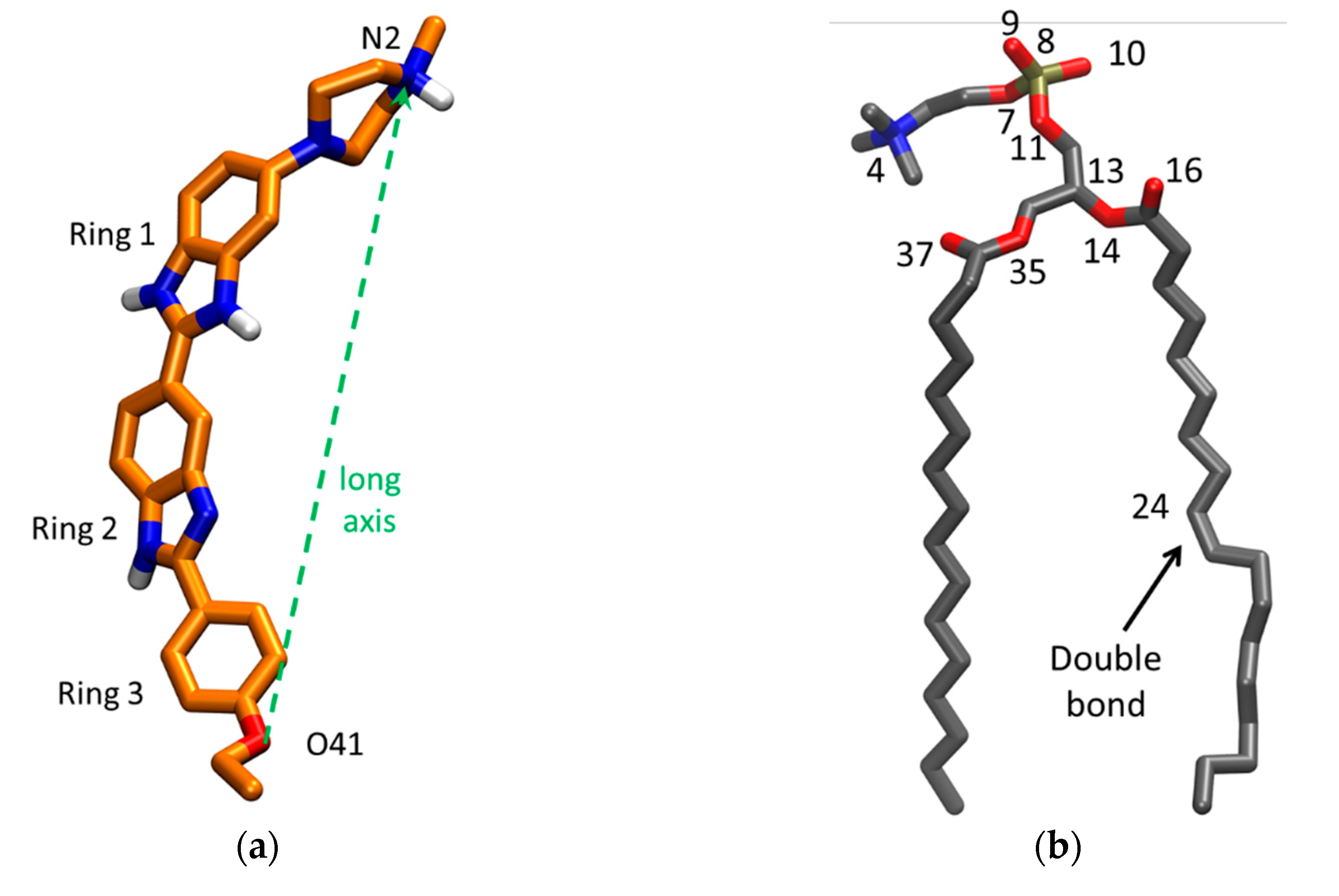
3.4. Quantum chemical calculations

Geometries of H33442 in different protonated forms were obtained by density functional theory (DFT) from optimizations using the hybrid exchange–correlation functional B3LYP [55,56] with the 6-31G(d,p) basis set. Solvent effects were considered by means of the implicit polarized continuum (PCM) [57,58] model. Frequency analysis confirmed that each optimized geometry was an energy minimum by the non-existence of imaginary frequencies. Free energies in solution were calculated at room temperature (T=298 K) with the thermal corrections calculated using the quasiharmonic oscillator approximation, where vibrational frequencies smaller than 100 cm−1 are raised to 100 cm−1 due to the failure of the harmonic oscillator model for low-frequency vibrational modes [59].
Partial charges of selected H33442 in different protonated forms were calculated from the optimized geometries, followed by a least-squares fit to the electrostatic potential obtained at the same theory level, according to the Merz-Singh-Kollman schemes [60,61]. All quantum calculations were performed with the Gaussian 16 package [62].

3.5. MD simulation details

MD simulation and trajectory analysis was carried out using GROMACS 5 [63,64,65]. The united-atom GROMOS 54a7 force field was used [66], with lipid parameters from Poger and Mark [67,68]. For H33342, the most stable structures obtained from the quantum chemical calculations for H(0), H(+1) and H(+2) were modeled using Automated Topology Builder [69,70,71]. We replaced the atomic charges generated by ATB with the values obtained as described in the previous subsection. The stability of the probe force field parameters was verified in simulations of each of three ionization states in water (not shown). A fully hydrated POPC bilayer, composed of 128 lipids and 5412 SPC waters [72] was built with standard GROMACS tools. For each ionization state, three different systems were generated and simulated, all of them with all four H33342 molecules. In two of these replicates (1 and 2 in Figure 5 and Figure S1), the probes were initially placed just outside the bilayer, 2 near each leaflet. In the other one (referred to as 3 in Figure 5 and Figure S1), H33442 molecules were placed in the POPC bilayer midplane. In the simulations with charged H33342, a corresponding number of chloride ions was added to the aqueous medium, to ensure electroneutrality.
All systems were simulated under NpT conditions at 298 K and 1 bar. Equilibration/ production run protocols and other simulation options were conducted as described elsewhere [73]. Each of the nine production runs was carried out for 200 ns. For visualization of structures and trajectories, VMD software was used [74].
The free energy of the system (ΔG), as a function of the reaction coordinate (defined as the distance between the center of mass of the H33442 molecule and the local center of mass of the POPC bilayer, i.e. calculated using only the POPC molecules whose locations in the bilayer plane were contained in a 1.1 nm radius cylinder centered on the solute), is derived from the PMF, obtained from a series of umbrella sampling (US) simulations [75]. For this purpose, a solute molecule, initially in the aqueous phase, is firstly pulled to the center of the bilayer (z = 0), with a rate of 0.0005 nm/ps and a force constant of 500 kJmol-1nm-2. Subsequently, a second pulling run was carried out, gently pulling in the opposite direction, using the same speed and force constant of the previous step, starting from z = 0 and ending at z = 4.0 nm. From this simulation, 41 configurations were extracted in which the molecule was approximately in each of the transverse positions between z = 0 and z = 4.0 nm, spaced 0.1 nm apart. This procedure was chosen to obtain the initial configurations for the umbrella sampling runs, avoiding the slow convergence of the free energy profiles observed in similar systems, when the final pulling is done from the water medium to the membrane interior [42] For the three H33442 forms, each of these 41 systems was simulated for 120 ns, using the same conditions as in the unrestrained runs, but imposing a harmonic restraint potential, centered in the reference position, with a force constant of 3000 kJmol-1nm-2. The resulting simulations were checked for convergence (Figures S3-S5) and analyzed using the Weighted Histogram Analysis Method [76,77] to produce the PMF profiles, using the last 80 ns of each run for sampling.

4. Conclusions

The results obtained for the association of H33342 with POPC membranes at distinct solute ionization states clearly show that lipophilicity cannot be directly estimated from solute hydrophobicity. The lipids that form biological membranes have a large variety of groups that can interact with the solutes, and biomembranes are very heterogeneous media that may accommodate solutes with distinct physico-chemical properties. This behaviour highlights the limitations of partition between water and water-immiscible non-polar solvents (such as octanol) when estimating the affinity for biomembranes. The limitations of such approaches become strikingly evident when the calculated P and D (octanol/water partition of the neutral form and the distribution of the ionization forms at a given pH value, respectively) is represented together with the observed KP as a function of pH for the case of H33342, Figure 12.
The calculated distribution between the aqueous media and octanol is close to the calculated partition coefficient between the two homogeneous solvents in the pH range 9-10 due to the higher abundance of H33342 neutral form, and decreases for lower and higher pH values where the charged forms become more abundant. A decrease of over 5 orders of magnitude is observed for LogD when the pH is changed from 9 to 3 (where forms +3 and +2 are the most abundant). In contrast, the partition coefficient between the aqueous media and POPC bilayers decreases by only one order of magnitude in this pH region.
The results obtained with the MD simulations allow the interpretation of the difference between partition to the homogeneous octanol solvent or to the heterogeneous and complex lipid bilayer. On the one hand, the distinct environments of the lipid bilayer are able to efficiently solvate solutes with distinct physico-chemical properties. On the other hand, glycerophospholipids (the most abundant in biomembranes) contain several charged groups and oxygens that may participate in electrostatic interactions. When amine groups become protonated, the decrease in hydrophobicity provided by the increase in charge is compensated by an increase in the number of hydrogen bonds that may be established with the acceptor groups in the membrane lipids, leading to small variations in the overall affinity for the membrane.
In conclusion, to estimate the local concentration of H33342 in lipid membranes, the overall hydrophobicity estimated from water/octanol partition cannot be used. The partition coefficients to the actual membranes must be used instead, or those provided in this work for POPC which is the most abundant lipid in biomembranes [14,15,16,17,18,19]. This procedure must be followed whenever the association of solutes with membrane proteins is considered [78], as is the case for the interaction with the efflux transporter P-glycoprotein of which Hoechst dyes are well known substrates [8,9]. Failure to do so will lead to apparent affinities for the membrane proteins that do not reflect the interactions established between the ligand and the protein [79]

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: Time variations of the center of mass positions of all individual molecules in each simulation; Figure S2: Average transverse distances to the bilayer center for selected atoms of POPC; Figure S3: PMF error and convergence analysis for H(0); Figure S4: PMF error and convergence analysis for H(+1); Figure S5: PMF error and convergence analysis for H(+2).

Author Contributions

Conceptualization, M.J.M.; methodology, H.A.L.F., J.P.P.R., L.M.S.L., M.J.M.; formal analysis, M.M.C., P.d.S., J.P.P.R., L.M.S.L., M.J.M.; investigation, M.M.C., H.A.L.F., P.d.S., J.S., J.P.P.R.; resources, J.P.P.R., L.M.S.L., M.J.M.; writing—original draft preparation, H.A.L.F., J.P.P.R., L.M.S.L., M.J.M.; writing—review and editing, all authors; supervision, H.A.L.F., M.J.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the European Regional Development Fund, through COMPETE2020-Operational Program for Competitiveness and Internationalization, and Portuguese funds via FCT-Fundação para a Ciência e a Tecnologia, under projects UIDB/00313/2020, UIDP/00313/2020, UIDB/50006/2020 and UIDP/50006/2020 (Portugal). H.A.L.F. was funded by Programa Operacional Regional do Centro (CENTRO-04-3559-FSE-000162) within the European Social Fund (ESF), and M.M.C. acknowledges support from FCT through fellowship 2022.11593.BD.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Source experimental and simulation data will be provided by the corresponding authors upon request.

Acknowledgments

The authors acknowledge the computational resources provided by the Laboratory for Advanced Computing at University of Coimbra (https://www.uc.pt/lca, accessed on 20 January 2023), funded by FCT I.P. under the Advanced Computing Projects 2021.09741.CPCA and CPCA/A1/407703/2021, on the platform Navigator.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A

Typical results obtained for the partition of H33342 to POPC liposomes at all studied pH values, based on the variation of H33342 fluorescence intensity (Figure A1) or on the variation of its fluorescence anisotropy (Figure A2).
Preprints 78429 g0a1
Figure A1. Typical results obtained for the variation of H33342 fluorescence emission intensity with the concentration of POPC in LUVs at different pH values. The lines are the best fit of a simple partition, equation (2).
Figure A1. Typical results obtained for the variation of H33342 fluorescence emission intensity with the concentration of POPC in LUVs at different pH values. The lines are the best fit of a simple partition, equation (2).
Preprints 78429 g0a1
Preprints 78429 g0a2
Figure A2. Typical results obtained for the variation of H33342 fluorescence anisotropy (λexc=340 nm, λem=500-510, 450-510, and 450-470 nm for pH=3, 4, and 6, respectively) with the concentration of POPC in LUVs at different pH values. The lines are the best fit of a simple partition, equation (3), with α M =2, 2, and 13 for pH=3, 4, and 6, respectively.
Figure A2. Typical results obtained for the variation of H33342 fluorescence anisotropy (λexc=340 nm, λem=500-510, 450-510, and 450-470 nm for pH=3, 4, and 6, respectively) with the concentration of POPC in LUVs at different pH values. The lines are the best fit of a simple partition, equation (3), with α M =2, 2, and 13 for pH=3, 4, and 6, respectively.
Preprints 78429 g0a2

References

  1. Weisenfeld, R.B. Mass Transport Kinetics of the DNA-Binding Dye Hoechst-33342 into Bovine Spermatozoa. Bioorg Med Chem 2007, 15, 6361–6366. [Google Scholar] [CrossRef] [PubMed]
  2. Lalande, M.E.; Ling, V.; Miller, R.G. Hoechst 33342 Dye Uptake as a Probe of Membrane Permeability Changes in Mammalian Cells. Proceedings of the National Academy of Sciences 1981, 78, 363–367. [Google Scholar] [CrossRef] [PubMed]
  3. Neuberger, A.; van Veen, H.W. Hoechst 33342 Is a Hidden “Janus” amongst Substrates for the Multidrug Efflux Pump LmrP. PLoS One 2015, 10, e0141991. [Google Scholar] [CrossRef] [PubMed]
  4. Tang, F.; Ouyang, H.; Yang, J.Z.; Borchardt, R.T. Bidirectional Transport of Rhodamine 123 and Hoechst 33342, Fluorescence Probes of the Binding Sites on P-Glycoprotein, across MDCK–MDR1 Cell Monolayers. J Pharm Sci 2004, 93, 1185–1194. [Google Scholar] [CrossRef]
  5. Clay, A.T.; Sharom, F.J. Lipid Bilayer Properties Control Membrane Partitioning, Binding, and Transport of P-Glycoprotein Substrates. Biochemistry 2013, 52, 343–354. [Google Scholar] [CrossRef]
  6. Bucevičius, J.; Lukinavičius, G.; Gerasimaitė, R. The Use of Hoechst Dyes for DNA Staining and Beyond. Chemosensors 2018, 6. [Google Scholar] [CrossRef]
  7. Alemán, C.; Namba, A.M.; Casanovas, J. Acid-Base and Electronic Structure-Dependent Properties of Hoechst 33342. J Biomol Struct Dyn 2005, 23, 29–36. [Google Scholar] [CrossRef]
  8. Shapiro, A.B.; Corder, A.B.; Ling, V. P-Glycoprotein-Mediated Hoechst 33342 Transport Out of the Lipid Bilayer. Eur J Biochem 1997, 250, 115–121. [Google Scholar] [CrossRef]
  9. Eckford, P.D.W.; Sharom, F.J. ABC Efflux Pump-Based Resistance to Chemotherapy Drugs. Chem Rev 2009, 109, 2989–3011. [Google Scholar] [CrossRef]
  10. Chufan, E.E.; Sim, H.-M.; Ambudkar, S. V Chapter Three - Molecular Basis of the Polyspecificity of P-Glycoprotein (ABCB1): Recent Biochemical and Structural Studies. In ABC Transporters and Cancer; Schuetz, J.D., Ishikawa, T., Eds.; Advances in Cancer Research; Academic Press, 2015; Vol. 125, pp. 71–96.
  11. Benzimidazole Derivatives - Drugbank Online. Available online: https://www.drugbank.ca/categories/DBCAT002403 (accessed on 12 June 2023).
  12. Imidazole Derivatives - Drugbank Online. Available online: https://www.drugbank.ca/categories/DBCAT002246 (accessed on 12 June 2023).
  13. Gaohua, L.; Miao, X.; Dou, L. Crosstalk of Physiological PH and Chemical PKa under the Umbrella of Physiologically Based Pharmacokinetic Modeling of Drug Absorption, Distribution, Metabolism, Excretion, and Toxicity. Expert Opin Drug Metab Toxicol 2021, 17, 1103–1124. [Google Scholar] [CrossRef]
  14. Pradas, I.; Huynh, K.; Cabré, R.; Ayala, V.; Meikle, P.J.; Jové, M.; Pamplona, R. Lipidomics Reveals a Tissue-Specific Fingerprint. Front Physiol 2018, 9. [Google Scholar] [CrossRef]
  15. Aviram, R.; Manella, G.; Kopelman, N.; Neufeld-Cohen, A.; Zwighaft, Z.; Elimelech, M.; Adamovich, Y.; Golik, M.; Wang, C.; Han, X.; et al. Lipidomics Analyses Reveal Temporal and Spatial Lipid Organization and Uncover Daily Oscillations in Intracellular Organelles. Mol Cell 2016, 62, 636–648. [Google Scholar] [CrossRef] [PubMed]
  16. Gerl, M.J.; Sampaio, J.L.; Urban, S.; Kalvodova, L.; Verbavatz, J.-M.; Binnington, B.; Lindemann, D.; Lingwood, C.A.; Shevchenko, A.; Schroeder, C.; et al. Quantitative Analysis of the Lipidomes of the Influenza Virus Envelope and MDCK Cell Apical Membrane. Journal of Cell Biology 2012, 196, 213–221. [Google Scholar] [CrossRef] [PubMed]
  17. Leidl, K.; Liebisch, G.; Richter, D.; Schmitz, G. Mass Spectrometric Analysis of Lipid Species of Human Circulating Blood Cells. Biochimica et Biophysica Acta (BBA) - Molecular and Cell Biology of Lipids 2008, 1781, 655–664. [Google Scholar] [CrossRef]
  18. Moreno, M.J.; Teles Martins, P.A.; Bernardino, E.F.; Abel, B.; Ambudkar, S. V Characterization of the Lipidome and Biophysical Properties of Membranes from High Five Insect Cells Expressing Mouse P-Glycoprotein. Biomolecules 2021, 11. [Google Scholar] [CrossRef] [PubMed]
  19. Klose, C.; Surma, M.A.; Simons, K. Organellar Lipidomics—Background and Perspectives. Curr Opin Cell Biol 2013, 25, 406–413. [Google Scholar] [CrossRef]
  20. Martins, P.T.; Velazquez-Campoy, A.; Vaz, W.L.C.; Cardoso, R.M.S.; Valério, J.; Moreno, M.J. Kinetics and Thermodynamics of Chlorpromazine Interaction with Lipid Bilayers: Effect of Charge and Cholesterol. J Am Chem Soc 2012, 134, 4184–4195. [Google Scholar] [CrossRef]
  21. Coreta-Gomes, F.M.; Martins, P.A.T.; Velazquez-Campoy, A.; Vaz, W.L.C.; Geraldes, C.F.G.; Moreno, M.J. Interaction of Bile Salts with Model Membranes Mimicking the Gastrointestinal Epithelium: A Study by Isothermal Titration Calorimetry. Langmuir 2015, 31, 9097–9104. [Google Scholar] [CrossRef]
  22. Rowe, E.S.; Zhang, F.; Leung, T.W.; Parr, J.S.; Guy, P.T. Thermodynamics of Membrane Partitioning for a Series of N-Alcohols Determined by Titration Calorimetry: Role of Hydrophobic Effects. Biochemistry 1998, 37, 2430–2440. [Google Scholar] [CrossRef]
  23. Martins, P.A.T.; Domingues, N.; Pires, C.; Alves, A.M.; Palmeira, T.; Samelo, J.; Cardoso, R.; Velazquez-Campoy, A.; Moreno, M.J. Molecular Crowding Effects on the Distribution of Amphiphiles in Biological Media. Colloids Surf B Biointerfaces 2019, 180, 319–325. [Google Scholar] [CrossRef]
  24. Beschiaschvili, G.; Seelig, J. Peptide Binding to Lipid Bilayers. Nonclassical Hydrophobic Effect and Membrane-Induced PK Shifts. Biochemistry 1992, 31, 10044–10053. [Google Scholar] [CrossRef] [PubMed]
  25. Loura, L.M.S.; Prates Ramalho, J.P. Fluorescent Membrane Probes’ Behavior in Lipid Bilayers: Insights from Molecular Dynamics Simulations. Biophys Rev 2009, 1, 141–148. [Google Scholar] [CrossRef]
  26. Loura, L.M.S.; Ramalho, J.P.P. Recent Developments in Molecular Dynamics Simulations of Fluorescent Membrane Probes. Molecules 2011, 16, 5437–5452. [Google Scholar] [CrossRef] [PubMed]
  27. Filipe, H.A.L.; Moreno, M.J.; Loura, L.M.S. The Secret Lives of Fluorescent Membrane Probes as Revealed by Molecular Dynamics Simulations. Molecules 2020, 25. [Google Scholar] [CrossRef]
  28. Debruycker, V.; Hutchin, A.; Masureel, M.; Ficici, E.; Martens, C.; Legrand, P.; Stein, R.A.; Mchaourab, H.S.; Faraldo-Gómez, J.D.; Remaut, H.; et al. An Embedded Lipid in the Multidrug Transporter LmrP Suggests a Mechanism for Polyspecificity. Nat Struct Mol Biol 2020, 27, 829–835. [Google Scholar] [CrossRef] [PubMed]
  29. Thaker, T.M.; Mishra, S.; Zhou, W.; Mohan, M.; Tang, Q.; Faraldo-Goméz, J.D.; Mchaourab, H.S.; Tomasiak, T.M. Asymmetric Drug Binding in an ATP-Loaded Inward-Facing State of an ABC Transporter. Nat Chem Biol 2022, 18, 226–235. [Google Scholar] [CrossRef]
  30. Thai, N.Q.; Tseng, N.-H.; Vu, M.T.; Nguyen, T.T.; Linh, H.Q.; Hu, C.-K.; Chen, Y.-R.; Li, M.S. Discovery of DNA Dyes Hoechst 34580 and 33342 as Good Candidates for Inhibiting Amyloid Beta Formation: In Silico and in Vitro Study. J Comput Aided Mol Des 2016, 30, 639–650. [Google Scholar] [CrossRef]
  31. Subramanian, N.; Schumann-Gillett, A.; Mark, A.E.; O’Mara, M.L. Probing the Pharmacological Binding Sites of P-Glycoprotein Using Umbrella Sampling Simulations. J Chem Inf Model 2019, 59, 2287–2298. [Google Scholar] [CrossRef]
  32. Singh, M.; Sur, S.; Rastogi, G.K.; Jayaram, B.; Tandon, V. Bi and Tri-Substituted Phenyl Rings Containing Bisbenzimidazoles Bind Differentially with DNA Duplexes: A Biophysical and Molecular Simulation Study. Mol Biosyst 2013, 9, 2541–2553. [Google Scholar] [CrossRef]
  33. Putman, M.; Koole, L.A.; van Veen, H.W.; Konings, W.N. The Secondary Multidrug Transporter LmrP Contains Multiple Drug Interaction Sites. Biochemistry 1999, 38, 13900–13905. [Google Scholar] [CrossRef]
  34. Ladinig, M.; Leupin, W.; Meuwly, M.; Respondek, M.; Wirz, J.; Zoete, V. Protonation Equilibria of Hoechst 33258 in Aqueous Solution. Helv Chim Acta 2005, 88, 53–67. [Google Scholar] [CrossRef]
  35. Swain, B.M.; Guo, D.; Singh, H.; Rawlins, P.B.; McAlister, M.; van Veen, H.W. Complexities of a Protonatable Substrate in Measurements of Hoechst 33342 Transport by Multidrug Transporter LmrP. Sci Rep 2020, 10, 20026. [Google Scholar] [CrossRef]
  36. MarvinSketch Version 22.9.0. Available online: http://www.chemaxon.com (accessed on 24 May 2023).
  37. Paketurytė, V.; Petrauskas, V.; Zubrienė, A.; Abian, O.; Bastos, M.; Chen, W.-Y.; Moreno, M.J.; Krainer, G.; Linkuvienė, V.; Sedivy, A.; et al. Uncertainty in Protein–Ligand Binding Constants: Asymmetric Confidence Intervals versus Standard Errors. European Biophysics Journal 2021, 50, 661–670. [Google Scholar] [CrossRef] [PubMed]
  38. Filipe, H.A.L.; Coreta-Gomes, F.M.; Velazquez-Campoy, A.; Almeida, A.R.; Peixoto, A.F.; Pereira, M.M.; Vaz, W.L.C.; Moreno, M.J. Synthesis and Characterization of a Lipidic Alpha Amino Acid: Solubility and Interaction with Serum Albumin and Lipid Bilayers. J Phys Chem B 2013, 117, 3439–3448. [Google Scholar] [CrossRef] [PubMed]
  39. Heiko Heerklotz The Microcalorimetry of Lipid Membranes. Journal of Physics: Condensed Matter 2004, 16, R441. [CrossRef]
  40. Goldberg, R.N.; Kishore, N.; Lennen, R.M. Thermodynamic Quantities for the Ionization Reactions of Buffers. J Phys Chem Ref Data 2002, 31, 231–370. [Google Scholar] [CrossRef]
  41. Elías-Wolff, F.; Lindén, M.; Lyubartsev, A.P.; Brandt, E.G. Computing Curvature Sensitivity of Biomolecules in Membranes by Simulated Buckling. J Chem Theory Comput 2018, 14, 1643–1655. [Google Scholar] [CrossRef]
  42. Filipe, H.A.L.; Moreno, M.J.; Róg, T.; Vattulainen, I.; Loura, L.M.S. How to Tackle the Issues in Free Energy Simulations of Long Amphiphiles Interacting with Lipid Membranes: Convergence and Local Membrane Deformations. Journal of Physical Chemistry B 2014, 118, 3572–3581. [Google Scholar] [CrossRef]
  43. Filipe, H.A.L.; Javanainen, M.; Salvador, A.; Galvão, A.M.; Vattulainen, I.; Loura, L.M.S.; Moreno, M.J. Quantitative Assessment of Methods Used To Obtain Rate Constants from Molecular Dynamics Simulations—Translocation of Cholesterol across Lipid Bilayers. J Chem Theory Comput 2018, 14, 3840–3848. [Google Scholar] [CrossRef]
  44. Magalhães, N.; Simões, G.M.; Ramos, C.; Samelo, J.; Oliveira, A.C.; Filipe, H.A.L.; Ramalho, J.P.P.; Moreno, M.J.; Loura, L.M.S. Interactions between Rhodamine Dyes and Model Membrane Systems&mdash;Insights from Molecular Dynamics Simulations. Molecules 2022, 27. [Google Scholar] [CrossRef]
  45. Oliveira, A.C.; Filipe, H.A.L.; Loura, L.M.S. Fluorescent Probes Cis- and Trans-Parinaric Acids in Fluid and Gel Lipid Bilayers: A Molecular Dynamics Study. Molecules 2023, 28. [Google Scholar] [CrossRef]
  46. Filipe, H.A.L.; Loura, L.M.S.; Moreno, M.J. Permeation of a Homologous Series of NBD-Labeled Fatty Amines through Lipid Bilayers: A Molecular Dynamics Study. Membranes (Basel) 2023, 13. [Google Scholar] [CrossRef] [PubMed]
  47. MacCallum, J.L.; Tieleman, D.P. Computer Simulation of the Distribution of Hexane in a Lipid Bilayer: Spatially Resolved Free Energy, Entropy, and Enthalpy Profiles. J Am Chem Soc 2006, 128, 125–130. [Google Scholar] [CrossRef] [PubMed]
  48. Paloncýová, M.; DeVane, R.; Murch, B.; Berka, K.; Otyepka, M. Amphiphilic Drug-Like Molecules Accumulate in a Membrane below the Head Group Region. J Phys Chem B 2014, 118, 1030–1039. [Google Scholar] [CrossRef] [PubMed]
  49. Kiametis, A.S.; Stock, L.; Cirqueira, L.; Treptow, W. Atomistic Model for Simulations of the Sedative Hypnotic Drug 2,2,2-Trichloroethanol. ACS Omega 2018, 3, 15916–15923. [Google Scholar] [CrossRef]
  50. Tang, P.K.; Chakraborty, K.; Hu, W.; Kang, M.; Loverde, S.M. Interaction of Camptothecin with Model Cellular Membranes. J Chem Theory Comput 2020, 16, 3373–3384. [Google Scholar] [CrossRef] [PubMed]
  51. Piasentin, N.; Lian, G.; Cai, Q. Evaluation of Constrained and Restrained Molecular Dynamics Simulation Methods for Predicting Skin Lipid Permeability. ACS Omega 2021, 6, 35363–35374. [Google Scholar] [CrossRef]
  52. Samelo, J.; Mora, M.J.; Granero, G.E.; Moreno, M.J. Partition of Amphiphilic Molecules to Lipid Bilayers by ITC: Low-Affinity Solutes. ACS Omega 2017, 2, 6863–6869. [Google Scholar] [CrossRef]
  53. Thermo Scientific Instructions - Hoechst 33342. Available online: https://assets.thermofisher.com/TFS-Assets/LSG/manuals/MAN0011717_Hoechst_33342_UG.pdf (accessed on 12 June 2023).
  54. Moreno, M.J.; Bastos, M.; Velazquez-Campoy, A. Partition of Amphiphilic Molecules to Lipid Bilayers by Isothermal Titration Calorimetry. Anal Biochem 2010, 399, 44–47. [Google Scholar] [CrossRef]
  55. Perdew, J.P. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys Rev B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
  56. Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J Chem Phys 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  57. Amovilli, C.; Barone, V.; Cammi, R.; Cancès, E.; Cossi, M.; Mennucci, B.; Pomelli, C.S.; Tomasi, J. Recent Advances in the Description of Solvent Effects with the Polarizable Continuum Model. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Academic Press, 1998; Vol. 32, pp. 227–261 ISBN 0065-3276.
  58. Cossi, M.; Barone, V. Time-Dependent Density Functional Theory for Molecules in Liquid Solutions. J Chem Phys 2001, 115, 4708–4717. [Google Scholar] [CrossRef]
  59. Ribeiro, R.F.; Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Use of Solution-Phase Vibrational Frequencies in Continuum Models for the Free Energy of Solvation. J Phys Chem B 2011, 115, 14556–14562. [Google Scholar] [CrossRef] [PubMed]
  60. Besler, B.H.; Merz Jr., K. M.; Kollman, P.A. Atomic Charges Derived from Semiempirical Methods. J Comput Chem 1990, 11, 431–439. [Google Scholar] [CrossRef]
  61. Singh, U.C.; Kollman, P.A. An Approach to Computing Electrostatic Charges for Molecules. J Comput Chem 1984, 5, 129–145. [Google Scholar] [CrossRef]
  62. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C. 01 2016.
  63. Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindah, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
  64. Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
  65. Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J Chem Theory Comput 2008, 4, 435–447. [Google Scholar] [CrossRef]
  66. Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; van Gunsteren, W.F. Definition and Testing of the GROMOS Force-Field Versions 54A7 and 54B7. European Biophysics Journal 2011, 40, 843–856. [Google Scholar] [CrossRef]
  67. Poger, D.; Van Gunsteren, W.F.; Mark, A.E. A New Force Field for Simulating Phosphatidylcholine Bilayers. J Comput Chem 2010, 31, 1117–1125. [Google Scholar] [CrossRef] [PubMed]
  68. Poger, D.; Mark, A.E. On the Validation of Molecular Dynamics Simulations of Saturated and Cis-Monounsaturated Phosphatidylcholine Lipid Bilayers: A Comparison with Experiment. J Chem Theory Comput 2010, 6, 325–336. [Google Scholar] [CrossRef]
  69. Malde, A.K.; Zuo, L.; Breeze, M.; Stroet, M.; Poger, D.; Nair, P.C.; Oostenbrink, C.; Mark, A.E. An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0. J Chem Theory Comput 2011, 7, 4026–4037. [Google Scholar] [CrossRef] [PubMed]
  70. Stroet, M.; Caron, B.; Visscher, K.M.; Geerke, D.P.; Malde, A.K.; Mark, A.E. Automated Topology Builder Version 3.0: Prediction of Solvation Free Enthalpies in Water and Hexane. J Chem Theory Comput 2018, 14, 5834–5845. [Google Scholar] [CrossRef] [PubMed]
  71. Koziara, K.B.; Stroet, M.; Malde, A.K.; Mark, A.E. Testing and Validation of the Automated Topology Builder (ATB) Version 2.0: Prediction of Hydration Free Enthalpies. J Comput Aided Mol Des 2014, 28, 221–233. [Google Scholar] [CrossRef] [PubMed]
  72. Berendsen, H.J.C.; Postma, J.P.M.; Gunsteren, W.F. van; Hermans, J. Interaction Models for Water in Relation to Protein Hydration. In Intermolecular Forces; Pullman, B., Ed.; Springer, Dordrecht, 1981; pp. 331–342.
  73. Filipe, H.A.L.; Santos, L.S.; Prates Ramalho, J.P.; Moreno, M.J.; Loura, L.M.S. Behaviour of NBD-Head Group Labelled Phosphatidylethanolamines in POPC Bilayers: A Molecular Dynamics Study. Physical Chemistry Chemical Physics 2015, 17, 20066–20079. [Google Scholar] [CrossRef]
  74. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J Mol Graph 1996, 14, 33–38. [Google Scholar] [CrossRef]
  75. Torrie, G.M.; Valleau, J.P. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling. J Comput Phys 1977, 23, 187–199. [Google Scholar] [CrossRef]
  76. Hub, J.S.; De Groot, B.L.; Van Der Spoel, D. G_wham—A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates. J Chem Theory Comput 2010, 6, 3713–3720. [Google Scholar] [CrossRef]
  77. Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J Comput Chem 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
  78. Moreno, M.J.; Salvador, A. Ligand’s Partition to the Lipid Bilayer Should Be Accounted for When Estimating Their Affinity to Proteins. Molecules 2023, 28. [Google Scholar] [CrossRef] [PubMed]
  79. Moreno, M.J.; Filipe, H.A.L.; Cunha, S.V.P.; Ramos, C.V.; Martins, P.A.T.; Abel, B.; Loura, L.M.S.; Ambudkar, S. V Interaction of a Homologous Series of Amphiphiles with P-Glycoprotein in a Membrane Environment - Contributions of Polar and Non-Polar Interactions. Pharmaceutics 2023, 15. [Google Scholar] [CrossRef] [PubMed]
Preprints 78429 g001
Figure 1. (a) Structures of one of the isomers of H33442 with overall charge +2. (b) Structure of POPC. In both structures, numbers of selected atoms (relevant for the MD analyses) are indicated, and oxygen and nitrogen atoms are depicted in red and blue, respectively. Carbon or united CHn atoms are shown in orange for H33442 or grey for POPC. Hydrogens bound to N atoms are shown in white. The phosphorus atom of POPC is displayed in ochre.
Figure 1. (a) Structures of one of the isomers of H33442 with overall charge +2. (b) Structure of POPC. In both structures, numbers of selected atoms (relevant for the MD analyses) are indicated, and oxygen and nitrogen atoms are depicted in red and blue, respectively. Carbon or united CHn atoms are shown in orange for H33442 or grey for POPC. Hydrogens bound to N atoms are shown in white. The phosphorus atom of POPC is displayed in ochre.
Preprints 78429 g001
Preprints 78429 g002
Figure 2. Variation of H33342 fluorescence intensity at 470 nm (a) and fluorescence anisotropy at 450-470 nm (●), 470-490 nm (●), and 490-510 nm (●) (b) with the concentration of POPC at pH=6. The values obtained for the partition coefficient were all similar, leading to 1.8(±0.6)×103. The average value obtained for all samples (N=6) and conditions is shown in Table 1.
Figure 2. Variation of H33342 fluorescence intensity at 470 nm (a) and fluorescence anisotropy at 450-470 nm (●), 470-490 nm (●), and 490-510 nm (●) (b) with the concentration of POPC at pH=6. The values obtained for the partition coefficient were all similar, leading to 1.8(±0.6)×103. The average value obtained for all samples (N=6) and conditions is shown in Table 1.
Preprints 78429 g002
Preprints 78429 g003
Figure 3. Titration curves and best fit parameters obtained for the titration of H33342 (5 µM in the ITC cell) with 10 µL additions of POPC LUVs (10 mM in the ITC syringe), at 25 °C in PBS containing 2 % (v/v) DMSO and at the pH values indicated.
Figure 3. Titration curves and best fit parameters obtained for the titration of H33342 (5 µM in the ITC cell) with 10 µL additions of POPC LUVs (10 mM in the ITC syringe), at 25 °C in PBS containing 2 % (v/v) DMSO and at the pH values indicated.
Preprints 78429 g003
Preprints 78429 g004
Figure 4. Structures of Hoechst 33342 species in water optimized at PCM-B3LYP/6-31G(d,p) level. Relative free energies values are in kcal mol-1. Non protonated nitrogen atoms are highlighted.
Figure 4. Structures of Hoechst 33342 species in water optimized at PCM-B3LYP/6-31G(d,p) level. Relative free energies values are in kcal mol-1. Non protonated nitrogen atoms are highlighted.
Preprints 78429 g004
Preprints 78429 g005
Figure 5. Final snapshots of production runs. Each row concerns a different ionization state (H(0), H(+1) and H(+2), respectively). Different columns refer to runs 1, 2 (with probes starting from water) and 3 (with probes starting in the bilayer midplane) in each ionization state, respectively.
Figure 5. Final snapshots of production runs. Each row concerns a different ionization state (H(0), H(+1) and H(+2), respectively). Different columns refer to runs 1, 2 (with probes starting from water) and 3 (with probes starting in the bilayer midplane) in each ionization state, respectively.
Preprints 78429 g005
Preprints 78429 g006
Figure 6. Mass density profiles of H33342 along the direction normal to the bilayer plane, for the three studied forms. The shown curves are the average of the behavior of all molecules (except the aggregated molecules in run 1 of H(+1)) across the last 100 ns of the different simulations.
Figure 6. Mass density profiles of H33342 along the direction normal to the bilayer plane, for the three studied forms. The shown curves are the average of the behavior of all molecules (except the aggregated molecules in run 1 of H(+1)) across the last 100 ns of the different simulations.
Preprints 78429 g006
Preprints 78429 g007
Figure 7. Average transverse distances to the bilayer center for the center of mass (COM) of different atoms/groups (defined in Figure 1) of H33342 (in columns) and, as reference, for different lipid atoms in probe-free bilayers (in dotted lines). Averaging and error estimation involved the 12 H33342 molecules (10 for H(+1)) simulated in the three replicates of each ionization state.
Figure 7. Average transverse distances to the bilayer center for the center of mass (COM) of different atoms/groups (defined in Figure 1) of H33342 (in columns) and, as reference, for different lipid atoms in probe-free bilayers (in dotted lines). Averaging and error estimation involved the 12 H33342 molecules (10 for H(+1)) simulated in the three replicates of each ionization state.
Preprints 78429 g007
Preprints 78429 g008
Figure 8. Angular distributions for the tilt of H33342 long axis, relative to the bilayer normal, for the three simulated ionization states (see Figure 1a for axis definition).
Figure 8. Angular distributions for the tilt of H33342 long axis, relative to the bilayer normal, for the three simulated ionization states (see Figure 1a for axis definition).
Preprints 78429 g008
Preprints 78429 g009
Figure 9. Fraction of time of hydrogen bonds between H33342 N-H donor groups and POPC oxygen atoms.
Figure 9. Fraction of time of hydrogen bonds between H33342 N-H donor groups and POPC oxygen atoms.
Preprints 78429 g009
Preprints 78429 g010
Figure 10. PMF profiles of the simulated H33442 forms (obtained discarding the first 40 ns from analysis), as a function of the distance z between the centers of mass of the probe and the bilayer.
Figure 10. PMF profiles of the simulated H33442 forms (obtained discarding the first 40 ns from analysis), as a function of the distance z between the centers of mass of the probe and the bilayer.
Preprints 78429 g010
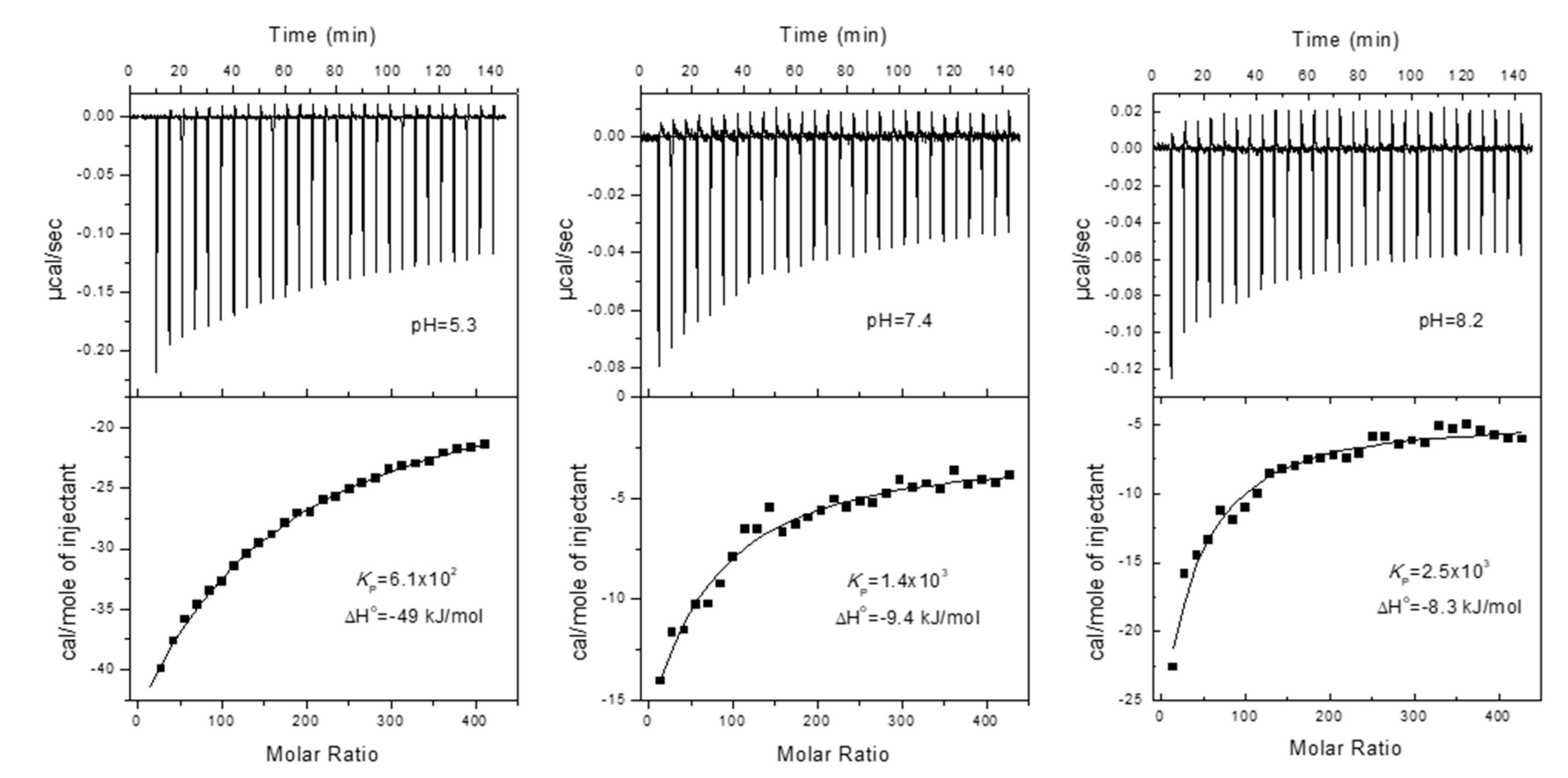
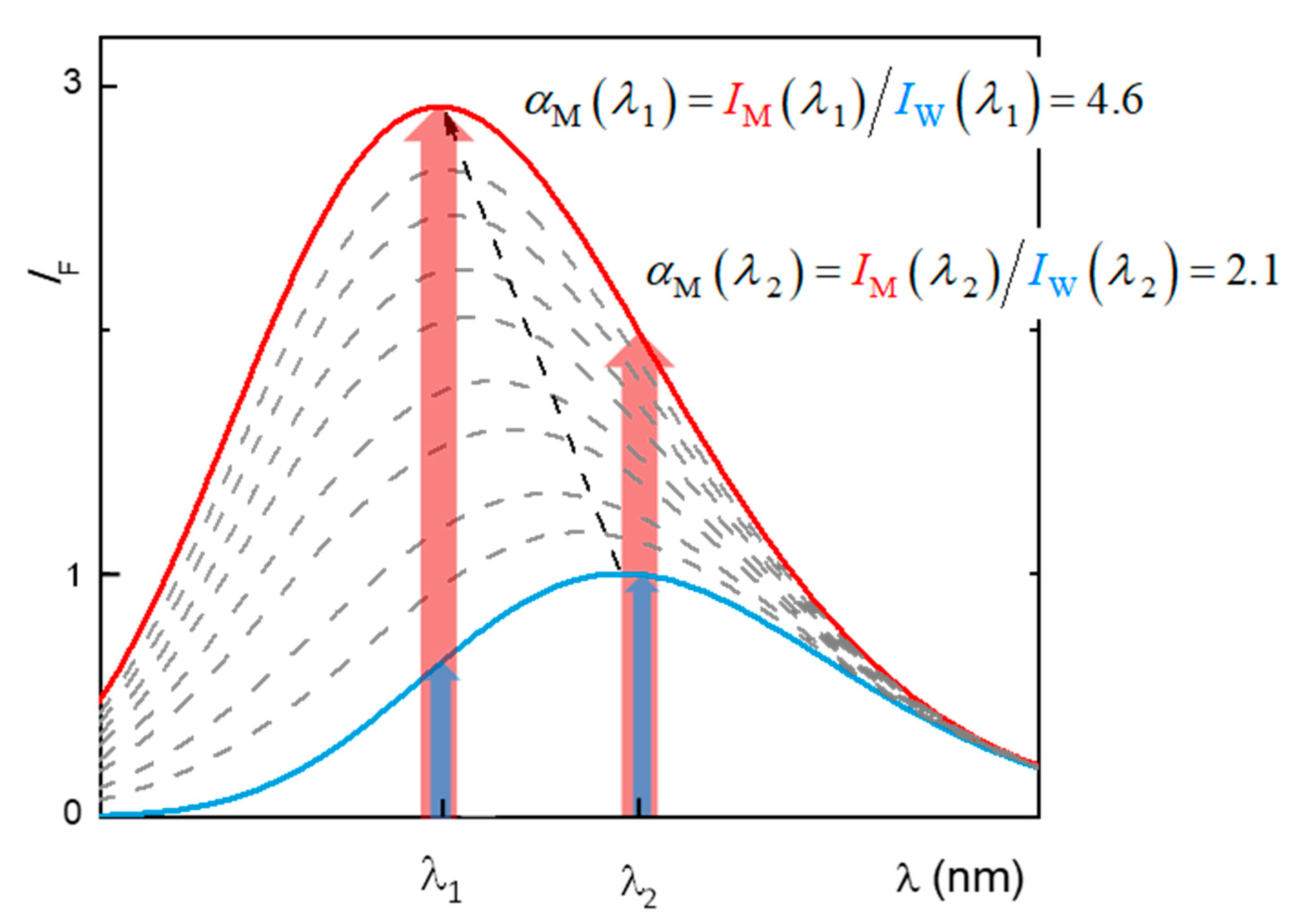
Preprints 78429 g011
Figure 11. Graphical exemplification of the method used to calculate the parameter α M for use in equation (3). The continuous lines represent the fluorescence emission spectra of the probe in the aqueous medium (blue) and in the membrane (red), and the dashed grey lines the spectra at different lipid concentrations. The highlighted wavelengths ( λ 1 and λ 2 ) correspond to hypothetical wavelengths selected for the use of the fluorescence anisotropy to calculate the partition coefficient, and thus where the parameter α M must be calculated.
Figure 11. Graphical exemplification of the method used to calculate the parameter α M for use in equation (3). The continuous lines represent the fluorescence emission spectra of the probe in the aqueous medium (blue) and in the membrane (red), and the dashed grey lines the spectra at different lipid concentrations. The highlighted wavelengths ( λ 1 and λ 2 ) correspond to hypothetical wavelengths selected for the use of the fluorescence anisotropy to calculate the partition coefficient, and thus where the parameter α M must be calculated.
Preprints 78429 g011
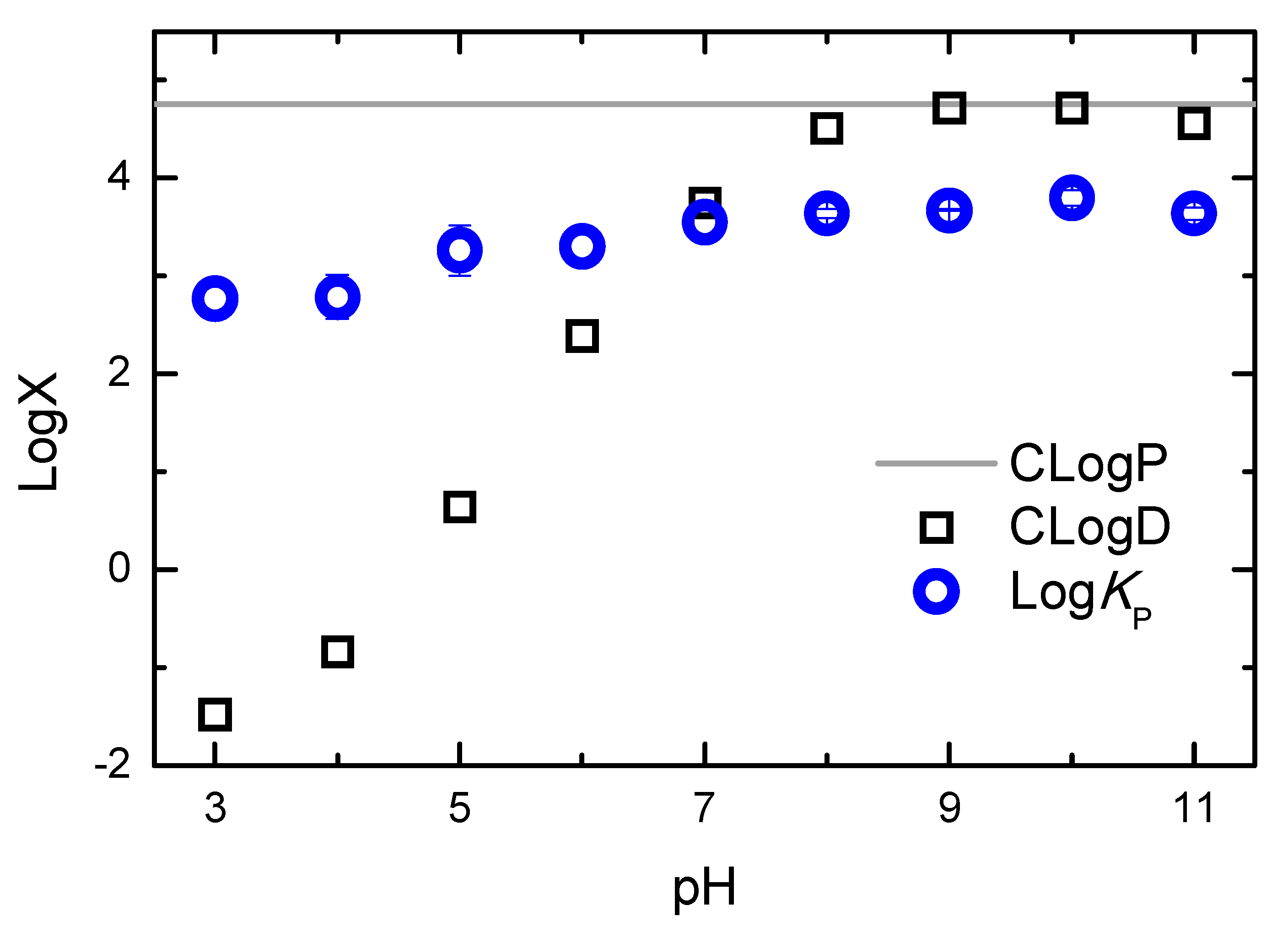
Preprints 78429 g012
Figure 12. Dependence of the calculated partition (CLogP) and distribution (CLogD) of H33342 between the aqueous medium and octanol, and of the partition coefficient measured experimentally between the aqueous medium and POPC bilayers (LogKP), as a function of the pH of the aqueous medium. The calculated parameters were obtained with the MarvinSketch software [36].
Figure 12. Dependence of the calculated partition (CLogP) and distribution (CLogD) of H33342 between the aqueous medium and octanol, and of the partition coefficient measured experimentally between the aqueous medium and POPC bilayers (LogKP), as a function of the pH of the aqueous medium. The calculated parameters were obtained with the MarvinSketch software [36].
Preprints 78429 g012
Table 1. Partition coefficient of H33342 towards POPC LUVs at different pH values. The average and standard deviation were calculated for the log KP because this is the variable with a normal distribution [37]; the average KP was then calculated from the average of log KP. The number of replicates (N) for each situation is indicated below the pH value.
Table 1. Partition coefficient of H33342 towards POPC LUVs at different pH values. The average and standard deviation were calculated for the log KP because this is the variable with a normal distribution [37]; the average KP was then calculated from the average of log KP. The number of replicates (N) for each situation is indicated below the pH value.
pH 3 4 5 6 7 8 9 10 11
N 4 5 3 6 6 4 2 4 4
log KP µ 2.8 2.8 3.3 3.3 3.6 3.6 3.7 3.8 3.6
σ 0.16 0.22 0.26 0.17 0.19 0.05 0.01 0.08 0.06
KP µ 5.8×102 6.1×102 2.6×103 2.0×103 3.8×103 4.4×103 4.7×103 6.3×103 4.3×103
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated