Joint Latency-Oriented, Energy Consumption, and Carbon Emission for Space-Air-Ground Integrated Network with New Designed Power Technology

Preprint

Article

Joint Latency-Oriented, Energy Consumption, and Carbon Emission for Space-Air-Ground Integrated Network with New Designed Power Technology

Altmetrics

Downloads

113

Views

Comments

A peer-reviewed article of this preprint also exists.

Yonghao Wang,

Bo Li^*,Jiahao He,Jiaxing Dai,Yuxin Yang,Yidong Liu

Yonghao Wang,

Bo Li^*,Jiahao He,Jiaxing Dai,Yuxin Yang,Yidong Liu

This version is not peer-reviewed

Submitted:

04 July 2023

Posted:

04 July 2023

You are already at the latest version

Alerts

Abstract

The ubiquitous connectivity for the space-air-ground integrated network (SAGIN) of the beyond fifth generation of communication and sixth generation of communication (B5G/6G) is envisaged to meet the needs for the demanded quality of service (QoS), green communication, and "dual carbon" target. However, the offloading and computation of massive latency-sensitive tasks dramatically increases the energy consumption of the network. Furthermore, the traditional power supply technology of the network base stations (BSs) enhances the carbon emission. To address these issues, we first propose a SAGIN architecture with energy harvesting devices, where the BS is powered by both renewable energy (RE) and the conventional grid. The BS explores wireless power transfer (WPT) technology to power the unmanned aerial vehicle (UAV) for stable network operation. RE sharing between neighbouring BSs is designed to fully utilize RE for reduce carbon emission. Secondly, on the basis of task offloading decision, UAV trajectory, and RE sharing ratio, we construct cost functions with joint latency-oriented, energy consumption, and carbon emission. Then, we develop a twin delayed deep deterministic policy gradient (TD3PG) algorithm based on deep reinforcement learning to minimize the cost function. Finally, simulation results demonstrate that the proposed algorithm outperforms the benchmark algorithm in terms of reducing latency, energy saving, and lower carbon emission.

Keywords:

Subject: Computer Science and Mathematics - Other

1. Introduction

To accommodate the diverse quality-of-service (QoS) requirements of a wide range of applications in various scenarios, future communication networks are envisioned to offer low latency and ubiquitous connectivity [1]. In particular, the space-air-ground integrated network (SAGIN) is considered a promising paradigm for future communication to provide large-scale coverage and network performance enhancement [2].

On the other hand, mobile edge computing (MEC) is considered one of the key technologies for future communication network severice for latency-sensitive tasks [3,4]. Meanwhile, the execution of tasks would consume a considerable amount of energy. Green communication in 6G should be manifested in reducing the total energy consumption in order to achieve energy efficiency goal [5]. In addition, The dual carbon goal of future communication networks is to reduce carbon emissions by 50% [6]. Thereby, joint latency-oriented for QoS guarantee, energy consumption for green communication and carbon reduction for dual carbon goal in SAGIN has attracted wide attention from both academia and industry.

Several studies have been put into reducing network latency for QoS guarantee. Peng et al. [7] consider two typical MEC architectures in a vehicular network and formulate multi-dimensional resource optimization problems, exploiting reinforcement learning (RL) to obtain the appropriate resource allocation decisions to achieve high delay/QoS satisfaction ratios. Through jointly optimizing computation offloading decision and computation resource allocation, Zhao et al. [8] effectively improve the system utility and computation time. Abderrahim et al. [9] propose an offloading scheme that improves network availability, while reducing the transmission delay of ultra-reliable low-latency communication packets in the terrestrial backhaul and satisfying different QoS requirements.

Furthermore, a few other studies have considered the issue of energy consumption in networks. Literature [10,11] consider a multi-user MEC system with the goal of minimizing the total system energy consumption over a finite time horizon. Chen et al. [12] investigate the task offloading problem in ultra-dense network and formulate it as a mixed integer nonlinear program which is NP-hard, which can reduce 20% of the task duration with 30% energy saving, compared with random and uniform task offloading schemes.

Some scholars have concentrated their attention on latency and energy consumption for the SAGIN network architecture. Guo et al. [13] investigate service coordination to guarantee the QoS in SAGIN service computing and propose an orchestration approach to achieve low cost reduction in service delay. To achieve a better latency/QoS for different 5G slices with heterogeneous requirements, Zhang et al. [14] offload smartly the traffic to the appropriate segment of SAGIN. In order to ensure QoS for airborne users as well as to reduce energy consumption, Chen et al. [15] design an energy-efficient data saving scheme with extensive simulations confirming the effectiveness of the proposed scheme in terms of both the energy consumption and the processing delay in SAGIN.

Although the aforementioned studies have done a considerable amount of exploration on the issues of latency reduction and energy consumption reduction, research in [16] highlights that the dense deployment of higher energy-demanding communication devices will keep pumping up the energy consumption of wireless access networks. Moreover, the future networks have to reduce carbon emission. Fortunately, energy harvesting technology converts ambient energy to electric energy, which can be used in cellular networks to help reduce the carbon footprint of wireless networks [17]. In particular, the approach to green cellular BS has been proposed, which involves the adoption of renewable energy (RE) resources [18].

Consequently, the subject of utilizing RE to power BS reduce the carbon footprint of the network attracted academic attention. Yuan et al. [19] propose an energy storage assisted RE supply solution to power the BS, in which a deep reinforcement learning (DRL) based regulating policy is utilized to flexibly regulate the battery’s discharging/charging. On the basis of off-grid cellular BSs powered by integrated RE, JAHID et al. [20] formulate a hybrid energy cooperation framework, which optimally determines the quantities of RE exchanged among BSs to minimize both related costs and greenhouse gas emissions. Despite the more advantages, RE harvesting technologies are still variable and intermittent compared to traditional grid power. An aggregate technology, which combines RE with traditional grid power, is the most promising option for reliably powering cellular infrastructure [21].

However, existing research efforts are limited to one or two aspects of the network in terms of reducing latency, energy saving, or access to new power supply technology. Meanwhile, few attention has been paid to the entire SAGIN with integrated power energy access technology. Apart from considered above, there are still a number of challenges facing SAGIN. First of all, the long-term performance of the network needs to be considered as the arrival, transmission, and processing of tasks is a stochastic and dynamic process over a period of time. DRL in artificial intelligence techniques can address problems with stochasticity and complexity, as well as dynamic problems. Secondly, due to the fact that the future communication is probably a cellular network capable of providing energy [22], it is extremely critical to power the UAV in order to maintain the sustainability of the network when device is powered. Fortunately, radio-frequency signal based wireless power transfer (WPT) can provide battery-equipped equipment with sustainable energy supply. For instance, literature [23,24,25,26] consider a wireless-powered multi-access network, where a hybrid access point powers the wireless devices via WPT.

Motivated by the above limitations and challenges, we inquire into two issues in SAGIN. One is how to combine latency-oriented, energy consumption, and carbon emission to model the objective function in SAGIN with new power access technology. The other is how the relevant influence factors affect latency, energy consumption and carbon emissions.

In this article, we first develop a SAGIN with a new designed power supply technology. In order to maintain the sustainability of the network, the BS explores the WPT to power the UAV. The UAV is able to dynamically adjust its trajectory to cope with task processing and charging. Joint the latency, energy consumption, and carbon emission is formulated the cost function. Obviously, our research target is to minimize the cost function.

The main contributions of this article can be summarized as follows:

We propose an architecture for SAGIN with a new designed power supply technology. This network offers ubiquitous connectivity while adapting to the requirements of high reliability and green communication.
We develop a cost function with a joint latency-oriented, energy consumption, and carbon emission, which facilitates to decrease the latency of task processing, the energy consumption and carbon footprint of the network through optimization.
We put forward a TD3PG method. This DRL-based algorithm is capable of sensing parameter changes in the network and dynamically updates the offloading decision.
We conduct experimental evaluations and comparisons. The proposed algorithm is compared with the other three benchmark algorithms. The results show that the proposed algorithm is outstanding in terms of reducing task latency, network energy saving, and lower carbon emision.

The rest of this article is organized as follows. In Section 2, the system model with SAGIN is presented. Section 3 provides the problem formulation. In Section 4, a TD3PG algorithm is designed to obtain the optimal values. Section 5 demonstrates the simulation results and performance analysis. Finally, Section 6 devotes to the conclusions.

2. System Model

A SAGIN is considered, which consists of M ground user devices, N BSs, K UAVs, and a low earth orbit (LEO) satellite. As shown in Figure 1, each BS, each UAV, and the LEO satellite is separately equipped with a server for providing the devices with computation services. Devices are randomly distributed on the ground, which satisfy

m \in M = {1, 2, \dots, M}

. BSs are deployed on buildings of height

H_{B S}

and satisfy

n \in N = {1, 2, \dots, N}

. The flight altitude of the UAV k is fixed as H. The communication range covers the preset range around itself, which satisfies

k \in K = {1, 2, \dots, K}

. It is assumed that a LEO satellite is available within the communication coverage at all times and the meteorological environment remains constant. The set of the time slot is indicated as

t \in T = {1, 2, \dots, T}

with the size of each time slot is

τ

Each BS is independently equipped with solar panels, wind turbine, backup battery and electricity converter to provide uninterrupted energy supply. Adjacent BSs are able to share energy by energy sharing line. In order to maintain the stable operation of the UAV, the BS is able to supply the UAV with energy via WPT.

Given that virtual reality, augmented reality, and mixed reality are the typical applications based on the 6G [27], it is assumed that each device has one total task which can be divided into a number of subtasks. The subtasks from device m may be respresented as

〈s_{m} (t), e_{m} (t), t_{m} (t)〉

, where

s_{m} (t)

and

e_{m} (t)

denote the subtask’s size (bit) and required CPU cycles per unit of data (cycles/bit) in time slot t, respectively.

t_{m} (t)

indicates the latency constraint for executing the subtask, which contains the latency for the transmission, computation, and waiting of the subtask. Subtasks follow a Poisson distribution with arrival rate

λ_{m} (t)

The relevant system models in SAGIN will be enumerated in the following.

2.1. Backup battery Model for BS

Denote

L_{n} (t)

as the electrical load for BS n in time slot t, which is related to the communication traffic

T_{n} (t)

[28]. Hence,

L_{n} (t)

can be expressed as

L_{n} (t) = δ_{0} + δ_{1} T_{n} (t),

(1)

where

δ_{0}

and

δ_{1}

are coefficients.

The BS backup battery is required to reserve capacity

b_{n}^{r e s} (t)

to meet the energy consumption for BS n electrical load during the fixed standby time

D_{n}^{r e s} (t)

in time slot t.

b_{n}^{r e s} (t)

can be represented as

b_{n}^{r e s} (t) = \int_{0}^{D_{n}^{r e s} (t)} L_{n} (τ) d τ .

(2)

During the time slot t, the harvested energy from RE by N BS backup batteries is

H (t) = [h_{1} (t), h_{2} (t), \dots, h_{N} (t)]

. The energy sharing to the adjacent BS is denoted as

E^{share} (t) = [e_{1}^{s h a r e} (t), e_{2}^{s h a r e} (t), \dots, e_{N}^{s h a r e} (t)]

. Let

B^{res} (t) = [b_{1}^{r e s} (t), b_{2}^{r e s} (t), \dots, b_{N}^{r e s} (t)]

denote the energy reserved by the backup battery to meet a fixed standby time at the current communication traffic of the BS.

E^{bs} (t) = [e_{1}^{b s} (t), e_{2}^{b s} (t), \dots, e_{N}^{b s} (t)]

is the energy consumption of each BS. Suppose the energy remaining in the backup battery is

B^{bs} (t) = [b_{1}^{b s} (t), b_{2}^{b s} (t), \dots, b_{N}^{b s} (t)]

. Then backup battery during the next time slot can be derivated as

B^{bs} (t + 1) = min {E^{gird} (t) + H (t) + B^{bs} (t) - E^{share} (t) - E^{bs} (t), B^{b a t t e r y}},

(3)

where

B^{b a t t e r y}

is the backup battery capacity.

E^{gird} (t)

is the energy supplied by power grid when RE harvesting is unable to maintain the BS energy consumption, which can be constructed as

E^{gird} (t) = [B^{res} (t) + E^{bs} (t) - H (t) + E^{share} (t) - B^{bs} {(t)]}^{+},

(4)

where

{[x]}^{+} = max {x, 0}

. Considering the cost and size of BS energy harvesting equipment, the optimal unit size is finitely large. On the other hand, battery lifetime

B^{l i f e}

is an another factor to be considered, which is related to the number of charge/discharge cycles. In this case, the following constraints are required to be satisfied as

\begin{matrix} B^{b a t t e r y} ⩾ \int_{0}^{D_{n}^{r e s} (t)} L^{m a x} d τ, \end{matrix}

(5a)

\begin{matrix} C P R = \frac{B^{l i f e} B^{b a t t e r y}}{C^{b a t t e r y}}, \end{matrix}

(5b)

\begin{matrix} C^{b a t t e r y} \leq C^{e x p e c t}, \end{matrix}

(5c)

where

L^{m a x}

is the maximum electrical load for the BS. Define

C P R

as the cost-performance ratio of the backup battery, which is as large as possible.

C^{b a t t e r y}

and

C^{e x p e c t}

denote the actual and the maximum expectation cost of the backup battery, respectively.

Furthermore, adjacent BSs are able to share energy by physical resistive power line connections to maximize RE utilization. This approach may be reasonable for energy sharing among BSs within small zones [20]. The remaining energy of the RE may be shared with other BSs. Then the sharing energy

E^{share} (t)

can be expressed as

E^{share} (t) = υ_{n} \cdot {[H (t) + B^{bs} (t) - B^{res} (t) - E^{bs} (t)]}^{+},

(6)

where

υ_{n}

is the RE transfer ratio with

υ_{n} \in [0, 1]

. When the backup batteries are fully charged, the excess RE

E^{exc} (t) = [e_{1}^{e x c} (t), e_{2}^{e x c} (t), \dots, e_{N}^{e x c} (t)]

will be discarded. Supposing that the loss factor for energy transfer between BSs is

η

, which satisfies

η \in [0, 1]

. Thus, the energy loss

E^{loss} (t) = [e_{1}^{l o s s} (t), e_{2}^{l o s s} (t), \dots, e_{N}^{l o s s} (t)]

can be expressed as

E^{loss} (t) = η E^{share} (t) + E^{exc} (t) .

(7)

It is crucial to reduce energy loss

E^{loss} (t)

in evaluating the reduction of carbon emission.

2.2. Communication Model

Each subtask can be offloaded to BS, UAV, or LEO satellites for execution in one of these ways in time slot t. Thereafter, the task communication model is described as follows.

2.2.1. Offloading to the BSs

Let

R_{m, n} (t)

denotes the wireless transmission rate between device m and BS n in time slot t, which can be expressed as

R_{m, n} (t) = B_{m, n} {log}_{2} [1 + \frac{p_{m} G_{m, n} (t) g_{m, n} (t)}{σ^{2} + ζ_{m^{'}, n^{'}} (t)}],

(8)

where

B_{m, n}

represents the channel bandwidth between device m and BS n.

p_{m}

is the transmission power of device m.

G_{m, n} (t)

is the path loss that is related to the distance

d_{m, n} (t)

between device m and BS n in time slot t.

g_{m, n} (t)

is the small-scale channel fading subject to Rayleigh fading.

σ^{2}

denotes the noise power.

ζ_{m^{'}, n^{'}} (t)

is the interference from the other BSs.

2.2.2. Offloading to the UAVs

If device m is in the communication coverage of UAV k in time slot t,

a_{m, k} (t) = 1

is assumed. Otherwise,

a_{m, k} (t) = 0

. As the altitude of the UAV is much higher than that of the devices, the line-of-sight channels of the UAV communication links are much more predominant [29]. The wireless channel of the UAV is considered as a free-space path loss model. Thereby the channel gain

g_{m, k} (t)

β_{0} {(d_{m, k} (t))}^{- α_{0}}

, where

β_{0}

denotes the channel gain at unit distance.

α_{0}

represents the path loss index.

d_{m, k} (t)

is the Euclidean distance between the m-

t h

device and the k-

t h

UAV. Hence, the transmission rate

R_{m, k} (t)

can be formulated as

R_{m, k} (t) = B_{m, k} {log}_{2} [1 + \frac{a_{m, k} (t) p_{m} g_{m, k} (t)}{σ^{2} + ζ_{m^{'}, k^{'}} (t)}],

(9)

where

B_{m, k}

is the channel bandwidth. The

ζ_{m^{'}, k^{'}} (t)

represents the co-channel interference from all the other UAVs.

2.2.3. Offloading to the LEO satellite

The channel conditions between the LEO satellite and ground devices are mainly affected by the communication distance and rainfall attenuation. Since the distance between LEO satellite and device remains almost unchanged, a fixed transmission rate

R_{m, s a t} (t)

between devices and the LEO satellite is adopted. It is usually lower than the tansmission rate between devices and UAV communication [30,31].

2.3. Computation Model

The task can be executed in four ways, executed locally, offloaded to BSs, offloaed to UAVs, or offloaded to the LEO satellite. Due to the small data size of the computation result, the delay and energy consumption for transmitting the computation result can be omitted [32].

2.3.1. Local Computation

The device is capable of varying CPU cycle frequency

f_{m} (t)

dynamically to obtain better system performance. Consequently, the latency of local task execution

t_{m}^{l} (t)

can be obtained as

t_{m}^{l} (t) = \frac{s_{m} (t) e_{m} (t)}{f_{m} (t)} + t_{m}^{l, w a i t} (t),

(10)

where

t_{m}^{l, w a i t} (t)

indicates the queuing delay of the task for the device. Assuming the energy consumption of per CPU cycle as

κ f_{m}^{2} (t)

, where

κ

is the CPU chip related switching capacitor [33], the energy consumption

E_{m}^{l} (t)

of the task execution at the device can be expressed as

E_{m}^{l} (t) = κ f_{m}^{2} (t) s_{m} (t) e_{m} (t) .

(11)

2.3.2. Offloading to the BSs

The BS has a relatively stable energy supply and a powerful CPU. If tasks are offloaded to the BS, they will be executed instantly without queueing. Denote that

f_{m, n} (t)

is the allocated computation resource for the n-

t h

BS. The task execution latency

t_{n}^{b s} (t)

for offloading to the BS can be given as

t_{n}^{b s} (t) = \frac{s_{m} (t)}{R_{m, n} (t)} + \frac{s_{m} (t) e_{m} (t)}{f_{m, n} (t)} .

(12)

The energy consumption

E_{n}^{b s} (t)

of the task execution at the BS can be obtained as

E_{n}^{b s} (t) = δ_{0} + δ_{1} s_{m} (t) .

(13)

2.3.3. Offloading to the UAVs

The task execution latency

t_{k}^{u a v} (t)

for offloading to the UAV can be expressed as

t_{k}^{u a v} (t) = a_{m, k} (t) [\frac{s_{m} (t)}{R_{m, k} (t)} + \frac{s_{m} (t) e_{m} (t)}{f_{m, k} (t)} + t_{k}^{u, w a i t} (t)],

(14)

where

f_{m, k} (t)

is the allocated computation resource for the k-

t h

UAV.

Define

e_{u a v}

as the energy consumption per unit of computation resources of the UAV. The energy consumption

E_{k}^{u a v} (t)

of the task execution at the UAV can be given as

E_{k}^{u a v} (t) = a_{m, k} (t) [\frac{p_{m} s_{m} (t)}{R_{m, k} (t)} + e_{u a v} s_{m} (t) e_{m} (t)] .

(15)

2.3.4. Offloading to the LEO satellite

Denote that

f_{m, s a t} (t)

is the allocated computation resource for the LEO satellite. The task execution latency

t_{m}^{s a t} (t)

for offloading to the LEO satellite can be expressed as

t_{m}^{s a t} (t) = \frac{s_{m} (t)}{R_{m, s a t} (t)} + \frac{s_{m} (t) e_{m} (t)}{f_{m, s a t} (t)} + t^{s, w a i t} (t) .

(16)

The energy consumption

E_{m}^{s a t} (t)

of the task execution at the LEO satellite can be obtained as

E_{m}^{s a t} (t) = \frac{p_{m} s_{m} (t)}{R_{m, s a t} (t)} + e_{s a t} s_{m} (t) e_{m} (t),

(17)

where

e_{s a t}

is the energy consumption per unit of computation resources of the LEO satellite.

2.4. WPT Model

In the case that UAV k is within the BS n energy transmission coverage in time slot t,

o_{k, n} (t) = 1

. Otherwise,

o_{k, n} (t) = 0

. In order to maintain the sustainability of the network, the BS explores the WPT to power the UAV. Linear energy harvesting model is adopted. Then the harvested energy of the UAV k can be expressed as

B_{k}^{H} (t) = \sum_{k = 1}^{K} o_{k, n} (t) χ P_{n} G_{n}^{t} G_{k}^{r} h_{n, k} (t) \cdot τ,

(18)

where

χ

denotes the energy conservation efficiency, which satisfies

χ \in (0, 1]

P_{n}

is the BS transmitting power.

G_{n}^{t}

and

G_{k}^{r}

are the antenna power gains of the BS transmitter and the UAV receiver, respectively.

h_{n, k} (t)

is the channel gain between the n-

t h

BS and the k-

t h

UAV in time slot t.

2.5. Flight Model

Continuous variables such as the average velocity

v_{k} (t)

and the directional angle

θ_{k} (t)

are considered to adjust the trajectory of the UAV k. Assuming that the horizontal position coordinates and the moving distance of UAV k in current time slot are

Ψ_{k} (t) = {[x_{k} (t), y_{k} (t)]}^{T}

and

d_{k} (t)

, respectively. The position coordinates of UAV k in the next time slot can be expressed as

\{\begin{matrix} x_{k} (t + 1) = x_{k} (t) + d_{k} (t) cos θ_{k} (t), \\ y_{k} (t + 1) = y_{k} (t) + d_{k} (t) sin θ_{k} (t) . \end{matrix}

(19)

Referring to [34], the propulsion power consumption of UAV can be modeled as

P [v (t)] = P_{0} (1 + 3 v^{2} (t) / U_{t i p}^{2}) + \frac{1}{2} d_{0} ρ s A v^{3} (t) + P_{1} {[\sqrt{1 + v^{4} (t) / 4 v_{0}^{4}} - v^{2} (t) / 2 v_{0}^{2}]}^{\frac{1}{2}},

(20)

where

P_{0}

and

P_{1}

are constants, representing the blade profile power and induced power in hovering status, respectively.

U_{t i p}

denotes the tip speed of the rotor blade.

v_{0}

is known as the mean rotor induced velocity in hover.

d_{0}

and s are the fuselage drag ratio and rotor solidity, respectively.

ρ

and A denote the air density and rotor disc area, respectively. The flight energy consumption of UAV k in time slot t can be given as

E_{k}^{F} (t) = \int_{t}^{t + τ} P [v_{k} (t)] d t .

(21)

The system model in SAGIN are enumerated in this section. In the following section, the cost function will be constructed.

3. Problem Formulation

How to integrate latency-oriented, energy consumption, and carbon emission to model the objective function in SAGIN is the key to solve the first issue. According to the system model mentioned above, the cost function is first constructed on the basis of system model and then the formulation of the problem is demonstrated in this section.

The network cost function

U (t)

is constructed by joint the total latency

T (t)

, energy consumption

E^{e c} (t)

, and carbon emission

C^{R E} (t)

, which can be represented as

U (t) = ϑ_{0} T (t) + ϑ_{1} E^{e c} (t) + ϑ_{2} C^{R E} (t),

(22)

where

ϑ_{0}

ϑ_{1}

, and

ϑ_{2}

represent the preference on latency, energy consumption, and carbon emission, respectively. And satisfy

ϑ_{0} + ϑ_{1} + ϑ_{2} = 1

T (t)

E^{e c} (t)

, and

C^{R E} (t)

are expressed as

T (t) = \sum_{\binom{m \in M,}{n \in N, k \in K}} [t_{m}^{l} (t) + t_{n}^{b s} (t) + t_{k}^{u a v} (t) + t_{m}^{s a t} (t)],

(23)

E^{e c} (t) = \sum_{\binom{m \in M,}{n \in N, k \in K}} [E_{m}^{l} (t) + E_{n}^{b s} (t) + E_{k}^{u a v} (t) + E_{m}^{s a t} (t) + E_{k}^{F} (t)],

(24)

C^{R E} (t) = \sum_{n \in N} ξ [h_{n} (t) - e_{n}^{l o s s} (t)],

(25)

where

ξ

is the conversion factor of carbon emission per unit of energy and is related to the type of energy source.

t_{m}^{l} (t)

t_{n}^{b s} (t)

t_{k}^{u a v} (t)

, and

t_{m}^{s a t} (t)

represent the time when the tasks are executed locally or offloaded to the computation server in time slot t, respectively. In particular, each subtask can only be executed in one of these ways.

E^{e c} (t)

includes energy consumption for tasks execution and UAV flight in time slot t.

C^{R E} (t)

is the reduction in carbon emissions through reducing traditional power gird energy consumption.

The network cost function is formulated into a minimization problem as the following.

Constraint (26b) and (26b) imply that the task is indivisible and can be executed locally or remotely at the computation server. (26c) constrains the latency limit of the task. Constraint (26d) defines the range of angles and velocities that control the UAV’s flight trajectory. (26e) ensures that the safety distance among different UAVs, where

∥\cdot∥

is the Euclidean norm. Constraint (26f) indicates that the minimum and maximum thresholds for the UAV and BS backup batteries, respectively. (26g) guarantees that the computation resources allocated to the task by the device and other computation servers do not exceed the maximum computation capacity. (26h) specifies the range of variables.

It is a challenge to solve the above problem, since the dynamic and complex characteristics of the network environment. It is crucial to design a satisfactory solution that is real-time and capable of handling high-dimensional dynamic parameters. Therefore, in the following section, DRL is used to learn network and to deal with optimization problem with various constraints.

\begin{matrix} min \sum_{t \in T} U (t) \end{matrix}

(26a)

\begin{matrix} s . t . & o_{m}^{L} (t), o_{m, n}^{N} (t), o_{m, k}^{K} (t), o_{m}^{s a t} (t) \in {0, 1}, \end{matrix}

(26b)

\begin{matrix} o_{m}^{L} (t) + \sum_{n = 1}^{N} o_{m, n}^{N} (t) + \sum_{k = 1}^{K} o_{m, k}^{K} (t) + o_{m}^{s a t} (t) = 1, \end{matrix}

(26c)

\begin{matrix} t_{m}^{l} (t), t_{n}^{b s} (t), t_{k}^{u a v} (t), t_{m}^{s a t} (t) \leq t_{m} (t), \end{matrix}

(26d)

\begin{matrix} 0 \leq θ_{k} (t) \leq 2 π, 0 \leq v_{k} (t) \leq v_{max}, \end{matrix}

(26e)

\begin{matrix} ∥Ψ_{k 1} (t) - Ψ_{k 2} (t)∥ \geq D_{min}, k 1 \neq k 2, \\ B^{b o t} \leq B_{k}^{K} (t) \leq B^{c a p a c i t y}, \end{matrix}

(26f)

\begin{matrix} B^{r e s} \leq B_{n}^{N} (t) \leq B^{b a t t e r y}, \\ f_{m} (t) \leq f_{m}^{max}, \sum_{m = 1}^{M} f_{m, k} (t) \leq f_{k}^{max}, \end{matrix}

(26g)

\begin{matrix} \sum_{m = 1}^{M} f_{m, n} (t) \leq f_{n}^{max}, \sum_{m = 1}^{M} f_{m, s a t} (t) \leq f_{s a t}^{max}, \end{matrix}

(26h)

\begin{matrix} \forall m \in M, n \in N, k \in K, t \in T . \end{matrix}

(26i)

4. Markov Chain Model based TD3PG Algorithm in SAGIN

DRL aims to learn award maximizing strategy by the interaction of intelligent agents with the environment. In order to solve the second issue with DRL, the cost function is reformulated as a Markov Decision Process (MDP). TD3PG, a DRL-based strategy, is proposed to optimize the objective problem by training the nearoptimal model.

4.1. MDP Formulation

A typical MDP with 4 elements tuple

〈S, A, M, R〉

, where

S

is the state space.

A

is the action space.

M

denotes the state transition function, which indicates the probability of the transition to next state

s_{t + 1}

after performing

(s_{t}, a_{t})

R

is the reward function. The detail descriptions of the elements in the tuple are as follows.

State space: State space is designed to store the DRL agent’s observations in the environment and to guide the generation of actions. The state space includes the remaining energy of the UAV $B_{k}^{K} (t)$ , the BS $B_{n}^{b s} (t)$ , the reserved energy for BS backup battery $B_{n}^{r e s} (t)$ , the current horizontal location of the UAV $Ψ_{k} (t)$ , and the remaining amount of the current task $s_{m} (t)$ . Then the system state space can be defined as

$s_{t} = {B_{k}^{K} (t), B_{n}^{b s} (t), B_{n}^{r e s} (t), Ψ_{k} (t), s_{m} (t)} .$

(27)

Action space: Action space is designed to store the actions performed by the DRL agent in the environment in order to obtain feedback from the environment and the next state. The action space contains the offloading decisions $o_{m}^{L} (t), o_{m, n}^{N} (t), o_{m, k}^{K} (t), o_{m}^{s a t} (t)$ (i.e., offloading task to local device, BS, UAV, or the LEO satellite). The navigation speed $v_{k} (t)$ and the rotation angle $θ_{k} (t)$ for controlling UAV trajectory are continuous value in the interval $[0, v_{max}]$ and $[0, 2 π]$ , respectively. $f_{m} (t) \in [f_{m}^{max} / 2, f_{m}^{max}]$ denotes the dynamic computation resources of the device. $υ_{n}$ is the proportion of shared RE harvested by BS. Therefore, the system action space can be expressed as

$a_{t} = {o_{m}^{L} (t), o_{m, n}^{N} (t), o_{m, k}^{K} (t), o_{m}^{s a t} (t), v_{k} (t), θ_{k} (t), f_{m} (t), υ_{n} (t)}$

(28)

Reward: Reward is the feedback from the environment to the DRL agent after performing the current action. The research goal is to minimize the cost function. The algorithm depends on the reward to evaluate its decisions by learning the SAGIN environment. Due to the fact that the goal of RL is a cumulative overall reward over time to maximize reward, the reward function is reformulated to be the negative value of the optimization cost function. Then the reward can be expressed as

$R_{t} = - U (t),$

(29)

where the coefficients $ϑ_{0}$ , $ϑ_{1}$ , and $ϑ_{2}$ in U are required to satisfy $ϑ_{0}, ϑ_{1} > 0$ and $ϑ_{2} < 0$ , respectively.

4.2. TD3PG Algorithm

Owing to the fact that the action space contains continuous variables, TD3PG is adopted, which is an off-policy algorithm based on the actor-critic structure for dealing with the optimization problems with the high-dimension action space [35].

Compared to the conventional actor-critic based deep deterministic policy gradient (DDPG), which would result in cumulative errors. TD3PG solves the former overestimation problem. It has two pairs of critic networks in which the smaller Q value of the two Q-functions is chosen to form the loss function in the Bellman equation. Hence, there is less overestimation in learning process. Moreover, the application of delayed policy technique enables TD3PG to less frequently update the actor network and the target network than the critic networks. In other words, the model does not update policy unless the model’s value function is updated sufficiently. The less frequent policy updates will bring a value evaluation with lower variance and produce a better policy [36].

Apart from the above, TD3PG is also able to smooth the value estimate by applying a smoothing technique for target policy that adds noise ( clipped random noise) to the target actions and average over mini-batches, as shown in

ϵ \sim clip (N (0, \tilde{ω}), - c, c) .

(30)

According to the structure of the TD3PG algorithm depicted in Figure 2, the TD3PG architecture contains one actor network and two critic networks. The actor network is parameterized by

θ_{π}

, and two critic networks by

θ_{Q 1}

and

θ_{Q 2}

, respectively.

The agent firstly observes the current state

s_{t}

and picks an action

a_{t}

via the actor network. After performing

a_{t}

in the environment, the agent is able to observe the immediate reward

R_{t}

and the next state

s_{t + 1}

. Then, the agent will select the policy that maximizes the cumulative reward, which converts the state

s_{t}

to the action

a_{t}

. At this point, the transition

〈s_{t}, a_{t}, R_{t}, s_{t + 1}〉

is obtained and stored in the replay memory for further sampling.

The training process of the TD3PG algorithm is summarized as Algorithm 1.

Algorithm 1 TD3PG algorithm.

Require: Training episode length:

m a x

e p i s o d e

. discount factor:

γ

.
Ensure: Loss, gradients.

1:: Initialize the actor network $π_{θ_{π}}$ with parameter $θ_{π}$ . Initialize the critic network $Q_{θ_{Q 1}}$ , $Q_{θ_{Q 2}}$ with parameters $θ_{Q 1}$ and $θ_{Q 2}$ , respectively.
2:: Initialize the target network by: $θ_{π}^{T} \leftarrow θ_{π}$ , $θ_{Q 1}^{T} \leftarrow θ_{Q 1}$ , $θ_{Q 2}^{T} \leftarrow θ_{Q 2}$ .
3:: Initialize replay buffer $R$ .
4:: for episode = 1 to $m a x$ - $e p i s o d e$ do
5:: Reset simulation parameters and obtain initial observation state s.
6:: for t = 1 to T do
7:: Get action after adding exploration noise $a_{t} \sim π (s_{t} | θ_{π}) + N (0, δ)$ .
8:: Obtain the reward $R_{t}$ and update $s_{t + 1}$ .
9:: Store the transition $〈s_{t}, a_{t}, R_{t}, s_{t + 1}〉$ in replay buffer $R$ .
10:: Sample a random mini-batch of V tuples from replay buffer $R$ .
11:: Compute greedy actions for next states through $\tilde{a} \leftarrow π (s_{t + 1} | θ_{π}^{T}) + ϵ$ , where $ϵ \sim clip (N (0, \tilde{ω}), - c, c)$ .
12:: Compute target value $y_{t}$ based on Eq. (31).
13:: Update the critics by minimizing the loss function Eq. (32).
14:: Update the actor network parameter $θ_{π}$ by using the sampled policy gradient Eq. (34).
15:: Update the target networks Eq. (35).
16:: end for
17:: end for

The minimum Q-value estimate of these two critic networks is used to calculate the target value

y_{t}

, which can be obtained by

y_{t} = R_{t} + γ \cdot min_{i = 1, 2} Q_{Q i} (s_{t + 1}, π (s_{t + 1} | θ_{π}^{T}) | θ_{Q i}^{T}),

(31)

where

γ

is a discount factor, ranging from 0 to 1.

The loss function of two critic networks can be defined as

L s (θ_{Q i}) = E [{(y_{t} - Q_{Q i} (s_{t}, a_{t} | θ_{Q i}))}^{2}], i = 1, 2 .

(32)

Then the gradient of loss function is calculated as

\nabla_{θ_{Q i}} L s (θ_{Q i}) = E [y_{t} - (Q (s_{t}, a_{t} | θ_{μ})) \nabla_{θ_{Q i}} Q (s_{t}, a_{t} | θ_{Q i})] .

(33)

The policy gradient of the actor network can be given as

\nabla_{θ_{π}} J \approx E [\nabla_{a} min_{i = 1, 2} Q (s_{t}, a_{t} | θ_{Q i}) |_{a_{t} = π (s_{t})} \nabla_{θ_{π}} π (s_{t} | θ_{π})] .

(34)

The parameters of the target networks will be updated by means of

\begin{matrix} θ_{π}^{T} \leftarrow ω θ_{π} + (1 - ω) θ_{π}^{T} \\ θ_{Q i}^{T} \leftarrow ω θ_{Q i} + (1 - ω) θ_{Q i}^{T}, i = 1, 2, \end{matrix}

(35)

where

ω

is a step size coefficient and satisfies

ω \in [0, 1]

4.3. Complexity Analysis

The proposed TD3PG algorithm contains both actor network and critic network. Therefore, the complexities of them are evaluated separately. Assuming that the actor network has

L^{a}

layers with

n_{l}

neuron nodes in the l-

t h

layer. Then the complexity of the l-

t h

layer is

O (n_{l - 1} n_{l} + n_{l} n_{l + 1})

[37]. The complexity of the actor network is

O (\sum_{l = 2}^{L^{a} - 1} (n_{l - 1} n_{l} + n_{l} n_{l + 1}))

. Assuming that the critic network has

L^{c}

layers with

m_{l}

neuron nodes in the j-

t h

layer, the complexity of the j-

t h

layer is

O (m_{j - 1} m_{j} + m_{j} m_{j + 1})

[37]. Similarly, the complexity of the critic network is

O (\sum_{j = 2}^{L^{c} - 1} (m_{j - 1} m_{j} + m_{j} m_{j + 1}))

. Hence, the overall computational complexity of the TD3PG algorithm is

O (\sum_{l = 2}^{L^{a} - 1} (n_{l - 1} n_{l} + n_{l} n_{l + 1}) + \sum_{j = 2}^{L^{c} - 1} (m_{j - 1} m_{j} + m_{j} m_{j + 1}))

, which is similar to that of the DDPG algorithm. In general, TD3PG algorithm is an improvement for DDPG algorithm, but it does not increase the complexity much.

5. Results and Discussion

In this section, numerical simulations are used to evaluate the performance of the proposed TD3PG algorithm. Specifically, the simulation settings and benchmark strategies are firstly elaborated. Afterwards, the analysis of test results is conducted.

5.1. Simulation Settings

We consider an experimental area of 800m × 800m in which M = 50 devices are uniformly distributed. The data size and latency requirements of each computation subtask obey a uniform distribution. Each device has a subtask in each time slot with the data size is randomly distributed in

U [3, 8]

MB. The latency requirements of the subtasks are randomly distributed in

U [0.8, 1.2]

s. There are N = 2 BSs, K = 3 UAVs and a LEO satellite in the experimental area, where the fixed altitude of the UAV is H = 100 m. The bandwidths of the UAV and BS are 5 and 20MHz, respectively. Corresponding simulation parameters are illustrated in Table 1.

To evaluate the performance of our proposed algorithm, we compare the proposed TD3PG algorithm with three conventional benchmarks.

DDPG Algorithm: DDPG also contains two types of neural networks, an actor network and a critic network, but only one critic network.

Full Offload: Tasks are all offloaded to the computation server for computation, and the computation server distributes computation resources evenly based on the number of connected devices.

Greedy on Edge Algorithm (Greedy-edge): Since edge computing has a low computation cost, the computation resources of the UAV can be fully utilized, resembling the “Greedy on edge” algorithm in literature [39]. In time slot t, 60% of the total tasks are offloaded to the UAV, which distributes computation resources evenly based on the number of connected devices.

5.2. Results and Analysis

As shown in Figure 3, combinations of four learning rates are presented to evaluate the impact of different learning rates. With the increase of episodes, the normalized cumulative reward value fluctuates with different learning rates. Until around 2000 episodes, the four cases of normalized cumulative reward have different convergence trends. The performance of the proposed algorithm is the best when

α_{π} = 0.0001

and

α_{μ} = 0.0001

, due to highest convergence reward curve among four cases.

In Figure 4, the impacts of different discount factors are evaluated. From the convergence results, the normalized cumulative reward in four cases gradually become smaller as

γ

keeps increasing. In particular, compared with

γ = 0.69

0.79

, and

0.89

, higher performance is exhibited when

γ = 0.99

. Hence,

γ = 0.99

is the best discount factor among the proposed different discount factors.

Figure 5 shows the variation of the network cost function with the number of devices under different benchmark algorithms. Both the proposed algorithm and DDPG algorithm demonstrate the good performance in terms of joint latency-oriented, energy consumption and carbon emission. Specifically, the value of the network cost function for both algorithms are always lower than other benchmarks for different number of devices and increases at a low rate as the number of devices increases. This is due to the fact that the proposed algorithm and the DDPG algorithm dynamically adjust the offloading strategy, optimize the trajectory of the UAV and the sharing ratio of the RE in real time, ultimately obtaining a lower value of the cost function. In particular, the cost function under the TD3PG algorithm is lower and shows better performance compared to the DDPG algorithm.

In Figure 6, with the exception of full offload, the total energy consumption under other benchmark strategies increases with the maximum computation capacity of the device. Due to the ability of the proposed algorithm and DDPG algorithm with dynamically adjusting the local computation resources according to the reward function, the total energy consumption has great performance when

f_{m a x}

is low. In particular, the proposed algorithm shows the better performance with

f_{m a x}

between 2.0GHz and 2.5GHz. However, the full offload policy offloads all tasks to the computation server with no significant change in total energy consumption.

Figure 7 compares the variation of the total network energy consumption with different energy consumption per unit of computation resource for LEO satellite

e_{s a t}

under different benchmark algorithms. With the increase of

e_{s a t}

, the total energy consumption under the proposed algorithm is always the lowest. The total energy consumption of the network under the greedy-edge algorithm is the highest. On the one hand, it has no better offloading decision. On the other hand, in terms of energy consumption, the devices unable to intelligently change the computation resource, resulting in increased energy consumption for local computation. Under the full offload benchmark algorithm, more tasks are offloaded to the LEO satellite for execution and the total energy consumption grows more significantly when

e_{s a t}

increases. The DDPG algorithm enables to dynamically adjust task offloading according to the reward value, with the rate of increase in total network energy consumption gradually decreasing as

e_{s a t}

grows. The high altitude of LEO satellite lead to more transmission latency. So a very little tasks will be offloaded to it. The variation in total network energy consumption with the proposed algorithm is slight when

e_{s a t}

increases. Similarly, the proposed algorithm demonstrates excellent performance as the energy consumption per unit computation resource for UAV

e_{u a v}

increases.

In order to illustrate the performance of the proposed algorithm in optimizing the UAV trajectory to reduce latency, three cases with different benchmark algorithms are analyzed. These three cases are trajectory optimization, trajectory fixed in one direction, and UAV flying in place, respectively. As shown in Figure 8, the lowest overall latency of the three cases is trajectory optimization, which reduces the overall latency by 2.93% compared to UAV flying in place and 5.78% compared to the overall time reduction for trajectory fixed in one direction. The total task latency under both the proposed algorithm and the DDPG algorithm is lower in each flight trajectory mode, significantly improving the latency/QoS. The greedy-edge and full offload algorithm show poor performance. The greedy-edge algorithm offloads a higher percentage of tasks to UAV, resulting in a higher task latency. Meanwhile, the local computation resources are not the maximum computation capability, which leads to longer computation time, which explains the lower total task latency of the full offload compared to the greedy-edge algorithm.

Since the UAV have limited battery, the remaining power of the UAV needs to be maintained as much as possible to ensure the sustainable operation of the network. Figure 9 shows the average residual power of the UAV at each time slot for different benchmark algorithms. Among these benchmark algorithms, both the proposed algorithm and DDPG algorithm employ WPT, which ensure that the UAV always has remaining power to maintain operation. However, the other two do not have WPT, so the power is quickly depleted and unable to maintain the sustainable operation of the network. It is worth noting that the energy consumed by UAV computation is not large compared to the energy consumed by UAV flight. Hence, the difference in the average remaining power of UAV under the remaining three benchmark algorithms is small. The greedy-edge algorithm and the full offload policy offload a large of tasks to the computation server, so the average remaining power of the UAV is lower. The proposed algorithm, on the other hand, integrates dynamic task offloading with UAV trajectory optimization, which not only maximize the relative residual power of UAV, but also enables UAV to replenish power through WPT when the power of UAV falls below a threshold value, maintaining sustainable network operation.

In order to evaluate the performance of the proposed algorithm in reducing the carbon emissions of the network, Figure 10 shows the average loss ratio of RE for different loss factors of energy transmission. The smaller the average loss rate of RE is, the more RE is utilized. And the more carbon emissions are reduced. As the two algorithms can intelligently optimize the sharing proportion

υ_{n} (t)

of RE, the proposed algorithm shows better performance compared to the DDPG algorithm. It is worth noting that the average loss ratio of RE under the DDPG algorithm at

η = 0.05

is higher than that

η = 0.1

. It may be that too much energy is carried over when too little energy is shared. When RE arrives in the next time slot, the total remaining energy exceeds the backup battery capacity, which leads to an increase in the amount of RE

e_{n}^{e x c} (t)

that is discarded.

6. Conclusions

In this article, a SAGIN scenario with new designed power technology is proposed firstly. A cost function is formulated with joint latency/QoS, green communication and peak carbon dioxide. Specifically, the cost function consists of task latency, energy consumption, and the carbon emissions of the BSs. To maintain the flight and computation energy consumption of the UAV, BSs explore WPT to power UAV to ensure the sustainability of the network. Then a TD3PG method is proposed to optimizing the cost function. Finally, the proposed algorithm is compared with three benchmark algorithms. Simulation results show that the approach improves the sustainability of the network, while offering advantages in terms of task latency and energy saving. By optimizing the UAV trajectory under this algorithm, the total task latency is reduced by 2.93% and 5.78% compared to single trajectory and no trajectory, respectively. The proposed algorithm also shows better performance when it comes to reducing the carbon emissions of the network. In the future, software defined network will be utilized to better optimize the energy resources and wireless resources in SAGIN.

Author Contributions

Y.W.: methodology, software, writing. B.L.: supervision, writing—reviewing and editing. J.H.: validation. J.D.: supervision. Y.L.: editing, Y.L.: original draft preparation. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Ningxia Autonomous Region key R&D plan project (general project) (2020BDE03006), Ningxia Natural Science Foundation (2019AAC03072), and the National Natural Science Foundation of China (61301145).

Conflicts of Interest

The authors declare no conflict of interest.

References

Cheng, N.; Quan, W.; Shi, W.; Wu, H.; Ye, Q.; Zhou, H.; Zhuang, W.; Shen, X.; Bai, B. A Comprehensive Simulation Platform for Space-Air-Ground Integrated Network. IEEE Wireless Communications 2020, 27, 178–185. [Google Scholar] [CrossRef]
Wang, Y.; Su, Z.; Ni, J.; Zhang, N.; Shen, X. Blockchain-Empowered Space-Air-Ground Integrated Networks: Opportunities, Challenges, and Solutions. IEEE Communications Surveys & Tutorials 2022, 24, 160–209. [Google Scholar]
Wang, C.; Yu, X.; Xu, L.; Jiang, F.; Wang, W.; Cheng, X. QoS-aware offloading based on communication-computation resource coordination for 6G edge intelligence. China Communications 2023, 20, 236–251. [Google Scholar] [CrossRef]
Feng, X.; Ling, X.; Zheng, H.; Chen, Z.; Xu, Y. Adaptive Multi-Kernel SVM With Spatial-Temporal Correlation for Short-Term Traffic Flow Prediction. IEEE Transactions on Intelligent Transportation Systems 2019, 20, 2001–2013. [Google Scholar] [CrossRef]
Zhao, B.; Cui, Q.; Liang, S.; Zhai, J.; Hou, Y.; Huang, X.; Pan, M.; Tao, X. Green concerns in federated learning over 6G. China Communications 2022, 19, 50–69. [Google Scholar] [CrossRef]
Cheshmehzangi, A.; Chen, H. Key Suggestions and Steps Ahead for China’s Carbon Neutrality Plan. In China’s Sustainability Transitions: Low Carbon and Climate-Resilient Plan for Carbon Neutral 2060; Springer Singapore: Singapore, 2021; pp. 189–206. [Google Scholar]
Peng, H.; Shen, X. Deep Reinforcement Learning Based Resource Management for Multi-Access Edge Computing in Vehicular Networks. IEEE Transactions on Network Science and Engineering 2020, 7, 2416–2428. [Google Scholar] [CrossRef]
Zhao, J.; Li, Q.; Gong, Y.; Zhang, K. Computation Offloading and Resource Allocation For Cloud Assisted Mobile Edge Computing in Vehicular Networks. IEEE Transactions on Vehicular Technology 2019, 68, 7944–7956. [Google Scholar] [CrossRef]
Abderrahim, W.; Amin, O.; Alouini, M.S.; Shihada, B. Latency-Aware Offloading in Integrated Satellite Terrestrial Networks. IEEE Open Journal of the Communications Society 2020, 1, 490–500. [Google Scholar] [CrossRef]
Dai, Y.; Zhang, K.; Maharjan, S.; Zhang, Y. Edge Intelligence for Energy-Efficient Computation Offloading and Resource Allocation in 5G Beyond. IEEE Transactions on Vehicular Technology 2020, 69, 12175–12186. [Google Scholar] [CrossRef]
Wang, F.; Xing, H.; Xu, J. Real-Time Resource Allocation for Wireless Powered Multiuser Mobile Edge Computing With Energy and Task Causality. IEEE Transactions on Communications 2020, 68, 7140–7155. [Google Scholar] [CrossRef]
Chen, M.; Hao, Y. Task Offloading for Mobile Edge Computing in Software Defined Ultra-Dense Network. IEEE Journal on Selected Areas in Communications 2018, 36, 587–597. [Google Scholar] [CrossRef]
Guo, Y.; Li, Q.; Li, Y.; Zhang, N.; Wang, S. Service Coordination in the Space-Air-Ground Integrated Network. IEEE Network 2021, 35, 168–173. [Google Scholar] [CrossRef]
Zhang, L.; Abderrahim, W.; Shihada, B. Heterogeneous Traffic Offloading in Space-Air-Ground Integrated Networks. IEEE Access 2021, 9, 165462–165475. [Google Scholar] [CrossRef]
Chen, M.; Hao, Y. Task Offloading for Mobile Edge Computing in Software Defined Ultra-Dense Network. IEEE Journal on Selected Areas in Communications 2018, 36, 587–597. [Google Scholar] [CrossRef]
Buzzi, S.; I, C.L.; Klein, T.E.; Poor, H.V.; Yang, C.; Zappone, A. A Survey of Energy-Efficient Techniques for 5G Networks and Challenges Ahead. IEEE Journal on Selected Areas in Communications 2016, 34, 697–709. [Google Scholar] [CrossRef]
Alqasir, A.M.; Kamal, A.E. Cooperative Small Cell HetNets With Dynamic Sleeping and Energy Harvesting. IEEE Transactions on Green Communications and Networking 2020, 4, 774–782. [Google Scholar] [CrossRef]
Malta, S.; Pinto, P.; Fernández-Veiga, M. Using Reinforcement Learning to Reduce Energy Consumption of Ultra-Dense Networks With 5G Use Cases Requirements. IEEE Access 2023, 11, 5417–5428. [Google Scholar] [CrossRef]
Yuan, H.; Tang, G.; Guo, D.; Wu, K.; Shao, X.; Yu, K.; Wei, W. BESS Aided Renewable Energy Supply Using Deep Reinforcement Learning for 5G and Beyond. IEEE Transactions on Green Communications and Networking 2022, 6, 669–684. [Google Scholar] [CrossRef]
Nabavi, S.A.; Motlagh, N.H.; Zaidan, M.A.; Aslani, A.; Zakeri, B. Deep Learning in Energy Modeling: Application in Smart Buildings With Distributed Energy Generation. IEEE Access 2021, 9, 125439–125461. [Google Scholar] [CrossRef]
Rubina Aktar, M.; Shamim Anower, M.; Zahurul Islam Sarkar, M.; Sayem, A.S.M.; Rashedul Islam, M.; Akash, A.I.; Rumana Akter Rume, M.; Moloudian, G.; Lalbakhsh, A. Energy-Efficient Hybrid Powered Cloud Radio Access Network (C-RAN) for 5G. IEEE Access 2023, 11, 3208–3220. [Google Scholar] [CrossRef]
Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Network 2020, 34, 134–142. [Google Scholar] [CrossRef]
Wang, F.; Xu, J.; Wang, X.; Cui, S. Joint Offloading and Computing Optimization in Wireless Powered Mobile-Edge Computing Systems. IEEE Transactions on Wireless Communications 2018, 17, 1784–1797. [Google Scholar] [CrossRef]
Zheng, K.; Jiang, G.; Liu, X.; Chi, K.; Yao, X.; Liu, J. DRL-Based Offloading for Computation Delay Minimization in Wireless-Powered Multi-Access Edge Computing. IEEE Transactions on Communications 2023, 71, 1755–1770. [Google Scholar] [CrossRef]
Zheng, K.; Jia, X.; Chi, K.; Liu, X. DDPG-Based Joint Time and Energy Management in Ambient Backscatter-Assisted Hybrid Underlay CRNs. IEEE Transactions on Communications 2023, 71, 441–456. [Google Scholar] [CrossRef]
Liu, J.; Zhao, X.; Qin, P.; Geng, S.; Meng, S. Joint Dynamic Task Offloading and Resource Scheduling for WPT Enabled Space-Air-Ground Power Internet of Things. IEEE Transactions on Network Science and Engineering 2022, 9, 660–677. [Google Scholar] [CrossRef]
Sun, L.; Pang, H.; Gao, L. Joint Sponsor Scheduling in Cellular and Edge Caching Networks for Mobile Video Delivery. IEEE Transactions on Multimedia 2018, 20, 3414–3427. [Google Scholar] [CrossRef]
Yong, P.; Zhang, N.; Hou, Q.; Liu, Y.; Teng, F.; Ci, S.; Kang, C. Evaluating the Dispatchable Capacity of Base Station Backup Batteries in Distribution Networks. IEEE Transactions on Smart Grid 2021, 12, 3966–3979. [Google Scholar] [CrossRef]
Hu, Q.; Cai, Y.; Yu, G.; Qin, Z.; Zhao, M.; Li, G.Y. Joint Offloading and Trajectory Design for UAV-Enabled Mobile Edge Computing Systems. IEEE Internet of Things Journal 2019, 6, 1879–1892. [Google Scholar] [CrossRef]
Hong, T.; Zhao, W.; Liu, R.; Kadoch, M. Space-Air-Ground IoT Network and Related Key Technologies. IEEE Wireless Communications 2020, 27, 96–104. [Google Scholar] [CrossRef]
Mao, S.; He, S.; Wu, J. Joint UAV Position Optimization and Resource Scheduling in Space-Air-Ground Integrated Networks With Mixed Cloud-Edge Computing. IEEE Systems Journal 2021, 15, 3992–4002. [Google Scholar] [CrossRef]
Lakew, D.S.; Tran, A.T.; Dao, N.N.; Cho, S. Intelligent Offloading and Resource Allocation in Heterogeneous Aerial Access IoT Networks. IEEE Internet of Things Journal 2023, 10, 5704–5718. [Google Scholar] [CrossRef]
Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K.B. A Survey on Mobile Edge Computing: The Communication Perspective. IEEE Communications Surveys & Tutorials 2017, 19, 2322–2358. [Google Scholar]
Zhan, C.; Zeng, Y. Aerial-Ground Cost Tradeoff for Multi-UAV-Enabled Data Collection in Wireless Sensor Networks. IEEE Transactions on Communications 2020, 68, 1937–1950. [Google Scholar] [CrossRef]
Huang, H.; Ye, Q.; Zhou, Y. 6G-Empowered Offloading for Realtime Applications in Multi-Access Edge Computing. IEEE Transactions on Network Science and Engineering 2023, 10, 1311–1325. [Google Scholar] [CrossRef]
Wang, Y.; Gao, Z.; Zhang, J.; Cao, X.; Zheng, D.; Gao, Y.; Ng, D.W.K.; Renzo, M.D. Trajectory Design for UAV-Based Internet of Things Data Collection: A Deep Reinforcement Learning Approach. IEEE Internet of Things Journal 2022, 9, 3899–3912. [Google Scholar] [CrossRef]
Gao, G.; Li, J.; Wen, Y. DeepComfort: Energy-Efficient Thermal Comfort Control in Buildings Via Reinforcement Learning. IEEE Internet of Things Journal 2020, 7, 8472–8484. [Google Scholar] [CrossRef]
Zhao, X.; Du, F.; Geng, S.; Fu, Z.; Wang, Z.; Zhang, Y.; Zhou, Z.; Zhang, L.; Yang, L. Playback of 5G and Beyond Measured MIMO Channels by an ANN-Based Modeling and Simulation Framework. IEEE Journal on Selected Areas in Communications 2020, 38, 1945–1954. [Google Scholar] [CrossRef]
Cheng, N.; Lyu, F.; Quan, W.; Zhou, C.; He, H.; Shi, W.; Shen, X. Space/Aerial-Assisted Computing Offloading for IoT Applications: A Learning-Based Approach. IEEE Journal on Selected Areas in Communications 2019, 37, 1117–1129. [Google Scholar] [CrossRef]

Figure 1. SAGIN scenario with new designed power supply.

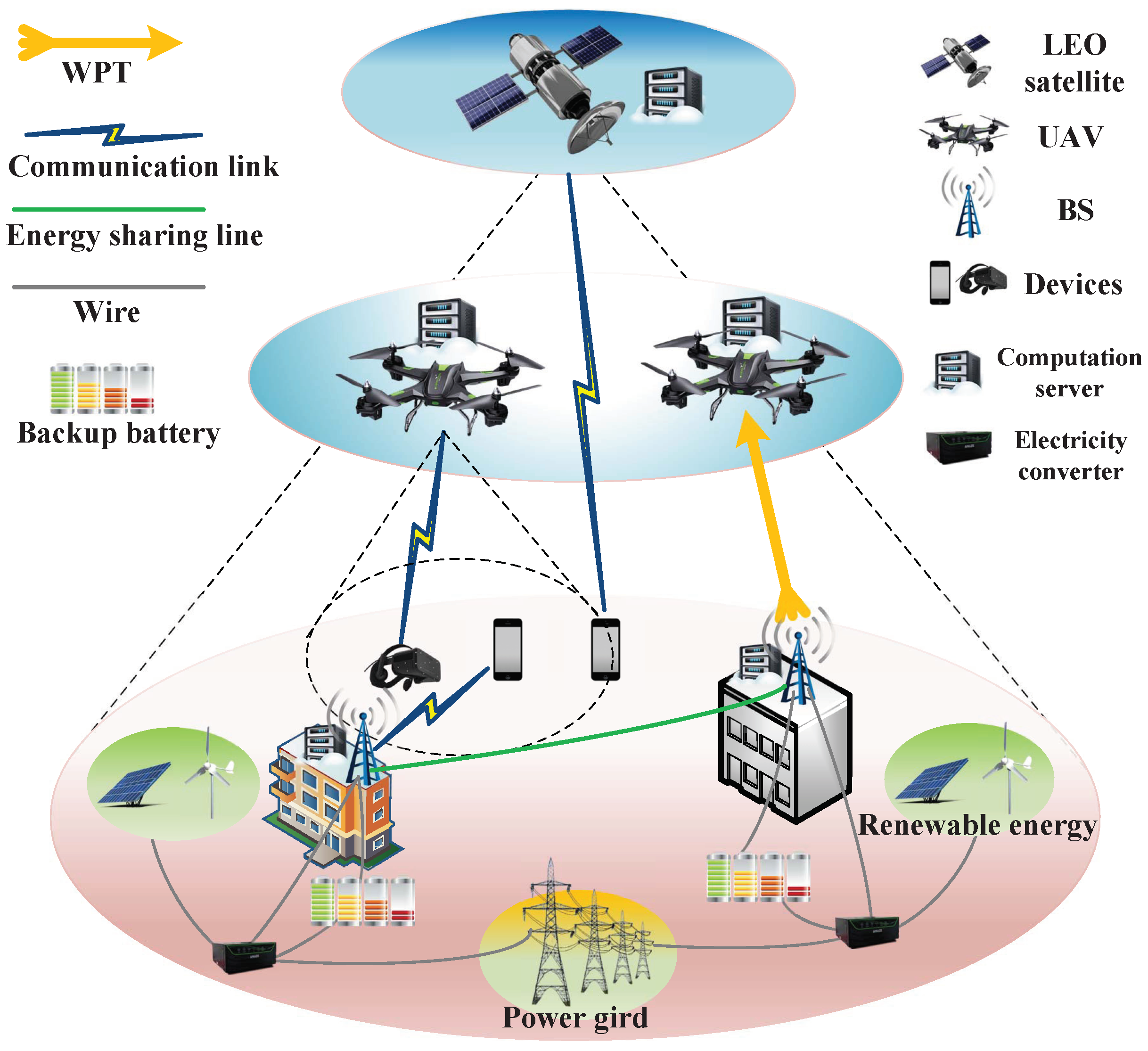
Figure 2. Structure of TD3PG algorithm.

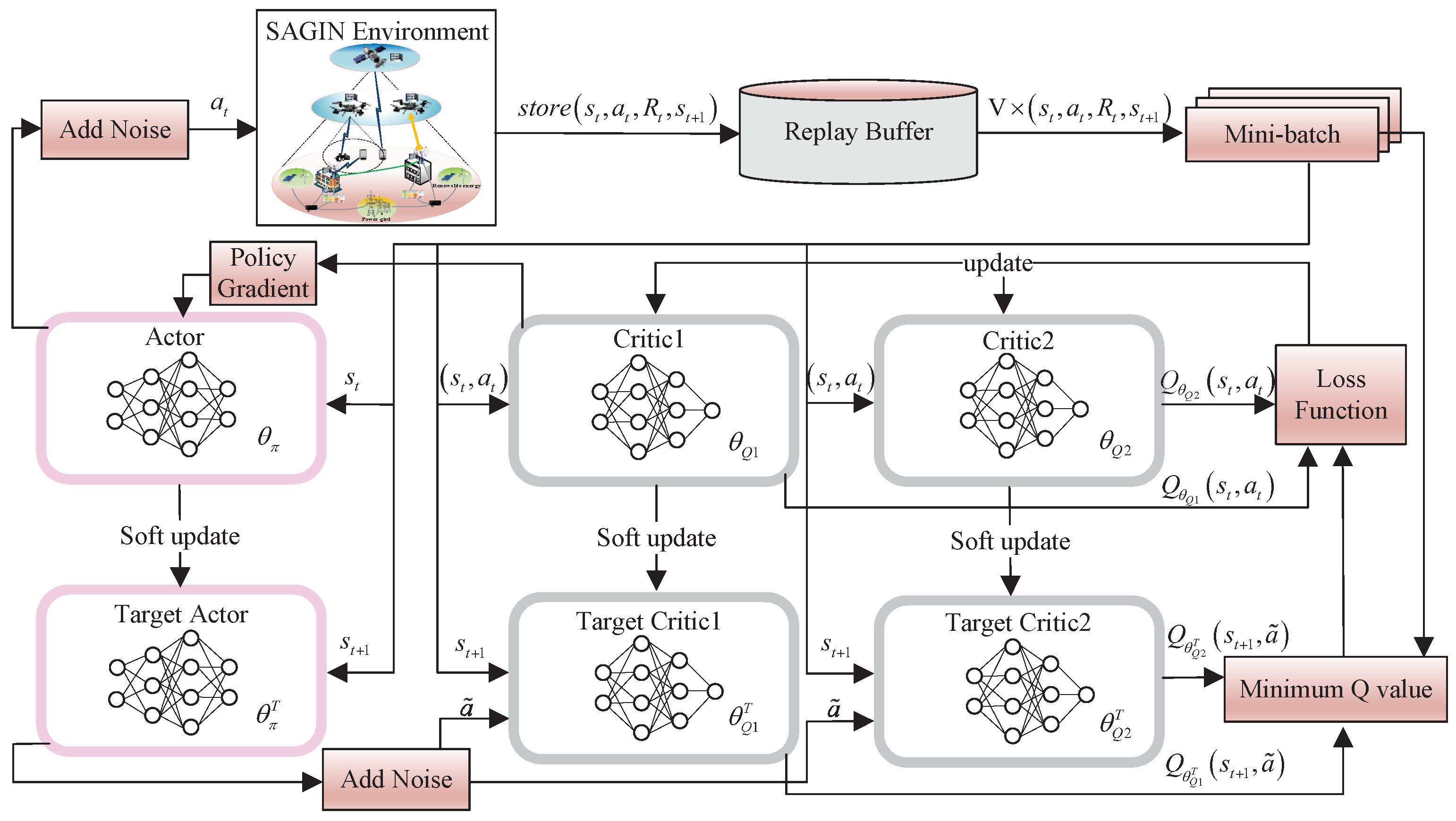
Figure 3. Impact of learning rate over training episodes.

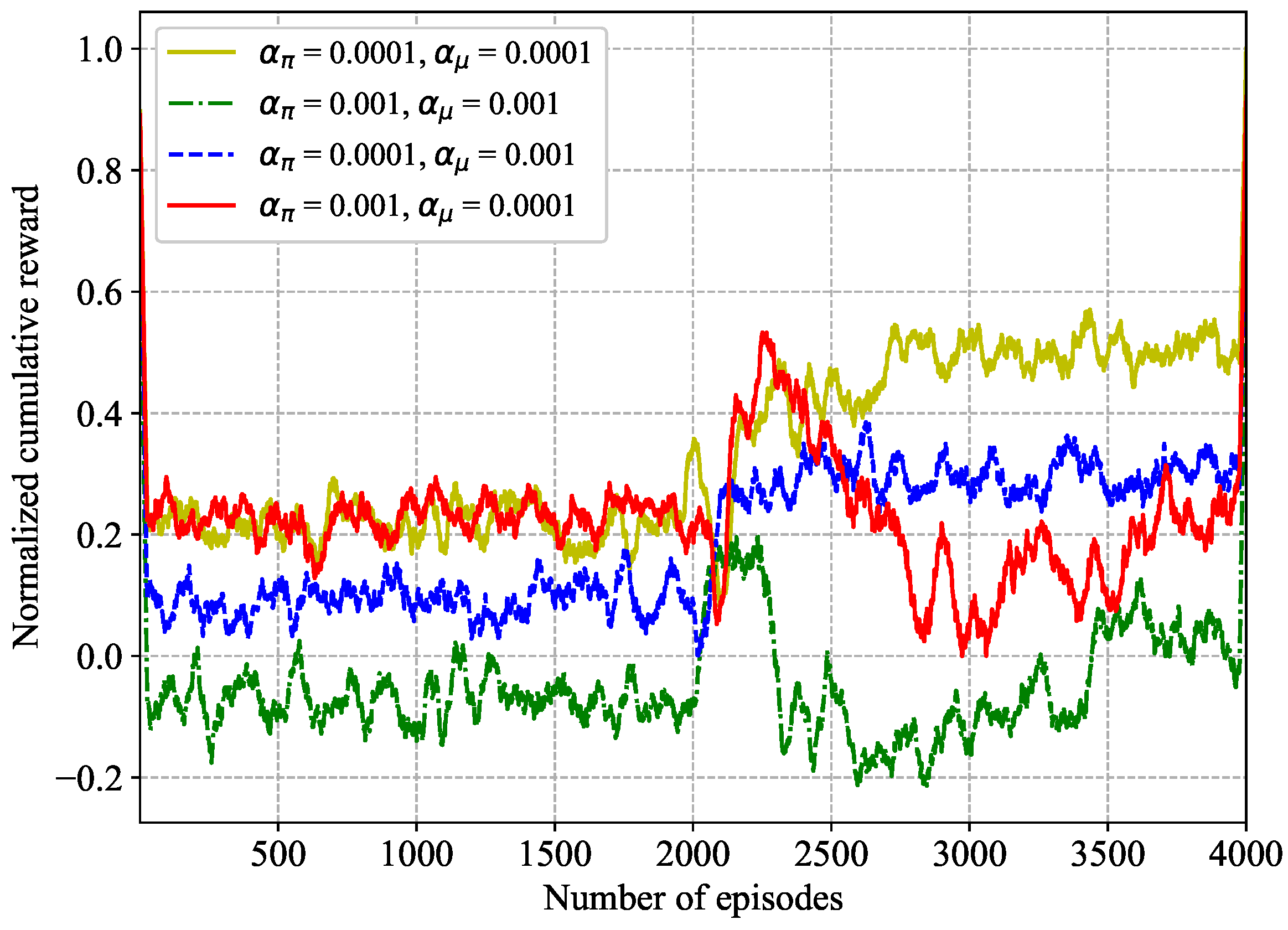
Figure 4. Impact of discount factor over training episodes.

Figure 5. Comparison of cost function with respect to the number of devices.

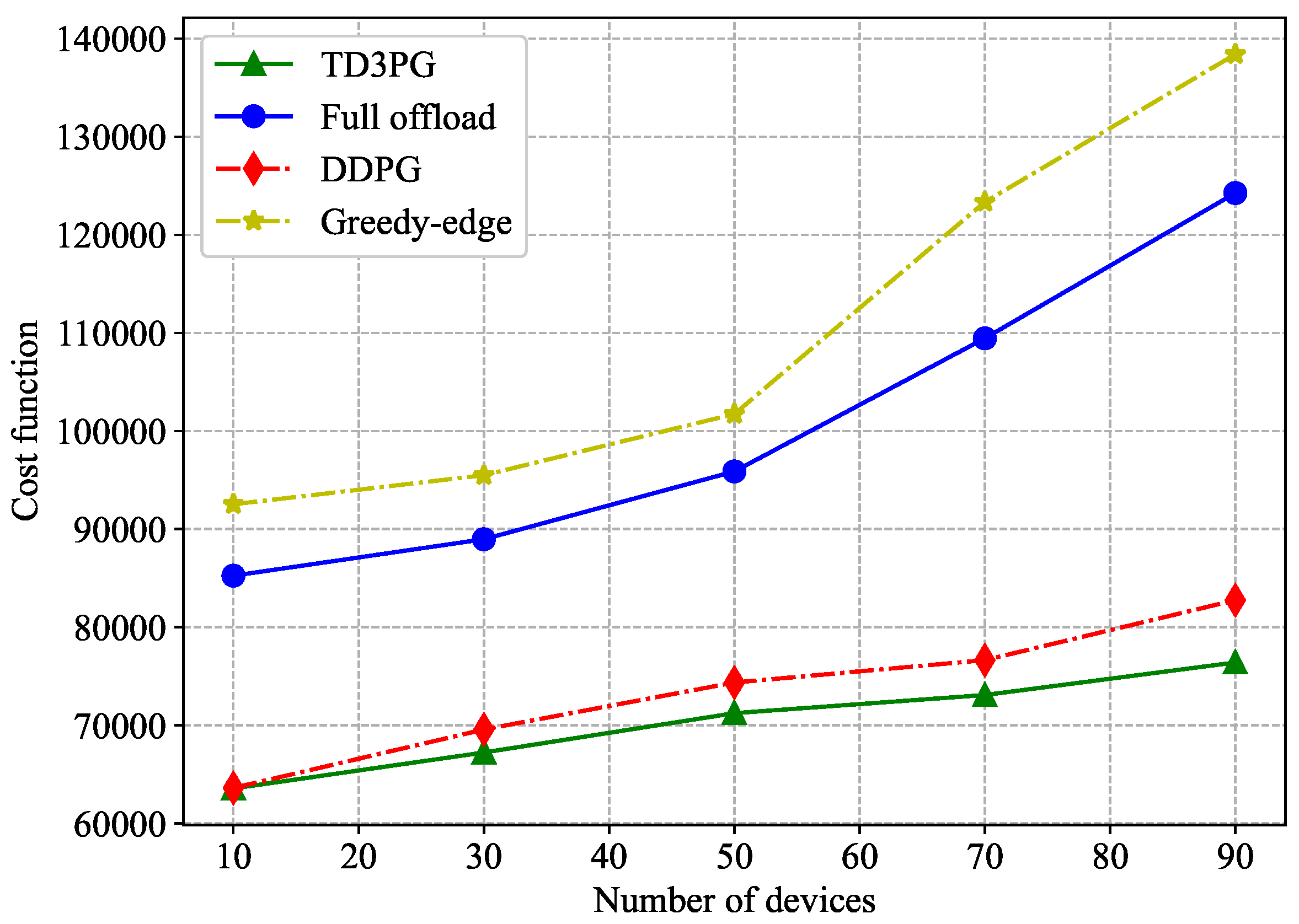
Figure 6. Comparison of total energy consumption for device with maximum computation capacity.

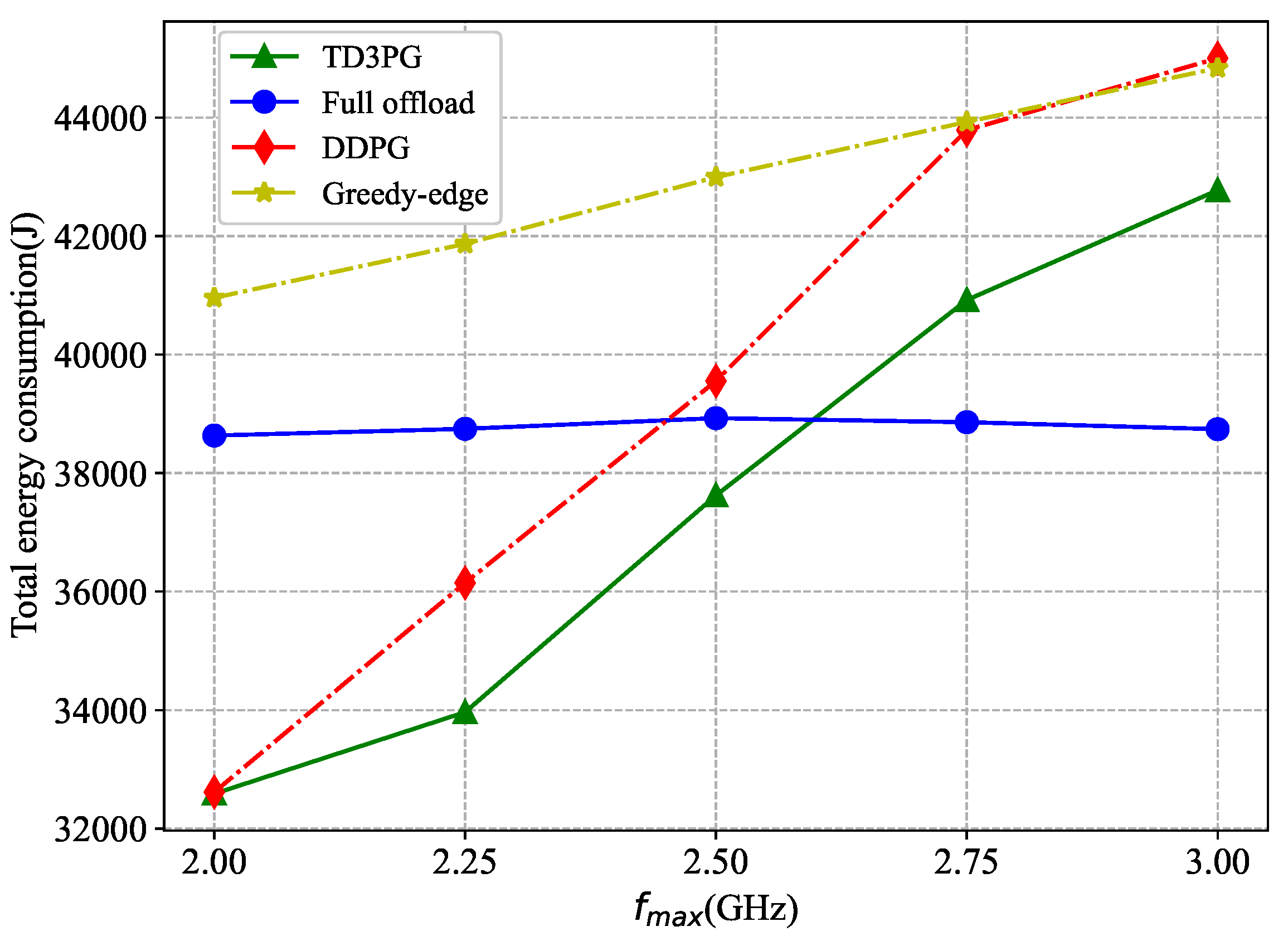
Figure 7. Comparison of the total energy consumption with the energy consumption per unit computation resource for LEO satellite.

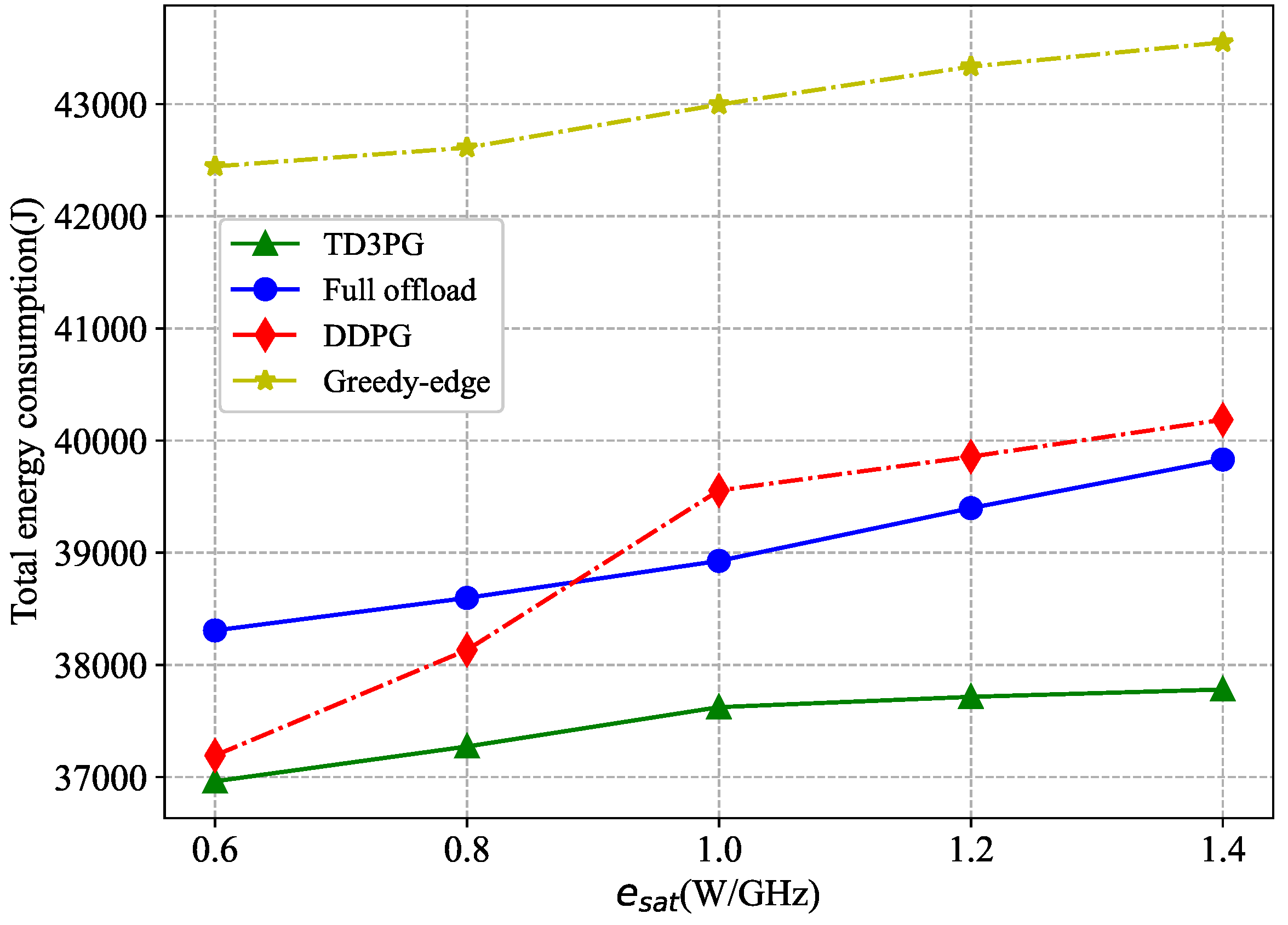
Figure 8. Comparison of total task latency with three trajectory settings.

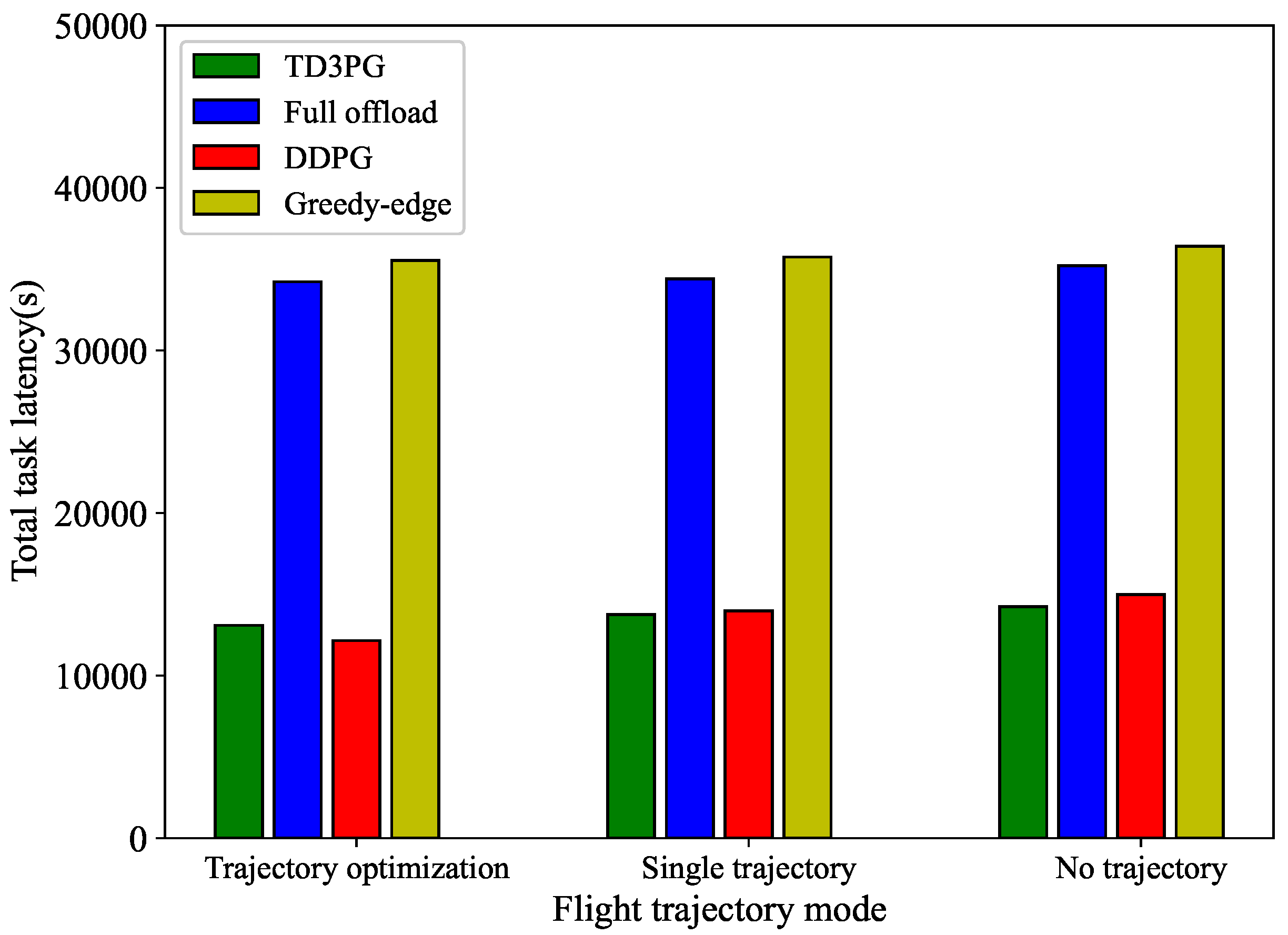
Figure 9. Comparison of average remaining power of UAV in each time slot.

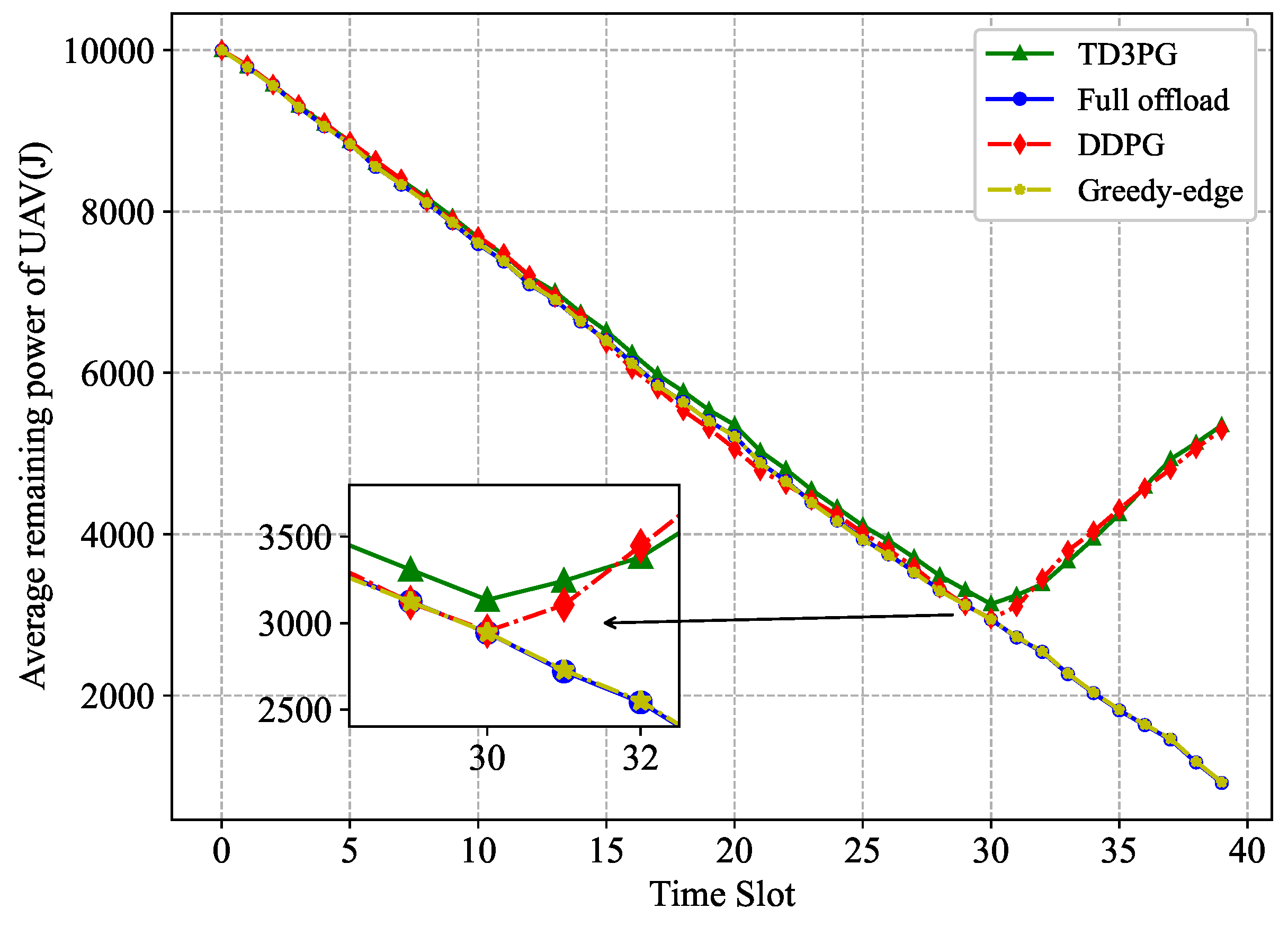
Figure 10. Comparison of average loss ratio of RE with the loss factor

η

Figure 10. Comparison of average loss ratio of RE with the loss factor

η

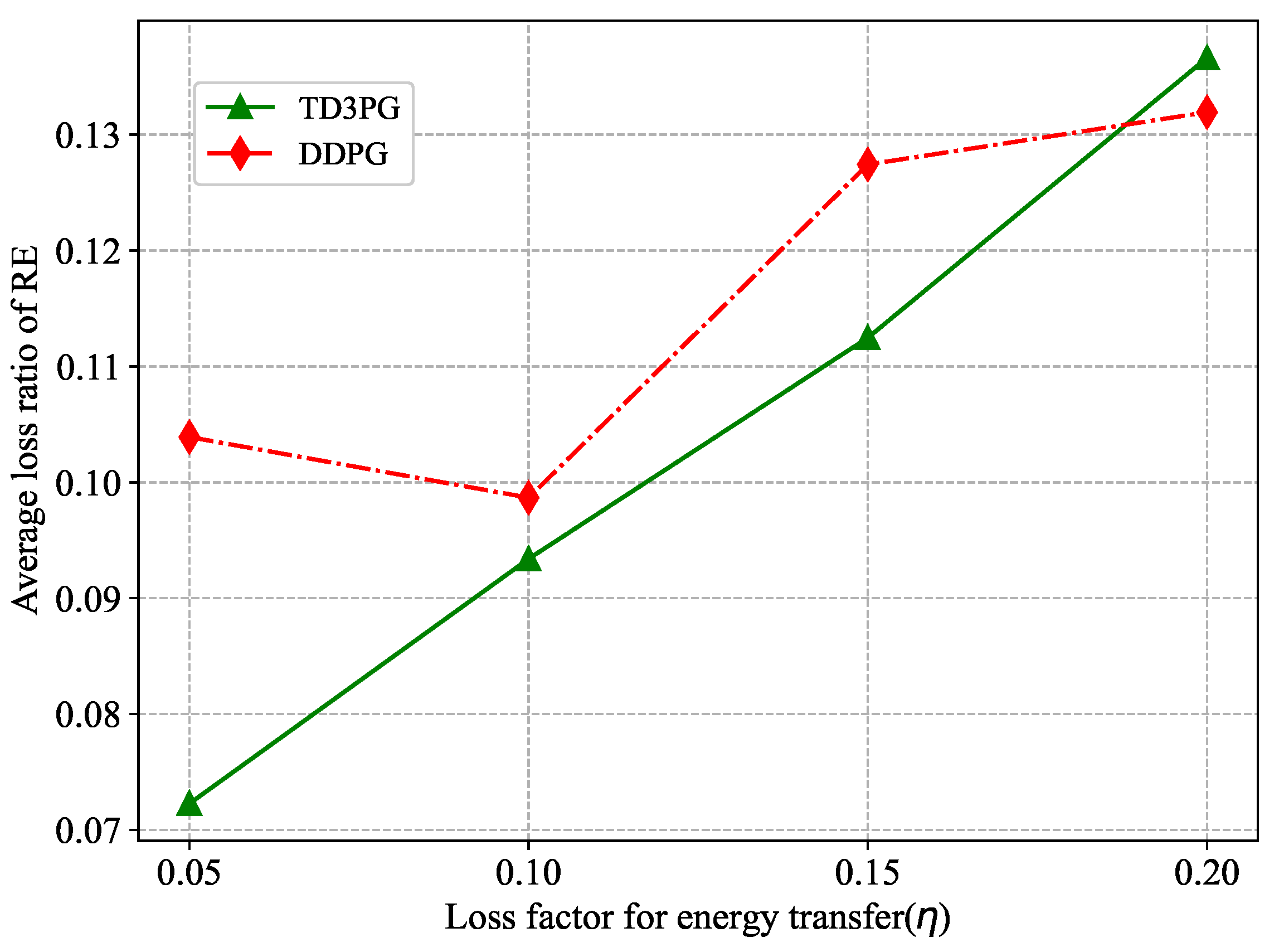
Table 1. Simulation Parameters.

Parameter	Value
Weight of UAV ( $m_{k}$ )	9.65kg
Safety distance among UAVs ( $D_{min}$ )	20m
Maximum speed of UAV ( $v_{m a x}$ )	30m/s
Path loss index [38] ( $α_{0}$ )	2
Device upload power ( $p_{m}$ )	100mW
CPU cycles required for each bit of data ( $e_{m}$ )	800 cycles/bit
Effective switched capacitance ( $κ$ )	$10^{- 27}$ J/Hz $^{3}$ /s
Energy conservation efficiency ( $χ$ )	0.9
Antenna power gains of the BS transmitter ( $G_{n}^{t}$ )	41dB
Antenna power gains of the UAV receiver ( $G_{k}^{r}$ )	41dB
Blade profile power in hovering status ( $P_{0}$ )	79.86W
Induced power in hovering status ( $P_{i}$ )	92.48W
Tip speed of the rotor blade ( $U_{t i p}$ )	120m/s
Mean rotor induced velocity in hover ( $v_{0}$ )	4.03m/s
Air density ( $ρ$ )	1.225kg/m $^{3}$
Rotor disc area (A)	0.503m $^{2}$
Fuselage drag ratio ( $d_{0}$ )	0.6
Rotor solidity (s)	0.05
Loss factor for energy transfer ( $η$ )	0.1
Energy consumption per unit of computation
resource for LEO satellite( $e_{s a t}$ )	1W/GHz
Energy consumption per unit of computation
resource for UAV( $e_{u a v}$ )	1.5W/GHz

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Joint Latency-Oriented, Energy Consumption, and Carbon Emission for Space-Air-Ground Integrated Network with New Designed Power Technology

Abstract

1. Introduction

2. System Model

2.1. Backup battery Model for BS

2.2. Communication Model

2.2.1. Offloading to the BSs

2.2.2. Offloading to the UAVs

2.2.3. Offloading to the LEO satellite

2.3. Computation Model

2.3.1. Local Computation

2.3.2. Offloading to the BSs

2.3.3. Offloading to the UAVs

2.3.4. Offloading to the LEO satellite

2.4. WPT Model

2.5. Flight Model

3. Problem Formulation

4. Markov Chain Model based TD3PG Algorithm in SAGIN

4.1. MDP Formulation

4.2. TD3PG Algorithm

4.3. Complexity Analysis

5. Results and Discussion

5.1. Simulation Settings

5.2. Results and Analysis

6. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe