Prerpints.org logo
Preprint
Article

Estimation of Reference Evapotranspiration in a Semi-Arid Region of Mexico

Altmetrics

Downloads

148

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 July 2023

Posted:

04 July 2023

You are already at the latest version

Alerts
Abstract
Reference evapotranspiration (ET0) is the first step in calculating crop irrigation demand, and numerous methods have been proposed to estimate this parameter. FAO-56 Penman-Monteith (PM) is the only standard method for defining and calculating ET0. However, it requires radiation, air temperature, atmospheric humidity, and wind speed data, limiting its application in regions where these data are unavailable; therefore, new alternatives are required. This study compared the accuracy of ET0 calculated with the Blaney-Criddle (BC) and Hargreaves-Samani (HS) methods versus PM using information from an automated weather station (AWS) and the NASA-POWER platform (NP) for different periods of time. The information collected corresponding at Module XII of the Lagunera Region Irrigation District 017, a semi-arid region in the North of Mexico. The HS method underestimated by 5.5 % the reference evapotranspiration (ET0) compared to the PM method during the period from March to August, and yielded the best fit in the different evaluation periods: daily, average, and 5-day cumulative; the latter showed the best values of inferential parameters. The information about maximum and minimum temperatures from the NP platform was suitable for estimating ET0 using the HS equation. This data source is a timely alternative, particularly in semi-arid regions where no data from weather stations are available.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

Reference evapotranspiration (ET0) is the evapotranspiration rate of a hypothetical reference crop (grass or alfalfa) with a height of 0.12 m, a fixed surface resistance of 70 s m-1, and an albedo of 0.23, homogeneous, well-watered, free from diseases and pests, growing vigorously, and providing complete shade to the soil [1,2,3]. ET0 measures atmospheric evaporation demand regardless of crop type, development, and management practices [4,5]. This variable is affected only by climatic factors [6] and can be calculated from meteorological data [2].
Estimating ET0 is the first step in the design, planning, and management of different irrigation systems [7,8]. In addition, it is relevant for calculating crop water requirements [9,10]. This parameter is the backbone of the agronomic design of any irrigation system, facilitates its operation (irrigation schedule and shifts), and allows planning water resource management, either in a basin [11] or in an irrigation district. Therefore, its accurate estimation is an essential step in water management, particularly in arid and semi-arid areas where water is scarce [12].
Given the temporal and spatial variability of the climate, several methods to estimate ET0 have been proposed, mainly empirical equations developed from field experiments and those based on theoretical approaches [11]. These methods include the evaporimeter tank and empirical equations, including the complete physical model (FAO-56 Penman-Monteith), the equation based on temperature (Blaney-Criddle, Thornthwaite, and Turc), and the one based on temperature and radiation (Hargreaves, Jensen-Haise, Priestley-Taylor, and FAO Radiation), among others [13].
The UN Food and Agriculture Organization (FAO) recommends the Penman-Monteith standard method described in the FAO-56 Manual because it can be used in arid, temperate, and tropical areas [14]. However, this method requires various meteorological input variables (temperature, solar radiation, relative humidity, and wind speed), which restrains its widespread use [15]. Therefore, its usefulness is limited in regions with no meteorological stations or shortage of input data [16], which are usually not available with the frequency and quality required [17]. The other equations can be used in regions with very little climatological information; such is the case of Hargreaves-Samani (HS) and Blaney-Criddle (BC) equations, which are the most common ones [18,19,20] and only require temperature as an input variable [21].
The accuracy of the HS and BC equations has been evaluated by several authors, comparing their results with the FAO-56 Penman-Monteith (PM) reference method; HS was the equation that attained the best fit in semi-arid regions [22,23]. Other authors state that the HS method works well in most climatic regions, except for wet areas where it tends to overestimate ET0 [8,24,25,26]. Since HS was developed empirically based on data from arid to subhumid environments, it may not fit well to conditions markedly different from those considered for its calibration, as is the case of wet climates [8]. On the other hand, the HS method underestimates ET0 for dry and windy areas because it does not include wind, and is seemingly more accurate when applied for 5- to 7-day averages than for daily time scales [27,28]. However, despite a fairly good performance of the HS equation in most applications, particularly irrigation planning, several authors have attempted to either recalibrate the HS coefficients or parameters [26,29] or modify the equation itself [30,31] aiming to improve its performance.
Given the scarcity of climatological data for some regions, there is also the possibility to estimate ET0 using gridded meteorological or reanalysis data [32,33,34]; these can be obtained from the following platforms: National Aeronautics and Space Administration - Prediction Of Worldwide Energy Resource (NASA-POWER) [17,35], Global Land Data Assimilation System (GLDAS) [36], Climate Forecast System ver. 2 (CFSv2) [37], North American Land Data Assimilation System (NLDAS) [38], and National Digital Forecast Database (NDFD) [39]. Some of these systems are global and others regional; the latter provides data at a finer spatio-temporal resolution [17], although this does not necessarily translate into high precision [40]. Currently, NASA-POWER is one of the most used platforms for estimating this variable [41,42,43]. The platform is free and easily accessible; it provides daily information on near-surface air temperature, precipitation, relative humidity, radiation, and wind direction and speed. In addition, data on these variables are arranged according to three different conditions: (1) “single point” with available time-series data based on geographic coordinates recorded and selected by the user; (2) “regional endpoint” that produces a time-series dataset for cells delimited by geographic coordinates selected by the user; and (3) “global endpoint” that produces long-term climatological averages at a global scale [44]. However, such NASA-POWER climate information requires evaluation and validation with data from in-situ weather stations for the area of interest [35].
This study aims to compare the accuracy of ET0 calculated with the BC and HS methods relative to the FAO-56 Penman–Monteith (PM) reference method, with data recorded by an automated weather station (AWS) and using the NASA-POWER (NP) platform, for different calculation periods.

2. Materials and Methods

2.1. Study Area and Data Collection

The climatic variables to calculate ET0 with empirical equations were recorded with a wireless Davis Vantage Pro 2 Plus AWS; it has a console that allows viewing all meteorological variables simultaneously [45], with a 30-minute update frequency.
The AWS belongs to Centro Nacional de Investigación Disciplinaria en Relación Agua, Suelo, Planta, Atmósfera (National Center for Disciplinary Research on Water, Soil, Plant, Atmosphere; CENID RASPA) of Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (National Institute of Forestry, Agricultural, and Livestock Research; INIFAP), within the facilities of an agricultural production unit located at Module XII of the Lagunera Region Irrigation District 017, at 1,110 m a.s.l and coordinates 25°47’00.32” N, 103°18’46.54” W (Figure 1).
The meteorological information used was daily averages for the period between 26 February (Julian day 57) and 09 August (Julian day 221) 2021 (n = 165). In the Lagunera Region Irrigation District 017, the main crops of the spring-summer cycle are grown In this period, including forage corn.
In addition, the meteorological variables were downloaded from the NASA-POWER climate website (National Aeronautics and Space Administration - Prediction of Worldwide Energy Resource; https://power.larc.nasa.gov). This website collects information from various sources: data recorded on site, satellite data, wind probes, and assimilated data systems [17].
The NASA-POWER (NP) weather data are based on a single assimilation model named GMAO (Global Modeling and Assimilation Office), starting from the MERRA-2 (Modern Era Retrospective-Analysis for Research and Applications) reanalysis dataset and the GEOS (Goddard Earth Observation System) data processing system [46,47]. Solar radiation is derived from the GEWEX SRB (Global Energy and Water Exchanges Project Surface Radiation Budget) project [48,49].
The horizontal resolution of the NP meteorological data source corresponds to a ½° × 5/8° latitude/longitude grid and the solar data sources come from a 1° × 1° latitude/longitude grid. The current version no longer reassigns data to a common grid; once the data are processed and filed, they are available through the NP service package. The meteorological data derive from NASA’s GMAO MERRA-2 and GEOS 5.12.4 FP-IT. The NP platform team processes GEOS data daily and combines them with MERRA-2 data, producing daily time series that yield low-latency products usually available in approximately two days (real-time). Energy flow data (solar irradiance, thermal IR, and cloud properties) derive from NASA’s GEWEX SRB Release 4-Integrated Product (R4-IP) file and CERES SYNIdeg and FLASHFlux projects. These data are processed daily and added to the daily time series, issuing products after approximately 4 days, almost in real time [50].
The main features of the NP system database are shown in Table 1.

2.2. Et0 Estimation with Empirical Equations

ET0 was estimated+++ through three empirical equations with different information requirements: an equation based on a complete physical model (PM); another, on solar temperature and radiation (HS); and the last one, on temperature, relative humidity, and wind speed (BC).

2.2.1. FAO-56 Penman – Monteith Method (Et0-PM)

ET0 was estimated daily with the FAO-56 Penman-Monteith method using Equation 1 [14,51]; this method is useful for arid, temperate, and tropical zones [11,14].
E T 0 − P M = 0.408 Δ ( R n − G ) + γ 900 T + 273 u 2 ( e s − e a ) Δ + γ ( 1 + 0.34 u 2 ) ,
where R n is net radiation at the reference crop surface (MJ m-2 d-1); G is soil heat flux (MJ m-2 d-1); u 2 is wind speed (m s-1); e s is saturation vapor pressure (kPa); e a is actual vapor pressure (kPa); e s − e a is vapor pressure deficit (kPa); Δ is the slope of the vapor saturation pressure curve (kPa °C-1); T is mean temperature (°C); and γ is the psychrometric constant (kPa °C-1). For daily time intervals, G values are relatively small and, therefore, this term was not included [14].

2.2.2. Hargreaves-Samani Method (Et0-HS)

The Hargreaves-Samani method estimates ET0 based on temperature data only (Equation 2) [52]. This equation was developed for semi-arid zones and is useful when solar radiation data are not available; however, as it is based on a few variables, its accuracy should be evaluated at the regional and local levels [53].
E T 0 − H S = K H ( T + K T ) R 0 ∗ ( T m a x − T m i n ) A H ,
where T is mean daily temperature (ºC); R 0 is extraterrestrial solar radiation (from tables, mm d-1); T m a x is maximum daily temperature (ºC); T m i n is minimum daily temperature (ºC); K H and K T are the empirical calibration parameters; and A H is a Hargreaves’ empirical exponent. This study used the original values proposed by Hargreaves and Samani [52]: K H   = 0.0023, K T = 17.78, and A H = 0.5.

2.2.3. Blaney-Criddle Method (Et0-BC)

The meteorological variables required to apply the Blaney-Criddle method are air temperature, relative humidity, and daytime wind speed (Equation 3) [54].
E T 0 − B C = a + b [ p ( 0.46 * T + 8.13 ) ] ,
where a and b are climatic calibration coefficients calculated with equations (4) and (5), respectively; p is mean annual percentage of daytime hours (value from tables, decimal); and T is mean temperature at 2 m height (ºC).
a = 0.0043 * R H m i n − n N − 1.41 ,
where R H M I N is minimum relative humidity (%); n N is the ratio between theoretical and actual sunlit hours (value from tables, decimal).
b = 0.082 − 0.0041 ( R H m i n ) + 1.07 ( n N ) + 0.066 ( u 2 ) − 0.006 ( R H m i n ) ( n N ) − 0.0006 ( R H m i n ) ( u 2 ) ,
where u 2 is mean wind speed at 2 m above ground (m s-1).

2.3. Inferential Evaluation Parameters

Table 2 shows the inferential parameters used for evaluating the empirical equations that estimate ET0 (HS and BC), considering the PM method as reference. Likewise, the climatic information of the NP platform was evaluated when calculating ET0 through the reference method (PMNP).
In the aboe equations, E i . s the estimated value using the empirical equation; O i is the value obtained with the reference method; E ¯ is the average of estimated values obtained with the empirical equation; O ¯ is the average of the values obtained with the reference method; and n is the number of observations.
Table 3 summarizes the criteria for interpreting the reliability coefficient [55].
ET0 was estimated in three different ways with empirical equations (daily, average, and 5-day cumulative) using a total of 165 observations. La ET0 promedio se determinó durante el período de 5 días, al igual que la ET0 acumulada.

3. Results and Discussion

The daily ET0 calculated by the PM method and with AWS meteorological data (Figure 2) had the peak value (8.8 mm d-1) on Julian day 126 (06 May 2021); on the same day, a wind speed of 5.0 m s-1 was recorded, which was higher than the average recorded over the study period (2.2 m s-1). On the other hand, the minimum ET0 (2.2 mm day-1) was recorded on Julian day 192 (11 July 2021) — the day that recorded a solar radiation value of 107.0 W m-2, lower than the average for the study period (282.8 W m-2). This low radiation was due to atypical conditions: high cloudiness (rainfall of 7.6 mm recorded) and high relative humidity (84.5 %). Some authors mention that wind speed and solar radiation are the climatic variables with the greatest influence on ET0 estimates in the study area [17]. Other authors reach the same conclusion when performing a sensitivity analysis in other regions [56,57,58].

3.1. Comparison of ET0 estimated by Empirical Equations versus the Reference Method

Table 4 shows monthly and total ET0 estimated using the empirical equations and the reference method (PM). Considering the month with the maximum ET0 (May, with the HS and PM_NP equations and June with the BC method) and the reference method (PM), HS yielded an ET0 value that was 6.6 % lower vs. PM; BC, 12.5 % lower; and PM_NP, 13.2 % higher. However, taking into account the month with the minimum ET0 (February) and the PM method, HS yielded an ET0 12.8 % higher vs. PM; BC, 6.8 % higher; and PM_NP, 14.2 % higher. It is observed that HS and BC underestimate ET0 over most of the study period, consistent with the findings reported by some authors for an agroclimatic region similar to the study area [59].
However, when considering total ET0 (whole study period) and the PM method, HS recorded an ET0 value 5.5 % lower vs. PM; BC, a value 15.6 % lower; and PM_NP, 10.6 % higher; therefore, HS was the equation that yielded values closest to the PM method. This is because HS considers temperature and radiation as the main energy sources that promote evapotranspiration [1,16].
The results in Table 4 indicate an overestimation of ET0 relative to the value obtained with the PM_NP method during the study period. The magnitude of this overestimation is related to the accuracy of each variable and has been reported only when using NP (NASA-POWER) data and the PM method [42,43,60].
Table 5 summarizes the relationship between the climatic variables recorded by the AWS and those obtained from the NP platform during the study period, where wind speed (WS) and solar radiation (SR) showed a low and moderate relationship, respectively. This same behavior has been reported by some authors for WS [17,35,61] and SR [62]. By contrast, Tmax and RH recorded a high ratio, and Tmin, a very high ratio. Some authors reported similar R2 values for Tmin and Tmax [46] and RH [17] to those obtained in the present study. WS was the variable that yielded the lowest R2. This highlights the multiple challenges in determining this variable; these include quality control of the measured data, since improving this aspect may return more accurate estimates [63].
Figure 3 depicts the bias in the data recorded by the automated weather station (AWS) relative to NP platform data for the following meteorological variables: temperature (maximum and minimum), relative humidity, solar radiation, and wind speed. It is observed that 44 % of the maximum temperature data evaluated (n = 165) were virtually unbiased, while 39 % of NP data overestimated Tmax by 2.1 °C to 7.5 °C, and the rest of the data (17 %) underestimated Tmax by 1.2 °C to 5.5 °C (Figure 3a). Regarding the minimum temperature, 39 % of the data evaluated showed bias values close to zero, while 46 % of the NP data overestimated Tmin by 1.6 °C to 5.1 °C and the rest (15 %) underestimated Tmin by 1.8 ºC to 5.3 °C (Figure 3b).
The less biased RH values (values close to zero) were observed in 16 % of the evaluated data; the NP platform underestimated RH by 3.0 % to 38.8 % in 76 % of the data, and the rest of the data (7 %) overestimated RH by 5.9 % to 14.9 % (Figure 3c). On the other hand, 45 % of the evaluated data showed the minimum differences in solar radiation bias (values between 0 MJ m-2 d-1 and 1.5 MJ m-2 d-1), while 36 % of the data overestimated radiation by 3.7 MJ m-2 d-1 to 17.2 MJ m-2 d-1, and the rest of the data (19 %) underestimated radiation by 2.9 MJ m-2 d-1 to 9.7 MJ m-2 d-1 (Figure 3d).
Finally, 50 % of the WS data showed bias values close to zero. It is also observed that most data (41 %) overestimated WS by 1.4 m s-1 to 2.9 m s-1, and the rest of the data (9 %) underestimated WS by 1.2 m s-1 to 3.3 m s-1 (Figure 3e).
Based on the above, the NP platform tends to overestimate Tmax, Tmin, SR, and WS, while it underestimates RH. This same behavior was reported by Jiménez et al. [17] in the study area for Tmin, WS, and RH [17].
Estimating the 5-day cumulative ET0 improved the values of R2, r, and c relative to daily ET0 and 5-day mean ET0. This behavior is consistent with the one reported by Jiménez et al. [17], who obtained better R2 and RMSE values when estimating 10-day mean ET0 versus daily data. Also, this way of estimating ET0 yielded reliability coefficients (c) rated as “very good” for BC and PM_NP, and “good” for HS. However, PM_NP showed the best R2, r, and c values, while HS yielded the best RMSE, PE, MBE, and b (Table 6). The latter parameter returned values close to 1, indicating that the estimated values are statistically similar to observed or reference values [8]. Some authors reported similar RMSE values (1.1 mm d-1) when comparing ET0 estimated by the HS equation and the PM method on a daily basis [59,64]. However, some authors recorded an RMSE (0.7 mm d-1) for 10-day mean data, which is similar to the RMSE value obtained in the present study for 5-day cumulative ET0 [17].
When graphically comparing the empirical equations versus the reference method (PM), daily ET0 and 5-day mean ET0 show a greater variability (Figure 4a and Figure 4b); the 5-day cumulative ET0 returned the best fit, with a lower variability of ET0 values between the empirical equations and the PM method (Figure 4c).
In addition, HS yielded a better fit than the reference method (PM) in the three ways of estimating ET0. Other authors have also reported a better fit with the HS equation relative to other methods and taking PM as a reference for arid and semi-arid regions [8,25,64]. This equation underestimates ET0 over most of the study period because the methods based on solar temperature and radiation do not include wind speed [11].

3.2. Comparison of estimated ET0 with observed (AWS) versus estimated (NP) data

Table 7 shows the results of the goodness-of-fit tests between ET0 calculated by PM and the HS and BC methods using maximum and minimum temperature data from the NP platform for the different calculation periods (daily, 5-day mean, and 5-day cumulative). The analyses of variance, with a 95% confidence interval (p-value <0.0001), indicate a significant linear relationship between the PM method and the HS_NP and BC_NP equations for the three calculation periods. HS_NP yielded the best values of inferential parameters versus BC_NP, except for R2 and r, in the daily ET0 estimate. This indicates that HS with NP temperature data is a suitable option for estimating ET0 for different periods. Besides, we found that the estimation percent error (PE) is lower than 5% with HS_NP for the three ET0 calculation periods. In addition, MBE is negative in the three periods, pointing to an underestimation with the HS_NP method. Some authors report this same ET0 underestimation effect in semi-arid regions during the winter-summer period [17,59].
The 5-day mean ET0 estimate recorded the best values in most statistical parameters relative to the mean daily ET0. However, the 5-day cumulative ET0 estimate recorded the best r and R2 values compared with the other two estimates (daily ETo and 5-day mean ETo). These good results are obtained because grouping ET0 over five days mitigates the variation in daily temperature associated with precipitation, wind speed, and cloudiness [65].
Figure 5 shows the dispersion of the calibrated HS method (HS_cal) relative to PM for the different ET0 calculation periods, depicting the best data fit obtained using data accumulated over five days.
The comparison of ET0 estimates with the HS equation using temperature data recorded by the AWS (HSAWS) and from the NP platform (HSNP) yielded a high correlation for daily ET0 (Figure 6a) and very high for the other two estimates (Figure 6b and Figure 6c); The 5-day cumulative ET0 recorded the highest R2. These R2 values indicate the feasibility of estimating ET0 using temperature data from the NP platform and using the HS formula [17,59,64].
The accuracy of ET0 calculated with methods BC and HS was compared versus the FAO-56 Penman–Monteith (PM) reference method using data from an automated weather station (AWS) and the NASA-POWER platform (NP). In this comparison, the HS equation returned the best fit in the different ways of estimating ET0: daily, 5-day mean, and 5-day cumulative, with the latter yielding the best fit. In addition, temperature data (maximum and minimum) from the NP platform were suitable for estimating ET0 with the HS equation.
The above results showed that NP data are suitable for cumulative ET0; therefore, NP is a reliable data source for programming medium- and low-frequency irrigation (sprinkler and surface irrigation), which are common in the study area. In addition, they provide spatially comprehensive data, unlike the point values recorded by weather stations [66]. The latter is an enormous advantage when studying large areas, such as irrigation districts, in addition to being freely accessible.

4. Conclusions

The Hargreaves-Samani (HS) method underestimated by 5.5 % the reference evapotranspiration (ET0) compared to the FAO-56 Penman-Monteith (PM) method during the period from March to August. This was because the calculation of ET0 with the HS equation does not consider wind speed, which influences the evapotranspiration rate some times during the year in the study area. Nonetheless, this method is an alternative for calculating ET0 in semi-arid regions for which only temperature records are available.
The HS equation yielded the best estimate relative to the reference method (PM) in the different ways of estimating ET0 during the spring-summer crop cycle; the 5-day cumulative ET0 showed the best fit. Therefore, this method is suitable for use with remote-sensing data to determine crop evapotranspiration (ETc) with 5-day temporal resolution images.
The maximum and minimum temperature data from the NASA–POWER (NP) platform was suitable for estimating ET0 with the HS equation. This data source is a timely alternative, particularly in semi-arid regions where no data from weather stations are available.

Funding

This research received no external funding.

Contributions of Authors

Conceptualization, M.A.B.-G. and G.D.-R.; methodology, M.A.B.-G., G.D.-R., and A.Q.-N.; formal analysis, M.A.B.-G., and G.D.-R.; research, M.A.B.-G., G.D.-R., and A.L.-P.; preparation of the original draft, G.D.-R.; writing, review, and editing, M.A.B.-G., A.Q.-N., A.L.-P., and J.E.-A.; supervision, M.A.B.-G. All authors have read and agree with the final manuscript version for publication.

Statement by the Institutional Review Board

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data are not publicly available because they are currently used in an ongoing thesis.

Acknowledgements

To the Consejo Nacional de Ciencia y Tecnología (National Council of Science and Technology, CONACYT) for financing the Ph. D. studies of G. D.-R. (Scholarship no. 765686) and to the GIS Water and Soil Laboratory at CENID-RASPA INIFAP for the use of the Automated Weather Station (AWS). María Elena Sánchez-Salazar translated the manuscript into English.

Conflicts of interest

The authors declare that they have no conflict of interest.

References

  1. Allen, R. G.; Pereira, L.; Raes, D.; Smith, M.; Crop evapotranspiration: Guidelines for computing crop requirements. Irrigation and Drainage paper No. 56, FAO. 1998. Available online: https://www.fao.org/3/x0490e/x0490e00.htm (accessed on 1 March 2022).
  2. Gong, L.; Xu, C.; Chen, D.; Halldin, S.; Chen, Y. D. Sensitivity of the Penman-Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J Hydrol 2006, 329(3-4), 620–629. [Google Scholar] [CrossRef]
  3. Pereira, L. S.; Alves, I.; Paredes, P. Crop and landscape water requirements. In Reference Module in Earth Systems and Environmental Sciences. Elsevier. 2022. [Google Scholar] [CrossRef]
  4. Peng, L.; Li, Y.; Feng, H. The best alternative for estimating reference crop evapotranspiration in different sub-regions of mainland China. Sci Rep. 2017, Rep 7, 5458. [Google Scholar] [CrossRef]
  5. Talebmorad, H.; Ahmadnejad, A.; Eslamian, S.; Askari, K. O. A.; Singh, V. P. Evaluation of uncertainty in evapotranspiration values by FAO56-Penman-Monteith and Hargreaves-Samani methods. Int J Hydrol Sci Technol. 2020, 10(2), 135–147. [Google Scholar] [CrossRef]
  6. Wen, C.; Shuanghe, S. H.; Chunfeng, D. Sensitivity of the Penman-Monteith Reference Evapotranspiration in Growing Season in the Northwest China. Int Conf Mult Technol. 2010. [Google Scholar] [CrossRef]
  7. Muhammad, M. K. I.; Shahid, S.; Ismail, T.; Harun, S.; Kisi, O.; Yaseen, Z. M. The development of evolutionary computing model for simulating reference evapotranspiration over Peninsular Malaysia. Theor Appl Clim. 2021, 144, 1419–1434. [Google Scholar] [CrossRef]
  8. Raziei, T.; Pereira, L. S. Estimation of ETo with Hargreaves–Samani and FAO-PM temperature methods for a wide range of climates in Iran. Agric Water Manag. 2013, 121, 1–18. [Google Scholar] [CrossRef]
  9. Gabr, M. E.-S. Management of irrigation requirements using FAO-CROPWAT 8.0 model: A case study of Egypt. Model Earth Syst Environ 2022, 8(3), 3127–3142. [Google Scholar] [CrossRef]
  10. Surendran, U.; Sushanth, C. M.; Joseph, E. J.; Al-Ansari, N.; Yasseen, Z. M. FAO CROPWAT Model-Based Irrigation Requirements for Coconut to Improve Crop and Water Productivity in Kerala, India. Sustainability. 2019, 11(18), 5132. [Google Scholar] [CrossRef]
  11. Ortiz, R. S.; Chile, A. M. Métodos de cálculo para estimar la evapotranspiración de referencia para el Valle de Tumbaco. Siembra. 2020, 7(1), 70–79. [Google Scholar] [CrossRef]
  12. Yamaç, S. S. Reference Evapotranspiration Estimation With kNN and ANN Models Using Different Climate Input Combinations in the Semi-arid Environment. J Agric Sci (Tarim Bilimleri Dergisi) 2021. [Google Scholar] [CrossRef]
  13. Sahoo, B.; Walling, I.; Deka, B. C.; Bhatt, B. P. Standardization of Reference Evapotranspiration Models for a Subhumid Valley Rangeland in the Eastern Himalayas. J Irrigat Drainage Eng. 2012, 138(10), 880–895. [Google Scholar] [CrossRef]
  14. Allen, R. G.; Pereira, L. S.; Raes, D.; Smith, M.; Evapotranspiración del cultivo: Guías para la determinación de los requerimientos de agua de los cultivos. FAO Riego y Drenaje Manual 56. 2006. Available online: https://www.fao.org/3/x0490s/x0490s00.htm (accessed on 15 May 2022).
  15. Borges, J. C. F.; Anjos, R. J.; Silva, T. J. A.; Lima, J. R. S.; Andrade, C. L. T. Métodos de estimativa da evapotranspiração de referência diária para a microrregião de Garanhuns, PE. Rev Bras Eng Agrí Amb 2012, 16(4), 380–390. [Google Scholar] [CrossRef]
  16. Woldesenbet, T. A.; Elagib, N. A. Spatial-temporal evaluation of different reference evapotranspiration methods based on the climate forecast system reanalysis data. Hydrol Process 2021, 36(6). [Google Scholar] [CrossRef]
  17. Jiménez, J. S. I.; Ojeda, B. W.; Inzunza, I. M. A.; Marcial, P. M. D. J. Analysis of the NASA-POWER system for estimating reference evapotranspiration in the Comarca Lagunera, Mexico. Ingeniería Agrícola y Biosistemas 2021, 13(2), 201–226. [Google Scholar] [CrossRef]
  18. Luo, Y.; Chang, X.; Peng, S.; Khan, S.; Wang, W.; Zheng, Q.; Cai, X. Short-term forecasting of daily reference evapotranspiration using the Hargreaves-Samani model and temperature forecasts. Agric Water Manag. 2014, 136, 42–51. [Google Scholar] [CrossRef]
  19. Perera, K. C.; Western, A. W.; Nawarathna, B.; George, B. Forecasting daily reference evapotranspiration for Australia using numerical weather prediction outputs. Agric For Meteorol. 2014, 194, 50–63. [Google Scholar] [CrossRef]
  20. Xiong, Y.; Luo, Y.; Wang, Y.; Traore, S.; Xu, J.; Jiao, X.; Fipps, G. Forecasting daily reference evapotranspiration using the Blaney-Criddle model and temperature forecasts. Arch Agron Soil Sci. 2015, 62(6), 790–805. [Google Scholar] [CrossRef]
  21. Goh, E. H.; Ng, J. L.; Huang, Y. F.; Yong, S. L. S. Performance of potential evapotranspiration models in Peninsular Malaysia. J Water Clim Change. 2021, 12(7), 3170–3186. [Google Scholar] [CrossRef]
  22. Fooladmand, H. R. Evaluation of some equations for estimating evapotranspiration in the south of Iran. Arch Agron Soil Sci. 2011, 57(7), 741–752. [Google Scholar] [CrossRef]
  23. Hafeez, M.; Ahmad, C. Z.; Akhtar, K. A.; Bakhsh, G. A.; Basit, A.; Tahira, F. Comparative Analysis of Reference Evapotranspiration by Hargreaves and Blaney-Criddle Equations in Semi-Arid Climatic Conditions. Curr Res Agri Sci. 2020, 7(2), 52–57. [Google Scholar] [CrossRef]
  24. Martinez, C. J.; Thepadia, M. Estimating Reference Evapotranspiration with Minimum Data in Florida. J Irrig Drain Eng. 2010, 136(7), 494–501. [Google Scholar] [CrossRef]
  25. Tabari, H. Evaluation of Reference Crop Evapotranspiration Equations in Various Climates. Water Resour Manage. 2010, 24, 2311–2337. [Google Scholar] [CrossRef]
  26. Lima, J. R. de S.; Antonino, A. C. D.; Souza, E. S. de; Hammecker, C.; Montenegro, S. M. G. L.; Lira, C. A. B. de O. Calibration of Hargreaves-Samani Equation for Estimating Reference Evapotranspiration in Sub-Humid Region of Brazil. J Water Resour Prot 2013, 05(12), 1–5. [Google Scholar] [CrossRef]
  27. Temesgen, B.; Eching, S.; Davidoff, B.; Frame, K. Comparison of Some Reference Evapotranspiration Equations for California. J Irrig Drain Eng. 2005, 131(1), 73–84. [Google Scholar] [CrossRef]
  28. Todorovic, M.; Karic, B.; Pereira, L. S. Reference evapotranspiration estimate with limited weather data across a range of Mediterranean climates. J Hydrol. 2013, 481, 166–176. [Google Scholar] [CrossRef]
  29. Shahidian, S.; Serralheiro, R. P.; Serrano, J.; Teixeira, J. L. Parametric calibration of the Hargreaves-Samani equation for use at new locations. Hydrol Process. 2012, 27(4), 605–616. [Google Scholar] [CrossRef]
  30. Sepaskhah, A. R.; Razzaghi, F. Evaluation of the adjusted Thornthwaite and Hargreaves-Samani methods for estimation of daily evapotranspiration in a semi-arid region of Iran. Arch Agron Soil Sci. 2009, 55(1), 51–66. [Google Scholar] [CrossRef]
  31. Hafeez, M.; Chatha, Z. A.; Bakhsh, A.; Basit, A.; Khan, A. A.; Tahira, F. Reference Evapotranspiration by Hargreaves and Modified Hargreaves Equations under Semi-Arid Environment. Curr Res Agri Sci. 2020, 7(2), 58–63. [Google Scholar] [CrossRef]
  32. Martins, D. S.; Paredes, P.; Raziei, T.; Pires, C.; Cadima, J.; Pereira, L. S. Assessing reference evapotranspiration estimation from reanalysis weather products. An application to the Iberian Peninsula. Int J Climatol 2016, 37(5), 2378–2397. [Google Scholar] [CrossRef]
  33. Paredes, P.; Martins, D. S.; Pereira, L. S.; Cadima, J.; Pires, C. Accuracy of daily estimation of grass reference evapotranspiration using ERA-Interim reanalysis products with assessment of alternative bias correction schemes. Agric Water Manag 2018, 210, 340–353. [Google Scholar] [CrossRef]
  34. Pelosi, A.; Terribile, F.; D’Urso, G.; Chirico, G. Comparison of ERA5-Land and UERRA MESCAN-SURFEX Reanalysis Data with Spatially Interpolated Weather Observations for the Regional Assessment of Reference Evapotranspiration. Water. 2020, 12(6), 1669. [Google Scholar] [CrossRef]
  35. Rodrigues, G. C.; Braga, R. P. Evaluation of NASA POWER Reanalysis Products to Estimate Daily Weather Variables in a Hot Summer Mediterranean Climate. Agronomy. 2021, 11(6), 1207. [Google Scholar] [CrossRef]
  36. Park, J.; Choi, M. Estimation of evapotranspiration from ground-based meteorological data and global land data assimilation system (GLDAS). Stoch Environ Res Risk Assess. 2015, 29, 1963–1992. [Google Scholar] [CrossRef]
  37. Tian, D.; Martinez, C. J.; Graham, W. D. Seasonal Prediction of Regional Reference Evapotranspiration Based on Climate Forecast System Version 2. J Hydrometeorol. 2014, 15(3), 1166–1188. [Google Scholar] [CrossRef]
  38. Peters, L. C. D.; Kumar, S. V.; Mocko, D. M.; Tian, Y. Estimating evapotranspiration with land data assimilation systems. Hydrol Process. 2011, 25(26), 3979–3992. [Google Scholar] [CrossRef]
  39. McEvoy, D. J.; Roj, S.; Dunkerly, C.; McGraw, D.; Huntington, J. L.; Hobbins, M. T.; Ott, T. Validation and Bias Correction of Forecast Reference Evapotranspiration for Agricultural Applications in Nevada. J Water Resour Plann Manage 2022, 148(11). [Google Scholar] [CrossRef]
  40. Blankenau, P. A.; Kilic, A.; Allen, R. An evaluation of gridded weather data sets for the purpose of estimating reference evapotranspiration in the United States. Agric Water Manag 2020, 242. [Google Scholar] [CrossRef]
  41. Ndiaye, P. M.; Bodian, A.; Diop, L.; Deme, A.; Dezetter, A.; Djaman, K.; Ogilvie, A. Trend and Sensitivity Analysis of Reference Evapotranspiration in the Senegal River Basin Using NASA Meteorological Data. Water. 2020, 12(7), 1957. [Google Scholar] [CrossRef]
  42. Negm, A.; Jabro, J.; Provenzano, G. Assessing the suitability of American National Aeronautics and Space Administration (NASA) agro-climatology archive to predict daily meteorological variables and reference evapotranspiration in Sicily, Italy. Agric For Meteorol. 2017, 244-245, 111–121. [Google Scholar] [CrossRef]
  43. Srivastava, P. K.; Singh, P.; Mall, R. K.; Pradhan, R. K.; Bray, M.; Gupta, A. Performance assessment of evapotranspiration estimated from different data sources over agricultural landscape in Northern India. Theor Appl Clim 2020, 140(1-2), 145–156. [Google Scholar] [CrossRef]
  44. Rodrigues, G. C.; Braga, R. P. Estimation of Daily Reference Evapotranspiration from NASA POWER Reanalysis Products in a Hot Summer Mediterranean Climate. Agronomy. 2021, 11(10), 2077. [Google Scholar] [CrossRef]
  45. Davis. Instrumentos climáticos de precisión. Catálogo Global. 2020. Available online: https://cdn.shopify.com/s/files/1/0515/5992/3873/files/Weather_Catalog_Spanish.pdf (accessed on 10 February 2020).
  46. White, J. W.; Hoogenboom, G.; Stackhouse, P. W.; Hoell, J. M. Evaluation of NASA satellite- and assimilation model-derived long-term daily temperature data over the continental US. Agric For Meteorol. 2008, 148(10), 1574–1584. [Google Scholar] [CrossRef]
  47. Zhang, T.; Chandler, W. S.; Hoell, J. M.; Westberg, D.; Whitlock, C. H.; Stackhouse, P. W. A Global Perspective on Renewable Energy Resources: Nasa’s Prediction of Worldwide Energy Resources (Power) Project. Proceedings of ISES World Congress 2007 2007, Vol.I-Vol.5, 2636–2640. [Google Scholar] [CrossRef]
  48. Monteiro, L. A.; Sentelhas, P. C.; Pedra, G. U. Assessment of NASA/POWER satellite-based weather system for Brazilian conditions and its impact on sugarcane yield simulation. Int J Climatol. 2017, 38(3), 1571–1581. [Google Scholar] [CrossRef]
  49. Zhang, T.; Stackhouse, P. W.; Gupta, S. K.; Cox, S. J.; Mikovitz, J. C. Validation and Analysis of the Release 3.0 of the NASA GEWEX Surface Radiation Budget Dataset. AIP Conference Proceedings. 2009. [Google Scholar] [CrossRef]
  50. National Aeronautics and Space Administration - Prediction Of Worldwide Energy Resource. 2023. Available online: https://power.larc.nasa.gov/ (accessed on 18 March 2023).
  51. Allen, R. G.; Pruitt, W. O.; Businger, J. A.; Fritschen, L. J.; Jensen, M. E.; Quinn, F. H. Capítulo 4 Evaporation and Transpiration in ASCE Handbook of Hydrology. 1996, pp. 125–252. Available online: https://doi.org/10.1061/9780784401385.ch04 (accessed on 13 April 2022).
  52. Hargreaves, G. H.; Samani, Z. A. Reference crop evapotranspiration from ambient air temperature. Appl Eng Agr. 1985, 1(2), 1–13. [Google Scholar] [CrossRef]
  53. Chávez, R. E.; González, C. G.; González, B. J. L.; Dzul, L. E.; Sánchez, C. I.; López, S. A.; Chávez, S. J. A. Uso de estaciones climatológicas automáticas y modelos matemáticos para determinar la evapotranspiración. Tecnol. y Cienc del Agua. 2013, 4, pp. 115–126. Available online: https://www.scielo.org.mx/pdf/tca/v4n4/v4n4a7.pdf (accessed on 23 June 2022).
  54. Doorenbos, J.; Pruitt, W. O.; Guidelines for predicting crop water requirements. Irrigation and Drainage Paper FAO-24. 1977. Available online: https://www.fao.org/publications/card/en/c/6bae3071-5d7b-5206-af5c-c9bfa1d9d1fe/ (accessed on 29 May 2022).
  55. Silva, G. H. da.; Dias, S. H. B.; Ferreira, L. B.; Santos, J. É. O.; Cunha, F. F. da. Performance of different methods for reference evapotranspiration estimation in Jaíba, Brazil. Rev Bras Eng Agrí Amb 2018, 22(2), 83–89. [Google Scholar] [CrossRef]
  56. Debnath, S.; Adamala, S.; Raghuwanshi, N. S. Sensitivity Analysis of FAO-56 Penman-Monteith Method for Different Agro-ecological Regions of India. Environ Process. 2015, 2, 689–704. [Google Scholar] [CrossRef]
  57. Jerszurki, D.; Moretti de Souza, J. L.; Ramos, S. L. de C. Sensitivity of ASCE-Penman-Monteith reference evapotranspiration under different climate types in Brazil. Clim Dyn 2019, 53(1-2), 943–956. [Google Scholar] [CrossRef]
  58. Ndiaye, P. M.; Bodian, A.; Diop, L.; Djaman, K. Sensitivity Analysis of the Penman-Monteith Reference Evapotranspiration to Climatic Variables: Case of Burkina Faso. J Water Resour Prot. 2017, 9, 1364–1376. [Google Scholar] [CrossRef]
  59. Villa, C. A. O.; Ontiveros, C. R. E.; Ruíz, A. O.; González, S. A.; Quevedo, T. J. A.; Ordoñez, H. L. M. Spatio-temporal variation of reference evapotranspiration from empirical methods in Chihuahua, Mexico. Ingeniería Agrícola y Biosistemas 2021, 13(1), 95–115. [Google Scholar] [CrossRef]
  60. Maldonado, W.; Valeriano, T. T. B.; de Souza, R. G. EVAPO: A smartphone application to estimate potential evapotranspiration using cloud gridded meteorological data from NASA-POWER system. Comput Electron Agric. 2019, 156, 187–192. [Google Scholar] [CrossRef]
  61. Duarte, Y. C. N.; Sentelhas, P. C. NASA/POWER and DailyGridded weather datasets—how good they are for estimating maize yields in Brazil? Int J Biometeorol. 2020, 64, 319–329. [Google Scholar] [CrossRef]
  62. Quansah, A. D.; Dogbey, F.; Asilevi, P. J.; Boakye, P.; Darkwah, L.; Oduro, K. S.; Sokama, N. Y. A.; Mensah, P. Assessment of solar radiation resource from the NASA-POWER reanalysis products for tropical climates in Ghana towards clean energy application. Sci Rep 2022, 12(1). [Google Scholar] [CrossRef]
  63. De Pondeca, M. S. F. V.; Manikin, G. S.; DiMego, G.; Benjamin, S. G.; Parrish, D. F.; Purser, R. J.; Wan, S. W.; Horel, J. D.; Myrick, D. T.; Lin, Y.; Aune, R. M.; Keyser, D.; Colman, B.; Mann, G.; Vavra, J. The Real-Time Mesoscale Analysis at NOAA’s National Centers for Environmental Prediction: Current Status and Development. Weather Forecasting. 2011, 26(5), 593–612. [Google Scholar] [CrossRef]
  64. Najmaddin, P. M.; Whelan, M. J.; Balzter, H. Estimating Daily Reference Evapotranspiration in a Semi-Arid Region Using Remote Sensing Data. Remote Sens. 2017, 9(8), 779. [Google Scholar] [CrossRef]
  65. Texeira, P.; Pannunzio, A.; Brenner, J. Calibración de la ecuación de Hargreaves para el cálculo de la evapotranspiración de cultivo de referencia (ETo) en Salto, Uruguay. Revista de Climatología. 2021, 21, 80–88. Available online: https://rclimatol.eu/wp-content/uploads/2021/06/Articulo21g.pdf (accessed on 23 June 2023).
  66. Kadhim, H.; Mohammed, R. Analysis of NASA POWER Reanalysis Products to Predict Temperature and Precipitation in Euphrates River Basin. J. Hydrol. 2023, 619, 129327. [Google Scholar] [CrossRef]
Preprints 78444 g001
Figure 1. Location of the automated weather station (AWS).
Figure 1. Location of the automated weather station (AWS).
Preprints 78444 g001
Preprints 78444 g002
Figure 2. Reference evapotranspiration estimated with the FA0-56 Penman–Monteith method using AWS meteorological data.
Figure 2. Reference evapotranspiration estimated with the FA0-56 Penman–Monteith method using AWS meteorological data.
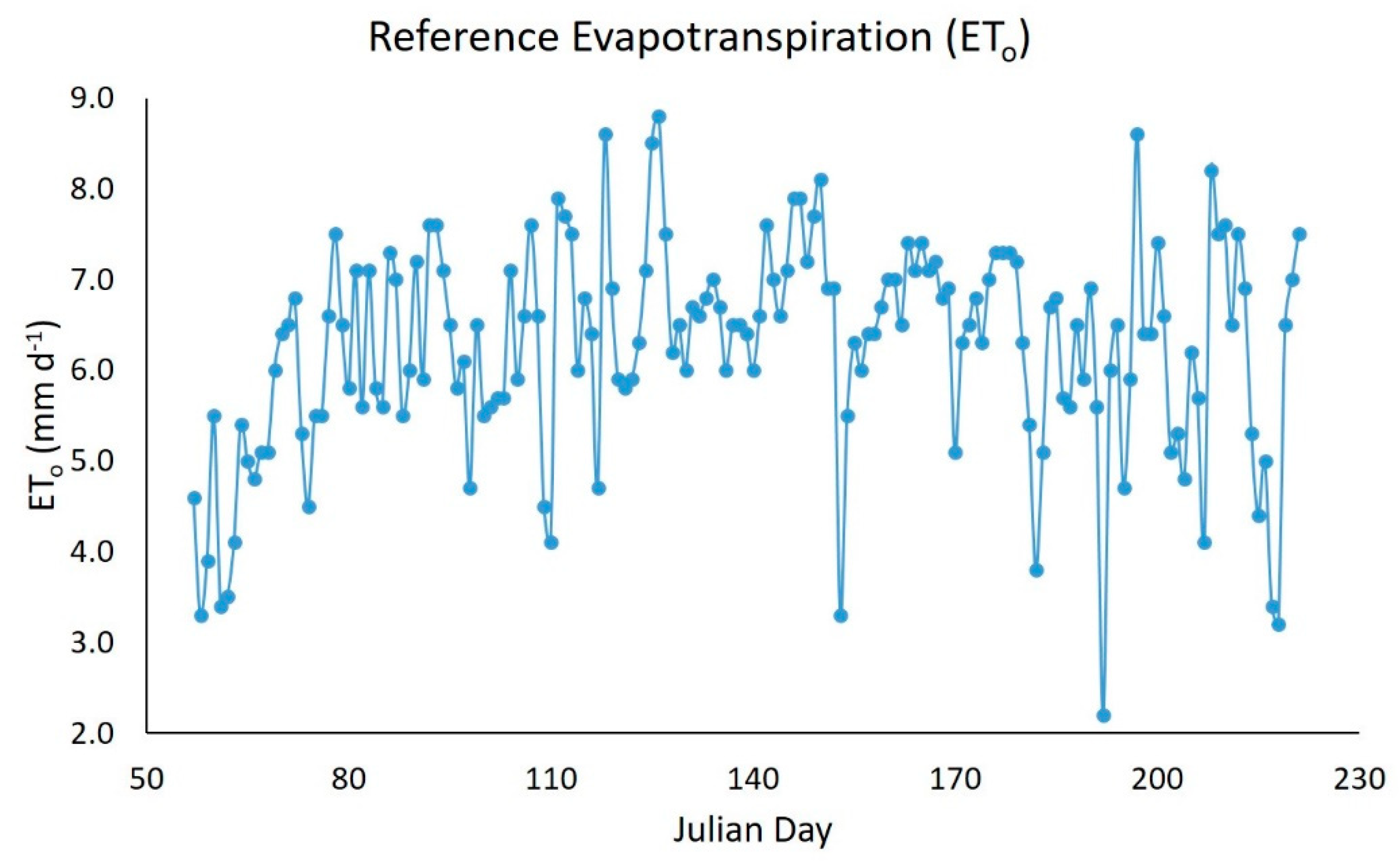
Preprints 78444 g002
Preprints 78444 g003
Figure 3. Bias between observed (AWS) and reference (NP) data for the meteorological variables Tmax, Tmin, RH, SR, and WS during the study period.
Figure 3. Bias between observed (AWS) and reference (NP) data for the meteorological variables Tmax, Tmin, RH, SR, and WS during the study period.
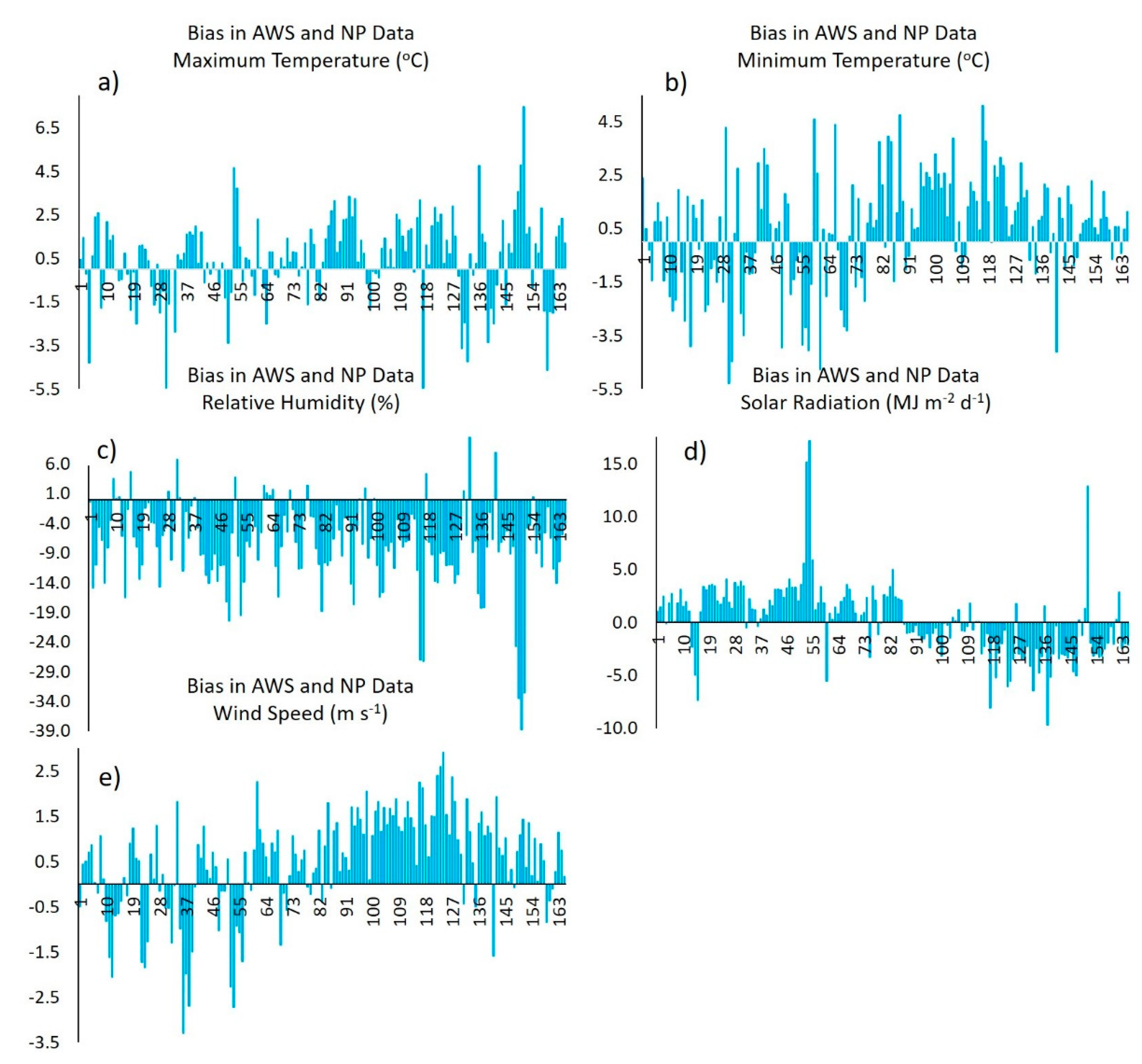
Preprints 78444 g003
Preprints 78444 g004
Figure 4. Different ways to estimate ET0 using empirical equations and the reference method (PM) during the study period.
Figure 4. Different ways to estimate ET0 using empirical equations and the reference method (PM) during the study period.
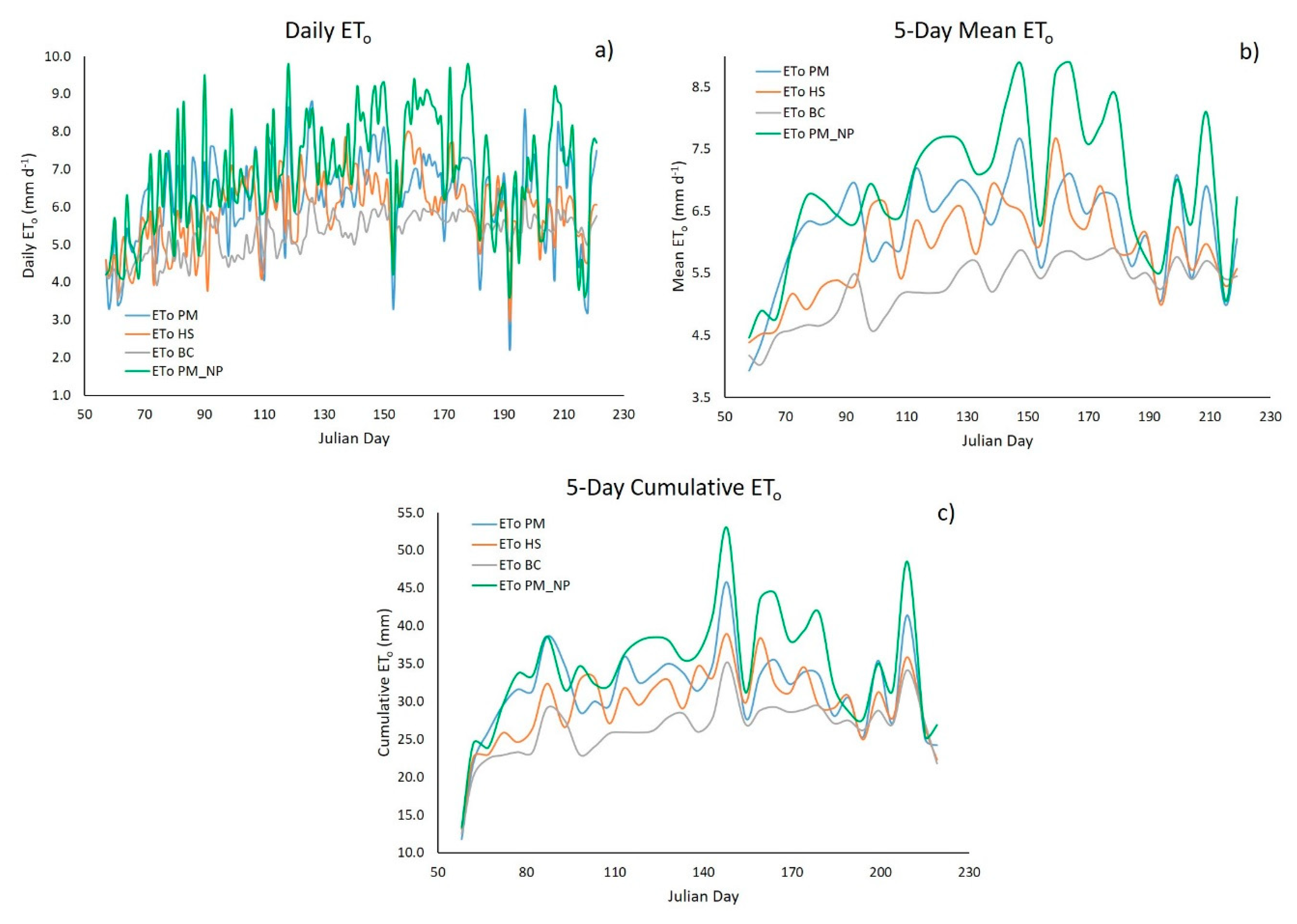
Preprints 78444 g004
Preprints 78444 g005
Figure 5. Dispersion plot of the calibrated HS method (HS_cal) relative to the FAO-56 Penman – Monteith (PM) reference method for the different ET0 calculation periods: daily (Figure 5a), 5-day mean, and 5-day cumulative (Figure 5b and Figure 5c, respectively).
Figure 5. Dispersion plot of the calibrated HS method (HS_cal) relative to the FAO-56 Penman – Monteith (PM) reference method for the different ET0 calculation periods: daily (Figure 5a), 5-day mean, and 5-day cumulative (Figure 5b and Figure 5c, respectively).
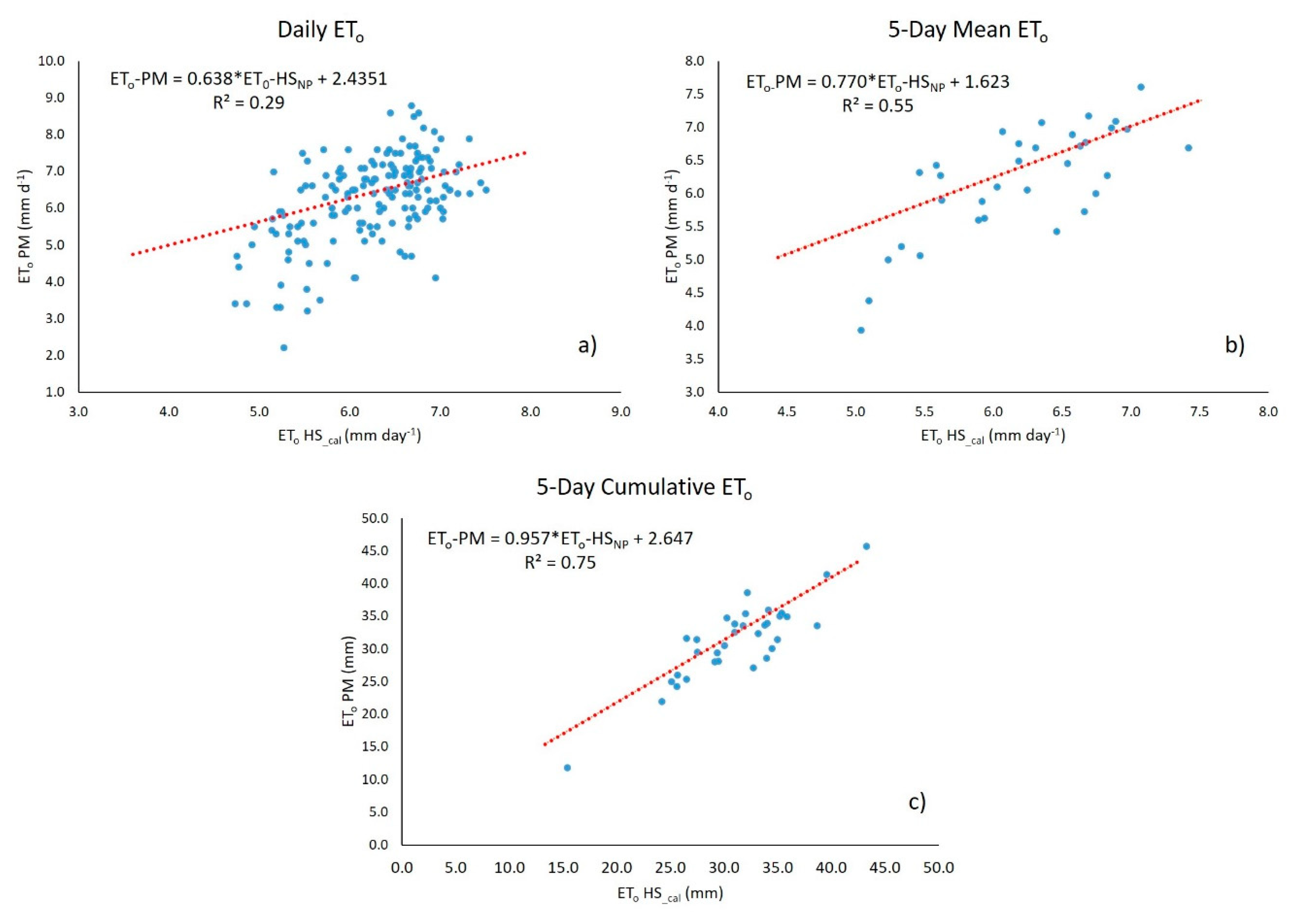
Preprints 78444 g005
Preprints 78444 g006
Figure 6. Linear relationship between ET0 estimates with the HS equation using temperature data from the AWS and the NP platform.
Figure 6. Linear relationship between ET0 estimates with the HS equation using temperature data from the AWS and the NP platform.
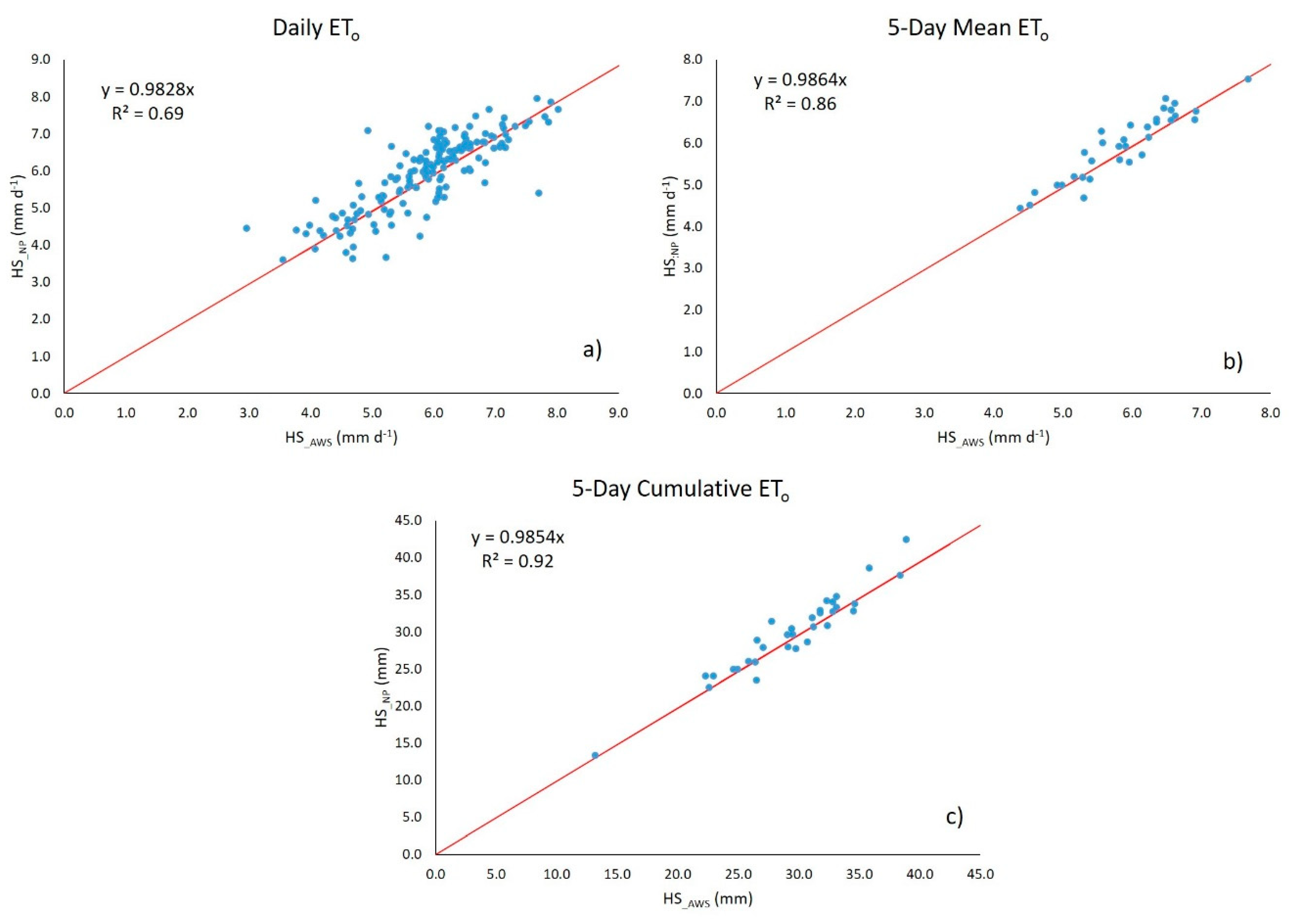
Preprints 78444 g006
Table 1. Features of the NASA-POWER (NP) system information.
Table 1. Features of the NASA-POWER (NP) system information.
Parameter Feature
Data period 1981 to date
Geographic range Global
Download format ASCII, CSV, GeoJSON and NetCDF
Temporal resolution Daily
Spatial resolution 0.5° × 0.5° (55.56 km × 55.56 km cell) for temperature (T), relative humidity (RH), and wind speed ( u 2 ). 1.0° × 1.0° for solar radiation and extraterrestrial solar radiation data.
Delayed data availability Approximately two days for temperature, relative humidity, and wind speed, and five days for solar radiation data.
Table 2. Equations and optimal values of inferential parameters.
Table 2. Equations and optimal values of inferential parameters.
Parameter Equation Optimal value
Coefficient of Determination ( R 2 ) R 2 = [ ∑ i = 1 n ( E i − E ¯ ) ( O i − O ¯ ) ] 2 ∑ i = 1 n ( E i − E ¯ ) 2 ∑ i = 1 n ( O i − O ¯ ) 2  (6) 1
Root Mean Error ( R M S E ) R M S E = ∑ i = 1 n ( E i − O i ) 2 n    (7) 0
Estimate Error Percentage ( P E ) P E = | E ¯ − O ¯ O ¯ | ∗ 100       (8) 0
Mean Error Bias ( M B E ) M B E = ∑ i = 1 n ( E i − O i ) n      (9) 0
Concordance Index ( d ) d = 1 − [ ∑ i = 1 n ( E i − O i ) 2 ∑ i = 1 n ( | E i − O ¯ | + | O i − O ¯ | ) 2 ]  (10) 1
Correlation coefficient ( r ) r = ∑ i = 1 n ( | O i − O ¯ | ) ( | E i − E ¯ | ) ∑ i = 1 n ( O i − O ¯ ) 2 ∑ i = 1 n ( E i − E ¯ ) 2   (11) 1
Reliability coefficient ( c ) c = r ∗ d            (12) 1
Regression coefficient ( b ) b = ∑ i = 1 n O i E i ∑ i = 1 n O i 2         (13) 1
Table 3. Criteria for interpreting the reliability coefficient.
Table 3. Criteria for interpreting the reliability coefficient.
Reliability coefficient Classification
> 0.85 Excellent
0.76 a 0.85 Very good
0.66 a 0.75 Good
0.61 a 0.65 Intermediate
0.51 a 0.60 Tolerable
0.41 a 0.50 Poor
< 0.40 Very poor
Table 4. Monthly and total ET0 estimated by empirical equations and the reference method (FAO-56 Penman–Monteith) during the study period.
Table 4. Monthly and total ET0 estimated by empirical equations and the reference method (FAO-56 Penman–Monteith) during the study period.
Variable Evaluation Period: 26 February to 09 August 2021
Feb Mar Abr May Jun Jul Aug Total
(n = 3) (n = 31) (n = 30) (n = 31) (n = 30) (n = 31) (n = 9) (n = 165)
ET0-PM (mm) 11.7 179.0 191.3 214.4 196.7 187.8 49.1 1,030.0
ET0-HS (mm) 13.2 154.8 180.8 200.3 195.5 179.6 48.7 972.9
ET0-BC (mm) 12.5 141.3 152.1 171.7 172.2 170.9 48.8 869.5
ET0-PM_NP (mm) 13.4 183.7 204.8 242.7 238.5 203.5 52.3 1,138.9
Table 5. Relationship between the meteorological variables recorded by the automated weather station (AWS) and obtained from the NP platform during the study period.
Table 5. Relationship between the meteorological variables recorded by the automated weather station (AWS) and obtained from the NP platform during the study period.
Climatic Variables Coefficient of Determination (R2)
Tmax_NP Tmin_NP RH_NP WS_NP SR_NP
Tmax_AWS 0.76
Tmin_AWS 0.81
RH_AWS 0.80
WS_AWS 0.27
SR_AWS 0.45
Tmax, maximum temperature; Tmin, minimum temperature; RH, relative humidity; WS, wind speed; SR = solar radiation.
Table 6. Comparison and inferential parameters to determine the ET0 equation that best fits the study area.
Table 6. Comparison and inferential parameters to determine the ET0 equation that best fits the study area.
Parameter Methods
HS BC PM_NP HS BC PM_NP HS BC PM_NP
Daily ET0  n = 165) 5-day mean ET0  n = 33) 5-day cumulative ET0  n = 33)
R 2 (Dimensionless) 0.29 0.43 0.53 0.44 0.47 0.73 0.69 0.76 0.84
R M S E (mm d-1) 1.1 1.3 1.2 0.7 1.1 0.9 3.8 5.8 4.6
P E (%) 5.5 15.6 10.6 5.2 15.3 10.6 5.5 15.6 10.6
M B E (mm d-1) -0.35 -0.97 0.66 -0.32 -0.95 0.66 -1.73 -4.86 3.30
d (Dimensionless) 0.94 0.99 0.98 0.85 1.00 0.94 0.86 1.00 0.94
r (Dimensionless) 0.54 0.65 0.73 0.66 0.69 0.85 0.83 0.87 0.91
c (Dimensionless) 0.51 0.65 0.72 0.56 0.66 0.81 0.71 0.83 0.86
B (Dimensionless) 0.9270 0.8257 1.0994 0.9416 0.8399 1.1073 0.9362 0.8349 1.1075
Table 7. Comparison and linear regression coefficients between ET0 calculated with the reference method (FAO-56 Penman – Monteith) and methods HS and BC with temperature data from the NP platform.
Table 7. Comparison and linear regression coefficients between ET0 calculated with the reference method (FAO-56 Penman – Monteith) and methods HS and BC with temperature data from the NP platform.
Parameter Methods
HS_NP BC_NP HS_NP BC_NP HS_NP BC_NP
Daily ET0  n = 165) 5-day mean ET0 (n =33) 5-day cumulative ET0 (n = 33)
R 2 (Dimensionless) 0.29 0.38 0.55 0.45 0.75 0.74
R M S E (mm d-1) 1.1 1.3 0.6 1.1 3.3 5.7
P E (%) 4.4 15.0 4.1 14.6 4.4 15.0
M B E (mm d-1) -0.28 -0.93 -0.26 -0.91 -1.38 -4.67
r (Dimensionless) 0.54 0.61 0.74 0.67 0.87 0.86
a (Dimensionless) 2.435 -0.359 1.623 0.732 2.647 -1.700
b (Dimensionless) 0.638 1.244 0.770 1.033 0.957 1.240
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated