Prerpints.org logo
Preprint
Article

Structural Optimization Design of Microfluidics Chips Based on Fast Sequence Pair Algorithm

Altmetrics

Downloads

108

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 July 2023

Posted:

06 July 2023

You are already at the latest version

Alerts
Abstract
The market for microfluidic chips is experiencing significant growth; however, their development is hindered by a complex design process and low efficiency. Enhancing microfluidic chips’ design quality and efficiency has emerged as an integral approach to foster their advancement. Currently, the existing structural design schemes lack careful consideration regarding the impact of chip area, microchannel length, and the number of intersections on chip design. This inadequacy leads to redundant chip structures resulting from the separation of layout and wiring design. This study proposes a structural optimization method for microfluidic chips to address these issues utilizing a simulated annealing algorithm. The simulated annealing algorithm generates an initial solution in advance using the fast sequence pair algorithm. Subsequently, an improved simulated annealing algorithm is employed to obtain the optimal solution for the device layout. During the wiring stage, an advanced wiring method is used to designate the high wiring area, thereby increasing the success rate of microfluidic chip wiring. Furthermore, the connection between layout and routing is reinforced through an improved layout adjustment method, which reduces the length of microchannels and the number of intersections. Finally, the effectiveness of the structural optimization approach is validated through six sets of test cases, successfully achieving the objective of enhancing the design quality of microfluidic chips.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Microfluidic technology is a scientific and technological system that integrates fundamental operational units, such as sample preparation, reaction, separation, and detection, into a chip, automating the analysis process [1,2,3]. The microfluidic chip serves as the primary platform for microfluidic technology, utilizing microfluidic channels and reaction chambers to process and manipulate small liquid volumes. Compared to traditional technology platforms, microfluidic chips enable faster completion of tasks that originally took hours, such as separation, isolation, and chemical and biological reactions, resulting in significantly improved detection efficiency [4,5,6].
The structure of a microfluidic chip primarily consists of a fluid layer and a control layer [7,8]. The fluid layer facilitates the reaction process of the experimental reagent. In contrast, the control layer connects to external pressure sources to regulate the flow and stoppage of the reagent within the fluid layer. The connection between the fluid layer and the control layer is established through microvalves, which serve as connectors and can also form devices within the microfluidic chip [9,10]. Figure 1 illustrates the chip's reaction device and the hybrid device featuring a microvalve. Microvalves are placed at intersections of microchannels based on experimental requirements. However, increasing microvalves results in greater design complexity for microfluidic chips [11,12,13].
Additionally, when the microchannel length is too long, the accuracy of biochemical experiments may be affected due to the excessive output of an external mechanical pump [14,15,16]. Moreover, an extensive chip area leads to material wastage [17,18,19]. Hence, the number of microchannel intersections, microchannel length, and chip area are critical indicators for evaluating the quality of chip structural design. Based on a Monte Carlo iterative solution strategy, the simulated annealing algorithm is a stochastic optimization algorithm commonly employed for combinatorial optimization problems [20,21]. Drawing inspiration from the annealing process of solid materials in physics, this algorithm provides an effective approximate solution for issues with non-deterministic polynomial (NP) complexity [22,23,24].
This paper focuses on the objective of structural optimization for microfluidic chips. To achieve this, the Fast Sequence Pair (FAST-SP) algorithm is utilized to generate the initial solution for the simulated annealing algorithm. Additionally, the cooling speed function of the simulated annealing algorithm is enhanced, thereby improving its convergence speed. Subsequently, the layout of devices and the routing of microchannels are integrated through layout adjustment using a chip layout quality evaluation function, which reduces the length of microchannels and the number of intersections. Finally, the comparison of data from six experiments demonstrates that the optimization algorithm proposed in this paper effectively enhances the design quality of microfluidic chips.

2. Structure optimization of a microfluidic chip.

2.1. Structural modeling of microfluidic chips

(1) Definition of a structural optimization problem
Problem input: experimental process, device summary, device connection relationship, and design constraints
Problem output: design results, including device layout and microchannel routing results.
Optimization objects: chip area, microchannel length, and number of microchannel intersections
Design goal: minimize the weighted sum of chip area, the length of microchannels, and the number of microchannel intersections.
(2) Structural design modeling
The structural design of microfluidic chips mainly includes device layout, channel routing, and device layout adjustment [25,26,27]. Figure 2 is the structural design modeling diagram of the microfluidic chip, and Figure 2a is the experimental sequence diagram, showing the observed reaction's specific flow and the device's connection relationship. Each node represents a particular operation, such as detection, mixing, etc. Figure 2b summarizes the experimental apparatus. Figure 2c is a schematic diagram of the device layout and channel routing of the microfluidic chip, where the grey channel is the microchannel of the chip.

2.2. Algorithm design

The FAST-SP algorithm represents the device layout's initial setting scheme in this paper. The exact position of each device on the microfluidic chip is calculated through the improved simulated annealing algorithm. The chip layout design scheme is output according to the change processes of heating, isothermal cooling, and search strategies. As shown in Figure 3, the algorithm design process is as follows:
Upon completion of the layout, wiring the microchannels directly would result in experimental redundancy. To address this issue, the devices intended for connection are sequentially linked end to end, utilizing line segments as microchannel lengths in accordance with the experimental sequence diagram. The number of microchannel intersections can be determined by counting the intersection points between these line segments. Once the routing phase is finalized, the optimized layout adjustment algorithm can be employed to rectify the device layout and microchannel routing. The optimized layout adjustment algorithm preserves the initial sequence generated by FAST-SP but adjusts the component spacing to allow for more routing possibilities. The objective is to eliminate unnecessary microchannel intersections, minimize the number of microvalves, and reduce the overall length of microchannels. Compared with the traditional sequence pair algorithm, the FAST-SP algorithm reduces the complexity of decoding time. After the longest common subsequence (LCS) algorithm is integrated, it speeds up the time to evaluate the layout of sequence pairs, making it more practical. Given a sequence pair, the structure's starting point, the device's width, and height, and the layout direction can be obtained, and then a configuration can be generated. The starting point refers to the position where the first device is placed. When calculating the relative position between devices, the device's size is required, and the layout direction is conducive to minimizing the area of the chip. This paper adopts the layout scheme from bottom left to top right.
It is relevant to generate a layout from sequence pairs and find the longest weighted common subsequence in two sequence pairs. Determining the x coordinate of each device is equivalent to calculating LCS (SX, SY), choosing the y coordinate of each device is equivalent to calculating LCS (SXR, SYR), and SXR is the inverse sequence of SX (Table 1 and Table 2). Device constraint relationship: each sequence unit in the sequence pair (SX, SY) represents each device. Given two devices a and b, in the sequences SX and SY, if a is before b, then a is on the left of b; In sequence SX, if a is before b; in sequence SY, if a is after b, then a is above b.
As shown in Figure 4, given a set of sequence pairs, the grid represents their corresponding constraint relationships. Draw a grid graph of n✕n, mark the grid lines from top to bottom with a positive sequence, and mark the grid lines from left to right with an inverse arrangement. Rotate -45° to obtain the oblique grid of sequence pairs<a c d b e> and<c d a c b>. Given this group of sequence pairs, the layout vertical constraint graph (VCG) and layout horizontal constraint graph (HCG) can be obtained according to the start and endpoints.
Lines 1–2 are used to initialize the width of n devices. Three lines search for the longest weighted common subsequence of SX and SY and calculate the x coordinate of each device. Lines 4–5 initialize the height of n devices. 6 rows to get the reverse-order column SXR of SX. Line 7 calculates the y-coordinate of each device according to the longest weighted common subsequence of SXR and SY.
1-2 lines represent vector blocks_order, which records the index of each device in S2. Line 3 initializes the vector length to 0, saving the maximum length of each device. Lines 4-5 indicate that the variable block is equivalent to the current device in S1. Six lines indicate that the index is the index of the current device in S2. The block's position in line 7 is defined as the position not occupied by other devices at first. Lines 9–12 update the lengths. The last quantity of 13 lines stores the determined total length.
(1) Calculate the weighted LCS width of two sequences, S1 and S2, and use the vector block order to record the index of each device in S2.
(2) Initialize vector lengths to 0 to store each device's maximum quantity (length or width).
(3) The variable block is defined as the current device in S1, and the index is the index of the current device in S2. All the items on the left of the block are arranged into intervals with the length of the block, and the block is then placed.
(4) The total length of the updated layout is length, and length [n] indicates the full length after n devices are determined.
(5) It is updated if the length [j] exceeds the current length.
Extract the LCS algorithm when S1=SX, S2=SY, and weights=width, which can define the x coordinate of the layout. Extract the LCS algorithm when S1=SXR, S2=SY, and weights=heights, which can define the y coordinate of the layout.
Example: from a sequence pair to a layout
Input: ① The sequence pair SX:<a c d b e>, SY:<c d a e b>; ②Layout direction: from bottom left; ③Layout starting point (0, 0); ④The dimensions of devices are shown in Table 3.
Solution process:
widths[a b c d e]=[8 4 4 4 4], heights[a b c d e]=[4 3 5 5 6]
Solve the x coordinate:
S1=SX=<a c d b e>, S2=SY=<c d a e b>
weights[a b c d e]=widths[a b c d e]=[8 4 4 4 4]
block_order[a b c d e]=[3 5 1 2 4]
lengths=[0 0 0 0 0]
i=1:block=a
Index=block_order[a]=3
positions [a]=lengths [index]=lengths [3]=0 //Calculate the current device position
t_span=positions [a]+weights [a]=0+8=8 //Determine the current device length
Update the length vector from index=3 to n=5, length=[0 0 8 8 8]. At the beginning of iterations 2-5, repeat the above operation. The x coordinate: positions [a b c d e]=[0 8 0 4 8], and the width of the layout W=lengths [5]=12.
Solve y coordinate:
S1=SXR=<e b d c a>, S2=SY=<c d a e b>
weights[a b c d e]=heights[a b c d e]=[4 3 5 5 6]
block_order[a b c d e]=[3 5 1 2 4]
lengths=[0 0 0 0 0]. 1-5 Iteration for 5 times in the way of finding the x coordinate, the height of the layout H=lengths [5]=9
Output: the layout area is: W=12✕9. The coordinates of the lower left corner of each device are a (0, 5), b (8, 6), c (0, 0), d (4, 0), and e (8, 0). The results are shown in Figure 5.

2.3. Layout calculation optimization

The traditional simulated annealing algorithm has the problem that the parameters greatly impact the experimental results, and the convergence quality is not high when dealing with layout problems [28,29,30]. For this reason, this paper improves the simulated annealing algorithm, and the main improvement strategies are divided into two types: ① change the factors of the algorithm itself; ②change the search strategy, speed up the search, and improve the search quality.
(1) Change of algorithm cooling function
The control methods of simulated annealing in temperature cooling are divided into rapid cooling mode (RSA) and general cooling mode (CSA).
RSA:T=T0/log(1+N); CSA: T=qT0+k, where q is the cooling rate and k is a constant.
Because of the shortcoming that the initial cooling rate of traditional simulated annealing is too fast to obtain the optimal global solution, this paper proposes an improved simulated annealing algorithm as shown in Formula 1:
T = T 0 × e − N 3 / T 0 2
T0 is the temperature at the initial time, N is the number of iterations required by the algorithm in the external cycle, and T is the current temperature.
As shown in Figure 6, during the iteration process, the improved simulated annealing algorithm (ISA) proposed in this paper decreases slowly at the high-temperature stage, realizing the global search of the algorithm, which is conducive to the generation of the optimal solution.
The slow cooling speed is easy to blame for the slow global convergence speed. Combining the FAST-SP algorithm and the simulated annealing algorithm can speed up the convergence. Therefore, the FAST-SP algorithm is improved as follows:
1) Use reverse transformation to select two device units and reverse all units between the two units.
2) Select three device units and switch the unit between the two device units to the back of the third unit.
(2) Change of algorithmic search strategy
1) Expand the recording function. During the implementation of the algorithm, the particularity of its selection probability may cause the problem that even if the optimal solution is generated, it may be abandoned. The extended recording function can save the optimal solution in this cycle for comparison with the results generated later.
Add a memory matrix (I) and a function (F) in the simulated annealing algorithm. Initially, there is an element i0 in I, and F = f (i0). When generating a new solution, each time a new solution (j) is obtained, compare F with f (j). If f (j) < F, let F=f (j), and store j in I. After the algorithm is completed, the optimal solution is compared with the solution recorded in I to select the optimal solution as the final solution of the algorithm.
2) For the solution of the initial solution, the simulated annealing algorithm with the recording function is used first. After the trial run of the entire algorithm is completed, the final result obtained is searched locally until the local algorithm search is conducted. Then the final solution, namely the optimal solution, is output.

2.4. Routing algorithm optimization

The wiring of microfluidic chips can be divided into two stages. In the first stage, the A* algorithm is mainly used for routing because there is no microchannel intersection [31,32,33]. If the wiring is successful, the result will be output. If the wiring fails, the second stage will be carried out. In the second stage, the microchannels are allowed to generate intersections during routing. Then the routing is carried out through the improved A* algorithm, adding additional generation value to the grid. Whether it is the first or second stage, the existing algorithms use routing based on the experimental response order [34,35,36]. Although the extra generation value of the routing grid can be iterated to get the routing scheme, the routing quality is not high.
As shown in Figure 7a, the blue box is a device, and the black line is a microchannel. When six devices are wired, a microchannel intersection will be generated, and the experimental reaction sequence is af, bf, and dcef. As shown in Figure 7b, the intersection disappears when the microchannel of connector f is wired first. It can be seen that key devices are essential to the results of microchannel wiring, and the probability that key devices can be wired in this area is higher than in other areas.
For this reason, in the wiring stage of a microfluidic chip, this paper gives priority to the wiring of devices with multiple microchannels, defines the high wiring area (in the red dotted box) to distinguish it from other regions, and then wires the chip microchannels based on the improved wiring algorithm. In addition, the main purpose of wiring is to shorten the length of the microchannel and speed up the biochemical reaction time in the microchannel. To this end, three types of wiring modes, as shown in Figure 8, can also be selected to reduce the number of cross-points in microchannels.

2.5. Adjustment algorithm optimization

The previous device layout and microchannel routing results must be adjusted in the layout adjustment phase. Fine-tune the devices while keeping the relative position of the devices unchanged in the congested area; that is, keep the sequence pair order intact. The congestion area contains most devices, microchannels, and microchannel intersections. After adjustment, the next iteration will be carried out if the layout and wiring results are better than the previous work. They will be discarded if they are not as good as the earlier work [37,38,39]. However, this method only adjusts the congestion area, and the adjustment spacing is too small, which affects the overall layout quality to a certain extent and may result in the failure of layout adjustment.
For this reason, when adjusting the device layout and microchannel routing, this paper adjusts the devices in all areas where there are microchannel intersections and multiple channels, moving two units of length to the left, down, or right while maintaining the same relative position and moving one unit of measurement for devices in areas where there is no microchannel intersection. The purpose is to provide space for machine and microchannel adjustment in other congested areas and ensure the algorithm can optimize the layout results without defects. If the result after adjustment is better than the previous scheme, the optimal solution will be output.

2.6. Improved algorithm flow

On the premise of device set and device connection relationships and with the device layout scheme obtained by the FAST-SP algorithm as the input, the following conditions are defined:
1: The distance between device mi and device mj on its right or above is defined as rx and axe.
2: The width and height of all device set spacing are defined as WX and WY. The constraint condition of elements between WX and WY is [emin, emax]. WX and WY form the initial solution S.
3: In the simulated annealing algorithm, the initial temperature is defined as T, the number of external cycles is N, the end temperature is Tend, the current temperature is T0, the chain length is L, and the quality function for evaluating the chip layout is E (S).
The algorithm flow is:
(1) Initialise WX and HY: emin < rx, rx < emax.
(2) Set the state variables S = (SX, SY, WX, HY) and the initial temperature T. When the initial test temperature exceeds the minimum temperature, the iteration starts.
(3) Adjust the state variable S -> S1, randomly generate the variables rx1 and ax1, and compare them with emin and emax. When rx1 < emin, let emin = rx1; When rx1 > emax, let emin = rx1. The ax1 is obtained in the same way.
(4) Utilise Metropolis guidelines [40,41,42]:
d f = E S ' − E S
P = 1 , d f < 0 exp ⁡ − d f / T , d f ≥ 0
P ' = 1 , d f < 0 exp ⁡ − d f / T 0 × e − N 3 / T 0 2 , d f ≥ 0
If df<0, the newly generated layout result will be accepted; otherwise, the new layout result will be obtained with probability exp (- df/T).
(5) Cool down. Use the new cooling rate function to cool down. Stop iterating and output the current result if T0 exceeds the end temperature.
Formula 4 is obtained by combining formulas 2 and 3. The improved simulated annealing algorithm proposed in this paper converges quickly and can get a better solution when facing more devices.
For example, the parameters emin = 3, emax = 5, T = 10000, Tend = 10-4, L = 200, and the cooling rate is 0.95.
Evaluate chip layout quality functions:
E S = α A + β B + γ C + θ C 2
where A is the chip layout area, B is the number of microchannel intersections, C is the length of the microchannel segment, and C2 is the square of the total segment. The main purpose is to minimize and enhance the length of the microchannel. Set the weight values of α to 1, β to 300, γ to 20, and θ to 0.001.
After the layout is completed, the A* algorithm can be used to find the shortest path after the layout. The input of the algorithm includes the following:
① non-negative edge weight graph G (WX, HY)
② A starting source node s
③ One target end node t
Then two sets, M and N, are introduced, where M contains the point of the shortest path that has been found and the length of the shortest route, and N is the point of the shortest path that has not been found and the distance from the point to the source node.
Initialize the two sets M and N, find the shortest path point from the N set, add it to the M set, then update the devices in the N set, iterate circularly until the end of the traversal, and find the best routing result of the microfluidic chip.

3. Experimental results and analysis

The comprehensive optimization algorithm proposed in this paper is compared with the manual layout and existing algorithms to verify its effectiveness. Among them, the existing algorithm uses the basic simulated annealing algorithm. The programming language used in this paper is C++.
As shown in Table 4, six groups of test cases were selected, with 16 PCR devices, 30, 45, and 60 InVitro-1~InVitro-3 devices, and 30 and 66 devices in ProteinSplit-1 and ProteinSplit-2, respectively. The experimental results show that the integrated optimization algorithm in this paper reduces the chip area by 17.6%, the microchannel length by 20.9%, and the number of microchannel intersections by 24.0% on average, compared with existing algorithms. From the improvement percentage, it can be concluded that when the number of devices is 45, the comprehensive optimization algorithm in this paper is optimal.
Figure 9, Figure 10 and Figure 11 compares the integrated optimization algorithm, the existing algorithm, and manual layout in the total chip area, the number of microchannel intersections, and the total length of microchannels. The figure shows the effectiveness of the integrated optimization algorithm in the structural design of microfluidic chips and the necessity of the mechanical structural optimization design of microfluidic chips.
The experimental results show that the optimization algorithm proposed in this paper can meet the automatic design requirements of microfluidic chips. The advantages of the optimization algorithm in the structural design of microfluidic chips are verified through the reduction of chip area, the shortening of microfluidic channels, and the reduction of the number of intersections.

4. Conclusions

This FAST-SP algorithm addresses the challenges in chip layout design. By leveraging the FAST-SP algorithm, the proposed method accelerates the convergence rate of the simulated annealing algorithm, enhances its cooling rate and search strategy, mitigates the impact of parameters on the outcomes, and improves convergence quality. This approach targets the limitations of existing layout design methods for microfluidic chips, which often lack global optimization capabilities. Additionally, it enhances the routing method to minimize the number of intersections between microchannels. The key contribution is strengthening the interaction between microchannel routing and device layout. Sixx test cases were reconducted to evaluate the proposed algorithm's effectiveness, with chip area, microchannel length, and the number of intersections serving as optimization objectives. The results clearly state the superiority of the optimization algorithm presented in this paper compared to existing design methods in these three areas. Notably, the experimental data reveal that when the number of devices reaches 45, the algorithm achieves the optimal improvement percentage, highlighting its capability to obtain optimal solutions and exhibit robustness. Through enhancements, the optimization algorithm achieves an average reduction of 17.6% in the total chip area, 20.9% in the overall microchannel length, and 24.0% in the number of microchannel intersections. These quantitative results unequivocally validate the effectiveness of the proposed optimization algorithm in optimizing the structure of microfluidic chips and enhancing their design quality paper, introducing an improved simulated annealing algorithm that builds upon the FAST-SP.

Author Contributions

Conceptualization, C.W. and B.Y.; methodology, C.W., and J.S.; software, J.S., and H.Y.M.A.; validation, C.W., H.Y.M.A., A.S.M.M.F.S., and B.Y.; formal analysis, B.Y.; investigation, J.S., and H.Y.M.A.; resources, B.Y.; data curation, C.W.; writing—original draft preparation, C.W., H.Y.M.A., and A.S.M.M.F.S.; writing review and editing, C.W. and B.Y.; visualization, C.W.; supervision, B.Y.; project administration, B.Y.; funding acquisition, C.W., and B.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Innovative Science and Technology Platform Project of Cooperation between Yangzhou City and Yangzhou University, China [grant number YZ2020266], the “Green Yang Golden Phoenix Project” in Yangzhou City [grant number YZLYJFJH2021YXBS098], the National Natural Science Foundation of China [grant number 52075138], the Natural Science Foundation of the Jiangsu Higher Education Institutions of China [grant number 22KJB150050], the Jiangsu Agricultural Science and Technology Innovation Fund [grant number CX(21)3162], the Science and Technology Planning Project of Yangzhou City [grant number YZ2022180], and the Market Supervision Administration Science and Technology Fund of Jiangsu Province [grant number KJ2023076].

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fu, E.; Wentland, L. A survey of 3D printing technology applied to paper microfluidics. Lab on a chip 2021, 22, 9–25. [Google Scholar] [CrossRef]
  2. Yin, B.; Yue, W.; Sohan, A.; Zhou, T.; Qian, C.; Wan, X. Micromixer with Fine-Tuned Mathematical Spiral Structures. ACS omega 2021, 6, 30779–30789. [Google Scholar] [CrossRef]
  3. Yin, B.; Wan, X.; Qian, C.; Sohan, A.; Wang, S.; Zhou, T. Point-of-Care Testing for Multiple Cardiac Markers Based on a Snail-Shaped Microfluidic Chip. Frontiers in chemistry 2021, 9, 741058. [Google Scholar] [CrossRef]
  4. Yin, B.F.; Wan, X.H.; Yang, M.Z.; Qian, C.C.; Sohan, A. Wave-shaped microfluidic chip assisted point-of-care testing for accurate and rapid diagnosis of infections. Military Medical Research 2022, 9, 8–21. [Google Scholar] [CrossRef]
  5. Yin, B.; Qian, C.; Wan, X.; Muhtasim Fuad Sohan, A.S.M.; Lin, X. Tape integrated self-designed microfluidic chip for point-of-care immunoassays simultaneous detection of disease biomarkers with tunable detection range. Biosensors & bioelectronics 2022, 212, 114429. [Google Scholar]
  6. Yin, B.; Wan, X.; Qian, C.; Sohan, A.; Zhou, T.; Yue, W. Enzyme Method-Based Microfluidic Chip for the Rapid Detection of Copper Ions. Micromachines (Basel) 2021, 12, 1380–1390. [Google Scholar] [CrossRef]
  7. Shin, W.; Kim, H.J. 3D in vitro morphogenesis of human intestinal epithelium in a gut-on-a-chip or a hybrid chip with a cell culture insert. Nature protocols 2022, 17, 910–939. [Google Scholar] [CrossRef]
  8. Zhang, Y.; Tseng, T.M.; Schlichtmann, U. Portable all-in-one automated microfluidic system (PAMICON) with 3D-printed chip using novel fluid control mechanism. Sci Rep 2021, 11, 19189–19199. [Google Scholar] [CrossRef] [PubMed]
  9. Aishan, Y.; Funano, S.I.; Sato, A.; Ito, Y.; Ota, N.; Yalikun, Y.; Tanaka, Y. Bio-actuated microvalve in microfluidics using sensing and actuating function of Mimosa pudica. Sci Rep 2022, 12, 7653–7664. [Google Scholar] [CrossRef] [PubMed]
  10. Gong, J.; Wang, Q.; Liu, B.; Zhang, H.; Gui, L. A Novel On-Chip Liquid-Metal-Enabled Microvalve. Micromachines (Basel) 2021, 12, 1051–1065. [Google Scholar] [CrossRef] [PubMed]
  11. Im, S.B.; Uddin, M.J.; Jin, G.J.; Shim, J.S. A disposable on-chip microvalve and pump for programmable microfluidics. Lab on a chip 2018, 18, 1310–1319. [Google Scholar] [CrossRef] [PubMed]
  12. Liu, W.; He, H.; Zheng, S.Y. Microfluidics in Single-Cell Virology: Technologies and Applications. Trends in biotechnology 2020, 38, 1360–1372. [Google Scholar] [CrossRef] [PubMed]
  13. Peshin, S.; Madou, M.; Kulinsky, L. Microvalves for Applications in Centrifugal Microfluidics. Sensors (Basel, Switzerland) 2022, 22, 8955–8991. [Google Scholar] [CrossRef] [PubMed]
  14. Hayes, B.; Smith, L.; Kabutz, H.; Hayes, A.C.; Whiting, G.L.; Jayaram, K.; MacCurdy, R. Rapid Fabrication of Low-Cost Thermal Bubble-Driven Micro-Pumps. Micromachines (Basel) 2022, 13, 1634–1655. [Google Scholar] [CrossRef] [PubMed]
  15. Gao, R.Z.; Hébert, M.; Huissoon, J.; Ren, C.L. µPump: An open-source pressure pump for precision fluid handling in microfluidics. HardwareX 2020, 7, e00096. [Google Scholar] [CrossRef]
  16. Bao, Q.; Zhang, J.; Tang, M.; Huang, Z.; Lai, L.; Huang, J.; Wu, C. A Novel PZT Pump with Built-in Compliant Structures. Sensors (Basel, Switzerland) 2019, 19, 1301–1316. [Google Scholar] [CrossRef]
  17. Tang, P.C.; Eriksson, O.; Sjögren, J.; Fatsis-Kavalopoulos, N.; Kreuger, J.; Andersson, D.I. A Microfluidic Chip for Studies of the Dynamics of Antibiotic Resistance Selection in Bacterial Biofilms. Frontiers in cellular and infection microbiology 2022, 12, 896149. [Google Scholar] [CrossRef]
  18. Reyes, D.R.; van Heeren, H. Proceedings of the First Workshop on Standards for Microfluidics. Journal of research of the National Institute of Standards and Technology 2019, 124, 1–22. [Google Scholar] [CrossRef]
  19. Tian, L.L.; Li, C.H.; Ye, Q.C.; Li, Y.F.; Huang, C.Z.; Zhan, L.; Wang, D.M.; Zhen, S.J. A centrifugal microfluidic chip for point-of-care testing of staphylococcal enterotoxin B in complex matrices. Nanoscale 2022, 14, 1380–1385. [Google Scholar] [CrossRef]
  20. Chantar, H.; Tubishat, M.; Essgaer, M.; Mirjalili, S. Hybrid Binary Dragonfly Algorithm with Simulated Annealing for Feature Selection. SN computer science 2021, 2, 295–306. [Google Scholar] [CrossRef]
  21. Pei, J.; Xu, L.; Huang, Y.; Jiao, Q.; Yang, M.; Ma, D.; Jiang, S.; Li, H.; Li, Y.; Liu, S.; et al. A Two-Step Simulated Annealing Algorithm for Spectral Data Feature Extraction. Sensors (Basel, Switzerland) 2023, 23, 893–908. [Google Scholar] [CrossRef] [PubMed]
  22. Benítez-Hidalgo, A.; Nebro, A.J.; Aldana-Montes, J.F. Sequoya: multiobjective multiple sequence alignment in Python. Bioinformatics (Oxford, England) 2020, 36, 3892–3893. [Google Scholar] [CrossRef] [PubMed]
  23. Meinecke, C.R.; Heldt, G.; Blaudeck, T.; Lindberg, F.W.; van Delft, F.; Rahman, M.A.; Salhotra, A.; Månsson, A.; Linke, H.; Korten, T.; et al. Nanolithographic Fabrication Technologies for Network-Based Biocomputation Devices. Materials (Basel, Switzerland) 2023, 16, 1046–1062. [Google Scholar] [CrossRef] [PubMed]
  24. Vlaic, S.; Conrad, T.; Tokarski-Schnelle, C.; Gustafsson, M.; Dahmen, U.; Guthke, R.; Schuster, S. ModuleDiscoverer: Identification of regulatory modules in protein-protein interaction networks. Sci Rep 2018, 8, 433–444. [Google Scholar] [CrossRef] [PubMed]
  25. Valverde, M.G.; Mille, L.S.; Figler, K.P.; Cervantes, E.; Li, V.Y.; Bonventre, J.V.; Masereeuw, R.; Zhang, Y.S. Biomimetic models of the glomerulus. Nature reviews. Nephrology 2022, 18, 241–257. [Google Scholar] [CrossRef] [PubMed]
  26. Zhang, J.; Tavakoli, H.; Ma, L.; Li, X.; Han, L.; Li, X. Immunotherapy discovery on tumor organoid-on-a-chip platforms that recapitulate the tumor microenvironment. Advanced drug delivery reviews 2022, 187, 114365. [Google Scholar] [CrossRef]
  27. Cho, S.; Lee, S.; Ahn, S.I. Design and engineering of organ-on-a-chip. Biomedical engineering letters 2023, 13, 97–109. [Google Scholar] [CrossRef]
  28. Jie, Y. Deep Learning-Guided Simulated Annealing for Designing Vocational High Educational System. Applied bionics and biomechanics 2022, 2022, 7187863. [Google Scholar] [CrossRef]
  29. Meng, X.; Wang, N.; Liu, J.; Liu, Q. An Improved Simulated Annealing-Based Decision Model for the Hybrid Flow Shop Scheduling of Aviation Ordnance Handling. Computational intelligence and neuroscience 2022, 2022, 1843675. [Google Scholar] [CrossRef]
  30. Pakela, J.M.; Tseng, H.H.; Matuszak, M.M.; Ten Haken, R.K.; McShan, D.L.; El Naqa, I. Quantum-inspired algorithm for radiotherapy planning optimization. Medical physics 2020, 47, 5–18. [Google Scholar] [CrossRef]
  31. Leber, A.; Dong, C.; Laperrousaz, S.; Banerjee, H.; Abdelaziz, M.; Bartolomei, N.; Schyrr, B.; Temelkuran, B.; Sorin, F. Highly Integrated Multi-Material Fibers for Soft Robotics. Advanced science (Weinheim, Baden-Wurttemberg, Germany) 2023, 10, e2204016. [Google Scholar] [CrossRef]
  32. Zeng, W.; Guo, L.; Xu, S.; Chen, J.; Zhou, J. High-Throughput Screening Technology in Industrial Biotechnology. Trends in biotechnology 2020, 38, 888–906. [Google Scholar] [CrossRef]
  33. Zabihihesari, A.; Hilliker, A.J.; Rezai, P. Fly-on-a-Chip: Microfluidics for Drosophila melanogaster Studies. Integrative biology : quantitative biosciences from nano to macro 2019, 11, 425–443. [Google Scholar] [CrossRef] [PubMed]
  34. Cheng, C.; Foxworthy, G.; Fridman, G. On-chip ionic current sensor. Applied physics. A, Materials science & processing 2021, 127, 314–324. [Google Scholar]
  35. Wei, C.; Zong, Y.; Jiang, Y. Bioinspired Wire-on-Pillar Magneto-Responsive Superhydrophobic Arrays. ACS Appl Mater Interfaces 2023, 15, 24989–24998. [Google Scholar] [CrossRef] [PubMed]
  36. Sakaguchi, K.; Akimoto, K.; Takaira, M.; Tanaka, R.I.; Shimizu, T.; Umezu, S. Cell-Based Microfluidic Device Utilizing Cell Sheet Technology. Cyborg and bionic systems (Washington, D.C.) 2022, 2022, 9758187. [Google Scholar] [CrossRef]
  37. Ducrée, J. Systematic review of centrifugal valving based on digital twin modeling towards highly integrated lab-on-a-disc systems. Microsystems & nanoengineering 2021, 7, 104–130. [Google Scholar]
  38. Sanka, R.; Lippai, J.; Samarasekera, D.; Nemsick, S.; Densmore, D. 3DμF - Interactive Design Environment for Continuous Flow Microfluidic Devices. Sci Rep 2019, 9, 9166–9176. [Google Scholar] [CrossRef]
  39. Honrado, C.; McGrath, J.S.; Reale, R.; Bisegna, P.; Swami, N.S.; Caselli, F. A neural network approach for real-time particle/cell characterization in microfluidic impedance cytometry. Analytical and bioanalytical chemistry 2020, 412, 3835–3845. [Google Scholar] [CrossRef]
  40. Ross, G.A.; Rustenburg, A.S.; Grinaway, P.B.; Fass, J.; Chodera, J.D. Biomolecular Simulations under Realistic Macroscopic Salt Conditions. The journal of physical chemistry. B 2018, 122, 5466–5486. [Google Scholar] [CrossRef]
  41. Song, C.; Du, Q.; Yang, S.; Feng, H.; Pang, H.; Li, C. Flexible joint parameters identification method based on improved tracking differentiator and adaptive differential evolution. The Review of scientific instruments 2022, 93, 084706. [Google Scholar] [CrossRef] [PubMed]
  42. Suh, D.; Radak, B.K.; Chipot, C.; Roux, B. Enhanced configurational sampling with hybrid non-equilibrium molecular dynamics-Monte Carlo propagator. The Journal of chemical physics 2018, 148, 14101–14110. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions, and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content.
Preprints 78497 g001
Figure 1. A device with microvalve structure: (a) Schematic diagram of a chip reaction device; (b) Schematic diagram of hybrid device.
Figure 1. A device with microvalve structure: (a) Schematic diagram of a chip reaction device; (b) Schematic diagram of hybrid device.
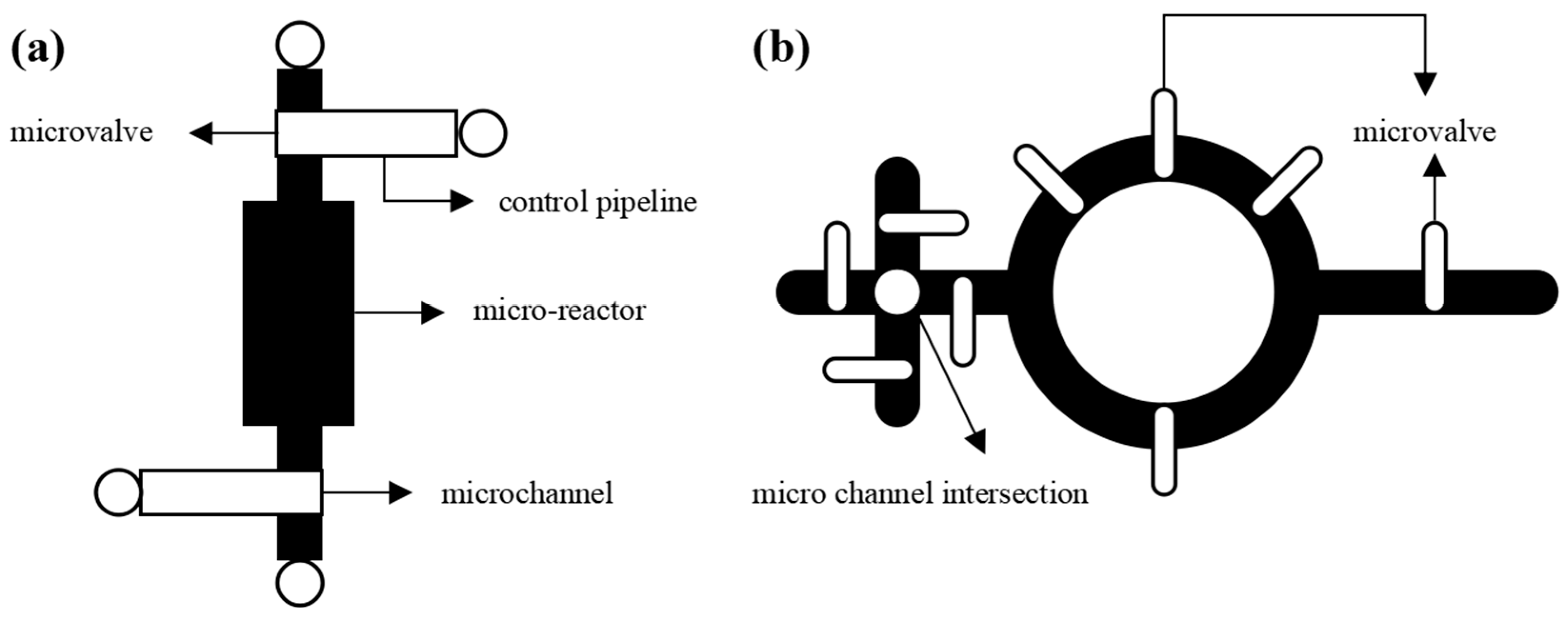
Preprints 78497 g001
Preprints 78497 g002
Figure 2. Structural design modeling of microfluidic chips: (a) Experimental sequence diagram; (b) Device summary; (c) Channel wiring diagram of chip device layout.
Figure 2. Structural design modeling of microfluidic chips: (a) Experimental sequence diagram; (b) Device summary; (c) Channel wiring diagram of chip device layout.
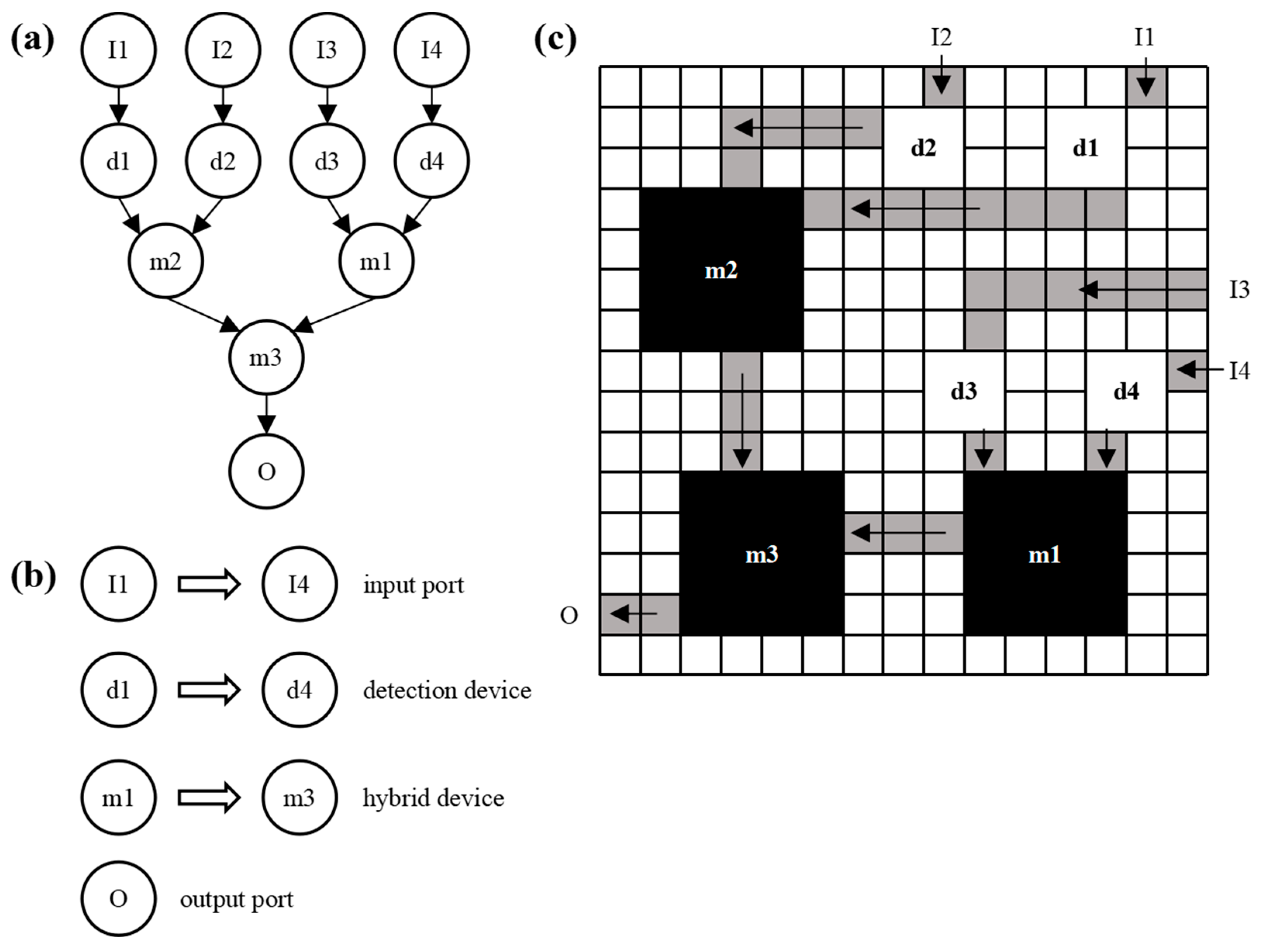
Preprints 78497 g002
Preprints 78497 g003
Figure 3. Algorithm design flow chart.
Figure 3. Algorithm design flow chart.
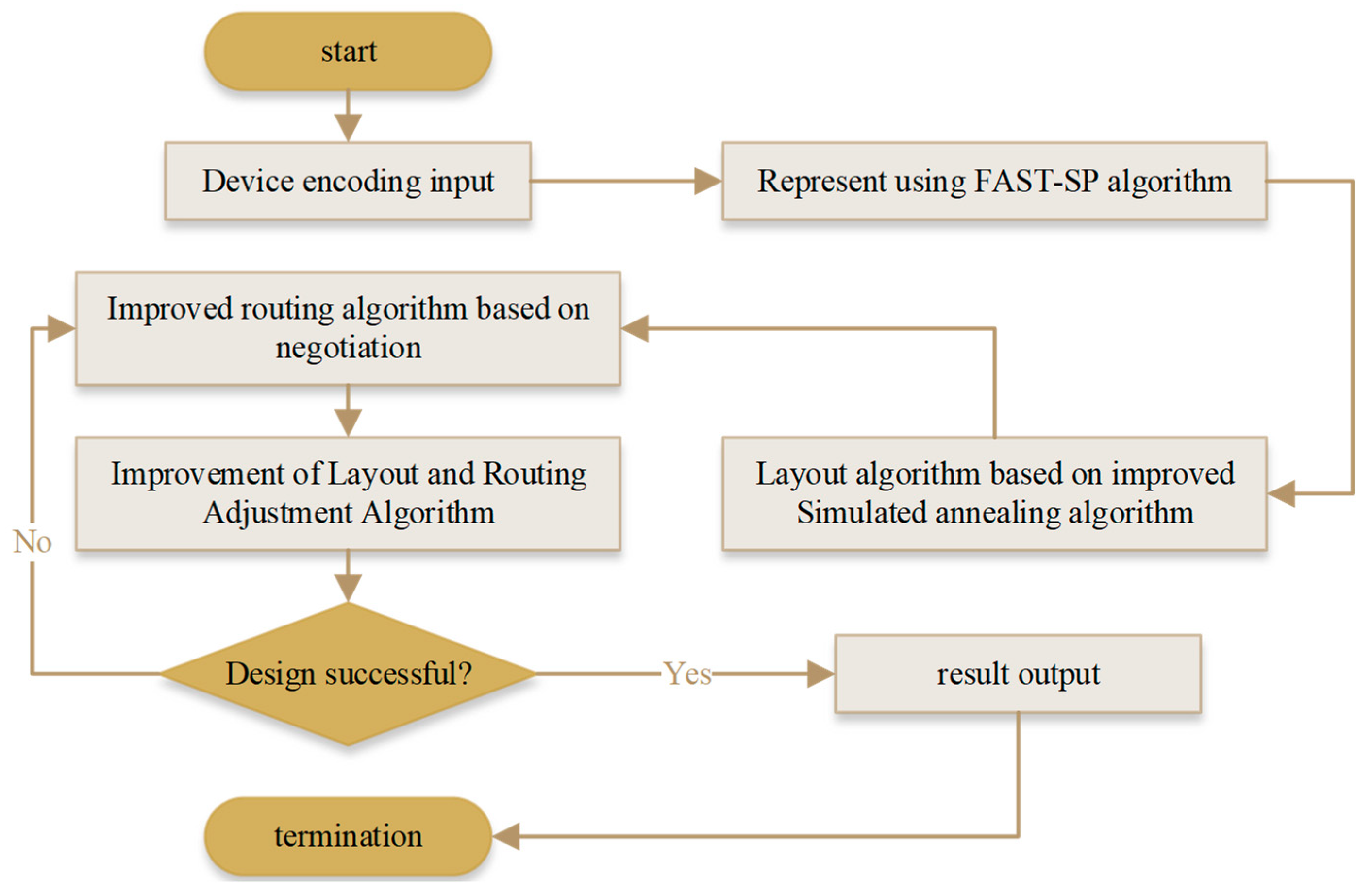
Preprints 78497 g003
Preprints 78497 g004
Figure 4. Sequence pair layout: (a) Skew network of sequence pairs; (b) Layout vertical constraint diagram; (c) Layout horizontal constraint diagram.
Figure 4. Sequence pair layout: (a) Skew network of sequence pairs; (b) Layout vertical constraint diagram; (c) Layout horizontal constraint diagram.
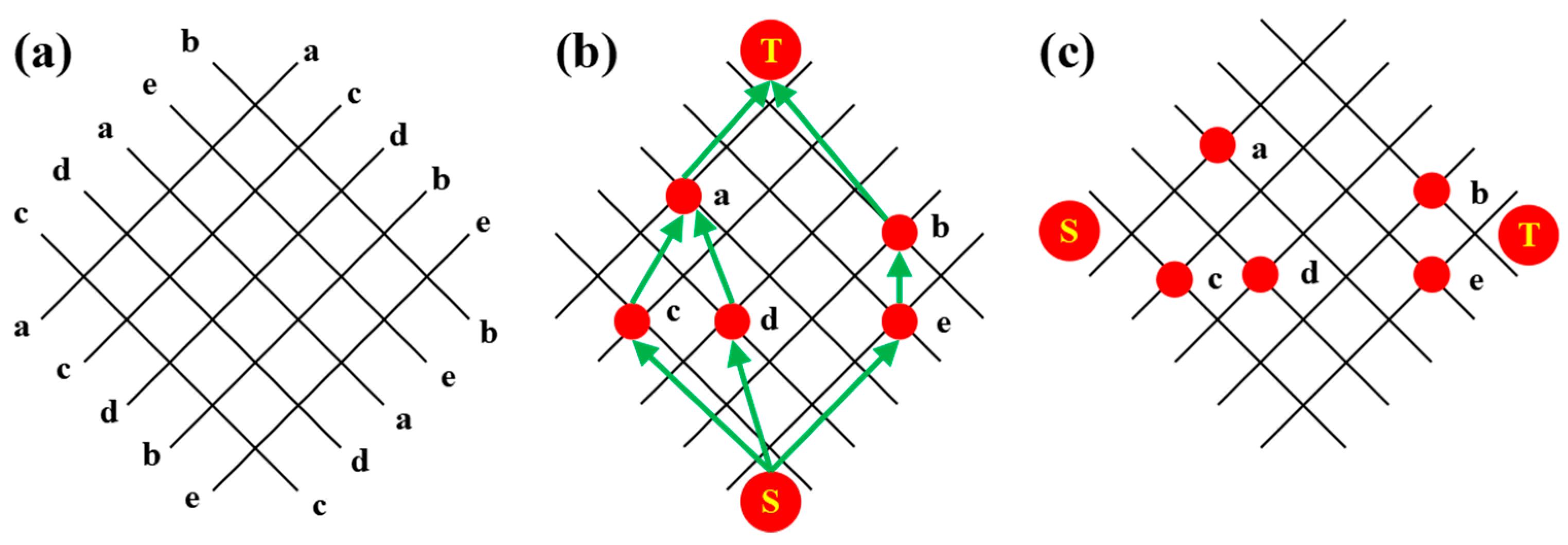
Preprints 78497 g004
Preprints 78497 g005
Figure 5. The layout result of the device is (a) before layout; (b) after layout.
Figure 5. The layout result of the device is (a) before layout; (b) after layout.
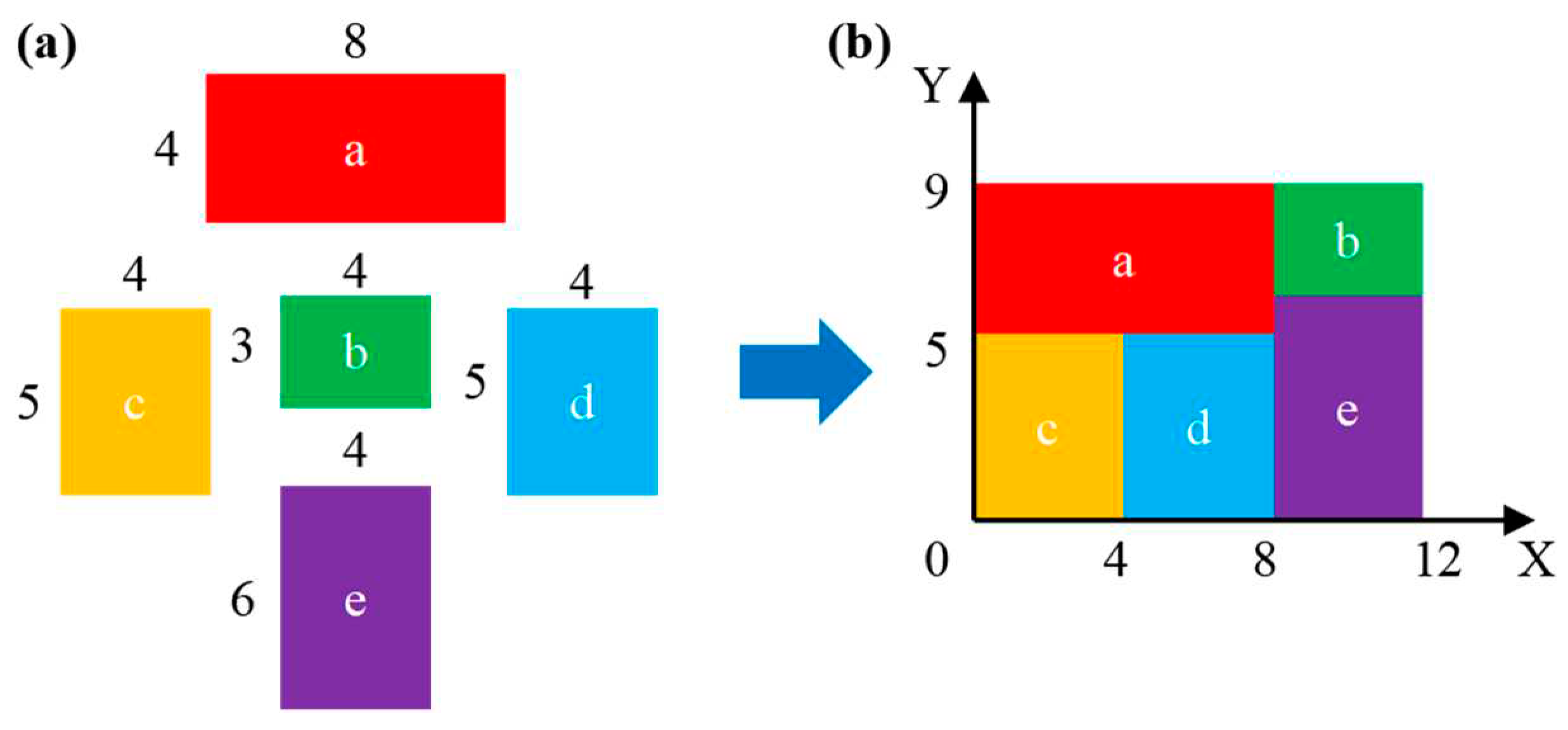
Preprints 78497 g005
Preprints 78497 g006
Figure 6. Cooling function curve, where CSA is the function curve of the available cooling mode, RSA is the function curve of the rapid cooling mode, and ISA is the function curve of the improved simulated annealing algorithm.
Figure 6. Cooling function curve, where CSA is the function curve of the available cooling mode, RSA is the function curve of the rapid cooling mode, and ISA is the function curve of the improved simulated annealing algorithm.
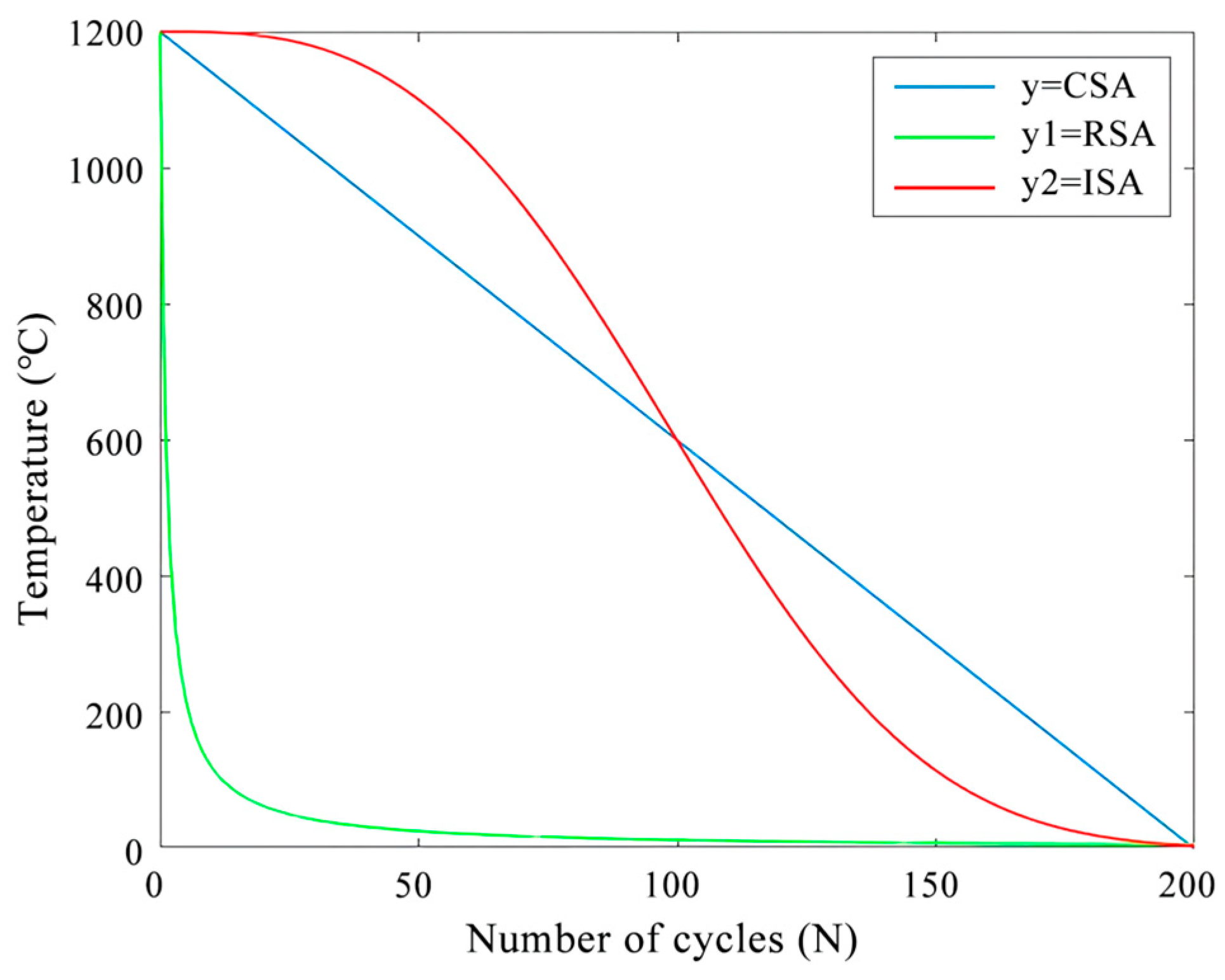
Preprints 78497 g006
Preprints 78497 g007
Figure 7. A schematic diagram of two types of wiring results: (a) There is an intersection; (b) No intersection exists.
Figure 7. A schematic diagram of two types of wiring results: (a) There is an intersection; (b) No intersection exists.
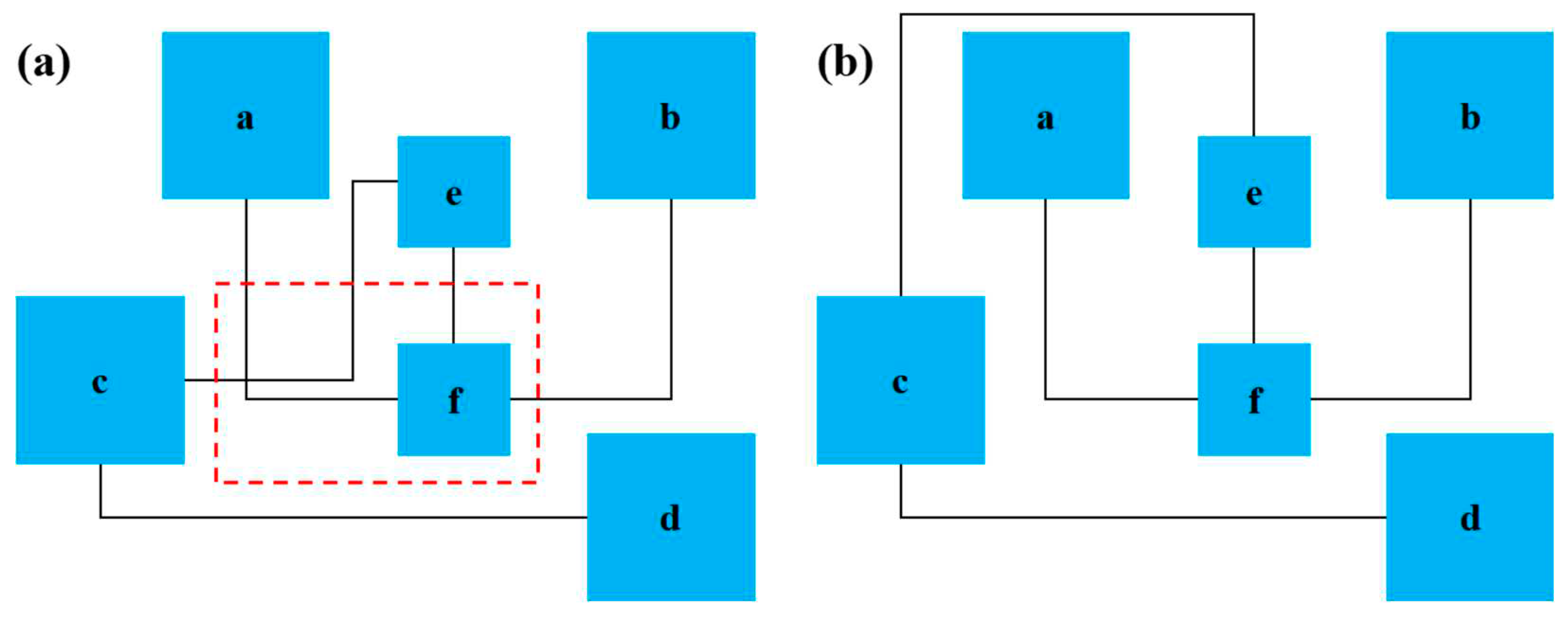
Preprints 78497 g007
Preprints 78497 g008
Figure 8. Wiring mode: (a) L-shaped wiring; (b) Z-wiring; (c) U-shaped wiring.
Figure 8. Wiring mode: (a) L-shaped wiring; (b) Z-wiring; (c) U-shaped wiring.
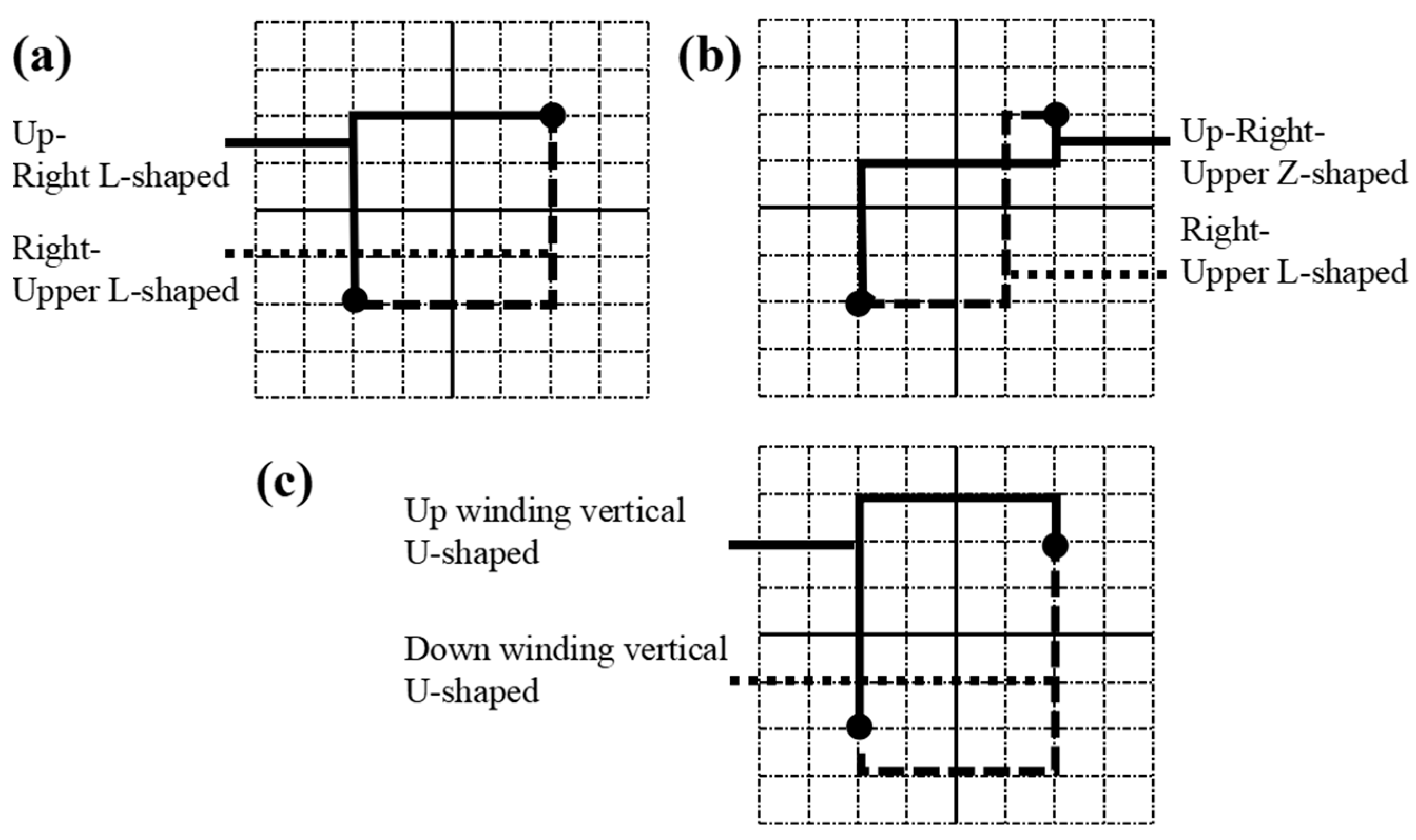
Preprints 78497 g008
Preprints 78497 g009
Figure 9. Comparison of three types of algorithms in total chip area.
Figure 9. Comparison of three types of algorithms in total chip area.
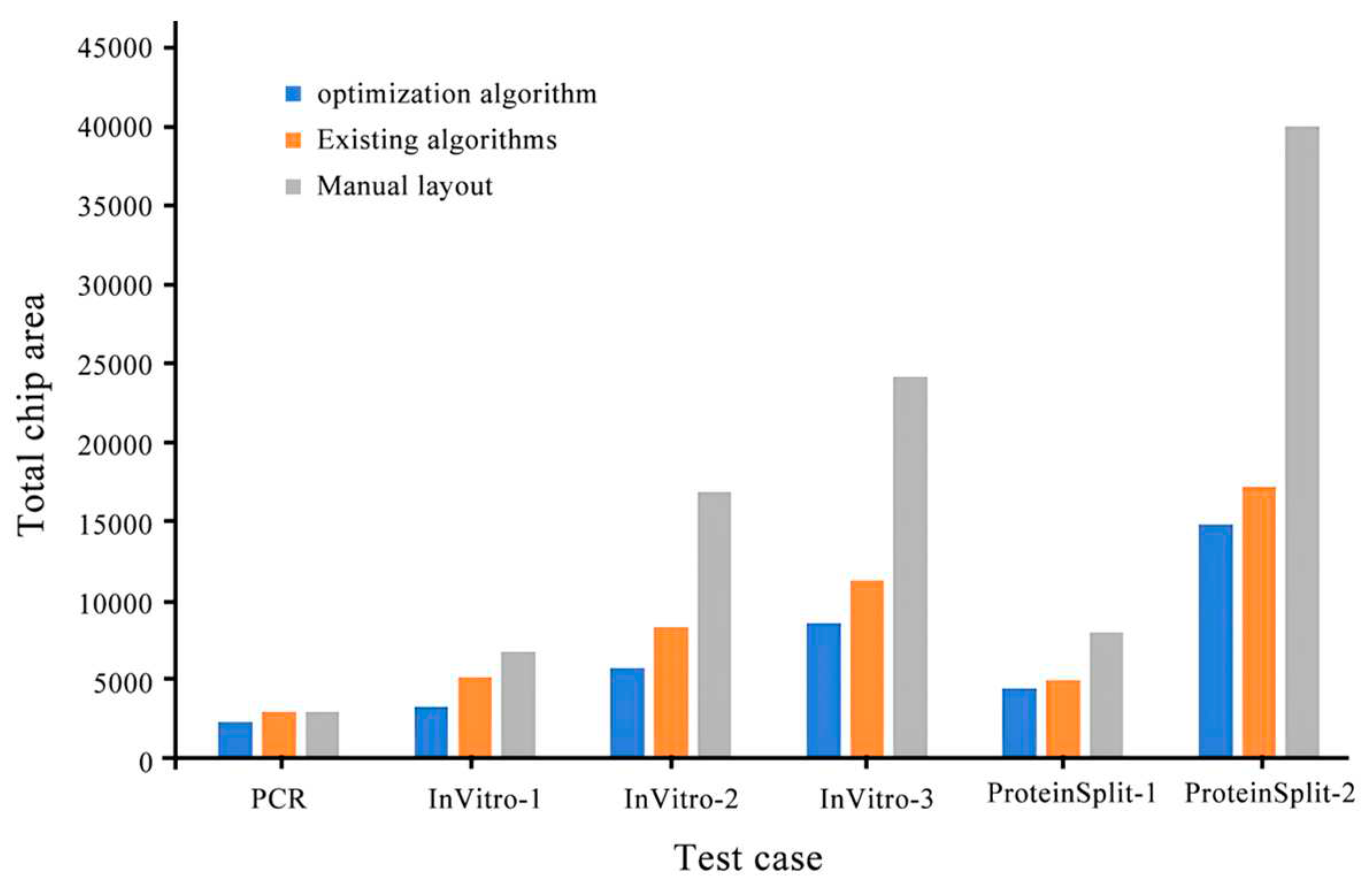
Preprints 78497 g009
Preprints 78497 g010
Figure 10. Comparison of three types of algorithms on the number of intersections.
Figure 10. Comparison of three types of algorithms on the number of intersections.
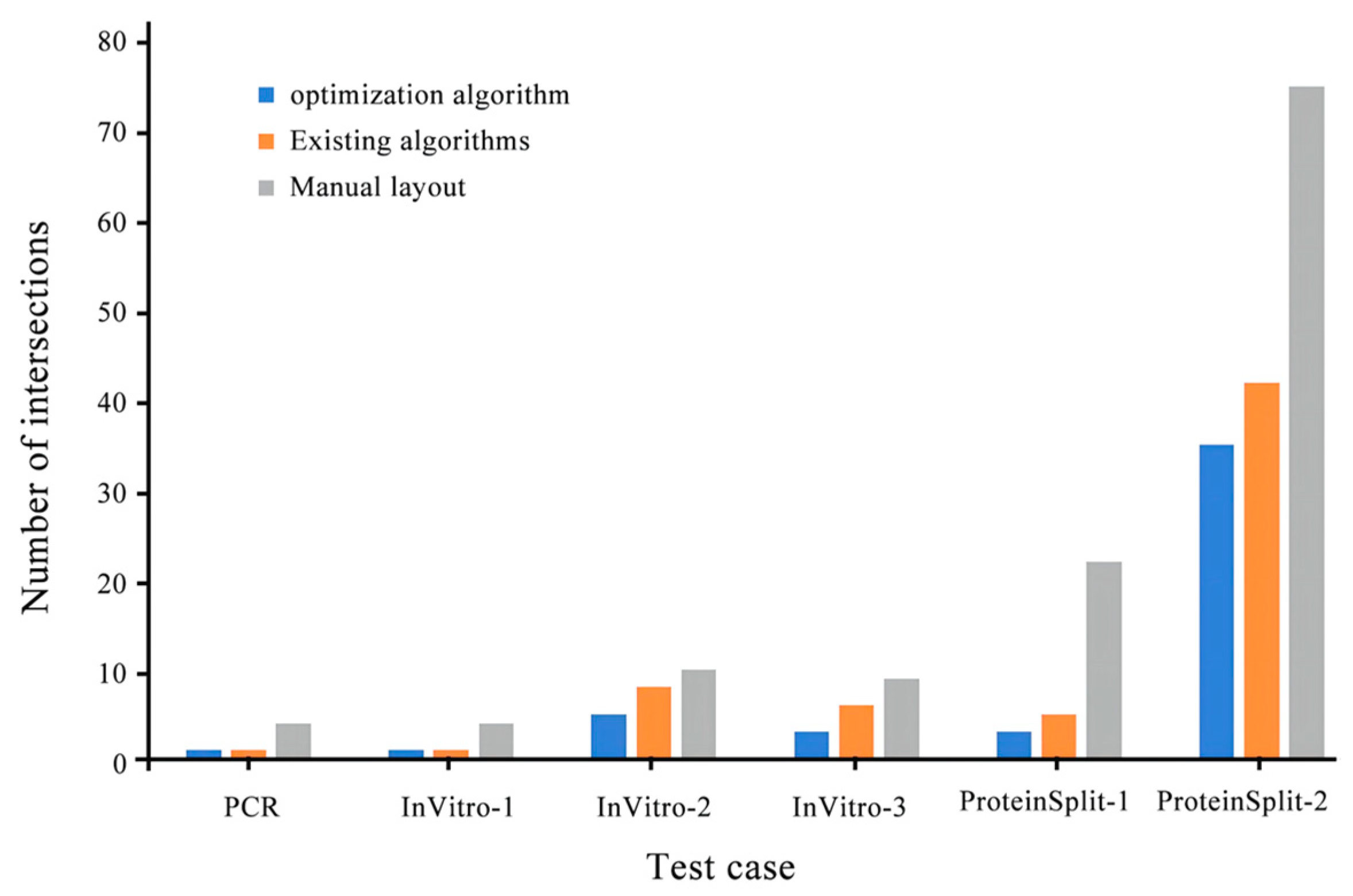
Preprints 78497 g010
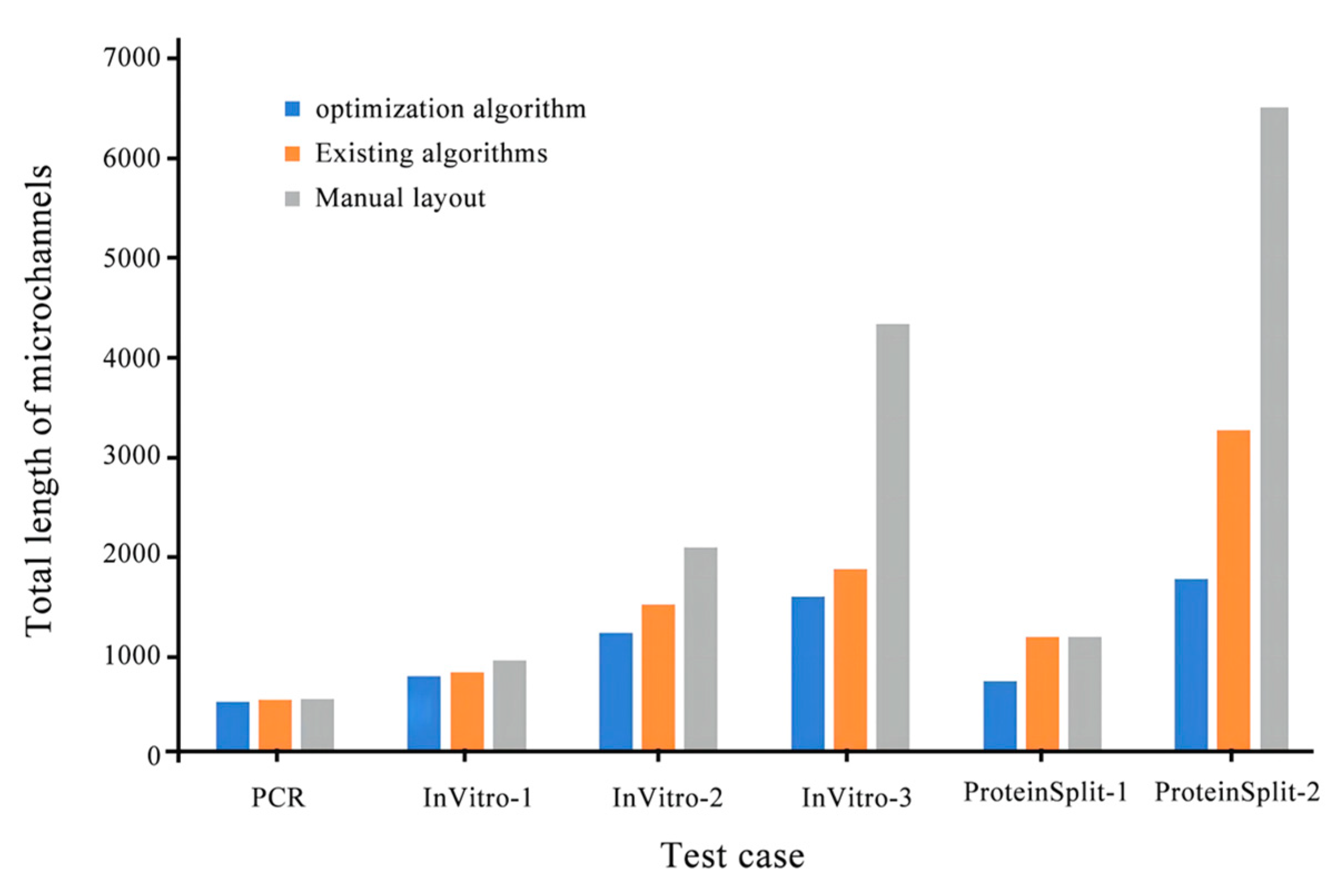
Preprints 78497 g011
Figure 11. Comparison of 3D algorithms on the total length of microchannels.
Figure 11. Comparison of 3D algorithms on the total length of microchannels.
Preprints 78497 g011
Table 1. Sequence pair algorithm.
Table 1. Sequence pair algorithm.
Input: sequence pair (SX, SY), width (length) of n devices, width [n] (heights [n])
Output: x (y) coordinates x_coords (y_coords), the W (H) dimension of the layout structure.
1. for(i = 1 to n)
2. weights [i] = widths [i] //Weight of device-width
3. (x_coords, W) = LCS (SX, SY, weights) //X coordinate, total width W
4. for(i = 1 to n)
5. weights [i] = heights [i] //Weight of device height
6. SXR[i]=SX[n+1-i] //Reverse SX
7. (y_coords, H) = LCS(SXR, SY, weights) //Y coordinate, total height H
Table 2. LCS algorithm.
Table 2. LCS algorithm.
Input: sequences S1 and S2, weights of n devices [n]
Output: position of each module, total length L
1. for(i =1 to n)
2. block_order[S2[i]]=i //Index of each device in S2
3. lengths[i]=0 //Total length initialization of all devices
4. for(i=1 to n)
5. block=S1[i] //Current device
6. index=block_order[block] //Index of current device in S2
7. positions[block]=lengths[index] //Calculate the position of the device
8. t_span=positions[block]+weights[block] //Determine the current fast length
9. for(j=index to n)
10. if(t_span>lengths[j])
11. lengths[j]=t_span //The length of the current device replaces the former
12. else break
13. L=lengths[n] //Total length
Table 3. Device dimensions.
Table 3. Device dimensions.
device widths heights
a 8 4
b 4 3
c 4 5
d 4 5
e 4 6
Table 4. Comparison of Experimental Results.
Table 4. Comparison of Experimental Results.
Test case Chip area
(Existing algorithm/optimization algorithm)		 Microchannel length
(Existing algorithm/optimization algorithm)		 Microchannel intersection
(Existing algorithm/optimization algorithm)		 Percent improvement
(%)
PCR 2958/2850 522/509 1/1 3.6
InVitro-1 5110/3906 802/765 1/1 23.5
InVitro-2 8232/5688 1485/1203 8/5 30.9
InVitro-3 11187/8460 1864/1568 6/3 24.3
ProteinSplit-1 4914/4422 1162/713 5/3 10.0
ProteinSplit-2 17030/14690 3247/1749 42/35 13.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated