Preprint
Article
A Walk Through Agn Country—For the Somewhat Initiated!
Altmetrics
Downloads
116
Views
71
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
04 July 2023
Posted:
05 July 2023
You are already at the latest version
Alerts
Abstract
Some key issues in AGN and galaxy formation are discussed. Very successful Unified Models explain much of the variety of AGN with orientation effects; ingredients are shadowing by a dusty “torus" and relativistic beaming. A spinoff result is described which is important for the formation of massive elliptical galaxies. It’s the most spectacular and unequivocal AGN feedback phenomenon known. This is the so-called “alignment effect" in powerful radio galaxies at z > 1. One of them is a BAL radio galaxy! I explain a very robust derivation of the reddening law for nuclear dust, which reveals a dearth of small grains. Then the quasistatic thin accretion disk model, thought by many to explain the energetically dominant optical/UV continuum, is thoroughly debunked. Much of this was known when the model was proposed 35 years ago. A new argument is given that trivially falsifies a huge superset of such models. It’s possible to see the central engine spectrum with the atomic and dust emission surgically removed! Few noticed this breakthrough work. The far IR dust emission in Cygnus A is 10% polarized, and so far high nuclear dust polarization is seen in all radio loud objects, but no radio quiet ones.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
Introduction to the content:
The first two parts of this essay derive from a meeting presentation, my task being to tell the origin story for the AGN spectroscopic unified model, and comment on various aspects of its development. There is a second aspect of geometrical unification of accreting supermassive black holes, by relativistic beaming. Beaming unification was a compelling and necessary idea, but plagued with statistical anomalies until Peter Barthel found the solution by “cheating"! He read outside his field! He read our optical polarization papers, and suddenly underwent a religious conversion and started the Unification Church. I joined the Church right away, and we preached that spectroscopic unification married Beaming Unification, and the two live happily together today.
I recount some of the sad and almost unbelievable history of modeling the energetically dominant Big Blue Bump continuum component in Quasars and other Type 1 AGN. The story is sad because vast theoretical effort has gone into modeling this Big Blue Bump continuum with optically thick, geometrically thin and quasistatic accretion disks, despite its gross inconsistency with the data. Cognitive dissonance was part of the model since the very beginning in the 1980s: it was pointed out explicitly at that time that the variability and polarization were comically at variance with predictions. Over the 40 years (and counting) of its “development," additional profound discrepancies have been discovered, not least of which is measurement of the surface brightness of the emitter with microlensing: it is an order of magnitude less than the value for opaque material that can fit the spectral energy distribution.
References for the variability, polarization, and surface brightness are Alloin et al. 1985 [1]; Antonucci 1988 [2], Antonucci, Kinney and Ford 1989 [3]; and Dexter and Agol 2011 [4].
Carl Sagan (1987) wrote, in The Burdens of Skepticism:
“In science it often happens that scientists say, `You know, that’s a really good argument; my position is mistaken,’ and then they actually change their minds and you never hear that old view from them again. They really do it."
“It doesn’t happen as often as it should, because scientists are human and change is sometimes painful. But it happens every day. I cannot recall the last time that happened in politics or religion."
[The Skeptical Inquirer 12, 1, 1987]
My experience has been that when I argue individually for the rough validity of the Unified Models, my audience finds me persuasive and tends to adopt it as a very helpful approximation, and to acknowledge its prodigious predictive power.
By contrast, I’ve had a great many opportunities in papers and talks to detail the profound falsification of the “standard" disk model. In that case, my listeners appear to be similarly moved by the force of the arguments, but revert their views within at most about three days. They then relax back into Magical Thinking. I’ve measured that time constant at meetings. Two or three days and the Ostrichs’ heads are back in the sand. They resume the nearly universal practice of referring to “the accretion disk" and the Big Blue Bump (BBB) optical/UV continuum component synonymously. I now stop reading when I get to such a statement in a paper. It means that the authors are unaware or uninterested in the observations.
I’ve made clear since my first critiques in the 1980s that accretion by black holes is almost certain to be the energy source for AGN; and that I’d bet my car that there is a flat isodensity contour somewhere in the inner accretion flow. But alas we are not looking at the photosphere of a disk which remotely resembles the standard version that almost everyone accepts, along with the scaling relations that it implies.
Instead of forcing my content to fit a structure, I will just take you on a walk through AGN country, and tell you about some things that interest me. In keeping with the intent of this volume, I will remind you of a precious opportunity to separate radiative from dynamical effects of an accreting massive black hole on its host. I will also draw attention to a spectacular body of knowledge about giant Elliptical galaxy star-formation in powerful radio galaxies at redshifts z ≲ 4, which illustrates
feedback in the clearest possible way, and at the greatest possible scale. This is the radio/optical
“alignment effect". (Tim Heckman tells me galaxy formation people pay no attention to this incredible
phenomenology, because they labor under the illusion that the extended optical light is just scattered
from hidden quasars!) I’ll give seemingly powerful testable arguments that something akin to a
latter-day monolithic collapse event (or cooling flood) occurs in certain powerful radio galaxies. I
will highlight a literal Broad Absorption Line (BAL) radio galaxy, not a quasar! — surely the most
spectacular GalacticWind ever seen. Yet these amazing aspects of AGN feedback are known to very
few people in that field, presumably due to the usual balkanization by sub-speciality that holds back
all fields of science.
Very fundamentally, the standard disk model predicts a proportionality between the characteristic temperature and the product . This is required of any model with thermal radiation from a fixed region set by (that is, ). This has been utterly falsified multiple times. In fact in the present paper, I explain how the reader can exclude such models with a figure perfect for a T-shirt: A mighty river of theory papers flowing for 40 years is negated by a simple observation based on published literature. An enterprising person can disprove that dependence on M and L...or anything else!
I introduce the reader to the five extant quasar spectra freed of the awful contamination from surrounding reprocessed emission in the various emission line regions and the dust torus. These spectra don’t look like the spectra of quasars which you have seen. But they do look very much like each other!
I will prove that many AGN are heavily absorbed by dust which is gray in the UV! You don’t have to believe this result, but if not, you have to give up an Axiom which may be dear to you!
Finally some recent and quite unexpected results are given regarding the wonderful Cygnus A radio galaxy, and on a very intriguing apparent difference between radio loud and radio quiet AGN. They tentatively differ systematically in their magnetic fields on pc scales!
2. How I became Mr. Doughnut. — the Spectroscopic Unified Model.
The AGN Mesoscale is my new name for the region around the dust sublimation radius through say the Narrow Line Region, where the AGN is still driving the car.
The discovery of the first hidden Type 1 nucleus with polarimetry, the Narrow Line Radio Galaxy 3C234.
2.1. “Take out the dark slide."
After I published the first hidden Type 1 spectrum in 1984, I met a fellow at a conference who excitedly and correctly described my paper, saying that he had discussed it in his journal club and he was sorry he didn’t remember the name of the author. When I confessed I was the author, he said, “Really? You’re Mister Doughnut?" Well here is how I found the doughnuts with the Type 1 nuclei inside.
When I was a grad student at U C Santa Cruz in the late 1970s, my eventual advisor, J S Miller, along with postdoc Gary Schmidt, were building an instrument that could sort photons by polarization as well as wavelength. At that time there had been very little spectropolarimetry of AGN. Perhaps it was considered overkill to get high spectral resolution, since AGN polarization was known only for identifying broadband processes like synchrotron emission and scattering. And so many photons would need to be collected! In fact, polarimetry was considered by most to be an esoteric fringe field.
I’d been considering asking Miller to take me on as a graduate student when I attended a AAS meeting and heard a talk by the director of Kitt Peak National Observatory, the famous Geoffrey Burbidge. His topic was the wonders that might be revealed by a truly giant telescope (say 8 m). On Burbidge’s grand agenda for the futuristic telescope, the last sub-sub-sub-topic was “Astrometry and polarimetry." Burbidge may have devoted a dependent clause of his talk to these two despised specialities, but I think it was really rather a grunt.
I knew that aside from the well-explored blazar class of synchrotron emitters, the percent polarizations of AGN are discouragingly low; 1% is considered to indicate an attractive target. And for spectropolarimetry, I knew that to achieve the same SNR in polarized light as total light, with 1% polarization, it would take an exposure longer by a factor of at least 20,000.
Also I wondered if such low polarization might be due to “weather," and carry no important information. Then in 1979, Stockman et al. (1979) [5] reported that the optical polarization “vector" in lobe-dominant radio quasars tends very strongly to align parallel with the kpc radio axis. That was electrifying to me because it meant that the very small optical polarizations were not meaningless weather, but something fundamental that connected the tiny optical region of perhaps a few a.u. to the giant radio lobes on scales billions of times larger. The rough axisymmetry is maintained from relativistic scales to intergalactic scales!
Joe took me on. I had no talent or interest in instrumentation or software, and when he showed me the precious incubating instrument, I could only nod and smile uncomfortably. It looked just like any other gray box of parts to my glazed eyes. I was no great observer, either. I prepared hugely and relied on incredibly detailed checklists. For example, before beginning an exposure, I read aloud solemnly, “Step 1. Open Dark Slide." Miller and Schmidt were both very intuitive at the telescope and I later learned that after that first run, Gary told Joe, “You’ve got to get rid of this guy. Did you see he had to read his checklist to figure out you have to open the dark slide?"
With linear polarimetry you get 3 of the 4 Stokes’ Parameters; instead of just I, you also measured Q and U simultaneously, with only slight loss of light. Joe and I, and I guess Gary, had a personality trait in common. We all wanted a free lunch. A stairway to heaven! We had little assurance that Q and U encoded a ton of interesting information, but we were all...optimistic guys.
2.2. Pay dirt: The Spectroscopic Unified Model, with obscuring torus and polar periscopic mirror.
Joe suggested Radio Galaxies for my thesis topic, which I eagerly accepted. We observed almost every dark run, at the modest-sized 3-m telescope of Lick Observatory. The site was poor, and the quantum efficiency was also low by today’s standards. When I expressed anxiety about the SNR situation, Joe said, “Think of it this way. We have a big telescope, only it’s in series instead of parallel." Our “Image Dissector Scanner" was a real Rube Goldberg device, but devilishly clever in using slightly persistent phosphors on the back of an image tube, which allowed the single channel detector to zip around, steered magnetically, and visit all the wavelength channels before they stopped glowing. The fact is, Lick was eating everyone’s lunch with that thing. It was before CCDs.
During each run we included a few of my radio galaxies, and it was discouraging work. A series of them showed P consistent with zero, or with just the polarization due to dichroic absorption in the Milky Way galaxy. The dominant signal was from stars in the host galaxies.
One advantage of that crazy instrument was that it truly counted photons, unlike CCDs, and you could see each one cause an increment in the flux in some wavelength channel in real time. The spectra for each polarization position angle were displayed on a small round green oscilloscope screen. Finally we observed 3C234, and we saw the photons come in, sometimes to the Ordinary Ray spectrum, and sometimes to the Extraordinary Ray. Any difference meant polarization was detected.
We sensed a possible detection such that the () ray was stronger than . I recall that we watched the photons barrel in and get counted, incrementing the displayed spectra. Ordinary. Ordinary. Extraordinary. Then we (or at least I) started rooting aloud for each +Q () photon, while cursing those at .
The Ordinary ray of the Q Stokes Parameter was getting farther ahead!
Finally Joe said calmly, “Pay dirt."
Because until that moment, we had nothing.
The 3C234 radio galaxy has a jet position angle of degrees, to which I’d assigned an uncertainty of , which was somewhat arbitrary and a bit generous. We measured a polarization position angle of , almost exactly orthogonal to the radio axis, and we eventually established a “perpendicular" class of AGN. That is, the optical polarization position angle in this group was perpendicular to the radio axis. That was opposite to the discovery of parallel polarization in quasars by Stockman et al. And the magnitude of P was at least ten times higher in the perpendicular group. It became clear that they were none other than the Type 2 spectral class members.
The total flux spectrum of 3C234 is shown in the present Figure 1.
At home, I made the present Figure 2, which shows the Ordinary minus Extraordinary ray, i.e. Stokes Q; and then the same for U. As a reminder, this un-normalized Q is the flux at (Ordinary) minus that at (Extraordinary) and U is the same except the ray is compared to the ray.
The Stokes spectra have been smoothed obviously, but it’s very clear that the [O III] 5007 Å line hardly shows up in the difference spectrum and is thus unpolarized. But the H line behaves differently! It is highly polarized, and accounting for unpolarized narrow components and starlight, the broad component polarization is a whopping %.
Emission lines are only intrinsically polarized in very special circumstances, so I realized this meant we went looking at a hidden broad line (high density; permitted lines only) region, through a periscopic mirror!
In scattering polarization, physics tells us that the perpendicular to the position angle is the direction of the photon’s last flight before being scattered into the line of sight. Thus these photons could have escaped the hidden nucleus only if they were travelling parallel to the radio axis. Since line emission is intrinsically quite isotropic, it follows that the other directions, the equatorial directions, must be blocked. That is, an opaque equatorial structure must be hiding the Type 1 nucleus. A correlary is that astronomers in those regions of the universe with polar views of 3C234 believe it is a Type 1 object, aka a Broad Line Radio Galaxy.
If this were to be generic, it would explain how radio galaxies could produce radio lobes without a visible central engine. Both spectral types do have the engine, and which type of object you saw was an accident.1
I may not know instrumentation but I know about data and systematic errors. Our setup symmetrized everything in time with respect to light paths, modulating at about 1 Hz, and the data from that instrument were clean. Furthermore we were meticulous about correcting for dichroic interstellar polarization contamination.
I gathered some clues about the wide applicability of the 3C234 scenario. While the spectropolarimetry paper didn’t come out until 1984, I’d published a short paper in Nature asserting the existence of a class of radio galaxies with a high perpendicular polarization two years earlier in 1982 [7]. I also reported there a parallel class, related to the radio quasars in Stockman et al. 1979 [5]; and the following year I did the same for Seyferts. (In the Seyfert case, the competition missed the parallel and perpendicular polarization alignment groups, because they combined Types 1 and 2, and took insufficient care with spurious signals due to interstellar polarization. In fact I only used their published data to find the alignments. I just analyzed it more carefully.
The geometry described “unified" the broad line (Type 1) and narrow line (Type 2) objects, both radio loud and radio quiet. (The language isn’t helping here, because the broad line objects actually have the narrow component as well.) The term “unified" is used very specifically: we asserted that if we changed our viewing angle relative to the AGN axis, the appearance and classification would change. Thus we may only have one physical class to try to understand. (The Broad Line or Type 1 radio galaxies can be considered just low luminosity radio quasars; and now the community recognizes that even powerful quasars are often observed in the Type 2 orientation.) We didn’t use the term obscuring “torus," but “thick disk," to avoid any implication regarding the outer boundary of the structure, or for that matter, of any particular physics at all. But I’ve fallen into the common usage of “torus" here. Keep in mind that the AGN torus is defined as the structure that blocks photons from the nucleus which are emitted in the equatorial directions, based on the radio axes, and nothing else at all. The torus-like shadowing can be realized by a variety of physical and kinematical models. The term is used loosely in the literature, leading to imaginary paradoxes at times.
2.3. NGC1068, the radio quiet prototype! why it’s good to know nothing.
Now we turn our attention to radio quiet AGN. We discovered the nature of the radio-quiet prototypical Type 2, NGC1068, in two steps. This was necessary because certain properties made the interpretation less obvious than for 3C234, though in retrospect the differences were very superficial. While smarter astronomers would not have been confused by this...alas the task fell to us. In step 1, published in 1983, we showed that the very strong host contribution caused the % polarization to be very low in the optical, with a lot of structure. The sharp rise towards the UV2 simply resulted from dilution of nuclear light by an old stellar population.
Correcting for the effects of the host produced a quasi-power law nuclear spectrum with constant 16% polarization. A very similar result was shown very soon afterwards by McLean et al. (1983) [8]. But I was fixated on one tiny bump in % polarization in the uncorrected P spectrum, just redward of Hb, that couldn’t be explained by the “upside down" stellar absorption lines; nor by dilution by low-polarization narrow emission lines. It was clearly present in the McLean et al. data too, but they didn’t mention it, and they concluded that the whole polarized continuum was due to synchrotron emission. In our 1983 paper, we mentioned that possibility but hedged, and favored Thomson scattering. Just as we had a big telescope by using our little one in series, we did the same with our brains, and published the polarized flux showing the Seyfert 1 only in 1985.
In almost all cases, huge host contamination makes life harder, but this was an exception. The excess in the bump in the UN-corrected % polarization spectrum is due to a redshifted broad and highly polarized H line component. It only showed up in the uncorrected P spectrum, because it reduced the starlight fraction at that wavelength. After starlight correction, since this scattered broad H has the same polarization as the nuclear continuum, it’s entirely invisible, and indeed one might assume the p is due to synchrotron radiation. Why was this “phantom" feature only conspicuous on the red side of narrow H? Because the scattered line is redshifted by the moving mirror effect. The mirror gas must be moving away from the nucleus at about 400 km/s, while the narrow line peaks are blueshifted by km/s relative to the systemic redshift.
So 1) look at your data carefully in every form you can think of, and 2) never get tired of staring at each bump and wiggle till you understand it.
When one looks through a cosmic mirror with polarimetry, the question arises as to the nature of the scatterers. The practical possibilities are dust grains and free electrons. In a sense, the former has greater plausibility because “dust has orders of magnitude higher cross-section than electrons, per gm of diffuse matter." Fortunately I wasn’t so steeped in this folklore, which is somewhat dubious anyway. It says that in fully ionized gas with a normal complement of standard Milky Way grains, dust would greatly dominate the scattering in the optical/UV region. But that’s not a common situation, and in hot or strongly irradiated media the dust is absent, and the mirror in NGC1068 is like that. Without going into all the arguments, I simply note that scattering by a mix of grain sizes like that in our Galactic disk scatters short wavelengths much more efficiently than long wavelengths, and can also introduce albedo features, especially in the Å region.
In NGC1068 all the evidence favors Thomson scattering in the central hundred pc, as we found in Miller and Antonucci (1983) [9] and Antonucci and Miller (1985) [10]. The former paper shows that while the observed % polarization is low in the optical in ground-based apertures rising steeply into the UV, careful correction of the effects of the unpolarized host galaxy leads to a nuclear continuum with wavelength-independent P at a much higher value, namely 16%. We must have done a fantastic job of correcting the optical light for host starlight because HST observations in the UV, past the starlight, show exactly that behavior (Figure 3). Note the overlay of total flux divided by the 0.16 fractional P from our 1985 paper, on top of the measured UV polarized flux. The match is perfect, without even any normalization.
That’s a signature of electron scattering, and in fact the polarized light looks exactly like a typical Type 1 with no shape changes. But in science one would like to prove things at least ten ways, and other strong arguments can be brought to bear. And as suggested by the “Proof" of beaming unification below, a direct argument is better than a consistency check. We suggested electron scattering for NGC1068, and that raised a flag for another reason. That process normally dominates the opacity only at very high temperatures, and by “normally" I mean in the common case of collisional ionization equilibrium. But we know that the putative scattering electrons couldn’t be very hot, or they would scatter—broaden any emission lines beyond recognition. We set a very conservative upper limit on their temperature of a million degrees, but a hundred thousand would have been justified.
Krolik and Kallman (1987) [11] then showed that the electron temperature could be low enough to fit the data, but only if the mirror gas were highly photoionized. (This is also concluded in Miller et al. (1991) [12], thanks to the wonderful late Bill Mathews.) And in that case, they said it must produce an enormous ∼keV equivalent-width Fe K line, whose energy would indicate extremely high ionization. This was a very dramatic prediction since nothing like that had ever been seen before. Conversely, they pointed out that if that prediction came true, then the gas producing the Fe lines would necessarily have significant Thomson scattering optical depth! (Their predicted line strength was raised further by Dave Band et al. (1990) [13], who added the contribution of resonant scattering.) The prediction was gloriously confirmed by subsequent X-ray observations. Even better, in a landmark paper by Ogle et al. (2003) [14], observations and analysis were presented from the Chandra CCD spectrometer, whose high spatial and spectral resolution resolved the X-ray narrow line region very well. Detailed analysis showed that indeed the emitting clouds must have about the anticipated product of Thomson depth and solid angle. Best of all, the radiative recombination continua directly indicated by their energy width that the electron temperature was also quite consistent (as low as) that required by the data.
After I left Santa Cruz, Miller and Bob Goodrich performed some very elegant and important observations, written up with a big assist by theorist Bill Mathews. The broad line profile in polarized flux from the nucleus must be a convolution of the intrinsic one and the electron thermal velocity distribution, and we didn’t know how big an effect the latter factor was. We didn’t know whether our mirror was hot or cold. So Joe and Bob decided to look at the nucleus as scattered by dust clouds a few hundred pc away. They knew dust scattering would reveal the true line profile. They succeeded in measuring it from three different off-nuclear dust clouds. The line was clearly narrower, as expected! And the polarized flux was much bluer than from the region where we identified electron scattering! Their amazing paper [12] is called “Multidirectional Views of the Active Nucleus of NGC1068.3
The mirror is quite interesting and exotic, but the amazing thing to me is that some mirrors associated high radio galaxies at relatively high z behave indistinguishably (see Figure 4 for the optical image). Figure 5 shows a near-perfect match between 3C256 and NGC1068. (Not shown in that figure is the Type 1 nucleus of NGC4151, crucially also indistinguishable to both of them.) In that former case, the tiny electron scattering cross-section is consequential, because these mirrors are 10 s of kpc in size, and such a mirror needs to have an enormous mass, of order Mo. It’s especially interesting because we argue for 3C256 (Dey et al. 1996 [15]) that that enormous mass of baryons is too cool for hydrostatic support. There is no rotational support either, so one wonders whether all that mass is undergoing some kind of monolithic collapse! This galaxy differs from the other “alignment-effect" radio galaxies in lacking a massive old stellar population.
If I’d been more sophisticated, I’d have discounted electron scattering in both NGC1068 and 3C256.
3. Unification of the Radio Loud AGN by Relativistic Beaming.
How the Spectral Unified Model saved the Beaming Unified Model, and then the two lived happily ever after. Two “proofs."
3.1. Self-calibration, Diffuse Emission, and “Proof" of Unification by Relativistic Beaming
When I was starting out in the 1970s, one of the many attractions of the field of AGN was Superluminal Motion. In low-frequency radio surveys of the sky, most of the extragalactic objects found turned out to be giant kpc double-lobed sources. Their steep radio spectra reflect the optically thin synchrotron emission from the lobes.
But a few were quite different, only showing point sources on the arc-second resolution maps of the day. These tiny but very bright little guys showed flat spectrum (self-absorbed) synchrotron emission, which invited examination with VLBI networks. Typically this revealed a stationary core and a string of dots on one side. Re-observation, say a year later in the rest frame, shockingly revealed that the dots had apparently moved transversely outward by perhaps 10 light years! And often a new dot was seen near the core.
Such behavior is reproducible without actual superluminal space motions in a special geometry: The dots have to be traveling along a line pointing nearly, but not exactly, at the Earth, and doing so at c! The effect has nothing to do with relativity; it’s simply that the light travel time of the dots for the second epoch was almost a year less, so the activity seems to be speeded way up.
That hypothesis seemed extravagant to some, particularly because none of these “blazars" could be interpreted as highly misaligned objects, which would be seen to move much more slowly. Blandford and Rees (1978) [16] explained4 that the misaligned sources would, however, appear much fainter (that is partly special relativity), and in fact were identical to the tiny pc-scale relatively faint cores of the giant doubles. After all, something must be feeding plasma and energy into those powerful lobes. (In the early days, the jets (feeding tubes) were not clearly seen in the images.)
You can see that in that case the superluminals would also have giant lobes, one perhaps projected on the other. When radio astronomers rudely pointed out (e.g. after Blandford spoke at the famous Pittsburgh meeting in 1978) that that was manifestly not the case, the theorists replied: Get some dynamic range! According to special relativity, those jets pointed at us are greatly boosted in flux, neatly accounting for their very high incidence at high flux levels.
Because interferometer maps of the day were severely limited in dynamic range, it was quite possible that rather bright lobes were present on arcsecond scales in association with the pc-scale blazar cores. They could have been lost in the poorly subtracted sidelobes of the greatly boosted compact jets. The boost can be very high because special relativistic aberration directs the radiation into a solid angle of order the inverse square of the bulk gamma factor of 10 or so; plus that factor (actually the similarly-valued Doppler factor) comes in two more times, via photon arrival rate and photon kinematic blueshift.
The low dynamic range was mostly the result of the ever-changing air column densities over, for example, the 27 VLA dishes. This introduced 54 scalar functions of time for the effects on amplitudes and (especially) on the phase delays over each dish. Radio astronomers are by far the champions at mustering the fortitude required to address data systematics with sophisticated software.5
It sounds bad that there are unknown scalar functions required to correct for the effect of the ever-changing atmospheric columns above each VLA dish. However, the total number of measured fringe visibilities (baselines) is of order , not , per integration record. This brings massive redundancy which can be exploited in favorable cases. The self-calibration algorithm was being developed very rapidly around 1980, and it largely eliminated the dynamic range limitation! Several groups began to look for diffuse emission associated with the superluminals, including a major effort by myself and J. Ulvestad. We observed or reprocessed data on all the blazars6 known at this time, generally detecting the expected diffuse emission. With strong arguments we convinced a lot of people of this Beaming Unified Model. An important part of our paper was citing and debunking the various counter-arguments in the air at the time. (That’s the essential step shamefully and consistently skipped by generations of accretion disk peddlers, as you’ll see below!)
As an aside, it was fortunate that this self-calibration algorithm is a highly iterative process. That was fortunate because it greatly prolonged the pleasure of discovering the diffuse emission in each source. You have all sat in the optometrist’s chair while s/he interrogated you with questions such as: “Now which is clearer...image A...? ...or B...?" while slipping in or out, say, a quarter of a diopter of correction.
The first several iterations of the self calibration map of very highly point source dominated objects shows you nothing but that point source. If you do reduce such data, be careful, because this program wants to please you. You start with a point source model and the program tweaks the phases to give it back to you. But if you aren’t careful it will simply erase all the diffuse emission, thinking that is what you want. Truly interferometry is an art, and the optimal operation of these powerful complex nonlinear algorithms differs depending on everything from source structure, to Fourier components sampled, to phase stability over the antennas as a function of coherence length, etc. It’s a wonder it works at all. The only near-certainty is that you need some SNR on every baseline time record or you will get garbage. Yet vast experience speaks to the consistency and fidelity of the results in most cases, as long as a skillful astronomer is driving the car.
I’d started to boast above about my 1985 paper with Ulvestad. I had occasion recently to re-read that paper carefully, and had quite an odd feeling of pride, but also the certain knowledge that 40 more years of practice have not made me a better astronomer.
Aside from general consistency of the detected diffuse emission matching expectations for projected double lobes, we claimed we could prove the idea was true! Our proof convinced at least the present writer. You might say I underwent a religious conversion, and never since doubted its qualitative correctness.
We said our proof has two axioms. First, the fluxes from the superluminal cores are in fact greatly boosted in our direction. That largely follows from special relativity and the linear superluminal VLBI sources, so no one wanted to give up that axiom. The second was that the diffuse emission detected was not highly directional. Most people were fine with that axiom as well. It would be hard to imagine such giant diffuse clouds moving near light speed and often the diffuse emission is two-sided. Optically thin synchrotron emission from a multi-zone source is not intrinsically highly anisotropic. It hardly seems that both diffuse components would be moving so relativistically in the same direction.
In most cases the diffuse emission we detected wasn’t extremely bright because, after all, the blazars were picked up mostly by their core flux. But several had sufficient diffuse flux that those objects would have made it into our low-frequency flux-limited catalogs even without their bright cores.
It would make no sense for all such objects to be pointing very nearly towards Earth. Of order a hundred times more would not be aimed so perfectly.7 So for each object among the several referred to in the previous paragraph, there should be intrinsically similar objects pointed away.
According to our two hypotheses, misdirected equivalents of these blazars with bright diffuse emission would have much weaker radio cores by Axiom 1; but the second Axiom assures us that they’d have the same diffuse flux and would have been included in the catalog anyway.
Since all these misdirected blazar equivalents are in the catalog, let’s look at what they could be. The entire 3C list for example only has around 500 sources, and many are Galactic objects. The other entries are...simplifying slightly...none other than the giant double quasars and radio galaxies! In fact, we said “many or most" of the others would have to be misdirected blazars.
All was not quite well in radio-astronomer-land however, as we shall see!
3.2. The Great Depolarization Asymmetry! Another Proof of beaming, but be careful what you wish for; Trouble with the cosmological principle; Peter Barthel Feels Uncomfortable;
Or, how the spectral Unified Model had to save the beaming Unified model, and the two lived happily ever after. This is a story I told in Antonucci 2012 [6]. It would be pointless to rewrite it.
Peter Barthel worked mostly on VLBI observations of superluminal sources in the 1980s, and he knew well that the beam model explained many properties such as superluminal motions and jet sidedness qualitatively. But he was (according to the title of his rumination for a conference [18]) “Feeling Uncomfortable" because one had to assume that a paradoxically large fraction of these sources in quasar samples have jet axes fortuitously close to the line of sight.8 Barthel later wrote a famous paper (Barthel, 1989 [19]) entitled “Are all quasars beamed?" suggesting that those quasars whose axes lie near the sky plane somehow fall out of quasar samples, and (inspired by the spectropolarimetry) in fact get classified as radio galaxies.
The general idea of beaming to explain superluminal motions and one-sided jets was accepted by most doubters as a result of two key back-to-back discovery papers in Nature, reporting on the so-called Lobe Depolarization Asymmetry. They are Laing (1988) [20] and Garrington et al. (1988) [21]. It was spectacular, inspired work. The wonderful astronomer and human being Peter Scheuer (1987) [22] described it in a section of a (basically unavailable) conference paper called, “Why relativistic beaming is true." (We’d know a lot more about radio sources today if Peter had been granted a reasonable time on Earth.)
Giant double radio quasars are rather similar to giant double radio galaxies, but there are differences. They tend to show one-sided, fairly bright arc-second-scale (>kpc) jets. Radio galaxy jets are hard to see and, when you can detect them, they are more similar in flux on the two sides. Both the Laing (1988) paper and the Garrington et al. (1988) paper studied samples of double-lobed quasars.
Some extremely clever person designed the VLA to work in scaled configurations. That is, the standard radio bands are separated by factors of three in frequency. The 27 antennas are laid out along railroad tracks, and periodically moved outward en-masse by factors of three in distance from the center. So to make images of spectral slopes or depolarization one can use for example the 20 cm band in the largest configuration ( km), and compare the result to mapping at a frequency in the 6 cm band with a 1/3 scale array! Of course with interferometry we just measure a finite sample of Fourier components of the image brightness distribution and only those components inform what you see in the image plane. With this plan the maps at the two frequencies would be based on the same Fourier components. (The clean algorithm tries to guess at what the unmeasured components would have been.)
The following sounds implausible not only because of the powerful result but because of various coincidences too weird to explain. These papers showed that in the 6 cm band observed with the more compact array configuration, in all cases I think, both lobes were shown to be highly polarized.
Sit down for this, though. In all, or perhaps nearly all cases, the 20 cm images showed that only one lobe is highly polarized in each quasar. It was always the “jetted" side, and the nearly inevitable interpretation was that this proved the jetted side is in fact the near side (a commonplace now...). It lies in the foreground of some polarization-angle scrambling medium, while the far side was almost completely depolarized, undoubtedly due to Faraday rotation measure gradients within each synthesized beam (angular resolution element). Aside from the breakthrough information this suggests to me that the diety or dieties possess a very jolly sense of humor to put the effect exactly in the parameter space observed; and in virtually every case that s/he/it/they designed the sources with the VLA in mind, to delight only us on Terra. I can’t prove it but I have heard that the former Astronomer Royal warned us that it would be really funny if nothing funny ever happened. But there is a limit to my credulity.
To recap, and blend in something else that delighted me: There is a very strong tendency for one radio lobe in double-lobed radio quasars to be depolarized at low frequencies (say the VLA A Configuration at 20 cm) by Faraday rotation within the observing beam...but only on the sides of the (single-jet) sources which lack the jet (Laing 1988; Garrington et al. 1988) [20,21]! Most people accepted that the depolarized lobe must be the more distant one, located behind a large-scale depolarizing magneto-ionic medium; thus the polarized lobe is on the near side, so that the jet is also on the near side, just as expected for the beam model!!
Church bells rang. But be careful what you wish for! The effect was way too strong! The first paper of the pair has this disclaimer: “The sources observed here must then be oriented within about of the line of sight...to generate sufficient asymmetry in path length..." to fit the depolarization data!9
Neither these authors nor the referees asked themselves what happened to the quasars oriented close to the sky plane! They were apparently blissfully unaware that we knew from optical spectropolarimetry that many of the high-inclination “quasars" are simply masquerading as FR II radio galaxies, which would have dropped out of samples restricted to quasars, as explained by Barthel 1989 [19]. Barthel had read outside his field, and found our polarization papers. There are many mysteries in one’s field which one simply can’t resolve without reading outside it.
4. The peculiar AGN Reddening law
Using only hard data, special relativity and the Copernican principle, we derived an extinction curve for radio quasars. We claim it’s the most robust determination of the law and mention some consequences, including the equally robust derived anisotropy as a function of wavelength throughout the electromagnetic spectrum. We need also to reassess the broad Hydrogen line spectra, in particular the very large Balmer to Ly ratios. This type of extinction totally dominates that of most radio loud objects, and plays a major role in most quiet ones which, however, often also have more standard reddening from dust outside the nucleus as well.
One can make a robust extinction curve by dividing the SEDs of objects of different extinction, if the comparison is between sources known to be intrinsically identical. That’s the key feature of the curve put forth here in Figure 6 from Gaskell et al. (2004) [23]. You needn’t believe my conclusion but I will specify what axioms you have to give up in that case.
We reported (Gaskell et al. 2004) on a study which was so well-designed, its dramatic result depended logically only on hard data, special relativity, and the Copernican principle. We studied a complete lobe-selected quasar sample. The fluxes from the radio lobes are manifestly at least approximately isotropic. In that situation (aside from small statistical effects), if a giant reorients a member of the sample it will have the same lobe flux and necessarily look like another member of the sample. The power of that idea is shown also by the very strong conclusions reached for High z 3Cs by Marin and Antonucci (2016) [24].
In the 2004 sample there was of course a wide range in core dominance. Quasars with strong radio cores show, to first order, linear superluminal jets. Special Relativity says the fluxes from such cores are highly boosted in our direction. The Copernican principle says there are many other quasars not so specially oriented. They must comprise the sample members with lower core dominance.
Thus to determine the polar diagram or anisotropy or extinction curve of any component, one need only divide the ones with weak cores by the ones with strong cores. The result is an extinction curve that is quite selective in the optical region, and quite flat in the near-UV. Small grains are evidently severely depleted.
Then we tested that curve as follows. Due to the wonderful work of Joann Baker, with advisor Richard Hunstead in a supporting role, we had up to 6 measured emission lines, going from Ly to H for every quasar. We divided those in the same way, according to core dominance to derive an independent line extinction curve.
It was identical in shape and normalization to the continuum curve.
Most reddening curves are only suggestive because there is no assurance the comparison objects are intrinsically identical. Since our papers, authors that cite reddening curves in the literature list ours among the others, all of which are of the latter type. There is no recognition that ours is the robust definitive one. In fact some people perceive that e.g. the SDSS curve supercedes or even disproves ours. Such is the level of scholarship in this field.
Since then our reddening curve has proven its plausibility and its worth.
I’ve come to realize that the AGN torus is almost certainly a winnowing machine. Every grain has a different sublimation radius and physics tells us only the large grains, being better radiators, reach and define the inner edge of the dusty torus. So I don’t consider the dearth of small grains required for our extinction curve to be a stretch; just the opposite.
There is another qualitative point of consistency. A major result from mid-infrared interferometry is that one tends not to resolve the tori in the equatorial direction, which is as expected for a pc-scale dusty gas with Av (Krolik and Begelman 1986, 1988) [25,26]. More often one resolves the Narrow Line Region in the polar direction (e.g. Bock et al. (2000) [27], which didn’t require interferometry for NGC1068). Although this emission is optically thin, it lacks the usual Silicate emission features due to small Silicate grains. That suggests the dust has passed through the torus crucible, losing small grains and perhaps the Si grains generally [28].
It was known to the ancients that the ratios of Ba line strengths to Ly are far above case B, and that only a curve shaped like ours could account for it and still have mostly the physics of Case B. Martin Gaskell et al. (2017) [29] have shown how well this works for the integrated line fluxes. They argue that the wings, which are said to be energetically insignificant, can be explained by a small Case C contribution. This is my optimistic broad-brush description, but there are many details about line profiles and transfer functions which must be considered. What I can defend is this: our extinction curve is manifest in the continuum and line spectra of AGN, and changes both significantly. Correction greatly reduces the anomalously high Balmer to Ly ratios. A piece of the puzzle which has yet to be rigorously incorporated is the energy budget and the infrared dust emission.
5. The Tragi-Comic Story of AGN Accretion Disk Modeling.
It’s been absolutely routine for the past 40 years to assert that accretion disk models can account for the optical/UV continua of AGN. In a recent example in Science magazine, C J Burke et al. (2021) [30] open their article as follows: “Accretion disks are present around growing supermassive black holes (SMBHs) found in active galactic nuclei (AGNs). Standard theory of radiatively-efficient accretion disks can reproduce the broad-band emission from AGNs ..."10
Yet one of those authors distinguished by intellectual honesty, when writing alone, states in a public funding application, “In marked contrast to models of accretion disks around stellar mass black holes, neutron stars, and in cataclysmic variables, existing theoretical models of accretion disks around supermassive black holes do a very poor job of explaining, never mind predicting, the observed properties of luminous active galactic nuclei (AGNs) [31]."
What’s going on here? The prestigious Science paper with the same author says the opposite. It also very strongly implies that with the model tweak presented, the theory applies to AGN. There is no mention of the counterarguments such as the factor of 10 too low surface brightness measured by microlensing (e.g. Dexter and Agol 2011) [4].
The Science paper purports to address just one of the many contradictions, and fails at that, though they do not say so. It attempts to explain the extremely rapid variability, but via an opacity/convection argument that applies only locally in the disk, which doesn’t help at all since the “problem" appears equally throughout the entire continuum supposedly produced by the model, covering several orders of magnitude in frequency. Finally, see their Figure 1, proposed as compelling, but in fact a terrible fit. Such is the level of scholarship in my field. This fancy paper is disingenuous in my opinion.
Perhaps the most fundamental prediction of the standard disk model is that the characteristic temperature is proportional to the one fourth power of L, and the inverse square root of M. We have methods of estimating M and we can also get the approximate BBB luminosity from observation. These scaling relations have been tested implicitly in many papers and explicitly in at least three: Courvoisier and Clavel 1991 [32], Bonning et al. 2007 [33] and Davis et al. 2007 [34]. See also Reimers (1989) [35] No sign of the predicted behavior is seen!
These papers had no noticeable effect on the consensus however!
I note that when the Courvoisier and collaborators debunked the disk model, they followed up with several very nice modeling papers based on generic shock cascades, which is consistent with the variability as well.
Let’s return to the BBB spectral energy distribution.
- Of course we can’t generally observe much past 1 Rydberg, and when we can, the data are affected by intergalactic absorption.
- Wavelength-dependent extinction is common as shown above for radio loud quasars, and this can’t be corrected reliably in individual objects.
- Often the host galaxy contributes and it is difficult to subtract it unambiguously.
All of these problems are avoided by the T-shirt method described below!
Let’s back up to my start in science. When I started out in the 1980s, I realized that quasar continuum spectra carry very little interpretable information. They are just rather generic looking broad convex lumps which one can fit by many functional forms with those properties. Many authors had already noted their generic nature, perhaps starting with Ward et al. (1987) [36].
Following the insights of Lynden-Bell (1969) [37], most workers agreed that to provide the luminosities observed in quasars, and the energies contained in radio lobes, black hole accretion was the only game in town. It was well-said, probably by M. Rees, that accreting supermassive black holes are by far the least amazing idea that fit the facts.
Following the suggestion of Shields (1978) [38], this idea was instantiated in the simplest possible way as quasistatic geometrically thin, optically thick accretion disks. The potential gradient was used to predict the temperature as a function of radius, and thus the SED. Soon as pioneered by M. Malkan (1983) [39], models incorporating these ideas were fit to observations of AGN.
Since the get-go, this paradigm required major cognitive dissonance. The quasistatic assumption is crucial to the models, but that was known to be comically violated by the speed and extremely broadband nature of their flux variations. The discrepancy is by several orders of magnitude, as discussed for example, by Alloin et al. (1985) [1]. Those authors explained that their observations of NGC1566 showed that the H emission line and the optical continuum vary on timescales of days, with a very tight upper limit on any temporal offset between the two time series. That means the ionizing continuum and the optical continuum vary extremely rapidly and closely in phase, utterly inconsistent with any viscous quasistatic flow.
Also in the 1980s, I pointed out that these models necessarily produce significant polarization in the disk plane. Since the radio jets (including the little ones in Seyferts) lie parallel to the polarization, essentially every thin disk model in the mighty river of such models that continues to flow today has as an essential feature: the requirement that the jets emerge from the sides of the disks!!! Such is the level of scholarship in my chosen field.
I discuss these and other horrible and palpable contradictions in Antonucci et al. (1989) [3], and many papers since. Almost no one cares.
Those of you who had the pleasure of knowing the late, great Bill Mathews of UC Santa Cruz will appreciate this story. I was complaining to him that this obviously erroneous model was accepted instantly and nearly universally, and told him about my commentaries and ongoing tests. He obviously agreed, but cut me off soon with the interjection:. “Oh you can’t stop that!"
The main topic of that 1989 paper was a search for the Lyman continuum absorption feature predicted for the standard disk by Kolykhalov and Sunyaev (1984) [40].
Blackbody accretion disks also predict a spectral slope of 1/3 over a wide frequency range with slightly more realistic physics. The spectral index remains positive. Since almost all quasars actually have negative spectral indices, Malkan fit the models not to the observed spectra but to the residual spectra after subtracting a notional steep power law extrapolated from the near infrared. But universal minima at and reverberation mapping show that the near-IR is dust reradiation of the primary continuum, which must drop like a stone shortward of . The community was convinced of this largely by a famous paper by Barvainis (1987) [41]; see also Clavel et al. 1989 [42]. Thus the extrapolation under the optical was...not legitimate.
Malkan also got about the same temperature for each object, evidently because he was interpreting an atomic feature as the exponential cutoff expected at the innermost stable circular orbit.
The next attempt I studied closely was by A Laor, and I found it very instructive in multiple ways. He fit a larger sample, crucially finding it advantageous to assume maximal spin. He concluded that the majority fit the models in the sense. It was an odd criterion because I’m sure, having examined a solar spectrum with great intrinsic SNR and high resolution, that I could use the method to rule out the G star model.
A cursory look at the analysis confirmed that the quasars that fit the criteria were basically the ones with low SNR. Still, I wondered how the luminous objects, necessarily with high mass and thus low temperature, managed to pass muster. As I read, I predicted silently and quickly confirmed that they were strongly biased at very high inclination to the line of sight. That combination of maximal spin and near inclination results in beaming highly blueshifted light towards the observer! Thus the quasistatic disk model was saved at the wee cost of the Copernican principle. It was slightly worse than that in the sense that if aligned with the matter accreting through the AGN torus, they would alas have been observed as Type 2 objects and not quasars.
Thus I saw that the lack of any sign of the expected relation could easily be subsumed into the many nuisance parameters like spin, inclination, host subtraction, reddening etc, not to mention the ever-ready designer Comptonization.
It now gets a lot worse. Laor and colleagues Netzer and Piran were apparently aware that the polarization of quasars was inconsistent with the high disk values based on the expected scattering dominated atmospheres. But only that the observed polarization was too low, and not that it was in the wrong direction!
They adjusted the atmospheric densities such that the optically emitting annuli would be absorption dominated, and produce low polarization, which would then rise strongly into the UV, which would be dominated by hotter annuli.
Malkan had noticed the sadly low observed % polarization too, and argued that the unified model censorship of edge-on quasars helped a lot by removing those which would have had the highest % polarization; then the magnitude distribution would supposedly be as predicted by the disk model.
None of these authors seemed to be aware that as I’d pointed out in papers in the 1980s, the polarization was in the wrong sense for a disk atmosphere, and they were thus wedded to the prediction that the jets emerge from the sides of the disks. That remains true of models being published today, though theorists don’t mention it. Some are aware of it because I bring it to their attention, but do not deem it worthy of mention in their papers. A random example is Mitchell et al. 2022 [43]. These particular authors comically crow that they’ve discovered some wee problem with their quasistatic disk theory, but hide the fact that much more powerful arguments have been published and spoken about at meetings for 40 years, which falsify a huge superset of models, including theirs. That style isn’t honest.
I knew Joe Miller understood the situation with regard to the erroneous sign of polarization of disk models, so I said to him (with tongue in cheek) “We know the polarization has the wrong sign, but all these authors have shown that it has the correct magnitude."
I knew his sardonic facial expression by that time. He just shook his head and said, “That doesn’t help when you’re balancing your check book."
Digression: I noted in print (Antonucci 1988; Antonucci et al. 1989 [2,3]) that the polarization direction in most quasars and other Type 1 objects, being parallel rather than perpendicular to the axis measured in the radio, negates the disk model. Next, Laor et al. (1990) [44], used the parallel polarizations as though they were perpendicular, an egregious error negating their whole study.
Next, I pointed out their error in 8 papers starting with Antonucci 1993 [45] and including Kishimoto et al. (2004) [46].
However, I read this recently in Capetti, Laor, Baldi, Robinson, and Marconi (2021) [47] “In contrast with our conclusion that the continuum and BLR polarization are produced by a single scattering medium, Kishimoto et al.. (2004) suggest that the optical polarization in quasars is produced by electron scattering within the accretion disk atmosphere...However, this interpretation is inconsistent with the PA of a disk atmosphere scattering, which is predicted to be perpendicular to the radio axis, rather than parallel, as observed."
They literally reversed history, stated that we’d made the error.
That same paper misrepresents the work I described in two equally epic ways.
They added two additional arguments, attributed them to our paper, and refuted them as well! One stated a completely fallacious reason for our attribution of the polarization to electron scattering, and another did the same for our identification of the Ba edge feature. These arguments were made up out of whole cloth.
When we expressed our dismay and asked for a correction they simply said no. So they win. I suppose any interested reader wouldn’t bother with our “true central engine" papers, after reading all that, and would perhaps share a chuckle with those worthies, take my group down a peg in their estimation, and miss our best ever result. Or so goes my feverish mind.
6. The Naked Central Engine Spectrum of Quasars.
The only 5 spectra you’ve ever seen of the quasar central-engine.
Polarimetry has allowed us to objectively remove all atomic and dust emission to reveal the true central engine spectra from to in the rest frame. It attracted virtually non-interest.
This is probably the best thing I’ve done, and I say that with the disclaimer that actually my then-postdoc Makoto Kishimoto did virtually everything. Thus this is not a boast.
Considering the fiasco of first principles theory, I thought a more phenomenological approach was in order both for observations and theory.
I thought a good starting point was to check the assumption of optically thick thermal emission. We know stars are optically thick, with higher temperatures inside, because wavelength of high opacity are seen in absorption. For quasars in which mildly relativistic motions and gravitational redshifts are expected, line features would be smeared out. Therefore we went after the Lyman continuum absorption feature, which was indeed predicted to be deeply in absorption (Kolykhalov and Sunyaev 1984) [40]. Theirs wasn’t a definitive calculation but a combination of results from the available stellar atmospheres with the lowest surface gravity.
Alas, quasar show no features of any kind at all at that location! We designed a powerful series of observations to maximize sensitivity to highly broadened edges using 8" slit widths for accurate photometry. We also got high resolution spectra of the edge positions to be sure to distinguish smoothed atmospheric edges from associated Lyman Limit Systems, and also of the Lyman region because a true atmospheric edge would not produce a strong sharp Lyman absorption line. Later attempts by others failed to take these precautions and, unbeknownst to those authors, produced only false positives.
It’s possible that Lyman edges, arising deep in the potential well, are inconspicuous because of heavy scattering and the disks are famously unstable in the inner annuli where they arise. While we designed our observations to detect even quite broad features that could decrease the contrast excessively, at least in principle. Thus we decided to check the behavior at the Ba edge position, which arises from much more distant annuli, alleviating all these concerns.
My philosophy throughout decades of testing the standard and non-standard disk models has been to give the model the benefit of every doubt, bacause it seems so attractive and natural. That would seem impossible to check for Ba continuum absorption to most people because at that very wavelength, one observes enormous Ba continuum emission from the broad line region. But perhaps the magic of polarization could save the day.
Digression into the lack of Lyman edge features in quasars.
It’d be worthwhile even today to read the discussion from our 1989 paper on the Lyman Limit region, because other mysteries are discussed, too. For example, every quasar shows enormous Ba continuum from the BLR. An epic number of free electrons combine to the orbital.
However, no electrons in any object detectably combine directly to !!! That jump has a much higher capture cross-section. What do you think of that? Optical depth effects can weaken the Lyman emission feature, but extensive experimentation fails to reveal any modeled cases where the continua are as perfectly smooth across 912 Å as any quasars.13
It gets worse. Photon counting arguments lead to a covering factor for recombination-line producing BLR clouds of at least 30%, if the Ly line or the Balmer lines have strong contributions from that process. (The latter are much stronger relative to Ly than for Case B recombinations, so some other processes probably occur, and non-standard reddening also plays a major role: Gaskell et al. 2004; Gaskell et al. 2017 [23,29].) Nevertheless a substantial covering factor in clouds opaque at the Lyman edge is required. If such clouds were larger than the 1 Ryd-emitting continuum region at least a large minority of quasars should show spectral cutoffs there. If instead the clouds comprise a fine mist composite spectra should show a robust partial absorption at 912 Å. Yet of the countless thousands of edge locations examined, I am unaware of a single intrinsic Lyman continuum absorption edge which can be identified with a BLR cloud. What do you think of that?
I can only assume that those objects in which our sight line passes through recombination-line producing clouds...drop out of the sample and aren’t called Type 1 AGN! A moment’s reflection identifies the only candidate for their observed properties: they must be classified as Type 2. That is, every such sight line must also pass through the torus. Thus as seen from the nucleus, the solid angle covered by recombination clouds must be a subset of that covered by the torus. Various colleagues have convinced me that the outer boundary of the recombination BLR is continuous with the inner boundary of the torus, largely from the reverberation transfer functions. But ionizing photons incident on the torus would produce recombination lines. I can only conclude that these BLR clouds are simply the name we give to the part of the torus which extends inside the sublimation radius. This is all discussed in Antonucci et al. 1989 [3], with some further considerations in Maiolino et al. 2001 [48].
We now return to the test of the behavior of the quasar central engine continuum at the Balmer edge position. Quasars generally tend to have a slight polarization which is parallel to the radio symmetry axis which is wavelength-independent (Antonucci 1988; Schmidt and Smith 2000; Kishimoto et al. 2003, 2004, 2008 [2,46,49,50,51]). The broad line polarizations can be similar, or somewhat different with structure inside the profiles. We sought and found 5 examples in which no polarization at all was detected in the lines. The slight 1% polarization in the continuum is exactly wavelength-independent
to the attainable accuracy. We propose and then show that this slight polarization is due to scattering.
Then there are two powerful arguments that the scattering is by free electrons rather than dust grains.
The first is the precise wavelength-independence of % polarization in the continuum, so that the
continuum polarized flux is identical in shape to the total flux. The second is that the scattering takes
place interior to the broad line region, since the broad lines are unpolarized. That places it well inside
the sublimation radius, so by definition, in a dust-free region.
Again we sought and found these five precious quasars, and by design their redshift put the desired Ba limit wavelength at the most convenient location in the observed frame; and which happened to have the slight polarization in the continuum only.
The polarized flux spectra are nothing but a noisier version of the total flux, but with the emission lines and bound-free continua magically removed!! See Kishimoto et al. (2003, 2004) [46,50].
Thus we produced the first ever spectra of the quasar central engines, isolated from all contaminating atomic emission! Virtually no one showed interest in these previous and unprecedented and unique spectra! We found that in all five cases the central engine spectra show the Balmer continuum in absorption. That is, they somewhat resemble the spectra of A stars! This is an extremely important result and proves that at least some of the central engine optical continuum arises in optically thick material with a normal temperature (or source function) gradient. That is, hotter inside!
Later we performed the same trick to find out what the central engine spectrum does in the near-IR, heretofore completely inaccessible underneath the dust emission which is ubiquitous longward of in the rest frame. Again, all five quasars behave the same way: A slope change occurs so that, whereas the spectral index of a fit to is almost always negative in the optical/UV, in the near IR it breaks to .
These are arguably the only known spectral features in the central engine spectrum and constitute a major advance, but it attracted virtually no community interest. Together with all the other constraints (such as microlensing surface) it tells us a lot about the emitter, that at least part of the light comes from optically thick gas (with heat dissipation at large optical depth) and effectively only partial covering (with dark regions in between the bright regions).
This is about all that I know about the quasar optical/UV continuum today. The nearly generic shape of the Big Blue Bump; the two localized features just described, the Ba Continuum absorption and the Near-IR turnover; and the grossly sub-blackbody surface brightness from microlensing. There is also sometimes a slope change near 1000 Å as well, though that is probably due to absorption by wind.
A way forward?
There is however a clue from a generic feature of the AGN SEDs. We recognized the emission mechanism for the infrared light in part by the fact that it has a feature (really two!) which is fixed in wavelength. Virtually every total-flux spectrum has a conspicuous minimum when plotted in energy () vs. log frequency at . Thus the IR emission cuts off sharply of . This is just what one would expect for dust emission, because the most abundant dust species sublimate at around 1500 K. (Similarly, though not quite so precisely, the dust bumps terminate in the sub-mm region.) That’s also quite understandable because dust anywhere in the host galaxy is heated to a few 10s of degrees.
What is the analogy for the Big Blue Bump? Until the polarization work described above, the low-frequency turnover was an open question because the BBB couldn’t be traced past due to the contaminating dust emission. However as explained above, we now know that the optical slope, approximately or so, breaks14 to +0.35 in the near-IR. Thus the BBB becomes energetically insignificant past that region (the slope being +1.35).
So it’s fair to say that the BBB begins around the same location that the dust emission ends. (The very narrow range of wavelength for the minimum is also suggestive of that, since otherwise the drop in the dust spectrum might not define it quite so well.)
Where does the BBB end at high frequencies? The answer to that is very remarkable as well because it is closely consistent from object to object. One generally observes, from the X-ray point of view, a Soft X-ray Excess: that is, the flux below keV in energy is usually well above the extrapolation from higher energy. If fit with a blackbody, whether or not physically appropriate, this excess gives a temperature of K, with very little dispersion.
Thus the BBB extends primarily from ( eV*) to a break at say 300 eV. Such behavior strongly suggests the controlling element is atomic physics rather than global conditions. Why this range is generic is not known at present. Of course efforts have been made to use this valuable clue, none totally successful so far.
Rapid broadband variability is a key property of AGN and it’s wise to make that part of the model rather than making the false and manifestly disastrous quasistatic assumption! To support the role of shocks, I note that Tidal Disruption Events are precious examples of supermassive black hole accretion, and shocks are very likely essential there. Note these two key references, simulating the prompt emission of TDEs: Huang et al. (2023) [53] and Ryu et al. (submitted, 2023) [54]. See Courvoisier and Türler (2005) [55] for a more qualitative description of how shock cascades might account for all the accretion radiation.
7. Disproof of the accretion disk and related models, suitable for illustration on a T-shirt. How to beat a dead horse.
I’ve written many papers over the decades pointing out robust falsifications of the disk model, and in this enterprise I’ve been largely alone and largely ignored.15 I’m sure this won’t change with this T-shirt argument, which I’ve also given before. Yet I claim it can disprove any model involving optically thick thermal emission from a fixed area, a huge superset of the standard disk models. This will be presented here in qualitative form in the hope that a more industrious person carries it out. Nevertheless if you are well acquainted with the data, you too may find it striking.
My hot dust lag argument is extremely valuable because it avoids all the limitations of direct observation of the BBB, enumerated in Sec. Section 5! True, it doesn’t tell you the shape of the BBB. But it tells you something incredibly valuable, it covers the entire BBB and it is immune to reddening and host galaxy contamination! It tells you that from the point of view of the innermost surviving dust grains the shape is extremely generic and thus independent of M and L and anything else! The standard disk model, and any optically thick thermal model in which the radiating area is proportional to , would not have that property!
Many excellent papers have presented reverberation distances between the BBB source and the hottest dust emission. The distances follow the expected just as one would expect from radiative equilibrium and sublimation. But the dispersion in the relation is interestingly low. The relation is so tight that this correlation provides an excellent standard candle for cosmology! See the VEILS project simulation in Hönig et al. (2017) [56].
In Koshida et al. (2014) [57], which covers luminosity range of around a factor of 300 in (their Fig. 10), they wrote a dispersion in hot dust lags in K band of 0.13 in the log. They assess the measurement uncertainty at 0.11, and note that there are several other sources of dispersion which must be present. Thus no intrinsic dispersion is detected, and they set a very generous upper limit at 0.10. This is indeed conservative because subtracting 0.11 in quadrature leaves 0.07. That’s still not the dispersion in the bolometric correction from to because that remaining error budget must also accommodate those introduced from V band variability, anisotropy of the BBB emission, extinction, host correction, geometry and inclination of the torus, etc. In the disk model, the anisotropy alone would easily contribute that much I think, leaving none (or less than none) for the effects of T.
The next paper in the series, Minezaki et al. (2019) [58] extends the luminosity range to four powers of ten (!) without a noticeable increase in dispersion, but no value is quoted there. Their Fig. 5 is suitable for a T-shirt. But they also show that using mid-IR or X-ray instead of V band (less susceptible to anisotropy, reddening, host subtraction, etc.) tightens the noose!
That’s very remarkable and has two implications. First, the innermost, hottest dust has extremely similar physical properties from object to object. The sublimation temperature is very sensitive to both composition of the grains and their sizes (and thus radiative efficiency). And the exact cutoff in the spectrum depends sensitively on grain size in another way: aside from the effect on T, small grains are not only hotter in a given radiation field, they also deviate from blackbody emission at given T as well.
So why does the emission radius follow so perfectly? I think it’s easy to understand why the grain properties are very generic. Far from the inner edge of the torus, there is a great variety of grain size and composition, and each grain has its own Rsub. But the torus is a winnowing machine: as the grains work their way inward, only those with the largest Rsub survive. The inner region must be made of the largest, most refractory grains, and these may well be the same in all objects. The closest grains are the toughest and they are just those large enough to emit with near blackbody efficiency.
I think this very likely explains the special AGN extinction curve deduced from the exceptionally well-designed study of Gaskell et al. (2004) [23]; that study compared the spectra of radio quasars from complete samples of isotropically (radio lobe) selected objects, as a function of core dominance. Arguably, given the VLBI properties, it matches objects subject only to the validity of special relativity and the Copernican principle. In fact, very remarkably, it’s shown in that paper that the spectral shape differences are truly due to reddening because one can make curves based on comparing 6 emission lines from Ly to Ha, which match the curves from the continua in both shape and normalization!
Now the fun really begins. None of the reverberation lag papers actually plots lag vs. BBB luminosity! Instead, for the latter, a convenient proxy is used: the (rest) V magnitude! This is not reasonable in principle and the tiny dispersion in the relation must mean that the bolometric correction from to must itself have a very small dispersion!
The V band indicates the flux at the very bottom of the BBB, very far from the peak in . If the BBB arises as optically thick thermal radiation from a fixed area, then the characteristic temperature depends sensitively on the black hole mass and Eddington ratio of luminosity. That is, . The bolometric correction from V to BBB then depends very sensitively on the characteristic temperature.
Thus for models of the type described, a very small dispersion would require an unrealistically small range in at any given . I haven’t proven quantitatively here that this leads to a contradiction, but instead leave that as an exercise.
8. Cygnus A Keeps on Giving — recent results on our glorious prototype
We are so fortunate to have such a prize as Cygnus A! Without checking the folklore again, I’ll tell you it’s very likely at least roughly true that :
• Despite the volume element and strong cosmological evolution, you’d need to go to a redshift of 1 to find another of it’s radio luminosity. The redshift of Cygnus is only 0.056. It’s claimed that in only one of 10,000 realizations of our universe would we be so lucky, and we think it’s largely a result of its rich environment (Barthel and Arnaud) [59].
• A slightly inebriated expert assured me that this legend is true: if Cygnus is above the horizon, you can map it in a VLA sidelobe, independent of the pointing. Even before the upgrade!
In this little section I’ll recount some results from our group over the past several years. First, our leader at the late Sofia airborne observatory, Enrique Lopez-Rodriguez, has helped build the only sensitive far-IR polarimeter this planet has ever deployed, then heroically and repeatedly soared into the stratosphere to make various discoveries, not least that the far-IR emission of Cygnus is 10% polarized. This is an unprecedented result in the field, and the interpretation came as a surprise to many.
Certainly one’s first thought might be synchrotron emission, and the IR SED had been modeled as such in multiple papers. I wasn’t convinced by the models because they were physically possible but not physically plausible. They required extreme and fortuitous homogeneity and global parameters to fit the very sharp sub-mm rise and the decline from the mid-IR to the near-IR. With the far-IR polarization measurement, it became clear that this is really emission from dust grains aligned by a globally coherent magnetic field. In the submillimeter region, the polarized flux of Cygnus A rises extremely steeply with frequency like the total sub-mm flux, the signature of dust emission. (The near-IR polarization is similar in magnitude but somewhat dissimilar in position angle, in fact falling exactly perpendicular to the radio jet.)
It seems very likely, especially considering analogous behavior in other objects, that the near-IR polarization is none other than the result of polar scattering of the unified model. That’s true of the optical too, where Ogle et al. [60] have revealed enormously broad lines in polarized flux. The optical scattering is only seen on scales of several arcsec.
While that large-scale scattering component isn’t seen easily in the near-IR, the polar (perpendicular) scattering is detectable with very high surface brightness on sub-arcsec scales at because this light penetrates a big kpc-scale dust lane, very similar to the situation in Centaurus A. They are discussed together with a third very similar case, 3C223.1, in Antonucci and Barvainis 1990 [61].
We (Enrique) have gone on to observe a heterogeneous handful of AGN, both radio-quiet and radio-loud, finding so far a perfect correspondence between those types and the detection and magnitude of polarization of the far dust emission polarization [62]. This remarkable result must be explored further to characterize it more fully and accumulate definitive statistics and, despite the loss of Sofia, prospects for that are bright. The reason is that mighty ALMA can cover enough of the crucial sub-mm range in many objects to look for the extremely rapid rise in polarized flux that proves the origin as dust emission.
This powerful discovery, if verified fully, is arguably our major clue to the reason for the radio-loud vs quiet classes. Our theoretical colleagues were sufficiently motivated to explore interpretations in our second paper. In particular it’s logically possible that the globally magnetized accretion flow on pc scales ultimately manifests in a relativistic or sometimes slow Seyfert-like jet; or that the opposite is true, and the jet instead magnetizes the dusty gas. Much exciting work to do for all here.
Next, we are close to settling the nature of the gas in the cm X-ray column, a typical value for Type 2 objects. Of course the X-rays really measure the heavy elements primarily, and much of that column resides in the dust grains themselves. But is the accompanying gas in the atomic or molecular phase?
Struve and Conway [63] have published beautiful and fascinating results from H I 21 cm observations with VLBI. Even the innermost counter-jet continuum component just 45 milliarcsec or pc from the core shows very strong H I absorption, with an equivalent width sufficient to account for such a column density if one assumed a reasonable spin temperature of K. Yet the absorption in front of the radio core is nearly two orders of magnitude smaller, and unable to account for the X-ray columns unless T-spin is K, which would be impossible to explain in our view. Yet that’s what the X-ray column measures for the core itself!
For many reasons, most importantly that such high columns are only observed in Type 2 AGN, it’s thought that the high X-ray columns are associated with the torus-like obscurer of the U M rather than say atomic gas inside the sublimation radius. Thus, absent sufficient atomic hydrogen column, we turn to the possibility of a molecular torus as the default possiblity. This must involve some exotic conditions however, because low-J CO rotational absorption lines have long been sought without success against the core in the millimeter region. The most recent limits come from ALMA observations at the position of the to 2 transition at rest-frame frequency of 230 GHz (Carilli et al. 2022 [64], and pc). No absorption is seen, and if the excitation of the low J states were thermal it’d be very conspicuous.
It’s been suggested based on much poorer limits that the low J states are depopulated as we are driven to extremely high rotation temperatures by the radiation of the radio core itself (Maloney et al. 1994) [65]. Great compactness is required, with almost the entire column within a few pc of the very compact 1.5 mm core. For comparison, this sublimation radius for blackbody grains which evaporate at 1500 K is estimated at pc. Once again we think that ALMA can test this with a search for absorption in a CO line near the atmospheric opacity cutoff. At that frequency the solid-angle averaged brightness temperature is much reduced relative to that at 230 GHz.
Finally Carilli et al. [64] report a beautiful-looking candidate torus in radio continuum emission. The proposed radiation mechanism of Bremsstrahlumg doesn’t seem tenable (Bagul et al. 2023), the nature of the detected torus is still in need of elucidation.
9. Summary
That was an arduous trek but we’ll take the bus back.
Spectroscopic Unification
The polarization properties of narrow line (Type 2) radio galaxies. Torus and mirror.
This Spectroscopic Unification seems to apply to most or all Seyfert galaxies and quasars (including radio loud ones). But at low to medium radio luminosity, there are plenty of radio galaxies which lack signs of copious realtime accretion, namely the Big Blue Bump continuum and the Broad Emission Lines.
Beaming Unification by Orientation in the Radio Loud Objects
Many properties of radio loud AGN, especially those of the Blazar class, are very nicely explained with an orientation-based Unified Model and bulk relativitic motion. Those with the directly visible or hidden BBB/BLR comprise one group, and those without comprise another. The many nuances are described systematically in e.g. Antonucci 2012.
The Peculiar AGN Reddening Law
Direct arguments are given that lobe-dominant radio quasars and radio galaxies must be intrinsically the same as matched blazars, only differing in orientation. We select a complete sample based on (∼isotropic) lobe flux, and then we can unify the sample objects of the various subtypes with high confidence.
Dividing the composites as described produces an anisotropy due to extinction which is highly chromatic in the visible, but quite flat in the UV. This indicates a dearth of small grains, as expected qualitatively from the winnowing action of the torus.
This reddening curve is then confirmed in a spectacular and independent way: we showed that using the six emission lines from Ly to H, we make a new curve. It is identical in shape and normalization to the continuum curve!
None of this precludes additional reddening by more normal dust in the host, and we find much evidence for it, especially in radio-quiet Seyfert galaxies, in keeping with their spiral hosts.
The Accretion Disk Model for the Big Blue Bump: Epic Magical Thinking.
The standard thin accretion disk model was proposed I’m the late 1970s and 80s to account for the Big Blue Bump continuum component, which dominates the luminosity of AGN.
Cognitive dissonance was part of this model since it was proposed. For example, the quasistatic assumption is comically at variance with observation. Similarly a scattering atmosphere of a thin disk with internal dissipation produces a polarization perpendicular to the radio jet, opposite to what we see. It was soon shown that actual data show no sign whatever of the basic expectation that the maximum disk temperature is proportional to the one fourth power of the luminosity and the negative square root of the mass. Other powerful arguments followed, but the non-viable disk model bandwagon meant nobody noticed!
The spectrum of the central engine, with atomic and dust emission removed!
Se Raser la Barbe!
There is little correlation between my own assessment of my papers and the attention they receive. This is the most remarkable example: the BBB is energetically dominant, but over most of its wavelength range from the near-IR to the EUV, it’s contaminated by reprocessed emission. We removed it over much of that range, and the message can be extended. But the work received virtually no notice. M. Kishimoto deserves the lion’s share of the credit.
Luckily the polarization in most quasars is wavelength-independent in the continuum, and we identified some cases in which the reprocessing features are unpolarized. Therefore the polarized flux looks just like a noisy version of the total flux, but without the contamination which heretofore prevented us from observing the bare central engine spectrum. The results were rather amazing and our five clear examples all behaved qualitatively the same way! They all show a broad absorption feature starting at exactly the right location for the Balmer jump. That strongly implies a contribution from an optically thick emitter with a source function gradient like those in stars, indicating dissipation at large optical depth.
We then looked in the near-IR, to try to find out what the BBB is doing under the ubiquitous hot dust emission. In all five cases, the polarized flux turns downward to reach by in the rest frame. The only non-contrived explanation is that the dust is unpolarized as perhaps expected for Type 1 (at low inclination), and the BBB turns over at those wavelengths. That is another intrinsic spectral feature of the BBB (Kishimoto et al. 2008).
Recall though that microlensing observations indicate a surface brightness an order of magnitude lower than required. If these observations, at much shorter rest wavelengths than the Balmer jump, are also from optically thick thermal radiation, it must be that the effective areal covering factor is much less than one.
Negating a mighty river of theory with a figure suitable for a T shirt.
The relationship between hot dust lags relative to BBB fluctuations has been demonstrated to have very small dispersion. It follows the expected relationship of lag time being proportional to the square root of luminosity, but more important here is the remarkably small dispersion.
However— can’t be measured—so the observers used as a proxy! It worked extremely well. But that’s completely unexpected for a huge superset of the standard disk models. It precludes any scenario in which the characteristic temperature is set by . In fact the “temperature" can’t depend much on anything at all, in most cases!
I consider that to be a profound result, but I leave the execution as an exercise for the reader.
The Magnificent Radio Galaxy Cygnus A—recent developments.
We’ve learned many new things about Cygnus A beyond its glorious and extremely energy-rich radio lobes.
This prototype source fulfills all aspect of unified models, with high perpendicular polarization of scattered light; a Type 1 spectrum in polarized flux; beautiful bicones of polarized UV flux from HST; highly polarized dust emission indicating a global magnetic field.
Other recent gossip is reported.
Funding
This research received no external funding.
Acknowledgments
Many astronomers provided comments on earlier versions of this paper. These people suffered the most: R. Barvainis, P. Ogle, E. Lopez-Rodriguez, A. Bagul, M. Gaskell. A. Bagul also kindly prepared most of the figures. D.L. Ceder made it much more intelligible.
Abbreviations
The following abbreviations are used in this manuscript:
| AGN | active galactic nucleus |
| UV | ultraviolet |
| BBB | Big Blue Bump |
| a.u. | astronomical unit(s) |
| CCD | Charge coupled device |
| HST | Hubble Space Telescope |
References
- Alloin, D.; Pelat, D.; Phillips, M.; Whittle, M. Recent spectral variations in the active nucleus of NGC 1566. Astrophysical Journal 1985, 288, 205–220. [Google Scholar] [CrossRef]
- Antonucci, R. Polarization of Active Galactic Nuclei and Quasars. In Proceedings of the Third George Mason Astrophysics Workshop, Fairfax, Virginia, USA, 14–16 October 1986; 1988; p. 26, ISBN 0-521-34246-5. [Google Scholar]
- Antonucci, R. R. J.; Kinney, A. L.; Ford, H. C. The Lyman Edge Test of the Quasar Emission Mechanism. Astrophysical Journal 1989, 342, 64. [Google Scholar] [CrossRef]
- Dexter, J.; Agol, E. Quasar Accretion Disks are Strongly Inhomogeneous. The Astrophysical Journal Letters 2011, 727, L24. [Google Scholar] [CrossRef]
- Stockman, H. S.; Angel, J. R. P.; Miley, G. K. Alignment of the optical polarization with the radio structure of QSOs. Astrophysical Journal 1979, 227, L55–L58. [Google Scholar] [CrossRef]
- Antonucci, R. A panchromatic review of thermal and nonthermal active galactic nuclei. Astronomical & Astrophysical Transactions 2012, 27, 557–602. [Google Scholar]
- Antonucci, R. R. J. Optical polarization position angle versus radio source axis in radio galaxies. Nature 1982, 299, 605–606. [Google Scholar] [CrossRef]
- McLean, I. S.; Aspin, C.; Heathcote, S. R.; McCaughrean, M. J. Is the polarization of NGC1068 evidence for a non-thermal source? Nature 1983, 304, 609–611. [Google Scholar] [CrossRef]
- Miller, J. S.; Antonucci, R. R. J. Evidence for a highly polarized continuum in the nucleus of NGC 1068. Astrophysical Journal 1983, 271, L7–L11. [Google Scholar] [CrossRef]
- Antonucci, R. R. J.; Miller, J. S. Spectropolarimetry and the nature of NGC 1068. Astrophysical Journal 1985, 297, 621–632. [Google Scholar] [CrossRef]
- Krolik, J.H.; Kallman, T.R.; Fe, K. Features as Probes of the Nuclear Reflection Region in Seyfert Galaxies. Astrophysical Journal 1987, 320, L5. [Google Scholar] [CrossRef]
- Miller, J. S.; Goodrich, R. W.; Mathews, William G. Multidirectional Views of the Active Nucleus of NGC 1068. Astrophysical Journal 1991, 378, 47. [Google Scholar] [CrossRef]
- Band, D.L.; Klein, R.I.; Castor, J.I.; Nash, J.K. Iron K-Shell Emission from NGC 1068. Astrophysical Journal 1990, 362, 90. [Google Scholar] [CrossRef]
- Ogle, P. M.; Brookings, T.; Canizares, C. R.; Lee, J. C.; Marshall, H. L. Testing the Seyfert unification theory: Chandra HETGS observations of NGC 1068. Astronomy and Astrophysics 2003, 402, 849–864. [Google Scholar] [CrossRef]
- Dey, Arjun; Cimatti, Andrea; van Breugel, Wil; Antonucci, Robert; Spinrad, Hyron; On the Origin of the Ultraviolet Continuum Emission from the High-Redshift Radio Galaxy 3C 256. Astrophysical Journal 1996, 465, 157. [CrossRef]
- Blandford, R. D.; Rees, M. J. Some comments on radiation mechanisms in Lacertids. Proceedings of Pittsburgh Conference on BL Lac Objects, Pittsburgh, PA, USA, 24–26 April 1978; 1978; pp. 328–341. [Google Scholar]
- Blandford, R.D.; Königl, A. Relativistic jets as compact radio sources. Astrophysical Journal 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Barthel, P.D. Feeling Uncomfortable. In Proceedings of the Workshop on Superluminal radio sources, Pasadena, CA, USA, 28–30 October 1986; Cambridge University Press: Cambridge, UK, 1987; pp. 148–154. [Google Scholar]
- Barthel, Peter D. Is Every Quasar Beamed? Astrophysical Journal 1989, 336, 606. [Google Scholar] [CrossRef]
- Laing, R. A. The sidedness of jets and depolarization in powerful extragalactic radio sources. Nature 1988, 331, 149–151. [Google Scholar] [CrossRef]
- Garrington, S. T.; Leahy, J. P.; Conway, R. G.; Laing, R. A. A systematic asymmetry in the polarization properties of double radio sources with one jet. Nature 1988, 331, 147–149. [Google Scholar] [CrossRef]
- Scheuer, P.A.G. Tests of beaming models. In Proceedings of the Workshop on Superluminal radio sources, Pasadena, CA, USA, 28–30 October 1986; Cambridge University Press: Cambridge, UK, 1987; pp. 104–113. [Google Scholar]
- Gaskell, C. Martin; Goosmann, René W.; Antonucci, R. J.; Whysong, David H.; The Nuclear Reddening Curve for Active Galactic Nuclei and the Shape of the Infrared to X-Ray Spectral Energy Distribution. The Astrophysical Journal 2004, 616, 147–156. [CrossRef]
- Marin, Frédéric; Antonucci, Robert; A Robust Derivation of the Tight Relationship of Radio Core Dominance to Inclination Angle in High Redshift 3CRR Sources. The Astrophysical Journal 2016, 830, 82. [CrossRef]
- Krolik, J. H.; Begelman, M. C. An X-ray heated wind in NGC 1068. Astrophysical Journal, Part 2 — Letters to the Editor 1986, 308, L55–L58. [Google Scholar] [CrossRef]
- Krolik, Julian H. Begelman, Mitchell C.; Molecular Tori in Seyfert Galaxies: Feeding the Monster and Hiding It. Astrophysical Journal 1988, 329, 702. [Google Scholar] [CrossRef]
- Bock, J. J. Neugebauer, G.; Matthews, K.; Soifer, B. T.; Becklin, E. E.; Ressler, M.; Marsh, K.; Werner, M. W.; Egami, E.; Blandford, R.; High Spatial Resolution Imaging of NGC 1068 in the Mid-Infrared. The Astronomical Journal 2000, 120, 2904–2919. [Google Scholar] [CrossRef]
- Ramos Almeida, Cristina; Ricci, Claudio; Nuclear obscuration in active galactic nuclei. Nature Astronomy 2017, 1, 679–689. [CrossRef]
- Gaskell, C. Martin; The case for cases B and C: intrinsic hydrogen line ratios of the broad-line region of active galactic nuclei, reddenings, and accretion disc sizes. Monthly Notices of the Royal Astronomical Society 2017, 467, 226–238. [Google Scholar]
- Burke, Colin J.; Shen, Yue; Blaes, Omer; Gammie, Charles F.; Horne, Keith; Jiang, Yan-Fei; Liu, Xin; McHardy, Ian M.; Morgan, Christopher W.; Scaringi, Simone; Yang, Qian; A characteristic optical variability time scale in astrophysical accretion disks. Science 2021, 373, 789–792.
- Blaes, O. Accretion Disks around Supermassive Black Holes with Realistic Opacity. NASA proposal id 21-ATP21-96. 2021. [Google Scholar]
- Courvoisier, T. J.-L.; Clavel, J. Observational constraints on disc models for quasars and Seyfert galaxies. Astronomy and Astrophysics 1991, 248, 389–394. [Google Scholar]
- Bonning, E. W.; Cheng, L.; Shields, G. A.; Salviander, S.; Gebhardt, K. Accretion Disk Temperatures and Continuum Colors in QSOs. The Astrophysical Journal 2007, 659, 211–217. [Google Scholar] [CrossRef]
- Davis, Shane W.; Woo, Jong-Hak; Blaes, Omer M.; The UV Continuum of Quasars: Models and SDSS Spectral Slopes. The Astrophysical Journal 2007, 668, 682–698. [CrossRef]
- Reimers, D.; Clavel, J.; Groote, D.; Engels, D.; Hages, H.J.; Naylor, T.; Wamsteker, W.; Hopp, U. The luminous quasar HS 1700+6416 and the shape of the “big bump" below 500 A. Astronomy and Astrophysics 1989, 218, 71–77. [Google Scholar]
- Ward, Martin; Elvis, Martin; Fabbiano, G.; Carleton, N.P.; Willner, S.P.; Lawrence, A.; The Continuum of Type 1 Seyfert Galaxies. I. A Single Form Modified by the Effects of Dust. Astrophysical Journal 1987, 315, 74. [CrossRef]
- Lynden-Bell, D. Galactic Nuclei as Collapsed Old Quasars. Nature 1969, 223, 690–694. [Google Scholar] [CrossRef]
- Shields, G. A. ; Thermal continuum from accretion disks in quasars. Nature 1978, 272, pp–706. [Google Scholar] [CrossRef]
- Malkan, M.A. The ultraviolet excess of luminous quasars. II. Evidence for massive accretion disks. Astrophysical Journal 1983, 268, 582–590. [Google Scholar] [CrossRef]
- Kolykhalov, P.I.; Sunyaev, R. A. Radiation of accretion disks in quasars and galactic nuclei. Advances in Space Research 1984, 3, 249–254. [Google Scholar] [CrossRef]
- Barvainis, Richard; Hot Dust and the Near-Infrared Bump in the Continuum Spectra of Quasars and Active Galactic Nuclei. Astrophysical Journal 1987, 320, 537. [CrossRef]
- Clavel, J.; Wamsteker, W.; Glass, I.S. Hot Dust on the Outskirts of the Broad-Line Region in Fairall 9. Astrophysical Journal 1989, 337, 236. [Google Scholar] [CrossRef]
- Mitchell, Jake A. J.; Done, Chris; Ward, Martin J.; Kynoch, Daniel; Hagen, Scott; Lusso, Elisabeta; Landt, Hermine; The SOUX AGN sample: Optical/UV/X-ray SEDs and the nature of the disc. MNRAS 2022. accepted.
- Laor, Ari; Netzer, Hagai; Piran, Tsvi; Massive thin accretion discs. II - Polarization. Monthly Notices of the Royal Astronomical Society 1990, 242, 560–569. [CrossRef]
- Antonucci, Robert; Unified models for active galactic nuclei and quasars. Annual Review of Astrononmy and Astrophysics 1993, 31, 473–521. [CrossRef]
- Kishimoto, Makoto; Antonucci, Robert; Boisson, Catherine; Blaes, Omer; The buried Balmer-edge signatures from quasars. Monthly Notices of the Royal Astronomical Society 2004, 345, 1065–1092.
- Capetti, Alessandro; Laor, Ari; Baldi, Ranieri, D.; Robinson, Andrew; Marconi, Alessandro; Spectropolarimetry of low redshift quasars: origin of the polarization and implications for black hole mass estimates. Monthly Notices of the Royal Astronomical Society 2021, 502, 5086–5103. [CrossRef]
- Maiolino, R.; Salvati, M.; Marconi, A.; Antonucci, R. R. J. The Ly-edge paradox and the need for obscured QSOs. Astronomy and Astrophysics 2001, 375, 25–29. [Google Scholar] [CrossRef]
- Schmidt, Gary D.; Smith, Paul S.; Evidence for Polarized Synchrotron Components in Radio-Optical Aligned Quasars. The Astrophysical Journal 2000, 545, 117–128. [CrossRef]
- Kishimoto, Makoto; Antonucci, Robert; Blaes, Omer; A first close look at the Balmer-edge behaviour of the quasar big blue bump. Monthly Notices of the Royal Astronomical Society 2003, 345, 253–260. [CrossRef]
- Kishimoto, Makoto; Antonucci, Robert; Blaes, Omer; Lawrence, Andy; Boisson, Catherine; Albrecht, Marcus; Leipski, Christian; The characteristic blue spectra of accretion disks in quasars as uncovered in the infrared. Nature 2008, 454, 492–494. [CrossRef]
- Goodman, Jeremy; Self-gravity and quasi-stellar object discs. Monthly Notice of the Royal Astronomical Society 2003, 339, 937–948. [CrossRef]
- Huang, Xiaoshan; Davis, DShane W.; Jiang, Yan-Fei; A Bright First Day for Tidal Disruption Event. The Astrophysical Journal 2023. submitted.
- Ryu, Taeho; Krolik, Julian; Piran, Tsvi; Noble, Scott; Avara, Mark; Shocks Power Tidal Disruption Events. The Astrophysical Journal 2023. submitted.
- Courvoisier, T. J.-. L; Tüler, M.; Cascades of shocks in active galactic nuclei and their radiation. Astronomy and Astrophysics 2005, 444, 417–424. [Google Scholar] [CrossRef]
- Hönig, S. F.; Watson, D.; Kishimoto, M.; Gandhi, P.; Goad, M.; Horne, K.; Shankar, F.; Banerji, M.; Boulderstone, B.; Jarvis, M.; Smith, M.; Sullivan, M. Cosmology with AGN dust time lags-simulating the new VEILS survey. Monthly Notices of the Royal Astronomical Society 2017, 464, 1693–1703. [Google Scholar] [CrossRef]
- Koshida, Shintaro; Minezaki, Takeo; Yoshii, Yuzuru; Kobayashi, Yukiyasu; Sakata, Yu; Sugawara, Shota; Enya, Keigo; Suganuma, Masahiro; Tomita, Hiroyuki; Aoki, Tsutomu; Peterson, Bruce A.; Reverberation Measurements of the Inner Radius of the Dust Torus in 17 Seyfert Galaxies. The Astrophysical Journal 2014, 788, 159.
- Minezaki, Takeo; Yoshii, Yuzur; Kobayashi, Yukiyasu; Sugawara, Shota; Sakata, Yu; Enya, Keigo; Koshida, Shintaro; Tomita, Hiroyuki; Suganuma, Masahiro; Soki, Tsutomu; Peterson, Bruce A.; Reverberation Measurements of the Inner Radii of the Dust Tori in Quasars. The Astrophysical Journal 2019, 886, 150.
- Barthel, P.D.; Arnaud, K.A. Anomalous radio-loudness of Cygnus A and other powerful radio galaxies. Monthly Notices of the Royal Astronomical Society 1996, 283, 45–49. [Google Scholar] [CrossRef]
- Ogle, P.M.; Cohen, M.H.; Miller, J.S.; Tran, H.D.; Fosbury, R.A.E.; Goodrich, R.W. Scattered Nuclear Continuum and Broad Ha in Cygnus A. The Astrophysical Journal 1997, 482, L37–L40. [Google Scholar] [CrossRef]
- Antonucci, Robert; Barvainis, Richard; Narrow-Line Radio Galaxies as Quasars in the Sky Plane. Astrophysical Journal Letters 1990, 363, L17. [CrossRef]
- Lopez-Rodriguez, Enrique; Kishimoto, Makoto; Antonucci, Robert; Begelman, Mitchell C.; Globus, Noemie; Blandford, Roger; On the origin of radio-loudness in active galactic nuclei using far-infrared polarimetric observations. The Astrophysical Journal 2023. accepted.
- Struve, C.; Conway, J. E. An H I absorbing circumnuclear disk in Cygnus A. Astronomy and Astrophysics 2010, 513, A10. [Google Scholar] [CrossRef]
- Carilli, Christopher L.; Perley, Richard A.; Perley, Daniel A.; Dhawan, Vivek; Decarli, Roberto; Evans, Aaron S.; Nyland, Kristina; A 4 kpc Molecular Gas Lane in Cygnus A. The Astrophysical Journal 2022, 937, 106.
- Maloney, Philip R.; Begelman, Mitchell C.; Rees, Martin J.; Radiative Excitation of Molecules near Powerful Compact Radio Sources. Astrophysical Journal 1994, 432, 606. [CrossRef]
| 1 | You will see below that this is the whole story for very luminous radio sources, but many weaker radio galaxies don’t participate in this scheme. Very detailed information can by found in a major review, Antonucci 2012 [6]. |
| 2 | **When I first showed Joe that starlight heavily dilutes the polarization and strongly affects the wavelength dependence, he pointed out to me that there were bumps in % polarization corresponding to the stellar absorption lines, due to reduced dilution compared to neighboring wavelengths. He said the % polarization plot “looks like a galaxy spectrum plotted upside down." |
| 3 | *I had the pleasure of showing their data at a meeting in 1986. Afterwards Chris McKee said to me, “I didn’t know telescopes were that powerful!" |
| 4 | *To be a bit more historically accurate, in 1978 there was little direct imaging evidence for fast superluminal motion, and these authors argued powerfully for the scenario using physical arguments based on data at other wavelengths as well. |
| 5 | *To this day X-ray astronomers mostly show uncalibrated count spectra because they are too lazy to deconvolve their line spread functions. They believe in X-ray exceptionalism, so only they are prevented from proper flux calibration. The published count spectra mainly show the “effective area" curve, and diabolically conceal the physical information. X-ray astronomers publish pages of these uninformative count spectra. |
| 6 | *The fast Superluminal radio sources are approximately the same objects as optical astronomers call blazars, based on their beamed synchrotron core emission which can swamp even the optical spectrum of the AGN. I’m not making an explicit distinction in this conversation-style condensed essay. That’s not adequate for research of course, and the subtleties are all discussed in e.g., Antonucci and Ulvestad 1985 and Wills et al. 1991, and my 1993 and 2012 reviews. The net effect here however is to diminish work by others, e.g., Browne et al. 1983, which used selection by VLBI speed. In general the present paper uses very incomplete and self-serving referencing, for which the author expects to pay in Pergatory. His major reviews of 1993 and 2012 are much better in this regard. |
| 7 | At this time a theory paper by Blandford and Königl (1979) [17] made me worry that these statistical arguments might be too naïve, due to a possible large intrinsic beaming angle resulting from non-co-linear motions. But all the data in hand suggested to me that if I did otherwise, I’d be too sophisticated. |
| 8 | Note though that he did not entitle his paper “Do all radio galaxies contain hidden quasars?" He did not make that superficially similar statement because he is a very smart guy. The answer to that question would be no, but the answer to the question he posed is still basically yes. |
| 9 | *The selection criteria in Laing (1988) [20] and in Garrington et al. (1988) [21] only slightly favored low-inclination sources. Ulvestad and I didn’t have this problem because we knew about the polarimetry, and we didn’t “know" that quasars should be considered separately from radio galaxies. Too much “knowledge" is as dangerous as too little. |
| 10 | We will see below that the disk model or anything resembling it is completely at odds with the spectral energy distribution. |
| 11 | *As we explain, the lack of any feature in quasar spectra at the Lyman edge position has other remarkable implications. Consider that the Broad emission Line Region could very reasonably be expected to absorb ionizing photons, and to produce Lyman continuum emission. Neither such effect has been documented even once to my knowledge, while they would seem to occur fairly generically. |
| 12 | ** After our paper was published, another paper claimed to see absorption in the Lyman continuum consistent with an origin in a disk atmosphere in a couple quasars. Those authors carelessly omitted a key test to distinguish edges from disk atmospheres from “associated" Lyman Limit Systems from foreground gas: kinematic and gravitational broadening would completely disguise the accompanying narrow absorption lines that a cloud would produce. We used that test to rule out the disk explanation for our candidates. Then Kinney and I later checked these others and alas they all showed the accompanying narrow absorption lines. |
| 13 | *This information comes to me mostly from a lifetime of challenging Gary Ferland to make Cloudy models that look like quasars in this part of the spectrum. |
| 14 | This break can’t be identified with the so-called self-gravity radius of an accretion disk, which would be at longer wavelengths. In fact it’s not clear how such a cutoff would arise in the accretion process, though self-gravity breakup would make sense if the disk ran backwards! Gas can break up due to self-gravity, but gravitating objects like stars would not obviously decompose and turn into a gas disk on the way in! See Goodman 2003 [52]. |
| 15 | An important exception is the work of Courvoisier and collaborators, starting with Courvoisier and Clavel (1991) [32]. These strong papers also attracted no attention. |
Figure 1.
Total flux spectrum of the narrow-line radio galaxy 3C234.
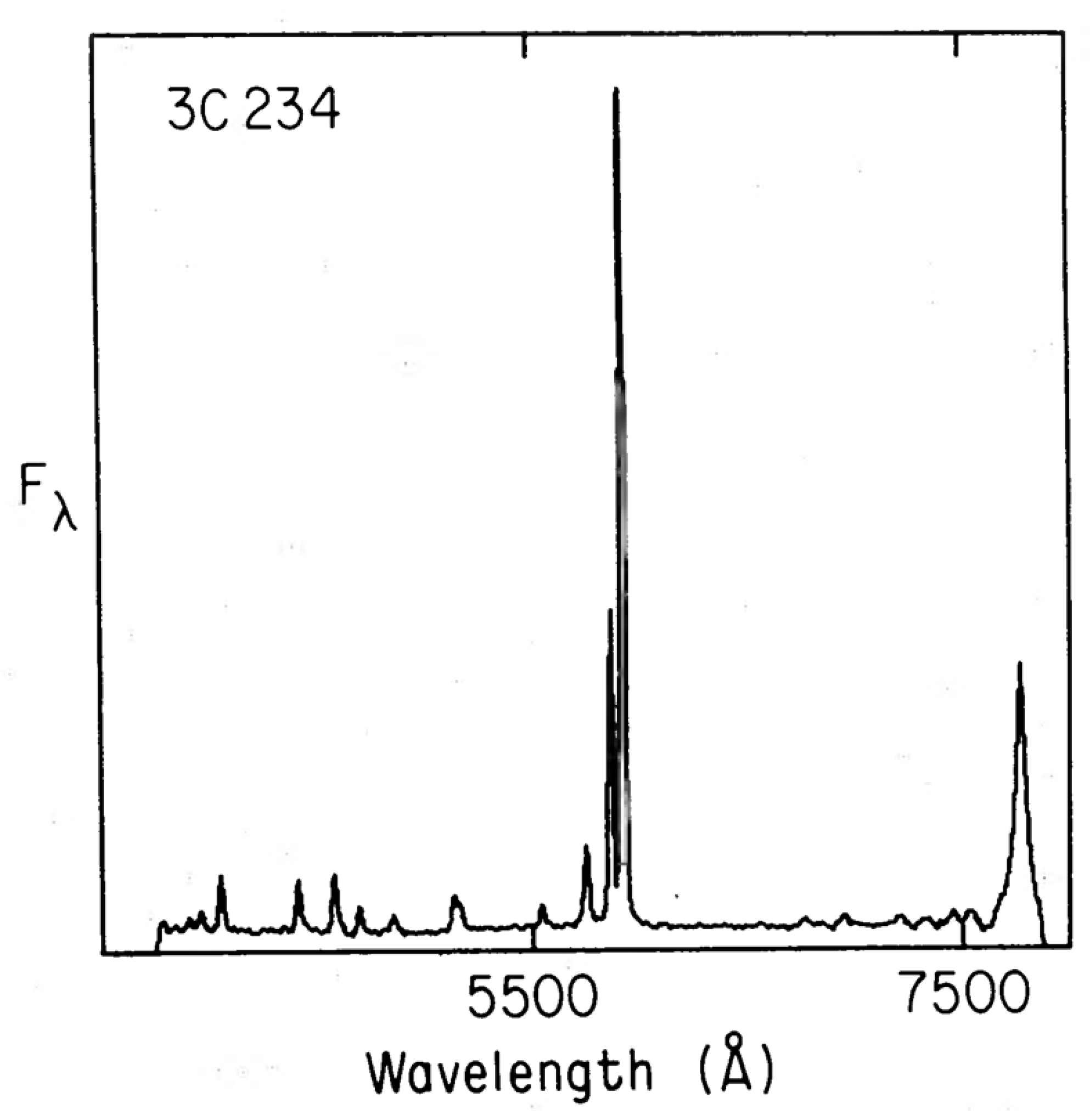
Figure 2.
The smoothed unnormalized Stokes parameters and count spectrum of 3C234.
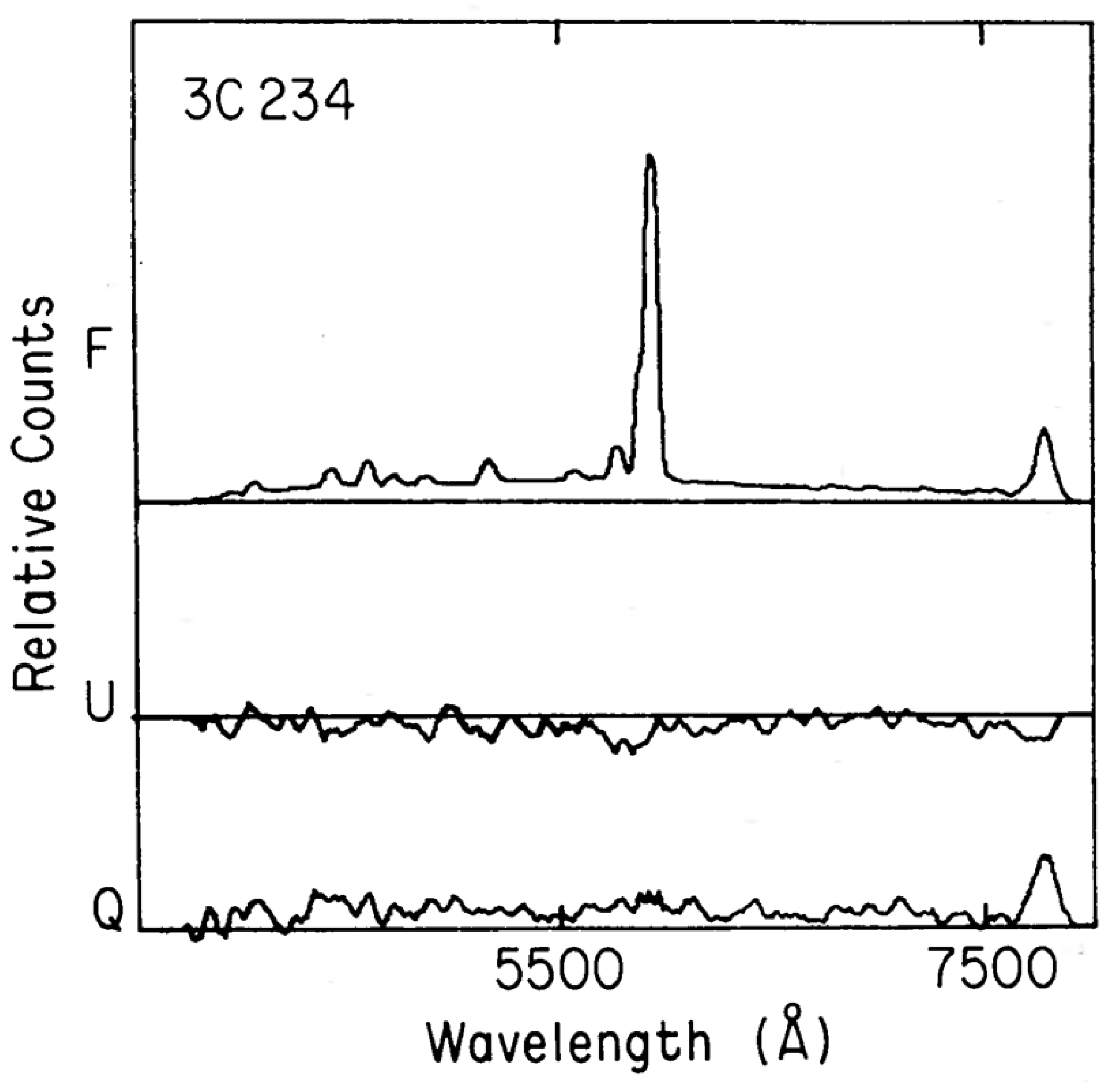
Figure 3.
NGC1068 ultraviolet polarized flux scaled by 1/0.16 and plotted over total flux. See text.
Figure 3.
NGC1068 ultraviolet polarized flux scaled by 1/0.16 and plotted over total flux. See text.
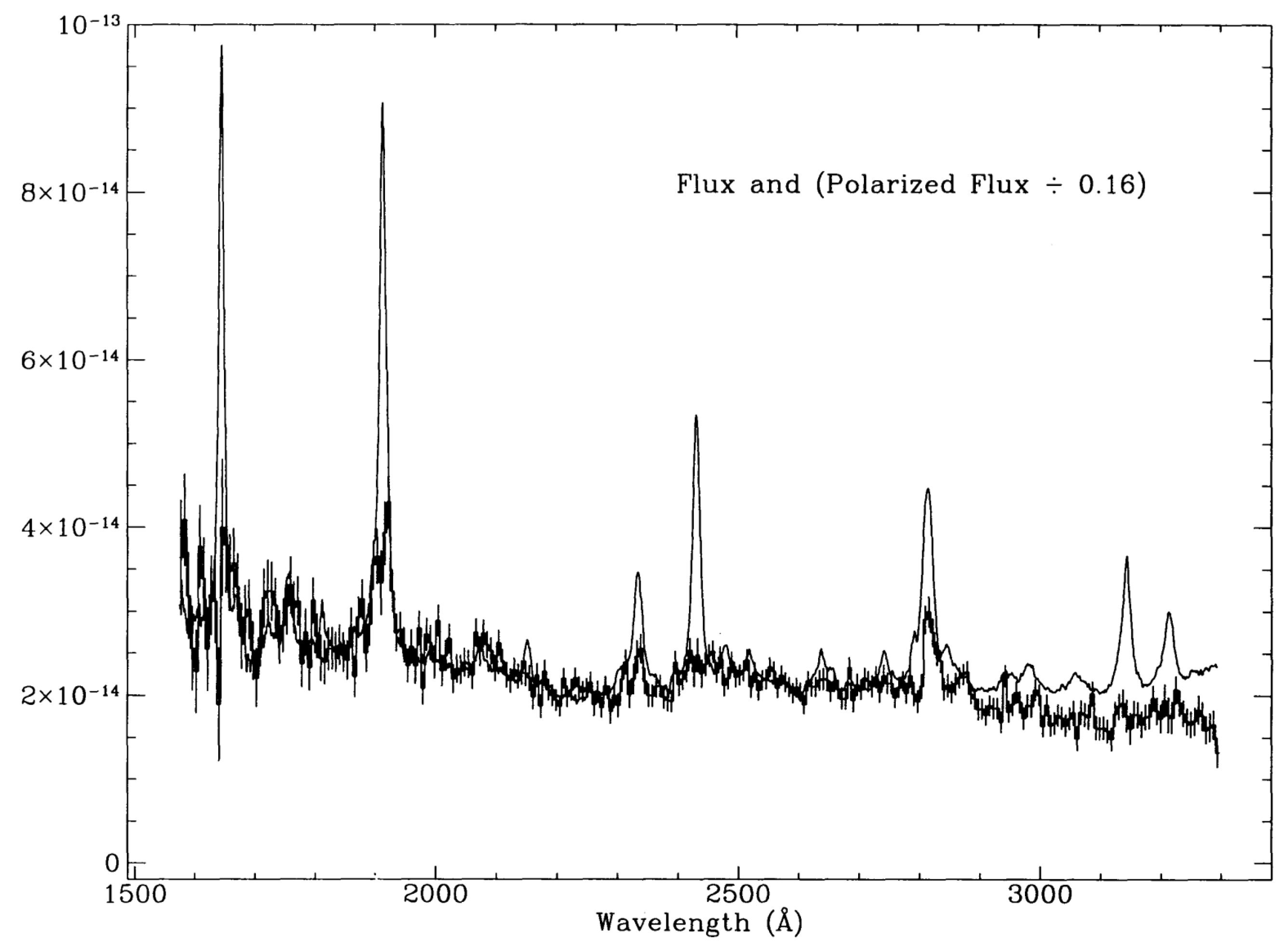
Figure 4.
Broadband image of 3C256 obtained by S. Djorgovski and H. Spinrad. See Dey et al. (1996) for details.
Figure 4.
Broadband image of 3C256 obtained by S. Djorgovski and H. Spinrad. See Dey et al. (1996) for details.
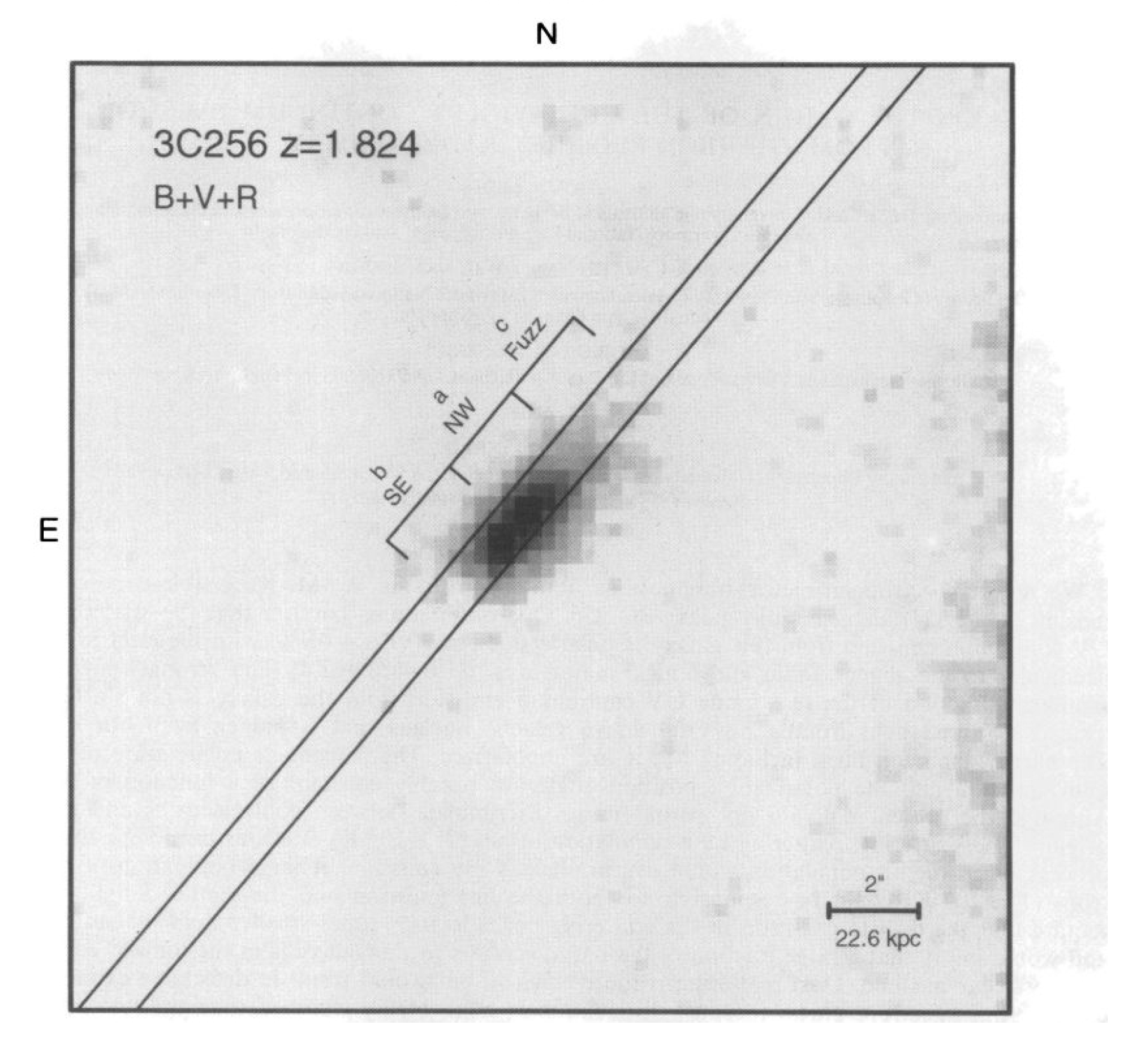
Figure 5.
Comparison of the rest frame UV continuum spectra of 3C256 and NGC1068 (from Antonucci, Hurt, & Miller 1994). The ordinate is labeled with the flux density scales for NGC1068 and 3C256 on the left and right axes, respectively. Note that the spectrum of 3C256 is sampled in a aperture () whereas the spectrum of NGC1068 is from a nuclear region of size (). See Dey et al. for additional details.
Figure 5.
Comparison of the rest frame UV continuum spectra of 3C256 and NGC1068 (from Antonucci, Hurt, & Miller 1994). The ordinate is labeled with the flux density scales for NGC1068 and 3C256 on the left and right axes, respectively. Note that the spectrum of 3C256 is sampled in a aperture () whereas the spectrum of NGC1068 is from a nuclear region of size (). See Dey et al. for additional details.
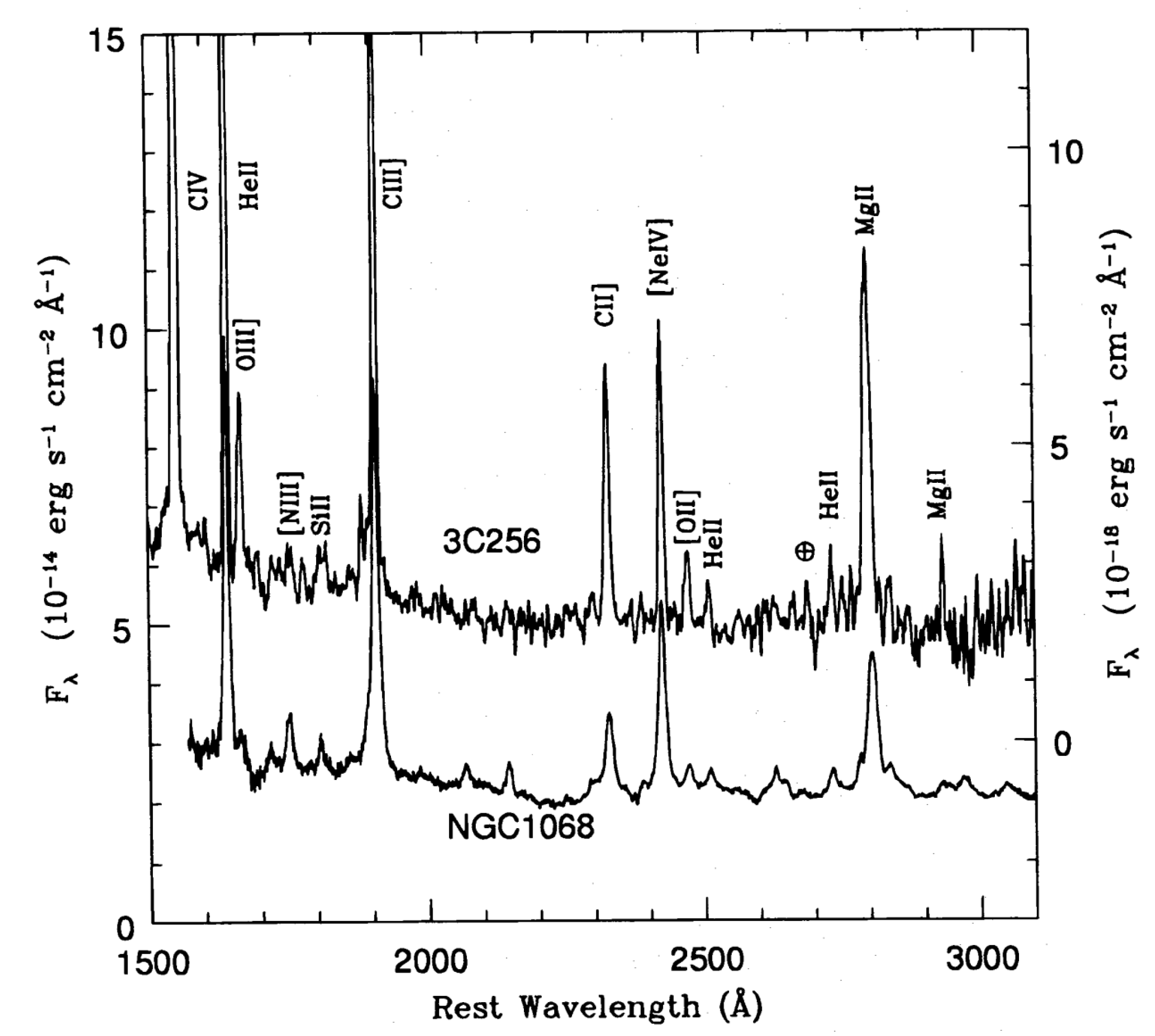
Figure 6.
Reddening curves from Gaskell et al. (2004) for composite spectra of various values of radio-core dominance. Filled triangles are from comparing with , and filled circles are from comparing with CSS. The open circles represent average BLR extinction values between face-on and edge-on (; CSS) objects. Theoretical reddening curves derived from CCM89 for and 3.1 are shown as dashed and solid curves, respectively.
Figure 6.
Reddening curves from Gaskell et al. (2004) for composite spectra of various values of radio-core dominance. Filled triangles are from comparing with , and filled circles are from comparing with CSS. The open circles represent average BLR extinction values between face-on and edge-on (; CSS) objects. Theoretical reddening curves derived from CCM89 for and 3.1 are shown as dashed and solid curves, respectively.
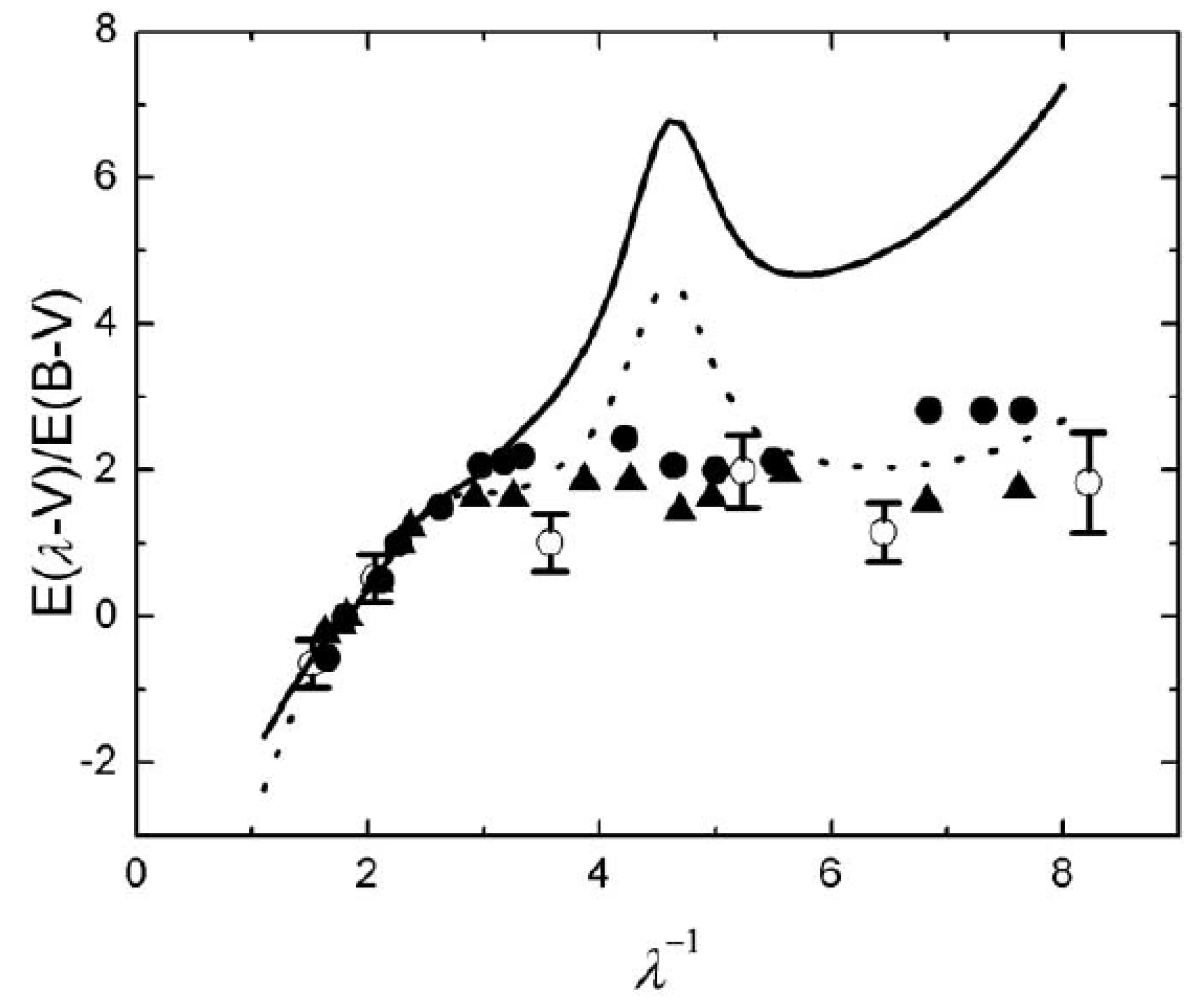
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




