Prerpints.org logo
Preprint
Article

General evaluation model for complex environment system

Altmetrics

Downloads

104

Views

26

Comments

0

Submitted:

04 July 2023

Posted:

05 July 2023

You are already at the latest version

Alerts
Abstract
Establishing an effective evaluation model to analyze the actual environmental level of the multi-indicator systems is an urgent challenge. However, due to the complexity of the environmental system, the factors that determine the practical system are usually interrelated. To solve this problem, many methods have been proposed and verified. However, the disadvantage of unreasonable weight determination and only single-indicator assessment limits the practical application of these analysis methods. Here, we established an optimized entropy weight model and integrate it with the fuzzy comprehensive evaluation (FCE) method to quantify the complex environmental system. By introducing the linear programming method into the entropy weight solution, we can obtain high accuracy weight values and strong resistance to extreme data. Theoretical and simulation results demonstrate that our method can enhance the precision of weight calculation and evaluation results for multi-factor systems. Our work develops an effective method to quantify the complex environment system comprehensively and is significant to real applications of evaluation method.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

As an important evaluation method, the comprehensive evaluation model has been widely applied in various fields, such as ecological civilization development level [1], environmental evaluation [2], ecosystem stability assessment [3] and water quality pollution evaluation [4]. This evaluation model can help researchers to quantify the environment system comprehensively. However, the practical environmental system is complex and its determining factors are often interrelated. Therefore, a single factor evaluation is insufficient to assess the status of practical system. However, most comprehensive evaluation models are usually used to assess single-factor systems, which fail to accurately capture the complexity of practical environmental systems [5]. Thus, the developing of effective evaluation model for multi-factors system is a crucial challenge.
In order to solve these issues and improve the performance of assessment, various methods have been proposed [6,7,8,9,10,11]. The traditional entropy weight (TEW) method has been proposed to obtain an objective weight based on the uncertainty of information. However, in situations where the differences in entropy are small, this method may yield excessively high weight values [12]. These results indicated that the TEW method has poor resistance to extreme values (data with a small difference in entropy). To effectively reduce the weight differences and enhance the resistance to extreme data, the improved entropy weight (IEW) method has been proven to optimize the entropy evaluation formula [13,14,15,16,17,18]. However, this method resulted in overcorrection of normal data weight, causing it to deviated from the law of consistency in entropy weight variation. Besides, this method is typically used in conjunction with single-factor evaluation (SFE) method, which is particularly suitable for systems with fewer or independent factors. But, for a complex systems with multiple factors, the SFE method may lack rationality due to the interrelationship between these factors. The fuzzy comprehensive evaluation (FCE) method utilizes the membership degree theory of fuzzy mathematical model to transform qualitative assessments into quantitative ones, can effectively evaluate complex environmental systems that are influenced by multiple predetermined factors [19,20,21,22,23,24,25]. However, literature [26,27] have pointed that the FCE method is greater subjectivity in weight determination, which results in lower accuracy of evaluation results.
In this paper, we establish an optimized improved entropy weight (OIEW) model and integrate it with the FCE method to achieve multi-factors system assessment. To improve the accuracy of weight determination and enhance the anti-interference ability in handling extreme data, we develop an objective function based on the law of consistency in entropy weight variation using the mathematical programming concepts. This single objective model can be effectively solved by the linear programming algorithm, which prevents normal data from being suppressed. Furthermore, our model can effectively realize the comprehensive evaluation of multi-factors system by integrating the FCE method. The theoretical and simulation results demonstrate that our model can enhance the precision of weight determination and evaluation outcomes. Our works provide theoretical guidance for the practical application in the complex system evaluation field.

2. Disadvantages of entropy evaluation method

The traditional entropy evaluation (TEW) method is an objective weighting method that employs the calculation of information entropy value (IEV) to determine the weight of each factor. In the calculation process, the evaluation results follow the law of consistency in entropy weight variation, whereby an increase in IEV corresponds with decrease the weight, and vice versa [28] (The detail calculation process see Appendix A). However, this method has poor resistance to extreme data and is greatly affected by outliers. To overcome this limitation, several studies [15,16,17,18] have proposed by incorporating a correction factor to enhance its robustness against extreme data. Although these corrections can enhance their robustness to extreme data, the correction factor will overcorrect the weight of normal data. To further describe the drawbacks of the entropy evaluation method, we utilize Table 1 to delineate the issues in weight determination within both TEW and IEW methods.
The yellow section in Table 1(a) shows the weights of extreme data (where minimal differences are observed among the IEV( H i )). It can be observed that the weights calculated by the TEW method are 0.0476 when the H i is 0.9999. However, a decreases of 0.005 in the IEV results in an approximate sixfold increase in the weights. The IEV exhibits minimal variation, whereas the TEW undergoes significant weight fluctuations. The weight formula [12] of the TEW method is displayed as follows
ω i = 1 − H i ∑ i = 1 n ( 1 − H i )
where w i refers the i-th weight calculated by TEW method. n is the number of evaluation factors. H i represents the IEV of the i-th factor.
According to Equation 1, the weights of TEW method are determined by 1 − H i , and this value retains the significant decimal places when the difference in IEV is small. To provide further clarification on the issue of inadequate resistance to extreme data by the TEW method, the weight ratio Q [12] is introduced in ours work.
Q = X i X d
Where X i is the i-th weight of evaluation method. For extreme data, H i and H d exhibits nearly equal values ( H i / H d ≈ 1 ), thus using 1 as the baseline is a suitable metric to assess the degree of weight variation. As the difference in the decimal part decreases, the deviation between Q and 1 will increase. The greater the deviation from 1, the more inconsistent the variation in entropy weight. Table 2(a) shows the calculated Q value of TEW method for extreme data. We use 0.9996 as a fixed comparison. It can be observed that the weight ratio Q exhibits obviously deviation from 1 when the H d is 0.9999, and the Q value is notably lower than 1 when H d is 0.9994. The difference in IEV is negligible, whereas the deviation of Q value from 1 is significant. These results further substantiate the inadequacy of the TEW method in weight calculation for extreme data.
To effectively solve this problem, the correct factor is used in TEW method [12,14,18]. Using the IEW1 method, as mentioned in the literature [18], we demonstrate the limitations of IEW method. The green section in Table 1(b) shows the influence of correction factor for normal data (where larger differences are observed among the IEV). It can be observed that the corresponding weights are 0.1579 and 0.1769 when H i is at 0.9890 and 0.8750, respectively. There is a significant disparity in H i , but the change in weight remains inconspicuous. The weight changes are smooth when the formula incorporating correction factor. To elucidate this phenomenon, we give the formula [18] of correction factor, as shown in follows
ω i ′ = 1 − H i + H ¯ ∑ i = 1 n ( 1 − H i + H ¯ )
where w i ′ refers the i-th weight calculated by IEW1 method. The average value H ¯ is the correct factor. It can be observed that the increase of the H ¯ results in an increment of the numerator. For the extreme data, this increment in the numerator will increase the integer part of the weight value while diminishing the influence of the decimal portion. Ignoring the effect of the fractional part will mitigate the deviation of Q from 1. Therefore, this correction approach can reduces the differences between weights and improves the resistance to extreme data. The green section in Table 2(b) shows the calculated Q value of IEW1 method for extreme data. It can be seen that a small fluctuation in the IEV results in a correspondingly minor deviation of the Q value from 1. This phenomenon demonstrates that the addition of correction factors can improve the resistance to extreme data.
However, the integer part also weakens the weight difference of normal data and leads to a larger relative error between the changes in weight values and IEV, as shown in Table 3. We examine the impact of adding or omitting correction factors on Q values within the same dataset. The TEW method exhibits a clear decreasing trend in Q value as H d decreases. However, the introduction of the correction factor H ¯ only slightly decrease the Q value for IEW1 method. Therefore, the correction factor will impact the weight of normal data.
It should be emphasized that we use 1 as the benchmark to measure the degree of deviation between Q and 1 to assess the accuracy of the evaluation method for extreme data, but this benchmark is not applicable to normal data. This is because that there exists a significant disparity between the H i and H d for normal data ( H i / H d ≫ 1 ), thus rendering 1 as a benchmark is inadequate to assess the weight variation. To assess the entropy weight variation of normal data, the G value is introduced as an evaluative tool for assessing consistency. Equation 4 is formula of G [29].
G = 1 n − 1 ∑ i = 1 n X i − X i + 1 − H i − H i + 1 X i − X i + 1 2
The G value is the standard deviation of the relative error between the differences in adjacent entropy values and those in weights. It denotes the consistency level of the entropy weight variation. A smaller value of G indicates a higher level of consistency, whereas a larger value of G signifies that the weights fail to meet the requirement for consistency. According to the calculation formula of standard deviation, G is a constant value. Table 4 shows the G value of different method for normal data and extreme data. It can be observed that the G value of IEW method is greatly higher than that of the TEW method. These results prove that the consistency of the TEW method is superior for normal data. But, the correction factor used in the IEW method overcompensates for normal data weights, leading to a violation of consistency principle.
Therefore, building an appropriate evaluation model is a pressing issue, which should not only optimize the correction factors to normal data but also enhance the anti-interference ability to extreme data. Moreover, the evaluation process must adhere to the principle of consistency in entropy weight variation.

3. Disadvantage of SFE method

Two crucial aspects must be considered during assessing the complex environment systems [30]. Firstly, assigning weights to each factor individually becomes more difficult when the system comprises many factors. Secondly, when these factors exhibit categorical or hierarchical relationships, determining weights at different levels will add complexity to the evaluation process. If all factors are measured on the same level, it will weaken the internal correlation of each attribute and result in meaningless evaluation outcomes. Therefore, the SFE method is insufficient for evaluating multi-factor systems.

4. Theoretical model construction

To enhance the robustness to extreme data and mitigate excessive correction in IEW method, we propose an optimized improved entropy weight (OIEW) method to improve the weight determination process. By utilizing linear programming methodology and adhering to the principle of consistency in entropy weight variation, a programming model is constructed to calculate the weight. Furthermore, the FCE method is introduced to the OIEW method to overcome the simplistic of SFE method and provides a comprehensive evaluation for multi-factors systems.

4.1. Construction of evaluation datasets and reference sets, as well as the determination of membership functions

Appropriate sets of evaluation criteria, datasets, and membership functions can effectively reflect the true condition of the evaluated objects and enhance the accuracy of the evaluation results. The detailed construction process see Appendix B and Appendix C.

4.2. OIEW method

The TEW method employs a single formula for weight calculation, which results in insufficient robustness against extreme data. Although correction factors can be applied to each factor, they still rely on a static weight calculation formula. As entropy variation is a dynamic process, it is necessary to use a dynamic solution method that adjusts weight calculations accordingly. Therefore, we transform the mathematical planning model into linear programming model by simplex algorithm.
The weights calculated using the correction factor have a significant impact on normal data. Therefore, we introduce the concept of linear programming and optimize the computation process by imposing specific constraints on each weight. As G value can effectively characterize the consistency of entropy weight variation, we select it as the objective function in our linear programming model. According to the Equation 4, it can be observed that the smaller the value of H i − H i + 1 − X i − X i + 1 results in a lower G value, thereby increasing the consistency. Therefore, we construct the objective function Z, which is defined as
Z = m i n H i − H i + 1 − X i − X i + 1
X i and H i represent the generalized weight value and IEV, respectively. When the constraints are satisfied, a smaller value of Z indicates more precise weights. The constraints of the objective function are specified as follows: (1) The total weight of all factors is 1; (2) The changes in weights are inversely proportional to the changes in IEV; (3) The weights X i should range from 0 to 1.
To facilitate comparison with the TEW and IEW methods, we replace X i with w i ′ ′ to denote the weights calculation in the OIEW method. Therefore, the formula of the OIEW model can be derived by synthesizing the aforementioned concepts.
Z = m i n H i − H i + 1 − w i ′ ′ − w i + 1 ′ ′ s . t . w i ′ ′ − w i + 1 ′ ′ H i − H i + 1 < 0 ∑ i = 1 n w i ′ ′ = 1 0 ≤ w i ′ ′ ≤ 1
By utilizing Equation 6 to calculate the weights, maximum consistency with the trend of information entropy changes can be ensured. To achieve stable data acquisition and simplify the calculation process, the single objective function problem is transformed into a linear programming model to optimize the weight calculation process (see Appendix D for the detailed description). The linear programming model that undergoes transformation is formulated as
min ∑ i = 1 n u i + v i ζ i − ϵ i H i − H i + 1 < 0 ∑ i = 1 n w i ′ ′ = 1 ζ i + ϵ i + u i − v i = H i − H i + 1 u i , v i , ζ i , ϵ i ≥ 0 0 ≤ w i ′ ′ ≤ 1 i
Where u i , v i represent two variables that characterize H i − H i + 1 − w i ′ ′ − w i + 1 ′ ′ . Where ζ i and ϵ i represent two variables that characterize w i ′ ′ − w i + 1 ′ ′ .
This linear programming model can be solved by the simplex method. Therefore, to achieve the optimal solution, we must first convert the inequality in formula 7 into the standard form of constraints, resulting in the following equation.
ζ i − ϵ i H i − H i + 1 + Γ i = 0
Where Γ i is relaxation variables. By introducing this relaxation variables, the inequality constraints of the linear programming problem can be transformed into equality constraints. Then, the optimal solution can be obtained through the simplex method. And, the weights calculated by the dynamic solution process of the simplex method can greatly comply with the principle of consistency in entropy weight variation.

4.3. OIEFC method

The evaluation of multi-factors system by SFE method lacks comprehensiveness. Therefore, we incorporate the FCE method into the OIEW method to establish a multi-factors evaluation model (we call it the OIEFC evaluation model). In this method, the multi-factor set is divided into multiple sub-factor sets, and the first-level FCE is conducted for each subset. Subsequently, the obtained first-level evaluation vectors are further utilized as a new factor set to conduct second-level FCE. By repeating the aforementioned process, it is feasible to carry out comprehensive evaluations at third, fourth, and even higher levels in order to obtain the final evaluation results. This evaluation method fully considers the interrelationships among factors, and the hierarchical processing enhances the significance of weights to yield more accurate evaluation results. In order to further enhance the comprehension of the evaluation process, we present the two-level FCE models an illustrative example. The two-level model include first and second evaluation level.
(1) Establish the second-level FCE matrix.
After obtaining the weight judgment matrix and the weight vector, the FCE matrix can be constructed (The weight judgment matrix obtained is presented in Appendix C). The comprehensive result at the current level are determined by fuzzy algorithm. The final evaluation results can be obtained through step-by-step calculations. The detailed method is as follows:
The FCE matrix is calculated based on fuzzy operations. According to weights formula and simplex algorithm, the FCE matrix of the second-level B p can be expressed as
B p = w → p ′ ′ · R p = w p 1 ′ ′ , w p 2 ′ ′ , w p 3 ′ ′ , … , w p n ′ ′ × r p 11 . . . r p 1 j . . . . . . . . . r p i 1 . . . r p i j = b p 1 , b p 2 , b p 3 , … , b p j W h e r e ( p = 1 , 2 , … , t , k = 1 , 2 , … , n )
Where p is p-th first level indicator, k is k-th second level indicator. w → p ′ ′ , and R p are the weight vector, and weight judgment matrix of the second-level factors corresponding to the p-th first-level indicator, respectively. w p k ′ ′ is the weight of the k-th secondary indicator corresponding to the p-th first-level indicator. b p α (where α =1,2, …,j) represents the overall membership of the α level corresponding to the p-th first-level indicator.
(2) Establish the first-level FCE matrix.
Then, the FCE matrix of second-level factors are taken as the weight judgment matrix of the first-level factors. And the membership of the corresponding first-level factor is determined by the comprehensive membership degree of the secondary factors. Therefore, the weight judgment matrix of the first-level factors U can be written as
U = b 11 . . . b 1 j . . . . . . . . . b p 1 b p α b p j . . . . . . . . . b t 1 . . . b t j = B 1 . . . B p . . . B t
Where U is the weight judgment matrix of the first-level indicators. b p α is the α -level membership of the p-th first-level indicator. By utilizing the weights of the second-level factors as raw data and applying the OIEW method, we can derive the weights of the first-level factors. Then, the FCE matrix of the first-level factors can be constructed. Ultimately, the evaluation of these indicators can be assessed by the principle of maximum membership degree. The evaluation model can be expressed as
L = S → · U = S 1 , … , S p , … , S t × B 1 . . . B p . . . B t = L 1 , . . . , L p , . . . , L t
Where L is the first-level FCE matrix. S → is the weights matrix of first level indicator, S p is the weights of p -th first level indicator. L p is overall membership of p-th first level. If L α = m a x L 1 , . . . , L p , . . . , L t , the level results of the environmental system are level α .

5. Results and Analysis

5.1. The accuracy of OIEW Method

Figure 1 shows the weight comparisons obtained by different methods for extreme data (a) and normal data (b). As shown in Figure 1(a), when extreme data conditions cause a decrease in IEV at equal intervals of 0.0001, the TEW method exhibits a linear increasing trend and produces weight values that differ significantly. This phenomenon demonstrates that the TEW method violates the principle of consistency of entropy weight variation. But, the slight decrease in extreme entropy calculated by the OIEW method does not result in a significant change in weight, and the overall trend remains stable. This finding is consistent with that of the IEW1 method, indicating that the OIEW method is equally robust to extreme data. Figure 1(b) presents a comparison for the normal data. When the IEV randomly decreases from 0.989 to 0.875, the weight value calculated by TEW method exhibits a obvious upward trend, indicating that the TEW method adheres to the principle of consistency of entropy weight variation for normal data. But the weight values calculated by the IEW1 method show a relatively stable trend, with only minor fluctuations ranging from 0.1579 to 0.1769. This result demonstrates that the IEW1 method overcorrects normal data and violates the principle of consistency. In contrast, the weight of the OIEW method doubles from 0.1140 to 0.2280 as IEV increase, thereby satisfying the principle of consistency of entropy weight variation.
Figure 2 compares the Q-value distribution of extreme data. We adopt H i = 0.9996 as a fixed benchmark to compare the weight ratio of other entropy values. It can be seen that the Q value of TEW method exhibits a deviation from the baseline and deviates significantly from 1 when there is only a small difference between H i and H d . This phenomenon indicates a substantial deviation in weight obtained by the TEW method, demonstrating its poor resistance to extreme data. However, the Q value of IEW1 and OIEW methods consistently remains at the baseline. These results demonstrate that IEW and OIEW methods are robust against extreme data.
To prove the consistency of entropy weight variation, we compare the G value of different method as shown in Figure 3. IEW1 [18], IEW2 [12] and IEW3 [14] method respend the entropy evaluation method with correction factor. It can be apparently seen that the G value of OIEW method is 1.9825 × 10 − 16 , which is greatly lower than the other four method, indicating its adherence to the principle of consistency in entropy weight variation. Furthermore, we can also observe that the G values with the correction factor for normal data exceed that of TEW method, demonstrating an overcorrection by the correction factor and consequent violation of consistency principle.
Therefore, compared with the TEW and IEW1 methods, the weight changes of the OIEW method remain a relatively stable when IEV changes slightly, but show a corresponding trend when the IEV decreases randomly. The Q value of the OIEW method exhibits stability with the baseline for extreme data, whereas the G value is significantly small for normal data. These results obviously demonstrate that the OIEW method not only effectively alleviates the excessive correction of normal data and improves the resistance to extreme data, but also adheres the theory of consistency in entropy weight variation with high precision.

5.2. The rationality of the OIEFC model

To evaluate the validity of the OIEFC method, a comprehensive evaluation is performed on the soil dataset from Shandong Province of Chinese Soil Database (HWSD)(was collected from 2009/01/01 to 2009/12/31, and updated from 2020-12-31) [31,32]. This dataset provides actual measured physical indicators and chemical indicators collected from 154 different sampling points (The dataset is provided by National Cryosphere Desert Data Center. (http://www.ncdc.ac.cn).). Referring to the current national standards of ’GB/T33469-2016: Quality Grade of Cultivated Land’ and ’Agricultural Soil Nutrient Grading Standard’, two first-level factors are selected, which are further subdivided into six second-level factors. The first-level factors are the physical and chemical properties of the soil. The second-level factors are the soil pH(PH), organic carbon content (OC), soil electrical conductivity (ECE), soil cation exchange rate (CEC), soil bulk density (BULK), and soil texture (TEX). These factors constitute the assessment factor system for soil quality.
Table 5 displays the IEV and weight values obtained from different evaluation methods. As can be observed from the table, when the difference between the IEVs of the two physical factors is small, there is a significant discrepancy in weight values calculated by the TEW method for BULK and TEX factors, which are 0.101 and 0.899, respectively. In contrast, the OIEFC method produces nearly consistent weight values for both indicators, demonstrating its robustness to extreme data when evaluating the complex systems. For chemical factors, it can be seen that the OIEW method demonstrates the corresponding change in response to changes in entropy values as the IEV decrease from 0.9837 to 0.6733, while the IEW1 method exhibits a relatively stable trend. These results fully prove the high accuracy of the OIEFC method in determining weights for factors in practical systems.
The evaluation results of soil quality and the proportion of soil utilization, which are obtained by the OIEFC method containing 154 soil data, are presented in Figure 4. The red area denotes the evaluation results of soil quality. From these bar chart, it can be observed that the soil quality level in Shandong Province is predominantly classified as Grade I (excellent), accounting for 66.22% of the total soil dataset. This is followed by Grade II (good) with a proportion of 18.92%. Grades III (moderate) and IV (poor) each account for 12.84%, while the smallest proportion belongs to Grade V (very poor) at only 0.68%. These analysis results indicate that the overall soil quality in Shandong Province meets an excellent standard. Compared to the 2020 soil distribution announced by Shandong Province (as shown in the blue area), the proportion of farmland (F) is 65.58%, while woodland (W), grassland (G), residential areas (R) and abandoned land (A) are 6.30%, 8.40%, and 18.60% and 1.12%, respectively. The predominant proportion of farmland further attests to the superior overall soil quality in Shandong Province, while the minimal proportion of abandoned land serves as evidence of poor soil quality. This findings fully validate the rationality and effectiveness of OIEFC method in practical system evaluation.
To further demonstrate the precision of the OIEFC method in multi-factor systems, we conducted a comparison with the SFE method adopted in [33]. Only the initial 30 samples from the Shandong soil dataset in the HWSD are selected to facilitate the comparison. Figure 5 shows the comparison results. Most of the line charts exhibit overlap, indicating that the evaluation results for both SFE and OIEFC method on these samples are congruent. However, there exist notable variances in the evaluation results for ID15 and 24-27. To further elucidate the disparities among these data points, we conduct an analysis of the physical and chemical characteristics of ID15 and ID24 samples, as presented in Table 6. The yellow section in Table 6 are actual measurement data obtained by HWSD dataset. This dataset provides raw physical and chemical indicators data. The soil’s physical and chemical properties of ID26 and ID27 are same as ID24. From the Table 6, we can find that the physical and chemical properties of ID15 and ID24 are nearly identical, indicating that their soil grades are equivalent. The actual measurement data show that most of the indicator values for samples ID15 and ID24 are at level IV or V, indicating a relatively poor soil condition(The indicator level is evaluated according to the current national standards of ’GB/T33469-2016: Quality Grade of Cultivated Land’ and ’Agricultural Soil Nutrient Grading Standard’). However, the calculated result obtained by the SFE method is rated as level II (good) as shown in green section in Table 6, which did not align with the actual situation. In contrast, the OIEFC method’s evaluation result is rated as level IV (poor), demonstrating greater accuracy. Therefore, with almost identical indicator weights, the OIEFC method outperforms the SFE method in terms of comprehensiveness and precision in soil evaluation.

6. Conclusion

In this paper, we conduct an optimized and improved entropy evaluation method to obtain more accurate weights. And, we also integrate our method with the FCE method to conduct a comprehensive evaluation for the multi-factor system. Theoretical and simulation results demonstrate that our method can enhance resistance to extreme data and improve the over-correction of normal data. Compared to the traditional method, our method is more adaptable to diverse information entropy conditions. Besides, it also provides a more comprehensive and accurate assessment results compared to the SFE method. Our works is instructive to quality evaluation for complex environment system, and provide guidance for the practical application in the complex system evaluation field.

Author Contributions

Conceptualization, M.Z.Y. and Y.X.W.; methodology, M.Z.Y.; software, Y.X.W.; validation, M.Z.Y., Y.X.W. and J.W.; formal analysis, M.Z.Y.; investigation, Y.G.; resources, J.J.S.; data curation, Z.G.W.; writing—original draft preparation, F.B.G.; writing—review and editing,M.Z.Y, Y.X.W. and J.W.; visualization, M.Z.Y.; supervision, J.W.; project administration, J.W.; funding acquisition, S.H.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (62105004); University Natural Science Research Project of Anhui Province (KJ2020A0308); Natural Science Foundation of Anhui Province (2108085MF200); University-level general projects of Anhui University of science and technology (QNYB2021-05, QNYB2021-10).

Data Availability Statement

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A: Calculation process of TEW method

The weight calculation using TEW method is outlined as follows:
(1) Construct the raw data matrix Y Suppose there are n evaluation indicators and μ evaluation factors. The raw data matrix Y can be expressed as
Y = y i j n × μ
Where y i j is the j-th raw data of i-th evaluate indicator.
(2) Normalization of raw data To mitigate the impact of the original data dimension, we normalized the raw data. The normalization process is as follows
P i j = y i j / ∑ j = 1 μ y i j
Where P i j is normalized factor values.
(3) Calculate the entropy value of each factor The information entropy value (IEV) of each indicators can be defined as follows
H i = − ∑ j = 1 μ P i j log P i j ln μ , i = 1 , 2 , … , n
Where H i is information entropy of i-th indicator. Considering the possibility of zero values in some original data, errors may occur during entropy calculation. To solve this problem, a small increment is added to the indicator value. (e.g. 10 − 4 ). This small value can prevent errors while preserving the integrity of the original data.
(4) Calculation of indicator weights
The weights assigned to each indicator can be determined upon completion of the IEV calculation.
w i = 1 − H i ∑ i = 1 n ( 1 − H i )
Where w i represents the weights of i-th indicator, and 0 ≤ w i ≤ 1 , ∑ i = 1 n w i = 1

Appendix B: Evaluation Data Set and evaluation criteria set Construction

The evaluation data set is a raw data matrix. The evaluation criteria for each indicator are included in the evaluation set, which is consistently divided into five levels. However, different from the conventional FCE method, each indicator adheres to a strict ranking standard. Thus, this paper utilizes national standards and ranks each evaluation factor in the form of intervals
F = f k 1 , f k 2 , … , f k 5 f k a = a k α , b k α ( k = 1 , 2 , … , n ; α = 1 , 2 , … , j )
Where F is evaluation set, f k 1 ∼ f k 5 represent five levels: I (excellent), II (good), III (moderate), IV (poor), and V (extremely poor). a k α , b k α represent the α -th rank and the upper and lower limits of the interval corresponding to the k-th indicator, respectively.

Appendix C: Membership determination

The membership can be determined by the membership function, which is dependent upon the evaluation level value of the evaluation set. The evaluation set is expressed in the form of intervals. Therefore, the membership function is established based on the correlation between factor values and various levels. To facilitate the representation of the membership function, it is advisable to arrange all rank intervals in descending order when considering the irregular arrangement of each rank interval. Ultimately, reverting to the original order after calculating the membership. Membership function are expressed as follow (1) a k α ≤ ρ ≤ b k α
r p k α ( ρ ) = m a x ( b k α ) − ρ m a x ( b k α ) − b k ( α − h ) a ( α − h ) k ≤ ρ ≤ b ( α − h ) k 1 a k α ≤ ρ ≤ b k α ρ a k ( α + g ) a ( α + g ) k ≤ ρ ≤ b ( α + g ) k ( h = 1 , 2 , … α − 1 ; g = 1 , 2 , … , j − α )
(2) ρ < m i n ( a k α )
r p k α ( ρ ) = ρ a k α ( α = 1 , 2 , … , j )
(3) ρ > m a x ( b k α )
r p k α = m a x ( b k α ) − ρ m a x ( b k α ) − b k ( α − h ) α = 1 , 2 , … , j − 1 1 , α = j
Where ρ is variable. r p k α is the membership of the p-th first indicator corresponding to the k-th secondary indicator at level a. a k ( α − h ) and b k ( α − h ) are the upper and lower limits of the h levels preceding level a for the k-th secondary indicator, respectively. a k ( α + g ) and b k ( α + g ) are the upper and lower limits of the g levels following level level a for the k-th secondary indicator, respectively.

Appendix D: Linearization of nonlinear programming problems

For certain nonlinear programming problems, it can be reformulated as linear programming problems to facilitate the solution process and ensure stable results. For instance, the following equation shows a nonlinear process
min δ 1 + δ 2 + … + δ n s . t . A δ ≤ b
where δ = δ 1 , δ 2 , … , δ n T is the matrices of the corresponding dimensions. A and b are vectors.
To convert the aforementioned issue into a linear programming problem, it is simply necessary to take note of the following fact when u i and v i equal and bigger than 0.
δ i = u i − v i | δ i | = u i + v i
Therefore, we can get u i = δ i + δ i 2 , v i = δ i − δ i 2 . By writing u = u 1 , u 2 , … , u n T , v = v 1 , v 2 , … , v n T , the aforementioned issue can be transformed into an equivalent form
min ∑ i = 1 n u i + v i s . t . A ( u − v ) ≤ b u , v ≥ 0
Here u ≥ 0 indicates that each component of the vector u is greater than or equal to 0.
Combining the above linearization conversion methods, we can substitute the subsequent variables for Equation 7.
H i − H i + 1 − ω ′ ′ i − ω ′ ′ i + 1 = μ i + ν i H i − H i + 1 − ω ′ ′ i − ω ′ ′ i + 1 = μ i − ν i
where H i , H i + 1 are the entropy values of the i-th known metric and its neighbors. w i ′ ′ and w i + 1 ′ ′ are the corresponding weight.
Introducing two new variables ζ i , ϵ i converts w i ′ ′ − w i + 1 ′ ′ and w i ′ ′ − w i + 1 ′ ′ equivalently, we can obtain
ω i ′ ′ − ω i + 1 ′ ′ = ζ i + ϵ i ω i ′ ′ − ω i + 1 ′ ′ = ζ i − ϵ i
Therefore, by utilizing the Equation D.4 and Equation D.5, we can linearize the weight difference between adjacent indicators to derive the relationship of new various, that is ζ i + ϵ i + u i − v i = H i − H i + 1 . However, since the constraints are imposed on each weight rather than the difference of the weights, and introducing new variables to represent separate weights would increase complexity, w i ′ ′ remains a variable in our model.
Bring the aforementioned equation into Equation 7, the linear programming model after variable substitution can be obtained
min ∑ i = 1 n u i + v i ζ i − ϵ i H i − H i + 1 < 0 ∑ i = 1 n w i ′ ′ = 1 ζ i + ϵ i + u i − v i = H i − H i + 1 u i , v i , ζ i , ϵ i ≥ 0 0 ≤ w i ′ ′ ≤ 1

References

  1. Hu, P. Evaluation algorithm of coastal city ecological civilization development level based on improved BP neural network. Journal of Environmental Management 2022, 321, 116039. [Google Scholar] [CrossRef]
  2. Lee, K.l.; Lin, S.c. A fuzzy quantified SWOT procedure for environmental evaluation of an international distribution center. Information Sciences 2008, 178, 531–549. [Google Scholar] [CrossRef]
  3. Zhang, R.; Zhang, X.; Yang, J.; Yuan, H. Wetland ecosystem stability evaluation by using Analytical Hierarchy Process (AHP) approach in Yinchuan Plain, China. Mathematical and Computer Modelling 2013, 57, 366–374. [Google Scholar] [CrossRef]
  4. Li, R.; Zou, Z.; An, Y. Water quality assessment in Qu River based on fuzzy water pollution index method. Journal of environmental sciences 2016, 50, 87–92. [Google Scholar] [CrossRef]
  5. Chen, J.F.; Hsieh, H.N.; Do, Q.H. Evaluating teaching performance based on fuzzy AHP and comprehensive evaluation approach. Applied Soft Computing 2015, 28, 100–108. [Google Scholar] [CrossRef]
  6. Yue-Ju, X.; Shu-Guang, L.; Yue-Ming, H.; Jing-Feng, Y. Soil quality assessment using weighted fuzzy association rules. Pedosphere 2010, 20, 334–341. [Google Scholar]
  7. Xie, L.; Zhong, J.; Chen, F.; Cao, F.; Li, J.; Wu, L. Evaluation of soil fertility in the succession of karst rocky desertification using principal component analysis. Solid Earth 2015, 6, 515–524. [Google Scholar] [CrossRef]
  8. Zhang, X.; Wang, C.; Li, E.; Xu, C. Assessment model of ecoenvironmental vulnerability based on improved entropy weight method. The Scientific World Journal 2014, 2014. [Google Scholar] [CrossRef]
  9. Liu, J.; Liu, C.; Han, W. Efficiently evaluating heavy metal urban soil pollution using an improved entropy-method-based TOPSIS model. Archives of environmental contamination and toxicology 2016, 71, 377–382. [Google Scholar] [CrossRef]
  10. Kucuker, D.M.; Giraldo, D.C. Assessment of soil erosion risk using an integrated approach of GIS and Analytic Hierarchy Process (AHP) in Erzurum, Turkiye. Ecological Informatics 2022, 71, 101788. [Google Scholar] [CrossRef]
  11. Heil, J.; Häring, V.; Marschner, B.; Stumpe, B. Advantages of fuzzy k-means over k-means clustering in the classification of diffuse reflectance soil spectra: A case study with West African soils. Geoderma 2019, 337, 11–21. [Google Scholar] [CrossRef]
  12. Deng, X.; Chen, C. A novel portfolio selection with prospect value constraint and distance measure of IFSs based on the improved entropy-weighted method. Journal of Intelligent & Fuzzy Systems 2020, 39, 3519–3543. [Google Scholar]
  13. He, Y.; Jiao, Z.; Yang, J. Comprehensive evaluation of global clean energy development index based on the improved entropy method. Ecological Indicators 2018, 88, 305–321. [Google Scholar] [CrossRef]
  14. Wang, S.; Xu, Y.; Wang, D.; Gao, B.; Lu, M.; Wang, Q. Effects of industry structures on water quality in different urbanized regions using an improved entropy-weighted matter-elementmethodology. Environmental Science and Pollution Research 2020, 27, 7549–7558. [Google Scholar] [CrossRef]
  15. Xu, H.; Ma, C.; Lian, J.; Xu, K.; Chaima, E. Urban flooding risk assessment based on an integrated k-means cluster algorithm and improved entropy weight method in the region of Haikou, China. Journal of hydrology 2018, 563, 975–986. [Google Scholar] [CrossRef]
  16. Deng, X.; Xu, Y.; Han, L.; Yu, Z.; Yang, M.; Pan, G. Assessment of river health based on an improved entropy-based fuzzy matter-element model in the Taihu Plain, China. Ecological Indicators 2015, 57, 85–95. [Google Scholar] [CrossRef]
  17. Zuo, L.; Dong, S.; Zhu, C.; Shu, L.; Han, G. A cloud resource evaluation model based on entropy optimization and ant colony clustering. The Computer Journal 2015, 58, 1254–1266. [Google Scholar] [CrossRef]
  18. Ouyang, S.; Liu, Z.W.; Li, Q.; Shi, Y.L. A new improved entropy method and its application in power quality evaluation. Advanced Materials Research. Trans Tech Publ 2013, 706, 1726–1733. [Google Scholar]
  19. Torbert, H.; Krueger, E.; Kurtener, D. Soil quality assessment using fuzzy modeling. International Agrophysics 2008, 22, 365–370. [Google Scholar]
  20. Liu, L.; Zhou, J.; An, X.; Zhang, Y.; Yang, L. Using fuzzy theory and information entropy for water quality assessment in Three Gorges region, China. Expert Systems with Applications 2010, 37, 2517–2521. [Google Scholar] [CrossRef]
  21. Qi, Y.; Wen, F.; Wang, K.; Li, L.; Singh, S. A fuzzy comprehensive evaluation and entropy weight decision-making based method for power network structure assessment. International Journal of Engineering, Science and Technology 2010, 2, 92–99. [Google Scholar] [CrossRef]
  22. Li, Z.w.; Huang, J.q.; Li, Y.y.; Guo, W.; Zhu, J.f. Assessment on soil fertility of Dongting Lake wetland area (China) based on GIS and fuzzy evaluation. Journal of Central South University 2011, 18, 1465–1472. [Google Scholar] [CrossRef]
  23. Khalili-Damghani, K.; Tavana, M.; Santos-Arteaga, F.J. A comprehensive fuzzy DEA model for emerging market assessment and selection decisions. Applied Soft Computing 2016, 38, 676–702. [Google Scholar] [CrossRef]
  24. Bo, L.; Cheng, S.; Li, D. Establishment and application of fuzzy comprehensive evaluation of green building design based on data mining. Journal of Intelligent & Fuzzy Systems 2020, 38, 6815–6823. [Google Scholar]
  25. Xie, Q.; Ni, J.Q.; Su, Z. Fuzzy comprehensive evaluation of multiple environmental factors for swine building assessment and control. Journal of Hazardous Materials 2017, 340, 463–471. [Google Scholar] [CrossRef] [PubMed]
  26. Zhang, X.; Wang, Y.; Xiang, Q.; Zhang, H.; Jiang, Z. Remanufacturability evaluation method and application for used engineering machinery parts based on fuzzy-EAHP. Journal of manufacturing systems 2020, 57, 133–147. [Google Scholar] [CrossRef]
  27. Alaoui, Y.L.; Tkiouat, M. Assessing the performance of microfinance lending process using AHP-fuzzy comprehensive evaluation method: Moroccan case study. International Journal of Engineering Business Management 2017, 9, 1847979017736692. [Google Scholar] [CrossRef]
  28. Ouyang, L.Y.; Chen, K.S.; Yang, C.M.; Hsu, C.H. Using a QCAC–Entropy–TOPSIS approach to measure quality characteristics and rank improvement priorities for all substandard quality characteristics. International Journal of Production Research 2014, 52, 3110–3124. [Google Scholar] [CrossRef]
  29. Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): when to use them or not. Geoscientific Model Development 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
  30. Liu, J.P.; Ji, Z.G. Evaluation of the single-factor approach to determining wave exposure. Journal of Coastal Research 2004, 20, 546–552. [Google Scholar]
  31. lin, L.; chao, L. Chinese soil data set based on world soil database (hwsd) (v1.1).
  32. Fischer, G.; Nachtergaele, F.; Prieler, S.; van Velthuizen, H.T.; Verelst, L.; Wiberg, D. Global Agro-ecological Zones Assessment for Agriculture (GAEZ 2008); IIASA: Laxenburg, Austria and FAO, Rome, Italy, 2008. [Google Scholar]
  33. Wei-Xin, L.; ZHANG, X.X.; Bing, W.; Shi-Lei, S.; Yan-Song, C.; Wen-Yang, P.; Da-Yong, Z.; CHENG, S.P. A comparative analysis of environmental quality assessment methods for heavy metal-contaminated soils. Pedosphere 2008, 18, 344–352. [Google Scholar]
Preprints 78483 g001
Figure 1. Weight comparison among different methods for extreme data (a) and normal data (b). IEV is the information entropy value. TEW, IEW1 and OIEW denote the traditional entropy weight method, the improved entropy weight method and the optimized improved entropy weight method, respectively. The blue numbers are the weight values corresponding to the information entropy.
Figure 1. Weight comparison among different methods for extreme data (a) and normal data (b). IEV is the information entropy value. TEW, IEW1 and OIEW denote the traditional entropy weight method, the improved entropy weight method and the optimized improved entropy weight method, respectively. The blue numbers are the weight values corresponding to the information entropy.
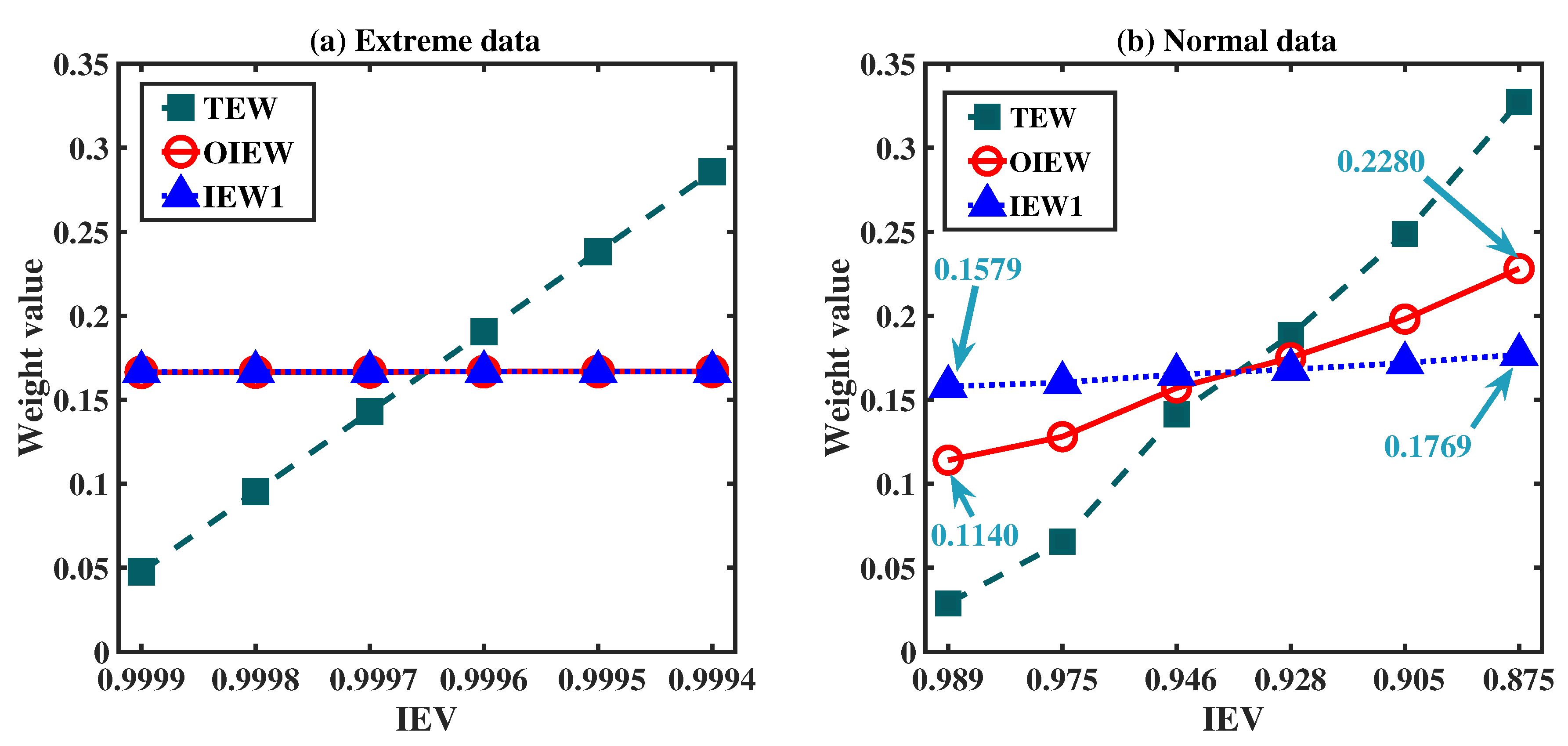
Preprints 78483 g001
Preprints 78483 g002
Figure 2. Q values of extreme data. H d is d-th information entropy value. The black baseline line is 1.
Figure 2. Q values of extreme data. H d is d-th information entropy value. The black baseline line is 1.
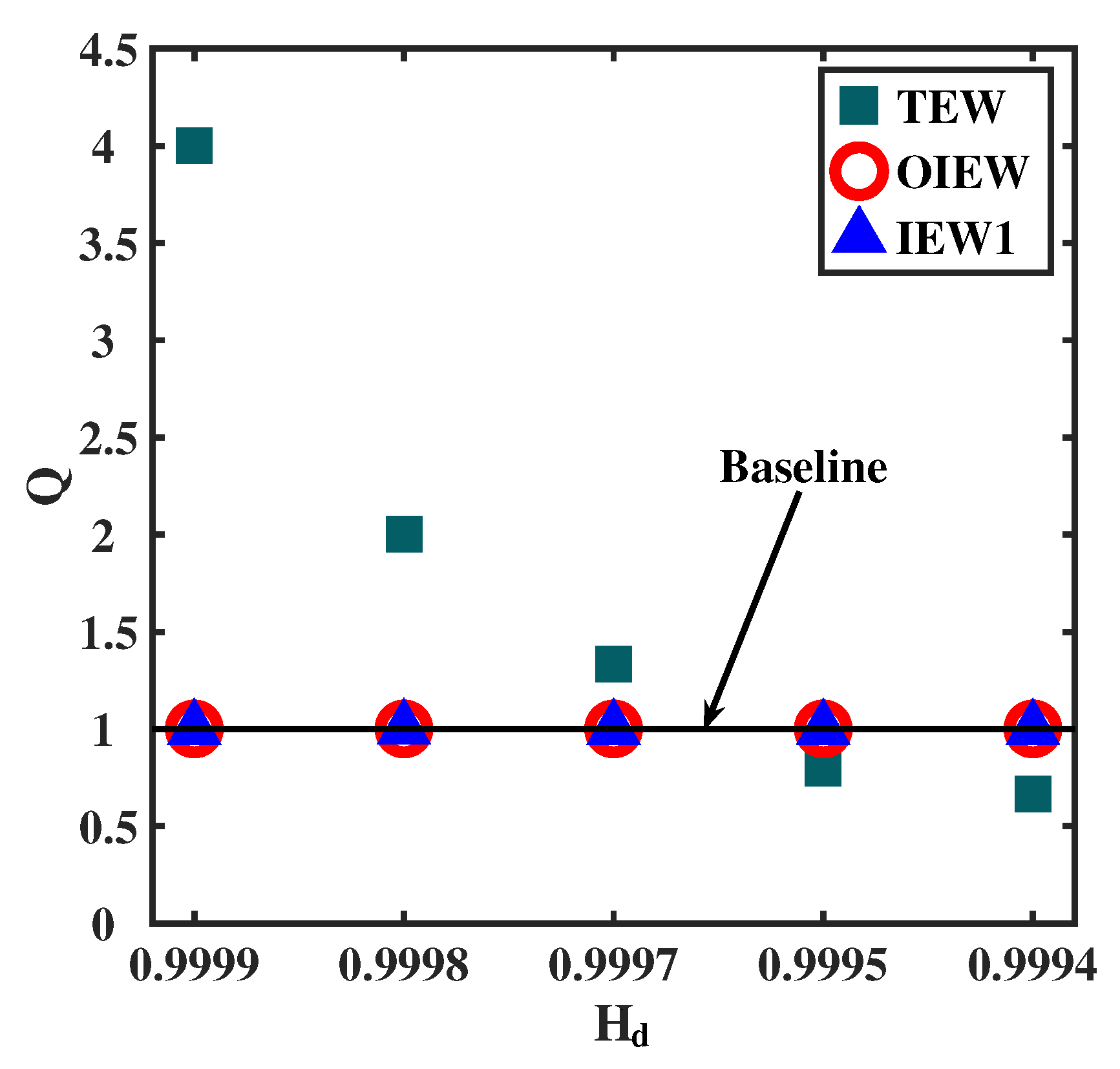
Preprints 78483 g002
Preprints 78483 g003
Figure 3. G values of normal data calculated by different EW methods.
Figure 3. G values of normal data calculated by different EW methods.
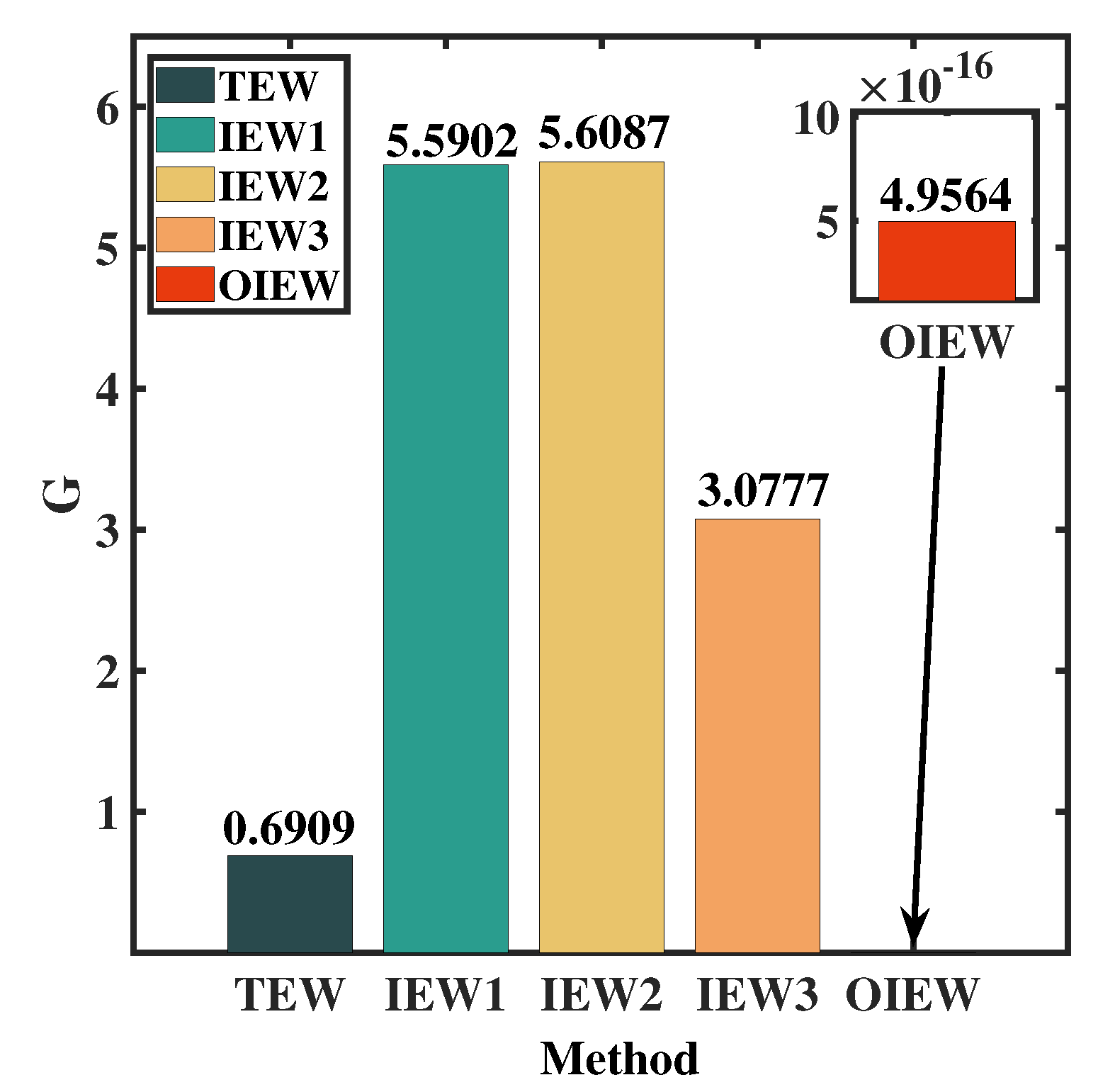
Preprints 78483 g003
Preprints 78483 g004
Figure 4. Soil evaluation results and soil utilization percentage. The orange bars are the evaluation grades. The blue bars represent land use types obtained from Shandong Province of Chinese Soil Database, including farmland (F), grassland (G), woodland (W), residential areas (R), and abandoned land (A). The soil evaluation results are divided into five levels: I (excellent), II (good), III (moderate), IV (poor), and V (extremely poor).
Figure 4. Soil evaluation results and soil utilization percentage. The orange bars are the evaluation grades. The blue bars represent land use types obtained from Shandong Province of Chinese Soil Database, including farmland (F), grassland (G), woodland (W), residential areas (R), and abandoned land (A). The soil evaluation results are divided into five levels: I (excellent), II (good), III (moderate), IV (poor), and V (extremely poor).
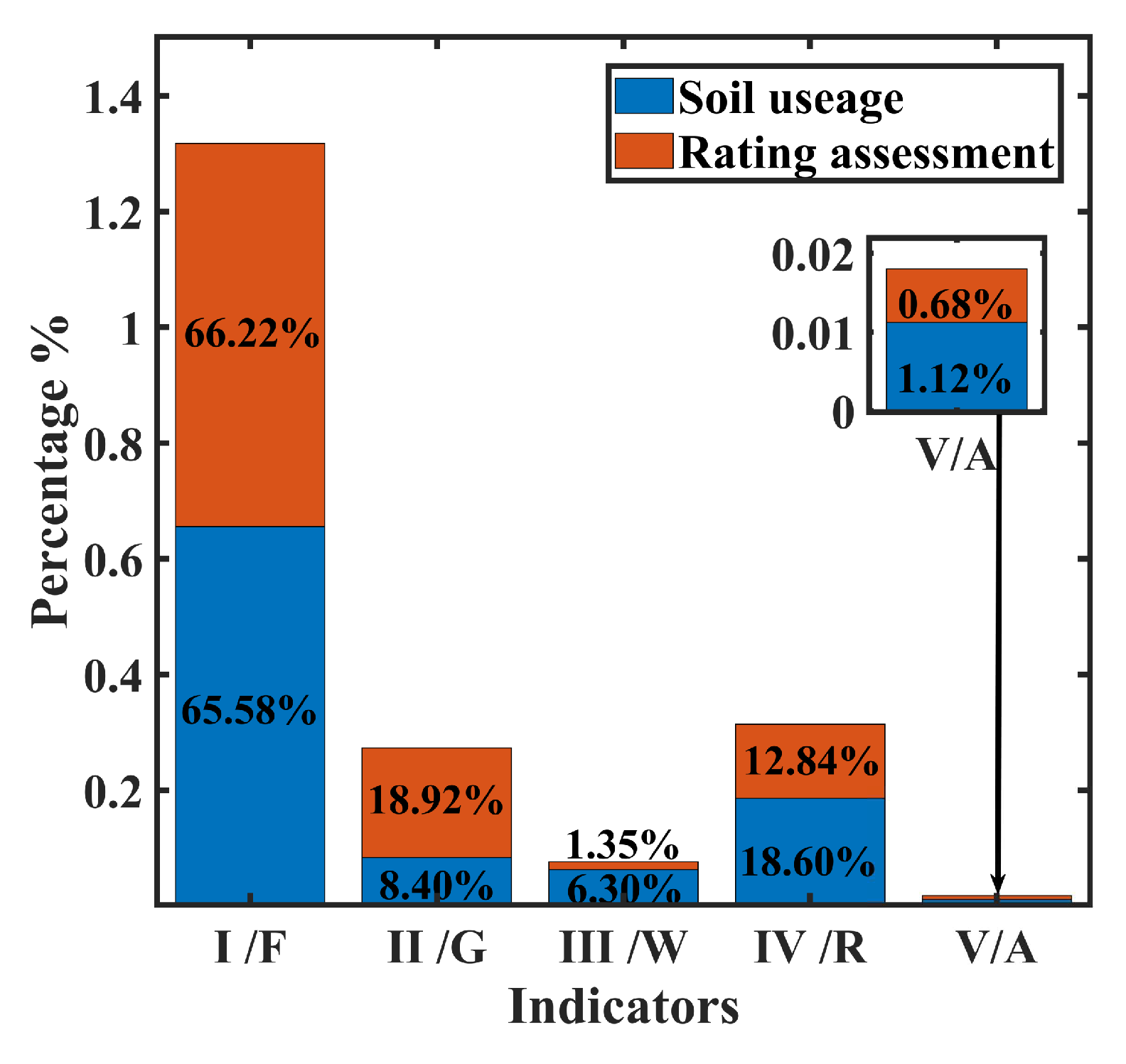
Preprints 78483 g004
Preprints 78483 g005
Figure 5. Comparison of evaluation results between SFE and OIEFC method. Sample ID is the serial number of the soil data. The blue dotted line and the red dashed line are the evaluation results calculated by the SFE method and OIEFC method, respectively. The magenta numbers indicate the serial numbers of the differential evaluation results.
Figure 5. Comparison of evaluation results between SFE and OIEFC method. Sample ID is the serial number of the soil data. The blue dotted line and the red dashed line are the evaluation results calculated by the SFE method and OIEFC method, respectively. The magenta numbers indicate the serial numbers of the differential evaluation results.
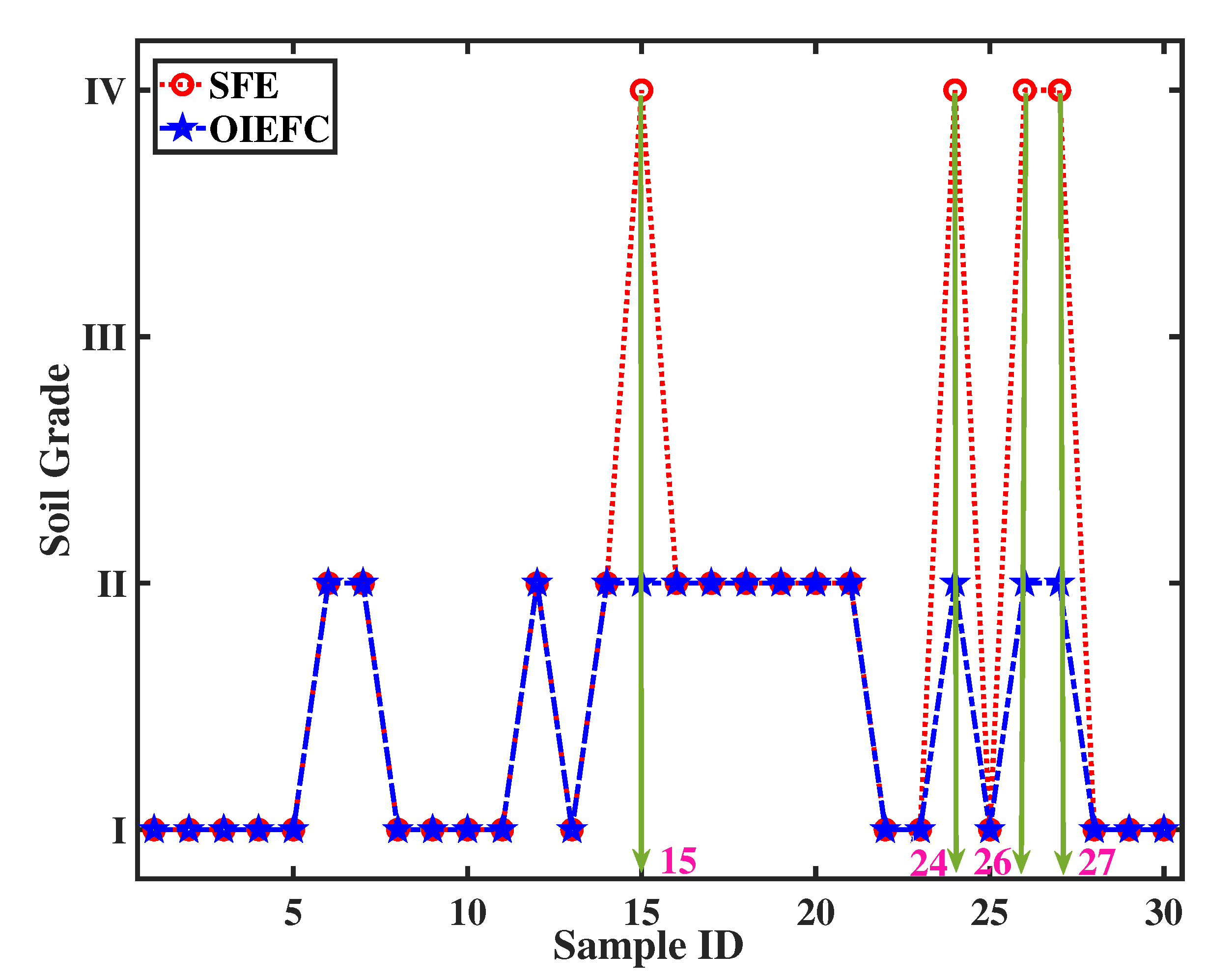
Preprints 78483 g005
Table 1. Weights of TEW method and IEW method. H i represents the i-th information entropy value (IEV). W T E W and W I E W 1 are the weight calculated by the TEW method and IEW1 method, respectively.
Table 1. Weights of TEW method and IEW method. H i represents the i-th information entropy value (IEV). W T E W and W I E W 1 are the weight calculated by the TEW method and IEW1 method, respectively.
Condition (a) Extreme data (b) Normal data
H i 0.9999 0.9998 0.9997 0.9996 0.9995 0.9994 0.989 0.975 0.946 0.928 0.905 0.875
W TEW 0.0476 0.0952 0.1429 0.1905 0.2381 0.2857 0.0288 0.0654 0.1414 0.1885 0.2487 0.3272
W IEW 1 0.1666 0.1666 0.1667 0.1667 0.1667 0.1667 0.1579 0.1602 0.1651 0.1681 0.1719 0.1769
Table 2. Q value of different EW methods for extreme data. The correct factor of IEW1 is approximately 0.99965.
Table 2. Q value of different EW methods for extreme data. The correct factor of IEW1 is approximately 0.99965.
Method (a) TEW method (b) IEW1 method
H i 0.9996 0.9996
H d 0.9999 0.9998 0.9997 0.9995 0.9994 0.9999 0.9998 0.9997 0.9995 0.9994
Q 4.002 2.001 1.333 0.8001 0.6668 1.0003 1.0002 1.0001 0.9999 0.9998
Table 3. Q value of different EW methods for normal data. The correct factor of IEW1 is 0.9305.
Table 3. Q value of different EW methods for normal data. The correct factor of IEW1 is 0.9305.
Method (a) TEW method (b) IEW1 method
H i 0.928 0.928
H d 0.989 0.975 0.946 0.905 0.875 0.989 0.975 0.946 0.905 0.875
Q 6.545 2.882 1.333 0.758 0.576 1.065 1.049 1.018 0.978 0.950
Table 4. G value of normal data. IEW1, IEW2 and IEW3 are the improved entropy weight method obtained by the literature [12,14,18].
Table 4. G value of normal data. IEW1, IEW2 and IEW3 are the improved entropy weight method obtained by the literature [12,14,18].
Method TEW IEW1 IEW2 IEW3
G 0.6909 5.5902 5.6087 3.0777
Table 5. Evaluation values for the chemical and physical indicators. The chemical indicators include organic carbon (OC), potential of hydrogen (PH), cation exchange capacity (CEC), and electrical conductivity (ECE). The physical indicators include soil texture (TEX) and soil bulk density (BULK). The weight values for each indicator should be discussed separately based on the second-level indicator classification.
Table 5. Evaluation values for the chemical and physical indicators. The chemical indicators include organic carbon (OC), potential of hydrogen (PH), cation exchange capacity (CEC), and electrical conductivity (ECE). The physical indicators include soil texture (TEX) and soil bulk density (BULK). The weight values for each indicator should be discussed separately based on the second-level indicator classification.
Indicator/Method IEV TEW IEW1 OIEW
Chemical
Indicator 		OC 0.9837 0.0447 0.2313 0.1752
PH 0.9979 0.0058 0.2278 0.161
CEC 0.9807 0.053 0.2321 0.1782
ECE 0.6733 0.8695 0.3089 0.4856
Physical TEX 0.8932 0.899 0.5327 0.5474
Indicator BULK 0.988 0.101 0.4763 0.4526
Table 6. Difference of evaluation results between ID15 and ID24. Actual measurement data obtained by HWSD dataset which provides raw physical and chemical indicators data for diverse soil indicators. Soil grade calculation results obtained by SFE and OIEFC method.
Table 6. Difference of evaluation results between ID15 and ID24. Actual measurement data obtained by HWSD dataset which provides raw physical and chemical indicators data for diverse soil indicators. Soil grade calculation results obtained by SFE and OIEFC method.
ID ID15 ID24
Actual measurement data Physical
indicator 		TEX 12 12
BULK 1.58 1.6
OC 0.3 0.63
Chemical
indicator 		PH 7.1 6.5
CEC 7 6
ECE 0.1 0.1
Calculation evaluation results SFE II II
OIEFC IV IV
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated