Prediction of Contact Fatigue Performance Degradation Trend Based on Multi-domain Features and Temporal Convolutional Network

Preprint

Article

Prediction of Contact Fatigue Performance Degradation Trend Based on Multi-domain Features and Temporal Convolutional Network

Altmetrics

Downloads

115

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 July 2023

Posted:

05 July 2023

You are already at the latest version

Alerts

Abstract

In order to realize the performance degradation trend prediction accurately, a prediction method based on multi-domain features and temporal convolutional network (TCN) is proposed. Firstly, construct a high-dimensional feature set in the multi-domain of vibration signals, and use comprehensive evaluation indicators to preliminarily screen performance degradation indexes with good sensitivity and strong trend. Secondly, the kernel principal component analysis (KPCA) method is adopted to eliminate redundant information between multi-domain features, and construct a health index (HI) based on convolutional auto-encoder (CAE) network. Thirdly, a TCN-based performance degradation trend prediction model is constructed, and direct multi-step prediction is used to predict the performance degradation trend of the monitored object. On this basis, the validity of the proposed method is verified using the bearing public data, and it is successfully applied to performance degradation trend prediction of rolling contact fatigue specimen. The results show that the feature set can be reduced from 14 dimensions to 4 dimensions by using KPCA, while 98.33% of the information of the original feature set is retained. Furthermore, the method of constructing HI based on CAE network is effective. The change process of the HI constructed truly reflects the performance degradation process of the rolling contact fatigue specimen. Compared with the two commonly used HI construction methods, auto-encoding (AE) network and gaussian mixture model (GMM), this method has obvious advantages. At the same time, the prediction model based on TCN can accurately predict the performance degradation of the rolling contact fatigue specimen with the root mean square error 0.0146 and the mean absolute error 0.0105, which has better performance and higher prediction accuracy than the prediction model based on the long short-term memory (LSTM) network and the gated recurrent unit (GRU). This method has general significance and may be extended to the performance degradation prediction of other mechanical equipment/parts.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

With the rapid progress of manufacturing technology, the structure of mechanical equipment becomes more and more complex, and the operating conditions of parts become more and more severe [1], and the probability of failure increases accordingly. Therefore, the predictive monitoring of mechanical equipment/components is particularly important. It is helpful for the scientific formulation of maintenance strategies and the health management of equipment. At the same time, the application of technologies such as the internet, smart sensors and wireless communication in the mechanical field enables more information to be collected. These massive data reflect the health status and performance changes of mechanical equipment/components, and contain rich information. It has prompted the field of mechanical health monitoring to enter the era of "big data". However, the existing fault diagnosis and early warning methods are difficult to reliably realize the fault diagnosis and early warning of the status of mechanical equipment/components under the background of massive data, which makes the data-driven mechanical equipment/component health monitoring technology arouse extensive attention of researchers [2,3]. Therefore, how to deeply mine and utilize historical and real-time data in massive data to accurately grasp the health status of mechanical equipment/components and accurately analyze its performance degradation trend has become one of the research hotspots in the condition monitoring field [4].

Contact fatigue is mainly due to damage caused by cyclic loading below the contact surface, until it extends to the surface to form pitting or spalling. The failure process is essentially the initiation and propagation of cracks. Contact fatigue strength is an important index that affects the service performance of basic components such as gears and bearings. At present, the only way to obtain the contact fatigue properties of materials is through rolling contact fatigue tests, which take a long time and are labor-intensive. Therefore, it is of great significance to realize the accurate prediction of the performance degradation trend of the rolling contact fatigue specimen. It can not only predict the fatigue failure time point of the specimens in advance and shorten the test time, but also enrich the ways to obtain the contact fatigue properties of the materials. That is to say, in the context of big data, the contact fatigue properties of materials can be obtained by analyzing historical data of materials, rather than relying only on rolling contact fatigue tests.

To realize the prediction of the degradation trend of the monitored objects, the core work mainly includes two parts. One is to construct a Health Index (HI) that can truly reflect the performance degradation process of the monitored object throughout its life cycle. The other is to build a predictive model that can accurately predict the changing trend of HI. In the construction of HI, one idea is to extract features from raw data and use them for state monitoring. This method is widely used, such as extracting single-domain multi-features, multi-domain multi-features, as well as directly extracting deep features from raw data, etc., and take the extracted features directly as HI or take the dimension-reduced features as HI [5,6,7,8,9,10,11,12]. Another idea is to divide the feature data into healthy samples and test samples based on the extracted features, measure the health degree of the test samples by calculating the similarity, and define the health degree as HI. The change process of the health degree is regarded as the process of performance degradation [13,14,15,16]. In addition, some researchers directly use the raw vibration signal as the input of the neural network [17,18,19,20], and use the deep features contained in the extracted signal as a HI. However, the first two methods have problems such as incomplete use of the state information of the monitored object and ignoring the nonlinear relationship between the characteristics. The third method needs to fully consider the operating characteristics of the monitored objects, because different monitored objects have different mechanical structures, operating environments and damage mechanisms. In terms of building degradation trend prediction models, most researchers use shallow machine learning methods such as support vector machine (SVM) and extreme learning machine (ELM) [21,22,23,24], or use the long short-term memory (LSTM) neural network, the gated recurrent unit (GRU) model and the deep learning method optimized on this basis [25,26,27,28,29,30,31,32]. However, it is difficult for shallow machine learning methods to fully exploit the correlation between data, which will have a great impact on the accuracy of prediction results. While for deep learning methods, as far as the current recurrent neural network model, it is most suitable for sequence data prediction and still difficult to perform a large number of parallel calculations due to the network structure, which affects the calculation speed of the model.

The vibration signal contains the most essential information of the operating state of the monitored object [33]. In this paper, a research on the performance degradation prediction of the rolling contact fatigue specimen based on the vibration signal is carried out. Aiming at the shortcomings of existing performance degradation prediction research, such as information loss when building HI, poor parallel computing performance and small receptive field when constructing prediction models, combined with the non-stationary and nonlinear vibration characteristics of the monitored object, as well as the timing characteristics of performance degradation, a performance degradation trend prediction method based on multi-domain features and temporal convolutional network (TCN) is proposed, and the effectiveness of the method is verified by using the bearing public data. On this basis, relying on the monitoring data of the rolling contact fatigue testing machine independently developed by the research group, the accurate performance degradation prediction of the rolling contact fatigue specimen is realized.

2. Theory and Method

2.1. Multi-domain Feature Extraction and Feature Screening

2.1.1. Multi-domain Feature Extraction

In view of the fact that the information contained in a single feature or single-domain feature has certain limitations, it cannot fully reflect the complete process of the performance degradation of the monitored object. Therefore, this paper extracts the vibration signal from time domain, frequency domain and time-frequency domain. Note that the discrete vibration signal value collected each time during the test is

x (n) = {x_{1}, x_{2}, x_{3}, \dots x_{N - 1}, x_{N}}

, where

N

is the number of sampling points each time. For the convenience of subsequent description, the extracted features are numbered.

Time domain analysis is to describe vibration signals through statistical features, including dimensional indicators and dimensionless indicators. In this paper, the 7 dimensional features extracted such as mean and root mean square value, and 6 dimensionless features extracted such as skewness index and kurtosis index are shown in Table 1 [34].

The frequency domain analysis is to transform the vibration signal into the frequency domain through Fourier Transform (FT), and then analyze the obtained signal spectrogram. Compared with time domain analysis, it can display more details of fault characteristics. In this paper, the 12 frequency domain features extracted such as the frequency amplitude mean and frequency amplitude variance are shown in Table 2 [34], where

s (k)

represents the spectrum obtained by the Fast Fourier Transform (FFT) of each sampled signal, and

f_{k}

represents the frequency value of the k-th spectral line.

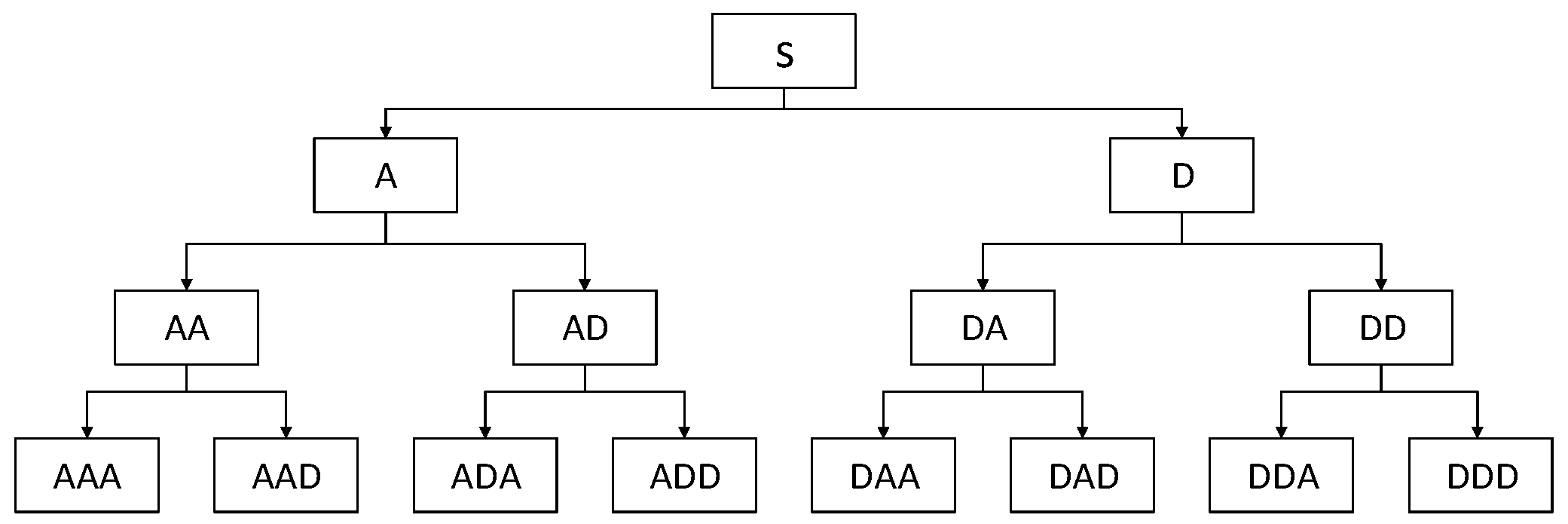
Time-frequency analysis can capture transient characteristics, making up for the limitation that a single time-domain analysis or frequency-domain analysis cannot fully reflect fault characteristics when dealing with complex non-stationary signals. In this paper, the wavelet packet transform is used to extract the time-frequency domain features of the vibration signal, and the wavelet basis selects the db3 function to decompose the signal in three layers, as shown in Figure 1.

After the original signal is decomposed by wavelet packet, the second norm of the node coefficient is called the node energy. When the monitored object fails, some node energy may change. Therefore, the ratio of the node energy to the total node energy in the corresponding decomposition layer is used as the time-frequency domain feature parameter.

e_{i} = {‖ c {(t)}_{i} ‖}_{2}

(1)

E_{i} = e_{i} / \sum_{m = 1}^{M} e_{m}

(2)

where

e_{i}

represents the energy of the i-th node coefficient;

c {(t)}_{i}

represents the wavelet packet coefficient of the i-th node decomposed at each layer; M represents the total number of nodes obtained by each layer decomposition.

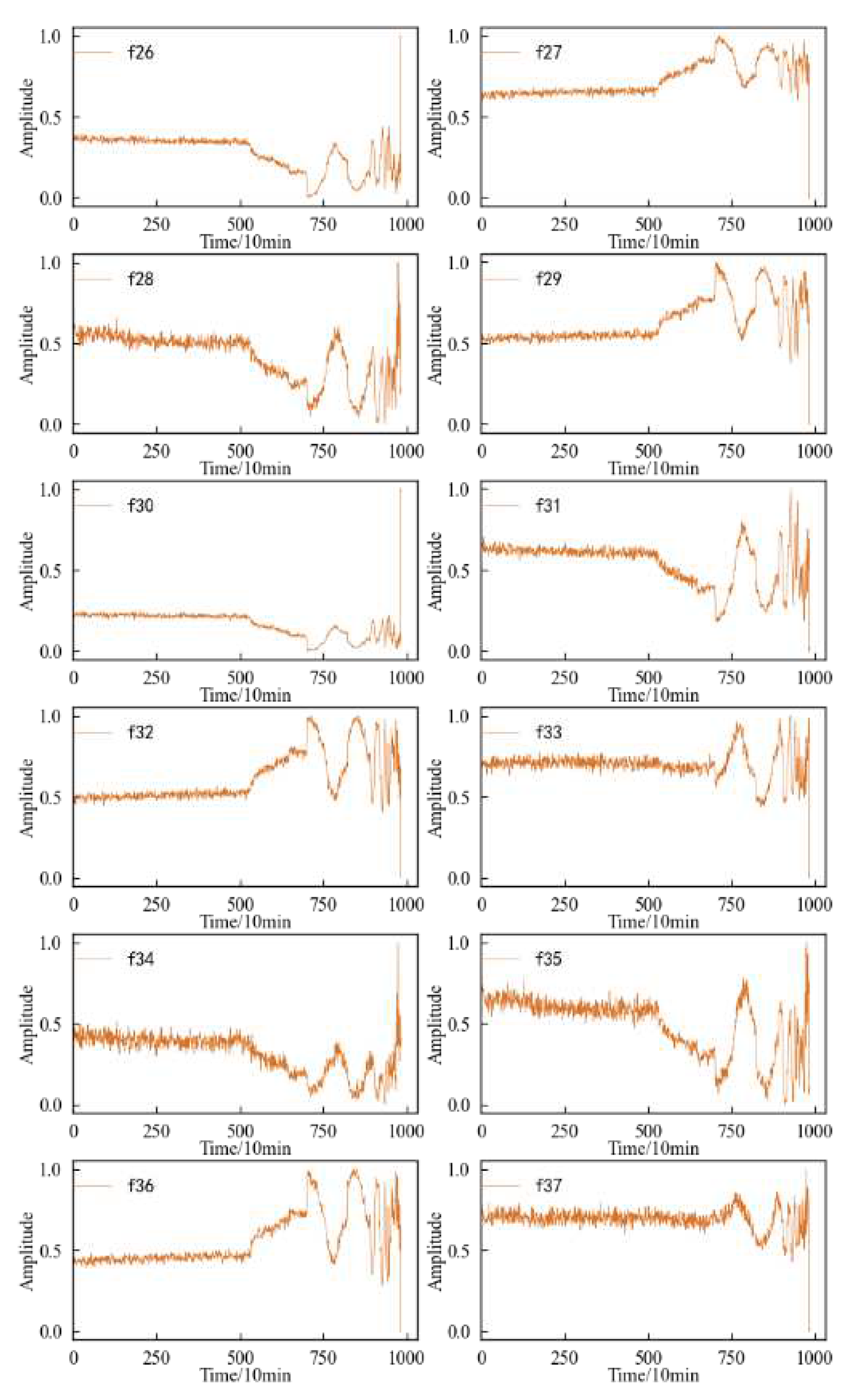
Considering the features number and the decomposition degree of the signal, this paper selects a total of 12 feature parameters of the energy ratio of each node in the second and third layers of the signal wavelet packet decomposition as the time-frequency domain features. According to the position of each nod e in the wavelet packet signal decomposition tree diagram shown in Figure 1, for the second layer and the third layer in order from left to right, the eigenvalues calculated by the coefficients of each node are numbered as f₂₆-f₂₉ and f₃₀-f₃₇.

2.1.2. Feature Screening

A total of 37 multi-domain features have been extracted based on the original vibration signal, but not every feature can well reflect the performance degradation process of the monitored object. Therefore, it is unscientific to screen features only based on the visualization results of features, and it is necessary to establish evaluation indicators to get the optimal feature set. In this paper, the monotonicity of features, the correlation between features and the trend evaluation index of features are integrated [35], and a comprehensive evaluation index Ch(F) is constructed for feature screening. It should be noted that, since the change of the feature may show a downward trend with time, and its trend value is negative, the trend value in formula (3) takes an absolute value.

\begin{array}{l} C h (F) = α_{1} M o n (F) + α_{2} \bar{C o n (F)} + α_{3} | T r e (F) | \\ s . t . \begin{matrix} \sum_{i = 1}^{3} α_{i} = 1 \end{matrix}, α_{i} > 0 \end{array}

(3)

where

α_{1} 、 α_{2} 、 α_{3}

represents the proportion of monotonicity, correlation mean and trend of the feature respectively, and its value can be optimized according to the service environment and performance degradation characteristics of the monitored object. The definitions of three evaluation indicators are shown in formulas (4), (5) and (6), respectively.

M o n (F) = \frac{1}{N - 1} | S (\frac{d}{d F} > 0) - S (\frac{d}{d F} < 0) |

(4)

\bar{C o n (F)} = \frac{1}{N} \sum_{j = 1}^{N} | C o n (F, F_{j}) |

(5)

T r e (\tilde{F}, \tilde{T}) = \frac{N (\sum_{i = 1}^{N} {\tilde{f}}_{i} {\tilde{t}}_{i}) - (\sum_{i = 1}^{N} {\tilde{f}}_{i}) (\sum_{i = 1}^{N} {\tilde{t}}_{i})}{\sqrt{[N \sum_{i = 1}^{N} {\tilde{f}}_{i}^{2} - {(\sum_{i = 1}^{N} {\tilde{f}}_{i})}^{2}] [N \sum_{i = 1}^{N} {\tilde{t}}_{i}^{2} - {(\sum_{i = 1}^{N} {\tilde{t}}_{i})}^{2}]}}

(6)

In formula (4),

N

represents the number of samples in the feature

F

;

d / d F

represents the derivation result of the feature F; S represents the number of

d / d F

is greater than zero or less than zero. In formula (5), if there are N feature sequences, the correlation between the feature and the features including itself can be obtained according to formula (7) (the correlation between the feature and itself is 1), and then the obtained value can be substituted into formula (5) can be used to obtain the mean correlation of features. In formula (6),

{\tilde{f}}_{i}

represents the i-th value in the rank sequence

\tilde{F}

of the feature sequence

F

;

{\tilde{t}}_{i}

represents the i-th value in the rank sequence

\tilde{T}

of the time series

T

C o n (F_{1}, F_{2}) = \frac{\sum_{i = 1}^{N} (f_{1, i} - {\bar{F}}_{1}) (f_{2, i} - {\bar{F}}_{2})}{\sqrt{\sum_{i = 1}^{N} {(f_{1, i} - {\bar{F}}_{1})}^{2} \sum_{i = 1}^{N} {(f_{2, i} - {\bar{F}}_{2})}^{2}}}

(7)

where

F_{1}, F_{2}

represents any two feature sequences;

N

represents the number of samples in the feature;

f_{1, i}

and

{\bar{F}}_{1}

represents the i-th eigenvalue and mean of the feature

F_{1}

, respectively;

f_{2, i}

and

{\bar{F}}_{2}

represents the i-th eigenvalue and mean of the feature

F_{2}

, respectively.

In order to get the features that are sensitive to the performance degradation process of the monitored object, the monotonicity, correlation mean and trend of 37 multi-domain features are calculated according to equations (4), (5) and (6). On this basis, the comprehensive evaluation index value of each feature is calculated according to formula (3), and the features with larger comprehensive evaluation index value are selected to form the optimal feature set.

2.2. Construction of Health Index

The construction of the HI is closely related to the extracted vibration signal characteristics, and the ideal HI can clearly reflect the performance degradation process of the monitored object in the whole life cycle. Aiming at the information loss problem faced by the existing one-dimensional HI, on the basis of above multi-domain feature extraction, this paper adopts kernel principal component analysis (KPCA) to reduce the feature dimension, and uses convolutional auto-encoding (CAE) network to build HI.

2.2.1. Feature Dimensionality Reduction Based on KPCA

The dimension of the preferred feature set obtained by the aforementioned method is still high, which will bring dimensional disaster to subsequent calculations. At the same time, there is coupling between the features of the high-dimensional feature set, which will lead to information duplication and overfitting. Therefore, it is necessary to reduce the dimension of the preferred feature set to retain as much effective information as possible while reducing the dimension of the feature set.

Considering the non-stationary and nonlinear characteristics of vibration signals in the process of performance degradation of most monitored objects, it is more general to select a dimension reduction method suitable for nonlinear operations for feature dimension reduction. In this paper, the KPCA method is used to reduce the dimension of the preferred feature set. This method uses the kernel function to effectively capture the nonlinear characteristics of the data [14], and non-linearly maps the linearly inseparable data in the low-dimensional space to the high-dimensional space, so as to realize the linearity of the data [36,37].

Let the original data set be

X_{1} = {x_{1}, x_{2}, \dots x_{n}}

, where

x_{i}

represents a sample, and each sample has m features, which is mapped

X_{1}

to a high-dimensional space

F

through a nonlinear mapping function

ϕ (x)

to get

ϕ (X_{1})

. Assuming that the mapping relationship has been decentralized, ie

\sum_{i = 1}^{n} ϕ (x_{i}) = 0

, the covariance matrix of

ϕ (X_{1})

is:

C = \frac{1}{n} ϕ (X_{1}) ϕ {(X_{1})}^{T}

(8)

Let the eigenvalue of C be

λ

and the eigenvector be

v

, then

λ v = C v

(9)

Since

1 / n

is a coefficient, it can be omitted. When

λ \neq 0

, combining equations (8) and (9), then

v = \frac{1}{λ} \sum_{i = 1}^{n} ϕ (x_{i}) ϕ {(x_{i})}^{T} \cdot v

(10)

Note that

ϕ {(x_{i})}^{T} \cdot v

is a scalar, so there is a set of coefficients

ω = {[ω_{1}, ω_{2}, \dots, ω_{n}]}^{T}

such that:

v = \sum_{j = 1}^{n} ω_{j} ϕ (x_{j}) = ϕ (X_{1}) ω

(11)

Combining formula (8) and formula (9), substituting formula (11) into formula (11) can be obtained:

λ ϕ (X_{1}) ω = ϕ (X_{1}) ϕ {(X_{1})}^{T} ϕ (X_{1}) ω

(12)

Multiply both ends of the above equation by

ϕ {(X_{1})}^{T}

, get:

λ ϕ {(X_{1})}^{T} ϕ (X_{1}) ω = ϕ {(X_{1})}^{T} ϕ (X_{1}) ϕ {(X_{1})}^{T} ϕ (X_{1}) ω

(13)

Define matrix

K = {(X_{1})}^{T} ϕ (X_{1})

, then

K

is a symmetric positive semi-definite matrix of

n \times n

order, Equation (13) can be simplified as:

λ ω = K ω

(14)

where

ω

and

λ

are the eigenvectors and eigenvalues of

K

, respectively.

Let the eigenvalue of

K

λ_{1} \geq λ_{2} \geq \dots \geq λ_{n}

, and take the first

p

eigenvalues to reduce the dimension. Normalize the eigenvectors in

F

, even if

v_{k}^{T} v_{k} = 1

(k = 1, 2, \dots, p)

, correspondingly, according to equations (11) and (14), get:

λ_{k} ω_{k}^{T} ω_{k} = 1 (k = 1, 2, \dots, p)

(15)

After obtaining the eigenvector of

K

, divide by

\sqrt{λ_{k}}

to achieve normalization.

And each principal component of

X_{1}

in space

F

is the projection of

ϕ (x_{i})

on the eigenvector

v_{l}

(l = 1, 2, \dots, n)

C

, namely:

ϕ {(x_{i})}^{T} v_{l} = \sum_{j = 1}^{n} ω_{l j} ϕ {(x_{i})}^{T} ϕ (x_{j}) = \sum_{j = 1}^{n} ω_{l j} K_{i j}

(16)

where

ω_{l j}

represents the j-th value in

ω_{l}

On this basis, the principal component can be obtained according to the matrix

K

and its eigenvector, and the kernel function

k (x, y)

is usually used to obtain

K

, namely:

K_{i j} = ϕ {(x_{i})}^{T} ϕ (x_{j}) = k (x_{i}, x_{j})

(17)

It should be noted that the above calculation process is carried out on the basis of

ϕ (X_{1})

decentralization, specifically:

\tilde{ϕ} (X_{1}) = ϕ (X_{1}) - I_{N} ϕ (X_{1})

(18)

where

I_{N}

represents

1 / N

multiplied by the

N \times N

-order identity matrix, and correspondingly, the result after decentralization of

K

is:

\tilde{K} = K - I_{N} K - K I_{N} + I_{N} K I_{N}

(19)

Therefore, the contribution rate of the k-th principal component in F is calculated by the ratio of

λ_{k}

\sum_{i = 1}^{n} λ_{i}

, and the contribution rate of the principal component represents the percentage of the information contained in the principal component to all the information in

ϕ (X_{1})

[38].

2.2.2. Construction of HI Based on CAE Network

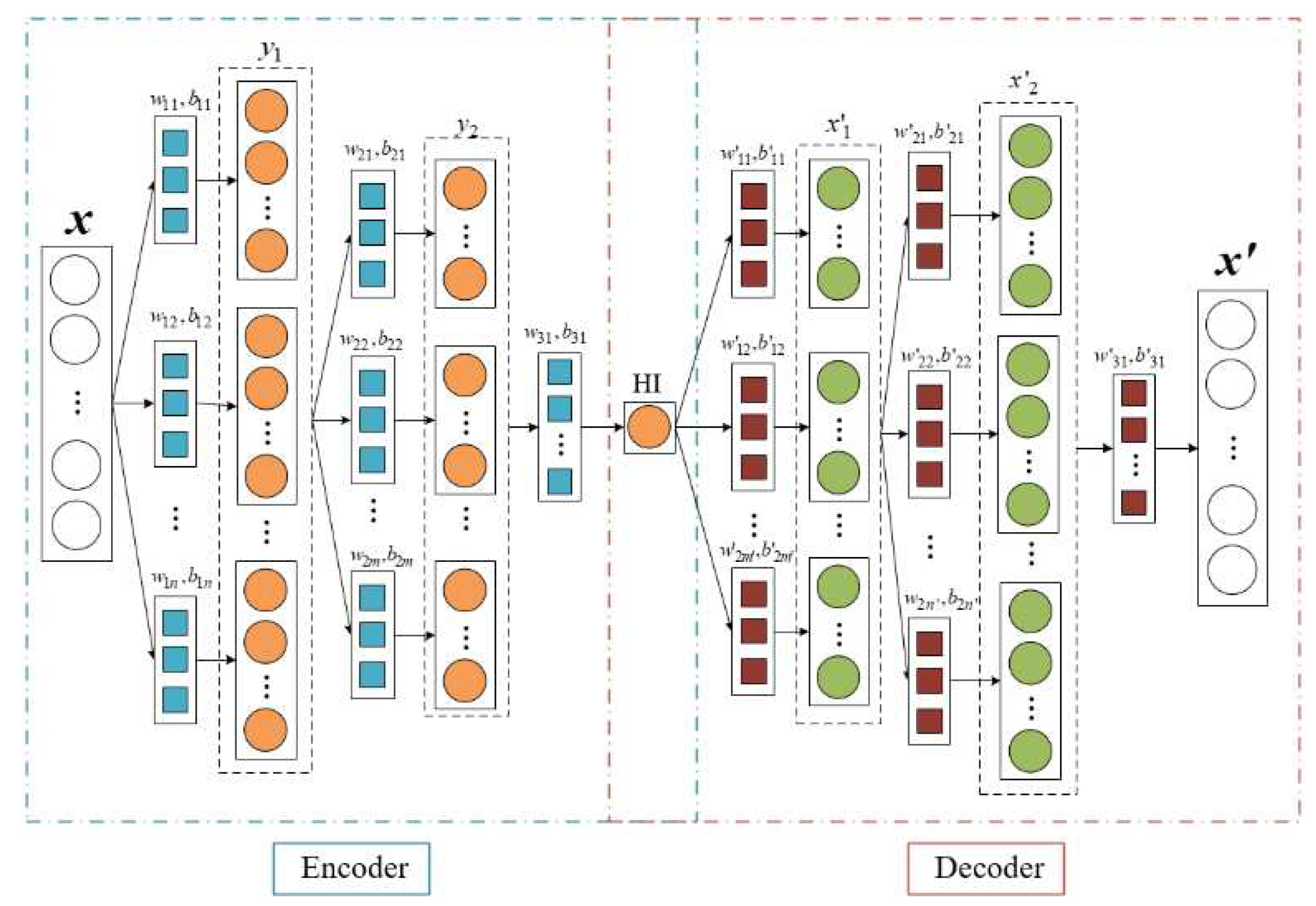
Convolution Auto Encoders (CAE) network is a network model derived from Auto Encoders (AE) network, which converts the encoding and decoding calculation process of data from conventional linear layers to convolution layers to better obtain data deep nonlinear information. The simple CAE network structure is shown in Figure 2.

In the encoding stage, the input information is encoded through multi-layer convolution operations, and finally a one-dimensional encoded feature is obtained. For a one-dimensional input sequence

x

, the one-dimensional convolution operation at each layer is as follows:

y_{k} = f (w_{k} \cdot x + b_{k})

(20)

where

w_{k}

represents the k-th convolution kernel of the convolutional layer;

b_{k}

represents the corresponding bias; “

\cdot

” represents the convolution operation;

f

represents the activation function.

In the decoding stage, the encoded features are used as input, and the dimension of the original information is reconstructed through layer-by-layer one-dimensional transposed convolution. The 1D transposed convolution operation for each layer is as follows:

x_{k}' = h (w'_{k} * y + b'_{k})

(21)

where

y

represents the input sequence of the transposed convolution;

w'_{k}

and

b'_{k}

represent the k-th convolution kernel and the corresponding bias of the transposed convolution, respectively; “

*

” represents the transposed convolution operation;

h

represents the activation function.

Compared with the fully connected layer in the ordinary AE network, this paper uses the convolution layer in the CAE network, which has stronger nonlinear mapping ability.

2.3. Performance Degradation Prediction

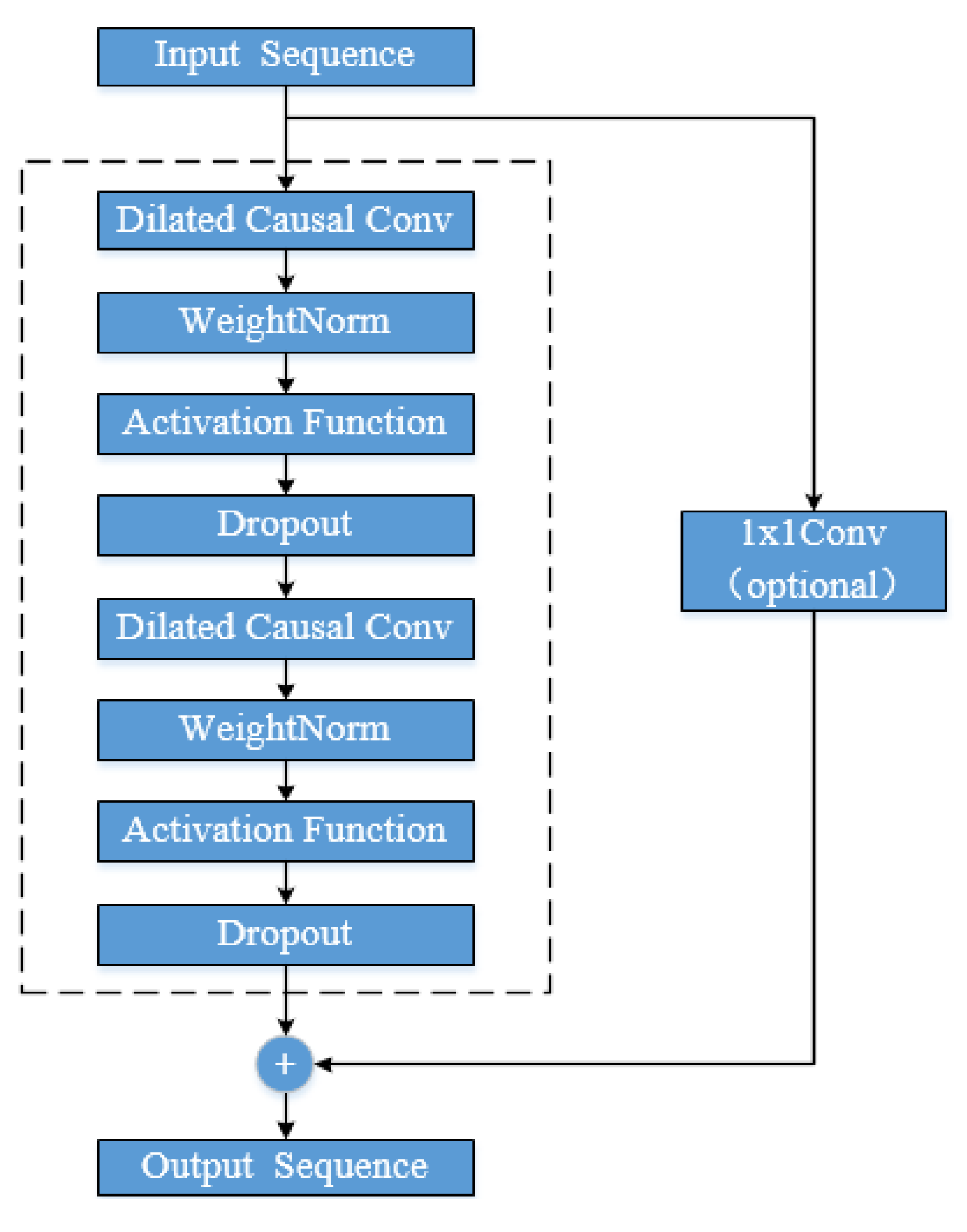
The HI constructed above can reflect the degradation process of the performance of the monitored object. Therefore, the prediction of the performance degradation trend of the monitored object is essentially the prediction of the HI value. HI is one-dimensional time series data that changes with time. Aiming at the shortcomings of the commonly used prediction models based on recurrent neural networks, such as low parallel computation and small receptive field for input data, this paper builds the performance degradation trend prediction model of the monitored object based on the Temporal Convolutional Network (TCN) and realizes the prediction. TCN adopts the structure of one-dimensional full convolution, causal convolution, dilated convolution and residual connection, which has the advantages of large receptive field, strong parallel computing and can weaken the gradient problem [39,40].

2.3.1. Temporal Convolutional Networks

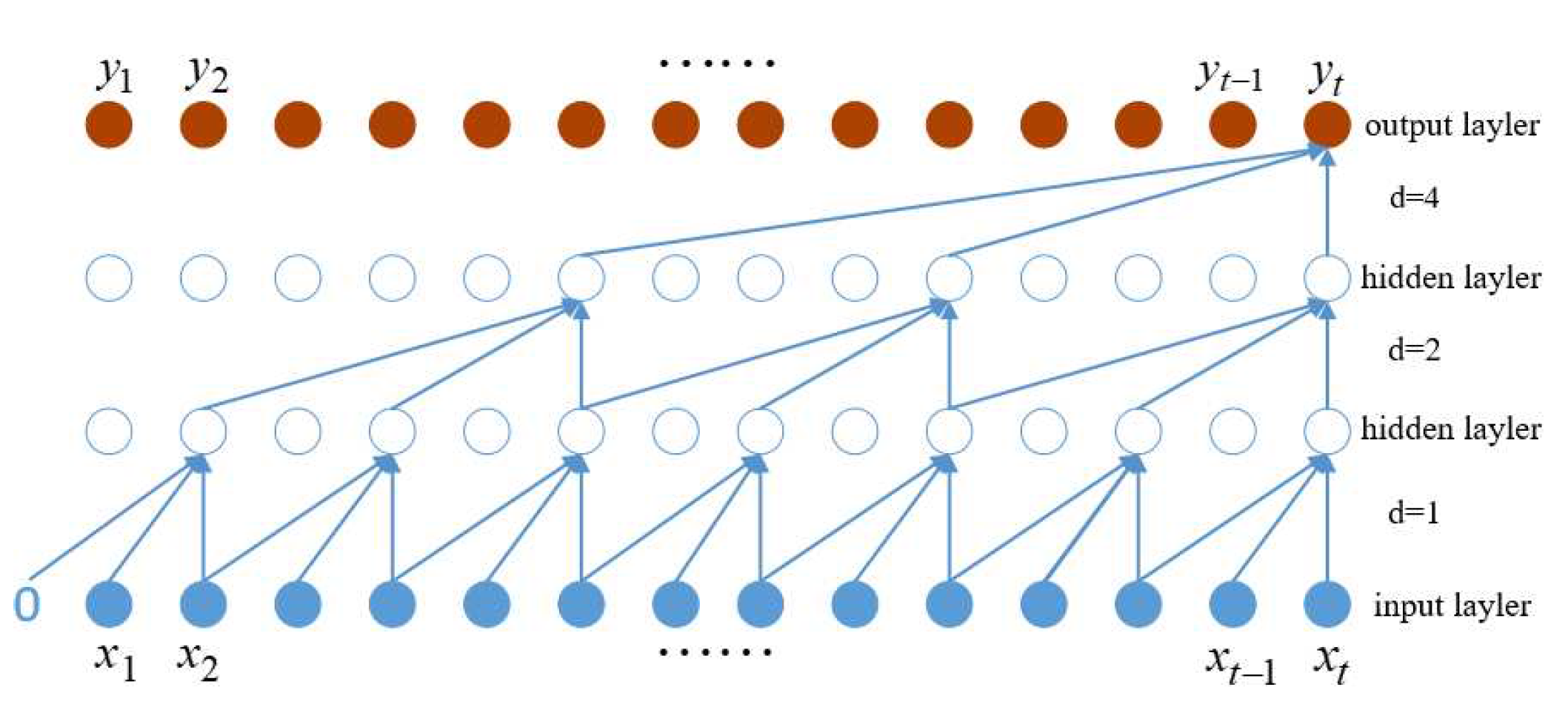
Figure 3 illustrates the combined process of representing one-dimensional full convolution, causal convolution, and dilated convolution with dilated causal convolution, where the input sequence is X = {x₁,x₁,⋯,x_t−1,x_t}, the output sequence after the three-layer one-dimensional dilated causal convolution operation with a convolution kernel size of 3 is Y = {y₁,y₁,⋯,y_t−1,y_t}, and the dilation coefficient in the convolution calculation

d \in N^{*}

, generally d = 2.

The receptive field is related to the size of the convolution kernel, the number of layers in the convolution calculation and the expansion coefficient. And its calculation formula is:

v = 1 + \sum_{i = 0}^{l - 1} (k - 1) \cdot b_{i}

(22)

where k represents the size of the convolution kernel; l represents the number of convolution layers in the network; b represents the base of the expansion coefficient, usually set b = 2.

In TCN, given a one-dimensional input sequence

x \in R^{n}

and a convolution kernel

f : {0, 1 \dots k - 1} \to R

, the calculation result of the dilated causal full convolution at position 3 of the sequence is:

F (s) = \sum_{i = 0}^{k - 1} f (i) \cdot x_{s - d \cdot i}

(23)

where

x_{s - d \cdot i}

represents the (

s - d \cdot i

)-th element in the previous layer, and the other parameters have the same meanings as before.

In addition, TCN uses residual block connection to increase the network depth. By connecting multiple residual blocks together, the gradient problem can be effectively weakened and the model receptive field can be further increased. The form of each residual block is shown in Figure 4.

2.3.2. Performance Degradation Prediction Based on TCN

Data-driven forecasting can be divided into single-step prediction and multi-step prediction. Since single-step prediction can only predict the value of the next moment, it is of little practical engineering significance. Therefore, this paper adopts multi-step prediction.

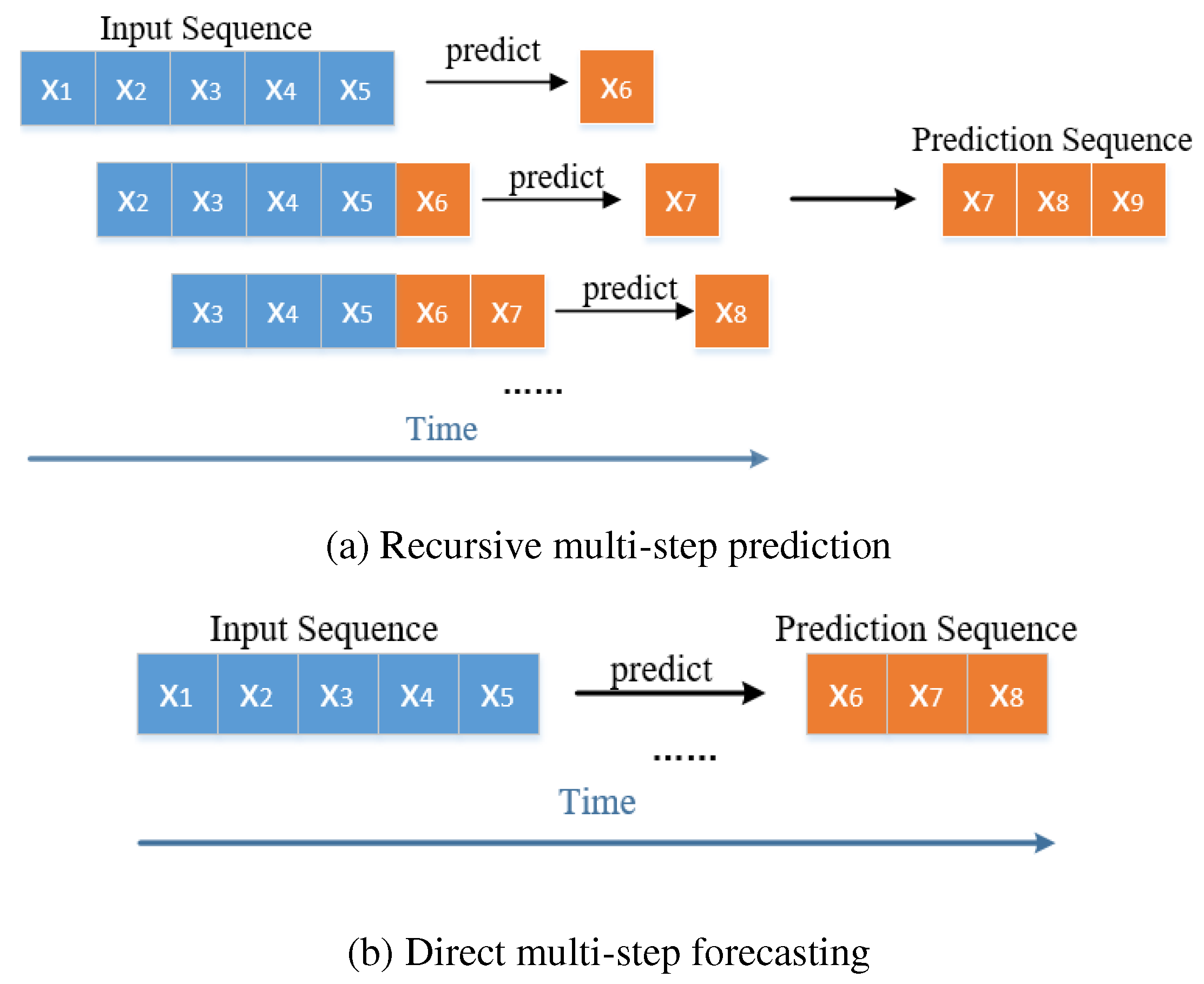
The strategy of multi-step forecasting is divided into direct forecasting and recursive forecasting [4], as shown in Figure 5. There is only one time point for each prediction in recursive prediction. Since the errors of each prediction will accumulate, it may eventually cause a large deviation between the predicted sequence and the actual value. While direct prediction is to predict the target sequence at one time. Since there are many time points for each prediction, the prediction model is required to be better. Comparing two forecasting strategies and considering the engineering application value, this paper chooses direct forecasting.

The process of using direct multi-step prediction to predict the performance degradation of the monitoring object is as follows: 1) Combine the HI samples number of the monitored objects, divide them into training sets and test sets according to an appropriate ratio, and use the spatial phase reconstruction technology to form the training set and test set of the prediction model respectively. And set the time step and prediction step of each input; 2) Set the key parameters of the prediction model and model training, input the training set into the prediction model, use the obtained predicted value and the actual value to calculate the error, and optimize the hyperparameters in the model through error backpropagation. This cycle is repeated until the set number of training times is reached or the prediction error reaches the threshold; 3) Input the test set into the trained model to obtain the predicted value, and calculate the evaluation index based on the error between the predicted value and the actual value, and evaluate the prediction ability of the model.

In this paper, the root mean square error (RMSE) and the mean absolute error (MAE) are used as the evaluation indicators of the model, and their calculation formulas are:

R M S E = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} {(\hat{y} - y)}^{2}}

(24)

M A E = \frac{1}{N} \sum_{i = 1}^{N} | \hat{y} - y |

(25)

where

\hat{y}

represents the predicted value of the model, and

y

represents the true value.

3. Verification

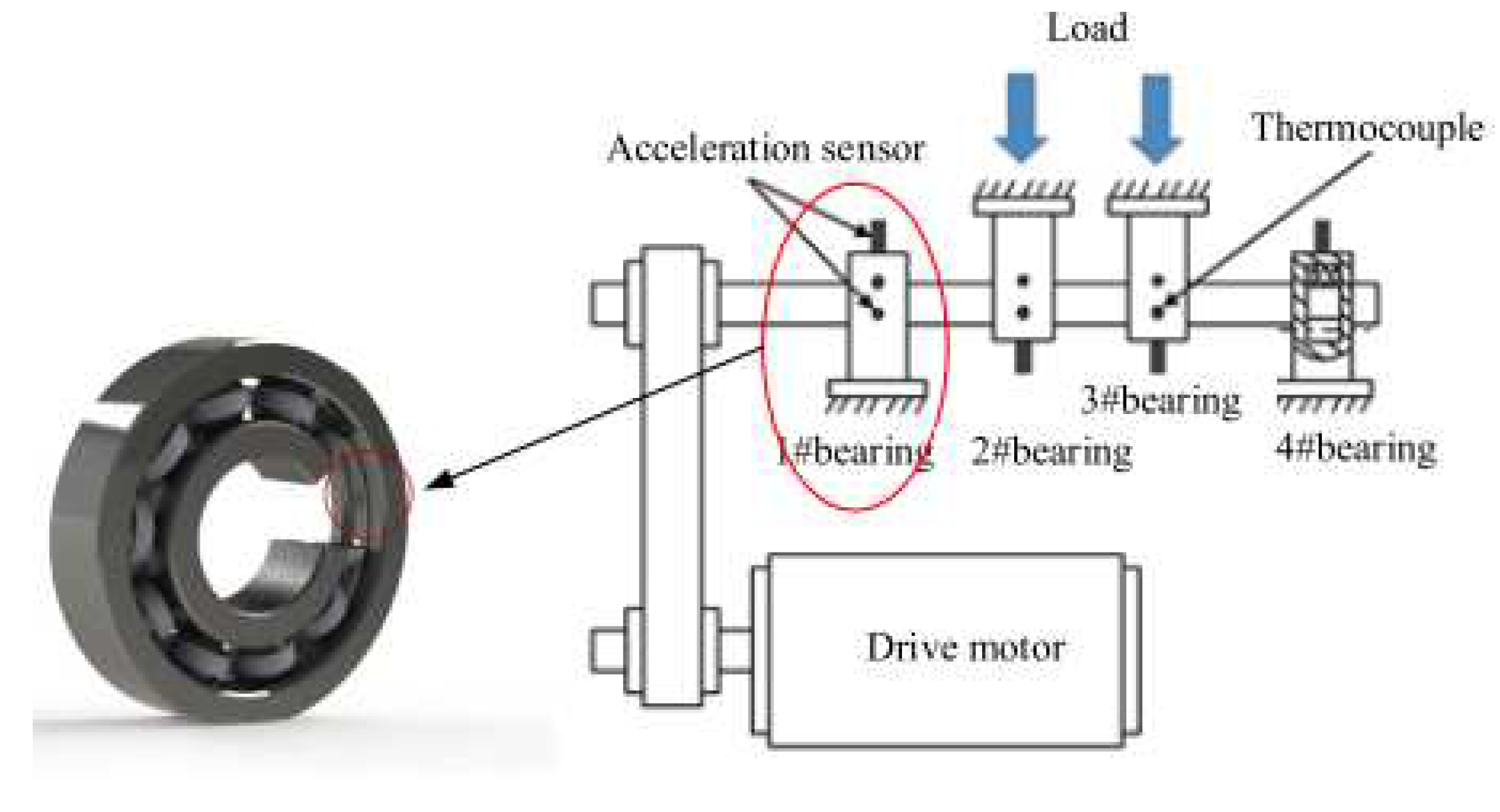
The data used in the verification test come from the rolling bearing life data set of the NSF I/UCR Intelligent System Maintenance Center in the United States. The structure of the test bench is shown in Figure 6. The DC motor drives the drive shaft to rotate with the speed 2000r/min. The applied radial load is 6000lbs (ie 2721.5kg), and four double-row cylindrical roller bearings (Rexnord ZA-2115) are installed on the drive shaft. The 353B33 high-sensitivity ICP accelerometer of PCB company and the 6062E acquisition card of NI company are used to collect the vibration signal of the bearing.

The bearing public data contains three test data, and the 2nd test data is used in this paper. Among them, the sampling frequency of the experiment is 20 kHz, data is collected every 10 minutes, and 20480 sampling points are collected each time. The test ran for a total of 8 days. The acceleration signals of the four bearings corresponded to the four channels in the data set respectively. Finally, the test ended when the outer ring of 1#bearing failed. A total of 984 times were collected. Therefore, a total of 984×20480 sampling points were collected.

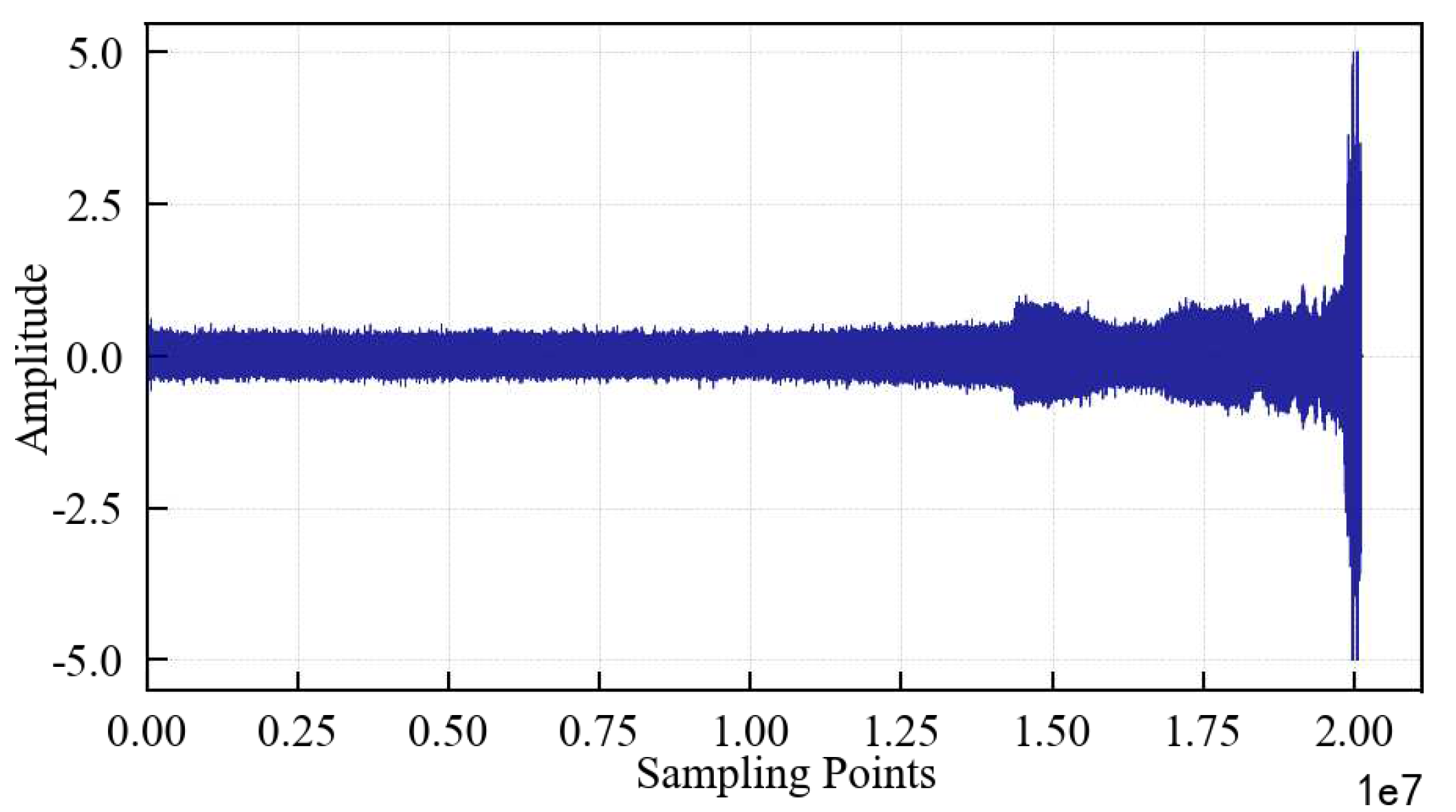
The change of the vibration signal during the whole life of the 1#bearing is shown in Figure 7. It can be seen that: 1) In the early stage of the test, the running state of the 1#bearing was relatively stable, and its vibration signal had no obvious abnormal change; 2) After a minor fault of the 1#bearing occurs, the amplitude of the vibration signal begins to increase; 3) With the progress of the test, the failure of the 1#bearing intensified, the vibration signal began to change abruptly, the amplitude further increased, and finally the 1#bearing suffered a serious outer ring failure, and the value of the vibration signal at the corresponding time also reflected this situation more clearly. The above phenomenon shows that it is feasible to analyze the bearing performance degradation trend based on the vibration signal. However, the degradation trend of the original vibration signal is not intuitive enough to better analyze the performance degradation process of the 1#bearing, and only when the 1#bearing fault is serious will it be reflected on the original vibration signal, which is obviously disadvantageous for the identification of early/weak faults. Therefore, it is necessary to analyze the performance degradation process of the 1#bearing through feature extraction.

3.1. Verification of Feature Screening Method

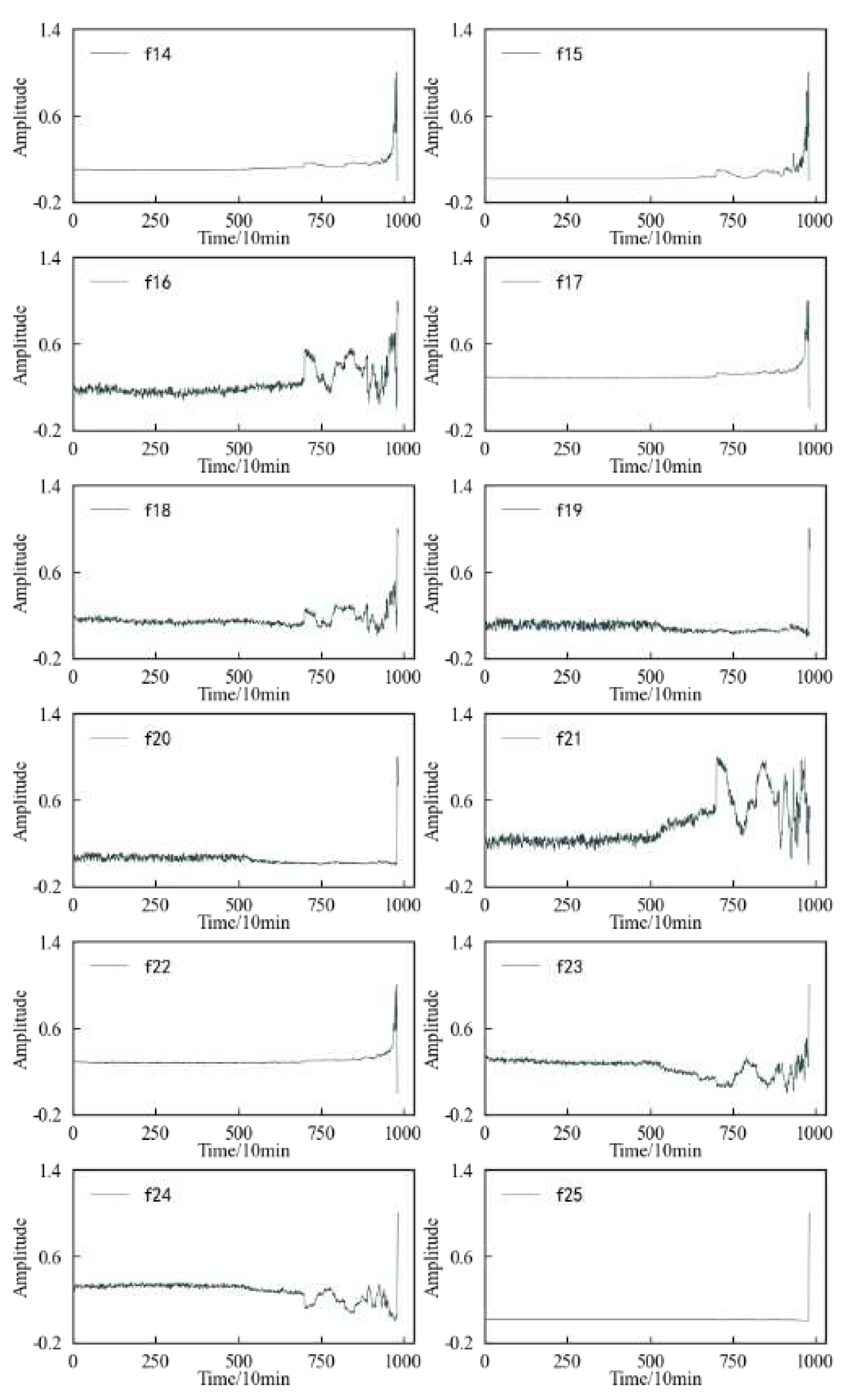
Combined with the experimental plan, an eigenvalue is calculated for the 20480 sampling points collected in a single time, and each eigenindex sequence consists of 984 values. According to Table 1 and Table 2, the change trends of the time domain and frequency domain characteristics in the whole life cycle of 1#bearing are shown in Figure 8 and Figure 9, respectively. Figure 10 shows the change trend of the time-frequency domain characteristics in the whole life cycle of the 1#bearing extracted according to equations (1) and (2). In order to visualize the change trend of each feature more conveniently, the features are normalized.

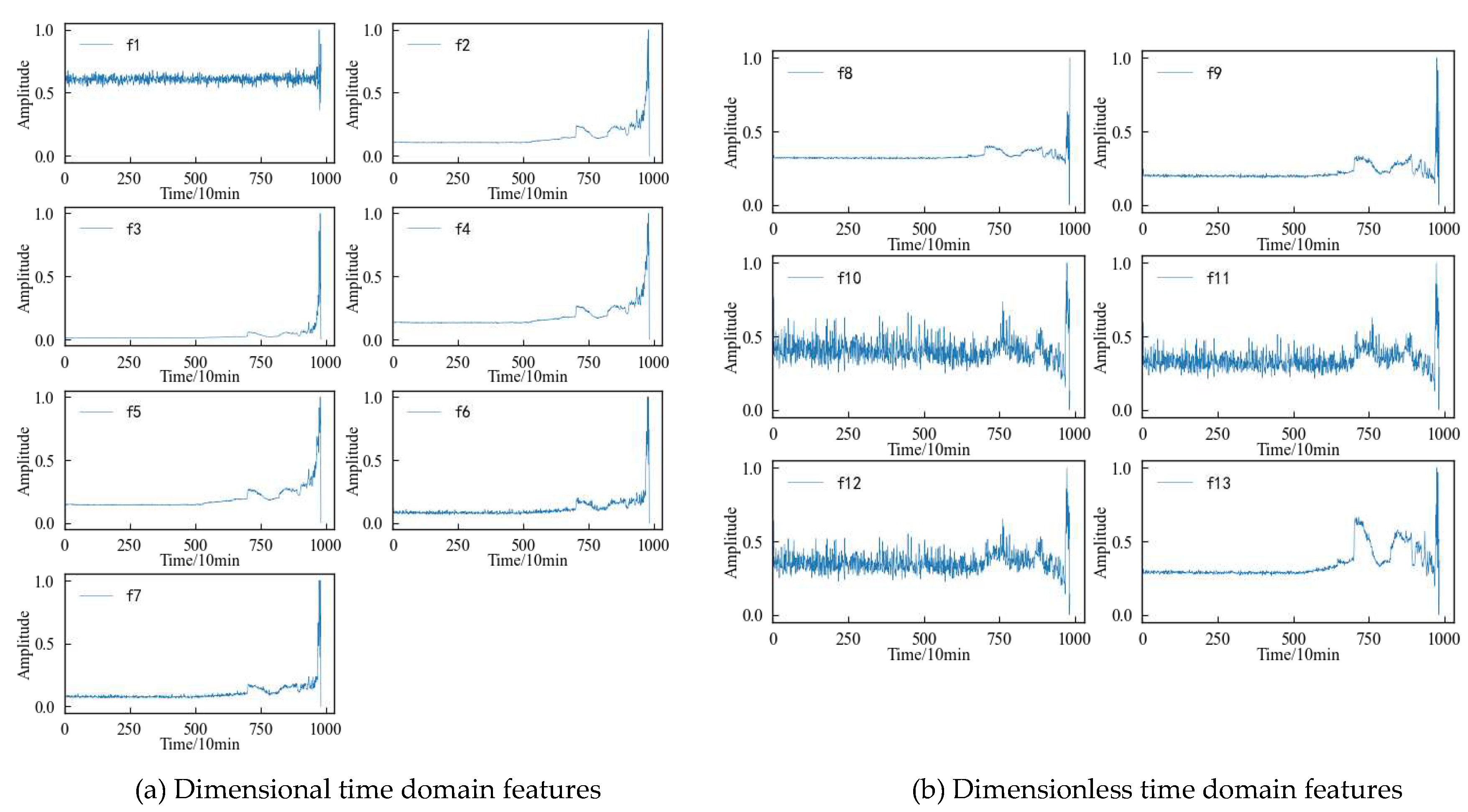
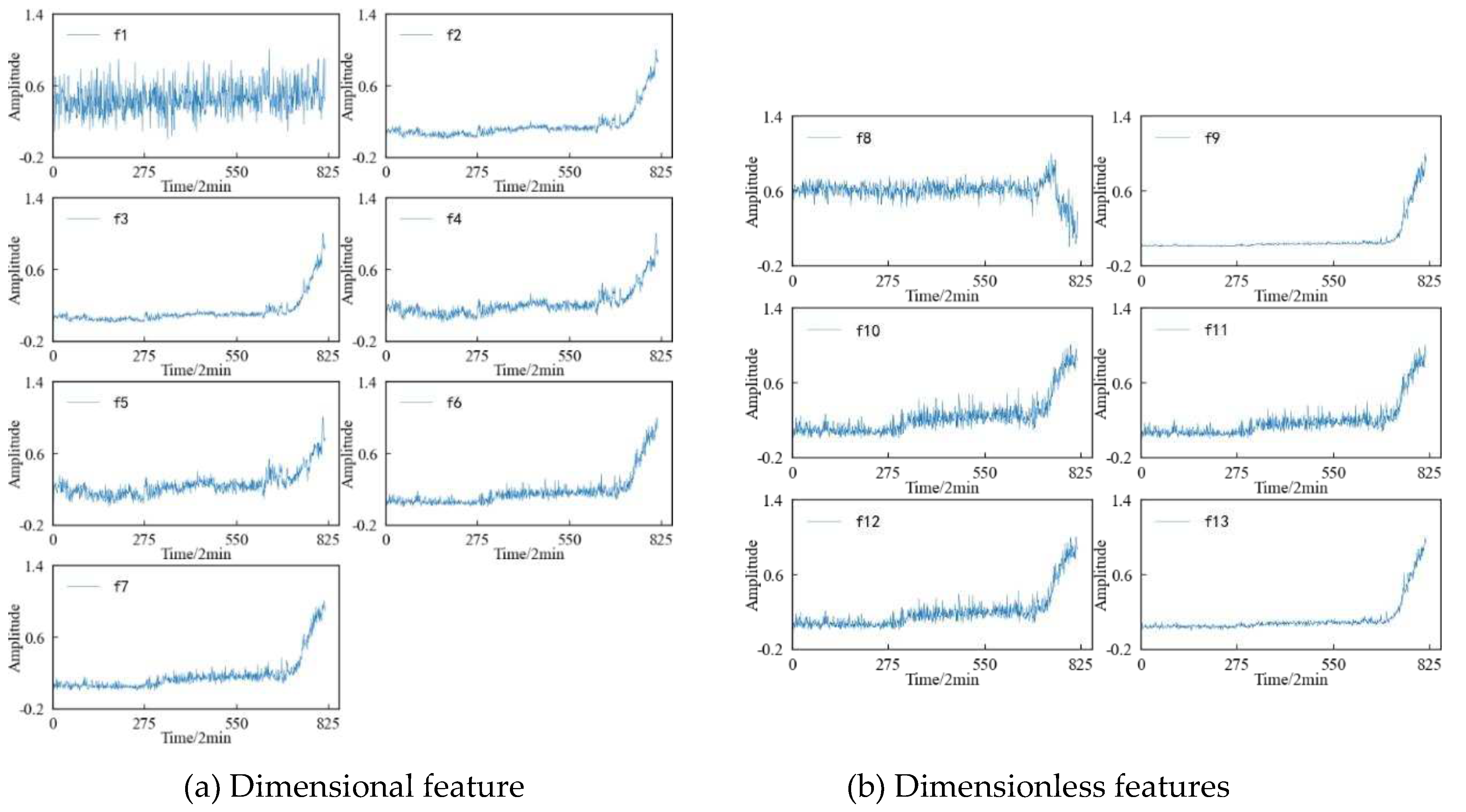
According to Figure 8, it can be found that the time-domain features can more intuitively reflect the performance degradation process of the 1#bearing than the original vibration signal, but not every time-domain feature can describe this process well. The 13 time-domain features can be divided into the following four categories according to the changing trend: 1) The first type of characteristic, such as the mean characteristic etc., although the amplitude fluctuates from the beginning of the test to the end of the test, it is not sensitive to the slight and moderate faults of the 1#bearing. Until the 1#bearing fails completely, its amplitude changes significantly; 2) The second type of features, such as skewness and kurtosis characteristics, is relatively stable in the early stage, which corresponds well with the running state of the 1#bearing, but is not sensitive enough to minor faults. After the 1#bearing is slightly damaged, the characteristics are not displayed in time, and can not show changes until the degree of failure is more serious; 3) The third type of characteristics, such as peak index, margin index and pulse index, etc., fluctuates violently from the beginning, and shows a certain change trend with the operation of the 1#bearing. But the fluctuation of this type of characteristics is too large, so that the change trend of the characteristics is not obvious enough to be submerged in it; 4) The changes of the fourth type of characteristics, such as the root mean square value, variance and root square amplitude, are similar to those of the second type in the early stage, but the difference is that when the 1#bearing has a slight fault, the amplitude of the characteristics also changes correspondingly. And with the deepening of the failure degree, this change will be more obvious, which can better reflect the performance degradation trend of the bearing during the entire life.

According to Figure 9, it can be found that the change process of the 12 frequency-domain features over time is not the same. Except for the frequency-domain feature 7, other features can change when the 1#bearing fails, which shows that the frequency domain features can better reflect the performance degradation process of the 1#bearing. However, some frequency domain features, such as frequency domain features 1, 2, 5 and 6, etc., decrease in amplitude after the 1#bearing failure, and further decrease over time until the performance degrades sharply and their amplitude fluctuates drastically.

According to Figure 10, it can be found that most of the time-frequency domain features do not reflect the performance degradation process of the 1#bearing well, and the trend is not obvious and the fluctuation is large.

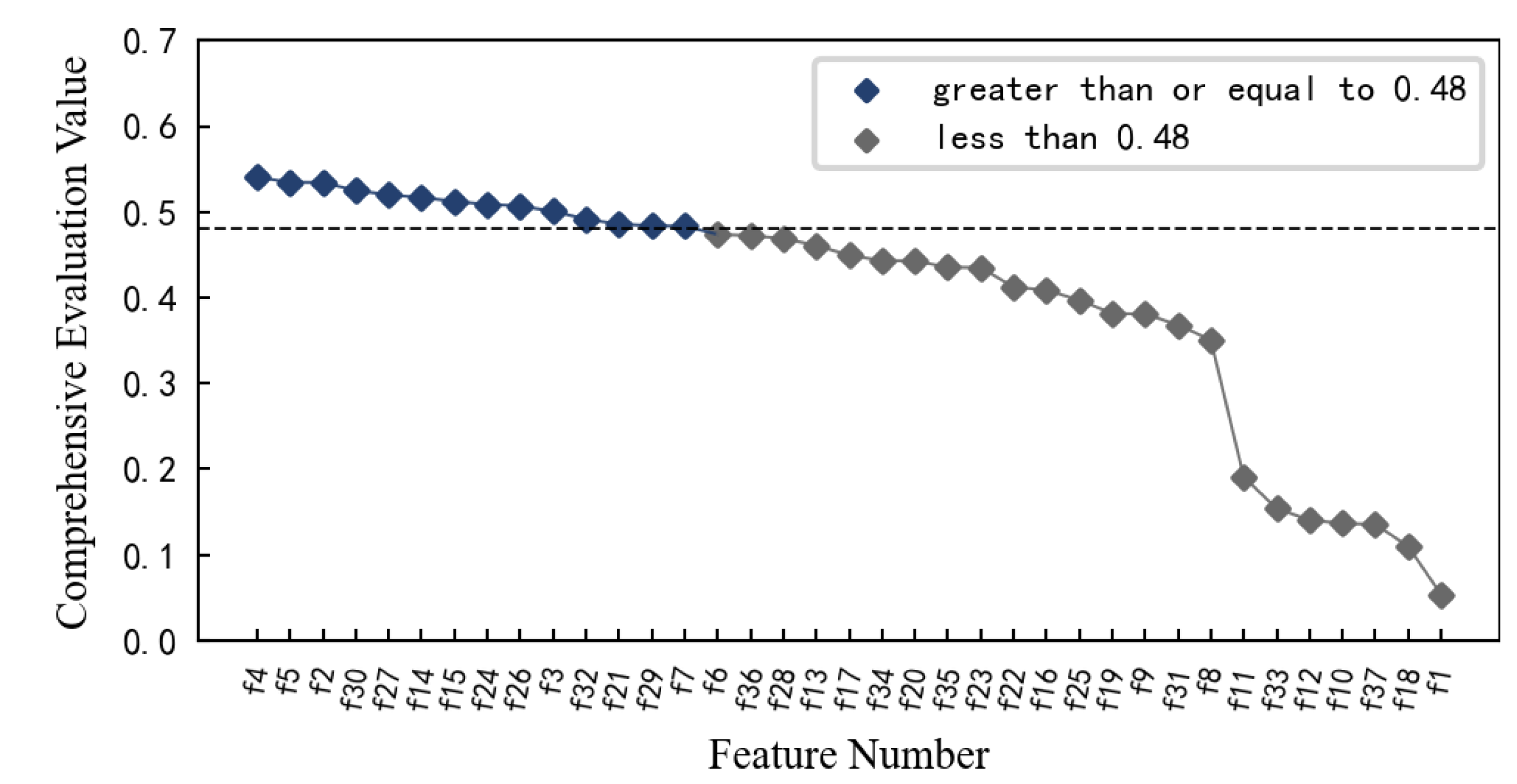
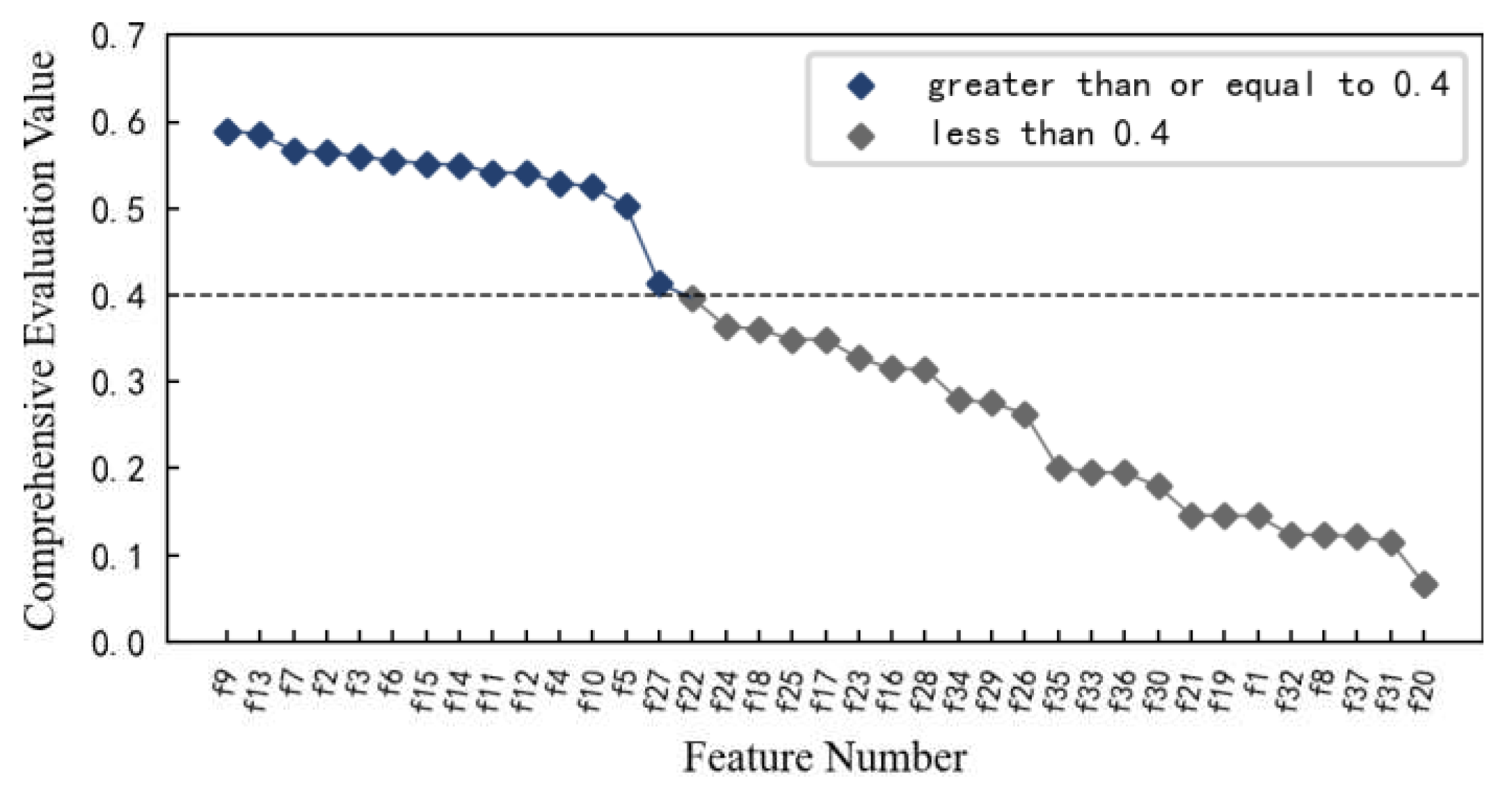
Therefore, the feature screening is carried out according to the aforementioned method. At this time, the performance degradation of the 1#bearing is paid attention to, and

α_{1} = 0 . 3

α_{2} = 0 . 3

α_{3} = 0 . 4

during the calculation, and the result is shown in Figure 11. If the mean value of the comprehensive evaluation value of 37 features is 0.4013 as the threshold, then the comprehensive evaluation value of 25 features is greater than or equal to 0.4013. However, combined with the changing trends of the aforementioned features, it is found that some of these 25 features fluctuate greatly or are relatively gentle in the changing process, such as features f₁₆ and f₂₂, etc. Therefore, considering the comprehensive evaluation value, degradation process of each feature and the dimension of the feature set, the features with the comprehensive evaluation value greater than or equal to 0.48 are reserved to form the optimal feature set, which includes 14 features such as features f₄, f₅ and f₂, etc. Among these features, even the feature f₇ with the smallest comprehensive evaluation value, when the 1#bearing is running well, its amplitude fluctuation is small. Although it is not sensitive enough to minor damage, it can also be reflected after obvious failure of the 1#bearing. Therefore, these 14 features can be used as the preferred feature set for performance degradation assessment of 1#bearing.

3.2. Verification of of HI Construction Method

The KPCA method is used to reduce the dimensionality of the aforementioned 14 preferred features. Firstly, the features of the low-dimensional space are mapped to the high-dimensional space. In this paper, the rbf radial basis function is selected as the kernel function. The specific type is the Gaussian kernel function, and its expression is:

k (x_{1}, x_{2}) = e x p (\frac{- {‖ x_{1} - x_{2} ‖}^{2}}{2 σ})

(26)

where

x_{1}

、

x_{2}

can be regarded as two feature sequences;

σ

is the kernel parameter.

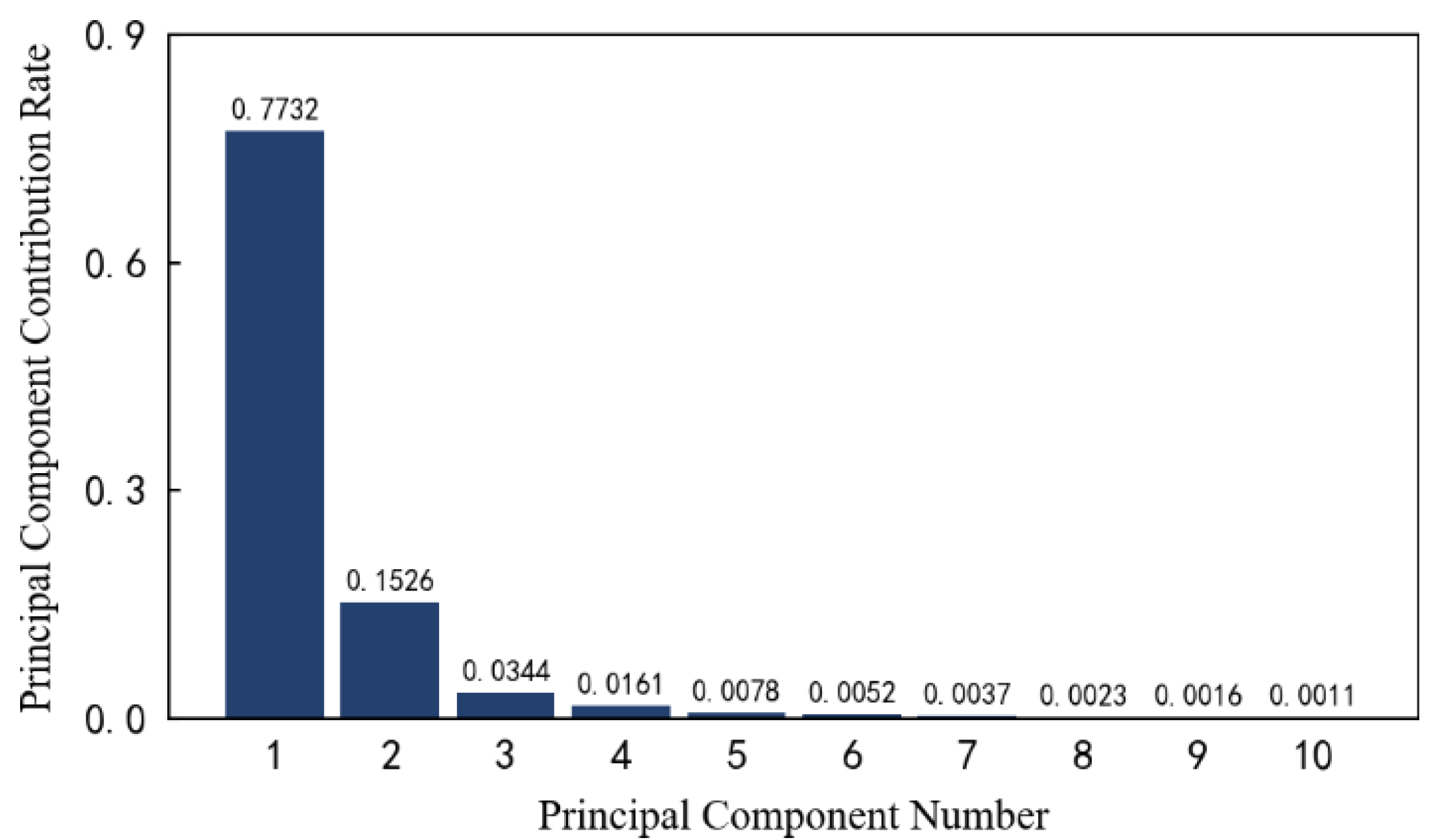
Secondly, the contribution rate of each principal component is calculated in a high-dimensional space. Taking the previous 10 principal components as an example, the respective contribution rates are shown in Figure 12. It can be seen that the first and second principal components occupy 77.32% and 15.26% of the original data information respectively. The larger the subsequent principal component number, the smaller the contribution rate, and gradually approach zero.

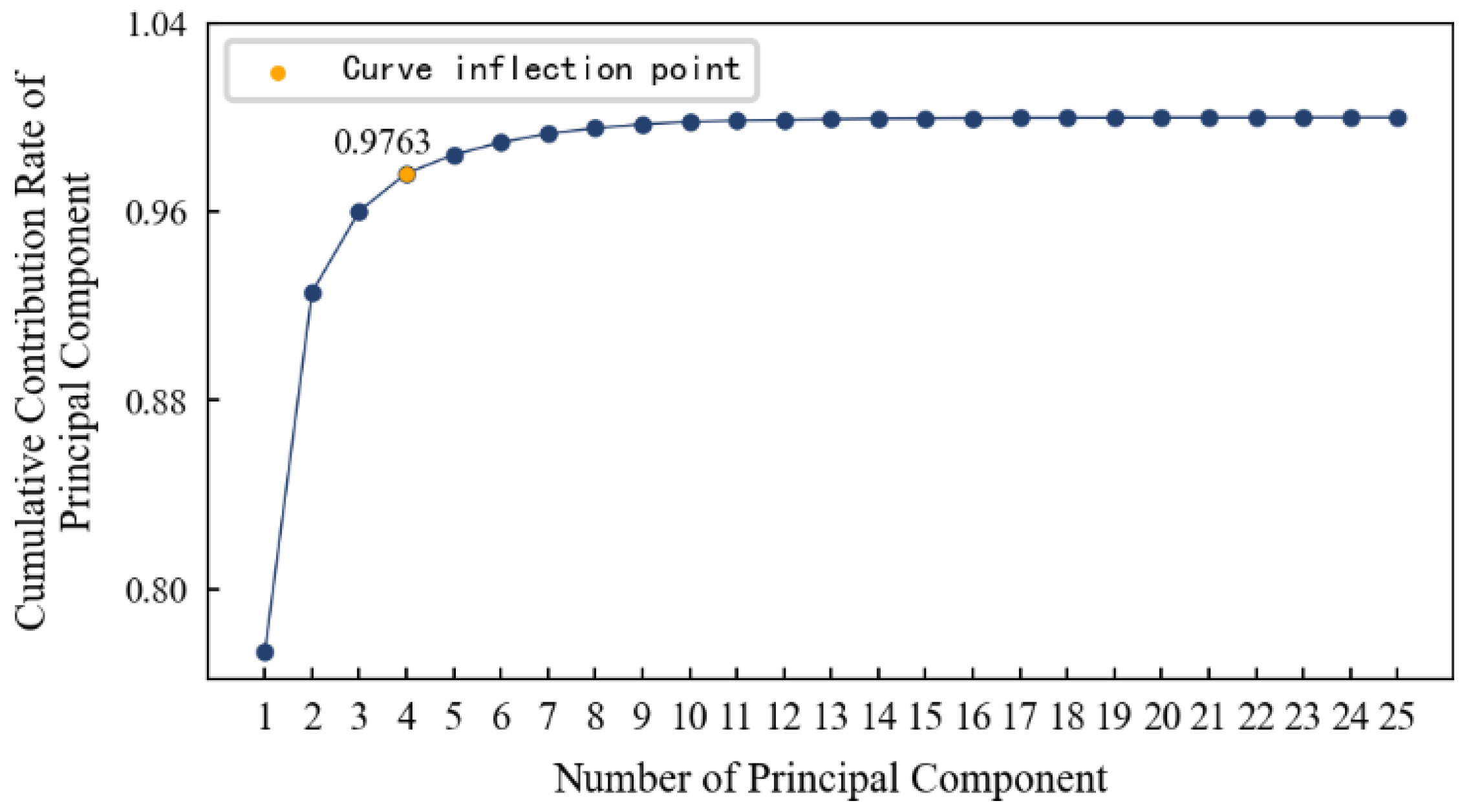
In order to determine the appropriate dimension, the cumulative contribution rate curve of the principal components is drawn as shown in Figure 13. It can be seen that: 1) With the increase of the principal components, the cumulative contribution rate of principal components becomes smooth after a large increase, and finally approaches 1 infinitely; 2) The inflection point of the curve is roughly at the fourth principal component. After that, even if the principal components number continues to increase, the cumulative contribution rate will not increase significantly. Therefore, this paper selects the first four principal components as the features after dimension reduction, and their cumulative contribution rate reaches 97.63%. That is to say, the features after dimension reduction contain 97.63% of the information of the original data, and it is the most appropriate that the dimension is reduced from 14 dimensions to 4 dimensions.

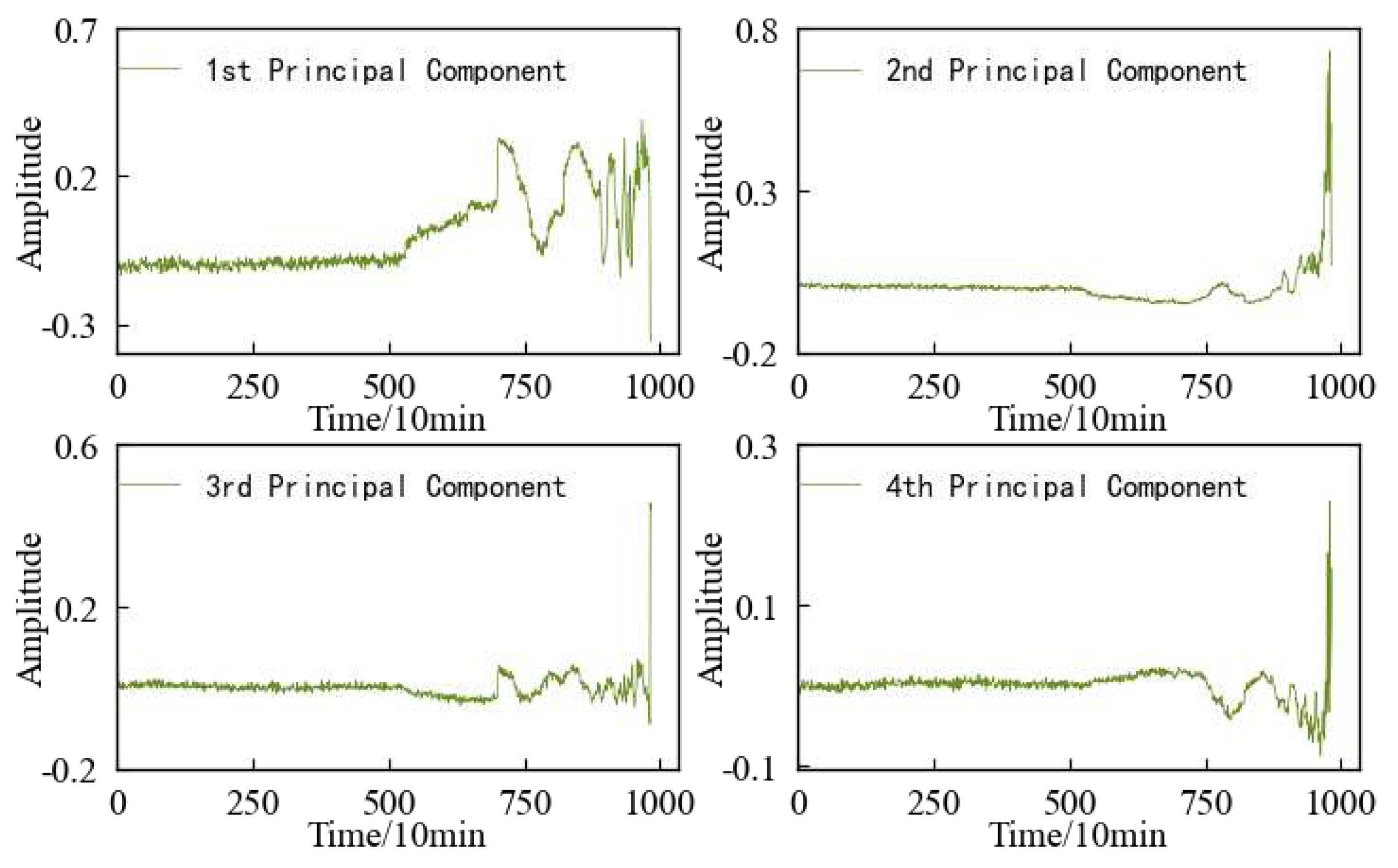
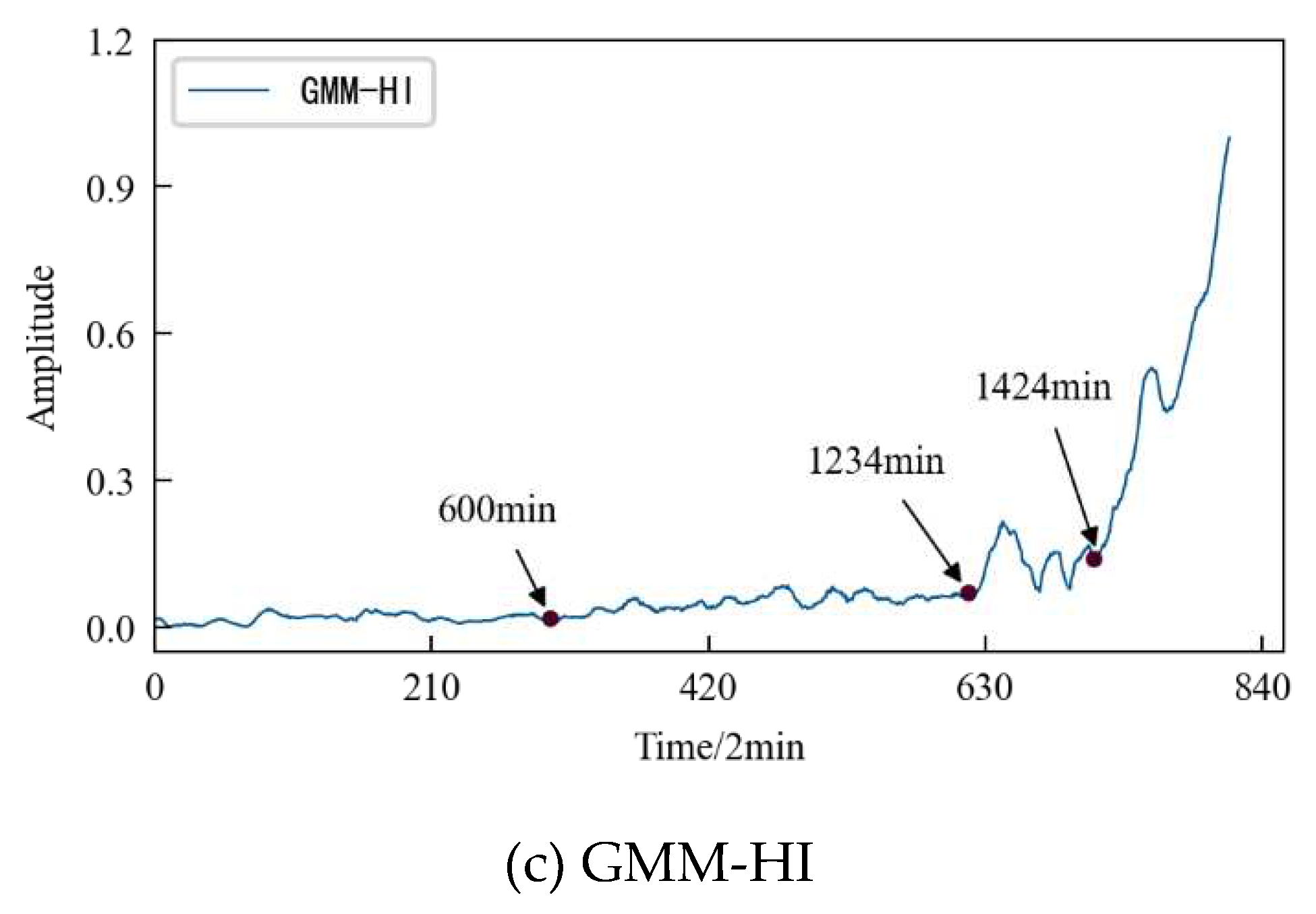
The variation trends of the first four main elements of 1#bearing are shown in Figure 14, which are used as the input value and target value of the CAE network for training, and the obtained encoded features are used as the HI of 1#bearing. For the convenience of comparison, the HI of 1#bearing is constructed using the Auto-Encoding (AE) network and the Gaussian Mixture Model (GMM) respectively. The HI obtained by three different methods is shown in Figure 15 after denoising and smoothing.

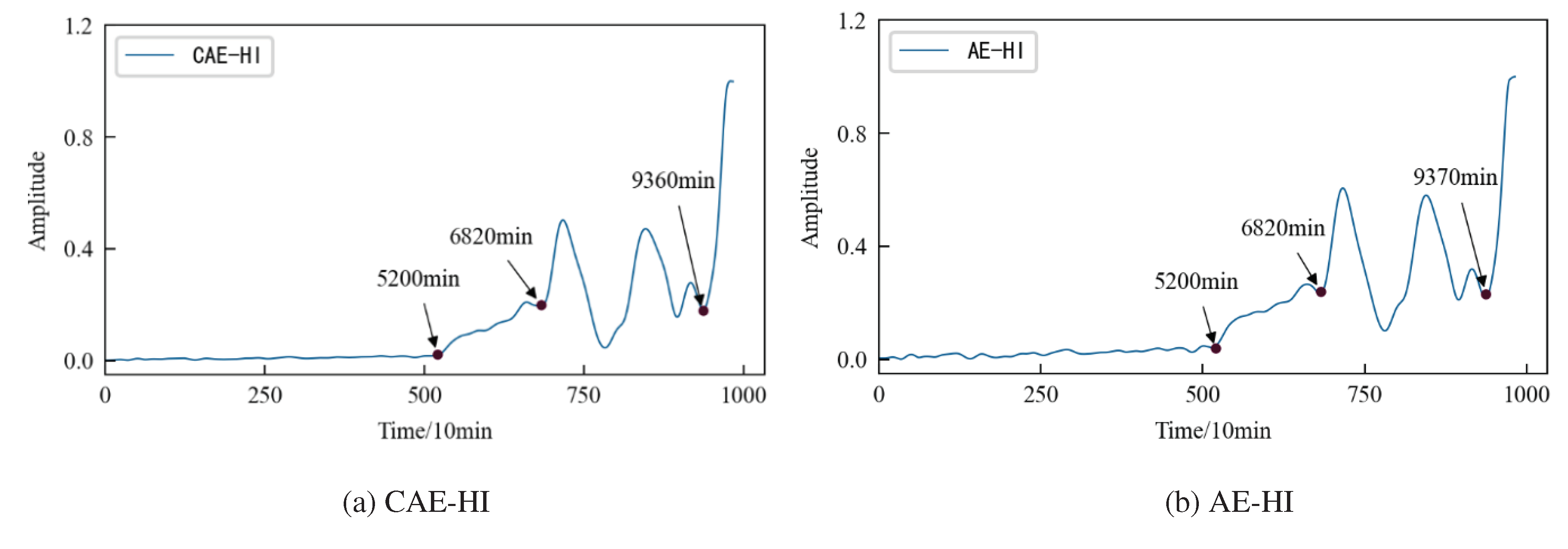
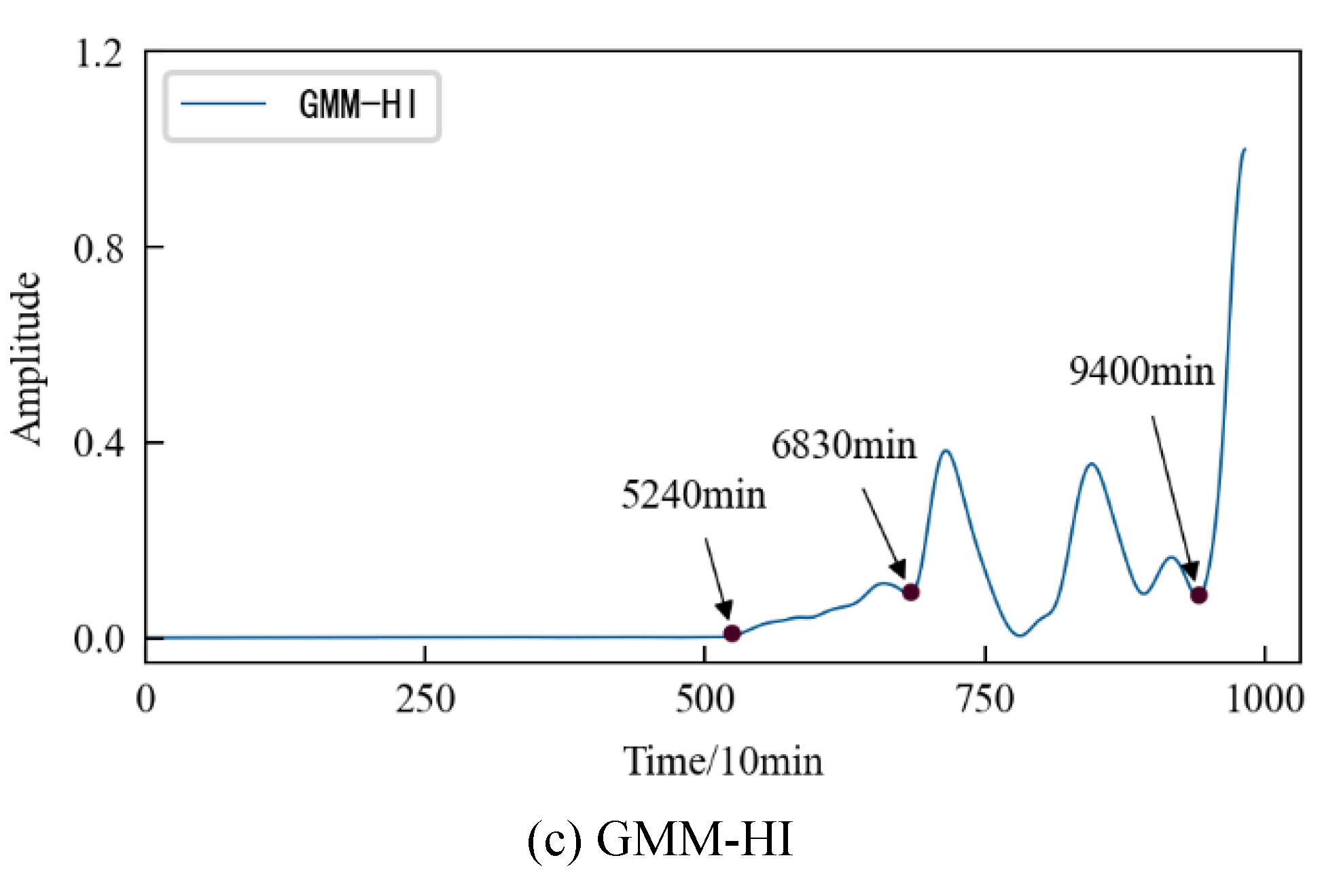
The comparative analysis shows that: 1) The HI constructed by three different methods show a consistent degradation trend, and the change process reflects the performance degradation process of 1#bearing. 2) In the early stage of the test, since the running state of the 1#bearing is relatively stable, the amplitude of its HI should be relatively stable on the whole. Considering the actual operation situation, the amplitude of the HI slightly fluctuates more in line with reality. Observing Figure 15, it is found that the early stage of GMM-HI is too stable and has almost no fluctuation. The early stage of AE-HI fluctuates greatly, which is different from the actual situation. While the early stage of CAE-HI is in line with the expectation of overall stability and slight fluctuation. 3) As the test progresses, the 1#bearing begins to be damaged, and the amplitude of the HI should show an increasing trend. Observing Figure 15, it is found that GMM-HI began to increase significantly after the 5240th minute, while AE-HI and CAE-HI began to increase after the 5200th minute. That is to say, 40 minutes ahead of GMM-HI. It is very important for the actual industrial production to be able to detect the early damage of the monitored object in time. From this level of analysis, it is obvious that AE-HI and CAE-HI are better. 4) When the 1#bearing fails, the amplitude of the HI should fluctuate greatly. Observing Figure 15, it is found that AE-HI and CAE-HI began to fluctuate greatly after the 6820th minute, while GMM-HI was delayed by 10 minutes. 5) As the test continues, the 1#bearing fails completely, and the amplitude of the HI should change sharply. Observing Figure 15, it was found that CAE-HI showed a steep change at the 9360th minute, while AE-HI and GMM-HI were delayed at the 9370th and 9400th minutes, respectively.

Therefore, whether from the qualitative analysis reflecting the early running state of the 1#bearing, or from the quantitative analysis of the 1#bearing damage and failure time point, the results show that the CAE-HI constructed in this paper is superior to AE-HI and GMM-HI.

Further, characteristic evaluation indicators, such as monotonicity and trend established by formula (4) and formula (6), can be used to evaluate the HI constructed by three different methods. The results are shown in Table 3. It can be seen that the CAE-HI constructed in this paper is better than AE-HI and GMM-HI.

3.3. Verification of Performance Degradation Prediction Model

Based on the TCN algorithm, the aforementioned direct multi-step prediction is used to predict the performance degradation trend of 1#bearing. By comparing with the prediction models constructed based on the Long Short-Term Memory (LSTM) network and the Gated Recurrent Unit (GRU) algorithm, the superiority of the performance degradation prediction method proposed in this paper is verified.

The HI of 1#bearing has a total of 984 data files, which are divided into training set and test set according to the ratio of 7:3, that is, the first 689 data files and the remaining 295 data files respectively form the training set and test set of the prediction model through spatial phase reconstruction technology. Set the time step of each input to 8 and the prediction step to 3. Set the size of the convolution kernel in the model to 3, the number of convolution layers to 4 and the expansion coefficient to 2. The number of iterations for training the model is 150, and the input batch size in each training is 10. The prediction results based on the TCN model are shown in Figure 16, which also shows the prediction results based on LSTM and GRU models. It should be noted that in order to prevent the model from overfitting, the number of hidden layers for training LSTM and GRU is set to 1, the maximum number of iterations is 100, and the dropout is 0.3.

According to Figure 16, it can be seen that: 1) The prediction models established by three different methods can make accurate performance degradation predictions of the 1#bearing, and the difference between the predicted values of three different methods at certain time points is very small or even the same; 2) In the failure stage of 1#bearing, the deviation between the predicted value and the actual value of two methods based on the LSTM algorithm and the GRU algorithm is large.

Further, combined with the evaluation indicators established by Equation (28) and Equation (29), the prediction models constructed by three different methods were evaluated, and the results are shown in Table 4. It can be seen that compared with the other two models, the performance degradation trend prediction model constructed based on TCN in this paper has better prediction performance and higher prediction accuracy.

4. Application

The feasibility of the performance degradation trend prediction method based on multi-domain features and TCN proposed in this paper is verified by using the bearing public data. Now, it is applied to predict the performance degradation trend of rolling contact fatigue specimen to further verify the effectiveness of the method.

4.1. Introduction of Rolling Contact Fatigue Test Equipment

According to "Rolling Contact Fatigue Test Method for Metal Materials" (YB/T 5345.2014) [41], the contact fatigue properties of materials are obtained by testing on a rolling contact fatigue testing machine. The research group successfully developed a rolling contact fatigue testing machine, as shown in Figure 17, which solved the problems of similar test technologies, such as discontinuous data collection, untraceable damage evolution and difficulty in accurately obtaining fatigue strength.

The testing machine is mainly composed of mechanical system, electrical system, vision system, measurement and control software system and lubrication system, etc. It can monitor the running state of the sample in real time. During the test, various sensors were installed to realize the measurement and control of key parameters such as vibration, load, oil temperature, rotational speed and torque. At the same time, an image acquisition system with independent intellectual property rights has been developed, which realizes real-time acquisition and accurate quantitative analysis of damage images.

4.2. Rolling Contact Fatigue Test

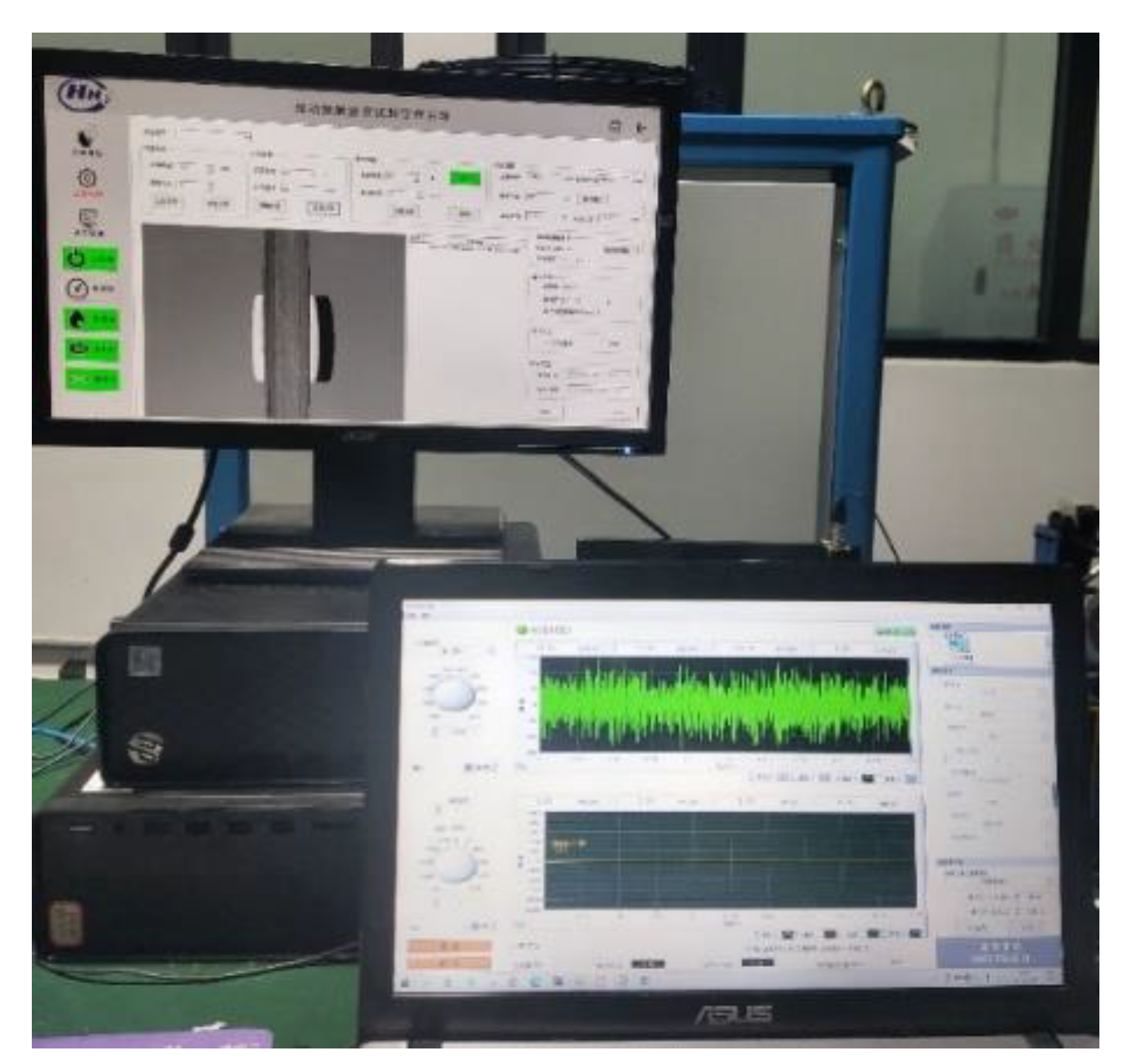
The test was carried out on the RCF-A type testing machine, as shown in Figure 18. The specimen and the accompanying specimen are processed according to the YB/T 5345.2014 test standard, the material is 40Cr, and the quenching and tempering process is used. During the test, set the rotational speed of the main shaft (specimen) to 1000 r/min, the rotational speed of the accompanying shaft (accompanying specimen) to 1100 r/min, the slip rate to be 10%, and the radial load to be 2071 N. The 1A307E accelerometer is installed on the headstock box by magnetic attraction (as shown in Figure 19), and the EM9118B-6/ICP data acquisition card is used to collect vibration signals. The control interface of the testing machine is shown in Figure 20.

The performance degradation of the specimen is a gradual process, and the period of rolling contact fatigue test is relatively long. In order to avoid too much repetitive information in the data, the vibration signal is collected by interval sampling during the test. The sampling frequency was 10 kHz, and the samples were collected every 2 min. The time of each collection was 1s. The collected data points were 10,000 until the specimen failed.

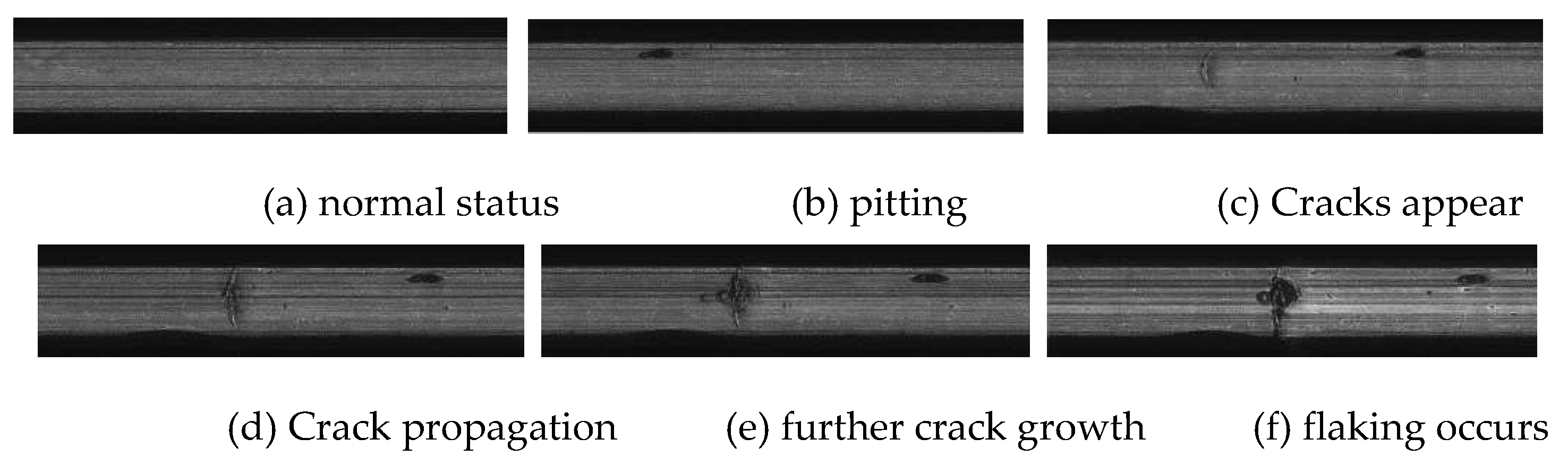
Finally, when the test went to 1632min, the contact fatigue failure of the specimen occurred. Figure 21 shows the good state and failure state of the specimen before and after the test. It can be seen that due to rolling contact fatigue, pitting corrosion and crack-induced spalling occurred at 1 and 2 in Figure 21(b), respectively. Although the naked eye cannot easily found, but with the help of the image acquisition system of the testing machine, the time of fatigue failure was accurately captured. Figure 22 is the acquired image information of the contact surface of the specimen at key time points, which truly records the evolution process of the contact surface of the sample from the initiation of fatigue damage to the appearance of cracks and then to spalling.

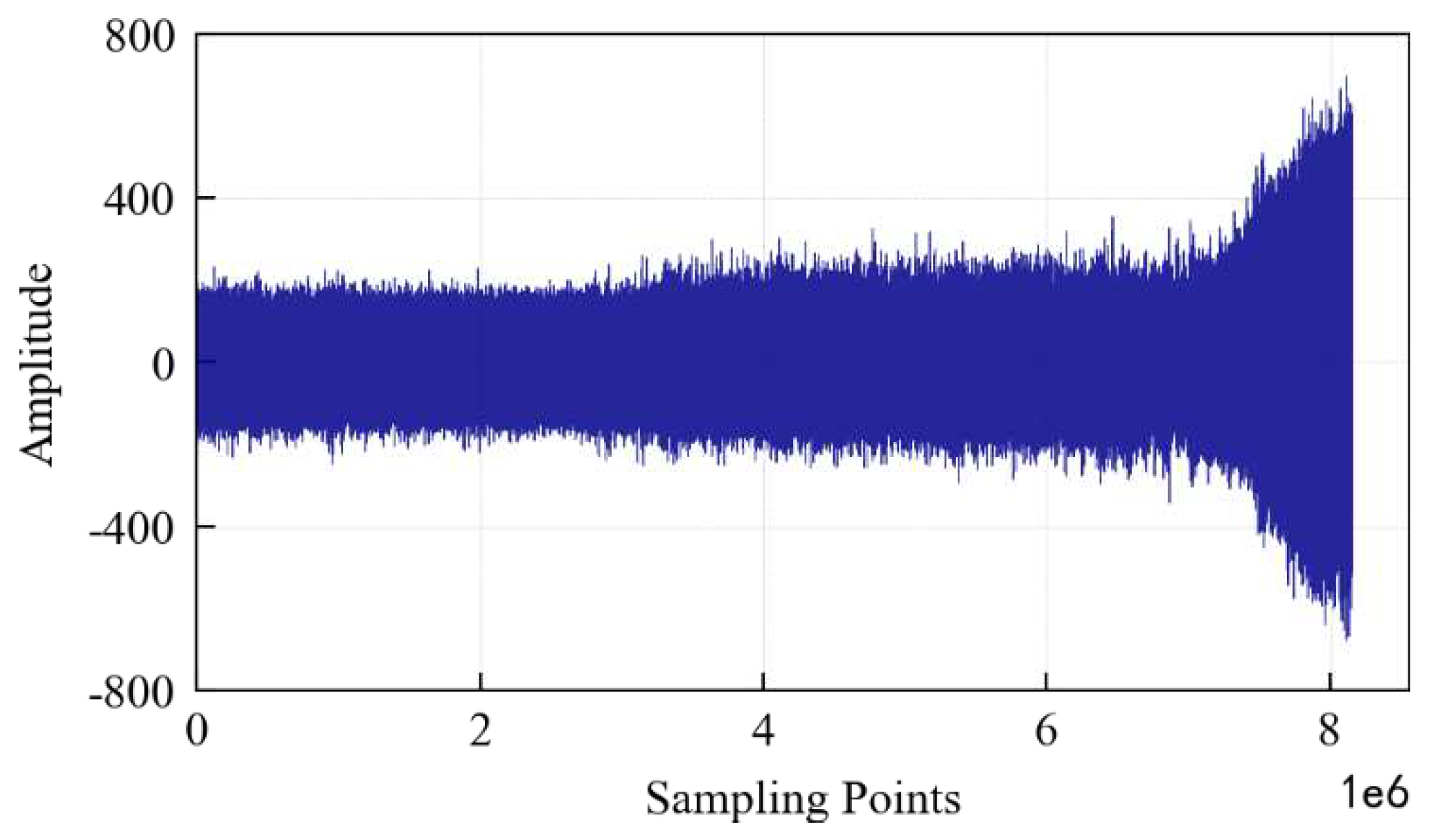
According to the above-mentioned test process and data collection method, if the data collected every 1s is a data file and each file contains 10,000 sampling points, then a total of 816 data files are obtained until the specimen fails. The vibration signal in the whole life cycle of the specimen is shown in Figure 23, which contains 8.16×10⁶ sampling points. It can be seen that: 1) From the beginning of the test to about 3×10⁶ sampling points, the value of the specimen vibration signal does not fluctuate much, indicating that the specimen is in a relatively stable state; 2) From 3×10⁶ to 7×10⁶ sampling points, the signal amplitude increases significantly. Fatigue pitting damage should have occurred in the specimen; 3) After 7×10⁶ sampling points, the signal amplitude continued to increase, indicating that cracks appeared on the surface of the specimen, and the crack area expanded rapidly. Finally, spalling was formed and the specimen failed completely.

4.3. Feature Screening

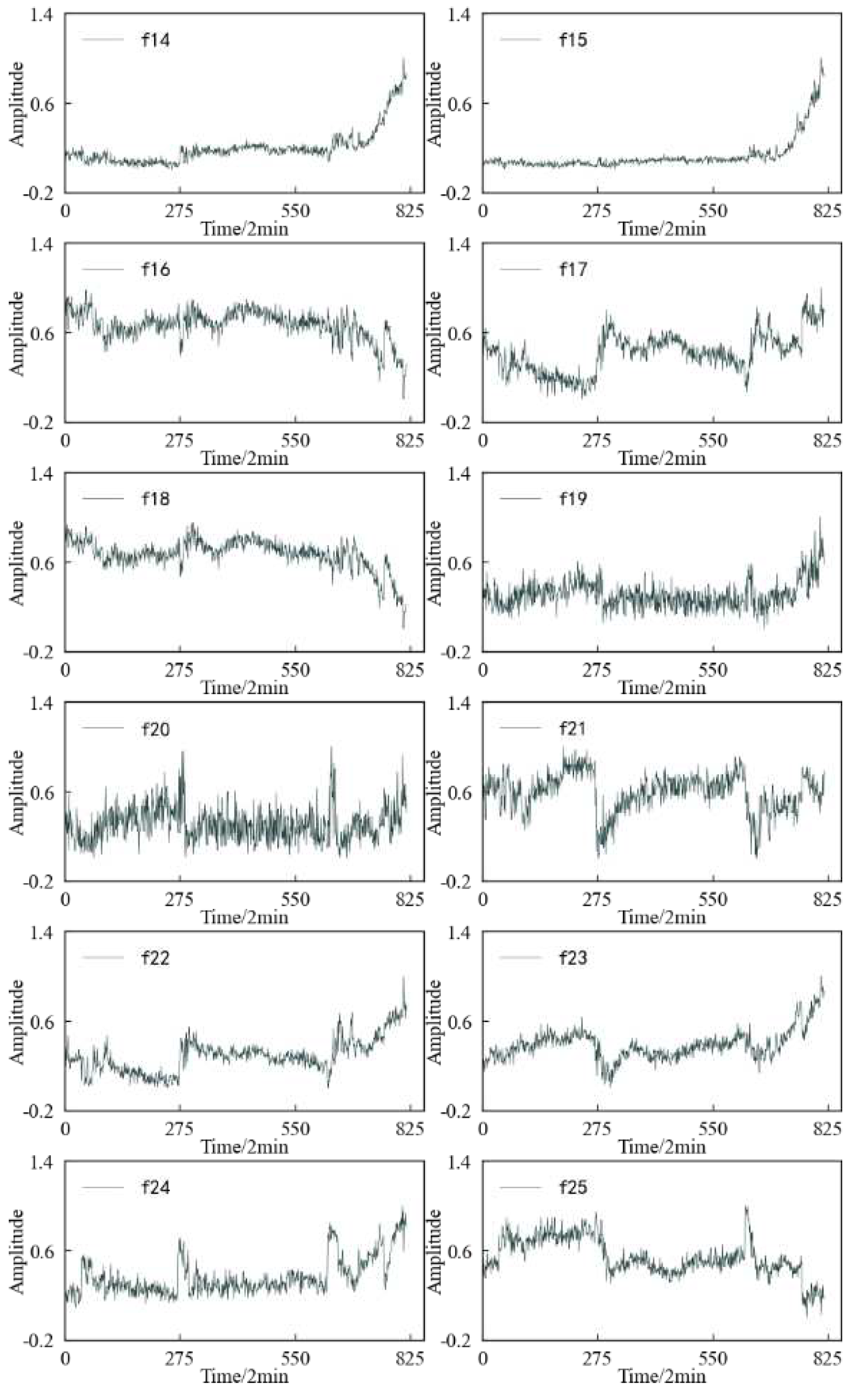
A feature value is calculated for the data points obtained at each sampling time, and each feature sequence has a total of 816 values. The variation trend of the time-domain characteristics of the specimen in the whole life cycle is shown in Figure 24. It can be seen that: 1) In the dimensioned time domain feature, the mean value feature is not sensitive to the contact fatigue of the specimen, and the amplitude changes of other features can better reflect the state change of the specimen compared with the original vibration. The signal is more timely and clear; 2) Among the dimensionless time domain features, in addition to the skewness index feature, other features can also better reflect the change process of the specimen from normal to failure.

Figure 25 shows the variation trend of the frequency-domain characteristics of the specimen in the whole life cycle. It can be found that in terms of reflecting the operating state of the specimen, the overall performance of the frequency domain features is not as good as the time domain features. Except for the amplitude mean and amplitude variance, other frequency domain features have large fluctuations in the whole life cycle. Although there is a certain trend in the performance degradation process of the specimen, this trend is not stable, and even jumps at some time points.

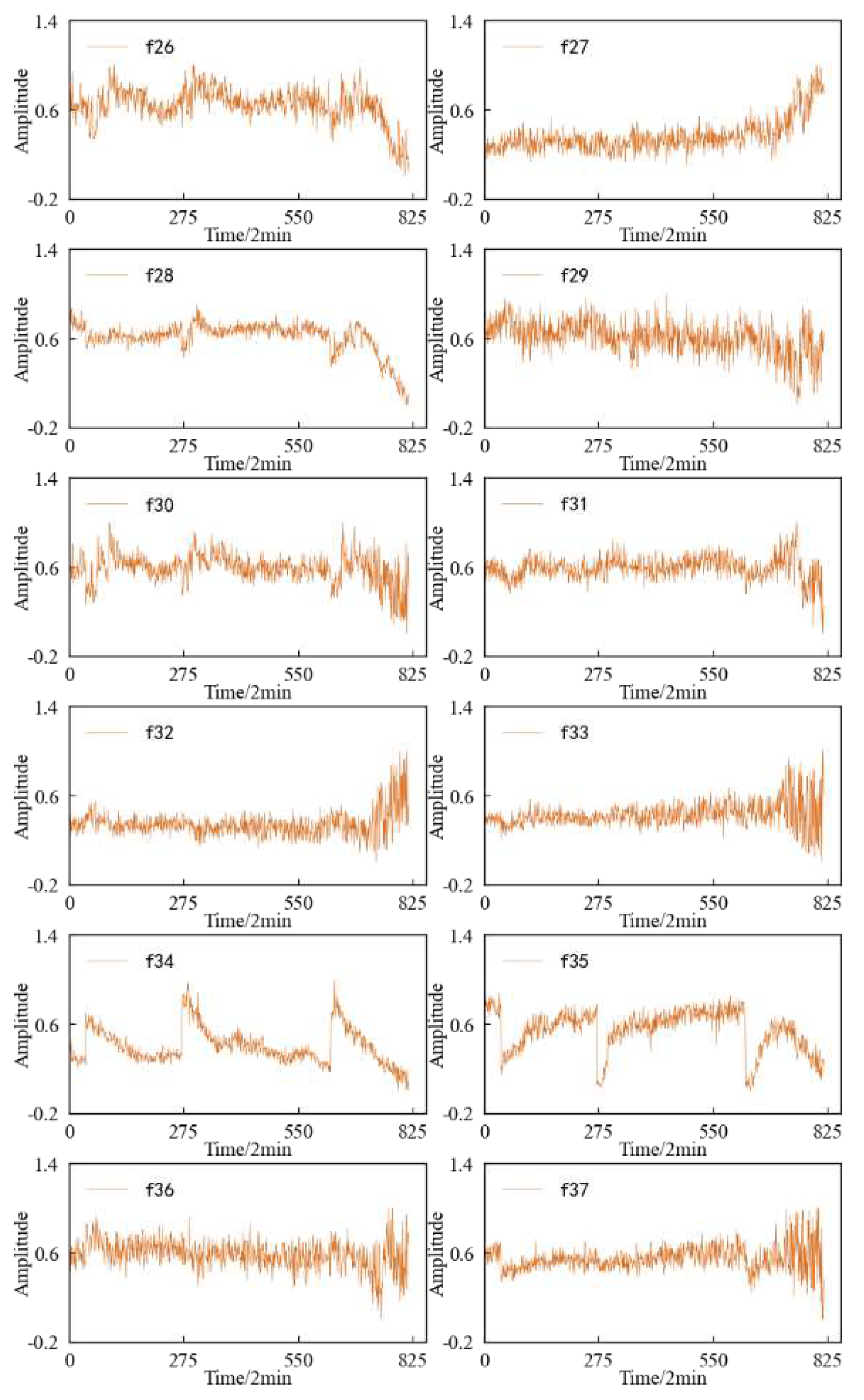
The three-layer wavelet packet decomposition is performed on the vibration signal of the specimen, and the obtained energy changes of each frequency band in the second layer and the third layer are shown in Figure 26. It can be found that most of the time-frequency domain features do not reflect the performance degradation process of the specimen well, and the trend is not obvious and the fluctuation is large.

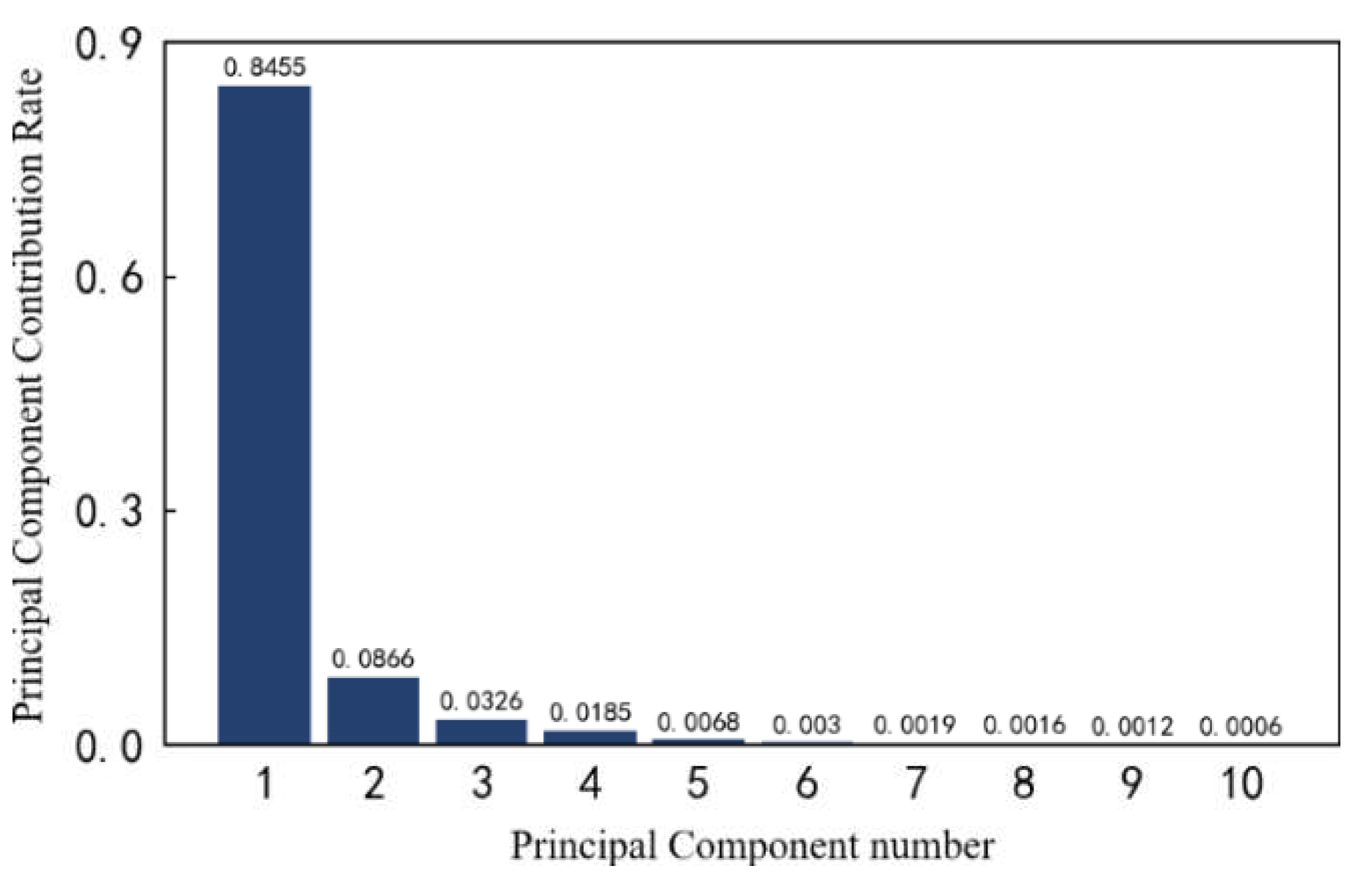
Similarly, in order to get the features that are sensitive to the contact fatigue degradation process of the specimen, the monotonicity, correlation mean and trend of 37 multi-domain features are calculated according to equations (4), (5) and (6). On this basis, the comprehensive evaluation index of each feature is calculated according to formula (3), and the result is shown in Figure 27. Considering the comprehensive evaluation value and degradation process of each feature, and considering the dimension of the feature set, the features with comprehensive evaluation value greater than or equal to 0.4 are reserved to form the optimal feature set, which includes 14 features such as feature, feature and feature. These preferred features can better reflect the performance degradation process of the specimen.

4.4. Feature Dimensionality Reduction

The rolling contact fatigue performance of the specimen is degraded, and its vibration signal also has non-stationary and nonlinear characteristics. The dimensionality reduction of the aforementioned 14 preferred features was carried out by using KPCA method.

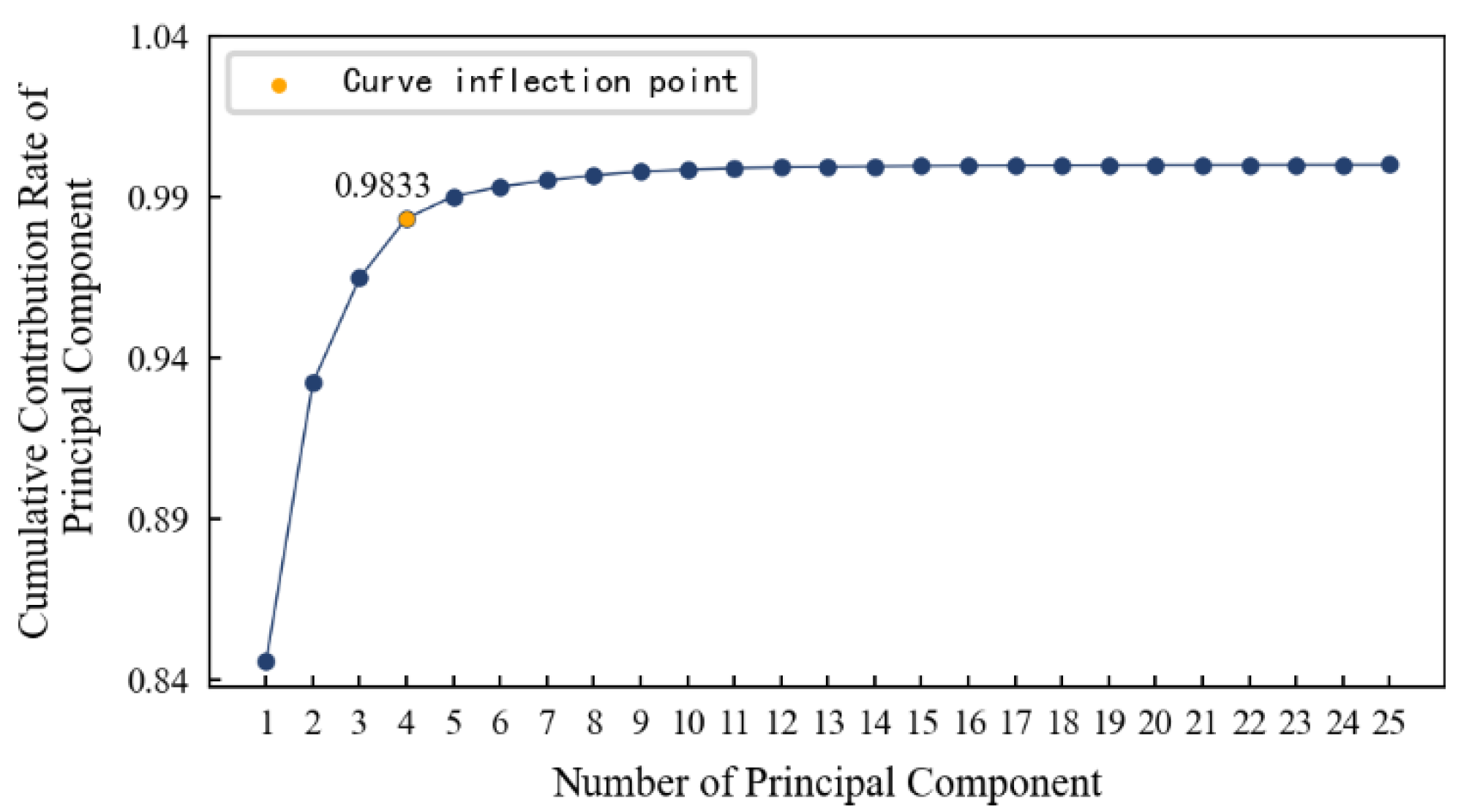
When mapping the features of the low-dimensional space to the high-dimensional space, the Gaussian kernel function shown in equation (26) is also selected, and the respective contribution rates of the first 10 principal components are calculated as shown in Figure 28. The plotted pivotal cumulative contribution rate curve is shown in Figure 29. It can be seen that: 1) As the number of principal components increases, the cumulative contribution rate of the principal components also increases, and more information is contained; 2) The inflection point of the curve is roughly at the fourth principal component. At this time, even if the number of principal components continues to increase, the cumulative contribution rate will not increase significantly. Therefore, it is most appropriate to reduce dimensions from 14 to 4.

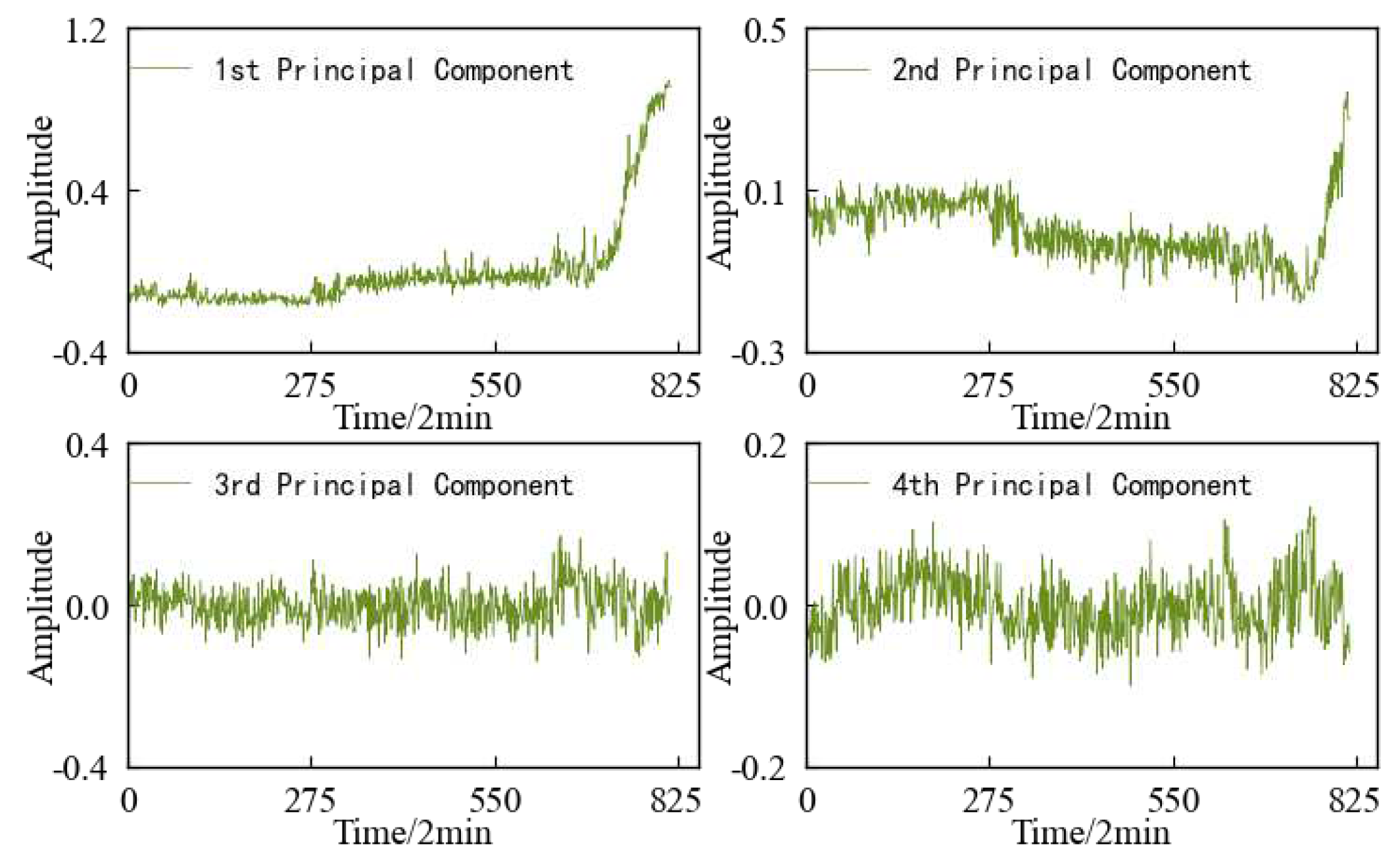
The variation trends of the first four principal components of the specimen are shown in Figure 30. Through feature dimensionality reduction, the optimal feature set of the specimen is reduced from 14 dimensions to 4 dimensions. The feature set after dimensionality reduction contains 98.33% of the information of the optimal feature set, achieving the purpose of reducing the dimension without losing a lot of information.

4.5. Construction of HI

The dimensionality-reduced features are used as the input value and target value of the CAE network for training, and the obtained encoded features are used as the HI of the specimen. Similarly, the AE network and the GMM were used to construct the HI of the specimen respectively for comparison. The HI obtained by three different methods were denoised and smoothed, as shown in Figure 31.

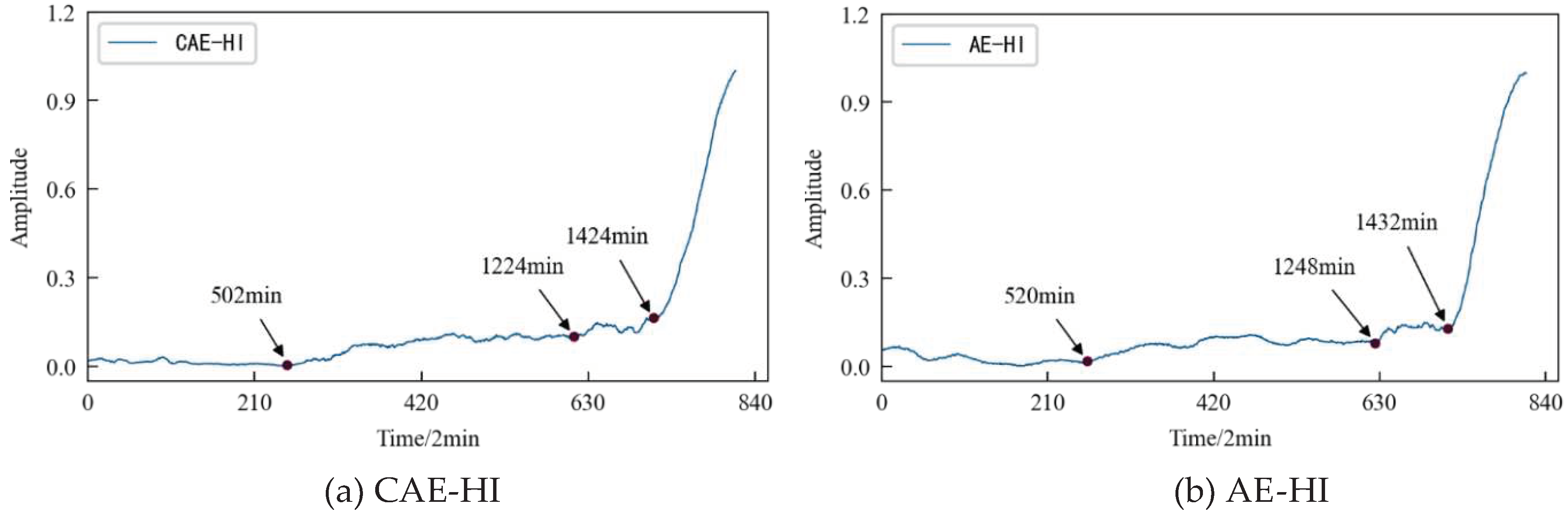
The comparative analysis shows that: 1) The HI constructed by three different methods show a consistent degradation trend, and the change process reflects the performance degradation process of the contact fatigue of the specimen, which is consistent with the process of rolling contact fatigue of the specimen in Figure 22. 2) In the early stage of the test, due to the relatively stable running state of the specimen, the amplitudes of HI were generally stable, but slightly fluctuated due to the influence of the test environmental conditions. 3) With the progress of the test, the specimen began to be damaged, and the amplitude of the HI showed an increasing trend. Observing Figure 31, it was found that AE-HI and GMM-HI began to increase significantly after 520min and 600min respectively, while CAE-HI began to show an increasing trend after 502min. That is to say, compared with AE-HI and GMM –HI, it was advanced by 18min and 98min respectively. Therefore, the HI construction method proposed in this paper has more advantages. 4) When the specimen has serious fatigue damage such as crack, the amplitude of the HI should fluctuate greatly. Observing Figure 31, it was found that CAE-HI began to fluctuate greatly after 1224 minutes, while the large fluctuations of AE-HI and GMM-HI were delayed by 24 minutes and 10 minutes, respectively. 5) With the continuous progress of the test, the fatigue failure of the specimen occurs, and the amplitude of the HI changes sharply. Observing Figure 31, it was found that CAE-HI and GMM-HI showed a steep change at 1424 min, while the abrupt change of AE-HI appeared at 1432 minute, and there was a lag.

In a word, whether from the qualitative analysis reflecting the early running state of the specimen or from the quantitative analysis of the time point of the fatigue damage and fatigue failure of the specimen, the results show that the CAE-HI constructed in this paper is superior to the AE-HI and GMM-HI. Therefore, the method of constructing HI based on CAE network is reasonable and effective, and this method has obvious advantages compared with AE network and GMM, two commonly used methods of constructing HI.

4.6. Performance Degradation Prediction of Rolling Contact Fatigue

Based on the TCN algorithm, the direct multi-step prediction is also used to performance degradation prediction of the rolling contact fatigue specimen. By comparing with the prediction models based on the LSTM algorithm and the GRU algorithm, the superiority of the proposed performance degradation trend prediction method is further verified.

The HI of specimen has a total of 816 data files, which are divided into training set and test set according to the ratio of 7:3, that is, the first 571 data files and the remaining 245 data files respectively form the training set and test set of the prediction model through spatial phase reconstruction technology. Other parameters are the same as that of the performance degradation prediction of 1#bearing.

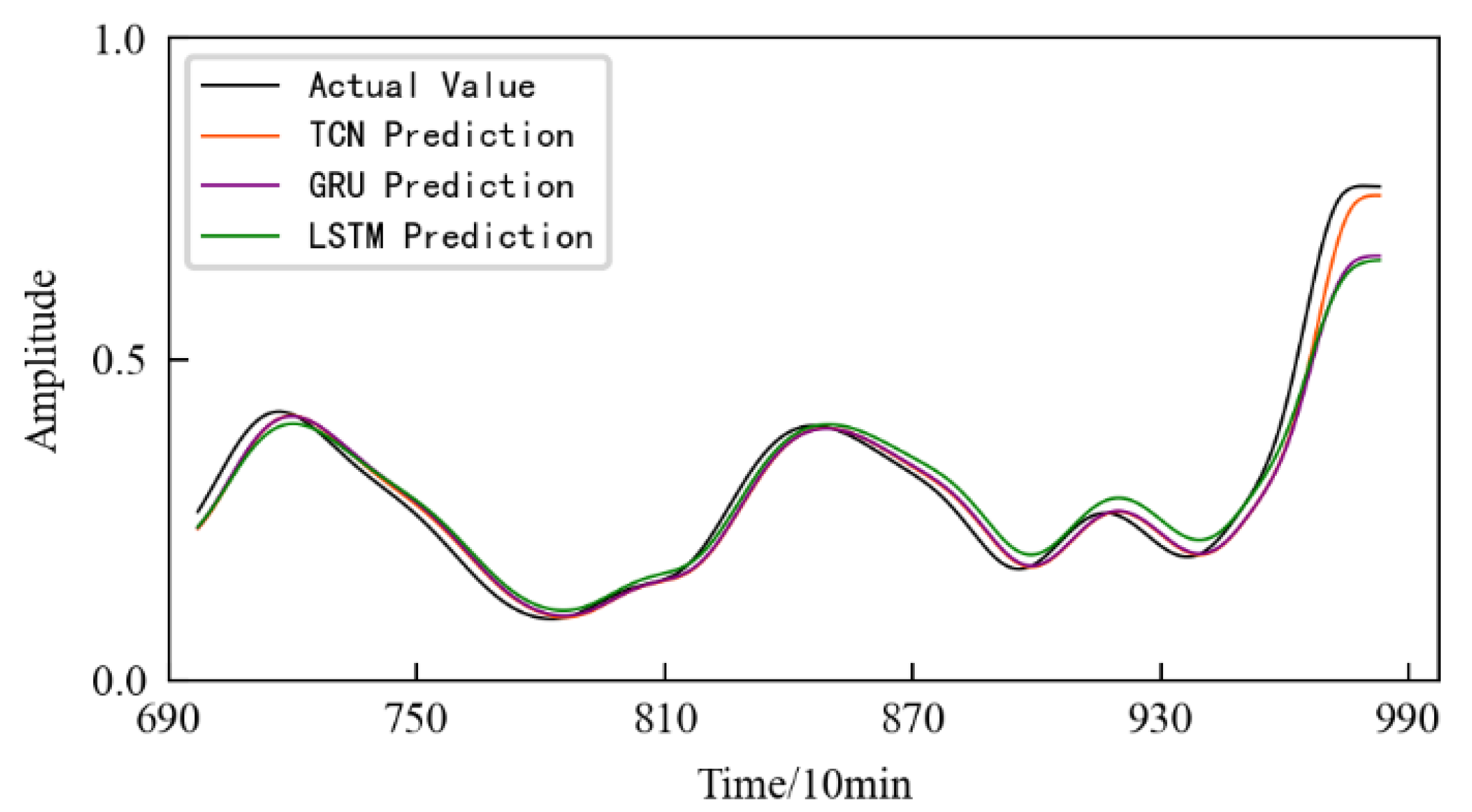
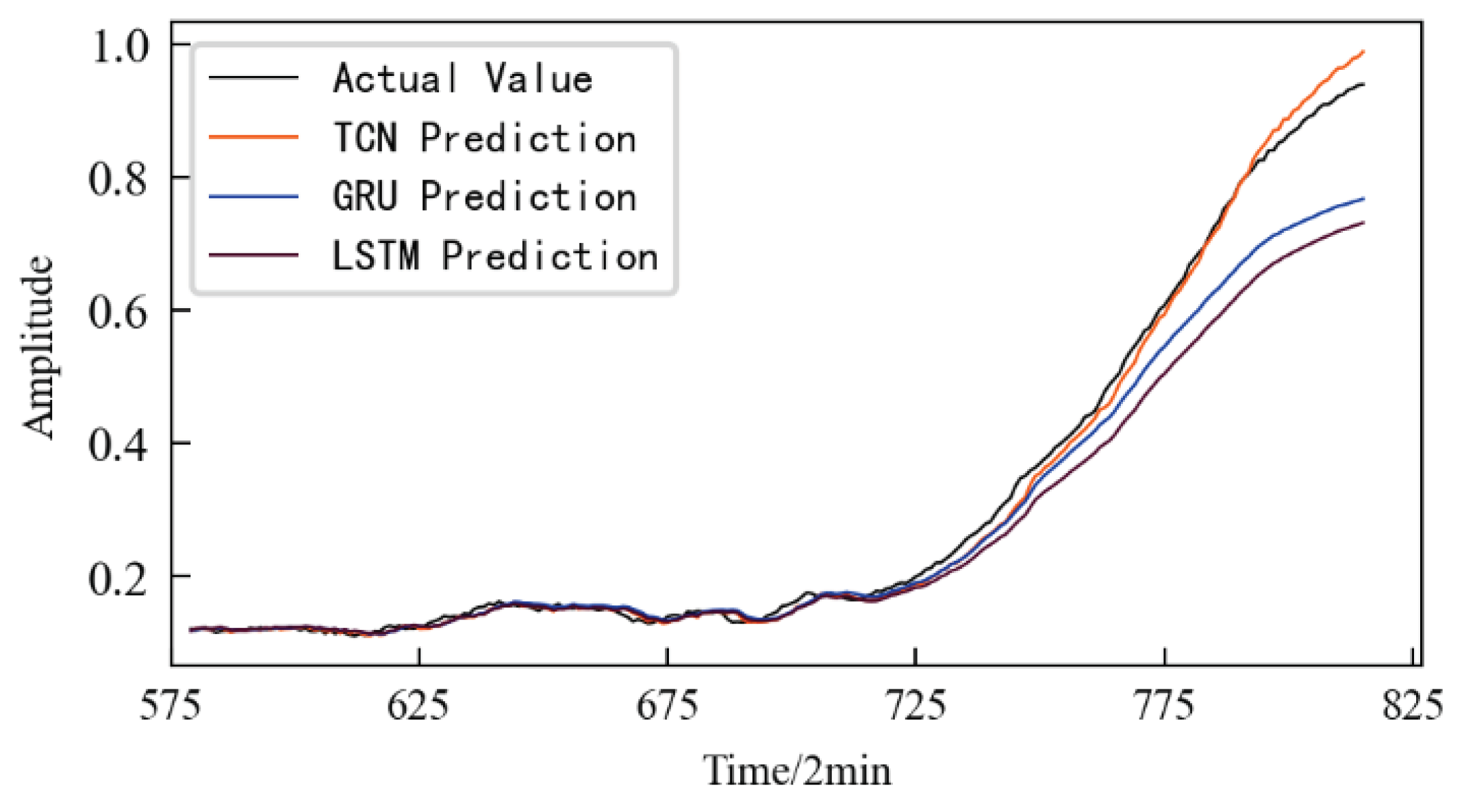
The prediction results based on the TCN model are shown in Figure 32, and the prediction starts from the 580th sampling time, that is, the 1160th minute. In order to illustrate the superiority of the method, the prediction results of two commonly used time series data prediction models, LSTM network and GRU, are also shown in Figure 32. The evaluation indicators of three different prediction models are shown in Table 5. It can be seen that the prediction model based on the TCN can well predict the performance degradation of the rolling contact fatigue specimen. Moreover, it is the best fit with the actual performance degradation curve, and the prediction accuracy is higher. At the same time, the model evaluation index is also the best among three models.

5. Discussion

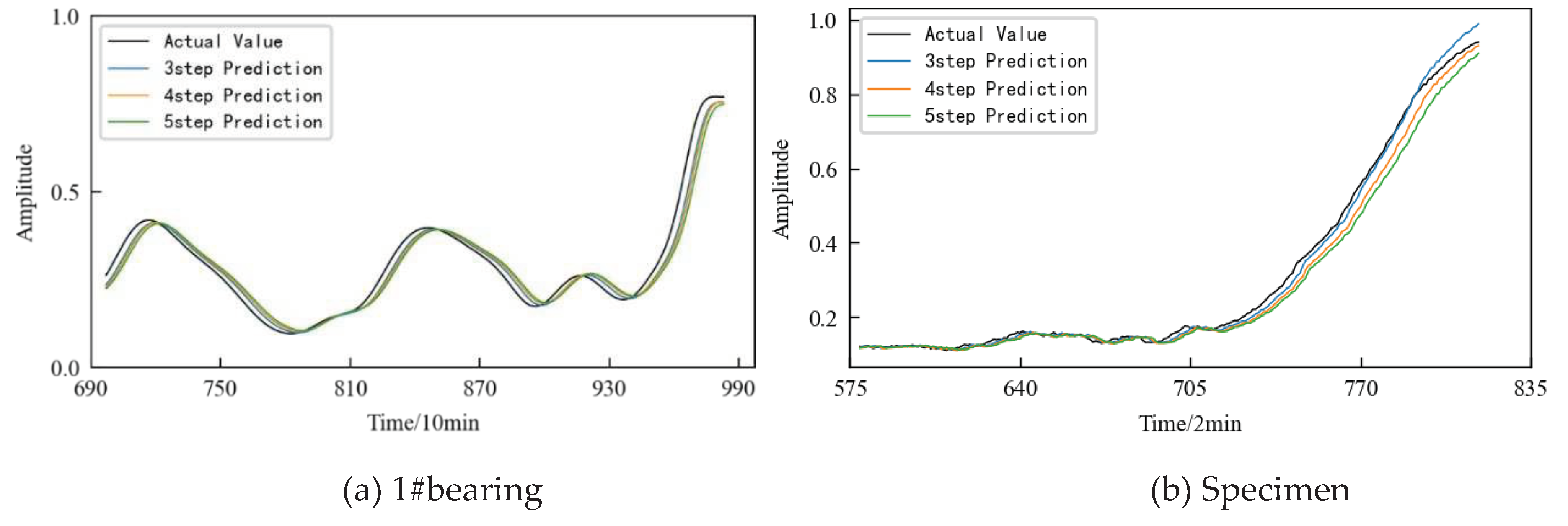
In practical applications, the number of predicted steps can be appropriately increased according to demand. Figure 33 shows the prediction results based on the TCN model in the prediction time period when the prediction steps are 3, 4, and 5 respectively. It can be seen that: 1) In the early stage of prediction, the difference between the predicted values under different prediction step sizes is small and close to the actual value; 2) With the passage of time, the variation range of the HI increases, and the predicted value begins to deviate from the actual value; 3) In the later stage of prediction, the prediction error increases. The larger the prediction step sizes is, the larger the error is.

Further, the evaluation indicators RMSE and MAE are used to quantitatively evaluate the prediction effect of the model. The evaluation index values of the models under the aforementioned three prediction steps are shown in Table 6. It can be seen that under the same other conditions, with the increase of the prediction step size each time, the error of the prediction results increases. Therefore, when predicting performance degradation trend of the monitored object, the prediction step size can be reasonably selected according to the actual demand under the premise of satisfying the prediction accuracy.

6. Conclusions

In this paper, a performance degradation prediction method based on multi-domain features and TCN is proposed and implemented, where comprehensively using theories and methods such as multi-feature fusion, feature space transformation and machine learning.

1) In terms of HI construction, in view of the information loss problem faced by the construction of one-dimensional HI based on multi-domain feature extraction, on the basis of multi-domain feature extraction, a method of using KPCA to reduce feature dimensionality and using CAE network to construct performance degradation HI is proposed. The results show that KPCA can reduce the dimension of the feature set, and retain more than 97% of the information of the original data. Furthermore, the change process of the HI constructed based on the CAE network truly reflects the performance degradation process of the monitored object. Compared with AE network and GMM, this method has obvious advantages.

2) In the aspect of prediction model construction, in view of the shortcomings of the commonly used prediction model based on recurrent neural network, such as low parallel computation and small receptive field of input data, a performance degradation trend prediction method based on multi-domain features and TCN is proposed. The results show that the prediction model constructed by the TCN algorithm can accurately predict the performance degradation trend of the monitored object, and the constructed prediction model has better performance and higher accuracy than the prediction models based on LSTM network and GRU.

The verification results of the bearing public data and the application results of the rolling contact fatigue show that the performance degradation prediction method based on multi-domain features and TCN proposed in this paper is feasible and effective. This method has general significance and can be extended to the performance degradation prediction of other mechanical equipment/components.

Author Contributions

Y.L. conceived this research; YB.L. built model, did experiments and data processing; Y.L. and YB.L. wrote the original draft preparation; editing and review on this article was completed by Y.L. and Y.Y.; Y.Y. is responsible for overseeing the progress and visualization of the article. All authors have read and agreed to the published version of the manuscript.

Funding

This research was founded by the National Natural Science Foundation of China (No.52075062), and Chongqing Municipal Education Commission Major Project of China (No.KJZD-M202001101).

Conflicts of Interest

The authors declare no conflict of interest. And the funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

Pei H, Hu C H, Si X S, et al. Review of machine learning based on remaining useful life prediction methods for equipment [J].Journal of Mechanical Engineering,2019,55(08):1-13.
Li X D, Zhang S C, Liu Y. Review of Rolling Contact Fatigue Life Prediction [J]. Aviation Precision Manufacturing Technology, 2017, 53(03):1-4.
Lei Y G, Jia F, Zhou X, et al. A deep learning-based method for machinery health monitoring with big data [J].Journal of Mechanical Engineering, 2015, 51(21):49-56.
Liu Z Y, Liu Y B, Yang F, et al. Remaining life prediction of contact fatigue based on optimized BP neural network model on Spark platform [J]. Journal of Chongqing University of Technology (Natural Science), 2021, 35(10):111-119.
Ahmad W, Khan S A, Kim J M. A hybrid prognostics technique for rolling element bearings using adaptive predictive models[J]. IEEE Transactions on Industrial Electronics, 2017, 65(2): 1577-1584.
Wu J, Wu C, Cao S, et al. Degradation data-driven time-to-failure prognostics approach for rolling element bearings in electrical machines[J]. IEEE Transactions on Industrial Electronics, 2018, 66(1): 529-539.
Zhu J K. Research on Prediction Method of Rolling Bearing Performance Degradation Trend Based on Deep Learning[D]. Chongqing Jiaotong University, 2021. [CrossRef]
Liu J H. Research on Prediction of Performance Degradation Trend of Wind Turbine Bearings[D]. North China Electric Power University (Beijing),2020.
Wang F T, Chen X T, Liu C X, et al. Reliability evaluation and life prediction of rolling bearing based on KPCA and WPHM[J]. Journal of Vibration, Measurement & Diagnosis, 2017,37(03): 476-483+626.
Zhang Y Q, Zou J H, Ma J. Rolling Bearing Residual Life Prediction Based on Grey Prediction Model with Multiple Degenerate Variables[J]. Journal of Detection & Control, 2019,41(03): 112-120.
Qiao W, Ni X, Wang L, et al. New degradation feature extraction method of planetary gearbox based on alpha stable distribution[J]. Journal of Mechanical Science and Technology, 2021, 35(1): 1-19.
Zhang B, Zhang S, Li W. Bearing performance degradation assessment using long short-term memory recurrent network[J]. Computers in Industry, 2019, 106: 14-29. [CrossRef]
Zheng X X, Qian Y Q, Wang S. GRU prediction for performance degradation of rolling bearings based on optimal wavelet packet and Mahalanobis distance[J]. Journal of Vibration and Shock, 2019, 106:14-29. [CrossRef]
Fang B. Research on Health Status Assessment Method of Rolling Bearings[D]. Harbin Institute of Technology, 2019.
Yang C, Yang X X, Li L F. Prediction of Bearing Performance Degradation Trend Based on Grey Relational Degree and ELM[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2019(11): 105-108.
Zhai W R. Study on Performance Degradation Evaluation of Shearer[D]. China University of Mining, 2020.
Jin Q, Wang Y R, Wang J. Planetary Gearbox Fault Diagnosis Based on Multiple Feature Extraction and Information Fusion Combine with Deep Learning[J]. China Mechanical Engineering, 2019,30(02): 196-204.
Chen X L, Wu C Z. Prediction for Rolling Bearing Performance Degradation Based on 1-DCNN[J]. Chinese Journal of Ordnance Equipment Engineering, 2021, 42(11): 222-227.
AlThobiani F, Ball A. An approach to fault diagnosis of reciprocating compressor valves using Teager–Kaiser energy operator and deep belief networks [J]. Expert Systems with Applications, 2014, 41(9): 4113-4122.
Zhao G Q, Ge Q Q, Liu X Y, et al. Fault feature extraction and diagnosis method based on deep belief network[J]. Chinese Journal of Scientific Instrument, 2016, 37(09): 1946-1953. [CrossRef]
Dai S W, Chen Q Q, Ding Y. Prediction for Rolling Bearing Remaining Life Based on Time Domain Features[J]. Computer Measurement & Control, 2019, 27(10): 60-63.
Shen Z J, Chen X F, He Z J, et al. Remaining Life Predictions of Rolling Bearing Based on Relative Features and Multivariable Support Vector Machine[J]. Journal of Mechanical Engineering, 2013, 49(02): 183-189.
Chen Q Q, Dai S W, DAI H D, et al. Performance degradation trend prediction of rolling bearings based on SPA-FIG and optimized ELM[J]. Journal of Vibration and Shock, 2020, 39(19): 187-194.
Mei W J, Gao Y, Du L, et al. Online sequential regularized correntropy criterion extreme learning machine on spark streaming signal prediction for electronic device degradation[J]. Chinese Journal of Scientific Instrument, 2019, 40(11): 212-224.
Zhou F N, Gao Y L, Wang J Y, et al. Early Diagnosis and Life Prognosis for Slowly Varying Fault Based on Deep Learning[J]. Journal of Shandong University (Engineering Science), 2017, 47(05): 30-37.
Zhang N. A Method of Rolling Bearings Life Prediction Based on Deep Belief Network[D]. Hunan University, 2018.
Yang Y, Zhang N, Cheng S J. Global parameters dynamic learning deep belief networks and its application in rolling bearing life prediction[J]. Journal of Vibration and Shock, 2019, 38(10): 199-205+249.
Janssens O, Slavkovikj V, Vervisch B, et al. Convolutional neural network based fault detection for rotating machinery[J]. Journal of Sound and Vibration, 2016, 377: 331-345.
SunS E, Yao L, Zhao Y. Time Series Data Fusion Algorithm Based on Convolutional Neural Network[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2021, 36(05): 136-142. [CrossRef]
Wang X, Wu J, Liu C, et al. Fault Time Series Prediction Based on LSTM Recurrent Neural Network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(04): 772-784.
Li F, Chen Y, Xiang W, et al. State degradation trend prediction based on quantum weighted long short-term memory neural network [J]. Chinese Journal of Scientific Instrument, 2018, 39(07): 217-225.
Wang P, Deng L, Tang B P, et al. Degradation trend prediction of rolling bearing based on auto-encoder and GRU neural network[J]. Journal of Vibration and Shock, 2020, 39(17): 106-111+133.
Lei Y, Jia F, Lin J, et al. An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data [J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3137-3147.
Li J. Research on State Evaluation Based on Similarity Analysis of Principal Curves in Manifold Space[D]. Chongqing University, 2017. [CrossRef]
Lei Y, Li N, Guo L, et al. Machinery health prognostics: A systematic review from data acquisition to RUL prediction[J]. Mechanical systems and signal processing, 2018, 104: 799-834.
Schölkopf B, Smola A, Müller K R. Kernel principal component analysis[C]//International conference on artificial neural networks. Springer, Berlin, Heidelberg, 1997: 583-588. [CrossRef]
Lee J M, Yoo C K, Choi S W, et al. Nonlinear process monitoring using kernel principal component analysis[J]. Chemical engineering science, 2004, 59(1): 223-234.
Yu S B, He J L, Wang R J, et al. Fault Diagnosis of Electromagnetic Three-level Inverter Based on Wavelet Packet Analysis and Probabiliatic Neural Networks [J]. Transactions of China Electrotechnical Society, 2016,31(17):102-112.
Bai S, Kolter J Z, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling [J]. arXiv preprint arXiv:1803.01271, 2018.
Yu C C, Ning Y Q, Qin Y, et al. Prediction of rolling bearing state degradation trend based on T-SNE sample entropy and TCN [J]. Chinese Journal of Scientific Instrument, 2019,40(08):39-46.
YB/T 5345.2014, Test Method for Rolling Contact Fatigue of Metallic Materials [S].

Figure 1. Schematic diagram of three-layer wavelet packet decomposition.

Figure 2. Schematic diagram of convolution auto encoder network.

Figure 3. Schematic diagram of dilated causal convolution operation.

Figure 4. Schematic diagram of residual block in TCN.

Figure 5. Multi-step forecasting.

Figure 6. Rolling bearing full life test bench.

Figure 7. Lifetime vibration signal of 1#bearing.

Figure 8. Variation trend of time domain feature.

Figure 9. Variation trend of frequency domain feature.

Figure 10. Variation trend of time-frequency domain features.

Figure 11. Comprehensive evaluation index of characteristics.

Figure 12. The contribution rate of the top 10 principal components.

Figure 13. The cumulative contribution rate of the principal components.

Figure 14. Variation trend of the top 4 principal components.

Figure 15. HI constructed by different methods.

Figure 16. Performance degradation prediction of 1#bearing based on different methods.

Figure 17. The structure of the self-developed RCF-A test machine.

Figure 18. Schematic diagram of the shaft box of the RCF-A test machine.

Figure 19. The installation position of the accelerometer.

Figure 20. The control interface of the RCF-A test machine.

Figure 21. Comparison of specimen before and after test.

Figure 22. Fatigue damage and evolution process of specimen surface.

Figure 23. Vibration signal during the whole life cycle of the specimen.

Figure 24. Variation trend of time domain feature.

Figure 25. Variation trend of frequency domain feature.

Figure 26. Variation trend of time-frequency domain features.

Figure 27. Comprehensive evaluation index value of each feature.

Figure 28. The contribution rate of the top 10 principal components.

Figure 29. The cumulative contribution rate of the principal components.

Figure 30. Variation trend of the top 4 principal components.

Figure 31. HI constructed by different methods.

Figure 32. Prediction results of different prediction models.

Figure 33. Prediction results based on TCN under different prediction step sizes.

Table 1. Time domain feature parameters.

No.	Feature	Calculation formula
Dimensional Time Domain Features
$f_{1}$	mean	$\bar{X} = \frac{1}{N} \sum_{i = 1}^{N} x_{i}$
$f_{2}$	rms value	$X_{r m s} = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} x_{i}^{2}}$
$f_{3}$	variance	$X_{var} = \frac{1}{N - 1} \sum_{i = 1}^{N} {(x_{i} - \bar{X})}^{2}$
$f_{4}$	absolute mean	${\bar{X}}_{a b s} = \frac{1}{N} \sum_{i = 1}^{N} \| x_{i} \|$
$f_{5}$	root amplitude	$X_{s r a} = {(\frac{1}{N} \sum_{i = 1}^{N} \sqrt{\| x_{i} \|})}^{2}$
$f_{6}$	peak	$X_{p} = \max_{1 \leq i \leq N} (\| x_{i} \|)$
$f_{7}$	peak-to-peak	$X_{p - p} = \max (x_{i}) - \min (x_{i})$
Dimensionless time domain features
$f_{8}$	skewness index	$X_{s k e w} = \frac{1}{N} \sum_{i = 1}^{N} {(x_{i} - \bar{X})}^{3} / X_{s t d}^{3}$
$f_{9}$	kurtosis index	$X_{k u r} = \frac{1}{N} \sum_{i = 1}^{N} {(x_{i} - \bar{X})}^{4} / X_{s t d}^{4}$
$f_{10}$	peak indicator	$X_{c - f} = X_{p} / X_{r m s}$
$f_{11}$	margin indicator	$X_{c l - f} = X_{p} / X s r a$
$f_{12}$	impulse indicator	$X_{i - f} = X_{p} / {\bar{X}}_{a b s}$
$f_{13}$	waveform indicator	$X_{s - f} = X_{r m s} / {\bar{X}}_{a b s}$

Table 2. Frequency domain feature parameters.

No.	Feature	Calculation formula
$f_{14}$	frequency amplitude mean	$F_{1} = \frac{1}{K} \sum_{k = 1}^{K} s (k)$
$f_{15}$	frequency amplitude variance	$F_{2} = \frac{1}{K - 1} \sum_{k = 1}^{K} {(s (k) - F_{1})}^{2}$
$f_{16}$	first-order center of gravity	$F_{3} = \sum_{k = 1}^{K} f_{k} s (k) / \sum_{k = 1}^{K} s (k)$
$f_{17}$	second-order center of gravity	$F_{4} = \sqrt{\frac{1}{K} \sum_{k = 1}^{K} {(f_{k} - F_{3})}^{2} s (k)}$
$f_{18}$	rms frequency	$F_{5} = \sqrt{\sum_{k = 1}^{K} f_{k}^{2} s (k) / \sum_{k = 1}^{K} s (k)}$
$f_{19}$	frequency domain features 1	$F_{6} = \sum_{k = 1}^{K} {(s (k) - F_{1})}^{3} / [K {(\sqrt{F_{2}})}^{3}]$
$f_{20}$	frequency domain features 2	$F_{7} = \sum_{k = 1}^{K} {(s (k) - F_{1})}^{4} / (K F_{2}^{2})$
$f_{21}$	frequency domain features 3	$F_{8} = \sum_{k = 1}^{K} f_{k}^{2} s (k) / \sqrt{\sum_{k = 1}^{K} s (k) \sum_{k = 1}^{K} f_{k}^{4} s (k)}$
$f_{22}$	frequency domain features 4	$F_{9} = F_{4} / F_{3}$
$f_{23}$	frequency domain features 5	$F_{10} = \sqrt{\sum_{k = 1}^{K} f_{k}^{4} s (k) / \sum_{k = 1}^{K} f_{k}^{2} s (k)}$
$f_{24}$	frequency domain features 6	$F_{11} = \sum_{k = 1}^{K} {(f_{k} - F_{3})}^{3} s (k) / (K F_{4}^{3})$
$f_{25}$	frequency domain features 7	$F_{12} = \sum_{k = 1}^{K} {(f_{k} - F_{3})}^{4} s (k) / (K F_{4}^{4})$

Table 3. Performance of HI constructed by different methods.

Evaluation indicator	CAE-HI	AE-HI	GMM-HI
Monotonicity	0.2513	0.2411	0.1801
Trend	0.9462	0.9430	0.9454

Table 4. Evaluation metrics for different prediction models.

Evaluation indicator	Predictive model
Evaluation indicator	TCN	LSTM	GRU
RMSE	0.0257	0.0385	0.0366
MAE	0.0187	0.0264	0.0234

Table 5. Evaluation index of different prediction models.

Evaluation indicators	Predictive model
Evaluation indicators	TCN	GRU	LSTM
RMSE	0.0146	0.0555	0.0744
MAE	0.0105	0.0308	0.0423

Table 6. Evaluation index of TCN model under different prediction step size.

Evaluation indicators	1#bearing			Specimen
	Prediction step size
	3	4	5	3	4	5
RMSE	0.0257	0.0333	0.0418	0.0146	0.0259	0.0393
MAE	0.0187	0.0243	0.0305	0.0105	0.0164	0.0270

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Prediction of Contact Fatigue Performance Degradation Trend Based on Multi-domain Features and Temporal Convolutional Network

Abstract

1. Introduction

2. Theory and Method

2.1. Multi-domain Feature Extraction and Feature Screening

2.1.1. Multi-domain Feature Extraction

2.1.2. Feature Screening

2.2. Construction of Health Index

2.2.1. Feature Dimensionality Reduction Based on KPCA

2.2.2. Construction of HI Based on CAE Network

2.3. Performance Degradation Prediction

2.3.1. Temporal Convolutional Networks

2.3.2. Performance Degradation Prediction Based on TCN

3. Verification

3.1. Verification of Feature Screening Method

3.2. Verification of of HI Construction Method

3.3. Verification of Performance Degradation Prediction Model

4. Application

4.1. Introduction of Rolling Contact Fatigue Test Equipment

4.2. Rolling Contact Fatigue Test

4.3. Feature Screening

4.4. Feature Dimensionality Reduction

4.5. Construction of HI

4.6. Performance Degradation Prediction of Rolling Contact Fatigue

5. Discussion

6. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe