Prerpints.org logo
Preprint
Article

Optimizing Vehicle Replacement in Sustainable Urban Freight Transportation Subject to Presence of Regulatory Measures

Altmetrics

Downloads

142

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 July 2023

Posted:

06 July 2023

You are already at the latest version

Alerts
Abstract
Since the 1990’s, studies and pilot tests have been conducted to reduce traffic, accidents, and pollution due to urban freight transport (UFT). These ended up in several policies, regulations, and restrictions for UFT, such as low emission zones, delivery time windows, and vehicle size and weight restrictions. However, issues in UFT under regulatory measures still persevere. This study introduces an optimization framework for deriving an optimal combination of various types of vehicles with different capacities for vehicle replacement in UFT. This framework allows an understanding of how an urban freight company with a limited budget efficiently satisfies its freight demand within an urban area in the presence of regulatory measures by urban administrators. The introduced formulation, which is a mixed-integer linear programming, will assist the operator in choosing the best investment strategy for introducing new vehicles of certain types and sizes, for operation in different zones, into its fleet while gaining economic benefits and having a positive impact on the liveability of the urban area. Furthermore, a sensitivity analysis is performed to consider the effects of specific uncertain parameters on the total cost. The numerical results show that the share of electric vehicles in the fleet increases, and they are more competitive than diesel vehicles.
Keywords: 
Subject: Environmental and Earth Sciences  -   Other

1. Introduction

The continuous growth of the urban population is a global phenomenon, with the European Union projecting an increase in the proportion of urban residents from 55% in 2018 to 68% by 2050 [1]. This rapid urbanization, coupled with the rise of globalization, economic development, e-commerce, and Omni channel retailing, has led to a significant surge in urban freight transportation (UFT) UFT [2,3]. However, this upsurge in UFT has also brought forth various challenges and concerns, including emissions, air and noise pollution, traffic congestion, accidents, and damage to road networks [3,4,5]. The implications of these issues are particularly pronounced in city centers, where a substantial portion of freight movement occurs. It is estimated that approximately 20-25% of truck travel distance in urban areas is dedicated to outgoing freight, 40-50% for incoming freight, and the remainder consists of movements between depots and destinations within the city [6]. Furthermore, city centers often face limited parking spaces and narrow streets, exacerbating the problems associated with freight delivery using large vehicles. The resulting congestion and emission issues not only hinder efficient freight transportation but also impact the livability and sustainability of these urban areas [7].
In response to the growing concerns surrounding UFT, various studies and pilot tests have been conducted since the 1990s to mitigate traffic, accidents, and pollution. These efforts have resulted in implementing policies, regulations, and restrictions for UFT operations, such as low emission zones, delivery time windows, and limitations on vehicle size and weight [8,9,10]. Consequently, access to city centers for certain types of vehicles has become restricted due to measures established by local authorities to improve traffic flow and reduce emissions [11,12,13]. As a result, urban freight operators must carefully consider these restrictions when determining their fleet composition. This involves selecting the appropriate number and types of vehicles with the necessary capacity and cost-effectiveness to meet customer demands within restricted areas and beyond. It is crucial for UFT companies to periodically assess and optimize their strategies for utilizing each vehicle type, minimizing associated costs, and maintaining service levels [13,14].
Despite the extensive research conducted in the field of UFT, there is a notable gap in addressing the challenges posed by regulatory measures imposed by urban policymakers on vehicle size and type for operating in different areas of a city. To bridge this gap, this study aims to guide urban freight operators in identifying the optimal fleet configuration and investment strategy for introducing new vehicles of specific types and sizes into their fleets to comply with regulatory measures. In pursuit of this goal, we present an innovative optimization framework designed to reconfigure the fleet of an urban freight transport operator over a planning period, taking into account the regulatory measures imposed by urban policymakers. The proposed framework considers vehicle characteristics and determines the appropriate number of vehicles of each type to be used, purchased, or salvaged in each year of the planning period. Notably, the framework addresses the novelty of incorporating urban restrictions set by policymakers regarding vehicle size and type in different zones of an urban area, as suggested by Maxner et al. [13].
By utilizing this optimization framework, urban freight operators can make informed decisions regarding fleet reconfiguration, ensuring compliance with regulatory measures while optimizing operational efficiency and cost-effectiveness. This study's outcomes can potentially enhance the sustainability and effectiveness of UFT operations within urban areas.
The rest of the paper is organized as follows: Section 2 reviews relevant literature; Section 3 describes the studied problem and its formulation; Section 4 covers the data sources and assumptions; Section 5 presents and discusses computational results; and Section 6 presents the conclusions and future research.

2. Literature review

2.1. Urban freight transport

UFT is fundamental for the economy of cities and the quality of life of those who live and work there. However, by providing necessary goods and services, freight transport has a detrimental impact on urban areas. To overcome these impacts, policymakers should promote regulatory measures for UFT that attempt to balance the economic, social, and environmental impacts of UFT operations [15,16].
Various regulatory measures, mainly to control the type, size, and load factor in terms of lower carbon emission, weight, volume, and the number of parcels to deliver to customer point of use, are already implemented to control UFT in the inner city [13,17]. Comi et al. [18] state that the goal of the regulatory measures is mainly social objectives, such as reducing congestion to expand accessibility and efficiency in goods delivery and related activities. The authors analyze the existing regulatory measures in Rome and Milan and present a theoretical framework to highlight and identify accessible regulations to control vehicle movements. Nuzzolo and Comi [12] analyzed the effectiveness of the measures set by Rome’s administrators on the types of freight vehicles in the inner city areas between 1999 and 2008. Under these enforced measures, they showed that the proportion of environmentally friendly vehicles in the freight fleet has increased over time. The use of electric vehicles (EVs) for delivering goods and parcels to customers in urban areas has received more attention from urban policymakers and private stakeholders[19,20,21,22]. For instance, small EVs could be a viable alternative for delivering goods and services within congested urban areas due to their small size and reduced environmental impact. Small EVs are more suitable for urban distribution and last-mile deliveries because of their battery limitations [23,24]. In another research study by Dablanc [25], the author studied the challenges of transporting goods in large European cities. The author proposes to fix and implement simple regulations in cities for UFT and indicates some decision-making processes, such as identifying measures based on truck age, environmental performance, weight, and size.
European Commission [26] presented and evaluated methods and measures mainly focused on optimizing the operation of truck fleets in a highly congested city level, such as the application of modern devices and appropriate administrative measures, on optimizing truck use in the cities toward achieving economic and environmental benefits. Implementing regulations based on the weight and dimensions of vehicles operating in cities could be a very effective measure. Lindholm [11] has concluded that the current models for UFT mainly focus on transport planning or short-time measures. The author identified the need to develop sustainable measures to manage the lack of applicable restrictions for a long-run perspective method in UFT.
In order to develop sustainable UFT with actionable strategies, the use of electric vehicles (EVs) for delivering goods and services to customers in urban areas has received increasing attention from urban planners and private stakeholders [11,22,27]. For instance, small EVs could be a viable alternative for delivering goods and services within congested urban areas due to their small size and reduced environmental impact.
A study by Lebeau, et al. [20] analyzed the total cost of ownership (TCO ) and competitiveness of light commercial vehicles and quadricycles in UFT. The study found electric quadricycles as a better solution to shift from light diesel vehicles to electric vehicles. The authors considered the effect of utilization level and battery life on TCO and the manner of changing the competitiveness of EVs in the future market. Crist [21] studied the TCO of internal combustion engine vehicles (ICEVs) and EVs and the effect of utilization levels on the competitiveness of those vehicles. The author shows that high levels of utilization have a positive impact on the vehicle's cost. The study shows that considering a 15-year planning horizon, EVs (vans) in France would cost about 4000 EUR less than diesel vehicles (DVs). Currently, EVs are more suitable for urban distribution and last-mile deliveries because of their battery limitations [23,24]. Nina [28] performed a cost-benefit analysis of C-segment passenger EVs in Portugal by considering the user and social factors. From a user point of view, it compares EVs with ICEVs by considering factors such as acquisition and re-sale, maintenance, energy, insurance, periodic inspection, and vehicle-to-grid. From a societal point of view, the author compared local and global greenhouse gas emissions between EVs and ICEVs. The work also considers the contribution of technologies, tax incentives, and governmental support in reducing energy import dependency as the most important goal.

2.2. Fleet replacement problem

The desire to determine an optimal charter to guide vehicle replacement, particularly in the urban freight fleet, has resulted in multiple studies. One basic approach to managing vehicle replacement is to find optimal replacement strategies by taking into account related total cost (TC) [29,30,31]. Redmer [32] developed a deterministic replacement model by considering the reduction in the utilization level by age. Rees et al. [33] proposed an optimization model for police patrol vehicle replacement analysis and planning by considering a network simulation model with probabilistic transition times. In another study, the authors present a vehicle replacement optimization model for the motor carrier by using actual data and presenting a sensitivity analysis to test the effect of changes in vehicle resale values and insurance cost [34]. Kim et al. [35] proposed an automobile replacement model for determining the optimal vehicle age by analyzing life cycle inventories for different vehicles. Their model considers several variables: material production, manufacturing, use, maintenance, and end-of-life environmental impact. Emiliano et al. [36] developed an optimization replacement by solving an integer linear programming problem to indicate different types and ages of diesel buses over a period of 50 years, considering budgetary and environmental constraints. The results show the possibility of emission reduction with a low annual budget using an optimal replacement policy.
In addition, several studies have investigated the combination of fleet replacement with fleet management problems, such as fleet sizing problem (FSP), composition problems (CP), and vehicle routing problem (VRP) [23,34,37,38,39,40,41]. Raposo et al. [42] have suggested a solution for the replacement problem that is combined with FSP by developing a global econometric replacement model. Their model mainly focuses on bus fleets' maintenance approach and related costs. Feng and Figliozzi [23] propose a deterministic, integer linear programming model combining the replacement problem with the FSP in commercial fleets, comparing EVs and DVs. In another study, the authors proposed an optimization framework to find the optimal mix in bus fleets by solving an integer linear programming model that combines the replacement problem with the FSP and VRP [38].
While various studies have been conducted on fleet replacement problems and achieving optimized vehicle replacement frameworks to some extent, to the best of our knowledge, no research has been carried out on regulatory restriction as an important factor in fleet replacement problems.

3. Problem description

3.1. Problem setting

In this paper, we assume that UFT operator wants to select the best strategy for the vehicle composition of their fleet over a specific planning time period. It is assumed that city administrators have regulated the size and type of vehicles that can operate in specific city zones. As a result, the operator must choose vehicles that comply with such restrictions. The city area is divided into different zones based on regulatory measures. In particular, we consider rectangular nested zones [43]. We assume the operator will use a single vehicle type in each zone for operational convenience. The operator must determine the best vehicle replacement strategy while minimizing its TC over a given planning period. Various factors, such as the characteristics of vehicles, related costs, and demand levels of each zone, are incorporated into the model. The model output will determine the type and number of vehicles of each size that needs to be purchased and used for operating in various city zones in each year of the planning period. In addition, it will determine the number of vehicles of any type and size that should be salvaged in any year of the planning time period. The derived model will assist the operator in deriving an efficient vehicle composition for its fleet for operating in different city zones.

3.2. Formulation of the problem

As stated previously, the objective is to minimize the TC of a fleet over a time period operating in a city area divided into different zones with different regulatory measures. The TC consists of different cost components such as energy, operation, maintenance, purchase, and emission costs. In all cases, the costs are accounted for at the beginning of the planning horizon.
The fleet composition is determined for the years t = 0, …, T. Given vehicle types k = 1, …, K, for allowed vehicle ages of the i = 0, …, Ak. The considered urban area is divided into z = 1, …, Z zones.
The decision variables are as follows:
  • x i t k z : number of vehicles of type k and age i used in zone z during year t;
  • y i t k : number of salvaged vehicles of type k and age i at the end of year t;
  • p t k : number of vehicles of type k purchased at the beginning of year t;
The objective function comprises all TC parcels, namely, the purchase costs, energy costs, maintenance costs, emission costs, and salvage revenue. In what follows, we describe each parcel of the cost.
Purchase Cost:
PC = ∑   k = 1 K ∑ t = 0 T − 1 v t k Z t k ( 1 + d r ) − t
v k , t is the purchase cost (EUR) per unit of type k vehicle at the end of year t. The discount rate d r accounts for the decreased value of money over time.
Energy Cost:
FC = ∑ z = 1 Z ∑ k = 1 K ∑ i = 0 A k − 1 ∑ t = 0 T − 1 f i t k z u i k t z x i t k z ( 1 + d r ) − t
f i t k z represents energy cost per kilometer (EUR /km) of vehicle type k of age i in year t in serving zone z, and u i k t z is the annual distance traveled (kilometer per year) of vehicle type k in zone z during year t.
The following formula, adapted from Daganzo [44], will be used for calculating the distance traveled by all vehicles in zone z during year t:
u i k t z ( n t z ) = 2 n t z r z c k + 0.57 n t z A z
r z is the average distance from the depot assigned to zone z to the center of the zone, c k is the number of customers that are served by vehicle type k, A z represents the area of zone z, and n t z represents the number of customers in zone z during year t.
Maintenance Cost:
MC = ∑ z = 1 Z ∑ k = 1 K ∑ i = 0 A k − 1 ∑ t = 0 T − 1 m i t k z u i k t z x i t k z ( 1 + d r ) − t
where m i , t , k represents per-km operation and maintenance cost (EUR/km) of vehicle type k of age i during the year t.
Emission Cost:
EC = ∑ z = 1 Z ∑ k = 1 K ∑ i = 0 A k − 1 ∑ t = 0 T − 1 e i t k z u i k t z x i t k z ( 1 + d r ) − t
where e i t k z represents CO2 emission cost (EUR/km) of vehicle k of age i, in year t and zone z.
Salvage revenue:
SR = ∑ k = 1 K ∑ i = 0 A k − 1 ∑ t = 0 T − 1 s i t k y i t k ( 1 + d r ) − t
where s i t k represents salvage revenue (EUR) of vehicle k of age i, in year t.
Labor cost:
LC = ∑ k = 1 K ∑ i = 0 A k − 1 ∑ t = 0 T − 1 l k t x i t k z ( 1 + d r ) − t
where l k t is labor cost (EUR/year) associated with a vehicle of type k.
Objective function:
Therefore, the objective function, TC, is as follows:
T C = ∑ k = 1 K   ∑ t = 0 T − 1   v k t p t k ( 1 + d r ) − t − ∑ k = 1 K   ∑ i = 1 A k   ∑ t = 0 T   s i t k y i t k ( 1 + d r ) − t +   + ∑ z = 1 Z   ∑ k = 1 K   ∑ i = 0 A k − 1 T − 1   ∑ t = 0 T   f i t k z + m i t k z + e i k z u i k t z x i t k z ( 1 + d r ) − t +   + ∑ k = 1 K   ∑ i = 0 A k − 1   ∑ t = 0 T − 1   l k t x i t k z ( 1 + d r ) − t
Now in the following, we present the constraints of the problem. The total of all newly purchased vehicles in period t must be lower than budget b t of that year:
∑ k = 1 K v kt p tk ≤ b t   ,   ∀ t ∈ { 0 , 1 , 2 , … , T − 1 }
Furthermore, the total kilometers traveled by all used vehicles cannot be lower than the demand of each zone every year:
∑ k = 1 K ∑ i = 0 A k − 1 c k x i t k z ⩾ d t z   ,   ∀ t ∈ { 0 , 1 , 2 , … , T − 1 } ,   ∀ z ∈ { 1 , 2 , … , Z }
where d t z represents the demand of zone z at each year t.
The number of newly available vehicles of type k and the number of newly purchased vehicles of type k ( p 0 , k ) , must be greater or equal to the number of used new vehicles of the corresponding type:
( p 0 , k + ∑ z = 1 Z h 0 , k ) ≥ ∑ z = 1 Z x 0 , 0 , k   ,   ∀ k ∈ { 1 , 2 , … , K }
where h 0 , k represent new vehicles of type k available in the existing fleet at the beginning of the planning period.
At the beginning of the planning horizon, the number of used and salvaged vehicles should be equal to the number of existing vehicles in each zone:
∑ z = 1 Z ( x i 0 k z + y i 0 k z ) = ∑ z = 1 Z h i k z   ,   ∀ i ∈ { 1 , 2 , … , A k } ,   ∀ k ∈ { 1 , 2 , … , K }
In any year of the planning horizon, the number of purchased vehicles of any type should be equal to the number of used new vehicles in that zone:
p t k = ∑ z = 1 Z x 0 t k z   , ∀ t ∈ { 1 , 2 , … , T } ,   ∀ k ∈ { 1 , 2 , … , K }
In each year, the number of used vehicles of any type should be equal to the number of used and salvaged vehicles of the following year:
∑ z = 1 Z x ( i − 1 ) ( t − 1 ) k z = ∑ z = 1 Z ( x i t k z + y i t k z ) ,   ∀ i ∈ { 1 , 2 , … , A k } ,   ∀ t ∈ { 1 , 2 , … , T } ,   k ∈ { 1 , 2 , … , K }
At the end of the last year of the planning horizon, all the vehicles will be sold:
x i T k z = 0 ,   ∀ i ∈ { 1 , 2 , … , A k − 1 } ,   ∀ k ∈ { 1 , 2 , … , K } ,   ∀ z ∈ { 1 , 2 , … , Z }
No vehicle will be used again when it reaches its maximum age:
x A k t k z = 0 ,   ∀ t ∈ { 1 , 2 , … , T } ,   ∀ k ∈ { 1 , 2 , … , K } ∀ z ∈ { 1 , 2 , … , Z }
No newly purchased vehicle will be salvaged in the first year of its lifetime:
y 0 t k z = 0 ,   ∀ t ∈ { 1 , 2 , … , T } ,   ∀ k ∈ { 1 , 2 , … , K }
At each period, the number of purchase, used, and salvaged vehicles of type k that are not allowed to operate in zone z must be zero:
p t k = x i t k z = y i t k z = 0 ,   ∀ t ∈ { 1 , 2 , … , T } ,   ∀ i ∈ { 1 , 2 , … , A k − 1 } ,   ∀ k ∈ K ∖ K z ,   ∀ z ∈ { 1 , 2 , … , Z }
K z is the set of vehicle types allowed to operate in zone z.
Finally, the decision variables can take only non-negative integer values:
p t k , x i t k z , y i t k z ∈ ℤ + = { 0 , 1 , 2 , … }
To minimize the TC, the following a mixed integer linear optimization problem needs to be solved:
{ m i n [ T C ]   s . t .   ( 9 ) − ( 19 )

4. Data sources and assumptions

This section describes the characteristics of the zones, vehicles, and demand considered in the model presented in the previous section.

4.1. Zones characterization

We assume the regulatory measures divide the city area into three different zones, denoted by z1, z2, and z3, respectively (Figure 1 and Table 1) [43]. Additionally, we consider zone z4 (out of zones) a suburban area where the depot point to supply the city can be placed. We presume the zones are nested with the same center and with the areas of A z .
We considered that the zones where the depots are localized are known to the operator. As shown in Figure 1, we characterized these known depot points with D1, D2, and D3, for zones z1 to z3, and D4 for the outside of all zones. We do not consider depot-related costs such as handling, storage, operations administration, and general administrative expenses [45].
Different scenarios are considered to assess the impact on TC of the number and location of depot points:
  • S1: each zone has its own depot points (D1, D2 and D3);
  • S2: depot points are located only in zone 2 and zone3 (D2 and D3);
  • S3: depot point is located only in zone 3 (D3);
  • S4: depot point is out of all zones and in the suburb of the city (D4);
  • S5: all vehicle types can access all zones, each with its own depot points (D1, D2, and D3).

4.2. Vehicle characterization

We consider three vehicle capacities (in m3): light (L), medium (M), and heavy (H). We consider a DV and an EV for each capacity. Thus, we consider a set of six vehicle types {LDV, LEV, MDV, MEV, HDV, HEV}, where LDV, for example, indicates a light diesel vehicle, and we denote this set of vehicles by k = {1, 2, …, 6}. The main characteristics of the vehicles are presented in Table 2, and the main input parameters to determine the TC are in Table 3.
A daily utilization level of 64 km is assumed for both DVs and EVs, equivalent to 16,064 km per year, considering 251 working days a year. We considered the planning horizon of 30 years. The EVs considered in this paper use Lithium-ion batteries, which have a longer lifetime and, according to Emiliano et al. [36], have a lifetime of 240,000 km, equivalent to 15 years, considering a maximum utilization level of 16,000 km/year. Considering the predicted daily utilization, we assume only one battery will be required during the 15 years’ lifetime of the EVs. We included the battery and any other technology costs of EVs in their purchase costs.
To calculate the energy cost (euro/km), we use the following formulas:
f i t k = 1.16 R k e f d . t   , ∀ t ∈ { 1 , 2 , … , T } , ∀ i ∈ { 1 , 2 , … , A k − 1 } ,   k = 1 , 3 , 5
f i t k = 0.16 Q k e f e . t   ,   ∀ t ∈ { 1 , 2 , … , T } ,   ∀ i ∈ { 1 , 2 , … , A k − 1 } ,   k = 2 , 4 , 6
R k (l/km) and Q k (kWh/km) represent the energy consumption of DVs and EVs, respectively, as shown in Table 3. The values 1.16 and 0.16 represent the energy cost of DVs in EUR/l and EVs in EUR/kWh, respectively. Parameters f d and f e are the inflation rates of fuel and electricity prices, respectively, about 6% and 3% per year. These numbers were inferred in accordance with the yearly history of fuel prices from 1981 to 2014 and electricity prices from 2001 to 2013 in Portugal [50].
According to Adeniran [53], the average amount of well-to-wheel-produced CO2 emission by DVs and EVs are about 2.63 kg/l and 0.47 kg/kWh, respectively. The value of CO2 emission of EVs is the result of various types of power generation technologies. The emission costs of DVs and EVs with age i are calculated as follows [53]:
e i D = 2.63 × R k × 0.001 × e c ,   ∀ t ∈ { 1 , 2 , … , T } ,   ∀ i ∈ { 1 , 2 , … , A k − 1 } ,   k = 1 , 3 , 5
e i E = 0.47 × Q k × 0.001 × e c ,   ∀ t ∈ { 1 , 2 , … , T } ,   ∀ i ∈ { 1 , 2 , … , A k − 1 } ,   k = 2 , 4 , 6
e c represents the CO2 emission cost of 25 EUR\ton [54].
For calculating salvage revenue, we use the following formula [21]:
s i t k = ( 1 − θ t k ) s ( i − 1 ) t k = v k ⋅ ( 1 − θ t k ) i ,   ∀ k ∈ K ,   ∀ i ∈ { 1 , … , A k − 1 } ,   ∀ t ∈ { 1 , … T }
θ t k is the depreciation rate of vehicle type k, which is assumed to be 15% [23] for DVs and 19% for EV, as reported in Ahani et al. [49]. The depreciation rate of EVs is less than that of DVs because of their rapid development and the less mature market of second-hand EVs. According to Lee at al. [55], the total maintenance cost of EVs is half the maintenance cost of DVs. Thus, we use the following linear functions to estimate the maintenance costs of light vehicles [49]:
m i t 1 = 0.2 + 0.04 × i , ∀ i ∈ { 0 , 1 , … , A k − 1 } ,   ∀ t ∈ { 1 , … T }  
m i t 2 = 0.1 + 0.02 × i , ∀ i ∈ { 0 , 1 , … , A k − 1 } ,   ∀ t ∈ { 1 , … T }  
We assume the maintenance costs of vehicles of size medium and heavy are as follows [56,57]:
m i t 3 = 1.5 m i t 1   , m i t 5 = 1.5 m i t 1  
m i t 4 = 1.5 m i t 2   , m i t 6 = 1.5 m i t 2
where m i t 3 and m i t 5 for MDVs and HDVs, respectively, and where m i t 4 and m i t 6 for MEVs and HEVs, respectively.
Finally, based on the regulatory measures, it is assumed that LDV and LEV (i.e., k = 1 and 2) can operate in zone z1, which is the most congested zone. In zone z2, LDV, LEV, MDV, and MEV (i.e., k = 1, 2, 3 and 4) can operate. Finally, all six types of vehicles LDV, LEV, MDV, MEV, HDV, and HEV (i.e., k = 1 to 6), can operate in zone z3.

4.3. Demand and fleet composition

We assume the company has an average daily demand of 270 customers distributed in the three zones, as shown in Table 4. The average demand of each customer is assumed to be 0.333 m3. Thus, based on the capacities given in Table 2, and considering that the vehicles operate fully loaded:
  • Light-size vehicles can serve c1 = 6 customers;
  • Medium-size vehicles can serve c2 = 12 customers;
  • Heavy vehicles can serve c3 = 36 customers.
In the first fleet configuration, the existing fleet composition is according to the demand and capacity of the vehicles assigned to each zone, comprising only DVs, with two and one years old vehicles (Table 4), and the operator has a budget of 500,000 EUR for purchasing new vehicles in each year of planning horizon; in the second configuration, there is no existing fleet, and the operator has a budget of 810000 EUR for purchasing new vehicles in each year.

5. Results and discussion

In this section, we report some experimental results for the presented optimization framework using the initial parameter and data described in the previous section as input parameters: total cost, fleet composition, and capacity. Additionally, an elasticity analysis is presented concerning several key parameters. The results comprise six scenarios regarding the locations of depot points combined with two existing fleet configurations. For every combination of scenario and fleet configuration, the optimization problem (20), which is a mixed integer linear optimization problem, is solved by solver Cplex of GAMS 2019 version 27.3 on a laptop computer with CPU Intel core i3-4030U 1.90 GHz and RAM of 4 GB running Windows 10 64-bits, and execution time needed to perform are close to 0.62 s.

5.1. Total cost

Figure 2 presents the results of the TC of each scenario and both existing fleet configurations. Whatever the scenario considered, the TC with an existing fleet is always higher than when the company has no vehicles in its existing fleet. This reflects that without an imposed existing fleet, the model can optimize its composition from the beginning of the planning horizon without the restriction of the existing fleet, thereby achieving lower costs. Considering the variation of the scenario, with or without the existing fleet, the TC increases from S1 to S4, which was expected, once the number of depot points is progressively reduced, increasing the distances between depots and clients.
Moreover, as expected, the TC in scenario S5 is the most reduced, which can be explained by the absence of regulatory measures and the presence of depot points in all zones. This occurs because the distances are reduced, and without restrictions, it is more economical to use larger vehicles (Figure 3).
Figure 3 compares the fleet composition, considering the average usage of vehicles between scenarios S1 and S5. It shows the changes in the number of light, medium, and heavy vehicles in different zones. Particularly in zone z1, the change from medium and heavy to light vehicles highlights the impact of regulatory measures.

5.2. Fleet composition

Table 5 shows the number of vehicles of different types used in the fleet at the beginning of the planning time horizon, their average number, and their final number when the operator has an existing fleet. The existing fleet has different size vehicles, but they are all diesel. However, at the beginning of the planning horizon, the model reconfigures the fleet composition according to the budget available and the existing fleet, originating the initial fleet.
As mentioned, different vehicles are permitted to operate in different zones: light DVs and EVs in zone z1; light and medium DVs and EVs in zone z2; and all types and sizes in zone z3. In all scenarios, in the final year of the planning time horizon, all DVs are replaced by EVs. Hence, the energy cost becomes the dominant factor in the TC, as EVs have lower energy costs than DVs. Moreover, reflecting the regulatory measures, in all scenarios except S5, zone z1 ended with LEVs, z2 with MEVs, and z3 with HEVs. In scenario S5, the lack of regulatory measures allowed the increase of the size of the vehicles in all zones, thus allowing economies of scale in the fleet.
Concluding, the regulatory measures determine the size of the vehicles, the bigger the best, and the energy cost associated with distance determines the motor type.
Table 6 shows the number of vehicles of different types used in the fleet at the beginning of the planning time horizon, their average number, and their final number when the operator does not have an existing fleet. In this case, the model suggests using different types of vehicles at the beginning of the planning horizon according only to the budget available. The results show that the fleet composition over the planning horizon is similar to the previous case with the existing fleet. Comparing Table 5 to Table 6, the initial fleets are identical in scenarios S2 to S4, suggesting it is worth updating the existing fleet because it minimizes TC in the long run. The swiftness of fleet reconfiguration depends on the budget available at the beginning of the planning horizon.

5.3. Capacity analysis

Figure 4 compares the average capacity over the planning horizon of each type, Dvs and EVs, for each scenario with an existing fleet. As shown, the average capacity of EVs is dominant in all scenarios except in Scenario S5. Scenario S5, where any vehicle size and type are free to operate in all zones, and each zone has its own depot, favors the usage of heavier diesel-powered vehicles, particularly in zone z3 (Figure 3). Furthermore, scenario S4 shows that the average EV capacity is greater than in other scenarios since the travel distance increased due to depot points outside the zones. Moreover, it shows that EVs have become more competitive regarding fleet capacity.

5.4. Elasticity analysis

As mentioned earlier, some input parameters have high uncertainty, which inevitably propagates to the TC. Therefore, we conducted an elasticity analysis on the EVs depreciation rate and the energy price growth rates for EVS and DVs. These parameters are particularly affected by uncertainty during the planning horizon. For that, we adopted the arc elasticity formula proposed by Allen [58].
E A ( T C , p ) = %   change   in   TC   %   change   in   parameter   p = p 1 + p 2 T C 1 + T C 2 × T C 2 − T C 1 p 2 − p 1
Elasticity analysis was done for different ranges of values to support the operator in defining which input parameter has the most significant impact on his fleet. The results of the elasticity analysis are shown in Table 7. The elasticity of the depreciation rate of EVs was calculated for three intervals of 10% to 20%, 14% to 24%, and 18% to 28%, as a low, medium, and high level of depreciation rate for all scenarios. For instance, for EVs depreciation rate between 10% and 20%, the elasticity for S1 scenario is 0.055, indicating that when the depreciation rate increases by 1%, the fleet TC increases by 5.5 %; the impact on the TC is 5.5 times higher compared with the rise on the depreciation rate. With or without an existing fleet, on average, a 1% increase in the depreciation rate leads to a rise of around 7% in the TC, which reveals the importance of the uncertainty associated with this parameter.
We also examined the elasticity of the growth rate of energy price for intervals of 2.91% to 8.73%, for DVs, and 1.44% to 4.33% for EVs, both with and without an existing fleet. Table 7 shows that the DVs energy price growth rate, when compared to EVs energy price growth rate, has a bigger impact on the fleet TC, independently of an existing fleet or not. When using DVs, the energy cost is higher, thus representing a more significant part of the TC. On average, an increase of 1% in the diesel price growth rate results in a rise of nearly 4% and 7% in the TC, respectively, with an without and existing fleet.

6. Conclusions

The quality of delivering and distributing goods to customers is of prime importance for companies. Thus choosing the best strategy for purchasing, using, and salvaging each vehicle size and type, electric or diesel-powered, while minimizing the related total cost and maintaining the quality of its service become a critical issue for an urban freight transportation company.
On the other hand, access to the city centers for certain types of vehicles might be restricted due to regulatory measures set by city authorities to ease traffic movements and reduce carbon emissions within such areas. This study contribution is a model to assist urban freight transport operators in optimizing their fleet composition, minimizing the total cost, and considering the regulatory measures regarding the size and type of vehicles and the possibility of operating in specific city areas defined by the city authorities. The developed framework considers the costs of acquiring vehicles, energy consumption, emissions, maintenance, salvage, and labor of different types of vehicles. The model output indicates the optimal composition of the fleet, namely, the number, size, and types of vehicles required for operating in the various city areas in the planning time horizon.
The results indicate that fleet composition vehicle size depends on regulatory measures, and the motor type, diesel or electric, depends on the trade-off between purchasing and operating costs. This means that, by reducing regulatory measures, the size of vehicles increases. Additionally, by reducing the number of depot points, the number of electric vehicles increases due to the rise in operating costs driven by increased travel distances. Moreover, the rate of fleet electrification depends on the existing fleet and the budget to purchase new vehicles.
An elasticity analysis was also performed to consider some input parameters' uncertainty. The results show that the total cost is highly exposed to changes in electric vehicle depreciation and diesel price growth rates. On average, an increase of 1% in the depreciation rate leads to an increase of almost 7% in the total cost; and a rise of 1% in the diesel price growth rate leads to an increase of nearly 6% in the total cost. As such, fleet operators must be very aware of the trends in the used electric vehicle market and the diesel price.
Finally, this work has some limitations that can be settled in future research. For example, the costs related to the depot points should also be considered in the total cost, multi-depot settings, and fleet assignment to each depot point. Moreover, the uncertain effects of other parameters using an optimization framework based on the portfolio theory, such as the one developed by Ahani et al. [49], need to be further investigated.

Author Contributions

Conceptualization, Parisa Ahani, Amílcar Arantes, Rohollah Garmanjani and Sandra Melo; Data curation, Parisa Ahani and Sandra Melo; Formal analysis, Parisa Ahani, Amílcar Arantes and Rohollah Garmanjani; Funding acquisition, Sandra Melo; Investigation, Parisa Ahani; Methodology, Parisa Ahani, Amílcar Arantes and Rohollah Garmanjani; Project administration, Sandra Melo; Resources, Amílcar Arantes; Supervision, Amílcar Arantes and Sandra Melo; Validation, Parisa Ahani and Rohollah Garmanjani; Writing – original draft, Parisa Ahani and Amílcar Arantes.

Data Availability Statement

Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. European Commission Urbanisation Worldwide. Available online: https://knowledge4policy.ec.europa.eu/foresight/topic/continuing-urbanisation/urbanisation-worldwide_en (accessed on 9 June 2020).
  2. Sheth, M.; Butrina, P.; Goodchild, A.; McCormack, E. Measuring Delivery Route Cost Trade-Offs between Electric-Assist Cargo Bicycles and Delivery Trucks in Dense Urban Areas. Eur. Transp. Res. Rev. 2019, 11, 12. [Google Scholar] [CrossRef]
  3. Bosona, T. Urban Freight Last Mile Logistics—Challenges and Opportunities to Improve Sustainability: A Literature Review. Sustain. 2020, 12, 8769. [Google Scholar] [CrossRef]
  4. Cardenas, I.; Borbon-Galvez, Y.; Verlinden, T.; Voorde, E. Van De; Vanelslander, T.; Dewulf, W. City Logistics, Urban Goods Distribution and Last Mile Delivery and Collection. Compet. Regul. Netw. Ind. 2017, 18. [Google Scholar] [CrossRef]
  5. Melacini, M.; Perotti, S.; Rasini, M.; Tappia, E. E-Fulfilment and Distribution in Omni-Channel Retailing: A Systematic Literature Review. Int. J. Phys. Distrib. Logist. Manag. 2018, 48, 391–414. [Google Scholar] [CrossRef]
  6. Macharis, C.; Kin, B. The 4 A’s of Sustainable City Distribution: Innovative Solutions and Challenges Ahead. Int. J. Sustain. Transp. 2017, 11, 59–71. [Google Scholar] [CrossRef]
  7. Letnik, T.; Hanžič, K.; Luppino, G.; Mencinger, M. Impact of Logistics Trends on Freight Transport Development in Urban Areas. Sustain. 2022, 14, 16551. [Google Scholar] [CrossRef]
  8. Riccardi, M.R.; Mauriello, F.; Sarkar, S.; Galante, F.; Scarano, A.; Montella, A. Parametric and Non-Parametric Analyses for Pedestrian Crash Severity Prediction in Great Britain. Sustainability 2022, 14, 3188. [Google Scholar] [CrossRef]
  9. Montella, A.; Marzano, V.; Mauriello, F.; Vitillo, R.; Fasanelli, R.; Pernetti, M.; Galante, F. Development of Macro-Level Safety Performance Functions in the City of Naples. Sustainability 2019, 11, 1871. [Google Scholar] [CrossRef]
  10. Ville, S.; Gonzalez-Feliu, J.; Dablanc, L. The Limits of Public Policy Intervention in Urban Logistics: Lessons from Vicenza (Italy). Eur. Plan. Stud. 2013, 21, 1528–1541. [Google Scholar] [CrossRef]
  11. Lindholm, M. Urban Freight Transport from a Local Authority Perspective-A Literature Review. Eur. Transp. - Trasp. Eur. 2013, 1–37. [Google Scholar]
  12. Nuzzolo, A.; Comi, A. Urban Freight Transport Policies in Rome: Lessons Learned and the Road Ahead. J. Urban. 2015, 8, 133–147. [Google Scholar] [CrossRef]
  13. Maxner, T.; Chiara, G.D.; Goodchild, A. Identifying the Challenges to Sustainable Urban Last-Mile Deliveries: Perspectives from Public and Private Stakeholders. Sustain. 2022, 14, 4701. [Google Scholar] [CrossRef]
  14. Masłowski, D.; Kulińska, E.; Komada, G. Impact of Alternative Forms of Transport on Urban Freight Congestion. Sustain. 2022, 14, 10972. [Google Scholar] [CrossRef]
  15. Anderson, S.; Allen, J.; Browne, M. Urban Logistics––How Can It Meet Policy Makers’ Sustainability Objectives? J. Transp. Geogr. 2005, 13, 71–81. [Google Scholar] [CrossRef]
  16. Browne, M.; Allen, J. Enhancing the Sustainability of Urban Freight Transport and Logistics. Transp. Commun. Bull. Asia Pacific 2011, 44, 1–19. [Google Scholar]
  17. Axelsson, J.; Jensen, C.; Johansson, H.; Lagercrantz, J.; Larsson, M.-O.; Lindman, K.; Ottosson, M.; Siira, J.; Stenström, M.; Vennersten, S.; et al. Final Evaluation Report Göteborg (TELLUS Project); 2005.
  18. Comi, A.; Site, P.D.; Filippi, F.; Marcucci, E.; Nuzzolo, A. Differentiated Regulation of Urban Freight Traffic: Conceptual Framework and Examples from Italy. In Proceedings of the 13th International Conference of Hong Kong Society for Transportation Studies: Transportation and Management; 2008; pp. 815–824.
  19. Barter, G.E.; Reichmuth, D.; Westbrook, J.; Malczynski, L.A.; West, T.H.; Manley, D.K.; Guzman, K.D.; Edwards, D.M. Parametric Analysis of Technology and Policy Tradeoffs for Conventional and Electric Light-Duty Vehicles. Energy Policy 2012, 46, 473–488. [Google Scholar] [CrossRef]
  20. Lebeau, P.; Macharis, C.; Van Mierlo, J.; Lebeau, K. Electrifying Light Commercial Vehicles for City Logistics? A Total Cost of Ownership Analysis. Eur. J. Transp. Infrastruct. Res. 2015, 15, 551–569. [Google Scholar] [CrossRef]
  21. Crist, P. Elecric Vehicles Revisited - Costs, Subsidies and Prospects; OECD Publishing: Paris, 2012. [Google Scholar]
  22. Tipagornwong, C.; Figliozzi, M. Analysis of Competitiveness of Freight Tricycle Delivery Services in Urban Areas. Transp. Res. Rec. 2014, 2410, 76–84. [Google Scholar] [CrossRef]
  23. Feng, W.; Figliozzi, M. An Economic and Technological Analysis of the Key Factors Affecting the Competitiveness of Electric Commercial Vehicles: A Case Study from the USA Market. Transp. Res. Part C Emerg. Technol. 2013, 26, 135–145. [Google Scholar] [CrossRef]
  24. Taefi, T.T.; Kreutzfeldt, J.; Held, T.; Konings, R.; Kotter, R.; Lilley, S.; Baster, H.; Green, N.; Laugesen, M.S.; Jacobsson, S.; et al. Comparative Analysis of European Examples of Freight Electric Vehicles Schemes—A Systematic Case Study Approach with Examples from Denmark, Germany, the Netherlands, Sweden and the UK. In Dynamics in Logistics - Proceedings of the 4th International Conference LDIC, 2014 Bremen, Germany; Kotzab, H., Pannek, J., Thoben, K.D., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 495–504. ISBN 9783319235127. [Google Scholar]
  25. Dablanc, L. Goods Transport in Large European Cities: Difficult to Organize, Difficult to Modernize. Transp. Res. Part A Policy Pract. 2007, 41, 280–285. [Google Scholar] [CrossRef]
  26. Behiri, W.; Belmokhtar-Berraf, S.; Chu, C. Urban Freight Transport Using Passenger Rail Network: Scientific Issues and Quantitative Analysis. Transp. Res. Part E Logist. Transp. Rev. 2018, 115, 227–245. [Google Scholar] [CrossRef]
  27. Pelletier, S.; Viswanath, P.; Mathew, M. Goods Distribution with Electric Vehicles : Review and Research Perspectives Goods; 2014.
  28. Nina, M. Introduction of Electric Vehicles in Portugal - A Cost-Benefit Analysis, Instituto Superior Técnico, Universidade de Lisboa, 2010.
  29. Eilon, S.; King, J.R.; Hutchinson, D.E. A Study in Equipment Replacement. J. Oper. Res. Soc. 1966, 17, 59–71. [Google Scholar] [CrossRef]
  30. Christer, A.H.; Goodbody, W. Equipment Replacement in an Unsteady Economy. J. Oper. Res. Soc. 1980, 31, 497–506. [Google Scholar] [CrossRef]
  31. Scarf, P.A.; Bouamra, O. Capital Equipment Replacement Model for a Fleet with Variable Size. J. Qual. Maint. Eng. 1999, 5, 40–49. [Google Scholar] [CrossRef]
  32. Redmer, A. Optimisation of the Exploitation Period of Individual Vehicles in Freight Transportation Companies. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 978–987. [Google Scholar] [CrossRef]
  33. Rees, L.P.; Clayton, E.R.; Taylor, B.W. A Network Simulation Model for Police Patrol Vehicle Maintenance and Replacement Analysis. Comput. Environ. Urban Syst. 1982, 7, 191–196. [Google Scholar] [CrossRef]
  34. Suzuki, Y.; Pautsch, G.R. A Vehicle Replacement Policy for Motor Carriers in an Unsteady Economy. Transp. Res. Part A Policy Pract. 2005, 39, 463–480. [Google Scholar] [CrossRef]
  35. Kim, H.C.; Keoleian, G.A.; Grande, D.E.; Bean, J.C. Life Cycle Optimization of Automobile Replacement: Model and Application. Environ. Sci. Technol. 2003, 37, 5407–5413. [Google Scholar] [CrossRef]
  36. Emiliano, W.; Alvelos, F.; Telhada, J.; Lanzer, E.A. An Optimization Model for Bus Fleet Replacement with Budgetary and Environmental Constraints. Transp. Plan. Technol. 2020, 43, 488–502. [Google Scholar] [CrossRef]
  37. Beaujon, G.J.; Turnquist, M.A. A Model for Fleet Sizing and Vehicle Allocation. Transp. Sci. 1991, 25, 17–45. [Google Scholar] [CrossRef]
  38. Li, L.; Lo, H.K.; Xiao, F.; Cen, X. Mixed Bus Fleet Management Strategy for Minimizing Overall and Emissions External Costs. Transp. Res. Part D Transp. Environ. 2018, 60, 104–118. [Google Scholar] [CrossRef]
  39. Redmer, A. Strategic Vehicle Fleet Management–a Joint Solution of Make-or-Buy, Composition and Replacement Problems. J. Qual. Maint. Eng. 2022, 28, 327–349. [Google Scholar] [CrossRef]
  40. Wu, P.; Hartman, J.C.; Wilson, G.R. An Integrated Model and Solution Approach for Fleet Sizing with Heterogeneous Assets. Transp. Sci. 2005, 39, 87–103. [Google Scholar] [CrossRef]
  41. Zheng, S.; Chen, S. Fleet Replacement Decisions under Demand and Fuel Price Uncertainties. Transp. Res. Part D Transp. Environ. 2018, 60, 153–173. [Google Scholar] [CrossRef]
  42. Raposo, H.; Farinha, J.T.; Ferreira, L.; Galar, D. An Integrated Econometric Model for Bus Replacement and Determination of Reserve Fleet Size Based on Predictive Maintenance. Eksploat. i Niezawodn. 2017, 19, 358–368. [Google Scholar] [CrossRef]
  43. Koç, Ç.; Bektaş, T.; Jabali, O.; Laporte, G. The Impact of Depot Location, Fleet Composition and Routing on Emissions in City Logistics. Transp. Res. Part B Methodol. 2016, 84, 81–102. [Google Scholar] [CrossRef]
  44. Daganzo, C.F. Modeling Distribution Problems with Time Windows: Part I. Transp. Sci. 1987, 21, 171–179. [Google Scholar] [CrossRef]
  45. Ghiani, G.; Laporte, G.; Musmanno, R. Introduction to Logistics Systems Management; 3rd ed.; John Wiley and Sons Ltd, 2022; ISBN 9781119789390.
  46. Meusalario.pt Compare Seu Salário. Available online: https://meusalario.pt/salario/compare-seu-salario?job-id=8322020000000/%5C#/ (accessed on 6 July 2020).
  47. NISSAN NISSAN E-NV200. Available online: https://www.nissan.pt/veiculos/novos-veiculos/e-nv200/preco-e-versoes.html (accessed on 6 May 2020).
  48. ACEA Average Age of the EU Vehicle Fleet, by Country. Available online: https://www.acea.auto/figure/average-age-of-eu-vehicle-fleet-by-country/ (accessed on 22 July 2020).
  49. Ahani, P.; Arantes, A.; Melo, S. A Portfolio Approach for Optimal Fleet Replacement toward Sustainable Urban Freight Transportation. Transp. Res. Part D Transp. Environ. 2016, 48, 357–368. [Google Scholar] [CrossRef]
  50. PORDATA Consumo de Energia Elétrica: Total e Por Setor de Atividade Económica. Available online: https://www.pordata.pt/Portugal (accessed on 22 July 2020).
  51. Zhang, J.; Wang, Z.; Liu, P.; Cui, D.; Li, X. Analysis on Influence Factors of Energy Consumption of Electric Vehicles Based on Real-World Driving Data. In Proceedings of the International Conference on Applied Energy 2019; Västerås, Sweden, 2019; pp. 12–15.
  52. Lois, D.; Wang, Y.; Boggio-Marzet, A.; Monzon, A. Multivariate Analysis of Fuel Consumption Related to Eco-Driving: Interaction of Driving Patterns and External Factors. Transp. Res. Part D Transp. Environ. 2019, 72, 232–242. [Google Scholar] [CrossRef]
  53. Adeniran, I.O. The Impacts of Sustainable Concepts in Urban Freight Distribution - A Courier, Express and Parcel Case Study, TUM - Technische Universität München, 2020.
  54. Gerlagh, R.; Heijmans, R.J.R.K.; Rosendahl, K.E. COVID-19 Tests the Market Stability Reserve. Environ. Resour. Econ. 2020, 76, 855–865. [Google Scholar] [CrossRef]
  55. Lee, D.Y.; Thomas, V.M.; Brown, M.A. Electric Urban Delivery Trucks: Energy Use, Greenhouse Gas Emissions, and Cost-Effectiveness. Environ. Sci. Technol. 2013, 47, 8022–8030. [Google Scholar] [CrossRef] [PubMed]
  56. City of Toronto - Fleet Services 2017 Performance Measurement & Benchmarking Report; Canada, 2019.
  57. Electrification Coalition Fleet Electrification Roadmap: Revolutionizing Transportation and Achieving Energy Security; Washington, D.C., 2010.
  58. Allen, R.G.D. The Concept of Arc Elasticity of Demand: I. Rev. Econ. Stud. 1934, 1, 226–229. [Google Scholar] [CrossRef]
Preprints 78665 g001
Figure 1. Characteristics of the zones.
Figure 1. Characteristics of the zones.
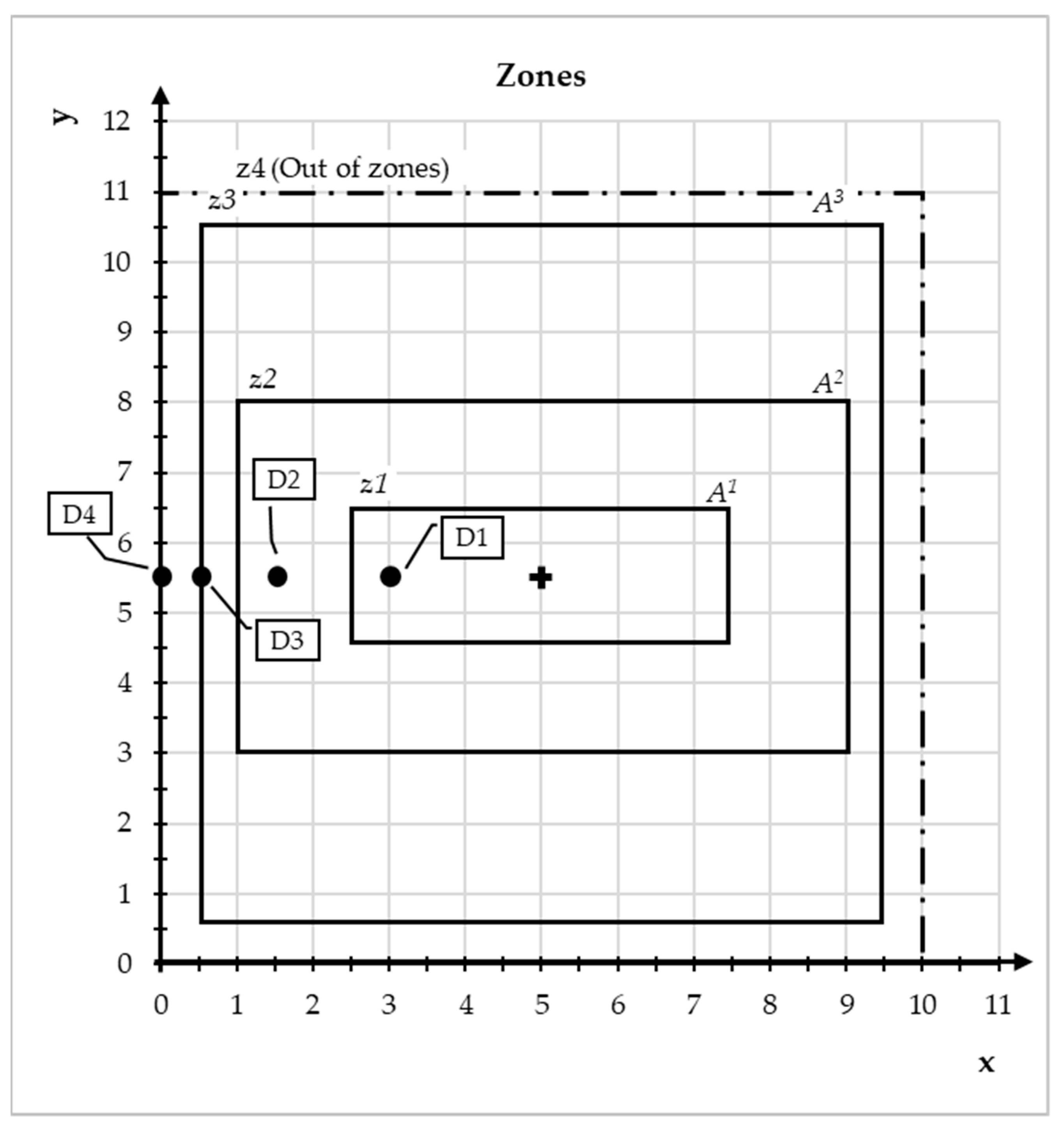
Preprints 78665 g001
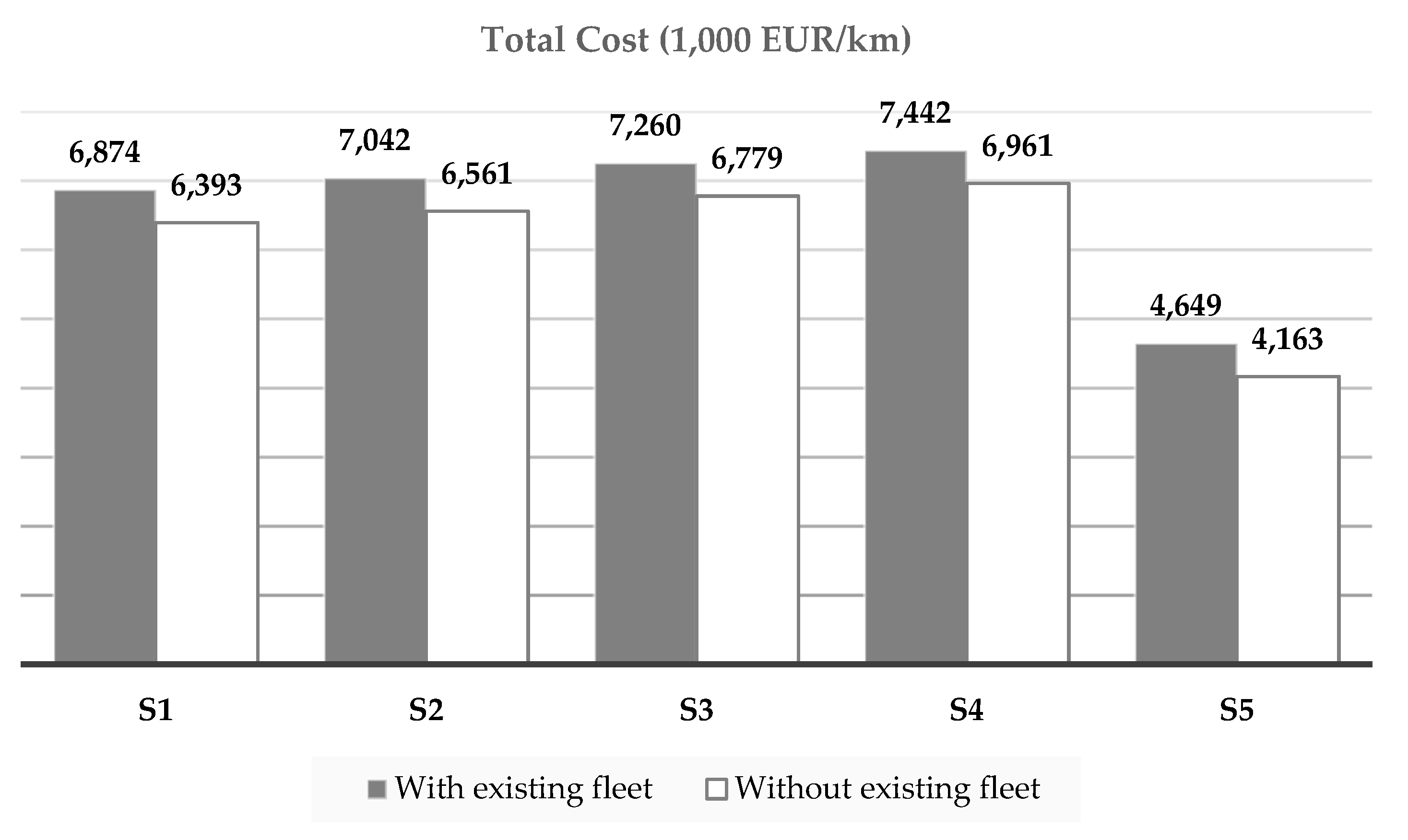
Preprints 78665 g002
Figure 2. Total cost for all scenarios with and without an existing fleet.
Figure 2. Total cost for all scenarios with and without an existing fleet.
Preprints 78665 g002
Preprints 78665 g003
Figure 3. Average fleet composition for scenarios S1 and S5 (with existing fleet).
Figure 3. Average fleet composition for scenarios S1 and S5 (with existing fleet).
Preprints 78665 g003
Preprints 78665 g004
Figure 4. The average capacity of each type for each scenario with an existing fleet.
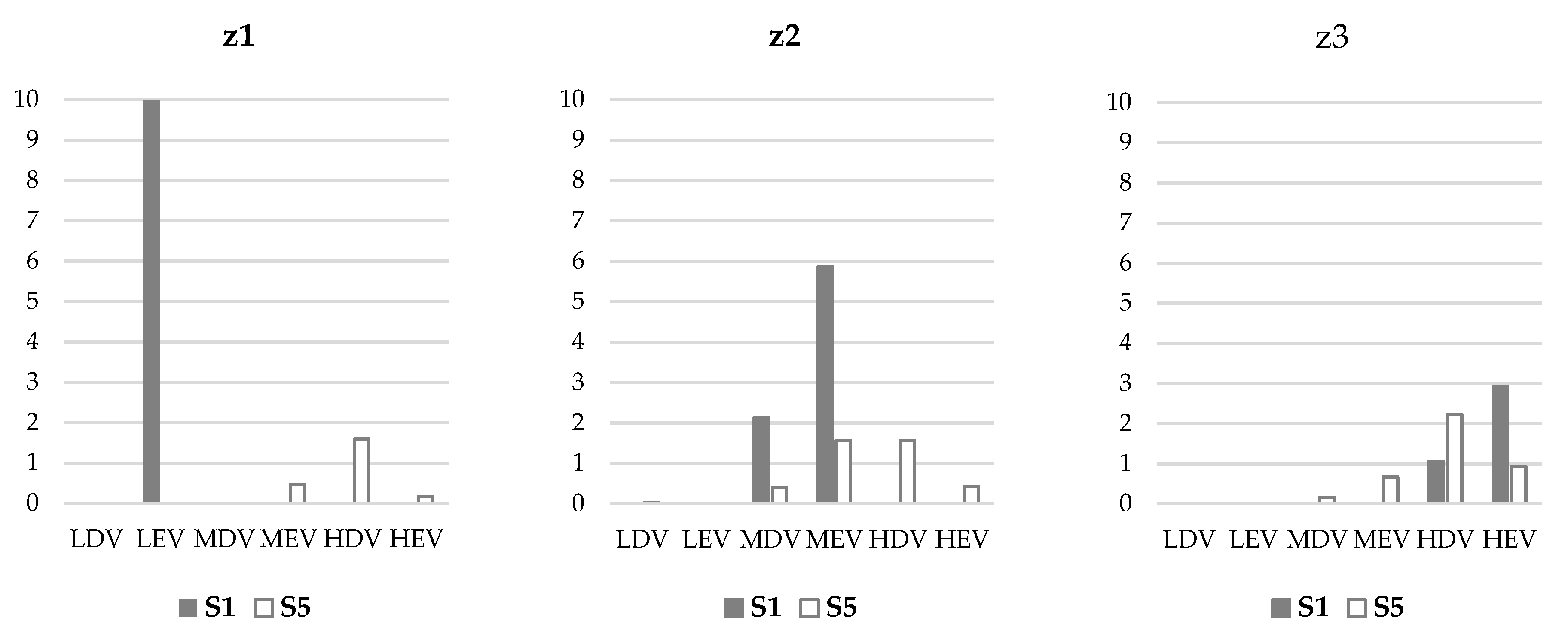
Figure 4. The average capacity of each type for each scenario with an existing fleet.
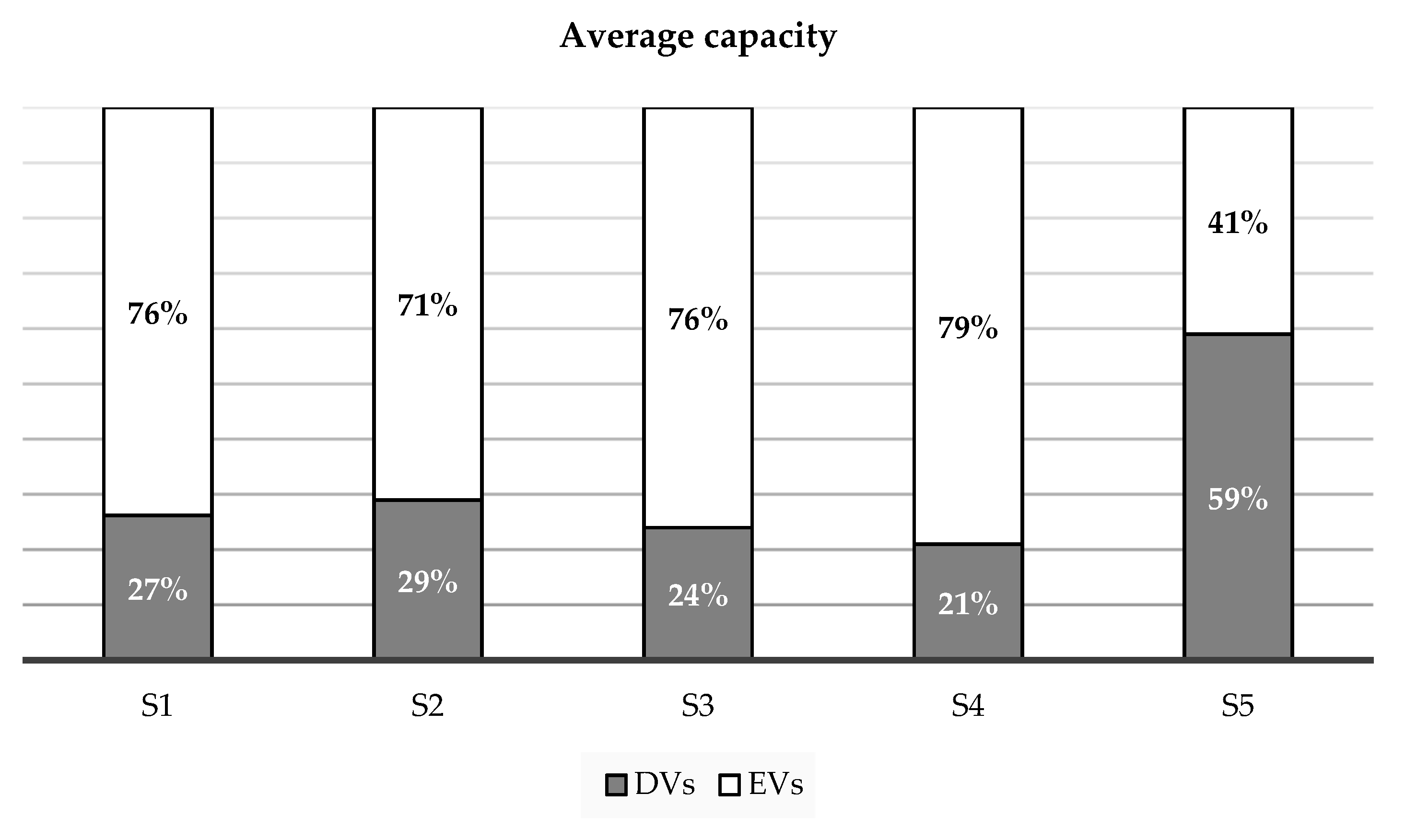
Preprints 78665 g004
Table 1. Characteristics of the zones.
Table 1. Characteristics of the zones.
Zone Coordinates (x, y) of the left-down corner of each zone
(km, km)		 Outer dimensions of each zone
(km x km)		 Area   of   each   zone   ( A z )
(km2)		 Coordinates (x, y) of each depot
(km, km)		 Distance   from   depots   to   the   center   of   the   zones   ( r z ) (km)
z1 2.5, 4.5 5 x 2 10 3.0, 5.5 2.0
z2 1.0, 3.0 8 x 5 30 1.5, 5.5 3.5
z3 0.5, 0.5 9 x 10 50 0.5, 5.5 4.5
Suburban zone (Out of zones) 0.0, 0.0 10 x 11 20 0.0, 5.5 5.0
Table 2. Characteristic of the vehicles.
Table 2. Characteristic of the vehicles.
k Vehicle Model Motor type Size type Capacity (m3) Price (euro) Driver salary (EUR/month) [46] Energy consumption
1 Renault New Kangoo Express [20] Diesel Light 2 13,600 750 5.2 l/100 km
2 Renault Kangoo ZE [20] Electric Light 2 21,150 750 15.5 kWh:100 km
3 Nissan NV200 [20] Diesel Medium 4 15,400 932 5.7 l/100 km
4 Nissan e-NV200 [47] Electric Medium 4 25,652 932 16.5 k Wh:100 km
5 Isuzu N-Series [23] Diesel Heavy 12 48,450 1068 17.47 l/100km
6 eStar (Navistar) [23] Electric Heavy 12 133,369 1068 50 kWh:100km
Table 3. Vehicles input parameters data.
Table 3. Vehicles input parameters data.
Parameter Diesel vehicle Electric vehicle
Maximum age (Ak) [23,48] 15
Discount rate(dr) [23] 6.50%
Working days in a year (Wd) 251
Planning time horizon(year) (t) [23] 30
Depreciation rate (θk) [23,49] 0.15 0.198
Energy cost growth rate (fd, fe) [50] 0.0582 0.0289
Energy consumption (Rk, Qk) [51,52] 0.062 l/km 0.145 kWh/km
Energy cost [50] 1.167 EUR/l 0.167 EUR/kWh
CO2 emissions (Well-to-Wheel) [53] 2.63 kg/l 0.47 kg/kWh
Table 4. Existing fleet composition.
Table 4. Existing fleet composition.
Zone Demand
(customer/day)		 LDV MDV HDV
z1 n1 = 60 10 - -
z2 n2 = 90 5 5 -
z3 n3 = 120 4 2 2
Total 270 19 1 7 2
1 Six vehicles of ages 0 to 2 years old, with two of each age. The remaining ones are of different ages.
Table 5. The average, initial, and final usage of different vehicle types under different scenarios with an existing fleet.
Table 5. The average, initial, and final usage of different vehicle types under different scenarios with an existing fleet.
Scenario Vehicle type Average usage Initial usage Final usage
z1 z2 z3 z1 z2 z3 z1 z2 z3
S1 LDV 0.033 0 0 1 0 0 0 0 0
LEV 9.967 0 0 9 0 0 10 0 0
MDV 0 2.133 0 0 8 0 0 0 0
MEV 0 5.867 0 0 0 0 0 8 0
HDV 0 0 1.067 0 0 4 0 0 0
HEV 0 0 2.933 0 0 0 0 0 4
S2 LDV 1.267 0 0 10 0 0 0 0 0
LEV 8.733 0 0 0 0 0 10 0 0
MDV 0 2.133 0 0 8 0 0 0 0
MEV 0 5.867 0 0 0 0 0 8 0
HDV 0 0 1.067 0 0 4 0 0 0
HEV 0 0 2.933 0 0 0 0 0 4
S3 LDV 0.7 0 0 10 0 0 0 0 0
LEV 9.3 0 0 0 0 0 10 0 0
MDV 0 1.6 0 0 8 0 0 0 0
MEV 0 6.4 0 0 0 0 0 8 0
HDV 0 0 1.067 0 0 4 0 0 0
HEV 0 0 2.933 0 0 0 0 0 4
S4 LDV 0.933 0 0 10 0 0 0 0 0
LEV 9.067 0 0 0 0 0 10 0 0
MDV 0 1.067 0 0 8 0 0 0 0
MEV 0 6.933 0 0 0 0 0 8 0
HDV 0 0 1.3 0 0 4 0 0 0
HEV 0 0 2.7 0 0 0 0 0 4
S5 LDV 0 0.033 0 0 1 0 0 0 0
LEV 0 0 0 0 0 0 0 0 0
MDV 0 0.4 0.167 0 1 1 0 0 0
MEV 0.467 1.567 0.667 0 0 0 2 2 1
HDV 1.6 1.567 2.233 2 2 3 0 0 0
HEV 0.167 0.433 0.933 0 0 0 1 2 3
Table 6. The average, initial, and final usage of different vehicle types under different scenarios without an existing fleet.
Table 6. The average, initial, and final usage of different vehicle types under different scenarios without an existing fleet.
Scenario Vehicle type Average usage Initial usage Final usage
z1 z2 z3 z1 z2 z1 z2 z3 z3
S1 LDV 0.133 0 0 4 0 0 0 0 0
LEV 9.867 0 0 6 0 0 10 0 0
MDV 0 2.133 0 0 8 0 0 0 0
MEV 0 5.867 0 0 0 0 0 8 0
HDV 0 0 1.067 0 0 4 0 0 0
HEV 0 0 2.933 0 0 0 0 0 4
S2 LDV 1.267 0 0 10 0 0 0 0 0
LEV 8.733 0 0 0 0 0 10 0 0
MDV 0 2.133 0 0 8 0 0 0 0
MEV 0 5.867 0 0 0 0 0 8 0
HDV 0 0 1.067 0 0 4 0 0 0
HEV 0 0 2.933 0 0 0 0 0 4
S3 LDV 0.7 0 0 10 0 0 0 0 0
LEV 9.3 0 0 0 0 0 10 0 0
MDV 0 1.6 0 0 8 0 0 0 0
MEV 0 6.4 0 0 0 0 0 8 0
HDV 0 0 1.067 0 0 4 0 0 0
HEV 0 0 2.933 0 0 0 0 0 4
S4 LDV 0.933 0 0 10 0 0 0 0 0
LEV 9.067 0 0 0 0 0 10 0 0
MDV 0 1.067 0 0 8 0 0 0 0
MEV 0 6.933 0 0 0 0 0 8 0
HDV 0 0 1.3 0 0 4 0 0 0
HEV 0 0 2.7 0 0 0 0 0 4
S5 LDV 0 0 0 0 0 0 0 0 0
LEV 0 0 0 0 0 0 0 0 0
MDV 0 0.433 0.167 0 2 1 0 0 0
MEV 0.467 1.567 0.667 0 0 0 2 2 1
HDV 1.6 1.567 2.333 2 2 3 0 0 0
HEV 0.167 0.433 0.933 0 0 0 1 2 3
Table 7. Elasticity analysis of TC for depreciation rate and energy price.
Table 7. Elasticity analysis of TC for depreciation rate and energy price.
Parameter Interval (%) Baseline value (%) S1 S2 S3 S4 S5
With an existing fleet with EVs depreciation rate 10 to 20 15 0.055 0.132 0.193 0.055 0.055
EVs depreciation rate 14 to 24 19.8 0.015 0.135 0.095 0.015 0.015
EVs depreciation rate 18 to 28 23 0.025 0.130 0.048 0.025 0.025
DVs energy price growth rate 2.91 to 8.73 5.82 0.069 0.005 0.004 0.069 0.069
EVs energy price growth rate 1.44 to 4.33 2.89 0.016 0.016 0.026 0.016 0.016
Without an existing fleet EVs depreciation rate 10 to 20 15 0.091 0.098 0.118 0.129 0.055
EVs depreciation rate 14 to 24 19.8 0.052 0.054 0.079 0.095 0.015
EVs depreciation rate 18 to 28 23 0.026 0.026 0.04 0.052 0.025
DVs energy price growth rate 2.91 to 8.73 5.82 0.069 0.068 0.063 0.061 0.132
EVs energy price growth rate 1.44 to 4.33 2.89 0.016 0.018 0.021 0.024 0.014
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated