Preprint
Article
An Analysis of CFD-DEM with Coarse Graining for Turbulent Particle-Laden Jet Flows
Altmetrics
Downloads
160
Views
40
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
05 July 2023
Posted:
06 July 2023
You are already at the latest version
Alerts
Abstract
This paper presents the results of simulations of particle-laden air-solid jet flow in long straight tubes using CFD-DEM, along with an analysis of coarse-graining. Although previous studies have used CFD-DEM for similar flows, these have typically been in a dilute flow regime where uncoupled simulations are accurate. However, fully coupled simulations can introduce issues, necessitating validation studies to ensure that all coupling parameters are effectively used and that the physics is accurately represented. This paper validates the simulations against two different experimental studies, with fluid Reynolds numbers between 10,000 and 40,000 and Stokes numbers between 5.6 and 50. Interestingly, the profiles of mean particle velocity exhibit fewer discrepancies as the Stokes number increases but more discrepancies for the root mean square velocity compared to the experiments. Particle number flux is consistent with the experiments after the nozzle exit. Coarse-graining is also applied to the same simulations, achieving relatively accurate results. However, as expected, scaling of contact collision frequencies, forces, and stresses cannot be achieved, meaning that coarse-graining may be useful for comparing designs or operating parameters on an industrial scale but falls short when measuring the total energy dissipation of one experiment.
Keywords:
Subject: Engineering - Chemical Engineering
1. Introduction
Two-phase dense particle-laden jets are found in many modern industrial applications, including jet mills, sandblasting, cold spray additive manufacturing, and a new innovative method for particle comminution called High-Pressure Slurry Ablation©. Such systems can be costly, both in equipment and time, to monitor and evaluate experimentally. Traditional experimental techniques may involve many design iterations and consider several operating parameters, where valuable information for optimization is collected at the end of the experiment or test, and midstream phenomena are difficult to measure and quantify. Monitoring particle collision statistics and the fluid flow fields inside industrial units is difficult, further decreasing the amount of information available for optimization.
For simple, diluted two-phase air-particle and water-particle flows, there are a few methods that can be used to quantify the particle and fluid flow fields, such as Laser Doppler velocimetry (LDV), Particle Image Velocimetry (PIV), and Planar Nephelometry (PN) [1,2,3,4,5,6]. All of these methods are limited to simplified flow problems where it is required to have a predictable path or sampling location for the particles and transparent containers and carrier fluids. Furthermore, once an additional phase is added to a flow, such as in air-liquid-particle flows, light refraction occurs at the free surface making these methods ineffective [7]. In summary, the experimental methods presented here can be used to collect results to validate this current work; however, they cannot be used when opaque three-phase systems and industrial flow optimization problems are considered.
Fully coupled CFD-DEM solvers are well developed and validated across many different flow regimes [8,9,10]. Although many CFD-DEM studies exist for two-phase jet flows, most are for applications in wear in which they implemented a dilute flow regime that is uncoupled [11,12,13,14]. In a dilute flow regime, with reasonable accuracy, it is possible to perform an uncoupled numerical simulation where only fluid-particle interactions are considered. The uncoupled approach drastically increases the simplicity of the flow problem, primarily because of fewer limitations of mesh cell size and the absence of forces, and therefore models, acting on the fluid and particles that can bring forth both instabilities and more complexity to the flow problem. Furthermore, one can track particles as a post-carrier-phase solution process with an uncoupled simulation. Other two-phase CFD-DEM numerical solutions found in the literature are for combustion applications, where the particles are assumed to be droplets [15].
In our preliminary study [16], a long straight tube was considered with a fully developed particle-laden air jet at a Reynolds number of and mass loading up to that was simulated using fully coupled un-resolved CFD-DEM approach. Samples of particle flux at axial and radial locations along the jet were compared to the experimental data of Hardalupas et al. [1]. The primary consideration for this work was the effect of the particle volume fraction on the fluid flow field because of the concern for accurate momentum coupling between the two phases. It was concluded that a CFD cell minimum side length of particle diameters could be used without changing results. However, it was also realized that the round/plane jet anomaly caused significant issues for the single-phase results in context to the two-phase problem that would not otherwise exist if this were a pure single-phase flow problem. As explained at length in Wilcox’s well-known book Turbulence Modelling for CFD [17], using the k- turbulence model for standard and plane jets produces agreeable results. Still, a spreading rate as high as 40% over the measured experimental values can be seen for round jets. Many solutions have already been proposed to solve this issue, such as adding a vortex stretching term by Pope [18] and changing the empirical coefficients in the works of Faghani et al. [19], Givi and Ramos [20], Morgans et al. [21], but no nozzle domain was included in the flow profiles presented in these works.
Because this work is used as a foundation for the study of industrial flow systems with fully coupled two-phase CFD-DEM simulations, it is required that the nozzle profile shape be included in the solution domain. This is partly due to the required location and initial parameters for particle insertion - particles could be inserted at the nozzle exit. However, this would require experimental data for each change in nozzle shape, which would be impractical for an industrial flow problem. Instead, work was performed to slightly modify the empirical constants in the standard Launder and Spalding [22] k- turbulence model from and to and . This approach circumvents the issue with spreading rates and has been used in the works by Faghani et al. [19] and also validated extensively in our previous work [23] by comparing the numerical results to the well-cited works of Bogusławski and Popiel [24] and Hardalupas et al. [1]. Therefore, in this current work, we use the modified k- model for our Hardalupas et al. [1] test cases and also perform an analysis comparing unmodified to modified k- for the Lau and Nathan [7] test cases for additional validation.
For CFD-DEM to be deemed an effective method, it is important to first ensure the accuracy of the models by comparing the numerical results to known experimental results. After validation is achieved for the simplified flows, more solver development into three-phase flows can be performed with the end goal of optimization of an industrial unit. Therefore, this work presents a validation study for CFD-DEM in the application of turbulent high-speed jets with a look into coarse-graining to help with the computational expense.
2. Numerical Methodology
The computational fluid dynamics (CFD) portion of the simulations is performed by discretization of the fluid domain into computational cells, where the incompressible Navier-Stokes equations are solved given the boundary conditions. The Navier-Stokes equations are highly non-linear partial differential equations and, therefore, require numerical models to be solved. This Eulerian framework for flow calculation is coupled with Newton’s equation of motion, using the velocity Verlet algorithm, for particle tracking in a Lagrangian framework of the discrete element method (DEM). The two frameworks exchange momentum as the simulation runs using averaging and interpolation methods.
2.1. CFD
The carrier phase is described by the multi-phase fully coupled Navier-Stokes Equations given by
where is the liquid phase volume fraction, defined as the ratio of the volume of fluid to the volume of the cell, is the liquid fluid velocity, is the mean solid particle velocity, is the liquid phase stress tensor, and f is an explicit force term that can be used to exchange momentum between the solid and carrier phase directly. The variable, , becomes either the void fraction, , or one, , depending on whether Set I(Model Bfull or B) or Set II (Model A) is used for coupling [25,26] under the CFDEM code, which will be explained further in Section 2.3[10]. The implicit momentum coupling term, , is given by
where is the volume of the cell and is the summation of all the forces acting on the fluid by the particles, which are defined in Section 2.3.
The liquid phase volume fraction, , is calculated by determining the volume of particles inside of the cell. The volume of particles inside the cell can be calculated exactly, but this would be extremely computationally expensive. Therefore, the particles’ volume is calculated using a model that divides the particles into 29 non-overlapping regions of equal volume. The centroid of the particle is then used to determine the respective cell in which the new region exists. The approach allows accurate modeling while also providing decreased computational expense. Finally, the volumes of all regions inside a cell are added to obtain the total volume of particles, from which the liquid phase volume fraction can be calculated given the cell volume. There are errors associated with using a model for volume fraction calculation in an unresolved coupled CFD-DEM simulation. However, they are kept at a minimum with a sufficiently large cell size compared to particle size. Calculation of volume fraction is critical for accurate momentum coupling, so through our previous work, where similar simulations are performed for jet flow, it was realized that a minimum cell side length of particle diameters provided consistent results [16].
Turbulence is modeled using the "standard" k- model of Launder and Spalding [22] with slight modifications to the empirical coefficients. The turbulence model is given by
where eddy viscosity is given by and the Boussinesq assumption is used to obtain
The turbulent kinetic energy is given by k, the variable, , is the turbulent dissipation rate, u is the fluid velocity, f is a damping function, and the turbulence length scale is given by [23]. The first term in Equation 6 is the deviatoric part and the second term is the isotropic part of the fluid stress tensor. The last term, k, is kinetic energy, which in OpenFOAM and most other CFD codes gets absorbed into pressure. Since we are exclusively considering incompressible flow, the following term becomes
but is still included on the CFD side for solution boundedness. It is worth noting that Equation 8 is not used to calculate the viscous particle force, as shown in Section 2.2. Instead, the deviatoric part of the fluid stress tensor is used for this calculation.
2.2. DEM
Lagrangian particle translations through time are governed by Newton’s Second Law.
Velocity Verlet integration is then used on these equations to calculate the new particle positions and velocities [27,28].
The pressure force is given by
where is provided by the divided void fraction model to be the total volume of solid particles (both whole and partial particle volumes) inside the cell.
The viscous force models the inter-molecular forces between the particle and fluid and is given by
where and, therefore,
as indicated in the CFDEM code [10].
The lift force is calculated from Archimedes’ principle by stating that a solid body (particle) in a fluid will experience an opposing force to gravity because of the density disparity between the particle and fluid. It is given by
The particle-particle interaction force, , has contribution of normal and tangential forces,
CFDEM software uses LIGGGHTS for particles, and the particle-particle contact model used is a non-linear dashpot type known as the Hertz-Mindlin model. Details about this contact model can be found in Di Renzo and Di Maio [29], Di Renzo and Di Maio [30]. The normal and tangential forces are contributions of spring and damping forces given, respectively, by
where is the stiffness coefficient, is the overlap distance, is the relative velocity between the two particles, and is the damping coefficient. Further information on these coefficients is found in Appendix A.
The contact model used for particle-wall normal and tangential interactions, , is the same as the particle-particle contact model given by Equations 15-17, which are further defined in the coarse graining Section 2.4.
The force due to drag is given by
where is the volume of the particle, is the relative velocity, is either cell or interpolated fluid velocity (depending on if point forcing or volume averaging is chosen for fluid-particle coupling force), and is the solid velocity. It should be noted that the solid velocity, , is the individual particle velocity when applying the force to the particles but is the average solid velocity of all particles inside a cell when applying the force to the fluid.
2.3. CFD-DEM Coupling
CFD-DEM coupling can be classified into unresolved and resolved methods. Fully resolved methods use an immersed boundary approach, where the particles are seen as a boundary condition for the CFD simulation. This method is restricted to larger particles that cover at least ten computational cells [10]. An unresolved approach uses the volume fraction of solids inside a cell and averaging methods to exchange momentum between the two phases. An unresolved method requires multiple particles to fit inside a computational cell. For our type of turbulent jet flow, a minimum cell side length of 1.86 particle diameters was found to be sufficient [16].
Coupling using an unresolved approach between the carrier (CFD) and particulate (DEM) phases can be performed in many ways. In CFDEM software, the coupling can be achieved using three similar methods, with the difference being in the methodology used for calculating viscous and pressure forces by setting the variable in Equation 2 equal to 1 or for Set I and Set II, respectively. The full description of the models is given in detail by Zhou et al. [26]. We tested Set I and Set II in these jet flow simulations and determined there were only minute differences in results. Set II goes against Newton’s third law and therefore Set I was chosen for the work. The summation of all forces for the coupling term in Set I are given by
where the viscous and pressure terms in the momentum equation are left unchanged as indicated by the variable in Equation 2.
2.4. Coarse Graining
Coarse-graining is a technique that allows a single particle (grain) to represent a cluster of multiple individual particles by scaling the size and contact parameters. Coarse-graining is very similar to the multiphase particle-in-cell (MPPIC) method. The difference is that MPPIC is more of a combination of a two-fluid model and uses indirect stress models, whereas coarse graining uses explicit DEM models for the stresses [31,32]. Even with the availability of modern computing resources, it is still costly to run simulations that include tens of millions of particles. With the coarse-graining approach, it is possible to reduce the tracking of, say, 20 million particles to tracking of million particles, where is a coarse-graining factor that is typically equal to two or three. Therefore, it would be a great benefit to realize that coarse-graining is an effective method.
While researchers are developing new coarse-graining models every year, this current work uses the technique currently implemented in CFDEM, which is proposed by Radl et al. [33]. The basic premise of this method is to equate the density, energy densities, translational velocity, and total rotational kinetic energy of the original and coarse-grained particles and merely scale the radius of the particles. [34]. This is performed by keeping the coefficient of restitution, coefficient of friction, density, and Young’s modulus constant while scaling the radius of the particles by a coefficient . Dimensional analysis and a significant amount of reduction is then performed to determine that particle contact forces using the Hertz-Minlin non-linear contact model can be scaled directly using Equation A4 and no other modification is needed. The full derivation is shown in Appendix A.
The scaling of particle coupling forces is performed slightly differently than for the contact forces. The drag force acting on the particles was previously stated in Equations 18-21. The drag coefficient is not scaled linearly with coarse-graining as shown through the term in Equations 19 and 21. Instead, it is scaled when calculating for total drag force using the total solid volume, , in Equation 18.
3. Simulation Setup
Seven simulations are performed for validation and are compared to the experimental work by Hardalupas et al. [1] and Lau and Nathan [7]. Table 1 summarizes particle, operating, and flow conditions for the selected validation cases.
3.1. Generalized CFD Setup
Due to the nature of CFD-DEM, a complete 3-D circular domain is needed to accurately capture the physics of the particles inside of the fluid domain. The geometries of domains considered in this work are described in Figure 1.
Discretization is performed by producing an all-hexahedral mesh using Cubit© meshing software. A mesh sensitivity analysis was performed in our previous work, where it was concluded that an average cell size of should be used. This produced a minimum side length for the smallest cells of 357 , which is well above the requirement of the minimum cell side length of 1.86 particle diameters as noted from our previous work [16]. This mesh resolution ensured that achieve mesh-independent results was achieved while also being large enough to allow the effective coupling to the Lagrangian phase [16]. Max orthogonality of all meshes is kept below 30, as defined as the deviation angle between the line connecting two cell centers and the face normal of one [35]. Skewness is kept below for all meshes as defined as , where is the distance to the common face center and is the distance between the two cell centers. Further mesh quality information can be found in Table 2.
Temporal discretization is performed using the first-order implicit Euler scheme. Spatial discretization is performed using a second-order linear upwind scheme for all velocity and turbulent fields. This native OpenFOAM scheme for spatial discretization uses upwind interpolation weights depending on the gradient of the fluid velocity [36]. The linear second-order scheme is used for all interpolations between cell centered to face center values. A final solver tolerance of is used for all scalar and vector fields.
Boundary conditions are shown in Table 3. For the velocity boundary condition, the mean velocity found in Table 1 is used to calculate a turbulence power-law profile. First, the maximum velocity is calculated by
and then the turbulence power law is used with this maximum velocity for the profile. A great description of the power law is given by Jaroslav [37]. The turbulence intensity is set to , turbulence mixing length is set to , and for all cases.
A wall function approach is used near the wall to allow larger cell sizes and achieve effective momentum coupling between the fluid and particulate phases. It is a continuous wall function modeled from Spalding’s equation that fits a curve of the relationship between and [23,38]. Typically, wall functions constructed using the Launder and Spalding methods require a first cell height that produces a in the logarithmic layer but OpenFOAM uses adaptive wall functions proposed by Kalitzin et al. [38], which obtains agreeable solutions from . A between 24 and 76 for all simulations is obtained as indicated in Table 2. Therefore, we are confident that the wall boundary layer is being effectively modeled, as was also validated in our previous publications [16,23].
3.2. Generalized DEM Setup
Typically, glass beads have a very high Young’s Modulus of Pascals (Pa). To fully resolve the particle collisions with this Young’s Modulus would require an extremely small time step, which is impractical and could be over times more computationally expensive depending on the leeway given for the critical time step criterion. Chen et al. [39] tested a wide range of Young’s Moduli, reducing them to , and concluded that although Young’s Modulus has significant effects on single particle collisions, the bulk behavior of particles in the system (a rotating drum) was conserved. Lommen et al. [40] performed a study testing the accuracy of reducing Young’s Modulus with the intent of speeding up DEM simulations. It was determined that, at a minimum, if Young’s Modulus is kept greater than or equal to Pa, there is no change in the simulation results. There are very small relative velocities with the simulations in this current work and, therefore, it is possible to reduce this Young’s Modulus even further. A comparison of simulations with a Young’s Modulus of and is first performed to determine if there is any effect of Young’s Modulus on simulation results. An average relative error of 0.06% for particle velocities and 1.49% for particle fluxes was realized, with the majority of an error occurring at the outer regions of the jet where particle flux approaches zero. Therefore, it was decided that a Young’s Modulus of would suffice to reduce the computational cost.
The coefficient values in the present study (except Young’s Modulus) are taken directly from Lorenz et al. [41] for glass beads in which experiments were performed colliding two nearly spherical glass particles. Poisson’s ratios for glass beads vary depending on the paper, but a value of is common throughout [42,43]. Tang et al. [43] performed a wonderful study on testing for these parameters between a glass bead and glass plate and found a Poisson’s ratio, , equal to , a coefficient of restitution, , equal to , a coefficient of friction, , equal to , and a coefficient of rolling friction, , equal to . Whether this transforms over to particle-particle contact is uncertain. Another study found a equal to about for varying sizes of glass beads in the range from 2 to 4 mm with the value decreasing with a reduction in glass beads size. These coefficients are not highly critical because the volume fraction of particles is sufficiently low, where the drag force will dominate the flow. This is another example of a need for research that has detailed and defined inputs for the material properties of the particles.
The experimental data at the nozzle exit is used to obtain particle insertion velocities and fluctuations. DEM particles are inserted on a surface and the insertion velocities and fluctuations do not vary along that surface. Therefore, the mean of the experimental velocities in the radial direction of the nozzle is used with the inputs shown in Table 4.
3.3. Hardalupas Et al. DEM Setup
The solids inserted into the system are "mono-sized" 40 and 80 µm spherical glass beads with the velocities given in Table 4. It should be noted that it is stated to be "mono-sized," but it is extremely difficult to obtain true mono-sized particles because of the expense and quantity needed for these types of experiments. Therefore, a size range is used, with the mean being the mono-sized value and a range small enough to be considered negligible to overall results. The 40 µm particles of a nominal range of 37-44 µm and the 80 µm have a nominal range of 60-95 µm. The information on the particle size distribution can be found in Hardalupas et al. [1].
3.4. Lau and Nathan DEM Setup
Polymer particles of density are used for this study with the inlet velocities given in Table 7 . These particles have an extremely low nominal range as compared to the particle size distribution (PSD) of Hardalupas et al. [1][7]. Other than the PSD of the particles, the paper does not go into details on the specific spheres used, but in a previous paper by Lau and Nathan, with what appears as the same setup, they state that they are Microbeads Spheromers [44]. The Microbead Spheromers are made with polymethylmethacrylate (acrylic). Polymethylmethacrylate has a density of 1.18 and Flexural Modulus Pascals. Similar to the Hardalupas et al. [1] test cases, we reduce the Young’s Modulus to for help with the computational expense. Poisson’s ratio of acrylic is about , and this is what is used in the DEM simulations. The coefficient of restitution is given by and coefficient of friction by , which are taken directly from Lorenz et al. [41] in which experiments are performed on the collision of two acrylic spheres. It is assumed that the coefficient of rolling friction is extremely low for these acrylic spheres, and therefore Coefficient of rolling friction, , is set to the low value of
3.5. Coupling Setup
Coupling is performed implicitly between the two phases. The soft sphere non-linear spring-dashpot contact model of Hertz-Mindlin is used. To fully model and ensure particles are observing one another, a DEM time-step lower than 20% Rayleigh and Hertzian critical timesteps is used [28]. This produces a very small timestep; therefore, a coupling interval to the CFD side is set to 10 to facilitate less computational expense while keeping the fluid Courant number less than . DEM time-steps and specifics for percentages of Rayleigh and Hertzian time-step criterion are shown in Table 4. The Gidaspow drag model is used, which combines the drag models of Ergun [45] and Wen and Yu [46]. The full model description can be found in Zhu et al. [47]. Pressure, viscous, and Archimedes lift forces are used and calculated from Equations 11, 13, and 14, respectively. Second-order linear interpolation is used to obtain face-centered values from cell centers for velocity, void fraction, and pressure in all calculations of forces on the particles.
4. Results and Discussion
Mesh sensitivity analysis was first performed to determine if the numerical solution is independent of domain discretization (mesh resolution). Three systematically refined meshes of , , and million elements were used with the same operating parameters. Richardson extrapolation was going to be used, but it was found that the solution differed so minutely that Richardson extrapolation would hold no quantitative value for the solution of mesh convergence. Instead, it was deemed that the medium mesh size of million elements would be used. Simulations were performed in our previous work that demonstrates a particle diameter to minimum side cell size ratio of up to particles diameters can be used while still conserving the accurate momentum exchange between the two phases.
4.1. Particle Full Development
A fully developed flow is critical in these simulations. If we did not have a fully developed flow before the outlet of a simulation, then particle flux and velocities would entirely depend on both the insertion location and initial velocities. It is difficult to conclude that the experimental work performed by Hardalupas et al. [1] is a fully developed flow. The pipe used in the study is in length with a Reynolds number of 13000. For single-phase flows, this Reynolds number is well into the turbulent zone; therefore, no laminar boundary layer forms and there will be a turbulent velocity profile. To further demonstrate this, an idealized entry length is calculated until fully developed flow by using an assumed velocity profile at the inlet and the classical solution developed by Latzko [48] given as
where for the circular tube. Calculating this, an entry length of is obtained for an idealized single-phase flow. The pipe used for Hardalupas et al. [1] is well above this entry length, but this does not indicate for certain that the particles are fully developed because of particle slippage during particle insertion and mixing. Indeed, this is briefly discussed in the paper when the results for the highest particle size () showed signs of a lack of fully developed flow. In the work performed by Mena and Curtis [49], it is postulated and concluded that 51 pipe diameters is sufficient for fully developed flow and they measure this by the use of pressure transducers placed periodically along the pipe. In the study, they use water as the carrier fluid; therefore, viscous effects are significantly higher than air and particle slip velocity would be less of a concern.
To the current authors’ knowledge, Lau and Nathan [44] and their future work of Lau and Nathan [7] are the only studies to test for fully developed flow. They perform particle experiments with and with identical Stokes numbers to test for particle slippage. They realized that the particle concentration and velocities converged to similar values and therefore concluded that was a sufficiently long enough nozzle for full flow development at Stokes numbers of and Reynolds numbers of 10000 and 20000. In the study performed by Hardalupas et al. [1], a Stokes number of and with a Reynolds number of 13000 is used. There is a possibility that with the larger Stokes number of 50 and the fact that Lau and Nathan [44] has a pipe length almost times that of Hardalupas et al. [1] that we may not have fully developed flow. Therefore, no conclusion can be realized.
To test for fully developed flow for the numerical Hardalupas et al. [1] test case, simulations were performed using merely the nozzle or pipe flow with the same operating parameters as previously outlined. Still, instead of particles inserted at , they are inserted at with sampling at locations at and negative , , , , , , , , , , and , as referenced from the nozzle exit with the positive in the flow direction. In addition, two simulations were performed to test for the location of full development and determine whether inlet velocity makes a significant difference in flow development.
It was realized that most of the flow development occurs in the first 40 nozzle diameters, where the last experiences very minute changes in all parameters (Figure 2). The inside of the nozzle for the Lau and Nathan (Lau3, Table 1 and Table 4) test case are also examined. It was realized that full development occurs in about the first 30 nozzle diameters with only minute differences observed in the last 10 nozzle diameters Figure 3.
4.2. Hardalupas Et al. Results
It is realized that the results at the nozzle exit for all the Hardalupas et al. [1] test cases provide a similar trend for the mean and root mean square velocity near the central regions of the jet stream. Still, towards the outer regions near the nozzle wall, it is observed that the particles move more towards a laminar shape profile rather than a more turbulent shape as demonstrated by the experiments (Figure 4a and Figure 5a). This is believed to be caused by the interpolation method used for velocity in particle-fluid interactions.
To achieve effective momentum coupling, we require a cell size with a minimum length side of at least times the particle diameter for these types of flow problems [16]. To model the boundary layer at the wall of a CFD simulation, we either need to fully integrate into the wall or use an algebraic function. To fully integrate to the wall, we require an extremely fine mesh with, at the very least, 8-10 cells located below the [23]. Achieving this, while also achieving effective momentum coupling, would require extremely small particles, far smaller than those used in many cases including the experimental studies considered in this current work. Therefore, a wall approach near the wall is used in this current work to accurately model the strong viscous effects on fluid velocity while achieving effective momentum coupling. That said, there isn’t a perfect solution here because there is also concern with fluid velocity and void fraction interpolation when calculating the drag particle-fluid coupling force. A wall function is used in this current work to model the fluid boundary layer in the larger cell. Still, for interpolation, that same wall function is not used for particle coupling parameter interpolation, but instead, a linear interpolation method.
In CFD-DEM, the interpolation method used is a linear cell point method. This method breaks each face into triangles to define tetrahedra and the cell center point; then, it cycles through the tetrahedra to determine where the point or particle cell point center is located. An inverse distance linear interpolation is then used from known velocity points of the cell centers. This produces a different distribution of coupling velocities than is modeled by our wall function. Optimally, we would want to use an interpolation method that follows the wall function but is out of this work’s scope.
Although there are discrepancies at the nozzle exit it is observed that further in the flowfield there are very similar trends between the numerical and experimental results for the lower (0.23) and higher (0.86) mass fractions, respectively.
In general, for the particle simulations (Hardalupas1 and Hardalupas2), discrepancies are observed at the nozzle exit associated with the interpolation method for both mean (rms) velocities and particle number fluxes (Figure 4a). As previously outlined, this can be attributed to the issues with the interpolation method near the wall. That being said, relative accuracy is achieved for the velocities where the general change in results between the two mass fractions is similar to that of the experiments. At location , similar slopes are achieved between all numerical and experimental results. The numerical results show a slight decrease in slope relative to the experimental results near the outer regions of the jet. At , higher mean velocities are observed for the numerical results with root mean square velocities closely following and smaller spread with the particle number fluxes. It is concluded that with particles, up to should see viable results for the case of optimization of an industrial unit, but anything further downstream would need more analysis. Work needs to be performed for pipe flows with wall functions in CFD-DEM to solve the interpolation issues, but it is observed that the particles “correct” themselves after they exit the nozzle. This could be attributed to having relatively low Stokes numbers, and therefore the particles closely follow the highly accurate and validated fluid flow where wall effects are not present.
For the particles, the same errors at the nozzle exit are observed because of interpolation for all fields but with the same relative accuracy or change in trends between the two mass fluxes (Figure 5ab). An interesting note for the nozzle exit is that with smaller mass loading (Hardalupas3), a particle number flux with a more flat profile than that of the larger mass loading (Hardalupas4) is observed. It is postulated that if mass loading continued to increase, a more triangular profile for particle number flux would be achieved. Further downstream, similar slopes in the results for mean velocity and particle number flux are observed but a significantly lower root mean square velocity for the numerical results. It is curious to note that these smaller particle trends line up quite well up to , but with the larger particles results can only be trusted up to . It can be concluded that as Stokes number increases, where the particles tend to "go their own path," the numerical results start deviating from the experimental results.
4.3. Lau and Nathan Single-Phase Results
The single-phase results for the Hardalupas et al. [1] test cases were validated in our previous work of Weaver and Mišković [23], but Lau and Nathan [7] results were not. Therefore, three different simulation setups were used to determine that single-phase results were accurate before adding the particulate phase. If this is not done, then there is a risk of obtaining a model that may have the perfect combination of parameters for the two-phase flow but not necessarily because each of the phases separately is accurate. This would make it difficult to conclude with any confidence that this model can be generally applied to other similar flows and accurately represents the physics.
All cases start with the Lau3 test case () but without the inclusion of particles. The default Launder and Spalding [22] k- is used for one case. For the second case, a change of the empirical coefficients is made to the turbulence model by and . This modification is researched and validated extensively in our previous work of Weaver and Mišković [23]. The third simulation uses the modified k- turbulence model but without the use of co-flow. This is to test the effect that co-flow has on these types of numerical simulations.
There is very little difference between all simulations at the nozzle exit for both mean and root mean square velocities as shown in Figure 6ad. At location , the unmodified k- turbulence model produces spreading that more closely follows the experiment for mean velocity, but the modified k- produces a drop in axial velocity that more closely matches the experiment. Therefore, it is up to the researcher to weigh the pros and cons of using the modified k-; whether it is important for accurate spreading or accurate axial drop in mean velocities. That being said, in the current authors’ previous work, it was found that both spreading rates and axial drop in mean velocity were both improved with the slight modification of the empirical coefficients [23] for two different sets of data provided by Bogusławski and Popiel [24] and Hardalupas et al. [1]. For root mean square velocities, the modified k- produces spreading rates that more closely match experiments at all sampling locations. There is no appreciable difference in all sampling locations in adding a co-flow to simulations. Considering all this, it was decided to use the modified k- with a co-flow for all subsequent simulations for the Lau and Nathan [7] test cases.
4.4. Lau and Nathan Results
As previously noted, there will be errors at the nozzle exit associated with the interpolation method and this also extends to the Lau and Nathan [7] results as indicated in Figure 7ab. A more laminar flow profile is realized for the mean particle velocity with a higher mean velocity in the central region while decreasing rapidly towards the wall relative to the experimental results. That being said, it is observed that the overall trend when changing the Stokes number agrees with the experimental results. For example, the lowest Stokes number has the highest mean particle velocity in the central region. Conversely, the highest Stokes number has the lowest mean particle velocity for both the experiments and numerical simulations (Figure 7a). At the location we observe a slightly steeper slope for the mean particle velocities and a slightly higher root mean square velocity with the same slope. It is interesting to note that mean particle velocity changes at depending on the Stokes number. In contrast, in the experiments, the normalized mean particle velocity minimally changes between Stokes numbers. This could be attributed to the errors at the nozzle exit, but this is difficult to postulate with confidence because we are not experiencing this behavior with the Hardalupas et al. [1] test cases.
4.5. Coarse Graining Results
Some DEM simulations use a large number of particles, upwards of 6 million. This would require a significant amount of compute cores to track and calculate all collisions between particles. Also, developing codes to have the ability to scale to a very large amount of compute cores can be difficult because of the issues associated with the slowed communication between compute nodes. To circumvent this, many researchers have turned to coarse-graining methods. The essence of coarse-graining is that multiple particles are represented as a single grain and then the grain is tracked through time. This significantly decreases the number of trajectories tracked throughout the system and, depending on the type of coarse-graining model, can reduce the number of tracking points by . We can see that with a coarse-graining factor of 2, , the example of 6 million particles reduces down to 750 thousand particles. This reduces overall computational cost significantly. Also, additional computational savings can be realized by increasing the integration time-step and the duration of the soft sphere collisions will generally be smaller by orders of magnitude [32].
As previously mentioned in Section 2.4, the type of coarse-graining used for this analysis was first proposed by Radl et al. [33] and further expanded to include the Hertz nonlinear contact model by Nasato et al. [34]. Radl et al. [33] conclude that the major hurdle in using a coarse-graining approach is to correctly compute the collision rate and inter-parcel or inter-grain stress, with there being no easy way to scale the interaction parameters in an inertial flow regime [33]. This conclusion is significant because it will be difficult to relate this current work collision frequencies, forces, and stresses from an unscaled system (no coarse-graining) to a scaled (coarse-grained) one. That being said, if overall trends are followed, we may find the usefulness of coarse-graining in an industrial application.
To optimize an industrial scale unit, a statistical analysis needs to be performed on parameters, including collision frequencies and forces acting on particles. Therefore, at first glance, it would seem that coarse-graining shouldn’t be used in this type of setting because of the disparity between inter-grain stresses from the un-scaled to scaled system. That being said, the goal of numerical simulations, and any experimental study for that matter, is to find the optimum setup through an analysis of changes in geometric and operating parameters. Since this is the ultimate practical goal, and it may not be necessary to obtain the exact answers of the physical space, we can, for example, compare two different geometries of an unscaled system to a scaled system using those same geometries.
To investigate the accuracy of coarse-graining, two sets of simulations with the same operating parameters as the Hardalupas1 case are performed. The first set of simulations is unscaled, while the second set is scaled. In each set, a plate is inserted at two different axial locations: and relative to the nozzle exit, resulting in four simulations in total. The collision frequencies and force statistics applied to particles when they hit the plate for both the and cases are then outputed. The ratio of results obtained from the and simulations is calculated and compared the ratios between the scaled and unscaled systems to determine the accuracy of coarse-graining. We then analyze the collision frequencies and mean/variances of the normal/tangential forces for all collisions (Figure 8a), and also analyzed the results grouped by location with intervals of on the plate. These results and then used to determine whether the coarse-graining method accurately predicted the results that follow the simulation trend of an unscaled system.
The ratios we are comparing for collision frequencies are given by
where and are the collision frequencies for the unscaled DEM method for simulations with 5D and 15D plate, respectively. and are the collision frequency for the scaled system with the coarse-graining factor of 2 for simulations with 5D and 15D plate, respectively. Similarly, for the force statistics we have
The collision frequencies and force statistics are then output for all collisions (Figure 8a) and concentric regions (Figure 8b), and calculated ratios and associated errors as shown in Table 5.
It should be noted, for completeness, that the percent error is calculated from the traditional formula given by
When analyzing all the collisions acting on the plate, it is realized that there is an error of less than for all parameters as indicated by Table 5. These results demonstrate accuracy in comparing ratios of scaled to un-scaled systems when analyzing all collisions on the plate.
To further analyze the trends of particle collisions with the plate, the collisions are independently considered within specific concentric regions on the plate as shown in Figure 8b and perform the same analysis of collision frequency and force statistics.
In Figure 9 the relative errors are plotted between the scaled and unscaled system ratios for each region. A slightly different conclusion than when analyzing all collisions can be realized. The majority of mean values have an error less than with the only region above being at with an error of just above . The highest errors in the force statistics are the variance errors which are in line with the collision frequency errors; most errors are observed in regions where the collision frequency is low. To investigate this further, (Figure 9b) shows individual collision frequencies for both unscaled and scaled systems at 5D and 15D plate positions with corresponding collision frequency ratio relative errors. It is realized that collision frequency is high near the center region with a very lower percentage error. Conversely, collision frequency is lowest in the outer regions with a relatively high percentage error. Considering all this, along with the very low error of less than for all collisions, it can be concluded that we have achieved relative accuracy that provides significant results for the practical application of an industrial flow problem.
A kernel density estimate plot (KDE) is then used to visualize the distribution of collisions on the plate (Figure 10). This plot uses a Gaussian smoothing algorithm to estimate the probability density function. This allows visualization of the distribution of particle impacts across the plate. It is realized that the probability of particle collisions between and are very comparable with the largest difference towards the outer regions as demonstrated when comparing at location (Figure 10b and Figure 10d). This reassuringly confirms the use of coarse-graining for an industrial flow optimization problem.
Of special interest is comparing the flow profiles both inside of the nozzle and outside of the jet. This could be beneficial in future simulations because if flow development occurs sooner for coarse-graining, that further reduces the computational cost by allowing a shorter nozzle.
Very little difference in the length of full development for the particles (Figure 11 in all parameters is observed. Furthermore, it is realized that there is also very little difference between the scaled and unscaled systems in the jetstream for all fields, with the highest error being observed for root mean square velocity (Figure 12).
If the desire is to optimize an industrial unit, then the goal is to pinpoint a design that performs better than another. Therefore, from a practical standpoint, if relatively accurate answers are achieved that follow the same trends as changes in the design of a physical system, then the goal can be reached from purely numerical simulations alone. With that in mind, coarse-graining is deemed a very useful tool in the optimization of an industrial unit for high-speed jet flows because of the significant reduction in simulation cost. That being said, these results and conclusions shouldn’t be realized for other types of systems, in particular, systems with a large amount of particle-particle collisions in a semi-quasi steady state inertial system that significantly dictates the bulk flow behavior.
5. Conclusion
This paper has performed fully coupled CFD-DEM simulations and validated them against two different experimental studies, namely Hardalupas et al. [1] and Lau and Nathan [7]. Coupling parameters, models, and operating conditions were all considered. However, issues were encountered with the interpolation method used in fully coupled simulations, which produced a more laminar profile shape for the particles at the nozzle exit. Future work can investigate this issue further.
For the Hardalupas et al. [1] test cases, a Stokes number of 50 can be trusted up to 10D from the nozzle exit, and a Stokes number of 10.27 can be trusted up to 20D if only mean and particle number fluxes are desired. The modified k-epsilon models are consistent with the Lau and Nathan [7] single-phase results, providing further validation of previous work [23]. For the Lau and Nathan [7] test cases at 10D, there was a slightly steeper slope for mean particle velocity with a higher root mean square velocity. Overall, it is concluded that CFD-DEM accuracy generally increases with increasing Stokes number up to 50, based on both studies.
Finally, it is noted that coarse-graining is a useful method for practical applications such as optimization of industrial-scale units, where relative results between designs are desired. However, if the goal is to measure the total energy dissipation of a single experiment, coarse-graining falls short.
Author Contributions
Conceptualization, D.W. and S.M.; methodology, D.W.; software, D.W; validation, D.W.; formal analysis, D.W; investigation, D.W; resources, S.M.; data curation, D.W.; writing—original draft preparation, D.W.; writing—review and editing S.M. and D.W; visualization, D.W; supervision, S.M.; project administration, S.M.; funding acquisition, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research is supported and funded by the MITACS Accelerate program and Disa Technologies (contract No. IT23227). We gratefully acknowledge the computing support of Compute Canada via their WestGrid program and ARC group at the University of British Columbia for providing the access to the Sockeye cluster.
Data Availability Statement
The cases, models, and data solutions are available at https://doi.org/10.6084/m9.figshare.15039798.v1.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results
Nomenclature
| liquid volume fraction, | |
| volume of fluid inside of a cell | |
| volume of particles inside of a cell | |
| volume of the cell | |
| total solid volume inside of a cell | |
| density of the fluid | |
| density of the particle | |
| velocity of the liquid | |
| average solid velocity inside of the cell | |
| particle velocity | |
| variable to change between model A (Set II) and model B (Set I) of CFD-DEM formulation | |
| p | pressure |
| liquid phase stress tensor | |
| implicit momentum coupling term | |
| f | explicit force term |
| summation of all forces inside of a cell | |
| k | fluid turbulent kinetic energy |
| fluid turbulent dissipation | |
| fluid viscosity | |
| fluid turbulent viscosity | |
| k- constant | |
| k- constant | |
| k- constant | |
| k- constant | |
| deviatoric part of the fluid stress tensor | |
| Kronecker delta | |
| particle mass | |
| g | gravity vector |
| pressure force | |
| viscous force | |
| lift force acting on the particle | |
| particle-particle interaction force | |
| particle-wall interaction force | |
| drag force | |
| moment of inertia of the particle | |
| rotational velocity of the particle | |
| torque acting on the particle | |
| normal contact force | |
| tangential contact force | |
| normal stiffness coefficient | |
| normal damping coefficient | |
| normal overlap distance | |
| normal relative velocity | |
| tangential stiffness coefficient | |
| tangential damping coefficient | |
| tangential overlap distance | |
| tangential relative velocity | |
| used for the calculation of drag to further simplify the equation | |
| relative velocity between the fluid and the solid, | |
| a coefficient of drag | |
| diameter the grain | |
| coarse grain factor | |
| shape factor | |
| particle Reynolds number | |
| particle shape factor | |
| fluid viscosity | |
| equivalent Young’s modulus | |
| equivalent particle radius | |
| particle radius on collision | |
| particle Young’s modulus for collisions | |
| Poisson’s ratio for collisions | |
| Poisson’s ratio for collisions | |
| grain (parcel) radius | |
| particle radius | |
| un-scaled (no coarse graining) system | |
| coarse graining factor of 2 | |
| non-dimensional wall distance | |
| non-dimensional velocity defined as the near-wall velocity divided by the shear velocity | |
| Collision frequency statistic for unscaled system using 5D plate | |
| Collision frequency statistic for unscaled system using 15D plate | |
| Collision frequency statistic for scaled system using 5D plate | |
| Collision frequency statistic for scaled system using 15D plate | |
| Normal or tangential force statistic for unscaled system using 5D plate | |
| Normal or tangential force statistic for unscaled system using 15D plate | |
| Normal or tangential force statistic for scaled system using 5D plate | |
| Normal or tangential force statistic for scaled system using 15D plate |
Appendix A
Dimensional analysis is used for the stiffness and damping coefficients to scale from the particles to the grains. The normal and tangential stiffness coefficients in the Hertz model are provided in the work of Di Renzo and Di Maio [29], Di Renzo and Di Maio [30] and given, respectively, by
where is the equivalent Young’s modulus, is an equivalent radius, is the normal overlap, is an equivalent shear modulus, is Poisson’s ratio, E is Young’s modulus, and R is the particle radius. Scaling particle radius by the factor we obtain
Plugging Equation A5 into Equations A1 and A2 we obtain the scaled stiffness coefficients given by
As shown by Equations A6 and A7, the stiffness coefficients are merely scaled by . The damping coefficients for the non-linear Hertz-Mindlin model are given in Hu et al. [50] by
Plugging Equation A5 into Equations A10 and A11 we demonstrate that and are also scaled by
To then calculate the scaling for the damping coefficient, we first need to determine the mass. We know that density is constant from the particles to the grains, so to obtain mass, we multiply density by the volume of the particle.
Plugging Equation A5 into A16 we obtain the grain mass by
Given Equation A12, we can then infer that the equivalent mass scales by
We can now calculate the scaled damping coefficients in normal and tangential directions by plugging Equations A14, A15, and A18 into Equations A8 and A9 and show that the damping coefficient is scaled by .
Based on the non-dimensional analysis work of Radl et al. [33] and Nasato et al. [34], a linear spring-dashpot model does not have a non-linear function of particle radius but only constant values for the stiffness and damping coefficients. We observe that after scaling grains’ radius, there is no need to additionally scale both the stiffness and damping parameters because they already scale with and , respectively. Therefore, merely the particle radius is scaled by the coarse-graining factor.
References
- Hardalupas, Y.; Taylor, A.; Whitelaw, J. Velocity and particle-flux characteristics of turbulent particle-laden jets. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 1989, 426, 31–78. [Google Scholar] [CrossRef]
- Levy, Y.; Lockwood, F.C. Velocity measurements in a particle laden turbulent free jet. Combustion and Flame 1981, 40, 333–339. [Google Scholar] [CrossRef]
- McComb, W.; Salih, S. Measurement of normalised radial concentration profiles in a turbulent aerosol jet, using a laser-doppler anemometer. Journal of Aerosol Science 1977, 8, 171–181. [Google Scholar] [CrossRef]
- Modarress, D.; Wuerer, J.; Elghobashi, S. An Experimental Study of a Turbulence Round Two-Phase Jet. Chemical Engineering Communications 1984, 28, 341–354. [Google Scholar] [CrossRef]
- Popper, J.; Abuaf, N.; Hetsroni, G. Velocity measurements in a two-phase turbulent jet. International Journal of Multiphase Flow 1974, 1, 715–726. [Google Scholar] [CrossRef]
- Shuen, J.S. A Theoretical and Experimental Investigation of Dilute Particle-Laden Turbulent Gas Jets (two-Phase Flow). Ph.D., The Pennsylvania State University, United States – Pennsylvania, 1984.
- Lau, T.C.W.; Nathan, G.J. The effect of Stokes number on particle velocity and concentration distributions in a well-characterised, turbulent, co-flowing two-phase jet. Journal of Fluid Mechanics 2016, 809, 72–110. [Google Scholar] [CrossRef]
- Fernandes, C.; Semyonov, D.; Ferrás, L.L.; Nóbrega, J.M. Validation of the CFD-DPM solver DPMFoam in OpenFOAM® through analytical, numerical and experimental comparisons. Granular Matter 2018, 20, 64. [Google Scholar] [CrossRef]
- Karimi, M.; Mostoufi, N.; Zarghami, R.; Sotudeh-Gharebagh, R. A new method for validation of a CFD–DEM model of gas–solid fluidized bed. International Journal of Multiphase Flow 2012, 47, 133–140. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD-DEM. Progress in Computational Fluid Dynamics, An International Journal 2012, 12, 140. [Google Scholar] [CrossRef]
- Mansouri, A.; Arabnejad, H.; Shirazi, S.; McLaury, B. A combined CFD/experimental methodology for erosion prediction. Wear 2015, 332-333, 1090–1097. [Google Scholar] [CrossRef]
- Nguyen, V.; Nguyen, Q.; Liu, Z.; Wan, S.; Lim, C.; Zhang, Y. A combined numerical–experimental study on the effect of surface evolution on the water–sand multiphase flow characteristics and the material erosion behavior. Wear 2014, 319, 96–109. [Google Scholar] [CrossRef]
- Pozzetti, G.; Peters, B. A numerical approach for the evaluation of particle-induced erosion in an abrasive waterjet focusing tube. Powder Technology 2018, 333, 229–242. [Google Scholar] [CrossRef]
- Wang, Q.; Huang, Q.; Sun, X.; Zhang, J.; Karimi, S.; Shirazi, S.A. Large Eddy Simulation of Slurry Erosion in Submerged Impinging Jets. Volume 3: Computational Fluid Dynamics; Micro and Nano Fluid Dynamics. American Society of Mechanical Engineers, 2020, p. V003T05A040. [CrossRef]
- Bazdidi-Tehrani, F.; Zeinivand, H. Presumed PDF modeling of reactive two-phase flow in a three dimensional jet-stabilized model combustor. Energy Conversion and Management 2010, 51, 225–234. [Google Scholar] [CrossRef]
- Weaver, D.; Miskovic, S. Analysis of Coupled CFD-DEM Simulations in Dense Particle-Laden Turbulent Jet Flow. Volume 2: Fluid Mechanics; Multiphase Flows; American Society of Mechanical Engineers: Virtual, Online, 2020. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence modeling for CFD, 3rd ed.; Number Book, Whole in 1, DCW Industries: La Cãnada, Calif, 2006. [Google Scholar]
- Pope, S.B. An explanation of the turbulent round-jet/plane-jet anomaly. AIAA Journal 1978, 16, 279–281. [Google Scholar] [CrossRef]
- Faghani, E.; Saemi, S.D.; Maddahian, R.; Farhanieh, B. On the effect of inflow conditions in simulation of a turbulent round jet. Archive of Applied Mechanics 2011, 81, 1439–1453. [Google Scholar] [CrossRef]
- Givi, P.; Ramos, J. On the calculation of heat and momentum transport in a round jet. International Communications in Heat and Mass Transfer 1984, 11, 173–182. [Google Scholar] [CrossRef]
- Morgans, R.C.; Dally, B.B.; Nathan, G.J.; Lanspeary, P.V.; Fletcher, D.F. Applications of the Revised Wilcox 1998 K-Omega Turbulence Model To A Jet In Co-Flow. CFD in the Minerals and Process Industries, 1999, p. 6.
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Computer Methods in Applied Mechanics and Engineering 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Weaver, D.S.; Mišković, S. A Study of RANS Turbulence Models in Fully Turbulent Jets: A Perspective for CFD-DEM Simulations. Fluids 2021, 6. [Google Scholar] [CrossRef]
- Bogusławski, L.; Popiel, C.O. Flow structure of the free round turbulent jet in the initial region. Journal of Fluid Mechanics 1979, 90, 531–539. [Google Scholar] [CrossRef]
- GmbH, D.C. About CFDEM(R)coupling; CFDEMresearch GmbH, 2017.
- Zhou, Z.Y.; Kuang, S.B.; Chu, K.W.; Yu, A.B. Discrete particle simulation of particle–fluid flow: model formulations and their applicability. Journal of Fluid Mechanics 2010, 661, 482–510. [Google Scholar] [CrossRef]
- Verlet, L. Computer "Experiments" on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Physical Review 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Otsubo, M.; O’Sullivan, C.; Shire, T. Empirical assessment of the critical time increment in explicit particulate discrete element method simulations. Computers and Geotechnics 2017, 86, 67–79. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F.P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chemical Engineering Science 2004, 59, 525–541. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F.P. An improved integral non-linear model for the contact of particles in distinct element simulations. Chemical Engineering Science 2005, 60, 1303–1312. [Google Scholar] [CrossRef]
- Andrews, M.; O’Rourke, P. The multiphase particle-in-cell (MP-PIC) method for dense particulate flows. International Journal of Multiphase Flow 1996, 22, 379–402. [Google Scholar] [CrossRef]
- Di Renzo, A.; Napolitano, E.; Di Maio, F. Coarse-Grain DEM Modelling in Fluidized Bed Simulation: A Review. Processes 2021, 9, 279. [Google Scholar] [CrossRef]
- Radl, S.; Radeke, C.; Khinast, J.G.; Sundaresan, S. Parcel-Based Approach for the Simulation of Gas-Particle Flows. CFD;, 2011; p. 11.
- Nasato, D.S.; Goniva, C.; Pirker, S.; Kloss, C. Coarse Graining for Large-scale DEM Simulations of Particle Flow – An Investigation on Contact and Cohesion Models. Procedia Engineering 2015, 102, 1484–1490. [Google Scholar] [CrossRef]
- Ishigaki, M.; Abe, S.; Sibamoto, Y.; Yonomoto, T. Influence of mesh non-orthogonality on numerical simulation of buoyant jet flows. Nuclear Engineering and Design 2017, 314, 326–337. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Computers in Physics 1998, 12, 620. [Google Scholar] [CrossRef]
- Jaroslav, S. Contribution to investigation of turbulent mean-flow velocity profile in pipe of circular cross-section. 35th Meeting of Departments of Fluid Mechanics and Thermomechanics;, 2016; p. 020010. [CrossRef]
- Kalitzin, G.; Medic, G.; Iaccarino, G.; Durbin, P. Near-wall behavior of RANS turbulence models and implications for wall functions. Journal of Computational Physics 2005, 204, 265–291. [Google Scholar] [CrossRef]
- Chen, H.; Xiao, Y.; Liu, Y.; Shi, Y. Effect of Young’s modulus on DEM results regarding transverse mixing of particles within a rotating drum. Powder Technology 2017, 318, 507–517. [Google Scholar] [CrossRef]
- Lommen, S.; Schott, D.; Lodewijks, G. DEM speedup: Stiffness effects on behavior of bulk material. Particuology 2014, 12, 107–112. [Google Scholar] [CrossRef]
- Lorenz, A.; Tuozzolo, C.; Louge, M.Y. Measurements of impact properties of small, nearly spherical particles. Experimental Mechanics 1997, 37, 292–298. [Google Scholar] [CrossRef]
- Sandeep, C.S.; Luo, L.; Senetakis, K. Effect of Grain Size and Surface Roughness on the Normal Coefficient of Restitution of Single Grains. Materials 2020, 13, 814. [Google Scholar] [CrossRef]
- Tang, H.; Song, R.; Dong, Y.; Song, X. Measurement of Restitution and Friction Coefficients for Granular Particles and Discrete Element Simulation for the Tests of Glass Beads. Materials 2019, 12, 3170. [Google Scholar] [CrossRef] [PubMed]
- Lau, T.C.; Nathan, G.J. Influence of Stokes number on the velocity and concentration distributions in particle-laden jets. Journal of Fluid Mechanics 2014, 757, 432–457. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow through Packed Columns. Chemical Engineering Process 1952, 48, 89–94. [Google Scholar]
- Wen, C.Y.; Yu, Y. Mechanics of fluidization. Chemical Engineering Progress Symposium Series 1966, 62, 100–111. [Google Scholar]
- Zhu, H.; Zhou, Z.; Yang, R.; Yu, A. Discrete particle simulation of particulate systems: Theoretical developments. Chemical Engineering Science 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Latzko, H. Warmubergang an einem Turbulenten. Z. Angew 1921, Math, 268–290. [Google Scholar]
- Mena, S.E.; Curtis, J.S. Experimental data for solid–liquid flows at intermediate and high Stokes numbers. Journal of Fluid Mechanics 2020, 883, A24. [Google Scholar] [CrossRef]
- Hu, G.; Hu, Z.; Jian, B.; Liu, L.; Wan, H. On the Determination of the Damping Coefficient of Non-linear Spring-dashpot System to Model Hertz Contact for Simulation by Discrete Element Method. Journal of Computers 2011, 6, 984–988. [Google Scholar] [CrossRef]
Figure 1.
Domains for Hardalupas et al. [1] and Lau and Nathan [7] test cases with nozzle diameters of and , respectively.
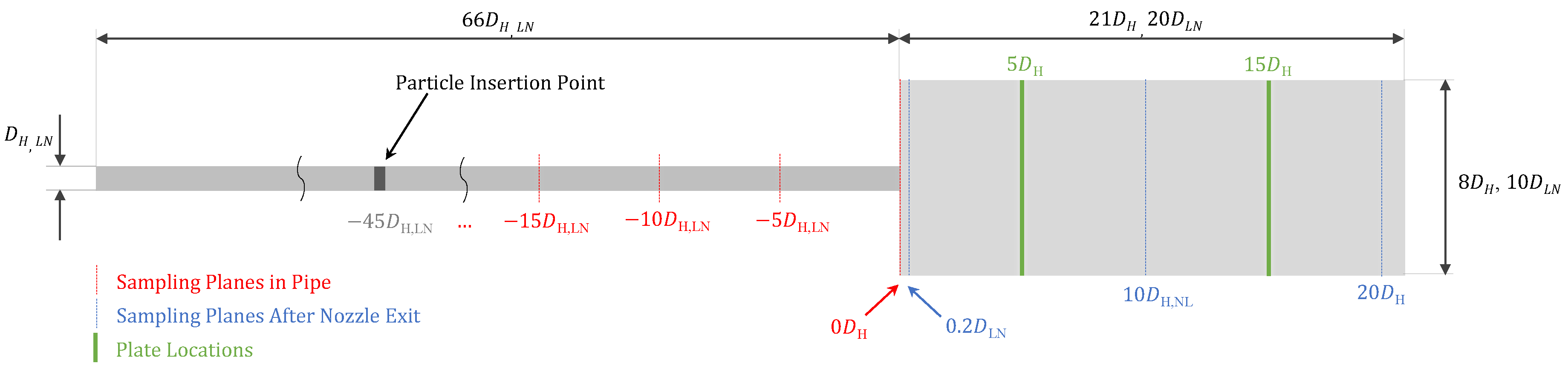
Figure 2.
Radial profiles for particle (ab) mean and (cd) root mean square velocity and (ef) number flux for fully developed flow at locations and negative , , , , , , , , , , and for a mean inlet velocity of (ace) and (dbf), respectively.
Figure 2.
Radial profiles for particle (ab) mean and (cd) root mean square velocity and (ef) number flux for fully developed flow at locations and negative , , , , , , , , , , and for a mean inlet velocity of (ace) and (dbf), respectively.
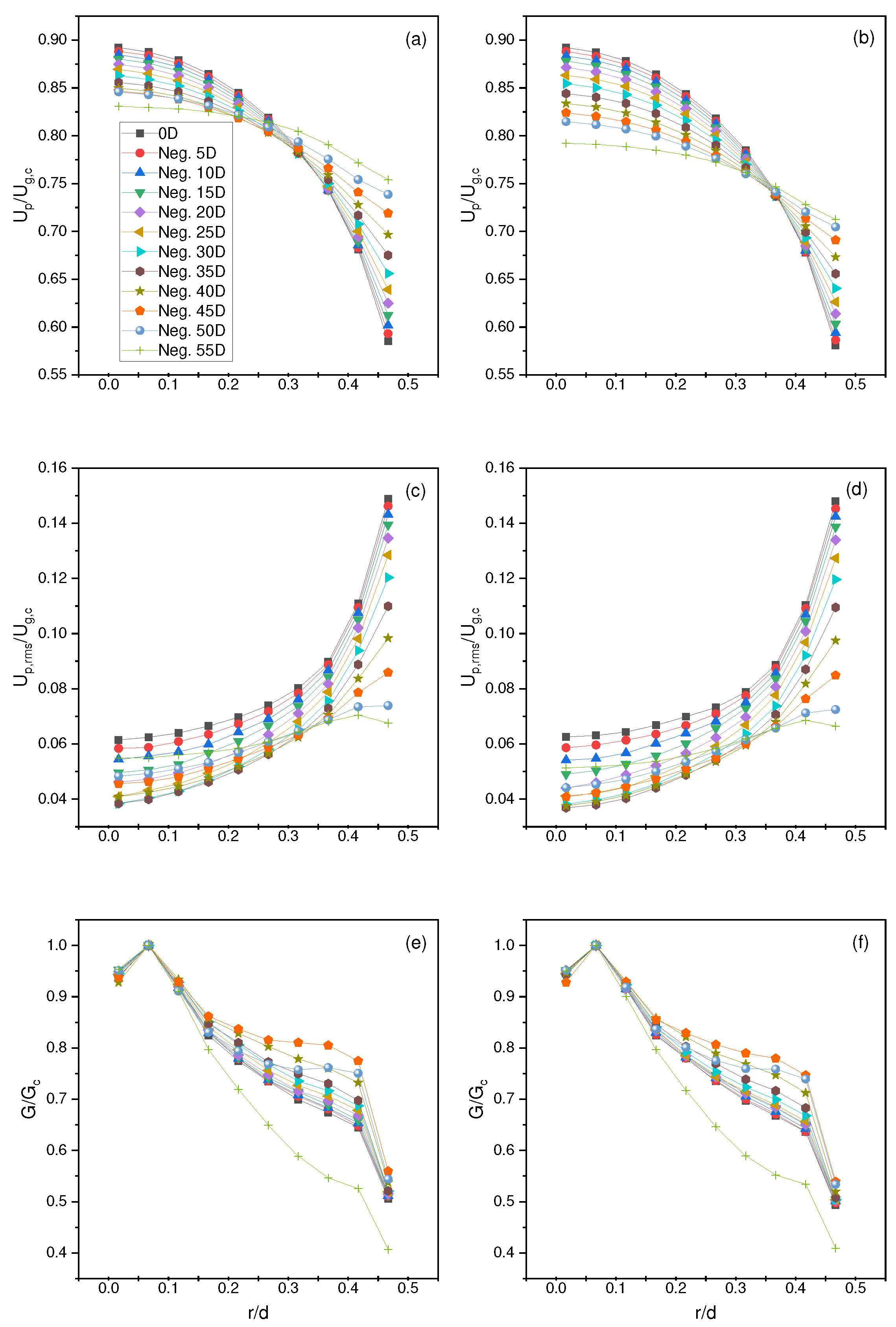
Figure 3.
Radial profiles of the particles’ (ab) velocities (c) and flux for locations of , negative , , , , , , , and from the nozzle exit for Lau3 simulation ().
Figure 3.
Radial profiles of the particles’ (ab) velocities (c) and flux for locations of , negative , , , , , , , and from the nozzle exit for Lau3 simulation ().
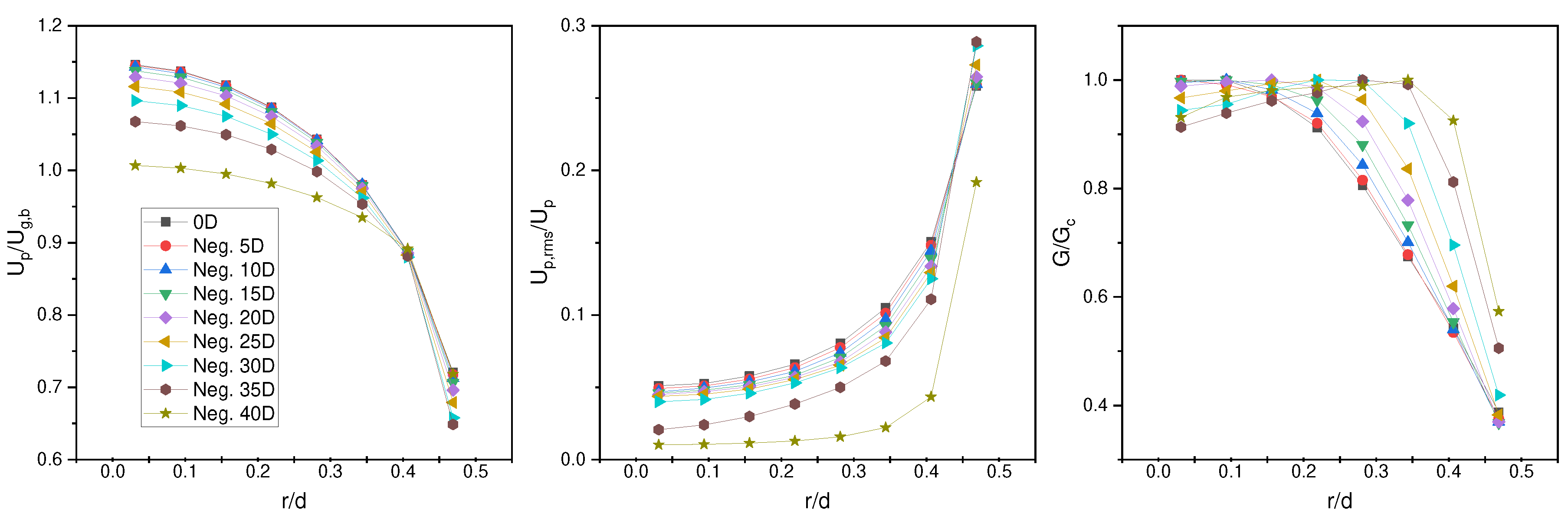
Figure 4.
Radial profiles for mean and root mean square velocity and particle flux at 0.1D (ab), 10D (cd), and 20D (ef) from the nozzle exit for simulation Hardalupas1,2 and experimental data of Hardalupas et al. [1] ( size particles).
Figure 4.
Radial profiles for mean and root mean square velocity and particle flux at 0.1D (ab), 10D (cd), and 20D (ef) from the nozzle exit for simulation Hardalupas1,2 and experimental data of Hardalupas et al. [1] ( size particles).
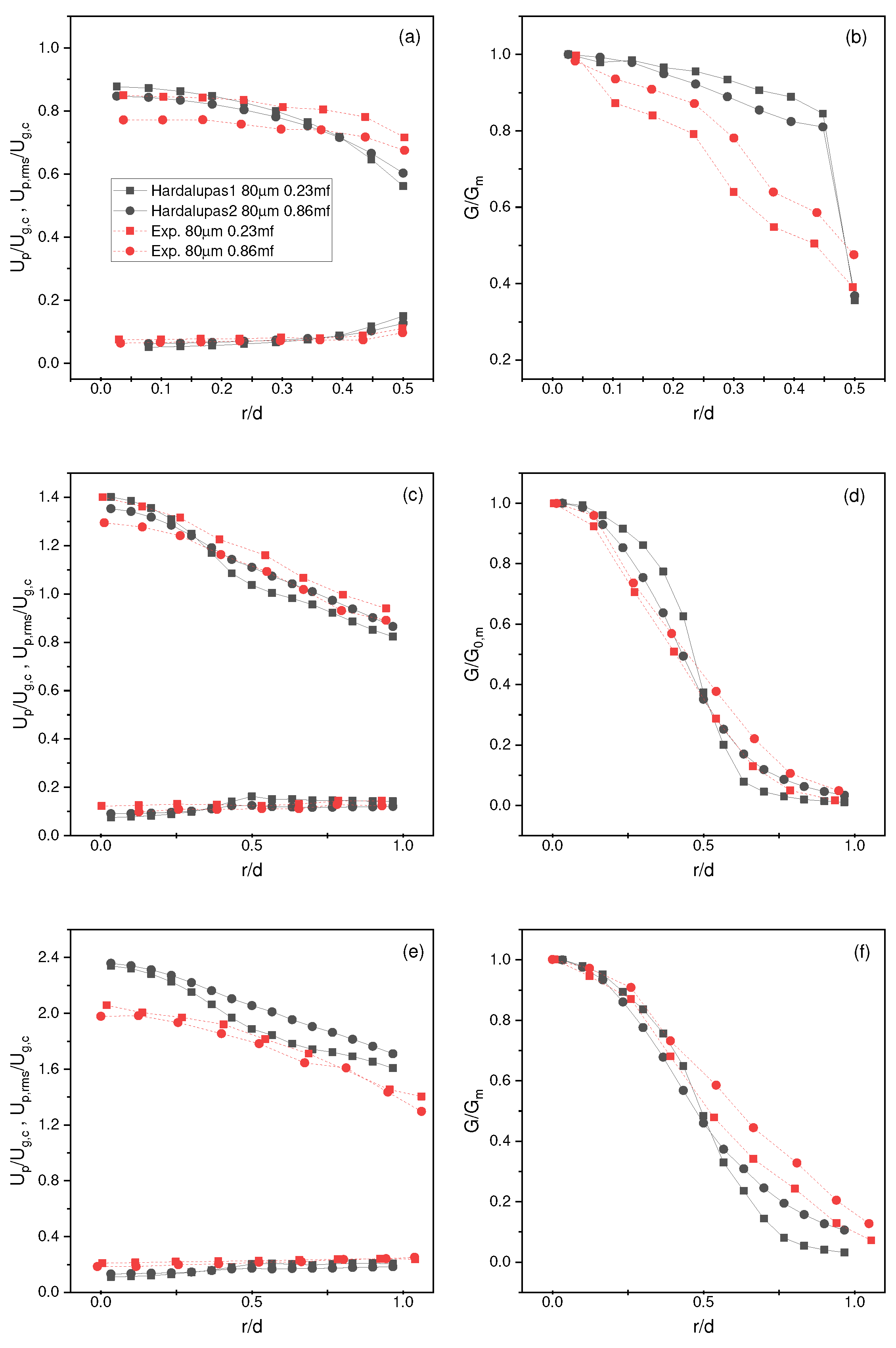
Figure 5.
Radial profiles for mean and root mean square velocity and particle flux at 0.1D (ab), 10D (cd), and 20D (ef) from the nozzle exit for simulation Hardalupas3,4 and experimental data of Hardalupas et al. [1] ( size particles).
Figure 5.
Radial profiles for mean and root mean square velocity and particle flux at 0.1D (ab), 10D (cd), and 20D (ef) from the nozzle exit for simulation Hardalupas3,4 and experimental data of Hardalupas et al. [1] ( size particles).
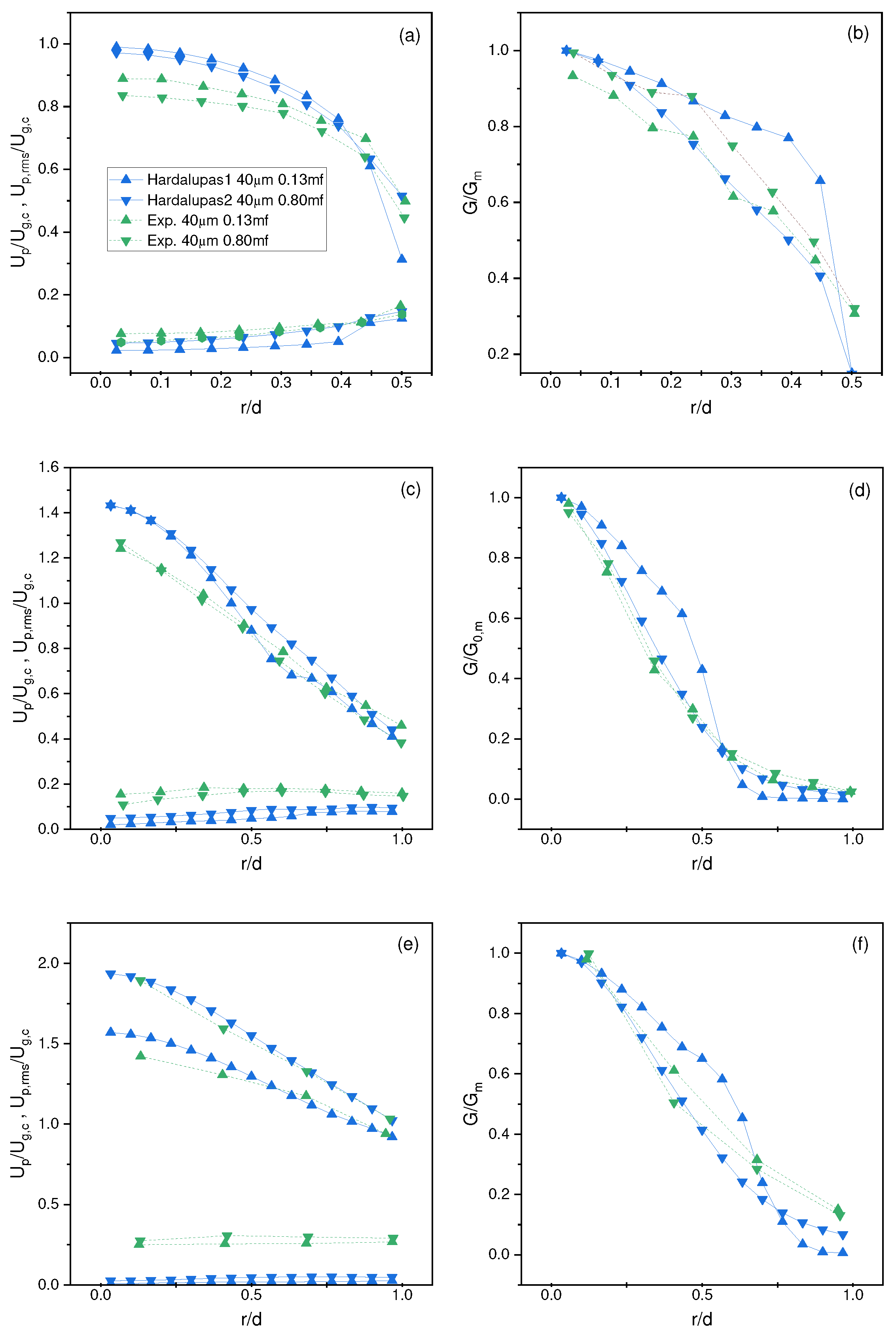
Figure 6.
Results for CFD comparison of turbulence models and experiments for (abc) mean and (def) root mean square velocity at 0.2D, 10D, and axial locations, respectively.
Figure 6.
Results for CFD comparison of turbulence models and experiments for (abc) mean and (def) root mean square velocity at 0.2D, 10D, and axial locations, respectively.
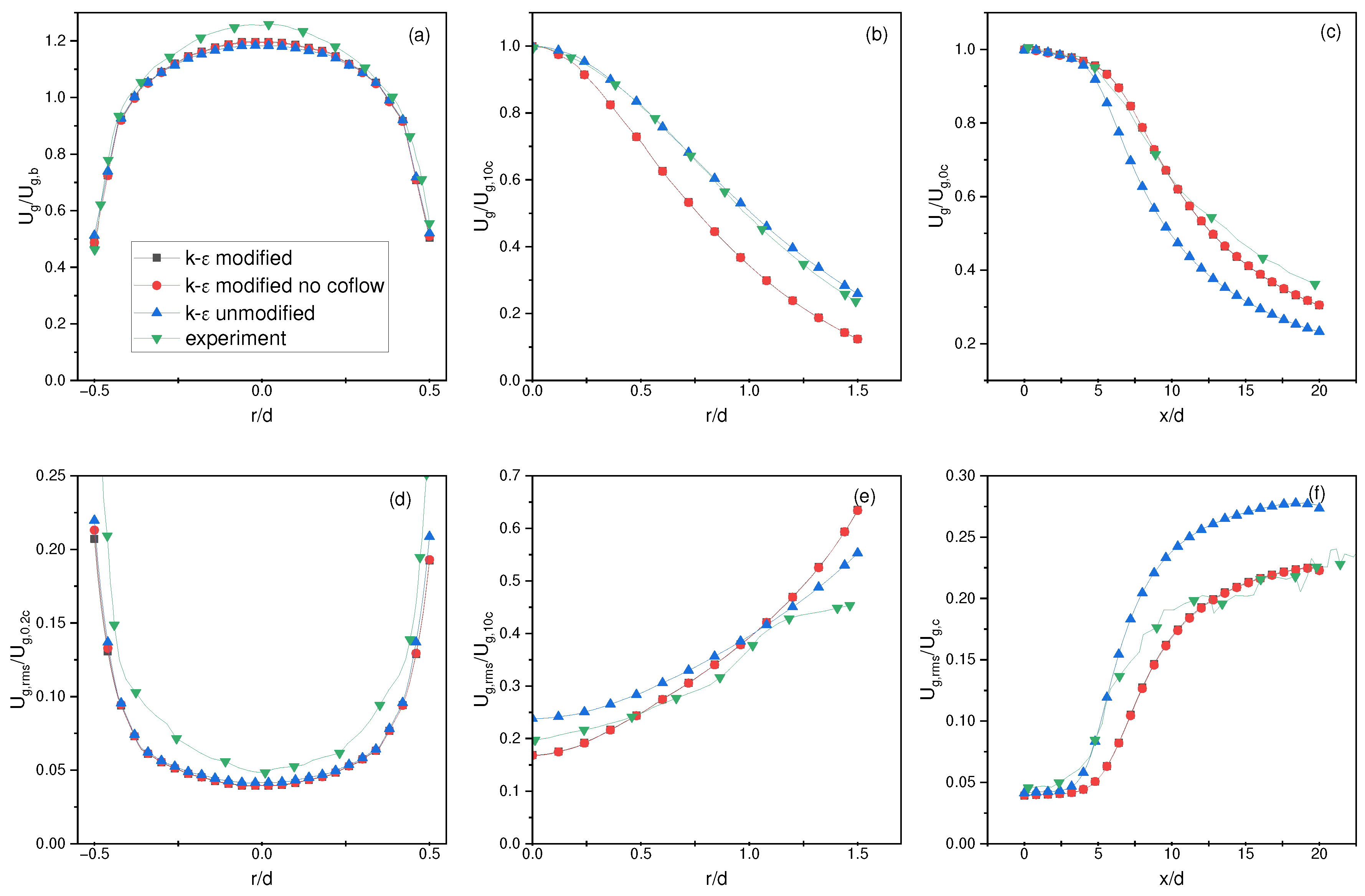
Figure 7.
Lau and Nathan [7] radial profiles for mean and root mean square velocity and particle flux at (ab) and (bc)
Figure 7.
Lau and Nathan [7] radial profiles for mean and root mean square velocity and particle flux at (ab) and (bc)
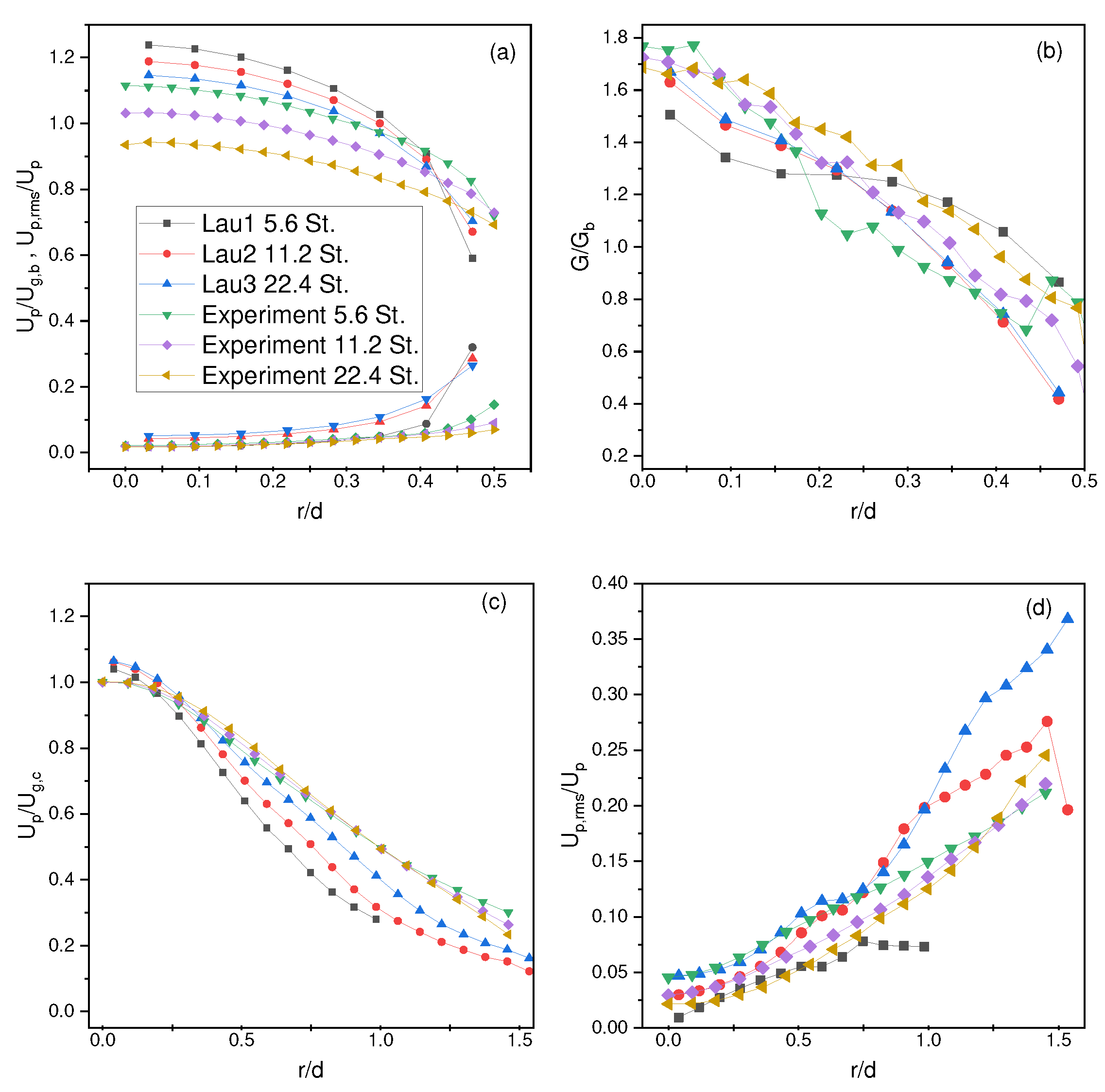
Figure 8.
A snapshot in time showing particles contacting the plate: (a) all collisions on a full plate (3.5D radius) and (b) collisions grouped by concentric regions with 0.5D width
Figure 8.
A snapshot in time showing particles contacting the plate: (a) all collisions on a full plate (3.5D radius) and (b) collisions grouped by concentric regions with 0.5D width
Figure 9.
%Error (a) between ratios of CG0 and CG2 and collision frequencies and (b) %Error for the collision frequency.
Figure 9.
%Error (a) between ratios of CG0 and CG2 and collision frequencies and (b) %Error for the collision frequency.
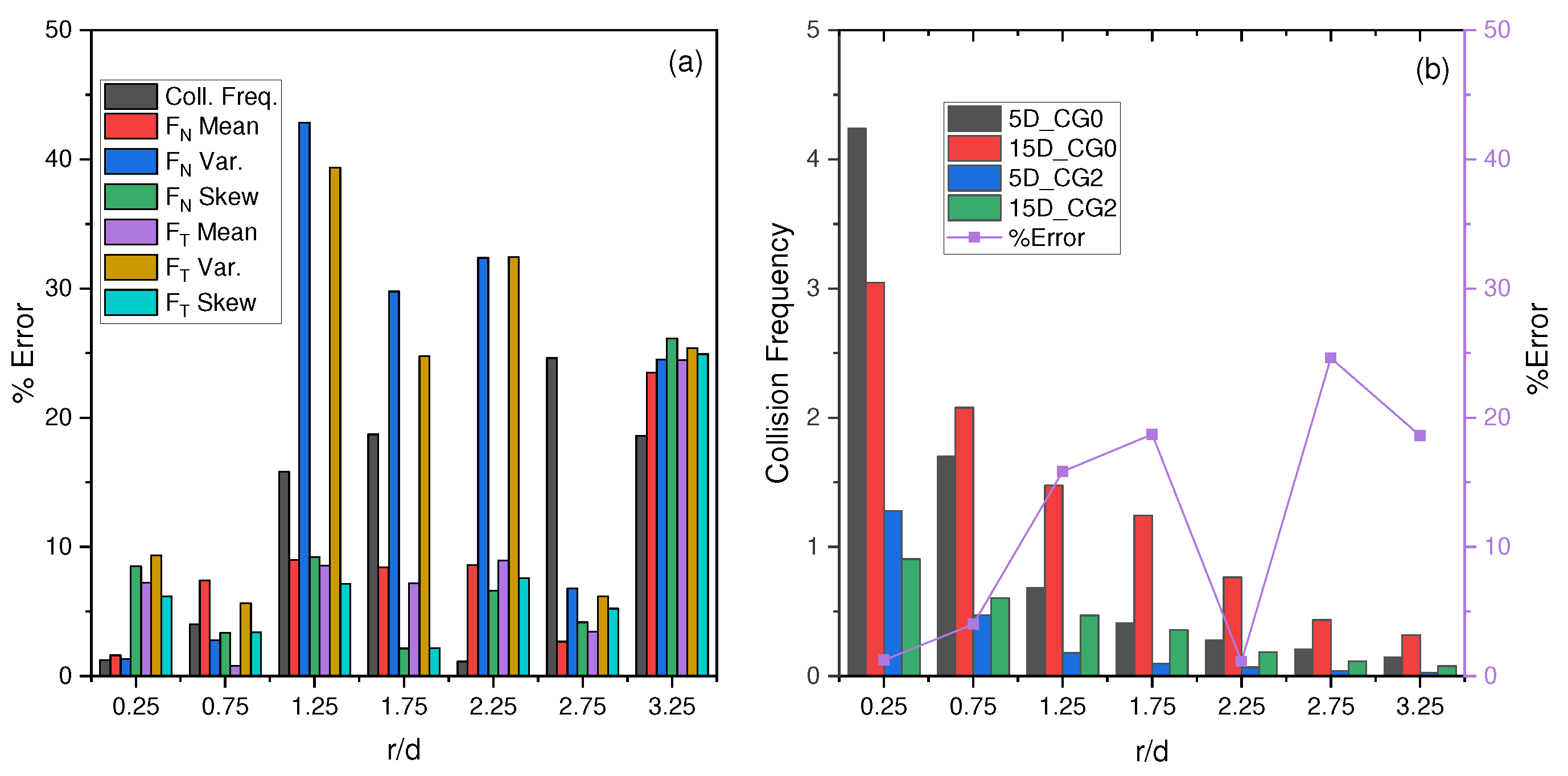
Figure 10.
A Kernel density estimate plot for collision frequency on the plate in the (a) unscaled 5D, (b) unscaled 15D, (c) scaled 5D, and (d) scaled 15D simulations
Figure 10.
A Kernel density estimate plot for collision frequency on the plate in the (a) unscaled 5D, (b) unscaled 15D, (c) scaled 5D, and (d) scaled 15D simulations
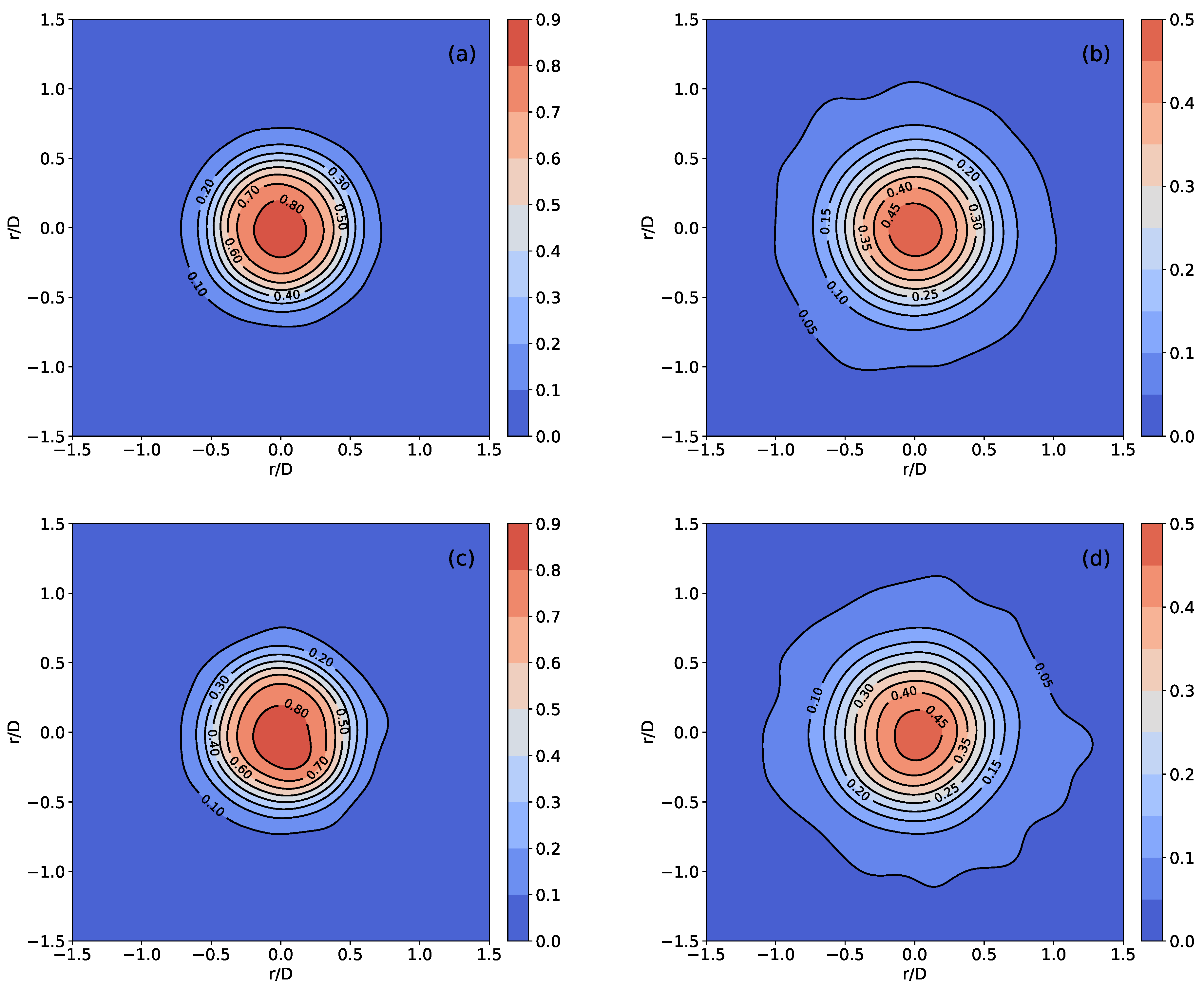
Figure 11.
Flow profiles for particle (ab) mean and (cd) root mean square velocity, and (ef) number flux at locations and negative , , , , , , and relative to the nozzle exit for CG0 and CG2, respectively.
Figure 11.
Flow profiles for particle (ab) mean and (cd) root mean square velocity, and (ef) number flux at locations and negative , , , , , , and relative to the nozzle exit for CG0 and CG2, respectively.
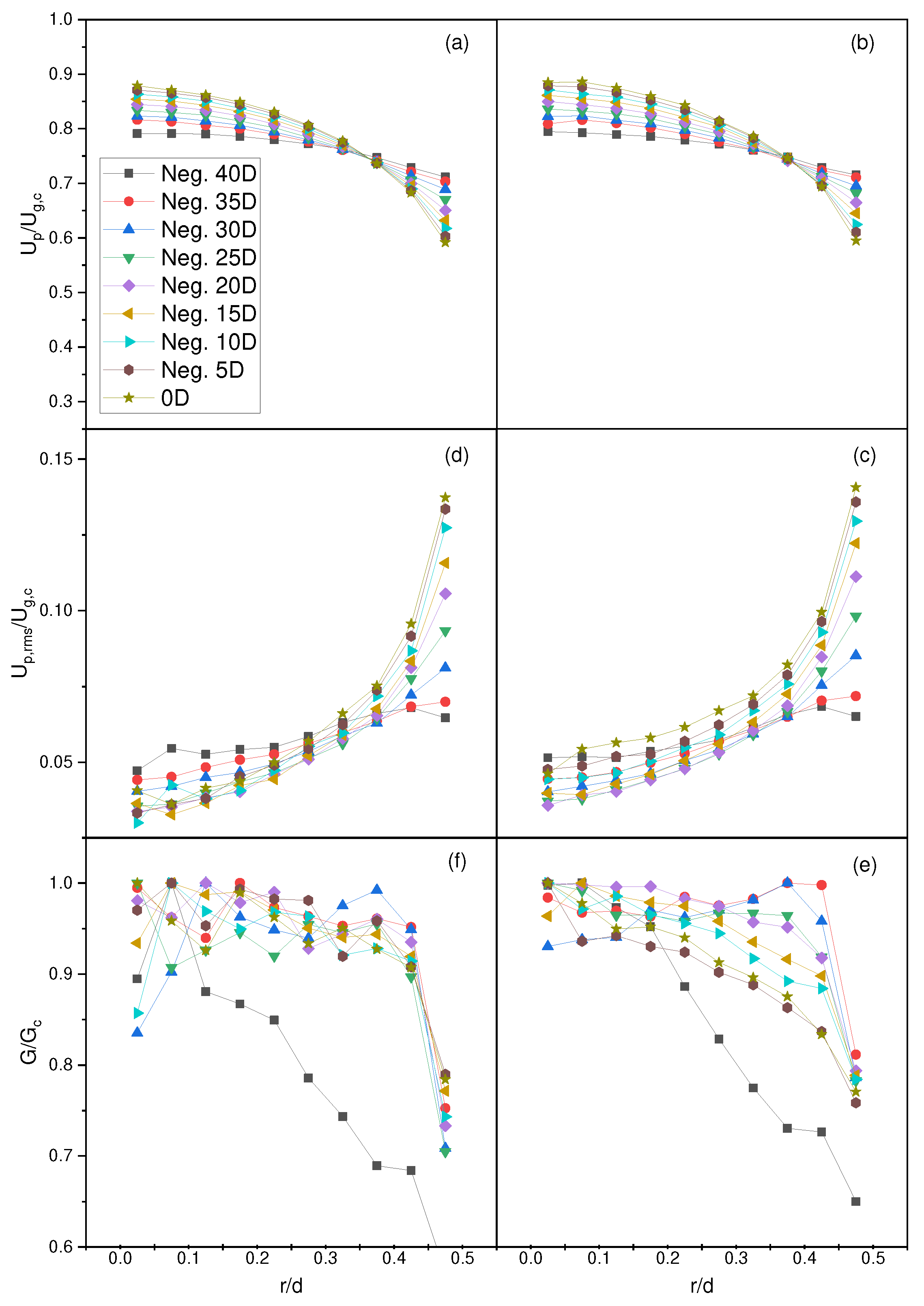
Figure 12.
Mean and root mean square particle velocity and particle number flux for locations , , , , , , , and relative to nozzle exit.
Figure 12.
Mean and root mean square particle velocity and particle number flux for locations , , , , , , , and relative to nozzle exit.
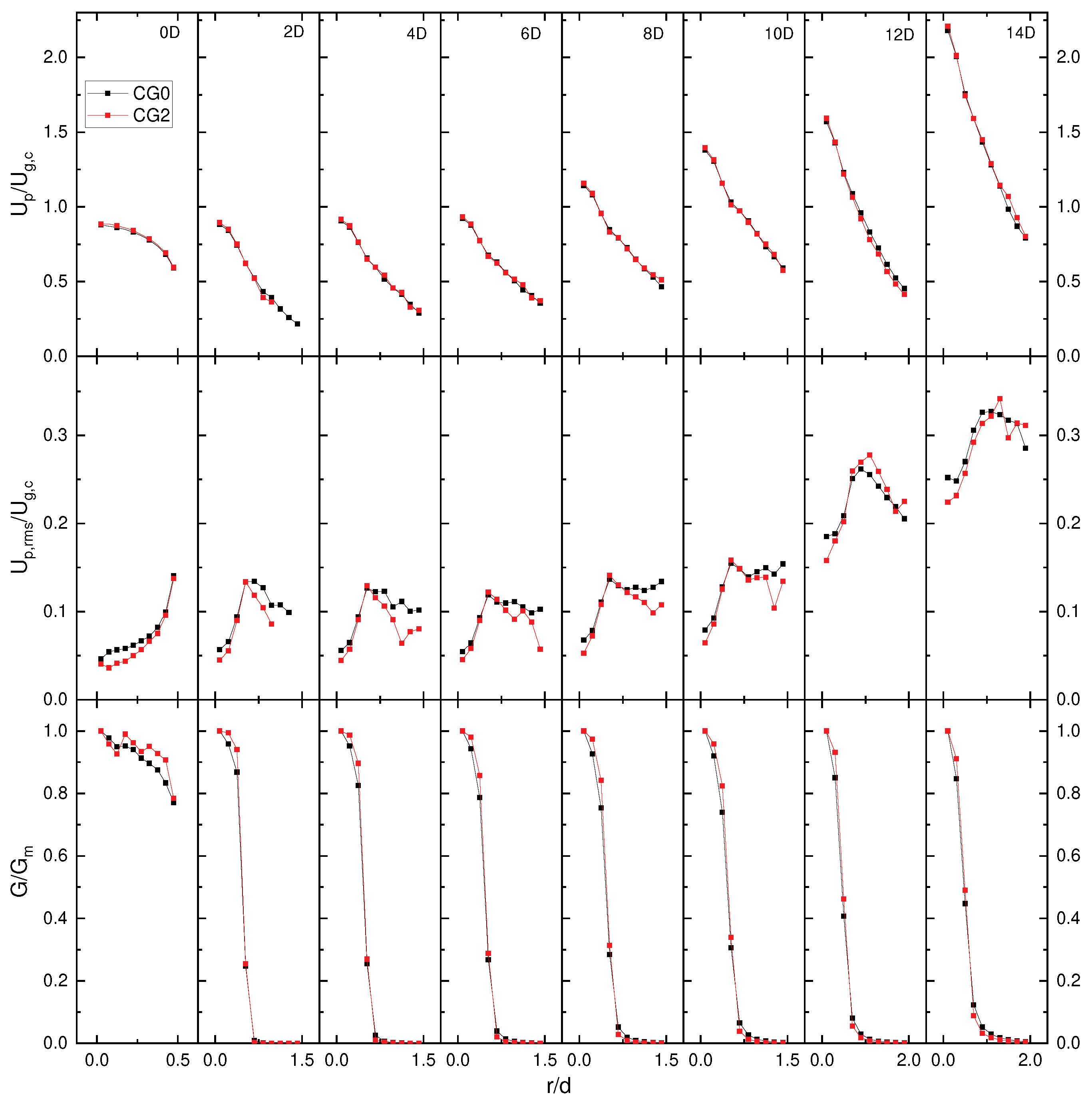
Table 1.
Summary of particle operating and flow conditions for the selected validation cases.
| Simulation | Particle | Particle | Mass | Gas Exit | Reynolds | Stokes |
| Name | Diameter, | Density, | Loading | Velocity, | Number | Number |
| Hardalupas1 | 80 | 2950 | 0.23 | 13 | 13000 | 50 |
| Hardalupas2 | 80 | 2950 | 0.86 | 13 | 13000 | 50 |
| Hardalupas3 | 40 | 2420 | 0.13 | 13 | 13000 | 10.27 |
| Hardalupas4 | 40 | 2420 | 0.80 | 13 | 13000 | 10.27 |
| Lau1 | 40 | 1200 | 0.40 | 12 | 10000 | 5.6 |
| Lau2 | 40 | 1200 | 0.40 | 24 | 20000 | 11.2 |
| Lau3 | 40 | 1200 | 0.40 | 48 | 40000 | 22.4 |
Table 2.
Mesh quality details.
| Experiment | Number | Orthogonality | Orthogonality | Skew | Average |
| Cells | Max | Average | Max | ||
| Hardalupas et al. [1] | 3806397 | 21.9 | 2.9 | 0.5 | 24 |
| Lau and Nathan [7] | 3440578 | 25.8 | 3.1 | 0.5 | 24-76 |
Table 3.
Summary of boundary conditions used in simulations.
| Location | Velocity | Pressure | Eddy Viscosity | Kinetic Energy | Epsilon |
| Wall | No Slip | Zero Gradient | Spalding Wall Func. | Zero Gradient | Epsilon Wall Func. |
| Inlet | Zero Gradient | Calculated | |||
| Outlet | Entrainment Vel. | Total Pressure | Calculated | Zero Gradient | Zero Gradient |
| Initial Freestream | Uniform 0 | Uniform 0 | 0 |
Table 4.
Particle initial mean and fluctuating velocities, DEM time-step, and percentage of Rayleigh and Hertz critical time-steps for each simulation.
Table 4.
Particle initial mean and fluctuating velocities, DEM time-step, and percentage of Rayleigh and Hertz critical time-steps for each simulation.
| Simulation | Inlet Velocity | Fluctuating | DEM | %Rayleigh, %Hertz |
| Name | (45D), | Velocity, | Time-Step, s | |
| Hardalupas1 | ||||
| Hardalupas2 | ||||
| Hardalupas3 | ||||
| Hardalupas4 | ||||
| Lau1 | ||||
| Lau2 | ||||
| Lau3 |
Table 5.
Ratios of 5D and 15D collision frequencies and normal and tangential force statistics for unscaled (CG0) and scaled (CG2) systems with their relative errors.
Table 5.
Ratios of 5D and 15D collision frequencies and normal and tangential force statistics for unscaled (CG0) and scaled (CG2) systems with their relative errors.
| Ratio | Col. Freq. | Mean | Var. | Skew | Mean | Var. | Skew |
| CG0 | 1.22 | 0.70 | 0.64 | 1.38 | 0.73 | 0.56 | 1.12 |
| CG2 | 1.25 | 0.68 | 0.62 | 1.42 | 0.75 | 0.55 | 1.10 |
| %Error | 2.39 | 3.10 | 3.78 | 3.56 | 3.81 | 1.04 | 1.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






