Prerpints.org logo
Preprint
Article

Splicing Measurement and Compensation of Straightness Errors for Ultra-Precision Guideways

Altmetrics

Downloads

131

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 July 2023

Posted:

07 July 2023

You are already at the latest version

Alerts
Abstract
The straightness error of guideway is one of the key indicators of ultra-precision machine, which plays an important role in the machining accuracy of work-piece. In order to measure straightness error of long distance ultra-precision guideway accurately, a splicing measurement for straightness error of guideway using high-precision flat mirror and displacement sensor was proposed in this paper, and the data splicing processing algorithm based on coordinate transformation was studied. Then comparative experiments on splicing measurement and direct measurement of straightness error were carried out on a hydrostatic guideway grinder. The maximum difference between the two measurements was about 0.3μm, which was far less than the straightness error of 5.8μm. The experiment demonstrated the correctness of the proposed splicing measurement method and data processing algorithm. To suppress the influence of straightness error on machining accuracy, a straightness error compensation algorithm based on error rotation transformation and vertical axis position correction was proposed, and the grinding experiment of a plane optics with size of 1400mm×500mm was carried out, whose flatness error after grinding was about 2.98μm. The straightness error of the grinding machine had been well suppressed.
Keywords: 
Subject: Engineering  -   Industrial and Manufacturing Engineering

1. Introduction

With the continuous development of industrial technology, long distance and high precision hydrostatic linear guideways are increasingly being applied in advanced manufacturing fields, such as large-diameter ultra-precision turning machines, ultra-precision grinder, coordinate measuring systems [1], etc. Straightness error is one of the most important geometric errors of the guideway, which not only affects the machining accuracy, but also affects the reliability and stability of the equipment during long-term operation [2]. In the process of equipment manufacturing, there are many methods which can effectively reduce the straightness error of the guideway, such as improving the flatness of the working surface [3], optimizing the fluid parameters in the slider [4], reducing hydraulic oil temperature fluctuations [5]. During the equipment debugging stage, by accurately measuring the straightness error of the guideway and compensating it in the CNC system, the straightness error of the guideway can be further reduced [6]. For machine tools such as ultra-precision lathes and grinders, the straightness error of the guideway will be copied onto the surface of the component, which affect the machining accuracy [7]. Therefore, measuring the straightness error accurately, analyzing the influence of straightness error on machining accuracy, establishing compensation algorithm for straightness error, and error compensating during the machining process are effective means to improve the machining accuracy of components [8].
There are many methods for measuring the straightness error of guideway. Ahmed Elmelegy measured the geometric error of machine with autocollimator and laser interferometer respectively, and analyzed the influence of different methods on the measurement results [9]. Vladas Vekteris researched the non-contact optical device for two-dimensional straightness measurement of machine, and presented the measuring principle and measuring transversal displacements of machine parts in two directions during their linear longitudinal motion [10]. Wang presented a simple and light-weight two-dimensional straightness measurement configuration based on optical knife-edge sensing, and analyzed the physical model of the configuration and performs simulations. The experiments results indicated that the configuration could achieve ±0.25µm within a ±40µm measurement range along a 40mm primary axial motion [11]. Zhang proposed a three-degrees-of-freedom measurement system based on the Faraday effect for simultaneously measuring two-dimensional straightness errors and their positions and analyzed the influence of angle error of the semitransparent mirror on straightness measurement [12]. Wang proposed a novel method for testing straightness error of long guideway by laser tracker, and researched the basic principle and testing processing, whose testing precision was about 0.4 µm/m [13]. Because of airflow disturbances, there were significant errors by optical interference for straightness measurement if the guideway was two long. Liu proposed a method for noise attenuation of straightness measurement based on laser collimation, and the signal noise was reduced by about 90% [14]. Li proposed a new straightness splicing method using the stable characteristic of angle between two adjacent sub-guide rails for long guideway when measuring straightness error by interferometer [15]. Yun proposed a rail corrugation measurement method based on coarse-to-refine data splicing method, which could acquire the wavebands of corrugation varied from 10 mm to 1 m [16].
In order to measure the straightness error of the long guideway in ultra-precision grinder accurately, a splicing measurement method using high-precision flat mirror and displacement sensor was proposed in this paper, and the mathematical model for straightness data stitching was established. By measurement experiments, the correctness and accuracy of the stitching model were verified. In order to further improve the machining accuracy of component, the straightness error compensation model was established. By the error compensation method, the flatness error of a large scale optics was grinded to 2.98µm.

2. Splicing measurement of straightness error

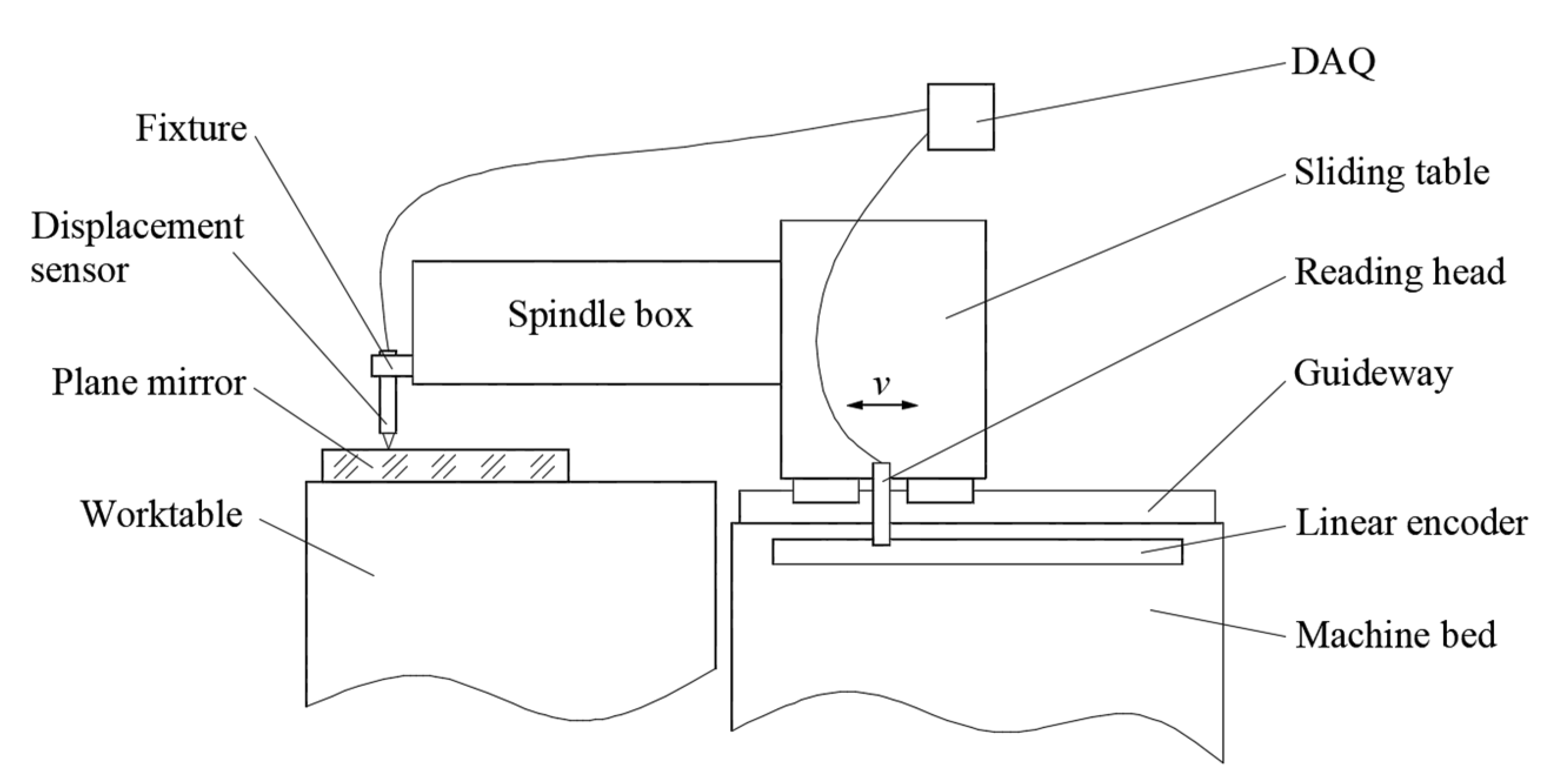
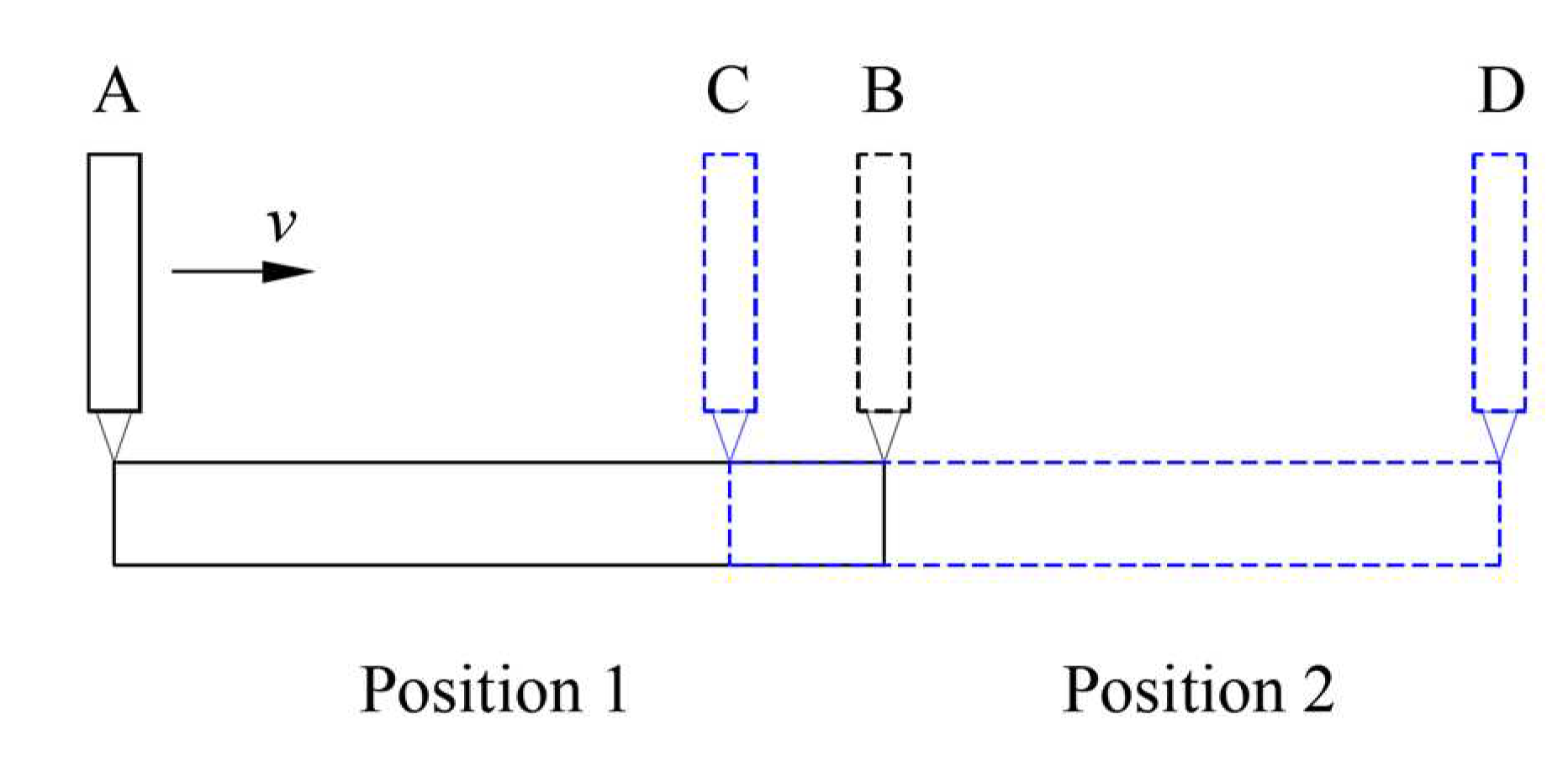
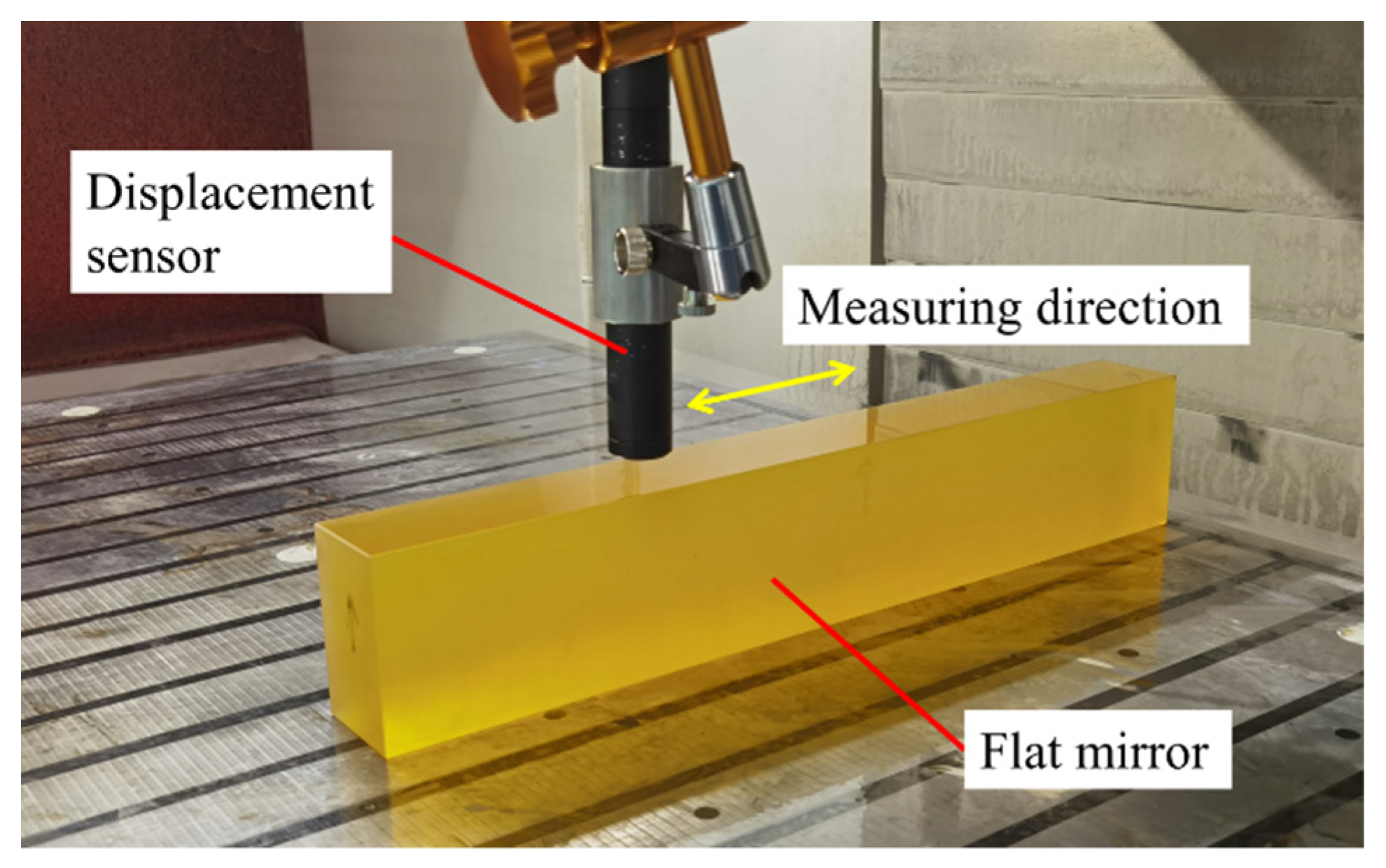
2.1. Principle of Splicing Measurement

The measurement process of guideway straightness error using high-precision flat mirror and displacement sensor is shown in Figure 1. The high-precision displacement sensor is fixed on the spindle and moves along the guideway with the slide table. The flat mirror is fixed on the machine table, and the displacement sensor measures on the surface of the mirror. If the flatness error of the mirror is much smaller than the straightness error of the guideway, the data acquired by the displacement sensor could be considered as the straightness error. To accurately obtain the straightness error at different positions of the guideway, a synchronous data acquisition card is used to collect the signal output by the displacement sensor and the grating ruler reading head.
It’s difficult to manufacture large size and high-precision flat mirror, so it’s almost impossible to directly measure the straightness of long guideway. In order to accurately measure the straightness error of long guideway, a segmented measurement method of the straightness error at different positions of the guideway was proposed. And the straightness error of the whole guideway was calculated by stitching algorithm based on coordinate transformation. The schematic diagram of segmented measurement of straightness error was shown in Figure 2. Firstly, the flat mirror was fixed at position 1, and the displacement sensor was moved along the mirror surface from point A to point B. In this process, the straightness error within the AB range was acquired, which could be represented by a data series (xi, yi) in the measurement coordinate system O1X1Y1, where i=1, 2, 3, …, n. Then the flat mirror was fixed at position 2, with a certain overlap area between position 2 and position 1. And the displacement sensor was moved along the mirror surface from point C to point D. Meantime the straightness error within the CD range was acquired, which could be represented by a data series (xj, yj) in the measurement coordinate system O2X2Y2, where j=1, 2, 3, …, m. Within the CB area, the straightness errors of the two measurements were consistent. As shown in Formula 1, after rotation and translation transformation, straightness error (xj, yj) of CB area measured with flat mirror fixed at position 2 was consistent with straightness error (xi, yi) of CB area measured with flat mirror fixed at position 1, where i=k, k+1, k+2, …, n, j=1, 2, 3, …, q. Bringing the measured data series (xi, yi) and data series (xj, yj) into formula 1, the rotation angle α and translation vector (a, b) could be solved based on the least square method. After rotation transformation by angle α and translation transformation by vector (a, b), the straightness error (xj, yj) of BD area was combined with the straightness error (xi, yi) of AB area, where i=1, 2, 3, …, n, j= q +1, q +2, q +3, …, m. And the combined data was the straightness error of full AD area.
[ x i y i ] = [ x j T y j T ] = [ cos α sin α − sin α cos α ] [ x j y j ] + [ a b ]

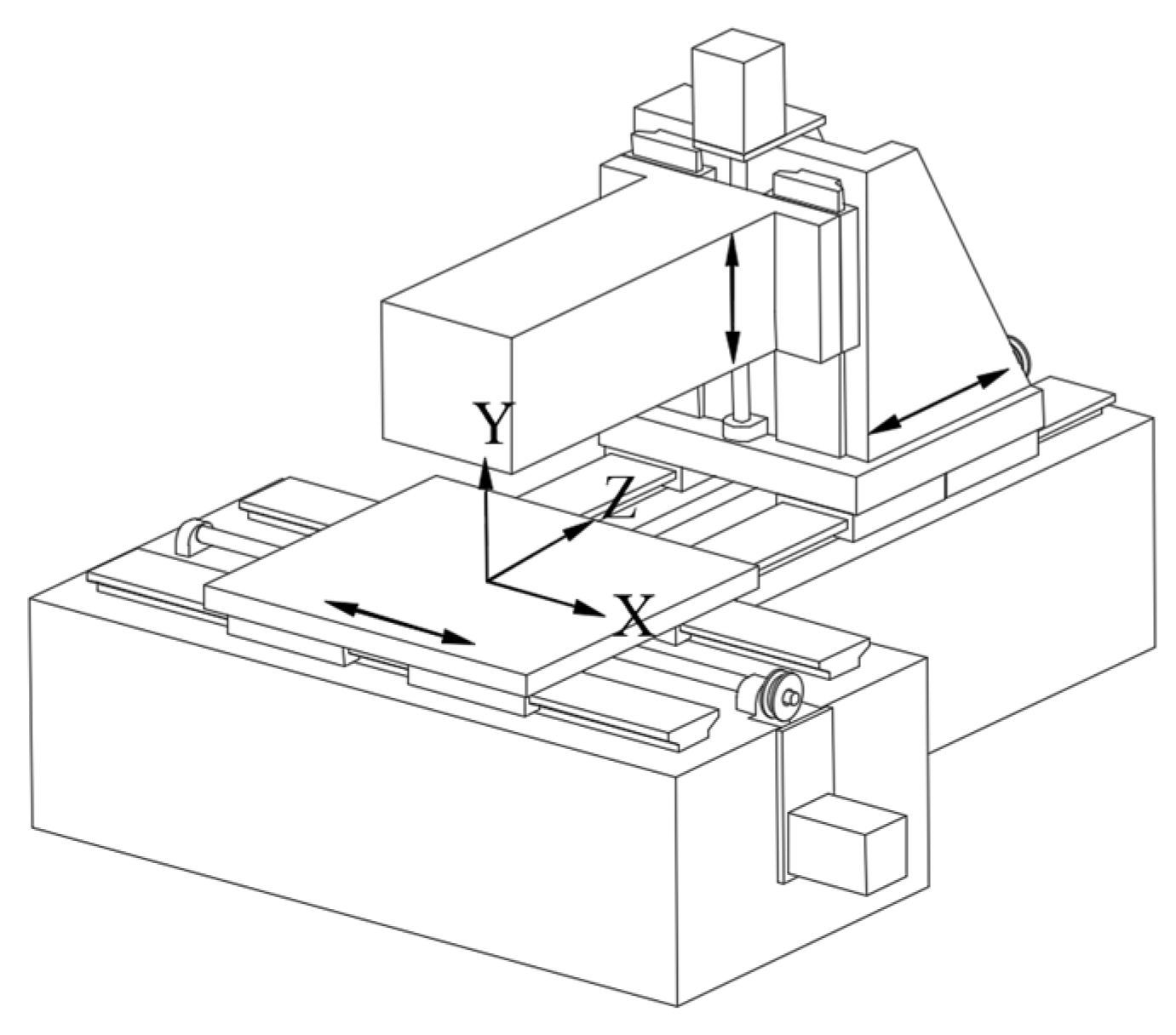
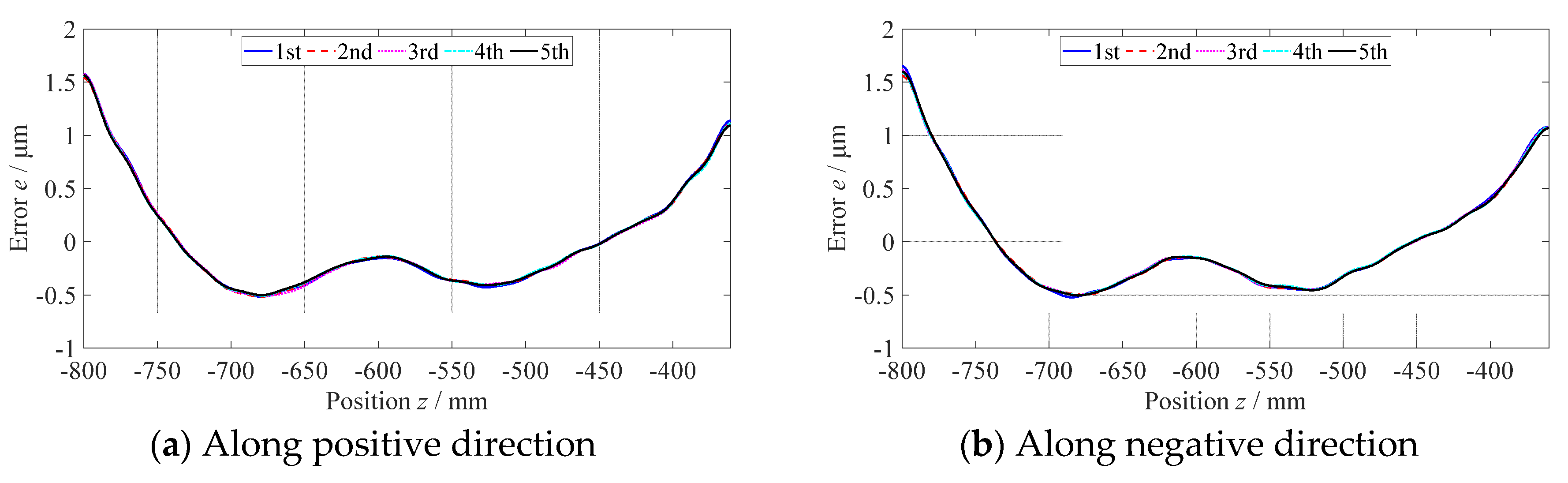
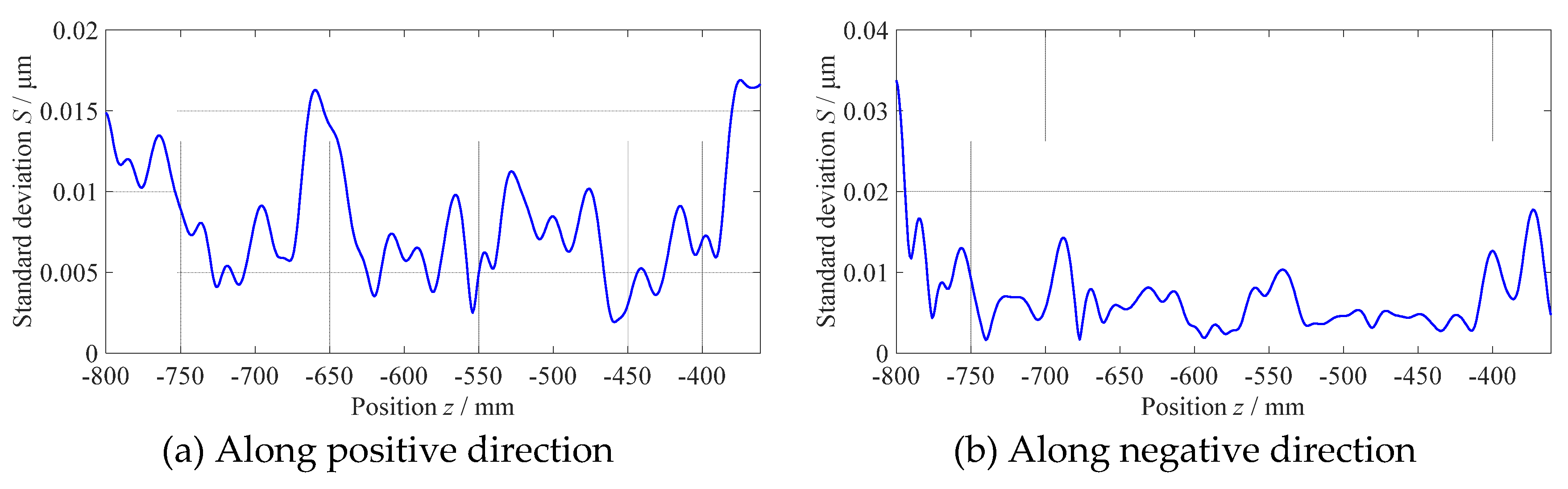
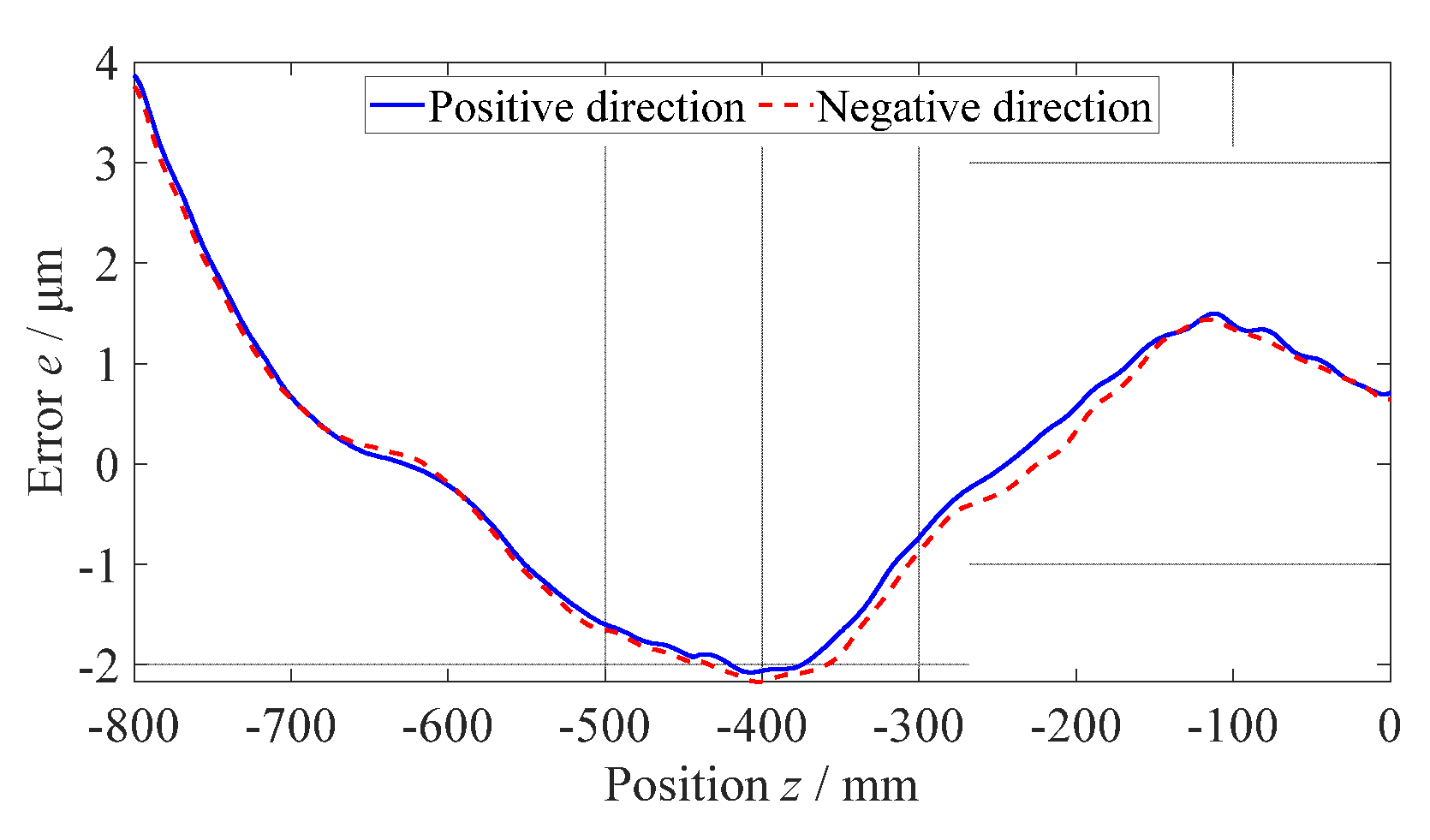
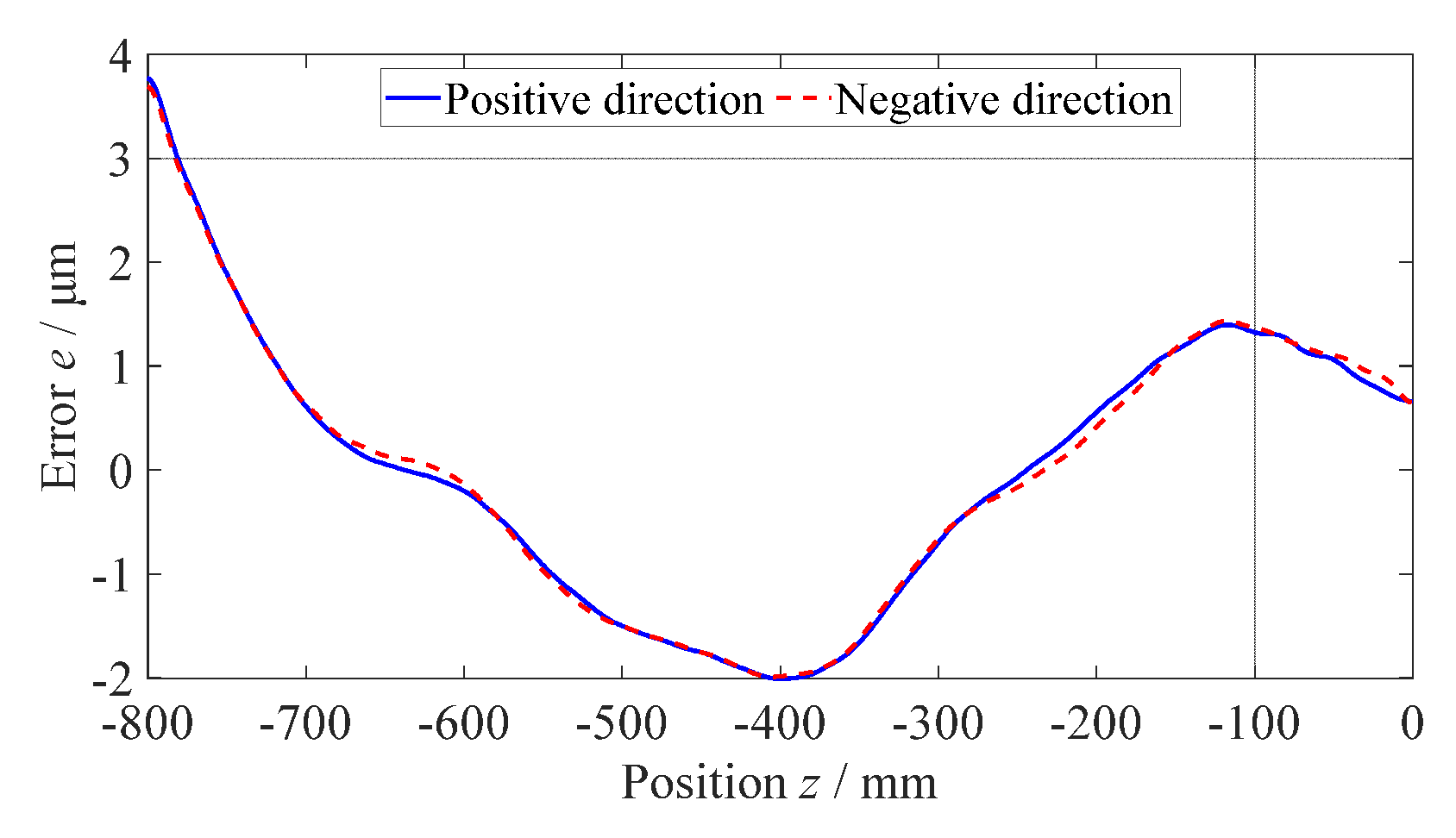
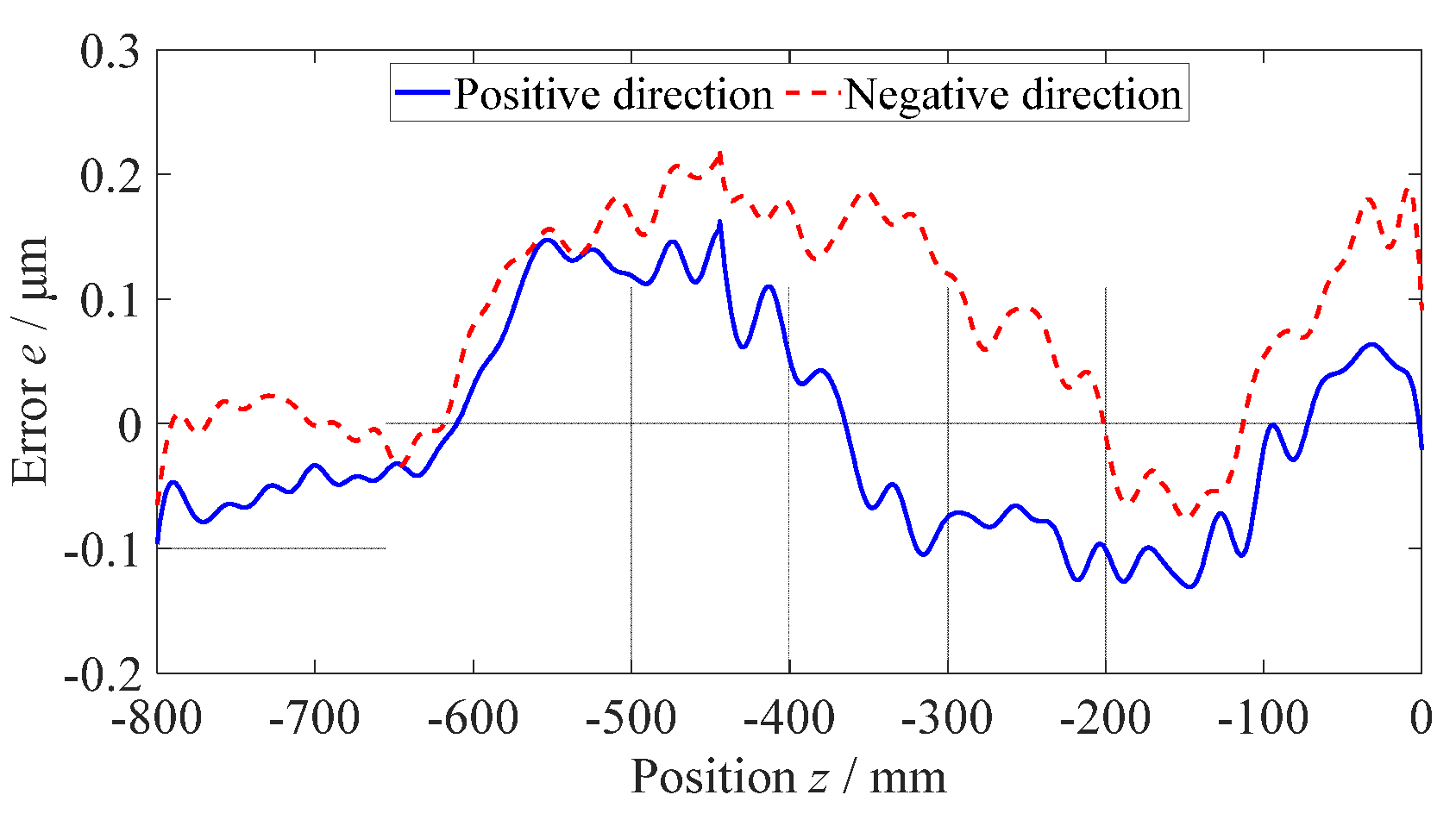
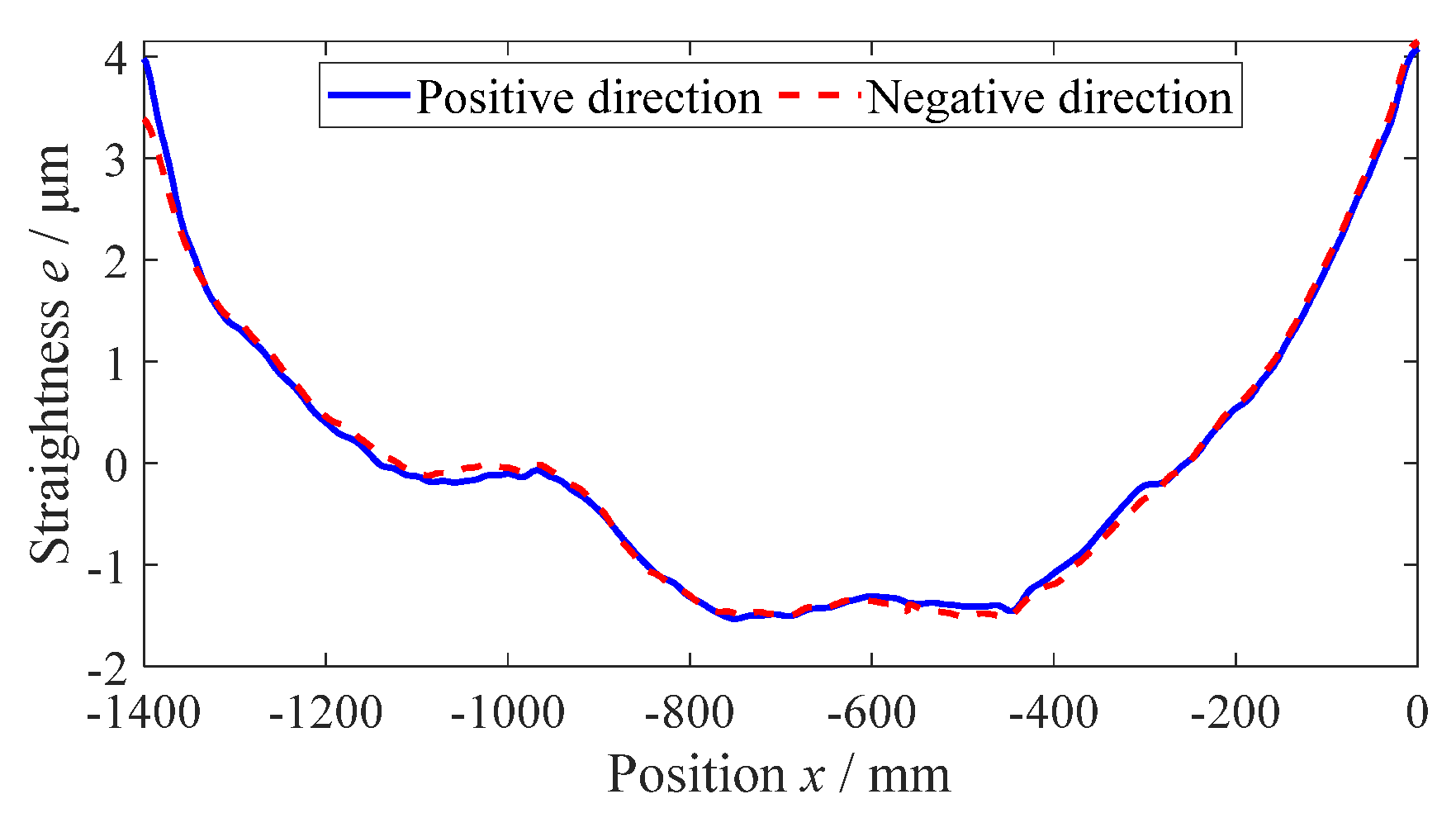
2.2. Experiments on measuring straightness error of guideways

In order to verify the correctness of the splicing measurement method, experiments of measuring straightness error were carried out on an ultra-precision grinding machine with hydrostatic guideways and position closed-loop feedback control. As shown in Figure 3, the length of X-axis, Z-axis and Y-axis were 1400mm, 800mm and 550mm, respectively. Firstly, the straightness error of Z-axis at Y-axis direction was measured using a flat mirror (No. 1) with size of 440mm × 40mm and flatness error of 0.08µm (Figure 4) and a spectral confocal displacement sensor with accuracy of 60nm, as shown in Figure 5. The flatness error of the mirror was much smaller than the straightness error of the guideway, so the influence on the measurement results could be ignored. The Z-axis was longer than the length of the flat mirror. It was necessary to measure the straightness error of the Z-axis guideway at two positions, which were -800mm~-360mm and -440mm~0mm in the machine coordinate system.
As shown in Figure 6, the straightness error of Z-axis at -800mm to -360mm position was measured for 5 times along the positive and negative directions respectively, with measuring velocity of 600mm/min and data sampling period of 100ms. When measuring along single direction, the results of five measurements of straightness error were consistent. According to formula 2, the repeatability standard deviation curve for 5 measurements was calculated and shown in Figure 7. The maximum repeatability standard deviation was not exceeding 0.04 μ m, which was far less than the straightness error. Using the same method, the straightness error at -440mm~0mm position was measured, as shown in Figure 8.
(a) Along positive direction
(b) Along negative direction
S ( z ) = 1 n − 1 ∑ i = 1 n [ e i ( z ) − e ( z ) ¯ ] 2
According to the above stitching processing algorithm, the straightness errors measured at position -800mm~-360mm and position -440mm~0mm were processed, as shown in Figure 9. Then the straightness error of whole Z-axis was directly measured by No.2 flat mirror with size of 840mm×40mm and flatness error of 0.12µm, as shown in Figure 10. The straightness error curve measured using the splicing method was the same as the straightness error curve directly measured. As shown in Figure 11, the maximum difference of straightness error between two measurement methods was approximately 0.3µm, which was far less than the straightness error of the guideway 5.8µm. Therefore, the segmented measurement and data splicing processing algorithm could be used for straightness error measurement of long guideway precisely.
The straightness error of X-axis was measured using No.2 flat mirror. The length of X-axis was 1400 mm, but that of flat mirror was 840 mm. It was necessary to measure the straightness error of the X-axis guideway at two positions, which were -1400mm~-560mm and -840mm~0mm in the machine coordinate system. After segmental measurement and data splitting process, the straightness error of whole X-axis was calculated, whose PV was approximately 5.5µm, as shown in Figure 12.

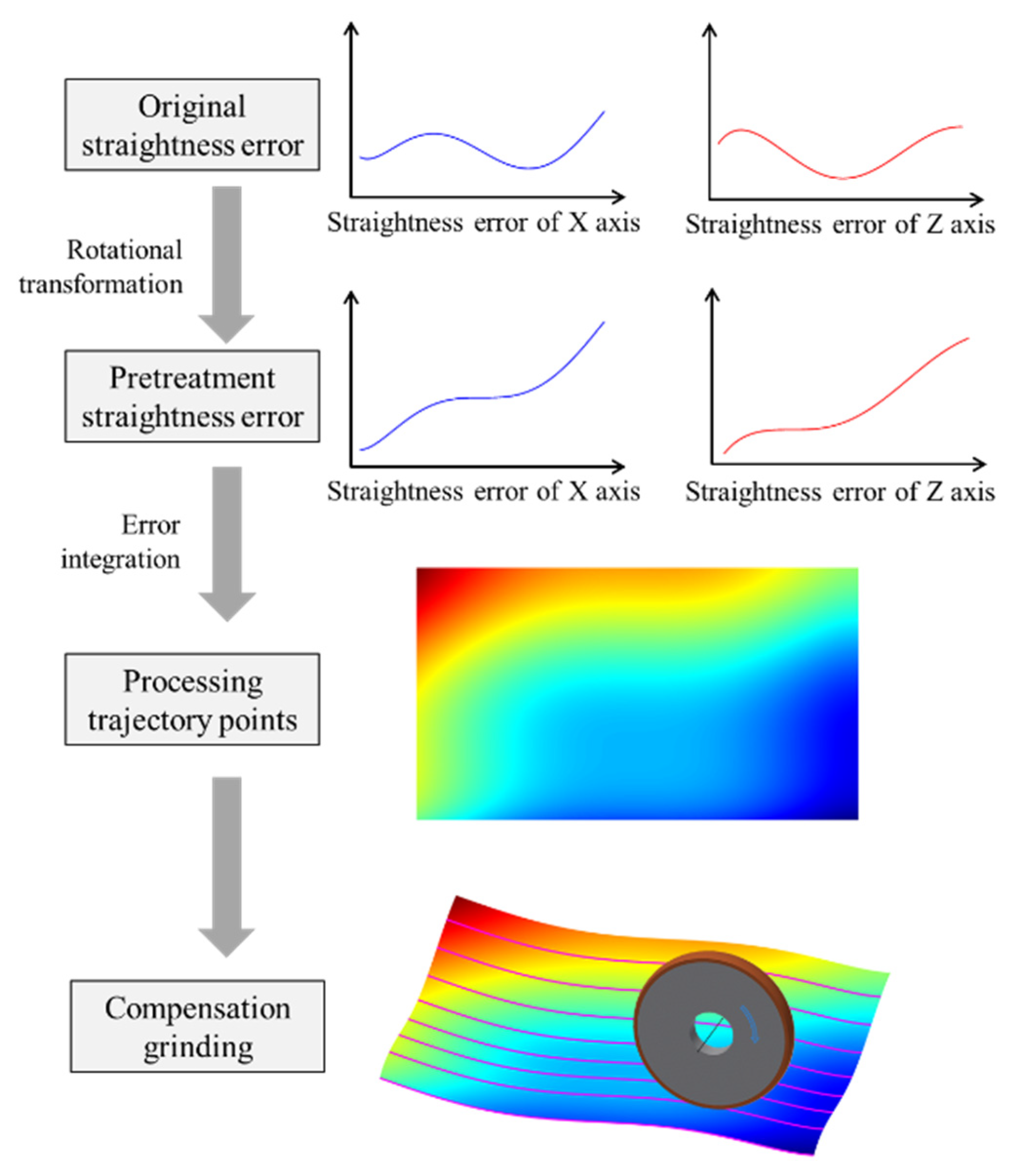
3. Compensation for Straightness Error of Guideways

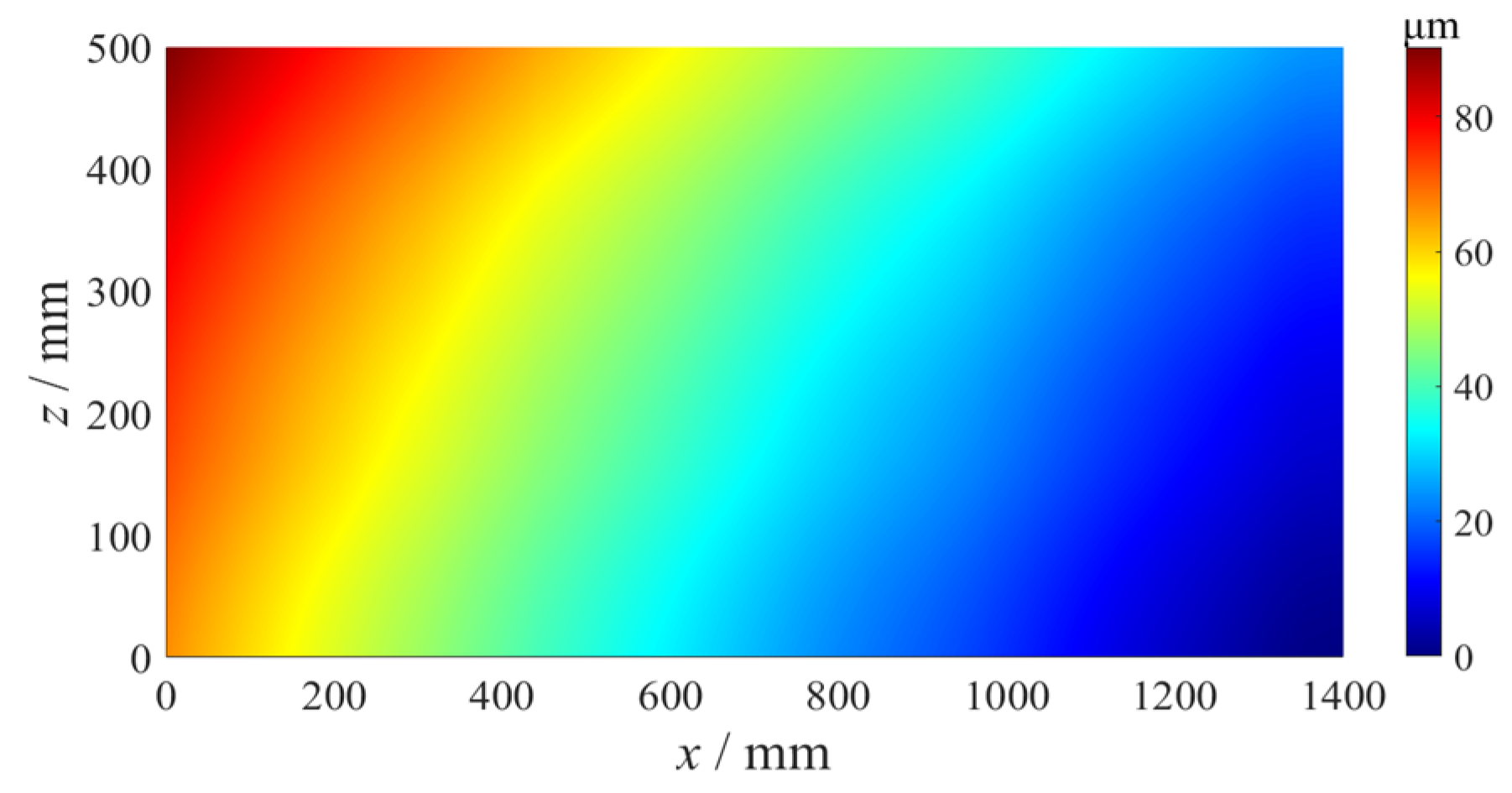
3.1. Analysis of Straightness Error Compensation

In the grinding process, the machined surface is formed according to the distance between the component and grinding wheel [17]. The straightness errors of the feed axes will be 1:1 copied on the component surface and reduce machining accuracy [18]. There are high-precision grating rulers for position measurement and closed-loop feedback control in ultra-precision machine, and the positioning errors of the feed axes are usually much smaller than the straightness errors. Therefore, it is possible to compensate the straightness errors of the X-axis and Z-axis by correcting the position of the Y-axis during processing [19], which can improve the machining accuracy of the component. In the compensation grinding process of flat optical element, due to that the straightness curves are not monotonic, the grinding wheel will move up and down with the distribution of straightness errors, and the reverse motion error of the Y-axis will reduce the compensation effect. To prevent the influence of reverse motion error on the component accuracy, a novel straightness error compensation method as shown in Figure 13 was proposed. Firstly, the straightness error curve would be rotated to be monotonic. Then, according to Formula 3, the error matrix E(i, j) of the whole machining area was calculated, where eX(i) was the rotated X-axis straightness data, and eZ(j) was the rotated Z-axis straightness data. Finally, according to the component positions in the machine coordinate, the error matrix ES(i, j) within the component area was cut out from error matrix E(i, j), which was used to 1:1 calculate the relative positions of the grinding wheel and the component in the grinding process. After grinding, the straightness error should be compensated.
E ( i , j ) = e X ( i ) + e Z ( j )

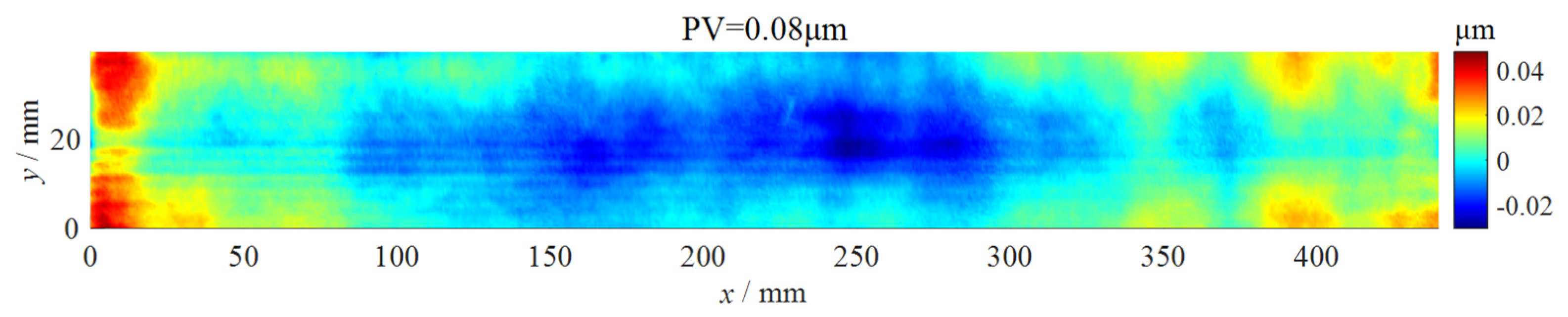
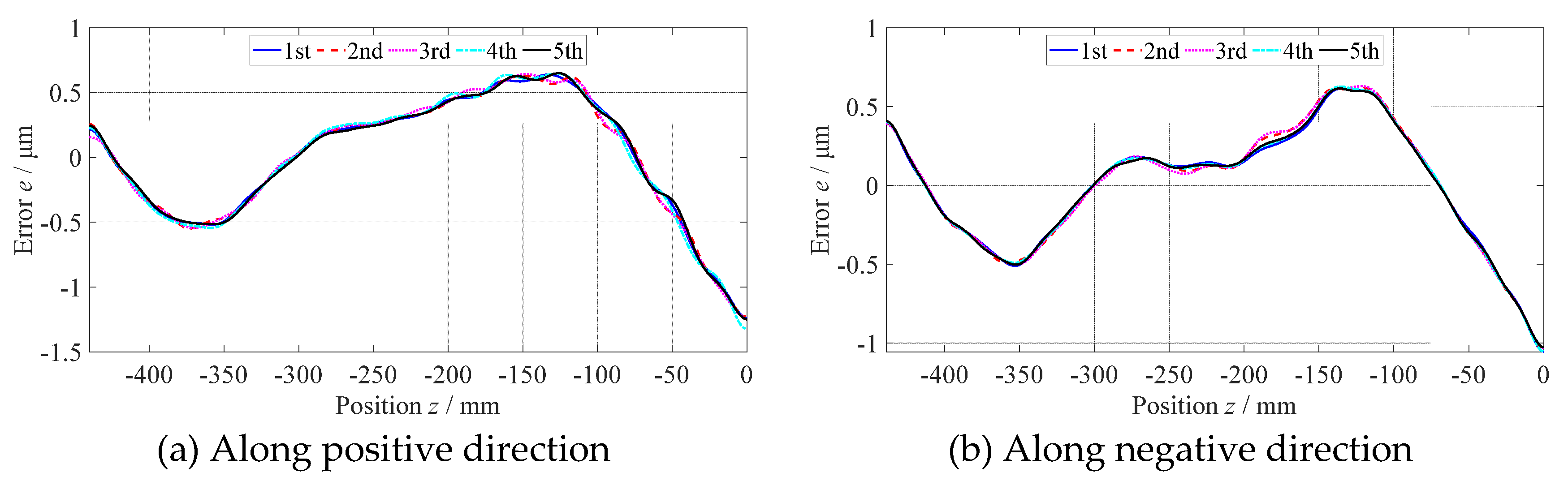
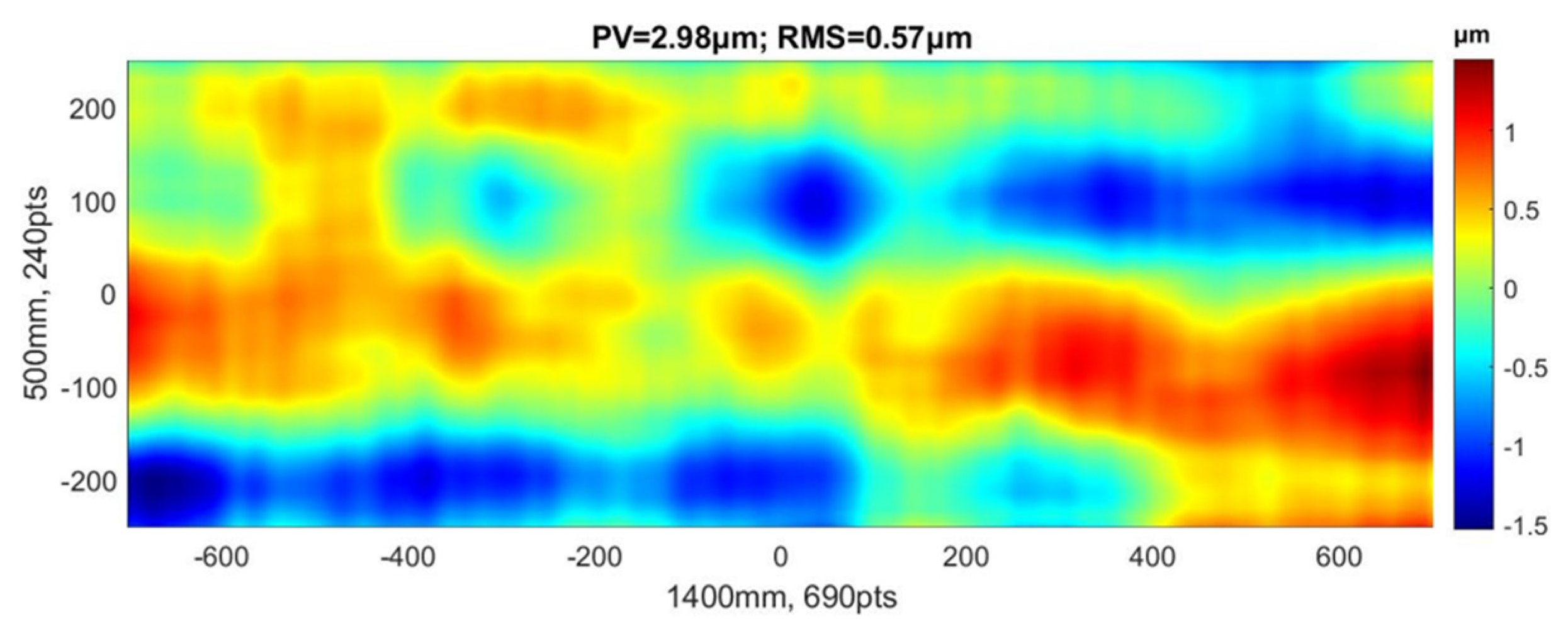
3.2. Compensation grinding experiment

The straightness errors compensation grinding experiment of flat fused quartz optical element with size of 1400mm × 500mm was carried out on the ultra-precision grinder, whose positioning error of the Y-axis was about 1.2µm measured by laser interferometer. The grinding parameters were shown in Table 1. According to the X-axis straightness error and Z-axis straightness error as shown in Figure 12 and Figure 9, the error matrix of the component area was calculated by Formula 3, as shown in Figure 15. After compensation grinding, the flatness error of optical element was measured by the above confocal displacement sensor, and the P-V value of flatness error was about 2.98µm as shown in Figure 16. The straightness error of the X-axis and Z-axis of the grinder had been well compensated.

4. Conclusions

In this paper, a segmented measurement method for straightness error of long distance guideway in ultra-precision grinder was proposed, as well as error data splicing algorithm based on coordinate transformation. Comparative measurement experiments of guideway straightness errors were carried out on an ultra-precision grinder. The maximum difference between the straightness errors of splicing measurement and direct measurement was about 0.3µm, which was far smaller than the straightness error of 5.8µm. It was accurate enough to measure guideway straightness error by the segmented measurement and data splicing algorithm. To reduce the influence of guideway straightness error on machining accuracy, the straightness error compensating method based on error curve rotation and Y-axis position correction was proposed. At the last, compensation grinding experiment of a flat fused quartz optical element with size of 1400mm × 500mm was carried out, and the P-V value of flatness error after grinding was about 2.98µm, which indicated that the compensation method had a well suppressive effect on the guideway straightness errors.

References

  1. Hong, H.B.; Yin, Y.H. Ontology-based conceptual design for ultra-precision hydrostatic guideways with human-machine interaction. Journal of Industrial Information Integration 2016, 2, 11–18. [Google Scholar] [CrossRef]
  2. Patricio, F.; Jose, J. Theoretical Analysis of Straightness Errors in Coordinate Measuring Machines (CMM) with Three Linear Axes. International Journal of Precision Engineering and Manufacturing 2021, 22, 63–72. [Google Scholar]
  3. Zha, J.; Lv, D.; Jia, Q.; Chen, Y.L. Motion straightness of hydrostatic guideways considering the ratio of pad center spacing to guide rail profile error wavelength. The International Journal of Advanced Manufacturing Technology 2016, 82, 2065–2073. [Google Scholar] [CrossRef]
  4. Shi, C.C.; Wang, Z.Z.; Peng, Y.F.; Lei, P.L.; Li, C.L. Quasi-static kinematics model for motion errors of closed hydrostatic guideways in ultra-precision machining. Precision Engineering 2021, 71, 90–102. [Google Scholar] [CrossRef]
  5. Lei, P.; Wang, Z.; Shi, C.; Peng, Y.; Lu, F. Simulation, Modeling and Experimental Research on the Thermal Effect of the Motion Error of Hydrostatic Guideways. Micromachines 2021, 12, 1445. [Google Scholar] [CrossRef] [PubMed]
  6. Feng, W.L.; Yao, X.D.; Arynov, A.; Yang, J.G. Straightness error compensation for large CNC gantry type milling centers based on B-spline curves modeling. International Journal of Machine Tools & Manufacture 2015, 88, 165–174. [Google Scholar]
  7. Sato, Y.; Fujlmoto, M.; Keita, R.; Kato, H.; Tasaki, R.; Ohishi, S. Designing and manufacturing of desktop type 5-axis NC precision grinder and its fundamental grinding characteristics. Journal of the Japan Society for Abrasive Technology 2021, 65, 153–161. [Google Scholar]
  8. Zheng, F.J.; Feng, Q.B.; Zhang, B.; Li, J.K.; Zhao, Y.Q. A high-precision laser method for directly and quickly measuring 21 geometric motion errors of three linear axes of computer numerical control machine tools. The International Journal of Advanced Manufacturing Technology 2020, 109, 1285–1296. [Google Scholar] [CrossRef]
  9. Ahmed, E.; Sarwat, Z. Comparative study of error determination of machine tools. The International Journal of Advanced Manufacturing Technology 2023, 124, 4575–4602. [Google Scholar]
  10. Vladas, V.; Mindaugas, J.; Vytautas, T. Optical device for straightness measurement. Applied Physics B: Lasers and Optics 2015, 121, 203–208. [Google Scholar]
  11. Wang, C.; Zhong, F.H.; Jonathan, D.E. Two-dimensional straightness measurement based on optical knife-edge sensing. Review of Scientific Instruments 2017, 88, 095109. [Google Scholar] [CrossRef] [PubMed]
  12. Zhang, E.Z.; Teng, X.Y.; Chen, B.Y.; Zhang, S.H.; Li, Z.Y. Three-degrees-of-freedom measurement system for measuring straightness errors and their position based on the Faraday effect. Applied Optics 2020, 59, 764–770. [Google Scholar] [CrossRef] [PubMed]
  13. Wang, X.K. Testing linearity error of long guideway by laser tracker. Applied Optics 2013, 34, 686–689. [Google Scholar]
  14. Liu, W.Z.; Zhang, C.; Duan, F.J.; Fu, X.; Bao, R.J.; Yan, M. A method for noise attenuation of straightness measurement based on laser collimation. Measurement 2021, 182, 109643. [Google Scholar] [CrossRef]
  15. Li, T.; Miao, D.J.; Li, L.F.; Li, J.S.; Zhong, W. Research on stitching method for segment straightness measurement of the long guideway. Acta Metrologica Sinica 2022, 43, 837–843. [Google Scholar]
  16. Teng, Y.; Liu, H.L.; Liu, J.W.; Wang, C.; Ma, Z. J. A Rail Corrugation Measurement Method Based on Data splicing. Measurement 2020, 107560. [Google Scholar] [CrossRef]
  17. Yu, S.M.; Yao, P.; Xu, J.M.; Wang, W.; Li, Y.M.; Chu, D.K.; Qu, S.H; Huang, C.Z. Profile error compensation in ultra-precision grinding of aspherical-cylindrical lens array based on the real-time profile of wheel and normal residual error. Journal of Materials Processing Technology 2023, 312, 117849. [Google Scholar] [CrossRef]
  18. Zha, J.; Xue, F.; Chen, Y.L. Straightness error modeling and compensation for gantry type open hydrostatic guideways in grinding machine. International Journal of Machine Tools and Manufacture 2017, 122, 1–6. [Google Scholar] [CrossRef]
  19. Deng, Y.J.; Jin, X.; Zhang, Z.J. A macro–micro compensation method for straightness motion error and positioning error of an improved linear stage. The International Journal of Advanced Manufacturing Technology 2015, 80, 1799–1806. [Google Scholar] [CrossRef]
Preprints 78693 g001
Figure 1. Principle of measuring straightness with flat mirror and displacement sensor
Figure 1. Principle of measuring straightness with flat mirror and displacement sensor
Preprints 78693 g001
Preprints 78693 g002
Figure 2. Schematic diagram of segmented measurement
Figure 2. Schematic diagram of segmented measurement
Preprints 78693 g002
Preprints 78693 g003
Figure 3. The three linear axes of ultra-precision grinding machine
Figure 3. The three linear axes of ultra-precision grinding machine
Preprints 78693 g003
Preprints 78693 g004
Figure 4. Flatness error of NO. 1 flat mirror
Figure 4. Flatness error of NO. 1 flat mirror
Preprints 78693 g004
Preprints 78693 g005
Figure 5. Measuring process of straightness error
Figure 5. Measuring process of straightness error
Preprints 78693 g005
Preprints 78693 g006
Figure 6. Straightness error of Z axis at -800mm~-360mm position
Figure 6. Straightness error of Z axis at -800mm~-360mm position
Preprints 78693 g006
Preprints 78693 g007
Figure 7. Repeatability standard deviation of straightness error
Figure 7. Repeatability standard deviation of straightness error
Preprints 78693 g007
Preprints 78693 g008
Figure 8. Straightness error of Z axis at -440mm~0mm position
Figure 8. Straightness error of Z axis at -440mm~0mm position
Preprints 78693 g008
Preprints 78693 g009
Figure 9. Straightness error after data splicing
Figure 9. Straightness error after data splicing
Preprints 78693 g009
Preprints 78693 g010
Figure 10. Straightness error measured by NO. 2 flat mirror
Figure 10. Straightness error measured by NO. 2 flat mirror
Preprints 78693 g010
Preprints 78693 g011
Figure 11. Difference between stitching measurement and direct measurement
Figure 11. Difference between stitching measurement and direct measurement
Preprints 78693 g011
Preprints 78693 g012
Figure 12. Straightness error of X axis
Figure 12. Straightness error of X axis
Preprints 78693 g012
Preprints 78693 g013
Figure 13. Principle of straightness error compensation
Figure 13. Principle of straightness error compensation
Preprints 78693 g013
Preprints 78693 g014
Figure 14. Grinding experiment of flat optics
Figure 14. Grinding experiment of flat optics
Preprints 78693 g014
Preprints 78693 g015
Figure 15. Grinding wheel motion trajectory points.
Figure 15. Grinding wheel motion trajectory points.
Preprints 78693 g015
Preprints 78693 g016
Figure 16. Flatness error of optics after grinding
Figure 16. Flatness error of optics after grinding
Preprints 78693 g016
Table 1. Grinding parameters
Table 1. Grinding parameters
Grinding wheel Coolant Grinding velocity Feed speed Grinding depth per time
Diamond wheel with grit size of 8µm~12µm Water 30m/s 5000mm/min 10µm
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated