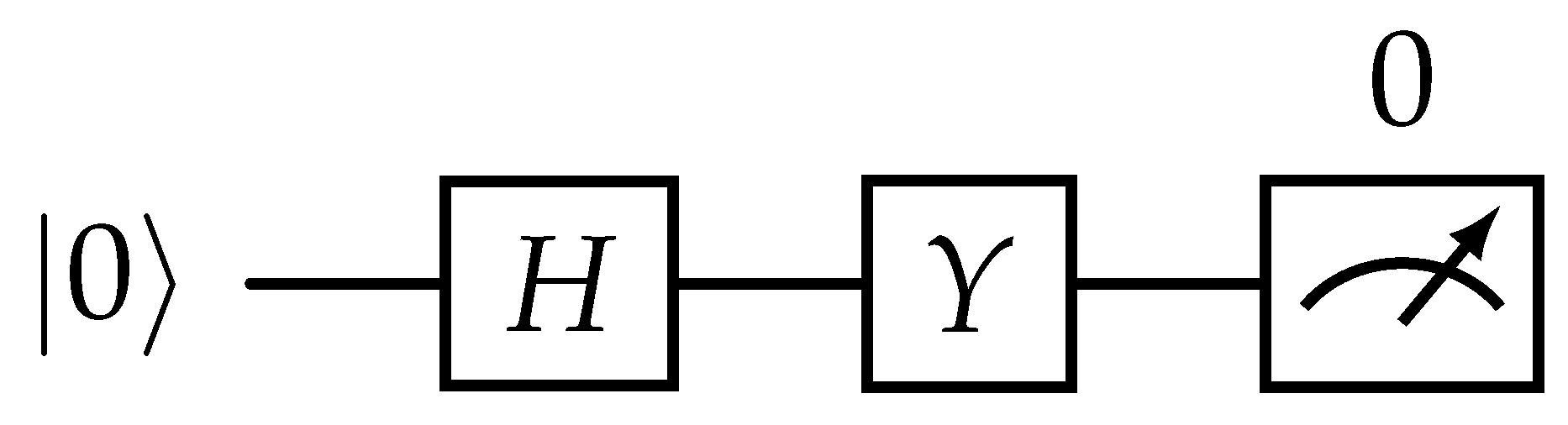Prerpints.org logo
Preprint
Article

Cross-pollinating Quantum Computing and Machine Learning for the Solution of Parameterized Problems in Computational Science and Engineering

Altmetrics

Downloads

136

Views

57

Comments

0

Submitted:

20 June 2023

Posted:

07 July 2023

You are already at the latest version

Alerts
Abstract
The potential of quantum computing for scientific and industrial breakthroughs is immense, however, we are still in the Noisy Intermediate-Scale Quantum (NISQ) era, where the currently available quantum devices contain small numbers of qubits, are very sensitive to environmental conditions and prone to quantum decoherence. Even so, existing NISQ computers have already been shown to outperform conventional computers on specific problems and the key question is how to make use of today’s NISQ devices to achieve quantum advantage in the field of computational science and engineering (CSE). In this direction, this work proposes a hybrid computing formulation by combining quantum computing with machine learning for accelerating the solution of parameterized linear systems in NISQ devices. In particular, it focuses on the Variational Quantum Linear Solver (VQLS), which is a hybrid quantum- classical algorithm for solving linear systems of equations. VQLS employs a short-depth quantum circuit to efficiently evaluate a cost function related to the system solution. The algorithm’s circuit consists of a quantum gate sequence (unitary operators) that involves a set of tunable parameters. Then, well-established classical optimizers are utilized to tune the parameters of the sequence in order to minimize the cost function, which is equivalent to finding the system solution at an acceptable level of accuracy. In this work, it is demonstrated that machine learning tools such as feed-forward neural networks and nearest-neighbor interpolation techniques can be successfully employed to accelerate the convergence of the VQLS algorithm towards the optimal values for the circuit parameters when applied to parameterized linear systems that need to be solved for multiple parameter instances.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Advancements in quantum computing (QC) are paving the way for a new age in simulations, promising to revolutionize several industry verticals, including communications, finance, medicine, materials, artificial intelligence, cryptography, etc., over the coming decades. The enormous potential for QC to tackle extremely complex issues is garnering ever greater interest as the capabilities of conventional computer systems are rapidly approaching their limits, and efforts globally to mount up the quantum race are intensifying. This disruptive and rapidly emerging new technology represents both a radical change in the laws of physics in computing as we know them and a huge, unimaginable opportunity, which is expected to result in significant changes to many aspects of modern life. Since its first conceptualization in the 1980s and early proof of principles for hardware in the 2000s, quantum computers can now be built with hundreds of qubits thanks to the progress made by companies, start-ups and corporations.
In contrast to classical computing, QC harnesses the laws of quantum mechanics to solve problems that are considered intractable for classical computers by exploiting counter-intuitive quantum physical phenomena like superposition and entanglement. Despite the fundamental differences between classical and quantum computing, any computational problem solvable by a classical computer can also be solved by a quantum computer, and vice versa, as stated by the Church-Turing thesis. However, certain quantum algorithms are demonstrated to have significantly lower time and/or memory complexity than corresponding known classical algorithms and are even expected to solve problems that no classical computer could in any feasible amount of time, a feat known as “quantum supremacy”. Examples include the famous Schor factoring algorithm [1] and the Grover search algorithm [2]. Therefore, the potential of quantum computing for scientific and industrial breakthroughs is immense, which justifies the considerable research devoted to its application in real-world problems.
Even though quantum technology is still in its infancy, the rapid development of quantum hardware and the enormous monetary investments made worldwide have led many to claim that the so-called Noisy-Intermediate Scale Quantum (NISQ) devices already in existence may soon outperform conventional computers. In short, NISQ devices are near-term quantum computers with insufficient physical qubits to execute effective error-correcting techniques. On a handful of problems created specifically for assessing the capabilities of quantum computers, it already has been demonstrated that existing NISQ computers outperform classical computers. The algorithms that run on these constrained devices may only need a few qubits, exhibit some noise resilience, and are frequently implemented as hybrid algorithms, where some operations are carried out on a quantum device and some on a classical computer. Particularly, the number of operations, or quantum gates, must be kept to a minimum since the more errors that are introduced into the quantum state during implementation, the greater the likelihood that the quantum state may decohere. Due to these restrictions, there are limits on the scope of algorithms that can be considered. Therefore, the crucial technological question is how to best utilize current NISQ technology to get a quantum advantage. Any such strategy must account for a limited number of qubits, limited connectivity of the qubits, and coherent and incoherent errors that limit quantum circuit depth.
In parallel, the field of computational science and engineering (CSE) is also exponentially growing, being inextricably linked to the quest of solving problems of rising complexity. In this environment, quantum computing is expected to bring tremendous breakthroughs to this field. Even to this day, many critical problems lay beyond our current computational capabilities and are deemed intractable even for the world’s most advanced supercomputers. Some examples are non-convex optimization problems, modeling physical systems at multiple length and/or time scales, molecular modeling, robust design problems, and others. With quantum computing coming to the fore, there is a silver lining in the computing world that one can finally solve such complex problems. Towards this direction, quantum variants of classical algorithms have been recently proposed for solving linear systems of algebraic equations [3] and differential equations [4], as well as for performing optimization [5,6] and machine learning [7,8,9] in quantum computers. All these problems lie at the heart of CSE and incorporating new quantum technologies may lead to unforeseeable advances in the field. Nevertheless, we are still in the NISQ era and there are still several obstacles and limitations that hinder the application of quantum algorithms in the field of CSE. Current state-of-the-art quantum technologies solve at best a very limited set of problems and it’s unlikely that there will be available general-purpose quantum computers in the near future that can solve problems more quickly than classical computers do. In addition, even quantum algorithms that are known to be faster than their classical counterparts most often require a fair amount of preparation done on a classical computer, either to set up the problem and/or interpret the answer.
Based on these, it becomes evident that quantum computing utilization requires efficient synergy with classical computing. In this regard, variational quantum algorithms (VQAs) have emerged as the leading strategy to obtain a quantum advantage on NISQ devices. VQAs are hybrid quantum-classical algorithms that consist of a parameterized quantum circuit, that is an ansatz of gates containing tunable parameters, and an optimization part performed on a classical computer to find the optimal values of the parameters in the circuit. Most prominent examples in this category include the VQLS algorithm [10,11] for solving linear systems of equations, the Quantum Approximate Optimization algorithm (QAOA) [5] and the Quantum Analytic Descent algorithm (QAD) [12] for optimization problems, as well as the Variational Quantum Eigensolver (VQE) [13], tasked with finding the lowest eigenvalue of a given matrix.
This work proposes a methodology that fuses hybrid quantum algorithms and in particular the VQLS algorithm, with machine learning to accelerate the solution of parameterized linear systems. Such systems arise frequently in CSE applications in the context of uncertainty propagation, parameter inference, optimization, or sensitivity analysis, since these problems are governed by parameterized partial differential equations that are converted to linear systems using numerical discretization methods (typically, finite element or finite difference methods). A general approach to treat these types of problems is to evaluate the system response for multiple parameter instances and post-process the results to extract relevant information on quantities of interest. However, this can be a computationally intensive process, especially when the linear systems under consideration are of high dimensionality. In this regard, this work explores the use of the VQLS algorithm as the main tool to solve parametrized linear systems and investigates ways to accelerate its convergence for a given snapshot of parameters by employing machine learning algorithms to efficiently deliver accurate predictions on the optimal circuit parameters of the corresponding linear system. The main intuition behind this approach is that successful initial prediction on the circuit parameters will reduce the number of iterations of the classical optimizer employed by the VQLS algorithm.
The paper is structured as follows: In Section 2 the fundamental principles of quantum computing are presented. Section 3 provides the mathematical and algorithmic background for the VQLS algorithm. Section 4 presents a methodology that utilizes machine learning to accelerate the convergence of the VQLS algorithm when used for solving parameterized linear systems. Section 5 demonstrates the proposed methodology in a set of numerical applications and, lastly, Section 5 summarizes the conclusions drawn from this work and discusses future research directions.

2. Basic Principles of Quantum Computing

Initially, we shall introduce the basic principles of quantum computing and specifically the well-established Circuit /or Gate paradigm, on which VQLS is based. Most famous algorithms, s.a. Shor’s for prime factoring [1] or HHL for linear systems [3], follow this paradigm.

2.1. Quantum Computation

A quantum computation is composed of three steps: input state preparation, transformations acting on this state and, finally, measurement of the output state. Due to the stochastic nature of quantum objects, the only way to gain part of the information hidden in a quantum state is by sampling, i.e. repeating the quantum algorithm several times and extracting probabilistic measures.
The elementary memory unit of QC is the qubit, a 2-level quantum system that can be prepared, manipulated and measured in a predefined way. Unlike a classical bit, which can take the distinct value of either 0 or 1, a qubit can be a linear combination — or superposition— of two orthogonal quantum states |0〉 and |1〉. Thus, using Dirac notation, a single-qubit system can be described as
| ψ 〉 = a | 0 〉 + b | 1 〉 ,
where the coefficients a , b ∈ C are called amplitudes of the state adhering to the constraint | a | 2 + | b | 2 = 1 .
Since not much can be achieved with a single-qubit system, multi-qubit systems can be produced by taking advantage of the peculiar quantum-mechanical properties of superposition and entanglement. Hence, an n-qubit state, which resides in a 2 n -dimensional complex Hilbert space, can be written as
| ψ 〉 = ∑ i = | 0 〉 2 n − 1 a i | i 〉 ,
where a i ∈ C , i = 1 , ⋯ , n the amplitudes following the normalization constraint 〈 ψ | ψ 〉 = ∑ i | a i | 2 = 1 . The probability of measuring a particular outcome, p i , is given by the squared magnitude of the corresponding amplitude, | a i | 2 . As mentioned, in order to calculate that probability, one has to repeatedly take measurements of output state.
Quantum computers use quantum gates, which are elementary operations that manipulate the quantum state of a system, to perform calculations. some of the most notable single-qubit gates are the Pauli gates X , Y , Z and the Hadamard gate H. These gates are represented by unitary matrices, denoted as U and preserve the inner product between quantum states.
An example of a single-qubit circuit is illustrated in Figure 1. Starting from state |0〉, a Hadamard gate is applied to the qubit, followed by a Pauli-Y gate. The resulting state is | ψ 〉 = Y H | 0 〉 = − i / 2 ( | 0 〉 − | 1 〉 ) . The measurement that determines whether the resulting state is k e t 0 occurs last. A measurement is a non-unitary operation which results with the qubit in either state |0〉 or |1〉. Due to the Hadamard gate, the probability of measuring the state |0〉 is p ( | 0 〉 ) = − i / 2 2 = 0.5 .
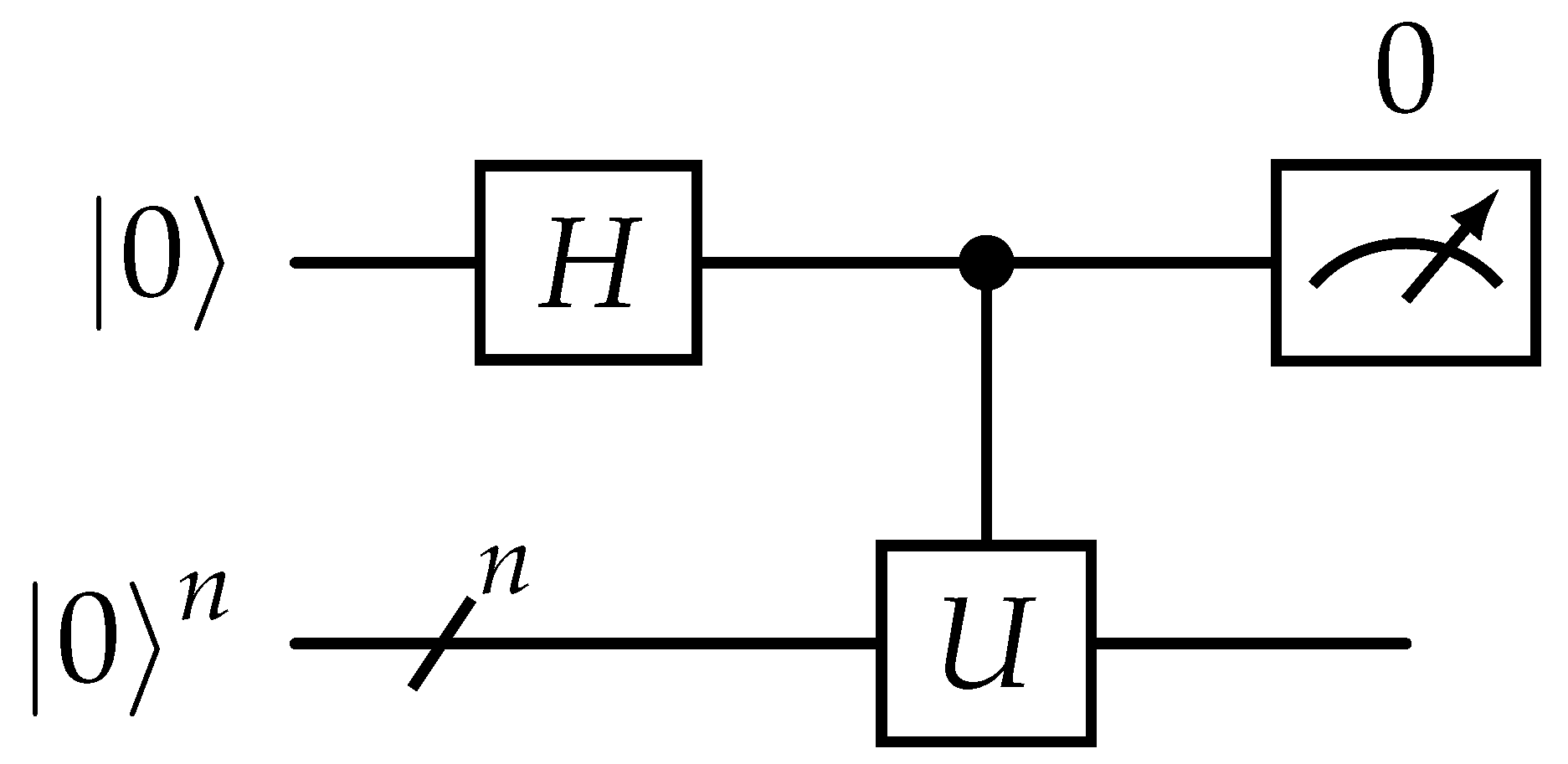
In general, multi-qubit state manipulation is achieved by use of unitary operators which evolve an initial state to a target state.
| ψ t 〉 = U | ψ 0 〉 ,
where U ∈ C 4 n . Quantum computers also utilize entanglement, a phenomenon where two or more qubits become physically correlated. In circuit computing, entanglement is introduced via controlled operations. Every unitary operator U ∈ C 4 n has a controlled form
C U = | 0 〉 〈 0 | ⊗ I + | 1 〉 〈 1 | ⊗ U ∈ C 4 n + 1 ,
which applies U conditionally on a target-qubit register, if a control-qubit has a |1〉 component. An example of a multi-qubit, controlled gate is illustrated in Figure 2, where the first qubit acts as control-qubit and the rest n qubits as targets.

2.2. Quantum Linear System Problem

When given a Linear System Problem (LSP) of N linear equations and N unknowns which can be expressed as A x = b , where x is the vector of unknowns, A the matrix of coefficients and b is the right-hand side vector, one can construct the Quantum Linear System Problem (QLSP) [14,15]
A | x 〉 = | b 〉 ,
where | b 〉 = b / ∥ b ∥ 2 is the normalized right-hand side and A the normalized matrix satisfying ∥ A ∥ ≤ 1 .
Although QLSP is practically a normalized version of the LSP, they are two distinct problems with latter being addressed mostly by quantum algorithms. The main difference is the requirement that both the input and output of a QLSP are given as quantum states. This means that any efficient algorithm for QLSP requires an efficient preparation of |b〉 and efficient readout of |x〉, both of which are open problems for the general case.
In the quantum linear systems algorithm literature, the term "efficient" usually refers to polylogarithmic complexity w.r.t the system size N. This means that Quantum algorithms like [16] solve the QLSP exponentially faster than even the fastest classical algorithms like Conjugate Gradient method. Solving and reading in quantum computing, though, are two completely distinct processes and as such, we must note though that in order to read out all the elements of |x〉, we would still require O ( N ) time, just as any efficient classical algorithm. Hence, a solution to QLSP should be used as a subroutine in an application where samples from vector x are useful, as discussed thoroughly in [17].

3. The VQLS algorithm

The Variational Quantum Linear Solver (VQLS) [10] is a Variational Hybrid Quantum-Classical (VHQC) algorithm used for solving QLSPs and designed with NISQ devices in mind. Given the QLSP A | x 〉 = | b 〉 , the quantum part of the algorithm uses a cost function which captures the similarity between vectors A | x 〉 and |b〉, by means of either a local or global Hamiltonian. Classical optimization schemes can be then utilized in order to minimize the Hamiltonian loss and finally terminate when a desired precision ϵ is reached.
Although variational algorithms are heuristic and complexity analysis of VQLS is a challenging open problem, the authors of [10] provided numerical simulations indicating efficient scaling in the linear system’s dimension N, condition number κ and desired absolute error ϵ w.r.t the exact solution. Specifically, they found evidence of (at worst) linear scaling in κ , logarithmic scaling in 1 / ϵ and polylogarithmic scaling in N [10].

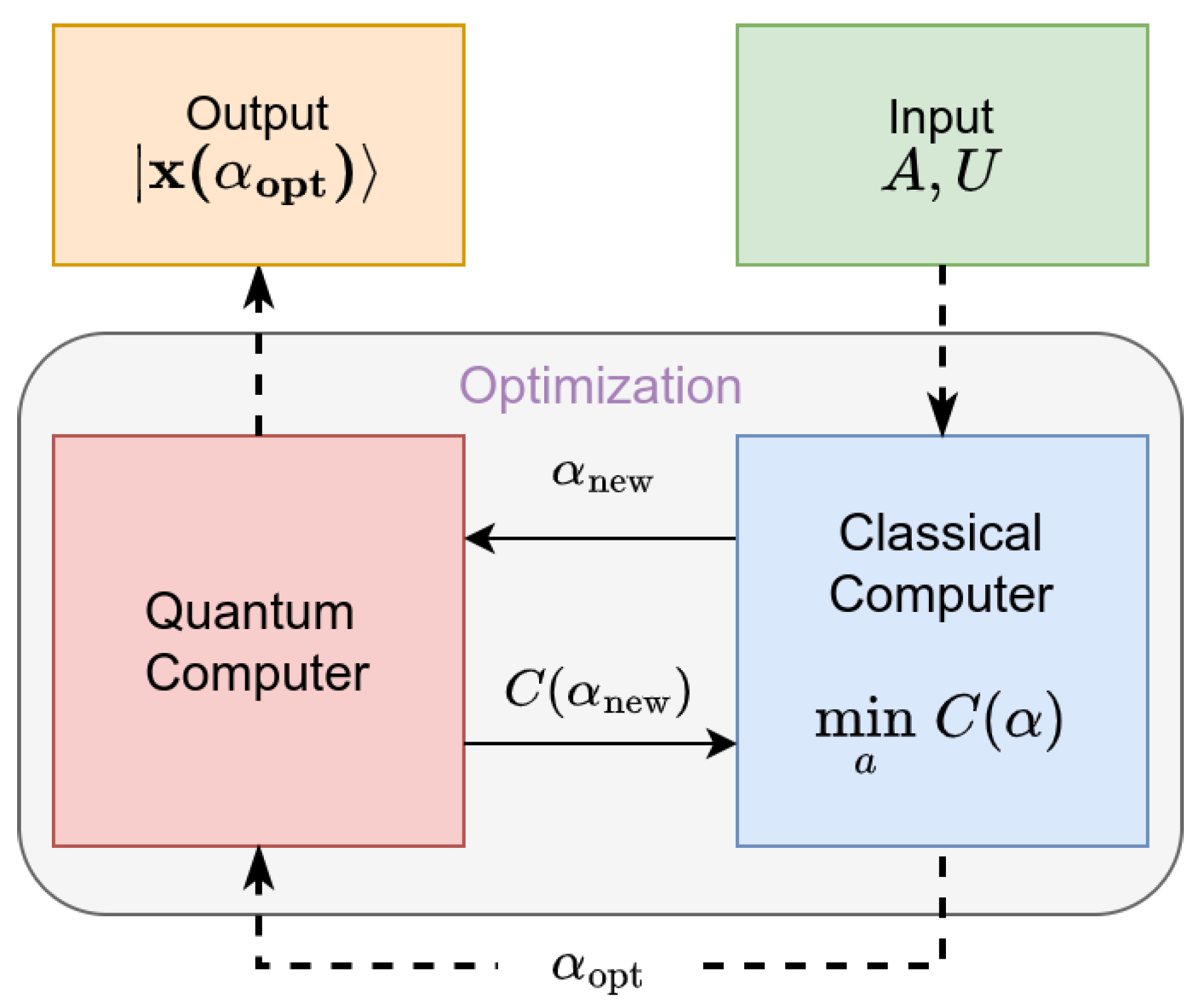
3.1. Overview

The algorithm requires the following as input: an efficient operator initializing a quantum state | b 〉 = U | 0 〉 , a vector of initial parameters α and a linear decomposition of the normalized matrix A = ∑ l = 1 L c l A l , with A l being unitary matrices and c l ∈ C . Intuitively, this linear decomposition into unitaries is essential to construct the required circuits since all quantum gates are unitary operators themselves. VQLS requires the following assumptions be made: L scales as O ( poly ( n ) ) , A has a finite condition number κ < ∞ , its spectral norm satisfies ∥ A ∥ ≤ 1 . The A l unitaries must additionally be implemented with efficient circuits, which in quantum computing terms, this usually implies a worst case polynomial dependence on n. Information over efficient decomposition method for sparse A can be found at [10]. The output is the quantum state |x〉 that approximately satisfies the system A x = b up to a constant factor. Parameters α in the ansatz V ( α ) are adjusted in a hybrid, quantum and classical optimization scheme until the cost C ( α ) (local or global) reaches a predefined threshold. Lastly, the optimized ansatz is applied to construct the solution state which may be measured in order to compute observable quantities of interest. 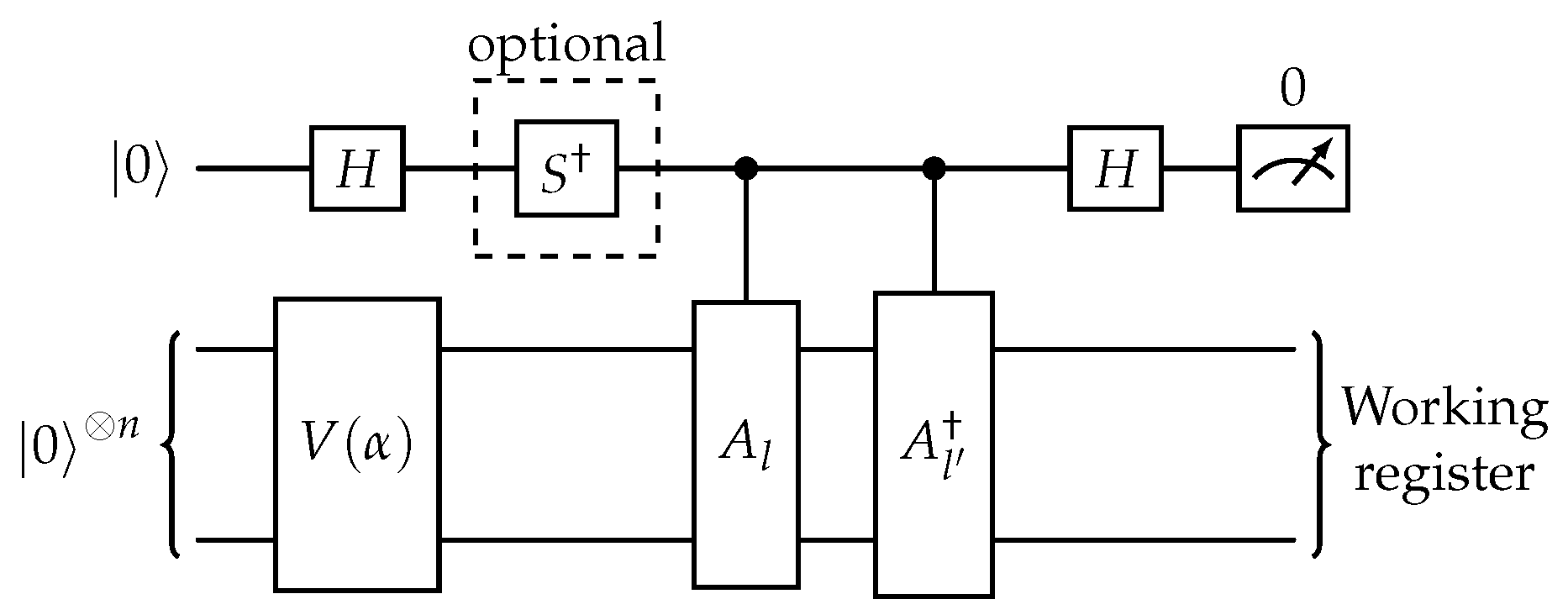An overview of the algorithm can be seen in Figure 3.
As mentioned, in order to solve the QLSP one must prepare a state |x〉 s.t. A | x 〉 is as close as possible to |b〉. In order to achieve that, VQLS employs an ansatz V ( α ) that prepares a candidate solution | x ( α ) 〉 = V ( α ) | 0 〉 . A parameter vector α is given as input to the quantum computer, which prepares | x ( α ) 〉 and runs an efficient quantum circuit that estimates a cost function C ( α ) . The cost function’s value quantifies how far the proposed state A | x 〉 deviates from the desired state |b〉. This value C ( α ) is then returned to the classical computer which adjusts parameters α according to a classical optimization algorithm, attempting to reduce the cost. The process is repeated until a termination condition of the form C ( α ) ≤ γ is achieved, at which point VQLS outputs the solution parameters α opt .
Finally, the optimal parameters α opt are given as input to the ansatz which computes the solution state | x ( α opt ) 〉 = V ( α opt ) | 0 〉 . Once the solution state is achieved we can finally measure quantities of interest in order to extract valuable information for the solution vector. The deviation of observable expectation values from those of the exact solution can be upper bounded based on the cost function.

3.1.1. VQLS Cost functions

According to [10], the cost functions can be described as expectation values of either global or local Hamiltonians. To avoid cumbersome notation, we will thereafter write | ψ 〉 = A | x 〉 = A | x ( α ) 〉 . As it is noted in [18], global functions may introduce barren plateaus in the energy field, which lead to exponentially vanishing gradients with respect to the number of qubits n. For improved trainability as n grows larger, the authors introduce local Hamiltonian, the normalized version of which is
C L = 〈 ψ | H L | ψ 〉 〈 ψ | ψ 〉 = 〈 Ψ ( α ) | H L | Ψ ( α ) 〉 ,
where | Ψ 〉 = | ψ 〉 ∥ | ψ 〉 ∥ is normalized. The effective Hamiltonian is
H L = U I − 1 n ∑ j = 1 n | 0 j 〉 〈 0 j | ⊗ I j ¯ U † ,
and | 0 j 〉 is the zero state on qubit j and I j ¯ the identity on all qubits but qubit j.

3.2. Cost evaluation

In order to estimate the cost C L one must evaluate each part of the fraction in Equation 6 separately, with the first and simpler term to evaluate being
〈 ψ | ψ 〉 = ∑ l l ′ L c l c l ′ * β l l ′
where
β l l ′ = 〈 0 | V † A l ′ † A l V | 0 〉 .
Also, for C L one needs to estimate the terms
δ l l ′ j = 〈 0 | V † A l ′ † U ( | 0 j 〉 〈 0 j | ⊗ I j ¯ ) U † A l V | 0 〉 ,
where index j implies application of corresponding operator to the j-th qubit, while j ¯ refers to every other qubit but j. By exploiting the fact that | 0 j 〉 〈 0 j | = 1 2 ( Z j + I j ) , 10 can be written as
δ l l ′ j = 1 2 〈 0 | V † A l ′ † U ( I j + Z j ) ⊗ I j ¯ U † A l V | 0 〉 = 1 2 ( β l l ′ + ζ l l ′ j ) ,
where
ζ l l ′ j = 〈 0 | V † A l ′ † U Z j ⊗ I j ¯ U † A l V | 0 〉
Taking the previous into account, the cost function finally becomes
C L = 1 2 − 1 2 n ∑ j n ∑ l l ′ L c l c l ′ * ζ l l ′ j ∑ l l ′ L c l c l ′ * β l l ′ ,
where each of the terms β l l ′ , ζ l l ′ i are computed by postprocessing the output of the circuits shown in Figure 4 and Figure 5 respectively.
The circuit in Figure 4 applies operator V on |0〉 and then, conditioned on the first qubit, applies two controlled operations, C A l followed by C A l ′ † . Finally, a measurement takes place in the ancilla circuit. The S † gate is added to the circuit when the imaginary part of the expectation value is needed. In a similar manner, the circuit of Figure 10 additionally applies the U † , C Z j and U operators. The case shown corresponds to j = 1 , when controlled-Z gate is applied to first qubit of working register. As before the S † gate is added to the circuit when the imaginary part of the expectation value is needed.

3.3. Ansatz

VQLS works by preparing the state | x 〉 = V ( α ) | 0 〉 . The unitary operator V ( α ) consists of a sequence of gates with trainable continuous parameters α = ( α 1 , ⋯ , α L ) and can more or less be expressed as
V ( α ) = G k L ( α L ) ⋯ G k i ( α i ) ⋯ G k 1 ( α 1 ) .
The discrete parameters k = ( k L , ⋯ , k 1 ) encode the types of gates and their placement in the circuit. Such empirical gate constructs are called ansatzes and are common in variational quantum algorithms in general.
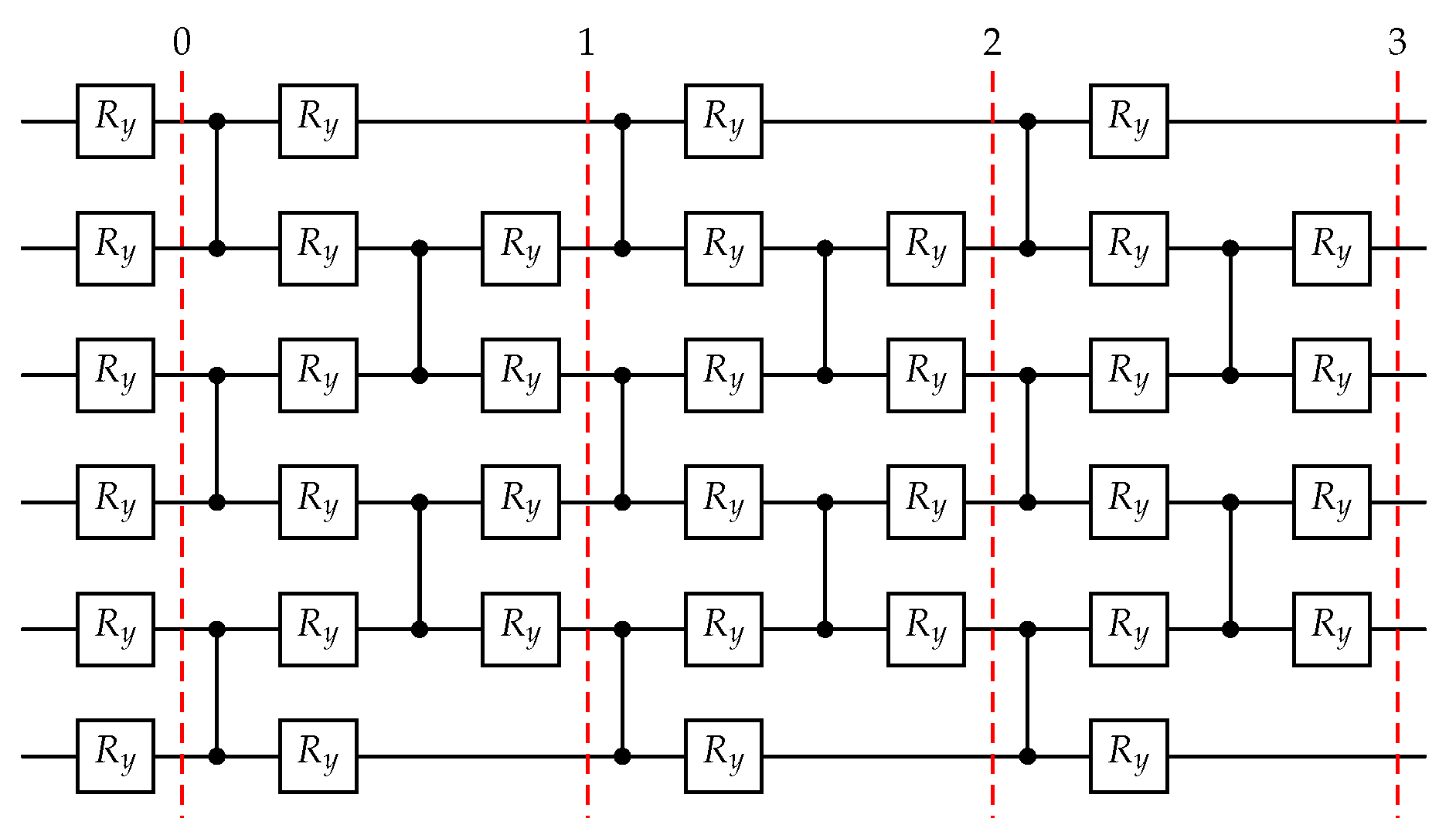
If k is constant, we are referring to "fixed-structure" ansatz, since one optimizes only over α . An example of fixed ansatz can be seen Figure 6. Although less versatile, fixed ansatzes are simpler than "variable-structure" ones, where one optimizes with respect to k as well. Lastly, another type that can be employed is the Quantum Alternating Operator Ansatz (QAOA) [19,20], which is known to be universal as the number of its layers tend to infinity [21,22].

4. AI-VQLS-solver: coupling Quantum Computing with machine learning to accelerate the solution of parameterized linear systems

In a multitude of applications, such as uncertainty propagation, parameter inference, optimization, sensitivity analysis etc. it is required to produce sufficient number of samples or solution datasets. These, in turn, require the solution of parametric linear systems, and besides the often unavoidable, immense matrix sizes, one has to deal with an overwhelming number of LSP instances which often exceed available computational resources. While quantum algorithms, and specifically VQLS, are expected to deal with the former challenge by exponentially reducing the computational complexity of individual LSPs, there still remains space for further acceleration of the overall parametric problem.
In this regard, it is essential to derive efficient methods that exploit the continuity of the LSP solution space with the respect to the parameters that produce the linear system, hereafter called physical parameters p ∈ R d . Starting from the linear system with equation A ( p ) · x = b , with A ( p ) being the parametrized system matrix, x the solution sought and b the right-hand side vector. The equivalent QLSP is the system with equation A ( p ) | x 〉 = | b 〉 . Finally, when a variational quantum algorithm such as VQLS is used as solver, the system takes the form
A ( p ) | x ( α ) 〉 = | b 〉 ,
where α = ( α 1 , ⋯ , α r ) ∈ R r the VQLS real parameter-vector and | x ( α ) 〉 the proposed solution of the QLSP. Using the cost function from Equation 6 the optimal parameters are obtained by the following minimization problem
α opt = arg min α C ( p , α ) = arg min α 〈 Ψ ( p , α ) H L | Ψ ( p , α ) 〉 ,
It is evident from Equation 16 that for every matrix A ( p ) , a search over parametric space R r is required in order to reach the solution | x ( α opt ) 〉 which minimizes the Hamiltonian cost C L .
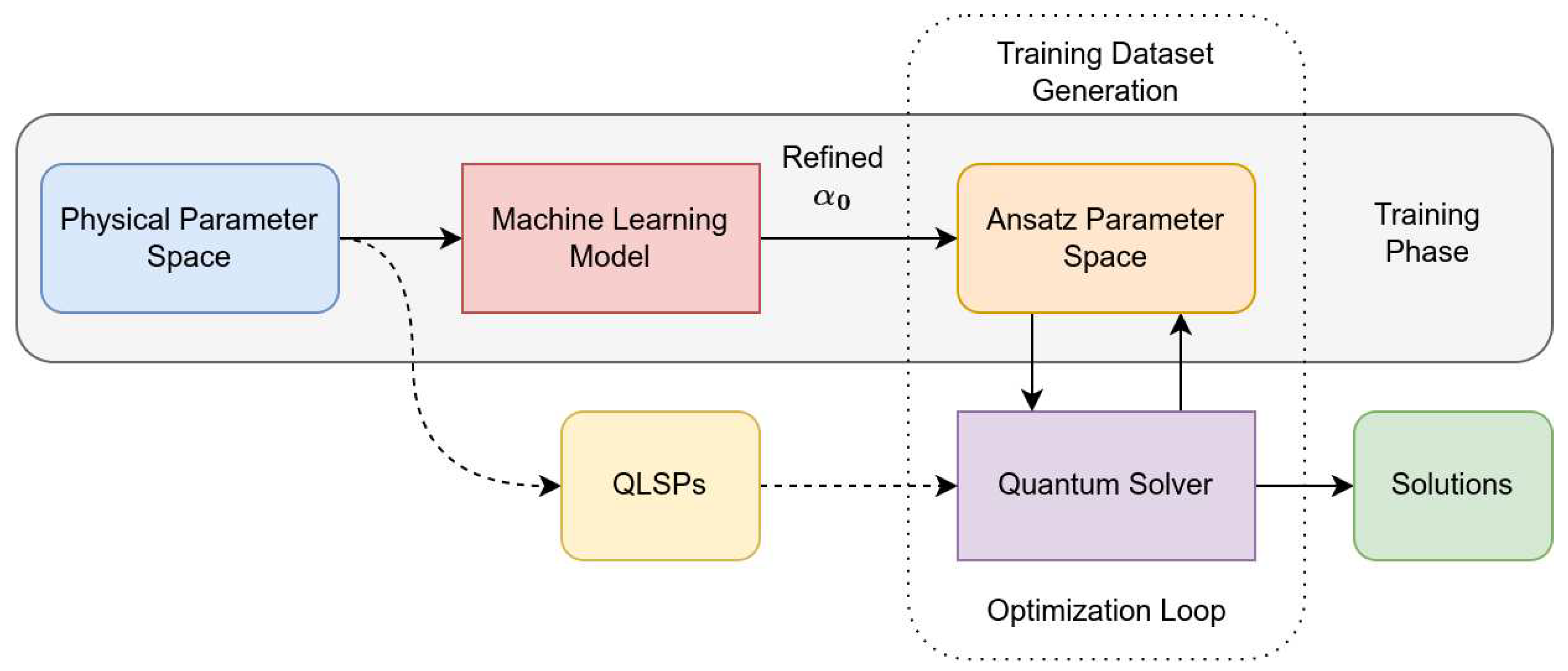
Our proposed scheme uses a machine-learning model M : R d → R r in order to propose refined initial guesses to the VQLS algorithm. Instead of letting the initial VQLS parameters be random or constant, we take advantage of the assumed continuity of the cost function C ( p , α ) , so that for every physical parameter p, a refined initial guess α 0 is proposed that is as close as possible to the optimal ones α 0 − α opt ≤ ϵ with some probability P M depending on the chosen model. The acceptable error ϵ between the proposed and optimal parameters is a hyperparameter for the overall scheme and depends on the value of the training loss.
Since, in general, no training dataset will be available, one has to initially rely on the usual workflow without refined initial parameter proposition i.e. α 0 i = S ( p i ) for i = 1 , ⋯ , N train using some generic strategy S . Once the first optimal solutions are produced, the model can be trained on the respective dataset ( p i , α opt i ) , i = 1 , ⋯ , N train . The trained model thereafter proposes refined initial parameters α 0 i = M ( p i ) for i = N train + 1 , ⋯ , N total . Again, N train is considered a hyperparameter which must be chosen to balance the trade-off between accuracy and training-time.
The overall scheme is presented in Figure 7. Initially, as noted, the scheme follows the dashed arrows generating the training data by solving the first N train QLSPs with the base-VQLS. Once the training dataset has been generated, the machine-learning model is trained with x i as input and α i as output. The computational scheme thereafter changes as indicated by the solid arrows, with the model now proposing refined initial VQLS parameters α i , which are closer to the optimal, thus reducing the optimization cost for a QLSP instance.
In the model architecture context, in order to minimize training time without adding to the overall execution time, it is desirable to choose a ML model M with low complexity and efficient scaling with respect to its output. In our scheme, the only hyperparameter that can be controlled in this regard is the complexity of the ansatz V and more specifically the dimension r of the ansatz parameter vector α . An ansatz that scales polynomially with the number of qubits is desirable because it enables one to construct models that remain efficient as the size of the system increases. Specifically, in our case r should scale at most as O ( poly ( n ) ) , where n the number of qubits required for the system, so that low-complexity, efficient ML models are sustainable. Some known ansatzes with polynomial qubit scaling include the Quantum Approximate Optimization Algorithm (QAOA) ansatz [5] and the Hardware-Efficient ansatz [23].

5. Numerical examples

To evaluate the performance of the proposed scheme we conducted the comparative experiments described in the subsequent section. The quantum circuit simulations were driven by the Qiskit open-source framework and specifically the statevector simulator [24]. The matrix generator for the parametric 2 n × 2 n QLSP is chosen to be
A ( p ) = 1 ξ I + 1 C ∑ j , k = 1 n c i j ( p ) ( X j ⊗ Z k ) ,
where n is the number of effective qubits used in the circuit, c i j ( p ) are coefficients that depend on the physical parameters p, while C , ξ are normalization constants. In both examples, the physical parameters p = ( p 0 , p 1 , p 2 ) T are uniformly distributed in a 3-dimensional unit cube D : [ 0 , 1 ] × [ 1 , 2 ] × [ 3 , 4 ] . At each example we compare pure VQLS schemes with ones that fall under our paradigm. Since the circuits are simulated, the comparison is conducted in relation to the required number of iterations to solve each instance of the parametric system. The parametric QLSP is discretized into a total of N total regular QLSPs, with equations
A ( p i ) | x ( α i ) 〉 = b ,
and i = 1 , ⋯ , N total . For all examples the right-hand side is set to | b 〉 = | 0 〉 ∈ C 2 n and the total number of solutions N total = 1000 .

5.1. Convergence and continuity

A main problem when using variational algorithms is that the Hamiltonian loss-functions and especially their local versions are inherently non-convex which increases the probability for different optimization paths with neighboring initial parameters to land astray at completely different local-minima. Furthermore, quantum ansatzes are inherently periodic, since most parametric quantum gates themselves are not bijective with respect to their parameters. In fact, quantum gates are essentially rotations with period of at most 4 π and the parameters themselves are rather angles of rotation in some complex Hilbert space. Thus, when an ansatz is deployed, in general there is often a multitude of parameter values that can produce the same state. Besides periodicity, an ansatz contains many different paths through which the quantum states are prepared, resulting in different quantum states that may possess the same properties and more specifically the same probability distribution when measured under a specific basis. Lastly, when dealing with real quantum processors, the unavoidable hardware noise will most definitely propagate through the optimization path resulting again in discontinuous optimal values.
Another source of discontinuities which may arise in low-qubit systems is over-parametrization of the quantum ansatz. The required number of parameters to fully span an n-qubit system’s Hilbert space is N span = O ( 2 n ) , whereas the number of parameters of an efficient ansatz usually scales as N ans = O ( poly ( n ) ) . Hence, as n → ∞ more often than not the optimization problem will be under-parametrized, since N ans ≪ N span . 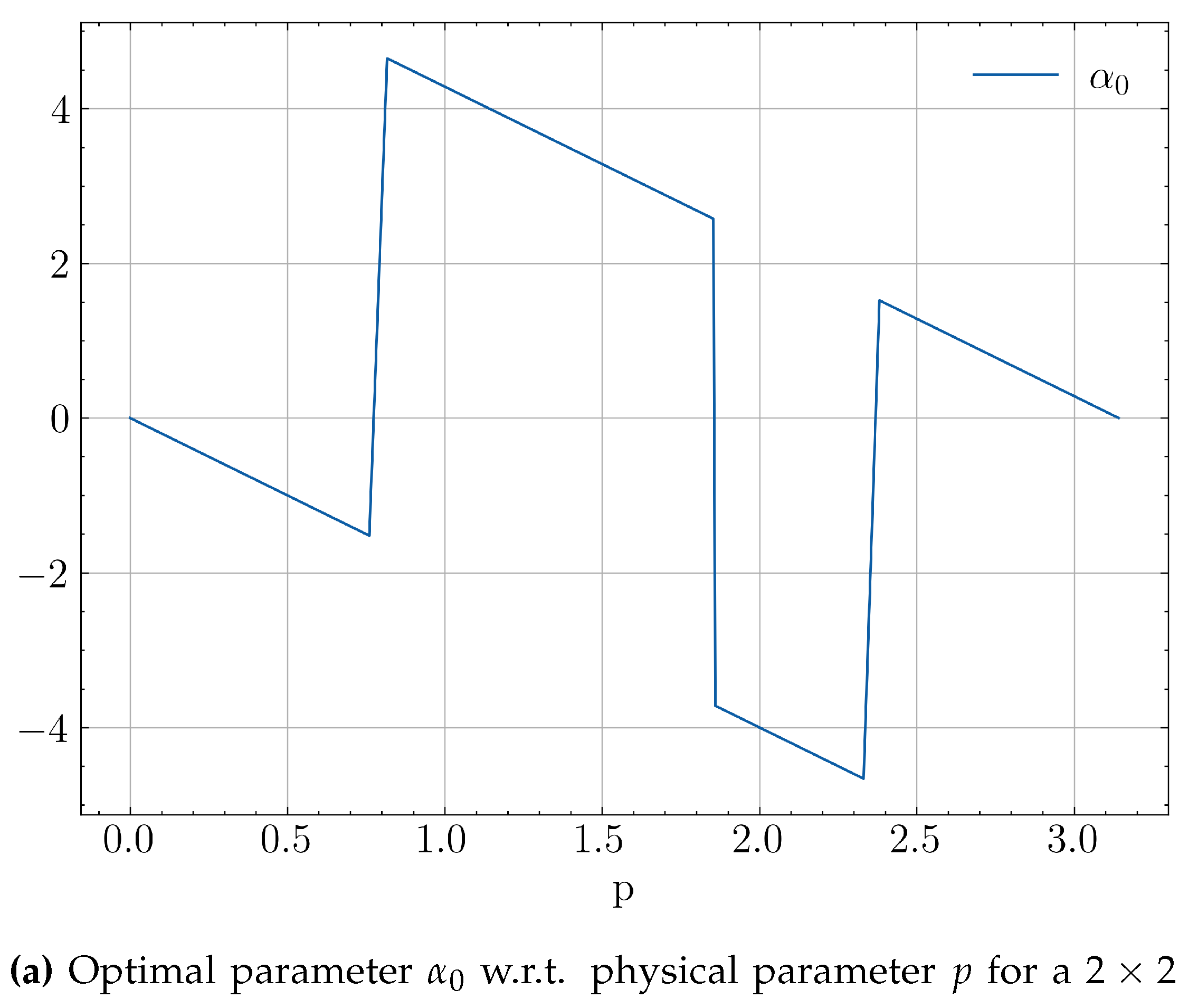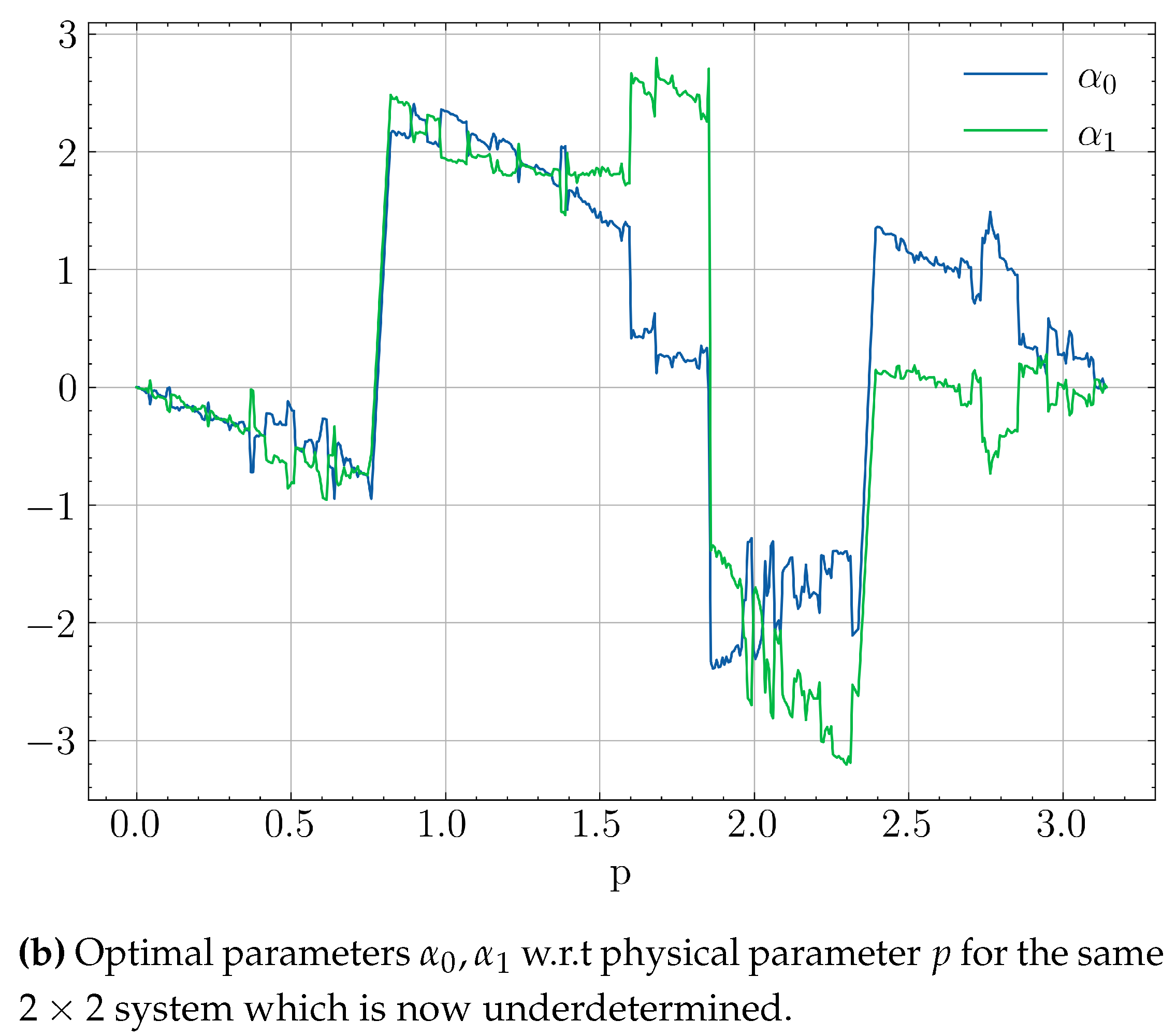In smaller systems, though, where the previous inequality is not guaranteed, one might eventually use more parameters than required. This will lead to an underdetermined system with infinite solutions w.r.t a portion of its parameters, giving optimizers more paths to explore, but also more ways to diverge from previous strategies. A the simple illustrative example of this behaviour can be seen in Figure 9. The discontinuities in Figure 9a are due to the periodicity of the non-convex Hamiltonian loss which allow jumps between different local minima. In Figure 9b which has more than required ansatz parameters, the system becomes underdetermined resulting in more discontinuities.
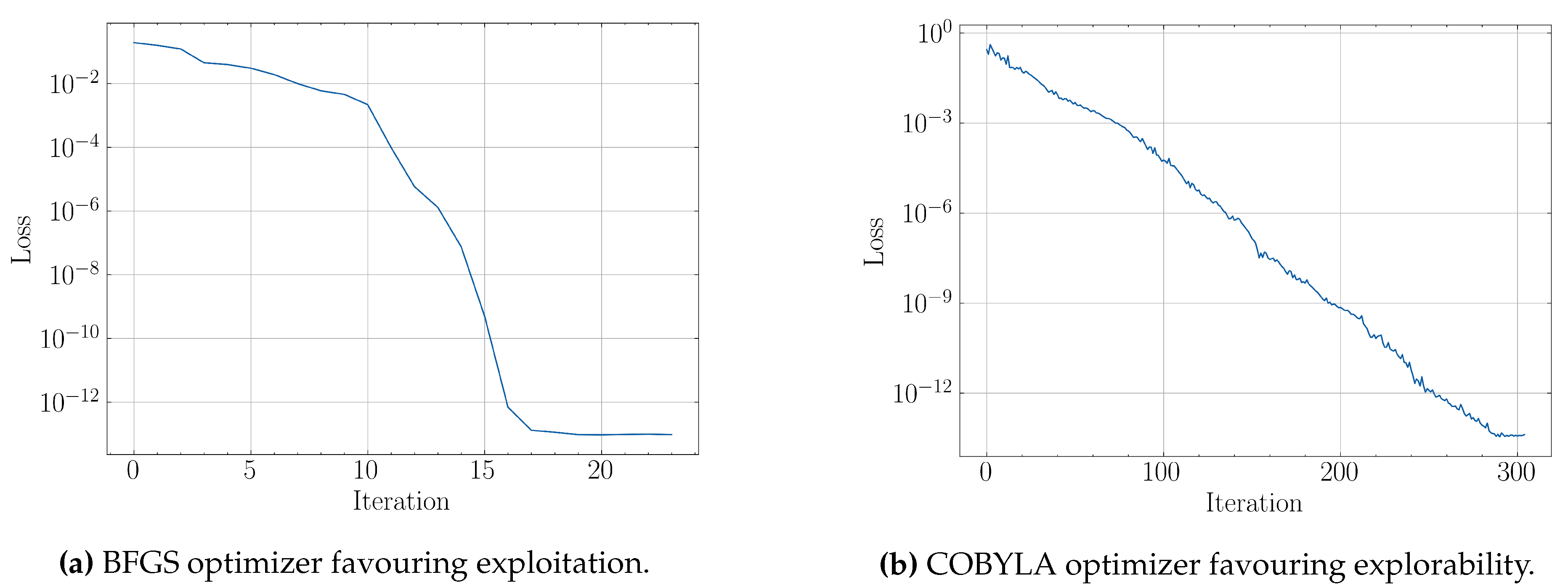
From the above, it is apparent that in order to ensure precision and suffice to simple, scalable model architectures, it is imperative to take into account any potential hindrances posed by aforementioned discontinuities, which can obstruct training and prediction to a substantial extent. Coherently, various classical optimizations schemes used in VQLS may introduce different convergence behaviours with respect to the utilized algorithm. When dealing with convergence alone, the only optimization property that matters is the execution time, where the fastest algorithm to reach a minimum loss, can be considered best for the given problem. In our case though, continuity is of equal importance, since we seek to not only reach a solution, but to force systems with close physical parameters p i , p j ∈ R d to produce output in the ansatz parameter space α opt i , α opt j ∈ R r in the same neighbourhood. An optimization algorithm that favours explorability instead of exploitation has a higher chance to visit different local minima during the optimization of concurrent, similar QLSPs and thus resulting in optimal parameter discontinuities with higher probability. In the subsequent experiments, we were confined to gradient-free optimizers in order to evaluate their sufficiency with respect to the potential discontinuities.

5.2. Example 1: two-qubit system

The first example consists of the QLSP in Equation 17 for n = 2 , which results in a parametric system of size 4 × 4 , with the coefficients c i j chosen as trigonometric functions of the physical parameters p 1 , p 2 , p 3 e.g. c 00 = cos ( p 1 + p 2 ) . For the solution of the QLSPs a BFGS optimizer was used with numerical first and second order derivatives approximation. 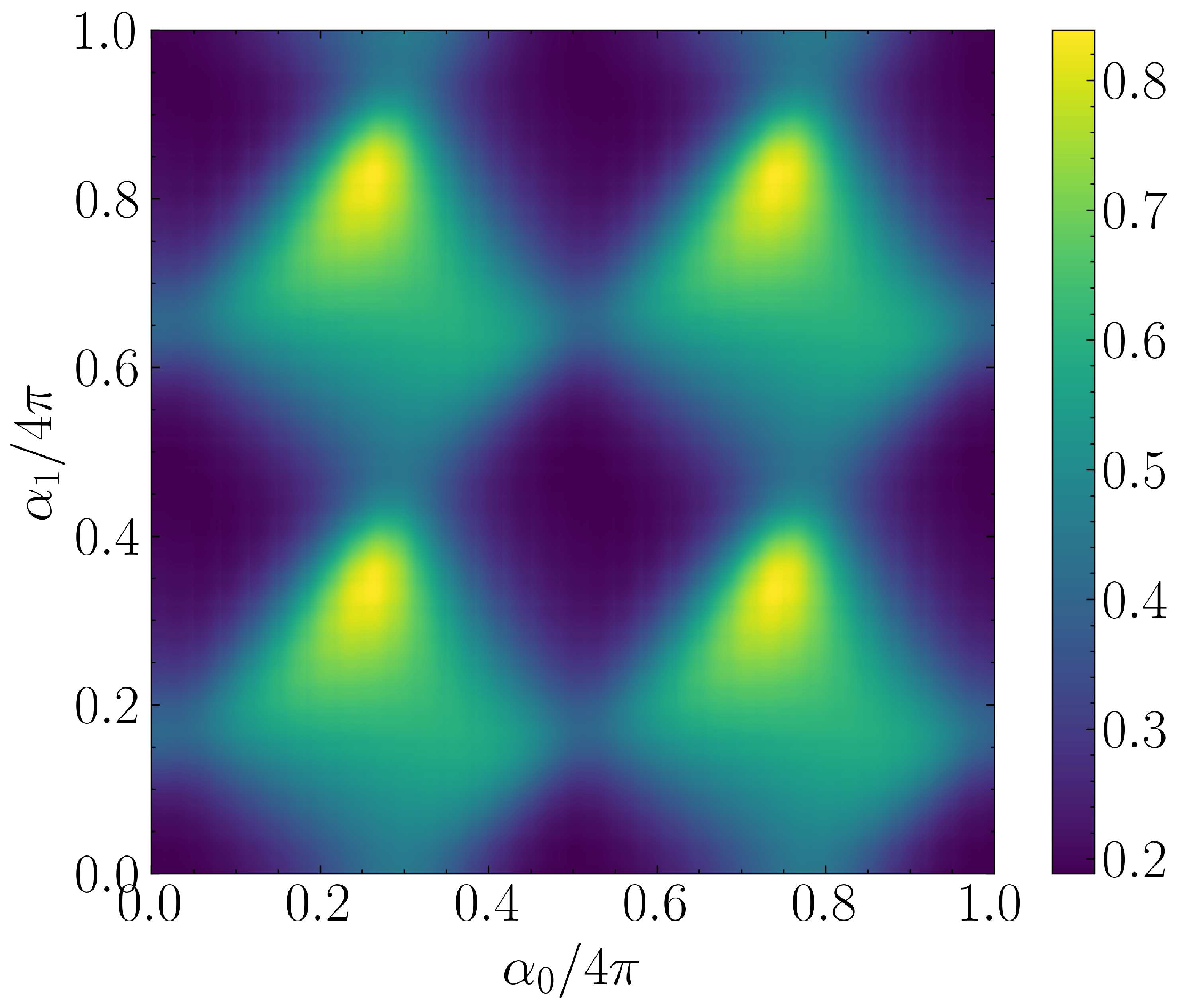The ansatz used in the example is shown in Figure 10
The Hamiltonian cost function for a given QLSP instance can be seen in Figure 11. We observe an intensive non-convex behariour and periodicity resulting in different local minima which may have hindered optimization algorithm to consistently extract continuous optimal solutions α opt i across all QLSP instances.
In this example, three strategies were implemented: in the first two the basic VQLS scheme was used with constant, α 0 i = 0 , and uniformly random, α 0 i ∼ U [ 0 , 1 ] , proposed initial parameters respectively, while the third strategy consists of a naive nearby scheme, where the proposed initial parameters for each linear system were the optimal parameters of the previous one α 0 i = α opt i − 1 . The nearby strategy requires an initial reordering of the QLSPs w.r.t the dimensions of the physical parameters. The latter strategy takes advantage of the continuity of the QLSP and requires that p i are mostly sorted at each dimension in order to avoid large gaps between the sought optimal ansatz parameters. This scheme is quite efficient in the sense that it does not require any training, N train = 1 , prior to its application and can be compared in a direct manner with the base VQLS.
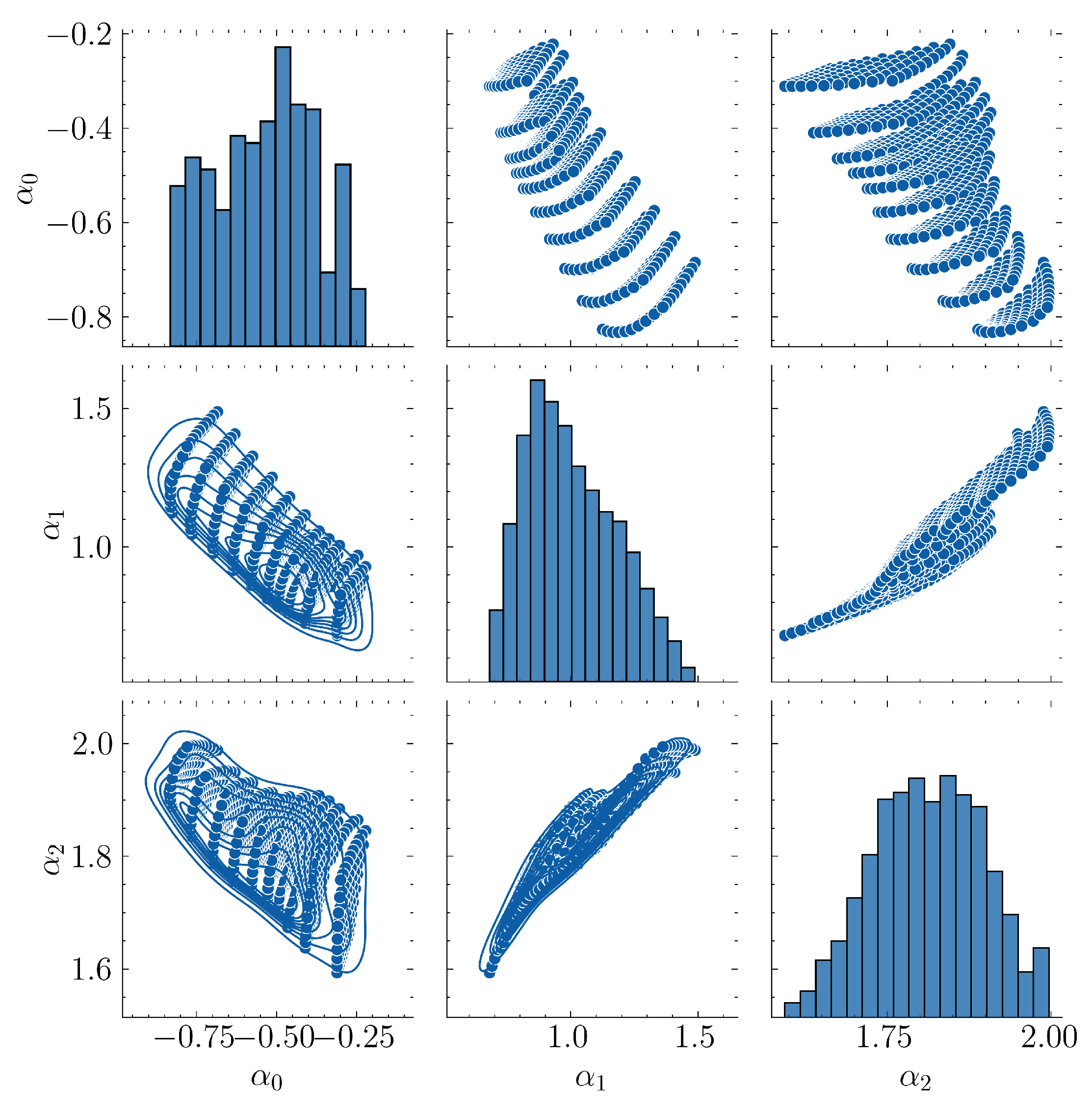
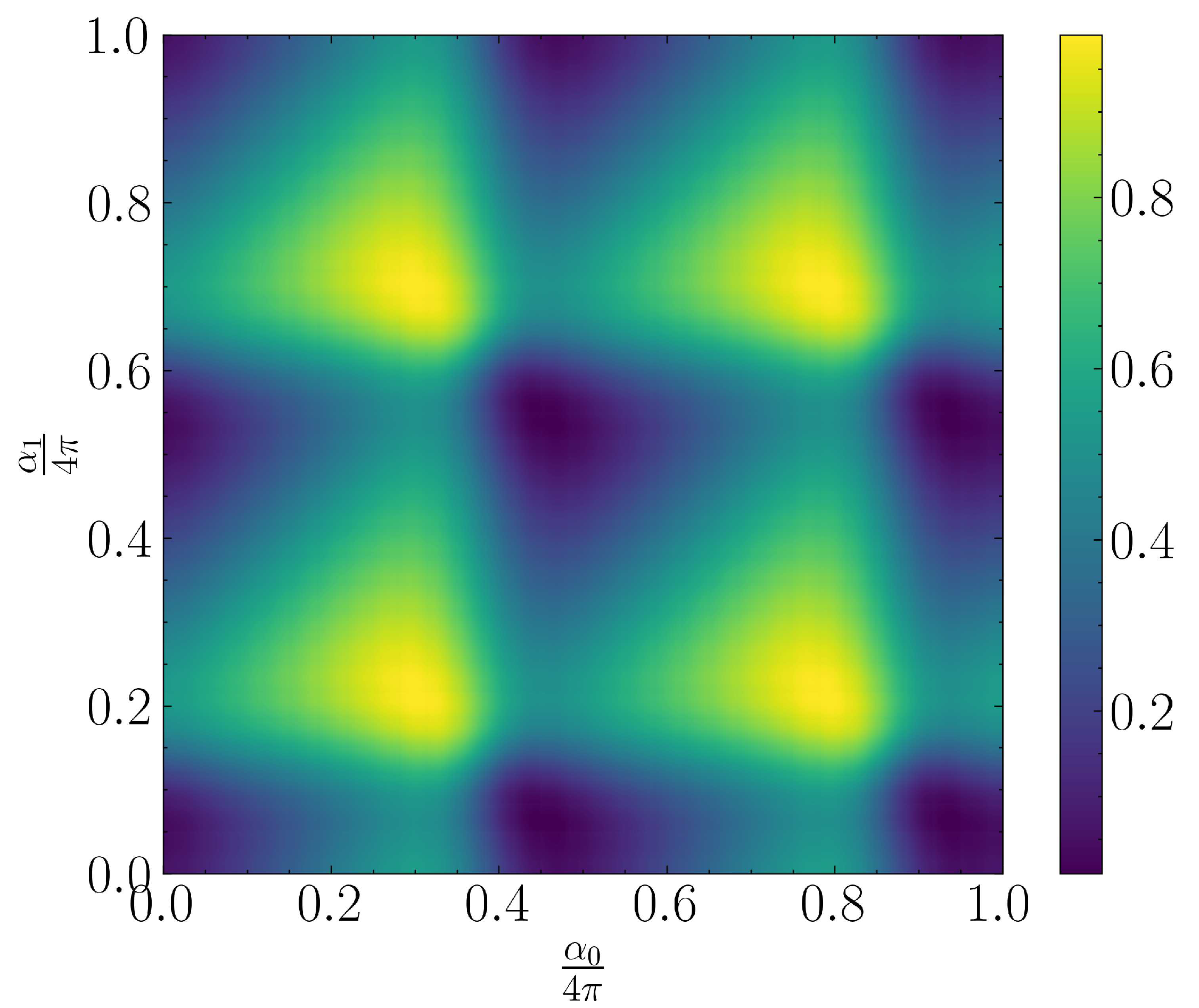
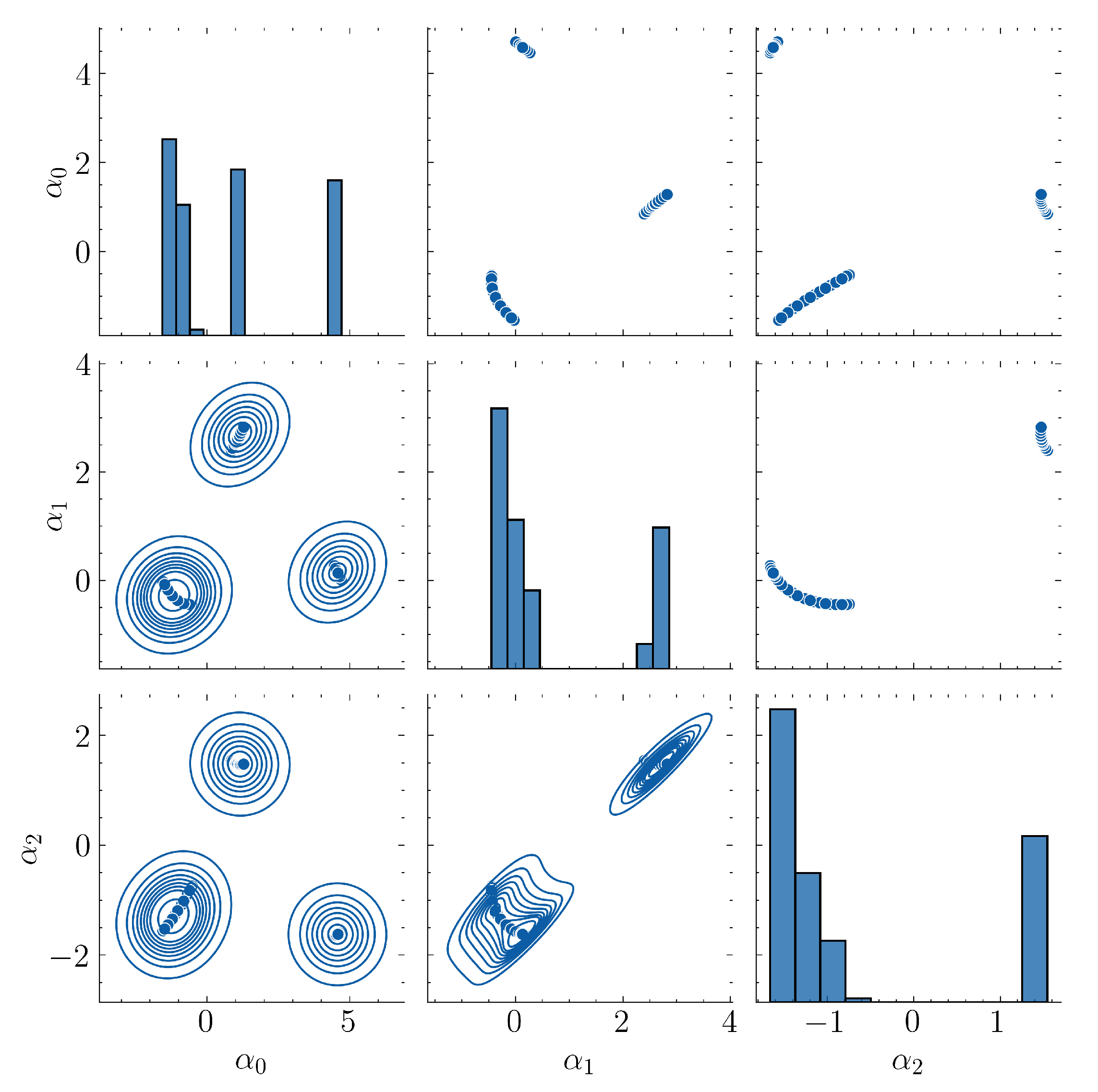
In Figure 12 one can see the joint probability distributions of the optimal parameters α opt , k i for k = 0 , 1 , 2 , i = 1 , ⋯ , 1000 for the 2 2 × 2 2 example of this section. In this example the dataset had no discontinuities which led to a trainable ML model.
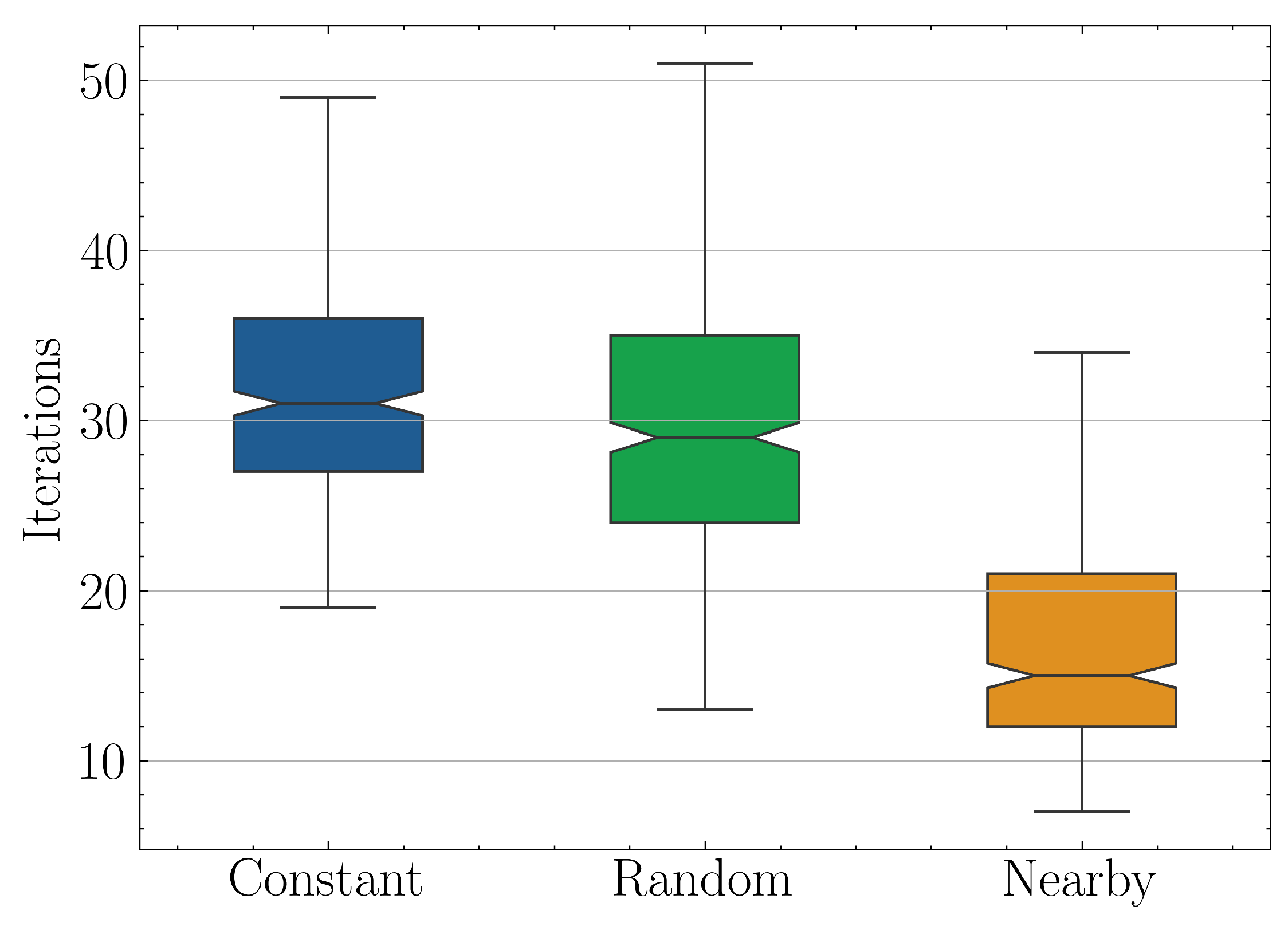
The comparative results of the three strategies can be summarized in Figure 13, where the required iterations distribution for solving one instance of the parametric QLSP A ( p i ) | x ( α i ) 〉 = | b 〉 are shown. On the left is the pure-VQLS scheme with constant initial ansatz parameters, in the middle a similiar approach but with random initialization and on the right the naive nearby approach, where the proposed ansatz parameters for each system is taken as the optimal of the previous. The speedup factor of the latter over first two schemes based on their median values is S ≈ 1.9 .

5.3. Example 2: three-qubit system

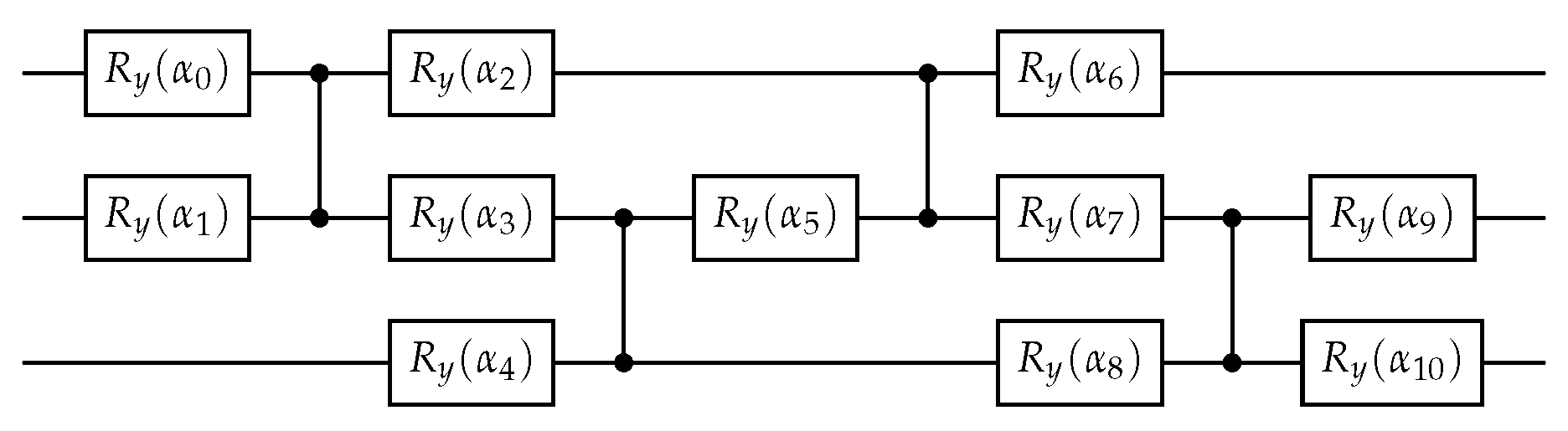
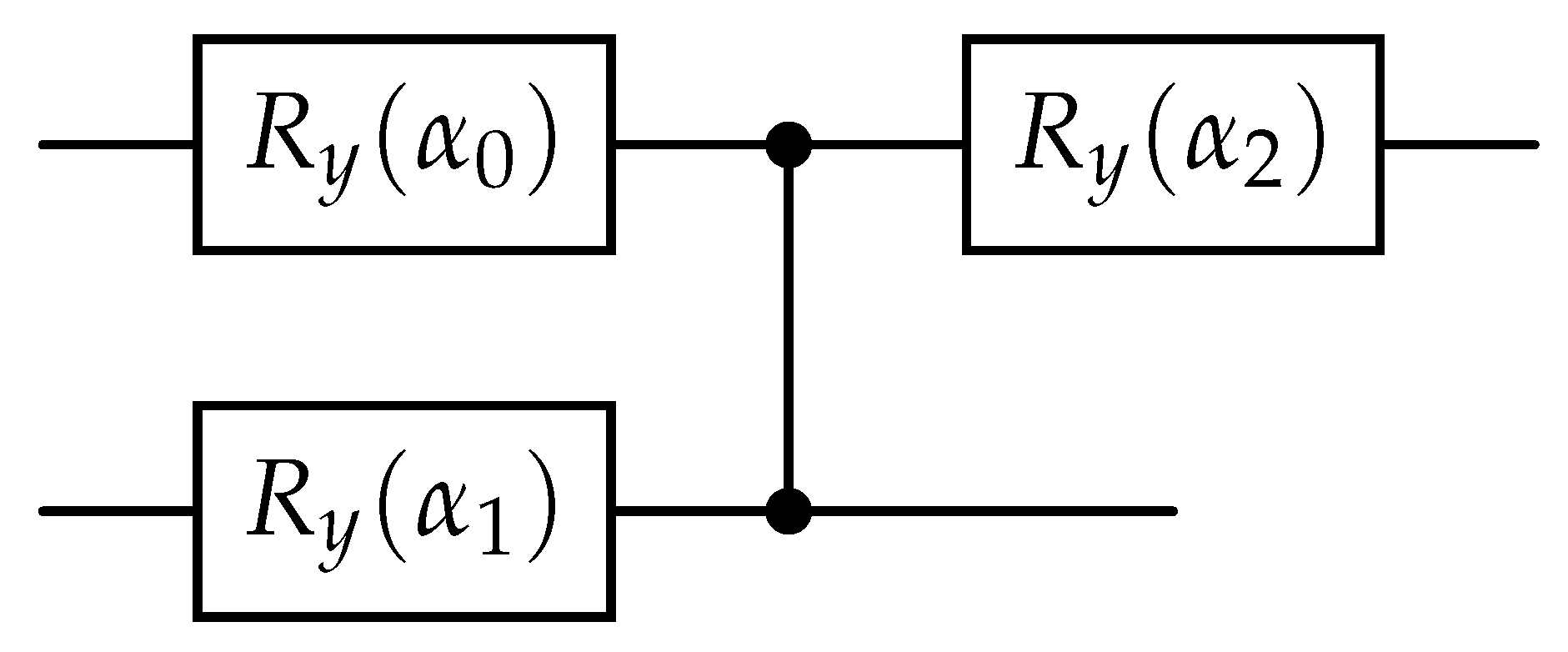
For the second example, a three-qubit system was chosen, which results in a parametric system of size 8 × 8 , with the coefficients c i j being polynomial functions of the physical parameters p i e.g c 00 = p 1 2 + p 0 2 . For the solution of the QLSPs a BFGS optimizer was used with numerical first and second order derivatives approximation. The 2-layered ansatz used for this example takes as input a vector α ∈ R 11 . Each angle a k , k = 0 , ⋯ , 10 is used as a parameter for the R y gates which are structured as shown in Figure 14. For the solution of the systems a BFGS optimizer was used with numerical first and second order derivatives approximation.
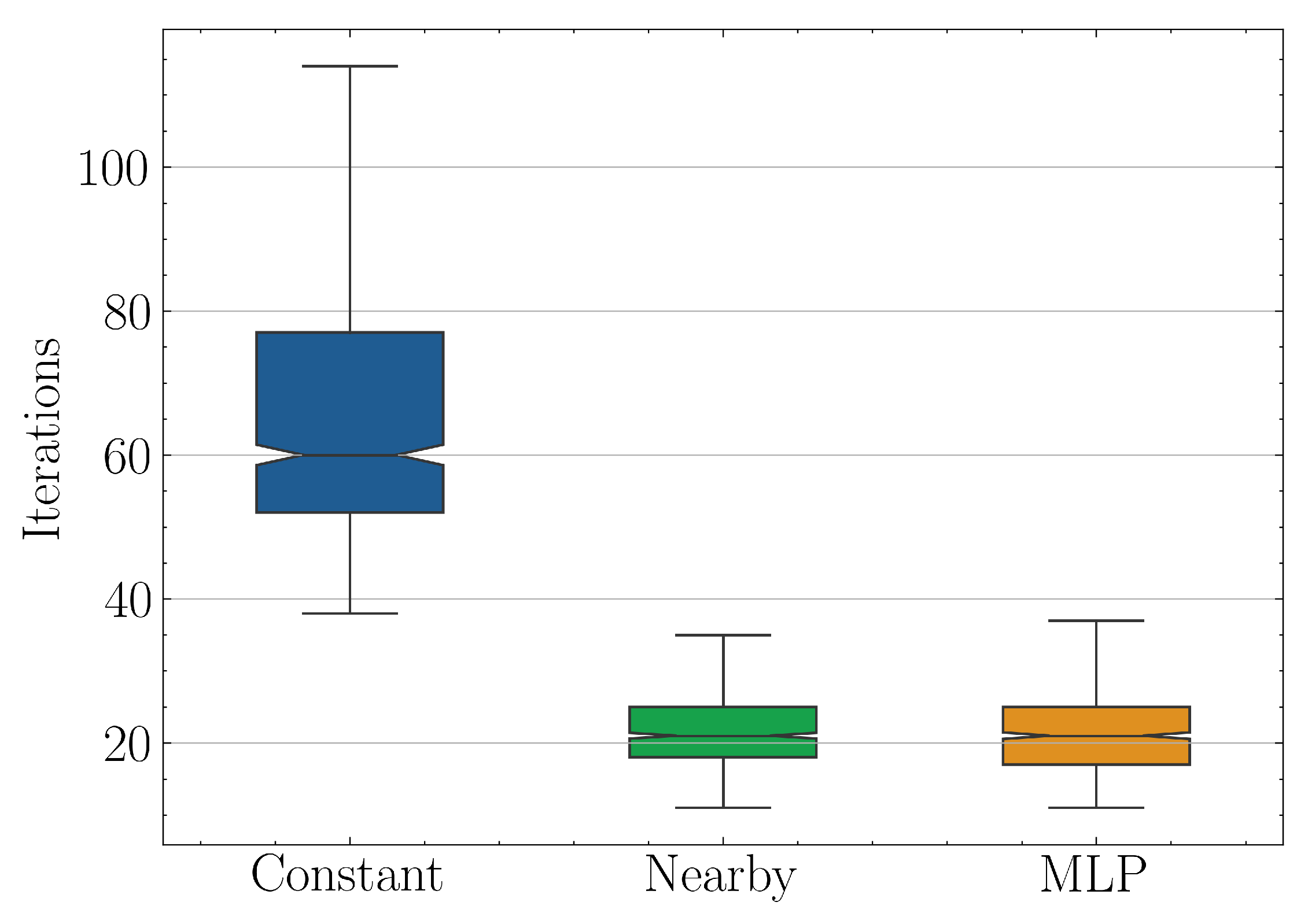
Three distinct strategies were compared, the first two are the pure VQLS scheme with constant initial parameters and the naive nearby scheme, as before. Additionally, as a third approach a simple MLP with 2 hidden layers was trained in the first N train = 100 samples using standard MSE loss and an Adam optimizer. In contrast to the nearby scheme, the optimal parameters used for training must cover the whole solution space in order to better approximate the manifold they reside in. In Figure 15, one can observe the non-convex Hamiltonian cost function C L for an instance of the QLSP. As in the first example, the Hamiltonian is non-convex resulting in different local minima, each one with similar loss values. This behaviour is expected when using local cost functions C L .
In Figure 12 one can see the joint probability distributions of the optimal parameters α opt , k i for k = 0 , 1 , 2 and i = 1 , ⋯ , 1000 for the 2 3 × 2 3 example of this section. In this example the dataset had no discontinuities which led to a trainable ML model.
Preprints 77196 g016
Figure 16. Pairwise joint probability distributions of optimal parameters α opt , k i , k = 0 , 1 , 2 , i = 1 , ⋯ , 1000 for example 5.3. In this example there are no discontinuities resulting in easier training of ML models.
Figure 16. Pairwise joint probability distributions of optimal parameters α opt , k i , k = 0 , 1 , 2 , i = 1 , ⋯ , 1000 for example 5.3. In this example there are no discontinuities resulting in easier training of ML models.
Preprints 77196 g016
The numerical results of the three strategies Constant, Nearby and MLP, are summarized in Figure 17. For each strategy, the graph shows the quartile distribution of the number of BFGS iterations required to reach a minimum Hamiltonian loss of at least C L min = 10 − 12 for a given QLSP instance. The last two strategies seemingly provide the same level of acceleration with speedup factor over the original algorithm being S ≈ 2.9 based on the median values. However, the MLP model didn’t outperform the naive Nearby method, since the mean square error, after an initial drop, usually was trapped in plateaus which were difficult to overcome without hyperparameter fine-tuning. Due to the fact that our experiments were simulated and did not include QPU runtimes, which are directly comparable to the time spend in fine-tuning, we were forced to be quite conservative with the latter. To our knowledge, unless one can use real quantum hardware and time metrics, it is not apparent how to take into account and compare the required MLP training time with respect to overall VQLS iterations. The assumption eventually made was that by using scalable models and as N → ∞ , which is the field quantum algorithms are supposed to excel, the model training time will be negligible with respect to the total solution time since t train / t total → 0 .
Regarding the low MLP performance, it seems that in order to outperform a naive nearby approach in such a small scale, a very delicate fine-tuning of the undermine the predictive ability of simple models played the most important role. Furthermore, the majority of the optimized parameters dataset α i cannot be used for training, as is common practice, since increasing the training data means that more solutions will be generated using the base VQLS scheme which is slower.

6. Conclusions and future work

Variational algorithms — specifically in our context VQLS algorithm — are designed for the noisy qubits of the current NISQ era. In order to solve the QLSP, VQLS optimizes classically a parametric ansatz w.r.t a quantumly computed Hamiltonian cost function.
Our proposed machine-learning scheme aims to accelerate the convergence of variational quantum algorithms when they are utilized as solvers in parametric problems by taking advantage of continuity. As a proof of concept, we showed that there is potential in that direction, since we managed to achieve a speed-up factor of up to 2.9. In the studied cases, the nearby shceme which combines both speed-up and simplicity seems to be preferable. We also demonstrated that when using gradient-free solvers, and especially ones which favour explorability, discontinuities in the optimal ansatz parameters emerge for various reasons, most prominently due to non-convexity of Hamiltonian loss and periodicity of quantum ansatzes w.r.t. their paramaters. This considerably handicaps the performance of machine learning models such as MLPs, a problem that should be addressed in the future in order to take full advantage of modern ML models.
A natural next step in order to overcome those hindrances is to use exact gradient-informed optimizers, which shall favour exploitation over exploration of parameter-space. Additionally, using domain constraint optimizers will help alleviate discontinuities related to the periodicity of the Hamiltonian. In particular, the use of natural gradient methods initially proposed in [25] for classical neural networks and their quantum counterparts [26] may provide sufficient robustness to the optimation process and in this way addressing the discontinuities originating from non-convex loss functions. An extensive evaluation of transformation-preprocessing techniques may also help significantly in this regard. Without doubt, increasing the scale of the experiments will allow bigger training datasets, which will in turn enable more complex, deeper machine learning models to be trained. Finally, experiments with real quantum hardware noise must be conducted so that similar obstructive phenomena are highlighted and addressed.

Author Contributions

Conceptualization, I.K. and K.A.; methodology, K.A.; software, K.A.; validation, I.K.; formal analysis, K.A.; investigation, K.A.; resources, G.S.; data curation, K.A.; writing—original draft preparation, K.A. and I.K.; writing—review and editing, G.S. and V.P.; visualization, K.A.; supervision, I.K. and V.P.; project administration, V.P.; funding acquisition, G.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the European Regional Development Fund of the European Union and Greek national funds through the Operational Program Competitiveness, Entrepreneurship and Innovation, under the call “RESEARCH–CREATE–INNOVATE“ project code: T2EDK-03206 Materialize.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Research data can be shared after justified request.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
QC Quantum Computing
QPU Quantum Processing Unit
CSE Computational Science & Engineering
MLP Multi-Layer Perceptron
NISQ Noisy Intermediate-Scale Quantum
(Q)LSP (Quantum) Linear System Problem
BFGS Broyden–Fletcher–Goldfarb–Shanno
HHL Harrow-Hassidim-Lloyd
VHQC Variational Hybrid Quantum-Classical
QAOA Quantum Alternating Operator Ansatz
QAOA Quantum Approximate Optimization Algorithm
VQE Variational Quantum Eigensolver
VQLS Variational Quantum Linear Solver
IBM International Business Machines

References

  1. Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM Review 1999, 41, 303–332. [Google Scholar] [CrossRef]
  2. Grover, L.K. Quantum Computers Can Search Arbitrarily Large Databases by a Single Query. Phys. Rev. Lett. 1997, 79, 4709–4712. [Google Scholar] [CrossRef]
  3. Harrow, A.W.; Hassidim, A.; Lloyd, S. Quantum Algorithm for Linear Systems of Equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef] [PubMed]
  4. Xin, T.; Wei, S.; Cui, J.; Xiao, J.; Arrazola, I.n.; Lamata, L.; Kong, X.; Lu, D.; Solano, E.; Long, G. Quantum algorithm for solving linear differential equations: Theory and experiment. Phys. Rev. A 2020, 101, 032307. [Google Scholar] [CrossRef]
  5. Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm Applied to a Bounded Occurrence Constraint Problem, 2014. [CrossRef]
  6. Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm, 2014. [CrossRef]
  7. Schuld, M.; Sinayskiy, I.; Petruccione, F. An introduction to quantum machine learning. Contemporary Physics 2015, 56, 172–185. [Google Scholar] [CrossRef]
  8. Dunjko, V.; Briegel, H.J. Machine learning & artificial intelligence in the quantum domain: A review of recent progress. Reports on Progress in Physics 2018, 81. [Google Scholar] [CrossRef]
  9. Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised learning with quantum-enhanced feature spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef] [PubMed]
  10. Bravo-Prieto, C.; LaRose, R.; Cerezo, M.; Subasi, Y.; Cincio, L.; Coles, P.J. Variational Quantum Linear Solver 2019. [CrossRef]
  11. Huang, H.Y.; Bharti, K.; Rebentrost, P. Near-term quantum algorithms for linear systems of equations with regression loss functions. New Journal of Physics 2021, 23. [Google Scholar] [CrossRef]
  12. Koczor, B.; Benjamin, S.C. Quantum analytic descent. Physical Review Research 2022, 4. [Google Scholar] [CrossRef]
  13. Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nature Communications 2014, 5. [Google Scholar] [CrossRef] [PubMed]
  14. Childs, A.M.; Kothari, R.; Somma, R.D. Quantum Algorithm for Systems of Linear Equations with Exponentially Improved Dependence on Precision. SIAM Journal on Computing 2017, 46, 1920–1950. [Google Scholar] [CrossRef]
  15. Dervovic, D.; Herbster, M.; Mountney, P.; Severini, S.; Usher, N.; Wossnig, L. Quantum linear systems algorithms: a primer, 2018. [CrossRef]
  16. Harrow, A.W.; Hassidim, A.; Lloyd, S. Quantum Algorithm for Linear Systems of Equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef] [PubMed]
  17. Aaronson, S. Read the fine print. Nature Physics 2015, 11, 291–293. [Google Scholar] [CrossRef]
  18. Cerezo, M.; Sone, A.; Volkoff, T.; Cincio, L.; Coles, P.J. Cost function dependent barren plateaus in shallow parametrized quantum circuits. Nature Communications 2021, 12. [Google Scholar] [CrossRef] [PubMed]
  19. Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm, 2014. [CrossRef]
  20. Hadfield, S.; Wang, Z.; O’Gorman, B.; Rieffel, E.G.; Venturelli, D.; Biswas, R. From the Quantum Approximate Optimization Algorithm to a Quantum Alternating Operator Ansatz. Algorithms 2017, 12, 34. [Google Scholar] [CrossRef]
  21. Wang, Z.; Hadfield, S.; Jiang, Z.; Rieffel, E.G. Quantum approximate optimization algorithm for MaxCut: A fermionic view. Phys. Rev. A 2018, 97, 022304. [Google Scholar] [CrossRef]
  22. Crooks, G.E. Performance of the Quantum Approximate Optimization Algorithm on the Maximum Cut Problem, 2018. [CrossRef]
  23. Kandala, A.; Mezzacapo, A.; Temme, K. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246. [CrossRef] [PubMed]
  24. Qiskit: An Open-source Framework for Quantum Computing, 2021. [CrossRef]
  25. Amari, S.i. Natural Gradient Works Efficiently in Learning. Neural Computation 1998, 10, 251–276, [https://direct.mit.edu/neco/article-pdf/10/2/251/813415/089976698300017746.pdf]. [Google Scholar] [CrossRef]
  26. Stokes, J.; Izaac, J.; Killoran, N.; Carleo, G. Quantum Natural Gradient. Quantum 2020, 4, 269. [Google Scholar] [CrossRef]
Preprints 77196 g001
Figure 1. Single-qubit circuit with initial state |0〉, followed by gate operations and finally a measurement.
Figure 1. Single-qubit circuit with initial state |0〉, followed by gate operations and finally a measurement.
Preprints 77196 g001
Preprints 77196 g002
Figure 2. Multi-qubit circuit with a controlled operation C U . U operator is applied in the second n-qubit register only when the control (first from above) qubit has a |1〉 component.
Figure 2. Multi-qubit circuit with a controlled operation C U . U operator is applied in the second n-qubit register only when the control (first from above) qubit has a |1〉 component.
Preprints 77196 g002
Preprints 77196 g003
Figure 3. Schematic diagram of VQLS algorithm from [10].
Figure 3. Schematic diagram of VQLS algorithm from [10].
Preprints 77196 g003
Preprints 77196 g004
Figure 4. Hadamard Test used to compute coefficients β l l ′ = 〈 0 | V † A l ′ † A l V | 0 〉 [10].
Figure 4. Hadamard Test used to compute coefficients β l l ′ = 〈 0 | V † A l ′ † A l V | 0 〉 [10].
Preprints 77196 g004
Preprints 77196 g005
Figure 5. Hadamard Test used to compute ζ l l ′ i coefficients as indicated in Equation 12 [10].
Figure 5. Hadamard Test used to compute ζ l l ′ i coefficients as indicated in Equation 12 [10].
Preprints 77196 g005
Preprints 77196 g006
Figure 6. Fixed-structure layered Ansatz for V ( α ) [10]. Each layer introduces R y ( a i ) -rotations (exploration) and controlled-Z operations acting on alternating pairs of neighbouring qubits (correlation). If the linear system is restricted to real numbers, R y gates are sufficient, since they don’t produce complex output. For fixed layer depth the number of variational parameters scales as O ( n ) . The example shows an ansatz with n = 6 qubits (linear system with size 2 6 × 2 6 ) and three layers.
Figure 6. Fixed-structure layered Ansatz for V ( α ) [10]. Each layer introduces R y ( a i ) -rotations (exploration) and controlled-Z operations acting on alternating pairs of neighbouring qubits (correlation). If the linear system is restricted to real numbers, R y gates are sufficient, since they don’t produce complex output. For fixed layer depth the number of variational parameters scales as O ( n ) . The example shows an ansatz with n = 6 qubits (linear system with size 2 6 × 2 6 ) and three layers.
Preprints 77196 g006
Preprints 77196 g007
Figure 7. Computational workflow for the machine-learning-enhanced VQLS scheme for parametric systems.
Figure 7. Computational workflow for the machine-learning-enhanced VQLS scheme for parametric systems.
Preprints 77196 g007
Preprints 77196 g008
Figure 8. Example of VQLS Hamiltonian loss C L for a 2 2 × 2 2 system per iteration. Note that BFGS algorithm uses internal iterations which are not shown in order to approximate the Hessian matrix.
Figure 8. Example of VQLS Hamiltonian loss C L for a 2 2 × 2 2 system per iteration. Note that BFGS algorithm uses internal iterations which are not shown in order to approximate the Hessian matrix.
Preprints 77196 g008
Preprints 77196 g009aPreprints 77196 g009b
Figure 9. Optimal ansatz parameters w.r.t physical parameteres for a 2 × 2 single-qubit system using the COBYLA method.
Figure 9. Optimal ansatz parameters w.r.t physical parameteres for a 2 × 2 single-qubit system using the COBYLA method.
Preprints 77196 g009aPreprints 77196 g009b
Preprints 77196 g010
Figure 10. Ansatz consisting of three parametric gates with angles α k , k = 0 , 1 , 2 for the 2 2 × 2 2 parametric QLSP example of 5.2.
Figure 10. Ansatz consisting of three parametric gates with angles α k , k = 0 , 1 , 2 for the 2 2 × 2 2 parametric QLSP example of 5.2.
Preprints 77196 g010
Preprints 77196 g011
Figure 11. Hamiltonian loss function C L w.r.t. input ansatz parameters α 0 , α 1 for a QLSP instance of example 5.2.
Figure 11. Hamiltonian loss function C L w.r.t. input ansatz parameters α 0 , α 1 for a QLSP instance of example 5.2.
Preprints 77196 g011
Preprints 77196 g012
Figure 12. Pairwise joint probability distributions of optimal parameters α opt , k i , k = 0 , 1 , 2 , i = 1 , ⋯ , 1000 for example 5.2.
Figure 12. Pairwise joint probability distributions of optimal parameters α opt , k i , k = 0 , 1 , 2 , i = 1 , ⋯ , 1000 for example 5.2.
Preprints 77196 g012
Preprints 77196 g013
Figure 13. Quartiles for the number of BFGS iterations required to solve an instance A ( p i ) | x ( α i ) 〉 = | b 〉 where A ( p i ) ∈ C 4 × 4 .
Figure 13. Quartiles for the number of BFGS iterations required to solve an instance A ( p i ) | x ( α i ) 〉 = | b 〉 where A ( p i ) ∈ C 4 × 4 .
Preprints 77196 g013
Preprints 77196 g014
Figure 14. Fixed-structure layered Ansatz with 11 parametric gates with angles α k , k = 0 , ⋯ , 10 for the 2 3 × 2 3 parametric QLSP example of 5.2.
Figure 14. Fixed-structure layered Ansatz with 11 parametric gates with angles α k , k = 0 , ⋯ , 10 for the 2 3 × 2 3 parametric QLSP example of 5.2.
Preprints 77196 g014
Preprints 77196 g015
Figure 15. Hamiltonian loss function C L w.r.t. input ansatz parameters α 0 , α 1 for a QLSP instance of example 5.3.
Figure 15. Hamiltonian loss function C L w.r.t. input ansatz parameters α 0 , α 1 for a QLSP instance of example 5.3.
Preprints 77196 g015
Preprints 77196 g017
Figure 17. Quartiles for the number of BFGS iterations required to solve QLSP instance A ( p i ) | x ( α i ) 〉 = | b 〉 , where A ( p i ) ∈ C 8 × 8 .
Figure 17. Quartiles for the number of BFGS iterations required to solve QLSP instance A ( p i ) | x ( α i ) 〉 = | b 〉 , where A ( p i ) ∈ C 8 × 8 .
Preprints 77196 g017
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated