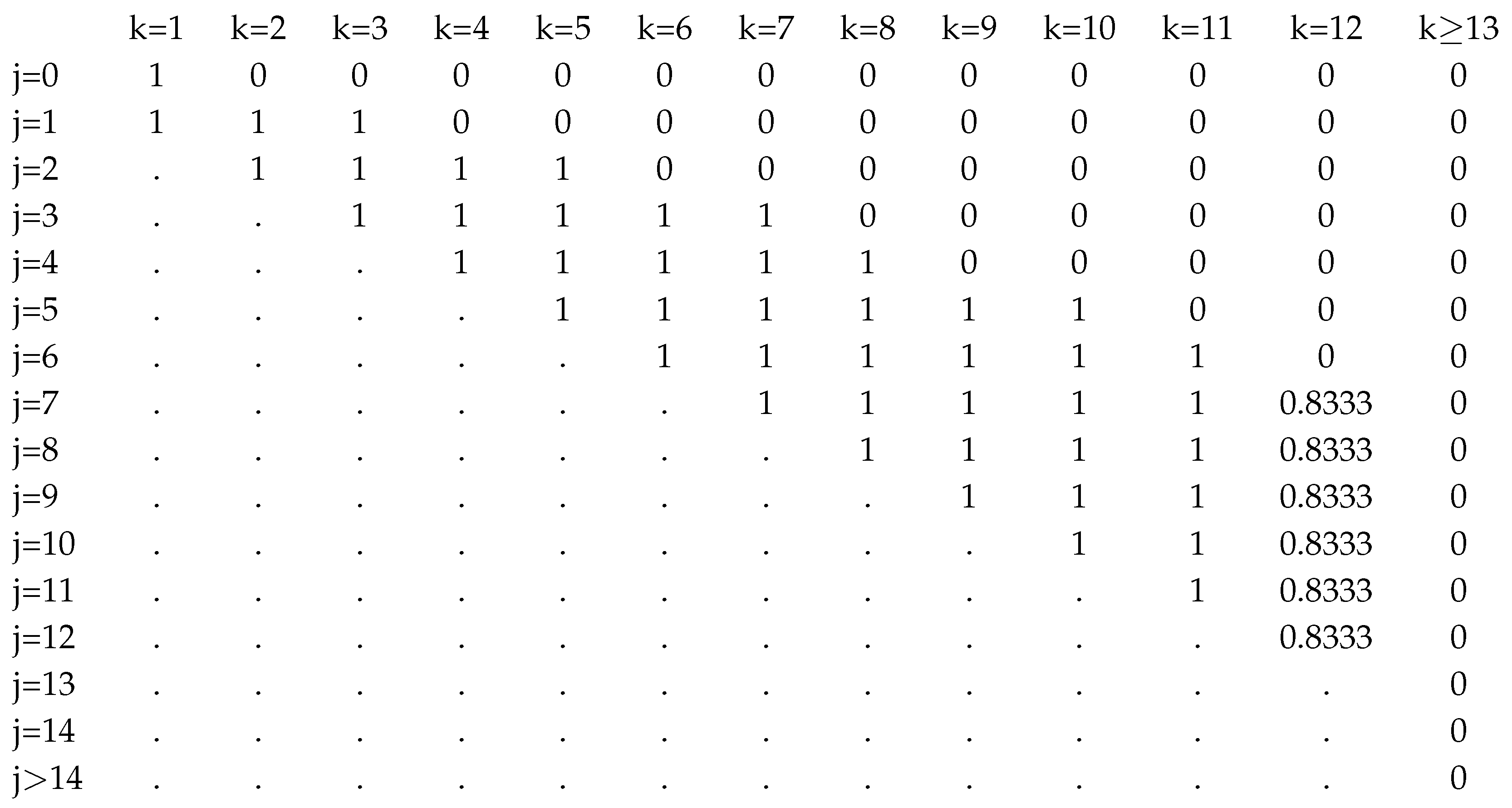1. Introduction
Opinion diffusion is a fundamental aspect of human interaction, playing a pivotal role in the spread of innovations, and the emergence of consensus. Understanding how opinions spread and evolve within social networks is crucial for comprehending the emergence of collective behavior, the formation of public opinion, and the polarization of societies.
Social sciences provide plenty of applications, where the importance of diffusion dynamics is studied and witnessed, like in marketing (see e.g. [
2,
12,
13]), agent-based modeling (see e.g. [
14]) and sociophysics, where the papers of Serge Galam serve as a guide for researchers (see e.g. [
9]).
Galam’s opinion diffusion model (see [
8]) provides a framework for investigating and understanding the dynamics of opinion formation in social systems. Galam’s model sheds light into the mechanisms that drive opinion dynamics. In particular, Galam’s model describes the formation of collective opinion convergence processes using concepts from statistical physics. To analyze them, along with several generalisations of the model, the authors of the current paper have proposed the alternatives in [
4] (showing some drawbacks when applying Galam’s model with a relatively small number of agents), and in [
5] (where a novel subset of agents, namely the
opinion leaders, are introduced, to duly represent a possible communication bias). Furthermore, additional literature covering a number of keynote issues can be found in [
9,
10,
11] and therein references.
The standard Galam’s model in [
8] assumes that individuals in a group influence and are influenced by their peers. After several iterations within repeated group discussions, each agent may consequently influence the opinion diffusion. Galam’s stylized model simplifies the complexity of opinions by considering a binary state, where individuals can adopt either of two possible opinions, thus allowing a straightforward mathematical analysis of the diffusion process.
We suggest a generalisation of Galam’s model and then offer evidence in an optimisation framework that some of the diffusion parameters can be successfully adjusted in order to steer the diffusion process. Combining Galam’s model with specific Linear Programming (LP) formulations, we take into account both theoretical and numerical results concerning the role of the model’s parameters, in order to better control the dynamics of the diffusion: namely we aim at maximizing the probability that an opinion can spread among agents.
The paper is organised as follows: the essential characteristics of Galam’s model [
8] are recapped in
Section 2. Then, in
Section 3, we present and discuss a generalisation of Galam’s model. The optimisation of the parameters of the new model via linear programming allows to speed up opinion diffusion at a fixed step of the process: the optimisation problem is discussed in
Section 4 while
Section 5 provides numerical examples of its resolution.
Section 6 discusses a dynamic programming extension of the optimisation problem that optimizes the values of the parameters along the whole diffusion process, till convergence.
Section 7 contains final remarks and concludes the paper.
2. Recap of Galam’s model
This section reviews the foundational elements of Galam’s model in [
8]. Think of a group of
N people (
agents), each of whom may hold one of two opposing views (let’s say, `+’ or `−’), regarding a specific issue. These agents meet, during several repeated rounds, within subgroups of smaller cardinality, to converse and possibly change one another’s minds.
Each agent at round (
time)
t has a probability
of being a member of a subgroup of size
k, being
L the maximum allowed size of groups. In the original formulation of Galam’s model the values
are exogenous parameters such that
Joining a group discussion at time t, any agent may, at the beginning of the subsequent time , modify their position (e.g. `+’ becomes `−’ or viceversa) in accordance with a unique law: the majority rule. Indeed, all agents in a subgroup take the position of the majority in that group in the end of time t. The rule for reversing opinion is slightly biased in favor of the negative opinion `−’, since tie breaks in favor of `−’. This may lead to a substantial bias in case the subgroup has an even number of members.
Calling
the probability that an agent opinion is `+’ at time
t, the probability of opinion `−’ is then
. The probability
is estimated in [
8] as
where
is the largest integer less or equal to
z, and
is the binomial coefficient
.
Let
(
) be the number of agents who at time step
t have opinion `+’ (`−’). Observe that for small values of
N, setting
, where
is the number of agents thinking `+’ at time
, for any
the quantity
may possibly differ from the `actual’ frequency of `+’, i.e.
(see [
4]). Nevertheless, the estimated probability
always lies in the interval
being
A relevant role in the model is taken by the value such that
when then ,
when then ,
when then ∀.
constitutes the threshold value such that when
is greater than
, then all agents will eventually have opinion `+’. Conversely, when
all the agents will definitely think `−’ if
. The value
is addressed as the
killing point of the model. In
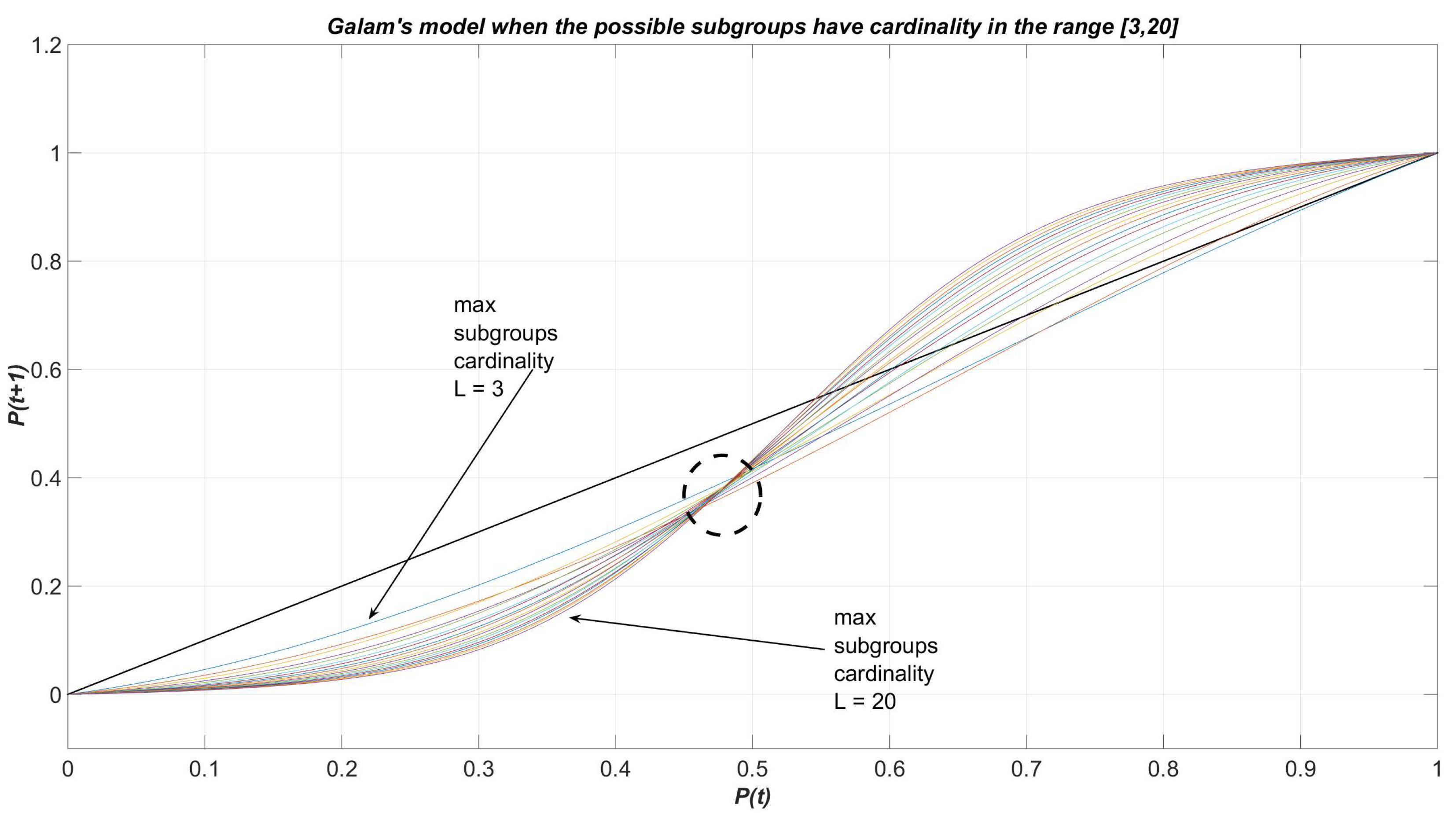
Figure 1 we can observe the dynamics described by relation (
1), when the largest cardinality
L of the subgroups takes integer values in the interval
and
, for any
k: for each of the 18 curves, the killing point is identified by the intersection with the bisector line other than the extreme points
and
. Observe that for small values of
L no killing point appears (or equivalently it coincides with the extreme point
).
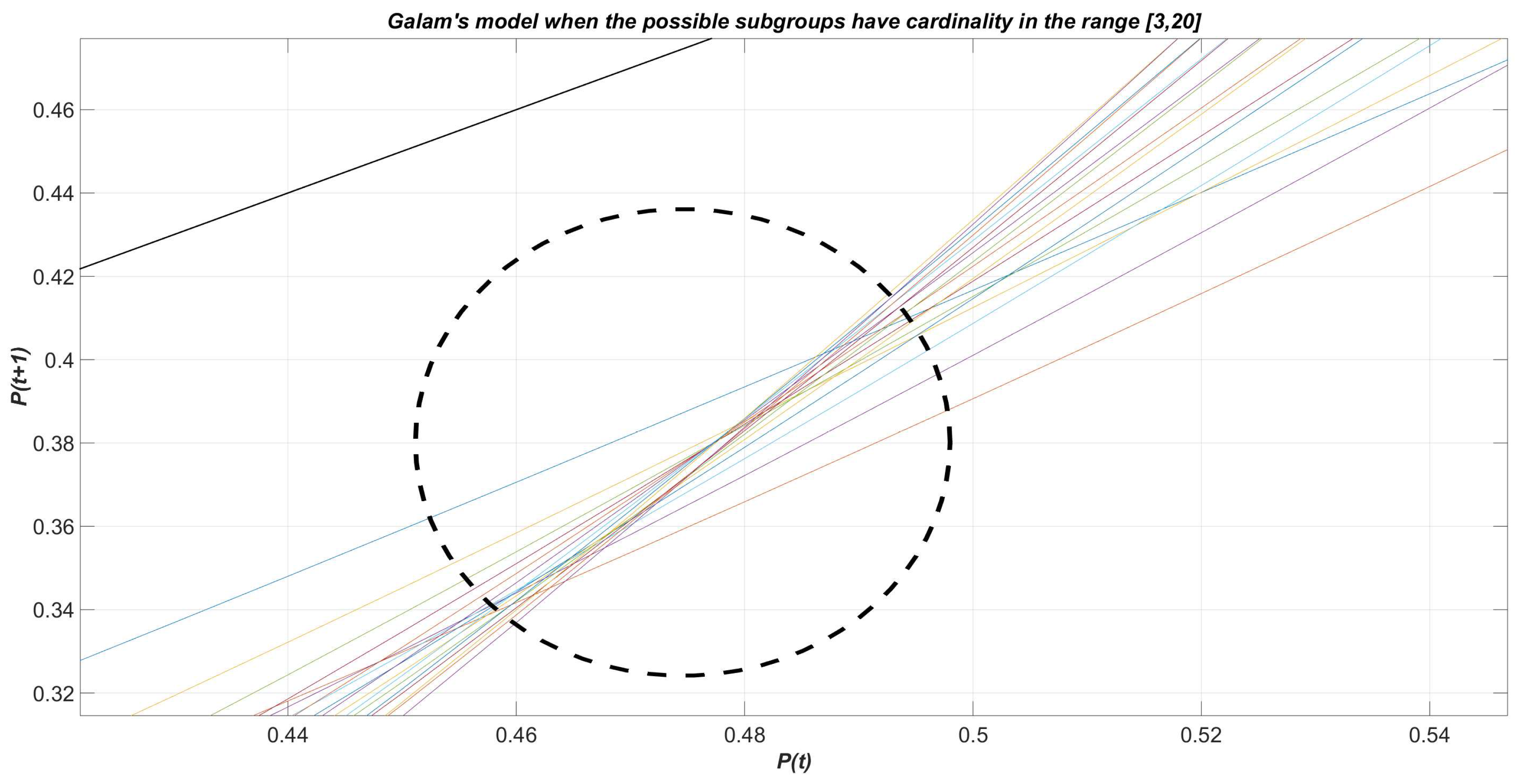
Figure 2 reports a zoom perspective of
Figure 1.
3. Capturing additional dynamics using a generalised Galam’s model
According to model (
1), a strict majority of members with positive opinion is a necessary and sufficient condition to have opinion + for all the subgroup members.
Since the ultimate choice in a group is frequently the product of a discussion, rather than a simple tally of the two opposing viewpoints in the group, a rule that is so rigorous yet so straightforward could not correctly reflect the actual opinion dynamics in practice. As an illustration, think about the propagation of political opinions. The probability that everyone in the group would share the same view (e.g. +) at the close of a conversation may rise
smoothly with the number of members who had that opinion prior to the meeting. As a second application, the reader may consider the audience of social networks, where the dynamics of information spreading was widely investigated in a dedicated literature (see, e.g. [
1]).
Accordingly, we suggest to generalise Galam’s model (
1) taking into account a softer dynamics of opinion change, i.e., without using rigid majority as a necessary and sufficient condition to shift the entire group to the same view. In particular, we assume that after the conversations, all agents in a group will have opinion + with a probability
that is dependent on the size
k of the group and the number
j of agents that had opinion + before the discussion. We use the following definition to model the relationship between the probabilities of having an opinion + before (i.e.
) and after (i.e.
) discussion (see [
3] for a preliminary version of the model):
Model (
2) generalises (
1), since it is possible to select indeed the probabilities
that exactly replicate model (
1) (see also
Figure 3):
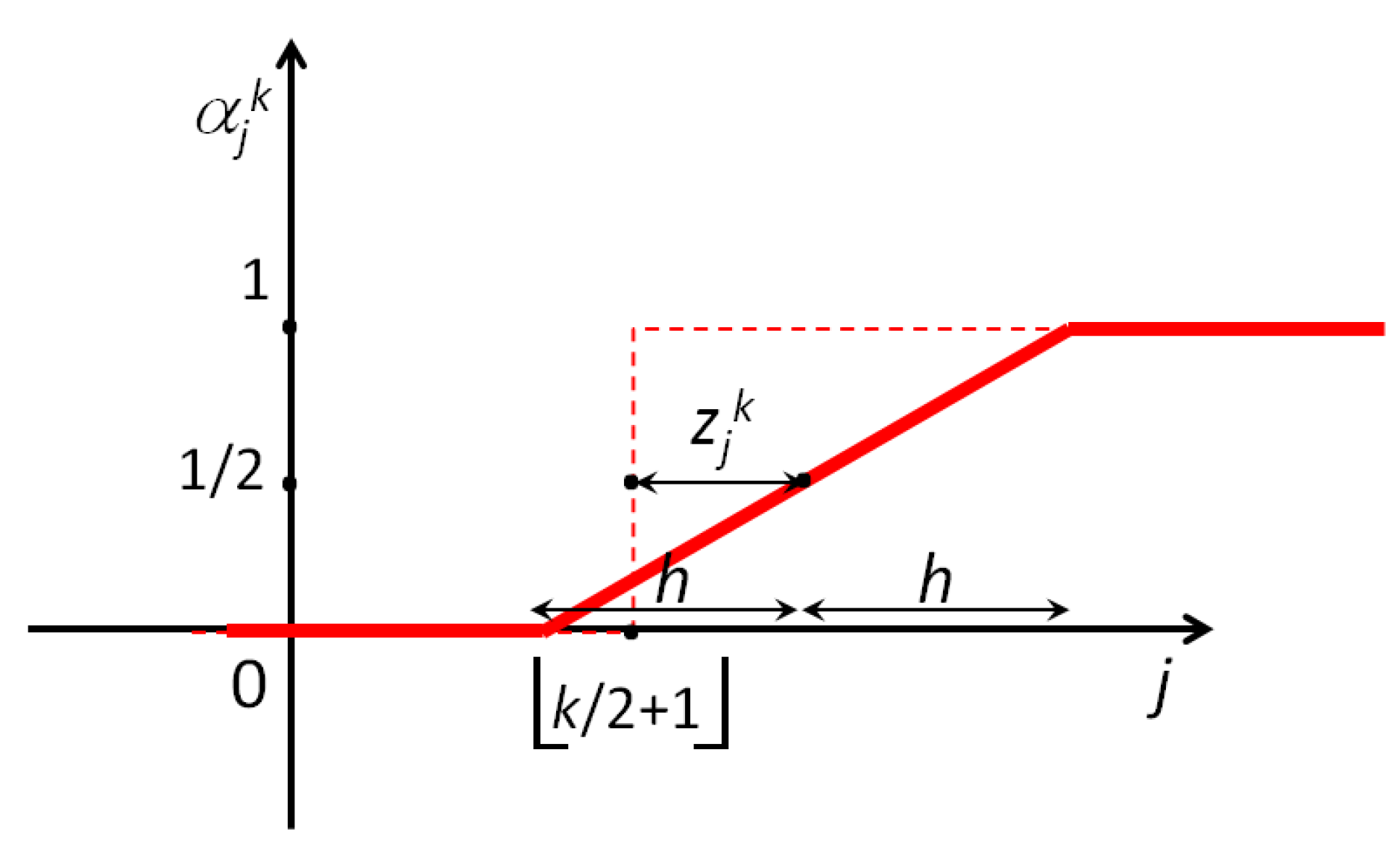
As mentioned, probabilities
should reasonably increase with the number
j of + in a subgroup, and decrease with respect to the size of the group
k. In this regard, it is reasonable to expect for the probability
to become negligible when the number
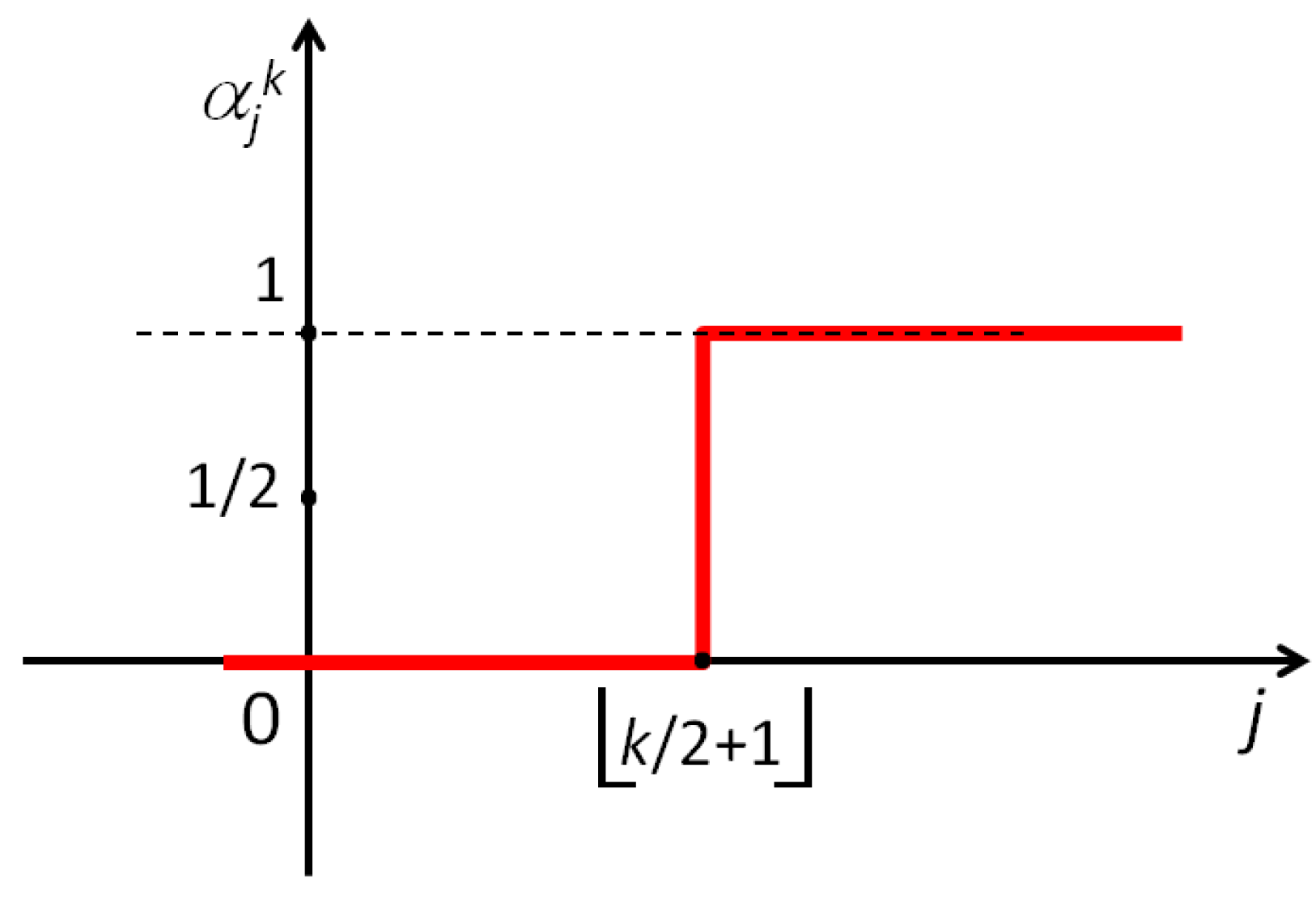
j of + in a subgroup is relatively small (i.e., much lower than the strict majority), and to become close to 1 as the number of + noticeably increases (i.e., higher than strict majority). In general, the probability that all agents in the subgroup will adopt the opinion + is conceivably a function rising from zero to one as
j increases. If we assume that this function of
j is linear, we may precisely define the probabilities
as (see
Figure 4)
When
, the probabilities defined in (
4) are exactly the same as in (
3) . The value of
in (
4) represents a shift (either positive or negative) from the value
, while the slope of the ramp in
Figure 4 is
.
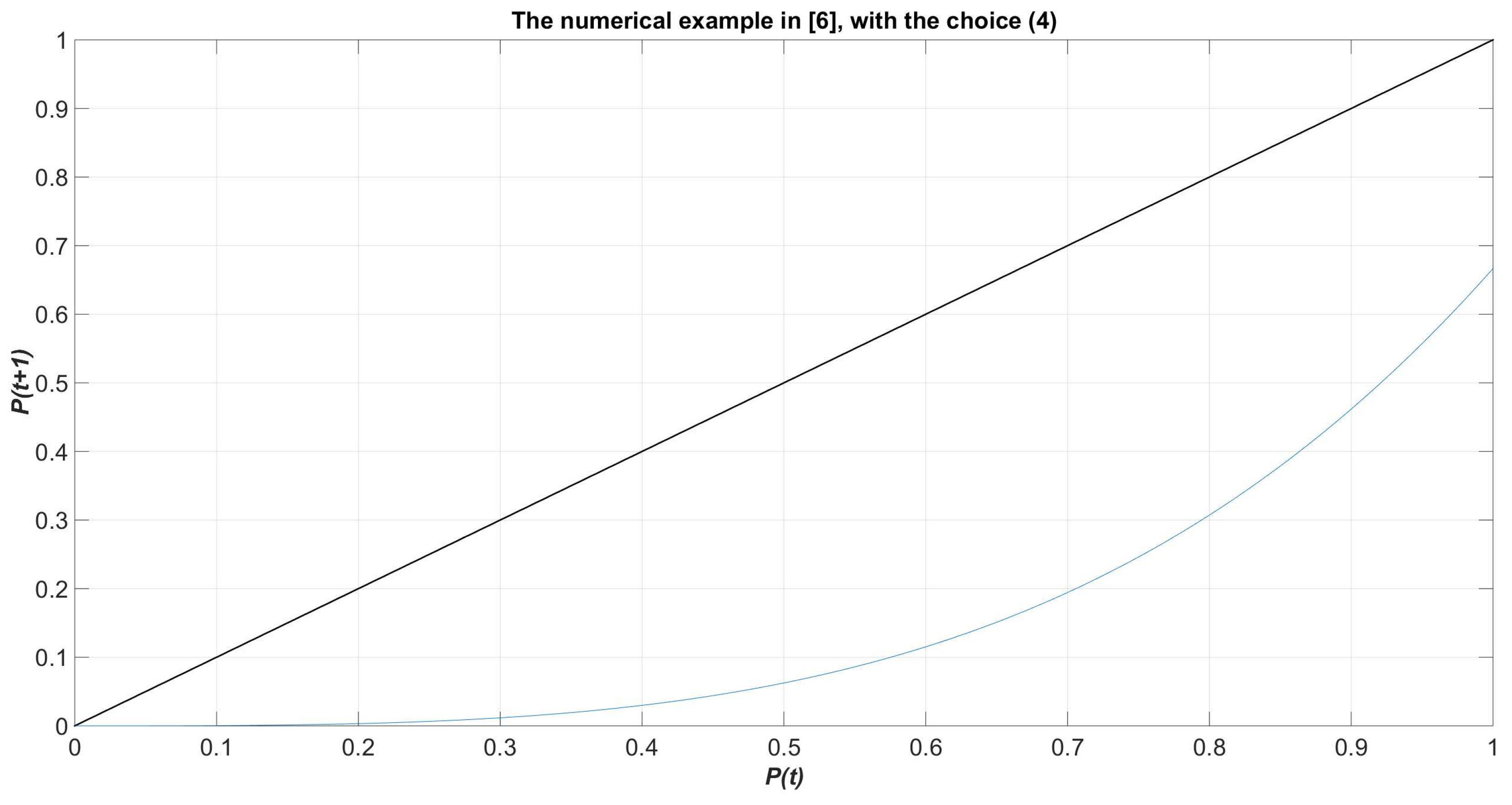
To better grasp the geometric insight behind the choice of the parameters in (
4), let us consider the simple numerical example reported in [
8], where
,
,
(and
for all
j and
k). As reported in [
8] the killing point (
) lies in between
and
(see
Figure 5). Then, we also have in
Figure 6 the model (
2) with the choice (
4), after setting
for any
j and
k. We can immediately infer that the dynamics of Galam’s model in [
8] is definitely spoiled when the choice for the coefficients
in (
3) is replaced by (
4). Equivalently, even in case
(complete consensus among agents to think +) then the choice (
4) imposes a
regression towards the stable point given by the origin.
Hence, the presence of a killing point for Galam’s model seems to be strictly related to the expression (
1), and introducing the coefficients
definitely spoils also the killing point. Moreover, we observe that, in case the majority rule is not explicitly applied in (
1), then the dynamics of the model is strongly altered.
Nevertheless, the model (
2) retains a number of properties and can suggest fruitful results, following both the next guidelines:
At least a couple of intriguing issues in applications can steer the choice of the coefficients , ranging from small–medium to large scale (number of agents) applications:
(One Period Analysis) we may assess values for so that, considering at time t the probability , we maximize the probability at time . In this regard, the values represent costs for steering the information among agents and fostering the positive opinion: the larger (i.e. higher costs) the larger the probability to convey a group to opinion `+’. Of course the combination of the proper values for each of the coefficients is strongly related to the value , the probabilities and the binomial coefficients ;
(Multi-Period Analysis) similarly to the previous item we may decide to select such that, considering again at time t the probability , we maximize the probability at time , and compute the entire sequence of intermediate probabilities.
The last two scenarios can be declined in a variety of contexts, including production and Marketing, where consumers play the role of agents and the aforementioned perspectives may be the answer to the question: what is (if any) the necessary extra effort in terms of advertising campaign, in order to promote a certain spread of the products or customers’ expectations on items ? In this regard the quantities
summarise the resulting effort, while from a mathematical programming perspective they represent unknowns to be assessed. This also suggest that a number of additional questions may arise adopting the model (
2), mapping relevant practical instances where a tentative forecast is sought in order to plan the use of (possibly scarce) resources to control the process of diffusion of the information. For the sake of brevity, we itemize below some proposals that are representative but not exhaustive:
(Feasibility Problem) given the value of and the target value , we may determine a set of values for the coefficients such that, starting at t from , at time we will have ;
(Focus Group Problem) given the value of and the target value and the time , we may be interested to determine a set of values for the coefficients such that , where are possible bounds, and . This scenario models a specific interest on those subgroups of cardinality k.
4. Single period maximization of diffusion
As from the analysis in
Section 3, one of the possible proposals to couple the dynamics described through the model (
2) with a single period optimization framework, is given by the following LP scheme:
The last optimization problem assumes that the value is given, so that both the objective function and the constraints are linear in the set . Though the meaning associated with the objective function is relatively clear, for the constraints some clarifications seem necessary, indeed:
the constraints (6) state that for a given dimension k of a subset, larger values of the number of agents thinking + imply a larger probability ;
similarly in the constraints (7), when the number of agents thinking + remains constant, the larger the set cardinality (i.e. k) the smaller the probability ;
the constraint (8) expresses the overall cost (i.e. it is a budget constraint) allowed to assess the probabilities , at time t;
since the quantities need to represent probabilities, they are required to fulfill also the constraint (9).
In order to avoid either infeasible or straightforward solutions for the optimization problem (5)–(9), the next lemmas gives some indications on the choice of the parameter
, for any
t (for a proof see [
3]).
Lemma 1.
Let be given the linear program (5)–(9) with the choice ( and )
Then, relations (10) satisfy the constraints (6)–(7) and (9). Moreover, if (10) also satisfies (8), then the value of the objective function in (5) coincides with in (1).
Note that Lemma 1 gives a clear idea of the fact that the solution of the linear program (5)–(9) is substantially nothing else but a generalization of (
1). Furthermore, the next result will give a precise indication on the possible values for the budget
in (8).
Lemma 2.
Let be given the optimization problem (5)–(9) and let be assigned as in (10), for any and . Then
Note that the right sides of (
11) explicitly give some hints for the selection of the parameter
in (8), both either in case
L is even or it is odd.
As regards some technicalities associated with the solution of the optimization problem (5)–(9), we observe that it is a continuously differentiable problem, where all the functions are linear. Hence, it is a convex problem, so that the set of all its solutions (possibly an empty set or a singleton) is a convex set. This implies that for any given pair of its solutions, all the points in the segment joining them will be solutions, too. Moreover, being a linear program, all its (possible) solutions will lie on vertices of the feasible set, and not in the interior of the feasible set. As well known, this makes its solution relatively simple (throughout any solver based on the Simplex method) and achievable in a polynomial time. Hence, large scale instances are easily tractable and allow for a scalable solution in a number of applications with a great number of agents (e.g. problems involving social media or large social groups).
We complete this section highlighting that one further generalization of the linear program (5)–(9) suggests to disaggregate the budget constraint and to replace the inequality (8) by the set of constraints
Observe that the value , for any k, represents a budget devoted to possibly affect the solution after working uniquely on the subsets of cardinality k. This increases the flexibility of the model without compromising its overall complexity (being the resulting model yet a linear program).
5. Preliminary numerical experience
This section is devoted to provide a numerical experience where the potentialities of the formulation (5)–(9) are exploited. In this regard, we limit our investigation to a couple of meaningful instances, being the first one a small scale (number of unknowns) problem, while the second one attempts to scale the first one scale by 100.
5.1. Small scale instance
As regards the value of the coefficients in (5)–(9), we consider for the small scale instance the following setting:
The above choice corresponds to possibly allow only subgroups of dimension 1, 3, 5, 7 and 9, with probabilities that include null values and possibly repeated values. Furthermore, we set the initial percentage of the population thinking `+’ to . Finally, in order to avoid an empty feasible set in (5)–(9) we also selected respectively the values and , based on Lemma 2. The outcomes of our numerical experience are obtained using the solver CPLEX 20.1.0.0 available on the platform https://neos-server.org/neos. We remark that CPLEX is definitely among the best and faster solvers for LP, along with the alternative solver BARON. Our numerical experience on the above two instances is summarized as follows:
-
: the problem (5)–(9) was coded using AMPL (A Mathematical Programming Language, see [
6] and [
7]). The
presolve tool in CPLEX eliminated 65 constraints from the formulation, so that the simplified problem reduced to 65 variables and 110 linear inequality constraints. As regards the final solution, CPLEX performed 13
dual simplex iterations (i.e. iterations of a method for LP which represents the counterpart of the Simplex method, after exploiting the duality theory), with an overall time for the solution not larger than a couple of seconds. Finally, the value of
found by the solver was
with the set of variables
given by
-
: again the problem (5)–(9) was coded using AMPL and the
presolve tool in CPLEX eliminated 65 constraints from the formulation, so that again the simplified problem reduced to 65 variables and 110 linear inequality constraints. CPLEX performed 18
dual simplex iterations with an overall time for computation similar to the case where it was
. Finally, the value of
found by the solver was
with the set of variables
given by the matrix
Note that allowing a larger value of the budget (say ), the solver was able to select a larger number of nonzero unknowns, so that the final value of was almost doubled with respect to the case . In real applications this turns to imply that, in order to obtain almost twice the effect of the previous case, on this instance twice the value of the budget must be allowed.
5.2. Large scale instance
Here we focus on the same instance of
Section 5.1, where conversely a larger number of unknowns is considered. The novel setting of the parameters for the solver are given as follows:
The above choice corresponds to possibly allow all the subgroups with the same probability, and again the initial percentage of the population thinking `+’ is equal to . Similarly to the small scale instance, we considered two values for the budget, being and . The computation is again performed adopting the solver CPLEX 20.1.0.0 on the Neos Server. The outcomes of the resulting two instances are summarized as follows:
-
: the problem (5)–(9) was coded using AMPL and the
presolve tool in CPLEX eliminated 501500 constraints from the formulation. The overall simplified problem contained 501500 variables and 1001000 linear inequality constraints. CPLEX performed 192
dual simplex iterations with a time of computation smaller than 20 seconds, showing that the linear model can easily scale the time of computation. The final value of
found by the solver was
with the set of variables
given by
: the outcomes have been much similar to the case where
, being 501500 the overall number of variables and 1001000 the linear inequality constraints. CPLEX performed 30854
simplex iterations with a time of computation smaller than 20 seconds, showing again that the linear model can easily scale the time of computation. The final value of
found by the solver was now
and we do not report the value of the unknowns for the sake of simplicity.
Observe that in both the last two examples, given that subgroups are allowed to be very large, despite relatively high budget values, the levels reached by the probabilities are very low.
As a general achievement, we can easily describe the pattern of the nonzero unknowns which was respected in all the four numerical tests reported above. In particular, we can easily prove that the solution of the formulation ()–(9) only fills the principal submatrix of unknowns of order , depending h on the value of the budget parameter along with the number of possible subgroups L. In the end, this also allows to easily assess a number of null unknowns, and possibly reduce the complexity of the overall formulation.
6. A Multi-Period Model
This section considers a multi-period reformulation of the Linear Program (5)-(9), in order to further generalize the model (
2). In particular, in place of the
single-period model (5)-(9), where at time step
t the quantity
is maximized starting from
, we can consider a
multi-period approach with the ultimate goal of maximizing
, being
T the time horizon. The latter approach is summarized in the next Nonlinear Program:
The previous Nonlinear Program includes the unknowns
which represent a larger number of variables with respect to (5)-(9). This implies that the larger the time horizon
T, the larger the number of unknowns of the resulting problem formulation. Moreover, as already remarked, (12)-(17) is a Nonlinear Program, which in general increases the difficulty of its solution. In particular, the nonlinearities in (13) might yield a nonconcave overall maximization problem, which implies that a certain number of local maxima (which are not global) might arise. In addition, unlike (5)-(9), the feasible set of (12)-(17) is no more a polyhedron, so that the final solutions not necessarily are located on the boundary of the feasible set. As a consequence, the choice of the starting value
in (13) becomes a key factor for at least a couple of reasons:
the sequence strongly depends on , in a similar fashion of the single-period formulation (5)-(9);
the choice of strongly affects the local maximum provided by the solver adopted for (12)-(17).
As regards the constraints (13), observe that they simply state a recursion for the function in (
2), at each time step. Moreover, the constraints (14), (15) and (17) have a similar meaning of the constraints (6), (7) and (9), for the single-period formulation. Finally, the budget constraints (16) have a possible double formulation, due to the multi-period scheme.
Proposition 1. Let the sequence be a global solution of (5)-(9), for any . Then, is a global solution of (12)-(17).
Proof. Observe that from relation (
2) we have the following equalities
Thus, considering that
is a constant value, the maximization in (
12) is equivalent to the maximization
Moreover, observe that if
is given,
depends only on the unknowns
and the maximization in (
5) is equivalent to
Now, suppose the sequence
is a solution of (5)-(9); then, it also satisfies (13) for
t, as well as (14), (15), (16) and (17). Thus, if the sequences
solve the problem (5)-(9), for
, then by (18) the values (19) are a feasible point of (12)-(17), satisfying also (18), i.e. (19) is a solution of (12)-(17). □
Lemma 3.
Let be a global solution of (5)-(9), for any , where the inequality (8) is replaced by the nonlinear inequality
Then, is also a global solution of (12)-(17), with (16) replaced by
Proof. The proof trivially follows the guidelines of the proof for Proposition 1. □
Lemma 4.
Let be a global solution of (5)-(9), for any , where the inequality (8) is replaced by the nonlinear inequality
and Φ is any convex function. Then, is also a feasible solution of (12)-(17), with (16) replaced by
being .
Proof. The convexity of
and the hypotheses imply
so that
also satisfy (
21). The rest of the proof follows the guidelines of the proof for Proposition 1. □
Remark 1.
Note that from Lemma 4, if the sequences , , are global solutions of (5)-(9) for , then the sequence is a feasible solution but possibly not a global solution of (12)-(17), with (16) replaced by
and .
6.1. A Numerical example
We provide here a very preliminary numerical example where the solution of the formulation (12)–(17) is considered, and the budget constraints (16) are replaced by the unique one (which aggregates possible different budgets at the epoches
)
Since the multi-period formulation is indeed nonlinear and possibly nonconvex, we preferred to preliminarily investigate its solutions through a renowned nonlinear (NLP) solver from the literature. In particular, we adopted Knitro 13.2.0 from the NEOS serve. Nevertheless, we are aware that since the problem might be nonconvex (unless the last property is explicitly proved to hold for (12)–(17)), the choice of the starting point by the NLP solver may be crucial, to both outreach an accurate final solution and to reduce the overall computational burden. The parameters of the two instances we considered are summarized as follows (respectively):
and
We will briefly show that due to the smaller budget (i.e.
) in the first scenario, it yields worse results (i.e. a smaller value of
) with respect to the second one. Indeed, adopting the first set of parameters for our multi-period formulation, Knitro presolver was able to eliminate 403 constraints and 1 variable, so that the final formulation included 395 variables and 660 constraints. Moreover, for the probabilities
we obtained the following nonmonotone sequence (due to the nonlinearity of the multi-period model)
Conversely, adopting the second set of parameters for our multi-period formulation, Knitro presolver was again able to eliminate 403 constraints and 1 variable, yielding for the probabilities the values
Again we observe a nonmonotone behaviour for the sequence , due to nonlinearities of the multi-period model. For the sake of completeness we remark that the solution of the last two nonlinear instances by Knitro required no more than 10 seconds each.
7. Conclusions
We studied the problem of possibly enhancing a standard dynamics from sociophysics (namely the model (
1)), using a mathematical programming perspective. We were interested about following a couple of lines of research. First we coupled the model (
1) with a LP scheme, in order to possibly control the probability
for a given probability
, after leveraging the unknowns
in (
2). The final value of these variables gives a measure of the effort which is required to steer the diffusion process of the opinion + for the subgroups of cardinality
k. The dynamics is strongly based on the idea of possibly maximizing
. A numerical experience is also reported in this regard, showing that the computational effort for solving LPs associated with this first proposal is definitely modest, even in case the solution of large instances is sought.
As a second task, we also extended the (one period) LP formulations to a more general multi-period formulation, being in this case necessary to compute the sequence for a given value of and for a given time horizon T. Some theoretical properties showing a connection between the solutions of both our proposals have been given, though much work yet requires to be carried on, including a wide numerical experience also in the multi-period case.
Funding
G.Fasano wishes to thank the CNR-INM - Institute of Marine Engineering, Italian National Research
Council, and the GNCS group within INδAM, for their support.
References
- Backstrom, L.; Huttenlocher, D.; Kleinberg, J.; Lan, X. Group formation in large social networks: membership, growth, and evolution. In Proceedings of the KDD 2006: The 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 44–54. [Google Scholar]
- Bass, F.M. A new product growth for model consumer durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Ellero, A.; Fasano, G.; Favaretto, D. An application of Linear Programming to Sociophysics Models. In Proceedings of the Modeling and Analysis of Complex Systems and Processes - MACSPro’2020, Venice, Italy, 22–24 October 2020; pp. 23–33. [Google Scholar]
- Ellero, A.; Fasano, G.; Sorato, A. A modified Galam’s model for word-of-mouth information exchange. Physica A 2009, 388, 3901–3910. [Google Scholar] [CrossRef]
- Ellero, A.; Fasano, G.; Sorato, A. Stochastic Model for Agents Interaction with Opinion–Leaders. Phys. Rev. E 2013, 87, 042806. [Google Scholar] [CrossRef] [PubMed]
- Fourer, R. Modeling Languages versus Matrix Generators for Linear Programming. ACM T Math. Softw. 1983, 9, 143–183. [Google Scholar] [CrossRef]
- Fourer, R. AMPL: A Modeling Language for Mathematical Programming, 2nd ed.; Scientific Pr.: San Francisco, CA, USA, 1996. [Google Scholar]
- Galam, S. Modelling rumors: the no plane pentagon french hoax case. Physica A 2003, 320, 571–580. [Google Scholar] [CrossRef]
- Galam, S. Sociophysics: A review of Galam models. Int. J. Mod. Phys. C 2008, 19, 409–440. [Google Scholar] [CrossRef]
- Galam, S. Sociophysics. A Physicists? Modeling of Psycho-Political Phenomena; Springer Science+Business Media: New York, NY, USA, 2012. [Google Scholar]
- Galam, S.; Jacobs, F. The role of inflexible minorities in the breaking of democratic opinion dynamics. Physica A 2007, 381, 366–376. [Google Scholar] [CrossRef]
- Moore, G. Crossing the Chasm; Harper Collins: New York, NY, USA, 1991. [Google Scholar]
- Rogers, E.M. Diffusion of Innovations, 5th ed.; The Free Press: New York, NY, USA, 2003. [Google Scholar]
- Schelling, T.C. Dynamic models of segregation. J. Math. Sociol. 1971, 1, 143–186. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
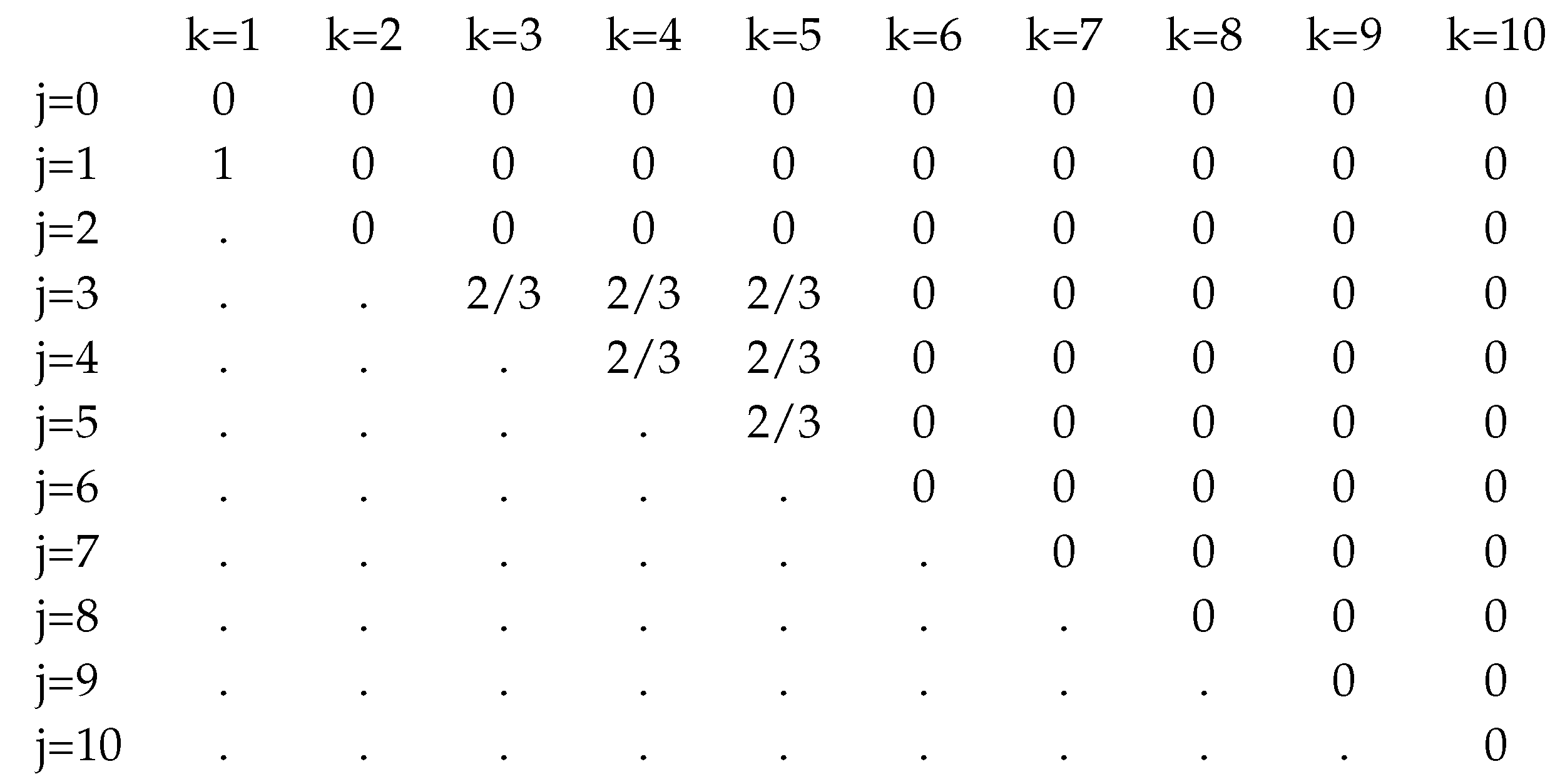
 Note that allowing a larger value of the budget (say ), the solver was able to select a larger number of nonzero unknowns, so that the final value of was almost doubled with respect to the case . In real applications this turns to imply that, in order to obtain almost twice the effect of the previous case, on this instance twice the value of the budget must be allowed.
Note that allowing a larger value of the budget (say ), the solver was able to select a larger number of nonzero unknowns, so that the final value of was almost doubled with respect to the case . In real applications this turns to imply that, in order to obtain almost twice the effect of the previous case, on this instance twice the value of the budget must be allowed.