Prerpints.org logo
Preprint
Article

PCa-Clf: A Classifier of Prostate Cancer Patients into Indolent and Aggressive Using Machine Learning

Altmetrics

Downloads

124

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 July 2023

Posted:

07 July 2023

You are already at the latest version

Alerts
Abstract
Accurately distinguishing between indolent and aggressive tumors is a crucial unmet need in the clinical management of prostate cancer (PCa). The traditional Gleason grading system has been utilized for this purpose; however, there is often ambiguity in classifying tumors with a Gleason grade of 7. Clinicians commonly resort to using secondary Gleason grades, such as 3+4 or 4+3, to classify these tumors as indolent or aggressive, respectively. Unfortunately, such classifications are prone to misinterpretation, leading to erroneous diagnoses and prognoses. To address this challenge, we investigated the application of Machine Learning (ML) techniques to classify PCa patients based on gene expression data sourced from The Cancer Genome Atlas. By comparing gene expression levels between indolent and aggressive tumors, we sought to identify distinctive features for developing and validating a range of ML algorithms and stacking techniques. The stacking based model achieved an impressive accuracy of 96% for all samples encompassing primary Gleason grades 6 to 10. Notably, when excluding Gleason grade 7 from the analysis, the accuracy further improved to 97%. This study underscores the effectiveness of the stacked ML algorithm for accurately classifying indolent versus aggressive PCa. Leveraging gene expression data and employing a combination of classifiers, this approach offers a powerful solution to address the unmet need in robustly distinguishing between different types of PCa tumors. Future implementation of this methodology may significantly impact clinical decision-making and patient outcomes in the management of prostate cancer.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Prostate cancer (PCa) is the most common solid tumor and the second most common cause of cancer death in men in the United States [1]. Treatment decisions for PCa patients are guided by various risk stratification algorithms [2]. These stratification algorithms identify and predict patients at high risk of developing aggressive diseases. Among the parameters used, the most potent predictor of PCa mortality is the Gleason grade (GG) [3,4], which ranges from 6 to 10. The majority of PCa are indolent, presenting GG 6. Thus, these cancers are associated with very low cancer-specific mortality rates, even in the absence of therapy. Localized high-grade (aggressive) with potential lethal PCa presents GG: 8 to 10. These tumors are aggressive, progress rapidly to metastatic disease, and are often lethal. Intermediated grade PCa presents GG 7. These cancers present a much more variable clinical course, with some behaving like GG 6 and others behaving like GG 8-10. Although current stratification protocols are moderately effective, significant challenges remain in classifying PCas into Indolent versus Aggressive tumors. A critical unmet need in the clinical management of prostate cancer (PCa) is the lack of algorithms to accurately distinguish truly indolent from aggressive tumors. Therefore, there is an urgent need for the development of algorithms that could accurately distinguish truly indolent cancers that could be safely monitored from aggressive cancers with lethal potential that could be prioritized for treatment.
PCa screening using the prostate-specific antigen (PSA) has led to earlier detection of PCa, with fewer men today presenting with metastatic disease [5]. However, although PSA has reduced mortality rate, it has also resulted in unintended consequences. The unintended consequences include over-diagnosis, which leads to overtreatment of patients with indolent PCa, which causes no harm even without treatment, and under-treatment of patients with aggressive disease. Concerns about PSA-based screening led to the U.S. Preventive Services Task Force issuing a D-grade recommendation for its use in 2012 [6]. Importantly, a U.S. Preventive Services Task Force review concluded that PSA-based screening results in either small or no reduction in prostate cancer-specific mortality [7]. PSA screening is also associated with harms related to subsequent treatments and evaluation - some of which may be unnecessary. These concerns have heightened the need to develop novel risk stratification algorithms to identify patients at high risk of developing aggressive tumors, which could be prioritized for treatment, and the discovery of molecular markers separating truly indolent tumors from aggressive tumors with lethal potential.
To address this critical unmet medical need, we propose the use of machine learning (ML) models for the classification of PCa patients into two groups: those with genuinely indolent tumors, which could be safely monitored, versus those with aggressive tumors, which could be prioritized for treatment, using gene expression data. Implementing ML promises to stratify patients more accurately and thus could guide therapeutic decision-making and eliminate the unintended consequences resulting from current protocols. Our working hypothesis is that genomic alterations in patients diagnosed with indolent and aggressive tumors could lead to measurable changes distinguishing the two patient groups. Thus, applying ML to genomics data would accurately distinguish the two patient groups. We addressed this hypothesis using gene expression data on patients diagnosed with indolent and aggressive PCa from The Cancer Genome Atlas (TCGA).

2. Experimental Materials and Methods

2.1. Source of Transcriptome and Clinical Datasets

We used publicly available gene expression and clinical data on indolent and aggressive PCa from the TCGA generated using RNA-Sequencing. The data were downloaded from the Genomics Data Commons portal using the data transfer tool [8]. Because the same TCGA barcode structure was used for both clinical data and transcriptome data, we used the barcode structure to integrate patient-based clinical data with sample-based genomics data [8]. The original gene expression data set included N = 547 samples distributed as follows: N = 45 samples as indolent (GG=6), 246 samples as intermediate (GG=7), 204 as aggressive with lethal potential (GG 8-10), and 52 control samples. After annotating gene expression data with clinical information, we used the American Urological Association classification protocol [9] to verify and validate tumor classification according to GG because GG =7 follows a variable clinical course. We used the protocol to assign the tumors to either indolent or aggressive consistent with the guidelines [10]. The tumor samples were either classified as 3 + 4 (primary + secondary) and assigned to GG =6 as indolent or 4 + 3 (primary + secondary), which are assigned to GG = 8-10 as aggressive; consistent with current classification guidelines [10].

2.2. Data Processing and Analysis for Gene Selection

We performed data quality control and processing steps on gene expression data containing 60,483 probes across 547 samples. We implemented counts per million (CPM) filter (>0) in R using the edgeR library to remove the rows with missing data (i.e., zero or very low gene expression values), such that each row had at least ≥ 30% data [11]. After applying the filter, the resulting dataset had 34,956 probes across 547 samples. 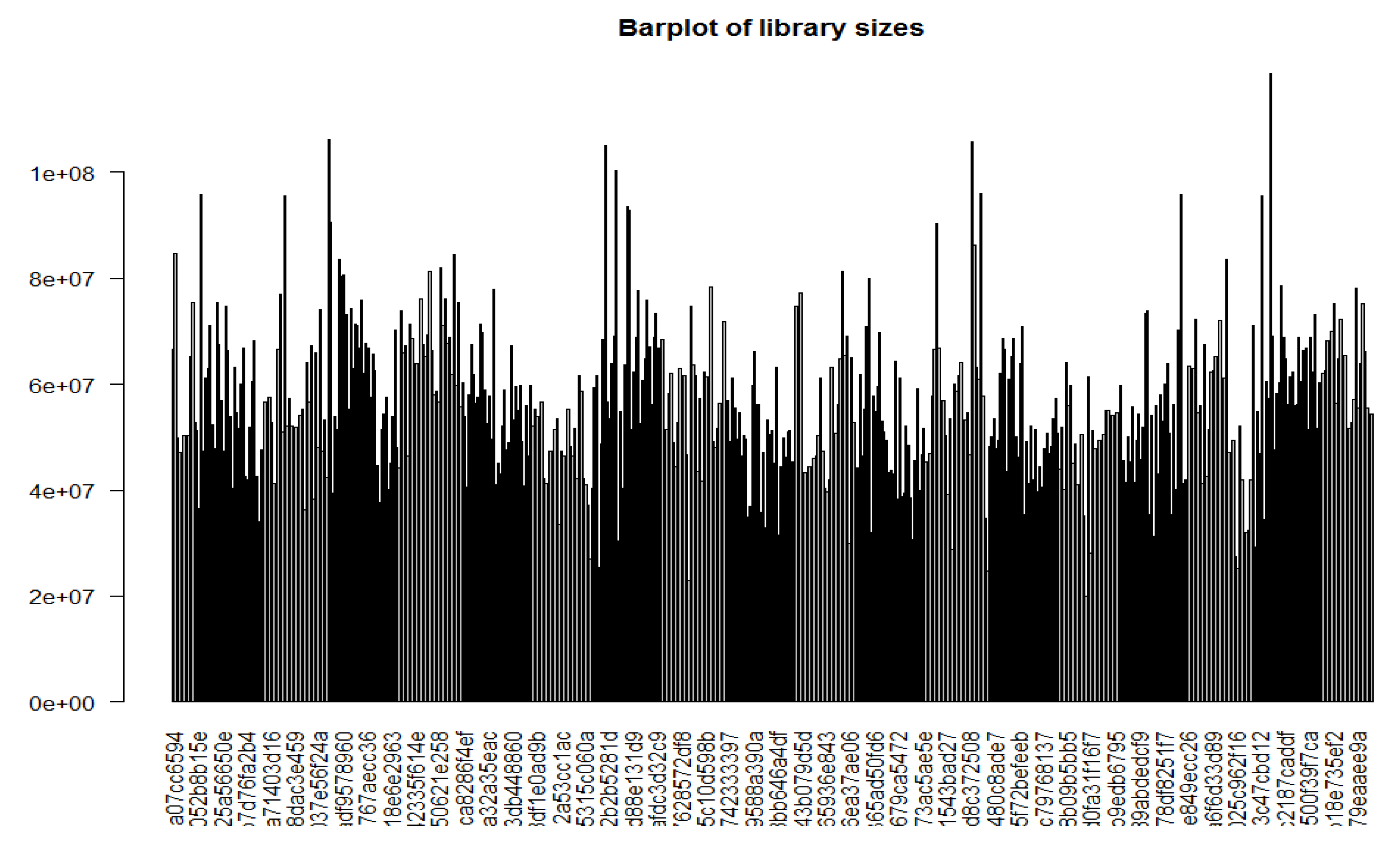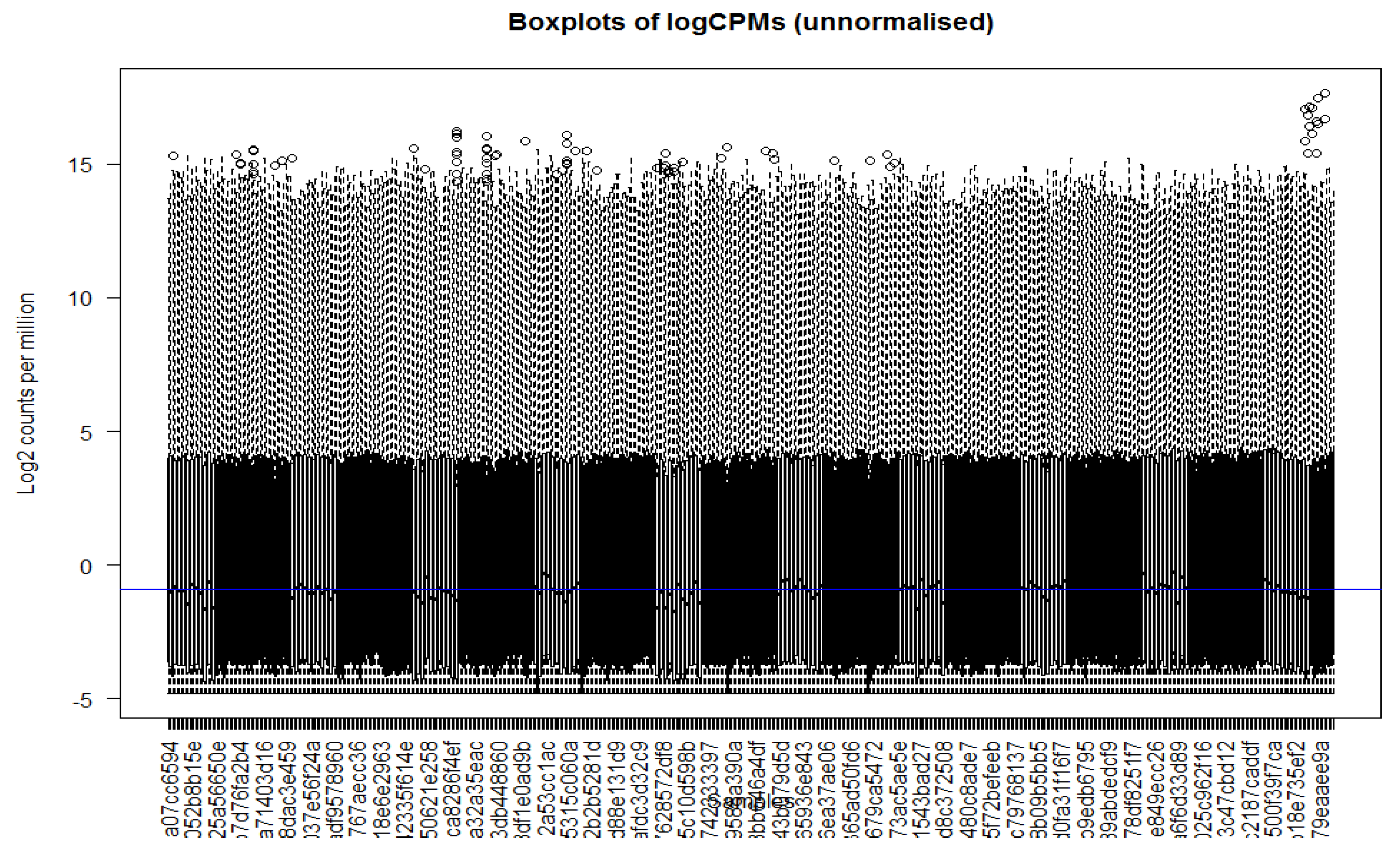In Figure 1, all the library sizes of samples in TCGA data are expressed using a barplot to see any major discrepancies between samples. It shows that the data quality is not good and is not normally distributed. As part of initial the normalization process, we applied a log scale transformation to the counts matrix. This scaling technique is commonly used to address the inherent variability and dynamic range of gene expression data. By applying the log transformation, we aimed to achieve a more balanced and comparable distribution of gene expression values across samples. Here, we used box plots to check the distribution of the read counts on the log2 scale. To address variations in library sizes among the samples containing gene expression data, we employed the cpm function to correct the data. This function calculates the log2 counts per million (log2 CPM) values, taking into account the total library size for each sample. Additionally, a small offset was added to the log2 CPM values to mitigate the issue of excessive zeros in the dataset. Figure 2 represents the boxplots of logCPM (log counts per million) before normalization.
Composition biases were eliminated between libraries and generated a set of normalization factors (the product of the library sizes and factors defining the effective library size) using the Trimmed Mean of M-values (TMM) [11]. This was implemented in R before performing statistical tests. We used 2 levels of analysis for gene selection (see sections 2.2.1 and 2.2.2). 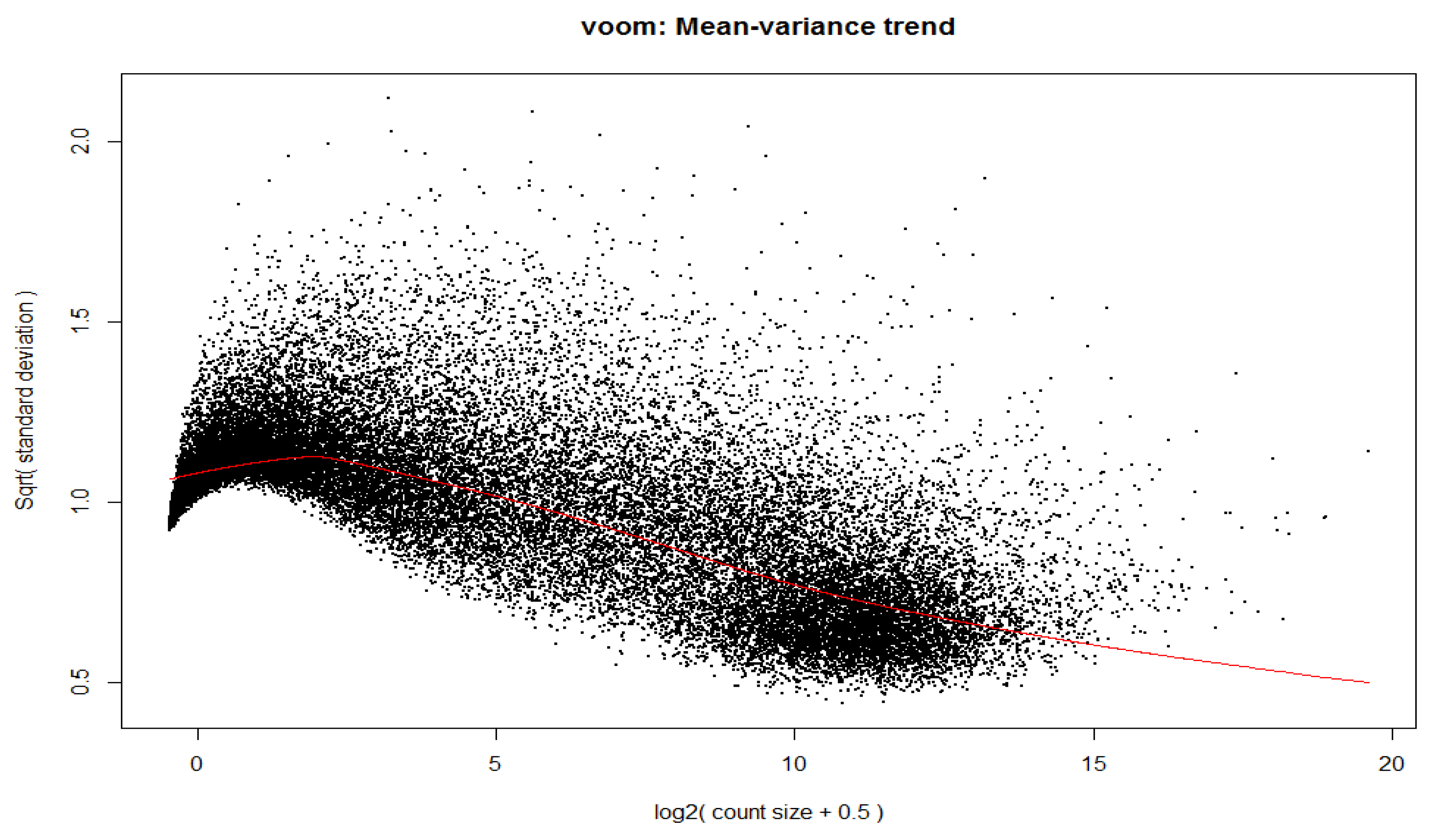Since there are many pipelines to analyze RNA-Seq data, we used a popular pipeline, the Limma package implemented in R, which offers the Voom function that transforms the read counts into logCPMs [12]. We then performed a Voom transformation and generated a mean-variance trend plot (shown in Figure 3). 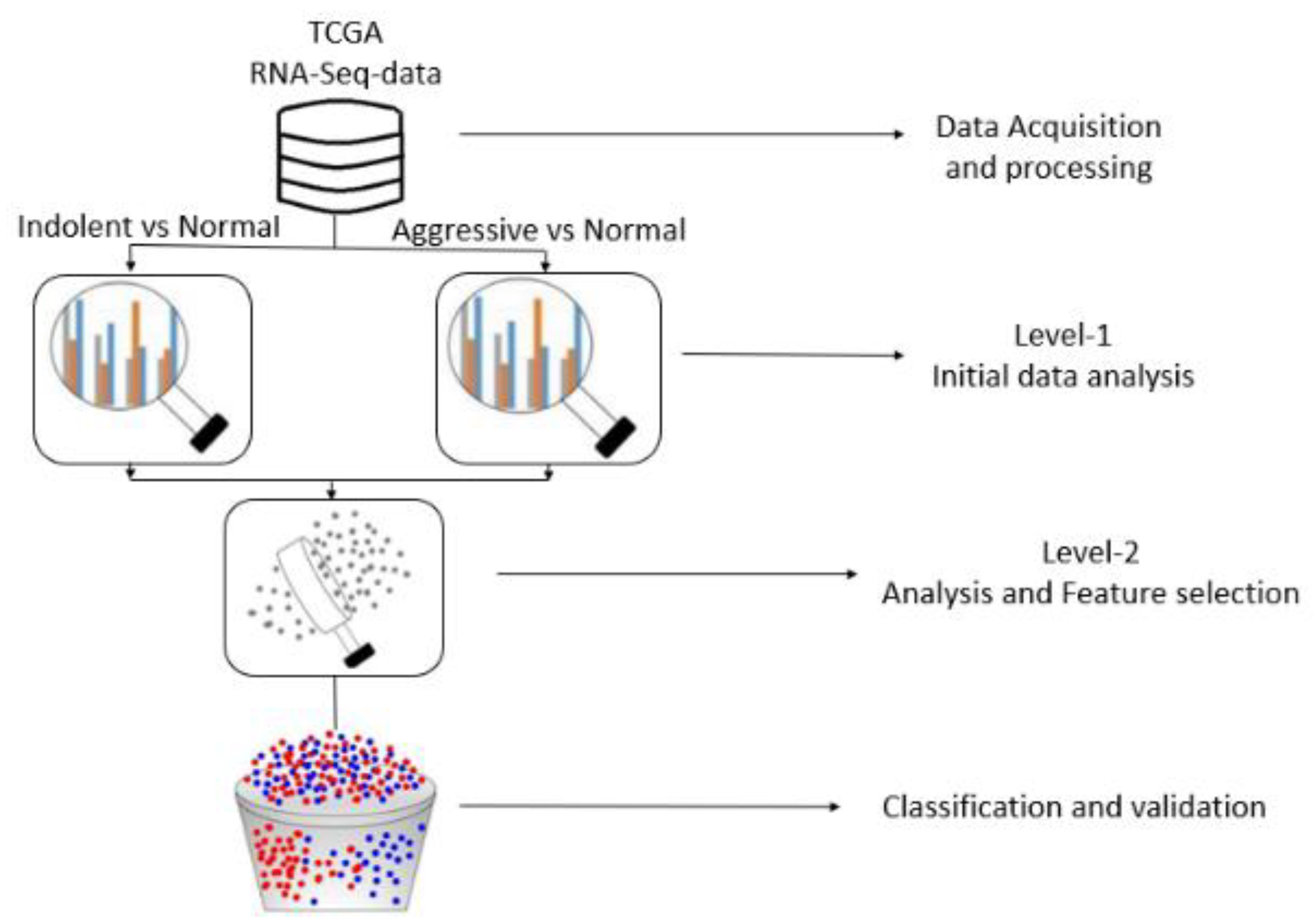Figure 4 depicts the study design and execution workflow flowchart of our project. This visual representation provides an overview of the key steps and processes involved in the project's methodology.

2.2.1. Level 1 Analysis

Using normalized data in R [13], we performed a level-1 analysis comparing gene expression levels between tumor samples and controls for indolent and aggressive PCa separately using the Limma package in R. We used this baseline analysis to discover a signature of genes significantly (p < 0.05) associated with each type of disease. A volcano plot was used to visualize the results. We used the false discovery rate (FDR) procedure to correct for multiple hypothesis testing [14]. The probes were ranked on p-values and –log fold change (-log FC). Significantly differentially expressed genes/probes between tumors and controls were considered to be associated with each type of PCa.

2.2.2. Level 2 Analysis

In level 2 analysis, we created a data set of genes significantly associated with both indolent and aggressive PCa. We performed several analysis strategies on the combined data set to identify significantly differentially expressed genes distinguishing indolent from aggressive PCa. First, we compared gene expression levels between patients with Gleason grade 6 and Gleason grade 8-10. Additionally, we compared gene expression levels between patients with Gleason grade 6, 7 (3+4) and patients with Gleason score 8-10, 7 (4+3). We also compared gene expression levels between patients presenting with Gleason grade 7, comparing gene expression levels between patients with Gleason grade 3+4 and patients with Gleason grade 4 + 3 separately. We used the FDR procedure for all the analyses to correct multiple hypothesis testing. The genes were ranked on p-values and –log fold change (-log FC). Significant genes, which are differentially expressed between disease states, were used as the features in the development and implementation of classification algorithms.

2.2.3. Feature Selection and Implementation of ML Algorithms

Developing, applying, and evaluating ML classifiers involved selecting probes/genes or features from gene expression data analysis using different cutoffs. The cutoffs were determined by the p-values and logFC values of significant genes identified in the analysis. We selected features at different threshold levels, abs(logFC) > 0.5, 0.7, 1, 1.5, and 2 to test and validate the classification algorithms. Using the Machine Learning literature, we selected five classifiers in Weka with different fundamental approaches: Logistic Model Tree (LMT), MultiClassClassifier, Stochastic Gradient Decent (SGD), Sequential Minimal Optimization (SMO), SimpleLogistic. We used the platform Weka 3.8.2 software [15] to implement the algorithms. We used a 10-fold cross-validation technique on all mentioned subsets to prevent overfitting, with metrics averaged over all 10 folds and tested on each classifier.
Apart from traditional feature selection using logFC and p-value, we also implemented a Genetic algorithm to extract important features from a subset (abs(logFC) > 0.5). Using this set of features, we tested the below classifiers obtained from scikit-learn package individually and the stacking technique [16,17,18,19,20,21].
(1)
Support Vector Machine (SVM).
(2)
Logistic Regression (LR).
(3)
Random Decision Forest (RF).
(4)
Extra Tree Classifier (ETC).
(5)
Gradient Boosting Classifier (GBC).
(6)
K nearest neighbor (KNN).
(7)
eXtreme Gradient Boosting (XGB).

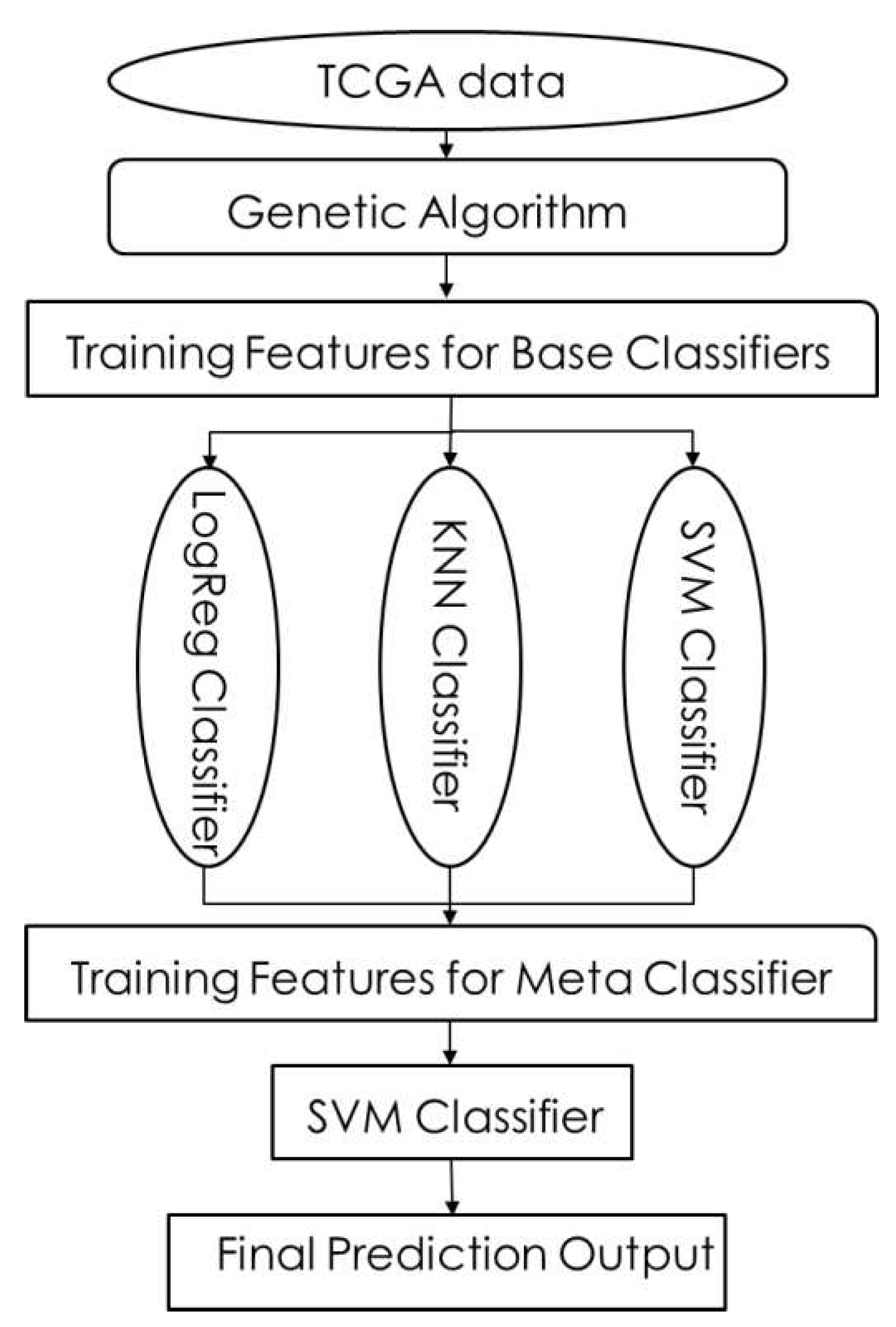
2.3. Stacking

In this investigation, we used the stacking technique to reduce the generalized error rate and increase the accuracy by combining the prediction probabilities [16,17,18,19,20,21].
There are two stages of learners in stacking. The first stage of classifiers is known as base classifiers, and the second stage of classifiers is considered meta classifiers. To find the meta classifiers and base classifiers to use in the second and first stages of the stacking framework, we examined seven different machine learning algorithms mentioned in the above section.
i) Support Vector Machine (SVM): SVM [22] is a machine learning classifier, which is defined by a separating hyperplane. The Support Vector Machine algorithm finds a hyperplane in an N-dimensional space that classifies each data point (where N is the number of features). Hyperplanes help in classifying data points and depend upon the number of features. If the number of features in a dataset is 2, then the hyperplane is just a line. If the number of features in a dataset is 3, then the hyperplane is a plane. If the number of features is greater than 3, then it would be difficult to imagine a hyperplane.
ii) Logistic Regression (LR): Logistic Regression [23] is a technique for analyzing data that determines the dependent output (outcome) when there are one or more independent variables. In several cases, the outcome variable (dependent) is a dichotomous variable in which there are only two possible outcomes. The goal is to find the best fitting model to describe the relationship between the dependent variable and the set of independent variables. The logistic sigmoid function is used to return a probability value by transforming the output, which can be mapped to discrete classes. Regularization techniques are used to avoid overfitting (any modification made to a learning algorithm is intended to reduce the generalization error).
iii) Random Decision Forest (RF): Random decision Forest [24] is a supervised machine learning algorithm that randomly creates and merges more than one decision tree into a forest. During training time, RF algorithm operates by constructing a multitude of decision trees and outputting the class that is a classification or mean prediction (regression) of individual trees. It adds additional randomness to the model of growing the trees. The best feature is searched among a random subset of features instead of searching for the most crucial feature while splitting a node. Random decision forests are an effective approach for mitigating the issue of overfitting to the training dataset. This technique addresses overfitting by constructing multiple decision trees on different subsets of the dataset. The collective predictions of these trees are then combined to form a mean prediction, which improves the overall accuracy of the forest and helps prevent overfitting.
iv) Extra Tree Classifier (ETC): The Extra Tree [25] method is also known as extremely randomized trees. An Extra Tree classifier’s main objective is to randomize the input features of a tree, where the large proportion of the variance of the induced tree depends on the choice of optimal cut-point. It constructs randomized decision trees from the original learning samples and uses the above-average decision to improve accuracy and avoid over-fitting. The method selects a cut point at random and drops the idea of using bootstrap copies of the training sample. Cut-point randomization often reduces the variance when the bootstrapping idea is dropped and can also lead to an advantage in terms of bias. This method has yielded state-of-the-art results in high-dimensional complex problems.
v) Gradient Boosting Classifier (GBC): GBC [26] is a machine learning technique used for classification and regression problems. It builds a model in a forward stage-wise fashion like other boosting methods. It allows for optimizing arbitrary differentiable loss functions. It involves three elements: (a) a loss function to be optimized, (b) a weak learner to make predictions, and (c) an additive model to add weak learners to minimize the loss function. The Gradient boosting classifier’s main objective is to minimize the model’s loss by adding weak learners in a stage-wise fashion using a similar procedure of Gradient descent. While adding a new weak learner, the existing weak learners in the model remain unchanged. To correct or improve the final output, the output of a new learner is added to the existing sequence of learners.
vi) K Nearest Neighbors (KNN): K nearest neighbor [27] is an algorithm that classifies new cases based on a similarity measure of all stored available instances. It has been used as a non-parametric statistical estimation and pattern recognition technique. A case is assigned to the common class among the K nearest neighbors, measured by a distance function and classified by a majority vote of its neighbors. If k=3, then the class is assigned to a class of its three nearest neighbors.
vii) eXtreme Gradient Boosting (XGB): The implementation of eXtreme Gradient Boosting [28] offers several advanced features for model tuning, algorithm enhancement, and computing environments. It can perform in three different forms of gradient boosting (Gradient Boosting (GB), Stochastic Gradient Boosting (GB), and Regularized Gradient Boosting (GB)). It is strong enough to support fine-tuning and the addition of regularization parameters. It uses the regularized model formalization to avoid overfitting and results in better performance. Moreover, XGB trains faster compared to other methods.
We performed five different stacking models listed below. The models were built and optimized using Scikit-learn [29]. We used 3 different models, as explained earlier in this section. The below-mentioned stacking models (SM-1, SM-2, SM-3, SM-4, and SM-5) were performed using two different datasets.
(1)
SM-1: LR, KNN, SVM as Base, SVM as Meta-classifier.
(2)
SM-2: LR, SVM, KNN, XGB as Base, XGB as Meta-classifier.
(3)
SM-3: LR, KNN, SVM as Base, XGB as Meta-classifier.
(4)
SM-4: RDF, LR, KNN as Base, GBC as Meta-classifier.
(5)
SM-5: RDF, LR, GBC as Base, KNN as Meta-classifier.

2.4. Model Selection and Correlation between ML and GG = Validation

To address our working hypothesis that genomic alterations in patients diagnosed with Indolent and aggressive tumors could lead to measurable changes distinguishing the two patient groups, we implemented 3 models to find and classify the crucial part of our hypothesis GG:7 (a grey area).

2.4.1. Model 1

In this model, we selected all the samples with Gleason Grade (6 and 3+4 indolent) versus (8-10 and 4+3 aggressive) for all log-fold change values (0.5, 0.7, 1, 1.5, and 2). Note that we assumed the samples with Gleason Grade: 7 (3+4) belong to Indolent and 7(4+3) belong to aggressive PCa. We applied the above machine learning algorithms (see section 2.2.3) to evaluate the classification of GG.

2.4.2. Model 2

Here, we used the samples with Gleason Grade (6 and 8-10) for all log-fold change values (0.5, 0.7, 1, 1.5, 2). We removed samples with GG=7 and trained Gleason Grade: 6 (Indolent) versus Gleason Grade 8, 9, and 10 (Aggressive) tumors using ML classifiers.

2.3. Model 3

This model used the samples with Gleason Grade (7) for all log-fold change values (0.5, 0.7, 1, 1.5, 2). We trained Gleason Grade: 7 (3+4) indolent versus Gleason Grade: 7 (4+3) aggressive tumors using the ML classifiers. Since we assumed GG: 7 as a grey area, we tried to use Model 2 as training and correctly classify samples with GG: 7 as a test set.

3. Performance Evaluation

We evaluated the performance of ML classifiers based on the results in 2 ways –
  • We created a set of classifier performance evaluation matrics with their names and definitions mentioned in Table 1 below.
  • We used the Principal component analysis (PCA) plot to check if the samples are correctly classified as Indolent and Aggressive. We should see a clear separation of samples in the plot if the classifiers predicted them correctly.

4. Results

From Figure 1 and our hypothesis, we assumed the crucial part GG: 7 is the grey area, leading to measurable changes between two patient groups. Implementing ML would accurately distinguish this grey area. As per section 2.4, we will compare 3 models with level 1 and level 2 analysis.

4.1. Level 1 Analysis

In the Level 1 analysis, we separately compared gene expression levels between tumor samples and controls for indolent and aggressive PCa.
  • This initial level-1 analysis for model 1 yielded 18,215 significantly (p < 0.05) and 21,042 significantly (p < 0.05) differentially expressed probes associated with Indolent and aggressive PCa, respectively. We used the Volcano plot (Figure 5) to discover a signature of genes significantly (p < 0.05) associated with each type of PCa.
  • This initial level-1 analysis for model 2 yielded 15,105 significantly (p < 0.05) and 20,712 significantly (p < 0.05) differentially expressed probes associated with Indolent and Aggressive PCa, respectively. We used the Volcano plot (Figure 6) to discover a signature of genes significantly (p < 0.05) associated with each disease state.
  • The initial level-1 analysis for model 3 yielded 5220 significantly (p < 0.05) and 3352 significantly (p < 0.05) differentially expressed probes associated with Indolent and Aggressive respectively. We then compared Indolent and Aggressive using the differentially expressed probes from earlier analysis and used the Volcano plot (Figure 7) to discover a signature of genes significantly (p < 0.05) associated with each disease state.

4.2. Level 2 Analysis

We used LogFC cutoff for all the models from level 1 analysis, and the significant probes were then matched to the corresponding gene symbols obtained from the Ensemble Biomart database. This analysis resulted in a certain number of genes mentioned in Table 2. These genes were used as features in the downstream analysis in level-2 and machine learning classification. Overall, the results confirmed our hypothesis that genomic alterations in patients diagnosed with indolent and aggressive tumors could lead to measurable changes distinguishing the two patient groups.

4.3. Classification Results

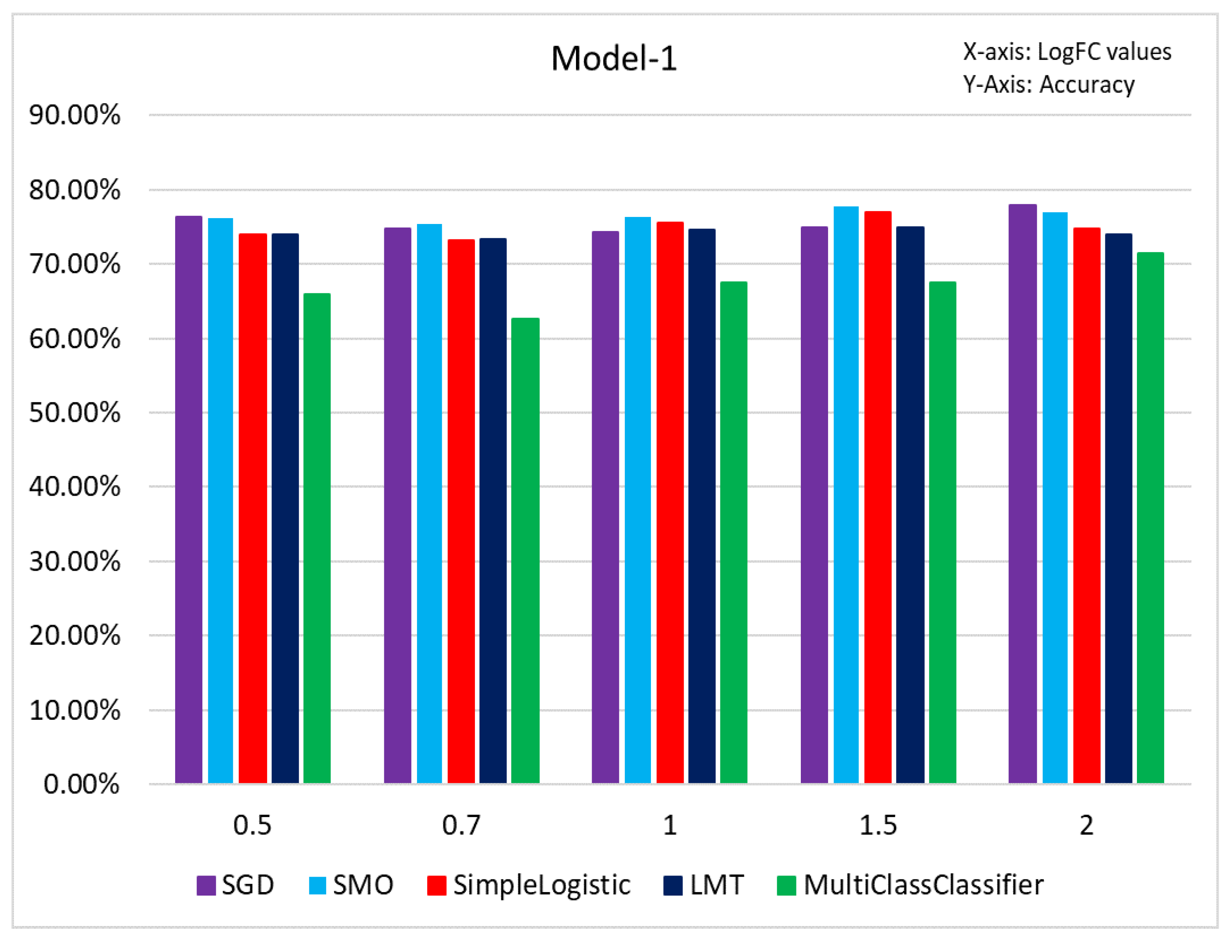
4.3.1. Model 1 Result:

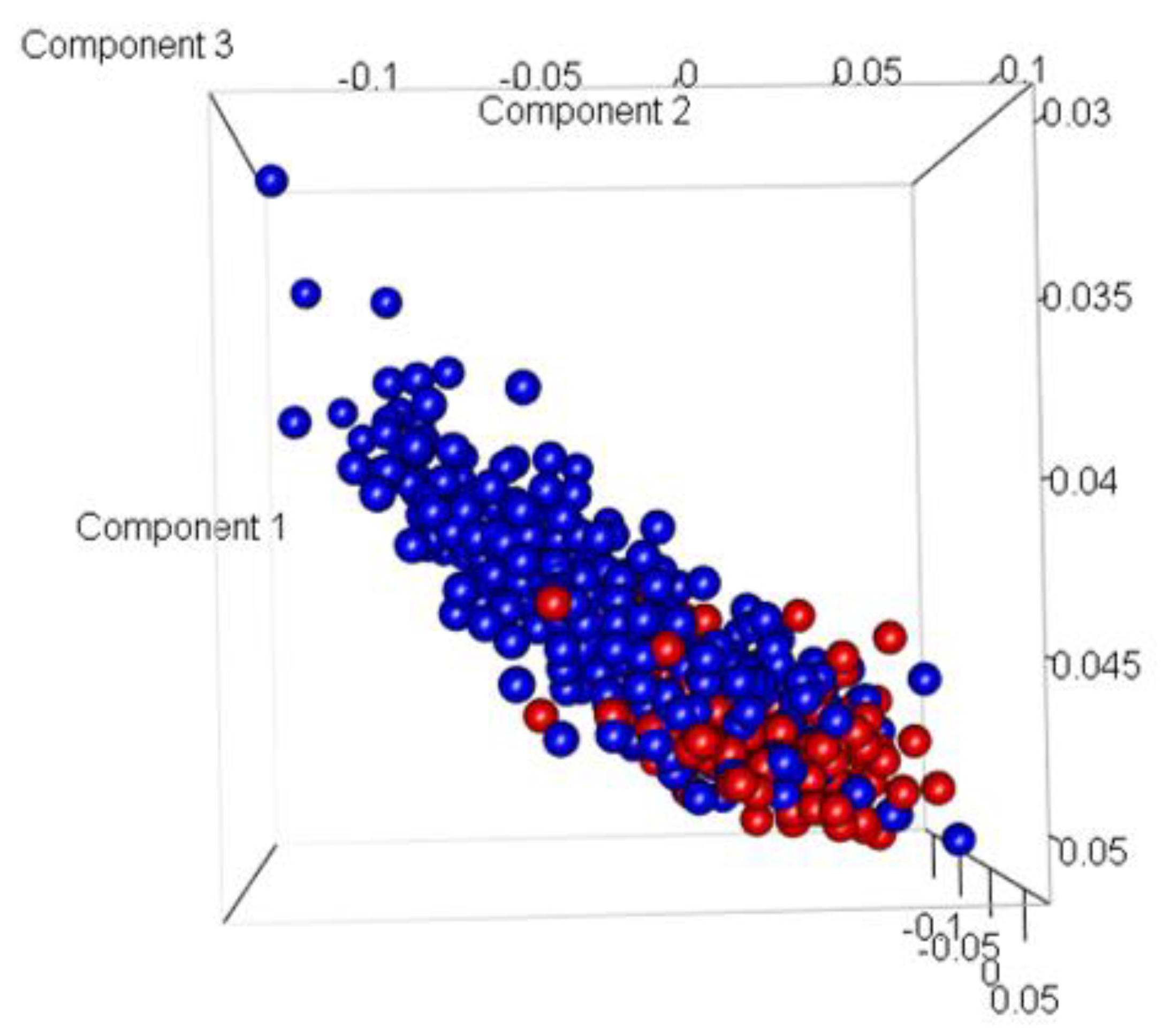
In this section, we selected all the samples with Gleason Grade (6, 7, 8, 9, 10) and applied ML classifiers at different threshold levels, abs(logFC) > 0.5, 0.7, 1, 1.5, and 2. The results of this investigation are presented in Figure 8. The SGD classifier achieved the highest accuracy for LogFC: 2 with 78.18%. MultiClassClassifier achieved the lowest accuracy for LogFC: 0.7, with 62.63%. 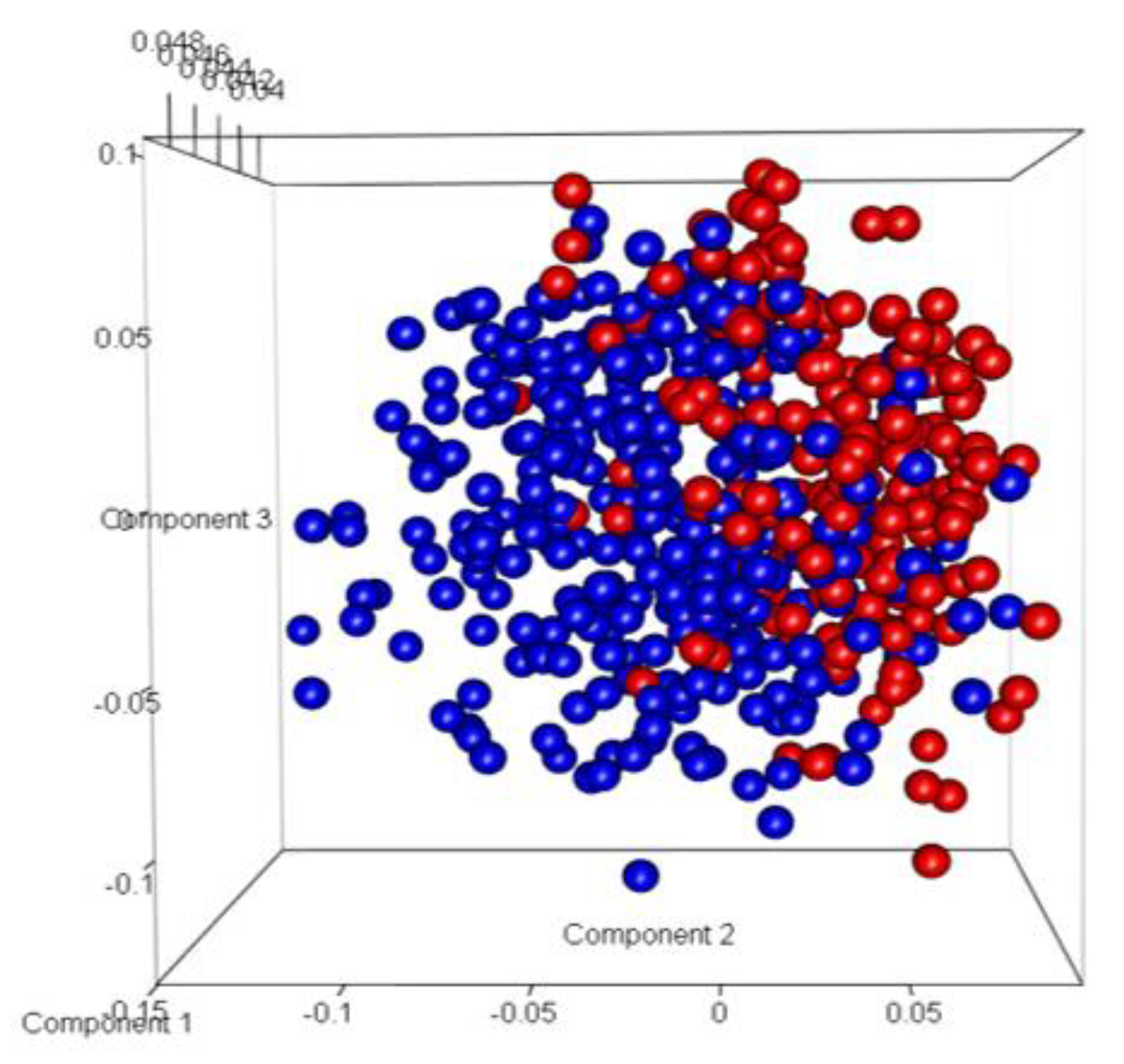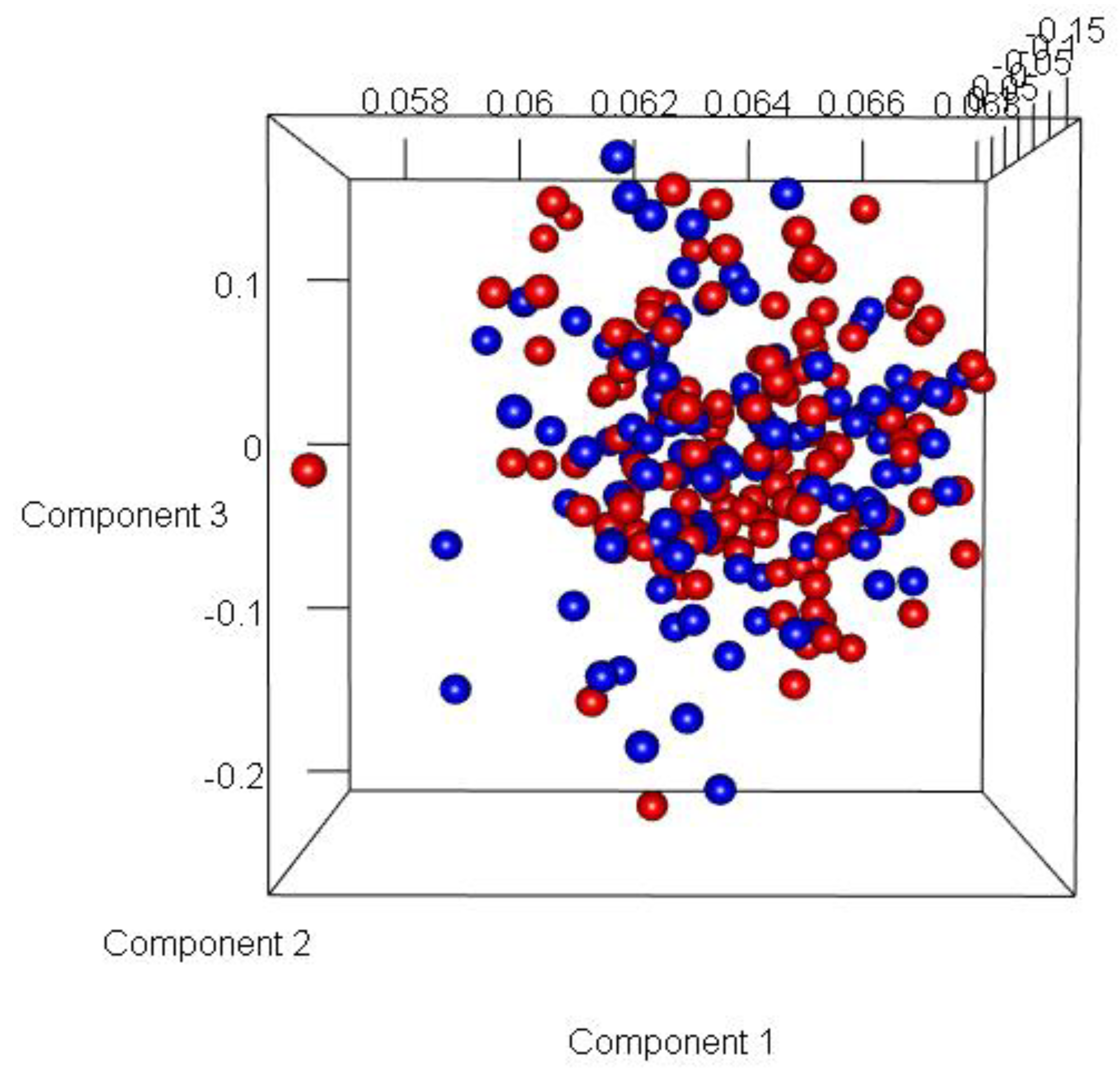Using the PCA plot to check if the samples were correctly represented as Indolent and Aggressive revealed a mixture and misclassification of samples (Figure 9). Most of the misclassification was attributed to GG =7.

4.3.2. Model 2 Result:

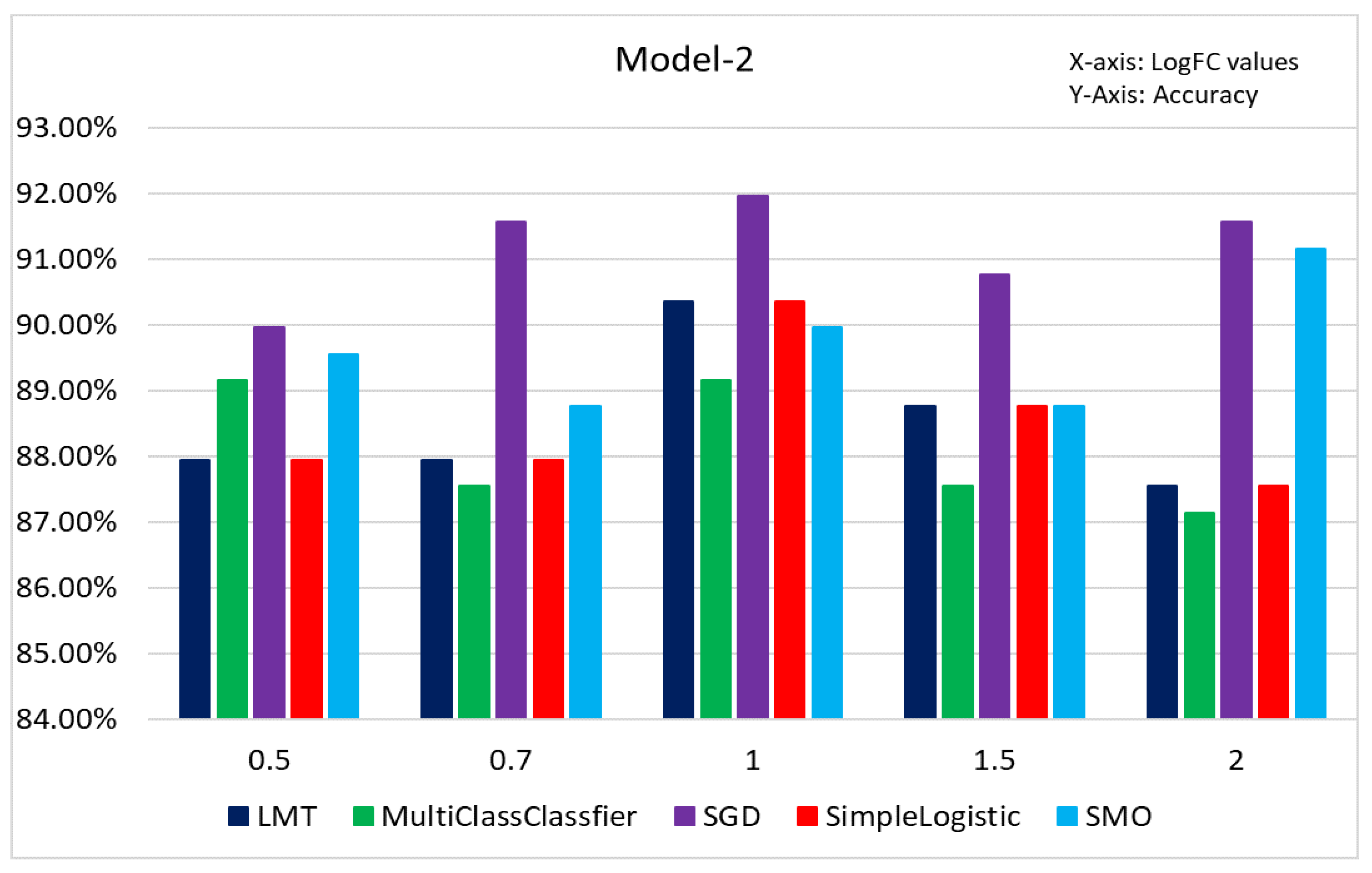
To address misclassification and improve the accuracy, we removed the samples with GG: 7 and applied machine learning classifiers to the rest of the samples (GG 6 versus GG 8-10) with different LogFC cutoffs. The results of this investigation are presented in Figure 10. The accuracy is improved significantly, and the misclassification error is reduced.
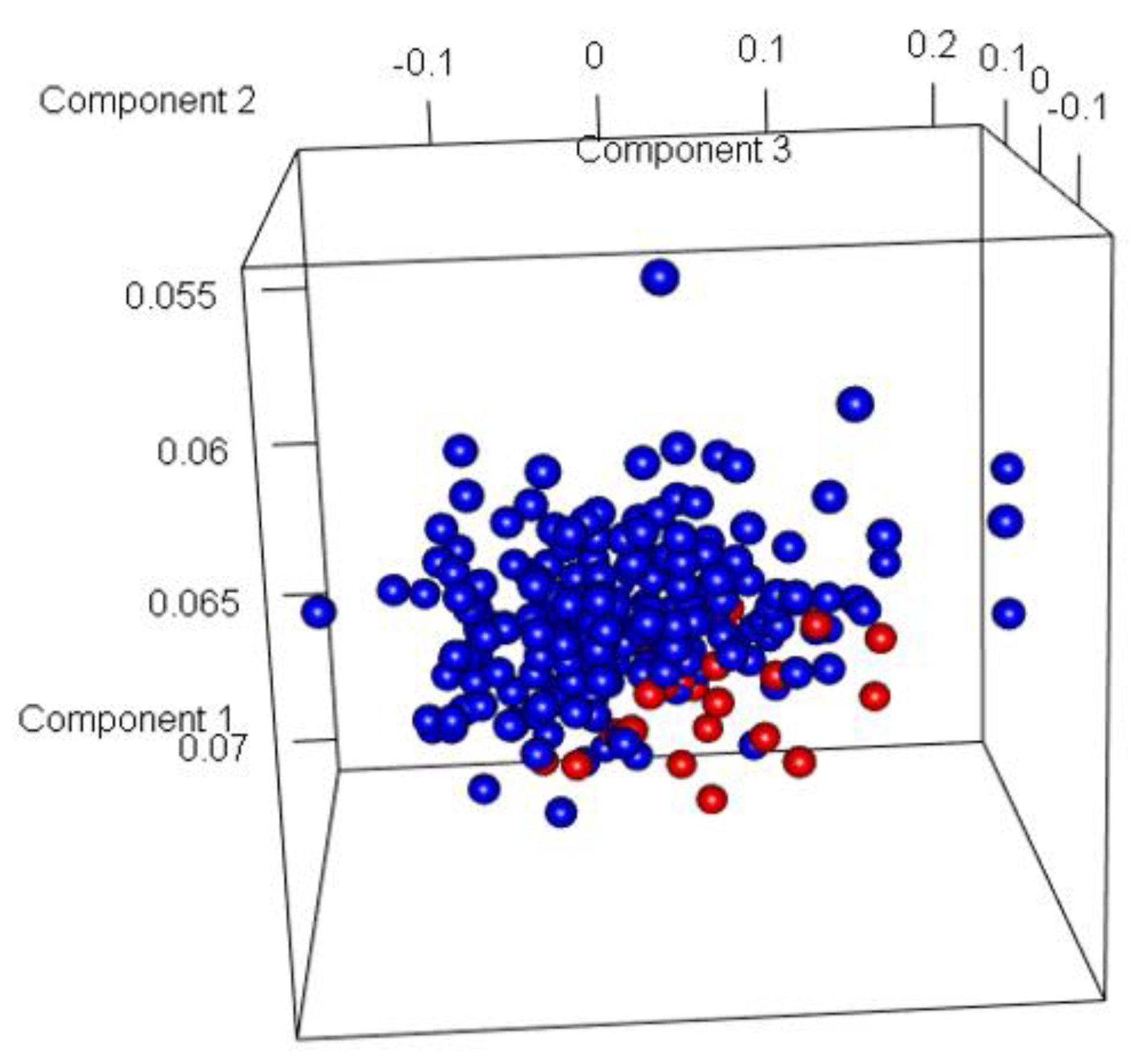
The SGD classifier obtained the highest accuracy for LogFC 1 at 91.97% and MultiClassClassifier with the lowest for LogFC 2 at 87.15%. PCA analysis (Figure 11) revealed that most of the samples with GG: 6, 8, 9, and 10 were correctly classified. Model 2 produced significantly higher accuracy and lower misclassification rates than Model 1.

4.3.3. Model 3 Result:

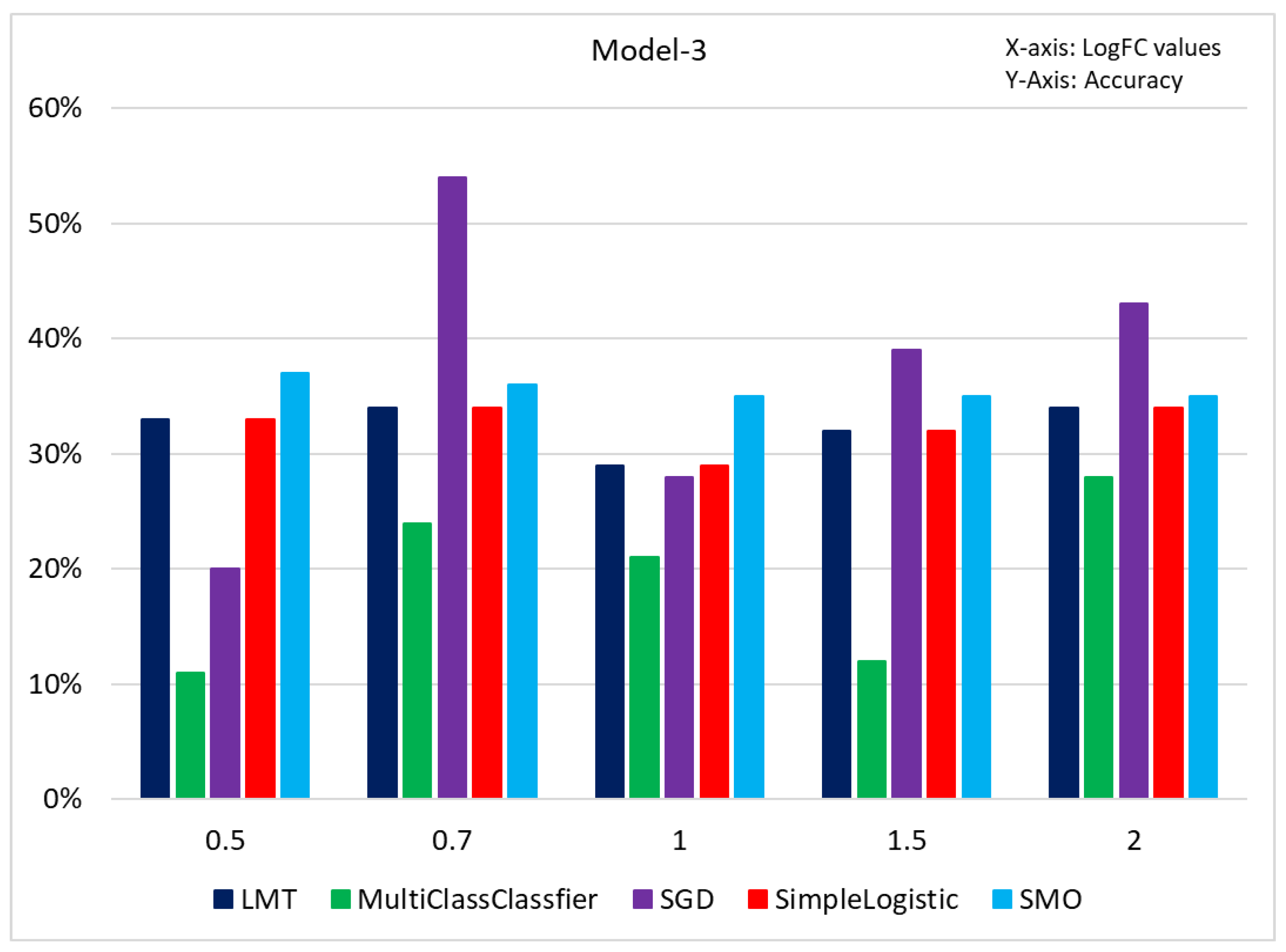
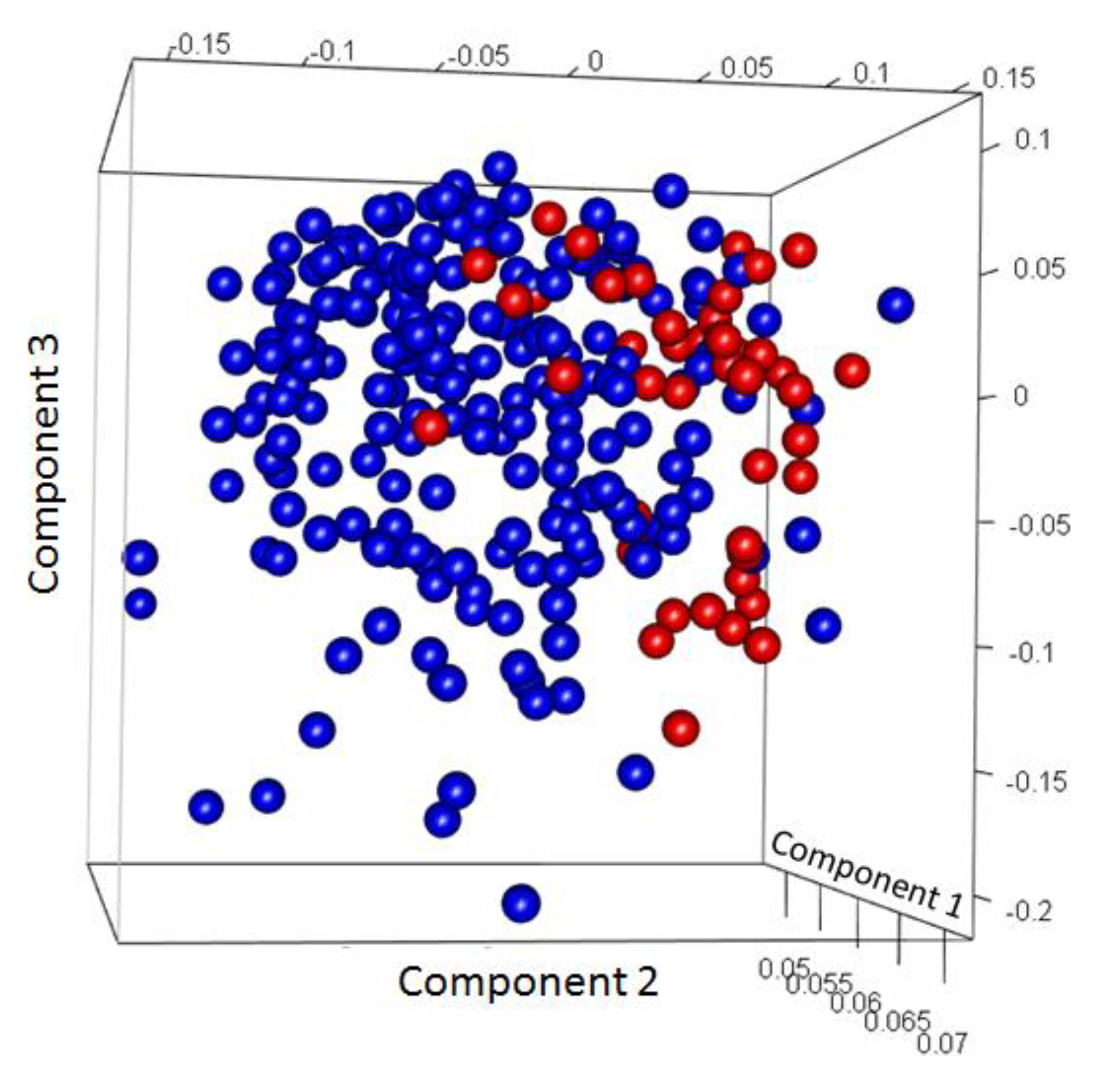
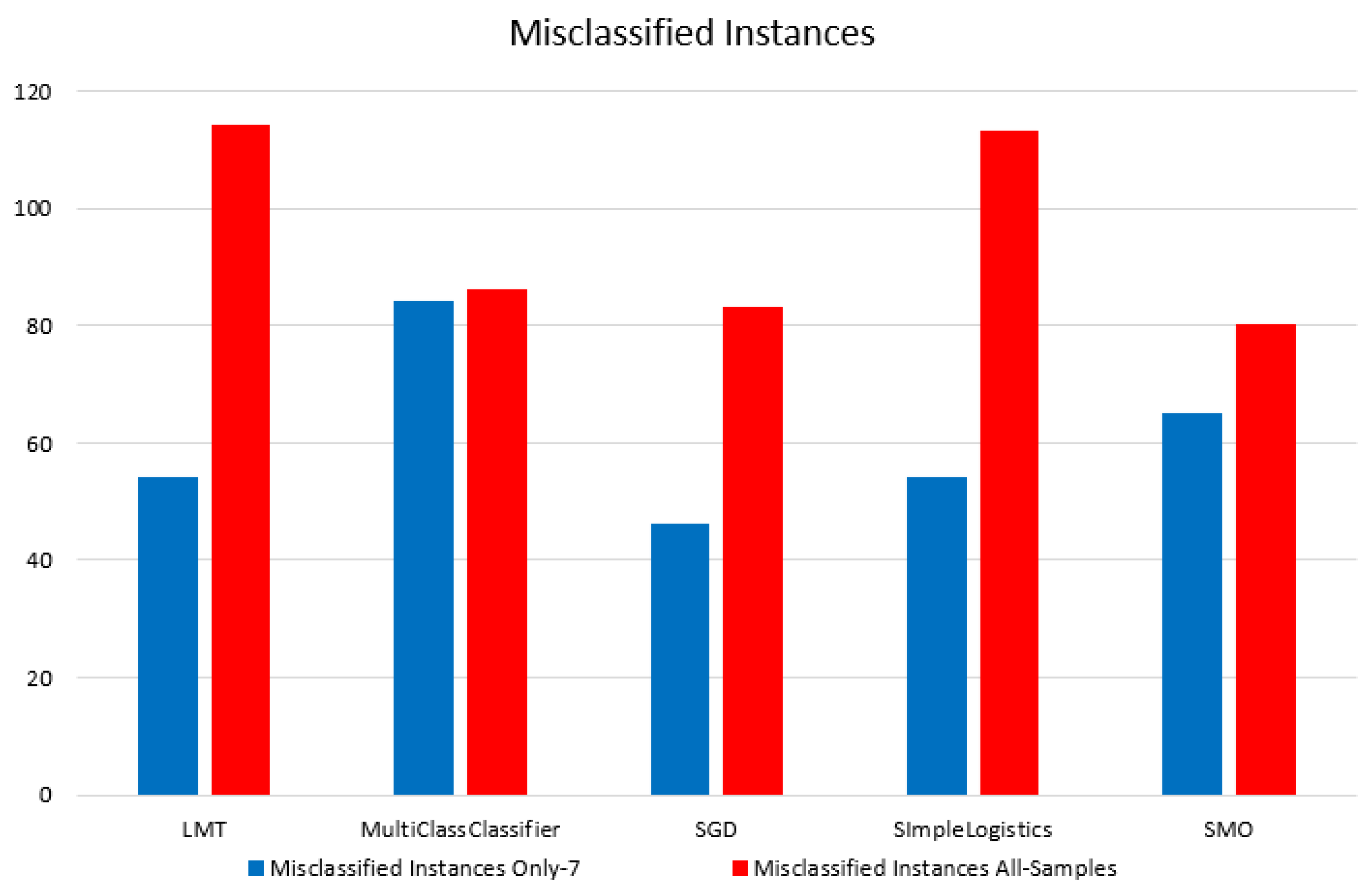
To further address the misclassification problem for samples with GG: 7, we applied machine learning classifiers to 3+4 Versus 4+3 samples using the same cutoffs as shown in the previous two models. The results of this investigation are presented in Figure 12. The accuracy was significantly lower, and the misclassification rate increased. PCA analysis (Figure: 13) revealed that most of the samples with GG: 7 were misclassified. Overall, the results of model 3 produced significantly lower accuracy and higher misclassification rates compared to Models 1 and 2, further confirming the part of our hypothesis that high misclassification was attributable to GG: 7.
As we hypothesized that GG: 7 is causing misclassification, we applied 10-fold-cross validation for all mentioned ML classifiers to samples with GG: 7 at different threshold levels, abs(logFC) > 0.5, 0.7, 1, 1.5, and 2. The highest and lowest accuracy was obtained by the SGD classifier for LogFC 0.7 with 54% and by MultiClassClassifier for LogFC 0.5 with 11%, respectively. Figure 14 shows that model 3 is misclassified compared to model 1 and model 2.
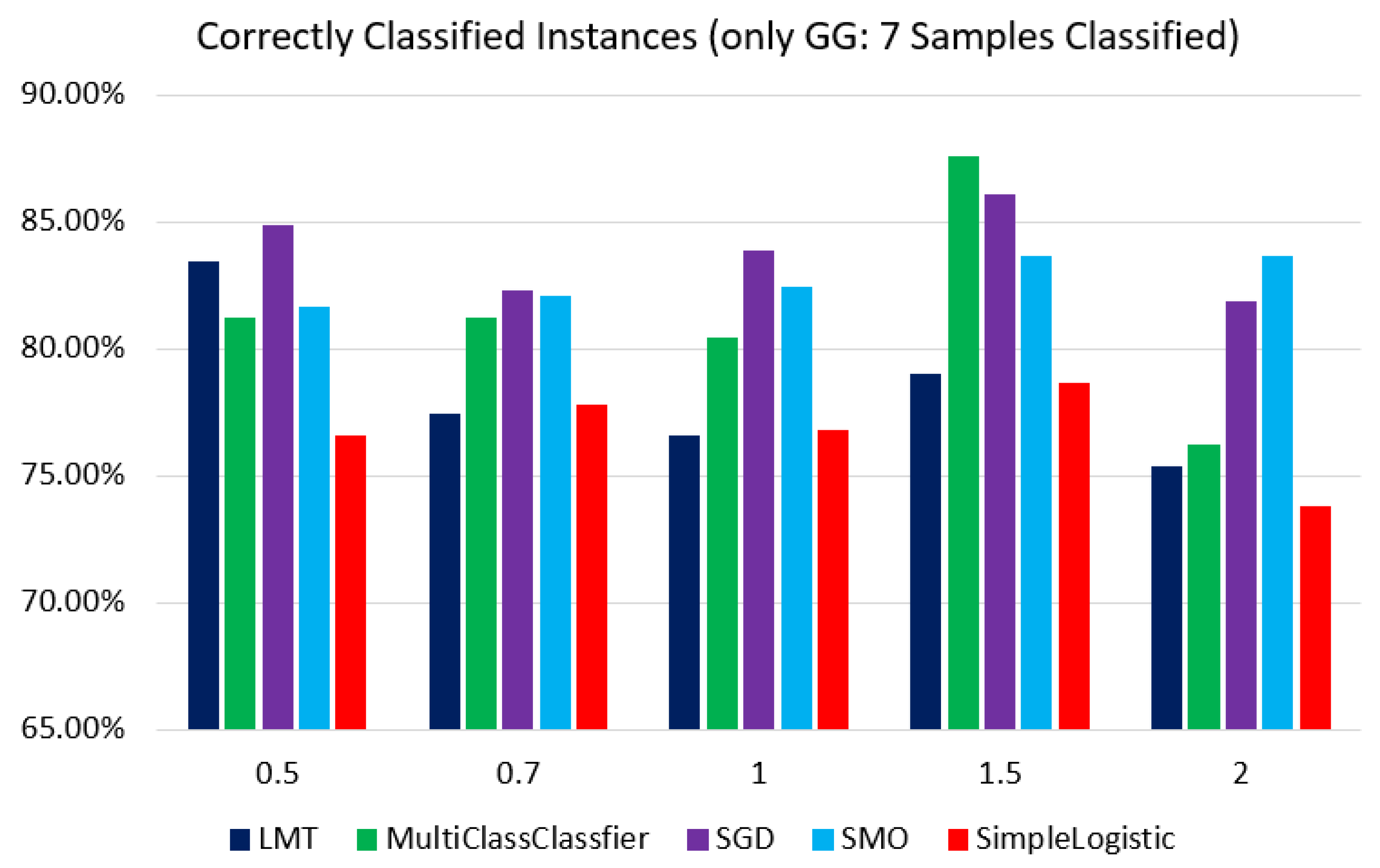
We implemented a supervised machine learning method to classify Model 3 by treating it as testing and Model 2 as training. The accuracy significantly improved for all LogFC values for all the five different classifiers in Weka. From Figure 15, the highest and lowest accuracy was obtained by MultiClassClassifier for LogFC 1.5 with 87.55% and by SimpleLogistic Classifier for LogFC 2 with 73.74%, respectively. From Table 3, we can say that the highest accuracy obtained by an individual classifier (SVM) using scikit-learn is 86%.

4.4. Stacking Results

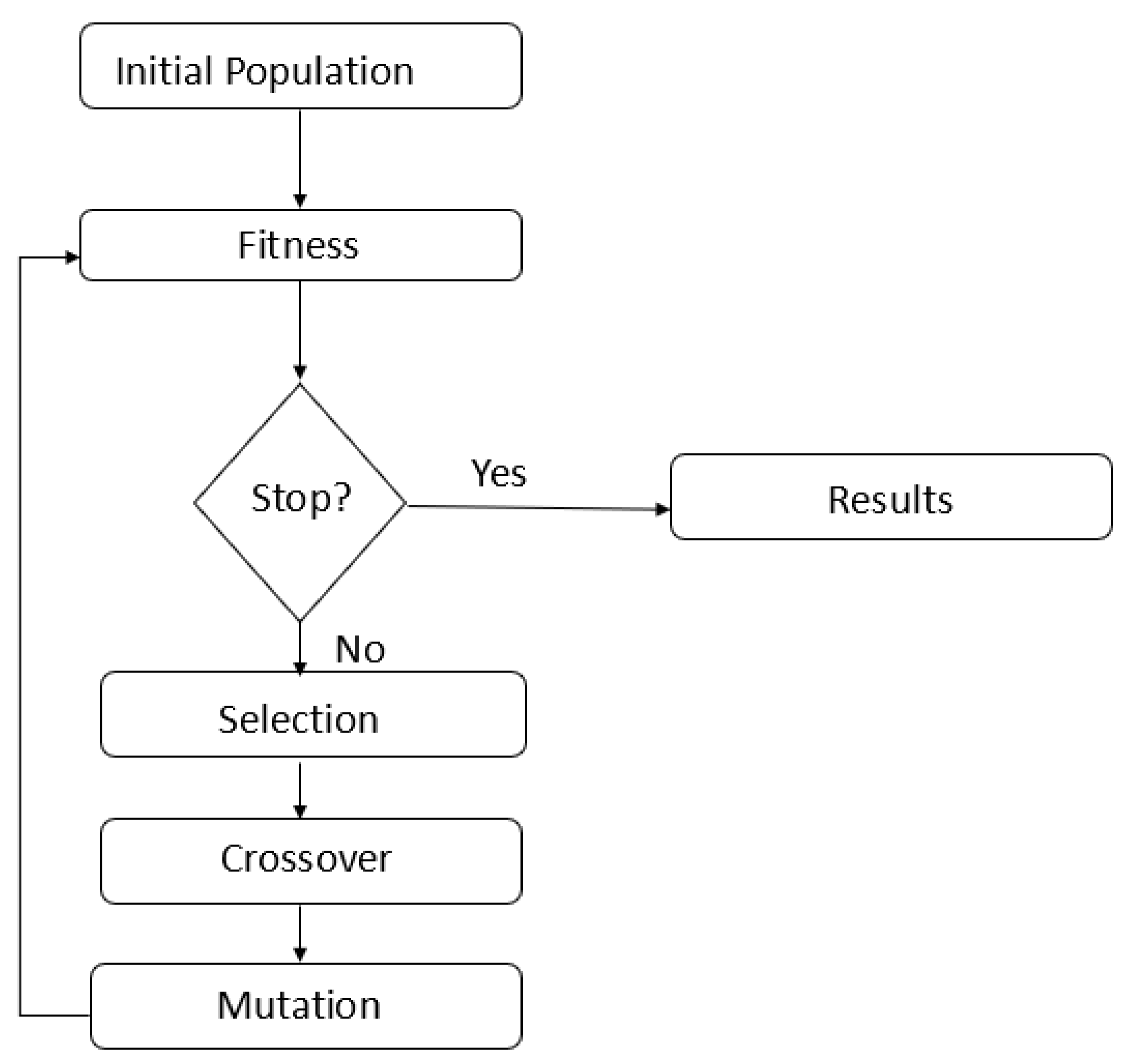
We increased the accuracy to 86% by correctly classifying samples with GG: 7. We implemented a Genetic Algorithm (GA) to reduce the number of features to identify the probes/genes that contribute to the disease. GA is a metaheuristic that gradually refines solutions through natural selection, where the best individuals are selected to produce offspring for the next generation. GA’s are used to generate high-quality solutions to optimization by relying on operators such as Selection, Crossover, and Mutation. In the optimization using GA, the parameters were set as: i) population size of 50, ii) elite rate of 5%, iii) crossover rate of 90%, and v) mutation rate of 50%. Figure 16 and Figure 17 represents the flowchart of GA and Stacking method. After applying a genetic algorithm, the resulting models contain 1020 (model 1) and 1681 (Model 2) genes. Later, we assumed that we could classify all the samples and increase our accuracy by using both models.

4.4.1. Model 1

In this section, we tried different combinations of base classifiers and meta classifiers using the stacking technique. Table 5 represents the performance metric of Model 1, and the highest accuracy was obtained by stacking model 1 (SM-1) with 96%. Then, we used the principal component analysis (PCA) plot to check if the samples were correctly represented as Indolent and Aggressive. From Figure 18, we observed that most of the samples were correctly classified.

4.4.2. Model 2

As per our assumption, we removed the samples with GG: 7 and applied the stacking technique with different combinations for the rest of the samples. The results are presented in Table 6. Model 2 was now more comparable to Model 1, and the highest accuracy was obtained by stacking model 1 (SM-1) with 97%. Almost all the samples were classified correctly (Figure 19). Due to our model's inability to achieve 100% accuracy, a few misclassified samples persisted within our models. Figure 17 shows the number of misclassified samples in GG:7 and Model 1 at different threshold levels, abs(logFC) > 0.5, 0.7, 1, 1.5, and 2.

5. Discussion

This study’s main purpose was to classify prostate cancer patients into Indolent tumors that could be safely monitored and Aggressive tumors with lethal potential that require immediate therapeutic intervention. We used GG to guide our modeling approach consistent with current standard operating procedures. The GG ranges from 6 to 10, and patients with GG: 7 (Gleason Grade: 3+4 and 4+3) are the most variable. Our investigation shows that using the current protocol based on GG alone could lead to misclassification errors. The practical consequence is that this could lead to unnecessary treatment of men with indolent tumors, a practice that could impair their quality of life and potentially economic well-being. Likewise, under-treatment due to misclassification could lead to loss of life in those who could otherwise be saved. However, we have shown that implementing ML algorithms could accurately classify cancer patients into Indolent and Aggressive. Most notably, our approach could be used to complement current protocols based on GG.
One of the challenges in using TCGA data is the unbalanced design nature of the studies, which causes some technical challenges when dealing with the dimensionality of the data and model fitting to a large number of variables. Several studies faced the same problem using TCGA datasets [30,31].
Lei Yang et al. [32] used Random walk with restart algorithm (RWRA) and Graph-regularized Nonnegative Matrix Factorization (GNMF) methods for molecular classification of prostate adenocarcinoma by the integrated somatic mutation profiles and molecular network. They analyze somatic point mutations in exome sequences from TCGA-prostate samples. The overall accuracy achieved was 82.54%.
One recent study [30] used RNA-seq expression data from the TCGA database containing breast samples. They used Stacked denoising Autoencoder (SDAE), PCA, KPCA, and differentially expressed gene methods to reduce the dimensionality. They also tried different methods like Artificial Neural Network (ANN), Support-Vector Machine (SVM), Support-Vector Machine (SVM) with linear kernel, and Support-Vector Machine with Radial basis function kernel (SVM-RBF). SVM-RBF’s highest accuracy was obtained using the SDAE method for dimensionality reduction, and the highest sensitivity was achieved by the ANN model, followed by the SDAE method. The SVM-RBF model obtains the highest specificity and precision. Glocuk et al. [31] aimed to increase accuracy by performing different dimensionality methods like PCA, KPCA, and NMF. They tried implementing a ladder network and found that it outperformed SDAE and AVM models. The accuracy achieved was 89.13%.
Takumi et al. [33] tried machine learning to diagnose prostate cancer using clinical data. They implemented an Artificial Neural Network (ANN) with the data and found that improvements need to be made before being suitable for clinical applications, although their model performed well. A recent study [34] implemented the SMOTE technique to increase the number of samples in the data set to deal with imbalanced classes. Using SMOTE, they created synthetic observations and equalized the class distribution. They applied the Recursive Feature Elimination (RFE) algorithm to reduce the number of features to identify the tumor. Later, they performed a logistic regression model using 5-fold cross-validation to minimize the false positive rate and improved the accuracy compared to previous machine learning attempts. The overall accuracy achieved was 85%.
In our study, we used Differential Expression analysis and Genetic Algorithm to reduce the number of features to identify the probes that contribute to the disease. We also performed different ML classifiers using 10-fold cross-validation to minimize the misclassification rate and improve accuracy compared to previous studies. Later, we used a stacking-based ML technique using a different combination of ML classifiers with 10-fold cross-validation and yielded better results (Model 1 with 96% for SM-1 and Model 2 with 97% for SM-1). The following table (Table 7) shows the comparison of the proposed method with the existing methods.

6. Conclusions

Our investigation demonstrates that genomic alterations in patients diagnosed with indolent and aggressive tumors could lead to measurable changes distinguishing the two patient groups; ML provides powerful tools with accuracy, specificity, and sensitivity for accurately distinguishing truly indolent tumors that could be safely monitored from aggressive tumors that require treatment. Further research is recommended to integrate genomic with somatic mutation data to classify indolent and aggressive PCa and identify drivers of disease aggressiveness using Machine Learning.

References

  1. Rodney, S., et al., Key papers in prostate cancer. Expert Rev Anticancer Ther, 2014. 14(11): p. 1379-84. [CrossRef]
  2. Watson, M.J., et al., Risk stratification of prostate cancer: integrating multiparametric MRI, nomograms and biomarkers. Future oncology (London, England), 2016. 12(21): p. 2417-2430. [CrossRef]
  3. Epstein, J.I., et al., The 2005 International Society of Urological Pathology (ISUP) Consensus Conference on Gleason Grading of Prostatic Carcinoma. Am J Surg Pathol, 2005. 29(9): p. 1228-42. [CrossRef]
  4. Epstein, J.I., et al., The 2014 International Society of Urological Pathology (ISUP) Consensus Conference on Gleason Grading of Prostatic Carcinoma: Definition of Grading Patterns and Proposal for a New Grading System. Am J Surg Pathol, 2016. 40(2): p. 244-52. [CrossRef]
  5. Lavi, A. and M. Cohen, [PROSTATE CANCER EARLY DETECTION USING PSA - CURRENT TRENDS AND RECENT UPDATES]. Harefuah, 2017. 156(3): p. 185-188.
  6. Moyer, V.A. Screening for Prostate Cancer: U.S. Preventive Services Task Force Recommendation Statement. Annals of Internal Medicine, 2012.
  7. Lin, K., et al., U.S. Preventive Services Task Force Evidence Syntheses, formerly Systematic Evidence Reviews, in Prostate-Specific Antigen-Based Screening for Prostate Cancer: An Evidence Update for the U.S. Preventive Services Task Force. 2011, Agency for Healthcare Research and Quality (US): Rockville (MD).
  8. National Cancer Institute. Genomic Data Commons Data Portal. 7 May 2020. Available online: https://portal.gdc.cancer.gov.
  9. American Urological Association. Clinically Localized Prostate Cancer: AUA/ASTRO/SUO Guideline. 2017. Available online: https://www.auanet.org/guidelines/prostate-cancer-clinically-localized-guideline.
  10. Chen, N. and Q. Zhou, The evolving Gleason grading system. Chinese journal of cancer research = Chung-kuo yen cheng yen chiu, 2016. 28(1): p. 58-64.
  11. Robinson, M.D. and A. Oshlack, A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biology, 2010. 11(3): p. R25. [CrossRef]
  12. Belinda Phipson, A.T. Matt Ritchie, Maria Doyle, Harriet Dashnow, Charity Law, RNA-seq analysis in R. 2016: p. 68.
  13. Belinda Phipson, A.T. Matt Ritchie, Maria Doyle, Harriet Dashnow, Charity Law, RNA-seq analysis in R. 2016.
  14. Li, J., et al., Normalization, testing, and false discovery rate estimation for RNA-sequencing data. Biostatistics (Oxford, England), 2012. 13(3): p. 523-538. [CrossRef]
  15. Brownlee, J. How to Run Your First Classifier in Weka. Machine Learning Mastery, 2014.
  16. Kuchi, A., et al., Machine learning applications in detecting sand boils from images. Array, 2019. 3-4: p. 100012. [CrossRef]
  17. Gattani, S., A. Mishra, and M.T. Hoque, StackCBPred: A stacking based prediction of protein-carbohydrate binding sites from sequence. Carbohydr Res, 2019. 486: p. 107857. [CrossRef]
  18. Hu, Q., et al. A Stacking-Based Approach to Identify Translated Upstream Open Reading Frames in Arabidopsis Thaliana. in Bioinformatics Research and Applications. 2015. Cham: Springer International Publishing. [CrossRef]
  19. Iqbal, S. and M. Hoque, PBRpredict-Suite: A Suite of Models to Predict Peptide Recognition Domain Residues from Protein Sequence. Bioinformatics (Oxford, England), 2018. 34.
  20. Mishra, A., P. Pokhrel, and M. Hoque, StackDPPred: A Stacking based Prediction of DNA-binding Protein from Sequence. Bioinformatics, 2018. 35. [CrossRef]
  21. Flot, M., et al., StackSSSPred: A Stacking-Based Prediction of Supersecondary Structure from Sequence. Methods in molecular biology (Clifton, N.J.), 2019. 1958: p. 101-122. [CrossRef]
  22. Vapnik, V.N. An overview of statistical learning theory. IEEE Transactions on Neural Networks, 1999. 10(5): p. 988-999. [CrossRef]
  23. Szilagyi, A. and J. Skolnick, Efficient prediction of nucleic acid binding function from low-resolution protein structures. J Mol Biol, 2006. 358(3): p. 922-33. [CrossRef]
  24. Tin Kam, H. Random decision forests. in Proceedings of 3rd International Conference on Document Analysis and Recognition. 1995.
  25. Geurts, P., D. Ernst, and L. Wehenkel, Extremely randomized trees. Machine Learning, 2006. 63(1): p. 3-42. [CrossRef]
  26. Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. The Annals of Statistics, 2001. 29(5): p. 1189-1232. [CrossRef]
  27. Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. The American Statistician, 1992. 46(3): p. 175-185. [CrossRef]
  28. Chen, T. and C. Guestrin, XGBoost: A Scalable Tree Boosting System. 2016. 785-794.
  29. Pedregosa, F., et al., Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research, 2012. 12.
  30. Danaee, P., R. Ghaeini, and D.A. Hendrix, A DEEP LEARNING APPROACH FOR CANCER DETECTION AND RELEVANT GENE IDENTIFICATION. Pac Symp Biocomput, 2017. 22: p. 219-229. [CrossRef]
  31. Golcuk, G., M.A. Tuncel, and A. Canakoglu. Exploiting Ladder Networks for Gene Expression Classification. in Bioinformatics and Biomedical Engineering. 2018. Cham: Springer International Publishing. [CrossRef]
  32. Yang, L., et al., Molecular classification of prostate adenocarcinoma by the integrated somatic mutation profiles and molecular network. Scientific reports, 2017. 7(1): p. 738-738. [CrossRef]
  33. Takeuchi, T., et al., Prediction of prostate cancer by deep learning with multilayer artificial neural network. Canadian Urological Association journal = Journal de l'Association des urologues du Canada, 2019. 13(5): p. E145-E150. [CrossRef]
  34. Casey, M., et al. A Machine Learning Approach to Prostate Cancer Risk Classification Through Use of RNA Sequencing Data. in Big Data – BigData 2019. 2019. Cham: Springer International Publishing. [CrossRef]
Preprints 78778 g001
Figure 1. Library sizes of all samples expressed using a barplot constitute data quality and unnormalized library sizes.
Figure 1. Library sizes of all samples expressed using a barplot constitute data quality and unnormalized library sizes.
Preprints 78778 g001
Preprints 78778 g002
Figure 2. Figure checks the read counts’ distribution on the log2 scale of logCPM (log counts per million) before normalization.
Figure 2. Figure checks the read counts’ distribution on the log2 scale of logCPM (log counts per million) before normalization.
Preprints 78778 g002
Preprints 78778 g003
Figure 3. Figure showing the voom transformation using a decision matrix and mean-variance trend.
Figure 3. Figure showing the voom transformation using a decision matrix and mean-variance trend.
Preprints 78778 g003
Preprints 78778 g004
Figure 4. Flowchart depicting study design and execution workflow. Only the genes significantly differentially expressed between tumors and controls discovered in the level 1 analysis were considered in the level 2 analysis.
Figure 4. Flowchart depicting study design and execution workflow. Only the genes significantly differentially expressed between tumors and controls discovered in the level 1 analysis were considered in the level 2 analysis.
Preprints 78778 g004
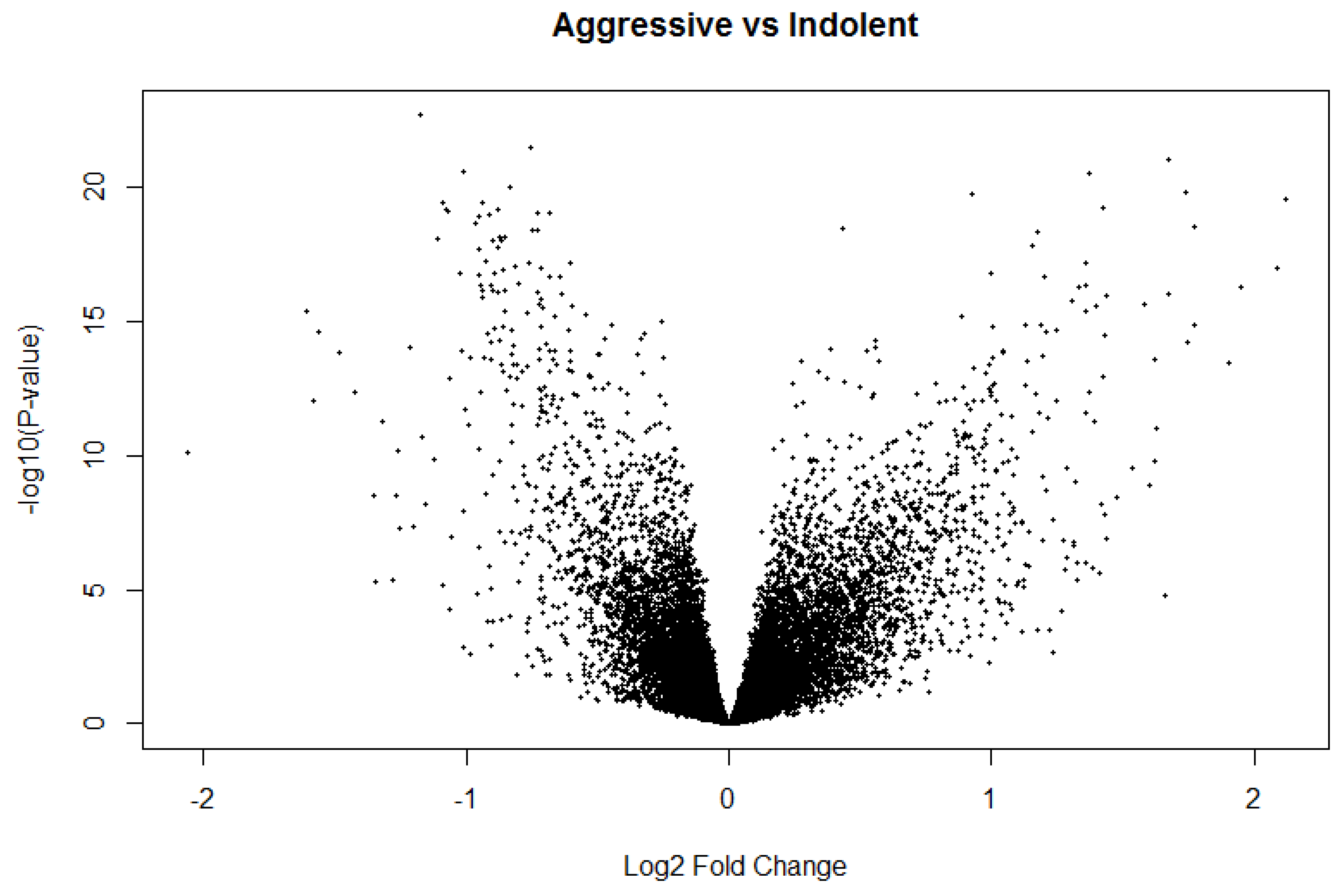
Preprints 78778 g005
Figure 5. Volcano plot from differential expression analysis using Limma package on Indolent vs. Aggressive PCa samples (Model 1).
Figure 5. Volcano plot from differential expression analysis using Limma package on Indolent vs. Aggressive PCa samples (Model 1).
Preprints 78778 g005
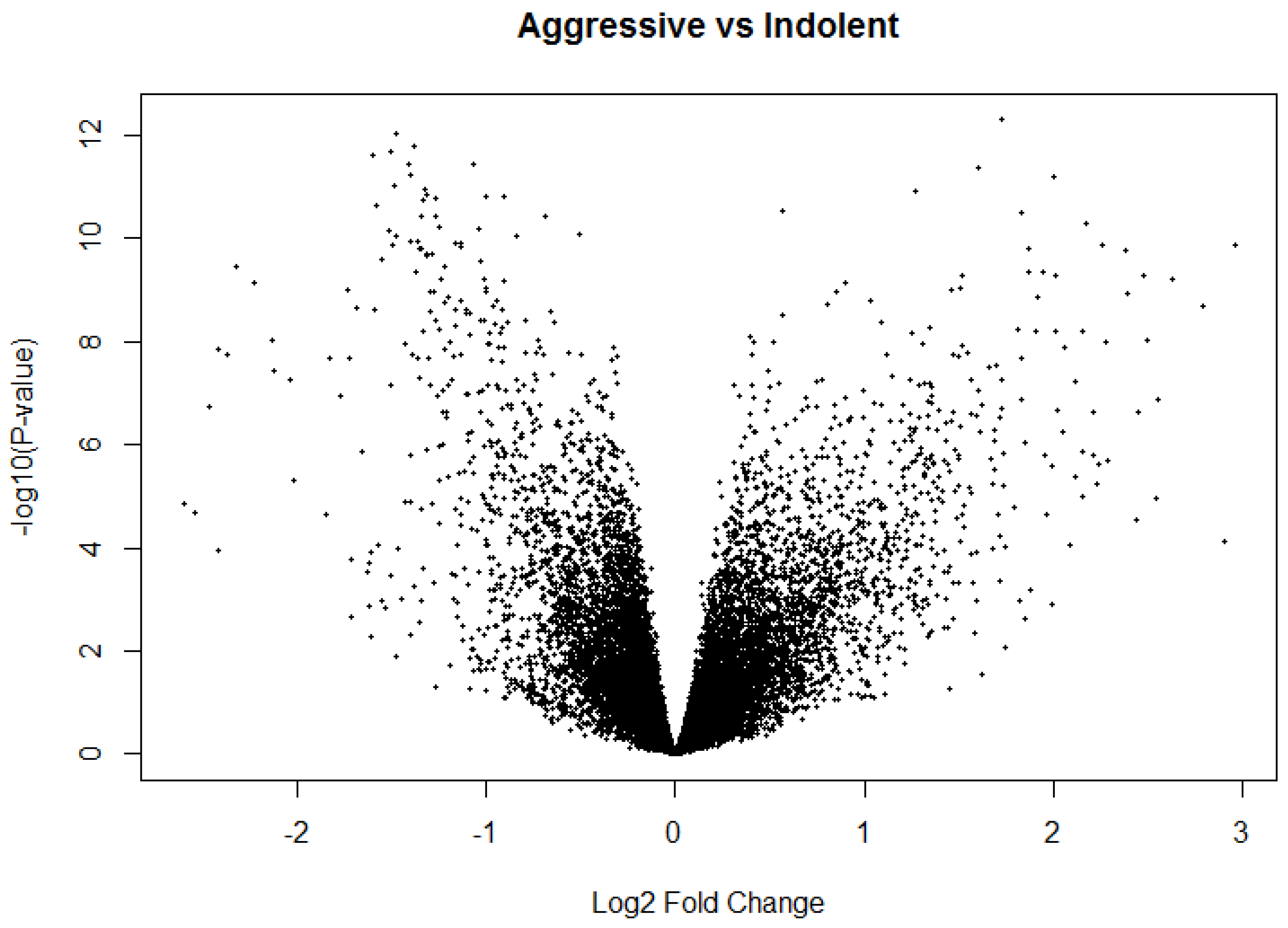
Preprints 78778 g006
Figure 6. Volcano plot from differential expression analysis using Limma package on Indolent vs. Aggressive PCa samples (Model 2).
Figure 6. Volcano plot from differential expression analysis using Limma package on Indolent vs. Aggressive PCa samples (Model 2).
Preprints 78778 g006
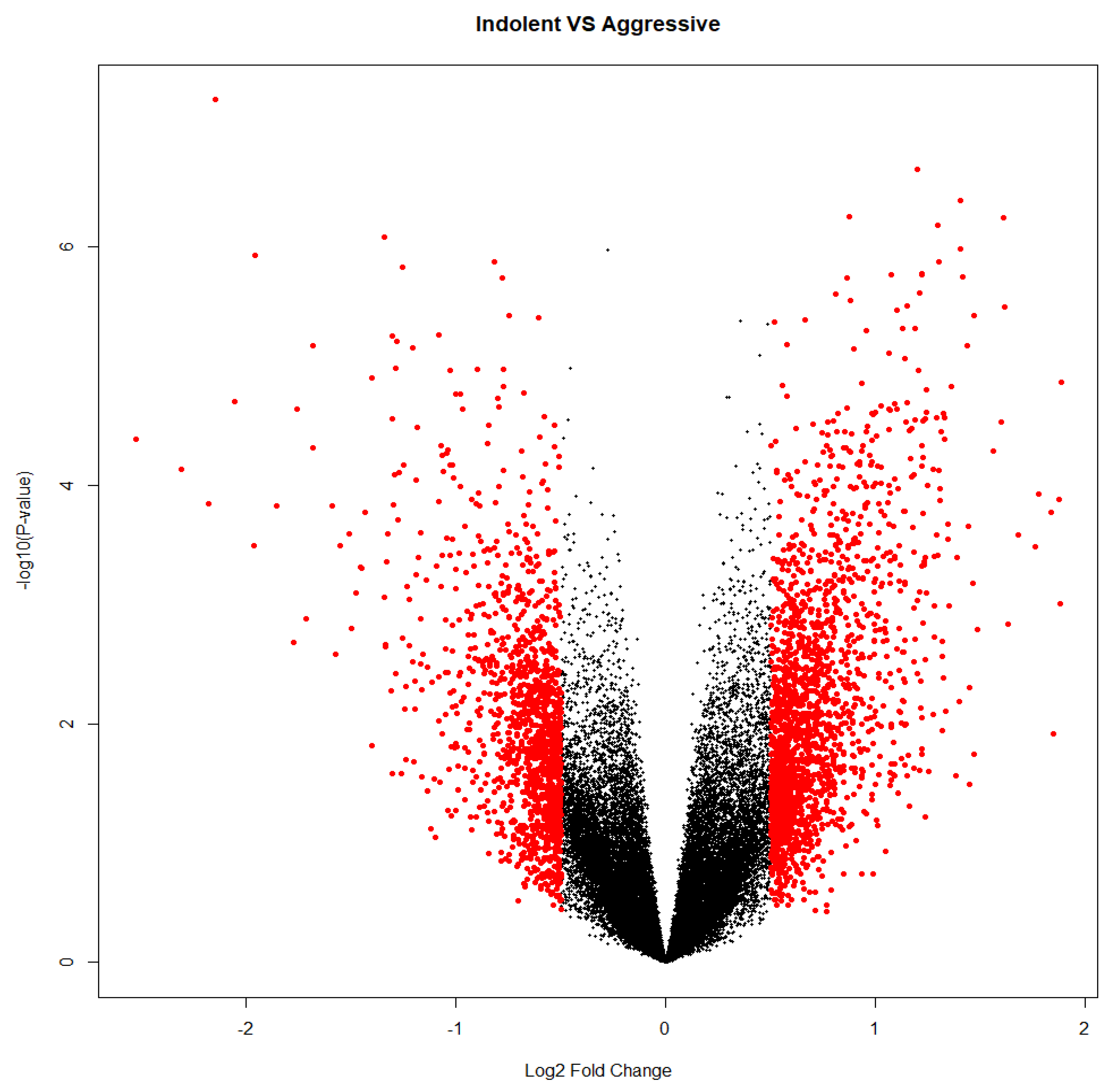
Preprints 78778 g007
Figure 7. Volcano plot from differential expression analysis using Limma package on Indolent vs. Aggressive PCa samples (Model 3).
Figure 7. Volcano plot from differential expression analysis using Limma package on Indolent vs. Aggressive PCa samples (Model 3).
Preprints 78778 g007
Preprints 78778 g008
Figure 8. Figure represents the accuracy percentage of Model 1 before classification.
Figure 8. Figure represents the accuracy percentage of Model 1 before classification.
Preprints 78778 g008
Preprints 78778 g009
Figure 9. Three dimensional Principal Component Analysis (PCA) plot of Model 1. (Here, Blue represents Indolent samples, and Red represents Aggressive samples).
Figure 9. Three dimensional Principal Component Analysis (PCA) plot of Model 1. (Here, Blue represents Indolent samples, and Red represents Aggressive samples).
Preprints 78778 g009
Preprints 78778 g010
Figure 10. Figure represents the accuracy percentage Model 2 before classification.
Figure 10. Figure represents the accuracy percentage Model 2 before classification.
Preprints 78778 g010
Preprints 78778 g011
Figure 11. Three dimensional Principal Component Analysis (PCA) plot of Model 2. (Here, Blue represents Indolent samples, and Red represents Aggressive samples).
Figure 11. Three dimensional Principal Component Analysis (PCA) plot of Model 2. (Here, Blue represents Indolent samples, and Red represents Aggressive samples).
Preprints 78778 g011
Preprints 78778 g012
Figure 12. The figure represents the accuracy percentage samples with GG: 7 before classification. Here x-axis represents log fold change values, and the y-axis represents accuracy.
Figure 12. The figure represents the accuracy percentage samples with GG: 7 before classification. Here x-axis represents log fold change values, and the y-axis represents accuracy.
Preprints 78778 g012
Preprints 78778 g013
Figure 13. Principal component analysis (PCA) plot of Model 3. (Here, Blue represents Indolent samples, and Red represents Aggressive samples).
Figure 13. Principal component analysis (PCA) plot of Model 3. (Here, Blue represents Indolent samples, and Red represents Aggressive samples).
Preprints 78778 g013
Preprints 78778 g014
Figure 14. Figure representing the misclassified instances in samples with both datasets (Samples with GG: 7 and Samples with GG: 6, 7, 8, 9, 10).
Figure 14. Figure representing the misclassified instances in samples with both datasets (Samples with GG: 7 and Samples with GG: 6, 7, 8, 9, 10).
Preprints 78778 g014
Preprints 78778 g015
Figure 15. Figure represents all the samples’ accuracy after classifying only samples with GG: 7 for 5 different classifiers with different log-fold change values.
Figure 15. Figure represents all the samples’ accuracy after classifying only samples with GG: 7 for 5 different classifiers with different log-fold change values.
Preprints 78778 g015
Preprints 78778 g016
Figure 16. Flowchart represents the implementation of the Genetic Algorithm.
Figure 16. Flowchart represents the implementation of the Genetic Algorithm.
Preprints 78778 g016
Preprints 78778 g017
Figure 17. Flowchart represents the implementation of Stacking.
Figure 17. Flowchart represents the implementation of Stacking.
Preprints 78778 g017
Preprints 78778 g018
Figure 18. Figure represents the principal component analysis of Model 1.
Figure 18. Figure represents the principal component analysis of Model 1.
Preprints 78778 g018
Preprints 78778 g019
Figure 19. Figure represents the principal component analysis of Model 2.
Figure 19. Figure represents the principal component analysis of Model 2.
Preprints 78778 g019
Table 1. Name and definition of the evaluation metric.
Table 1. Name and definition of the evaluation metric.
Name of Metric Definition
True Positive (TP) Correctly predicted positive samples
True Negative (TN) Correctly predicted negative samples
False Positive (FP) Incorrectly predicted positive samples
False Negative (FN) Incorrectly predicted negative samples
Recall/Sensitivity/True Positive Rate (TPR) T P T P + F N
Specificity/True Negative Rate (TNR) T N T N + F P
Fall-out Rate/False Positive Rate (FPR) F P F P + T N
Miss Rate/False Negative Rate (FNR) F N F N + T P
Accuracy (ACC) T P + T N F P + F P + T N + F N
Balanced Accuracy (Bal_ACC) 1 2 ( T P T P + F N + T N T N + F P )
Precision T P T P + F P
F1 score (Harmonic mean of precision and recall) 2 T P 2 T P + F P + F N
Mathews Correlation Coefficient (MCC) T P * T N − ( F P * F N ) T P + F N * T P + F P * T N + F P * ( T N + F N )
Table 2.  Representation of the number of genes and Log-fold change values for Model-1, Model-2, and Model-3.
Table 2.  Representation of the number of genes and Log-fold change values for Model-1, Model-2, and Model-3.
LogFC cutoff No. of Genes
Model-1 Model-2 Model-3
0.5 2074 3513 513
0.7 821 2028 381
1 213 836 174
1.5 24 186 25
2 3 52 5
Table 3. Performance of various classifiers for Model 1 after classifying samples with GG: 7.
Table 3. Performance of various classifiers for Model 1 after classifying samples with GG: 7.
Metric/
Method		 LR ETC KNN SVM GBC RF XGB
Sensitivity 0.85 0.93 0.86 0.91 0.91 0.92 0.90
Specificity 0.67 0.49 0.59 0.69 0.54 0.51 0.67
Bal. Acc. 0.76 0.72 0.72 0.90 0.72 0.71 0.80
Accuracy 0.80 0.82 0.79 0.86 0.82 0.82 0.85
Precision 0.88 0.84 0.86 0.90 0.86 0.85 0.89
F1 score 0.87 0.88 0.86 0.90 0.88 0.88 0.89
MCC 0.50 0.84 0.45 0.61 0.49 0.49 0.61
Table 5. Performance of various Stacking methods for Model 1.
Table 5. Performance of various Stacking methods for Model 1.
Method/
Metric		 Sensitivity Specificity Accuracy Precision F1 Score MCC Balanced
Accuracy
SM-1 0.99 0.85 0.96 0.95 0.97 0.88 0.92
SM-2 0.96 0.83 0.93 0.95 0.95 0.81 0.87
SM-3 0.97 0.84 0.93 0.95 0.96 0.84 0.91
SM-4 0.98 0.68 0.91 0.90 0.94 0.74 0.83
SM-5 0.94 0.81 0.91 0.94 0.94 0.74 0.87
Table 6. Performance of various Stacking methods for Model 2.
Table 6. Performance of various Stacking methods for Model 2.
Method/
Metric		 Sensitivity Specificity Accuracy Precision F1 Score MCC Balanced
Accuracy
SM-1 0.98 0.90 0.97 0.99 0.98 0.87 0.94
SM-2 0.95 0.79 0.94 0.97 0.96 0.72 0.91
SM-3 0.96 0.79 0.95 0.97 0.97 0.72 0.92
SM-4 0.98 0.62 0.94 0.95 0.96 0.66 0.80
SM-5 0.98 0.59 0.93 0.95 0.96 0.64 0.78
Table 7. Performance comparison with the existing methods.
Table 7. Performance comparison with the existing methods.
Methods Accuracy
Yang et al. [32] 82.54%.
Danaee et al. [30] 89.13%.
Casey et al. [34] 85.00%
Proposed Method (SM1) 96.00%
Proposed Method (SM2) 97.00%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated