Prerpints.org logo
Preprint
Article

An Unsupervised Machine Learning Approach for Monitoring Data Fusion and Health Indicator Construction

Altmetrics

Downloads

129

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 July 2023

Posted:

10 July 2023

You are already at the latest version

Alerts
Abstract
The prediction of system degradation is very important as it serves as an important basis for the formulation of condition-based maintenance strategies. An effective health indicator (HI) plays a key role in the prediction of system degradation as it enables vital information for critical tasks ranging from fault diagnosis to remaining useful life prediction. To address this issue, a method for monitoring data fusion and health indicator construction based on autoencoder (AE) and long short-term memory (LSTM) network is proposed to improve the predictability and effectiveness of health indicator in this study. Firstly, an unsupervised method and overall framework for HI construction is built based on deep autoencoder and LSTM neural network. The neural network is trained fully based on the normal operating monitoring data and then the construction error of the AE model is adopted as the health indicator of the system. Secondly, we propose related machine learning techniques for monitoring data processing to overcome the issue of data fusion, like mutual information for sensor selection and t-distributed stochastic neighbor embedding (T-SNE) for operating condition identification, etc. Thirdly, in order to verify the performance of the proposed method, experiments are conducted based on CMAPSS dataset and results are compared with algorithms of principal component analysis (PCA) and vanilla autoencoder model. Result shows that LSTM-AE model outperforms the PCA and Vanilla-AE model in metrics of monotonicity, trendability, prognosability and fitness. Fourthly, in order to analyze the impact of the time step of the LSMT-AE model on HI construction, we construct and analyze the system HI curve under different time steps of 5, 10, 15, 20, and 25 cycles. Finally, the results demonstrate that the proposed method for HI construction can effectively characterize the health state of system, which is helpful for further failure prognostics and converting the scheduled maintenance into condition-based maintenance.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

In the field of Prognostics and Health Management (PHM) [1], real-time prediction of equipment degradation is crucial as it serves as an important basis for developing Condition Based Maintenance (CBM) strategies [2]. However, in most cases, the data measured by the monitoring system cannot track the degradation status of the system. Therefore, a model that can predict system degradation or a quantifiable indicator is needed to evaluate the health status of the system, such as the system health indicator (HI). HI reflects the current health status of the system and is an important basis for predicting the trend of system fault development and performance degradation, which can be used to estimate the time when the system reaches failure [3]. Therefore, constructing a reasonable and accurate system HI is an important foundation for developing CBM strategies. For example, HI plays an important role in anomaly detection [4], remaining useful life (RUL) prediction [5], and health state prediction [6], and the effectiveness of the implementation in these fields heavily depends on HI construction [7].
The construction of HI can be divided into two types: model-based methods and data-driven methods, or directly using parameters with clear physical meanings in the system, such as the crack length of mechanical devices and the vibration amplitude of rotating machinery. Among them, model-based methods require in-depth analysis of system characteristics and the establishment of physical failure models based on this, which usually requires rich domain knowledge[8]. Currently, with the development of data collection and storage technology, data-driven methods have become the mainstream method for constructing HI. The core idea is to fuse multiple measurement data to obtain the comprehensive HI of the system.
The evaluation of system health status can be summarized into two questions: what data to use, and how to process and analyze the data. Usually, the most easily obtained data for a system are its monitoring data, which are time series data typically. The monitoring data of the system actually reflect many characteristics of the system, and by deeply mining the system monitoring data, a large amount of relevant information about the system’s health status can be obtained. For example, in [9], several data-driven models have been proposed and applied for diagnostics and prognostics purposes in complex systems based on monitoring data. In [10], a PHM model for the prediction components failures and system lifetime is proposed by combining monitoring data, time-to-failure data and background engineering knowledge of the systems. Likewise, in [11], the degradation index of rolling bearing is constructed based on the monitoring data.
Regarding the issue of HI construction, a certain number of researchers have adopted traditional machine learning methods such as principal component analysis [12], quantitative programming [13], support vector machines [14], hidden Markov model [15], and Bayesian linear regression [16]. In recent years, with the massive accumulation of data and the development of computer hardware, as an important branch of machine learning, deep learning technology has been rapidly developed. Currently, deep learning techniques have been applied to HI construction in relevant literature, including: vanilla neural network [17], recurrent neural network (RNN) [18], long short term memory network [19, 20], convolutional neural network [21, 22], and generative adversarial network [23] et al.
Among the current numerous deep learning methods, autoencoder is a kind of unsupervised learning method, which is essentially a custom-built neural network architecture. The architecture of autoencoder consists of decoder and encoder. It was first proposed by Rumelhart et al. and is mainly used for data dimension reduction [24]. Deep autoencoder is a multi-layer feedforward neural network with narrow middle and wide ends. It compresses the input data into a low dimensional projection through the encoder, and then reconstructs the output data through the decoder, trying to make them similar enough. Thus, the dimension of input data can be reduced in a hierarchical manner, achieving high-quality data reconstruction. With the development of autoencoder methods, derivative methods such as denoising autoencoder [25], sparse autoencoder [26] and stacked autoencoder [27], et al. have been invented. In the field of PHM research, autoencoder has also been gradually applied to anomaly detection [28, 29], RUL prediction [30] , fault diagnosis [31, 32] and health status assessment [33].
For HI construction, we have a basic assumption that when the system’s health status deteriorates, the monitoring data of the system will gradually deviate from the range of normal data, and the more system performance degrades, the greater the degree of deviation. Therefore, the autoencoder can successfully reconstruct normal data samples after training, but for the abnormal data of the system and the monitoring data after system degradation, an autoencoder model is expected to get a large reconstruction error, and the more serious the system degradation, the larger the reconstruction error should be. Based on this, it is reasonable to use autoencoder to build system HI based on system monitoring data. However, as mentioned earlier, the monitoring data of the system are typical time series data, and methods mentioned above do not fully consider the time series characteristics of monitoring data and the correlation between variables. LSTM neural network is a kind of recurrent neural network, which is specially designed to solve the vanishing gradient problem existing in general RNN. It can learn the relationship between variables in time series, capture the time series characteristics of monitoring data, and better realize the encoding and decoding of time series data.
On the other hand, for time series analysis, sensor selection, also known as feature selection, is one of the important factors that determine the final effect, which plays a vital role in the quantitative analysis of data. At present, for the feature analysis of the time series of HI, in most cases, the selection of variables is mainly done manually by observing the trend, amplitude, noise and other characteristics of the variables, which has problems such as strong subjectivity, inability to quantitatively analyze, and inaccuracy[34]. To solve this problem, a sensor selection method based on mutual information (MI) is proposed to determine the input data of Autoencoder. Mutual information is a measure of the interdependence between two variables, which indicates how much information is shared between two variables[35]. The greater the mutual information between two variables, the stronger the correlation they are [36]. It has become one of the important methods for feature selection to calculate and analyze the mutual information of features, judge the correlation between features, and then select the features with strong correlation with target variables[37]. However, for feature extraction and analysis of time series, one of the main problems of mutual information-based methods is to seek for suitable target variables, that is, the key of mutual information- based methods is to identify an appropriate target data. In most cases, there is no intuitive and directly available target information and the existing literature and researches are mainly focus on the improvement of feature extraction algorithm based on mutual information itself. To solve the above problems, we propose a target information extraction method based on PCA dimensionality reduction. On this basis, a mutual information method coupled with target variables is constructed to distinguish and extract applicable monitoring sensor data.
In view of above situation, we propose an HI construction method based on deep autoencoder, which is used to assess system health status based on high-dimensional monitoring time series data. The model is composed of a neural network composed of an encoder and a decoder, and LSTM is used to optimize the autoencoder network structure. While extracting the information of monitoring time series data, the method can complete the bidirectional mapping of data between high dimensional feature space and low dimensional latent space. The autoencoder compresses the time series into a low dimensional space, and then uses the decoder to reconstruct the compressed data, minimize the reconstruction error, and construct the HI of the system by the degree of the reconstruction error.
To sum up, we propose an HI construction method based on LSTM and autoencoder neural networks for the health assessment of complex system. This method is a data-driven approach that uses system health operating data to train neural networks, and uses the reconstruction error of the decoder as the basis for HI construction. To verify the effectiveness of the method, we conduct HI construction experiments based on the CMAPSS dataset and compared with the most widely used PCA dimensionality reduction method for extracting HI from multiple metrics. In summary, the contributions of this research are as follows:
(1) We propose a construction method of system HI based on Autoencoder and LSTM neural network. As the system gradually degrades and reaches failure, the monitoring data will gradually deviate from the normal range. Based on this assumption, the LSTM neural network is used to obtain the data series characteristics of the system monitoring data, and the system health index is constructed according to the reconstruction error of the Autoencoder.
(2) We design a specific technical process for implementing HI construction based on the above theoretical methods. In this process, we focus on data processing of sensor selection and operating condition identification, and propose a sensor selection method based on mutual information and operating condition identification method based on t-distributed stochastic neighbor embedding.
(3) The effectiveness of the proposed method is verified based on a publicly available aviation engine operation dataset. The experimental results are compared with other methods to verify the feasibility of the proposed method. Through qualitative and quantitative analysis, it is shown that the proposed method does not require the establishment of an accurate mathematical model for the system, and can effectively achieve the health status assessment of the system.
The remainder of this paper is organized as follows. In Section 2, we describe the architecture of the proposed system and introduce the theoretical foundation of the methodology. Results of the experiments are presented and discussed in Section 3. Finally, the conclusions and future work are set out in Section 4.

2. Methodology

2.1. Overall framework

The key to conducting system health assessment is to establish a system health assessment model, that is, to establish a mapping relationship between multidimensional monitoring variables and system HI. In the actual process, the system will operate alternately under different working conditions, and due to the different operating states of the system, there may be significant differences in the monitoring data of the system. On the other hand, under different operating conditions, the degradation rate and failure threshold of the system also vary, which will increase the difficulty of evaluating the health status. Based on the idea of divide and conquer, a system HI construction method and process, as shown in Figure 1, are proposed for these multiple working conditions system health assessment problem. It mainly includes the following steps: Step 1, select sensor data for health assessment, which contains rich information and can reflect system degradation; Step 2, divide the working conditions based on sensor data and classify the data samples according to different working conditions; Step 3, establish health assessment models based on autoencoder for different working conditions and calculate the comprehensive HI; Step 4, integrate the comprehensive HI of all monitoring data in chronological order to obtain the system degradation curve in the form of HI sequences.

2.2. Deep autoencoder

An autoencoder is an unsupervised neural network with training in two stages. It can simplify high-dimensional data into low-dimensional data, and then reconstruct low-dimensional data into high-dimensional input vectors. In the process, the reconstructed high-dimensional vectors are made as close to high-dimensional input vectors as possible. On this basis, a deep autoencoder builds a deep model through superposition. The hidden state of the upper layer is taken as the input of the lower layer. The model is trained with greedy learning layer by layer. Its basic structure is as shown in Figure 2. In this case, the encoder is used to transform the high-dimensional data in the input layer into the low-dimensional data in the hidden layer. Meanwhile, the decoder reconstructs the low-dimensional data in the hidden layer into the high-dimensional data in the output layer. Through constant training, the autoencoder structure can deliver reconstructed output that is approximate to the original input. This is mainly intended to denoise the data and extract its truly useful features.
When the data X are input into the encoder, they are transformed by dimension reduction layer by layer until the bottleneck layer is reach, because the number of nodes in the encoder’s neural network decreases layer by layer. Next, the decoder is used to expand such data into   X ^ . The difference between the input X and the output   X ^ is taken as the optimization objective function to adjust the parameters of the neural network, so as to guarantee their approximation as much as possible. To be specific, the input data are assumed to be X, so that the output of the encoder is:
h ( X ) = σ ( W ( E N ) X + b ( E N ) )
where σ is the encoder activation function, and W(EN) and b(EN) are the encoder’s neural network weight matrix and bias vector, respectively. The output of the decoder is:
  X ^ = σ ( W ( D E ) h ( X ) + b ( D E ) )
where W(DE) and b(DE) are the decoder’s neural network weight matrix and bias vector, respectively. To the autoencoder as a whole, the reconstruction error to be minimized can be expressed as:
D ( X , X ^ ) = ‖ X − X ^ ‖ 2
While searching for the parameters needed to minimize the reconstruction error, the autoencoder can gradually adjust the parameters of the network to achieve the permissible convergence value of the reconstruction error, that is:
W ( E N ) , b ( E N ) , W ( D E ) , b ( D E ) = arg min ‖ X − X ^ ‖ 2

2.3. Long Short-Term Neural Network

Long short-term memory (LSTM) is a special type of a recurrent neural network. With the series data as its input, an RNN recurs in the evolution direction of a series, and has all nodes linked. Normally, it is trained by a back propagation through time (BPTT) algorithm. Nevertheless, the inference rules of a BPTT algorithm make it very easy for an error gradient to cause nonlinear behaviors such as vanishing or exploding gradients after the back propagation of multiple time steps. The LSTM neural network relies on gate control to combine short- and long-term memories, which resolves the problem of a vanishing gradient to some extent [38]. The internal structure of an LSTM neural network unit is given in Figure 3.
An LSTM unit consists of three gates, that is, input, forget and output. The input and output gates are used to control the input and output activation of the memory unit, respectively. The forget gate can update the state of the unit. The module formed by these gates guarantees that the error travels in the form of a constant instead of a product in the network. This can resolve the problem of a vanishing or exploding gradient. The parameters of the unit are updated by the following equations:
f t = sgmoid ( W x f ⋅ x t + W h f ⋅ h t − 1 + b f )
i t = sgmoid ( W x i ⋅ x t + W h i ⋅ h t − 1 + b i )
C ⌣ t = tanh ( W x a ⋅ x t + W h a ⋅ h t − 1 + b a )
o t = sgmoid ( W x o ⋅ x t + W h o ⋅ h t − 1 + b o )
C t = f t ⊗ C t − 1 + i t ⊗ C ⌣ t
h t = o t ⊗ tanh ( C t )
where ht-1 and Ct-1 are the output and the state of the unit at the previous time; xt is the input at the current time; f, i, and o are the forget, input, and output gates, respectively; ft is the forget control signal for the state of the unit at the previous time; ft ⊗ Ct-1 is the information kept at the previous time; C ⌣ t is the state of the candidate unit at the current time; it is the control signal of C ⌣ t ; ht-1 is the final output; ot is the output control signal; Wx is the link matrix of input and hidden layers; Wh is the link matrix of output and hidden layers; and ⊗ is the dot product between matrices.

2.4. Sensor Selection based on mutual information

Mutual information is a measure of the interdependence between two variables, which mainly represents the correlation between two variables. Assuming that the joint probability distribution of two variables X and Y is p ( x , y ) , and their marginal probability distribution is p ( x ) and p ( y ) respectively, then mutual information M I ( X , Y ) is the relative entropy of the joint probability distribution p ( x , y ) and the marginal probability distribution p ( x ) and p ( y ) , and is defined as follows:
M I ( X , Y ) = − ∫ x ∫ y f x , y ( x , y ) log f x , y ( x , y ) f x ( x ) f y ( y ) d x d y
When variables X and Y are completely independent or mutually independent, their mutual information is 0. The greater the mutual information between two variables, the stronger the correlation between them. In data processing, sensors with large mutual information with the target variable should be selected to improve the prediction of the algorithm. At the same time, features with small mutual information should be eliminated to reduce data redundancy, which is the so-called feature selection based on maximum correlation and minimum redundancy.
In the application of the mutual information method, the probability density estimation function can be used to approximate the marginal probability distribution to simplify the above formula:
M I ( X , Y ) = − 1 N ∑ i = 1 N log f ^ x , y ( x i , y i ) f ^ x ( x i ) f ^ y ( y i )
where f ^ x ( x i ) and f ^ y ( y i ) are the joint probability distributions of X and Y respectively, f ^ x , y ( x i , y i ) is the joint probability density estimation function, and N is the number of data samples.

2.5. Operating condition identification based on T-SNE

The idea of T-SNE is to convert the Euclidean distance between data points into conditional probability, and then use the conditional probability to measure the similarity between data points. The greater the similarity, the closer the distance between data points is. The advantage of measuring the distance between samples in the form of probability is that in the process of mapping from high-dimensional space to low-dimensional space, although the distance between sample points may vary due to spatial differences, it can still maintain the relative distance between sample points, so that the originally distant sample points still maintain a relatively far distance. Specifically, for the sample point xi, in the original high-dimensional space, its similarity to other sample points such as xj can be expressed by the conditional probability pj/i and pi/j of the Gaussian distribution as:
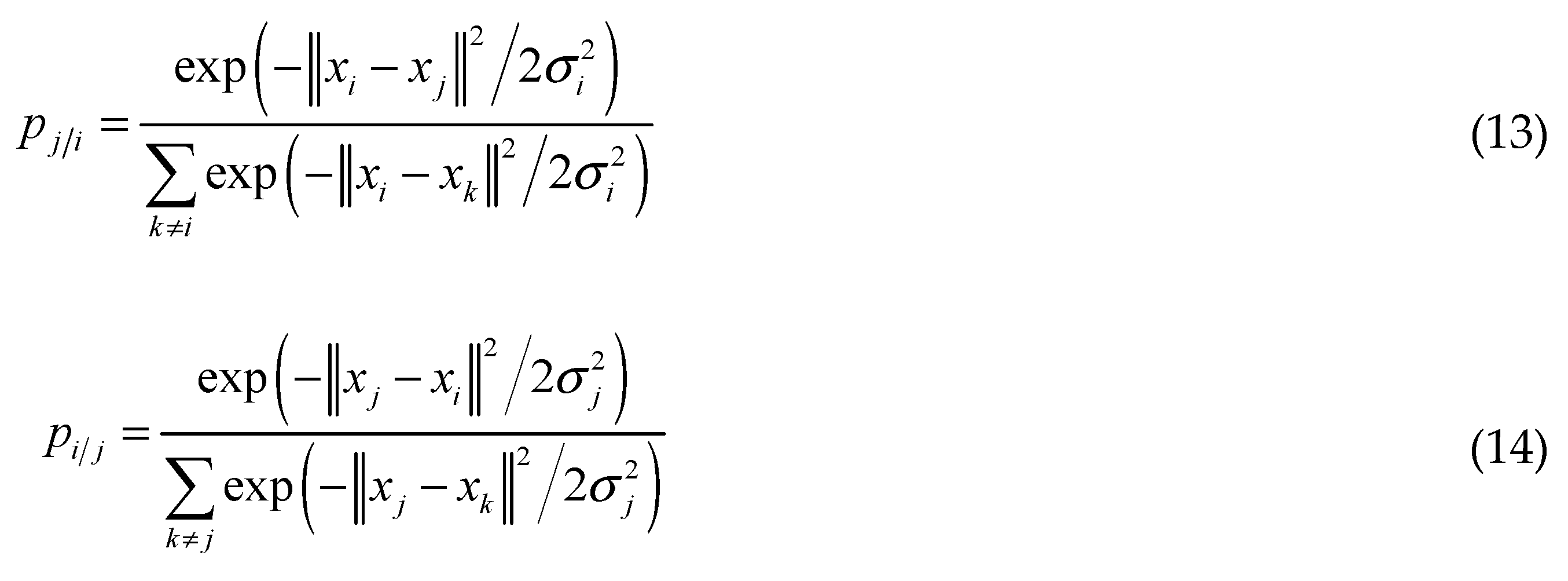Preprints 78877 i001 where k is the number of nearest neighbors of each point, σi and σj are the Gaussian variances of xi and xj respectively. Then the symmetric joint probability distribution of data points in the original space is:
Preprints 78877 i002 where N is the size of the data. The variance σ in formulas 13 and 14 is calculated by binary search of perplexity Prep(Pi), which is a manually defined parameter. Its function is to measure the number of points around each point in the effective domain that can form a smooth epidemic, and it is defined as follows:
Preprints 78877 i003 where H(Pi) is the Shannon entropy of Pi and is defined as follow:
Preprints 78877 i004
In the low dimensional space after dimensionality reduction, the mapping points of sample points xi and xj are ti and tj. Assuming that the symmetric joint probability distribution between the two is represented by qij, it can be expressed as:
Preprints 78877 i005 where, k and l respectively represent any two different points in a low dimensional space, defined by a t-distribution with a degree freedom of 1, which makes the points within the same cluster aggregate more tightly and the points in different clusters more distant.

2.6. Reconstruction error as health indicator

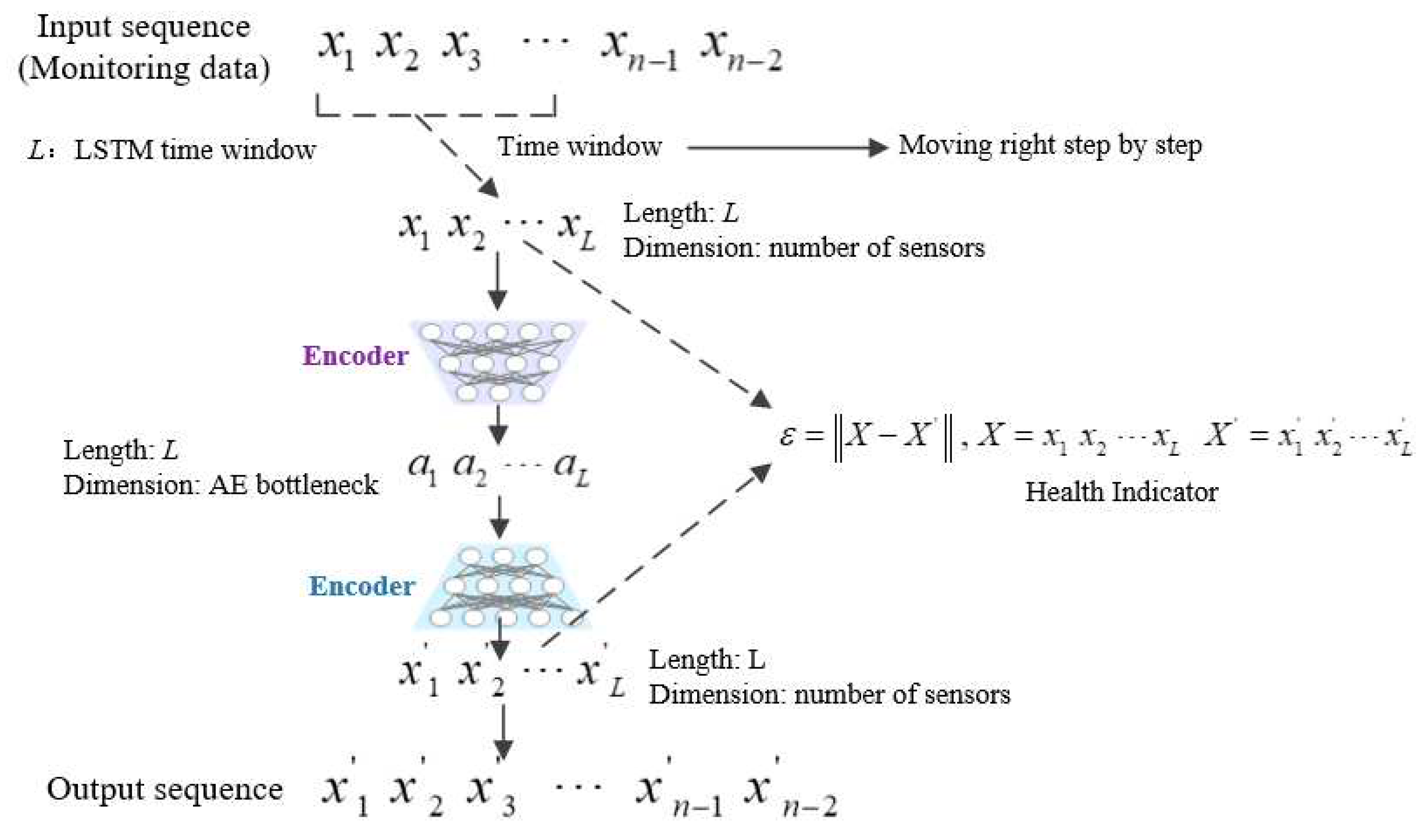
In the training process of LSTM-AE, we only use monitoring data of the initial state of the system, that is, the health status data of the system. Figure 4 shows the workflow of HI construction based on LSTM-AE. Among them, L is the length of the LSTM time window, which is one of the hyperparameters of the model. For the monitoring data of the system, the time window with a length of L will gradually move to the right and intercept the time series with a length of L (the dimension of the time series depends on the number of sensors used). Then, the time series X is calculated by the decoder and encoder to obtain another encoded time series X ' .
As only normal data is used in the training process of autoencoder. When the system state gradually deteriorates, the autoencoder model has poor reconstruction ability for the deviated monitoring data as it has not seen any data after state deviation. Therefore, the reconstruction error for the monitoring data of the system will gradually increase [39]. In the method proposed in this paper, the reconstruction error of system monitoring data using LSTM-AE will be used as HI and is defined as follow:
ε = ‖ X − X ' ‖   ,   X = x 1   x 2   ⋯ x L     X ' = x 1 '   x 2 ' ⋯ x L '
where, L is the length of LSTM time window, X is the input data, and X ' is the data reconstructed by Autoencoder.
Preprints 78877 g004
Figure 4. Workflow of HI construction based on LSTM-AE.
Figure 4. Workflow of HI construction based on LSTM-AE.
Preprints 78877 g004

3. Experiments

To verify the effectiveness of the method proposed in this paper, the LSTM-AE based HI construction method is validated using the C-MAPSS aircraft engine performance degradation simulation dataset published by NASA. The methods of sensor selection based on MI and T-SNE based Operating condition identification are applied. The effectiveness of the method is compared and analyzed with algorithms like PCA and Vanilla AE. All simulation experiments are carried out in Pycharm 2021 (Community Edition) environment on a PC with an AMD Ryzen 7 3700X 8-core CPU and 16GB memory.

3.1. C-MAPPS Datasets

As shown in Figure 5, a structure diagram of the aero-engine based on C-MAPSS contains several components such as a fan, combustion chamber, high/low pressure booster, turbine, nozzle, and so on[40].
The C-MAPSS dataset consists of four sub-datasets (FD001 to FD004), each corresponding to different working conditions and fault modes. As shown in Table 1, FD001 and FD003 contain one operating condition, while FD002 and FD004 both contain six operating conditions. FD001 and FD002 have one fault mode, while FD003 and FD004 both have two fault modes. The number of engines in the dataset from FD001 to FD004 is 100, 260, 100, and 249, respectively. In this dataset, there are a total of 21 different sensors used to measure the working condition, including physical information collected from different locations during the operating cycle of the aircraft engine (such as temperature, pressure, speed, etc.).
During data processing as shown in Figure 6, the data taken from the first 50 cycles of each engine were regarded as normal data, and only the normal data of each engine were used in the training of an autoencoder.

3.2. Data Preprocessing

Due to the different measurement intervals of different sensors, the data needs to be normalized to make all sensor data ranges consistent, so as to achieve better prediction effect. We adopt Z-score standardization to normalize the input data:
X ' = X − X ¯ σ
where, X is the time series data, X ¯ and σ are the average and variance of X respectively, and X ' is the normalized monitoring data.
Figure 7 shows the normalized change trend of the original data of FD001, FD002, FD003 and FD004 in the C-MAPSS dataset. From Figure 4, it can be seen that the sensor data of FD001 and FD003 show a clear upward or downward trend, while FD002 and FD004 cannot see a clear pattern. The reason for this problem is that, as mentioned earlier, there are six different operating conditions in the FD002 and FD004 datasets. During the entire life cycle of the engine, the engine operates alternately between different operating conditions. For the situations of FD002 and FD004, the T-SNE method proposed in section 2.5 should be used to prepare for the identification and division of such alternating operating conditions.

3.3. Sensor Selection

For the Feature selection problem of time series based on mutual information, one of the difficulties is to find appropriate target variables [41]. For monitoring data, in most cases, the monotonicity and predictability of sensors cannot be guaranteed, nor can they fully reflect the health and degradation of the system. Therefore, it is not possible to randomly select a sensor signal as the target variable. To address this issue, we propose a time series target variable construction method based on PCA. Firstly, the PCA method is applied to reduce the dimensionality of multidimensional time series variables, and then the obtained principal components are smoothed. After that, the smoothed principal component is taken as the target variable of Mutual information. In this way, the obtained target variable can represent the overall performance change of the system. Figure 8 shows the degradation trajectory of engines from numbers 1 to 100 in datasets FD001 and FD003. It can be seen from the figure that by extracting the system degradation curve as the target variable, the monotonicity and Irreversible process of the variable can be guaranteed, and the health state of the system can be reflected to a certain extent.
The Mutual information correlation between different sensors and target variables is analyzed by taking engine 1 in FD001 dataset as an example. It should be noted that some sensor signals in the monitoring data are constant values, which do not change with engine operation, such as s1, s5, s6, s10, s16, s18, and s19. After removing these data, a total of 14 sensor signals are obtained in the C-MAPSS dataset. Further, in order to reduce the redundancy between data, based on the feature selection idea of maximum correlation and minimum redundancy [42]. Before feature selection, some variables with high redundancy among themselves are removed according to the value of mutual information between variables. After the above selection, Table 2 shows the mutual information values of 9 different sensors with the target variable.
It can be seen from Table 3 that the five sensors with high mutual information with the target variable are s7, s9, s11, s12 and s13, corresponding to total pressure at high-pressure Compressor outlet, physical core speed, static pressure at high-pressure compressor outlet, ratio of fuel flow to Ps30 and corrected fan speed respectively, as shown in Table 3.

3.4. Operating Condition Identification

The C-MAPSS dataset FD002 and FD004 contain six different operating conditions, which continuously alternate between each operating condition during the working process. In order to build a system HI, real-time and accurate identification of system operating conditions is necessary. We propose and apply the T-SNE method for real-time operating condition recognition of the monitoring data for dataset FD002 and FD004.
We conduct operating condition identification on the FD002 and FD004 datasets based on the five sensor signals selected in section 3.3. Figure 9 shows the effects of FD002 and FD004 using the T-SNE method for condition identification, respectively. From the graph, it can be seen that the data points of different operating conditions are effectively separated into different regions. The T-SNE method can accurately identify the engine operating conditions and preserve the general structure of the monitoring data.
Based on this, we can effectively normalize and process the monitoring data of this variable working condition. Thus, we can divide and normalize the data of FD002 and FD004 in section 3.2, and obtain the sensor change trend shown in Figure 10. From the graph, it can be seen that the monitoring data curve obtained has a clear upward or downward trend, eliminating the impact of variable operating conditions on data processing.

3.5. Performance Metrics

For HI construction, a set of metrics that can describe the quality of HI is needed, including monotonicity, trendability, and prognosability [43, 44]. Among them, monotonicity represents the potential positive or negative trend of features. Assuming that the system does not undergo maintenance, it should be monotonic on the timeline for degraded features. The definition of monotonicity is as follows:
m o n o t o n i c i t y = 1 M ∑ j = 1 M | ∑ k = 1 N j − 1 sgn ( x j ( k + 1 ) − x j ( k ) ) N j − 1 |
where M is the number of HIs, N j is the length of the jth HI, x j ( k + 1 ) and x j ( k ) are the values of the jth HI at time of k + 1 and k , respectively. In PHM, the value of monotonicity is between 0 and 1, and the closer it is to 1, the more monotonic the predictor is, which is more beneficial for prediction.
Trendability measures the similarity among the trajectories of the HI in multiple run-to-failure experiments. Generally, Pearson correlation is used to describe whether a set of HI has the same basic trend, and its calculation methods are as follows:
t r e n d a b i l i t y = min j , k | corr ( x j , x k ) | ,         j , k = 1 , … , M
where M is the number of HI, x j and x k are the values of the jth and kth HI respectively, corr ( ) is the Pearson correlation function. When the lengths of x j and x k are different, interpolation processing is required. The value of trendability is between 0 and 1. The closer it approaches the value of 1, the better its predictability.
Prognosability reflects the dispersion of HI between faults and normal states, specifically:
p r o g n o s a b i l i t y = exp ( − std j ( x j ( N j ) ) mean j | x j ( 1 ) − x j ( N j ) | ) ,       j = 1 , 2 , ⋯ M
where M is the number of HIs, N j is the length of the jth HI, x j is the value of the jth HI, std j is the standard deviation function, mean j is the average function. The value of prognosability is between 0 and 1. The closer it is to 1, the better its predictability.
The fitness is the weighted sum of the three predictive indicators mentioned above:
f i t n e s s = w m × M o n o t o n i c i t y + w t × T r e n d a b i l i t y + w p × P r o g n o s a b i l i t y
where w m , w t , w p are the weight values, which are all equal to 1 in this paper.

3.6. Health indicator evaluation

To verify the effectiveness of the proposed method, experiments are conducted on the four sets of data in the C-MAPSS, FD001, FD002, FD003, and FD004. Among them, FD002 and FD004 contain six different operating conditions. Comparative analysis is conducted with PCA and Vanilla AE, two widely used HI construction methods. Table 4 shows the performance of the three methods on the four datasets.
From Table 5, it can be seen that the LSTM-AE method has achieved better results than PCA and Vanilla AE in terms of monotonicity, trendability, prognosability, and fitness. Except for the two metrics of trendability and prognosability, it is slightly lower than the PCA method on the FD001 and FD003 datasets. In addition, we also notice that the PCA method performed well on the FD001 and FD003 datasets, but on the FD002 and FD004 datasets, the prognosability metric are almost equal to 0, which indicates that the PCA method has weak data processing ability for variable operating conditions.
In order to more intuitively demonstrate the predictive effects of the three methods, we visualize the HI curves of the engines obtained from the three methods in four datasets, as shown in Figure 11. From Figure 11, we can see that the PCA method has a certain upward trend in HI during the initial operation phase of the system during the long-life cycle, while Vanilla AE and LSTM AE are relatively stable in the initial stage. From the perspective of system degradation, the system has a good state in the initial stage, and HI should theoretically remain relatively stable at this time. Therefore, we believe that compared to PCA methods, AE based methods can better reflect the degradation status of the system. On the other hand, comparing the HI curves of Vanilla AE and LSTM-AE, it can be seen that due to the time series characteristics of monitoring data learned by LSTM neural networks, their HI curves are more stable and smoother compared to Vanilla AE, thus having better predictive performance.
The LSTM-AE model and Vanilla AE neural network structure used in this article are the same, including input layer, three encoding layers, intermediate layer, three decoding layers, and output layer. The detailed network layer structure and hyperparameter settings are shown in Table 5 and Table 6, respectively, with the LSTM-AE model using a time step of 20 cycles.
Table 5. Neural Network Structures of LSTM-AE and Vanilla AE.
Table 5. Neural Network Structures of LSTM-AE and Vanilla AE.
Model Neural Network Name Neuron number
Input layer LSTM Input 5
Decoder LSTM Hidden layer 128
Decoder LSTM Hidden layer 64
Decoder LSTM Hidden layer 32
Middle layer LSTM Bottleneck 8
Encoder LSTM Hidden layer 32
Encoder LSTM Hidden layer 64
Encoder LSTM Hidden layer 128
Output layer Dense Output 5
Table 6. Hyperparameters of neural networks.
Table 6. Hyperparameters of neural networks.
Hyperparameters Value
Batch size 128
Learning rate 0.001
Optimizer Adam
Loss Mae
Epochs 200
Dropout rate 0.5

3.7. The effect of LSTM time step on predictive performance

For LSTM-AE model, time step is one of the most important hyperparameters, which directly affects the prediction performance of HI construction. To analyze the impact of different time steps on the HI performance of the system, we compare the performance of the LSTM-AE model under different time steps. Table 7 shows the comparison of time steps of 5, 10, 15, 20, 25, and 30 cycles, respectively.
From Table 7, we can see that increasing the time step size can obviously improve the predictive performance of HI. However, it should be noted that for the time step, when it is too long, the predictive performance of HI will deteriorate. For example, when the step size reaches 25 cycles, the relevant metric decreases. The reason for this phenomenon is that when the time step is too large, the time series information of system degradation contained within a single step range is too much, resulting in the model learning too vague degradation information. Because a single time step may contain information about the normal, degraded, and failed states of the system. Therefore, special attention should be paid to the hyperparameter of time step.
Figure 12 shows the sensor data measurement of the LSTM-AE model with a time step of 20 cycles before and after AE reconstruction. The reconstructed sensor data are the s7, s9, s11, s12, and s13 sensor signals of the first engine in the FD001, FD002, FD003, and FD004 datasets. From the figure, it can be seen that the sensor signal reconstructed by the LSTM-AE model basically coincides with the original signal in the initial stage. As the engine operating cycles increase, the reconstructed signal gradually deviates from the original signal. At this time, the engine gradually deviates from the normal operating state, and the reconstruction error (HI) also gradually increases, reflecting the changes in the system operating state.

4. Conclusion

In this paper we propose an HI construction method based on autoencoder and long short-term memory neural network. The proposed method LSTM-AE is an unsupervised method as the model is fully trained based on the system normal operating monitoring data, which the abnormal data is not needed. The constructiong error of the AE model is adopted as the system HI. We built the overall framework for the monitoring data fusion and HI construction based on LSTM-AE and the data processing workflow including the tecniques like mutual information for sensor selection and t-distributed stochastic neighbor embedding for operating condition identification, etc. The predictability and effectiveness of the constructed HI is validated in the experiments section of the paper.
Regarding future work, we plan to apply our proposal in hybrid autoencoder architectures, such as deep adversarial autoencoders (AAE) as AAE can learn better representations and extract more robust features. Another direction of future work is to develop new indicators for prognostics. For example, instead of directly constructing HI for prognostics, to explore indicators of feature importance that are interrelated for prognostics features might be promising.

References

  1. Y. Hu, X. Miao, Y. Si, E. Pan, and E. Zio, “Prognostics and health management: A review from the perspectives of design, development and decision,” Reliability Engineering & System Safety, vol. 217, p. 108063, 2022-1-1 2022. [CrossRef]
  2. E. Quatrini, F. Costantino, G. Di Gravio, and R. Patriarca, “Condition-Based Maintenance—An Extensive Literature Review,” in Machines. vol. 8, 2020. [CrossRef]
  3. K. L. Tsui, N. Chen, Q. Zhou, Y. Hai, W. Wang, and S. Wu, “Prognostics and Health Management: A Review on Data Driven Approaches,” Mathematical Problems in Engineering, vol. 2015, p. 793161, 2015-1-1 2015. [CrossRef]
  4. A. A. Bataineh, A. Mairaj and D. Kaur, “Autoencoder based Semi-Supervised Anomaly Detection in Turbofan Engines,” International journal of advanced computer science & applications, vol. 11, 2020-1-1 2020.. [CrossRef]
  5. K. T. P. Nguyen and K. Medjaher, “An automated health indicator construction methodology for prognostics based on multi-criteria optimization,” ISA Transactions, vol. 113, pp. 81-96, 2021. [CrossRef]
  6. P. Wen, S. Zhao, S. Chen, and Y. Li, “A generalized remaining useful life prediction method for complex systems based on composite health indicator,” Reliability Engineering & System Safety, vol. 205, p. 107241, 2021-1-1 2021. [CrossRef]
  7. L. Xiao, J. Tang, X. Zhang, E. Bechhoefer, and S. Ding, “Remaining useful life prediction based on intentional noise injection and feature reconstruction,” Reliability Engineering & System Safety, vol. 215, p. 107871, 2021-1-1 2021. [CrossRef]
  8. D. D., L. H. Q., W. Z., and G. X., “A Survey on Model-Based Distributed Control and Filtering for Industrial Cyber-Physical Systems,” IEEE Transactions on Industrial Informatics, vol. 15, pp. 2483-2499, 2019-1-1 2019. [CrossRef]
  9. S. Cofre-Martel, E. Lopez Droguett and M. Modarres, “Big Machinery Data Preprocessing Methodology for Data-Driven Models in Prognostics and Health Management,” in Sensors. vol. 21, 2021. [CrossRef]
  10. R. Rocchetta, Q. Gao, D. Mavroeidis, and M. Petkovic, “A robust model selection framework for fault detection and system health monitoring with limited failure examples: Heterogeneous data fusion and formal sensitivity bounds,” Engineering Applications of Artificial Intelligence, vol. 114, p. 105140, 2022-1-1 2022. [CrossRef]
  11. W. Zhu, G. Ni, Y. Cao, and H. Wang, “Research on a rolling bearing health monitoring algorithm oriented to industrial big data,” Measurement, vol. 185, p. 110044, 2021-1-1 2021. [CrossRef]
  12. Y. Zhang, Y. Xin, Z. Liu, M. Chi, and G. Ma, “Health status assessment and remaining useful life prediction of aero-engine based on BiGRU and MMoE,” Reliability Engineering & System Safety, vol. 220, p. 108263, 2022. [CrossRef]
  13. L. Guo, Y. Yu, A. Duan, H. Gao, and J. Zhang, “An unsupervised feature learning based health indicator construction method for performance assessment of machines,” Mechanical Systems and Signal Processing, vol. 167, p. 108573, 2022-1-1 2022. [CrossRef]
  14. M. M. Manjurul Islam, A. E. Prosvirin and J. Kim, “Data-driven prognostic scheme for rolling-element bearings using a new health index and variants of least-square support vector machines,” Mechanical Systems and Signal Processing, vol. 160, p. 107853, 2021-1-1 2021. [CrossRef]
  15. S. Wang, J. Chen, H. Wang, and D. Zhang, “Degradation evaluation of slewing bearing using HMM and improved GRU,” Measurement, vol. 146, pp. 385-395, 2019-1-1 2019. [CrossRef]
  16. Z. Lyu, G. Wang and C. Tan, “A novel Bayesian multivariate linear regression model for online state-of-health estimation of Lithium-ion battery using multiple health indicators,” Microelectronics Reliability, vol. 131, p. 114500, 2022-1-1 2022. [CrossRef]
  17. Y. Wu, M. Yuan, S. Dong, L. Lin, and Y. Liu, “Remaining useful life estimation of engineered systems using vanilla LSTM neural networks,” Neurocomputing, vol. 275, pp. 167-179, 2018-1-1 2018. [CrossRef]
  18. L. Chen, G. Xu, S. Zhang, W. Yan, and Q. Wu, “Health indicator construction of machinery based on end-to-end trainable convolution recurrent neural networks,” Journal of Manufacturing Systems, vol. 54, pp. 1-11, 2020-1-1 2020. [CrossRef]
  19. Y. Cheng, K. Hu, J. Wu, H. Zhu, and X. Shao, “A convolutional neural network based degradation indicator construction and health prognosis using bidirectional long short-term memory network for rolling bearings,” Advanced Engineering Informatics, vol. 48, p. 101247, 2021-1-1 2021. [CrossRef]
  20. Z. Ye and J. Yu, “Health condition monitoring of machines based on long short-term memory convolutional autoencoder,” Applied Soft Computing, vol. 107, p. 107379, 2021-1-1 2021. [CrossRef]
  21. P. Li, Z. Zhang, R. Grosu, Z. Deng, J. Hou, Y. Rong, and R. Wu, “An end-to-end neural network framework for state-of-health estimation and remaining useful life prediction of electric vehicle lithium batteries,” Renewable and Sustainable Energy Reviews, vol. 156, p. 111843, 2022-1-1 2022. [CrossRef]
  22. M. Marei, S. E. Zaatari and W. Li, “Transfer learning enabled convolutional neural networks for estimating health state of cutting tools,” Robotics and Computer-Integrated Manufacturing, vol. 71, p. 102145, 2021-1-1 2021. [CrossRef]
  23. S. Behera and R. Misra, “Generative adversarial networks based remaining useful life estimation for IIoT,” Computers & Electrical Engineering, vol. 92, p. 107195, 2021-1-1 2021. [CrossRef]
  24. P. Li, Y. Pei and J. Li, “A comprehensive survey on design and application of autoencoder in deep learning,” Applied Soft Computing, vol. 138, p. 110176, 2023-1-1 2023. [CrossRef]
  25. P. Vincent, H. Larochelle, Y. Bengio, and P. A. Manzagol, “Extracting and Composing Robust Features with Denoising Autoencoders,” in Machine Learning, Proceedings of the Twenty-Fifth International Conference (ICML 2008), Helsinki, Finland, June 5-9, 2008, 2008.
  26. D. She, M. Jia and M. G. Pecht, “Sparse auto-encoder with regularization method for health indicator construction and remaining useful life prediction of rolling bearing,” Measurement Science and Technology, vol. 31, p. 105005, 2020-1-1 2020. [CrossRef]
  27. F. Xu, Z. Huang, F. Yang, D. Wang, and K. L. Tsui, “Constructing a health indicator for roller bearings by using a stacked auto-encoder with an exponential function to eliminate concussion,” Applied Soft Computing, vol. 89, p. 106119, 2020-1-1 2020. [CrossRef]
  28. J. Jakubowski, P. Stanisz, S. Bobek, and G. J. Nalepa, “Anomaly Detection in Asset Degradation Process Using Variational Autoencoder and Explanations,” in Sensors. vol. 22, 2022. [CrossRef]
  29. H. D. Nguyen, K. P. Tran, S. Thomassey, and M. Hamad, “Forecasting and Anomaly Detection approaches using LSTM and LSTM Autoencoder techniques with the applications in supply chain management,” International Journal of Information Management, vol. 57, p. 102282, 2021-1-1 2021. [CrossRef]
  30. T. Han, J. Pang and A. C. C. Tan, “Remaining useful life prediction of bearing based on stacked autoencoder and recurrent neural network,” Journal of Manufacturing Systems, vol. 61, pp. 576-591, 2021-1-1 2021. [CrossRef]
  31. Z. Yang, B. Xu, W. Luo, and F. Chen, “Autoencoder-based representation learning and its application in intelligent fault diagnosis: A review,” Measurement, vol. 189, p. 110460, 2022-1-1 2022. [CrossRef]
  32. X. Wu, Y. Zhang, C. Cheng, and Z. Peng, “A hybrid classification autoencoder for semi-supervised fault diagnosis in rotating machinery,” Mechanical Systems and Signal Processing, vol. 149, p. 107327, 2021-1-1 2021. [CrossRef]
  33. H. Lee, H. J. Lim and A. Chattopadhyay, “Data-driven system health monitoring technique using autoencoder for the safety management of commercial aircraft,” Neural Computing and Applications, vol. 33, pp. 3235-3250, 2021-1-1 2021. [CrossRef]
  34. J. Li, W. Ren and M. Han, “Mutual Information Variational Autoencoders and Its Application to Feature Extraction of Multivariate Time Series,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 36, p. 2255005, 2022-1-1 2022. [CrossRef]
  35. H. Stögbauer, P. Grassberger and A. Kraskov, “Estimating mutual information,” Physical Review E, vol. 69, p. 066138, 2004-6-23 2004. [CrossRef]
  36. C. Pascoal, M. R. Oliveira, A. Pacheco, and R. Valadas, “Theoretical evaluation of feature selection methods based on mutual information,” Neurocomputing, vol. 226, pp. 168-181, 2017-1-1 2017. [CrossRef]
  37. J. Cheng, J. Sun, K. Yao, M. Xu, and Y. Cao, “A variable selection method based on mutual information and variance inflation factor,” Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, vol. 268, p. 120652, 2022-1-1 2022. [CrossRef]
  38. W. Zaremba, I. Sutskever and O. Vinyals, “Recurrent neural network regularization,” arXiv preprint arXiv:1409.2329, 2014-1-1 2014. [CrossRef]
  39. de Pater and M. Mitici, “Developing health indicators and RUL prognostics for systems with few failure instances and varying operating conditions using a LSTM autoencoder,” Engineering Applications of Artificial Intelligence, vol. 117, p. 105582, 2023-1-1 2023. [CrossRef]
  40. S. A., G. K., S. D., and E. N., “Damage propagation modeling for aircraft engine run-to-failure simulation,” in 2008 International Conference on Prognostics and Health Management, 2008, pp. 1-9.
  41. U. M. Khaire and R. Dhanalakshmi, “Stability of feature selection algorithm: A review,” Journal of King Saud University-Computer and Information Sciences, vol. 34, pp. 1060-1073, 2022-1-1 2022. [CrossRef]
  42. H. Peng, F. Long and C. Ding, “Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy,” IEEE Transactions on pattern analysis and machine intelligence, vol. 27, pp. 1226-1238, 2005-1-1 2005. [CrossRef]
  43. C. Liu, J. Sun, H. Liu, S. Lei, and X. Hu, “Complex engineered system health indexes extraction using low frequency raw time-series data based on deep learning methods,” Measurement, vol. 161, p. 107890, 2020-1-1 2020. [CrossRef]
  44. M. L. Baptista, K. Goebel and E. M. P. Henriques, “Relation between prognostics predictor evaluation metrics and local interpretability SHAP values,” Artificial Intelligence, vol. 306, p. 103667, 2022-1-1 2022. [CrossRef]
Preprints 78877 g001
Figure 1. Autoencoder based health status assessment process.
Figure 1. Autoencoder based health status assessment process.
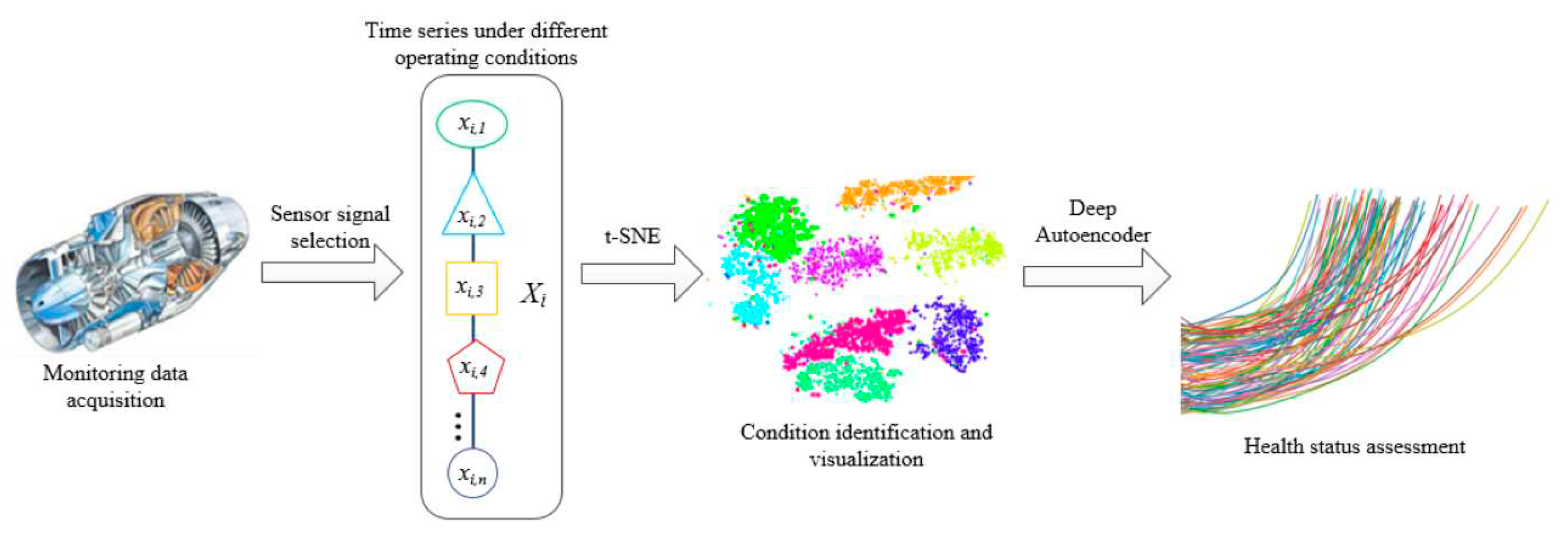
Preprints 78877 g001
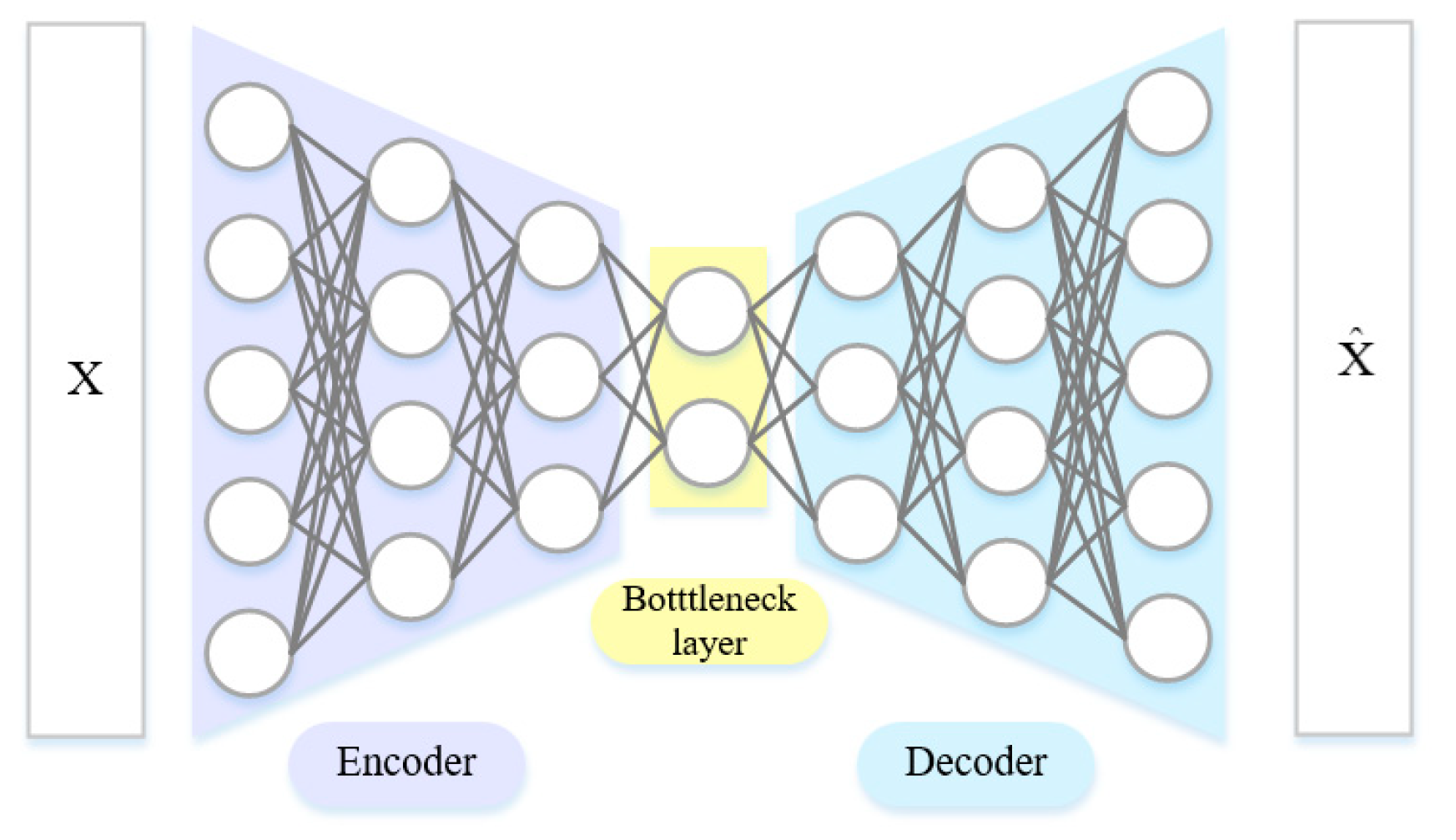
Preprints 78877 g002
Figure 2. Deep autoencoder.
Figure 2. Deep autoencoder.
Preprints 78877 g002
Preprints 78877 g003
Figure 3. Structure of a long short-term memory network unit.
Figure 3. Structure of a long short-term memory network unit.
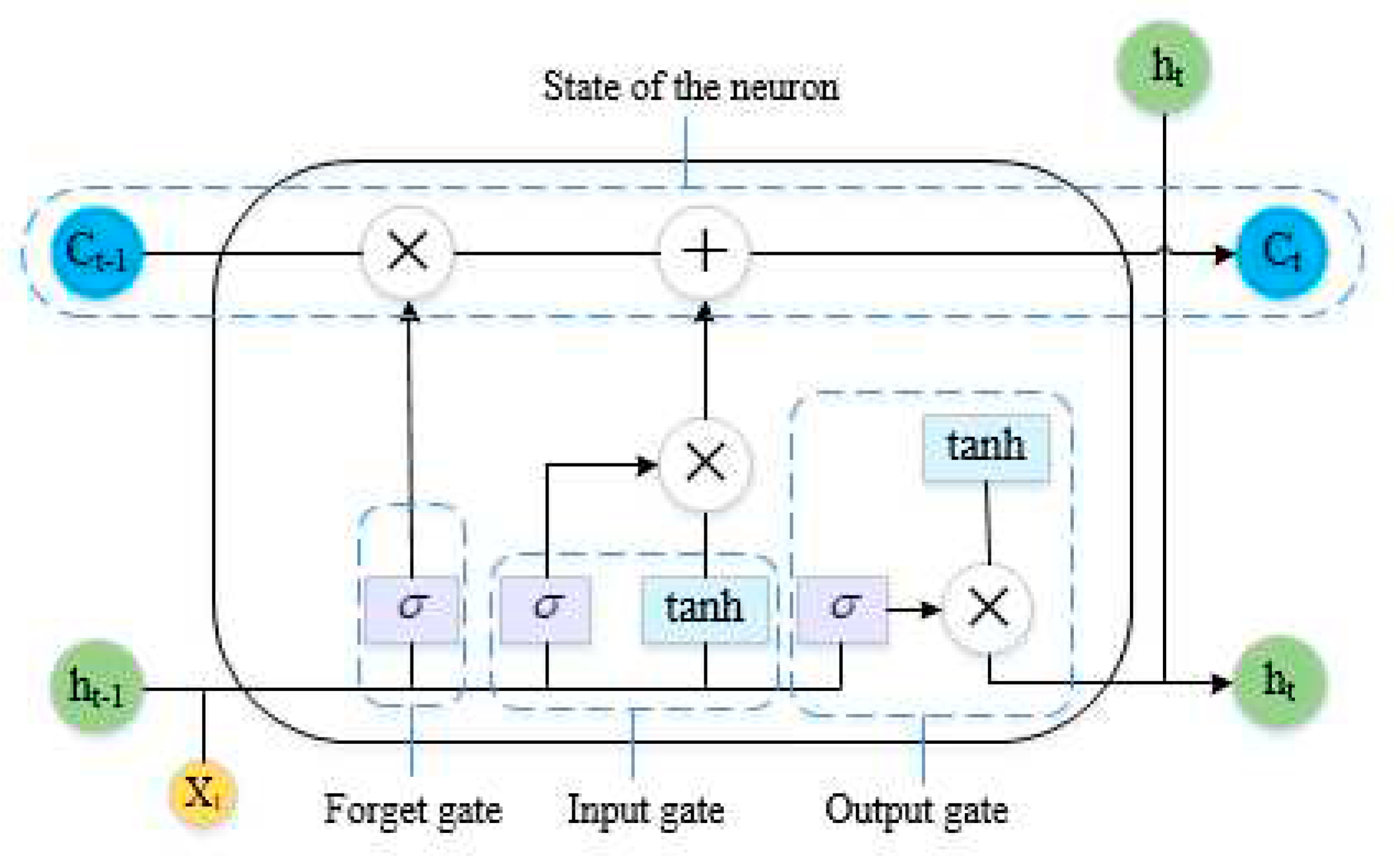
Preprints 78877 g003
Preprints 78877 g005
Figure 5. Structure diagram of a commercial modular aero-propulsion system.
Figure 5. Structure diagram of a commercial modular aero-propulsion system.
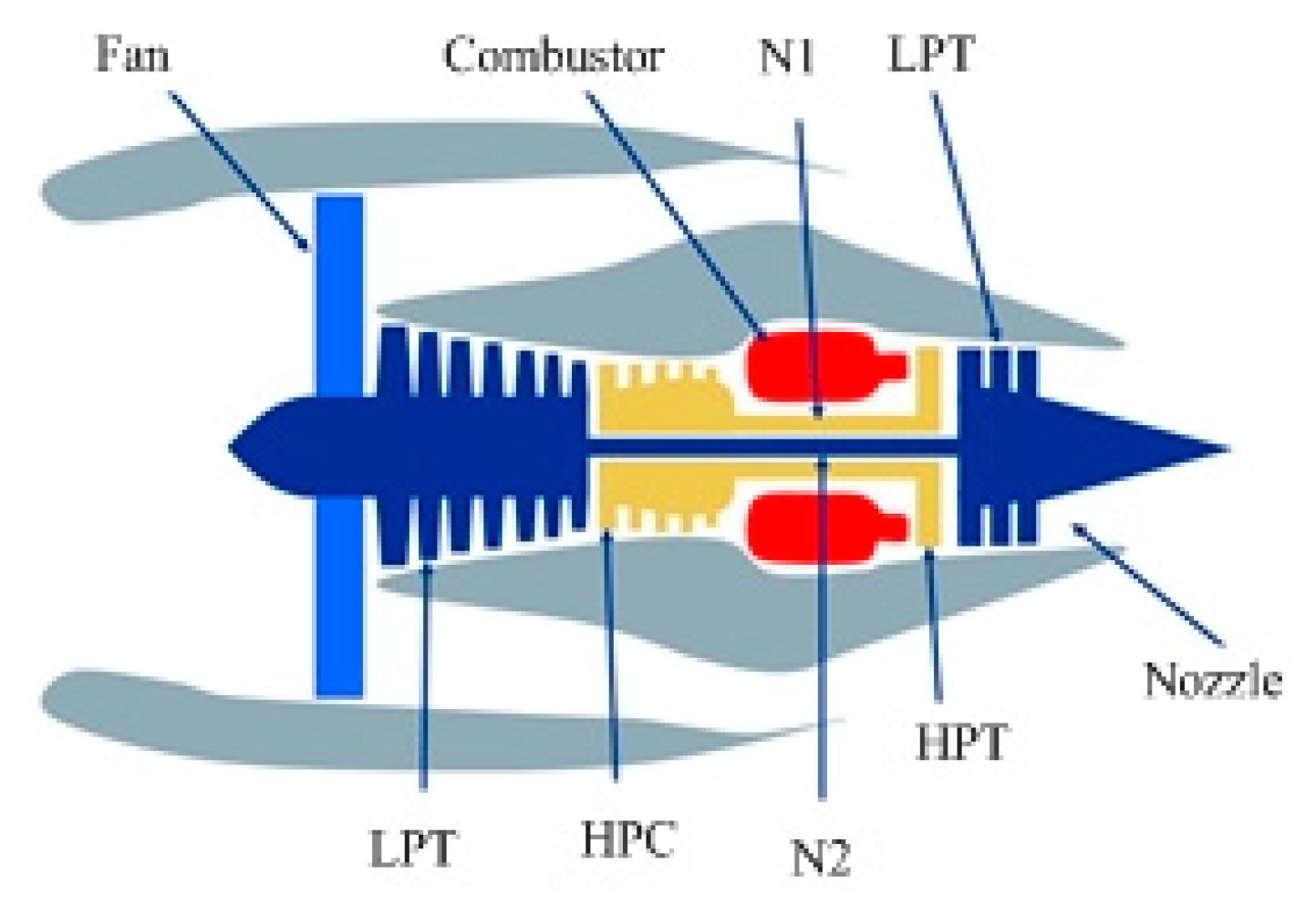
Preprints 78877 g005
Preprints 78877 g006
Figure 6. Data partition in the full lifecycle of engine.
Figure 6. Data partition in the full lifecycle of engine.
Preprints 78877 g006
Preprints 78877 g007
Figure 7. Normalized C-MAPSS sensor monitoring data from FD001 to FD004.
Figure 7. Normalized C-MAPSS sensor monitoring data from FD001 to FD004.
Preprints 78877 g007
Preprints 78877 g008
Figure 8. Trends in principal component of FD001 and FD003.
Figure 8. Trends in principal component of FD001 and FD003.
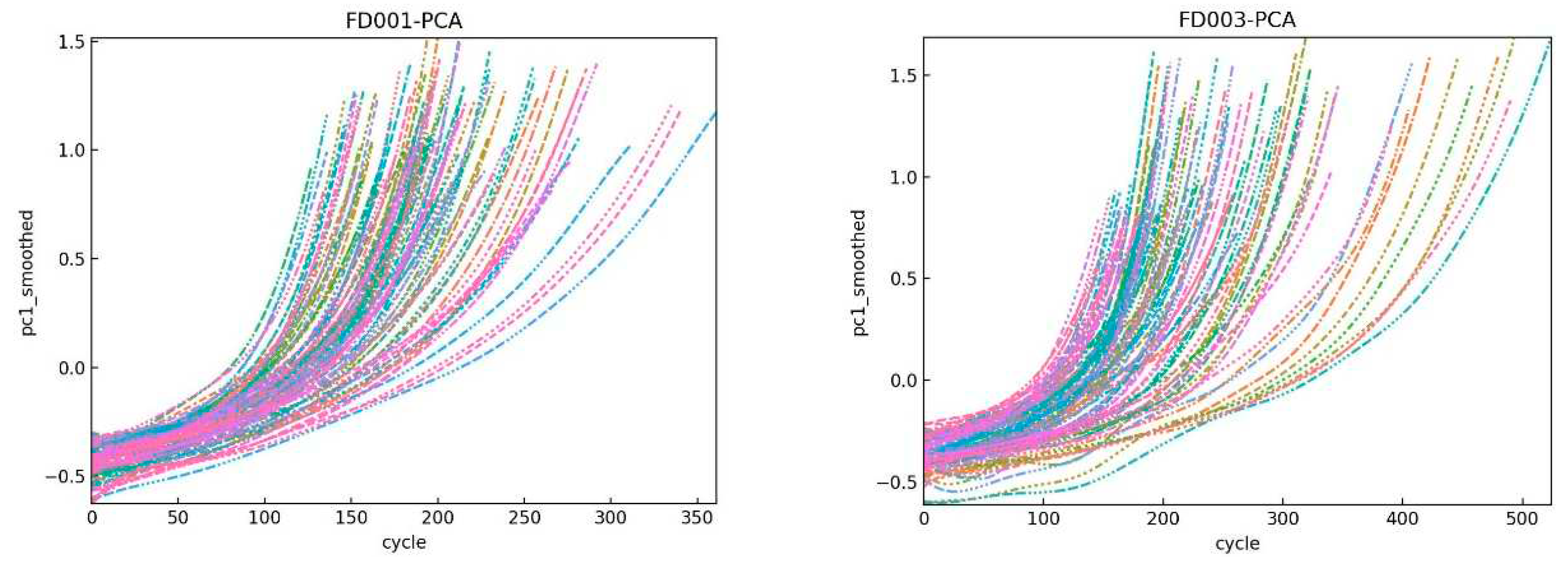
Preprints 78877 g008
Preprints 78877 g009
Figure 9. Clustering results of 6 operating conditions, with a sample size of 5000 cycles. Left-hand plot is FD002, and the right-hand plot is FD004.
Figure 9. Clustering results of 6 operating conditions, with a sample size of 5000 cycles. Left-hand plot is FD002, and the right-hand plot is FD004.
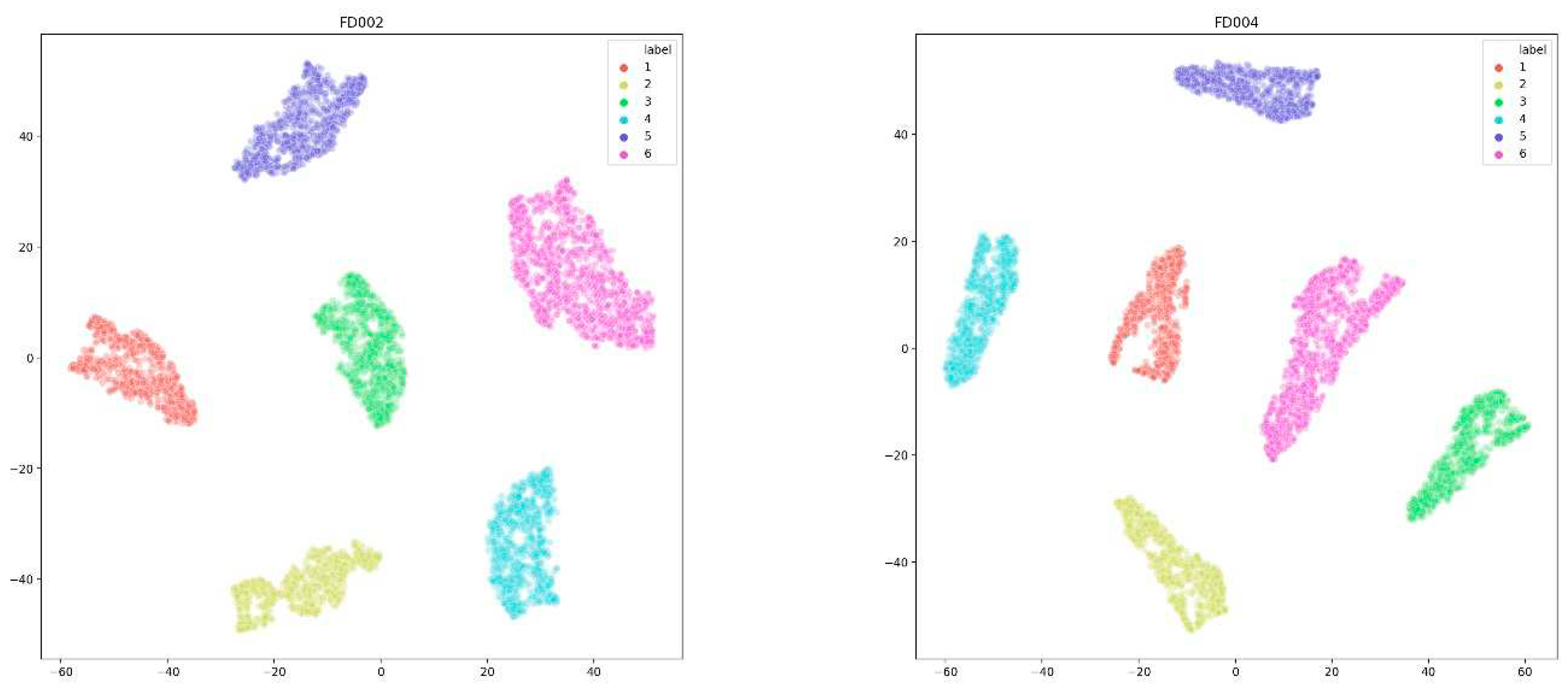
Preprints 78877 g009
Preprints 78877 g010
Figure 10. FD002 and FD004 monitoring data after condition identification and normalization.
Figure 10. FD002 and FD004 monitoring data after condition identification and normalization.
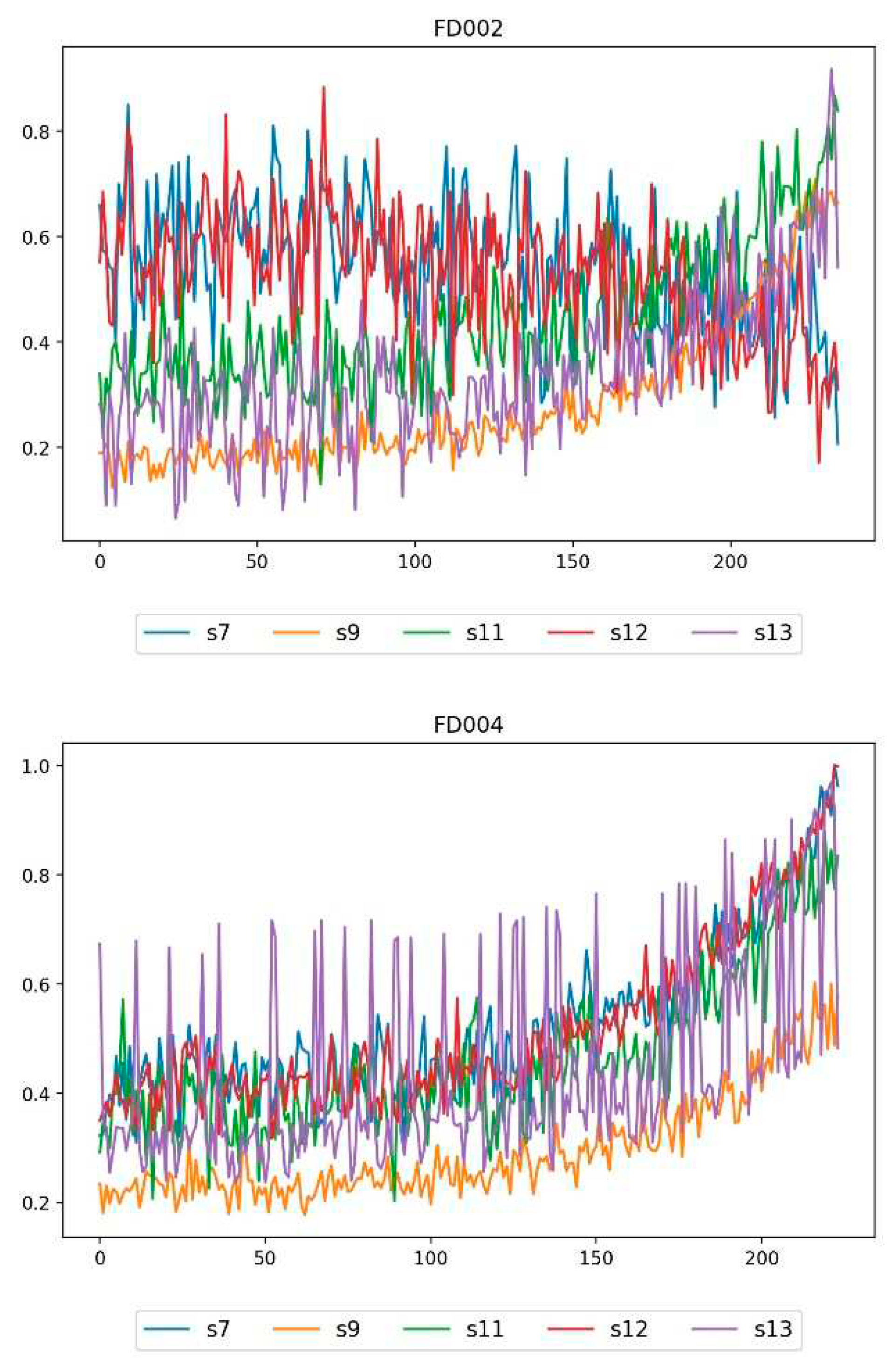
Preprints 78877 g010
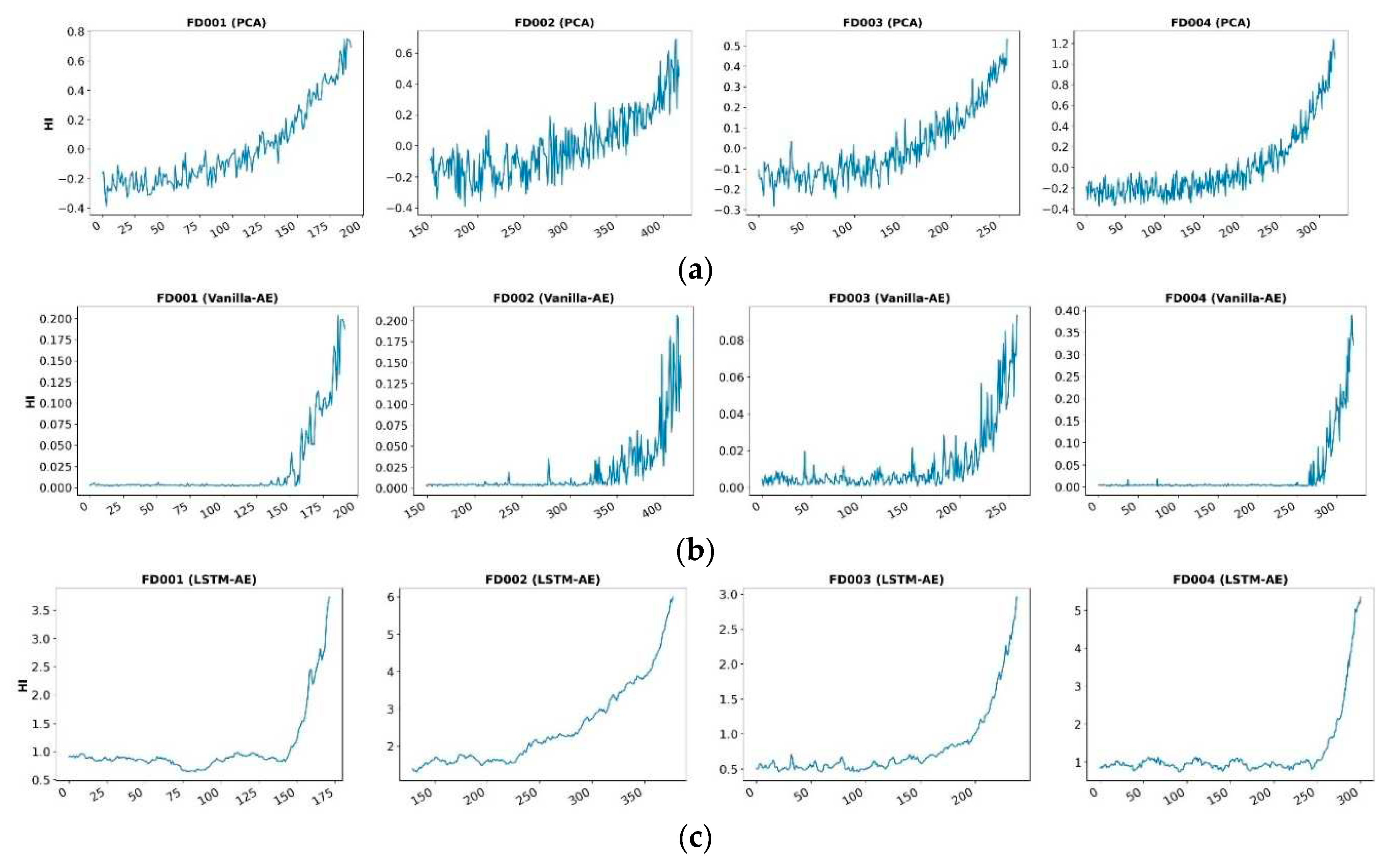
Preprints 78877 g011
Figure 11. HIs built on (a) PCA, (b) Vanilla-AE and (c) LSTM-AE residuals for four test degradation profiles belonging to dataset FD001, FD002, FD003 and FD004.
Figure 11. HIs built on (a) PCA, (b) Vanilla-AE and (c) LSTM-AE residuals for four test degradation profiles belonging to dataset FD001, FD002, FD003 and FD004.
Preprints 78877 g011
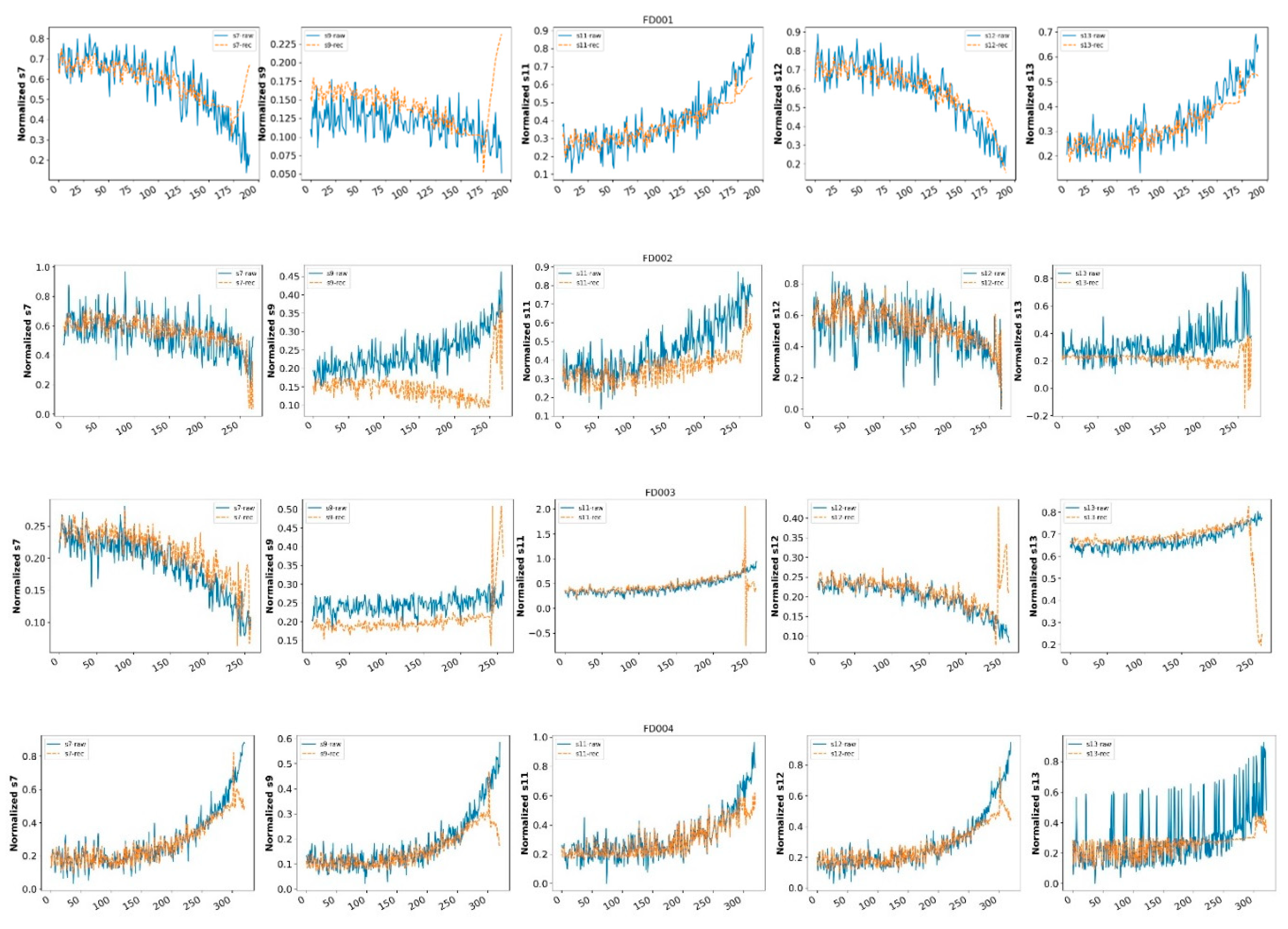
Preprints 78877 g012
Figure 12. Actual and reconstructed sensor measurements with the LSTM-AE —s7、s9、s11、s12 and s13 of FD001, FD002, FD003 and FD004.
Figure 12. Actual and reconstructed sensor measurements with the LSTM-AE —s7、s9、s11、s12 and s13 of FD001, FD002, FD003 and FD004.
Preprints 78877 g012
Table 1. Basic information of C-MAPSS dataset.
Table 1. Basic information of C-MAPSS dataset.
Datasets FD001 FD002 FD003 FD004
Operating condition 1 6 1 6
Fault mode 1 1 2 2
Number of engines 100 260 100 249
Table 2. Mutual information between sensor signal and target variable.
Table 2. Mutual information between sensor signal and target variable.
Sensor number Value of MI
s2 0.570
s7 0.697
s8 0.597
s9 1.000
s11 0.951
s12 0.705
s13 0.682
s17 0.485
s20 0.506
Table 3. Selected engine sensor for HI construction.
Table 3. Selected engine sensor for HI construction.
Sensor number Description Units
s7 Total pressure at High-Pressure Compressor outlet kpa
s9 Physical core speed rpm
s11 Static pressure at High-Pressure Compressor outlet kpa
s12 Ratio of fuel flow to Ps30 —
s13 Corrected fan speed rpm
Table 4. Results of performance of PCA, Vanilla-AE and LSTM-AE for FD001, FD002, FD003 and FD004.
Table 4. Results of performance of PCA, Vanilla-AE and LSTM-AE for FD001, FD002, FD003 and FD004.
Predictor FD001 　 FD002
Mono Tren Prog Fitness 　 Mono Tren Prog Fitness
PCA 0.335 0.892 0.855 2.082 0.194 0.0004 0.751 0.9454
Vanilla-AE 0.246 0.796 0.818 1.860 0.142 0.419 0.617 1.178
LSTM-AE 0.449 0.890 0.841 2.180 　 0.446 0.861 0.822 2.129
Predictor FD003 FD004
Mono Tren Prog Fitness 　 Mono Tren Prog Fitness
PCA 0.330 0.805 0.701 1.836 0.169 0.0002 0.581 0.7502
Vanilla-AE 0.215 0.640 0.496 1.351 0.15 0.383 0.529 1.062
LSTM-AE 0.419 0.718 0.605 1.742 　 0.272 0.387 0.641 1.300
monotonicity –mono–, trendability –tren–, prognosability –prog– and Fitness.
Table 7. Results of performance of Vanilla-AE for time step 5, 10, 15,20 and 25cycles.
Table 7. Results of performance of Vanilla-AE for time step 5, 10, 15,20 and 25cycles.
Time step
(cycle)		 FD001 　 FD002
Mono Tren Prog Fitness 　 Mono Tren Prog Fitness
5 0.298 0.880 0.852 2.030 0.184 0.356 0.537 1.077
10 0.313 0.801 0.739 1.853 0.296 0.776 0.657 1.729
15 0.406 0.709 0.795 1.910 0.358 0.791 0.648 1.797
20 0.449 0.890 0.841 2.180 0.446 0.861 0.822 2.129
25 0.448 0.886 0.817 2.151 　 0.358 0.772 0.729 1.859
Time step
(cycle)		 FD003 FD004
Mono Tren Prog Fitness 　 Mono Tren Prog Fitness
5 0.329 0.845 0.561 1.735 0.216 0.371 0.549 1.136
10 0.383 0.860 0.330 1.573 0.284 0.454 0.610 1.348
15 0.418 0.707 0.545 1.670 0.316 0.406 0.614 1.336
20 0.419 0.718 0.605 1.742 0.272 0.387 0.641 1.300
25 0.448 0.820 0.441 1.709 　 0.323 0.188 0.453 0.964
monotonicity –mono–, trendability –tren–, prognosability –prog– and Fitness.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated