Preprint
Concept Paper
Meaningfully Averaging Unbounded Functions
Altmetrics
Downloads
916
Views
269
Comments
0
This version is not peer-reviewed
Submitted:
26 March 2024
Posted:
27 March 2024
You are already at the latest version
Alerts
Abstract
In this paper we want meanignfully average an "infinite collection of objects covering an infinite expanse of space". For any n∈ ℕ, set A⊆ℝⁿ and set B⊆ℝ where (A,P) is a Polish space, we illustrate this quote with an everywhere, surjective function f∶A→B. The problem is no meaningful expected value of f (e.g., w.r.t the Lebesgue or Hausodorff measure) on Borel sets has a finite value, since the graph of f in any n-dim. interval which covers a subset of A×B has countably infinite points. (The Hausdorff measure of countably infinite points is +∞, where the expected value of f is undefined due to division by infinity.) To fix this, we need the most generalized and "meaningful" expected value; however, consider the following issue. Suppose for n∈ ℕ, set A⊆ℝⁿ and function f∶A→ℝⁿ. If set A is Borel; B* is the set of all Borel measurable function in ℝᴬ for all A⊆ℝⁿ, and B** is the set of all f∈B* with a finite-valued expected value—w.r.t the Hausdorff measure—then B** is a shy subset of B*. Hence a "positive measure" of Borel measurable functions needs to have a finite expected value to increase the chance that everywhere, surjective f:A→B has a finite expectation. To fix this issues, we wish to find a unique and "natural" extension of the expected value—w.r.t the Hausdorff measure—on bounded functions to unbounded/bounded f, which takes finite values only, so B** is a non-shy subset of B*. Note, we haven't found evidence suggesting mathematicians have thought of this problem; however, it's assumed, in general, there's no meaningful way of averaging functions which cover an infinite expanse of space. Note, we haven’t found evidence suggesting mathematicians thought of this problem; however, it’s assumed, in general, there’s no meaningful way of averaging functions which cover an infinite expanse of space. Regardless, we’ll choose a sequence of bounded functions using a "choice function". Note, we find the "choice function" using a question with criteria in §2.4. Also, in §3 and §4, we attempt to answer this question that should "choose" a sequence of bounded functions that a) meaningfully averages everywhere, surjective functions and b) obtains a finite average from a "positive measure" of Borel measurable functions.
Keywords:
Subject: Computer Science and Mathematics - Analysis
1. Introduction
According to an article in Quanta Magazine [1] Wood writes, "No known mathematical procedure can meaningfully average an infinite number of objects covering an infinite expanse of space in general. The path integral is more of a physics philosophy than an exact mathematical recipe." If , set , and set where is a Polish space, the quote can be illustrated by an everywhere, surjective , i.e. a function defined on a topological space where the restriction of f to any non-empty open subset is surjective (2.3, crit. 3a). Note, everywhere, surjective functions, e.g. f, have been well studied [2,3,4]; however, their expected values (w.r.t the Lebesgue or Hausdorff measure) have not. Moreover, a meaningful average of f (e.g. w.r.t the Lebesgue or Hausdorff measure) is non-finite, since the graph of f in any n-dimensional interval which covers a subset of has countably infinite points. (This means the average is undefined, since the Hausdorff measure of countably infinite points is , and the expected value—w.r.t the Hausdorff measure—is undefined due to division by infinity.) To fix this, we want the most generalized "meaningful" average, so the expected value of f is "natural" and finite. In 4 and 5, we explore a constructive approach where the average is unique, finite, and "meaningful" (3.3 & 3.4) for all functions in a non-shy or "positive measure" subset (def. 3) of the set of all Borel measurable functions. The reason we want this is to increase the chances of obtaining a finite average from an everywhere, surjective function . The rest is explained in the next paragraph. (Note the functions must be Borel measurable, since these functions are most useful [5].)
Suppose for , set and the function . If A is Borel, note the expected value of f, w.r.t the d-dimensional Hausdorff measure (i.e., d is the Hausdorff dimension of A), is undefined when the Hausdorff-dimension (of A)-dimensional Hausdorff measure (of also A) is either , zero or the function f is unbounded (def. 4,5 & 6). Infact, if is the set of all Borel measurable functions in (for all the sets —i.e, def. 7) and is the set of all with a finite expected value, then is a shy "measure zero" (def. 2) subset of . This means "almost no" Borel measurable functions have a finite expected value. Specifically, within the definition of —we want to manipulate the expected value of f to be finite—such that is a non-shy (i.e., prevelant or neither prevelant nor shy[6]) subset of .
This can be done by taking the expected value of a sequence of bounded functions which converge to bounded/unbounded f. A sequence of bounded functions with a meaningful average is chosen using a "choice function". We find this "choice function" from answering a question which has four criteria: a) the chosen sequence of bounded functions converge to f at a rate linear or super-linear to the rate non-equivalent sequences of bounded functions converge also to f; b) The expected value of the sequence of bounded & equivalent bounded functions are finite; c) When set is the set of all where the choice function chooses a unique set of equivalent bounded functions satisfying (a) and (b), then Q is a non-shy "positive measure" subset of ; and d) out of all the functions which satisfy (a), (b) and (c) we choose the one with the simplest form. Note, the expected value for the chosen sequence of bounded functions should be a unique and "natural" extension of the original expected value (w.r.t Hausdorff measure) on bounded f, which takes finite values only.
We do this by defining a sequence of sets called ★-sequence of sets (def. 8), where the ★-sequences of sets converge to the graph of f rather than A. Otherwise, the generalized expected value of f w.r.t to a ★-sequence (def. 9) cannot be finite for f in a non-shy subset of Borel measurable functions. Moreover, since there are graphs of functions with multiple ★-sequences of sets, s.t.the generalized expected values of f w.r.t each ★-sequence are different and non-unique (depending on the starred-sequence chosen)—we must have a choice function which chooses a unique set of equivalent ★-sequences with the same, unique expected value.
Therefore, when defining the choice function, we ask a question in 3.4 where with previous sections; we define equivalent & non-equivalent ★-sequences of sets for 3.1, and "natural" extensions of expected values for 3.3. We attempt to answer the question in 3.4—similar to the one two paragraphs before—by redefining linear/super-linear convergence (def. 16) in terms of entropy, samples and "pathways", where samples are derived by taking a point from each partition of a ★-sequence of sets, where the partitions have equal Hausdorff measure—§ 4. Since all samples have finite points; we take a "pathway" of line segments between the nearest point to each start-point of all segments in the pathway (i.e., the pathway should intersect every point once), where in def. 19 we exclude segments with lengths which are outliers [7]. The procedure is similar to the ones used in computers to graph functions [8]. We also take the length of each of the line segments in the "pathway", multiplying all lengths by a constant so they add up to one (i.e. a discrete probability distribution). We take the supremum of the Entropy of the distribution [9] w.r.t all "pathways" to redefine def. 16 as def. 20, where the redefined definition is used to create a choice function in 5.1.
2. Preliminary Definitons/Motivation
There are other constructive approaches to finding a unique and "natural" extension of the average that takes a finite value for additional functions. Before beginning, consider the following mathematical definitions:
2.1. Preliminary Definitions
Let X be a completely metrizable topological vector space.
Definition 1
(Prevalent Subset of X). A Borel set is said to be prevalent if there exists a Borel measure μ on X such that:
- for some compact subset C of X, and
- the set has full μ-measure (that is, the complement of has measure zero) for all .
More generally, a subset F of X is prevalent if F contains a prevalent Borel Set. Also note:
Definition 2
(Shy Subset of X). The complement of a prevalent set is called a shy set.
such that we define:
Definition 3
(Non-Shy Subset of X). A subset of X that is prevalent or neither prevalent nor shy.
Furthermore, suppose we define:
Definition 4
(Hausdorff Measure). Let be a metric space, . For every , define the diameter of C as:
We define:
The Hausdorff Outer Measure is defined by
If and such that , where the Euler’s Gamma function is Γ and constant is:
when and E is a Borel set we have that
such that is related to the α-dimensional Lebesgue Measure.
Definition 5
(Hausdorff Dimension). The Hausdorff Dimension of E is defined by where:
Therefore, we can use definitions 1, 2, 4 to prove or disprove:
Theorem 1.
The set of Borel measurable, unbounded functions forms a prevalent subset of the set of all Borel measurable functions.
Note 1
(Notes on Theorem 1). By measurable function, we mean the pre-image of any subset of (under a measurable function) is in the Borel sigma algebra. (Note function f on set A is unbounded when there is no such that for all ):
however, we’re unsure if theorem 1 is correct. Despite this, we could prove or disprove theorem 1 using the paper on prevalence in [6].
If the theorem is true, it is easier to show a shy subset of Borel measurable, unbounded function have finite expected values (see the next definition). Hence, a shy subset of all Borel measurable function, including bounded Borel functions, have finite expected values.
We, therefore, define the expected value w.r.t the Hausdorff measure to be the following:
Definition 6
(Expected Value of f).If , where set , the expected value of function (using def. 4 and 5) is
where we can see there are cases where is undefined or infinite (e.g. is zero, or f is unbounded). In this case, if topological vector space X is (see ) where we define such that:
Definition 7
(The set of all measurable functions). is the set of all Borel measurable functions in for all the sets . This can also be described as:
Thus, we must prove:
Theorem 2.
If set is the set of all (def. 7) with a finite , then is a shy subset of .
Note 2
(Note on Theorem 2). We’re not sure how to prove theorem 2; however, we refer to an answer from @Mathe at the last page of this citation [10],
"We can follow the argument presented in example 3.6 of [6]:
Because a function can always be represented as we only consider whether positive functions have a mean value. We consider the case of a set A with finite positive measure. In this context having a mean means having a finite integral, and not being integrable means having an infinite integral.
Take (measurable functions over A) let P denote the one-dimensional subspace of consisting of constant functions (assuming the Hausdorff measure on A) and let (measurable functions over A with no finite integral)
If denotes the Lebesgue measure over P, for any fixed
Meaning P is a 1-dimensional probe of F, so F is a 1-prevalent set. (In other terms, the set of measurable functions over A with no finite integral or mean, forms a prevalent subset of the set of all measurable functions in . Therefore, using def. 2, the set of measurable functions with a finite integral or mean forms a shy subset of all Borel measurable functions in .)
2.2. Extended Expected Values
Here are four ways to extend (def. 4 & 5) in (def. 6), so when f is bounded, if is the set of all where extended expected values are finite, then set (i.e., thm. 2):
- 1.
-
Defining a (exact) dimension function; i.e., , that’s monotonically increasing, strictly positive and right continuous, such that when D denotes the diameter of a ball in a covering for the definition of the Hausdorff Measure, we replace with so : the h-Hausdorff measure, is positive and finite. This leads to the extended expected value , where:Note, however, not all A has dimension function h which leads to:
- 2.
- If A is fractal but has no gauge function, we could use this paper [11] which is an extension of the Lebesgue density theorem and this paper [12] which is an extension of the Hausdorff measure using Hyperbolic Cantor sets. Note, however, when A is non-fractal (e.g. countably infinite) or f is unbounded, there is a possibility that the expected value is infinite or undefined. Hence,
- 3.
- In the case f is unbounded and fractal, we could use [13], which applies a Henstock-Kurzweil type integral (i.e., -HK integral) on a measure Metric Space. This coincides with unbounded functions with finite improper Riemman integrals, including bounded functions with finite Lebesgue integrals, bounded function with finite integrals w.r.t the Hausdorff measure, or function with finite Henstock-Kurzweil integrals.
2.3. Examples
If , set and function , we want to apply the definitions of 3, 4, and 5 for the following examples:
- (a)
-
If , where set , set and is a Polish space, the most important example is any everywhere, surjective . Note f is everywhere, surjective when (i.e., the image of f) for every . (This is a nice example of "infinite number of objects covering an infinite expanse of space" described by Wood [1].) Note is undefined, since the graph of f in each n-dimensional interval which covers the subset of is countably infinite [14]. In other words, usingis undefined because of division by (i.e, ).Further, we assume using 2.2, crit. 1, there is no (exact) dimension function of A where is positive & finite, since A is unbounded. Furthermore, the graph of f might be "too chaotic" for extensions of the Lebesgue Density Theorem [11], the Hausdorff measure using Hyperbolic Cantor Sets [12], or the Henstock-Kurzweil integral on the Metric Space [13].
- (b)
-
A simpler, more explicit example is , gcd is the greatest common divisor, and where:For instance, point is a point in the graph of f (since and , making ). Also, point is a point in the graph of f (since and , making ); however, point is not in the graph of f (since ).Note the function in eq. 5 is bounded; however, the expected value & extensions are undefined. (Using def. 6, we know but , which makes :undefined by division of .) Further, we assume using 2.2, crit. 1, there is no (exact) dimension function of A where is finite. Worse, A isn’t "fractal" enough for extensions of the Lebesgue Density Theorem [11], the Hausdorff measure using Hyperbolic Cantor Sets [12], or the Henstock-Kurzweil integral on the Metric Space [13].
- (c)
- An extremely simple example is and . This function is unbounded and has an undefined expected value, even with the improper Riemann integral since:is (when , , and ) or (when , , and ), making the expected value undefined.
3. Attempt to Answer Thesis
Suppose for , set and function . Moreover, is the h-Hausdorff measure (2.2, crit. 1) where h is the dimension function, and is the set of all Borel measurable functions in .
(Note for the definitions below, I prefer the generalized extensions of (def. 6) in 2.2, crit. 2 & 3. Unfortunately, I’m unsure how to describe most of these generalized measures. If possible, replace the h-Hausdorff measure with 2.2, crit. 2 or crit. 3)
Definition 8.
(★-Sequence of Sets).
When we define a sequence of sets , where h is the dimension function (2.2, crit. 1), then if:
- (a)
-
The set theoretic limit of is the graph of f (i.e., convergesto the graph of f) such thatwith the graph of f being:such that the set-theoretic limit of should be:
- (b)
- For all , where is the h-Hausdorff measure (2.2, crit. 1):
- (c)
- we define sequence of functions where such that:
we have is a ★-sequence of setsorstarred-sequence of sets.
One ★-sequence of sets of on (2.3, crit. 3c) is:
Another example of a ★-sequence of sets of where:
using (2.3, crit. 3b) is the following:
another example is:
Note this leads to a new extension of the expected value where when set (def. 7) is the set of all , there exists at least one starred-sequence of sets (of the graph of f) s.t.the extended expected value of f is finite, is a non-shy subset of .
Definition 9.
(Generalized Expected Value).
If is a ★-sequence of sets (def. 8), the generalized expected value of f w.r.t is (when it exists) where:
Using example Section 3, we find that when :
- (a)
- (b)
- for
and the generalized expected value is:
We can see from example Section 2.3 crit. 3c, the average was once undefined but now we’ve "chosen" a ★-sequence which gives a finite expected value.
3.1. Equivalent and Non-Equivalent ★-Sequences of Sets
Suppose we define the following:
Definition 10.
(Set ).
Set is the set of all f, where the generalized expected value—w.r.t at least one starred sequence—exists.
The following are definitions of equivelant and non-equivelant starred-sequences of sets:
Definition 11.
(Non-Equivalent Starred-Sequences of Sets).
All starred-sequences of sets (in a set of ★-sequences of sets) are non-equivalent, if there exists an (def. 10), where the generalized expected values of f (def. 9) w.r.t each starred-sequence of sets has two or more different values (e.g., defined and undefined values are different). See Figure 1.
Definition 12.
(Equivalent Starred-Sequences of Sets).
All starred-sequences of sets (in the set of ★-sequences of sets) are equivalent, if we get for all (def. 10); the generalized expected value of f (def. 9) w.r.t each starred-sequence of sets has the same value. See Figure 2.
However, proving that two or more starred-sequences of sets are non-equivalent or equivalent (using def. 12 or 11) is tedious, since we constantly compute def. 9. Therefore, we ask the following:
3.1.1. Question 1
Is there are a simpler definition of equivalent and non-equivalent ★-sequences of sets?
3.1.2. Possible Answer
For the sake of brevity, suppose starred-sequences (i.e., def. 8), such that , , and
Definition 13.
(Equivalent Starred-Sequences of Sets [Revisited]).
Starred-sequence of sets and are equivalent, if there exists a , where for all , there exists a , where if is the (exact) dimension function (2.2, crit. 1) of and is the -Hausdorff measure:
and also for all , there exists a , where if is the (exact) dimension function of and is the -Hausdorff measure (2.2, crit. 1) then:
Note we denote these equivalent starred-sequence of sets as
Definition 14.
(Multiple Equivalent Starred-Sequences of Sets [Revisited]).
All starred-sequences of sets in:
are equivalent, if for all where , and are equivelant (def. 13). We also state the former as:
Theorem 3.
If starred-sequences of sets in:
are equivalent (def. 14), then for all where , the generalized means of f w.r.t the ★-sequences (def. 9) have the same mean value. In other words:
Note this is similar to def. 12.
Definition 15.
(Non-Equivalent Starred-Sequences of Sets [Revisited]).
All starred-sequences of sets in
are non-equivalent, if def. 14 is false, meaning for all where , there exists an , where for all there is either a , where if is the (exact) dimension function (2.2, crit. 1) of , and is the -Hausdorff measure:
or for all there exists a , where if is the (exact) dimension function of , and is the -Hausdorff measure (, crit. 1) then:
3.2. Motivation For Sec. 3.4
If the set (def. 7) is the set of all where we choose a ★-sequence of sets of the graph of f (def. 8)—where the generalized expected value of f, w.r.t the chosen starred-sequence, is finite—then is a non-shy subset of . However, consider the following problem:
Theorem 4.
If set , is the set of all where the generalized expected values of f w.r.t two or more non-equivalent ★-sequences of sets (def. 15) have different values, then is a non-shy subset of (def. 7).
This means "almost all" measurable functions have several generalized expected values depending on the starred-sequence chosen. Therefore, we need to choose a unique ★-sequence of sets where the new extended expected value is an "meaningful" extension of (def. 6).
3.3. Essential Definitions for a "Meaningful" Expected Value
Suppose and are non-equivelant starred-sequences of sets (def. 8 & 15): we have the following is essential for a "natural" extension of the expected value.
Definition 16.
(Linear & Super-linear Convergence of a ★-Sequence of Sets To That Of Another ★-Sequence of Sets).
If we define function , where and for any linear , where , is the Big-O notation, and:
where if the following is true:
then converges to the graph of f: i.e.,
at alinearorsuper-linearrate compared to that of .
Now we may combine the previous definitions into a main question with an answer that solves the thesis [1].
3.4. Main Question
Does there exist a choice function that chooses a unique set (of equivalent ★-sequences of sets—def. 14) such that:
- (a)
- The chosen starred-sequences of sets converge to at a rate linear or super-linear (def. 16) to the rate non-equivalent ★-sequences of sets (def. 15) converge to
- (b)
- The generalized expected value (def. 9) of f w.r.t the chosen (and equivalent) starred-sequences of sets (def. 14) is finite.
- (c)
- When set (def. 7) is the set of all such that the choice function chooses a unique set of equivalent ★-sequences of sets satisfying (3a) and (3b), then Q is a non-shy subset (def. 3) of (i.e., def. 7).
- (d)
- Out of all the choice functions which satisfy (3a), (3b) and (3c), we choose the one with the simplest form, meaning for each choice function fully expanded, we take the one with the fewest variables/numbers (excluding those with quantifiers)?
Note 3.
(Notes On Question)Note, the unique set of equivalent and chosen starred-sequences of sets is defined using notation , where is a starred-sequence in . Therefore, after we define the choice function, the answer should be —using def. 9 (when it exists):
Also, consider three things:
- (a)
- If the solution to the main question is extraneous, what other criteria can be included to get a unique choice function? (Note if the solution is always extraneous, we want to replace “equivelant starred-sequences of sets” with the following: ”the set of all ★-sequences of sets, where the generalized expected values of f w.r.t each starred-sequence is the same”.)
- (b)
- The h-Hausdorff measure (2.2, crit. 1) isn’t the most generalized measure in 2.2. How do we use the other measures in 2.2 to answer the thesis[2] of this paper?
- (c)
- How do we change the definitions and main question in 3 of this paper to counter Wood’s statement [1] which states, "No known mathematical procedure can meaningfully average an infinite number of objects covering an infinite expanse of space in general" by finding an exact mathematical recipe that does otherwise.
4. Preliminaries to Solve Main Question of Section 2.4 (in Current Form)
Suppose h is the dimension function, is the h-Hausdorff measure (2.2, crit. 1), and is the starred-sequence of sets (def. 8). We will use an alternative approach to definition 16 so we can define a choice function which solves the main question. Read from the second sentence of the last paragraph of the intro of 1 for a summary. Also, refer to sec. 3 and 4 of [15] for examples: (the cited paper uses sets instead of the graphs of functions).
While reading, keep in mind the following questions:
- (a)
- How do we use mathematica code to illustrate § 4 and 5?
- (b)
- Is there a more efficient solution to 3.4?
- (c)
- If 3.4 should be changed, (see note 3) what else should be 3.4? What is the most efficient solution to the improved version of 3.4? Would this meaningfully average an everywhere, surjective function (2.3, crit. 3a)?
4.1. Preliminary Definitions
Definition 17.
(Uniform coverings of each term of a ★-sequence of sets).
We define uniform ε coverings of each term of as a group of pair-wise disjoint sets which cover (for some ), such when taking dimension function h of , we want of each pair-wise disjoint set to have the same value , where and the total sum of of the coverings is minimized. In shorter notation, if
- The element
- The set is arbitrary and uncountable.
and set Ω is defined as:
then for every , the set of uniform ε coverings is defined using where ω “enumerates" all possible uniform ε coverings of for every .
Definition 18.
(Sample of the uniform coverings of each term of a ★-sequence of sets).
The sample of uniform ε coverings of each term of is the set of points where for every and , we take a point from each pair-wise disjoint set in the uniform ε coverings of (def. 17). In shorter notation, if
- The element
- The set is arbitrary and uncountable.
and set is defined as:
then for every , the set of all samples of the set of uniform ε coverings is defined using , such that ψ “enumerates" all possible samples of .
Definition 19.
(Entropy on the sample of uniform coverings of each term of ★-sequence of sets).
Since there are finitely many points in the sample of the uniform ε coverings of each term of (def. 18), we:
- (a)
-
Take a "pathway" of line segments between all points in each sample (def. 18), such that if we define the following:
- i.
- is the ceiling function
- ii.
- is the Euclidean-distance between points and
- iii.
-
The sequence:contains all points in the "original" sample where we define a "pathway" for which we:
- (A)
- Choose a point
- (B)
- Take a point from (excluding ) with smallest euclidean distance from point . We denote this point where we take . (If more than one point has the smallest Euclidean distance from , we take either point).
- (C)
- Take a point in (excluding and ) with smallest euclidean distance from . We denote this point , where we take . (If more than one point has the smallest Euclidean distance from , we take either point).
- (D)
- Take a point in (excluding , , and ) with smallest euclidean distance from . We denote this point then take . (If more than one point has the smallest Euclidean distance from , we take either point).
- (E)
- Repeat the process excluding points etc. until all points in the sample are "denoted". (This should occur times.)
- iv.
-
is a subset of with the largest cardinality, where we take the subset of i-values where has the -th smallest Euclidean distance from (compared to every point in ) such that is not an outlier [7] ofIn other words:
- (A)
- For all , we want to be the largest subset of for which w-values are all i-values satisfying def. 19, criteria 3(a)iv.
- v.
- Combining everything in def. 19, crit. 3a, we ultimately want all lengths between every point in the "pathway" (def. 18) satisfying def. 19, crit. 3(a)iv. We call this:
- (b)
- Using def. 19, crit. 3(a)v, normalize into a discrete probability distribution. This is defined as:
- (c)
- (d)
-
Take where is maximized. Call this, where:with eq. 24 the entropy of the sample of uniform ε coverings of .
Definition 20.
1.
2.
3.
(Starred-Sequence of sets converging Sublinearly, Linearly, or Superlinearly to A compared to that of another ★-Sequence).
Suppose we define starred-sequences of sets and , where for aconstant greater than zero and variable , we say:
- (a)
-
Using def. 18 and 19, suppose we have:then (using) we get
- (b)
-
From def. 18 and 19, suppose we have:then (using) we have:
If using and we have that:
we say converges to A at a ratesuperlinearto that of .
If using equations and (where we swap in and with ) we have that:
we then say converges to A at a ratesublinearto that of .
If using equations , , , and (such for the two latter, we swap
in and with ) we haveboth:
- (a)
- or does not equal zero
- (b)
- or does not equal zero
and say converges to A at a ratelinearto that of .
5. Attempt to Answer Main Question of Section 2.4 (in Current Form)
5.1. Choice Function
Suppose we define the following:
- 1.
- is a starred-sequence of sets (def. 8) which satisfies (1), (2), and (3) of the main question in 3.4
- 2.
-
, where G is the graph of f; i.e.,is the set of the starred-sequences of sets that have finite generalized mean (def. 9).
- 3.
- is an element butnotan element in the set of equivalent starred-sequences of sets (def. 14) of where using note 3, we can represent this criteria as:
Further note, from def. 20, if we take:
and from def. 20, we take:
the choice function (which we’ll later define on pg. , thm. 5) should immediately choose when:
- 1.
-
For all when defining the set of all values of the m-th coordinate of (i.e., —where, unlike cit.[15] §4, we focus on the domain of to get "n" instead of ""), then when , we either want:
- (a)
- and .
- (b)
- and .
- (c)
- and .
- (d)
- and .
- 2.
-
If the center of the universe is a chosen point , where:then for all , there exists , s.t.for all , when set is a collection of all the values of the m-th co-ordinate of , such that (again, unlike cit.[15] §4, we focus on the domain of to get "n" instead of ""), we must get:
where, using absolute value function and , when set is a collection of all the values of the m-th co-ordinate of , for , when we define:
and
criteria (1) is achieved, using eq. 37, when:
such that, for all :
such that, for all :
where we consider the following:
5.2. Question:
How do we create a choice function which solves the question in sec. 3.4 using , , , , and or equations 32, 33, 34, 39 and 41 resp.?
5.3. "Attempt" to answer the Question
(Note the attempt might be wrong but could offer hints to how the solution would appear).
Suppose and the chosen coordinate for the center of the universe (i.e., eq. 35) is the origin, where for all :
Using equations , , , , and (i.e., eq. 32, 33, 34, 39 and 41) with the absolute value function and the nearest integer function , we define:
where using , the choice function should be the following:
Theorem 5.
page:16 If we define:
where for , we define to be the same as when swapping "" with "" (for eq. & ) and sets with (for eq. 32–44), then for constant and variable , if:
and:
then for all (5.1, crit. 3), if:
Note 4.
(Explanation of Theorem 5)The theorem 5 is similar to the methods used in def. 20 crit. 1a and 1b— and —and def. 20 crit. 2 and crit. 4—linear/superlinear convergence—where:
such that we replace:
note the changes to def. 20, crit. 2 were made, so is "large enough" compared to , with non-equivalent to (e.g., when , should be and never give which increases at a smaller rate than that of "small" , e.g.:
or smaller than that of "large" ; e.g.,
Moreover, in and of thm. 5, we add constant and variable so if either
- 1.
- (i.e., using a related limit to eq. 47, division by zero is undefined).
- 2.
- (i.e., using a related limit to eq. 47, division by zero is undefined).
- 3.
- 4.
-
(i.e., similar to of eq. 45, with no variable and , where we apply a related limit to eq. 47 that’s undefined sinceis an undefined empty set.)
- 5.
- 6.
-
(i.e., similar to of eq. 45, with no variable and , where we apply a related limit to eq. 47 that’s undefined sinceis an undefined empty set.)
- 7.
- (i.e., infinite number succeeding are smaller than original , where such should be eliminated).
the limit in eq. 47 still exists.
5.4. Questions Regarding , and [Revisited]
- How do we use mathematica code to illustrate § 4 and 5?
- Is there a more efficient solution to 3.4?
- If 3.4 should be changed, (see note 3) what else should be 3.4? What is the most efficient solution to the improved version of 3.4? Would this meaningfully average an everywhere, surjective function (2.3, crit. 3a)?
References
- C.,W. Mathematicians Prove 2D Version of Quantum Gravity ReallyWorks. Quanta Magazine. https://www. quantamagazine.org/mathematicians-prove-2d-version-of-quantum-gravity-really-works-20210617/.
- Bernardi, C.; Rainaldi. Everywhere surjections and related topics: Examples and counterexamples, 2018. https://lematematiche.dmi.unict.it/index.php/lematematiche/article/view/1478/1042.
- Bernardi, C. Graphs of real functions with pathological behaviors, 2016, [arXiv:math.HO/1602.07555]. [CrossRef]
- Bernal-González, L.; Pellegrino, D.; Seoane-Sepúlveda, J. Linear subsets of nonlinear sets in topological vector spaces. Bulletin (New Series) of the American Mathematical Society 2014, 51. [CrossRef]
- (https://mathoverflow.net/users/4832/nate eldredge), N.E. Why do probabilists take random variables to be Borel (and not Lebesgue) measurable? MathOverflow, [https://mathoverflow.net/q/31609]. https: //mathoverflow.net/q/31609.
- Ott, W.; Yorke, J.A. Prevelance. Bulletin of the American Mathematical Society 2005, 42, 263–290. https: //www.ams.org/journals/bull/2005-42-03/S0273-0979-05-01060-8/S0273-0979-05-01060-8.pdf. [CrossRef]
- John, R. Outlier. https://en.m.wikipedia.org/wiki/Outlier.
- Emily. How do computers draw function graphs? Mathematics Stack Exchange, https://math.stackexchange. com/q/634338.
- M., G. 2 ed.; Springer New York: New York [America];, 2011; pp. 61–95. https://ee.stanford.edu/~gray/it. pdf. [CrossRef]
- Mathe. Mean of a function in Rn. Matchmaticians, https://matchmaticians.com/storage/answer/101942 /matchmaticians-7gatrd-file-1.pdf.
- B., B.; A., F. Analogues Of The Lebesgue Density Theorem For Fractal Sets Of Reals And Integers. https: //www.ime.usp.br/~afisher/ps/Analogues.pdf.
- B., B.; A., F. Ratio Geometry, Rigidity And The Scenery Process For Hyperbolic Cantor Sets. https: //arxiv.org/pdf/math/9405217.pdf.
- Corrao, G. AN HENSTOCK-KURZWEIL TYPE INTEGRAL ON A MEASURE METRIC SPACE. https: //core.ac.uk/download/pdf/53287889.pdf.
- (https://mathoverflow.net/users/87856/arbuja), A. Finding an explicit, bijective function that satisfies the following properties? MathOverflow, [https://mathoverflow.net/q/451445]. https://mathoverflow.net/q/ 451445.
- Krishnan, B. Mean of Unbounded Sets Using Method Similar To Conditional Expectation. ResearchGate, https://www.researchgate.net/publication/376597571.
| [1] | If the set (def. 7) is the set of all , with an unique and "meaningful" extension of the expected value—w.r.t the Hausdorff measure—on bounded functions to bounded/unbounded f taking finite values, then should be non-shy subset of
|
| [2] | If the set (def. 7) is the set of all , with an unique and "meaningful" extension of the expected value—w.r.t the Hausdorff measure—on bounded functions to bounded/unbounded f taking finite values, then should be non-shy subset of
|
| [3] | If the set (def. 7) is the set of all , with an unique and "meaningful" extension of the expected value—w.r.t the Hausdorff measure—on bounded functions to bounded/unbounded f taking finite values, then should be non-shy subset of
|
Figure 1.
Below , , are non-equivalent starred sequences of sets, where is all circles and is the generalized expected value of f w.r.t either ★-sequence of sets (def. 8)
Figure 1.
Below , , are non-equivalent starred sequences of sets, where is all circles and is the generalized expected value of f w.r.t either ★-sequence of sets (def. 8)
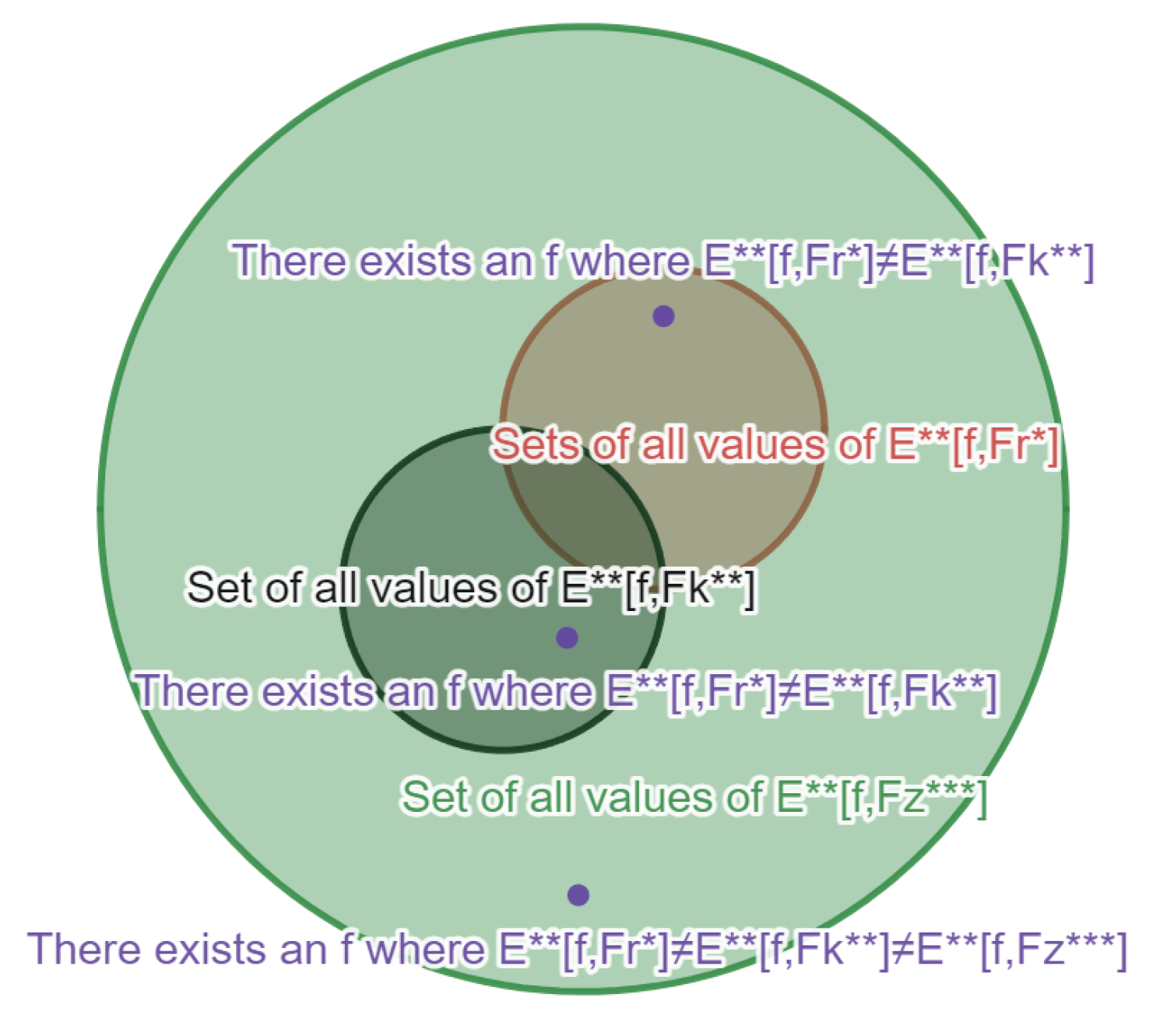
Figure 2.
Below , , are equivalent starred sequences of sets, where is the entire circle and is the generalized expected value of f w.r.t either ★-sequence of sets (def. 8)
Figure 2.
Below , , are equivalent starred sequences of sets, where is the entire circle and is the generalized expected value of f w.r.t either ★-sequence of sets (def. 8)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





