Prerpints.org logo
Preprint
Article

Quartz-Enhanced Photoacoustic Spectroscopy Assisted by Partial Least-Squares Regression for Multi-Gas Measurements

Altmetrics

Downloads

137

Views

58

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 July 2023

Posted:

10 July 2023

You are already at the latest version

Alerts
Abstract
We report on the use of quartz-enhanced photoacoustic spectroscopy (QEPAS) for multi-gas detection. Photo-acoustic (PA) spectra of mixtures of water (H2O), ammonia (NH3) and methane (CH4) were measured in the mid-infrared (MIR) wavelength range using a MIR (mid-infrared) optical parametric oscillator (OPO) light source. Highly overlapping absorption spectra is a common challenge for gas spectroscopy. To mitigate this, we use a partial least-squares regression (PLS) method to estimate the mixing ratio and concentrations of the individual gasses. The concentration range explored in the analysis varies from a few parts-per-million (ppm) to thousands of ppm. Spectra obtained from HITRAN and experimental single-molecule reference spectra of each of the molecular species were acquired and used as training data sets. These spectra were used to generate simulated spectra of the gas mixtures (linear combinations of the reference spectra). Here in this proof-of-concept experiment we demonstrate that after an absolute calibration of the QEPAS cell, the PLS analyses could be used to determine concentrations of single molecular species with a relative accuracy within a few % for mixtures of H2O, NH3 and CH4 and with an absolute sensitivity of approximately 300(±50) ppm/V, 50(±5) ppm/V and 5(±2) ppm/V for water, ammonia and methane, respectively. Thus, demonstrating that QEPAS assisted by PLS is a powerful approach to estimate concentrations of individual gas components with considerable spectral overlap, which is a typical scenario for real-life adoptions and applications.
Keywords: 
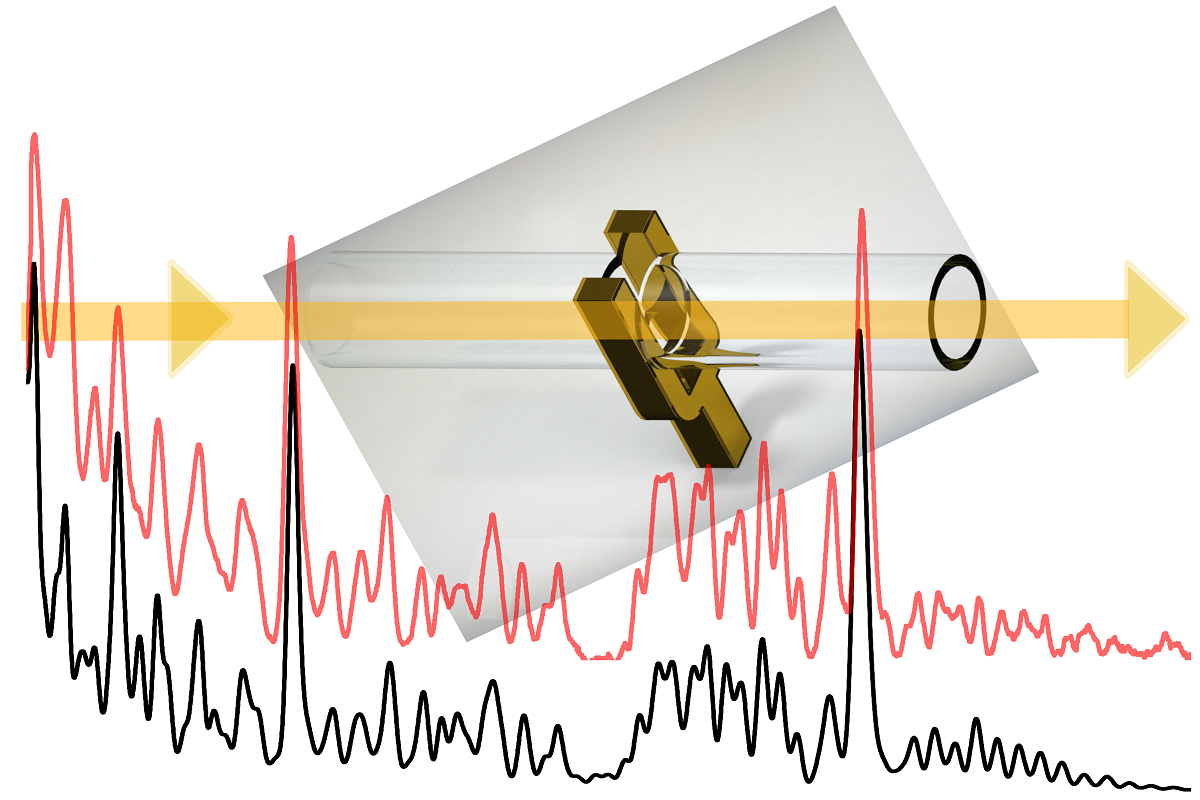
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Multi-gas detection devices that can detect a wide range of gasses and gas concentrations are highly attractive since they significantly enhance safety in various environments and can help enforce regulations with respect to allowable emission and concentrations of various gasses. There is an unmet need for for accurate trustworthy gas detection devices [1,2,3]. Multi-gas sensors are valuable for real-life applications, where multiple gases may be present or where gas concentrations can vary significantly, such as in process-control applications, airborne pollutants, medical diagnostics, and in general for monitoring industrial and urban emissions of greenhouse gasses [4,5,6,7,8,9,10]. Having a single device for detecting multiple gasses saves time during gas monitoring activities. Instead of having to use multiple detectors sequentially or wait for results from different devices, a multi-gas detection system can provide immediate and simultaneous measurements of several gasses [11,12]. This allows for quicker responses to potential gas leaks or unsafe conditions, enabling faster decision-making and remedial actions.
Optical spectroscopy is particularly useful for gas sensing, including gas concentration estimation [13,14,15]. Of the many optical spectroscopic methods developed during the past century, photoacoustic spectroscopy (PAS) [16,17,18,19,20] has attracted considerable interest due to its powerful, yet simple, trace-gas detection method and capability to detect multiple gases with a single device. The PAS method is different from other optical absorption-based methods, where the absorbed energy translates into kinetic energy, which forms an acoustic wave that can be detected with a simple pressure transducer [16,21,22]. A variant of PAS is quartz-enhanced photoacoustic spectroscopy (QEPAS), which was introduced in 2002 [22], and is today an established spectroscopic technique [23,24,25,26,27,28,29]. For QEPAS the generated acoustic wave is detected using a quartz tuning fork (QTF) with a high quality factor ( Q > 10 3 at atmospheric pressures) and an eigenfrequency matching the laser modulation frequency [22,30]. The PAS/QEPAS technique is however not an absolute technique and requires calibration using certified reference gas samples. Further absolute gas concentration measurements with PAS becomes highly nontrivial in complex gas-mixtures and detailed knowledge about the chemical gas composition of the complete gas matrix is needed. This entails that absolute environmental gas-concentration measurements can only be achieved upon applying a correction factor to the PAS signal, which will depend on the gas matrix. For example, the presence of water vapor in a gas sample acts as a buffer for the relaxation process, and thereby enhances, or diminishes, the generated sound waves [25,31,32,33,34]. Furthermore, in many situations, multi-gas measurements are made difficult if not impossible due to strongly overlapping spectra. Therefore most experimental PAS demonstrations have been conducted using a single gas in a simple N 2 matrix and only recently application for real-life situations have been addressed [12,18,25]. However, it has been demonstrated that both identification and concentration estimation can be made possible using multivariate analysis (MVA), such as partial least-squares regression (PLS) together with gas matrix correction factors [12,37]. PLS is a machine learning technique that is widely used for regression and classification tasks. PLS combines elements of both principal component analysis (PCA) and multiple linear regression to handle situations where there are high-dimensional datasets with multicollinearity.
In this work we demonstrate QEPAS measurements of "complex" gas mixtures with (0 - 12000) ppm/V water vapor (H 2 O), 2 - 100 ppm/V methane (CH 4 ), and 50-300 ppm/V ammonia. The measurements are all acquired in the mid-infrared (MIR) region from 2.85 μ m to 3.50 μ m enabled by a home-built wavelength-tuneable optical parametric oscillator (OPO). Note that our system is capable of scanning a much broader wavelength range, and thus capable of exciting more trace gasses with the same setup. To estimate the mixing ratios and concentrations a PLS model was trained with both HITRAN spectra and experimental PAS spectra for single components and synthetic spectra of mixtures and tested on experimental acquired PAS spectra of different mixtures of gasses. The PLS algorithm was trained to estimate the gas mixture ratio. Hereby the concentration of all gasses in the mixture can be estimated by having just one known gas concentration. The motivation for using HITRAN spectra as training data is that instead of acquiring PAS training data, which can involve measuring many calibration data of different concentrations and be time consuming, one simply download spectra from the HITRAN database and train the PLS model. Hereby any gas mixtures (within the wavelength range available) can in principle be identified and mixing ratios can be estimated.

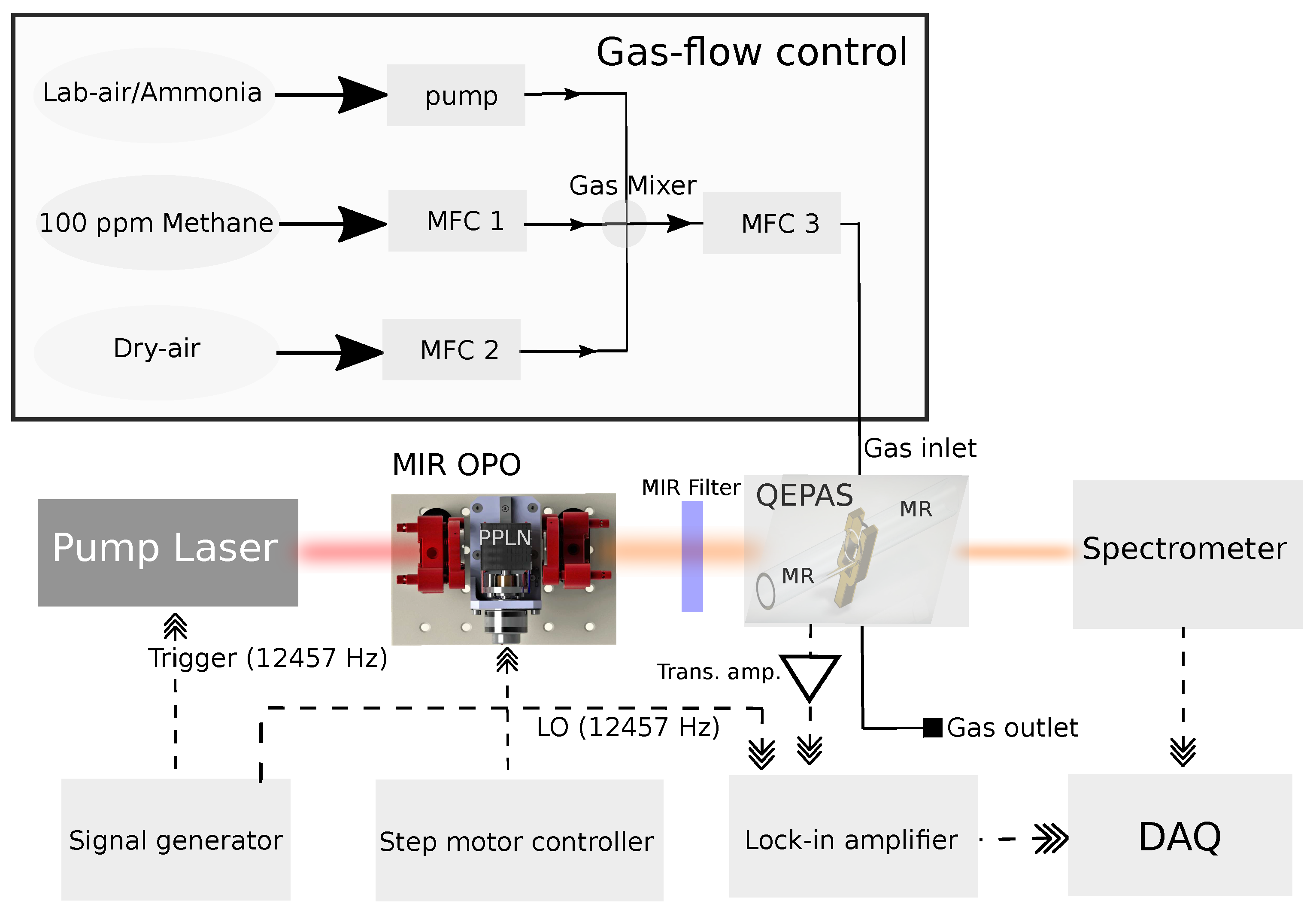
2. Experimental setup

The experimental setup is shown in Figure 1. The main parts in the setup includes a home built mid-infrared (MIR) nanosecond pulsed OPO, a QEPAS sensor module (ADM01, Thorlabs), optical detectors for power measurement, humidity/temperature/pressure sensors, a mass-flow control system, and a lock-in amplifier and an oscilloscope for data acquisition. The MIR pump source is based on an actively Q-switched nanosecond Nd:YAG pump laser (BrightSolution), which emits 15 ns pulses at a center wavelength of 1064 nm with a repetition rate of 12.457 kHz matching the resonant frequency of the QEPAS cell. The 1064 nm pulses are focused into a 40 mm long fan-out structured periodically poled lithium niobate crystal (PPLN) (HC Photonics) placed inside a 55 mm long linear cavity with a waist of approximately 150 μ m. By translating the PPLN crystal with a step motor MIR light from 2.85 μ m to 3.55 μ m with 50 mW of mean optical output power was generated. This wavelength range matches ro-vibrational lines of water (H 2 O), ammonia (NH 3 ) and methane (CH 4 ). More details on the MIR OPO can be found in [25]. The QEPAS module contains a quartz tuning fork (QTF) with an eigenfrequency of f 0 = 12457 Hz and a quality factor of ∼ 5300 ± 50 at 1 atm [30]. The QTF is piezo-electrically active in the mechanical mode for which the two prongs oscillate 180 degrees out of phase (asymmetrical stretching mode) [22,28]. Acoustic coupling is further improved by two microresonator (MR) tubes each having a length of 12.4 mm. In- and out coupling of the MIR light through the module happens through two BaF 2 windows with a combined transmittance of ∼ 0.9 . [17,22,25,26,27,28,36].
The gas-flow control is realized using triplet mass-flow controllers (Brooks 0254, MFCs). Two MFCs are used for setting the in-flow rate of dry-air/N 2 and 100 ppmV CH 4 in N 2 . Lab-air and ammonia (NH 3 ) gas flow is combined with a valve-controlled inlet that enables suction of wet laboratory air and NH 3 into the QEPAS cell using a mini vacuum pump with variable flow rate. The humidity is measured with a commercial humidity sensor (Extech RH25, measurement accuracy 0.3%) and verified by fitting HITRAN spectra to the acquired PAS spectra, while the ammonia has a completely unknown concentration. The combined gas flow is led through a third MFC, which is used to monitor and log the total gas flow to the QEPAS module, thus estimating the concentrations of the mixed gasses with an uncertainty of ± 5%. Data processing is enabled by a lock-in amplifier receiving the electrical local oscillator signal from the active laser Q-switch with an integration time of 30 ms. The lock-in amplifier demodulates the PA output signal of the transimpedance amplifier build-in the QEPAS using a 1-f configuration (i.e. amplitude modulation) [11]. The output from the lock-in amplifier is digitized using a fast 12-bit oscilloscope and spectra in the 2.85 μ m-3.5 μ m is obtained as function of scanning time as shown in Figure 2.

3. Partial least squares regression

Partial Least Squares (PLS) is a machine learning technique that is widely used for regression and classification tasks. PLS is a statistical method that finds a linear regression model by projecting the predicted variables and the observable variables to a new space [37]. PLS can be thought of as a hybrid between multiple linear regression and principal component analysis (PCA). In PLS, the predictor variables are first transformed into a set of latent variables using singular value decomposition. These latent variables are then used to predict the response variable in a multiple linear regression model. Thus, PLS is different than simple linear regression in that it projects the variables to a new space, where the variance is maximized along one direction in the variable hyperplane. This makes the method more powerful for fitting spectra than other fitting approaches. For example PCA is not well suited for identifying gas mixtures in complex spectra, where one gas component completely dominates the measured spectrum, and here the PLS method performs well and can establish the actual mixture ratio with high fidelity. However, the PLS regression method is not without its limitations. It is sensitive to the scaling of the predictor variables and can be influenced by outliers in the data. It is also not suitable for cases where the predictor variables are highly correlated with the response. The general form of the PLS equation can be written as:
Y ^ = X B + C ,
where Y ^ is the predicted response, X is the matrix of predictor variables, B is the matrix of regression coefficients, and C is the intercept term. The matrix B is obtained by performing singular value decomposition on the predictor matrix X. In this work the PLS method is used to estimate the mixing ratio, thus the gas concentrations of the three gasses (H 2 O, NH 3 and CH 4 ), where they have a very high degree of spectral overlap. The validity of the method has already been shown in the literature for QEPAS spectroscopy [12] and was verified to establish well-fitting spectra for both two-gas mixtures and three-gas mixtures with highly overlapping spectra. With the main difference between our work and the work presented in ref. [12] is the use of HITRAN and PAS spectra acquired in a much broader wavelength range, thus more spectral lines are used in our PLS method, which potential gives more information about the complete gas matrix and any potential pollutants that might influence the estimation. However, this also adds to the complexity of the analysis. The PLS method used here is an implementation from the scikit-learn community [38]. A training data set was developed using either the measured single-gas PAS spectra or HITRAN spectra as reference spectra, as shown in Figure 2. The main motivation for using HITRAN spectra is that instead of acquiring PAS training data, which can be time consuming, one simply download spectra from the HITRAN database to train the PLS model. This will in principle enable estimation of any gases (within the wavelength range available) and mixing ratios. The PLS algorithm was trained with a data set of 5000 artificial spectra composed of the three reference spectra using random ratios of the gas-mixture, with a small amount of white noise added. Thus, the algorithm was trained to estimate the gas mixture ratio of the three gasses. The PAS technique is not an absolute technique and therefore calibration of the acquired PAS signal is required against a known gas sample. We use the obtained lock-in voltage signal for 100 ppm/V methane in N 2 to set the expected PAS voltage level for 100 ppm/V water and ammonia. The PAS data and HITRAN data can now be used to estimate the concentration of unknown mixtures of these gasses and be used to train the PLS method. These are shown in Figure 2.

4. Results

The acquired PAS spectra for training of the PLS are shown in Figure 2 together with absorption spectra from HITRAN. The HITRAN data is convolved with a Gaussian instrument profile of 5 cm − 1 . Thus, shows that our QEPAS sensor has a spectral resolution bandwidth of 5 cm − 1 . The pressure used for these simulations are 1013 mbar and at a temperature of 25 ∘ C. These parameters closely resemble experimental conditions in our lab. Prior to the PLS analysis, the experimental data is post-processed to make them useful for training and validation as well as to be compared with the PLS model trained with the corresponding HITRAN data. The raw spectral data is acquired as function of time and subsequently the time x-axis is transformed into a wavelength x-axis using the Sellmeier equation for PPLN [39]. The absolute wavelength of the probe light is also measured using a calibrated optical spectrum analyzer (OSA205C, Thorlabs) to establish the start and end of the wavelength x-axis. It was confirmed that the wavelength of the scans conforms very well with the Sellmeier equation. However, we found for some of the acquired spectra small deviation and nonlinear behavior of the transformation from time to wavelength, which is related to heating effects of the PPLN crystal and acceleration-deacceleration of the stepping motor. To make the experimental data useful and give reliable predictions using both experimental PAS data and HITRAN for training we therefore shift the wavelength axis in the start and end to secure maximum overlap between with HITRAN and experimental PAS data. 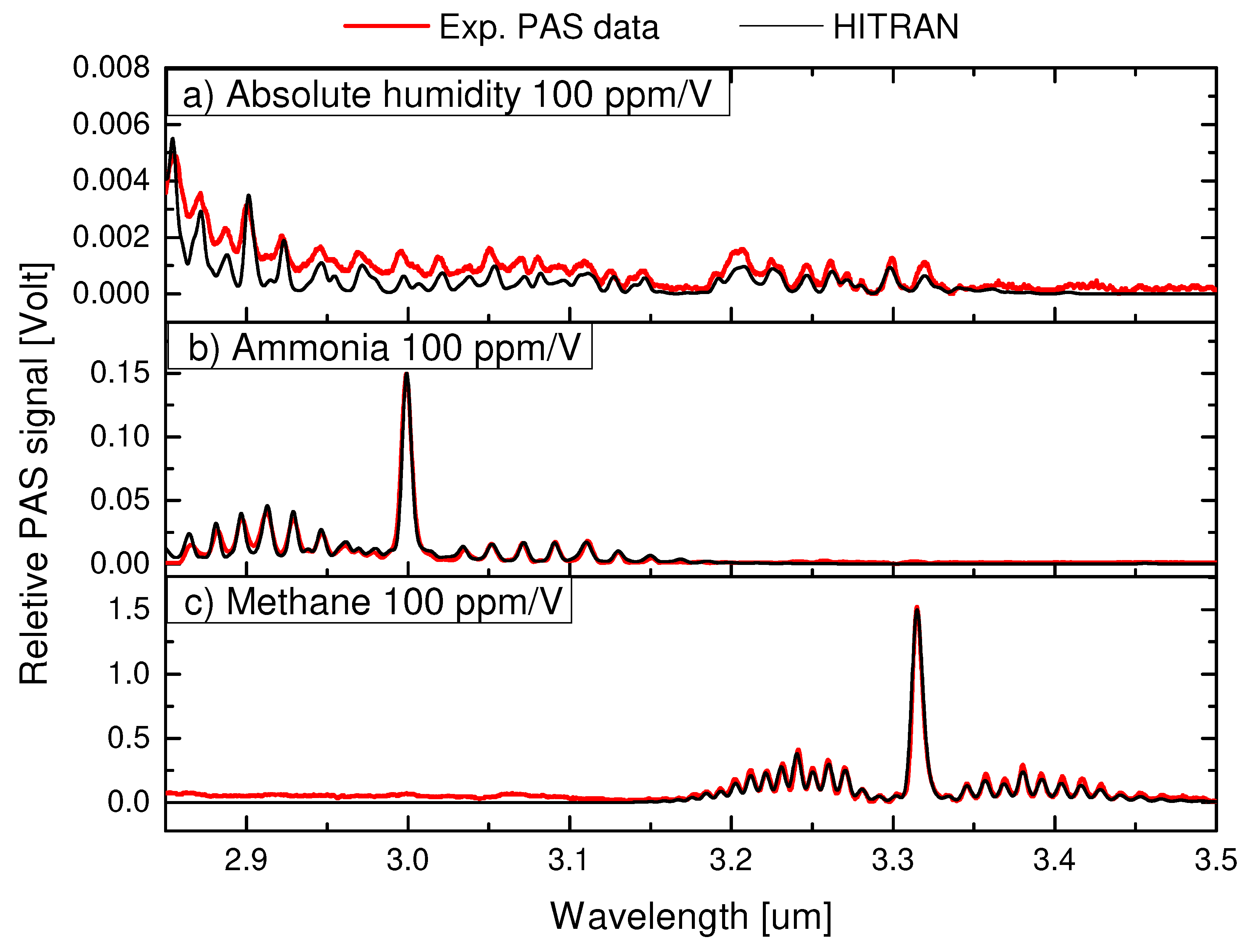Continuous measurement of the wavelength is being implemented for future work to improve this.

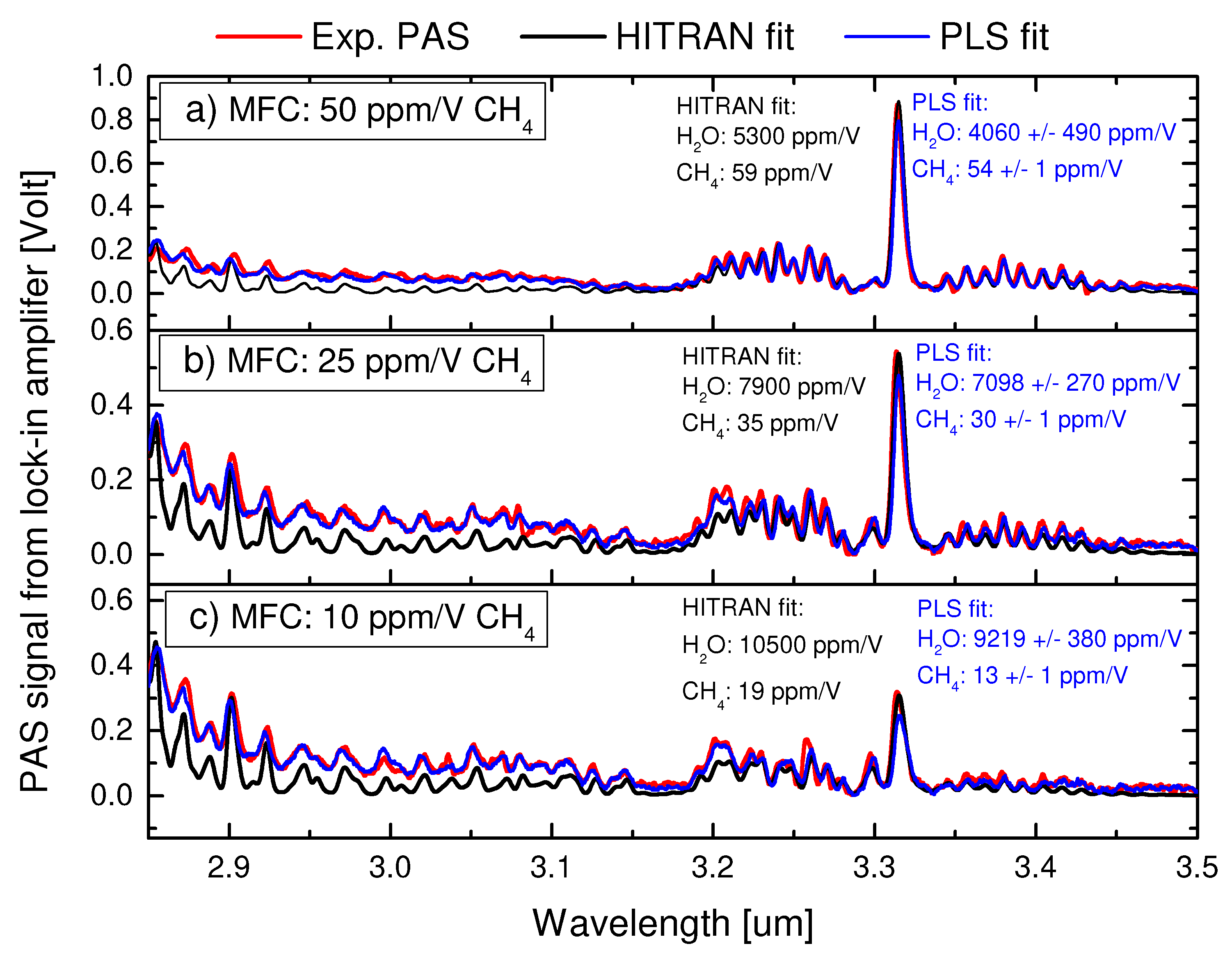
4.1. Performance and calibration of the PLS method

The PAS spectra in Figure 3 shows test data containing gas mixtures of water and methane with known concentrations. The ambient concentration of water in the lab-air is approximately 10400 ppm/V measured with a humidity sensor. The methane concentration with an uncertainty of ±5% is estimated using the gas flow into the QEPAS. For the data shown in Figure 3 we used flow ratios of 50/50, 25/75 and 10/90, resulting in methane concentrations of 50(±2.5) ppm/V, 25(±1.25) ppm/V and 10(±0.5) ppm/V, respectively. In Figure 3 (black traces) HITRAN data are directly fitted to the PAS data to estimate the concentrations of water and methane. The concentration of the water and methane were also estimated by the PLS algorithm trained on a linear combination of 5000 experimental training PAS spectra, the training data is shown in Figure 2a,c, and superimposed with Gaussian noise to mimic experimental variations. The experimental spectra were normalized in the prediction step, which was found to significantly improve prediction reliability of the PLS implementation. We find that both the HITRAN and PLS fitting overestimates the methane concentrations. The reason for this is that the measured PA signal is gas-matrix dependent, meaning that PA-based trace-gas sensors, while they can be extremely sensitive, can quickly become inaccurate without adequate calibration of the necessary gas-matrix corrections. Most prominent, and relevant for real-life adaptation of PA sensors, are the presence of water vapor which acts as a catalyst for the molecular relaxation process. The ro-vibrational relaxation is a result of inelastic scattering between the excited molecule and other molecules in the gas matrix. The existence of water vapor strongly mediates the relaxation process, which can result in a misleading enhancement or in some cases attenuation of the PA signal [25,33]. This demands that absolute environmental gas-concentration measurements can only be achieved upon correction for the water content.

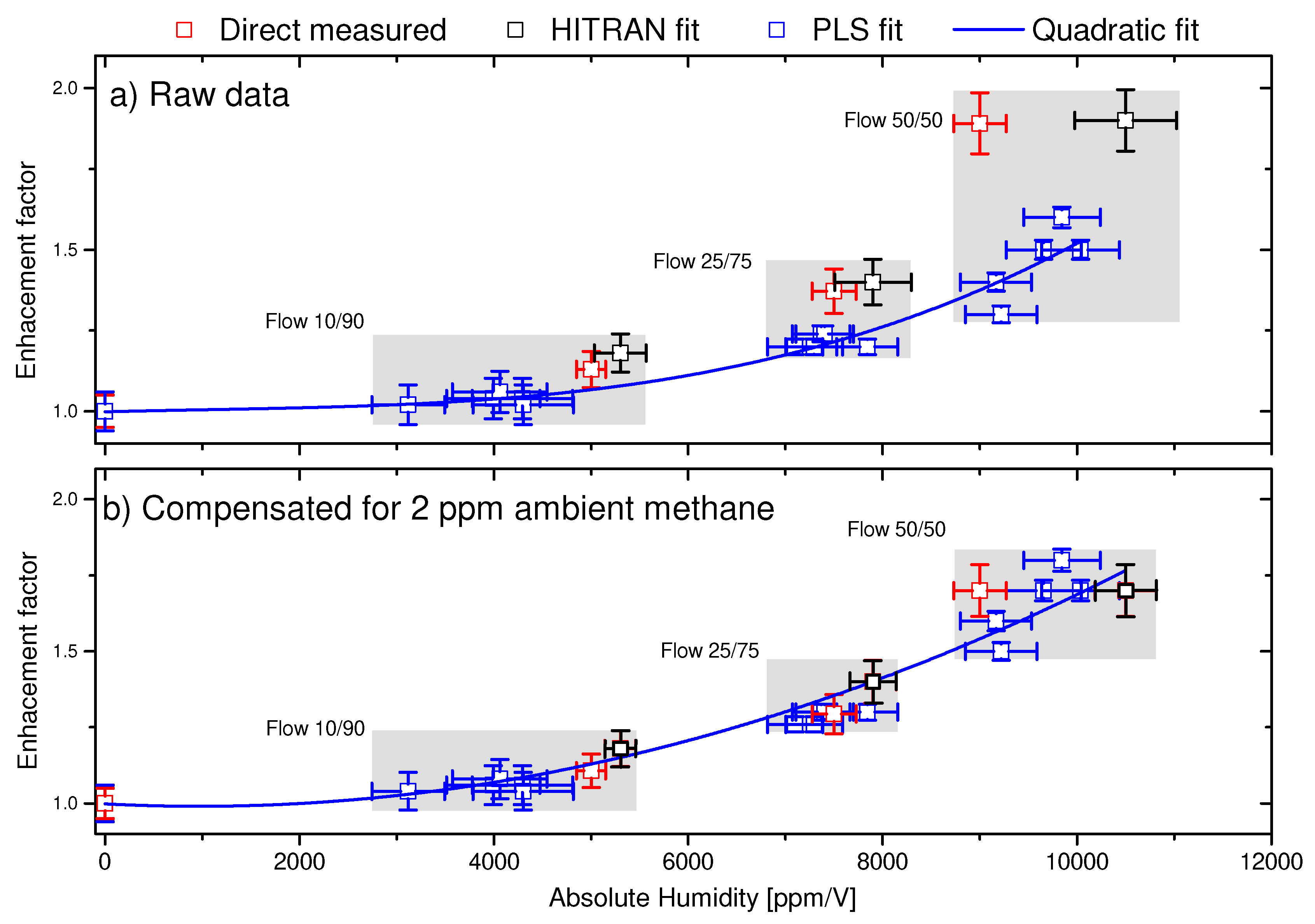
4.2. Water correction factors for absolute calibration of the PLS method

Figure 3 demonstrates how the presence of water molecules enhances the PA signal of methane. In the literature the enhancement has previously been demonstrated to be both gas- and wavelength dependent and the factor does not necessarily seem to be a simple linear function of absolute humidity as also demonstrated here [25]. The measured enhancement factor is depicted in Figure 4a as function of absolute humidity. The humidity was measured by a relative humidity sensor (Extech RH25, measurement accuracy 3%). Using a high-end calibrated humidity sensor we confirm that the measurement accuracy is indeed within 3%. We found that while acquiring the experimental PAS data the humidity fluctuates slightly in our lab between 9000 ppm/V and 12000 ppm/V. We apply three different methods for estimating the water enhancement factor; by fitting directly with the PAS voltage signal from the lock-in amplifier followed by normalization to the voltage level for 100 ppm/V-N 2 concentration, by fitting with HITRAN data, and by using the PLS training methods. For this we use two models one trained with 5000 experimental PAS spectra and a second model trained with 2500 experimental spectra + 2500 HITRAN spectra. We find that within the range of humidity’s used in this work that the enhancement factor shows a quadratic growths and the PA signal for methane is seen to be enhanced by more than a factor of 1.75 as a result of absolute humidity level of approximately 10000 ppm/V. Note that similar quadratic behavior has also been demonstrated for ammonia detection with PAS [40]. The standard deviation (STD) across all four fitting methods are for 10/90 flow ratio: 711 ppm/V for water and 2.5 ppm/V for methane, for 25/75 flow ratio: 290 ppm/V for water and 2.6 ppm/V for methane and for 50/50 flow ratio: 540 ppm/V for water and 2.9 ppm/V for methane. Figure 3 and Figure 4a strongly underlines that absolute PA-based concentration measurements in humidity conditions, necessarily involves a highly sensitive measurement of the absolute humidity level. Thus, a sensitive humidity measurement can either be done directly using the PA effect, or more conveniently, by embedding humidity sensors [25,32].
Besides estimating the water enhancement factor we also estimate the natural abundance of methane in our lab-air. The lab-air is used for diluting the ammonia and methane gasses and to mimic a real-life environment with varying humidity’s. Not shown here but from the comparison of HITRAN spectra with the PAS spectra we find that the lab-air also contains approximately 2 ppm/V of methane. This offset needs to be taken into account since the PLS method will underestimate the concentration, while fitting directly with HITRAN (or the PAS voltage) will overestimate the concentration of methane. In Figure 4b we apply the compensation and find that the STD for the estimation of methane across all fitting methods are indeed improved for all three flow cases. Explicitly we find a STD for 10/90 flow ratio: of 1 ppm/V, for 25/75 flow ratio: of 1.2 ppm/V for methane and for 50/50 flow ratio: of 2.5 ppm/V, respectively. Taking the ambient methane into account the estimated concentrations in Figure 3a: For HITRAN fitting 58 (± 3) ppm/V and PLS fitting 53 (± 3) ppm/V. Figure 3b: HITRAN fitting 34 (± 2) ppm/V and PLS fitting 31 (± 2) ppm/V. Figure 3c HITRAN fitting 17 (± 1) ppm/V and PLS fitting 13 (± 1) ppm/V. Within the measurement uncertainties both fitting methods is found to agree well. Thus, the estimated gas mixture ratios show good correspondence with the experimentally estimated mixtures. However, the trained PLS algorithm seems in general to have a slightly lower estimate of the concentrations compared to the direct fitting with HITRAN data. This is because the HITRAN data does not take into account the background signal that the training and test data are containing. This can clearly be seen using 5000 combinations of HITRAN spectra for training the PLS algorithm, where we find that the estimation becomes very inaccurate and gives concentrations estimates for Figure 3a of 8457/76 ppm/V, Figure 3b 12560/66 ppm/V and Figure 3c 15376/50 ppm/V for water/methane, respectively. Thus, to enable the direct use of HITRAN data for training of the PLS algorithm and use them on experimental PAS data one need to baseline correct the experimental data. The baseline correction involves removing the underlying baseline signal that can obscure the true spectral features. Various mathematical algorithms, such as polynomial fitting, was employed and tested for baseline correction. The goal was to improve peak detection, and enable more reliable quantification of the concentrations using the HITRAN spectra. However, in practice we found that using the experimental PAS spectra for training always gave higher accuracy.
We notice that using different trained PLS models on the same training data gives slightly different results, as seen in Figure 4. This is due to the adding of random Gaussian noise that was superimposed to the simulated spectra. We find that for the 5 PLS models trained on experimental spectra a STD of 12% for water in the 1000-5000 ppm/V range, and 4% in 7000-12000 ppm/v, respectively. For methane the PLS concentration estimations has a relative uncertainty with a STD of 6% at the 10 ppm/V level and a STD of 2% for concentrations higher than 20 ppm/V. However, we are confident that our PLS algorithm together with the water correction and methane compensation gives the correct estimates of the mixing ratios between water and methane within the uncertainties of our measurements and training of the models. In the following section we will use the calibration of the PLS algorithm to estimate the unknown mixtures of water, ammonia and methane.

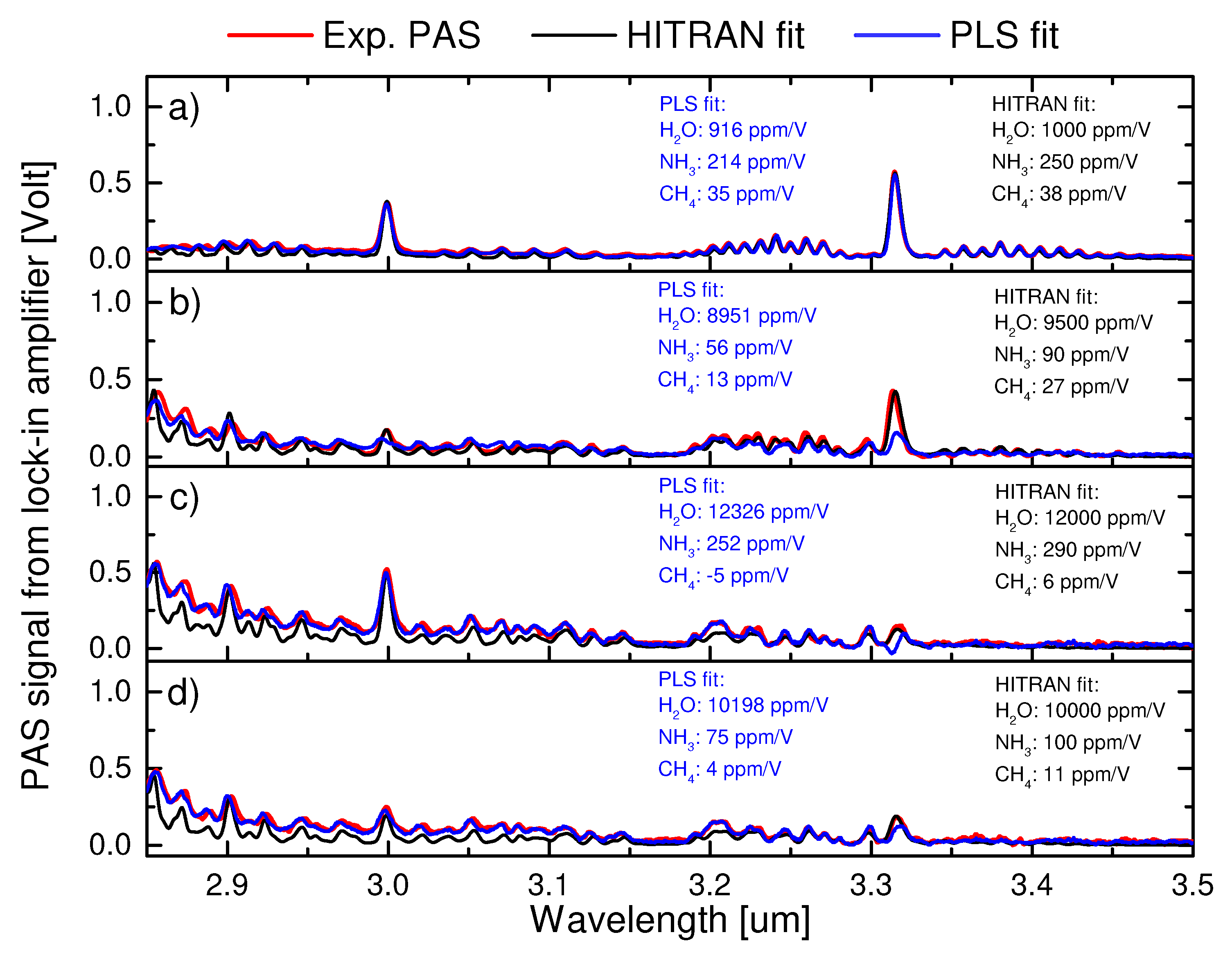
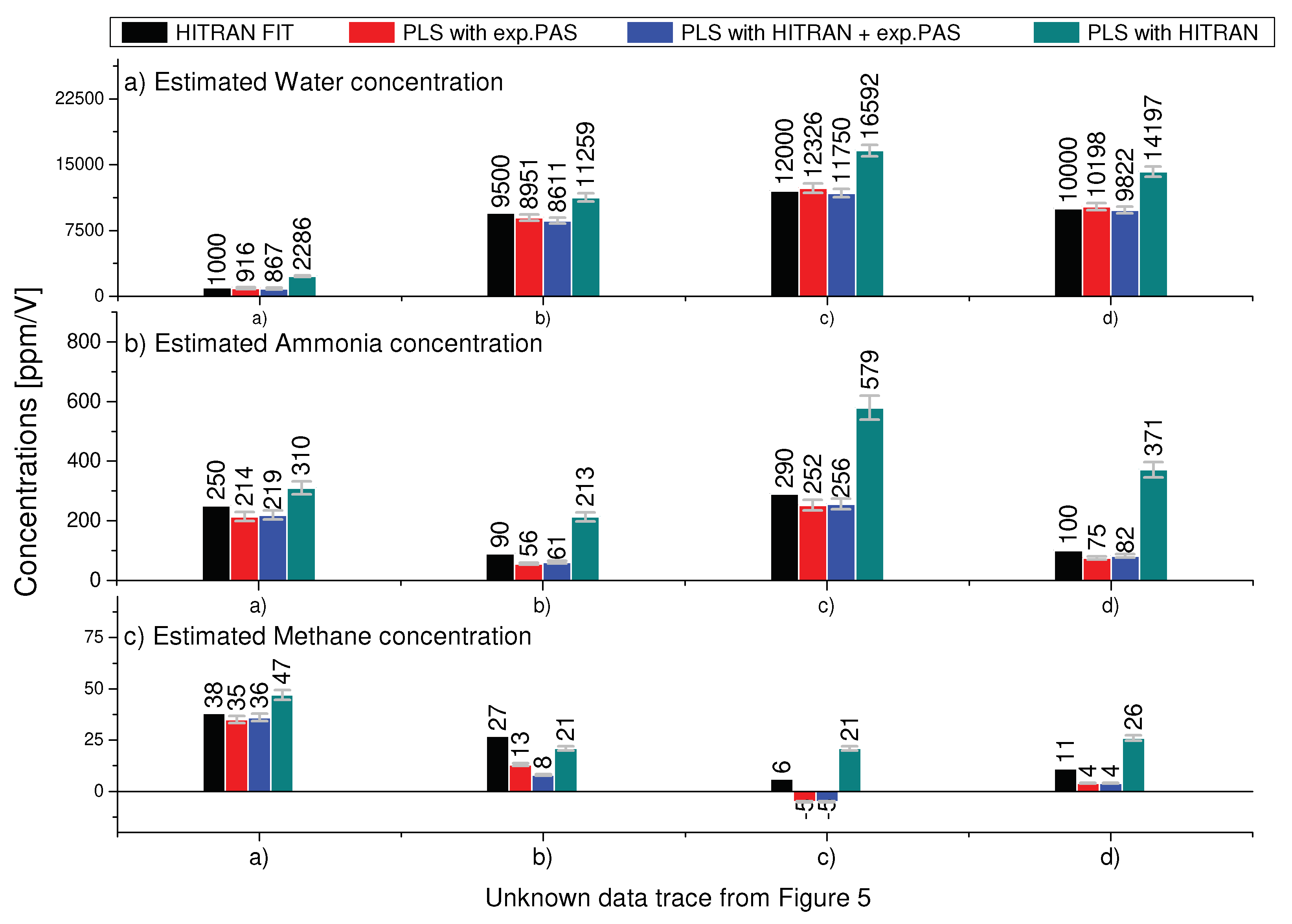
4.3. Performance of the PLS method on unknown mixtures of water, ammonia and methane

The PAS spectra shown in Figure 5 depicts the test data containing unknown mixtures of water, ammonia and methane. As can be seen the mixtures with the three gas components has high spectral overlap. In the following we make a benchmark test of the relative accuracy of the PLS method compared with direct fitting with HITRAN spectra. The two main effects that can influence the performance and accuracy of the PLS method is high concentration of water relative to ammonia and methane concentrations and deviations in the wavelength axis compared to the training spectra. The four gas mixtures displayed in Figure 5 are chosen as extreme cases to evaluate the performance of the PLS algorithm. The PLS method was again implemented using a standard training-test approach. The training data set was built starting from the three reference spectra for water, ammonia and methane, as shown in Figure 2. The data set then expanded by means of calculating a linear combinations of 5000 reference spectra with superimposing Gaussian noise distributions. Based on the above calibration of the PLS method for the known concentrations we can estimate the concentrations of the unknown mixtures. We make the assumption that the water enhancement factor of ammonia has a similar behavior as methane. Figure 5a shows data for a low concentration of water and relatively similar PAS signal strength for ammonia and methane with minimal deviation in the wavelength (less than 0.2 nm) axis compared to the training/HITRAN data. Keeping in mind that the Q-branch peak of methane is 10.4 times higher than the Q-branch of ammonia (as shown in Figure 2). We find that the PLS method and HITRAN fitting agrees very well within the measurements uncertainties as shown in Figure 6. The overall estimation of the water, ammonia and methane concentrations with the PLS method has a accuracy of 92%, 86% and 92%, respectively, relative to the HITRAN fitting. In Figure 5b the water content is increased to 9000 ppm/V hereby diluting the concentration of ammonia and methane. In this case we find that the relative accuracy of the estimation of water concentration has increased to 94% compared to the HITRAN fitting. Meanwhile the accuracy of the ammonia and methane concentrations has decreased to 62% and 48%, respectively. This decrease in accuracy is due to the relativity low concentration of ammonia and methane. For methane it is mainly because of the mismatch between the wavelength axis of the test spectra and the training spectra. Comparing Figure 5b with the training data in Figure 2c we find that the experimental PAS spectra is shifted approximately 2 nm to the left in the 3.2 to 3.35 μ m range. This can be seen from Figure 5b and is the reason that the PLS fitting for methane becomes very inaccurate and underestimated the presents of methane. Note that the experimental conditions are very similar for the experimental PAS spectra shown in Figure 3b, where the wavelength deviation is less than 0.2 nm. We apply the same three gas trained PLS method to the data in Figure 3b and find concentrations of 7196 ppm/V, -4 ppm/V and 30 ppm/V for water, ammonia and water, respectively. Thus, we conclude that the main reason for the inaccuracies shown in Figure 5b is due to the deviation of wavelength axis compared to the training/HITRAN spectra and that in order for the PLS to estimate with high accuracy the deviation in wavelength should be less than 1 nm. In Figure 5c,d the deviation is less than 0.5 nm and we continue with the investigation of how very asymmetric mixing ratio affect the accuracy of the PLS method. In this case the concentrations of ammonia and methane becomes relative low compared to the water content. The water spectra will therefore dominate the trained PLS model due to the high level of spectral overlap with ammonia and methane. To test this behavior and make an estimation of the PLS methods lower accuracy (sensitivity) limit we increase the amount of water and ammonia. Thus diluting the content of methane at the same time. This is depicted in Figure 5c where we find that the PLS method is making a completely wrong estimation of the concentration by estimating it to be negative (-5 ppm/V). Due to this apparent wrong estimation of the methane concentration the PLS method predicts a 3% higher concentration of water relative to the HITRAN fitting. This fitting behavior is in general very different from the fitting behavior that we have seen in the previous cases in Figure 3 and Figure 4, where the HITRAN fitting always estimated higher concentrations. It suggests that for high concentrations of water and for relatively low concentrations of ammonia and methane the PLS algorithm are using the ammonia and methane coefficients as a free parameter to make a better fit of the water spectra. This is clearly seen from the fact that the relative precision between the PLS method and HITRAN fitting becomes higher in this case. Therefore to estimate the accuracy and sensitivity we dilute the concentration of water and ammonia by purging with methane as shown in Figure 5d. It can be seen than the PLS method now gives only positive coefficients for the estimation of the concentrations. However, the estimations of ammonia and methane are still underestimated relative to the HITRAN fitting while the water is overestimated with 2%. If we apply the enhancement and correction factors found in Figure 4 for the calibration of absolute concentrations of methane, we find a methane concentration of 3 (±2) ppm/V and 5(±2) ppm/V for the PLS method and HITRAN fitting, respectively. Thus, the estimations of the contractions with the two methods are in good agreement within the measurements uncertainties. By applying the same water correction factor from Figure 4b to the estimated ammonia concentration we find that the absolute concentration should be approximately 50(±10) ppm/V and 67(±10) ppm/V for the PLS method and HITRAN fitting, respectively. We conclude from these measurement and tests that the absolute sensitivity of the three gas training PLS is approximately 300(±50) ppm/V, 50(±5) ppm/V and 5(±2) ppm/V for water, ammonia and methane, respectively.

5. Discussion

The PLS algorithm was trained to estimate the gas mixture ratio. Thus by proper normalization of the data the concentration of all gasses in the mixture can then be estimated by having just one known gas concentration, in our case methane reference gas with a concentration of 100 ppm/V. The performance of the different trained PLS models are summarized in Figure 6. The error-bars are a sum of the uncertainties of the gas preparation, PAS measurement and the PLS analysis. Three PLS models were trained as shown by the color code. Red columns: trained with 5000 experimental PAS spectra, Blue columns: with 2500 experimental PAS spectra + 2500, and Green columns: 5000 HITRAN spectra. Ideally, we aimed in this pilot study to apply HITRAN spectra for the training of the PLS model. However, we found that the direct use of HITRAN becomes highly inaccurate and overestimates the concentrations as shown in Figure 6. This is because the HITRAN spectra does not take into account the relaxation mechanisms, which are both gas- and wavelength dependent, and potential error-sources such as electrical noise and background signals that arises from stray light. The relaxation mechanisms can by proper calibration, as shown in Figure 4, indeed be taken into account, as also demonstrated here. While the noise sources and background signals are more tedious to compensate for and is the main reason for the failure to train the PLS algorithm with only HITRAN spectra. The background signals of the experimental PAS spectra changes slightly over time. However, we try to compensate for this by realigning the MIR laser light through the QEPAS cell during a measurement series. As an alternative method we also investigated baseline subtraction using higher order polynomial fitting. This resulted in a slightly higher overall uncertainty in the estimation of the concentrations and in general we found that the direct use of the HITRAN spectra overestimated the concentration with 10-15%.

6. Conclusions

In conclusion, the combination of QEPAS with PLS was proven to be a strong method for the estimation of gas concentrations in complex mixtures. The mixing ratios and concentrations were estimated using PLS models trained with both HITRAN and experimental PAS spectra for single components and synthetic spectra of mixtures. The training data was built starting from the single reference spectra and was enlarged by means of simulated spectra, calculated as linear combinations of reference ones. Gaussian noise was superimposed to the simulated spectra to consider the experimental noise involved in the measurements. An absolute sensitivity, after correction for water enhancement factors and ambient methane, of approximately 500(±50) ppm/V, 50(±5) ppm/V and 5(±2) ppm/V for water, ammonia and methane, respectively, was demonstrated.
By employing PLS to PAS sensors, concentration levels of many different target gases can be estimated simultaneously, based on their unique spectral fingerprints. We foresee that this approach holds great promise for many different applications, such as environmental monitoring and industrial safety, providing a non-invasive and efficient solution for detecting and quantifying gases in real-time and therefore might become a valuable tool in advancing gas detection technologies and addressing critical challenges in various fields.

Author Contributions

Methodology, A.N.R., B.L.T. and M.L.; software, A.N.R., B.L.T. and J.B.C.; validation, A.N.R. and M.L.; formal analysis, A.N.R and M.L.; investigation, A.N.R. and M.L.; resources, J.C.P. and M.L.; data curation, A.N.R. and M.L.; writing–original draft preparation, A.N.R. and M.L.; writing–review and editing, A.N.R., J.B.C., J.C.P.,, M.L.; visualization, A.N.R. and M.L.; supervision, M.L.; project administration, J.C.P. and M.L.; funding acquisition, J.C.P., M.L.

Funding

This work is funded by the Innovation Fund Denmark (IFD) under case no. 0140-00011B (UP-CEMS) and the Danish Agency for Institutions and Educational Grants.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

The data leading to the results of this work is available from the authors upon reasonable requests.

Abbreviations

The following abbreviations are used in this manuscript:
PPLN periodically poled lithium niobate crystal
PLS Partial least-squares regression
MFC Mass-flow controller
MIR Midinfrared
OPO Optical parametric oscillator
PA Photoacoustic
PAS Photoacoustic spectroscopy
QEPAS Quartz-enhanced photoacoustic spectroscopy
QTF Quartz tuning fork
FTIR Fourier-transform infrared spectroscopy

References

  1. Refaat, T.F.; Ismail, S.; Koch, G.J.; Rubio, M.; Mack, T.L.; Notari, A.; Collins, J.E.; Lewis, J.; De Young, R.; Choi, Y.; et al. Backscatter 2-μm Lidar Validation for Atomospheric CO2 Differential Absorption Lidar Applications. IEEE Trans. Geosci. Remote Sens. 2011, 49, 572–580. [Google Scholar] [CrossRef]
  2. Feng, S.; Farha, F.; Li, Q.; Wan, Y.; Xu, Y.; Zhang, T.; Ning, H. Review on Smart Gas Sensing Technology. Sensors 2019, 19, 3760. [Google Scholar] [CrossRef] [PubMed]
  3. Nazemi, H.; Joseph, A.; Park, J.; Emadi, A. Advanced Micro- and Nano-Gas Sensor Technology: A Review. Sensors 2019, 19, 1285. [Google Scholar] [CrossRef] [PubMed]
  4. Amann, A.; Poupart, G.; Telser, S.; Ledochowski, M.; Schmid, A.; Mechtcheriakov, S. Applications of breath gas analysis in medicine. Int. J. Mass Spectrom. 2004, 239, 227–233. [Google Scholar] [CrossRef]
  5. Lassen, M.; Baslev-Harder, D.; Brusch, A.; Nielsen, O. S.; Heikens, D.; Persijn, S.; Petersen, J.C. Photo-acoustic sensor for detection of oil contamination in compressed air systems. Opt. Express 2017, 25, 1806–1814. [Google Scholar] [CrossRef] [PubMed]
  6. Jongma, R.T.; Boogaarts, M.G.; Holleman, I.; Meijer, G. Trace gas detection with cavity ring down spectroscopy. Rev. Sci. Instrum. 1995, 66, 2821–2828. [Google Scholar] [CrossRef]
  7. Wilson, A. Application of electronic-nose technologies and VOC-biomarkers for the noninvasive early diagnosis of gastrointestinal diseases. Sensors 2018, 18, 2613. [Google Scholar] [CrossRef]
  8. Yuan, Z., et al. Trace-level, multi-gas detection for food quality assessment based on decorated silicon transistor arrays. Advanced materials, 2020, 32.21: 1908385. [CrossRef]
  9. Lewen, Z.; Zhirong, Z.; Qianjin, W.; Pengshuai, S.; Bian, W.; Tao, P.; Sigrist, M. W. A sensitive carbon monoxide sensor for industrial process control based on laser absorption spectroscopy with a 2.3 μm distributed feedback laser. Optics and Lasers in Engineering, 2022 152, 106950. [CrossRef]
  10. Strahl, T.; Herbst, J.; Lambrecht, A.; Maier, E.; Steinebrunner, J.; Wöllenstein, J. Methane leak detection by tunable laser spectroscopy and mid-infrared imaging. Applied Optics, 2021 60(15), C68-C75. [CrossRef]
  11. Lamard, L.; Balslev-Harder, D.; Peremans, A.; Petersen, J.C.; Lassen, M. Versatile photoacoustic spectrometer based on a mid-infrared pulsed optical parametric oscillator. Appl. Opt. 2019, 58, 250–256. [Google Scholar] [CrossRef] [PubMed]
  12. Zifarelli, A.; Giglio, M.; Menduni, G.; Sampaolo, A.; Patimisco, P.; Passaro, V. M. N.; Wu, H.; Dong, L.; Spagnolo, V. Partial Least-Squares Regression as a Tool to Retrieve Gas Concentrations in Mixtures Detected Using Quartz-Enhanced Photoacoustic Spectroscopy. Anal. Chem. 2020, 92, 11035–11043. [Google Scholar] [CrossRef]
  13. Werle, P.; Slemr, F.; Maurer, K.; Kormann, R.; Mücke, R.; Jänker, B. Near- and mid-infrared laser-optical sensors for gas analysis. Opt. Lasers Eng. 2002, 37, 101–114. [Google Scholar] [CrossRef]
  14. Bogue, R. Detecting gases with light: a review of optical gas sensor technologies, Sensor Review, 2015 35 2, 133–140. [CrossRef]
  15. Hodgkinson, J.; Tatam, R. P. Optical gas sensing: a review. Meas. Sci. Technol. 2013, 24, 012004. [Google Scholar] [CrossRef]
  16. Manohar, S.; Razansky, D. Photoacoustics: a historical review. Adv. Opt. Photon. 2016, 8, 586–617. [Google Scholar] [CrossRef]
  17. Spagnolo, V.; Patimisco, P.; Borri, S.; Scamarcio, G.; Bernacki, B. E.; Kriesel, J. Part-per-trillion level SF6 detection using a quartz enhanced photoacoustic spectroscopy-based sensor with single-mode fiber-coupled quantum cascade laser excitation. Opt. Lett. 2012, 37, 4461–4463. [Google Scholar] [CrossRef] [PubMed]
  18. Palzer, S. Photoacoustic-Based Gas Sensing: A Review. Sensors 2020, 20, 2745. [Google Scholar] [CrossRef]
  19. Popa, C. Ethylene Measurements from Sweet Fruits Flowers Using Photoacoustic Spectroscopy. Molecules 2019, 24, 1144. [Google Scholar] [CrossRef]
  20. Mikkonen, T., Luoma, D., Hakulinen, H., Genty, G., Vanninen, P. and Toivonen, J. Detection of gaseous nerve agent simulants with broadband photoacoustic spectroscopy. Journal of Hazardous Materials. 2022 , 440, p.129851. [CrossRef]
  21. Westergaard, P. G.; Lassen, M. All-optical detection of acoustic pressure waves with applications in photoacoustic spectroscopy. Applied Optics, 2016 55(29), 8266–8270. [CrossRef]
  22. Kosterev, A.A.; Bakhirkin, Y.A.; Curl, R.F.; Tittel, F.K. Quartz-enhanced photoacoustic spectroscopy. Opt. Lett. 2002, 27, 1902–1904. [Google Scholar] [CrossRef]
  23. Sampaolo, A.; Menduni, G.; Patimisco, P.; Giglio, M.; Passaro, V.M.; Dong, L.; Wu, H.; Tittel, F.K.,; Spagnolo, V. Quartz-enhanced photoacoustic spectroscopy for hydrocarbon trace gas detection and petroleum exploration. Fuel 2020, 277, 118118. [CrossRef]
  24. Tomberg, T.; Vainio, M.; Hieta, T.; Halonen, L. Sub-parts-per-trillion level sensitivity in trace gas detection by cantilever-enhanced photo-acoustic spectroscopy. Sci. Rep. 2018, 8, 1–7. [Google Scholar] [CrossRef] [PubMed]
  25. Christensen, J.B.; Høgstedt, L.; Friis, S.M.M.; Lai, J.-Y.; Chou, M.-H., Balslev-Harder, D., Petersen, J.C.; Lassen, M. Intrinsic spectral resolution limitations of QEPAS sensors for fast and broad wavelength tuning. Sensors 2020, 20, 4725. [CrossRef]
  26. Lassen, M.; Lamard, L.; Feng, Y.; Peremans, A.; Petersen, J.C. Off-axis quartz-enhanced photoacoustic spectroscopy using a pulsed nanosecond mid-infrared optical parametric oscillator. Opt. Lett. 2016, 41, 4118–4121. [Google Scholar] [CrossRef]
  27. Hayden, J.; Baumgartner, B.; Waclawek, J.P.; Lendl, B. Mid-infrared sensing of CO at saturated absorption conditions using intracavity quartz-enhanced photoacoustic spectroscopy. Appl. Phys. B 2019, 125, 159. [Google Scholar] [CrossRef] [PubMed]
  28. Patimisco, P.; Sampaolo, A.; L. Dong, L.; Tittel, F.K.; Spagnolo, V. Recent advances in quartz enhanced photoacoustic sensing. Appl. Phys. Rev. 2018, 5, 011106. [CrossRef]
  29. Li, B.; Menduni, G.; Giglio, M.; Patimisco, P.; Sampaolo, A.; Zifarelli, A.; Dong, L. Quartz-enhanced photoacoustic spectroscopy (QEPAS) and Beat Frequency-QEPAS techniques for air pollutants detection: a comparison in terms of sensitivity and acquisition time. 2023 Photoacoustics, 100479. [CrossRef]
  30. Friedt, J.M.; Carry, E. Introduction to the quartz tuning fork. Am. J. Phys. 2007, 75, 415–422. [Google Scholar] [CrossRef]
  31. Lang, B.; Breitegger, P.; Brunnhofer, G.; Valero, J.P.; Schweighart, S.; Klug, A.; Hassler, W.; Bergmann, A. Molecular relaxation effects on vibrational water vapor photoacoustic spectroscopy in air. Appl. Phys. B 2020, 126, 1–18. [Google Scholar] [CrossRef]
  32. Elefante, A.; Menduni, G.; Rossmadl, H.; Mackowiak, V.; Giglio, M.; Sampaolo, A.; Patimisco, P.; Passaro, V.; Spagnolo, V. Environmental Monitoring of Methane with Quartz-Enhanced Photoacoustic Spectroscopy Exploiting an Electronic Hygrometer to Compensate the H2O Influence on the Sensor Signal. Sensors 2020, 20, 2935. [Google Scholar] [CrossRef]
  33. Müller, M.; Rück, T.; Jobst, S.; Pangerl, J.; Weigl, S.; Bierl, R.; Matysik, F. M. An algorithmic approach to compute the effect of non-radiative relaxation processes in photoacoustic spectroscopy. Photoacoustics 2022, 26, 100371. [Google Scholar] [CrossRef] [PubMed]
  34. Wysocki, G.; Kosterev, A.A.; Tittel, F.K. Influence of molecular relaxation dynamics on quartz-enhanced photoacoustic detection of CO 2 at λ= 2 μm. Appl. Phys. B 2006, 2006 85, 301–306. [Google Scholar] [CrossRef]
  35. Yin, X.; Dong, L.; Zheng, H.; Liu, X.; Wu, H.; Yang, Y.; Ma, W.; Zhang, L.; Yin, W.; Xiao, L.; Jia, S. Impact of humidity on quartz-enhanced photoacoustic spectroscopy based CO detection using a near-IR telecommunication diode laser. Sensors 2016, 16, 162. [Google Scholar] [CrossRef]
  36. Petra, N.; Zweck, J.; Kosterev, A.A.; Minkoff, S.E.; Thomazy, D. Theoretical analysis of a quartz-enhanced photoacoustic spectroscopy sensor. Appl. Phys. B 2009, 94, 673–680. [Google Scholar] [CrossRef]
  37. Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: a basic tool of chemometrics. Chemometrics and intelligent laboratory systems 2001, 2, 109–130. [Google Scholar] [CrossRef]
  38. Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011. scikit-learn.org.
  39. Umemura, N.; Matsuda, D.; Mizuno, T.; Kato, K. Sellmeier and thermo-optic dispersion formulas for the extraordinary ray of 5 mol.% MgO-doped congruent LiNbO 3 in the visible, infrared, and terahertz regions. Applied optics 2014, 53(25), 5726–5732. [CrossRef]
  40. Schilt, S.; Thévenaz, L.; Niklès, M.; Emmenegger, L.; Hüglin, C. Ammonia monitoring at trace level using photoacoustic spectroscopy in industrial and environmental applications. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2004, 60(14), 3259–3268. [CrossRef]
Preprints 78960 g001
Figure 1. Block diagram of the main parts of the experimental setup. Actively Q-switched 1064 nm ns pump laser. QEPAS: Quartz-enhanced PAS. MIR OPO: Mid-infrared (MIR) pulsed optical parametric oscillator. MFC: Mass-flow controller. MIR filter for removing the pump. DAQ: Signal generator for trigger signal for the 1064 nm pump laser and generating the local oscillator (both at 12.457 kHZ) for the lock-in amplifier. The downmixed signal is then acquired by an oscilloscope. The generated MIR wavelength is measured with an optical spectrometer.
Figure 1. Block diagram of the main parts of the experimental setup. Actively Q-switched 1064 nm ns pump laser. QEPAS: Quartz-enhanced PAS. MIR OPO: Mid-infrared (MIR) pulsed optical parametric oscillator. MFC: Mass-flow controller. MIR filter for removing the pump. DAQ: Signal generator for trigger signal for the 1064 nm pump laser and generating the local oscillator (both at 12.457 kHZ) for the lock-in amplifier. The downmixed signal is then acquired by an oscilloscope. The generated MIR wavelength is measured with an optical spectrometer.
Preprints 78960 g001
Preprints 78960 g002
Figure 2. Training data for the PLS analysis for a) Water (H 2 O), b) Ammonia (NH 3 ) and c) Methane (CH 4 ). The red curves show the experimental measured PAS spectra. The black curves shows the spectra from the HITRAN database convolved with a Gaussian instrument profile of 5 cm − 1 . For ammonia and methane, the R-, Q- and P-branch are clearly observed. The y-axis is given as the measured/estimated PAS voltage and equals a concentration of 100 ppm/V for each of the three gasses. The scaling levels of the PAS signal for H 2 O and NH 3 are estimated using 100 ppm/V of CH 4 in N 2 .
Figure 2. Training data for the PLS analysis for a) Water (H 2 O), b) Ammonia (NH 3 ) and c) Methane (CH 4 ). The red curves show the experimental measured PAS spectra. The black curves shows the spectra from the HITRAN database convolved with a Gaussian instrument profile of 5 cm − 1 . For ammonia and methane, the R-, Q- and P-branch are clearly observed. The y-axis is given as the measured/estimated PAS voltage and equals a concentration of 100 ppm/V for each of the three gasses. The scaling levels of the PAS signal for H 2 O and NH 3 are estimated using 100 ppm/V of CH 4 in N 2 .
Preprints 78960 g002
Preprints 78960 g003
Figure 3. Test data containing a mixture of known water and methane concentrations. The red curves are the experimental PAS data and the black curves are the HITRAN fitted spectra with corresponding coefficients. The blue traces are the fitted PLS method with coefficients. The model was trained on combinations of 5000 experimental PAS spectra with superimposed Gaussian noise. The concentration of methane was controlled using the MFC and the water humidity was measured by the humidity sensor. a) 50 ppm/V (± 2.5 ppm) of methane and 5000 ppm/V (± 250 ppm) of water humidity. b) 25 ppm/V (± 1.25 ppm) and 7500 ppm/V (± 375 ppm) of absolute humidity. c) 10 ppm/V (± 0.5 ppm) of methane and 9000 ppm/V (± 450 ppm) of absolute humidity.
Figure 3. Test data containing a mixture of known water and methane concentrations. The red curves are the experimental PAS data and the black curves are the HITRAN fitted spectra with corresponding coefficients. The blue traces are the fitted PLS method with coefficients. The model was trained on combinations of 5000 experimental PAS spectra with superimposed Gaussian noise. The concentration of methane was controlled using the MFC and the water humidity was measured by the humidity sensor. a) 50 ppm/V (± 2.5 ppm) of methane and 5000 ppm/V (± 250 ppm) of water humidity. b) 25 ppm/V (± 1.25 ppm) and 7500 ppm/V (± 375 ppm) of absolute humidity. c) 10 ppm/V (± 0.5 ppm) of methane and 9000 ppm/V (± 450 ppm) of absolute humidity.
Preprints 78960 g003
Preprints 78960 g004
Figure 4. a) Enhancement factor of the methane signal as a function of absolute humidity. Four flow settings (ratios between the methane and lab-air) were used for this data: 100/0, 10/90, 25/75 and 50/50, respectively. Three different methods are used to estimate the enhancement factor as shown with the color code. The shaded areas show the uncertainty area for the estimation of water and methane concentrations across the three different methods. The fitted blue curves are quadratic functions. b) Same data as in a) compensated for 2 ppm of ambient methane. Note that the uncertainty area is decreased by compensation for the ambient methane.
Figure 4. a) Enhancement factor of the methane signal as a function of absolute humidity. Four flow settings (ratios between the methane and lab-air) were used for this data: 100/0, 10/90, 25/75 and 50/50, respectively. Three different methods are used to estimate the enhancement factor as shown with the color code. The shaded areas show the uncertainty area for the estimation of water and methane concentrations across the three different methods. The fitted blue curves are quadratic functions. b) Same data as in a) compensated for 2 ppm of ambient methane. Note that the uncertainty area is decreased by compensation for the ambient methane.
Preprints 78960 g004
Preprints 78960 g005
Figure 5. Test data for the PLS analysis of unknown concentrations of water, ammonia and methane. The red traces are the experimental PAS spectra and the black are the HITRAN spectra. The HITRAN spectra are fitted with the coefficients shown in black typing. The blue traces are the fitted PLS method using the coefficients shown in blue typing. The PLS model was trained on combinations of 5000 experimental PAS spectra with a superimposed Gaussian noise (0.01).
Figure 5. Test data for the PLS analysis of unknown concentrations of water, ammonia and methane. The red traces are the experimental PAS spectra and the black are the HITRAN spectra. The HITRAN spectra are fitted with the coefficients shown in black typing. The blue traces are the fitted PLS method using the coefficients shown in blue typing. The PLS model was trained on combinations of 5000 experimental PAS spectra with a superimposed Gaussian noise (0.01).
Preprints 78960 g005
Preprints 78960 g006
Figure 6. Summary of the different PLS models for estimating the unknown concentrations of a) water, b) ammonia and c) methane. The black columns are the fitted coefficients for the HITRAN spectra for comparison. Red columns: PLS trained on experimental PAS spectra. Blue columns: mix of HITRAN and experimental spectra. Green columns: HITRAN spectra. The errors-bars are given by the estimated measurement and systematic uncertainties.
Figure 6. Summary of the different PLS models for estimating the unknown concentrations of a) water, b) ammonia and c) methane. The black columns are the fitted coefficients for the HITRAN spectra for comparison. Red columns: PLS trained on experimental PAS spectra. Blue columns: mix of HITRAN and experimental spectra. Green columns: HITRAN spectra. The errors-bars are given by the estimated measurement and systematic uncertainties.
Preprints 78960 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated